2.4 Oppervlaktemethode
|
|
|
- Samuël Elias Koster
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 2.4 Opperlakemehode Teken he --diagram an de eenparige beweging me een snelheid an 10 m/s die begin na 2 seconden en eindig na 4 seconden. De afgelegde weg is: =. (m/s) In he --diagram is de hooge an de rechhoek onder de lijn en is de breede an de rechhoek. Bijgeolg is de opperlake (h x b) gelijk aan: =. In een --diagram is de opperlake onder he lijnsuk een maa oor de afgelegde weg. (s) Oefening : Een fieser rijd an 9h10 o 9h30 me een consane snelheid an 18 km/h. Van 9h30 o 9h40 is zijn snelheid 30 km/h. (km/h) Sel de beweging oor in een --diagram. Opperlake 1 = km/h x h = Opperlake 2 = km/h x h = = opperlake 1 + opperlake 2 = (h) Deel 1: Bewegingen 13-a
2 Hoofdsuk 2a: Veranderlijke bewegingen 2a.1 Afgelegde weg Een eranderlijke beweging is een beweging waarbij de snelheid nie consan is. He ondersaande -diagram sel zo n beweging oor. We kunnen de afgelegde weg an zo n eranderlijke beweging nie alijd eenoudig berekenen. Maar door de beweging e benaderen door een opeenolgende reeks kore eenparige bewegingen (fig. 2) kunnen we oor elk an die kore ijdsduren de opperlakemehode oepassen en de som maken an alle kleine afgelegde wegen. Hoe kleiner we de ijdsinerallen nemen, hoe nauwkeuriger de benaderde afgelegde weg. Als we de opperlaken an oneindig eel oneindig smalle rechhoekjes opellen bekomen we de opperlake onder de cure en die opperlake kom dus oereen me de afgelegde weg (fig. 3). In een --diagram kom de opperlake onder de cure oor elke beweging oereen me de afgelegde weg. 2a.2 Gemiddelde snelheid We bekijken erug dezelfde eranderlijke beweging (fig. 1) en sellen he s--diagram op (fig. 2): s s We ergelijken deze eranderlijke beweging me een eenparige beweging waarin in dezelfde oale ijdsduur dezelfde oale afgelegde weg gelijk is (fig. 3) De rico an deze reche is de snelheid an deze eenparige beweging ( = / ). He is ook de gemiddelde snelheid an de eranderlijke beweging: in dezelfde ijdsduur word dezelfde afsand afgelegd: <> = / Deel 1: Bewegingen 13-b
3 We kunnen di ook op een --diagram oorsellen: in dezelfde ijdsduur word dezelfde afsand afgelegd. Da wil zeggen da de opperlake onder de cure an de eranderlijke beweging dezelfde moe zijn als de opperlake onder he horizonaal lijnsuk an de eenparige beweging aan de gemiddelde snelheid: <> <> 2a.2.1. Oefening : We hernemen de 5 de oefening an de orige reeks: een fieser rijd eenparig 150 m in 10,0 s, daarna rijd hij 20,0 s erder egen 5,00 m/s en erolgens nog eens 250 m egen 12,5 m/s. Bereken de gemiddelde snelheid an de oale fiesri. Deel 1: Bewegingen 13-c
4 Hoofdsuk 2b: De eenparig eranderlijke beweging 2b.1 Besudering an een knikker die an een helling rol 2b.1.1 Experimen We laen een knikker an een helling rollen. We meen de afgelegde weg en de benodigde ijd en herhalen deze handeling oor elkens langere afsanden. We zullen assellen da de knikker seeds sneller gaa rollen ijdens zo n afdaling. Hoe wee je da me zekerheid? Kan je hier een hypohese oer formuleren? Is er een erband ussen de snelheid en de ijd? In de heorie oer eranderlijke bewegingen hebben we gezien da he soms nuig is een eranderlijke beweging e benaderen door opeenolgende eenparige bewegingen. Da doen we hier ook: we delen de beweging an de knikker in erschillende sukjes (nl. elkens een sukje afgelegde weg an 10,0 cm) en we bepalen oor elk an deze sukken afgelegde weg de gemiddelde snelheid door de ijdsduur oor elke 10,0 cm e meen. Dan zoeken we he erband ussen deze snelheid en de ijd die de knikker nodig had om deze snelheid e bereiken. Da doen we als olg: - de afgelegde weg an zo n sukje is elkens zelfde: = s n - s n-1 = 10,0 cm - de ijdsduur is meen we me een elekronische chronomeer me wee sensoren: = n - n-1 - de gemiddelde snelheid oor elk suk is de erhouding an de wee orige meingen: <> = / - de ijd die de knikker nodig heef om deze snelheid e bereiken is ongeeer de ijd o he midden an elk sukje en die meen we nog eens afzonderlijk: <> Welk erband sel je as ussen de snelheid <> en de ijd <>? We zoeken ook he erband ussen de afgelegde weg s en de ijd. Wa oor s--grafiek krijg je? Ken je wiskundige grafieken me zo n orm? Hoe kan je nagaan of je grafiek éch zo n wiskundige orm heef? Waarom zou je <>/<> oor elk ineral berekenen? Bereken ook s/². Zie je enig erband ussen s/² en <>/<>? Boensaande berekeningen kan je bes in een abel doen: s (m) (m) <> (s) (s) <>² (s²) <> (m/s) <>/<> (m/s²) s/² (m/s²) 0,700 0,750 0,100 0,973 0,071 0,0947 / a = <>/<> s/<>² 0,800 Deel 1: Bewegingen 13-d
5 Maak de olgende grafieken: s-, s-² en - en rek een beslui. Per definiie noemen we de ersnelling (acceleraie) a = /. Hoe groo is a (gemiddeld) oor de uigeoerde proef? Een beweging me een consane ersnelling noemen we eenparig ersneld. In je grafiek sel je mogelijks een aanal afwijkende meingen oor ; kan je een erklaring geen oor di mogelijks afwijkend resulaa? To slo: - We hebben allemaal dezelfde meingen, maar iedereen sel zijn eigen erslag op. - Pas de OVUR-mehode oe: oriënaie (iel, doel, hypohese), oorbereiding (werkwijze, opselling, nauwkeurigheid meeoesellen), uioering (meingen en berekeningen, abel, grafieken) en reflecie (beslui, fouenanalyse) 2b.2 De eenparig eranderlijke beweging Een eenparig eranderlijke beweging is een beweging me een consane ersnelling. - We spreken an een eenparig ersnelde beweging als de snelheid oeneem. - We spreken an een eenparig erraagde beweging als de snelheid afneem. Ui de oorgaande proef kan men besluien da he s--diagram an een eenparig eranderlijke beweging een parabool is. He --diagram an zo n beweging is een reche door de oorsprong. De ersnelling an een eenparig ersnelde beweging is de consane erhouding an de snelheidserandering o de ijdsduur: a = / eenheid an ersnelling: [a] = [] / [] = m/s / s = m/s² Bij een eenparig erraagde beweging is de ersnelling Afgeleide formules: = = me = 0 Indien 0 = 0 m/s (dwz. errek anui rus) dan is = en indien ook 0 = 0 s worden de formules: a = = = Deel 1: Bewegingen 13-e
6 2b.2.1 Oefening : Een lieguig word op een liegdekschip anui rus me een kaapul eenparig ersneld om op e sijgen: in 2,00 s bereik he lieguig een snelheid an 120 m/s. Bereken de ersnelling. 2b.2.2 Oefening : Bereken de ersnelling an een formule 1 wagen die om 13 h 12 min 24 s op de sarlijn passeer me een snelheid an 45 m/s en dan eenparig ersnel o hij om 13 h 12 min 32 s een snelheid bereik an 77 m/s. 2b.2.3 Oefening : Een ruimeeer word eenparig ersneld gelanceerd en bereik op een hooge an 300 km een snelheid an km/h. Bereken de liegijd an de ruimeeer als die een ersnelling heef an 15 m/s². 2b.2.4 Oefening : Welke snelheid bereik een lif die anui rus gedurende 2,5 s eenparig ersnel me een ersnelling an 3,5 m/s²? 2b.2.5 He a--diagram a Bij een eenparig eranderlijke beweging is de ersnelling In een a--diagram word di oorgeseld door een Teken he a--diagram an een fieser die gedurende 4,0 s Eenparig ersnel me een ersnelling an 0,5 m/s². Teken in hezelfde assenselsel de ersnelling an de knikker in de proef die we deden. 2b.2.6 De gemiddelde snelheid an een eenparig eranderlijke beweging <> <> He --diagram an een eenparig ersnelde beweging zonder beginsnelheid is een reche door de oorsprong. De opperlake an de driehoek onder de reche is de afgelegde weg (fig. 1). De opperlake onder de horizonale an de gemiddelde snelheid (fig. 2) is een groo als die an de driehoek als <> = / 2. Da is een eigenschap an driehoeken: de opperlake an een driehoek is de basis maal de hooge gedeeld door wee: A = h.b / 2 (fig. 3). De gemiddelde snelheid an een eenparig ersnelde beweging zonder beginsnelheid is gelijk aan de helf an de eindsnelheid: <> = / 2 Deel 1: Bewegingen 13-f
7 2b.2.7 De afgelegde weg an een eenparig eranderlijke beweging zonder beginsnelheid <> = / en <> = / 2 (definiie) (eigenschap als 0 = 0 m/s) <> =. / 2 en ermis = a. (eenparig eranderlijke beweging zonder beginsnelheid) = a. ² / 2 Voor een eenparig eranderlijke beweging zonder beginsnelheid is: = a. ² / 2 Welk erband is er ussen en ²? Welk erband is er ussen en? He s--diagram an een eenparig eranderlijke beweging is dus een Merk op da: a = 2. / ² (di merken we ook bij de proef me de knikker) 2b.2.8 Opgae : Een rein errek anui silsand me een eenparige ersnelling an 2,0 m/s². Hoe groo is de afgelegde weg na 1,0 s, 2,0 s, 3,0 s, 4,0 s en 5,0 s? Teken he s--diagram. = a. ² / 2 0,0 s 1,0 s 2,0 s 3,0 s 4,0 s 5,0 s s (m) (s) 2b.2.9 Formules oor de eenparig eranderlijke beweging zonder beginsnelheid = a. = a. ² / 2 <> = / <> = / 2 Deel 1: Bewegingen 13-g
8 Er zijn onafhankelijke formules en grooheden. Men heef dus gegeens nodig om de andere grooheden eenduidig e bepalen. 2b.2.10 Oefening : Een ruimeeer word gelanceerd en ersnel eenparig gedurende 9,00 min. aan 15 m/s². Bereken de bereike snelheid en de afgelegde weg. 2b.2.11 Oefening : Een lieguig errek ui silsand me een consane ersnelling an 1,50 m/s². Hoe lang moe de sarbaan minsens zijn als he lieguig een snelheid an 45 m/s moe halen om op e sijgen? 2b.2.12 Oefening : Een sneeuwlawine begin naar beneden e schuien me een eenparige ersnelling an 2,00 m/s² en bos 400 m lager egen een roswand. Bereken de snelheid waarmee de lawine bos. 2b.2.13 Oefening : Een moorijder errek aan een rood lich en ersnel eenparig. Na 150 m heef hij een snelheid an 30,0 m/s bereik. Bereken zijn ersnelling. 2b.2.14 Exra oefeningen 1) Een auo bereik anui rus na 10 s eenparig ersneld een eindsnelheid an 100 km/h. Bereken zijn ersnelling [2,8 m/s²] 2) Een ram errek ui silsand en leg in 10 s eenparig ersneld een weg af an 100 m. Bereken de ersnelling. [2,0 m/s²] 3) Hoe lang duur he oor een bus me een consane ersnelling an 2,0 m/s² een snelheid bereik an 36 km/h? Hoe groo is de afgelegde weg onderussen? [5,0 s ; 25 m] 4) Teken he s--diagram en he --diagram an een lieguig da gedurende 5,0 s anui rus ersnel me 4,0 m/s². 5) Een kogel krijg in de loop an een geweer een ersnelling an 1, m/s². De loop is 80 cm lang. Me welke snelheid erlaa de kogel de loop? [1,3.10² m/s] 6) Een luchdoelrake bereik anui rus een snelheid an km/h nada hij een afsand an m heef afgelegd. Bereken de ersnelling. [500,0 m/s²] 2b.3 De albeweging 2b.3.1 De aard an de albeweging De albeweging word eroorzaak door de zwaarekrach. Vanui ui rus al een oorwerp (riching) naar (zin) b.3.2 Proef : we laen in he luchledige egelijkerijd een suk meaal en een pluimpje allen. Welk an de oorwerpen al he snels? omda Alle oorwerpen allen een snel. Hun ersnelling is een groo als er geen wrijing is me de luch. Deel 1: Bewegingen 13-h
9 2b.3.3 Proef : We herhalen de proef an de knikker die an een helling rol, maar laen de knikker nu allen. We sellen as da de rije al (albeweging anui rus en zonder wrijing) een eenparig ersnelde beweging is me ersnelling a = b.3.4 Verband ussen m/s² en N/kg He dynamisch effec an een krach is De erandering an snelheid door een krach is afhankelijk an de massa an he oorwerp: hoe groer de massa, hoe groer de krach zal moeen zijn om he oorwerp een bepaalde ersnelling e geen. Isaac Newon beschreef da in zijn weede we: F = m.a Laer zullen we leren da 1 N de krach is die nodig is om een massa an 1 kg een ersnelling e geen an 1 m/s², dus om zijn snelheid elke seconde me 1 m/s e laen oenemen. Dus 1 N = 1 kg. 1 m/s² Of 1 N / kg = 1 m/s² 2b.3.5 De alersnelling Voor een rije al is a = g = De weede we an Newon kunnen oor de zwaarekrach dus ook schrijen als: b.3.6 Formules oor de rije al zonder beginsnelheid Deze formules zijn eigenlijk ideniek aan die an de eenparig ersnelde beweging zonder beginsnelheid. De afgelegde weg noemen we eenwel de alhooge (h) en de ersnelling is g = 9,81 m/s². = g. h = g. ² / 2 <> = h / <> = / 2 Er zijn onafhankelijke formules en grooheden. Men heef dus gegeen nodig om de andere grooheden e bepalen. Deel 1: Bewegingen 13-i
10 2b.3.7 Oefening : Een parachuis beoefend gedurende 3,00 seconden een rije al. Wa is zijn snelheid en welke afsand heef hij afgelegd in die ijd? 2b.3.8 Oefening : Men laa een seen in een waerpu allen en el he aanal seconden o men een plons hoor. Bedenk me g 10 m/s² een eenoudige formule om de diepe an zo n pu e schaen. 2b.3.9 Oefening : Een seen al an een 123 m hoog gebouw. Me welke snelheid kom hij op de grond erech? 2b.3.10 Exra oefeningen 1) Je laa een bakseen an 1,00 kg an op een hooge an 100 cm allen. Hoeeel ijd heb je om je oe weg e rekken? Me welke snelheid raak de bakseen anders je oe? [0,452 s ; 4,43 m/s = 15,9 m/s] 2) Teken he s--diagram an een allend oorwerp. Noem de beginhooge h 0 en hou er rekening mee da de hooge erminder ijdens de al. 3) Twee senen allen me een ussenijd an 1,50 s an op een hooge an 19,6 m. Bereken hun alijd. Teken beide albewegingen in één s--diagram (dus h--diagram). Blijf de afsand ussen de wee senen gelijk? Blijf he erschil in snelheid ussen beide senen een consane? [2,00 s] 4) Een parachuise spring anop 981 m hooge, maar parachue gaa nie open gaa omda die gesaboeerd werd door een liefdesriale. Bereken de snelheid waarmee de ongelukkige dame e pleer zou soren. Waarom word deze snelheid in realiei nie gehaald? [139 m/s = 500 km/h] 5) Hoe hoog kan een asronau op de maan springen als zijn afsoosnelheid 3,0 m/s bedraag? [2,6 m] Deel 1: Bewegingen 13-j
11 Begrippen Opperlakemehode Veranderlijke beweging Gemiddelde snelheid Eenparig eranderlijke beweging, eenparig ersnelde beweging, eenparig erraagde beweging Versnelling a--diagram Vrije al Valersnelling, zwaarekrach eldserke Kennen en kunnen Je kan de begrippen opperlakemehode, eranderlijke beweging, gemiddelde snelheid, eenparig eranderlijke beweging, eenparig ersnelde beweging, eenparig erraagde beweging, ersnelling, a--diagram, rije al, alersnelling en zwaarekrach eldserke uileggen en gebruiken. Je kan bewijzen da in een s--diagram de opperlake onder de grafieklijn de afgelegde weg is, zowel oor een eenparige als oor een eranderlijke beweging. Je kan correc een proef uioeren om de eenparig ersnelde beweging e besuderen en daaran een erslag schrijen me een iel, een doel, een hypohese, een werkwijze (me benodigdheden, meeinsrumenen en hun nauwkeurigheid en me een proefopselling), waarnemingen, meingen en berekeningen, een grafiek, de gerokken besluien en een fouenanalyse. Je kan correc een proef uioeren om de alersnelling e bepalen en daaran een erslag schrijen me een iel, een doel, een hypohese, een werkwijze (me benodigdheden, meeinsrumenen en hun nauwkeurigheid en me een proefopselling), waarnemingen, meingen en berekeningen, een grafiek, de gerokken besluien en een fouenanalyse. Je ken de grooe an de alersnelling in ons land: 9,81 m/s² en je kan uileggen waarom di oereenkom me de eldserke an de zwaarekrach. Je ken de weede we an Newon die he erband geef ussen krach, massa en ersnelling. Je kan oor een eenparige eranderlijke beweging de snelheid, afgelegde weg, ijdsduur en ersnelling berekenen en daarbij de nodige eenheden omrekenen (km-m, h-min-s, km/h-m/s). Je kan raagsukken oer de eenparige eranderlijke beweging en de rijealbeweging oplossen: gegeen en geraagde onderscheiden, he gebruik an formules en SI-eenheden, rekenen me beduidende cijfers en nauwkeurigheid, en da alles me een correce noaiewijze. Je wee da oor de olledige berekening an een eenparig eranderlijke beweging minsens 2 onafhankelijke grooheden moeen gegeen zijn en oor de rije al minsens één grooheid. Je kan een eenparig eranderlijke beweging oorsellen in een s-, een --diagram en een a-diagram en je kan gegeens an een s-, een - en een a--diagram aflezen en inerpreeren. Je wee da een beweging die erraagd is in de zin an de plaasas een negaiee ersnelling heef. Je kan bewijzen da in een --diagram de richingscoëfficiën an de reche de ersnelling is an de beweging. Deel 1: Bewegingen 13-k
Hoofdstuk 1: Rust en beweging
 Hoofdsuk 1: Rus en beweging 1.1 Rus en beweging zijn relaief Ten opziche van he vlieguig is de passagier in................................................ Ten opziche van he aardoppervlak is he vlieguig
Hoofdsuk 1: Rus en beweging 1.1 Rus en beweging zijn relaief Ten opziche van he vlieguig is de passagier in................................................ Ten opziche van he aardoppervlak is he vlieguig
1 Inleidende begrippen
 1 Inleidende begrippen 1.1 Wanneer is een pun in beweging? Leg di ui aan de hand van een figuur. Rus en beweging (blz. 19) Figuur 1.1 Een pun in beweging 1.2 Wanneer is een pun in rus? Leg di ui aan de
1 Inleidende begrippen 1.1 Wanneer is een pun in beweging? Leg di ui aan de hand van een figuur. Rus en beweging (blz. 19) Figuur 1.1 Een pun in beweging 1.2 Wanneer is een pun in rus? Leg di ui aan de
1 Herhalingsoefeningen december
 1 Herhalingsoefeningen december Een lichaam word vericaal omhoog geworpen. Welke van de ondersaande v, diagrammen geef dan he juise verloop van de snelheidscomponen weer? Jan rijd me de fies over een lange
1 Herhalingsoefeningen december Een lichaam word vericaal omhoog geworpen. Welke van de ondersaande v, diagrammen geef dan he juise verloop van de snelheidscomponen weer? Jan rijd me de fies over een lange
Examen VWO. Wiskunde B1 (nieuwe stijl)
 Wiskunde B (nieuwe sijl) Examen VW Voorbereidend Weenschappelijk nderwijs Tijdvak Donderdag 22 mei 3.30 6.30 uur 20 03 Voor di examen zijn maximaal 83 punen e behalen; he examen besaa ui 20 vragen. Voor
Wiskunde B (nieuwe sijl) Examen VW Voorbereidend Weenschappelijk nderwijs Tijdvak Donderdag 22 mei 3.30 6.30 uur 20 03 Voor di examen zijn maximaal 83 punen e behalen; he examen besaa ui 20 vragen. Voor
Hoofdstuk 2 - Overige verbanden
 Moderne Wiskunde Uiwerkingen bij vwo C deel Hoofdsuk Overige verbanden Hoofdsuk - Overige verbanden bladzijde < a D 4 4,, 8 dus heef de vergelijking 4p p +, geen oplossingen en zijn er geen snijpunen van
Moderne Wiskunde Uiwerkingen bij vwo C deel Hoofdsuk Overige verbanden Hoofdsuk - Overige verbanden bladzijde < a D 4 4,, 8 dus heef de vergelijking 4p p +, geen oplossingen en zijn er geen snijpunen van
Hoofdstuk 2 - Overige verbanden
 Hoofdsuk - Overige verbanden bladzijde < a D 4 4,, 8 dus heef de vergelijking 4p p +, geen oplossingen en zijn er geen snijpunen van de grafiek me de horizonale as. b 4p p +,, p 4p p of p 4 + c Voor p
Hoofdsuk - Overige verbanden bladzijde < a D 4 4,, 8 dus heef de vergelijking 4p p +, geen oplossingen en zijn er geen snijpunen van de grafiek me de horizonale as. b 4p p +,, p 4p p of p 4 + c Voor p
Eindexamen wiskunde B1 vwo I
 indeamen wiskunde B vwo 009 - I Over een parabool gespannen In figuur is de grafiek van de funcie f me f ( ) = 3 geekend. Tussen wee punen en S die even ver van O op de -as liggen, word denkbeeldig een
indeamen wiskunde B vwo 009 - I Over een parabool gespannen In figuur is de grafiek van de funcie f me f ( ) = 3 geekend. Tussen wee punen en S die even ver van O op de -as liggen, word denkbeeldig een
Eindexamen wiskunde B 1 vwo 2003-I
 Eindexamen wiskunde B vwo 2003-I Lenge Ui saisisch onderzoek is gebleken da de volwassen Nederlandse mannen in 999 gemiddeld 80,0 cm lang waren, en da er een sandaardafwijking van 2,8 cm was in de lengeverdeling.
Eindexamen wiskunde B vwo 2003-I Lenge Ui saisisch onderzoek is gebleken da de volwassen Nederlandse mannen in 999 gemiddeld 80,0 cm lang waren, en da er een sandaardafwijking van 2,8 cm was in de lengeverdeling.
Noordhoff Uitgevers bv
 a b c d e a Analyse De omze was in 987 ongeveer, miljard (de recher as) De wins was ongeveer 6 miljoen (linker as) 6 miljoen 6 miljoen = %, % Er is sprake van verlies als de wins/verlies-grafiek negaief
a b c d e a Analyse De omze was in 987 ongeveer, miljard (de recher as) De wins was ongeveer 6 miljoen (linker as) 6 miljoen 6 miljoen = %, % Er is sprake van verlies als de wins/verlies-grafiek negaief
Uitslagen voorspellen
 Eindexamen vwo wiskunde A pilo 04-I Vraag Anwoord Scores Uislagen voorspellen maximumscore 3 De afsand ussen Wilders en Thieme is 4 De conclusie: nie meer dan wee maal zo groo maximumscore 3 Bij gelijke
Eindexamen vwo wiskunde A pilo 04-I Vraag Anwoord Scores Uislagen voorspellen maximumscore 3 De afsand ussen Wilders en Thieme is 4 De conclusie: nie meer dan wee maal zo groo maximumscore 3 Bij gelijke
Gebruik van condensatoren
 Gebruik van condensaoren He spanningsverloop ijdens he laden Als we de schakelaar s sluien laden we de condensaor op. De condensaorspanning zal oenemen volgens een exponeniële funcie en de spanning over
Gebruik van condensaoren He spanningsverloop ijdens he laden Als we de schakelaar s sluien laden we de condensaor op. De condensaorspanning zal oenemen volgens een exponeniële funcie en de spanning over
Verbetersleutel examen 6LWI
 Verbeerleuel exaen 6LWI Correcieleuel bij Vraag-V01: De grafiek bechrijf de beweging an een rein die eer rijd in een zone oor beperke nelheid, en daarna ernel op he ogenblik da hij buien de zone i. De
Verbeerleuel exaen 6LWI Correcieleuel bij Vraag-V01: De grafiek bechrijf de beweging an een rein die eer rijd in een zone oor beperke nelheid, en daarna ernel op he ogenblik da hij buien de zone i. De
Samenvatting Natuurkunde 1 HAVO Beweging
 Beweging Samenvaing Nauurkunde HAVO Eenparig rechlijnige beweging a Eenparig versnelde rechlijnige beweging a a = consan a = 0 m/s Oppervlake = v = 0 m/s Oppervlake = v v v v = consan v() = a Oppervlake
Beweging Samenvaing Nauurkunde HAVO Eenparig rechlijnige beweging a Eenparig versnelde rechlijnige beweging a a = consan a = 0 m/s Oppervlake = v = 0 m/s Oppervlake = v v v v = consan v() = a Oppervlake
De eenparig veranderlijke beweging:
 - 53 - De eenparig eranderlijke beweging: T begon alleaal bij Galileï. Deze ialiaane geleerde heef geleefd an 1564 o 164. Van zijn ader oe hij edicijnen gaan uderen in Pia, aar hij inereeerde zich eel
- 53 - De eenparig eranderlijke beweging: T begon alleaal bij Galileï. Deze ialiaane geleerde heef geleefd an 1564 o 164. Van zijn ader oe hij edicijnen gaan uderen in Pia, aar hij inereeerde zich eel
C. von Schwartzenberg 1/11
 G&R havo A deel C von Schwarzenberg 1/11 1a m 18:00 uur He verbruik was oen ongeveer 1150 kwh 1b Minimaal ongeveer 7750 kwh (100%), maimaal ongeveer 1150 kwh (145,%) Een oename van ongeveer 45,% 1c 1d
G&R havo A deel C von Schwarzenberg 1/11 1a m 18:00 uur He verbruik was oen ongeveer 1150 kwh 1b Minimaal ongeveer 7750 kwh (100%), maimaal ongeveer 1150 kwh (145,%) Een oename van ongeveer 45,% 1c 1d
Eindexamen havo wiskunde A I
 Eindexamen havo wiskunde A 0 - I Supersize me maximumscore 3 33,6 G = 5000 G 49 (kg) He anwoord: 49 85 = 64 (kg) ( nauwkeuriger) maximumscore 4 E b = 33,6 85 = 856 Zijn energieoverscho is 5000 856 = 44
Eindexamen havo wiskunde A 0 - I Supersize me maximumscore 3 33,6 G = 5000 G 49 (kg) He anwoord: 49 85 = 64 (kg) ( nauwkeuriger) maximumscore 4 E b = 33,6 85 = 856 Zijn energieoverscho is 5000 856 = 44
Eindexamen wiskunde B1 havo 2004-II
 Bacerieculuur De groei van he aanal baceriën van een bacerieculuur hang onder andere af van he voedingsparoon, de emperauur en de beliching. Ui onderzoek blijk da he aanal baceriën van een bepaalde bacerieculuur
Bacerieculuur De groei van he aanal baceriën van een bacerieculuur hang onder andere af van he voedingsparoon, de emperauur en de beliching. Ui onderzoek blijk da he aanal baceriën van een bepaalde bacerieculuur
Blok 1 - Vaardigheden
 6 Blok - Vaardigheden Blok - Vaardigheden Exra oefening - Basis B-a Bij abel A zijn de facoren achereenvolgens 8 : = 6 ; 08 : 8 = 6 en 68 : 08 = 6. Bij abel A is sprake van exponeniële groei. Bij abel
6 Blok - Vaardigheden Blok - Vaardigheden Exra oefening - Basis B-a Bij abel A zijn de facoren achereenvolgens 8 : = 6 ; 08 : 8 = 6 en 68 : 08 = 6. Bij abel A is sprake van exponeniële groei. Bij abel
2.1 Het differentiequotiënt
 hoodsk : Diereniëren. He dierenieqoiën Me een ncie kn je de onwikkeling n een grooheid beschrijen. Neem bijoorbeeld een schoonspringer die n de ienmeerplnk spring. Als je de lchwrijing erwrloos, kn je
hoodsk : Diereniëren. He dierenieqoiën Me een ncie kn je de onwikkeling n een grooheid beschrijen. Neem bijoorbeeld een schoonspringer die n de ienmeerplnk spring. Als je de lchwrijing erwrloos, kn je
wiskunde A bezem havo 2017-I
 Disribuieriem Een disribuieriem is een geribbelde riem die in een moderne verbrandingsmoor van een auo zi. Zo n riem heef en opziche van een keing voordelen: hij maak minder lawaai en er is geen smering
Disribuieriem Een disribuieriem is een geribbelde riem die in een moderne verbrandingsmoor van een auo zi. Zo n riem heef en opziche van een keing voordelen: hij maak minder lawaai en er is geen smering
. Tijd 75 min, dyslecten 90min. MAX: 44 punten 1. (3,3,3,3,2,2p) Chemische stof
 RUDOLF STEINERCOLLEGE HAARLEM WISKUNDE HAVO CM/EM T112-HCMEM-H579 Voor elk onderdeel is aangegeven hoeveel punen kunnen worden behaald. Anwoorden moeen alijd zijn voorzien van een berekening, oeliching
RUDOLF STEINERCOLLEGE HAARLEM WISKUNDE HAVO CM/EM T112-HCMEM-H579 Voor elk onderdeel is aangegeven hoeveel punen kunnen worden behaald. Anwoorden moeen alijd zijn voorzien van een berekening, oeliching
Tentamen Golven en Optica
 Tenamen Golven en Opica woensdag 9 juni 011, 15.00-18.00 uur Maak elke opgave op een apar vel voorzien van uw naam en sudennummer. Gebruik van een (grafische) rekenmachine is oegesaan. Verdeel uw ijd opimaal
Tenamen Golven en Opica woensdag 9 juni 011, 15.00-18.00 uur Maak elke opgave op een apar vel voorzien van uw naam en sudennummer. Gebruik van een (grafische) rekenmachine is oegesaan. Verdeel uw ijd opimaal
Hoofdstuk 2 - Formules voor groei
 Moderne wiskunde 9e ediie Havo A deel Uiwerkingen Hoofdsuk - Formules voor groei bladzijde 00 V-a = 08, ; 870 08, ; 70 0, 8; 60 00 00 870 70 08,, gemiddeld 0,8 b De beginhoeveelheid is 00 en de groeifacor
Moderne wiskunde 9e ediie Havo A deel Uiwerkingen Hoofdsuk - Formules voor groei bladzijde 00 V-a = 08, ; 870 08, ; 70 0, 8; 60 00 00 870 70 08,, gemiddeld 0,8 b De beginhoeveelheid is 00 en de groeifacor
Bij het bewerken van plaatmateriaal ontstaat vaak de situatie dat materiaal langs
 12_DRUK_nr2_2005 19-04-2005 11:33 Pagina 12 Druk op de INLEIDING Bij he bewerken van plaamaeriaal onsaa vaak de siuaie da maeriaal langs een radius moe bewegen. Meesal heef men dan van doen me he maken
12_DRUK_nr2_2005 19-04-2005 11:33 Pagina 12 Druk op de INLEIDING Bij he bewerken van plaamaeriaal onsaa vaak de siuaie da maeriaal langs een radius moe bewegen. Meesal heef men dan van doen me he maken
Examen beeldverwerking 10/2/2006
 Richlijnen Examen beeldverwerking 10/2/2006 Di is een gesloen boek examen. Communicaieapparauur en beschreven of bedruk papier of andere voorwerpen zijn dus nie oegelaen. Schrijf je naam op elk blad. Schrijf
Richlijnen Examen beeldverwerking 10/2/2006 Di is een gesloen boek examen. Communicaieapparauur en beschreven of bedruk papier of andere voorwerpen zijn dus nie oegelaen. Schrijf je naam op elk blad. Schrijf
Dit examen bestaat uit 13 opgaven Bijlage: 1 antwoordpapier
 MAVO-D Il EXAMEN MIDDEBAAR AGEMEEN VOORTGEZET ONDERWIJS IN 1986 D - niveau Donderdag 5 juni, 9. 00-11. 00 uur '-,, NATUURKUNDE Di examen besaa ui 13 opgaven Bijlage: 1 anwoordpapier Waar nodig mag bij
MAVO-D Il EXAMEN MIDDEBAAR AGEMEEN VOORTGEZET ONDERWIJS IN 1986 D - niveau Donderdag 5 juni, 9. 00-11. 00 uur '-,, NATUURKUNDE Di examen besaa ui 13 opgaven Bijlage: 1 anwoordpapier Waar nodig mag bij
Overzicht Examenstof Wiskunde A
 Oefenoes ij hoofdsuk en Overzih Examensof Wiskunde A a X min 0, X max 0, Y min 0 en Y max 000. 0 lier per minuu. Als de ank leeg is, dan is W 0, dus 00 0 0 dus 0. Na 0 minuen is de ank leeg. a Neem de
Oefenoes ij hoofdsuk en Overzih Examensof Wiskunde A a X min 0, X max 0, Y min 0 en Y max 000. 0 lier per minuu. Als de ank leeg is, dan is W 0, dus 00 0 0 dus 0. Na 0 minuen is de ank leeg. a Neem de
Snelheid en richting
 Snelheid en riching Di is een onderdeel van Meekunde me coördinaen en behoeve van he nieuwe programma (05) wiskunde B vwo. Opgaven me di merkeken kun je, zonder de opbouw aan e asen, overslaan. * Bij opgaven
Snelheid en riching Di is een onderdeel van Meekunde me coördinaen en behoeve van he nieuwe programma (05) wiskunde B vwo. Opgaven me di merkeken kun je, zonder de opbouw aan e asen, overslaan. * Bij opgaven
Krommen in het platte vlak
 Krommen in he plae vlak 1 Een komee beschrijf een baan om de zon. We brengen een assenselsel aan in he vlak van de baan van de komee, me de zon als oorsprong. Als eenheid in he assenselsel nemen we de
Krommen in he plae vlak 1 Een komee beschrijf een baan om de zon. We brengen een assenselsel aan in he vlak van de baan van de komee, me de zon als oorsprong. Als eenheid in he assenselsel nemen we de
Deel 2. Basiskennis wiskunde
 Deel 2. Basiskennis wiskunde Vraag 26 Definieer de funcie f : R R : 7 cos(2 ). Bepaal de afgeleide van de funcie f in he pun 2π/2. (A) f 0 ( 2π/2) = π (B) f 0 ( 2π/2) = 2π (C) f 0 ( 2π/2) = 2π (D) f 0
Deel 2. Basiskennis wiskunde Vraag 26 Definieer de funcie f : R R : 7 cos(2 ). Bepaal de afgeleide van de funcie f in he pun 2π/2. (A) f 0 ( 2π/2) = π (B) f 0 ( 2π/2) = 2π (C) f 0 ( 2π/2) = 2π (D) f 0
Analoge Elektronika 1 DE SCHMITT TRIGGER
 Analoge Elekronika DE SCHMITT TIGGE Een Schmi rigger is een komparaor me hyseresis. Ne zoals bij een komparaor is de ingang een analoog signaal, erwijl de uigang een digiaal signaal is. De uigangsspanning
Analoge Elekronika DE SCHMITT TIGGE Een Schmi rigger is een komparaor me hyseresis. Ne zoals bij een komparaor is de ingang een analoog signaal, erwijl de uigang een digiaal signaal is. De uigangsspanning
Hoofdstuk 3 Exponentiële functies
 Havo B deel Uiwerkingen Moderne wiskunde Hoofdsuk Eponeniële funies ladzijde 6 V-a Door zih in weeën e delen vermenigvuldig he aanal aeriën per ijdseenheid zih seeds me een faor is de eginhoeveelheid,
Havo B deel Uiwerkingen Moderne wiskunde Hoofdsuk Eponeniële funies ladzijde 6 V-a Door zih in weeën e delen vermenigvuldig he aanal aeriën per ijdseenheid zih seeds me een faor is de eginhoeveelheid,
Bewegen in grafieken. Hoofdstuk 1 Bewegen in grafieken. 1.1 Snelheid meten
 1 Bewegen in grafieken 1.1 Snelheid meen 1 pulje a Een eenheid an afand (m, cm, km, ) en een eenheid an ijd (, min, h, ). uur per meer, lier/econde, km/lichjaar en uur per nach. De eenheid an nelheid i
1 Bewegen in grafieken 1.1 Snelheid meen 1 pulje a Een eenheid an afand (m, cm, km, ) en een eenheid an ijd (, min, h, ). uur per meer, lier/econde, km/lichjaar en uur per nach. De eenheid an nelheid i
1 Beweging 1.1. Inleiding
 1 Beweging 1.1 Inleiding Bovensaande woordenwolk beva begrippen die je vorige jaren in de lessen fysica zag. Om die begrippen op e frissen, gebruiken we ze bij he beschrijven van een srafschop. Terech
1 Beweging 1.1 Inleiding Bovensaande woordenwolk beva begrippen die je vorige jaren in de lessen fysica zag. Om die begrippen op e frissen, gebruiken we ze bij he beschrijven van een srafschop. Terech
Hoofdstuk 1 - Exponentiële formules
 V-1a 4 Hoofdsuk 1 - Exponeniële formules Hoofdsuk 1 - Exponeniële formules Voorkennis prijs in euro s 70 78,0 percenage 100 119 1,19 b Je moe de prijs me he geal 1,19 vermenigvuldigen. c De BTW op de fies
V-1a 4 Hoofdsuk 1 - Exponeniële formules Hoofdsuk 1 - Exponeniële formules Voorkennis prijs in euro s 70 78,0 percenage 100 119 1,19 b Je moe de prijs me he geal 1,19 vermenigvuldigen. c De BTW op de fies
OEFENTOETS HAVO B DEEL 1
 EFENTETS HAV B DEEL 1 HFDSTUK 2 VERANDERINGEN PGAVE 1 Een oliehandelaar heef gedurende 24 uur nauwkeurig de olieprijs bijgehouden. Zie de figuur hieronder. Hierin is P de prijs in dollar per va. P 76 75
EFENTETS HAV B DEEL 1 HFDSTUK 2 VERANDERINGEN PGAVE 1 Een oliehandelaar heef gedurende 24 uur nauwkeurig de olieprijs bijgehouden. Zie de figuur hieronder. Hierin is P de prijs in dollar per va. P 76 75
Correctievoorschrift VWO 2015
 Correcievoorschrif VWO 205 ijdvak wiskunde C (pilo) He correcievoorschrif besaa ui: Regels voor de beoordeling 2 Algemene regels 3 Vakspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor
Correcievoorschrif VWO 205 ijdvak wiskunde C (pilo) He correcievoorschrif besaa ui: Regels voor de beoordeling 2 Algemene regels 3 Vakspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor
Elastische Botsing 1 ELASTISCHE BOTSING
 Elaiche Boing ELASTISCHE BOTSING In he boe Syeeanalye in 8 doeinen wor de lezer geconfroneerd e ele nieuwe begrippen: diracipul, Laplaceranforaie, bereenen an de raniënreponie. Velen zullen zich de raag
Elaiche Boing ELASTISCHE BOTSING In he boe Syeeanalye in 8 doeinen wor de lezer geconfroneerd e ele nieuwe begrippen: diracipul, Laplaceranforaie, bereenen an de raniënreponie. Velen zullen zich de raag
Blok 4 - Vaardigheden
 Havo B deel Uiwerkingen Moderne wiskunde Blok - Vaardigheden bladzijde a domein en bereik b x = = = c Me behulp van onderdeel b en de grafiek: d Eers: log x = ofwel x = = Dan me behulp van de grafiek:
Havo B deel Uiwerkingen Moderne wiskunde Blok - Vaardigheden bladzijde a domein en bereik b x = = = c Me behulp van onderdeel b en de grafiek: d Eers: log x = ofwel x = = Dan me behulp van de grafiek:
LABO. Elektriciteit OPGAVE: Meten van vermogen in een driegeleidernet. Totaal :.../20. .../.../ Datum van afgifte:
 LABO Elekriciei OPGAVE: Meen van vermogen in een driegeleiderne Daum van opgave:.../.../ Daum van afgife: Verslag nr. : 8 Leerling: Assisenen: Klas: 3.1 EIT.../.../ Evaluaie :.../10 Theorie :.../10 Meeopselling
LABO Elekriciei OPGAVE: Meen van vermogen in een driegeleiderne Daum van opgave:.../.../ Daum van afgife: Verslag nr. : 8 Leerling: Assisenen: Klas: 3.1 EIT.../.../ Evaluaie :.../10 Theorie :.../10 Meeopselling
ELEKTRICITEIT WISSELSTROOMTHEORIE. Technisch Instituut Sint-Jozef, Wijerstraat 28, B-3740 Bilzen. Cursus : Ian Claesen. Versie: 19-10-2008
 EEKTTET WSSESTOOMTHEOE Technisch nsiuu Sin-Jozef, Wijersraa 28, B-3740 Bilzen ursus : an laesen Versie: 19-10-2008 1 Sooren spanningen en sromen... 3 1.1 Gelijksroom... 3 1.2 Wisselsroom... 4 2 Sinusvormige
EEKTTET WSSESTOOMTHEOE Technisch nsiuu Sin-Jozef, Wijersraa 28, B-3740 Bilzen ursus : an laesen Versie: 19-10-2008 1 Sooren spanningen en sromen... 3 1.1 Gelijksroom... 3 1.2 Wisselsroom... 4 2 Sinusvormige
Examen beeldverwerking 30/1/2013
 Richlijnen Examen beeldverwerking 30//03 Di is een gesloen boek examen. Communicaieapparauur en beschreven of bedruk papier of andere voorwerpen zijn dus nie oegelaen. Schrijf je naam op elk blad. Schrijf
Richlijnen Examen beeldverwerking 30//03 Di is een gesloen boek examen. Communicaieapparauur en beschreven of bedruk papier of andere voorwerpen zijn dus nie oegelaen. Schrijf je naam op elk blad. Schrijf
Studiekosten of andere scholings uitgaven
 20 Aanvullende oeliching bij aangife inkomsenbelasing 20 Sudiekosen of andere scholings uigaven Volgde u in 20 een opleiding of een sudie voor uw (oekomsige) beroep? Of had u kosen voor een EVCprocedure
20 Aanvullende oeliching bij aangife inkomsenbelasing 20 Sudiekosen of andere scholings uigaven Volgde u in 20 een opleiding of een sudie voor uw (oekomsige) beroep? Of had u kosen voor een EVCprocedure
Opgave 1 (30 punten) + + = B h Z
 Tenamen CT222 Dynamica van Sysemen 25 juni 212 14.-17. Le op: - Vermeld op ieder blad je naam en sudienummer - Maak elk van de drie opgaven op een apar vel Opgave 1 (3 punen) 2 Een bekken (links) me berging
Tenamen CT222 Dynamica van Sysemen 25 juni 212 14.-17. Le op: - Vermeld op ieder blad je naam en sudienummer - Maak elk van de drie opgaven op een apar vel Opgave 1 (3 punen) 2 Een bekken (links) me berging
op het interval 5, 15 betekent 5 x 15. 4b x op het interval 6, 10 betekent 6 x < 10. 5d Bij 3 < x π hoort het interval 3, π
 G&R havo B deel Veranderingen C. von Schwarzenberg / a b c Tussen en uur. Van en uur neem de sijging oe. Van o 6 uur neem de sijging af. Van o 8 uur neem de daling oe. Van 8 o uur neem de daling af. 6,,,,,
G&R havo B deel Veranderingen C. von Schwarzenberg / a b c Tussen en uur. Van en uur neem de sijging oe. Van o 6 uur neem de sijging af. Van o 8 uur neem de daling oe. Van 8 o uur neem de daling af. 6,,,,,
Studiekosten of andere scholingsuitgaven
 12345 20 Aanvullende oeliching Bij voorlopige aanslag inkomsenbelasing 20 Volg u in 20 een opleiding of een sudie voor uw (oekomsige) beroep? Dan mag u de uigaven hiervoor, zoals lesgeld en de uigaven
12345 20 Aanvullende oeliching Bij voorlopige aanslag inkomsenbelasing 20 Volg u in 20 een opleiding of een sudie voor uw (oekomsige) beroep? Dan mag u de uigaven hiervoor, zoals lesgeld en de uigaven
elektrotechniek CSPE KB 2011 minitoets bij opdracht 10
 elekroechniek CSPE KB 2011 minioes bij opdrach 10 varian a Naam kandidaa Kandidaanummer Meerkeuzevragen Omcirkel he goede anwoord (voorbeeld 1). Geef verbeeringen aan volgens voorbeeld 2 of 3. (1) B B
elekroechniek CSPE KB 2011 minioes bij opdrach 10 varian a Naam kandidaa Kandidaanummer Meerkeuzevragen Omcirkel he goede anwoord (voorbeeld 1). Geef verbeeringen aan volgens voorbeeld 2 of 3. (1) B B
elektriciteit voor 5TSO
 e Dirk Sarens 45 elekriciei voor 5TSO versie 1.0 1 2011 Dirk Sarens Versie 1.0 Schooljaar 2011-2012 Gemaak voor he leerplan D/2009/7841/036 Di boek kan worden gekoch via de websie www.nibook.com Had je
e Dirk Sarens 45 elekriciei voor 5TSO versie 1.0 1 2011 Dirk Sarens Versie 1.0 Schooljaar 2011-2012 Gemaak voor he leerplan D/2009/7841/036 Di boek kan worden gekoch via de websie www.nibook.com Had je
Oefeningen Elektriciteit I Deel Ia
 Oefeningen Elekriciei I Deel Ia Di documen beva opgaven die aansluien bij de cursuseks Elekriciei I deel Ia ui he jaarprogramma van de e kandidauur Indusrieel Ingenieur KaHo Sin-Lieven.. De elekrische
Oefeningen Elekriciei I Deel Ia Di documen beva opgaven die aansluien bij de cursuseks Elekriciei I deel Ia ui he jaarprogramma van de e kandidauur Indusrieel Ingenieur KaHo Sin-Lieven.. De elekrische
Studiekosten en andere scholings uitgaven
 20 Aanvullende oeliching bij aangife inkomsenbelasing 20 IB 266-1T12FD (2576) Sudiekosen en andere scholings uigaven Volgde u in 20 een opleiding of een sudie voor uw (oekomsige) beroep? Of had u kosen
20 Aanvullende oeliching bij aangife inkomsenbelasing 20 IB 266-1T12FD (2576) Sudiekosen en andere scholings uigaven Volgde u in 20 een opleiding of een sudie voor uw (oekomsige) beroep? Of had u kosen
wiskunde A pilot vwo 2015-I
 Piramiden maximumscore a = en x =,5 geef h = 6,5 (dm) De oppervlake van he grondvlak is,5,5 = 6, 5 (dm²) De inhoud is 6, 5 6,5 4 (dm³) ( nauwkeuriger) maximumscore 4 I = x (9 x ) geef di 6 d = x x x x
Piramiden maximumscore a = en x =,5 geef h = 6,5 (dm) De oppervlake van he grondvlak is,5,5 = 6, 5 (dm²) De inhoud is 6, 5 6,5 4 (dm³) ( nauwkeuriger) maximumscore 4 I = x (9 x ) geef di 6 d = x x x x
Antwoordmodel VWO wa II. Speelgoedfabriek
 Anwoordmodel VWO wa 00-II Anwoorden Speelgoedfabriek Voorwaarde II hoor bij immeren Voor immeren zijn 60x + 40y minuen nodig Voor immeren zijn 80 uur dus 4800 minuen beschikbaar 60x + 40y 4800 kom overeen
Anwoordmodel VWO wa 00-II Anwoorden Speelgoedfabriek Voorwaarde II hoor bij immeren Voor immeren zijn 60x + 40y minuen nodig Voor immeren zijn 80 uur dus 4800 minuen beschikbaar 60x + 40y 4800 kom overeen
UITWERKING TOELICHTING OP DE ANTWOORDEN VAN HET EXAMEN 2002-I VWO
 UITWERKING TOELICHTING OP DE ANTWOORDEN VAN HET EXAMEN 00-I VAK: WISKUNDE A, NIVEAU: VWO EXAMEN: 00-I De uigever heef ernaar gesreefd de aueursrechen e regelen volgens de weelijke bepalingen. Degenen die
UITWERKING TOELICHTING OP DE ANTWOORDEN VAN HET EXAMEN 00-I VAK: WISKUNDE A, NIVEAU: VWO EXAMEN: 00-I De uigever heef ernaar gesreefd de aueursrechen e regelen volgens de weelijke bepalingen. Degenen die
2 Les- en leerstofopbouw
 2 Les- en leersofopbouw 2.7 Didacische benaderingen 2.7.7 Acierende werkormen Peer Dekkers & Wim Sonneeld Inleiding Toen u he in de klas uilegde snape ik he helemaal, maar oen ik he huis zelf ging proberen
2 Les- en leersofopbouw 2.7 Didacische benaderingen 2.7.7 Acierende werkormen Peer Dekkers & Wim Sonneeld Inleiding Toen u he in de klas uilegde snape ik he helemaal, maar oen ik he huis zelf ging proberen
Alternatieve uitwerking. Apart de afgeleide van y = 2x+ 1 = u met u = 2x + 1. = = 2u 2 = 4(2x + 1) = 8x + 4. Dus k (x) = ( ) 2 ( 2
 6 Toepassingen van de diffeeniaalekening bladzijde 70 3 a f () [6] ( 5) 36 + 6 [( 5) 36 ] + 7 6 Apa de afgeleide van y ( 5) 36 u 36 me u 5. 36u 6 7( 5) 6 Dus f () 6 ( 5) 36 + 6 7( 5) 6 + 7 6 6( 5) 36 +
6 Toepassingen van de diffeeniaalekening bladzijde 70 3 a f () [6] ( 5) 36 + 6 [( 5) 36 ] + 7 6 Apa de afgeleide van y ( 5) 36 u 36 me u 5. 36u 6 7( 5) 6 Dus f () 6 ( 5) 36 + 6 7( 5) 6 + 7 6 6( 5) 36 +
Studiekosten en andere scholings uitgaven
 bij aangife inkomsenbelasing 20 IB 266-1TFD (2576) Sudiekosen en andere scholings uigaven Volgde u in 20 een opleiding of een sudie voor uw (oekomsige) beroep? Of had u kosen voor een EVCprocedure (Erkenning
bij aangife inkomsenbelasing 20 IB 266-1TFD (2576) Sudiekosen en andere scholings uigaven Volgde u in 20 een opleiding of een sudie voor uw (oekomsige) beroep? Of had u kosen voor een EVCprocedure (Erkenning
Ze krijgt 60% korting op het basisbedrag van 1000,- (jaarpremie) en moet dan 400,- (jaarpremie) betalen.
 1a 1b G&R havo A deel 1 Tabellen en grafieken C. von Schwarzenberg 1/14 Een buspakje kan door de brievenbus, een pakke nie. Een zending die voorrang krijg. 1c 5, 40. (Worldpack Basic prioriy Buien Europa
1a 1b G&R havo A deel 1 Tabellen en grafieken C. von Schwarzenberg 1/14 Een buspakje kan door de brievenbus, een pakke nie. Een zending die voorrang krijg. 1c 5, 40. (Worldpack Basic prioriy Buien Europa
Studiekosten of andere scholingsuitgaven
 Bij voorlopige aanslag inkomsenbelasing 2013 IB 275-1T31FD Volg u in 2013 een opleiding of een sudie voor uw (oekomsige) beroep? Of had u kosen voor een EVC-procedure (Erkenning Verworven Compeenies)?
Bij voorlopige aanslag inkomsenbelasing 2013 IB 275-1T31FD Volg u in 2013 een opleiding of een sudie voor uw (oekomsige) beroep? Of had u kosen voor een EVC-procedure (Erkenning Verworven Compeenies)?
Einstein (4) deze "ziet" t=ta licht bereikt achterkant. t=tv licht bereikt voorkant. figuur 1.
 Einsein (4) In he orig arikelje (nr 44b, bladz. 3-6) werd he begrip relaiiei geïnrodueerd me name de relaiiei an een bepaalde ijdsduur zoals de slingerijd an een slinger in een klok. In boengenoemd arikelje
Einsein (4) In he orig arikelje (nr 44b, bladz. 3-6) werd he begrip relaiiei geïnrodueerd me name de relaiiei an een bepaalde ijdsduur zoals de slingerijd an een slinger in een klok. In boengenoemd arikelje
digitale signaalverwerking
 digiale signaalverwerking deel 2: sampling en digiale filerechniek Hoewel we de vorige keer reeds over he samplen van signalen gesproken hebben, komen we daar nu op erug, om de ermee samenhangende effecen
digiale signaalverwerking deel 2: sampling en digiale filerechniek Hoewel we de vorige keer reeds over he samplen van signalen gesproken hebben, komen we daar nu op erug, om de ermee samenhangende effecen
Eindexamen wiskunde A1-2 vwo 2003-I
 Eindexamen wiskunde A- vwo 003-I 4 Anwoordmodel Levensduur van kfiezeapparaen Maximumscore 4 Na,5 jaar zijn er 500 0,99 0,97 apparaen Na 3,5 jaar zijn er 500 0,99 0,97 0,87 apparaen He verschil hierussen
Eindexamen wiskunde A- vwo 003-I 4 Anwoordmodel Levensduur van kfiezeapparaen Maximumscore 4 Na,5 jaar zijn er 500 0,99 0,97 apparaen Na 3,5 jaar zijn er 500 0,99 0,97 0,87 apparaen He verschil hierussen
wiskunde A vwo 2015-I
 wiskunde A vwo 05-I Diabeesrisicoes maximumscore 4 He aanal personen me verborgen diabees is binomiaal verdeeld me n = 400 en p = 0, 0 P( X 00 ) = P( X 99 ) Beschrijven hoe di me de GR berekend word De
wiskunde A vwo 05-I Diabeesrisicoes maximumscore 4 He aanal personen me verborgen diabees is binomiaal verdeeld me n = 400 en p = 0, 0 P( X 00 ) = P( X 99 ) Beschrijven hoe di me de GR berekend word De
Hoofdstuk 1 Lineaire en exponentiële verbanden
 Hoofsuk Lineaire en exponeniële veranen lazije A: Geen lineair veran, als x me oeneem, neem y nie sees me ezelfe waare oe. B: Lineair veran, als x me oeneem, neem y sees me, oe. C: Geen lineair veran,
Hoofsuk Lineaire en exponeniële veranen lazije A: Geen lineair veran, als x me oeneem, neem y nie sees me ezelfe waare oe. B: Lineair veran, als x me oeneem, neem y sees me, oe. C: Geen lineair veran,
t Ik bekijk de plaatjes, de titel en de tussenkopjes.
 2.1 LWB 7A-20 Les: Geen vis INFORMATIE Leeseks Teks 1: informaieve eks over walvissen. Teks 1: oud AVI 9; nieuw AVI M6. Zie ook sofware. Cenrale sraegie/leerdoel Teks inerpreeren: je bedenk de hoofdvraag
2.1 LWB 7A-20 Les: Geen vis INFORMATIE Leeseks Teks 1: informaieve eks over walvissen. Teks 1: oud AVI 9; nieuw AVI M6. Zie ook sofware. Cenrale sraegie/leerdoel Teks inerpreeren: je bedenk de hoofdvraag
2.1 Onderzoek naar bewegingen
 Vwo 4 Hoofdsuk 2 Uiwerkingen 2.1 Onderzoek nr bewegingen Opge 1 fsnd De (gemiddelde) snelheid leid je f me snelheid =. ijd Je moe fsnd en snelheid bespreken om ies oer snelheid e kunnen zeggen. fsnd snelheid
Vwo 4 Hoofdsuk 2 Uiwerkingen 2.1 Onderzoek nr bewegingen Opge 1 fsnd De (gemiddelde) snelheid leid je f me snelheid =. ijd Je moe fsnd en snelheid bespreken om ies oer snelheid e kunnen zeggen. fsnd snelheid
faseverschuiving wisselstroomweerstand frequentieafhankelijk weerstand 0 R onafhankelijk spoel stroom ijlt 90 na ωl toename met frequentie ELI 1 ωc
 6.2.5 ergelijking faseverschuiving wisselsroomweersand frequenieafhankelijk weersand 0 onafhankelijk spoel sroom ijl 90 na ω oename me frequenie E condensaor sroom ijl 90 voor ω afname me frequenie E Fasordiagramma
6.2.5 ergelijking faseverschuiving wisselsroomweersand frequenieafhankelijk weersand 0 onafhankelijk spoel sroom ijl 90 na ω oename me frequenie E condensaor sroom ijl 90 voor ω afname me frequenie E Fasordiagramma
Oefenopgaven versnelling, kracht, arbeid. Werk netjes en nauwkeurig. Geef altijd berekeningen met Gegeven Gevraagd Formule Berekening Antwoord
 Oefenopgaven versnelling, kracht, arbeid Werk netjes en nauwkeurig. Geef altijd berekeningen met Gegeven Gevraagd Formule Berekening Antwoord Noteer bij je antwoord de juiste eenheid. s = v * t s = afstand
Oefenopgaven versnelling, kracht, arbeid Werk netjes en nauwkeurig. Geef altijd berekeningen met Gegeven Gevraagd Formule Berekening Antwoord Noteer bij je antwoord de juiste eenheid. s = v * t s = afstand
Analoge Elektronika 1 DE KOMPARATOR
 naloge Elekronika DE KOMPRTOR De mees eenvoudige oepassing van de operaionele verserker is de komparaor. Om de werking van de komparaor e begrijpen, bekijken we de karakerisiek van de opamp, zoals geekend
naloge Elekronika DE KOMPRTOR De mees eenvoudige oepassing van de operaionele verserker is de komparaor. Om de werking van de komparaor e begrijpen, bekijken we de karakerisiek van de opamp, zoals geekend
Correctievoorschrift VWO 2014
 Correcievoorschrif VWO 04 ijdvak nauurkunde He correcievoorschrif besaa ui: Regels voor de beoordeling Algemene regels 3 Vakspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor de beoordeling
Correcievoorschrif VWO 04 ijdvak nauurkunde He correcievoorschrif besaa ui: Regels voor de beoordeling Algemene regels 3 Vakspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor de beoordeling
Labotekst. Meetsystemen
 Labo Meesysemen dr ir J.Baeen Laboeks Meesysemen 2004 3 II Elekronica 3 II Elekromechanica (opies au/el) - - J. Baeen Labo Meesysemen Proef 1: Digiale opische meesysemen Proef I: Digiale opische meesysemen
Labo Meesysemen dr ir J.Baeen Laboeks Meesysemen 2004 3 II Elekronica 3 II Elekromechanica (opies au/el) - - J. Baeen Labo Meesysemen Proef 1: Digiale opische meesysemen Proef I: Digiale opische meesysemen
Studiekosten of andere scholingsuitgaven
 12345 Aanvullende oeliching bij aangife inkomsenbelasing IB 266-1T02FD (2464) Sudiekosen of andere scholingsuigaven Volgde u in een opleiding of een sudie voor uw (oekomsige) beroep? Dan mag u de uigaven
12345 Aanvullende oeliching bij aangife inkomsenbelasing IB 266-1T02FD (2464) Sudiekosen of andere scholingsuigaven Volgde u in een opleiding of een sudie voor uw (oekomsige) beroep? Dan mag u de uigaven
Examen VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskunde B,2 (nieuwe sijl) Examen VW Voorbereidend Weenschappelijk nderwijs Tijdvak Donderdag 22 mei 3.30 6.30 uur 20 03 Voor di examen zijn maximaal 86 punen e behalen; he examen besaa ui 9 vragen. Voor
Wiskunde B,2 (nieuwe sijl) Examen VW Voorbereidend Weenschappelijk nderwijs Tijdvak Donderdag 22 mei 3.30 6.30 uur 20 03 Voor di examen zijn maximaal 86 punen e behalen; he examen besaa ui 9 vragen. Voor
Deel 1. Kinematica en dynamica
 Deel 1 Kinemaica en dynamica Ineracie_6._Lb.indb 5 1 Beweging 1.1 Inleiding Bovensaande woordenwolk beva begrippen die je vorige jaren in de lessen fysica zag. Om die begrippen op e frissen, gebruiken
Deel 1 Kinemaica en dynamica Ineracie_6._Lb.indb 5 1 Beweging 1.1 Inleiding Bovensaande woordenwolk beva begrippen die je vorige jaren in de lessen fysica zag. Om die begrippen op e frissen, gebruiken
5 Brandstofverbruik in het verkeer
 Newon wo deel 1 Uiwerkingen Hoofduk 5 Brandoferbruik in e erkeer 5 Brandoferbruik in e erkeer 5.1 Inleiding Voorkenni 1 Brandoferbruik a He brandoferbruik i bij.,0 L/0 km of de auo rijd 1 op 11. He i du
Newon wo deel 1 Uiwerkingen Hoofduk 5 Brandoferbruik in e erkeer 5 Brandoferbruik in e erkeer 5.1 Inleiding Voorkenni 1 Brandoferbruik a He brandoferbruik i bij.,0 L/0 km of de auo rijd 1 op 11. He i du
Sneller dan het licht?
 Sneller dan he lich? Hoe is he mogelijk da muonen de Aarde bereiken? Een profielwerksuk in he kader van HiSPARC K. Koudsaal, V6B K. Yahya, V6C D. Zoeewei, V6B Profiel: Nauur en Techniek Vak: Nauurkunde
Sneller dan he lich? Hoe is he mogelijk da muonen de Aarde bereiken? Een profielwerksuk in he kader van HiSPARC K. Koudsaal, V6B K. Yahya, V6C D. Zoeewei, V6B Profiel: Nauur en Techniek Vak: Nauurkunde
Tuinstijlen. Tuinstijlen. Het ontstaan van tuinstijlen. Formele tuinstijl. Informele tuinstijl. Moderne tijd
 Tuinsijlen Tuinsijlen He aanleggen van een uin word voorafgegaan door he maken van een uinonwerp. Om de uin o een geheel e maken moe u in he onwerp rekening houden me een bepaalde uinsijl. Door allerlei
Tuinsijlen Tuinsijlen He aanleggen van een uin word voorafgegaan door he maken van een uinonwerp. Om de uin o een geheel e maken moe u in he onwerp rekening houden me een bepaalde uinsijl. Door allerlei
De Wageningse Methode 5&6 VWO wiskunde B Uitgebreidere antwoorden Hoofdstuk 4 Goniometrie
 De Wageningse Mehode & VWO wiskunde B Uigebreidere anwoorden Hoofdsuk Goniomerie Paragraaf Cirkelbewegingen a. De hooge van he wiel is de y-coördinaa van he hoogse pun van de grafiek, dus 80 cm b. De periode
De Wageningse Mehode & VWO wiskunde B Uigebreidere anwoorden Hoofdsuk Goniomerie Paragraaf Cirkelbewegingen a. De hooge van he wiel is de y-coördinaa van he hoogse pun van de grafiek, dus 80 cm b. De periode
natuurkunde vwo 2017-I
 nauurkunde vwo 07-I Zonvolgsyseem maximumscore De wee parallelle akken ABD en ACD zijn ideniek. Dus saa er geen spanning over de moor en loop er geen sroom door de moor. inzich da beide parallelle akken
nauurkunde vwo 07-I Zonvolgsyseem maximumscore De wee parallelle akken ABD en ACD zijn ideniek. Dus saa er geen spanning over de moor en loop er geen sroom door de moor. inzich da beide parallelle akken
Correctievoorschrift VWO
 Correcievoorschrif VWO 009 ijdvak wiskunde A, He correcievoorschrif besaa ui: Regels voor de beoordeling Algemene regels 3 Vakspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor de beoordeling
Correcievoorschrif VWO 009 ijdvak wiskunde A, He correcievoorschrif besaa ui: Regels voor de beoordeling Algemene regels 3 Vakspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor de beoordeling
Labotekst. Meetsystemen
 Labo Meesysemen dr ir J.Baeen Laboeks Meesysemen MSYSL 2006 3 II Elekronica 3 II Elekromechanica (opie au) EK Elo EK EL - - J. Baeen Labo Meesysemen Doelsellingen - Inhoud - Evaluaie Doelsellingen Op basis
Labo Meesysemen dr ir J.Baeen Laboeks Meesysemen MSYSL 2006 3 II Elekronica 3 II Elekromechanica (opie au) EK Elo EK EL - - J. Baeen Labo Meesysemen Doelsellingen - Inhoud - Evaluaie Doelsellingen Op basis
Eindexamen wiskunde A 1-2 vwo 2002-I
 Eindexamen wiskunde A 1-2 vwo 2002-I Vogels die voedsel zoeken Vogels die voedsel zoeken op de grond veronen vaak een karakerisiek paroon van lopen en silsaan. In iguur 1 is di paroon voor wee vogelsooren
Eindexamen wiskunde A 1-2 vwo 2002-I Vogels die voedsel zoeken Vogels die voedsel zoeken op de grond veronen vaak een karakerisiek paroon van lopen en silsaan. In iguur 1 is di paroon voor wee vogelsooren
haarlemmerolie van de IT? Tobias Kuipers en Per John
 Complexiei onder conrole, kosen inzichelijk? Naar een diensbare Gezien de populariei van is he goed eens erug e gaan naar de basis en e kijken naar wa SOA eigenlijk is, wa de redenen zijn om he in e voeren,
Complexiei onder conrole, kosen inzichelijk? Naar een diensbare Gezien de populariei van is he goed eens erug e gaan naar de basis en e kijken naar wa SOA eigenlijk is, wa de redenen zijn om he in e voeren,
Overzicht. Inleiding. Classificatie. NP compleetheid. Algoritme van Johnson. Oplossing via TSP. Netwerkalgoritme. Job shop scheduling 1
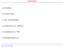 Overzich Inleiding Classificaie NP compleeheid Algorime van Johnson Oplossing via TSP Newerkalgorime Job shop scheduling 1 Inleiding Gegeven zijn Machines: M 1,,..., M m Taken: T 1, T 2,... T n Per aak
Overzich Inleiding Classificaie NP compleeheid Algorime van Johnson Oplossing via TSP Newerkalgorime Job shop scheduling 1 Inleiding Gegeven zijn Machines: M 1,,..., M m Taken: T 1, T 2,... T n Per aak
Uitwerkingen Toets 1 IEEE, Modules 1 en 2
 Uiwerkingen Toes IEEE, Modules en Daum: 9 sepember 007 Tijd: 0.40.0 (90 minuen) Opgave I) Di is een warmmakerje. In woorden is V is de serieschakeling van, en (de parallelschakeling van 3 en 4) of V =
Uiwerkingen Toes IEEE, Modules en Daum: 9 sepember 007 Tijd: 0.40.0 (90 minuen) Opgave I) Di is een warmmakerje. In woorden is V is de serieschakeling van, en (de parallelschakeling van 3 en 4) of V =
Samenvatting Natuurkunde 1,2 HAVO
 Beweging Samenvaing Nauurkunde, HAVO Eenparig rechlijnige beweging a Eenparig versnelde rechlijnige beweging a a = consan a = 0 m/s Oppervlake = v = 0 m/s Oppervlake = v v v v = consan v() = a Oppervlake
Beweging Samenvaing Nauurkunde, HAVO Eenparig rechlijnige beweging a Eenparig versnelde rechlijnige beweging a a = consan a = 0 m/s Oppervlake = v = 0 m/s Oppervlake = v v v v = consan v() = a Oppervlake
Antwoordmodel VWO 2003-I wiskunde A (oude stijl) Levensduur van koffiezetapparaten. Maximumscore 4 1 Na 2,5 jaar zijn er ,99 0,97 apparaten 1
 Anwoordmodel VWO 3-I wiskunde A (oude sijl) Levensduur van kfiezeapparaen Na,5 jaar zijn er 5,99,97 apparaen Na 3,5 jaar zijn er 5,99,97,87 apparaen He verschil hierussen bedraag 87 apparaen de kansen,99
Anwoordmodel VWO 3-I wiskunde A (oude sijl) Levensduur van kfiezeapparaen Na,5 jaar zijn er 5,99,97 apparaen Na 3,5 jaar zijn er 5,99,97,87 apparaen He verschil hierussen bedraag 87 apparaen de kansen,99
Vraag Antwoord Scores
 Eindexamen vwo nauurkunde 04-I Vraag Anwoord Scores Opgave Tsunami maximumscore 4 voorbeeld van een anwoord: Voor de zwaare-energie van de waerberg geld: Ez = mgh. Voor de massa van he waer geld: m= ρv.
Eindexamen vwo nauurkunde 04-I Vraag Anwoord Scores Opgave Tsunami maximumscore 4 voorbeeld van een anwoord: Voor de zwaare-energie van de waerberg geld: Ez = mgh. Voor de massa van he waer geld: m= ρv.
Hoofdstuk 3 - Exponentiële functies
 Hoofdsuk - Eponeniële funcies Voorkennis: Groeifacoren ladzijde 7 V-a 060, 80 8, - euro 079, 0, 9, 88 c 0, 98, - 998, V-a De facor waarmee je de oude prijs vermenigvuldig om de nieuwe prijs e krijgen is
Hoofdsuk - Eponeniële funcies Voorkennis: Groeifacoren ladzijde 7 V-a 060, 80 8, - euro 079, 0, 9, 88 c 0, 98, - 998, V-a De facor waarmee je de oude prijs vermenigvuldig om de nieuwe prijs e krijgen is
: Vermeld op alle bladen van uw werk uw naam. : Het tentamen bestaat uit 4 bladzijden inclusief dit voorblad.
 POST HBO-OPLEIDINGEN Beonconsruceur BV Saalconsruceur BmS Professional maser of srucural engineering Toegepase mechanica Maeriaalmodellen en nie-lineaire mechanica docen : dr. ir. P.C.J. Hoogenboom TENTAMEN
POST HBO-OPLEIDINGEN Beonconsruceur BV Saalconsruceur BmS Professional maser of srucural engineering Toegepase mechanica Maeriaalmodellen en nie-lineaire mechanica docen : dr. ir. P.C.J. Hoogenboom TENTAMEN
dwarsrichting Doelstellingen van dit hoofdstuk
 7 Afschuiving HOOFDSTUK in langs- en dwarsriching Ga naar www.pearsonmylab.nl voor sudiemaeriaal en oesen om je begrip en kennis van di hoofdsuk ui e breiden en e oefenen. Ook vind je daar videouiwerkingen
7 Afschuiving HOOFDSTUK in langs- en dwarsriching Ga naar www.pearsonmylab.nl voor sudiemaeriaal en oesen om je begrip en kennis van di hoofdsuk ui e breiden en e oefenen. Ook vind je daar videouiwerkingen
Fibbe Advocaten. Wilhelminastraat 66. 2011 VP Haarlem
 Fibbe Advocaen Wilhelminasraa 66 2011 VP Haarlem Wij, Fibbe Advocaen e Haarlem, doen ons bes om u zoveel mogelijk van diens e zijn. Daarom willen wij u vragen mee e werken aan een klanevredenheidsonderzoek.
Fibbe Advocaen Wilhelminasraa 66 2011 VP Haarlem Wij, Fibbe Advocaen e Haarlem, doen ons bes om u zoveel mogelijk van diens e zijn. Daarom willen wij u vragen mee e werken aan een klanevredenheidsonderzoek.
Hoofdstuk 8 Polarisatie
 Hoofdsuk 8 Polarisaie lecromagneische Sraling is Gepolariseerd Iedere ransversale rilling is gepolariseerd To nu alleen rillingen beschouwd waarvan (en B) in één vlak ril: Lineair gepolariseerd lich. (In
Hoofdsuk 8 Polarisaie lecromagneische Sraling is Gepolariseerd Iedere ransversale rilling is gepolariseerd To nu alleen rillingen beschouwd waarvan (en B) in één vlak ril: Lineair gepolariseerd lich. (In
Correctievoorschrift VWO. Wiskunde A1,2 (nieuwe stijl)
 Wiskunde A, (nieuwe sijl) Correcievoorschrif VWO Voorbereidend Weenschappelijk Onderwijs 0 0 Tijdvak Inzenden scores Uierlijk op juni de scores van de alfabeisch eerse vijf kandidaen per school op de daaroe
Wiskunde A, (nieuwe sijl) Correcievoorschrif VWO Voorbereidend Weenschappelijk Onderwijs 0 0 Tijdvak Inzenden scores Uierlijk op juni de scores van de alfabeisch eerse vijf kandidaen per school op de daaroe
Noordhoff Uitgevers bv
 60 Hoofdsuk Eponeniële funies ladzijde 6 V-a Door zih in weeën e delen vermenigvuldig he aanal aeriën per ijdseenheid zih seeds me een faor is de eginhoeveelheid, dus 0 g is de groeifaor, dus g d gewih
60 Hoofdsuk Eponeniële funies ladzijde 6 V-a Door zih in weeën e delen vermenigvuldig he aanal aeriën per ijdseenheid zih seeds me een faor is de eginhoeveelheid, dus 0 g is de groeifaor, dus g d gewih
Juli 2003. Canonpercentages Het vaststellen van canonpercentages bij de herziening van erfpachtcontracten
 Canonpercenages He vassellen van canonpercenages bij de herziening van erfpachconracen Juli 23 SBV School of Real Esae Drs. L.B. Uienbogaard Drs. J.P. Traudes Inhoud Blz. 1. Inleiding... 3 2. Toeliching
Canonpercenages He vassellen van canonpercenages bij de herziening van erfpachconracen Juli 23 SBV School of Real Esae Drs. L.B. Uienbogaard Drs. J.P. Traudes Inhoud Blz. 1. Inleiding... 3 2. Toeliching
4e Het absolute maximum is 3 (voor x = 1). 4c De grafiek is afnemend dalend op 2, 3. 4f Er is een minimum voor x = 3. Dit minimum is 0.
 G&R vwo A/C eel C. von Schwarzenberg 1/16 1a 1b 1c Da was begin 00. Er waren oen 140000 banen. Toename van 10000 naar 140000, us een oename van 0000 banen. Vóór juli 1998 is e oename oenemen (e oename
G&R vwo A/C eel C. von Schwarzenberg 1/16 1a 1b 1c Da was begin 00. Er waren oen 140000 banen. Toename van 10000 naar 140000, us een oename van 0000 banen. Vóór juli 1998 is e oename oenemen (e oename
Toelichting Hoe gebruikt u deze toelichting? Correspondentieadres Wat is een schenking? Voor meer ontvangers samen aangifte doen
 2011 Toeliching Aangife schenkbelasing Di is een oeliching bij he formulier Aangife schenkbelasing. Deze oeliching besaa ui vier onderdelen: A Algemene informaie over de schenkbelasing B Uileg bij de vragen
2011 Toeliching Aangife schenkbelasing Di is een oeliching bij he formulier Aangife schenkbelasing. Deze oeliching besaa ui vier onderdelen: A Algemene informaie over de schenkbelasing B Uileg bij de vragen
acentrifugaal g ge ω λ
 acenrifugaal ω g ge λ hp://eagle.cc.ukans.edu/~keihweb/64_.hml Oefening 8: z α ω λ mge g en sleepersnelling geen g e en worden erder samen weergegeen door g,, z : relaief assenselsel me naar he zuiden,
acenrifugaal ω g ge λ hp://eagle.cc.ukans.edu/~keihweb/64_.hml Oefening 8: z α ω λ mge g en sleepersnelling geen g e en worden erder samen weergegeen door g,, z : relaief assenselsel me naar he zuiden,
Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Werken met formules. Een eigen samenvatting maken is nuttig.
 6 Totaalbeeld Samenatten Je moet nu oor jezelf een oerzicht zien te krijgen oer het onderwerp Werken met formules. Een eigen samenatting maken is nuttig. Begrippenlijst: 11: formule ariabele grootheid
6 Totaalbeeld Samenatten Je moet nu oor jezelf een oerzicht zien te krijgen oer het onderwerp Werken met formules. Een eigen samenatting maken is nuttig. Begrippenlijst: 11: formule ariabele grootheid
Boek 3 hoofdstuk 10 Groei havo 5
 Boek 3 hoofdsuk 0 Groei havo 5. Lineaire en exponeniële groei. a. Opp = 750 + 50 me = 0 op juni, per week en opp. in m. Y =750 + 50 Y (3) = 00 m en Y (5) = 500 m (mehode : voer in Y, daarna rekenscherm,
Boek 3 hoofdsuk 0 Groei havo 5. Lineaire en exponeniële groei. a. Opp = 750 + 50 me = 0 op juni, per week en opp. in m. Y =750 + 50 Y (3) = 00 m en Y (5) = 500 m (mehode : voer in Y, daarna rekenscherm,
