Algemeen geformuleerd: a a a b) wanneer we machten met hetzelfde grondtal op elkaar delen, bijv. a
|
|
|
- Dries Thys
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Theorie mchtsverheffen, worteltreen en logritmen (gedeelte uit hoofdstu vn Ro Flohr (00). Bsiswisunde voor sttistie. Den Hg: Acdemic Service). Mchtsverheffen en worteltreen In deze rgrf esreen we de eweringen mchtsverheffen en worteltreen en reiden we de getlverzmeling vn rtionle getllen Q uit tot de verzmeling vn lle reële getllen R. Mchten Voor el getl geldt: , wrij el ositief geheel getl is. We zien dt de herhlde otelling vn uitmondt in een vermenigvuldiging, nders gezegd: de sommen, enz. worden geschreven ls de roducten, enz. Anloog hiern leidt de herhlde vermenigvuldiging vn el getl tot het mchtsverheffen:...., wrij el ositief geheel getl is. Vooreelden: We definiëren de volgende egrien: in de uitdruing noemen we het grondtl, de e exonent en de mcht (reciezer: de mcht vn of tot de mcht ). In het vooreeld vn eteent dit: is het grondtl, is de exonent en is tot de mcht. Eigenschen vn mchten ) wnneer we mchten met hetzelfde grondtl met elr vermenigvuldigen, ijv., dn rijgen we een mcht met hetzelfde grondtl en een exonent die gelij is n de som vn de oorsronelije exonenten. G mr n: ( ). Algemeen geformuleerd: ) wnneer we mchten met hetzelfde grondtl o elr delen, ijv. :, dn rijgen we een mcht met hetzelfde grondtl en een exonent die gelij is n het verschil vn de
2 oorsronelije exonenten. G mr n: ) ( :. Algemeen geformuleerd: : c) uit het ovenstnde volgt: 0 : en ) ( :. We unnen de regel voor het delen oo fleiden uit die voor het vermenigvuldigen. Immers, indien geldt, geldt oo : en :. Vervolgens ijen we nr d) de mcht vn een mcht, ijvooreeld 6. We zien dt we de exonenten moeten vermenigvuldigen, immers 6. Algemeen geformuleerd: e) de mcht vn een roduct, ijvooreeld Er geldt dus lijr dt (wellicht ten overvloede wijzen we ero, dt een vermenigvuldiging o verschillende mnieren n worden weergegeven:. ). Algemeen geformuleerd: r r r f) de mcht vn een uotiënt, ijvooreeld. We zien dt, lgemeen geformuleerd: r r r Smengevt:..., wrij el ositief geheel getl is. : 0 r r r r r r n.. - ij 0 hoort de voorwrde 0, omdt 0 0 niet gedefinieerd is -wnneer de grondtllen verschillend zijn, gn de ovenstnde regels niet o, vergelij: en
3 : Ogve..) ) h) ) i) 0 j) ).. c) d) 0 0 l). e). 0 f) m).. g) n) Worteltreen In het ovenstnde heen we de egrien grondtl, exonent en mcht leren ennen. Bij mchtsverheffen gt het om het vinden vn de mcht, gegeven een eld grondtl en een elde exonent. Een vrgstu dt etreing heeft o mchtsverheffen, heeft nmelij de vorm?. Wnneer de exonent en de mcht gegeven zijn mr het grondtl niet, rijgen we een vrgstu vn de vorm?. Een r vooreelden:?. Het ntwoord is wnt.?. Het ntwoord is wnt.?. Het ntwoord is wnt. Bij dit soort vrgstuen zoeen we dus het grondtl en de ewering die hierij hoort heet worteltreen. Kijen we nog even nr het eerste vooreeld?, dn is de vrg: wel getl tot de tweede mcht (of: in het wdrt) is gelij n? Nu geldt zowel dt ls en omdt we ons eeren tot de ositieve uitomst, definiëren we het volgende: de tweedemchtswortel vn is het niet-negtieve getl wrvoor geldt dt. We schrijven dit ls volgt:, wrin we het wortelteen, de wortelexonent en het ereenen vn het worteltreen noemen (i..v. schrijven we doorgns gewoon, wnneer de wortelexonent niet vermeld wordt gt het dus om een tweedemchtswortel). Ogve..) ) f) 6 ) 00 g) 0 c) 6 h) 6 00 i) d)
4 j) 6 e) 6 Het nemen vn een tweedemchtswortel is dus de omgeeerde (inverse) ewering vn het wdrteren, zo geldt ijvooreeld wnt. Dit eteent, dt het getl onder het wortelteen groter dn of gelij n nul moet zijn. Immers, stel dt gelij is n een getl, dn moet dus gelden dt. Mr omdt een wdrt vn een getl een ositief getl olevert, n dit niet het gevl zijn. We unnen nu in het lgemeen definiëren: de (tweedemchts)wortel vn een getl 0 is het getl wrvoor geldt dt 0 en. In de vooreelden en de ogven tot nog toe wm het worteltreen recies uit : de uitomst ws telens een getl dt gewdrteerd het getl onder het wortelteen oleverde. Er zijn echter tlloze vooreelden te edenen wrij dit niet het gevl is. In zo n gevl roeren we zoveel mogelij wdrten in het getl onder het wortelteen o te soren om de wortel te unnen vereenvoudigen. Neem ijvooreeld 0 ; nu is 6 en 6, dus de uitomst vn 0 moet ergens tussen en in liggen. Dit eteent dt 0 geen geheel getl ls uitomst heeft (verdero zullen we zien dt de uitomst vn 0 oo geen reu is!). Om de wdrten in het getl 0 o te soren, unnen we een herhlde deling uitvoeren, wrij we eerst zoveel mogelij door delen, dn door enz. We rijgen in het gevl vn 0 dn: 0: 0 0: : : : Dit houdt in dt we 0 unnen schrijven ls het roduct. Drdoor geldt 0 6. Controle: ls 0 6, dn moet gelden: 6 0. Welnu, (dt gelij is n, volgt direct uit de definitie vn worteltreen: is het getl dt, gewdrteerd, olevert, m..w. ). O dezelfde wijze unnen we 00 vereenvoudigen: Controle: Ogve..) Vereenvoudig o dezelfde wijze de volgende wortels: ) f) ) g) 00 c) h) d) 0 i) e) 6 j) 00 Anloog n hetgeen hiervoor gezegd is over worteltreen t..v. gehele getllen, unnen we wortels vn reuen ereenen res. vereenvoudigen. Zo geldt ijvooreeld:
5 wnt 6 6 en wnt Bij het vereenvoudigen zorgen we er voor dt, indien er in de noemer geen wdrt vooromt, we dr een wdrt rijgen door teller en noemer met hetzelfde getl te vermenigvuldigen. Bijvooreeld: (er stt in de noemer l een wdrt) 6 mr en Ogve..) Vereenvoudig de volgende reuen: ) d) ) c) e) Tot nog toe heen we het gehd over tweedemchtswortels ( of ), oo wel vierntswortels genoemd. Drnst estn er oo hogeremchtswortels wrij de wortelexonent is. Vooreelden: wnt wnt wnt wnt en oo wnt wnt wnt wnt mr estt niet omdt een ositieve uitomst heeft, nmelij. Zo omen we tot de volgende mogelijheden: de wortelexonent is een de wortelexonent is een
6 het getl onder het wortelteen is ositief het getl onder het wortelteen is negtief even getl oneven getl even ositief ositief oneven ositief ositief even negtief estt niet oneven negtief negtief Het ereenen en vereenvoudigen vn hogeremchtswortels verloot nloog n de wijze wro dit hieroven voor tweedemchtswortels is uiteengezet. Vooreelden: ) ) 6 d) wnt 6 c) e) wnt g) wnt h) 0 wnt mr: i) 6 estt niet. f) wnt 6 Ogve..) Vereenvoudig res. ereen de volgende wortels: ) e) 6 ) f) c) 6 6 g) 6 d) 0 h) 6 Uit hetgeen we hieroven eschreven heen met etreing tot worteltreen, unnen we het volgende fleiden: 6 6 ); wnneer we nu de gelijheid 6 in de vorm vn mchten met grondtl schrijven, rijgen we: 6 6. We unnen 6 6 dus schrijven ls. Algemeen geformuleerd: (voor el ositief grondtl ). Zo geldt ijvooreeld (controle: ). Nemen we voor ijvooreeld het getl, dn rijgen we:
7 wnt of, nders gezegd, wnt. Omgeeerd geldt ijvooreeld dt en. Dit ltste levert ij terugreenen het volgende resultt o:.. We sreen in deze gevllen vn geroen mchten, ngezien de exonent een reu is (in het ltste vooreeld ). Enele vooreelden ter toelichting: en omgeeerd: (of: ) We unnen oo te men rijgen met negtieve geroen exonenten. Vergelij het volgende vooreeld:. Omgeeerd n geschreven worden ls Vooreelden (odrcht: schrijf ls mcht) (odrcht: schrijf ls wortel) ( ) 0 ( ) Ogve..6) Schrijf ls wortel res. ls mcht: ) f) ) g) ( ). c) x h)
8 i) d) 0 e) j) 0.. Irrtionle getllen en de verzmeling vn reële getllen R In rgrf. heen we eerst N (de verzmeling vn ntuurlije getllen) uitgereid tot Z (de verzmeling vn gehele getllen), en vervolgens Z weer uitgereid tot Q (de verzmeling vn rtionle getllen). Door het invoeren vn de ewering worteltreen, zien we ons genoodzt om onieuw tot een uitreiding vn onze getlverzmeling over te gn. Zo heen we onder meer het getl leren ennen. Nu n geen geheel getl zijn, ngezien en. moet dus tussen en liggen ( ). Mr we unnen ntonen dt oo geen rtionl getl vn de vorm is (d.w.z. een getl dt ls een reu geschreven n worden). Bewijs vn de stelling dt geen rtionl getl is. Stel dt geschreven n worden ls een niet vereenvoudigre reu. Dn geldt volgens de definitie vn een tweedemchtswortel dt, dus oo en. Dit eteent dt een even getl is (g mr n: ls je een getl met vermenigvuldigt, rijg je ltijd een even getl, ijv. mr oo 6 ). Mr ls een even getl is, moet dt oo zijn (ls oneven zou zijn, zou - het roduct vn twee oneven getllen oo oneven zijn). Omdt een even getl is, mogen we schrijven: r. Wnneer we dit invullen in, dn rijgen r, dus r, dus we r ofwel r. Dit eteent dt een even getl is. Mr dn is oo een even getl. Het gevolg is dt de reu vereenvoudigr is, ngezien zowel ls even getllen zijn. Mr dit is in strijd met onze veronderstelling dt een niet vereenvoudigre reu is. Conclusie: is geen rtionl getl. is een vooreeld vn een irrtionl getl. Om het onderscheid tussen rtionle getllen (getllen die ls een reu geschreven unnen worden) en irrtionle getllen (wrij dt niet het gevl is) te verduidelijen, geven we vn de volgende getllen de decimle schrijfwijze (d.w.z. met cijfers chter de omm)
9 0... mr: We zien dt sommige rtionle getllen (, 0, ) een eindige decimle ontwieling heen (het ntl cijfers chter de omm stot o een geven moment omdt de deling ogt ) en dt ndere rtionle getllen (,, ) een oneindige decimle ontwieling 0 heen mr wel een reeterend troon vertonen (vnf een eld unt in de decimle ontwieling dt er getl verschillend n zijn is er sre vn een zich herhlende rees vn getllen). We zien oo dt dit ltste niet geldt voor : de cijfers chter de omm gn tot in lle eeuwigheid door zonder zichzelf te reeteren. Om dit nog eens goed voor het voetlicht te rengen, geven we hieronder de decimle schrijfwijze vn twee ndere irrtionle getllen, nl. het getl e (zie hoofdstu 6) en het getl (het getl dt de verhouding weergeeft tussen de omtre vn een cirel en de middellijn ervn): e Hoeveel cijfers chter de omm er oo verschijnen, er is geen terugerend troon te eennen! U unt zich misschien wel voorstellen dt het enige tijd heeft geduurd voordt irrtionle getllen getllen die in zeere zin ltijd ongrijr lijven ls echte getllen werden gezien (net zols de ccettie vn negtieve getllen niet vn de ene o de ndere dg is gegn). Zo schrijft de Duitse wisundige Michel Stifel in zijn Arithmetic Integr uit : On the other hnd, other considertions comel us to deny tht irrtionl numers re numers t ll. To wit, when we see to suject them to numertion [deciml reresenttion] we find tht they flee wy eretully, so tht not one of them cn e rehended recisely in itself Now tht cnnot e clled true numer which is of such nture tht it lcs recision..therefore, just s n infinite numer is not numer, so n irrtionl numer is not true numer, ut lies hidden in ind of cloud of infinity (Kline: ). Wnneer we de irrtionle getllen toevoegen n de verzmeling vn rtionle getllen Q, dn rijgen we de verzmeling vn lle reële getllen R : R...,,...,,...,,...,,...,0,...,,...,,...,,...,... De volgende uitreiding, nmelij die met de imginire en comlexe getllen, vlt uiten het este vn dit oe. De solute wrde vn een getl Soms zijn we voorl geïnteresseerd in de fstnd vn een getl tot het getl 0 o de getllenlijn. In dt gevl n het teen (+ of -) uiten eschouwing worden gelten, wnt de fstnd vn ijvooreeld - tot 0 is dezelfde ls die vn tot 0, nmelij. Dit n zich voordoen wnneer we de fwijingen ten ozichte vn een eld unt (v het unt 0) willen weten, los vn de vrg of het fwijingen nr oven of nr eneden etreft. In de wisunde sreen we in dit gevl vn de solute wrde (of modulus) vn een getl dt wordt ngegeven door twee verticle streen. We definiëren drom het volgende: onder de solute wrde vn een getl verstn we het getl zelf, met weglting vn het er voor stnde teen. Enele vooreelden zijn:
10 . Logritmen In rgrf. heen we gezien dt een vrgstu dt etreing heeft o mchtsverheffen vn de vorm? is, terwijl het ij worteltreen de vorm? etreft. Anders gezegd, ij mchtsverheffen zoeen we de mcht (oo wel rgument genoemd) en ij worteltreen? het grondtl. We unnen echter oo o zoe zijn nr de exonent wrij de vorm hoort. Het zoeen vn de exonent noemen we logritme nemen. We noteren dit ls volgt: ls, dn is log. Dit eteent: log is de exonent wrtoe we moeten verheffen om te rijgen. M..w., log en omen o hetzelfde neer. Wnneer we log invullen ( sustitueren ) in log rijgen we: wruit lijt dt inderdd de exonent is wrtoe we moeten verheffen om te rijgen. Verder sreen we f dt wnneer het grondtl gelij is n 0, we ortweg log schrijven, log eteent dus hetzelfde ls smen: ls geldt dn is - mchtsverheffen het ereenen vn - worteltreen het ereenen vn - logritme nemen het ereenen vn 0 log. We vtten het ovenstnde ls volgt log Wnneer we ls cijfervooreeld nemen, dn omt - mchtsverheffen neer o het uitvoeren vn de ereening (de uitomst is tot de mcht, nl. het getl ) - worteltreen o het uitvoeren vn de ereening (de uitomst is het grondtl ) - en logritme nemen o het uitvoeren vn de ereening log (de uitomst is de exonent ) Vooreelden: ) log wnt f) log 0 wnt 0 0 ) log6 wnt 6 g) log 0 wnt 0 0 c) log00 log00 wnt 0 00 h) log 6 wnt 6 6 d) log 0. wnt 0 0. i) log wnt 0 6 e) log0 wnt 0 0 j) log wnt Ogve..) ) log f) log ) log6 c) log d) log g) log 0.0 h) log 0 i) log 6
11 e) log j) log Voor de volledigheid geven we hieronder nog de regels die gelden voor logritmen wrij we gemshlve uitgn vn het grondtl 0 (hoewel de conclusies geldig zijn voor el grondtl). Regel : log log log log loglog Om n te tonen dt dit zo is, schrijven we: 0 0 (dit volgt uit regel ). Nu men we gerui vn de regel dt Dn volgt hieruit en uit de definitie vn logritme dt: log log 0 0. Linerlid en rechterlid zijn dus n elr gelij, dus is regel juist. Regel : log log log 0 We geruien dezelfde redenering ls ij regel, lleen ssen we hier de regel 0 0 log log loglog 0 toe. We rijgen dn: uit log log log volgt 0 0 en dit omt neer log 0 o. Liner- en rechterlid zijn n elr gelij, dus is regel juist. Regel : log n nlog Afleiding: o dezelfde wijze, lleen met ehul vn de regel n 0 0. Uit n log n log nlog volgt n log log n n n n, dus. Uit de gelijheid vn liner- en rechterlid concluderen we dt regel juist is. n n N.B. Omdt en, volgt hieruit en uit regel dt log log log en n n log log log. n log c Regel : log c log We volgen weer dezelfde werwijze met ehul vn de regel Uit. log c log c volgt log c log log c (ruiselings vermenigvuldigen). We mogen log vervolgens schrijven: c logc log logc c logc log logc wruit (er definitie) volgt:. Liner- en rechterlid zijn n elr gelij, dus is regel juist. Met ehul vn regel unnen we o een willeeurig grondtl overgn hetgeen goed vn 0 log 6 log 6 s n omen. Zo is log 6 met ehul vn regel te herschrijven ls, 0 log log hetgeen met ehul vn de reenmchine eenvoudig uit te reenen is (het ntwoord is ongeveer. en de controle is: , dus ongeveer 6). Ter fsluiting vn deze rgrf volgen nog enele vooreelden wrij de ovenstnde regels unnen worden toegest (dit soort ogven n v o verschillende mnieren ogelost worden).
12 Vooreelden: log ) log log log log log 00 log log0 0 ) 0 log (controle: 00 ) 0 log c) Gegeven is: log 0., log 6 0. en log 0. (fgerond). Bereen met ehul vn deze gegevens: log, log, log en log. ntwoorden: 6 log log log 6 log 0.0 log log 6 log log6. log log log log.0 log log 6 6 log log log 6 log d)?. O de lts vn het vrgteen moet omen te stn: fgerond. (controle: ) log log 6 log. log log en dit is log Uitweringen en ntwoorden: Ogve..) ), wnt ) - c) 6 d) e) f) wnt g) wnt h) wnt i) 0 wnt j) wnt ) wnt.. l) wnt m) 0 wnt... 0
13 n) 6 wnt Ogve..) ) wnt f) wnt ) 0 g) c) h) 6 0 wnt wnt 6 6 d) 0 i) wnt e) wnt 6 j) 6 Ogve..) ) wnt ) 6 wnt 6 c) wnt d) 0 e) f) g) 0 h) 6 i) j) Ogve..) ) ntwoord: 6 60 wnt 6 of 6 ) ntwoord: 6 wnt 6 6 c) ntwoord: wnt d) ntwoord: 0 e) ntwoord: Ogve..) ) ntwoord: ) ntwoord: wnt c) ntwoord: estt niet wnt 6
14 6 d) ntwoord: wnt e)ntwoord: wnt f) ntwoord: wnt g) ntwoord: 0 wnt h) ntwoord: 0 wnt en 0 0 Ogve..6 ) f) ) g) (wnt ) c) x h) (wnt ) d) i) (wnt ) e) j) 0 (wnt ) 0 Ogve..) ) f) ) g) - c) h) wnt d) i) wnt e) 0 j) wnt
Getallenverzamelingen
 Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Hoofdstuk 0: algebraïsche formules
 Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
In dit hoofdstuk introduceren we de hoofdrolspelers van het college: eindige automaten.
 9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
Het kwadraat van een tweeterm a+b. (a+b)²
 Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Rekenregels van machten
 4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
Rekenen in Ê. Module De optelling. Definitie
 Module 1 Rekenen in Ê 1.1 De optelling Definitie Het resultt vn de optelling vn reële getllen en b noemen we de som vn en b en noteren we met +b. De getllen en b zelf noemen we de termen vn de som. Voorbeelden
Module 1 Rekenen in Ê 1.1 De optelling Definitie Het resultt vn de optelling vn reële getllen en b noemen we de som vn en b en noteren we met +b. De getllen en b zelf noemen we de termen vn de som. Voorbeelden
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
 Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
opgaven formele structuren procesalgebra
 opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
Formeel Denken 2012 Uitwerkingen Tentamen
 1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
REKENEN MACHTEN MET. 5N4p EEBII 2013 GGHM
 REKENEN MET MACHTEN Np EEBII 0 GGHM Inhoud Herhlin: Eponentiele roei... Netieve Mchten... Geroken mchten... Etr Oefeninen... 9 Hoere-mchts functies... 0 Overzicht vn de reels... Herhlin: Eponentiële roei
REKENEN MET MACHTEN Np EEBII 0 GGHM Inhoud Herhlin: Eponentiele roei... Netieve Mchten... Geroken mchten... Etr Oefeninen... 9 Hoere-mchts functies... 0 Overzicht vn de reels... Herhlin: Eponentiële roei
Hoofdstuk 2: Bewerkingen in R
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
2) Kegelsneden (in basisvorm)
 ) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
is het koppel dat overeenkomt met het eindpunt van λ.op ax by = a a b x y = a b = x y a b ax by bx + ay = a b
 1 Tweedimensionle Euclidische ruimte 11 Optelling, verschil en sclire vermenigvuldiging = ( b, ) b, is de verzmeling vn lle koppels reële getllen { } Zols we ons de reële getllen kunnen voorstellen ls
1 Tweedimensionle Euclidische ruimte 11 Optelling, verschil en sclire vermenigvuldiging = ( b, ) b, is de verzmeling vn lle koppels reële getllen { } Zols we ons de reële getllen kunnen voorstellen ls
Hoofdstuk 11. Kwadraatresten Inleiding
 Hoofdstuk 11 Kwdrtresten 11.1 Inleiding In Hoofdstuk 6 hebben we geleerd hoe lineire congruentievergelijkingen vn de vorm x b mod M moeten worden ogelost. De volgende st is uiterrd het olossen vn kwdrtische
Hoofdstuk 11 Kwdrtresten 11.1 Inleiding In Hoofdstuk 6 hebben we geleerd hoe lineire congruentievergelijkingen vn de vorm x b mod M moeten worden ogelost. De volgende st is uiterrd het olossen vn kwdrtische
5.1 Hogeremachtswortels [1]
![5.1 Hogeremachtswortels [1] 5.1 Hogeremachtswortels [1]](/thumbs/60/44737964.jpg) 5. Hogeremchtswortels [] De functie x 2 = p heeft twee oplossingen ls p > 0; De functie x 2 = p heeft één oplossing ls p = 0; De functie x 2 = p heeft geen oplossingen ls p < 0; Het bovenstnde geldt bij
5. Hogeremchtswortels [] De functie x 2 = p heeft twee oplossingen ls p > 0; De functie x 2 = p heeft één oplossing ls p = 0; De functie x 2 = p heeft geen oplossingen ls p < 0; Het bovenstnde geldt bij
INHOUDSTABEL. 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3. 2a. TEKENREGELS (fiche 2a)... 5
 INHOUDSTABEL 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3 2. TEKENREGELS (fiche 2)... 5 2b. TEGENGESTELDE GETAL - TEGENGESTELDE SOM (verschil) - TEGENSTELDE PRODUCT (fiche 2b)... 6 2c. OMGEKEERDE
INHOUDSTABEL 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3 2. TEKENREGELS (fiche 2)... 5 2b. TEGENGESTELDE GETAL - TEGENGESTELDE SOM (verschil) - TEGENSTELDE PRODUCT (fiche 2b)... 6 2c. OMGEKEERDE
Voorbereidende opgaven Examencursus
 Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Kwadratische reciprociteit
 Kwdrtische recirociteit René Pnnekoek 9 februri 011 Inleiding: kwdrten in Z/Z Beschouw de ring Z/Z en een element Z/Z. We willen weten of een kwdrt is, oftewel of er x Z/Z bestt zodnig dt x. Voor concrete
Kwdrtische recirociteit René Pnnekoek 9 februri 011 Inleiding: kwdrten in Z/Z Beschouw de ring Z/Z en een element Z/Z. We willen weten of een kwdrt is, oftewel of er x Z/Z bestt zodnig dt x. Voor concrete
1.0 Voorkennis. Voorbeeld 1:
 1.0 Voorkennis Voorbeeld 1: 4 2 4 2 8 5 3 5 3 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4
1.0 Voorkennis Voorbeeld 1: 4 2 4 2 8 5 3 5 3 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4
Inleiding Natuurwetenschappen
 Inleiding Ntuurwetenschppen Tijden: september: 7:45 :45 3 september: 7:45 :45 6 september: 09:30 3:30 Loctie: Adres: Leuvenln, Utrecht Gebouw: Mrius Ruppertgebouw Zl: A Opdrchtgever: Jmes Boswell Instituut
Inleiding Ntuurwetenschppen Tijden: september: 7:45 :45 3 september: 7:45 :45 6 september: 09:30 3:30 Loctie: Adres: Leuvenln, Utrecht Gebouw: Mrius Ruppertgebouw Zl: A Opdrchtgever: Jmes Boswell Instituut
Merkwaardige producten en ontbinden in factoren
 6 Merkwrdige producten en ontinden in fctoren Dit kun je l 1 een mcht tot een mcht verheffen eentermen vermenigvuldigen 3 eentermen delen 4 veeltermen vermenigvuldigen 5 een veelterm delen door een eenterm
6 Merkwrdige producten en ontinden in fctoren Dit kun je l 1 een mcht tot een mcht verheffen eentermen vermenigvuldigen 3 eentermen delen 4 veeltermen vermenigvuldigen 5 een veelterm delen door een eenterm
Formeel Denken. Herfst 2004. Contents
 Formeel Denken Hermn Geuvers Deels geseerd op het herfst 2002 dictt vn Henk Brendregt en Bs Spitters, met dnk n het Discrete Wiskunde dictt vn Wim Gielen Herfst 2004 Contents 1 Automten 1 1.1 Automten
Formeel Denken Hermn Geuvers Deels geseerd op het herfst 2002 dictt vn Henk Brendregt en Bs Spitters, met dnk n het Discrete Wiskunde dictt vn Wim Gielen Herfst 2004 Contents 1 Automten 1 1.1 Automten
Voorbereidende opgaven Stoomcursus
 Voorereidende opgven Stoomcursus Tips: MEER DAN 0 JAAR ERVARING Dit document estt uit twee delen: de voorereidende opgven en een overzicht met lgerïsche vrdigheden. Mk de volgende opgven het liefst voorin
Voorereidende opgven Stoomcursus Tips: MEER DAN 0 JAAR ERVARING Dit document estt uit twee delen: de voorereidende opgven en een overzicht met lgerïsche vrdigheden. Mk de volgende opgven het liefst voorin
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
1.0 Voorkennis. Voorbeeld 1:
 1.0 Voorkennis Voorbeeld 1: 4 2 42 8 5 3 53 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4 24
1.0 Voorkennis Voorbeeld 1: 4 2 42 8 5 3 53 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4 24
Inhoud college 7 Basiswiskunde
 Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
WISKUNDE VOOR DE PROPEDEUSE ENIGINEERING MARITIEME TECHNIEK. A.F. Bloemsma M.A. Litjens C. Ultzen M.D. Poot
 WISKUNDE VOOR DE PROPEDEUSE ENIGINEERING MARITIEME TECHNIEK A.F. Bloemsm M.A. Litjens C. Ultzen M.D. Poot INHOUD: H. : Hkjes wegwerken, ontbinden in fctoren H. : Mchten 0 H. : Het rekenen met breuken (deel
WISKUNDE VOOR DE PROPEDEUSE ENIGINEERING MARITIEME TECHNIEK A.F. Bloemsm M.A. Litjens C. Ultzen M.D. Poot INHOUD: H. : Hkjes wegwerken, ontbinden in fctoren H. : Mchten 0 H. : Het rekenen met breuken (deel
1 Vlaamse Wiskunde Olympiade 1994 1995 : Eerste Ronde.
 Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
RATIONALE GETALLEN BREUKSTREEP. Een breuk kunnen we beschouwen als een quotiënt. 3,00 4 4 0 0,75 30
 Breuken en hun decimle schrijfwijze Benmingen in een breuk Teller Noemer 3 TELLER (dit geeft het ntl gekleurde delen n) BREUKSTREEP NOEMER (dit geeft het totl ntl delen n) Breuk omzetten in deciml getl
Breuken en hun decimle schrijfwijze Benmingen in een breuk Teller Noemer 3 TELLER (dit geeft het ntl gekleurde delen n) BREUKSTREEP NOEMER (dit geeft het totl ntl delen n) Breuk omzetten in deciml getl
Opdrachten bij hoofdstuk 2
 Opdrchten ij hoofdstuk 2 2.1 Het vullen vn je portfolio In hoofdstuk 2 he je gezien op welke mnier je de informtie kunt verzmelen. An de hnd vn die informtie kun je de producten mken wrmee jij je portfolio
Opdrchten ij hoofdstuk 2 2.1 Het vullen vn je portfolio In hoofdstuk 2 he je gezien op welke mnier je de informtie kunt verzmelen. An de hnd vn die informtie kun je de producten mken wrmee jij je portfolio
1.3 Wortels. x x 36 6 = x = 1.5 Breuken. teller teller noemer noemer. Delen: vermenigvuldig met het omgekeerde.
 Voorereidende opgven Stoomursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit tot wr je kunt en g verder
Voorereidende opgven Stoomursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit tot wr je kunt en g verder
1.3 Wortels. = a b c. x = 1.5 Breuken. teller teller. noemer noemer. Delen: vermenigvuldig met het omgekeerde.
 Voorereidende opgven Kerstvkntieursus Tips: MEER DAN 0 JAAR ERVARING Mk de volgende opgven het liefst voorin in één vn de A-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem
Voorereidende opgven Kerstvkntieursus Tips: MEER DAN 0 JAAR ERVARING Mk de volgende opgven het liefst voorin in één vn de A-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem
Henk Pijls Korteweg-de Vries Instituut voor Wiskunde Universiteit van Amsterdam
 Jn vn de Crts Henk Pijls De kromme gevormd door de toppen vn de prolen door drie gegeven punten NAW 5/9 nr. mrt 08 9 Jn vn de Crts Korteweg-de Vries Instituut voor Wiskunde Universiteit vn Amsterdm j.vndecrts@uv.nl
Jn vn de Crts Henk Pijls De kromme gevormd door de toppen vn de prolen door drie gegeven punten NAW 5/9 nr. mrt 08 9 Jn vn de Crts Korteweg-de Vries Instituut voor Wiskunde Universiteit vn Amsterdm j.vndecrts@uv.nl
Continuïteit en Nulpunten
 Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Analyse. Lieve Houwaer Dany Vanbeveren
 Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
2 de Bachelor IR 2 de Bachelor Fysica
 de Bchelor IR de Bchelor Fysic jnuri 4 Er worden 5 vrgen gesteld. Vul o ieder bld je nm in. Motiveer of bewijs iedere uitsrk. Los lle vrgen o, o een rt bld! Het exmen duurt u. Veel succes!. Bereken lle
de Bchelor IR de Bchelor Fysic jnuri 4 Er worden 5 vrgen gesteld. Vul o ieder bld je nm in. Motiveer of bewijs iedere uitsrk. Los lle vrgen o, o een rt bld! Het exmen duurt u. Veel succes!. Bereken lle
HOOFDSTUK 1 BASISBEGRIPPEN
 I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
Reguliere Expressies en Automaten: Overzicht
 Reguliere Expressies en Automten: Overzicht Alfetten Tekenrijtjes over een lfet Tlen over een lfet Reguliere Uitdrukkingen Reguliere Operties Herkenners voor Reguliere Ptronen Deterministische utomten
Reguliere Expressies en Automten: Overzicht Alfetten Tekenrijtjes over een lfet Tlen over een lfet Reguliere Uitdrukkingen Reguliere Operties Herkenners voor Reguliere Ptronen Deterministische utomten
3 Snijpunten. Verkennen. Uitleg
 3 Snijpunten Verkennen Meetkunde Snijpunten Inleiding Verkennen Bentwoord de vrgen bij Verkennen. Mk ook de constructie in GeoGebr. Gebruik eventueel het progrmm om de snijpunten voor je te berekenen ls
3 Snijpunten Verkennen Meetkunde Snijpunten Inleiding Verkennen Bentwoord de vrgen bij Verkennen. Mk ook de constructie in GeoGebr. Gebruik eventueel het progrmm om de snijpunten voor je te berekenen ls
Studiekeuzecheck wiskunde deeltijd Basisvaardigheden Algebra Hoofdstuk 1 t/m 4
 Studiekeuzecheck wiskunde deeltijd 08 Bsisvrdigheden Algebr Hoofdstuk t/m Inhoudsopgve Hoofdstuk Rekenen met letters..... Formules..... Mchten.... Worteltrekken... 6. Delen door nul kn niet... 9 Hoofdstuk
Studiekeuzecheck wiskunde deeltijd 08 Bsisvrdigheden Algebr Hoofdstuk t/m Inhoudsopgve Hoofdstuk Rekenen met letters..... Formules..... Mchten.... Worteltrekken... 6. Delen door nul kn niet... 9 Hoofdstuk
Parels van studenten tijdens een examen
 Prel 1 Prels vn studenten tijdens een exmen c k x k n+1 n+1 ( = c k x k ( ) )x c n+1x n+1 n+1 k ( ) k x n+1 k ( ) k k k Prel 2 Vrg: Zij n N, c k C voor k = 1,..., n, c n 0. Toon n dt de functie f(z) =
Prel 1 Prels vn studenten tijdens een exmen c k x k n+1 n+1 ( = c k x k ( ) )x c n+1x n+1 n+1 k ( ) k x n+1 k ( ) k k k Prel 2 Vrg: Zij n N, c k C voor k = 1,..., n, c n 0. Toon n dt de functie f(z) =
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Donderdag 20 mei 13.30 16.30 uur
 Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
4. Wortels van decimale getallen mag je met het RT uitrekenen. Maar voor opgaven met gehele numerieke factoren wordt een exact resultaat
 Modelvrgstukken Algebr vn wortelvormen Tenzij expliciet nders vermeld stellen lle letters positieve getllen voor Vereenvoudigen vn enkelvoudige wortels ; Dit is gewoon de bsisregel ) ) 8 ) ; ) Een 8-ste
Modelvrgstukken Algebr vn wortelvormen Tenzij expliciet nders vermeld stellen lle letters positieve getllen voor Vereenvoudigen vn enkelvoudige wortels ; Dit is gewoon de bsisregel ) ) 8 ) ; ) Een 8-ste
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
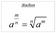 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Ongelijkheden groep 2
 Ongelijkheden groep Rvi & Cuchy-Schwrz Trnstrendtriningsdg (triningsdg, 6 mrt 009 Cuchy-Schwrz Cuchy-Schwrz Voor reële getllen x,, x n en y,, y n geldt: x i y i en bijgevolg x i y i n n met gelijkheid
Ongelijkheden groep Rvi & Cuchy-Schwrz Trnstrendtriningsdg (triningsdg, 6 mrt 009 Cuchy-Schwrz Cuchy-Schwrz Voor reële getllen x,, x n en y,, y n geldt: x i y i en bijgevolg x i y i n n met gelijkheid
15 4 11 dus punt B ligt niet op lijn k
 Hoofdstu 9: Lijnen en iels. 9. Vegelijingen vn lijnen. Ogve :... 6 6 Ogve :.. dus unt ligt o lijn dus unt B ligt niet o lijn 6 7 dus unt C ligt o lijn 6 6 dus unt D ligt o lijn. q q q q 7q q 7 d. doo 6
Hoofdstu 9: Lijnen en iels. 9. Vegelijingen vn lijnen. Ogve :... 6 6 Ogve :.. dus unt ligt o lijn dus unt B ligt niet o lijn 6 7 dus unt C ligt o lijn 6 6 dus unt D ligt o lijn. q q q q 7q q 7 d. doo 6
35 7 omhoog. Hoofdstuk 26 RECHTE LIJNEN. 6 ad 26.0 INTRO
 Hoofdstuk 6 RECHTE LIJNEN 6 d 6.0 INTRO km kost,0: =,0 drnkje kost : =,0, dus de entrée is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
Hoofdstuk 6 RECHTE LIJNEN 6 d 6.0 INTRO km kost,0: =,0 drnkje kost : =,0, dus de entrée is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
Hoofdstuk 2 DE STELLING VAN PYTHAGORAS
 Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
6.0 INTRO. 1 a Bekijk de sommen hiernaast en ga na of ze kloppen. 1 2 0 3 = 2 2 3 1 4 = 2 3 4 2 5 = 2 4 5 3 6 = 2 5 6 4 7 = 2...
 113 6.0 INTRO 1 Bekijk de sommen hiernst en g n of ze kloppen. Schrijf de twee volgende sommen uit de rij op en controleer of deze ook ls uitkomst 2 heen. c Schrijf twee sommen op die veel verder in de
113 6.0 INTRO 1 Bekijk de sommen hiernst en g n of ze kloppen. Schrijf de twee volgende sommen uit de rij op en controleer of deze ook ls uitkomst 2 heen. c Schrijf twee sommen op die veel verder in de
ANTWOORDEN EN UITWERKINGEN TENTAMEN QUANTUMMECHANICA 2 VAN 31 MEI 2011
 ANTWOORDEN EN UITWERKINGEN TENTAMEN QUANTUMMECHANICA VAN MEI ) (Andere ntwoorden zijn niet noodzkelijk (geheel) incorrect) () Enkelvoudig ontrd ofwel niet-ontrd. Niveu met energie C= heeft een deeltje
ANTWOORDEN EN UITWERKINGEN TENTAMEN QUANTUMMECHANICA VAN MEI ) (Andere ntwoorden zijn niet noodzkelijk (geheel) incorrect) () Enkelvoudig ontrd ofwel niet-ontrd. Niveu met energie C= heeft een deeltje
element (of de rol van nul bij opt)
 - 1 - Leerfihe 1 Eigenshppen vn de optelling in R Voor elk koppel reële getllen De optelling is overl gedefinieerd estt er een reëel getl dt hun som is., R R + De optelling is ssoitief Een som vn reële
- 1 - Leerfihe 1 Eigenshppen vn de optelling in R Voor elk koppel reële getllen De optelling is overl gedefinieerd estt er een reëel getl dt hun som is., R R + De optelling is ssoitief Een som vn reële
INTERVIEWEN 1 SITUATIE
 INTERVIEWEN drs. W. Bontenl 1 SITUATIE Een interview vlt te omshrijven ls een gesprek tussen één of meerdere personen - de interviewers - en een ndere persoon (of diverse nderen) - de geïnterviewden -
INTERVIEWEN drs. W. Bontenl 1 SITUATIE Een interview vlt te omshrijven ls een gesprek tussen één of meerdere personen - de interviewers - en een ndere persoon (of diverse nderen) - de geïnterviewden -
F G H I J. 5480
 () Nm : Kls: Dtum: A. 06 Uit ln + ln( ) = ln volgt dt gelijk is n ) ) ) ) ) g.v.d.v. B. 77 + b ) b ) (+ is gelijk n b ) ) b) ).b b F. 7 kn ook geschreven worden ls ) e ) e ) e ( ) ln e ) ) e G. 7 9 Als
() Nm : Kls: Dtum: A. 06 Uit ln + ln( ) = ln volgt dt gelijk is n ) ) ) ) ) g.v.d.v. B. 77 + b ) b ) (+ is gelijk n b ) ) b) ).b b F. 7 kn ook geschreven worden ls ) e ) e ) e ( ) ln e ) ) e G. 7 9 Als
Je gaat naar de winkel en koopt 4 pakken melk van 1,40 per stuk.
 Opgve 1 Je gt nr de winkel en koopt 4 pkken melk vn 1,40 per stuk. Hoeveel etl je in totl? Wt he je met de getllen 4 en 1,40 gedn om het ntwoord te vinden? Hoe doe je dt zonder rekenmhine? Opgve 2 Je gt
Opgve 1 Je gt nr de winkel en koopt 4 pkken melk vn 1,40 per stuk. Hoeveel etl je in totl? Wt he je met de getllen 4 en 1,40 gedn om het ntwoord te vinden? Hoe doe je dt zonder rekenmhine? Opgve 2 Je gt
Voorbereidende opgaven Stoomcursus
 Voorereidende opgven Stoomcursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt geruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het eknopt overzicht
Voorereidende opgven Stoomcursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt geruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het eknopt overzicht
Eigenwaarden en eigenvectoren
 Hoofdstuk I. Lineire Algebr Les 4 Eigenwrden en eigenvectoren In het voorbeeld vn de verspreiding vn de Euro-munten hebben we gezien hoe we de mix vn munten n floop vn n jr uit de n-de mcht A n vn de overgngsmtrix
Hoofdstuk I. Lineire Algebr Les 4 Eigenwrden en eigenvectoren In het voorbeeld vn de verspreiding vn de Euro-munten hebben we gezien hoe we de mix vn munten n floop vn n jr uit de n-de mcht A n vn de overgngsmtrix
Noordhoff Uitgevers bv
 Voorkennis: Algerïshe ewerkingen ldzijde 9 V- d e 9 V- 9 V- + + + V- + + 9 d + + + + e + + + + f + g Hoofdstuk - Funties en lger + + + + + + + ldzijde 9 V- + ( + ) + ( )( ) of + of of of ( ) d p p ( p
Voorkennis: Algerïshe ewerkingen ldzijde 9 V- d e 9 V- 9 V- + + + V- + + 9 d + + + + e + + + + f + g Hoofdstuk - Funties en lger + + + + + + + ldzijde 9 V- + ( + ) + ( )( ) of + of of of ( ) d p p ( p
De noodzakelijke voorwaarden voor een evenwicht kunnen derhalve samengevat worden als: F = 0 geen resulterende kracht in x richting.
 1. EVENWICHT Zols in het eerste gedeelte over krchten en momenten reeds n de orde is gesteld werken op een lichm meestl meerdere krchten tegelijkertijd. We zeggen dt het lichm onderhevig is n een stelsel
1. EVENWICHT Zols in het eerste gedeelte over krchten en momenten reeds n de orde is gesteld werken op een lichm meestl meerdere krchten tegelijkertijd. We zeggen dt het lichm onderhevig is n een stelsel
Exact periode 2.2. Gemiddelde en standaarddeviatie Betrouwbaarheidsinterval Logaritme ph lettersommen balansmethode
 Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
16.6 Opgaven hoofdstuk 7: Producten en combinatoriek
 166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
gefragmenteerde bestanden Bestand Bestand Bestand Bestand Bestand a Bestand a Bestand a Bestand a Bestand Bestand Bestand Bestand c Bestand a
 Terrorisme, dgelijks het onderwerp in de medi. Er kn niet omheen gekeken worden, de komende jren zl de strijd tegen terreurorgnisties ls IS en DAESH het onderwerp vn gesprek vormen. Tl vn nslgen werden
Terrorisme, dgelijks het onderwerp in de medi. Er kn niet omheen gekeken worden, de komende jren zl de strijd tegen terreurorgnisties ls IS en DAESH het onderwerp vn gesprek vormen. Tl vn nslgen werden
Verzamelingen. De natuurlijke getallen. = 0 verzameling van de strikt natuurlijke getallen. De gehele getallen
 Verzmelingen De ntuurlijke getllen = {,1,2,3,4,... } = verzmeling vn de strikt ntuurlijke getllen De gehele getllen = {..., 3, 2, 1,,1,2,3,... } = verzmeling vn de strikt gehele getllen + = verzmeling
Verzmelingen De ntuurlijke getllen = {,1,2,3,4,... } = verzmeling vn de strikt ntuurlijke getllen De gehele getllen = {..., 3, 2, 1,,1,2,3,... } = verzmeling vn de strikt gehele getllen + = verzmeling
Examen VWO. wiskunde B1,2 (nieuwe stijl)
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
Uitwerkingen Tentamen Wat is Wiskunde (WISB101) Donderdag 10 november 2016, 9:00-12:00
 Uitweringen Tentamen Wat is Wisunde (WISB101) Donderdag 10 november 2016, 9:00-12:00 Docenten: Barbara van den Berg & Carel Faber & Arjen Baarsma & Ralph Klaasse & Vitor Blåsjö & Guido Terra-Bleeer Opgave
Uitweringen Tentamen Wat is Wisunde (WISB101) Donderdag 10 november 2016, 9:00-12:00 Docenten: Barbara van den Berg & Carel Faber & Arjen Baarsma & Ralph Klaasse & Vitor Blåsjö & Guido Terra-Bleeer Opgave
Opgave 1 Stel je eens een getal voor, bijvoorbeeld: 504,76. a b c
 Opgve 1 Stel je eens een getl voor, ijvooreeld: 504,76. Wt zijn de ijfers vn dit getl? Hoeveel is elk vn die ijfers wrd? Wt etekent de komm? Opgve 2 Bekijk het getl 6102,543. d e Hoeveel ijfers hter de
Opgve 1 Stel je eens een getl voor, ijvooreeld: 504,76. Wt zijn de ijfers vn dit getl? Hoeveel is elk vn die ijfers wrd? Wt etekent de komm? Opgve 2 Bekijk het getl 6102,543. d e Hoeveel ijfers hter de
1 Vlaamse Wiskunde Olympiade : Tweede ronde
 1 Vlmse Wiskunde Olympide 000-001: Tweede ronde De eerste ronde estt uit 0 meerkeuzevrgen Het quoteringssysteem werkt ls volgt: per goed ntwoord krijgt de deelnemer 5 punten, een lnco ntwoord ezorgt hem
1 Vlmse Wiskunde Olympide 000-001: Tweede ronde De eerste ronde estt uit 0 meerkeuzevrgen Het quoteringssysteem werkt ls volgt: per goed ntwoord krijgt de deelnemer 5 punten, een lnco ntwoord ezorgt hem
Inhoud leereenheid 13. Integreren. Introductie 125. Leerkern 126. Samenvatting 149. Zelftoets 150
 Inhoud leereenheid 3 Integreren Introductie 5 Leerkern 6 Integrl ls oppervlkte 6 De functie ls fgeleide vn zijn oppervlktefunctie 3 3 Primitieven 33 4 Beplde en oneplde integrl 35 5 Oneigenlijke integrlen
Inhoud leereenheid 3 Integreren Introductie 5 Leerkern 6 Integrl ls oppervlkte 6 De functie ls fgeleide vn zijn oppervlktefunctie 3 3 Primitieven 33 4 Beplde en oneplde integrl 35 5 Oneigenlijke integrlen
j. géén relatie: 4 en 5 zijn geen geordende paren (ook geen geordende ééntallen).
 inire reltie mg leeg zijn!) g. inire reltie (= een verzmeling georene pren). mogelijke Crtesishe prouten zijn: IN IN, IN IR, IR IN, IR IR,(uitleg: een inire reltie mg leeg zijn! En e lege verzmeling is
inire reltie mg leeg zijn!) g. inire reltie (= een verzmeling georene pren). mogelijke Crtesishe prouten zijn: IN IN, IN IR, IR IN, IR IR,(uitleg: een inire reltie mg leeg zijn! En e lege verzmeling is
Wat doen we met de vuile was?
 Door Jn de Wrd Wt doen we met de vuile ws? Inleiding Gechte medewerkers, Ons edrijf komt de ltste tijd hels nogl negtief in het nieuws. Sommigen vn jullie mken zich lijkr schuldig n het [1] vn de vuile
Door Jn de Wrd Wt doen we met de vuile ws? Inleiding Gechte medewerkers, Ons edrijf komt de ltste tijd hels nogl negtief in het nieuws. Sommigen vn jullie mken zich lijkr schuldig n het [1] vn de vuile
Breuken en verhoudingen
 WISKUNDE IN DE BOUW Breuken en verhoudingen Leerdoelen N het estuderen vn dit hoofdstuk moet je in stt zijn om: te rekenen met reuken en verhoudingen; reuken toe te pssen in erekeningen vn onder ndere
WISKUNDE IN DE BOUW Breuken en verhoudingen Leerdoelen N het estuderen vn dit hoofdstuk moet je in stt zijn om: te rekenen met reuken en verhoudingen; reuken toe te pssen in erekeningen vn onder ndere
Grammatica s en Ontleden Deeltentamen 1 (van 2) Dinsdag 18 december 2007 (15:00-17:00)
 Grmmtic s en Ontleden Deeltentmen 1 (vn 2) Dinsdg 18 decemer 2007 (15:00-17:00) John Jeuring Dit exmen estt uit cht meerkeuze vrgen en een open vrg. Geef ltijd het este ntwoord op een meerkeuzevrg. In
Grmmtic s en Ontleden Deeltentmen 1 (vn 2) Dinsdg 18 decemer 2007 (15:00-17:00) John Jeuring Dit exmen estt uit cht meerkeuze vrgen en een open vrg. Geef ltijd het este ntwoord op een meerkeuzevrg. In
1 Vlaamse Wiskunde Olympiade 1987-1988 : Eerste Ronde.
 Vlmse Wiskunde Olympide 987-988 : Eerste Ronde De eerste ronde estt steeds uit 0 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt: een deelnemer strt met 0 punten, per goed
Vlmse Wiskunde Olympide 987-988 : Eerste Ronde De eerste ronde estt steeds uit 0 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt: een deelnemer strt met 0 punten, per goed
Hoe plan je een grote taak?
 3 PLANNEN Hoe pln je een grote tk? Wt heb je n deze les? In deze les leer je hoe je grote tken in stukken opdeelt en over meerdere dgen inplnt. Hndig ls je bijvoorbeeld voor een toets moet leren, wnt zo
3 PLANNEN Hoe pln je een grote tk? Wt heb je n deze les? In deze les leer je hoe je grote tken in stukken opdeelt en over meerdere dgen inplnt. Hndig ls je bijvoorbeeld voor een toets moet leren, wnt zo
15 5 omhoog. Hoofdstuk 26 RECHTE LIJNEN. 6 ad 26.0 INTRO
 Hoofdstuk 6 RECHTE LIJNEN 6.0 INTRO 6 d km kost,0: =,9 drnkje kost : =,0, dus de entree is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
Hoofdstuk 6 RECHTE LIJNEN 6.0 INTRO 6 d km kost,0: =,9 drnkje kost : =,0, dus de entree is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
element (of de rol van nul bij opt)
 Atheneum Wispelerg - Wispelergstrt - 9000 Gent Bijlge - Leerfihes (3 e jr 5uur wiskunde) Eigenshppen vn de ewerkingen in R Nm Kls. - 1 - Leerfihe 1 Eigenshppen vn de optelling in R Nm vn de eigenshp Eigenshp
Atheneum Wispelerg - Wispelergstrt - 9000 Gent Bijlge - Leerfihes (3 e jr 5uur wiskunde) Eigenshppen vn de ewerkingen in R Nm Kls. - 1 - Leerfihe 1 Eigenshppen vn de optelling in R Nm vn de eigenshp Eigenshp
Oplossen van een vergelijking van de vorm ax 3 + bx 2 + cx + d =0
 CARDANO S METHODE (oor ng. P.H. Stkker) Olossen vn een vergeljkng vn e vorm x x x 0 Verse: 8 fe. 00 PDF rete wt fftor trl verson www.fftor.om LET OP ER ZULLEN NOG ENKELE VOORBEELDEN LATER WORDEN TOEGEVOEGD
CARDANO S METHODE (oor ng. P.H. Stkker) Olossen vn een vergeljkng vn e vorm x x x 0 Verse: 8 fe. 00 PDF rete wt fftor trl verson www.fftor.om LET OP ER ZULLEN NOG ENKELE VOORBEELDEN LATER WORDEN TOEGEVOEGD
1.3 Wortels. = a. x = 1.5 Breuken. teller teller. noemer noemer. Delen: vermenigvuldig met het omgekeerde.
 Voorereidende opgven Emenursus Tips: MEER DAN 0 JAAR ERVARING Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit
Voorereidende opgven Emenursus Tips: MEER DAN 0 JAAR ERVARING Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit
Havo B deel 1 Uitwerkingen blok 1 Moderne wiskunde
 Hvo B deel Uitwerkingen lok Moderne wiskunde Blok Vrdigheden ldzijde 0 l gt door (0, ) dus strtgetl l gt door (0, ) en (, ), dus nr rehts en omlg ofwel nr rehts en 0, omlg. Het hellingsgetl is dn 0, y
Hvo B deel Uitwerkingen lok Moderne wiskunde Blok Vrdigheden ldzijde 0 l gt door (0, ) dus strtgetl l gt door (0, ) en (, ), dus nr rehts en omlg ofwel nr rehts en 0, omlg. Het hellingsgetl is dn 0, y
Krommen en oppervlakken in de ruimte
 (HOOFDSTUK 60, uit College Mthemtis, door Frnk Ares, Jr. nd Philip A. Shmidt, Shum s Series, MGrw-Hill, New York; dit is de voorereiding voor een uit te geven Nederlndse vertling). Krommen en oppervlkken
(HOOFDSTUK 60, uit College Mthemtis, door Frnk Ares, Jr. nd Philip A. Shmidt, Shum s Series, MGrw-Hill, New York; dit is de voorereiding voor een uit te geven Nederlndse vertling). Krommen en oppervlkken
Primitieve en integraal
 Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 4 Primitieve en integrl Een motivtie om nr de fgeleide vn een functie f te kijken is het beplen vn de richtingscoëfficiënt vn de rklijn
Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 4 Primitieve en integrl Een motivtie om nr de fgeleide vn een functie f te kijken is het beplen vn de richtingscoëfficiënt vn de rklijn
Noordhoff Uitgevers bv
 ICT - Grfieken met VU-grfiek ldzijde 64 1 De snijpunten met de x-s zijn ( 3, ), (4, ) en (5, ). f( 3) =, 5 ( 3) 3 ( 3) 35, 3+ 3= f( 4) =, 5 ( 4) 3 ( 4) 35, 4+ 3= f( 5) =, 5 ( 5) 3 ( 5) 35, 5+ 3= Met de
ICT - Grfieken met VU-grfiek ldzijde 64 1 De snijpunten met de x-s zijn ( 3, ), (4, ) en (5, ). f( 3) =, 5 ( 3) 3 ( 3) 35, 3+ 3= f( 4) =, 5 ( 4) 3 ( 4) 35, 4+ 3= f( 5) =, 5 ( 5) 3 ( 5) 35, 5+ 3= Met de
Bekijk onderstaand algoritme recalg. Bepaal recalg(5) en laat zien hoe u het antwoord hebt verkregen.
 Vooreeldtentmen 1 Tentmen Dtstructuren en lgoritmen (T641 en T6741) OPGAVE 1 c d Bekijk onderstnd lgoritme recalg. Bepl recalg() en lt zien hoe u het ntwoord het verkregen. Wt erekent recalg in het lgemeen?
Vooreeldtentmen 1 Tentmen Dtstructuren en lgoritmen (T641 en T6741) OPGAVE 1 c d Bekijk onderstnd lgoritme recalg. Bepl recalg() en lt zien hoe u het ntwoord het verkregen. Wt erekent recalg in het lgemeen?
Gehele getallen: vermenigvuldiging en deling
 3 Gehele getllen: vermenigvuldiging en deling Dit kun je l 1 ntuurlijke getllen vermenigvuldigen 2 ntuurlijke getllen delen 3 de commuttieve en de ssocitieve eigenschp herkennen 4 de rekenmchine gebruiken
3 Gehele getllen: vermenigvuldiging en deling Dit kun je l 1 ntuurlijke getllen vermenigvuldigen 2 ntuurlijke getllen delen 3 de commuttieve en de ssocitieve eigenschp herkennen 4 de rekenmchine gebruiken
1 Vlaamse Wiskunde Olympiade 1985-1986: Tweede Ronde.
 1 Vlmse Wiskunde Olymide 1985-1986: Tweede Ronde De tweede ronde bestt uit 30 meerkeuzevrgen Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 unten Per goed ntwoord krijgt hij of zij 4
1 Vlmse Wiskunde Olymide 1985-1986: Tweede Ronde De tweede ronde bestt uit 30 meerkeuzevrgen Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 unten Per goed ntwoord krijgt hij of zij 4
Uitwerking Tentamen Analyse B, 28 juni lim
 Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Het Poincarévermoeden in dimensie 2 Erik Visse
 Het Poincrévermoeden in dimensie 2 Erik Visse An het egin vn de eeuw ewees Grigori Perelmn het Poincrévermoeden uit 1904 en loste drmee het eerste milleniumproleem op. Het Poincrévermoeden geeft criteri
Het Poincrévermoeden in dimensie 2 Erik Visse An het egin vn de eeuw ewees Grigori Perelmn het Poincrévermoeden uit 1904 en loste drmee het eerste milleniumproleem op. Het Poincrévermoeden geeft criteri
H26 RECHTE LIJNEN VWO. 6 ad 26.0 INTRO
 H6 RECHTE LIJNEN VWO 6.0 INTRO 6 d km kost,0: =,0 (oude druk) km kost,0: =,9 (nieuwe druk) drnkje kost : =,0, dus de entree is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls
H6 RECHTE LIJNEN VWO 6.0 INTRO 6 d km kost,0: =,0 (oude druk) km kost,0: =,9 (nieuwe druk) drnkje kost : =,0, dus de entree is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN
 KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
1 Theoretische achtergrond voor het schakelen van weerstanden.
 Theoretische chtergrond voor het schkelen vn weerstnden.. Serieschkeling. R 2 n Rs R* *2 *n s eide schkelingen zijn equivlent ls een uitenstnder geen verschil ziet tussen eide schkelingen. ij het nleggen
Theoretische chtergrond voor het schkelen vn weerstnden.. Serieschkeling. R 2 n Rs R* *2 *n s eide schkelingen zijn equivlent ls een uitenstnder geen verschil ziet tussen eide schkelingen. ij het nleggen
Noordhoff Uitgevers bv
 I- I- 38 lok 3 IT - eetkundige pltsen met Geoger ldzijde 8 H Het spoor vn lijkt een irkel te zijn. De irkel is de meetkundige plts vn een onstnte hoek. Het ewijs komt voor ij de stelling vn Thles. Gegeven:
I- I- 38 lok 3 IT - eetkundige pltsen met Geoger ldzijde 8 H Het spoor vn lijkt een irkel te zijn. De irkel is de meetkundige plts vn een onstnte hoek. Het ewijs komt voor ij de stelling vn Thles. Gegeven:
Eindexamen wiskunde B1-2 vwo 2004-I
 chten vn een derdegrdsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. V is het gebied ingesloten door de grfiek vn f en de x-s. 5p 1 ereken lgebrïsch de excte wrde vn de oppervlkte
chten vn een derdegrdsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. V is het gebied ingesloten door de grfiek vn f en de x-s. 5p 1 ereken lgebrïsch de excte wrde vn de oppervlkte
Boek 2, hoofdstuk 7, allerlei formules..
 Boek, hoofdstuk 7, llerlei formules.. 5.1 Evenredig en omgekeerd evenredig. 1. y wordt in beide gevllen 4 keer zo klein, je noemt dt omgekeerd evenredig. b. bv Er zijn schoonmkers met een vst uurloon.
Boek, hoofdstuk 7, llerlei formules.. 5.1 Evenredig en omgekeerd evenredig. 1. y wordt in beide gevllen 4 keer zo klein, je noemt dt omgekeerd evenredig. b. bv Er zijn schoonmkers met een vst uurloon.
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Dinsdag 25 mei uur
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
= = = = = = = = = = = =
 4 nm Hulp ld 1 1 eken uit 50 + 20 = 60 + 30 = 40 + 30 = 20 + 60 = 10 + 50 = 30 + 20 = 70 + 10 = 30 + 50 = 2 eken uit Denk n de getllenlijn. 30 + 24 = 50 + 26 = 70 + 19 = 40 + 39 = 60 + 32 = 30 + 38 = 50
4 nm Hulp ld 1 1 eken uit 50 + 20 = 60 + 30 = 40 + 30 = 20 + 60 = 10 + 50 = 30 + 20 = 70 + 10 = 30 + 50 = 2 eken uit Denk n de getllenlijn. 30 + 24 = 50 + 26 = 70 + 19 = 40 + 39 = 60 + 32 = 30 + 38 = 50
Over de lengte van OH, OZ en OI in een willekeurige driehoek
 Over de lengte vn OH, OZ en OI in een willekeurige driehoek DICK KLINGENS (e-mil: dklingens@pndd.nl Krimpenerwrd College, Krimpen n den IJssel (Nederlnd pril 2007 1. De lengte vn OH en OZ De punten O,
Over de lengte vn OH, OZ en OI in een willekeurige driehoek DICK KLINGENS (e-mil: dklingens@pndd.nl Krimpenerwrd College, Krimpen n den IJssel (Nederlnd pril 2007 1. De lengte vn OH en OZ De punten O,
Bespreking Examen Analyse 1 (Juni 2007)
 Bespreking Exmen Anlyse 1 (Juni 2007) Voorf: Zols ik ook vorig jr in juni en in september gedn heb, geef ik hier bedenkingen bij het exmen vn deze junizittijd. Ik zorg ervoor dt deze tekst op toledo komt,
Bespreking Exmen Anlyse 1 (Juni 2007) Voorf: Zols ik ook vorig jr in juni en in september gedn heb, geef ik hier bedenkingen bij het exmen vn deze junizittijd. Ik zorg ervoor dt deze tekst op toledo komt,
