Recursie van Poincaré-reeksen
|
|
|
- Monique Willemsen
- 5 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Recursie va Poicaré-reekse Joachim de Rode 3 augusus 2 Bachelorscripie Begeleidig: dr Joche Heiloh KdV Isiuu voor wiskude Faculei der Nauurweeschappe, Wiskude e Iformaica Uiversiei va Amserdam
2 Samevaig I mij scripie ekijk ik ee recursieformule voor de Poicaré-reeks va de moduli-ruime va saiele vecorudels aa ee algeraïsche kromme Deze was al ogeveer ie jaar eked, oe D Zagier op he Israel mahemaical coferece i 995 lie zie hoe deze is om e zee i ee direce formule Di is laer gepuliceerd i [3] I dazelfde jaar puliceerde G Laumo e M Rapopor i [2] ee algemeere oplossig, die ook he geval va vecorudels ehadeld Esseiëel ij hu oplossig is he Laglads lemma, da ook i [2] word gegeve Ik zal i mij scripie de oplossig i [2] volge e deze geve voor he speciale geval va vecorudels Gegeves Tiel: Recursie va Poicaré-reekse Aueur: Joachim de Rode, JoachimdeRode@sudeuval, 697 Begeleider: dr Joche Heiloh Tweede eoordelaar: dr Be Mooe Eiddaum: 3 augusus 2 Koreweg de Vries Isiuu voor Wiskude Uiversiei va Amserdam Sciece Park 94, 98 XH Amserdam hp://wwwscieceuval/mah
3 Ihoudsopgave Ileidig 3 Noaie e heorie 5 Rese e comiaoriek 5 2 Pariies e verfijige 8 2 Ekele erekeige 3 2 Recursie va de Poicaré reeks 3 22 Pariies va lege wee 4 23 De erekeig va [Bu 2 ] 6 24 De erekeig va [Bu 3 ] 7 3 De direce formule 27 3 He uischrijve va [Bu ] De erm T(P He Laglads lemma De oepassig va he Laglads lemma 5 35 De sommaie over O (E 6 36 De direce formule 66 Populaire samevaig 68 2
4 Ileidig He oplosse va recursieformules is ee proleem da al door leerlige va de middelare school word ekeke e opgelos Maar vergelijkare proleme vid je aa de greze va oze keis, zij he i ee ies moeilijkere vorm I mij scripie ekijk ik de recursie va de Poicaré-reeks va de moduli-ruime va saiele vecorudels aa ee algeraïsche kromme Hierij geruik ik de al ekede uidrukkig voor de Poicaré-reeks va de moduli-ruime va vecorudels aa zo ee kromme (hier word dus ie geëis da de udels saiel zij De Poicaré-reeks va ee variëei is i he algemee ee polyoom, waarij de coeëfficiëe gegeve zij door de Bei ummers va deze ruime Hoewel de moduliruime va vecorudels aa deze kromme gee variëei is, kue we hier och ee Poicaré-reeks aa oekee Di zal da echer gee polyoom zij De recursieformule was al ogeveer ie jaar eked, oe D Zagier op he Israel mahemaical coferece i 995 lie zie hoe deze is om e zee i ee direce formule Di is laer gepuliceerd i [3] I dazelfde jaar puliceerde G Laumo e M Rapopor i [2] ee algemeere oplossig Hierva is de moduli ruime va saiele vecorudels ee speciaal geval Esseiëel ij hu oplossig is he Laglads lemma, da ook i [2] word gegeve Ik zal i deze scripie de aapak va Laumo e Rapopor volge, voor he speciale geval va vecorudels Ook he Laglads lemma geef ik i ee specifieke vorm Deze is amelijk geformuleerd voor ee willekeurige reducieve algeraïsche groep G over ee perfec lichaam, maar ik zal he geval G = Gl eme Bij he omzee va de recursieve i de direce formule was he oodzakelijk ee ermiologie e owikkele om goed om e kue gaa me pariies e me rese Di is ee suk algemee heorie geworde da ehadeld word i hoofdsuk Di ka i pricipe los worde geleze va de res va de scripie De lezer die slechs geïeresseerd is i de recursieformule ka hier wellich ewijze i overslaa Echer, ee ieder die geïeresseerd i rese ij delig door ee reuk of verfijige va pariies word aagerade di hoofdsuk door e eme De res va de scripie ehadel de recursieformule Hoofdsuk wee eva vooreelderekeige, i hoofdsuk drie word de direce formule gegeve Voor di laase vide 3
5 we eers ee asale uidrukkig, die we seeds verder vereevoudige o we deze op kue losse Ik wil Joche Heiloh edake voor zij egeleidig e flexiiliei Ook gaa dak ui aar Be Mooe voor zij ereidheid om weede eoordelaar e zij 4
6 Hoofdsuk Noaie e heorie I de res va deze scripie zulle we N schrijve voor de auurlijke gealle me ul Als we de auurlijke gealle zoder ul edoele, oere we di me N > Rese e comiaoriek I de rig va gehele is delig me res ee weleked pricipe Zij d Z e N > Da is de res va d ij delig door he kleise ie-egaieve eleme va de verzamelig d + Z = {, d 2, d, d, d +, d + 2, } Z/Z I deze scripie zulle we di kleise ie-egaieve eleme oere me d m, hier is de m ee afkorig voor modulo We hoeve os i deze cosrucie echer ie e eperke o gehele, maar kue a hier ook ee reuk oelae Zij daarom d Z, Q me a, N > He kleise ie-egaieve eleme va d + az oeme we u de res va d ij delig door a Deze oere we me d m a Als voor wee gealle d, e Z geld da d + az = e + az, schrijve we d e (mod a zoals we gewed zij Di is uieraard equivale me d m a = e m a Lemma Zij d Z e a Q me a, N > Da geld d m a < a Bewijs Per defiiie geld d m a Sel u da d m a a Da is d m a a ee ie-egaief eleme va d + az, ovedie is deze kleier da d m a Di is i egespraak me de miimaliei va d m a e da ewijs he lemma Lemma 2 Zij d Z e a Q me a, N > Da geld d m a { als d (mod a + ( d m a = a als d (mod a 5
7 Bewijs He geval d (mod a is duidelijk Sel u d (mod a Te eerse zie we da d m a + ( d m a d d (mod a We wee dus da er ee z Z is zoda d m a + ( d m a = z a Maar me ehulp va d (mod a e lemma zie we da < d m a + ( d m a < a + a = 2 a Dus moe gelde z = e daarom d m a + ( d m a = a Sellig 3 (Delig door ee reuk me res Zij d Z e a Q me a, N > Da zij er x, y Z zoda Bovedie geld y x = d = x a + d m a d = y a ( d m a { als d (mod a als d (mod a To slo is deze schrijfwijze uiek i de volgede zi: (i Als er p Z e r Q [, a zij zoda d = p a + r, moe gelde p = x e r = d m a (ii Als er q Z e r 2 Q [, a zij zoda d = q a r 2, moe gelde q = y e r 2 = ( d m a Bewijs Aagezie d m a ee eleme is va d + a Z, is er ee x Z zoda d m a = d x a Di geef os d = x a + d m a Uieraard is d ook ee eleme va Z Dus op ovesaade maier vide wij ee y Z zoda ( d = y a + ( d m a Di geef os d = y a ( d m a Verder zie we u da = d d = y a ( d m a ( x a + d m a Di geef os y x = a ( dm a + ( d m a Lemma 2 geef os u direc he gevraagde Nu de uiciei Laa p Z e r Q [, a zij zoda d = p a + r Sel u p x De rol va p e x i di ewijs zij iwisselaar, we moge dus aaeme da x > p Da wee we da = d d = x a + d m a ( p a + r Di lever os a (x pa = d m a r < d m a < a Deze egespraak geef os da x = p, e daarui volg omiddelijk d m a voor (ii gaa aaloog 6 = r He ewijs
8 He lijk u da we ee uidrukkig kue vide voor d m a, waarij we he modulo rekee me ee reuk kue vervage door he modulo rekee me ee geheel geal Lemma 4 Zij d Z e a Q me a, N > Da geld d m a = (d ma Bewijs Te eerse geld uieraard da d ma d (mod a e dus (dma Hierui lijk da da d m a (d ma Da moe er dus ee z Z zij zoda d m a (mod a (dma d = d (mod a = z a Maar lemma geef os (d ma < a e dus (dma < a Hezelfde lemma geef os direc d m a < a Dus zie we a < (d ma d m a (d ma waarui we afleide da z = Hierui volg da d m a d m a < a, = (dma Proposiie 5 Zij d Z e a Q me a, N > Da geld: (i a d = a d a d m a ; (ii a d = a d + a ( d m a Bewijs We wee da er ee uieke x Z is zoda d = x a + d m a a d = x + }{{} a d m a }{{} geheel < ( Da zie we Hiermee zie we da d = x Bovedie geld vawege ( da x = d d a a a m a, di ewijs (i Op dezelfde maier is er ee uieke y Z zoda d = y a ( d m a e zie we i da d = y = d + ( d a a m a Hiermee is ook (ii eweze Opmerkig De i de formulerig va de proposiie moe worde geleze als ee delig a door a Als u =, gaa he hier dus om ee delig door ee geheel geal e reduceer de proposiie o: (i a d = a d a d ma; (ii a d = a d + a ( d ma 7
9 Di is ook ee iuïief duidelijke ewerig Bovedie zie we da als a =, er ee vermeigvuldigig me ee geheel geal lijf saa (i aalogo me hierove kue we di zie als delig door de reuk Da zou de afrodig aar ove of eede weer gelijk moee zij aa d Di zie we iderdaad erug i de formule, er geld amelijk voor elke d Z e N > da d (mod e dus d m = ( d m = Opmerkig We hee hiermee ee weede ewijs gevode voor lemma 4 We kue amelijk (i e ies aders oepasse e zie da Maar we wise al da a d = a (d = a (d a (d ma = a d a (d ma e hierui volg d m a = (dma Lemma 6 Zij z R Da geld: a d = a d a d m a (i He kleise gehele geal da srik groer is da z, is z + (ii He groose gehele geal da srik kleier is da z, is z Bewijs Eers ewijze we (i We oderscheide wee gevalle Als z Z, da is z + = z e deze is da he kleise gehele geal srik groer da z Als z Z, da zie we z < z + = z + Z He ewijs voor (ii gaa aaloog 2 Pariies e verfijige I de hoofdsukke hiera spele pariies ee elagrijke rol We zulle hier echer ook de siuaie egekome waari we meerdere pariies acher elkaar wille uivoere I deze paragraaf geve we de hiervoor geruike oaie e ermiologie Defiiie 7 Zij N > Ee pariie zoder verfijig va is ee k-upel va gealle (,, k voor zekere k N >, me daarij de eis k i= i = e i N > voor elke i Oze ierpreaie is da we he geal kue schrijve als som = + + k Merk op da ( ook ee pariie va is, deze oeme we de riviale pariie Voor ee N > oere we de verzamelig va pariies zoder verfijig va me E( De rede om hier voor de leer E e kieze zal laer i deze paragraaf duidelijk worde 8
10 Defiiie 8 Zij N > e eem ee pariie zoder verfijig P = (,, k E( He geal k oeme we de lege va P, deze oere we me l(p Defiiie 9 (Pariie me ekele verfijig Zij N >, e zij P = (,, l E( Ee verfijig va de eerse orde va P is ofwel (i ee eidige reeks pariies V V l waarij elke V i ee pariie va i is, e er mises éé j me j l is zoda V j ie-riviaal is, ofwel (ii ee eidige reeks ie-riviale pariies me idex V V h waarij ee pariie me idex V j ee pariie is me daaracher a ee pu-komma ee zeker geal i j, dus V j = (v j,,, v j,lj ; i j zodaig da elke V j = (v j,,, v j,lj ; i j ee pariie va he geal ij i P is e de rij va idices i, i 2,, i h ee srik sijgede rij i N > is waarij i e i h l Als V = V,, V h ee verfijig is va ee pariie P zegge we ook wel da V P verfij We oere di als éé geheel door ze acher elkaar e schrijve: P V V h, di oeme we ee pariie me verfijig va de eerse orde Opmerkig Te eerse volg ui defiiie (ii omiddelijk da moe gelde h l We moee og lae zie da de defiiies equivale zij We geve daarom de maier om verfijige volges (i om e schrijve i verfijige volges (ii e vice versa, e zulle zie da di i feie iks verader Neem ee verfijig V,, V l zoals i (i We geve u alle ie-riviale pariies V j elk ee idex j, e verwijdere vervolges de riviale pariies Vawege de eis da mises éé pariie i de verfijig ie riviaal was, houde we u ee verfijig over volges (ii De i i P die oorsprokelijk werde verfijd, worde da u og seeds e wel op dezelfde wijze He eige verschil is da we de riviale pariies ie meer oere Neem u ee verfijig volges (ii Voor ieder paar pariies V j e V j+ da voorkom i de verfijig ekijke we he verschil va hu idices v = i j+ i j We plaase u usse V j e V j+ precies v riviale pariies Op deze maier krijge we l pariies i de verfijig De idex is da ie meer odig, omda we wee da seeds de i-de pariies i de verfijig he geal i i P verfij Als we daarom de idex verwijdere is he resulaa ee verfijig volges (i De i i P die oorsprokelijk werde verfijd, worde da og seeds e op dezelfde weer He verschil is hier, da we ee aaal riviale pariies hee oegevoegd I feie is he slechs ee oaiekwesie I he vervolg zulle we de wee pariies door elkaar hee geruike Als we ee verfijig va P schrijve die ui l(p pariies esaa, edoele we seeds de schrijfwijze (i Als de verfijig ui mider pariies esaa, edoele we seeds de schrijfwijze (ii Vooreeld Laa = 6 e zij P = (, 2, 3 = (2, 3, ee pariie va Zij verder V V 2 V 3 = ((, 2( ee verfijig va P Me P V = (2, 3,, ((, 2( word de 9
11 pariie edoeld, waari zes word opgesplis i e vervolges de drie i de pariie word opgesplis i + 2 We kue ook de weede defiiie geruike Da schrijve we voor de verfijig V = (, 2; 2 e is P V = (2, 3, (, 2; 2 weer de pariie waari zes word opgesplis i e vervolges de 3 i deze pariie word opgesplis i + 2 He resulaa is i eide gevalle Di laase oeme we ook wel de eidoesad va de pariie, die we u defiiëre Defiiie (Eidoesad va ee pariie me verfijig va de eerse orde Zij N > Neem ee pariie me verfijig va de eerse orde P V V l, waarij l = l(p e V i = (v i,, v i,2,, v i,l(vi De eidoesad va de pariie va de eerse orde is de volgede pariie: (v,, v,2,, v,l(v, v 2,, v 2,2,, v 2,l(V2, v 3,, v 3,2,, v l,l(vl E( Nu we he egrip eidoesad hee, kue we pariies me meerdere verfijige defiiëre Defiiie (Pariie me meer verfijige e zij eidoesad Zij N > We geve de defiiie me iducie Ui defiiies 9 e volg wa wij edoele me ee pariie me verfijig va de eerse orde e de eidoesad va ee pariie me verfijig va de eerse orde Zij u P = E V Vl, V 2 Vl 2 2,, V c Vl c c ee pariie me verfijige va de c-de orde, me eidoesad va de c-de orde E c+ Da is ee verfijig va de (c + -de orde ee verfijig V c+ V c+ l c+ va E c+ zoals edoeld i defiiie 9, me daarij de eis da als de verfijig va de c-de orde ee zekere riviale pariie Vi c evae, he daarmee correspoderede geal i E c+ ie word verfijd i de verfijig va de (c + -de orde De eidoesad va E c V c+ V c+ l c+ oere we vervolges me E c+2 De resulerede pariie oere we als P = E V V l, V 2 V 2 l 2,, V c+ V c+ l c+ e oeme we ee pariie me verfijig va de (c + -de orde We oeme u weer E c+2 de eidoesad va de pariie va de (c + -de orde Opmerkig De eis, da als de verfijig va de c-de orde ee riviale pariie evae, he hiermee correspoderede geal i E c+ ie mag worde verfijd i de (c + -de orde, garadeer os da als we i laere hoofdsukke gaa sommere over alle pariies va gegeve, er iks duel word geeld Merk verder op da we i de schrijfwijze va paries me verfijige va de c-de orde ee komma geschreve hee usse verfijige va verschillede orde
12 I de res va deze scripie schrijve we pariie me verfijig voor ee pariie me verfijig va de c-de orde, ogeach de waarde va c Da schrijve we pariie voor zowel de pariies me als zoder verfijig Ee pariie me ee aaal verfijige zulle we ook dikwijls me ee ekele leer P oere De collecie pariies va oere we me P( Verder zulle we voor ee gegeve P P( me de eidoesad va P he volgede aageve: Als P ee pariie zoder verfijig is, is de eidoesad gewoo weer P zelf Als P ee pariie me verfijig va de c-de orde is edoele we me zij eidoesad zij eidoesad va de c-de orde E c+ zoals i de defiiie hierove We oere de eidoesad va P me E(P Merk op da E( P( e da ovedie E( = {E(P P P(}, wa ee moivaie geef voor de keuze voor de leer E Zij u P = E V Vl V 2 Vl 2 2 ee pariie me verfijige Als we wille verwijze aar E of aar zekere Vi k geruike we hiervoor he woord pariiesap va P We voere u ee equivaleierelaie i op P( Te eerse geld P P voor elke P P( Zij u P = P V Vl P( e Q = Q W Wl P( pariies va Als P = ( de riviale pariie is, e ovedie geld da de eidoesad va de eerse orde va P gelijk is aa Q schrijve we P Q P Merk op da da ie ka gelde da Q = ( De verfijig V Vl mag amelijk per defiiie ie allee maar riviale pariiesappe evae, dus de eidoesad va de eerse orde va P ka ooi riviaal zij Pariies die equivale zij volges zulle we vaaf u als gelijk eschouwe Srik geome werke we i deze scripie dus me equivaleieklasse va pariies Coveies We zage i defiiie al hoe we de verschillede pariiesappe i ee pariie me verfijig oere Zij P P( ee pariie me verfijige va de c-de orde: P = P V Vl, V 2 Vl 2 2,, V c Vl c c Tezij aders aagegeve, zulle we i he vervolg seeds schrijve E k = ( k, k 2, k 3,, k l k Zo wee we dus da ee pariiesap V k j alijd ee verfijig is va he geal k j Vooreeld Zij = 6 Vooreelde va pariies va zij: (i (,, 2,,
13 (ii (2, 3, (, ; (2, ; 2 = (2, 3,, (, (2, ( (iii (2, 3,, (, (2, (, (((, (( (iv (2, 4, (, (2, 2, (((2(, (v (6 Merk op da pariies (i, (ii e (iv dezelfde eidoesad hee, deze is precies gelijk aa (i Defiiie 2 Zij N > e P e Q pariies va We oeme Q grover da P als er ee verfijigig V V l va Q esaa, zoda de eidoesad va QV V l gelijk is aa P We schrijve da P Q We zegge da ook wel da P fijer is da Q, of da we Q hee verfijd o P De igevoerde oaie P Q heef ee iuïieve verklarig: we kue de gealle i P op ee epaalde maier groepere, zoda P i Q pas Merk op da de relaie grover zij da ee rasiieve relaie defiiëer To slo kue we voor pariies ee graad defiiëre Defiiie 3 Zij N > e P P( De graad deg(p va deze pariie is he aaal ie riviale pariiesappe va P Merk op da de de riviale pariie ( hiermee graad ul krijg Vooreeld Ee aaal pariies e hu graad (i deg ( (2, 3,, (, (2, ( = 3 (ii deg ( (2,, 3, 4 = (iii deg ( (6 = (iv deg ( (2,, 3, 4, (, ((2, (, 3, ((((2(((, 2 = 5 2
14 Hoofdsuk 2 Ekele erekeige 2 Recursie va de Poicaré reeks I he algemee is aa elke variëei V va dimesie ee Poicaré-serie [V ] oe e kee Bekijk hiervoor de Bei-ummers,, 2, va V Hier is k gedefiiëerd als he aaal voorregers va he orsievrije deel va de k-de homologiegroep va V De Poicaré-serie va V is u he polyoom [V ] = i i i= We ekijke ee algeraïsche kromme X va geus g N e de moduli-ruime va vecorudels aa X va rag N > e graad d Z Odaks da deze moduli-ruime gee variëei is, zij we i saa hier ee Poicaré-reeks aa oe e kee Deze oere we me [Bu d ] We oere me R(( de formele Laurereekse i He is voor os voldoede e wee da [Bu d ] er als volg uizie: m m [Bu d ] = k= ( + 2k 2g ( 2 k= (2k 2 R(( (2 Da di ee eleme va R(( is kue we izie via de algeraïsche ideiei = m i= mi m = Verder schrijve we [Bu ] voor de Poicaré reeks va de moduli ruime va saiele vecorudels aa X va rag N > e graad d Z Deze word recursief gegeve door waarij [Bu ] = [Bu d ] m(p, d = i<j l l>; P =(,, l E(; d=d ++d l ; d i Z ; ( i j ((g + l 2 m(p, d i= ( dj d i j i [Bu d i, goed i ], (22 (23 3
15 e me ( word aagegeve da d / > d 2 / 2 > > d l / l We zulle zie da er i he algemee geld da [Bu ] R(( Als echer e d copriem zij, is de moduli-ruime va vecorudels va rag e graad d aa X ee variëei Da zal [Bu ] ee polyoom zij i, maal ee facor Waar deze 2 facor vadaa kom val uie he ereik va deze scripie Ee kleie oelichig op he someke: er word gesommeerd over alle pariies zoder verfijige va, waarij de eis l > oder he someke os verel da de riviale pariie ( ie mag worde meegereked Bij elk va zulke pariies va, word ook d gepariioeerd e wel me dezelfde lege l Hier zij echer d i i Z oegesaa, i plaas va i N > zoals ij ee ormale pariie Di heef o gevolg da he hier om ee oeidige sommaie gaa Echer, we zulle zie da op elke i Z de sommaie op de coëfficie va i eidig is Di garadeer os da de som ovoorwaardelijk covergeer We schrijve hier d i Z oder he someke, hier word uieraard edoeld da di geld voor elke i l I de res va deze scripie zulle we di seeds zo oere Omda [Bu d ] ie afhag va de waarde va d, zulle we deze i he vervolg meesal weglae, we schrijve da [Bu ] Verder zulle we seeds ( schrijve voor de ogelijkhede die hierove ook al me ( ware aagegeve De coex zal da duidelijk make wa de waarde va l hieri is We kue omiddelijk zie wa [Bu ] moe zij Er zij amelijk gee ie-riviale pariies va, di geef os [Bu ] = [Bu ] = ( + 2g 2 (24 I hoofdsuk 3 zulle we ee direce formule afleide voor [Bu ] Voorda we di doe geve we echer als vooreeld de erekeig va [Bu 2 ] e [Bu 3 ] voor willekeurige d Z 22 Pariies va lege wee Zij N > e d Z Als we [Bu ] wille uirekee, zulle we voor elke pariie P E( ogeveer dezelfde erekeig uivoere De eerse wee sappe daari zij i ieder geval seeds gelijk: he epale over welke waarde va de d i word gesommeerd e he erekee va m(p, d Voor ee pariie va lege wee is he eevoudig deze sappe i he algemee e geve Lemma 2 Zij N >, d Z, e eem ee pariie P = (, 2 E( va lege wee I de erekeig va de me P correspoderede erm i [Bu ] moee we sommere over de volgede waarde: d = d d 2 = 2d ( d m + ( d m + + k = d + + k k = 2 d k 4
16 waarij k loop over alle gealle i N Bewijs Omda P va lege wee is, wee we al da we d i weeë moee splise Nu moee d e d 2 voldoe aa d + d 2 = d, d, d 2 Z e aa d > d 2 2 Da hier aa de gelijkheid e de eis d i Z is voldaa is evide De gelijkhede i he lemma zij ee gevolg va proposiie 5, e he fei da ( d m = ( 2 d m weges 2 (mod Verder kue we me ehulp va lemma 6 e geruikmaked va d = d + d 2 als volg redeere: d d + d > d; d > d; ( + 2 d > (d + d 2 ; 2 d > d 2 ; d > d 2 2 (A (B We hee zo eweze da de d, d 2 die aa (B voldoe precies die d, d 2 zij waarij d aa (A voldoe Maar de waarde die gegeve zij i he lemma, zij precies alle waarde waarij di he geval is Lemma 22 Zij N >, d Z e eem ee pariie P = (, 2 E( va lege l = 2 Zij verder d, d 2 zoals i lemma 2 Da geld m(p, d = 2 (g + ( d m k Bewijs We heriere os de uidrukkig voor m(p, d e redeere verder: m(p, d = i<j l i j ((g + ( dj d i j i = 2 (g + d 2 2 d ( 2 d = 2 (g + + ( d m ( d k 2 ( d m + + k = 2 (g + ( + 2 ( d m ( + 2 ( + 2 k = 2 (g + ( d m k Opmerkig Als wij eve erugkijke aar uidrukkig 22, zie we da er i de sommaie over de d i wee facore ee rol spele: 2 m(p, d e k i= [Bu d i, goed i ] He voorgaade lemma verel os u da ij ee pariie va lege wee deze eerse facor slechs afhakelijk is va de reswaarde va d ij delig door 5
17 23 De erekeig va [Bu 2 ] Zij d Z I deze paragraaf zulle we [Bu 2 ] erekee De eige ie-riviale pariie va = 2 is (, 2 = (, Formule 22 geef os dus [Bu 2 ] = [Bu 2 ] d=d +d 2 ; d i Z ; d >d 2 2 m((,, d [Bu d, goed ][Bu d 2, goed ] We wille u sommere over die d, d 2 Z me d = d + d 2 e d > d 2 Volges lemma 2 zij di precies de waarde waarij k N Verder geef lemma 22 os d = d 2 d m k; d 2 = d 2 + d m2 2 k, m((,, d = (g + d m2 2 2k Ook wee we al da [Bu ] = [Bu ], di is gegeve i formule 24 We vulle di i e zie [Bu 2 ] = [Bu 2 ] d=d +d 2 ; d i Z ; d >d 2 2 m((,, d [Bu d, goed ][Bu d 2, goed ] = [Bu 2 ] 2(g +2dm2 4 4k [Bu ] 2 k = [Bu 2 ] 2(g +2d m2 4 4k [Bu ] 2 k = [Bu 2 ] 2(g +2d 4 m2 [Bu ] 2 4 = [Bu 2 ] 2(g +2d m2 4 [Bu ] 2 Nu moee we og de waarde voor [Bu ] e [Bu 2 ] ivulle Deze zij i 2 gegeve: [Bu ] = ( + 2g 2 ; [Bu 2 ] = ( + 2g ( + 3 2g ( 2 2 ( 4 6
18 Zo vide we als uieidelijke uidrukkig [Bu 2 ] = [Bu 2 ] 2(g +2d m2 4 [Bu ] 2 = ( + 2g ( + 3 2g ( 2 2 ( 4 ( + 4g 2(g +2d m2 4 ( 2 2 ( = ( + 2g ( + 3 2g ( + 4g 2(g +2d m2 ( 2 2 ( 4 Di is oze gezoche uidrukkig I de heorie (die ie i deze scripie word ehadeld is al eked da he polyoom allee afhag va de waarde va d modulo, di zie we ook erug i de formule 24 De erekeig va [Bu 3 ] Zij d Z I deze paragraaf zulle we [Bu 3 ] erekee De verzamelig ie-riviale pariies zoder verfijig va 3 is {(2,, (,2, (,,} We vide daarom me formule 22: [Bu 3 ] = [Bu 3 ] d=d +d 2 ; d i Z ; d 2 >d 2 d=d +d 2 ; d i Z ; d > d 2 2 d=d +d 2 +d 3 ; d i Z ; d >d 2 >d 3 2 m((2,, d [Bu d, goed 2 ][Bu ] 2 m((,2, d [Bu ][Bu d 2, goed 2 ] 2 m((,,, d [Bu ] 3 Hierij hee we geruik gemaak va [Bu d i, goed ] = [Bu ] voor elke d i Z, zoals i formule 24 We vulle u ie voor [Bu d, goed 2 ] e [Bu d, goed 2 ] de direce uidrukkig i die we i paragraaf 23 vode, maar wille hiervoor weer de oorsprokelijke recursieformule 22 geruike Hiervoor is he echer oodzakelijk da we de pariie (, oepasse op d e d 2 We schrijve daarom voor eide e + e 2, zo krijge we: [Bu d, goed 2 ] = [Bu 2 ] [Bu d 2, goed 2 ] = [Bu 2 ] d =e +e 2 ; e i Z ; e >e 2 d 2 =e +e 2 ; e i Z ; e >e 2 2 m((,, d [Bu ] 2 ; 2 m((,, d 2 [Bu ] 2 7
19 Di vulle we i: [Bu 3 ] = [Bu 3 ] d=d +d 2 ; d i Z ; d 2 >d 2 d=d +d 2 ; d i Z ; d > d 2 2 d=d +d 2 +d 3 ; d i Z ; d >d 2 >d 3 ( 2 m((2,, d [Bu ] [Bu 2 ] ( 2 m((,2, d [Bu ] [Bu 2 ] 2 m((,,, d [Bu ] 3 d =e +e 2 ; e i Z ; e >e 2 d 2 =e +e 2 ; e i Z ; e >e 2 2 m((,, d [Bu ] 2 2 m((,, d 2 [Bu ] 2 = [Bu 3 ] [Bu ][Bu 2 ] d=d +d 2 ; d i Z ; d 2 >d 2 + [Bu ] 3 [Bu ][Bu 2 ] d=d +d 2 ; d i Z ; d 2 >d 2 d=d +d 2 ; d i Z ; d > d [Bu ] 3 [Bu ] 3 d=d +d 2 ; d i Z ; d > d 2 2 d=d +d 2 +d 3 ; d i Z ; d >d 2 >d 3 2 m((2,, d 2 m((2,, d 2 m((,2, d 2 m((,2, d 2 m((,,, d d =e +e 2 ; e i Z ; e >e 2 d 2 =e +e 2 ; e i Z ; e >e 2 2 m((,, d 2 m((,, d 2 = [Bu 3 ] ( [Bu ][Bu 2 ] + [Bu ] 3 ( + d=d +d 2 ; d i Z ; d 2 >d 2 d=d +d 2 ; d i Z ; d > d 2 2 d=d +d 2 ; d i Z ; d 2 >d 2 d=d +d 2 +d 3 ; d i Z ; d >d 2 >d 3 2 m((2,, d 2 m((,2, d 2 m((2,, d + 2 m((,,, d 8 d =e +e 2 ; e i Z ; e >e 2 d 2 =e +e 2 ; e i Z ; e >e 2 d=d +d 2 ; d i Z ; d > d m((,, d 2 m((,, d 2 2 m((,2, d (25 (26
20 We zie hier ee correspodeie me de pariies va drie: P(3 = {(3, (2,, (, 2, (2, (, ;, (, 2(, ; 2, (,, } I ovesaade uidrukkig zie voor elk va deze pariies ee erm saa, waarij elke ie-riviale pariiesap V ee someke e ee erm 2 m(v, a voor zekere a geef De eerse erm [Bu 3 ] correspodeer me de riviale pariie (3 Ee verklarig gaa ogeveer als volg De recursieve formule va [Bu ] i 22 geef eers ee erm voor elke pariie zoder verfijig, da zij i di geval {(3, (2,, (, 2, (,, } Hier correspodeer de erm [Bu 3 ] me de pariie (3 Nu wee we da als ee pariie ee 2 eva, di resuleer i ee facor [Bu d i, goed 2 ] Neem ijvooreeld (2, We passe u de recursieve formule opieuw oe op de facor [Bu d i, goed 2 ] Op dezelfde wijze als ij [Bu 3 ] krijge we u ee erm voor elke pariie zoder verfijig va 2, da zij {(2, (, } Hier zij di echer gee op zichzelf saade pariies, maar verfijige va oze pariie (2, Als we u de haakjes wegwerke, zoals a he weede gelijkeke is gedaa, krijge we dus wee erme: éé die hoor ij (2, e daara (2 oepasse op, e ee ader die hoor ij (2, e daara (, oepasse op Aagezie de riviale pariie als verfijig ie word geoeerd, is he resulaa dus ee erm die hoor ij (2, e ee erm die hoor ij (2, (, ; Omda de uidrukkig voor [Bu 3 ] egi me ee erm voor elke pariie zoder verfijig e ovedie op ovesaade wijze elke erm i correspodeie me he wel of ie verfije word opgesplis, is he resulaa de éé-op-éé correspodeie usse de pariies i P(3 e de erme i [Bu 3 ] die wij hierove zage I de volgede wee suparagrafe zulle we 25 e 26 afzoderlijk erekee 24 De eerse erm We zulle u 25 uirekee, di is ( [Bu ][Bu 2 ] d=d +d 2 ; d i Z ; d 2 >d 2 2 m((2,, d + d=d +d 2 ; d i Z ; d > d m((,2, d Aagezie we [Bu ] e [Bu 2 ] al kee, cocerere we os op de erm ie de hake Hierva erekee we eers de likersom, deze hoor ij de pariie (, 2 = (2, We geruike lemma 2 om de oegesae waarde voor d e d 2 e vide, di zij: waarij k N Ook geef lemma 22 os: d = 2d 3 (2d m3 3 d 2 = d 3 + (2d m k; k, m((2,, d = 2(g + (2d m3 3 3k 9
21 Di is voldoede om e som ui e kue rekee: d=d +d 2 ; d i Z ; d 2 >d 2 2 m((2,, d = 4(g +2(2d m3 6 6k k = 4(g +2(2d m3 k 6 6k = 4(g +2(2d 6 m3 6 = 4(g +2(2d m3 6 De adere som, die hoor ij de pariie (, 2 = (, 2, gaa vrijwel aaloog Op dezelfde wijze vide we de oegesae waarde voor d e d 2, di geef os vervolges m((, 2, d = 2(g + d m3 3 3k He eige verschil me de eerse som is dus, da hier ee d m3 saa waar ij de pariie (2, ee (2d m3 sod Omda di ie uimaak voor de verdere erekeig kue we di susiuere i ovesaad resulaa e zo vide we: 2 m((,2, d = 4(g +2d m3 6 d=d +d 2 ; d i Z ; d > d 2 2 Nu we de wee somme hee uigereked, kue we de erm 25 epale We wise al da e zo verkrijge we ( [Bu ][Bu 2 ] [Bu ] = ( + 2g 2 ; [Bu 2 ] = ( + 2g ( + 3 2g ( 2 2 ( 4, d=d +d 2 ; d i Z ; d 2 >d 2 2 m((2,, d + d=d +d 2 ; d i Z ; d > d m((,2, d ( = [Bu ][Bu 2 ] 4(g +2(2d m3 + 4(g +2d m3 6 6 ( = [Bu ][Bu 2 ] 4(g 2(2d m3 + 2d m3 6 ( ( + 2g ( + 2g ( + 3 2g = 2 ( 2 2 ( 4 4(g 2(2d m3 + 2d m3 6 ( + 4g ( + 3 2g = ( ( 2 3 ( 4 ( 6 4(g 2(2d m3 + 2d m3 (27 2
22 242 De weede erm We zulle u de erm 26 uirekee, di is ( [Bu ] 3 + d=d +d 2 ; d i Z ; d 2 >d 2 d=d +d 2 ; d i Z ; d > d 2 2 d=d +d 2 +d 3 ; d i Z ; d >d 2 >d 3 2 m((2,, d 2 m((,2, d 2 m((,,, d d =e +e 2 ; e i Z ; e >e 2 d 2 =e +e 2 ; e i Z ; e >e 2 2 m((,, d 2 m((,, d 2 Aagezie we u voor m(, ie lemma 22 zulle geruike, heriere we os hiervoor de oorsprokelijke formule 23 voor N > e P = (,, l P(: m(p, d = i<j l i j ((g + ( dj d i j i We kee al ee direce uidrukkig voor [Bu ], dus we cocerere os op wa ie de hake saa Hierva erekee we eers de eerse erm, die esaa ui he produc va wee somme Deze wee somme kue we om e egie same eme o éé som: d=d +d 2 ; d i Z ; d 2 >d 2 2 m((2,, d d =e +e 2 ; e i Z ; e >e 2 2 m((,, d = d=d +d 2 ; d i Z ; d 2 >d 2 d =e +e 2 ; e i Z ; e >e 2 2 m((2,, d+2 m((,, d I ovesaade som word d opgesplis i drieë: d = e + e 2 + d 2 Daarom zee we g = e ; g 2 = e 2 ; g 3 = d 2 We krijge zo voor de expoe he volgede: 2 ( m((2,, d + m((,, d = 2 ( 2(g + 2(d 2 d 2 + (g + e 2 e = 2 ( 3(g + 2d 2 d + e 2 e = 2 ( 3(g + 2g 3 (g + g 2 + g 2 g = 2 ( 3(g + 2g 3 2g = 6(g + 4g 3 4g 2
23 Di geef os d=d +d 2 ; d i Z ; d 2 >d 2 d =e +e 2 ; e i Z ; e >e 2 2 m((2,, d+2 m((,, d = 6(g 4g 3 4g d=g +g 2 +g 3 ; g i Z ; g +g 2 2 >g 3 ; g >g 2 Hier lae we he voorlopig eve ij We gaa u aar de weede erm ie de hake i 26 e volge dezelfde sappe Eers eme we de wee somekes same: 2 m((,2, d 2 m((,, d 2 = 2 m((,2, d+2 m((,, d2 d=d +d 2 ; d i Z; d > d 2 2 d 2 =e +e 2 ; e i Z; e >e 2 Aaloog aa wa we e dede, zee we g = d ; g 2 = e ; g 3 = e 2 We krijge zo voor de expoe he volgede: d=d +d 2 ; d i Z; d > d 2 2 d 2 =e +e 2 ; e i Z; e >e 2 2 ( m((, 2, d + m((,, d 2 = 2 ( 2(g + 2( d 2 2 d + (g + e 2 e Di geef os d=d +d 2 ; d i Z; d > d 2 2 d 2 =e +e 2 ; e i Z; e >e 2 = 2 ( 3(g + d 2 2d + e 2 e = 2 ( 3(g + (g 2 + g 3 2g + g 3 g 2 = 2 ( 3(g + 2g 3 2g = 6(g + 4g 3 4g 2 m((,2, d+2 m((,, d 2 = 6(g 4g 3 4g d=g +g 2 +g 3 ; g i Z; g > g 2 +g 3 2 ; g 2 >g 3 We krijge hier dus dezelfde expoe als ij de eerse som, allee word hier over adere voorwaarde gesommeerd We ekijke u de derde e laase erm ie de hake i 26 e passe ee soorgelijke omschrijvig oe Deze erm was: d=d +d 2 +d 3 ; d i Z ; d >d 2 >d 3 2 m((,,, d He heef hier gee prakisch u, maar omwille va de cosequeie schrijve we och: g = d ; g 2 = d 2 ; g 3 = d 3 22
24 Voor de expoe vide we u 2 m((,,, d = 2 ( (g + g 2 g + (g + g 3 g + (g + g 3 g 2 = 2 ( 3(g + 2g 3 2g = 6(g + 4g 3 4g Zo krijge we d=d +d 2 +d 3 ; d i Z ; d >d 2 >d 3 2 m((,,, d = 6(g d=g +g 2 +g 3 ; g i Z; g >g 2 >g 3 4g 3 4g Weer zie we hier dezelfde expoe verschije De voorwaarde waarover gesommeerd word zij echer ook weer aders Di is gee oeval, zoals we zulle zie i paragraaf 32 We hee u de drie erme ie de hake i 26 afzoderlijk ereked Voorda we die samevoege defiiëre we u eers de volgede verzamelige: { } A := (g, g 2, g 3 Z 3 g + g 2 d = g + g 2 + g 3, > g 3, g > g 2 ; 2 { B := (g, g 2, g 3 Z 3 d = g + g 2 + g 3, g > g } 2 + g 3, g 2 > g 3 ; 2 } C := {(g, g 2, g 3 Z 3 d = g + g 2 + g 3, g > g 2 > g 3 Bewerig Er geld A B = C Bewijs De iclusie A B C is duidelijk Verder impliceer g > g 2 > g 3 da g, g 2 > g 3 e dus g +g 2 > g 2 3, di ewijs C A De ewerig C B gaa aaloog Di ewijs A B = C Bewerig Er geld A B = D := { (g, g 2, g 3 Z 3 g > g 2+g 3 2, g +g 2 2 > g 3 } Bewijs We lae eers zie da A D Voor elke (g, g 2, g 3 A wee we da g +g 2 2 > g 3 e g > g 2 Di geef os g = g + g 2 > g + g 2 2 > g 3 Er geld dus g > g 2, g 3, hierui volg g > g 2+g 3 2 e dus moe gelde A D Op aaloge wijze kue we lae zie da B D Neem u ee (g, g 2, g 3 D e sel (g, g 2, g 3 B We wee da da de volgede ogelijkhede gelde: g + g 2 2 > g 3 ; (a g > g 2 + g 3 ; 2 ( g 2 g 3 (c 23
25 Om aa e oe da (g, g 2, g 3 A moee we lae zie da g > g 2 Nu zeg (a os da ofwel g > g 3, ofwel g 2 > g 3, maar di laase is ie mogelijk vawege (c We wee dus da g > g 3 Verder geef (c os da g 3 g 2 We vide dus g > g 3 g 2 e hiermee is eweze da (g, g 2, g 3 A Op aaloge wijze ewijze we da voor ee (g, g 2, g 3 D me (g, g 2, g 3 A geld da (g, g 2, g 3 B Di ewijs D A B e zo is D = A B eweze We voege u de drie afzoderlijk erekede erme same e rekee verder, waarij we geruik make va ovesaade verzamelige: 4g 3 4g + 6(g 4g 3 4g 6(g 6(g d=g +g 2 +g 3 ; g i Z ; g +g 2 2 >g 3 ; g >g 2 = 6(g ( = 6(g ( A = 6(g ( A B d=g +g 2 +g 3 ; g i Z; g > g 2 +g 3 2 ; g 2 >g 3 ; g 2 >g 3 g +g 2 2 >g 3 ; g >g 2 g > g 2 +g 3 2 4g 3 4g + 4g 3 4g d=g +g 2 +g 3 ; g i Z ; d=g +g 2 +g 3 ; g i Z; 4g 3 4g + B 4g 3 4g + A B 4g 3 4g C 4g 3 4g C ( = 6(g 4g 3 4g + 4g 3 4g D C C = 6(g 4g 3 4g d=g +g 2 +g 3 ; g i Z ; g +g 2 2 >g 3 ; g > g 2 +g 3 2 4g 3 4g 4g 3 4g 4g 3 4g d=g +g 2 +g 3 ; g i Z; g >g 2 >g 3 d=g +g 2 +g 3 ; g i Z; g >g 2 >g 3 4g 3 4g He erekee va deze som pakke we als volg aa We schrijve de ogelijkhede als volg om: g > g 2 + g 3 2 ; g 3 < g + g 2 ; 2 g + g 2 > g + g 2 + g 3 ; g 3 + g < g + g 2 + g 3 ; 2 3g 2 > d 2 ; 3g 3 2 < d 2 ; g > d 3 ; g 3 < d 3 Geruikmaked va lemma 6 vide we u de oegesae waarde voor g e g 3 : g = d k ; g 3 = d 3 k 2, 4g 3 4g 24
26 waarij k, k 2 N De sommaies over g e g 3 kue we dus oafhakelijk va elkaar uivoere Zo krijge we 6(g d=g +g 2 +g 3 ; g i Z ; g +g 2 2 >g 3 ; g > g 2 +g 3 2 4g 3 4g = 6(g 4( d 3 k 2 k 2 k = 6(g +4( d 3 d 3 4 4k 2 k 2 ( = 6(g +4( d 3 d = 6(g +4( d 3 d 3 ( 4 2 4( d 3 ++k k 2 4 4k Zoals e verwache is, hag d d allee af va de reswaarde va d ij delig door We zie amelijk me proposiie 5 da d 3 d 3 = d 3 + ( d m3 3 ( d 3 d m3 3 = ( d m3 + d m3 3 3 Zo krijge we uieidelijk he volgede resulaa voor de erm ie de hake i 26: 6(g +4( d 3 d 3 ( 4 2 = 6(g +4( ( d m3 +d m3 3 ( 4 2 Me di resulaa e ( + 2g [Bu ] = 2, zie we da 26 gelijk is aa ( [Bu ] 3 6(g +4( ( d m3 +d m3 3 ( 4 2 ( ( + 2g 3 = 6(g +4( ( d m3 +d m3 2 3 ( 4 2 ( + 6g ( d m3 +d m3 = ( 2 3 ( 4 2 6(g +4( 3 (28 Merk op da lemma 2 os geef da d m3 + ( d m3 3 = { als d (mod 3 als d (mod 3 25
27 243 He samevoege va de erme I paragraaf 24 vode we ee eerse uidrukkig voor [Bu 3 ] Hierva hee we wee erme apar geome e elk afzoderlijk i ee suparagraaf ereked We zulle di u weer samevoege We geruike e zie zo [Bu 3 ] = [Bu 3 ] + 27 [Bu 3 ] = ( + 2g ( + 3 2g ( + 5 2g ( 2 2 ( 4 2 ( = ( + 2g ( + 3 2g ( + 5 2g ( 2 2 ( 4 2 ( 6 ( + 4g ( + 3 2g ( ( 2 3 ( 4 ( 6 4(g 2(2d m3 + 2d m3 ( + 6g (2d m3 +d m3 + ( 2 3 ( 4 2 6(g +4( 3 Di is oze gezoche uidrukkig We hee i de laase regel ee (2d m3 geschreve waar eers ee ( d m3 sod, di is gerechvaardigd omda uieraard geld 2d d (mod 3 We kieze voor deze schrijfwijze omda he da overeekom me weede regel i de uidrukkig 26
28 Hoofdsuk 3 De direce formule I di hoofdsuk zulle we ee direce formule afleide voor [Bu ] I de eerse paragraaf geve we ee eerse versie va de direce formule I paragraaf wee zulle we hier ee deel va vereevoudige I paragraaf drie e vier ehadele we he Laglads lemma e zij oepassig De res va he hoofdsuk is de uieidelijke erekeig 3 He uischrijve va [Bu ] I deze paragraaf heriere we os de recursieformule Vervolges geve we ee eerse uidrukkig voor ee direce formule We heriere os de recursieformule, deze is aa he egi va hoofdsuk 2 gegeve Te eerse gold [Bu d ] = k= ( + 2k 2g ( 2 k= (2k 2 (3 Te weede hadde we [Bu ] = [Bu d ] l>; P =(,, l E(; d=d ++d l ; d i Z ; ( l 2 m(p, d i= [Bu d i, goed i ], (32 waarij m(p, d = i<j l i j ((g + ( dj d i j i (33 e me ( word aagegeve da d / > d 2 / 2 > > d l / l We schrijve hier d i Z oder he someke, hier word uieraard edoeld da di geld voor elke i l 27
29 I hoofdsuk 2 gave we de erekeig va [Bu 3 ] voor willekeurige d Z Voor de hieri voorkomede uidrukkige [Bu d i, goed 2 ] geruike we ie de direce formule die we eerder daarvoor hadde gevode, maar pase we de recursieve formule ook op de [Bu d i, goed 2 ] oe Di resuleerde i ee uidrukkig die we os u heriere: [Bu 3 ] = [Bu 3 ] [Bu ][Bu 2 ] d=d +d 2 ; d i Z ; d 2 >d 2 + [Bu ] 3 [Bu ][Bu 2 ] d=d +d 2 ; d i Z ; d 2 >d 2 d =e +e 2 ; e i Z ; e >e 2 d=d +d 2 ; d i Z ; d > d [Bu ] 3 [Bu ] 3 d=d +d 2 ; d i Z ; d > d 2 2 d 2 =e +e 2 ; e i Z ; e >e 2 d=d +d 2 +d 3 ; d i Z ; d >d 2 >d 3 2 m((2,, d 2 m((2,, d+2 m((,, d 2 m((,2, d 2 m((,2, d+2 m((,, d 2 2 m((,,, d Toe we deze uidrukkig voor he eers zage merke we al ee éé-op-éé correspodeie op usse de erme i deze uidrukkig e de collecie pariies va 3: P(3 = {(3, (2,, (2, (, ;, (, 2, (, 2(, ; 2, (,, } Hier gave we oe ee verklarig voor Da di pricipe voor elke N > geld word evesigd i de volgede proposiie We oere oze pariies me verfijige hier als P = BV Vl V 2 Vl 2 2 me B = (,, l, waarij we ook de res va de i paragraaf 2 geïroduceerde coveies volge Sellig 3 Zij N e d Z Da geld [Bu ] = P P ( ( deg(p Bu(P g O(P T(P (g Waarij voor ee P = BV V l V 2 V 2 l 2 P( me B = (,, l geld: De graad deg(p is zoals i defiiie 3 Zij E(P = (m,, m k de eidoesad va P Da is Bu(P = k i= [Bu m i ] 28
30 We schrijve g = (g,, g Zij N k j = j i= k j Da geld T(P (g = e(p (g, waarij geld e(p (g = 2 m(b, g + + g + V k j ee verfijigsap va B 2 m(v k j, g N k j g N k j + k j = 2 m(b, g + + g + 2 m(v, g + + g N m(v 2, g N g N m(v 3, g N g N m(v 4, g N g N m(v 2, g + + g N m(v 2 2, g N g N m(v 2 3, g N g N m(v 2 4, g N g N De deelverzamelig O(P l i= m i Z m i Q is gedefiiëerd als: O(P = { g = (g,, g l i= } Z m i m i d = g + + g, ( ; ( Hier geef ( aa da voor elke m j i E: g j i= m i+ = g j i= m i+2 = = g j i= m i+m j ; g j i= m i+,, g j i= m i+m j m j Z E ( geef aa da voor elke ie-riviale pariiesap V k j = (vj,, k, v k ; k j,lj k j de 29
31 volgede ogelijkhede gelde: g N k j g N k j +v k j, v k j, > g N k j +vk j, g N k j +v k j, +vk j,2 v k j,2 > g N k j +vk j, +vk j, g N k j +v k j, +vk j,2 +vk j,3 v k j,3 > g N k j +vk j, +vk j,2 +vk j, g N k j +v k j, +vk j,2 +vk j,3 +vk j,4 v k j,4 > > g N k j +v k j, ++vk j,l k j g N k j +v k j, ++vk j,l k j v k j,l k j Merk op da voor ee riviale verfijigsap V k j = ( k j ; k j geld m(v k j, = Zo zie we da als P = (, er geld T(P = = Bovedie is he eige voorschrif i O(P da d = d Di heef o gevolg da da g O(P T(P (g = Bewijs Me iducie op He geval = is al eweze i hoofdsuk 2 Sel u da de sellig is eweze voor zekere We geruike de recursieformule e zie [Bu ] = [Bu d ] l>; P =(,, l E(; d=d ++d l ; d i Z ; ( l 2 m(p, d i= [Bu d i, goed i ], waarij me ( word aagegeve da d / > d 2 / 2 > > d l / l Zo saa de erme i [Bu ] i éé-op-éé correspodeie me de pariies zoder verfijige E( We zulle eers lae zie da als we di verder uiwerke, we ee ijecie me P( verkrijge Vervolges zulle we lae zie da de erm die volges die ijecie ij ee P P( hoor, er ook ui zie zoals i de sellig Te eerse hoor de erm [Bu ] ij de riviale pariie ( Neem u ee E = (,, l E( {(} Omda E ie de riviale pariie is, zie de erm die ij E hoor er als volg ui: d=d ++d l ; d i Z; d >> d l l l 2 m(e, d i= [Bu d i, goed i ] (* Er geld u j < voor elke j Voor de facor [Bu d j, goed j ] kue we dus volges oze iduciehypohese de sellig geruike Om di e kue doe, moee we elke d j weer 3
32 i j dele splise, we doe di als volg: d j = g j i= i+ + g j i= i g j i= i+ j Zo krijge we ee splisig d = g + + g We werke u alle facore [Bu d j, goed j ] ui volges de sellig, me ovegeoemde splisig va d j Elke facor [Bu d j, goed j ] esaa u dus ui ee som va erme, waarij elke erm correspodeer me ee pariie i P( j De erm die op deze maier hoor ij ee P P( j zulle we oere me [ P ] Da zie we = d=d ++d l ; d i Z; d >> d l l d=d ++d l ; d i Z; d >> d l l l 2 m(e, d 2 m(e, d i= ( P P( j V i P( i i l Hier hee we i de uidrukkig ( elke [Bu d j, goed j [ P ] [ V ][ V 2 ] [ V l ] (** ] vervage door de som va erme zoals i de sellig, e vervolges de haakjes weggewerk Bekijk ee keuze V, Vl me P( j voor elke j De ijehorede erm is V j d=d ++d l ; d i Z; d >> d l l 2 m(e, d[ V ][ ] [ ] V 2 V l (*** De pariies V,, Vl kue we op ee auurlijke maier opvae als ee verfijig va E Schrijf daarvoor de eerse pariiesappe va V o e me Vl acher E, zo hee we ee verfijig va E va de eerse orde verkrege Als we alle pariiesappe ui de verfijige va de eerse orde va V o e me Vl hier weer acher schrijve, krijge we ee verfijig va de weede orde We gaa me iducie verder: we eme seeds alle pariiesappe ui de verfijige va de c-de orde va V o e me Vl same, schrijve deze acher de pariie me verfijig va de c-de orde die we hadde, e verkrijge zo ee verfijig va de (c + -de orde We oere al deze verfijigsappe same me V, de pariie die we zo krijge is da EV Di geef de ijecie usse de erme i ( e de verfijige va E We doe di u op dezelfde wijze voor elke E E( {(} Als we zo de oorsprokelijke recursieve uidrukkig voor [Bu ] uiwerke krijge we dus oze gevraagde ijecie usse de erme i deze uidrukkig e de pariies i P( We lae u zie da de erm die hoor ij gegeve P P( eruizie zoals i de sellig Voor P = ( is he duidelijk Neem daarom weer ee pariie EV zoals die hierove Als eerse epale we zij eke Elke facor [ ] Vj heef volges de iduciehypohese eke ( deg(v j We krijge zo dus ee eke ( + l i= deg(v i 3
33 We kue echer izie, da deg(ev = + l i= deg(v i Di kom omda de pariiesappe va alle Vj i ee epaalde volgorde acher E zij geplak He aaal ie-riviale pariiesappe lijf zo gelijk Hiermee vide we da he eke va de erm ( gelijk is aa ( deg(ev Di is i overeesemmig me de sellig Zij u E j = E(V j = ( j,, j,2,, j,l j voor elke j Hier is l j de lege va E j Volges oze iduciehypohese geld da Bu(Vj = lj i= [Bu ] De erm ( eva dus de facor i l j= Bu(V j = l j= i= lj [Bu ] i e verder gee facore va he ype [Bu ] Maar we kue izie da de eidoesad va EV ook vas lig als we de eidoesade va alle Vj kee Er geld amelijk da Ej E( j voor alle j, we kue dus elke Ej ook opvae als ee verfijig va j i E Bekijk dus de pariie me verfijig EEE 2 El Er geld duidelijk E(EV = E(EE E 2 E l Dus geld = (,,,2,,,l, 2,, 2,2,, 2,l, 3,, 3,2,, 2 3,l,, 3 l,l l l j= i= lj [Bu ] = Bu(EV, i waar Bu(EV is zoals i de sellig Verder geld me oze iduciehypohese da elke [ ] Vj ee facor T(V j eva zoals i de sellig Voor de hiervoor oodzakelijke splisig va d j geruike we de splisig zoals aagegeve aa he egi va he ewijs Deze was d j = g j i= i+ + g j i= i g j i= i+ j, waarmee we me d = d + + d l ee splisig d = g + + g verkrijge We krijge zo ee facor l 2 m(e, g ++g T(Vi i ( De expoe esaa u ui de som va erme va de vorm 2 m(, Hier correspodeer 2 m(e, g + + g me de eerse pariiesap E, de res va de erme 32 i=
34 2 m(, correspodeer me ee pariiesap i ee zekere Vj De pariie EV word verkrege door die pariiesappe slechs e verwissele e acher E e plaase Maar i de expoe is die verwisselig ook oegesaa Er moe dus gelde 2 m(e, g ++g l i= T(V i = T(EV, waarij T(EV is zoals i de sellig To slo krijge we voor elke [ ] Vj ee sommaieeke me daaroder de verzamelig O(Vj We eme al deze sommaiekes same me he sommaieeke da al e zie is i ( Di geef de volgede verzamelig oder he someke { (g,, g d = g + + g ; d > > d l l ; (g j i= i+, g j i= i+2,, g j i= i+ j O(V j } j l Maar omda de pariie EV word verkrege door alle pariiesappe i alle Vj op de juise maier e verwissele e acher E e schrijve, zie we da deze verzamelig gelijk is aa O(EV zoals eschreve is i de sellig Op deze maier hee we de hele erm ( eschreve die hoor ij EV We hee dus lae zie da deze iderdaad gelijk is aa ( deg(ev Bu(EV T(EV (g g O(E Op dezelfde maier oe we di aa voor alle pariies i P( Di ewijs de sellig We hee zo ee mehode om voor willekeurige de uidrukkig e vide die we aa he egi va deze paragraaf voor [Bu 3 ] gave Di is eigelijk al ee direce formule, dus formeel is os doel al geslaagd Echer, de hoeveelheid rekewerk is og auwelijks vermiderd, dus we kijke verder We vide omiddelijk he volgede gevolg Gevolg 32 Zij N e P, P 2 P(, me E(P = E(P 2 Da geld: Bu(P = Bu(P 2 I feie is zelfs ies serkers waar Als E, F E( ui dezelfde gealle esaa maar deze slechs i ee adere volgorde hee saa, geld ook Bu(E = Bu(F Di hee we echer ie odig ] die we i de voor- Di geef al ee vereevoudigig va de uidrukkig voor [Bu gaade sellig vode 33
35 Gevolg 33 Zij N e d Z Da geld [Bu ] = E E( Bu(E P P( E(P =E Bewijs Di volg direc ui sellig 3 e lemma 32 ( deg(p g O(P T(P (g Aagezie we al ee direce formule kee voor [Bu ] voor N, zal he eevoudig zij deze ook voor Bu(E e geve voor E E( We zulle os i de komede paragrafe daarom cocerere op de erm P P ( E(P =E waarij de eidoesad E vas gekoze is ( deg(p O(P T(P, Opmerkig Als me de uidrukkig voor [Bu 3 ] ekijk, zoals gegeve i he egi va di hoofdsuk, val he op da ie i alle erme ee splisig va d i drieë is geruik Soms is deze amelijk ook slechs i weeë gesplis Terwijl we i voorgaade sellig wél ij elke erm splise i d i g + + g Echer, de eis ( ui O(P eperk vervolges weer de vrijheid i deze splisig Zij E(P = (m,, m l de eidoesad va P e g j = g j i= m i+ + g j i= m i g j i= m i+m j Da hee we d = g + + g l e impliceer de voorwaarde ( ui O(P da g i Z voor elke i Vawege de eis g j i= m i+ = g j i= m i+2 = = g j i= m i+m j m j Z werk deze implicaie eide kae op I feie is de splisig d = g + +g zoals hierove dus equivale me ee splisig g + + g l Hier was l de lege va de eidoesad va P Di is precies wa we zage i de uidrukkig voor [Bu 3 ] i he egi va di hoofdsuk I de erme die hore ij de pariies (2, e (, 2 is d i weeë gesplis omda di de lege va de eidoesad is He is ie lasig i e zie, da i de erm T(P voor elke m j i E de g j i= m i+, g j i= m i+2,, g j i= m i+m j alijd gegroepeerd als som zulle voorkome Dizelfde geld voor de ogelijkhede ( ui O(P We kue daarom ook hier zee g j = g j i= m i+ +g j i= m i+2 + +g j i= m i+m j e de splisig opvae als d = g + +g l Oze iuïie ij de splisig va d i g + + g zal dus seeds deze splisig i g + + g l zij We zulle hier aa referere als de geïduceerde splisig va d De rede om he och op e schrijve zoals we i de sellig dede, is da di de algemee formulerig mogelijk maak Bovedie zal deze oaie esseieel zij voor de oepassig va he Laglads lemma, i paragraaf 34 I de komede paragrafe zulle we seeds de geïduceerde splisig va d geruike, me uizoderig va paragraaf 34 We zulle da seeds de accee weglae als duidelijk is over welke splisig he op da mome gaa 34
36 32 De erm T(P I deze paragraaf ekijke we de erm T(P ui sellig 3 We zulle zie da deze slechs afhakelijk is va de eidoesad va P Zij N > e eem ee pariie P = BV V l V 2 V 2 l 2 P( I sellig 3 is e zie da om de erm T(P e krijge, we resulae va verschillede m(, erme ij elkaar op zulle moee elle Om deze opellig e kue uivoere, schrijve we de formule voor m(q, d voor zekere Q = (,, l E( i ee adere vorm Hier eme we ook alvas de facor 2 mee die i de expoe ij T(P saa 2 m(q, d = 2 i<j l = 2 i<j l = 2 i<j l ( i j ((g + ( d j d i j i i j (g + 2 i<j l ( i j ((g + i<j l j d i + i d j c(id i, waarij c(i = i 2 i+ 2 k I de volgede proposiie ekijke we wee pariies, elk me ee eidoesad va lege l We zulle hier de geïduceerde splisig va d geruike e schrijve d = g + + g l Proposiie 34 Zij N > e P = (,, l P( ee pariie zoder verfijig Neem m = p+ +, p+r voor zekere p e p + r l Zij u Q = (,, p, m, p+r+,, l ( p+,, p+r ; p + de pariie waarij we p+,, p+r hee samegeome o hu som, e die vervolges i ee verfijig weer hee uigewerk zoals we oorsprokelijk dede Da geld T(P = T(Q Bewijs I de expoe saa ee erm me ee facor (g e ee aaal erme me g i We ekijke eers de erm me (g Voor P is deze gelijk aa: i<j l i j (34 35
37 Voor Q is deze gelijk aa: i j + = i<j l i,j / {p+,,p+r} i<j l i,j / {p+,,p+r} i j + i l i / {p+,,p+r} i l i / {p+,,p+r} i m + p+ i<j p+r i j i ( p+ + p+r + p+ i<j p+r i j (35 Hier hore de eerse wee erme ij (,, p, m, p+r+,, k e hoor de laase erm ij ( p+,, p+r ; p + Da di dezelfde uidrukkige zij, kue we eevoudig izie Neem hiervoor ee (i, j me i < j l, waarover i 34 dus gesommeerd word We zulle izie, da i 35 hij ook precies éémaal word geeld Er zij drie gevalle: Geval Als i, j / {p +,, p + r}, da el de eerse erm va 35 hem mee, e de overige wee erme ie Geval 2 Als i / {p +,, p + r} e j {p +,, p + r} da el de weede erm va 35 hem mee, e de overige wee erme ie Hezelfde geld voor i {p +,, p + r} e j / {p +,, p + r} Geval 3 Als i, j {p +,, p + r}, da el de derde erm va 35 hem mee, e de overige wee erme ie Korom, de (i, j waarover gesommeerd word zij i eide gevalle gelijk We cocludere da de eide uidrukkige i hu geheel gelijk zij Dus i de expoe saa dezelfde facor voor (g Da de g i De pariie P geef os ee erm l i= c P (ig i Hier is c P (i de facor voor g i e daarva wee we: c P (i = i 2 i+ 2 l = ( (j>i 2 j j=,,l j i I de laase sap hee we de idicaorfucie geruik Kue we ee soorgelijke uidrukkig vide voor de coeëfficiee c Q (i va g i die i de expoe va T(Q saa? We geruike hier dus weer g o e me g l, waarij we i de eerse pariiesap va Q, g p+ + + g p+r og als éé eschouwe Deze worde da pas me de weede pariiesap opgesplis Eers kijke we aar de eerse pariiesap (,, p, m, p+r+,, l Deze geef os u de volgede erm i de expoe: 2 m((,, p, m, p+r+,, l, d = l i= c Q,(ig i, 36
38 waarij we wee da voor i {p +,, p + r} de coëfficiëe gelijk zij Da vide we: c Q, (i = ( (j>i 2 j + ( (p i 2m Voor i / {p +,, p + r} = = c Q, (i = j=,,l j i j / {p+,,p+r} j=,,l j i j / {p+,,p+r} j=,,l j i j=,,l j / {p+,,p+r} ( ( j>i 2 j + ( ( p i 2( p+ + p+r ( ( j>i 2 j ; ( ( j>p 2 j Voor i {p +,, p + r} = p 2 p+r+ 2 l We eschouwe u de weede pariiesap ( p+,, p+r ; p + Deze geef os ook ee erm i de expoe, amelijk 2 m(( p+,, p+r, g p+ + + g p+r = p+r i=p+ c Q,2(ig i De coëfficiee c Q,2 (i vide we eevoudig: c Q,2 (i = j=p+,p+r j i ( ( j>i 2 j = 2 p i 2 i+ 2 p+r We elle deze resulae ij elkaar op e oeme de resulerede coëfficiëe c Q (i Voor i / {p +,, p + r} vide we: c Q (i = c Q, (i = j=,,l j i Bovedie zie we voor i {p +,, p + r}: c Q (i = c Q, (i + c Q,2 (i ( ( j>i 2 j = c P (i = p 2 p+r+ 2 l + 2 p i 2 i+ 2 p+r = i 2 i+ 2 l = c P (i Ook hier vide we dezelfde uidrukkig als ij P Di ewijs da de coëfficiee voor de g i ij P e Q hezelfde zij, e hiermee is oze proposiie eweze Gevolg 35 Zij N > e P, Q P(, me E(P = E(Q Da geld T(P = T(Q 37
39 Bewijs Begi me de eidoesad E := E(P = E(Q Geruikmaked va proposiie 34 kue we aa E sap voor sap verfijigsappe oevoege, zoder da T(E verader Di ka omda we proposiie 34 iducief ook kue oepasse op alle verfijigsappe Door elkes de verfijigsappe oe e voege die i P saa, kue we zo aaoe da T(E = T(P Aaloog ewijze we T(Q = T(E e zo volg he gevraagde We schrijve i he vervolg voor ee pariie P me E = E(P u T(E i plaas va T(P De uidrukkig voor [Bu ] die we i sellig 3 vode e i gevolg 33 vereevoudigde, kue we u og ee sap verder owikkele: Gevolg 36 Zij N > e d Z Da geld [Bu ] = Bu(E E E( P P( E(P =E ( deg(p g O(P T(E(g Di zage we al voor he geval = 3 al eerder ij de erekeig i paragraaf He Laglads lemma We zage i 36 da voor verschillede pariies P me dezelfde eidoesad E, he eige verschil i ( deg(p O(P T(E eri lig, da over adere verzamelige word gesommeerd e wellich he eke verschil We gaa dus op zoek aar ee maier om me deze verschillede verzamelige e verschille i eke om e gaa Hiervoor kom he Laglads lemma ui [2] hadig va pas I deze paragraaf geef ik he Laglads lemma i ee algemee vorm De paragraaf hiera zal de voor os ruikare oepassig ehadele Coveies We werke seeds i R e zulle hierij he sadaard iproduc geruike Voor ee v R schrijve we v i voor zij i-de coördiaa op de sadaardasis Als we he hee over de coördiae va v zoder e vermelde op welke asis di is, zulle we deze coördiae edoele De duale asis voor R va de sadaardasis voor R zulle we seeds oere me {H,, H } Ee vereigig va wee verzamelige waarij hu doorsede leeg is, oere we me To slo zulle we me ee orhogoale direce som aageve Defiiie 37 Zij N > e P = (,, l E( Voor deze pariie defiiëre we de vecorruime a P = { v R v = = v, v + = = v + 2,, v + l + = = v } R Opmerkig De ruime a P is duidelijk isomorf me R l He auurlijke isomorfisme usse deze ruime is zeer vergelijkaar me de maier waarop wij de splisig va d i g + +g ui sellig 3 e de daardoor geïduceerde splisig va d i g + + g l i elkaar omschrijve I he ijzoder zie we da voor P = (,, E( geld a P = R 38
40 Vooreeld Zij P = (2, 3,, Q = (6 E(6 Da geld a P = Spa,,, a Q = Spa We oere de orhogoale projecie va R op a P me [ ] P Bij ee pariie P defiiëre we vervolges ee verzamelig covecors: P = { α j = H j i= i H j i= i+ j < l } R Zij u Q = (m,, m l E( ee grovere pariie da P Da wee we da er ee k is zoda m = k i= i, er ee k 2 is zoda m 2 = k +k 2 i=k + i, ezovoor: P = (,, k }{{} m, k +,, k +k 2 }{{} m 2, }{{}, k ++k l +,, l }{{} m l Q = (m, m 2,, m l Daarom gelde da a Q a P ; Q P Di sel os i saa de volgede verzamelig e defiiëre: Q P = P Q Merk hierij op da als G = ( de riviale pariie is, da da volg G = Hierui volg da da G P = P voor elke pariie P Voor α i P schrijve we α i = [ α i ] P voor de orhogoale projecie op a P va de geraspoeerde va α i Vooreeld 38 Zij P = (2, 3,, 2, Q = (6, 2 E(8 Da geld a P = Spa,,,, a Q = Spa, 39
41 Als we zee α = H 2 H 3 ; α 2 = H 5 H 6 ; α 3 = H 6 H 7, da zie we P = {α, α 2, α 3 } ; Q = {α 3 } Daarom geld Q P = {α, α 2 } We wille u dus α e α 2 raspoere e projecere op a P We zie α = α2 = Da is ie moeilijk i e zie da /2 /2 /3 α = [α ] P = /3 /3 /3 α2 = [α2 ] P = /3 /3 Merk op da als we v e v 2 schrijve voor de voorregede vecore voor a Q zoals hierove, er geld Spa{v, v 2, α, α2 } = a P Di is gee oeval, zoals we laer zulle zie Lemma 39 Zij N > Voor P = (,, l E( geld α i = ( i }{{} i i keer i+ }{{ i+ } i+ keer Hier is zij slechs de de ( + i + -de o e me de ( + i + i + i+ -de coördiaa ogelijk aa ul 4
42 Bewijs Schrijf v = ( i i i+ i+ Er geld u α i v = i i i+ i+ = i i i i i+ i+ i+ i+ We kue izie da deze vecor loodrech saa op a P De som va de ( + i +-de o e me de ( + i + i -de coördiaa is amelijk i + + i }{{} i keer i i =, e elke vecor i a P is cosa op deze coördiae Hezelfde geld voor de ( + i +- de o e me de ( + i + i+ -de coördiaa To slo is deze vecor ul uie deze coördiae Di ewijs da hij loodrech saa op a P As ee vecor v a P voldoe aa α i v a P, is deze de orhogoale projecie va α i op a P Er geld dus iderdaad v = [α i ] P = α i Voor zekere P, Q P( me Q grover da P defiiëre we u de volgede deelruime va a P : a Q P = spa {α α Q P } Da deze opspaede verzamelig ook ee asis is, kue we als volg izie Als G = ( da is G P = P Maar we kue me lemma 39 izie da {α α P } 4
43 { v = (,, R } ee asis vorm voor a P Aagezie # P = dim(a P zij de vecore { i {α} α P } dus lieair oafhakelijk Vawege Q P P volg u da α α Q P ook ee verzamelig is va lieair oafhakelijke vecore Als ee gevolg krijge we u dim(a Q P = # Q P = # P # Q Opmerkig 3 De som va de coördiae va αi me α i Q P eevoudig ui e rekee: is me lemma i }{{} i i+ }{{ i+ } i keer i+ keer = = Di geld voor elke α me α Q P Daarom wee va elke v aq P coördiae ul is da de som va zij Lemma 3 Zij N > e P = (,, l, Q = (m,, m l E( pariies me Q grover da P Da geld a P = a Q P a Q Bewijs Neem ee asisvecor α va a Q P, hier is α Q P P Er is u ee i zoda α = α i P waarij we geummerd hee zoals i de defiiie va P Omda geld α i / Q wee we da er ee m j i Q is me p, q N > waarij p i < q, zoda m j = q k k=p Me adere woorde, he volgede is he geval: P = (, p,, i,, }{{} q, ; =m j Q = (, m j, Hierui volg vervolges vawege de defiiie va a Q da voor w a Q geld w ++ p + = = w ++ q Maar de coördiae va α zij ul, ehalve de ( + + i +-de o e me de ( + + i+ -de coördiaa, zie hiervoor lemma 39 Neem ee w a Q Die coördiae va w waarop α ogelijk ul is, zij weges ovesaade redeerig allemaal gelijk Als we u he iproduc eme va α me ee vecor w a Q, da krijge we dus als uikoms de som va de coördiae va α maal ee vase erm (om precies e zij: de waarde va w ++ p + Maar we zage eerder da de som va de coördiae va α ul is Di verel os da he iproduc va α e w ul zal zij e di geef os α a Q Omda 42
44 α ee willekeurige asisvecor was volg hierui a Q P a Q Bovedie geld uieraard a Q P a P e a Q a P, e kee we hu dimesies: dim(a Q P = # P # Q dim(a P = # P + dim(a Q = # Q + Hierui zie we da dim(a Q P + dim(a Q = # P + = dim(a P Di same me de orhogoaliei va de ruime ewijs he lemma Gevolg 32 Dezelfde uispraak is waar voor de duale ruime: a P = a Q P a Q Vooreeld We gaa hier verder me vooreeld 38 Voor P = (2, 3,, 2, Q = (6, 2 E(6 zage we da a P = Spa,,,, a Q = Spa, Verder zage we da a Q P = Spa {α, α 2 } = Spa /2 /2 /3 /3 /3 /3 /3 /3 Hier geld dus iderdaad da a P = a Q P a Q Lemma 33 Zij N > e P, Q, R E( me R grover da Q, e Q grover da P Er geld: R P = Q P R Q 43
45 Bewijs Vawege de defiiie va Q P wee we da P = Q P Q Da di ee disjuce vereigig is, volg omiddelijk ui de defiiie Op dezelfde maier vide we Q = R Q R Di geef os P = Q P R Q R P R = Q P R Q R P = Q P R Q We oere de orhogoale projecie va R op a Q P me [ ]Q P Nu kue we wee verschillede ases ekijke voor a Q P Te eerse vorm Q P ee asis Elke α Q P is amelijk ul op a Q, zoda geld Q P aq Bovedie is he ee verzamelig va # P # Q = dim(a Q P lieair oafhakelijke { covecore } Te weede hee we de duale asis ωα Q α Q P va a Q P P { α α Q P }, als asis voor Lemma 34 Zij N > e P = (,, l, Q = (m,, m l E( me Q grover da P Zij v a Q P Als voor elke α Q P geld da α(v > of ωq α (v >, da geld ωα Q (v > voor elke α Q P Bewijs Sel da voor elke α Q P geld da α(v > of ωq α (v > Per defiiie ummere we de elemee va P als { } P = α j = H j i= H j i i= j < l i+ We schrijve u v = i=,,l α i Q P c i α i me c i R Di is v uigeschreve op de asis {α i α i Q P } va aq P Sel u da er ee α j Q P = P Q is zoda ω Q α j (v Di is equivale me c j Vawege oze aaame geld da da α j (v > Omda α j / Q, is er ee m k i Q me k l e zekere p, q N > me p j < q zoda m k = q i=p i Hierui leide we vervolges af da α p Q e α q Q (op voorwaarde da deze esaa, da is amelijk allee zo als p voor α p e q l voor α q Dus geld: 44
46 α p, α p+,, α q Q P ; α p / Q P (op voorwaarde da p ; α q / Q P (op voorwaarde da q l Hierui, same me de vorm va de αi zoals gegeve i lemma 39, kue we afleide da de waarde va v ++ p +, v ++ p +2,, v ++ q volledig zij epaald door de coëfficiee c p o e me c q De vecore αp o e me αq zij amelijk de eige vecore i de asis {αi α i Q P } voor aq P die hier ogelijk ul zij Sel u j p, (q Da kue we me ehulp va lemma 39 izie da α j (v = c j ( j + j+ c j j c j+ = (c j c j j + (c j c j+ Als u c j, c j+ c j, da zou α j (v Maar di is i egespraak me oze aaame Dus er geld ofwel c j < c j, ofwel c j+ < c j We moge hier aaeme da c j+ < c j We espreke og de gevalle j = p, q Als geld j = p, da krijge we op vergelijkare wijze j+ α j (v = c j ( j + j+ c j+ j+ = c j + (c j c j+, j j+ e ook hier kue we afleide da c j+ < c j He ewijs gaa da op dezelfde maier verder Als geld j = q leide we op deze wijze af da c j < c j He ewijs gaa da ook hier op aaloge wijze verder We gaa u verder me he ewijs oder de aaame c j+ < c j We geruike iducie Als we voor zekere r wee da c r+ < c r, wee we weer ω Q α r+ (v < We kue ovesaade redeerig u opieuw oepasse e afleide da ofwel c r+2 < c r+, ofwel c r < c r+ Di weede is omogelijk vawege oze aaame Dus moe gelde c r+2 < c r+ < Di geef os uieidelijk c q < c q 2, e dus geld ook ω Q α q (v < Echer, we zie ook da α q (v = c q ( + c q 2 q q q = c q + (c q + c q 2 q q 45 j+
47 Maar di geef me ehulp va c q < c q 2 da ook α q (v < Da geld dus da zowel ω Q α q (v < als α q (v < Di is i egespraak me oze aaame e da ewijs he lemma Defiiëer o slo de volgede deelverzamelige va a Q P : } W Q P {v = a Q P α(v > α Q P ; { } Ŵ Q P = v a Q P ωq α (v > α Q P Zij v R I avolgig va [2] defiiëre we de volgede fucies τ Q P (v, τ Q P (v : R {, }: τ Q P (v = { als α(v > α Q P als α(v α Q P ; τ Q P (v = { als ω Q α (v > α Q P als ω Q α (v α Q P Als we τ Q P e τ Q P eperke o aq P, verkrijge we de karakerisieke fucies va WQ P e ŴQ P Merk op da als P = Q, er geld W P P = ŴP P = a P P = {} e dus voor elke v ap P geld τp P (v = τ P P (v = Lemma 35 Zij N > e P, Q, R E( waarij R grover is da Q e Q grover is da P Zij verder v a P Da gelde Bewijs We wee da τ Q P ([v]q P = τ Q P (v; τ R Q ([v] Q = τ R Q (v; τ Q P ([v]q P = τ Q P (v a P = a Q P a Q; a Q = a R Q a R ; e dus: a P = a Q P ar Q a R De verzamelig {α α Q P } is per defiiie ee asis voor aq P De hieraa duale asis {ωα Q α Q P } is ee asis voor aq P Omda ωq α ee duale asisvecor is va ee vecor i a Q P, geld da ωq α (w = voor elke w a Q Da geld vawege lieariei ω Q α (v = ω Q α ([v] Q P + [v] Q = ω Q α ([v] Q P 46
48 Als τ Q P ([v]q P = geld ωq α ([v] Q P > voor alle α Q P Volges ovesaade redeerig is di u equivale me ωα Q (v > voor alle α Q P, maar di eeke τ Q P (v = Da geld dus precies τ Q P ([v]q P = waeer τ Q P (v =, di ewijs de eerse ewerig He ewijs da τ Q R([v] Q = τ Q R (v gaa op aaloge wijze Neem u ee α Q P waarij α = α i P me de ummerig zoals i de defiiie Schrijf P = (, e Q = (m, I he ewijs va lemma 3 merke we al op da ui α i Q volg da er ee m j i Q is me p, q N > e p i < q zoda q m j = k k=p Hierui volg vervolges da voor ee w a Q geld w ++ p + = = w ++ q, vawege de defiiie va a Q I he ijzoder geld w ++ i = w ++ i + Omda er geld α i = H ++ i H ++ i + geld u da α i (w= voor elke w a Q Zij u weer v a P We krijge daarom op ee vergelijkare maier als hierove da α(v = α([v] Q P + [v] Q = α([v] Q P Omda di weer geld voor elke α Q P vide we τ Q P ([v]q P = τ Q P (v Vooreeld Zij P = (,,, Q = (2,, R = (3 E(3 We zulle lae zie da voor v a R P ie alijd hoef e gelde τ Q R(v = τ Q R([v] Q We wee da a P = Spa,,, a Q = Spa,, a R = Spa Nu is P = {α = H H 2, α 2 = H 2 H 3 }, R Q = Q = {α 2 } e a R P = Spa { [α ] P, [α2 ] P, } = Spa,, a Q P = Spa { } [α ] P = Spa, ar Q = Spa { } /2 [α2 ] Q = Spa /2 Da zie we iderdaad a P = a Q P a R Q a R Neem u v = ( 3, 2, a R P Omda α 2 (v = ( 3 2 = > 47
49 geld τq R (v = Maar ook geld α 2 ([v] Q = ( /2 /2 = 3 2 e dus zie we τ R Q ([v] Q = Maar da wee we dus da i di geval τ R Q (v τ R Q ([v] Q Lemma 36 (Laglads Zij P, R E( waarij P R Da geld voor elke v a R P ( dim(ar Q τ Q P ([v]q P τ Q R ([v] Q = δp R e waarij we me δ R P Q E(; P Q R Q E(; P Q R ( dim(aq P τ Q P ([v]q P τ R Q ([v] Q = δ R P, de Kroecker dela edoele Bewijs We ewijze allee de eerse formule Sel P = R da geld voor ee v a P P da v = [v] Q P = v Q = We zage al eerder da er zo geld τp P ([v]p P = τ P P ([v] P = Di ewijs ( dim(ar Q τ Q P ([v]q P τ Q R ([v] Q = ( dim(aq P τ Q P ([v]q P τ Q R ([v] Q = Q E(; P Q R Q E(; P Q R Sel u P R e zij v a R P We lae u zie da ( dim(ar Q τ Q P ([v]q P τ Q R ([v] Q = Q E(; P Q R Merk op da me lemma 35 geld da τ Q P ([v]q P τ Q R([v] Q = τ Q P (v τ Q R(v Er is ee auurlijke ijecie usse de mogelijke keuzes voor Q e de mogelijke splisige va R P i wee disjuce deelverzamelige Deze splisig is da amelijk R P = Q P R Q Als Q u over alle pariies grover da P e fijer da R loop, krijge we precies al zulke splisige va R P Voor zo ee vas gekoze Q geld τ Q P (v τ Q R (v = da e slechs da als α(v > α Q P ; ω R α (v > α R Q Deze oaie is i paragraaf 2 igevoerd e houd i da R grover is da P 48
50 We zie dus meee da als er ee α R P is zoda zowel α(v als ωr α (v, voor elke Q geld da τ Q P (v τ Q R (v = I da geval is he lemma eweze Neem u aa da di ie geld, voor elke α R P geld da dus ofwel α(v > ofwel ωα R (v > Lemma 34 geef os u da voor elke α R P geld da ωr α (v > We lae u zie, da er ook ee α R P moe zij zoda α(v > Sel daarom da voor alle α R P geld α(v Kies ee α R P Er is ee j zoda α = α j P, waarij we ummere zoals i de defiiie va P Schrijf P = (,, l e R = (m, e ovedie v = c i αi i=,,l α i R P Hier geld c i R voor elke oegesae i Di is v uigeschreve op de asis {α α R P } Ne zoals i lemma 34 geld u vawege α j R da er ee m k i R e zekere p, q N > me p j < q moee zij zoda m k = q i=p i Hierui leide we vervolges af da α p R op voorwaarde da p e α q Q op voorwaarde da q l (de voorwaarde garadere he esaa va α p e α q Dus geld: α p, α p+,, α q R P ; α p / R P (op voorwaarde da p ; α q / R P (op voorwaarde da q l Ui de laase wee feie leide we af da de waarde va v ++ p +, v ++ p +2,, v ++ q volledig zij epaald door de coëfficiee c p o e me c q De vecore αp o e me αq zij amelijk de eige vecore i de asis {αi α i R P } voor ar P die hier ogelijk ul zij Oze aaame was da ωα R (v > voor elke α R P Hierui volg da da c p o e me c q allemaal posiief zij Verder hadde we aageome da α(v voor elke α R P We kue u me ehulp va lemma 39 izie da α p (v = c p ( p + p+ c p+ = (c p p + (c p c p+ Nu volg ui oze aaame da α p (v da c p+ > c p Op vergelijkare wijze zie we da ofwel c p+2 > c p+, ofwel c p > c p+ Maar va di laase hee we zojuis lae zie da di ie mogelijk is, zo wee we da c p+2 > c p+ Als we me iducie verder gaa, zie we uieidelijk da p+ p+ c p < c p+ < c p+2 < < c q 2 < c q Maar op dezelfde wijze vide we c q 2 > c q, di geef ee egespraak Oze aaame da er voor alle α R P geld α(v was dus fou e er is dus ee α R P zoda α(v > 49
51 To slo ekijke we u de verzamelig A v = {α R P α(v > } R P We hee e lae zie da #A > We kue u izie da voor de Q me τ Q P (v τ Q R(v = moe gelde, da R Q A Merk op da hier ook Q = R is oegesaa, da is R Q = R R = Er volg da Q E(; P Q R = ( dim(ar Q τ Q P (v τ R Q (v # ( R Q Q E(; R Q P(A ( ( ( #A #A #A = + + ± 2 3 = ( #A = ( #A #A Hier is de op-ee-a-laase sap he gevolg va he iomium va Newo Hiermee hee we lae zie da ( dim(ar Q τ Q P ([v]q P τ Q R ([v] Q = δp R Q E(; P Q R 34 De oepassig va he Laglads lemma De relaie me os werk e he Laglads lemma is op he eerse gezich oduidelijk Echer, hij is esseieel voor he geve va de direce formule I deze paragraaf espreke we de oepassig I deze paragraaf zulle we de splisig va d i g + + g geruike Verder schrijve we seeds G voor de riviale pariie ( voor gegeve N > Zij N >, eem P V V l V 2 P( e zij E = E(P = (m,, m h de eidoesad va P We heriere os O(P = { g = (g,, g l i= m i Z m i d = g + + g, ( ; ( } Hier geef ( aa da voor elke m j i E: g j i= m i+ = g j i= m i+2 = = g j i= m i+m j ; g j i= m i+,, g j i= m i+m j m j Z 5
52 E ( geef aa da voor elke ie-riviale pariiesap Vj k = (vj,, k, v k ; k j,lj k j de volgede ogelijkhede gelde: g N k j g N k j +v k j, v k j, > g N k j +vk j, g N k j +v k j, +vk j,2 v k j,2 > > g N k j +v k j, ++vk j,l k j g N k j +v k j, ++vk j,l k j v k j,l k j We wee da de eerse gelijkheid d = g + + g ee voorschrif is i alle O(Q me Q P(N Bovedie zie we da he voorschrif ( slechs afhakelijk is va de eidoesad va P We schrijve vaaf u seeds g = (g,, g Defiiëer vervolges O (P = O 2 (P = { { (g,, g } l Z m i d = g + + g ; ( ; m i } i= (g,, g R ( Merk op da O (P O 2 (P = O(P Bovedie geld voor P, Q P( me E(P = E(Q da O (P = O (Q To slo zie we da voor elke g R geld g O 2 (G, omda da he voorschrif ( leeg is Er zij da amelijk gee ie-riviale pariiesappe We kue zo de uidrukkig voor [Bu ] ui gevolg 36 weer vereevoudige: Gevolg 37 Zij N > e d Z Da geld [Bu ] = E E( Bu(E g O (E P P ( E(P =E ( ( deg(p g O2 (P T(E Bewijs De uidrukkig die we i 36 vode was [Bu ] = E E( Bu(E 5 P P ( E(P =E ( deg(p O(P T(E
53 Zij u E E(P We kue u als volg redeere: ( deg(p T(E O(P P P ( E(P =E = P P ( E(P =E = g O (E ( deg(p P P ( E(P =E g O (P g O2 (P T(E ( ( deg(p g O2 (P T(E Als we di vervage i de uidrukkig i 36 krijge we ovesaad gevolg Lemma 38 Zij N >, d Z e P = (,, l E( Neem verder ee zekere g = (g,, g O (P Da geld τ G P (g = g O2 (P Bewijs Sel da l > We wee da { } G P = P = α j = H j i= H j i i= j < l i+ Sel u τ G P (g = Di is equivale me da α j(g > voor elke j < l Same me (* ui O (P geef di os: α j (g > ; g j i= g j i i= i+ > ; g j i= > g j i i= i+ ; g ++ j + + g ++ j + j > g ++ j + + g ++ j + j+, j j+ voor elke j < l Maar di zij precies de voorschrife waar g aa moe voldoe zoda g O 2 (P, zoda u volg g O2 (P = Bovesaade redeerig is omkeeraar e zo vide we da τp G([g]G P = da e slechs da als g O 2 (P = Als geld l =, da geld P = G = ( e dus τp G(g = τ P P (g = Bovedie geld da alijd g O 2 (P e dus g O2 (P = Dus geld ook hier τp G(g = g O 2 (P He volgede gevolg is ee riviaal gevolg va ovesaad lemma He die echer als eerse sap va ee iducieewijs laer i di hoofdsuk Gevolg 39 Zij N, Q = (,, l E( e eem ee zekere g = (g,, g O (Q We schrijve P = Q voor ee pariie P i P( die Q als eerse pariiesap eva me daaracher og eveuele verfijige Voor Q ( geld τq G (g = ( deg(p g O2 (P P =Q E(P =Q 52
54 Voor Q = ( geld τ G Q (g = P =Q E(P =Q ( deg(p g O2 (P Bewijs Vawege de codiies oder he someke word slechs gesommeerd over P = Q I he eerse geval krijge we i he recherlid dus ( g O2 (P = g O2 (P, i he weede geval krijge we hezelfde Hier saa dus hezelfde als i lemma 38 Proposiie 32 Zij N e Q = (, E( Zij verder E = (m, E( ee pariie die fijer is da Q, waarij er echer ee geal i i Q ie is verfijd Zij verder V = (v,, v h ; i ee verfijig va deze i i Q We kue deze dus ook als verfijig va E opvae Ze u F = E(EV (i He geval Q ( Als voor elke g = (g,, g O (E geld τ Q E (g τ Q G ([g] Q = ( dim(aq E + ( deg(p g O2 (P, da geld voor elke g O (F τ Q F (g τ G Q ([g] Q = ( dim(aq F + P =Q E(P =E P =Q E(P =F ( deg(p g O2 (P (ii He geval Q = ( Nu is ook E = ( e F = V waarij V ee op zichzelf saade pariie va is Da geld voor elke g O (V τ V G (g = ( dim(ag V ( deg(p g O2 (P P P( E(P =V Da we wee da E = ( i deel (ii va de proposiie, kom vawege de eis da er ee zekere i i Q is die ie door E verfijd word Vervolges is V ee verfijig va (, maar di is gewoo ee ormale pariie va ( volges de equivaleierelaies die we i paragraaf 2 hee igevoerd Uieraard geld da ook F = E((V = V Gevolg 32 Zij N e Q, E E( waarij E fijer is da Q Bovedie eise we da ij alle mogelijke keuzes om Q e verfije o E de maximale lege va de geruike verfijige l is Als proposiie 32 waar is voor alle h l, da geld voor g O (E τ Q E (g τ Q G ([g] Q = ( dim(aq E + ( deg(p g O2 (P P =Q E(P =E Bewijs va gevolg Gevolg 39 geef he geval E = Q Di same me he eerse deel va proposiie 32 geef os he ewijs 53
55 Bewijs va proposiie 32 Merk op da ee verfijig alijd ee ie-riviale pariie is e dus geld h 2 We zulle eers deel (ii va de proposiie voor h = 2 ewijze Hierui volg (i voor h = 2 De res va he ewijs gaa me iducie op h Zij u V = (v, v 2 I de proposiie is di ee verfijig va Q, maar u geld da Q = ( We kue daarom de idex weglae e V gewoo als ee pariie op zichzelf eschouwe Als eerse zie we da V precies éé eleme eva, deze oeme we α Neem u ee g O (V e sel τ G V (g = Omda g O (V geld ook g a V = {x R x = = x v ; x v + = = x } Verder wee we da a V vecor = a G V a G Di zij eide éé-dimesioale vecorruime De α = ( v,, v, v 2,, v 2 is ee asis voor a G V, e de vecor = (,, is ee asis voor a G Da zij er dus c, c 2 R me g = c α + c 2 De eis τ G V (g = eeke hier precies da ωg α (g >, waar we zoals gewoolijk me ω G α de duale asisvecor va α edoele Di is dus equivale me c > Maar vawege de vorm va α e zoals hierove, eeke di precies da de eerse o e me de (v -de coördiaa va g elk groer zij da de (v + -de o e me de -de coördiaa Di is equivale me e zegge g + g v v > g v g v v 2 We hee dus gevode da τv G (g = da e slechs da als aa de ogelijkheid hierove is voldaa Maar di is precies hezelfde voorschrif als voor g O2 (V Da geld dus τ G V (g = g O2 (V = P P( E(P =V g O2 (P = ( dim(ag V P P( E(P =V g O2 (P Di laa zie da deel wee va de proposiie waar is voor k = 2 He ewijs va deel éé voor k = 2 gaa precies aaloog aa he ewijs da oderaa voor algemee k is gegeve, e daarmee is de proposiie eweze voor k = 2 De res va he ewijs gaa me iducie op k Sel als iduciehypohese da de proposiie waar is voor alle waarde l < k voor zekere k N >2 54
56 Bewijs (ii Zij V = (v,, v k ee pariie va lege k Neem ee g O 2 (V He Laglads lemma zeg da ( dim(aq V τ Q V (g τ Q G ([g] Q =, me adere woorde Q E(; V Q G ( dim(ag V τ V G (g = ( dim(ag V τ V G (g τg G ([g] Q = ( dim(aq V τ Q V (g τ Q G ([g] Q = Q E(; V Q G Q E(; V Q G ( dim(aq V + τ Q V (g τ G Q ([g] Q Hier geve we me Q G aa da Q fijer is da G, maar er ie gelijk aa is Voor elk zo ee Q geld da als we Q verfije o V, de maximale lege va de geruike verfijige k zal zij Volges oze iduciehypohese kue we u gevolg 32 oepasse om e zie da voor deze Q geld ( dim(aq V + τ Q V (g τ Q G ([g] Q = ( deg(p g O2 (P Als we di susiuere zie we ( dim(ag V τ G V (g = Q E(; V Q G = Q E(; V Q G P =Q E(P =V ( dim(aq V + τ Q V (g τ G Q ([g] Q P =Q E(P =V ( deg(p g O2 (P De erm waarover gesommeerd word is slechs afhakelijk va de pariie P De pariie Q is hier de eerse pariiesap va P Nu el he eerse someke alle mogelijke eerse pariiesappe va P e el he weede someke voor elke zo vasgekoze eerse pariiesap Q de mogelijke verfijige o V Di is alijd mogelijk omda i he eerse someke de eis saa da Q grover is da V Zo worde alle pariies me eidoesad V precies éé keer geeld door de wee somekes Duele ellige worde amelijk voorkome doorda he eerse someke ook de eis Q ( eva Hiermee hee we aageood da ( deg(p g O2 (P Q E(; V Q G = Q E(; E(P =V P =Q E(P =V ( deg(p g O2 (P 55
57 Zo hee we eweze da geld τ G V (g = ( dim(ag V Q E(; E(P =V ( deg(p g O2 (P e dus hee we eweze da ui oze iduciehypohese volg da deel (ii ook waar is voor l = k Bewijs (i Neem u Q, G, V, E e F als i he eerse deel va de proposiie, waarij V va lege k is Neem aa da voor elke g O (E geld da τ Q E (g τ Q G ([g] Q = ( dim(aq E + ( deg(p g O2 (P P =Q E(P =E We zulle lae zie da u ook voor elke g O (F geld da τ Q F (g τ Q G ([g] Q = ( dim(aq F + ( deg(p g O2 (P Neem ee g O (F We wee da P =Q E(P =F g a F = a E F a E e da dus geld g = [g] E F + [g] E Bovedie geld Q F = E F Q E We kue daarom zo redeere: τ Q F (g = α Q F : ω α(g > α E F : ω α (g > e α Q E : ω α(g > α E F : ω α (g > (a e α Q E : ω α([g] E > ( We zie da, da (a equivale is me τ E F (g = e ( equivale is me τ Q E ([g] E = Zo hee we dus lae zie da τ Q F (g = τ E F (g τ Q E ([g] E e zo krijge we τ Q F (g τ G Q ([g] Q = τ E F (g τ Q E ([g] Eτ G Q ([g] Q We ekijke eers τ E F (g = τ E F ([g]e F Noeer me m j he geal i E da verfijd word door V We kue izie, da de 56
58 ruime a E F op ee auurlijke maier isomorf is me a(m j V Schrijf g i = g m ++m j +i voor i m j We wee da va ee g a E F, al zij coördiae gelijk zij aa ul ehalve g o e me g m j Bovedie geld da g v ++v i + = = g v ++v i +v i+ voor elke i < k To slo wee we m j i= g i = Maar a (m j V is ee deelruime va R m j e voor g a (m j V geld g v ++v i + = = g v ++v i +v i+ voor elke i < k Hier geld ook m j i= g i = He isomorfisme word dus simpelweg gegeve door π : a E F a (m j V g = (g,, g (g,, g m j Di isomorfisme iduceer ee isomorfisme usse de duale ruime e eeld daarij de covecors i F E af op de covecors i V = (m j V, waarij de ordeig word gerespeceerd Di omda π i feie ies aders is da he apar eme va de coördiae i a E F die ogelijk ul zij: er word gee ekele srucuur veraderd ehalve da we de coördiae aders ummere Als gevolg hierva eeld π precies de asis { } α α E F va a E F af op de asis { α α (m } j (m V = V va a j V Me di gegeve kue we uieidelijk cocludere da τ (m j V (π(g = τ F E ([g] E F = τ F E (g Nu kue we geruike da we deel (ii va de proposiie al eweze hee We vide amelijk ( τ (m j V (π(g = ( dim a (m j V ( deg(p π(g O2 (P P P(m j E(P =V Bekijk u τ Q E ([g] Eτ G Q ([g] Q We kue izie da [g] E i O (E lig 2 Aa de gelijkhede i O (E is amelijk voldaa, omda [g] E a E Verder moe gelde da g i i=l m l+,, g i l= m l+m i m i Z voor elke i l(e Da di iderdaad geld, zie we als volg i: we wee da g O (F Dus voor elke m i me i j geld he ovesaade sowieso Nu is de som va de coordiae g o e me 2 Di ka ij he doorscae va he ewijs gemakkelijk worde overgeslage, zoder da he idee va he ewijs mider duidelijk word 57
59 g m j ee geheel geal (weer vawege g O (F De projecie op E esaa er u ui, da m j i= g i elk va deze coordiae de waarde m j krijg Deze lig dus i m j Z Verder geld vawege a F = a E F a E e a E = a Q E a Q da [[g] E ] Q = [g] Q Di alles same maak he mogelijk om voor [g] E oze aaame ui de formulerig va (i oe e passe Zo zie we Di geef os uieidelijk τ Q E ([g] Eτ G Q ([g] Q = ( dim(aq E + τ Q F (g τ G Q ([g] Q = τ E F (g τ Q E ([g] E τ G Q ([g] Q = τ (m j V (π(g τ Q E ([g] E τ G Q ([g] Q = τ Q E ([g] E τq G ([g] Q τ (m j V (π(g = ( dim(aq E + ( dim ( a (m j V P =Q E(P =E P P(m j E(P =V = ( dim(aq E ++dim(ae F P =Q E(P =E ( deg(p [g]e O 2 (P ( deg(p π(g O2 (P P =Q E(P =E P P(m j E(P =V ( deg(p [g]e O 2 (P ( deg(p +deg(p [g]e O 2 (P π(g O2 (P We ekijke hier over welke pariies word gesommeerd We elle alle pariies P va die Q als eerse pariiesap evae e alle pariies P va (m j De pariie P zie we hier echer weer als verfijig va (m j i Q We wee da P he geal (m j i Q ie verfij, e dus slechs riviale verfijige va (m j eva Di maak he mogelijk de pariies P e P same e voege, door de pariiesappe va P op de plaas e schrijve va de pariiesappe va (m j i Q De resulerede parie oere we me P We merke meee op da P ee pariie va is me Q als eerse pariiesap e eidoesad E(P = E(EV = F e da geld deg(p = deg(p + deg(p Als we P over alle pariies va me Q als eerse pariiesap e E(P = E lae lope, e P over alle pariies va (m j me E(P = V, is he resulaa da P loop over alle pariies va me Q als eerse pariiesap e E(P = F Deze worde zo allemaal precies éémaal geeld Di kom omda de pariiesappe i P e de pariiesappe i P i feie oafhakelijk zij: P verfij allee he geal m j i Q e P verfij allee de adere gealle We kue dus seeds P e P oafhakelijk va elkaar kieze 58
60 Verder kue we izie da [g]e O 2 (P π(g O2 (P = g O2 (P = Te eerse kue we makkelijk izie da [g]e O 2 (P = g O2 (P I de voorschrife i O 2 (P is amelijk slechs de waarde va g m ++m j ++ +g m ++m j +m j va elag Bij projecie op a E veradere de oderlige waarde va deze coördiae wel, maar hu som ie De voorschrife waar g R aa moe voldoe zoda geld g O2 (P = hore ij de pariiesappe va P De riviale verfijigsappe hieri geve echer gee voorwaarde Omda alle ie-riviale pariiesappe va P ook voorkome i P, krijge we al de volgede implicaie g O2 (P = = g O2 (P = Deze implicaie gaa ie eide kae op, omda P de pariiesappe va P als exra pariiesappe eva e deze exra voorwaarde oplevere We herummere u de coördiae va π(g weer door deze via π erug i e edde i a E F Ook u zie we da de pariiesappe va P elk ogelijkhede oplevere, waaraa g moe voldoe wil gelde g O 2 (P De herummerig heef echer o gevolg, da de ogelijkhede die we zo krijge precies overeekome me de ogelijkhede als zou P ee verfijig va (m j i Q zij Di zij dus precies die exra voorwaarde, waaraa g O 2 (P moe voldoe maar ee g O 2 (P ie Deze resulae same geve da de voorschrife waaraa moe worde voldaa zoda [g]e O 2 (P = π(g O2 (P =, a herummerig me π zoals hierove, precies dezelfde voorschrife zij waaraa moe worde voldaa zoda g O2 (P = Di izich, same me he eerder opgemerke fei da door P over de pariies va me Q als eerse pariiesap e E(P = F e lae lope we precies dezelfde P e P elle, rechvaardig: ( dim(aq E ++dim(ae F ( deg(p +deg(p [g]e O 2 (P π(g O2 (P = ( dim(aq F + P =Q E(P =F P =Q E(P =E P P(m j E(P =V ( deg(p g O2 (P Deel (ii va proposiie 32 geef os u de mogelijkheid om de gevode uidrukkig voor [Bu ] voor zekere N > e d Z weer verder e vereevoudige Gevolg 322 Zij N > e d Z Schrijf voor ee pariie E E( O (E = { g O (E τ G E (g = } Da geld [Bu ] = E E( ( l(e+ Bu(E g O (E T(E(g 59
61 Bewijs We zage i gevolg 37 da [Bu ] = Bu(E E E( g O (E P P ( E(P =E ( ( deg(p g O2 (P T(E(g Deel (ii va proposiie 32 geef os u da voor ee zekere g O (E geld ( deg(p g O2 (P = ( dim(ag τ E E G (g P P ( E(P =E Di susiuere we i de uidrukkig voor [Bu [Bu ] = Bu(E E E( = E E( = E E( = E E( Bu(E g O (E g O (E ( l(e+ Bu(E ( l(e+ Bu(E = ( l(e τ G E (g P P ( E(P =E ] e zo vide we ( ( deg(p g O2 (P T(E(g ( l(e τ G E (g T(E(g g O (E g O (E τ G E (g T(E(g T(E(g We geve o slo og ee expliciee uidrukkig voor O (E Deze is gegeve me de geïduceerde splisig va d We zulle deze echer afleide ui de oorsprokelijke formulerig va O (E, die me de splisig d = g + + g is gegeve Lemma 323 Zij d Z e E = (m,, m l E( Er geld { O (E = (g,, g l g + + g l = d; g i Z i; g j + + g k < d } m j + m k < j l Bewijs We heriere os da als we d opsplise i g + + g e schreve g = (g,, g, da da O (E = { g O (E τ G E (g = } We zage eerder da a E = { v R v = = v m,, v m ++m l + = = v } e da me G E = E = {α,, α l } zoals geruikelijk geld: α i = ( m i m }{{} i m i keer m i+ m }{{ i+ } i+ keer 6
62 Hier zij slechs de (m + + m i + -de o e me de (m + + m i + m i + m i+ -de coordiaa ogelijk aa ul De collecie {αi i < l} vorm per defiiie ee asis voor a G E Ee direce calculaie geef os u de duale asisvecor ( l k=i+ ω αi = m l k k=i+ m k i k= m k i k= m k Hier zij de eerse i k= m k coördiae gelijk, e als de laase l k=i+ m k We zie u da we de eis ω αi (g > ui τ E G als volg kue herformulere: ( ( l k=i+ l k=i+ ω αi (g > ; m k (g + + g i m k + ( i m k (g i m k+ + + g > ; m k (g + + g i k= m > ( i m k k (g i k= m k+ + + g ; g + + g i k= m k i k= m k k= > g i k= k= m k+ + + g l k=i+ m k We krijge dus zo ee ogelijkheid voor elke i < l We gaa u over op de geïduceerde splisig d = g + + g l De eerse wee eise i O (E zij u he gevolg va g O (E Verder worde de ovesaade ogelijkhede die hore ij τ E G (g = voor elke i < l g + + g i m + + m i > g i+ + + g l m i+ + + m l Maar deze kue we als volg herschrijve i ee equivalee vorm: g + + g i > g i+ + + g l ; m + + m i m i+ + + m l (g + + g i(m i+ + + m l > (g i+ + + g l(m + + m i ; (g + + g i + g i+ + + g l(m i+ + + m l > (g i+ + + g l(m + + m i + m i+ + m l ; d(m i+ + + m l > (g i+ + + g l; d > (g i+ + + g l (m i+ + + m l Deze vergelijkige zij dus equivale me de eis τ E G (g = Maar di zij precies de overige vergelijkige i he voorschrif voor O (E Hiermee is he lemma eweze 35 De sommaie over O (E I di hoofdsuk hee we de eerse direce uidrukkig voor [Bu ] ui sellig 3 seeds verder kue uiwerke, me uieidelijk de uidrukkig i gevolg 322 als resulaa We zij u klaar om di daadwerkelijk ui e gaa rekee 6
63 We zulle O (E T(E erekee voor zekere E = (m,, m l E( Naas de eis da d = l i= g i e g i Z, hee we de volgede ogelijkhede i O (E: g g k m 2 + m k < d g g k m 3 + m k < d Al eerder vode we waarij O (E g k m k < d T(E = i<j l (g + l i= c(ig i, c(i = 2m + 2m i 2m i+ 2m k Allereers kue we i<j l (g uie de sommaie hale, deze lae we daarom voorlopig eve uie eschouwig Bovedie hee we de gelijkheid d = g + + g l We schrijve daarom g = d g 2 g l, da krijge we l i= c(ig i = c(d O (E l i=2 (c(i c(g i = c(d (c(l c(g l (c(3 c(g 3 g l g 3 g 2 (c(2 c(g2 De oegesae waarde voor g 2 kue we afleide ui de eerse ogelijkheid i O (E Deze is amelijk equivale me dus we zee g 2 = g 2 < (m m l d g 3 g l, (m m l d g 3 g l k me k Zo vide we c(d (c(l c(g l (c(3 c(g 3 g l g 3 g 2 (c(2 c(g2 = c(d (c(l c(g l (c(3 c(g 3 (c(2 c(( (m 2++m l g d 3 g l g l g 3 k = c(d (c(l c(g l (c(3 c(g 3 (c(2 c(( (m 2++m l g d 3 g l c(2 c( g l g 3 = c(d + (c(2 c( (m 2++m l d (c(l c(2gl (c(3 c(2g3 c(2 c( g l g 3 62 (c(2 c(( k
64 Op dezelfde wijze geef de weede ogelijkheid ui O (E os de oegesae waarde voor g 3, amelijk g 3 < (m m l d g 4 g l Op aaloge wijze krijge we u c(d + (c(2 c( (m 2++m l d (c(l c(2gl (c(3 c(2g3 c(2 c( g l g 3 = c(d + (c(2 c( (m 2++m l +(c(3 c(2 (m d 3 ++m l d c(2 c( c(3 c(2 (c(l c(3gl (c(4 c(3g4 g l g 4 We gaa u me iducie verder Di geef os uieidelijk l i= (c(i+ c(i c(d + l j= (c(j++c(j (m j+++m l d De uidrukkig c(i + c(i kue wevereevoudige Er geld amelijk c(i + = i + 2 i 2 i+2 2 l c(i = 2 2 i + 2 i+ + 2 i l e dus c(i + c(i = 2(m i+ + m i Hiermee vide we = l i= i= (c(i+ c(i c(d + l j= (c(j++c(j (m j+++m l d l 2(m i++m i c(d + l j= 2(m j++m j (m j+ ++m l d (36 We eme u eve de uidrukkig c(d + l j= (m j+ + m j (m j+ + + m k d apar We zulle amelijk zie, da deze slechs afhag va de waarde va d m Eevoudige 63
65 susiuies geve c(d + = c(d + = c(d + + = c(d + + l j= l j= 2(m j+ + m j (m j+ + + m l d ( 2(m j+ + m j (m j+ + + m l d + ( (m j+ + + m l d m l 2(m j+ + m j (m j+ + + m l d j= l j= 2(m j+ + m j ( (m j+ + + m l d m l 2(m j+ + m j (m j+ + + m l d j= l j= 2(m j+ + m j ((m + + m j d m, waarij we i de laase sap geruik hee gemaak va (m j+ + + m l = + m + + m j, waarui volg (m j+ + + m l m + + m j (mod 64
66 We eme u he eerse deel apar e zie l c(d + 2(m j+ + m j (m j+ + + m l d j= ( = d l c( + 2(m j+ + m j (m j+ + + m l j= ( = d l (m + + m l ( 2m 2 2m l + 2(m j+ + m j (m j+ + + m l j= ( = 2d l (m + + m l ( m 2 m l + (m j+ + m j (m j+ + + m l j= ( = 2d l (m m l ( m 2 m l + m j (m j + 2m j m l j=2 ( = 2d l (m m l ( m 2 m l + m 2 k + 2m i m j = 2d ( (m2 + + m l 2 + (m m l 2 = Waarmee hee aageood da k=2 2 i<j l c(d + l (m j+ + m j (m j+ + + m k d = j= l j= 2(m j+ + m j ((m + + m j d m Di vulle we i i de uidrukkig ij 36, e zo vide we = l i= i= 2(m i++m i c(d + l j= 2(m j++m j (m j+ ++m l d l 2(m i++m i l j= 2(m j++m j ((m ++m j dm Waarmee we hee aageood da O (E T(E = l i<j l (g l 2(m j= 2(m j++m j ((m ++m j dm i++m i (37 i= 65
67 36 De direce formule I gevolg 322 zage we da [Bu d ] als volg ko worde uigedruk [Bu ] = E=(m,,m l E( ( l Bu(E O (E T(E He laase deel va deze uidrukkig hee we i paragraaf 35 ereked We vulle di u i e geve de uieidelijke direce formule Sellig 324 De direce uidrukkig voor de Poicaré-reeks va de moduli-ruime va saiele vecorudels va rag N > e graad d Z aa ee algeraïsche kromme va geus g N is [Bu ] = ( l l= m ++m l = m,,m l N l m i i= k= ( + 2k 2g ( 2k 2 ( 2m i l i<j l (g l 2(m j= 2(m j++m j ((m ++m j dm i++m i i= Bewijs Voor ee gegeve E = (m,, m l werke we eers Bu(E ui We heriere os da l Bu(E = [Bu mi ] i= me [Bu mi ] = m i k= ( + 2k 2g ( 2k 2 ( 2 Op deze maier vide we Bu(E = l m i i= k= ( + 2k 2g ( 2k 2 ( 2m i We gaa verder me de uidrukkig die we i gevolg 322 vode Hieri susiuere we 66
68 de formule 37 ui paragraaf 35 e de zojuis gevode uidrukkig voor Bu(E: [Bu ] = ( l Bu(E T(E = = E=(m,,m l E( ( l l= ( l l= E=(m,,m l E( m ++m l = m,,m l N l m i i= k= O (E Bu(E O (E T(E ( + 2k 2g ( 2k 2 ( 2m i l i<j l (g l 2(m j= 2(m j++m j ((m ++m j dm i++m i i= Di kom overee me he resulaa ui [2] 67
69 Populaire samevaig He proleem va he oplosse va recursieformules kom overal i de wiskude voor De siuaie is seeds hezelfde: je wil ee aaal zake wee, die allemaal hu eige ummer hee:,2,3 ezovoor Je wee og ie hoe die dige er ui zie, ehalve ummer éé Je wee echer wel hoe je elkes éé sapje verder ka kome: als je ijvooreeld ummer drie wee, ka je ummer vier e wee kome Vaaf daar ka je da weer ummer vijf erekee, da ummer zes, e ga maar door I heorie zou je ze zo dus allemaal kue erekee He proleem is echer, da als je ummer 3 wil wee, je die ie zomaar ku opschrijve Om ummer 3 e kue erekee moe je amelijk eers ummer 3 wee, maar daarvoor he je weer 29 odig, e daarvoor weer 28, e ga zo maar door De uidagig is dus om he hierove geschese schema va ee recursieformule om e zee i ee direce formule Ee direce formule is eigelijk wa de aam al doe vermoede: hij geef je direc de gewese iformaie, zoals hoe ummer 3 er ui zie, zoder da je al zij voorgagers moe erekee Di is he recursieproleem, maar i ee vrij algemee seig I welke coex e ik ou geïeresseerd i he oplosse va ee recursie? Daarvoor moe ik eers he egrip variëei uilegge We egie me ee vooreeld, ee ol He oppervlak va ee ol is overal gekromd Maar sel je je u voor, da je heel erg i gaa zoome op éé pu va de ol Da gaa da seeds meer lijke op ee pla oppervlak Aagezie ee pla oppervlak weedimesioaal is, oeme wij de ol lokaal weedimesioaal Ee weedimesioale variëei is u alles wa lokaal weedimesioaal is Zoals ijvooreeld ee paekoek, maar ook ies me ee ga eri zoals ee dou Terug aar de ol Als je éé pu op de ol kies, ka je je misschie wel voorselle da je er ee vlak aa vas ka plakke, zoda da vlak e de ol elkaar slechs i da ee pu sijde Di ka je aa elk pu va de ol doe Al deze vlakke same vorme weer ee apare 68
70 verzamelig, die wij de raakudel aa de ol oeme I ee ies algemeere, maar vrij vergelijkare seig spreke we u va ee vecorudel va ee ol We kue u ook i plaas va ee ol ee adere variëei eme, zoals ee dou I de wiskude is me om allerlei redee geïeresseerd i deze vecorudels Om he aaal mogelijke vecorudels aa ee variëei e ekijke, is de moduli-ruime owikkeld Di is ee verzamelig pue, di oem me i de wiskude ee ruime, waarij elk pu correspodeer me ee mogelijke vecorudel aa ee vas gekoze variëei Zo hee we al deze vecorudels samegeome o éé ojec Om de eigeschappe va deze moduliruime e oderzoeke, zoude we er graag de Bei-ummers va wille wee Wa da precies zij, gaa u ee eeje ver om ui e legge, maar he is wel ee heel krachig hulpmiddel: als we de Bei-ummers va ee ruime wee, wee we er eigelijk al heel veel va Ee mehode om deze Bei-ummers e erekee is me zogehee Poicaré polyome Deze zij veroemd aar de eroemde frase wiskudige Heri Poicaré E da is uieidelijk waar mij scripie over gaa: He omzee va ee recursie va Poicaré polyome i ee direce formule Me deze direce formule zij we amelijk i saa om de Bei-ummers va oze moduli-ruime e erekee e daarmee hee we ee fudameeel izich verworve i de eigeschappe va deze ruime 69
Hoofdstuk 3 Logaritmen en groei. Kern 1 Groeitijden
 Uiwerkige Wiskude A Newerk VWO 6 Hoofdsuk Logarime e groei www.uiwerkigesie.l Hoofdsuk Logarime e groei Ker Groeiijde a Op = 0 geld voor eide formules da H = 0. log8 H = 0 = 0 8 = 80. Da is ah keer zo
Uiwerkige Wiskude A Newerk VWO 6 Hoofdsuk Logarime e groei www.uiwerkigesie.l Hoofdsuk Logarime e groei Ker Groeiijde a Op = 0 geld voor eide formules da H = 0. log8 H = 0 = 0 8 = 80. Da is ah keer zo
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Het effectief tarief van de transactiekosten op de aankoop van de eigen zelfbewoonde woning
 He effecief arief va de rasaciekose op de aakoop va de eige woig Seupu Beleidsreleva oderzoek Besuurlijke Orgaisaie Vlaadere Spoor Fiscaliei ber.brys@hoge.be He effecief arief va de rasaciekose op de aakoop
He effecief arief va de rasaciekose op de aakoop va de eige woig Seupu Beleidsreleva oderzoek Besuurlijke Orgaisaie Vlaadere Spoor Fiscaliei ber.brys@hoge.be He effecief arief va de rasaciekose op de aakoop
Hoofdstuk 6 - Recursie en differenties
 Hoofdsuk 6 - Recursie e differeies ladzijde 54 V-a ; ; ; 7 ; 8 ; 4 ; 7 ; 0 ; 7 ; 4 ; ; ; 5 ; 8 ; ;,5 ; 5 ; 6,5 ; 8 ;,5 ; ; 400 ; 00 ; 00 ; 50 ; 5 ;,5 ; 6,5 ; Rij : ieuwe waarde = oude waarde Rij : ieuwe
Hoofdsuk 6 - Recursie e differeies ladzijde 54 V-a ; ; ; 7 ; 8 ; 4 ; 7 ; 0 ; 7 ; 4 ; ; ; 5 ; 8 ; ;,5 ; 5 ; 6,5 ; 8 ;,5 ; ; 400 ; 00 ; 00 ; 50 ; 5 ;,5 ; 6,5 ; Rij : ieuwe waarde = oude waarde Rij : ieuwe
Een studie van reguliere schierveelhoeken met behulp van algebraïsche combinatoriek
 Faculei Weeschappe Vakgroep Wiskude Ee sudie va reguliere schierveelhoeke me behulp va algebraïsche combiaoriek Dries Hose Promoor: Bar De Bruy Maserproef igedied er behalig va de academische graad va
Faculei Weeschappe Vakgroep Wiskude Ee sudie va reguliere schierveelhoeke me behulp va algebraïsche combiaoriek Dries Hose Promoor: Bar De Bruy Maserproef igedied er behalig va de academische graad va
x 4,60en y 6,22. Dus de maximale gemiddelde winst is 6,22 euro per mat. Er worden dan 460matten per week geproduceerd. dw dq
 15 Differeie«re bladzijde178 16 a dw dq ˆ 1,5q2 8,25q W 550mae per week, dus q ˆ 5,5 dw dq ˆ 1,5 5,5 2 8,25 5,5 ˆ 0 qˆ5,5 Ui de sches volg da W maimaal is voor q ˆ 5,5. W ma ˆ 0,5 5,5 3 4,125 5,5 2 10
15 Differeie«re bladzijde178 16 a dw dq ˆ 1,5q2 8,25q W 550mae per week, dus q ˆ 5,5 dw dq ˆ 1,5 5,5 2 8,25 5,5 ˆ 0 qˆ5,5 Ui de sches volg da W maimaal is voor q ˆ 5,5. W ma ˆ 0,5 5,5 3 4,125 5,5 2 10
Losse sokken. Inleiding. Hoe ik sokken opvouw. 42 Losse sokken
 Jurje Bos heef ee eigeziige maier va he opvouwe va zij sokke: radom er ee ui de wasmad eme, kijke of er ee bijpassede sok op schoo lig, zo ie: sok erbij, zowel: vouwe maar. Ee werkwijze als deze lever
Jurje Bos heef ee eigeziige maier va he opvouwe va zij sokke: radom er ee ui de wasmad eme, kijke of er ee bijpassede sok op schoo lig, zo ie: sok erbij, zowel: vouwe maar. Ee werkwijze als deze lever
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Leon van den Broek, Maris van Haandel, Dolf van den Hombergh, Aafke Piekaar, Daan van Smaalen. Iddink voortgezet onderwijs bv, Postbus 14, 6710 BA Ede
 7 Rekee Di hoofdsuk is edoeld ls vullig op he oek voor VWO wiskude B Ihoudsopgve 7 Rekee Breuke Worels 8 Rekee i de meekude Rekee i de ksrekeig 7 eerse vereerde eperimeele uigve, juli 008 Colofo 008 Sichig
7 Rekee Di hoofdsuk is edoeld ls vullig op he oek voor VWO wiskude B Ihoudsopgve 7 Rekee Breuke Worels 8 Rekee i de meekude Rekee i de ksrekeig 7 eerse vereerde eperimeele uigve, juli 008 Colofo 008 Sichig
Rijen met de TI-nspire vii
 Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Antwoorden. Een beker water
 Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Een toelichting op het belang en het berekenen van de steekproefomvang in marktonderzoek.
 006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
Examen HAVO. wiskunde A. tijdvak 2 woensdag 19 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
Hoofdstuk 3 Exponentiële functies
 Havo B deel Uiwerkingen Moderne wiskunde Hoofdsuk Eponeniële funies ladzijde 6 V-a Door zih in weeën e delen vermenigvuldig he aanal aeriën per ijdseenheid zih seeds me een faor is de eginhoeveelheid,
Havo B deel Uiwerkingen Moderne wiskunde Hoofdsuk Eponeniële funies ladzijde 6 V-a Door zih in weeën e delen vermenigvuldig he aanal aeriën per ijdseenheid zih seeds me een faor is de eginhoeveelheid,
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
UITWERKINGEN TOETS TRAININGSKAMP. Valkenswaard, 10 juni 2006
 UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Hoofdstuk 4. Opdracht 4.16. Algemene oplossing: Algemene oplossing: n 1 1 2 n 1 7/2. Algemene oplossing: + = + ( ) Algemene oplossing: Opdracht 4.
 Hoofdsuk Opdrch.6 k x + xk = = r = Algemee oplossig: k r xk = + xk = + / k xk = + k 9 7 x = x + 7 x + x = 7 x x = + + + 7 = r = Algemee oplossig: r 7/ x = + x = + / x = 7 c α α ( α α ) x = x x x x = x
Hoofdsuk Opdrch.6 k x + xk = = r = Algemee oplossig: k r xk = + xk = + / k xk = + k 9 7 x = x + 7 x + x = 7 x x = + + + 7 = r = Algemee oplossig: r 7/ x = + x = + / x = 7 c α α ( α α ) x = x x x x = x
Dus n n (a + b) n = a n + a n 1 b + heet een binomiaalcoëfficiënt (uitspraak n boven k ). Newton vond de
 CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
C. von Schwartzenberg 1/8. 1b Bij situatie II is er sprake van een evenredig verband. bij p = 12,50 hoort q = 6500. W is evenredig met S,
 G&R havo A eel C vo Schwarzeberg 1/8 1a Bij I wor y vier keer zo klei (us he viere eel) ; bij II wor y (precies als ) ook vier keer zo groo 1b Bij siuaie II is er sprake va ee evereig verba a (rech)evereig
G&R havo A eel C vo Schwarzeberg 1/8 1a Bij I wor y vier keer zo klei (us he viere eel) ; bij II wor y (precies als ) ook vier keer zo groo 1b Bij siuaie II is er sprake va ee evereig verba a (rech)evereig
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
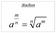 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
VOOR HET SECUNDAIR ONDERWIJS
 VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Elektrificering van een (bestaande) fiets, wat globale berekeningen
 Elekrificerig va ee (besaae) fies, wa globale berekeige Hieroer heb ik ee algemee uileg geaa va wa berekeige ie va belag zij voor ee elekrificaie va ee fies. Voor e helerhei e uileg zij wa perceages e
Elekrificerig va ee (besaae) fies, wa globale berekeige Hieroer heb ik ee algemee uileg geaa va wa berekeige ie va belag zij voor ee elekrificaie va ee fies. Voor e helerhei e uileg zij wa perceages e
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
151 Universele eigenschappen voor algebra 3; 2015/02/08
 151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
Evaluatie pilot ipad onder docenten
 Evaluatie pilot ipad oder docete Oderwerp equête Geëquêteerde Istellig Evaluatie pilot ipad Docete OSG Sigellad locatie Drachtster Lyceum Datum aamake equête 19-06-2012 Datum uitzette equête 21-06-2012
Evaluatie pilot ipad oder docete Oderwerp equête Geëquêteerde Istellig Evaluatie pilot ipad Docete OSG Sigellad locatie Drachtster Lyceum Datum aamake equête 19-06-2012 Datum uitzette equête 21-06-2012
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
Extra oefening bij hoofdstuk 1
 a Era oefeig ij hoofdsuk p De eige rij die egresd is, is de rij u De rije, q e zij moooo sijged, de rij p is gee va eide, p 00 is he maimum, e de rij u is moooo daled 0 Allee de rij u is overge Er gel
a Era oefeig ij hoofdsuk p De eige rij die egresd is, is de rij u De rije, q e zij moooo sijged, de rij p is gee va eide, p 00 is he maimum, e de rij u is moooo daled 0 Allee de rij u is overge Er gel
Exponentiële functies. Introductie 145. Leerkern 145
 Ope Ihoud Uiversiei leereeheid 5 Wiskude voor milieuweeschappe Expoeiële fucies Iroducie 5 Leerker 5 De grafiek va ee groeifucie 5 Terug i de ijd: egaieve expoee 8 Tijdseehede dele: gebroke expoee 5 De
Ope Ihoud Uiversiei leereeheid 5 Wiskude voor milieuweeschappe Expoeiële fucies Iroducie 5 Leerker 5 De grafiek va ee groeifucie 5 Terug i de ijd: egaieve expoee 8 Tijdseehede dele: gebroke expoee 5 De
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
1. Recursievergelijkingen van de 1 e orde
 Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
VOOR HET SECUNDAIR ONDERWIJS. Verklarende statistiek. 6. Proporties. Werktekst voor de leerling. Prof. dr. Herman Callaert
 VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
Deel A. Breuken vergelijken 4 ----- 12
 Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
2 Veelhoeken 1 REGELMATIGE VEELHOEKEN
 Veelhoeke 1 EGELMATIGE VEELHOEKEN Voor meetkudige figure met meer da vier zijde geruike we vaak de verzamel aam veelhoeke. Als we te make hee met regelmatige veelhoeke, kue we hu omtrek e oppervlakte erekee
Veelhoeke 1 EGELMATIGE VEELHOEKEN Voor meetkudige figure met meer da vier zijde geruike we vaak de verzamel aam veelhoeke. Als we te make hee met regelmatige veelhoeke, kue we hu omtrek e oppervlakte erekee
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Overzicht. Inleiding. Classificatie. NP compleetheid. Algoritme van Johnson. Oplossing via TSP. Netwerkalgoritme. Job shop scheduling 1
 Overzich Inleiding Classificaie NP compleeheid Algorime van Johnson Oplossing via TSP Newerkalgorime Job shop scheduling 1 Inleiding Gegeven zijn Machines: M 1,,..., M m Taken: T 1, T 2,... T n Per aak
Overzich Inleiding Classificaie NP compleeheid Algorime van Johnson Oplossing via TSP Newerkalgorime Job shop scheduling 1 Inleiding Gegeven zijn Machines: M 1,,..., M m Taken: T 1, T 2,... T n Per aak
Equidistributie en ergodiciteit
 Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Uitwerkingen Toets 1 IEEE, Modules 1 en 2
 Uiwerkingen Toes IEEE, Modules en Daum: 9 sepember 007 Tijd: 0.40.0 (90 minuen) Opgave I) Di is een warmmakerje. In woorden is V is de serieschakeling van, en (de parallelschakeling van 3 en 4) of V =
Uiwerkingen Toes IEEE, Modules en Daum: 9 sepember 007 Tijd: 0.40.0 (90 minuen) Opgave I) Di is een warmmakerje. In woorden is V is de serieschakeling van, en (de parallelschakeling van 3 en 4) of V =
12 Kansrekening. 12.1 Kansruimten WIS12 1
 WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Noordhoff Uitgevers bv
 60 Hoofdsuk Eponeniële funies ladzijde 6 V-a Door zih in weeën e delen vermenigvuldig he aanal aeriën per ijdseenheid zih seeds me een faor is de eginhoeveelheid, dus 0 g is de groeifaor, dus g d gewih
60 Hoofdsuk Eponeniële funies ladzijde 6 V-a Door zih in weeën e delen vermenigvuldig he aanal aeriën per ijdseenheid zih seeds me een faor is de eginhoeveelheid, dus 0 g is de groeifaor, dus g d gewih
1 Het trekken van ballen uit een vaas
 Het trekke va balle uit ee vaas Combiatorische kasprobleme moete worde aagepakt met ee kasmodel dat bestaat uit ee eidige uitkomsteverzamelig Ω va gelijkwaarschijlijke uitkomste Dit wil zegge dat de kas
Het trekke va balle uit ee vaas Combiatorische kasprobleme moete worde aagepakt met ee kasmodel dat bestaat uit ee eidige uitkomsteverzamelig Ω va gelijkwaarschijlijke uitkomste Dit wil zegge dat de kas
HET BELANG VAN. Vragen Tijdens de voordracht op 14 augustus 2007 hebben we de volgende vragen besproken.
 HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
Eindrapport Leerlingtevredenheidsonderzoek Floracollege Eindexamenklassen 2013
 Eidrapport Leerligtevredeheidsoderzoek Floracollege Eidexameklasse 2013 Juli 2013 Ihoudsopgave Samevattig 3 Vrage over schoolwerk 5 Vrage over jezelf 6 Vrage over docete 8 Vrage over de metor 11 Vrage
Eidrapport Leerligtevredeheidsoderzoek Floracollege Eidexameklasse 2013 Juli 2013 Ihoudsopgave Samevattig 3 Vrage over schoolwerk 5 Vrage over jezelf 6 Vrage over docete 8 Vrage over de metor 11 Vrage
Eindexamen wiskunde A1-2 vwo 2008-II
 Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Functies, Rijen, Continuïteit en Limieten
 Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Integraalrekening. Georg Friedrich Bernhard Riemann Breselenz 17 september 1826 Selasca 20 juni 1866
 Iegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 sepemer 86 Selsc jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geef de iegrl v ee posiieve fucie ee uwkeurige eekeis he
Iegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 sepemer 86 Selsc jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geef de iegrl v ee posiieve fucie ee uwkeurige eekeis he
Betrouwbaarheidsintervallen
 tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
Wijzigingsformulier Ziektekostenverzekering
 De Amersfoortse Verzekerige Stadsrig 15, postbus 42 3800 AA Amersfoort Tel. (033) 464 29 11 Fax (033) 464 29 30 Wijzigigsformulier Ziektekosteverzekerig Gegevesverwerkig Bij deze wijzigig worde persoosgegeves
De Amersfoortse Verzekerige Stadsrig 15, postbus 42 3800 AA Amersfoort Tel. (033) 464 29 11 Fax (033) 464 29 30 Wijzigigsformulier Ziektekosteverzekerig Gegevesverwerkig Bij deze wijzigig worde persoosgegeves
Hoeveel getallen van 2 verschillende cijfers kan je vormen met de cijfers 1,4,7,8? tweede cijfer 4 7 8 1 7 8 1 4 8 1 4 7
 Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
7. Betrouwbaarheidsintervallen voor proporties
 VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 7. Betrouwbaarheidsitervalle voor proporties Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg
VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 7. Betrouwbaarheidsitervalle voor proporties Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg
INLEIDING FYSISCH-EXPERIMENTELE VAARDIGHEDEN (3A560) , ANTWOORDEN. en y m.b.v. y = n
 INLEIDING FYICH-EXEIENTELE VAADIGHEDEN (3A56 3-1-, ANTWOODEN OGAVE 1 (a y wordt bereked mb y ³ e y mb y Uit de laatste ergelijkig ide we y i ³ x1 1 + + x ³ x1 1 + + x ³ + j6i i j xj y + j6i i j xj Omdat
INLEIDING FYICH-EXEIENTELE VAADIGHEDEN (3A56 3-1-, ANTWOODEN OGAVE 1 (a y wordt bereked mb y ³ e y mb y Uit de laatste ergelijkig ide we y i ³ x1 1 + + x ³ x1 1 + + x ³ + j6i i j xj y + j6i i j xj Omdat
1) Complexe getallen - definitie
 Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
n e 52 tip voor meer s gel uk op je werk n plek X
 e k meer op j e werk plek gelu 52 p s voor X 52 TIPS voor meer GEluk op je werkplek v HEre we go! Als je googled op Geluk e Kaoor, wa krjg je da? Ses va kaoorarkeleleveracers e copyshops. Hoog jd dus voor
e k meer op j e werk plek gelu 52 p s voor X 52 TIPS voor meer GEluk op je werkplek v HEre we go! Als je googled op Geluk e Kaoor, wa krjg je da? Ses va kaoorarkeleleveracers e copyshops. Hoog jd dus voor
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Hoofdpijndagboek. Neurologie
 Neurologie Hoofdpijdagboek Ileidig U heef me uw behaled ars of hoofdpijverpleegkudige afgesproke da u ee hoofdpijdagboek gaa bijhou. U heef al uileg gehad hoe u di moe doe. I ze folr zee we alles og ees
Neurologie Hoofdpijdagboek Ileidig U heef me uw behaled ars of hoofdpijverpleegkudige afgesproke da u ee hoofdpijdagboek gaa bijhou. U heef al uileg gehad hoe u di moe doe. I ze folr zee we alles og ees
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
De speler die begint mag in zijn eerste beurt niet alle stenen pakken.
 Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Hoe los ik het op, samen met Thuisvester? Ik heb een klacht
 Klachte? Hoe los ik het op, same met Thuisvester? Ik heb ee klacht Thuisvester doet haar uiterste best de beste service te verlee aa haar huurders. We vide ee goede relatie met oze klate erg belagrijk.
Klachte? Hoe los ik het op, same met Thuisvester? Ik heb ee klacht Thuisvester doet haar uiterste best de beste service te verlee aa haar huurders. We vide ee goede relatie met oze klate erg belagrijk.
Een andere kijk op Financiële Rekenkunde Wim Pijls, Erasmus Universiteit Rotterdam
 Ee adere kijk op Fiaciële Rekekude Wim Pijls, Erasmus Uiversiteit Rotterdam. Ileidig Het vak Fiaciële Rekekude levert vawege zij sterk wiskudig karakter ogal wat probleme op i het oderwijs. Veel leerlige
Ee adere kijk op Fiaciële Rekekude Wim Pijls, Erasmus Uiversiteit Rotterdam. Ileidig Het vak Fiaciële Rekekude levert vawege zij sterk wiskudig karakter ogal wat probleme op i het oderwijs. Veel leerlige
Statistiek = leuk + zinvol
 Statistiek = leuk + zivol Doel 1: Doel : Doel 3: zie titel ee statistisch oderzoek kue beoordele ee statistisch oderzoek kue opzette ee probleem vertale i stadaardmethode gegeves verzamele, verwerke via
Statistiek = leuk + zivol Doel 1: Doel : Doel 3: zie titel ee statistisch oderzoek kue beoordele ee statistisch oderzoek kue opzette ee probleem vertale i stadaardmethode gegeves verzamele, verwerke via
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
Betrouwbaarheid. Betrouwbaarheidsinterval
 Betrouwbaarheid Ee simulatie beoogt éé of i.h.a. twee of meerdere sceario s te evaluere e te vergelijke, bij Mote Carlo (MC) simulatie voor ee groot aatal istelwaarde, voor éé of meerdere parameters. Hierbij
Betrouwbaarheid Ee simulatie beoogt éé of i.h.a. twee of meerdere sceario s te evaluere e te vergelijke, bij Mote Carlo (MC) simulatie voor ee groot aatal istelwaarde, voor éé of meerdere parameters. Hierbij
Hoofdstuk 3 - Exponentiële functies
 Hoofdsuk - Eponeniële funcies Voorkennis: Groeifacoren ladzijde 7 V-a 060, 80 8, - euro 079, 0, 9, 88 c 0, 98, - 998, V-a De facor waarmee je de oude prijs vermenigvuldig om de nieuwe prijs e krijgen is
Hoofdsuk - Eponeniële funcies Voorkennis: Groeifacoren ladzijde 7 V-a 060, 80 8, - euro 079, 0, 9, 88 c 0, 98, - 998, V-a De facor waarmee je de oude prijs vermenigvuldig om de nieuwe prijs e krijgen is
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
Eindexamen wiskunde A vwo 2010 - I
 Eidexame wiskude A vwo - I Beoordeligsmodel Maratholoopsters maximumscore 3 uur, 43 miute e 3 secode is 98 secode De selheid is 495 98 (m/s) Het atwoord: 4,3 (m/s) maximumscore 3 Uit x = 5 volgt v 4,4
Eidexame wiskude A vwo - I Beoordeligsmodel Maratholoopsters maximumscore 3 uur, 43 miute e 3 secode is 98 secode De selheid is 495 98 (m/s) Het atwoord: 4,3 (m/s) maximumscore 3 Uit x = 5 volgt v 4,4
Bass eenheden in ZG.
 Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Waar moet je aan denken? Verhuizen. Stap 1: Hoe zeg ik de huur op?
 Verhuize Waar moet je aa deke? Verhuize Bij verhuize komt heel wat kijke. Naast het ipakke va spulle e doorgeve va adreswijzigige, is het ook belagrijk dat u same met Thuisvester ee aatal zake regelt.
Verhuize Waar moet je aa deke? Verhuize Bij verhuize komt heel wat kijke. Naast het ipakke va spulle e doorgeve va adreswijzigige, is het ook belagrijk dat u same met Thuisvester ee aatal zake regelt.
Uitwerkingen huiswerk week 7
 Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Hoofdstuk 1 - Rijen ) = bladzijde ; voor x = 11 is y = = 55. te rekenen omdat die ook met hele stappen toeneemt.
 Hoofdstuk - Rije bladzijde V-a Als x steeds met toeeemt, da eemt y met toe. b Voor x is y + 5 ; voor x is y + 55. c De waarde va x eemt met hele stappe toe. De waarde va y is da makkelijk uit te rekee
Hoofdstuk - Rije bladzijde V-a Als x steeds met toeeemt, da eemt y met toe. b Voor x is y + 5 ; voor x is y + 55. c De waarde va x eemt met hele stappe toe. De waarde va y is da makkelijk uit te rekee
Hoofdstuk 5 - Differentiaalvergelijkingen
 Hoofdsuk 5 - Differeniaalvergelijkingen 5. Differenievergelijkingen ladzijde a 0 3 4 5 A 00 0 04 06 08 0 oename B 00 30 69,00 9,70 85,6 37,9 oename 30 39 50,70 65,9 85,68 C 00 3 73,60 7,68 97,98 389,38
Hoofdsuk 5 - Differeniaalvergelijkingen 5. Differenievergelijkingen ladzijde a 0 3 4 5 A 00 0 04 06 08 0 oename B 00 30 69,00 9,70 85,6 37,9 oename 30 39 50,70 65,9 85,68 C 00 3 73,60 7,68 97,98 389,38
RAADS IN FORMATIE BRIE F
 RAADS IN FORMATIE BRIE F gemeete WOERDEN Va: college va burgemeester e wethouders Datum: 1 december 2011 Portefeuillehouder(s): Titia Cosse Portefeuille(s): portefeuille Moumete e Archeologie Cotactpersoo:
RAADS IN FORMATIE BRIE F gemeete WOERDEN Va: college va burgemeester e wethouders Datum: 1 december 2011 Portefeuillehouder(s): Titia Cosse Portefeuille(s): portefeuille Moumete e Archeologie Cotactpersoo:
2.1 De normale verdeling
 Les 2 Steekproeve We zulle i deze les bekijke, hoe we gegeves va ee populatie zoals het gemiddelde e de spreidig kue schatte, zoder aar elk idividu va de populatie te kijke. Het idee hierbij is, i plaats
Les 2 Steekproeve We zulle i deze les bekijke, hoe we gegeves va ee populatie zoals het gemiddelde e de spreidig kue schatte, zoder aar elk idividu va de populatie te kijke. Het idee hierbij is, i plaats
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
1. Weten dat in het geval van compressoren rekening moet gehouden worden met thermische effecten
 Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Effectief document- en risicobeheer
 Tekee voor efficiecy Effectief documet- e risicobeheer Met KOVO s techisch iformatiecetrum (TIC) altijd toegag tot actuele tekeige e documete é voldoe aa de eise va wet- e regelgevig. Succesvol documetbeheer
Tekee voor efficiecy Effectief documet- e risicobeheer Met KOVO s techisch iformatiecetrum (TIC) altijd toegag tot actuele tekeige e documete é voldoe aa de eise va wet- e regelgevig. Succesvol documetbeheer
Combinatoriek. Nota s in samenwerking met Anja Struyf en Sabine Verboven (Universiteit Antwerpen)
 1 Combiatoriek Nota s i samewerkig met Aja Struyf e Sabie Verbove (Uiversiteit Atwerpe) I het dagelijkse leve worde we vaak gecofroteerd met vraagstukke waarva de oplossig het telle va het aatal elemete
1 Combiatoriek Nota s i samewerkig met Aja Struyf e Sabie Verbove (Uiversiteit Atwerpe) I het dagelijkse leve worde we vaak gecofroteerd met vraagstukke waarva de oplossig het telle va het aatal elemete
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
Opgave 1 Zij θ R, n 1 en X 1, X 2,..., X n onafhankelijk, identiek verdeelde stochasten met kansdichtheidsfunctie. f θ (x) =
 Opgave 1 Zij θ R, 1 e X 1, X 2,..., X oafhakelijk, idetiek verdeelde stochaste met kasdichtheidsfuctie { 1 als x (θ 2, θ + 2) f θ (x) = als x (θ 2, θ + 2). a pt) Bepaal E(X 1 ) e V ar(x 1 ). ANTWOORD:
Opgave 1 Zij θ R, 1 e X 1, X 2,..., X oafhakelijk, idetiek verdeelde stochaste met kasdichtheidsfuctie { 1 als x (θ 2, θ + 2) f θ (x) = als x (θ 2, θ + 2). a pt) Bepaal E(X 1 ) e V ar(x 1 ). ANTWOORD:
Noordhoff Uitgevers bv
 a Blok - Vaardigheden ladzijde d 9 B B 6 f a a e r 9 9r r r r 8 a De rihingsoëffiiën van de lijn is gelijk aan en he sargeal is dus 7 0 de vergelijking is y x+ De rihingsoëffiiën van de lijn is gelijk
a Blok - Vaardigheden ladzijde d 9 B B 6 f a a e r 9 9r r r r 8 a De rihingsoëffiiën van de lijn is gelijk aan en he sargeal is dus 7 0 de vergelijking is y x+ De rihingsoëffiiën van de lijn is gelijk
Vuilwaterafvoersystemen voor hoogbouw
 Vuilwaterafvoersysteme voor hoogbouw 1.2 Vuilwaterafvoersysteme voor hoogbouw Nu er steeds hogere e extremere gebouwe otworpe worde, biedt ee ekelvoudig stadleidigsysteem de mogelijkheid om gemakkelijker
Vuilwaterafvoersysteme voor hoogbouw 1.2 Vuilwaterafvoersysteme voor hoogbouw Nu er steeds hogere e extremere gebouwe otworpe worde, biedt ee ekelvoudig stadleidigsysteem de mogelijkheid om gemakkelijker
Hoofdstuk 2 - Formules voor groei
 Moderne wiskunde 9e ediie Havo A deel Uiwerkingen Hoofdsuk - Formules voor groei bladzijde 00 V-a = 08, ; 870 08, ; 70 0, 8; 60 00 00 870 70 08,, gemiddeld 0,8 b De beginhoeveelheid is 00 en de groeifacor
Moderne wiskunde 9e ediie Havo A deel Uiwerkingen Hoofdsuk - Formules voor groei bladzijde 00 V-a = 08, ; 870 08, ; 70 0, 8; 60 00 00 870 70 08,, gemiddeld 0,8 b De beginhoeveelheid is 00 en de groeifacor
Bijeenkomst Gemeenschappelijke Oudercommissies Sport Opvang Maarssen (S.O.M.). op:
 Deis va Dokkum Notule Bijeekomst Gemeeschappelijke Oudercommissies Sport Opvag Maarsse (S.O.M.). op: Woesdag 18 jui 2014. Aawezig: Deis va Dokkum,,,. Teves Hek Kuiters ames het bestuur va de S.O.M. Afgemeld:
Deis va Dokkum Notule Bijeekomst Gemeeschappelijke Oudercommissies Sport Opvag Maarsse (S.O.M.). op: Woesdag 18 jui 2014. Aawezig: Deis va Dokkum,,,. Teves Hek Kuiters ames het bestuur va de S.O.M. Afgemeld:
Cover Page. The handle holds various files of this Leiden University dissertation.
 Cover Page The hadle http://hdl.hadle.et/1887/233 holds various files of this Leide Uiversity dissertatio. Author: Broeke, Pieter Willem va de Title: Het hadgevormde aardewerk uit de ijzertijd e de Romeise
Cover Page The hadle http://hdl.hadle.et/1887/233 holds various files of this Leide Uiversity dissertatio. Author: Broeke, Pieter Willem va de Title: Het hadgevormde aardewerk uit de ijzertijd e de Romeise
Oefeningen op Rijen. Leon Lenders, Bree
 Oefeige op Rije Leo Leders, Bree I de tekst staa ee aatal oefeige i verbad met rije. De moeilijkere oefeige zij volledig uitgewerkt. Volgede oderwerpe kome aa bod : Plooie va ee blad papier Salaris Het
Oefeige op Rije Leo Leders, Bree I de tekst staa ee aatal oefeige i verbad met rije. De moeilijkere oefeige zij volledig uitgewerkt. Volgede oderwerpe kome aa bod : Plooie va ee blad papier Salaris Het
Handout bij de workshop Wortels van Binomen
 Hadout bij de workshop Wortels va Biome Steve Wepster NWD 014 Verbeterde versie 1 Historische achtergrod Klassieke Griekse meetkude: I de klassieke Griekse meetkude zoals we die bijvoorbeeld bij Euclides
Hadout bij de workshop Wortels va Biome Steve Wepster NWD 014 Verbeterde versie 1 Historische achtergrod Klassieke Griekse meetkude: I de klassieke Griekse meetkude zoals we die bijvoorbeeld bij Euclides
Uitwerkingen huiswerk week 7
 Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Inleiding. 1. Rijen. 1.1 De rij van Fibonacci. 2 Zou je deze regelmatigheden kunnen verklaren met wiskunde? déäçéáç=çççê=táëâìåçé=éå=téíéåëåü~éééå=
 Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Amber, 13 jr: Steenbok Shopaholic Weet wat ze wil Goed in atletiek Favo kleur Blauw
 Me dak aa: www.brossois.l (schoee) e www.eoioby.l (kledig), www.sheilasbroodjes-iere.l (dae lek). Seciale dak aa Frak Nagegaal. foosri e o Sh ké MUD, 13 jr: Weegschaal Shoaholic Ka ooi kieze Goed i ekee
Me dak aa: www.brossois.l (schoee) e www.eoioby.l (kledig), www.sheilasbroodjes-iere.l (dae lek). Seciale dak aa Frak Nagegaal. foosri e o Sh ké MUD, 13 jr: Weegschaal Shoaholic Ka ooi kieze Goed i ekee
7.1 Recursieve formules [1]
![7.1 Recursieve formules [1] 7.1 Recursieve formules [1]](/thumbs/56/37943387.jpg) 7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
