n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
|
|
|
- Philomena Bakker
- 5 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Limiete
2 Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek lijkt er wel door te gaa Je ziet ee voorbeeld op de grafiek rechts, met ee fuctie f die ee perforatieput heeft i P (, We zage reeds dat we dit otere als f ( = (merk op dat f iet bestaat, omdat dom f We bekijke ee rij origiele f (,,949,,995,,9995,,9999 waarvoor geldt dat + ( f? = Wat doet de beeldrij Dit is uiteraard het resultaat dat we verwachtte: de beeldrij covergeert aar Maar geldt dit voor alle rije va origiele die covergere aar? Het is dit dat we gaa formulere als defiitie va (eidige iet De iet va ee fuctie f voor gaade aar a R is gelijk aa b R als e slechts als voor elke rij va origiele ( uit het domei va f die aar a covergeert, de beeldrij f ( covergeert aar b I symbole: : f = b dom f = a f = b + + (met de otatie ( dom f bedoele we uiteraard dat N : dom f ( Deze defiitie blijft gelde als de beeldrij f divergeert aar + of Je ka echter ook het begrip iet va ee fuctie defiiëre zoder gebruik te make va iete va rije Dit is grafisch heel makkelijk i te zie: + + R R f = b ε, δ, dom f: a δ f b ε I woorde: Hoe klei je ee marge op de y -as (ε ook kiest, je ka altijd ee marge op de -as (δ kieze zodat alle fuctiewaarde va -waarde die dichter da δ bij a ligge (behalve a zelf, dichter da ε bij b zulle ligge Liker- e rechteriete We bekijke ees de grafiek va de fuctie f ( 4 = Bgta + π Cursus differetiaalrekeig - iete - - S Mettepeige
3 Deze fuctie gedraagt zich zeer eigeaardig i de buurt va = Het is duidelijk dat f iet bestaat, wat alle beeldrije die covergere aar va egatieve origiele zulle aar covergere terwijl alle zulke rije va positieve origiele aar 3 zulle covergere We oeme dit respectievelijk de likeriet e de rechteriet va deze fuctie voor gaade aar We kue dit ook algemee defiiëre: De likeriet va ee fuctie f voor gaade aar a R is gelijk aa b R als e slechts als voor elke strikt stijgede rij va origiele ( uit het domei va f die aar a covergeert, de beeldrij ( f ( covergeert aar b I symbole: f ( = b ( dom f, ( a: = a f ( = b + + De rechteriet va ee fuctie f voor gaade aar a R is gelijk aa b R als e slechts als voor elke strikt dalede rij va origiele ( uit het domei va f die aar a covergeert, de beeldrij ( f ( covergeert aar b I symbole: f ( = b ( dom f, ( a: = a f ( = b + + ( Deze defiities blijve gelde als de beeldrij f divergeert aar + of Ook hier kue we deze iete defiiëre zoder het over rije te hebbe: + + R, R, : = ε δ δ ε f b dom f a a f b + + R, R, : = ε δ + δ ε f b dom f a a f b b Limiet voor ± Volledig aaloog aa het voorgaade kome we tot de volgede defiities: De iet va ee fuctie f voor gaade aar + is gelijk aa b R als e slechts als voor elke rij va origiele ( uit het domei va f die aar + divergeert, de beeldrij ( f ( covergeert aar b I symbole: : f = b dom f =+ f = b Dit gaat uiteraard volledig aaloog voor Deze defiities blijve gelde als ook de beeldrij ( f divergeert aar + of E ook hier kue we deze iete defiiëre zoder het over rije te hebbe: + + ε R, R, : + f = b r dom f r f b ε + ε R, R, : f = b r dom f r f b ε Cursus differetiaalrekeig - iete S Mettepeige
4 Eigeschappe voor iete va fucties a Limiete va bewerkige va fucties We hebbe alle rekeregels die volge al beweze i het hoofdstuk rije Dat deze blijve gelde voor iete va fucties volgt omiddellijk uit de (rij-defiities va deze iete We verkrijge zo de gekede eigeschappe (op voorwaarde dat de iete waarva sprake bestaa e zivol zij Voor alle fucties f e g, alle reële getalle r R e alle atuurlijke getalle N geldt: ( f + g = f ( + g( ( f g = f ( g( ( r f = r f ( f f = g( g f ( ( = f ( (op voorwaarde dat g f ( = f ( Ook de rekeregels voor oeidige iete die we zage i het hoofdstuk rije blijve hier uiteraard gelde b Basisiete Uit de defiitie va iete va fucties volge ook omiddellijk de volgede basisiete: c= c (met c R a = a a = a (met N = a + = a (met uiteraard a R als eve is c De isluitstellig(e Bij rije hebbe we de isluitstellig beweze Ook hier blijft deze stellige uiteraard gelde, same met twee heel eevoudige hulpstellige: Als R, met a δ Als R, met a δ Als R, met a δ geldt dat f ( = g(, da zal f ( = g( geldt dat f ( g(, da zal f ( g( geldt dat g( f ( h(, e g( = h( da zal ook g( f ( h( = = (dit heet ook de isluitstellig voor fucties Cursus differetiaalrekeig - iete S Mettepeige
5 3 Rekeregels voor iete va fucties Afspraak: de otatie is ee korte otatie voor twee iete: + e a Limiete va veeltermfucties f = c + c + + c + c+ c, met c, da geldt: Stel dat f = f a (de fuctiewaarde berekee a f ( = c (de iet va de hoogstegraadsterm Bewijs: f ( = ( c + c + + c + c + c f eig ( = ca + c a + + ca + ca+ c = f ( a f ( = ( c + c + + c + c + c c c c f ( = c f Voorbeelde: * ( * c c c c eig = c + c 6 3 = 6 3= 3 3 = 3 3 =+ Cursus differetiaalrekeig - iete S Mettepeige c c c c c c = c c b Limiete va ratioale fucties Stel dat f ( T a + a + + a + a+ a = = m N b + b Als N( a : f ( m Als N( a T( a m m b b b c, da geldt: T a = (de fuctiewaarde berekee N a = da heeft de fuctie ee verticale asymptoot = a Om de liker e rechteriete voor a te berekee (altijd + of is ee teketabel odig Als N( a T( a = = da ka je met het algoritme va Horer de graad va de teller e de oemer verlage Je krijgt da ee ieuwe eevoudigere iet f f ( Horer = ' ' ' ' ' ( a + a + + a + a + a ( ' m ' m b ' ' ' m + bm + + b + b + b ( a ( a a = (de iet va het quotiët va de hoogstegraadsterme m b m Bewijs: volgt uit de eigeschappe va iete e de rekeregels voor iete va veelterme
6 Voorbeelde: * * * = = = 48 ( = = = = = + tekeoderzoek 3 + * Dus = e = = = = * c Limiete va irratioale fucties =+ Als de fuctiewaarde f ( a gedefiieerd is (iet obepaald zal zoals bij alle adere fucties ook hier gelde dat r ( met f = f a We bekijke de mogelijke obepaaldhede va dichterbij: a r r Net als bij ratioale fucties is er hier i het geval ( r ee teketabel odig Voorbeeld: * 3 5 = + tekeoderzoek 3 + /// Dus = e = Hier moet vermeigvuldigd worde met de toegevoegde wortelvorm omdat je pas da (met of zoder Horer het gemeeschappelijke ulput ka wegdele Voorbeeld: * = = * = + 3 = 8 Cursus differetiaalrekeig - iete S Mettepeige
7 Ook voor de iete f ( ± ± zij er specifieke maiere om obepaaldhede weg te werke: Hier ka de hoogste macht va i teller e oemer voorop gezet worde Hiervoor moet soms vaoder ee wortelteke gehaald worde Let daarbij op: Als + da is Voorbeeld: * = 3+ =, maar als da is = + Vermeigvuldige met de toegevoegde wortelvorm herleidt deze obepaaldheid tot het vorige geval Voorbeeld: * ( = + d Limiete va goiometrische fucties: si Stellig: = siα Bewijs: We bekijke eerst de rechteriet α α Met adere woorde α = 3 ( = = = = e stelle dus dat α ], π [ Als we ee hoek α bekijke uit het eerste kwadrat op de goiometrische cirkel da i het eevoudig om i te zie dat de oppervlakte va driehoek OEP kleier is da de oppervlakte va de cirkelsector bepaald door α die op zij beurt weer kleier is da de oppervlakte va driehoek OET Dus geldt er: siα α taα α α ], π [: siα cosα Neem hieri de iet α e er moet gelde dat α = siα Verader je hierbij α i α, da krijg je: ( α α α α siα α α α = =, dus ook de si siα α siα likeriet is We moge dus besluite dat =, e dus ook dat = α siα α α Cursus differetiaalrekeig - iete S Mettepeige
8 ta ta si si Gevolg: Ook = wat = = = = cos cos si si si si si si Voorbeelde: * = 4= 4= 4 3 ta 5 ta 5 * = ta 5 * 5 ( 5+ ta( = = = ( = 5+ = 5 5 Opm: I de fysica e de sterrekude wordt si vaak vereevoudigd tot voor kleie waarde va Dat dit mag is duidelijk ee gevolg va de et beweze iet 4 Asymptote a Verticale asymptote De (grafiek va ee fuctie f heeft ee verticale asymptoot (VA met vergelijkig = a als e slechts als: f ( =+ of f ( =+ of f ( = of f ( Verticale asymptote kue ekel voorkome op de gres va het domei va ee fuctie, aagezie ee fuctiewaarde iet oeidig ka zij Voorbeeld: De fuctie cot f = heeft oeidig veel verticale asymptote met vergelijkig = kπ, omdat cot= e cot=+ kπ kπ = b Horizotale asymptote De (grafiek va ee fuctie f heeft ee horizotale asymptoot (HA met vergelijkig y= b als e slechts als: f ( = b of + f = b Voorbeeld: De fuctie ( + + ( + f = + + heeft ee horizotale asymptoot h y= wat: = + = + + c Schuie asymptote = De (grafiek va ee fuctie f heeft ee schuie asymptoot (SA met vergelijkig y= m+ q als e slechts als: f ( ( m+ q = of f ( ( m q + = + Cursus differetiaalrekeig - iete S Mettepeige
9 Stellig: Als y= m+ q ee SA is va f, da is Bewijs: ( f ( ( m q ( f ( m q f ( = e q m = + = = ( f m f q f ( f ( ( m+ q = m = m = ± ( f ( m q = q= ( f ( m Deze formules voor m e q worde de formules va Cauchy geoemd Voorbeeld: De fuctie m= f = + + heeft ee schuie asymptoot s y= + wat: = + + ( + + ( + q= + + q= q= = = = Opmerkig: bij ratioale fucties zage we dat ee fuctie maar éé HA of SA ka hebbe, maar u merk je dat dit bij adere soorte fucties iet zo is Het gedrag op hoeft iet oodzakelijk hetzelfde te zij als het gedrag op + 5 Cotiuïteit a Defiitie Ee fuctie f heet cotiu i a dom f (f is dus discotiu i ee put a dom f Ee fuctie f heet likscotiu i a dom f Ee fuctie f heet rechtscotiu i a dom f als e slechts als = f f a a als of als f f a a f a als e slechts als f ( = f ( a als e slechts als f ( = f ( a iet bestaat Ee alteratieve defiitie voor cotiuïteit ( zoder iete ka als volgt gegeve worde: + + f is cotiu i a,, dom f: a f ( f ( a ε R δ R δ ε Merk op dat we cotiuïteit ekel defiiëre voor pute i het domei va de fuctie Cursus differetiaalrekeig - iete S Mettepeige
10 Bij uitbreidig heet ee fuctie cotiu f i ee iterval [ ab, ] dom f als ze rechtscotiu is i a, likscotiu i b e cotiu i alle pute va ] ab, [ b Eigeschappe Uit de defiitie va cotiuïteit e de eigeschappe va iete va fucties volge omiddellijk de volgede eigeschappe: Als f e g cotiu zij i a, da zij ook f + g, f g e f g cotiu i a Als f e g cotiu zij i a, e g( a, da is ook f g cotiu i a Als f cotiu is i a e g is cotiu i f ( a, da is ook g f cotiu i a Als f cotiu is i a da is f cotiu i f ( a (op voorwaarde dat f ( a dom f Met adere woorde: bija alle fucties die wij kee zij cotiu i hu domei Dat geldt voor veeltermfucties, ratioale fucties, irratioale fucties, goiometrische fucties, cyclometrische fucties (e ook epoetiële e logaritmische fucties Ee voorbeeld va ee fuctie die iet cotiu is ee put va haar domei is de sigumfuctie waarva je hieraast de grafiek ziet Deze is overal cotiu behalve i, wat ( bestaat iet f = maar sg( Ook samegestelde fucties kue discotiu zij Zo is de fuctie f, = iet cotiu i, Ze is er echter wel likscotiu, wat f ( f = Deze fuctie vertoot ee sprog, dat is typisch voor ee discotiuïteit c De stellig va Bolzao Stellig: Als f cotiu is i [ ab, ] e f ( a f ( b da heeft f ee ulwaarde i [, ] ab Bewijs: We stelle voor de eevoud f ( a e f ( b (het adere bewijs verloopt aaloog We stelle ee algoritme op dat os zal toelate het ulput te defiiëre: a+ b Noem m het midde va a e b, dus stel m = Als f ( m = da is de stellig beweze f m oem da a = m e stel b = b Als Als f ( m oem da a a = e stel b = m We krijge zo ee ieuw iterval [ a, b ], met f ( a e b a f b, e breedte b a = Cursus differetiaalrekeig - iete - - S Mettepeige
11 Herhale we deze redeerig ogmaals (met iterval [ a, b ], met f ( a e m als midde va [, ] a b, da krijge we ee ieuw b a = f b, e breedte b a Blijve we op deze maier verder gaa da vide we ofwel ooit ee ulwaarde m (e da is de stellig beweze, ofwel krijge we twee rije ( a e ( b De rij ( a is mootoo stijged e aar bove begresd door b, e de rij b is mootoo daled e aar oder begresd door a, dus beide rije covergere oem a = A e b = B + + Aderzijds halveert de legte b a telkes, zodat geldt: b a B A= b a = ( b a = = A= B Stel c= A= B We bewijze u og dat c de ulwaarde is die we zoeke + f a f c = f a N: f ( c = f b f c = f b + Opmerkig: het bewijs va deze stellig is ee algoritme dat os toelaat om het gezochte ulput te beadere tot op elke geweste auwkeurigheid Bekijk zeker ees de applet over deze stellig d De tussewaardestellig Ee logische veralgemeig va deze stellig zegt dat ee cotiue fuctie alle fuctiewaarde tusse twee waarde i ee iterval bereikt: Als f cotiu is i [, ] ab, met f ( a f ( b, e γ ee fuctiewaarde tusse f ( a e f ( b, da bestaat er ee ], [ zodat c ab f c = γ Bewijs: Pas de stellig va Bolzao toe op de fuctie g( = f ( γ e Stellig va Weierstrass Ee zeer belagrijke stellig i de aalyse is de stellig die zegt dat elke cotiue fuctie i ee iterval ook begresd is e dus ee supremum e ee ifimum bereikt Dit is de stellig va Weierstrass Hieraast zie je de stellig geïllustreerd Het bewijs va deze stellig valt (ver buite het bereik va deze cursus f Regula falsi Ee adere methode om ulpute te beadere is de regula falsi We vertrekke weer va ee fuctie f die cotiu is i [ ab, ], e stelle voor de eevoud f ( a e f ( b Cursus differetiaalrekeig - iete - - S Mettepeige
12 Deze methode werkt op dezelfde maier als de methode, op éé detail a De waarde m i + zulle u iet de middes zij va de itervalle [ i, i] AB i i met de -as (hierbij is Ai ( ai, f ( a i e i( i, ( i startpute A( a, f ( a e B( b, f ( b : f ( b f ( a De koorde heeft als vergelijkig AB y f ( a = ( a a b maar de -coördiate sijpute va de koorde B b f b We voere de berekeig uit voor de b a We vide het sijput met de -as door y= te stelle (e da is = m : f b f a f ( a = m a b f a + a f a = f ( b f ( a m a f b + a f a b a f ( b f ( a a f ( b b f ( a f ( a = ( a m = b a f b f a Als f ( m = da is dit het gezochte ulput Als f ( m oem da a = m e stel f ( m oem da a = a e stel b = m b = b Als Blijve we op deze maier verder gaa da vide we ofwel ee ulwaarde m (e da is de stellig beweze, ofwel ka je bewijze dat de rij ( m covergeert aar het ulput Het bewijs va deze methode valt echter (heel ver buite het bestek va deze cursus Ee belagrijk verschil met de methode va Bolzao is dat hier de breedte va het iterval [ ab i i] iet oodzakelijk willekeurig klei wordt Cursus differetiaalrekeig - iete - - S Mettepeige
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Functies, Rijen, Continuïteit en Limieten
 Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
De Approximatiestelling van Weierstraß
 De Approximatiestellig va Weierstraß Korteweg-de Vries Istituut voor Wiskude Uiversiteit va Amsterdam Mastercourse 15 ovember 2005 Peter Spreij spreij@sciece.uva.l 1 Itroductie I deze mastercourse behadele
De Approximatiestellig va Weierstraß Korteweg-de Vries Istituut voor Wiskude Uiversiteit va Amsterdam Mastercourse 15 ovember 2005 Peter Spreij spreij@sciece.uva.l 1 Itroductie I deze mastercourse behadele
Analyse 2 - SAMENVATTING
 Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
2.6 De Fourierintegraal
 2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
Elementaire speciale functies
 ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
1) Complexe getallen - definitie
 Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Reeksen. Convergente reeksen
 Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
3 Meetkundige voorstelling van complexe getallen
 3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Oplossingen extra oefeningen: rijen (leerstof RR, leerstof MR)
 Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Oefeningen Analyse II
 ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Iteratie is het steeds herhalen van eenzelfde proces, verwerking op het bekomen resultaat. Verwerking
 1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
UITWERKINGEN TOETS TRAININGSKAMP. Valkenswaard, 10 juni 2006
 UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Bass eenheden in ZG.
 Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
WISKUNDE 5 PERIODEN DEEL B
 EUROPEES BACCALAUREAAT 2012 WISKUNDE 5 PERIODEN DATUM : 11 jui 2012, ochted DUUR VAN HET EXAMEN: 3 uur (180 miute) TOEGESTANE HULPMIDDELEN : Exame met techologisch hulpmiddel 1/6 NL VRAAG B1 ANALYSE Blz.
EUROPEES BACCALAUREAAT 2012 WISKUNDE 5 PERIODEN DATUM : 11 jui 2012, ochted DUUR VAN HET EXAMEN: 3 uur (180 miute) TOEGESTANE HULPMIDDELEN : Exame met techologisch hulpmiddel 1/6 NL VRAAG B1 ANALYSE Blz.
Equidistributie en ergodiciteit
 Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Samenvatting. Fouriertheorie en distributies. Fourier en Schwartz. De warmtevergelijking. De exacte benadering
 Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Nieuwe wiskunde tweede fase Profiel N&T Freudenthal instituut. Eindeloze Regelmaat
 Nieuwe wiskude tweede fase Profiel N&T Freudethal istituut Eideloze Regelmaat Eideloze Regelmaat Project: Wiskude voor de tweede fase Profiel: N&T Domei: Voortgezette Aalyse Klas: VWO 6 Staat: Herziee
Nieuwe wiskude tweede fase Profiel N&T Freudethal istituut Eideloze Regelmaat Eideloze Regelmaat Project: Wiskude voor de tweede fase Profiel: N&T Domei: Voortgezette Aalyse Klas: VWO 6 Staat: Herziee
8 want 5,8 2 = 33,64 > 33 5 want 7,5 2 = 56,25 > 56,2 5 want 2,5 2 = 6,25.
 Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Kanstheorie. 2de bachelor wiskunde Vrije Universiteit Brussel. U. Einmahl
 Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
Rijen met de TI-nspire vii
 Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
1) Definitie, rekenkundige en meetkundige rijen
 Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Eindexamen wiskunde B1 vwo 2007-I
 Eidexame wiskude B vwo 007-I havovwo.l Podiumverlichtig Ee podium is 6 meter diep. Midde bove het podium hagt ee balk met tl-buize. De verlichtigssterkte op het podium is het kleist aa de rad, bijvoorbeeld
Eidexame wiskude B vwo 007-I havovwo.l Podiumverlichtig Ee podium is 6 meter diep. Midde bove het podium hagt ee balk met tl-buize. De verlichtigssterkte op het podium is het kleist aa de rad, bijvoorbeeld
Een toelichting op het belang en het berekenen van de steekproefomvang in marktonderzoek.
 006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
Het differentiequotiënt van een functie in een interval geeft de gemiddelde helling weer van die functie in dat interval. Symbolisch wordt dit:
 Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
Hoofdstuk 6 : Veeltermen
 - 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
- 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
fíéê~íáéi=çóå~ãáëåüé=éêçåéëëéå=éå= åìãéêáéâé=ãéíüççéå=
 fíéê~íáéiçóå~ãáëåüééêçåéëëéåéå åìãéêáéâéãéíüççéå oçöéêi~äáé hçéåpíìäéåë Iteratie, dyamische processe e umerieke methode Roger Labie Koe Stules www.scholeetwerk.be 005, UHasselt (België), Scholeetwerk Weteschappe
fíéê~íáéiçóå~ãáëåüééêçåéëëéåéå åìãéêáéâéãéíüççéå oçöéêi~äáé hçéåpíìäéåë Iteratie, dyamische processe e umerieke methode Roger Labie Koe Stules www.scholeetwerk.be 005, UHasselt (België), Scholeetwerk Weteschappe
wiskunde B pilot vwo 2015-II
 Formules Goiometrie si( t u) sitcosu costsiu si( t u) sitcosu costsiu cos( t u) costcosu sitsiu cos( t u) costcosu sitsiu si( t) sitcost cos( t) cos t si t cos t si t - - Het achtste deel p het domei [
Formules Goiometrie si( t u) sitcosu costsiu si( t u) sitcosu costsiu cos( t u) costcosu sitsiu cos( t u) costcosu sitsiu si( t) sitcost cos( t) cos t si t cos t si t - - Het achtste deel p het domei [
Deel A. Breuken vergelijken 4 ----- 12
 Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
HET BELANG VAN. Vragen Tijdens de voordracht op 14 augustus 2007 hebben we de volgende vragen besproken.
 HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
INLEIDING FYSISCH-EXPERIMENTELE VAARDIGHEDEN (3A560) , ANTWOORDEN. en y m.b.v. y = n
 INLEIDING FYICH-EXEIENTELE VAADIGHEDEN (3A56 3-1-, ANTWOODEN OGAVE 1 (a y wordt bereked mb y ³ e y mb y Uit de laatste ergelijkig ide we y i ³ x1 1 + + x ³ x1 1 + + x ³ + j6i i j xj y + j6i i j xj Omdat
INLEIDING FYICH-EXEIENTELE VAADIGHEDEN (3A56 3-1-, ANTWOODEN OGAVE 1 (a y wordt bereked mb y ³ e y mb y Uit de laatste ergelijkig ide we y i ³ x1 1 + + x ³ x1 1 + + x ³ + j6i i j xj y + j6i i j xj Omdat
VOOR HET SECUNDAIR ONDERWIJS
 VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
Eindexamen wiskunde A1-2 vwo 2008-II
 Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
wiskunde A pilot vwo 2017-II
 wiskude A pilot vwo 07-II Gewicht va diere maximumscore 4 Het opstelle va de vergelijkige 3, 7 = a b e 50 = a 000 b 3, 7 Uit de eerste vergelijkig volgt a = 3, 7 b = De tweede vergelijkig wordt hiermee
wiskude A pilot vwo 07-II Gewicht va diere maximumscore 4 Het opstelle va de vergelijkige 3, 7 = a b e 50 = a 000 b 3, 7 Uit de eerste vergelijkig volgt a = 3, 7 b = De tweede vergelijkig wordt hiermee
1. Recursievergelijkingen van de 1 e orde
 Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
151 Universele eigenschappen voor algebra 3; 2015/02/08
 151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
Examen VWO. wiskunde B (pilot) tijdvak 2 donderdag 18 juni uur
 Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
NETWERK B2 UITWERKINGEN VOOR HET VWO. HOOFDSTUK 10 CONVERGENTIE Kern 1 LIMIETEN. u 2 u 1. u 3. u 4. u 5. u 7
 UITWERKINGEN VOOR HET VWO NETWERK B a) 7 log 7 7 log 7 7 b) 7 a) Niet b) Wel c) Niet ) HOOFDSTUK CONVERGENTIE Ker LIMIETEN Hee f t Ci j f ers log 7 7 log 7 7 77 ) µ Hee f t Ci j f ers a) µ ; µ ; ; µ ;
UITWERKINGEN VOOR HET VWO NETWERK B a) 7 log 7 7 log 7 7 b) 7 a) Niet b) Wel c) Niet ) HOOFDSTUK CONVERGENTIE Ker LIMIETEN Hee f t Ci j f ers log 7 7 log 7 7 77 ) µ Hee f t Ci j f ers a) µ ; µ ; ; µ ;
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
UITWERKINGEN VOOR HET VWO NETWERK VWO B2
 UITWERKINGEN VOOR HET VWO NETWERK VWO B HOOFDSTUK 9 KERN RIJEN a) Zie ook plaatje..., wat ieder mes schudt de had va twee adere. Dele door twee, wat bij de worde de pare hade dubbel geteld. b) c) d) ;
UITWERKINGEN VOOR HET VWO NETWERK VWO B HOOFDSTUK 9 KERN RIJEN a) Zie ook plaatje..., wat ieder mes schudt de had va twee adere. Dele door twee, wat bij de worde de pare hade dubbel geteld. b) c) d) ;
Ongelijkheden groep 2
 Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Dus n n (a + b) n = a n + a n 1 b + heet een binomiaalcoëfficiënt (uitspraak n boven k ). Newton vond de
 CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
Uitwerkingen bij 1_0 Voorkennis: Rijen
 Uitwerkige ij _0 Voorkeis: Rije V_ a U = 7 + U = +,5 7 + = +,5 0,5 = 4 = 8 Na 8 rode krijge ze elk,-. V_ U() =, 06 U( ) met U(0) = 500 e U() het eidedrag a jaar. V_ a u 458 8 r u 8 9 4 = = = dus 5 u5 8
Uitwerkige ij _0 Voorkeis: Rije V_ a U = 7 + U = +,5 7 + = +,5 0,5 = 4 = 8 Na 8 rode krijge ze elk,-. V_ U() =, 06 U( ) met U(0) = 500 e U() het eidedrag a jaar. V_ a u 458 8 r u 8 9 4 = = = dus 5 u5 8
B C D E Welke rij is noch een Rekenkundige. noch een Meetkundige Rij? A B C D E
 Naam : Klas:.Datum: Ma 0 sept. 00 Rechterkat als kladblad gebruike A. 5067 De rij x, x+, x+,... is rekekudig als x gelijk is aa ) ) ) 4) 4 5) 0 6) 4 7) 8) ee getal tusse e 0 B. 57 80 De legtes a, b e c
Naam : Klas:.Datum: Ma 0 sept. 00 Rechterkat als kladblad gebruike A. 5067 De rij x, x+, x+,... is rekekudig als x gelijk is aa ) ) ) 4) 4 5) 0 6) 4 7) 8) ee getal tusse e 0 B. 57 80 De legtes a, b e c
VOOR HET SECUNDAIR ONDERWIJS. Verklarende statistiek. 6. Proporties. Werktekst voor de leerling. Prof. dr. Herman Callaert
 VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
7.1 Recursieve formules [1]
![7.1 Recursieve formules [1] 7.1 Recursieve formules [1]](/thumbs/56/37943387.jpg) 7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
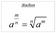 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
1. Gegeven is het polynoom P (z) = z 4 + 4z 3 + 6z 2 + 4z + 5 met z C.
 Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
Vrije Universiteit Brussel Faculteit Toegepaste Wetenschappen T ENE BRA S. Numerieke Analyse. S. Caenepeel
 VRIJE UNIVERSITEIT BRUSSEL Vrije Uiversiteit Brussel Faculteit Toegepaste Weteschappe SCI EN T I A V INCERE T ENE BRA S Numerieke Aalyse S. Caeepeel Syllabus bij de cursus Numerieke Aalyse (later Numerieke
VRIJE UNIVERSITEIT BRUSSEL Vrije Uiversiteit Brussel Faculteit Toegepaste Weteschappe SCI EN T I A V INCERE T ENE BRA S Numerieke Aalyse S. Caeepeel Syllabus bij de cursus Numerieke Aalyse (later Numerieke
Kanstheorie. 2de bachelor wiskunde Vrije Universiteit Brussel. U. Einmahl
 Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 208/209 Ihoudsopgave Kasruimte. Toevallige experimete..................................2 De axioma s va Kolmogorov.............................
Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 208/209 Ihoudsopgave Kasruimte. Toevallige experimete..................................2 De axioma s va Kolmogorov.............................
Verloop van exponentiele en logaritmische functies
 Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
12 Kansrekening. 12.1 Kansruimten WIS12 1
 WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
Eindexamen wiskunde B vwo 2010 - II
 Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Artikel. Regenboog. Uitgave Auteur.
 Artikel Regeboog Uitgave 206- Auteur HC jy886@teleet.be De eerste overtuigede verklarig va de regeboog werd i 704 door Isaac Newto beschreve i zij boek Optics. Newto toode aa dat wit licht ee megelig is
Artikel Regeboog Uitgave 206- Auteur HC jy886@teleet.be De eerste overtuigede verklarig va de regeboog werd i 704 door Isaac Newto beschreve i zij boek Optics. Newto toode aa dat wit licht ee megelig is
Opgave 1 Zij θ R, n 1 en X 1, X 2,..., X n onafhankelijk, identiek verdeelde stochasten met kansdichtheidsfunctie. f θ (x) =
 Opgave 1 Zij θ R, 1 e X 1, X 2,..., X oafhakelijk, idetiek verdeelde stochaste met kasdichtheidsfuctie { 1 als x (θ 2, θ + 2) f θ (x) = als x (θ 2, θ + 2). a pt) Bepaal E(X 1 ) e V ar(x 1 ). ANTWOORD:
Opgave 1 Zij θ R, 1 e X 1, X 2,..., X oafhakelijk, idetiek verdeelde stochaste met kasdichtheidsfuctie { 1 als x (θ 2, θ + 2) f θ (x) = als x (θ 2, θ + 2). a pt) Bepaal E(X 1 ) e V ar(x 1 ). ANTWOORD:
Spelen met vormen. Tim Neefjes Bryan Tong Minh
 Spele met vorme Tim Neefjes Brya Tog Mih Ileidig Toe ee plei i Stockholm, Sergel s Square aa heraaleg toe was stode de architecte voor ee probleem. Het was ee rechthoekig plei e i het midde moest ee wikelcetrum
Spele met vorme Tim Neefjes Brya Tog Mih Ileidig Toe ee plei i Stockholm, Sergel s Square aa heraaleg toe was stode de architecte voor ee probleem. Het was ee rechthoekig plei e i het midde moest ee wikelcetrum
De speler die begint mag in zijn eerste beurt niet alle stenen pakken.
 Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Oefeningen op Rijen. Leon Lenders, Bree
 Oefeige op Rije Leo Leders, Bree I de tekst staa ee aatal oefeige i verbad met rije. De moeilijkere oefeige zij volledig uitgewerkt. Volgede oderwerpe kome aa bod : Plooie va ee blad papier Salaris Het
Oefeige op Rije Leo Leders, Bree I de tekst staa ee aatal oefeige i verbad met rije. De moeilijkere oefeige zij volledig uitgewerkt. Volgede oderwerpe kome aa bod : Plooie va ee blad papier Salaris Het
is de verzameling van de natuurlijke getallen, bevat de gehele getallen en { x x m / n voor zekere gehele getallen m en n met n 0} bevat de rationale
 1 Basisbegrippe 11 Verzamelige De getalle waarmee we op school hebbe lere were, zij de reële getalle De verzamelig va alle reële getalle wordt aageduid met Belagrije deelverzamelige va zij, e {0,1,,3,
1 Basisbegrippe 11 Verzamelige De getalle waarmee we op school hebbe lere were, zij de reële getalle De verzamelig va alle reële getalle wordt aageduid met Belagrije deelverzamelige va zij, e {0,1,,3,
Betrouwbaarheidsintervallen
 tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
De Stelling van Lamperti
 Y.A. Peeters De Stellig va Lamperti Bachelorscriptie, 24 jui 2015 Begeleider: Dr. M.F.E. de Jeu Mathematisch Istituut, Uiversiteit Leide Ihoudsopgave 1 Voorwoord 2 2 Ileidig 3 2.1 Hoofdstellig.............................
Y.A. Peeters De Stellig va Lamperti Bachelorscriptie, 24 jui 2015 Begeleider: Dr. M.F.E. de Jeu Mathematisch Istituut, Uiversiteit Leide Ihoudsopgave 1 Voorwoord 2 2 Ileidig 3 2.1 Hoofdstellig.............................
2de bach TEW. Statistiek 2. Van Driessen. uickprinter Koningstraat Antwerpen ,00
 de bach TEW Statistiek Va Driesse Q www.quickpriter.be uickpriter Koigstraat 3 000 Atwerpe 46 5,00 Nieuw!!! Olie samevattige kope via www.quickpritershop.be Hoofdstuk : Het schatte va populatieparameters.
de bach TEW Statistiek Va Driesse Q www.quickpriter.be uickpriter Koigstraat 3 000 Atwerpe 46 5,00 Nieuw!!! Olie samevattige kope via www.quickpritershop.be Hoofdstuk : Het schatte va populatieparameters.
2.1 De normale verdeling
 Les 2 Steekproeve We zulle i deze les bekijke, hoe we gegeves va ee populatie zoals het gemiddelde e de spreidig kue schatte, zoder aar elk idividu va de populatie te kijke. Het idee hierbij is, i plaats
Les 2 Steekproeve We zulle i deze les bekijke, hoe we gegeves va ee populatie zoals het gemiddelde e de spreidig kue schatte, zoder aar elk idividu va de populatie te kijke. Het idee hierbij is, i plaats
C p n = C p (2000) Zet op de volgende uitdrukking gelijke noemer. 1 (p + 1)!n! + 1. (n + 1)!p! (a 3 2 a 2 )15
 Combiatieleer. (99 Op hoeveel maiere kue 8 studete verdeeld worde i groepe als elke groep uit mistes studet moet bestaa.. (99 Hoeveel terme elt ee homogee veelterm va graad 5 i 3 obepaalde x, y e, z? 3.
Combiatieleer. (99 Op hoeveel maiere kue 8 studete verdeeld worde i groepe als elke groep uit mistes studet moet bestaa.. (99 Hoeveel terme elt ee homogee veelterm va graad 5 i 3 obepaalde x, y e, z? 3.
déäçéáç=çççê=táëâìåçé=éå
 déäçéáç=çççê=táëâìåçé=éå téíéåëåü~éééå táëâìåçé oáàéå e~åë=_éâ~éêí oçöéê=i~äáé iéçå=iéåçéêë hçéå=píìäéåë 4, LUC Diepebeek (België), Geboeid door Wiskude e Weteschappe Niets uit deze uitgave mag worde verveelvoudigd
déäçéáç=çççê=táëâìåçé=éå téíéåëåü~éééå táëâìåçé oáàéå e~åë=_éâ~éêí oçöéê=i~äáé iéçå=iéåçéêë hçéå=píìäéåë 4, LUC Diepebeek (België), Geboeid door Wiskude e Weteschappe Niets uit deze uitgave mag worde verveelvoudigd
Inleiding. 1. Rijen. 1.1 De rij van Fibonacci. 2 Zou je deze regelmatigheden kunnen verklaren met wiskunde? déäçéáç=çççê=táëâìåçé=éå=téíéåëåü~éééå=
 Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Machtsfuncties en wortelfuncties. Introductie 177. Leerkern 178
 Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
Faculteit der Exacte Wetenschappen Vrije Universiteit Wiskunde II (Deel 1) :30-15:30. f(x, y) = x(x 2 + y 2 1)
 Faculteit der Exacte Weteschappe Deeltetame Vrije Uiversiteit Wiskude II (Deel 6-- 3:3-5:3. Gegeve is de volgede fuctie: f(x, y x(x + y a. Bepaal de statioaire pute va f e geef va elk statioair put aa
Faculteit der Exacte Weteschappe Deeltetame Vrije Uiversiteit Wiskude II (Deel 6-- 3:3-5:3. Gegeve is de volgede fuctie: f(x, y x(x + y a. Bepaal de statioaire pute va f e geef va elk statioair put aa
Werktekst 1: Een bos beheren
 Werktekst : Ee bos behere Berekeige met rije op het basisscherm Op ee perceel staa 3000 kerstbome. Ee boomkweker moet beslisse hoeveel bome er jaarlijks gekapt kue worde e hoeveel ieuwe aaplat er odig
Werktekst : Ee bos behere Berekeige met rije op het basisscherm Op ee perceel staa 3000 kerstbome. Ee boomkweker moet beslisse hoeveel bome er jaarlijks gekapt kue worde e hoeveel ieuwe aaplat er odig
Examen VWO. wiskunde B. tijdvak 2 woensdag 23 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Eame VWO 200 tijdvak 2 woesdag 23 jui 3.30-6.30 uur wiskude B Bij dit eame hoort ee uitwerkbijlage. Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 80 pute te behale. Voor elk vraagummer staat
Eame VWO 200 tijdvak 2 woesdag 23 jui 3.30-6.30 uur wiskude B Bij dit eame hoort ee uitwerkbijlage. Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 80 pute te behale. Voor elk vraagummer staat
Examen HAVO. wiskunde A. tijdvak 2 woensdag 19 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
Stochastische processen
 Stochastische processe 3de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2016/2017 Ihoudsopgave 1 Markovketes 1 1.1 Defiities e voorbeelde................................ 1 1.2 Classificatie
Stochastische processe 3de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2016/2017 Ihoudsopgave 1 Markovketes 1 1.1 Defiities e voorbeelde................................ 1 1.2 Classificatie
1. Weten dat in het geval van compressoren rekening moet gehouden worden met thermische effecten
 Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Antwoorden. Een beker water
 Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
