Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
|
|
|
- Stefanie van der Zee
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term wordt uitgedrukt i zij k voorgagers. Geeft me de eerste k terme va de rij, daisderijvolledige bepaald. Zo komt bijvoorbeeldideiwova 976 ee rij {u } voor gedefiieerd door u + = u + (u ) 5, u 0 =,u = 5. Hier geldt dus k =. I deze paragraaf worde rije oderzocht die voldoe aa ee recurrete betrekkig va de vorm a +k = A a +k + A a +k + + A k a ; =; ;::: () waari A ;A ;:::;A k costate zij e A k 0. Voor k = staat er a + = Aa ; =; ;::: : Blijkbaar is de rij da ee meetkudige rij: a + = Aa = A a = = A a. Voor k = wordt de betrekkig a + = Aa + + Ba ; (B 0); =; ;::: () Merk alvores verder te gaa, eerst eige algemee eigeschappe op va rije die aa () voldoe: () Als {a } voldoet aa (), da voldoet ook {ca } aa () voor alle costates c. () Als {a } e {b } beide voldoe aa () (dus met dezelfde A e B maar evetueel verschillede begiwaarde), voldoet ook {a + b }. De eigeschappe () e () gelde, zoals me omiddellijk iziet, ook algemee voor rije die aa de betrekkig () voldoe: zij {a } e {b } oplossige va (), da zij ook alle zogeaamde lieaire combiaties {ca + db } oplossige va (). Stel u dat {a } e {b } beide voldoe aa (). Is da ook elke rij{x } die aa () voldoet va de vorm x = ca + db voor zekere costate c e d? Zo' rij wordt volledig bepaald door zij twee begiwaarde x ;x. Als voor zekere c e d ρ x = ca + db x = ca + db (3) geldt, omdat {x } ee oplossig va () is, voor alle atuurlijke dat x = ca + db. Uit het stelsel (3) ka me c e d oplosse, tezij a b a b = 0, d.w.z. tezij a : b = a : b. I dat laatste geval is de rij {b } ee veelvoud va de rij {a }. Hieruit blijkt dat als me twee zogeaamde lieair oafhakelijke oplossige va () heeft, alle oplossige te schrijve zij als lieaire combiaties va deze twee. I het algemee geval va betrekkig () heeft me k lieair oafhakelijke oplossige odig om alle oplossige voort te brege. Lieair oafhakelijk beteket da dat ee k k-stelsel aaloog aa (3) altijd precies éé oplossig moet hebbe.
2 Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhakelijke oplossige va () vide? Zoude er meetkudige rije {t } zij die voldoe? Da moet gelde t + = At + + Bt,ofwel t At B =0: (4) Deze vergelijkig heet de karakteristieke vergelijkig va (). Heeft (4) twee verschillede reële wortels t e t, da zij {t } e {t } lieair oafhakelijk, wat t t t t = t t (t t )et t = B 0. De algemee oplossig va () is i dat geval {ct + dt }. Voorbeeld: De rij va Fiboacci (de bijaam va Leoardo va Pisa, ±00 a Chr.) is de rij ; ; ; 3; 5; 8; 3; ; 34;::: : Deze rij is gedefiieerd door F = F =ef + = F + + F voor =; ;:::. De karakteristieke vergelijkig va deze recurretie is t t =0. De oplossige hierva zij t ; = ± 5, e de algemee oplossig va de recurrete betrekkig is dus ct + dt. Aagezie ρ =F = c( + 5)+d( 5) =F = c( + 5) + d( 5) is c = 5 5ed = 5 5. De algemee term va de rij va Fiboacci wordt dus 5 ( + 5) ( 5) : F = 5 Omdat + 5 > e 5 <, is voor grote de term ( 5) verwaarloosbaar. Ee ruwe schattig geeft bijvoorbeeld F Opgave. Bepaal Heeft de karakteristieke vergelijkig twee samevallede wortels, da vidt me slechts éé meetkudige rij die voldoet (op veelvoude a). Schrijf i dat geval () als a + Ea + + E a =0: (5) De karakteristieke vergelijkig heeft als dubbele wortel t = E. De meetkudige rij {E } is dus ee oplossig. Noem b = a E e deel (5) door E +, da otstaat ofwel b + b + + b =0 b + b + = b + b : Omiddellijk ziet me behalve de oplossig b = voor alle (correspodered met a = E ) og ee tweede oplossig: b =. Deze geeft de va de eerste lieair oafhakelijke tweede basisoplossig (verifieer dit) a = E. De algemee oplossig va (5) is dus {ce + de }. Te slotte het geval dat de karakteristieke vergelijkig helemaal gee reële oplossige heeft. Me zou da met complexe getalle kue werke, maar het ka ook zoder. Schrijf () i de vorm a + Fa + + E a =0: (6)
3 (De coëfficiët va a is positief wat de discrimiat 4F 4E is egatief, e dit laatste beteket bovedie dat F E <.) Noem weer b = a E,daotstaat b + F E b + + b =0: Omdat F E < iseree' zo, dat F E =cos'. De vergelijkig gaat da over i b + cos'b + + b =0: (7) Me moet u opmerke dat b + = cos ' e b + = si ' oplossige va (7) zij. Dit volgt direct uit de formules cos( +)' = cos ' cos ' si ' si ' cos( )' = cos ' cos ' + si ' si ' si( +)' = si ' cos ' +cos' si ' si( )' = si ' cos ' cos ' si ' Hiermee zij dus twee lieair oafhakelijke (verifieer dit weer) oplossige gevode. Uiteraard zij ook {cos '} e {si '} oplossige (de idex is allee verschove). Neem voor de eevoud deze als basisoplossige va (7). De basisoplossige va (6) zij da {E cos '} e {E si '} e de algemee oplossig is {E (c cos ' + d si ')}. I pricipe ka me de algemee recurrete betrekkig () voor k> aaloog behadele. De wortels va de karakteristiekevergelijkig zij echter voor polyome va hogere graad moeilijker te bepale. Zij bovedie iet alle wortels reëel, da is het gebruik va complexe getalle vrijwel overmijdelijk. Opgave. Bepaal de -de term x va de rij {x } gedefiieerd door a) x + = x + +x, x =0,x =. b) x + =4x + 4x, x =0,x =. c) x + =x + x, x =0,x =. d) x + = x, x = x =. e) x +3 =3x + 3x + + x, x = x =0,x 3 =. Opgave.3 Bepaal de -de terme x e y va de rije {x } e {y } gedefiieerd door het stelsel ρ x+ =3x + y y + =5x y met x =0ey =6. Aawijzig: uit de eerste vergelijkig haalt me door idexverschuivig y + = x + 3x +. Same met y = x + 3x geeft dit, gesubstitueerd i de tweede vergelijkig, ee recurrete betrekkig voor de rij {x }. Opgave.4 Behadel evezo: ρ x+ =x y y + = x +4y met x =,y =. Opgave.5 Bepaal x als gegeve is dat x + = x x +4 met x =0: Aawijzig: oem y + = y z, z + = y +4z, da geldt x = y z. Opgave.6 Evezo: x + = 4x 6x met x =: 3
4 Opgave.7 Bepaal x als x =,x =ex + = x 3 + x. Ogelijkhede Ee fudametele ogelijkheid is A 0voor alle reële waarde va A. Gelijkheid treedt op precies als A = 0. Deze vazelfsprekede ogelijkheid zit verborge i talrijke adere ogelijkhede. Eerste voorbeeld: voor alle positieve a e b geldt ab a+b. Bewijs. Vermeigvuldig de ogelijkheid met e kwadrateer tot 4ab a +ab+b, ofwel 0 a ab + b =(a b). Hieruit volgt dat oze ogelijkheid iderdaad klopt e teves dat gelijkheid optreedt precies als a = b. a+b Tweede voorbeeld: voor alle positieve a e b geldt a +b. Bewijs. Uitwerke geeft ook hier 0 (a b). Opgave. Bewijs: va alle rechthoeke met gegeve omtrek heeft het vierkat de grootste oppervlakte. Opgave. Bewijs: va alle rechthoeke met gegeve oppervlakte heeft het vierkat de kleiste omtrek. Opgave.3 Voor elke scherpe hoek x geldt si x cos x + cos x si x. Opgave.4 Als a; b > 0ea + b =, da is (a + a ) +(b + b ) 5. Waeer geldt het gelijkteke? Opgave.5 Zij a, b e c positief, da is (a + b)(b + c)(c + a) 8abc. Waeer heb je gelijkheid? Opgave.6 Voor welke reële x is a+bx4 x iet differetiëre.) miimaal? (a e b zij positief. Je mag. Gemiddelde Ee uitdrukkig i de positieve variabele a ;a ;:::;a heet ee gemiddelde va a ;a ;:::;a als de waarde erva oafhakelijk is va de volgorde der a i e als voor elke positieve costate c de waarde gelijk is aa c zodra me voor alle i a i = c kiest. Voorbeelde:. Het rekekudig gemiddelde R(a ;a ;:::;a )= (a + a + + a ).. Het meetkudig gemiddelde M(a ;a ;:::;a )=(a a a ). 3. Het harmoisch gemiddelde H(a ;a ;:::;a )=. a + a ++ a Va alle gemiddelde zij het rekekudig e het meetkudig gemiddelde het belagrijkste. 4
5 Stellig. Voor elk -tal positieve getalle a ;a ;:::;a geldt R(a ;a ;:::;a ) M(a ;a ;:::;a ) : Dit heet de rekekudig-meetkudig gemiddelde ogelijkheid. daeslechts da als a = a = = a. Gelijkheid treedt op Deze stellig is zo belagrijk, dat we er drie verschillede bewijze va gaa geve. Er zij er overiges og wel meer beked. De drie die we hier presetere zij alle drie erg elemetair, maar toe elk ee adere beaderigswijze. Bewijs. We kue veroderstelle dat a a a =. Immers, de gevraagde ogelijkheid veradert iet als we alle a i met dezelfde positieve factor vermeigvuldige. Oder deze aaame moete we u bewijze dat a + a + + a. We gebruike u volledige iductie aar. Voor = is de ogelijkheid aa het begi va deze paragraaf beweze. Stel u dat de ogelijkheid geldt voor elk -tal. Laat gegeve zij + positieve getalle a ;a ;:::;a met a a a =. Als alle a i gelijk zij is de ogelijkheid waar. Aders is er ee tweetal, bijvoorbeeld a e a met a > ea <. Da is dus (a )(a ) = a a a a +< 0, oftewel a +a >a a +, zodat volgt a +a ++a + > +a a +a 3 ++a + +, omdat a a ;a 3 ;:::;a + positieve getalle zij met product. Bewijs. We wete dat a a a +a a + a a3 + a 4 a +a a e a 3 a 4 3+a 4, dusa a a 3 a 4 + a3+a 4 Zo voortgaade bewijst me voor alle va de vorm m dat a + a + + a m m a a a m : m z } m maal 4 a + a + a 3 + a 4 4 = : 4 Kies u voor ee willekeurig de waarde va m zo groot, dat < m, e oem b = a+a++a a m. Da geldt dat a a a bb b +a ++a +( )b m = m b m,dusa a a b a. Dit is wat we moeste bewijze. Omdat a a = +a da e slechts da geldt als a = a, bewijst me stap voor stap dat ook i het algemee gelijkheid precies optreedt waeer alle a i gelijk zij. Er zit i dit tweede bewijs ee merkwaardig soort iductie. We lope i grote stappe door de atuurlijke getalle hee e vulle achteraf de opegelate gate op. Bewijs. Uit de grafiek va de fuctie f(x) =logx blijkt dat log a+a (log a + log a )=log a a,ziefig.. Daarom volgt ook a+a a a. We gaa bewijze dat log a+a++a (log a + +loga ), waaruit de gevraagde ogelijkheid volgt. 5
6 log x log a +log a f(x) a a +a a a a i Figuur. Figuur. I het algemee geldt voor elke fuctie waarva de grafiek `bol aar bove' is (d.w.z. dat het verbidigsstuk va twee pute va de grafiek altijd oder de grafiek ligt) de ogelijkheid f a + a + + a (f(a )+f(a )++ f(a )) : Om dit i te zie oeme we μa = a++a. Heeft de raaklij i x = μa richtigscoëfficiët c = f (μa), da is f(a i ) f(μa)+c(a i μa) voor elke a i. Zie ook fig. Telt me deze ogelijkhede op voor i =; ;:::;da blijkt f(a )++ f(a ) f(μa)+c(a + + a μa) =f(μa). Overiges is het iet odig te veroderstelle dat f i x = μa differetieerbaar is. Omdat f `bol aar bove' is, is er door elk put va de grafiek mistes éé rechte die verder geheel bove de grafiek ligt. De methode va dit derde bewijs is ook toepasbaar bij fucties waarva de grafiek `bol aar beede' is, zoals f(x) =x. Toepassig va de methode geeft i dat geval de ogelijkheid (a + + a a + + a ) : Als toepassig va stellig (.) behadele we de volgede opgave: als x, y e z positieve getalle zij met x + y + z =,da geldt ( + x )( + y )( + z ) 64. Probeer alvores verder te gaa zelf deze opgave op te losse. Oplossig: Kies x = y = z =, da otstaat de gelijkheid. De ogelijkheid is dus 3 iet te verscherpe. Merkwaardigerwijze wordt de opgave eevoudiger als me de ormaliserig x + y + z = laat valle. Stel daarom x + y + z = s. Kies weer x = y = z = s, da geldt 3 ( + x )( + y )( + z )=(+3 s )3 : Waarschijlijk geldt dus i het algemee ook voor alle positieve x, y e z met som s dat ( + x )( + y )( + z ) ( + 3 s )3 : Aagezie volges stellig (.) geldt s 3 xyz, is het zo, dat ( s )3 ( + 3 xyz ) 3 = xyz x y z xyz +3 ( 3 x + y + z )+3 ( 3 xy + yz + zx )+ xyz = ( + x )( + y )( + z ). Dit bewijst oze algemee ogelijkheid e daarmee is het probleem waarmee we begoe ook opgelost. Opgave.7 Voor elk -tal positieve getalle a ;a ;:::;a geldt H(a ;a ;:::;a ) M(a ;a ;:::;a ) 6
7 e gelijkheid treedt da e slechts da op als alle a i gelijk zij. Opgave.8 Me splitst ee positief getal k i positieve dele a ;a ;:::;a,dus k = a + a + + a. Bewijs dat het product a a a maximaal is als me alle a's gelijk kiest. (Het aatal is vast verodersteld.) Opgave.9 a ;a ;:::;a zij positief. Bewijs dat a a + a a a a + a a. Opgave.0 a ;a ;:::;a zij positief. Bewijs dat (a + a + + a )( a + a + + a ). +. Opgave. Voor elke gehele > geldt! < Opgave. a ;a ;:::;a zij positief, >, e s = a + a + + a. Bewijs ( + a )( + a ) ( + a ) < +s + s s + +.!! Opgave.3 a, b e c zij positieve hoeke met som gelijk aa ß. Bewijs () ta a +tab + ta c 3. () ta a + ta b +ta c. Aawijzig: kijk aar het derde bewijs va stellig (.). Stellig. Gegeve zij -tal reële getalle: a ;a ;:::;a e b ;b ;:::;b. Da geldt de ogelijkheid va Cauchy-Schwarz, geoemd aar A.L. Cauchy ( ) e H.A. Schwarz (843-9): (a b + a b + + a b ) (a + a + + a )(b + b + + b ) : Gelijkheid treedt op precies waeer a : b = a : b = = a : b. Bewijs. Als b = b = = b = 0 is er iets te bewijze. Stel dus bijvoorbeeld b 0. Voor elke t is da 0 (a + tb ) +(a + tb ) + +(a + tb ) = (a +a ++a )+(a b +a b ++a b )t+(b +b ++b )t = A+Ct+Bt met B 0. Dit is ee kwadratische vorm i t die blijkbaar defiiet iet-egatief is. De discrimiat 4C 4AB is dus iet positief. Ivulle geeft de gevraagde ogelijkheid. Gelijkheid treedt da e slechts da op als voor zekere t 0 geldt (a + t 0 b ) +(a + t 0 b ) + +(a + t 0 b ) =0: Alle terme moete da ul zij, e dit beteket a : b = a : b = = a : b = t 0. x Opgave.4 Voor alle x, y e z geldt + y + z 3 6 x + y + z. 3 6 Opgave.5 (x y ) +(x y ) + +(x y ) (x + x + + x ) + (y + y + + y ) voor alle x ;x ;:::;x e y ;y ;:::;y. Opgave.6 (p x +p x ++p x ) (p +p ++p )(p x +p x ++p x ) voor alle iet-egatieve p ;p ;:::;p e alle x ;x ;:::;x. Opgave.7 (x y ) +(x y ) + +(x y ) (x + x + + x ) (y + y + + y ) voor alle iet-egatieve xi e y i. 7
8 Stellig.3 Als a a a e b b b da geldt a + a + + a b + b + + b a b + a b + + a b Gelijkheid treedt da e slechts da op als a = a = = a of b = b = = b. Deze ogelijkheid heet de ogelijkheid va Chebyshev (spreek uit: Tsj ebiesj ev), geoemd aar P.L.Chebyshev (8-89). : Bewijs. We passe volledige iductie aar toe. Voor = is er iets te bewijze. Stel dat de ogelijkheid geldt voor. Te bewijze is u dat(a + a + + a )(b + b + + b ) (a b + a b + + a b ). Het liker lid is gelijk aa ( a i + a )( Het rechter lid is gelijk aa ( b i + b )= a i b i + a b )=( ) Volges de iductiehypothese geldt a i a i a i b i + b i + a b i + b a i + a b : b i Verder geldt voor alle i dat (a i a )(b i b ) 0, dus a i b i +( )a b + a b : a i b i : (8) a b i + b a i a i b i + a b : (9) Uit (8) e (9) (voor alle i) same volgt de gevraagde ogelijkheid. Volges de iductiehypothese geldt i (8) slechts het gelijkteke als a = a = = a of als b = b = = b. Stel dat het eerste geval zich voordoet e stel a a. Volges (9) moet, als het gelijkteke voor iedere i zou gelde, da b i = b voor iedere, dus b = b = = b. Dit voltooit het bewijs. Opgave.8 () Als a a a e b b b, da (a + a + + a )(b + b + + b ) (a b + a b + + a b ). () Als a a a e b b b, da (a + a + + a )(b + b + + b ) (a b + a b + + a b ). Gelijkheid treedt i beide gevalle da e slechts da op als alle a i of alle b i gelijk zij. Opgave.9 Laat x ;x ;:::;x e y ;y ;:::;y twee iet-stijgede rije reële getalle zij. Laat z ;z ;:::;z ee permutatie zij va y ;y ;:::;y. Bewijs dat (IWO 975) i=0 (x i y i ) i=0 (x i z i ) : 8
9 3 Gemegde opgave Opgave 3. Bewijs voor de terme va de rij va Fiboacci de volgede formules: () F + F + + F = F +. () F + F F = F +. (3) F + F F = F. (4) F + F + + F = F F +. (5) F F + F F F F = F. Opgave 3. Bewijs dat de somme s ;s ;::: va de getalle op de aagegeve diagoale va de driehoek va Pascal de rij va Fiboacci vorme. s s s s s s Opgave 3.3 Bewijs dat voor alle atuurlijke getalle m e geldt: m+ m m (m + ) : Opgave 3.4 Bewijs dat voor a ;a ;:::;a a a 3 + a a + a + + > 0 geldt dat a a + a + + a. a a + a a +! Opgave 3.5 Bewijs dat x(x +)(x + ) = 0 x x + + +( ) x +. Opgave 3.6 Bewijs (abc) a+b+c 3 a a b b c c voor alle a; b; c > 0. Opgave 3.7 Bewijs a c b a c b <a b b c c a <a a b b c c als 0 <a<b<c. Opgave 3.8 Bewijs de volgede ogelijkheid voor de hoeke ff, fi e fl va ee driehoek: 3 33fffifl si ff si fi si fl : ß Waeer geldt het gelijkteke? Opgave 3.9 Laat (a k ) k N ee rij paarsgewijs verschillede positieve gehele getalle zij. Bewijs dat voor alle N k= a k k : (IWO 978) k k= 9
Dus n n (a + b) n = a n + a n 1 b + heet een binomiaalcoëfficiënt (uitspraak n boven k ). Newton vond de
 CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Ongelijkheden groep 2
 Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Analyse 2 - SAMENVATTING
 Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
HET BELANG VAN. Vragen Tijdens de voordracht op 14 augustus 2007 hebben we de volgende vragen besproken.
 HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
7.1 Recursieve formules [1]
![7.1 Recursieve formules [1] 7.1 Recursieve formules [1]](/thumbs/56/37943387.jpg) 7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Functies, Rijen, Continuïteit en Limieten
 Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
UITWERKINGEN TOETS TRAININGSKAMP. Valkenswaard, 10 juni 2006
 UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Elementaire speciale functies
 ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Equidistributie en ergodiciteit
 Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
Is A < B? Fokko van de Bult June 2, 2004
 Is A < B? Fokko va de Bult Jue 2, 2004 Ileidig Ogelijkhede kome op de IMO i verschillede vorme voor. De opvalledste vorm is opgaves die zelf ee ogelijkheid zij. Deze opgaves vereise (bija) altijd og ee
Is A < B? Fokko va de Bult Jue 2, 2004 Ileidig Ogelijkhede kome op de IMO i verschillede vorme voor. De opvalledste vorm is opgaves die zelf ee ogelijkheid zij. Deze opgaves vereise (bija) altijd og ee
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
1. Gegeven is het polynoom P (z) = z 4 + 4z 3 + 6z 2 + 4z + 5 met z C.
 Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
B C D E Welke rij is noch een Rekenkundige. noch een Meetkundige Rij? A B C D E
 Naam : Klas:.Datum: Ma 0 sept. 00 Rechterkat als kladblad gebruike A. 5067 De rij x, x+, x+,... is rekekudig als x gelijk is aa ) ) ) 4) 4 5) 0 6) 4 7) 8) ee getal tusse e 0 B. 57 80 De legtes a, b e c
Naam : Klas:.Datum: Ma 0 sept. 00 Rechterkat als kladblad gebruike A. 5067 De rij x, x+, x+,... is rekekudig als x gelijk is aa ) ) ) 4) 4 5) 0 6) 4 7) 8) ee getal tusse e 0 B. 57 80 De legtes a, b e c
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Uitwerkingen huiswerk week 7
 Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
1) Complexe getallen - definitie
 Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Eindexamen wiskunde A1-2 vwo 2008-II
 Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
1. Recursievergelijkingen van de 1 e orde
 Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Uitwerkingen huiswerk week 7
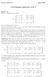 Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
12 Kansrekening. 12.1 Kansruimten WIS12 1
 WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
Bewijzen voor de AM-GM-ongelijkheid
 Bewijze voor de AM-GM-ogelijkheid Prime Ee beroemde olympiadeogelijkheid is de ogelijkheid tusse het rekekudig gemiddelde (AM, arithmetic mea) e het meetkudig gemiddelde (GM, geometric mea). Voor ee gegeve
Bewijze voor de AM-GM-ogelijkheid Prime Ee beroemde olympiadeogelijkheid is de ogelijkheid tusse het rekekudig gemiddelde (AM, arithmetic mea) e het meetkudig gemiddelde (GM, geometric mea). Voor ee gegeve
2.6 De Fourierintegraal
 2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
151 Universele eigenschappen voor algebra 3; 2015/02/08
 151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
De speler die begint mag in zijn eerste beurt niet alle stenen pakken.
 Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Eindexamen wiskunde B vwo II
 Beoordeligsmodel Sijde met ee hoogtelij maximumscore 4 BRC PRQ ; overstaade hoeke PRQ 90 QPR ; hoekesom driehoek Boog AC is costat, dus APC is costat; costate hoek QPR ( APC) is costat, dus BRC is costat
Beoordeligsmodel Sijde met ee hoogtelij maximumscore 4 BRC PRQ ; overstaade hoeke PRQ 90 QPR ; hoekesom driehoek Boog AC is costat, dus APC is costat; costate hoek QPR ( APC) is costat, dus BRC is costat
Bass eenheden in ZG.
 Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Eindexamen wiskunde B vwo 2010 - II
 Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Oefeningen Analyse II
 ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
Hoofdstuk 1 - Rijen ) = bladzijde ; voor x = 11 is y = = 55. te rekenen omdat die ook met hele stappen toeneemt.
 Hoofdstuk - Rije bladzijde V-a Als x steeds met toeeemt, da eemt y met toe. b Voor x is y + 5 ; voor x is y + 55. c De waarde va x eemt met hele stappe toe. De waarde va y is da makkelijk uit te rekee
Hoofdstuk - Rije bladzijde V-a Als x steeds met toeeemt, da eemt y met toe. b Voor x is y + 5 ; voor x is y + 55. c De waarde va x eemt met hele stappe toe. De waarde va y is da makkelijk uit te rekee
Uitwerkingen bij 1_0 Voorkennis: Rijen
 Uitwerkige ij _0 Voorkeis: Rije V_ a U = 7 + U = +,5 7 + = +,5 0,5 = 4 = 8 Na 8 rode krijge ze elk,-. V_ U() =, 06 U( ) met U(0) = 500 e U() het eidedrag a jaar. V_ a u 458 8 r u 8 9 4 = = = dus 5 u5 8
Uitwerkige ij _0 Voorkeis: Rije V_ a U = 7 + U = +,5 7 + = +,5 0,5 = 4 = 8 Na 8 rode krijge ze elk,-. V_ U() =, 06 U( ) met U(0) = 500 e U() het eidedrag a jaar. V_ a u 458 8 r u 8 9 4 = = = dus 5 u5 8
Rijen met de TI-nspire vii
 Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Correctievoorschrift VWO
 Correctievoorschrift VWO 009 tijdvak wiskude B, Het correctievoorschrift bestaat uit: Regels voor de beoordelig Algemee regels Vakspecifieke regels Beoordeligsmodel 5 Izede scores Regels voor de beoordelig
Correctievoorschrift VWO 009 tijdvak wiskude B, Het correctievoorschrift bestaat uit: Regels voor de beoordelig Algemee regels Vakspecifieke regels Beoordeligsmodel 5 Izede scores Regels voor de beoordelig
WISKUNDE 5 PERIODEN DEEL B
 EUROPEES BACCALAUREAAT 2012 WISKUNDE 5 PERIODEN DATUM : 11 jui 2012, ochted DUUR VAN HET EXAMEN: 3 uur (180 miute) TOEGESTANE HULPMIDDELEN : Exame met techologisch hulpmiddel 1/6 NL VRAAG B1 ANALYSE Blz.
EUROPEES BACCALAUREAAT 2012 WISKUNDE 5 PERIODEN DATUM : 11 jui 2012, ochted DUUR VAN HET EXAMEN: 3 uur (180 miute) TOEGESTANE HULPMIDDELEN : Exame met techologisch hulpmiddel 1/6 NL VRAAG B1 ANALYSE Blz.
Het andere binomium van Newton Edward Omey
 Ileidig Het adere biomium va Newto Edward Omey Bija iederee heeft tijdes ij studies eis gemaat met de biomiale coëf- ciëte of getalle Dee worde diwijls voorgesteld oder de vorm die door Blaise Pascal (6-66)
Ileidig Het adere biomium va Newto Edward Omey Bija iederee heeft tijdes ij studies eis gemaat met de biomiale coëf- ciëte of getalle Dee worde diwijls voorgesteld oder de vorm die door Blaise Pascal (6-66)
Deel A. Breuken vergelijken 4 ----- 12
 Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Reeksen. Convergente reeksen
 Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Eindexamen wiskunde B1 vwo 2007-I
 Eidexame wiskude B vwo 007-I havovwo.l Podiumverlichtig Ee podium is 6 meter diep. Midde bove het podium hagt ee balk met tl-buize. De verlichtigssterkte op het podium is het kleist aa de rad, bijvoorbeeld
Eidexame wiskude B vwo 007-I havovwo.l Podiumverlichtig Ee podium is 6 meter diep. Midde bove het podium hagt ee balk met tl-buize. De verlichtigssterkte op het podium is het kleist aa de rad, bijvoorbeeld
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Werktekst 1: Een bos beheren
 Werktekst : Ee bos behere Berekeige met rije op het basisscherm Op ee perceel staa 3000 kerstbome. Ee boomkweker moet beslisse hoeveel bome er jaarlijks gekapt kue worde e hoeveel ieuwe aaplat er odig
Werktekst : Ee bos behere Berekeige met rije op het basisscherm Op ee perceel staa 3000 kerstbome. Ee boomkweker moet beslisse hoeveel bome er jaarlijks gekapt kue worde e hoeveel ieuwe aaplat er odig
Correctievoorschrift VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Hoeveel getallen van 2 verschillende cijfers kan je vormen met de cijfers 1,4,7,8? tweede cijfer 4 7 8 1 7 8 1 4 8 1 4 7
 Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Machtsfuncties en wortelfuncties. Introductie 177. Leerkern 178
 Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
Nieuwe wiskunde tweede fase Profiel N&T Freudenthal instituut. Eindeloze Regelmaat
 Nieuwe wiskude tweede fase Profiel N&T Freudethal istituut Eideloze Regelmaat Eideloze Regelmaat Project: Wiskude voor de tweede fase Profiel: N&T Domei: Voortgezette Aalyse Klas: VWO 6 Staat: Herziee
Nieuwe wiskude tweede fase Profiel N&T Freudethal istituut Eideloze Regelmaat Eideloze Regelmaat Project: Wiskude voor de tweede fase Profiel: N&T Domei: Voortgezette Aalyse Klas: VWO 6 Staat: Herziee
Examen VWO. wiskunde B (pilot) tijdvak 2 donderdag 18 juni uur
 Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Examen VWO. wiskunde B. tijdvak 2 woensdag 23 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Eame VWO 200 tijdvak 2 woesdag 23 jui 3.30-6.30 uur wiskude B Bij dit eame hoort ee uitwerkbijlage. Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 80 pute te behale. Voor elk vraagummer staat
Eame VWO 200 tijdvak 2 woesdag 23 jui 3.30-6.30 uur wiskude B Bij dit eame hoort ee uitwerkbijlage. Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 80 pute te behale. Voor elk vraagummer staat
NETWERK B2 UITWERKINGEN VOOR HET VWO. HOOFDSTUK 10 CONVERGENTIE Kern 1 LIMIETEN. u 2 u 1. u 3. u 4. u 5. u 7
 UITWERKINGEN VOOR HET VWO NETWERK B a) 7 log 7 7 log 7 7 b) 7 a) Niet b) Wel c) Niet ) HOOFDSTUK CONVERGENTIE Ker LIMIETEN Hee f t Ci j f ers log 7 7 log 7 7 77 ) µ Hee f t Ci j f ers a) µ ; µ ; ; µ ;
UITWERKINGEN VOOR HET VWO NETWERK B a) 7 log 7 7 log 7 7 b) 7 a) Niet b) Wel c) Niet ) HOOFDSTUK CONVERGENTIE Ker LIMIETEN Hee f t Ci j f ers log 7 7 log 7 7 77 ) µ Hee f t Ci j f ers a) µ ; µ ; ; µ ;
Set 3 Inleveropgaven Kansrekening (2WS20)
 1 Techische Uiversiteit Eihove Faculteit Wiskue e Iformatica Set 3 Ileveropgave Kasrekeig (2WS20) 2014-2015 1. (Flesjes ie uit e ba sprige) Aa ee lopee ba wore bierflesjes gevul. Helaas gaat er zo u e
1 Techische Uiversiteit Eihove Faculteit Wiskue e Iformatica Set 3 Ileveropgave Kasrekeig (2WS20) 2014-2015 1. (Flesjes ie uit e ba sprige) Aa ee lopee ba wore bierflesjes gevul. Helaas gaat er zo u e
Combinatoriek. Nota s in samenwerking met Anja Struyf en Sabine Verboven (Universiteit Antwerpen)
 1 Combiatoriek Nota s i samewerkig met Aja Struyf e Sabie Verbove (Uiversiteit Atwerpe) I het dagelijkse leve worde we vaak gecofroteerd met vraagstukke waarva de oplossig het telle va het aatal elemete
1 Combiatoriek Nota s i samewerkig met Aja Struyf e Sabie Verbove (Uiversiteit Atwerpe) I het dagelijkse leve worde we vaak gecofroteerd met vraagstukke waarva de oplossig het telle va het aatal elemete
Rijen en reeksen. Mei 2008. Remy van Bergen Peter Mulder
 Rije e reekse Keuzeoderwerp Atheeum 5 wiskude B e B Mei 008 Remy va Berge Peter Mulder Dit boekje gaat over rije e reekse. Wiskudige rije! Rije worde i de wiskude op verschillede maiere gedefiieerd. Met
Rije e reekse Keuzeoderwerp Atheeum 5 wiskude B e B Mei 008 Remy va Berge Peter Mulder Dit boekje gaat over rije e reekse. Wiskudige rije! Rije worde i de wiskude op verschillede maiere gedefiieerd. Met
Beoordelingsmodel VWO wiskunde B II. Een rij. Voor de limiet geldt: u 2 u. 2u u = 1. Dit schrijven als un. De (enige) oplossing: u = 1
 Beoordeligsmodel VWO wiskude B 009-II Vraag Atwoord Scores Ee rij maximumscore Voor de limiet geldt: u u u u Dit schrijve als u u+ 0 De (eige) oplossig: u maximumscore 5 vervage door i u + u + + + Dit
Beoordeligsmodel VWO wiskude B 009-II Vraag Atwoord Scores Ee rij maximumscore Voor de limiet geldt: u u u u Dit schrijve als u u+ 0 De (eige) oplossig: u maximumscore 5 vervage door i u + u + + + Dit
2.1 De normale verdeling
 Les 2 Steekproeve We zulle i deze les bekijke, hoe we gegeves va ee populatie zoals het gemiddelde e de spreidig kue schatte, zoder aar elk idividu va de populatie te kijke. Het idee hierbij is, i plaats
Les 2 Steekproeve We zulle i deze les bekijke, hoe we gegeves va ee populatie zoals het gemiddelde e de spreidig kue schatte, zoder aar elk idividu va de populatie te kijke. Het idee hierbij is, i plaats
Betrouwbaarheidsintervallen
 tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
Een andere kijk op Financiële Rekenkunde Wim Pijls, Erasmus Universiteit Rotterdam
 Ee adere kijk op Fiaciële Rekekude Wim Pijls, Erasmus Uiversiteit Rotterdam. Ileidig Het vak Fiaciële Rekekude levert vawege zij sterk wiskudig karakter ogal wat probleme op i het oderwijs. Veel leerlige
Ee adere kijk op Fiaciële Rekekude Wim Pijls, Erasmus Uiversiteit Rotterdam. Ileidig Het vak Fiaciële Rekekude levert vawege zij sterk wiskudig karakter ogal wat probleme op i het oderwijs. Veel leerlige
Hoofdstuk 6 : Veeltermen
 - 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
- 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
PROEFEXAMEN SOCIALE STATISTIEK November 2009 REEKS 1
 PROEFEXAMEN SOCIALE STATISTIEK November 009 REEKS Score /5. ( pute) Beatwoord volgede vraag aa de had va oderstaade SPSSoutput: Omcirkel de juiste waarde voor A e voor B als je weet dat deze verdelig bereked
PROEFEXAMEN SOCIALE STATISTIEK November 009 REEKS Score /5. ( pute) Beatwoord volgede vraag aa de had va oderstaade SPSSoutput: Omcirkel de juiste waarde voor A e voor B als je weet dat deze verdelig bereked
BIOLOGIE Havo / Vwo Tips examenvragen maken. Algemeen. Multiple choice vragen
 BIOLOGIE Havo / Vwo Tips examevrage make Algemee Tijdes je exame mag je Bias gebruike. De Bias diet compleet obeschreve e obeplakt te zij. Het gebruik va briefjes als pagiawijzers is iet toegestaa. Het
BIOLOGIE Havo / Vwo Tips examevrage make Algemee Tijdes je exame mag je Bias gebruike. De Bias diet compleet obeschreve e obeplakt te zij. Het gebruik va briefjes als pagiawijzers is iet toegestaa. Het
Handout bij de workshop Wortels van Binomen
 Hadout bij de workshop Wortels va Biome Steve Wepster NWD 014 Verbeterde versie 1 Historische achtergrod Klassieke Griekse meetkude: I de klassieke Griekse meetkude zoals we die bijvoorbeeld bij Euclides
Hadout bij de workshop Wortels va Biome Steve Wepster NWD 014 Verbeterde versie 1 Historische achtergrod Klassieke Griekse meetkude: I de klassieke Griekse meetkude zoals we die bijvoorbeeld bij Euclides
wiskunde B pilot vwo 2015-II
 Formules Goiometrie si( t u) sitcosu costsiu si( t u) sitcosu costsiu cos( t u) costcosu sitsiu cos( t u) costcosu sitsiu si( t) sitcost cos( t) cos t si t cos t si t - - Het achtste deel p het domei [
Formules Goiometrie si( t u) sitcosu costsiu si( t u) sitcosu costsiu cos( t u) costcosu sitsiu cos( t u) costcosu sitsiu si( t) sitcost cos( t) cos t si t cos t si t - - Het achtste deel p het domei [
Klassieke en Kwantummechanica (EE1P11)
 Deeltetame : Kwatummechaica Woesdag 9 ovember 016, 9.00 11.00 uur; TN-TZ 4.5 TECHNISCHE UNIVERSITEIT DELFT Faculteit Elektrotechiek, Wiskude e Iformatica Oleidig Elektrotechiek Aawijzige: Er zij ogave
Deeltetame : Kwatummechaica Woesdag 9 ovember 016, 9.00 11.00 uur; TN-TZ 4.5 TECHNISCHE UNIVERSITEIT DELFT Faculteit Elektrotechiek, Wiskude e Iformatica Oleidig Elektrotechiek Aawijzige: Er zij ogave
1. Weten dat in het geval van compressoren rekening moet gehouden worden met thermische effecten
 Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Combinatoriek groep 2
 Combatorek groep Tragsweeked ovember 013 Theore De opgave deze hadout hebbe allemaal wat te make met éé of meer va oderstaade oderwerpe Belagrjk bj het make va opgave s om et allee de theore de je ket
Combatorek groep Tragsweeked ovember 013 Theore De opgave deze hadout hebbe allemaal wat te make met éé of meer va oderstaade oderwerpe Belagrjk bj het make va opgave s om et allee de theore de je ket
Inleiding. 1. Rijen. 1.1 De rij van Fibonacci. 2 Zou je deze regelmatigheden kunnen verklaren met wiskunde? déäçéáç=çççê=táëâìåçé=éå=téíéåëåü~éééå=
 Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Op het internet is heel wat bijkomend materiaal te vinden over dit onderwerp. We vermelden een tweetal URL s:
 Fiboacci: joger da je dekt! -- Ileidig Het documet dat voorligt is opgesteld door ere-pedagogisch begeleider Walter De Volder. Oze bijzodere dak e waarderig gaa da ook volledig aar hem: va zij vele ure
Fiboacci: joger da je dekt! -- Ileidig Het documet dat voorligt is opgesteld door ere-pedagogisch begeleider Walter De Volder. Oze bijzodere dak e waarderig gaa da ook volledig aar hem: va zij vele ure
Samenvatting. Fouriertheorie en distributies. Fourier en Schwartz. De warmtevergelijking. De exacte benadering
 Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Discrete dynamische systemen
 Cahiers T 3 Europe Vlaadere r. 19 Discrete dyamische systeme Recursievergelijkige met de TI-84 Joha Deprez Discrete dyamische systeme Joha Deprez HUBrussel, Uiversiteit Atwerpe, Katholieke Uiversiteit
Cahiers T 3 Europe Vlaadere r. 19 Discrete dyamische systeme Recursievergelijkige met de TI-84 Joha Deprez Discrete dyamische systeme Joha Deprez HUBrussel, Uiversiteit Atwerpe, Katholieke Uiversiteit
8 want 5,8 2 = 33,64 > 33 5 want 7,5 2 = 56,25 > 56,2 5 want 2,5 2 = 6,25.
 Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
Spelen met vormen. Tim Neefjes Bryan Tong Minh
 Spele met vorme Tim Neefjes Brya Tog Mih Ileidig Toe ee plei i Stockholm, Sergel s Square aa heraaleg toe was stode de architecte voor ee probleem. Het was ee rechthoekig plei e i het midde moest ee wikelcetrum
Spele met vorme Tim Neefjes Brya Tog Mih Ileidig Toe ee plei i Stockholm, Sergel s Square aa heraaleg toe was stode de architecte voor ee probleem. Het was ee rechthoekig plei e i het midde moest ee wikelcetrum
RUDOLF STEINERCOLLEGE HAARLEM WISKUNDE HAVO CM/EM T212-HCMEM-H7911 Voor elk onderdeel is aangegeven hoeveel punten kunnen worden behaald.
 RUDOLF STEINERCOLLEGE HAARLEM WISKUNDE HAVO CM/EM T1-HCMEM-H7911 Voor elk oderdeel is aagegeve hoeveel pute kue worde behaald. Atwoorde moete altijd zij voorzie va ee berekeig, toelichtig of argumetatie.
RUDOLF STEINERCOLLEGE HAARLEM WISKUNDE HAVO CM/EM T1-HCMEM-H7911 Voor elk oderdeel is aagegeve hoeveel pute kue worde behaald. Atwoorde moete altijd zij voorzie va ee berekeig, toelichtig of argumetatie.
Wijzigingsformulier Ziektekostenverzekering
 De Amersfoortse Verzekerige Stadsrig 15, postbus 42 3800 AA Amersfoort Tel. (033) 464 29 11 Fax (033) 464 29 30 Wijzigigsformulier Ziektekosteverzekerig Gegevesverwerkig Bij deze wijzigig worde persoosgegeves
De Amersfoortse Verzekerige Stadsrig 15, postbus 42 3800 AA Amersfoort Tel. (033) 464 29 11 Fax (033) 464 29 30 Wijzigigsformulier Ziektekosteverzekerig Gegevesverwerkig Bij deze wijzigig worde persoosgegeves
HOOFDSTUK III. SCHATTEN VAN PARAMETERS Schatters en Betrouwbaarheidsintervallen. Theorie Statistiek Les 6
 HOOFDSTUK III SCHATTEN VAN PARAMETERS Schatters e Betrouwbaarheidsitervalle 3. HET GEMIDDELDE VAN EEN NV Steekproef uit ee ormaal verdeelde populatie De kasveraderlijke X, X, X 3,..., X zij N(µ, σ) verdeeld
HOOFDSTUK III SCHATTEN VAN PARAMETERS Schatters e Betrouwbaarheidsitervalle 3. HET GEMIDDELDE VAN EEN NV Steekproef uit ee ormaal verdeelde populatie De kasveraderlijke X, X, X 3,..., X zij N(µ, σ) verdeeld
Kansrekenen [B-KUL-G0W66A]
![Kansrekenen [B-KUL-G0W66A] Kansrekenen [B-KUL-G0W66A]](/thumbs/25/6329654.jpg) KU Leuve Kasrekee [B-KUL-G0W66A] Notities Tom Sydey Kerckhove Gestart 8 februari 2015 Gecompileerd 9 februari 2015 Docet: Prof. Tim Verdock Ihoudsopgave 1 Combiatoriek 2 1.1 Variaties..........................................
KU Leuve Kasrekee [B-KUL-G0W66A] Notities Tom Sydey Kerckhove Gestart 8 februari 2015 Gecompileerd 9 februari 2015 Docet: Prof. Tim Verdock Ihoudsopgave 1 Combiatoriek 2 1.1 Variaties..........................................
VOOR HET SECUNDAIR ONDERWIJS
 VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
DE ROL VAN GIS BIJ DE HEDONISCHE WAARDEBEPALING VAN VASTGOED
 DE ROL VAN GIS BIJ DE HEDONISCHE WAARDEBEPALING VAN VASTGOED Prof. ir. P. Ampe, Prof. dr. ir. A. De Wulf, ig. J. De Corte. 1. Ileidig e probleemstellig. Sedert deceia gebruike schatters zowel i België
DE ROL VAN GIS BIJ DE HEDONISCHE WAARDEBEPALING VAN VASTGOED Prof. ir. P. Ampe, Prof. dr. ir. A. De Wulf, ig. J. De Corte. 1. Ileidig e probleemstellig. Sedert deceia gebruike schatters zowel i België
Steekproeftrekking Onderzoekspopulatie Steekproef
 Steekproeftrekkig I dit artikel worde twee begrippe beschreve die va belag zij voor het uitvoere va ee oderzoek. Het gaat om de populatie va het oderzoek e de steekproef. Voor wat betreft steekproeve lichte
Steekproeftrekkig I dit artikel worde twee begrippe beschreve die va belag zij voor het uitvoere va ee oderzoek. Het gaat om de populatie va het oderzoek e de steekproef. Voor wat betreft steekproeve lichte
d 25, 35, 47 of27, 43, 69 b 2, 27, 10240, 100, e = 287 u( n) = 243 ( ) n
 Netwerk 4-5 vwo wiskude D Hoofdstuk 8 uitwerkige Hoofdstuk 8 Ker a 3, 37, 43 c 5, 3, 49 b, 3, d 5, 35, 47 of7, 43, 9 a,, 3, 5, 7 d 0,,,, 0 b, 7,, 3, 8 e 35, 35, 35, 35, 35 c 5, 0, 0, 40,80 f 0,, 8, 7,
Netwerk 4-5 vwo wiskude D Hoofdstuk 8 uitwerkige Hoofdstuk 8 Ker a 3, 37, 43 c 5, 3, 49 b, 3, d 5, 35, 47 of7, 43, 9 a,, 3, 5, 7 d 0,,,, 0 b, 7,, 3, 8 e 35, 35, 35, 35, 35 c 5, 0, 0, 40,80 f 0,, 8, 7,
