Verloop van exponentiele en logaritmische functies

Maat: px

Weergave met pagina beginnen:

Download "Verloop van exponentiele en logaritmische functies"

Oscar Maes
6 jaren geleden
Aantal bezoeken:

1 Verloop v epoetiele e loritmische fucties

2 ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked We herhle ekele belrijke eieschppe: Alle epoetiële fucties hebbe hetzelfde domei e hetzelfde beeld: R \ : domep = R, bldep = R Alle rfieke door het put (, ) Als ],[ d is ep ee dlede fuctie, ls > d is ep ee stijede fuctie Alle epoetiële fucties hebbe de -s ls horizotle symptoot:, d is lim =, e Als ],[ + ls >, d is lim = b) Defiitie e rfiek v loritmische fucties f ( ) =, wrbij + c We oeme c de -loritme v b ls e slechts ls eldt dt = b I symbole wordt deze defiitie: \,, : c R b R c R lob= c = b Rekereels Voor loritme elde de volede rekereels: b, R \,, y R, r R : R \ Deze fuctie wordt lo r r = lo = lo ( ) y = lo+ loy lo lo loy y = r lo = r lo lo= b b lo lo Opm: Stelli heeft ls omiddellijk evol dt ook eldt dt: N : lo = lo Ee loritmische fuctie is ee fuctie met voorschrift wordt ook vk eoteerd ls lo = lo, wrbij + f R \ Deze fuctie Het is omiddellijk duidelijk dt lo e ep elkrs iverse fuctie zij (voor lle + R \ ) Cursus verloop ep e lo fies - - S Mettepeie

3 Hierst st ekele rfieke v loritmische fucties eteked We herhle ekele belrijke eieschppe: Alle loritmische fucties hebbe hetzelfde domei e hetzelfde beeld: R \ : domlo = R, bldlo = R Alle rfieke door het put (, ) I symbole: + R \ :, lo Als ],[ d is lo ee dlede fuctie, ls > d is lo ee stijede fuctie Alle loritmische fucties hebbe de y -s ls horizotle symptoot: Als ],[, d is ls >, d is > lim lo > lim lo Brise & tuurlijke loritme =+, e = Loritme met rodtl oeme we Brise loritme Bij loritme met dit rodtl hoef je de iet te schrijve (et zols je de bij ee vierktswortel ook iet schrijft) Loritme met ls rodtl het trscedete etl e ( e=, ) oeme we tuurlijke loritme, of Neperise loritme Hier oteer je ook ee rodtl mr ebruik je ipv lo het symbool l (dit stt voor loritmus turlis) Dt het etl e zeer belrijk is volt uit de volede prrf ) Afeleide v epoetiele e loritmische fucties ) Afeleide v epoetiële fucties De defiitie v feleide zet dt f' ( ) Voor epoetiële fucties (met f' = lim Merk op dt De limiet = ( + ) f f lim f ( ) = ) wordt dit: f' ( ) = lim = lim +, dit is de richtiscoëfficiët v de rklij i put P (,) lim bestt dus e is ekel fhkelijk v de wrde v e We defiiëre u het etl e zó dt lim = I dt evl zl dus elde dt D( e ) = e Uit de rekereels v mchte e loritme, e de kettireel, volt d ook direct dt: l l l D = D e = D e = e l = l + Hieruit volt dus ook metee dt eldt: R \ : lim = l Cursus verloop ep e lo fies S Mettepeie

4 b) Afeleide v loritmische fucties Steued op het vorie e de kettireel kue we u ook heel eevoudi de tuurlijke loritme fleide: D ( l ) ( l ) ( l ) e = D e = e D = D = D = Voor loritmische fucties met ee der rodtl ebruike we rekereel : l l l ( lo ) l ( l ) D = D = D = l l l Belrijke evole (voor de cursus iterlrekei) D( l ) D( l k ) + =, wt ls = =, e D l = D( l ) = = R eldt D( l) D( l) Als + + k = k c) Het etl e ders bekeke R eldt + k + k + ( + + k) + k = + k = + k Stelli: e= lim + + Bewijs: D( ) stel= ( +) ( +) l l l l = lim = lim = > > Stelle we u =, d is is = e eldt dt + (omdt ) We krije: > * lim l lim l llim lim e + + = + = + = + = (*: Dt lim e l v plts moe wissele lit het feit dt l ee cotiue fuctie is ) Opm : Het bewijs v deze stelli eldt ook voor de likerlimiet, dus ook e= lim + < Stel je z= (dus zl d) Afeleide v f z ls ± ) d eldt dus ook dt e lim( z) z z = + Als f e beide fleidbre fucties zij, d eldt voor de feleide v de fuctie lf lf lf D f = D e = D e = e D lf + = f lf D+ f Df = f Df f Deze op het eerste zicht iewikkelde formule k eevoudi othoude worde door te beseffe dt de feleide bestt uit twee terme De eerste term bekom je door tweede term door f te leide ls mchtsfuctie f : f f te leide ls epoetiële fuctie, de Cursus verloop ep e lo fies S Mettepeie

5 e) Ee eevoudie differetilverelijki Stelli: f' ( ) k f ( ) =, met k R f ( ) = be k, met b R Bewijs: : f' ( ) D( be k ) be k k kbe k k f ( ) : = = = = k ( e ) f ( ) k k k k f e f' f ke e k f f ke D b k = = = = R k k e e e 3) Ekele belrijke vullede stellie ivm limiete ) Herhli: de stellie v Rolle e Lre Stelli (Rolle): f is cotiu i [ b, ], fleidbr i ] b, [, e f ( ) = f ( b) c ] b[ f Stelli (Lre): f is cotiu i [ b, ], fleidbr i ] b, [ c ] b, [: f' b) De middelwrdestelli v Cuchy =, : ' = f b f b De middelwrdestelli v Lre k verlemeed worde tot de volede stelli, die d de (verlemeede) middelwrdestelli v Cuchy wordt eoemd Stelli: Zij f e cotiu i [ b, ] e fleidbr i ] b, [, e eldt ] b[ ( ) f ( b) f ( ) f' c ] b, [: = ( b) ( ) ', : ', d: Bewijs: Defiieer de fucties h( ) f ( ) k ( ) i [ b, ] e fleidbr i ] b, [ We kieze u k zodt h( ) = h( b), dit k wt: f ( b) f ( ) h( ) = h( b) f ( ) + k ( ) = f ( b) + k ( b) k = ( b) ( ) ( ( b) ( ) wt ] b, [: ' ( ) dus is strikt stijed of dled i [ b, ] ) f' De stelli v Rolle zet dus c ] b, [: h' f' k ' k ' c) De reels v de l Hôpitl = +, met prmeter k R, d zij l deze fucties cotiu = + = = De middelwrdestelli v Cuchy wordt eielijk llee ebruikt i het volede bewijs: Stelli: Zij f ( ) = ( ) =, mr zo dt B B { } ( ) e ' ( ), d eldt: Bewijs: Neem B\ { } c ], [ : f f' lim = ' : \ : ', met f e fleidbr i,, met >, d eldt er wees de stelli v Cuchy: f f f f' c = = ' c Neem je hieri de limiet voor, d zl ook c, dus: f f' c f' lim = lim = c ' c ' Cursus verloop ep e lo fies S Mettepeie

6 Deze stelli ket twee veelebruikte uitbreidie (we vrde deze zoder bewijs): Stelli: Als limf ( ) = lim( ) =, of limf ( ) lim( ) B \{ }, zodt B { } ( ) (Deze stelli eldt ook ls ± ) = =± e f e zij fleidbr i ee f \ : ', d eldt: lim 3 3 f' = lim ' e e 3 Voorbeeld: lim = lim = 3 H Soms is het hdi om de loritme te eme v ee limiet, om het rekewerk te vereevoudie: Voorbeeld: om lim te berekee stel je lim = L llim = ll ll= lim l = lim l Vi ee kleie kustreep kue we hierop de reel v l Hôpitl te kue toepsse: l + ll= lim = lim = lim ( ) = L= e = H Cursus verloop ep e lo fies S Mettepeie

Vergelijkbare documenten

0 niet gedefinieerd is).

0 niet gedefinieerd is). 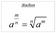Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels