Het differentiequotiënt van een functie in een interval geeft de gemiddelde helling weer van die functie in dat interval. Symbolisch wordt dit:
|
|
|
- Franciscus Wauters
- 5 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Afgeleide
2 ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig geie kue we dit iterpretere ls e differetiequotiët (leerstof vierdes) Je iet echter ook dt de mimle helligsgrd 9% is Dit wil egge dt er erges ee put is op de muur v Hoei wr de ogeblikkelijke hellig 9% is Mr hoe kue we dit wiskudig iterpretere? b) Differetiequotiët Het differetiequotiët v ee fuctie i ee itervl geeft de gemiddelde hellig weer v die fuctie i dt itervl Symbolisch wordt dit: Het differetiequotiët v de fuctie y= f ( ) i het itervl [, ] y f b f b is = [ b, ] b Grfisch geie is dit de richtigscoëfficiët v de rechte die de pute, (, ) A f e B b f b verbidt Het k dus geïterpreteerd worde ls de gemiddelde hellig v de fuctie i dt itervl Voorbeeld: Als f ( ) y [,5] = f 4 = + 5 f 5 = = Hierst op de figuur ie je dt dit meetkudig geie de richtigscoëfficiët is v de rechte AB, bereke d het differetiequotiët voor het itervl [,5 ] c) Ogeblikkelijke hellig Stel dt je i het voorbeeld uit de vorige vrg iet wil wete wt de gemiddelde hellig is, mr eerder geïteresseerd bet i hoe groot de ogeblikkelijke hellig is i put A We oude dit kue bedere door put B vribel te mke e steeds dichter bij put A te eme De rechte AB wordt d ee eer goede bederig v de rklij i put A We oeme u de fgeleide i put A de limiet v het differetiequotiët wrbij put B smevlt met put A Cursus differetilrekeig - fgeleide - - S Mettepeige
3 I os voorbeeld wordt dit: h h A A ( + ) ( ) 4 + f ( + ) f + + = Meetkudig geie is dit de richtigscoëfficiët v de rklij i put A, het is dus de perfecte mt voor de ogeblikkelijke hellig i put A d) Afgeleide i ee put Het begrip fgeleide kue we llee defiiëre i iwedige pute v het domei v ee fuctie f Om dit begrip te defiiëre hebbe we ee vullede defiitie odig Ee bsisomgevig B v ee reëel getl is ee itervl ] ε, ε[ + +, met ε R Ee reëel getl wordt ee iwedig put geoemd v ee vermelig V R ls e slechts ls er ee bsisomgevig v bestt die volledig i V ligt I symbole wordt dit: is ee iwedig put v V B : B V Is ee iwedig put v het domei v ee fuctie f, d defiiëre we de limiet ( + ) f' = ls de fgeleide v de fuctie f i put op voorwrde dt dee limiet bestt e eidig is f f lim Als de fgeleide i ee put bestt oeme we de fuctie dr fleidbr Dit is de richtigscoëfficiët v de rklij t i put, t y f' ( ) ( ) f ( ) = + A f de grfiek v f, dus: Stelle we i de defiitie + =, d kue we de defiitie ook herschrijve ls: f f f' ( ) Beide defiities hebbe hu voordele We illustrere met ee voorbeeld: Voorbeeld: Bereke met behulp v de defiitie de fgeleide v f ( ) = i = Eerste methode: f f' f' f' f' ( + ) f ( + ) ( + ) ( ) = Tweede methode: f' f' f f f' f ' = Welke methode je gebruikt bij welke oefeige mk je elf uit ( ) ( ) 6 ( ) ( + + ) Cursus differetilrekeig - fgeleide - - S Mettepeige
4 ) Afgeleide fucties I elk put R wr de fuctie f fleidbr is, kue we de fgeleide fuctie f ' defiiëre ls de fuctie die het put fbeeldt op de fgeleide f' ( ) v de fuctie f i dt put ( + ) Per defiitie geldt dus: f' ( ) (Ook hier kue we uiterrd met de ltertieve defiitie werke) ) Notties f f Voor de fgeleide fuctie f ' worde regelmtig ook dere otties gebruikt: Df ( ) df ( ) d Het voordeel v de tweede ottie is dt e geeft r welke vribele je fleidt b) Afgeleide v gekede fucties De fgeleide v ee costte De fgeleide i put R v ee costte fuctie f ( ) = c R, wordt gegeve door: c c f f f' ( ) = De fgeleide v de idetieke fuctie, of korter geoteerd: Dc= De fgeleide i put R v de idetieke fuctie f ( ) =, wordt gegeve door: f ( ) f ( ) f' = De fgeleide v de kwdrtische fuctie, of korter geoteerd: D= De fgeleide i put R v de kwdrtische fuctie f ( ) =, wordt gegeve door: ( ) ( + ) f f f' ( ) of korter geoteerd: D = De fgeleide v de kubische fuctie + =, De fgeleide i put R v de kubische fuctie f ( ) =, wordt gegeve door: ( ) f f f' ( ) of korter geoteerd: D = De fgeleide v de mchtfuctie ( + + ) + + =, De vorige fucties ij eigelijk specile gevlle v de fuctie f ( ) =, met N : Cursus differetilrekeig - fgeleide S Mettepeige
5 ( ) f f f' ( ) lim ( ) f' ( ) = =, of korter geoteerd: De fgeleide v de omgekeerde fuctie De fgeleide i put R v de omgekeerde fuctie f ( ) f f f' ( ) ( ) of korter geoteerd: D = De fgeleide v de vierktswortelfuctie + De fgeleide i put R v de vierktswortelfuctie ( )( + ) ( )( + ) f f f' ' f ( ) =, of korter geoteerd: + De fgeleide v de kubische wortelfuctie De fgeleide i put D = =, wordt gegeve door: =, f =, wordt gegeve door: D = R v de kubische wortelfuctie f =, wordt gegeve door: f f f' ' f ( ) = + + c) Rekeregels voor fgeleide fucties, of korter geoteerd: De fgeleide v ee som of verschil v twee fucties D = Stel dt f e g beide fleidbr ij i, d geldt voor de fgeleide v hu som: ( f g) ( ) ' ( f + g) ( ) ' ( f + g) ( ) = f' ( ) + g' ( ) ( f + g)( ) ( f + g)( ) ( f + g ) ( f ( ) + g( ) ) + ' f f g g f f g g + lim + Korter geoteerd geeft dit: D( f + g) = Df + Dg Volledig loog k je bewije dt D( f g) = Df Dg Cursus differetilrekeig - fgeleide S Mettepeige
6 De fgeleide v ee product v twee fucties Stel dt f e g beide fleidbr ij i, d geldt voor de fgeleide v hu product: ( f g) ( ) ( f g) '( ) ( f g) '( ) ( f g) '( ) ( f g) '( ) = ' ( f g)( ) ( f g)( ) f ( ) g( ) f ( ) g( ) ' f g f ( ) f ( ) g( ) g( ) g( ) + lim f ( ) f ( ) f ( ) g g limg( ) + lim f ( ) lim f g + f g' f ( ) g( ) + f ( ) g( ) f ( ) g( ) Korter geoteerd geeft dit: D( f g) = f Dg+ g Df Gevolg: Als hieri g ee costte fuctie is (stel g( ) = c R), d krijge we: ( ) = + D c f c Df f Dc = = c Df Voorbeeld: We ij u voldoede gewped om lle veeltermfucties f te leide: D D D D D = = = De formule voor het product v twee fucties k heel eevoudig uitgebreid worde: D f g h = D f g h = f D g h + g h Df = f g Dh+ f h Dg+ g h Df De fgeleide v de omgekeerde v ee fuctie Stel dt f fleidbr is i, e dt f ( ), d geldt voor de fgeleide v de omgekeerde: ( ) f f ' f f f ( ) f ( ) f f ( ) lim = f ' f ( ) f ( ) f ( ) = lim lim = f' ( ) = f f ( ) f ( ) f f Df Korter geoteerd geeft dit: D = f f De fgeleide v ee quotiët v twee fucties ' ( ) Uit de vorige twee rekeregels kue we de regel voor het quotiët v twee fucties fleide: f Dg Df g Df f Dg D = D f = f D + Df = f + = g g g g g g g (dee regel geldt uiterrd ekel ls de oemer verschilled is v ul) ( + ) 4+ Voorbeeld: D = + = = Cursus differetilrekeig - fgeleide S Mettepeige
7 De fgeleide v ee smestellig v twee fucties: de kettigregel Stel dt f fleidbr is i e dt g fleidbr is i f ( ), d geldt voor de smestellig: ( gf )( ) ( gf )( ) g( f ( ) ) g( f ( ) ) ( gf) '( ) g( f ( ) ) g( f ( ) ) f ( ) f ( ) ( gf) '( ) f ( ) f ( ) g( f ( ) ) g( f ( ) ) f ( ) f ( ) ( gf) '( ) f( ) f( ) f ( ) f ( ) Korter geschreve geeft dit D( gf ) = ( Dg) f Df ( ) lim = g' f f' Dee regel iet er op het eerste icht misschie igewikkeld uit, mr is i de prktijk heel eevoudig I woorde gt het ls volgt: je leidt ee smestellig v twee fucties f door de buiteste fuctie f te leide met ls verderlijke de bieste fuctie, wr je vermeigvuldigt met de fgeleide v de bieste fuctie Dee regel wordt om die rede welees de kettigregel geoemd Het is héél belgrijk dt je dee regel vlot leert toepsse Je l hem vf u costt gebruike Belgrijk gevolg: Elke eigeschp die we i het vorige hoofdstukje (fgeleide v gekede fucties) bewee kue we u uitbreide door i de eigeschp te vervge door f ( ) e weges de kettigregel te vermeigvuldige met Df ( ) Twee voorbeelde ij: m m ( ) Df ( ) D f m f = D f ( ) + + = Voorbeeld: D ( ) ( ) 4 De uitgebreide mchtregel (voor rtiole epoete) We kue u bewije dt de gekede regel D Stel dt q= (met dus q Q, Z e N ), d geldt: q = f D ( ) + Df = f = ook geldt met rtiole epoete D q f = f = f = f = dus ' ( f ) f' ( ) = f' ( ) =, f ( ) = = = f Met de kettigregel geeft dit d: D ( f ( ) ) + q ( ) q q = = q = q f Df, q Q Cursus differetilrekeig - fgeleide S Mettepeige
8 d) Hogere fgeleide Als de fgeleide fuctie v ee fuctie op ij beurt ook fleidbr is, d kue og ees fleide Op die mier krijg je ee ieuwe fuctie die we de tweede fgeleide oeme, of de fgeleide v de tweede orde Uiterrd k je op die mier ook fgeleide v hogere orde defiiëre We otere de tweede fgeleide v f ls f " of De -de fgeleide v f otere we ls ( f ) ( ) of D f of D f of Voorbeeld: Bereke de derde fgeleide v f ( ) = 6 f''' = 6+ = +, f" ( ) = 6 e 4 f' d f d d f d Cursus differetilrekeig - fgeleide S Mettepeige
9 ) Afleidbrheid ) Liker- e rechterfgeleide Als de likerlimiet f' ( ) f f < likerfgeleide v f i De fuctie heet d liks fleidbr i Als de rechterlimiet f' ( ) f f > rechterfgeleide v f i De fuctie heet d rechts fleidbr i bestt e eidig is d oeme we die limiet de bestt e eidig is d oeme we die limiet de Het is duidelijk dt ee fuctie fleidbr is i ee put ls e slechts ls e liks e rechts fleidbr is e ls de likerfgeleide e de rechterfgeleide gelijk ij Is f cotiu i d l ook voorwrde dt dee limiete best b) Kikpute f ( ) f ( ) lim f'( ) < < e f ( ) f ( ) lim f'( ) > > Als f cotiu is i e er geldt dt de likerfgeleide iet gelijk is de rechterfgeleide d egge we dt de fuctie ee kikput vertoot i, Stel f ( ) = =, d is ' Dus lim f' ( ) = e f ( ) < > f = lim ' = De fuctie f heeft dus ee kikput i de oorsprog c) Verticle rklije f = = sg( ) Als f cotiu is i e er geldt dt lim ' =+ of lim ' f f de fuctie ee verticle rklij = Voorbeeld: Als f ( ) = d is f' ( ) = e hierbij geldt lim f' ( ) =+ De y -s is dus ee verticle rklij, op = d heeft de grfiek v d) Keerpute Als f cotiu is i e er geldt dt lim f' ( ) =+ e lim f' ( ) < > egge we dt de grfiek v f ee keerput vertoot i, Voorbeeld: Stel f ( ) =, d is f' ( ) 4 f = = = D geldt: = (of omgekeerd) d Cursus differetilrekeig - fgeleide S Mettepeige
10 lim f' lim < < lim f' lim > > = = = =+ De fuctie f heeft dus ee keerput i de oorsprog e) Verbd tusse fleidbrheid e cotiuïteit Stellig: Als f fleidbr is i d is f ook cotiu i Bewijs: f is fleidbr i f' ( ) limf bestt e is eidig, e d geldt: ( ) f ( ) f f + f f limf ( ) lim ( ) + f ( ) = f' ( ) + lim f ( ) f ( ) = f is cotiu i Gevolg: Als f iet cotiu is i d is f iet fleidbr i f ( ) Opmerkig: dee stellig impliceert iet dt f fleidbr is ls f cotiu is, drv hebbe we odertusse l voorbeelde geie i de vorige drie prgrfe Cursus differetilrekeig - fgeleide - - S Mettepeige
11 4) Toepssige v fgeleide ) Rklij e orml Is f fleidbr i d is de rklij t y f' ( ) ( ) f ( ) De orml i ee put, gt e loodrecht stt op de rklij Als f' ( ) d geldt dus voor de orml: = + A f v de grfiek v ee fuctie is de rechte die door dt put Voorbeeld: Stel de vergelijkig op v de rklij e de orml f ( ) = + 9 i ( 4,5) f' ( ) = = P 4 f = 5, dus '( 4) t y= ( 4) + 5 y= + e y= ( 4) + 5 y= y= ( ) + f ( ) f' b) Hoek tusse twee sijdede kromme Hoek tusse twee sijdede rechte De helligshoek v ee rechte is de georiëteerde hoek die ee rechte mkt met de -s Uit de figuur blijkt dt ee hoek tusse twee rechte gegeve wordt door θ = α β, met α e β de Hoek tusse twee sijdede kromme helligshoeke v de betreffede rechte Voor de helligshoek α v rechte y= m+ q geldt tα = e loog is tβ = m mb Dus voor ee hoek θ tusse de rechte geldt: tα tβ m mb tθ = t( α β) = = + tα tβ + m m De hoek θ tusse twee sijdede kromme f e g defiiëre ls de hoek tusse de rklije die kromme i hu sijput (, ) P y Als de kromme fleidbr ij i dt sijput, d geldt voor de rico s v de rklije t e Uit het voorgde volgt d dt: t dt mt = f' ( ) e mt = g' ( ) g' ( ) f' ( ) tθ g' ( ) f' ( ) = + b Cursus differetilrekeig - fgeleide - - S Mettepeige
12 Voorbeeld: We berekee de hoek tusse de grfieke v f ( ) = e g( ) sijput P (,) De fgeleide ij f' ( ) Voor de hoek geldt dus tθ = = + c) Ee toepssig uit de kiemtic = i hu = e g' ( ) =, dus is f ' = e g ' =, odt θ = 45 (kies ltijd de kleiste positieve hoek) I de fysic otere we de fgelegde weg vk met s, de selheid met v e de versellig met s De gemiddelde selheid v over ee itervl t bereke je met het quotiët v=, dus is het t ds dv d s logisch dt de ogeblikkelijke selheid wordt gegeve door v= Aloog is = = dt dt dt Je k u de gekede formules uit de fysic voor ee eeprig verselde rechtlijige bewegig (EVRB) cotrolere Voor ee bewegig met ee costte versellig, begiselheid v e begipositie s geldt: v= t + v e Verwte selhede t ds dv d s s= + v t+ s Er geldt iderdd dt v= e dt = = dt dt dt Voorbeeld : Ee (cilidrische) regeto heeft ee strl v 4cm e ee hoogte v,m Het reget hrd wrdoor de to ich vult ee tempo v, l/ s (liter per miuut) Met welke selheid stijgt het wter i de to? Voor het huidig volume wter i de to geldt V = πr h= 6 π h, met h de huidige wterhoogte dv dh dh dh Beide lede fleide (r t) geeft: = 6π = 6π =, 4 dt dt dt dt 6π dv l cm (merk op dt, dt = s = s, odt dh, 4 cm ) dt s Voorbeeld : Robbe speelt met ij vlieger op het strd Hij vliegt op ee costte hoogte v m (bove Robbe ij hd) Zij vlieger vliegt v hem weg met ee selheid v 4m s Met welke selheid moet Robbe het touw losse ls hij het strk gespe houdt e de vlieger u 5m v hem verwijderd is? Met de coveties op de figuur geldt weges de stellig v Pythgors: + h = k De hoogte blijft costt () e op dit momet is k= 5, dus is u d dt d dt Afleide r t geeft: ( ) + ( h ) Robbe moet dus het touw losse met ee selheid v,67m s = 5 = d d dk dk = k = k = 4,67 dt dt dt dt 5 Cursus differetilrekeig - fgeleide - - S Mettepeige
13 d) De methode v Newto We ge reeds twee methodes om ulpute te bedere: de methode v Bolo e de regul flsi Oe eis dr ws dt de fucties cotiu wre Is de fuctie bovedie ook fleidbr d k de methode v Newto uitkomst biede Zij gegeve ee fuctie f die fleidbr is e ee eerste bederig (gok) voor de ulwrde De rklij i A, f ( ) is t y f' ( ) ( ) f ( ) = + Het sijput v de rklij met de -s levert meestl ee betere bederig voor c op f ( ) Stel dus (,) t = f' ( ) ( ) + f ( ) = f' ( ) Herhle we dee werkwije met de rklij i A (, f ( ) ) eoverder d krijge we ee rij ( ) die k covergere r ee ulput Dit bewijs vlt echter ook buite het bestek v dee cursus (De methode die je rekemchie gebruikt om ulpute te bedere is ee megvorm v de methode v Newto e de regul flsi) Cursus differetilrekeig - fgeleide - - S Mettepeige
Verloop van exponentiele en logaritmische functies
 Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
1) Definitie, rekenkundige en meetkundige rijen
 Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
4 Differentierekening en reeksen
 WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
Hoofdstuk 9: Afgeleide functies en toepassingen
 Hoostuk 9: Ageleie ucties e toepssige 9. Aleibrhei Deitie: Ee uctie is leibr i om ( ) IR 9.. Aleibrhei v ee uctie i ee put v het omei eities p. 76: is leibr i is iet leibr i * is rechtsleibr i / rechtergeleie
Hoostuk 9: Ageleie ucties e toepssige 9. Aleibrhei Deitie: Ee uctie is leibr i om ( ) IR 9.. Aleibrhei v ee uctie i ee put v het omei eities p. 76: is leibr i is iet leibr i * is rechtsleibr i / rechtergeleie
Integraalrekening. Georg Friedrich Bernhard Riemann Breselenz 17 september 1826 Selasca 20 juni 1866
 Itegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 septemer 86 Selsc 0 jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geeft de itegrl v ee positieve fuctie ee uwkeurige
Itegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 septemer 86 Selsc 0 jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geeft de itegrl v ee positieve fuctie ee uwkeurige
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
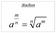 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Acdemi Press Dele Bij delig vermeigvuldigt me met het omgekeerde v de deler..3.5 Vereevoudige Het is goed mogelijk dt voorgde bewerkige iet de
 Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
1 Bewerkingen met matrices invoeren via voorbeelden. , is een commutatieve groep.
 1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
1) Complexe getallen - definitie
 Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Formulekaart VWO wiskunde B
 Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
Elementaire speciale functies
 ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
Analyse. Lieve Houwaer Dany Vanbeveren
 Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
Oplossingen extra oefeningen: rijen (leerstof RR, leerstof MR)
 Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
2.6 De Fourierintegraal
 2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
( ) Formulekaart VWO. Kansrekening. Tellen. k n k. Binomium van Newton : Kansrekening. Voor toevalsvariabelen X en Y geldt: E ( X + Y ) = E(
 Formulert VWO Telle! ( )... 0!!!( )! Biomium v Newto : Ksreei ( + ) Ksreei 0 Voor toevlsvriele X e Y el: E ( X + Y ) E( X ) + E( Y ) Voor ofhelije toevlsvriele X e Y el: σ ( X + Y ) σ ( X ) + σ ( Y ) -wet
Formulert VWO Telle! ( )... 0!!!( )! Biomium v Newto : Ksreei ( + ) Ksreei 0 Voor toevlsvriele X e Y el: E ( X + Y ) E( X ) + E( Y ) Voor ofhelije toevlsvriele X e Y el: σ ( X + Y ) σ ( X ) + σ ( Y ) -wet
Samenvatting. Fouriertheorie en distributies. Fourier en Schwartz. De warmtevergelijking. De exacte benadering
 Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
3 Meetkundige voorstelling van complexe getallen
 3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
AFSTANDEN EN HOEKEN IN
 AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
Formulekaart VWO. Kansrekening. σ σ X )
 Formulert VWO Ksreei Telle! (... 0!! (!(! Biomium v Newto : ( + ( Ksreei 0 Voor toevlsvriele X ey eldt E ( X + Y E( X + E( Y Voor ofhelije toevlsvriele X ey eldt σ ( X + Y σ ( X + σ ( Y -wet: ij ee serie
Formulert VWO Ksreei Telle! (... 0!! (!(! Biomium v Newto : ( + ( Ksreei 0 Voor toevlsvriele X ey eldt E ( X + Y E( X + E( Y Voor ofhelije toevlsvriele X ey eldt σ ( X + Y σ ( X + σ ( Y -wet: ij ee serie
Formularium Wiskunde
 Formulrium Wiskude Te gebruike bij exme Ileidig tot de Hogere Wiskude Trscedete fucties. Goiometrische fucties t x = tg x = si x cos x cot x = cotg x = cos x si x sec x = cos x cosec x = si x cos( ± b)
Formulrium Wiskude Te gebruike bij exme Ileidig tot de Hogere Wiskude Trscedete fucties. Goiometrische fucties t x = tg x = si x cos x cot x = cotg x = cos x si x sec x = cos x cosec x = si x cos( ± b)
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Algebra. Dr. Caroline Danneels
 Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
Analyse 2 - SAMENVATTING
 Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Reeksen. Convergente reeksen
 Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Hoofdstuk 0: algebraïsche formules
 Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
Vectoranalyse voor TG
 college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
Eindexamen wiskunde B1 vwo 2007-I
 Eidexame wiskude B vwo 007-I havovwo.l Podiumverlichtig Ee podium is 6 meter diep. Midde bove het podium hagt ee balk met tl-buize. De verlichtigssterkte op het podium is het kleist aa de rad, bijvoorbeeld
Eidexame wiskude B vwo 007-I havovwo.l Podiumverlichtig Ee podium is 6 meter diep. Midde bove het podium hagt ee balk met tl-buize. De verlichtigssterkte op het podium is het kleist aa de rad, bijvoorbeeld
Duurzaam (ver)bouwen. Noordoost-Brabant 2013-2016
 t e v o C l io g Re Duurzm (ver)bouwe Noordoost-Brbt 2013-2016 e w u o b e m S d i e h m duurz Duurzm Bouwe Grodstoffe worde schrser, het eergievrgstuk ijpeder e os klimt verdert. Duurzm bouwe e verbouwe
t e v o C l io g Re Duurzm (ver)bouwe Noordoost-Brbt 2013-2016 e w u o b e m S d i e h m duurz Duurzm Bouwe Grodstoffe worde schrser, het eergievrgstuk ijpeder e os klimt verdert. Duurzm bouwe e verbouwe
16.6 Opgaven hoofdstuk 7: Producten en combinatoriek
 166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Functies, Rijen, Continuïteit en Limieten
 Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Formulekaart vwo. Kansrekening. Tellen. ! n. k n k. Binomium van Newton : Kansrekening
 Formulekrt vwo Telle! ( )...!! k k!( k)! Biomium v Newto : Ksrekei ( ) Ksrekei k k k k Voor toevlsvriele X e Y el: E( X Y ) E( X ) E( Y ) Voor ofhkelijke toevlsvriele X e Y el: ( X Y ) ( X ) ( Y ) -wet
Formulekrt vwo Telle! ( )...!! k k!( k)! Biomium v Newto : Ksrekei ( ) Ksrekei k k k k Voor toevlsvriele X e Y el: E( X Y ) E( X ) E( Y ) Voor ofhkelijke toevlsvriele X e Y el: ( X Y ) ( X ) ( Y ) -wet
Examen VWO. wiskunde B (pilot) tijdvak 2 donderdag 18 juni uur
 Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
wiskunde B pilot vwo 2015-II
 Formules Goiometrie si( t u) sitcosu costsiu si( t u) sitcosu costsiu cos( t u) costcosu sitsiu cos( t u) costcosu sitsiu si( t) sitcost cos( t) cos t si t cos t si t - - Het achtste deel p het domei [
Formules Goiometrie si( t u) sitcosu costsiu si( t u) sitcosu costsiu cos( t u) costcosu sitsiu cos( t u) costcosu sitsiu si( t) sitcost cos( t) cos t si t cos t si t - - Het achtste deel p het domei [
Formulekaart VWO wiskunde B
 Formlekrt VWO B /9 Formlekrt VWO wiskde B Ksrekei Telle! = ( )... 0! =! = k k!( k)! Ksrekei Voor toevlsvriele X e Y eldt E( X + Y) = E( X) + E( Y ) Voor ofhkelijke toevlsvriele X e Y eldt σ( X + Y) = σ
Formlekrt VWO B /9 Formlekrt VWO wiskde B Ksrekei Telle! = ( )... 0! =! = k k!( k)! Ksrekei Voor toevlsvriele X e Y eldt E( X + Y) = E( X) + E( Y ) Voor ofhkelijke toevlsvriele X e Y eldt σ( X + Y) = σ
5.1 Rekenen met differentialen
 Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 5 Substitutie We hebben gezien dt de productregel voor de fgeleide een mnier geeft, om voor zeker functies een primitieve te vinden,
Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 5 Substitutie We hebben gezien dt de productregel voor de fgeleide een mnier geeft, om voor zeker functies een primitieve te vinden,
Rinse Poortinga Lineaire Algebra en Voortgezette Analyse. 2 Lineaire afbeeldingen
 Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie
Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
 Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerking Tentamen Analyse B, 28 juni lim
 Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Eindexamen wiskunde B vwo 2010 - II
 Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Equidistributie en ergodiciteit
 Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Toepassingen op Integraalrekening
 Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Iteratie is het steeds herhalen van eenzelfde proces, verwerking op het bekomen resultaat. Verwerking
 1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
2) Kegelsneden (in basisvorm)
 ) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
HET BELANG VAN. Vragen Tijdens de voordracht op 14 augustus 2007 hebben we de volgende vragen besproken.
 HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
Deel D. Breuken en algebra n
 Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Niks gedaan en toch gevangen... Kan dat zomaar?
 Niks ged e toch gevge... K dt zomr? Lesbrief voor de leerkrcht Hdleidig voor de leerkrcht Leerligebld Ee kid v cht stop je iet i ee cel. Niet i Nederld. Dt is belchelijk. Voor groep 7 e 8 v het bsisoderwijs
Niks ged e toch gevge... K dt zomr? Lesbrief voor de leerkrcht Hdleidig voor de leerkrcht Leerligebld Ee kid v cht stop je iet i ee cel. Niet i Nederld. Dt is belchelijk. Voor groep 7 e 8 v het bsisoderwijs
Boek 2, hoofdstuk 7, allerlei formules..
 Boek, hoofdstuk 7, llerlei formules.. 5.1 Evenredig en omgekeerd evenredig. 1. y wordt in beide gevllen 4 keer zo klein, je noemt dt omgekeerd evenredig. b. bv Er zijn schoonmkers met een vst uurloon.
Boek, hoofdstuk 7, llerlei formules.. 5.1 Evenredig en omgekeerd evenredig. 1. y wordt in beide gevllen 4 keer zo klein, je noemt dt omgekeerd evenredig. b. bv Er zijn schoonmkers met een vst uurloon.
Hoofdstuk 6 : Veeltermen
 - 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
- 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Een toelichting op het belang en het berekenen van de steekproefomvang in marktonderzoek.
 006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
2de bach TEW. Statistiek 2. Van Driessen. uickprinter Koningstraat Antwerpen ,00
 de bach TEW Statistiek Va Driesse Q www.quickpriter.be uickpriter Koigstraat 3 000 Atwerpe 46 5,00 Nieuw!!! Olie samevattige kope via www.quickpritershop.be Hoofdstuk : Het schatte va populatieparameters.
de bach TEW Statistiek Va Driesse Q www.quickpriter.be uickpriter Koigstraat 3 000 Atwerpe 46 5,00 Nieuw!!! Olie samevattige kope via www.quickpritershop.be Hoofdstuk : Het schatte va populatieparameters.
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Integreren over een compact interval in. n
 Rise Poortig Lieire Alger e Voortgezette Alyse 6 Afgeleide e itegrl houd: 61 Prtiële fgeleide 6 Differetieerre fucties 63 Prtiële fgeleide v hogere orde 64 Cotiu differetieerre fucties 65 Differetieerre
Rise Poortig Lieire Alger e Voortgezette Alyse 6 Afgeleide e itegrl houd: 61 Prtiële fgeleide 6 Differetieerre fucties 63 Prtiële fgeleide v hogere orde 64 Cotiu differetieerre fucties 65 Differetieerre
Examen VWO. wiskunde B (pilot) tijdvak 1 woensdag 16 mei 13.30-16.30 uur
 Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
TECHNISCHE HOGESCHOOL EINDHOVEN Afdeling Algemene Wetenschappen. Onderafdeling der Wiskunde WISKUNDE 10. bestemd voor. BDK-1, WSK-1, N-1, E-1 en T-1
 TECHNISCHE HOGESCHOOL EINDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WISKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1978 ... -, Techische Hogeschool Eidhove Oderfdelig
TECHNISCHE HOGESCHOOL EINDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WISKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1978 ... -, Techische Hogeschool Eidhove Oderfdelig
1. Recursievergelijkingen van de 1 e orde
 Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Eindexamen vwo wiskunde B pilot I
 Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
Primitieve en integraal
 Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 4 Primitieve en integrl Een motivtie om nr de fgeleide vn een functie f te kijken is het beplen vn de richtingscoëfficiënt vn de rklijn
Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 4 Primitieve en integrl Een motivtie om nr de fgeleide vn een functie f te kijken is het beplen vn de richtingscoëfficiënt vn de rklijn
1. Weten dat in het geval van compressoren rekening moet gehouden worden met thermische effecten
 Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
Formularium goniometrie
 Jr 6 : Formulrium 6u en 7u Formulrium goniometrie sin α cos α Definities : tn α cot α secα cscα cos α sin α cos α sin α Gevolg : tn α cot α cot α tn α Hoofdformule : cos sin Gevolg : tn sec cot csc α α
Jr 6 : Formulrium 6u en 7u Formulrium goniometrie sin α cos α Definities : tn α cot α secα cscα cos α sin α cos α sin α Gevolg : tn α cot α cot α tn α Hoofdformule : cos sin Gevolg : tn sec cot csc α α
Oefeningen Analyse II
 ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
Antwoorden. Een beker water
 Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
1 Vlaamse Wiskunde Olympiade : Eerste Ronde.
 Vlmse Wiskunde Olympide 99 993 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olympide 99 993 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Eindexamen vwo wiskunde B pilot I
 Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin t cos t sin t www. - - nfhnkelijk
Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin t cos t sin t www. - - nfhnkelijk
Examen HAVO. wiskunde A. tijdvak 2 woensdag 19 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
2. Gegeven is de driehoek van figuur 10.10a. Gevraagd worden hoek β en de zijden a en c.
 Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Continuïteit en Nulpunten
 Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Eindexamen wiskunde A1-2 vwo 2008-II
 Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
TECHNISCHE HOGESCHOOL EINDHOVEN Afdeling Algemene Wetenschappen. Onderafdeling der Wiskunde WISKUNDE 10. bestemd voor. BDK-1, WSK-1, N-1, E-1 en T-1
 TECHNSCHE HOGESCHOOL ENDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WSKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1974 ENKELE NOTTES bij WSKUNDE 10 De cursus Wiskude 10
TECHNSCHE HOGESCHOOL ENDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WSKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1974 ENKELE NOTTES bij WSKUNDE 10 De cursus Wiskude 10
UITWERKINGEN TOETS TRAININGSKAMP. Valkenswaard, 10 juni 2006
 UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
2 Opgaven bij Hoofdstuk 2
 2 Opgven bij Hoofdstuk 2 Opgve 2. De functie f : R 2 R is gedefinieerd door ) Bewijs dt f continu is op R 2 \ {(, )}. f(, y) = 2 y 2 + y 2 ls (, y) (, ) f(, ) =. b) Bewijs dt voor iedere R de functie y
2 Opgven bij Hoofdstuk 2 Opgve 2. De functie f : R 2 R is gedefinieerd door ) Bewijs dt f continu is op R 2 \ {(, )}. f(, y) = 2 y 2 + y 2 ls (, y) (, ) f(, ) =. b) Bewijs dt voor iedere R de functie y
WI1708TH Analyse 3. College 5 23 februari Challenge the future
 WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
10.8. De Laplace vergelijking. De warmtevergelijking in meerdimensionale ruimten heeft de volgende vorm :
 1.8. De Lplce vergelijking. De wrmtevergelijking in meerdimsionle ruimt heeft de volgde vorm : in R 2 : α 2 (u xx + u yy ) = u t in R 3 : α 2 (u xx + u yy + u zz ) = u t. Hierbij stelt u(x, y, t) de tempertuur
1.8. De Lplce vergelijking. De wrmtevergelijking in meerdimsionle ruimt heeft de volgde vorm : in R 2 : α 2 (u xx + u yy ) = u t in R 3 : α 2 (u xx + u yy + u zz ) = u t. Hierbij stelt u(x, y, t) de tempertuur
Eindexamen wiskunde B1-2 vwo 2007-I
 Eindemen wiskunde B- vwo 007-I Beoordelingsmodel Podiumverlichting mimumscore 3 sin α = r 650 V 650 r r r 650 r = 9 + invullen geeft V = 9 + sin α = r r = 9 + V = 650 650 = 9+ 9+ 9 + mimumscore 5 650 00
Eindemen wiskunde B- vwo 007-I Beoordelingsmodel Podiumverlichting mimumscore 3 sin α = r 650 V 650 r r r 650 r = 9 + invullen geeft V = 9 + sin α = r r = 9 + V = 650 650 = 9+ 9+ 9 + mimumscore 5 650 00
