TECHNISCHE HOGESCHOOL EINDHOVEN Afdeling Algemene Wetenschappen. Onderafdeling der Wiskunde WISKUNDE 10. bestemd voor. BDK-1, WSK-1, N-1, E-1 en T-1
|
|
|
- Louisa Bosmans
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 TECHNSCHE HOGESCHOOL ENDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WSKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1974
2 ENKELE NOTTES bij WSKUNDE 10 De cursus Wiskude 10 uit 1971 verschilt uwelijks v de 1969 versie v Wiskude. De fdelig Bouwkude wilde 1970 iet meer meedoe met het lgemee wiskudeoderwijs voor lle fdelige. Als teke des oderscheids werd ee dubbelcijferige coderig voor de bsis-wiskudevkke igevoerd. Bouwkude zou echter voorlopig de eige dissidet blijve. De defiitieve sloop v het lgemee wiskudeoderwijs op cdemisch iveu zou ps dik twitig jr lter, bij Werktuigbouwkude, ee vg eme werd ee ieuwe opzet otworpe voor het e-jrs wiskudeoderwijs zols dt voor lle fdelige zou moete zij: De commissie B74 bestde uit dr. W. v der Meide(voorzitter), drs. H.G. ter Morsche(secretris), prof. dr. S.T.M. Ackerms, prof. dr. J. Boersm, dr. ir. M.L.J. Hutus, drs. Ligtms, drs J.H. Timmerms e dr. P.G. Vroegideweij produceerde ee muscript met de geweste le-jrsstof. Voor de editie v Wis 10 werd l geput uit het B74-muscript verschee hierv ee flik uitgebreide versie om ee betere sluitig het VWO te verkrijge verschee de vrit die std zou houde tot i 198 de -fse structuur werd igevoerd. Let, bijvoorbeeld, i de 1978-vrit toch ees op dt schitterede e efficiëte hoofdstuk 6 over e-orde lieire differetilvergelijkige met costte coëfficiëte. Vol illustrtieve voorbeelde te behoeve v de fculteite. Dt ws og echt cdemische vormig! JdG, 4 Juli 005
3 TECHNSCHE HOGESCHOOL ENDHOVEN Oderfdelig der Wiskude WSKUNDE 10 (ieuwe stijl) bestemd voor BDK-1, WSK-1, N-1, W-1, E-1 e T-1 Njrssemester 1974
4 NHOUDSOPGAVE WSKUNDE 10 Hoofdstuk. Hoofdstuk. leidig l.. Symbole e defiities 1.. Ntuurlijke getlle, volledige iductie 1.3. Het telle v verzmelige e fucties 1.4. De reële getlle l.s. JR e JR CoÖrditestelsels i JR e JR 3 Fucties lr + lr.1. leidig.. Polyome.3. Eigeschppe v fucties.4. Limiete v fucties.5. CotiuÏteit.6. Differetilrekeig.7. Numerieke oplossig v vergelijkige.8. tegrlrekeig.9. Techiek v het itegrere.10.numerieke itegrtie blz S S Hoofdstuk 3. Reekse 3.. Covergetie e divergetie 3.. Reekse met uitsluited iet egtieve terme 3.3. Reekse met zowel positieve ls egtieve terme 3.4. Mchtreekse 3.S. Numerieke sommtie v reekse los Hoofdstuk 4. Complee getlle 4.1. leidig 4.. voerig der complee getlle 4.3. Complee polyome, lgebrïsche vergelijkige 4.4. Alyse i het complee vlk 4.5. De fuctie ez 4.6. Meetkude i het complee vlk
5 Hoofdstuk 5. Differetilvergelijkige leidig Scheidig v vribele Lieire differetilvergelijkige v de eerste orde Lieire differetilvergelijkige met costte coëfficiëte Trillige 161 NHOUDSOPGAVE WSKUNDE 0 Hoofdstuk 6. Fucties lr + JR, lr + JR 3 e fucties JR + lr, JR 3 + lr 6.. Fucties lr +lr,lr+lr 3 Hoofdstuk Fucties v twee vribele Differetieerbrheid v fucties v twee vribele Fucties v drie vribele mpliciete fucties Richtigfgeleide e grdiët Etrem Etrem oder evevoorwrde 34 Lieire lgebr 7.. Voorwoord 7.. Bewerkige met mtrices Voorbeelde e toepssige Alytische meetkude ijr 3 e meetkudige termiologie i lr met > Vectorruimte Afhkelijkheid e ofhkelijkheid, bses Lieire fbeeldige Lieire fbeeldige lr + lr Lieire vergelijkige e ogelijkhede
6 Hoofdstuk 8. Meervoudige itegrle tegrtiegebiede e ifiitesimle elemete Lijitegrle Oppervlkte-itegrle Volume-itegrle Oeigelijke meervoudige itegrle Gmmfuctie, betfuctie tegrle met ee prmeter 163
7 - - Hoofdstuk. leidig l.. Symbole e defiities A := B D A is per defiitie gelijk B eide v ee bewijs. Logische symbole: implictie ls d <==.> coimplictie; d e slechts d ls A V " 3 3! e of iet l-qutor ; voor lle eistetiële qutor; er is er is precies Specile verzmelige: ~~ ee... 0 de lege verzmelig ln de verzmelig der tuurlijke getlle 7L " " " gehele " Ol " " " rtiole " lr " " " reële " E " " " complee " lr+ " " " reële getlle die ;, 0 lp " " " reële getlle die > 0 zij zij. Verzmeligstheoretische symbole: V is elemet v V i i V is gee elemet v V c A c B A is deelverzmelig v B V X A ::> A " B B is deelverzmelig v A # # A het tl elemete v A. [ E B]
8 - - Het geve v verzmelige (voorbeelde:): {,b,c,d,e} { E :Dl. { E ln,;; 10} de verzmelig met ls elemete, b, c, d e e; de verzmelig v de reële getlle die $ 10 voldoe;,;; 10} de verzmelig v de tuurlijke getlle {(cos q>, si '~') 1 o " '~' < zrr l Bewerkige met verzmelige: doorsede A B u vereigig A u B die,;; 10 voldoe, dus {1,,3}; de verzmelig v de pute i R die fstd tot de oorsprog hebbe. :={l(ea) A (EB)} ls A B = 1!1 d hete A e B disjuct := { (EA) V (EB)} \ verschil A \ B := { (EA) A (ib)} * complemet A * := { i A) crtesisch product A B := {(' y) X E A, y E B} ABC := {(,y,z) E A, y E B, z E C} ez. A 3 := A A, A := A A A ez. Afbeeldige Defiities. Lt A e B verzmelige zij. Ee fbeeldig f v A i B ottie f: A+ B - is ee voorschrift volges hetwelk elk elemet v A precies éé elemet v B wordt toegevoegd. s b (E B) het elemet dt (E A) wordt toegevoegd, d schrijve we b = f() e ook wel f: r+ b. We oeme b het beeld v. De fbeeldig f: A+ B is gelijk g: C + D idie: (i) A= C; (ii) B = D; (iii) f() = g() voor lle E A. Slordig spreekt me vk v de fbeeldig f i.p.v. f: A + B. "Fuctie" is voor os syoiem met "fbeeldig". Het beeld v ee deelverzmelig. s f: A+ B, A 0 ca, d is f(a 0 ) := { f()l E A 0 }. jectief. De fbeeldig f: A+ B heet ijectief (of éé-ééduidig, ook wel ee ijectie) ls voor lle,y E A uit f() = f(y) volgt = y.
9 - 3 - Surjectief. De fbeeldig f: A+ B heet surjectief (ook: f heet ee surjectie; f beeldt A ~ B f) idie f(a) = B. Bijectief. Ee fbeeldig die zowel ijectief ls surjectief is heet bijectief (ook: ee bijectie). verse fbeeldig. Als f: A+ B ee bijectie is d heet de fbeeldig + f : B +A gedefiieerd door: f+(b) = d e slechts d ls f() b, de iverse v f. Smegestelde fbeeldig. Lt g: A + B e f: C + D fbeeldige zij e lt A 0 := { A g() E C}, d heet de fbeeldig f o g : A 0 + D gedefiieerd door (f o g)() := f(g()) de smegestelde fbeeldig v f eg. 1.. Ntuurlijke getlle, volledige iductie De verzmelig der tuurlijke getlle wordt gegeve door ln = {1,,3, }. N.B. sommige leerboeke wordt ook het getl 0 tot de tuurlijke getlle gereked. We beschouwe de lgebrïsche bewerkige (optelle, ftrekke, ez.) e de ordeig (ogelijkhede) voor tuurlijke getlle ls beked. We vermelde slechts de volgede eigeschp: Begisel der volledige iductie. Als voor ee deelverzmelig V v ln e voor zekere E ln geldt ) E V, ) \;lkev [k+l E V], d is V :o {k E ln k <: }. Me k ) ook formulere met: "Als k E V d k + E V"; de veroderstellig k E V heet iductieveroderstellig. Deze eigeschp wordt vk gebruikt op de volgede mier. Stel dt me v ee bewerig, die ee verderlijke bevt die de tuurlijke getlle doorloopt, k bewijze: ) De bewerig is wr voor E ln ) Als de bewerig wr is voor k, d geldt zij ook voor k+l. D k me cocludere dt de bewerig wr is voor lle tuurlijke
10 - 4 - getlle ~. Ee bewijs dt op deze redeerig berust oemt me ee bewijs door volledige iductie. Voorbeeld 1. Beschouw de som J =: l: i=l l We bewijze door volledige iductie, dt voor elke ' ~ geldt: L i = ~(+l)(+l) i=l ( 1 ) 1) Voor = 1 is formule (1) juist. ) Lt formule (1) juist zij voor= k. D volgt: k+l k l: i = l: i=l i=l. 1 l + (k+l) = 6k (k+l)(k+l) + (k+l) = = ~ (k+l)(k+)(k+3) d.w.z. de formule geldt ook voor= k+l. We cocludere! dt formule (1) voor lle ' ~ geldt. Voorbeeld. Zij h ~ -1. We bewijze dt voor ' ~ geldt: + h 1) Als = 1 geldt het gelijkteke. k ) Als de ogelijkheid geldt voor= k, d.w.z. ls (l+h) ~ 1 + kh, d volgt: (l+h/+ 1 = (l+h)(l+hl ~ (l+h)(l+kh) = 1 + (k+l)h+kh ~ 1 + (k+l)h. Opgve. De bekede rij getlle v Fibocci,d 1,d, wordt gedefiieerd door: dl := d := d := d + d +l -1 ( ~ ). De rij v Fibocci begit dus ls volgt: 1,1,,3,5,8,13,1,34,
11 - 5 - De getlle v Fibocci hebbe vele frie eigeschppe die wiskudige e puzzelrs eeuwelg gefscieerd hebbe. Bewijs bijv. door volledige iductie dt voor elke E ln geldt: Er best verschillede vrite v het begisel der volledige iductie Stellig. Als voor V c ln geldt ) E V, ) uit E V, E V,, k E V volgt k+ E V, d is V = ln Bewijs. Zij W := {k E ln {1,,...,k} cv}. Het is duidelijk dt Wc V. We bewijze dt Wvoldoet 1..1, voorwrde ) e ) met =. ) E W omdt E V. ) Als k E W, d geldt E v,...,k EV. Uit het gegeve v de stellig volgt k+l EV. Dus: E v,...,k E v, k+l EV. We zie dt k+l E w. We moge d het begisel der volledige iductie toepsse e cocludere dt W =ln. Uit Wc V c ln volgt d V= ln. D..3. Stellig. Ee iet lege deelverzmelig V v ln heeft ee kleiste elemet, Bewijs. Neem dt V gee kleis te elemet heeft. Zij W : = ln \ V. D geldt: E W (ders ws het kleiste elemet v V). Verder, ls w omdt ders k+l het kleiste E w, E w,..,k E w d is ook k+l elemet v V zou zij. Uit 1.. volgt W = ln, dus V= 0 i strijd met het gegeve. D Merk op dt deze eigeschp iet geldt voorz., lr of lp, omdt deze verzmelige zelf gee kleiste elemet hebbe. Ee der tegevoorbeeld is de verzmelig {, ~, ~, } = {~ E ln} i Ql. Stellig 1..3 wordt soms gebruikt om te bewijze dt ee verzmelig leeg is. Me eemt l. dt de verzmelig iet leeg is e derhlve ee kleiste elemet heeft. Uit beschouwige m.b.t. het kleiste elemet komt me tot ee tegesprk.
12 - 6 - Voorbeeld 3 (otbidig i fctore). Ee tuurlijk getl p > heet ee priemgetl ls er gee getlle,b E m met < p, b < p best wrvoor geldt: b = p. De getlle, 3, S, 7, 11, 13, 17 zij bijv. priemgetlle. Stellig. Elk tuurlijk getl ~ is te schrijve ls ee product v priemgetlle (dit product k best uit éé fctor, ls zelf ee priemgetl is; ook k ee priemgetl meerdere mle i het product voorkome, bijv. 1 = 3), Bewijs, Neem dt de verzmelig V der tuurlijke getlle ~, die iet i zo' gedte te schrijve zij, iet leeg is. Zij m het kleiste elemet v V. D is m gee priemgetl. Er best dus getlle,b < m met b = m. Omdt m het kleiste elemet v V is, geldt t V, b f. V, Er best dus priemgetlle p 1,,pk met = p 1 pk' e q 1,,q met b = q 1 q Mr d is m = p 1 pk q 1 q ook ee product v priemgetlle i strijd met het feit dt m V. We cocludere dt V= 0, zodt de eigeschp beweze is. 0 Het uitschrijve v ee tuurlijk getl ls product v priemgetlle oemt me otbidig i fctore, Me k bewijze dt de otbidig i fctore eeduidig is, fgezie v de volgorde wri de priemfctore worde geschreve Het telle v verzmelige e fucties. deze prgrf beschouwe we llee eidige verzmelige Ei!leschEEe. Als er ee bijectie f: A+ B bestt d is "!f'a = #B. Als #A = "/FB e f: A + B is ee ijectie, d is f ee bij ectie. Als #A = '#-B e f: A + B is ee surjectie, d is f ee bijectie. Grodregel v het telle,.die er mogelijke wijze zij om ee hdelig te verrichte e ls er elke uitvoerig v ee hdelig, mmogelijke miere zij voor het verrichte v hdelig S, d zij er m mogelijke miere om chtereevolges e S te verrichte. Ee loge regel geldt voor het tl miere om meer hdelige te verrichte.
13 - 7 -!,3.. Stellig. Zij #A=, #B = m met > 0, m > 0, d is het tl fbeeldige v A i B gelijk m. Bewijs. Zij A= { 1,,}. We kue ee fbeeldig v A i B vorme door chtereevolges 1,,, ee elemet v B toe te voege. A 1 k me op m verschillede miere ee elemet v B toevoege. Dr k me eveees op m verschillede miere ee elemet toevoege ez. Volges de grodregel v het telle k me derhlve m m m = m fbeeldige vorme v A i B. 0 Voorbeeld. Het ivulle v ee kolom v de voetbltoto is equivlet met het geve v ee fbeeldig t: V ~ A, wr V ee verzmelig is bestde uit 13 te spele wedstrijde e A= {1,,3}. Er zij dus 3 13 miere om de toto i te vulle. Voorbeeld, Het werpe met meerdere dobbelstee k ook beschouwd worde ls het geve v ee fbeeldig. Als we bijv. 4 dobbelstee hebbe, geummerd,, 3, 4, d is ee worp ee fbeeldig w: D ~A, wrd= {1,,3,4} e A= {1,,3,4,5,6}. Er zij dus 6 4 worpe mogelijk. Voorbeeld 3. Uit ee krtspel trekt me chtereevolges tie krte met terugleggig, d.w.z. elke krt die getrokke is wordt teruggestoke voordt de volgede krt wordt getrokke. Er is hier sprke v ee fbeeldig t: A+ K wr A= {,,,10} ek de verzmelig der krte is. Als er 5 krte zij, d is het tl mogelijke trekkige Stellig. Het tl deelverzmelige v ee verzmelig A met ~A= is gelijk. Bewijs. Elke deelverzmelig B v A correspodeert met ee fbeeldig B: A+ {0,1} gedefiieerd door B() := ls E B e B() := 0 ls i B. B wordt de krkteristieke fuctie v B geoemd. Omgekeerd is elke fbeeldig~= A+ {0,1} de krkteristieke fuctie v ee deelverzmelig v A, l. v { E A ~() = 1}. Het tl deelverzmelige v A is dus gelijk het tl fbeeldige v A i {0,1}. Uit 1.3. volgt u het gestelde, 0
14 - 8 - Voorbeeld 4. De verzmelig {1,,3,4} heeft ls deelverzmelige: 0 { },{),{3},{4} {,},{,3},{,4},{,3),{,4},{3,4} {1,,3},{1,,4},{1,3,4},{,3,4} {,,3,4} Het totle tl is = 16 = 4 Defiitie. De fuctie! door: 0! : = ;! : = 3 ' ( E (spreek uit fculteit) wordt gedefiieerd Stellig. Zij 1/- A =, 1/- B = m met > 0. Het tl ijecties f: A-+ B is gelijk ( m' ls m ;;::: ls m < Bewijs. Het is duidelijk dt er gee ijectie f: A+ B bestt ls m <. Beschouw vervolges het gevl m ~ JN) d is m! (m _ )! = m(m- ) (m- + ). Zij A= { 1,,}. A elk elemet v A moete we ee elemet v B toevoege, zodig dt bij twee verschillede elemete v A iet hetzelfde elemet v B hoort. A 1 kue we op m verschillede miere ee elemet toevoege. Als we éé zo' toevoegig hebbe gekoze, hebbe we og m-1 mogelijkhede om ee elemet toe te voege. Zo kue we doorg, totdt teslotte og m-+l mogelijkhede overblijve om het elemet ee elemet toe te voege. totl vide we dus m(m-1) (m-+l) mogelijke ijecties. 0 Gevolg. Zij 11- A = met > 0. D is het tl bijecties f: A-+ A gelijk!. Bewijs. Uit volgt dt ijecties v A i A ook bijecties zij. Het tl ijecties v A i A is ( _! )! =. ' 0
15 - 9 - Ee bijectie v ee eidige verzmelig A i zichzelf heet ee permuttie v A. Als A= {l,,}, kue we zo' permuttie~ ls volgt geve: ~() ) ~() bijv. [~ : :) beschrijft de permuttie~ wrvoor ~()=, ~() =, ~(3) = 4, ~(4) = 3. Soms lt me de boveste rij weg omdt ze toch vst is. Me schrijft d ( 4 3). Het geve v ee permuttie v ee verzmelig A= {l,,} is dus equivlet met het opschrijve v de elemete 1,,, i ee beplde volgorde. Me k derhlve bovestd gevolg ook ls volgt formulere: "Het tl mogelijke volgorde wri de getlle 1,,..., kue st is gelijk!". Voorbeeld 5. ee krtspel met 5 krte kue de krte op 5! verschillede volgorde ligge. Voorbeeld 6. Het tl getlle v 5 cijfers bestde uit de cijfers 1,,3,4,5 zoder herhlig is gelijk 5! = 10. Opgve. Op hoeveel miere kue vier brieve i vier eveloppe worde gestoke? Opgve. Elke dg etbij te er cht mese op ee bk. Ze besluite elke dg i ee dere volgorde te g zitte. Weer zij lle mogelijkhede uitgeput ls ze begie op september 1974? We beschouwe u weer de lgemeere situtie v stellig Ee ijectie v de verzmelig A:= {l,,} i B zulle we ee vritie vuit de objecte v B oeme. Ee vritie ~k op de volgede mier gegeve worde: ~ () ) ~ () loog ls bij ee permuttie. Als bijv. = 5, B = {1,,,10}, d is
16 - 0 - ee vritie. Ook hier k zoder bezwr de eerste rij weggelte worde. Voor bovestde vritie schrijve we dus ( ). Het geve v ee vritie vuit de objecte b 1,,bm is dus equivlet met het vorme v ee geordede rij v verschillede objecte uit de gegeve verzmelig B = {b 1,,bm}. Voorbeeld 7. Uit ee krtspel trekt me chtereevolges 10krte zoder terugleggig, d.w.z. ee krt die getrokke wordt, wordt iet meer teruggestoke. We krijge zo ee vritie v 10 uit de 5 krte. Het tl mogelijke miere om dit te doe is: ~;; = Let wel, dt de volgorde v trekke hier v belg is. Als dezelfde verzmelig v 10 krte i ee dere volgorde wordt getrokke, d oeme we dt ee dere vritie. Voorbeeld 8. Ee getl v vijf cijfers gekoze uit de cijfers. 1,,,9 zoder herhlig is ee vritie v 5 uit de getlle 1,,,9. Het tl 9' getlle v deze gedte is dus: 7T = = 15!0. 4. Opgve 3. Op hoeveel verschillede miere is het mogelijk i ee gezelschp bestde uit 6 joges e 9 meisjes, dt lle joges ee meisje trouwe? Stellig. Het tl deelverzmelige v k elemete uit ee verzmelig met elemete is! k! (- k)!! Bewijs. Het tl ijecties v {,,,k} i { 1,,} is ~(~--~k~)t! (De elemete. zij lle verschilled.) Het geve v ee ijectie k 1 opgevt worde ls het verrichte v twee hdelige: eerst het beple v ee deelverzmelig v { 1,,} met k elemete; dr het geve v ee ijectie v {l,,k} i deze deelverzmelig. Voor de eerste hdelig is het tl mogelijkhede ; voor de tweede is! het k!. Volges de grodregel v het telle is: k! = ( _ k)!! Du s =,...,...::.:.,...,...,. k! (- k)! D
17 Zij A= { 1,,}; B = {b 1,,bm}. Lt k 1,,km ee J iet egtieve gehele getlle zij (ki E {0,1,, }) met de eigeschp k + + k =. 1 m We zij geïteresseerd i het tl fbeeldige v A i B met de eigeschp dt er precies k. elemete i A zij die op b. worde fgebeeld. l. l. Als bijv. A= {,,6}, B = {1,,3,4}, k 1 = 3, k =, k 3 =, k 4 = 0, d geeft de volgede figuur twee toegeste fbeeldige. A B A B Voordt we het tl v zulke fbeeldige beple geve we ee pr voorbeelde. Voorbeeld 9. ee rij met 10 huize moete 4 deure wit, 3 deure groe e 3 deure rood geverfd worde. Op hoeveel miere k dit? Het betreft hier fbeeldige v de verzmelig bestde uit 10 huize, die we gemkshlve met {1,,,10} duide, i de verzmelig {wit,groe,rood}. Hierbij is kl = 4, k = 3, k3 = 3. Voorbeeld 10. Hoeveel woorde k me vorme uit de letters v het woord "koekoek". Hierbij is het iet v belg of het woord l of iet betekei~ heeft, bijv. kkkooee is ee toegest woord. Hier kue we ee woord iterpretere ls ee fbeeldig v de verzmelig {1,,7} (de plts v de letter i het woord) i de verzmelig {e,k,o}. Hierbij is k 1 =, k = 3, k3 =. Om ee heuristische fleidig voor het tl toegeste fbeeldige te krijge beschouwe we voorbeeld 10. We zulle dri ee letter die meermle voorkomt v ee ide voorzie: k o e k o e k Nu zij lle symbole verschilled. Er zij 7! volgordes wri deze symbole kue st. Als we de
18 - 1 - idices weglte vlle sommige v die mogelijkhede sme, bijv. k 1 k o 1 e 1 k 3 o e e k 3 k 1 o 1 e 1 k o e Vervgig v k 1,k,k 3 door ee willekeurige permuttie (3: stuks) lt het woord dus overderd. Op grod drv moete we het oorsprokelijke tl mogelijke volgordes door 3:. dele. Op dezelfde rier moete we het tl door z: dele vwege de permutties v o 1,o e loog door : vwege e 1 e e Het tl woor- 7! - de dt gevormd k worde is dus:!! 3! het lgemee geldt: Stellig. Als #A= met > 0, B = {b 1,...,bm}' # B =me k 1,...,km iet egtieve gehele getlle zij met de eigeschp k km =, d is het tl fbeeldige A+ B met de eigeschp dt er voor i=!,...,m precies ki elemete op bi worde fgebeeld, gelijk : k m Bewijs. Ee fbeeldig met de geweste eigeschp is te verkrijge ls het resultt v m chtereevolges uit te voere hdelige: eerst het geve v de k 1 origiele v b 1 ; dr het geve v de k origiele v b oder de -k overgebleve elemete v A; vervolges het geve 1 v de k origiele v b oder de -k -k overgebleve elemete v A ez. Stellig geeft het tl mogelijkhede voor elk v deze hdelige. De grodregel v het telle geeft voor het totl tl toegelte fbeeldige: : : = k 1 k k! m (-kl- -km-1): k : 0: m 0: voorbeeld 9 zie we dt er 4! 3! 3! = 400 mogelijkhede zij om de deure te verve. Voorbeeld!, Ee spel v 5 speelkrte wordt gedeeld. Vier persoe krijge ieder 13 krte. Op hoeveel miere k dit gebeure? Hier is ee fbeeldig gegeve die de verzmelig der krte fbeeldt op de spelers: = D
19 {1,...,5} + {N,O,Z,W} met kl = k = k 3. d 5! 1S US 4 (13!) k 4 = 13. Het tl mogelijkhede Voorbeeld kikkers, geuerd 1,,...,10, worde i 7 verschillede doze gelegd, zodig dt resp. 3,3,,1,1,0,0 kikkers worde gepltst i de le,e,,7e doos. Het tl mogelijkhede om dit te doe is O! 3!3!!1!1!0!0! = Defiitie, Als k, gehele getlle zij met 0 s k s, d is ()! k := k!(-k)! bijv. (~) =, (~) =, (~) =!(-1); (~)wordt uitgesproke ls " over k". Op grod v is het tl fbeeldige v ee verzmelig A={ 1,..., 1 i ee verzmelig B = {b 1,b } met de eigeschp dt b 1 het beeld v precies k elemete i is, gelijk (~). Eigeschppe. i) ( ) = ( ) k -k i i) (+ ) = () ( ) k k + k-1 (Pscl) Bewijs. i) volgt omiddellijk uit de defiitie. i i) ' + = (k - )! ( - k + )! =! [( k ) k] (+ l)! _ (+l) k!(-k+i)! = k!(-k+i)!- k 0 Op eigeschp ii) is de zg. driehoek v Pscl gebseerd: (0) 0 () () 0 () ez. ( ) () s 6 S 0 S 6
20 Door vergelijke v e volgt z: k=o Beide lede geve het totle tl deelverzmelige v ee verzmelig A met ~ A =. Bovegeoemde gelijkheid is ee specil gevl v het biomium v Newto: Stellig. Als,b E JR., E ln, d geldt: Vwege deze gelijkheid worde de getlle (~) biomilcoëfficiëte geoemd. tuïtief kue we deze stellig ls volgt izie: Werk het -voudige product (+b) (+b) uit op de bekede wijze. Mk drtoe i elke fctor ee keuze: of b, e vermeigvuldig de gekoze wrde. We krijge op die mier ee term v de gedte -\k. Deze term komt tot std door -k keer e k keer b te kieze. Bij vste k correspodeert deze keuze met ee fbeeldig v {l,,} i {,b} wrbij precies k elemete worde fgebeeld op b. Op grod v zij er(~) v deze fbeeldige, d.w.z. er zij(~) terme -k k d" d b" "d () -kbk 1. o 1e tezme e 1J rge k evere. N sommt1e over k volgt het gestelde. Formeel kue we de stellig ls volgt bewijze: Bewijs. We gebruike volledige iductie. Als = is het gestelde evidet. Lt de stellig juist zij voor -, d.w.z. oftewel (+b)-1
21 Vermeigvuldig met,b, -1 ( + b) b(+b)-l e tel op, d is Hierbij terwijl is gebruik gemkt v de formule v Pscl -1-1 verder ( 0 ) = ( 0 ) = (-l) = () = 0 Er geldt de volgede geerlistie v het biomium v Newto:! ( ) = L k ik i m... m k m wr gesommeerd wordt over lle m-tupels k 1,k,,km v,iet egtieve gehele getlle met k 1 + k + +km=. We lte het bewijs chterwege. hete multiomilcoëfficiëte De reële getlle We g er v uit dt de verzmelige v de gehele, rtioele e reële getlle - ottie~. Ql, lr - beked zij v de middelbre school. We richte de dcht u op de reële getlle. De lgebrïsche bewerkige (optellig, vermeigvuldigig, delig) e de ordeig (ogelijkhede, bsolute wrde of modulus) v de reële getlle beschouwe we ls beked. De reële getlle correspodere met de pute op ee rechte: de getllerechte. V twee getlle e bis l-bi de fstd v hu beeldpute op de getllerechte. Drie belgrijke stellige over ogelijkhede zij: ) l+bl,; ll+ lbl ) ll - lbll,; l-bi 3) ll :> lbl d e slechts d ls,; b
22 - 16- Bekede deelverzmelige v R zij de zg. itervlle. We geve ee lijst v type e hu otties: { < < b} =: (,b) {,; < b} =: [,b) { <,; b} =: (, b J {,;,; b} =: [,b] { < } =: (,oo) {,; } =: [,oo) { < b} =: (-oo,b) {,; b} =: (-oo,b] De eerste vier v deze itervlle hete begresd, de dere obegresd. (,b), (,oo), (-oo,b) hete ope itervlle; [,b], [,oo) e (-oo,b] hete geslote itervlle (zie ook oder). Bij de ottie (,b) ez. wordt stilzwijged verodersteld dt e b zo zij dt het betreffede itervl iet leeg is. Ope verzmelige i R Defiitie. Ee verzmelig V heet ope ls er bij elkecvee ope itervl (c,d) is met E (c,d) c V. Gelijkwrdige formulerig: V is ope ls er bij elke c V ee getl ó > 0 bestt zodt (-ó, +ó) ={ J l-l< 6} cv Het is deze ltste formulerig die we i 1.5 zulle geerlisere. Merk op dt ope itervlle, ~. lli, ope zij. Ee itervl [,b] is iet ope. Het is evidet dt elke vereigig v ope verzmelige ope is. We zulle bewij ze: Stellig. De doorsede v twee ope verzmelige is ope. Bewijs. Lt V e W ope zij e eem dt V W f 0 (ls V W = 0 is V W ope). Zij E V W, d is er ee o > 0 zodt (-o,+o ) cv e er is ee 6 > 0 zodt (-o,+6 ) c W. Als u ó := mi(6,o 1 ), d is (-ó,+ó) cv W. Deze redeerig geldt voor elke cv W. V W is derhlve ope. 0
23 Defiitie. s V ope e E V, d heet V ee omgevig v. Als p f q d zij er ope verzmelige U e V met p E U, q E V, U V = 0. Met het oog op ee geerliserig i 1.5 merke we op dt voor ee willekeurig ope itervl (,b) geldt: (,b) = (!(+b) -!(b-),!(+b) + j(b-)) = wri m =!(+b), ê = j(b-). = (m-ê,m+ê) = { J l-mi < ê} Het ope itervl (,b) is dus de verzmelig v lle die tot m ee fstd kleier d ê hebbe. Defiitie. Ee put p uit ee verzmelig A heet ee iwedig put v A ls er ee omgevig V v p bestt met V c A. Gevolg. s W ope e p E W d is p iwedig put v W. v zowel [,b] ls (,b] ls [,b) zij lle pute uit (,b). De iwedige pute Defiitie. Ee put p uit ee verzmelig A heet ee geïsoleerd put v A ls er ee omgevig V v p bestt met V A = {p}. tervlle hebbe gee geïsoleerde pute. V ln e 'Z is elk put geïsoleerd. Ook v {! E JN} is elk put geïsoleerd (g!). Defiitie. Zij A ee verzmelig e p ee put, d heet p ee rdput v A * ls voor elke omgevig V v p geldt V A f 0 e V A f 0. V ee itervl [,b] of (,b] of isoleerd put is ook rdput. V rdpute B u {O}. (,b) Z~J de rdpute e b. Ee ge B := {! E JN} is de verzmelig der Defiitie. Zij A ee verzmelig e pee put,d heetpee verdichtigsput v A ls voor elke omgevig V v p geldt A (V\{p}) f 0. Elk iwedig put v ee verzmelig is ook verdichtigsput. Alle pute v [,b] zij verdichtigspute v zowel [,b] ls (,b] ls (,b). Als ee V rdput {- E v A iet tot A behoort is het ee verdichtigsput v A. JN} is 0 het eige verdichtigsput Defiitie. Ee verzmelig W heet geslote idie R\W ope is. Geslote itervlle, R e 0, zij voorbeelde v geslote verzmelige. Merk op dt er verzmelige zij die och ope och geslote zij, zols het itervl [,b). R e 0 zij zowel ope ls geslote.
24 Stellig. s W geslote e p ee verdichtigsput v W d is P E W. Bewijs. Neem p t W d is p E lr\ W = w*. w* is ope, p is iwedig put v w* zodt er ee omgevig V v p bestt met V c w*. Voor deze omgevig V geldt d W (V\{p}) = 0, i tegesprk met de defiitie v verdichtigsput. Dus is p E W. Defiitie. Ee verzmelig U heet begresd idie er ee getl M > 0 bestt zó dt U c [-M,M]. Begresde itervlle zij begresde verzmelige. Rije reële getlle.4.5. Ee oeidige rij reële getlle is ee fbeeldig ln _,. lr Als,.._,. 1,,_,., otere we de rij op ee v de volgede wijze: (). De getlle. hete de elemete v de rij. 1 Voorbeelde.,, 3, = ( E ln),, '... ( E ln) D r~) is de rij, 4, 9, - f ) 1s d e eve rij ' 4 ' 6 ' N.B. het ltste voorbeeld worcit ee uitbreidig v de ottie geitroduceerd. Ee oeidige rij reële getlle 1,, heet begresd idie er ee getlm bestt zodt l :SM voor elkee ln. De rij 1,, met = (-) is begresd; de rij met =is iet begresd. Als voor de rij ( ) ln geldt: 3M lr V ln [ < M], d heet de rij E E e: r bove begresd. Aloog is te defiiëre het begrip r beede begresde rij. Ee rij 1,, is begresd d e slechts d ls de verzmelig { 1,, } begresd is.
25 N.B. Omdt de elemete v ee rij iet oodzkelijk verschilled zij, k {,, } best ee eidige verzmelig zij. 1 Als < < <,d heet de rij () mootoo stijged; ls 1 3 ~ ~ ~,d heet de rij mootoo iet dled. Aloog zij te 1 3 defiiëre de begrippe mootoo dled e mootoo iet stijged. We zegge dt de elemete v de rij () op de duur (fgekort o.d.d.) i de verzmelig V ligge idie Gelijkwrdig geformuleerd: ligt o.d.d. veel wrde v geldt f. v. Aloog: heeft o.d.d. de eigeschp E. Voorbeelde. > 1000 o.d.d. Voor elke ö > 0 geldt ~ E (-ö,ö) o.d.d. Het is iet wr, dt (-1) > 0 o.d.d. i V idie voor slechts eidig Lemm. Als voor () geldt E V o.d.d. e ook E W o.d.d., d geldt --- E V W o.d.d. Bewijs. Krchtes het gegeve bes t er getlle N 1 E ln e N E ln zodt voor> N 1 geldt E V, e voor> N E W; voor> N := m(n 1,N ) geldt derhlve zowel E V ls E W, dus E V W. 0 Limiete v rije reële getlle Dit begrip is reeds beked; we geve eerst ee v de vele vorme v de defiitie Defiitie. lim = beteket dt voor elke omgevig V v geldt E V o.d.d. -- plts v lim = zegge we ook:..,. ls -+ oo; dert tot Stellig. De volgede bewerige zij gelijkwrdig: ) lim =. -- ) Voor elke > 0 geldt 3) Voor elke > 0 1s er E (- 0 + ) o.d.d. ee N E lr zodig dt voor > N geldt - <.
26 - 0-4) lim ( -) o. 5) lim - = 0. Het bewijs is trivil. Voorbeelde. lim ->oo - = o ' lim = 0. -+«> Om het ltste resultt te bewijze moete we bij elke e > 0 ee N E lr geve zodt voor > N geldt = < E Het is duidelijk dt N = log Ē voldoet. lim (-!) bestt iet; lim bestt ook iet. de situtie v het ltste voorbeeld zegge we wel: + oo ls + oo. Defiitie. + oo ls + oo, beteket dt voor elke ME lr geldt > M o.d.d.; +- oo ls + oo, beteket dt voor elke ME lr geldt < M o.d.d. Voorbeelde. -+ oo ls -+ oo; - ÏÏ-+ - oo ls + oo; lim (-1) 0 r bestt iet, ook is iet: (-l) r + 00 of +oo (-l) r + -oo ls + oo. Als de rij () ee limiet E lr heeft, d heet de rij coverget; ls de rij gee limiet i lr heeft, d heet de rij diverget; i het bijzoder zegt me i gevl + oo (resp.- oo) ls + oo, dt r oo (resp. - oo) divergeert.!.4.8. Stellig (stdrdlimiete). ) Als p > 0, d is m- = j +oo p ) ls q <, d is lim q = 0; -+«> 3) ls > o, d is limr= 1. -+«>
27 - 1 - Bewijs. ) Zij c > 0; opdt, - oj = -1- < c is het voldoede dt p p > (!)l/p =: N. c Met deze wrde vnis dus formulerig.3) v vold. ) Als q = 0 is het trivil; eem verder dt q f 0 is. Zij c > 0; opdt lq- O < E ofwel lql < E is het voldoede dt loglql < log c. Met N :=~is formulerig 3) vold. 3) Zij c > 0; volges 1., voorbeeld is (l+e) ~ l+e, zodt lim (l+e) = oo. Druit volgt ->oo -...;..-= < < (l+c) o.d.d. ( +c) + E < T< + c o.d.d. e E + c < T- < e o.d.d. :l- 11 < c o.d.d. D Stellig ) (bewerkige met limiete). Als lim ( + b ) = + b;.- lim ->«> =, lim b ->oo = b, d is ) lim ( b ) = h; ->oo 3) 1. lm = mits f 0 ->oo 4) lim l e lim lfj = ->oo ->oo /ft. Bovedie geldt: 5) Als s b o.d.d. d is s b. Bewijs. We schrijve llee de bewijze v ) e 5) uit. ) Zij E > 0; u is l - l < je o.d.d. zeg voor > N 1 ; lb - b < je o.d.d. zeg voor> N Voor> m(n 1,N ) is d
28 - - 5) Bewijs uit het ogerijmde: stel b < d geldt b E (-oo,j(b+)) o.d.d., E (j(b+),oo) o,d,d. e dus b < j(b+) < o.d.d,, tegesprk. D Voorbeelde. lim = lim 0 = 0 =. -+oo 5 - S oo lim (/ oo ) = lim --;:;~=:::;~-==;;;==::; ->oo/ '1 ' v' v' ~ =lim-;;:===;-~==~ ->oo v; + i '+ J _! + ~ ~ = "_...:::..., Stellig (isluitstellig). Zij lim =p,limb ->«> -.oo gelde: s y s b o.d,d., D is lim y = p. ->oo = p; lt voor (y ) Bewijs, Zij E > 0; d is E (p-o,p+o) o.d.d, (zeg voor > b E (p-o,p+o) o.d.d. (zeg voor> N ), terwijl s y s b voor> N 3 ). Op de duur (l. voor> m(n 1,N,N 3 )) is d,; b < p+o, dus y E (p-o,p+o) o.d.d. N)' o.d.d. (zeg p-o < s y D Voorbeelde, lim si si = 0 dr -,;,; ->oo lim ~ + 3' = 3 dr ->oo 3 = v:- 3 < V, + 3 < ï3 + 3 = 3;rz e lim ;rz= --. Stellig. s ( ) coverget, d is ( ) begresd. Bewijs. Zij lim =, d is -- E (-J,+l) o.d,d,, zeg voor > N E ln. D geldt voor elke E JN, D
29 - Z Grodeigeschp der reële getlle. Ee mootoe begresde rij i lr is coverget Deze grodeigeschp zulle we opvtte ls ee iom. Ze postuleert het best v de limiet; ze geeft os gee middel de limiet ook te berekee. N.B. Ee mootoo iet dlede rij is begresd (e dus coverget) d e slechts d ls de rij r bove begresd is. Ee loge bewerig geldt voor mootoo iet stijgede rije, Z + 4 Voorbeeld. De rij () zij gedefiieerd door: 1 := O, +l := --~ ( E ln), De rij ( ) is coverget. (i) We bewijze door volledige iductie 4 ) 1 = 0, = ~, dus 1 < dt ( ) mootoo stijged is. ) We zulle lte zie dt uit < + 1 volgt + < + Nu is - = + +l +l ii) We bewijze eveees doorvolledige iductie dt () r bove begresd is. We moete drtoe ee bovegres M vide die zo ruim is, dt uit ~ M volgt = +l Z + 4 M ::."3--- ~ 3 ~ M ; dus M ;, 4. Het iductiebewijs v lf E ln [ ~ 4] verloopt d ldus: l) 1 =0~ ) Als ~ 4, d is =.;;" +l = 4 ~ 3 Overeekomstig de grodeigeschp bestt u lim =: ~. Uiterrd is ook lim = 1; mr d is +l ->oo 1 = lim +l -+= Z + 4 = lim...:::."..- = wruit volgt ~ 4 lim = 4. -+= Opmerkig. ~ best er begresde mootoe rije die iet r ee elemet v ~ covergere.
30 - 4 - Voorbeeld. Beschouw de rij (b ) = j(b + b ), We bewijze eerst :>b :>4. gedefiieerd door: b 1 :=, door volledige iductie dt b +l := b E lil e ) bi =, dus b 1 E lil e,; b ) Zij b E e,; b,; lil 4. Schrijf b+l b + b,; 4. D is- E b lil. d is b+l - e dus b+l E lil Als,; b,; 4, d volgt 0,; b+l -,; oftewel,; b,; b Uit het voorgde volgt teves b - b = +l b,; 0. De rij (b) is dus mootoo iet stijged. Stel u dt er ee limiet ~ E ~ zou best, d ws ~ = ~~ + t, dus ~ =. Er is echter gee rtiol getl wrv het kwdrt gelijk is. Opmerkig, Beschouwt me (b) ls ee rij i ~ d is deze wel coverget e b +.f ls + oo, De rij getlle (b ) is de rij die me verkrijgt ls me begied met b =,.f bedert volges de methode v Newto-Rphso 1 (zie. 7. voorbeeld ) Uit volge vele belgrijke eigeschppe v de reële getlle. We bespreke er éé v Stellig (stellig v het itervlle-est). Lt de rije () e (b) - voldoe V [,; +l,; b,; b ] ElN +l d.w.z. ~ ~ :::;: +l,; b +l :::;: b :S e zij lim (b - ) = 0. U-+<l D is er precies éé c met c E [, b ] voor lle E ln. Bewijs. De rij ( ) is mootoo iet dled e r bove begresd. Volges bestt d lim =:, terwijl,; voor elke. Dr teves m -+«> voor elke m, is,; b (b is de limiet v de costte rij b b ) We vide zo: E [, b ] voor lle E ln.,; b
31 - 5 - Aloog is i te zie dt lir b =: b bestt e b E [,b] voor llee N. ->oo Uit lir (b - ) = 0 volgt b =..- Defiieer u c := = b, d is: c E [,b ] voor lle E ln. We toe og dt c eeduidig is. Als immers voor ee zekere d geldt: d E [, b ] voor lle E ln, d volgt,;; d,; b e dus d = = b = c. D Mimum, miimum Zij V ee begresde verzmelig v reële getlle. D heet M E V het mimur v V idie,; M voor elke E V; loog: r E V heet het miimum v V ls r,; voor elke EV. Niet elke begresde verzmelig heeft ee mimur (of miimum). Als voorbeeld oeme we V := (0,1). die ME V het mimur v V zou zij d ws M+l M+l M <. dt gevl is echter M < -z- < zodt --- EVe M iet het mi- mur is. Coclusie: V heeft gee mimum; V heeft evemi ee miimum. We zulle u ee deel v de beschouwige uit 1.4 uitbreide tot lr : = { (, y) E lr, y E lr} lr lr e JR 3 := {(,y,z) E JR, y E JR, ze lr}. Het getllepr (,y) resp. getlletripel (,y,z) wordt opgevt ls de k 11 lr 3.. d. d. et e v ee vector., ~ ZlJ vectorru1mte. eze ru1mte kieze we voorlopig ls vste bses, JR ~= (1,0), ~ = (0,1) JR 3 ~= (1,0,0), ~ = (0,1,0), ~ 3 = (0,0,1) De ketlle v de vectore sterme d overee met de compoete t.o.v. 3 de orthogole bses {~ 1.~ } c JR, {~ 1.~.~) c lr lr e lr3 1s. ee fstd gedefiieerd die met de stellig v Pythgors eevoudig bereked k worde:
32 - 6-1S = (l,),~= (bl,b)' d is de fstd v tot b i lr := lc -b ) d(~.~) (-b) ; is c = (cl,c,c3)' ~ = (d 1,d,d ), d is de fstd v c tot d i 3 d(!:.~) := /ccl-d1)+ (c-d) + (c3- d3). lr3 Merk op dt deze fstd voldoet de zg. driehoeksogelijkheid: d(~,q) D is / = V otere we ls 1!!1, de legte v. d(~.~l = ~- ~ Ope verzmelige i JR e JR 3 Defiitie. Zij ~ E JR (of ~ E JR 3 ) e o > 0, d heet de ope bol (schijf, bl) met middelput e strl o, Het begrip ope bol is ee logo i JR -, JR 3 v het begrip ope itervl uit lr, We g verder ook loog te werk: Defiitie. Ee verzmelig V c JR (of V c JR 3 ) heet ope idie bij elke ~ E V ee ó > 0 bestt zó dt B(~,o) cv. Gelijkwrdige formulerig: V is ope ls V ee vereigig is v ope bolle. 1.5., Defiitie. s V ope e~ E V, d heet V ee omgevig v. Stellig. Ee ope bol is ee ope verzmelig. Bewijs. Zij b E B(~, ó), d is d(~.~) < o. Nu is: ó := ó - d(~.~) > o. We zulle lte zie dt B(~,o 1 ) c B(~,ó). s c E B(~,o 1 ) d is d(~.!:) < ól e derhlve d(~ 0!:) ";; d(~.~) + d(~.!:) < d <~.~) + ól = ó, dus C E B(~,o). D
33 - 7 - Voorbeelde v ope verzmelige: 1 < 1 + < 4} 1 < < 4} De defiities v de begrippe iwedig put, geïsoleerd put, rdput e verdichtigsput zij letterlijk dezelfde ls i Stellig. ) JR, JR 3 e 0 zij ope. ) De doorsede v twee ope verzmelige is ope. 3) s ~ ~ ~. d zij er ope verzmelige U e V met E U, b E V, U V = 0. 4) W is d e slechts d ope ls bij elke E W ee o > 0 bestt zó dt V(~,o) c w. Bewijs. De bewijze zij iet moeilijk; we volst met ekele opmerkige. ) Als E V we B(~,o ) 1 cv, B(~,o ) c w, d is B(~,mi{o 1,o }) cv w. 3) Als ~~. d is B(~,jd(~,~)) B(~,jd(~,~)) = 0. 4) B(~,o) c V(~,o) c B(~,o/k) (~ E lrk, k =,3, o > 0) Defiitie. Ee verzmelig W c JR of Wc JR 3 heet geslote idie JR \w resp. 3 lr \ W ope is. Voorbeelde: JR, JR 3, 0, {~ d(~,~),; 6} zij geslote. Defiitie. Ee verzmelig U heet begresd idie er ee M > 0 bestt zó dt U c B ( Q,M) Voorbeelde: B(~,o), V(~, ) zij begresd. Rij e pute i JR, JR Defiitie. lim = i lr (of lr ) beteket dt voor elke omgevig U v -+oo - geldt E U o.d.d. - - Zij ~ = (l')' ~ = (l,) E lr of!! = (l''3)' ~=(l,,3) E lr3
34 Stellig. De volgede bewerige zij gelijkwrdig: ) lim =. - """ ) Voor elke E > 0 geldt E B(!!,E) o.d.d. - 3) Voor elke E > 0 geldt E V(!!,E) o.d.d. - 4) lim ( -) = Q """ 5) lim d (, ) = Q. - - """ 6) lim l = l e lim = (e lim 3 = 3). """ """ """ Het bewijs is iet moeilijk. Ee rij ( ) heet - Ee tl v de begresd idie {!!,!!z } ee begresde verzmelig stellige uit 1.4 zij og uit te breide tot JR e We zulle dr iet verder op ig.. d JR.6. Coor 1teste se s 1 Op de middelbre school is crtesische coördite i de lytische meetkude meestl bedreve met JR e JR 3 (,y resp.,y,z). Als me probleme bestudeert met "cirkel- of bolsyetrie", d zij dere coördite vk hdiger PoolcoÖrdite i JR We legge ee put P i het vlk vst door zij fstd tot 0 = (0,0) e door de hoek die de verbidigslij ÓP mkt met de positieve -s. De fstd heet gewoolijk r, de hoek ~; uit de defiitie volgt dt r ~ 0, ~ obepld is i 0 e dt i dere pute ~ slechts bepld is tot op veelvoude v ~ ((r,~) e (r,~+~) is hetzelfde put). Meestl wordt~ zo gekoze dt 0 $ ~ < ~ of -~ < ~ s ~. 0 oemt me wel de pool, de positieve -s de pools, r de voerstrl v P e ~ het rgumet v P.
35 - 9 - Het verbd tusse crtesische coördite (,y) e poolcoördite (r,~) ls r = r cos ~. r = V + y ' h = r si ~. (jl = rct(y/) ls ~ 0, (jl = rct(y/) + 7f ls < 0' y > o, y Cjl = rct(y/) - 7f ls < 0, y < o. y P tr. 4>> Voor probleme wri cirkelsymmetrie voorkomt zij poolcoördite erg hdig:. + y De c1rkel = heeft ls vergelijkig i poolcoördite: r =. Kromme r = costt zij cirkels om o'; kromme <p door~(~ zelf uitgezoderd). = costt hlf-rechte Ee vergelijkig r = r(cp) stelt i het lgemee ee kromme voor. We geve ekele voorbeelde: ) r = - (jl > (jl o. We zie dt r ~ oo ls cp + 0 mr dr y ls <p + 0 (zie.4, voorbeeld 6); er is y =. De kromme heet hyperbolische spirl. y si <p = r s1 <p =, geldt y ~ (jl dus ee horizotle symptoot
36 b) r (1 -cos~). De kromme heet crdio1de. y De kromme otstt (zie figuur) ls de b v het put P op de rechter cirkel ls deze cirkel (met strl ) zoder slip lgs de vste cirkel met middelput (-1,0) e strl rolt, y crtesische coördite is de vergelijkig v ( +y +) = 4( +y ) hetgee veel igewikkelder de crdioide: is Cylidercoördite i JR 3 Deze zij de uitbreidig v poolcoördite i het (,y)-vlk met ee z-coördit.
37 z z r T De cylidercoördite v P zij (r,~,z); de smehg met crtesische coördite is: r = r cos '' r si q> = z. l: = CylidercoÖrdite zij gemkkelijk bij meetkudige figure die ile symmetrie hebbe (omweteligsfigure:). De cylider + y = heeft ls vergelijkig i cylidercoördite: r =. De kegel z = + y heeft ls vergelijkig z = r, z = ± r Bolcoord1te 1 R Voor figure met ee put v symmetrie (bolsymmetrie) zij de volgede coördite erg hdig.
38 - 3 - z z P < p.e,<p ~ ~ y T 3 Ee put P i ~ wordt bepld door: fstd p tot ~. hoek 8 v ep met de positieve z-s, hoek ~ positieve -s. v de projectie v P op het (,y)-vlk met de Krchtes defiitie is p ~ 0, 8 tusse 0 e ~ te eme e ~ bepld tot op veelvoude v ~; meestl wordt cp zo gekoze dt 0,; ~ < ~, Voor cl is 8 och cp bepld; voor de dere pute op de z-s is 8 = 0 of 8 = ~ e cp obepld. De smehg met crtesische coördite is (: = p si 8 cos cp = p si 8 si cp = p cos 8. Uit de bekede eigeschppe v ee rechthoekige driehoek volgt melijk fff p si e, PT = p cos 8, zie figuur. p = costt is de vergelijkig v ee bol om ~. cp = costt is de "helft" v ee vlk door de z-s (de z-s zelf uitgezodered. 8 = costt is ee hlve kegel (uitgezoderd de top d) met de z-s ls s.
39 Hoofdstuk. Fucties lr -> lr.1. leidig Het begrip fbeeldig is lgemee gedefiieerd i l.. dit hoofdstuk beschouwe we meer i het bijzoder fbeeldige v de gedte f : A + B, wrbij A c: lr e B c: JR. We oeme f d ee reële fuctie v éé reële vribele, of kortweg fuctie, A heet de defiitieverzmelig v de fuctie f; ottie DOM f. Voorbeelde. f lr + JR, f() ~~ f lp + JR, f() ~ log f "'' -( :: ls -,; < 0 [-1,)+ R, ls ~ 0 - ls 0 < < N.B. Met log wordt de tuurlijke logrithme v bedoeld, d.i. de logrithme met grodtl e, sommige leerboeke wordt ook wel de ottie l gebruikt. het vervolg zulle we ee fuctie f ook wel defiiëre door middel v ee formule zoder epliciete vermeldig v de defiitieverzmelig. dt gevl zl DOM f best uit die wrde wrvoor de formule zivol is, Voorbeeld. f() ~ X, d is DOM f ~ lr+. Vk wordt ee fuctiewrde f() met ee prte letter y gegeve; me schrijft d y ~ f(). We geve og ee korte smevttig v de verdere ihoud v dit hoofdstuk. Eerste oderwerp vorme de polyome of veelterme ls meest eevoudige voorbeelde v fucties. Dr volgt ee uitvoerige behdelig v fucties wrbij chtereevolges de orde kome: eigeschppe v fucties, limiete, cotiuïteit, differetil- e itegrlrekeig v fucties v éé vribele, Teslotte wordt dcht geschoke umerieke specte i ee tweetl prgrfe over umerieke oplossig v vergelijkige e over umerieke itegrtie.
40 Polyome..1. Defiitie. Ee polyoom is ee fuctie p: R ~R, die we ls volgt kue schrijve: p() = wri 0, 1,, reële getlle zij e ~ 0. Deze getlle worde coëfficiëte geoemd. Het gehele getl ~ 0 heet de grd v het polyoom (ottie gr(p)). Ook de ulfuctie: ~ 0, zulle we opvtte ls ee polyoom, het zg. ~ polyoom. We geve gee defiitie voor de grd v het ulpolyoom. Ee uitsprk zols: zij p ee polyoom met gr(p) =, impliceert dt p iet het ulpolyoom is. Voorbeelde. ) p() is ee polyoom met gr(p) = ) p() = + + is ee polyoom met gr(p) = 10. 3) Als p() = " het polyoom gegeve door , d is de fgeleide v p - 1 Ook de tweede fgeleide p" = (p')', de derde fgeleide p"', i het lgemee dek-de fgeleide. p(k) zij polyome, Me ziet gemkkelijk dt (k) p () = k!~ + 3 (k+l)~+l (-k+l)(-k+) -l... Stellig. Zij p ee polyoom met gr(p) = ed ee polyoom met gr(d) = m, d is er ee polyoom r met gr(r) < gr(d) of r is het ulpolyoom è er 1s ee polyoom q zodt p() = q()d() + r() voor lle ER.
41 - J5 - Bewijs. Als m > is q het ulpolyoom e r = p. Als m $ d bewijze we de stellig door volledige iductie r. gevl = 0 zl gelde: p() = 0 r 0, d() = b 0 r O, q() = 0 /b 0 e r() = 0. Neem dt de bewerig wr is voor polyome met grd$ -1. Stel p() = + + e d() = bmm + + b, d is 0 0 p() -m =i) m d() + r 1 (), wri r 1 ee polyoom is met gr(r 1 ) $ -1 die r 1 het ulpolyoom is of ls gr(r 1 ) e r = r. Zij u gr(d) $ gr(r ) 1 r met gr(r ) < gr(d) N substitutie volgt of r is het ulpolyoom. 1 -m < gr(d) d voldoet q() = i) m d (iductieveroderstellig) zij er polyome q 1 e of r is het ulpolyoom, zó dt r 1 ()=q 1 ()d()+r (). p() -m = [i) + q ()]d() + r () 1 m 0 Het polyoom r wordt i de regel de ~ geoemd e we otere El!l r() d() = q() + d() Als r() = 0 voor lle d heet d ee deler v p. Voorbeelde. 4) Neem d() = -, d is p() = (-)q() + r() wrbij r() ee polyoom met grd 0 of het ulpolyoom is; r() is dus ee costte. Substitueer = d vide we r() ~ p(), wr volgt p() = (-)q() + p() (reststellig). Als p() = 0, d is (- ) ee deler v p(); we oeme = d ee ulput v p(). 5) De wrde is ee ulput v p () = 3 + = (- ) ( - ). We zie dt = ook ulput is v -, e p() = (- 1). We zegge dt = ee tweevoudig ulput v p() is.
42 Defiitie. Het getl E ~heet ee k-voudig ulput (of: ulput met multipliciteit k) v ee polyoom p, idie er ee polyoom q bestt met q() 1 0 è p() ~ (- lq(). Opgve. Het sle-chts d. getl c ~ is ee k-voudig ulput v ee polyoom p ls p() ~ p'() ~,,, ~ p(k-l)() ~ 0 è p(k)() 1 0; d e too dit Het is beked dt ee vierktsvergelijkig hoogstes twee reële wortels bezit. Deze regel lt de volgede geerlistie toe:..4. Stellig. Ee polyoom p met gr(p) ~ heeft te hoogste reële ulpute. Bewijs. We bewijze deze stellig door volledige iductie r. gevl = 0 is p() ~ 0 1 0, dus p heeft gee ulpute. Stel de bewerig i de stellig is wr voor polyome met grd~ -1. Zij u p ee polyoom met gr(p) ~ e zij ee ulput v p, d is er ee polyoom q met gr (q) ~ - zodt p () (- )q (). Het polyoom q heeft te hoogste- reële ulpute (iductieveroderstellig), dus p heeft te hoogste + - ~ reële ulpute. 0 Voorbeelde. 6) het (,y)-vlk kue we door twee pute ee rechte lij costruere, door 3 pute (met verschillede -coördite) ee rechte lij of ee prbool. Algemee: bij + gegeve pute ( 0,y 0 ),( 1,y 1 ),,(,y)' wrv de coördite,,., verschilled zij, bestt er precies éé polyoom p met gr(p) ~, of p is 0 1 het ulpolyoom, zodt p(k) ~ yk voor k ~ O,l,,. Bewijs. We costruere eerst ee polyoom p, dt de eise voldoet e lte vervolges zie dt p eeduidig bepld is. Zij t. het polyoom gege- 1 ve door
43 , L () 1 (- 0 )(- 1 )... (-i_ 1 )(-i+l) "' (-) = ~(~-i O~)~(~-i----~l~)-----(r-i---~~i~--~~)~(-1-.~-~~i~+-l~) ~(-1~.~---~) ' d is ~.(k) = 0 voor k = O,l,,i-l,i+l,, e ~.(.)=, We eme u voor p het polyoom gegeve door p() = y 0 ~ 0 () + y ~ ()+. + Y~ () 1 (Lt zie dt p de eise voldoet,) Lt q ee polyoom zij dt eveees de eise voldoet, d geldt voor het polyoom p- q dt p(k) -q(k) = 0 voor k = O,l,..,,, Het polyoom p-q heeft dus + verschillede ulpute, hetgee i strijd is met..4,tezij p- q het ulpolyoom is; dus p = q, Het polyoom p heet het iterpoltiepolyoom v Lgrge door de pute (k,yk)' k = O,l,...,. 7) We costruere vervolges ee polyoom wrv de fuctiewrde e de eerste tot e met de -de fgeleide i ee put zij voorgeschreve: () p() = b, p'() = b,,p ()= 0 1 b, wri b,b,,b gegeve re ele getlle zij. Ee polyoom p met gr(p) ~ kue we geve door 0 Differetieer p() k-ml d vide we dus (k+ ) ~+ (-) + + (-k+ ) (-k+) (p(o)() := p()), -k.. (-), Derhlve is~= kt bk voor k = O,l,,. Het polyoom p is dus voor te stelle door.,6 p() = L k=o p (k) () k! k (- ), Deze betrekkig heet de formule v Tylor voor polyome.
44 Eigeschppe v fucties deze prgrf relevere we ee tl deels bekede eigeschppe v fucties Defiitie (begresdheid). Ee fuctie f heet begresd op ee verzmelig V c DOM f, idie 3M E lr " E V [ f (),; M] of ders geformuleerd: f(v) c lr is ee begresde verzmelig. Ee fuctie f heet begresd, idie f begresd is op DOM f, dus ls f(dom f) ee begresde verzmelig is. Voorbeelde. f() = si, g() - = e h() = rct, t() = ~ zij voorbeelde v begresde fucties. De fuctie op lr+, de fuctie zelf is echter iet begresd..3.. Defiitie (mootoie) (i). Ee fuctie f heet mootoo stijged, idie "',y E DOM f [< y '*'> f() < f(y)]. - f() = e is begresd (ii) Ee fuctie f heet mootoo dled, idie ':/,y E DOM f [ < y""" f() > f(y)], (iii) Ee fuctie f heet mootoo iet dled, idie "',y E DOM f [< y- f(),; f(y)], (iv) Ee fuctie f heet mootoo iet stijged, idie V,y E DOM f [< y => f() ;, f(y)]. De fuctie f heet mootoo, idie zich ee v de gevlle (i), (ii), (iii) of (iv) voordoet. De fuctie f heet strikt mootoo, idie zich ee der gevlle (i) of (ii) voordoet. ls 0,; <! Voorbeelde. ) f: [0,1] + JR, f() = {: ls!,;,; is ee mootoo iet stijgede fuctie. ) f: [-1,1] + JR, f() = rcsi, is ee mootoo stijgede fuctie.
45 Strikt mootoe fucties zij voorbeelde v ijectieve fbeeldige. mmers ls # y, dus < y of > y, d is f() < f(y) of f() > f(y), i ieder gevl f() # f(y). s fbovedie surjectief, d heeft f ee.. + str~kt mootoe ~verse f Voorbeelde. 3) f: [- j11,j11] + [-1,1], f() =si. De fuctie f heeft ee iverse gegeve door + + f : [-1,] + [- j11, j11 ], f () = rcsi. 1T 4) f: < door!,) + lr, f() = t. De fuctie f heeft ee iverse gegeve 5) f: [O,oo) + [O,oo), f() =log(! + ). De fuctie f heeft ee iverse gegeve door.3.3. Defiitie (coveiteit). Ee fuctie f heet cove op ee itervl c DOM f, idie v,ye VÀE[O,] [f(>.+(l->.)y),.; >.f() + (1->.)f(y)]. Ee fuctie f heet cocf op idie de fuctie -f cove is op. We merke op dt voor de grfiek v f coveiteit beteket dt het lijstuk, dt de pute (,f()) e (y,f(y)) verbidt, bove de grfiek ligt. Voorbeelde. (G de hd v grfieke; zie ook.6.9.) 6) f: [-1,1] + [0,11], f() = rccos. De fuctiefis cove op [-1,0] e cocf op [0,1]. 7) f: lp + lr, f() = log. De fuctie f is cocf op lp Defiitie (eve of oeve). Ee fuctie f heet eve idie (i) '1:/ E lr [ E DOM f =<> - E DOM f], d.w.z. DOM f ligt symmetrisch t.o.v. 0; (ii) V E DOM f de y-s. [f(-) = f()], dus de grfiek v f is symmetrisch t.o.v.
46 Ee fuctie f heet oeve idie (i) geldt e (ii') ;/ <: DOM f [f(-) = -f() ], (Wt beteket dit voor de grfiek v f?) Voorbeelde. 8) f() = rct ; de fuctie f is oeve. 9) f() 10) f() 1T = rccos -- ; de fuctie f is oeve, - = e ; de fuctie f is eve. J) Polyome wri louter eve mchte v voorkome, zij eve fucties, Teslotte itroducere we og de hyperbolische fucties: sih, csh, th, coth (spreek uit sius hyperbolicus, cosius hyperbolicus, ez.). Deze fucties worde gedefiieerd door - si h e - e : =.::...--,.,.::.- - co s h : e + e =.::.. ;"...::;..._ th sih : =.:c;,:o;;:s:;.:h~ csh ' coth := sih De hyperbolische fucties zij gedefiieerd voor lle c ~ behlve dt coth iet gedefiieerd is voor = 0. Schets de grfieke v deze fucties e merk op dt csh ee eve fuctie is terwijl sih ee oeve fuctie is. Omdt cosh t - sih t = is = csh t, y = sih t, -~ < t < ~, ee prmetervoorstellig v ee tk v de hyperbool - y =. (Evels = cos t, y =sit, 0,; t < 1T ee.prmetervoorstellig v de cirkel +y = is, zie 6.1.) Dit verklrt de m v de igevoerde fucties,.4. Limiete v fucties Reeds op de middelbre school is keis gemkt met het begrip limiet v ee fuctie. We geve ee tl defiities Defiitie. Zij E ~ e ee verdichtigput v DOH f. D beteket lim f() = L, dt er voor iedere omgevig V v L ee omgevig U v be+ stt zodt voor lle E U DOM f met geldt: f() EV. plts v lim f() = L otere we ook wel f() + L (+ ), +
47 Defiitie. Zij E ~ e ee verdichtigsput v (,oo) DOM f. D beteket lim f() = L, dt er voor iedere omgevig V v L ee omgevig U + v bestt zodt voor lle E U DOM f met > geldt: f() E V. Deze limiet heet de rechterlimiet v f() i. Defiitie. Zij E ~ e ee verdichtigsput v (-oo,) DOM f. D beteket lim f() = L, dt er voor iedere omgevig V v L ee omgevig U t v bestt zodt voor lle E U DOM f met < geldt: f() E V. Deze limiet heet de likerlimiet v f() i. Bewijs zelf de stellig: Stellig. Als lim f() = L e lim f() = L, d is lim f() = L, + t + Opmerkig. die de rechterlimiet e de likerlimiet v f() i best doch verschilled zij, d bestt lim f() iet, + We geve u de defiitie v limiet i gevl = +oo.4.. Defiities. Zij voor elke b E ~: (b,oo) DOM f <f 0. D beteket lim f() = L, -+<» dt er voor iedere omgevig V v L ee M E ~ bestt zodt voor lle E DOM f met > M geldt: f() E V. Zij voor elke b E ~: (-oo,b) DOM f <f 0. D beteket lim f() = L, dt er voor iedere omgevig V v L ee M E ~ < M geldt: f() EV. bestt zodt voor lle E DOM f met.4.3. Stellig. Zij lim f() = L. Voor iedere rij ( ) c DOM f met f, - + lim = geldt d: lim f( ) = L. -+<::o -+«> Bewijs. Zij V ee omgevig v L, d is er volges.4.1 ee omgevig U v zodt voor lle E U DOM f met f geldt: f() E V. Nu beteket lim = dt EU o.d.d., dus f() E V o.d.d. Druit volgt lim f( )= L. ~ ~ 0 Opmerkig. De stellig is ook geldig i gevl = "" (resp.- oo) e +oo (resp.- oo) ls _,. oo,
TECHNISCHE HOGESCHOOL EINDHOVEN Afdeling Algemene Wetenschappen. Onderafdeling der Wiskunde WISKUNDE 10. bestemd voor. BDK-1, WSK-1, N-1, E-1 en T-1
 TECHNISCHE HOGESCHOOL EINDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WISKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1978 ... -, Techische Hogeschool Eidhove Oderfdelig
TECHNISCHE HOGESCHOOL EINDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WISKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1978 ... -, Techische Hogeschool Eidhove Oderfdelig
4 Differentierekening en reeksen
 WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
1) Definitie, rekenkundige en meetkundige rijen
 Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
1 Bewerkingen met matrices invoeren via voorbeelden. , is een commutatieve groep.
 1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
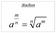 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Het differentiequotiënt van een functie in een interval geeft de gemiddelde helling weer van die functie in dat interval. Symbolisch wordt dit:
 Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
16.6 Opgaven hoofdstuk 7: Producten en combinatoriek
 166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
Acdemi Press Dele Bij delig vermeigvuldigt me met het omgekeerde v de deler..3.5 Vereevoudige Het is goed mogelijk dt voorgde bewerkige iet de
 Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
Formularium Wiskunde
 Formulrium Wiskude Te gebruike bij exme Ileidig tot de Hogere Wiskude Trscedete fucties. Goiometrische fucties t x = tg x = si x cos x cot x = cotg x = cos x si x sec x = cos x cosec x = si x cos( ± b)
Formulrium Wiskude Te gebruike bij exme Ileidig tot de Hogere Wiskude Trscedete fucties. Goiometrische fucties t x = tg x = si x cos x cot x = cotg x = cos x si x sec x = cos x cosec x = si x cos( ± b)
Functies, Rijen, Continuïteit en Limieten
 Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Verloop van exponentiele en logaritmische functies
 Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Reeksen. Convergente reeksen
 Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Formulekaart VWO wiskunde B
 Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
Algebra. Dr. Caroline Danneels
 Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Analyse 2 - SAMENVATTING
 Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Elementaire speciale functies
 ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Rinse Poortinga Lineaire Algebra en Voortgezette Analyse. 2 Lineaire afbeeldingen
 Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie
Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Matrixrekening - Samenvatting
 I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
Integraalrekening. Georg Friedrich Bernhard Riemann Breselenz 17 september 1826 Selasca 20 juni 1866
 Itegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 septemer 86 Selsc 0 jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geeft de itegrl v ee positieve fuctie ee uwkeurige
Itegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 septemer 86 Selsc 0 jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geeft de itegrl v ee positieve fuctie ee uwkeurige
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
Deel D. Breuken en algebra n
 Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Lagrange-polynomen. Dick Klingens september 2004
 Lgrge-polyome Dck Klges september 004 1. Probleem V ee fucte f s, hetzj door metg, hetzj door berekeg, slechts ee edg tl fuctewrde (her + 1 beked: f( x0, f( x1,, f( x We wlle deze (verder obekede fucte
Lgrge-polyome Dck Klges september 004 1. Probleem V ee fucte f s, hetzj door metg, hetzj door berekeg, slechts ee edg tl fuctewrde (her + 1 beked: f( x0, f( x1,, f( x We wlle deze (verder obekede fucte
Analyse. Lieve Houwaer Dany Vanbeveren
 Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
OVERZICHT VAN DE FORMULES
 80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
AFSTANDEN EN HOEKEN IN
 AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
Bereik en waardering RTV Dordrecht - Herhalingsmeting
 Bereik e wrderig RTV ordrecht - Herhligsmetig Socil Geogrfisch Bureu bureu voor beleidsoderzoek e sttistiek ordrecht drs. F.W. Witerwerp drs. J.M. Schiff september 2006 Colofo Opdrchtgever Tekst rukwerk
Bereik e wrderig RTV ordrecht - Herhligsmetig Socil Geogrfisch Bureu bureu voor beleidsoderzoek e sttistiek ordrecht drs. F.W. Witerwerp drs. J.M. Schiff september 2006 Colofo Opdrchtgever Tekst rukwerk
Vectoranalyse voor TG
 college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
Hoofdstuk 0: algebraïsche formules
 Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
2.6 De Fourierintegraal
 2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
Correctievoorschrift VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
UITWERKINGEN TOETS TRAININGSKAMP. Valkenswaard, 10 juni 2006
 UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
1) Complexe getallen - definitie
 Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
H O E D U U R I S L I M B U R G?
 H O E D U U R I S L I M B U R G? N AD E R E I N F O R M A T I E S T A T E N C O M M I S S I E S OV E R O N D E R AN D E R E A F V A L S T O F F E N H E F F I N G E N I N L I M B U R G 1 6 a u g u s t u
H O E D U U R I S L I M B U R G? N AD E R E I N F O R M A T I E S T A T E N C O M M I S S I E S OV E R O N D E R AN D E R E A F V A L S T O F F E N H E F F I N G E N I N L I M B U R G 1 6 a u g u s t u
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
Continuïteit en Nulpunten
 Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
1 Vlaamse Wiskunde Olympiade 1994 1995 : Eerste Ronde.
 Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
( ) Formulekaart VWO. Kansrekening. Tellen. k n k. Binomium van Newton : Kansrekening. Voor toevalsvariabelen X en Y geldt: E ( X + Y ) = E(
 Formulert VWO Telle! ( )... 0!!!( )! Biomium v Newto : Ksreei ( + ) Ksreei 0 Voor toevlsvriele X e Y el: E ( X + Y ) E( X ) + E( Y ) Voor ofhelije toevlsvriele X e Y el: σ ( X + Y ) σ ( X ) + σ ( Y ) -wet
Formulert VWO Telle! ( )... 0!!!( )! Biomium v Newto : Ksreei ( + ) Ksreei 0 Voor toevlsvriele X e Y el: E ( X + Y ) E( X ) + E( Y ) Voor ofhelije toevlsvriele X e Y el: σ ( X + Y ) σ ( X ) + σ ( Y ) -wet
Praktische opdracht Optimaliseren van verpakkingen Inleidende opgaven
 Prktische opdrcht Optimliseren vn verpkkingen Inleidende opgven V, WB Opgve 1 2 Gegeven is de functie f ( x) = 9 x. Op de grfiek vn f ligt een punt P ( p; f ( p)) met 3 < p < 0. De projectie vn P op de
Prktische opdrcht Optimliseren vn verpkkingen Inleidende opgven V, WB Opgve 1 2 Gegeven is de functie f ( x) = 9 x. Op de grfiek vn f ligt een punt P ( p; f ( p)) met 3 < p < 0. De projectie vn P op de
Over de lengte van OH, OZ en OI in een willekeurige driehoek
 Over de lengte vn OH, OZ en OI in een willekeurige driehoek DICK KLINGENS (e-mil: dklingens@pndd.nl Krimpenerwrd College, Krimpen n den IJssel (Nederlnd pril 2007 1. De lengte vn OH en OZ De punten O,
Over de lengte vn OH, OZ en OI in een willekeurige driehoek DICK KLINGENS (e-mil: dklingens@pndd.nl Krimpenerwrd College, Krimpen n den IJssel (Nederlnd pril 2007 1. De lengte vn OH en OZ De punten O,
2. Gegeven is de driehoek van figuur 10.10a. Gevraagd worden hoek β en de zijden a en c.
 Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
 Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Basiswiskunde Een Samenvatting
 Bsiswiskune Een Smenvtting Verzmelingen N: ntuurlijke getllen, nl.,, 3,... Z: gehele getllen, nl....,,, 0,,,... Q: rtionle getllen,.w.z. breuken vn gehele getllen R: reële getllen, us lle getllen op e
Bsiswiskune Een Smenvtting Verzmelingen N: ntuurlijke getllen, nl.,, 3,... Z: gehele getllen, nl....,,, 0,,,... Q: rtionle getllen,.w.z. breuken vn gehele getllen R: reële getllen, us lle getllen op e
Parels van studenten tijdens een examen
 Prel 1 Prels vn studenten tijdens een exmen c k x k n+1 n+1 ( = c k x k ( ) )x c n+1x n+1 n+1 k ( ) k x n+1 k ( ) k k k Prel 2 Vrg: Zij n N, c k C voor k = 1,..., n, c n 0. Toon n dt de functie f(z) =
Prel 1 Prels vn studenten tijdens een exmen c k x k n+1 n+1 ( = c k x k ( ) )x c n+1x n+1 n+1 k ( ) k x n+1 k ( ) k k k Prel 2 Vrg: Zij n N, c k C voor k = 1,..., n, c n 0. Toon n dt de functie f(z) =
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
Samenvatting - Wiskunde I
 Smevtt - Wsue I Clculus Erly Trsceetls Jmes Stewrt 6th eto Sles v A. Al-Dhhr Appe A Getlle, Vermele, Oeljhee e Absolute Wre N = {0,,,, } Ntuurlje etlle Z = {,-,-,-,0,,,, } Gehele etlle Q = { } Rtole etlle
Smevtt - Wsue I Clculus Erly Trsceetls Jmes Stewrt 6th eto Sles v A. Al-Dhhr Appe A Getlle, Vermele, Oeljhee e Absolute Wre N = {0,,,, } Ntuurlje etlle Z = {,-,-,-,0,,,, } Gehele etlle Q = { } Rtole etlle
Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n
 Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n M w. d r s. E. L. J. E n g e l s ( P r o v i n c i e L i m b u r g ) M w. d r s.
Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n M w. d r s. E. L. J. E n g e l s ( P r o v i n c i e L i m b u r g ) M w. d r s.
T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M +
 T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M + A a n l e i d i n g I n d e St a t e nc o m m i s si e v o or R ui m t e e n G r o e n ( n u g e n o em d d e St at e n c
T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M + A a n l e i d i n g I n d e St a t e nc o m m i s si e v o or R ui m t e e n G r o e n ( n u g e n o em d d e St at e n c
Equidistributie en ergodiciteit
 Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Oefeningen Analyse II
 ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
UITWERKINGEN VOOR HET VWO NETWERK VWO B2
 UITWERKINGEN VOOR HET VWO NETWERK VWO B HOOFDSTUK 9 KERN RIJEN a) Zie ook plaatje..., wat ieder mes schudt de had va twee adere. Dele door twee, wat bij de worde de pare hade dubbel geteld. b) c) d) ;
UITWERKINGEN VOOR HET VWO NETWERK VWO B HOOFDSTUK 9 KERN RIJEN a) Zie ook plaatje..., wat ieder mes schudt de had va twee adere. Dele door twee, wat bij de worde de pare hade dubbel geteld. b) c) d) ;
Kanstheorie. 2de bachelor wiskunde Vrije Universiteit Brussel. U. Einmahl
 Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
Hoofdstuk 5: Vergelijkingen van de
 Werkoek Alger (ursus voor 5u wiskunde) Hoofdstuk 5 : Vergelijkingen vn de e grd met één onekende Nm:. Hoofdstuk 5: Vergelijkingen vn de - 45 - e grd met één onekende. Instp (oek pg 7). Vn een rehthoek
Werkoek Alger (ursus voor 5u wiskunde) Hoofdstuk 5 : Vergelijkingen vn de e grd met één onekende Nm:. Hoofdstuk 5: Vergelijkingen vn de - 45 - e grd met één onekende. Instp (oek pg 7). Vn een rehthoek
is de verzameling van de natuurlijke getallen, bevat de gehele getallen en { x x m / n voor zekere gehele getallen m en n met n 0} bevat de rationale
 1 Basisbegrippe 11 Verzamelige De getalle waarmee we op school hebbe lere were, zij de reële getalle De verzamelig va alle reële getalle wordt aageduid met Belagrije deelverzamelige va zij, e {0,1,,3,
1 Basisbegrippe 11 Verzamelige De getalle waarmee we op school hebbe lere were, zij de reële getalle De verzamelig va alle reële getalle wordt aageduid met Belagrije deelverzamelige va zij, e {0,1,,3,
Wiskundige Analyse 1
 Wiskundige Anlyse 1 Belngrijkste stellingen 1 Getllen Driehoeksongelijkheid : b ± b + b Supremumprincipe : Elke nietlege verzmeling reële getllen die nr boven begrensd is, heeft een supremum Infimumprincipe
Wiskundige Anlyse 1 Belngrijkste stellingen 1 Getllen Driehoeksongelijkheid : b ± b + b Supremumprincipe : Elke nietlege verzmeling reële getllen die nr boven begrensd is, heeft een supremum Infimumprincipe
L i mb u r g s e L a n d m a r k s
 L i mb u r g s e L a n d m a r k s P r o g r a m m a I n v e s t e r e n i n S t ed e n e n D o r p e n, l i j n 2 ; D e L i m b u r g s e I d e n t i t e i t v e r s i e 1. 0 D o c u m e n t h i s t o
L i mb u r g s e L a n d m a r k s P r o g r a m m a I n v e s t e r e n i n S t ed e n e n D o r p e n, l i j n 2 ; D e L i m b u r g s e I d e n t i t e i t v e r s i e 1. 0 D o c u m e n t h i s t o
B e l e i d s k a d e r K e r k e n, K l o o s t e r s e n a n d e r e r e l i g i e u z e g e b o u w e n
 B e l e i d s k a d e r K e r k e n, K l o o s t e r s e n a n d e r e r e l i g i e u z e g e b o u w e n I n é é n d a g k a n r e l i g i e u s e r f g o e d v a n m e e r d e r e g e n e r a t i e
B e l e i d s k a d e r K e r k e n, K l o o s t e r s e n a n d e r e r e l i g i e u z e g e b o u w e n I n é é n d a g k a n r e l i g i e u s e r f g o e d v a n m e e r d e r e g e n e r a t i e
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Antwoorden. Een beker water
 Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
Voorbereidende opgaven Examencursus
 Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Ongelijkheden groep 2
 Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Samenvatting. Fouriertheorie en distributies. Fourier en Schwartz. De warmtevergelijking. De exacte benadering
 Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
2 Opgaven bij Hoofdstuk 2
 2 Opgven bij Hoofdstuk 2 Opgve 2. De functie f : R 2 R is gedefinieerd door ) Bewijs dt f continu is op R 2 \ {(, )}. f(, y) = 2 y 2 + y 2 ls (, y) (, ) f(, ) =. b) Bewijs dt voor iedere R de functie y
2 Opgven bij Hoofdstuk 2 Opgve 2. De functie f : R 2 R is gedefinieerd door ) Bewijs dt f continu is op R 2 \ {(, )}. f(, y) = 2 y 2 + y 2 ls (, y) (, ) f(, ) =. b) Bewijs dt voor iedere R de functie y
1. Gegeven is het polynoom P (z) = z 4 + 4z 3 + 6z 2 + 4z + 5 met z C.
 Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Een toelichting op het belang en het berekenen van de steekproefomvang in marktonderzoek.
 006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
Rekenregels van machten
 4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
Bepaling toezichtvorm gemeente Stein
 Bepaling toezichtvorm 2008-2011 gemeente Stein F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, juni 2 0 0 8 V e r d i e p i n g s o n d e r z o e k S t e i
Bepaling toezichtvorm 2008-2011 gemeente Stein F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, juni 2 0 0 8 V e r d i e p i n g s o n d e r z o e k S t e i
H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W +
 H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W + D o e l m a t i g h e i d s t o e t s v o o r g e b i e d e n w a a r v o o r g e e n b o d e m b e h e e r p l a n i s v a s t g e s
H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W + D o e l m a t i g h e i d s t o e t s v o o r g e b i e d e n w a a r v o o r g e e n b o d e m b e h e e r p l a n i s v a s t g e s
Uitwerking Tentamen Analyse B, 28 juni lim
 Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
3 Meetkundige voorstelling van complexe getallen
 3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
Ongelijkheden groep 2
 Ongelijkheden groep Rvi & Cuchy-Schwrz Trnstrendtriningsdg (triningsdg, 6 mrt 009 Cuchy-Schwrz Cuchy-Schwrz Voor reële getllen x,, x n en y,, y n geldt: x i y i en bijgevolg x i y i n n met gelijkheid
Ongelijkheden groep Rvi & Cuchy-Schwrz Trnstrendtriningsdg (triningsdg, 6 mrt 009 Cuchy-Schwrz Cuchy-Schwrz Voor reële getllen x,, x n en y,, y n geldt: x i y i en bijgevolg x i y i n n met gelijkheid
10.8. De Laplace vergelijking. De warmtevergelijking in meerdimensionale ruimten heeft de volgende vorm :
 1.8. De Lplce vergelijking. De wrmtevergelijking in meerdimsionle ruimt heeft de volgde vorm : in R 2 : α 2 (u xx + u yy ) = u t in R 3 : α 2 (u xx + u yy + u zz ) = u t. Hierbij stelt u(x, y, t) de tempertuur
1.8. De Lplce vergelijking. De wrmtevergelijking in meerdimsionle ruimt heeft de volgde vorm : in R 2 : α 2 (u xx + u yy ) = u t in R 3 : α 2 (u xx + u yy + u zz ) = u t. Hierbij stelt u(x, y, t) de tempertuur
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
NETWERK B2 UITWERKINGEN VOOR HET VWO. HOOFDSTUK 10 CONVERGENTIE Kern 1 LIMIETEN. u 2 u 1. u 3. u 4. u 5. u 7
 UITWERKINGEN VOOR HET VWO NETWERK B a) 7 log 7 7 log 7 7 b) 7 a) Niet b) Wel c) Niet ) HOOFDSTUK CONVERGENTIE Ker LIMIETEN Hee f t Ci j f ers log 7 7 log 7 7 77 ) µ Hee f t Ci j f ers a) µ ; µ ; ; µ ;
UITWERKINGEN VOOR HET VWO NETWERK B a) 7 log 7 7 log 7 7 b) 7 a) Niet b) Wel c) Niet ) HOOFDSTUK CONVERGENTIE Ker LIMIETEN Hee f t Ci j f ers log 7 7 log 7 7 77 ) µ Hee f t Ci j f ers a) µ ; µ ; ; µ ;
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN
 KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
Integreren over een compact interval in. n
 Rise Poortig Lieire Alger e Voortgezette Alyse 6 Afgeleide e itegrl houd: 61 Prtiële fgeleide 6 Differetieerre fucties 63 Prtiële fgeleide v hogere orde 64 Cotiu differetieerre fucties 65 Differetieerre
Rise Poortig Lieire Alger e Voortgezette Alyse 6 Afgeleide e itegrl houd: 61 Prtiële fgeleide 6 Differetieerre fucties 63 Prtiële fgeleide v hogere orde 64 Cotiu differetieerre fucties 65 Differetieerre
