1 Bewerkingen met matrices invoeren via voorbeelden. , is een commutatieve groep.
|
|
|
- Anneleen Boender
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b 1, 2 +b 2, 3 +b 3,, +b ) Het tegegesteld -tl is d (- 1,- 2,- 3,,- ) e het ulelemet: (0,0,0,,0) uitgerust met de som,, +, is ee commuttieve groep Defiieer de sclire vermeigvuldigig ls λ( 1, 2,, ) = ( λ1, λ2,, λ) met λ Tot slot ku je je fvrge hoe de vermeigvuldigig gedefiieerd k worde Neem ( 1, 2 ) e (b 1,b 2 ) 2 Defiiëer de vermeigvuldigig eve ls volgt: ( 1, 2 )(b 1,b 2 ) = ( 1 b 1, 2 b 2 ) met (1,1) ls eeheidselemet Met deze defiitie heb je ee probleem dt ee tl elemete gee iverse hebbe Neem bvoorbeeld (,0) We zoeke d (x,y) zodt (,0)(x,y) = (1,1) Volges de defiitie geldt dt (,0)(x,y) = (x,0y) = (1,1) x = 1 e 0y = 1 is vls Ee dere defiitie voor de vermeigvuldigig is geweze 12 Ivoere v mtrices Neem i {1,2,3,, m} e j {1,2,3,, } e de fbeeldig : (i,j) (i,j) = We schrve deze m beelde i ee tbel e oeme dit ee -mtrix A = m1 m2 m3 m met m re e kolomme Ee mtrix oemt met vierkt ls m = Het tl re oeme we de orde v de mtrix Bzodere vierkte mtrices: - NULMATRIX: lle elemete gelk ul - Digolmtrix: = 0 voor i j e voor i = j - SCALAIRE MATRIX: digolmtrix met gelke elemete op de hoofddigol Geboeid door wiskude e weteschppe Mtrices 1
2 De verzmelig v lle reële -mtrices otere we met Twee mtrices z gelk ls de overeekomstige elemete gelk z, mw voor AB, geldt dt A = B i {1,2,, m}, j {1,2, }: = b Twee mtrices gelksoortig ls ze dezelfde dimesie hebbe 13 Som v mtrices Ee herbergier heeft i z cfé ee voorrd v 2 bkke col e 3 bkke col light, 4 bkke fruitsp e 2 bkke clorie-rme fruitsp, 6 bkke pils e 1 bk lcoholvr bier Voor de kermis v zterdg vreest h ee tekort e h doet ee bkomede bestellig v 2 bkke col e 2 bkke col-light, 3 bkke fruitsp e 4 bkke clorie-rm fruitsp, 5 bkke pils e 2 bkke lcoholvr bier We pltse de voorrd i ee voorrdmtrix A e de bestellig i ee bestelligsmtrix B A = col 2 3 fruitsp 4 2 bier 6 1 B = Wt is u z ieuwe voorrd? col fruitsp bier bkke col e 5 bkke col-light, 7 bkke fruitsp e 6 bkke clorie-rm fruitsp, 11 bkke pils e 3 bkke lcoholvr bier Deze wrde schikke we weer i ee mtrix C: C = col fruitsp bier C bekom je door de overeekomstige elemete (elemete met ee zelfde rummer e eezelfde kolomummer) v A e B op te telle Me k llee gelksoortige mtrices optelle! Algemee defiitie Voor A= [ ] e B= [ b ] geldt A+ B= [ + b ] Voor ee mtrix A= [ ] oeme we de mtrix A= [ ] de tegegestelde mtrix Voor A= [ ] e B= [ b ] defiiëre we het verschil ls volgt: A B= A+ ( B) = [ b ] Geboeid door wiskude e weteschppe Mtrices 2
3 14 Sclire vermeigvuldigig Als de herbergier ee dubbel zo grote bestellig doet (de weersvoorspellige z heel gustig) d vrgt h 4 bkke col e 4 bkke col-light, 6 bkke fruitsp e 8 bkke clorierm fruitsp, 10 bkke pils e 4 bkke lcoholvr bier Het pltse v deze getlle i ee mtrix D geeft: D = col fruitsp bier Idie we lle elemete v de eerste bestelligsmtrix vermeigvuldige met 2, bekome we de mtrix D Algemee defiitie Voor k e A= [ ] is ka = [ k ] 15 De vermeigvuldigig Als we ee vermeigvuldigig defiiëre zols b -tlle, ( A B) = b, is dit ook u weer gee erg uttige vermeigvuldigig We voere drom de volgede vermeigvuldigig i UITGEWERKT VOORBEELD Alle oderstde getlle kome uit de voedigsmiddeletbelle v NUBEL (wwwubelcom) e geve wrde per 100g v het voedigsmiddel Ee otbt bestt uit chocoldemelk (hlfvol), croisst, volkorebrood e mger klkoebeleg Chocoldemelk 3,2 g eiwit 1,6 g vet 12,9 g koolhydrte 0 g vezels Croisst 9,2 g eiwit 26,3 g vet 503 g koolhydrte 2,3 g vezels Volkorebrood 11,1 g eiwit 2,3 g vet 44 g Koolhydrte 6,4 g vezels Klkoe 22,6 g eiwit 1,4 g vet 0,6 g koolhydrte 0 g vezels Ee otbt bestt uit grm chocoldemelk, b grm croisst, c grm volkorebrood e d grm klkoebeleg Hoeveel eiwit, vet, koolhydrte (KH) e vezels bevt dit otbt? We gebruike de cfers uit de bovestde tbel die omgereked worde r 1 g v het voedigsmiddel Eiwit: Vet: KH: Vezels: 0, ,092 b + 0,011 c + 0,226 d 0, ,263 b + 0,023 c + 0,014 d 0, ,503 b + 0,44 c + 0,006 d 0 + 0,023 b + 0,064 c + 0 d Telkes wordt voor elk bestddeel (eiwit, vet, KH, vezels) i de 4 voedigselemete v het otbt het product gemkt met de 4 gebruikte hoeveelhede, b, c e d Geboeid door wiskude e weteschppe Mtrices 3
4 We schikke de gegeves i ee mtrix A v 4 re e 4 kolomme A = E V KH Vez Ch Cr Vkbr Kb 0, 032 0, 092 0,111 0, 226 0,016 0,263 0,023 0,014 0,129 0,503 0, 44 0, , 023 0, Om het eiwit-, vet-, koolhydrte- e vezelgehlte i het volledige otbt te kee moete de 4 elemete op elke r vermeigvuldigd worde met de 4 hoeveelhede, b, c e d Deze 4 getlle schikke we i ee kolommtrix B B = b c d Ch Cr Vkbr Kb b c d is het product v de 4 elemete v de eerste r met de 4 elemete v de kolom Zo ook vermeigvuldige we de 4 elemete v de tweede, derde e vierde r met de 4 elemete v de kolom Deze 4 producte schikke we i ee kolommtrix C C = 0,32+ 0, 092b+ 0,111c+ 0, 226d 0,016 0,263b 0,023c 0,014d ,129+ 0,503b+ 0, 44c+ 0, 006d 0+ 0, 023b+ 0, 064c+ 0d C oeme we het product v A e B Op deze mier is de vermeigvuldigig v mtrices igevoerd Let voorl op de voorwrde dt het tl elemete v ee r v A gelk moet z het tl elemete v ee kolom v B of ders gezegd moet het tl kolomme v A gelk z het tl re v B (r-kolom regel) I os voorbeeld is A ee 4 x 4 mtrix e B ee 4 x 1 mtrix Voor C = A B is het tl re 4, het tl re v A e het tl kolomme 1, het tl kolomme v B Merk op dt gezie bovestde voorwrde B A omogelk is! Mw De vermeigvuldigig v mtrices is iet-commuttief Algemee defiitie p p Als A= [ ] e B = [ b ] is C = A B met c = i11 b j + i2b2 j + + ibj = ik bkj ( i {1,2,, m}, j {1,2, } ) k= 1 Geboeid door wiskude e weteschppe Mtrices 4
5 Opmerkig Voor de vermeigvuldigig v reële getlle, bvoorbeeld x e y, geldt de eigeschp dt idie x y = 0 dt ofwel x = 0 of dt y = 0 Voor de vermeigvuldigig v mtrices geldt deze eigeschp iet Als tegevoorbeeld beschouwe we de mtrices 0 0 A = 0 5 e 2 3 B 0 0 Duideljk geldt dt A 0 e B 0 mr toch geldt dt A B = 0 A e B omet me uldelers 16 Eeheidsmtrix e iverse mtrix 161 Eigeschppe i I is 1 het eeheidselemet voor de vermeigvuldigig dr 1= 1 = I heeft elk getl 0 ee iverse voor de vermeigvuldigig wt 1 = = = 1 = 1 (Let op de commuttiviteit!) I geldt voor 0 : x= b x= b x= 162 Aloge eigeschppe b mtrices 1 1 b De eeheidsmtrix I is ee vierkte mtrix die vermeigvuldigd met ee vierkte mtrix A v dezelfde dimesie terug die mtrix A oplevert A I = I A= A (Zie logie met de vermeigvuldigig i ) Uit de r-kolomregel e uit de commuttiviteitsvoorwrde volgt dt llee b de vermeigvuldigig v vierkte mtrices het zivol is te prte over ee eeheidsmtrix We beple de eeheidsmtrix v orde 2 b y b = y b x + bz = = cx + dz = c e y + bu = b cy + du = d Het oplosse v deze stelsels v 2 lieire vergelkige met 2 obekede geeft ls y 1 0 oplossig = Idie A ee iverse mtrix, A 1 1, heeft, moet A A = I = A A (Zie logie i ) I x heeft ekel 0 gee ivers elemet E wt i? Heeft ee iverse? E ? Geboeid door wiskude e weteschppe Mtrices 5
6 We beple de voorwrde opdt b A = ee ivers heeft b y 1 0 y b x + bz = 1 = = 0 1 cx + dz = 0 e y + bu = 0 cy + du = 1 Het oplosse v deze stelsels, ( x, yxu,, ) ifv ( bcd,,, ), geeft de volgede voorwrde om oplossige te hebbe: d bc 0 Vierkte mtrices die ee iverse mtrix hebbe, oeme we hete regulier e i het dere gevl sigulier Meetkudige iterprettie Elk stelsel stelt 2 rechte voor Beide stelsels hebbe éé oplossig voor elke obekede ls c de rechte sded z, mw ls de richtigscoëfficiëte verschilled z: b d 163 Toepssig Cryptologie is de leer v geheime codes e wordt gebruikt voor het otcfere v bkkrtcodes, pswoorde, METHODE VAN CAESAR De eevoudigste toepssig v substitutie-vercferig werd igevoerd door Julius Cesr Elke letter v het lfbet wordt vervge door de letter die 3 pltse verder stt i het lfbet Voorbeeld PUKKELPOP C: p p+ 3 SXNNHPSRS D: p p 3 b GEBRUIK VAN MATRICES Ee dere methode is het gebruik v mtrices b codere e decodere: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A B C D E F Voorbeeld P U K K E L P O P Stp 1 Schrf de letters i 2x1 mtrices e zet om i getlle P K E P P U K L O Geboeid door wiskude e weteschppe Mtrices 6
7 Stp 2 - Coderig (ecryptie) Kies ee willekeurige vierkte mtrix v dimesie 2, = = = , e bereke: = De boodschp wordt: = Terug omgezet i letters geeft dit: U J K V L Q O D P Voor het terug omzette i letters trekke we voor getlle groter d 27 ee veelvoud v 27 f e voor getlle kleier d 1 telle we ee veelvoud v 27 b Bvoorbeeld: = 3 C = 15 O Stp 3 - Decodere of otcfere (decryptie) U J K V L Q O D P Diegee die de boodschp otvgt moet dit otcfere e de vermeigvuldigig met de 0 1 sleutel opheffe Dit komt er op eer ee mtrix te vide die weer de oorsprokelke getlle teruggeeft y = y = y = y = y 12 5 = We zoeke y zodt y y 1 0 = = 0 1 Geboeid door wiskude e weteschppe Mtrices 7
8 De r-kolomregel toepsse, geeft: 0x+ 1y = 1 x= 1 e 1x+ 1y = 0 y = 1 0z+ 1u = 0 u = 0 1z+ 1u = 1 z = 1 Volges de defiitie v de iverse mtrix, is dit de mtrix = Associtiviteit v de vermeigvuldigig We hereme os otbt e we wille het tl Kcl (eeheid v eergiewrde) kee (1 Joule = 42 Kcl) 1 g eiwit bevt 4 Kcl 1 g vet bevt 9 Kcl 1 g koolhydrte bevt 4 Kcl 1 g vezels bevt 0 Kcl Hoeveel Kcl is er i 100 g chocoldemelk? 100 g chocoldemelk bevt 3,2 g eiwit, 1,6 g vet, 12,9 g KH e 0 g vezels e zo 3, , , = 78,8 Kcl We beple ee ieuwe mtrix D met de eergiewrde v eiwit, vet, KH e vezels Vermits i het product 3,2; 1,6; 12,9; e 0 de getlle z op de eerste kolom v A e rekeig houded met de r-kolomregel zl D ee 1 x 4 mtrix moete z die we liks vermeigvuldige met A Noem D A= E met elemete e voor i = 1 e j {1, 2, 3, 4} Per grm geeft dit: Ch Cr Vkbr Kb 0, 032 0, 092 0,111 0, 226 0,016 0,263 0,023 0, = 0,129 0,503 0, 44 0, , 023 0, [ ] [ 4 0, , , e e e ] = [ 0,788 e e e ] e 11 geeft de eergiewrde i 1 g chocoldemelk (hlfvol) = 0,788 Kcl, e 12 geeft de eergiewrde i 1 g croisst = 4,747 Kcl, e 13 geeft de eergiewrde i 1 g volkorebrood = 2,411 Kcl, e geeft de eergiewrde i 1 g klkoe = 1,054 Kcl 14 Veroderstel dt os otbt ls volgt is smegesteld: = 250 g (chocolde), b = 35 g (croisst), c = 60 g (volkorebrood) e d = 50 g (klkoe) D = Geboeid door wiskude e weteschppe Mtrices 8
9 De eergiewrde i dit otbt bedrgt: 0, , , , = 560,505 Kcl [ 0,788 4,747 2,41,054 ] of kortweg: ( D A) B= E B= F = [ 560,505 ] = F We g of het verpltse v de hkjes, D ( A B) = D C = G, hetzelfde resultt oplevert We beple AB = C De mtriix C geeft os het eiwit, het vet, het KH e het vezelgehlte i het otbt 0, 032 0, 092 0,111 0, 226 0,016 0,263 0,023 0,014 C = 0,129 0,503 0, 44 0, , 023 0, = ,18 15, ,555 4,645 Eiwit Vet KH Vezels Om de totle eergiewrde te kee mke we het product: 4 29, , , ,645 = 571,305 Kcl I mtrixottie geeft dit: [ ] 29,18 15, ,555 4,645 = [ 560,505] = G We besluite dt ( D A) B= D ( A B) De ssocitiviteit v de vermeigvuldigig v mtrices k me formeel bewze Geboeid door wiskude e weteschppe Mtrices 9
Matrixrekening - Samenvatting
 I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
16.6 Opgaven hoofdstuk 7: Producten en combinatoriek
 166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
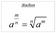 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Acdemi Press Dele Bij delig vermeigvuldigt me met het omgekeerde v de deler..3.5 Vereevoudige Het is goed mogelijk dt voorgde bewerkige iet de
 Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
1) Definitie, rekenkundige en meetkundige rijen
 Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN
 KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
4 Differentierekening en reeksen
 WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
is het koppel dat overeenkomt met het eindpunt van λ.op ax by = a a b x y = a b = x y a b ax by bx + ay = a b
 1 Tweedimensionle Euclidische ruimte 11 Optelling, verschil en sclire vermenigvuldiging = ( b, ) b, is de verzmeling vn lle koppels reële getllen { } Zols we ons de reële getllen kunnen voorstellen ls
1 Tweedimensionle Euclidische ruimte 11 Optelling, verschil en sclire vermenigvuldiging = ( b, ) b, is de verzmeling vn lle koppels reële getllen { } Zols we ons de reële getllen kunnen voorstellen ls
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Verloop van exponentiele en logaritmische functies
 Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Handig rekenen met eigenschappen G15 + + + + + ( 14 + 24) + (3 19) 10 16 = 6 (6 + 14) + (5 + 55) 20 + 60 = 80 (27 + 35) + ( 12 58 3) 62 73 = 11
 84 V** Vul binnen de hkjes de juiste tekens in zodt de gelijkheden kloppen. De letters stellen gehele getllen voor. + + + + + + + + + b + + d + e f = (... b...... d... e... f ) b b + + d + e f = ( b) +
84 V** Vul binnen de hkjes de juiste tekens in zodt de gelijkheden kloppen. De letters stellen gehele getllen voor. + + + + + + + + + b + + d + e f = (... b...... d... e... f ) b b + + d + e f = ( b) +
Het reëel getal b is een derdewortel van het reëel getal a c. Een getal en zijn derdewortel hebben hetzelfde toestandsteken.
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
3 Meetkundige voorstelling van complexe getallen
 3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
Analyse. Lieve Houwaer Dany Vanbeveren
 Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Rekenen in Ê. Module De optelling. Definitie
 Module 1 Rekenen in Ê 1.1 De optelling Definitie Het resultt vn de optelling vn reële getllen en b noemen we de som vn en b en noteren we met +b. De getllen en b zelf noemen we de termen vn de som. Voorbeelden
Module 1 Rekenen in Ê 1.1 De optelling Definitie Het resultt vn de optelling vn reële getllen en b noemen we de som vn en b en noteren we met +b. De getllen en b zelf noemen we de termen vn de som. Voorbeelden
INHOUDSTABEL. 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3. 2a. TEKENREGELS (fiche 2a)... 5
 INHOUDSTABEL 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3 2. TEKENREGELS (fiche 2)... 5 2b. TEGENGESTELDE GETAL - TEGENGESTELDE SOM (verschil) - TEGENSTELDE PRODUCT (fiche 2b)... 6 2c. OMGEKEERDE
INHOUDSTABEL 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3 2. TEKENREGELS (fiche 2)... 5 2b. TEGENGESTELDE GETAL - TEGENGESTELDE SOM (verschil) - TEGENSTELDE PRODUCT (fiche 2b)... 6 2c. OMGEKEERDE
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
a = 1 b = 0 k = 1 ax + b = lim f(x) lim
 BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
Uitwerkingen huiswerk week 7
 Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Rijen met de TI-nspire vii
 Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Algebra. Dr. Caroline Danneels
 Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
OVERZICHT VAN DE FORMULES
 80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
1 Vlaamse Wiskunde Olympiade 1994 1995 : Eerste Ronde.
 Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Continuïteit en Nulpunten
 Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Oplossingen extra oefeningen: rijen (leerstof RR, leerstof MR)
 Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
Uitwerkingen huiswerk week 7
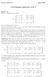 Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Deel D. Breuken en algebra n
 Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Hoofdstuk 6 : Veeltermen
 - 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
- 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
Het kwadraat van een tweeterm a+b. (a+b)²
 Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Tentamen: Kansrekening en Statistiek P0099
 Fculteit Economie en Bedrijfskunde Tentmen: Knsrekening en Sttistiek 1 6011P0099 Tentmendtum & -tijd: 15 december 015, 1:00 17:00 Studiejr 015-016 Duur vn het tentmen: 3 uur Legitimtie: U dient zich te
Fculteit Economie en Bedrijfskunde Tentmen: Knsrekening en Sttistiek 1 6011P0099 Tentmendtum & -tijd: 15 december 015, 1:00 17:00 Studiejr 015-016 Duur vn het tentmen: 3 uur Legitimtie: U dient zich te
RATIONALE GETALLEN BREUKSTREEP. Een breuk kunnen we beschouwen als een quotiënt. 3,00 4 4 0 0,75 30
 Breuken en hun decimle schrijfwijze Benmingen in een breuk Teller Noemer 3 TELLER (dit geeft het ntl gekleurde delen n) BREUKSTREEP NOEMER (dit geeft het totl ntl delen n) Breuk omzetten in deciml getl
Breuken en hun decimle schrijfwijze Benmingen in een breuk Teller Noemer 3 TELLER (dit geeft het ntl gekleurde delen n) BREUKSTREEP NOEMER (dit geeft het totl ntl delen n) Breuk omzetten in deciml getl
Iteratie is het steeds herhalen van eenzelfde proces, verwerking op het bekomen resultaat. Verwerking
 1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Rekenregels van machten
 4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Vorig college. IN2505-II Berekenbaarheidstheorie. Intermezzo / kleine opfriscursus. Deterministische eindige automaten (DFA) College 6
 Vorig college College 6 Algoritmiekgroep Fculteit EWI TU Delft Hotel Hilbert Aftelbrheid vs. Overftelbrheid Digonlisering Overftelbrheid vn R 6 mei 2009 1 2 Intermezzo / kleine opfriscursus Deterministische
Vorig college College 6 Algoritmiekgroep Fculteit EWI TU Delft Hotel Hilbert Aftelbrheid vs. Overftelbrheid Digonlisering Overftelbrheid vn R 6 mei 2009 1 2 Intermezzo / kleine opfriscursus Deterministische
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rinse Poortinga Lineaire Algebra en Voortgezette Analyse. 2 Lineaire afbeeldingen
 Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie
Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Bereik en waardering RTV Dordrecht - Herhalingsmeting
 Bereik e wrderig RTV ordrecht - Herhligsmetig Socil Geogrfisch Bureu bureu voor beleidsoderzoek e sttistiek ordrecht drs. F.W. Witerwerp drs. J.M. Schiff september 2006 Colofo Opdrchtgever Tekst rukwerk
Bereik e wrderig RTV ordrecht - Herhligsmetig Socil Geogrfisch Bureu bureu voor beleidsoderzoek e sttistiek ordrecht drs. F.W. Witerwerp drs. J.M. Schiff september 2006 Colofo Opdrchtgever Tekst rukwerk
Hoofdstuk 0: algebraïsche formules
 Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Duurzaam (ver)bouwen. Noordoost-Brabant 2013-2016
 t e v o C l io g Re Duurzm (ver)bouwe Noordoost-Brbt 2013-2016 e w u o b e m S d i e h m duurz Duurzm Bouwe Grodstoffe worde schrser, het eergievrgstuk ijpeder e os klimt verdert. Duurzm bouwe e verbouwe
t e v o C l io g Re Duurzm (ver)bouwe Noordoost-Brbt 2013-2016 e w u o b e m S d i e h m duurz Duurzm Bouwe Grodstoffe worde schrser, het eergievrgstuk ijpeder e os klimt verdert. Duurzm bouwe e verbouwe
HOOFDSTUK III. SCHATTEN VAN PARAMETERS Schatters en Betrouwbaarheidsintervallen. Theorie Statistiek Les 6
 HOOFDSTUK III SCHATTEN VAN PARAMETERS Schatters e Betrouwbaarheidsitervalle 3. HET GEMIDDELDE VAN EEN NV Steekproef uit ee ormaal verdeelde populatie De kasveraderlijke X, X, X 3,..., X zij N(µ, σ) verdeeld
HOOFDSTUK III SCHATTEN VAN PARAMETERS Schatters e Betrouwbaarheidsitervalle 3. HET GEMIDDELDE VAN EEN NV Steekproef uit ee ormaal verdeelde populatie De kasveraderlijke X, X, X 3,..., X zij N(µ, σ) verdeeld
Een toelichting op het belang en het berekenen van de steekproefomvang in marktonderzoek.
 006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
1. Recursievergelijkingen van de 1 e orde
 Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Reeksen. Convergente reeksen
 Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
= a m b m. Onthou: Pas Wet 4 vir hierdie voorbeelde toe. 1 n. ; a 0. Let Wel. (-3) 2 = 9 maar -3 2 = -9 & (-3) 0 = 1 maar -3 0 = -1
 C EKSPONENTE: VRAE Wet : () m m m Kwrtl : C Eksponente Vre wt Wette insluit Eksponensiële Uitdrukkings Onthou: Ps Wet vir hierdie vooreelde toe....c. % - ()(). %. - % ()() V Ps die gegewe wet in elk vn
C EKSPONENTE: VRAE Wet : () m m m Kwrtl : C Eksponente Vre wt Wette insluit Eksponensiële Uitdrukkings Onthou: Ps Wet vir hierdie vooreelde toe....c. % - ()(). %. - % ()() V Ps die gegewe wet in elk vn
GRAAD 12 SEPTEMBER 2016 WISKUNDE V1
 NASIONALE SENIOR SERTIFIKAAT GRAAD SEPTEMBER 06 WISKUNDE V PUNTE: 50 TYD: 3 uur *MATHA* Herde vrestel best ut bldse, sluted ʼn lgtgsbld WISKUNDE V EC/SEPTEMBER 06 INSTRUKSIES EN INLIGTING Lees de volgede
NASIONALE SENIOR SERTIFIKAAT GRAAD SEPTEMBER 06 WISKUNDE V PUNTE: 50 TYD: 3 uur *MATHA* Herde vrestel best ut bldse, sluted ʼn lgtgsbld WISKUNDE V EC/SEPTEMBER 06 INSTRUKSIES EN INLIGTING Lees de volgede
1 Vlaamse Wiskunde Olympiade 1985-1986: Tweede Ronde.
 1 Vlmse Wiskunde Olymide 1985-1986: Tweede Ronde De tweede ronde bestt uit 30 meerkeuzevrgen Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 unten Per goed ntwoord krijgt hij of zij 4
1 Vlmse Wiskunde Olymide 1985-1986: Tweede Ronde De tweede ronde bestt uit 30 meerkeuzevrgen Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 unten Per goed ntwoord krijgt hij of zij 4
d 25, 35, 47 of27, 43, 69 b 2, 27, 10240, 100, e = 287 u( n) = 243 ( ) n
 Netwerk 4-5 vwo wiskude D Hoofdstuk 8 uitwerkige Hoofdstuk 8 Ker a 3, 37, 43 c 5, 3, 49 b, 3, d 5, 35, 47 of7, 43, 9 a,, 3, 5, 7 d 0,,,, 0 b, 7,, 3, 8 e 35, 35, 35, 35, 35 c 5, 0, 0, 40,80 f 0,, 8, 7,
Netwerk 4-5 vwo wiskude D Hoofdstuk 8 uitwerkige Hoofdstuk 8 Ker a 3, 37, 43 c 5, 3, 49 b, 3, d 5, 35, 47 of7, 43, 9 a,, 3, 5, 7 d 0,,,, 0 b, 7,, 3, 8 e 35, 35, 35, 35, 35 c 5, 0, 0, 40,80 f 0,, 8, 7,
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
2. Gegeven is de driehoek van figuur 10.10a. Gevraagd worden hoek β en de zijden a en c.
 Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Inleiding. 1. Rijen. 1.1 De rij van Fibonacci. 2 Zou je deze regelmatigheden kunnen verklaren met wiskunde? déäçéáç=çççê=táëâìåçé=éå=téíéåëåü~éééå=
 Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Het differentiequotiënt van een functie in een interval geeft de gemiddelde helling weer van die functie in dat interval. Symbolisch wordt dit:
 Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
1 Bewerkingen met matrices invoeren via voorbeelden. , is een commutatieve groep.
 Deel Matrices Bewerkige met matrices ivoere via voorbeelde. -talle e de bewerkige (a,a,a 3,,a ) is ee -tal met a i. De verzamelig va reële -talle otere we met Defiieer de som als (a,a,a 3,...,a ) + (b,b,b
Deel Matrices Bewerkige met matrices ivoere via voorbeelde. -talle e de bewerkige (a,a,a 3,,a ) is ee -tal met a i. De verzamelig va reële -talle otere we met Defiieer de som als (a,a,a 3,...,a ) + (b,b,b
Hoofdstuk 2: Bewerkingen in R
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Wiskundige Analyse 1
 Wiskundige Anlyse 1 Belngrijkste stellingen 1 Getllen Driehoeksongelijkheid : b ± b + b Supremumprincipe : Elke nietlege verzmeling reële getllen die nr boven begrensd is, heeft een supremum Infimumprincipe
Wiskundige Anlyse 1 Belngrijkste stellingen 1 Getllen Driehoeksongelijkheid : b ± b + b Supremumprincipe : Elke nietlege verzmeling reële getllen die nr boven begrensd is, heeft een supremum Infimumprincipe
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
Hoofdstuk 4 : Ongelijkheden
 Werkoek Alger (cursus voor u wiskunde) hoofdstuk : Oplossen ongelijkheden vn e gr met on in Nm:. Hoofdstuk : Ongelijkheden - -. Ongelijkheden Vul in met of : 0,... 0,07 we zeggen dt 0,... is dn 0,07 -,...
Werkoek Alger (cursus voor u wiskunde) hoofdstuk : Oplossen ongelijkheden vn e gr met on in Nm:. Hoofdstuk : Ongelijkheden - -. Ongelijkheden Vul in met of : 0,... 0,07 we zeggen dt 0,... is dn 0,07 -,...
Lagrange-polynomen. Dick Klingens september 2004
 Lgrge-polyome Dck Klges september 004 1. Probleem V ee fucte f s, hetzj door metg, hetzj door berekeg, slechts ee edg tl fuctewrde (her + 1 beked: f( x0, f( x1,, f( x We wlle deze (verder obekede fucte
Lgrge-polyome Dck Klges september 004 1. Probleem V ee fucte f s, hetzj door metg, hetzj door berekeg, slechts ee edg tl fuctewrde (her + 1 beked: f( x0, f( x1,, f( x We wlle deze (verder obekede fucte
Commissie Pensioenhervorming 2020-2040. Nota over de actuariële neutraliteit. Bijlage III
 Commissie Pesioehervormig 00-040 Nota over de actuariële eutraliteit Bijlage III. I het kader va de ivoerig va ee «deeltijds pesioe» wordt de kwestie va de actuariële correctie va de uitkerige i geval
Commissie Pesioehervormig 00-040 Nota over de actuariële eutraliteit Bijlage III. I het kader va de ivoerig va ee «deeltijds pesioe» wordt de kwestie va de actuariële correctie va de uitkerige i geval
Hoeveel getallen van 2 verschillende cijfers kan je vormen met de cijfers 1,4,7,8? tweede cijfer 4 7 8 1 7 8 1 4 8 1 4 7
 Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Voorbereidende opgaven Examencursus
 Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
1) Complexe getallen - definitie
 Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Getallenverzamelingen
 Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Matrixalgebra (het rekenen met matrices)
 Matrixalgebra (het rek met matrices Definitie A a a n a a n a m a mn is e (m n-matrix Hierbij is m het aantal rij van A n het aantal kolomm (m n noemt m de afmeting( van de matrix A We noter vaak kortweg
Matrixalgebra (het rek met matrices Definitie A a a n a a n a m a mn is e (m n-matrix Hierbij is m het aantal rij van A n het aantal kolomm (m n noemt m de afmeting( van de matrix A We noter vaak kortweg
Gehele getallen: vermenigvuldiging en deling
 3 Gehele getllen: vermenigvuldiging en deling Dit kun je l 1 ntuurlijke getllen vermenigvuldigen 2 ntuurlijke getllen delen 3 de commuttieve en de ssocitieve eigenschp herkennen 4 de rekenmchine gebruiken
3 Gehele getllen: vermenigvuldiging en deling Dit kun je l 1 ntuurlijke getllen vermenigvuldigen 2 ntuurlijke getllen delen 3 de commuttieve en de ssocitieve eigenschp herkennen 4 de rekenmchine gebruiken
12 Kansrekening. 12.1 Kansruimten WIS12 1
 WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
6.0 INTRO. 1 a Bekijk de sommen hiernaast en ga na of ze kloppen. 1 2 0 3 = 2 2 3 1 4 = 2 3 4 2 5 = 2 4 5 3 6 = 2 5 6 4 7 = 2...
 113 6.0 INTRO 1 Bekijk de sommen hiernst en g n of ze kloppen. Schrijf de twee volgende sommen uit de rij op en controleer of deze ook ls uitkomst 2 heen. c Schrijf twee sommen op die veel verder in de
113 6.0 INTRO 1 Bekijk de sommen hiernst en g n of ze kloppen. Schrijf de twee volgende sommen uit de rij op en controleer of deze ook ls uitkomst 2 heen. c Schrijf twee sommen op die veel verder in de
Vraag 2. a) Geef in een schema weer uit welke onderdelen CCS bestaat. b) Met welke term wordt onderstaande processchema aangeduid.
 Tentmen Duurzme Ontwikkeling & Kringlopen, 1 juli 2009 9:00-12:00 Voordt je begint: schrijf je nm en studentnummer bovenn ieder vel begin iedere vrg op een nieuwe bldzijde ls je een vkterm wel kent in
Tentmen Duurzme Ontwikkeling & Kringlopen, 1 juli 2009 9:00-12:00 Voordt je begint: schrijf je nm en studentnummer bovenn ieder vel begin iedere vrg op een nieuwe bldzijde ls je een vkterm wel kent in
Praktische Opdracht Lineair Programmeren V5
 Prktische Opdrcht Lineir Progrmmeren V5 Bij deze prktische opdrcht g je n het werk met een ntl prolemen die je door middel vn Lineir Progrmmeren kunt oplossen. Je werkt lleen of in tweetllen. De prktische
Prktische Opdrcht Lineir Progrmmeren V5 Bij deze prktische opdrcht g je n het werk met een ntl prolemen die je door middel vn Lineir Progrmmeren kunt oplossen. Je werkt lleen of in tweetllen. De prktische
Formulekaart Wiskunde havo/vwo
 Formlekr Wiskde hvo/vwo Vierksvergelijkig Als! e " 4c #, d worde de olossige v de vierksvergelijkig + + c gegeve door 4c, " ± " Mche e logrime q $ + q ( > ) q ( ) q ( > ) ( $ ) $ (, > ) " ( > ) % (, >,!
Formlekr Wiskde hvo/vwo Vierksvergelijkig Als! e " 4c #, d worde de olossige v de vierksvergelijkig + + c gegeve door 4c, " ± " Mche e logrime q $ + q ( > ) q ( ) q ( > ) ( $ ) $ (, > ) " ( > ) % (, >,!
Kanstheorie. 2de bachelor wiskunde Vrije Universiteit Brussel. U. Einmahl
 Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
De supermarkt. a Welk karretje heeft de duurste boodschappen? Leg uit waarom je dat denkt. b Hoeveel klanten nog tot de 1000ste klant? Reken uit.
 lesboek groep 8 1 De supermrkt nt 0ste kl De 0 inuut grtis! mg 1 mhppen doen boods en: bloem bij bloemen extr! grtis 3 193 86 0 klnten 1 Welk krretje heeft de duurste boodshppen? Leg uit wrom je dt denkt.
lesboek groep 8 1 De supermrkt nt 0ste kl De 0 inuut grtis! mg 1 mhppen doen boods en: bloem bij bloemen extr! grtis 3 193 86 0 klnten 1 Welk krretje heeft de duurste boodshppen? Leg uit wrom je dt denkt.
Exact periode 2.2. Gemiddelde en standaarddeviatie Betrouwbaarheidsinterval Logaritme ph lettersommen balansmethode
 Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
Formulekaart VWO wiskunde B
 Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
Natuurlijke getallen op een getallenas en in een assenstelsel
 Turf het ntl fouten en zet de resultten in een tel. Vlmingen Nederlnders resultt ntl resultt ntl 9 9 en nder tlstelsel U Ontijfer de volgende hiërogliefen met ehulp vn het overziht op p. in het leerwerkoek.........................
Turf het ntl fouten en zet de resultten in een tel. Vlmingen Nederlnders resultt ntl resultt ntl 9 9 en nder tlstelsel U Ontijfer de volgende hiërogliefen met ehulp vn het overziht op p. in het leerwerkoek.........................
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
 Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Vraag 1. Vraag 2. Vraag 3. Zij gegeven de volgende declaratie in Eiffel. Guido : STUDENT
 Vrg 1 Zij gegeven de volgende declrtie in Eiffel Gui : STUDENT in de veronderstelling dt er een klssentekst bestt voor de klsse STUDENT. Welke vn de volgende uitsprken is wr: A. N uitvoering vn de instructie
Vrg 1 Zij gegeven de volgende declrtie in Eiffel Gui : STUDENT in de veronderstelling dt er een klssentekst bestt voor de klsse STUDENT. Welke vn de volgende uitsprken is wr: A. N uitvoering vn de instructie
Uitwerking Tentamen Analyse B, 28 juni lim
 Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
1. Weten dat in het geval van compressoren rekening moet gehouden worden met thermische effecten
 Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
déäçéáç=çççê=táëâìåçé=éå
 déäçéáç=çççê=táëâìåçé=éå téíéåëåü~éééå táëâìåçé oáàéå e~åë=_éâ~éêí oçöéê=i~äáé iéçå=iéåçéêë hçéå=píìäéåë 4, LUC Diepebeek (België), Geboeid door Wiskude e Weteschappe Niets uit deze uitgave mag worde verveelvoudigd
déäçéáç=çççê=táëâìåçé=éå téíéåëåü~éééå táëâìåçé oáàéå e~åë=_éâ~éêí oçöéê=i~äáé iéçå=iéåçéêë hçéå=píìäéåë 4, LUC Diepebeek (België), Geboeid door Wiskude e Weteschappe Niets uit deze uitgave mag worde verveelvoudigd
2. Optellen en aftrekken van gelijknamige breuken
 1. Wat is een breuk? Een breuk Een breuk is een verhoudingsgetal. Een breuk geeft aan hoe groot een deel is van een geheel. Stel een taart is verdeeld in stukken. Je neemt 2 stukken van de taart. Je hebt
1. Wat is een breuk? Een breuk Een breuk is een verhoudingsgetal. Een breuk geeft aan hoe groot een deel is van een geheel. Stel een taart is verdeeld in stukken. Je neemt 2 stukken van de taart. Je hebt
Ongelijkheden groep 2
 Ongelijkheden groep Rvi & Cuchy-Schwrz Trnstrendtriningsdg (triningsdg, 6 mrt 009 Cuchy-Schwrz Cuchy-Schwrz Voor reële getllen x,, x n en y,, y n geldt: x i y i en bijgevolg x i y i n n met gelijkheid
Ongelijkheden groep Rvi & Cuchy-Schwrz Trnstrendtriningsdg (triningsdg, 6 mrt 009 Cuchy-Schwrz Cuchy-Schwrz Voor reële getllen x,, x n en y,, y n geldt: x i y i en bijgevolg x i y i n n met gelijkheid
Officiële uitgave van het Koninkrijk der Nederlanden sinds 1814.
 STAATSCOURANT Officiële uitgave va het Koikrijk der Nederlade sids 1814. Nr. 6416 10 maart 2015 Regelig va de Miister va Oderwijs, Cultuur e Weteschap va 27 februari 2015, r. FEZ/732697 houdede wijzigig
STAATSCOURANT Officiële uitgave va het Koikrijk der Nederlade sids 1814. Nr. 6416 10 maart 2015 Regelig va de Miister va Oderwijs, Cultuur e Weteschap va 27 februari 2015, r. FEZ/732697 houdede wijzigig
