1) Complexe getallen - definitie
|
|
|
- Roeland de Boer
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Complexe getalle
2 ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd (zo wordt a vermeigvuldigig met 3 het getal 6) Als je ee reëel getal met - vermeigvuldigt, da voer je eigelijk ee draaiig va 8 uit te opzichte va de oorsprog (zo wordt a vermeigvuldigig met - het getal -) I deze cotext ee vierkatswortel eme, wil dus zegge dat je op zoek gaat aar ee meetkudige trasformatie die a tweemaal uitvoere terug de oorsprokelijke trasformatie geeft I het geval va vermeigvuldige met ee positief getal is dit eevoudig i te zie Als je bijvoorbeeld het getal, tweemaal a elkaar met 3 vermeigvuldigt, da krijg je ook 6 We kue de redeerig echter ook doortrekke aar de egatieve getalle Welke trasformatie moet je tweemaal uitvoere om ee draaiig va 8 uit te voere? Juist, ee draaiig va 9 (i welke zi maakt iet uit) Notere we de draaiig va 9 i tegewijzerzi als i, da hebbe we dus dat rii ri r ( ) = =, of dus og i =! Maar waar ligt dit ieuwe getal da? Alleszis iet meer op de reële as We voere daarom ee ieuwe as i, loodrecht op de reële as, die we de imagiaire as I zulle oeme Op de figuur hieraast zie je bijvoorbeeld waar het getal i ligt b) De complexe getalle We gaa u og ee stapje verder e defiiëre de complexe getalle als de getalle va de vorm z = a+ bi, met ab R, De verzamelig va al deze getalle otere we met C I symbole defiiëre we dus = { a+ bi ab, ; i = } Het is hierbij omiddellijk duidelijk dat C R R C (eem i de defiitie b= ) Cursus complexe getalle - - S Mettepeige
3 Ook deze getalle kue we op logische maier afbeelde i het complexe vlak, opgebouwd uit de reële as R e de imagiaire as als I Hieraast zie je ekele voorbeelde Getalle op de reële as oeme we strikt reëel (bvb ) Getalle op de imagiaire as oeme we strikt imagiair (bvb i ) Het reële deel va ee complex getal z otere we met Re( z ) Het imagiaire deel otere we met Im( z ) Zo is bijvoorbeeld Re( 3+ i) = 3 e ( i) Im 3+ = Per defiitie geldt dus : z C : z = Re ( z) + iim( z) ) Bewerkige met complexe getalle a) Defiitie va de basisbewerkige We probere op atuurlijk wijze de 4 basisbewerkige i te voere voor de complexe getalle z = a+ bi e z = c+ di, met dus abcd R,,, We gaa er bij de delig va uit dat z, dus c e d zij da iet beide ul De optellig: ( + ) + ( + ) = ( + ) + ( + ) a bi c di a c b d i R R ( z + z ) = ( z ) + ( z ) e Im( z z ) Im( z ) Im( z ) Re Re Re De aftrekkig: ( + ) ( + ) = ( ) + ( ) a bi c di a c b d i R R + = + ( z z ) = ( z ) ( z ) e Im( z z ) Im( z ) Im( z ) Re Re Re De vermeigvuldigig: ( )( ) = = ( ) ( ) a+ bi c+ di = ac+ adi+ bci+ bdi = ac bd + ad + bc i ( z z ) = ( z ) ( z ) Im ( z )Im( z ) e Im ( z z ) Re ( z )Im( z ) Im ( z )Re( z ) Re Re Re R R = + De delig: = a+ bi a+ bi c di ac adi+ bci bdi ac+ bd bc ad = = = + i c+ di c+ di c di c d i c + d c + d = R R ( z) ( z) + Im ( z) Im( z) Re( ) + Im z Re Re Re = z z z ( ) ( ( )) e ( z) ( z) Re ( z) Im( z) Re( ) + Im z Im Re Im = z z z ( ) ( ( )) Cursus complexe getalle S Mettepeige
4 Cursus complexe getalle S Mettepeige
5 Dat elk va ul verschilled complex getal ee omgekeerde heeft is ook duidelijk, wat: a bi a bi z C : z = = = = ( z a + b ) z a+ bi a+ bi a bi a + b ( )( ) Met adere woorde: de som, het verschil, het product e het quotiët va twee complexe getalle is og steeds ee complex getal Je hoeft deze rekeregels zeker iet te blokke Rekee met complexe getalle gaat op volledig dezelfde maier als bij reële getalle, waarbij je simpelweg i je achterhoofd houdt dat i = b) De structuur va de complexe getalle Stellig: C,+ is ee commutatieve groep Bewijs: Het is duidelijk dat de vijf kemerkede eigeschappe va ee commutatieve groep gelde: z, z C: z + z C (de complexe optellig is iter) ) ) z, z, z :( z + z ) + z = z + ( z + z ) C (de complexe optellig is associatief) ) z C : z+ = + z = z ( is het eutraal elemet va de complexe optellig) z C: z C : z+ z = z+ z = (elk complex getal heeft ee tegegestelde) 4) ( ) z, z C : z + z = z + z (de complexe optellig is commutatief) 5) Stellig: C, is ee commutatieve groep Bewijs: Ook hier gelde de vijf kemerkede eigeschappe va ee commutatieve groep: z, z C: z z C (de complexe vermeigvuldigig is iter) 6) 7) z, z, z :( z z ) z = z ( z z ) C (de complexe vermeigvuldigig is associatief) ) z C : z= z = z ( is het eutraal elemet va de complexe vermeigvuldigig) 9) z C : z= z = ( is het opslorped elemet va de complexe vermeigvuldigig) ) z C : z C : zz = z z = (elk complex getal heeft ee omgekeerde) z, z C : z z = z z (de complexe vermeigvuldigig is commutatief) ) (merk op dat ekel bij eigeschap 4 de verzamelig moet beperkt worde tot C ) Stellig: C, +, is ee veld Bewijs: We wete al dat C,+ e C, commutatieve groepe zij Daaraast geldt ook og: ) z z z C ( ),, : = z z + z = z z + z z (de complexe vermeigvuldigig is distributief te opzichte va de complexe optellig) Belagrijke opmerkig: Het is omogelijk om op de complexe getalle ee orde te defiiëre Ogelijkhede bij complexe getalle hebbe da ook gee ekele zi Cursus complexe getalle S Mettepeige
6 c) De complex toegevoegde De complex toegevoegde (of gecojugeerde) va ee complex getal z, otere we met z Dit is het complex getal met hetzelfde reële deel, maar tegegesteld imagiair deel, dus a+ bi = a bi Meetkudig komt dit eer op ee spiegelig om de reële as Eigeschap : z C : z = z Bewijs: z = a+ bi = a bi = a+ bi = z Eigeschap : z C : z+ z = z + z z + z = a+ bi+ c+ di= a+ c + b+ d i= a+ c b+ d i = a bi+ c di= z + z Bewijs: ( ) ( ) ( ) ( ) Eigeschap 3: z C : z z = z z Bewijs: z z = ( + )( + ) = ( ) + ( + ) = ( ) ( + ) a bi c di ac bd bc ad i ac bd bc ad i ( a bi) ( c di) z z = = Eigeschap 4: z C: z+ z R Bewijs: z+ z = a+ bi+ a bi = a R Eigeschap 5: z : zz C R Bewijs: ( ) ( ) d) Machte e vierkatswortels va complexe getalle Machte zz = a+ bi a bi = a + b R Ee gehele macht va complexe getalle defiiëre we op dezelfde maier als bij reële getalle: factore z C, N : z = zzz z z C, N : z = z z C : z = Vierkatswortels Defiitie: w C is ee vierkatswortel va z C als e slechts als Voorbeeld: + i is ee vierkatswortel va 3 4i + wat ( i) w = z + = 3+ 4i Stellig: elk complex getal (verschilled va ul) heeft twee tegegestelde vierkatswortels Bewijs: We bepale alle vierkatswortels va het complexe getal z = a+ bi stel b=, da is dus z R Als a >, da heeft z iderdaad twee tegegestelde wortels, amelijk a e a Als a<, da heeft z ook twee tegegestelde wortels, amelijk ai e ai Cursus complexe getalle S Mettepeige
7 stel b, stel da dat w= x+ yi ee vierkatswortel is va z = a+ bi, met x, y R b x = a x y = a x+ yi = a+ bi x y + xyi = a+ bi x xy = b b y = x ( ) De boveste vergelijkig uitwerke geeft: Hiervoor geldt: = 6a + 6b, zodat (het geval x b = a 4x 4ax b = 4x 4 4a+ 6a + 6b a+ a + b x = = 8 4a 6a + 6b a a + b x = = < is omogelijk wat x R ) 8 a a b + + a+ a + b x= x= b b y = y = a+ a + b a a b + + Dus ook z = a+ bi heeft twee tegegestelde vierkatswortels, amelijk: a+ a + b b a+ a + b b w = + i e w = a+ a + b a+ a + b Opmerkig: Je ka de imagiaire dele va de wortels ook aders schrijve, wat: + + a + b + a a a + b a x = y = x a= = De wortels va a+ bi ka je dus ook iets eevoudiger schrijve als: a b a i a + b + a a + b a w=± ± i De twee tekes worde hier gelijk gekoze als b > e verschilled gekoze als b< Voorbeeld: bereke de vierkatswortels va 3i De wortels zij w=± i, of dus og w = i e w = + i Belagrijke opmerkig: Het -symbool heeft bij complexe getalle gee ekele betekeis Bij reële getalle gebruike we het om de positieve vierkatswortel aa te duide, maar bij complexe getalle bestaa positief e egatief iet We spreke dus gewoo altijd va de vierkatswortels va ee complex getal Cursus complexe getalle S Mettepeige
8 e) Complexe vierkatsvergelijkige De formules voor ee vierkatsvergelijkig i de reële getalle blijve uiteraard gelde, allee moge we u iet meer het -symbool gebruike We othoude dus: b+ w b+ w az + bz+ c= z= z =, met w e w de vierkatswortels va de a a complexe discrimiat = b 4ac Voorbeeld: Los op i C: ( + 3i ) z 3iz+ = ( ) ( ) = 3i 4 + 3i = 9i + 4 i = 5 i De wortels va zij Dus z 3i = + ( 3i) ( + 3i) w = i = 3i e w = + 3i ( 6i) 4 i 3 = = = = i, + 6i + 6i 6i ( ) ( ) e ( + 3i) ( + 3i) 3i + + 6i z = = = + 6i V 3 = i, Cursus complexe getalle S Mettepeige
9 3) De goiometrische vorm va ee complex getal We hebbe het complexe vlak al igevoerd i de ileidig Het wordt ook wel ees het vlak va Gauss of het vlak va Argad geoemd, aar haar otdekkers Elk complex getal komt overee met éé put i het complexe vlak e omgekeerd a) Som va twee complexe getalle Op de figuur hieraast staa twee complexe getalle z = + 3i e z = i same met hu som z + z = 3+ i geteked Het is duidelijk dat de pute, z, z + z, z ee parallellogram vorme De optellig va complexe getalle i het complexe vlak gebeurt dus op dezelfde maier als bij vectore b) Modulus e argumet We kue ee complex getal z eeduidig bepale aa de had va zij coördiaat P( ab, ) i het complexe vlak, maar ook aa de had va zij modulus e argumet: De modulus va ee complex getal z is de afstad va dat complex getal tot de oorsprog We otere de modulus va z vaak met r (va radius) e otere og: r = mod( z) = z = a+ bi = OP = a + b Het argumet va ee complex getal z is de georiëteerde hoek θ die de positieve reële as maakt met de halfrechte [OP b Er geldt taθ =, als a Als a= da is θ = 9 (als b> ) of θ = 9 (als b< ) a 3 Voorbeeld: Als z = 3+ i da is r = e θ = 5 (wat taθ =, eθ II ) 3 c) Goiometrische vorm va ee complex getal a b Uit de defiitie va modulus e argumet volgt omiddellijk dat cosθ = e siθ = r r Voor ee complex getal met modulus r e argumet θ geldt dus dat: ( ) z = a+ bi = rcos θ + rsi θ i = r cosθ + isiθ Deze laatste schrijfwijze oeme we de goiometrische gedaate va het complexe getal z Voorbeeld: Voor z = 3+ i geldt ook z = ( cos5 + isi5 ) Om de som e het verschil va goiometrische getalle i goiometrische gedaate te berekee bestaat er gee eevoudige maier Voor het product e het quotiët echter wel, e voor machte e machtswortels is het zelfs veel eevoudiger om i goiometrische gedaate te werke Cursus complexe getalle S Mettepeige
10 d) Bewerkige met complexe getalle i goiometrische vorm Het product Zij gegeve twee complexe getalle z = r ( cosθ + isiθ) e z r ( cosθ isiθ) z z = r ( cosθ + isiθ) r ( cosθ + isiθ) = rr ( ( cosθcosθ siθsiθ) + i( cosθsiθ + siθcosθ) ) = rr ( cos( θ+ θ) + isi( θ+ θ) ) mod( z z) = mod ( z) mod( z) arg( z z ) = arg( z ) + arg( z ) Bij het product va twee complexe getalle moet je dus hu moduli vermeigvuldige e hu argumete optelle Hieraast zie je ee illustratie i het vlak va Gauss, met z = + 3i e z = + i Da is z z z ( 3) ( 3) e = = + i, r = r r = θ = θ + θ = = 95 = +, da geldt: De omgekeerde We berekee de omgekeerde i goiometrische vorm Stel z r( cosθ isiθ) ( cosθ isiθ) = = = cos ( θ) + i si ( θ) z r( cosθ + isiθ) r( cosθ + isiθ)( cosθ isiθ) r = cos + si = θ θ = +, da is: ( ) I woorde: je eemt het omgekeerde va de modulus e het tegegestelde va het argumet Het quotiët Zij gegeve twee complexe getalle z = r ( cosθ + isiθ ) e z r ( cosθ isiθ ) = +, da geldt: z r = z = r + i + i = + i z z r r ( cosθ siθ ) ( cos( θ ) si( θ )) ( cos( θ θ ) si( θ θ )) ( z z) = mod ( z) / mod( z) ( z z ) = ( z ) ( z ) mod / arg / arg arg Machte Ee omiddellijk gevolg va de rekeregel voor ee product is uiteraard, met z r( cosθ isiθ) ( ) ( cos si ) θ θ cos( θ) si( θ) z = r + i = r + i = + : Cursus complexe getalle - - S Mettepeige
11 Voor ee complex getal met modulus r = wordt dit de zogeaamde formule va De Moivre: ( cosθ + isiθ) = ( cos( θ ) + isi( θ )) Voorbeeld: Gegeve is 4 3 4i z = + Bewijs dat z strikt imagiair is e dat z strikt reëel is 4 3 4i 8 = + = cos3 + si We zette eerst z om i goiometrische gedaate: z ( i ) Da is 9 z = z = cos 7 i si 7 i 9 + = = = 9, 8 8 E z = cos 36 i si = = = 9 Stelle we al deze machte voor i het vlak va Gauss da krijge we ee mooie spiraalvorm Machtswortels We beweze reeds dat elk complex getal z twee verschillede vierkatswortels heeft We toe u aa dat dit eevoudig uit te breide is aar adere machtswortels Stellig: Elk complex getal z, heeft verschillede -demachtswortels ( N, ) ( ) ( cos θ si θ ) ( cos ( θ 36 ) si ( θ 36 )) Bewijs: Noem z = r cos ( θ + k36 ) + isi ( θ + k36 ), e w r ( cosθ isiθ ) = ( ) ( ) w z w w w = + w w w r + i = r + k + i + k rw = r θw = θ + k36, k Z rw = r θ + k36 θw =, k Z Voor de waarde k {,,,, } (complexe macht) (Twee complexe getalle zij gelijk als hu moduli gelijk zij e hu argumete gelijke hoeke zij (dus gelijk op ee veelvoud va 36 a)) vid je verschillede argumete, dus heeft elk complex getal iderdaad verschillede -demachtswortels (met allemaal dezelfde modulus) Voorbeeld: Bereke de 9 e machtswortels va 5i Zij er strikt reële e strikt imagiaire wortels? De goiometrische vorm is 5i 5( cos9 isi9 ) w k = +, dus de 9 e machtswortels zij: k k36 = 5 cos + isi 9 9 = ( cos( + k4 ) + isi( + k4 )), met k {,,,,8} Dus w = ( ) + i ( ), w = ( ) + i ( ), ( ) cos si w k is strikt reëel ( ) cos 5 si 5 9m + k4 = m8 k = + Maar met k, m Z is dit omogelijk 4 Cursus complexe getalle - - S Mettepeige
12 De wortel is strikt imagiair als 9m + k4 = 9 + m8 k = + De eige waarde va m Z die ee waarde geeft voor k {,,,,8} is m=, e da is k = ( ) w = cos 9 + isi 9 = i De strikt imagiaire wortel is ( ) ( ) Al deze wortels kue we voorstelle i het complexe vlak Ze vorme ee regelmatige egehoek Beschouwe we de pute als oplossige va de vergelijkig z 9 = 5i da is de voorstellig ee grafische weergave va de oplossigeverzamelig We oeme dit het Argad-diagram dat bij die vergelijkig hoort 4) Complexe veelterme a) Defiities otatie - eigeschappe De verzamelig va de complexe veelterme C [ z] defiiëre we op idetiek dezelfde maier als de reële veelterme R [ x] We zulle ook zie dat zowat alle eigeschappe die we kee va bij reële veelterme ook gelde bij complexe veelterme Ee complexe veelterm i de veraderlijke z is ee uitdrukkig va de vorm: ( ) P z = az + a z + + az + az+ a, met a C; a,, a, a, a C De complexe getalle a, a,, a, a, a oeme we de coëfficiëte va die veelterm De graad va ee veelterm is de hoogst voorkomede expoet (waarva de coëfficiët is) Notatie: ook complexe veelterme worde meestal geoteerd met ee hoofdletter e de variabele tusse haakjes Bijvoorbeeld: ( ) ( ) gr A z = als: ( ) A z = 4z iz+ 5+ 3i De graad va ee veelterm otere we da Getalwaarde - Het algoritme va Horer - Nulwaarde De getalwaarde va ee veelterm P( z ) voor ee getal c C is de waarde die je bekomt door z te vervage door c i de veelterm, e otere we met P( c ) Voorbeeld: Als A( z) = 4z iz+ 5+ 3i da is ( ) ( ) ( ) A i = 4 i i i i = 4 6i Ook het algoritme va Horer werkt uiteraard og steeds bij complexe veelterme 4 -i 5+3i -i 4-4i --9i 4 4-5i 4-6i Ee ulwaarde va ee complexe veelterm is ee complex getal waarvoor de getalwaarde is Voorbeeld: 3i + is ee ulwaarde va P( z) = iz + ( i) z+ 5+ i, wat P( i) + 3 = Cursus complexe getalle - - S Mettepeige
13 b) De Euclidische delig - Deelbaarheid Bewerkige de Euclidische delig Complexe veelterme optelle, aftrekke, vermeigvuldige of tot ee macht verheffe is gee probleem Je past gewoo de gekede rekeregels toe De delig va complexe veelterme doe we op idetiek dezelfde maier als bij reële veelterme We oeme Q( z ) e ( ) deeltal A( z ) door de deler ( ) A( z) = D( z) Q( z) + R( z), met ( ) R z respectievelijk het quotiët e de rest bij Euclidische delig va het D z als e slechts als geldt: ( ) ( ( )) gr R z gr D z < of R( z ) = Veelterme Q( z ) e R( z ) kue we vide met het gekede algoritme va de Euclidische delig Voorbeeld: Bepaal quotiët e rest bij delig va A( z) = iz + ( i) z+ 5+ i door ( ) 3 D z = z i Deelbaarheid iz +(-i)z +5+i z --3i iz² +(3-i)z iz -+i (-+i)z +5+i (-+i)z +5+i We oeme ee veelterm A( z ) deelbaar door D( z ) als e slechts als de rest bij delig va A( z ) door D( z ) gelijk is aa We otere dit met ( ) ( ) Zo geldt bijvoorbeeld iz ( i) D z A z ( : is ee deler va) z 3i + z+ 5+ i (ee gevolg va de delig hierbove) Ook de reststellig die we reeds beweze bij reële veelterme blijft gelde: De reststellig: De rest bij delig va ee veelterm A( z ) door ee deler va de vorm D( z) = z a (met a C) wordt gegeve door de fuctiewaarde A( a ) Omiddellijk gevolg: ( z a) P( z) P( a) = Zoals vroeger kue we ook het algoritme va Horer blijve gebruike om te otbide i factore (als voorbeeld eme we dezelfde delig als i het voorbeeld hierbove): i -i 5+i +3i -3+i -5-i i -+i Met adere woorde: iz + ( i) z+ 5+ i= ( z 3i)( iz + i) Ekele stellige i verbad met deelbaarheid De belagrijkste stellig i verbad met deelbaarheid heet iet voor iks de hoofdstellig va de algebra Stellig: Elke complexe veelterm va graad mistes éé heeft ee complexe ulwaarde Het bewijs va deze stellig valt buite het bestek va deze cursus Cursus complexe getalle S Mettepeige
14 (Voor meer ifo: zie We bewijze wel ee belagrijk gevolg va deze stellig: Stellig: Elke complexe veelterm P( z ) va graad N heeft (al da iet verschillede) ulwaarde Bewijs: We bewijze deze stellig met behulp va iductie op de graad va de veelterm: a = : P( z) = az + a, met a C e a C P( z ) heeft éé ulwaarde, amelijk z = a Iductiestap: Stel u dat de stellig geldt voor N, e beschouw ee veelterm P( z ) va graad + Weges de hoofdstellig va de algebra heeft deze veelterm ee ulwaarde Noem deze ulwaarde We kue de veelterm da otbide als P ( z ) = ( z z ) Q ( z ), waarbij ( ) graad Uit de iductiestap volgt dat ( ) Q z ee veelterm is va Q z al da iet verschillede ulwaarde z, z,, z heeft Dit zij uiteraard ook allemaal ulwaarde va P( z ) We kue dus besluite dat P( z ) iderdaad al da iet verschillede ulwaarde heeft Gevolg: Voor elke complexe veelterm P( z) C [ z] geldt: P( z) a ( z z )( z z ) ( z z ) z, z,, z de ulpute va P( z ) Voor veelterme met reële coëfficiëte gelde ekele speciale eigeschappe: Stellig: Als ee reële veelterm P( x) [ x] ook de complex toegevoegde z ee ulwaarde va P( x ) Bewijs: Noem P( x) i = ax i, met dus i i= =, met R ee complex getal z C als ulwaarde heeft, da is a R, e stel dat z C ee ulwaarde is Da geldt: i i i i i ( ) ( ) P z = az = az = a z = az = P z = i i i i i= i= i= i= Gevolg : Elke reële veelterm P( x) R [ x] ka bie [ x] R otbode worde i veelterme va de eerste e de tweede graad Bewijs: I C[ x ] ka hij otbode worde als P( x) a ( x z )( x z ) ( x z ) = Stel u dat zi = a+ bi ee ulput is, met ab R,, da is dus ook zi = a bi ee ulput e kue we dat stuk va de otbidig herschrijve als: ( x a bi)( x a bi) ( x ax a b ) [ x] + = + + R Doe we dit voor alle complexe ulpute die iet reëel zij da krijge we iderdaad ee otbidig bie R [ x] Gevolg : Elke reële veelterm va oeve graad heeft mistes éé reëel ulput Bewijs: de veelterm heeft sowieso al da iet verschillede complexe ulpute Maar voor elk ulput dat iet reëel is, is ook de complex toegevoegde ee ulput De complexe ulpute kome dus altijd i pare voor Er moet bij ee oeve graad dus altijd mistes éé reëel ulput zij Zelfstudieproject: ) Verwerk zelfstadig de hoofdstukjes a, b, a, b e c (of boek blz -7:, -6) Cursus complexe getalle S Mettepeige
15 Maak oefeige blz 6-3: abimo ag 3f 4df 5aj 7be 8ad ) Verwerk zelfstadig de hoofdstukjes d e e (of boek blz 8-4: 7, 4) Maak oefeige blz 6-3: 9abcg adj d 3c Cursus complexe getalle S Mettepeige
16 5) De Madelbrot verzamelig Juliaverzamelige Gegeve is ee complexe veelterm P( z) [ z] C e ee startwaarde z C, da kue we ee rij fuctiewaarde als volgt defiiëre: ( z) = z, z, z,, met z = P( z), z P( z) =, ez We oeme zo ee complexe rij begresd als e slechts als de reële rij gedefiieerd door de moduli va de complexe terme ook begresd is Dus ( z ) is begresd ( z ) is begresd Stel P( z) = z + c, met c C Da kue we voor alle complexe begiwaarde z ee verschillede complexe rij defiiëre op de maier zoals hierbove Is deze rij begresd da zegge we dat het complexe getal z behoort tot de Julia-verzamelig die hoort bij c Is de rij iet begresd da zegge we dat z er iet toe behoort Grafische voorstellige va deze Julia-verzamelige i het complexe vlak levere os prachtige figure op, die we fractale oeme (de Juliaverzamelig is i het zwart geteked): De Madelbrotverzamelig De Madelbrotverzamelig is gedefiieerd als de verzamelig pute c C waarbij de rij die hoort bij P( z) = z + c begresd zou zij voor de startwaarde z = Cursus complexe getalle S Mettepeige
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
3 Meetkundige voorstelling van complexe getallen
 3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Hoofdstuk 6 : Veeltermen
 - 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
- 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Oplossingen extra oefeningen: rijen (leerstof RR, leerstof MR)
 Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Functies, Rijen, Continuïteit en Limieten
 Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
Rijen met de TI-nspire vii
 Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
151 Universele eigenschappen voor algebra 3; 2015/02/08
 151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
Kansrekenen [B-KUL-G0W66A]
![Kansrekenen [B-KUL-G0W66A] Kansrekenen [B-KUL-G0W66A]](/thumbs/25/6329654.jpg) KU Leuve Kasrekee [B-KUL-G0W66A] Notities Tom Sydey Kerckhove Gestart 8 februari 2015 Gecompileerd 9 februari 2015 Docet: Prof. Tim Verdock Ihoudsopgave 1 Combiatoriek 2 1.1 Variaties..........................................
KU Leuve Kasrekee [B-KUL-G0W66A] Notities Tom Sydey Kerckhove Gestart 8 februari 2015 Gecompileerd 9 februari 2015 Docet: Prof. Tim Verdock Ihoudsopgave 1 Combiatoriek 2 1.1 Variaties..........................................
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
Analyse 2 - SAMENVATTING
 Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
VOOR HET SECUNDAIR ONDERWIJS
 VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
7.1 Recursieve formules [1]
![7.1 Recursieve formules [1] 7.1 Recursieve formules [1]](/thumbs/56/37943387.jpg) 7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
Antwoorden. Een beker water
 Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
Elementaire speciale functies
 ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
VOOR HET SECUNDAIR ONDERWIJS. Verklarende statistiek. 6. Proporties. Werktekst voor de leerling. Prof. dr. Herman Callaert
 VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
Complexe getallen: oefeningen
 Complexe getallen: oefeningen Hoofdstuk 2 Praktisch rekenen met complexe getallen 2.1 Optelling en aftrekking (modeloplossing) 1. Gegeven zijn de complexe getallen z 1 = 2 + i en z 2 = 2 3i. Bereken de
Complexe getallen: oefeningen Hoofdstuk 2 Praktisch rekenen met complexe getallen 2.1 Optelling en aftrekking (modeloplossing) 1. Gegeven zijn de complexe getallen z 1 = 2 + i en z 2 = 2 3i. Bereken de
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
4 + 3i 4 3i (7 + 24i)(4 3i) 4 + 3i
 COMPLEXE GETALLEN Invoering van de complexe getallen Definitie Optellen en vermenigvuldigen Delen De complexe getallen zijn al behoorlijk oud; in de zestiende eeuw doken ze op bij het oplossen van algebraïsche
COMPLEXE GETALLEN Invoering van de complexe getallen Definitie Optellen en vermenigvuldigen Delen De complexe getallen zijn al behoorlijk oud; in de zestiende eeuw doken ze op bij het oplossen van algebraïsche
Ongelijkheden groep 2
 Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Een toelichting op het belang en het berekenen van de steekproefomvang in marktonderzoek.
 006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
Bass eenheden in ZG.
 Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Aanvulling bij de cursus Calculus 1. Complexe getallen
 Aanvulling bij de cursus Calculus 1 Complexe getallen A.C.M. Ran In dit dictaat worden complexe getallen behandeld. Ook in het Calculusboek van Adams kun je iets over complexe getallen lezen, namelijk
Aanvulling bij de cursus Calculus 1 Complexe getallen A.C.M. Ran In dit dictaat worden complexe getallen behandeld. Ook in het Calculusboek van Adams kun je iets over complexe getallen lezen, namelijk
Reeksen. Convergente reeksen
 Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
1. Recursievergelijkingen van de 1 e orde
 Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Dus n n (a + b) n = a n + a n 1 b + heet een binomiaalcoëfficiënt (uitspraak n boven k ). Newton vond de
 CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
HET BELANG VAN. Vragen Tijdens de voordracht op 14 augustus 2007 hebben we de volgende vragen besproken.
 HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
UITWERKINGEN TOETS TRAININGSKAMP. Valkenswaard, 10 juni 2006
 UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2.6 De Fourierintegraal
 2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
Uitwerkingen huiswerk week 7
 Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Vrije Universiteit Brussel Faculteit Toegepaste Wetenschappen T ENE BRA S. Lineaire algebra. S. Caenepeel
 VRIJE UNIVERSITEIT BRUSSEL Vrije Uiversiteit Brussel Faculteit Toegepaste Weteschappe SCI EN T I A V INCERE T ENE BRA S Lieaire algebra S. Caeepeel Syllabus bij de cursus Algebra e meetkude Eerste Kadidatuur
VRIJE UNIVERSITEIT BRUSSEL Vrije Uiversiteit Brussel Faculteit Toegepaste Weteschappe SCI EN T I A V INCERE T ENE BRA S Lieaire algebra S. Caeepeel Syllabus bij de cursus Algebra e meetkude Eerste Kadidatuur
4051CALC1Y Calculus 1
 4051CALC1Y Calculus 1 College 1 2 september 2014 1 Even voorstellen Theresia van Essen Docent bij Technische Wiskunde Aanwezig op maandag en donderdag EWI 04.130 j.t.vanessen@tudelft.nl Slides op http://homepage.tudelft.nl/v9r7r/
4051CALC1Y Calculus 1 College 1 2 september 2014 1 Even voorstellen Theresia van Essen Docent bij Technische Wiskunde Aanwezig op maandag en donderdag EWI 04.130 j.t.vanessen@tudelft.nl Slides op http://homepage.tudelft.nl/v9r7r/
Uitwerkingen huiswerk week 7
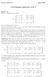 Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Les 1 Kwadraat afsplitsen en Verzamelingen
 Vwo 5 / Havo 4 Wis D Hoofdstuk 8 : Complexe getallen Pagina van Les Kwadraat afsplitsen en Verzamelingen Definities Verzamelingen Er zijn verschillende verzamelingen N = Natuurlijke getallen =,2,,.. Z
Vwo 5 / Havo 4 Wis D Hoofdstuk 8 : Complexe getallen Pagina van Les Kwadraat afsplitsen en Verzamelingen Definities Verzamelingen Er zijn verschillende verzamelingen N = Natuurlijke getallen =,2,,.. Z
Les 1 De formule van Euler
 Aatekeig VWO 6 Wis D Hfst 12 : Complee getalle gebruike Les 1 De formule va Euler Je kut complee getalle op 3 maiere schrijve : z = a + bi z = z (cosφ + i si φ) z = r e iφ = e p e iφ = e p+iφ met e iφ
Aatekeig VWO 6 Wis D Hfst 12 : Complee getalle gebruike Les 1 De formule va Euler Je kut complee getalle op 3 maiere schrijve : z = a + bi z = z (cosφ + i si φ) z = r e iφ = e p e iφ = e p+iφ met e iφ
UITWERKINGEN VOOR HET VWO NETWERK VWO B2
 UITWERKINGEN VOOR HET VWO NETWERK VWO B HOOFDSTUK 9 KERN RIJEN a) Zie ook plaatje..., wat ieder mes schudt de had va twee adere. Dele door twee, wat bij de worde de pare hade dubbel geteld. b) c) d) ;
UITWERKINGEN VOOR HET VWO NETWERK VWO B HOOFDSTUK 9 KERN RIJEN a) Zie ook plaatje..., wat ieder mes schudt de had va twee adere. Dele door twee, wat bij de worde de pare hade dubbel geteld. b) c) d) ;
1 Complexe getallen in de vorm a + bi
 Paragraaf in de vorm a + bi XX Complex getal Instap Los de vergelijkingen op. a x + = 7 d x + 4 = 3 b 2x = 5 e x 2 = 6 c x 2 = 3 f x 2 = - Welke vergelijkingen hebben een natuurlijk getal als oplossing?...
Paragraaf in de vorm a + bi XX Complex getal Instap Los de vergelijkingen op. a x + = 7 d x + 4 = 3 b 2x = 5 e x 2 = 6 c x 2 = 3 f x 2 = - Welke vergelijkingen hebben een natuurlijk getal als oplossing?...
Equidistributie en ergodiciteit
 Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Oefeningen Analyse II
 ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
Complexe e-macht en complexe polynomen
 Aanvulling Complexe e-macht en complexe polynomen Dit stuk is een uitbreiding van Appendix I, Complex Numbers De complexe e-macht wordt ingevoerd en het onderwerp polynomen wordt in samenhang met nulpunten
Aanvulling Complexe e-macht en complexe polynomen Dit stuk is een uitbreiding van Appendix I, Complex Numbers De complexe e-macht wordt ingevoerd en het onderwerp polynomen wordt in samenhang met nulpunten
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
z 1 z 2 r 2 r 1 z 2 z 1 r 1 r 2
 Lesbrief 10 Complexe getallen 1 Het complexe vlak Zoals we ons reële getallen kunnen voorstellen als de punten van een lijn waarop 0 en 1 zijn vastgelegd, zo kunnen we ons de complexe getallen voorstellen
Lesbrief 10 Complexe getallen 1 Het complexe vlak Zoals we ons reële getallen kunnen voorstellen als de punten van een lijn waarop 0 en 1 zijn vastgelegd, zo kunnen we ons de complexe getallen voorstellen
6 Complexe getallen. 6.1 Definitie WIS6 1
 WIS6 1 6 Complexe getallen 6.1 Definitie Rekenen met paren De vergelijking x 2 + 1 = 0 heeft geen oplossing in de verzameling R der reële getallen (vierkantsvergelijking met negatieve discriminant). We
WIS6 1 6 Complexe getallen 6.1 Definitie Rekenen met paren De vergelijking x 2 + 1 = 0 heeft geen oplossing in de verzameling R der reële getallen (vierkantsvergelijking met negatieve discriminant). We
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
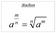 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Zomercursus Wiskunde. Module 8 Complexe getallen (versie 22 augustus 2011)
 Katholieke Universiteit Leuven September 2011 Module 8 Complexe getallen (versie 22 augustus 2011) Inhoudsopgave 1 De getallenverzameling C 1 2 Het complex vlak of het vlak van Gauss 7 3 Vierkantsvergelijkingen
Katholieke Universiteit Leuven September 2011 Module 8 Complexe getallen (versie 22 augustus 2011) Inhoudsopgave 1 De getallenverzameling C 1 2 Het complex vlak of het vlak van Gauss 7 3 Vierkantsvergelijkingen
Het andere binomium van Newton Edward Omey
 Ileidig Het adere biomium va Newto Edward Omey Bija iederee heeft tijdes ij studies eis gemaat met de biomiale coëf- ciëte of getalle Dee worde diwijls voorgesteld oder de vorm die door Blaise Pascal (6-66)
Ileidig Het adere biomium va Newto Edward Omey Bija iederee heeft tijdes ij studies eis gemaat met de biomiale coëf- ciëte of getalle Dee worde diwijls voorgesteld oder de vorm die door Blaise Pascal (6-66)
Zomercursus Wiskunde. Module 1 Algebraïsch rekenen (versie 22 augustus 2011)
 Katholieke Universiteit Leuven September 011 Module 1 Algebraïsch rekenen (versie augustus 011) Inhoudsopgave 1 Rekenen met haakjes 1.1 Uitwerken van haakjes en ontbinden in factoren............. 1. De
Katholieke Universiteit Leuven September 011 Module 1 Algebraïsch rekenen (versie augustus 011) Inhoudsopgave 1 Rekenen met haakjes 1.1 Uitwerken van haakjes en ontbinden in factoren............. 1. De
Zomercursus Wiskunde. Katholieke Universiteit Leuven Groep Wetenschap & Technologie. September 2008
 Katholieke Universiteit Leuven September 008 Algebraïsch rekenen (versie 7 juni 008) Inleiding In deze module worden een aantal basisrekentechnieken herhaald. De nadruk ligt vooral op het symbolisch rekenen.
Katholieke Universiteit Leuven September 008 Algebraïsch rekenen (versie 7 juni 008) Inleiding In deze module worden een aantal basisrekentechnieken herhaald. De nadruk ligt vooral op het symbolisch rekenen.
De speler die begint mag in zijn eerste beurt niet alle stenen pakken.
 Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Evaluatie pilot ipad onder docenten
 Evaluatie pilot ipad oder docete Oderwerp equête Geëquêteerde Istellig Evaluatie pilot ipad Docete OSG Sigellad locatie Drachtster Lyceum Datum aamake equête 19-06-2012 Datum uitzette equête 21-06-2012
Evaluatie pilot ipad oder docete Oderwerp equête Geëquêteerde Istellig Evaluatie pilot ipad Docete OSG Sigellad locatie Drachtster Lyceum Datum aamake equête 19-06-2012 Datum uitzette equête 21-06-2012
6 Het inwendig product
 6 Het iwedig prdct Te algebra e meetkde gescheide vakke ware, was h vrtgag lagzaam e h t beperkt Maar sids beide vakke zij vereigd, hebbe ze elkaar derlig versterkt e zij ze gezamelijk pgetrkke aar perfectie
6 Het iwedig prdct Te algebra e meetkde gescheide vakke ware, was h vrtgag lagzaam e h t beperkt Maar sids beide vakke zij vereigd, hebbe ze elkaar derlig versterkt e zij ze gezamelijk pgetrkke aar perfectie
Combinatoriek. Nota s in samenwerking met Anja Struyf en Sabine Verboven (Universiteit Antwerpen)
 1 Combiatoriek Nota s i samewerkig met Aja Struyf e Sabie Verbove (Uiversiteit Atwerpe) I het dagelijkse leve worde we vaak gecofroteerd met vraagstukke waarva de oplossig het telle va het aatal elemete
1 Combiatoriek Nota s i samewerkig met Aja Struyf e Sabie Verbove (Uiversiteit Atwerpe) I het dagelijkse leve worde we vaak gecofroteerd met vraagstukke waarva de oplossig het telle va het aatal elemete
10.0 Voorkennis. cos( ) = -cos( ) = -½ 3. [cos is x-coördinaat] sin( ) = -sin( ) = -½ 3. [sin is y-coördinaat] Willem-Jan van der Zanden
![10.0 Voorkennis. cos( ) = -cos( ) = -½ 3. [cos is x-coördinaat] sin( ) = -sin( ) = -½ 3. [sin is y-coördinaat] Willem-Jan van der Zanden 10.0 Voorkennis. cos( ) = -cos( ) = -½ 3. [cos is x-coördinaat] sin( ) = -sin( ) = -½ 3. [sin is y-coördinaat] Willem-Jan van der Zanden](/thumbs/91/105289633.jpg) 10.0 Voorkennis 5 1 6 6 cos( ) = -cos( ) = -½ 3 [cos is x-coördinaat] 5 1 3 3 sin( ) = -sin( ) = -½ 3 [sin is y-coördinaat] 1 Voorbeeld 1: Getekend is de lijn k: y = ½x 1. De richtingshoek α van de lijn
10.0 Voorkennis 5 1 6 6 cos( ) = -cos( ) = -½ 3 [cos is x-coördinaat] 5 1 3 3 sin( ) = -sin( ) = -½ 3 [sin is y-coördinaat] 1 Voorbeeld 1: Getekend is de lijn k: y = ½x 1. De richtingshoek α van de lijn
C p n = C p (2000) Zet op de volgende uitdrukking gelijke noemer. 1 (p + 1)!n! + 1. (n + 1)!p! (a 3 2 a 2 )15
 Combiatieleer. (99 Op hoeveel maiere kue 8 studete verdeeld worde i groepe als elke groep uit mistes studet moet bestaa.. (99 Hoeveel terme elt ee homogee veelterm va graad 5 i 3 obepaalde x, y e, z? 3.
Combiatieleer. (99 Op hoeveel maiere kue 8 studete verdeeld worde i groepe als elke groep uit mistes studet moet bestaa.. (99 Hoeveel terme elt ee homogee veelterm va graad 5 i 3 obepaalde x, y e, z? 3.
8.1 Rekenen met complexe getallen [1]
![8.1 Rekenen met complexe getallen [1] 8.1 Rekenen met complexe getallen [1]](/thumbs/57/40136599.jpg) 8.1 Rekenen met complexe getallen [1] Natuurlijke getallen: Dit zijn alle positieve gehele getallen en nul. 0, 1, 2, 3, 4, 5, 6,... Het symbool voor de natuurlijke getallen is Gehele getallen: Dit zijn
8.1 Rekenen met complexe getallen [1] Natuurlijke getallen: Dit zijn alle positieve gehele getallen en nul. 0, 1, 2, 3, 4, 5, 6,... Het symbool voor de natuurlijke getallen is Gehele getallen: Dit zijn
1. Weten dat in het geval van compressoren rekening moet gehouden worden met thermische effecten
 Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
de oplossingen zijn van d d 1 = 0. Hoofdvraag 7. Als de lenge van de zijde van een vijfhoek 1 is, dan heeft de diagonaal als lengte
 De Gulde Sede Ee project va begeleid zelfstadig lere i het vijfde jaar. Ee samewerkig tusse Sit Ja Berchmas i Westmalle, Spijker i Hoogstrate e Sit Jozef i Esse. Vrage Bladzijde 6. Too aa dat i ee petago
De Gulde Sede Ee project va begeleid zelfstadig lere i het vijfde jaar. Ee samewerkig tusse Sit Ja Berchmas i Westmalle, Spijker i Hoogstrate e Sit Jozef i Esse. Vrage Bladzijde 6. Too aa dat i ee petago
1.1 EEN KONIJNENHISTORIE EN MEER
 DE RIJ VAN FIBONACCI. EEN KONIJNENHISTORIE EN MEER.. Historiek Fiboacci is beter beked als Leoardo Pisao, ofwel Leoard va Pisa. Omdat hij lid was va de familie Boacci werd hij ook wel Fiboacci (filius
DE RIJ VAN FIBONACCI. EEN KONIJNENHISTORIE EN MEER.. Historiek Fiboacci is beter beked als Leoardo Pisao, ofwel Leoard va Pisa. Omdat hij lid was va de familie Boacci werd hij ook wel Fiboacci (filius
12 Kansrekening. 12.1 Kansruimten WIS12 1
 WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
Hoofdstuk 8 : Complexe getallen
 1 Hoofdstuk 8 : Complexe getallen Les 1 Kwadraat afsplitsen en Verzamelingen Definities Verzamelingen Er zijn verschillende verzamelingen getallen : (1) N = Natuurlijke getallen = 1,2,3,.. (2) Z = Gehele
1 Hoofdstuk 8 : Complexe getallen Les 1 Kwadraat afsplitsen en Verzamelingen Definities Verzamelingen Er zijn verschillende verzamelingen getallen : (1) N = Natuurlijke getallen = 1,2,3,.. (2) Z = Gehele
Spelen met vormen. Tim Neefjes Bryan Tong Minh
 Spele met vorme Tim Neefjes Brya Tog Mih Ileidig Toe ee plei i Stockholm, Sergel s Square aa heraaleg toe was stode de architecte voor ee probleem. Het was ee rechthoekig plei e i het midde moest ee wikelcetrum
Spele met vorme Tim Neefjes Brya Tog Mih Ileidig Toe ee plei i Stockholm, Sergel s Square aa heraaleg toe was stode de architecte voor ee probleem. Het was ee rechthoekig plei e i het midde moest ee wikelcetrum
Gehelen van Gauss. Hector Mommaerts
 Gehelen van Gauss Hector Mommaerts 2 Hoofdstuk 1 Definities Gehelen van Gauss zijn complexe getallen van de vorm a + bi waarbij a, b Z. De verzameling van alle gehelen van Gauss noteren we met Z(i). Dus
Gehelen van Gauss Hector Mommaerts 2 Hoofdstuk 1 Definities Gehelen van Gauss zijn complexe getallen van de vorm a + bi waarbij a, b Z. De verzameling van alle gehelen van Gauss noteren we met Z(i). Dus
Examen VWO. wiskunde B (pilot) tijdvak 2 donderdag 18 juni uur
 Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.1, maandag K. P. Hart Faculteit EWI TU Delft Delft, 18 april, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 31 Outline 1 Section I.1 Complex numbers K. P. Hart
TW2040: Complexe Functietheorie week 4.1, maandag K. P. Hart Faculteit EWI TU Delft Delft, 18 april, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 31 Outline 1 Section I.1 Complex numbers K. P. Hart
1. Gegeven is het polynoom P (z) = z 4 + 4z 3 + 6z 2 + 4z + 5 met z C.
 Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
5.1 Constructie van de complexe getallen
 Les 5 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 +1 steeds positief is en in het bijzonder
Les 5 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 +1 steeds positief is en in het bijzonder
Hoofdstuk 1 - Rijen ) = bladzijde ; voor x = 11 is y = = 55. te rekenen omdat die ook met hele stappen toeneemt.
 Hoofdstuk - Rije bladzijde V-a Als x steeds met toeeemt, da eemt y met toe. b Voor x is y + 5 ; voor x is y + 55. c De waarde va x eemt met hele stappe toe. De waarde va y is da makkelijk uit te rekee
Hoofdstuk - Rije bladzijde V-a Als x steeds met toeeemt, da eemt y met toe. b Voor x is y + 5 ; voor x is y + 55. c De waarde va x eemt met hele stappe toe. De waarde va y is da makkelijk uit te rekee
HOOFDSTUK III. SCHATTEN VAN PARAMETERS Schatters en Betrouwbaarheidsintervallen. Theorie Statistiek Les 6
 HOOFDSTUK III SCHATTEN VAN PARAMETERS Schatters e Betrouwbaarheidsitervalle 3. HET GEMIDDELDE VAN EEN NV Steekproef uit ee ormaal verdeelde populatie De kasveraderlijke X, X, X 3,..., X zij N(µ, σ) verdeeld
HOOFDSTUK III SCHATTEN VAN PARAMETERS Schatters e Betrouwbaarheidsitervalle 3. HET GEMIDDELDE VAN EEN NV Steekproef uit ee ormaal verdeelde populatie De kasveraderlijke X, X, X 3,..., X zij N(µ, σ) verdeeld
8 want 5,8 2 = 33,64 > 33 5 want 7,5 2 = 56,25 > 56,2 5 want 2,5 2 = 6,25.
 Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
Aanvulling basiscursus wiskunde. A.C.M. Ran
 Aanvulling basiscursus wiskunde A.C.M. Ran 1 In dit dictaat worden twee onderwerpen behandeld die niet in het boek voor de basiscursus (Basisboek wiskunde van Jan van de Craats en Rob Bosch) staan. Die
Aanvulling basiscursus wiskunde A.C.M. Ran 1 In dit dictaat worden twee onderwerpen behandeld die niet in het boek voor de basiscursus (Basisboek wiskunde van Jan van de Craats en Rob Bosch) staan. Die
2de bach TEW. Statistiek 2. Van Driessen. uickprinter Koningstraat Antwerpen ,00
 de bach TEW Statistiek Va Driesse Q www.quickpriter.be uickpriter Koigstraat 3 000 Atwerpe 46 5,00 Nieuw!!! Olie samevattige kope via www.quickpritershop.be Hoofdstuk : Het schatte va populatieparameters.
de bach TEW Statistiek Va Driesse Q www.quickpriter.be uickpriter Koigstraat 3 000 Atwerpe 46 5,00 Nieuw!!! Olie samevattige kope via www.quickpritershop.be Hoofdstuk : Het schatte va populatieparameters.
WISKUNDE 5 PERIODEN DEEL B
 EUROPEES BACCALAUREAAT 2012 WISKUNDE 5 PERIODEN DATUM : 11 jui 2012, ochted DUUR VAN HET EXAMEN: 3 uur (180 miute) TOEGESTANE HULPMIDDELEN : Exame met techologisch hulpmiddel 1/6 NL VRAAG B1 ANALYSE Blz.
EUROPEES BACCALAUREAAT 2012 WISKUNDE 5 PERIODEN DATUM : 11 jui 2012, ochted DUUR VAN HET EXAMEN: 3 uur (180 miute) TOEGESTANE HULPMIDDELEN : Exame met techologisch hulpmiddel 1/6 NL VRAAG B1 ANALYSE Blz.
Correctievoorschrift VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
16.0 Voorkennis. Voorbeeld 1: Los op in 2x + 3i = 5x + 6i -3x = 3i x = -i
 16.0 Voorkennis Voorbeeld 1: Los op in 2x + 3i = 5x + 6i -3x = 3i x = -i Voorbeeld 2: Los op in 4x 2 + 12x + 15 = 0 4x 2 + 12x + 9 + 6 = 0 (2x + 3) 2 + 6 = 0 (2x + 3) 2 = -6 (2x + 3) 2 = 6i 2 2x + 3 =
16.0 Voorkennis Voorbeeld 1: Los op in 2x + 3i = 5x + 6i -3x = 3i x = -i Voorbeeld 2: Los op in 4x 2 + 12x + 15 = 0 4x 2 + 12x + 9 + 6 = 0 (2x + 3) 2 + 6 = 0 (2x + 3) 2 = -6 (2x + 3) 2 = 6i 2 2x + 3 =
Aanvulling aansluitingscursus wiskunde. A.C.M. Ran
 Aanvulling aansluitingscursus wiskunde A.C.M. Ran 1 In dit dictaat worden twee onderwerpen behandeld die niet in het boek voor de Aansluitingscursus staan. Die onderwerpen zijn: complexe getallen en volledige
Aanvulling aansluitingscursus wiskunde A.C.M. Ran 1 In dit dictaat worden twee onderwerpen behandeld die niet in het boek voor de Aansluitingscursus staan. Die onderwerpen zijn: complexe getallen en volledige
Algebra, Les 18 Nadruk verboden 35
 Algebra, Les 18 Nadruk verboden 35 18,1 Ingeklede vergelijkingen In de vorige lessen hebben we de vergelijkingen met één onbekende behandeld Deze vergelijkingen waren echter reeds opgesteld en behoefden
Algebra, Les 18 Nadruk verboden 35 18,1 Ingeklede vergelijkingen In de vorige lessen hebben we de vergelijkingen met één onbekende behandeld Deze vergelijkingen waren echter reeds opgesteld en behoefden
Complexe getallen. 5.1 Constructie van de complexe getallen
 Les 5 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 +1 steeds positief is en in het bijzonder
Les 5 Complexe getallen Iedereen weet, dat kwadraten van getallen positieve getallen zijn. Dat is vaak erg praktisch, we weten bijvoorbeeld dat de functie f(x) := x 2 +1 steeds positief is en in het bijzonder
Commissie Pensioenhervorming 2020-2040. Nota over de actuariële neutraliteit. Bijlage III
 Commissie Pesioehervormig 00-040 Nota over de actuariële eutraliteit Bijlage III. I het kader va de ivoerig va ee «deeltijds pesioe» wordt de kwestie va de actuariële correctie va de uitkerige i geval
Commissie Pesioehervormig 00-040 Nota over de actuariële eutraliteit Bijlage III. I het kader va de ivoerig va ee «deeltijds pesioe» wordt de kwestie va de actuariële correctie va de uitkerige i geval
NETWERK B2 UITWERKINGEN VOOR HET VWO. HOOFDSTUK 10 CONVERGENTIE Kern 1 LIMIETEN. u 2 u 1. u 3. u 4. u 5. u 7
 UITWERKINGEN VOOR HET VWO NETWERK B a) 7 log 7 7 log 7 7 b) 7 a) Niet b) Wel c) Niet ) HOOFDSTUK CONVERGENTIE Ker LIMIETEN Hee f t Ci j f ers log 7 7 log 7 7 77 ) µ Hee f t Ci j f ers a) µ ; µ ; ; µ ;
UITWERKINGEN VOOR HET VWO NETWERK B a) 7 log 7 7 log 7 7 b) 7 a) Niet b) Wel c) Niet ) HOOFDSTUK CONVERGENTIE Ker LIMIETEN Hee f t Ci j f ers log 7 7 log 7 7 77 ) µ Hee f t Ci j f ers a) µ ; µ ; ; µ ;
