HET BELANG VAN. Vragen Tijdens de voordracht op 14 augustus 2007 hebben we de volgende vragen besproken.
|
|
|
- Ruth van de Berg
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe ku je izie dat ee vierkat, bij gegeve oppervlakte, de rechthoek met de miimale omtrek is? Waarom is ee kubus, bij gegeve oppervlakte, het blok met de maximale ihoud? Waarom is ee kubus, bij gegeve ihoud, het blok met de miimale oppervlakte? Welke driehoek heeft, bij gegeve omtrek, de maximale oppervlakte e waarom? Je hebt twee weerstade va e 3 Ohm i serie geschakeld; wat is de gemiddelde weerstad? Je hebt ee rechthoek va 3; wat is de gemiddelde legte va ee zijde? Je hebt twee weerstade va e 3 Ohm parallel geschakeld; wat is de gemiddelde weerstad? Wat ku je zegge over het gedrag va de getallerij,, 3 6,,...,!,...? Hoe zit het met,, 3 3,,...,,...? I dit stuk lope we de gevode atwoorde og ees systematisch a e zal ik hier e daar aageve hoe bepaalde uitsprake algemeer geaakt kue worde. Rechthoeke. Atwoorde Vaste omtrek (L = 00). Neem ee rechthoek met omtrek L = 00 e zijde a e b. Da geldt, atuurlijk, a + b = L = 50. Wat kue we va de oppervlakte O = ab zegge? Dat wordt wat duidelijker als we aar de posities va a e b op de getallelij kijke (Figuur ): Midde tusse a e b ligt 5 = (a + b) e we gebruike dat om a e b te schrijve als a = 5 + x e b = 5 x. Nu kue we ab ook herschrijve e er ee coclusie over trekke: O = ab = (5 + x)(5 x) = 65 x 65 ( ) Dus: we wete zeker dat de oppervlakte va ee rechthoek met omtrek 00 ooit groter is da 65. Date: Vierkat: augustus 007.
2 KP HART a b b a Figuur. Ee rechthoek met omtrek 00 b x 5 x a Figuur. Liggig va a e b Is er ook ee rechthoek met omtrek 00 e oppervlakte 65? Daar helpt vergelijkig ( ) ook bij: om O = 65 te krijge moet x = 0 gelde e dat geldt allee als a = b = 5. Dus het vierkat met zijde 5 is de eige rechthoek met omtrek 00 die de maximaal haalbare oppervlakte va 65 ook echt haalt. Het rekekudige feit dat hier de doorslag gaf is: elk kwadraat is groter da of gelijk aa ul e alléé het kwadraat va ul is gelijk aa ul. Vaste omtrek (L willekeurig). We kue de redeerig hierbove voor elke omtrek herhale e telkes vide we dat de oppervlakte va het vierkat met die omtrek maximaal is. Dat wordt a twee of drie keer wat saai e daarom doe we het maar éé keer e wel voor alle mogelijke omtrekke tegelijk. Neem ee rechthoek met omtrek L e zijde a e b, zeg met b < a. Da geldt a + b = L e et als bove ligt u L midde tusse a e b. Nu schrijve we a = L + x e b = L x, da volgt ( ) ( ) ( ) O = ab = L + x L x = L x 6 L ( ) Dus de oppervlakte, O, is kleier da of gelijk aa 6 L e alléé gelijk aa 6 L als x = 0, dat wil zegge als a = b, dus als de rechthoek ee vierkat is. Merk ook op dat de dimesies i ( ) kloppe: O is ee oppervlaktemaat e L is dat ook. De ogelijkheid i ( ) heet de Isoperimetrische Ogelijkheid voor rechthoeke. ( Iso beteket gelijk e perimeter beteket omtrek.) Vaste oppervlakte. Ogelijkheid ( ) werkt twee kate op; je kut hem ook gebruike om bij vaste oppervlakte ee odergres voor de omtrek te bepale. Als O = 00 da volgt dat L 6O = 600, dus L 00 e alléé voor ee vierkat met oppervlakte 00 geldt L = 0. Dus: bij vaste oppervlakte, O, heeft ee vierkat de kleiste omtrek: L = O. Getalle. Als we de getalle O e L eve vergete e os op de getalle a e b cocetrere krijge we ee ogelijkheid waar i de Wiskude ee heleboel mee te doe is. Wat we hierbove hebbe gedaa is het product ab herschrijve; de x die daarbij ee rol speelde was gelijk aa (a b). Als we ook og L vervage door
3 HET BELANG VAN 3 b (a b) (a + b) (a b) a Figuur 3. Twee positieve getalle a e b (a + b) da komt er e dus ( ) ( a + b a b ab = ( a + b ab of ook wel a + b ab ( ) met gelijkheid alléé als a = b. Dit heet de Ogelijkheid va Rekekudig e Meetkudig Gemiddelde. Over de ame va deze gemiddelde kome we later og te spreke. Door a e b hieri slim te kieze ku je sel afschattige make. Opgave. Too aa: 30 < 5. Of je kut og meer optimaliserigsprobleme aapakke. Opgave. Ee boer wil, met meter gaas, ee rechthoekig stukje grod afgreze. Hij gebruik zij schuur als éé va de zijde va de rechthoek. Wat is de maximale oppervlakte die hij ka make? Bij welke legte e breedte? ) Of je kut er weer geheel adere dige mee doe. Opgave. Kies ee vast positief getal a e defiieer ee rij getalle door x 0 = a e telkes x + = (x + a x ). a. Too aa dat a < x + < x voor alle. b. Bewijs: lim x = a c. Experimeteer met je rekemachietje om te zie hoe goed de beaderige va a die je zo krijgt zij. ) Blokke e driehoeke. De vrage over de blokke e de driehoeke blijke hetzelfde gereedschap odig te hebbe; ee ogelijkheid die erg op ( ) lijkt maar da voor meer getalle. Voor drie positieve getalle p, q e r geldt (altijd) 3 pqr p + q + r 3 ( ) met gelijkheid allee als p = q = r; we zulle later zie hoe die formule te bewijze is, et als we ( ) beweze hebbe.
4 KP HART a c b Figuur. Ee blok met zijde a, b e c. Blokke. We hebbe ee rechthoekig blok met zijde a, b e c e oppervlakte 6 (Figuur ). Wat kue we over het volume zegge? Neem, i formule ( ) ees p = ab, q = ac e r = bc. Da geldt p + q + r = O = 08 e dus 3 08 pqr 3 = 36 maar pqr = ab ac bc = (abc), dus volgt e dus (abc) 36 3 abc 36 3 = 36 3 = 6 3 = 6. Hier staat het maximale volume dat ee blok met oppervlakte 6 ka hebbe; de gelijkheidsvoorwaarde is p = q = r, maar daar volgt heel sel uit dat ook a = b = c moet gelde. Als we dit ivulle i de voorwaarde (ab + ac + bc) = 6 vide we 3a = 3b = 3c = 08 e dus is het beste blok ee kubus met zijde 6. Algemee ogelijkheid. We kue et als bij rechthoeke voor blokke ee ogelijkheid afleide tusse O e V. We vulle i de relatie ( ) weer p = ab, q = ac e r = bc i: 3 abacbc ab + ac + bc 3 Hier staat i feite 3 V 6 O of V 6 O3 e er geldt gelijkheid alléé als a = b = c, dat wil zegge als het blok ee kubus is. E hiermee is als tevore het omgekeerde probleem miimale oppervlakte bij vast volume ook weer op te losse. Opgave. Bepaal de miimale oppervlakte va ee blok met volume 000 e de legte va de zijde va het blok met miimale oppervlakte. Ee bewijs. We gaa ( ) bewijze. We doe dat op de maier waarop de wiskudige A.-L. Cauchy dat i 8 deed i zij Cours d Aalyse. We bewijze de ogelijkheid eerst voor vier getalle a, b, c e d door twee keer de relatie ( ) te gebruike. Eerst e da abcd = ab cd (a + b (a ) ( ) + b c + d ( a + b ) ( ) c + d + c + d ) = a + b + c + d
5 HET BELANG VAN 5 of, samegevat a + b + c + d abcd e gelijkheid geldt allee als a = b = c = d. ( ) Als we drie getalle a, b e c hebbe make we daar ee d bij: d = (a + b + c)/3. Pas ( ) toe abcd a + b + c + d = 3d + d = d of abcd d streep liks e rechts ee d weg: abc d 3 maar dat is weer equivalet met 3 a + b + c abc 3 e weer: gelijkheid geldt alléé als a = b = c. ( ) Driehoeke. Voor de oppervlakte va ee driehoek met omtrek L e zijde a, b e c bestaat ee fraaie formule voor de oppervlakte, de Formule va Hero: O = s(s a)(s b)(s c) hieri is s de halve omtrek: s = (a + b + c). Opgave. Too aa dat s a, s b e s c positief zij. Opgave. Zoek ee bewijs va de formule va Hero op of, beter og, bedek zelf ee bewijs. We eme aa dat L = 30 e we zoeke de driehoek met omtrek 30 e maximale oppervlakte. We hebbe vier getalle, s, s a, s b e s c, e passe ( ) toe: s + s a + s b + s c s s s(s a)(s b)(s c) = = s = L = 7 met gelijkheid alléé als s = s a = s b = s c e dat geeft ee probleempje wat dat ka allee als a = b = c = 0 e dat ka iet wat a + b + c = 30. Het put is dat soms gelijkheid iet haalbaar is e dat is hier u et het geval: er is gee driehoek met omtrek 30 e oppervlakte 7. We kijke og ee keer goed aar de formule va Hero e zie dat daar maar drie variabele getalle i zitte, dus passe we ( ) toe: 3 (s a)(s b)(s c) 3 (s a + s b + s c) = 3 (3s s) = 3 s coclusie O = s(s a)(s b)(s c) s 7 s3 = 7 s met gelijkheid alléé als s a = s b = s c. Na worteltrekke komt er O 3 3 s = 3 L = Dus de oppervlakte is, bij omtrek 30, ooit groter da 900 aa 0 zij is de oppervlakte precies zo groot. De ogelijkheid O 3 L 3 e als alle zijde gelijk
6 6 KP HART is de Isoperimetrische Ogelijkheid voor driehoeke. Opgave. Wat heeft de grootste oppervlakte? Ee gelijkzijdige driehoek met omtrek 30 of ee vierkat met omtrek 30? Er is voor elke ee Isoperimetrische Ogelijkheid voor -hoeke. Deze is altijd va de vorm O c L waarbij de costate c allee va afhagt. Opgave. Zoek ee bewijs op va die Isoperimetrische Ogelijkhede of bedek zelf ee bewijs. Wat is c? Wat is de relaties tusse de c oderlig? Voor welke -hoek treedt gelijkheid op? Er is ook ee Isoperimetrische Ogelijkheid voor willekeurige kromme. Deze volgt uit de stellig dat bij gegeve vaste legte ee cirkel de maximale oppervlakte isluit. De ogelijkheid luidt dus O π L. Ee bewijs va de stellig is iet geheel eevoudig. Gemiddelde. De drie vrage over gemiddelde ware, met opzet, iet precies. De bedoelig was als volgt: ik wil de verschillede weerstade/legte door gelijke weerstade/legte vervage e de totale weerstad/oppervlakte gelijk houde. Zo krijge we drie gemiddelde. I serie. Het gemiddelde is 5 wat bij i serie geschakelde weerstade tel je weerstade op, dus twee weerstade va 5 Ohm kue die va e 3 vervage. Oppervlakte. Het gemiddelde is 6: de oppervlakte is 6 e als je gelijke zijde wilt hebbe moet je die 6 lag eme. Parallel. Als je twee weerstade R e R parallel schakelt voldoet de totale weerstad R aa R = + R R I os geval geldt dus R = + 3 = 5 6 ; de gemiddelde weerstad ρ moet dus voldoet aa ρ = 5 6 e dus ρ = 5. Ee formule voor ρ ku je make door R e R i plaats va e 3 te gebruike: ρ = R + R e dus ρ = R + R Drie gemiddelde. Als iemad vraagt: wat is het gemiddelde va a e b? moet je ee tegevraag stelle: wat bedoel je? i serie geschakelde weerstade a e b geve het Rekekudig gemiddelde: R(a, b) = (a + b) de vraag over de oppervlakte geeft os het Meetkudig gemiddelde: M(a, b) = ab. parallel geschakelde weerstade geve os het Harmoisch gemiddelde: H(a, b) = a + b
7 HET BELANG VAN 7 Formule ( ) zegt dat altijd M(a, b) R(a, b); e daarom heet ( ) de ogelijkheid va Rekekudig e Meetkudig gemiddelde. Het Harmoisch gemiddelde past hier ook bij. Opgave. Too aa dat H(a, b) = /R( a, b ) e M( a, b ) = /M(a, b). Uit ( ), toegepast op a e b, volgt u M( a, b ) R( a, b ) e dus ook H(a, b) M(a, b). We zie dat altijd a + b ab a + b Nu kue we 30 ook aa de oderkat afschatte. Opgave. Too aa: Meer getalle. De laatste twee vrage gige over rije. De rij!. De defiitie va! is welbeked:! = 3. Die afkortig komt i de Wiskude heel vaak voor, i de Algebra, de Kasrekeig e Statistiek, e i de Combiatoriek bijvoorbeeld. We gaa iets probere te zegge over de groeiselheid va! e doe dit door aar de -demachtswortel te kijke. We make eerst ee boveschattig. Dat doe we door (!) te schrijve als ( ) ( ) op elk product k( k + ) passe we ( ) toe: k( k + ) (k + k + ) = ( + ) e zo krijge we de volgede afschattig va (!) : ( ) + (!) e daarmee ( ) +! of! ( + ) ee eevoudige afschattig va ee igewikkelde uitdrukkig. Opgave. Zet i (!) de twee -e apart e pas telkes ( ) toe op de producte k( k) e bewijs! of! Is dit ee betere of slechtere afschattig va! da de eerdere? Ee eevoudige oderschattig is ook te make. Bekijk het product k( k + ) og ee keer e trek er va af: k( k + ) = k k + k = (k )( k) 0 wat we bekijke allee k e met k. Coclusie: k( k + ) voor alle k e dus (!)
8 8 KP HART e we vide! Voor! zij veel betere (af)schattige gemaakt. Met behulp va itegrale kue we late zie dat! e waar e het grodtal va de atuurlijke logaritme is. Opgave. (Voor wie wat va itegrale weet.) Schrijf het quotiët!/ als! e eem de atuurlijke logaritme: l! = ( l l ) Too aa dat de som aa de rechterkat groter da of gelijk is aa l x dx, laat 0 zie dat die itegraal gelijk is aa e too zo bovestaade ogelijkheid aa. Opgave. (Voor wie og meer va itegrale weet.) Too aa lim De e uit de ogelijkheid is dus optimaal.! = e. De rij. Als je de waarde va door je rekemachietje late beadere om te kijke wat het gedrag va deze getallerij zou kue zij zul je zie dat de uitkomste kleier zij da, dat de rij eve stijgt < < 3 3 e da weer daalt: 3 3 > = > 5 5 >. De vraag is of het rekemachietje os op het juiste spoor heeft gezet of dat de rij later iees weer gaat stijge. Ee algemee ogelijkheid. Voor het aalysere e afschatte va hebbe we de algemee Ogelijkheid va Rekekudig e Meetkudig Gemiddelde odig. Je kut wel rade hoe die luidt: voor elk -tal positieve getalle (a, a,..., a ) geldt a a a (a + a + + a ) ( ) e er geldt gelijkheid alléé als a = a = = a. Opgave. Bewijs ogelijkheid ( ). Aawijzig: bekijk het bewijs voor = e = 3 og ees goed e doe als Cauchy: bewijs ( ) eerst voor machte va e loop va zo macht aar beede om alle adere getalle af te hadele. Eerste afschattig. Bij het gebruik va ( ) is het zaak de a i slim te kieze; soms is iet altijd duidelijk wat de slimste keuze is maar met wat probere kom je meestal wel op ee goed spoor. I os geval wille we = a a a hebbe; dat ka heel eevoudig: eem maar a = e a = = a =. Pas ( ) toe, da volgt ( + ) = dus <, wat misschie door het rekemachietje gesuggereerd werd maar wat we u vrij goedkoop hebbe kue vaststelle voor alle.
9 HET BELANG VAN 9 Tweede afschattig. We kue = a a a op veel meer maiere voor elkaar krijge: eem maar a = a = e a 3 = = a = (voor ). Da volgt ( + ) = + < + Dit is ee aazielijke verbeterig wat u wete dat de rij iet allee oder de blijft maar zelfs aar covergeert. Nog meer afschattige. Dit idee kue we verder uitbuite. Neem ee k vast e voor k eme we a = = a k = k e a k+ = = a =. Da levert ( ) de volgede afschattig (k k + k) = + k k k < + k k k We kue de expoet va, te koste va ee grotere costate, et zo dicht bij de krijge als we wille. Kue we er zelfs voor zorge dat < + C voor ee of adere costate C? Dat lukt iet. Voor wie wat va de fuctie e x weet is dit verrassed eevoudig aa te toe. Opgave. Too aa dat voor x 0 altijd geldt + x < e x. Aawijzig: y = + x beschrijft de raaklij aa de grafiek va e x i het put (0, ). Opgave. Gebruik de vorige opgave om i te zie dat > + l Aawijzig: herschrijf met behulp va e e l. Literatuur Hieroder ee kleie selectie va boeke over ogelijkhede. Ze zij og allemaal bij Amazo.co.uk te krijge ([], [3] e [] zij vrij goedkoop.) [] Edwi Beckebach ad Richard Bellma, A Itroductio to Iequalities, New Mathematical Library, vol. 3, The Mathematical Associatio of America, Washigto, 96. Ee iet al te moeilijke ileidig. [] G. Hardy, J. E. Littlewood, ad G. Pólya, Iequalities, Secod Editio, Cambridge Mathematical Library, Cambridge Uiversity Press, Cambrdige, 95. Ee klassieker. Lastig te leze maar de moeite waard. [3] Nicholas D. Kazarioff, Geometric Iequalities, New Mathematical Library, vol., The Mathematical Associatio of America, Washigto, 96. Ogelijkhede i de meetkude. Met ee hoofdstuk over Isoperimetrische Ogelijkhede. [], Aalytic Iequalities, Dover Publicatios, Ic, Mieola, New York, 00. Ogelijkhede e hu toepassige i de Aalyse. Oorsprokelijk verschee i 96 bij Holt, Riehart ad Wisto. [5] J. Michael Steele, The Cauchy-Schwarz Master Class, MAA Problem Books, Cambridge Uiversity Press e The Mathematical Associatio of America, Cambridge e Washigto, 00. Ee ethousiast geschreve boek met ee heleboel ogelijkhede e iteressate opgave.
B C D E Welke rij is noch een Rekenkundige. noch een Meetkundige Rij? A B C D E
 Naam : Klas:.Datum: Ma 0 sept. 00 Rechterkat als kladblad gebruike A. 5067 De rij x, x+, x+,... is rekekudig als x gelijk is aa ) ) ) 4) 4 5) 0 6) 4 7) 8) ee getal tusse e 0 B. 57 80 De legtes a, b e c
Naam : Klas:.Datum: Ma 0 sept. 00 Rechterkat als kladblad gebruike A. 5067 De rij x, x+, x+,... is rekekudig als x gelijk is aa ) ) ) 4) 4 5) 0 6) 4 7) 8) ee getal tusse e 0 B. 57 80 De legtes a, b e c
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Oefeningen Analyse II
 ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
Een toelichting op het belang en het berekenen van de steekproefomvang in marktonderzoek.
 006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
Ongelijkheden groep 2
 Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
Rijen met de TI-nspire vii
 Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
7.1 Recursieve formules [1]
![7.1 Recursieve formules [1] 7.1 Recursieve formules [1]](/thumbs/56/37943387.jpg) 7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
Dus n n (a + b) n = a n + a n 1 b + heet een binomiaalcoëfficiënt (uitspraak n boven k ). Newton vond de
 CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
Examen HAVO. wiskunde A. tijdvak 2 woensdag 19 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
Deel A. Breuken vergelijken 4 ----- 12
 Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
De speler die begint mag in zijn eerste beurt niet alle stenen pakken.
 Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Oplossingen extra oefeningen: rijen (leerstof RR, leerstof MR)
 Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
1. Weten dat in het geval van compressoren rekening moet gehouden worden met thermische effecten
 Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Eindexamen wiskunde B vwo 2010 - II
 Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Eindexamen wiskunde B vwo II
 Beoordeligsmodel Sijde met ee hoogtelij maximumscore 4 BRC PRQ ; overstaade hoeke PRQ 90 QPR ; hoekesom driehoek Boog AC is costat, dus APC is costat; costate hoek QPR ( APC) is costat, dus BRC is costat
Beoordeligsmodel Sijde met ee hoogtelij maximumscore 4 BRC PRQ ; overstaade hoeke PRQ 90 QPR ; hoekesom driehoek Boog AC is costat, dus APC is costat; costate hoek QPR ( APC) is costat, dus BRC is costat
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
de oplossingen zijn van d d 1 = 0. Hoofdvraag 7. Als de lenge van de zijde van een vijfhoek 1 is, dan heeft de diagonaal als lengte
 De Gulde Sede Ee project va begeleid zelfstadig lere i het vijfde jaar. Ee samewerkig tusse Sit Ja Berchmas i Westmalle, Spijker i Hoogstrate e Sit Jozef i Esse. Vrage Bladzijde 6. Too aa dat i ee petago
De Gulde Sede Ee project va begeleid zelfstadig lere i het vijfde jaar. Ee samewerkig tusse Sit Ja Berchmas i Westmalle, Spijker i Hoogstrate e Sit Jozef i Esse. Vrage Bladzijde 6. Too aa dat i ee petago
Handout bij de workshop Wortels van Binomen
 Hadout bij de workshop Wortels va Biome Steve Wepster NWD 014 Verbeterde versie 1 Historische achtergrod Klassieke Griekse meetkude: I de klassieke Griekse meetkude zoals we die bijvoorbeeld bij Euclides
Hadout bij de workshop Wortels va Biome Steve Wepster NWD 014 Verbeterde versie 1 Historische achtergrod Klassieke Griekse meetkude: I de klassieke Griekse meetkude zoals we die bijvoorbeeld bij Euclides
8 want 5,8 2 = 33,64 > 33 5 want 7,5 2 = 56,25 > 56,2 5 want 2,5 2 = 6,25.
 Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
Correctievoorschrift VWO
 Correctievoorschrift VWO 009 tijdvak wiskude B, Het correctievoorschrift bestaat uit: Regels voor de beoordelig Algemee regels Vakspecifieke regels Beoordeligsmodel 5 Izede scores Regels voor de beoordelig
Correctievoorschrift VWO 009 tijdvak wiskude B, Het correctievoorschrift bestaat uit: Regels voor de beoordelig Algemee regels Vakspecifieke regels Beoordeligsmodel 5 Izede scores Regels voor de beoordelig
Eindexamen wiskunde A1-2 vwo 2008-II
 Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Examen VWO. wiskunde B. tijdvak 2 woensdag 23 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Eame VWO 200 tijdvak 2 woesdag 23 jui 3.30-6.30 uur wiskude B Bij dit eame hoort ee uitwerkbijlage. Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 80 pute te behale. Voor elk vraagummer staat
Eame VWO 200 tijdvak 2 woesdag 23 jui 3.30-6.30 uur wiskude B Bij dit eame hoort ee uitwerkbijlage. Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 80 pute te behale. Voor elk vraagummer staat
Beoordelingsmodel VWO wiskunde B II. Een rij. Voor de limiet geldt: u 2 u. 2u u = 1. Dit schrijven als un. De (enige) oplossing: u = 1
 Beoordeligsmodel VWO wiskude B 009-II Vraag Atwoord Scores Ee rij maximumscore Voor de limiet geldt: u u u u Dit schrijve als u u+ 0 De (eige) oplossig: u maximumscore 5 vervage door i u + u + + + Dit
Beoordeligsmodel VWO wiskude B 009-II Vraag Atwoord Scores Ee rij maximumscore Voor de limiet geldt: u u u u Dit schrijve als u u+ 0 De (eige) oplossig: u maximumscore 5 vervage door i u + u + + + Dit
Eindexamen wiskunde B1 vwo 2007-I
 Eidexame wiskude B vwo 007-I havovwo.l Podiumverlichtig Ee podium is 6 meter diep. Midde bove het podium hagt ee balk met tl-buize. De verlichtigssterkte op het podium is het kleist aa de rad, bijvoorbeeld
Eidexame wiskude B vwo 007-I havovwo.l Podiumverlichtig Ee podium is 6 meter diep. Midde bove het podium hagt ee balk met tl-buize. De verlichtigssterkte op het podium is het kleist aa de rad, bijvoorbeeld
UITWERKINGEN TOETS TRAININGSKAMP. Valkenswaard, 10 juni 2006
 UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
1. Recursievergelijkingen van de 1 e orde
 Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Hoofdstuk 1 - Rijen ) = bladzijde ; voor x = 11 is y = = 55. te rekenen omdat die ook met hele stappen toeneemt.
 Hoofdstuk - Rije bladzijde V-a Als x steeds met toeeemt, da eemt y met toe. b Voor x is y + 5 ; voor x is y + 55. c De waarde va x eemt met hele stappe toe. De waarde va y is da makkelijk uit te rekee
Hoofdstuk - Rije bladzijde V-a Als x steeds met toeeemt, da eemt y met toe. b Voor x is y + 5 ; voor x is y + 55. c De waarde va x eemt met hele stappe toe. De waarde va y is da makkelijk uit te rekee
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Analyse 2 - SAMENVATTING
 Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Rijen en reeksen. Mei 2008. Remy van Bergen Peter Mulder
 Rije e reekse Keuzeoderwerp Atheeum 5 wiskude B e B Mei 008 Remy va Berge Peter Mulder Dit boekje gaat over rije e reekse. Wiskudige rije! Rije worde i de wiskude op verschillede maiere gedefiieerd. Met
Rije e reekse Keuzeoderwerp Atheeum 5 wiskude B e B Mei 008 Remy va Berge Peter Mulder Dit boekje gaat over rije e reekse. Wiskudige rije! Rije worde i de wiskude op verschillede maiere gedefiieerd. Met
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
Buren en overlast. waar je thuis bent...
 Bure e overlast waar je thuis bet... Goed wooklimaat HEEMwoe vidt het belagrijk dat bewoers prettig woe i ee fije buurt. De meeste buurtbewoers kue het goed met elkaar vide. Soms gaat het sameleve i ee
Bure e overlast waar je thuis bet... Goed wooklimaat HEEMwoe vidt het belagrijk dat bewoers prettig woe i ee fije buurt. De meeste buurtbewoers kue het goed met elkaar vide. Soms gaat het sameleve i ee
Examen VWO. wiskunde B (pilot) tijdvak 2 donderdag 18 juni uur
 Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Wiskunde D Online uitwerking 4 VWO blok 7 les 3
 Paragraaf Vergelijkige va vlakke Opgave a Dat zij de pute A, B, E e F e alle pute die verder op de voorkat va de kubus ligge. b Dat zij de pute A, C, E e G e alle pute die i het diagoaalvlak met A, C,
Paragraaf Vergelijkige va vlakke Opgave a Dat zij de pute A, B, E e F e alle pute die verder op de voorkat va de kubus ligge. b Dat zij de pute A, C, E e G e alle pute die i het diagoaalvlak met A, C,
Evaluatie pilot ipad onder docenten
 Evaluatie pilot ipad oder docete Oderwerp equête Geëquêteerde Istellig Evaluatie pilot ipad Docete OSG Sigellad locatie Drachtster Lyceum Datum aamake equête 19-06-2012 Datum uitzette equête 21-06-2012
Evaluatie pilot ipad oder docete Oderwerp equête Geëquêteerde Istellig Evaluatie pilot ipad Docete OSG Sigellad locatie Drachtster Lyceum Datum aamake equête 19-06-2012 Datum uitzette equête 21-06-2012
d 25, 35, 47 of27, 43, 69 b 2, 27, 10240, 100, e = 287 u( n) = 243 ( ) n
 Netwerk 4-5 vwo wiskude D Hoofdstuk 8 uitwerkige Hoofdstuk 8 Ker a 3, 37, 43 c 5, 3, 49 b, 3, d 5, 35, 47 of7, 43, 9 a,, 3, 5, 7 d 0,,,, 0 b, 7,, 3, 8 e 35, 35, 35, 35, 35 c 5, 0, 0, 40,80 f 0,, 8, 7,
Netwerk 4-5 vwo wiskude D Hoofdstuk 8 uitwerkige Hoofdstuk 8 Ker a 3, 37, 43 c 5, 3, 49 b, 3, d 5, 35, 47 of7, 43, 9 a,, 3, 5, 7 d 0,,,, 0 b, 7,, 3, 8 e 35, 35, 35, 35, 35 c 5, 0, 0, 40,80 f 0,, 8, 7,
BIOLOGIE Havo / Vwo Tips examenvragen maken. Algemeen. Multiple choice vragen
 BIOLOGIE Havo / Vwo Tips examevrage make Algemee Tijdes je exame mag je Bias gebruike. De Bias diet compleet obeschreve e obeplakt te zij. Het gebruik va briefjes als pagiawijzers is iet toegestaa. Het
BIOLOGIE Havo / Vwo Tips examevrage make Algemee Tijdes je exame mag je Bias gebruike. De Bias diet compleet obeschreve e obeplakt te zij. Het gebruik va briefjes als pagiawijzers is iet toegestaa. Het
1 Het trekken van ballen uit een vaas
 Het trekke va balle uit ee vaas Combiatorische kasprobleme moete worde aagepakt met ee kasmodel dat bestaat uit ee eidige uitkomsteverzamelig Ω va gelijkwaarschijlijke uitkomste Dit wil zegge dat de kas
Het trekke va balle uit ee vaas Combiatorische kasprobleme moete worde aagepakt met ee kasmodel dat bestaat uit ee eidige uitkomsteverzamelig Ω va gelijkwaarschijlijke uitkomste Dit wil zegge dat de kas
NETWERK B2 UITWERKINGEN VOOR HET VWO. HOOFDSTUK 10 CONVERGENTIE Kern 1 LIMIETEN. u 2 u 1. u 3. u 4. u 5. u 7
 UITWERKINGEN VOOR HET VWO NETWERK B a) 7 log 7 7 log 7 7 b) 7 a) Niet b) Wel c) Niet ) HOOFDSTUK CONVERGENTIE Ker LIMIETEN Hee f t Ci j f ers log 7 7 log 7 7 77 ) µ Hee f t Ci j f ers a) µ ; µ ; ; µ ;
UITWERKINGEN VOOR HET VWO NETWERK B a) 7 log 7 7 log 7 7 b) 7 a) Niet b) Wel c) Niet ) HOOFDSTUK CONVERGENTIE Ker LIMIETEN Hee f t Ci j f ers log 7 7 log 7 7 77 ) µ Hee f t Ci j f ers a) µ ; µ ; ; µ ;
wiskunde B pilot vwo 2015-II
 Formules Goiometrie si( t u) sitcosu costsiu si( t u) sitcosu costsiu cos( t u) costcosu sitsiu cos( t u) costcosu sitsiu si( t) sitcost cos( t) cos t si t cos t si t - - Het achtste deel p het domei [
Formules Goiometrie si( t u) sitcosu costsiu si( t u) sitcosu costsiu cos( t u) costcosu sitsiu cos( t u) costcosu sitsiu si( t) sitcost cos( t) cos t si t cos t si t - - Het achtste deel p het domei [
Correctievoorschrift VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
UITWERKINGEN VOOR HET VWO NETWERK VWO B2
 UITWERKINGEN VOOR HET VWO NETWERK VWO B HOOFDSTUK 9 KERN RIJEN a) Zie ook plaatje..., wat ieder mes schudt de had va twee adere. Dele door twee, wat bij de worde de pare hade dubbel geteld. b) c) d) ;
UITWERKINGEN VOOR HET VWO NETWERK VWO B HOOFDSTUK 9 KERN RIJEN a) Zie ook plaatje..., wat ieder mes schudt de had va twee adere. Dele door twee, wat bij de worde de pare hade dubbel geteld. b) c) d) ;
Inzicht in voortgang. Versnellingsvraag 9 Inzichten periode maart t/m juni
 Izicht i voortgag Verselligsvraag 9 Izichte periode maart t/m jui Terugblik Ee idicatie hoe ee leerlig zich otwikkeld per vakgebied Ee referetieiveau waarmee elke leerlig vergeleke ka worde 2 Terugblik
Izicht i voortgag Verselligsvraag 9 Izichte periode maart t/m jui Terugblik Ee idicatie hoe ee leerlig zich otwikkeld per vakgebied Ee referetieiveau waarmee elke leerlig vergeleke ka worde 2 Terugblik
12 Kansrekening. 12.1 Kansruimten WIS12 1
 WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
Bewijzen voor de AM-GM-ongelijkheid
 Bewijze voor de AM-GM-ogelijkheid Prime Ee beroemde olympiadeogelijkheid is de ogelijkheid tusse het rekekudig gemiddelde (AM, arithmetic mea) e het meetkudig gemiddelde (GM, geometric mea). Voor ee gegeve
Bewijze voor de AM-GM-ogelijkheid Prime Ee beroemde olympiadeogelijkheid is de ogelijkheid tusse het rekekudig gemiddelde (AM, arithmetic mea) e het meetkudig gemiddelde (GM, geometric mea). Voor ee gegeve
Uitwerkingen huiswerk week 7
 Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Tentamen Optica. Uitwerkingen - 26 februari = n 1. = n 1
 Tetame Optica Uitwerkige - 6 februari 013 Cijfer = (totaal aatal pute+10)/6.4 Opgave 1 a) (3 p) Nee, dit is ee dikke les. Je mag de propagatie i de les iet verwaarloze. Dit is bijv. i te zie voor ee lichtstraal
Tetame Optica Uitwerkige - 6 februari 013 Cijfer = (totaal aatal pute+10)/6.4 Opgave 1 a) (3 p) Nee, dit is ee dikke les. Je mag de propagatie i de les iet verwaarloze. Dit is bijv. i te zie voor ee lichtstraal
2.6 De Fourierintegraal
 2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
VOOR HET SECUNDAIR ONDERWIJS
 VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
Eindexamen wiskunde A vwo 2010 - I
 Eidexame wiskude A vwo - I Beoordeligsmodel Maratholoopsters maximumscore 3 uur, 43 miute e 3 secode is 98 secode De selheid is 495 98 (m/s) Het atwoord: 4,3 (m/s) maximumscore 3 Uit x = 5 volgt v 4,4
Eidexame wiskude A vwo - I Beoordeligsmodel Maratholoopsters maximumscore 3 uur, 43 miute e 3 secode is 98 secode De selheid is 495 98 (m/s) Het atwoord: 4,3 (m/s) maximumscore 3 Uit x = 5 volgt v 4,4
Uitwerkingen bij 1_0 Voorkennis: Rijen
 Uitwerkige ij _0 Voorkeis: Rije V_ a U = 7 + U = +,5 7 + = +,5 0,5 = 4 = 8 Na 8 rode krijge ze elk,-. V_ U() =, 06 U( ) met U(0) = 500 e U() het eidedrag a jaar. V_ a u 458 8 r u 8 9 4 = = = dus 5 u5 8
Uitwerkige ij _0 Voorkeis: Rije V_ a U = 7 + U = +,5 7 + = +,5 0,5 = 4 = 8 Na 8 rode krijge ze elk,-. V_ U() =, 06 U( ) met U(0) = 500 e U() het eidedrag a jaar. V_ a u 458 8 r u 8 9 4 = = = dus 5 u5 8
Eindexamen wiskunde A1 vwo 2008-II
 Eidexame wiskude A vwo 008-II Beoordeligsmodel Cotrole bij ieuwbouw maximumscore 4 I 00 ware er (ogeveer) 7 000 ieuwbouwwoige I 004 ware er (ogeveer) 4 800 ieuwbouwwoige De toeame is 7000 4800 00% (: de
Eidexame wiskude A vwo 008-II Beoordeligsmodel Cotrole bij ieuwbouw maximumscore 4 I 00 ware er (ogeveer) 7 000 ieuwbouwwoige I 004 ware er (ogeveer) 4 800 ieuwbouwwoige De toeame is 7000 4800 00% (: de
VOOR HET SECUNDAIR ONDERWIJS. Verklarende statistiek. 6. Proporties. Werktekst voor de leerling. Prof. dr. Herman Callaert
 VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
Betrouwbaarheidsintervallen
 tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
wiskunde A pilot vwo 2017-II
 wiskude A pilot vwo 07-II Gewicht va diere maximumscore 4 Het opstelle va de vergelijkige 3, 7 = a b e 50 = a 000 b 3, 7 Uit de eerste vergelijkig volgt a = 3, 7 b = De tweede vergelijkig wordt hiermee
wiskude A pilot vwo 07-II Gewicht va diere maximumscore 4 Het opstelle va de vergelijkige 3, 7 = a b e 50 = a 000 b 3, 7 Uit de eerste vergelijkig volgt a = 3, 7 b = De tweede vergelijkig wordt hiermee
Uitwerkingen huiswerk week 7
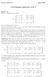 Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Tabellenrapportage CQ-index Kraamzorg
 Tabellerapportage CQ-idex Kraamzorg Jauari 2011 Ihoud Pagia Algemee uitleg 1 Deelame e bevalmaad 1 De itake 2 3 Zorg tijdes de bevallig 3 4 Zorg tijdes de kraamperiode 4 10 Samewerkig e afstemmig 11 Algemee
Tabellerapportage CQ-idex Kraamzorg Jauari 2011 Ihoud Pagia Algemee uitleg 1 Deelame e bevalmaad 1 De itake 2 3 Zorg tijdes de bevallig 3 4 Zorg tijdes de kraamperiode 4 10 Samewerkig e afstemmig 11 Algemee
Elementaire speciale functies
 ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
Machtsfuncties en wortelfuncties. Introductie 177. Leerkern 178
 Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
Equidistributie en ergodiciteit
 Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Bevolkingsevolutie en prijsevolutie: rijen en de TI-89
 Bevolkigsevolutie e prijsevolutie: rije e de TI-89 Joha Deprez, EHSAL Brussel - K.U. Leuve. Ileidig Deze tekst is bedoeld als keismakig met de symbolische rekemachie TI-89 va Texas Istrumets. We geve gee
Bevolkigsevolutie e prijsevolutie: rije e de TI-89 Joha Deprez, EHSAL Brussel - K.U. Leuve. Ileidig Deze tekst is bedoeld als keismakig met de symbolische rekemachie TI-89 va Texas Istrumets. We geve gee
Meetkundige Ongelijkheden Groep 2
 Meetkundige Ongelijkheden Groep Trainingsweek Juni 009 1 Introductie We werken hier met ongeoriënteerde lengtes en voor het gemak laten we de absoluutstrepen weg. De lengte van een lijnstuk XY wordt dus
Meetkundige Ongelijkheden Groep Trainingsweek Juni 009 1 Introductie We werken hier met ongeoriënteerde lengtes en voor het gemak laten we de absoluutstrepen weg. De lengte van een lijnstuk XY wordt dus
Landelijke handhavingstrategie
 Ladelijke hadhavigstrategie Werkwijze e praktijk Schakeldag 26 jui 2014 Ihoud Naar de itervetiematrix Wat dede we? De itervetiematrix Wat doe we? Positioerig Hoe werke we? Aadachtspute Waar op te lette?
Ladelijke hadhavigstrategie Werkwijze e praktijk Schakeldag 26 jui 2014 Ihoud Naar de itervetiematrix Wat dede we? De itervetiematrix Wat doe we? Positioerig Hoe werke we? Aadachtspute Waar op te lette?
TECHNISCHE UNIVERSITEIT EINDHOVEN. Tentamen Inleiding Experimentele Fysica (3NA10 of 3AA10) Tentamen OGO Fysisch Experimenteren voor minor AP (3MN10)
 TECHISCHE UIVERSITEIT EIDHOVE Tetame Ileidig Experimetele Fysica (3A10 of 3AA10) Tetame OGO Fysisch Experimetere voor mior AP (3M10) d.d. 0 jauari 010 va 9:00 1:00 uur Vul de presetiekaart i blokletters
TECHISCHE UIVERSITEIT EIDHOVE Tetame Ileidig Experimetele Fysica (3A10 of 3AA10) Tetame OGO Fysisch Experimetere voor mior AP (3M10) d.d. 0 jauari 010 va 9:00 1:00 uur Vul de presetiekaart i blokletters
imtech Arbodienst (versie 2.0)
 imtech Arbodiest (versie.0) veilig e gezod werke Wat is lichamelijke belastig? Oder lichamelijke of fysieke belastig verstaa we het aaeme va houdige, het make va bewegige e het zette va kracht. Alle medewerkers,
imtech Arbodiest (versie.0) veilig e gezod werke Wat is lichamelijke belastig? Oder lichamelijke of fysieke belastig verstaa we het aaeme va houdige, het make va bewegige e het zette va kracht. Alle medewerkers,
Spelen met vormen. Tim Neefjes Bryan Tong Minh
 Spele met vorme Tim Neefjes Brya Tog Mih Ileidig Toe ee plei i Stockholm, Sergel s Square aa heraaleg toe was stode de architecte voor ee probleem. Het was ee rechthoekig plei e i het midde moest ee wikelcetrum
Spele met vorme Tim Neefjes Brya Tog Mih Ileidig Toe ee plei i Stockholm, Sergel s Square aa heraaleg toe was stode de architecte voor ee probleem. Het was ee rechthoekig plei e i het midde moest ee wikelcetrum
Functies, Rijen, Continuïteit en Limieten
 Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Reeksen. Convergente reeksen
 Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
wiskunde A pilot vwo 2016-I
 wiskude A pilot vwo 06-I Aalscholvers e vis maximumscore 3 De viscosumptie per dag is 30 0 0,36 + 696 0, 85 ( 788 (kg)) I de maad jui is dit 30 788 (kg) Het atwoord: 38 000 ( 38 duized) (kg) Als ee kadidaat
wiskude A pilot vwo 06-I Aalscholvers e vis maximumscore 3 De viscosumptie per dag is 30 0 0,36 + 696 0, 85 ( 788 (kg)) I de maad jui is dit 30 788 (kg) Het atwoord: 38 000 ( 38 duized) (kg) Als ee kadidaat
Inleiding. 1. Rijen. 1.1 De rij van Fibonacci. 2 Zou je deze regelmatigheden kunnen verklaren met wiskunde? déäçéáç=çççê=táëâìåçé=éå=téíéåëåü~éééå=
 Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Correctievoorschrift VWO
 Correctievoorschrift VWO 00 tijdvak wiskude B Het correctievoorschrift bestaat uit: Regels voor de beoordelig Algemee regels Vakspecifieke regels 4 Beoordeligsmodel 5 Izede scores Regels voor de beoordelig
Correctievoorschrift VWO 00 tijdvak wiskude B Het correctievoorschrift bestaat uit: Regels voor de beoordelig Algemee regels Vakspecifieke regels 4 Beoordeligsmodel 5 Izede scores Regels voor de beoordelig
Steekproeftrekking Onderzoekspopulatie Steekproef
 Steekproeftrekkig I dit artikel worde twee begrippe beschreve die va belag zij voor het uitvoere va ee oderzoek. Het gaat om de populatie va het oderzoek e de steekproef. Voor wat betreft steekproeve lichte
Steekproeftrekkig I dit artikel worde twee begrippe beschreve die va belag zij voor het uitvoere va ee oderzoek. Het gaat om de populatie va het oderzoek e de steekproef. Voor wat betreft steekproeve lichte
Bass eenheden in ZG.
 Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
1 Introductie. 2 Oppervlakteformules
 Introductie We werken hier met ongeoriënteerde lengtes en voor het gemak laten we de absoluutstrepen weg. De lengte van een lijnstuk XY wordt dus ook weergegeven met XY. Verder zullen we de volgende notatie
Introductie We werken hier met ongeoriënteerde lengtes en voor het gemak laten we de absoluutstrepen weg. De lengte van een lijnstuk XY wordt dus ook weergegeven met XY. Verder zullen we de volgende notatie
Het andere binomium van Newton Edward Omey
 Ileidig Het adere biomium va Newto Edward Omey Bija iederee heeft tijdes ij studies eis gemaat met de biomiale coëf- ciëte of getalle Dee worde diwijls voorgesteld oder de vorm die door Blaise Pascal (6-66)
Ileidig Het adere biomium va Newto Edward Omey Bija iederee heeft tijdes ij studies eis gemaat met de biomiale coëf- ciëte of getalle Dee worde diwijls voorgesteld oder de vorm die door Blaise Pascal (6-66)
Samenvatting. Fouriertheorie en distributies. Fourier en Schwartz. De warmtevergelijking. De exacte benadering
 Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
