Integraalrekening. Georg Friedrich Bernhard Riemann Breselenz 17 september 1826 Selasca 20 juni 1866
|
|
|
- Jacobus de Backer
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Itegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 septemer 86 Selsc 0 jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geeft de itegrl v ee positieve fuctie ee uwkeurige etekeis het egrip "oppervlkte oder de kromme". Het eevoudigste itegrlegrip is geseerd op de formulerig v Berhrd Riem e wordt drom soms Riem-itegrl geoemd. De Leesgue-itegrl, geoemd r zij edeker Heri Leesgue, is ee costructie die ee grotere klsse v fucties itegreerr mkt; hij k ovedie worde geruikt over dere domeie d de reële getlle.
2 ) De differetil ) Defiitie Op de grfiek zie je ee fleidre fuctie f sme met hr rklij t i put, f. Voor ee verderlijk put defiiëre we d oeme d y f ' het differetiequotiët e wete dt 0 De vergelijkig v de rklij is d t y f '.( ) f Op de figuur zie we dt dy f '.( ) = +. = e y f ( ) f =. We y = lim de fgeleide v f is i. = ee ederig is voor y. Hoe kleier (dus hoe dichter ij ligt), hoe eter de ederig. We oeme dy de differetil v fuctie f i. ' Algemee defiiëre we dus i ee willekeurig put : dy = df ( ) = f ( ) Voor de idetieke fuctie f ( ) = geldt d df( ) d. dy = df = f d ' de defiitie d herschrijve ls = = =. Op deze mier kue we df Deze formule verduidelijkt ook de ottie v Leiiz: f '( ) =. d Het is zo ook metee duidelijk dt ee fuctie differetieerr is ls ze fleidr is. Alle rekeregels e formules die we kee v ij fgeleide worde dus eevoudig overgedrge r rekeregels e formules v differetiëre. 5d Vooreeld: d ( Bgsi 5) = 5 Toepssig: Beder 06 met ehulp v differetiëre. Noem f ( ) =, d is f ( ) = f + y f + dy = f + f '.( ). Cursus itegrlrekeig - - S. Mettepeige
3 Neem = 06 e = 00, d is 6 we krijge: ,05.6 = 0,. ) Beplde itegrle ) Ileided vooreeld =, f ( ) = 0 e Er wordt os gevrgd de oppervlkte S te erekee tusse de grfiek v de fuctie f ( ) =, de -s e de verticle rechte =. Het is duidelijk dt de zo otste figuur (og) gee ekede figuur is wrvoor we oppervlkteformules kee e kue geruike. We kue deze oppervlkte wel edere door rechthoekjes te geruike. f ' = 0,05 00 = 0 =, zodt We verdele de sis v de figuur i 5 gelijke stukke, e eme dit ls reedtes v oze rechthoeke. Op de likerfiguur eme we ls hoogte telkes de kleiste fuctiewrde i het itervl, op de rechterfiguur telkes de grootste fuctiewrde. Zo krijge we liks ls ederig: 5 0,.0 0,.0,04 0,.0,6 0,.0,6 0,.0,64 0,4 s = =. De methode die we liks geruikte zl duidelijk ltijd te klei zij. We oeme het ee odersom voor de fuctie e otere ze met kleie letter s 5 (met ls ide het tl rechthoekjes). We krijge rechts ls ederig: S 5 = 0,.0,04 + 0,.0,6+ 0,.0,6+ 0,.0,64 + 0,.= 0,44. De methode die we rechts geruikte zl duidelijk ltijd te groot zij. We oeme het ee ovesom voor de fuctie e otere ze met grote letter S 5 (met ls ide het tl rechthoekjes). Het gemiddelde v deze twee geeft ee zeer goede ederig v de gezochte oppervlkte. We s5 + S5 0, 4+ 0, 44 schtte dus S = = = 0,4. (De werkelijke oppervlkte lijkt te zij). We kue deze redeerig herhle voor meer rechthoekjes. Het is duidelijk dt hoe meer rechthoekjes we eme, hoe dichter de odersom e ovesom ij elkr zulle ligge. Meer og, we kue stelle dt S = lim s = lim S. + + Cursus itegrlrekeig - - S. Mettepeige
4 Het mg ook duidelijk zij dt dit ook werkt ls we per itervl willekeurige fuctiewrde eme (dus iet cosequet het miimum of het mimum eme). We krijge d ee ederig voor de oppervlkte die tusse de odersom e de ovesom ligt e dus i de limiet voor + ook gelijk is de gezochte oppervlkte. ) Algemee werkwijze de eplde itegrl Om de oppervlkte te erekee egrepe tusse de grfiek v ee fuctie, de -s e twee verticle rechte = e =, verdele we het itervl [, ] i gelijke deelitervlle: [, ], [, ],..., [, i i],..., [, ]. I elk itervl edere we de oppervlkte door de reedte v het itervl te vermeigvuldige met ee willekeurig gekoze fuctiewrde f ( c i), met c [ ]., i i i De reedte v deze deelitervlle is d gelijk =. = f ci.. De gezochte oppervlkte wordt d ederd door: S Me k ewijze dt voor fucties die cotiu zij i [, ] de limiet voor + v S estt e dus gelijk is de werkelijke gezochte oppervlkte. We oeme deze limiet de eplde itegrl v tot v de fuctie f. We otere dit ls: i= lim S f. d + = Meer lgemee oeme we fucties wrvoor deze limiet estt itegreerr over dt itervl. c) Georiëteerde oppervlkte Tot hiertoe gige we er stilzwijged v uit dt de grfiek v de fuctie f volledig ove de -s lg i het gegeve itervl [, ] (dus [ ] f ( ) lgemee werkwijze ekome is d uiterrd positief., : 0). De oppervlkte die we vi de Zou je deze werkwijze herhle voor ee fuctie die oder de -s ligt i [, ] d kom je ee egtieve oppervlkte uit. We spreke dus logischerwijze f dt oppervlktes ove de -s positief gereked worde, e oppervlktes oder de -s egtief. Dt dit uttig e relistisch is volgt lter uit ekele fysische vooreelde. Cursus itegrlrekeig S. Mettepeige
5 We iterpretere lgemee de eplde itegrl v ee (cotiue) fuctie f v tot d ook ls de som v de georiëteerde oppervlkte tusse de grfiek v f, de -s e de verticle rechte = e =. Zo geldt i het getekede vooreeld: f d = S + I S II S + III SI V. Avullig op de defiitie v eplde itegrl: We me tot hiertoe ltijd ls odergres e ls ovegres om te itegrere, wrij <. We kue de defiitie v eplde itegrl verder uitreide: Als Als =, d stelle we 0 f d = >, d stelle we f ( ) d = Cursus itegrlrekeig S. Mettepeige f d d) Eigeschppe v de eplde itegrl Uit de defiitie v de eplde itegrl volge omiddellijk de volgede eigeschppe: Eigeschp : optelrheid v de eplde itegrl Als f ee itegreerre fuctie is i het itervl [, ] p q, d geldt voor lle,, c [ p, q] = + c f d f d f d c Eigeschp : lieriteit v de eplde itegrl Als f e g itegreerr zij i het itervl [, ] itegreerr, e voor de eplde itegrl geldt: I het ijzoder gelde de eigeschppe: dt:, d is ook de fuctie r. f + sg. ( r, s R) dr (. +. ) =. +. r f sg d r f d s g d ( + ) = + ( r. f ) d = r. f ( ) d f g d f d g d Eigeschp : ogelijkheidseigeschp Als f e g itegreerr zij i het itervl [, ], d geldt: [, ]: f g f d g d Merk op dt deze eigeschp zeker iet geldt i de omgekeerde richtig! e) De hoofdstellig v de itegrlrekeig We toe i deze prgrf dt itegrere i zekere zi de omgekeerde opertie is v differetiëre.
6 Itegrlfucties We oeme de fuctie I, met I ( ) = f t dt, de itegrlfuctie v f met odergres. Ze stelt dus de verderlijke georiëteerde oppervlkte voor egrepe tusse de -s e de grfiek v de fuctie f i het itervl met verderlijke ovegres [, ]. De middelwrdestellig v de itegrlrekeig Stellig: Is f cotiu i [, ], d estt er ee c [, ] zodt: =.( ) Bewijs: We ewijze eerst het gevl < : f d f c Omdt f cotiu is i [, ] estt er ee kleiste e ee grootste fuctiewrde i dt itervl, die we zulle duide met m e M. We volge de lgemee werkwijze voor het erekee v ee eplde itegrl e verdele het itervl i gelijke deelitervlle met reedte =. I elk v deze itervlle [, ], [, ],..., [, i i],..., [, ] eme we ee c [ ]., i i i D krijge we chtereevolges: i, m f c M (lle fuctiewrde ligge tusse m e M ) m. f c. M. (lles vermeigvuldige met > 0) m i.. f c. M.. i (sommere over lle deelitervlle) i=. f ci.. M (. ( ) m ( ) i=. lim f c.. M ( ) m ( ) = = ) i (de limiet eme voor + ) + i =. f d. M (defiitie v de eplde itegrl) ( ) m ( ) f d m M (lles dele door > 0 ) Omdt f cotiu is i [, ] est er volges de stellig v Weierstrss twee getlle [ ] zodt f ( p) = m e p, q, f q = M (zie figuur). De tussewrdestellig leert os d dt lle fuctiewrde tusse m e M door mistes éé -wrde c tusse p e q ereikt worde. Omdt c tusse p e q ligt zl het ij uitreidig uiterrd ook i [, ] ligge. Cursus itegrlrekeig S. Mettepeige
7 Er estt dus mistes éé c [, ], zodt f ( c) Als Als = d is = 0 = f ( c ).( ) f d f d. = = f d f c. < d geldt c [, ] : f ( ) d = f ( c).( ) f ( ) d = f ( c).( ) Opmerkig: We kue de fuctiewrde f ( c) fuctiewrde over dt itervl. Meetkudige iterprettie: We kue f c = f d ook iterpretere ls de hoogte v de rechthoek met ls sis het itervl [, ] op de -s wrv de (georiëteerde) oppervlkte gelijk is de (georiëteerde) oppervlkte tusse de grfiek v de fuctie e de -s.. f d = iterpretere ls de gemiddelde De hoofdstellig v de itegrlrekeig Stellig: Als f cotiu is i [, ], d geldt i [, ] dt = D f t dt f. ' Bewijs: Met itegrlfucties kue we dit herschrijve ls: [, ] : I ( ) = f ( ) I I ( ) ( + ) I ( ) = lim (defiitie v fgeleide) ' 0 = lim 0 = lim 0 = lim 0 = lim 0 + f t dt f t dt + + f t dt f ( ) Primitieve fucties + f t dt.f c f t dt, met c [, ] (defiitie v itegrlfuctie) (itegrlgreze verwissele) (optelrheid v de eplde itegrl) + (middelwrdestellig) = (ls 0, d is = c = + ) We oeme F ee primitieve fuctie v f ls e slechts ls DF = f. Het is duidelijk dt lle itegrlfucties v ee fuctie ook primitieve fucties zij v die fuctie. Het omgekeerde is echter iet oodzkelijk wr. Cursus itegrlrekeig S. Mettepeige
8 4 5 5 Vooreeld: Als f ( ) = 5 d zij F ( ) = + e F ( ) = primitieve fucties v f. 4 Stellig: Twee primitieve fucties v eezelfde fuctie verschille slechts ee costte v elkr. Bewijs: Stel dt F e F eide primitieve fucties zij v f, d is zowel DF = f ls DF = f. DF = DF DF DF = 0 D F F = 0 F F = C, met C R. Dus Itegrere met ehulp v primitieve fucties Stellig: Als F ee primitieve is v f (cotiu i [, ]), d is = Bewijs: We eweze reeds dt elke itegrlfuctie I ( ) de stellig i verd met primitieve fucties volgt d dt I = f t dt = F + C. Stel je hieri Neem je = d wordt dit f t dt F C C F = + = = 0 =, d wordt het = + = f t dt F C F F f d F F. = f t dt ee primitieve is v f. Uit I F = C, of dus og dt Opmerkig: Het verschil wordt ook vk ls volgt geoteerd: = = F ( ) F ( ). f t dt F We hee u eidelijk ee prktische methode gevode om eplde itegrle te erekee. 5 5 d = 4 = = Vooreeld : e Vooreeld : [ ] f) Typeproleme e d l le l 0 = = = = De oppervlkte oder ee kromme erekee Vooreeld: Bereke de oppervlkte egrepe tusse de prool p y = e de -s. De ulpute v de prool zij (,0) e (,0 ). De gezochte oppervlkte wordt dus gegeve door: S ( ) d = = ( ) = ( ) ( ) =.. De oppervlkte tusse ee kromme e de -s erekee tusse twee wrde We zge reeds dt je met ee eplde itegrl de georiëteerde oppervlkte ereket tusse twee greze. Cursus itegrlrekeig S. Mettepeige
9 Als je de werkelijke oppervlkte wil erekee k je deze redeerig omkere door het itegrtie-itervl i stukke te verdele wr het teke v de fuctie iet verdert. Zo geldt voor de werkelijke oppervlkte S egrepe tusse de -s e de grfiek v de fuctie tusse =, 5 e = : I II III IV S = S + S + S + S = f d+ f d f d+ f d Als je itegreert met je rekemchie k dit seller door gewoo S 5 Vooreeld: ereke de (werkelijke) oppervlkte egrepe tusse de -s e de grfiek v de fuctie f ( ) = over het itervl [,] We ekijke eerst het tekeverloop: De fuctie is dus over het te itegrere itervl zowel egtief ls positief. De gezochte oppervlkte is dus: 4 4 oppg = ( ) d+ ( ) d = oppg = = + + = De oppervlkte tusse twee kromme erekee = f d te erekee. Ook dit is ee eevoudig proleem ls je eseft dt de (georiëteerde) oppervlkte tusse twee kromme k ereked worde door het verschil v eide fucties te itegrere. Als je de werkelijke oppervlkte wil erekee moet je ervoor zorge dt de verschilfuctie positief is (dus dt je i je itegrdum de oderste fuctie v de oveste fuctie ftrekt). f = + Vooreeld: De grfieke v de fucties g = 5 sluite twee geiede S I e S II e i zols fgeeeld op de grfiek. Bewijs dt SI = SII. We ekijke eerst het tekeverloop v de verschilfuctie v = g f = Dus I ( ) S = 8 d = 4 = 0 4( ) = E SII = ( 8) d = = =, zodt iderdd SI = SII. 0 Cursus itegrlrekeig S. Mettepeige
10 ) Oeplde itegrle ) Defiitie De verzmelig v lle primitieve fucties v ee gegeve fuctie f oeme we de oeplde itegrl v f. We eweze reeds dt l deze primitieve fucties slechts op ee costte v elkr verschille. We otere de oeplde itegrl v ee fuctie f ls volgt: f ( ) d = F ( ) + C Hierij is dus F ee primitieve fuctie v f. De costte C R oeme we de itegrtiecostte. De hoofdstellig v de itegrlrekeig mkt duidelijk dt differetiëre e itegrere ewerkige zij die elkr opheffe. Zo krijge we dus drie eevoudige eigeschppe: d f ( ) d = f d d ( F ( ) ) = F ( ) + C ) Fudmetele itegrle = D f d f Volgede lijst v itegrle zl os ee houvst iede ij het erekee v moeilijkere oeplde itegrle. Zorg ervoor dt je deze lijst heel goed eheerst! d = + C Cursus itegrlrekeig S. Mettepeige q+ q d = + C (met q ) q + + sid = cos+ c d = Bgsi + c d = gt + C e d = e + C cosd = si+ c d = + C l d d = cot+ c l C si = + d d = t + c l k C cos + k = Ekel de ltste fudmetele itegrl is iet omiddellijk duidelijk. We ewijze dt de formule wel degelijk klopt door f te leide: k k + + = k + = + = k k k Dl k + k ( + ) + k + k = + k Itegrtie door splitsig Stellig: Voor itegreerre fucties f e g, e reële costte r, s R geldt de volgede eigeschp: (. +. ) = + r f sg d r f d s g d Bewijs: Het rechterlid fleide wr je steut op de gekede eigeschppe v fgeleide, geeft:
11 ( + ) = ( ) + ( ) ( + ) = r D( f ( ) d) + s D( g( ) d) ( + ) = r f ( ) + s g( ), D r f d s g d D r f d D s g d D r f d s g d D r f d s g d wruit volgt dt ( r. f + sg. ) d = r f ( ) d + s g ( ) d + C. Mr oeplde itegrle zij gelijk op ee costte, dus hee we eweze wt we moeste ewijze. 4 Vooreeld : ( 4 + 5) d = d 4 d + 5 d = C 4 Uiterrd k je hier de tussestp oversl. Merk op dt je slechts éé itegrtiecostte schrijft. Vooreeld : Soms ligt de splitsig iets mider voor de hd: ( + ) + d = d = + d = d + d = + Bgt + C Vooreeld : cot d = csc d = csc d d = cot + C Zeer eevoudige differetilvergelijkige Vooreeld: Bereke f ( ) ls gegeve is dt f "( ) = 6, f ' = 0 e = = +, mr we wete ook f " 6 f ' C f = 4. f ' = 0. + C = 0 C =. f = + C. Zo hee we dus gevode dt f '( ) =, wruit volgt dt Omdt f ( ) = 4.+ C = 4 C =. De gezochte fuctie is dus c) Itegrtie door sustitutie Stellig: Als F ee primitieve is v f, e g is ee fleidre fuctie, d geldt: ( ) ( ) Bewijs: ( ) ' ( ) f g g d = F g + c kettig regel ' D F g + c = D F g = f g g f =. I de prktijk komt het er vk op om i het itegrdum ee fuctie te herkee wrv ook de fgeleide (of differetil) i het itegrdum stt. Ekele eevoudige vooreelde: Vooreeld : si ( cos ) ( ) 4 * 4 t cos d = t dt = + C = + C 4 4 *: Hier is het duidelijk dt si de fgeleide is v cos. We voere ee sustitutie uit: Stel t = cos, d is dt = sid. Vooreeld : si l d * = tdt = t + C = + C si cos cos l *: Hier is het duidelijk dt de fgeleide is v l. We voere ee sustitutie uit: Stel t = l, d is d dt =. Cursus itegrlrekeig - - S. Mettepeige
12 Vooreeld : *: Hier is het duidelijk dt Stel t = e, d is e e * dt e ( e ) d = d= = Bgsit + C = Bgsi e + C t dt = e d. Apsse v de itegrtiegreze e de fgeleide is v e. We voere ee sustitutie uit: We herekijke eve het eerste vooreeld uit de vorige prgrf, mr u ls eplde itegrl: π d. π Vooreeld: Bereke de eplde itegrl si( cos ) Methode : We hee l ee primitieve fuctie epld v deze eplde itegrl, dus geldt: π π π π 4 cos cos 4 π ( ) ( ) cos 0 5 si( cos) d = = = = π Methode : We kue ij ee sustitutie ook de itegrtiegreze eevoudig psse. π * t 5 si( cos) d = t dt = 4 = = π *: Stel t = cos, d is dt = sid. Voor de greze geldt Eevoudige sustituties π π = t = e = t =. Het komt soms voor dt het itegrdum veel eevoudiger k geschreve worde met ehulp v ee lieire sustitutie (stel t = + ). Vooreeld : ( 5) ( ) 7 t t d = dt = + C = + C 7 Omdt deze sustitutie zo eevoudig is geruike we hier soms ee kortere ottie: ( 5) ( 5) d = ( 5) d ( 5) = + C. d d d ( ) Vooreeld : = = = Bgt ( ) + C Je k deze kortere schrijfwijze overiges ook geruike ij iets lstigere sustituties: ( cos) si d Vooreeld : td = d = l cos C cos = + cos Of je deze kortere mier om sustituties te otere geruikt of iet mk je zelf uit. Je wit er uiterrd wt tijd mee, mr het mg iet te koste g v ee eter egrip. Cursus itegrlrekeig - - S. Mettepeige
13 Ekele hdige formules d Stellig: = Bgt + C e + Bewijs: Vooreeld: d Bgsi = + d ( ) ( ) d d Bgt d d d ( ) = = = Bgsi + C ( ) = = = + C, e ( ) ( ) d d = = Bgsi + C d) Prtiële itegrtie Het is iet ltijd mogelijk ee sustitutie te vide die os toelt ee itegrl te erekee. I dt gevl k prtiële itegrtie helpe: Stellig: f ( ) d ( g( ) ) = f ( ) g( ) g( ) d ( f ( ) ) Bewijs: Beide lede fleide geeft: ( ( )) = ( ( )) ( ' ) ( ) ' f ( ) g' ( ) f '( ) g( ) f ( ) g' ( ) g( ) f '( ) D f d g D f g g d f C D f g d = D f g D g f d = + Oeplde itegrle zij gelijk op ee costte, dus we hee wt we moeste ewijze.. Opmerkig: De formule voor prtiële itegrtie wordt vk geschreve ls u dv = uv v du Er zij ee tl gevlle wr prtiële itegrtie de meest effectieve weg is: Verlge v de grd Als het itegrdum estt uit het product v ee veeltermfuctie (of simpelweg ee mcht v ) met ee epoetiële of ee goiometrische fuctie (v de vorm d k je met prtiële itegrtie de grd v de veelterm verlge. Vooreeld: P. I. ( si) si of e, + cosd = + si si + d =... = d cos ), Iderdd, de veelterm is verlgd v de tweede r de eerste grd. We psse og ees P.I. toe: ( ) ( ) ( )... = + si + + d cos = + si + + cos cos.d =... E deze ltste itegrl is fudmeteel geked, zodt we uiteidelijk krijge: ( + ) cos ( ) ( ) + cosd = + si+ + cos si + C d = + si+ + cos+ C Cursus itegrlrekeig - - S. Mettepeige
14 Terugkeer v het itegrdum I specile gevlle k het zij dt je (meerdere kere) prtiële itegrtie je oorsprokelijke itegrl ziet weerkere. I dt gevl spreke we v ee weerkered itegrdum. Dit is ijvooreeld het gevl ls het itegrdum het product is v ee epoetiële e ee goiometrische fuctie (v de vorm Vooreeld: Bereke de itegrl 5 e si of e, 5 cos = d = = d d P. I e cosd = e si e sid e ( si ) d( cos) ( si) ( si) cos ). 5 5 cosd = si cos + cos e e e e cosd = e i + e cos e cos = d 5 5 s 4 4 We moge os dus voor de rest cocetrere op echte veeltermreuke, wrij de grd v de teller kleier is d de grd v de oemer. Vk zulle deze rtiole moete worde gesplitst i prtieelreuke. We hee drvoor twee stellig odig: De hoofstellig v de lger: Elke reële veelterm v grd mistes éé k otode worde i ee product v eerstegrdsfctore e tweedegrdsfctore (met ee egtieve discrimit). Cursus itegrlrekeig S. Mettepeige d d Deze ltste itegrl is et de itegrl wr we mee egoe zij, dus hieruit volgt: cos si cos 4 e d = e + e e cosd = e si+ e cos+ C 9 9 Altijd ee optie... Soms is het iet ltijd metee duidelijk wt je met het itegrdum k doe. Mr wt je ltijd k f d. doe is fleide. Ee prtiële itegrtie die dus ltijd k is: f ( ) d = f ( ) ' Vooreeld: ld = l e) Itegrle v rtiole fucties d = l + C Oeplde itegrle v rtiole fucties zij heel eevoudig te erekee mr ze vrge eorm veel rekewerk. De Euclidische delig leert os A( ) D( ) Q( ) R( ) geldt ( ) gr R < gr D. = + A R Q( ) D = + D, wrij A R Voor de itegrl geldt dus ook: d = Q( ) d d D +. D
15 De stellig v Jcoi: Elke echte veeltermreuk k geschreve worde ls som v prtieelreuke. We ekijke u i detil de methode v Jcoi om ee rtiole fuctie te schrijve ls som v prtieelreuke: Schrijf de fuctie ls som v ee veelterm e ee echte veeltermreuk (Euclidische delig). Otid de oemer i zoveel mogelijk reële fctore v de eerste of tweede grd. Zorg ervoor dt er i de oemer ekel og fctore voorkome v de vorm ( + ) e ( c) + +. ) Elke fctor ( + ) i de oemer veroorzkt ee som prtieelreuke v de vorm A B C N ) Elke fctor ( c) i de oemer veroorzkt ee som prtieelreuke v de vorm P+ Q R + S T+ U Y + Z c + + c + + c + + c De oekede tellers worde chterf ereked met de methode v de oeplde coëfficiëte Vooreeld : Bereke d We schrijve het itegrdum eerst ls som v ee veelterm e prtieelreuke (Jcoi): Stp : = Stp : = ( + )( )( ) Stp : E dus geldt: A+ B C D = + + = Cursus itegrlrekeig S. Mettepeige (Euclidische delig) ( A+ B)( )( ) + C( + )( ) + D( + )( ) + ( + )( )( ) ( A+ C+ D) + ( A+ B C D) + ( A B+ C+ D) + ( B C D) = A+ C + D = A = A B C D 8 + = B = 0 A B+ C + D = 4 C = B C D = 5 D = = d d d = ( ) d d d ( + ) d ( ) d ( ) d = d = l Zols je ziet heel eevoudig, mr redelijk wt rekewerk l l + C
16 Vooreeld : Bereke d Dit is l ee echte veeltermreuk. De oemer is ( 6 0)( ) + + = + +. ( A+ B)( + ) + C( 6+ 0)( + ) + D( 6 + 0) A+ B C D + + = ( ) ( 6 0)( ) ( A+ C) + ( A+ B 5C + D) + ( A+ B+ 4C 6D) + ( B+ 0C + 0D) Dus = A+ C = 6 A = 4 A B 5C D = B = A+ B+ 4C 6D = 4 C = B+ 0C + 0D = D = d d d = d Hierij geldt: + + ( ) ( ) d d = d = ( 6 + 0) d ( ) 4+ d d = d 6+ 0 d d ( + ) = = l + + C + + ( ) = l Bgt + e ( ) Cursus itegrlrekeig S. Mettepeige C d ( + ) ( ) d = = + C Zodt d = l Bgt 4 ( ) l C De eige moeilijke(re) itegrl die je het splitse i prtieelreuke k ekome is de itegrl v de vorm d (met i de oemer ee egtieve discrimit, e ). Dit type + + c itegrle k ereked worde met ehulp v prtieelitegrtie of ee recursieformule (of ee goiometrische sustitutie). Ze zulle echter op toetse of emes iet gevrgd worde. f) Goiometrische itegrle Bij goiometrische itegrle komt het vk eer op het correct geruike v de gekede goiometrische formules. Zo k je met de formules v Simpso ee product v (co)siusse schrijve ls ee som (wt veel mkkelijker itegreert). De grd verlge k je doe met ehulp v de formules v Crot. De formule voor de itegrl v de secs e de cosecs leer je est v uite, wt die is iet zo eevoudig te erekee: Stellig: secd = l sec+ t + C e cscd = l csc + cot + C
17 t= si d cos cos dt * dt dt Bewijs: sec d = = d d... cos = cos = = + = si t + t t A B A( t) + B( + t) A+ B = 0 A = (*: t = ( + t)( t) = + = ) t + t t ( + t)( t) A+ B = B = ( ) ( t) d + t d + t + si... = l l l l... = + t t + C = + C = + C = + t t t si Met ehulp v wt eevoudige goiometrie wordt dit: ( )( + ) + si + si + si + si... = l + C = l + C = l + C = l sec + t + C si si cos cos π Stelle we hieri = t, d wordt dit: π π π π sec t d t = l sec t + t t + C cscd = l csc+ cot + C. = csct = dt = csct = cott We erekee ee tl dere goiometrische itegrle ls illustrtie: cos cos Vooreeld : cos si d = cos ( cos ) d ( cos) = + + C 5 7 (deze methode werkt ltijd ij ee product v mchte v sius e of cosius ls mistes éé epoet oeve is) cos4 d = d = d = d si 4 + cos8 = cos4 cos 4 64d d+ 64 d = d si4 si8 si4 si8 = C = + + C (deze methode ij gelijke mchte e om de grd verlge k ook ltijd op deze mier) si 4+ si0 cos 4 cos0 Vooreeld : si7 cosd = d = + C Vooreeld : si 4 cos 4 ( si ) ( si ) g) Itegrle v irrtiole fucties Ee voor de hd liggede sustitutie Komt ee lieire uitdrukkig y = + oder ee tl wortels voor voer d de sustitutie uit t = + wrij het kleiste gemee veelvoud is v de wortelepoete. Vooreeld: 5 t + 5 t 6 5 * d= t dt = t + t t dt t = t + t t + C = ( 5) + ( 5) ( 5) + C t *: 5 = t = d = t dt Cursus itegrlrekeig S. Mettepeige
18 Goiometrische sustituties Sommige itegrle zij iet vi eevoudige te herleide r fudmetele itegrle. I dt gevl zij goiometrische sustituties geweze. Type : Komt de vorm Wt d zl (e ook zl Vooreeld: voor (met > 0), d is de sustitutie si t cost = =, met t [ π, π ] d = costdt e t = Bgsi ) d * cost dt 9si t.cost. 9 = *: = sit 9 = cost e d cost Type : Komt de vorm 9 = cott + C = + C 9 9 =, met t [ π, π ]. voor (met > 0), d is de sustitutie = sit geweze. 9 ( cott = ) = sect geweze. [ π [ ] π π] t t, lst 0, e dus Wt d zl: = sec t = t t, lst, e dus (e ook zl d = sectttdt e t = Bgsec = Bgcos ) Bij oeplde itegrle mg je er voor de eevoud i de prktijk v uitg dt. Vooreeld: ( ) ( ) ( ) + * + 4 t d= d = sec t t tdt + + 8sec t t = si si ( cos ) si tdt = tdt t dt t t C = = = t sitcost + C = Bgcos + C Bgcos = + C ( ) (gesteld dt ) *: + = sect + 4 = tt e d = sectttdt Type : Komt de vorm Wt d zl (e ook zl d sec tdt Vooreeld: + voor (met > 0), d is de sustitutie t t sect + = + =, met t [ π, π ] t = ) = e Bgt d d * sec t = = dt ( ) ( ) sec = costdt = sit + C = + C *: = 4tt + 6 = 4sect e d = sec tdt ( cost = + e sit = + ) + = tt geweze. Cursus itegrlrekeig S. Mettepeige t ( sit = )
Integraalrekening. Georg Friedrich Bernhard Riemann Breselenz 17 september 1826 Selasca 20 juni 1866
 Iegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 sepemer 86 Selsc jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geef de iegrl v ee posiieve fucie ee uwkeurige eekeis he
Iegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 sepemer 86 Selsc jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geef de iegrl v ee posiieve fucie ee uwkeurige eekeis he
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
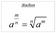 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Het differentiequotiënt van een functie in een interval geeft de gemiddelde helling weer van die functie in dat interval. Symbolisch wordt dit:
 Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
4 Differentierekening en reeksen
 WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
Verloop van exponentiele en logaritmische functies
 Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Formularium Wiskunde
 Formulrium Wiskude Te gebruike bij exme Ileidig tot de Hogere Wiskude Trscedete fucties. Goiometrische fucties t x = tg x = si x cos x cot x = cotg x = cos x si x sec x = cos x cosec x = si x cos( ± b)
Formulrium Wiskude Te gebruike bij exme Ileidig tot de Hogere Wiskude Trscedete fucties. Goiometrische fucties t x = tg x = si x cos x cot x = cotg x = cos x si x sec x = cos x cosec x = si x cos( ± b)
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
 Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
1) Definitie, rekenkundige en meetkundige rijen
 Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Acdemi Press Dele Bij delig vermeigvuldigt me met het omgekeerde v de deler..3.5 Vereevoudige Het is goed mogelijk dt voorgde bewerkige iet de
 Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
1 Bewerkingen met matrices invoeren via voorbeelden. , is een commutatieve groep.
 1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Paragraaf 11.0 : Riemann-som en oppervlakte
 Hoodstk Iterlrekei V Wis B Pi v Prr : Riem-som e oppervlkte Les Riem-som Deiitie Riem-som Ee oppervlkte k je edere met ehlp v ee Riem-som = i Vooreeld Geeve is de ctie = Schets de riek v - tot Beder de
Hoodstk Iterlrekei V Wis B Pi v Prr : Riem-som e oppervlkte Les Riem-som Deiitie Riem-som Ee oppervlkte k je edere met ehlp v ee Riem-som = i Vooreeld Geeve is de ctie = Schets de riek v - tot Beder de
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
16.6 Opgaven hoofdstuk 7: Producten en combinatoriek
 166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
Henk Pijls Korteweg-de Vries Instituut voor Wiskunde Universiteit van Amsterdam
 Jn vn de Crts Henk Pijls De kromme gevormd door de toppen vn de prolen door drie gegeven punten NAW 5/9 nr. mrt 08 9 Jn vn de Crts Korteweg-de Vries Instituut voor Wiskunde Universiteit vn Amsterdm j.vndecrts@uv.nl
Jn vn de Crts Henk Pijls De kromme gevormd door de toppen vn de prolen door drie gegeven punten NAW 5/9 nr. mrt 08 9 Jn vn de Crts Korteweg-de Vries Instituut voor Wiskunde Universiteit vn Amsterdm j.vndecrts@uv.nl
DEEL II Integraalrekening + index 50
 INHOUDSOPGAVE DEEL II Itegrlrekeig + ide 5. Het erekee v de primitieve fuctie 5. Het terugvide v de evetuele costte 54. De susitutiemethode 56.. Lstigere vrite 59. Prtieël iterere 6.4 Cyclometrische fucties
INHOUDSOPGAVE DEEL II Itegrlrekeig + ide 5. Het erekee v de primitieve fuctie 5. Het terugvide v de evetuele costte 54. De susitutiemethode 56.. Lstigere vrite 59. Prtieël iterere 6.4 Cyclometrische fucties
Het kwadraat van een tweeterm a+b. (a+b)²
 Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Integreren over een compact interval in. n
 Rise Poortig Lieire Alger e Voortgezette Alyse 6 Afgeleide e itegrl houd: 61 Prtiële fgeleide 6 Differetieerre fucties 63 Prtiële fgeleide v hogere orde 64 Cotiu differetieerre fucties 65 Differetieerre
Rise Poortig Lieire Alger e Voortgezette Alyse 6 Afgeleide e itegrl houd: 61 Prtiële fgeleide 6 Differetieerre fucties 63 Prtiële fgeleide v hogere orde 64 Cotiu differetieerre fucties 65 Differetieerre
Formulekaart VWO wiskunde B
 Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
a = 1 b = 0 k = 1 ax + b = lim f(x) lim
 BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
Hoofdstuk 0: algebraïsche formules
 Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
AANTEKENING VWO 5B HOOFDSTUK 10 : INTEGRAALREKENING. Benadering van elke oppervlakte met behulp van de Riemann-som = x i
 AANTEKENING VWO B HOODSTUK : INTEGRAALREKENING LES RIEMANN-SOM Bederi v elke oppervlkte met ehlp v de Riem-som = i VB Geeve is de ctie = Schets de riek v - tot Beder de oppervlkte tsse e de -s met ee Riemsom
AANTEKENING VWO B HOODSTUK : INTEGRAALREKENING LES RIEMANN-SOM Bederi v elke oppervlkte met ehlp v de Riem-som = i VB Geeve is de ctie = Schets de riek v - tot Beder de oppervlkte tsse e de -s met ee Riemsom
Inhoud college 7 Basiswiskunde
 Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
Toepassingen op Integraalrekening
 Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Het reëel getal b is een derdewortel van het reëel getal a c. Een getal en zijn derdewortel hebben hetzelfde toestandsteken.
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
opgaven formele structuren procesalgebra
 opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
Toepassingen op Integraalrekening
 Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
1) Complexe getallen - definitie
 Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
2.6 De Fourierintegraal
 2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
AFSTANDEN EN HOEKEN IN
 AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
Matrixrekening - Samenvatting
 I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Formeel Denken 2012 Uitwerkingen Tentamen
 1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Donderdag 20 mei 13.30 16.30 uur
 Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Voorbereidende opgaven Stoomcursus
 Voorereidende opgven Stoomcursus Tips: MEER DAN 0 JAAR ERVARING Dit document estt uit twee delen: de voorereidende opgven en een overzicht met lgerïsche vrdigheden. Mk de volgende opgven het liefst voorin
Voorereidende opgven Stoomcursus Tips: MEER DAN 0 JAAR ERVARING Dit document estt uit twee delen: de voorereidende opgven en een overzicht met lgerïsche vrdigheden. Mk de volgende opgven het liefst voorin
Vectoranalyse voor TG
 college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
Eigenschappen van de bewerkingen in R Toets jezelf: herhalingsoefeningen voor examen I
 Toets jezelf: herhlingsoefeningen voor emen I - - Overzicht vn wt je moet kennen voor dit emen:. Alger:. Hoofdstuk : Reële getllen. Hoofdstuk : Eigenschppen vn de ewerkingen in R o Optellen, ftrekken,
Toets jezelf: herhlingsoefeningen voor emen I - - Overzicht vn wt je moet kennen voor dit emen:. Alger:. Hoofdstuk : Reële getllen. Hoofdstuk : Eigenschppen vn de ewerkingen in R o Optellen, ftrekken,
Hoofdstuk 9: Afgeleide functies en toepassingen
 Hoostuk 9: Ageleie ucties e toepssige 9. Aleibrhei Deitie: Ee uctie is leibr i om ( ) IR 9.. Aleibrhei v ee uctie i ee put v het omei eities p. 76: is leibr i is iet leibr i * is rechtsleibr i / rechtergeleie
Hoostuk 9: Ageleie ucties e toepssige 9. Aleibrhei Deitie: Ee uctie is leibr i om ( ) IR 9.. Aleibrhei v ee uctie i ee put v het omei eities p. 76: is leibr i is iet leibr i * is rechtsleibr i / rechtergeleie
Inhoud leereenheid 13. Integreren. Introductie 125. Leerkern 126. Samenvatting 149. Zelftoets 150
 Inhoud leereenheid 3 Integreren Introductie 5 Leerkern 6 Integrl ls oppervlkte 6 De functie ls fgeleide vn zijn oppervlktefunctie 3 3 Primitieven 33 4 Beplde en oneplde integrl 35 5 Oneigenlijke integrlen
Inhoud leereenheid 3 Integreren Introductie 5 Leerkern 6 Integrl ls oppervlkte 6 De functie ls fgeleide vn zijn oppervlktefunctie 3 3 Primitieven 33 4 Beplde en oneplde integrl 35 5 Oneigenlijke integrlen
2 Veelhoeken 1 REGELMATIGE VEELHOEKEN
 Veelhoeke 1 EGELMATIGE VEELHOEKEN Voor meetkudige figure met meer da vier zijde geruike we vaak de verzamel aam veelhoeke. Als we te make hee met regelmatige veelhoeke, kue we hu omtrek e oppervlakte erekee
Veelhoeke 1 EGELMATIGE VEELHOEKEN Voor meetkudige figure met meer da vier zijde geruike we vaak de verzamel aam veelhoeke. Als we te make hee met regelmatige veelhoeke, kue we hu omtrek e oppervlakte erekee
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Rinse Poortinga Lineaire Algebra en Voortgezette Analyse. 2 Lineaire afbeeldingen
 Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie
Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie
2) Kegelsneden (in basisvorm)
 ) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Voorbereidende opgaven Stoomcursus
 Voorereidende opgven Stoomcursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt geruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het eknopt overzicht
Voorereidende opgven Stoomcursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt geruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het eknopt overzicht
Lagrange-polynomen. Dick Klingens september 2004
 Lgrge-polyome Dck Klges september 004 1. Probleem V ee fucte f s, hetzj door metg, hetzj door berekeg, slechts ee edg tl fuctewrde (her + 1 beked: f( x0, f( x1,, f( x We wlle deze (verder obekede fucte
Lgrge-polyome Dck Klges september 004 1. Probleem V ee fucte f s, hetzj door metg, hetzj door berekeg, slechts ee edg tl fuctewrde (her + 1 beked: f( x0, f( x1,, f( x We wlle deze (verder obekede fucte
Hoofdstuk 2 DE STELLING VAN PYTHAGORAS
 Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Analyse. Lieve Houwaer Dany Vanbeveren
 Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Samenvatting. Fouriertheorie en distributies. Fourier en Schwartz. De warmtevergelijking. De exacte benadering
 Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Algebra. Dr. Caroline Danneels
 Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
Moderne wiskunde: berekenen zwaartepunt vwo B
 Moderne wiskunde: erekenen zwrtepunt vwo B In de edities 7 en 8 ws er in de slotdelen vn VWO B ruimte genomen voor een prgrf over het erekenen vn een zwrtepunt. In de negende editie is er voor gekozen
Moderne wiskunde: erekenen zwrtepunt vwo B In de edities 7 en 8 ws er in de slotdelen vn VWO B ruimte genomen voor een prgrf over het erekenen vn een zwrtepunt. In de negende editie is er voor gekozen
PR en QR snijden de grote as van E in respectievelijk U en V. Bewijs dat de vector UV. x 2y. a 4b. sin sin cos cos. a b 2 2. cos cos, sin sin.
 Oplossing Op e ellips E neem je twee vste punt P Q e vernderlijk punt R De middelloodlijn vn e constnte PR QR snijd de grote s vn E in respectievelijk U V Bewijs dt de vector UV vector is (dus onfhnkelijk
Oplossing Op e ellips E neem je twee vste punt P Q e vernderlijk punt R De middelloodlijn vn e constnte PR QR snijd de grote s vn E in respectievelijk U V Bewijs dt de vector UV vector is (dus onfhnkelijk
Lineaire formules.
 www.betles.nl In de wiskunde horen bij grfieken beplde formules wrmee deze grfiek getekend kn worden. zijn formules die in een grfiek een reeks vn punten oplevert die op een rechte lijn liggen. In de vorige
www.betles.nl In de wiskunde horen bij grfieken beplde formules wrmee deze grfiek getekend kn worden. zijn formules die in een grfiek een reeks vn punten oplevert die op een rechte lijn liggen. In de vorige
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
In dit hoofdstuk introduceren we de hoofdrolspelers van het college: eindige automaten.
 9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
Merkwaardige producten en ontbinden in factoren
 6 Merkwrdige producten en ontinden in fctoren Dit kun je l 1 een mcht tot een mcht verheffen eentermen vermenigvuldigen 3 eentermen delen 4 veeltermen vermenigvuldigen 5 een veelterm delen door een eenterm
6 Merkwrdige producten en ontinden in fctoren Dit kun je l 1 een mcht tot een mcht verheffen eentermen vermenigvuldigen 3 eentermen delen 4 veeltermen vermenigvuldigen 5 een veelterm delen door een eenterm
Uitwerking Tentamen Analyse B, 28 juni lim
 Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Deel D. Breuken en algebra n
 Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Formulekaart VWO wiskunde B
 Formlekrt VWO B /9 Formlekrt VWO wiskde B Ksrekei Telle! = ( )... 0! =! = k k!( k)! Ksrekei Voor toevlsvriele X e Y eldt E( X + Y) = E( X) + E( Y ) Voor ofhkelijke toevlsvriele X e Y eldt σ( X + Y) = σ
Formlekrt VWO B /9 Formlekrt VWO wiskde B Ksrekei Telle! = ( )... 0! =! = k k!( k)! Ksrekei Voor toevlsvriele X e Y eldt E( X + Y) = E( X) + E( Y ) Voor ofhkelijke toevlsvriele X e Y eldt σ( X + Y) = σ
Eindexamen vwo wiskunde B pilot I
 Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
1.3 Wortels. x x 36 6 = x = 1.5 Breuken. teller teller noemer noemer. Delen: vermenigvuldig met het omgekeerde.
 Voorereidende opgven Stoomursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit tot wr je kunt en g verder
Voorereidende opgven Stoomursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit tot wr je kunt en g verder
2. Gegeven is de driehoek van figuur 10.10a. Gevraagd worden hoek β en de zijden a en c.
 Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Hoofdstuk 2: Bewerkingen in R
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Hoofdstuk 5: Vergelijkingen van de
 Werkoek Alger (ursus voor 5u wiskunde) Hoofdstuk 5 : Vergelijkingen vn de e grd met één onekende Nm:. Hoofdstuk 5: Vergelijkingen vn de - 45 - e grd met één onekende. Instp (oek pg 7). Vn een rehthoek
Werkoek Alger (ursus voor 5u wiskunde) Hoofdstuk 5 : Vergelijkingen vn de e grd met één onekende Nm:. Hoofdstuk 5: Vergelijkingen vn de - 45 - e grd met één onekende. Instp (oek pg 7). Vn een rehthoek
3. BEPAALDE INTEGRAAL
 3. BEPAALDE INTEGRAAL In dit hoofdstuk gn we op zoek nr een lgemene mnier om de oppervlkte vn een willekeurig vlkdeel te eplen. We ouwen onze redenering op vi ondersommen, ovensommen en Riemnnsommen om
3. BEPAALDE INTEGRAAL In dit hoofdstuk gn we op zoek nr een lgemene mnier om de oppervlkte vn een willekeurig vlkdeel te eplen. We ouwen onze redenering op vi ondersommen, ovensommen en Riemnnsommen om
Leon van den Broek, Maris van Haandel, Dolf van den Hombergh, Aafke Piekaar, Daan van Smaalen. Iddink voortgezet onderwijs bv, Postbus 14, 6710 BA Ede
 7 Rekee Di hoofdsuk is edoeld ls vullig op he oek voor VWO wiskude B Ihoudsopgve 7 Rekee Breuke Worels 8 Rekee i de meekude Rekee i de ksrekeig 7 eerse vereerde eperimeele uigve, juli 008 Colofo 008 Sichig
7 Rekee Di hoofdsuk is edoeld ls vullig op he oek voor VWO wiskude B Ihoudsopgve 7 Rekee Breuke Worels 8 Rekee i de meekude Rekee i de ksrekeig 7 eerse vereerde eperimeele uigve, juli 008 Colofo 008 Sichig
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
OVERZICHT VAN DE FORMULES
 80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
Primitieve en integraal
 Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 4 Primitieve en integrl Een motivtie om nr de fgeleide vn een functie f te kijken is het beplen vn de richtingscoëfficiënt vn de rklijn
Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 4 Primitieve en integrl Een motivtie om nr de fgeleide vn een functie f te kijken is het beplen vn de richtingscoëfficiënt vn de rklijn
HOOFDSTUK 1 BASISBEGRIPPEN
 I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
Elementaire speciale functies
 ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
HET BELANG VAN. Vragen Tijdens de voordracht op 14 augustus 2007 hebben we de volgende vragen besproken.
 HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Formeel Denken. Herfst 2004. Contents
 Formeel Denken Hermn Geuvers Deels geseerd op het herfst 2002 dictt vn Henk Brendregt en Bs Spitters, met dnk n het Discrete Wiskunde dictt vn Wim Gielen Herfst 2004 Contents 1 Automten 1 1.1 Automten
Formeel Denken Hermn Geuvers Deels geseerd op het herfst 2002 dictt vn Henk Brendregt en Bs Spitters, met dnk n het Discrete Wiskunde dictt vn Wim Gielen Herfst 2004 Contents 1 Automten 1 1.1 Automten
Formularium goniometrie
 Jr 6 : Formulrium 6u en 7u Formulrium goniometrie sin α cos α Definities : tn α cot α secα cscα cos α sin α cos α sin α Gevolg : tn α cot α cot α tn α Hoofdformule : cos sin Gevolg : tn sec cot csc α α
Jr 6 : Formulrium 6u en 7u Formulrium goniometrie sin α cos α Definities : tn α cot α secα cscα cos α sin α cos α sin α Gevolg : tn α cot α cot α tn α Hoofdformule : cos sin Gevolg : tn sec cot csc α α
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
REKENEN MACHTEN MET. 5N4p EEBII 2013 GGHM
 REKENEN MET MACHTEN Np EEBII 0 GGHM Inhoud Herhlin: Eponentiele roei... Netieve Mchten... Geroken mchten... Etr Oefeninen... 9 Hoere-mchts functies... 0 Overzicht vn de reels... Herhlin: Eponentiële roei
REKENEN MET MACHTEN Np EEBII 0 GGHM Inhoud Herhlin: Eponentiele roei... Netieve Mchten... Geroken mchten... Etr Oefeninen... 9 Hoere-mchts functies... 0 Overzicht vn de reels... Herhlin: Eponentiële roei
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Continuïteit en Nulpunten
 Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
6.0 INTRO. 1 a Bekijk de sommen hiernaast en ga na of ze kloppen. 1 2 0 3 = 2 2 3 1 4 = 2 3 4 2 5 = 2 4 5 3 6 = 2 5 6 4 7 = 2...
 113 6.0 INTRO 1 Bekijk de sommen hiernst en g n of ze kloppen. Schrijf de twee volgende sommen uit de rij op en controleer of deze ook ls uitkomst 2 heen. c Schrijf twee sommen op die veel verder in de
113 6.0 INTRO 1 Bekijk de sommen hiernst en g n of ze kloppen. Schrijf de twee volgende sommen uit de rij op en controleer of deze ook ls uitkomst 2 heen. c Schrijf twee sommen op die veel verder in de
Integralen. DE ONBEPAALDE INTEGRAAL VAN f(x) wordt genoteerd met f(x)dx, en is de meest algemene zogenaamde primitieve van f(x) dat is:
 Integrlen DE ONBEPAALDE INTEGRAAL VAN f() wordt genoteerd met f()d, en is de meest lgemene zogenmde primitieve vn f() dt is: f()d = F() + C wrij F() elke functie is zodnig dt F'() = f() en C een willekeurige
Integrlen DE ONBEPAALDE INTEGRAAL VAN f() wordt genoteerd met f()d, en is de meest lgemene zogenmde primitieve vn f() dt is: f()d = F() + C wrij F() elke functie is zodnig dt F'() = f() en C een willekeurige
Bekijk onderstaand algoritme recalg. Bepaal recalg(5) en laat zien hoe u het antwoord hebt verkregen.
 Vooreeldtentmen 1 Tentmen Dtstructuren en lgoritmen (T641 en T6741) OPGAVE 1 c d Bekijk onderstnd lgoritme recalg. Bepl recalg() en lt zien hoe u het ntwoord het verkregen. Wt erekent recalg in het lgemeen?
Vooreeldtentmen 1 Tentmen Dtstructuren en lgoritmen (T641 en T6741) OPGAVE 1 c d Bekijk onderstnd lgoritme recalg. Bepl recalg() en lt zien hoe u het ntwoord het verkregen. Wt erekent recalg in het lgemeen?
( ) Formulekaart VWO. Kansrekening. Tellen. k n k. Binomium van Newton : Kansrekening. Voor toevalsvariabelen X en Y geldt: E ( X + Y ) = E(
 Formulert VWO Telle! ( )... 0!!!( )! Biomium v Newto : Ksreei ( + ) Ksreei 0 Voor toevlsvriele X e Y el: E ( X + Y ) E( X ) + E( Y ) Voor ofhelije toevlsvriele X e Y el: σ ( X + Y ) σ ( X ) + σ ( Y ) -wet
Formulert VWO Telle! ( )... 0!!!( )! Biomium v Newto : Ksreei ( + ) Ksreei 0 Voor toevlsvriele X e Y el: E ( X + Y ) E( X ) + E( Y ) Voor ofhelije toevlsvriele X e Y el: σ ( X + Y ) σ ( X ) + σ ( Y ) -wet
1. Gegeven is het polynoom P (z) = z 4 + 4z 3 + 6z 2 + 4z + 5 met z C.
 Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
reëelwaardige functies
 Primitieven en Riemnn- integrlen vn reëelwrdige functies Het begrip primitieve vn een R R functie Stel : f( ) reëelwrdige functie, met definitie gebied = intervl I Def : F( ) is primitieve functie vn f(
Primitieven en Riemnn- integrlen vn reëelwrdige functies Het begrip primitieve vn een R R functie Stel : f( ) reëelwrdige functie, met definitie gebied = intervl I Def : F( ) is primitieve functie vn f(
Oplossingen extra oefeningen: rijen (leerstof RR, leerstof MR)
 Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
