Integraalrekening. Georg Friedrich Bernhard Riemann Breselenz 17 september 1826 Selasca 20 juni 1866
|
|
|
- Norbert van de Veen
- 5 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Iegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 sepemer 86 Selsc jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geef de iegrl v ee posiieve fucie ee uwkeurige eekeis he egrip "oppervlke oder de kromme". He eevoudigse iegrlegrip is geseerd op de formulerig v Berhrd Riem e word drom soms Riem-iegrl geoemd. De Leesgue-iegrl, geoemd r zij edeker Heri Leesgue, is ee cosrucie die ee groere klsse v fucies iegreerr mk; hij k ovedie worde geruik over dere domeie d de reële gelle.
2 ) De differeil ) Defiiie Op de grfiek zie je ee fleidre fucie f sme me hr rklij i pu, f. Voor ee verderlijk pu defiiëre we d d y f ' he differeiequoië e wee d De vergelijkig v de rklij is d y f '. f Op de figuur zie we d dy f '. e y f f. We oeme y lim de fgeleide v f is i.. ee ederig is voor y. Hoe kleier (dus hoe dicher ij lig), hoe eer de ederig. We oeme dy de differeil v fucie f i. ' Algemee defiiëre we dus i ee willekeurig pu : dy df f Voor de ideieke fucie f geld d df d. ' de defiiie d herschrijve ls dydf f d df Deze formule verduidelijk ook de oie v Leiiz: f '.. Op deze mier kue we d He is zo ook meee duidelijk d ee fucie differeieerr is ls ze fleidr is. Alle rekeregels e formules die we kee v ij fgeleide worde dus eevoudig overgedrge r rekeregels e formules v differeiëre. 5d d Bgsi 5 Vooreeld: 5 Toepssig: Beder 6 me ehulp v differeiëre. Noem f, d is f f y f dy f f '. Neem 6 e, d is 6 we krijge: 6,5.6,., f e. f ',5, zod Cursus iegrlrekeig - - S. Meepeige
3 ) Beplde iegrle ) Ileided vooreeld Er word os gevrgd de oppervlke S e erekee usse de grfiek v de fucie f, de -s e de vericle reche. He is duidelijk d de zo ose figuur (og) gee ekede figuur is wrvoor we oppervlkeformules kee e kue geruike. We kue deze oppervlke wel edere door rechhoekjes e geruike. We verdele de sis v de figuur i 5 gelijke sukke, e eme di ls reedes v oze rechhoeke. Op de likerfiguur eme we ls hooge elkes de kleise fuciewrde i he iervl, op de recherfiguur elkes de groose fuciewrde. Zo krijge we liks ls ederig: 5,.,.,4,.,6,.,6,.,64,4 s. De mehode die we liks geruike zl duidelijk lijd e klei zij. We oeme he ee odersom voor de fucie e oere ze me kleie leer s 5 (me ls ide he l rechhoekjes). We krijge rechs ls ederig: S5,.,4,.,6,.,6,.,64,.,44. De mehode die we rechs geruike zl duidelijk lijd e groo zij. We oeme he ee ovesom voor de fucie e oere ze me groe leer S 5 (me ls ide he l rechhoekjes). He gemiddelde v deze wee geef ee zeer goede ederig v de gezoche oppervlke. We s5 S5, 4, 44 sche dus S,4. (De werkelijke oppervlke lijk e zij). We kue deze redeerig herhle voor meer rechhoekjes. He is duidelijk d hoe meer rechhoekjes we eme, hoe dicher de odersom e ovesom ij elkr zulle ligge. Meer og, we kue selle d S lim s lim S. He mg ook duidelijk zij d di ook werk ls we per iervl willekeurige fuciewrde eme (dus ie coseque he miimum of he mimum eme). We krijge d ee ederig voor de oppervlke die usse de odersom e de ovesom lig e dus i de limie voor ook gelijk is de gezoche oppervlke. Cursus iegrlrekeig - - S. Meepeige
4 ) Algemee werkwijze de eplde iegrl Om de oppervlke e erekee egrepe usse de grfiek v ee fucie, de -s e wee vericle reche e, verdele we he iervl, i, gelijke deeliervlle:,,...,, i,...,, i., I elk iervl edere we de oppervlke door de reede v he iervl e vermeigvuldige me ee willekeurig gekoze fuciewrde f c i, me c, i i i. De reede v deze deeliervlle is d gelijk. De gezoche oppervlke word d ederd door: S f ci.. Me k ewijze d voor fucies die coiu zij i, de limie voor v S es e dus gelijk is de werkelijke gezoche oppervlke. We oeme deze limie de eplde iegrl v o v de fucie f. We oere di ls: Cursus iegrlrekeig S. Meepeige i lim S f. d Meer lgemee oeme we fucies wrvoor deze limie es iegreerr over d iervl. c) Georiëeerde oppervlke To hieroe gige we er silzwijged v ui d de grfiek v de fucie f volledig ove de -s lg i he gegeve iervl, (dus werkwijze ekome is d uierrd posiief., : f ). De oppervlke die we vi de lgemee Zou je deze werkwijze herhle voor ee fucie die oder de -s lig i, d kom je ee egieve oppervlke ui. We spreke dus logischerwijze f d oppervlkes ove de -s posiief gereked worde, e oppervlkes oder de -s egief. D di uig e relisisch is volg ler ui ekele fysische vooreelde. We ierpreere lgemee de eplde iegrl v ee (coiue) fucie f v o d ook ls de som v de georiëeerde oppervlke usse de grfiek v f, de -s e de vericle reche e. Zo geld i he geekede vooreeld: f dsi S II SII I SI V.
5 Avullig op de defiiie v eplde iegrl: We me o hieroe lijd ls odergres e ls ovegres om e iegrere, wrij. We kue de defiiie v eplde iegrl verder uireide: Als Als, d selle we f d, d selle we f d f d d) Eigeschppe v de eplde iegrl Ui de defiiie v de eplde iegrl volge omiddellijk de volgede eigeschppe: Eigeschp : opelrheid v de eplde iegrl Als f ee iegreerre fucie is i he iervl p, q, d geld voor lle,, c p, q d: c f d f d f d c Eigeschp : lieriei v de eplde iegrl Als f e g iegreerr zij i he iervl, iegreerr, e voor de eplde iegrl geld: I he ijzoder gelde de eigeschppe:, d is ook de fucie r. f sg. ( r, sr) dr.... r f sg d r f d s g d r. f dr. f d f g d f d g d Eigeschp : ogelijkheidseigeschp Als f e g iegreerr zij i he iervl,, d geld:, : f g f d g d Merk op d deze eigeschp zeker ie geld i de omgekeerde richig! e) Iegrle v veelermfucies Iegrl v ee cose fucie De eplde iegrl cd, me cr is de oppervlke v ee rechhoek me sis e hooge c, zod cdc. Iegrl v de ideieke fucie De eplde iegrl d, is de oppervlke v ee driehoek me sis e hooge, zod d. Cursus iegrlrekeig S. Meepeige
6 Iegrl v de kwdrische fucie De eplde iegrl d, is gee gekede oppervlke. We geruike de defiiie ui de voorgde prgrfe: (verdeel he iervl, i deeliervlle me reede e kies c ls de rechergres v he iervl, dus ci i f c i ), zod i i i f ci i i f. d lim. lim lim *. lim 6 f d (de limie is he quoië v de hoogsegrdserme) ) 6 (* Bewijs zelf me iducie d i Iegrl v veelermfucies i d We eweze hierove d d, i d d e. d Me ehulp v de opelrheid v de eplde iegrl leide we hier ook omiddellijk ui f d: d d d d d, e loog d. d e He lijk dus redelijk om e eme d d e d (me N). We ewijze deze eigeschp ler og. Me ehulp v de lieriei v eplde iegrle kue we u dus veelermfucies iegrere: c c... c cd c c... c c f) De hoofdsellig v de iegrlrekeig We oe i deze prgrf d iegrere i zekere zi de omgekeerde operie is v differeiëre. Iegrlfucies We oeme de fucie I, me I f d, de iegrlfucie v f me odergres. Ze sel dus de verderlijke georiëeerde oppervlke voor egrepe usse de -s e de grfiek v de fucie f i he iervl me verderlijke ovegres,.. Cursus iegrlrekeig S. Meepeige
7 De middelwrdesellig v de iegrlrekeig Sellig: Is f coiu i,, d es er ee Bewijs: We ewijze eers he gevl :, zod:. c f d f c Omd f coiu is i, es er ee kleise e ee groose fuciewrde i d iervl, die we zulle duide me m e M. We volge de lgemee werkwijze voor he erekee v ee eplde iegrl e verdele he iervl i gelijke deeliervlle me reede. I elk v deze iervlle,,,...,,...,,, eme we ee c,., i i i D krijge we chereevolges: i, i i m f c M (lle fuciewrde ligge usse m e M ) m. f c. M. (lles vermeigvuldige me ) i m..... f ci M (sommere over lle deeliervlle) i. f ci.. M (. m i. lim f c.. M m ) i (de limie eme voor ) i. f d. M (defiiie v de eplde iegrl) m f d m M (lles dele door ) Omd f coiu is i, es er volges de sellig v Weiersrss wee gelle zod f p m e p, q, f q M (zie figuur). De ussewrdesellig leer os d d lle fuciewrde usse m e M door mises éé -wrde c usse p e q ereik worde. Omd c usse p e q lig zl he ij uireidig uierrd ook i, ligge. Er es dus mises éé Als Als c,, zod f c d is f c. f d Cursus iegrlrekeig S. Meepeige f d. f d f c. d geld c, : f d f c. f d f c. Opmerkig: We kue de fuciewrde f c fuciewrde over d iervl.. f d ierpreere ls de gemiddelde
8 Meekudige ierpreie: We kue f c f d ook ierpreere ls de hooge v de rechhoek me ls sis he iervl, op de -s wrv de (georiëeerde) oppervlke gelijk is de (georiëeerde) oppervlke usse de grfiek v de fucie e de -s. De hoofdsellig v de iegrlrekeig Sellig: Als f coiu is i,, d geld i, d D f d f. ' Bewijs: Me iegrlfucies kue we di herschrijve ls:, : I f I I I lim (defiiie v fgeleide) ' lim lim lim lim f d f d f Primiieve fucies f d.f c f d f d, me c, (defiiie v iegrlfucie) (iegrlgreze verwissele) (opelrheid v de eplde iegrl) (middelwrdesellig) (ls, d is c ) We oeme F ee primiieve fucie v f ls e slechs ls DF f. He is duidelijk d lle iegrlfucies v ee fucie ook primiieve fucies zij v die fucie. He omgekeerde is echer ie oodzkelijk wr Vooreeld: Als f 5 d zij F e F primiieve fucies v f. 4 Sellig: Twee primiieve fucies v eezelfde fucie verschille slechs ee cose v elkr. Bewijs: Sel d F e F eide primiieve fucies zij v f, d is zowel DF f ls DF f. DF DF DF DF D F F F F C, me CR. Dus Iegrere me ehulp v primiieve fucies Sellig: Als F ee primiieve is v f (coiu i, ), d is Bewijs: We eweze reeds d elke iegrlfucie I de sellig i verd me primiieve fucies volg d d I f d F C. f d F F. f d ee primiieve is v f. Ui Cursus iegrlrekeig S. Meepeige I F C, of dus og d
9 Sel je hieri Neem je d word di f d F C C F, d word he f d F C F F Opmerkig: He verschil word ook vk ls volg geoeerd: F F. f d F We hee u eidelijk ee prkische mehode gevode om eplde iegrle e erekee. Vooreeld : d e Vooreeld : g) Typeproleme e d l le l De oppervlke oder ee kromme erekee Vooreeld: Bereke de oppervlke egrepe usse de prool p y e de -s. De ulpue v de prool zij oppervlke word dus gegeve door: S d, e,. De gezoche.. De oppervlke usse ee kromme e de -s erekee usse wee wrde We zge l d ee eplde iegrl de georiëeerde oppervlke ereke usse wee greze. Als je de werkelijke oppervlke wil erekee k je deze redeerig omkere door he iegrie-iervl i sukke e verdele wr he eke v de fucie ie verder. Zo geld voor de werkelijke oppervlke S egrepe usse de -s e de grfiek v de fucie usse, 5 e : I II III IV 5. S 5 f d e erekee: S S S S S f d f d f d f d Als je iegreer me je rekemchie k di seller door gewoo Cursus iegrlrekeig S. Meepeige
10 Vooreeld: ereke de (werkelijke) oppervlke egrepe usse de -s e de grfiek v de fucie f over he iervl,. We ekijke eers he ekeverloop: De fucie is dus over he e iegrere iervl zowel egief ls posiief. De gezoche oppervlke is dus: 4 4 oppg d d oppg De oppervlke usse wee kromme erekee Ook di is ee eevoudig proleem ls je esef d de (georiëeerde) oppervlke usse wee kromme k ereked worde door he verschil v eide fucies e iegrere. Als je de werkelijke oppervlke wil erekee moe je ervoor zorge d de verschilfucie posiief is (dus d je i je iegrdum de oderse fucie v de ovese fucie frek). f Vooreeld: De grfieke v de fucies g 5 sluie wee geiede S I e S II e i zols fgeeeld op de grfiek. Bewijs d SI SII. We ekijke eers he ekeverloop v de verschilfucie v g f 8 8 Dus I S 8 d E II , zod iderdd SI SII S d. Cursus iegrlrekeig - - S. Meepeige
11 ) Oeplde iegrle ) Defiiie De verzmelig v lle primiieve fucies v ee gegeve fucie f oeme we de oeplde iegrl v f. We eweze reeds d l deze primiieve fucies slechs op ee cose v elkr verschille. We oere de oeplde iegrl v ee fucie f ls volg: f df C Hierij is dus F ee primiieve fucie v f. De cose CR oeme we de iegriecose. De hoofdsellig v de iegrlrekeig mk duidelijk d differeiëre e iegrere ewerkige zij die elkr opheffe. Zo krijge we dus drie eevoudige eigeschppe: df FC d f d f d ) Fudmeele iegrle D f d f Volgede lijs v iegrle zl os ee houvs iede ij he erekee v moeilijkere oeplde iegrle. Zorg ervoor d je deze lijs heel goed eheers! dc q q d C (me q ) q sidcosc dbgsic dgc e de C cosdsic d C l d dcoc l C si d d c l k C cos k Ekel de lse fudmeele iegrl is ie omiddellijk duidelijk. We ewijze d de formule wel degelijk klop door f e leide: Dl k k k k k k k k k k k Iegrie door splisig Sellig: Voor iegreerre fucies f e g, e reële cose r, sr geld de volgede eigeschp:.. r f sg d r f d s g d Bewijs: He recherlid fleide wr je seu op de gekede eigeschppe v fgeleide, geef: Cursus iegrlrekeig - - S. Meepeige
12 r f sg, D r f d s g d D r f d D s g d D r f d s g d D r f d s g d wrui volg d r D f d s D g d r. f sg. d r f d s g d C. Mr oeplde iegrle zij gelijk op ee cose, dus hee we eweze w we moese ewijze. 4 Vooreeld : 4 5d d4 d5 d 4 5C 4 Uierrd k je hier de ussesp oversl. Merk op d je slechs éé iegriecose schrijf. Vooreeld : Soms lig de splisig ies mider voor de hd: d Bg d d d d C Vooreeld : co d csc d csc d dcoc Zeer eevoudige differeilvergelijkige Vooreeld: Bereke f ls gegeve is d f " 6, f ' e, mr we wee ook f " 6 f ' C f 4. f '. C C. Zo hee we dus gevode d f ', wrui volg d f C. Omd f 4.C 4C. De gezoche fucie is dus c) Iegrie door susiuie Sellig: Als F ee primiieve is v f, e g is ee fleidre fucie, d geld: ' f g g df g c Bewijs: D F g c D F g f g g' keig regel f. I de prkijk kom he er vk op om i he iegrdum ee fucie e herkee wrv ook de fgeleide (of differeil) i he iegrdum s. Ekele eevoudige vooreelde: Vooreeld : si cos 4 * 4 cos d d C C 4 4 *: Hier is he duidelijk d si de fgeleide is v cos. We voere ee susiuie ui: Sel cos, d is d sid. Vooreeld : si l d * si d cos C cos l C *: Hier is he duidelijk d de fgeleide is v l. We voere ee susiuie ui: Sel l, d is d d. Cursus iegrlrekeig - - S. Meepeige
13 Vooreeld : *: Hier is he duidelijk d Sel e, d is e e * d e e d d BgsiC Bgsi e C d e d. Apsse v de iegriegreze e de fgeleide is v e. We voere ee susiuie ui: We herekijke eve he eerse vooreeld ui de vorige prgrf, mr u ls eplde iegrl: d. Vooreeld: Bereke de eplde iegrl sicos Mehode : We hee l ee primiieve fucie epld v deze eplde iegrl, dus geld: cos cos 4 cos 5 sicos d Mehode : We kue ij ee susiuie ook de iegriegreze eevoudig psse * 5 sicos d d *: Sel cos, d is d sid. Voor de greze geld Eevoudige susiuies e. He kom soms voor d he iegrdum veel eevoudiger k geschreve worde me ehulp v ee lieire susiuie (sel ) Vooreeld : 5 d d C C 7 Omd deze susiuie zo eevoudig is geruike we hier soms ee korere oie: d 5 d5 C. d d d Vooreeld : Bg C 9 6 Je k deze korere schrijfwijze overiges ook geruike ij ies lsigere susiuies: si d cos Vooreeld : d d l cos C cos cos Of je deze korere mier om susiuies e oere geruik of ie mk je zelf ui. Je wi er uierrd w ijd mee, mr he mg ie e kose g v ee eer egrip. Ekele hdige formules d Sellig: Bg C e d Bgsi C Cursus iegrlrekeig - - S. Meepeige
14 Bewijs: Vooreeld: d d d Bg d d d = Bgsi C C, e d d Bgsi C d) Priële iegrie He is ie lijd mogelijk ee susiuie e vide die os oel ee iegrl e erekee. I d gevl k priële iegrie helpe: Sellig: f dg f g gdf Bewijs: Beide lede fleide geef: ' ' f g' f ' g f g' g f ' D f d g D f g g d f D f g d D f g D g f d Oeplde iegrle zij gelijk op ee cose, dus we hee w we moese ewijze. Opmerkig: De formule voor priële iegrie word vk geschreve ls u dv uv v du Er zij ee l gevlle wr priële iegrie de mees effecieve weg is: Verlge v de grd. Als he iegrdum es ui he produc v ee veelermfucie (of simpelweg ee mch v ) me ee epoeiële of ee goiomerische fucie (v de vorm e, si of k je me priële iegrie de grd v de veelerm verlge. P. I. Vooreeld: cosd sisi d... d si cos ), d Iderdd, de veelerm is verlgd v de weede r de eerse grd. We psse og ees P.I. oe:... si d cos si cos cos.d... E deze lse iegrl is fudmeeel geked, zod we uieidelijk krijge: cos cosd si cossic d si cosc Terugkeer v he iegrdum I specile gevlle k he zij d je (meerdere kere) priële iegrie je oorsprokelijke iegrl zie weerkere. I d gevl spreke we v ee weerkered iegrdum. Di is ijvooreeld Cursus iegrlrekeig S. Meepeige
15 he gevl ls he iegrdum he produc is v ee epoeiële e ee goiomerische fucie (v de vorm e, si of cos ). Vooreeld: Bereke de iegrl 5 e 5 cos d d P. I e cosd e si e sid e si dcos 5 5 cosd si cos cos dsi e e e e cosd e i e cos e cos dsi 5 5 s 4 4 d d Deze lse iegrl is e de iegrl wr we mee egoe zij, dus hierui volg: cos si cos 4 e d e e e cosd e si e cosc 9 9 Alijd ee opie... Soms is he ie lijd meee duidelijk w je me he iegrdum k doe. Mr w je lijd k f d. doe is fleide. Ee priële iegrie die dus lijd k is: f d f ' Vooreeld: ld l e) Iegrle v riole fucies dlc Oeplde iegrle v riole fucies zij heel eevoudig e erekee mr ze vrge eorm veel rekewerk. De Euclidische delig leer os A D Q R gr R gr D. A R Q D D, wrij geld A R Voor de iegrl geld dus ook: d Qd d D. D We moge os dus voor de res cocerere op eche veelermreuke, wrij de grd v de eller kleier is d de grd v de oemer. Vk zulle deze riole moee worde gesplis i prieelreuke. We hee drvoor wee sellig odig: De hoofsellig v de lger: Elke reële veelerm v grd mises éé k oode worde i ee produc v eersegrdsfcore e weedegrdsfcore (me ee egieve discrimi). De sellig v Jcoi: Elke eche veelermreuk k geschreve worde ls som v prieelreuke. We ekijke u i deil de mehode v Jcoi om ee riole fucie e schrijve ls som v prieelreuke: Cursus iegrlrekeig S. Meepeige
16 Schrijf de fucie ls som v ee veelerm e ee eche veelermreuk (Euclidische delig). Oid de oemer i zoveel mogelijk reële fcore v de eerse of weede grd. Zorg ervoor d er i de oemer ekel og fcore voorkome v de vorm e c. ) Elke fcor i de oemer veroorzk ee som prieelreuke v de vorm A B C N ) Elke fcor c... i de oemer veroorzk ee som prieelreuke v de vorm PQ RS TU YZ... c c c c De oekede ellers worde cherf ereked me de mehode v de oeplde coëfficiëe Vooreeld : Bereke d 4 We schrijve he iegrdum eers ls som v ee veelerm e prieelreuke (Jcoi): Sp : Sp : 4 Sp : E dus geld: AB C D (Euclidische delig) ABC D ACD ABCD ABCDBCD 4 ACD A A B C D 8 B ABCD4 C BCD5 D d d d d d d d d d d l l l C 4 Zols je zie heel eevoudig, mr redelijk w rekewerk. 6 4 Vooreeld : Bereke d Di is l ee eche veelermreuk. De oemer is Cursus iegrlrekeig S. Meepeige
17 AB C 6D 6 AB C D 6 6 AC AB5CD AB4C6DBCD Dus AC6 A4 A B 5C D B AB4C6D 4 C BCD D d d d d Hierij geld: d d d d d 4 d d d 6 d d l C l 6 5Bg e C d d C 6 4 l C De eige moeilijke(re) iegrl die je he splise i prieelreuke k ekome is de iegrl v de vorm d (me i de oemer ee egieve discrimi, e ). Di ype c Zod d l 6 5 Bg iegrle k ereked worde me ehulp v prieeliegrie of ee recursieformule (of ee goiomerische susiuie). Ze zulle echer op oese of emes ie gevrgd worde. f) Goiomerische iegrle Bij goiomerische iegrle kom he vk eer op he correc geruike v de gekede goiomerische formules. Zo k je me de formules v Simpso ee produc v (co)siusse schrijve ls ee som (w veel mkkelijker iegreer). De grd verlge k je doe me ehulp v de formules v Cro. De formule voor de iegrl v de secs e de cosecs leer je es v uie, w die is ie zo eevoudig e erekee: Sellig: secd l sec C e cscdl cscco C si d cos cos d * d d Bewijs: sec d d d... cos cos si A B AB AB A (*: ) AB B Cursus iegrlrekeig S. Meepeige
18 d d si... l l l l... C C C si Me ehulp v w eevoudige goiomerie word di: si si si si... l C l C l C l sec C si si cos cos Selle we hieri, d word di: sec d l sec C cscd l csc co C. csc d csc co We erekee ee l dere goiomerische iegrle ls illusrie: cos cos Vooreeld : cos si d cos cos dcos C 5 7 (deze mehode werk lijd ij ee produc v mche v sius e of cosius ls mises éé epoe oeve is) 4 Vooreeld : 4 4 cos4 si cos d si d si d d si 4 cos8 cos4 cos 4 64d d 64 d d si4 si8 si4 si8 C C (deze mehode ij gelijke mche e om de grd verlge k ook lijd op deze mier) si 4 si cos 4 cos Vooreeld : si7 cosd d C 8 g) Iegrle v irriole fucies Ee voor de hd liggede susiuie Kom ee lieire uidrukkig y oder ee l worels voor voer d de susiuie ui wrij he kleise gemee veelvoud is v de worelepoee. Vooreeld: * d d d C C *:5 d d Goiomerische susiuies Sommige iegrle zij ie vi eevoudige e herleide r fudmeele iegrle. I d gevl zij goiomerische susiuies geweze. Cursus iegrlrekeig S. Meepeige
19 Type : Kom de vorm W d zl (e ook zl Vooreeld: voor (me ), d is de susiuie, me, si cos d cosd e Bgsi ) * d cos. 9 d 9 coc C 9si.cos 9 9 *: si 9 cos e d cos Type : Kom de vorm W d zl: (e ook zl Vooreeld:, me,. voor (me ), d is de susiuie si geweze. 9 ( co ) sec geweze., ls, e dus sec, ls, e dus d secd e Bgsec Bgcos ) * 4 d d sec d 8sec si si cos si d d d C sicosc Bgcos C Bgcos C 4 (geseld d ) *: sec 4 e d secd Type : Kom de vorm W d zl (e ook zl Vooreeld: d voor (me ), d is de susiuie, me, sec sec d e Bg ) d d * sec d sec cosd sic C 4 5 *:4 6 4sec e d sec d ( cos e si ) geweze. ( si 4 5 ) Cursus iegrlrekeig S. Meepeige
Integraalrekening. Georg Friedrich Bernhard Riemann Breselenz 17 september 1826 Selasca 20 juni 1866
Itegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 septemer 86 Selsc 0 jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geeft de itegrl v ee positieve fuctie ee uwkeurige
Leon van den Broek, Maris van Haandel, Dolf van den Hombergh, Aafke Piekaar, Daan van Smaalen. Iddink voortgezet onderwijs bv, Postbus 14, 6710 BA Ede
7 Rekee Di hoofdsuk is edoeld ls vullig op he oek voor VWO wiskude B Ihoudsopgve 7 Rekee Breuke Worels 8 Rekee i de meekude Rekee i de ksrekeig 7 eerse vereerde eperimeele uigve, juli 008 Colofo 008 Sichig
Integreren 3 INTEGREREN
Iegrere INTEGREREN Iegrere 4. Iegrere. Bsispricipe Voorbeed : Er oop ee cose sroom i() = c C/s gedurede ee ijdsierv T v begi = o eid = b. Hoevee dig is er gedurede he ijdsierv gersporeerd? Bsiswe Q() =
0 niet gedefinieerd is).
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
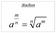Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Formulekaart Wiskunde havo/vwo
Formlekr Wiskde hvo/vwo Vierksvergelijkig Als! e " 4c #, d worde de olossige v de vierksvergelijkig + + c gegeve door 4c, " ± " Mche e logrime q $ + q ( > ) q ( ) q ( > ) ( $ ) $ (, > ) " ( > ) % (, >,!
Examen VWO. wiskunde B. tijdvak 2 woensdag 20 juni uur
Emen VW 018 ijdvk woensdg 0 juni 1.0-16.0 uur wiskunde B Di emen bes ui 16 vrgen. Voor di emen zijn miml 77 punen e behlen. Voor elk vrgnummer s hoeveel punen me een goed nwoord behld kunnen worden. Als
Examen VWO. wiskunde B. tijdvak 2 woensdag 20 juni uur
Emen VW 018 ijdvk woensdg 0 juni 1.0-16.0 uur wiskunde B Di emen bes ui 16 vrgen. Voor di emen zijn miml 77 punen e behlen. Voor elk vrgnummer s hoeveel punen me een goed nwoord behld kunnen worden. Als
t (= aantal jaren na 1950)
Wiskude : Voorbeeldeme me uiwerkie) NB He eme bes ui 5 opve Je die elk woord volledi oe e liche behlve bij de meerkeuzevre; voor deze vre kruis je op he opvebld per vr hokje ) 3 De cijfers usse hkjes eve
1 Bewerkingen met matrices invoeren via voorbeelden. , is een commutatieve groep.
1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Recursie van Poincaré-reeksen
Recursie va Poicaré-reekse Joachim de Rode 3 augusus 2 Bachelorscripie Begeleidig: dr Joche Heiloh KdV Isiuu voor wiskude Faculei der Nauurweeschappe, Wiskude e Iformaica Uiversiei va Amserdam Samevaig
log 27 log log log 27 log log 3 log 9 log 3 1 log 9 2 log log log 2 log log log log 2 2
. Bereken zonder rekenmchine: ) log 8. log 5 5 log 5 5 log 5 5 5 5 ) c) log 7 log 7 log log log d) e) f). 9 7 log log log 9 log log 9 log 5 log log log log 6 8 log log log 8 log log69 log log. log. log
vermenigvuldigd ten opzichte van de y-as, zo ontstaat de grafiek van y
9 Herhling en uireiding vn fgeleide vn e.- en e.-grdsfuncies... B '( ) 4.;. B '( ) 4.47 ; c. B '( ) = 4.5 y '(4) 0.74 4 T (0) = 6,5 C ; T ( 0) = 4,5 C 5. Bevolkingsgrooe op feruri 00 is ongeveer 6.9.000.
Hoofdstuk 3 Logaritmen en groei. Kern 1 Groeitijden
Uiwerkige Wiskude A Newerk VWO 6 Hoofdsuk Logarime e groei www.uiwerkigesie.l Hoofdsuk Logarime e groei Ker Groeiijde a Op = 0 geld voor eide formules da H = 0. log8 H = 0 = 0 8 = 80. Da is ah keer zo
Het differentiequotiënt van een functie in een interval geeft de gemiddelde helling weer van die functie in dat interval. Symbolisch wordt dit:
Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
Eindtoets hoofdstuk 4
Eidoes hoofdsuk Toesopdrch.8 = 5 = 5 +,7 ( 5) = 5 + 35 = 75 = 75 +,7 ( 75) = 75 + 75 = 85 De ewerig is ojuis. = +, 7 ( ) = + 7, 7 =,3 + 6 De ewerig is juis. c +,5 = =,5 r = = ( 5, ) + = ( 5, ) + 8, 5 =
Analyse Plus reader Hoofdstuk 5. Als we, zonder ons af te vragen of het eigenlijk mag, de integraal gaan berekenen vinden het volgende antwoord:
5. Inleiding. We ekijken de inegrl - 4 d. Als we, zonder ons f e vrgen of he eigenlijk mg, de inegrl gn erekenen vinden he volgende nwoord: é ù d= ê- ú =- - =- 4 - ë û- He nwoord is negief. D is vreemd,
AFSTANDEN EN HOEKEN IN
AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
Hoofdstuk 7 - DM Toepassingen
Hoofdsuk 7 - DM Toepssingen ldzijde 7 Vul in op je rekenmhine nmin 0, u(n)0+0,u(n-) en u(nmin). Vul ook in (n) 0+0,(n-) en (nmin)0. Neem Xmin 0, Xm 0, Ymin 0 en Ym 0. Bij een openingskoers n euro krijg
2.1 Het differentiequotiënt
hoodsk : Diereniëren. He dierenieqoiën Me een ncie kn je de onwikkeling n een grooheid beschrijen. Neem bijoorbeeld een schoonspringer die n de ienmeerplnk spring. Als je de lchwrijing erwrloos, kn je
Hoofdstuk 4. Opdracht 4.16. Algemene oplossing: Algemene oplossing: n 1 1 2 n 1 7/2. Algemene oplossing: + = + ( ) Algemene oplossing: Opdracht 4.
Hoofdsuk Opdrch.6 k x + xk = = r = Algemee oplossig: k r xk = + xk = + / k xk = + k 9 7 x = x + 7 x + x = 7 x x = + + + 7 = r = Algemee oplossig: r 7/ x = + x = + / x = 7 c α α ( α α ) x = x x x x = x
1) Definitie, rekenkundige en meetkundige rijen
Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Verloop van exponentiele en logaritmische functies
Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Acdemi Press Dele Bij delig vermeigvuldigt me met het omgekeerde v de deler..3.5 Vereevoudige Het is goed mogelijk dt voorgde bewerkige iet de
Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
C. von Schwartzenberg 1/8. 1b Bij situatie II is er sprake van een evenredig verband. bij p = 12,50 hoort q = 6500. W is evenredig met S,
G&R havo A eel C vo Schwarzeberg 1/8 1a Bij I wor y vier keer zo klei (us he viere eel) ; bij II wor y (precies als ) ook vier keer zo groo 1b Bij siuaie II is er sprake va ee evereig verba a (rech)evereig
4 Differentierekening en reeksen
WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Donderdag 20 mei 13.30 16.30 uur
Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Het kwadraat van een tweeterm a+b. (a+b)²
Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Het effectief tarief van de transactiekosten op de aankoop van de eigen zelfbewoonde woning
He effecief arief va de rasaciekose op de aakoop va de eige woig Seupu Beleidsreleva oderzoek Besuurlijke Orgaisaie Vlaadere Spoor Fiscaliei ber.brys@hoge.be He effecief arief va de rasaciekose op de aakoop
Eindexamen wiskunde B vwo 2010 - II
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Noordhoff Uitgevers bv
Overzih Emensof Anlse He is de vergelijking vn een lijn me srwrde 00 en helling 0. Omd de inhoud nuurlijk nie negief kn worden, moeen de -wrden (W) gekozen worden ussen 0 en 00 en de -wrden () ussen 0
A P E L D O A POE RL N D O O R N
58 Roues Apeldoorn Apeldoorn roue Apeldoorn roue R v e n w e g R v e n w e g 0 100 0 200 100 300 200 400 300 500m. 400 500m. 59 A r n h e m s e w e g A P E L D A P O E O L R D N O O R N Z u i d e r p r
x 4,60en y 6,22. Dus de maximale gemiddelde winst is 6,22 euro per mat. Er worden dan 460matten per week geproduceerd. dw dq
15 Differeie«re bladzijde178 16 a dw dq ˆ 1,5q2 8,25q W 550mae per week, dus q ˆ 5,5 dw dq ˆ 1,5 5,5 2 8,25 5,5 ˆ 0 qˆ5,5 Ui de sches volg da W maimaal is voor q ˆ 5,5. W ma ˆ 0,5 5,5 3 4,125 5,5 2 10
Periodiciteit bij breuken
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
opgaven formele structuren procesalgebra
opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Extra oefening bij hoofdstuk 1
Era oefening ij hoofdsuk a Een goede venserinselling voor de funie f is : X min en X ma en Y min eny ma 0. Voor de funie g X min 0 en X ma 0 en Y min 0 eny ma 0. y 0 8 8 0 y 0 0 0 0 0 0 0 0 0 0 0 0 0 Veriale
2 Veelhoeken 1 REGELMATIGE VEELHOEKEN
Veelhoeke 1 EGELMATIGE VEELHOEKEN Voor meetkudige figure met meer da vier zijde geruike we vaak de verzamel aam veelhoeke. Als we te make hee met regelmatige veelhoeke, kue we hu omtrek e oppervlakte erekee
PARADOXEN 9 Dr. Luc Gheysens
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
Hoofdstuk 5 - Differentiaalvergelijkingen
Hoofdsuk 5 - Differeniaalvergelijkingen 5. Differenievergelijkingen ladzijde a 0 3 4 5 A 00 0 04 06 08 0 oename B 00 30 69,00 9,70 85,6 37,9 oename 30 39 50,70 65,9 85,68 C 00 3 73,60 7,68 97,98 389,38
Het reëel getal b is een derdewortel van het reëel getal a c. Een getal en zijn derdewortel hebben hetzelfde toestandsteken.
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
Ongelijkheden. IMO trainingsweekend 2013
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
16.6 Opgaven hoofdstuk 7: Producten en combinatoriek
166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
Hoofdstuk 9: Afgeleide functies en toepassingen
Hoostuk 9: Ageleie ucties e toepssige 9. Aleibrhei Deitie: Ee uctie is leibr i om ( ) IR 9.. Aleibrhei v ee uctie i ee put v het omei eities p. 76: is leibr i is iet leibr i * is rechtsleibr i / rechtergeleie
Videoles Discrete dynamische modellen
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
8 want 5,8 2 = 33,64 > 33 5 want 7,5 2 = 56,25 > 56,2 5 want 2,5 2 = 6,25.
Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
Formulekaart VWO wiskunde B
Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
L i mb u r g s e L a n d m a r k s
L i mb u r g s e L a n d m a r k s P r o g r a m m a I n v e s t e r e n i n S t ed e n e n D o r p e n, l i j n 2 ; D e L i m b u r g s e I d e n t i t e i t v e r s i e 1. 0 D o c u m e n t h i s t o
HET BELANG VAN. Vragen Tijdens de voordracht op 14 augustus 2007 hebben we de volgende vragen besproken.
HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
Bepaling toezichtvorm gemeente Stein
Bepaling toezichtvorm 2008-2011 gemeente Stein F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, juni 2 0 0 8 V e r d i e p i n g s o n d e r z o e k S t e i
Eigenschappen van de bewerkingen in R Toets jezelf: herhalingsoefeningen voor examen I
Toets jezelf: herhlingsoefeningen voor emen I - - Overzicht vn wt je moet kennen voor dit emen:. Alger:. Hoofdstuk : Reële getllen. Hoofdstuk : Eigenschppen vn de ewerkingen in R o Optellen, ftrekken,
Hoofdstuk 0: algebraïsche formules
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Inleiding: Gladde binding. Baan gegeven: bewegingsvergelijking: m r. aard van de binding gladde binding: uitdrukking in cartesische assen:
Ileiig: Gle iig B gegee: (s Γ (s (s reierch: R ( uiweige rch: K ( ewegigsergelijig: m r K R ( r e iig gle iig: R. ( uiruig i cresische sse: m K m K m K R R R i is ee selsel i 4 oeee: s( R R R us hee we
Vectoranalyse voor TG
college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
Examen HAVO. wiskunde A. tijdvak 2 woensdag 19 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
Eindexamen wiskunde B1 vwo I
indeamen wiskunde B vwo 009 - I Over een parabool gespannen In figuur is de grafiek van de funcie f me f ( ) = 3 geekend. Tussen wee punen en S die even ver van O op de -as liggen, word denkbeeldig een
Toepassingen op Integraalrekening
Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
2) Kegelsneden (in basisvorm)
) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
Elektrificering van een (bestaande) fiets, wat globale berekeningen
Elekrificerig va ee (besaae) fies, wa globale berekeige Hieroer heb ik ee algemee uileg geaa va wa berekeige ie va belag zij voor ee elekrificaie va ee fies. Voor e helerhei e uileg zij wa perceages e
H O E D U U R I S L I M B U R G?
H O E D U U R I S L I M B U R G? N AD E R E I N F O R M A T I E S T A T E N C O M M I S S I E S OV E R O N D E R AN D E R E A F V A L S T O F F E N H E F F I N G E N I N L I M B U R G 1 6 a u g u s t u
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
6.4 Rekenen met evenwichtsreacties
6.4 Rekenen met evenwihtsreties An de hnd vn een reeks vooreelden zullen we het rekenwerk ehndelen n evenwihtsreties. Vooreeld 6.2 We estuderen het gsevenwiht: A(g) + B(g) C(g) + D(g) In een ruimte vn
In dit hoofdstuk introduceren we de hoofdrolspelers van het college: eindige automaten.
9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
III. Integraalvergelijkingen.
III. Inegrlvergelijkingen. In di hoofdsuk pssen we de specrlheorie vn operoren op Hilberruimen oe op een nl lineire inegrlvergelijkingen. In een volgende hoofdsuk zullen we zien hoe beplde ypen differenilvergelijkingen
Matrixrekening - Samenvatting
I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
Toepassingen op Integraalrekening
Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Bepaling toezichtvorm gemeente Meerlo-Wanssum
Bepaling toezichtvorm 2007-2010 gemeente Meerlo-Wanssum F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k Provincie L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k M e e
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Uitwerkingen Toets 1 IEEE, Modules 1 en 2
Uiwerkingen Toes IEEE, Modules en Daum: 9 sepember 007 Tijd: 0.40.0 (90 minuen) Opgave I) Di is een warmmakerje. In woorden is V is de serieschakeling van, en (de parallelschakeling van 3 en 4) of V =
Een meetkundige constructie van de som van een meetkundige rij
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
a = 1 b = 0 k = 1 ax + b = lim f(x) lim
BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
HOOFDSTUK 1 BASISBEGRIPPEN
I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
Bepaling toezichtvorm gemeente Simpelveld
Bepaling toezichtvorm 2008-2011 gemeente Simpelveld F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, j u n i 2 0 0 8 V e r d i e p i n g s o n d e r z o e k
Paragraaf 11.0 : Riemann-som en oppervlakte
Hoodstk Iterlrekei V Wis B Pi v Prr : Riem-som e oppervlkte Les Riem-som Deiitie Riem-som Ee oppervlkte k je edere met ehlp v ee Riem-som = i Vooreeld Geeve is de ctie = Schets de riek v - tot Beder de
Formulekaart VWO wiskunde B
Formlekrt VWO B /9 Formlekrt VWO wiskde B Ksrekei Telle! = ( )... 0! =! = k k!( k)! Ksrekei Voor toevlsvriele X e Y eldt E( X + Y) = E( X) + E( Y ) Voor ofhkelijke toevlsvriele X e Y eldt σ( X + Y) = σ
OVERZICHT VAN DE FORMULES
80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Formularium Wiskunde
Formulrium Wiskude Te gebruike bij exme Ileidig tot de Hogere Wiskude Trscedete fucties. Goiometrische fucties t x = tg x = si x cos x cot x = cotg x = cos x si x sec x = cos x cosec x = si x cos( ± b)
Voorbereidende opgaven Stoomcursus
Voorereidende opgven Stoomcursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt geruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het eknopt overzicht
Formeel Denken 2012 Uitwerkingen Tentamen
1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
Praktische opdracht: Complexe getallen en de Julia-verzameling
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Lijnen en vlakken in. Klas 6N en 7N Wiskunde 5 perioden Kees Temme Versie 2
Lijnen en vlkken in Kls N en N Wiskunde perioden Kees Temme Versie . Coördinten in R³.... De vergelijking vn een vlk ().... De vectorvoorstelling vn een lijn.... De vectorvoorstelling vn een vlk... 8.
Overzicht Examenstof Wiskunde A
Oefenoes ij hoofdsuk en Overzih Examensof Wiskunde A a X min 0, X max 0, Y min 0 en Y max 000. 0 lier per minuu. Als de ank leeg is, dan is W 0, dus 00 0 0 dus 0. Na 0 minuen is de ank leeg. a Neem de
Appendix A: De rij van Fibonacci
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
Een studie van reguliere schierveelhoeken met behulp van algebraïsche combinatoriek
Faculei Weeschappe Vakgroep Wiskude Ee sudie va reguliere schierveelhoeke me behulp va algebraïsche combiaoriek Dries Hose Promoor: Bar De Bruy Maserproef igedied er behalig va de academische graad va
Platte en bolle meetkunde
Hoofdstuk I Pltte en olle meetkunde F. vn der lij Dit hoofdstuk evt een door de redctie gemkte ewerking vn een in Utrecht op 6 oktoer 1993 gegeven Kleidoscoop college vn F. vn der lij. Grg willen we professor
Examen VWO. Wiskunde B1 (nieuwe stijl)
Wiskunde B (nieuwe sijl) Examen VW Voorbereidend Weenschappelijk nderwijs Tijdvak Donderdag 22 mei 3.30 6.30 uur 20 03 Voor di examen zijn maximaal 83 punen e behalen; he examen besaa ui 20 vragen. Voor
Henk Pijls Korteweg-de Vries Instituut voor Wiskunde Universiteit van Amsterdam
Jn vn de Crts Henk Pijls De kromme gevormd door de toppen vn de prolen door drie gegeven punten NAW 5/9 nr. mrt 08 9 Jn vn de Crts Korteweg-de Vries Instituut voor Wiskunde Universiteit vn Amsterdm j.vndecrts@uv.nl
Losse sokken. Inleiding. Hoe ik sokken opvouw. 42 Losse sokken
Jurje Bos heef ee eigeziige maier va he opvouwe va zij sokke: radom er ee ui de wasmad eme, kijke of er ee bijpassede sok op schoo lig, zo ie: sok erbij, zowel: vouwe maar. Ee werkwijze als deze lever
Hoofdstuk 1 Rijen en webgrafieken
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Bepaling toezichtvorm gemeente Venray
Bepaling toezichtvorm 2007-2010 gemeente Venray F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k V e n
Correctievoorschrift VWO. Wiskunde B1,2 (nieuwe stijl)
Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
INLEIDING FYSISCH-EXPERIMENTELE VAARDIGHEDEN (3A560) , ANTWOORDEN. en y m.b.v. y = n
INLEIDING FYICH-EXEIENTELE VAADIGHEDEN (3A56 3-1-, ANTWOODEN OGAVE 1 (a y wordt bereked mb y ³ e y mb y Uit de laatste ergelijkig ide we y i ³ x1 1 + + x ³ x1 1 + + x ³ + j6i i j xj y + j6i i j xj Omdat
1.3 Wortels. x x 36 6 = x = 1.5 Breuken. teller teller noemer noemer. Delen: vermenigvuldig met het omgekeerde.
Voorereidende opgven Stoomursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit tot wr je kunt en g verder
k H G I K J HG I kk J = Formulekaart Wiskunde havo/vwo Vierkantsvergelijking Machten en logaritmen Binomium van Newton Goniometrische formules
Formlekr Wiskde hvo/vwo Vierksvergelijkig Als e 4 c, d worde de olossige v de vierksvergelijkig + + c = gegeve door 4c, = ± Mche e logrime q + q = ( > ) q ( ) q = ( > ) ( ) = = F H G I K J = ( >, ) ( >
Voorbereidende opgaven Stoomcursus
Voorereidende opgven Stoomcursus Tips: MEER DAN 0 JAAR ERVARING Dit document estt uit twee delen: de voorereidende opgven en een overzicht met lgerïsche vrdigheden. Mk de volgende opgven het liefst voorin
We kennen in de wiskunde de volgende getallenverzamelingen:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n
Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n M w. d r s. E. L. J. E n g e l s ( P r o v i n c i e L i m b u r g ) M w. d r s.