DEEL II Integraalrekening + index 50
|
|
|
- Leona Hendriks
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 INHOUDSOPGAVE DEEL II Itegrlrekeig + ide 5. Het erekee v de primitieve fuctie 5. Het terugvide v de evetuele costte 54. De susitutiemethode 56.. Lstigere vrite 59. Prtieël iterere 6.4 Cyclometrische fucties 64.5 Breuksplitsig 67.6 De eplde itegrl (deel ) 69.7 Riemsomme 7 4. De eplde itegrl (deel ) Gemiddelde fuctiewrde 8 4. Beplde itegrle e oppervlkte 8 4. Lstigere eplde itegrle Oppervlkte tusse twee fucties Oppervlkte tusse twee fucties, Itegrtie r y toe Ihoudserekeige: Omwetelige Ihoudserekeige: Slicig Ihoudserekeige: Omweteligsvlk tusse f() e g() Booglegte 9 4. Oppervlkte v lichme Zwrteput Areid 98 diverse opgve uit Getl e Ruimte VWO B4. 5
2 .. Het erekee v de primitieve fuctie Het proces v itegrtie is i de eerste plts het vide v de primitieve (oorsprokelijke) fuctie die hoort ij ee gegeve fgeleide fuctie. Het proces dt leidt v fgeleide tot primitieve fuctie oemt me itegrere. I de Egelse e Amerikse litertuur vidt je de term "tiderivte" e me defiieert de "tiderivte" d ook ls volgt: Ee fuctie F() is ee tiderivte v ee fuctie f() ls: F'() = f() voor lle i het domei v f. De verzmelig v "tiderivtes" oemt me de oeplde itegrl v f, met ichtemig v, voorgesteld door: f() Het -symool oemt me het itegrl-teke e de fuctie f() de itegrd e verrd de vriele wrr geitegreerd wordt. Algemee geldt de defiitie: f() = F() + C Vooreelde die dit illustrere: = + C, wt de fgeleide v is weer 6 = + C =.5 + C cos() = si() + C Feitelijk drie we het differetieer-proces u weer om: we kee de fgeleide e vrge os f welke fuctie ooit geleidt heeft tot deze fgeleide. De techiek die we hierij geruike is prim i regels te vtte, doch eige routie i het vide v de primitieve op grod v 'gezod verstd' regt os dikwijls seller tot het resultt. Voor de lstigere gevlle, geruike we ee 'echte techiek'. De ottie dy e zij fkomstig uit de differetilrekeig e het werke met differetile. We zulle er hier iet verder op i g. Hieroder (volgede pgi) vidt je de meest elgrijke oeplde itegrle: dwz ls ee fgeleide eked is, is hiermee de primitieve sel gevode. Het spreekt voor zich dt de eige cotrole is: opieuw differetiere. Itegrl-formules: C,, rtiol. e: C cos( k) si( k) C k si( k) cos( k) C k 5
3 Wt is de rol v de Costte? De costte moet ij het primitivere wel worde meegeome omdt er vele primitieve zij die differetiere dezelfde fgeleide oplevere. Dergelijke primitieve verschille i getlwrde die differetiere wegvlle. Om ij het itegrtie-proces dit i ogeschouw te eme, eemt me de costte mee, die lter middels ee eked put zo mogelijk ee wrde k krijge: Vooreeld: Itegreer de fuctie f() = + e epl de primitieve die teves door put (,) gt: Oplossig: f() = +... dus F(X) = C g door (,) => = C dus C = Ook ij dit proces est ekele regels zols we die eerder ij limiete gezie hee: Costte-regel: kf() = k f() Regel voor egtieve itegrle: - f() = - f() Som e verschilregel: [ f() + g() ] = f() + g() [ f() - g() ] = f() - g() Term-voor-term itegrtie: ( + + c) = ( ) + + c = (/) c + C Vooreeld ( 5) 5 C.5 C 5 C.5 5 C Vooreeld C Vooreeld ( ) C Vooreeld ( ) l( ) C 5
4 Oderstde oefeige moet je wel echt mke om het itegrtie-proces i de vigers te krijge.!! OEFENSTOF. Los de volgede itegrle op: ) = ) 6 = c) - 4 = d) (/) = e) (/) = f) -si() = g) (5/ ) = h) (- - (/ )) = i) ( ) =. Los de volgede itegrle op: ) ( ) t c) ( ) ) ( t ) dt d) ( ) e ) (4si ) y dy f ) ( cos( ) si( )) 5
5 . Het terugvide v de evetuele Costte: Iitil Vlue Prolems Uit deze itegrtievooreelde lijkt steeds ee Costte te otst; dt hee we eerder gezie. Idie st ee fgeleide fuctie ook ee (strt)put eked is, is het mogelijk ivullig te geve deze costte. Vooreeld Ee voorwerp vlt met ee versellig v 9,8 m/s. Als het voorwerp gee egiselheid hd (t t=, V=), wt is zij selheid t secode? dv 9,8 dt dv dt 9,8 dt dt V 9,8 t C. Agezie V()= C V 9,8t Vooreeld Ee fuctie heeft ls fgeleide dy/ =,4 +. Het origieel (de primitieve) gt door (,5). Vid deze. dy,4 dy (, 4 ) 4 y, C. Door(,5) 4 y,,9 Vooreeld Ee projectiel schiet me omhoog vf ee m hoog pltform. De vgsselheid = 6m/s. Hoe hoog komt dit projectiel secode? ds dv d s v, e dt dt dt d s ds gegeve: 9,8 m / s, () 6 m / s, s() m dt dt ds 9,8 dt dt dt ds ds 9,8 t C, () 6 C 6 dt dt ds 9,8t 6 dt Nu ogmls itegrere om s te vide. ds dt ( 9,8 t 6) dt dt s 4,9t 6 t C, s() s t t 4,9 6 N secode: s () 4,9() 6() 48,9 m 54
6 OEFENINGEN. Bereke de volgede 'iitil vlue-prolems' e los hu cotte op.. dy 5, y() 6. dy, y() c. dy, y() - d. dy, y() - e. dy /, y(-) -5 f. dr si( ), r() d g. d y dy 6, () 4, y() h. d y dy 6, () 6, y(). ds I oderstde formules zij de selhede v dt I oderstde opgve vidt je de selheid e iitiele positie v putmss's lgs ee rechte lij. Wr zitte deze mss's op tijdtip t? ) ds v 9,8t 5, dt s() ) ds v t, dt s(,5) 4 c) ds v si( t), dt s() d) ds t v cos( ), s( ) dt 55
7 . De sustitutiemethode Tot op dit momet zij we i stt om eevoudige itegrle terug te vide e op te losse. Het wordt lstiger ls i de itegrd ee product v twee fucties of stt, of de gegeve fgeleide het resultt is v het toepsse v de kettigregel. We egie met die ltste. Vooreeld: Zoek de primitieve v de fuctie: f() = (4 - ). () Het is duidelijk dt dit te leze ls u. met u = 4 - De primitieve v u ws ( eig deke...) f u u u.5 ( ), met 4 F( ) u C dus met igevulde u krijg je: F( ) (4 ) C Echter ls je dit differetieert. otstt: df.5 f ( ) (4 ) e dt stod er iet.. Eigelijk moete we het itegrtieproces zodig toepsse zodt de kettigregel weer wordt meegeome. dy dy du De kettigregel og eve.. du Dit eteket dt je de itegrl zó herschrijft dt wordt omgezet i du... Het vooreeld og ees... Zoek de primitieve v de fuctie: f() = (4 - ). Nu zegge we dit: Bereke de primitieve v f ( ) 4.5 () f ( ) u u, met u 4.5 () f ( ) u. du () Agezie: u=4- geldt: 4 e dus = du (G!!) 4.5 (4) Dus krijg je: F( ) u du (5) u du, 4 geeft 4 4 u du u met u 4 (6) Zó. De lstigheid zit 'm i het omzette v r du. Hierdoor wordt.h.w. de kettigregel recht ged e i omgekeerde volgorde weer 'verreket'. 56
8 Ee mkkelijk vooreeld: 5 ( ) zou je kue herschrijve tot: 5 ( u) met: du u ( ) du D wordt de oplosre itegrl: ( ) ( ) u du u C C Ee der vooreeld 5 zou je kue herschrijve tot: u met: du u ( 5) du D wordt de oplosre itegrl: ( 5) u u du udu u C C 8 Nog ee vooreeld: cos( ) zou je kue herschrijve tot: cos( u) met: du u ( ) du D wordt de oplosre itegrl: cos( u) cos( u) du cos( u) du si( u) C si( ) C Nog ee vooreeld: si( ) si( ) zou je kue herschrijve tot: si( u) met: du D wordt de oplosre itegrl: u du u u du u du u c c si( ) si( ) si( ) cos( ) cos( ) Het is duidelijk dt dit mooie gevlle zij. Immers i het vooreeld hierove rk je op ee elegte mier de fctor kwijt zijde het restproduct v de kettigregel. 57
9 Ee dere vorm (ook og erg (...veel te... )gustig eigelijk).. ( ) ( ) zou je kue herschrijve tot: u du omdt: du D wordt de oplosre itegrl: u ( ), dus du ( ) du ( ) ( ) 6 6 u du u du u C u C C Lstigere vorme eise veel meer keis v lger e v stdrd oplossige. Meestl komt het erop eer dt me de itegrl proeert te herschrijve zodt deze oplosr wordt. Als dt lles iet meer lukt, is llee de umerieke ederig og mogelijk Het recept voor de sustitutiemethode is dus deze:. Defiieer welk fuctie-deel u() is e differetieer deze prt.. Eeml vstgesteld wt u() is, is eked wie du/ is e dus hoe je door du k vervge.. Losse fctore k me uite de itegrtie hle; zeker dige ls pi. 4. Itegreer de fuctie. VOORBEELD Itegreer ( 5) du u dus du ( 5), : e dus =, of og mooier: 4 du =. ( 5) 4 u du e dt is: 4 4 u ( 5) Proeer ees zelf: OEFENINGEN ) ( 4) ) c) 8 ( ) d) ( t 4t )( t t) dt e) ( 4) ds f ) ds g) l(4 ) 5s 4 r h) r dr 8 i) l( ) j) 5 58
10 .. Lstigere vrite Gegeve de fuctie t(). Deze k je herschrijve tot de reuk si()/cos(). We g lte zie hoe me t() k primitivere. y t( ), vidt: t( ) si( ) du () t() =, u = cos(), si( ), -du si( ) cos( ) si( ) () Dus: t( ) du cos( ) cos( ) () e du l cos( ) c cos( ) De truc zit hem i het slim splitse. Hieroder ee vooreeld dt het mechisme duidelijk mkt; het feitelijke gevl is veel mkkelijker te primitievere. 4 y vidt:. Simpel twoord: c. 4 du () e dus: u =,, du=,,5du= (),5 udu 4 () e ws,5(,5u ) met u= geeft: c. Vooreeld: Bereke cos ( ). tw: cos ( ) cos( ) cos ( ) cos( )( si ( )) Dus: Noem u=si() e du cos ( ) cos( )( si ( )) ( ) u u c, = si( ) (si( )) c 4 =cos(), du=cos(). u du Bereke zelf : ) t( ) ) si ( ) c) d) e e) si ( )cos( ) f) l( ) 59
11 .. Prtieel itegrere. Deze gevceerde mier v itegrtie is ee pssed twoord op het terugdrie v de product e quotiet-regel. Hoewel vele itegrle toch llee umeriek oplosr zij, e ee lgerisch twoord uitgeslote is, k met deze methode og wel het e.e.. ereikt worde. Veroderstel dt we moete primitievere: y=e ( + 4). Het moge direct duidelijk zij dt sustitutie hier iet de orde is. Immers zulle de eide fctore iet elkrs fgeleide kue zij. Beschouw: y=u v. Bereke de primitieve. d(u v) dv du () y= u v, u v, e dus ook: dv d(u v) du u v u dv d( uv) v du () Primitiveer lle lede liks e rechts: u dv d( uv) v du u dv u v v du Het prtiële zit hem i dt me slechts deels itegreert. Dus ls je ee fuctie ls ove moet itegrere, stelt je ee lijstje op v u, dies fgeleide, v e dies fgeleide. D ps je deze omgewerkte productregel toe. Bereke e ( 4) u 4, du v e, dv e Regel toepsse: u dv u v v du ( 4) e ( 4) e e = ( 4) e e = ( 4) e e c So fr, so good. Je moet wel slim kieze wie je voor f eemt e wie d dg/ wordt. Doe je het verkeerd om, d zl de tweede itegrl eroerder zij d wr je mee ego. Bereke e ( 4) u e, du e v 4, dv ( 4) Regel toepsse: u dv u v v du ( 4) ( 4) ( 4 ) e e e e toe... 6
12 Nog ee die lstiger is: Bereke l( ) u l( ), du 4 v, dv 4 Regel toepsse: u dv u v v du, Bereke primitieve v l() 4 4 l( ) l( ) = l( ) = l( ) c 4 6 Opdrcht: Cotroleer dit twoord door te differetiere. Opdrcht: Kies f e g epres verkeerd om e otdek wt er mis gt. Teslotte: Meerdere prtiele stppe kue odig zij... Dt is ee kwestie v goed kieze é geduld... Bereke de primtieve v e Bereke u e dus du = v=,5e wt dv = e. dus:. e,5e,5e og 's... e u e dus du v,5 e wt dv,5 e. dus: e,5e, 5e, 5e =,5e,5 e,5 e =,5e,5 e, 5 e c Met deze methode k me eevoudige itegrle oplosse: Los op: l( ) () Geruik u dv u v v du é l() = l() () u=l(), du= v= dv= () l( ) l( ) du = l( ) 6
13 Ee listige e lstige... Itegreer de volgede fuctie: f()=l(). l( ) () Voor de sustitutiemethode zoek je steeds r ee vorm wri u e zij fgeleide is te vide: du kies: u =,5du () slimme: l() =,5l( )!!! G dt dit klopt! () Nu kue we dus schrijve: du l( ),5l( ) e met sus v,5 e u:,5l( u) du,5 l( u) du Wete dt l( u) du u l( u) u...,5( u l( u) u) c. (4) Terugsustitutie:,5( l( ) ),5 l(),5 (5) Dus othoudt: c c l( ),5 l(),5 c Ditzelfde hd ook simpeler gekud met prtiele itegrtie: dv du l( ) We geruike: u u v v dv u l( ), dus = e = dus v=,5 l( ) l( ),5,5,5 l( ),5 Je ziet dt itegrere soms op ee simpele, soms omslchtige mier tot std komt. Bereke zelf: ) f ( ) cos( ) ) f ( ) l( ) c) f ( ) l( ) e) f ( ) l ( ) (pittige!!) f) ( )si( ) l( ) g) l( ) h) c. 6
14 Som e v hiervoor toch mr eve uitgewerkt... Itegreer l ( ). dv du () We geruike: u u v v e l( ),5 l( ),5 c du () u=l ( ), (l( )) l ( ) dv Dus v,5 dv du () u u v v geruike: l ( ) l ( ),5,5 l ( ) l ( ),5,5 l ( ). (4) Het proces og ees herhle met de tweede itegrl: du dv v (5) u=l ( ), (l( )) l( ) Dus,5 dus... igevuld: (6) l ( ),5,5 l ( ) = l ( ),5,5 l ( ), 5,5 l( ) = l ( ),5,5 l ( ),5 l( ) = l ( ),5,5 l ( ),5,5 l( ),5 c = (7) l ( ) l ( ) l( ) c pffff Eigelijk zou ee derde itegrtiestp odig zij voor die ltste itegrl. Gelukkig ws dt imiddels ee 'oude' ekede. 6
15 .4 Cyclometrische fucties..4.. Iverse fucties. Iverse fucties kue llee est, ls me de rol v y e k vewissele. Immers is ee fuctie llee v toepssig ls ij elke keuze v slechts éé wrde v y hoort. Ee fuctie v y= heeft ls iverse y. Ee siuscurve k me wel spiegele i de lij y= (rolverwisselig) mr mits ie het domei -pi/ tot pi/. De iverse v si() is rcsi(). De iverse v cos() is rccos(). De iverse v t() is rct(). Iversefucties zij overiges iet de fucties: t( ) etc.. Verwrrede ottie: t - () is de iverse v t() e (t()) - eteket We espreke rct() gedefiieerd tusse y=-pi/ e pi/. We poge de reuk te primitivere. dt, =t(t) => t ( t), => = t ( t) dt t ( t) dus: ( t ( t) dt) ( dt) dt t ( t) t ( t) e dt t. Dus sustitutie v door t(t) levert t op. Agezie we =t(t) hee geoemd, moet t rct() zij. Coclusie: dt rct( ) c. De primitieve v deze reuk leidt tot rct(t). t( ) Othoudt: t( u) du l(cos( u)) c Othoudt: Othoudt: Othoudt: u du rct u u du rcsi u u du rccos u u Voorl de eerste twee kome we og wel ees tege. Zo guw wortels i de reuk ee rol spele, wordt het lstiger. 64
16 Wt vooreelde v differetierig Differetieer f()= rct(,5) du opl: u=,5, dus,5, f(u)= rct(u) df,5 = u (,5 ) Differetieer f()=rct( ) du, f(u)=rct(u) df = 4 u ( ) opl: u=, dus Wt vooreelde v itegrtie Er zij twee miere v werke: () Werk de reuk om tot, l zo: 5 Bereke () ( ) 9 ( ) = = 9 9 ( ) du u= ) e, dus du 5 5 dus krijg je: du rct 9 u 9 u 5 rct () Met de gegeve formule: 5 5, ( ) ( ) dus u=(-) e =, met formule: u du rct u 5 5 Dus otstt: rct( ) rct klr. 65
17 Bereke. 4 () Herschrijf de fuctie zodt de vorm otstt... u () dus: 4,5 4 du (4) u =,5,,5 du (5) du 6 du,5 u u (6) 6rct(,5)+c. (7) Cotrole:Differetieer 6rct(,5) = 6,5 (,5 ), 5( ) 4 u Bereke. Allee u seller met formule: du rct 4 u () Herschrijf de fuctie zodt de vorm otstt... u () dus: 4 (4) e dus otstt rct( ) c 6rct(,5)+c. Ee vergelijkre pk geld voor rcsi e rccos. Oefee Itegreer: Itegreer: ) ) c) d) e)
18 .5. Breuksplitsig Als ltste zou het hdig zij om veel voorkomede reuke te herkee e om te zette i stdrd itegrle. Er zij vier type reuke: I De oemer is te schrijve ls ( ) p q II De oemer is te schijve ls ( p) III De oemer is te schrijve ls ( p)( q). IIII De oemer is v ee lgere mcht d de teller e k dus worde uitgedeeld. I Het eerste type: I) 45 Nu splitst me de reuk, zodt sustitutie k: 4 5 ) ) Het eerste deel wordt du, met du ( 4) e wordt u dus l( 45) 4) Het tweede deel: 5 (5rct( )) ( ) 5) Dus de hele oplossig wordt: l( 4 5) (5rct( )) ( ) c II) Het tweede type: ( ) ( ) ( ) 5 ( ) ( ) 5 ( ) ( ) l( ) 5 c 67
19 Bij de derde mier moet me de oemer kue schrijve ls ee product v twee fctore. (+p)(+q). III Het derde type: re-rrge... I) 4 Nu splitst me de reuk, i eevoudigere reuke: ) 4 Ofwel: ( ) ( ) e, dus moet gelde: ( )( ) ( )( ) (+)+(+)=-, dus +++=-, (+)++=-. Coclusie: +=, +=- Ee eevoudig stelsel met =-,5 e =,5. (los zelf op!) Los u op:,5,5 ( ) ( ),5l( ),5l( ) C IV Het vierde type: 4 Bereke :. 6 4 dele door, levert op: ++, dus 4 6,5 6 l( ) C Opgve: (komed uit G&R, deel VWO B4 (editie 7) Itegreer : ) ) c) d)
20 .6 De eplde itegrl (deel ) I dit hoofdstuk kijke we r de eplde itegrl: de itegrl die.h.w. is opgeslote tusse twee greze. We lichte dit toe dhv ee vooreeld: Uit de medische wereld is eked hoe me het volume loed k eple dt het hrt per miuut k wegpompe. Het is duidelijk dt deze hoeveelheid epld wordt door de omstdighede wri de ptiet verkeert: Coditie, ctiviteit, hrt-toestd ed. Me ijecteert i de loed ee vloeistof, juist voordt het hrt wordt ereikt: i de ders dus. Deze vloeistof k me hrt-pssge mete e zodig i-eeld rege zodt de cocetrtie v deze test-stof gedetecteerd wordt. Veroderstel dt ee megsel i éé ijectie ls prop wordt igercht; verloop v tijd meet me de cocetrtie v deze test-vloeistof ls iets-uitgesmeerde curve: verschil i stroomselheid e ee zekere 'retetie-tijd' mke deze curve-vorm e dies tijdstip v verschije. Horizotl zie we de tijd i secode. Vertikl de cocetrtie i mg/liter loed. Hoe kome we u te wete welke 'slgkrcht', gemete i liters per miuut het hrt heeft? Me hteert de volgede formule: 'Crdic-output' = 6 hoeveelheid teststof i mg oppervlkte oder de curve Uitgewerkt: met ls oppervlkte: mg. l - sec: 6 mg 6 l sec l l sec sec mi sec mi mg l Veroderstel verder dt de tel de volgede wrde heeft ( fleze) secods: mg. secods mg Me k u de oppervlkte vststelle door i de curve.h.w. kleie rechthoeke te kieze die de curve zo goed mogelijk volge: 69
21 (de streepjes kome iet geheel overee met de telwrde..) De totle oppervlkte oder de curve is dus voor te stelle ls de som v de kleie rechthoekjes. Horizotl zij de rechthoekjes groot, vertikl geldt hu fuctiewrde. We hee os u edied v rechthoekjes die zo zij eergezet dt de ovezijde i het midde op de juiste hoogte is. Me k er ook voor kieze steeds de likerkt of rechterkt ls hoogte te houde. Dit leidt logischerwijs tot over- e oderschttige v de oppervlkte. Totle oppervlkte is hier f(6) + f(8) +... f() = 57.6 mg.sec/liter Dit gegeve k me fleze de grfiek; f(6)=,4 e vermeigvuldigd met levert dt,8 op. etc... Zo vid me 57,6 mg sec/liter Ageome dt me met 5.6 mg stof ego e dit igevuld i de eerder geoemde formule geeft: = 5.8 liter/miuut 57.6 Wt leert os dit vooreeld? Dt me i sommige situties de oppervlkte oder ee curve odig heeft e deze diet te edere met kleie rechthoekjes. Deze techiek ekijke we iets preciezer. Beked is dt de fgelegde weg v ee projectiel met selheid v, te vide is door: S = v t. Om ee idruk te krijge v de fgelegde weg v ee projectiel gedurede de eerste secode kue we per secode kijke hoevér het projectiel is. Me schiet ee projectiel de lucht i met de formule: v = 6-9,8t. We geruike deze lkjes methode om te zie of we de fgelegde weg gedurede de eerste drie secode kue vide. We eme eerst de likergreze. () Er zij drie itervlle = sec. () Afstd = f() ofwel (6-9,8()) = 6m Afstd = f() ofwel (6-9,8()) = 5,m Afstd = f() ofwel (6-9,8()) = 4,4m Sme: 45.6m. Zou me u iet de likergreze mr de rechtergreze v dt itervl eme: () Afstd = f() ofwel (6-9,8()) = 5,m Afstd = f() ofwel (6-9,8()) = 4,4m Afstd = f() ofwel (6-9,8()) =,6m 7
22 Sme: 4.m. Dt scheelt ogl erg veel.. Het mkt u og VEEL uit of je de fuctiewrde liks of rechts v itervl kiest. I oderstde tel zie we de uitkomste v deze erekeig ij het verkleie v het itervl. Dus ipv secode,,5 secode etc... Atl suitervlle Legte likergres gehoude rechtergres gehoude 45,6 4. 6,5 44,5 48,55,5 49,58 4, 4,5 47,74 44,6 48,6 46,8 44,98 96, 46,6 45,44 9,6 46, 45,67 Het zl iet verze dt me ij og kleiere itervlle i eide kolomme gelijke wrde zl vide. Dit proces zl covergere r de wrde 46 m. Vooreeld. Het vide v de ihoud v ee ol door plkke te eme die op 'dmschijve' lijke. We g uit v de formule: f()=(6 - ), hetgee ee hlve cirkel is. Het domei loopt d v -4 tot 4., =. Wt we erekee geldt voor de totle ol! Zie figuur: De ihoud v elke schijf: is (f(c)) (loog r ) De som v l deze ihoude zl zij ( = ): ij c: (6-(-4) )= ij c: (6-(-) )=7 ij c (6-(-) )= ij c4: (6-(-) )=5 ij c5: (6-() )=6 ij c6: (6-() )=5 ij c7: (6-() )= ij c8: (6-() )=7 Sme: 84. De echte ihoud is 4 r , Coclusie: Door het kieze v itervlle, mkt het i het egi uit of je de liker- of rechtergres eemt ls (fuctie)hoogte. 7
23 Als me steeds kleiere itervlle kiest, is dit verschil steeds kleier e me k zich voorstelle dt i ee limiet-situtie dit verschil zelfs ul is. Dit ltste is ee grote verdieste geweest v de Duitser Riem. Op deze mier k me trouwes ook de gemiddelde wrde v ee fuctie vststelle op ee zeker trject. Vooreeld: We zoeke de gemiddelde fuctiehoogte v de prool y = op het itervl [-,]. We verdele het stuk i zesse e eme steeds het midde! v elke stf. Elk itervl is / reed; dus Gemiddelde wrde: {(-5/6) + (-/6) + (-/6) + (/6) + (/6) + (5/6) }/6 =7/6=,4 Welu: Om ee lg verhl te ekorte: de eerder geoemde wiskudige Riem heeft zich met de wiskudige chtergrod v de som v rechthoeke ezig gehoude e hiervoor de itegrlrekeig flik gevuld. I essetie zit de zk zo i elkr:. Me stelt vst dt de oppervlkte oder ee curve diet te worde epld e geruikt hierij de rechthoek-pk.. Me verdeelt het trject i stroke met eezelfde reedte. Elke rechthoek is zo gekoze dt het midde erv de curve rkt/sijdt. Die hoogte is dus f(k). Vermeigvuldigd met levert de opppervlkte v die rechthoek 4. Er otstt ee som v rechthoeke f() met ls reedte e f() ls hoogte. Voor de som eme we het teke. Oppervlktev deze rechthoeke wordt d k f ( ) k 7
24 .7 RiemSomme. k f ( ) k Me oemt deze uitdrukkig ee Riemsom. Dit is de leidig om te kome tot de eplde itegrl zols we l zge. Toch is het werke met de Riemsom iet llee leidig; het toot i tl gevlle hoe het mechisme i elkr steekt. Me cummuleert de producte v fuctiewrde met ijehorede reedte. Stel me moet de som eple v de oppervlkte oder de prool y = - op het domei [-,] met itervlreedte =,: We eme d de fuctiewrde hlverwege die stfreedte dus f(,) e f(,) De totle oppervlkte zl ogeveer zij: f(-,9) + f(-,7) +... f(,9) I de GRM reket me die zó uit: sum(seq(f()*,, strt, ed, )) sum(seq(( - )*.,, -.9,.9,.)) Atwoord:,4 De sleutelwoorde sum e seq, vidt me i de 'ctlog' v de GRM. We kue u de Riem som geruike voor de eplig v oppervlkte e de ectere itegrl; hetgee eigelijk het limietgevl is v die Riemsom. OEFENSTOF I l deze gevlle is het hdig de situte eve te schetse of te plotte met de GRM.. Geruik de GRM om de Riemsom te eple v: De oppervlkte tusse de curve: y = + e de lij y =. Geruik ee =,.. Geruik de GRM om de Riemsom te eple v: De oppervlkte tusse de curve: y = (5- ) - 4 e de -s. Geruik ee =,. Je het de selheidsfuctie v(t) = t - t Vidt de fgelegde weg v de eerste 5 secode door de Riemsom te eme v die eerste vijf secode. Kies =,5 e eem de fuctiehoogte egied ij,5 e d steeds,5 verder. (de ltste zit dus op 4,75) 4. Me ijecteert ee ptiet ee hoeveelheid v 5 mg kleurstof teeide de eerder geoemde 'crdic output' te wete te kome. Me meet de volgede gegeves: secods ij. kleurstof coc secods ij. kleurstof coc De resultte st i de grfiek hieroder. 7
25 ) Verid zelf de pute tot ee vloeiede kromme. Om de crdic output te vide, moet je dus de reedte v de kolom (hier : ) vermeigvuldige met het midde v elke kolom. Mk dus ee schttig v deze fuctiewrde i het midde v elke kolom. Deze optellig levert som v rechthoekjes die ij ederig gelijk is de hoeveel mg kleurstof. hoeveelheidmgkleurstof Deze oppervlkte A vul je i de formule : crdic output = 6 OppervlkteA ) Doe dt. 5 Om de ihoud v ee ol te vide k je geruik mke v de cirkel: y 6. Hiermee epl je de fuctiehoogte voor ee kwrtcirkel. Neem reedte v,5 e kies zo 8 stroke. ( de cirkel heeft r=4). ) De ihoud estt uit 'dmschijve', met strl f() e ihoud (f()) Bereke de ihoud v de ol ) Vergelijk je twoord met (4/)r ls klopped twoord. ================================================================ De Riemsom heeft ee kemerkede vorm. k f ( ) k I het volgede deel g we de stp mke r de eplde itegrl; eigelijk eme we de limiet v de Riemsom door het itervlletje r te lte dere. 74
26 TOEVOEGING: Riemsomme met de GRM Otdek eve hoe je GRM i dit verd werkt: De fuctie seq ( ) (sequece) seq (,,,4,) geeft ls uitkomst de rij {,,,,4} seq (,,,4,) geeft ls uitkomst de rij {,,4,9,6} seq (,,,,) geeft ls uitkomst de rij { 8,7} Dus ls je dát sommeert met de fuctie sum: sum (seq (,,,4,)) geeft ls uitkomst sum (seq (,,,4,)) geeft ls uitkomst sum (seq (,,,,)) geeft ls uitkomst 5 e dt klopt ook ls het gt om de optellig v de eerdere getlle. Als het gt om ee fuctie wroder je oppervlk wil wete, zij deze uitkomste te hoog! Bekijk de eerste: y =. Je wil wete wt de oppervlkte is oder deze curve v = tot =4.. De stroke zij reed = e hoog f(), dus egied ij = tot =4 sum (seq (,,, 4,)) = (teveel!). De stroke zij reed =,5 e hoog f(), dus egied ij =.5 tot =.75 sum (seq (*,5,,.5,.75,.5)) = 8 (goed). De stroke zij reed =, e hoog f(), dus egied ij =. tot =.9 sum (seq (*,,,.,.9,.)) = 8 (goed) 4. De stroke zij reed =, e hoog f(), dus egied ij =. tot =.99 sum (seq (*,,,.,.99,.)) =... lg deke lijft dus 8. OPM Dt de ltste uitkomste steeds 8 geve. is omdt de fuctie mooi rechtlijig is. Bij iets ls of of zo, zl dt ders ligge.. OPM Besef je dt de strook die reed is, strt ij strtput +,5 e eidigt ij eidput -,5. Hoe kleier je eemt. hoe ecter. 75
27 4. De eplde itegrl (deel ) I dit deel v de theorie, mke we de stp v de Riem-sommtie r de eplde itegrl. We zoude dit klkkeloos kue meedele, iets dt i os wiskudeoek toch vk geeurd, mr hier poog ik iets meer egrip te creere voor de chterliggede gedchte.. Zoder ewijs is de som v de eerste gehele getlle, kwdrte e derde mchte: i. ii. k iii. k ( ) k k k k ( )( 6 ( ) De formule ii vertelt os de som v de eerste kwdrte e de formule iii de som v de eerste derde-mchte. Deze hee we l eve odig! De verdieste v Riem zij dt hij deze wiskude heeft uitgeouwd e otdekte dt ls me de limiet m v dergelijke somme, me steeds dezelfde oppervlkte vod, ogecht of je ij de rechthoekjes u de likerkt, het midde, dwel de rechterkt ls hoogte kiest. Zowr ee opzierede uitkomst! Voorwrde (kemerked voor het limiet-deke) is dt me zich de reedte v de rechthoekjes zo klei mogelijk (dered r ) voorstelt. De formele defiities he ik u weggelte mr i essetie zegt me: Als de 'reedte' v het rechthoekje P (de orm gehete) kleier is d ee zekere, d is het verschil v deze gevode som v l die rechthoeke met de echte oppervlkte I kleier d ee zekere e (epsilo). I vkjrgo: P f ( c) I k Weer ders gesteld: Als je de reedte v die rechthoekjes gewoo hééél klei eemt, zl de fwijkig v wt je op deze mier uitreket ij iks fwijke v de echte wrde... We oeme I de eplde itegrl v f over het trject [,] e zegge dt f itegreerr is over [,] e zegge dt de Riemitegrl covergeert r ee vste wrde I. Nottie: lim f ( c) f ( ) P k Dus i gewoo Nederlds: De som v de oppervlkte oder ee curve op ee vst e zeker trject [,] k me zie ls de eplde (vwege het vste trject) itegrl over [,] f(). Weéér ders: Als je dus ee oppervlkte oder ee curve wil wete, k je de Riem-som geruike, mr ook de zogemde 'eplde itegrl'. 76
28 Vooreeld I Me eplt de fgelegde weg vuit de selheidsfuctie v(t) = 6-9,8t Welke weg is fgelegd v t= tot t=? Er zij u drie miere v pk mogelijk: I Het is meetkudig ee trpezium, dus losse we het u meetkudig op. Opp,5( )( f ( ) f ( )),5( )((6 9,8() 6 9,8()) (6 9,8() 6 9,8() 8,8 m. II III We geruike de Riemsom Breedte strookjes:, strtput,, eidput,9, dus: sum( seq((6 9,8 ),, X,,,,9,,) Oplossig: 8,8m. We geruike de eplde itegrl e psse de methode toe: F() - F(). Die legge we hier geheel uit! Opp (6 9,8 t) dt 6t 4,9t C (6() 4,9() 6* 4,9() C C m Het is klip e klr duidelijk dt de meetkudige oplossig vk iet zl lukke; zo mooi zij de curves dikwijls iet. Ook k je wel egrijpe dt zelfs methode é het vk lte fwete, omdt er gee formule eked is die ee eplde curve eschrijft. me mkt d óf ee model dt redelijk goed pst, of me vervlt tot umerieke ederigsmethode. Vooreeld II Zoek de oppervlkte oder de curve f() = op het trject [,]. Oplossig: () We oeme o =, e = () We eme steeds de rechtergres ls fuctiewrde voor de zijkt v ee rechthoek. (reket mkkelijker) 77
29 () Noem c =, c =, c =, c = ez (4) De fuctie ws: f() = dus de eerste oppervlkte is: f(c) = f() = () = () = () (5) De tweede oppervlkte is: f(c) = f() = () = () (6) De -de oppervlkte is d: f(c) = f() = () = () (7) De som v deze oppervlkte is d: S f ( c ) k ( ) k k k ( ) k ( )( ). omdt = met ls legte tl rechth. 6 ( )( ). 6 ( ) We kome d tot de slotsom dt de oppervlkte S te schrijve is ls: S. 6 Geruik mked v de defiitie v de eplde itegrl: f ( ) lim f ( c ) P k 78
30 vide ls oppervlkte oder de curve: lims lim. 6. lim 6.( ) 6 Agezie we egoe met het trject ij =, e eidigde ij =, vlt u op dt me voor de oppervlkte k eme te eerste de primitieve e wel op het put. Oppervlk oder y= loped v = tot = is dus (/) Als je deze hele procedure herhlt voor de oppervlkte oder deze curve v = tot ee zekere =, d krijg je uiterrd de uitkomst: (/) Dit eteket dt ls me de oppervlkte wil hee oder ee curve f()= loped v = tot =, me k volst door de primitieve F() te vermidere met F(). Immers ws de primitieve v de fuctie (/). f ( ) lim S F( ) F( ) Dus dit eteket i de prktijk dt de oppervlkte sel wordt gevode door:. itegrtie. formule opstelle F() e F() e. v elkr ftrekke. F() - F(). Ook i dit verhl, wr we proere het e.e.. wt meer te toe, ediee we os teslotte iet v deze limiet-defiities e sommtieregels voor oppervlkte. Het is wel dkzij Riem dt we kue eschikke over de ee tl veelgeruikte itegrtieregels. Merk op dt de itegrtiecostte ij deze eplde itegrle iet v elg is: me vidt de oppervlkte door F() + C -(F() + C) dus F() - F(). te doe. De Costte vlle tege elkr weg. Uit dit vooreeld lijkt vrij duidelijk dt de eplde itegrl v r, mkkelijk k worde gevode door de primitieve fuctie F te eple voor F(). Immers lijkt Oppervlkte = F() -. Als ook zo de oppervlkte voor r k worde gevode (F() - ) d k me emelijk mke dt de oppervlkte v r dus te vide is door: 79
31 F() - F() uit te rekee. 8
32 OEFENSTOF. Bereke de wrde v deze eplde itegrle: 4 ). 5 ). c). d) si( ). Bepl de oppervlkte dt is igeslote door: ) de -s, de lij =4 e f ( ) ( ) ) de y-s, de -s, de lij = e f ( ) cos( ) c) de y-s, de -s, de lij = e f( ) d) de y-s, de -s, de lij = e f ( ). Geruik de GRM om de volgede fucties te plotte. Zoek ij elk v he uit wt de gevrgde oppervlkte is oder de curve op het gegeve trject. 5 ) f ( ) 5, Bepl f ( ) 4 4 ) f ( ), Bepl f ( ), f ( ), f ( ) / c) f ( ) si( ), Bepl f ( ) d) f ( ) l( ), Bepl f ( ) 4. Gegeve de prool: y = Bepl f ( ). Wt gt er mis? 5. Dit wetede.. og ees.. 4 ) ( ), Bepl ( ) f f 4 ) ( ), Bepl ( ) f f ) ( ), Bepl ( ) c f f 8
33 Itegrl regels. ) f ( ). ) f ( ). - f ( ). ) k. f ( ). k. f ( ). 4) f ( ). g( ). ( f ( ) g( )). 5) f ( ). g( ). ( f ( ) g( )). c 6) f ( ). f ( ). f ( ). c 4. Gemiddelde fuctiewrde. Me k de gemiddelde fuctie wrde v ee curve uitrekee door i gedchte de oppervlkte ode de curve te verdele i eideloos veel strookjes met reedte e de volgede gemiddelde te eple: f ( c ) f ( c) f ( c)... f ( c) gemwrde f ( ck ) k f( c ) k k f( c ) f ( c ) De epressie f ( c ) geldt ls Riemsom Nu geldt ook: k k k k v(f) = f ( ck ) f ( ) k k Ee wiskudig theorem zegt ook dt er op het trject [,] ltijd ee f(c) zl zij die ect gelijk is de gevode gemiddelde wrde v(f). k 8
34 Ee eis is wel dt we prte over cotiue fucties. Met deze keis is het mogelijk vst te stelle wt de gemiddelde wrde is v ee fuctie verloop e drmee geldt ook de volgede stellig: f(c) ( - ) = f ( ) Bereke voor de oderstde fucties voor welke hu gemiddelde fuctiewrde gelijk is die f(c). ) f ( ), op itervl [, ] ) f ( ), op itervl [,] c) f ( ) si( ), op itervl [, ] d) f ( ) 4, op itervl [, ] 8
35 4. Beplde itegrle e de totle oppervlkte. Idie me de oppervlkte ereket v het vlk oder de curve v cos() tusse de greze e /, mv de volgede itegrl, vide we: / / cos( ) [si( ) C] si( / ) si( / ) () / / Merk op dt doordt we ee vlk oder de -s eple, we ee egtieve oppervlkte krijge. Geometrisch is metee duidelijk dt dt ls moet worde geleze. Toch schuilt hieri ee gevr. Bereke de oppervlkte oder de curve cos() v tot. cos( ) [si( ) C] si( ) si() () Toch is die oppervlkte ook. Door het 'tege elkr wegvlle' v positieve e egtieve oppervlkke, otst rre twoorde. Me diet dus te itegrere tot de ulpute: / cos( ) cos( ) cos( ) / [si( ) C] si( / ) si() / [si( ) C] si( ) si( / ) / OEFENING Bereke de volgede eplde itegrle; los eerst de ulpute op:,5 4 ) ( 4) ) ( ) 4 c) ( ) d) ( 6 8) 4 e) ( ) f ) -4 7 u g) dv h) 4 v v du 5,5 u i) ( ) j) ( ) t k) ( ) dt - t 8 84
36 4. Lstigere eplde itegrle De techiek is die v hierove, de itegrtietechiek v eerdere prgrfe. ez. Bereke ect: ) ) c) d) e) f ) 6 6, g) Gegeve de fuctie f()= ( i) Bereke de opp v het vlkdeel dt wordt igeslote door f, de -s e de lij =. (ii) Het vlkdeel W wordt igeslote door f, de -s e de lij =p met p>, zodig dt Oppervlkte(W)=. Bereke p. h) Bereke ect i) Bereke ect i) Bereke ect
37 4.4 Oppervlkte tusse twee fucties. Gegeve de fucties y = e de lij y = +. Me teket deze i éé grfiek. Nu wille we de oppervlkte wete die tusse de grfieke i ligt. Me eige vereeldig k me zich ideke dt die gevode k worde door de oppervlkte oder de lij te vermidere met die oder de prool. Uiterrd moete we rekeig houde met de sijpute ls itegrtiegreze. Uitgewerkt: Opp l( ) f ( ) ( ),5 () ( ),5() () {,5( ) ( ) 8 4 {,5 }. (,666) 4,5 Belgrijke opmerkige.. Me moet goed zie welke fuctie me v welke ftrekt.. Me itegreert het verschil v de fucties.. Me itegreert v sijput r sijput, ook rekeig houded met evetuele tusseliggede ulpute. Het is du goed mogelijk dt me het trject - i meer d stukke moet hkke om de juiste oppervlkte te vide. OEFENEN ) f ( ), e g( ) -s e y-s f g ) ( ) cos ( ), e ( ) -s c f g 4 ) ( ), e ( ) -s e y-s d) f ( ), e g( ) 4 -s e y-s 86
38 4.5 Oppervlkte tusse twee fucties, Itegrtie r y toe. Soms is het hdig, soms zelfs oodzkelijk om te itegrere r y toe i plts v r toe. Me diet d de fucties om te zette ls ee fuctie v y r i r y. Vooreeld: Vrg: Vid de oppervlkte tusse de wortelfuctie de rechte lij e de -s!! f() = e g() = - ; Zie opgve hiervoor voor het twoord. Als we deze fuctie zoude schrijve ls ee fuctie r y: f(y)= = y e g(y) = = y + ; De oppervlkte die tusse de fucties e de - e y-s ligt:. Het v toepssig zijde sijput : y = y + -> =4,y=.. Stel itegrl r y op: Opp ( y y ) dy [,5y y y ] 8 4 Wrom ko dt iet op de 'ormle' mier?. Het woord is te zie i de ovestde grfiek. Me k est het stuk ove de -s uitrekee door oppervlkte oder de wortelfuctie te vermidere met die oder de rechte lij. Immers is het stuk odr de lij ee driehoek met ee ij fleesre oppervlkte. Vooreeld Neem de fuctie y = 8l() e y = 4(); Vidt de geslote oppervlkte tusse de eide grfieke e de -s. (zie grfiek) 87
39 Omzette r fuctie v y e d verschil v de fucties itegrere: y y /8 y 8l( ) l( ) e 8 y y y Sijput : (.4,5.7) umeriek epld. 5.7 y /8 y Opp ( e ) dy 6 y /8 5.7 [8 e y ] OEFENINGEN. Zoek de hdigste mier om de oppervlkte te eple: ) f() =, g( ).5, lij y y ) y=, c) f() =, g( ) 4, -s. Het vlkdeel V wordt igeslote door de grfiek v f() = e de lij y = 6 - e de y-s. ) Bereke ect de oppervlkte v V. ) De lij =p verdeelt V i twee gelijke dele met gelijke oppervlkte. Bereke p i twee decimle. Gegeve de fuctie: f( ). Het vlkdeel V wordt igeslote door de grfiek v f e de lij y=-,5 ) Bereke de oppervlkte v V. ) De oppervlkte v vlkdeel W, igeslote door f, lij y=+ e de lije = e =p met p>, is totl gelijk. Wt is de wrde v p Het vlkdeel V wordt igeslote door de grfiek v f( ), de -s de y-s e de lije =8 e y=8 Lij = verdeelt vlk V i twee stukke i de verhoudig : (likerdeel is groter d rechterdeel). Bereke lgerisch de wrde v Gegeve de fucties: f ( ) e g( ) 4 g de -e y-s e de lij =. ) Bereke oppervlkte V. Vlk V wordt egrest door f, 88
40 4.6 Ihoudserekeige: Omwetelige I dit hoofdstuk kijke we r de ihoudseplig v lichme. De ihoud v deze lichme kue op verschillede miere worde ereked. Zodr het gt om mooie geometriche lichme, zij er stdrd formules voor hde zols voor cylider, kegel, etc... Zodr de lichme ee grilliger vorm krijge zulle we de itegrlrekeig moete geruike om deze ihoude og te erekee. Voorwrde is wel dt de fucties cotiue zij op het te itegrere itervl, de uitwedige vorm ee fuctie is hetzij v, hetzij v y. Ee simpel vooreeld. Me ereket de ihoud v ee cylider die op zij kt ligt: Feitelijk ee soort uis die de -s cetrl ls s heeft. De uis is 4 cm reed, 5 cm lg. De -s i deze impressie komt 'r je toe' e de y-s gt omhoog. De figuur k me zich voorstelle ls ee vlk egrest door de lij y=, de -s e de lij =5: die me rod wetelt rod die -s. Door het rodwetele otst ee lichm dt dezelfde ihoud heeft ls i figuur. De ihoud zou me mkkelijk kue vide met hr = 5 =. Als we itegrlrekeig geruike, stelt me zich voor dt de ihoud is opgeouwd uit cirkelvormige plkjes die 'oeidig' du zij e hu volume sme zl eveees die v de cylider zij: Ihoud = r f ( ) ( ( )) () 4 Zou de lij y= schuier lope, zols y =,+, d otstt ee kegel zoder top ls omweteligslichm (zols dt heet). 5 ) G dt de ihoud hierv is: 5 5,4 (, ) (, 4, ),, 667 ) Cotroleer dt met je meetkudekeis v kegels. 89
41 Feitelijk is ee omweteligslichm te vide door ls strl de fuctiewrde te kieze op elke i dt itervl. De itegrl estt eigelijk uit vele cirkelvormige plkjes die tesme het omweteligslichm mke. Ihoud omweteligslichm: f ( ) (,5 ) g( ) (,7 ) Omwetele : p I ( f ( )) ( g( )) Vooreeld Bewijs dt de ihoud v elke kegel, met hoogte e grodstrl r gevode k worde door de formule Gh/ te geruike. De eschrijvede is te zie ls y =. (>) Bewijs: () Hoogte h loopt lgs de -s. Strl r = h => = r/h () Klopt. h h h h ( r) ( f ( )) ( ) h r h h h r h Vooreeld Welk ihoud heeft het lichm dt otstt ls me de wortelfuctie y = roteert om de - s. Me eme het trject v tot 4. Atwoord: 4 4 ( ) =.5 8 Vooreeld Zelfde vrg, mr u wil me het vlk tusse de fuctie e de lij y= lte rotere Er otstt u ee soort hol voorwerp met ee gt eri. (G!) Vidt opieuw de ihoud.. Vergeet iet dt de lij y= de wortelfuctie sijdt i (,) dus het itegrtie-itervl wordt [,4] ipv [,4]. Atwoord: 4 Ihoud ( ) () 4 ( ) [,5 ] 4 OEFENSTOF 4. Bereke de ihoud v de curve y = () die me lt rotere om de -s, op het trject [,4]. Bereke de ihoud v het omweteligslichm (6- ) op het trject [,4] om de -s. Welke vorm otstt? 9
42 . Bewijs dt de ihoud v ee ol met formule: overeekomt met 4 r y r tusse greze -r e r, door middel v omwetelig rod de -s. 4. Bereke de ihoud die otstt ls me () lt wetele om de lij y=. Neem het trject [,4]. Teke de situtie Psop! Nu wordt de itegrl ( ) 4. Me heeft de fuctie y = /. Me wil het vertikle deel v de fuctie wetele om de y-s!! Dus de fuctie wordt = /y e de itegrl: 4 ( ) y Mk de erekeig verder f. 5. Me roteert de prool =y om de lij =. op trject [,] De itegrl wordt dus: ( y ) dy Mk de erekeig verder f. 6. Bereke de ihoud v het olsegmet B dt wordt eslote door vlk V te wetele om de -s. V ligt tusse de ol e rechts v de lij. Formule v de ol: y r 7. Wr moet me ee (kogelrode) ol sijde om 7 ihoude te krijge die ect eve groot zij. Me mg llee de ol vertikl i plkke sijde. Neem de formule: y r, met r =.(Ntiole Weteschpsquiz) 8. Het vlkdeel V wordt igeslote door de lij y=,5, de -s, e de lije =8 e =p. Me kiest p : <p<8. Door V te wetele om d e-s otstt ee fgekotte kegel. Voor welke wrde v p is dies ihoud gelijk 78? 9. Bereke het volume dt wordt epld door het rodwetele v het vlk rod de y-s dt zit tusse de y-s, de fuctie, e de lije y= e y=4. Teke eerst y de situtie!. Me roteert ee vlk dt wordt epld door de prool: =y +. Rottie-s is de lij =. Het edoelde vlk loopt v = tot =. Je mkt u geruik v ( ) ( ) I y dy Leg uit e voer uit. 9
43 4.7 Ihoudserekeige: SLICING. Feitelijk dezelfde pk; llee er is gee sprke v rottie. Als me i ee lichm ee reltie k legge tusse de doorsede op eig put e de ijehorede -wrde, k me ook met de itegrl de ihoud eple. Neem de pyrmide met de put i de oorsprog. Zie figuur Als we eme dt ij =c geldt: legte grodvlk =reedte grodvlk =. D zl de oppervlkte A zij. Dus ij eige =h: A = (f(c)) D wordt de ihoud: h h h ( A) ( ) h Aloog Gh V elg is hier tuurlijk hoe schui je de lije kiest. Het idee hierchter is dt iet elke ihoud otstt door rodwetelig v vlkdele, mr opgeouwd is uit ee som v oppervlkte. Stel ee liggede prool voor i het y vlk. Op elke reedte stelt me ee gelijkzijdige driehoek op: Wt is de ihoud v het volume dt otstt ls me zo v = tot =4 de prool 'vult' met deze driehoeke? () De prool otstt uit =y, y () De legte v de grodlij v elke driehoek is dus () Elke gelijkzijdige driehoek met zijde heeft opp: A( ) 4 (4) 4 4 Alle oppervlkte sme zij d: d ( 4 ) 4 4 d 4 9
44 4.8 Ihoudserekeige: Omweteligsvlk tusse f() e g() Merk op dt er ee groot verschil is tusse: ( f ( ) g( )) e ( ( )) ( ( )) f g Allee de tweede geeft het juiste omweteligslichm om de -s. G dt!! De eerste geeft ee der resultt: l de omwetelig v ee fstd die het verschil is tusse f() e g(). Er otstt d ook gee 'hol' lichm.! Dus de tweede pk levert os het juiste omweteligslichm. Vooreeld: f ( ) (,5 ) g( ) (,7 ) Omwetele : p I ( f ( )) ( g( )) Bereke zelf de ihoud v deze odemloze loempot.. OEFENSTOF. Bereke de ihoud v het omweteligslichm tusse de fucties f()= e g() =, op trject [,4]. Idem voor f()=l() e de lij y= op trject [,]. Idem voor f() = e -,4 e de lij y= op trject [,sijput] 9
45 4.9 Booglegte Nu we veel meer wete v itegrle wordt het ook rdig om ees dere dige met itegrle uit te rekee. Zo k me de legte v ee kromme eveees eple met ee juiste itegrl. Ndeel is dt deze itegrle vk umeriek moete worde opgelost. Techiek: Uit dit simpele pltje lijkt dt de ooglegte over het kleie trjectje v ederd k worde door ( +y ). Pythgors dus. Vooreeld: Wt is de ooglegte v de fuctie y=f() op trject [,]? Oplossig: () Bederig v de ooglegte mv Pythgors: ( +y ). Dit klopt eter rmte me steeds kleier kiest. dus ooglegte g = ( +y ) () y y y Dus lle ooglegte sme: f '( ) Deze itegrle zij meestl llee umeriek oplosr. Je eplt dus eerst de fgeleide v deze fuctie. D los je de itegrl op. Vooreeld: Bereke de ooglegte v y=-/8 + op [-,] () dy/ = -/4 () g = (+(-,5 ))= (+/6 )= () Met GRM fit (f(),x,odergres,ovegres) = fit ((+/6 ),X,-,) =, 94
46 e Vooreeld: Bereke de ooglegte v de fuctie y = l() tusse = e =. Opl: y=l() geeft dy/ = /, dus Legte = ( ) 9,4 Me voert deze fuctie i op de GRM e eplt de itegrl met FIt OEFENSTOF. Bepl de ooglegte v de fuctie y=si() op trject [,]. Bepl de ooglegte v de fuctie y=,5 op trject [-,4]. Bepl de ooglegte v de fuctie y=(6- ) op trject [-4,4] Cotrole: het moet ee hlve cirkel zij! 4. Bepl de ooglegte v de fuctie y=+ op trject [,6] 4. Oppervlkte v lichme. Net zols de ooglegte mkkelijk te vide is, k me ook g wt de oppervlkte is v ee lichm. Me deke zich i dt ee lichm is 'gesede' i ee tl plkke met dikte. De legte v de wd: is de fuctie f() e k worde ederd ls ooglegte. Feitelijk is dt de 'hoogte 'v de plk. Me vidt de wd v deze plk ls rh dus ls Riemsom: De Riemsom v l deze plkjes wordt: f ( k) ( f '( k)) ofwel ls limiet: k Oppervlk f ( k) ( f '( k)) Leze ls: Alle plkjes met cirkelomtrek: f()ooglegte: e hoogte=f() (=f()) e dikte ooglegte. Odks dt de wd v zo' plk iet mooi recht lijkt te zij, vlt dit ezwr weg door met ee zeer kleie te werke wrdoor je eigelijk ee plk v ee rechte uis lijkt uit te rekee. 95
47 OEFENSTOF. Bereke de oppervlkte v de vorm die otstt ls me y=,5 omwetelt op trject [,4]. Bereke de oppervlkte v de vorm die otstt ls me y=si() omwetelt op trject [,] 96
48 4. Zwrteput. Het is mogelijk om met ehulp v itegrle het zwrteput v pltte vorme ect te eple. Ook v ruimtelichme k het zwrteput worde epld. Voor het eple v het zwrteput he je twe ederige odig. I I het zwrteput deke me zich i dt lle mss zich cocetreert i dt ee put. I de figuur lijkt dt Z te zij. II Het krchtmomet M is het product v Xz e Oppervlkte V. Immers dekt me zich de gehele oppervlkte v vlk V gecocetreerd i Z. Dit levert de volgede epressie op: M O( v) f ( ) z z Me k de gehele oppervlkte ook verdele i stroke met ee reedte e hoogte f(). Elke strook heeft zij eige Momet: M = f(). De som v l die stroke levert ee Riem-chtige epressie op, die idie me de strookreedte lt dere tot, overgt i deze itegrl: M f ( ) Als me eide epressie elkr gelijk stelt, vid me voor Xz: f ( ) f ( ) z z f ( ) f ( ) Uit deze etrekkig vid me de -coordit v het zwrteput. Op dezelfde wijze k me de y-coordit v het zwrteput vide. Dit ltste is mider werk; de oppervlkte v vlk V heeft me l l. Dus eerst rolverwisselig e y, e d: y dy dy y z z dy dy Vooreeld Bepl zwrteput v het vlk ove de curve y= e de lij y=4. Oppervlkte = (4 ) Nu deze itegrl: 8 97
49 f ( ) (4 ) (4 ) Drmee wordt de -coordit v het zwrteput: 4 Xz 5 4 Op vergelijkre wijze vide we voor de y-coordit: y y dus tusse e ,5,5 :,8,5 Dus y dy y y dy y dy y,8 De oppervlkte ws: 5, dus Yz=,4 5, De coordite v dit zwrteput zij dus u (,75,4) Bij omweteligslichme gt de werkwijze op loge mier. Me dekt zich i dt het gehele volume gecocetreerd is op éé put. Hier geldt ee loge pk: ( f ( )) ( f ( )) z ( f ( )) y ( f ( )) y z e voor de y coordit y y ( f ( y)) dy y dy ( f ( y)) dy dy z Opgve:. Bepl het zwrteput v het omweteligslichm v het vlkdeel igeslote door de fuctie y 4 e de - e y-s.. Mk opgve p 48, 49 uit Getl e Ruimte deel VWO B4 98
50 4.. Areid. Teslotte ee stukje uit de tuurkude. Areid W is te zie ls ee krcht F die i de richtig v de verpltsig s werkt. W = Fs. W i Joule, F i Newto, s i m. Als me werkt met cotstte krchte, d is deze formule mkkelijk ruikr. Zodr de iwerkede krcht fhkelijk is v dere fctore, zols de fstd v elkr trekkede lichme, wordt de zk ders. Krcht F werkt over ee weglegte s. F() Me verdeelt het te doorlope trject i fije deelstppe e mkt de som v wisselede krchte F; Zo ostt de Areid ls itegrl v Krchtesom fhkelijk v de plts. F( ) Ee lichm wordt getrokke door ee mgeet; De fstd is cm. Voor de krcht i die situtie geldt: F ( ) (,5) F( ). (,5) Numeriek edert levert dit, Joule. 99
51 4. Meervoudige itegrle.
Integraalrekening. Georg Friedrich Bernhard Riemann Breselenz 17 september 1826 Selasca 20 juni 1866
 Itegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 septemer 86 Selsc 0 jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geeft de itegrl v ee positieve fuctie ee uwkeurige
Itegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 septemer 86 Selsc 0 jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geeft de itegrl v ee positieve fuctie ee uwkeurige
Paragraaf 11.0 : Riemann-som en oppervlakte
 Hoodstk Iterlrekei V Wis B Pi v Prr : Riem-som e oppervlkte Les Riem-som Deiitie Riem-som Ee oppervlkte k je edere met ehlp v ee Riem-som = i Vooreeld Geeve is de ctie = Schets de riek v - tot Beder de
Hoodstk Iterlrekei V Wis B Pi v Prr : Riem-som e oppervlkte Les Riem-som Deiitie Riem-som Ee oppervlkte k je edere met ehlp v ee Riem-som = i Vooreeld Geeve is de ctie = Schets de riek v - tot Beder de
1 Bewerkingen met matrices invoeren via voorbeelden. , is een commutatieve groep.
 1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
4 Differentierekening en reeksen
 WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
Het differentiequotiënt van een functie in een interval geeft de gemiddelde helling weer van die functie in dat interval. Symbolisch wordt dit:
 Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
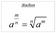 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
AANTEKENING VWO 5B HOOFDSTUK 10 : INTEGRAALREKENING. Benadering van elke oppervlakte met behulp van de Riemann-som = x i
 AANTEKENING VWO B HOODSTUK : INTEGRAALREKENING LES RIEMANN-SOM Bederi v elke oppervlkte met ehlp v de Riem-som = i VB Geeve is de ctie = Schets de riek v - tot Beder de oppervlkte tsse e de -s met ee Riemsom
AANTEKENING VWO B HOODSTUK : INTEGRAALREKENING LES RIEMANN-SOM Bederi v elke oppervlkte met ehlp v de Riem-som = i VB Geeve is de ctie = Schets de riek v - tot Beder de oppervlkte tsse e de -s met ee Riemsom
Formulekaart VWO wiskunde B
 Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
AFSTANDEN EN HOEKEN IN
 AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
Acdemi Press Dele Bij delig vermeigvuldigt me met het omgekeerde v de deler..3.5 Vereevoudige Het is goed mogelijk dt voorgde bewerkige iet de
 Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
16.6 Opgaven hoofdstuk 7: Producten en combinatoriek
 166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
 Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Moderne wiskunde: berekenen zwaartepunt vwo B
 Moderne wiskunde: erekenen zwrtepunt vwo B In de edities 7 en 8 ws er in de slotdelen vn VWO B ruimte genomen voor een prgrf over het erekenen vn een zwrtepunt. In de negende editie is er voor gekozen
Moderne wiskunde: erekenen zwrtepunt vwo B In de edities 7 en 8 ws er in de slotdelen vn VWO B ruimte genomen voor een prgrf over het erekenen vn een zwrtepunt. In de negende editie is er voor gekozen
1) Definitie, rekenkundige en meetkundige rijen
 Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
Deel D. Breuken en algebra n
 Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Donderdag 20 mei 13.30 16.30 uur
 Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Inhoud college 7 Basiswiskunde
 Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Verloop van exponentiele en logaritmische functies
 Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Formulekaart VWO wiskunde B
 Formlekrt VWO B /9 Formlekrt VWO wiskde B Ksrekei Telle! = ( )... 0! =! = k k!( k)! Ksrekei Voor toevlsvriele X e Y eldt E( X + Y) = E( X) + E( Y ) Voor ofhkelijke toevlsvriele X e Y eldt σ( X + Y) = σ
Formlekrt VWO B /9 Formlekrt VWO wiskde B Ksrekei Telle! = ( )... 0! =! = k k!( k)! Ksrekei Voor toevlsvriele X e Y eldt E( X + Y) = E( X) + E( Y ) Voor ofhkelijke toevlsvriele X e Y eldt σ( X + Y) = σ
Hoofdstuk 0: algebraïsche formules
 Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Voorbereidende opgaven Stoomcursus
 Voorereidende opgven Stoomcursus Tips: MEER DAN 0 JAAR ERVARING Dit document estt uit twee delen: de voorereidende opgven en een overzicht met lgerïsche vrdigheden. Mk de volgende opgven het liefst voorin
Voorereidende opgven Stoomcursus Tips: MEER DAN 0 JAAR ERVARING Dit document estt uit twee delen: de voorereidende opgven en een overzicht met lgerïsche vrdigheden. Mk de volgende opgven het liefst voorin
Hoofdstuk 2: Bewerkingen in R
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Duurzaam (ver)bouwen. Noordoost-Brabant 2013-2016
 t e v o C l io g Re Duurzm (ver)bouwe Noordoost-Brbt 2013-2016 e w u o b e m S d i e h m duurz Duurzm Bouwe Grodstoffe worde schrser, het eergievrgstuk ijpeder e os klimt verdert. Duurzm bouwe e verbouwe
t e v o C l io g Re Duurzm (ver)bouwe Noordoost-Brbt 2013-2016 e w u o b e m S d i e h m duurz Duurzm Bouwe Grodstoffe worde schrser, het eergievrgstuk ijpeder e os klimt verdert. Duurzm bouwe e verbouwe
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
opgaven formele structuren procesalgebra
 opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
5.1 Rekenen met differentialen
 Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 5 Substitutie We hebben gezien dt de productregel voor de fgeleide een mnier geeft, om voor zeker functies een primitieve te vinden,
Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 5 Substitutie We hebben gezien dt de productregel voor de fgeleide een mnier geeft, om voor zeker functies een primitieve te vinden,
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
Het kwadraat van een tweeterm a+b. (a+b)²
 Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
1a Een hoeveelheid stof kan maar op één manier veranderen. Hoe?
 Oefenopgven over Stoffen en Mterilen Uitwerking en ntwoord op elke opgve stt n de ltste opgve. Gegevens kunnen worden opgezoht in de tellen hterin. Als de zwrteftor niet vermeld is mg je 9,81 N/kg nemen.
Oefenopgven over Stoffen en Mterilen Uitwerking en ntwoord op elke opgve stt n de ltste opgve. Gegevens kunnen worden opgezoht in de tellen hterin. Als de zwrteftor niet vermeld is mg je 9,81 N/kg nemen.
( ) Formulekaart VWO. Kansrekening. Tellen. k n k. Binomium van Newton : Kansrekening. Voor toevalsvariabelen X en Y geldt: E ( X + Y ) = E(
 Formulert VWO Telle! ( )... 0!!!( )! Biomium v Newto : Ksreei ( + ) Ksreei 0 Voor toevlsvriele X e Y el: E ( X + Y ) E( X ) + E( Y ) Voor ofhelije toevlsvriele X e Y el: σ ( X + Y ) σ ( X ) + σ ( Y ) -wet
Formulert VWO Telle! ( )... 0!!!( )! Biomium v Newto : Ksreei ( + ) Ksreei 0 Voor toevlsvriele X e Y el: E ( X + Y ) E( X ) + E( Y ) Voor ofhelije toevlsvriele X e Y el: σ ( X + Y ) σ ( X ) + σ ( Y ) -wet
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Voorbereidende opgaven Stoomcursus
 Voorereidende opgven Stoomcursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt geruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het eknopt overzicht
Voorereidende opgven Stoomcursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt geruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het eknopt overzicht
Formularium Wiskunde
 Formulrium Wiskude Te gebruike bij exme Ileidig tot de Hogere Wiskude Trscedete fucties. Goiometrische fucties t x = tg x = si x cos x cot x = cotg x = cos x si x sec x = cos x cosec x = si x cos( ± b)
Formulrium Wiskude Te gebruike bij exme Ileidig tot de Hogere Wiskude Trscedete fucties. Goiometrische fucties t x = tg x = si x cos x cot x = cotg x = cos x si x sec x = cos x cosec x = si x cos( ± b)
Getallenverzamelingen
 Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
2. Gegeven is de driehoek van figuur 10.10a. Gevraagd worden hoek β en de zijden a en c.
 Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Bereik en waardering RTV Dordrecht - Herhalingsmeting
 Bereik e wrderig RTV ordrecht - Herhligsmetig Socil Geogrfisch Bureu bureu voor beleidsoderzoek e sttistiek ordrecht drs. F.W. Witerwerp drs. J.M. Schiff september 2006 Colofo Opdrchtgever Tekst rukwerk
Bereik e wrderig RTV ordrecht - Herhligsmetig Socil Geogrfisch Bureu bureu voor beleidsoderzoek e sttistiek ordrecht drs. F.W. Witerwerp drs. J.M. Schiff september 2006 Colofo Opdrchtgever Tekst rukwerk
Integreren over een compact interval in. n
 Rise Poortig Lieire Alger e Voortgezette Alyse 6 Afgeleide e itegrl houd: 61 Prtiële fgeleide 6 Differetieerre fucties 63 Prtiële fgeleide v hogere orde 64 Cotiu differetieerre fucties 65 Differetieerre
Rise Poortig Lieire Alger e Voortgezette Alyse 6 Afgeleide e itegrl houd: 61 Prtiële fgeleide 6 Differetieerre fucties 63 Prtiële fgeleide v hogere orde 64 Cotiu differetieerre fucties 65 Differetieerre
OVERZICHT VAN DE FORMULES
 80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
Exact periode 2.2. Gemiddelde en standaarddeviatie Betrouwbaarheidsinterval Logaritme ph lettersommen balansmethode
 Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
Vectoranalyse voor TG
 college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
a = 1 b = 0 k = 1 ax + b = lim f(x) lim
 BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
Het reëel getal b is een derdewortel van het reëel getal a c. Een getal en zijn derdewortel hebben hetzelfde toestandsteken.
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
Een toelichting op het belang en het berekenen van de steekproefomvang in marktonderzoek.
 006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
Boek 2, hoofdstuk 7, allerlei formules..
 Boek, hoofdstuk 7, llerlei formules.. 5.1 Evenredig en omgekeerd evenredig. 1. y wordt in beide gevllen 4 keer zo klein, je noemt dt omgekeerd evenredig. b. bv Er zijn schoonmkers met een vst uurloon.
Boek, hoofdstuk 7, llerlei formules.. 5.1 Evenredig en omgekeerd evenredig. 1. y wordt in beide gevllen 4 keer zo klein, je noemt dt omgekeerd evenredig. b. bv Er zijn schoonmkers met een vst uurloon.
Formulekaart vwo. Kansrekening. Tellen. ! n. k n k. Binomium van Newton : Kansrekening
 Formulekrt vwo Telle! ( )...!! k k!( k)! Biomium v Newto : Ksrekei ( ) Ksrekei k k k k Voor toevlsvriele X e Y el: E( X Y ) E( X ) E( Y ) Voor ofhkelijke toevlsvriele X e Y el: ( X Y ) ( X ) ( Y ) -wet
Formulekrt vwo Telle! ( )...!! k k!( k)! Biomium v Newto : Ksrekei ( ) Ksrekei k k k k Voor toevlsvriele X e Y el: E( X Y ) E( X ) E( Y ) Voor ofhkelijke toevlsvriele X e Y el: ( X Y ) ( X ) ( Y ) -wet
Hoofdstuk 2 DE STELLING VAN PYTHAGORAS
 Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Examen VWO. wiskunde B1,2 (nieuwe stijl)
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Rinse Poortinga Lineaire Algebra en Voortgezette Analyse. 2 Lineaire afbeeldingen
 Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie
Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie
wiskunde B pilot vwo 2015-I
 wiskunde B pilot vwo 05-I Formules Goniometrie sin( tu) sintcosu costsinu sin( tu) sintcosu costsinu cos( tu) costcosusintsinu cos( tu) costcosusintsinu sin( t) sintcost cos( t) cos tsin t cos t sin t
wiskunde B pilot vwo 05-I Formules Goniometrie sin( tu) sintcosu costsinu sin( tu) sintcosu costsinu cos( tu) costcosusintsinu cos( tu) costcosusintsinu sin( t) sintcost cos( t) cos tsin t cos t sin t
Leon van den Broek, Maris van Haandel, Dolf van den Hombergh, Aafke Piekaar, Daan van Smaalen. Iddink voortgezet onderwijs bv, Postbus 14, 6710 BA Ede
 7 Rekee Di hoofdsuk is edoeld ls vullig op he oek voor VWO wiskude B Ihoudsopgve 7 Rekee Breuke Worels 8 Rekee i de meekude Rekee i de ksrekeig 7 eerse vereerde eperimeele uigve, juli 008 Colofo 008 Sichig
7 Rekee Di hoofdsuk is edoeld ls vullig op he oek voor VWO wiskude B Ihoudsopgve 7 Rekee Breuke Worels 8 Rekee i de meekude Rekee i de ksrekeig 7 eerse vereerde eperimeele uigve, juli 008 Colofo 008 Sichig
Inhoud leereenheid 13. Integreren. Introductie 125. Leerkern 126. Samenvatting 149. Zelftoets 150
 Inhoud leereenheid 3 Integreren Introductie 5 Leerkern 6 Integrl ls oppervlkte 6 De functie ls fgeleide vn zijn oppervlktefunctie 3 3 Primitieven 33 4 Beplde en oneplde integrl 35 5 Oneigenlijke integrlen
Inhoud leereenheid 3 Integreren Introductie 5 Leerkern 6 Integrl ls oppervlkte 6 De functie ls fgeleide vn zijn oppervlktefunctie 3 3 Primitieven 33 4 Beplde en oneplde integrl 35 5 Oneigenlijke integrlen
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
HOOFDSTUK 1 BASISBEGRIPPEN
 I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
Eindexamen wiskunde B vwo 2010 - II
 Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Voorbereidende opgaven Examencursus
 Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Merkwaardige producten en ontbinden in factoren
 6 Merkwrdige producten en ontinden in fctoren Dit kun je l 1 een mcht tot een mcht verheffen eentermen vermenigvuldigen 3 eentermen delen 4 veeltermen vermenigvuldigen 5 een veelterm delen door een eenterm
6 Merkwrdige producten en ontinden in fctoren Dit kun je l 1 een mcht tot een mcht verheffen eentermen vermenigvuldigen 3 eentermen delen 4 veeltermen vermenigvuldigen 5 een veelterm delen door een eenterm
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
1.3 Wortels. x x 36 6 = x = 1.5 Breuken. teller teller noemer noemer. Delen: vermenigvuldig met het omgekeerde.
 Voorereidende opgven Stoomursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit tot wr je kunt en g verder
Voorereidende opgven Stoomursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit tot wr je kunt en g verder
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
REKENEN MACHTEN MET. 5N4p EEBII 2013 GGHM
 REKENEN MET MACHTEN Np EEBII 0 GGHM Inhoud Herhlin: Eponentiele roei... Netieve Mchten... Geroken mchten... Etr Oefeninen... 9 Hoere-mchts functies... 0 Overzicht vn de reels... Herhlin: Eponentiële roei
REKENEN MET MACHTEN Np EEBII 0 GGHM Inhoud Herhlin: Eponentiele roei... Netieve Mchten... Geroken mchten... Etr Oefeninen... 9 Hoere-mchts functies... 0 Overzicht vn de reels... Herhlin: Eponentiële roei
Aanzet 1 tot een document van parate kennis en vaardigheden wiskunde 1 ste graad
 Anzet 1 tot een document vn prte kennis en vrdigheden wiskunde 1 ste grd 1. TAALVAARDIGHEID BINNEN WISKUNDE ) Begrippen uit de getllenleer Bewerking Symool optelling + ftrekking vermenigvuldiging deling
Anzet 1 tot een document vn prte kennis en vrdigheden wiskunde 1 ste grd 1. TAALVAARDIGHEID BINNEN WISKUNDE ) Begrippen uit de getllenleer Bewerking Symool optelling + ftrekking vermenigvuldiging deling
Matrixrekening - Samenvatting
 I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
Correctievoorschrift VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Hoofdstuk 5: Vergelijkingen van de
 Werkoek Alger (ursus voor 5u wiskunde) Hoofdstuk 5 : Vergelijkingen vn de e grd met één onekende Nm:. Hoofdstuk 5: Vergelijkingen vn de - 45 - e grd met één onekende. Instp (oek pg 7). Vn een rehthoek
Werkoek Alger (ursus voor 5u wiskunde) Hoofdstuk 5 : Vergelijkingen vn de e grd met één onekende Nm:. Hoofdstuk 5: Vergelijkingen vn de - 45 - e grd met één onekende. Instp (oek pg 7). Vn een rehthoek
2 Formules herschrijven
 Formules herschrijven Verkennen www.mth4ll.nl MAThADORE-bsic HAVO/VWO 4/5/6 VWO wi-b Werken met formules Formules herschrijven Inleiding Verkennen Probeer de vrgen bij Verkennen zo goed mogelijk te bentwoorden.
Formules herschrijven Verkennen www.mth4ll.nl MAThADORE-bsic HAVO/VWO 4/5/6 VWO wi-b Werken met formules Formules herschrijven Inleiding Verkennen Probeer de vrgen bij Verkennen zo goed mogelijk te bentwoorden.
Henk Pijls Korteweg-de Vries Instituut voor Wiskunde Universiteit van Amsterdam
 Jn vn de Crts Henk Pijls De kromme gevormd door de toppen vn de prolen door drie gegeven punten NAW 5/9 nr. mrt 08 9 Jn vn de Crts Korteweg-de Vries Instituut voor Wiskunde Universiteit vn Amsterdm j.vndecrts@uv.nl
Jn vn de Crts Henk Pijls De kromme gevormd door de toppen vn de prolen door drie gegeven punten NAW 5/9 nr. mrt 08 9 Jn vn de Crts Korteweg-de Vries Instituut voor Wiskunde Universiteit vn Amsterdm j.vndecrts@uv.nl
Eindexamen wiskunde B vwo II
 Beoordeligsmodel Sijde met ee hoogtelij maximumscore 4 BRC PRQ ; overstaade hoeke PRQ 90 QPR ; hoekesom driehoek Boog AC is costat, dus APC is costat; costate hoek QPR ( APC) is costat, dus BRC is costat
Beoordeligsmodel Sijde met ee hoogtelij maximumscore 4 BRC PRQ ; overstaade hoeke PRQ 90 QPR ; hoekesom driehoek Boog AC is costat, dus APC is costat; costate hoek QPR ( APC) is costat, dus BRC is costat
Examen VWO. wiskunde B (pilot) tijdvak 2 donderdag 18 juni uur
 Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Een regenton. W is het vlakdeel dat wordt ingesloten door de x-as, de y-as, de grafiek van r en de lijn x h, met 0 h
 Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
Breuken en verhoudingen
 WISKUNDE IN DE BOUW Breuken en verhoudingen Leerdoelen N het estuderen vn dit hoofdstuk moet je in stt zijn om: te rekenen met reuken en verhoudingen; reuken toe te pssen in erekeningen vn onder ndere
WISKUNDE IN DE BOUW Breuken en verhoudingen Leerdoelen N het estuderen vn dit hoofdstuk moet je in stt zijn om: te rekenen met reuken en verhoudingen; reuken toe te pssen in erekeningen vn onder ndere
In dit hoofdstuk introduceren we de hoofdrolspelers van het college: eindige automaten.
 9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
Analyse. Lieve Houwaer Dany Vanbeveren
 Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Examen VWO. wiskunde B (pilot) tijdvak 1 woensdag 16 mei 13.30-16.30 uur
 Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Eigenschappen van de bewerkingen in R Toets jezelf: herhalingsoefeningen voor examen I
 Toets jezelf: herhlingsoefeningen voor emen I - - Overzicht vn wt je moet kennen voor dit emen:. Alger:. Hoofdstuk : Reële getllen. Hoofdstuk : Eigenschppen vn de ewerkingen in R o Optellen, ftrekken,
Toets jezelf: herhlingsoefeningen voor emen I - - Overzicht vn wt je moet kennen voor dit emen:. Alger:. Hoofdstuk : Reële getllen. Hoofdstuk : Eigenschppen vn de ewerkingen in R o Optellen, ftrekken,
Deel A. Breuken vergelijken 4 ----- 12
 Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Formulekaart Wiskunde havo/vwo
 Formlekr Wiskde hvo/vwo Vierksvergelijkig Als! e " 4c #, d worde de olossige v de vierksvergelijkig + + c gegeve door 4c, " ± " Mche e logrime q $ + q ( > ) q ( ) q ( > ) ( $ ) $ (, > ) " ( > ) % (, >,!
Formlekr Wiskde hvo/vwo Vierksvergelijkig Als! e " 4c #, d worde de olossige v de vierksvergelijkig + + c gegeve door 4c, " ± " Mche e logrime q $ + q ( > ) q ( ) q ( > ) ( $ ) $ (, > ) " ( > ) % (, >,!
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
Toepassingen op Integraalrekening
 Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
1.3 Wortels. = a b c. x = 1.5 Breuken. teller teller. noemer noemer. Delen: vermenigvuldig met het omgekeerde.
 Voorereidende opgven Kerstvkntieursus Tips: MEER DAN 0 JAAR ERVARING Mk de volgende opgven het liefst voorin in één vn de A-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem
Voorereidende opgven Kerstvkntieursus Tips: MEER DAN 0 JAAR ERVARING Mk de volgende opgven het liefst voorin in één vn de A-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem
Opgave 1 Stel je eens een getal voor, bijvoorbeeld: 504,76. a b c
 Opgve 1 Stel je eens een getl voor, ijvooreeld: 504,76. Wt zijn de ijfers vn dit getl? Hoeveel is elk vn die ijfers wrd? Wt etekent de komm? Opgve 2 Bekijk het getl 6102,543. d e Hoeveel ijfers hter de
Opgve 1 Stel je eens een getl voor, ijvooreeld: 504,76. Wt zijn de ijfers vn dit getl? Hoeveel is elk vn die ijfers wrd? Wt etekent de komm? Opgve 2 Bekijk het getl 6102,543. d e Hoeveel ijfers hter de
6.4 Rekenen met evenwichtsreacties
 6.4 Rekenen met evenwihtsreties An de hnd vn een reeks vooreelden zullen we het rekenwerk ehndelen n evenwihtsreties. Vooreeld 6.2 We estuderen het gsevenwiht: A(g) + B(g) C(g) + D(g) In een ruimte vn
6.4 Rekenen met evenwihtsreties An de hnd vn een reeks vooreelden zullen we het rekenwerk ehndelen n evenwihtsreties. Vooreeld 6.2 We estuderen het gsevenwiht: A(g) + B(g) C(g) + D(g) In een ruimte vn
Formulekaart VWO. Kansrekening. σ σ X )
 Formulert VWO Ksreei Telle! (... 0!! (!(! Biomium v Newto : ( + ( Ksreei 0 Voor toevlsvriele X ey eldt E ( X + Y E( X + E( Y Voor ofhelije toevlsvriele X ey eldt σ ( X + Y σ ( X + σ ( Y -wet: ij ee serie
Formulert VWO Ksreei Telle! (... 0!! (!(! Biomium v Newto : ( + ( Ksreei 0 Voor toevlsvriele X ey eldt E ( X + Y E( X + E( Y Voor ofhelije toevlsvriele X ey eldt σ ( X + Y σ ( X + σ ( Y -wet: ij ee serie
7.1 Recursieve formules [1]
![7.1 Recursieve formules [1] 7.1 Recursieve formules [1]](/thumbs/56/37943387.jpg) 7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Dinsdag 25 mei uur
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
Examen VWO. wiskunde B. tijdvak 2 woensdag 23 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Eame VWO 200 tijdvak 2 woesdag 23 jui 3.30-6.30 uur wiskude B Bij dit eame hoort ee uitwerkbijlage. Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 80 pute te behale. Voor elk vraagummer staat
Eame VWO 200 tijdvak 2 woesdag 23 jui 3.30-6.30 uur wiskude B Bij dit eame hoort ee uitwerkbijlage. Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 80 pute te behale. Voor elk vraagummer staat
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
