NUMERIEKE WISKUNDE, 1-ste deel Inleiding in de Numerieke Analyse. Department of Mathematics. November door
|
|
|
- Cecilia Timmermans
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 .5.5 grfiek f 3 de grds 6 de grds 9 de grds 5 de grds ÍÒ Ú Ö Ø Ø¹ÍØÖ Ø 0.5 Deprtment of Mthemtics NUMERIEKE WISKUNDE, -ste deel Inleiding in de Numerieke Anlyse door Numerieke Wiskunde Groep Deprtement Wiskunde Universiteit Utrecht November 0
2
3 Voorwoord Numeriek Wiskunde. Een numeriek wiskundige ontwerpt en nlyseert rekenschem s (lgoritmen) voor het numeriek oplossen vn (gewoonlijk) rekenintensieve rekenproblemen. Hij let drbij op efficiëntie (met het rekenschem produceert een computer snel de oplossing) nuwkeurigheid (de oplossing is nuwkeurig binnen vn te voren opgegeven foutgrenzen) betrouwbrheid (er is een zekere grntie dt de gewenste nuwkeurigheid ook ddwerkelijk gehld wordt) robuustheid (de performnce (d.w.z., efficiëntie, nuwkeurigheid, betrouwbrheid) wordt ook gehld voor nburige problemen) De rekenschem s moeten geïmplementeerd worden voor verwerking op een computer. Dit is het werkterrein vn de informticus. En ze kunnen voor zekere toepssingen geoptimliseerd worden. Dit is het werkterrein vn de computtionl scientist. De grenzen tussen Numerieke Wiskunde en Informtic en Computtionl Science is vg: de efficiëntie vn een rekenschem hngt f vn de rchitectuur vn de computer wrop het schem moet drien en wt efficiënt is en nuwkeurig hngt f vn de toepssing. De rekenschem s zijn numeriek en niet symbolisch, d.w.z., de geproduceerde oplossingen bestn uit getllen. Voor nlyse ten behoeve vn inzicht, voorspellingen, beleid, ontwerp, etc., worden de oplossingen gewoonlijk gevisuliseerd middels grfieken of nimties. In het weerprtje in het 8 uur journl zijn de beelden vn het weer vn fgelopen dg foto s (stellietbeelden), mr de beelden met pijlen die de windrichting ngeven, lijnen vn gelijke luchtdruk, bewegende wolkenprtijen, etc., dus de beelden die het weer voorspellen zijn nimties verkregen met rekenschem s ls boven bedoeld. De cursus. Het doel vn deze cursus is tweeledig. (i) Voor eenvoudige problemen de functies in deze cursus zijn reëelwrdig en gedefiniëerd op een reëel intervl willen we lten zien wt efficiëntie, nuwkeurigheid, betrouwbrheid en robuustheid is en welke overwegingen een rol spelen bij het fleiden vn schem s met dergelijke eigenschppen. (ii) Verder zullen we benderingstrtegiën bekijken die vk de bsis vormen voor rekenschem s voor ingewikkeldere problemen. Bij tl vn mthemtische problemen is de excte oplossing niet in hndzme vorm te vinden. Zo is f(x)dx mr voor reltief weinig functies f ls getlwrde te beplen, zijn differentilvergelijkingen nog zeldzmer in eindige termen vn elementire functies oplosbr en zijn wortels vn vergelijkingen f(x) = 0 slechts zelden te beplen. En de oplossingen vn deze problemen worden zelfs ongedefiniëerd ls men vn de optredende functies slechts in een ntl punten de wrden kent, terwijl dit bijv. bij de experimentele wetenschppen toch een veel voorkomende situtie is. In dit college, en in vervolg colleges, zullen wij lten zien hoe men de genoemde problemen benderd kn oplossen door de optredende functies te benderen door functies uit zinnige functieklssen wrvoor de gestelde problemen wèl oplosbr zijn. Belngrijke vrgen die hierbij een rol zullen spelen zijn: Wt is (een bovengrens voor) de fout in de numerieke bendering; Wt zijn de kosten verbonden n het berekenen vn deze bendering; i
4 Wt is het effect op het eindresultt vn fouten in de ingngsgegevens en vn fouten die gemkt worden door het rekenen in eindige precisie. Het dictt. Dit dictt is een bewerking vn een collegedictt geschreven door A. vn der Sluis en M. de Gee. Verschillende leden vn de numerieke wiskunde groep, i.h.b. G. Sleijpen en R. Stevenson, hebben drn bijgedrgen. ii
5 Inhoudsopgve Voorwoord i Interpoltie.0 Inleiding Lineire interpoltie Lgrnge interpoltie Interpoltie met functiewrden en fgeleiden Inverse (lineire) interpoltie Numerieke differentitie 5. Eenvoudige formules. Effect vn frondfouten Nuwkeuriger formules Experimenteel gevonden functiewrden Foutschttingen bij numerieke processen 0 3. Fouten Afrondfouten Foutvoortplnting Representtiefouten Extrpoltieprocessen Numerieke integrtie Inleiding De trpeziumregel Automtische integrtie en Romberg schem s Andere kwdrtuurformules Convergentie vn kwdrtuurschem s A Interpoltie met fgeleiden 5 B Rombergschem s 53 C De Euler Mc-Lurin reeks 55 Vrgstukken 57 Interpoltie Numerieke differentitie Foutschttingen bij numerieke processen Numerieke integrtie Index 74
6 INTERPOLATIE Interpoltie.0 Inleiding Een bsis element in de numerieke wiskunde is het benderen vn een functie f door een ndere functie f uit een geschikte functieklsse. Wnneer bijvoorbeeld f slechts bekend is in een ntl punten, kn dn deze f, die ook in tussengelegen punten gedefiniëerd is, gebruikt worden om de wrde vn f in zo n tussenpunt te benderen of om de extremen, de integrl of de fgeleide vn f te benderen. Ook wnneer f in principe in ieder punt beschikbr is, mr moeilijk te evlueren vlt, kn f hier voor gebruikt worden. Vk zijn de functies f oplosingen vn differentilvergelijkingen en kunnen de functiewrden lleen (en ook nog mr lleen bij bendering) berekend worden in zekere rekenpunten. Bij bijvoorbeeld de weersvoorspellingen berekent men de tempertuur lleen om de 5 minuten. Of zijn functiewrden lleen bekend in zekere meetpunten (de tempertuur vn gisteren is lleen gemeten in een ntl meetsttions). In dit hoofdstuk benderen we f door een interpoltiepolynoom, d.w.z. een polynoom dt met f overeenstemt in een ntl (steun)punten.. Lineire interpoltie.a Zij < b twee punten in R en f een functie die gedefiniëerd is op [, b]. Lt verder c en d twee verschillende punten zijn in [, b]. Het lineire interpoltiepolynoom vn f op de steunpunten c en d is dn gedefiniëerd ls het eerste grds polynoom p dt in c en d dezelfde wrde nneemt ls f. Men gt snel n dt het bedoelde polynoom gegeven wordt door oftewel p(x) = f(c) + x c (f(d) f(c)) () d c p(x) = x d c d f(c) + x c f(d). () d c Grfisch komt dit er op neer dt men op [, b] de grfiek vn f bendert door de rechte lijn door de punten (c, f(c)) en (d, f(d)). Lineire interpoltie is een veel nuwkeuriger proces dn de meeste mensen denken. Beschouw bijvoorbeeld volgend tbelletje vn de sinus. x 35 o 36 o 37 o 38 o 39 o sin(x) Stel eens dt we sin(37 o ) niet gekend hdden en deze door lineire interpoltie uit sin(36 o ) en sin(38 o ) hdden willen beplen. Dn ws er uitgekomen , hetgeen slechts 9 eenheden vn de vijfde deciml verschilt vn het wre ntwoord. Dit is eigenlijk wel een verrssend resultt, en er rijzen dn ntuurlijk meteen vrgen, zols - zou je ook voor ndere rgumenten dn 37 o zo n goed resultt krijgen; - zou dt ook zo zijn op ndere intervllen [c, d] met d c = ; - wt gebeurt er op lngere of kortere intervllen; - hoe zit dit bij ndere functies.
7 . Lineire interpoltie grfiek f grfiek p f(x) p(x) c x d Figuur : De grfiek vn een functie f en vn een lineir interpoltie polynoom p vn f..b Kortom, ls je een functie bendert met een ndere wil je weten wt de fout ongeveer is en wr die vn fhngt. Voor lineire interpoltie doet de volgende stelling hierover een uitsprk (hierin duidt een nottie ls [, b, c, d] het gesloten intervl n opgespnnen door de uitersten vn het rijtje, b, c, d en evenzo ], b, c, d[ het bijbehorende open intervl;, b, c, d hoeven drbij geen stijgend rijtje voor te stellen; met nme is dus bijv. [5, 3] toegestn met dezelfde betekenis ls [ 3, 5]). Stelling.. Lt c en d punten in [, b] zijn met c d. Zij f C[, b], en lt f en f bestn op ], b[. Dn geldt voor het lineire interpoltiepolynoom p vn f op de steunpunten c en d, en voor elke x [, b] dt er een ξ ]c, d, x[ is, zo dt f(x) p(x) = (x c)(x d) f (ξ). (3) Bewijs. Als x = c of x = d, dn is f(x) p(x) = 0 en kn men ξ willekeurig kiezen. Zij dus nu x c, x d. Dn is er, voor deze vste wrde vn x, een getl q zo dt Beschouw voor deze vste q de functie f(x) p(x) = q(x c)(x d). ϕ : t f(t) p(t) q(t c)(t d). Hiervoor geldt: ϕ(c) = ϕ(d) = ϕ(x) = 0. Volgens de stelling vn Rolle zijn er minstens twee (verschillende) punten y en z in ]c, d, x[ zodt ϕ (y) = ϕ (z) = 0. Opnieuw volgens Rolle is er ook een ξ ]y, z [, dus ξ ]c, d, x[, zo dt ϕ (ξ) = 0. Wegens ϕ (t) = f (t) q volgt nu q = f (ξ).
8 4 INTERPOLATIE Opmerking.. Hoewel we p een inter poltiepolynoom noemen kunnen we p ntuurlijk ook gebruiken om te extrpoleren (dt wil zeggen, het benderen vn f(x) met p(x) voor x / [c, d]). Stelling.. doet dn nog steeds een uitsprk over de fout..c Als we ons beperken tot echte interpoltie (dus x [ c, d]), dn kunnen we met stelling.. eenvoudig een bovengrens voor de bsolute interpoltiefout vinden: Stelling.. Zij f C[c,d], f C ]c,d[. Definiëer R f (c,d) = f p,[c,d] (= sup{ (f p)(x) : x [c,d]}), wrbij p het lineire interpoltiepolynoom is vn f op de steunpunten c en d. Dn geldt 8 (d c) inf f (x) R f (c,d) ] c, d[ 8 (d c) sup f (x). ] c, d[ I.h.b. geldt voor vste m = d+c dt lim (d c) 0 R f (c,d) 8 (d c) = f (m). Bewijs. Dit volgt eenvoudig uit mx x [c,d] (x c)(x d) = (m c)(m d) = 8 (d c), R f (c,d) f(m) p(m), en, voor de ltste bewering, een toepssing vn de insluitstelling voor limieten. In woorden zegt bovenstnde stelling dus dt, indien f (m) 0, de mximle fout bij lineire interpoltie symptotisch fneemt met het kwdrt vn de fstnd tussen de steunpunten. Voorbeeld.. Neem f(x) = sin(x) (voortn x in rdilen). In onderstnde tbel stn voor verschillende wrden vn m = c+d en d c de wrden vn R sin (c, d) gegeven (op de regel met R ) en de fctor wrmee R sin (c, d) gereduceerd wordt ls bij vste wrde vn m de wrde vn d c gehlveerd wordt (op de regels met red ). m\(d c) R red R red R red R red We zien, dt in de eerste drie rijen de reductiefctor het getl 4 heel rdig bendert. Dt in de derde rij de reductiefctoren wt verder vn 4 fliggen wordt verklrd doordt de tweede fgeleide vn de sinus op de intervllen [0, 0.], [0.05, 0.5] en [0.075, 0.5] in reltieve zin sterk vriëert. In de vierde rij ziet men een reductiefctor 8 opdoemen. Men kn inderdd bewijzen dt deze fctor symptotisch juist is (zie prgrf.d).
9 . Lgrnge interpoltie 5.D Opgve.. Zij f een voldoend vk differentiëerbre functie, en zij p het lineire interpoltiepolynoom vn f op de punten c d. Lt zien dt voor lle x en ]x,c,d[ er een η ], c, d, x[ is met f(x) p(x) = (x c)(x d)[f () + ( x+c+d 3 )f (η)]. (4) Anwijzing: Het bewijs loopt nloog n dt vn stelling..; bedenk dt voor de overeenkomstig gedefiniëerde functie ϕ ook nog geldt: ϕ () = 0. Opgve.. In de situtie vn opgve.., en met ζ := x+c+d 3 het zwrtepunt vn c, d en x, lt zien dt er een θ ],ζ[ en een φ ]η,θ[ zijn, zo dt f(x) p(x) = (x c)(x d)[f (ζ) + ( ζ)(θ η)f (φ)] (5) Merk op door willekeurig dicht bij ]x,c,d[ te nemen dt dit betekent dt ξ uit (3) ongeveer gelijk is n het zwrtepunt vn x en de steunpunten c en d. Lt zien dt indien f een derde grds polynoom is er zelfs gelijkheid geldt. Opgve..3 In de situtie vn opgve.. en met m = d+c, bewijs dt indien f (m) = 0 er geldt 8 7 R f (c,d) lim = f (m). (d c) 0 3(d c) 3 Verklr hiermee de fctor 8 in de ltste rij vn de tbel in.c. (Merk op dt het rekenwerk nzienlijk vereenvoudigt ls men m = 0 veronderstelt. G n dt dit geen wezenlijke beperking is.). Lgrnge interpoltie.a Als ntuurlijke generlistie vn lineire interpoltie kn men de pproximtie beschouwen vn een functie f door een n-de grds polynoom p, zodnig dt de wrden vn f en p in een voorf gegeven n + -tl verschillende punten x 0,...,x n overeenstemmen. Men spreekt dn vn n-de orde Lgrnge interpoltie. Een polynoom p dt n deze eisen voldoet is gemkkelijk n te geven, en wel in een vorm die een duidelijke generlistie vn () is: wrin p(x) = n f(x k )L k n (x) (6) k=0 L k n (x) = (x x 0) (x x k )(x x k+ ) (x x n ) (x k x 0 ) (x k x k )(x k x k+ ) (x k x n ). (7) Immers, L k n heeft voor elke k de grd n, en L k n (x i ) = 0 voor i k, L k n (x k ) =, zodt p(x i ) = f(x i ) voor i = 0,...,n. Het polynoom p is het Lgrnge interpoltiepolynoom vn f op de steunpunten x 0,...,x n.
10 6 INTERPOLATIE Opmerking.. Het polynoom p is uniek. Immers zij p een nder n-de grds polynoom dt met f overeenstemt op de verschillende punten x 0,...,x n. Dn is p p een n-de grds polynoom met n + verschillende nulpunten, hetgeen betekent dt p p = 0. Het rechterlid vn (6) is de Lgrnge representtie vn p. (Elk polynoom heeft tlloze representties; vergelijk bijvoorbeeld () en ().). De polynomen L k n uit (7) zijn de Lgrnge coëfficiënten; zij hngen slechts f vn x 0,...,x n, en niet vn f. In de litertuur worden ze vk geschreven ls L k n (x) = ω(x) (x x k )ω (x k ) met ω(x) = n (x x i ). Stelling.. lt zich eenvoudig generliseren. Het bewijs lten we chterwegen: het loopt geheel nloog n dt vn stelling... Stelling.. Lt x 0,...,x n verschillende punten zijn in [, b]. Lt f C[, b], en lt f, f,...,f (n+) bestn op ], b[. Dn geldt voor het bijbehorende interpoltiepolynoom p en voor elke x [, b] dt er een ξ ]x 0,x,...,x n,x[ is, zo dt f(x) p(x) = (x x 0 )(x x ) (x x n ) f(n+) (ξ) (n + )!. (8) Opmerking.. Wt betreft het punt ξ in stelling.. kn men weer bewijzen dt ( ) ξ n x + x i, (9) n + dus ξ is ongeveer het zwrtepunt vn x,x 0,x,...,x n (Vergelijk opgve..) i=0 i=0.b Een belngrijk gevl krijgt men ls de fstnd tussen twee opeenvolgende steunpunten steeds gelijk is, zeg gelijk n h. Dn nummert men de steunpunten zo dt x k = x 0 + kh voor k = 0,...,n. Men noemt dit equidistnte Lgrnge interpoltie. Schrijven we nu x = x 0 + qh, dn krijgt men: L k n (x) = q (q (k ))(q (k + )) (q n) ( ) n k k!(n k)! (0) voor k = 0,...,n. Merk op dt het rechterlid vn (0) onfhnkelijk is vn h, hetgeen betekent dt de coëfficiënten hergebruikt kunnen worden wnneer de stpgrootte h vernderd wordt..c Stel dt een functie f gegeven is voor x = 0, 0., 0., etc. Als we dn met 4 punts interpoltie f(0.65) willen beplen kunnen we dt bijv. doen met ls steunpunten 0.4 t/m 0.7, 0.5 t/m 0.8 of 0.6 t/m 0.9. Zou dt verschil uitmken? We proberen dit eens voor f(x) = e x. Men krijgt dn resp ; ; , zodt f p = ; ; Dus ls we de steunpunten zo kiezen dt het interpoltiepunt x in het middelste deelintervl ligt krijgen we het beste resultt. Is dit verschil stelselmtig? Bekijken we eens de restterm (x x 0 )(x x ) (x x n ) f(n+) (ξ) (n + )! ()
11 . Lgrnge interpoltie 7 Wnneer f (n+) op de gezmenlijke interpoltie intervllen slechts weinig vriëert, hetgeen geen onredelijke nnme is ngezien men meestl interpoleert op kleine intervllen, dn wordt het gedrg vn de fout in fhnkelijkheid vn x voornmelijk bepld door het gedrg vn het polynoom (x x 0 )(x x ) (x x n ). In het equidistnte gevl dt we zojuist beschouwden hebben we x i = x 0 + ih. Schrijven we weer x = x 0 + qh dn krijgen we (x x 0 )(x x ) (x x n ) = h n+ q(q ) (q n). () Voor n =,,3,4,5 zijn de grfieken vn q(q ) (q n) in figuur geschetst. De e e e e e e e e+00.00e+00.00e e e e e+0.3e e e+0.4e e+0.69e e Figuur : De grfiek vn de functies q q(q ) (q n) voor n =,, 3,4, 5,6 met drin de wrden vn lokle extrem (in drie decimlen). wrden vn de lokle extrem zijn in de tekening ngegeven. Het blijkt dt deze extrem inderdd het kleinst zijn midden op het interpoltie intervl zodt men bij lngzm vriërende f (n+) dus inderdd mg verwchten dt de interpoltiefouten het kleinst zijn in het (of een) middelste interpoltie intervl. Hiermee moet men dn
12 8 INTERPOLATIE bij de keuze vn de steunpunten rekening proberen te houden. Buiten het intervl [0, n] groeit het rechterlid vn () snel ls functie vn q. Dit verklrt de veel grotere fout bij extrpoltie..d Bij functies die men in de prktijk tegenkomt zijn de hogere fgeleiden vk bijzonder ingewikkelde uitdrukkingen, wrbij het vrijwel ondoenlijk is te schtten hoe groot de wrden wel kunnen worden. Toch kn men zich wel een indruk verschffen vn de wrden vn f (n+). Een vn de methoden drvoor werkt ls volgt: Stel: We kennen de functiewrden in een (groot) ntl punten x 0,...,x n,x n+,..., (die we eenvoudigheidshlve in volgorde vn grootte genummerd denken: x 0 < x < ). Lt p 0 het n-de orde interpoltiepolynoom zijn op x 0,...,x n, dn kunnen we de wrde vn het polynoom en die vn de functie vergelijken in het punt x n+. We vinden zodoende de wrde vn f (n+) in n punt ξ 0 [x 0, x n+ ]: f (n+) (ξ 0 ) = (n + )! (x n+ x 0 )(x n+ x ) (x n+ x n ) [f(x n+) p 0 (x n+ )]. (3) Evenzo vindt men uitgnde vn het interpoltiepolynoom p op x,...,x n+ en de functiewrde in x n+ de wrde vn f (n+) in n ξ [x, x n+ ] etc. f ( ξ ) f ( ξ ) f ( ξ 0 ) x 0 x x x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 0 Figuur 3: De grfiek vn de functie f loopt door de punten (ξ i, f (ξ i)). Vn deze punten weten we dt ze op de horizontle lijnstukjes liggen (het i-de punt ligt ergens op het i-de lijnstukje). Stel nu eens dt deze ldus verkregen wrden f (n+) (ξ i ) een gldjes verlopende rij vormen en lten we deze, lthns in gedchten, eens grfisch uitzetten d.m.v. horizontle lijnstukjes op de hoogte f (n+) (ξ i ) boven het intervl [x i, x i+n+ ] (zie figuur 3 voor n = ). Dn snijdt de grfiek vn f (n+) l deze horizontle lijnstukjes en men hoopt dt
13 . Lgrnge interpoltie 9 hij binnen de ngegeven strook loopt. Op die mnier krijgt men dn een indruk vn de wrden vn f (n+). Men kn dit beschouwen ls een bedenkelijke gng vn zken, mr men doet hetzelfde wnneer men, om enig zicht op het verloop vn een lstige functie te krijgen, een ntl functiewrden beplt (zie figuur 4) en dn nneemt dt het verloop door de getrokken kromme wordt weergegeven en niet door de gestippelde. Figuur 4: Als we vn een functie een ntl wrden kennen (gemrkeerd met o ), dn nemen we n dt de grfiek vn de vn de functie meer lijkt op de getrokken kromme dn op de gestippelde..e Tot dusver hebben we ons bezig gehouden met de fout die je bij interpoltie mkt ls je gebruik mkt vn excte functiewrden. In werkelijkheid heb je die vrijwel nooit. Zo moet men er in het voorbeeld in.a mee rekening houden dt er (frond)fouten ter grootte vn 0 6 op de functiewrden kunnen zitten. Het is een essentiële numeriek wiskundige vrgstelling bij llerhnde numerieke processen hoe dergelijke ingngsfouten in het resultt doorwerken. We gn dt nu n voor interpoltie. We merken eerst op dt ls we n+ punts interpoltie toepssen op een polynoom f vn grd hoogstens n, we wegens opmerking.. f zelf terug krijgen. In het bijzonder geldt dit voor f(x) =. Bijgevolg geldt de interessnte reltie: n k=0 L k n(x) = voor lle x. I.h.. zijn echter niet lle Lgrnge coëfficiënten positief, zodt n k=0 L k n(x). Stel nu dt de functiewrden f(x k ) met fouten ǫ k belst zijn, ǫ k ǫ. Deze werken in het interpoltieresultt door ls L k n (x)ǫ k, en dt is hoogstens ǫ L k n (x). Deze grens kn bereikt worden; nmelijk, ls ǫ k net telkens ± ǫ is met het teken vn L k n (x). Als nu mx x Lk n (x) veel groter dn zou zijn zouden fouten in de f(x k ) dus zeer versterkt kunnen doorwerken. Bij equidistnte interpoltie (d.w.z. x k = x 0 + kh) met niet l te veel punten vlt dit echter nog l mee. Onderstnd geven we voor dit gevl bovengrenzen voor n k=0 L k n(x) in fhnkelijkheid vn n en vn de ligging vn x ten
14 0 INTERPOLATIE opzichte vn x 0,...,x n. x [x 0, x ] x [x, x ] x [x, x 3 ] x [x 3, x 4 ] x [x 4, x 5 ] n = n =.5.5 n = n = n = Men ziet hieruit nog dt deze wrden bij stijgende n lngzm oplopen. Men kn bewijzen (zie bijvoorbeeld Ntnson, Constructive Function Theory, vol. III, Theorem ) dt voor willekeurige x 0 < < x n, mx x [ x 0, x n ] k=0 n L k n (x) > ln(n + ) 8 π (4).F Veronderstel dt we geïnteresseerd zijn in de wrde vn een functie f in een punt x, en dt de functie slechts bekend is in de punten < x < x 0 < x < wrbij x (x 0,x ). Indien we niet tevreden zijn met het resultt vn een zeker Lgrnge interpoltie polynoom op een neengesloten rijtje steunpunten wronder x 0 en x, dn kunnen we slechts hopen een betere bendering te krijgen door meer steunpunten toe te voegen die evenwel verder verwijderd zijn vn x. Bij equidistnte steunpunten, efficiënte berekeningswijzen vn het Lgrnge interpoltiepolynoom wrbij de steunpunten in de volgorde x 0,x,x,... dnwel x 0, x, x, x,... worden toegevoegd stn bekend ls Newton s voorwrtse formule respectievelijk Guß voorwrtse formule (zie vrgstuk 9). Op grond vn inzichten verkregen in.c kunnen we voor vste grd n, nnemende dt f (n+) lngzm vriëert, vn de Guß formule betere resultten verwchten. De vrg is of er voor n convergentie optreedt vn het resultt vn interpoltie nr f(x). Dit blijkt slechts onder bijzondere voorwrden het gevl te zijn. Zo is bij Newton s voorwrtse formule een noodzkelijke (niet eens voldoende) voorwrde dt f regulier (d.w.z. differentiëerbr) is in het complexe hlfvlk Rez x 0. En bij de formule vn Guß moet f zelfs in het hele complexe vlk regulier zijn. Voor een functie ls +x, die op de reële s C is, kn dus eenvoudig geen convergentie optreden bij Guß, en ook niet bij Newton ls x 0 < 0, wegens de singulriteiten voor x = ±i. Uit het hieronder gegeven voorbeeld blijkt zelfs dt wnneer men met het verhogen vn de orde tegelijkertijd de fstnd tussen de steunpunten verkleint convergentie geen uitgemkte zk is: Voorbeeld.. [Runge] Zij p n het Lgrnge interpoltie polynoom vn de functie +x op de punten x (n) k = 5+k 0 n, k = 0,,...,n. Er geldt lim n p n (x) = f(x) dn en slechts dn ls 5 5 log x ξ dξ < 5 5 log x i dξ x < , zie figuur 5. Problemen ls in bovenstnd voorbeeld worden veroorzkt door (4). Voor een overzicht vn positieve resultten ngnde convergentie vn interpoltieschem s bij het verhogen vn de orde, zie P.J. Dvis, Interpoltion nd Approximtion, Ch. IV. Een voldoende voorwrde voor uniforme convergentie is ruwweg dt de fstnd tussen het betreffende gebied en de singulriteiten groot genoeg is. Deze fstnd beplt immers de grootte vn de fgeleiden.
15 .3 Interpoltie met functiewrden en fgeleiden.5 grfiek f 3 de grds 6 de grds 9 de grds 5 de grds Figuur 5: De getrokken kromme is de grfiek vn de functie f : x /( + x ). De ndere krommen zijn de grfieken vn Lgrnge interpoltie polynomen op steunpunten die equidistnt verdeeld liggen tussen 5 en +5. De benderingskwliteit verbetert in het midden bij toenemend ntl steunpunten, terwijl die n de rnd verslechtert. Opgve.. Zij f C[,b], x (n) k = + k b n, k = 0,...,n. Bender f door p n gedefinieerd ls het stuksgewijs lineir interpoltie polynoom op de intervllen [x (n) k,x(n) k+ ]. Bewijs dt lim n f p n,[,b] = 0..3 Interpoltie met functiewrden en fgeleiden.3a De Tylor polynomen. Een heel bekende methode om een functie te benderen met een polynoom is het gebruiken vn de Tylor ontwikkeling. Als eigenlijke benderingsmethode wordt deze techniek in de numerieke wiskunde niet zo vk gebruikt; veel belngrijker echter is zijn rol in de nlyse vn ndere numerieke processen. We vtten hier kort enige resultten uit de nlyse smen. Stelling.3. Lt c een punt in het intervl [, b] zijn, en f C n [, b]. Het n-de orde Tylor polynoom p n vn f in c is gegeven door p n (x) = n (x c) k f(k) (c). k! k=0 Voor x [,b] geldt voor de restterm R n (x) = f(x) p n (x) dt ) R n (x) = x c (x t) n (f (n) (t) f (n) (c))dt (= o((x c) n ) (x c)). (n )!
16 INTERPOLATIE Als zelfs f C n+ [c, x], dn b) R n (x) = x c (x t) n f (n+) (t)dt (= O((x c) n+ ) (x c)). n! en er bestt dn een, x fhnkelijke, ξ ]c, x[ zodt c) R n (x) = (x c)n+ f (n+) (ξ) (n + )! Opmerking.3. Er geldt p n (k) (c) = f (k) (c) voor k = 0,...,n. Bovenstnde stelling doet geen uitsprk over convergentie vn R n (x) nr nul voor n..3b Interpoltie in het lgemeen. In het lgemene gevl stelt men zich bij interpoltie de opgve om bij een functie f een polynoom p te construeren, zodnig dt in een ntl gegeven steunpunten niet lleen de wrden vn f en p overeenstemmen, mr ook de wrden vn een ntl vn hun fgeleiden. Het ntl fgeleiden mg per steunpunt verschillen. Het zl duidelijk zijn, dt zowel Lgrnge interpoltie ls pproximtie met Tylor polynomen bijzondere gevllen zijn. We bekijken hiertoe een rij (x 0,x,...,x n ) getllen x i die niet lleml verschillend wrden hoeven te hebben. Zo komt in de rij (0,0,,,,0) de wrde 0 drie ml voor en de wrde twee ml. Nottie.3. Lt (x 0,x,...,x n ) een rij getllen zijn. We zeggen dt p = f op (x 0,x,...,x n ) ls p(x i ) = f(x i ) voor lle i = 0,...,n en bovendien p (j) (x i ) = f (j) (x i ) ls de wrde vn x i j + of meer keer voorkomt in de rij (x 0,x,...,x n ). We nemen hierbij n dt f in de x i gedefiniëerd is en in dt punt ook voldoende vk differentiëerbr is. Dus met p = f op (0,0,,,,0) bedoelen we dt p(0) = f(0), p (0) = f (0), p (0) = f (0), (immers 0 komt drie ml voor in de rij (0,0,,,,0)), p() = f() en p () = f (), ( komt twee ml voor) en p( ) = f( ). Stelling.3. Lt (x 0,x,...,x n ) een rij getllen zijn. Dn is er een uniek polynoom p vn grd hoogstens n wrvoor p = f op (x 0,x,...,x n ): deze p wordt het interpoltie polynoom voor f op (x 0,x,...,x n ) genoemd. Anders dn bij pproximtie met Lgrnge en Tylor polynomen is in dit lgemene gevl een expliciete gednte vn het interpoltiepolynoom niet zo eenvoudig n te geven. We volstn drom met het geven vn bovenstnd resultt over existentie, uniciteit en onderstnd resultt over de restterm. De bewijzen vn deze stellingen kn men vinden in Bijlge A. In deze bijlge (in het bewijs vn Stelling A.3) en in Vrgstuk 9 wordt overigens een recursieve definitie gegeven voor het interpoltiepolynoom, wrin het interpoltiepolynoom uitgedrukt wordt in lger grds interpoltiepolynomen, d.w.z, in polynomen die f in één punt minder interpoleren. Met behulp vn deze uitdrukking (een generlistie vn de voorwrtse Newton formule ls vermeld in.f) kn je polynoomwrden gemkkelijk en efficiënt berekenen.
17 .4 Inverse (lineire) interpoltie 3 Opmerking.3. Een essentieel element bij lgemene interpoltie is, dt men in ieder steunpunt slechts een neengesloten stel fgeleiden, beginnend vnf de nulde (de functiewrde zelf) mg nemen. Als men dt niet doet, zijn existentie en uniciteit niet ltijd gegrndeerd. Voorbeeld.3. Er bestt geen eerste grds polynoom met p(0) =, p (0) = en er bestn er oneindig veel vn de tweede grd die n deze eisen voldoen. Nst Lgrnge interpoltie (x i x j lle i j) en Tylor polynomen (x i = x 0 lle i) heeft ook het gevl x i = x i+ (lle i, i + n) en x i x j lle i j een fzonderlijke nm; men spreekt dn vn Hermite interpoltie. Stelling.3.3 Lt (x 0,x,...,x n ) een rij getllen zijn. Zij p het polynoom vn grd hoogstens n dt gelijk is n f op (x 0,x,...,x n ). Als f C[, b] en f (n+) bestt op ], b[, dn bestt er voor elke x [, b] een ξ ]x 0,...,x n,x[ zodnig dt f(x) p(x) = (x x 0 )(x x ) (x x n ) f(n+) (ξ) (n + )! (5) Als voor de ξ in stelling.. geldt ook hier weer (9). Er is bijvoorbeeld precies een polynoom p vn grd hoogstens 5 zodt p = f op (0,0,0,,,). Voor dit polynoom is er voor iedere x R een ξ tussen 0, en x zodt.4 Inverse (lineire) interpoltie f(x) p(x) = x 3 (x )(x (ξ) )f(6). 6! Bij het tbelletje in.a vn de sinus zou men zich de vrg kunnen stellen: voor welke wrde vn x heeft sin(x) de wrde ? De vrg kn benderd bentwoord worden door de tbel vn rechts nr links te lezen en lineir te interpoleren in Men vt dus de wrden vn de sinus op ls rgumenten, de wrden vn x ls functiewrden, en interpoleert in feite op de inverse functie, in dit gevl de boogsinus. Dit heet drom inverse interpoltie. Met (), en m.b.v. de wrden vn sin(36 o ) en sin(37 o ) vinden we in dit gevl x = o. Hoe nuwkeurig is dit ntwoord? Met stelling.. vinden we voor de fout: f (ξ) = f (ξ), wrin f echter niet de sinus, mr de inverse functie is. Vn de sinus kennen we de inverse functie, mr in het lgemeen is de inverse niet expliciet bekend. Een mogelijkheid biedt dn invers differentiëren. Voor een inverteerbre en voldoend gldde functie g, zij y = g(x) en dus x = g (y). Door de reltie g g = Id te differentiëren m.b.v. de kettingregel vindt men (g ) (y) = g (x). Hiermee verkrijgt men (g ) (y) = d ( dy g (g (y)) ) = g (g (y)) d dy (g (y)) (g (g (y))) = g (x) (g (x)) 3 (6)
18 4 INTERPOLATIE Met g(x) = sin(x) kunnen wij nu de fout schtten, wrbij we dn ook g (x) = cos(x) nodig hebben. Wegens cos 36 o = 0.809, cos 37 o = vinden we ls bovengrens voor de fout /(0.8) rdilen grden. Het juiste ntwoord is grden, en de fout o.
19 5 Numerieke differentitie. Eenvoudige formules. Effect vn frondfouten.a Vnwege de definitie f f(x (x 0 ) = lim 0 +h) f(x 0 ) h 0 h zou men f (x 0 ) kunnen benderen met het eindige quotiënt, een zogenmde differentie quotiënt. Als we schrijven f (x 0 ) = f(x 0 + h) f(x 0 ) h + R (h), (7) dn is R (h) de fout bij de stpgrootte h. Annemend dt f C [x 0,x 0 + h], vinden we door f(x 0 + h) in een Tylor reeks te ontwikkelen een uitdrukking voor R (h): R (h) = h f (ξ), met ξ tussen x 0 en x 0 + h. (8) Voor h klein zl f (ξ) niet veel verschillen vn f (x 0 ), en we zien dt, indien f (x 0 ) 0, symptotisch de fout liner met h fneemt. x 0 h x 0 x 0 +h x 0 h x 0 x 0 +h Figuur 6: De richting vn de rklijn ( ) n de grfiek ( ) vn de functie f is de fgeleide f (x) die we willen benderen. De richting vn de koorde ( ) in het rechter figuur doet dt veel beter dn die in het linker figuur..b Uit het linker pltje in figuur 6 zien we dt het quotiënt in (7) niet zo n goede keuze is. Veel betere resultten kunnen we verwchten vn de in het rechter pltje gesuggereerde bendering. We schrijven f (x 0 ) = f(x 0 + h) f(x 0 h) h + R (h). (9) Als de derde fgeleide vn f bestt en continu is vinden we door f(x 0 +h) en f(x 0 h) volgens Tylor te ontwikkelen in x 0 de restterm R (h) = h 6 f (ξ), x 0 h < ξ < x 0 + h. (0) De fout gt nu inderdd veel sneller nr nul voor h 0, nl. indien f (x 0 ) 0, symptotisch met het kwdrt vn de stpgrootte h.
20 6 NUMERIEKE DIFFERENTIATIE.C Lten we voor verschillende stpgrootten h, rekenend met zes cijfers, eens de fgeleiden vn de exponentiële functie e x in x 0 = beplen met behulp vn (9). x e x h bendering fout We zien dt voor dlende h de bendering nvnkelijk beter wordt, mr drn verslechtert. De reden voor dit verschijnsel is niet moeilijk n te geven. Voor bijv. h = hebben we de volgende situtie: f(x 0 + h) =.700 f(x 0 h) = Bij het ftrekken vllen de eerste drie cijfers tegen elkr weg, en we houden er slechts drie over. Dit heeft de volgende consequenties: De oorspronkelijke wrden vn f zijn belst met frondfouten. De bsolute grootte vn deze fouten is hoogstens 5.0 6, en de reltieve fouten zijn dus hoogstens / De bsolute frondfout in het verschil kn dus oplopen tot (nmelijk bij tegengestelde tekens vn de frondfouten), hetgeen een reltieve fout in het verschil veroorzkt vn / , dt is dus 000 ml zo groot ls de mximle reltieve fout in de f-wrden. Dit effect wordt ntuurlijk sterker nrmte h kleiner wordt. We zijn hier ngelopen tegen bekend probleem in de numerieke wiskunde: Het ftrekken vn twee bijn even grote getllen. Voor de benderingsformule (9) betekent dit dt de te bereiken nuwkeurigheid gelimiteerd is. Enerzijds wil je h zo klein mogelijk hebben om de rest klein te mken; nderzijds mg h niet klein zijn om bovengenoemde reden. Er zl dus een optimle wrde vn h zijn wrbij de uitkomst zo nuwkeurig mogelijk is. Angezien de frondfout onbekend is kunnen we deze wrde niet beplen. Wel kn men een mjornt, d.w.z. bovengrens, vn de fout minimliseren, en wel ls volgt. Lt de wrden vn f belst zijn met frondfouten hoogstens ǫ. Dit levert dn een bijdrge vn hoogstens S (h) = ǫ/h tot de bsolute fout in de numerieke bendering voor f (x 0 ). De tweede bijdrge is de restterm R (h) ls in (0). De totle fout wordt dus gemjoreerd door de grootheid ϕ(h) die gegeven wordt door ϕ(h) = ǫ h + h 6 m ()
21 . Nuwkeuriger formules 7 wrin m een mjornt is voor f (x) op een voldoend grote mr ook weer niet l te grote omgeving [x 0 h 0, x 0 + h 0 ] vn x 0. Deze functie heeft een minimum ǫ m voor h = 3 3ǫ/m. Wnneer voor deze h geldt h h 0 dn beschouwt men hem ls de optimle. In het voorbeeld met e x vinden we zo met x 0 =, ǫ = 5.0 6, h 0 = 0., m = 3.3 dt h = en φ(h) = D De tweede fgeleide kunnen we benderen door met (9) eerst f (x 0 + h) en f (x 0 h) te benderen, en hiermede vervolgens de bendering f (x 0 + h) f (x 0 h) h voor f (x 0 ) te construeren. Met enig rekenen en Tylor vinden we () f (x 0 ) = f(x 0 + h) f(x 0 ) + f(x 0 h) h + R 3 (h), R 3 (h) = h f(4) (ξ). (3).E De effecten vn frondfouten zijn nu nog ernstiger. Anloog n.c vinden we nu S 3 (h) = 4ǫ h ls bovengrens voor het effect vn de frondfouten in de f-wrde op de numerieke bendering voor f (x 0 ) en dt loopt snel op bij dlende h. Formule (3) levert met h = 0.0 en de tbel vn.c voor f () een wrde.70 en voor h = 0. een wrde.7. Men kn een nlogon vn () opstellen, en vindt dn een optimle foutschtting voor h 0...F Formules (9) en (3) zijn equidistnte formules. Een generlistie vn (3) wordt gegeven door wrin f (x 0 ) = h f(x 0 + h ) (h + h )f(x 0 ) + h f(x 0 h ) h h (h + h )/ + R 4 (h,h ) (4) R 4 (h,h ) = h f (ξ ) h f (ξ ), ξ (x 0,x 0 + h ) en ξ (x 0 h,x 0 ). (5) 3(h + h ) Merk op dt i.h.. slechts R 4 (h,h ) = O(mx{h,h }).. Nuwkeuriger formules De formules in sectie. zijn enigzins dhoc fgeleid en hebben geen erge hoge nuwkeurigheidsorde. Een systemtischer mnier, wrmee ook hogere nuwkeurigheidsorden bereikt kunnen worden (ls we fzien vn het effect vn frondfouten), is de te differentiëren functie te benderen met een Lgrnge interpoltiepolynoom p n op steunpunten {x k : 0 k n} en dit polynoom te differentiëren. M.b.v. de Lgrnge representtie uit (6) krijgt men zo f (i) () p (i) n () = n k=0 L (i) kn ()f(x k) (6) wrbij de coëfficiënten L (i) kn () dus onfhnkelijk zijn vn f. Duidelijk is dt de bendering (6) slechts zinnig is voor i n. Angezien (6) exct is voor f P n, kunnen
22 8 NUMERIEKE DIFFERENTIATIE we voor vste {x k : 0 k n}, i en, de fctoren L (i) kn () behlve door differentitie vn de Lgrnge coëfficiënten ook beplen door een stelsel vn n + vergelijkingen op te lossen dt verkregen wordt door voor f(x) chtereenvolgens,x,... x n te nemen. Men kn eenvoudig ntonen dt dit stelsel een unieke oplossing heeft. Voor equidistnte puntenrijen {x k }, i = n en met h de fstnd tussen opvolgende steunpunten krijgt men de volgende formules: f (x 0 + h) [f(x ) f(x 0 )]/h (7) f (x ) [f(x ) f(x ) + f(x 0 )]/h (8) f (x + h) [f(x 3) 3f(x ) + 3f(x ) f(x 0 )]/h 3 (9) etc., welke voor voldoend gldde f een restterm O(h ) hebben. Formules met een restterm vn hogere orde kn men verkrijgen door de techniek uit deze sectie met n > i toe te pssen. Een voorbeeld vn een dergelijke formule met n = 4 en i = is f () [f( h) 8f( h) + 8f( + h) f( + h)] (30) h met restterm O(h 4 ). De coëfficiënt voor f() blijkt hier nul te zijn..3 Experimenteel gevonden functiewrden Wnneer men een functie f wil differentiëren wrvn men slechts experimenteel gevonden functiewrden kent dn kunnen de tot dusverre ontwikkelde differentitieformules wel heel slecht uit de bus komen. Voorbeeld.3. Stel dt men vn de functie f(x) = +x door meting functiewrden beplt voor x k = + k 0 (k = 0,... 4), en dt de resultten vn onderstnde tbel worden verkregen. Men ziet dt de meetfout circ bedrgt. Bendert men nu f (0.60) met behulp vn de formule (30) dn vindt men f (0.60).0, hetgeen 0% fout is. x f(x) Een ndere npk is nu dt we f niet benderen met een 4-de grds polynoom en dt differentiëren (zols in (30)), mr dt we een lineire functie zo goed mogelijk n de gevonden functiewrden npssen, en dn die lineire functie differentiëren. 4 k=0 g(x k) ls norm op functies gedefiniëerd op de punten x k, Kiezen we g = dn levert elementir rekenwerk dt de beste bendering vn f door een lineire functie gegeven wordt door x α 0β α β 0 α 0 α α x + α β 0 α β α 0 α α wrbij α 0 = n +, α = x k, α = x k, β 0 = f(x k ) en β = f(x k )x k. Het minimliseren vn de fstnd in bovenstnde norm is bekend ls de kleinste kwdrten
23 .3 Experimenteel gevonden functiewrden 9 methode. Het differentiëren vn het verkregen lineir polynoom levert nu de bendering f (0.6) α 0β α β 0 = 0.99 hetgeen een heel wt beter resultt is dn wt eerder werd α 0 α α verkregen. Op soortgelijke wijze kn men, ls men wt meer punten heeft, f npssen n een polynoom vn hogere grd, en dt dn differentiëren.
24 0 3 FOUTSCHATTINGEN BIJ NUMERIEKE PROCESSEN 3 Foutschttingen bij numerieke processen 3. Fouten 3.A Vrijwel ltijd zl het resultt vn een numerieke bendering vn een grootheid α niet exct zijn. De mte wrin vn α fwijkt, kunnen we uitdrukken in - de fout: α - de bsolute fout: α - de (bsolute) reltieve fout: α α De fout zelf is doorgns onbekend (wnt nders zou men het wre ntwoord α ook kunnen vinden). Men is vk l blij ls men een mjornt (d.w.z. bovengrens) voor de bsolute fout heeft. Zo weet men dt de bsolute fouten in de sinustbel uit.a hoogstens 0 6 zijn, mr de (gewone, bsolute, reltieve) fout zelf kent men niet. Het is dn ook onjuist te zeggen dt deze tbel de sinuswrden oplevert met een fout vn 0 6 : de wrden worden opgeleverd met een onbetrouwbrheid vn 0 6. Wij zullen dit onderscheid verder steeds nhouden. Onder onbetrouwbrheid (respectievelijk reltieve onbetrouwbrheid) verstn we dus bovengrenzen (mjornten) voor de bsolute (respectievelijk reltieve) fout. Eigenschp. (bewijs dit zelf): heeft onbetrouwbrheid ǫ = α + ǫ, ǫ ǫ, heeft reltieve onbetrouwbrheid ǫ = α( + ǫ ), ǫ ǫ. 3.B Foutfilosofie. Het is doorgns niet interessnt om een onbetrouwbrheid erg nuwkeurig op te geven: de mededeling, dt een reltieve onbetrouwbrheid.% is, is nuwelijks inhoudsrijker dn dt hij % is. Het is ntuurlijk wel vn belng, te weten of hij % dn wel 5% is, wnt nu is er onderhnd sprke vn een verschil in orde vn grootte. Hetzelfde geldt ntuurlijk voor de (bsolute) onbetrouwbrheid. Voorbeeld 3.. We bekijken weer dezelfde sinus-tbel uit.a, mr nu met wt meer decimlen om in het vervolg frondfouten te kunnen verwrlozen. x sin(x) 35 o o o o o Pssen wij nu lineire interpoltie toe met steunpunten 36 o en 38 o om sin(37 o ) te benderen, dn vinden we sin(37 o ) , wrin dus een fout zit vn Als bovengrens voor de fout vinden we met stelling..: fout 8 (4π/360) sin(38 o ) = Als mjornt voor de fout is deze informtie veel te nuwkeurig. Immers, we zien hieruit dt de 7 in de vierde deciml vn het berekende ntwoord misschien wel een 6 of een 8 hd moeten zijn, en dt lle volgende cijfers betekenisloos zijn. Dezelfde conclusie hd men kunnen trekken ls er een onbetrouwbrheid vn ws gegeven.
25 3. Fouten Een nder spect dt door het bovenstnde voorbeeld goed geïllustreerd wordt, is dt vn de overbodige decimlen. Dikwijls geven rekenpprten (computers, pocketclcultors, etc.) de uitkomst stndrd in de -voor hen- grootst mogelijke nuwkeurigheid, dt wil zeggen, in het mximl beschikbre ntl cijfers. Echter doordt een pproximtieproces is toegepst, gebeurt het mr zelden dt l deze cijfers inderdd ook juist zijn. Als men, zols in het bovenstnde voorbeeld, een ntwoord heeft met een onbetrouwbrheid vn ongeveer 0.000, dn is het n te bevelen om in een verslg niet meer dn 4 of 5 cijfers chter de komm te vermelden, dus in bovenstnd gevl of 0.607; men hndhft zo de onbetrouwbrheid op ongeveer hetzelfde niveu (deze wordt resp ), en vlt de lezer niet lstig met overbodige cijfers. Het is geen goede gewoonte om (zols nogl eens nbevolen wordt) een uitkomst f te ronden op een zodnig ntl cijfers dt het resultt gelijk is n het wre ntwoord fgerond op dit ntl cijfers. Dt zou bijvoorbeeld betekenen dt een uitkomst met een onbetrouwbrheid 0.000, moet worden fgerond op 0.43, met een onbetrouwbrheid De onbetrouwbrheid kn zo dus nzienlijk toenemen. Het is ook geen goede gewoonte het ntl correcte cijfers te hnteren ls mt voor de nuwkeurigheid vn een uitkomst. Immers, een uitkomst =.9999 voor een grootheid α = heeft geen enkel correct cijfer, mr is wel redelijk nuwkeurig. Omgekeerd geldt ntuurlijk wel, dt een groot ntl correcte cijfers (fgezien vn eventuele nullen voorn) een kleine reltieve onbetrouwbrheid grndeert. Zelfs indien men over een uitkomst met een kleine reltieve onbetrouwbrheid beschikt (zeg 0 0 ) dn is het nog niet ltijd verstndig om de eerste tien relevnte cijfers (dt zijn de cijfers die overblijven n weglting vn eventuele nullen voorn) ook lle te geven. Dikwijls is de lezer niet geïnteresseerd in een dergelijke nuwkeurigheid. Smenvttend: - Geef vn het resultt niet meer cijfers dn er nodig zijn om de onbetrouwbrheid ongeveer op hetzelfde niveu te hndhven. - Geef vn het resultt niet meer cijfers dn er gewenst worden. - Geef vn de reltieve of bsolute onbetrouwbrheid één, of hoogstens twee, relevnte cijfers. 3.C De bronnen vn fouten kunnen globl worden ingedeeld in drie groepen: - modelfouten - representtiefouten - frondfouten Modelfouten ontstn ls men trcht de fysische (of economische, biologische, technische) reliteit te beschrijven door middel vn een wiskundige vergelijking; vk worden hierbij kleine (en soms ook niet zo kleine) effecten verwrloosd. In het lgemeen zijn deze fouten vrij klein bij problemen uit de fysic, mr nzienlijk groter bij problemen uit de economie of de biologie. Deze fouten vllen eigenlijk buiten het kder vn de numerieke wiskunde. Representtiefouten ontstn doordt men het wiskundige probleem, dt ls model vn het fysische (economische, enz.) probleem dient, en wrvn men de oplossing niet kn beplen, vervngt door een nburig probleem dt men wel kn oplossen. Voorbeeld: men vervngt een fgeleide door een differentiequotiënt, zie hoofdstuk. Heel
26 3 FOUTSCHATTINGEN BIJ NUMERIEKE PROCESSEN vk hebben representtiefouten een beplde struktuur. Een belngrijke tk vn de numerieke wiskunde houdt zich bezig met het opsporen en uitbuiten vn deze struktuur. Zie verder sectie 3.4 en sectie 3.5. Afrondfouten ontstn doordt men rekenpprten slechts in eindige precisie rekenen. Zie verder sectie Afrondfouten 3.A Afrondfouten ontstn doordt rekenpprten niet met de verzmeling R vn reële getllen werken, mr met een eindige deelverzmeling Q vn Q. De elementen vn Q worden mchinegetllen genoemd. Gewoonlijk heeft deze verzmeling de volgende vorm Q = {y = ±.d...d s β e : d i {0,...,β }, d > 0 tenzij y = 0, e Z, m e M}. Hierbij heet ±.d...d s de mntisse, en e de exponent (t.o.v. het grondtl β). Computers rekenen meestl binir, d.w.z. β =, hoewel er ook wel hexdecimle rithmetiek toegepst wordt, d.w.z. β = 6. In het binire gevl zijn typische wrden (IEEE stndrd) s = 4, m = 5 en M = 8 (enkelvoudige precisie), dnwel s = 53, m = 0 en M = 04 (dubbele precisie). Rekenmchines rekenen meestl deciml (β = 0). Typische wrden zijn s = 0, m = 98, M = 00. Onder het bereik vn een mchine verstt men de verzmeling { R q q } {0} wrin q en q het kleinste resp. grootste positieve getl in Q is. Getllen binnen dit bereik kunnen door de mchine in goede reltieve precisie worden weergegeven. Als bij een berekening een uitkomst ontstt met bsolute wrde groter dn q dn spreekt men vn overflow. Vk wordt er dn een foutmelding gegenereerd, echter sommige rekenmchines leveren zonder verdere wrschuwing ±q f. Bij een uitkomst ongelijk n 0 in ] q, q [ (underflow) wordt doorgns op 0 fgerond zonder verdere wrschuwing. Eigenschp. (Bewijs dit zelf) Zij α 0 een getl dt binnen het bereik vn de mchine ligt. Zij het getl in Q (of een vn de twee getllen in Q) het dichtst bij α. Als de mchine α frondt tot, spreken we vn een correcte fronding. Dn heeft een reltieve fout vn hoogstens β s. In het lgemeen zl n iedere bewerking +,,, / en sin, cos, exp, enzovoort, vn getllen in Q het excte resultt niet meer in Q zitten. Er zl dus (opnieuw) fgerond moeten worden. Op deze wijze ontstt in grotere progrmm s een hele keten vn frondfouten, die bovendien op elkr inwerken. Hierin vlt meestl geen struktuur te ontdekken. Het beste dt men kn bereiken is het geven vn een bovengrens voor de uiteindelijke frondfout (dt is het totle effect vn lle voorfgnde frondingen) in het eindresultt. 3.B In prktijk komt het reltief zelden voor dt de begrenzingen vn het mchinebereik een rol spelen; bovendien, ls dit wel het gevl is, kn men zich drtegen wpenen door het inbouwen vn controles in het progrmm.
27 3. Afrondfouten 3 We nemen drom n dt het volgende geldt: Er bestt een (klein) getl ξ, de reltieve mchine precisie, en een functie rd (round) : R Q zo dt voor elk reëel getl α geldt rd(α) = α( + ξ) met ξ ξ (3) en bovendien voor elke Q rd() =, (3) met de fsprk, dt getllen die men vn buiten in het rekenpprt invoert, door rd worden fgebeeld in Q. We nemen verder n dt de optelopertie + die de mchine uitvoert op getllen en b uit Q ls resultt levert + b = rd( + b) = ( + b)( + ξ), ξ ξ en nloog voor de mchineoperties,, /. D.w.z., we veronderstellen een optimle rithmetiek. Om dit te reliseren wordt er intern met één of meerdere extr cijfers gerekend. 3.C Om te lten zien hoe frondfoutennlyse werkt, bekijken we nu het voorbeeld vn het optellen vn een ntl mchinegetllen 0,..., n, in deze volgorde. Allereerst tellen we 0 en op: Hierbij wordt opgeteld, enzovoort: 0 + = ( 0 + )( + ξ ), ξ ξ. ( 0 + ) + = (( 0 + )( + ξ ) + )( + ξ ) = S, ξ i ξ, i =,; (( 0 + ) + ) + 3 = ((( 0 + )( + ξ ) + )( + ξ ) + 3 )( + ξ 3 ) = S 3 ξ i ξ, i =,,3. (Om de uitdrukking nog enigszins overzichtelijk te houden, nemen we n = 3.) We krijgen zo: S 3 = 0 ( + ξ )( + ξ )( + ξ 3 ) + ( + ξ )( + ξ )( + ξ 3 )+ + ( + ξ )( + ξ 3 ) + 3 ( + ξ 3 ). We merken nu op dt er zeker een ξ 4 is met ξ 4 ξ zo dt ( + ξ )( + ξ )( + ξ 3 ) = ( + ξ 4 ) 3 (g n), en evenzo is er een ξ 5 met ξ 5 ξ, zo dt S 3 = 0( + ξ 4 ) 3 + ( + ξ 4 ) 3 + ( + ξ 5 ) + 3 ( + ξ 3 ). (33) Bijgevolg, ls S 3 de wre som voorstelt, geldt S 3 S 3 = 0 [( + ξ 4 ) 3 ] + [( + ξ 4 ) 3 ] + [( + ξ 5 ) ] + 3 ξ 3 Nu geldt [(+ξ 4 ) 3 ] = 3ξ 4 +3ξ 4 +ξ3 4 3ξ 4 en [(+ξ 5 ) ] = ξ 5 +ξ 5 ξ 5 zodt, indchtig de foutfilosofie uit 3.B, S 3 S 3 < ( )ξ. Het teken < wordt uitgesproken ls kleiner dn of ongeveer gelijk n.
28 4 3 FOUTSCHATTINGEN BIJ NUMERIEKE PROCESSEN 3.D We constteren dt het ons weinig gebt heeft l de optredende ξ s door middel vn indices vn elkr te onderscheiden; dit blijkt vk het gevl te zijn bij frondfoutennlyse. We lten drom deze indices meestl weg. Dit betekent dn wel dt een en hetzelfde symbool ξ een ntl verschillende wrden kn representeren, zelfs binnen één formule. We mken drom de volgende nottiefsprk: Bij frondfoutennlyse zl ξ steeds een getl voorstellen met bsolute wrde kleiner dn of gelijk n ξ, mr iedere keer dt ξ voorkomt, kn hij een ndere wrde hebben. Met deze fsprk krijgen we voor de berekende som S 3 S 3 = ((( 0 + )( + ξ) + )( + ξ) + 3 )( + ξ) = = 0 ( + ξ) 3 + ( + ξ) 3 + ( + ξ) + 3 ( + ξ) (34) (vergelijk (33)). We hebben hier l stilzwijgend gebruik gemkt vn een volgende nottiefsprk: Een reltie ls f(ξ) = g(ξ), met f en g functies vn R nr R, moet in de frondfouten nlyse gelezen worden ls: bij elke ξ, ξ ξ, is er een ξ, ξ ξ, zodt f(ξ ) = g(ξ ). Merk op, dt volgens deze fsprk het = teken geen symmetrische reltie weergeeft. Het symbool ξ is dus vergelijkbr met de ordesymbolen o en O vn Lndu. Zo geldt er (g n!) ξ = ξ mr niet Dit is vergelijkbr met mr niet ξ = ξ. O(x ) = O(x) (x 0) O(x) = O(x ) (x 0). G ook n, dt de volgende uitdrukkingen juist zijn: ξ ξ = ξ ( + ξ)( + ξ) = ( + ξ). 3.E Bij frondfoutennlyse komen we blijkbr llerlei mchten vn ( + ξ) tegen, ook negtieve en niet gehele mchten, en we willen weten, hoever die vn f kunnen liggen. In eerste bendering (dt wil zeggen voor ξ 0, k vst) geldt ( + ξ) k kξ (35) (eerste orde Tylor bendering). De vrg is voor welke wrden vn k dit bij een vste wrde vn ξ nog bruikbr is. Hierover doet het volgende lemm een uitsprk.
29 3. Afrondfouten 5 Lemm 3.. Zij k R. Dn geldt + kx ( + x) k + kx( + kx) voor k en kx (36) kx ( + x) k kx( kx) voor k en kx. (37) Bewijs. Noem f(x) = ( + x) k ( + kx). Dn geldt f(0) = 0, f (x) 0 voor x 0 en k en f (x) 0 voor x 0 en k. Hiermee volgt de linker ongelijkheid in (36). Angnde de rechter ongelijkheid in (36) merken we op dt + x e x voor lle x R, zodt voor k 0, kx geldt ( + x) k e kx = + kx + k x + kx + k x ( + kx3 + k x k3 x 3 ) ( ) = + kx k x, en dus is de rechter ongelijkheid in (36) bewezen. De linker ongelijkheid in (37) volgt uit ( + x) k ( kx) e kx e kx =. De rechter ongelijkheid volgt m.b.v. (36) uit ( + x) k + kx = kx + k x + kx. We zien hieruit dt ls kξ (en dit is heel vk het gevl) de reltie (35) in de zin vn de foutfilosofie bevredigend vervuld is, en evenzo de reltie kξ (38) ( + ξ) k (merk op dt de ξ s links en rechts tegengesteld teken hebben). 3.F Toepssingen. G n dt in het lgemeen geldt: Eigenschp. Zij Sn de door het rekenpprt geleverde bendering voor de som S n = n i=0 i, gesommeerd vnf 0. Dn S n S n < (n 0 + n (n + i) i )ξ. i= Opgve 3.. Zij 0,..., n een stel mchinegetllen en S n = n i=0 i. Men kn deze getllen uiterrd in llerlei volgordes optellen, en krijgt dn steeds verschillende berekende wrden Sn. Toon n dt de onbetrouwbrheid in S n zols deze gegeven wordt door eigenschp 3.F miniml is ls men de getllen optelt in volgorde vn opklimmende bsolute wrde. Opgve 3.. Men kn de getllen 0,..., n ook ls volgt optellen:
Hoofdstuk 0: algebraïsche formules
 Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Uitwerking Tentamen Analyse B, 28 juni lim
 Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Primitieve en integraal
 Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 4 Primitieve en integrl Een motivtie om nr de fgeleide vn een functie f te kijken is het beplen vn de richtingscoëfficiënt vn de rklijn
Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 4 Primitieve en integrl Een motivtie om nr de fgeleide vn een functie f te kijken is het beplen vn de richtingscoëfficiënt vn de rklijn
Continuïteit en Nulpunten
 Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Analyse. Lieve Houwaer Dany Vanbeveren
 Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Tentamen Numerieke Wiskunde (WISB251)
 1 Tentmen Numerieke Wiskunde (WISB251) Mk één opgve per vel en schrijf op ieder vel duidelijk je nm en studentnummer. Lt duidelijk zien hoe je n de ntwoorden komt. Onderstnde formules en stellingen mg
1 Tentmen Numerieke Wiskunde (WISB251) Mk één opgve per vel en schrijf op ieder vel duidelijk je nm en studentnummer. Lt duidelijk zien hoe je n de ntwoorden komt. Onderstnde formules en stellingen mg
== Modeluitwerking tentamen Analyse 1 == Maandag 14 januari 2008, u
 == Modeluitwerking tentmen Anlyse == Mndg 4 jnuri 8, 4.-7.u. Formuleer de Tussenwrdestelling. Als f :, b] R continu is en s R ligt tussen f en fb, dn bestt er een c, b] met fc = s. b Toon n, dt de vergelijking
== Modeluitwerking tentmen Anlyse == Mndg 4 jnuri 8, 4.-7.u. Formuleer de Tussenwrdestelling. Als f :, b] R continu is en s R ligt tussen f en fb, dn bestt er een c, b] met fc = s. b Toon n, dt de vergelijking
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
2 Opgaven bij Hoofdstuk 2
 2 Opgven bij Hoofdstuk 2 Opgve 2. De functie f : R 2 R is gedefinieerd door ) Bewijs dt f continu is op R 2 \ {(, )}. f(, y) = 2 y 2 + y 2 ls (, y) (, ) f(, ) =. b) Bewijs dt voor iedere R de functie y
2 Opgven bij Hoofdstuk 2 Opgve 2. De functie f : R 2 R is gedefinieerd door ) Bewijs dt f continu is op R 2 \ {(, )}. f(, y) = 2 y 2 + y 2 ls (, y) (, ) f(, ) =. b) Bewijs dt voor iedere R de functie y
Bespreking Examen Analyse 1 (Juni 2007)
 Bespreking Exmen Anlyse 1 (Juni 2007) Voorf: Zols ik ook vorig jr in juni en in september gedn heb, geef ik hier bedenkingen bij het exmen vn deze junizittijd. Ik zorg ervoor dt deze tekst op toledo komt,
Bespreking Exmen Anlyse 1 (Juni 2007) Voorf: Zols ik ook vorig jr in juni en in september gedn heb, geef ik hier bedenkingen bij het exmen vn deze junizittijd. Ik zorg ervoor dt deze tekst op toledo komt,
2. Gegeven is de driehoek van figuur 10.10a. Gevraagd worden hoek β en de zijden a en c.
 Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
Parels van studenten tijdens een examen
 Prel 1 Prels vn studenten tijdens een exmen c k x k n+1 n+1 ( = c k x k ( ) )x c n+1x n+1 n+1 k ( ) k x n+1 k ( ) k k k Prel 2 Vrg: Zij n N, c k C voor k = 1,..., n, c n 0. Toon n dt de functie f(z) =
Prel 1 Prels vn studenten tijdens een exmen c k x k n+1 n+1 ( = c k x k ( ) )x c n+1x n+1 n+1 k ( ) k x n+1 k ( ) k k k Prel 2 Vrg: Zij n N, c k C voor k = 1,..., n, c n 0. Toon n dt de functie f(z) =
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
 Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Examen VWO. wiskunde B1,2 (nieuwe stijl)
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
5.1 Rekenen met differentialen
 Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 5 Substitutie We hebben gezien dt de productregel voor de fgeleide een mnier geeft, om voor zeker functies een primitieve te vinden,
Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 5 Substitutie We hebben gezien dt de productregel voor de fgeleide een mnier geeft, om voor zeker functies een primitieve te vinden,
Wiskundige Analyse 1
 Wiskundige Anlyse 1 Belngrijkste stellingen 1 Getllen Driehoeksongelijkheid : b ± b + b Supremumprincipe : Elke nietlege verzmeling reële getllen die nr boven begrensd is, heeft een supremum Infimumprincipe
Wiskundige Anlyse 1 Belngrijkste stellingen 1 Getllen Driehoeksongelijkheid : b ± b + b Supremumprincipe : Elke nietlege verzmeling reële getllen die nr boven begrensd is, heeft een supremum Infimumprincipe
Inhoud college 7 Basiswiskunde
 Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
Praktische opdracht Optimaliseren van verpakkingen Inleidende opgaven
 Prktische opdrcht Optimliseren vn verpkkingen Inleidende opgven V, WB Opgve 1 2 Gegeven is de functie f ( x) = 9 x. Op de grfiek vn f ligt een punt P ( p; f ( p)) met 3 < p < 0. De projectie vn P op de
Prktische opdrcht Optimliseren vn verpkkingen Inleidende opgven V, WB Opgve 1 2 Gegeven is de functie f ( x) = 9 x. Op de grfiek vn f ligt een punt P ( p; f ( p)) met 3 < p < 0. De projectie vn P op de
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
3 Snijpunten. Verkennen. Uitleg
 3 Snijpunten Verkennen Meetkunde Snijpunten Inleiding Verkennen Bentwoord de vrgen bij Verkennen. Mk ook de constructie in GeoGebr. Gebruik eventueel het progrmm om de snijpunten voor je te berekenen ls
3 Snijpunten Verkennen Meetkunde Snijpunten Inleiding Verkennen Bentwoord de vrgen bij Verkennen. Mk ook de constructie in GeoGebr. Gebruik eventueel het progrmm om de snijpunten voor je te berekenen ls
is het koppel dat overeenkomt met het eindpunt van λ.op ax by = a a b x y = a b = x y a b ax by bx + ay = a b
 1 Tweedimensionle Euclidische ruimte 11 Optelling, verschil en sclire vermenigvuldiging = ( b, ) b, is de verzmeling vn lle koppels reële getllen { } Zols we ons de reële getllen kunnen voorstellen ls
1 Tweedimensionle Euclidische ruimte 11 Optelling, verschil en sclire vermenigvuldiging = ( b, ) b, is de verzmeling vn lle koppels reële getllen { } Zols we ons de reële getllen kunnen voorstellen ls
ANTWOORDEN EN UITWERKINGEN TENTAMEN QUANTUMMECHANICA 2 VAN 31 MEI 2011
 ANTWOORDEN EN UITWERKINGEN TENTAMEN QUANTUMMECHANICA VAN MEI ) (Andere ntwoorden zijn niet noodzkelijk (geheel) incorrect) () Enkelvoudig ontrd ofwel niet-ontrd. Niveu met energie C= heeft een deeltje
ANTWOORDEN EN UITWERKINGEN TENTAMEN QUANTUMMECHANICA VAN MEI ) (Andere ntwoorden zijn niet noodzkelijk (geheel) incorrect) () Enkelvoudig ontrd ofwel niet-ontrd. Niveu met energie C= heeft een deeltje
Routeplanning middels stochastische koeling
 Routeplnning middels stochstische koeling Modellenprcticum 2008 Stochstische koeling of Simulted nneling is een combintorisch optimlistielgoritme dt redelijke resultten geeft in ingewikkelde situties.
Routeplnning middels stochstische koeling Modellenprcticum 2008 Stochstische koeling of Simulted nneling is een combintorisch optimlistielgoritme dt redelijke resultten geeft in ingewikkelde situties.
Inleiding Natuurwetenschappen
 Inleiding Ntuurwetenschppen Tijden: september: 7:45 :45 3 september: 7:45 :45 6 september: 09:30 3:30 Loctie: Adres: Leuvenln, Utrecht Gebouw: Mrius Ruppertgebouw Zl: A Opdrchtgever: Jmes Boswell Instituut
Inleiding Ntuurwetenschppen Tijden: september: 7:45 :45 3 september: 7:45 :45 6 september: 09:30 3:30 Loctie: Adres: Leuvenln, Utrecht Gebouw: Mrius Ruppertgebouw Zl: A Opdrchtgever: Jmes Boswell Instituut
Exact periode 2.2. Gemiddelde en standaarddeviatie Betrouwbaarheidsinterval Logaritme ph lettersommen balansmethode
 Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
2 Verwisselingsstellingen en oneigenlijke integralen
 2 Verwisselingsstellingen en oneigenlijke integrlen 2.1 Verwisseling vn de differentitievolgorde Lt V een open deelverzmeling vn R 2 zijn, en f : V R een reëelwrdige funtie op V die prtieel differentieerbr
2 Verwisselingsstellingen en oneigenlijke integrlen 2.1 Verwisseling vn de differentitievolgorde Lt V een open deelverzmeling vn R 2 zijn, en f : V R een reëelwrdige funtie op V die prtieel differentieerbr
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Dinsdag 25 mei uur
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
Keuze van het lagertype
 Keuze vn het lgertype Beschikbre ruimte... 35 Belstingen... 37 Grootte vn de belsting... 37 Richting vn de belsting... 37 Scheefstelling... 40 Precisie... 40 Toerentl... 42 Lgergeruis... 42 Stijfheid...
Keuze vn het lgertype Beschikbre ruimte... 35 Belstingen... 37 Grootte vn de belsting... 37 Richting vn de belsting... 37 Scheefstelling... 40 Precisie... 40 Toerentl... 42 Lgergeruis... 42 Stijfheid...
1 Vlaamse Wiskunde Olympiade 1985-1986: Tweede Ronde.
 1 Vlmse Wiskunde Olymide 1985-1986: Tweede Ronde De tweede ronde bestt uit 30 meerkeuzevrgen Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 unten Per goed ntwoord krijgt hij of zij 4
1 Vlmse Wiskunde Olymide 1985-1986: Tweede Ronde De tweede ronde bestt uit 30 meerkeuzevrgen Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 unten Per goed ntwoord krijgt hij of zij 4
INHOUDSTABEL. 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3. 2a. TEKENREGELS (fiche 2a)... 5
 INHOUDSTABEL 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3 2. TEKENREGELS (fiche 2)... 5 2b. TEGENGESTELDE GETAL - TEGENGESTELDE SOM (verschil) - TEGENSTELDE PRODUCT (fiche 2b)... 6 2c. OMGEKEERDE
INHOUDSTABEL 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3 2. TEKENREGELS (fiche 2)... 5 2b. TEGENGESTELDE GETAL - TEGENGESTELDE SOM (verschil) - TEGENSTELDE PRODUCT (fiche 2b)... 6 2c. OMGEKEERDE
Correctievoorschrift VWO. Wiskunde B1 (nieuwe stijl)
 Wiskunde B (nieuwe stijl) Correctievoorschrift VWO Voorbereidend Wetenschppelijk Onderwijs 0 0 Tijdvk Inzenden scores Vul de scores vn de lfbetisch eerste vijf kndidten per school in op de optisch leesbre
Wiskunde B (nieuwe stijl) Correctievoorschrift VWO Voorbereidend Wetenschppelijk Onderwijs 0 0 Tijdvk Inzenden scores Vul de scores vn de lfbetisch eerste vijf kndidten per school in op de optisch leesbre
4. Wortels van decimale getallen mag je met het RT uitrekenen. Maar voor opgaven met gehele numerieke factoren wordt een exact resultaat
 Modelvrgstukken Algebr vn wortelvormen Tenzij expliciet nders vermeld stellen lle letters positieve getllen voor Vereenvoudigen vn enkelvoudige wortels ; Dit is gewoon de bsisregel ) ) 8 ) ; ) Een 8-ste
Modelvrgstukken Algebr vn wortelvormen Tenzij expliciet nders vermeld stellen lle letters positieve getllen voor Vereenvoudigen vn enkelvoudige wortels ; Dit is gewoon de bsisregel ) ) 8 ) ; ) Een 8-ste
a = 1 b = 0 k = 1 ax + b = lim f(x) lim
 BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
Eindexamen wiskunde B1-2 vwo 2004-I
 chten vn een derdegrdsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. V is het gebied ingesloten door de grfiek vn f en de x-s. 5p 1 ereken lgebrïsch de excte wrde vn de oppervlkte
chten vn een derdegrdsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. V is het gebied ingesloten door de grfiek vn f en de x-s. 5p 1 ereken lgebrïsch de excte wrde vn de oppervlkte
Kwadratische reciprociteit
 Kwdrtische recirociteit René Pnnekoek 9 februri 011 Inleiding: kwdrten in Z/Z Beschouw de ring Z/Z en een element Z/Z. We willen weten of een kwdrt is, oftewel of er x Z/Z bestt zodnig dt x. Voor concrete
Kwdrtische recirociteit René Pnnekoek 9 februri 011 Inleiding: kwdrten in Z/Z Beschouw de ring Z/Z en een element Z/Z. We willen weten of een kwdrt is, oftewel of er x Z/Z bestt zodnig dt x. Voor concrete
Examen VWO. wiskunde B (pilot) tijdvak 1 woensdag 16 mei 13.30-16.30 uur
 Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
WISKUNDE VOOR DE PROPEDEUSE ENIGINEERING MARITIEME TECHNIEK. A.F. Bloemsma M.A. Litjens C. Ultzen M.D. Poot
 WISKUNDE VOOR DE PROPEDEUSE ENIGINEERING MARITIEME TECHNIEK A.F. Bloemsm M.A. Litjens C. Ultzen M.D. Poot INHOUD: H. : Hkjes wegwerken, ontbinden in fctoren H. : Mchten 0 H. : Het rekenen met breuken (deel
WISKUNDE VOOR DE PROPEDEUSE ENIGINEERING MARITIEME TECHNIEK A.F. Bloemsm M.A. Litjens C. Ultzen M.D. Poot INHOUD: H. : Hkjes wegwerken, ontbinden in fctoren H. : Mchten 0 H. : Het rekenen met breuken (deel
Vectoranalyse voor TG
 college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
2 ). Door steeds de functiewaarde aan de linkerkant te kiezen, krijgen we de benaderingsformule
 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse Les 9 Numerieke integrtie In de prktijk is het mr zelden het gevl dt we een functie expliciet kunnen primitiveren. Voorbeelden hiervoor
Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse Les 9 Numerieke integrtie In de prktijk is het mr zelden het gevl dt we een functie expliciet kunnen primitiveren. Voorbeelden hiervoor
Uitwerking herkansing Functies en Reeksen
 Uitwerking herknsing Functies en Reeksen 3 jnuri 14, 9: - 1: uur Opgve 1 () De functie ' is prtieel differentieerbr, met prtiële fgeleiden @'.x; y/ D.1; 1/T en @x @' @y.x; y/ D. v; v/t : Deze prtiële fgeleiden
Uitwerking herknsing Functies en Reeksen 3 jnuri 14, 9: - 1: uur Opgve 1 () De functie ' is prtieel differentieerbr, met prtiële fgeleiden @'.x; y/ D.1; 1/T en @x @' @y.x; y/ D. v; v/t : Deze prtiële fgeleiden
Rekenen in Ê. Module De optelling. Definitie
 Module 1 Rekenen in Ê 1.1 De optelling Definitie Het resultt vn de optelling vn reële getllen en b noemen we de som vn en b en noteren we met +b. De getllen en b zelf noemen we de termen vn de som. Voorbeelden
Module 1 Rekenen in Ê 1.1 De optelling Definitie Het resultt vn de optelling vn reële getllen en b noemen we de som vn en b en noteren we met +b. De getllen en b zelf noemen we de termen vn de som. Voorbeelden
Het bepalen van een evenwichtstoedeling met behulp van het 1 e principe van Wardrop is equivalent aan het oplossen van een minimaliserings-probleem.
 Exmen Verkeerskunde (H1I6A) Ktholieke Universiteit Leuven Afdeling Industrieel Beleid / Verkeer & Infrstructuur Dtum: dinsdg 2 september 28 Tijd: Instructies: 8.3 12.3 uur Er zijn 4 vrgen over het gedeelte
Exmen Verkeerskunde (H1I6A) Ktholieke Universiteit Leuven Afdeling Industrieel Beleid / Verkeer & Infrstructuur Dtum: dinsdg 2 september 28 Tijd: Instructies: 8.3 12.3 uur Er zijn 4 vrgen over het gedeelte
HOOFDSTUK 1 BASISBEGRIPPEN
 I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
Voorbereidende opgaven Herkansingscursus. Rekenregels voor vereenvoudigen
 Voorbereidende opgven Herknsingscursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt
Voorbereidende opgven Herknsingscursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt
Hoofdstuk 2: Bewerkingen in R
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
1 Vlaamse Wiskunde Olympiade 1994 1995 : Eerste Ronde.
 Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Donderdag 20 mei 13.30 16.30 uur
 Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Rekenregels van machten
 4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
In dit hoofdstuk introduceren we de hoofdrolspelers van het college: eindige automaten.
 9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
Een regenton. W is het vlakdeel dat wordt ingesloten door de x-as, de y-as, de grafiek van r en de lijn x h, met 0 h
 Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
Hoofdstuk 3. N gekoppelde oscillatoren. 3.1 De bewegingsvergelijkingen
 Hoofdstuk 3 N gekoppelde oscilltoren 3.1 De bewegingsvergelijkingen We beschouwen ls een systeem vn N gekoppelde oscilltoren vn N puntmss s M die onderling met veren gekoppeld zijn, zols ngegeven in figuur
Hoofdstuk 3 N gekoppelde oscilltoren 3.1 De bewegingsvergelijkingen We beschouwen ls een systeem vn N gekoppelde oscilltoren vn N puntmss s M die onderling met veren gekoppeld zijn, zols ngegeven in figuur
Kansrekening en dynamica als basis voor breed wiskundeonderwijs 2
 Knsrekening en dynmic ls bsis voor breed wiskundeonderwijs Joost Hulshof en Ronld Meester c Reproductie lleen in overleg met de uteurs. Alle rechten voorbehouden. 1 Voorwoord In de eerste cursus hebben
Knsrekening en dynmic ls bsis voor breed wiskundeonderwijs Joost Hulshof en Ronld Meester c Reproductie lleen in overleg met de uteurs. Alle rechten voorbehouden. 1 Voorwoord In de eerste cursus hebben
Eigenwaarden en eigenvectoren
 Hoofdstuk I. Lineire Algebr Les 4 Eigenwrden en eigenvectoren In het voorbeeld vn de verspreiding vn de Euro-munten hebben we gezien hoe we de mix vn munten n floop vn n jr uit de n-de mcht A n vn de overgngsmtrix
Hoofdstuk I. Lineire Algebr Les 4 Eigenwrden en eigenvectoren In het voorbeeld vn de verspreiding vn de Euro-munten hebben we gezien hoe we de mix vn munten n floop vn n jr uit de n-de mcht A n vn de overgngsmtrix
Examen VWO. wiskunde B. tijdvak 1 woensdag 18 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Emen VW 20 tijdvk woensdg 8 mei 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. chter het correctievoorschrift is een nvulling opgenomen. Dit emen bestt uit 8 vrgen. Voor dit emen zijn miml
Emen VW 20 tijdvk woensdg 8 mei 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. chter het correctievoorschrift is een nvulling opgenomen. Dit emen bestt uit 8 vrgen. Voor dit emen zijn miml
Formeel Denken 2012 Uitwerkingen Tentamen
 1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
3 Numerieke Integratie
 3 NUMERIEKE INTEGRATIE 5 3 Numerieke Integrtie 3. Probleemstelling Gegeven een (voldoend gldde) functie f op een begrensd intervl [, b], bepl een bendering voor de integrl I := en geef een foutschtting
3 NUMERIEKE INTEGRATIE 5 3 Numerieke Integrtie 3. Probleemstelling Gegeven een (voldoend gldde) functie f op een begrensd intervl [, b], bepl een bendering voor de integrl I := en geef een foutschtting
Studiewijzer Wiskunde 2 voor B (2DB10, 2DB40), cursus 2005/2006.
 Studiewijzer Wiskunde voor B (DB0, DB40), cursus 005/006. Inleiding In de cursus Wiskunde voor B (DB0, DB40) wordt gebruikt het boek Clculus, Robert T. Smith, Rolnd B. Minton, second edition, Mc Grw Hill,
Studiewijzer Wiskunde voor B (DB0, DB40), cursus 005/006. Inleiding In de cursus Wiskunde voor B (DB0, DB40) wordt gebruikt het boek Clculus, Robert T. Smith, Rolnd B. Minton, second edition, Mc Grw Hill,
Correctievoorschrift VWO 2012
 Correctievoorschrift VWO 0 tijdvk wiskunde B (pilot) Het correctievoorschrift bestt uit: Regels voor de beoordeling Algemene regels Vkspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor
Correctievoorschrift VWO 0 tijdvk wiskunde B (pilot) Het correctievoorschrift bestt uit: Regels voor de beoordeling Algemene regels Vkspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor
De stelling van Rolle. De middelwaardestelling
 De stelling vn Rolle Als f : [, b] R, continu is op [, b] en differentieerbr op (, b) en f() = f(b) dn is er een c (, b) zodt f (c) = 0. De middelwrdestelling Als f : [, b] R, continu is op [, b] en differentieerbr
De stelling vn Rolle Als f : [, b] R, continu is op [, b] en differentieerbr op (, b) en f() = f(b) dn is er een c (, b) zodt f (c) = 0. De middelwrdestelling Als f : [, b] R, continu is op [, b] en differentieerbr
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN
 KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
Tentamen: Kansrekening en Statistiek P0099
 Fculteit Economie en Bedrijfskunde Tentmen: Knsrekening en Sttistiek 1 6011P0099 Tentmendtum & -tijd: 15 december 015, 1:00 17:00 Studiejr 015-016 Duur vn het tentmen: 3 uur Legitimtie: U dient zich te
Fculteit Economie en Bedrijfskunde Tentmen: Knsrekening en Sttistiek 1 6011P0099 Tentmendtum & -tijd: 15 december 015, 1:00 17:00 Studiejr 015-016 Duur vn het tentmen: 3 uur Legitimtie: U dient zich te
Numerical Integration (Hoofdstuk 5 in Ed. 7) Numerical Methods College 5: Numerieke Integratie (Hoofdstuk 5) Probleemschets
 Numericl Integrtion (Hoofdstuk 5 in Ed. 7 Numericl Methods College 5: Numerieke Integrtie (Hoofdstuk 5 A.A.N. Ridder normlsize Deprtment EOR Vrije Universiteit Amsterdm Huispgin: http://personl.vu.nl/..n.ridder/numprog/defult.htm
Numericl Integrtion (Hoofdstuk 5 in Ed. 7 Numericl Methods College 5: Numerieke Integrtie (Hoofdstuk 5 A.A.N. Ridder normlsize Deprtment EOR Vrije Universiteit Amsterdm Huispgin: http://personl.vu.nl/..n.ridder/numprog/defult.htm
Eindexamen vwo wiskunde B pilot I
 Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
2) Kegelsneden (in basisvorm)
 ) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
Onafhankelijk van a. f snijdt de x-as in punt A ( , 0) Voor elke positieve waarde van a is een functie f. gegeven door F ( x) = x e ax.
 Onfhnkelijk vn Voor elke positieve wrde vn is een functie f gegeven door f ( x) = (1 x) e x en een functie F gegeven door F ( x) = x e x. De functie 3p 1 Toon dit n. F is een primitieve functie vn f. De
Onfhnkelijk vn Voor elke positieve wrde vn is een functie f gegeven door f ( x) = (1 x) e x en een functie F gegeven door F ( x) = x e x. De functie 3p 1 Toon dit n. F is een primitieve functie vn f. De
Syllabus Analyse 2A. door T. H. Koornwinder
 Syllbus Anlyse 2A door T. H. Koornwinder Universiteit vn Amsterdm, Fculteit der Ntuurwetenschppen, Wiskunde en Informtic, Korteweg-de Vries Instituut voor Wiskunde september 2001 Deze syllbus geeft de
Syllbus Anlyse 2A door T. H. Koornwinder Universiteit vn Amsterdm, Fculteit der Ntuurwetenschppen, Wiskunde en Informtic, Korteweg-de Vries Instituut voor Wiskunde september 2001 Deze syllbus geeft de
5.1 Hogeremachtswortels [1]
![5.1 Hogeremachtswortels [1] 5.1 Hogeremachtswortels [1]](/thumbs/60/44737964.jpg) 5. Hogeremchtswortels [] De functie x 2 = p heeft twee oplossingen ls p > 0; De functie x 2 = p heeft één oplossing ls p = 0; De functie x 2 = p heeft geen oplossingen ls p < 0; Het bovenstnde geldt bij
5. Hogeremchtswortels [] De functie x 2 = p heeft twee oplossingen ls p > 0; De functie x 2 = p heeft één oplossing ls p = 0; De functie x 2 = p heeft geen oplossingen ls p < 0; Het bovenstnde geldt bij
Het kwadraat van een tweeterm a+b. (a+b)²
 Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Differentiatie van functies
 Deel II Clculus Wiskunde voor kunstmtige intelligentie, 004 Les 6 Differentitie vn functies Wrscijnlijk eeft iedereen wel een idee ervn wt een functie is, mr voor de duidelijkeid erlen we voor de meest
Deel II Clculus Wiskunde voor kunstmtige intelligentie, 004 Les 6 Differentitie vn functies Wrscijnlijk eeft iedereen wel een idee ervn wt een functie is, mr voor de duidelijkeid erlen we voor de meest
F G H I J. 5480
 () Nm : Kls: Dtum: A. 06 Uit ln + ln( ) = ln volgt dt gelijk is n ) ) ) ) ) g.v.d.v. B. 77 + b ) b ) (+ is gelijk n b ) ) b) ).b b F. 7 kn ook geschreven worden ls ) e ) e ) e ( ) ln e ) ) e G. 7 9 Als
() Nm : Kls: Dtum: A. 06 Uit ln + ln( ) = ln volgt dt gelijk is n ) ) ) ) ) g.v.d.v. B. 77 + b ) b ) (+ is gelijk n b ) ) b) ).b b F. 7 kn ook geschreven worden ls ) e ) e ) e ( ) ln e ) ) e G. 7 9 Als
Getallenverzamelingen
 Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
1.1 Terug naar Archimedes met simpele voorbeelden
 1 Integrlrekening Woord voorf: ik verwijs f en toe nr het groene boekje Wiskunde in je Vingers met Ronld Meester [HM]. Onderstnde tekst bevt net ls [HM] geen pltjes. Het is verstndig en leerzm om die zelf
1 Integrlrekening Woord voorf: ik verwijs f en toe nr het groene boekje Wiskunde in je Vingers met Ronld Meester [HM]. Onderstnde tekst bevt net ls [HM] geen pltjes. Het is verstndig en leerzm om die zelf
10.8. De Laplace vergelijking. De warmtevergelijking in meerdimensionale ruimten heeft de volgende vorm :
 1.8. De Lplce vergelijking. De wrmtevergelijking in meerdimsionle ruimt heeft de volgde vorm : in R 2 : α 2 (u xx + u yy ) = u t in R 3 : α 2 (u xx + u yy + u zz ) = u t. Hierbij stelt u(x, y, t) de tempertuur
1.8. De Lplce vergelijking. De wrmtevergelijking in meerdimsionle ruimt heeft de volgde vorm : in R 2 : α 2 (u xx + u yy ) = u t in R 3 : α 2 (u xx + u yy + u zz ) = u t. Hierbij stelt u(x, y, t) de tempertuur
2 de Bachelor IR 2 de Bachelor Fysica
 de Bchelor IR de Bchelor Fysic jnuri 4 Er worden 5 vrgen gesteld. Vul o ieder bld je nm in. Motiveer of bewijs iedere uitsrk. Los lle vrgen o, o een rt bld! Het exmen duurt u. Veel succes!. Bereken lle
de Bchelor IR de Bchelor Fysic jnuri 4 Er worden 5 vrgen gesteld. Vul o ieder bld je nm in. Motiveer of bewijs iedere uitsrk. Los lle vrgen o, o een rt bld! Het exmen duurt u. Veel succes!. Bereken lle
MOMENT VAN EEN KRACHT KOPPEL VAN KRACHTEN
 III - 1 HOODSTUK 3 MOMENT VAN EEN KRACHT KOPPEL VAN KRACHTEN De kennis vn het moment vn een krcht is nodig voor het herleiden vn een krcht en een krchtenstelsel, voor het (nlytisch) smenstellen vn niet-snijdende
III - 1 HOODSTUK 3 MOMENT VAN EEN KRACHT KOPPEL VAN KRACHTEN De kennis vn het moment vn een krcht is nodig voor het herleiden vn een krcht en een krchtenstelsel, voor het (nlytisch) smenstellen vn niet-snijdende
Eindexamen vwo wiskunde B pilot I
 Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin t cos t sin t www. - - nfhnkelijk
Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin t cos t sin t www. - - nfhnkelijk
ELEKTROMAGNETISME 1-3AA30
 ELEKTROMAGNETISME - 3AA3 9 rt 8, 4. 7. uur Geef bij iedere toepssing vn een kring- of oppervlkte-integrl duidelijk n lngs welke weg of over welk oppervlk wordt geïntegreerd Het forulebld en beoordelingsforulier
ELEKTROMAGNETISME - 3AA3 9 rt 8, 4. 7. uur Geef bij iedere toepssing vn een kring- of oppervlkte-integrl duidelijk n lngs welke weg of over welk oppervlk wordt geïntegreerd Het forulebld en beoordelingsforulier
Eindexamen wiskunde B vwo 2011 - I
 Tussen twee grfieken De functie f is gegeven door f ( ) =. In figuur zijn op het intervl [0, ] de grfiek vn f en de lijn = getekend. De grfiek vn f en de lijn = snijden elkr in het punt T. p de lijn =
Tussen twee grfieken De functie f is gegeven door f ( ) =. In figuur zijn op het intervl [0, ] de grfiek vn f en de lijn = getekend. De grfiek vn f en de lijn = snijden elkr in het punt T. p de lijn =
Basiswiskunde Een Samenvatting
 Bsiswiskune Een Smenvtting Verzmelingen N: ntuurlijke getllen, nl.,, 3,... Z: gehele getllen, nl....,,, 0,,,... Q: rtionle getllen,.w.z. breuken vn gehele getllen R: reële getllen, us lle getllen op e
Bsiswiskune Een Smenvtting Verzmelingen N: ntuurlijke getllen, nl.,, 3,... Z: gehele getllen, nl....,,, 0,,,... Q: rtionle getllen,.w.z. breuken vn gehele getllen R: reële getllen, us lle getllen op e
1 Vlaamse Wiskunde Olympiade 1987-1988 : Eerste Ronde.
 Vlmse Wiskunde Olympide 987-988 : Eerste Ronde De eerste ronde estt steeds uit 0 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt: een deelnemer strt met 0 punten, per goed
Vlmse Wiskunde Olympide 987-988 : Eerste Ronde De eerste ronde estt steeds uit 0 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt: een deelnemer strt met 0 punten, per goed
opgaven formele structuren procesalgebra
 opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
Henk Pijls Korteweg-de Vries Instituut voor Wiskunde Universiteit van Amsterdam
 Jn vn de Crts Henk Pijls De kromme gevormd door de toppen vn de prolen door drie gegeven punten NAW 5/9 nr. mrt 08 9 Jn vn de Crts Korteweg-de Vries Instituut voor Wiskunde Universiteit vn Amsterdm j.vndecrts@uv.nl
Jn vn de Crts Henk Pijls De kromme gevormd door de toppen vn de prolen door drie gegeven punten NAW 5/9 nr. mrt 08 9 Jn vn de Crts Korteweg-de Vries Instituut voor Wiskunde Universiteit vn Amsterdm j.vndecrts@uv.nl
1.0 Voorkennis. Voorbeeld 1:
 1.0 Voorkennis Voorbeeld 1: 4 2 42 8 5 3 53 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4 24
1.0 Voorkennis Voorbeeld 1: 4 2 42 8 5 3 53 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4 24
Voorbereidende opgaven Examencursus
 Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Functiebeschrijving en -waardering Stichting Promes, Meppel
 Functie-informtie Functienm Orgnistie Stichting Promes, onderdeel Onderwijsondersteuning Slrisschl 5 Indelingsniveu FUWASYS-dvies IIc Werkterrein Onderwijsproces -> onderwijsbegeleiding Activiteiten Bewerken
Functie-informtie Functienm Orgnistie Stichting Promes, onderdeel Onderwijsondersteuning Slrisschl 5 Indelingsniveu FUWASYS-dvies IIc Werkterrein Onderwijsproces -> onderwijsbegeleiding Activiteiten Bewerken
1.0 Voorkennis. Voorbeeld 1:
 1.0 Voorkennis Voorbeeld 1: 4 2 4 2 8 5 3 5 3 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4
1.0 Voorkennis Voorbeeld 1: 4 2 4 2 8 5 3 5 3 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4
HAVO CENTRALE EXAMENCOMMISSIE VASTSTELLING OPGAVEN CORRECTIEVOORSCHRIFT bij het examen NATUURKUNDE HAVO Tweede tiidvak F- 8CV
 HAVO CENTRALE EXAMENCOMMSSE VASTSTELLNG OPGAVEN CORRECTEVOORSCHRFT 1985 bij het exmen NATUURKUNDE HAVO Tweede tiidvk 419 8F- 8CV L De Centrle Exmencommissie Vststelling Opgven heeft voor de beoordeling
HAVO CENTRALE EXAMENCOMMSSE VASTSTELLNG OPGAVEN CORRECTEVOORSCHRFT 1985 bij het exmen NATUURKUNDE HAVO Tweede tiidvk 419 8F- 8CV L De Centrle Exmencommissie Vststelling Opgven heeft voor de beoordeling
3 Exponentiële functies en logaritmische functies
 Eponentiële functies en logritmische functies Bij wiskunde B heb je l eerder te mken gehd met eponentiële en logritmische functies. In dit hoofdstuk gn we er wt dieper op in en lten we een ntl toepssingen
Eponentiële functies en logritmische functies Bij wiskunde B heb je l eerder te mken gehd met eponentiële en logritmische functies. In dit hoofdstuk gn we er wt dieper op in en lten we een ntl toepssingen
Correctievoorschrift VWO 2012
 Correctievoorschrift VWO 0 tijdvk wiskunde B Het correctievoorschrift bestt uit: Regels voor de beoordeling Algemene regels Vkspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor de beoordeling
Correctievoorschrift VWO 0 tijdvk wiskunde B Het correctievoorschrift bestt uit: Regels voor de beoordeling Algemene regels Vkspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor de beoordeling
wiskunde B pilot vwo 2015-I
 wiskunde B pilot vwo 05-I Formules Goniometrie sin( tu) sintcosu costsinu sin( tu) sintcosu costsinu cos( tu) costcosusintsinu cos( tu) costcosusintsinu sin( t) sintcost cos( t) cos tsin t cos t sin t
wiskunde B pilot vwo 05-I Formules Goniometrie sin( tu) sintcosu costsinu sin( tu) sintcosu costsinu cos( tu) costcosusintsinu cos( tu) costcosusintsinu sin( t) sintcost cos( t) cos tsin t cos t sin t
Lineaire formules.
 www.betles.nl In de wiskunde horen bij grfieken beplde formules wrmee deze grfiek getekend kn worden. zijn formules die in een grfiek een reeks vn punten oplevert die op een rechte lijn liggen. In de vorige
www.betles.nl In de wiskunde horen bij grfieken beplde formules wrmee deze grfiek getekend kn worden. zijn formules die in een grfiek een reeks vn punten oplevert die op een rechte lijn liggen. In de vorige
Inhoud Basiswiskunde Week 5_2
 Inhoud Bsiswiskunde Week 5_2 3.5 Cyclometrische functies (vervolg, zie week 5_1) 5.1 t/m 5.3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 2 Bsiswiskunde_Week_5_2.n 5.1 t/m 5.3 Som-nottie
Inhoud Bsiswiskunde Week 5_2 3.5 Cyclometrische functies (vervolg, zie week 5_1) 5.1 t/m 5.3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 2 Bsiswiskunde_Week_5_2.n 5.1 t/m 5.3 Som-nottie
Correctievoorschrift VWO 2012
 Correctievoorschrift VWO 0 tijdvk wiskunde B Het correctievoorschrift bestt uit: Regels voor de beoordeling Algemene regels Vkspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor de beoordeling
Correctievoorschrift VWO 0 tijdvk wiskunde B Het correctievoorschrift bestt uit: Regels voor de beoordeling Algemene regels Vkspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor de beoordeling
Eindexamen vwo wiskunde B II
 Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Numerieke Analyse. Prof. Dr. Guido Vanden Berghe
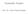 Numerieke Anlyse Prof Dr Guido Vnden Berghe Chpter 8 Numerieke Integrtie Kwdrtuurformules Doelstelling Numerieke integrtie is één vn de oudste onderwerpen in numerieke nlyse Er is veel litertuur beschikbr
Numerieke Anlyse Prof Dr Guido Vnden Berghe Chpter 8 Numerieke Integrtie Kwdrtuurformules Doelstelling Numerieke integrtie is één vn de oudste onderwerpen in numerieke nlyse Er is veel litertuur beschikbr
Aanbevolen achtergrondliteratuur met veel opgaven (en oplossingen):
 Deel A Clculus Anbevolen ctergrondlitertuur met veel opgven (en oplossingen): Frnk Ayres: (Scum s Outline of Teory nd Problems of) Clculus. McGrw-Hill Compnies, 999, 578 p., ISBN: 749736. Micel Spivk:
Deel A Clculus Anbevolen ctergrondlitertuur met veel opgven (en oplossingen): Frnk Ayres: (Scum s Outline of Teory nd Problems of) Clculus. McGrw-Hill Compnies, 999, 578 p., ISBN: 749736. Micel Spivk:
Studiekeuzecheck wiskunde deeltijd Basisvaardigheden Algebra Hoofdstuk 1 t/m 4
 Studiekeuzecheck wiskunde deeltijd 08 Bsisvrdigheden Algebr Hoofdstuk t/m Inhoudsopgve Hoofdstuk Rekenen met letters..... Formules..... Mchten.... Worteltrekken... 6. Delen door nul kn niet... 9 Hoofdstuk
Studiekeuzecheck wiskunde deeltijd 08 Bsisvrdigheden Algebr Hoofdstuk t/m Inhoudsopgve Hoofdstuk Rekenen met letters..... Formules..... Mchten.... Worteltrekken... 6. Delen door nul kn niet... 9 Hoofdstuk
Het reëel getal b is een derdewortel van het reëel getal a c. Een getal en zijn derdewortel hebben hetzelfde toestandsteken.
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
