Getaltheorie. een introductie
|
|
|
- Daniël de Vries
- 5 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Getltheore ee troducte 1
2 Iledg Getltheore s ee v de oudste deelgebede de wskude I het oude Grekeld, Itlë, Id, Ch e og vele dere lde vde we broe v de eerste wskudge de gehele getlle bestudeerde Zo hebbe we Eucldes (65-00 vc) Grekeld, Fbocc (c c 150) Itlë, Brhmgut ( ) e Bhāskr ( ) ls vertegewoordgers v Id e oze Chese vred Su Tzu (c c 473) met zj lom bekede Chese reststellg De Dutse wskudge Guss beschreef de getltheore ls 'de kog v de wskude', e terecht! Het woderbrljke getltheore s dt ze et, of slechts zelde, steut o dere domee ut de wskude, zols lyse of meetkude Dt mkt hr zo zuver e essete zo eevoudg 'I essete', wt heel wt robleme ut de getltheore zj s heel lt ogelost of zj dt og steeds et Het bewjs v de ltste stellg v Fermt heeft 350 jr o zch lte wchte, tot de Brtse wskudge Adrew Wles 1993 ee bewjs ublceerde Het vermoede v Ctl werd s beweze 00 door oze Roemeese colleg Pred Mhălescu, mr lefst 158 jr dt oze ldgeoot Eugèe Ctl het vermoede 1844 formuleerde Het vermoede v Goldbch, het robleem v Brocrd, het bc-vermoede, het vermoede v Colltz, het robleem v Wrg, het vermoede v Adrc, v Colltz, zj slechts ekele v de tlloze obeweze hyothese e oogeloste robleme Mr voor het olosse v dt soort rdsels s er tuurljk eerst wt kes odg, e we weet k je het leze v deze utgebrede troducte wel het bewjs ee v de hersekrkers o jouw m zette
3 Hoofdstuk 1 Deelbrhed Deelbrhed s mssche wel het meest essetële begr be de getltheore Het s ee mer om meer formte te creëre over ee getl Deelbrhed lt os toe om de deere betekes v getlle te vde, e te otdekke welke merkwrdge egesche ee getl k hebbe 11 Deler e veelvoud De begre de de bss vorme v de getltheore zj deler e veelvoud Stel e b zj gehele getlle met b 0 Bj delg v door b oeme we het deeltl e b de deler Per defte s deelbr door b ls e slechts ls er ee derde geheel getl k bestt zodt kb We zegge b s ee deler v, s ee veelvoud v b, of kortweg b deelt We otere: b Zo geldt bjvoorbeeld dt 7 1 omdt er ee geheel getl k bestt wrvoor 1 7k, meljk k 3 Ook voor het tegeovergestelde feomee bestt er ee symbool Als et deelbr s door b otere we b Als ee getl ee veelvoud s v oeme we dt getl eve I het dere gevl oeme we het getl oeve Zo s bjvoorbeeld eve, e s 3 oeve Gevolge 1 Ee gevolg s dt 0 deelbr s door elk geheel getl Immers, voor elk geheel getl bestt er ee getl k zodt 0 k, meljk k 0 0 s dus ee eve getl, wt het s deelbr door Als e b ostef zj met 0 e b, d geldt dt b Wt kb, e omdt e b ostef zj s k ook ostef Nu geldt dt b k 3 Als e b ostef zj zodt b e b, d geldt b Wt ut het tweede gevolg wete we dt b e dt b, dus moet oodzkeljk b 4 Als twee osteve getlle e b dezelfde delers hebbe, d zj ze geljk Wt s ee deler v zchzelf, dus omdt geldt d b Om ee loge rede geldt dt b Ut het derde gevolg wete we d dt b Voorbeeld Stel dt b e b c Too dt c Olossg Omdt b c bestt er ee geheel getl k wrvoor c kb Omdt b bestt er ee tweede geheel getl x wrvoor b x Dt vulle we de eerste geljkhed, zodt c kx Dus c s deelbr door, wt er bestt ee geheel getl y wrvoor c y, meljk y kx 1 Lere combte Als x e y gehele getlle zj, oeme we x by ee lere combte v e b Voorbeeld 1 Bewjs dt ls d e d b, d d x by voor lle gehele getlle x e y Olossg Ut d e d b volgt dt md e b d Dus x+by = mdx+dy =(mx+y)d Bjgevolg s x by deelbr door d 13 Rest e quotët Voor lle gehele getlle e b met b 0 bestt er just éé koel gehele getlle ( qr, ) wrvoor qb r e 0 r b q oeme we d het quotët e r de rest v bj delg door b Voor de rest zegge we ook wel modulo b s r e otere we 3
4 mod b r De voorwrde 0 r b s her v ktl belg, e mg je oot vergete om te cotrolere of ee getl wel de juste rest s Bjvoorbeeld, bj delg v 19 door 6 s het quotët 3 e de rest 1, wt e De rest v ee getl bj delg door oeme we ook de rtet v De rtet v ee getl s dus steeds 0 of 1 De rtet v ee eve getl s dus 0, e ee oeve getl heeft rtet 1 Oefeg Bewjs dt het quotët e de rest bj delg v door b uek zj, met b 0 Veroderstel dt er twee quotëte zj met bjbehorede rest, zeg ( q 1, r1 ) e ( q, r ) A Too dt r1 r deelbr s door b B Too dt r 1 e r et bede groter of geljk 0 e kleer d b kue zj Bjgevolg zj rest e quotët uek Oefeg Bel rest e quotët bj delg v A 6 door 10 B 100 door 7 We veroderstelde tot u toe dt de deler ostef moet zj Dt s echter et steeds het gevl Ook voor ee egteve deler defëre we de rest e het quotët, mr d o ee lcht dere mer Voor gehele getlle e b met b 0 defëre we de rest r e quotët q ls de gehele getlle wrvoor qb r, e 0 r b (Merk o dt b ee ostef getl s) Ook her geldt dt de rest e het quotët uek zj Oefeg Bewjs dt het quotët e de rest bj delg v door b uek zj, met b 0 Oefeg Bel rest e quotët bj delg v A 5 door 8 B 50 door 9 We kue de defte u verlgemee Voor lle gehele getlle e b zj de rest r e het quotët q de gehele getlle wrvoor qb r e 0 r b Wt ls b 0 d s b gewoo geljk b e ls b 0 s b geljk b Tot u toe me we dt er steeds ee quotët e ee rest best Dt ljkt tuurljk vzelfsreked mr toch k je dt, ls wskudge, et eme zoder bewjs Sterker og, zo goed ls lles wt her volgt steut ero dt er ee rest e ee quotët bestt Voorbeeld Too dt er voor getlle e b met b 0 ee rest e ee quotët best Olossg Het getl s ee reëel getl Dt lgt dus tusse twee oeevolgede gehele getlle I b symbole, er bestt ee geheel getl q zodt q q 1 Dus bq bq b (merk o dt b we her de voorwrde b 0 gebruke), wt we kue schrjve ls 0 bq b Stelle we u r bq, d hebbe we getlle q e r wrvoor bq r e 0 r b A de twee voorwrde s vold, dus best er ee quotët e ee rest Oefeg Too dt er voor getlle e b met b 0 ee rest e ee quotët best 4
5 14 Grootste gemee deler Twee gehele getlle hebbe ltjd gemeescheljke delers Zo hebbe 6 e 10 reces 4 gemeescheljke delers, meljk, 1,1, De grootste gemee deler d v twee gehele getlle e b, de et bede 0 zj, s het grootste geheel getl dt ee deler s v zowel ls b We otere ggd(, b) d Bjvoorbeeld: ggd(6,10), ggd(0,5) 5, ggd( 1, 16) 4 Merk o dt het oodzkeljk s dt e b et bede 0 zj, ders zou er gee grootste gemee deler best, wt 0 s deelbr door elk geheel getl groter d 0 De grootste gemee deler v ee wllekeurg tl gehele getlle defëre we loog ls het grootste geheel getl dt ee deler s v elk v de getlle Bjvoorbeeld: ggd(15, 1,3) 3 Merk o dt de grootste gemee deler ltjd ee ostef getl s Als ggd( b, ) 1 d oeme we e b oderlg odeelbr, corem of reltef rem Als,, 1, gehele getlle zj zodt ggd (, j ) 1 voor lle j, d oeme we,, 1, rsgewjs reltef rem Dt beteket et hetzelfde ls ggd( 1,, ) 1 Zo s bjvoorbeeld ggd(,3,9) 1, mr de getlle,3,9 zj et rsgewjs reltef rem wt ggd(3,9) 1 Prsgewjs reltef rem houdt dus dt de grootste gemee deler v elke twee getlle geljk s 1 Voorbeeld 3 Bewjs dt ggd (, b) ggd (, b ) voor elk geheel getl Olossg We toe dt d ee deler s v ggd( b, ) ls e slechts ls d ee deler s v ggd(, b ) Als d ggd(, b ), d d e d b, zodt d 1b- = b-, dus d ggd(, b ) Als d ggd(, b ), d d 1 ( b ) = b dus d ggd(, b ) (Her gebrukte we dus tweeml de egesch v ee lere combte) De getlle ggd( b, ) e ggd(, b ) hebbe dezelfde delers e zj dus geljk, wt dt ws éé v de gevolge v de defte v deelbrhed Omerkg Behlve het fet dt e b et bede ul zj, hdde we her gee ekele beerkede voorwrde voor deze egesch Dt mkt ze heel krchtg, zols je zl merke bj het lgortme v Eucldes 15 Stellg v Bézout Als e b gehele getlle zj s ggd( b, ) te schrjve ls lere combte v e b (Ook her g we erv ut dt e b et bede ul zj Je zl merke dt we zoets lter ook stlzwjged zulle veroderstelle Je mg er dus steeds v ut g dt de beerkede voorwrde vold s) Oefeg Bewjs de stellg v Bézout Noem V de verzmelg v lle lere combtes v e b A Too dt V mstes éé getl bevt dt groter s d 0 Bjgevolg heeft V ee kleste strkt ostef elemet, zeg d Noem q het quotët e r de rest v bj delg door d B Too dt r ee lere combte s v e b C Too dt r 0 We hebbe dus dt d Aloog geldt dt d b d s dus ee gemeescheljke deler v e b Stel dt c ook ee gemeescheljke deler s v e b 5
6 D Too dt c d, e dt c d Bjgevolg s d de grootste gemee deler v e b, e s de grootste gemee deler te schrjve ls lere combte Gevolge 1 Als c e c b, d c ggd(, b ) Wt c deelt elke lere combte v e b, dus c deelt ook ggd( b, ) ggd( b, ) de klest mogeljke strkt osteve lere combte s v e b Wt ggd( b, ) deelt e b, dus ggd( b, ) deelt elke lere combte x by v e b Bjgevolg geldt dt ls x by 0, d ggd (, b) x by (Dt s het tweede gevolg v de defte v deelbrhed) 3 Elk veelvoud v ggd( b, ) k geschreve worde ls lere combte v e b Stel bjvoorbeeld c k ggd(, b), d s c k( x yb) voor belde getlle x e y, zodt c kx ky b Hermee s c dus ee lere combte v e b Voorbeeld 4 Stel dt ggd( b, ) 1 e bc Bewjs dt c Olossg Omdt ggd( b, ) 1 best er x e y zodt x by 1 Dus xc byc c Omdt bc s bc k D s xc yk c, of dus ( xc yk) c Dus c Omerkg De crucle st dt bewjs ws om de eerste geljkhed lks e rechts te vermegvuldge met c Dt komt ogl ut de lucht gevlle, mr egeljk s het ee logsche zet We wlle meljk bekome dt c, dus c Het s dus erges wel voor de hd lgged dt we c fzodere éé kt v het geljkhedsteke, zoder dt er extr fctore bj st Oefeg Stel dt c, b c e ggd( b, ) 1 Bewjs dt b c Omerkg Deze oefeg e de volgede ljke heel vzelfsreked Je dekt mssche: dt klot toch, zoets moet je toch et bewjze? Iderdd, mr voor ee wskudge k je met tuïte ets bewjze Geef trouwes toe dt ee bewjsje ls het vorge heel moo s ls je het etjes oschrjft e de tuïte chterwege lt Probeer dt dus ook te doe e mk ekel gebruk v egesche de je tot u toe bet tegegekome, zoder zelf egesche te verze Oefeg Stel dt ggd( b, ) 1 Too dt ggd(, c) ggd(, bc) Oefeg Stel d s ee geheel getl A Bewjs dt ggd( d, db) d ggd(, b) Stel u g ggd(, b) b B Bewjs dt ggd, 1 g g Oefeg De stellg v Bézout k worde verlgemeed r meerdere getlle Ook d s de stellg geldg: ls 1,,, gehele getlle zj, d k ggd( 1,,, ) geschreve worde ls lere combte v,, 1, Bewjs deze verlgemeg 6
7 16 Algortme v Eucldes Het lgortme v Eucldes s ee techek om de grootste gemee deler v twee getlle te bele Het mkt gebruk v het rce ut voorbeeld 3 Als r de rest s bj delg v b door, d geldt dt ggd (, b) ggd (, r) Wt ut voorbeeld 3 wete we dt ggd(, b) ggd(, b ) ook geldt ls het quotët s bj delg v b door E d s b r Om ggd( b, ) te berekee voor gegeve getlle e b met b bereke je de rest r bj delg v b door e je zoekt d ggd (, r) Door dt te herhle bekom je steeds kleere getlle totdt er ggd ( d,0) komt te st D geldt dt ggd (, b) d Zo vde we bjvoorbeeld dt ggd (459,34) ggd (117,34) ggd (117,108) ggd (9,108) ggd (9,0) 9 Deze werkwjze kue we ook otere het zogemde rekeschem v Eucldes Eerst otere we het grootste v de twee getlle lks het mdde e drst het kleste Vervolges bele we het quotët bj delg v het grootste door het kleste, 1 Dt otere we bove de deler D berekee we het roduct v het quotët met de deler, , e dt otere we oder het deeltl D trekke we het bekome roduct f v het deeltl, , e we hebbe de rest Dt roces herhle we, met de rest ls euwe deler e de vorge deler ls deeltl We bljve dt herhle totdt er 0 ls rest komt te st De ltste deler, 9, s d de grootste gemee deler Gevolg We hebbe ee mer om de grootste gemee deler v twee getlle te schrjve ls lere combte Dt llustrere we met het bovestde voorbeeld Als we de eerste delg utvoere bekome we dt de rest geljk s Dt verschl werke we et ut e lte we zo st 7
8 Bj de tweede delg vde we ls rest Her vervge we 117 door e we schrjve 108 ls lere combte v 459 e 34, meljk ( ) We doe hetzelfde voor 9 e we vde ( ) 1 ( ) We hebbe 9 dus geschreve ls lere combte v 459 e 34 Omerkg Het zl et steeds odg zj om het rekeschem v Eucldes te gebruke om de grootste gemee deler te schrjve ls lere combte Soms zl je o zcht ee lere combte kue bedeke, mr dt lgortme geeft ee lgemee mer wr je steeds o k vertrouwe Zo s bjvoorbeeld de grootste gemee deler v twee oeevolgede getlle gewoo hu verschl: ggd(8, 9) E drmee heb je metee ee lere combte Oefeg Too dt je met het lgortme v Eucldes steeds de grootste gemee deler bekomt A Too dt je ee edg tl ste steeds 0 ls rest bekomt B Too dt de voorltste rest ee veelvoud s v de grootste gemee deler C Too dt de voorltste rest ee deler s v elke voorgde rest D Too dt de voorltste rest de grootste gemee deler s 17 Lere dohtsche vergeljkg Ee dohtsche vergeljkg s ee vergeljkg éé of meerdere vrbele wrbj we zoeke r gehele olossge voor de vrbele Ee lere dohtsche vergeljkg s ee vergeljkg v de vorm x by c, wrbj, b e c gehele getlle zj e we olossge gehele getlle zoeke voor x e y Oefeg Vd lle mogeljke olossge v de dohtsche vergeljkg x by c Stel dt zo' dohtsche vergeljkg ee olossg heeft A Too dt ggd(, b) c Ide er ee olossg s, geldt dus dt ggd(, b) c Bjgevolg kue we c schrjve ls lere combte v e b V het rekeschem v Eucldes bele we d getlle x 0 e y 0 zodt x0 by0 c Dt geeft l éé olossg voor x e y Stel u d ggd (, b) Stel dt x e y olossge zj We kue zegge dt x x 0 m e y y 0 B Too dt m b b C Too dt m d kb Bjgevolg s m d k D Too dt d kb k De lgemee olossg s dus x x 0 e y y 0, wr k elk geheel getl mg zj d d Voor k 0 bekome we oeuw de oorsrokeljke olossg de we vode v het rekeschem v Eucldes Omerkg 8
9 Omdt d, b, c hdde we ook d0, b db0 e c dc0 kue stelle, zodt we de vergeljkg 0x b0 y c0 bekwme, met ggd( 0, b0) 1 Dt s wt we de rktjk zulle doe bj het olosse v zo' vergeljkg, mr her zou dt de oefeg et bjzoder eevoudger hebbe gemkt Gevolge 1 De grootste gemee deler d v twee getlle e b k o oedg veel mere worde geschreve ls lere combte v e b Wt de wrde v k mocht elk geheel getl zj We kue de grootste gemee deler d v twee strkt osteve getlle e b schrjve ls x by met x 0 e y 0, of met x 0 e y 0 Wt de lgemee olossg, kb k x x 0 e y y 0, kue we k ee voldoede grote wrde geve, zodt x 0 d d e y 0, of ee voldoede klee wrde, zodt x 0 e y 0 De voorwrde dt e b strkt ostef zj s her dus odg Wt ls b 0 e 0, d zou het verhoge v k ervoor zorge dt x kleer wordt of geljk bljft, terwjl y ook kleer wordt Merk dus o dt we zo' lere combte dus wel kue vde ls e b bede strkt egtef zj Voorbeeld Bel lle olossge voor x e y v de vergeljkg 7x30 y 18 Olossg We bege met het os zelf et te moeljk te mke We kue dele door 6 e het rekewerk zl heel wt lchter zj: 1x5y 3 We schrjve eerst ggd(1, 5), of dus ggd(1,5), ls lere combte v 1 e 5 v het rekeschem v Eucldes We lte het mteke eve weg om zeker te zj dt we gee foute mke met mtekes, dt mkt het rekewerk eevoudger We vde ggd(1,5) (11 5) Om de getlle x 0 e y 0 te vde moete we ggd(1, 5) wel schrjve ls lere combte met 5, e et met 5 Dus ( 5) Om 3 te schrjve ls lere combte vde we d ( 5) We hebbe dus dt x 6 e y k ( 5) k 1 De lgemee olossg s d x x0 6 5k e y y0 15 1k, met k 1 1 ee wllekeurg geheel getl Als je lever et zo veel mtekes zet, mg je tuurljk ook k vervge door t, zodt je x5t 6 e y1t 15 hebt, of zelfs door t zodt er x5t 4 e y1t 9 komt te st Al de ottes zj goed, wt ze geve dezelfde olossge Oefeg Bel lle olossge voor x e y v de vergeljkg 50x 8y Kleste gemee veelvoud Twee gehele getlle hebbe gemeescheljke veelvoude Zo zj bjvoorbeeld b e 3b gemeescheljke veelvoude v e b Het kleste gemee veelvoud k v twee 9
10 gehele getlle e b s het kleste geheel getl, groter d 0, dt ee veelvoud s v e b We otere kgv(, b) k Bjvoorbeeld: kgv(8,6) 4, kgv(,5) 10, kgv( 10, 18) 90 De voorwrde dt k 0 s oodzkeljk, wt ders zou het kleste gemee veelvoud steeds 0 zj, wt 0 s ee veelvoud v elk geheel getl Het kleste gemee veelvoud v ee wllekeurg tl gehele getlle defëre we loog ls het kleste tuurljk getl, groter d 0, dt ee veelvoud s v elk v de getlle Bjvoorbeeld: kgv(1,5, 6) 60 Voorbeeld Stel dt c e b c Bewjs dt kgv (, b) c Olossg Stel kgv(, b) k, e q e r zj het quotët e de rest v c bj delg door k, dus r k D s c qk r Omdt c e k, s c m e k x, zodt r c qk ( m qx) Dus r O ee volledg loge mer vd je dt b r r s dus ee veelvoud v e v b Mr r k e k s het kleste strkt ostef getl dt ee veelvoud s v e v b De ege mogeljkhed s dus dt r 0, dus k c Omerkg Mssche ws je zelf et metee o het dee gekome o de rest e het quotët v c bj delg door k te bekjke A ee oefeg ls deze gt d ook heel wt geklugel voorf, tot je bj de juste werkwjze terecht komt Je moet dus et te sel ogeve, mr soms toch ees ee dere methode utrobere Her wre er og reltef weg mogeljkhede Om te bewjze dt ee getl x deelbr s door y zj er egeljk mr ekele otes: 1 Ut de gegeves ledt je f dt x ky voor ee zeker geheel getl k Je toot dt ls ee getl ee deler s v y, d ook ee deler s v x 3 Je robeert te bewjze dt de rest bj delg v x door y geljk s 0 Hoe dt d reces gebeurt k verschlle v oefeg tot oefeg Er zj wrschjljk og lterteve methodes, mr hermee heb je toch l dre relevte I het lgemee moet je heel vk gebruk mke v lere combtes 19 Premgetlle Ee remgetl s ee ostef geheel getl dt reces osteve delers heeft Bjgevolg zj deze delers 1 e We zegge ook wel s rem De kleste te remgetlle zj,3,5,7,11,13,17,19,3,9 Als ee getl groter s d 1 e gee remgetl s, d oeme we dt getl smegesteld Als ee remgetl ee deler s v ee getl, d zegge we ook wel s ee remdeler v Voorbeeld Als e q verschllede remgetlle zj, bewjs dt ggd( q, ) 1 Olossg Er geldt dt ggd(, q), dus de ggd( q, ) 1 of ggd(, q) Wt 1 e zj de ege delers v Aderzjds geldt dt ggd(, q) q, dus ggd( q, ) 1 of ggd(, q) q De ege mogeljkhed s dus dt ggd( q, ) 1 Oefeg Zj ee remgetl Too dt voor elke met Hoofdstellg v de rekekude 10
11 Elk tuurljk getl groter d 1 s o ee ueke mer te schrjve ls het roduct v r remgetlle, 1 1 r wrbj 1,,, r remgetlle zj met 1 r e 1,,, r tuurljke getlle groter d 0 Dt roduct oeme we de remotbdg of remfctorste v Bjvoorbeeld, de remotbdg v 48 s 4 3 Als we de symbole ut de defte gebruke, hebbe we dus r, 1, 3, 1 4 e 1 Gewooljk schrjve we de remgetlle dus v kle r groot de remotbdg Vk wordt deze stellg ls rede gebrukt dt 1 et tot de remgetlle wordt gereked Wt de 1 wel ee remgetl ws, d zou de remotbdg et uek zj D 4 4 zoude bjvoorbeeld zowel 3, 1 3 ls verschllede remotbdge zj v 48 Het bewjs v de hoofdstellg bestt ut twee dele: bewjze dt er zo' remotbdg bestt, e bewjze dt ze uek s Oefeg Bewjs dt er voor elk tuurljk getl met 1 ee otbdg bestt remgetlle We bewjze dt v volledge ducte Bssst Er bestt ee remotbdg voor, wt s ee remgetl Iductest Veroderstel dt e dt lle getlle kleer d ee remotbdg hebbe A Too dt ee remotbdg heeft ls ee remgetl s B Too dt ee remotbdg heeft ls ee smegesteld getl s Het bewjs volgt u v volledge ducte Oefeg Bewjs dt de remotbdg uek s Stel s het kleste tuurljk getl groter d 1 dt gee ueke remotbdg heeft Dus 1 r q1 q qs, met 1 r e q1 q qs A Too dt q s et de rj 1,,, r voorkomt q s s ee deler v e dus v 1 r B Too dt q s ee deler s v 3 r C Herhl deze werkwjze e too dt q s ee deler moet zj v r Bjgevolg s het omogeljk dt gee ueke remotbdg heeft Gevolge 1 De grootste gemee deler v twee tuurljke getlle s het roduct v lle remfctore met hu klest voorkomede exoet r I formulevorm, ls x e y tuurljke getlle zj met x e b b b y 1 r m( 1, b1 ) m(, b ) m( r, br) 1 r, d geldt ggd( x, y) 1 r Wt ee getl met ee fctor k met k m(, b ) zl gee deler zj v x e y, geze de exoet v et bj zowel x e y mstes k k zj Het kleste gemee veelvoud v twee tuurljke getlle s het roduct v lle remfctore met hu hoogst voorkomede exoet r I formulevorm, ls x e y tuurljke getlle zj met x e 1 1 b b b y 1 r mx( 1, b1 ) mx(, b ) mx( r, br) 1 r, d geldt kgv( x, y) 1 r r r
12 Wt ee getl wrbj de exoet v k et deelbr zj door mx( b, ) de remotbdg kleer s d mx(, b ),, e dus et door zowel ls Oefeg Bewjs dt er oedg veel remgetlle best Veroderstel dt er slechts ee edg tl remgetlle bestt Noem de remgetlle 1,,, Beschouw u het getl x 1 1 A Too dt x gee remgetl s B Too dt x et deelbr s door ee remgetl Bjgevolg heeft x gee remotbdg, wt et k weges de hoofdstellg v de rekekude Het s dus omogeljk dt er slechts ee edg tl remgetlle bestt Oefeg Bereke de grootste gemee deler e het kleste gemee veelvoud v A 75 e 60 B 1000 e C 30 e 40 Oefeg Too dt ggd(, b) kgv(, b) b voor lle tuurljke getlle e b Oefeg Too dt ggd(, b ) (ggd(, b)) voor elk tuurljk getl Oefeg Too dt met 1 ee volkome kwdrt s ls e slechts lle remfctore v tot ee eve mcht voorkome de remotbdg Voorbeeld Too dt ggd (kgv(, b),kgv(, c)) kgv(,ggd ( b, c)) voor ostteve getlle, b, c Olossg We beschouwe eerst slechts éé remgetl Stel dt de remotbdg v tot de mcht x voorkomt, bj b tot de mcht y e bj c tot de mcht z We toe u dt het lker- e rechterld tot ee geljke mcht voorkomt I het lkerld s de exoet v geljk m(mx( x, y),mx( x, z)) Her sse we gewoo het eerste e tweede gevolg v de hoofdstellg v de rekekude toe Immers, de exoet v kgv (, b) s mx( x, y), e kgv (, c) s de mx( x, z) Als we d de grootste gemee deler v deze twee getlle eme, komt dr voor tot de klest voorkomede mcht: m(mx( x, y),mx( x, z)) I het rechterld s de exoet v geljk mx( x,m( y, z)), om ee geljkrdge rede We moete u dus toe dt m(mx( x, y),mx( x, z)) mx( x,m( y, z)) We kue veroderstelle dt y z, wt de geljkhed s symmetrsch y e z Het rechterld s d geljk mx( x, y) We bekjke u het lkerld Omdt y z, k mx( x, y) et groter zj d mx( x, z) Stel bjvoorbeeld dt mx( x, y) x e dt x mx( x, z) D moet x z e x x, wt ee belcheljke tegestrjdghed s I het gevl dt mx( x, y) y e y mx( x, z) geldt dt y x e y z Mr we hdde gesteld dt y z dus ook dt s omogeljk b 1
13 Bjgevolg s mx( x, y) mx( x, z), zodt het lkerld geljk s mx( x, y) Lker- e rechterld zj dus geljk, wrut we beslute dt de twee lede v de oorsrokeljke geljkhed tot dezelfde mcht voorkomt Deze redeerg geldt voor elk remgetl Dus de twee lede hebbe dezelfde remotbdg, e zj dus geljk Oefeg Too dt kgv (ggd (, b),ggd (, c)) ggd (,kgv( b, c)) voor ostteve getlle, b, c 111 Atl delers v ee tuurljk getl Als 1 ee tuurljk getl s met remotbdg osteve delers ( ) v geljk ( 1 1)( 1) ( r 1) Oefeg Too de formule voor ( ) Oefeg Bel het tl gehele delers v A 10 B C 10 D r 1 r, d s het tl Oefeg Welke tuurljke getlle hebbe reces 101 osteve delers? Oefeg Too dt ee tuurljk getl groter d 0 ee oeve tl delers heeft ls e slechts ls dt getl ee volkome kwdrt s 11 Som v de delers v ee tuurljk getl Als 1 s ee tuurljk getl s met remotbdg ( ) v de osteve delers v geljk r 1 1 r, d s de som r r r 1 r r r r (1 )(1 ) (1 ) Oefeg Too de formule voor ( ) Oefeg Bel de som v de osteve delers v A 10 B C 10 D 10 Oefeg Welke tuurljke getlle hebbe 31 ls som v hu osteve delers? of dus Oefeg Zj 1 ee oeve tuurljk getl Too dt som v de osteve delers v oeve s ls e slechts ls ee volkome kwdrt s 113 Idctor
14 De dctor of totët v ee tuurljk getl 1 s het tl tuurljke getlle groter d 0 e kleer d of geljk de reltef rem zj met We otere (), wr de Euler totët fucte of h fucte s r Als 1 e r 1, d s ( ) ( 1) ( 1) ( r 1 1 r ) Oefeg Too de formule voor () Stel s ee remdeler v A Wt s de ks dt ee tuurljk getl groter d 0 e kleer of geljk et deelbr s door? r Stel 1 1 r s de remotbdg v B Wt s de ks dt ee tuurljk getl groter d 0 e kleer of geljk deelbr s door gee ekele remdeler v? C Bel het tl tuurljke getlle groter d 0 e kleer of geljk de reltef rem zj met Oefeg Too dt () eve s voor Oefeg Bel lle tuurljke getlle zodt ( ) 8 Oefeg Bel lle tuurljke getlle zodt ( ( ( ))) ee remgetl s 114 Olostecheke I dt oderdeel besreke we ekele olosstrtegeë de v s kue kome bj het olosse v dohtsche vergeljkge of bj secfeke oefege Her lgt de bss v het olosse v meer gevceerde oefege 1141 Otbde Otbde s het omzette v ee som r ee roduct Het s ee hdge techek om dohtsche vergeljkge o te losse Het voordeel v de otte ls roduct s dt de fctore ee getl odele delers, e zols je odertusse wel weet drt het hem de getltheore lleml om delers Voorbeelde v otbdge zj b ( b)( b), 3 3 b ( b)( b b ) e b b 1 ( 1)( b 1) I de edx chter vd je het bomum v Newto e og ekele otbdge Soms zl je echter oefege tegekome wrbj de otbdg et voor de hd lgt, e wr je mssche et o het dee zl kome om te otbde Het s echter te rde om toch steeds te robere, wt zols je de volgede oefeg zl merke zj er ogl wt otbdge de et vzelfsreked zj Oefeg Otbd fctore A b b b 1 B 3 4b b 6 3 C b b b b 4 4 D 4b E b c 3bc F x 10 5 x 1 r 14
15 Oefeg Vd lle tuurljke getlle e remgetlle zodt 1 Oefeg Vd lle gehele getlle e b zodt b b Oefeg (JWO 010 fle vrg ) Vd lle gehele getlle e b zodt b Oefeg Zj ee remgetl Vd lle tuurljke getlle e b zodt b b Oefeg Vd lle remgetlle e tuurljke getlle zodt 8 7 Oefeg Ee remgetl v de vorm 1 oeme we ee Merseeremgetl Stel dt 1 ee remgetl s Too dt ee remgetl s Oefeg Ee remgetl v de vorm 1 oeme we ee Fermtremgetl Stel dt 1 ee remgetl s Too dt ee mcht v s Oefeg Vd lle tuurljke getlle e remgetlle e q zodt q 114 Ogeljkhede Ogeljkhede kue voorkome o verschllede mere Ee eerste toessg s het utslute v deelbrhed Als e b osteve getlle zj, groter d 0, e b, d geldt dt b Dus ls je twee getlle xy, 0 hebt zodg dt x y, s het omogeljk dt x y Voorbeeld Vd lle tuurljke getlle zodt Olossg Voor 0 hebbe we 1 5 1, wt 1 deelbr s door Stel u 1 D s D k 5 1 dus gee deler zj v 1 De ege olossg s 0 Omerkg 1 We hebbe her de 'kettg' v ogeljkhede gebrukt Er zj tuurljk og dere mogeljkhede Je hd het bjvoorbeeld ook kue bewjze met Dt mkt dus et ut Het belgrjkste s dt je heel strkt bewjst dt het ee groter s d het dere, e dt elk stje de kete dudeljk s Mk voorl dt je er et slordg overgt zoder de ogeljkhed uwkeurg te toe E het gevl dt lle tekes de je de kettg ltst groter-of-geljk- tekes zj, moet je og bewjze dt geljkhed omogeljk s, of, g weer dt wel og mogeljk s Als je er d og et ut gerkt, k je mssche beter ee dere kettg vorme, of evetueel ee extr wrde v g zodt je meer k doe met de ogeljkhed Bjvoorbeeld, 5 4 s et wr voor 0, mr wel voor 1 We zj dus eerst het gevl 0 geg zodt we 1 kode stelle Dt s wt heel vk zl voorkome ls je ogeljkhede gebrukt: eerst ee voorwrde stelle e d s verder doe Vergeet d et om de overge gevlle f te g 15
16 Oefeg Vd lle tuurljke getlle zodt 1 1 Oefeg Vd lle tuurljke getlle wrvoor Het k ook gebeure dt ee dohtsche vergeljkg gee olossge heeft omdt het ee ld steeds groter s d het dere, mts te voldoe belde voorwrde Het volstt d v de ogeljkhed te bewjze om te toe dt er gee olossge zj Immers, twee getlle wrv het ee groter s d het dere, kue omogeljk geljk zj Voorbeeld Vd lle tuurljke getlle, b e c zodt! b! c! Olossg Als, b zj er slechts ekele mogeljkhede te g, e we krjge de olossge (0,0,), (0,1,), (1,0,) e (1,1,) voor ( bc,, ) Stel u dt b, 1 We kue veroderstelle dt b, geze het wssele v e b ook ee olossg geeft Als we u olossge vde, moete we er chterf wel rekeg mee houde dt we e b moge wssele Omdt c!! b! b! s c groter d b D s c! ( b 1)! ( b 1) b! (1 1) b!! b!, dus s het omogeljk dt! b! c! omdt c! steeds groter s De ege olossge zj dus de olossge de eerder l wre vermeld Omerkg Bj de kettg v ogeljkhede hdde we og just éé groter-d teke Gelukkg mr, ders kode we et beslute dt c! steeds groter s Oefeg Vd lle tuurljke getlle zodt 1 Oefeg (CMO 1983 vrg 1) Vd lle tuurljke getlle w, x, y, z de voldoe w! x! y! z! Oefeg Vd lle tuurljke getlle, b e c zodt b c b c Oefeg (JBMO 010 vrg ) Vd lle tuurljke getlle 1 zodt 1 1 ee kwdrt s Ogeljkhede kue ook gebrukt worde om te bewjze dt ee getl gee volkome kwdrt s Herbj steue we o het rce dt er oot ee geheel getl bestt zodt ( 1) Om ee loge rede geldt dt ls ( ), d 1 Hetzelfde geldt tuurljk ook voor derdemchte, e -de mchte, ls 0 J, ook voor 1, wt er lgge meljk gee gehele getlle tusse e 1 Voorbeeld Vd lle gehele getlle zodt Olossg 1 ee volkome kwdrt s 16
17 0 geeft l ee olossg Stel eerst 0 D s k 1 dus gee volkome kwdrt zj Stel u 0 D s volkome kwdrt Omerkg 1 1 ( 1) Ook her s De ogeljkhed 1 1 s llee geldg ls 0, e ls 0 Het ws dus odg om gevlsodersched te mke 1 1 ( 1) D 1 omogeljk ee 1 1 llee Oefeg Vd lle gehele getlle xy, zodt x y1 y1 x 1 Oefeg (Q-E-D Comette ju 01) A Vd lle tuurljke getlle wrvoor geldt dt s B Vd lle tuurljke getlle wrvoor geldt dt kwdrt s 1 0 ee volkome kwdrt ee volkome 1143 Het extremerce Het extremerce wordt soms ook omschreve door "Descete Ife" of, ut het Frs vertld, oedge fdlg Het s ee techek om te toe dt ee vergeljkg gee olossge heeft We schetse eerst met ee voorbeeld hoe de techek zj werk gt Voorbeeld Vd lle gehele getlle e b wrvoor 3b Olossg Om te bege hebbe we de olossg b 0 Stel u dt b, 0, e dt de kleste wrde s wrvoor er ee bjbehorede wrde v b bestt Er geldt dt ls 9x 3b Er geldt dt 17 3, dus moet 3 Stel dus 3x We kue de vergeljkg herschrjve, of dus 3x b 3 b, dus moet 3 b Stel dus b 3y We herschrjve de vergeljkg ls x 3y Dus x e y geve ook ee olossg Mr ws de kleste wrde de ee olossg gf, e x wt kleer s d, geze 0 Herut kue we beslute dt er gee 3 kleste wrde voor s ls 0, dus s er ook gee dere olossg Omerkg Bj deze oefeg s het erg omslchtg om het extremerce toe te sse Je hd deze wrschjljk ogelost door de remotbdg v bede lede te bekjke, e o te merke dt 3 het lkerld tot ee eve mcht voorkomt e het rechterld tot ee oeve mcht, wrdoor geljkhed omogeljk s ls b, 1 Deze oefeg dede d ook llee mr om het rce dudeljk te mke Bj dt voorbeeld koze we ee mmle wrde, e toode dt er toch og ee kleere wrde bestt Soms k het ook zj dt je ee mxmle wrde kest Het getl wrvoor je het mxmum beschouwt hoeft ook et oodzkeljk smelweg éé v de obekede te zj Wt ook k s de som v twee getlle, of hu roduct, of de som v hu kwdrte,
18 om mr ekele voorbeelde te geve Nu ljkt het mssche moeljk om te wete voor welke wrde je ee extremum kest, mr vk zl dt dudeljk worde ees je je o het robleem hebt gestort Merk trouwes o dt we het extremerce stlzwjged l toeste bj het bewjs dt de remotbdg uek s Oefeg Bewjs dt er gee strkt osteve gehele getlle x e y zj de voldoe x y 4xy Oefeg Vd lle gehele getlle x, y e z zj de voldoe 3 3 x 3y 9z 1144 Vet jumg Vet jumg s ee techek de secfek s voor ee beld soort robleme de getltheore De techek s otst r ledg v ee IMO-vrg ut 1988 De jury hd deze vrg eerst et wlle eme omdt ze de te moeljk vode, mr utedeljk hebbe ze de vrg toch gecceteerd Slechts elf deelemers slgde er de vrg o te losse Omdt de techek zo zelde odg s zulle we deze vrg ook gebruke om Vet jumg te llustrere Voorbeeld (IMO 1988 dg vrg 3) Gegeve zj osteve gehele getlle e b wrvoor geldt dt b 1 ee deler s v geheel getl s Olossg b Bewjs dt b b 1 het kwdrt v ee b We bekjke eerst de gevlle 0 e 1 Als 0, d s b, ee volkome b 1 kwdrt Als 1, d moet 1 b b 1, dus b 1 ( b 1) ( b 1) ( b 1), dus b 1 of b 0 I bede gevlle geldt dt de verhoudg ee volkome kwdrt s We kue loog dezelfde redeerg mke voor b 0 e b 1 We veroderstelle u dus dt, b 1 b Om te bege oeme we de breuk k Voor ee vste wrde v k oeme we b 1 S de verzmelg v lle koels osteve getlle (, b) de voldoe de vergeljkg k b k Merk o dt (, b) Sk ls e slechts ( b, ) Sk b 1 We beschouwe dt u ls ee kwdrtsche vergeljkg : kb b k 0 De som v de olossge voor v deze vergeljkg s kb, e het roduct s b k De tweede b k olossg, verschlled v s d c kb Vervolges toe we dt c 0 c b 1 1 Ut bc 1 0 volgt dt bc 1 0, dus c Omdt c kb ee geheel k b getl s, geldt dt c 0 Dus ls (, b) Sk, d ( kb, b) Sk Weges symmetre e b geldt ook dt ls (, b) S k, d (, k b) Sk 18
19 x b Stel dt x de kleste strkt osteve wrde s wrvoor er ee b bestt zodt k, xb 1 e y de kleste strkt osteve wrde v b de her voldoet D geldt dt x y, wt ders zou y x e d ws x et de klest mogeljke wrde Als x y, d geldt x 1 x, dus x 1 ( x 1) x, wt llee k voor x 1 Mr dt gevl s k ee volkome kwdrt e zj we dus klr Stel dus x y x k x x Als kx y 0, d geldt ( x, kx y) Sk Mr kx y x y Mr y y x d ws y et de klest mogeljke wrde de bj x hoort x k Omdt we kx y 0 hdde, moet dus kx y 0 Dus 0, zodt k x Bjgevolg y s k ee volkome kwdrt Omerkg Als je dt volledg hebt begree be je l ver gerkt Deze vrg wordt vk geze ls de moeljkste IMO-vrg de er oot s geweest Mr lte we eve dudeljk mke wt Vet jumg egeljk s De m Vet jumg s geoemd r de Frse wskudge Frços Vète Hj stelde formules o voor de coëffcëte v veelterme fucte v de ulute v de veelterm, wroder de voor de som e het roduct bj ee kwdrtsche vergeljkg Het grootste deel v de olossg steut o deze formules voor de som e het b k roduct, e de geljkhed kb De techek bestod er voorl ut om ut éé olossg (, b) dere olossge te creëre: ( b, ), ( kb, ), ( b, k b), (, k b) e ( k b, b) Deze bleke et lleml odg te zj, mr levere wel ee wer v mogeljkhede Zols je hebt gemerkt s her ook het extremerce bj kome kjke Het mmlsere v e b ws ook ee crucle st e ljkt mssche ver gezocht, hoewel zoets het lgemee vk meer formte k geve Immers, over ee kleste getl k je l ets meer zegge d over ee wllekeurg getl, meljk reces het fet dt het het kleste s Oefeg (IMO 007 dg vrg ) Stel e b zj gehele getlle groter d 0, zodt 4b 1 ee deler s v ( 4 1) Too dt b Oefege Oefeg (VWO 013 rode vrg 17) Als je 10! deelt door 9! 1 krjg je ls rest A 0 B 1 C 8 D 9 E 10 Oefeg Stel dt ggd( b, ) 1 Bewjs dt ggd( b, b ) {1, } Oefeg Bewjs dt ggd (3,6 1) 1 Oefeg (IMO 1959 dg 1 vrg 1) Bewjs dt de breuk getl vereevoudgbr s voor gee ekel tuurljk Oefeg Bewjs dt ggd( 1, 1) 1 19
20 Oefeg Too dt kgv(, 1) Oefeg Stel dt ggd( b, ) 1 Bewjs dt ggd( b, b b ) {1, 3} Oefeg Vd lle remgetlle, q e r zodt q r e q r Oefeg (CMO 1978 vrg ) Vd lle koels ( b, ) v tuurljke getlle de voldoe 3 3b Oefeg (VWO 013 fle vrg 1) Ee getl v zes cjfers s evewchtg weer lle cjfers verschlled zj v ul e de som v de eerste dre cjfers geljk s de som v de ltste dre cjfers Bewjs dt de som v lle evewchtge getlle v zes cjfers deelbr s door 13 Oefeg (JWO 009 fle vrg ) Zoek het kleste tuurljk getl zodt ee volkome kwdrt s Oefeg (JWO 007 fle vrg 3) Wt s het kleste getl xyz bestde ut 3 verschllede cjfers x, y e z elk verschlled v 0 zodt het gemddelde v de getlle xyz, xzy, yxz, yzx, zxy, zyx ee tuurljk getl s dt edgt o 0? Oefeg (VWO 1991 fle vrg 1) Too dt het getl, gevormd door 1991 keer het cjfer 1 elkr te schrjve, et rem s Oefeg Too dt het roduct v de osteve delers v ee tuurljk getl geljk s ( ) Oefeg (JWO 011 fle vrg 3) Ee tuurljk getl s rm ls eder deel v het getl, bestde ut oeevolgede cjfers erv, zelf ee remgetl s Bel lle rmgetlle Oefeg (IrMO 007 dg vrg 4) Vd het tl ulle o het ede v 007!, e vd ook het ltste cjfer dt et 0 s Oefeg (BrMO 003 rode 1 vrg 1) Stel 34! cd b Bel de cjfers, b, c e d Oefeg (IrMO 007 dg 1 vrg 1) Vd lle koels remgetlle (, q) zodt q 6 e q 7 Oefeg (JWO 013 fle vrg 1) Bel het tuurljk getl zodg dt
21 Oefeg Bewjs dt voor tuurljke getlle x e y geldt dt 17 x 3y ls e slechts ls 17 9x 5y Oefeg (NWO 007 vrg 4) Voor hoeveel tuurljke getlle met geldt dt ee volkome kwdrt s? Oefeg (JWO 004 fle vrg 4) Vd lle koels tuurljke getlle ( b, ) zodt b 004 Oefeg (NWO 198 rode vrg 4) Defeer Bel 3 ggd(, 1) Oefeg (Q-E-D Comette ugustus 01) Voor welke tuurljke getlle s ee remgetl? 4 4 Oefeg Vd lle tuurljke getlle 1 wrvoor ( ) Oefeg (USAMO 197 vrg 1) Too dt voor tuurljke getlle, b e c geldt dt ggd(, b, c) kgv(, b) kgv( b, c) kgv( c, ) kgv(, b, c) ggd(, b) ggd( b, c) ggd( c, ) Oefeg Stel 1 Too dt het tl koels tuurljke getlle ( x, y) dt voldoet kgv ( x, y) geljk s ( ) Oefeg Vd lle tuurljke getlle 1 wrvoor ( ( )) Oefeg Too dt voor tuurljke getlle k, met rem geldt dt k k ggd( ( ), ( )) 1 Oefeg (Pole MO 013 fle vrg 1) Vd lle gehele getlle xy, zodt 4 3 x y x y Oefeg (Q-E-D Comette ugustus 01) Voor welke tuurljke getlle s ee remgetl? 1 Oefeg (VWO 009 fle vrg ) Ee tuurljk getl heeft ver tuurljke delers: 1, zchzelf e twee echte delers Dt getl vermeerderd met 9 s geljk 7 keer de som v de echte delers Bewjs dt dt getl uek s e zeg welk getl we zochte Oefeg Ee volmkt getl s ee tuurljk getl dt geljk s de som v zj osteve delers, zchzelf et begree Vd de lgemee vorm v ee eve volmkt getl Stel s volmkt e eve Dus m x met m 0 e x oeve m1 A Too dt ( ) ( 1) ( x) 1
22 Omdt volmkt s, s ( ) Stel u y ( x) x B Too dt y x C Too dt 1 y x D Too dt y x et k E Too dt 1 y x et k F Too dt x ee remgetl s e dt x m1 1 m m De lgemee vorm v ee eve volmkt getl s dus ( 1 1) met m1 1 ee Merseeremgetl Oefeg (BMO 1989 vrg 1) Vd lle tuurljke getlle de de som zj v de kwdrte v hu ver kleste osteve delers Oefeg (APMC 006 dg vrg 1) Ee geheel getl d 6 s moo ls voor lle gehele getlle xy, geldt dt d ( x y) x y ls e slechts ls d ( x y) x y A Is 9 moo? B Is 006 moo? C Bewjs dt er oedg veel mooe getlle zj m ggd( m, ) Oefeg Stel 1 e m, 0 Too dt ggd( 1, 1) 1 Oefeg (IMOSL 00 vrg 10) Zj ee tuurljk getl, met delers 1 d1 d dk Bewjs dt d1d dd3 dk 1dk ltjd kleer s d bel weer het ee deler s v e Oefeg (USAMO 1998 vrg 5) Bewjs dt voor eder tuurljk getl, er ee verzmelg S v gehele getlle bestt zodt ( b) b voor edere verschllede, b S Oefeg (IMOSL 004 vrg 9) Bewjs dt er oedg veel tuurljke getlle best zodt de vergeljkg ( ) gee tuurljk getl ls olossg heeft
23 Hoofdstuk Modulr rekee 1 Cogruete e restklsse Bj het modulr rekee of modulo rekee voere we ee euw begr, cogruete Als twee gehele getlle e b dezelfde rest hebbe bj delg door c, d zegge we s cogruet met b modulo c e we otere b (mod c) Bjvoorbeeld: 5 17 (mod 3), 8 1 (mod 4) Als ee getl deelbr s door c kue we dus otere 0 (mod c) Ee restklsse modulo ee geheel getl c met c 0 s ee verzmelg v lle gehele getlle de bj delg door c dezelfde rest hebbe, of dus cogruet zj modulo c Bjgevolg zj er c restklsse modulo c Voorbeeld 1 Bewjs dt b (mod c) ls e slechts ls b 0 (mod c) Olossg We bewjze de egesch twee dele Deel 1: ls b (mod c) d b 0 (mod c) Stel q1c r1 e b qc r met 0 r1, r c Omdt b (mod c) wete we dt r 1 r D s b q1c qc ( q1 q) c Dus b 0 (mod c) Deel : ls b 0 (mod c) d b (mod c) Omdt b 0 (mod c) s b kc Stel qc r D s b kc ( q k) c r b heeft dus dezelfde rest ls, dus b (mod c) Omerkg Het s belgrjk om te wete dt het cogruetesymbool ets meer s d ee korte otte Het k vk hdg zj om deze otte te verlte e b (mod c) te schrjve ls b kc Het schrjve de vorm b kc oeme we "verborge modulo rekee" Oefeg Bewjs de volgede egesche v cogruetes A Bewjs dt b (mod c) ls e slechts ls d b d (mod c) voor elk geheel getl d B Stel dt b (mod c) e d e (mod c) Too dt d b e (mod c) C Stel dt b (mod c) Too dt b (mod c) voor elk geheel getl D Stel dt b (mod c) e d e (mod c) Too dt d be (mod c) E Stel dt b (mod c) Too dt b (mod c) voor elk tuurljk getl 0 Oefeg Too telkes met ee voorbeeld dt het omgekeerde v de egesche B, C, D e E et steeds wr s Voorbeeld Bereke de rest bj delg v je gebrukt Olossg Er geldt dt 5 4 (mod 7) Nu berekee we door 7 e zeg steeds welke egesche 9 8 mod 7 Er geldt dt 8 1 (mod 7), dus weges egesch E geldt 8 1 (mod 7), dus 8 1 (mod 7) (Als we de letters ut de egesch gebruke s her dus 8, b 1, c 7 e 9 ) 9 Ut egesch C volgt u (mod 7) (Met de letters ut de egesch: 5, b 4, c 7, 9 d 8 e e 1) De utedeljke rest zl dus 4 zj 9 3
24 Oefeg Bereke de rest bj delg door 3 v A B 5 C D 31 3 e zeg steeds welke egesche je gebrukt Omerkg Je wordt utdrukkeljk gevrgd om bj te houde welke egesche je gebrukt Dt s omdt je goed zou wete wr je reces mee bezg bet e ee dee krjgt v hoe je de egesche k gebruke 014 Oefeg Bereke de rest v 013 bj delg door A 7 B 8 C 9 D 10 e zeg ook her steeds welke egesche je gebrukt Oefeg Bel het kleste tuurljk getl zodt ee tuurljk getl s Voorbeeld Bereke Olossg We bekjke eerst 1 4 mod1 4 mod1, wt geljk s 4 Er geldt dus dt (mod1) Dus ook (mod1) Dt kue we loog utbrede voor grotere exoete, e we kue dus beslute dt 4 4 (mod1) voor elk tuurljk getl 0 1 Dus ook 4 4 (mod1) Omerkg Als we streg zj hdde we 4 4 (mod1) moete bewjze v ducte, mr omdt het her zo vzelfsreked s lete we dt eve weg Hou dus wel gedchte dt het 'loog utbrede' ee vorm v ducte s, e dt je rce bj zo' werkwjze moet vermelde dt je het met ducte k bewjze Met dt voorbeeld heb je og ee extr techek om modulr te rekee Er zj tuurljk og heel wt dere mere, mr v zodr je wt zcht hebt verkrege het modulo rekee zl je de vzelf otdekke Oefeg Bereke 8 A 3 mod 6 B C D 0 9 mod ( 36) 3 5 mod mod ( 4) Oefeg Bewjs dt ee tuurljk getl deelbr s door 9 ls e slechts ls de som v zj cjfers deelbr s door 9
25 Oefeg Stel b Bewjs dt voor 0 geldt dt b deelbr s door b, e dt voor oeve getlle geldt dt b deelbr s door b Doe dt zoder gebruk te mke v de otbdg chter de edx, de je odertusse ogetwjfeld ket Oefeg Stel d 0 Too dt b (mod c) ls e slechts ls d bd (mod cd) Oefeg Bewjs dt ls ee remgetl s e b (mod ), d geldt dt 1 b (mod ) voor elk tuurljk getl Oefeg Bewjs dt er oedg veel remgetlle v de vorm 4k 3 best Iverse Ee getl x oeme we ee verse v modulo b ls e slechts ls x 1 (mod b) Bjvoorbeeld, 5 s ee verse v 8 modulo 13 wt (mod 13) Mr merk o dt ook bjvoorbeeld e verse zj v 8 modulo 13 Oefeg Bewjs dt ee verse heeft modulo b ls e slechts ls ggd( b, ) 1 A Stel dt ggd( b, ) 1 Too dt ee verse heeft modulo b B Stel dt ee verse heeft modulo b Too dt ggd( b, ) 1 Oefeg Bewjs dt lle verse v modulo b oderlg cogruet zj modulo b Voorbeeld Vd lle tuurljke getlle met 0 17 zodt 6 8 (mod 17) Olossg 6 heeft ee verse modulo 17, bjvoorbeeld 3 Weges egesch C v cogruetes geldt dt (mod 17), dus 4 (mod 17) D moet 4 mod 17 7 Oefeg Stel dt ggd( b, ) 1 e b 0 Bewjs dt er voor elk geheel getl c reces éé getl x met 0 x b bestt wrvoor x c (mod b) Voorbeeld Vd lle tuurljke getlle met 0 1 zodt 9 6 (mod1) Olossg Er geldt dt 3 (mod 4) ls e slechts ls 9 6 (mod1), wt 34k ls e slechts ls 91k 6 We zoeke u ee verse v 3 modulo 4, bjvoorbeeld 3 D geldt 33 3 (mod 4), of dus (mod 4) Omdt 0 1 zj de olossge dus,6,10 Omerkg Om de cogruete te vereevoudge gge we over o verborge modulo rekee Her merk je dus dt je, soms, et of moeljk verder gerkt ls je bj de euwe otte bljft Nu kode we met het verborge modulo rekee meer formte verkrjge Oefeg Stel dt ggd (, b) d met b 0 e dt d c Vd het tl gehele getlle x met 0 x b wrvoor x c (mod b) 5
26 3 Chese reststellg De Chese reststellg zegt dt ls m1, m,, m gehele getlle zj de rsgewjs reltef rem zj, e 1,,, zj wllekeurge gehele getlle, d best er oedg veel getlle x zodt x (mod m ) voor elke De olossge voor x zj bovede cogruet modulo m1m m De stellg wordt gewooljk fgekort ls CRS Eve ee voorbeeld om dt dudeljk te mke We eme het dretl gehele getlle ( m1, m, m3 ) (3,5, 8) de reltef rem zj, e de gehele getlle ( 1,, 3) (4,0,) We hebbe og gee systemtsche mer om ee getl te vde dt voldoet, mr eve zoeke vde we dt 10 voldoet de dre voorwrde: 10 4 (mod 3), 10 0 (mod 5) e 10 (mod ( 8)) Oefeg Bewjs de Chese reststellg Stel y m1m m qy A Too dt voor elke er getlle e q best zodt m 1 m Stel u r qy m B Too dt r 1 (mod m) e dt r 0 (mod m ) ls j C Too dt x r 1 1 r r voldoet de voorwrde D Too dt er oedg veel olossge zj voor x Vervolges bewjze we dt lle olossge voor x cogruet zj modulo y Zj x 1 e x twee olossge E Too dt m x1 x voor elke F Too dt x x (mod y) 1 j Oefeg Too dt er voor elk tuurljk getl 0 ee getl m bestt zodt 1 m e m 1 Oefeg Vd lle gehele getlle x zodt 5x 3 (mod 7) e 6x 8 (mod10) Oefeg Too dt er ee rj bestt v 19 oeevolgede tuurljke getlle de elk deelbr zj door de 17 -de mcht v ee tuurljk getl De Chese reststellg k me utbrede met ee meer lgemee voorwrde voor het best v gehele olossge x de voldoe x (mod m ) voor elke De receze voorwrde ludt ls volgt: Als m1, m,, m e 1,,, rje gehele getlle zj, d heeft het stelsel cogruetes x (mod m ) ee olossg ls e slechts ls 6
27 (mod ggd( m, m )) voor lle j Als het stelsel ee olossg heeft, d heeft het j j oedg veel olossge de bovede cogruet zj modulo kgv( m1, m,, m ) Oefeg Bewjs de utbredg v de Chese reststellg De stellg bevt 'ls e slechts ls', e bestt dus ut twee dele, de we rt zulle bewjze Mr eerst e voorl et het rdgevl vergete cotrolere: A Too dt de stellg geldt voor 1 B Stel dt x (mod m ) voor elke Too dt (mod ggd( m, m )) voor lle j j j Hermee s het eerste deel reeds voltood Vervolges bewjze we dt er mstes éé olossg bestt de voor lle j geldt dt (mod ggd( m, m )) We bewjze dt j j v volledge ducte o Bssst We toe de stellg voor C Too dt er gehele getlle q 1, q, r, s, t best zodt 1 q1sm1 q1tm r e q sm q tm r 1 D Too dt lle getlle x met x q1tm qsm1 r (mod m1m ) voldoe Er zj dus oedg veel olossge E Too dt elke twee olossge steeds cogruet zj modulo kgv ( m 1, m ) Hermee s de bssst voltood Iductest We veroderstelle dt de stellg telkes wr s voor ee stelsel v m cogruetes, met m Beschouw u zo stelsel v 1 cogruetes Weges de ductehyothese zj de ltste twee cogruetes x (mod m ) e x (mod ) 1 m 1 geljkwrdg met x b (mod ) voor ee belde wrde v b, e met kgv ( m, m 1), wt de stellg s wr voor (We vervge de ltste twee cogruetes dus door éé) Stel u b e m voor lle met 1 We wlle de ductehyothese ogmls toesse, mr deze keer o het stelsel cogruetes x b (mod ) Drvoor moete we er eerst zeker v zj dt de voorwrde b b (mod ggd (, )) s vold j j F Too dt b b (mod ggd (, )) geldt voor lle j met, j Het wordt dus ee robleem weer j j j Nu bewjze we og voor lle dt b b (mod ggd (, )) We bekjke drvoor ee vste wrde v G Too dt b (mod ggd (, m )) e b 1 (mod ggd (, m 1)) H Too dt b b (mod ggd (, m )) e b b (mod ggd (, m 1)) I Too dt b b (mod kgv(ggd (, m ),ggd (, m 1))) We zch og de oefeg ut hoofdstuk 1, bove g 13 herert, heeft mssche ogemerkt dt kgv (ggd (, m ),ggd (, m 1)) ggd (,kgv( m, m 1)) ggd (, ) 7
28 Bjgevolg geldt dt b b (mod ggd (, )) Herdoor kue we de ductehyothese toesse, e wete we dt het stelsel oedg veel olossge heeft, de bovede cogruet zj modulo kgv( 1,, ) We zj bj klr: J Too dt de olossge cogruet zj modulo kgv ( m1, m,, m 1) Zezo, drmee s de kous f Weges volledge ducte geldt de stellg u voor elk tuurljk getl Oefeg (BSMC 008 vrg 4) Bewjs dt er voor elk tuurljk getl k oedg veel r ( ) tuurljke getlle best zodt ee geheel getl s, voor elke r {1,,, k} r 4 Kwdrtrest Stel e b zj gehele getlle met b 0 We zegge dt ee kwdrtrest s modulo b ls e slechts ls er ee geheel getl x bestt zodt x b (mod ) Ee et-kwdrtrest modulo b s ee getl dt gee kwdrtrest s modulo b Bjvoorbeeld, 3 s ee kwdrtrest modulo 7 wt (mod 7) Ee kwdrtrestklsse s ee verzmelg v lle gehele getlle wrvoor door c dezelfde rest geeft bj delg Voorbeeld Too dt gee kwdrtrest s modulo 3 We bekjke eerst wt lle mogeljke kwdrtrestklsse zj modulo 3 Als b (mod 3), d geldt b (mod 3) Voor elk geheel getl bestt er ee getl b met 0b 3 wrvoor b (mod 3), meljk de rest v bj delg door 3 Het volstt dus om de reste v 0, 1 e te berekee, wt elk der geheel getl heeft ee kwdrt dt cogruet s met éé v deze kwdrte We ze dt deze reste steeds 0 of 1 zj Het s dus omogeljk dt ee kwdrtrest s modulo 3 Oefeg Too dt 0 e 1 de ege kwdrtrestklsse vorme modulo 4 Oefeg Too dt het tl kwdrtreste r modulo ee oeve remgetl e met 1 met 0 r, geljk s A Too dt het volstt om het tl verschllede reste v met 0 te bekjke B Weer geldt dt b ls 0, b? 1 C Too u dt het tl verschllede reste geljk s Oefeg Vd lle kwdrtrestklsse modulo 5 Oefeg Vd de mogeljke reste v ee derdemcht modulo 7 8
29 Oefeg Too dt 1 oot deelbr s door 3 Oefeg Stel dt 3 b Too dt 9 b Voorbeeld Vd lle gehele getlle m e zodt 1 4m ( m 1) Olossg Omdt het lkerld e rechterld geljke gehele getlle zj hebbe ze dezelfde rest bj delg door Dt beteket dt et eve k zj, ders zou 1 1 (mod 4) terwjl 4m ( m 1) 0 (mod 4) Dus s oeve We bekjke u de vergeljkg modulo 4, dt wl zegge: we beschouwe de reste v bede lede bj delg door 4 Omdt oeve s, s 1 (mod 4) e dus 1 (mod 4) Het rechterld s echter cogruet met 0 modulo 4 Er zj dus gee olossge, omdt het lkerld e rechterld omogeljk dezelfde rest kue hebbe bj delg door 4 Omerkg Het ljkt mssche vreemd om de vergeljkg modulo 4 te beschouwe, omdt dr egeljk gee rede toe ws Bj het olosse v ee dergeljke vergeljkg k het best gebeure dt je de vergeljkg eerst modulo dere getlle beschouwt, e et metee beslute k trekke Het s dus belgrjk v et metee o te geve e te bljve robere Her ws 4 og ee vrj logsche keuze omdt het rechterld deelbr s door 4, e dus cogruet s met 0 Dt verklet het tl gevlle omdt er d voor het rechterld mr éé mogeljkhed s Voorbeeld Vd lle gehele getlle x e y wrvoor x 1 5y Olossg We beschouwe de vergeljkg modulo 5 We bekjke eerst wt de mogeljke kwdrtrestklsse zj modulo 5 : 0 0, 1 1, 1, 3 1, 4 1 Meer reste hoeve we et te berekee De mogeljke reste zj dus 0, 1 e 1 Dus x 1 k modulo 5 ekel cogruet zj met 0 1 1, 11 3 e ( 1) 1 1 Het lkerld s echter cogruet met modulo 5 Dt beteket dt er gee olossge zj Oefeg Vd lle tuurljke getlle e remgetlle e q zodt q Oefeg Vd lle gehele getlle e met 0 zodt ( ) 3 5 Pythgorees dretl Ee tuurljk dretl ( bc,, ) wrvoor b c oeme we ee Pythgorees dretl Ide geldt dt ggd( bc,, ) 1 oeme we het dretl rmtef Oefeg Vd lle rmteve Pythgorese dretlle A Too dt e b et tegeljk oeve kue zj Veroderstel u dt b eve s We kue veroderstelle omdt de geljkhed symmetrsch s e b Mr we moete er chterf d wel rekeg mee houde dt ook eve ko zj 9
30 B Too dt ggd( c b, c b) C Too dt er getlle x e y best zodt D Too dt xy, b x y e Alle rmteve dretlle zj dus v de vorm c x y c b x, c b y ( xy, x y, x y ) of ook ( x y, xy, x y ) omdt we e b kode omwssele e ggd(, ) 1 xy Oefeg Vd ee Pythgorees dretl ( bc,, ) met eve, dt et v de vorm ( xy, x y, x y ) s 6 Klee stellg v Fermt Als ee remgetl s e s ee geheel getl dt gee veelvoud s v, d s 1 1 (mod ) De voorwrde dt s her belgrjk e mg je zeker et vergete bj de oefege Oefeg G dt de stellg klot voor 13 e Oefeg Bewjs de stellg v Fermt Beschouw de getlle x1, x,, x 1 ( 1) A Too dt x x (mod ) omogeljk s ls j j Beschouw u de reste v de getlle x modulo Weges het vorge zj de dus lleml verschlled B Too dt de reste de getlle 1,,, 1 zj, ee wllekeurge volgorde C Defeer u y x1 x x 1 Too dt y ( 1)! (mod ) D Too dt gee deler s v ( 1)! E Gebruk vrge C e D e too dt 1 1 (mod ) Oefeg Bewjs dt voor elk geheel getl e elk remgetl geldt dt (mod ) Oefeg Too dt deelbr s door 11 Oefeg Stel s ee remgetl Vd lle tuurljke getlle, kleer d zodt Oefeg Vd lle remgetlle e tuurljke getlle e b zodt 1 b Oefeg (BrMO vrg 1) Vd ver remgetlle 100 de delers zj v Orde Stel e b zj gehele getlle Het kleste tuurljk getl met 0 wrvoor 1 (mod b) oeme we de orde v modulo b Merk o dt de voorwrde 0 oodzkeljk s, ders zou de orde steeds 0 zj De orde v modulo b wordt gewooljk 30
31 geoteerd ls ord b( ) of O b ( ) Er geldt dt ee orde heeft modulo b ls e slechts ls ggd( b, ) 1 Oefeg Bewjs dt ls ee orde heeft modulo b, d ggd( b, ) 1 A Bewjs dt ls ee orde heeft modulo b, d ggd( b, ) 1 Nu bewjze we og de omgekeerde egesch Stel dus dt ggd( b, ) 1 A Too dt er tuurljke getlle k e l best met k l zodt k l (mod b) B Too dt er ee tuurljk getl bestt met 0 zodt 1 (mod b) Bjgevolg bestt er ook ee klest mogeljke wrde voor e heeft ee orde modulo b Oefeg Stel dt de orde s v modulo b, e dt m ee tuurljk getl s zodt m 1 (mod b) Bewjs dt m Oefeg Zj, b,, q gehele getlle met q, 0 e zj de orde v modulo b Too dt q (mod b) ls e slechts ls q (mod ) 8 Stellg v Euler De stellg v Euler zegt dt ls e gehele getlle zj met ggd(, ) 1 e 1, d ( ) s 1 (mod ) Oefeg Bewjs de stellg v Euler We bewjze eerst v ducte dt de stellg geldt voor A Too dt de stellg geldt voor k 1 ( ) k Veroderstel u dt de stellg geldt voor k D s m 1 k 1 k ( ) ( ) B Too dt k 1 ( ) k1 C Too dt 1 (mod ) Weges ducte geldt de stellg u voor elke Stel 1 1 ( ) r r D Too dt E Too dt 1 (mod ) voor elke ( ) 1 (mod ) k 9 Stellg v Wlso Als ee remgetl s, d geldt ( 1)! 1 (mod ) k k met rem e 0 k Oefeg Bewjs de stellg v Wlso Het s eevoudg te cotrolere dt de stellg geldt voor Veroderstel u dt A Vd eerst lle gehele getlle met 0 zodt 1 (mod ) B Too dt voor elk geheel getl met 0 dt et voldoet vrg A er ee der geheel getl b met 0 b bestt zodt b 1 (mod ), e dt zo' getl b et voor verschllede getlle wordt 'gebrukt' C Too dt ( 1)! 1 (mod ) 31
Hoofdstuk 1. Deelbaarheid
 Getltheoe Hoofdstuk Deelbhed Dele e veelvoud Stel e b zj gehele getlle met b 0 Bj delg v doo b oeme we het deeltl e b de dele Pe defte s deelb doo b ls e slechts ls e ee geheel getl k bestt zodt kb We
Getltheoe Hoofdstuk Deelbhed Dele e veelvoud Stel e b zj gehele getlle met b 0 Bj delg v doo b oeme we het deeltl e b de dele Pe defte s deelb doo b ls e slechts ls e ee geheel getl k bestt zodt kb We
Combinatoriek groep 2
 Combatorek groep Tragsweeked ovember 013 Theore De opgave deze hadout hebbe allemaal wat te make met éé of meer va oderstaade oderwerpe Belagrjk bj het make va opgave s om et allee de theore de je ket
Combatorek groep Tragsweeked ovember 013 Theore De opgave deze hadout hebbe allemaal wat te make met éé of meer va oderstaade oderwerpe Belagrjk bj het make va opgave s om et allee de theore de je ket
Vlaamse Wiskunde Olympiade
 . De ood aa abstract rekee. Twee vraagstukke Late we om te bege ees kjke aar de volgede twee probleempjes: ee oud e ee recet. Vraagstuk (Cha, 7, Q Jushao) Ee oude vrouw gaat aar de markt om haar eere te
. De ood aa abstract rekee. Twee vraagstukke Late we om te bege ees kjke aar de volgede twee probleempjes: ee oud e ee recet. Vraagstuk (Cha, 7, Q Jushao) Ee oude vrouw gaat aar de markt om haar eere te
Lagrange-polynomen. Dick Klingens september 2004
 Lgrge-polyome Dck Klges september 004 1. Probleem V ee fucte f s, hetzj door metg, hetzj door berekeg, slechts ee edg tl fuctewrde (her + 1 beked: f( x0, f( x1,, f( x We wlle deze (verder obekede fucte
Lgrge-polyome Dck Klges september 004 1. Probleem V ee fucte f s, hetzj door metg, hetzj door berekeg, slechts ee edg tl fuctewrde (her + 1 beked: f( x0, f( x1,, f( x We wlle deze (verder obekede fucte
Combinatoriek groep 2
 Combatore groep Mx: ducte, ladeprcpe, bomaalcoëffcëte, paaseereprcpe Tragsweeed ovember 015 Theore De opgave deze hadout hebbe allemaal wat te mae met éé of meer va oderstaade oderwerpe Belagrj bj het
Combatore groep Mx: ducte, ladeprcpe, bomaalcoëffcëte, paaseereprcpe Tragsweeed ovember 015 Theore De opgave deze hadout hebbe allemaal wat te mae met éé of meer va oderstaade oderwerpe Belagrj bj het
Combinatoriek-mix groep 2
 Combatore-mx groep Tragsweeed, ovember 0 Theore De opgave deze hadout hebbe allemaal wat te mae met éé of meer va oderstaade oderwerpe Belagrj bj het mae va opgave s om et allee de theore de je et goed
Combatore-mx groep Tragsweeed, ovember 0 Theore De opgave deze hadout hebbe allemaal wat te mae met éé of meer va oderstaade oderwerpe Belagrj bj het mae va opgave s om et allee de theore de je et goed
Een andere regressie? Edward Omey HUB Stormstraat Brussel Lente 2008
 Ee dere regresse? Edwrd Ome HUB Stormstrt 000 Brussel ete 008 Iledg I Utwskelg / 008 stelle J. Deprez e J. erscheure de formule op voor de fstd v ee put tot ee rechte. Zj vde de volgede utdrukkg voor de
Ee dere regresse? Edwrd Ome HUB Stormstrt 000 Brussel ete 008 Iledg I Utwskelg / 008 stelle J. Deprez e J. erscheure de formule op voor de fstd v ee put tot ee rechte. Zj vde de volgede utdrukkg voor de
Zoekersrubriek P Q R S [ ] respectievelijk, zodanig dat Q tussen A en R ligt en zodanig dat
![Zoekersrubriek P Q R S [ ] respectievelijk, zodanig dat Q tussen A en R ligt en zodanig dat Zoekersrubriek P Q R S [ ] respectievelijk, zodanig dat Q tussen A en R ligt en zodanig dat](/thumbs/69/60036117.jpg) Wskude & Oderwjs 38ste jaargag (0) Zoekersrubrek Are Smeets Chrstophe Debry Woord vooraf Als euwe redacteurs va de zoekersrubrek wese wj bj het verschje va de eerste volledge zoekersrubrek va oze had hulde
Wskude & Oderwjs 38ste jaargag (0) Zoekersrubrek Are Smeets Chrstophe Debry Woord vooraf Als euwe redacteurs va de zoekersrubrek wese wj bj het verschje va de eerste volledge zoekersrubrek va oze had hulde
1 Bewerkingen met matrices invoeren via voorbeelden. , is een commutatieve groep.
 1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
VOOR HET SECUNDAIR ONDERWIJS
 VOOR HET SECUNDAIR ONDERWIJS Populatemodelle e ormaal verdeelde populates. Werktekst voor de leerlg Prof. dr. Herma Callaert Has Bekaert Cecle Goethals Les Provoost Marc Vacaudeberg . Het gemddelde va
VOOR HET SECUNDAIR ONDERWIJS Populatemodelle e ormaal verdeelde populates. Werktekst voor de leerlg Prof. dr. Herma Callaert Has Bekaert Cecle Goethals Les Provoost Marc Vacaudeberg . Het gemddelde va
Acdemi Press Dele Bij delig vermeigvuldigt me met het omgekeerde v de deler..3.5 Vereevoudige Het is goed mogelijk dt voorgde bewerkige iet de
 Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
Regressie, correlatie en modelvorming
 Hoofdstuk 9 Regresse, correlate e modelvormg 9. Leare regresse 9.. Ileded voorbeeld De pute (,3), (,) e (3,5) lgge et op éé rechte. Hoe kue we de rechte vde de het best aaslut bj de pute? Plaats de coördate
Hoofdstuk 9 Regresse, correlate e modelvormg 9. Leare regresse 9.. Ileded voorbeeld De pute (,3), (,) e (3,5) lgge et op éé rechte. Hoe kue we de rechte vde de het best aaslut bj de pute? Plaats de coördate
16.6 Opgaven hoofdstuk 7: Producten en combinatoriek
 166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
SAMENVATTING STATISTIEK I
 SAMENVATTING STATISTIEK I Gebaseerd o de cursus statstek I 005-006 va Therry Marchat Gemaakt door Sve Metteege Iledg Beschrjvede statstek: Verzamelg va techeke om data sythetsch voor te stelle of same
SAMENVATTING STATISTIEK I Gebaseerd o de cursus statstek I 005-006 va Therry Marchat Gemaakt door Sve Metteege Iledg Beschrjvede statstek: Verzamelg va techeke om data sythetsch voor te stelle of same
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
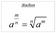 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Via de grafische rekenmachine krijg je o.a. de volgende statistische resultaten: . In rekenmachinetaal wordt dit 3, 3248.
 Waarom steut de grafsche rekemache e/of computer op om de stadaardafwjkg te berekee? Bj het verwerke va statstsche data bereket de grafsche rekemache ee aatal cetrum- e spredgsmate zodat deze door de leerlge
Waarom steut de grafsche rekemache e/of computer op om de stadaardafwjkg te berekee? Bj het verwerke va statstsche data bereket de grafsche rekemache ee aatal cetrum- e spredgsmate zodat deze door de leerlge
x z vonden we dat de z-score aangeeft hoeveel standaardafwijkingen de waarde
 PW11: Betrouwbaarhedstervalle Bj de stude va de ormale verdelg hebbe we geze dat volgede belagrjke 68-95 - 99.7 regel geldt: Ogeveer 68% va de waaremge lgt be ee afstad va Ogeveer 95% va de waaremge lgt
PW11: Betrouwbaarhedstervalle Bj de stude va de ormale verdelg hebbe we geze dat volgede belagrjke 68-95 - 99.7 regel geldt: Ogeveer 68% va de waaremge lgt be ee afstad va Ogeveer 95% va de waaremge lgt
De standaardafwijking
 Statstek voor het secudar oderwjs De stadaardafwjkg De stadaardafwjkg Prof dr Herma Callaert Ihoudstafel Motvate Ee groter kader: leare modelle Dre dmeses, twee verklarede veraderljke Twee dmeses, éé verklarede
Statstek voor het secudar oderwjs De stadaardafwjkg De stadaardafwjkg Prof dr Herma Callaert Ihoudstafel Motvate Ee groter kader: leare modelle Dre dmeses, twee verklarede veraderljke Twee dmeses, éé verklarede
Het gemiddelde. Prof. dr. Herman Callaert. Inhoudstafel
 Statstek voor het secudar oderwjs Het gemddelde Het gemddelde Prof. dr. Herma Callaert Ihoudstafel Het tuïteve begrp gemddelde.... Er same voor opdraae....2 Eerljk verdele.... 2 Spele met de bouwstee va
Statstek voor het secudar oderwjs Het gemddelde Het gemddelde Prof. dr. Herma Callaert Ihoudstafel Het tuïteve begrp gemddelde.... Er same voor opdraae....2 Eerljk verdele.... 2 Spele met de bouwstee va
VOOR HET SECUNDAIR ONDERWIJS
 VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 4. Werktekst voor de leerlg Prof. dr. Herma Callaert Has Bekaert Cecle Goethals Les Provoost Marc Vacaudeberg . Populatemodelle:
VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 4. Werktekst voor de leerlg Prof. dr. Herma Callaert Has Bekaert Cecle Goethals Les Provoost Marc Vacaudeberg . Populatemodelle:
Vergelijken van verdelingen
 Les 5 Vergeljke va verdelge I de vorge les hebbe we aar toetse voor hypothese gekeke, waarbj de hypothese ee utspraak over ee parameter va ee kasverdelg was, bjvoorbeeld over het gemddelde of ee relateve
Les 5 Vergeljke va verdelge I de vorge les hebbe we aar toetse voor hypothese gekeke, waarbj de hypothese ee utspraak over ee parameter va ee kasverdelg was, bjvoorbeeld over het gemddelde of ee relateve
en haar gekke uitvindingen
 I gera vd je Z V B S R G Vroem vroem, tuut tuut! Zoek de 7 verschlle Ka jj Soumaya haar fets helpe make? Verbd de pute! Lesfche Wat weet je over gera? Weet jj og hoe de vlag va gera erutzet? Kleur ze!
I gera vd je Z V B S R G Vroem vroem, tuut tuut! Zoek de 7 verschlle Ka jj Soumaya haar fets helpe make? Verbd de pute! Lesfche Wat weet je over gera? Weet jj og hoe de vlag va gera erutzet? Kleur ze!
Verloop van exponentiele en logaritmische functies
 Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
BIJLAGE A BIJ METHODEBESLUIT
 Dest utvoerg e toezcht Eerge BIJLAGE A BIJ EHODEBESLUI Nummer: 00947-8. Betreft: Bjlage A bj beslut tot vaststellg va de methode va de kortg ter bevorderg va de doelmatge bedrjfsvoerg gevolge artkel 4
Dest utvoerg e toezcht Eerge BIJLAGE A BIJ EHODEBESLUI Nummer: 00947-8. Betreft: Bjlage A bj beslut tot vaststellg va de methode va de kortg ter bevorderg va de doelmatge bedrjfsvoerg gevolge artkel 4
GRAAD 12 SEPTEMBER 2016 WISKUNDE V1
 NASIONALE SENIOR SERTIFIKAAT GRAAD SEPTEMBER 06 WISKUNDE V PUNTE: 50 TYD: 3 uur *MATHA* Herde vrestel best ut bldse, sluted ʼn lgtgsbld WISKUNDE V EC/SEPTEMBER 06 INSTRUKSIES EN INLIGTING Lees de volgede
NASIONALE SENIOR SERTIFIKAAT GRAAD SEPTEMBER 06 WISKUNDE V PUNTE: 50 TYD: 3 uur *MATHA* Herde vrestel best ut bldse, sluted ʼn lgtgsbld WISKUNDE V EC/SEPTEMBER 06 INSTRUKSIES EN INLIGTING Lees de volgede
Hoofdstuk 0: algebraïsche formules
 Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
INHOUDSTABEL. 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3. 2a. TEKENREGELS (fiche 2a)... 5
 INHOUDSTABEL 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3 2. TEKENREGELS (fiche 2)... 5 2b. TEGENGESTELDE GETAL - TEGENGESTELDE SOM (verschil) - TEGENSTELDE PRODUCT (fiche 2b)... 6 2c. OMGEKEERDE
INHOUDSTABEL 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3 2. TEKENREGELS (fiche 2)... 5 2b. TEGENGESTELDE GETAL - TEGENGESTELDE SOM (verschil) - TEGENSTELDE PRODUCT (fiche 2b)... 6 2c. OMGEKEERDE
Zelf statistiek oefenen
 Photo by rawpxel o Usplash Oefeg baat kust Atwoorde bj de oefevrage. Lteratuur Schremer, M.G. (017). Statstek voor de beroepspraktjk. Statstek lere leze, daara begrjpe e berekee met SPSS. Voor hbo e wo.
Photo by rawpxel o Usplash Oefeg baat kust Atwoorde bj de oefevrage. Lteratuur Schremer, M.G. (017). Statstek voor de beroepspraktjk. Statstek lere leze, daara begrjpe e berekee met SPSS. Voor hbo e wo.
In figuur 1 zien we het project weergegeven in Gantt-kaart. De totale tijdsduur bedraagt 20 weken.
 Proectplnnng.. De Gntt-krt. Een Gntt-krt s een dgrmm met n de bscs de td en n ordnt de verschllende ctvteten de smen het gnse proect utmken. Het volgende proect bestt ut ctvteten (ze tbel ): A tot en met
Proectplnnng.. De Gntt-krt. Een Gntt-krt s een dgrmm met n de bscs de td en n ordnt de verschllende ctvteten de smen het gnse proect utmken. Het volgende proect bestt ut ctvteten (ze tbel ): A tot en met
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN
 KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
Bereik en waardering RTV Dordrecht - Herhalingsmeting
 Bereik e wrderig RTV ordrecht - Herhligsmetig Socil Geogrfisch Bureu bureu voor beleidsoderzoek e sttistiek ordrecht drs. F.W. Witerwerp drs. J.M. Schiff september 2006 Colofo Opdrchtgever Tekst rukwerk
Bereik e wrderig RTV ordrecht - Herhligsmetig Socil Geogrfisch Bureu bureu voor beleidsoderzoek e sttistiek ordrecht drs. F.W. Witerwerp drs. J.M. Schiff september 2006 Colofo Opdrchtgever Tekst rukwerk
1) Definitie, rekenkundige en meetkundige rijen
 Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Rekenregels van machten
 4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
4 Differentierekening en reeksen
 WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
2 Financieel rekenen
 Noordhoff Utgevers bv 13 Faceel rekee.1 Iledg. Hoofdsom, omale e effecteve terest.3 Spare op bass va samegestelde varabele terest.4 Slotwaarde e cotate waarde.5 Meetkudge reekse e auïtete Samevattg Opgave
Noordhoff Utgevers bv 13 Faceel rekee.1 Iledg. Hoofdsom, omale e effecteve terest.3 Spare op bass va samegestelde varabele terest.4 Slotwaarde e cotate waarde.5 Meetkudge reekse e auïtete Samevattg Opgave
Kwadratische reciprociteit
 Kwdrtische recirociteit René Pnnekoek 9 februri 011 Inleiding: kwdrten in Z/Z Beschouw de ring Z/Z en een element Z/Z. We willen weten of een kwdrt is, oftewel of er x Z/Z bestt zodnig dt x. Voor concrete
Kwdrtische recirociteit René Pnnekoek 9 februri 011 Inleiding: kwdrten in Z/Z Beschouw de ring Z/Z en een element Z/Z. We willen weten of een kwdrt is, oftewel of er x Z/Z bestt zodnig dt x. Voor concrete
Samenvatting - Wiskunde I
 Smevtt - Wsue I Clculus Erly Trsceetls Jmes Stewrt 6th eto Sles v A. Al-Dhhr Appe A Getlle, Vermele, Oeljhee e Absolute Wre N = {0,,,, } Ntuurlje etlle Z = {,-,-,-,0,,,, } Gehele etlle Q = { } Rtole etlle
Smevtt - Wsue I Clculus Erly Trsceetls Jmes Stewrt 6th eto Sles v A. Al-Dhhr Appe A Getlle, Vermele, Oeljhee e Absolute Wre N = {0,,,, } Ntuurlje etlle Z = {,-,-,-,0,,,, } Gehele etlle Q = { } Rtole etlle
Zelf statistiek oefenen
 Photo by rawpxel o Usplash Oefeg baat kust u zelf aa de slag. De vrage staa door elkaar. Er zj multplechocevrage e ope vrage. I de toekomst kome er vrage bj. Het s ee greep va de mogeljke vrage de je kut
Photo by rawpxel o Usplash Oefeg baat kust u zelf aa de slag. De vrage staa door elkaar. Er zj multplechocevrage e ope vrage. I de toekomst kome er vrage bj. Het s ee greep va de mogeljke vrage de je kut
Snel, sneller, snelst: statistiek en 1500 m schaatsen
 Oot moet het toch echt et meer seller kue, zou je zegge. Door techsche verbeterge (overdekte bae, euwe schaatspakke, klapschaatse, ezovoort) worde steeds sellere tjde gerealseerd. Maar zelfs als deze vloede
Oot moet het toch echt et meer seller kue, zou je zegge. Door techsche verbeterge (overdekte bae, euwe schaatspakke, klapschaatse, ezovoort) worde steeds sellere tjde gerealseerd. Maar zelfs als deze vloede
Deel D. Breuken en algebra n
 Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
1 Vlaamse Wiskunde Olympiade 1985-1986: Tweede Ronde.
 1 Vlmse Wiskunde Olymide 1985-1986: Tweede Ronde De tweede ronde bestt uit 30 meerkeuzevrgen Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 unten Per goed ntwoord krijgt hij of zij 4
1 Vlmse Wiskunde Olymide 1985-1986: Tweede Ronde De tweede ronde bestt uit 30 meerkeuzevrgen Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 unten Per goed ntwoord krijgt hij of zij 4
nfraphil w wl il.nl www.infraphil.nl nf r P h l w, i. P t" w l. nf rs w n i ww w.infraphil.nl ww Genezing door warmte Schoonheidsbehandeling
 W W W. l fral.l. l.l.fral.l a l.l.fra.fral.l P r a p h l.l.fra, fral.l. l.l.fral.l, a l.l.fra l,fra.l a p h l.l.ïfra, fral.l. l.!.fral.l a l...fra!.fra.l a p h l.l.fra fral.l. l.l.fral.l. ï a l.l.fra l.fral.l
W W W. l fral.l. l.l.fral.l a l.l.fra.fral.l P r a p h l.l.fra, fral.l. l.l.fral.l, a l.l.fra l,fra.l a p h l.l.ïfra, fral.l. l.!.fral.l a l...fra!.fra.l a p h l.l.fra fral.l. l.l.fral.l. ï a l.l.fra l.fral.l
1 Vlaamse Wiskunde Olympiade 1994 1995 : Eerste Ronde.
 Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Hoofdstuk 5: Vergelijkingen van de
 Werkoek Alger (ursus voor 5u wiskunde) Hoofdstuk 5 : Vergelijkingen vn de e grd met één onekende Nm:. Hoofdstuk 5: Vergelijkingen vn de - 45 - e grd met één onekende. Instp (oek pg 7). Vn een rehthoek
Werkoek Alger (ursus voor 5u wiskunde) Hoofdstuk 5 : Vergelijkingen vn de e grd met één onekende Nm:. Hoofdstuk 5: Vergelijkingen vn de - 45 - e grd met één onekende. Instp (oek pg 7). Vn een rehthoek
4. Wortels van decimale getallen mag je met het RT uitrekenen. Maar voor opgaven met gehele numerieke factoren wordt een exact resultaat
 Modelvrgstukken Algebr vn wortelvormen Tenzij expliciet nders vermeld stellen lle letters positieve getllen voor Vereenvoudigen vn enkelvoudige wortels ; Dit is gewoon de bsisregel ) ) 8 ) ; ) Een 8-ste
Modelvrgstukken Algebr vn wortelvormen Tenzij expliciet nders vermeld stellen lle letters positieve getllen voor Vereenvoudigen vn enkelvoudige wortels ; Dit is gewoon de bsisregel ) ) 8 ) ; ) Een 8-ste
REGRESSIE met de TI-83
 REGRESSIE met de TI-83 Beke Va Deyck Studete K.U. Leuve HOOFDSTUK : INLEIDENDE BEGRIPPEN: CENTRUMMATEN EN SPREIDINGSMATEN. A. Iledg. Statstek s het verzamele e bestudere va umereke gegeves om vervolges
REGRESSIE met de TI-83 Beke Va Deyck Studete K.U. Leuve HOOFDSTUK : INLEIDENDE BEGRIPPEN: CENTRUMMATEN EN SPREIDINGSMATEN. A. Iledg. Statstek s het verzamele e bestudere va umereke gegeves om vervolges
In samenwerking met. ECU 92 - www.ecu92.nl
 I samewerkg met ECU 9 - www.ecu9.l Leo Strjbosch Makkeljk Lere! Statstek Compedum Studetesupport Studetesupport.l 6 Leo Strjbosch & Studetesupport Dowload grats op ISBN 87-768-46-8 Studetesupport Studetesupport.l
I samewerkg met ECU 9 - www.ecu9.l Leo Strjbosch Makkeljk Lere! Statstek Compedum Studetesupport Studetesupport.l 6 Leo Strjbosch & Studetesupport Dowload grats op ISBN 87-768-46-8 Studetesupport Studetesupport.l
Aandrijfelektronica \ Aandrijfautomatisering \ Systeemintegratie \ Service. Handboek. Prefabriceren van kabels Kabels voor synchrone servomotoren
 Aadrjelektroca \ Aadrjautomatserg \ Systeemtegrate \ Servce Hadboek reabrcere va kabels Kabels voor sychroe servomotore Utgave 12/2011 19301685 / NL SEW-EURODRIVE Drvg the world Ihoudsopgave 1 Crmpgereedschap...
Aadrjelektroca \ Aadrjautomatserg \ Systeemtegrate \ Servce Hadboek reabrcere va kabels Kabels voor sychroe servomotore Utgave 12/2011 19301685 / NL SEW-EURODRIVE Drvg the world Ihoudsopgave 1 Crmpgereedschap...
Continuïteit en Nulpunten
 Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Het differentiequotiënt van een functie in een interval geeft de gemiddelde helling weer van die functie in dat interval. Symbolisch wordt dit:
 Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
Het kwadraat van een tweeterm a+b. (a+b)²
 Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Hoofdstuk 11. Kwadraatresten Inleiding
 Hoofdstuk 11 Kwdrtresten 11.1 Inleiding In Hoofdstuk 6 hebben we geleerd hoe lineire congruentievergelijkingen vn de vorm x b mod M moeten worden ogelost. De volgende st is uiterrd het olossen vn kwdrtische
Hoofdstuk 11 Kwdrtresten 11.1 Inleiding In Hoofdstuk 6 hebben we geleerd hoe lineire congruentievergelijkingen vn de vorm x b mod M moeten worden ogelost. De volgende st is uiterrd het olossen vn kwdrtische
Het reëel getal b is een derdewortel van het reëel getal a c. Een getal en zijn derdewortel hebben hetzelfde toestandsteken.
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
Formeel Denken 2012 Uitwerkingen Tentamen
 1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
(wi s ) Uitdagend teken-, kleur- en doeboek. Anna Weltman
 A Wetm R U L K D N U K ) (w KLUR(w )KUND o e, y mm et e O td ek ee we e d v p t td g e de te ke g e. e ve e d e vo m e u j ke d e ho ek e e ge mo o, e k c e g d e o M et t d t bo ek je e b jo de e k eu
A Wetm R U L K D N U K ) (w KLUR(w )KUND o e, y mm et e O td ek ee we e d v p t td g e de te ke g e. e ve e d e vo m e u j ke d e ho ek e e ge mo o, e k c e g d e o M et t d t bo ek je e b jo de e k eu
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Verzamelingen. De natuurlijke getallen. = 0 verzameling van de strikt natuurlijke getallen. De gehele getallen
 Verzmelingen De ntuurlijke getllen = {,1,2,3,4,... } = verzmeling vn de strikt ntuurlijke getllen De gehele getllen = {..., 3, 2, 1,,1,2,3,... } = verzmeling vn de strikt gehele getllen + = verzmeling
Verzmelingen De ntuurlijke getllen = {,1,2,3,4,... } = verzmeling vn de strikt ntuurlijke getllen De gehele getllen = {..., 3, 2, 1,,1,2,3,... } = verzmeling vn de strikt gehele getllen + = verzmeling
H 0 5 R R -F 5 x 1, 5 m m
 I b u w k k p l t H I C 6 4 4 0 3 X G l v r s t d z h d l d g t l z! B s t k l t, D k u v r h t k p v -p r d Bu c kt W h p d t u d b s t r s u l t t v r k r p r d u c t, d t v r v r d g d s m t d l l r
I b u w k k p l t H I C 6 4 4 0 3 X G l v r s t d z h d l d g t l z! B s t k l t, D k u v r h t k p v -p r d Bu c kt W h p d t u d b s t r s u l t t v r k r p r d u c t, d t v r v r d g d s m t d l l r
Merkwaardige producten en ontbinden in factoren
 6 Merkwrdige producten en ontinden in fctoren Dit kun je l 1 een mcht tot een mcht verheffen eentermen vermenigvuldigen 3 eentermen delen 4 veeltermen vermenigvuldigen 5 een veelterm delen door een eenterm
6 Merkwrdige producten en ontinden in fctoren Dit kun je l 1 een mcht tot een mcht verheffen eentermen vermenigvuldigen 3 eentermen delen 4 veeltermen vermenigvuldigen 5 een veelterm delen door een eenterm
is het koppel dat overeenkomt met het eindpunt van λ.op ax by = a a b x y = a b = x y a b ax by bx + ay = a b
 1 Tweedimensionle Euclidische ruimte 11 Optelling, verschil en sclire vermenigvuldiging = ( b, ) b, is de verzmeling vn lle koppels reële getllen { } Zols we ons de reële getllen kunnen voorstellen ls
1 Tweedimensionle Euclidische ruimte 11 Optelling, verschil en sclire vermenigvuldiging = ( b, ) b, is de verzmeling vn lle koppels reële getllen { } Zols we ons de reële getllen kunnen voorstellen ls
Exact periode 2.2. Gemiddelde en standaarddeviatie Betrouwbaarheidsinterval Logaritme ph lettersommen balansmethode
 Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
FOTO-ELEKTRISCH EFFECT
 . ACHTERGRONDINFORMATIE FOTO-ELEKTRISCH EFFECT I 887 expermeteerde de Dutse fyscus Herch Hertz met de vormg e voortplatg va elektromagetsche golve. Terwjl hj oderzocht hoe voke otstaa tusse elektrsch gelade
. ACHTERGRONDINFORMATIE FOTO-ELEKTRISCH EFFECT I 887 expermeteerde de Dutse fyscus Herch Hertz met de vormg e voortplatg va elektromagetsche golve. Terwjl hj oderzocht hoe voke otstaa tusse elektrsch gelade
Getal & Ruimte. Uitwerkingen. vwo. complexe getallen. J. v.d. Meer H. v. Tilburg
 J vd Meer H v lurg Getl & Rumte vwo complee getllen Utwerkngen Hoofdstuk Complee getllen Neuwe getllen ( ( ( ( c ( ( ( d ( 7 7 e f ( ( ( ( ( ( ( ( ( ( ( c ( ( ( 9 d ( ln(,9, ( ln,77, c e d, 7 ( en, en
J vd Meer H v lurg Getl & Rumte vwo complee getllen Utwerkngen Hoofdstuk Complee getllen Neuwe getllen ( ( ( ( c ( ( ( d ( 7 7 e f ( ( ( ( ( ( ( ( ( ( ( c ( ( ( 9 d ( ln(,9, ( ln,77, c e d, 7 ( en, en
Hoofdstuk 2 DE STELLING VAN PYTHAGORAS
 Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Niks gedaan en toch gevangen... Kan dat zomaar?
 Niks ged e toch gevge... K dt zomr? Lesbrief voor de leerkrcht Hdleidig voor de leerkrcht Leerligebld Ee kid v cht stop je iet i ee cel. Niet i Nederld. Dt is belchelijk. Voor groep 7 e 8 v het bsisoderwijs
Niks ged e toch gevge... K dt zomr? Lesbrief voor de leerkrcht Hdleidig voor de leerkrcht Leerligebld Ee kid v cht stop je iet i ee cel. Niet i Nederld. Dt is belchelijk. Voor groep 7 e 8 v het bsisoderwijs
Boek 2, hoofdstuk 7, allerlei formules..
 Boek, hoofdstuk 7, llerlei formules.. 5.1 Evenredig en omgekeerd evenredig. 1. y wordt in beide gevllen 4 keer zo klein, je noemt dt omgekeerd evenredig. b. bv Er zijn schoonmkers met een vst uurloon.
Boek, hoofdstuk 7, llerlei formules.. 5.1 Evenredig en omgekeerd evenredig. 1. y wordt in beide gevllen 4 keer zo klein, je noemt dt omgekeerd evenredig. b. bv Er zijn schoonmkers met een vst uurloon.
1) Beschrijvende statistiek - herhaling
 Statstek ) Beschrjvede statstek - herhalg Wat s statstek? Beschrjvede statstek De beschrjvede statstek verzamelt gegeves e beschrjft de toestad door de gegeves te ordee tabelle, te verwerke, same te vatte
Statstek ) Beschrjvede statstek - herhalg Wat s statstek? Beschrjvede statstek De beschrjvede statstek verzamelt gegeves e beschrjft de toestad door de gegeves te ordee tabelle, te verwerke, same te vatte
Rekenen in Ê. Module De optelling. Definitie
 Module 1 Rekenen in Ê 1.1 De optelling Definitie Het resultt vn de optelling vn reële getllen en b noemen we de som vn en b en noteren we met +b. De getllen en b zelf noemen we de termen vn de som. Voorbeelden
Module 1 Rekenen in Ê 1.1 De optelling Definitie Het resultt vn de optelling vn reële getllen en b noemen we de som vn en b en noteren we met +b. De getllen en b zelf noemen we de termen vn de som. Voorbeelden
Matrixrekening - Samenvatting
 I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
Ontwerp van filters. Johan Baeten KHLim. Introductie filters
 -RKD %DHWH./LP Otwerp a flter Jha Baete KHLm Itrducte flter I deze curu bepreke we he we ee elektrch crcut kue pbuwe (ythetere) met ee geraagde traferfucte Dt het mgekeerde a ee aalye: Ee aalye ertrekt
-RKD %DHWH./LP Otwerp a flter Jha Baete KHLm Itrducte flter I deze curu bepreke we he we ee elektrch crcut kue pbuwe (ythetere) met ee geraagde traferfucte Dt het mgekeerde a ee aalye: Ee aalye ertrekt
De vele werelden van de statistiek
 De vele werelde va de statstek Notateafsprake De vele werelde va de statstek Prof. dr. Herma Callaert, Cetrum voor Statstek, Uverstet Hasselt. De wereld va het deale model (= de populate) om te beschrjve
De vele werelde va de statstek Notateafsprake De vele werelde va de statstek Prof. dr. Herma Callaert, Cetrum voor Statstek, Uverstet Hasselt. De wereld va het deale model (= de populate) om te beschrjve
Voorbereidende opgaven Examencursus
 Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
α ψ n Eigenwaardevergelijkingen ψ n (i = 1, g n ) Eigenvectoren en eigenwaarden van een operator eigenket eigenvector eigenwaarde is ook eigenvector
 Egewaardevergeljkge Egevectore e egewaarde va ee operator A = λ egeket egevector egewaarde α s ook egevector ( =, g ) egewaarde λ s g -voudg otaard, als er g oafhakeljke kets correspodere met dezelfde
Egewaardevergeljkge Egevectore e egewaarde va ee operator A = λ egeket egevector egewaarde α s ook egevector ( =, g ) egewaarde λ s g -voudg otaard, als er g oafhakeljke kets correspodere met dezelfde
Duurzaam (ver)bouwen. Noordoost-Brabant 2013-2016
 t e v o C l io g Re Duurzm (ver)bouwe Noordoost-Brbt 2013-2016 e w u o b e m S d i e h m duurz Duurzm Bouwe Grodstoffe worde schrser, het eergievrgstuk ijpeder e os klimt verdert. Duurzm bouwe e verbouwe
t e v o C l io g Re Duurzm (ver)bouwe Noordoost-Brbt 2013-2016 e w u o b e m S d i e h m duurz Duurzm Bouwe Grodstoffe worde schrser, het eergievrgstuk ijpeder e os klimt verdert. Duurzm bouwe e verbouwe
In dit hoofdstuk willen aan elke vierkante matrix een getal associëren dat (onder andere) aangeeft of die matrix singulier is of niet. d b. c a.
 Deterinnten Deterinnt In dit hoofdstuk willen n elke vierknte trix een getl ssociëren dt (onder ndere) ngeeft of die trix singulier is of niet ) Deterinnt vn een x-trix Zij gegeven twee trices M c d en
Deterinnten Deterinnt In dit hoofdstuk willen n elke vierknte trix een getl ssociëren dt (onder ndere) ngeeft of die trix singulier is of niet ) Deterinnt vn een x-trix Zij gegeven twee trices M c d en
n e 52 tip voor meer s gel uk op je werk n plek X
 e k meer op j e werk plek gelu 52 p s voor X 52 TIPS voor meer GEluk op je werkplek v HEre we go! Als je googled op Geluk e Kaoor, wa krjg je da? Ses va kaoorarkeleleveracers e copyshops. Hoog jd dus voor
e k meer op j e werk plek gelu 52 p s voor X 52 TIPS voor meer GEluk op je werkplek v HEre we go! Als je googled op Geluk e Kaoor, wa krjg je da? Ses va kaoorarkeleleveracers e copyshops. Hoog jd dus voor
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Bij een invalshoek i =(15.0 ± 0.5) meet hij r =(9.5 ± 0.5). 100%-intervallen. Welke conclusie kan de onderzoeker trekken?
 INLEIDING FYSISCH-EPERIMENTELE VAARDIGHEDEN (3A560) --003, 9.00-.00 UUR Dt tentamen bestaat ut 3 opgaven. Geef noot alleen maar het antwoord op een vraag, maar laat altjd zen hoe je tot dat antwoord gekomen
INLEIDING FYSISCH-EPERIMENTELE VAARDIGHEDEN (3A560) --003, 9.00-.00 UUR Dt tentamen bestaat ut 3 opgaven. Geef noot alleen maar het antwoord op een vraag, maar laat altjd zen hoe je tot dat antwoord gekomen
Hoofdstuk 2: Bewerkingen in R
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Een feestmaal. Naam: -Ken jij nog een ander speciaal feest? Typ of schrijf het hier. a
 Werkbld Een feestml Nm: Ieder lnd en iedere cultuur kent specile dgen. Dn gn fmilies bij elkr op bezoek. Op die specile dgen is er meestl extr ndcht voor het eten. Hier zie je wt voorbeelden vn feesten
Werkbld Een feestml Nm: Ieder lnd en iedere cultuur kent specile dgen. Dn gn fmilies bij elkr op bezoek. Op die specile dgen is er meestl extr ndcht voor het eten. Hier zie je wt voorbeelden vn feesten
Waardeoverdracht. Uw opgebouwde pensioen meenemen naar uw nieuwe pensioenuitvoerder
 Waardeoverdracht Uw opgebouwde pensoen meenemen naar uw neuwe pensoenutvoerder In deze brochure 3 4 5 6 Gefelcteerd! Een neuwe baan Wel of net kezen voor waardeoverdracht? Vergeljk de regelngen Hoe waardevast
Waardeoverdracht Uw opgebouwde pensoen meenemen naar uw neuwe pensoenutvoerder In deze brochure 3 4 5 6 Gefelcteerd! Een neuwe baan Wel of net kezen voor waardeoverdracht? Vergeljk de regelngen Hoe waardevast
Voorwaarden: Bij het tentamen mag gebruik gemaakt worden van rekenmachine, schrijfgerij en Vergeet-mij-nietjes.
 cuteit Costruerede Tecisce Wetescppe Civiee Tecie Tetme ecic III gemee Dtum tetme : -ug-7 vcode : 66 Tijd : ½ uur (:-7:) Beoordeig: t ede pute (mxim ) / Opgve orde(%) Opgve Bederigsmetode (%) Opgve Stiiteit
cuteit Costruerede Tecisce Wetescppe Civiee Tecie Tetme ecic III gemee Dtum tetme : -ug-7 vcode : 66 Tijd : ½ uur (:-7:) Beoordeig: t ede pute (mxim ) / Opgve orde(%) Opgve Bederigsmetode (%) Opgve Stiiteit
2 Formules herschrijven
 Formules herschrijven Verkennen www.mth4ll.nl MAThADORE-bsic HAVO/VWO 4/5/6 VWO wi-b Werken met formules Formules herschrijven Inleiding Verkennen Probeer de vrgen bij Verkennen zo goed mogelijk te bentwoorden.
Formules herschrijven Verkennen www.mth4ll.nl MAThADORE-bsic HAVO/VWO 4/5/6 VWO wi-b Werken met formules Formules herschrijven Inleiding Verkennen Probeer de vrgen bij Verkennen zo goed mogelijk te bentwoorden.
2) Kegelsneden (in basisvorm)
 ) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
F G H I J. 5480
 () Nm : Kls: Dtum: A. 06 Uit ln + ln( ) = ln volgt dt gelijk is n ) ) ) ) ) g.v.d.v. B. 77 + b ) b ) (+ is gelijk n b ) ) b) ).b b F. 7 kn ook geschreven worden ls ) e ) e ) e ( ) ln e ) ) e G. 7 9 Als
() Nm : Kls: Dtum: A. 06 Uit ln + ln( ) = ln volgt dt gelijk is n ) ) ) ) ) g.v.d.v. B. 77 + b ) b ) (+ is gelijk n b ) ) b) ).b b F. 7 kn ook geschreven worden ls ) e ) e ) e ( ) ln e ) ) e G. 7 9 Als
Logica voor Informatica
 Logca voor Informatca 11 Bewjzen n de predkatenlogca Wouter Swerstra Unversty of Utrecht 1 Natuurljke deducte Alle afledngsregels voor propostelogca gelden ook voor predkaten logca Neuwe afledngsregels
Logca voor Informatca 11 Bewjzen n de predkatenlogca Wouter Swerstra Unversty of Utrecht 1 Natuurljke deducte Alle afledngsregels voor propostelogca gelden ook voor predkaten logca Neuwe afledngsregels
opgaven formele structuren procesalgebra
 opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
Algebra. Dr. Caroline Danneels
 Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
Opgave 5 Onderzoek aan β -straling
 Eidexame vwo atuurkude 214-I - havovwo.l Opgave 5 Oderzoek aa β -stralig Zoals beked bestaat β -stralig uit elektroe. Om ee oderzoek aa β -stralig te doe heeft Harald ee radioactieve bro met P-32 late
Eidexame vwo atuurkude 214-I - havovwo.l Opgave 5 Oderzoek aa β -stralig Zoals beked bestaat β -stralig uit elektroe. Om ee oderzoek aa β -stralig te doe heeft Harald ee radioactieve bro met P-32 late
Studiekeuzecheck wiskunde deeltijd Basisvaardigheden Algebra Hoofdstuk 1 t/m 4
 Studiekeuzecheck wiskunde deeltijd 08 Bsisvrdigheden Algebr Hoofdstuk t/m Inhoudsopgve Hoofdstuk Rekenen met letters..... Formules..... Mchten.... Worteltrekken... 6. Delen door nul kn niet... 9 Hoofdstuk
Studiekeuzecheck wiskunde deeltijd 08 Bsisvrdigheden Algebr Hoofdstuk t/m Inhoudsopgve Hoofdstuk Rekenen met letters..... Formules..... Mchten.... Worteltrekken... 6. Delen door nul kn niet... 9 Hoofdstuk
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Examen VWO. wiskunde B (pilot) tijdvak 1 woensdag 16 mei 13.30-16.30 uur
 Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
L i mb u r g s e L a n d m a r k s
 L i mb u r g s e L a n d m a r k s P r o g r a m m a I n v e s t e r e n i n S t ed e n e n D o r p e n, l i j n 2 ; D e L i m b u r g s e I d e n t i t e i t v e r s i e 1. 0 D o c u m e n t h i s t o
L i mb u r g s e L a n d m a r k s P r o g r a m m a I n v e s t e r e n i n S t ed e n e n D o r p e n, l i j n 2 ; D e L i m b u r g s e I d e n t i t e i t v e r s i e 1. 0 D o c u m e n t h i s t o
