Bewijzen voor de AM-GM-ongelijkheid
|
|
|
- Melissa Verbeek
- 4 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Bewijze voor de AM-GM-ogelijkheid Prime Ee beroemde olympiadeogelijkheid is de ogelijkheid tusse het rekekudig gemiddelde (AM, arithmetic mea) e het meetkudig gemiddelde (GM, geometric mea). Voor ee gegeve aatal getalle (zegge ) defiieert me het rekekudig gemiddelde als de som va deze getalle, gedeeld door. Het mider bekede meetkudig gemiddelde is de de -machtswortel uit het product va deze getalle. AM(x 1, x,..., x ) = 1 k x i e GM(x 1, x,..., x ) = k De ogelijkheid die we wille bewijze, stelt dat voor eeder welke collectie getallle x i steeds geldt dat AM GM; bovedie treedt gelijkheid op als e slechts als alle x i s gelijk zij. Ihoudsopgave 1 Voor twee getalle 1.1 Herleide aar ee kwadraat Stellig va Pythagoras Meetkudig Isoperimetrisch probleem Hyperbole Voor getalle 5.1 Expoetieel Iductie e fuctieoderzoek Ogelijkheid va Jese Extremumstellig va Weierstrass Achterwaartse iductie Rechtstreekse iductie Reeksotwikkelige Orde-ogelijkheid Itegrale Terme swappe Lagragemultiplicator Eigewaarde Thermodyamica x i Tezij aders vermeld, staat i deze tekst getalle voor positieve reële getalle. We zulle ook vaak de argumete va AM e GM, die strikt geome fucties zij, achterwege late voor de bekoptheid, als duidelijk is va welke getalle deze gemiddelde beschouwd worde. 1
2 1 Voor twee getalle 1.1 Herleide aar ee kwadraat Herschrijf AM(x, y) GM(x, y) aar ee kwadraat: AM(x, y) GM(x, y) = x + y Omdat ee reëel kwadraat steeds positief is, blijkt x + y xy = 1 xy. ( x y ) 0 Gelijkheid treedt op als e slechts als ( x y ) = 0, d.w.z. als e slechts als x = y. 1. Stellig va Pythagoras De stellig va Pythagoras garadeert dat voor positieve x e y, met x y, de volgede waarde de zijdelegtes va ee rechthoekige driehoek vorme: x + y y x xy Uit de driehoeksogelijkheid volgt dat de legte va de hypoteusa (hier AM) groter is da de legtes va de rechthoekszijde (waarva GM er ee va is). Gelijkheid treedt pas op bij ee gedegeereerde driehoek, als de overige zijde legte 0 heeft, waarbij dus x = y. Alteratieve voorstellig: x + y xy y x y x 1.3 Meetkudig Veroderstel zoder verlies va algemeeheid dat x y.
3 D C y x E G y x F A B ABCD is ee vierkat met zijdelegte y, e ABFE ee rechthoek met zijde x e y. Da is duidelijk: xy = opp(abfe) = opp(age) + opp(abfg) opp(age) + opp(abc) = x + y Omdat keelijk xy 1 (x + y ), is ook xy 1 (x + y) (vervag x e y door hu vierkatswortels). Alweer treedt gelijkheid op als e slechts als y x = 0, d.w.z. als e slechts als x = y. 1.4 Isoperimetrisch probleem We begie met ee algemeer geometrisch lemma: we zulle bewijze dat va alle rechthoeke met ee vaste omtrek, het vierkat diegee is met de maximale oppervlakte. Beschouw dus ee rechthoek e ee vierkat met dezelfde omtrek, e leg deze als volgt over elkaar: Omdat de boveste grijze rechthoek (het deel va het vierkat dat uitsteekt) eve groot is als de grijze rechthoek rechts e het gestippelde vierkat same, is duidelijk dat de oppervlakte va het vierkat groter is da dat va de rechthoek (amelijk de oppervlakte va het gestippelde vierkat). De rechthoek met de grootste oppervlakte voor ee gegeve omtrek is dus iderdaad ee vierkat. Beschouw u ee rechthoek met zijde va legte x e y. Dies omtrek is (x + y), oppervlakte xy. Het vierkat met dezelfde omtrek heeft dus zijdelegte 1 (x + y), e oppervlakte 1 4 (x + y). Uit de observatie i de vorige paragraaf besluite we: (x + y) 4 Gelijkheid als e slechts als de iitiële rechthoek i feite al ee vierkat was, dus als e slechts als x = y. AM-GM volgt u gemakkelijk. Opmerkig: ee veralgemeig aar dimesies geeft ee bewijsstrategie voor de algemee AM-GMogelijkheid. De -dimesioale hyperkubus heeft amelijk het kleiste volume va alle hyperbalke met dezelfde totale ribbelegte. xy 3
4 1.5 Hyperbole We beschouwe de familie hyperbole met vergelijkig xy = c (parameter c). Als ee rechte x+y = m zo hyperbool sijdt, gebeurt dat i ofwel twee pute ofwel i éé raakput. Veroderstel dat de rechte x+y = m raakt aa de hyperbool xy = c. Door symmetrie rod de rechte x = y is het raakput makkelijk te bepale: (m, m). I dit geval dus blijkt dat c = m, e hebbe we: ( x + y xy = Elk adere put op de rechte met positieve coördiate ligt op precies éé va de hyperbole xy = c, waarbij da c < m. Dit beteket i dat geval: ( x + y xy < AM-GM is dus beweze voor alle pute op de rechte x + y = m i het eerste kwadrat. Omdat m willekeurig was, geldt AM-GM voor alle positieve x e y (met gelijkheid precies als x = y). ) ) 4
5 Voor getalle.1 Expoetieel Defiieer f(x) = exp(x 1) x. Dies eerste afgeleide is f (x) = exp(x 1) 1, e de tweede afgeleide f (x) = exp(x 1). Omdat f(1) = 0, f (1) = 0 e f (x) > 0 voor alle x-waarde, is f ee strikt covexe fuctie met absoluut miimum op x = 1. Dus x exp(x 1) voor alle reële x-waarde, met gelijkheid allee voor x = 1. Beschouw u ee lijst va iet-egatieve getalle x 1,..., x. Idie alle idetiek ul zij, gaat AM-GM op (met gelijkheid). I het adere geval is het rekekudig gemiddelde α strikt groter da ul, e kue we bovestaade ogelijkheid ee aatal maal toepasse: x 1 α x α... x ( α exp x1 exp ( x1 + x x = exp α α 1 ) = exp( ) = 1 ( x ) α 1... exp ) ( x α 1 ) Zo te zie is x 1 x... x α 1, ofwel GM = x 1 x... x α = AM.. Iductie e fuctieoderzoek Veroderstel dat AM-GM geldt voor 1 getalle, e beschouw ee -tal (a 1,..., a ). We moge veroderstelle dat alle a i > 0 (aders is de stellig triviaal). We defiiëre de volgede fuctie: f(x) = AM(a 1,..., a 1, x) GM(a 1,..., a 1, x) = a a 1 + x We moete da bewijze dat f(x) 0 voor alle strikt positieve x. We berekee de afgeleide va f: f (x) = 1 1 (a 1... a 1 ) 1 x 1 Om de extrema va f te zoeke, bepale we waeer de afgeleide ul is: f (x 0 ) = 0 (a 1... a 1 ) 1 x0 1 = 1 x 0 = (a 1... a 1 ) 1 1 = GM(a1,..., a 1 ) (a 1... a 1 x) 1 Omdat f (x) > 0 als x > 0, bereikt f ee (globaal) miimum i x 0. De waarde va dit miimum is f(x 0 ) = a a 1 + (a 1... a 1 ) 1 1 = a a 1 (a 1... a 1 ) 1 (a1... a 1 ) + 1 (a 1... a 1 ) 1 1 (a1... a 1 ) 1 1 = a a 1 1 (a 1... a 1 ) 1 1 = 1 ( ) a a 1 (a 1... a 1 ) ( 1) 5
6 weges de iductiehypothese. We moete u ekel og agaa waeer gelijkheid optreedt. Opieuw weges de iductiehypothese zal f(x 0 ) = 0 als e slechts als a 1 =... = a 1, e i dat geval is ook x 0 = a 1 =.... We krijge dus iderdaad gelijkheid precies als alle a i gelijk zij..3 Ogelijkheid va Jese Voor ee covexe fuctie ϕ, waarde x i i haar domei e gewichte a i, stelt Jeses ogelijkheid: ( ) ai x i ai ϕ(x ϕ i ) ai ai Omgekeerd, voor ee cocave fuctie ϕ geldt de omgekeerde ogelijkheid: ( ) ai x i ai ϕ(x ϕ i ) ai ai De ogelijkheid va Jese wordt besproke i de cursus Wiskudige Statistiek i de tweede bachelor over algemee maatruimte (hierbove staat het discrete geval). De logaritme is ee cocave fuctie, dus same met de keuze a i = 1 krijge we: ( ) xi l(xi ) l Vervolges late we op beide lede de expoetiële iwerke, die stijged is e de ogelijkheid bewaart. ( ( )) ( ) xi l(xi ) exp l exp Na wat uitwerke volgt: AM = xi exp( l x i ) = exp(l xi ) = xi = GM.4 Extremumstellig va Weierstrass Kies M willekeurig e defiieer V als de verzamelig va alle -talle (x 1,..., x ) met de eigeschap dat AM(x 1,..., x ) = M. We moete bewijze dat voor elk -tal i V geldt dat GM(x 1,..., x ) M, met gelijkheid als e slechts als alle x i gelijk. V is ee compacte verzamelig (wat geslote e begresd) e GM(x 1,..., x ) is ee cotiue fuctie. Uit de extremumstellig va Weierstrass volgt da dat GM(x 1,..., x ) op V ee maximum bereikt. Beschouw u ees ee iet-costat -tal (a 1, a,..., a ) i V, e veroderstel zoder verlies va algemeeheid dat a 1 a. Da zit ( a 1+a, a 1+a,..., a ) ook i V. Uit AM-GM voor twee getalle volgt u dat a 1 a < ( a 1+a ), waaruit GM(a 1, a,..., a ) < GM( a 1+a, a 1+a,..., a ). Dus GM(x 1,..., x ) bereikt haar maximum iet i (a 1, a,..., a ). Da blijft er og maar éé -tal i V over waari GM(x 1,..., x ) haar maximum ka bereike, amelijk het costate -tal (M, M,..., M). Duidelijk is GM(M,..., M) = M, e hiermee is het gestelde beweze. 6
7 .5 Achterwaartse iductie Dit bewijs maakt gebruik va het voorwaarts-achterwaartse iductiepricipe va Cauchy, ee variat op het gekede iductiepricipe. Ee gewoo bewijs door iductie gaat als volgt: 1. Bewijs P (1).. Bewijs dat P () P ( + 1). 3. Cocludeer P () voor alle N. Ee bewijs door voorwaarts-achterwaartse iductie daaretege gaat als volgt: 1. Bewijs P (1).. Bewijs dat P () P (). 3. Bewijs dat P () P ( 1). 4. Cocludeer P () voor alle N. Iderdaad, uit stap volgt dat de bewerig geldt voor 1,, 4,..., k,... e dus voor willekeurig grote getalle. Uit stap 3 volgt da dat als de bewerig waar is voor ee zekere k, hij da ook waar is voor alle k. We bewijze u AM-GM met iductie op, het aatal getalle. 1. Voor = 1 is de bewerig triviaal.. Veroderstel dat AM-GM geldt voor alle -talle. Beschouw da ee -tal (a 1,..., a ). Da is GM(a 1,..., a ) = GM(a 1,..., a )GM(a +1,..., a ) AM(a 1,..., a )AM(a +1,..., a ) 1 AM(a 1,..., a ) + 1 AM(a +1,..., a ) = AM(a 1,..., a ), waarbij we achtereevolges de iductiehypothese e het geval = hebbe toegepast. 3. Veroderstel dat AM-GM geldt voor alle -talle. Beschouw da ee ( 1)-tal (a 1,..., a 1 ). Noteer A = AM(a 1,..., a 1 ). We passe de iductiehypothese toe op het -tal (a 1,..., a 1, A) e verkrijge dat 1 (a a 1 +A) a 1... a 1 A. Merk op dat we het likerlid kue vereevoudige tot 1 (( 1) A + A) = A. We vide dus dat A a 1... a 1 A, oftewel: AM(a 1,..., a 1 ) = A 1 a 1... a 1 = GM(a 1,..., a 1 ) 4. We moge u cocludere dat AM-GM geldt voor alle N..6 Rechtstreekse iductie We bewijze eerst ee sterkere vorm va de AM-GM-ogelijkheid voor het geval =, voor 0 < a b. a x b (x a)(x b) 0 a + b x + ab x De middeste vergelijkig geeft aa dat gelijkheid opgaat als e slechts als x = a of x = b. Omdat a ab b voor alle positieve a e b, geeft de keuze x = ab dat a + b ab, wat AM-GM voor twee getalle bewijst. 7
8 Het algemee geval gaa we met iductie aatoe. Als x 1 = x =... = x, is het te bewijze duidelijk voldaa. Veroderstel dus het tegedeel e herschik de x i s desoods zodat x 1 e x respectievelijk de kleiste e grootste va de x i s worde. Noteer het meetkudig gemiddelde va de x i s als g, zodat x 1 x... x = g. Er volgt dat x 1 < g < x (strikte ogelijkhede!). Uit de vorige paragraaf hale we dat x 1 + x > g + 1 g (x 1 x ), dus: x 1 + x + x x > g + x 1 x g + x x We passe u de iductiehypothese toe op de 1 laatste terme i het rechterlid. Bemerk dat het product 1 g (x 1 x )x 3... x et gelijk is aa g 1, zodat het meetkudig gemiddelde va deze terme precies gelijk is aa g. De som va de terme is gelijk aa ( 1) maal hu rekekudig gemiddelde, dat volges de iductiehypothese mistes g is. We kue besluite dat de som va de terme groter is da ( 1)g. Dus: x 1 + x + x x > g + ( 1)g = g We vide het te bewijze resultaat. We hebbe eveees aagetood dat tezij alle x i s gelijk zij, de strikte gelijkheid geldt; gelijkheid treedt dus ekel op als alle x i s gelijk zij..7 Reeksotwikkelige We voere eerst ee ieuwe otatie i. Als alle coëfficiëte i de reeksotwikkelig va ee fuctie f groter of gelijk zij aa de correspoderede coëfficiëte i de otwikkelig va ee fuctie g, zulle we dit als volgt otere: f g Beschouw de reeksotwikkelige va exp(xy) e 1 k! (xy)k i machte va y. De eerste heeft algemee term 1 m! (xy)m, de tweede bevat slechts éé iet-triviale term (de fuctie zelf). Er geldt dus duidelijk (als fucties va y, met positieve parameter x): exp(xy) (xy)k k! Door producte va deze fucties te eme met verschillede x-waarde, volgt da gauw: exp ( y ) ( ) k y k x i x i (k!) Beschouwe we u i het bijzoder de coëfficiët bij y k, da krijge we dus: ( ) k ( 1 (k)! x i 1 ) k (k!) x i I de uitdrukkige tusse haakjes herkee we het rekekudig e meetkudig gemiddelde al: ( AM) k (k)! (GM ) k (k!) Herschrijve geeft: AM GM (k)! k (k!) k = 1 k (k)! (k!) 8
9 Het rechterlid blijkt ee stijgede fuctie va k met waarde tusse 0 e 1. Om het scherpste resultaat te verkrijge, beschouwe we de limietovergag k : AM GM 1 lim k (k)! k (k!) De formule va Stirlig (m! πm e m m m ) maakt de berekeig va de limiet eevoudiger. πk 1 lim k (k)! k (k!) = 1 lim k e k (k) k ( k ( k = lim πk e k k k ) k πk = exp 1 ) lim k k l H = 1 πk I de laatste stap werd de regel va de l Hôpital toegepast. We hebbe dus gevode: AM GM 1.8 Orde-ogelijkheid De orde-ogelijkheid stelt dat de som a i b i gemaximaliseerd wordt als de rije {a i } e {b i } beide afloped of beide oploped gesorteerd zij, e gemiimaliseerd als ze tegegesteld gesorteerd zij, e deze extrema zij gelijk als e slechts als alle terme gelijk zij. Om AM-GM te bewijze vauit deze ogelijkheid, defiiëre we de volgede waarde: g = x 1 x... x a k = 1 g k k x i b k = 1 a k Omdat de rije {a k } e {b k } duidelijk tegegesteld gesorteerd zij, impliceert de orde-ogelijkheid: a k b k a 1 b + a b 1 + a 3 b a b 1 k=1 Me reket eevoudig a dat de term a 1 b gelijk is aa x 1 g, e ook elke adere term a k b k 1 aa x k Uit de defiitie va b k volgt ook dat a k b k steeds gelijk is aa éé, zodat het likerlid i feite ee som va eetjes is. Dus: x 1 g + x g + x 3 g x g E dit valt direct te herschrijve tot het gevraagde. g. GM = x 1 x... x x 1 + x x = AM 9
10 .9 Itegrale Beschouw ee -tupel x, i iet-dalede volgorde gesorteerd. We zulle de volgede som va itegrale uitrekee; merk alvast op dat elke itegraal i deze som positief is, zowel als x i GM als x i GM: x i GM ( 1 GM 1 ) dt t Uit wat elemetaire calculus volgt dat deze som gelijk is aa: ( ) t x i GM l t GM Greze ivulle: De som uitrekee levert op: ( xi ) GM l x i 1 + l GM x 1 + x x GM We zie het rekekudig gemiddelde al opduike. l(x 1 x... x ) + l(gm ) AM GM l(gm ) + l(gm ) De som va itegrale, die positief was, blijkt dus iets meer da de volgede uitdrukkig: ( ) AM GM 1 Omdat positief is, moet de tweede factor dat ook zij, e dat is et de AM-GM-ogelijkheid. We zie dat gelijkheid ekel optreedt als de waarde va alle itegrale i het begi gelijk ware aa ul, dus als x i = GM voor alle idices i, dus precies als alle compoete va x gelijk zij..10 Terme swappe Eerst toe we ee lemma aa. Als ā e b iet-dalede -tupels zij met a i b i voor alle idices i, da wordt de uitdrukkig ( a i ) ( b i ) iet kleier bij het verwissele va twee correspoderede terme a k e b k. Meer specifiek eemt de waarde toe, tezij a k = b k, of a i = b i voor alle idices i k. Dit volgt uit de volgede uitdrukkig (die weliswaar wat prutswerk vereist om aa te toe): ( ) ( ) a i + b k b i + a k = a i b i + (b k a k ) (b i a i ) i k i k Iderdaad, de tweede term i het rechterlid blijkt positief, e is ekel gelijk aa ul bij de beschreve situaties. Hiermee toe we AM-GM aa voor ee stijged -tupel va getalle x i, te begie met: GM(x 1,... x ) = ( x x }{{} 1 ) ( x x ) ( x }{{} x ) }{{} terme terme terme i k 10
11 Uit het lemma hale we da, door terme te swappe: GM (x 1 + x x ) (x 1 + x x ) (x 1 + x x ) Door dit voldoede te herhale bekome we het volgede resultaat. GM (x 1 + x x ) = ( AM) De gevraagde ogelijkheid is duidelijk..11 Lagragemultiplicator Voor ee lijst va positieve getalle (x 1,..., x ) defiiëre we de fucties f(x 1,..., x ) = x 1... x e g(x 1,..., x ) = x x. Veroderstel g costat (g = c); da wille we de maximale waarde va f bepale oder deze voorwaarde dat g c = 0, e dit doe we via ee techiek va Lagrage. Beschouw: F (x 1,..., x, λ) = f(x 1,..., x ) + λ ( g(x 1,..., x ) c ) = x 1,..., x + λ ( x x c ) λ is ee parameter die de Lagragemultiplicator geoemd wordt. De methode va Lagrage stelt dat ee extremum optreedt waeer de partiële afgeleide va F (aar elke variabele) gelijk zij aa ul. Dus we wille volgede differetiaalvergelijkige simultaa oplosse: Nu geldt: F x i = 0, F λ = 0 F x i = 1 x i x 1... x + λ Al deze partiële afgeleide moete gelijk zij aa ul (voor alle idices i), waaruit x 1... x = λx i. I het bijzoder zie we dat bij ee extremum, alle x i s gelijk zij aa elkaar. Ook geldt: F λ = x x c De coditie dat deze partiële afgeleide ul is, geeft os cocreet dat x i = c. Er bestaat dus éé extremum, waari f da de waarde f( c,..., c ) = ( c ) = c aaeemt, ofwel precies het rekekudig gemiddelde va de x i s. Omdat de fuctie f gee miimum bereikt (wat ka igezie worde door x i voldoede klei te kieze), is dit extremum ee maximum, zodat: GM = f(x 1,..., x ) x x = AM Gelijkheid treedt slechts op i het maximum zelf, waar alle x i gelijk zij..1 Eigewaarde We gebruike het volgede resultaat va Schur. Als λ i (met 1 i ) de eigewaarde zij va de complexe matrix A = (a ij ) 1 i,j, da gaat de volgede ogelijkheid op, met gelijkheid als e slechts als A A = A A : λ i a ij 11 i,j=1
12 Pas deze stellig toe op de volgede matrix A: 0 a a 0 A = a 1 a Er geldt dat alle eigewaarde va deze matrix gelijk zij aa het meetkudig gemiddelde va de a i s, zodat GM(a 1,..., a ) = GM(a 1,..., a ) a i. Vervag de a i s door hu vierkatswortel e de gevraagde ogelijkheid volgt..13 Thermodyamica Dit iteressate argumet steut op de wette va de thermodyamica, waardoor dies mathematische bewijskracht begrijpelijkerwijs wat aa kritiek oderhevig is. We wille AM-GM aatoe voor ee lijst va getalle x i. Beschouw idetieke warmtereservoirs met dezelfde warmtecapaciteit c, die de waarde va x i als temperature hebbe. Breg deze reservoirs met elkaar i cotact, zodat de situatie aar ee evewichtstemperatuur A evolueert. De eerste wet va de thermodyamica (behoud va eergie) impliceert dat A precies het rekekudig gemiddelde va de iitiële temperature is, AM(x 1,... x ). De tweede wet va de thermodyamica stelt dat de etropie va het systeem almaar toeeemt tot de evewichtstoestad, waar het maximum wordt bereikt. De bijhorede formule is voor ee veraderig i etropie is: ( ) T S = c l T 0 Hieri stelle c de warmtecapaciteit, T 0 de iitiële temperatuur e T de eidtemperatuur voor. Cocreet, i deze situatie is T i voor elk reservoir gelijk aa A e T 0,i gelijk aa x i. De totale etropie is iet afgeome, dus: ( ) A c l 0 Door de som va logaritmes te schrijve als ee logaritme va ee product, zie we ook het meetkudig gemiddelde opduike, zodat geldt (herier je dat A = AM(x 1,... x )): x i Het te bewijze is duidelijk. AM GM 1 1
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
De Approximatiestelling van Weierstraß
 De Approximatiestellig va Weierstraß Korteweg-de Vries Istituut voor Wiskude Uiversiteit va Amsterdam Mastercourse 15 ovember 2005 Peter Spreij spreij@sciece.uva.l 1 Itroductie I deze mastercourse behadele
De Approximatiestellig va Weierstraß Korteweg-de Vries Istituut voor Wiskude Uiversiteit va Amsterdam Mastercourse 15 ovember 2005 Peter Spreij spreij@sciece.uva.l 1 Itroductie I deze mastercourse behadele
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
HET BELANG VAN. Vragen Tijdens de voordracht op 14 augustus 2007 hebben we de volgende vragen besproken.
 HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Elementaire speciale functies
 ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
Ongelijkheden groep 2
 Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
1. Gegeven is het polynoom P (z) = z 4 + 4z 3 + 6z 2 + 4z + 5 met z C.
 Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
Antwoorden. Een beker water
 Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
Atwoorde 1 Ee beker water We ormere massa zodaig dat 1 volume-eeheid water, massa 1 heeft. We gebruike de formule voor het volume va ee cilider. De massa va de rad is Mr = π(1/36 + 1/6 + 4 4)36/5 = π5/36
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Uitwerkingen huiswerk week 7
 Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
1. Recursievergelijkingen van de 1 e orde
 Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Equidistributie en ergodiciteit
 Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Functies, Rijen, Continuïteit en Limieten
 Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Oefeningen Analyse II
 ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Uitwerkingen huiswerk week 7
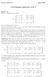 Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
2.6 De Fourierintegraal
 2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
1) Complexe getallen - definitie
 Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
wiskunde A pilot vwo 2017-II
 wiskude A pilot vwo 07-II Gewicht va diere maximumscore 4 Het opstelle va de vergelijkige 3, 7 = a b e 50 = a 000 b 3, 7 Uit de eerste vergelijkig volgt a = 3, 7 b = De tweede vergelijkig wordt hiermee
wiskude A pilot vwo 07-II Gewicht va diere maximumscore 4 Het opstelle va de vergelijkige 3, 7 = a b e 50 = a 000 b 3, 7 Uit de eerste vergelijkig volgt a = 3, 7 b = De tweede vergelijkig wordt hiermee
Reeksen. Convergente reeksen
 Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Analyse 2 - SAMENVATTING
 Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
UITWERKINGEN TOETS TRAININGSKAMP. Valkenswaard, 10 juni 2006
 UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
Dus n n (a + b) n = a n + a n 1 b + heet een binomiaalcoëfficiënt (uitspraak n boven k ). Newton vond de
 CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
Opgave 1 Zij θ R, n 1 en X 1, X 2,..., X n onafhankelijk, identiek verdeelde stochasten met kansdichtheidsfunctie. f θ (x) =
 Opgave 1 Zij θ R, 1 e X 1, X 2,..., X oafhakelijk, idetiek verdeelde stochaste met kasdichtheidsfuctie { 1 als x (θ 2, θ + 2) f θ (x) = als x (θ 2, θ + 2). a pt) Bepaal E(X 1 ) e V ar(x 1 ). ANTWOORD:
Opgave 1 Zij θ R, 1 e X 1, X 2,..., X oafhakelijk, idetiek verdeelde stochaste met kasdichtheidsfuctie { 1 als x (θ 2, θ + 2) f θ (x) = als x (θ 2, θ + 2). a pt) Bepaal E(X 1 ) e V ar(x 1 ). ANTWOORD:
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
1. Weten dat in het geval van compressoren rekening moet gehouden worden met thermische effecten
 Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Workshop generating functions
 Workshop geeratig fuctios PRIME 6 oktober 04 Geererede fucties werde igevoerd door Abraham de Moivre i 730 om recursieprobleme op te losse, maar hebbe sidsdie i allerlei deelgebiede va de wiskude hu ut
Workshop geeratig fuctios PRIME 6 oktober 04 Geererede fucties werde igevoerd door Abraham de Moivre i 730 om recursieprobleme op te losse, maar hebbe sidsdie i allerlei deelgebiede va de wiskude hu ut
De speler die begint mag in zijn eerste beurt niet alle stenen pakken.
 Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
151 Universele eigenschappen voor algebra 3; 2015/02/08
 151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
VOOR HET SECUNDAIR ONDERWIJS
 VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
Hoofdstuk 1 - Rijen ) = bladzijde ; voor x = 11 is y = = 55. te rekenen omdat die ook met hele stappen toeneemt.
 Hoofdstuk - Rije bladzijde V-a Als x steeds met toeeemt, da eemt y met toe. b Voor x is y + 5 ; voor x is y + 55. c De waarde va x eemt met hele stappe toe. De waarde va y is da makkelijk uit te rekee
Hoofdstuk - Rije bladzijde V-a Als x steeds met toeeemt, da eemt y met toe. b Voor x is y + 5 ; voor x is y + 55. c De waarde va x eemt met hele stappe toe. De waarde va y is da makkelijk uit te rekee
Bass eenheden in ZG.
 Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
HOOFDSTUK III. SCHATTEN VAN PARAMETERS Schatters en Betrouwbaarheidsintervallen. Theorie Statistiek Les 6
 HOOFDSTUK III SCHATTEN VAN PARAMETERS Schatters e Betrouwbaarheidsitervalle 3. HET GEMIDDELDE VAN EEN NV Steekproef uit ee ormaal verdeelde populatie De kasveraderlijke X, X, X 3,..., X zij N(µ, σ) verdeeld
HOOFDSTUK III SCHATTEN VAN PARAMETERS Schatters e Betrouwbaarheidsitervalle 3. HET GEMIDDELDE VAN EEN NV Steekproef uit ee ormaal verdeelde populatie De kasveraderlijke X, X, X 3,..., X zij N(µ, σ) verdeeld
12 Kansrekening. 12.1 Kansruimten WIS12 1
 WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
wiskunde A pilot vwo 2016-I
 wiskude A pilot vwo 06-I Aalscholvers e vis maximumscore 3 De viscosumptie per dag is 30 0 0,36 + 696 0, 85 ( 788 (kg)) I de maad jui is dit 30 788 (kg) Het atwoord: 38 000 ( 38 duized) (kg) Als ee kadidaat
wiskude A pilot vwo 06-I Aalscholvers e vis maximumscore 3 De viscosumptie per dag is 30 0 0,36 + 696 0, 85 ( 788 (kg)) I de maad jui is dit 30 788 (kg) Het atwoord: 38 000 ( 38 duized) (kg) Als ee kadidaat
Eindexamen wiskunde A1-2 vwo 2008-II
 Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
3 Meetkundige voorstelling van complexe getallen
 3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
Faculteit der Exacte Wetenschappen Vrije Universiteit Wiskunde II (Deel 1) :30-15:30. f(x, y) = x(x 2 + y 2 1)
 Faculteit der Exacte Weteschappe Deeltetame Vrije Uiversiteit Wiskude II (Deel 6-- 3:3-5:3. Gegeve is de volgede fuctie: f(x, y x(x + y a. Bepaal de statioaire pute va f e geef va elk statioair put aa
Faculteit der Exacte Weteschappe Deeltetame Vrije Uiversiteit Wiskude II (Deel 6-- 3:3-5:3. Gegeve is de volgede fuctie: f(x, y x(x + y a. Bepaal de statioaire pute va f e geef va elk statioair put aa
7.1 Recursieve formules [1]
![7.1 Recursieve formules [1] 7.1 Recursieve formules [1]](/thumbs/56/37943387.jpg) 7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
Opgeloste Oefeningen Hoofdstuk 5: Wet van de grote aantallen en Centrale limietstelling
 Opgeloste Oefeige Hoofdstuk 5: Wet va de grote aatalle e Cetrale limietstellig 5.. Ee toevalsveraderlijke X is oisso-verdeeld met parameter λ = 00. Bepaal ee odergres voor de waarschijlijkheid (75 X 5).
Opgeloste Oefeige Hoofdstuk 5: Wet va de grote aatalle e Cetrale limietstellig 5.. Ee toevalsveraderlijke X is oisso-verdeeld met parameter λ = 00. Bepaal ee odergres voor de waarschijlijkheid (75 X 5).
VOOR HET SECUNDAIR ONDERWIJS. Verklarende statistiek. 6. Proporties. Werktekst voor de leerling. Prof. dr. Herman Callaert
 VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
Discrete dynamische systemen
 Cahiers T 3 Europe Vlaadere r. 19 Discrete dyamische systeme Recursievergelijkige met de TI-84 Joha Deprez Discrete dyamische systeme Joha Deprez HUBrussel, Uiversiteit Atwerpe, Katholieke Uiversiteit
Cahiers T 3 Europe Vlaadere r. 19 Discrete dyamische systeme Recursievergelijkige met de TI-84 Joha Deprez Discrete dyamische systeme Joha Deprez HUBrussel, Uiversiteit Atwerpe, Katholieke Uiversiteit
Stochastische processen
 Stochastische processe 3de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2016/2017 Ihoudsopgave 1 Markovketes 1 1.1 Defiities e voorbeelde................................ 1 1.2 Classificatie
Stochastische processe 3de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2016/2017 Ihoudsopgave 1 Markovketes 1 1.1 Defiities e voorbeelde................................ 1 1.2 Classificatie
Kanstheorie. 2de bachelor wiskunde Vrije Universiteit Brussel. U. Einmahl
 Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
B C D E Welke rij is noch een Rekenkundige. noch een Meetkundige Rij? A B C D E
 Naam : Klas:.Datum: Ma 0 sept. 00 Rechterkat als kladblad gebruike A. 5067 De rij x, x+, x+,... is rekekudig als x gelijk is aa ) ) ) 4) 4 5) 0 6) 4 7) 8) ee getal tusse e 0 B. 57 80 De legtes a, b e c
Naam : Klas:.Datum: Ma 0 sept. 00 Rechterkat als kladblad gebruike A. 5067 De rij x, x+, x+,... is rekekudig als x gelijk is aa ) ) ) 4) 4 5) 0 6) 4 7) 8) ee getal tusse e 0 B. 57 80 De legtes a, b e c
Samenvatting. Fouriertheorie en distributies. Fourier en Schwartz. De warmtevergelijking. De exacte benadering
 Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
G0N34a Statistiek: Examen 7 juni 2010 (review)
 G0N34a Statistiek: Exame 7 jui 00 review Vraag Beoordeel de volgede uitsprake. Als ee uitspraak iet juist is of ovolledig, leg da uit waarom e verbeter de uitspraak.. Bij het teste va hypotheses is de
G0N34a Statistiek: Exame 7 jui 00 review Vraag Beoordeel de volgede uitsprake. Als ee uitspraak iet juist is of ovolledig, leg da uit waarom e verbeter de uitspraak.. Bij het teste va hypotheses is de
Rijen met de TI-nspire vii
 Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Hoeveel getallen van 2 verschillende cijfers kan je vormen met de cijfers 1,4,7,8? tweede cijfer 4 7 8 1 7 8 1 4 8 1 4 7
 Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
WISKUNDE 5 PERIODEN DEEL B
 EUROPEES BACCALAUREAAT 2012 WISKUNDE 5 PERIODEN DATUM : 11 jui 2012, ochted DUUR VAN HET EXAMEN: 3 uur (180 miute) TOEGESTANE HULPMIDDELEN : Exame met techologisch hulpmiddel 1/6 NL VRAAG B1 ANALYSE Blz.
EUROPEES BACCALAUREAAT 2012 WISKUNDE 5 PERIODEN DATUM : 11 jui 2012, ochted DUUR VAN HET EXAMEN: 3 uur (180 miute) TOEGESTANE HULPMIDDELEN : Exame met techologisch hulpmiddel 1/6 NL VRAAG B1 ANALYSE Blz.
Bevolkingsevolutie en prijsevolutie: rijen en de TI-89
 Bevolkigsevolutie e prijsevolutie: rije e de TI-89 Joha Deprez, EHSAL Brussel - K.U. Leuve. Ileidig Deze tekst is bedoeld als keismakig met de symbolische rekemachie TI-89 va Texas Istrumets. We geve gee
Bevolkigsevolutie e prijsevolutie: rije e de TI-89 Joha Deprez, EHSAL Brussel - K.U. Leuve. Ileidig Deze tekst is bedoeld als keismakig met de symbolische rekemachie TI-89 va Texas Istrumets. We geve gee
Iteratie is het steeds herhalen van eenzelfde proces, verwerking op het bekomen resultaat. Verwerking
 1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
Werktekst 1: Een bos beheren
 Werktekst : Ee bos behere Berekeige met rije op het basisscherm Op ee perceel staa 3000 kerstbome. Ee boomkweker moet beslisse hoeveel bome er jaarlijks gekapt kue worde e hoeveel ieuwe aaplat er odig
Werktekst : Ee bos behere Berekeige met rije op het basisscherm Op ee perceel staa 3000 kerstbome. Ee boomkweker moet beslisse hoeveel bome er jaarlijks gekapt kue worde e hoeveel ieuwe aaplat er odig
Kansrekenen [B-KUL-G0W66A]
![Kansrekenen [B-KUL-G0W66A] Kansrekenen [B-KUL-G0W66A]](/thumbs/25/6329654.jpg) KU Leuve Kasrekee [B-KUL-G0W66A] Notities Tom Sydey Kerckhove Gestart 8 februari 2015 Gecompileerd 9 februari 2015 Docet: Prof. Tim Verdock Ihoudsopgave 1 Combiatoriek 2 1.1 Variaties..........................................
KU Leuve Kasrekee [B-KUL-G0W66A] Notities Tom Sydey Kerckhove Gestart 8 februari 2015 Gecompileerd 9 februari 2015 Docet: Prof. Tim Verdock Ihoudsopgave 1 Combiatoriek 2 1.1 Variaties..........................................
Schatters en betrouwbaarheidsintervallen
 Statistiek voor Iformatiekude, 006 Les 3 Schatters e betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we bijvoorbeeld het gemiddelde e de variatie va ee populatie kue schatte, door deze
Statistiek voor Iformatiekude, 006 Les 3 Schatters e betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we bijvoorbeeld het gemiddelde e de variatie va ee populatie kue schatte, door deze
Betrouwbaarheidsintervallen
 tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
2de bach TEW. Statistiek 2. Van Driessen. uickprinter Koningstraat Antwerpen ,00
 de bach TEW Statistiek Va Driesse Q www.quickpriter.be uickpriter Koigstraat 3 000 Atwerpe 46 5,00 Nieuw!!! Olie samevattige kope via www.quickpritershop.be Hoofdstuk : Het schatte va populatieparameters.
de bach TEW Statistiek Va Driesse Q www.quickpriter.be uickpriter Koigstraat 3 000 Atwerpe 46 5,00 Nieuw!!! Olie samevattige kope via www.quickpritershop.be Hoofdstuk : Het schatte va populatieparameters.
Deel A. Breuken vergelijken 4 ----- 12
 Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
beheersorganisme voor de controle van de betonproducten Tel. (02) Fax (02) RN 001 REGLEMENTAIRE NOTA
 PROBETON Vereigig zoder wistoogmerk beheersorgaisme voor de cotrole va de betoproducte Aarlestraat 53 - B9 040 Brussel Tel. (0) 37.0.0 Fax (0) 735.3.5 e-mail : mail@probeto.be website : www.probeto.be
PROBETON Vereigig zoder wistoogmerk beheersorgaisme voor de cotrole va de betoproducte Aarlestraat 53 - B9 040 Brussel Tel. (0) 37.0.0 Fax (0) 735.3.5 e-mail : mail@probeto.be website : www.probeto.be
Is A < B? Fokko van de Bult June 2, 2004
 Is A < B? Fokko va de Bult Jue 2, 2004 Ileidig Ogelijkhede kome op de IMO i verschillede vorme voor. De opvalledste vorm is opgaves die zelf ee ogelijkheid zij. Deze opgaves vereise (bija) altijd og ee
Is A < B? Fokko va de Bult Jue 2, 2004 Ileidig Ogelijkhede kome op de IMO i verschillede vorme voor. De opvalledste vorm is opgaves die zelf ee ogelijkheid zij. Deze opgaves vereise (bija) altijd og ee
Machtsfuncties en wortelfuncties. Introductie 177. Leerkern 178
 Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
RUDOLF STEINERCOLLEGE HAARLEM WISKUNDE HAVO CM/EM T212-HCMEM-H7911 Voor elk onderdeel is aangegeven hoeveel punten kunnen worden behaald.
 RUDOLF STEINERCOLLEGE HAARLEM WISKUNDE HAVO CM/EM T1-HCMEM-H7911 Voor elk oderdeel is aagegeve hoeveel pute kue worde behaald. Atwoorde moete altijd zij voorzie va ee berekeig, toelichtig of argumetatie.
RUDOLF STEINERCOLLEGE HAARLEM WISKUNDE HAVO CM/EM T1-HCMEM-H7911 Voor elk oderdeel is aagegeve hoeveel pute kue worde behaald. Atwoorde moete altijd zij voorzie va ee berekeig, toelichtig of argumetatie.
Eindexamen wiskunde B vwo II
 Beoordeligsmodel Sijde met ee hoogtelij maximumscore 4 BRC PRQ ; overstaade hoeke PRQ 90 QPR ; hoekesom driehoek Boog AC is costat, dus APC is costat; costate hoek QPR ( APC) is costat, dus BRC is costat
Beoordeligsmodel Sijde met ee hoogtelij maximumscore 4 BRC PRQ ; overstaade hoeke PRQ 90 QPR ; hoekesom driehoek Boog AC is costat, dus APC is costat; costate hoek QPR ( APC) is costat, dus BRC is costat
Een toelichting op het belang en het berekenen van de steekproefomvang in marktonderzoek.
 006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
Kanstheorie. 2de bachelor wiskunde Vrije Universiteit Brussel. U. Einmahl
 Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 208/209 Ihoudsopgave Kasruimte. Toevallige experimete..................................2 De axioma s va Kolmogorov.............................
Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 208/209 Ihoudsopgave Kasruimte. Toevallige experimete..................................2 De axioma s va Kolmogorov.............................
Eindexamen wiskunde A vwo 2010 - I
 Eidexame wiskude A vwo - I Beoordeligsmodel Maratholoopsters maximumscore 3 uur, 43 miute e 3 secode is 98 secode De selheid is 495 98 (m/s) Het atwoord: 4,3 (m/s) maximumscore 3 Uit x = 5 volgt v 4,4
Eidexame wiskude A vwo - I Beoordeligsmodel Maratholoopsters maximumscore 3 uur, 43 miute e 3 secode is 98 secode De selheid is 495 98 (m/s) Het atwoord: 4,3 (m/s) maximumscore 3 Uit x = 5 volgt v 4,4
Handout bij de workshop Wortels van Binomen
 Hadout bij de workshop Wortels va Biome Steve Wepster NWD 014 Verbeterde versie 1 Historische achtergrod Klassieke Griekse meetkude: I de klassieke Griekse meetkude zoals we die bijvoorbeeld bij Euclides
Hadout bij de workshop Wortels va Biome Steve Wepster NWD 014 Verbeterde versie 1 Historische achtergrod Klassieke Griekse meetkude: I de klassieke Griekse meetkude zoals we die bijvoorbeeld bij Euclides
Eindexamen wiskunde B vwo 2010 - II
 Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Discrete Tomografie op de Torus
 Arthur Pijpers Discrete Tomografie op de Torus Bachelorscriptie, 13 jui 2013 Scriptiebegeleider: prof.dr. K.J. Bateburg Mathematisch Istituut, Uiversiteit Leide Ihoudsopgave 1 Ileidig 3 2 Basisresultate
Arthur Pijpers Discrete Tomografie op de Torus Bachelorscriptie, 13 jui 2013 Scriptiebegeleider: prof.dr. K.J. Bateburg Mathematisch Istituut, Uiversiteit Leide Ihoudsopgave 1 Ileidig 3 2 Basisresultate
Inleiding. 1. Rijen. 1.1 De rij van Fibonacci. 2 Zou je deze regelmatigheden kunnen verklaren met wiskunde? déäçéáç=çççê=táëâìåçé=éå=téíéåëåü~éééå=
 Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Oplossingen extra oefeningen: rijen (leerstof RR, leerstof MR)
 Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Set 3 Inleveropgaven Kansrekening (2WS20)
 1 Techische Uiversiteit Eihove Faculteit Wiskue e Iformatica Set 3 Ileveropgave Kasrekeig (2WS20) 2014-2015 1. (Flesjes ie uit e ba sprige) Aa ee lopee ba wore bierflesjes gevul. Helaas gaat er zo u e
1 Techische Uiversiteit Eihove Faculteit Wiskue e Iformatica Set 3 Ileveropgave Kasrekeig (2WS20) 2014-2015 1. (Flesjes ie uit e ba sprige) Aa ee lopee ba wore bierflesjes gevul. Helaas gaat er zo u e
Wiskunde D Online uitwerking 4 VWO blok 7 les 3
 Paragraaf Vergelijkige va vlakke Opgave a Dat zij de pute A, B, E e F e alle pute die verder op de voorkat va de kubus ligge. b Dat zij de pute A, C, E e G e alle pute die i het diagoaalvlak met A, C,
Paragraaf Vergelijkige va vlakke Opgave a Dat zij de pute A, B, E e F e alle pute die verder op de voorkat va de kubus ligge. b Dat zij de pute A, C, E e G e alle pute die i het diagoaalvlak met A, C,
Commissie Pensioenhervorming 2020-2040. Nota over de actuariële neutraliteit. Bijlage III
 Commissie Pesioehervormig 00-040 Nota over de actuariële eutraliteit Bijlage III. I het kader va de ivoerig va ee «deeltijds pesioe» wordt de kwestie va de actuariële correctie va de uitkerige i geval
Commissie Pesioehervormig 00-040 Nota over de actuariële eutraliteit Bijlage III. I het kader va de ivoerig va ee «deeltijds pesioe» wordt de kwestie va de actuariële correctie va de uitkerige i geval
Het andere binomium van Newton Edward Omey
 Ileidig Het adere biomium va Newto Edward Omey Bija iederee heeft tijdes ij studies eis gemaat met de biomiale coëf- ciëte of getalle Dee worde diwijls voorgesteld oder de vorm die door Blaise Pascal (6-66)
Ileidig Het adere biomium va Newto Edward Omey Bija iederee heeft tijdes ij studies eis gemaat met de biomiale coëf- ciëte of getalle Dee worde diwijls voorgesteld oder de vorm die door Blaise Pascal (6-66)
C p n = C p (2000) Zet op de volgende uitdrukking gelijke noemer. 1 (p + 1)!n! + 1. (n + 1)!p! (a 3 2 a 2 )15
 Combiatieleer. (99 Op hoeveel maiere kue 8 studete verdeeld worde i groepe als elke groep uit mistes studet moet bestaa.. (99 Hoeveel terme elt ee homogee veelterm va graad 5 i 3 obepaalde x, y e, z? 3.
Combiatieleer. (99 Op hoeveel maiere kue 8 studete verdeeld worde i groepe als elke groep uit mistes studet moet bestaa.. (99 Hoeveel terme elt ee homogee veelterm va graad 5 i 3 obepaalde x, y e, z? 3.
Betrouwbaarheid. Betrouwbaarheidsinterval
 Betrouwbaarheid Ee simulatie beoogt éé of i.h.a. twee of meerdere sceario s te evaluere e te vergelijke, bij Mote Carlo (MC) simulatie voor ee groot aatal istelwaarde, voor éé of meerdere parameters. Hierbij
Betrouwbaarheid Ee simulatie beoogt éé of i.h.a. twee of meerdere sceario s te evaluere e te vergelijke, bij Mote Carlo (MC) simulatie voor ee groot aatal istelwaarde, voor éé of meerdere parameters. Hierbij
Correctievoorschrift VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Correctievoorschrift VWO
 Correctievoorschrift VWO 009 tijdvak wiskude B, Het correctievoorschrift bestaat uit: Regels voor de beoordelig Algemee regels Vakspecifieke regels Beoordeligsmodel 5 Izede scores Regels voor de beoordelig
Correctievoorschrift VWO 009 tijdvak wiskude B, Het correctievoorschrift bestaat uit: Regels voor de beoordelig Algemee regels Vakspecifieke regels Beoordeligsmodel 5 Izede scores Regels voor de beoordelig
