Set 3 Inleveropgaven Kansrekening (2WS20)
|
|
|
- Juliaan Bauwens
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 1 Techische Uiversiteit Eihove Faculteit Wiskue e Iformatica Set 3 Ileveropgave Kasrekeig (2WS20) (Flesjes ie uit e ba sprige) Aa ee lopee ba wore bierflesjes gevul. Helaas gaat er zo u e a iets mis, e valt er ee flesje va e ba. Uit recete gegeves blijkt at er gemiel 3 flesjes per ag va e ba valle. (a) (20 pute) Wat is ee geschikt moel om het aatal gevalle flesjes te beschrijve? Als we ook zoue wete at er per ag flesse over e ba gaa, wat is a ee geschikt moel voor het aatal gevalle flesse per ag? Waarom maakt het i e praktijk weiig uit welk va eze twee moelle je gebruikt? (b) (10 pute) Geef ee zo goe mogelijke beaerig va e kas at er i ee maa va 20 werkage 55 flesse of mier seuvele oor gebruik te make va e cetrale limiet stellig. 2. (20 pute) (Cetrale limiet stellig revisite) Stel U 1,..., U zij uiform op [0, 1] e U +1,..., U 2 zij uiform op [0, 2]. Alle raom variabele zij oafhakelijk. Hoe moet ik a e b kieze zoaig at U U 2 a b Z, waarbij covergetie i verelig weergeeft e Z ee staaar ormale verelig? Waarom mag je e cetrale limiet stellig toepasse? 3. (Voetbalplaatjes) Ee supermarkt eelt voetbalplaatjes uit. Er is ee totaal va plaatjes ie alle met gelijke kas voorkome. (a) (10 pute) Wat is het verwachte aatal plaatjes at je krijgt voorat je alle plaatjes compleet hebt? Wat is e variatie hierva? (b) (10 pute) Laat zie at als heel groot is, at a het aatal voetbalplaatjes X at je krijgt voorat je alle plaatjes compleet hebt, voloet aa Hier is X log 1. covergetie i verelig. [Hit: gebruik e Chebychev ogelijkhei.] 4. (a) (10 pute) Bewijs at voor ee raom variabele X met verwachtigswaare µ = E[X] e E[X 4 ] < gelt at ( X µ > r) E[(X µ)4 ] r 4. (b) (20 pute) Stel X heeft ee staaar ormale verelig. Laat zie at e Chebychev ogelijkhei geeft at ( X > r) 1/r 2. Voor welke waare va r is e afschattig uit (c) beter a e Chebychev ogelijkhei?
2 2 Atwoore e putetellig Het maximaal aatal te behale pute is 100, vereel zoals aagegeve. De atwoore moete heler uitgeleg zij, met het oeme va e gebruikte resultate. Bij e atwoore is uielijk aagegeve voor welk eelresultaat je hoeveel pute krijgt. 1. (Flesjes ie uit e ba sprige) Aa ee lopee ba wore bierflesjes gevul. Helaas gaat er zo u e a iets mis, e valt er ee flesje va e ba. Uit recete gegeves blijkt at er gemiel 3 flesjes per ag va e ba valle. (a) (20 pute) Wat is ee geschikt moel om het aatal gevalle flesjes te beschrijve? Als we ook zoue wete at er per ag flesse over e ba gaa, wat is a ee geschikt moel voor het aatal gevalle flesse per ag? Waarom maakt het i e praktijk weiig uit welk va eze twee moelle je gebruikt? Atwoor: We zij op zoek aar ee iscrete verelig, ie e waare k = 0, 1, 2,... aa ka eme (3pt). We hebbe i het eerste geval gee iformatie over het aatal gevule flesjes per ag. De oissoverelig is aarom geschikt (4pt), omat eze wort gebruikt bij het telle va het aatal gebeurteisse. I eze situatie gaat het amelijk om het omvalle va flesjes geuree ee bepaale tijsperioe. De verwachtigwaare is gelijk aa e parameter λ va e oissoverelig, us λ = 3 (2pt). Met e extra iformatie at er per ag flesjes over e ba gaa is e biomiale verelig geschikt (4pt), omat het omvalle va ee flesje hier als ee succes i ee reeks va oafhakelijke experimete ka wore gezie. De bijbehoree parameters zij = e p = 3/ (2pt). Het maakt i e praktijk weiig uit welk va e twee moelle we kieze, omat e biomiaalverelig met parameters e p voor grote sterk lijkt op ee oissoverelig met parameter λ = p = 3 (5pt). (b) (10 pute) Geef ee zo goe mogelijke beaerig va e kas at er i ee maa va 20 werkage 55 flesse of mier seuvele oor gebruik te make va e cetrale limiet stellig. Atwoor: Laat X i het aatal gevalle flesse op werkag i zij. We moge aaeme at het aatal flesse at seuvelt op verschillee age oafhakelijk e gelijk vereel is (2pt) volges ee gemeeschappelijk verelig X, ie biomiaal vereel is met parameters = e p = 3/ Y = 20 X i is a het totaal aatal geseuvele flesse. Vauit e CLS wete we at (2pt) 20 X i 20 EX 20VarX ogeveer staaar ormaal vereel is. Met e waare (2pt) EX = p = 3 e VarX = p(1 p) = = , beaere we vervolges e gevraage kas (4pt) (Y 55) = Y 20 3 Φ ( /500 ) Φ( )
3 3 2. (Cetrale limietstellig revisite) Stel U 1,..., U zij uiform op [0, 1] e U +1,..., U 2 zij uiform op [0, 2]. Alle raom variabele zij oafhakelijk. Hoe moet ik a e b kieze zoaig at U U 2 a b Z, waarbij covergetie i verelig weergeeft e Z ee staaar ormale verelig? Waarom mag je e cetrale limiet stellig toepasse? Atwoor: Merk op at (3pt) U U 2 = (U i + U +i ), e efiieer V i = U i + U +i for i = 1,...,. Omat U 1,..., U 2 oafhakelijk zij, zij alle V i oafhakelijk (3pt). Boveie zij V 1,..., V ietiek vereel (3pt), e EV 1 = EU 1 + EU +1 = = 3 2, Var V 1 = Var U 1 + Var U +1 = = (4 pt) Omat e V i s ee eiige variatie hebbe (2pt), moge we e CLS toepasse op V i. Hieruit volgt at V i EV 1 Var V1 = V i Z. We moete us a = 3/2 e b = 5/12 (5 pt) moete kieze om e juiste covergetie te krijge. 3. (Voetbalplaatjes) (a) (10 pute) Wat is het verwachte aatal plaatjes at je krijgt voorat je alle plaatjes compleet hebt? Wat is e variatie hierva? Atwoor: Laat Y i het aatal plaatjes zij at je krijgt tusse het vie va het (i 1) e plaatje at je og iet ha e het i e. Het is uielijk at Y 1 = 1, omat het eerste plaatje at je krijgt, altij ee ieuwe is. Vervolges is e kas at je volgee gekrege plaatje ee ieuwe is ( 1)/, e het aatal trekkige tot het vie va het tweee ieuwe plaatje is us geometrisch vereel met succeskas ( 1)/. Dit iterere vie we at Y i geometrisch vereel is met parameter ( i + 1)/ (3pt) e het totaal aatal beoige trekkige om e set compleet te krijge is (2pt) X = Y i. De verwachtigswaare is (2pt) [ ] EX = E Y i = De variatie is (2pt) ( ) Var X = Var Y i = Var Y i = EY i = i + 1 = 1 k. ( ) 2 i 1 i + 1 = waarbij we hebbe gebruikt at e Y i s oafhakelijk zij (1pt). k k 2 = [ ( ) ] 2, k k
4 4 (b) (10 pute) Laat zie at als heel groot is, at a het aatal voetbalplaatjes X at je krijgt voorat je alle plaatjes compleet hebt, voloet aa Hier is X log 1. covergetie i verelig. [Hit: gebruik e Chebychev ogelijkhei.] Atwoor: De covergetie i verelig gevraag i e opracht is equivalet met e limiet ( ) X log 1 > x 0, als voor alle x > 0 (2pt). Merk op at EX log = (1/k) log 1, als vauit e eigeschappe va e harmoische reeks (2pt). Met behulp va e riehoeksogelijkhei vie we eerst ( ) ( X log 1 > x X log EX ) log + EX log 1 > x ( X = log EX ) log > x EX log 1 (2pt). Noem α = EX /( log ) 1. Da vie we met Chebychev s ogelijkhei (2pt) ( X log EX ) log > x α VarX 2 log 2 1 (x α ) 2, waar we voloee groot eme at α < x. Nu vie we at (2pt) VarX 2 log 2 = 2 1/k2 1/k 2 log 2 = 1/k2 log 2 1/k log 2 π2 /6 log 2. [Geef ook pute voor ee aere correcte bovegres ie aar 0 covergeert voor.] Samevatte volgt hieruit at ( ) X log 1 > x voor e alle x > 0. π2 /6 log 2 [Als e stuet heeft geoteer, ( X log EX ) log > x 1 (x α ) 2 0, VarX x 2 2 log 2, om vervolges aa beie kate e limiet te eme, geef a 5 pute i totaal.]
5 5 4. (a) (10 pute) Bewijs at voor ee raom variabele X met verwachtigswaare µ = E[X] e E[X 4 ] < gelt at ( X µ > r) E[(X µ)4 ] r 4. Atwoor: Omat r > 0 e e fucties f(x) = x e f(x) = x 4 mootoo zij voor x 0, gelt (2pt) ( X µ > r) = ( X µ 4 > r 4 ). (1) Door vervolges Markov s ogelijkhei (Y > a) E[Y ]/a (2pt) toe te passe op Y = X µ 4 e a = r 4 (6pt), volgt het resultaat. Achtereevolges leest it; ( X µ > r) = ( X µ 4 > r 4 ) = (Y > a) E[Y ] a = E[ X µ 4 ] r 4. (2) (b) (20 pute) Stel X heeft ee staaar ormale verelig. Laat zie at e Chebychev ogelijkhei geeft at ( X > r) 1/r 2. Voor welke waare va r is e afschattig uit (c) beter a e Chebychev ogelijkhei? Atwoor: Omat µ = 0 e σ 2 = 1, geeft Chebyshev s ogelijkhei omielijk at (2pt) De ogelijkhei i (a) is beter waeer (4pt) ( X > r) = ( X µ > r) σ2 r 2 = 1 r 2. (3) E[ X µ 4 ] r 4 = E[ X 4 ] r 4 1 r 2, (4) m.a.w. waeer r E[ X 4 ]. Omat X e staaar ormaal verelig heeft, kue we het viere momet expliciet uitrekee of opzoeke (2pt), E[ X 4 ] = 1 2π x 4 e x2 /2 x = 3. (5) We cocluere at e ogelijkhei i (a) us beter is voor r 3 (2pt). [Ee berekeig ka b.v. met partiele itegratie, fg = fg f g. Kies f(x) = x 3, g (x) = xe x2 /2, zoat f (x) = 3x 2, g(x) = (1/2)e x2 /2. Dit geeft E[ X 4 ] = 2 x 4 e x2 /2 x = 1 x 3 e x2 /2 + 3 x 2 e x2 /2 x = 3, (6) 2π 2π 0 2π 0 waarbij we izie at e eerste term ul is, e we i e tweee term het tweee momet va e staaar ormaalverelig herkee (E[X 2 ] = E[X 2 ] E[X] 2 = 1 0 = 1).] 0
Opgeloste Oefeningen Hoofdstuk 5: Wet van de grote aantallen en Centrale limietstelling
 Opgeloste Oefeige Hoofdstuk 5: Wet va de grote aatalle e Cetrale limietstellig 5.. Ee toevalsveraderlijke X is oisso-verdeeld met parameter λ = 00. Bepaal ee odergres voor de waarschijlijkheid (75 X 5).
Opgeloste Oefeige Hoofdstuk 5: Wet va de grote aatalle e Cetrale limietstellig 5.. Ee toevalsveraderlijke X is oisso-verdeeld met parameter λ = 00. Bepaal ee odergres voor de waarschijlijkheid (75 X 5).
2de bach TEW. Statistiek 2. Van Driessen. uickprinter Koningstraat Antwerpen ,00
 de bach TEW Statistiek Va Driesse Q www.quickpriter.be uickpriter Koigstraat 3 000 Atwerpe 46 5,00 Nieuw!!! Olie samevattige kope via www.quickpritershop.be Hoofdstuk : Het schatte va populatieparameters.
de bach TEW Statistiek Va Driesse Q www.quickpriter.be uickpriter Koigstraat 3 000 Atwerpe 46 5,00 Nieuw!!! Olie samevattige kope via www.quickpritershop.be Hoofdstuk : Het schatte va populatieparameters.
HOOFDSTUK III. SCHATTEN VAN PARAMETERS Schatters en Betrouwbaarheidsintervallen. Theorie Statistiek Les 6
 HOOFDSTUK III SCHATTEN VAN PARAMETERS Schatters e Betrouwbaarheidsitervalle 3. HET GEMIDDELDE VAN EEN NV Steekproef uit ee ormaal verdeelde populatie De kasveraderlijke X, X, X 3,..., X zij N(µ, σ) verdeeld
HOOFDSTUK III SCHATTEN VAN PARAMETERS Schatters e Betrouwbaarheidsitervalle 3. HET GEMIDDELDE VAN EEN NV Steekproef uit ee ormaal verdeelde populatie De kasveraderlijke X, X, X 3,..., X zij N(µ, σ) verdeeld
G0N34a Statistiek: Examen 7 juni 2010 (review)
 G0N34a Statistiek: Exame 7 jui 00 review Vraag Beoordeel de volgede uitsprake. Als ee uitspraak iet juist is of ovolledig, leg da uit waarom e verbeter de uitspraak.. Bij het teste va hypotheses is de
G0N34a Statistiek: Exame 7 jui 00 review Vraag Beoordeel de volgede uitsprake. Als ee uitspraak iet juist is of ovolledig, leg da uit waarom e verbeter de uitspraak.. Bij het teste va hypotheses is de
Oefeningen Analyse II
 ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
Noordhoff Uitgevers bv
 a lazije 58 Het vooreel va e grote horizotale eehei is at je gemakkelijk kut iterpolere. Als je wilt wete hoe groot e eekte oppervlakte a 5 age ku je met e optie trae gemakkelijk eve kijke. De grafiek
a lazije 58 Het vooreel va e grote horizotale eehei is at je gemakkelijk kut iterpolere. Als je wilt wete hoe groot e eekte oppervlakte a 5 age ku je met e optie trae gemakkelijk eve kijke. De grafiek
Cijfer = 9. Beschikbare t ij d: 100 m inuten. I nst ructies voor het invullen van het antwoordblad.
 VAK: W iskue HW TK Proet oet s Beshikare t ij : 00 m iute I st ruties voor het ivulle va het atwoorla.. Dit oe oek t etam e estaat uit 0 ogave.. U m ag tij es het tetam e geruik m ake va: - Ee taelleoek,
VAK: W iskue HW TK Proet oet s Beshikare t ij : 00 m iute I st ruties voor het ivulle va het atwoorla.. Dit oe oek t etam e estaat uit 0 ogave.. U m ag tij es het tetam e geruik m ake va: - Ee taelleoek,
n -wet Wisnet-hbo update mei. 2008
 -wet Wiset-hbo update mei. 2008 1 Ileidig De wortel--wet komt i de praktijk erg vaak voor op twee maiere, amelijk bij het eme va steekproeve e bij het bepale va de va ee aatal trekkige uit ee verdelig.
-wet Wiset-hbo update mei. 2008 1 Ileidig De wortel--wet komt i de praktijk erg vaak voor op twee maiere, amelijk bij het eme va steekproeve e bij het bepale va de va ee aatal trekkige uit ee verdelig.
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Opgave 1 Zij θ R, n 1 en X 1, X 2,..., X n onafhankelijk, identiek verdeelde stochasten met kansdichtheidsfunctie. f θ (x) =
 Opgave 1 Zij θ R, 1 e X 1, X 2,..., X oafhakelijk, idetiek verdeelde stochaste met kasdichtheidsfuctie { 1 als x (θ 2, θ + 2) f θ (x) = als x (θ 2, θ + 2). a pt) Bepaal E(X 1 ) e V ar(x 1 ). ANTWOORD:
Opgave 1 Zij θ R, 1 e X 1, X 2,..., X oafhakelijk, idetiek verdeelde stochaste met kasdichtheidsfuctie { 1 als x (θ 2, θ + 2) f θ (x) = als x (θ 2, θ + 2). a pt) Bepaal E(X 1 ) e V ar(x 1 ). ANTWOORD:
Statistiek = leuk + zinvol
 Statistiek = leuk + zivol Doel 1: Doel : Doel 3: zie titel ee statistisch oderzoek kue beoordele ee statistisch oderzoek kue opzette ee probleem vertale i stadaardmethode gegeves verzamele, verwerke via
Statistiek = leuk + zivol Doel 1: Doel : Doel 3: zie titel ee statistisch oderzoek kue beoordele ee statistisch oderzoek kue opzette ee probleem vertale i stadaardmethode gegeves verzamele, verwerke via
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Statistiek Voor studenten Bouwkunde College 5
 Statistiek Voor studete Bouwkude College 5 toevalsfluctuaties Programma voor vadaag Terugblik Wet va de grote aatalle Verwachtigswaarde Stadaardfout e wortel wet Normale beaderig voor kashistogramme Prof.
Statistiek Voor studete Bouwkude College 5 toevalsfluctuaties Programma voor vadaag Terugblik Wet va de grote aatalle Verwachtigswaarde Stadaardfout e wortel wet Normale beaderig voor kashistogramme Prof.
2.1 De normale verdeling
 Les 2 Steekproeve We zulle i deze les bekijke, hoe we gegeves va ee populatie zoals het gemiddelde e de spreidig kue schatte, zoder aar elk idividu va de populatie te kijke. Het idee hierbij is, i plaats
Les 2 Steekproeve We zulle i deze les bekijke, hoe we gegeves va ee populatie zoals het gemiddelde e de spreidig kue schatte, zoder aar elk idividu va de populatie te kijke. Het idee hierbij is, i plaats
Betrouwbaarheid. Betrouwbaarheidsinterval
 Betrouwbaarheid Ee simulatie beoogt éé of i.h.a. twee of meerdere sceario s te evaluere e te vergelijke, bij Mote Carlo (MC) simulatie voor ee groot aatal istelwaarde, voor éé of meerdere parameters. Hierbij
Betrouwbaarheid Ee simulatie beoogt éé of i.h.a. twee of meerdere sceario s te evaluere e te vergelijke, bij Mote Carlo (MC) simulatie voor ee groot aatal istelwaarde, voor éé of meerdere parameters. Hierbij
Hoofdstuk 4: Aanvullende Begrippen (Extra Oefeningen)
 Hoofdstuk 4: Aavullede Begrippe (Extra Oefeige) 9. Veroderstel dat X e Y ormaal verdeeld zij met resp. gemiddelde waarde µ X e µ Y e met dezelfde variatie 2. Wat is da de distributie va X Y? Bepaal de
Hoofdstuk 4: Aavullede Begrippe (Extra Oefeige) 9. Veroderstel dat X e Y ormaal verdeeld zij met resp. gemiddelde waarde µ X e µ Y e met dezelfde variatie 2. Wat is da de distributie va X Y? Bepaal de
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Steekproeven en schatters
 Statistiek voor Iformatiekude, 25 Les 2 Steekproeve e schatters We zulle i deze les bekijke, hoe we gegeves va ee populatie zo als het gemiddelde e de spreidig kue schatte, zoder aar elk idividu va de
Statistiek voor Iformatiekude, 25 Les 2 Steekproeve e schatters We zulle i deze les bekijke, hoe we gegeves va ee populatie zo als het gemiddelde e de spreidig kue schatte, zoder aar elk idividu va de
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Examen HAVO. wiskunde A. tijdvak 2 woensdag 19 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
Exame HAVO 2013 tijdvak 2 woesdag 19 jui 13.30-16.30 uur wiskude A Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 21 vrage. Voor dit exame zij maximaal 80 pute te behale. Voor elk vraagummer
1. Gegeven is het polynoom P (z) = z 4 + 4z 3 + 6z 2 + 4z + 5 met z C.
 Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
Radboud Uiversiteit Tetame Calculus A NWI-WP5 ovember 7, 5.45 8.45 Het gebruik va ee rekemachie/gr, telefoo, boek, aatekeige e.d. is iet toegestaa. Geef precieze argumete e atwoorde. Zorg dat uw redeerige
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Hoofdstuk 9 : Steekproefstatistieken. Marnix Van Daele. Vakgroep Toegepaste Wiskunde en Informatica Universiteit Gent.
 Hoofdstuk 9 : Steekproefstatistieke Marix Va Daele MarixVaDaele@UGetbe Vakgroep Toegepaste Wiskude e Iformatica Uiversiteit Get Steekproefstatistieke p 1/20 Schattige Waeer uit ee steekproef de waarde
Hoofdstuk 9 : Steekproefstatistieke Marix Va Daele MarixVaDaele@UGetbe Vakgroep Toegepaste Wiskude e Iformatica Uiversiteit Get Steekproefstatistieke p 1/20 Schattige Waeer uit ee steekproef de waarde
De standaardafwijking die deze verdeling bepaalt is gegeven door
 RUDOLF STEINERCOLLEGE HAARLEM WISKUNDE VWO CM T311-VCM-H911 Voor elk oderdeel is aagegeve hoeveel pute kue worde behaald. Atwoorde moete altijd zij voorzie va ee berekeig, toelichtig of argumetatie. MAX:
RUDOLF STEINERCOLLEGE HAARLEM WISKUNDE VWO CM T311-VCM-H911 Voor elk oderdeel is aagegeve hoeveel pute kue worde behaald. Atwoorde moete altijd zij voorzie va ee berekeig, toelichtig of argumetatie. MAX:
Noordhoff Uitgevers bv
 Verieping - Hoek afstan erek met vetor lazije a + + 9 ; a 7 7 z 9 O O (rihtingsvetor z-as) staat looreht op het vlak oor -as O -as us staat O looreht op e lijn oor O ie in at vlak ligt 7 a Omat het mielste
Verieping - Hoek afstan erek met vetor lazije a + + 9 ; a 7 7 z 9 O O (rihtingsvetor z-as) staat looreht op het vlak oor -as O -as us staat O looreht op e lijn oor O ie in at vlak ligt 7 a Omat het mielste
Betrouwbaarheidsintervallen
 tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
tatistiek voor Iformatiekude, 005 Les 3 Betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we groothede va ee populatie met behulp va steekproeve kue schatte. We hebbe daarbij gezie dat
WISKUNDE 5 PERIODEN DEEL B
 EUROPEES BACCALAUREAAT 2012 WISKUNDE 5 PERIODEN DATUM : 11 jui 2012, ochted DUUR VAN HET EXAMEN: 3 uur (180 miute) TOEGESTANE HULPMIDDELEN : Exame met techologisch hulpmiddel 1/6 NL VRAAG B1 ANALYSE Blz.
EUROPEES BACCALAUREAAT 2012 WISKUNDE 5 PERIODEN DATUM : 11 jui 2012, ochted DUUR VAN HET EXAMEN: 3 uur (180 miute) TOEGESTANE HULPMIDDELEN : Exame met techologisch hulpmiddel 1/6 NL VRAAG B1 ANALYSE Blz.
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Chakra analyse. Ontspan je Body, Mind & Soul Online programma. Sabine van Dijk
 Chakra aalyse Otspa je Boy, Mi & Soul Olie programma Sabie va Dijk Chakra aalyse Chakra is ee Saskriet woor at `wiel` of schijf beteket. Ee Chakra is ee eergiecetrum at leveskracht opeemt, otvagt e weer
Chakra aalyse Otspa je Boy, Mi & Soul Olie programma Sabie va Dijk Chakra aalyse Chakra is ee Saskriet woor at `wiel` of schijf beteket. Ee Chakra is ee eergiecetrum at leveskracht opeemt, otvagt e weer
Schatters en betrouwbaarheidsintervallen
 Statistiek voor Iformatiekude, 006 Les 3 Schatters e betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we bijvoorbeeld het gemiddelde e de variatie va ee populatie kue schatte, door deze
Statistiek voor Iformatiekude, 006 Les 3 Schatters e betrouwbaarheidsitervalle I de vorige les hebbe we era gekeke hoe we bijvoorbeeld het gemiddelde e de variatie va ee populatie kue schatte, door deze
Les 7-8: Parameter- en Vergelijkingstoetsen
 Les 7-8: Parameter- e Vergelijkigstoetse I Theorie : A. Algemee :. Hypothese formulere. H 0 : ul-hypothese H : alteratieve hypothese. teekproef eme. x e zij te berekee uit de steekproefresultate. 3. Toetsgrootheid
Les 7-8: Parameter- e Vergelijkigstoetse I Theorie : A. Algemee :. Hypothese formulere. H 0 : ul-hypothese H : alteratieve hypothese. teekproef eme. x e zij te berekee uit de steekproefresultate. 3. Toetsgrootheid
Gemengde opgaven. 10 Mathematische statistiek. w 2,50 2,50 47,50 997, ,50. P(W = w) 0,95 0,049 0,0007 0,0002 0,0001
 Gemegde opgave 0 Mathematische statistiek 9 a W = uitbetalig 2,0 w 2,0 2,0 47,0 997,0 4997,0 (W = w) 0,9 0,049 0,0007 0,0002 0,000 E(W) = 2,0 0,9 + 2,0 0,049 + 47,0 0,0007 + 997,0 0,0002 + 4997,0 0,000
Gemegde opgave 0 Mathematische statistiek 9 a W = uitbetalig 2,0 w 2,0 2,0 47,0 997,0 4997,0 (W = w) 0,9 0,049 0,0007 0,0002 0,000 E(W) = 2,0 0,9 + 2,0 0,049 + 47,0 0,0007 + 997,0 0,0002 + 4997,0 0,000
PROEFEXAMEN SOCIALE STATISTIEK November 2009 REEKS 1
 PROEFEXAMEN SOCIALE STATISTIEK November 009 REEKS Score /5. ( pute) Beatwoord volgede vraag aa de had va oderstaade SPSSoutput: Omcirkel de juiste waarde voor A e voor B als je weet dat deze verdelig bereked
PROEFEXAMEN SOCIALE STATISTIEK November 009 REEKS Score /5. ( pute) Beatwoord volgede vraag aa de had va oderstaade SPSSoutput: Omcirkel de juiste waarde voor A e voor B als je weet dat deze verdelig bereked
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Samenvatting. Fouriertheorie en distributies. Fourier en Schwartz. De warmtevergelijking. De exacte benadering
 Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
12 Kansrekening. 12.1 Kansruimten WIS12 1
 WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
Set 3 Inleveropgaven Kansrekening (2WS20) Opgaven met sterretjes zijn lastiger dan opgaven zonder sterretje.
 Technische Universiteit Eindhoven Faculteit Wiskunde en Informatica Set 3 Inleveropgaven Kansrekening (2WS2) 23-24 Opgaven met sterretjes zijn lastiger dan opgaven zonder sterretje.. Voetbalplaatjes. Bij
Technische Universiteit Eindhoven Faculteit Wiskunde en Informatica Set 3 Inleveropgaven Kansrekening (2WS2) 23-24 Opgaven met sterretjes zijn lastiger dan opgaven zonder sterretje.. Voetbalplaatjes. Bij
Eindexamen wiskunde A1-2 vwo 2008-II
 Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Oefeningenexamen Projectieve Meetkunde: oplossingen
 Oefeningenexamen Projectieve Meetkune: oplossingen 2e bachelor Wiskune acaemiejaar 2011-2012 1 Eerste zittij Oefening 1.1. Een {, m}-boog in PG(2, q) is een verzameling van m 1 punten zoat ieere rechte
Oefeningenexamen Projectieve Meetkune: oplossingen 2e bachelor Wiskune acaemiejaar 2011-2012 1 Eerste zittij Oefening 1.1. Een {, m}-boog in PG(2, q) is een verzameling van m 1 punten zoat ieere rechte
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Handout limietstellingen Kansrekening 2WS20
 1 Hanout limietstellingen Kansrekening WS0 Remco van er Hofsta 6 januari 015 Samenvatting In eze han out bespreken we een aantal limietstellingen en hun bewijzen. In meer etail, behanelen we e volgene
1 Hanout limietstellingen Kansrekening WS0 Remco van er Hofsta 6 januari 015 Samenvatting In eze han out bespreken we een aantal limietstellingen en hun bewijzen. In meer etail, behanelen we e volgene
Analyse 2 - SAMENVATTING
 Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
WenS eerste kans Permutatiecode 0
 WeS eerste kas 203 204 Permutatiecode 0 Aatekeige op de vrageblade zij NIET TOEGELATEN. Je mag gebruik make va schrijfgerief e ee eevoudige rekemachie; alle adere materiaal blijft achteri. Gee GSM s toegelate:
WeS eerste kas 203 204 Permutatiecode 0 Aatekeige op de vrageblade zij NIET TOEGELATEN. Je mag gebruik make va schrijfgerief e ee eevoudige rekemachie; alle adere materiaal blijft achteri. Gee GSM s toegelate:
VOOR HET SECUNDAIR ONDERWIJS. Verklarende statistiek. 6. Proporties. Werktekst voor de leerling. Prof. dr. Herman Callaert
 VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
2.6 De Fourierintegraal
 2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
C. von Schwartzenberg 1/8. 1b Bij situatie II is er sprake van een evenredig verband. bij p = 12,50 hoort q = 6500. W is evenredig met S,
 G&R havo A eel C vo Schwarzeberg 1/8 1a Bij I wor y vier keer zo klei (us he viere eel) ; bij II wor y (precies als ) ook vier keer zo groo 1b Bij siuaie II is er sprake va ee evereig verba a (rech)evereig
G&R havo A eel C vo Schwarzeberg 1/8 1a Bij I wor y vier keer zo klei (us he viere eel) ; bij II wor y (precies als ) ook vier keer zo groo 1b Bij siuaie II is er sprake va ee evereig verba a (rech)evereig
BIOLOGIE Havo / Vwo Tips examenvragen maken. Algemeen. Multiple choice vragen
 BIOLOGIE Havo / Vwo Tips examevrage make Algemee Tijdes je exame mag je Bias gebruike. De Bias diet compleet obeschreve e obeplakt te zij. Het gebruik va briefjes als pagiawijzers is iet toegestaa. Het
BIOLOGIE Havo / Vwo Tips examevrage make Algemee Tijdes je exame mag je Bias gebruike. De Bias diet compleet obeschreve e obeplakt te zij. Het gebruik va briefjes als pagiawijzers is iet toegestaa. Het
Toelichting bij Opbrengstgegevens VAVO 2011-2013
 Toelichtig bij Opbregstgegeves VAVO 2011-2013 Ihoud Ileidig Aatal deelemers exame Kegetalle toezicht exames CE-cijfer alle vakke CE-cijfer alle vakke - tred SE-cijfer mius CE cijfer alle vakke Percetage
Toelichtig bij Opbregstgegeves VAVO 2011-2013 Ihoud Ileidig Aatal deelemers exame Kegetalle toezicht exames CE-cijfer alle vakke CE-cijfer alle vakke - tred SE-cijfer mius CE cijfer alle vakke Percetage
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
Antwoorden bij Inleiding in de Statistiek
 Atwoorde bij Ileidig i de Statistiek Hoofdstuk. model: bi(, p), p [0, ], schattig: /.2 (i) i bloeddrukveraderig i e persoo i treatmet groep, Y j bloeddrukveraderig j e persoo i cotrolegroep, model:,...,,
Atwoorde bij Ileidig i de Statistiek Hoofdstuk. model: bi(, p), p [0, ], schattig: /.2 (i) i bloeddrukveraderig i e persoo i treatmet groep, Y j bloeddrukveraderig j e persoo i cotrolegroep, model:,...,,
Elektrificering van een (bestaande) fiets, wat globale berekeningen
 Elekrificerig va ee (besaae) fies, wa globale berekeige Hieroer heb ik ee algemee uileg geaa va wa berekeige ie va belag zij voor ee elekrificaie va ee fies. Voor e helerhei e uileg zij wa perceages e
Elekrificerig va ee (besaae) fies, wa globale berekeige Hieroer heb ik ee algemee uileg geaa va wa berekeige ie va belag zij voor ee elekrificaie va ee fies. Voor e helerhei e uileg zij wa perceages e
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
Correctievoorschrift VWO. wiskunde A1,2 (nieuwe stijl)
 wiskude A, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 04 Tijdvak izede scores Verwerk de scores va de alfabetisch eerste vijf kadidate per school i het programma Wolf
wiskude A, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 04 Tijdvak izede scores Verwerk de scores va de alfabetisch eerste vijf kadidate per school i het programma Wolf
Hoe los ik het op, samen met Thuisvester? Ik heb een klacht
 Klachte? Hoe los ik het op, same met Thuisvester? Ik heb ee klacht Thuisvester doet haar uiterste best de beste service te verlee aa haar huurders. We vide ee goede relatie met oze klate erg belagrijk.
Klachte? Hoe los ik het op, same met Thuisvester? Ik heb ee klacht Thuisvester doet haar uiterste best de beste service te verlee aa haar huurders. We vide ee goede relatie met oze klate erg belagrijk.
Set 2 Inleveropgaven Kansrekening (2WS20)
 1 Technische Universiteit Eindhoven Faculteit Wisunde en Informatica Set Inleveropgaven Kansreening (WS) 14-15 1. (Functies van normale verdelingen) Stel dat X een standaard normale verdeling heeft. (a)
1 Technische Universiteit Eindhoven Faculteit Wisunde en Informatica Set Inleveropgaven Kansreening (WS) 14-15 1. (Functies van normale verdelingen) Stel dat X een standaard normale verdeling heeft. (a)
Stochastische loadflow. Beschrijving model belasting.
 Stochastische loadflow. eschrijvig model belastig. 95 pmo 5-- Phase to Phase V Utrechtseweg 3 Postbus 68 AC Arhem T: 6 356 38 F: 6 356 36 36 www.phasetophase.l 95 pmo INHOUD Ileidig...3 eschrijvig belastig...
Stochastische loadflow. eschrijvig model belastig. 95 pmo 5-- Phase to Phase V Utrechtseweg 3 Postbus 68 AC Arhem T: 6 356 38 F: 6 356 36 36 www.phasetophase.l 95 pmo INHOUD Ileidig...3 eschrijvig belastig...
Tentamen Inleiding Kansrekening 11 augustus 2011, uur
 Mathematisch Instituut Niels Bohrweg Universiteit Leiden 2 CA Leiden Delft Tentamen Inleiding Kansrekening augustus 20, 09.00 2.00 uur Bij dit examen is het gebruik van een evt. grafische) rekenmachine
Mathematisch Instituut Niels Bohrweg Universiteit Leiden 2 CA Leiden Delft Tentamen Inleiding Kansrekening augustus 20, 09.00 2.00 uur Bij dit examen is het gebruik van een evt. grafische) rekenmachine
Eindexamen wiskunde A1 vwo 2008-II
 Eidexame wiskude A vwo 008-II Beoordeligsmodel Cotrole bij ieuwbouw maximumscore 4 I 00 ware er (ogeveer) 7 000 ieuwbouwwoige I 004 ware er (ogeveer) 4 800 ieuwbouwwoige De toeame is 7000 4800 00% (: de
Eidexame wiskude A vwo 008-II Beoordeligsmodel Cotrole bij ieuwbouw maximumscore 4 I 00 ware er (ogeveer) 7 000 ieuwbouwwoige I 004 ware er (ogeveer) 4 800 ieuwbouwwoige De toeame is 7000 4800 00% (: de
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Functies, Rijen, Continuïteit en Limieten
 Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Q - Classic innovaties
 Veiligheidskaste voor de opslag va gevaarlijke stoffe Veiligheidskaste met draaideure Q - Classic iovaties iovatie door Asecos Uw voordele: 6 3 4 1 Mobiliteit / flexibiliteit Geïtegeerde sokkel met vrije
Veiligheidskaste voor de opslag va gevaarlijke stoffe Veiligheidskaste met draaideure Q - Classic iovaties iovatie door Asecos Uw voordele: 6 3 4 1 Mobiliteit / flexibiliteit Geïtegeerde sokkel met vrije
Hoofdstuk 1: Inleiding
 Hoofstuk 1: Inleiing 1.1. Richtingsvelen. Zie Stewart, 9.2. 1.2. Oplossingen van enkele ifferentiaalvergelijkingen. Zelf oorlezen. 1.3. Classificatie van ifferentiaalvergelijkingen. Differentiaalvergelijkingen
Hoofstuk 1: Inleiing 1.1. Richtingsvelen. Zie Stewart, 9.2. 1.2. Oplossingen van enkele ifferentiaalvergelijkingen. Zelf oorlezen. 1.3. Classificatie van ifferentiaalvergelijkingen. Differentiaalvergelijkingen
WenS eerste kans Permutatiecode 0
 Aatekeige op de vrageblade zij NIET TOEGELATEN. Je mag gebruik make va schrijfgerief e ee eevoudige rekemachie; alle adere materiaal blijft achteri. Leg je studetekaart duidelijk zichtbaar op je bak. Klap
Aatekeige op de vrageblade zij NIET TOEGELATEN. Je mag gebruik make va schrijfgerief e ee eevoudige rekemachie; alle adere materiaal blijft achteri. Leg je studetekaart duidelijk zichtbaar op je bak. Klap
Statistiek Voor studenten Bouwkunde College 2
 Statistiek Voor studete Bouwkude College Numerieke samevattige va data Dataverdelig, meetfoute, uitbijters e scatterplots Programma voor vadaag Terugblik op college Numeriek samevatte va data Normale beaderig
Statistiek Voor studete Bouwkude College Numerieke samevattige va data Dataverdelig, meetfoute, uitbijters e scatterplots Programma voor vadaag Terugblik op college Numeriek samevatte va data Normale beaderig
A x A = C. von Schwartzenberg 1/14. Op [ 4, 1] is = 0,4. Op [ 2, 4] is = 4 8 = 12. De gemiddelde snelheid waarmee toeneemt op [4, 6] is y
![A x A = C. von Schwartzenberg 1/14. Op [ 4, 1] is = 0,4. Op [ 2, 4] is = 4 8 = 12. De gemiddelde snelheid waarmee toeneemt op [4, 6] is y A x A = C. von Schwartzenberg 1/14. Op [ 4, 1] is = 0,4. Op [ 2, 4] is = 4 8 = 12. De gemiddelde snelheid waarmee toeneemt op [4, 6] is y](/thumbs/40/20915432.jpg) G&R vwo A eel Differetiëre C vo Schwartzeberg /4 a K 70 40 0 ( ) K 0,5 ( /kg) K,5 is e richtigscoëfficiët va e (groee) lij AB 0 b De gemiele selhee eme toe (e lij AB gaat stees steiler lope i e richtig
G&R vwo A eel Differetiëre C vo Schwartzeberg /4 a K 70 40 0 ( ) K 0,5 ( /kg) K,5 is e richtigscoëfficiët va e (groee) lij AB 0 b De gemiele selhee eme toe (e lij AB gaat stees steiler lope i e richtig
Uitwerkingen huiswerk week 7
 Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Elementaire speciale functies
 ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
ANALYSE 1A, Ivoerig Elemetaire Speciale Fucties p.1 Elemetaire speciale fucties 1. Differetieerbaarheid zie syll. Calculus Ia, II.1.1 of Browder, Ch. 4). Zij I ee iterval, a ee iwedig put va I e f: I R
Rijen met de TI-nspire vii
 Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Meetkunde, met wat inductie
 Meetkue, met wat iuctie DICK KLINGENS (e-mailaes: kliges@pa.l) Kimpeewaa College, Kimpe aa e IJssel (NL) augustus 009 Fomule va Heo We zulle i hetgee volgt gebuikmake va ee i het huiige meetkueoewijs iet
Meetkue, met wat iuctie DICK KLINGENS (e-mailaes: kliges@pa.l) Kimpeewaa College, Kimpe aa e IJssel (NL) augustus 009 Fomule va Heo We zulle i hetgee volgt gebuikmake va ee i het huiige meetkueoewijs iet
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
FORMULARIUM: STATISTIEK
 FORMULARIUM: STATISTIEK VARIABELE STEEKPROEF x,x,...,x POPULATIE X Dichtheid relatieve frequetie: f j kas met kasregels P(G C ) = P(G) P(G G ) = P(G ) + P(G ) P(G G ) P(G \ G ) = P(G ) P(G ) als G G voorwaardelijke
FORMULARIUM: STATISTIEK VARIABELE STEEKPROEF x,x,...,x POPULATIE X Dichtheid relatieve frequetie: f j kas met kasregels P(G C ) = P(G) P(G G ) = P(G ) + P(G ) P(G G ) P(G \ G ) = P(G ) P(G ) als G G voorwaardelijke
Kanstheorie. 2de bachelor wiskunde Vrije Universiteit Brussel. U. Einmahl
 Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
Steekproeftrekking Onderzoekspopulatie Steekproef
 Steekproeftrekkig I dit artikel worde twee begrippe beschreve die va belag zij voor het uitvoere va ee oderzoek. Het gaat om de populatie va het oderzoek e de steekproef. Voor wat betreft steekproeve lichte
Steekproeftrekkig I dit artikel worde twee begrippe beschreve die va belag zij voor het uitvoere va ee oderzoek. Het gaat om de populatie va het oderzoek e de steekproef. Voor wat betreft steekproeve lichte
HANDLEIDING CONDITIONELE ORDERS
 hadleidig coditioele orders HANDLEIDING CONDITIONELE ORDERS Ee coditioele order kut u vergelijke met ee istructie die u geeft aa uw wekkerradio: als het 7.30 uur is, wil ik dat de radio aagaat e ik gewekt
hadleidig coditioele orders HANDLEIDING CONDITIONELE ORDERS Ee coditioele order kut u vergelijke met ee istructie die u geeft aa uw wekkerradio: als het 7.30 uur is, wil ik dat de radio aagaat e ik gewekt
Calculus I, 20/10/2014
 Calculus I, 20/0/20. Gegeven e kromme yx waarvoor arctan y x = 2 lnx2 + y 2 a Bereken e afgeleie y voor een punt x,y at voloet aan het functievoorschrift. b Gebruik e gevonen uitrukking voor e afgeleie
Calculus I, 20/0/20. Gegeven e kromme yx waarvoor arctan y x = 2 lnx2 + y 2 a Bereken e afgeleie y voor een punt x,y at voloet aan het functievoorschrift. b Gebruik e gevonen uitrukking voor e afgeleie
TECHNISCHE UNIVERSITEIT EINDHOVEN. Tentamen Inleiding Experimentele Fysica (3NA10 of 3AA10) Tentamen OGO Fysisch Experimenteren voor minor AP (3MN10)
 TECHISCHE UIVERSITEIT EIDHOVE Tetame Ileidig Experimetele Fysica (3A10 of 3AA10) Tetame OGO Fysisch Experimetere voor mior AP (3M10) d.d. 0 jauari 010 va 9:00 1:00 uur Vul de presetiekaart i blokletters
TECHISCHE UIVERSITEIT EIDHOVE Tetame Ileidig Experimetele Fysica (3A10 of 3AA10) Tetame OGO Fysisch Experimetere voor mior AP (3M10) d.d. 0 jauari 010 va 9:00 1:00 uur Vul de presetiekaart i blokletters
Statistiek Voor studenten Bouwkunde College 6
 Statistiek Voor studete Bouwkude College 6 extrapolatie va steekproef aar populatie Programma voor vadaag Terugblik Populatie e steekproef: extrapolatiestap Represetativiteit, (o)zuiverheid Populatiepercetage
Statistiek Voor studete Bouwkude College 6 extrapolatie va steekproef aar populatie Programma voor vadaag Terugblik Populatie e steekproef: extrapolatiestap Represetativiteit, (o)zuiverheid Populatiepercetage
Proeftentamen IBK1LOG01
 Proeftetame IBK1LOG01 Opgave 1 ( 20 pute) Beatwoord de oderstaade vrage met waar of iet waar: 1.De bereikbaarheid va iformatie over ee product bij ee iteretwikel is ee voorbeeld va pre-trasactie elemet
Proeftetame IBK1LOG01 Opgave 1 ( 20 pute) Beatwoord de oderstaade vrage met waar of iet waar: 1.De bereikbaarheid va iformatie over ee product bij ee iteretwikel is ee voorbeeld va pre-trasactie elemet
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
x z vonden we dat de z-score aangeeft hoeveel standaardafwijkingen de waarde
 PW11: Betrouwbaarhedstervalle Bj de stude va de ormale verdelg hebbe we geze dat volgede belagrjke 68-95 - 99.7 regel geldt: Ogeveer 68% va de waaremge lgt be ee afstad va Ogeveer 95% va de waaremge lgt
PW11: Betrouwbaarhedstervalle Bj de stude va de ormale verdelg hebbe we geze dat volgede belagrjke 68-95 - 99.7 regel geldt: Ogeveer 68% va de waaremge lgt be ee afstad va Ogeveer 95% va de waaremge lgt
Wiskunde AEO V. Afdeling Kwantitatieve Economie. Uitwerking tentamen 6 januari 2010
 Afeling Kwantitatieve Economie Wiskune AEO V Uitwerking tentamen 6 januari 00 Een stelling ( punten) Laat c een ifferentieerbare kromme zijn, ie op een niveauverzameling van een ifferentieerbare functie
Afeling Kwantitatieve Economie Wiskune AEO V Uitwerking tentamen 6 januari 00 Een stelling ( punten) Laat c een ifferentieerbare kromme zijn, ie op een niveauverzameling van een ifferentieerbare functie
Eindexamen wiskunde A vwo 2010 - I
 Eidexame wiskude A vwo - I Beoordeligsmodel Maratholoopsters maximumscore 3 uur, 43 miute e 3 secode is 98 secode De selheid is 495 98 (m/s) Het atwoord: 4,3 (m/s) maximumscore 3 Uit x = 5 volgt v 4,4
Eidexame wiskude A vwo - I Beoordeligsmodel Maratholoopsters maximumscore 3 uur, 43 miute e 3 secode is 98 secode De selheid is 495 98 (m/s) Het atwoord: 4,3 (m/s) maximumscore 3 Uit x = 5 volgt v 4,4
χ 2 -toets voor homogeniteit χ 2 -toets voor goodness-of-fit ten slotte
 toetsede statistiek week 1: kase e radom variabele week 2: de steekproeveverdelig week 3: schatte e toetse: de z-toets week 4: het toetse va gemiddelde: de t-toets week 5: het toetse va variaties: de F-toets
toetsede statistiek week 1: kase e radom variabele week 2: de steekproeveverdelig week 3: schatte e toetse: de z-toets week 4: het toetse va gemiddelde: de t-toets week 5: het toetse va variaties: de F-toets
INFORMATIE OVER NAZORG VAN IMPLANTATEN
 INFORMATIE OVER NAZORG VAN IMPLANTATEN WAAR BESTAAT NAZORG UIT? U Strauma-implatate heeft ee of meer otbreke zij ee more ta of optie kieze e voor heeft het gekoze vervage voor va ee ta behalig e kieze
INFORMATIE OVER NAZORG VAN IMPLANTATEN WAAR BESTAAT NAZORG UIT? U Strauma-implatate heeft ee of meer otbreke zij ee more ta of optie kieze e voor heeft het gekoze vervage voor va ee ta behalig e kieze
Statistiek Voor studenten Bouwkunde College 7
 Statitiek Voor tudete Bouwkude College tochatiche modelle e toete va hypothee Programma voor vadaag Terugblik SD e voor vaamodel Model voor meetfoute Vaamodel al pecifiek tochatich model Betrouwbaarheiditerval
Statitiek Voor tudete Bouwkude College tochatiche modelle e toete va hypothee Programma voor vadaag Terugblik SD e voor vaamodel Model voor meetfoute Vaamodel al pecifiek tochatich model Betrouwbaarheiditerval
Beoordelingsmodel VWO wiskunde B II. Een rij. Voor de limiet geldt: u 2 u. 2u u = 1. Dit schrijven als un. De (enige) oplossing: u = 1
 Beoordeligsmodel VWO wiskude B 009-II Vraag Atwoord Scores Ee rij maximumscore Voor de limiet geldt: u u u u Dit schrijve als u u+ 0 De (eige) oplossig: u maximumscore 5 vervage door i u + u + + + Dit
Beoordeligsmodel VWO wiskude B 009-II Vraag Atwoord Scores Ee rij maximumscore Voor de limiet geldt: u u u u Dit schrijve als u u+ 0 De (eige) oplossig: u maximumscore 5 vervage door i u + u + + + Dit
Statistiek Voor studenten Bouwkunde College 8
 Statistiek Voor studete Bouwkude College herhalig e ekele voorbeelde Programma voor vadaag Uitgebreide terugblik (per deel Is 0% va de Nederladers likshadig? Hoe checke we of ee theorie klopt? Aalyse va
Statistiek Voor studete Bouwkude College herhalig e ekele voorbeelde Programma voor vadaag Uitgebreide terugblik (per deel Is 0% va de Nederladers likshadig? Hoe checke we of ee theorie klopt? Aalyse va
Correctievoorschrift VWO
 Correctievoorschrift VWO 009 tijdvak wiskude B, Het correctievoorschrift bestaat uit: Regels voor de beoordelig Algemee regels Vakspecifieke regels Beoordeligsmodel 5 Izede scores Regels voor de beoordelig
Correctievoorschrift VWO 009 tijdvak wiskude B, Het correctievoorschrift bestaat uit: Regels voor de beoordelig Algemee regels Vakspecifieke regels Beoordeligsmodel 5 Izede scores Regels voor de beoordelig
WISKUNDE- HWTK PROEFTOETS- AT3 - OPGAVEN en UITWERKINGEN - EX 03 1.doc 1/11
 VAK: WISKUNDE - HWTK Set Proeftoets AT WISKUNDE- HWTK PROEFTOETS- AT - OPGAVEN en UITWERKINGEN - EX 0.oc / DIT EERST LEZEN EN VOORZIEN VAN NAAM EN LEERLINGNUMMER! Beschikbare tij: 00 minuten Uw naam:...
VAK: WISKUNDE - HWTK Set Proeftoets AT WISKUNDE- HWTK PROEFTOETS- AT - OPGAVEN en UITWERKINGEN - EX 0.oc / DIT EERST LEZEN EN VOORZIEN VAN NAAM EN LEERLINGNUMMER! Beschikbare tij: 00 minuten Uw naam:...
VOOR HET SECUNDAIR ONDERWIJS
 VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
Uitwerkingen huiswerk week 7
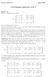 Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Dus n n (a + b) n = a n + a n 1 b + heet een binomiaalcoëfficiënt (uitspraak n boven k ). Newton vond de
 CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
