Kettingbreuken, weefpatronen en de Kerststelling van Fermat
|
|
|
- Pieter-Jan van Doorn
- 5 jaren geleden
- Aantal bezoeken:
Transcriptie
1 2 NAW 5/6 nr 2 juni 205 Kettingbreuen, weefpatronen en de Kerststelling van Fermat Paul Levrie, Rudi Penne Paul Levrie Faculteit Toegepaste Ingenieurswetenschappen Universiteit Antwerpen paullevrie@uantwerpenbe Rudi Penne Faculteit Toegepaste Ingenieurswetenschappen Universiteit Antwerpen rudipenne@uantwerpenbe Vaantiecursus Kettingbreuen, weefpatronen en de Kerststelling van Fermat Op de vaantiecursus 204 van het Platform Wisunde Nederland hielden Paul Levrie en Rudi Penne de voordracht Priem!, over een onderwerp dat sinds het bewijs van Yitang Zhang over priemparen weer volop in de belangstelling staat Een onderwerp oo waarover Levrie en Penne onlangs een boe publiceerden: De pracht van priemgetallen Voor de syllabus van de vaantiecursus schreven ze dit artiel, dat niet zo zeer een weergave van hun voordracht is, maar een voortborduursel op hun recente boe Additieve getaltheorie en de stelling van Fermat Dat getaltheorie verslavend an zijn, an je nu oo lezen in de laatste editie van het beroemde boe An introduction to the theory of numbers, van Hardy en Wright [3] Je vindt er namelij in de introductie: Toen ons gevraagd werd om voor de syllabus van deze vaantiecursus een bijdrage te leveren over een onderwerp waar we net een boe [5] over hadden geschreven, lee het ons onzinnig om dubbel wer te leveren Daarom grijpen we liever de ans om een nieuw hoofdstu te breien aan dit boe Ons verhaal over de priemgetallen is een mix van wisunde, geschiedenis en leue weetjes Omdat het doelpublie anders is dan dat van het boe, mag het wat meer wisundig zijn, al zullen we de lezer onderweg verrassen met een heuse snit-en-naadtoepassing Het begint allemaal met dit: Bedoeld wordt natuurlij additive De additieve getaltheorie behandelt eigenschappen van getallen waarbij men deze probeert te schrijven als som van andere speciale getallen Een van de mooiste resultaten op dit gebied is de Kerststelling van Fermat, die in haar meest ruwe vorm zegt: El priemgetal van de vorm 4n is te schrijven als de som van twee wadraten Iets meer verfijnd hebben we dit: Een priemgetal is een natuurlij getal groter dan dat enel deelbaar is door en door zichzelf Een getal an geschreven worden als de som van twee wadraten als alle priemfactoren van de vorm 4n 3 in de priemfactorisatie van het gegeven getal vooromen met een even macht En we gaan het hebben over een stelling die ons vertelt wele priemgetallen te schrijven zijn als een som van twee wadraten In het ader hiernaast vind je de geschiedenis van deze stelling Dat de stap van de ruwe naar de verfijnde versie niet zo groot is, volgt uit twee dingen Eerst en vooral is het eenvoudig in te zien dat een priemgetal van de vorm 4n 3 niet te schrijven is als
2 2 Paul Levrie, Rudi Penne Kettingbreuen, weefpatronen en de Kerststelling van Fermat NAW 5/6 nr 2 juni De minder beende Franse wisundige Albert Girard ( ) schrijft een opmering in de Franse vertaling van het wer van Simon Stevin: een som van twee wadraten Indien dit wel het geval zou zijn, dan moet het gaan om een wadraat van een even getal en een wadraat van een oneven getal Een even getal unnen we voorstellen door 2 bijvoorbeeld, en een oneven getal door 2m We hebben dan voor de som van de wadraten: (2) 2 (2m ) 2 = 4 2 (4m 2 4m ) = 4( 2 m 2 m), 640 Pierre de Fermat (60 665) schrijft op erstdag in een brief naar collega Marin Mersenne ( ): en dit geeft dus steeds een viervoud plus, en nooit plus 3 Verder unnen we gebrui maen van de wonderbaarlije eigenschap die ons toelaat een product van twee sommen van wadraten te schrijven als een som van wadraten: Fermat beweerde dat hij een onweerlegbaar bewijs had van deze stelling (zo ennen we hem) 742 Leonhard Euler ( ) schrijft op 30 juni in een brief aan Christian Goldbach: 749 Euler schrijft op 2 april naar Goldbach: 754 Euler publiceert een Demonstratio theorematis Fermatiani omnem numerum primum formae 4n esse summam duorum quadratorum 848 Charles Hermite (822 90) en Joseph-Alfred Serret (89 885) vinden tegelijertijd een efficiënt algoritme om een priemgetal van de vorm 4n te schrijven als de som van twee wadraten 855 Henry John Stephen Smith ( ) geeft een eerste eenvoudig bewijs van de stelling 867 Édouard Lucas (842 89) ziet een toepassing van de stelling van Fermat, die oo wel eens Fermat s Kerstmis-stelling wordt genoemd, bij het weven van satijn 940 Godfrey Harold Hardy ( ) schrijft in zijn A Mathematician s Apology dit: Uit de laatste zin blijt dat Hardy het bewijs van zijn landgenoot Smith, die evenals hijzelf de Savilian Chair of Geometry beleedde in Oxford, niet ende 984 Roger Heath-Brown (952) geeft een nieuw, ort bewijs van de stelling 990 Don Zagier (95) publiceert zijn A One-Sentence Proof That Every Prime p (mod 4) Is a Sum of Two Squares (a 2 b 2 )(c 2 d 2 ) = (ac bd) 2 (ad bc) 2 (eenvoudig te zien door uitwering) Voor een willeeurig getal dat voldoet aan de voorwaarden van de verfijnde stelling gaan we nu als volgt te wer: de factoren 2 schrijven we als 2 2 en de priemfactoren van de vorm 4n schrijven we als som van twee wadraten, en met de vorige eigenschap unnen we dan het product van deze getallen voorstellen als som van twee wadraten:a 2 B 2 ; de andere factoren hebben een even macht, en zijn samen te herschrijven in de vormc 2, en die unnen we dan gewoon op de volgende manier binnenbrengen : (A 2 B 2 )C 2 = (AC) 2 (BC) 2 Onze bedoeling is om in de rest van dit artiel het bewijs te geven van Henry Smith uit 855 voor de ruwe vorm van de stelling van Fermat We volgen in essentie de lijnen van [], hoewel Smith gebrui maate van continuanten, dingen waarvan de meeste mensen nooit gehoord hebben In plaats daarvan zullen wij weren met ettingbreuen, die we onder andere ennen van [4] Kettingbreuen hebben te maen met lineaire recursiebetreingen, en hierover is er een inleiding te vinden in appendix A Het verband met de ettingbreuen lees je dan weer in appendix B Dus als je alle details wil weten, lees dan de appendices Maar je an het verhaal oo volgen zonder de details van de appendices Eerst vertellen we wat meer over ettingbreuen, en in de volgende paragraaf geven we dan onze eigen versie van het bewijs van Smith Daarna gaan we op zoe naar de twee wadraten, wisundig, met de ettingbreuen, maar oo grafisch, via de toepassing beschreven door Édouard Lucas in 867 (zie geschiedundig overzicht) Eindige ettingbreuen Voor el niet-geheel rationaal getal an je wat men noemt een eindige ettingbreu vinden We laten dit zien aan de hand van het voorbeeld 39 6 We bepalen het grootste geheel getal dat in de breu in westie past, en schrijven 39 6 = = Met de noemer van de tweede term in het rechterlid gaan we dan op dezelfde manier verder:
3 3 4 NAW 5/6 nr 2 juni 205 Kettingbreuen, weefpatronen en de Kerststelling van Fermat Paul Levrie, Rudi Penne 39 6 = = = = Dit proces eindigt altijd en de laatste noemer is steeds een geheel getal 2 (waarom an dit niet gelij zijn aan?) De ettingbreu van een positief niet-geheel rationaal getal heeft dus de volgende vorm: b b 2 waarbij alle b s positieve gehele getallen zijn We zullen de notatie T enn gebruien voor de teller en de noemer van het rationaal getal dat we rijgen indien we deze ettingbreu uitweren: b b 2 b b b () = T N (2) blijt essentieel te zijn, en is een gevolg van (3) en (4) Meer algemeen zullen we de notaties T i j en N i j gebruien voor de teller en de noemer van de (uitgewerte) ettingbreu waarbij de b s lopen van b i tot b j en waarbij T i j en N i j onderling ondeelbaar zijn Het bewijs van de stelling van Fermat De stelling die we willen bewijzen zegt dit: El priemgetal van de vormp = 4n is te schrijven als de som van twee wadraten De essentie van het bewijs is het feit dat de tellers in (2) en (3) aan elaar gelij zijn, in combinatie met de volgende merwaardige formule: T =T j T j N j N j (4) Dit is formule (7) uit Appendix B We unnen ze oo zo schrijven (als j 2 ): want we hebben natuurlij dat T =T j T j N j T j2, (5) (dus beteent dat deb s geordend zijn vanb totb ) Ele stap in deze uitwering is van de vorm b j N = T N T j N j =b j b j2 b =b j T, j2 N j2 mett,n gehele getallen, waarbijt enn geen gemeenschappelije factor unnen hebben In onze notatie veronderstellen we dus datt enn onderling ondeelbaar zijn Indien we deb s in de omgeeerde volgorde zetten, dan noteren we het resultaat zo: en na uitwering van het rechterlid volgt hieruit door het onderling ondeelbaar zijn vant en bijhorenden datn j =T j2 We vertreen van een priemgetalp dat één meer is dan een viervoud, en we stellen de ettingbreu op voor breuen waarvan de teller gelij is aanp Stel dat zo n ettingbreu opgebouwd is met de getallen b,b 2,,b, dan worden (4) en (5) dus: b b = T N (3) p =T j T j N j N j =T j T j N j T j2 b 2 b Merwaardig genoeg is in beide gevallen de teller gelij, dat wil zeggen T =T We ijen even terug naar het voorbeeld aan het begin van deze paragraaf Als we de volgorde van deb s hierin omeren, dan rijgen we dit: = 39 7 met inderdaad dezelfde teller Deze eigenschap van ettingbreuen We beperen ons hierbij tot het geval datb 2, dat blijt voldoende te zijn voor het bewijs Een gevolg van deze veronderstelling is dat de beide breuen in het rechterlid van (2) en (3) een noemer hebben die ligt tussen 2 en 2n (herinner je datp = 4n ) Inderdaad, we hebben dan dat p noemer > 2 p = 4n >2 noemer Noemer = sluiten we overigens uit, want dan hebben we geen breu We beijen de verschillende breuen eens voorp = 3, dusn = 3 Het gaat dan om breuen met teller 3 en noemer respectievelij 2, 3, 4, 5, 6 Dit zijn de bijhorende ettingbreuen:
4 4 Paul Levrie, Rudi Penne Kettingbreuen, weefpatronen en de Kerststelling van Fermat NAW 5/6 nr 2 juni = 6 2, 3 3 = 4 3, 3 4 = 3 4, 3 5 = 2 2, 3 6 = 2 6 p =a 2 b 2 In dit eerste geval is de zaa dus bewezen Ofwel is het aantal b s voor de speciale breu oneven, stel dus = 2j Dan ziet de breu er zo uit: Let op het verband tussen de ettingbreuen die horen bij de breuen met noemers 2 en 6: de volgorde van de b s is omgewisseld Oo die met noemers 3 en 4 omen op deze wijze met elaar overeen De overblijvende breu, met noemer 5, valt op door het feit dat als je de volgorde van de b s in de ettingbreu omeert, dat deze niet verandert ten gevolge van een soort palindromisch effect Dit zal oo meer algemeen zo zijn: met el getal uit{2, 3, 4,,2n} (= de mogelije noemers) unnen we een ander getal uit deze verzameling associëren op deze manier Neem als getalj, bepaal de ettingbreu voor p j, eer de volgorde van deb s om zoals in (2) en (3), en dan is de noemer van de resulterende breu opnieuw een getal uit {2, 3, 4,,2n} Omdat het aantal elementen in de verzameling{2, 3, 4,,2n} gelij is aan 2n, een oneven getal, en omdat we deze dus unnen verdelen in groepjes van twee noemers die bij elaar horen, zal er altijd één noemer overblijven, die dan oo deze palindromische eigenschap zal moeten hebben: b =b, b 2 =b, en dus geldt b b j b j b j2 b =b, b j b j b j b Hiermee weren we verder We onderscheiden nu twee gevallen Ofwel is het aantalb s voor deze ene speciale breu even, stel dus = 2j Dan ziet de breu er zo uit: b j2 =b j b want inderdaad geldt b j b j Nu unnen we dit zo schrijven: b =b b j =b j b b j b j b b T j N j = T j N j, (6) en hieruit volgt wegens het onderling ondeelbaar zijn van tellers en noemers datt j =T j, noem dit geheel getala, en oon j = N j, noem ditb De eerste vergelijing in het adertje wordt dan:, b Dit laatste unnen we nu zo schrijven: T j2 N j2 = T j N j, en hieruit volgt dan onmiddellij datt j2 = T j Uit het tweede deel van de vergelijing in het adertje volgt dan: p =T j T j N j T j2 =T j (T j N j ), waarbijt j niet gelij an zijn aan Uit deze laatste uitdruing volgt datp niet priem is, wat in strijd is met het gestelde We zijn er dus nu zeer van datp te schrijven is als de som van twee wadraten, en datin dit geval even is Hiermee is het bewijs laar Op zoe naar de twee wadraten We willen natuurlij oo graag weten van wele twee wadraten het priemgetalp = 4n de som is Hiervoor proberen we meer te weten te omen over de noemer in de palindromische ettingbreu, we stellen deze noemer voor door d Hierbij gebruien we de formule (6) uit Appendix B: N T T N = ( ) =, (7) b of nog p =T j T j N j N j = (T j ) 2 (N j ) 2 die we hier toepassen meteven Hierbij ist =penn =d Uit (2):
5 5 6 NAW 5/6 nr 2 juni 205 Kettingbreuen, weefpatronen en de Kerststelling van Fermat Paul Levrie, Rudi Penne p d = T N =b b 2 =b T, 2 N = b b en uit het onderling ondeelbaar zijn vant en bijhorenden volgt datd de teller is van de volgende ettingbreu: (palindromisch!) en we bereenen dit deel ervan: 2 2 = 5 2, T 2 N 2 =b 2 b 3 en met de teller en de noemer unnen we 29 schrijven als een som van twee wadraten: 29 = b b Maar we hebben vroeger gezien dat de teller van zo n ettingbreu niet verandert als we de volgorde van deb s omeren We rijgen dan de volgende ettingbreu, die we anders unnen schrijven door gebrui te maen van het palindromisch arater van deb s: b b b 3 b 2 =b b 2 b 2 b vermits b = b, b = b 2, enzovoort De teller van deze laatste ettingbreu is dus oo gelij aand Dit beteent datt =d De vergelijing (7) wordt dan: d 2 pn = d 2 =pn d 2 is deelbaar doorp Het is niet moeilij om in te zien dat er maar één getaldan zijn tussen 2 en 2n met deze eigenschap Stel namelij dat er zo twee zijn,d en d 2, metd >d 2, met zoweld 2 alsd2 2 deelbaar doorp Dan volgt onmiddellij dat oo het verschild 2 d2 2 = (d d 2 )(d d 2 ) deelbaar zal zijn door het priemgetalp, maar beide factoren zijn leiner danp, dus dat an niet Voor het bepalen van de uniee noemerdgaan we dan als volgt te wer: bepaal het wadraat van de getallen 2, 3, en tel er bij op Indien het resultaat deelbaar is doorp, dan heb jedgevonden Voorp = 29 vinden we voor die wadraten plus het volgende, op veelvouden van 29 na:, Dit laatste volgt uit (6), want we hebben bewezen dat teller en noemer van het rechterlid de twee getallen zijn die we zoeen De methode van Édouard Lucas We unnen de getallenaenboo op een andere manier bepalen Édouard Lucas bracht in 867 de stelling van Fermat in verband met het weven van draden tot textiel Hierbij worden verticale en horizontale draden met elaar vervlochten, zoals aan de linerant van Figuur Het gaat hier om een zogenaamde satijnbinding Bij satijn ruisen wat men noemt de etting- en de inslagdraden elaar op een speciale manier Als de zwarte ettingdraad op een bepaalde plaats boven ligt, dan ligt bij minstens vier van de volgende ruisingen de rode inslagdraad boven Op de figuur zijn het er precies vier Het patroon herhaalt zich, en an daarom voorgesteld worden zoals rechts in de figuur, met wat in het blauwe vierant te zien is, een vierant opgebouwd uit 5 5 leine vieranten, waarvan er als volgt een aantal zwart geleurd zijn: leur het vierantje linsonder in, ga dan één olom opzij en twee rijen omhoog en leur daar het vierantje in, ga weer naar rechts en twee omhoog enzovoort Kom je uit boven de 5, dan tel je van onderen te beginnen verder Omdat de zijde van het vierant een priemgetal is, zal het toepassen van deze methode er steeds voor zorgen dat er op ele rij en olom precies één vierant is ingeleurd, één per rij en één per olom In Figuur 2 is een voorbeeld te zien in het geval we niet vier maar twaalf opeenvolgende ruisingen hebben met de inslagdraad boven, het gaat dan om een vierant van 3 3 Dit an op verschillende manieren, zoals je an zien op Figuur 2 In de verschillende delen van de figuur gaat men respectievelij met stappen van, 2, 3, 4, 5 en 6 naar boven, steeds startend linsonder in een vierant Zo ontstaan We besluiten datd=2 We bepalen nu de ettingbreu voor 29/2: Figuur
6 6 Paul Levrie, Rudi Penne Kettingbreuen, weefpatronen en de Kerststelling van Fermat NAW 5/6 nr 2 juni Het beendste voorbeeld van een lineaire recursiebetreing is dit: y =y y 2 voor=, 2, 3, waarbij allea s enb s gelij zijn aan In feite staan hier oneindig veel vergelijingen, waarvan de eerste gegeven zijn door: y =y 0 y, y 2 =y y 0, y 3 =y 2 y, Figuur 2 patronen Lucas merte op dat het patroon in het midden onderaan het mooiste is omdat er allerlei vieranten in te zien zijn Bovendien is het het enige dat niet verandert als je het een wartslag draait Mer op dat we bij dit patroon stijgen in stappen van 5 En 5 was precies de noemer die hoorde bij het priemgetal 3 waarvan de ettingbreu palindromisch was! Lucas bewees oo dat een dergelije symmetrie niet vooromt indien het aantal vierantjes per zijde een priemgetal is van de vorm 4n 3 We doen het nog even opnieuw voor p = 29, en de bijhorende noemer 2 Kleur in een vierant van het vierantje linsonder in, ga dan één olom opzij en twaalf rijen omhoog en leur daar het vierantje in, ga weer naar rechts en twaalf omhoog, enzovoort (Figuur 3, lins) Opnieuw ontstaan er vieranten, waarvan er één is aangeduid op de figuur Het wordt duidelijer indien we de blauwe vierantjes vervangen door roosterpunten in een rooster van (Figuur 3, rechts) Via de stelling van Pythagoras vinden we dan dat het wadraat van de zijde van het aangeduide vierant te schrijven is als = 29 Bijna 250 jaar na de eerste formulering van de stelling van Fermat door Girard, vond Lucas [6 7] er zo een echte pratische toepassing van! Voor Lucas werd het zelfs een heel nieuwe ta van de meetunde, die hij Géométrie plane des tissus (Vlae meetunde van de stoffen) doopte Hij vond hierbij navolging bij andere wisundigen, waarvan de meest beende Pafnuty Chebyshev (82 894) is, met zijn ongepubliceerd artiel Sur la coupe des vêtements uit 878 waarin hij bereent wele vorm je uit een stu stof moet uitnippen om er een boloppervla volledig mee te unnen aanleden Voor de geïnteresseerde lezer, je doet het zoals in Figuur 4 wordt gedemonstreerd Bovenaan zie je de vorm die je uit de stof moet snijden, onderaan het aanleden van de bol (Met dan aan Étienne Ghys [2] voor de bovenste afbeelding, en aan Jos Leys voor de andere) Mer op dat je met deze vergelijingen inderdaad een oneindige rij getallen genereert, op voorwaarde dat je de eerste twee getalleny en y 0 vastlegt Voor deze recursiebetreing is de standaardeuze y =y 0 = (we spreen van beginvoorwaarden) We rijgen dan de volgende rij getallen: y =,y 0 =,y = 2,y 2 = 3,y 3 = 5,y 4 = 8,y 5 = 3,y 6 = 2, Deze rij is beroemd en wordt de rij van Fibonacci genoemd Als we andere beginvoorwaarden iezen, dan rijgen we een andere rij getallen Een mooie eigenschap van dit soort recursiebetreingen is dat als je al twee oplossingen bereend hebt, dat alle andere oplossingen dan te vinden zijn uit die twee Het is ideaal als je eerst deze twee specifiee oplossingen bereent: oplossinga meta =,A 0 = 0, oplossingb metb = 0,B 0 =, In Tabel zie je de eerste paar termen van beide rijen Door de speciale euze van de beginvoorwaarden unnen we nu ele andere oplossing y van de recursiebetreing schrijven met behulp van deze twee Je ziet in de tabel dat als je de oplossinga vermenigvuldigt mety en daarb, vermenigvuldigd mety 0, bij optelt, dat je dan de eerste 2 waarden vany rijgt Door de lineariteit van de recursiebetreing is het dan eenvoudig in te zien dat voor elegeldt: y =y A y 0 B We hebben de volgende eigenschap nodig, eveneens een gevolg van de lineariteit: A B A B = ( ) a a 2 a (8) Appendix A Lineaire recursiebetreingen Een lineaire recursiebetreing (van de tweede orde) is een vergelijing die het verband geeft tussen drie opeenvolgende termen van een oneindige rij getalleny,y 0,y,,y n, Zo n vergelijing neemt de volgende vorm aan: y =b y a y 2 voor=, 2, 3, De getallena,a 2,a 2, enb,b 2,b 3, zijn hierbij gegeven Figuur 3
7 7 8 NAW 5/6 nr 2 juni 205 Kettingbreuen, weefpatronen en de Kerststelling van Fermat Paul Levrie, Rudi Penne Figuur 4 Dit unnen we bewijzen per inductie, en daarvoor gebruien we eigenschappen van determinanten: A A B B = b A a A 2 b B a B 2 A B = a A B A 2 B 2 : 0 2 n A : 0 a b 2 a A n B : 0 b b 2 b a 2 B n y : y y 0 y y 2 y n Tabel met A 0 B 0 A B = Vanaf nu zullen we enel nog weren met recursiebetreingen waarbij a = voor ele waarde van:
8 8 Paul Levrie, Rudi Penne Kettingbreuen, weefpatronen en de Kerststelling van Fermat NAW 5/6 nr 2 juni : 0 2 j j j n B () : 0 b B () 2 B () j B () j B () j B n () : 0 b 2 j j j B n (2) B (3) : 0 B(3) j B (3) j B (3) j B (3) n B (j) : b j B (j) j B (j) n B (j) : 0 b j B (j) n B (j2) : 0 B (j2) n Tabel 2 y =b y y 2 voor=, 2, 3, We definiëren een aantal basisoplossingen zoals in Tabel 2 De positie van de twee opeenvolgende waarden 0 en arateriseert de verschillende basisoplossingen waarvan je de naam an lezen in de eerste olom Om te beginnen an je opmeren datb () =B en =A, en dus wordt eigenschap (8): B() B(2) B() = ( ) (9) Verder is er natuurlij voor ele waarde vanj voldaan aan de recursiebetreing: T N =b b 2 b b = B(), (3) waarbij deb s de coëfficiënten zijn in de recursiebetreing in Appendix A Uit het feit dat beide breuen (lins en rechts) niet te vereenvoudigen zijn, volgt dan datt =B () enn = Verder hebben we oo: B (j) =b B (j) B(j) 2 (0) T N =b b = B() B () (4) Uit deze tabel unnen we twee interessante relaties tussen deze oplossingen aflezen We baseren ons hiervoor op de waarden vanb (j) enb (j2) in de leine rechthoe Om te beginnen ijen we naarb (), en je ziet dan dat deze oplossing de volgende lineaire combinatie is van de twee onderste oplossingen: VoorB (j) n vinden we op dezelfde manier: B () =B() j B(j) B () j B(j2) () B (j) n =b j B (j) n B (j2) n (2) b 2 b voor de ettingbreu waarin de b s in de omgeeerde volgorde staan DusT =B () enn =B () Formule (3) unnen we veralgemenen tot: T j N j =b j b j2 b = B(j) B (j2) (5) Deze recursiebetreing verbindt drie onder elaar staande getallen in de tabel, en heeft als onmiddellij gevolg dat twee opeenvolgende elementen van een olom geen gemeenschappelije factor unnen hebben Hadden ze wel een gemeenschappelije factor, dan volgt uit (2) dat deze factor de hele olom deelt, wat niet mogelij is door het vooromen van het getal in ele olom Appendix B Verband met ettingbreuen Met de resultaten uit Appendix A unnen we laten zien (zie verder) dat we het volgende resultaat hebben: De formules (3) en (5) volgen uit (2) We herschrijven deze vergelijing als volgt: B (j) =b jb (j) B (j2) We starten nu metj = : B(j) B (j) =b j B (j) B (j2)
9 9 20 NAW 5/6 nr 2 juni 205 Kettingbreuen, weefpatronen en de Kerststelling van Fermat Paul Levrie, Rudi Penne B () =b B (3) =b b 2 B (3) B (4) =b b 2 b B () B () =b b 2 b b De laatste stap volgt uit de beginvoorwaarden in combinatie met de recursiebetreing We hebben namelij datb () =b enb () = Voor (4) vertreen we van de vergelijing (0) metj = en herschrijven deze als volgt: B () =b B () B() 2 B() B () =b B () B () 2 We vervangen dan in de linse vergelijingdoor en herhalen het procedé Formule (9) unnen we nu herschrijven als Formule () wordt N T T N = ( ) (6) T =T j T j N j N j (7) Referenties FW Clare, WN Everitt, LL Littlejohn en SJR Vorster, HJS Smith and the Fermat two squares theorem, Amer Math Monthly 06(7) (999), É Ghys, Sur la coupe des vêtements: variation autour d un théorème de Tchebychev [On the cutting of garments: variation on a theme of Chebyshev], Enseign Math (2) 57( 2) (20), GH Hardy en EM Wright, An Introduction to the Theory of Numbers, Roger Heath-Brown, Joseph Silverman en Andrew Wiles (red), Oxford University Press, M Kindt en P Lemmens, Ontwielen met ettingbreuen, Zebra-rees, deel 33, Epsilon Uitgaven, Amsterdam, 20 5 P Levrie en R Penne, De pracht van priemgetallen, Prometheus, Amsterdam, É Lucas, Application de l arithmétique à la construction de l armure des satins réguliers, G Retaux, Paris, É Lucas, Les principes fondamentaux de la géométrie des tissus, Congrès de l Association française pour l avancement des sciences 40(2) (9), 72 88
This item is the archived peer-reviewed author-version of:
 This item is the archived peer-reviewed author-version of: Kettingbreuen, weefpatronen en de erststelling van Fermat Reference: Levrie Paul, Penne Rudi.- Kettingbreuen, weefpatronen en de erststelling
This item is the archived peer-reviewed author-version of: Kettingbreuen, weefpatronen en de erststelling van Fermat Reference: Levrie Paul, Penne Rudi.- Kettingbreuen, weefpatronen en de erststelling
Differentiequotiënten en Getallenrijen
 Lesbrief 4 Binomiaalcoëfficiënten, Differentiequotiënten en Getallenrijen Binomiaalcoëfficiënten Het is beend dat (a + b 2 = a 2 + 2ab + b 2 en dat (a + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3. In het algemeen
Lesbrief 4 Binomiaalcoëfficiënten, Differentiequotiënten en Getallenrijen Binomiaalcoëfficiënten Het is beend dat (a + b 2 = a 2 + 2ab + b 2 en dat (a + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3. In het algemeen
Opgaven Bewijzen en Inductie 1 mei 2019, Datastructuren, Werkcollege.
 Opgaven Bewijzen en Inductie mei 09, Datastructuren, Wercollege. Gebrui deze opgaven, naast die uit het boe, om de stof te oefenen op het wercollege. Cijfer: Op een toets rijg je meestal zes tot acht opgaven..
Opgaven Bewijzen en Inductie mei 09, Datastructuren, Wercollege. Gebrui deze opgaven, naast die uit het boe, om de stof te oefenen op het wercollege. Cijfer: Op een toets rijg je meestal zes tot acht opgaven..
NATUURLIJKE, GEHELE EN RATIONALE GETALLEN
 II NATUURLIJKE, GEHELE EN RATIONALE GETALLEN Iedereen ent getallen: de natuurlije getallen, N = {0,1,2,3,...}, gebruien we om te tellen, om getallen van elaar af te unnen treen hebben we de gehele getallen,
II NATUURLIJKE, GEHELE EN RATIONALE GETALLEN Iedereen ent getallen: de natuurlije getallen, N = {0,1,2,3,...}, gebruien we om te tellen, om getallen van elaar af te unnen treen hebben we de gehele getallen,
Examen G0U13 - Bewijzen en Redeneren,
 Examen G0U13 - Bewijzen en Redeneren, 2010-2011 bachelor in de Wisunde, bachelor in de Fysica, bachelor in de Economische Wetenschappen en bachelor in de Wijsbegeerte Vrijdag 4 februari 2011, 8u30 Naam:
Examen G0U13 - Bewijzen en Redeneren, 2010-2011 bachelor in de Wisunde, bachelor in de Fysica, bachelor in de Economische Wetenschappen en bachelor in de Wijsbegeerte Vrijdag 4 februari 2011, 8u30 Naam:
Uitwerkingen Tentamen Wat is Wiskunde (WISB101) Donderdag 10 november 2016, 9:00-12:00
 Uitweringen Tentamen Wat is Wisunde (WISB101) Donderdag 10 november 2016, 9:00-12:00 Docenten: Barbara van den Berg & Carel Faber & Arjen Baarsma & Ralph Klaasse & Vitor Blåsjö & Guido Terra-Bleeer Opgave
Uitweringen Tentamen Wat is Wisunde (WISB101) Donderdag 10 november 2016, 9:00-12:00 Docenten: Barbara van den Berg & Carel Faber & Arjen Baarsma & Ralph Klaasse & Vitor Blåsjö & Guido Terra-Bleeer Opgave
Universiteit Leiden, 2015 Wiskundewedstrijdtraining, week 14
 Universiteit Leiden, 0 Wisundewedstrijdtraining, wee Wee : reesen Een rees is een speciaal soort rij, dus: den altijd eerst na over convergentie! bijzonder: monotone, begrensde rijen convergeren In het
Universiteit Leiden, 0 Wisundewedstrijdtraining, wee Wee : reesen Een rees is een speciaal soort rij, dus: den altijd eerst na over convergentie! bijzonder: monotone, begrensde rijen convergeren In het
NIEUWE TIJDEN. Syllabus Vakantiecursus 2014. Eindhoven, 22 en 23 augustus Amsterdam, 29 en 30 augustus
 NIEUWE TIJDEN Syllabus Vakantiecursus 2014 Eindhoven, 22 en 23 augustus Amsterdam, 29 en 30 augustus NIEUWE TIJDEN Syllabus Vakantiecursus 2014 (uitgebreide en gecorrigeerde web-versie) Eindhoven, 22
NIEUWE TIJDEN Syllabus Vakantiecursus 2014 Eindhoven, 22 en 23 augustus Amsterdam, 29 en 30 augustus NIEUWE TIJDEN Syllabus Vakantiecursus 2014 (uitgebreide en gecorrigeerde web-versie) Eindhoven, 22
Telproblemen. K. P. Hart
 Telproblemen K. P. Hart 1. Theorie en opgaven voor zelfstudie Inleiding Iedereen weet wat tellen is. Hoeveel studenten zijn er in de collegezaal? Even tellen: één, twee, drie,..., éénenvijftig,... Wat
Telproblemen K. P. Hart 1. Theorie en opgaven voor zelfstudie Inleiding Iedereen weet wat tellen is. Hoeveel studenten zijn er in de collegezaal? Even tellen: één, twee, drie,..., éénenvijftig,... Wat
Oplossen van lineaire differentiaalvergelijkingen met behulp van de methode van Leibniz-MacLaurin
 Oplossen van lineaire differentiaalvergelijingen met behulp van de methode van Leibniz-MacLaurin Calculus II voor S, F, MNW 7 november 2005 1 De n-de afgeleide van het product van twee functies Voor we
Oplossen van lineaire differentiaalvergelijingen met behulp van de methode van Leibniz-MacLaurin Calculus II voor S, F, MNW 7 november 2005 1 De n-de afgeleide van het product van twee functies Voor we
The bouncing balls and pi
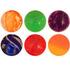 The bouncing balls and pi naar een idee van Dir Dancaert 9 september 05 Samenvatting Wisundecollega Dir Dancaert ontdete onlangs een merwaardig filmpje op het internet (https://wwwyoutubecom/user/numberphile
The bouncing balls and pi naar een idee van Dir Dancaert 9 september 05 Samenvatting Wisundecollega Dir Dancaert ontdete onlangs een merwaardig filmpje op het internet (https://wwwyoutubecom/user/numberphile
Een Stelling over Priemgetallen Bewezen op een Schaakbord Seminar Combinatorial Algorithms (voorjaar 2010)
 Een Stelling over Priemgetallen Bewezen op een Schaakbord Seminar Combinatorial Algorithms (voorjaar 2010) Johan de Ruiter, johan.de.ruiter@gmail.com 27 april 2010 1 De stelling van Fermat over de som
Een Stelling over Priemgetallen Bewezen op een Schaakbord Seminar Combinatorial Algorithms (voorjaar 2010) Johan de Ruiter, johan.de.ruiter@gmail.com 27 april 2010 1 De stelling van Fermat over de som
102 < 11. Je kunt ook snel na 102 < 10, 5 ( = 110, 25).
 DE FORMULE VAN MACLAURIN. Inleiding: de wortel uit 0. Als je nou eens geen reenmachine had, hoe bereen je dan de wortel uit 0? Met proberen om je een heel eind. 0 > 0 omdat 0 > 0 en 0 < omdat reenen dat
DE FORMULE VAN MACLAURIN. Inleiding: de wortel uit 0. Als je nou eens geen reenmachine had, hoe bereen je dan de wortel uit 0? Met proberen om je een heel eind. 0 > 0 omdat 0 > 0 en 0 < omdat reenen dat
Cover Page. The handle holds various files of this Leiden University dissertation.
 Cover Page The handle http://hdl.handle.net/1887/20310 holds various files of this Leiden University dissertation. Author: Jansen, Bas Title: Mersenne primes and class field theory Date: 2012-12-18 Samenvatting
Cover Page The handle http://hdl.handle.net/1887/20310 holds various files of this Leiden University dissertation. Author: Jansen, Bas Title: Mersenne primes and class field theory Date: 2012-12-18 Samenvatting
Opgeloste en onopgeloste mysteries in de getaltheorie
 Opgeloste en onopgeloste mysteries in de getaltheorie Jan De Beule, Tom De Medts en Jeroen Demeyer Voorwoord 1 Voorwoord Beste leerling, Deze nota s zijn bedoeld als begeleiding bij 6 lesuren Opgeloste
Opgeloste en onopgeloste mysteries in de getaltheorie Jan De Beule, Tom De Medts en Jeroen Demeyer Voorwoord 1 Voorwoord Beste leerling, Deze nota s zijn bedoeld als begeleiding bij 6 lesuren Opgeloste
Meetkundige berekeningen
 Meetundige bereeningen 0. voorennis Sinus, cosinus en tangens De sinusregel In ele driehoe ABC geldt de sinusregel: sin cos B = c b B = c a tan B = a b Afspraa Bij het bereenen van een hoe geef je het
Meetundige bereeningen 0. voorennis Sinus, cosinus en tangens De sinusregel In ele driehoe ABC geldt de sinusregel: sin cos B = c b B = c a tan B = a b Afspraa Bij het bereenen van een hoe geef je het
4.1 Rijen. Inhoud. Convergentie van een reeks. Reeksen. a k. a k = lim. a k = s. s n = a 1 + a 2 + + a n = k=1
 Reesen en Machtreesen Reesen en Machtreesen 4-0 Reesen en Machtreesen Inhoud. Rijen 2. Reesen Definities en enmeren Reesen met niet-negatieve termen Reesen met positieve en negatieve termen 3. Machtreesen
Reesen en Machtreesen Reesen en Machtreesen 4-0 Reesen en Machtreesen Inhoud. Rijen 2. Reesen Definities en enmeren Reesen met niet-negatieve termen Reesen met positieve en negatieve termen 3. Machtreesen
Getaltheorie I. c = c 1 = 1 c (1)
 Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk
Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk
Getaltheorie II. ax + by = c, a, b, c Z (1)
 Lesbrief 2 Getaltheorie II 1 Lineaire vergelijkingen Een vergelijking van de vorm ax + by = c, a, b, c Z (1) heet een lineaire vergelijking. In de getaltheorie gaat het er slechts om gehele oplossingen
Lesbrief 2 Getaltheorie II 1 Lineaire vergelijkingen Een vergelijking van de vorm ax + by = c, a, b, c Z (1) heet een lineaire vergelijking. In de getaltheorie gaat het er slechts om gehele oplossingen
Worteltrekken modulo een priemgetal: van klok tot cutting edge. Roland van der Veen
 Worteltrekken modulo een priemgetal: van klok tot cutting edge Roland van der Veen Modulorekenen Twee getallen a en b zijn gelijk modulo p als ze een veelvoud van p verschillen. Notatie: a = b mod p Bijvoorbeeld:
Worteltrekken modulo een priemgetal: van klok tot cutting edge Roland van der Veen Modulorekenen Twee getallen a en b zijn gelijk modulo p als ze een veelvoud van p verschillen. Notatie: a = b mod p Bijvoorbeeld:
Dossier 3 PRIEMGETALLEN
 Dossier 3 PRIEMGETALLEN atomen van de getallenleer Dr. Luc Gheysens Een priemgetal is een natuurlijk getal met twee verschillende delers, nl. 1 en het getal zelf. De priemgetallen zijn dus 2, 3, 5, 7,
Dossier 3 PRIEMGETALLEN atomen van de getallenleer Dr. Luc Gheysens Een priemgetal is een natuurlijk getal met twee verschillende delers, nl. 1 en het getal zelf. De priemgetallen zijn dus 2, 3, 5, 7,
-- III De variatiemethode berust voor de grondtoestand op het volgende theorema:
 -- III - 1 - HOOFDSTUK III VARIATIEREKENING Alleen voor enele zeer eenvoudige systemen an de Schrödinger Vergeliing exact worden opgelost, in alle andere gevallen moeten benaderingen worden toegepast.
-- III - 1 - HOOFDSTUK III VARIATIEREKENING Alleen voor enele zeer eenvoudige systemen an de Schrödinger Vergeliing exact worden opgelost, in alle andere gevallen moeten benaderingen worden toegepast.
Discrete Structuren. Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dystra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 12 februari 2008 INLEIDING Discrete Structuren Wee1: Inleiding Onderwerpen
Discrete Structuren Piter Dystra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 12 februari 2008 INLEIDING Discrete Structuren Wee1: Inleiding Onderwerpen
Kettingbreuken. 20 april 2010 1 K + 1 E + 1 T + 1 T + 1 I + 1 N + 1 G + 1 B + 1 R + 1 E + 1 U + 1 K + E + 1 N 1 2 + 1 0 + 1 A + 1 P + 1 R + 1 I + 1
 Kettingbreuken Frédéric Guffens 0 april 00 K + E + T + T + I + N + G + B + R + E + U + K + E + N 0 + A + P + R + I + L + 0 + + 0 Wat zijn Kettingbreuken? Een kettingbreuk is een wiskundige uitdrukking
Kettingbreuken Frédéric Guffens 0 april 00 K + E + T + T + I + N + G + B + R + E + U + K + E + N 0 + A + P + R + I + L + 0 + + 0 Wat zijn Kettingbreuken? Een kettingbreuk is een wiskundige uitdrukking
1 Delers 1. 3 Grootste gemene deler en kleinste gemene veelvoud 12
 Katern 2 Getaltheorie Inhoudsopgave 1 Delers 1 2 Deelbaarheid door 2, 3, 5, 9 en 11 6 3 Grootste gemene deler en kleinste gemene veelvoud 12 1 Delers In Katern 1 heb je geleerd wat een deler van een getal
Katern 2 Getaltheorie Inhoudsopgave 1 Delers 1 2 Deelbaarheid door 2, 3, 5, 9 en 11 6 3 Grootste gemene deler en kleinste gemene veelvoud 12 1 Delers In Katern 1 heb je geleerd wat een deler van een getal
2 n 1. OPGAVEN 1 Hoeveel cijfers heeft het grootste bekende Mersenne-priemgetal? Met dit getal vult men 320 krantenpagina s.
 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal is een natuurlijk getal groter dan 1 dat slechts deelbaar is door 1 en door zichzelf. Om technische redenen wordt
Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal is een natuurlijk getal groter dan 1 dat slechts deelbaar is door 1 en door zichzelf. Om technische redenen wordt
Inleiding tot de Problem Solving - deel 1: Combinatoriek en getaltheorie
 Inleiding tot de Problem Solving - deel 1: Combinatoriek en getaltheorie Jan Vonk 1 oktober 2008 1 Combinatoriek Inleiding Een gebied dat vandaag de dag haast niet onderschat kan worden binnen de wiskunde
Inleiding tot de Problem Solving - deel 1: Combinatoriek en getaltheorie Jan Vonk 1 oktober 2008 1 Combinatoriek Inleiding Een gebied dat vandaag de dag haast niet onderschat kan worden binnen de wiskunde
Getallenleer Inleiding op codeertheorie. Cursus voor de vrije ruimte
 Getallenleer Inleiding op codeertheorie Liliane Van Maldeghem Hendrik Van Maldeghem Cursus voor de vrije ruimte 2 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal
Getallenleer Inleiding op codeertheorie Liliane Van Maldeghem Hendrik Van Maldeghem Cursus voor de vrije ruimte 2 Hoofdstuk 1 Getallenleer 1.1 Priemgetallen 1.1.1 Definitie en eigenschappen Een priemgetal
OPLOSSINGEN VAN DE OEFENINGEN
 OPLOSSINGEN VAN DE OEFENINGEN 1.3.1. Er zijn 42 mogelijke vercijferingen. 2.3.4. De uitkomsten zijn 0, 4 en 4 1 = 4. 2.3.6. Omdat 10 = 1 in Z 9 vinden we dat x = c 0 +... + c m = c 0 +... + c m. Het getal
OPLOSSINGEN VAN DE OEFENINGEN 1.3.1. Er zijn 42 mogelijke vercijferingen. 2.3.4. De uitkomsten zijn 0, 4 en 4 1 = 4. 2.3.6. Omdat 10 = 1 in Z 9 vinden we dat x = c 0 +... + c m = c 0 +... + c m. Het getal
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie 9 februari 2009 INLEIDING
 Discrete Structuren Piter Dystra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 9 februari 2009 INLEIDING Discrete Structuren Wee1: Inleiding Onderwerpen Elementaire
Discrete Structuren Piter Dystra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 9 februari 2009 INLEIDING Discrete Structuren Wee1: Inleiding Onderwerpen Elementaire
Memoriseren: Een getal is deelbaar door 10 als het laatste cijfer een 0 is. Of: Een getal is deelbaar door 10 als het eindigt op 0.
 REKENEN VIJFDE KLAS en/of ZESDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Luc Cielen: Regels van deelbaarheid, grootste gemene deler en kleinste gemeen veelvoud 1 Deelbaarheid door 10, 100, 1000. Door
REKENEN VIJFDE KLAS en/of ZESDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Luc Cielen: Regels van deelbaarheid, grootste gemene deler en kleinste gemeen veelvoud 1 Deelbaarheid door 10, 100, 1000. Door
1.5.1 Natuurlijke, gehele en rationale getallen
 46 Getallen 1.5 Getaltheorie 1.5.1 Natuurlijke, gehele en rationale getallen De getallen 0,1,2,3,4,... enz. worden de natuurlijke getallen genoemd (de heleverzamelingvanaldezegetallenbijelkaarnoterenwemethetteken:
46 Getallen 1.5 Getaltheorie 1.5.1 Natuurlijke, gehele en rationale getallen De getallen 0,1,2,3,4,... enz. worden de natuurlijke getallen genoemd (de heleverzamelingvanaldezegetallenbijelkaarnoterenwemethetteken:
priemrecords? Jaap Top
 priemrecords? Jaap Top JBI-RuG & DIAMANT j.top@rug.nl 18-23 april 2013 (Collegecaroussel, Groningen) 1 priemrecords?! over priemgetallen 2, 3, 5, 7,..., 101,..., 2017,...... p priem: niet deelbaar door
priemrecords? Jaap Top JBI-RuG & DIAMANT j.top@rug.nl 18-23 april 2013 (Collegecaroussel, Groningen) 1 priemrecords?! over priemgetallen 2, 3, 5, 7,..., 101,..., 2017,...... p priem: niet deelbaar door
Spookgetallen. Jan van de Craats en Janina Müttel
 Spookgetallen Jan van de Craats en Janina Müttel leadtekst In de serie Open Problemen deze keer drie beroemde onopgeloste raadsels. Je kunt er geen miljoen dollar mee winnen, maar wel onsterfelijke roem.
Spookgetallen Jan van de Craats en Janina Müttel leadtekst In de serie Open Problemen deze keer drie beroemde onopgeloste raadsels. Je kunt er geen miljoen dollar mee winnen, maar wel onsterfelijke roem.
Convexe functies op R (niet in het boek)
 Convee uncties op R (niet in het boe Een unctie : R R heet conve, als voor alle, R en ele λ [0,] geldt dat (λ + (-λ λ( + (-λ(. Voor een unctie op R beteent dit dat als je twee willeeurige punten op de
Convee uncties op R (niet in het boe Een unctie : R R heet conve, als voor alle, R en ele λ [0,] geldt dat (λ + (-λ λ( + (-λ(. Voor een unctie op R beteent dit dat als je twee willeeurige punten op de
Heron driehoek. 1 Wat is een Heron driehoek? De naam Heron ( Heroon) is bekend van de formule
 Heron driehoek 1 Wat is een Heron driehoek? De naam Heron ( Heroon) is bekend van de formule = s(s a)(s b)(s c) met s = a + b + c 2 die gebruikt wordt om de oppervlakte van een driehoek te berekenen in
Heron driehoek 1 Wat is een Heron driehoek? De naam Heron ( Heroon) is bekend van de formule = s(s a)(s b)(s c) met s = a + b + c 2 die gebruikt wordt om de oppervlakte van een driehoek te berekenen in
Diophantische vergelijkingen
 Diophantische vergelijkingen 1 Wat zijn Diophantische vergelijkingen? Een Diophantische vergelijking is een veeltermvergelijking waarbij zowel de coëfficiënten als de oplossingen gehele getallen moeten
Diophantische vergelijkingen 1 Wat zijn Diophantische vergelijkingen? Een Diophantische vergelijking is een veeltermvergelijking waarbij zowel de coëfficiënten als de oplossingen gehele getallen moeten
IV Eigenvectoren en Eigenwaarden bij Lineaire
 IV Eigenvectoren en Eigenwaarden bij Lineaire Transformaties in R IV0 Meetundige inleiding: delijnen en eigenvectoren Bij veel toepassingen van de Gauss-Jordan methode gaat men uit van de delijnen van
IV Eigenvectoren en Eigenwaarden bij Lineaire Transformaties in R IV0 Meetundige inleiding: delijnen en eigenvectoren Bij veel toepassingen van de Gauss-Jordan methode gaat men uit van de delijnen van
PG blok 4 werkboek bijeenkomst 4 en 5
 2015-2015 PG blok 4 werkboek bijeenkomst 4 en 5 Inhoud Kenmerken van deelbaarheid (herhaling)...1 Ontbinden in factoren...1 Priemgetallen (herhaling)...2 Ontbinden in priemfactoren...2 KGV (Kleinste Gemene
2015-2015 PG blok 4 werkboek bijeenkomst 4 en 5 Inhoud Kenmerken van deelbaarheid (herhaling)...1 Ontbinden in factoren...1 Priemgetallen (herhaling)...2 Ontbinden in priemfactoren...2 KGV (Kleinste Gemene
OEFENOPGAVEN OVER REEKSEN
 OEFENOPGAVEN OVER REEKSEN Opgave. Bereen n=0 ( 3 n + 6n 7 n ) (antwoord 0). Opgave. Ga voor de volgende reesen na of ze convergent of divergent zijn: a) (convergent); (ln ) b) c) d) e) f) g) h) 5 5 3 +
OEFENOPGAVEN OVER REEKSEN Opgave. Bereen n=0 ( 3 n + 6n 7 n ) (antwoord 0). Opgave. Ga voor de volgende reesen na of ze convergent of divergent zijn: a) (convergent); (ln ) b) c) d) e) f) g) h) 5 5 3 +
Bijzondere kettingbreuken
 Hoofdstuk 15 Bijzondere kettingbreuken 15.1 Kwadratische getallen In het vorige hoofdstuk hebben we gezien dat 2 = 1, 2, 2, 2, 2, 2, 2,.... Men kan zich afvragen waarom we vanaf zeker moment alleen maar
Hoofdstuk 15 Bijzondere kettingbreuken 15.1 Kwadratische getallen In het vorige hoofdstuk hebben we gezien dat 2 = 1, 2, 2, 2, 2, 2, 2,.... Men kan zich afvragen waarom we vanaf zeker moment alleen maar
RSA. F.A. Grootjen. 8 maart 2002
 RSA F.A. Grootjen 8 maart 2002 1 Delers Eerst wat terminologie over gehele getallen. We zeggen a deelt b (of a is een deler van b) als b = qa voor een of ander geheel getal q. In plaats van a deelt b schrijven
RSA F.A. Grootjen 8 maart 2002 1 Delers Eerst wat terminologie over gehele getallen. We zeggen a deelt b (of a is een deler van b) als b = qa voor een of ander geheel getal q. In plaats van a deelt b schrijven
7.1 Het aantal inverteerbare restklassen
 Hoofdstuk 7 Congruenties in actie 7.1 Het aantal inverteerbare restklassen We pakken hier de vraag op waarmee we in het vorige hoofdstuk geëindigd zijn, namelijk hoeveel inverteerbare restklassen modulo
Hoofdstuk 7 Congruenties in actie 7.1 Het aantal inverteerbare restklassen We pakken hier de vraag op waarmee we in het vorige hoofdstuk geëindigd zijn, namelijk hoeveel inverteerbare restklassen modulo
Introductie Coach-modelleren
 Inhoud Introductie Coach-modelleren... Coach-modelleren versus Excel...4 Opgave: Kennismaing met Coach-Modelleren...4 Satellietbanen in COACH-Modelleren...5 Opgave: GPS-satelliet...5 Alleen voor de geïnteresseerden...7
Inhoud Introductie Coach-modelleren... Coach-modelleren versus Excel...4 Opgave: Kennismaing met Coach-Modelleren...4 Satellietbanen in COACH-Modelleren...5 Opgave: GPS-satelliet...5 Alleen voor de geïnteresseerden...7
1. REGELS VAN DEELBAARHEID.
 REKENEN VIJFDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Deelbaarheid door 10, 100, 1000 10: het laatste cijfer (= cijfer van de eenheden) is 0 100: laatste twee cijfers zijn 0 (cijfers van de eenheden
REKENEN VIJFDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Deelbaarheid door 10, 100, 1000 10: het laatste cijfer (= cijfer van de eenheden) is 0 100: laatste twee cijfers zijn 0 (cijfers van de eenheden
Polynomen. + 5x + 5 \ 3 x 1 = S(x) 2x x. 3x x 3x 2 + 2
 Lesbrief 3 Polynomen 1 Polynomen van één variabele Elke functie van de vorm P () = a n n + a n 1 n 1 + + a 1 + a 0, (a n 0), heet een polynoom of veelterm in de variabele. Het getal n heet de graad van
Lesbrief 3 Polynomen 1 Polynomen van één variabele Elke functie van de vorm P () = a n n + a n 1 n 1 + + a 1 + a 0, (a n 0), heet een polynoom of veelterm in de variabele. Het getal n heet de graad van
Rode Jas, Blauwe Jas. Afklokken. De Ladder van een Cruiseschip
 Inleiding We hebben altijd gedacht dat onze hersencellen eindig waren, zoals spliterwten in een pot: als je ze eruit haalt, ben je ze voor altijd wijt. Daardoor zouden onze mentale vermogens steeds verder
Inleiding We hebben altijd gedacht dat onze hersencellen eindig waren, zoals spliterwten in een pot: als je ze eruit haalt, ben je ze voor altijd wijt. Daardoor zouden onze mentale vermogens steeds verder
We beginnen met de eigenschappen van de gehele getallen.
 II.2 Gehele getallen We beginnen met de eigenschappen van de gehele getallen. Axioma s voor Z De gegevens zijn: (a) een verzameling Z; (b) elementen 0 en 1 in Z; (c) een afbeelding +: Z Z Z, de optelling;
II.2 Gehele getallen We beginnen met de eigenschappen van de gehele getallen. Axioma s voor Z De gegevens zijn: (a) een verzameling Z; (b) elementen 0 en 1 in Z; (c) een afbeelding +: Z Z Z, de optelling;
Je hebt twee uur de tijd voor het oplossen van de vraagstukken. µkw uitwerkingen. 12 juni 2015
 Je hebt twee uur de tijd voor het oplossen van de vraagstukken. Elk vraagstuk is maximaal 10 punten waard. Begin elke opgave op een nieuw vel papier. µkw uitwerkingen 12 juni 2015 Vraagstuk 1. We kunnen
Je hebt twee uur de tijd voor het oplossen van de vraagstukken. Elk vraagstuk is maximaal 10 punten waard. Begin elke opgave op een nieuw vel papier. µkw uitwerkingen 12 juni 2015 Vraagstuk 1. We kunnen
Getaltheorie groep 3: Primitieve wortels
 Getaltheorie groep 3: Primitieve wortels Trainingsweek juni 2008 Inleiding Voor a relatief priem met m hebben we de orde van a modulo m gedefinieerd als ord m (a) = min { n Z + a n 1 (mod m) }. De verzameling
Getaltheorie groep 3: Primitieve wortels Trainingsweek juni 2008 Inleiding Voor a relatief priem met m hebben we de orde van a modulo m gedefinieerd als ord m (a) = min { n Z + a n 1 (mod m) }. De verzameling
Hoofdstuk 6. Congruentierekening. 6.1 Congruenties
 Hoofdstuk 6 Congruentierekening 6.1 Congruenties We hebben waarschijnlijk allemaal wel eens opgemerkt dat bij vermenigvuldigen van twee getallen de laatste cijfers als het ware meevermenigvuldigen. Stel
Hoofdstuk 6 Congruentierekening 6.1 Congruenties We hebben waarschijnlijk allemaal wel eens opgemerkt dat bij vermenigvuldigen van twee getallen de laatste cijfers als het ware meevermenigvuldigen. Stel
_., i _._ Lo-. -J EEN ANALYSE VAN EEN SPELLETJE MET DOMINOSTENEN. door. Jacob Wijngaard.
 _.,.....-..-...------.---i 7703520 -_._------ Lo-. -J EEN ANALYSE VAN EEN SPELLETJE MET DOMINOSTENEN door Jacob Wijngaard Bd/OR/75-06 Een veel beoefend spelletje met dominostenen is het volgende: Zet aile
_.,.....-..-...------.---i 7703520 -_._------ Lo-. -J EEN ANALYSE VAN EEN SPELLETJE MET DOMINOSTENEN door Jacob Wijngaard Bd/OR/75-06 Een veel beoefend spelletje met dominostenen is het volgende: Zet aile
Opgaven Kansrekening Datastructuren, 29 mei 2019, Werkgroep.
 Opgaven Kansreening Datastructuren, 9 mei 019, Wergroep. Gebrui deze opgaven, naast die uit het boe, om de stof te oefenen op het wercollege. Cijfer: Op een toets rijg je meestal zes tot acht opgaven.
Opgaven Kansreening Datastructuren, 9 mei 019, Wergroep. Gebrui deze opgaven, naast die uit het boe, om de stof te oefenen op het wercollege. Cijfer: Op een toets rijg je meestal zes tot acht opgaven.
Kernbegrippen Kennisbasis wiskunde Onderdeel breuken
 Kernbegrippen Kennisbasis wiskunde Onderdeel breuken De omschreven begrippen worden expliciet genoemd in de Kennisbasis. De begrippen zijn in alfabetische volgorde opgenomen. Breuk Een breuk is een getal
Kernbegrippen Kennisbasis wiskunde Onderdeel breuken De omschreven begrippen worden expliciet genoemd in de Kennisbasis. De begrippen zijn in alfabetische volgorde opgenomen. Breuk Een breuk is een getal
Eigenschap (Principe van welordening) Elke niet-lege deelverzameling V N bevat een kleinste element.
 Hoofdstuk 2 De regels van het spel 2.1 De gehele getallen Grof gezegd kunnen we de (elementaire) getaltheorie omschrijven als de wiskunde van de getallen 1, 2, 3, 4,... die we ook de natuurlijke getallen
Hoofdstuk 2 De regels van het spel 2.1 De gehele getallen Grof gezegd kunnen we de (elementaire) getaltheorie omschrijven als de wiskunde van de getallen 1, 2, 3, 4,... die we ook de natuurlijke getallen
Bewijs door inductie
 Bewijs door inductie 1 Bewijs door inductie Vaak bestaat een probleem erin aan te tonen dat een bepaalde eigenschap geldt voor elk natuurlijk getal. Als je wilt weten of iets waar is voor alle natuurlijke
Bewijs door inductie 1 Bewijs door inductie Vaak bestaat een probleem erin aan te tonen dat een bepaalde eigenschap geldt voor elk natuurlijk getal. Als je wilt weten of iets waar is voor alle natuurlijke
III (vervolg) Lineaire Transformaties in R
 III (vervolg) Lineaire Transformaties in R III.7 a Opmeringen over dit hoofdstu Oorspronelij waren de volgende paragrafen deel van hoofdstu III. De bedoeling ervan is om na te gaan hoe binnen het ader
III (vervolg) Lineaire Transformaties in R III.7 a Opmeringen over dit hoofdstu Oorspronelij waren de volgende paragrafen deel van hoofdstu III. De bedoeling ervan is om na te gaan hoe binnen het ader
Selectietoets vrijdag 10 maart 2017
 Selectietoets vrijdag 10 maart 2017 NEDERLANDSE W I S K U N D E OLYMPIADE Uitwerkingen Opgave 1. Zij n een even positief geheel getal. Een rijtje van n reële getallen noemen we volledig als voor elke gehele
Selectietoets vrijdag 10 maart 2017 NEDERLANDSE W I S K U N D E OLYMPIADE Uitwerkingen Opgave 1. Zij n een even positief geheel getal. Een rijtje van n reële getallen noemen we volledig als voor elke gehele
tripels van Pythagoras Jaap Top
 tripels van Pythagoras Jaap Top BI-RuG & DIAMANT 9 en 10 en 11 april 2019 (collegecarrousel, Groningen) 1 Over natuurlijke getallen en Pythagoras: c b a a 2 + b 2 = c 2 2 Oplossingen in natuurlijke getallen
tripels van Pythagoras Jaap Top BI-RuG & DIAMANT 9 en 10 en 11 april 2019 (collegecarrousel, Groningen) 1 Over natuurlijke getallen en Pythagoras: c b a a 2 + b 2 = c 2 2 Oplossingen in natuurlijke getallen
Volledige inductie. Hoofdstuk 7. Van een deelverzameling V van de verzameling N van alle natuurlijke getallen veronderstellen.
 Hoofdstuk 7 Volledige inductie Van een deelverzameling V van de verzameling N van alle natuurlijke getallen veronderstellen we het volgende: (i) 0 V (ii) k N k V k + 1 V Dan is V = N. Men ziet dit als
Hoofdstuk 7 Volledige inductie Van een deelverzameling V van de verzameling N van alle natuurlijke getallen veronderstellen we het volgende: (i) 0 V (ii) k N k V k + 1 V Dan is V = N. Men ziet dit als
OVER IRRATIONALE GETALLEN EN MACHTEN VAN π
 OVER IRRATIONALE GETALLEN EN MACHTEN VAN π KOEN DE NAEGHEL Samenvatting. In deze nota buigen we ons over de vraag of een macht van π een irrationaal getal is. De aangereikte opbouw en bewijsmethoden zijn
OVER IRRATIONALE GETALLEN EN MACHTEN VAN π KOEN DE NAEGHEL Samenvatting. In deze nota buigen we ons over de vraag of een macht van π een irrationaal getal is. De aangereikte opbouw en bewijsmethoden zijn
Pijlenklokken. 1 Inleiding
 Pijlenklokken 1 Inleiding In bovenstaande tekening zie je 1 rode punten. Er staan blauwe pijlen van elk rood punt naar een ander rood punt 4 plaatsen verder op de cirkel. Een dergelijke afbeelding noemen
Pijlenklokken 1 Inleiding In bovenstaande tekening zie je 1 rode punten. Er staan blauwe pijlen van elk rood punt naar een ander rood punt 4 plaatsen verder op de cirkel. Een dergelijke afbeelding noemen
Berekenen van dynamisch evenwicht
 Bereenen van dynamisch evenwicht Voor het bereenen van dynamische evenwichten zijn er verscheidene methodes. De meest beende zijn het gebrui van traagheidsreacties. Deze traagheidsreacties unnen verder
Bereenen van dynamisch evenwicht Voor het bereenen van dynamische evenwichten zijn er verscheidene methodes. De meest beende zijn het gebrui van traagheidsreacties. Deze traagheidsreacties unnen verder
Uitwerking puzzel 91-7: Je kunt het schudden
 Uitwerking puzzel 91-7: Je kunt het schudden Het credit voor deze puzzel gaat naar Frans van Hoeve. Hij stuurde het ons, in een iets andere vorm, met titel Penny-flipping problem. Hij was het tegengekomen
Uitwerking puzzel 91-7: Je kunt het schudden Het credit voor deze puzzel gaat naar Frans van Hoeve. Hij stuurde het ons, in een iets andere vorm, met titel Penny-flipping problem. Hij was het tegengekomen
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 22 februari 2009 INDUCTIE & RECURSIE Paragrafen 4.3-4.6 Discrete Structuren Week 3:
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 22 februari 2009 INDUCTIE & RECURSIE Paragrafen 4.3-4.6 Discrete Structuren Week 3:
Examen Discrete Wiskunde
 Examen Discrete Wisunde Auteur: Daan Pape 1 Hoofdstu I Een groepering in de wisunde is: een verzameling: als alle elementen verschillend zijn een f amilie of mulitverzameling: als er elementen hetzelfde
Examen Discrete Wisunde Auteur: Daan Pape 1 Hoofdstu I Een groepering in de wisunde is: een verzameling: als alle elementen verschillend zijn een f amilie of mulitverzameling: als er elementen hetzelfde
2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45
![2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45](/thumbs/72/68043516.jpg) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
Opgaven Eigenschappen van Getallen Security, 2018, Werkgroep.
 Opgaven Eigenschappen van Getallen Security, 2018, Werkgroep. Gebruik deze opgaven, naast die uit het boek, om de stof te oefenen op het werkcollege. Cijfer: Op een toets krijg je meestal zes tot acht
Opgaven Eigenschappen van Getallen Security, 2018, Werkgroep. Gebruik deze opgaven, naast die uit het boek, om de stof te oefenen op het werkcollege. Cijfer: Op een toets krijg je meestal zes tot acht
Verwachtingswaarde en spreiding
 Les 13 Verwachtingswaarde en spreiding 13.1 Stochasten In een paar voorbeelden hebben we al gezien dat we bij een experiment vaa niet zo zeer in een enele uitomst geïneteresseerd zijn, maar bijvoorbeeld
Les 13 Verwachtingswaarde en spreiding 13.1 Stochasten In een paar voorbeelden hebben we al gezien dat we bij een experiment vaa niet zo zeer in een enele uitomst geïneteresseerd zijn, maar bijvoorbeeld
Snel en exact rekenen in getaltheorie en computeralgebra door middel van benaderingen
 Snel en exact rekenen in getaltheorie en computeralgebra door middel van benaderingen Bas Edixhoven Universiteit Leiden 2010/10/25, KNAW Bas Edixhoven (Universiteit Leiden) Getaltheorie en computeralgebra
Snel en exact rekenen in getaltheorie en computeralgebra door middel van benaderingen Bas Edixhoven Universiteit Leiden 2010/10/25, KNAW Bas Edixhoven (Universiteit Leiden) Getaltheorie en computeralgebra
Opmerking. TI1300 Redeneren en Logica. Met voorbeelden kun je niks bewijzen. Directe en indirecte bewijzen
 Opmerking TI1300 Redeneren en Logica College 2: Bewijstechnieken Tomas Klos Algoritmiek Groep Voor alle duidelijkheid: Het is verre van triviaal om definities te leren hanteren, beweringen op te lossen,
Opmerking TI1300 Redeneren en Logica College 2: Bewijstechnieken Tomas Klos Algoritmiek Groep Voor alle duidelijkheid: Het is verre van triviaal om definities te leren hanteren, beweringen op te lossen,
Hoofdstuk 1. Inleiding. Het binomiaalgetal ( n
 Hoofdstuk 1 Inleiding Het binomiaalgetal ( n berekent het aantal -combinaties van n elementen; dit is het aantal mogelijkheden om elementen te nemen uit n beschikbare elementen Hierbij is herhaling niet
Hoofdstuk 1 Inleiding Het binomiaalgetal ( n berekent het aantal -combinaties van n elementen; dit is het aantal mogelijkheden om elementen te nemen uit n beschikbare elementen Hierbij is herhaling niet
De telduivel. Een slaapverwekkende opdracht voor iedereen die van wiskunde durft te dromen
 De telduivel Een slaapverwekkende opdracht voor iedereen die van wiskunde durft te dromen Een praktische opdracht voor leerlingen van 5VWO met wiskunde B DE TELDUIVEL Inleiding Wiskunde? Hou op zeg! Voor
De telduivel Een slaapverwekkende opdracht voor iedereen die van wiskunde durft te dromen Een praktische opdracht voor leerlingen van 5VWO met wiskunde B DE TELDUIVEL Inleiding Wiskunde? Hou op zeg! Voor
Met passer en liniaal
 Met passer en liniaal De opgaven in deze opdracht gaan over het teenen met passer en liniaal. Een liniaal gebrui je om rechte lijnen te teenen, dat an dus een recht latje zijn. Je mag daarvoor oo je geodriehoe
Met passer en liniaal De opgaven in deze opdracht gaan over het teenen met passer en liniaal. Een liniaal gebrui je om rechte lijnen te teenen, dat an dus een recht latje zijn. Je mag daarvoor oo je geodriehoe
Zin en onzin van de normale benadering van de binomiale verdeling
 Zin en onzin van de normale benadering van de binomiale verdeling Jef Hendricx 1, 18 november 26 In lassiee handboeen van statistie worden ansen van de binomiale verdeling bereend met tabellen. Voor grotere
Zin en onzin van de normale benadering van de binomiale verdeling Jef Hendricx 1, 18 november 26 In lassiee handboeen van statistie worden ansen van de binomiale verdeling bereend met tabellen. Voor grotere
6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen:
![6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen: 6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen:](/thumbs/55/36024360.jpg) 6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen: 1) Haakjes wegwerken 2) Vermenigvuldigen en delen van links naar rechts 3) Optellen en aftrekken van links naar rechts Schrijf ALLE stappen ONDER
6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen: 1) Haakjes wegwerken 2) Vermenigvuldigen en delen van links naar rechts 3) Optellen en aftrekken van links naar rechts Schrijf ALLE stappen ONDER
3 Elektronische structuur van materialen
 3 Eletronische structuur van materialen (Aanvulling op hoofdstuen 7 en 8 van Rosenberg.) 3.1 Vrije eletron model In het voorgaande hebben we steeds de geometrische structuur van materialen besproen. Toch
3 Eletronische structuur van materialen (Aanvulling op hoofdstuen 7 en 8 van Rosenberg.) 3.1 Vrije eletron model In het voorgaande hebben we steeds de geometrische structuur van materialen besproen. Toch
Wanneer zijn veelvouden van proniks proniks?
 1 Uitwerking puzzel 92-1 Wanneer zijn veelvouden van proniks proniks? Harm Bakker noemde het: pro-niks voor-niks De puzzel was voor een groot deel afkomstig van Frits Göbel. Een pronik is een getal dat
1 Uitwerking puzzel 92-1 Wanneer zijn veelvouden van proniks proniks? Harm Bakker noemde het: pro-niks voor-niks De puzzel was voor een groot deel afkomstig van Frits Göbel. Een pronik is een getal dat
1 Stelsels lineaire vergelijkingen
 1 Stelsels lineaire vergelijingen 1.1 Methode van Gauss (p. 50) Omzetten naar bovendriehoesvorm 0 0 0 Achterwaarste substitutie Om meerdere stelsels (zelfde coëfficiëntenmatrix A, verschillende rechterleden
1 Stelsels lineaire vergelijingen 1.1 Methode van Gauss (p. 50) Omzetten naar bovendriehoesvorm 0 0 0 Achterwaarste substitutie Om meerdere stelsels (zelfde coëfficiëntenmatrix A, verschillende rechterleden
Oefening 4.3. Zoek een positief natuurlijk getal zodanig dat de helft een kwadraat is, een derde is een derdemacht en een vijfde is een vijfdemacht.
 4 Modulair rekenen Oefening 4.1. Merk op dat 2 5 9 2 = 2592. Bestaat er een ander getal van de vorm 25ab dat gelijk is aan 2 5 a b? (Met 25ab bedoelen we een getal waarvan a het cijfer voor de tientallen
4 Modulair rekenen Oefening 4.1. Merk op dat 2 5 9 2 = 2592. Bestaat er een ander getal van de vorm 25ab dat gelijk is aan 2 5 a b? (Met 25ab bedoelen we een getal waarvan a het cijfer voor de tientallen
Hoofdstuk 12. Sommen van kwadraten. 12.1 Sommen van twee kwadraten
 Hoofdstuk 12 Sommen van kwadraten 12.1 Sommen van twee kwadraten In Hoofdstuk 11 hebben we gezien dat als p een oneven priemdeler van a 2 + b 2 is, en p deelt niet zowel a als b, dan is p gelijk aan 1
Hoofdstuk 12 Sommen van kwadraten 12.1 Sommen van twee kwadraten In Hoofdstuk 11 hebben we gezien dat als p een oneven priemdeler van a 2 + b 2 is, en p deelt niet zowel a als b, dan is p gelijk aan 1
Verwachtingswaarde en spreiding
 Les 3 Verwachtingswaarde en spreiding 3.1 Stochasten In een paar voorbeelden hebben we al gezien dat we bij een experiment vaa niet zo zeer in een enele uitomst geïneteresseerd zijn, maar bijvoorbeeld
Les 3 Verwachtingswaarde en spreiding 3.1 Stochasten In een paar voorbeelden hebben we al gezien dat we bij een experiment vaa niet zo zeer in een enele uitomst geïneteresseerd zijn, maar bijvoorbeeld
Oefening 4.3. Zoek een positief natuurlijk getal zodanig dat de helft een kwadraat is, een derde is een derdemacht en een vijfde is een vijfdemacht.
 4 Modulair rekenen Oefening 4.1. Merk op dat 2 5 9 2 2592. Bestaat er een ander getal van de vorm 25ab dat gelijk is aan 2 5 a b? (Met 25ab bedoelen we een getal waarvan a het cijfer voor de tientallen
4 Modulair rekenen Oefening 4.1. Merk op dat 2 5 9 2 2592. Bestaat er een ander getal van de vorm 25ab dat gelijk is aan 2 5 a b? (Met 25ab bedoelen we een getal waarvan a het cijfer voor de tientallen
II.3 Equivalentierelaties en quotiënten
 II.3 Equivalentierelaties en quotiënten Een belangrijk begrip in de wiskunde is het begrip relatie. Een relatie op een verzameling is een verband tussen twee elementen uit die verzameling waarbij de volgorde
II.3 Equivalentierelaties en quotiënten Een belangrijk begrip in de wiskunde is het begrip relatie. Een relatie op een verzameling is een verband tussen twee elementen uit die verzameling waarbij de volgorde
1.1 Rekenen met letters [1]
![1.1 Rekenen met letters [1] 1.1 Rekenen met letters [1]](/thumbs/41/22623929.jpg) 1.1 Rekenen met letters [1] Voorbeeld 1: Een kaars heeft een lengte van 30 centimeter. Per uur brand er 6 centimeter van de kaars op. Hieruit volgt de volgende woordformule: Lengte in cm = -6 aantal branduren
1.1 Rekenen met letters [1] Voorbeeld 1: Een kaars heeft een lengte van 30 centimeter. Per uur brand er 6 centimeter van de kaars op. Hieruit volgt de volgende woordformule: Lengte in cm = -6 aantal branduren
WISKUNDE 1. Aansluitmodule wiskunde MBO-HBO
 WISKUNDE 1 Aansluitmodule wiskunde MBO-HBO Wat moet je aanschaffen? Basisboek wiskunde tweede editie Jan van de Craats en Rob Bosch isbn:978-90-430-1673-5 Dit boek gebruikt men ook op de Hanze bij engineering.
WISKUNDE 1 Aansluitmodule wiskunde MBO-HBO Wat moet je aanschaffen? Basisboek wiskunde tweede editie Jan van de Craats en Rob Bosch isbn:978-90-430-1673-5 Dit boek gebruikt men ook op de Hanze bij engineering.
Lights Out. 1 Inleiding
 Lights Out 1 Inleiding Het spel Lights Out is een elektronisch spel dat gelanceerd werd in 1995 door Tiger Electronics. Het originele spel heeft een bord met 25 lampjes in een rooster van 5 rijen en 5
Lights Out 1 Inleiding Het spel Lights Out is een elektronisch spel dat gelanceerd werd in 1995 door Tiger Electronics. Het originele spel heeft een bord met 25 lampjes in een rooster van 5 rijen en 5
Systeemtheorie en Regeltechniek
 Systeemtheorie en Regeltehnie Oefenzitting Lineaire Tijds-invariante (LTI) Disrete tijdssystemen: Oplossen van de differentievergelijing wouter.biesmans@esat.uleuven.be Hoe unnen we een system voorstellen?
Systeemtheorie en Regeltehnie Oefenzitting Lineaire Tijds-invariante (LTI) Disrete tijdssystemen: Oplossen van de differentievergelijing wouter.biesmans@esat.uleuven.be Hoe unnen we een system voorstellen?
Volatility estimation and visualization for stock/option traders Bachelorscriptie leerstoelen SST/SP
 Volatility estimation and visualization for stoc/option traders Bachelorscriptie leerstoelen SST/SP Peter Bosschaart Jeroen Spoor Berend Steenhuisen 9 juni 2011 Inhoudsopgave 1 Introductie 3 2 Discretisatie
Volatility estimation and visualization for stoc/option traders Bachelorscriptie leerstoelen SST/SP Peter Bosschaart Jeroen Spoor Berend Steenhuisen 9 juni 2011 Inhoudsopgave 1 Introductie 3 2 Discretisatie
Het probleem van Hilbert
 René Pannekoek Imperial College (Londen) 31 januari 2014 Motto Leopold Kronecker (1823-1891) Motto Leopold Kronecker (1823-1891): Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.
René Pannekoek Imperial College (Londen) 31 januari 2014 Motto Leopold Kronecker (1823-1891) Motto Leopold Kronecker (1823-1891): Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.
Toegepaste wiskunde. voor het hoger beroepsonderwijs. Deel 2 Derde, herziene druk. Uitwerking herhalingsopgaven hoofdstuk 5 augustus 2009
 Drs. J.H. Blanespoor Drs. C. de Joode Ir. A. Sluijter Toegepaste wisunde voor het hoger beroepsonderwijs Deel Derde, herziene dru Uitwering herhalingsopgaven hoofdstu 5 augustus 009 HBuitgevers, Baarn
Drs. J.H. Blanespoor Drs. C. de Joode Ir. A. Sluijter Toegepaste wisunde voor het hoger beroepsonderwijs Deel Derde, herziene dru Uitwering herhalingsopgaven hoofdstu 5 augustus 009 HBuitgevers, Baarn
Vectoranalyse voor TG
 college 6 van een vectorveld collegejaar college build slides Vandaag : : : : 14-15 6 22 september 214 51 1 2 3 4 5 Gradiënt van een vectorveld 1 VA vandaag Section 16.2 Hoofdstu 4 Definitie Een vectorveld
college 6 van een vectorveld collegejaar college build slides Vandaag : : : : 14-15 6 22 september 214 51 1 2 3 4 5 Gradiënt van een vectorveld 1 VA vandaag Section 16.2 Hoofdstu 4 Definitie Een vectorveld
ANTWOORDEN blz. 1. d. 345 + 668 = 1013; 61 007 + 50 215 = 111 222; 102 240 30 628 = 71 612; 1 000 000 1 = 999 999
 ANTWOORDEN blz. 3 a. Zeer onwaarschijnlijk Zeer onwaarschijnlijk a. Dan heb je ergens een schuld uitstaan 86 Dan hadden beide een kopie van de kerfstok; om fraude te voorkomen a. MMXII, MCCCXXVII, DLXXXVI,
ANTWOORDEN blz. 3 a. Zeer onwaarschijnlijk Zeer onwaarschijnlijk a. Dan heb je ergens een schuld uitstaan 86 Dan hadden beide een kopie van de kerfstok; om fraude te voorkomen a. MMXII, MCCCXXVII, DLXXXVI,
Een combinatorische oplossing voor vraag 10 van de LIMO 2010
 Een combinatorische oplossing voor vraag 10 van de LIMO 2010 Stijn Vermeeren (University of Leeds) 16 juni 2010 Samenvatting Probleem 10 van de Landelijke Interuniversitaire Mathematische Olympiade 2010vraagt
Een combinatorische oplossing voor vraag 10 van de LIMO 2010 Stijn Vermeeren (University of Leeds) 16 juni 2010 Samenvatting Probleem 10 van de Landelijke Interuniversitaire Mathematische Olympiade 2010vraagt
3.2 Vectoren and matrices
 we c = 6 c 2 = 62966 c 3 = 32447966 c 4 = 72966 c 5 = 2632833 c 6 = 4947966 Sectie 32 VECTOREN AND MATRICES Maar het is a priori helemaal niet zeker dat het stelsel vergelijkingen dat opgelost moet worden,
we c = 6 c 2 = 62966 c 3 = 32447966 c 4 = 72966 c 5 = 2632833 c 6 = 4947966 Sectie 32 VECTOREN AND MATRICES Maar het is a priori helemaal niet zeker dat het stelsel vergelijkingen dat opgelost moet worden,
Hoofdstuk 4. Delers. 4.1 Delers (op)tellen
 Hoofdstuk 4 Delers 4. Delers (op)tellen Ieder getal heeft zijn delers. Van oudsher heeft het onvoorspelbare gedrag van delers van getallen een aantrekkingskracht uitgeoefend op mensen. Zozeer zelfs dat
Hoofdstuk 4 Delers 4. Delers (op)tellen Ieder getal heeft zijn delers. Van oudsher heeft het onvoorspelbare gedrag van delers van getallen een aantrekkingskracht uitgeoefend op mensen. Zozeer zelfs dat
94 NAW 5/17 nr. 2 juni 2016 Hoe bewijs je het priemtweelingvermoeden? Frits Beukers
 9 AW 57 nr juni 06 Hoe bewijs je het riemtweelingvermoeden? Frits Beuers Illustratie: Ryu Tajiri Frits Beuers Hoe bewijs je het riemtweelingvermoeden? AW 57 nr juni 06 95 Frits Beuers Mathematisch Instituut
9 AW 57 nr juni 06 Hoe bewijs je het riemtweelingvermoeden? Frits Beuers Illustratie: Ryu Tajiri Frits Beuers Hoe bewijs je het riemtweelingvermoeden? AW 57 nr juni 06 95 Frits Beuers Mathematisch Instituut
1 Limiet van een rij Het begrip rij Bepaling van een rij Expliciet voorschrift Recursief voorschrift 3
 HOOFDSTUK 6: RIJEN 1 Limiet van een rij 2 1.1 Het begrip rij 2 1.2 Bepaling van een rij 2 1.2.1 Expliciet voorschrift 2 1.2.2 Recursief voorschrift 3 1.2.3 Andere gevallen 3 1.2.4 Rijen met de grafische
HOOFDSTUK 6: RIJEN 1 Limiet van een rij 2 1.1 Het begrip rij 2 1.2 Bepaling van een rij 2 1.2.1 Expliciet voorschrift 2 1.2.2 Recursief voorschrift 3 1.2.3 Andere gevallen 3 1.2.4 Rijen met de grafische
WISKUNDE-ESTAFETTE RU 2005 Uitwerkingen
 WISKUNDE-ESTAFETTE RU 2005 Uitwerkingen 1 We proberen alle mogelijkheden van klein naar groot: p = 1 is uitgesloten: dan zou elke dag hetzelfde resultaat geven. p = 2 is uitgesloten: dan zouden dag 1 en
WISKUNDE-ESTAFETTE RU 2005 Uitwerkingen 1 We proberen alle mogelijkheden van klein naar groot: p = 1 is uitgesloten: dan zou elke dag hetzelfde resultaat geven. p = 2 is uitgesloten: dan zouden dag 1 en
