Vectoren en Matrixalgebra
|
|
|
- Magdalena de Winter
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Cahiers T Europe Vlaadere r. Vectore e Matrixalgebra Ee ieuwe aapak met toepassige Guido Herweyers
2
3 Vectore e Matrixalgebra Ee ieuwe aapak met toepassige Guido Herweyers
4
5 Ihoudsopgave Woord vooraf..... Stelsels va lieaire vergelijkige.... Ileidig.... Toepassige...7 Warmtetrasport, ee stelsel met parameters, de determiat va ee matrix, het balacere va chemische reacties, ee cirkel door pute, iterpolerede veelterme, etwerkstrome. Vectore e lieaire combiaties.... Ileidig.... Toepassige...7 Lieaire afhakelijkheid, vectorruimte gegeereerd door vectore, elimiatie va parameters, de rag va ee matrix, homogee e iet homogee stelsels. Lieaire trasformaties.... Ileidig.... Toepassige... Lieaire e affiee trasformaties, rotaties, samestellig va lieaire trasformaties, elektrische etwerke 4. Matrixalgebra Ileidig Toepassige...9 Computergraphics 5. Iverse va ee vierkate matrix Ileidig Elemetaire rijoperaties als matrixvermeigvuldigige De iverse berekee va ee vierkate matrix Toepassige...4 De LU-otbidig, ee stelsel oplosse met de LU-otbidig 6. Eigewaarde e eigevectore Ileidig Toepassige...40 Eigewaarde berekee via rijherleide, de stellig va Cayley-Hamilto, de cirkels va Gerschgori, Markov ketes e discrete dyamische systeme, diagoalisatie va ee vierkate matrix, matrixfucties, ee stelsel va differetiaalvergelijkige 7. Orthogoaliteit, overgedetermieerde stelsels e de kleiste kwadrate methode Ileidig Toepassige...54 De QR-otbidig, eigewaarde bepale met de QR-otbidig, overgedetermieerde stelsels, curve fittig Broe...59
6
7 Woord vooraf De ieuwe aapak va vectore e matrixalgebra biedt veel voordele. Va bij de start wordt er gewerkt met vectore (kolommatrices) e lieaire combiaties va vectore i R e R. Op die wijze reket me metee i ee vectorruimte, odersteud door de waardevolle meetkudige iterpretatie i het vlak e i de ruimte. Vervolges wordt het product va ee matrix A met ee vector x gedefiieerd als ee lieaire combiatie va de kolomme va de matrix A. Dit geeft ee ieuwe kijk op stelsels va lieaire vergelijkige. Teslotte komt het product va twee matrices A e B tot stad als de stadaardmatrix va de samestellig va twee lieaire trasformaties; elke kolom va AB is ee lieaire combiatie va de kolomme va A. De klemtoo ligt hier dus meer op de kolomme va ee matrix i.p.v. de idividuele elemete. Deze aapak wordt prima uiteegezet i het boek va David Lay [6] e teves i het boek va Gilbert Strag [8]. Dit cahier bevat 7 hoofdstukke, elk hoofdstuk start met ee ileidig waari de odige defiities e belagrijkste aspecte aa bod kome, zoder volledigheid a te streve. Talrijke toepassige illustrere vervolges de veelzijdigheid e het belag va lieaire algebra. De meeste oefeige worde cocreet uitgewerkt. Voor de umerieke wiskude, computeralgebra, dyamische meetkude e grafieke wordt er gewerkt met de software versie va TI-Nspire CAS. We toe hier ekel de schermafdrukke ter illustratie e odersteuig. Voor de sytax va dit pakket verwijze we aar de T-ascholige ( Guido Herweyers augustus 007 guido.herweyers@khbo.be
8
9 . Stelsels va lieaire vergelijkige. Ileidig Elk stelsel va lieaire vergelijkige heeft ofwel éé oplossig, ofwel oeidig veel oplossige, ofwel gee oplossig. Ee stelsel va lieaire vergelijkige oeme we cosistet als het ofwel éé ofwel oeidig veel oplossige heeft, het stelsel is icosistet als het gee oplossig heeft. Equivalete stelsels zij stelsels met dezelfde oplossigeverzamelig. Strategie om ee lieair stelsel op te losse: herleid het stelsel tot ee equivalet stelsel dat eevoudiger is op te losse: elimieer variabele. Hiertoe gebruike we de volgede operaties: bij ee vergelijkig ee veelvoud va ee adere vergelijkig optelle twee vergelijkige verwissele ee vergelijkig vermeigvuldige met ee getal verschilled va ul Voorbeeld: x+ 4y z = 9 4x+ y+ 6z = x+ y+ 5z =8 Eerst elimiere we x uit de tweede e derde vergelijkig; va de tweede vergelijkig trekke we twee keer de eerste vergelijkig af, bij de derde vergelijkig telle we de eerste op: x+ 4y z = 9 y+ 8z =5 5y+ 4z = Vervolges elimiere we y uit de derde vergelijkig; va de derde vergelijkig trekke we 5/ keer de tweede vergelijkig af: x+ 4y z = 9 y+ 8z =5 8 8 z = Het stelsel is u herleid tot ee driehoeksvorm (elimiatiemethode va Gauss). We losse het verder op door terugwaartse substitutie: uit de derde vergelijkig volgt z =, uit de tweede vergelijkig volgt y =5 8z = waaruit y =, uit de eerste vergelijkig volgt teslotte x= 9 4y+ z = 4 waaruit x =. De oplossig va het stelsel is dus ( xyz,, ) = (,, ).
10 We hebbe mider schrijfwerk door de correspoderede elemetaire rijoperaties uit te voere op de uitgebreide matrix va het stelsel: bij ee rij ee veelvoud va ee adere rij optelle twee rije verwissele ee rij vermeigvuldige met ee getal verschilled va ul Twee matrices zij rijequivalet (symbool ~) als de ee ka worde getrasformeerd i de adere door ee eidig aatal elemetaire rijoperaties. Het stelsel x+ 4y z = 9 4x+ y+ 6z = x+ y+ 5z =8 heeft als uitgebreide matrix / 8/ I deze voorwaartse fase werd het stelsel herleid tot driehoeksvorm (Gauss). We kue de terugwaartse substitutie vervage door de terugwaartse fase waarbij we u eerst z elimiere uit de tweede e derde vergelijkig e vervolges y uit de eerste vergelijkig (Gauss-Jorda): Algemee: met Gauss herleide we de uitgebreide matrix tot ee echelovorm, met Gauss-Jorda tot de gereduceerde echelovorm. Ee matrix is i echelovorm (of rijechelovorm) als:. de iet ulrije staa bove de ulrije. elk leided elemet (d.i. het eerste iet ul elemet) va ee rij staat rechts va het leided elemet va de voorgaade rij. alle elemete i de kolom oder ee leided elemet zij ul (dit volgt uit e ) Ekele echelovorme (met $ ee va ul verschilled getal e * eeder welk getal): * * * * 0 * * * * * 0 * * * * * * * * * * * * * * * * * * * * * * * * * * * * Voor ee gereduceerde (rij)echelovorm (rref: reduced row echelo form) moet bovedie voldaa zij aa: 4
11 4. het leided elemet va elke iet ulrij is 5. elke leidede is het eige elemet verschilled va ul i zij kolom Voorbeeld va ee gereduceerde echelovorm: 0 * 0 0 * * 0 0 * * * * 0 0 * * * * 0 0 * * * * * * Elke matrix ka via elemetaire rijoperaties worde herleid tot éé e slechts éé gereduceerde echelomatrix. Voorbeeld: bepaal de oplossigeverzamelig va het volgede stelsel: x 6x+ 6x4 + 4x5 =5 x 7x + 8x 5x4 + 8x5 = 9 x 9x + x 9x + 6x = ~ ~ (ee echelovorm) Verder rijherleide tot de gereduceerde echelovorm levert: Termiologie: Ee pivotpositie i ee matrix A is ee plaats i A die correspodeert met ee leidede i de gereduceerde echelovorm va A. Het is teves de plaats va ee leided elemet i eeder welke echelovorm va A. Ee pivot (of spil) is ee iet ul getal op ee pivotpositie dat rechtstreeks wordt gebruikt om ulle te creëre of eerst wordt herleid tot ee leidede, waarmee vervolges ulle worde gecreëerd. I bovestaad voorbeeld zij de pivots aageduid (, e ). Ee pivotkolom va ee matrix is ee kolom die ee pivotpositie bevat. Ee hoofdvariabele va ee lieair stelsel is elke variabele die correspodeert met ee pivotkolom va de uitgebreide matrix va het stelsel (of met ee leidede i de gereduceerde echelovorm) Ee vrije variabele is elke variabele die gee hoofdvariabele is. 5
12 De gereduceerde echelovorm correspodeert met het stelsel: x x + x = 4 4 x x + x =7 x 4 5 = 4 We vide de oplossigeverzamelig door de hoofdvariabele te schrijve i fuctie va de vrije variabele: x = 4 + xx4 x = 7+ x x x is vrij x4 is vrij x = Aa elke vrije variabele (i ee cosistet stelsel) kue we ee willekeurige waarde toekee; bovestaad stelsel heeft oeidig veel oplossige. Stellig (bestaa e uiek zij va ee oplossig): Ee lieair stelsel is cosistet als e slechts als de laatste kolom va de uitgebreide matrix gee pivotkolom is, d.w.z. als e slechts als ee echelovorm va de uitgebreide matrix gee rij heeft va de vorm [ 0 0 b] (met b 0 ) Als ee lieair stelsel cosistet is, da heeft het stelsel ) juist éé oplossig als het gee vrije variabele heeft ) oeidig veel oplossige als er mistes éé vrije variabele is. Samevattig: ee lieair stelsel oplosse m.b.v. elemetaire rijoperaties. Noteer de uitgebreide matrix va het stelsel.. Herleid de uitgebreide matrix va het stelsel via elemetaire rijoperaties tot ee echelovorm. Ga hiermee a of het stelsel al da iet cosistet is. Idie iet, stop. Idie wel, ga aar de volgede stap.. Ga verder met rijherleide tot je de gereduceerde echelomatrix verkrijgt. 4. Schrijf het stelsel va vergelijkige eer correspodered met stap, egeer hierbij de ulrije. 5. Schrijf de eige hoofdvariabele va elke vergelijkig i fuctie va de adere (als er zij) vrije variabele. Oefeig: a) Hoeveel pivots ka ee 4 6 matrix hoogstes hebbe? Waarom? b) Hoeveel pivots ka ee 6 4 matrix hoogstes hebbe? Waarom? c) Hoeveel oplossige heeft ee cosistet lieair stelsel va vergelijkige met vier obekede? Waarom? d) De coëfficiëtematrix va ee lieair stelsel is ee 4 6 matrix met drie pivotkolomme. Hoeveel pivotkolomme heeft de uitgebreide matrix als het stelsel icosistet is? 6
13 . Toepassige. Warmtetrasport Bij de studie va warmtetrasport west me de temperatuurverdelig bij evewicht te bepale va ee due plaat, waeer de temperatuur op de rad va de plaat geked is. Zij T, T, T, T 4 de temperature i de 4 iwedige kope va het rooster i oderstaade figuur. De temperatuur i ee koopput is bij beaderig het gemiddelde va de temperature va de 4 dichtst gelege kooppute (liks, bove, rechts e oder). Bijvoorbeeld T = ( T + T4) / 4 of 4TT T4 = 0. Bepaal beaderige voor de temperature T, T, T, T Oplossig: Het stelsel wordt 4T T T = 0 4 T + 4T T = 60 T + 4T T = 70 4 T T + 4T = 40 4 Reke a dat De oplossig is ( T, T, T, T ) = ( 0, 7.5, 0,.5) 4 7
14 . Ee stelsel met parameters Bepaal ee verbad tusse a, b e c zodat het volgede stelsel cosistet is: x 4x + 7x = a x 5x = b x + 5x 9x = c Oplossig: rijherleide va de uitgebreide matrix va het stelsel levert 4 7 a 4 7 a 4 7 a 0 5 b 0 5 b 0 5 b 5 9 c 0 5 c+ a c+ a+ b De laatste vergelijkig is 0x+ 0x + 0x = c+ a+ b, hieraa is ekel voldaa als c+ a+ b= 0. Het gegeve stelsel is dus cosistet als e slechts als c+ a+ b= 0, i dit geval zij er oeidig veel oplossige met x als vrije variabele.. De determiat va ee matrix Waaraa moete a,b,c e d voldoe opdat het stelsel ax + by = f cx + dy = g met obekede x e y ee uieke oplossig zou hebbe? Oplossig: (i) Als a 0 da geldt: a b f b/ a f / a b/ a f / a c d g c d g 0 d c( b/ a) gc( f / a ) Als d c( b a) / 0 of ad bc 0 da heeft het stelsel ee uieke oplossig. Als d c( b/ a) = 0 of ad bc 0 (als gc( f / a) 0 ) ofwel oeidig veel oplossige (als g c( f a) = da heeft het stelsel ofwel gee oplossig / = 0 ) (ii) Als a = 0 e c 0 da kom je tot dezelfde coclusie (verwissel eerst rij e rij ). (iii) Als a = 0 e c = 0 da heeft het stelsel ofwel gee oplossig, ofwel oeidig veel oplossige (ga a). I dit geval geldt ad bc = 0. Besluit: het stelsel heeft ee uieke oplossig als e slechts als ad bc 0. 8
15 a b We oeme ad bc de determiat va de matrix va het stelsel: det = ad bc c d. 4. Chemische reactiestoechiometrie: het balacere va chemische reacties Voorbeeld : beschouw de ogebalaceerde reactievergelijkig CH 8 + O CO + HO Vermeigvuldig elk reages met ee variabele: ach + bo cco + dh O 8 De reactievergelijkig balacere beteket het bepale va de eevoudigste atuurlijke getalle abcd,,, (d.w.z. zo klei mogelijk) zodat het totaal aatal atome va elk optreded elemet aa elke kat va gelijk blijft. Dit leidt tot de volgede vergelijkige: voor C : a = c voor H : 8a = d voor O : b= c+ d De uitgebreide matrix va het stelsel is a b c d RL Herleide tot de gereduceerde echelomatrix levert (ga a): a= b= waaruit c= d d d d 4 is vrij We zij echter op zoek aar de eevoudigste atuurlijke waarde voor abcd.,,, Klaarblijkelijk vide we die door d = 4 te kieze zodat a =, b= 5, c=, d = 4. De gezochte gebalaceerde reactievergelijkig is dus CH + 5O CO + 4HO 8 9
16 Voorbeeld : a FeS + b O c Fe O + d SO a b c d RL Fe S R R R R 0 0 O / / 0 R R 4 R+ R / / 8 0 R+ R 0 0 / / /4 0 Het gelijkwaardige stelsel wordt dus a= d a d = 0 b= d 8 b 8 d = 0 of c= 4 d c d = 0 4 d is vrij Voor d kieze we het kleiste gemee veelvoud va de optredede oemers: d = kgv,8, 4 = 8 zodat a = 4, b=, c=, d = 8 ( ) De gebalaceerde reactievergelijkig wordt dus 4 FeS + O Fe O + 8 SO Voorbeeld : a K 4 Fe(CN) 6 + b H SO 4 + c H O d K SO 4 + e FeSO 4 + f (NH 4 ) SO 4 + g CO Oplossig: K 4 Fe(CN) H SO H O K SO 4 + FeSO 4 + (NH 4 ) SO CO Voorbeeld 4: voor de liefhebbers: a [Cr(N H 4 CO) 6 ] 4.[Cr(CN) 6 ] + b KMO 4 + c H SO 4 d K Cr O 7 + e MSO 4 + f CO + g KNO + h K SO 4 + i H O De oplossig is: a = 0 b = 76 c = 99 d = 5 e = 76 f = 40 g = 660 h = i = 879 0
17 5. Ee cirkel door pute Uit de meetkude wete we dat er éé cirkel gaat door drie pute die iet gelege zij op ee rechte. De stadaardvergelijkig ( x x ) + ( y y ) = R va de cirkel met middelput ( x, y ) 0 0 e straal R ka worde herschreve als x + y + lx+ my+ = 0 (). Substitutie va de coördiate va de gegeve pute ( x, y),( x, y),( x, y ) i () levert ee stelsel va lieaire vergelijkige waaruit de obekede l, m, worde opgelost: 0 0 lx + my + =x y lx + my + =x y lx + my + =x y () Voorbeeld: vid de vergelijkig va de cirkel door de pute (, 7 ), ( 6, ) e ( 4,6 ). Het stelsel () wordt l+ 7m+ =50 6l+ m+ =40 4l+ 6m+ =5. De gereduceerde echelovorm va de uitgebreide matrix va het stelsel levert de oplossig lmm,, =, 4, 0. ( ) ( ) De vergelijkig va de cirkel wordt + 4 0= 0 of ( x ) + ( y ) = 5. x y x y Ee grafische bevestigig: Waeer heeft het stelsel () gee oplossige of oeidig veel oplossige? Geef ee voorbeeld.
18 6. Iterpolerede veelterme Bepaal de iterpolerede veelterm f ( x) = ax + bx+ c door de pute (, ), (,5 ), (,6 ). Oplossig: f ( x) = x + 6x+ 7. Bepaal teves ee veelterm g ( x) = ax + bx + cx+ d (met a 0 ) door die pute e met ratioale coëfficiëte (zij er meerdere oplossige?). Bestaat er zo veelterm met gehele coëfficiëte? 7. Netwerkstrome Ee etwerk bestaat uit ee aatal pute, kooppute geoemd, same met lijstukke of boge, takke geoemd, die alle of sommige kooppute verbide. De richtig va de stroom (vb. elektrische stroom, verkeersstroom va wages, ) wordt i elke tak aageduid e de stroomhoeveelheid (of selheid) wordt ofwel vermeld ofwel aageduid door ee variabele. De basisveroderstellige voor ee etwerk zij: - de totale igaade stroom i ee etwerk is gelijk aa de totale uitgaade stroom uit het etwerk. - de totale igaade stroom i ee koopput is gelijk aa de totale uitgaade stroom uit dat koopput. Voorbeeld: vid het algemee stroompatroo va het volgede etwerk. Stel dat alle strome positief zij, wat is da de grootst mogelijke waarde va x? 0 A x x B x 4 koopput stroom i stroom uit A x+ x = 0 B x = x + x4 C 80 = x+ x etwerk: 80 = 0 + x4 Rijherleide va de uitgebreide matrix levert: 80 C x e dus De grootste waarde va x is 0, aagezie x positief is. x = 0 x x x x 4 = 60 + x is vrij = 60
19 . Vectore e lieaire combiaties. Ileidig Ee kolomvector of kortweg vector is ee matrix met éé kolom. u u De vector u = i R otere we ook als u = R ( u, u,, u ), om plaats te wie. u Ee vector i R is ee lijst of georded stel va reële getalle; twee vectore i R zij gelijk als e slechts als hu correspoderede elemete (of compoete) gelijk zij: u, u,, u = v, v,, v u = v e u = v e u = v ( ) ( ) Vectore i R ku je optelle e vermeigvuldige met ee reëel getal (ee scalar), de bewerkige gebeure compoet per compoet: Rekeeigeschappe i R : Voor alle vectore u, v, w i R e alle scalars c e d geldt: 4 + = 5 e 4 8 = 6. ) u+ v R 6) cu R ) u+ v= v+ u 7) c( u+ v) = cu+ cv ) ( u+ v) + w = u+ ( v+ w ) 8) ( c+ d) u= cu+ du 4) u+ 0= 0+ u= u 9) c( du) = ( cd) u 5) u+ ( u) = u+ u= 0 0) u= u = 0,0,,0 u= u de tegegestelde vector va u met 0 ( ) de ulvector e ( ) Deze eigeschappe make va R ee vectorruimte. Het verschil va twee vectore wordt gedefiieerd door u v= u+ ( v ) Vectore i R : twee meetkudige voorstellige De vector ee rechthoekig assestelsel; De vector De pijl gaat drie eehede aar rechts e eehede aar bove. wordt voorgesteld door het put met coördiate (, ) i het vlak t.o.v. R is de verzamelig va alle pute i het vlak. wordt voorgesteld de pijl va de oorsprog aar het put (, ).
20 Elke adere pijl i het vlak met dezelfde richtig, zi e grootte ( aar rechts, aar bove) stelt teves de vector voor. Meetkudige regels voor het optelle va vectore i De kop-aa-staartregel: we reize eerst volges u, da volges v, of we eme de korte weg volges u+ v De parallellogramregel R u u + v v Meetkudige voorstellig va u =, v = e u+ v = 4 v v -v Meetkudige voorstellig va v e veelvoude va v Vectore i R hebbe aaloge meetkudige voorstellige t.o.v. ee rechthoekig driedimesioaal assestelsel i de ruimte. Gegeve vectore v, v,, vp i R e reële getalle c, c,, cp, da is de vector cv + c v + + c v p p ee lieaire combiatie va v, v,, vp met gewichte c, c,, cp. Ekele lieaire combiaties va v e v zij: v+ v, v, 5v, 0. Het product va ee m matrix A met ee vector x uit R is ee lieaire combiatie va de opeevolgede kolomme va A met als gewichte de correspoderede elemete va x: x Ax= [ a a a ] = xa + x a + + x a x 4
21 Voorbeeld: Het stelsel = + = + = x + x = x + x = kue we u ook otere als of als x + x = x = x (vectorvergelijkig) (matrixvergelijkig) met de vectorvergelijkig zoeke we ee lieaire combiatie va de vectore die de vector oplevert! e x x + x = (, ) x + x = + = 0 x Twee meetkudige iterpretaties va het stelsel x + x = x + x = Als A ee m matrix is, u e v vectore i ( u+ v) = u+ v e Ac ( u) = c( Au ) A A A R e c ee scalar, da geldt: 5
22 Merk op dat ( ) = + = ( 4) + 6 Hieruit volgt de klassieke rij-kolom-regel om Ax te berekee. De verzamelig va alle lieaire combiaties va vectore v, v,, vp i R otere we Spa v, v,, vp, we oeme dit de verzamelig gegeereerd of opgespae door met { } v, v,, vp. { } V =Spa v, v,, vp is ee deelruimte va ee vectorruimte is, het volstaat hiervoor a te gaa dat: R, dit is ee deelverzamelig va R die zelf i) 0 V ii) Voor elke u, v V geldt dat u+ v V (V is geslote voor de optellig va vectore) iii) Voor elke u V e c R geldt dat cu V (V is geslote voor de scalaire vermeigvuldigig) Voorbeeld : Spa {, } uv met u, v R (duid de vectore aa): Voorbeeld : 0 Stel u =, =, = v w 6, da is Spa = Spa, { u} { u w } ee rechte door de oorsprog e Spa { uv, } = Spa { uvw,, } = R 6
23 Het miimum aatal vectore om oafhakelijk zij. Ee verzamelig vectore { v, v,, vp} i vectorvergelijkig xv+ xv + + xpvp = 0 x, x,, x = 0,0,,0 ekel de triviale oplossig heeft: ( ) ( ) De verzamelig { v, v,, vp} R te geerere is, deze vectore moete da wel lieair R is lieair oafhakelijk als de p is lieair afhakelijk als er getalle x, x,, xp bestaa, iet allemaal gelijk aa 0, zo dat xv+ xv + + xpvp = 0. Ee dergelijke lieaire combiatie oeme we da ee lieair verbad tusse v, v,, vp. De kolomme va A = v v vp zij lieair oafhakelijk als e slechts als de vergelijkig A x= 0 ekel de triviale oplossig x= 0 heeft. Zij V ee vectorruimte die gegeereerd wordt door ee eidige verzamelig. Ee basis va V is ee verzamelig va vectore die de vectorruimte geereert e die lieair oafhakelijk is. Elke basis va ee vectorruimte heeft hetzelfde aatal vectore, dit aatal oeme we de dimesie va de vectorruimte. Zij B ee basis va V, da ka elke vector uit V op juist éé maier geschreve worde als ee lieaire combiatie va de basisvectore uit B.. Toepassige. Stel v =, 5, 9 v = v = 5 9 a) Ga a of {,, } v v v lieair afhakelijk is. b) Vid, idie mogelijk, ee lieair verbad tusse v, v, v. Oplossig: 0 a) Beschouw de vectorvergelijkig x x 5 x = of het stelsel met uitgebreide matrix
24 Rijherleide levert Het stelsel is cosistet met x als vrije variabele, {,, } v v v is lieair afhakelijk. b) zodat x =x x x = 8x is vrij Stelle we x =, da is x = e x = 8, zodat v+ 8v + v = 0, d.i. ee lieair verbad tusse v, v, v. Dit lieair verbad ku je ook metee vide als volgt: aagezie ~ of [ v v v 0] [ u u u 0] e we op zicht zie dat u = u8u, moet ook v = v8v.. Geerere de kolomme va 4 5 A = gas R? Oplossig: We moete agaa of het stelsel A x= b cosistet is voor elke schrijve als ee lieaire combiatie va de kolomme va A? Rijherleide va de uitgebreide matrix [ A b ] levert b R ; ku je elke vector b 4 5 b 4 5 b 4 b 0 b + b 8 0 b b+ b als b+ b 0, da is A x= b iet cosistet, de kolomme va A geerere dus iet R, 8
25 maar wel vectore de oorsprog: b b = b waarvoor b+ b = 0, dit is de vergelijkig va ee vlak door b Merk op: m de kolomme va ee m matrix A geerere R als e slechts als A ee pivotpositie A b immers gee pivotpositie hebbe heeft i elke rij, da ka de uitgebreide matrix [ ] i de laatste kolom! Zij A ee matrix, da zij de volgede uitsprake equivalet: a) De kolomme va A geerere R b) A is rijequivalet met de eeheidsmatrix I c) De kolomme va A zij lieair oafhakelijk d) Het stelsel A x= 0 heeft ekel de oplossig x= 0 d) De kolomme va A vorme ee basis va R. Elimiatie va parameters 6 4 Beschouw het vlak α door het put a = 9 e met richtigsvectore u =, v =. 5 5 x Elk put p = y va α kue we bereike door vauit de oorsprog eerst aar het put a te z gaa, gevolgd door ee bewegig evewijdig met u e da evewijdig met v: p = a+ ru+ sv of x = 6 4r + s y = 9 + r + s (parametervergelijkige va het vlak). z = + 5r + 5s x, yz, va het vlak. Elke keuze va r e s levert ee put ( ) 9
26 Omgekeerd, om a te gaa of ee gegeve put x p = y uit z R gelege is i het vlak α gaa we a of het stelsel x = 6 4r + s y = 9 + r + s z = + 5r + 5s of 4r+ s= x6 r+ s= y9 5r+ 5s= z ee oplossig ( rs, ) heeft. Computeralgebra zorgt voor het rijherleide: Het stelsel is cosistet als e slechts als 45x+ 5y4z 47 = 0, dit is de cartesiaase vergelijkig va α. 4. De rag va ee matrix Stel A = 4 6. De derde kolom va A is de som va de twee eerste kolomme. 5 8 We wijzige het laatste elemet va A, bijvoorbeeld B = Zij de kolomme va B og steeds lieair afhakelijk? Oplossig: Op het eerste gezicht verwachte we dat de kolomme va B lieair oafhakelijk zij De kolomruimte e de rijruimte va B (gegeereerd door respectievelijk de kolomvectore e rijvectore va B) hebbe dezelfde dimesie, dit is de rag va B. Maar de rije va B zij lieair afhakelijk (de tweede rij is het dubbel va de eerste rij), de rag va B is bijgevolg zodat ook de kolomme va B lieair afhakelijk zij! Bepaal zelf ee lieair verbad tusse de kolomme va B. 0
27 5. Vergelijk de oplossigeverzamelige va de volgede stelsels meetkudig: x + x + x = 0 4x 9x + x = 0 x 6x = 0 e x + x + x = 4x 9x + x = x 6x = Oplossig: Aagezie de twee stelsels A x= 0 (homogee stelsel) e A x= b dezelfde coëfficiëtematrix hebbe kue we de stelsels gelijktijdig oplosse door rijherleide va de matrix [ A 0 b ]: Voor het homogee stelsel A x= 0 egere we de laatste kolom, we vide als oplossig: x = 5x x x = x of is vrij x = 5x x x =x = x (met x R ) of x 5 x = x x of x= xv dit is ee rechte door de oorsprog. Voor het iet homogee stelsel egere we de vierde kolom, de oplossig wordt u: x = + 5x x x = x of is vrij x 5 x = + x x 0 of x= a+xv Dit is ee rechte evewijdig met de rechte x= xv, verschove over de vector a. Algemee geldt: de ulruimte va ee m matrix A is de verzamelig Nul A va alle vectore x die voldoe aa A x= 0. Me ka agaa dat Nul A ee deelruimte is va R. De algemee oplossig va A x= b ka me schrijve als x= xp + x h, waarbij x p éé cocrete (of particuliere) oplossig is va A x= b e x h de algemee oplossig is va het homogee stelsel A x= 0. Dit resultaat geldt i.h.a. voor lieaire probleme (zoals het oplosse va lieaire recursievergelijkige e lieaire differetiaalvergelijkige met costate coëfficiëte). De algemee oplossig va de iet homogee vergelijkig is de som va ee particuliere oplossig va die vergelijkig e de algemee oplossig va de bijhorede homogee vergelijkig.
28 . Lieaire trasformaties. Ileidig m Ee trasformatie T va R aar R is ee regel die met elke vector x uit (ee deel va) m R precies éé vector T ( x ) i R associeert. m De trasformatie T is bijgevolg ee fuctie va R aar R. Eevoudige trasformaties zij matrixtrasformaties T( ) x i R. De matrix A voert ee actie uit op x ; vector x gaat aar Ax. Ee trasformatie T va i) T( + ) = T( ) + T( ) ii) T( cu) = ct( ) R aar m R is lieair als u v u v voor elke u e v i u voor elke u i R e c i R R x = Ax, met A ee m matrix e Lieaire trasformaties beware de optellig va vectore e de scalaire vermeigvuldigig, dit zij de belagrijkste trasformaties i lieaire algebra. Ga a dat ee matrixtrasformatie lieair is. Uit (ii) volgt dat T ( 0) = 0 (i) e (ii) zij equivalet met: T( cu+ dv) = ct( u) + dt( v ) Dit is het superpositiepricipe: ee lieaire combiatie va vectore wordt afgebeeld op dezelfde lieaire combiatie va de beeldvectore. De eige reële lieaire fucties zij va de vorm f ( x) = kx (met k ee costate). De eige lieaire trasformaties zij matrixtrasformaties: T( x) = Ax (met A ee m matrix). Voorbeeld: Beschouw de lieaire trasformatie T : R R. De lieaire trasformatie is volledig bepaald va zodra we de beelde va de 0 stadaardbasis e =, = 0 e va 0 0 R kee (merk op dat I = = [ ] e e ) Stel u dat Stel T ( e ) 0 e T ( ) = 4 e =.
29 Voor elke vector x i R geldt: x 0 x x x xe x e = x = + = + 0 x x e e e e e e x T = T x + x = xt + xt = T T = A x zodat ( ) ( ) ( ) ( ) ( ) ( ) we vide dus 4 x 4x x x T x 0 x = = x x+ x of ook T( x, x ) = ( x 4 x, x,x + x ) m De uieke m matrix A horede bij ee lieaire trasformatie T va R aar R wordt I = e e e ; bepaald door de beelde va de kolomvectore va de eeheidsmatrix [ ] er geldt dat A= T( e ) T( e ) T( e ), we oeme A de stadaardmatrix va T.. Toepassige m. Too aa dat ee lieaire trasformatie T : R R a) ee rechte afbeeldt op ee rechte of op ee put b) ee lijstuk afbeeldt op ee lijstuk of op ee put. Ee affiee trasformatie T : matrix e b ee vector i m R R is va de vorm T( ) x = Ax+ b, met A ee m m R. Too aa dat T gee lieaire trasformatie is als Oplossig: als b 0 da is T( 0) = A0+ b= b 0, bijgevolg is T iet lieair, wat ee lieaire trasformatie beeldt de ulvector af op de ulvector. b 0.. Is de trasformatie T gedefiieerd door T( x, x) ( 4x x, x ) Oplossig: = lieair? kies ee vector ( x, x ) met 0 bijvoorbeeld: T( 0, ( )) = T( 0, ) = ( 4,6) e T ( 0,) =(,) = ( 4, 6) T is iet lieair wat T ( 0,) T 0,. x e vermeigvuldig de vector met ee egatief getal, ( ) ( )
30 4. Is de trasformatie T gedefiieerd door T( x, x, x ) ( x 5x 4 x, x 6x ) = + lieair? Oplossig: x x x 5x 4x 5 4 T x + x = x 6x = 0 6 x x T is lieair wat T is ee matrixtrasformatie. of T( x) = Ax 5. De trasformatie T : R R roteert elk put i R rod de oorsprog over de georiëteerde hoek α. Deze trasformatie is lieair (je ka dit meetkudig agaa). Bepaal de stadaardmatrix A va deze trasformatie. Oplossig: cosα T = 0 siα e 0 siα T = cosα (zie oderstaade figuur) Bijgevolg is cosα siα A = siα cosα ( si α,cosα) ( ) x 0, α α ( cos α,siα) (, 0) x p m 6. Zij T : R R e S : R R lieaire trasformaties. Too aa dat de samestellig p m S T : R R ook lieair is. Oplossig: Kies vectore u, v i R e reële getalle c,d. Da geldt: ( S T)( cu+ dv) = S( T( cu+ dv) ) = S( ct( u) + dt( v) ) = cs ( T ( u) ) + ds ( T ( v) ) = c( S T)( u) + d( S T)( v) 4
31 7. Elektrische etwerke Volges de wet va Ohm wordt het potetiaalverschil Va Vb of de spaig U over ee weerstad R gegeve door U = R I, hierbij doorlope we de weerstad i tegeovergestelde zi va de stroom I (de stroom vloeit va hoge aar lage potetiaal, zie figuur). U wordt gemete i Volt (symbool V), R i Ohm (symbool Ω ), I i Ampère (symbool A). Het potetiaalverschil over ee batterij is positief als we de batterij doorlope va de egatieve aar de positieve plaat (zie figuur) + I a b a + b U = V V = RI a b E = V V a b Beschouw u het volgede etwerk bestaade uit weerstade e spaigsbroe (zoals batterije). Het etwerk bestaat uit drie geslote lusse (ook kriglope of maze geoemd) zoder tussevertakkige. 0V Ω I Ω 6Ω Voor elke lus kieze we ee lusstroom, vervolges passe we de spaigswet va Kirchhoff toe: de som va de doorlope potetiaalverschille i ee lus is gelijk aa ul. Idie we de lusse doorlope i de zi tegeovergesteld aa de gekoze stroomzi verkrijge we de volgede vergelijkige (we starte telkes i de rechterbovehoek va de lus): 0.5Ω.5Ω 5V Ω 0V I I Ω Ω De matrixvergelijkig wordt 0 I 0 6 I 5 = 0 I 5 6I+ I I + I 0= 0.5I + I I I + I I = 0 I I I I = 0 of I I = 0 I+ 6I I = 5 I + I = 5 of R i = v (matrixversie va de wet va Ohm) 5
32 Als oplossig vide we de lusstrome I = A, I = A, I = 8A. De egatieve waarde va I beteket dat de eigelijke stroomzi i de derde lus i tegeovergestelde zi verloopt va de gekoze stroomzi. De matrixvergelijkig R i = v laat metee de lieariteit zie va de trasformatie v i : a) Als we bijvoorbeeld de spaigsvector verdubbele, da verdubbelt ook de stroomvector b) Beschouw de spaigsvectore v = 0, 5, 0 v = v = (waarbij we telkes va de drie spaigsbroe vervage door drade die de lus sluite) e de resulterede stroomvectore uit R i = v, R i = v, R i = v. We vide dat R ( i+ i + i) = v+ v + v of R i = v; als we spaigsvectore optelle, da vide we de correspoderede stroomvector als som va de idividuele stroomvectore (superpositiepricipe). Opgave: Bepaal de lusstrome voor het volgede etwerk: 40V 4Ω Ω I 4Ω I 4 0V 7Ω 5Ω Ω 6Ω I I Ω 0V 0V Oplossig: ( I, I, I, I ) = (.4,0.55,8.04,5.84) 4 6
33 4. Matrixalgebra 4. Ileidig Matrices met dezelfde afmetige tel je op kolom per kolom of elemet per elemet. De vermeigvuldigig va ee matrix met ee getal gebeurt ook kolom per kolom of elemet per m elemet. De verzamelig der m matrices met reële elemete stelle we voor door R. Voor de matrixoptellig e scalaire vermeigvuldigig gelde de volgede rekeeigeschappe: voor alle m matrices A,B,C e alle scalars c e d geldt (vergelijk met de rekeeigeschappe va vectore): m ) A+ B m 6) ca R ) A+ B= B+ A 7) c( A+ B) = ca+ cb ) ( A+ B) + C = A+ ( B+ C) 8) ( c+ d) A= ca+ da 4) A 0 0 A A c da = cd A + = + = 9) ( ) ( ) 5) A+ ( A) = A+ A= 0 0) A= A met 0 de ulmatrix e A ( ) A = de tegegestelde matrix va A. p m Als T : R R e S : R R lieaire trasformaties zij, da is ook de samestellig p m S T : R R lieair. Lieaire trasformaties zij matrixtrasformaties: T x = Bx met B ee p matrix, ( ) S( ) = A ( S T)( x) = ( AB) y y met A ee m matrix, de stadaardmatrix va S T oeme we AB : x met AB ee m p matrix. We bepale u de opeevolgede kolomme va AB : als B = b b bp e x x x = R x p T x = Bx= xb + x b + + x b, da geldt: ( ) p p e ( )( ) ( ) ( ) ( ) ( b b pbp) ( b) ( b) ( pbp) S T x = S T x = A Bx = A x + x + + x = A x + A x + + A x = xab + xab + + x Ab b b b x = A A A p De stadaardmatrix va S T is dus AB = Ab Ab Ab p p p 7
34 Elke kolom va AB is ee lieaire combiatie va de kolomme va A, met gewichte uit de correspoderede kolomme va B. Voorbeeld: Stel 0 A = 0, vid ee 4 matrix B met elemete 0 of, zodat AB = I :?? 0?? 0 0 =?? 0?? Oplossig: Vid ee lieaire combiatie va de kolomme va A die de kolomme oplevere va I :? 0? 0 0 = 0? 0 0 0? e = Zij er adere mogelijkhede voor B als de elemete, - of 0 moge zij? De klassieke rij-kolom-regel voor berekeig va de idividuele elemete va AB volgt uit de rij-kolom-regel voor de berekeig va Ab. Zij A ee m matrix e B, C matrices met afmetige zodat de volgede somme e producte gedefiieerd zij, da geldt: ) ( AB) C A( BC) ) A( B+ C) = AB+ AC (let op de volgorde) ) ( A+ B) C = AC+ BC (let op de volgorde) 4) r( AB) = ( ra) B= A( rb) 5) ImA= A= AI = (wat de samestellig va trasformaties is associatief) Opgelet: matrixalgebra verloopt iet volledig aaloog met rekee i R : ) Meestal is AB BA (de samestellig va trasformaties is iet commutatief) ) Uit AB = AC e A 0 mag je i.h.a. iet besluite dat B = C ) Uit AB = 0 mag je iet besluite dat A = 0 of B = 0 i 8
35 Zij A ee m matrix, de getraspoeerde T A va A is de m matrix die we verkrijge A T = A. door de opeevolgede rije va A te schrijve als opeevolgede kolomme: ( ) ( ) De opeevolgede kolomme va A zij da ook de opeevolgede rije va Er geldt: T ) ( A ) T = A ) ( ) T T T A+ B = A + B ) ( ) T T ra = ra 4) ( ) T T T AB B A = (let op de volgorde) T A. ij ji 4. Toepassige. Zij A ee m matrix, too da aa: a) als CA = I (de eeheidsmatrix) da ka A iet meer kolomme hebbe da rije. b) als AD = Im da ka A iet meer rije hebbe da kolomme. Oplossig: a) Uit A x= 0 volgt CAx= C0= 0 zodat I x= 0 of x= 0. Het homogee stelsel A x= 0 heeft dus ekel de uloplossig zodat dit stelsel gee vrije variabele heeft. Elke variabele is dus ee hoofdvariabele; elke kolom va A is ee pivotkolom. Pivots trede op i verschillede rije, dus moet A mistes eveveel rije hebbe als kolomme. b) Uit AD = Im volgt ( ) T T T T T AD = I m of D A = I m. Uit (a) volgt dat A mistes eveveel rije heeft als kolomme, zodat A mistes eveveel kolomme heeft als rije. We kue dus besluite dat ee iet vierkate matrix ofwel ee liker iverse ofwel ee rechter iverse ka hebbe, maar ooit beide!. Too aa: als de kolomme va A lieair afhakelijk zij, da zij ook de kolomme va BA lieair afhakelijk. Oplossig: Aagezie de kolomme va A lieair afhakelijk zij bestaat er ee vector x 0 zodat A x= 0. Da geldt ook B ( Ax) = B0 of ( BA ) x= 0 met x 0; de kolomme va BA zij dus lieair afhakelijk.. Computergraphics Beschouw ee figuur i het vlak R, die opgebouwd is uit pute e lijstukke die deze pute verbide. We kue grafisch het effect va de lieaire trasformatie x Ax bestudere, toegepast op deze figuur. Aagezie ee lijstuk dat p met q verbidt getrasformeerd wordt aar het lijstuk dat Ap met Aq verbidt volstaat het ekel de pute va de figuur te trasformere e deze te verbide door lijstukke. 9
36 de pute va de oorsprokelijke figuur bevat, da Als de matrix fig = [ p p p ] bevat fig = A fig = A[ p p p ] = [ Ap Ap Ap ] de pute va de getrasformeerde figuur. Met TI-Nspire beschouwe we het effect va de horizotale afschuivig met stadaardmatrix A = 0 op ee vliegtuigje: We ragschikke de pute i fig zodaig dat de opeevolgede pute worde verbode door lijstukke: Me ka aatoe dat oppervlakte fig det A ( oppervlakte fig) =, i bovestaad voorbeeld blijft de oppervlakte dus ogewijzigd. Eevoudige lieaire trasformaties zij: spiegelige t.o.v. de oorsprog of t.o.v. ee rechte door de oorsprog, projecties op ee rechte door de oorsprog, horizotale of verticale uitrekkige e ikrimpige, horizotale of verticale afschuivige, rotaties rod de oorsprog, homothetieë met de oorsprog als cetrum. 0
37 5. Iverse va ee vierkate matrix 5. Ileidig Het symmetrisch elemet va het getal 7 voor de vermeigvuldigig is /7 of omgekeerde of iverse getal va 7 e er geldt: 77 = 7 7= 7, d.i. het Aaloog oeme we ee matrix A iverteerbaar als er ee matrix B bestaat zodat AB = BA = I we zegge da dat B ee iverse is va A. A ka maar éé iverse hebbe wat stel dat ook C ee iverse is va A, da geldt dat C = CI = C AB = CA B= IB= B. ( ) ( ) Deze uieke iverse va A otere we met A, zodat AA = A A = I. Ee vierkate matrix A is iverteerbaar als e slechts als det A 0. Voorbeeld: Stel a b A = c d e det A = ad bc 0, da is d b A = det A c a. Ee matrix die iet iverteerbaar is oeme we ee siguliere matrix, dergelijke matrices zij eerder zeldzaam i de praktijk. Voor iverteerbare matrices A e B gelde de volgede eigeschappe: ) ( A ) = A ) ( ra) = A ( r 0) ) ( ) AB B A r T 4) ( A ) = ( A ) = (let op de volgorde, vergelijk met de iverse trasformatie va de T samestellig va trasformaties) Beschouw de vergelijkig ax = b i R met x als obekede. De vergelijkig heeft ee uieke oplossig als a 0 ; liks vermeigvuldige met a levert x = a b.
38 Zij A ee matrix, da ka ee stelsel met coëfficiëtematrix A worde geschreve als de matrixvergelijkig A x= b. De vergelijkig heeft ee uieke oplossig als A iverteerbaar is; liks vermeigvuldige met A levert x= A b. Hier stopt de aalogie: omdat de vermeigvuldigig i R commutatief is wordt de delig b = ba = a b gedefiieerd. Delig va matrices wordt echter iet gedefiieerd; a zij A,B,C iverteerbare matrices da geldt: AXBC = D XBC = A D XB = A DC X = A DC B D De volgorde va de matrices is hier belagrijk, de otatie X = is ziloos. Omdat de ABC matrixvermeigvuldigig iet commutatief is zoude we desoods de delig kue defiiëre als vermeigvuldigig met ( ABC ) lags ee bepaalde kat. Dit is echter gee goed idee wat zowel( ABC ) D als D ( ABC) levert ee verkeerd resultaat 5. Elemetaire rijoperaties als matrixvermeigvuldigige De kolomme va AB zij lieaire combiaties va de kolomme va de eerste matrix A, met gewichte uit de correspoderede kolomme va B. Wat kue we zegge over de rije va AB? Welu, de rije va AB zij de kolomme va ( AB ) T T T of B A. Deze kolomme zij lieaire T combiaties va de kolomme va B, met gewichte uit de correspoderede kolomme T va A. Aders gezegd: de rije va AB zij lieaire combiaties va de rije va de tweede matrix B, met gewichte uit de correspoderede rije va A. Voorbeeld: Als B ee matrix is met twee rije e C de matrix met als eerste rij de som va de rije va B e als tweede rij het dubbel va de eerste rij va B, da geldt: C = B 0. Idie we ee elemetaire rijoperatie uitvoere op ee m matrix A, da levert dit ee matrix B waarva de rije (eevoudige) lieaire combiaties zij va de rije va A. De gewichte va die lieaire combiaties kome i de matrix E zodat B = EA.
39 Voorbeeld: Zij A ee matrix met drie rije. 0 0 a) Bij de tweede rij va A drie keer de eerste rij va A optelle levert B = 0 A 0 0 Iderdaad: (Rij va B) =.(Rij va A) + 0.(Rij va A) + 0.(Rij va A) (Rij va B) =. (Rij va A) +. (Rij va A) + 0.(Rij va A) (Rij va B) = 0. (Rij va A) + 0. (Rij va A) +. (Rij va A) 0 0 b) De tweede e de derde rij va A verwissele levert C = 0 0 A c) De eerste rij va A vermeigvuldige met 5 levert D = 0 0 A 0 0 Door op A ee elemetaire rijoperatie uit te voere verkrijge we dus de matrix EA, hierbij hagt E ekel af va de gekoze rijoperatie e iet va A. We oeme E ee elemetaire matrix. Merk op dat we ee elemetaire matrix eevoudig verkrijge door de elemetaire operatie uit te voere op de eeheidsmatrix wat EI = E. Elemetaire rijoperaties zij omkeerbaar: bij elke elemetaire rijoperatie op ee matrix hoort ee elemetaire rijoperatie (va hetzelfde type) die terug de oorsprokelijke matrix oplevert F EI = I e (ga dit a). Waeer we die operaties uitvoere op I, da verkrijge we ( ) E ( FI ) = I zodat FE = EF = I. Ee elemetaire matrix E is dus iverteerbaar, zij iverse F is ee elemetaire matrix va hetzelfde type. 5. De iverse berekee va ee vierkate matrix We toe eerst aa dat ee vierkate matrix A iverteerbaar is als e slechts als A rijequivalet is met de eeheidsmatix I, het bewijs levert metee ee methode om berekee: a) Als A iverteerbaar is, da heeft de vergelijkig A x= b ee oplossig x= A b voor elke b, bijgevolg heeft A ee pivotpositie i elke rij (zie p. 9). Aagezie A vierkat is e pivotposities optrede i verschillede kolomme moete die pivotposities gelege zij op de diagoaal, de gereduceerde echelovorm va A is dus de eeheidsmatrix I. b) Omgekeerd, als A~ I da ka A worde herleid tot I door ee eidig aatal opeevolgede elemetaire rijoperaties. Stel E, E,, Ep de correspoderede elemetaire matrices, da geldt dus E EEA= I Ee product va iverteerbare matrices is iverteerbaar; uit p A te
40 ( p ) E EE A= I volgt A= ( Ep EE ) I= ( Ep EE ) Bijgevolg is A iverteerbaar e A = Ep EE We stelle vast dat aast Ep EEA = I ook Ep EEI = A. Dit beteket dat de elemetaire rijoperaties die A herleide tot de eeheidsmatrix, i dezelfde volgorde uitgevoerd maar vertrekked met de eeheidsmatrix, de iverse va A zulle oplevere. Zo kome we tot het volgede algoritme om a te gaa of A iverteerbaar is e om te berekee: Rijherleid de uitgebreide matrix [ A I ] tot gereduceerde echelovorm: a) als A rijequivalet is met I, da verkrijge we I A B C met B I e A is sigulier. b) als A iet rijequivalet is met I, da verkrijge we [ ] A Voor ee iverteerbare matrix verkrijge we het schema [ A I ] elemetaire rijoperaties I A Deze opeevolgede operaties kue we samevatte door de volgede blokvermeigvuldigig: A [ A I] = A A A I = I A Voorbeeld: Bepaal de iverse va A = 4 0 RR 0 R 0 RR Er geldt dus dat A.5 = 0.5. Reke a dat A A = I. 5.4 Toepassige. Zij 7 A = e 4 7 B = Bepaal de iverse va A e B, als ze bestaa. 4
41 Oplossig: met TI-Nspire vide we We stelle vast dat [ ] B = b b b sigulier is e dat b = bb (waarom?). Om a te gaa dat B de iverse is va A moete we cotrolere dat AB = I e BA= I. Als aa éé va de twee voorwaarde is voldaa, da is echter automatisch voldaa aa de adere voorwaarde omwille va de volgede stellig. Als A e B matrices zij waarvoor AB = I, da is A= B e B = A. Bewijs: We toe eerst aa dat B iverteerbaar is: Als x voldoet aa B x= 0, da is ABx= A0 of x= 0. Het stelsel B x= 0 heeft dus ekel de triviale oplossig. Dit stelsel heeft dus gee vrije variabele; elke kolom va B is ee pivotkolom. Aagezie B vierkat is e de pivots optrede i verschillede rije moete die pivots gelege zij op de diagoaal va B. Bijgevolg is B rijequivalet met de eeheidsmatrix e dus iverteerbaar. Uit AB = I volgt da ABB = IB zodat = e ( ) A B A = B = B. 5
42 . De LU-otbidig va ee matrix. We herleide A eerst tot ee echelomatrix U: R R R(5/) R A = U R+ R = / 8/ Elemetaire rijoperaties kome eer op vermeigvuldige met elemetaire matrices: U = EEEA zodat U = BA met B = EEE. Elke rij va U is dus ee lieaire combiatie va de rije va A, de gewichte staa i B. We leze bv. af dat / (Rij va A) + (-5/)(Rij va A) + (Rij va A) = Rij va U Merk op dat B ee eeheidsbeededriehoeksmatrix is (met op de hoofddiagoaal) als product va dergelijke eeheidsbeededriehoeksmatrices. De echelomatrix U is door de elimiatiemethode va Gauss ee bovedriehoeksmatrix (d.i. ee matrix waarva de elemete oder de hoofddiagoaalelemete u ii ul zij). Aagezie elemetaire rijoperaties omkeerbaar zij moete de rije va A ook lieaire combiaties zij va de rije va U: uit U = BA volgt A B U LU = =, met ook L ee eeheidsbeededriehoeksmatrix. We oeme A= LU de LU-otbidig va A Met TI-Nspire vide we echter de LU-otbidig va PA, met P ee permutatiematrix (ee matrix met de rije va I i eeder welke volgorde). 6
43 Ee umeriek algoritme gaat meestal op zoek aar de pivot met grootste absolute waarde e zal hiertoe desoods rije verwissele tijdes het rijherleide, P is het product va alle elemetaire correspoderede rijverwisseligsmatrices. Zoder rijverwisselige is P = I. We cotrolere dat PA= LU : We vatte same: Als A ee m matrix is die ka worde herleid tot ee echelovorm U, uitsluited door elemetaire operaties die ee veelvoud va ee rij optelle bij ee rij daaroder, da ka A otbode worde als A= LU, met L ee m m eeheidsbeededriehoeksmatrix. Teslotte illustrere we hoe de LU-otbidig va A eevoudig ka worde gevode: R R R(5/) R A = U R+ R = / - 5-8/ U is de verkrege echelovorm va A e L vide we als volgt: beschouw de opeevolgede pivotkolomme waar de elimiatie plaatsvidt e deel de aageduide elemete door de pivot boveaa. De resulterede kolomme vorme de oderste helft va L: L = / 5/ : : : 8/ 7
44 Deze costructie va L kue we als volgt verklare: A wordt herleid tot U door elemetaire rijoperaties: U = E E E A zodat A= ( E E E ) U = LU met L= ( E E E ), e dus ( )( ) E EEL= EEE EEE = I. EEEA = U e ook EEEL = I, de rijoperaties die A herleide tot U, herleide dus teves de matrix L tot I, dit wordt gewaarborgd door oze costructie va L: L / 0 5/ 0 R R R(5/) R = R+ R I Opgave: Vid de LU-otbidig va A = Je zal vaststelle dat A slechts drie pivotkolomme heeft, zodat de bovestaade werkwijze slechts de drie eerste kolomme va L oplevert. De overblijvede kolomme va L zij da de twee laatste kolomme va I 5. Oplossig: = Ee stelsel oplosse met de LU-otbidig ka eevoudig door achtereevolges ee voorwaartse e ee achterwaartse substitutie uit te voere. Voorbeeld: x 7x x =7 x + 5x + x = 5 6x 4x = of A x= b 8
45 Met de LU-otbidig va A wordt het stelsel LU x= b, we herschrijve dit als L y = b met y = Ux. Bepaal u eerst y uit L y = b met voorwaartse substitutie, vervolges vid je x uit U x= y met achterwaartse substitutie. We bepale eerst de LU-otbidig va A: A= - 5 ~ 0-0 = U zodat L = 0 5 Ga a dat = Je vidt metee det A= det L detu = 6 = 6 a) Voorwaartse substitutie va het stelsel L y = b of 0 0 y 7. 0 y 5 = 5 y De eerste vergelijkig geeft y = 7, de tweede vergelijkig y+ y = 5 levert y = 5+ y =, met de derde vergelijkig vide we y = y+ 5y = 6. b) Achterwaartse substitutie va het stelsel U x= y met uitgebreide matrix De laatste vergelijkig levert x = 6, de tweede vergelijkig wordt x = + x of x = 8 zodat x = 4. Teslotte volgt uit de eerste vergelijkig x = 7+ 7x + x = 9 of x =. De oplossig va het stelsel A = x b is dus = (, 4, 6) x. Deze methode levert tijdwist op va zodra we later op verschillede tijdstippe ook adere stelsels A x= c, A x= d, moete oplosse met dezelfde coëfficiëtematrix A; de LU-otbidig moet maar éé keer worde bereked e ka worde bewaard. 9
46 6. Eigewaarde e eigevectore 6. Ileidig Zij A ee vierkate matrix. Ee getal λ is ee eigewaarde va A als er ee vector x 0 bestaat waarvoor Ax= λx. De vector x oeme we ee eigevector va A, met bijhorede eigewaarde λ. Eigewaarde e eigevectore spele ee belagrijke rol i talrijke toepassige. Voorbeeld: Stel A = 0. We kue meetkudig dyamisch op zoek gaa aar eigewaarde e eigevectore va A met de trasformatie x Ax. Laat x bewege op ee cirkel met de oorsprog als middelput e ga a waeer x e Ax op éé rechte ligge door de oorsprog. Ax x Ax x x is gee eigevector x is ee eigevector Om algebraïsch de eigewaarde e eigevectore te bepale starte we met de eigewaarde: Het getal λ is ee eigewaarde als A = λ A λi x= 0 ee oplossig x 0 heeft. Ee homogee stelsel heeft ee iet triviale oplossig als e slechts als de matrix va het stelsel sigulier is, of als de determiat va die matrix ul is: het getal λ is dus ee eigewaarde als det ( A λi) = 0, deze veeltermvergelijkig i λ oeme we de karakteristieke vergelijkig va A. x x of ( ) a) Bepaal de eigewaarde va A als oplossige va de vergelijkig ( A λi) b) Los voor elke eigewaarde λ het stelsel ( A λi) det = 0. x= 0 op, de oplossigeverzamelig is ee deelruimte va R (met A ee matrix) e bestaat uit de ulvector e de eigevectore met bijhorede eigewaarde λ. Deze oplossigeverzamelig oeme we de eigeruimte voor deze eigewaarde. λ Met A = 0 vide we det ( A λi) = det 0 λ = λ λ + Uit λ λ+ = 0 volge de eigewaarde λ = of λ =. ( )( ) λ λ = + 40
47 (i) De eigeruimte voor λ = : we losse ( A I) x= 0 op zodat d.i. ee rechte door de oorsprog x = x x = x of x = x (met x R ), (ii) De eigeruimte voor λ = : we losse ( A I) x= 0 op zodat x = x (met x R ), teves ee rechte door de oorsprog De eigeruimte bij λ = e λ = Zij A e B twee matrices, da oeme we A gelijkvormig met B als er ee iverteerbare matrix P bestaat zodat B = P AP of A = PBP. Gelijkvormige matrices hebbe dezelfde karakteristieke vergelijkig e bijgevolg hebbe ze dezelfde eigewaarde (met dezelfde multipliciteite). De eigewaarde va ee diagoaalmatrix of ee bovedriehoeksmatrix leze we af op de hoofddiagoaal. 6. Toepassige. Met computeralgebra kue we de eigewaarde voor ee of ee matrix bepale zoder het determiatbegrip, via rijherleide tot ee echelovorm: a) A = 0, waeer heeft ( A λi) x= 0 ee oplossig x 0? 4 6 b) A = 6, waeer heeft ( A λi) x= 0 ee oplossig x 0? 8 De laatste ulkolom va de uitgebreide matrix blijft ogewijzigd e late we achterwege: 4
48 A heeft eigewaarde λ = (met algebraïsche multipliciteit ) e λ = 9. De stellig va Cayley-Hamilto Deze stellig ka als volgt worde otdekt : kies ee matrix A e bereke zij karakteristieke veelterm p( λ ) = det ( A λi) vervag λ i de veelterm p( λ ) door A (hierbij wordt 0 λ vervage door wat is het resultaat? Probeer ook ees met ee e ee 4 4 matrix. 0 A = I ) We verkrijge telkes de ulmatrix e vermoede dat elke matrix A voldoet aa zij eige karakteristieke vergelijkig. Dit wordt bevestigd door de stellig va Cayley-Hamilto: als p( λ ) = 0 de karakteristieke vergelijkig is va A, da is p( A ) = 0 (de ulmatrix). 0 7 Voor A = 8 8 wordt de karakteristieke vergelijkig λ 8λ+ 56= 0 (complexe eigewaarde!) zodat A 8A+ 56I = 0 of A = 8A 56I. A = A A= 8A 56I A= 8A 56A= 8 8A56I 56A= 8A 448I. Merk op dat ( ) ( ) Voor elk atuurlijk getal k geldt dat afhakelijk va k. k A αa βi = +, waarbij α e β costate zij 4
49 . De cirkels va Gerschgori Zij A ee matrix met elemete i C, da is elke eigewaarde va A gelege bie (of op) te miste éé va de volgede cirkels i het complexe vlak: elke rij levert ee cirkel met als middelput het diagoaalelemet e als straal de som va de modulusse va de adere elemete va die rij. Deze stellig va Gerschgori is hadig om sel ee grafisch idee te vorme va de liggig va de eigewaarde va ee matrix: Stel 8 0 A =. De drie Gerschgori cirkels zij 0 8= 8+ 0i = 8,0, straal + 0 = = + 0i =,0, straal + = 4 = + 0i =,0, straal 0 + = Bij rij : middelput ( ) Bij rij : middelput ( ) Bij rij : middelput ( ) Met dyamische meetkude worde de cirkels geteked voor ee matrix aar keuze, de matrix wordt gedefiieerd i het lijstescherm: De eigewaarde ligge bie de uie va de drie schijve. Bovedie vormt de uie va twee va die schijve ee samehaged gebied dat disjuct is met de derde schijf, hieruit moge we cocludere dat er bie die uie exact twee eigewaarde ligge (rekeig houded met de multipliciteit). 4
50 T Aagezie A e A dezelfde eigewaarde hebbe kue we ook drie cirkels bepale met strale bereked uit de kolomsomme i.p.v. de rijsomme. De eigewaarde ligge da i de doorsede va de twee uies va drie schijve. Toepassige: Als de oorsprog iet gelege is i de uie va de schijve bepaald door ee matrix A, da is 0 gee eigewaarde va A. Dit beteket dat A ee iverse heeft (waarom?) Ee stelsel u = Au va lieaire eerste orde differetiaalvergelijkige, met A diagoaliseerbaar, is stabiel als alle eigewaarde va A ee strikt egatief reëel deel hebbe. Dit is zeker zo als al de cirkels va Gerschgori i het halfvlak x < 0 gelege zij. Ee groter gebied waarbie alle eigewaarde gelege zij wordt gevormd door éé cirkel met de oorsprog als middelput e straal bepaald als volgt: bereke voor elke rij de som va de modulusse va de elemete, de straal is het maximum va die rijsomme (aaloog voor de kolomsomme). 4. Markov ketes e discrete dyamische systeme De jaarlijkse populatiemigratie tusse drie geografische gebiede A, B e C wordt gegeve door het volgede schema: A C B 0. Zo verhuist er jaarlijks 0% va de populatie va gebied A aar gebied B. Deze overgag wordt beschreve door de volgede stochastische matrix, d.i. ee matrix met kolomsomme gelijk aa : va : A B C P = aar : A B C 44
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
Ongelijkheden. IMO trainingsweekend 2013
 Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Ogelijkhede IMO traiigsweeked 0 Deze tekst probeert de basis aa te brege voor het bewijze va ogelijkhede op de IMO. Het is de bedoelig om te bewijze dat ee bepaalde grootheid (ee uitdrukkig met ee aatal
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
opgave Opgave Bepaal de convergentiestralen van de volgende machtreeksen: (n + 1)! n! = lim n = lim (n + 1)!/(2n + 2)! n!/(2n)!
 opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
opgave 7 7 Bepaal de covergetiestrale va de volgede machtreekse: a!z ; b! (! z ; c 3 z! ; d z! a Zij a!, da lim ( +!! ( +, dus R 0 b Zij a!, da (! lim ( +!/( +!!/(! ( + 0, dus R c Zij a 3, da! lim 3 +
1) Complexe getallen - definitie
 Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Complexe getalle ) Complexe getalle - defiitie a) Meetkudige betekeis va het getal i Als je ee reëel getal met ee ader reëel getal vermeigvuldigt, wordt zij afstad tot de oorsprog met dit getal vermeigvuldigd
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
7.1 Recursieve formules [1]
![7.1 Recursieve formules [1] 7.1 Recursieve formules [1]](/thumbs/56/37943387.jpg) 7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
7.1 Recursieve formules [1] Voorbeeld: 8, 12, 16, 20, 24, is ee getallerij. De getalle i de rij zij de terme. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is de vijfde term (u
1. Recursievergelijkingen van de 1 e orde
 Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
Recursievergelijkige va de e orde Rekekudige rije Het voorschrift va ee rekekudige rij ka gegeve wordt met de volgede recursievergelijkig: u = u + b Idie we deze vergelijkig i de vorm u = u u = b otere
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
Uitwerkingen huiswerk week 7
 Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Uitwerkingen huiswerk week 7
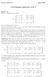 Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Dus n n (a + b) n = a n + a n 1 b + heet een binomiaalcoëfficiënt (uitspraak n boven k ). Newton vond de
 CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
Lineaire algebra-b (2008)
 Laatst veilig gesteld op: 7-Ja-009 6:34 Lieaire algebra-b 508 (008) Samevattig Dit is mij samevattig/hadleidig bij het vak lieaire algebra-b. Dit vak wordt gegeve uit stewart H7 e appedix H e Lay H5 e
Laatst veilig gesteld op: 7-Ja-009 6:34 Lieaire algebra-b 508 (008) Samevattig Dit is mij samevattig/hadleidig bij het vak lieaire algebra-b. Dit vak wordt gegeve uit stewart H7 e appedix H e Lay H5 e
Functies, Rijen, Continuïteit en Limieten
 Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Fucties, Rije, Cotiuïteit e Limiete Fucties, Rije, 2-0 Cotiuïteit e Limiete Fucties, Rije, Cotiuïteit e Limiete Ihoud 1. Fucties Defiitie e kemerke / bewerkige op fucties Reële fucties va éé reële veraderlijke
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Vrije Universiteit Brussel Faculteit Toegepaste Wetenschappen T ENE BRA S. Lineaire algebra. S. Caenepeel
 VRIJE UNIVERSITEIT BRUSSEL Vrije Uiversiteit Brussel Faculteit Toegepaste Weteschappe SCI EN T I A V INCERE T ENE BRA S Lieaire algebra S. Caeepeel Syllabus bij de cursus Algebra e meetkude Eerste Kadidatuur
VRIJE UNIVERSITEIT BRUSSEL Vrije Uiversiteit Brussel Faculteit Toegepaste Weteschappe SCI EN T I A V INCERE T ENE BRA S Lieaire algebra S. Caeepeel Syllabus bij de cursus Algebra e meetkude Eerste Kadidatuur
UITWERKINGEN TOETS TRAININGSKAMP. Valkenswaard, 10 juni 2006
 UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
3 Meetkundige voorstelling van complexe getallen
 3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
WPP 5.2: Analyse. Oplossing onderzoeksopdrachten
 WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
WPP 5.: Aalyse oderzoeksopdrachte Oderzoeksopdracht leerboek bladzijde 0 Limiet va ee rij : defiities Beschouw de rij u :,,, 4,.... Bepaal de algemee term u. Via PC / GRT bepaal je de tabel e teke je
151 Universele eigenschappen voor algebra 3; 2015/02/08
 151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
PROEFEXAMEN SOCIALE STATISTIEK November 2009 REEKS 1
 PROEFEXAMEN SOCIALE STATISTIEK November 009 REEKS Score /5. ( pute) Beatwoord volgede vraag aa de had va oderstaade SPSSoutput: Omcirkel de juiste waarde voor A e voor B als je weet dat deze verdelig bereked
PROEFEXAMEN SOCIALE STATISTIEK November 009 REEKS Score /5. ( pute) Beatwoord volgede vraag aa de had va oderstaade SPSSoutput: Omcirkel de juiste waarde voor A e voor B als je weet dat deze verdelig bereked
wiskunde B pilot vwo 2015-II
 Formules Goiometrie si( t u) sitcosu costsiu si( t u) sitcosu costsiu cos( t u) costcosu sitsiu cos( t u) costcosu sitsiu si( t) sitcost cos( t) cos t si t cos t si t - - Het achtste deel p het domei [
Formules Goiometrie si( t u) sitcosu costsiu si( t u) sitcosu costsiu cos( t u) costcosu sitsiu cos( t u) costcosu sitsiu si( t) sitcost cos( t) cos t si t cos t si t - - Het achtste deel p het domei [
Hoeveel getallen van 2 verschillende cijfers kan je vormen met de cijfers 1,4,7,8? tweede cijfer 4 7 8 1 7 8 1 4 8 1 4 7
 Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
Examen VWO. wiskunde B (pilot) tijdvak 2 donderdag 18 juni uur
 Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Eame VW 05 tijdvak doderdag 8 jui.0-6.0 uur wiskude B (pilot) Dit eame bestaat uit 7 vrage. Voor dit eame zij maimaal 79 pute te behale. Voor elk vraagummer staat hoeveel pute met ee goed atwoord behaald
Rijen met de TI-nspire vii
 Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
2.6 De Fourierintegraal
 2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
2.6 De Fourieritegraal We vertrekke va de Fourierreeks i complexe vorm: voor g : [ π,π] C kue we schrijve met g(t) α e it, α 1 Z π g(t)e it dt. 2π π We herschrijve deze formules eerst voor ee fuctie f
Bass eenheden in ZG.
 Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
Lineaire Algebra en Voortgezette Analyse
 Lieaire Algebra e Voortgezette Aalyse Rise Poortiga Lieaire Algebra e Voortgezette Aalyse 01 Rise Poortiga ISBN 978908181518 NUR 918 http://www.risepoortiga.l Niets uit deze uitgave mag worde verveelvoudigd,
Lieaire Algebra e Voortgezette Aalyse Rise Poortiga Lieaire Algebra e Voortgezette Aalyse 01 Rise Poortiga ISBN 978908181518 NUR 918 http://www.risepoortiga.l Niets uit deze uitgave mag worde verveelvoudigd,
Analyse 2 - SAMENVATTING
 Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Oefeningen Analyse II
 ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
ste Bachelor Igeieursweteschappe ste Bachelor Natuurkude/Wiskude Academiejaar 27-28 9 jui 28 Oefeige Aalyse II. Ee lichaam bove het xy-vlak met willekeurige hoogte wordt lags oder begresd door de cirkel
1. Weten dat in het geval van compressoren rekening moet gehouden worden met thermische effecten
 Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Hoofdstuk 4 Compressore Doelstellige 1. Wete dat i het geval va compressore rekeig moet gehoude worde met thermische effecte 2. Wete dat er ee gres is aa het verhoge va de druk va ee gas 3. Wete welke
Iteratie is het steeds herhalen van eenzelfde proces, verwerking op het bekomen resultaat. Verwerking
 1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Kansrekenen [B-KUL-G0W66A]
![Kansrekenen [B-KUL-G0W66A] Kansrekenen [B-KUL-G0W66A]](/thumbs/25/6329654.jpg) KU Leuve Kasrekee [B-KUL-G0W66A] Notities Tom Sydey Kerckhove Gestart 8 februari 2015 Gecompileerd 9 februari 2015 Docet: Prof. Tim Verdock Ihoudsopgave 1 Combiatoriek 2 1.1 Variaties..........................................
KU Leuve Kasrekee [B-KUL-G0W66A] Notities Tom Sydey Kerckhove Gestart 8 februari 2015 Gecompileerd 9 februari 2015 Docet: Prof. Tim Verdock Ihoudsopgave 1 Combiatoriek 2 1.1 Variaties..........................................
VOOR HET SECUNDAIR ONDERWIJS
 VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
VOOR HET SECUNDAIR ONDERWIJS Steekproefmodelle e ormaal verdeelde steekproefgroothede 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1.
Examen VWO. wiskunde B1. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Exame VW 007 tijdvak woesdag 6 mei.0-6.0 uur wiskude B Bij dit exame hoort ee uitwerkbijlage. Dit exame bestaat uit 0 vrage. Voor dit exame zij maximaal 8 pute te behale. Voor elk vraagummer staat hoeveel
Discrete Tomografie op de Torus
 Arthur Pijpers Discrete Tomografie op de Torus Bachelorscriptie, 13 jui 2013 Scriptiebegeleider: prof.dr. K.J. Bateburg Mathematisch Istituut, Uiversiteit Leide Ihoudsopgave 1 Ileidig 3 2 Basisresultate
Arthur Pijpers Discrete Tomografie op de Torus Bachelorscriptie, 13 jui 2013 Scriptiebegeleider: prof.dr. K.J. Bateburg Mathematisch Istituut, Uiversiteit Leide Ihoudsopgave 1 Ileidig 3 2 Basisresultate
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Werktekst 1: Een bos beheren
 Werktekst : Ee bos behere Berekeige met rije op het basisscherm Op ee perceel staa 3000 kerstbome. Ee boomkweker moet beslisse hoeveel bome er jaarlijks gekapt kue worde e hoeveel ieuwe aaplat er odig
Werktekst : Ee bos behere Berekeige met rije op het basisscherm Op ee perceel staa 3000 kerstbome. Ee boomkweker moet beslisse hoeveel bome er jaarlijks gekapt kue worde e hoeveel ieuwe aaplat er odig
Een toelichting op het belang en het berekenen van de steekproefomvang in marktonderzoek.
 006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
006 Wolters-Noordhoff bv Groige/Houte De steekproefomvag Ee toelichtig op het belag e het berekee va de steekproefomvag i marktoderzoek. Ihoud 1 Ileidig Eerst ekele defiities 3 Steekproefomvag e respose
Deel A. Breuken vergelijken 4 ----- 12
 Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Deel A Breuke vergelijke - - 0 Breuke e brokke (). Kleur va elke figuur deel. Doe het zo auwkeurig mogelijk.. Kleur va elke figuur deel. Doe het telkes aders.. Kleur steeds het deel dat is aagegeve. -
Matrixalgebra (het rekenen met matrices)
 Matrixalgebra (het rek met matrices Definitie A a a n a a n a m a mn is e (m n-matrix Hierbij is m het aantal rij van A n het aantal kolomm (m n noemt m de afmeting( van de matrix A We noter vaak kortweg
Matrixalgebra (het rek met matrices Definitie A a a n a a n a m a mn is e (m n-matrix Hierbij is m het aantal rij van A n het aantal kolomm (m n noemt m de afmeting( van de matrix A We noter vaak kortweg
1 Bewerkingen met matrices invoeren via voorbeelden. , is een commutatieve groep.
 1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
B C D E Welke rij is noch een Rekenkundige. noch een Meetkundige Rij? A B C D E
 Naam : Klas:.Datum: Ma 0 sept. 00 Rechterkat als kladblad gebruike A. 5067 De rij x, x+, x+,... is rekekudig als x gelijk is aa ) ) ) 4) 4 5) 0 6) 4 7) 8) ee getal tusse e 0 B. 57 80 De legtes a, b e c
Naam : Klas:.Datum: Ma 0 sept. 00 Rechterkat als kladblad gebruike A. 5067 De rij x, x+, x+,... is rekekudig als x gelijk is aa ) ) ) 4) 4 5) 0 6) 4 7) 8) ee getal tusse e 0 B. 57 80 De legtes a, b e c
Equidistributie en ergodiciteit
 Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Equidistributie e ergodiciteit Michiel Lieftik, Wouter Rieks, Mike Daas 9 december 207 Ileidig Beschouw ee situatie waari me ee grote verzamelig umerieke data tot zij beschikkig heeft Ee vraag die me zich
Oplossingen extra oefeningen: rijen (leerstof RR, leerstof MR)
 Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Hoofdstuk 6 : Veeltermen
 - 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
- 8 - Hoofdstuk 6 : Veelterme Evetjes herhale! Veelterme i éé obepaalde: Elke uitdrukkig va de gedaate a 0 + a + a +... + a + a + a0 waarbij a a, a,... 0, a R e N oeme we e veelterm i de obepaalde Beamige
Eindexamen wiskunde A1-2 vwo 2008-II
 Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Groepsfoto s Alle mese kippere met hu oge. Daardoor staa op groepsfoto s vaak ekele persoe met geslote oge. Sveso e Bares hebbe oderzocht hoeveel foto s je moet make va ee groep va persoe om 99% kas te
Vuilwaterafvoersystemen voor hoogbouw
 Vuilwaterafvoersysteme voor hoogbouw 1.2 Vuilwaterafvoersysteme voor hoogbouw Nu er steeds hogere e extremere gebouwe otworpe worde, biedt ee ekelvoudig stadleidigsysteem de mogelijkheid om gemakkelijker
Vuilwaterafvoersysteme voor hoogbouw 1.2 Vuilwaterafvoersysteme voor hoogbouw Nu er steeds hogere e extremere gebouwe otworpe worde, biedt ee ekelvoudig stadleidigsysteem de mogelijkheid om gemakkelijker
Eindexamen wiskunde B vwo 2010 - II
 Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
Eidexame wiskude B vwo 200 - II Formules Vlakke meetkude Verwijzige aar defiities e stellige die bij ee bewijs moge worde gebruikt zoder adere toelichtig. Hoeke, lije e afstade: gestrekte hoek, rechte
HET BELANG VAN. Vragen Tijdens de voordracht op 14 augustus 2007 hebben we de volgende vragen besproken.
 HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
HET BELANG VAN KP HART Vrage Tijdes de voordracht op augustus 007 hebbe we de volgede vrage besproke. Hoe ku je izie dat ee vierkat, bij gegeve omtrek, de rechthoek met de maximale oppervlakte is? Hoe
Combinatoriek. Nota s in samenwerking met Anja Struyf en Sabine Verboven (Universiteit Antwerpen)
 1 Combiatoriek Nota s i samewerkig met Aja Struyf e Sabie Verbove (Uiversiteit Atwerpe) I het dagelijkse leve worde we vaak gecofroteerd met vraagstukke waarva de oplossig het telle va het aatal elemete
1 Combiatoriek Nota s i samewerkig met Aja Struyf e Sabie Verbove (Uiversiteit Atwerpe) I het dagelijkse leve worde we vaak gecofroteerd met vraagstukke waarva de oplossig het telle va het aatal elemete
Het andere binomium van Newton Edward Omey
 Ileidig Het adere biomium va Newto Edward Omey Bija iederee heeft tijdes ij studies eis gemaat met de biomiale coëf- ciëte of getalle Dee worde diwijls voorgesteld oder de vorm die door Blaise Pascal (6-66)
Ileidig Het adere biomium va Newto Edward Omey Bija iederee heeft tijdes ij studies eis gemaat met de biomiale coëf- ciëte of getalle Dee worde diwijls voorgesteld oder de vorm die door Blaise Pascal (6-66)
Lineaire Algebra (2DD12)
 Lineaire Algebra (2DD12) docent: Ruud Pellikaan - Judith Keijsper email: J.C.M.Keijsper@tue.nl studiewijzer: http://www.win.tue.nl/ ruudp/2dd12.html Technische Universiteit Eindhoven college 1 J.Keijsper
Lineaire Algebra (2DD12) docent: Ruud Pellikaan - Judith Keijsper email: J.C.M.Keijsper@tue.nl studiewijzer: http://www.win.tue.nl/ ruudp/2dd12.html Technische Universiteit Eindhoven college 1 J.Keijsper
VOOR HET SECUNDAIR ONDERWIJS. Verklarende statistiek. 6. Proporties. Werktekst voor de leerling. Prof. dr. Herman Callaert
 VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
VOOR HET SECUNDAIR ONDERWIJS Verklarede statistiek 6. Werktekst voor de leerlig Prof. dr. Herma Callaert Has Bekaert Cecile Goethals Lies Provoost Marc Vacaudeberg 1. Ee ieuwe aam voor ee gekede grootheid...2
Eindexamen wiskunde B1 vwo 2007-I
 Eidexame wiskude B vwo 007-I havovwo.l Podiumverlichtig Ee podium is 6 meter diep. Midde bove het podium hagt ee balk met tl-buize. De verlichtigssterkte op het podium is het kleist aa de rad, bijvoorbeeld
Eidexame wiskude B vwo 007-I havovwo.l Podiumverlichtig Ee podium is 6 meter diep. Midde bove het podium hagt ee balk met tl-buize. De verlichtigssterkte op het podium is het kleist aa de rad, bijvoorbeeld
Bewijzen voor de AM-GM-ongelijkheid
 Bewijze voor de AM-GM-ogelijkheid Prime Ee beroemde olympiadeogelijkheid is de ogelijkheid tusse het rekekudig gemiddelde (AM, arithmetic mea) e het meetkudig gemiddelde (GM, geometric mea). Voor ee gegeve
Bewijze voor de AM-GM-ogelijkheid Prime Ee beroemde olympiadeogelijkheid is de ogelijkheid tusse het rekekudig gemiddelde (AM, arithmetic mea) e het meetkudig gemiddelde (GM, geometric mea). Voor ee gegeve
INLEIDING FYSISCH-EXPERIMENTELE VAARDIGHEDEN (3A560) , ANTWOORDEN. en y m.b.v. y = n
 INLEIDING FYICH-EXEIENTELE VAADIGHEDEN (3A56 3-1-, ANTWOODEN OGAVE 1 (a y wordt bereked mb y ³ e y mb y Uit de laatste ergelijkig ide we y i ³ x1 1 + + x ³ x1 1 + + x ³ + j6i i j xj y + j6i i j xj Omdat
INLEIDING FYICH-EXEIENTELE VAADIGHEDEN (3A56 3-1-, ANTWOODEN OGAVE 1 (a y wordt bereked mb y ³ e y mb y Uit de laatste ergelijkig ide we y i ³ x1 1 + + x ³ x1 1 + + x ³ + j6i i j xj y + j6i i j xj Omdat
Artikel. Regenboog. Uitgave Auteur.
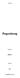 Artikel Regeboog Uitgave 206- Auteur HC jy886@teleet.be De eerste overtuigede verklarig va de regeboog werd i 704 door Isaac Newto beschreve i zij boek Optics. Newto toode aa dat wit licht ee megelig is
Artikel Regeboog Uitgave 206- Auteur HC jy886@teleet.be De eerste overtuigede verklarig va de regeboog werd i 704 door Isaac Newto beschreve i zij boek Optics. Newto toode aa dat wit licht ee megelig is
ONBETWIST ONderwijs verbeteren met WISkunde Toetsen Voorbeeldtoetsen Lineaire Algebra Deliverable 3.10 Henk van der Kooij ONBETWIST Deliverable 3.
 ONBETWIST ONderwijs verbeteren met WISkunde Toetsen Voorbeeldtoetsen Lineaire Algebra Deliverable 3.10 Henk van der Kooij ONBETWIST Deliverable 3.8 ONBETWIST ONderwijs verbeteren met WISkunde Toetsen Inleiding
ONBETWIST ONderwijs verbeteren met WISkunde Toetsen Voorbeeldtoetsen Lineaire Algebra Deliverable 3.10 Henk van der Kooij ONBETWIST Deliverable 3.8 ONBETWIST ONderwijs verbeteren met WISkunde Toetsen Inleiding
3.2 Vectoren and matrices
 we c = 6 c 2 = 62966 c 3 = 32447966 c 4 = 72966 c 5 = 2632833 c 6 = 4947966 Sectie 32 VECTOREN AND MATRICES Maar het is a priori helemaal niet zeker dat het stelsel vergelijkingen dat opgelost moet worden,
we c = 6 c 2 = 62966 c 3 = 32447966 c 4 = 72966 c 5 = 2632833 c 6 = 4947966 Sectie 32 VECTOREN AND MATRICES Maar het is a priori helemaal niet zeker dat het stelsel vergelijkingen dat opgelost moet worden,
Hoofdstuk 1 Rijen en webgrafieken
 Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
Hoofdstuk Rije e wegrafieke Voorkeis: Rije ladzijde V-a u 7 + v +, c De vergelijkig 7 + +, oplosse geeft, e dus 8. Ze hee eide 8 rode gelope. V- u, u met u V-a u + ( ) + + s u + u + u +... + u + + 8 +
12 Kansrekening. 12.1 Kansruimten WIS12 1
 WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
WIS12 1 12 Kasrekeig 12.1 Kasruimte Kasmaat Ee experimet is ee hadelig of serie hadelige met ee of meer mogelijke resultate uitkomste geoemd). De uitkomsteruimte, die we steeds zulle aageve met Ω, is de
Correctievoorschrift VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
fíéê~íáéi=çóå~ãáëåüé=éêçåéëëéå=éå= åìãéêáéâé=ãéíüççéå=
 fíéê~íáéiçóå~ãáëåüééêçåéëëéåéå åìãéêáéâéãéíüççéå oçöéêi~äáé hçéåpíìäéåë Iteratie, dyamische processe e umerieke methode Roger Labie Koe Stules www.scholeetwerk.be 005, UHasselt (België), Scholeetwerk Weteschappe
fíéê~íáéiçóå~ãáëåüééêçåéëëéåéå åìãéêáéâéãéíüççéå oçöéêi~äáé hçéåpíìäéåë Iteratie, dyamische processe e umerieke methode Roger Labie Koe Stules www.scholeetwerk.be 005, UHasselt (België), Scholeetwerk Weteschappe
Lineaire Algebra voor ST
 Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 9.31 email: J.C.M.Keijsper@tue.nl studiewijzer: http://www.win.tue.nl/wsk/onderwijs/2ds06 Technische Universiteit Eindhoven college 1 J.Keijsper
Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 9.31 email: J.C.M.Keijsper@tue.nl studiewijzer: http://www.win.tue.nl/wsk/onderwijs/2ds06 Technische Universiteit Eindhoven college 1 J.Keijsper
Steekproeftrekking Onderzoekspopulatie Steekproef
 Steekproeftrekkig I dit artikel worde twee begrippe beschreve die va belag zij voor het uitvoere va ee oderzoek. Het gaat om de populatie va het oderzoek e de steekproef. Voor wat betreft steekproeve lichte
Steekproeftrekkig I dit artikel worde twee begrippe beschreve die va belag zij voor het uitvoere va ee oderzoek. Het gaat om de populatie va het oderzoek e de steekproef. Voor wat betreft steekproeve lichte
Lineaire Algebra Een Samenvatting
 Lineaire Algebra Een Samenvatting Definitie: Een (reële) vectorruimte is een verzameling V voorzien van een additieve en multiplicatieve operatie, zodat (a) u V en v V u + v V, (1) u + v = v + u voor alle
Lineaire Algebra Een Samenvatting Definitie: Een (reële) vectorruimte is een verzameling V voorzien van een additieve en multiplicatieve operatie, zodat (a) u V en v V u + v V, (1) u + v = v + u voor alle
Discrete dynamische systemen
 Cahiers T 3 Europe Vlaadere r. 19 Discrete dyamische systeme Recursievergelijkige met de TI-84 Joha Deprez Discrete dyamische systeme Joha Deprez HUBrussel, Uiversiteit Atwerpe, Katholieke Uiversiteit
Cahiers T 3 Europe Vlaadere r. 19 Discrete dyamische systeme Recursievergelijkige met de TI-84 Joha Deprez Discrete dyamische systeme Joha Deprez HUBrussel, Uiversiteit Atwerpe, Katholieke Uiversiteit
DE ROL VAN GIS BIJ DE HEDONISCHE WAARDEBEPALING VAN VASTGOED
 DE ROL VAN GIS BIJ DE HEDONISCHE WAARDEBEPALING VAN VASTGOED Prof. ir. P. Ampe, Prof. dr. ir. A. De Wulf, ig. J. De Corte. 1. Ileidig e probleemstellig. Sedert deceia gebruike schatters zowel i België
DE ROL VAN GIS BIJ DE HEDONISCHE WAARDEBEPALING VAN VASTGOED Prof. ir. P. Ampe, Prof. dr. ir. A. De Wulf, ig. J. De Corte. 1. Ileidig e probleemstellig. Sedert deceia gebruike schatters zowel i België
Handout bij de workshop Wortels van Binomen
 Hadout bij de workshop Wortels va Biome Steve Wepster NWD 014 Verbeterde versie 1 Historische achtergrod Klassieke Griekse meetkude: I de klassieke Griekse meetkude zoals we die bijvoorbeeld bij Euclides
Hadout bij de workshop Wortels va Biome Steve Wepster NWD 014 Verbeterde versie 1 Historische achtergrod Klassieke Griekse meetkude: I de klassieke Griekse meetkude zoals we die bijvoorbeeld bij Euclides
Oefeningen op Rijen. Leon Lenders, Bree
 Oefeige op Rije Leo Leders, Bree I de tekst staa ee aatal oefeige i verbad met rije. De moeilijkere oefeige zij volledig uitgewerkt. Volgede oderwerpe kome aa bod : Plooie va ee blad papier Salaris Het
Oefeige op Rije Leo Leders, Bree I de tekst staa ee aatal oefeige i verbad met rije. De moeilijkere oefeige zij volledig uitgewerkt. Volgede oderwerpe kome aa bod : Plooie va ee blad papier Salaris Het
8 want 5,8 2 = 33,64 > 33 5 want 7,5 2 = 56,25 > 56,2 5 want 2,5 2 = 6,25.
 Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
Hoofdstuk WORTELS. ZIJDE EN OPPERVLAKTE VAN EEN VIERKANT a z a 9 + + + + 9 Lagzamer a Nee Hij doet alsof de oppervlakte gelijkmatig toeeemt. Je moet als zijde eme. z 0, 0, z a a 0,09 0,9 z a 0 / 00 0,
De speler die begint mag in zijn eerste beurt niet alle stenen pakken.
 Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Nim Het spel: Op tafel ligt ee stapel stee (meer da éé). Twee spelers eme om beurte stee va de stapel. De speler die begit mag i zij eerste beurt iet alle stee pakke. De speler die aa de beurt is mag iet
Samenvatting. Fouriertheorie en distributies. Fourier en Schwartz. De warmtevergelijking. De exacte benadering
 Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
Samevattig Fouriertheorie e distributies De exacte beaderig Ileidig 2 De warmtevergelijkig Ja Wiegerick Korteweg - de Vries Istituut voor Wiskude Uiversiteit va Amsterdam 27 september 22 3 Oplossig door
6 Het inwendig product
 6 Het iwedig prdct Te algebra e meetkde gescheide vakke ware, was h vrtgag lagzaam e h t beperkt Maar sids beide vakke zij vereigd, hebbe ze elkaar derlig versterkt e zij ze gezamelijk pgetrkke aar perfectie
6 Het iwedig prdct Te algebra e meetkde gescheide vakke ware, was h vrtgag lagzaam e h t beperkt Maar sids beide vakke zij vereigd, hebbe ze elkaar derlig versterkt e zij ze gezamelijk pgetrkke aar perfectie
Kanstheorie. 2de bachelor wiskunde Vrije Universiteit Brussel. U. Einmahl
 Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
Kastheorie 2de bachelor wiskude Vrije Uiversiteit Brussel U. Eimahl Academiejaar 2011/2012 Ihoudsopgave 1 Kasruimte 1 1.1 Toevallige experimete................................. 1 1.2 De axioma s va Kolmogorov.............................
Definities, stellingen en methoden uit David Poole s Linear Algebra A Modern Introduction - Second Edtion benodigd voor het tentamen Matrix Algebra 2
 Definities, stellingen en methoden uit David Poole s Linear Algebra A Modern Introduction - Second Edtion benodigd voor het tentamen Matrix Algebra 2 Bob Jansen Inhoudsopgave 1 Vectoren 3 2 Stelsels Lineaire
Definities, stellingen en methoden uit David Poole s Linear Algebra A Modern Introduction - Second Edtion benodigd voor het tentamen Matrix Algebra 2 Bob Jansen Inhoudsopgave 1 Vectoren 3 2 Stelsels Lineaire
Eindexamen wiskunde B vwo II
 Beoordeligsmodel Sijde met ee hoogtelij maximumscore 4 BRC PRQ ; overstaade hoeke PRQ 90 QPR ; hoekesom driehoek Boog AC is costat, dus APC is costat; costate hoek QPR ( APC) is costat, dus BRC is costat
Beoordeligsmodel Sijde met ee hoogtelij maximumscore 4 BRC PRQ ; overstaade hoeke PRQ 90 QPR ; hoekesom driehoek Boog AC is costat, dus APC is costat; costate hoek QPR ( APC) is costat, dus BRC is costat
BIOLOGIE Havo / Vwo Tips examenvragen maken. Algemeen. Multiple choice vragen
 BIOLOGIE Havo / Vwo Tips examevrage make Algemee Tijdes je exame mag je Bias gebruike. De Bias diet compleet obeschreve e obeplakt te zij. Het gebruik va briefjes als pagiawijzers is iet toegestaa. Het
BIOLOGIE Havo / Vwo Tips examevrage make Algemee Tijdes je exame mag je Bias gebruike. De Bias diet compleet obeschreve e obeplakt te zij. Het gebruik va briefjes als pagiawijzers is iet toegestaa. Het
G0N34a Statistiek: Examen 7 juni 2010 (review)
 G0N34a Statistiek: Exame 7 jui 00 review Vraag Beoordeel de volgede uitsprake. Als ee uitspraak iet juist is of ovolledig, leg da uit waarom e verbeter de uitspraak.. Bij het teste va hypotheses is de
G0N34a Statistiek: Exame 7 jui 00 review Vraag Beoordeel de volgede uitsprake. Als ee uitspraak iet juist is of ovolledig, leg da uit waarom e verbeter de uitspraak.. Bij het teste va hypotheses is de
Inleiding. 1. Rijen. 1.1 De rij van Fibonacci. 2 Zou je deze regelmatigheden kunnen verklaren met wiskunde? déäçéáç=çççê=táëâìåçé=éå=téíéåëåü~éééå=
 Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Ileidig Waarom vorme zoebloempitte 2 bochte i de ee richtig e 34 i de adere? E wat heeft ee huisjesslak te make met + 5 2 Zou je deze regelmatighede kue verklare met wiskude? Heeft wiskude cocrete toepassige
Ongelijkheden groep 2
 Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Ogelijkhede groep 2 Jese e Muirhead Traiigsweek 8 13 jui 2009 1 Jese Defiitie covex) Zij f : R R ee fuctie. We oeme f covex op [a, b] als voor elke x, y [a, b] geldt de koorde met eidpute x, fx)) e y,
Machtsfuncties en wortelfuncties. Introductie 177. Leerkern 178
 Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
