MEETKUNDE 5 Cirkels en cilinders
|
|
|
- Diana Verstraeten
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 MEETKUNDE 5 Cirkels en ilinders M22 De irkel 254 M23 De ilinder
2 M22 De irkel Cirkel en elementen vn een irkel 781 E Geef de nm vn de ngeduide delen in de irkel. Y X O T S het middelpunt een koorde de strl de dimeter een middelpuntshoek een middellijn O:... [XY]:... OS :... XT :... SOT:... XT: E Mk de tekening. Teken C(M,2 m) Duid op de irkel een punt n en teken C(,4 m) M 2 m 4 m 783 B Teken telkens twee vershillende irkels die de punten en B evtten. B B 254 M22 De irkel
3 784 B Mk de tekening. Teken [B] zodt B = 6 m. Teken C(,4 m) en C(B,3 m). Twee snijpunten Hoeveel snijpunten heen de twee irkels?... Wnneer B > 7 m. (som vn de strlen) J, wnneer B = 7 m. (som vn de strlen) d Wnneer heen de irkels geen snijpunten?... e Kunnen de irkels ook juist één snijpunt heen?... Verklr m 6 m B 3 m 785 B Teken C(M,2,5 m) Teken in de irkel een koorde [B] zodt B = 3 m. Teken een koorde [CD] zodt B//CD. Teken een middelpuntshoek BME vn m B M 50 E C D De irkel M22 255
4 786 B Mk de tekening. Teken C(O, 2 m). Teken twee koorden [XY] en [PQ] zodt XY = PQ = 3 m. Meet de middelpuntshoeken XOY en POQ. De middelpuntshoeken zijn even groot: XÔY = PÔQ d Wt stel je vst?... X Y P O Q 787 B Mk de tekening. Teken C(,3 m). Teken twee middelpuntshoeken BK en KD zodt BK = KD. Meet de koorden [BK] en [DK]. De koorden zijn even lng: BK = DK. d Wt stel je vst?... K B D 788 V* Teken een ssenstelsel. d e Teken de punten (6,1), B(8,5) en C(4,7). Teken driehoek BC. Mk een vierknt wrij [C] een digonl is en [B] een zijde. Teken een irkel door de hoekpunten vn het vierknt. Geef de oördinten vn lle roosterpunten met gehele oördinten die op de irkel liggen. F(6,7); G(8,3); H(4,1); I(2,5) 256 M22 De irkel
5 789 V* Mk de tekening. Teken C(M,3 m) en C(M,5 m). Teken in de kleine irkel twee vershillende middellijnen B en CD zodt, B, C en D op de irkel liggen. Teken in de grote irkel middellijn EF B en noem de snijpunten met de kleine irkel G en H. d Geef de meest pssende nm vn de volgende vierhoeken: ruit rehthoek prllellogrm vierknt FBE:... CBD:... DFCE:... HBG: V* Bereken de middelpuntshoek vn de vershillende vlkken in dit Rd vn fortuin. 360 : 12 = 30 Elke middelpuntshoek is B Hoe groot is een middelpuntshoek vn één stuk trt uit een ronde trt voor zes personen die elk evenveel krijgen? 360 : 6 = V* Teken C(M, 3 m) Teken de middelpuntshoeken MB = 60, BMC = 90 en CMD = 180. Hoe groot is D? Hoeveel proent vn de irkel wordt door elke middelpuntshoek epld? (rond f op één deiml) 16,7 % 50 % 25 % 8,3 % MB:... CMD:... BMC:... DM: V* Mevrouw De Keyser wil in hr tuin een rond zwemd met een dimeter vn 3 meter pltsen. Ze wil vnuit de punten, B en C het zwemd heleml kunnen zien. Bereken de dimeter vn het zwemd op de tekening (pgin 258). Teken het zwemd op de plttegrond. De irkel M22 257
6 getekende lengte (m) werkelijke lengte (m) lengte shl De dimeter vn de irkel op de plttegrond moet dn 2 m zijn. (300 m : 150) ,5 m tuin 9 m keuken 3 m B woonkmer C 6 m 9 m Omtrek, oppervlkte en volume 794 E Bereken de omtrek. Rond je resultt f op twee deimlen. Een irkel met een strl vn 3,5 m. O = 2 π r = 2 π 3,5 m = 21,99 m C(O, 2 m) O = 2 π r = 2 π 2 m = 12,57 m Een irkel met een dimeter vn 4 dm. O = 2 π r = 2 π 2 dm = 12,57 dm 795 V*** Bereken de omtrek vn een irkel die een oppervlkte vn 28,27 m² heeft. r = _ S π = 28,27 m 2 = 3 m _ π... O = 2 π r = 2 π 3 m = 18,85 m... De irkel heeft een omtrek vn 18,85 m M22 De irkel
7 796 E Bereken de oppervlkte. Rond je resultt f op twee deimlen. Een irkel met een strl vn 2 m. S = π r 2 = π 2 2 m 2 = 12,57 m 2 C(,5 m) S = π r 2 = π 5 2 m 2 = 78,54 m 2 Een irkel met een dimeter vn 400 mm. S = π r 2 = π mm 2 = ,71 mm V*** Bereken de oppervlkte vn een irkel die een omtrek vn 3,14 m heeft. r = O : (2 π) = 3,14 m : (2 π) = 0,5 m S = π r 2 = π 0,5 2 m 2 = 0,79 m 2 De irkel heeft een oppervlkte vn 0,79 m B Hmsters kunnen zih heerlijk uitleven in hun loopwieltje. Hoeveel meter loopt een hmster ls het wieltje 150 keer ronddrit? De strl vn het wieltje is 10 m. 150 O = π r = π 10 m = 9424,78 m = 94,25 m De hmster loopt 94,25 m B Hoeveel keer moet het kleine tndwiel (met een strl vn 5 m) drien om het grote tndwiel (met een strl vn 15 m) één keer rond te lten drien. O groot = 2 π r = 2 π 15 m = 94,25 m O klein = 2 π r = 2 π 5 m = 31,42 m 94,25 m : 31,42 m = 3 Het kleine tndwiel moet 3 keer drien om één keer rond het grote te drien B Bekijk het reuzenrd in het pretprk. Hoe groot is de middelpuntshoek tussen twee opeenvolgende stngen? 360 : 16 = 22,5 Elke middelpuntshoek is 22,5. Welke fstnd leg je f ls je drie keer heleml rond ent gegn? De strl vn het rd is 30 meter. 3 O = 3 2 π r = 3 2 π 30 m = 565,49 m Je legt 565,49 m f. De irkel M22 259
8 801 B Bekijk de voorstelling vn twee vershillende feesttfels. 2 m 1,6 m n welke tfel kn het grootst ntl gsten zitten? Eerste tfel: O = 2 2 m + 2 π r = 4 m + 2 π 1 m = 10,28 m Tweede tfel: O = 2 π r = 2 π 1,6 m = 10,05 m n de eerste tfel kunnen de meeste personen zitten. Welke tfel heeft de grootste oppervlkte? Eerste tfel: S = π r m 2 m = π 1 2 m m 2 = 7,14 m 2 Tweede tfel: S = π r 2 = π 1,6 2 m 2 = 8,04 m 2 De tweede tfel heeft de grootste oppervlkte. 802 V* Bereken de werkelijke omtrek en de oppervlkte vn de volgende figuur. Rond je resultten f op twee deimlen. O S = 3 m + 2 π r m = 3 m + 2 π 1,6 m m = 21,05 m = π r 2 ( + B) h + + h _ 2 _ m 1,6 m 3 m = π 1,6 2 m (3 m + 5 m) 3 m 5 m 3 m 2 + _ 2... = 8,04 m m 2 + 7,5 m m 4 m 3 m = 27,54 m V** Hoeveel keer meer drien de kleine wieltjes ten opzihte vn de grote wielen? De kleine wieltjes heen een dimeter vn 8 m en de grote wielen vn 30 m. O groot = π d = π 30 m = 94,25 m O klein = π d = π 8 m = 25,13 m 94,25 m : 25,13 m = 3,75 De kleine wieltjes drien 3,75 keer meer dn de grote M22 De irkel
9 804 V** Bereken de oppervlkte vn het witte deel in de gegeven figuur. S grote irkel = π r 2 = π 3 2 m 2 = 28,27 m S kleine irkel = 5 π r 2 = 5 π 1 2 m 2 = 15,71 m ,27 m 2 15,71 m 2 = 12,56 m m 2 m 2 m Het witte deel heeft een oppervlkte vn 12,56 m V** Bereken in elke figuur de oppervlkte vn het donker gekleurde deel. Rond je resultten f op twee deimlen. 28 m 44 m 3,5 m 2,5 m 5 m S groot vierknt = 44 m 44 m = 1936 m 2... S klein vierknt = 28 m 28 m = 784 m 2... S irkel = π r 2 = π 14 2 m 2 = 615,75 m 2... S gekleurd = 1936 m m 2 615,75 m 2... _ 5 m 3,5 m 2 = 8,75 m 2 S... driehoek = S irkel = π r 2 = π 1,25 2 m 2... = 4,91 m 2... S gekleurd = 8,75 m 2 4,91 m 2... = 536,25 m 2 De irkel heeft een dimeter vn 60 m. De rehthoek is 56 m lng en 10 m reed. = 3,84 m 2 S irkel = π r 2 = π 30 2 m 2 = 2827,43 m 2... S rehthoek = 56 m 10 m = 560 m 2... S gekleurd = 2827,43 m m 2... = 2267,43 m 2... De irkel M22 261
10 806 V*** Gegeven: Hoeveel proent vn het vierknt wordt door de irkel edekt? (rond f op een geheel) 3 m S vierknt = z 2 = 3 2 m 2 = 9 m 2... Welke figuur heeft de grootste omtrek? S irkel = π r 2 = π 1,5 2 m 2 = 7,07 m ,07 m 2 : 9 m 2 = 0,7855 = 79 %... De irkel edekt 79 % vn het vierknt.... Omtrek vierknt Omtrek irkel O = 4z = 4 3 m = 12 m O = 2 π r = 2 π 1,5 m = 9,42 m Het vierknt heeft de grootste omtrek. M23 De ilinder 807 E Geef telkens de meest pssende nm voor de ruimtefiguren die je in de volgende foto s herkent. d e kegel ilinder prism ilinder pirmide f g h i ilinder pirmide prism kegel M23 De ilinder
11 808 B Bereken het volume. Rond f op twee deimlen. Een ilinder vn 5 m hoog met een strl vn 2 m. V = π r 2 h = π 2 2 m 2 5 m 7,5 m = 62,83 m 3 23 m 4,5 m 2 m V = π r 2 h = π 1 2 m 2 4,5 m V = π r 2 h = π 3,75 2 m 2 23 m... = 14,14 m 3 = 1016,11 m B Deze tnkwgen levert stookolie. Hoeveel liter stookolie kn hij in één keer vervoeren? De tnk heeft een dimeter vn 2 m en is 10 m lng. V = π r 2 h = π 10 2 dm dm = ,93 dm 3 = ,93 l De tnkwgen kn ,93 l in één keer vervoeren B Een verflik heeft een dimeter vn 8,6 m en is 10 m hoog. Bereken de inhoud vn dit lik in liter. V = π r 2... h = π 0,43 2 dm 2 1 dm = 0,58 dm 3 = 0,58 l Om de hele zijknt vn het lik zit een etiket. S = 2 π... r h = 2 π 4,3 m 10 m = 270,18 m 2 Bereken de oppervlkte vn dit etiket.... Welke inhoud hoort ij een drie keer zo hoog lik? V = 3 0,58... l = 1,74 l d Welke inhoud heeft een lik wrvn de dimeter d = 2,5 8,6... m = 21,5 m r = 21,5 m : 2 = 10,75 m = 1,075 dm 2,5 keer zo groot is? V = π r 2... h = π 1,075 2 dm 2 1 dm = 3,63 dm 3 = 3,63 l 811 V* Een regenput heeft een dimeter vn 2 m en is 4 m diep. Hij is voor 3 _ 4 gevuld. Hoeveel liter wter kn er nog ij? V = 1 _ 4 π r 2 h = 1 _ 4 π 10 2 dm 2 40 dm = 3141,59 dm 3 = 3141,59 l... Er kn nog 3141,59 l wter ij in de regenput V* Zjne heeft een doos wspoeder gekoht. De doos is 19 m lng, 9 m reed en 22 m hoog. Omdt de doos eshdigd is, wil ze het wspoeder overgieten in een emmertje dt ze nog in de kst heeft stn. Het emmertje heeft een dimeter vn 19 m en is 14 m hoog. Kn l het wspoeder vn de doos in het emmertje?... V doos = l h = 19 m 9 m 22 m = 3762 m 3... V emmertje = π r 2 h = π 9,5 2 m 2 14 m = 3969,40 m ,40 m³ > 3762 m³ Het wspoeder kn in het emmertje.... De ilinder M23 263
12 813 V** Een lndouwer heeft 180 melkkoeien die gemiddeld 20 l melk geven per dg. Die melk wordt om de twee dgen opgehld. Zijn melktnk heeft een dimeter vn 2 m. Hoe lng moet die tnk minstens zijn om lle melk vn twee dgen te kunnen ewren? (rond f op één deiml) V melk per dg = l = 3600 l per twee dgen: 7200 l h = V : (π r 2 ) = 7200 dm 3 : ( π 10 2 dm 2 ) = 22,92 dm De tnk moet minstens 2,3 m lng zijn V*** Uit deze ks is een stuk gesneden met een middelpuntshoek vn 40. Bereken hoeveel m³ ks er nog overlijft ls je weet dt de strl vn de ks 10 m is en de hoogte 5 m. Middelpuntshoek 40 etekent één negende vn de hele ilinder. Er lijft nog ht negende over. V = _ 8 9 π r 2 h = _ 8 9 π 10 2 m 2 5 m = 1396,26 m 3 Er lijft nog 1396,26 m³ vn de ks over V*** In een ilindervormig ekergls met een dimeter vn 4 m stt een vloeistof 16 m hoog. Deze vloeistof wordt overgegoten in een ekergls met een dimeter vn 8 m. Hoe hoog stt de vloeistof in dit ekergls? Rond zinvol f. V vloeistof = π r 2 h = π 2 2 m 2 16 m = 201,06 m 3 h = V : (π r 2 ) = 201,06 m 3 : (π 4 2 m 2 ) = 4,01 m De vloeistof stt 4,0 m hoog in het tweede ekergls V*** Een oktil wordt in een ilindervormig gls gegoten. Het gls is 12 m hoog en heeft een strl vn 3 m. De oktil estt uit twee vershillende lgen: Een lg suikersiroop vn 3 m en een lg fruitsp vn 8 m. Bereken uit hoeveel ml suikersiroop en uit hoeveel ml fruitsp de oktil estt. V siroop = π r 2 h = π 3 2 m 2 3 m = 84,82 m 3 = 84,82 ml V fruitsp = π r 2 h = π 3 2 m 2 8 m = 226,19 m 3 = 226,19 ml Hoeveel kuusvormige ijslokjes met een rie vn 2 m kun je nog in het gls doen zonder dt het gls overloopt? V luht = π r 2 h = π 3 2 m 2 1 m = 28,27 m 3 V ijsklontje = z 3 = 2 3 m 3 = 8 m 3 28,27 m 3 : 8 m 3 = 3,53 Er kunnen nog 3 ijslokjes ij in het gls. Hoeveel m³ vn het gls is dn nog niet gevuld? 28,27 m m 3 = 4,27 m 3 er lijft nog 4,27 m 3 luht over in het gls 817 B Bereken de oppervlkte vn: een ilinder met een strl vn 6 m en een hoogte vn 20 m. S = 2 π r π r h = 2 π 6 2 m π 6 m 20 m = 980,18 m 2 de hoeveelheid krton in een w-rolletje. De dimeter is 4,5 m en de hoogte 10 m. S = 2 π r h = 2 π 2,25 m 10 m = 141,37 m het etiket vn een onservenlik met een dimeter vn 10 m en een hoogte vn 12 m. S = 2 π r h = 2 π 5 m 12 m = 376,99 m M23 De ilinder
De cirkel M22. het middelpunt een koorde de straal de diameter een middelpuntshoek een middellijn. 2 cm 4 cm. Cirkel en elementen van een cirkel
 M De irkel Cirkel en elementen vn een irkel 781 E Geef de nm vn de ngeduide delen in de irkel. Y X O T S het middelpunt een koorde de strl de dimeter een middelpuntshoek een middellijn O:... [XY]:... OS
M De irkel Cirkel en elementen vn een irkel 781 E Geef de nm vn de ngeduide delen in de irkel. Y X O T S het middelpunt een koorde de strl de dimeter een middelpuntshoek een middellijn O:... [XY]:... OS
Cirkels en cilinders
 5 irkels en cilinders it kun je l 1 middelpunt en strl in een cirkel nduiden 2 de oppervlkte vn vlkke figuren berekenen 3 het volume vn een prism berekenen Test jezelf Elke vrg heeft mr één juist ntwoord.
5 irkels en cilinders it kun je l 1 middelpunt en strl in een cirkel nduiden 2 de oppervlkte vn vlkke figuren berekenen 3 het volume vn een prism berekenen Test jezelf Elke vrg heeft mr één juist ntwoord.
Opgave 1. Waarom kun je bij het Noorden twee getallen neerzetten? Geldt dit ook voor andere windrichtingen? Hoeveel graden hoort er bij het Oosten?
 Opgve 1 Hier zie je een windroos met de windrihtingen er in getekend. Hij is verder verdeeld in 360 hoekjes, elk vn die hoekjes heet 1 grd. Bij het Noorden (N) hoort 0 grden (en dus ook 360 grden). file:
Opgve 1 Hier zie je een windroos met de windrihtingen er in getekend. Hij is verder verdeeld in 360 hoekjes, elk vn die hoekjes heet 1 grd. Bij het Noorden (N) hoort 0 grden (en dus ook 360 grden). file:
3 Snijpunten. Verkennen. Uitleg
 3 Snijpunten Verkennen Meetkunde Snijpunten Inleiding Verkennen Bentwoord de vrgen bij Verkennen. Mk ook de constructie in GeoGebr. Gebruik eventueel het progrmm om de snijpunten voor je te berekenen ls
3 Snijpunten Verkennen Meetkunde Snijpunten Inleiding Verkennen Bentwoord de vrgen bij Verkennen. Mk ook de constructie in GeoGebr. Gebruik eventueel het progrmm om de snijpunten voor je te berekenen ls
MEETKUNDE 1 Basisbegrippen
 MEETKUNE sisegrippen M Een klslokl vol meetkunde M nzihten M sisegrippen vn de meetkunde 7 M4 Onderlinge ligging vn rehten 74 M5 Eigenshppen in vernd met evenwijdigheid en loodrehte stnd vn rehten in het
MEETKUNE sisegrippen M Een klslokl vol meetkunde M nzihten M sisegrippen vn de meetkunde 7 M4 Onderlinge ligging vn rehten 74 M5 Eigenshppen in vernd met evenwijdigheid en loodrehte stnd vn rehten in het
Meet de lengte en de breedte van de rechthoek.
 M15 Rechthoek en lk 692 E Je kunt hieronder eenvoudig de oppervlkte vn een rechthoek vinden door de ruitjes te tellen. Elk ruitje is 1 cm². Hoe groot is de oppervlkte vn deze rechthoek?... 693 B Bereken
M15 Rechthoek en lk 692 E Je kunt hieronder eenvoudig de oppervlkte vn een rechthoek vinden door de ruitjes te tellen. Elk ruitje is 1 cm². Hoe groot is de oppervlkte vn deze rechthoek?... 693 B Bereken
Noordhoff Uitgevers bv
 Voorkennis: Algerïshe ewerkingen ldzijde 9 V- d e 9 V- 9 V- + + + V- + + 9 d + + + + e + + + + f + g Hoofdstuk - Funties en lger + + + + + + + ldzijde 9 V- + ( + ) + ( )( ) of + of of of ( ) d p p ( p
Voorkennis: Algerïshe ewerkingen ldzijde 9 V- d e 9 V- 9 V- + + + V- + + 9 d + + + + e + + + + f + g Hoofdstuk - Funties en lger + + + + + + + ldzijde 9 V- + ( + ) + ( )( ) of + of of of ( ) d p p ( p
Toetsopgaven vwo B deel 3 hoofdstuk 10
 Toetsopgven vwo deel 3 hoofdstuk 10 Opgve 1 In de figuur hiernst zie je 15 kubusjes met ribbe. e punten,, en zijn hoekpunten vn een kubusje, punt is het midden vn een ribbe en de punten en delen een ribbe
Toetsopgven vwo deel 3 hoofdstuk 10 Opgve 1 In de figuur hiernst zie je 15 kubusjes met ribbe. e punten,, en zijn hoekpunten vn een kubusje, punt is het midden vn een ribbe en de punten en delen een ribbe
Lijnen en vlakken in. Klas 6N en 7N Wiskunde 5 perioden Kees Temme Versie 2
 Lijnen en vlkken in Kls N en N Wiskunde perioden Kees Temme Versie . Coördinten in R³.... De vergelijking vn een vlk ().... De vectorvoorstelling vn een lijn.... De vectorvoorstelling vn een vlk... 8.
Lijnen en vlkken in Kls N en N Wiskunde perioden Kees Temme Versie . Coördinten in R³.... De vergelijking vn een vlk ().... De vectorvoorstelling vn een lijn.... De vectorvoorstelling vn een vlk... 8.
Hoofdstuk 2 DE STELLING VAN PYTHAGORAS
 Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Onafhankelijk van a. f snijdt de x-as in punt A ( , 0) Voor elke positieve waarde van a is een functie f. gegeven door F ( x) = x e ax.
 Onfhnkelijk vn Voor elke positieve wrde vn is een functie f gegeven door f ( x) = (1 x) e x en een functie F gegeven door F ( x) = x e x. De functie 3p 1 Toon dit n. F is een primitieve functie vn f. De
Onfhnkelijk vn Voor elke positieve wrde vn is een functie f gegeven door f ( x) = (1 x) e x en een functie F gegeven door F ( x) = x e x. De functie 3p 1 Toon dit n. F is een primitieve functie vn f. De
Overzicht eigenschappen en formules meetkunde
 Overziht eigenshppen en formules meetkunde 1 iom s Rehten en hoeken 3 riehoeken 4 Vierhoeken Op de volgende ldzijden vind je de eigenshppen en formules die je in de eerste grd geleerd het en deze die in
Overziht eigenshppen en formules meetkunde 1 iom s Rehten en hoeken 3 riehoeken 4 Vierhoeken Op de volgende ldzijden vind je de eigenshppen en formules die je in de eerste grd geleerd het en deze die in
Eindexamen vwo wiskunde B pilot I
 Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin t cos t sin t www. - - nfhnkelijk
Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin t cos t sin t www. - - nfhnkelijk
Krommen en oppervlakken in de ruimte
 (HOOFDSTUK 60, uit College Mthemtis, door Frnk Ares, Jr. nd Philip A. Shmidt, Shum s Series, MGrw-Hill, New York; dit is de voorereiding voor een uit te geven Nederlndse vertling). Krommen en oppervlkken
(HOOFDSTUK 60, uit College Mthemtis, door Frnk Ares, Jr. nd Philip A. Shmidt, Shum s Series, MGrw-Hill, New York; dit is de voorereiding voor een uit te geven Nederlndse vertling). Krommen en oppervlkken
Pak jouw passer en maak de afstand tussen de passerpunten 3 cm.
 Psser en irkel Verkennen Opgve 1 Op de foto hiernst wordt met ehulp vn een psser een irkel getekend. Pk jouw psser en mk de fstnd tussen de psserpunten 3 m. Teken een punt M en zet drin de stlen punt vn
Psser en irkel Verkennen Opgve 1 Op de foto hiernst wordt met ehulp vn een psser een irkel getekend. Pk jouw psser en mk de fstnd tussen de psserpunten 3 m. Teken een punt M en zet drin de stlen punt vn
MEETKUNDE 3 Vierhoeken
 MEETKUNDE 3 Vierhoeken M11 Vierhoeken in de ruimte 8 M1 Vierhoeken tekenen 1 M13 Kuus en lk 14 M14 Metriek stelsel M15 Rehthoek en lk 3 M16 Vierknt en kuus 8 M17 Trpezium, prllellogrm en ruit 3 7 M111
MEETKUNDE 3 Vierhoeken M11 Vierhoeken in de ruimte 8 M1 Vierhoeken tekenen 1 M13 Kuus en lk 14 M14 Metriek stelsel M15 Rehthoek en lk 3 M16 Vierknt en kuus 8 M17 Trpezium, prllellogrm en ruit 3 7 M111
Aanzet 1 tot een document van parate kennis en vaardigheden wiskunde 1 ste graad
 Anzet 1 tot een document vn prte kennis en vrdigheden wiskunde 1 ste grd 1. TAALVAARDIGHEID BINNEN WISKUNDE ) Begrippen uit de getllenleer Bewerking Symool optelling + ftrekking vermenigvuldiging deling
Anzet 1 tot een document vn prte kennis en vrdigheden wiskunde 1 ste grd 1. TAALVAARDIGHEID BINNEN WISKUNDE ) Begrippen uit de getllenleer Bewerking Symool optelling + ftrekking vermenigvuldiging deling
Basisbegrippen. Test jezelf Elke vraag heeft maar één juist antwoord. Controleer je antwoord in de correctiesleutel. balk cilinder kubus
 sisegrippen Dit kun je l de enmingen vn vershillende soorten driehoeken en vierhoeken geruiken een kuus, een lk en een ilinder herkennen evenwijdige en snijdende rehten herkennen sherpe, stompe en rehte
sisegrippen Dit kun je l de enmingen vn vershillende soorten driehoeken en vierhoeken geruiken een kuus, een lk en een ilinder herkennen evenwijdige en snijdende rehten herkennen sherpe, stompe en rehte
MEETKUNDE 4 Driehoeken
 MEETKUNDE 4 Driehoeken M18 Driehoeken in de ruimte 38 M19 Driehoeken tekenen 4 M0 Merkwrdige lijnen in een 44 M1 Omtrek, oppervlkte en volume 47 37 M18 Driehoeken in de ruimte 738 E Vul n. In KLM zijn
MEETKUNDE 4 Driehoeken M18 Driehoeken in de ruimte 38 M19 Driehoeken tekenen 4 M0 Merkwrdige lijnen in een 44 M1 Omtrek, oppervlkte en volume 47 37 M18 Driehoeken in de ruimte 738 E Vul n. In KLM zijn
Examen VWO. wiskunde B. tijdvak 1 woensdag 18 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Emen VW 20 tijdvk woensdg 8 mei 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. chter het correctievoorschrift is een nvulling opgenomen. Dit emen bestt uit 8 vrgen. Voor dit emen zijn miml
Emen VW 20 tijdvk woensdg 8 mei 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. chter het correctievoorschrift is een nvulling opgenomen. Dit emen bestt uit 8 vrgen. Voor dit emen zijn miml
Moderne wiskunde: berekenen zwaartepunt vwo B
 Moderne wiskunde: erekenen zwrtepunt vwo B In de edities 7 en 8 ws er in de slotdelen vn VWO B ruimte genomen voor een prgrf over het erekenen vn een zwrtepunt. In de negende editie is er voor gekozen
Moderne wiskunde: erekenen zwrtepunt vwo B In de edities 7 en 8 ws er in de slotdelen vn VWO B ruimte genomen voor een prgrf over het erekenen vn een zwrtepunt. In de negende editie is er voor gekozen
Examen VWO. wiskunde B (pilot) tijdvak 1 woensdag 16 mei 13.30-16.30 uur
 Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Rangschik van klein naar groot. Vul aan. Meet de lengte van onderstaande voorwerpen.
 582 Rngshik vn klein nr groot. 583 Vul n. 0,3 km 500 m 200 000 m 25 000 dm... 0,3 m 40 m 12 dm 240 mm... 1 mm is... mm kleiner dn 1 m. 8 m is... m kleiner dn 1 m. d 9 92 70 47 3 m is... mm kleiner dn 1
582 Rngshik vn klein nr groot. 583 Vul n. 0,3 km 500 m 200 000 m 25 000 dm... 0,3 m 40 m 12 dm 240 mm... 1 mm is... mm kleiner dn 1 m. 8 m is... m kleiner dn 1 m. d 9 92 70 47 3 m is... mm kleiner dn 1
Meetkunde 1 Ruimtemeetkunde
 Meetkunde 1 Ruimtemeetkunde M1 Ruimtelijke situties voorstellen in een vlk 180 M2 De pirmide, de kegel en de ol 18 M Het volume vn een pirmide, een kegel en een ol 190 179 M1 1 Titel Ruimtelijke situties
Meetkunde 1 Ruimtemeetkunde M1 Ruimtelijke situties voorstellen in een vlk 180 M2 De pirmide, de kegel en de ol 18 M Het volume vn een pirmide, een kegel en een ol 190 179 M1 1 Titel Ruimtelijke situties
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Donderdag 20 mei 13.30 16.30 uur
 Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Eindexamen vwo wiskunde B II
 Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
2. Gegeven is de driehoek van figuur 10.10a. Gevraagd worden hoek β en de zijden a en c.
 Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Examen VWO 2012. wiskunde B. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exmen VWO 2012 tijdvk 1 woensdg 16 mei 13.30-16.30 uur wiskunde B Bij dit exmen hoort een uitwerkbijlge. Dit exmen bestt uit 17 vrgen. Voor dit exmen zijn mximl 78 punten te behlen. Voor elk vrgnummer
Exmen VWO 2012 tijdvk 1 woensdg 16 mei 13.30-16.30 uur wiskunde B Bij dit exmen hoort een uitwerkbijlge. Dit exmen bestt uit 17 vrgen. Voor dit exmen zijn mximl 78 punten te behlen. Voor elk vrgnummer
Natuurlijke getallen op een getallenas en in een assenstelsel
 Turf het ntl fouten en zet de resultten in een tel. Vlmingen Nederlnders resultt ntl resultt ntl 9 9 en nder tlstelsel U Ontijfer de volgende hiërogliefen met ehulp vn het overziht op p. in het leerwerkoek.........................
Turf het ntl fouten en zet de resultten in een tel. Vlmingen Nederlnders resultt ntl resultt ntl 9 9 en nder tlstelsel U Ontijfer de volgende hiërogliefen met ehulp vn het overziht op p. in het leerwerkoek.........................
Getallenverzamelingen
 Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
1 Vlaamse Wiskunde Olympiade : Eerste Ronde.
 Vlmse Wiskunde Olympide 99 993 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olympide 99 993 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Bewerkingen met eentermen en veeltermen
 5 Bewerkingen met eentermen en veeltermen Dit kun je l 1 werken met letters ls onekenden, ls vernderlijken en om te verlgemenen 2 een tel mken ij een situtie 3 de fsprken over lettervormen toepssen 4 oppervlkteformules
5 Bewerkingen met eentermen en veeltermen Dit kun je l 1 werken met letters ls onekenden, ls vernderlijken en om te verlgemenen 2 een tel mken ij een situtie 3 de fsprken over lettervormen toepssen 4 oppervlkteformules
1a Een hoeveelheid stof kan maar op één manier veranderen. Hoe?
 Oefenopgven over Stoffen en Mterilen Uitwerking en ntwoord op elke opgve stt n de ltste opgve. Gegevens kunnen worden opgezoht in de tellen hterin. Als de zwrteftor niet vermeld is mg je 9,81 N/kg nemen.
Oefenopgven over Stoffen en Mterilen Uitwerking en ntwoord op elke opgve stt n de ltste opgve. Gegevens kunnen worden opgezoht in de tellen hterin. Als de zwrteftor niet vermeld is mg je 9,81 N/kg nemen.
Zwaartepunt en traagheid
 Nslgwerk deel 8 wrtepunt en trgheid Uitgve 2016-1 uteur HC hugocleys@icloud.com Inhoudsopgve 1 wrtepunt 4 1.1 Inleiding wrtepunt vn een lichm....................... 4 1.2 Momentenstelling..................................
Nslgwerk deel 8 wrtepunt en trgheid Uitgve 2016-1 uteur HC hugocleys@icloud.com Inhoudsopgve 1 wrtepunt 4 1.1 Inleiding wrtepunt vn een lichm....................... 4 1.2 Momentenstelling..................................
Een regenton. W is het vlakdeel dat wordt ingesloten door de x-as, de y-as, de grafiek van r en de lijn x h, met 0 h
 Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
Hoofdstuk 8 - Ruimtefiguren
 Voorkennis V-1a De oppervlakte van ABC is 12 5 : 2 = 0 m 2. zijde kwadraat AB = 12 144 AC = 5 BC = 25 169 d BC = 169 = 1 m De omtrek van ABC is 5 12 1 = 0 m. BD = 12 4 = 8 m De oppervlakte van BCD is 8
Voorkennis V-1a De oppervlakte van ABC is 12 5 : 2 = 0 m 2. zijde kwadraat AB = 12 144 AC = 5 BC = 25 169 d BC = 169 = 1 m De omtrek van ABC is 5 12 1 = 0 m. BD = 12 4 = 8 m De oppervlakte van BCD is 8
H. 10 Goniometrie Basisbegrippen. a c. Gemeenschappelijke Propedeuse Engineering WISKUNDE H.10
 H. 10 Goniometrie 10.1 Bsisegrippen Regelmtig voeren we erekeningen uit, wrin één of meerdere hoeken voorkomen. Voor een sherpe hoek kunnen we 3 goniometrishe verhoudingen definiëren. Deze lten zih het
H. 10 Goniometrie 10.1 Bsisegrippen Regelmtig voeren we erekeningen uit, wrin één of meerdere hoeken voorkomen. Voor een sherpe hoek kunnen we 3 goniometrishe verhoudingen definiëren. Deze lten zih het
Spiegelen, verschuiven en draaien in het vlak
 2 Spiegelen, vershuiven en drien in het vlk it kun je l 1 de iddelloodlijn vn een lijnstuk herkennen en tekenen 2 een hoek eten en tekenen 3 de issetrie vn een hoek herkennen en tekenen 4 de oördint vn
2 Spiegelen, vershuiven en drien in het vlk it kun je l 1 de iddelloodlijn vn een lijnstuk herkennen en tekenen 2 een hoek eten en tekenen 3 de issetrie vn een hoek herkennen en tekenen 4 de oördint vn
de Wageningse Methode Antwoorden H24 GONIOMETRIE VWO 1
 H GONIOMETRIE VWO.0 INTRO 6 km : 0.000 = cm b b Driehoek PQB is gelijkvormig met driehoek VHB, de 00 vergrotingsfctor is 0 = 7. Dus PQ = 680 = 0, dus zeilt ze 0 meter 7 in minuten. Dt is,8 km/u.. HOOGTE
H GONIOMETRIE VWO.0 INTRO 6 km : 0.000 = cm b b Driehoek PQB is gelijkvormig met driehoek VHB, de 00 vergrotingsfctor is 0 = 7. Dus PQ = 680 = 0, dus zeilt ze 0 meter 7 in minuten. Dt is,8 km/u.. HOOGTE
Eindexamen wiskunde B vwo 2011 - I
 Tussen twee grfieken De functie f is gegeven door f ( ) =. In figuur zijn op het intervl [0, ] de grfiek vn f en de lijn = getekend. De grfiek vn f en de lijn = snijden elkr in het punt T. p de lijn =
Tussen twee grfieken De functie f is gegeven door f ( ) =. In figuur zijn op het intervl [0, ] de grfiek vn f en de lijn = getekend. De grfiek vn f en de lijn = snijden elkr in het punt T. p de lijn =
Beste leerling. De auteurs
 Voor wie kopiëren wil: U vindt dit oek goed en wenst er kopieën vn te mken. edenk dn ook eens: dt zowel uitgever ls uteurs met de oprengst ervn hun kosten moeten dekken; dt kopiëren zonder toestemming
Voor wie kopiëren wil: U vindt dit oek goed en wenst er kopieën vn te mken. edenk dn ook eens: dt zowel uitgever ls uteurs met de oprengst ervn hun kosten moeten dekken; dt kopiëren zonder toestemming
Eindexamen vwo wiskunde B pilot I
 Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
CIRKELS EN BOLLEN. Klas 7N Wiskunde 5 perioden K. Temme
 CIRKELS EN BOLLEN Kls 7N Wiskunde 5 perioden K. Temme INHOUDSOPGAVE. DE VERGELIJKING VAN EEN BOL.... DE SNIJCIRKEL VAN EEN BOL EN EEN VLAK... 5. DE CIRKEL DOOR PUNTEN... 7. DE BOL DOOR GEGEVEN PUNTEN...
CIRKELS EN BOLLEN Kls 7N Wiskunde 5 perioden K. Temme INHOUDSOPGAVE. DE VERGELIJKING VAN EEN BOL.... DE SNIJCIRKEL VAN EEN BOL EN EEN VLAK... 5. DE CIRKEL DOOR PUNTEN... 7. DE BOL DOOR GEGEVEN PUNTEN...
1 Vlaamse Wiskunde Olympiade 1994 1995 : Eerste Ronde.
 Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
In dit hoofdstuk introduceren we de hoofdrolspelers van het college: eindige automaten.
 9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
Examen VWO. wiskunde B. tijdvak 2 woensdag 20 juni uur. Bij dit examen hoort een uitwerkbijlage.
 Emen VWO 202 tijdvk 2 woensdg 20 juni 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. Dit emen bestt uit 7 vrgen. Voor dit emen zijn miml 8 punten te behlen. Voor elk vrgnummer stt hoeveel
Emen VWO 202 tijdvk 2 woensdg 20 juni 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. Dit emen bestt uit 7 vrgen. Voor dit emen zijn miml 8 punten te behlen. Voor elk vrgnummer stt hoeveel
1 Vlaamse Wiskunde Olympiade : Tweede ronde
 1 Vlmse Wiskunde Olympide 000-001: Tweede ronde De eerste ronde estt uit 0 meerkeuzevrgen Het quoteringssysteem werkt ls volgt: per goed ntwoord krijgt de deelnemer 5 punten, een lnco ntwoord ezorgt hem
1 Vlmse Wiskunde Olympide 000-001: Tweede ronde De eerste ronde estt uit 0 meerkeuzevrgen Het quoteringssysteem werkt ls volgt: per goed ntwoord krijgt de deelnemer 5 punten, een lnco ntwoord ezorgt hem
436 = _ 135 11_ 33 = 2_ 12 = _ 1 19 = 1 19 = _ 19 _ 10 _ 11 _ 2 4 = _ 1. Reken uit. Reken uit.
 V** Voor 540 euro krijg je op de nk 4 pond. 540 Noteer de verhouding vn het ntl euro tot het ntl pond.............. 4 10 en epl de sisreuk. 5 : 10 0,55 Voor 5 euro krijg je 0,5 pond. 100 : 10 1,511 Je
V** Voor 540 euro krijg je op de nk 4 pond. 540 Noteer de verhouding vn het ntl euro tot het ntl pond.............. 4 10 en epl de sisreuk. 5 : 10 0,55 Voor 5 euro krijg je 0,5 pond. 100 : 10 1,511 Je
Meetkunde 2 Spiegelen, verschuiven en draaien in het vlak
 Meetkunde 2 Spiegelen, vershuiven en drien in het vlk M4 Spiegelingen herkennen en tekenen 200 M5 Eigenshppen vn de spiegeling 205 M6 Symmetrie 208 M7 Vershuivingen herkennen en tekenen 210 M8 Eigenshppen
Meetkunde 2 Spiegelen, vershuiven en drien in het vlk M4 Spiegelingen herkennen en tekenen 200 M5 Eigenshppen vn de spiegeling 205 M6 Symmetrie 208 M7 Vershuivingen herkennen en tekenen 210 M8 Eigenshppen
Meetkunde 2 Spiegelen, verschuiven en draaien in het vlak
 Meetkunde 2 Spiegelen, vershuiven en drien in het vlk M4 Spiegelingen herkennen en tekenen 200 M5 Eigenshppen vn de spiegeling 205 M6 Symmetrie 208 M7 Vershuivingen herkennen en tekenen 210 M8 Eigenshppen
Meetkunde 2 Spiegelen, vershuiven en drien in het vlk M4 Spiegelingen herkennen en tekenen 200 M5 Eigenshppen vn de spiegeling 205 M6 Symmetrie 208 M7 Vershuivingen herkennen en tekenen 210 M8 Eigenshppen
MEETKUNDE 2 Lengte - afstand - hoeken
 MTKUN 2 Lengte - fstnd - hoeken M7 Lengtemten en meetinstrumenten 186 M8 Lengte en fstnd 187 M9 Gelijke fstnden 194 M10 Hoeken meten en tekenen 198 185 M7 1 Titel Lengtemten en meetinstrumenten 579 Vul
MTKUN 2 Lengte - fstnd - hoeken M7 Lengtemten en meetinstrumenten 186 M8 Lengte en fstnd 187 M9 Gelijke fstnden 194 M10 Hoeken meten en tekenen 198 185 M7 1 Titel Lengtemten en meetinstrumenten 579 Vul
Junior Wiskunde Olympiade 2012-2013: de tweede ronde
 Junior Wiskunde Olympide 0-03: de tweede ronde Volgende enderingen kunnen nuttig zijn ij het oplossen vn sommige vrgen.,44 3,73 5,36 π 3,46.ls + =en =3,dnis gelijkn () 5 () 6 () 3 () 9 (E) 3.Hetgetl (
Junior Wiskunde Olympide 0-03: de tweede ronde Volgende enderingen kunnen nuttig zijn ij het oplossen vn sommige vrgen.,44 3,73 5,36 π 3,46.ls + =en =3,dnis gelijkn () 5 () 6 () 3 () 9 (E) 3.Hetgetl (
03 02 11 12 dagen. Ongeopend: 22 01 2014. 1 juni 1 juli
 lok les en C Hoelng is het houdr? in de winkelwgen houdrheidsdtum onsumeren innen 0 0 dgen zterdg jnuri 0 Ongeopend: 0 0 Ongeopend: 0 jr Ongeveer mnden 8 0 dgen C Reken met tijd. het is nu over dgen is
lok les en C Hoelng is het houdr? in de winkelwgen houdrheidsdtum onsumeren innen 0 0 dgen zterdg jnuri 0 Ongeopend: 0 0 Ongeopend: 0 jr Ongeveer mnden 8 0 dgen C Reken met tijd. het is nu over dgen is
Lengteverandering bij temperatuurverandering.
 2 Uitzetting. Opgve 2.1 Lengteverndering ij tempertuurverndering. De ene stof zet sterker uit dn de ndere. Deze mterileigenshp wordt ngegeven met de lineire uitzettingsoëffiiënt (α). De lineire uitzettingsoëffiiënt
2 Uitzetting. Opgve 2.1 Lengteverndering ij tempertuurverndering. De ene stof zet sterker uit dn de ndere. Deze mterileigenshp wordt ngegeven met de lineire uitzettingsoëffiiënt (α). De lineire uitzettingsoëffiiënt
Toepassingen op Integraalrekening
 Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Eindexamen vwo wiskunde B I
 Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Praktische opdracht Optimaliseren van verpakkingen Inleidende opgaven
 Prktische opdrcht Optimliseren vn verpkkingen Inleidende opgven V, WB Opgve 1 2 Gegeven is de functie f ( x) = 9 x. Op de grfiek vn f ligt een punt P ( p; f ( p)) met 3 < p < 0. De projectie vn P op de
Prktische opdrcht Optimliseren vn verpkkingen Inleidende opgven V, WB Opgve 1 2 Gegeven is de functie f ( x) = 9 x. Op de grfiek vn f ligt een punt P ( p; f ( p)) met 3 < p < 0. De projectie vn P op de
9 Roosterdam. 700 m x 1000 m = m 2 = 0,7 km = 3400 m = 3,4 km
 9 Roosterdm 700 m x 000 m 700.000 m 0,7 km 700 + 000 400 m,4 km,4 km x km,8 km,4 + 6,8 km De lengte en reedte zijn in het e gevl keer zo groot ls in het e gevl De omtrek wordt dn keer zo groot, de,4 0,7
9 Roosterdm 700 m x 000 m 700.000 m 0,7 km 700 + 000 400 m,4 km,4 km x km,8 km,4 + 6,8 km De lengte en reedte zijn in het e gevl keer zo groot ls in het e gevl De omtrek wordt dn keer zo groot, de,4 0,7
Formulekaart VWO wiskunde B1 en B2
 Formulekrt VWO wiskunde B en B2 De Formulekrt Wiskunde hvo/vwo is gepubliceerd in Uitleg, Gele Ktern nr. 2, CEVO- 98/257. Deze versie vn de Formulekrt is die officiële versie. Vierkntsvergelijking Als
Formulekrt VWO wiskunde B en B2 De Formulekrt Wiskunde hvo/vwo is gepubliceerd in Uitleg, Gele Ktern nr. 2, CEVO- 98/257. Deze versie vn de Formulekrt is die officiële versie. Vierkntsvergelijking Als
Formularium Wiskunde 1 ste graad
 Kls: Nm: Formulrium Wiskunde 1 ste grd Vkwerkgroep Wiskunde T. I. SINT-LAURENS MARIA MIDDELARES Ptrongestrt 51 9060 Zelzte Tel. (09)45 7 1 Fx (09)45 40 65 Internet: http://tislmm.pndor.be E-mil: so.tislmm.zelzte@frcrit.org
Kls: Nm: Formulrium Wiskunde 1 ste grd Vkwerkgroep Wiskunde T. I. SINT-LAURENS MARIA MIDDELARES Ptrongestrt 51 9060 Zelzte Tel. (09)45 7 1 Fx (09)45 40 65 Internet: http://tislmm.pndor.be E-mil: so.tislmm.zelzte@frcrit.org
e f l a b t 18 k 0,25 15 c p 5 16 c p temperatuur C 18 temperatuur C
 Formules geruiken 7 1 5,00 j j 2 4,00 j 3 9,6 48 10 4,8 4,8 2 9,6 4 60 0,10 6 2de 60 10 6 60 0,05 3 60 20 3 60 5 12 60 0,2 12 d 90 0,10 9 90 10 9 e 90 0,05 4,5 90 20 4,5 f 90 5 18 90 0,2 18 g 75 10 7,5
Formules geruiken 7 1 5,00 j j 2 4,00 j 3 9,6 48 10 4,8 4,8 2 9,6 4 60 0,10 6 2de 60 10 6 60 0,05 3 60 20 3 60 5 12 60 0,2 12 d 90 0,10 9 90 10 9 e 90 0,05 4,5 90 20 4,5 f 90 5 18 90 0,2 18 g 75 10 7,5
Toepassingen op Integraalrekening
 Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Toepssingen op Integrlrekening ) Oppervlktes vn vlkke figuren erekenen De meest voor de hnd liggende toepssing vn integrlrekening is uiterrd de reden wrom ze is ingevoerd, nmelijk het erekenen vn oppervlktes
Antwoorden Natuurkunde Hoofdstuk 1
 Antwoorden Ntuurkunde Hoofdstuk 1 Antwoorden door Dn 2719 woorden 3 pril 2016 4,3 2 keer eoordeeld Vk Methode Ntuurkunde Systemtishe ntuurkunde 1.1 Grootheden en eenheden Opgve 1 Kwntittieve metingen zijn
Antwoorden Ntuurkunde Hoofdstuk 1 Antwoorden door Dn 2719 woorden 3 pril 2016 4,3 2 keer eoordeeld Vk Methode Ntuurkunde Systemtishe ntuurkunde 1.1 Grootheden en eenheden Opgve 1 Kwntittieve metingen zijn
Eindexamen wiskunde B1-2 vwo 2004-I
 chten vn een derdegrdsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. V is het gebied ingesloten door de grfiek vn f en de x-s. 5p 1 ereken lgebrïsch de excte wrde vn de oppervlkte
chten vn een derdegrdsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. V is het gebied ingesloten door de grfiek vn f en de x-s. 5p 1 ereken lgebrïsch de excte wrde vn de oppervlkte
15 5 omhoog. Hoofdstuk 26 RECHTE LIJNEN. 6 ad 26.0 INTRO
 Hoofdstuk 6 RECHTE LIJNEN 6.0 INTRO 6 d km kost,0: =,9 drnkje kost : =,0, dus de entree is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
Hoofdstuk 6 RECHTE LIJNEN 6.0 INTRO 6 d km kost,0: =,9 drnkje kost : =,0, dus de entree is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
De oppervlakte van de rechthoek uit de vorige opgave hangt van dezelfde variabelen af.
 Opgve 1 Vn twee korte en twee lnge luifers is een rehthoek geleg. Omt je geen fmetingen weet hngt e omtrek vn eze rehthoek f vn twee vrielen, nmelijk lengtekorteluif er en lengtelngeluif er. Welke formule
Opgve 1 Vn twee korte en twee lnge luifers is een rehthoek geleg. Omt je geen fmetingen weet hngt e omtrek vn eze rehthoek f vn twee vrielen, nmelijk lengtekorteluif er en lengtelngeluif er. Welke formule
1 Vlaamse Wiskunde Olympiade 1987-1988 : Eerste Ronde.
 Vlmse Wiskunde Olympide 987-988 : Eerste Ronde De eerste ronde estt steeds uit 0 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt: een deelnemer strt met 0 punten, per goed
Vlmse Wiskunde Olympide 987-988 : Eerste Ronde De eerste ronde estt steeds uit 0 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt: een deelnemer strt met 0 punten, per goed
Zelfstudie practicum 1
 Zelfstudie prtium 1 1.8 Gegeven is de volgende expressie:. () Geef de wrheidstel vn deze expressie. () Minimliseer de gegeven expressie. () Geef een poort implementtie vn de expressie vn onderdeel ().
Zelfstudie prtium 1 1.8 Gegeven is de volgende expressie:. () Geef de wrheidstel vn deze expressie. () Minimliseer de gegeven expressie. () Geef een poort implementtie vn de expressie vn onderdeel ().
15 a b
 Formules geruiken 7 1 20 79:4 20 2 158 2 79 158 3 237 sinsppels 3 79 237 40 itroenen d 79:2 40 4 14 pkken melk 79:6 13,1 fgerond 14 pkken 5 30 kg 237:8 30 kg 6 krtjes d 30:5 6 krtjes e 38,70 f 6 6,45 38,70
Formules geruiken 7 1 20 79:4 20 2 158 2 79 158 3 237 sinsppels 3 79 237 40 itroenen d 79:2 40 4 14 pkken melk 79:6 13,1 fgerond 14 pkken 5 30 kg 237:8 30 kg 6 krtjes d 30:5 6 krtjes e 38,70 f 6 6,45 38,70
Noordhoff Uitgevers bv
 I- I- 38 lok 3 IT - eetkundige pltsen met Geoger ldzijde 8 H Het spoor vn lijkt een irkel te zijn. De irkel is de meetkundige plts vn een onstnte hoek. Het ewijs komt voor ij de stelling vn Thles. Gegeven:
I- I- 38 lok 3 IT - eetkundige pltsen met Geoger ldzijde 8 H Het spoor vn lijkt een irkel te zijn. De irkel is de meetkundige plts vn een onstnte hoek. Het ewijs komt voor ij de stelling vn Thles. Gegeven:
35 7 omhoog. Hoofdstuk 26 RECHTE LIJNEN. 6 ad 26.0 INTRO
 Hoofdstuk 6 RECHTE LIJNEN 6 d 6.0 INTRO km kost,0: =,0 drnkje kost : =,0, dus de entrée is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
Hoofdstuk 6 RECHTE LIJNEN 6 d 6.0 INTRO km kost,0: =,0 drnkje kost : =,0, dus de entrée is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
Opgave 1 Je ziet hier twee driehoeken op een cm-rooster. Beide driehoeken zijn omgeven door eenzelfde
 Oppervlkte vn riehoeken Verkennen Opgve 1 Je ziet hier twee riehoeken op een m-rooster. Beie riehoeken zijn omgeven oor eenzelfe rehthoek. nme: Imges/hv-me7-e1-t01.jpg file: Imges/hv-me7-e1-t01.jpg Hoeveel
Oppervlkte vn riehoeken Verkennen Opgve 1 Je ziet hier twee riehoeken op een m-rooster. Beie riehoeken zijn omgeven oor eenzelfe rehthoek. nme: Imges/hv-me7-e1-t01.jpg file: Imges/hv-me7-e1-t01.jpg Hoeveel
Hoofdstuk 8 : De Cirkel
 - 163 - Hoofdstuk 8 : De Cirkel Eventjes herhalen!!!! De cirkel met middelpunt O en straal r is de vlakke figuur die de verzameling is van alle punten die op een afstand r van O liggen. De schijf met middelpunt
- 163 - Hoofdstuk 8 : De Cirkel Eventjes herhalen!!!! De cirkel met middelpunt O en straal r is de vlakke figuur die de verzameling is van alle punten die op een afstand r van O liggen. De schijf met middelpunt
Eindexamen wiskunde B1-2 vwo 2007-I
 Eindemen wiskunde B- vwo 007-I Beoordelingsmodel Podiumverlichting mimumscore 3 sin α = r 650 V 650 r r r 650 r = 9 + invullen geeft V = 9 + sin α = r r = 9 + V = 650 650 = 9+ 9+ 9 + mimumscore 5 650 00
Eindemen wiskunde B- vwo 007-I Beoordelingsmodel Podiumverlichting mimumscore 3 sin α = r 650 V 650 r r r 650 r = 9 + invullen geeft V = 9 + sin α = r r = 9 + V = 650 650 = 9+ 9+ 9 + mimumscore 5 650 00
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Examen VWO. wiskunde B1,2. tijdvak 2 woensdag 20 juni uur. Bij dit examen hoort een uitwerkbijlage.
 Eamen VW 007 tijdvak woensdag 0 juni 13.30-16.30 uur wiskunde 1, ij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 17 vragen. Voor dit eamen zijn maimaal 81 punten te behalen. Voor elk vraagnummer
Eamen VW 007 tijdvak woensdag 0 juni 13.30-16.30 uur wiskunde 1, ij dit eamen hoort een uitwerkbijlage. Dit eamen bestaat uit 17 vragen. Voor dit eamen zijn maimaal 81 punten te behalen. Voor elk vraagnummer
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Dinsdag 25 mei uur
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
3 Reken uit (met cijferen of kolomsgewijs) = = = = = = 4 Van verhaal naar rekentaal
 LES 1 3 Reken uit (met cijferen of kolomsgewijs) 5 374 = 6 517 = 8 345 = 9 462 = 4 623 = 7 219 = 4 Vn verhl nr rekentl Reken uit met cijferen of kolomsgewijs. Vder koopt een ndere uto. Hij etlt cht mnden
LES 1 3 Reken uit (met cijferen of kolomsgewijs) 5 374 = 6 517 = 8 345 = 9 462 = 4 623 = 7 219 = 4 Vn verhl nr rekentl Reken uit met cijferen of kolomsgewijs. Vder koopt een ndere uto. Hij etlt cht mnden
Permanente kennis 3de trimester 4de jaar Grootheden en eenheden BASISGROOTHEDEN
 Permnente kennis 3de trimester 4de jr Grooteden en eeneden BASISGROOTHEDEN Bsisgrooteid Symool Eeneid lengte l meter m mss m kilogrm kg tijd t seonde s elektrise stroom I mpère A AFGELEIDE GROOTHEDEN EN
Permnente kennis 3de trimester 4de jr Grooteden en eeneden BASISGROOTHEDEN Bsisgrooteid Symool Eeneid lengte l meter m mss m kilogrm kg tijd t seonde s elektrise stroom I mpère A AFGELEIDE GROOTHEDEN EN
Oefeningen Analyse I
 1ste Kndidtuur Burgerlijk Ingenieur Ademiejr 001-00 1ste semester 11 jnuri 00 Oefeningen Anlyse I 1. Bereken de volgende ieten d n x(ln x ) x 0 x 0 e x os x ln( 1+x 1 x ) x x 3 y 4 (x,y) (0,0) x + y n
1ste Kndidtuur Burgerlijk Ingenieur Ademiejr 001-00 1ste semester 11 jnuri 00 Oefeningen Anlyse I 1. Bereken de volgende ieten d n x(ln x ) x 0 x 0 e x os x ln( 1+x 1 x ) x x 3 y 4 (x,y) (0,0) x + y n
Lijn, lijnstuk, punt. Verkennen. Uitleg. Opgave 1
 Lijn, lijnstuk, punt Verkennen Opgve 1 Je ziet hier een pltje vn spoorrils vn een modelspoorn. De rils zijn evestigd op dwrsliggers. Hoe liggen de rils ten opziht vn elkr? Hoe liggen de dwrsliggers ten
Lijn, lijnstuk, punt Verkennen Opgve 1 Je ziet hier een pltje vn spoorrils vn een modelspoorn. De rils zijn evestigd op dwrsliggers. Hoe liggen de rils ten opziht vn elkr? Hoe liggen de dwrsliggers ten
= = = = = = = =
 0 ld nm Hulp Reken uit met cijferen 0 Reken uit met splitsen Honderdvouden ij elkr en dn de rest ij elkr. + 0 = 0 + = 0 + = 0 + 0 = + 0 = 0 + 0 = 0 + = 0 + = Honderdvouden vn elkr f en dn de rest vn elkr
0 ld nm Hulp Reken uit met cijferen 0 Reken uit met splitsen Honderdvouden ij elkr en dn de rest ij elkr. + 0 = 0 + = 0 + = 0 + 0 = + 0 = 0 + 0 = 0 + = 0 + = Honderdvouden vn elkr f en dn de rest vn elkr
Eindexamen wiskunde B1-2 vwo 2007-II
 ier tappen ij het tappen van bier treden verschillen op in de hoeveelheid bier per glas. Uit onderzoek blijkt dat de hoeveelheid bier die per glas getapt wordt bij benadering normaal verdeeld is met een
ier tappen ij het tappen van bier treden verschillen op in de hoeveelheid bier per glas. Uit onderzoek blijkt dat de hoeveelheid bier die per glas getapt wordt bij benadering normaal verdeeld is met een
6 116 = 696. som: = som: = som: = zo groot één 0 erbij = = 7 600
 LES 1 Reken uit (met cijferen of kolomsgewijs) 5 74 = 1 87 8 45 = 2 76 4 62 = 2 492 6 517 = 12 9 462 = 4 158 7 219 = 1 5 4 Vn verhl nr rekentl Reken uit met cijferen of kolomsgewijs. Vder koopt een ndere
LES 1 Reken uit (met cijferen of kolomsgewijs) 5 74 = 1 87 8 45 = 2 76 4 62 = 2 492 6 517 = 12 9 462 = 4 158 7 219 = 1 5 4 Vn verhl nr rekentl Reken uit met cijferen of kolomsgewijs. Vder koopt een ndere
Hoofdstuk 11B - Meetkundig redeneren
 Voorkennis V-1a = 180 80 35 = 65 E = 360 90 90 10 = 78 J = 360 107 73 107 = 73 De tegenover elkaar liggende hoeken van deze vierhoek zijn gelijk, dus deze vierhoek is een parallellogram. V-a V-3a Figuur
Voorkennis V-1a = 180 80 35 = 65 E = 360 90 90 10 = 78 J = 360 107 73 107 = 73 De tegenover elkaar liggende hoeken van deze vierhoek zijn gelijk, dus deze vierhoek is een parallellogram. V-a V-3a Figuur
Parate kennis wiskunde
 Heilige Mgdcollege Dendermonde Prte kennis wiskunde 4 Lt A Lt B Wet A Wet B Ec C Vkgroep wiskunde Hemco Dit document is edoeld ls smenvtting vn wt ls prte kennis wordt ngenomen ij nvng vn het tweede jr
Heilige Mgdcollege Dendermonde Prte kennis wiskunde 4 Lt A Lt B Wet A Wet B Ec C Vkgroep wiskunde Hemco Dit document is edoeld ls smenvtting vn wt ls prte kennis wordt ngenomen ij nvng vn het tweede jr
Noordhoff Uitgevers bv
 V-1a d e 128 Voorkennis D C B N A K L Vierhoek ABCD is een vierkant. Vierhoek KLMN is een rehthoek en vierhoek PQRS is een parallellogram. De oppervlakte van vierhoek KLMN is 7 3 4 5 28 roostervierkantjes.
V-1a d e 128 Voorkennis D C B N A K L Vierhoek ABCD is een vierkant. Vierhoek KLMN is een rehthoek en vierhoek PQRS is een parallellogram. De oppervlakte van vierhoek KLMN is 7 3 4 5 28 roostervierkantjes.
Aanzet 1 tot een document van parate kennis en vaardigheden wiskunde 1 ste graad
 Anzet 1 tot een document vn prte kennis en vrdigheden wiskunde 1 ste grd 1. TAALVAARDIGHEID BINNEN WISKUNDE ) Begrippen uit de getllenleer Bewerking Symbool optelling + ftrekking vermenigvuldiging deling
Anzet 1 tot een document vn prte kennis en vrdigheden wiskunde 1 ste grd 1. TAALVAARDIGHEID BINNEN WISKUNDE ) Begrippen uit de getllenleer Bewerking Symbool optelling + ftrekking vermenigvuldiging deling
OP GETAL EN RUIMTE KUN JE REKENEN
 OP GETAL EN RUIMTE KUN JE REKENEN Welke wiskunde moet ik kiezen? Dit jr moet je gn kiezen welke wiskunde je wilt gn volgen in de bovenbouw. Hieronder kun je lezen wt wiskunde A, en D inhouden. Wiskunde
OP GETAL EN RUIMTE KUN JE REKENEN Welke wiskunde moet ik kiezen? Dit jr moet je gn kiezen welke wiskunde je wilt gn volgen in de bovenbouw. Hieronder kun je lezen wt wiskunde A, en D inhouden. Wiskunde
Hoofdstuk 1. De cirkel. 1.1 Middellijn, koorde en apothema. 1.2 Middelpuntshoek en omtrekshoek
 e irkel. iddellijn, koorde en apothema. iddelpuntshoek en omtrekshoek.3 Raaklijn aan een irkel.3. Raaklijn in een punt van een irkel.3. Raaklijnen uit een punt aan een irkel.4 Onderlinge ligging van twee
e irkel. iddellijn, koorde en apothema. iddelpuntshoek en omtrekshoek.3 Raaklijn aan een irkel.3. Raaklijn in een punt van een irkel.3. Raaklijnen uit een punt aan een irkel.4 Onderlinge ligging van twee
Lucht in je longen. Streep de foute woorden door. Hoe komt lucht in je longen? Zet een cirkel om de dieren met longen.
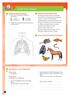 9 Luht in je longen Hoe komt luht in je longen? = longen = middenrif Kleur op de tekening de volgende onderdelen: Streep de foute woorden door. Ons lihm heeft zuurstof / kooldioxide nodig. Bij het indemen
9 Luht in je longen Hoe komt luht in je longen? = longen = middenrif Kleur op de tekening de volgende onderdelen: Streep de foute woorden door. Ons lihm heeft zuurstof / kooldioxide nodig. Bij het indemen
C 1 C 2. 42 blok 6. Er zijn 1440 tegels nodig.
 42 blok 6 C De zomervkntie komt ern! Voor de zomervkntie moet het zwembd in de gemeente Dorpstein gebruiksklr worden gemkt. Het 4 meter brede tegelpd rondom het zwembd moet vn nieuwe tegels vn 50 bij 50
42 blok 6 C De zomervkntie komt ern! Voor de zomervkntie moet het zwembd in de gemeente Dorpstein gebruiksklr worden gemkt. Het 4 meter brede tegelpd rondom het zwembd moet vn nieuwe tegels vn 50 bij 50
Examen VWO. wiskunde B1,2 (nieuwe stijl)
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
Bijlage 2 Gelijkvormigheid
 ijlge Gelijkvormigheid eze bijlge hoort bij het hoofdstuk e krcht vn vectoren juli 0 Opgven gemrkeerd met kunnen worden overgeslgen. Uitgve juli 0 olofon 0 ctwo uteurs d Goddijn, Leon vn den roek, olf
ijlge Gelijkvormigheid eze bijlge hoort bij het hoofdstuk e krcht vn vectoren juli 0 Opgven gemrkeerd met kunnen worden overgeslgen. Uitgve juli 0 olofon 0 ctwo uteurs d Goddijn, Leon vn den roek, olf
Bewerkingen met eentermen en veeltermen
 5 Bewerkingen met eentermen en veeltermen Dit kun je l 1 werken met letters ls onekenden, ls vernderlijken en om te verlgemenen 2 een tel mken ij een situtie 3 de fsprken over lettervormen toepssen 4 oppervlkteformules
5 Bewerkingen met eentermen en veeltermen Dit kun je l 1 werken met letters ls onekenden, ls vernderlijken en om te verlgemenen 2 een tel mken ij een situtie 3 de fsprken over lettervormen toepssen 4 oppervlkteformules
van basis tot Handleiding limiet Meetkunde
 Mrk De Feyter Filip Geeurickx Jn Thoelen Roger Vn Nieuwenhuyze ewerkt voor het gemeenschpsonderwijs door Wendy Luyckx o Roefs rtoons Dve Vnroye vn sis tot limiet Hndleiding Meetkunde 1 voorwoord ISN: 978
Mrk De Feyter Filip Geeurickx Jn Thoelen Roger Vn Nieuwenhuyze ewerkt voor het gemeenschpsonderwijs door Wendy Luyckx o Roefs rtoons Dve Vnroye vn sis tot limiet Hndleiding Meetkunde 1 voorwoord ISN: 978
UNIFORM HEREXAMEN MULO tevens TOELATINGSEXAMEN VWO/HAVO/NATIN 2008
 MINISTERIE VN ONERWIJS EN VOLKSONTWIKKELING EXMENUREU UNIFORM HEREXMEN MULO tevens TOELTINGSEXMEN VWO/HVO/NTIN 008 VK : WISKUNE TUM : TIJ : ------------------------------------------------------------------------------------------------------------------------
MINISTERIE VN ONERWIJS EN VOLKSONTWIKKELING EXMENUREU UNIFORM HEREXMEN MULO tevens TOELTINGSEXMEN VWO/HVO/NTIN 008 VK : WISKUNE TUM : TIJ : ------------------------------------------------------------------------------------------------------------------------
Een feestmaal. Naam: -Ken jij nog een ander speciaal feest? Typ of schrijf het hier. a
 Werkbld Een feestml Nm: Ieder lnd en iedere cultuur kent specile dgen. Dn gn fmilies bij elkr op bezoek. Op die specile dgen is er meestl extr ndcht voor het eten. Hier zie je wt voorbeelden vn feesten
Werkbld Een feestml Nm: Ieder lnd en iedere cultuur kent specile dgen. Dn gn fmilies bij elkr op bezoek. Op die specile dgen is er meestl extr ndcht voor het eten. Hier zie je wt voorbeelden vn feesten
Je gaat naar de winkel en koopt 4 pakken melk van 1,40 per stuk.
 Opgve 1 Je gt nr de winkel en koopt 4 pkken melk vn 1,40 per stuk. Hoeveel etl je in totl? Wt he je met de getllen 4 en 1,40 gedn om het ntwoord te vinden? Hoe doe je dt zonder rekenmhine? Opgve 2 Je gt
Opgve 1 Je gt nr de winkel en koopt 4 pkken melk vn 1,40 per stuk. Hoeveel etl je in totl? Wt he je met de getllen 4 en 1,40 gedn om het ntwoord te vinden? Hoe doe je dt zonder rekenmhine? Opgve 2 Je gt
Praktische Opdracht Lineair Programmeren V5
 Prktische Opdrcht Lineir Progrmmeren V5 Bij deze prktische opdrcht g je n het werk met een ntl prolemen die je door middel vn Lineir Progrmmeren kunt oplossen. Je werkt lleen of in tweetllen. De prktische
Prktische Opdrcht Lineir Progrmmeren V5 Bij deze prktische opdrcht g je n het werk met een ntl prolemen die je door middel vn Lineir Progrmmeren kunt oplossen. Je werkt lleen of in tweetllen. De prktische
