Meetkunde 2 Spiegelen, verschuiven en draaien in het vlak
|
|
|
- Edith Brouwer
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Meetkunde 2 Spiegelen, vershuiven en drien in het vlk M4 Spiegelingen herkennen en tekenen 200 M5 Eigenshppen vn de spiegeling 205 M6 Symmetrie 208 M7 Vershuivingen herkennen en tekenen 210 M8 Eigenshppen vn de vershuiving 216 M9 riingen herkennen en tekenen 218 M10 Eigenshppen vn de driing 224 M11 e puntspiegeling
2 M4 1 Titel Spiegelingen herkennen en tekenen 609 E Teken het spiegeleeld t.o.v. de rehte m vn: de punten, en het lijnstuk [] m m = de driehoek d de rehthoek m m 610 E Teken het spiegeleeld t.o.v. de rehte m vn: de punten, en de vierhoek het vierknt = m m = m 611 Kleur het spiegeleeld vn het vierknt: rood n spiegeling t.o.v. groen n spiegeling t.o.v. y luw n spiegeling t.o.v. p y p 200 M4 Spiegelingen herkennen en tekenen
3 612 V* oördinten ij de spiegeling. Teken het spiegeleeld vn de rehthoek met y ls spiegels. enoem je spiegeleelden ls volgt: ', ', ' en '. Teken het spiegeleeld vn de rehthoek met ls spiegels. enoem je spiegeleelden ls volgt: '', '', '' en ''. y epl de oördinten: oördint vn het oorspronkelijke punt oördint vn het punt dt gespiegeld wordt t.o.v. de s oördint vn het punt dt gespiegeld wordt t.o.v. de y s (...,...) '(...,...) ''(...,...) (...,...) '(...,...) ''(...,...) (...,...) '(...,...) ''(...,...) (...,...) '(...,...) ''(...,...) d e f g h Wt geeurt er met de oördint ls je spiegelt t.o.v. de s? e oördint verndert niet n een spiegeling t.o.v. de -s. Wt geeurt er met de y oördint ls je spiegelt t.o.v. de s? e y oördint verndert vn teken n een spiegeling t.o.v. de -s. Wt geeurt er met de oördint ls je spiegelt t.o.v. de y s? e oördint verndert vn teken n een spiegeling t.o.v. de y-s. Wt geeurt er met de y oördint ls je spiegelt t.o.v. de y s? e y oördint verndert niet n een spiegeling t.o.v. de y-s. Vul de tel in. oördint vn het oorspronkelijke punt ( 37,18) (0, 75) oördint vn het punt dt gespiegeld wordt t.o.v. de s oördint vn het punt dt gespiegeld wordt t.o.v. de y s ( 37, 18) (37,18) (0,75) (0, 75) ( 34,0) ( 34,0) (34,0) ( 67, 91) ( 67,91) (67, 91) Spiegelingen herkennen en tekenen M4 201
4 613 Teken de spiegelssen, en ls je weet dt: s (P) = P' s (P) = P'' s (P) = P''' P P P P 614 epl het snijpunt P vn de spiegelssen. s () = ' s y () = ' ' P ' 615 E Is de figuur ' het eeld vn de figuur door een spiegeling t.o.v. de rehte? Indien j, teken dn de spiegels. ' ' ' ' ' ' j neen j ' ' ' ' ' ' ' 616 V* e rehte is de spiegels. Kleur het spiegeleeld vn de luwe driehoek groen. H [E] [] [] E S G ([]) =... S H ([E]) = S E ([H]) = d S (H) = e S G (H) = f g h i j S... E ([]) = [HG] S... G () = E S... G ([) = [ S... E () = S... () = H G E 202 M4 Spiegelingen herkennen en tekenen
5 617 Zijn de punten en t.o.v. dezelfde spiegels gespiegeld? Zo j, teken de spiegels. Zo neen, verklr wrom niet. Neen, de spiegelssen vllen niet smen d e = f =... Neen, het punt (= ') ligt niet op Neen, het punt (= ') ligt niet op de spiegels vn ['] de spiegels vn ['] 618 Teken het spiegeleeld vn de hlfrehte [ t.o.v. rehte.... d Neen, de spiegelssen vllen niet smen.... Hoeveel punten moet je spiegelen om het spiegeleeld vn een hlfrehte te kunnen tekenen?... Het grenspunt. Welk punt vn de hlfrehte moet je ltijd spiegelen? Wt is het spiegeleeld vn een snijpunt met de spiegels en de hlfrehte?... d Welk punt he je gespiegeld ls het grenspunt op de spiegels ligt?... 2 Het snijpunt zelf. Een willekeurig punt. e Wt merk je op ls de rehte loodreht op de spiegels stt? Het eeld vn de hlfrehte stt loodreht op de spiegels en de drger vn de hlfrehte vlt smen met de drger vn het eeld Spiegelingen herkennen en tekenen M4 203
6 619 V* Spiegel, door zo weinig mogelijk punten te spiegelen, de rehten en t.o.v. rehte m. Noem de spiegeleelden en. = m m 620 V* Je speelt iljrt. Je wenst met l vi de ovenste nd l te rken. it wil zeggen dt de speell eerst de ovenste nd rkt en drn speell. Mk de onstrutie. TIP: Je moet nr het spiegeleeld vn t.o.v. de ovenste nd mikken. ' 621 V** Je speelt iljrt. Je geeft geen effet. Je wenst met l, l te rken. Nu moet l ehter eerst twee nden rken. Eerst nd I en dn nd II. Mk de onstrutie. TIP: Je moet nr het spiegeleeld vn l mikken. ' nd II nd I 204 M4 Spiegelingen herkennen en tekenen
7 M5 Eigenshppen vn de spiegeling 622 E Gegeven: s M ([]) = [''] 5 m = 5 m '' =... Welke eigenshp vn de spiegeling he je geruikt om dit ntwoord te vinden? e spiegeling ehoudt de lengte vn een lijnstuk. 623 E Is de figuur het eeld vn de figuur door een spiegeling t.o.v. de rehte? Verklr wrom (niet). ' ' ' J... Neen. e lengte lijft niet ewrd. 624 Is figuur het eeld vn figuur door een spiegeling? Zo j, teken dn de spiegels Zo nee, verklr wrom niet.... Neen.... e oriënttie vn hoeken is niet omgekeerd Neen, de oriënttie vn hoeken werd niet omgekeerd d Neen, de lengte lijft niet ewrd V* Is figuur het eeld vn figuur door een spiegeling? Zo j, teken dn de spiegels Zo nee, verklr wrom niet Neen, de lengte lijft niet ewrd Eigenshppen vn de spiegeling M5 205
8 626 Spiegel zo weinig mogelijk punten t.o.v. de rehte m om het eeld vn de vierhoeken te vinden. Rehthoek. m Hoeveel punten he je gespiegeld? Welke eigenshp(pen) vn de spiegeling he je geruikt? Een spiegeling ehoudt de evenwijdigheid. Een spiegeling ehoudt de lengte vn een lijnstuk. Een spiegeling ehoudt de grootte vn een hoek Ruit EGH. 2 E m E H H G G Hoeveel punten he je gespiegeld? Welke eigenshp(pen) vn de spiegeling he je geruikt? Een spiegeling ehoudt de evenwijdigheid. Een spiegeling ehoudt de lengte vn een lijnstuk, grootte vn een hoek Trpezium KLMN. Hoeveel punten moet je ten minste spiegelen om een trpezium te spiegelen? ontroleer door te tekenen. 2 2 K L N M Welke eigenshp(pen) vn de spiegeling he je geruikt? M L K N Een spiegeling ehoudt de evenwijdigheid. Een spiegeling ehoudt de lengte vn een lijnstuk, grootte vn een hoek M5 Eigenshppen vn de spiegeling
9 627 V* Gegeven: // en. Vul in:... Spiegel de rehte, en t.o.v. rehte. Steun op de eigenshppen vn de spiegeling. Hoeveel punten moet je spiegelen? Twee // Vul in:... en V* Het eeld vn een ruit n een spiegeling is een Wrom is geen ruit? e spiegels is geen rehte. ruit ' ' ' ' m 629 V* Wrom is het spiegeleeld vn het huis niet mooi reht? e spiegels stn niet lleml op één rehte lijn V** Vn de driehoek zijn twee hoekpunten fgeknipt. Teken het zwrtepunt (het snijpunt vn de drie zwrtelijnen) vn deze driehoek ls een zwrtelijn gegeven is. TIP: Teken een spiegels en zoek het spiegeleeld vn de lijnstukken. Z G z Eigenshppen vn de spiegeling M5 207
10 M6 Symmetrie 631 Zijn de figuren symmetrish? Teken lle mogelijke symmetriessen J d e f J Neen Neen J J 632 Zijn de figuren symmetrish? Teken lle mogelijke symmetriessen. J J Neen (hoofden zijn niet symmetrish) d e f J Neen Neen M6 Symmetrie
11 633 Mk de figuren symmetrish. 634 Teken de symmetriessen in de vlkke figuren. 635 V* Lees ndhtig de zinnen. Zijn ze wr of niet wr? Vereter de zinnen die fout zijn. zinnen wr niet wr Een driehoek met twee even lnge zijden heeft twee symmetriessen. Een driehoek met twee even lnge zijden heeft één symmetries Een driehoek met drie even lnge zijden heeft drie symmetriessen Een driehoek met één symmetries is gelijkenig.... d e f... Een driehoek met twee symmetriessen is gelijkzijdig.... Een gelijkzijdige driehoek heeft drie symmetriessen. Een driehoek met juist twee symmetriessen estt niet.... Een driehoek met twee even grote hoeken heeft drie symmetriessen. Een driehoek met twee even grote hoeken heeft één symmetries Een driehoek wrij de drie hoeken een vershillende grootte heen is symmetrish. Een driehoek met drie even grote hoeken is symmetrish Symmetrie M6 209
12 636 Teken de volledige figuur ls je weet dt een symmetries is. M7 Vershuivingen herkennen en tekenen 637 E mirkel de wre uitsprken. t _ (T) = V e t _ (I) = L I L K M t _ (M) = L t _ (P) = V f t _ PQ (P) = Q g t _ PQ () = Z P T V d t _ (L) = M h t _ PQ (M) = T Z Q 638 E e vershuiving wordt epld door de vetor. Vershuif de punten X en Y. X Y X Y 210 M7 Vershuivingen herkennen en tekenen
13 639 E e vershuiving wordt epld door de vetor KL. Vershuif de punten M, N, en P. K M N P 640 e vershuiving wordt epld door de vetor XY. Teken de punten,, en. L M N X P Y 641 V* Vershuif het vierknt volgens t _ Noem je eeldpunten,, en. epl de oördinten.... X(...,...) 1 6 Y(...,...) 6 10 (...,...) 2 1 '(...,...) XY y X Y (...,...) '(...,...) (...,...) '(...,...) (...,...) '(...,...)... Wt geeurt er telkens met de oördint ij deze vershuiving? Noteer dit ij de pijl. ij de -oördint wordt steeds 5 opgeteld. Wt geeurt er met de y oördint ij deze vershuiving? Noteer dit ij de pijl. ij de y-oördint wordt steeds 4 opgeteld. epl de oördinten vn E en zonder de punten te tekenen. t _ (E) = E' en t _ XY XY () = ' (0 + 5, 6 + 4) = E (5,10) E(0,6) E'... (4 + 5, ) = (9,1) (4, 3) '... Vershuivingen herkennen en tekenen M7 211
14 642 V* Vershuif de vijfhoek E volgens vetor w. y 4 E w E 4 epl de oördinten vn,,, en E. epl de oördinten vn,,, en E. epl de oördint vn het eindpunt vn de vetor die de vershuiving eplt. d e f g h i j _ w 8 7 (...,...) (...,...) (...,...) (...,...) (...,...) E(...,...) ereken: '(...,...) '(...,...) '(...,...) '(...,...) E'(...,...) Het vershil vn de oördint vn en de oördint vn Het vershil vn de oördint vn en de oördint vn Het vershil vn de oördint vn E en de oördint vn E ekijk de oördint vn elk punt en zijn eeld. Wt stel je vst? ereken het vershil vn de -oördint vn het eginpunt vn de vetor en de -oördint vn het eindpunt vn de vetor. ereken: Het vershil vn de y oördint vn en de y oördint vn Het vershil vn de y oördint vn en de y oördint vn Het vershil vn de y oördint vn E en de y oördint vn E ekijk de y oördint vn elk punt en zijn eeld. Wt stel je vst? ereken het vershil vn de y-oördint vn het eginpunt vn de vetor en de y-oördint vn het eindpunt vn de vetor. ereken de oördint vn S en vn T zonder de punten te tekenen en t _ (S) = S' en t _ (T) = T'. S( 5,3) S'... T(1, 6) T w Weetje Een vershuiving _ w (7,5) toepssen etekent: de vershuiving wrij het eginpunt ls oördint (0,0) heeft en ls eindpunt oördint (7,5). 5 (-2) = = 7 4 (-3) = 7 ij de oördint wordt steeds 7 opgeteld om het eeld te vinden. 7 0 = = = 5 4 (-1) = 5 ij de y oördint wordt steeds 5 opgeteld om het eeld te vinden. 5 0 = 5 (-5 + 7, 3 + 5) = S (2,8) (1 + 7, ) = T (8,-1) w 212 M7 Vershuivingen herkennen en tekenen
15 643 V*** Ps op figuur een vershuiving _ v ( 2, 13) toe. Je vindt figuur 1. rn ps je op 1 een vershuiving _ w ( 6, 5) toe en je vindt figuur 2. (eze vetoren heen ls eginoördint (0,0)) Teken de pijlen vn figuur nr figuur 2. J (-8,8) ekom je een vershuiving?... Zo j, wt is de oördint?... y 8 ig E E ig E ig (...,...) '(...,...) ''(...,...) (...,...) '(...,...) ''(...,...) _ v ( 2,13) _ w ( 6, 5) (...,...) '(...,...) ''(...,...) (...,...) '(...,...) ''(...,...) E(...,...) E'(...,...) E''(...,...) 8 8 (...,...) 644 V*** Jn pst op ig. een vershuiving _ u (0, 5) toe. Hij vindt ig. 1. Ndien pst hij op ig. 1 een vershuiving _ v (5, 0) toe en vindt ig. 2. p deze ltste figuur pst hij _ w ( 5, 5) toe en ekomt uiteindelijk ig. 3. Mk een shem vn de vershillende vershuivingen. Geef de oördinten vn volgende vershuivingen: (0 + 5, 5 + 0) = (5,5) (5 +(-5), 0 + (-5)) = (0,-5) ( , ) =(0,0) (-5,0) vershuiving ig. nr ig. 2 : vershuiving ig. 1 nr ig. 3 : vershuiving nr 3 : d vershuiving 2 nr 1 : Vershuivingen herkennen en tekenen M7 213
16 645 Werden de punten en door een zelfde vershuiving vershoven? Zo j, vershuif het punt volgens dezelfde vershuiving. Zo nee, verklr wrom niet. J d... Neen,... de vershuivingen heen een vershillende zin. e Neen, de vershuivingen heen een vershillende rihting. f... Neen,... de vershuivingen heen een vershillende lengte. 646 nderzoek de figuren. Is ig. het eeld vn door een vershuiving? Zo j, teken de vetor die deze vershuiving eplt. Zo neen, verklr wrom niet. d e f J... P g..., d, e: de hoekpunten worden niet volgens dezelfde vershuiving vershoven (lengte is vershillend) f: de figuur is gespiegeld Q T U J 647 Zijn de eweringen wr of niet wr? Ruiter is het shuifeeld vn ruiter door de vershuiving t _. Wr Ruiter is het shuifeeld vn ruiter door de vershuiving t _. Niet wr Ruiter is het shuifeeld vn ruiter door de vershuiving t _. Wr d Ruiter is het shuifeeld vn ruiter door de vershuiving t _. Wr e Ruiter I is het shuifeeld vn ruiter H door de vershuiving t _. Niet wr f Ruiter E is het shuifeeld vn ruiter door de vershuiving t _. Niet wr I H E 214 M7 Vershuivingen herkennen en tekenen
17 648 Hieronder vind je Sky nd wter vn M.. Esher Kn vogel 2 het eeld zijn vn vogel 1 door een vershuiving? Zo j: teken de vetor u. Kn vogel 3 het eeld zijn vn vogel 1 door een vershuiving? Zo j: teken de vetor v. Kn vis 2 het eeld zijn vn vis 3 door een vershuiving? Zo j: teken de vetor w. d Kn vis 2 het eeld zijn vn vis 1 door een vershuiving? Zo j: teken de vetor t. 1 _ v _ u _ t _ w ehoud het ptroon en mk de tekening f. 650 E e vershuiving wordt epld door vetor LS. Vershuif het lijnstuk. L S S L S L 651 E e vershuiving wordt epld door vetor PV. Vershuif de driehoek. P V P V P V Vershuivingen herkennen en tekenen M7 215
18 M8 Eigenshppen vn de vershuiving 652 Teken het eeld vn het vierknt volgens t _ XY. Vershuif zo weinig mogelijk punten om je eeld te vinden. Hoeveel punten he je vershoven? Welke eigenshppen he je toegepst? e vershuiving ehoudt de lengte vn een lijnstuk. e vershuiving ehoudt de evenwijdigheid vn rehten. Een lijnstuk en zijn eeld n een vershuiving zijn evenwijdig. e vershuiving ehoudt de hoekgrootte. 653 Vershuif telkens de rehte m volgens t _ P. P P m X Y m P d m Wt is de onderlinge ligging vn een rehte en zijn shuifeeld? Een rehte en zijn shuifeeld zijn evenwijdig. Hoeveel punten moet je ten minste vershuiven om het eeld vn een rehte te vinden? Eén m 654 V* Teken t _ (m), t _ (p) en t _ (r). Noem de eelden m, p en r. P m P R m p R p r = r 655 Teken X Y Z door een vershuiving met X [ en Z [ zo dt de zijden vn X Y Z en vn XYZ twee n twee even lng en evenwijdig zijn. X Y X Y Z Z 216 M8 Eigenshppen vn de vershuiving
19 656 Een tekenr heeft enkele fouten gemkt ij het vershuiven vn zijn tekening. Vereter de fouten op de tekening. 657 Vul het ptroon verder n. figuur 1 figuur 2 figuur 3 figuur 4 figuur 5 Hoe kun je ig. 1 op ig. 2 feelden? oor een spiegeling. Hoe kun je ig. 1 op ig. 3 feelden? oor twee spiegelingen over evenwijdige spiegelssen en of door een vershuiving t. 658 Is figuur ' het eeld vn figuur door een vershuiving? Zo j, teken de vetor die de vershuiving eplt. Zo neen, verklr wrom niet. ' ' ' d J K ' L Neen de lengte en hoekgrootte e werden niet ewrd ' f Neen de oriënttie vn hoeken werd omgekeerd R S J Neen het eeld vn het lijnstuk is niet evenwijdig n het origineel J ' Eigenshppen vn de vershuiving M8 217
20 659 V* Voer twee spiegelingen n elkr uit. d e S ( ) = S y ( ) = Hoe kun je nog ekomen? Δ """ is het shuifeeld vn driehoek Wt is de onderlinge ligging vn de twee spiegelssen? e spiegelssen zijn evenwijdig Vul n: e smenstelling vn twee spiegelingen wrvn de spiegelssen evenwijdig zijn is een. vershuiving (t _ ) y 660 V** nderzoek. Je krijgt twee punten en en een rehte. p die rehte eweegt een punt. Voor elke stnd vn kun je een prllellogrm tekenen. Het punt is ijgevolg ook een ewegend punt. p welke figuur eweegt het punt? (eze oefening kun je uittesten met geoger.) Punt eweegt op een rehte evenwijdig n. M9 riingen herkennen en tekenen 661 epl de drihoeken. r (0,......) (fig. ) = fig. ' r (0,......) (fig. ) = fig. ' fig. fig. fig. fig. 90 of of M9 riingen herkennen en tekenen
21 662 ver welke hoek drit de grote wijzer? Vn uur tot uur Vn uur tot uur Vn uur tot uur Vn uur tot uur : 60 = 6 p één minuut drit de grote wijzer over een hoek vn E Voer de driing uit. Zoek het eeld vn de punten, en. r (0, 60 ) ' 10 minuten 10 (-6 ) = minuten 30 (-6 ) = minuut 1 (-6 ) = minuten 50 (-6 ) = E Voer de driing uit. Zoek het eeld vn [] r (0,95 ) ([]) ' ' ' ' 665 E Voer de driing uit. r (0,45 ) ([E]) r (0, 45 ) ( ) ' ' E' E ' ' riingen herkennen en tekenen M9 219
22 666 Vul in. r (, 60 ) () =... H r (, 180 ) () = r (H, 120 ) () = d e f H r (H,...) () = r (,...) (H) = r (, 120 ) (...) = H G E 667 nderzoek of het eeld is vn. door r (, 70 ) door r (, 40 ) door r (, 75 ) ' ' ' J Neen, de drizin is fout. 40 i.p.v. 40. Neen, de hoekgrootte is fout: 105 i.p.v V* Hnne heeft de volgende driingen uitgevoerd. Wt is fout gelopen? r (,50 ) ([]) = [''] r (, 50 ) ( ) = e drizin is fout. Het lijnstuk is in wijzerzin gedrid i.p.v. in tegenwijzerzin ' '. Punten en zijn over een hoek vn gedrid, mr Hnne heeft ij het drien vn punt hr geodriehoek verkeerd fgelezen en gedrid over een hoek vn 130. e punten werden gedrid over een hoek vn V* Voer de driingen uit. r (,90 ) () = ' r (, 270 ) () = '' Wt merk je op? Het punt en het punt vllen smen Tel de solute wrden vn de twee drihoeken ij elkr op. Wt stel je vst? e som vn de solute wrden vn de twee driingshoeken is ' = " 220 M9 riingen herkennen en tekenen
23 670 V* Hoeveel grden moet het rd drien om: 5 In wijzerzin vn positie 1 nr positie 2 te gn? In tegenwijzerzin vn positie 1 nr positie 2 te gn? In wijzerzin vn positie 1 nr positie 4 te gn? d In tegenwijzerzin vn postitie 1 nr positie 4 te gn? V* e rde drit in 365 dgen rond de zon in tegenwijzerzin. epl de plts vn de rde n 146 dgen = = = ntwoord: n dgen is..... de rde gedrid rond de zon met een hoek vn V* e mn drit in 27,3 dgen rond de rde in tegenwijzerzin. epl de plts vn de mn n 21 dgen. 27,3 360 = = ,3 = 92, ' M' Z 148 M V** Geef de kleinst mogelijke drihoek in tegenwijzerzin vn een driing die de figuur op zihzelf feeldt : 9 = : 4 = : 4 = riingen herkennen en tekenen M9 221
24 674 V* Welk vn de onderstnde figuren kn niet ontstn door een driing vn een vn de ndere figuren? Verklr je ntwoord. figuur 1 figuur 2 figuur 3 figuur 4 J Neen Neen J is het snijpunt vn de digonlen vn het vierknt.... r (, 180 ) ig. 4 = ig. 1 r (, 180 ) ig. 4 = ig. 1 r (, 180 ) ig. 1 = ig. 4 r (, 180 ) ig. 1 = ig V* Een krnestuurder kreeg vn zijn opdrhtgever de volgende instrutie: Verplts de stenen over een hoek vn 120. Ter pltse merkt hij dt er een oom in de weg stt. Hoe kn de krnestuurder toh zijn opdrht uitvoeren zonder de oom om te hkken? Teken dit. e krnestuurder kn de stenen over een hoek vn 240 drien. ( = 240 ) stenen oom krn krn stenen 676 V* Kun je fig. 1 op fig. 2 feelden door een driing? Kun je fig. 3 op fig. 4 feelden door een driing? Zo j, teken het entrum en de drihoek. Noteer de driing. J r (0, 120 ) Neen M9 riingen herkennen en tekenen
25 677 V* e figuur is het drieeld vn de figuur. Rond welk entrum werd de figuur gedrid? Hoe groot is de driingshoek? Noteer je ntwoord met symolen. r (, 50 ) r (, 45 ) V** Het vierknt kn door vershillende driingen op vierknt fgeeeld worden. Noteer deze driingen. Teken telkens het entrum. r(, 90 ) r(, 180 ) r(, 90 ) r(, 270 ) r(, 180 ) r(, 270 ) V** p de eerste figuur kun je zien hoe een ij dnst om n te tonen wr de voedselron is. e zon en de voedselron vormen een hoek vn 120. Het kwispelende deel vn de dns vormt ijgevolg ook een hoek vn 120 met de vertile s vn het honingrt. ovenknt kst zon Welke situtie pst ij deze ijendns? ovenknt kst onderknt kst Teken een overeenkomstige ijendns op de ijenrt. 120 onderknt kst kst 120 voedselron Weetje ijen ommunieren door te dnsen. ls een werkster netr gevonden heeft vertelt ze de plts n de ndere ijen door te dnsen. Ze voert een ronde dns uit ls de loemen in de direte omgeving vn de ijenkorf stn en een kwispeldns ls de loemen verder verwijderd zijn. e hoek vn het rehte (kwispelende) stukje vn de dns met de vertile s vn het ijenrt komt overeen met de hoek tussen de loemen en de zon. Hoe meer ze kwispelt, hoe verder de voedselron verwijderd is. riingen herkennen en tekenen M9 223
26 M10 Eigenshppen vn de driing 680 Een rehthoek met een oppervlkte vn 100 m² wordt gedrid over een hoek vn m2 e driing ehoudt de lengte vn een lijnstuk. Wt is de oppervlkte vn het drieeld?... Welke eigenshp he je geruikt? Een vierknt met een oppervlkte vn 36 m² wordt gedrid over een hoek vn m e driing ehoudt de lengte vn een lijnstuk. Wt is de lengte vn de zijde vn het drieeld?... Welke eigenshp he je geruikt? Gegeven: r (, 90 ) Gevrgd: Kleur het drieeld vn de gekleurde driehoek. 683 Kleur het eeld vn de luwe zeshoek door de driing. r (, 120 ) groen r (, 120 ) rood r (E,180 ) roze E 684 Teken door zo weinig mogelijk punten te drien r (K, 70 ) ( ) = ''''. Hoeveel punten he je gedrid om het eeld te vinden. Twee Welke eigenshp(pen) vn de driing he je geruikt?. e driing ehoudt de lengte vn een lijnstuk e driing ehoudt de loodrehte stnd vn rehten e driing ehoudt de evenwijdigheid vn rehten K 224 M10 Eigenshppen vn de driing
27 685 V* Teken de volgende figuur in de rij. Verklring: je moet telkens 1 trpezium drien over 90 rond. ' V* epl het drieeld vn de rehte, en. r (0,80 ) Gegeven: // ' Y' ' X' X Y // Vul in: '... ' en '... '. 687 V** Het smenstellen vn spiegelingen met snijdende spiegelssen. Voer de volgende spiegelingen n elkr uit: S ( ) = ''' S y ( ''') = '''''' S z ( '''''') = ''''''''' y u z Hoe kun je driehoek """ nog ekomen? Je kunt driehoek onmiddellijk feelden op driehoek door een driing. Hoe kun je driehoek nog ekomen? oor een spiegeling t.o.v. de rehte u t.o.v. de rehte u. Eigenshppen vn de driing M10 225
28 688 Het drieeld vn de ruit is fout. n welke eigenshppen wordt er niet voldn?. e drihoek is..... vershillend Hierdoor lijft de lengte vn de lijnstukken niet ehouden en verndert ook de grootte vn de hoeken M11 e puntspiegeling 689 V* Teken: s () s (). Wt is het punt vn figuur? e puntspiegeling vn het lijnstuk met spiegelpunt. e puntspiegeling vn het prllellogrm met spiegelpunt.. Het punt is.... het symmetriepunt vn dit vierknt. 690 V* Teken s (ig. ). 226 M11 e puntspiegeling
29 691* Teken r (, 180 ) ( ) en noem de eeldpunten, en. epl de oördinten (...,...) (...,...) (...,...) Wt merk je op? '(...,...) '(...,...) '(...,...) e - oördint en de y - oördint krijgen een tegengesteld teken y V* ereken de oördinten. oördint (35, 8) (0,14) ( 30,7) (8,92) ( 5,7) oördint n driing rond de oorsprong over 180 oördint n een puntspiegeling met de oorsprong ls entrum oördint n een driing rond de oorsprong over 360 ( 35,8) ( 35,8) (35, 8) (0, 14) (0, 14) (0,14) (30, 7) (30, 7) ( 30,7) ( 8, 92) ( 8,-92) (8,92) (5, 7) (5,-7) ( 5,7) 693 V* Het smenstellen vn spiegelingen met loodreht op elkr stnde spiegelssen. Voer de volgende spiegelingen n elkr uit: S ( ) = ( ) S y ( ) = ( """) Hoe kun je de driehoek in een keer op de driehoek feelden? Met een driing over 180 met de oorsprong ls entrum of een puntspiegeling met ls spiegelpunt de oorsprong V* Zijn de figuren elkrs eeld door een puntspiegeling? Zo j, duid het entrum n. y d j j neen e f j j neen e puntspiegeling M11 227
30 695 V* nderzoek. Teken, indien mogelijk, in de nevenstnde figuren de symmetriepunten in luw en de symmetriessen in het rood. Heen lle symmetrishe figuren een symmetriepunt? Neen Zijn lle figuren met een symmetriepunt symmetrish? Neen Teken: s m () = ' t _ y () = ' r (0, 70 ) () = ' Weetje e spiegeling, vershuiving en driing zijn vooreelden vn trnsformties. Voor elke trnsformtie heeft elk punt slehts één eeldpunt. Hoeveel spiegeleelden vn he je getekend? Eén Hoeveel shuifeelden vn he je getekend? Eén Hoeveel drieelden vn he je getekend? Eén m X Y 697 Is het eeld vn de figuur het resultt vn een spiegeling, een driing of een vershuiving? e figuren zijn elkrs eeld door een driing met entrum M11 e puntspiegeling
31 698 V* Vul in. lle driehoeken in de ster zijn gelijkzijdig. L G K H M E J I s KL () =... s... KH([JI]) = [LG] t _ MH d t _ EJ (G)=... ([L) =... e r (M, 60 ) (I) =... f r (, 60 ) (J) =... g s LI ( GH) =... h t _ LM ( GL) =... i r (K, 120 ) () =... j s GJ... = [HI] k t _ I... = L l ([LK]) (G) () M r (H, 180 )... = I (of S MH of S KM ) [LG J I Δ KEJ Δ GHM M 699 V* nderzoek. = 90 = Kunnen en het resultt zijn vn eenzelfde spiegeling? Zo j, teken de spiegels. Zo neen, verklr wrom niet J Kunnen en het resultt zijn vn eenzelfde vershuiving? Indien j, teken dn de vetor vn deze vershuiving. Neen Zo neen, verklr wrom niet. Elk punt wordt op dezelfde mnier vershoven. ls één punt op zihzelf wordt fgeeeld, dn worden lle punten op zihzelf fgeeeld Kunnen en het resultt zijn vn eenzelfde driing? Zo j, epl het entrum en de driingshoek vn deze driing. J. Het entrum is en de driingshoek is 90 of -270 Zo neen, verklr wrom niet. e puntspiegeling M11 229
32 700 V* nderzoek de vershillende ptronen. ntdek op welke mnier ze gevormd werden. Kun je de driing, de vershuiving en of de spiegeling vinden? uid de gegevens n op de tekening. ntwerp zelf je eigen ehngppier. Teken een eenvoudig motief. Voer hierop een spiegeling uit. Vershuif vervolgens het spiegeleeld. Tenslotte dri je het shuifeeld. Eigen ontwerp vn de leerlingen 701 V* Kun je een vlinder door een spiegeling feelden op een ndere vlinder? Zo j, duid de vlinders n en teken de spiegels. d s (vlinder1) = vlinder Kun je een vlinder door een vershuiving feelden op een ndere vlinder? Zo j, duid de vlinders n en teken de vetor. t (vlinder3) = vlinder Kun je een vlinder door een driing feelden op een ndere vlinder? Zo j, duid de vlinders n en teken de drihoek. r(, 120 ) (vlinder 5) = vlinder Kun je een vlinder door een puntspiegeling feelden op een ndere vlinder? Zo j, duid de vlinders n en teken het spiegelpunt. s (vlinder 6) = vlinder M11 e puntspiegeling
Meetkunde 2 Spiegelen, verschuiven en draaien in het vlak
 Meetkunde 2 Spiegelen, vershuiven en drien in het vlk M4 Spiegelingen herkennen en tekenen 200 M5 Eigenshppen vn de spiegeling 205 M6 Symmetrie 208 M7 Vershuivingen herkennen en tekenen 210 M8 Eigenshppen
Meetkunde 2 Spiegelen, vershuiven en drien in het vlk M4 Spiegelingen herkennen en tekenen 200 M5 Eigenshppen vn de spiegeling 205 M6 Symmetrie 208 M7 Vershuivingen herkennen en tekenen 210 M8 Eigenshppen
Spiegelen, verschuiven en draaien in het vlak
 2 Spiegelen, vershuiven en drien in het vlk it kun je l 1 de iddelloodlijn vn een lijnstuk herkennen en tekenen 2 een hoek eten en tekenen 3 de issetrie vn een hoek herkennen en tekenen 4 de oördint vn
2 Spiegelen, vershuiven en drien in het vlk it kun je l 1 de iddelloodlijn vn een lijnstuk herkennen en tekenen 2 een hoek eten en tekenen 3 de issetrie vn een hoek herkennen en tekenen 4 de oördint vn
Overzicht eigenschappen en formules meetkunde
 Overziht eigenshppen en formules meetkunde 1 iom s Rehten en hoeken 3 riehoeken 4 Vierhoeken Op de volgende ldzijden vind je de eigenshppen en formules die je in de eerste grd geleerd het en deze die in
Overziht eigenshppen en formules meetkunde 1 iom s Rehten en hoeken 3 riehoeken 4 Vierhoeken Op de volgende ldzijden vind je de eigenshppen en formules die je in de eerste grd geleerd het en deze die in
Beste leerling. De auteurs
 Voor wie kopiëren wil: U vindt dit oek goed en wenst er kopieën vn te mken. edenk dn ook eens: dt zowel uitgever ls uteurs met de oprengst ervn hun kosten moeten dekken; dt kopiëren zonder toestemming
Voor wie kopiëren wil: U vindt dit oek goed en wenst er kopieën vn te mken. edenk dn ook eens: dt zowel uitgever ls uteurs met de oprengst ervn hun kosten moeten dekken; dt kopiëren zonder toestemming
MEETKUNDE 1 Basisbegrippen
 MEETKUNE sisegrippen M Een klslokl vol meetkunde M nzihten M sisegrippen vn de meetkunde 7 M4 Onderlinge ligging vn rehten 74 M5 Eigenshppen in vernd met evenwijdigheid en loodrehte stnd vn rehten in het
MEETKUNE sisegrippen M Een klslokl vol meetkunde M nzihten M sisegrippen vn de meetkunde 7 M4 Onderlinge ligging vn rehten 74 M5 Eigenshppen in vernd met evenwijdigheid en loodrehte stnd vn rehten in het
Basisbegrippen. Test jezelf Elke vraag heeft maar één juist antwoord. Controleer je antwoord in de correctiesleutel. balk cilinder kubus
 sisegrippen Dit kun je l de enmingen vn vershillende soorten driehoeken en vierhoeken geruiken een kuus, een lk en een ilinder herkennen evenwijdige en snijdende rehten herkennen sherpe, stompe en rehte
sisegrippen Dit kun je l de enmingen vn vershillende soorten driehoeken en vierhoeken geruiken een kuus, een lk en een ilinder herkennen evenwijdige en snijdende rehten herkennen sherpe, stompe en rehte
Noordhoff Uitgevers bv
 I- I- 38 lok 3 IT - eetkundige pltsen met Geoger ldzijde 8 H Het spoor vn lijkt een irkel te zijn. De irkel is de meetkundige plts vn een onstnte hoek. Het ewijs komt voor ij de stelling vn Thles. Gegeven:
I- I- 38 lok 3 IT - eetkundige pltsen met Geoger ldzijde 8 H Het spoor vn lijkt een irkel te zijn. De irkel is de meetkundige plts vn een onstnte hoek. Het ewijs komt voor ij de stelling vn Thles. Gegeven:
De cirkel M22. het middelpunt een koorde de straal de diameter een middelpuntshoek een middellijn. 2 cm 4 cm. Cirkel en elementen van een cirkel
 M De irkel Cirkel en elementen vn een irkel 781 E Geef de nm vn de ngeduide delen in de irkel. Y X O T S het middelpunt een koorde de strl de dimeter een middelpuntshoek een middellijn O:... [XY]:... OS
M De irkel Cirkel en elementen vn een irkel 781 E Geef de nm vn de ngeduide delen in de irkel. Y X O T S het middelpunt een koorde de strl de dimeter een middelpuntshoek een middellijn O:... [XY]:... OS
Opgave 1. Waarom kun je bij het Noorden twee getallen neerzetten? Geldt dit ook voor andere windrichtingen? Hoeveel graden hoort er bij het Oosten?
 Opgve 1 Hier zie je een windroos met de windrihtingen er in getekend. Hij is verder verdeeld in 360 hoekjes, elk vn die hoekjes heet 1 grd. Bij het Noorden (N) hoort 0 grden (en dus ook 360 grden). file:
Opgve 1 Hier zie je een windroos met de windrihtingen er in getekend. Hij is verder verdeeld in 360 hoekjes, elk vn die hoekjes heet 1 grd. Bij het Noorden (N) hoort 0 grden (en dus ook 360 grden). file:
MEETKUNDE 4 Driehoeken
 MEETKUNDE 4 Driehoeken M18 Driehoeken in de ruimte 38 M19 Driehoeken tekenen 4 M0 Merkwrdige lijnen in een 44 M1 Omtrek, oppervlkte en volume 47 37 M18 Driehoeken in de ruimte 738 E Vul n. In KLM zijn
MEETKUNDE 4 Driehoeken M18 Driehoeken in de ruimte 38 M19 Driehoeken tekenen 4 M0 Merkwrdige lijnen in een 44 M1 Omtrek, oppervlkte en volume 47 37 M18 Driehoeken in de ruimte 738 E Vul n. In KLM zijn
Natuurlijke getallen op een getallenas en in een assenstelsel
 Turf het ntl fouten en zet de resultten in een tel. Vlmingen Nederlnders resultt ntl resultt ntl 9 9 en nder tlstelsel U Ontijfer de volgende hiërogliefen met ehulp vn het overziht op p. in het leerwerkoek.........................
Turf het ntl fouten en zet de resultten in een tel. Vlmingen Nederlnders resultt ntl resultt ntl 9 9 en nder tlstelsel U Ontijfer de volgende hiërogliefen met ehulp vn het overziht op p. in het leerwerkoek.........................
MEETKUNDE 5 Cirkels en cilinders
 MEETKUNDE 5 Cirkels en ilinders M22 De irkel 254 M23 De ilinder 262 253 M22 De irkel Cirkel en elementen vn een irkel 781 E Geef de nm vn de ngeduide delen in de irkel. Y X O T S het middelpunt een koorde
MEETKUNDE 5 Cirkels en ilinders M22 De irkel 254 M23 De ilinder 262 253 M22 De irkel Cirkel en elementen vn een irkel 781 E Geef de nm vn de ngeduide delen in de irkel. Y X O T S het middelpunt een koorde
Werkkaarten GIGO 1184 Elektriciteit Set
 Werkkrten GIGO 1184 Elektriiteit Set PMOT 2006 1 Informtie voor de leerkrht Elektriiteit is één vn de ndhtsgeieden ij de nieuwe kerndoelen voor ntuur en tehniek: 42 De leerlingen leren onderzoek doen n
Werkkrten GIGO 1184 Elektriiteit Set PMOT 2006 1 Informtie voor de leerkrht Elektriiteit is één vn de ndhtsgeieden ij de nieuwe kerndoelen voor ntuur en tehniek: 42 De leerlingen leren onderzoek doen n
Bijlage 2 Gelijkvormigheid
 ijlge Gelijkvormigheid eze bijlge hoort bij het hoofdstuk e krcht vn vectoren juli 0 Opgven gemrkeerd met kunnen worden overgeslgen. Uitgve juli 0 olofon 0 ctwo uteurs d Goddijn, Leon vn den roek, olf
ijlge Gelijkvormigheid eze bijlge hoort bij het hoofdstuk e krcht vn vectoren juli 0 Opgven gemrkeerd met kunnen worden overgeslgen. Uitgve juli 0 olofon 0 ctwo uteurs d Goddijn, Leon vn den roek, olf
Lijn, lijnstuk, punt. Verkennen. Uitleg. Opgave 1
 Lijn, lijnstuk, punt Verkennen Opgve 1 Je ziet hier een pltje vn spoorrils vn een modelspoorn. De rils zijn evestigd op dwrsliggers. Hoe liggen de rils ten opziht vn elkr? Hoe liggen de dwrsliggers ten
Lijn, lijnstuk, punt Verkennen Opgve 1 Je ziet hier een pltje vn spoorrils vn een modelspoorn. De rils zijn evestigd op dwrsliggers. Hoe liggen de rils ten opziht vn elkr? Hoe liggen de dwrsliggers ten
HOOFDSTUK 1 BASISBEGRIPPEN
 I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
Aanzet 1 tot een document van parate kennis en vaardigheden wiskunde 1 ste graad
 Anzet 1 tot een document vn prte kennis en vrdigheden wiskunde 1 ste grd 1. TAALVAARDIGHEID BINNEN WISKUNDE ) Begrippen uit de getllenleer Bewerking Symool optelling + ftrekking vermenigvuldiging deling
Anzet 1 tot een document vn prte kennis en vrdigheden wiskunde 1 ste grd 1. TAALVAARDIGHEID BINNEN WISKUNDE ) Begrippen uit de getllenleer Bewerking Symool optelling + ftrekking vermenigvuldiging deling
Hoofdstuk 2 DE STELLING VAN PYTHAGORAS
 Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Hoofdstuk DE STELLING VAN PYTHAGORAS INHOUD. De stelling vn Pythgors formuleren 98. Meetkundige voorstellingen 06. De stelling vn Pythgors ewijzen 09. Rekenen met Pythgors. Construties.6 Pythgors in de
Bewerkingen met eentermen en veeltermen
 5 Bewerkingen met eentermen en veeltermen Dit kun je l 1 werken met letters ls onekenden, ls vernderlijken en om te verlgemenen 2 een tel mken ij een situtie 3 de fsprken over lettervormen toepssen 4 oppervlkteformules
5 Bewerkingen met eentermen en veeltermen Dit kun je l 1 werken met letters ls onekenden, ls vernderlijken en om te verlgemenen 2 een tel mken ij een situtie 3 de fsprken over lettervormen toepssen 4 oppervlkteformules
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
 Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
1a Een hoeveelheid stof kan maar op één manier veranderen. Hoe?
 Oefenopgven over Stoffen en Mterilen Uitwerking en ntwoord op elke opgve stt n de ltste opgve. Gegevens kunnen worden opgezoht in de tellen hterin. Als de zwrteftor niet vermeld is mg je 9,81 N/kg nemen.
Oefenopgven over Stoffen en Mterilen Uitwerking en ntwoord op elke opgve stt n de ltste opgve. Gegevens kunnen worden opgezoht in de tellen hterin. Als de zwrteftor niet vermeld is mg je 9,81 N/kg nemen.
MEETKUNDE 2 Lengte - afstand - hoeken
 MTKUN 2 Lengte - fstnd - hoeken M7 Lengtemten en meetinstrumenten 186 M8 Lengte en fstnd 187 M9 Gelijke fstnden 194 M10 Hoeken meten en tekenen 198 185 M7 1 Titel Lengtemten en meetinstrumenten 579 Vul
MTKUN 2 Lengte - fstnd - hoeken M7 Lengtemten en meetinstrumenten 186 M8 Lengte en fstnd 187 M9 Gelijke fstnden 194 M10 Hoeken meten en tekenen 198 185 M7 1 Titel Lengtemten en meetinstrumenten 579 Vul
Toetsopgaven vwo B deel 3 hoofdstuk 10
 Toetsopgven vwo deel 3 hoofdstuk 10 Opgve 1 In de figuur hiernst zie je 15 kubusjes met ribbe. e punten,, en zijn hoekpunten vn een kubusje, punt is het midden vn een ribbe en de punten en delen een ribbe
Toetsopgven vwo deel 3 hoofdstuk 10 Opgve 1 In de figuur hiernst zie je 15 kubusjes met ribbe. e punten,, en zijn hoekpunten vn een kubusje, punt is het midden vn een ribbe en de punten en delen een ribbe
Hoofdstuk 2: Bewerkingen in R
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Opgave 1 Je ziet hier twee driehoeken op een cm-rooster. Beide driehoeken zijn omgeven door eenzelfde
 Oppervlkte vn riehoeken Verkennen Opgve 1 Je ziet hier twee riehoeken op een m-rooster. Beie riehoeken zijn omgeven oor eenzelfe rehthoek. nme: Imges/hv-me7-e1-t01.jpg file: Imges/hv-me7-e1-t01.jpg Hoeveel
Oppervlkte vn riehoeken Verkennen Opgve 1 Je ziet hier twee riehoeken op een m-rooster. Beie riehoeken zijn omgeven oor eenzelfe rehthoek. nme: Imges/hv-me7-e1-t01.jpg file: Imges/hv-me7-e1-t01.jpg Hoeveel
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Donderdag 20 mei 13.30 16.30 uur
 Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
H. 10 Goniometrie Basisbegrippen. a c. Gemeenschappelijke Propedeuse Engineering WISKUNDE H.10
 H. 10 Goniometrie 10.1 Bsisegrippen Regelmtig voeren we erekeningen uit, wrin één of meerdere hoeken voorkomen. Voor een sherpe hoek kunnen we 3 goniometrishe verhoudingen definiëren. Deze lten zih het
H. 10 Goniometrie 10.1 Bsisegrippen Regelmtig voeren we erekeningen uit, wrin één of meerdere hoeken voorkomen. Voor een sherpe hoek kunnen we 3 goniometrishe verhoudingen definiëren. Deze lten zih het
Getallenverzamelingen
 Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Noordhoff Uitgevers bv
 86 Verdieping Regelmatige figuren 1a e figuur heeft 12 hoekpunten. lke hoek is 150. Ja, ze zijn allemaal 150. d e zijden zijn 2,5 m. e Ja, ze zijn allemaal even lang. 2a en regelmatige driehoek is een
86 Verdieping Regelmatige figuren 1a e figuur heeft 12 hoekpunten. lke hoek is 150. Ja, ze zijn allemaal 150. d e zijden zijn 2,5 m. e Ja, ze zijn allemaal even lang. 2a en regelmatige driehoek is een
Meetkunde 4 Congruentie
 Meetkunde 4 ongruentie M0 ongruente figuren 6 M ongruente driehoeken 68 M ewijzen met ongruente driehoeken 76 M3 igenshp en onstrutie vn de middelloodlijn vn een lijnstuk 85 M4 igenshp en onstrutie vn
Meetkunde 4 ongruentie M0 ongruente figuren 6 M ongruente driehoeken 68 M ewijzen met ongruente driehoeken 76 M3 igenshp en onstrutie vn de middelloodlijn vn een lijnstuk 85 M4 igenshp en onstrutie vn
MEETKUNDE 3 Vierhoeken
 MEETKUNDE 3 Vierhoeken M11 Vierhoeken in de ruimte 8 M1 Vierhoeken tekenen 1 M13 Kuus en lk 14 M14 Metriek stelsel M15 Rehthoek en lk 3 M16 Vierknt en kuus 8 M17 Trpezium, prllellogrm en ruit 3 7 M111
MEETKUNDE 3 Vierhoeken M11 Vierhoeken in de ruimte 8 M1 Vierhoeken tekenen 1 M13 Kuus en lk 14 M14 Metriek stelsel M15 Rehthoek en lk 3 M16 Vierknt en kuus 8 M17 Trpezium, prllellogrm en ruit 3 7 M111
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Noordhoff Uitgevers bv
 Voorkennis: Algerïshe ewerkingen ldzijde 9 V- d e 9 V- 9 V- + + + V- + + 9 d + + + + e + + + + f + g Hoofdstuk - Funties en lger + + + + + + + ldzijde 9 V- + ( + ) + ( )( ) of + of of of ( ) d p p ( p
Voorkennis: Algerïshe ewerkingen ldzijde 9 V- d e 9 V- 9 V- + + + V- + + 9 d + + + + e + + + + f + g Hoofdstuk - Funties en lger + + + + + + + ldzijde 9 V- + ( + ) + ( )( ) of + of of of ( ) d p p ( p
Meetkunde 1 Ruimtemeetkunde
 Meetkunde 1 Ruimtemeetkunde M1 Ruimtelijke situties voorstellen in een vlk 180 M2 De pirmide, de kegel en de ol 18 M Het volume vn een pirmide, een kegel en een ol 190 179 M1 1 Titel Ruimtelijke situties
Meetkunde 1 Ruimtemeetkunde M1 Ruimtelijke situties voorstellen in een vlk 180 M2 De pirmide, de kegel en de ol 18 M Het volume vn een pirmide, een kegel en een ol 190 179 M1 1 Titel Ruimtelijke situties
1 Serieschakeling. Rs I I I RS I ... I I I
 Hoofdstuk 4 Het shkelen vn weerstnden Serieshkeling Us U s I I * I 2* I 2... n* In * I 2* I... n* I S I I 2 s 2... n * I 2* I n* I... I I I s is steeds groter dn de grootste. weerstnden gelijk dn over
Hoofdstuk 4 Het shkelen vn weerstnden Serieshkeling Us U s I I * I 2* I 2... n* In * I 2* I... n* I S I I 2 s 2... n * I 2* I n* I... I I I s is steeds groter dn de grootste. weerstnden gelijk dn over
middelloodlijnen werkschrift naam:
 werkshrift middelloodlijnen nm: 1 Disuswerpen Hiernst zie je, vn ovenf, de setor wrinnen een disuswerper zijn shijf moet gooien. De shl is 1:1000. Het wereldreord disuswerpen is sinds 6 juni 1986 in hnden
werkshrift middelloodlijnen nm: 1 Disuswerpen Hiernst zie je, vn ovenf, de setor wrinnen een disuswerper zijn shijf moet gooien. De shl is 1:1000. Het wereldreord disuswerpen is sinds 6 juni 1986 in hnden
Cirkels en cilinders
 5 irkels en cilinders it kun je l 1 middelpunt en strl in een cirkel nduiden 2 de oppervlkte vn vlkke figuren berekenen 3 het volume vn een prism berekenen Test jezelf Elke vrg heeft mr één juist ntwoord.
5 irkels en cilinders it kun je l 1 middelpunt en strl in een cirkel nduiden 2 de oppervlkte vn vlkke figuren berekenen 3 het volume vn een prism berekenen Test jezelf Elke vrg heeft mr één juist ntwoord.
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Dinsdag 25 mei uur
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
Lijnen en vlakken in. Klas 6N en 7N Wiskunde 5 perioden Kees Temme Versie 2
 Lijnen en vlkken in Kls N en N Wiskunde perioden Kees Temme Versie . Coördinten in R³.... De vergelijking vn een vlk ().... De vectorvoorstelling vn een lijn.... De vectorvoorstelling vn een vlk... 8.
Lijnen en vlkken in Kls N en N Wiskunde perioden Kees Temme Versie . Coördinten in R³.... De vergelijking vn een vlk ().... De vectorvoorstelling vn een lijn.... De vectorvoorstelling vn een vlk... 8.
6.1 Schaduw gevormd door een puntvormige
 6 Schduwvorming 6.1 Schduw gevormd door een Vroeger geruikte men een zonnewijzer ls uurwerk. Die steunde op de verndering vn de schduw nrgelng de stnd vn de zon. A B Fig. 2.12 Een schduw kn gevormd worden
6 Schduwvorming 6.1 Schduw gevormd door een Vroeger geruikte men een zonnewijzer ls uurwerk. Die steunde op de verndering vn de schduw nrgelng de stnd vn de zon. A B Fig. 2.12 Een schduw kn gevormd worden
Parate kennis wiskunde
 Heilige Mgdcollege Dendermonde Prte kennis wiskunde 4 Lt A Lt B Wet A Wet B Ec C Vkgroep wiskunde Hemco Dit document is edoeld ls smenvtting vn wt ls prte kennis wordt ngenomen ij nvng vn het tweede jr
Heilige Mgdcollege Dendermonde Prte kennis wiskunde 4 Lt A Lt B Wet A Wet B Ec C Vkgroep wiskunde Hemco Dit document is edoeld ls smenvtting vn wt ls prte kennis wordt ngenomen ij nvng vn het tweede jr
Eindexamen wiskunde B1-2 vwo 2004-I
 chten vn een derdegrdsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. V is het gebied ingesloten door de grfiek vn f en de x-s. 5p 1 ereken lgebrïsch de excte wrde vn de oppervlkte
chten vn een derdegrdsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. V is het gebied ingesloten door de grfiek vn f en de x-s. 5p 1 ereken lgebrïsch de excte wrde vn de oppervlkte
Proefexemplaar. Mark De Feyter Filip Geeurickx Jan Thoelen Roger Van Nieuwenhuyze Eric Willockx. Wendy Luyckx Els Sas.
 Mrk De Feyter Filip Geeurickx Jn Thoelen Roger Vn Nieuwenhuyze Eric Willockx EWERkt voor het GO! onderwijs vn de Vlmse Gemeenschp door Wendy Luyckx Els Ss RTooNS Dve Vnroye Proefexemplr Leerwerkoek Trnsformties
Mrk De Feyter Filip Geeurickx Jn Thoelen Roger Vn Nieuwenhuyze Eric Willockx EWERkt voor het GO! onderwijs vn de Vlmse Gemeenschp door Wendy Luyckx Els Ss RTooNS Dve Vnroye Proefexemplr Leerwerkoek Trnsformties
Hoofdstuk 2 Vlakke meetkunde
 Opstap eellijn, hoogtelijn, samen 180 en samen 360 O-1a P 60º R d O-2a O-3a d P x x Q e drie deellijnen van de driehoek gaan inderdaad door één punt. M O Zie opdraht O-2a. U S V T UV is de hoogtelijn op
Opstap eellijn, hoogtelijn, samen 180 en samen 360 O-1a P 60º R d O-2a O-3a d P x x Q e drie deellijnen van de driehoek gaan inderdaad door één punt. M O Zie opdraht O-2a. U S V T UV is de hoogtelijn op
Merkwaardige producten en ontbinden in factoren
 6 Merkwrdige producten en ontinden in fctoren Dit kun je l 1 een mcht tot een mcht verheffen eentermen vermenigvuldigen 3 eentermen delen 4 veeltermen vermenigvuldigen 5 een veelterm delen door een eenterm
6 Merkwrdige producten en ontinden in fctoren Dit kun je l 1 een mcht tot een mcht verheffen eentermen vermenigvuldigen 3 eentermen delen 4 veeltermen vermenigvuldigen 5 een veelterm delen door een eenterm
Noordhoff Uitgevers bv
 V-1a d V-2a 102 ladzijde 138 In werkelijkheid zijn er 3 rien evenwijdig aan rie. In figuur 1 zijn die rien ook evenwijdig getekend. In figuur 2 zijn deze rien zo getekend dat ze elkaar alle vier in hetzelfde
V-1a d V-2a 102 ladzijde 138 In werkelijkheid zijn er 3 rien evenwijdig aan rie. In figuur 1 zijn die rien ook evenwijdig getekend. In figuur 2 zijn deze rien zo getekend dat ze elkaar alle vier in hetzelfde
Het kwadraat van een tweeterm a+b. (a+b)²
 Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Hoofdstuk 5 - Tekenen en zien
 avo deel 1 Uitwerkingen Moderne wiskunde oofdstuk 5 - ekenen en zien ladzijde 138 V-1a d In werkelijkheid zijn er 3 rien evenwijdig aan rie. In figuur 1 zijn die rien ook evenwijdig getekend. In figuur
avo deel 1 Uitwerkingen Moderne wiskunde oofdstuk 5 - ekenen en zien ladzijde 138 V-1a d In werkelijkheid zijn er 3 rien evenwijdig aan rie. In figuur 1 zijn die rien ook evenwijdig getekend. In figuur
Eigenschappen van driehoeken
 5 igenschappen van driehoeken it kun je al een hoek meten de verschillende soorten driehoeken definiëren 3 de verschillende soorten hoeken definiëren 4 de eigenschappen van de verschillende soorten hoeken
5 igenschappen van driehoeken it kun je al een hoek meten de verschillende soorten driehoeken definiëren 3 de verschillende soorten hoeken definiëren 4 de eigenschappen van de verschillende soorten hoeken
6.0 INTRO. 1 a Bekijk de sommen hiernaast en ga na of ze kloppen. 1 2 0 3 = 2 2 3 1 4 = 2 3 4 2 5 = 2 4 5 3 6 = 2 5 6 4 7 = 2...
 113 6.0 INTRO 1 Bekijk de sommen hiernst en g n of ze kloppen. Schrijf de twee volgende sommen uit de rij op en controleer of deze ook ls uitkomst 2 heen. c Schrijf twee sommen op die veel verder in de
113 6.0 INTRO 1 Bekijk de sommen hiernst en g n of ze kloppen. Schrijf de twee volgende sommen uit de rij op en controleer of deze ook ls uitkomst 2 heen. c Schrijf twee sommen op die veel verder in de
Rangschik van klein naar groot. Vul aan. Meet de lengte van onderstaande voorwerpen.
 582 Rngshik vn klein nr groot. 583 Vul n. 0,3 km 500 m 200 000 m 25 000 dm... 0,3 m 40 m 12 dm 240 mm... 1 mm is... mm kleiner dn 1 m. 8 m is... m kleiner dn 1 m. d 9 92 70 47 3 m is... mm kleiner dn 1
582 Rngshik vn klein nr groot. 583 Vul n. 0,3 km 500 m 200 000 m 25 000 dm... 0,3 m 40 m 12 dm 240 mm... 1 mm is... mm kleiner dn 1 m. 8 m is... m kleiner dn 1 m. d 9 92 70 47 3 m is... mm kleiner dn 1
Examen VWO. wiskunde B (pilot) tijdvak 1 woensdag 16 mei 13.30-16.30 uur
 Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Diagonaalvlakken. Verkennen. Uitleg. Opgave 1
 Wiskune eerste fse HAVO/VWO Meten en tekenen Ruimtelijke figuren Digonlvlkken Verkennen Opgve 1 Hier zie je pkjes Choomel. Neem n t elk vn ie pkjes e vorm heeft vn een lk vn 5,5 m ij 4,0 m ij 9,5 m. Er
Wiskune eerste fse HAVO/VWO Meten en tekenen Ruimtelijke figuren Digonlvlkken Verkennen Opgve 1 Hier zie je pkjes Choomel. Neem n t elk vn ie pkjes e vorm heeft vn een lk vn 5,5 m ij 4,0 m ij 9,5 m. Er
Wiskunde voor 1 havo/vwo
 Wiskunde voor 1 hvo/vwo Deel 2 Versie 2013 Smensteller 2013 Het uteursreht op dit lesmteril erust ij Stihting Mth4All. Mth4All is derhlve de rehtheende zols edoeld in de hieronder vermelde retive ommons
Wiskunde voor 1 hvo/vwo Deel 2 Versie 2013 Smensteller 2013 Het uteursreht op dit lesmteril erust ij Stihting Mth4All. Mth4All is derhlve de rehtheende zols edoeld in de hieronder vermelde retive ommons
1 Vlaamse Wiskunde Olympiade : Eerste Ronde.
 Vlmse Wiskunde Olympide 99 993 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olympide 99 993 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Noordhoff Uitgevers bv
 V-1a / V-2a e Voorkennis Zie e figuur hieroner. Zie e figuur hieroner. De lijn n en het punt P kunnen ook aan e anere kant van lijn l liggen. Zie e figuur hieroner. P Zie e figuur hieroven. In vierhoek
V-1a / V-2a e Voorkennis Zie e figuur hieroner. Zie e figuur hieroner. De lijn n en het punt P kunnen ook aan e anere kant van lijn l liggen. Zie e figuur hieroner. P Zie e figuur hieroven. In vierhoek
Eindexamen vwo wiskunde B II
 Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
INHOUDSTABEL. 1. TRANSFORMATIES (fiche 1) SYMMETRIE (fiche 2) MERKWAARDIGE LIJNEN IN EEN DRIEHOEK (fiche 3)...6
 INHOUDSTBEL 1. TRNSFORMTIES (fiche 1)...3 2. SYMMETRIE (fiche 2)...4 3. MERKWRDIGE LIJNEN IN EEN DRIEHOEK (fiche 3)...6 4. VLKKE FIGUREN: DRIEHOEKEN (fiche 4)...7 5. VLKKE FIGUREN: BIJZONDERE VIERHOEKEN
INHOUDSTBEL 1. TRNSFORMTIES (fiche 1)...3 2. SYMMETRIE (fiche 2)...4 3. MERKWRDIGE LIJNEN IN EEN DRIEHOEK (fiche 3)...6 4. VLKKE FIGUREN: DRIEHOEKEN (fiche 4)...7 5. VLKKE FIGUREN: BIJZONDERE VIERHOEKEN
3 Snijpunten. Verkennen. Uitleg
 3 Snijpunten Verkennen Meetkunde Snijpunten Inleiding Verkennen Bentwoord de vrgen bij Verkennen. Mk ook de constructie in GeoGebr. Gebruik eventueel het progrmm om de snijpunten voor je te berekenen ls
3 Snijpunten Verkennen Meetkunde Snijpunten Inleiding Verkennen Bentwoord de vrgen bij Verkennen. Mk ook de constructie in GeoGebr. Gebruik eventueel het progrmm om de snijpunten voor je te berekenen ls
In dit hoofdstuk introduceren we de hoofdrolspelers van het college: eindige automaten.
 9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
9 2 Eindige utomten In dit hoofdstuk introduceren we de hoofdrolspelers vn het college: eindige utomten. 2.1 Deterministische eindige utomten We eginnen met een vooreeld. Vooreeld 2.1 Beschouw het volgende
van basis tot Handleiding limiet Meetkunde
 Mrk De Feyter Filip Geeurickx Jn Thoelen Roger Vn Nieuwenhuyze ewerkt voor het gemeenschpsonderwijs door Wendy Luyckx o Roefs rtoons Dve Vnroye vn sis tot limiet Hndleiding Meetkunde 1 voorwoord ISN: 978
Mrk De Feyter Filip Geeurickx Jn Thoelen Roger Vn Nieuwenhuyze ewerkt voor het gemeenschpsonderwijs door Wendy Luyckx o Roefs rtoons Dve Vnroye vn sis tot limiet Hndleiding Meetkunde 1 voorwoord ISN: 978
Onafhankelijk van a. f snijdt de x-as in punt A ( , 0) Voor elke positieve waarde van a is een functie f. gegeven door F ( x) = x e ax.
 Onfhnkelijk vn Voor elke positieve wrde vn is een functie f gegeven door f ( x) = (1 x) e x en een functie F gegeven door F ( x) = x e x. De functie 3p 1 Toon dit n. F is een primitieve functie vn f. De
Onfhnkelijk vn Voor elke positieve wrde vn is een functie f gegeven door f ( x) = (1 x) e x en een functie F gegeven door F ( x) = x e x. De functie 3p 1 Toon dit n. F is een primitieve functie vn f. De
1 Vlaamse Wiskunde Olympiade : Tweede ronde
 1 Vlmse Wiskunde Olympide 000-001: Tweede ronde De eerste ronde estt uit 0 meerkeuzevrgen Het quoteringssysteem werkt ls volgt: per goed ntwoord krijgt de deelnemer 5 punten, een lnco ntwoord ezorgt hem
1 Vlmse Wiskunde Olympide 000-001: Tweede ronde De eerste ronde estt uit 0 meerkeuzevrgen Het quoteringssysteem werkt ls volgt: per goed ntwoord krijgt de deelnemer 5 punten, een lnco ntwoord ezorgt hem
6.4 Rekenen met evenwichtsreacties
 6.4 Rekenen met evenwihtsreties An de hnd vn een reeks vooreelden zullen we het rekenwerk ehndelen n evenwihtsreties. Vooreeld 6.2 We estuderen het gsevenwiht: A(g) + B(g) C(g) + D(g) In een ruimte vn
6.4 Rekenen met evenwihtsreties An de hnd vn een reeks vooreelden zullen we het rekenwerk ehndelen n evenwihtsreties. Vooreeld 6.2 We estuderen het gsevenwiht: A(g) + B(g) C(g) + D(g) In een ruimte vn
Pak jouw passer en maak de afstand tussen de passerpunten 3 cm.
 Psser en irkel Verkennen Opgve 1 Op de foto hiernst wordt met ehulp vn een psser een irkel getekend. Pk jouw psser en mk de fstnd tussen de psserpunten 3 m. Teken een punt M en zet drin de stlen punt vn
Psser en irkel Verkennen Opgve 1 Op de foto hiernst wordt met ehulp vn een psser een irkel getekend. Pk jouw psser en mk de fstnd tussen de psserpunten 3 m. Teken een punt M en zet drin de stlen punt vn
element (of de rol van nul bij opt)
 Atheneum Wispelerg - Wispelergstrt - 9000 Gent Bijlge - Leerfihes (3 e jr 5uur wiskunde) Eigenshppen vn de ewerkingen in R Nm Kls. - 1 - Leerfihe 1 Eigenshppen vn de optelling in R Nm vn de eigenshp Eigenshp
Atheneum Wispelerg - Wispelergstrt - 9000 Gent Bijlge - Leerfihes (3 e jr 5uur wiskunde) Eigenshppen vn de ewerkingen in R Nm Kls. - 1 - Leerfihe 1 Eigenshppen vn de optelling in R Nm vn de eigenshp Eigenshp
Blok 4 - Vaardigheden
 Blok - Vrdigheden ldzijde 0 Dt geldt voor h, len m ; de grfieken zijn symmetrish in de y -s. Die zijn tegengesteld; ijvooreeld g( ) g () De grfiek is symmetrish in de oorsprong. funtie symmetrie in de
Blok - Vrdigheden ldzijde 0 Dt geldt voor h, len m ; de grfieken zijn symmetrish in de y -s. Die zijn tegengesteld; ijvooreeld g( ) g () De grfiek is symmetrish in de oorsprong. funtie symmetrie in de
Rekenregels van machten
 4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
Examen VWO. wiskunde B1,2 (nieuwe stijl)
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
1 Vlaamse Wiskunde Olympiade 1987-1988 : Eerste Ronde.
 Vlmse Wiskunde Olympide 987-988 : Eerste Ronde De eerste ronde estt steeds uit 0 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt: een deelnemer strt met 0 punten, per goed
Vlmse Wiskunde Olympide 987-988 : Eerste Ronde De eerste ronde estt steeds uit 0 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt: een deelnemer strt met 0 punten, per goed
Examen VWO 2012. wiskunde B. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exmen VWO 2012 tijdvk 1 woensdg 16 mei 13.30-16.30 uur wiskunde B Bij dit exmen hoort een uitwerkbijlge. Dit exmen bestt uit 17 vrgen. Voor dit exmen zijn mximl 78 punten te behlen. Voor elk vrgnummer
Exmen VWO 2012 tijdvk 1 woensdg 16 mei 13.30-16.30 uur wiskunde B Bij dit exmen hoort een uitwerkbijlge. Dit exmen bestt uit 17 vrgen. Voor dit exmen zijn mximl 78 punten te behlen. Voor elk vrgnummer
= = = = = = = =
 0 ld nm Hulp Reken uit met cijferen 0 Reken uit met splitsen Honderdvouden ij elkr en dn de rest ij elkr. + 0 = 0 + = 0 + = 0 + 0 = + 0 = 0 + 0 = 0 + = 0 + = Honderdvouden vn elkr f en dn de rest vn elkr
0 ld nm Hulp Reken uit met cijferen 0 Reken uit met splitsen Honderdvouden ij elkr en dn de rest ij elkr. + 0 = 0 + = 0 + = 0 + 0 = + 0 = 0 + 0 = 0 + = 0 + = Honderdvouden vn elkr f en dn de rest vn elkr
1.3 Wortels. x x 36 6 = x = 1.5 Breuken. teller teller noemer noemer. Delen: vermenigvuldig met het omgekeerde.
 Voorereidende opgven Stoomursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit tot wr je kunt en g verder
Voorereidende opgven Stoomursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-shriften die je gt geruiken tijdens de ursus. Als een som niet lukt, werk hem dn uit tot wr je kunt en g verder
Examen VWO. wiskunde B. tijdvak 2 woensdag 20 juni uur. Bij dit examen hoort een uitwerkbijlage.
 Emen VWO 202 tijdvk 2 woensdg 20 juni 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. Dit emen bestt uit 7 vrgen. Voor dit emen zijn miml 8 punten te behlen. Voor elk vrgnummer stt hoeveel
Emen VWO 202 tijdvk 2 woensdg 20 juni 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. Dit emen bestt uit 7 vrgen. Voor dit emen zijn miml 8 punten te behlen. Voor elk vrgnummer stt hoeveel
Eindexamen vwo wiskunde B pilot I
 Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin t cos t sin t www. - - nfhnkelijk
Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin t cos t sin t www. - - nfhnkelijk
Een regenton. W is het vlakdeel dat wordt ingesloten door de x-as, de y-as, de grafiek van r en de lijn x h, met 0 h
 Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
element (of de rol van nul bij opt)
 - 1 - Leerfihe 1 Eigenshppen vn de optelling in R Voor elk koppel reële getllen De optelling is overl gedefinieerd estt er een reëel getl dt hun som is., R R + De optelling is ssoitief Een som vn reële
- 1 - Leerfihe 1 Eigenshppen vn de optelling in R Voor elk koppel reële getllen De optelling is overl gedefinieerd estt er een reëel getl dt hun som is., R R + De optelling is ssoitief Een som vn reële
INTERVIEWEN 1 SITUATIE
 INTERVIEWEN drs. W. Bontenl 1 SITUATIE Een interview vlt te omshrijven ls een gesprek tussen één of meerdere personen - de interviewers - en een ndere persoon (of diverse nderen) - de geïnterviewden -
INTERVIEWEN drs. W. Bontenl 1 SITUATIE Een interview vlt te omshrijven ls een gesprek tussen één of meerdere personen - de interviewers - en een ndere persoon (of diverse nderen) - de geïnterviewden -
Opgave 1 Stel je eens een getal voor, bijvoorbeeld: 504,76. a b c
 Opgve 1 Stel je eens een getl voor, ijvooreeld: 504,76. Wt zijn de ijfers vn dit getl? Hoeveel is elk vn die ijfers wrd? Wt etekent de komm? Opgve 2 Bekijk het getl 6102,543. d e Hoeveel ijfers hter de
Opgve 1 Stel je eens een getl voor, ijvooreeld: 504,76. Wt zijn de ijfers vn dit getl? Hoeveel is elk vn die ijfers wrd? Wt etekent de komm? Opgve 2 Bekijk het getl 6102,543. d e Hoeveel ijfers hter de
Bewerkingen met eentermen en veeltermen
 5 Bewerkingen met eentermen en veeltermen Dit kun je l 1 werken met letters ls onekenden, ls vernderlijken en om te verlgemenen 2 een tel mken ij een situtie 3 de fsprken over lettervormen toepssen 4 oppervlkteformules
5 Bewerkingen met eentermen en veeltermen Dit kun je l 1 werken met letters ls onekenden, ls vernderlijken en om te verlgemenen 2 een tel mken ij een situtie 3 de fsprken over lettervormen toepssen 4 oppervlkteformules
Noordhoff Uitgevers bv
 V-1a / 52 V-2a e Voorkennis Zie e figuur hieroner. Zie e figuur hieroner. De lijn n en het punt P kunnen ook aan e anere kant van lijn l liggen. Zie e figuur hieroner. P m l Zie e figuur hieroven. In vierhoek
V-1a / 52 V-2a e Voorkennis Zie e figuur hieroner. Zie e figuur hieroner. De lijn n en het punt P kunnen ook aan e anere kant van lijn l liggen. Zie e figuur hieroner. P m l Zie e figuur hieroven. In vierhoek
Inhoudsmaten. Verkennen. Uitleg. Opgave 1. Dit is een kubus met ribben van 1 m lengte. Hoeveel bedraagt de inhoud ervan?
 Inhousmten Verkennen Opgve 1 Dit is een kuus met rien vn 1 m lengte. Hoeveel ergt e inhou ervn? Kun je e nm kuieke meter ls eenhei vn inhou verklren? In hoeveel kleinere kuussen is eze kuieke meter vereel?
Inhousmten Verkennen Opgve 1 Dit is een kuus met rien vn 1 m lengte. Hoeveel ergt e inhou ervn? Kun je e nm kuieke meter ls eenhei vn inhou verklren? In hoeveel kleinere kuussen is eze kuieke meter vereel?
2 De kracht van vectoren
 De krcht vn vectoren Dit is een ewerking vn Meetkunde met coördinten lok Punten met gewicht vn d Goddijn ten ehoeve vn het nieuwe progrmm (015) wiskunde vwo. Opgven met dit merkteken kun je zonder de opouw
De krcht vn vectoren Dit is een ewerking vn Meetkunde met coördinten lok Punten met gewicht vn d Goddijn ten ehoeve vn het nieuwe progrmm (015) wiskunde vwo. Opgven met dit merkteken kun je zonder de opouw
Hoofdstuk 2 Vlakke meetkunde
 Opstap Hoeken, driehoeken en vierhoeken O-1a P = 65 R O-2a O-3a O-4a P A De driehoek is een gelijkzijdige driehoek. M Q P + + N Q De lengte van OP is 3,5 m. De oppervlakte van ^MNO is MN OP : 2 5,4 3,5
Opstap Hoeken, driehoeken en vierhoeken O-1a P = 65 R O-2a O-3a O-4a P A De driehoek is een gelijkzijdige driehoek. M Q P + + N Q De lengte van OP is 3,5 m. De oppervlakte van ^MNO is MN OP : 2 5,4 3,5
Noordhoff Uitgevers bv
 ldzijde f () Er is geen symmetrie in een vertile lijn. Alle rklijnen heen een positief hellingsgetl. Wrshijnlijk (0, 0). d f () e - ICT - Rklijnen ldzijde Geruik dt d y om de hellingsgetllen vn de rklijnen
ldzijde f () Er is geen symmetrie in een vertile lijn. Alle rklijnen heen een positief hellingsgetl. Wrshijnlijk (0, 0). d f () e - ICT - Rklijnen ldzijde Geruik dt d y om de hellingsgetllen vn de rklijnen
Aanzet 1 tot een document van parate kennis en vaardigheden wiskunde 1 ste graad
 Anzet 1 tot een document vn prte kennis en vrdigheden wiskunde 1 ste grd 1. TAALVAARDIGHEID BINNEN WISKUNDE ) Begrippen uit de getllenleer Bewerking Symbool optelling + ftrekking vermenigvuldiging deling
Anzet 1 tot een document vn prte kennis en vrdigheden wiskunde 1 ste grd 1. TAALVAARDIGHEID BINNEN WISKUNDE ) Begrippen uit de getllenleer Bewerking Symbool optelling + ftrekking vermenigvuldiging deling
Antwoorden Natuurkunde Hoofdstuk 1
 Antwoorden Ntuurkunde Hoofdstuk 1 Antwoorden door Dn 2719 woorden 3 pril 2016 4,3 2 keer eoordeeld Vk Methode Ntuurkunde Systemtishe ntuurkunde 1.1 Grootheden en eenheden Opgve 1 Kwntittieve metingen zijn
Antwoorden Ntuurkunde Hoofdstuk 1 Antwoorden door Dn 2719 woorden 3 pril 2016 4,3 2 keer eoordeeld Vk Methode Ntuurkunde Systemtishe ntuurkunde 1.1 Grootheden en eenheden Opgve 1 Kwntittieve metingen zijn
Eindexamen vwo wiskunde B I
 Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Krommen en oppervlakken in de ruimte
 (HOOFDSTUK 60, uit College Mthemtis, door Frnk Ares, Jr. nd Philip A. Shmidt, Shum s Series, MGrw-Hill, New York; dit is de voorereiding voor een uit te geven Nederlndse vertling). Krommen en oppervlkken
(HOOFDSTUK 60, uit College Mthemtis, door Frnk Ares, Jr. nd Philip A. Shmidt, Shum s Series, MGrw-Hill, New York; dit is de voorereiding voor een uit te geven Nederlndse vertling). Krommen en oppervlkken
opgaven formele structuren procesalgebra
 opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
opgven formele struturen proeslger Opgve 1. (opgve 3.3.7 op p.97 vn het ditt 2005) Een mier moet vn links voor onder nr rehts hter oven op een kuus, met ties (rehts), (hter), en (oven). Uitwerking vn opgve
Om welke reden heeft een kwak relatief grote ogen?
 Route K - Volière en fznterie Strt ij de volière; de vrgen 1 t/m 6 gn over een ntl grote Europese vogels. De vrgen over de ndere dieren vn deze route hoeven niet in de juiste volgorde te stn. Dt komt omdt
Route K - Volière en fznterie Strt ij de volière; de vrgen 1 t/m 6 gn over een ntl grote Europese vogels. De vrgen over de ndere dieren vn deze route hoeven niet in de juiste volgorde te stn. Dt komt omdt
Lucht in je longen. Streep de foute woorden door. Hoe komt lucht in je longen? Zet een cirkel om de dieren met longen.
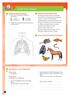 9 Luht in je longen Hoe komt luht in je longen? = longen = middenrif Kleur op de tekening de volgende onderdelen: Streep de foute woorden door. Ons lihm heeft zuurstof / kooldioxide nodig. Bij het indemen
9 Luht in je longen Hoe komt luht in je longen? = longen = middenrif Kleur op de tekening de volgende onderdelen: Streep de foute woorden door. Ons lihm heeft zuurstof / kooldioxide nodig. Bij het indemen
Eigenschappen van de bewerkingen in R Toets jezelf: herhalingsoefeningen voor examen I
 Toets jezelf: herhlingsoefeningen voor emen I - - Overzicht vn wt je moet kennen voor dit emen:. Alger:. Hoofdstuk : Reële getllen. Hoofdstuk : Eigenschppen vn de ewerkingen in R o Optellen, ftrekken,
Toets jezelf: herhlingsoefeningen voor emen I - - Overzicht vn wt je moet kennen voor dit emen:. Alger:. Hoofdstuk : Reële getllen. Hoofdstuk : Eigenschppen vn de ewerkingen in R o Optellen, ftrekken,
De oppervlakte van de rechthoek uit de vorige opgave hangt van dezelfde variabelen af.
 Opgve 1 Vn twee korte en twee lnge luifers is een rehthoek geleg. Omt je geen fmetingen weet hngt e omtrek vn eze rehthoek f vn twee vrielen, nmelijk lengtekorteluif er en lengtelngeluif er. Welke formule
Opgve 1 Vn twee korte en twee lnge luifers is een rehthoek geleg. Omt je geen fmetingen weet hngt e omtrek vn eze rehthoek f vn twee vrielen, nmelijk lengtekorteluif er en lengtelngeluif er. Welke formule
UNIFORM HEREXAMEN MULO tevens TOELATINGSEXAMEN VWO/HAVO/NATIN 2008
 MINISTERIE VN ONERWIJS EN VOLKSONTWIKKELING EXMENUREU UNIFORM HEREXMEN MULO tevens TOELTINGSEXMEN VWO/HVO/NTIN 008 VK : WISKUNE TUM : TIJ : ------------------------------------------------------------------------------------------------------------------------
MINISTERIE VN ONERWIJS EN VOLKSONTWIKKELING EXMENUREU UNIFORM HEREXMEN MULO tevens TOELTINGSEXMEN VWO/HVO/NTIN 008 VK : WISKUNE TUM : TIJ : ------------------------------------------------------------------------------------------------------------------------
Noorderpoortcollege School voor MBO Stadskanaal. Reader. Reader Wiskunde MBO Niveau 4 Periode. M. van der Pijl. Transfer Database
 Noorderpoortollege Shool voor MBO Stdsknl Reder Reder Wiskunde MBO Niveu 4 Periode 12 M. vn der Pijl Trnsfer Dtse ThiemeMeulenhoff ontwikkelt leermiddelen voor Primir Onderwijs, Algemeen Voortgezet Onderwijs,
Noorderpoortollege Shool voor MBO Stdsknl Reder Reder Wiskunde MBO Niveu 4 Periode 12 M. vn der Pijl Trnsfer Dtse ThiemeMeulenhoff ontwikkelt leermiddelen voor Primir Onderwijs, Algemeen Voortgezet Onderwijs,
Geef een tegenvoorbeeld als de uitspraak niet waar is. Als a een positief getal is, dan is a negatief.
 V* Vul n. ( ) 7 7 7 7 7 7 9 9 9 9 9 9 7 7 7 7 7 7 V** Is de uitsprk wr of niet wr? Geef een tegenvoorbeeld ls de uitsprk niet wr is. b d e ls een positief getl is, dn is negtief. = dn = ls b een negtief
V* Vul n. ( ) 7 7 7 7 7 7 9 9 9 9 9 9 7 7 7 7 7 7 V** Is de uitsprk wr of niet wr? Geef een tegenvoorbeeld ls de uitsprk niet wr is. b d e ls een positief getl is, dn is negtief. = dn = ls b een negtief
Opgaven met dit merkteken kun je zonder de opbouw aan te tasten, overslaan.
 2 Verschuiven Dit is een ewerking vn Meetkunde met coördinten Blok Punten met gewicht vn Ad Goddijn ten ehoeve vn het nieuwe progrmm (2014) wiskunde B vwo. Opgven met dit merkteken kun je zonder de opouw
2 Verschuiven Dit is een ewerking vn Meetkunde met coördinten Blok Punten met gewicht vn Ad Goddijn ten ehoeve vn het nieuwe progrmm (2014) wiskunde B vwo. Opgven met dit merkteken kun je zonder de opouw
Antwoorden Doeboek 21 Kijk op kegelsneden. Rob van der Waall en Liesbeth de Clerck
 Antwoorden Doeboek 1 Kijk op kegelsneden Rob vn der Wll en Liesbeth de Clerk 1 De 3 4 ) 5 Een 6 Als 7 8 ) 9 De Nee, lle punten die 1 entimeter vn het midden liggen, liggen op de irkel. gevrgde figuur bestt
Antwoorden Doeboek 1 Kijk op kegelsneden Rob vn der Wll en Liesbeth de Clerk 1 De 3 4 ) 5 Een 6 Als 7 8 ) 9 De Nee, lle punten die 1 entimeter vn het midden liggen, liggen op de irkel. gevrgde figuur bestt
wedstrijden, dus totaal 1 n ( n 1)
 Hoofdstuk : Comintoriek.. Telprolemen visuliseren Opgve :. ;. voordeel: een wegendigrm is compcter ndeel: ij een wegendigrm moet je weten dt je moet vermenigvuldigen terwijl je ij een oomdigrm het ntl
Hoofdstuk : Comintoriek.. Telprolemen visuliseren Opgve :. ;. voordeel: een wegendigrm is compcter ndeel: ij een wegendigrm moet je weten dt je moet vermenigvuldigen terwijl je ij een oomdigrm het ntl
