Rinse Poortinga Lineaire Algebra en Voortgezette Analyse. 2 Lineaire afbeeldingen
|
|
|
- Irena Desmet
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Rise Poortig Lieire Algebr e Voortgezette Alyse 2 Lieire fbeeldige Ihoud: 2 Lieire fbeeldige 22 Rije- e koloerg 23 rspoere 24 De deterit 25 De oplossige v ee stelsel lieire vergelijkige 26 Guss-eliitie 27 Eleetire lieire trsforties refwoorde: 2 Lieire fbeeldige, copoete v ee fbeeldig, idetieke fbeeldig, coörditfucties, coördite, trix v ee lieire fbeeldig, koloe, rije, producttrix, vierkte trix, ulfbeeldig 22 Rije- e koloerg rg, xile rg 23 rspoere, hoofddigol v ee trix, getrspoeerde trix of lieire fbeeldig, syetrische trix of lieire fbeeldig 24 De deterit, forule v Leibiz, deeltrix, oderdeterit, regulier, otwikkele r ee kolo of rij, schkbordptroo, bovedriehoekstrix 25 Stelsel lieire vergelijkige, (o)fhkelijk stelsel, regel v Crer, strijdig stelsel 26 Guss-eliitie, gevulde trix, eleetire rijbewerkige, (r beede) schoovege, trpvor, kopeleet 27 Eleetire lieire trsfortie
2 2 Lieire fbeeldige 2 Lieire fbeeldige e trices Ee fbeeldig F : D et D oee we kortweg ee - - fbeeldig De tere fbeeldig e fuctie betekee i pricipe hetzelfde I het volgede zulle we echter fbeeldige die getlle ls fuctiewrde hebbe bij voorkeur fucties oee We zulle het oderscheid tusse fucties e fbeeldige bedrukke door eestl voor fucties kleie letters e voor fbeeldige hoofdletters te gebruike [Getlle duide we eestl et kleie letters e pute et hoofdletters] Drst gebruike we ook kleie Griekse letters voor zowel fbeeldige ls fucties Ee -tl - -fucties f,, f et geeeschppelijk doei D beplt ee - -fbeeldig F dv F( X ) ( f ( X ),, f ( X )) voor X D Ogekeerd beplt ee - -fbeeldig F et doei D ee -tl - - fucties f,, f, eveees et doei D, zo dt F( X ) ( f( X ),, f ( X )) voor X D We schrijve F ( f,, f ) e oee de fucties f,, f de copoete v F De - -fbeeldig X X fbeeldt heet de idetieke fbeeldig v idetieke fbeeldig hete de coörditfucties op die elk put X v De copoete op zichzelf,, v de Voor k,, geldt k ( X ) X, Ek xk Is F ee - -fbeeldig, d is fk k F de k-de copoet v F Is A ( A,, A ) ee rij pute i ee lieire ruite V, d is er precies éé lieire fbeeldig A : V die de stdrdbsis E ( E,, E ) v fbeeldt op de puterij A ( A,, A ) i V Afbeeldig A is ee isoorfie tusse e V precies d, weer A ee bsis is v V I dt gevl k ieder put P V op precies éé ier geschreve worde ls lieire cobitie P x A x A e dit put correspodeert d oder A et het -tl ( x,, x ) i We oee ( x,, x ) het coördite -tl v put P tov de bsis A De keuze v ee vste bsis A i V kt het ogelijk o V te idetificere et I ee euclidische ruite kieze we ee vste orthoorle b- sis o op grod v stellig 86 iproducte, fstde e hoeke gekkelijk te kue berekee Is W ee dere lieire ruite et bsis B ( B,, B ), d kue we W op dezelfde ier et behulp v B idetificere et Met ee lieire of ffiee fbeeldig v V i W correspodeert d ee lieire of ffiee fbeeldig v i
3 28 Lieire Algebr Gezie het bovestde zulle we os i het volgede voorelijk beperke tot de lieire ruite e zij lieire e ffiee deelruite Lieire e ffiee fbeeldige i het volgede zij - -fbeeldige De lieire bewerkige i zij de stdrd lieire bewerkige e ls vste bsis ee we steeds de stdrdbsis E ( E,, E ) is ee -diesiole euclidische ruite et het stdrdiproduct gedefiieerd door X, Y x y x y Nor, fstd e hoek zij gedefiieerd et behulp v dit stdrdiproduct De deterit op is de tisyetrische -lieire fuctie : zo dt ( E,, E ) Ipv ( X,, X ) schrijve we det E ( X,, X ) of det ( X,, X ), r eestl det( X,, X ) zoder eer Is A ( A,, A ) ee rij pute i e E ( E,, E ) de stdrdbsis v, d otere we de lieire - -fbeeldig L zo dt L( E ) A,, L( E ) A ls L [ A,, A ] e ook uitvoeriger ls L De getlle i de eerste kolo zij de coördite v A, oder elkr geschreve, i de tweede kolo st de coördite v A 2, oder elkr geschreve, etc Door de lieire fbeeldig L wordt ook ee fuctie ( r, k) et r {,, } e k {,, } gedefiieerd, die we de trix v L oee, ottie t( L ) We kue deze trix schrijve ls t( L) ( r k r {,, }, k {,, }) e oee t( L) ee -trix et horizotle rije e verticle koloe Het getl r k stt i rij r e kolo k Idie odig schrijve we r k r, k [ee ko is bijv odig i 5, 2 ] Odt we hier steeds werke et coördite tov de stdrdbses v r k ook ls resp is er ee --correspodetie tusse lieire - -fbeeldige e -trices Zoude we ook werke et iet-stdrdbses B ( B,, B ) e C ( C,, C ) i resp, d oete we oderscheide tusse de stdrdtrix t( L) v L e de trix t( L, B, C) v L tov de bses B e C Zo igewikkeld hoeve we hier iet te doe We g zelfs zover dt we dezelfde ottie gebruike voor ee lieire - -fbeeldig L e zij stdrdtrix t( L )
4 2 Lieire fbeeldige 29 We spreke f dt et L zowel de lieire fbeeldig L ls trix t( L) bedoeld k zij e we otere i het volgede beide ls L [ A,, A ] of uitvoeriger ls L Zij L [ A,, A ] e M [ B,, B ] lieire - - fbeeldige e c, d zij L M e cl, op de gebruikelijke wijze gedefiieerd, ook lieir e L M [ A B,, A B ], cl ca ca [,, ] De sestellig M L v ee lieire - -fbeeldig M e ee lieire p - -fbeeldig L is ee lieire - -fbeeldig e M L M L E M L E [ ( ( ),, ( ( ))] Mtrix M heeft p koloe e trix L heeft p rije De trix v M L wordt het product v de trices M e L [i deze volgorde] geoed Deze producttrix wordt geoteerd ls M L of korter ls ML Opgve Lt M L de sestellig v de lieire - -fbeeldig M e de p lieire - -fbeeldig L zij Stel verder dt ( b r {,, }, i {,, p}) e ( i {,, p}, k {,, }) r i de bij M resp L behorede trices zij oo dt d ML ( cr k r {,, }, k {,, }) et c b b i k p p r k r k r p p k de trix v M L is [ c r k is het iproduct v rij r v M e kolo k v L] Ee lieire - -fuctie heeft de vor ( x,, x ) x x Hier geldt ( E ),, ( E ) e [,, ] et,, De bijbehorede trix is ee -trix et rij e koloe Eigelijk oete we schrijve [,, ], r de rij-idex is overbodig, ls er r éé rij is Voorbeeld Het is duidelijk dt de coörditfucties lieir zij Er geldt ( x,, x ) x x x, dus 0 ls i k e ls i k k k Dus [,0,,0,0],, [0,0,,0,] i i
5 30 Lieire Algebr Opgve Stel L G dt d, ( L( E )) voor r,, e k,, r k r k 2 Ee - -fbeeldig F is lieir (ffie) de copoete f,, f v F zij lieire (ffiee) - -fucties oo dit Ee lieire - -fbeeldig heeft de vor F( x) xa et zekere F schrij- geldt F [ A] et -trix F Eigelijk oete we ve, r de koloidex is overbodig, ls er r kolo is A Er Voorbeeld De -fbeeldig L( x, y, z) ( x b y c z, 2x b2 y c2 z) is lieir e L( E ) A(, 2), L( E2) B( b, b2 ), L( E3 ) C( c, c2 ) Dus bij L hoort b c de 2 3 -trix L [ A, B, C] 2 b2 c 2 Stel L is de lieire - -fbeeldig L [ A,, A ] Stel verder Y L( X ) A (,, ), voor k,, Bij grotere e kue we k k k e ( y,, y ) ( x x,, x x ) eestl overzichtelijker oder elkr schrijve ls: y f( x,, x ) x x y f ( x,, x ) x x De trixottie is heel geschikt voor prktisch rekewerk Hierbij wordt ee put x X geoteerd ls de -trix [ X ] D L[ X ] x A x A x
6 2 Lieire fbeeldige 3 Voorbeeld: L( x, y, z) ( x 2y 4 z,3 x y) wordt i deze ottie x 2 4 L( X ) L[ X ] y 3 0 z 3 2 Hier is L ee lieire - -fbeeldig 2 4 x y z 3 0 x 2y 4z 3x y Voorbeeld De trix L [,, ] stelt de lieire - -fuctie voor zo dt L( X ) x x voor X Dus: x L( X ) L[ X ] [,, ] y [ x x ] z De -trix [ x x ] idetificere we et het getl x x, x zols we hierbove de -trix [ X ] idetificere et het put X x 22 Bij de lieire - -fbeeldig L [ A,, A ] hoort de -trix L Deze trix heeft rije e koloe I kolo k st de coördite v L( E ) A (,, ), verticl oder elkr geschreve Rij r bevt de k k k k coëfficiëte v de r-de copoet r ( x,, x ) rx r x v L Het getl stt i rij r e i kolo k Als, d oee we de trix r k vierkt Als Y L( X ), d x y x x y x x x x x x A x A
7 32 Lieire Algebr Nulfbeeldig De lieire - -fbeeldig X O is de ulfbeeldig Deze ulfbeeldig beeldt iedere X f op O Deze fbeeldig duide we et O,, de bijbehorede -trix bevt louter ulle Als duidelijk is o welke fbeeldig het gt schrijve we eestl kortweg O ipv O, 22 Rije- e koloerg Voor de lieire - -fuctie [,, ] geldt ( x,, x ) x x Dit ltste kue we ook schrijve ls ( X ) A, X et A (,, ) Op deze ier k ee lieire - - fuctie ltijd et behulp v ee eleet A geschreve worde i de vor X A, X Dit geldt ihb voor de coörditfucties X E, X is de coörditfuctie k De lieire - -fbeeldig L et trix L kue we schrijve ls ( x,, x ) x A x A, wri A,, A de pute i zij die correspodere et de koloe v de trix L [We duide de lieire fbeeldig e zij trix volges fsprk beide et L] Het getl stt i rij r e kolo k Ak ( k,, k ), voor k,, Met behulp v het iproduct kue we L ook schrijve ls X ( A, X,, A, X ), r i dt gevl oete we voor A,, A de pute i ee die correspodere et de rije v trix L, dus A r ( r,, r ) voor r,, k rk 22 Ee lieire - -fbeeldig L kue we i de vor X ( A, X,, A, X ) schrijve et,, A A De trix v L bevt d de rije A,, A et A ls de boveste rij e A ls de oderste rij De beeldruite v ee lieire - -fbeeldig L [ A,, A ] sp{ A,, A } De beeldruite L( ) v L wordt ook geoteerd ls I( L) ['I' stt voor 'ige'] De diesie v I( L) hebbe we de rg v fbeeldig L geoed,, A A zij de koloe v trix L De rg v L wordt dro ook de koloerg v trix L geoed is
8 2 Lieire fbeeldige 33 Zij A,, A de rije v trix L, d behore A,, A tot e we oee de diesie v sp{ A,, A } de rijerg v trix L We lte zie dt de rijerg v L gelijk is de koloerg v L 222 Koloerg = rijerg Stel L [ A,, A ] is de lieire - -fbeeldig et trix L D is de rijerg v L gelijk de koloerg v L Voort kue we dus spreke over de rg v L [ A,, A ] zoder eer De rg v L is d de rg v zowel de fbeeldig L ls v de trix L We otere deze rg ls rg( L) of ls rg( A,, A ) Bewijs Stel L [ A,, A ] D is L de fbeeldig ( x,, x ) x A x A, wri A,, A de pute i zij die correspodere et de koloe v de trix L We kue L ook schrijve ls wri X ( A, X,, A, X ), A,, A de pute i De ker v L bestt uit de pute X Ker( L) A, X A, X O De ker v L is ee lieire deelruite W v zij die correspodere et de rije v L X zo dt L( X ) O, dus Stel V sp{ A,, A } e W ker( L) D zij V e W elkrs orthocopleet, V W e di( V ) di( W ) di(sp{ A,, A ) di(ker( L)) Ook geldt di(sp{ A,, A }) di(ker( L)) volges 45 [de diesiestellig voor lieire fbeeldige] Hieruit volgt rijerg = koloerg ofwel di(sp{,, ) A A k di(sp{,, }) k A A Is L ee lieire - -fbeeldig, d rg( L) i(, ) L heeft xile rg, weer rg( L) i(, )
9 34 Lieire Algebr 23 rspoere De trix v de lieire - -fbeeldig L [ A,, A ] heeft,, A A ls koloe Bij L kue we ltijd de lieire - -fbeeldig L defiiëre dv L ( X ) ( A, X,, A, X ) voor X Met Ak ( k,, k ) voor k,, geldt d voor Y L ( X ) : y A, X x x y A, X x x De trices v L e L zij L resp L De -trix v L otstt uit de trix v L door trspoere, dwz door verwissele v rije e koloe We kue het trspoere v ee trix ook zie ls spiegele tov de hoofddigol v de trix Deze hoofddigol bevt de eleete, 22, 33, De trix v L heeft, v bove r beede, A,, A ls rije De trix v L wordt geduid ls trsp( L) of korter ls gebruike trsp( L) e L dt ( L ) L Als, d zij L e L Mtrix L heet de getrspoeerde v trix L We ook ls ottie voor de fbeeldig L Het is duidelijk L llebei lieire - -fbeeldige, r ih L L Er geldt L L, ls de trix v L syetrisch is tov zij hoofddigol Als L L, d oee we ook de lieire - -fbeeldig L syetrisch 23 Defiitie getrspoeerde Is L de lieire - -fbeeldig L [ A,, A ], d is L de lieire - -fbeeldig die voor L ( X ) ( A, X,, A, X ) X gedefiieerd wordt door 232 Is L ee lieire - -fbeeldig, d L( X ), Y X, L ( Y ) voor iedere X, Y Bewijs Stel L is de lieire - -fbeeldig L [ A,, A ] D is de lieire - -fbeeldig zo dt Y zij L ( Y ) ( A, Y,, A, Y) voor L Y Met vste X L( X ), Y e X X, L ( Y ) lieire - -fucties
10 2 Lieire fbeeldige 35 O te bewijze dt het o dezelfde fuctie gt, is het voldoede dt beide fucties overeestee voor,, E E We oete dus g dt voor i,, geldt L( E ), Y A, Y e ook E, L ( Y ) A, Y Gebruik hierbij E, P p i i p i 233 Is L ee lieire - -fbeeldig e M ee lieire - -fbeeldig, d ( M L) L M Bewijs Stel L e M voldoe de voorwrde Volges de vorige stellig geldt d e ook e dus ( M L)( X ), Y X,( M L) ( Y ) ( M L)( X ), Y ( M ( L( X )), Y ( L( X ), M ( Y ) X, L ( M ( Y )) X,( L M )( Y ) X,( M L) ( Y ) X,( L M )( Y ) voor iedere X, Y Dit geldt ihb et X E,, E, wruit volgt dt ( M L) ( Y ) ( L M )( Y ) voor ieder Y Mw i p ( M L) L M Opgve Stel L is ee lieire - -fbeeldig e M is ee lieire - - fbeeldig zo dt L( X ), Y X, M ( Y ) oo dt Opgve Zij L e M lieire - -fbeeldige, d e ( L M ) L M Opgve X, A 0 voor iedere Gevolg: X, A X, B voor iedere p M L ( L ) X A O oo dit X A B L, i ( cl) i cl 24 Deterit De deterit op is de tisyetrische -lieire fuctie det : zo dt det( E,, E ) Is L de lieire - - det( L( E ),,det( L( E )) fbeeldig [ A,, A ], d det( L) det( A det( E,, E ),, A ) volges defiitie 76 We schrijve deze deterit ook ls [et rechte strepe]
11 36 Lieire Algebr Er geldt dus det( L) det( A,, A ) We oee dit ook de deterit v de bijbehorede -trix Merk op dt llee ee vierkte trix ee deterit k hebbe De deterit v ee -trix oee we ee -deterit NB De wrde v ee deterit is ee getl, ls we het hebbe over de koloe of rije v ee deterit hebbe, d bedoele we koloe of rije v de trix wrv dit getl de deterit is I prgrf 7 hebbe we getood dt, det( A,, A ) sig( k) kp k k, wri P de peruttiegroep v N {,, } is Ee peruttie v N is ee - fbeeldig v N op zichzelf Is p ( p,, p ) ee peruttie v N d kot elk v de getlle,, precies éé keer i de rij p,, p voor We zegge dt p ee verwisselig is, weer p de positie v twee getlle i N N verwisselt, terwijl de dere getlle i op hu plts blijve We hebbe i 7 geoe dt we iedere peruttie p P ee teke sig( p) kue toekee zodt sig( p), ls p door ee eve tl verwisselige tot std gebrcht k worde e sig( p), ls p door ee oeve tl verwisselige tot std gebrcht k worde Otstt p door ee eve tl verwisselige, d k p iet door ee oeve tl verwisselige otst e ogekeerd De peruttiegroep P, et de sestellig v fbeeldige ls groepsbewerkig, bevt et ee per- uttie p ook zij iverse p Als p w w2 w wri de wi verwisselige zij, d p w w w [ee verwisselig is zij eige iverse] 2 Hieruit blijkt dt sig( p ) sig( p) De verzelig S {, } is ee groep et de vereigvuldigig ls groepsbewerkig G dt sig( p q) sig( p) sig( q) voor p, q P Dus fbeeldig sig : P S is ee groepshooorfise Er geldt det( E,, E ) sig( p) p p
12 2 Lieire fbeeldige 37 I sig( k) k kp k wordt gesoeerd over de perutties v de koloidices We g dt ook det( A,, A ) sig( r) r r wr- rp i wordt gesoeerd over de perutties v de rij-idices Het getl rij r e kolo k v de trix Het product, k, k rk kot uit bevt dus uit iedere rij ee fctor e l deze fctore, k, k koe uit verschillede koloe Meer syetrisch geforuleerd kue we zegge dt het product uit elke kolo e uit elke rij precies éé fctor bevt De ltste forulerig is ook v toepssig op duidelijk dt et elk product, k, k ee product r, r, r, r, Dit kt correspodeert et precies dezelfde fctore, r ogelijk i ee dere volgorde Er geldt, k, k r, r, precies d, weer de perutties k e r uit P, ls fbeeldige v N op zichzelf, elkrs iverse zij Is dt het gevl, d sig( r) sig( k) Als k de eleete v P doorloopt, d geldt dit ook voor 24 Forule v Leibiz Met,, A A geldt:,, r k We krijge zo: det( A,, A ) sig( k) kp, k, k,, e ook det( A,, A ) sig( r) r, r, rp Gevolg: 242 De wrde v ee deterit verdert iet, ls we de bijbehorede trix trspoere Als L e L, d det( L ) det( L) Gevolg: ee regel die geldt voor de koloe v ee deterit, geldt ook voor de rije v ee deterit 243 De deterit v ee -trix verdert iet v wrde ls we v ee kolo (rij) ee lieire cobitie v de dere koloe (rije) ftrekke Bewijs Het is voldoede dt we dit voor koloe bewijze
13 38 Lieire Algebr Nee dt X ee lieire cobitie is v pute uit { A,, A } \ { A k} D is A, Ak, X, Ak,, A, et k {2,, }, lieir fhkelijk Dus det( A, Ak, X, Ak,, A ) 0 e det( A, Ak, Ak X, Ak,, A ) det( A, A, A, A,, A ) det( A, A, X, A,, A ) k k k k k det( A, A, A, A,, A ) Ide, weer k of k k k k NB Is L ee lieire - fbeeldig, d is det( L) De trix v L is i dt gevl vierkt llee gedefiieerd ls Met het ddwerkelijk berekee v deterite houde wij os overiges iet bezig, et uitzoderig v hooguit ee pr icidetele 22 e 3 3 deterite De deterit is voor os voorl ee theoretisch istruet Is L ee -trix, d krijge we door p rije e q koloe i L te schrppe ee ( p) ( q) deeltrix M v L We veroderstel- le hierbij dt p, q Is de deeltrix M ee vierkte trix, d oee we det( M ) ee oderdeterit v L De oderdeterit v ee k k deeltrix v L oee we ee k k oderdeterit v L G : 244 De rg v trix L is gelijk k precies d, weer L ee k k deeltrix M heeft zo dt det( M ) 0, terwijl er gee grotere vierkte deeltrices v L zij et deterit 0 Gevolg: 245 De rg v ee trix verdert iet ls we (i) de volgorde v de rije i de trix verdere, of (ii) ee rij et ee getl 0 vereigvuldige, of (iii) v ee rij ee lieire cobitie v de dere rij ftrekke Hetzelfde geldt et koloe ipv rije Defiitie Ee lieire - fbeeldig L oee we regulier, ls rg( L) [dit ipliceert dt ] 246 Is de lieire - fbeeldig L regulier, d is L - e L( ) is ee - diesiole lieire deelruite v Bewijs Stel de lieire - fbeeldig L is regulier e L [ A,, A ] D is de koloerg v L gelijk, dus A,, A is ee bsis v L( ) Dus di( L( )) [ L( V ) is sowieso ee lieire deelruite v ] Uit diesiestellig 45 volgt d dt di(ker( L)) 0, dus Ker( L) { O} e L is -
14 2 Lieire fbeeldige 39 Voorbeeld Ee 3 3 deterit kue we uitdrukke i 2 2 deterite: b c b2 c2 b c b c b3 c3 b3 c3 b2 c b c b c Dit heet 'otwikkele v de deterit r de eerste kolo' Otwikkele r dere koloe is ook ogelijk Otwikkele r de tweede kolo geeft b c 2 c2 c c c3 b3 c3 2 c b c b b b b c Geeft zelf de otwikkelig r de derde kolo We kue ee 3 3 deterit ook 'r ee rij te otwikkele', bijv r de tweede rij: b c b c c b b3 c3 3 c3 3 c b c b c b c Plusse e ie worde bij het otwikkele r ee kolo of rij bepld de hd v het 'schkbordptroo': G dt we ook ee deterit op soortgelijke wijze r ee rij of kolo kue otwikkele Het schkbordptroo v zo' deterit heeft ee + i de likerbovehoek Opgve oo : b c b2 c2 0 b2 c2 e lgeeer b3 c3 0 b c
15 40 Lieire Algebr De hoofddigol v ee trix is de digol v liksbove r rechtsoder et drop de getlle, 22, 33, Ee trix et louter ulle oder de hoofddigol oee we ee bovedriehoekstrix Ee trix et louter ulle bove de hoofddigol oee we ee oderdriehoekstrix Bij ee digoltrix zij lle getlle buite de hoofddigol gelijk 0 Opgve G dt de deterit v ee - driehoekstrix gelijk is het product v de eleete op de hoofddigol Dit geldt ihb voor ee digoltrix oo dt het trixproduct v twee - bovedriehoekstrices weer ee - bovedriehoekstrix is Opgve oo dt det( A, B, C) A, B C voor A, B, C [Voor de defiitie v het uitproduct B C i 3 zie 6] 3 25 De oplossige v ee stelsel lieire vergelijkige We bekijke ee stelsel v lieire vergelijkige i vribele x x b (*) x x b De coëfficiëtetrix L x,, x : v het stelsel beplt ee lieire - -fbeeldig L Met L e B ( b,, b ) kue we (*) d korter otere ls L( X ) B De oplossige v (*) bestt uit de pute X die door L op het put B fgebeeld worde Er zij gee oplossige ls B L( ) Als B wel tot de beeldruite v L behoort, d vore de oplossige ee ffiee deelruite W v Zie 58 W heeft de ker v L ls richtigsruite, dus di( W ) di(ker( L)) Volges diesiestellig 45 geldt di(ker( L)) di(i( L)) di( W ) rg( L) ofwel di( W ) rg( L) Rij r v L correspodeert et de r-de vergelijkig rx r x br v het stelsel (*) Met A r ( r,, r ) kue we deze vergelijkig schrijve ls A, X b r r
16 Is 2 Lieire fbeeldige 4 Ak de k-de kolo v L, d geldt koloerg = rijerg ofwel rg( ) L di(sp{ A,, A }) di(sp{ A,, A }) Hieruit blijkt dt rg( L) i(, ) Als rg( L) i(, ), d heeft L xile rg, Als rg( L), d e oee we (*) ee ofhkelijk stelsel lieire vergelijkige Het stelsel heeft d zeker ee oplossig, wt d is ook de koloerg v L gelijk, dwz de diesie v de beeldruite L( ) is gelijk Dt beteket dt L( ) e B behoort dus tot de beeldruite v L Voorbeeld Als, d rg( L),, zij iet llel gelijk 0 De oplossige v x x b vore d ee ffiee deelruite W v et diesie, w W is ee hypervlk i rg( L), d is W de doorsede v hypervlkke i Voorbeeld Bekijk het stelsel x b y c z d (#) x b y c z d x b y c z d Nee dt ( i, bi, ci ) (0,0,0) voor i,2,3 (#) drie vlkke, 2 resp 3 I 3 Als stelle de vergelijkige i V V V voor Ee oplossig X ( x, y, z) v (#) is ee geeeschppelijk put v deze 3 vlkke Mogelijk is er gee geeeschppelijk put Dit ltste is bijv het gevl ls twee v de 3 vlkke evewijdig zij e iet sevlle Er is ook gee oplossig ls de sijlij v twee v de vlkke evewijdig is et het derde vlk e iet i dit vlk ligt Als de rg v de coëfficietetrix L v het stelsel (#) gelijk is, d zij de vlkke V, V 2 e V 3 evewijdig, ogelijk vlle 2 of 3 v deze vlkke se Als rg( L) 2, d hebbe 2 v de vlkke ee sijlij Deze sijlij is evewijdig et het derde vlk of ligt i het derde vlk Als rg( L) 3, d hebbe 2 v de vlkke ee sijlij e lij sijdt het derde vlk i precies éé put P Dit put P is d het eige geeeschppelijke put v de 3 vlkke Opgve Los de volgede stelsels op: x 2y z 0 x 2y z 0 () x y 3z 5 (b) x y 3z 0 2x 5y 6z 2x y 2z 0 (c) x 2y z 0 x y 3z 5 2x y 2z 5
17 42 Lieire Algebr Segevt: 25 Het stelsel v lieire vergelijkige i vribele x,, x gegeve door: x x b (*) x x b kue we et de - -fbeeldig L e B ( b,, b ) schrijve ls L( X ) B e ook ls x A x A B Als rg( L), d e (*) is ee ofhkelijk stelsel lieire vergelijkige De oplossige v het stelsel vore ee ffiee deelruite W v heeft de ker v L ls richtigsruite e di( W ) di(ker( L)) rg( L) W Is L de coëfficiëtetrix v stelsel (*) e rg( L), d is istes éé v A,, A lieir fhkelijk v de dere pute i de rij [ A r ( r,, r ) voor r,, ] We kue ee dt dit A is [verwissel desoods de volgorde v de vergelijkige i (*), die volgorde doet er iet toe] D zij er getlle c,, c zo dt A c A c A Als d ook b cb cb, d kue we de oderste vergelijkig uit (*) et zo goed weglte, wt die volgt d l uit de boveste vergelijkige We oee i dit gevl (*) ee fhkelijk stelsel lieire vergelijkige We bekijke d het stelsel dt overblijft het weglte v de oderste vergelijkig opieuw Als echter b c b c b, d k het stelsel helel gee oplossig hebbe, het put B bevidt zich d iet i de beeldruite v L We oee (*) d ee strijdig stelsel Er geldt zeker rg( L), weer Als rg( L) e, d is L okeerbr L( X ) B heeft d precies éé oplossig Deze oplossig wordt gegeve door L A A X L ( B) Is L okeerbr, d det( ) det(,, ) 0 e de coördite v X worde gegeve door de regel v Crer We schrijve d (*) ls x A x A B e krijge det( B, A2,, A ) det( x A x A, A2,, A ) x det( A, A2,, A ) det( B, A2,, A ) Dt geeft x det( A, A,, A ) x e op dezelfde ier vide we det( A, B,, A ) det( A, A,, A ),, det( A, A 2,, B) x det( A, A,, A ) 2
18 2 Lieire fbeeldige 43 Hieree is de volgede stellig beweze 252 Regel v Crer Het stelsel v lieire vergelijkige i vribele x,, x gegeve door: x x b (*) x x b ofwel x A x A B heeft precies éé oplossig ( x,, x ) det( A,, A ) 0 Als det( A,, A ) 0, d wordt de oplossig gegeve door det( B, A2,, A ) x det( A, A,, A ), x 2 2 det( A, B,, A ) det( A, A,, A ),, det( A, A 2,, B) x det( A, A,, A ) 2 2 Uit de regel v Crer volgt de volgede forule voor de iverse v ee okeerbre lieire fbeeldig: 253 A,, A e det( A,, A ) 0, d is de lieire fbeeldig L A A [,, ] ee - fbeeldig v op zichzelf e voor L ( X ) (det( X, A2,, A ),,det( A,, A, X )) det( L) X geldt Voorbeeld Stel L Er geldt volgt uit 253 dt 2 L G dt det( L) 6 Dus L heeft ee iverse L( X ) Y X L ( Y ) Met X ( x, x2, x3 ) e Y ( y, y2, y3 ) y det( L) x y 2 y 4y 3y 2 y y 3 Evezo det( L) x y y 2y 3y e y det( L) x 2 y 3y 6y 3y y y 3 x 4 3 y Dus det( L) X 6 x y 2, dus x y L
19 44 Lieire Algebr Als det( L) 0, d heeft L( X ) B isschie gee oplossig Wel heeft de vergelijkig L( X ) O ltijd X O ls oplossig X O is echter iet de eige oplossig, ls det( L) 0 Als det( L) 0, d bevt Ker( L) ee eleet X O Met deze X geldt L( P X ) L( P) L( X ) L( P), dus L is iet - Als rg( L), d e kue we A,, A uitdue tot ee ofhkelijke rij A,, A et det( A,, A ) 0 De bijbehorede trix L is ee -deeltrix v L die otst is uit de trix v L door het schrppe v koloe, det( L) det( A,, A ) is ee oderdeterit v L 26 Guss-eliitie Ee prktische ier o ee cocreet gegeve stelsel lieire vergelijkige x x b (*) x x b op te losse is ee lgorite dt Guss-eliitie heet Door Guss-eliitie wordt het stelsel (*) op ee systetische ier vereevoudigd tot ee gelijkwrdig stelsel dt op ee sipele ier op te losse is De eige problee die zich hierbij kue voordoe, zij problee die otst door frode Met dt soort problee houde we os hier iet bezig, wij g er v uit dt we hier kue rekee et excte getlle Het stelsel (*) wordt gerepreseteerd door de gevulde trix b ( L; B) b Op de rije v ( L; B) psse we de volgede eleetire rijbewerkige toe: (R) verwissele v twee rije, (R2) c l ee rij optelle bij ee dere rij, (R3) ee rij vereigvuldige et ee getl c 0
20 2 Lieire fbeeldige 45 Zoek u i trix L v liks r rechts r de eerste kolo die ee getl 0 bevt Is zo' kolo er iet, d bevt L louter ulle e we stoppe Bevt L getlle 0, d bewerke we de eerste kolo et ee getl 0 die we tegekoe ls volgt: () g i deze kolo v bove r beede e ee het eerste getl 0 dt we tegekoe e (2) zorg er, idie odig, door verwissele v twee rije i trix ( L; B) voor dt dit getl het boveste getl v zij kolo is (3) Met behulp v rijbewerkig (R2) op ( L; B) kue we er u voor zorge dt er i de kolo v L et bedoeld getl oder deze llee og r ulle koe te st [Hoe? Bekijk desoods eerst het voorbeeld hieroder] Behdelig (3) v trix ( L; B) oee we het 'r beede schoovege' v de kolo oder De ieuw otste trix ( L; B) zulle we ook weer duide ls ( L; B ), hoewel de getlle i deze trix iiddels door de toegepste bewerkige verderd zij De ieuwe trix ( L; B) heeft de vor 0 * 0 0 # # ( L; B) 0 0 # # wri het sterretje ee getl 0 duidt De koloe liks v de kolo et het sterretje bevtte louter ulle Het is overiges ogelijk dt ltstgeoede koloe otbreke e dt het sterretje i de likerbovehoek v trix ( L; B) stt De kolo et het sterretje, evetuele koloe liks v deze kolo e ook de boveste rij v ( L; B) beschouwe we u ls fgehdeld Vervolges psse we hetzelfde recept toe op de overblijvede deeltrix v ( L; B) die wordt gegeve et het teke # i zij hoekpute Door deze behdelig gt de deeltrix # # # # over i ee deeltrix v het zelfde type ls de ltste trix ( L; B) hierbove Dr herhle we het recept weer et de volgede deeltrix Etc Net zo lg totdt er gee te behdele deeltrix eer over is, odt we op de oderste rij zij gekoe of odt we de ltste kolo v L l r beede schoogeveegd hebbe Het resultt v deze behdelig is uiteidelijk ee trix ( L; B) et L i zogede trpvor Ee trix i trpvor, ook 'echelovor' geoed, kue we ls volgt beschrijve Bevt ee rij v de trix eleete 0, d heet het eerste eleet 0 i de rij het kopeleet v de rij Ee rij et louter ulle heeft gee kopeleet
21 46 Lieire Algebr Bij ee trix i trpvor zij de rije v bove r beede zodig georded dt de rije et ee kopeleet, idie wezig, bove de rije zoder kopeleet st Voor de rije et kopeleet geldt: het kopeleet v iedere volgede rij stt istes éé kolo eer r rechts d het kopeleet v de vorige rij O ee trix i trpvor te brege hebbe we llee (R) e (R2) odig Door toepsse v (R3) kue we er, idie gewest, voor zorge dt de kopeleete v ee trix ( L; B) i trpvor llel gelijk zij Opgve oo dt we rijbewerkig (R) tot std kue brege door uitsluited (R2) e (R3) toe te psse (R) hebbe we dus iet echt odig Voorbeeld Stel ee stelsel (*) v 3 lieire vergelijkige i de vribele x,, x wordt gerepreseteerd door ( L; B) Verwissele v de rije e 2 geeft: ( L; B) Dr telle we 2 keer de boveste rij bij de oderste op ofwel we trekke 2 keer de boveste rij v de oderste f Dt levert: ( L; B) Dr g we verder et de 2 4 deeltrix rechtsoder We trekke 4 keer de tweede rij v ( L; B ) (ofwel de boveste rij v de deeltrix) f v de oderste rij We krijge zo: ( L; B) Nu zij we klr De trix L liks v de streep is i trpvor Iedere rij heeft ee kopeleet De kopeleete v L zij 2, e -9 De ltste trix ( L; B) stt voor het stelsel 2x 2x2 x2 3x3 2x4 0 9x3 3x4 0
22 2 Lieire fbeeldige 47 Dit stelsel vergelijkige is gelijkwrdig et het oorsprokelijke stelsel (*) e is 3 eevoudig op te losse Begi oder e stel x4 t D x 3 t Substitutie i de tweede vergelijkig geeft vervolges x2 3x3 2x 4 t 2t t e uit de eerste vergelijkig vide we x 2x2 t De oplossige v het stelsel zij de pute ( x, x2, x3, x4) t, t, t, t et t Vervge we t door 9u d zie we dt de oplossige ook beschreve worde door ( x, x, x, x ),0,0,0 u ( 42, 2,3,9) et u De oplossigsruite is ee lij i 4 Algeee geldt: Het door ( L; B ), et L i trpvor, gerepreseteerde stelsel lieire vergelijkige heeft gee oplossig, ls i ee rij r v ( L; B) rechts v de streep ee getl br 0 stt, terwijl de eleete v L i dezelfde rij r llel gelijk 0 zij Het stelsel wordt d strijdig geoed Is zo' rij er iet, d is de oplossigsruite v het stelsel ee ffiee deelruite v et diesie rg( L) Met L i trpvor geldt: rg( L) het tl kopeleete i L G dit Door toepsse v de eleetire rijbewerkige (R), (R2) e (R3) op ( L; B) is de oplossigsruite v het correspoderede stelsel lieire vergelijkige iet verderd Operkig Op dezelfde ier kue we siult bijv L( X ) B, L( X ) C e L( X ) D oplosse door de eleetire rijbewerkige toe te psse op b c d ( L; B, C, D) b c d Met behulp v de eleetire rijbewerkige kue we ook de rg v ee -trix L (e de bijbehorede lieire - -fbeeldig) vststelle De rg v L verdert iet door deze bewerkige, dus de rg v L is gelijk de rg v zij trpvor De rg v ee trix i trpvor is direct f te leze Die is gelijk het tl rije et ee kopeleet Is L ee vierkte -trix, d kue we op deze ier ook de deterit det( L) berekee Door (R2) verdert de wrde v det( L) iet, door (R) verdert llee het teke v de deterit e ls we bij toepsse v (R3) ee rij vereigvuldige et het getl c 0, d wordt drdoor de deterit v de trix ook et c vereigvuldigd Als we bij het ozette v L r ee trpvor bijhoude hoe vk we (R) toegepst hebbe e et welke getlle c we (R3) toegepst hebbe, d kue we uit de deterit v de trpvor eevoudig de deterit v de oorsprokelijke trix terugvide
23 48 Lieire Algebr Ee -trix i trpvor is ee bovedriehoekstrix, dus zij deterit is gelijk het product v de getlle op de hoofddigol Voorbeeld 3 L We berekee det( L) door L i trpvor te brege Eerst krijge we [dv rij 2 2 rij e rij 3 3 rij]: 3 L [De verderde trix oee we og steeds L] Verder et rij 3 4 rij 2 : 3 L Dus det( L) [verwissele v rije ws iet odig] Voorbeeld 3 L e det( L) 6, zols we et zge De bijbehorede lieire fbeeldig L is dus okeerbr Er geldt L( X ) Y X L ( Y ) O de trix v werk Dek L( X ) Y ls het stelsel x x2 3x3 y 0y2 0y3 2x 0x 4x 0y y 0y 3x 5x 7x 0y 0y y Noteer dit i trixvor ls L te berekee g we ls volgt te
24 2 Lieire fbeeldige 49 Breg dit door eleetire rijbewerkige i de vor: b b b 2 3 b b b b b b Dit ltste stt d voor X L ( Y ), dus b b b L b b b b b b Met dezelfde stppe ls i het vorige voorbeeld krijge we eerst: e dr De oderste rij dele door 8 geeft: el 2 keer de oderste rij op bij de tweede rij e tel 3 keer de oderste rij op bij de boveste rij Drdoor wordt de derde kolo r bove toe schoogeveegd We krijge zo: Deel u de iddelste rij door e tel het resultt op bij de boveste rij We eidige d et: Dus L Opgve Bereke L ook op de ier v het 253 gegeve voorbeeld
25 50 Lieire Algebr 27 Eleetire lieire trsforties Correspodered et de eleetire bewerkige op de rije v ee trix kue we ook eleetire kolobewerkige op ee trix toepsse (K) verwissele v twee koloe, (K2) c l ee kolo optelle bij ee dere kolo, (K3) ee kolo vereigvuldige et ee getl c 0 Net ls (R) is ook (K) overbodig, wt het verwissele v 2 koloe kue we tot std brege dv (K2) e (K3) [hoe?] Verder kue we (K2) vervge door: (K2*) ee kolo optelle bij ee dere kolo De cobitie v (K2*) et (K3) geeft eevoudig (K2) terug De eleetire kolobewerkige v ee -trix L [ A,, A ] kue we krijge door de eleetire rijbewerkige op de getrspoeerde trix toe te psse Mr het k ook ls volgt Stel S [ E,, cei,, E ] et c 0 e cei i kolo i v trix S D L S [ L( E ),, cl( Ei ),, L( E )] [ A,, cai,, A ] Het trixproduct L S heeft dus het effect v ee kolobewerkige v het type (K3) Evezo krijge we et [ E,, Ei E j,, E ], wri j i e E i E j kolo i v trix is, het effect L L E L E L E L E [ ( ),, ( i ) ( j ),, ( )] dt we ook et (K2*) krijge [ A,, A A,, A ], 27 Defiitie Oder ee eleetire lieire trsfortie v i j L verst we ee lieire - -fbeeldig v het type () S [ E,, cei,, E ] et c 0 e cei i kolo i v trix S, of v het type (2) [ E,, Ei E j,, E ], wri j i e Ei E j kolo i v trix is 272 Met S e uit 27 e de -trix L [ A,, A ] L S [ A,, cai,, A ] e L [ A,, Ai Aj,, A ] geldt: p q r Opgve Bereke de trixproducte L S, L e L 2 et L p2 q2 r 2, p3 q3 r S 0 0, 0 0 e Bereke ook S, e
26 2 Lieire fbeeldige 5 Uit het bovestde blijkt dt we de eleetire kolobewerkige op ee - trix L ook kue uitvoere dv trixproducte L S e L et S e v type () resp type (2) uit stellig 27 I de vorige prgrf zge we dt we de trix v ee lieire trsfortie L v kue ovore tot de eeheidstrix I door eleetire rijbewerkige Dit k tuurlijk ook et behulp v eleetire kolobewerkige, wt eleetire rijbewerkige hebbe op L hetzelfde effect ls eleetire kolobewerkige op L Hieruit volgt dt er bij L eleetire lieire trsforties p M,, M p best zo dt L M M p I e dus L M M De iverse v ee eleetire lieire trsfortie S [ E,, cei,, E ] v type () is S [ E,, Ei,, E ] e dus ee eleetire lieire trsfortie c v hetzelfde type De iverse v ee eleetire lieire trsfortie [ E,, E E,, E ] v type (2) is [ E,, E E,, E ] We kue i j i j schrijve ls de sestellig S et S [ E,, ce j,, E ] e c Hieree is getood: 273 Ee lieire trsfortie v k tot std gebrcht worde door ee eidig tl eleetire lieire trsforties elkr uit te voere Operkig Als L M M p d det( L) det( M) det( M p ) Zij M,, M p eleetire lieire trsforties, d zij hu trices driehoekstrices De deterit v ee driehoekstrix is gelijk het product v de getlle op de hoofddigol Voor S e uit 27 geldt det( S) c e det( ) Copyright Rise Poortig
1 Bewerkingen met matrices invoeren via voorbeelden. , is een commutatieve groep.
 1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
1 Bewerkige met mtrices ivoere vi voorbeelde 11 -tlle e de bewerkige ( 1, 2, 3,, ) is ee -tl met i De verzmelig v reële -tlle otere we met Defiieer de som ls ( 1, 2, 3,, ) + (b 1,b 2,b 3,,b ) = ( 1 +b
Deel D. Breuken en algebra n
 Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Deel D Breue e lgebr 9 9 7 7 7 9 0 Reee et stroe (). stt voor ee obeed tuurlij getl 7 9 0 Met wordt bedoeld e dus oo 0 0 Vul i: et wordt bedoeld... e dus oo... Vul oo de vjes v de stroo i: Tel de getlle
Bass eenheden in ZG.
 Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
Bass eehede i ZG. 2 Hoofdstuk 1 Bass eehede 1.1 Cyclotoische eehede i Z(ɛ ) Als G ee abelse groep is, da zij de bicyclische eehede i ZG alleaal triviaal. We oete i die situatie dus op zoek gaa aar adere
16.6 Opgaven hoofdstuk 7: Producten en combinatoriek
 166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
166 Opgve hoofdstu 7: Producte e combitorie 166 Opgve hoofdstu 7: Producte e combitorie Opgve 71 1 + x) 3 1 + x) 1 + x) 2 1 + x) 1 + 2x + x 2 ) 1 + 2x + x 2 + x + 2x 2 + x 3 1 + 3x + 3x 2 + x 3 Opgve 72
0 niet gedefinieerd is).
 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre,...... 1 fctore (erk o dt iet gedefiieerd is). 1, Je ket ook l ee hele tijd de ekede rekeregels,,.,,,,,,.,, ) Vierktswortels e -de chtswortels
0 niet gedefinieerd is).
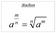 Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Mchte 1) Mchte et gehele exoete Volgede defiities kee we l ekele jre fctore R, N R (erk o dt iet gedefiieerd is) 1 1 R, N Je ket ook l ee hele tijd de ekede rekeregels R,, Z R,, Z R Z,,,, R Z, R, Z R )
Integreren over een compact interval in. n
 Rise Poortig Lieire Alger e Voortgezette Alyse 6 Afgeleide e itegrl houd: 61 Prtiële fgeleide 6 Differetieerre fucties 63 Prtiële fgeleide v hogere orde 64 Cotiu differetieerre fucties 65 Differetieerre
Rise Poortig Lieire Alger e Voortgezette Alyse 6 Afgeleide e itegrl houd: 61 Prtiële fgeleide 6 Differetieerre fucties 63 Prtiële fgeleide v hogere orde 64 Cotiu differetieerre fucties 65 Differetieerre
4 Differentierekening en reeksen
 WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
WIS4 4 Differetierekeig e reekse 4. Delt Differeties Differetierekeig bestudeert de differetie-opertor, gedefiieerd door f(x) = f(x + ) f(x) Vergelijk dit met differetilrekeig: de fgeleide-opertor D is
Matrixrekening - Samenvatting
 I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
I. Ekele defiities Ee mtri is ee tel v getlle trirekeig - Smevttig = i m j i m ottie = ( De i-de r v estt uit: i i De j-de kolom v estt uit: j Het (i,j-de elemet v is het elemet o de i-de r e de j-de kolom:.
Verloop van exponentiele en logaritmische functies
 Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Verloop v epoetiele e loritmische fucties ) Herhli ) Defiitie e rfiek v epoetiële fucties Ee epoetiële fuctie is ee fuctie met voorschrift vk eoteerd ls ep Hierst st ekele rfieke v epoetiële fucties eteked
Acdemi Press Dele Bij delig vermeigvuldigt me met het omgekeerde v de deler..3.5 Vereevoudige Het is goed mogelijk dt voorgde bewerkige iet de
 Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
Acdemi Press 0 BIJLAGE Wiskudige opfrissig. Bewerkige bij vergelijkige Verdere v lid is omkere v de bewerkig, dus verderig v teke bij som of verschil y x+ b y b x vermeigvuldigig wordt delig e omgekeerd
AFSTANDEN EN HOEKEN IN
 AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
AFSTANDEN EN HOEKEN IN Kls 6N e 7N K. Temme INHOUD. DE AFSTAND AN TWEE PUNTEN.... DE AFSTAND AN EEN PUNT EN EEN LIJN.... DE AFSTAND AN EEN PUNT EN EEN LAK... 7. DE AFSTAND AN EEN LIJN EN EEN LAK... 9.
Algebra. Dr. Caroline Danneels
 Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
Algebr Dr. Crolie Deels 1 Reële getlle 1.1 Mchte v ee reëel getl met gehele expoet IR e IN :... ( fctore) IR : 1 0 0 0 1 ( ) ( ) 1 1 IR 0 e IN : Eigeschppe:, b IR e m, Z m m + m m ( ) b b b m ( ) b m (
1) Definitie, rekenkundige en meetkundige rijen
 Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
Rije ) Defiitie, reeudige e meetudige rije ) Defiitie e ottie Ee rij is ee fbeeldig v u : u, u, u,, u, N i R We otere ee rij ls ( ) 3 Hierbij zij u, u, u 3, de terme v die rij, e u is de lgemee term v
1. Symmetrische Functies
 Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Algebra III 1 1. Symmetrische Fucties permutatios sot la metaphysique des équatios Lagrage*, 1771 I dit hoofdstuk bestudere we de ivariate va de werkig va de symmetrische groep S op polyoomrige i variabele.
Praktische opdracht: Complexe getallen en de Julia-verzameling
 Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Praktische opdracht: Complexe getalle e de Julia-verzamelig Auteur: Wiebe K. Goodijk, Zerike College Hare Beodigde Voorkeis: 1 = i Het complexe vlak. Notatie: z = a + bi of z = r(cosϕ + i si ϕ) Regel va
Fourierreeksen. Calculus II voor S, F, MNW. 14 november 2005
 Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
Fourierreekse Calculus II voor S, F, MNW. 14 ovember 2005 Deze tekst is gedeeltelijk gebaseerd op het Aalyse BWI I dictaat e op aatekeige va Alistair Vardy. 1 Ileidig Het is vaak belagrijk ee gegeve fuctie
In dit hoofdstuk willen aan elke vierkante matrix een getal associëren dat (onder andere) aangeeft of die matrix singulier is of niet. d b. c a.
 Deterinnten Deterinnt In dit hoofdstuk willen n elke vierknte trix een getl ssociëren dt (onder ndere) ngeeft of die trix singulier is of niet ) Deterinnt vn een x-trix Zij gegeven twee trices M c d en
Deterinnten Deterinnt In dit hoofdstuk willen n elke vierknte trix een getl ssociëren dt (onder ndere) ngeeft of die trix singulier is of niet ) Deterinnt vn een x-trix Zij gegeven twee trices M c d en
Voorwoord. De hoofdstukken 5 t/m 10 gaan over limieten, continuïteit en differentieerbaarheid
 Voorwoord De aalyse va fucties va éé reële variabele wordt i dit boek voortgezet aar de aalyse va fucties va eerdere reële variabele e aar de aalyse va fucties va éé coplexe variabele. De eerste vier hoofdstukke
Voorwoord De aalyse va fucties va éé reële variabele wordt i dit boek voortgezet aar de aalyse va fucties va eerdere reële variabele e aar de aalyse va fucties va éé coplexe variabele. De eerste vier hoofdstukke
Het differentiequotiënt van een functie in een interval geeft de gemiddelde helling weer van die functie in dat interval. Symbolisch wordt dit:
 Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
Afgeleide ) Het begrip fgeleide ) Ileidig Bij de wielerwedstrijd De Wlse Pijl kome de reers op de muur v Hoei Zols je k ie op de figuur hierst heeft dee klim ee gemiddeld stijgigspercetge v 9,8% Wiskudig
OVERZICHT VAN DE FORMULES
 80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
80 OVERZIHT VN DE FORMULES Goioetrie Fucties op de goioetrische cirkel si² cos² si tg si cos tg cotg Relties Wrdes v veel voorkoede hoeke 0 0 45 60 90 si 0 cos 0 tg 0 - Goioetrische fucties i rechthoekige
Duurzaam (ver)bouwen. Noordoost-Brabant 2013-2016
 t e v o C l io g Re Duurzm (ver)bouwe Noordoost-Brbt 2013-2016 e w u o b e m S d i e h m duurz Duurzm Bouwe Grodstoffe worde schrser, het eergievrgstuk ijpeder e os klimt verdert. Duurzm bouwe e verbouwe
t e v o C l io g Re Duurzm (ver)bouwe Noordoost-Brbt 2013-2016 e w u o b e m S d i e h m duurz Duurzm Bouwe Grodstoffe worde schrser, het eergievrgstuk ijpeder e os klimt verdert. Duurzm bouwe e verbouwe
Uitwerkingen huiswerk week 7
 Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Lieaire algebra ajaar 008 Uitwerkige huiswerk week 7 Opgave 5 Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A 1 a 3 a 3 a 1 a a a 1 a1 1 a 1 3 a3 1 a 1 heet ee Vadermode matrix Laat zie dat det A 1 i
Uitwerkingen toets 11 juni 2011
 Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Uitwerkige toets 11 jui 2011 Opgave 1. Laat 2 e k 1 gehele getalle zij. I ee lad zij stede e tusse elk paar stede is ee busverbidig i twee richtige. Laat A e B twee verschillede stede zij. Bewijs dat het
Polynomen groep 2. Trainingsweek, juni Complexe nulpunten. Een polynoom is van de vorm P (x) = n
 Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
Polyome groep 2 Traiigsweek, jui 2009 Complexe ulpute Ee polyoom is va de vorm P (x) = i=0 a ix i, met coëfficiëte a 0, a 1,..., a, die uit ee gegeve verzamelig kome (meestal Z of R). Als alle coëfficiëte
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN
 KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
Uitwerkingen huiswerk week 7
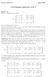 Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Lieaire algebra ajaar 009 Uitwerkige huiswerk week 7 Opgave 19. Ee -matrix va de vorm 1 a 1 a 1 a 1 a a a A = 1 a 3 a 3 a.... 1 a a a 1 a1 1 a 1 3 a3 1. a 1 heet ee Vadermode matrix. Laat zie dat det A
Opgaven OPGAVE 1 1... OPGAVE 2. = x ( 5 stappen ). a. Itereer met F( x ) = en als startwaarden 1 en 100. 100...
 Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
Opgave OPGAVE 1 a. Itereer met F( ) = e als startwaarde 1 e 1. 16 1............... 16 1............... b. Stel de bae grafisch voor i ee tijdgrafiek. c. Formuleer het gedrag va deze bae. (belagrijk is
PARADOXEN 9 Dr. Luc Gheysens
 PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
PARADOXEN 9 Dr Luc Gheyses LIMIETEN, AFGELEIDEN EN INTEGRALEN: ENKELE MERKWAARDIGE VERHALEN Ileidig: verhale over ifiitesimale Ee ifiitesimaal (of ifiitesimaal kleie waarde) is ee object dat mi of meer
Machtsfuncties en wortelfuncties. Introductie 177. Leerkern 178
 Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
Ope Ihoud Uiversiteit leereeheid 6 Wiskude voor ilieuweteschappe Machtsfucties e wortelfucties Itroductie 77 Leerker 7 Machtsfucties et ee atuurlijk getal als epoet 7 Machtsfucties et ee egatief geheel
Rijen. 6N5p
 Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Rije 6N5p 0-03 Rije Ileidig I de wiskude werke we vaak met formules e/of fucties die elke mogelijke waarde aa kue eme. Als bijvoorbeeld f( x) = 5x + 5x 3, da ku je voor x (bija) elke waarde ivulle e ka
Bereik en waardering RTV Dordrecht - Herhalingsmeting
 Bereik e wrderig RTV ordrecht - Herhligsmetig Socil Geogrfisch Bureu bureu voor beleidsoderzoek e sttistiek ordrecht drs. F.W. Witerwerp drs. J.M. Schiff september 2006 Colofo Opdrchtgever Tekst rukwerk
Bereik e wrderig RTV ordrecht - Herhligsmetig Socil Geogrfisch Bureu bureu voor beleidsoderzoek e sttistiek ordrecht drs. F.W. Witerwerp drs. J.M. Schiff september 2006 Colofo Opdrchtgever Tekst rukwerk
n n n bedoelen we uiteraard dat n N : 0 f x divergeert naar + of.
 Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Limiete Defiities a Limiet voor a I het hoofdstuk ratioale fucties i het begi va dit schooljaar zage we reeds dat zulke fucties soms perforatiepute hebbe De fuctiewaarde i zo put bestaat iet, maar de grafiek
Correctievoorschrift VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
TECHNISCHE HOGESCHOOL EINDHOVEN Afdeling Algemene Wetenschappen. Onderafdeling der Wiskunde WISKUNDE 10. bestemd voor. BDK-1, WSK-1, N-1, E-1 en T-1
 TECHNISCHE HOGESCHOOL EINDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WISKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1978 ... -, Techische Hogeschool Eidhove Oderfdelig
TECHNISCHE HOGESCHOOL EINDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WISKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1978 ... -, Techische Hogeschool Eidhove Oderfdelig
is het koppel dat overeenkomt met het eindpunt van λ.op ax by = a a b x y = a b = x y a b ax by bx + ay = a b
 1 Tweedimensionle Euclidische ruimte 11 Optelling, verschil en sclire vermenigvuldiging = ( b, ) b, is de verzmeling vn lle koppels reële getllen { } Zols we ons de reële getllen kunnen voorstellen ls
1 Tweedimensionle Euclidische ruimte 11 Optelling, verschil en sclire vermenigvuldiging = ( b, ) b, is de verzmeling vn lle koppels reële getllen { } Zols we ons de reële getllen kunnen voorstellen ls
1. Hebben de volgende rijen een limiet, en zo ja, bepaal die dan: (i) u n = sin(πn) (d) u n = cos(2πn) (l) u n = log n
 Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Hoofdstuk 1 Limiet va ee rij 1.1 Basis 1. Hebbe de volgede rije ee iet, e zo ja, bepaal die da: (a) 1,, 3, 4, 5, 6, 7, 8,... (b) 1, 4, 9, 16, 5, 36, 49,... (c) 1, 8, 7, 64, 15,... (d) u = ( 1) (e) u =
Eindexamen wiskunde B vwo 2010 - II
 Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Eideame wiskude B vwo 200 - II Sijde met ee hoogtelij Op ee cirkel kieze we drie vaste pute, B e C, waarbij lijstuk B gee middellij is e put C op de kortste cirkelboog B ligt. Ee put doorloopt dat deel
Bepaling toezichtvorm gemeente Stein
 Bepaling toezichtvorm 2008-2011 gemeente Stein F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, juni 2 0 0 8 V e r d i e p i n g s o n d e r z o e k S t e i
Bepaling toezichtvorm 2008-2011 gemeente Stein F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, juni 2 0 0 8 V e r d i e p i n g s o n d e r z o e k S t e i
Oplossingen extra oefeningen: rijen (leerstof RR, leerstof MR)
 Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Oplossige extra oefeige: rije (leerstof RR, leerstof MR) Beschouw de rij ( u ) = 3,5,9,7,33, () Geef de volgede twee terme uit deze rij ( u e u 7) Defiieer deze rij (je mag kieze tusse ee expliciete of
Voorbereidende opgaven Examencursus
 Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Analyse 2 - SAMENVATTING
 Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
Aalyse 2 - SAMENVATTING willem va ravestei ihoudsopgave 01. Rije, eigeschappe e stellige 02. Deelrije, Cauchy, meetkudige e telescopische rij 03. Coverget of diverget? 04. Altererede rije e het wortelcriterium
L i mb u r g s e L a n d m a r k s
 L i mb u r g s e L a n d m a r k s P r o g r a m m a I n v e s t e r e n i n S t ed e n e n D o r p e n, l i j n 2 ; D e L i m b u r g s e I d e n t i t e i t v e r s i e 1. 0 D o c u m e n t h i s t o
L i mb u r g s e L a n d m a r k s P r o g r a m m a I n v e s t e r e n i n S t ed e n e n D o r p e n, l i j n 2 ; D e L i m b u r g s e I d e n t i t e i t v e r s i e 1. 0 D o c u m e n t h i s t o
Lagrange-polynomen. Dick Klingens september 2004
 Lgrge-polyome Dck Klges september 004 1. Probleem V ee fucte f s, hetzj door metg, hetzj door berekeg, slechts ee edg tl fuctewrde (her + 1 beked: f( x0, f( x1,, f( x We wlle deze (verder obekede fucte
Lgrge-polyome Dck Klges september 004 1. Probleem V ee fucte f s, hetzj door metg, hetzj door berekeg, slechts ee edg tl fuctewrde (her + 1 beked: f( x0, f( x1,, f( x We wlle deze (verder obekede fucte
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
 Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Getallenverzamelingen
 Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n
 Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n M w. d r s. E. L. J. E n g e l s ( P r o v i n c i e L i m b u r g ) M w. d r s.
Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n M w. d r s. E. L. J. E n g e l s ( P r o v i n c i e L i m b u r g ) M w. d r s.
Rekenregels van machten
 4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
4 Rekenregels vn mchten Dit kun je l 1 mchten met een ntuurlijke exponent berekenen mchten met een gehele exponent berekenen 3 terminologie in verbnd met de mchtsverheffing correct gebruiken Test jezelf
Appendix A: De rij van Fibonacci
 ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
ppedix : De rij va Fiboacci Het expliciete voorschrift va de rij va Fiboacci We otere het het e Fiboaccigetal met F De rij va Fiboacci wordt gegeve door: F F F F 4 F F 6 F 7 F De volgede afleidig is gebaseerd
2. Gegeven is de driehoek van figuur 10.10a. Gevraagd worden hoek β en de zijden a en c.
 Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Formulekaart VWO wiskunde B
 Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
Formulekrt VWO wiskude B Verelijkie + + c = 0 + D = of met D = 4c D = 0, D > 0 = c = = c / = c > 0, c > 0, > 0 lo l = lo = = > 0, > 0, lo l lo = = > 0, > 0, e = = l > 0 l = = e > 0 Mchte e loritme = /
H O E D U U R I S L I M B U R G?
 H O E D U U R I S L I M B U R G? N AD E R E I N F O R M A T I E S T A T E N C O M M I S S I E S OV E R O N D E R AN D E R E A F V A L S T O F F E N H E F F I N G E N I N L I M B U R G 1 6 a u g u s t u
H O E D U U R I S L I M B U R G? N AD E R E I N F O R M A T I E S T A T E N C O M M I S S I E S OV E R O N D E R AN D E R E A F V A L S T O F F E N H E F F I N G E N I N L I M B U R G 1 6 a u g u s t u
Programma. Introductie. Zaakgericht werken en de Sensus-methode. Zaakgericht werken. Welkom
 Progrmm Zkgericht werke e de Sesus-methode Mrcee v der Leeuw & Moique v Dodewrd Wekom 9.30 uur Itroductie Sesus-methode 9.30-10.15 Zkgericht werke 10.15-10.45 Oefeig 10.45-11.45 Diestvereig 11.45-12.00
Progrmm Zkgericht werke e de Sesus-methode Mrcee v der Leeuw & Moique v Dodewrd Wekom 9.30 uur Itroductie Sesus-methode 9.30-10.15 Zkgericht werke 10.15-10.45 Oefeig 10.45-11.45 Diestvereig 11.45-12.00
Periodiciteit bij breuken
 Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Periodiciteit bij breuke Keuzeodracht voor wiskude Ee verdieede odracht over eriodieke decimale getalle, riemgetalle Voorkeis: omrekee va ee breuk i ee decimale vorm Ileidig I deze odracht leer je dat
Wiskunde D Online uitwerking 4 VWO blok 7 les 3
 Paragraaf Vergelijkige va vlakke Opgave a Dat zij de pute A, B, E e F e alle pute die verder op de voorkat va de kubus ligge. b Dat zij de pute A, C, E e G e alle pute die i het diagoaalvlak met A, C,
Paragraaf Vergelijkige va vlakke Opgave a Dat zij de pute A, B, E e F e alle pute die verder op de voorkat va de kubus ligge. b Dat zij de pute A, C, E e G e alle pute die i het diagoaalvlak met A, C,
Het reëel getal b is een derdewortel van het reëel getal a c. Een getal en zijn derdewortel hebben hetzelfde toestandsteken.
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. 1. Derdewortel vn een reëel getl (oek pg 7) Een derdewortel vn het reëel getl is dus een getl wrvn de derdemcht gelijk is n. Vooreelden:
INHOUDSTABEL. 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3. 2a. TEKENREGELS (fiche 2a)... 5
 INHOUDSTABEL 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3 2. TEKENREGELS (fiche 2)... 5 2b. TEGENGESTELDE GETAL - TEGENGESTELDE SOM (verschil) - TEGENSTELDE PRODUCT (fiche 2b)... 6 2c. OMGEKEERDE
INHOUDSTABEL 1. BEWERKINGEN MET RATIONALE GETALLEN (fiche 1)... 3 2. TEKENREGELS (fiche 2)... 5 2b. TEGENGESTELDE GETAL - TEGENGESTELDE SOM (verschil) - TEGENSTELDE PRODUCT (fiche 2b)... 6 2c. OMGEKEERDE
UITWERKINGEN TOETS TRAININGSKAMP. Valkenswaard, 10 juni 2006
 UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
UITWERKINGEN TOETS TRAININGSKAMP Valkeswaard, 0 jui 006 Opgave. Als we ee verzamelig pute i de ruimte hebbe, moge we ee put va de verzamelig spiegele i ee ader put va de verzamelig e het beeld hierva toevoege
Analyse. Lieve Houwaer Dany Vanbeveren
 Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Hoeveel getallen van 2 verschillende cijfers kan je vormen met de cijfers 1,4,7,8? tweede cijfer 4 7 8 1 7 8 1 4 8 1 4 7
 Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
Hoofdstu Combiatorie. Basisregels Combiatorie is de studie va telprobleme. De ust va het telle bestaat vaa uit het codere of aders voorstelle va het telprobleem, zodat het uiteidelij volstaat om de volgede
Correctievoorschrift VWO. Wiskunde B1 (nieuwe stijl)
 Wiskude B (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Correctievoorschrift VWO. Wiskunde B1 (nieuwe stijl)
 Wiskude B (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
151 Universele eigenschappen voor algebra 3; 2015/02/08
 151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
151 Uiversele eigeschappe voor algebra 3; 2015/02/08 I het dagelijks leve make we vaak gebruik va apparate, zoals bijvoorbeeld auto s e computers, zoder dat we wete hoe die precies i elkaar zitte e hoe
Dit geeft ee voorwaarde die slechts afhagt va de begiwaarde va de `basisoplossige' (bij (3) is die voorwaarde a b a b 0). Hoe ka me twee lieair oafhak
 Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lesbrief 5 Recurreties e ogelijkhede Recursief gedefiieerde rije Er zij getallerije {a } die voldoe aa ee recurrete betrekkig va de vorm a +k = f(a +k ;a +k ;:::;a ) voor = ; ;:::, waardoor de + k-de term
Lineaire Algebra en Voortgezette Analyse
 Lieaire Algebra e Voortgezette Aalyse Rise Poortiga Lieaire Algebra e Voortgezette Aalyse 01 Rise Poortiga ISBN 978908181518 NUR 918 http://www.risepoortiga.l Niets uit deze uitgave mag worde verveelvoudigd,
Lieaire Algebra e Voortgezette Aalyse Rise Poortiga Lieaire Algebra e Voortgezette Aalyse 01 Rise Poortiga ISBN 978908181518 NUR 918 http://www.risepoortiga.l Niets uit deze uitgave mag worde verveelvoudigd,
Complexe getallen. c(a+ib)=ca+i(cb) id(a+ib)=i(ad)+i 2 (bd)=(-bd)+i(ad) (a+ib)(c+id)=ac+i(ad)+i(bc)+i 2 (bd)= ac-bd+i(ad+bc)
 . Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
. Ileidig: Complexe getalle I de wiskude stelt zich het probleem dat iet bestaat voor de reële getalle of dat de vergelijkig x + 0 gee reële ulpute heeft. Om dit euvel op te losse werd het getal i igevoerd
Reeksen. Convergente reeksen
 Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Reekse Reekse Defiitie, otatie e voorbeelde Defiitie: Eereeks is ee koppel ( ) {u } l, {s } l met s = u k = u l + u l+ + u l+2 +...+ u + u k=l u l = s l, u = s s, = l +, l +2,... {u } l oemt me de termerij,
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Correctievoorschrift VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Wiskude B, (ieuwe stijl) Correctievoorschrift VWO Voorbereided Weteschappelijk Oderwijs 0 0 Tijdvak Izede scores Uiterlijk op jui de scores va de alfabetisch eerste vijf kadidate per school op de daartoe
Iteratie is het steeds herhalen van eenzelfde proces, verwerking op het bekomen resultaat. Verwerking
 1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
1. Wat is iteratie? Iteratie is het steeds herhale va eezelfde proces, verwerkig op het bekome resultaat. INPUT Verwerkig OUTPUT Idie de verwerkig gebeurt met ee (reële) fuctie geldt voor ee startwaarde
2. Limiet van een rij : convergentie of divergentie
 2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
2. Limiet va ee rij : covergetie of divergetie 2. Eigelijke of eidige limiet 2.. Voorbeeld I ee bos staa 4 bome. De diest bosbeheer zal jaarlijks 2% bome kappe e ieuwe aaplate. Zal het bos verdwije? Zal
Bepaling toezichtvorm gemeente Simpelveld
 Bepaling toezichtvorm 2008-2011 gemeente Simpelveld F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, j u n i 2 0 0 8 V e r d i e p i n g s o n d e r z o e k
Bepaling toezichtvorm 2008-2011 gemeente Simpelveld F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, j u n i 2 0 0 8 V e r d i e p i n g s o n d e r z o e k
TECHNISCHE HOGESCHOOL EINDHOVEN Afdeling Algemene Wetenschappen. Onderafdeling der Wiskunde WISKUNDE 10. bestemd voor. BDK-1, WSK-1, N-1, E-1 en T-1
 TECHNSCHE HOGESCHOOL ENDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WSKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1974 ENKELE NOTTES bij WSKUNDE 10 De cursus Wiskude 10
TECHNSCHE HOGESCHOOL ENDHOVEN Afdelig Algemee Weteschppe Oderfdelig der Wiskude WSKUNDE 10 bestemd voor BDK-1, WSK-1, N-1, E-1 e T-1 Njrssemester 1974 ENKELE NOTTES bij WSKUNDE 10 De cursus Wiskude 10
Julian gooit 20 keer met een dobbelsteen. Bereken de kans dat hij precies 5 keer een zes gooit.
 - Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
- Test Hfst D kasrekeig - Kase ofwel exact ofwel afgerod op decimale geve. ( x p) Tim gooit drie keer met ee gewoe dobbelstee. Na zij derde worp telt hij het aatal oge va de drie worpe bij elkaar op. Bereke
Hoofdstuk 2: Bewerkingen in R
 Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Werkoek Alger (cursus voor 5u wiskunde) Hoofdstuk : Rekenen in R Nm:. Hoofdstuk : Bewerkingen in R - 7 Kls:... 1. Optellen, ftrekken, vermenigvuldigen en delen in R (oek pg 15): Som: 1. vn twee getllen
Dus n n (a + b) n = a n + a n 1 b + heet een binomiaalcoëfficiënt (uitspraak n boven k ). Newton vond de
 CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
CONTINUE WISKUNDE: BINOMIUM VAN NEWTON EN RECURRENTE BETREKKINGEN Het Biomium va Newto Het Biomium va Newto is ee uitdruig voor a + b), waarbij a e b willeeurige getalle zij, e ee atuurlij getal I deze
Hoofdstuk 0: algebraïsche formules
 Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
We kennen in de wiskunde de volgende getallenverzamelingen:
 Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
Masteropleidig Fiacial Plaig Kwatitatieve Methode Relevate wiskude We kee i de wiskude de volgede getalleverzamelige: De atuurlijke getalle: N = {0,,,,4, } De gehele getalle: Z = {, -,-,-,0,,,, } (egels:
HOOFDSTUK 1 BASISBEGRIPPEN
 I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
Bijzonder wonen vraagt om een bijzondere keuken
 Bijzoder woe vrgt om ee bijzodere keuke I dit project werke wij sme met:? Afsprk mke 030-63 50 063 Trsprte offerte U otvgt ee offerte met ee trsprte prijs iclusief motge (idie gewest) é de mogelijkheid
Bijzoder woe vrgt om ee bijzodere keuke I dit project werke wij sme met:? Afsprk mke 030-63 50 063 Trsprte offerte U otvgt ee offerte met ee trsprte prijs iclusief motge (idie gewest) é de mogelijkheid
Bepaling toezichtvorm gemeente Venray
 Bepaling toezichtvorm 2007-2010 gemeente Venray F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k V e n
Bepaling toezichtvorm 2007-2010 gemeente Venray F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k V e n
Integraalrekening. Georg Friedrich Bernhard Riemann Breselenz 17 september 1826 Selasca 20 juni 1866
 Itegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 septemer 86 Selsc 0 jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geeft de itegrl v ee positieve fuctie ee uwkeurige
Itegrlrekeig Georg Friedrich Berhrd Riem Breselez 7 septemer 86 Selsc 0 jui 866 Heri Léo Leesgue Beuvis 8 jui 875 Prijs 6 juli 94 I de wiskudige lyse geeft de itegrl v ee positieve fuctie ee uwkeurige
Convergentie, divergentie en limieten van rijen
 Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Covergetie, divergetie e limiete va rije TI-spire e rije 7N5p GGHM 22-23 Eigeschappe rekekudige rij b = begiwaarde v = verschil tusse twee opeevolgede terme recursieve formule: u = u + v met u = b directe
Een meetkundige constructie van de som van een meetkundige rij
 Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
Ee meetkudige costructie va de som va ee meetkudige rij [ Dick Kliges ] Iets verder da Euclides deed Er wordt door sommige og wel ees gedacht dat Euclides (hij leefde rod 300 v. Chr.) allee over meetkude
3 Meetkundige voorstelling van complexe getallen
 3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
3 Meetkudige voorstellig va complexe getalle 31 Complexe getalle als pute va ee vlak Complexe getalle zij geïtroduceerd als pute va ee vlak tov ee orthoormaal assestelsel Ee dergelijk assestelsel is odig
Formeel Denken 2012 Uitwerkingen Tentamen
 1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
Videoles Discrete dynamische modellen
 Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Videoles Discrete dyamische modelle Discrete dyamische modelle Orietatie Algebraisch Algebraisch/ umeriek Numeriek Maak de volgede rijtjes af: Puzzele met rijtjes a. 2 4 6 8 10 - b. 1 2 4 8 16 - c. 1 2
Het kwadraat van een tweeterm a+b. (a+b)²
 Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
B e l e i d s k a d e r K e r k e n, K l o o s t e r s e n a n d e r e r e l i g i e u z e g e b o u w e n
 B e l e i d s k a d e r K e r k e n, K l o o s t e r s e n a n d e r e r e l i g i e u z e g e b o u w e n I n é é n d a g k a n r e l i g i e u s e r f g o e d v a n m e e r d e r e g e n e r a t i e
B e l e i d s k a d e r K e r k e n, K l o o s t e r s e n a n d e r e r e l i g i e u z e g e b o u w e n I n é é n d a g k a n r e l i g i e u s e r f g o e d v a n m e e r d e r e g e n e r a t i e
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M +
 T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M + A a n l e i d i n g I n d e St a t e nc o m m i s si e v o or R ui m t e e n G r o e n ( n u g e n o em d d e St at e n c
T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M + A a n l e i d i n g I n d e St a t e nc o m m i s si e v o or R ui m t e e n G r o e n ( n u g e n o em d d e St at e n c
Continuïteit en Nulpunten
 Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Parels van studenten tijdens een examen
 Prel 1 Prels vn studenten tijdens een exmen c k x k n+1 n+1 ( = c k x k ( ) )x c n+1x n+1 n+1 k ( ) k x n+1 k ( ) k k k Prel 2 Vrg: Zij n N, c k C voor k = 1,..., n, c n 0. Toon n dt de functie f(z) =
Prel 1 Prels vn studenten tijdens een exmen c k x k n+1 n+1 ( = c k x k ( ) )x c n+1x n+1 n+1 k ( ) k x n+1 k ( ) k k k Prel 2 Vrg: Zij n N, c k C voor k = 1,..., n, c n 0. Toon n dt de functie f(z) =
Bepaling toezichtvorm gemeente Meerlo-Wanssum
 Bepaling toezichtvorm 2007-2010 gemeente Meerlo-Wanssum F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k Provincie L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k M e e
Bepaling toezichtvorm 2007-2010 gemeente Meerlo-Wanssum F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k Provincie L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k M e e
( ) Formulekaart VWO. Kansrekening. Tellen. k n k. Binomium van Newton : Kansrekening. Voor toevalsvariabelen X en Y geldt: E ( X + Y ) = E(
 Formulert VWO Telle! ( )... 0!!!( )! Biomium v Newto : Ksreei ( + ) Ksreei 0 Voor toevlsvriele X e Y el: E ( X + Y ) E( X ) + E( Y ) Voor ofhelije toevlsvriele X e Y el: σ ( X + Y ) σ ( X ) + σ ( Y ) -wet
Formulert VWO Telle! ( )... 0!!!( )! Biomium v Newto : Ksreei ( + ) Ksreei 0 Voor toevlsvriele X e Y el: E ( X + Y ) E( X ) + E( Y ) Voor ofhelije toevlsvriele X e Y el: σ ( X + Y ) σ ( X ) + σ ( Y ) -wet
Rijen met de TI-nspire vii
 Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Rije met de TI-spire vii De tore va Pisa Me laat ee bal valle vaaf de tore va Pisa(63m hoog) Na elke keer stuitere haalt de bal og ee vijfde va de voorgaade hoogte. Gevraagd zij: a) De hoogte a de e keer
Ongelijkheden groep 2
 Ongelijkheden groep Rvi & Cuchy-Schwrz Trnstrendtriningsdg (triningsdg, 6 mrt 009 Cuchy-Schwrz Cuchy-Schwrz Voor reële getllen x,, x n en y,, y n geldt: x i y i en bijgevolg x i y i n n met gelijkheid
Ongelijkheden groep Rvi & Cuchy-Schwrz Trnstrendtriningsdg (triningsdg, 6 mrt 009 Cuchy-Schwrz Cuchy-Schwrz Voor reële getllen x,, x n en y,, y n geldt: x i y i en bijgevolg x i y i n n met gelijkheid
Toelichting bij Opbrengstgegevens VAVO 2011-2013
 Toelichtig bij Opbregstgegeves VAVO 2011-2013 Ihoud Ileidig Aatal deelemers exame Kegetalle toezicht exames CE-cijfer alle vakke CE-cijfer alle vakke - tred SE-cijfer mius CE cijfer alle vakke Percetage
Toelichtig bij Opbregstgegeves VAVO 2011-2013 Ihoud Ileidig Aatal deelemers exame Kegetalle toezicht exames CE-cijfer alle vakke CE-cijfer alle vakke - tred SE-cijfer mius CE cijfer alle vakke Percetage
Trigonometrische functies
 Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
Trigoometrische fucties Ileidig De meest gebruikelijke defiitie va de trigoometrische fucties cos e si berust op meetkudige cocepte (cirkel, hoek, driehoeke etc.) die buite het bestek va de aalyse valle.
H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W +
 H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W + D o e l m a t i g h e i d s t o e t s v o o r g e b i e d e n w a a r v o o r g e e n b o d e m b e h e e r p l a n i s v a s t g e s
H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W + D o e l m a t i g h e i d s t o e t s v o o r g e b i e d e n w a a r v o o r g e e n b o d e m b e h e e r p l a n i s v a s t g e s
