2 ). Door steeds de functiewaarde aan de linkerkant te kiezen, krijgen we de benaderingsformule
|
|
|
- Martina Wouters
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse Les 9 Numerieke integrtie In de prktijk is het mr zelden het gevl dt we een functie expliciet kunnen primitiveren. Voorbeelden hiervoor zijn de Guss-functie e x die in de sttistiek en knsrekening en bij probbilistische modellen een belngrijke rol speelt, mr ook de functie sin(x) x die we bij de Fourier trnsformtie vker zijn tegen gekomen heeft geen primitieve die zonder integrl te schrijven is. Verder is de situtie bij de integrtie vk vergelijkbr met de discrete Fourier trnsformtie, nmelijk dt we een functie lleen mr in sommige (discrete) punten kennen, bijvoorbeeld door een meting. Om in deze situtie niettemin integrlen te kunnen berekenen, zijn numerieke benderingsmethoden belngrijk. De mnier vn npk hierbij is enigszins voor de hnd liggend, wnt we hebben de integrl gedefinieerd ls limiet vn een bendering met smlle rechthoeken en gn dit nu op een of ndere mnier omdrien. 9.1 Constnte fstnden De eenvoudigste methoden om een integrl op het intervl [, b] numeriek te benderen, gebruiken een onderverdeling vn het intervl in even grote stukken x en benderen de oppervlkte vn f(x) op het deelintervl x door een rechthoek. Voor de hoogte vn de rechthoek zijn er ntuurlijk verschillende mogelijkheden, voor de hnd liggend zijn de functiewrde n de linkerknt vn het intervl, n de rechterknt vn het intervl, of in het midden vn het intervl. Om de integrl f(x) dx te berekenen, delen we het intervl [, b] in N delen vn lengte x, dus is x = b N. De rndpunten vn de deelintervllen noemen we x,..., x N, wrbij x i := + i x, dn is x = en x N = b. Als we de hoogte vn de rechthoek op het deelintervl [x i, x i ] door de wrde n de linkerknt benderen, is dit f(x i ), n de rechterknt hebben we f(x i ) en in het midden is het f(x i x ). Door steeds de functiewrde n de linkerknt te kiezen, krijgen we de benderingsformule f(x i ) x = b N (f(x ) + f(x 1 ) f(x N )). Net zo geeft de functiewrde n de rechterknt vn het deelintervl de formule f(x i ) x = b N (f(x 1) + f(x ) f(x N )). Als we een goede bendering willen hebben, moeten we x zeker redelijk klein kiezen, mr dn kunnen we ervn uitgn dt f(x) op de meeste vn de deelintervllen monotoon (stijgend of dlend) is. In zo n gevl is de bendering vn de functiewrde op een deelintervl door de wrde n een vn de rnden 115
2 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse zeker slechter dn de bendering door de wrde in het midden vn het deelintervl. Drom krijgt men bijn ltijd een betere bendering door de wrde in het midden te kiezen, dus door f(x i x ) x = b N ( f(x 1 x ) + f(x x ) f(x N x ) Meestl wordt deze formule de rechthoek-regel genoemd, mr soms vllen ook de formules met de wrden n de linker- of rechterknt vn het deelintervl onder deze nm. Het idee bij de rechthoek-regel is in principe dt we de functie f(x) door een stuksgewijs constnte functie benderen wrvoor we de integrl mkkelijk uit kunnen rekenen. Mr we kennen ntuurlijk betere benderingen vn een functie f(x) dn door stuksgewijs constnte functies. Om de nottie iets eenvoudiger te houden, kijken we lleen mr nr één deelintervl en noemen de grenzen hiervn weer en b. De eerstvolgende soort vn functies die beter zijn dn constnte functies zijn lineire functies. Als we een functie f(x) op een intervl [, b] door een lineire functie willen benderen, is de meest voor de hnd liggende keuze hiervoor de lijn door de twee rndpunten, dus de lijn door de punten (, f()) en (b, f(b)). De oppervlkte wrmee we onze functie benderen is dn geen rechthoek meer mr een trpezium met hoogte f() n de ene knt en hoogte f(b) n de ndere. Mr de oppervlkte vn dit trpezium is gewoon 1 b (f() + f(b)) x = (f() + f(b)). Als we nu weer nr de combintie vn meerdere deelintervllen kijken, moeten we de oppervlkten vn de trpeziums bij elkr optellen, dit geeft dn 1 (f(x i) + f(x i )) x ). = x 1 (f() + f(x 1) + f(x 1 ) + f(x ) f(x N ) + f(b)) = b N N (f() + f(b) + f(x i )) Deze benderingsformule voor een integrl heet de trpezium-regel. In Figuur I.4 zijn de benderingen vn de integrl onder de stndrdnormlverdeling f(x) := 1 π e x met behulp vn de rechthoek-regels en de trpeziumregel te zien. Het linkerpltje geeft de rechthoeken met wrden n de linkeren n de rechterknt. Omdt f(x) op het intervl [, ] strikt dlend is, geeft de wrde n de linkerknt steeds een te grote en de wrde n de linkerknt steeds een te kleine wrde. Het middelste pltje lt zien dt de wrde in 116
3 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse het midden vn het deelintervl l een betere bendering geeft, en het rechterpltje mkt duidelijk dt de trpezium-regel een nog betere bendering geeft x x x Figuur I.4: Rechthoek-regels en trpezium-regel. We zijn vn de rechthoek-regel nr de trpezium-regel gekomen, door een functie door een stuksgewijs lineire functie in plts vn een stuksgewijs constnte functie te benderen. Mr in het kder vn de Tylor reeksen hebben we l gezien dt we functies steeds beter door veeltermen vn hogere grd kunnen benderen. Drom is de volgende voor de hnd liggende stp, de functie f(x) op een deelintervl [x i, x i ] door een kwdrtische functie te benderen. Het idee is dn weer, de oppervlkte onder de prbool ls bendering vn de oppervlkte onder de grfiek vn f(x) te zien. Mr de oppervlkte onder een prbool kunnen we mkkelijk beplen, en het is zelfs voldoende ls we dit voor de stndrd-prbool f(x) = x berekenen. Voor f(x) := x geldt dt f(x) dx = = b x dx = 1 x b = 1 (b ) = 1 (b )( + b + b ) 1 ( + ( + b) + b ) = b ( + 4( + b 6 ) + b ) = b + b (f() + 4f( 6 ) + f(b)). Mr dezelfde vergelijking b f(x) dx = 6 (f() + 4f(+b ) + f(b)) geldt ook voor een geschlde prbool f(x) := c x en omdt we en b willekeurig hebben gekozen geldt dit ook voor een lngs de x-s verschoven prbool. En ook ls we lngs de y-s verschuiven, dus vn f(x) tot f(x) + d over gn, klopt het nog steeds, omdt f(x) + d dx = f(x) dx + (b )d en ook b +b b 6 (f()+d+4(f( )+d)+f(b)+d) = 6 (f()+4f(+b )+f(b))+(b )d. Het idee is nu dt we de functie f(x) op het intervl [, b] benderen door de prbool die door de drie punten (, f()), ( +b, f(+b )) en (b, f(b)) loopt. De oppervlkte onder deze prbool berekenen we met behulp vn de boven gegeven formule en we nemen dit ls bendering voor de oppervlkte onder de 117
4 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse grfiek vn f(x). Dit geeft dus de benderingsformule b + b (f() + 4f( 6 ) + f(b)) en we weten dt deze voor kwdrtische veeltermen zelfs exct is. De formule b +b 6 (f() + 4f( ) + f(b)) stt ook bekend ls Keplers vtregel. Omdt Kepler n nleiding vn zijn (tweede) huwelijk ontevreden ws over de methode hoe de inhoud vn een vt wijn bepld werd (meten met behulp vn een stf door het spongt) wilde hij een eenvoudige formule vinden om het volume vn een vt te beplen. Zijn idee ws, het volume ls volume vn een rottielichm te berekenen, wrbij de helft vn de doorsnede vn het vt rond een s tussen bodem en deksel roteert. r m = f( +b ) r = f() r b = f(b) Gemeten werd de strl r = f() vn de bodem, de strl r b = f(b) vn de deksel en de strl r m = f( +b ) in het midden vn het vt en ntuurlijk de hoogte h = b vn het vt. Het roterende oppervlk A benderde Kepler nu op twee mnieren: Een keer door de te grote rechthoek met hoogte r m en breedte h en een keer door de twee trpeziums tussen r en r m en tussen r m en r b, die smen een te kleine wrde opleveren. en een keer door twee te kleine trpeziums. Dit gf de ongelijkheden (b )r m A b r + r m + b r m + r b = b 4 (r +r m +r b ). Het ltste idee ws nu, een gemiddelde vn de twee benderingen vn A te nemen, wrbij de rechthoek gewicht 1 en de trpeziums gewicht krijgen, omdt de trpeziums een onderverdeling in twee stukken gebruiken. Dit geeft de bendering A 1 ((b )r m + b (r + r m + r b )) = b 6 (r + 4r m + r b ) en dit is precies wt we boven hebben gevonden. Het volume vn het vt wordt op een soortgelijke mnier benderd: Als de rechthoek roteert geeft dit een cilinder en ls de trpeziums roteren 118
5 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse geeft dit twee kegelstompen. Ook deze volumes worden weer met de gewichten 1 : gemiddeld, en dit geeft de benderingsformule voor het volume. V = π 9 (b )(r + 5r m + r b + r r m + r m r b ) Als we nu weer het intervl [, b] in meerdere deelintervllen [x i, x i ] vn breedte x opsplitsen en op elk deelintervl Keplers vtregel toepssen, krijgen we 1 6 (f(x i) + 4f( x i + x i ) + f(x i )) x 1 = 6 (f(x i) + 4f(x i x ) + f(x i)) x = x ( f() + 4f(x 1 x 6 ) + f(x 1) + f(x 1 ) + 4f(x x ) +f(x ) f(x N ) + 4f(x N x ) ) + f(b) = b 6N ( f() + f(b) + N f(x i ) + 4 f(x i x ) en dit stt bekend ls de Simpson-regel. Dit is de typische mnier hoe in zkrekenmchines integrlen uitgerekend worden. Nu dt we een keer op stp zijn kn ons ntuurlijk niets meer hinderen om ook eens een bendering door een derdegrds-veelterm te proberen. Een soortgelijke redenering ls boven lt zien dt het voldoende is om de functie f(x) := x te bekijken. Er geldt f(x) dx = = b 4 = b 8 x dx = 1 4 x4 b = 1 4 (b4 4 ) = 1 4 (b )( + b + b + b ) 1 ( + ( + b + b (f() + f( ) + ( + b ) + b ) ) + f( + b ) + f(b)). Als we dit nu weer op deelintervllen gn toepssen, krijgen we 1 8 (f(x i) + f( x i + x i ) + f( x i + x i ) + f(x i )) x ( ) = b N f() + f(b) + f(x i ) + (f(x i 8N x) + f(x i 1 x)) en dit heet de Newton 8-regel. Het is trouwens zo dt ook de Simpson-regel l exct voor derdegrds-veeltermen is, mr dit is eigenlijk een beetje toevl, 119 )
6 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse omdt zekere termen bij het uitwerken vn de Simpson-regel voor f(x) := x tegen elkr wegvllen. Op een soortgelijke mnier kunnen we doorgn met benderingen door vierdegrds-, vijfdegrds- en hogere veeltermen. Dit geeft de zogeheten Newton-Cotes-formules, wrbij voor een vste N het intervl [, b] in N even grote stukken vn lengte x = b N onderverdeelt wordt. Vervolgens wordt door de N + 1 punten (x i, f(x i )) met x i := + i x een veelterm vn grd N gelegd en de oppervlkte onder f(x) bendert door de oppervlkte onder de grfiek vn deze veelterm. Men krijgt op deze mnier steeds een formule vn de vorm b m w i f( + i x) voor zekere gewichten w i een een noemer m. De volgende tbel geeft de gewichten en noemers voor N = 1,,..., 6: i= N m w i nm trpezium-regel Simpson-regel Newton- 8 -regel Milne-regel Weddle-regel Ntuurlijk worden ook deze formules weer op onderverdelingen vn het intervl [, b] in deelintervllen toegepst. Het probleem hierbij is, dt de nuwkeurigheid niet meer zo snel toeneemt, terwijl frondingsfouten bij veeltermen vn hogere grd een steeds grotere rol gn spelen. Wt men in plts vn een bendering vn de functie door veeltermen vn steeds hogere grd in de prktijk meestl toepst, zijn dptieve methoden. Het idee is, met een eenvoudige methode zo ls de trpezium-regel of (hooguit) de Simpson-regel op een redelijk grove onderverdeling te beginnen en deze vervolgens te verfijnen. Op stukken wr de verfijning bijn geen verndering meer oplevert (d.w.z. de verndering ligt binnen de gewenste nuwkeurigheid), is de bendering blijkbr l heel goed en hoeven we hier niets meer n te vernderen. Drentegen gn we op deelstukken wr de verfijning wel een grotere verndering oplevert nog verder verfijnen, tot dt we ook hier de gewenste nuwkeurigheid bereiken. Een bekende methode vn deze soort is de Romberg-methode die veel toegepst wordt. We gn nu een pr vn de genoemde methoden vergelijken, door de integrl 1 I := e x dx π 1
7 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse vn de stndrdnormlverdeling met verwchtingswrde en stndrdfwijking 1 te benderen. Omdt de normlverdeling symmetrisch ten opzichte vn het nulpunt is, geeft deze integrl de helft vn de kns, dt bij een normlverdeling een gebeurtenis binnen keer de stndrdfwijking vn de verwchtingswrde vlt. Uit de sttistiek weten we, dt deze kns ongeveer 95% is. De op 16 decimlen fgeronde wrde vn de integrl is I = De volgende tbel geeft de benderingen vn de integrl met de rechthoekregel (voor het midden vn het deelintervl), met de trpezium-regel en met de Simpson-regel. In elk gevl worden onderverdelingen in N = 4, 8, 16,, 64 deelintervllen bekeken. N rechthoek trpezium Simpson We zien dt de rechthoek-regel en de trpezium-regel in dit gevl ongeveer even goed scoren, met 64 deelintervllen hebben we een bendering met een nuwkeurigheid vn 1 5 bereikt. Mr met de Simpson-regel bereiken we deze nuwkeurigheid l met 4 deelintervllen en met elke verdubbeling vn het ntl deelintervllen komt er ongeveer één juiste cijfer erbij. 9. Guss kwdrtuur Tot nu toe hebben we een integrl steeds met een formule vn de vorm b N w i f(x i ) bendert, wrbij x i = + i x. De punten x i wr we de functie evlueren noemen we ook de roosterpunten. De Newton- Cotes methoden zijn dus lleml methoden met roosterpunten met constnte fstnden. Het is ntuurlijk ngenm om hiermee te werken, mr n de ndere knt is het eigenlijk een onnodige beperking. Het lgemene idee chter de zogeheten Guss kwdrtuur-methoden is, de integrl f(x) dx te benderen door een formule vn de vorm w i f(x i ) wrbij de roosterpunten x i geschikt gekozen punten in het intervl [, b] zijn en de w i zekere gewichten. Het doel is hierbij, x i en w i zo te kiezen dt de formule voor veeltermen vn zo hoog mogelijke grd exct zijn. Om de nottie te vereenvoudigen, speciliseren we het intervl [, b] nu tot het intervl [, 1]. We zullen lter zien, hoe we weer terug nr een lgemeen intervl komen. 11
8 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse Legendre-veeltermen We hebben l in het kder vn de Fourier trnsformtie nr inproducten vn functies gekeken, een voorbeeld hiervn is Φ(f(x), g(x)) := f(x) g(x) dx. Het doel is, een orthogonl stelsel vn veeltermen ten opzichte vn dit inproduct te vinden. Hiervoor beginnen we met p (x) := 1 en zien dt p 1 (x) := x l loodrecht op p (x) stt. Vervolgens beplen we p (x) met Φ(p (x), p (x)) = en Φ(p (x), p 1 (x)) = door de projecties vn f(x) = x op p (x) en p 1 (x) vn x f te trekken. Er geldt Φ(x, p (x)) = x dx = en Φ(x, p 1 (x)) = en wegens Φ(p (x), p (x)) = is de projectie vn x op p (x) dus 1 p (x). De veelterm x 1 stt dus loodrecht op p (x) en op p 1 (x). Op een soortgelijke mnier kn men nu doorgn en voor elke n een veelterm p n (x) beplen die loodrecht op de eerder gevonden p m (x) met m < n stt. Dit is de Grm-Schmidt orthogonlistie methode. Echter lt zich een orthogonl stelsel vn veeltermen ook op een rechtstreekse mnier vinden, nmelijk de Legendre-veeltermen. De Legendre-veelterm p n (x) vn grd n is gedefinieerd door p n (x) := 1 n n! d n dx n (x 1) n, p (x) = 1. Dit betekent dt we p n (x) krijgen door de n-de fgeleide vn de veelterm (x 1) n te berekenen. Omdt (x 1) n een veelterm vn grd n is, levert de n-de fgeleide inderdd een veelterm vn grd n. Men gt nu n dt voor de Legendre-veeltermen geldt dt p n (x)p m (x) dx = ls m n en p n (x)p n (x) dx = n + 1, met ndere woorden zijn de Legendre-veeltermen een orthogonl stelsel ten opzichte vn het inproduct Φ. Een belngrijke reltie om de Legendre-veeltermen te berekenen is de recursie formule (n + 1)p n+1 (x) = (n + 1)xp n (x) np n (x). Met p (x) = 1 en p 1 (x) = x lten zich hieruit de eerste Legendre-veeltermen snel berekenen: p (x) = 1 (x 1) p (x) = 1 (5x x) p 4 (x) = 1 8 (5x4 x + ) p 5 (x) = 1 8 (6x5 7x + 15x) p 6 (x) = 1 16 (1x6 15x x 5) 1
9 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse De Guss-Legendre methode Wt hebben de Legendre-veeltermen nu met numerieke integrtie te mken? Het ntwoord is, dt we de nulpunten vn de Legendre-veeltermen ls roosterpunten x i kiezen. Er lt zich nmelijk ook ntonen, dt de n-de Legendreveelterm p n (x) in het intervl [, 1] precies n verschillende nulpunten heeft. Voor p 1 (x) is dit bijvoorbeeld x 1 = en voor p (x) zijn dit x 1 = 1 en x = 1. We kiezen nu eerst een vst ntl N vn roosterpunten, en kiezen ls roosterpunten x 1,..., x N de nulpunten vn p N (x). De gewichten w 1,..., w N gn we nu zo beplen, dt de formule w i f(x i ) voor veeltermen vn grd, 1,..., N 1 exct is. Dit is mogelijk omdt we het met een stelsel vn N lineire vergelijkingen in de N onbekende w 1,..., w N te mken hebben, met ls vergelijkingen w i x j i = x j dx voor j =, 1,..., N 1. Men gt n dt de determinnt vn de mtrix vn dit stelsel vergelijkingen ongelijk n is en het stelsel drom een eenduidige oplossing heeft. De bewering is nu, dt met deze keuze vn roosterpunten x i en gewichten w i, de formule w i f(x i ) voor elke veelterm f(x) vn grd hoogstens N 1 exct is. Dit zien we ls volgt in: Zij f(x) een veelterm vn grd m N 1, dn kunnen we f(x) met behulp vn een strtdeling schrijven ls f(x) = p N (x)g(x) + r(x) wrbij de grden vn g(x) en r(x) hoogstens N 1 zijn. An de ene knt geldt nu f(x) dx = p N (x)g(x) dx + r(x) dx = r(x) dx omdt p N(x)x m dx = voor lle m < N, wnt x m is een lineire combintie vn de p k (x) met k m en deze stn lleml loodrecht op p N (x). An de ndere knt is w i f(x i ) = w i p N (x i )g(x i ) + w i r(x i ) = w i r(x i ) 1
10 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse omdt de x i de nulpunten vn p N (x) zijn, dus p N (x i ) = voor lle i. Mr de gewichten w i zijn juist zo gekozen dt r(x) dx = N w i r(x i ) voor veeltermen r(x) vn grd hoogstens N 1, en bij elkr genomen zegt dit dt inderdd f(x) dx = N w i f(x i ). De methode om een integrl met deze roosterpunten en gewichten te benderen, heet de Guss-Legendre methode. Merk op dt de roosterpunten x i en de gewichten w i lleen mr vn het gekozen ntl N vn roosterpunten fhngt, mr niet vn de functie f(x). Voor gegeven N kunnen de x i en w i dus een keer uitgerekend en tot de benodigde nuwkeurigheid opgeslgen worden. De volgende tbel geeft de roosterpunten x i en de gewichten w i vn de Guss- Legendre-methode voor N = 1,..., 4 met een nuwkeurigheid vn 6 decimlen. Merk op dt met N = 4 veeltermen vn grd 7 nog exct uitgewerkt worden. N i x i w i We zijn bij de Legendre-veeltermen ervn uit gegn dt we een integrl op het intervl [, 1] willen berekenen. Mr een integrl op een lgemeen intervl [, b] kunnen we door een eenvoudige substitutie op dit intervl terug brengen, er geldt: Met u = b x b+ b b is x = x(u) = u + b+ en dx = b du. Als u vn tot 1 loopt, loopt x vn tot b en er geldt dus: f(x) dx = b f(x(u)) du = b Als we de Guss-Legendre methode weer op de integrl I := f(x) dx met f(x) := 1 e x π f ( b u + b + ) vn de stndrdnormlverdeling willen toepssen, is de substitutie gewoon een verschuiving om 1, dus we berekenen de integrl door I := 1 π e (x+1) dx. Voor N = hebben we x 1 = 1, x = 1 en w 1 = w = 1. Als we hiermee de integrl I zonder verdere onderverdeling vn het intervl benderen, krijgen du. 14
11 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse we I f(x 1 + 1) + f(x + 1) = en dit is een fwijking vn slechts.5%. Voor N = hebben we x 1 = 5, x =, x = 5 en w 1 = 5 9, w = 8 9, w = 5 9. In dit gevl krijgen we I w 1 f(x 1 +1)+w f(x +1)+w f(x +1) = en dit is een fwijking vn.4%. De Guss-Legendre methode is een specil gevl vn een lgemenere klsse vn methode, die onder de nm Guss kwdrtuur vllen. Hierbij gt het om het benderen vn integrlen vn de vorm ρ(x)f(x) dx voor een zekere gewichtsfunctie ρ(x) die in het gevl vn de Guss-Legendre methode ρ(x) = 1 is. Deze gewichtsfunctie kn men ook in het inproduct inbouwen, dit is dn Φ(f(x), g(x)) := ρ(x)f(x)g(x) dx. Voor zekere functies ρ(x) krijgt men ook in dit gevl een stelsel vn orthogonle veeltermen. Voorbeelden zijn: ρ(x) = 1 1 x op [, 1] geeft de Chebyshev-veeltermen, ρ(x) = e x op [, ] geeft de Lguerre-veeltermen, ρ(x) = e x op [, ] geeft de Hermite-veeltermen. Anloog met het gevl vn de Legendre-veeltermen worden in elk gevl de nulpunten vn deze veeltermen ls roosterpunten gekozen en de gewichten zo bepld, zo dt de formule ρ(x)f(x) dx = N w i f(x i ) exct is voor veeltermen f(x) vn grd hoogstens N Functies vn meerdere vribelen We hebben in de vorige les gezien, dt we integrlen over functies vn meerdere vribelen in principe uit kunnen werken door in elkr geschkelde gewone integrties. Hetzelfde geldt ook voor de numerieke integrtie, we kunnen de integrties voor de verschillende vribelen chter elkr uitvoeren, wrbij we voor elke 1-dimensionle integrtie onze fvoriete benderingsmethode gebruiken. We gn dit nu eens n de hnd vn een functie f(x, y) vn vribelen voor de Simpson-regel en de Guss-Legendre methode uitschrijven. -dimensionle Simpson-regel De 1-dimensionle Simpson-regel geeft voor een onderverdeling vn het intervl [, b] in N deelintervllen de benderingsformule b 6 ( f() + f(b) + wrbij x = b N, x i = + i x en x i 1 N = x i x. f(x i ) + 4 f(x i 1 ) Als we nu een integrtie vn een functie met meerdere vribelen willen benderen, kunnen we de Simpson-regel op de enkele 1-dimensionle integrties toepssen. Voor een functie f(x, y) vn twee vribelen op de rechthoek R = ) 15
12 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse [, b] [c, d], wrbij we het intervl [, b] in N stukken vn lengte x = b N en het intervl [c, d] in M stukken vn lengte y = d c M onderverdelen, geeft dit: d ( ) f(x, y) da = f(x, y) dx dy R c c c ( ) d N b c N (f(, y) + f(b, y) + f(x i, y) + 4 f(x i 1, y) = b ( d d f(, y) dy + f(b, y) dy N c c N d ) d + f(x i, y) dy + 4 f(x i 1, y) dy In elke integrl in deze formule moeten we nu nog de Simpson-regel op de y- coördint toepssen, dit betekent dt elke integrl in vier termen opgesplitst moet worden. De uiteindelijke formule ziet er niet zo erg mooi uit, mr is wel nuttig: f(x, y) da R (b )(d c) NM f(, c) + f(, d) + M + f(b, c) + f(b, d) + f(b, y j ) + 4 N + +4 j=1 (f(x i, c) + f(x i, d)) + 4 N (f(x i 1, c) + f(x i 1, d)) + 8 M j=1 M j=1 M j=1 f(, y j ) + 4 f(b, y j 1 ) M j=1 N f(x i, y j ) + 8 M j=1 f(, y j 1 ) M j=1 f(x i 1, y j ) + 16 dy f(x i, y j 1 ) M j=1 f(x i 1 De beste mnier om de -dimensionle Simpson-regel te onthouden is, de verdeling vn de gewichten in het schem vn roosterpunten te bekijken. De 1-dimensionle Simpson-regel heeft de rij vn gewichten 1, 4,, 4,...,, 4, 1. In dimensies moeten we nu de gewichten voor de twee coördinten met elkr vermenigvuldigen, dit geeft n de rnden gewichten 1, 4,, 4,...,, 4, 1 (omdt we met 1 vermenigvuldigen) en drtussen fwisselend rijen, 8, 4, 8,..., 4, 8, (ls we met vermenigvuldigen) en 4, 16, 8, 16,..., 8, 16, 4 (ls we met 4 vermenigvuldigen). Als we voor de punten x i en y j doorgetrokken lijnen nemen en voor de punten x i 1 en y j 1 stippellijnen, ziet het schem vn gewichten op de roosterpunten er zo uit ls in Figuur I.4., y j 1 ) 16
13 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse Figuur I.4: Gewichten voor -dimensionle Simpson-regel. -dimensionle Guss-Legendre methode Bij de Guss-Legendre methode ziet de situtie er eigenlijk iets overzichtelijker uit. Voor een 1-dimensionle integrl hebben de benderingsformule w i f(x i ) wrbij x i de nulpunten vn de Legendre-veelterm p N (x) vn grd N zijn en de w i de bijhorende gewichten. Als we nu veronderstellen dt we voor de x-richting en de y-richting de Guss-Legendre methode vn dezelfde grd N toepssen, hebben we y i = x i en krijgen voor de integrtie over de vierknt R := [, 1] [, 1]: ( ) ( 1 N ) f(x, y) da = f(x, y) dx dy w i f(x i, y) dy R = w i f(x i, y) dy w j f(x i, y j ) = j=1 w i w j f(x i, y j ). Deze formule betekent dt we over de functiewrden in de roosterpunten (x i, y j ) met 1 i, j N middelen, wrbij de functiewrde in het punt (x i, y j ) het gewicht w i w j krijgt. Voor N = 4 hebben we de nulpunten x 1 = y 1 =.86116, x = y =.9981, x = y =.9981, x 4 = y 4 =.86116, en de gewichten w 1 = w 4 =.47855, w = w = Hieruit volgt, dt er mr verschillende gewichten voor de roosterpunten zijn, nmelijk w 1 w 1 = w 1 w 4 = w 4 w 1 = w 4 w 4 =.11, w 1 w = w 1 w = w w 1 = w w 4 = w w 1 = w w 4 = w 4 w = w 4 w =.685, w w = w w = w w = w w = We krijgen dus een pltje vn roosterpunten en gewichten zo ls in Figuur I w i j=1
14 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse y 4 y x 1 x x x 4 y : gewicht.11 : gewicht.685 : gewicht.4594 y 1 Figuur I.44: Roosterpunten en gewichten voor -dimensionle Guss-Legendre methode met N = 4. Specile methoden In het (belngrijke) -dimensionle gevl zijn er ook nog lterntieve methoden, die een goede bendering opleveren. Het idee dt we bij de trpezium-regel hdden, ws dt we de functie tussen twee punten door een lijn benderen. Mr net zo ls twee punten in het vlk een lijn eenduidig beplen, leggen drie punten in de -dimensionle ruimte een vlk eenduidig vst. Als we dus drie (verschillende) punten P 1 = (x 1, y 1 ), P = (x, y ), P = (x, y ) in het x y-vlk kiezen, is er een eenduidig vlk in R dt de drie punten (x 1, y 1, f(x 1, y 1 )), (x, y, f(x, y )) en (x, y, f(x, y )) bevt. Het idee is, dt we de functie f(x, y) op het driehoek dt door de drie punten P 1, P, P opgespnnen is, door dit vlk benderen. Bij deze methode zou men verwchten dt de bendering lleen mr voor lineire functies exct is. Er is echter een trucje, wrmee zelfs kwdrtische functies nog exct berekend worden, nmelijk door in plts vn de hoekpunten P 1, P, P vn de driehoek de functiewrden in de middelpunten vn de zijden te nemen, dus in de punten 1 (P 1 + P ), 1 (P + P ), 1 (P + P 1 ). Dit lijkt op de rechthoek-regel in het 1-dimensionle gevl, wr we ls gemiddelde functiewrde de functiewrde in het midden nemen. Mr bij een driehoek hebben we drie zijden, dus drie gemiddelde functiewrden op de zijden en het gemiddelde vn deze functiewrden geeft inderdd een goede bendering voor de integrl. Het idee is dus dt we voor een driehoek D met hoekpunten P 1, P, P en oppervlkte opp(d) de integrl vn f(x, y) op D benderen door D f(x, y) da opp(d) (f( P 1 + P ) + f( P + P ) + f( P + P 1 )) en men kn bewijzen dt deze bendering voor kwdrtische functies exct is, d.w.z. voor functies vn de vorm f(x, y) = x + bxy + cy + dx + ey + f. 18
15 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse P P 1 +P D P +P P 1 P P 1 +P We gn dit eens n het voorbeeld vn de driehoek D met hoekpunten P 1 = (, ), P = (1, ) en P = (, 1) en de functie f(x, y) := xy checken. Er geldt opp(d) = 1, f(p 1+P ) = f( 1, ) =, f(p +P ) = f( 1, 1 ) = 1 4, f(p +P 1 ) = f(, 1 ) =, dus geeft de bendering het resultt D f(x, y) da = 1 4. An de ndere knt geeft de expliciete integrtie x xy dy dx = = 1 ( 1 xy 1 x ) dx = 1 x(1 x) dx (x x + x ) dx = 1 (1 x x x4 ) 1 = 1 ( ) = = 1 4. Op een soortgelijke mnier gt men n dt de bendering ook voor de functies f(x, y) = x en f(x, y) = y exct is. Verder komt men vn de specile driehoek D tot een willekeurige driehoek door een verschuiving en een lineire trnsformtie en men ziet dt bij deze trnsformties de integrl en de bendering op dezelfde mnier vernderen. Dit is voldoende om te lten zien dt de benderingsformule inderdd voor kwdrtische veeltermen exct is. Als we nu over een rechthoek willen integreren, is het ntuurlijk enigszins voor de hnd liggend, de rechthoek in twee driehoeken te delen, en de formule voor driehoeken op deze twee driehoeken toe te pssen. Als men dit doet, gebeurt er iets soortgelijks ls bij de Simpson-regel, nmelijk er vllen derdegrds-termen tegen elkr weg en deze bendering is zelfs nog voor kubische functies f(x, y) exct. Voor de rechthoek R = [, b] [c, d] krijgt men zo de bendering ( (b )(d c) f(x, y) da f( + b + b, c) + f( R 6, d) + f(, c + d ) + f(b, c + d ) + f( + b, c + d ) ). 19
16 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse y d c b x Dt deze bendering inderdd voor derdegrds-veeltermen in x en y werkt, ziet men bijvoorbeeld door nrekenen voor de functies f(x, y) = x, x y, xy, y op de vierknt [, 1] [, 1]. Verschuiving en schling mkt ook hier geen verschil in de geldigheid vn de formule. Ook in het meerdimensionle gevl worden in de prktijk vk dptieve methoden gebruikt. Men begint met een redelijk grove onderverdeling vn het gebied in driehoeken (een zogeheten tringultie) en verfijnd deze op gebieden wr een verfijning nog fwijkingen boven de gewenste nuwkeurigheid oplevert. Methoden ls deze vllen onder het begrip vn eindige elementen methoden. 9.4 Monte-Crlo methoden Voorl in de numerieke integrtie vn functies met meerdere vribelen worden inmiddels vk methoden toegepst die een toevlsgenertor gebruiken. Het idee hierbij is simpel: Als x 1, x,... toevllig volgens een uniforme verdeling op het intervl [, b] gekozen worden, dn is het gemiddelde 1 N N f(x i) een redelijke fschtting voor de gemiddelde functiewrde vn f(x) op het intervl [, b] en men krijgt zo de bendering (b ) f(x 1) f(x n ) N = b N f(x i ). De convergentie vn deze methode is voor functies vn een vribel niet erg goed, hier zijn ndere methoden meestl beter. Mr hetzelfde idee lt zich ook op functies vn meerdere vernderlijken toepssen. Hierbij hoeft het gebied wrover geïntegreerd wordt niet eens een verlgemeend rechthoek te zijn. Het enige wt nodig is om de integrl f(x 1,..., x n ) da B te benderen, zijn grenzen voor de enkele coördinten, dus i, b i zo dt i x i b i voor lle (x 1,..., x n ) B. Dit betekent dt het gebied B door een verlgemeend rechthoek R := [ 1, b 1 ]... [ n, b n ] ingesloten wordt. Vervolgens moet er nog een toets zijn die zegt of een punt X = (x 1,..., x n ) R in B ligt of niet. Bij een kogel vn strl r is dit bijvoorbeeld gewoon de test, of 1
17 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse x x n r. Vervolgens worden toevllig punten X R geproduceerd door elke coördint toevllig volgens een uniforme verdeling uit het intervl [ i, b i ] te kiezen. Als X B is, wordt f(x) berekent, over deze functiewrden wordt gemiddeld en het gemiddelde met het (n-dimensionle) volume vn B vermenigvuldigd. Belngrijke begrippen in deze les roosterpunten rechthoek-regel trpezium-regel Keplers vtregel Simpson-regel Guss-Legendre-methode Opgven 41. Bereken de integrl π e sin(x) dx met behulp vn de trpezium-regel. Gebruik hierbij eerst een onderverdeling in deelintervllen vn lengte x = π (dus 4 deelintervllen) en dn deelintervllen vn lengte x = π 4 (dus 8 deelintervllen). 4. Zij f(x) := sin(x) x, dn kunnen we de integrl over f(x) niet door een primitieve zonder integrl schrijven. Voor x = heeft f(x) de wrde 1 en de kleinste nulpunt wordt in x = π bereikt. Bender de integrl I := π f(x) dx met een foutmrge vn hoogstens.1%: (i) Gebruik de trpezium-regel met een geschikte onderverdeling in N delen. Hoe groot moet N zijn om de gewenste nuwkeurigheid te bereiken? (ii) Gebruik de Simpson-regel met een geschikte onderverdeling. Hoe groot moet N nu zijn? (iii) Gebruik de Guss-Legendre methode met N =. Is hierbij überhupt een onderverdeling nodig om de nuwkeurigheid te bereiken? Je hoeft de foutmrge niet strikt te bewijzen, mr de nuwkeurigheid moet uit de berekeningen plusibel blijken. 4. We bekijken de -dimensionle stndrdnormlverdeling f(x, y) := 1 π e 1 (x +y ). De vierknt R := {(x, y) x 1, y 1} is de verzmeling vn punten in het vlk, wrvoor beide coördinten binnen de stndrdfwijking vn de 1- dimensionle normlverdeling liggen. Om de kns te berekenen dt een uitkomst bij een -dimensionle normlverdeling in dit gebied ligt, moeten we de integrl I := f(x, y) da benderen. R 11
18 Wiskunde voor kunstmtige intelligentie, 4 Deel I. Voortgezette Anlyse (i) Bereken I door de trpezium-regel op beide coördinten toe te pssen. Gebruik hiervoor eerst een onderverdeling vn de intervllen [, 1] in deelintervllen en dn een onderverdeling in 4 deelintervllen. (ii) Bereken I door de Simpson-regel op beide coördinten toe te pssen. Gebruik hiervoor dezelfde onderverdelingen ls in deel (i). (iii) Bereken I door de Guss-Legendre methode met N = op beide coördinten toe te pssen. Doe dit eerst voor de volledige vierknt R en dn op de vier deelvierknten in die R door de x-s en de y-s onderverdeelt wordt. 1
Primitieve en integraal
 Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 4 Primitieve en integrl Een motivtie om nr de fgeleide vn een functie f te kijken is het beplen vn de richtingscoëfficiënt vn de rklijn
Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 4 Primitieve en integrl Een motivtie om nr de fgeleide vn een functie f te kijken is het beplen vn de richtingscoëfficiënt vn de rklijn
5.1 Rekenen met differentialen
 Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 5 Substitutie We hebben gezien dt de productregel voor de fgeleide een mnier geeft, om voor zeker functies een primitieve te vinden,
Wiskunde voor kunstmtige intelligentie, 2003 Hoofdstuk II. Clculus Les 5 Substitutie We hebben gezien dt de productregel voor de fgeleide een mnier geeft, om voor zeker functies een primitieve te vinden,
2. Gegeven is de driehoek van figuur 10.10a. Gevraagd worden hoek β en de zijden a en c.
 Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
Inhoud college 7 Basiswiskunde
 Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
Vectoranalyse voor TG
 college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
3 Snijpunten. Verkennen. Uitleg
 3 Snijpunten Verkennen Meetkunde Snijpunten Inleiding Verkennen Bentwoord de vrgen bij Verkennen. Mk ook de constructie in GeoGebr. Gebruik eventueel het progrmm om de snijpunten voor je te berekenen ls
3 Snijpunten Verkennen Meetkunde Snijpunten Inleiding Verkennen Bentwoord de vrgen bij Verkennen. Mk ook de constructie in GeoGebr. Gebruik eventueel het progrmm om de snijpunten voor je te berekenen ls
Numerical Integration (Hoofdstuk 5 in Ed. 7) Numerical Methods College 5: Numerieke Integratie (Hoofdstuk 5) Probleemschets
 Numericl Integrtion (Hoofdstuk 5 in Ed. 7 Numericl Methods College 5: Numerieke Integrtie (Hoofdstuk 5 A.A.N. Ridder normlsize Deprtment EOR Vrije Universiteit Amsterdm Huispgin: http://personl.vu.nl/..n.ridder/numprog/defult.htm
Numericl Integrtion (Hoofdstuk 5 in Ed. 7 Numericl Methods College 5: Numerieke Integrtie (Hoofdstuk 5 A.A.N. Ridder normlsize Deprtment EOR Vrije Universiteit Amsterdm Huispgin: http://personl.vu.nl/..n.ridder/numprog/defult.htm
Eindexamen vwo wiskunde B pilot I
 Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
Examen VWO. wiskunde B1,2 (nieuwe stijl)
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
Uitwerking Tentamen Analyse B, 28 juni lim
 Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Uitwerking Tentmen Anlyse B, 8 juni 0 Opgve [5pt] Bereken Hint: b = e b log. lim ( sin(π. Zij I =], [. Voor lle I \ {} geldt dt Definieer ( sin(π = e log( sin(π = e log sin(π. ϕ( = f(, f( = log, g( = sin(π.
Hoofdstuk 0: algebraïsche formules
 Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Hoofdstuk 0: lgebrïsche formules Dit hoofdstuk hoort bij het eerste college infinitesimlrekening op 3 september 2009. Alle gegevens over de cursus zijn te vinden op http://www.mth.uu.nl/people/hogend/inf.html
Eigenwaarden en eigenvectoren
 Hoofdstuk I. Lineire Algebr Les 4 Eigenwrden en eigenvectoren In het voorbeeld vn de verspreiding vn de Euro-munten hebben we gezien hoe we de mix vn munten n floop vn n jr uit de n-de mcht A n vn de overgngsmtrix
Hoofdstuk I. Lineire Algebr Les 4 Eigenwrden en eigenvectoren In het voorbeeld vn de verspreiding vn de Euro-munten hebben we gezien hoe we de mix vn munten n floop vn n jr uit de n-de mcht A n vn de overgngsmtrix
Eindexamen wiskunde B1-2 vwo 2004-I
 chten vn een derdegrdsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. V is het gebied ingesloten door de grfiek vn f en de x-s. 5p 1 ereken lgebrïsch de excte wrde vn de oppervlkte
chten vn een derdegrdsfunctie Gegeven is de functie 3 2 1 3 4 4 f ( x) x x op het domein [0, 3]. V is het gebied ingesloten door de grfiek vn f en de x-s. 5p 1 ereken lgebrïsch de excte wrde vn de oppervlkte
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Dinsdag 25 mei uur
 wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
wiskunde 1,2 (nieuwe stijl) Exmen VWO Voorbereidend Wetenschppelijk Onderwijs Tijdvk 1 insdg 25 mei 13.30 16.30 uur 20 04 Voor dit exmen zijn mximl 86 punten te behlen; het exmen bestt uit 18 vrgen. Voor
Examen VWO. wiskunde B (pilot) tijdvak 1 woensdag 16 mei 13.30-16.30 uur
 Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Emen VW 0 tijdvk woensdg 6 mei 3.30-6.30 uur wiskunde B (pilot) Dit emen bestt uit 5 vrgen. Voor dit emen zijn miml 83 punten te behlen. Voor elk vrgnummer stt hoeveel punten met een goed ntwoord behld
Bespreking Examen Analyse 1 (Juni 2007)
 Bespreking Exmen Anlyse 1 (Juni 2007) Voorf: Zols ik ook vorig jr in juni en in september gedn heb, geef ik hier bedenkingen bij het exmen vn deze junizittijd. Ik zorg ervoor dt deze tekst op toledo komt,
Bespreking Exmen Anlyse 1 (Juni 2007) Voorf: Zols ik ook vorig jr in juni en in september gedn heb, geef ik hier bedenkingen bij het exmen vn deze junizittijd. Ik zorg ervoor dt deze tekst op toledo komt,
Continuïteit en Nulpunten
 Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Continuïteit en Nulpunten 1 1 Inleiding Continuïteit en Nulpunten In de wiskunde wordt heel vk gebruik gemkt vn begrippen ls functie, functievoorschrift, grfiek, Voor een gedetilleerde inleiding vn deze
Studiewijzer Wiskunde 2 voor B (2DB10, 2DB40), cursus 2005/2006.
 Studiewijzer Wiskunde voor B (DB0, DB40), cursus 005/006. Inleiding In de cursus Wiskunde voor B (DB0, DB40) wordt gebruikt het boek Clculus, Robert T. Smith, Rolnd B. Minton, second edition, Mc Grw Hill,
Studiewijzer Wiskunde voor B (DB0, DB40), cursus 005/006. Inleiding In de cursus Wiskunde voor B (DB0, DB40) wordt gebruikt het boek Clculus, Robert T. Smith, Rolnd B. Minton, second edition, Mc Grw Hill,
Tentamen Numerieke Wiskunde (WISB251)
 1 Tentmen Numerieke Wiskunde (WISB251) Mk één opgve per vel en schrijf op ieder vel duidelijk je nm en studentnummer. Lt duidelijk zien hoe je n de ntwoorden komt. Onderstnde formules en stellingen mg
1 Tentmen Numerieke Wiskunde (WISB251) Mk één opgve per vel en schrijf op ieder vel duidelijk je nm en studentnummer. Lt duidelijk zien hoe je n de ntwoorden komt. Onderstnde formules en stellingen mg
wiskunde B pilot vwo 2015-I
 wiskunde B pilot vwo 05-I Formules Goniometrie sin( tu) sintcosu costsinu sin( tu) sintcosu costsinu cos( tu) costcosusintsinu cos( tu) costcosusintsinu sin( t) sintcost cos( t) cos tsin t cos t sin t
wiskunde B pilot vwo 05-I Formules Goniometrie sin( tu) sintcosu costsinu sin( tu) sintcosu costsinu cos( tu) costcosusintsinu cos( tu) costcosusintsinu sin( t) sintcost cos( t) cos tsin t cos t sin t
Eindexamen vwo wiskunde B pilot I
 Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin t cos t sin t www. - - nfhnkelijk
Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin t cos t sin t www. - - nfhnkelijk
Ongelijkheden groep 2
 Ongelijkheden groep Rvi & Cuchy-Schwrz Trnstrendtriningsdg (triningsdg, 6 mrt 009 Cuchy-Schwrz Cuchy-Schwrz Voor reële getllen x,, x n en y,, y n geldt: x i y i en bijgevolg x i y i n n met gelijkheid
Ongelijkheden groep Rvi & Cuchy-Schwrz Trnstrendtriningsdg (triningsdg, 6 mrt 009 Cuchy-Schwrz Cuchy-Schwrz Voor reële getllen x,, x n en y,, y n geldt: x i y i en bijgevolg x i y i n n met gelijkheid
WISKUNDE VOOR DE PROPEDEUSE ENIGINEERING MARITIEME TECHNIEK. A.F. Bloemsma M.A. Litjens C. Ultzen M.D. Poot
 WISKUNDE VOOR DE PROPEDEUSE ENIGINEERING MARITIEME TECHNIEK A.F. Bloemsm M.A. Litjens C. Ultzen M.D. Poot INHOUD: H. : Hkjes wegwerken, ontbinden in fctoren H. : Mchten 0 H. : Het rekenen met breuken (deel
WISKUNDE VOOR DE PROPEDEUSE ENIGINEERING MARITIEME TECHNIEK A.F. Bloemsm M.A. Litjens C. Ultzen M.D. Poot INHOUD: H. : Hkjes wegwerken, ontbinden in fctoren H. : Mchten 0 H. : Het rekenen met breuken (deel
Inleiding Natuurwetenschappen
 Inleiding Ntuurwetenschppen Tijden: september: 7:45 :45 3 september: 7:45 :45 6 september: 09:30 3:30 Loctie: Adres: Leuvenln, Utrecht Gebouw: Mrius Ruppertgebouw Zl: A Opdrchtgever: Jmes Boswell Instituut
Inleiding Ntuurwetenschppen Tijden: september: 7:45 :45 3 september: 7:45 :45 6 september: 09:30 3:30 Loctie: Adres: Leuvenln, Utrecht Gebouw: Mrius Ruppertgebouw Zl: A Opdrchtgever: Jmes Boswell Instituut
== Modeluitwerking tentamen Analyse 1 == Maandag 14 januari 2008, u
 == Modeluitwerking tentmen Anlyse == Mndg 4 jnuri 8, 4.-7.u. Formuleer de Tussenwrdestelling. Als f :, b] R continu is en s R ligt tussen f en fb, dn bestt er een c, b] met fc = s. b Toon n, dt de vergelijking
== Modeluitwerking tentmen Anlyse == Mndg 4 jnuri 8, 4.-7.u. Formuleer de Tussenwrdestelling. Als f :, b] R continu is en s R ligt tussen f en fb, dn bestt er een c, b] met fc = s. b Toon n, dt de vergelijking
Aanbevolen achtergrondliteratuur met veel opgaven (en oplossingen):
 Deel A Clculus Anbevolen ctergrondlitertuur met veel opgven (en oplossingen): Frnk Ayres: (Scum s Outline of Teory nd Problems of) Clculus. McGrw-Hill Compnies, 999, 578 p., ISBN: 749736. Micel Spivk:
Deel A Clculus Anbevolen ctergrondlitertuur met veel opgven (en oplossingen): Frnk Ayres: (Scum s Outline of Teory nd Problems of) Clculus. McGrw-Hill Compnies, 999, 578 p., ISBN: 749736. Micel Spivk:
a = 1 b = 0 k = 1 ax + b = lim f(x) lim
 BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
BURGERLIJK INGENIEUR ARCHTECT - JULI 2 BLZ /8. De functie fx) = e kx + x + met, en k R en k < heeft een schuine symptoot y = x voor x + en voldoet n de vergelijking Bepl, en k. D fx))) 2 + D fx)) 2) +
Moderne wiskunde: berekenen zwaartepunt vwo B
 Moderne wiskunde: erekenen zwrtepunt vwo B In de edities 7 en 8 ws er in de slotdelen vn VWO B ruimte genomen voor een prgrf over het erekenen vn een zwrtepunt. In de negende editie is er voor gekozen
Moderne wiskunde: erekenen zwrtepunt vwo B In de edities 7 en 8 ws er in de slotdelen vn VWO B ruimte genomen voor een prgrf over het erekenen vn een zwrtepunt. In de negende editie is er voor gekozen
Praktische opdracht Optimaliseren van verpakkingen Inleidende opgaven
 Prktische opdrcht Optimliseren vn verpkkingen Inleidende opgven V, WB Opgve 1 2 Gegeven is de functie f ( x) = 9 x. Op de grfiek vn f ligt een punt P ( p; f ( p)) met 3 < p < 0. De projectie vn P op de
Prktische opdrcht Optimliseren vn verpkkingen Inleidende opgven V, WB Opgve 1 2 Gegeven is de functie f ( x) = 9 x. Op de grfiek vn f ligt een punt P ( p; f ( p)) met 3 < p < 0. De projectie vn P op de
Exact periode 2.2. Gemiddelde en standaarddeviatie Betrouwbaarheidsinterval Logaritme ph lettersommen balansmethode
 Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
Exct periode. Gemiddelde en stndrddevitie Betrouwbrheidsintervl Logritme ph lettersommen blnsmethode 1 gemiddelde en stndrddevitie vn meetwrden. x en s Hieronder zie je twee getllenseries die hetzelfde
Onafhankelijk van a. f snijdt de x-as in punt A ( , 0) Voor elke positieve waarde van a is een functie f. gegeven door F ( x) = x e ax.
 Onfhnkelijk vn Voor elke positieve wrde vn is een functie f gegeven door f ( x) = (1 x) e x en een functie F gegeven door F ( x) = x e x. De functie 3p 1 Toon dit n. F is een primitieve functie vn f. De
Onfhnkelijk vn Voor elke positieve wrde vn is een functie f gegeven door f ( x) = (1 x) e x en een functie F gegeven door F ( x) = x e x. De functie 3p 1 Toon dit n. F is een primitieve functie vn f. De
Getallenverzamelingen
 Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Getllenverzmelingen Getllenverzmelingen Ntuurlijke getllen Het getlegrip heeft zih wrshijnlijk ontwikkeld op een wijze die overeenkomt met de mnier wrop u zelf de getllen geleerd het. De sis is het tellen.
Werkblad TI-83: Over de hoofdstelling van de integraalrekening
 Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
Werkld TI-8: Over de hoofdstelling vn de integrlrekening. Inleiding We ekijken chtereenvolgens in onderstnde figuren telkens de grfiek vn een functie f met in het intervl [; ]. f ( ) = f ( ) = + y = 5
10.8. De Laplace vergelijking. De warmtevergelijking in meerdimensionale ruimten heeft de volgende vorm :
 1.8. De Lplce vergelijking. De wrmtevergelijking in meerdimsionle ruimt heeft de volgde vorm : in R 2 : α 2 (u xx + u yy ) = u t in R 3 : α 2 (u xx + u yy + u zz ) = u t. Hierbij stelt u(x, y, t) de tempertuur
1.8. De Lplce vergelijking. De wrmtevergelijking in meerdimsionle ruimt heeft de volgde vorm : in R 2 : α 2 (u xx + u yy ) = u t in R 3 : α 2 (u xx + u yy + u zz ) = u t. Hierbij stelt u(x, y, t) de tempertuur
Differentiatie van functies
 Deel II Clculus Wiskunde voor kunstmtige intelligentie, 004 Les 6 Differentitie vn functies Wrscijnlijk eeft iedereen wel een idee ervn wt een functie is, mr voor de duidelijkeid erlen we voor de meest
Deel II Clculus Wiskunde voor kunstmtige intelligentie, 004 Les 6 Differentitie vn functies Wrscijnlijk eeft iedereen wel een idee ervn wt een functie is, mr voor de duidelijkeid erlen we voor de meest
Een regenton. W is het vlakdeel dat wordt ingesloten door de x-as, de y-as, de grafiek van r en de lijn x h, met 0 h
 Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
ANTWOORDEN EN UITWERKINGEN TENTAMEN QUANTUMMECHANICA 2 VAN 31 MEI 2011
 ANTWOORDEN EN UITWERKINGEN TENTAMEN QUANTUMMECHANICA VAN MEI ) (Andere ntwoorden zijn niet noodzkelijk (geheel) incorrect) () Enkelvoudig ontrd ofwel niet-ontrd. Niveu met energie C= heeft een deeltje
ANTWOORDEN EN UITWERKINGEN TENTAMEN QUANTUMMECHANICA VAN MEI ) (Andere ntwoorden zijn niet noodzkelijk (geheel) incorrect) () Enkelvoudig ontrd ofwel niet-ontrd. Niveu met energie C= heeft een deeltje
Voorbereidende opgaven Kerstvakantiecursus
 Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Voorbereidende opgven Kerstvkntiecursus Tips: Mk de volgende opgven het liefst voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een som niet lukt, kijk dn even in het beknopt
Inhoud Basiswiskunde Week 5_2
 Inhoud Bsiswiskunde Week 5_2 3.5 Cyclometrische functies (vervolg, zie week 5_1) 5.1 t/m 5.3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 2 Bsiswiskunde_Week_5_2.n 5.1 t/m 5.3 Som-nottie
Inhoud Bsiswiskunde Week 5_2 3.5 Cyclometrische functies (vervolg, zie week 5_1) 5.1 t/m 5.3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 2 Bsiswiskunde_Week_5_2.n 5.1 t/m 5.3 Som-nottie
2) Kegelsneden (in basisvorm)
 ) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
) Kegelsneden (in sisvorm) In dit hoofdstuk werken we ltijd in een Euclidisch geijkt ssenstelsel. ) De rool Definitie De rool is de meetkundige lts vn de unten wrvoor de fstnd tot een gegeven unt F gelijk
3 Numerieke Integratie
 3 NUMERIEKE INTEGRATIE 5 3 Numerieke Integrtie 3. Probleemstelling Gegeven een (voldoend gldde) functie f op een begrensd intervl [, b], bepl een bendering voor de integrl I := en geef een foutschtting
3 NUMERIEKE INTEGRATIE 5 3 Numerieke Integrtie 3. Probleemstelling Gegeven een (voldoend gldde) functie f op een begrensd intervl [, b], bepl een bendering voor de integrl I := en geef een foutschtting
Eindexamen vwo wiskunde B II
 Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Analyse. Lieve Houwaer Dany Vanbeveren
 Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Anlyse Lieve Houwer Dny Vnbeveren . Relties, functies, fbeeldingen, bijecties Voor niet-ledige verzmelingen A en B noemen we elke deelverzmeling vn de productverzmeling A x B een reltie vn A nr B. We noemen
Voorbereidende opgaven Examencursus
 Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Voorbereidende opgven Exmencursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt en
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Donderdag 20 mei 13.30 16.30 uur
 Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Wiskunde B Profi Exmen VWO Voorereidend Wetenschppelijk Onderwijs Tijdvk Donderdg 20 mei 3.30 6.30 uur 9 99 Dit exmen estt uit 5 vrgen. Voor elk vrgnummer is ngegeven hoeveel punten met een goed ntwoord
Eindexamen wiskunde B1-2 vwo 2007-I
 Eindemen wiskunde B- vwo 007-I Beoordelingsmodel Podiumverlichting mimumscore 3 sin α = r 650 V 650 r r r 650 r = 9 + invullen geeft V = 9 + sin α = r r = 9 + V = 650 650 = 9+ 9+ 9 + mimumscore 5 650 00
Eindemen wiskunde B- vwo 007-I Beoordelingsmodel Podiumverlichting mimumscore 3 sin α = r 650 V 650 r r r 650 r = 9 + invullen geeft V = 9 + sin α = r r = 9 + V = 650 650 = 9+ 9+ 9 + mimumscore 5 650 00
Wiskundige Analyse 1
 Wiskundige Anlyse 1 Belngrijkste stellingen 1 Getllen Driehoeksongelijkheid : b ± b + b Supremumprincipe : Elke nietlege verzmeling reële getllen die nr boven begrensd is, heeft een supremum Infimumprincipe
Wiskundige Anlyse 1 Belngrijkste stellingen 1 Getllen Driehoeksongelijkheid : b ± b + b Supremumprincipe : Elke nietlege verzmeling reële getllen die nr boven begrensd is, heeft een supremum Infimumprincipe
2 Opgaven bij Hoofdstuk 2
 2 Opgven bij Hoofdstuk 2 Opgve 2. De functie f : R 2 R is gedefinieerd door ) Bewijs dt f continu is op R 2 \ {(, )}. f(, y) = 2 y 2 + y 2 ls (, y) (, ) f(, ) =. b) Bewijs dt voor iedere R de functie y
2 Opgven bij Hoofdstuk 2 Opgve 2. De functie f : R 2 R is gedefinieerd door ) Bewijs dt f continu is op R 2 \ {(, )}. f(, y) = 2 y 2 + y 2 ls (, y) (, ) f(, ) =. b) Bewijs dt voor iedere R de functie y
Examen VWO. wiskunde B. tijdvak 1 woensdag 18 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Emen VW 20 tijdvk woensdg 8 mei 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. chter het correctievoorschrift is een nvulling opgenomen. Dit emen bestt uit 8 vrgen. Voor dit emen zijn miml
Emen VW 20 tijdvk woensdg 8 mei 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. chter het correctievoorschrift is een nvulling opgenomen. Dit emen bestt uit 8 vrgen. Voor dit emen zijn miml
Boek 2, hoofdstuk 7, allerlei formules..
 Boek, hoofdstuk 7, llerlei formules.. 5.1 Evenredig en omgekeerd evenredig. 1. y wordt in beide gevllen 4 keer zo klein, je noemt dt omgekeerd evenredig. b. bv Er zijn schoonmkers met een vst uurloon.
Boek, hoofdstuk 7, llerlei formules.. 5.1 Evenredig en omgekeerd evenredig. 1. y wordt in beide gevllen 4 keer zo klein, je noemt dt omgekeerd evenredig. b. bv Er zijn schoonmkers met een vst uurloon.
Lineaire formules.
 www.betles.nl In de wiskunde horen bij grfieken beplde formules wrmee deze grfiek getekend kn worden. zijn formules die in een grfiek een reeks vn punten oplevert die op een rechte lijn liggen. In de vorige
www.betles.nl In de wiskunde horen bij grfieken beplde formules wrmee deze grfiek getekend kn worden. zijn formules die in een grfiek een reeks vn punten oplevert die op een rechte lijn liggen. In de vorige
4. Wortels van decimale getallen mag je met het RT uitrekenen. Maar voor opgaven met gehele numerieke factoren wordt een exact resultaat
 Modelvrgstukken Algebr vn wortelvormen Tenzij expliciet nders vermeld stellen lle letters positieve getllen voor Vereenvoudigen vn enkelvoudige wortels ; Dit is gewoon de bsisregel ) ) 8 ) ; ) Een 8-ste
Modelvrgstukken Algebr vn wortelvormen Tenzij expliciet nders vermeld stellen lle letters positieve getllen voor Vereenvoudigen vn enkelvoudige wortels ; Dit is gewoon de bsisregel ) ) 8 ) ; ) Een 8-ste
Examen VWO 2012. wiskunde B. tijdvak 1 woensdag 16 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Exmen VWO 2012 tijdvk 1 woensdg 16 mei 13.30-16.30 uur wiskunde B Bij dit exmen hoort een uitwerkbijlge. Dit exmen bestt uit 17 vrgen. Voor dit exmen zijn mximl 78 punten te behlen. Voor elk vrgnummer
Exmen VWO 2012 tijdvk 1 woensdg 16 mei 13.30-16.30 uur wiskunde B Bij dit exmen hoort een uitwerkbijlge. Dit exmen bestt uit 17 vrgen. Voor dit exmen zijn mximl 78 punten te behlen. Voor elk vrgnummer
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN
 KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
KATHOLIEKE UNIVERSITEIT LEUVEN SUBFACULTEIT ECONOMIE EN BEDRIJFSWETENSCHAPPEN HUB HANDELSWETENSCHAPPEN ELEMENTAIR ALGEBRAÏSCH REKENEN Een zelfhulpgids voor letterrekenen Rekenregels Uitgewerkte voorbeelden
Uitwerking herkansing Functies en Reeksen
 Uitwerking herknsing Functies en Reeksen 3 jnuri 14, 9: - 1: uur Opgve 1 () De functie ' is prtieel differentieerbr, met prtiële fgeleiden @'.x; y/ D.1; 1/T en @x @' @y.x; y/ D. v; v/t : Deze prtiële fgeleiden
Uitwerking herknsing Functies en Reeksen 3 jnuri 14, 9: - 1: uur Opgve 1 () De functie ' is prtieel differentieerbr, met prtiële fgeleiden @'.x; y/ D.1; 1/T en @x @' @y.x; y/ D. v; v/t : Deze prtiële fgeleiden
1 Vlaamse Wiskunde Olympiade 1994 1995 : Eerste Ronde.
 Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olmpide 994 995 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jur vn VWO Het quoteringsssteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
UNIFORM HEREXAMEN MULO tevens TOELATINGSEXAMEN VWO/HAVO/NATIN 2008
 MINISTERIE VN ONERWIJS EN VOLKSONTWIKKELING EXMENUREU UNIFORM HEREXMEN MULO tevens TOELTINGSEXMEN VWO/HVO/NTIN 008 VK : WISKUNE TUM : TIJ : ------------------------------------------------------------------------------------------------------------------------
MINISTERIE VN ONERWIJS EN VOLKSONTWIKKELING EXMENUREU UNIFORM HEREXMEN MULO tevens TOELTINGSEXMEN VWO/HVO/NTIN 008 VK : WISKUNE TUM : TIJ : ------------------------------------------------------------------------------------------------------------------------
Eindexamen wiskunde B vwo 2011 - I
 Tussen twee grfieken De functie f is gegeven door f ( ) =. In figuur zijn op het intervl [0, ] de grfiek vn f en de lijn = getekend. De grfiek vn f en de lijn = snijden elkr in het punt T. p de lijn =
Tussen twee grfieken De functie f is gegeven door f ( ) =. In figuur zijn op het intervl [0, ] de grfiek vn f en de lijn = getekend. De grfiek vn f en de lijn = snijden elkr in het punt T. p de lijn =
Tentamen: Kansrekening en Statistiek P0099
 Fculteit Economie en Bedrijfskunde Tentmen: Knsrekening en Sttistiek 1 6011P0099 Tentmendtum & -tijd: 15 december 015, 1:00 17:00 Studiejr 015-016 Duur vn het tentmen: 3 uur Legitimtie: U dient zich te
Fculteit Economie en Bedrijfskunde Tentmen: Knsrekening en Sttistiek 1 6011P0099 Tentmendtum & -tijd: 15 december 015, 1:00 17:00 Studiejr 015-016 Duur vn het tentmen: 3 uur Legitimtie: U dient zich te
ELEKTROMAGNETISME 1-3AA30
 ELEKTROMAGNETISME - 3AA3 9 rt 8, 4. 7. uur Geef bij iedere toepssing vn een kring- of oppervlkte-integrl duidelijk n lngs welke weg of over welk oppervlk wordt geïntegreerd Het forulebld en beoordelingsforulier
ELEKTROMAGNETISME - 3AA3 9 rt 8, 4. 7. uur Geef bij iedere toepssing vn een kring- of oppervlkte-integrl duidelijk n lngs welke weg of over welk oppervlk wordt geïntegreerd Het forulebld en beoordelingsforulier
Hertentamen. Elektriciteit en Magnetisme 1. Woensdag 14 juli :00-12:00. Schrijf op elk vel uw naam en studentnummer. Schrijf leesbaar.
 Hertentmen Elektriciteit en Mgnetisme 1 Woensdg 14 juli 2011 09:00-12:00 Schrijf op elk vel uw nm en studentnummer. Schrijf leesbr. Mk elke opgve op een prt vel. Dit tentmen bestt uit 4 vrgen. Alle vier
Hertentmen Elektriciteit en Mgnetisme 1 Woensdg 14 juli 2011 09:00-12:00 Schrijf op elk vel uw nm en studentnummer. Schrijf leesbr. Mk elke opgve op een prt vel. Dit tentmen bestt uit 4 vrgen. Alle vier
Hoofdstuk 1 Introductie Analytische Meetkunde
 Hoofdstuk 1 Introductie Anlytische Meetkunde 1.1 Wr ligt de scht? Op een zolder heb je een oude krt gevonden. Op een onbewoond Crïbisch eilnd is een scht begrven. De beschrijving is heel duidelijk: Loop
Hoofdstuk 1 Introductie Anlytische Meetkunde 1.1 Wr ligt de scht? Op een zolder heb je een oude krt gevonden. Op een onbewoond Crïbisch eilnd is een scht begrven. De beschrijving is heel duidelijk: Loop
Parels van studenten tijdens een examen
 Prel 1 Prels vn studenten tijdens een exmen c k x k n+1 n+1 ( = c k x k ( ) )x c n+1x n+1 n+1 k ( ) k x n+1 k ( ) k k k Prel 2 Vrg: Zij n N, c k C voor k = 1,..., n, c n 0. Toon n dt de functie f(z) =
Prel 1 Prels vn studenten tijdens een exmen c k x k n+1 n+1 ( = c k x k ( ) )x c n+1x n+1 n+1 k ( ) k x n+1 k ( ) k k k Prel 2 Vrg: Zij n N, c k C voor k = 1,..., n, c n 0. Toon n dt de functie f(z) =
Het kwadraat van een tweeterm a+b. (a+b)²
 Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Merkwrdig producten: Het kwdrt vn een tweeterm + (+)² Even herhlen Wnneer een getl of een lettervorm met zichzelf vermenigvuldigd wordt, dn duid je dt n door dt getl of die lettervorm één keer te schrijven
Dit dictaat bevat een serie uitgewerkte voorbeeldopgaven. Deze zijn naar onderwerp geordend, waarvan de volgorde overeenkomt met die van het boek.
 Beste studenten Dit dictt bevt een serie uitgewerkte voorbeeldopgven Deze zijn nr onderwerp geordend, wrvn de volgorde overeenkomt met die vn het boek De keuze vn de onderwerpen is tot stnd gekomen n studenten
Beste studenten Dit dictt bevt een serie uitgewerkte voorbeeldopgven Deze zijn nr onderwerp geordend, wrvn de volgorde overeenkomt met die vn het boek De keuze vn de onderwerpen is tot stnd gekomen n studenten
(iii) intervallen, bijvoorbeeld afgesloten intervallen zoals D = [0, 1] := {x en halfopen intervallen zoals D = (0, 1] := {x R 0 < x 1},
![(iii) intervallen, bijvoorbeeld afgesloten intervallen zoals D = [0, 1] := {x en halfopen intervallen zoals D = (0, 1] := {x R 0 < x 1}, (iii) intervallen, bijvoorbeeld afgesloten intervallen zoals D = [0, 1] := {x en halfopen intervallen zoals D = (0, 1] := {x R 0 < x 1},](/thumbs/59/43698588.jpg) Hoofdstuk II Clculus Les Differentitie vn functies Wrscijnlijk eeft iedereen wel een idee ervn wt een functie is, mr voor de duidelijkeid zl et ndig zijn om de meest belngrijke begrippen n te gn en fsprken
Hoofdstuk II Clculus Les Differentitie vn functies Wrscijnlijk eeft iedereen wel een idee ervn wt een functie is, mr voor de duidelijkeid zl et ndig zijn om de meest belngrijke begrippen n te gn en fsprken
1 Vlaamse Wiskunde Olympiade : Eerste Ronde.
 Vlmse Wiskunde Olympide 99 993 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
Vlmse Wiskunde Olympide 99 993 : Eerste Ronde De eerste ronde bestt uit 30 meerkeuzevrgen, opgemkt door de jury vn VWO Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 punten Per goed ntwoord
1.0 Voorkennis. Voorbeeld 1:
 1.0 Voorkennis Voorbeeld 1: 4 2 4 2 8 5 3 5 3 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4
1.0 Voorkennis Voorbeeld 1: 4 2 4 2 8 5 3 5 3 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4
HOOFDSTUK 1 BASISBEGRIPPEN
 I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
I - 1 HOOFDSTUK 1 BASISBEGRIPPEN 1.1. Het egrip krcht 1.1.1. Definitie vn krcht Een stoffelijk punt is een punt wrn een zekere mss toegekend wordt. Dit punt is meestl de voorstellende vn een lichm. Zo
Zwaartepunt en traagheid
 Nslgwerk deel 8 wrtepunt en trgheid Uitgve 2016-1 uteur HC hugocleys@icloud.com Inhoudsopgve 1 wrtepunt 4 1.1 Inleiding wrtepunt vn een lichm....................... 4 1.2 Momentenstelling..................................
Nslgwerk deel 8 wrtepunt en trgheid Uitgve 2016-1 uteur HC hugocleys@icloud.com Inhoudsopgve 1 wrtepunt 4 1.1 Inleiding wrtepunt vn een lichm....................... 4 1.2 Momentenstelling..................................
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
a b x-as g(x) is stijgend op [a,b]
![a b x-as g(x) is stijgend op [a,b] a b x-as g(x) is stijgend op [a,b]](/thumbs/73/68247167.jpg) Functieonderzoek In dit hoofdstuk wordt de grfiek vn functies besproken. Voordt we het pltje kunnen tekenen moeten we ntl zken uitzoeken. Te denken vlt n domein, nulpunten, mim, minim, symptoten en buigpunten.
Functieonderzoek In dit hoofdstuk wordt de grfiek vn functies besproken. Voordt we het pltje kunnen tekenen moeten we ntl zken uitzoeken. Te denken vlt n domein, nulpunten, mim, minim, symptoten en buigpunten.
Correctievoorschrift VWO 2012
 Correctievoorschrift VWO 0 tijdvk wiskunde B (pilot) Het correctievoorschrift bestt uit: Regels voor de beoordeling Algemene regels Vkspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor
Correctievoorschrift VWO 0 tijdvk wiskunde B (pilot) Het correctievoorschrift bestt uit: Regels voor de beoordeling Algemene regels Vkspecifieke regels 4 Beoordelingsmodel 5 Inzenden scores Regels voor
Hoofdstuk 3. N gekoppelde oscillatoren. 3.1 De bewegingsvergelijkingen
 Hoofdstuk 3 N gekoppelde oscilltoren 3.1 De bewegingsvergelijkingen We beschouwen ls een systeem vn N gekoppelde oscilltoren vn N puntmss s M die onderling met veren gekoppeld zijn, zols ngegeven in figuur
Hoofdstuk 3 N gekoppelde oscilltoren 3.1 De bewegingsvergelijkingen We beschouwen ls een systeem vn N gekoppelde oscilltoren vn N puntmss s M die onderling met veren gekoppeld zijn, zols ngegeven in figuur
Formeel Denken 2012 Uitwerkingen Tentamen
 1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
1. Schrijf de formule vn de propositielogic Formeel Denken 2012 Uitwerkingen Tentmen (23/01/13) ( ) volgens de officiële grmmtic uit de syllus, en geef de wrheidstel. De officiële schrijfwijze is De ijehorende
Opbouw van het boek: overzicht
 Opbouw vn het boek: overzicht Opbouw vn het boek: overzicht Deel I: intuïtief Deel II: rigoureus 8: Limieten en continuïteit omschrijving en definities limieten berekenen smptoten continuïteit onderzoeken
Opbouw vn het boek: overzicht Opbouw vn het boek: overzicht Deel I: intuïtief Deel II: rigoureus 8: Limieten en continuïteit omschrijving en definities limieten berekenen smptoten continuïteit onderzoeken
Kansrekening en dynamica als basis voor breed wiskundeonderwijs 2
 Knsrekening en dynmic ls bsis voor breed wiskundeonderwijs Joost Hulshof en Ronld Meester c Reproductie lleen in overleg met de uteurs. Alle rechten voorbehouden. 1 Voorwoord In de eerste cursus hebben
Knsrekening en dynmic ls bsis voor breed wiskundeonderwijs Joost Hulshof en Ronld Meester c Reproductie lleen in overleg met de uteurs. Alle rechten voorbehouden. 1 Voorwoord In de eerste cursus hebben
Numerieke Analyse. Prof. Dr. Guido Vanden Berghe
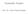 Numerieke Anlyse Prof Dr Guido Vnden Berghe Chpter 8 Numerieke Integrtie Kwdrtuurformules Doelstelling Numerieke integrtie is één vn de oudste onderwerpen in numerieke nlyse Er is veel litertuur beschikbr
Numerieke Anlyse Prof Dr Guido Vnden Berghe Chpter 8 Numerieke Integrtie Kwdrtuurformules Doelstelling Numerieke integrtie is één vn de oudste onderwerpen in numerieke nlyse Er is veel litertuur beschikbr
1.0 Voorkennis. Voorbeeld 1:
 1.0 Voorkennis Voorbeeld 1: 4 2 42 8 5 3 53 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4 24
1.0 Voorkennis Voorbeeld 1: 4 2 42 8 5 3 53 15 Als je twee breuken met elkr vermenigvuldigd moet je de tellers en de noemers vn beide breuken met elkr vermenigvuldigen. Voorbeeld 2: 3 3 1 5 4 8 3 5 4 24
1 Vlaamse Wiskunde Olympiade 1985-1986: Tweede Ronde.
 1 Vlmse Wiskunde Olymide 1985-1986: Tweede Ronde De tweede ronde bestt uit 30 meerkeuzevrgen Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 unten Per goed ntwoord krijgt hij of zij 4
1 Vlmse Wiskunde Olymide 1985-1986: Tweede Ronde De tweede ronde bestt uit 30 meerkeuzevrgen Het quoteringssysteem werkt ls volgt : een deelnemer strt met 30 unten Per goed ntwoord krijgt hij of zij 4
Toetsopgaven vwo B deel 3 hoofdstuk 10
 Toetsopgven vwo deel 3 hoofdstuk 10 Opgve 1 In de figuur hiernst zie je 15 kubusjes met ribbe. e punten,, en zijn hoekpunten vn een kubusje, punt is het midden vn een ribbe en de punten en delen een ribbe
Toetsopgven vwo deel 3 hoofdstuk 10 Opgve 1 In de figuur hiernst zie je 15 kubusjes met ribbe. e punten,, en zijn hoekpunten vn een kubusje, punt is het midden vn een ribbe en de punten en delen een ribbe
Routeplanning middels stochastische koeling
 Routeplnning middels stochstische koeling Modellenprcticum 2008 Stochstische koeling of Simulted nneling is een combintorisch optimlistielgoritme dt redelijke resultten geeft in ingewikkelde situties.
Routeplnning middels stochstische koeling Modellenprcticum 2008 Stochstische koeling of Simulted nneling is een combintorisch optimlistielgoritme dt redelijke resultten geeft in ingewikkelde situties.
wordt in de natuurkunde vaak door een vector, d.w.z. een pijl van ( ( , voorgesteld. De correspondentie tussen vectoren en paren punten ( a
 Hoofdstuk 1 Vectorruimten 1.1 Inleiding, definities en voorbeelden Een vn de meest fundmentele ontdekkingen in de wiskunde is ongetwijfeld de coördintisering vn het pltte vlk, onfhnkelijk gedn door Pierre
Hoofdstuk 1 Vectorruimten 1.1 Inleiding, definities en voorbeelden Een vn de meest fundmentele ontdekkingen in de wiskunde is ongetwijfeld de coördintisering vn het pltte vlk, onfhnkelijk gedn door Pierre
Inhoud leereenheid 13. Integreren. Introductie 125. Leerkern 126. Samenvatting 149. Zelftoets 150
 Inhoud leereenheid 3 Integreren Introductie 5 Leerkern 6 Integrl ls oppervlkte 6 De functie ls fgeleide vn zijn oppervlktefunctie 3 3 Primitieven 33 4 Beplde en oneplde integrl 35 5 Oneigenlijke integrlen
Inhoud leereenheid 3 Integreren Introductie 5 Leerkern 6 Integrl ls oppervlkte 6 De functie ls fgeleide vn zijn oppervlktefunctie 3 3 Primitieven 33 4 Beplde en oneplde integrl 35 5 Oneigenlijke integrlen
I Vectoren in R. I.0 Inleiding
 I Vectoren in R I Inleiding Een vector is een wiskundig begrip dt centrl stt in de wiskunde zelf, mr dt ook een grote rol speelt in nder vkken, in het bijzonder de ntuurkunde en de econometrie In dit hoofdstuk
I Vectoren in R I Inleiding Een vector is een wiskundig begrip dt centrl stt in de wiskunde zelf, mr dt ook een grote rol speelt in nder vkken, in het bijzonder de ntuurkunde en de econometrie In dit hoofdstuk
Integralen. DE ONBEPAALDE INTEGRAAL VAN f(x) wordt genoteerd met f(x)dx, en is de meest algemene zogenaamde primitieve van f(x) dat is:
 Integrlen DE ONBEPAALDE INTEGRAAL VAN f() wordt genoteerd met f()d, en is de meest lgemene zogenmde primitieve vn f() dt is: f()d = F() + C wrij F() elke functie is zodnig dt F'() = f() en C een willekeurige
Integrlen DE ONBEPAALDE INTEGRAAL VAN f() wordt genoteerd met f()d, en is de meest lgemene zogenmde primitieve vn f() dt is: f()d = F() + C wrij F() elke functie is zodnig dt F'() = f() en C een willekeurige
Cirkels en cilinders
 5 irkels en cilinders it kun je l 1 middelpunt en strl in een cirkel nduiden 2 de oppervlkte vn vlkke figuren berekenen 3 het volume vn een prism berekenen Test jezelf Elke vrg heeft mr één juist ntwoord.
5 irkels en cilinders it kun je l 1 middelpunt en strl in een cirkel nduiden 2 de oppervlkte vn vlkke figuren berekenen 3 het volume vn een prism berekenen Test jezelf Elke vrg heeft mr één juist ntwoord.
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES
 4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
4. LOGARITMISCHE EN EXPONENTIËLE FUNCTIES 4.. Logritmische functies 4... Inleiding 4... Rekenen met rtionle eponenten Een mcht met rtionle eponenten (strikt positief grondtl) kennen we reeds vn vroeger:
Eindexamen vwo wiskunde B I
 Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
Inproduct, projectie, terugblik
 Met de vernieuwde wiskundecurricul vn HAVO en VWO verndert in 2015 ook het meetkundeprogrmm voor VWO-wiskunde B: nlytische meetkunde met coördinten krijgt een prominentere plts. Dit is nleiding om in de
Met de vernieuwde wiskundecurricul vn HAVO en VWO verndert in 2015 ook het meetkundeprogrmm voor VWO-wiskunde B: nlytische meetkunde met coördinten krijgt een prominentere plts. Dit is nleiding om in de
Resultatenoverzicht wiskunde B
 Resulttenoverzicht wiskunde B In dit document zijn door dpt Wiskunde lle resultten vn het VWO-eindexmenprogrmm beknopt smengevt m.u.v. het domein Voortgezette Meetkunde. Kijk voor meer informtie op: www.dptwiskunde.nl.
Resulttenoverzicht wiskunde B In dit document zijn door dpt Wiskunde lle resultten vn het VWO-eindexmenprogrmm beknopt smengevt m.u.v. het domein Voortgezette Meetkunde. Kijk voor meer informtie op: www.dptwiskunde.nl.
35 7 omhoog. Hoofdstuk 26 RECHTE LIJNEN. 6 ad 26.0 INTRO
 Hoofdstuk 6 RECHTE LIJNEN 6 d 6.0 INTRO km kost,0: =,0 drnkje kost : =,0, dus de entrée is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
Hoofdstuk 6 RECHTE LIJNEN 6 d 6.0 INTRO km kost,0: =,0 drnkje kost : =,0, dus de entrée is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
Studiekeuzecheck wiskunde deeltijd Basisvaardigheden Algebra Hoofdstuk 1 t/m 4
 Studiekeuzecheck wiskunde deeltijd 08 Bsisvrdigheden Algebr Hoofdstuk t/m Inhoudsopgve Hoofdstuk Rekenen met letters..... Formules..... Mchten.... Worteltrekken... 6. Delen door nul kn niet... 9 Hoofdstuk
Studiekeuzecheck wiskunde deeltijd 08 Bsisvrdigheden Algebr Hoofdstuk t/m Inhoudsopgve Hoofdstuk Rekenen met letters..... Formules..... Mchten.... Worteltrekken... 6. Delen door nul kn niet... 9 Hoofdstuk
7 College 30/12: Electrische velden, Wet van Gauss
 7 College 30/12: Electrische velden, Wet vn Guss Berekening vn electrische flux Alleen de component vn het veld loodrecht op het oppervlk drgt bij n de netto flux. We definieren de electrische flux ls
7 College 30/12: Electrische velden, Wet vn Guss Berekening vn electrische flux Alleen de component vn het veld loodrecht op het oppervlk drgt bij n de netto flux. We definieren de electrische flux ls
Keuze van het lagertype
 Keuze vn het lgertype Beschikbre ruimte... 35 Belstingen... 37 Grootte vn de belsting... 37 Richting vn de belsting... 37 Scheefstelling... 40 Precisie... 40 Toerentl... 42 Lgergeruis... 42 Stijfheid...
Keuze vn het lgertype Beschikbre ruimte... 35 Belstingen... 37 Grootte vn de belsting... 37 Richting vn de belsting... 37 Scheefstelling... 40 Precisie... 40 Toerentl... 42 Lgergeruis... 42 Stijfheid...
Hoe plan je een grote taak?
 3 PLANNEN Hoe pln je een grote tk? Wt heb je n deze les? In deze les leer je hoe je grote tken in stukken opdeelt en over meerdere dgen inplnt. Hndig ls je bijvoorbeeld voor een toets moet leren, wnt zo
3 PLANNEN Hoe pln je een grote tk? Wt heb je n deze les? In deze les leer je hoe je grote tken in stukken opdeelt en over meerdere dgen inplnt. Hndig ls je bijvoorbeeld voor een toets moet leren, wnt zo
Oefeningen. 1 Ga na of de gegeven functie een oplossing is van de gegeven differentiaalvergelijking. (g) y = y x 2. (a) xy = 2y ; y = 5x 2
 Oefeningen 1 G n of de gegeven functie een oplossing is vn de gegeven differentilvergelijking. () xy = 2y ; y = 5x 2 (b) (x + y) dx + y dy = 0 ; y = 1 x2 2x (c) y + y = 0 ; y = 3 sin x 4 cos x 2 Zoek een
Oefeningen 1 G n of de gegeven functie een oplossing is vn de gegeven differentilvergelijking. () xy = 2y ; y = 5x 2 (b) (x + y) dx + y dy = 0 ; y = 1 x2 2x (c) y + y = 0 ; y = 3 sin x 4 cos x 2 Zoek een
Antwoorden Natuurkunde Hoofdstuk 1
 Antwoorden Ntuurkunde Hoofdstuk 1 Antwoorden door Dn 2719 woorden 3 pril 2016 4,3 2 keer eoordeeld Vk Methode Ntuurkunde Systemtishe ntuurkunde 1.1 Grootheden en eenheden Opgve 1 Kwntittieve metingen zijn
Antwoorden Ntuurkunde Hoofdstuk 1 Antwoorden door Dn 2719 woorden 3 pril 2016 4,3 2 keer eoordeeld Vk Methode Ntuurkunde Systemtishe ntuurkunde 1.1 Grootheden en eenheden Opgve 1 Kwntittieve metingen zijn
Voorbereidende opgaven Herkansingscursus. Rekenregels voor vereenvoudigen
 Voorbereidende opgven Herknsingscursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt
Voorbereidende opgven Herknsingscursus Tips: Mk de voorbereidende opgven voorin in één vn de A4-schriften die je gt gebruiken tijdens de cursus. Als een opdrcht niet lukt, werk hem dn uit tot wr je kunt
Zomercursus Wiskunde
 Ktholieke Universiteit Leuven September 0 Module Integrtietechnieken: substitutie en prtiële integrtie (versie ugustus 0) Module : Integrtietechnieken: substitutie en prtiële integrtie Inhoudsopgve Primitieve
Ktholieke Universiteit Leuven September 0 Module Integrtietechnieken: substitutie en prtiële integrtie (versie ugustus 0) Module : Integrtietechnieken: substitutie en prtiële integrtie Inhoudsopgve Primitieve
