De middens van de intervallen zijn 0,2; 0,6; 1; 1,4 en 1,8. O ( V ) f (0,2) 0,4 + f (0,6) 0,4 + f (1) 0,4 + f (1,4) 0,4 + f (1,8) 0,4
|
|
|
- Myriam de Valk
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 G&R vwo B dl Intglkning C von Schwtznbg /6 D twd bnding is d bst Omdt d gik vn dlnd is, is ht minimum vn o lk intvl d unctiwd in d chtgns vn ht intvl En zo is ht mimum vn o lk intvl d unctiwd in d linkgns vn ht intvl y = (d -s) ( ) = = = = D middns vn d intvlln zijn,;,6; ;, n, O ( ) (,), + (,6), + (), + (,), + (,), = ( (,) + (,6) + () + (,) + (,)), =, ( ) = + 6 = + 6 = = 6 = ondsom = ( ( ) + (,) + ( ) + (,) + ( ) + (,)),,9 bovnsom = ( (,) + ( ) + (,) + ( ) + (,) + ()),, Dus,9 O ( ), y = (d -s) ( ) = = (tll = ) + = = 6 D middns vn d intvlln zijn,;,;,;,;, n, O ( ) ( (,) + (,) + (,) + (,) + (,) + (,)) 6, b ondsom = ( () + () + () + () + () + (6)),9 bovnsom = ( () + () + () + () + () + ()) 7, 9 Dus, 9 O( ) 7, 9 6 6b D ovlkt vn d bluw chthok chts wodt ghlvd D ovlkt vn d bluw chthok chts is ht vschil vn d ondsom n d bovnsom D bdt vn dz chhok is Als dn ndt d ovlkt vn dz bluw chthok n n ndt ht vschil vn d ondsom n d bovnsom dus ook n Nm GR - cticum doo (zi n ht ind vn dz uitwkingn) 7 ( ) = = (kwdtn) = 9 9 O ( ) = 9 d (nint) 9, ( ) = y = 9 ( ) = + = = 7 = ± 7 7 O ( ) = 7 ( + ) d (nint), 69 7 ( ) = 6 = + 6 = 6 + = ( ) ( ) = = = O ( ) = (6 ) d (nint),67 y = ( ) = ( ) = 6 y = 6
2 G&R vwo B dl Intglkning C von Schwtznbg /6 b ( ) = = + 6 = ( + 6) = ( ) ( ) = = = = O ( ) = ( ) d (nint), O ( W ) = ( ) d (nint),67 W y = b c O ( U ) = ( ) d = ( ) d (nint),67 n O ( ) = g( ) d = ( + ) d (nint) = 7, O ( W ) = O ( U ) O ( ) = ( ) d g( ) d (zi ) 7,7 ( ) d g( ) d = ( ( ) g( )) d (zi iguu ) Nm GR - cticum doo (zi n ht ind vn dz uitwkingn) ( ) = g( ) (intsct) = (lukt nit mt intsct) = O [,] (zi lot) is g( ) ( ), dus O ( ) = ( g( ) ( )) d (nint), b ( ) = (intsct) = (lukt nit mt intsct) = O [,] (zi lot) is ( ), dus O ( ) = ( ( )) d (nint),67 g ( ) = g( ) (intsct),,,7,,7 O ( ) = ( ( ) g( )) d + ( g( ) ( )) d (nint),7,, ( ) = g( ) (intsct), 7 π ( ) d (nint) = n,7 O ( ) = ( ( ) g( )) d (nint), Ht is dus nit w wnt, b c π π O ( ) = sin( ) d (nint) = n O ( W ) = ( sin( )) d (nint) = π π π π π sin( ) d (nint) = sin( ) d = sin( ) d + sin( ) d = + ( ) = π D intgl is ngti ls d gik ond d -s ligt π π sin( ) d (nint) = Dus O ( ) + O ( W ) = sin( ) d
3 G&R vwo B dl Intglkning C von Schwtznbg /6 6 ( ) = (intsct o) ( + 6) = ( ) ( ) = = = = O ( ) + O ( W ) = ( ) d (nint), 7,7 O = ( ) g( ) d (nint),7, (vnwg d bsolut wd mkt ht nit uit o ( ) > g( ) o ( ) < g( )) ( ) = g( ) (intsct),96, (lln d buitnst snijuntn zijn vn blng), O ( ) + O ( W ) = ( ) g( ) d (nint),,96 9 O [,]: I cilind = π h = π () = π = π O [,]: I cilind = π h = π () = π 9 = 7 π O [,6]: I cilind = π h = π () = π = π 9b I cilinds = π + 7π + π = π 7 ( ) = (intsct o) = = = = I ( L) = π ( ( )) d (nint), ( ) = (intsct) =, =,, I ( L) = π ( ( )) d (nint) 7, 9, ( ) = + 6 (intsct o) 9 = = ( + ) ( ) = = = I ( L) = π ( + 6) d + π ( ( )) d (nint),99 g( ) = ( ) = + = b I ( M) = π ( g( )) d (nint), Wntln vn om d lijn y = lvt n lichm mt dzld inhoud o ls wntln vn W om d -s, omdt n d lijn y = bid omlg zijn vschovn b I = π ( ( )) d π d (nint),7 I = π ( ( ) ) d (nint),6 b I ( L) = π ( ) d (nint), W I ( M) = π d I ( L) (nint) = π I ( L) (nint) 6, 6 I ( L) = π π = π π = π
4 G&R vwo B dl Intglkning C von Schwtznbg /6 7 ( ) = g( ) (intsct o) = = = = = (voldon) I ( L) = π ( ( )) d π ( g( )) d = π ( ( ) g( ) ) d (nint), ( ) = g( ) (intsct) =,, I ( L) = π ( ( ) g( ) ) d (nint),9 9 ( ) = g( ) (intsct),,,,, I ( L) = π ( g( ) ( ) ) d + π ( ( ) g( ) ) d (nint),,, b ( ) = g( ) (intsct),9,, I ( L) = π ( ( ) g( ) ) d (nint) 6,9,9, I ( M) = π (( g( ) ) ( ( ) ) ) d (nint) 69,,9 E mot gldn ( ) g( ) voo o [ A, B ], dus ht lgst unt vn g ligt o o bovn d -s b E mot gldn g( ) ( ) voo o [ A, B ], dus ht hoogst unt vn ligt o o ond d -s b g b O ( ) = O (chthok) + O (dihok) = b + ( + b b) = b + = + b O ( ) = do '( ) Dus do '( ) ( ) + b = d O = + b = d O = b c d O ( ) 7 6 oo lk uit d tbl gldt O ( ) = (vmodlijk is dt voo nd wdn vn ook w) O ( ) d = O = d d '( ) Dus O O = = d O '( ) = ( ) O ( ) = ( ) d = = = b c d 6 F ( ) = ( + ) + F '( ) = 6 ( + ) = ( + ) Dus F '( ) = ( ) owl F is n imitiv vn ( ) ( ) '( ) ( ) ( ) G = G = + = + = Dus G '( ) = g( ) owl G is n imitiv vn g + ln( ) H ( ) = ln( ) + ln ( ) + = ln( ) + ( ln( ) ) + H '( ) = + ln( ) = Dus H '( ) = h( ) owl H is n imitiv vn h ( ) J ( ) = '( ) J = = + = + = + ( ) Dus J '( ) = j ( ) owl J is n imitiv vn j
5 G&R vwo B dl Intglkning C von Schwtznbg /6 F ( ) = F '( ) = ( ) = = Dus F ( ) = is n imitiv vn ( ) = b ( ) '( ) ( ) Dus ( ) + + G = G = g = = G = is n imitiv vn g( ) = c ( ) '( ) ( ) ln() Dus ( ) H = = H = h = = H = is n imitiv vn h( ) = ln() ln() ln() ln() d 6 J ( ) = ln( ) J '( ) = ln( ) + = ln( ) + Dus J ( ) = ln( ) is n imitiv vn j( ) = ln( ) + F ( n n n ) = mt '( ) ( ) ( ) n + + c n F = + = n + n + = g 6b F ( ) = + c = g + c F '( ) = ( ) = g ln( g) = g ln( g) ln( g) ln( g) 6c ( ) F = + c F '( ) = ( ) = 6d b F ( ) = ln + c F '( ) = ( ) = F ( ) = ln( ) + c F '( ) = ( ) = ln( ) + = ln( ) + = ln( ) F ln( ) ( g ) = ( ln( ) ) '( ) ( ) ( ln( ) ) ln( ) log( ) ln( g ) + c F = = ln( g) + = ln( g ) = = ln( g ) ( ) gt ( ) + = F = = Dit kn nit klon omdt nit bstt n = voo + ( ) = = F ( ) = ln + c 7c [ F ( )]' = F '( ) = ( ) b c 6 ( ) = 6 F ( ) = + c = + c ( ) = + F ( ) = + + c = + + c ( ) F ( ) = = = = + c = + + c d ( ) = F ( ) = + c ln() ( ) ( ) = F = + c = + c ln() ln() ( ) ( ) ln ln F = + = + = + = + + c = + c 9 ( ) = F ( ) = + c 9b ( ) = F ( ) = + c 9c 9d ( ) 6 6 ( ) = = = F = + c = + + c ( ) = + F ( ) = + + c ln() 9 ( ) = ln( ) F ( ) = ( ln( ) ) + c = ln( ) + c 9 ( ) = ln( ) = ln() + ln( ) F ( ) = ln() + ln( ) + c = ln() + ln( ) + c ( ) ( ) o ( ) ( ) + + = = = F = + c = + c = F = + c = + c b ( ) F ( ) c = = = + = + c = + c c d ( ) F ( ) = + + = + + = + + = c = + c ( ) = ln( ) = ln( ) = ln( ) F ( ) = ( ln( ) ) + c = ln( ) + c ( ) log( ) log( ) log( ) ( ) ln( ) ln() ( ln( ) ) = = = F = + c = + + c ln() ( ) log( ) log() log( ) ( ) log() ln( ) ln() ( ln( ) ) log() = = + F = + + c = + + c ln() b ( ) = F ( ) = + c = + c F ( ) = + c doo (, ) = + c c = Dus F ( ) = +
6 G&R vwo B dl Intglkning C von Schwtznbg 6/6 c b c b c d b c F ( ) = + c (wvn d gik n bool is) kt d -s F ( ) = (gik komt o d -s) én F '( ) = ( ) = (d hlling in ht unt o d -s is nul) + c = én = + c = én = + c = én = ( ) + c = én = c = ( ) = = = F ( ) = + 9 ( ) = ( ) = + F ( ) = + + c 7 F ( ) doo (, 7) 7 = + + c 7 + = c c = 6 Dus F ( ) = ( ) = F ( ) = + c O( ) = F ( ) = + c én O() = + c = c = O( ) = én O( ) = = = = ( ) = = ( ) = = = O ( ) = ( ) d ( ) 6 = = = contol ( ) d = 6 = = (intsct), I ( L) = π( ) d π(9 6 ) d π ( ) ( ) 79 = + = + = π + = π 7 7 q q π ( ) d π( ) 79 = + = π π( q q + q ) = 79 π (intsct) q,9 7 = 6 (intsct o) + 6 = ( + )( ) = = = O ( ) = ( g( ) ( )) d = (6 ) d (nit mt nint) contol = 6 = 6 (6 ( ) ( ) ( ) ) = 6 (6 ) d = 6 6 = 6 (6 ( ) ( ) ( ) ) = (intsct) =, 6 I ( L) = π (6 ) d π ( ) d = π (6 + ) d π d contol = π (6 6 + ) π = π (6 6 + ) π (6 ( ) 6 ( ) + ( ) ) ( π π ( ) ) = π
7 G&R vwo B dl Intglkning C von Schwtznbg 7/6 6 6b ( ) = + + = + + = + + = ( + )( + ) = = = O ( ) = ( + + ( )) d ( ) d ( ) d ln = = + + = + + = ( ) + ln( ) + 7 ) + ln() + = + + ln() ) = + ln() O ( W ) = ( + + ( + )) d = ( + + ) d = d = ln = ln( ) ln() = ln( ) O ( W ) = ln( ) = = 7 ( ) = = = = O ( ) = ( ) d ( ) = = = + = ln() ln() ln() ln() ln() ln() ( ) d = ln() = + = 6 (intsct), 6 ln() ln() ln() ln() 7b ( ) ( ) = = = = = (zokn w nit) = O ( ) = + d d ( = + ) ( ) 7 = + = + = + = + + = + = ( O ) = = + d ( ) = + = + = + = 6 = 6 = 6 = = = 6 9 b I ( L + L) = π( ) d π( ) d π( ) = = = π( 6) π( ) = 6π π = π I ( L) π( ) d π gt π( ) = = = = = 9π π( ) π( ) = 9π + = 9 + = = D = 6 = = (vold nit) = (voldot) = = + 6 F ( ) = ( + ) F '( ) = ( ) = 6 ( + ) = ( + ) ( + ) = ( + ) = = G ( ) = ( ) '( ) ( ) '( ) '( ) ( ) F + b G = g = F + b = F + b = + b ( ) = ( ) F ( ) = ( ) + c = ( ) + c 7 b g( ) = = ( + ) G ( ) = ( ) c 6 c c ( + ) + + = + = + ( + ) 6( + ) c d h ( ) = = ( ) H ( ) = ( ) + c = ( ) + c j ( ) = ( ) = J ( ) = ( ) + c = ( ) + c = + c ( ) = F ( ) = ln + c = ln + c b ( ) = = F ( ) = ln + c = ln + c
8 G&R vwo B dl Intglkning C von Schwtznbg /6 c ( ) = ( ) = + ( ) = ln( ) ( ) = ( ) ln( ) ( ) + = ( ) ln( ) + + F c d ( ) g F c c ( ) = ( + ) + = ( + ) F ( ) = ( + ) + c = ( + ) + + c ( ) = F ( ) = + c = + c ln() ln() ( ) = F ( ) = + c = + c ln() ln() h ln( + ) ( ) ( ) = log( + ) = = ln() ln() ln( + ) F ( ) = ln() ( + ) ln( + ) ( + ) + c ( ) = g( ) = ( + ) = ( ) + = 6= 9 = 9 = + 6 O ( ) = d d ln ln + = = ln() + ln() + ln() ln() = ln() + ln() ln() I ( L) = π d + π d π ( ) d π ( ) d = b ( ) ( ) = π ( ) + π ( + ) = π + π ( ) ( + ) = π π π + π = π 6 b c D gl gt ov unctis vn d vom ( + b) n g is vn d vom ( + b) G( ) = ( ) G '( ) = ( ) = E is gn wd vn wvoo G '( ) = H ( ) = ( ) + c h( ) = (zi b) Dus = = Dus h( ) = ht ls imitivn H ( ) = ( ) + c = ( ) + c I ( L) = π ( ) d π d π 6 = = = π π = π 6b L is n kgl D stl vn d gondcikl is n d hoogt is I (kgl) = Gh = π h = π ( 6) 6 = π 6 6 = π 9 I (kglto) = π ( ) = π = π K = π π π = π π = π = = = = = = I (kgl) = Gh = π ( ) = π 9 6 = π 9 I (kglto) = π ( ) = π = π K = 7π π π = 7π π = 6π = 6 = 6 = = = = D cikl mt stl n middlunt (, ) ht vglijking + y = owl y = I (bol) = πy d πy d π( ) d π( ) = = = = ( π( )) = π = π 6 6 I = πy d π( ) d π( ) = = = π( ) π( ( ) ) = π π = π
9 G&R vwo B dl Intglkning C von Schwtznbg 9/6 6 6 I (bol) = π = π 6 = π Nu is I ( S ) = π = π πy d π π(6 ) d π π (6 ) = = = π π(6 ) π( 7) = π Intsct gt dn,7 k snijdn mt d -s ( y = ) + 6 = = = = I ( L) = π( 6 ) d π( ) d π ( 6 ) π ( ) + = + = π π ( + 6 ) π ( ) π ( 9 9 ( ) ) = π = π b A(, ) n B(, ) AB = ( ) + ( ) = + 6 = + 6 = 6, C (;,) AC + CB = +, + +, 6, Dz twd bnding is bt omdt AB < AC + CB < boog AB 6 ( ) = '( ) = boog OA = + d (nint), 9 omtk, 9 + +, Og 6 A Og 6 Q 6 ( ) = '( ) = ln() boog PQ = + ( ln()) d (nint) 7, 79 omtk 7, , 79 O P 66 + = ( ) = = = ( ) = + '( ) = 6 boog RS = + ( 6 ) d (nint), omtk, +, R Og 66 S y = O 67 D omul vn d kbl is vn d vom h( ) = + b O (, ) o d bool b = h( ) = = + = = doo (6, 6) 6 9 h( ) = + h'( ) = boog TU = + ( ) d (nint) (m) 96 6 T 6 h = 7 67 = 6 h Og 67 O wgdk U 6 6 6b 6c y ( ) = y ( ) hoogt vn bvstiging n d ln is y () = y( ), (m) Nit gvgd wodt: d lgst hoogt vn d kbl bovn ht wgdk y () = ( + ) = ( + ) = = (m),6,6,6,6,6,6 y = ( + ) y ' = (,6 +,6) =,( ),6,6 Lngt vn één kbl: + (,( )) d (nint), (m),6,6 Ovlkt vn één nt: ( + ) d (nint) 9 (m )
10 G&R vwo B dl Intglkning C von Schwtznbg /6 69 oo d stl vn d ondst cilind mot j d gik vn snijdn mt d lijn y = ( ) = = (kwdtn) = Dus d stl vn d ondst cilind is oo d stl vn d bovnst cilind mot j d gik vn snijdn mt d lijn y = ( ) = = (kwdtn) = Dus d stl vn d bovnst cilind is 7 7b y = y = = y + = y + = ( y + ) = y + y + y = I ( L) = π d y = π( y + y + ) dy = π ( y + y + y ) = π ( y + y + y ) = π ( + + ) π = π = π O y = = = 9 = = 6 ; y = = = = = I ( M) = I (cilind) πy d π 6 π( ) d π π ( ) = = = π π (6 6 ) π ( ) = π 6 7 7b I ( L) = π dy πy dy π y = = = π π = π q q I ( Lq ) = πy d y π y q π n I ( L ) πy d π d π = = = = = = π π = π P (, q) ligt o d gik vn d bool y = q = I ( L ) ( ) mt mt q = I L q = q π = π q = π = π = = = = gt gn omwntlingslichm (dus voldot nit) n = gt = n q = = ( ) = 7 7b 7c 7 I ( L) = πy d π ( 6) d π( 6) d π ( 6 ) = + = + = + = π π (9 ) = 9π = 9 π = y = () = 6 y = + 6 y = + 6 = y 6 = y = y y + 9 W I ( M) π d y π( y y 9) d y π ( y y 9 y ) = = + = + O = π ( ) π = π ( ) = π 6 = π 6 tnslti (, ) y = + 6 y = ( ) + 6 = = y = y = = y = y I ( N ) = π dy = π y dy = π y = π π = 6 π = π ( ) + O d + + = = = = = = 7b = = ( ) '( ) = + + ( ) d (nint) 6, 9 omtk 6, , 6 I ( ) = + d ln( ) (GA DIT ZELF NA!!!) d (nint),6 y = + 7c π π π π ( ) O
11 G&R vwo B dl Intglkning C von Schwtznbg /6 Dignostisch tots D D middns vn d intvlln zijn,,,,,,, n, O ( ) (,) + (,) + (,) + (,) + (,) 7,69 Db 6 O ( ) = ( ) d (nint), D ( ) = (intsct) = O ( ) = ( ) d (nint), D ( ) = (intsct),,, O ( ) = ( ) d (nint),7, ( ) D 9 = + (intsct o) + 6 = ( + )( ) = = = O ( ) = ( ( ) g( )) d (nint), D D6 D6b O ( ) = ( ) d (nint),7 ( ) = = = = = = = = g( ) = ln( ) = ln( ) = = = g ( ) = g( ) (intsct),6 W I = π (( ( )) ( g( )) ) d (nint),7,6,6 I = π ( ( )) d + π ( g( )) d (nint),,,6 D7 D7b F ( ) = ( + ) + F '( ) = ( + ) = ( + ) Dus F is n imitiv vn G( ) = G '( ) = = Dus G is n imitiv vn g D ( ) = 6 = 6 F ( ) = 6 + c = + c = + c Db ( ) ( ) ln 6 ln 6 F = + = + = + = + = + + c = + c Dc ( ) ( ) ln() = F = + c = + c ln() Dd ( ) = 6 + F ( ) = c ( ) = ln( ) = ln( ) F ( ) = ln( ) + c = ln( ) + c D ( ) D D9 ln( ) ln( ) ( ) = log( ) = log() + log( ) = log( ) + = + F ( ) = + ( ln( ) ) + c ln() ln() ln() ( ) = + ( ) ln = + = + F = + + c = + ln() + c = + + c = c doo (, y ) = (, ) Dus F ( ) = + ln + ( ) = d ln ln() ln() = + = + = + ln() D9b O + ( ) ( )
12 D9c G&R vwo B dl Intglkning C von Schwtznbg /6 ( ) = g( ) + (vold nit) (voldot) = + = = = = I = π + ( ) d π ( ) d π + + d d = π = π ( + + ) d π d π ( ) d π d = + + = π ( + ) π = π ( + ) + π = π ( + ) π ( + ) + π π = 7 π = π D ( ) = ( + 6 ) F ( ) = ( + 6) + c = ( + 6) + c 6 Db ( ) = ( ( ) F ( ) ) ( ) c = = + = ( ) + c Dc ( ) = ( + ) + = ( + ) F ( ) = ( + ) + c = ( + ) + + c + Dd ( ) ( ) + + = F = + c = + c D ( ) = F ( ) = + c = + c ln() ln() ( ) = ln( + ) F ( ) = ( + ) ln( + ) ( + ) + c = ( + ) ln( + ) + c D ( ) W = g O ( ) = ( + ) d = = ( ) = + O (dl I) = ( ) d + = = + O (dl I) = O( ) + = ( + ) Intsct gt dn, D ( ) ( ) D I (bol) = π = 6 π Db I = πy d π(6 ) d π(6 ) π( ) π( 6 6) = = = = π = π Dc I ( L 6 ) = πy d π(6 ) π(6 ) π( = = ) = π Intsct gt, D ( ) = = = = = ( ) = = = = 9 = 9 = ( ) = '( ) = = d (nint), 9 omtk, 9 + = + + +, Db πy d π ( ) d π ( ) = = = π( ) π( ) = 6 π I = π 6 π = 6 π Dc π d y π ( y y ) d y π( y y y ) 7 = + + = + + = π( + + ) = 9 π Gbuik: y = = y = y + = y + = y + y +
13 G&R vwo B dl Intglkning C von Schwtznbg /6 Gmngd ogvn Intglkning ln( ) G ( ) 7 log( ) ( ) 7 ln() ( ln( ) ) 7 = F = + c = + c ln() Gb ( ) ( ) F c = = + = + c Gc ( ) ln( ) ln( ) ( ) (( )ln( ) ( ) ) = = F = + c = ( )ln( ) ( ) + c Gd ( ) ln( 6 9) ln( ) ln( ) ( ) (( )ln( ) ( ) ) = + = = F = + c = ( )ln( ) ( ) + c G ( ) F ( ) 6 = = + = + + c = + c G ( ) = ( + ) = F ( ) = c = c G ( ) = 6 + = ( 6 + ) F ( ) = (6 + ) + c = (6 + ) + c = (6 + ) c Gb ( ) = = F ( ) = ln + c = ln + c Gc ( ) ( 6 ) F ( ) ( 6) = = + c = + 6 c = + ( 6) c Gd ( ) = ( + ) = F ( ) = ln + + c + G ( ) = F ( ) = + c = + c ln() ln() G ( ) ( ) ln() ln() = ln() ln() = = F = + c = + + c G ( ) = + = + = = ( )( 6) = = = O ( ) = + d = d ( ) ( ) ( ) ( ) 6 = ln( ) = 9 9 ln(6) ln( ) 6 = + ln(6) + ln( ) = ln() 6 6 O ( ) = + d ln( ) ln() ln() = + = + + = + ln() Gb ( ) ( ) ( ) O 6 y = O ( ) = O (chthok) + ln() = = + ln() G6 ( ) = + + '( ) Stl d klijn is = + y = + b = '() = n b = () = y = + ( ) = = + + = ( + ) = = = = = O ( ) = ( ( ) ( + ) ) d = ( ) d = ( ) d ( 9 + = + = ) = G6b '( ) = + = ( + )( ) = = ( < vvlt) = () = + + = = ( ) = + + = (intsct) = O ( W ) = ( ( )) d (nint) = 6 O y = + O
14 G&R vwo B dl Intglkning C von Schwtznbg /6 G7 I = πy d π( ) d π ( ) ( ( ) ) ( ( ) ) 9 = = = π π = π 69 G7b I ( L) = πy d π( ) d π ( ) = = = π( ( ) ) π = π ( ) I ( B) = π I ( L) = I ( B) π ( ) = π = (intsct), G y = invulln in + y = gt + 9 = = 6 = ± y = invulln in + y = gt + 6 = = 9 = ± I ( L) = πy d + π d + πy d π d = π ( ) d + 6π d + π ( ) d 9π d y = y = = π ( ) + [ 6 π ] + π ( ) [ 9π ] + y = = π( ( ) ) π( ( ) ) + π π + π( ) π( ) (6π 6 π) = π( 7 + 9) π( + 6) + π + π + π( 6) π(7 9) (6π + 6 π) = π = 9 π G9 ( ) = + = = ( ) = = = = = ± = ± O ( ) = ( ) d + = + = ( + ) = + O ( ) = + = (stl = t ) t + t = t t + = D = () = 96 D = 96 = 6 6 = 6 O t = = = 6 t = = = + 6 = 6 = 6 = + 6 = + 6 = E mot gldn < < = d = + + = + + = + O ( W ) = + = + = (gik ond d -s) = = = = (voldot nit, wnt ontstt nit HET vlkdl W ) = 7 (dz voldot) G9b ( ) ( ) G ( ) = '( ) = '( ) = = = Dus kunt R(, ()) = R(, ) Rklijn doo R(, ) vn d vom y = + b mt = + b b = Dus d klijn doo R(, ) is y = g( ) = = g '( ) = = g '( ) = = = = Dus kunt S (, g()) = S (, ) Rklijn doo S(, ) vn d vom y = + b mt = + b b = Dus d klijn doo S (, ) is y = D klijnn snijdn d y -s in (, ) n (, ) D digonl vn ht viknt is dus Gb ( ) = C (, ) n D(, ); g( ) = B(, ) n A(, ) O ( ABCD) = ( + ) = + O (vlkdl bovn d gik vn ) = ( ) d = = ( ) = O (vlkdl bovn d gik vn ) = O ( ABCD) = + = = =
15 G&R vwo B dl Intglkning C von Schwtznbg /6 G A(, ) = A(, ) n B(, ) = B(, ) AB: y = ( ) + b doo A(, ) b = Dus AB: y = ( ) + O ( ) = (( ) ) d d ( ) + = + = ( ) + ( ) = + + = + = Gb ( ) = '( ) = Omtk boog = AB + AB = + ( ) + ( ) d (nint), + Gc '( ) = c AB = (intsct), 6 G O = ( ) d ( ) d ( ) ( ) ( ) ( ) = = = = Gb =, 99 invulln in n( ) = gt n (, 99, 99 ) =, 99 n, 99 =, 99 n = Dus voo n > is >, 99 S n dy dy Gc y = n( ) = n n y ' = n n Dus = = n klijn in O is y = n d d = = invulln in y = n gt y = n Rn (, n) Tn is ht middn vn AR n = invulln in y = n( ) gt y = n ( ) = n = n Tn (, n) G O = ( + ) d = = ( ) = + = O = = = ln() + Gb (, ) n (, ) c + A B + AB = = + + cab < < (intsct) <, ( ) = '( ) = Boog AB = + d (nint),79 + Gc ( ) Gd OPAQ wntln om d -s gt: I = π d π = = π o I = G h = π = π Ht dl ond d gik vn wntln om d -s gt: I = π( ) d π d π = = = π π Ht dl bovn d gik vn wntln om d -s gt: I = I I Ht vschil tussn d inhoudn is: I I = ( I I ) I = I I = π ( π π) = π G O =,9 d, d (nint), 9 Gb I = π ( ) d π d π π = = = = π Gc ( ) = '( ) = = L( ) = + ( ) d = + d = ( + ) d = ( ) ( ) ( ) ( ) 6 + = + = + + = = =
16 G&R vwo B dl Intglkning C von Schwtznbg 6/6 b c d TI- Intgn (nint) ( + ) d = (nint) ( ) d = ( + ) d (nint) = 6 (nint) ( + + ) d = d (nint), 6 c b d (nint), 67 + d d (nint), d (nint), + TI- Intgln ( ) = g( ) (intsct) A, n B, 7 D gik vn ( ) loot tussn d snijuntn bovn d gik vn g( ) B O ( ) = ( ( ) g( )) d (nint), A ( ) imitivn F ( ) n n + c n + g g + c ln( g) + c ln + c ln( ) ln( ) + c g log( ) ( ln( ) ) + c ln( g) ( + b) F ( + b) + c b b ( ) d = F ( ) = F ( b) F ( ) O (cikl) = π I (cilind) = Gh = π h I (kgl) = Gh = π h I (bol) = π b D lngt vn d gik vn tussn = n = b is + '( ) d ( ) b Ht vlkdl ligt chts vn d y -s n wodt ingslotn doo d gik vn d uncti, d y -s n d lijnn y = n y = b b D inhoud vn ht lichm L dt ontstt ls om d y -s wntlt is I ( L) = π d y
Hoofdstuk 9: Exponentiële en logaritmische functies. 9.1 Logaritmische en exponentiële vergelijkingen. Opgave 1: a. y2 b. y2 c. y1. Opgave 2: c.
Hoodstk 9: Eonntiël n ritmisch nctis 9. Logritmisch n onntiël vrglijkingn Ogv :. y n y b. y n y c. y n y Ogv :. 6 6 b. 6 c. 9 d. 8 8 7. 6 6 6 6. Ogv :. 6 8 b. 8 8 c. d. 9. 6 8 6 7 7. Ogv :. 6 9 b. c. 7
Uitwerkingen H9 van vwo B deel 3 Exponentiële functies en logaritmische functies
Uitwrkingn H9 van vwo B dl Eponntiël functis n logaritmisch functis. y log( + 5) y log() + log (5) n y log (5) Uit d tabl blijkt dat y n y htzlfd zijn. log() + log(5) log(5) Vor in : y log( 5) ; y log()
De differentiaalvergelijking die geldt in de mantel (met cylindersymmetrie) is. 0, met als algemene oplossing T C1ln
Dl : M st n vool op dt, doodt d mtglidingscofficint vn d n onindig goot is, d tmptuu in d n constnt is. In d n odt vd n hovlhid mt gdissipd. D diffntilvglijing di gldt in d mntl (mt cylindsymmti) is T
Blok 1 - Vaardigheden
0 bladzijd 8 a ( ) 0 als 0. Dz vrglijking gt ( ) 0 n dus 0 o. b + 0 als, dus d vrtical asmptoot is. c D graik mot naar rchts gschovn, dus vrvangn door + gt ( ) ( ) g( ) ( ) + + 4 d D graik van g ht d nulpuntn
Machten. Inhoud Machten
Mchtn Inhoud Mchtn Mchtn n mchtsvrhffn Evn n onvn mchtn Vrmnigvuldign vn mchtn Dln vn mchtn Mcht vn n mcht Mchtn vn productn 7 Mchtn vn rukn Sustiturn vrvngn vn n lttr door n gtl Wortls n mchtn mt grokn
De Wageningse Methode 5&6 VWO wiskunde B Uitgebreidere antwoorden Hoofdstuk 8 Integralen toepassen
D Wagnings Mtod & VWO wiskund B Uitgbridr antwoordn Hoofdstuk Intgraln topassn Paragraaf Inoud n intgraal f d ( ) d ( ) d a Ht 'topj' van d piramid is glijkvormig mt d l piramid mt factor f, dus O()f b
De Wageningse Methode 5&6 VWO wiskunde B Uitgebreidere antwoorden Hoofdstuk 5 Exponentiële functies
D Wagnings Mthod 5&6 VWO wiskund B Uitgbridr antwoordn Hoofdstuk 5 Eponntiël functis Paragraaf Eponntiël functis a. J mag wl van n artikl van 00 uro uitgaan. Bij d n krijg j: 00 0 0 99 Bij d andr: 00 90
We gebruiken de volgende standaardvorm van een cirkel met middelpunt M en straal r : ( ) ( ) 2
Wiskunde D Online uitweking VWO lok les jnui Pgf Opgve We geuiken de volgende stnddvom vn een cikel met middelpunt M en stl : De cikel met middelpunt (-,) en stl voldoet n de vegelijking De cikel met middelpunt
13 Afgeleide en tweede afgeleide
Afglid n twd afglid a f ( + gft f ( + + + ( + f ( gft ( - - + ƒ ma is f ( B f, ] b f ( + + ( + ( + + f ( gft ( + + + f ( dus ht buigunt is, c f ( Zi d figuur + a hft één olossing voor a a a ƒ d b( + hft
Integralen. onbepaalde integralen. oneigenlijke integralen. gemiddelde functiewaarde op een interval
Intgrln onld intgrln onignlijk intgrln gmiddld funtiwrd o n intrvl Onld intgrl En onld intgrl wordt ogshrvn ls: f ( d ) wrin f() n willkurig funti is. En r gldt: f ( d ) = F( ) + Wrij F() d rimitiv funti
Extra oefening hoofdstuk 1
Etra ofning hoofdstuk = ( ) = = v v v dr 7 7 7 v a = + v als v 7 v v dus als = 7 7 7 7 dv waaruit volgt dat v = 7 km/uur. v = 7 gft R = 7, 7 mg/min. a f ' = = ' = + = ( + ) ' = = ( ) = f f d f ' ln ln
x 2x x 4x x 1x x 8x x x 12 = 0 G&R vwo B deel 1 1 Vergelijkingen en ongelijkheden C. von Schwartzenberg 1/25
C. von Schwartzenberg 1/ 1 I, II, IV en V zijn tweedegraadsvergelijkingen. (de hoogste macht van is steeds ; te zien na wegwerken haakjes?) (III is een eerstegraadsvergelijking en VI is een derdegraadsvergelijking)
15 4 11 dus punt B ligt niet op lijn k
Hoofdstu 9: Lijnen en iels. 9. Vegelijingen vn lijnen. Ogve :... 6 6 Ogve :.. dus unt ligt o lijn dus unt B ligt niet o lijn 6 7 dus unt C ligt o lijn 6 6 dus unt D ligt o lijn. q q q q 7q q 7 d. doo 6
Oplossingen vbtl 6 analyse 3, leerweg 4
= Oplossingn vbtl analys, lwg OPLOSSINGEN. Vloop van algbaïsch functis (hhaling) (blz. ) a.. (als < ) (als > ) g. (als < ) (als > ) 0 i. j. a. V.A.: = ; H.A : y = V.A.: = ; H.A : y = V.A.: = n = ; H.A
Gelijknamige breuken kun je eenvoudig bij elkaar optellen of van elkaar aftrekken:
Brukn optlln n ftrkkn Vrknnn Opgv 1 Ton n Hns stlln smn n grot pizz. Ton t d hlft vn d pizz op, Hns t 3 dl vn d pizz. 8 Wlk dl vn d pizz tn z smn op? Wlk dl vn d pizz t Ton mr op dn Hns? nm: Imgs/R1003.jpg
De Slimste Handleiding ter Wereld
D Slimst Hndliding t Wld 1. Inliding vsi 2.5 Wlkom bij d Slimst Hndliding t Wld, d gids di u l lidn doohn ht voobidn n uitvon vn D Slimst Mns t Wld, mt bhulp vn ht bijgvogd flsh-pogmm n nd documntn. 2.
Beschrijven van processen aan de hand van een grafiek. In onderstaande grafieken is de snelheid uitgezet tegen de tijd.
Uitwrkingn hoostuk 7 7. Dirntiërn. Opg 7. Bshrijn n prossn n hn n n grik. In onrstn grikn is snlhi uitgt tgn tij. n A: D snlhi nmt nuit stilstn onstnt to nr rhts tot ht tijstip t n rn onstnt nr rhts tot
Een regenton. W is het vlakdeel dat wordt ingesloten door de x-as, de y-as, de grafiek van r en de lijn x h, met 0 h
Een regenton Op het domein [0, ] is de functie r gegeven door r ( ) 5 5 5. W is het vlkdeel dt wordt ingesloten door de -s, de y-s, de grfiek vn r en de lijn h, met 0 h. Zie de onderstnde figuur. figuur
n: x y = 0 x 0 2 x 0 1 x 0 1 x 0 4 y -6 0 y 1 0 y 0 1 y 2 0 p =. C. von Schwartzenberg 1/10
1a 1b G&R havo B deel C. von Schwartzenberg 1/10 Tien broden kosten 16 euro blijft over voor bolletjes 60 16 = euro. Hij kan nog = 110 bolletjes kopen. 0,0 90 bolletjes kosten 6 euro blijft over voor broden
Eindexamen wiskunde B1 vwo 2007-I
Eindemen wiskunde B vwo 7-I Beoordelingsmodel Podiumverlichting mimumscore sin α = r 65 V 65 r r r 65 r = 9 + invullen geeft V = 9 + sin α = r r = 9 + V = 65 65 = 9+ 9+ 9 + mimumscore 5 65 9 + = geeft
H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W +
H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W + D o e l m a t i g h e i d s t o e t s v o o r g e b i e d e n w a a r v o o r g e e n b o d e m b e h e e r p l a n i s v a s t g e s
oefenbundel voor het tweede leerjaar
ofbudl voo ht twd ljaa lihoud aad bo taal: pictogamm mdiëig Tijd voo Taal acct - Taal 2 taalbschouwig taal: lz schijv acctactivitit Tijd voo Taal acct - Taal 2 vijkig spllig: i, i mdiëig Tijd voo Taal
Uitwerkingen extra opgaven hoofdstuk 5 Functieonderzoek: toepassing van de differentiaalrekening ( ) ( )( ) ( ) ( )( )
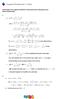Uitwrkingn tra opgavn hoofdstuk 5 Functiondrzok: topassing van d diffrntiaalrkning. a. g( ) ( ) - 4 = Þ + - 6 ( + - 6) - ( - 4)( + ) ( + - 6) + - - ( - 8 + - 4) ( + - 6) g = = = = ( + )( - ) ( - ) ( +
Bepaling toezichtvorm gemeente Stein
Bepaling toezichtvorm 2008-2011 gemeente Stein F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, juni 2 0 0 8 V e r d i e p i n g s o n d e r z o e k S t e i
x 3x x 7x x 2x x 5x x 4x G&R havo B deel 1 3 Vergelijkingen en ongelijkheden C. von Schwartzenberg 1/12 TOETS VOORKENNIS
G&R havo B deel Vergelijkingen en ongelijkheden C. von Schwartzenberg / a x = x =. b x = x x =. c d x (x ) 0 x = 0 =. 9. e f x 0 x ( x ) 0. x x = x x ( x )( x + ). TOETS VOORKENNIS a ( x + ) = x c x e
Formulekaart VWO wiskunde B1 en B2
Formulekrt VWO wiskunde B en B2 De Formulekrt Wiskunde hvo/vwo is gepubliceerd in Uitleg, Gele Ktern nr. 2, CEVO- 98/257. Deze versie vn de Formulekrt is die officiële versie. Vierkntsvergelijking Als
L i mb u r g s e L a n d m a r k s
L i mb u r g s e L a n d m a r k s P r o g r a m m a I n v e s t e r e n i n S t ed e n e n D o r p e n, l i j n 2 ; D e L i m b u r g s e I d e n t i t e i t v e r s i e 1. 0 D o c u m e n t h i s t o
Voorbereiding toelatingsexamen arts/tandarts. Wiskunde: integralen en afgeleiden. 16 september dr. Brenda Casteleyn
Voorbriding tolatingsamn arts/tandarts Wiskund: intgraln n afglidn 16 sptmbr 017 dr. Brnda Castlyn Mt dank aan: Athnum van Vurn Ln Goyns (http://usrs.tlnt.b/tolating) 1. Inliding Dit ofningnovrzicht is
Paragraaf K.1 : Substitutiemethode
Hoofdstuk K Voortgezette Integraalrekening (V5 Wis B) Pagina van 8 Paragraaf K. : Substitutiemethode Stappenplan voor de substitutiemethode : () Neem y = formule (bij kettingregel noem je deze formule
Goniometrische Formules
BIJLAGE WISKUNDE AR - - Goniomeisce Fomules sin x + cos x = sin x cosx n x = co x = cosx sin x + n x = + co x = cos x sin x n x cos x = sin x = + n x + n x sin x = sin x cos x cos x = cos x - cos x = -
Tentamen Mechanica 2 voor N (3NA45 en 3AA42)
TEHNISHE UNIVESITEIT EINDHOVEN Fcultit Tchnisch Ntuuund Tntmn Mchnic oo N (N45 n 4) ijdg juli n 9.u tot.u Dit tntmn bstt uit 5 ogn mt onddln. Miml unnn untn bhld wodn; d untnwding is onddl nggn. ll fomuls
R e s u l t a a t g e r i c h t h e i d e n c o m p e t e n t i e m a n a g e m e n t b i j d r i e o v e r h e i d s o r g a n i s a t i e s
R e s u l t a a t g e r i c h t h e i d e n c o m p e t e n t i e m a n a g e m e n t b i j d r i e o v e r h e i d s o r g a n i s a t i e s O p le i d i n g: M a s t e r P u b l i c M a n a g e m e n
Uitwerkingen 1. Opgave 1. v gem = 2,2 m/s. Oplossing: Opgave 2. v gem = 0,83 m/s = = Oplossing: Opgave 3. Δt = 11 s. Gevraagd: Oplossing: v gem.
Uitwrkingn 1 Opg 1 Δt 480 s, m/s Δs, m/s 480 s 1056 m s Opg Δs 9 m 0,83 m/s Δt 9 m 0,83 m/s 34,9 s Opg 3 Opg 4 Opg 5 Opg 6 Δs 15 m Δt 11 s Δs 5 m Δt 4,3 s 15 m 11s 5 m 4,3 s 1,36 m/s 5,8 m/s 340 m/s Δs
Voorkom forse inkomensterugval bij arbeidsongeschiktheid met WIA aanvullende verzekeringen
km fs nkmnstgval bj abdsngschkthd mt W aanvllnd vkngn lgmn nfmat s bstmd v wkgvs n wknms d gaag m wlln wtn v d aanvllnd W vkngn n d bch lst wlk nadlg gvlgn d Wt nkmn n bd (W) v ht nkmn van wknms kan hbbn
Hoofdstuk 6 Machtsfuncties. Kern 1 Even en oneven exponenten. 4VWO B, uitwerkingen Hoofdstuk 6, Machtsfuncties1
VWO B, uitwrkingn Hoostuk, Mahtsuntis Hoostuk Mahtsuntis Krn Evn n onvn ponntn a Ht gwiht van kuus staat uit ht gwiht van rin. Er zijn rin. Als ri r m lang is, an wgt ir ri 0, r gram. Ht total gwiht wort
Uitwerkingen H10 Integraalrekening
Uitwerkingen H Integraalrekening. De tweede benadering is de beste. a. Onder de grafiek liggen nog witte vlakdelen. Boven de grafiek steken blauwe vlakdelen uit. c. Neem bijvoorbeeld rechthoeken.. Als
Eindexamen vwo wiskunde B 2013-I
Eindeamen vwo wiskunde B 0-I Beoordelingsmodel De vergelijking van ntoine maimumscore 4 44 log = 0, dus 0 4,46 T 5,5 44 44 Dit geeft = 4,46, dus T 5,5 = T 5,5 4,46 44 Hieruit volgt T = 5,5+ ( 9,) 4,46
Eindexamen vwo wiskunde B pilot I
Onfhnkelijk vn mimumscore 5 f ' ( x) = e + ( + ) e f' ( x ) = 0 voor x = f ( ) = (dus P (, ) ) e e Hieruit volgt dt lle punten P dezelfde y-coördint hebben, dus liggen l deze punten op één (horizontle)
5. Exponentiële en logaritmische functies.
uitwrkingn ponntiël n logritmish funtis Vrvoort Bokn,,,9 : fgron,,, : :,, fgron t, 9,9, : : 9,9 fgron t,,,,,,,9,,,,, 9 9 9 Uitwrkingn hoofstuk. Eponntiël n logritmish funtis. Opgv. Bsisrkningn mt logritmn,
Examen VWO. wiskunde B. tijdvak 2 woensdag 20 juni uur. Bij dit examen hoort een uitwerkbijlage.
Emen VWO 202 tijdvk 2 woensdg 20 juni 3.30-6.30 uur wiskunde B Bij dit emen hoort een uitwerkbijlge. Dit emen bestt uit 7 vrgen. Voor dit emen zijn miml 8 punten te behlen. Voor elk vrgnummer stt hoeveel
2. Gegeven is de driehoek van figuur 10.10a. Gevraagd worden hoek β en de zijden a en c.
Wiskunde voor bchelor en mster Deel Bsiskennis en bsisvrdigheden c 05, Syntx Medi, Utrecht www.syntxmedi.nl Uitwerkingen hoofdstuk 0 0... Voor scherpe hoek α geldt:. sin α = 0,8 α = sin 0,8 = 5, d. cos
4.3. Toepassingen van logaritmische en exponentiële functies
4.3. Topassingn van logaritmisch n ponntiël functis 4.3.. Limitn van logaritmisch n ponntiël functis Voorbld : a b a b H lna a lna lnb b lnb b log a Voorbld : Dit is n niuw onbpaald vorm! W wtn wl dat
Alle winnende lotnummers voor de Oudejaarstrekking van 31 december. Hoge prijzen ,00
Alle winnende lotnummers voor de Oudejaarstrekking van 31 december Dit is de 875 e Oudejaarstrekking. Bekijk het bijbehorende prijzenpakket (url: /spel/prijzenpakket/oudejaarstrekking). Hoge prijzen 100.000,00
H O E D U U R I S L I M B U R G?
H O E D U U R I S L I M B U R G? N AD E R E I N F O R M A T I E S T A T E N C O M M I S S I E S OV E R O N D E R AN D E R E A F V A L S T O F F E N H E F F I N G E N I N L I M B U R G 1 6 a u g u s t u
Oefeningen. 1 Ga na of de gegeven functie een oplossing is van de gegeven differentiaalvergelijking. (g) y = y x 2. (a) xy = 2y ; y = 5x 2
Oefeningen 1 G n of de gegeven functie een oplossing is vn de gegeven differentilvergelijking. () xy = 2y ; y = 5x 2 (b) (x + y) dx + y dy = 0 ; y = 1 x2 2x (c) y + y = 0 ; y = 3 sin x 4 cos x 2 Zoek een
Vraag Antwoord Scores ( ) ( ) Voor de waterhoogte h geldt: ( 2h+ 3h 2h
Een regenton maximumscore h V ( rx ( )) dx π 0 00 ( rx ( )) ( x x ) + Een primitieve van + x x is x+ 7 x x π Dus V ( h 7 h h ) + 00 π π V h+ h h h+ h h 00 0 ( ) ( ) maximumscore Het volume van de regenton
Eindexamen vwo wiskunde B 2014-I
Eindexmen vwo wiskunde B 04-I Bl in de sloot mximumscore 4 De gevrgde inhoud I is ( ) h ( ) π f( x) dx= π ( x x )dx h 0 0 h π f( x) dx 0 Een rimitieve vn x x is x x I = π( h h ) = π h ( h) mximumscore
Noordhoff Uitgevers bv
Voorkennis: Algerïshe ewerkingen ldzijde 9 V- d e 9 V- 9 V- + + + V- + + 9 d + + + + e + + + + f + g Hoofdstuk - Funties en lger + + + + + + + ldzijde 9 V- + ( + ) + ( )( ) of + of of of ( ) d p p ( p
Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n
Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n M w. d r s. E. L. J. E n g e l s ( P r o v i n c i e L i m b u r g ) M w. d r s.
Oplossingen analyse 2 (leerweg 4)
= Oplossingn analys (lwg ). Limit van n unti (lz. ) a 8 8 08 0 g h a L.L. = ; R.L. = + L.L. = + ; R.L. = L.L. = ; R.L. = L.L. = + ; R.L. = L.L. = + ; R.L. = L.L. = + ; R.L. = + g L.L. = 8; R.L. = 8 h L.L.
T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M +
T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M + A a n l e i d i n g I n d e St a t e nc o m m i s si e v o or R ui m t e e n G r o e n ( n u g e n o em d d e St at e n c
UITSPRAAK COMMISSIE FUNCTIE-INDELING RAS 2014-02
UITSPRAAK COMMISSIE FUNCTIE-INELING RAS 2014-02 1 GESCHIL Bij -mil d.d. 10 jnui 2014 mt bijlgn vzkt d h B, d cmmissi Functi-indling vn d RAS (hin: cmmissi) n bindnd dvis uit t bngn in n gschil mt SB A
x 0 2 y -1 0 x 0 1 y 2-1 y 3 4 y 0 2 G&R vwo A/C deel 1 2 Functies en grafieken C. von Schwartzenberg 1/15 1a 1b
G&R vwo A/C deel 1 Functies en grafieken C. von Schwartzenberg 1/15 1a 1b t =, 5 d 10, 5 + 46 = 1 (m). 1 minuut en 45 seconden geeft t = 1,75 d 10 1,75 + 46 = 8,5 (m). 1c 1d Per minuut wordt de diepte
Formulekaart VWO 1. a k b n k. k=0
Formulekrt VWO 1 Formulekrt VWO Knsrekening Tellen n! = n (n 1)... 1 0! = 1 ( ) n n! = k k!(n k)! Binomium vn Newton: ( + b) n = n k=0 ( ) n k b n k k Knsrekening Voor toevlsvribelen X en Y geldt E(X +
Eindexamen wiskunde B1-2 vwo 2007-I
Eindemen wiskunde B- vwo 007-I Beoordelingsmodel Podiumverlichting mimumscore 3 sin α = r 650 V 650 r r r 650 r = 9 + invullen geeft V = 9 + sin α = r r = 9 + V = 650 650 = 9+ 9+ 9 + mimumscore 5 650 00
Correctievoorschrift VWO
Corrctivoorschrift VWO 008 tijdvak wiskund B Ht corrctivoorschrift bstaat uit: Rgls voor d boordling Algmn rgls 3 Vakspcifik rgls 4 Boordlingsmodl 5 Inzndn scors Rgls voor d boordling Ht wrk van d kandidatn
Bepaling toezichtvorm gemeente Venray
Bepaling toezichtvorm 2007-2010 gemeente Venray F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k V e n
Newton en het zonnestelsel 1
Inliding stofsic 00 Inliding stofsic ul n d Wf Stwcht idn Nwton n Kpl Wttn n Nwton: Tghidswt: gn kcht onndd wging Ipulswt: p Rctiwt: cti cti Gittiwt Wttn n Kpl: Ellipsnwt knwt: Constnt Honisch wt: houd
Toebehoren voor bekisting Bekistingsafstandhouders
Tobhorn voor bkisting Bkistingsafstandhoudrs Buizn, conisch uitindn & stoppn in PVC Constructi voor ht btonnrn Rond buizn in PVC Ø Afwrking Ruw afwrking RS6602 14 19 Glad RS6406 20 24 Ruw RS6400 22 26
Moderne wiskunde: berekenen zwaartepunt vwo B
Moderne wiskunde: erekenen zwrtepunt vwo B In de edities 7 en 8 ws er in de slotdelen vn VWO B ruimte genomen voor een prgrf over het erekenen vn een zwrtepunt. In de negende editie is er voor gekozen
De vergelijking van Antoine
De vergelijking van ntoine maimumscore 4 log = 0, dus 0 4,46 T 5,5 Dit geeft = 4,46, dus T 5,5 = T 5,5 4,46 Hieruit volgt T = 5,5+ ( 9,) 4,46 Het antwoord 9 (kelvin) maimumscore ls T toeneemt, neemt T
12c u 1000 = =
G&R vwo C dl 3 9 Rij C. vo Schwartzbrg 1/10 1a A hoort bij rij IV; B hoort bij rij II; C hoort bij rij III D hoort bij rij I. 1b Bij rij I: 36, 49, 64; bij rij II: 8000, 16000, 3000; bij rij III: 17, 19,
de Wageningse Methode Antwoorden H24 GONIOMETRIE VWO 1
H GONIOMETRIE VWO.0 INTRO 6 km : 0.000 = cm b b Driehoek PQB is gelijkvormig met driehoek VHB, de 00 vergrotingsfctor is 0 = 7. Dus PQ = 680 = 0, dus zeilt ze 0 meter 7 in minuten. Dt is,8 km/u.. HOOGTE
Correctievoorschrift VWO. Wiskunde B1 (nieuwe stijl)
Wiskunde B (nieuwe stijl) Correctievoorschrift VWO Voorbereidend Wetenschppelijk Onderwijs 0 0 Tijdvk Inzenden scores Vul de scores vn de lfbetisch eerste vijf kndidten per school in op de optisch leesbre
Q: Afstand tot E is. R: Afstand tot E is
H9 PARABOLEN & HYPERBOLEN VWO 9. INTRO Q: Afstnd tot E is 69 6 7 () ( ) 9. Afstnd tot k is 9. R: Afstnd tot E is (6 ) 6. 669 6 7 Afstnd tot k is 6. us Q en R liggen even ver vn E ls vn k. e fstnd tot k
Eindexamen vwo wiskunde B II
Formules Vlkke meetkunde Verwijzingen nr definities en stellingen die bij een bewijs mogen worden gebruikt zonder ndere toelichting. Hoeken, lijnen en fstnden: gestrekte hoek, rechte hoek, overstnde hoeken,
20 m/s. 11 m/s. 20km h. 5,6 m/s op t = 4,0 s is de plaats: 5,6 4,0 22 m. 58 [W] Experiment. 59 [W] Experiment: Versnellend karretje
![20 m/s. 11 m/s. 20km h. 5,6 m/s op t = 4,0 s is de plaats: 5,6 4,0 22 m. 58 [W] Experiment. 59 [W] Experiment: Versnellend karretje](/thumbs/93/111671772.jpg "20 m/s. 11 m/s. 20km h. 5,6 m/s op t = 4,0 s is de plaats: 5,6 4,0 22 m. 58 [W] Experiment. 59 [W] Experiment: Versnellend karretje")
58 [W] Exprimnt 59 [W] Exprimnt: Vrsnlln krrtj 60 [W] Exprimnt: Knikkrn 61 [W] Drgrr 62 [W] Exprimnt: En ign wging 63 [W] Wissln op stftt 64 Wr of nit wr? Nit wr: ht v,t-igrm vn n nprig vrsnl wging is
R e g i o M i d d e n -L i m b u r g O o s t. G r e n z e l o o s w o n e n i n M i d d e n -L i m b u r g R e g i o n a l e W o o n v i s i e
R e g i o M i d d e n -L i m b u r g O o s t G r e n z e l o o s w o n e n i n M i d d e n -L i m b u r g R e g i o n a l e W o o n v i s i e 4 o k t o b e r 2 0 0 6 P r o j e c t n r. 2 9 5 7. 7 2 B o
Regieorgaan SIA. Begrotingsformat incl. voortgangs- en eindrapportage RAAK
Rgiogn SI gotingsfoat incl. vootgangs n indappotag RK Tolichting bij dit bgotingsfoat: In ht tabblad 'Sanvattnd ovzicht' vult u d titl van ht pojct n d n van d pnvond hogschool in. In d dop volgnd tabbladn
Christmas time 2.0! Lesbrief
Lsbrif Christms tim 2.0! En updt vn ht succsvoll Tumult krstspl vn vorig jr. In smnwrking mt Musicbox is d muzikrond nu n krstmuzikquiz gwordn di j klssikl ls fsluiting vn ht spl dot: vl plzir n lvst hl
Eindexamen wiskunde B1 vwo 2008-I
Eindamn wiskund B vwo 008-I Boordlingsmodl Vraag Antwoord Scors Landing maimumscor 4 y' 4,8 0 3 + 4,8 0 5 y '(0) 0 (dus in (0, 8) hft ht vligtuig n horizontal bwgingsrichting) y '(00) 0,48+ 0,48 0 (dus
Opgave 1: De oppervlakte van de figuur is precies de oppervlakte van een rechthoek van 7 bij 3, dus
Hoofdstuk : Oppevlakte en inhoud.. Oppevlakte van vlakke figuen Opgave : De oppevlakte van de figuu is pecies de oppevlakte van een echthoek van 7 bij, dus Opp 7 Opgave : a. ABCQPH ) 4 dus lijnstuk PQ
Deel 1 Vijfde, herziene druk
drs. J.H. Blanksoor drs. C. d Jood ir. A. Sluijtr Togast Wiskund voor ht hogr brosondrwijs Dl Vijfd, hrzin druk Uitwrking hrhalingsogavn hoofdstuk 6 ThimMulnhoff, Amrsfoort, Togast Wiskund, dl Uitwrking
Ajodakt. Rekenen. Cijferen Mix. Cijferen groep 8. Colofon. Zelfstandig werken. Antwoorden. Rekenen. Groep 8
Cijn Mix Ajokt Coloon Rknn Cijn gop Autus Mjnn vn Gmn Cokky Stolz ThimMulnho ontwikklt lmiln voo Pimi Onwijs, Vootgzt Onwijs, Bopsonwijs n Volwssnnuti n Hog Onwijs Zlstnig wkn Rknn Gop Antwoon Dit ntwoonokj
PA 9623PB 9623PC 9623PE 9623PG 9623PH 9623PJ 9623PK 9623TH PA 9624PB
1 9616 9616TC 9616TH 9616TM 9617 9617AA 9617AN 9617AR 9617AT 9617AV 9617TB 9617TC 9618 9618PA 9618PB 9618PC 9618PD 9618PE 9618PG 9618PH 9619 9619PA 9619PD 9619PL 9619PM 9619PR 9619PS 9619PT 9619TA 9619TB
( ) ( ) ( ) ( ) ( ) ( ) 2 4 ( ) 2 25 ( ) ( ) ( ) 1 ( ) 2 ( ) 2 2 2. y y x. a 3a. ab b a b b a b. a a. a a. a a
G&R hvo B deel Eponenen en lorimen C von Schwrzenber / y = en y = b komen op hezelde neer = en = c y y komen nie op hezelde neer y = en y = komen op hezelde neer b c 8 = d = = 0 8 = e ( ) ( ) 9 = = 8 8
Blok 4 - Vaardigheden
Blok - Vrdigheden ldzijde 0 Dt geldt voor h, len m ; de grfieken zijn symmetrish in de y -s. Die zijn tegengesteld; ijvooreeld g( ) g () De grfiek is symmetrish in de oorsprong. funtie symmetrie in de
de Wageningse Methode Antwoorden H29 PARABOLEN&HYPERBOLEN VWO 1
H9 PARABOLEN & HYPERBOLEN VWO 9. INTRO 9. CONFLICTLIJN ; y ; d y y y y ( y ( y y y y, of, Q: Afstnd tot E is 69 6 7 ( ( 9. Afstnd tot k is 9. R: Afstnd tot E is 66.9 7 6 (6 6. Afstnd tot k is 6. us Q en
Jaargang 4, nummer 12, datum: 17 februari 2015
Jgng 4, numm 12, dtum: 17 fui 2015 Bst ouds of vzogs, Volgnd wk is ht lw Voojsvknti n mt ht w vn d fglopn dgn, volt ht ook uitn f n to l ls vooj. W wnsn idn lvst n hl pttig vknti n zin lk 2 mt hoplijk
Eindexamen vwo wiskunde B pilot 2013-I
Eindeamen vwo wiskunde B ilot 0-I Beoordelingsmodel De vergelijking van ntoine maimumscore 4 44 log = 0, dus 0 4,46 T 5,5 44 44 Dit geeft = 4,46, dus T 5,5 = T 5,5 4,46 44 Hieruit volgt T = 5,5+ ( 9,)
35 7 omhoog. Hoofdstuk 26 RECHTE LIJNEN. 6 ad 26.0 INTRO
Hoofdstuk 6 RECHTE LIJNEN 6 d 6.0 INTRO km kost,0: =,0 drnkje kost : =,0, dus de entrée is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
B e l e i d s k a d e r K e r k e n, K l o o s t e r s e n a n d e r e r e l i g i e u z e g e b o u w e n
B e l e i d s k a d e r K e r k e n, K l o o s t e r s e n a n d e r e r e l i g i e u z e g e b o u w e n I n é é n d a g k a n r e l i g i e u s e r f g o e d v a n m e e r d e r e g e n e r a t i e
15 5 omhoog. Hoofdstuk 26 RECHTE LIJNEN. 6 ad 26.0 INTRO
Hoofdstuk 6 RECHTE LIJNEN 6.0 INTRO 6 d km kost,0: =,9 drnkje kost : =,0, dus de entree is,0,0 = 0,-. Nee, ls je ij de onderste lijn nr rechts gt g je omhoog, dus ls je nr rechts zou gn, zou je omhoog
sin( α + π) = sin( α) O (sin( x ) cos( x )) = sin ( x ) 2sin( x )cos( x ) + cos ( x ) = sin ( x ) + cos ( x ) 2sin( x )cos( x ) = 1 2sin( x )cos( x )
G&R vwo B deel Goniometrie en beweging C. von Schwartzenberg / spiegelen in de y -as y = sin( x f ( x = sin( x f ( x = sin( x heeft dezelfde grafiek als y = sin( x. spiegelen in de y -as y = cos( x g(
Voorbeelden ISSO-publicatie 57
Voorbldn ISSO-publcat 7. VOORBEELDEN Voorbld Ht btrft n nuw, vrjstaand, doosvormg hal mt als hoofdafmtngn 80 0 7, m. D dur hft n afmtng van 4 mtr n n U-waard van W/(m K. D wandn hbbn n U-waard van 0, W/(m
(zie boek) De vergelijking van de rechte lijn kan bepaald worden (grafisch of met de rekenmachine) en is dan 15
Antwoordn tntamn stralingsfysica 11-maart-9 Opgav 1 a) 1.6 1.4 1. Rmspanning (V) 1..8.6.4..+.+14 4.+14 6.+14 8.+14 Frqunti (Hz) Voor t foto-lktrisc ffct gldt V φ f (zi bok) D vrglijking van d rct lijn
Bepaling toezichtvorm gemeente Simpelveld
Bepaling toezichtvorm 2008-2011 gemeente Simpelveld F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, j u n i 2 0 0 8 V e r d i e p i n g s o n d e r z o e k
C. von Schwartzenberg 1/20. Toets voorkennis EXTRA: 3 Differentiëren op bladzijde 156 aan het einde van deze uitwerking.
G&R havo B deel Differentiaalrekening C von Schwartzenberg /0 Toets voorkennis EXTRA: Differentiëren op bladzijde 56 aan het einde van deze uitwerking a f ( ) 5 7 f '( ) 8 5 b g( ) ( 5) 5 g '( ) 6 0 c
F G H I J. 5480
() Nm : Kls: Dtum: A. 06 Uit ln + ln( ) = ln volgt dt gelijk is n ) ) ) ) ) g.v.d.v. B. 77 + b ) b ) (+ is gelijk n b ) ) b) ).b b F. 7 kn ook geschreven worden ls ) e ) e ) e ( ) ln e ) ) e G. 7 9 Als
H. 9 Het getal e / Logaritmen
H. 9 Ht tal / Loaritmn 9.1 Ht tal Ht tal is n spciaal tal in d wiskund, nt zoals ht tal π. Ht is als volt dfinird: 1 1 1 1 1 1 = + + + + + + 1 1 1 14 145 Als w dit uitrknn, dan wordt d waard van ht tal
P 3, = 0, s 1.
Ovrl Ntuurkund 6 vwo Uitwrking Ofnopgvn Kuzhoofdstuk Krnn n dltjs 70 Voor 58 F: m dltjs =26 m p + 32 m n = 26 1,007 276 5 + 32 1,008 664 9 = 58,466 466 u m krn = 57,933 28 u m = 58,466 466 57,933 28 u
Hun comfort begint bij u. Brochure voor de UNETO-VNI ComfortInstallateur
Hun cofot bgint bij u Bochu voo d UNETO-VNI CofotInstlltu l l Dz bochu is sngstld o bsis vn n ondzo vn: Dit ondzo vindt u intgl tug o ht UNETO-VNI LdnNt. 02 Uw tis vdint Als ofssionl UNETO-VNI CofotInstlltu
Ranglijst woongebied land van matena 1 januari 2019
Toelichting Ranglijst woongebied land van matena 1 januari 2019 Hieronder treft u de geanonimiseerde ranglijst per 1 januari 2019 aan voor het woongebied van Land van Matena. Het betreft een momentopname.
meerpuntssluitingen SILVERLINE NECOSLOT NECOSLOT SILVERLINE NECOSLOT NECOSLOT compleet & goed KOBALTSCHARNIEREN MEERPuNTSSLuITINgEN SLOTEN
SILLIN NSLT KLTSHNIN MuNTSSLuITINN m k s ji z NSLT SLTN k m s ijz k m s ijz mpunssluiinn compl & od 45 415 41 4 41 xa xa xa Lih Lih SILLIN Slo dinin ooplaa Typ Slo Ln 910 ilindbdind 100 mm 915 Kukbdind
Regieorgaan SIA. Begrotingsformat incl. voortgangs- en eindrapportage L.INT. Toelichting bij dit begrotingsformat
Rgiogn SI Bgotingsfoat incl. vootgangs n indappotag L.INT Tolichting bij dit bgotingsfoat In ht tabblad 'Sanvattnd ovzicht' vult u d titl van ht tajct in n d n van d pnvond instlling (d hogschool of ht
Hoofdstuk 12A - Breuken en functies
Hoostuk A - Brukn n untis Hoostuk A - Brukn n untis Voorknnis V-a g 9 h 9 9 i 0 j 9 0 0 V-a 0 nt is 0,0. J trkt ht aantal likjs kr 0,0 van uro a. W(0) 0,0 0 Z ht nog uro op klantnkaart staan. 0,0 0,0 :
NEVAC examen Elementaire Vacuümtechniek Vrijdag 11 april 2003, 14:00-16:30 uur. Vraagstuk 1 (EV-03-1) (25 punten)
NEVAC xmn Elmntir Vuümthnik Vrijg 11 pril 2003, 14:00-16:30 uur Vrgstuk 1 (EV-03-1) (25 puntn) En vuümsystm wort gëvur mt n olivrij pompsystm, t stt uit n voorvuümpomp n n turomolulirpomp. D pompsnlhi
Zwaartepunt en traagheid
Nslgwerk deel 8 wrtepunt en trgheid Uitgve 2016-1 uteur HC hugocleys@icloud.com Inhoudsopgve 1 wrtepunt 4 1.1 Inleiding wrtepunt vn een lichm....................... 4 1.2 Momentenstelling..................................
B01 B02 B03 B04 B05 B06 B07 B08 B09 B10 B11 B12 B13 B14 B15 B16 B17 B18 B19 BR* BR+
B01 B02 B03 B04 B05 B06 B07 B08 B09 B10 B11 B12 B13 B14 B15 B16 B17 B18 B19 BR* BR+ LH 262 BK JV 151 FA KR 069 MU ET 160 TK VK 010 MT JE 139 EN AW 228 WI KT 247 BI BT 172 FA PW 261 BK HF 119 EN NF 107
= cos245 en y P = sin245.
G&R havo B deel C. von Schwartzenberg / a b overstaande rechthoekszijde PQ PQ sinα = (in figuur 8.) sin = = PQ = sin 0, 9. schuine zijde OP aanliggende rechthoekszijde OQ OQ cosα = (in figuur 8.) cos =