TW2020 Optimalisering
|
|
|
- Lucas Michiels
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
2 Definitie Een boom is een samenhangende graaf zonder circuits. Een bos is een verzameling bomen. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
3 Definitie Een boom is een samenhangende graaf zonder circuits. Een bos is een verzameling bomen. Of: een bos is een graaf zonder circuits. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
4 Definitie Een boom is een samenhangende graaf zonder circuits. Definitie Een bos is een verzameling bomen. Of: een bos is een graaf zonder circuits. Laat G = (V, E) een graaf zijn. Een opspannende boom (spanning tree) van G is een boom T = (V, F ) met F E. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
5 Definitie Een boom is een samenhangende graaf zonder circuits. Definitie Een bos is een verzameling bomen. Of: een bos is een graaf zonder circuits. Laat G = (V, E) een graaf zijn. Een opspannende boom (spanning tree) van G is een boom T = (V, F ) met F E. Anders gezegd, een opspannende boom van G is een deelgraaf van G die alle punten van G verbindt en geen circuits bevat. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
6 Voorbeeld Een opspannende boom van de Petersen graaf (in zwart): Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
7 Voorbeeld Een andere opspannende boom van de Petersen graaf (in zwart): Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
8 Probleem Minimum Opspannende Boom (Minimum Spanning Tree) Gegeven: samenhangende graaf G = (V, E) en lengtefunctie l : E R Vind: een opspannende boom T = (V, F ) van G met minimale lengte l(t ) = l(e) e F Elke samenhangende graaf heeft tenminste één opspannende boom. Toepassing: netwerk ontwerp. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
9 Prim-Dijkstra methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) en lengtefunctie l : E R Definitie δ(u) is de verzameling lijnen die precies één eindpunt in U hebben Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
10 Prim-Dijkstra methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) en lengtefunctie l : E R Definitie δ(u) is de verzameling lijnen die precies één eindpunt in U hebben Algoritme Kies willekeurig punt v 1 U 1 := {v 1 } F 1 := Voor k = 1, 2,..., V 1 Kies een lijn ek δ(u k ) met minimale lengte Uk+1 := U k e k Fk+1 := F k {e k } Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
11 Prim-Dijkstra methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) en lengtefunctie l : E R Definitie δ(u) is de verzameling lijnen die precies één eindpunt in U hebben Algoritme Kies willekeurig punt v 1 U 1 := {v 1 } F 1 := Voor k = 1, 2,..., V 1 Kies een lijn ek δ(u k ) met minimale lengte Stelling Uk+1 := U k e k Fk+1 := F k {e k } (V, F V ) is een minimum opspannende boom van G Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
12 Voorbeeld Vind een minimum opspannende boom in de volgende graaf m.b.v. de Prim-Dijkstra methode: Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
13 Lemma (1) De volgende uitspraken zijn equivalent voor een graaf G = (V, E): 1 G is een boom (is samenhangend en bevat geen circuit) 2 G is samenhangend en E = V 1 3 G bevat geen circuit en E = V 1 4 G bevat een uniek pad tussen elk tweetal punten Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
14 Lemma (2) Als G = (V, E) samenhangend is, (V, F ) een opspannende boom van G en e E \ F dan zijn de volgende twee uitspraken waar: 1 (V, F {e}) heeft een uniek circuit C Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
15 Lemma (2) Als G = (V, E) samenhangend is, (V, F ) een opspannende boom van G en e E \ F dan zijn de volgende twee uitspraken waar: 1 (V, F {e}) heeft een uniek circuit C 2 voor elke lijn f van C is (V, F \ {f } {e}) ook een opspannende boom van G e Voorbeeld: lijn e toevoegen geeft een uniek circuit; lijn f weglaten geeft weer een opspannende boom. f Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
16 Definitie Een bos (V, F ) is een bos van G = (V, E) als F E. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
17 Definitie Een bos (V, F ) is een bos van G = (V, E) als F E. Stelling (12.1) Laat (V, F ) een bos van G = (V, E) zijn, U een samenhangende component van (V, F ) en e δ(u) een lijn met minimale lengte over alle lijnen in δ(u), dan bestaat er een opspannende boom van G die de lijnen in F {e} bevat en die minimaal is over alle opspannende bomen van G die de lijnen in F bevatten. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
18 Definitie Een bos (V, F ) is een bos van G = (V, E) als F E. Stelling (12.1) Laat (V, F ) een bos van G = (V, E) zijn, U een samenhangende component van (V, F ) en e δ(u) een lijn met minimale lengte over alle lijnen in δ(u), dan bestaat er een opspannende boom van G die de lijnen in F {e} bevat en die minimaal is over alle opspannende bomen van G die de lijnen in F bevatten. Stelling Het algoritme van Prim-Dijkstra vindt een minimum opspannende boom. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
19 Stelling Het algoritme van Prim-Dijkstra heeft een looptijd van O( V 2 ). Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
20 Stelling Het algoritme van Prim-Dijkstra heeft een looptijd van O( V 2 ). Bewijs Houd voor elk punt v V \ U k de lengte f (v) bij van een kortste lijn {u, v} met u U k. Er zijn V iteraties. In elke iteratie is er O( V ) tijd nodig om een punt v V \ U k met minimale f (v) te vinden. In elke iteratie is er O( V ) tijd nodig om de labels van de buren van dit punt v aan te passen. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
21 Stelling Het algoritme van Prim-Dijkstra heeft een looptijd van O( V 2 ). Bewijs Stelling Houd voor elk punt v V \ U k de lengte f (v) bij van een kortste lijn {u, v} met u U k. Er zijn V iteraties. In elke iteratie is er O( V ) tijd nodig om een punt v V \ U k met minimale f (v) te vinden. In elke iteratie is er O( V ) tijd nodig om de labels van de buren van dit punt v aan te passen. Het algoritme van Prim-Dijkstra geïmplementeerd met Fibonacci Heaps lost het minimum opspannende boom probleem op in tijd O( E + V log( V )). Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
22 Borůvka s methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) met lengtefunctie l : E R. Neem voor het gemak aan dat alle lijnen verschillende lengtes hebben. Algoritme F := while F < V 1 laat U 1,..., U k de componenten van (V, F ) zijn for i = 1,..., k kies een lijn e i δ(u i ) van minimum lengte F := F {e1,..., e k } Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
23 Borůvka s methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) met lengtefunctie l : E R. Neem voor het gemak aan dat alle lijnen verschillende lengtes hebben. Algoritme F := while F < V 1 laat U 1,..., U k de componenten van (V, F ) zijn for i = 1,..., k kies een lijn e i δ(u i ) van minimum lengte F := F {e1,..., e k } Stelling Borůvka s algoritme vindt een minimum opspannende boom (V, F ) van G. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
24 Borůvka s methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) met lengtefunctie l : E R. Neem voor het gemak aan dat alle lijnen verschillende lengtes hebben. Algoritme F := while F < V 1 laat U 1,..., U k de componenten van (V, F ) zijn for i = 1,..., k kies een lijn e i δ(u i ) van minimum lengte F := F {e1,..., e k } Stelling Borůvka s algoritme vindt een minimum opspannende boom (V, F ) van G. Stelling De looptijd van Borůvka s algoritme is O( E log( V )). Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
25 Voorbeeld Vind een minimum opspannende boom in de volgende graaf m.b.v. Borůvka s methode: Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
26 Kruskals methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) met lengtefunctie l : E R. Algoritme F := for k = 1, 2,..., V 1 Kies een lijn e k E \ F met minimale lengte waarvoor (V, F {e k }) een bos is F := F {ek } Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
27 Kruskals methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) met lengtefunctie l : E R. Algoritme Stelling F := for k = 1, 2,..., V 1 Kies een lijn e k E \ F met minimale lengte waarvoor (V, F {e k }) een bos is F := F {ek } Kruskals algoritme vindt een minimum opspannende boom (V, F ) van G. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
28 Kruskals methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) met lengtefunctie l : E R. Algoritme Stelling F := for k = 1, 2,..., V 1 Kies een lijn e k E \ F met minimale lengte waarvoor (V, F {e k }) een bos is F := F {ek } Kruskals algoritme vindt een minimum opspannende boom (V, F ) van G. Stelling Kruskals algoritme kan geïmplementeerd worden zodat de looptijd O( E log( V )) is. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
29 Voorbeeld Vind een minimum opspannende boom in de volgende graaf m.b.v. Kruskals algoritme: Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
30 Probleem Maximum Gewicht Bos (Maximum Weight Forest) Gegeven: graaf G = (V, E) en gewichtsfunctie w : E R + Vind: een bos B = (V, F ) van G met maximum gewicht w(e) e F Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
31 Probleem Maximum Gewicht Bos (Maximum Weight Forest) Gegeven: graaf G = (V, E) en gewichtsfunctie w : E R + Vind: een bos B = (V, F ) van G met maximum gewicht w(e) e F Definieer een lengtefunctie l : E R + met l(e) = W w(e) waar W = max e E w(e). Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
32 Probleem Maximum Gewicht Bos (Maximum Weight Forest) Gegeven: graaf G = (V, E) en gewichtsfunctie w : E R + Vind: een bos B = (V, F ) van G met maximum gewicht w(e) e F Definieer een lengtefunctie l : E R + met l(e) = W w(e) waar W = max e E w(e). Voor een samenhangende graaf G = (V, E) is (V, F ) een maximum gewicht bos m.b.t. w dan en slechts dan als (V, F ) een minimum opspannende boom is m.b.t. l. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
33 Probleem Maximum Gewicht Bos (Maximum Weight Forest) Gegeven: graaf G = (V, E) en gewichtsfunctie w : E R + Vind: een bos B = (V, F ) van G met maximum gewicht w(e) e F Definieer een lengtefunctie l : E R + met l(e) = W w(e) waar W = max e E w(e). Voor een samenhangende graaf G = (V, E) is (V, F ) een maximum gewicht bos m.b.t. w dan en slechts dan als (V, F ) een minimum opspannende boom is m.b.t. l. Voor een niet-samenhangende graaf G = (V, E) vormen de minimum opspannende bomen van de samenhangende componenten van G m.b.t. l een maximum gewicht bos m.b.t. w. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
34 Kruskals methode voor het vinden van een maximum gewicht bos van een graaf G = (V, E) met gewichtsfunctie w : E R. Algoritme F := while er een lijn bestaat die aan F toegevoegd kan worden zonder een circuit te creëren Vind zo n lijn van maximum gewicht en voeg die lijn toe aan F Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
35 Kruskals methode voor het vinden van een maximum gewicht bos van een graaf G = (V, E) met gewichtsfunctie w : E R. Algoritme F := while er een lijn bestaat die aan F toegevoegd kan worden zonder een circuit te creëren Vind zo n lijn van maximum gewicht en voeg die lijn toe aan F Kruskals algoritme is een voorbeeld van een greedy algoritme: het maakt in elke iteratie de keuze die direkt het meeste profijt oplevert. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
36 Kruskals methode voor het vinden van een maximum gewicht bos van een graaf G = (V, E) met gewichtsfunctie w : E R. Algoritme F := while er een lijn bestaat die aan F toegevoegd kan worden zonder een circuit te creëren Vind zo n lijn van maximum gewicht en voeg die lijn toe aan F Kruskals algoritme is een voorbeeld van een greedy algoritme: het maakt in elke iteratie de keuze die direkt het meeste profijt oplevert. Het Maximum Gewicht Bos probleem is een voorbeeld van een matroïde probleem. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
37 Kruskals methode voor het vinden van een maximum gewicht bos van een graaf G = (V, E) met gewichtsfunctie w : E R. Algoritme F := while er een lijn bestaat die aan F toegevoegd kan worden zonder een circuit te creëren Vind zo n lijn van maximum gewicht en voeg die lijn toe aan F Kruskals algoritme is een voorbeeld van een greedy algoritme: het maakt in elke iteratie de keuze die direkt het meeste profijt oplevert. Het Maximum Gewicht Bos probleem is een voorbeeld van een matroïde probleem. Alle matroïde problemen kunnen opgelost worden met een greedy algoritme. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
38 Een matroïde bestaat uit een eindige verzameling E en een verzameling I van deelverzamelingen van E die independent sets worden genoemd. Definitie Een matroïde (matroid) is een paar (E, I) met E een eindige verzameling en I een verzameling van deelverzamelingen van E, zodanig dat: (i) Als A I en B A dan is B I. (ii) Als A, B I en A < B dan is er een element e E zodanig dat A {e} I. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
39 Voorbeeld Als G = (V, E) een graaf is en I = {F E (V, F ) bevat geen circuit} dan is (E, I) een matroïde (een graphic matroid). Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
40 Voorbeeld Als G = (V, E) een graaf is en I = {F E (V, F ) bevat geen circuit} dan is (E, I) een matroïde (een graphic matroid). Voorbeeld Als A een m n matrix is met: S de verzameling van kolommen van A; F = {F S de kolommen in F zijn lineair onafhankelijk} dan is (S, F) een matroïde (een matric matroid). Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
41 Elke matroïde (E, I) heeft een bijbehorend probleem: gegeven een gewichtsfunctie w : E R, vind een independent set van maximum gewicht. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
42 Elke matroïde (E, I) heeft een bijbehorend probleem: gegeven een gewichtsfunctie w : E R, vind een independent set van maximum gewicht. Deze problemen kunnen allemaal opgelost worden met het greedy algoritme. Algoritme F := while E Kies e E met maximum gewicht w(e) Verwijder e uit E. if F {e} I Voeg e toe aan F Uitvoer: F De uitvoer F is een independent set van maximum gewicht. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
43 Vraag Hoeveel opspannende bomen heeft een volledige graaf met n punten? Stelling (Formule van Cayley) Het aantal verschillende bomen met n gelabelde punten is n n 2. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
44 Vraag Hoeveel opspannende bomen heeft een volledige graaf met n punten? Stelling (Formule van Cayley) Het aantal verschillende bomen met n gelabelde punten is n n 2. Leo 2 2 van Iersel (TUD) TW2020 Optimalisering oktober / 25
45 Definitie Een Prüfer rij is een rij van lengte n 2 bestaande uit getallen uit {1,..., n} Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
46 Definitie Een Prüfer rij is een rij van lengte n 2 bestaande uit getallen uit {1,..., n} Gegeven een gelabelde boom T, kun je als volgt een unieke Prüfer rij bepalen: Laat 1, 2,..., n de labels van de punten van T zijn. Een blad is een punt met graad één. Algoritme Vind het blad b met kleinste label; voeg de buur van b toe aan de Prüfer rij; verwijder b uit de boom; herhaal de voorgaande stappen totdat er twee punten over zijn. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
47 Algoritme Vind het blad b met kleinste label; voeg de buur van b toe aan de Prüfer rij; verwijder b uit de boom; herhaal de voorgaande stappen totdat er twee punten over zijn. Voorbeeld Vind de Prüfer rij van de onderstaande boom Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25 7
48 Algoritme Vind het blad b met kleinste label; voeg de buur van b toe aan de Prüfer rij; verwijder b uit de boom; herhaal de voorgaande stappen totdat er twee punten over zijn. Voorbeeld Vind de Prüfer rij van de onderstaande boom Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25 7
49 Gegeven een Prüfer rij a = (a 1, a 2,..., a n 2 ), kun je als volgt een unieke gelabelde boom bepalen: Algoritme L := (1, 2,..., n) Creëer punten met labels 1, 2,..., n Herhaal de volgende stappen totdat L = 2 Laat l het eerste label in L zijn dat niet in a voor komt Laat a1 het eerste element van a zijn Verbind het punt met label l met het punt met label a1 Verwijder l uit L en a1 uit a Laat L = {l 1, l 2 } Verbind het punt met label l 1 met het punt met label l 2 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
50 Stelling Er is een bijectie tussen bomen met puntlabels 1,..., n en Prüfer rijen van lengte n 2. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
51 Stelling Er is een bijectie tussen bomen met puntlabels 1,..., n en Prüfer rijen van lengte n 2. Stelling (Formule van Cayley) Het aantal verschillende bomen met n gelabelde punten is n n 2. Dus een volledige graaf heeft n n 2 opspannende bomen. Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober / 25
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 27 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 27 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 maart 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 maart 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 9 Leo van Iersel Technische Universiteit Delft 11 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 11 november 2015 1 / 22 Mededelingen Huiswerk 2 nagekeken Terug
TW2020 Optimalisering Hoorcollege 9 Leo van Iersel Technische Universiteit Delft 11 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 11 november 2015 1 / 22 Mededelingen Huiswerk 2 nagekeken Terug
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 11 Leo van Iersel Technische Universiteit Delft 25 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 25 november 2015 1 / 28 Vandaag Vraag Voor welke problemen
TW2020 Optimalisering Hoorcollege 11 Leo van Iersel Technische Universiteit Delft 25 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 25 november 2015 1 / 28 Vandaag Vraag Voor welke problemen
Discrete Wiskunde, College 12. Han Hoogeveen, Utrecht University
 Discrete Wiskunde, College 12 Han Hoogeveen, Utrecht University Dynamische programmering Het basisidee is dat je het probleem stap voor stap oplost Het probleem moet voldoen aan het optimaliteitsprincipe
Discrete Wiskunde, College 12 Han Hoogeveen, Utrecht University Dynamische programmering Het basisidee is dat je het probleem stap voor stap oplost Het probleem moet voldoen aan het optimaliteitsprincipe
Minimum Opspannende Bomen. Algoritmiek
 Minimum Opspannende Bomen Inhoud Het minimum opspannende bomen probleem Een principe om een minimum opspannende boom te laten groeien Twee greedy algoritmen + tijd en datastructuren: Het algoritme van
Minimum Opspannende Bomen Inhoud Het minimum opspannende bomen probleem Een principe om een minimum opspannende boom te laten groeien Twee greedy algoritmen + tijd en datastructuren: Het algoritme van
Grafen. Indien de uitgraad van ieder punt 1 is, dan bevat de graaf een cykel. Indien de ingraad van ieder punt 1 is, dan bevat de graaf een cykel.
 Grafen Grafen Een graaf bestaat uit een verzameling punten (ook wel knopen, of in het engels vertices genoemd) en een verzameling kanten (edges) of pijlen (arcs), waarbij de kanten en pijlen tussen twee
Grafen Grafen Een graaf bestaat uit een verzameling punten (ook wel knopen, of in het engels vertices genoemd) en een verzameling kanten (edges) of pijlen (arcs), waarbij de kanten en pijlen tussen twee
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 12 Leo van Iersel Technische Universiteit Delft 7 december 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 december 2016 1 / 25 Volgende week: Study guide Vragenuurtje
TW2020 Optimalisering Hoorcollege 12 Leo van Iersel Technische Universiteit Delft 7 december 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 december 2016 1 / 25 Volgende week: Study guide Vragenuurtje
l e x e voor alle e E
 Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 5 Leo van Iersel Technische Universiteit Delft 12 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 12 oktober 2016 1 / 31 Dualiteit Dualiteit: Elk LP probleem heeft
TW2020 Optimalisering Hoorcollege 5 Leo van Iersel Technische Universiteit Delft 12 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 12 oktober 2016 1 / 31 Dualiteit Dualiteit: Elk LP probleem heeft
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 21 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 21 oktober 2015 1 / 20 Deze week: algoritmes en complexiteit
TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 21 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 21 oktober 2015 1 / 20 Deze week: algoritmes en complexiteit
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 5 Leo van Iersel Technische Universiteit Delft 2 oktober 206 Leo van Iersel (TUD) TW2020 Optimalisering 2 oktober 206 / 3 Dualiteit Dualiteit: Elk LP probleem heeft een
TW2020 Optimalisering Hoorcollege 5 Leo van Iersel Technische Universiteit Delft 2 oktober 206 Leo van Iersel (TUD) TW2020 Optimalisering 2 oktober 206 / 3 Dualiteit Dualiteit: Elk LP probleem heeft een
Discrete Structuren. Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Hebzucht loont niet altijd
 Thema Discrete wiskunde Hoe verbind je een stel steden met zo weinig mogelijk kilometers asfalt? Hoe maak je een optimaal computernetwerk met kabels die maar een beperkte capaciteit hebben? Veel van zulke
Thema Discrete wiskunde Hoe verbind je een stel steden met zo weinig mogelijk kilometers asfalt? Hoe maak je een optimaal computernetwerk met kabels die maar een beperkte capaciteit hebben? Veel van zulke
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TUE) en Centrum Wiskunde & Informatica (CWI) 3 en 6 februari 2014 Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TUE) en Centrum Wiskunde & Informatica (CWI) 3 en 6 februari 2014 Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 26 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 26 oktober 2016 1 / 28 Deze week: analyseren van algoritmes Hoe
TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 26 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 26 oktober 2016 1 / 28 Deze week: analyseren van algoritmes Hoe
Tentamen Discrete Wiskunde 1 10 april 2012, 14:00 17:00 uur
 Tentamen Discrete Wiskunde 0 april 0, :00 7:00 uur Schrijf je naam op ieder blad dat je inlevert. Onderbouw je antwoorden, met een goede argumentatie zijn ook punten te verdienen. Veel succes! Opgave.
Tentamen Discrete Wiskunde 0 april 0, :00 7:00 uur Schrijf je naam op ieder blad dat je inlevert. Onderbouw je antwoorden, met een goede argumentatie zijn ook punten te verdienen. Veel succes! Opgave.
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 en 13 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 en 13 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 13 Leo van Iersel Technische Universiteit Delft 9 december 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 december 2015 1 / 13 Vraag Wat moet ik kennen en kunnen voor
TW2020 Optimalisering Hoorcollege 13 Leo van Iersel Technische Universiteit Delft 9 december 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 december 2015 1 / 13 Vraag Wat moet ik kennen en kunnen voor
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 3 Leo van Iersel Technische Universiteit Delft 21 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 21 september 2016 1 / 36 LP: Lineair Programmeren min x 1 2
TW2020 Optimalisering Hoorcollege 3 Leo van Iersel Technische Universiteit Delft 21 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 21 september 2016 1 / 36 LP: Lineair Programmeren min x 1 2
Elfde college algoritmiek. 10 mei Algoritme van Dijkstra, Gretige Algoritmen
 lgoritmiek 019/lgoritme van ijkstra lfde college algoritmiek 10 mei 019 lgoritme van ijkstra, Gretige lgoritmen 1 lgoritmiek 019/ynamisch programmeren Programmeeropdracht 3 Lange Reis 0 10 10 1 1 100 0
lgoritmiek 019/lgoritme van ijkstra lfde college algoritmiek 10 mei 019 lgoritme van ijkstra, Gretige lgoritmen 1 lgoritmiek 019/ynamisch programmeren Programmeeropdracht 3 Lange Reis 0 10 10 1 1 100 0
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 9 Leo van Iersel Technische Universiteit Delft 16 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 16 november 2016 1 / 28 Vandaag Integer Linear Programming (ILP)
TW2020 Optimalisering Hoorcollege 9 Leo van Iersel Technische Universiteit Delft 16 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 16 november 2016 1 / 28 Vandaag Integer Linear Programming (ILP)
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 3 Leo van Iersel Technische Universiteit Delft 21 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 21 september 2016 1 / 36 LP: Lineair Programmeren min x 1 2
TW2020 Optimalisering Hoorcollege 3 Leo van Iersel Technische Universiteit Delft 21 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 21 september 2016 1 / 36 LP: Lineair Programmeren min x 1 2
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 1 Leo van Iersel Technische Universiteit Delft 7 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 september 2016 1 / 40 Opzet vak Woensdag: hoorcollege 13:45-15:30
TW2020 Optimalisering Hoorcollege 1 Leo van Iersel Technische Universiteit Delft 7 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 september 2016 1 / 40 Opzet vak Woensdag: hoorcollege 13:45-15:30
Transport-, Routing- en Schedulingproblemen. Wi4062TU / Wi487TU / a86g. Uitwerkingen 08-04-2005
 Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 08-04-2005 1 Transportprobleem Onderdeel a Fabriek 1 kan 120 ton staal fabriceren in 40 uur. Voor fabriek 2 is dit 150
Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 08-04-2005 1 Transportprobleem Onderdeel a Fabriek 1 kan 120 ton staal fabriceren in 40 uur. Voor fabriek 2 is dit 150
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 2 Leo van Iersel Technische Universiteit Delft 14 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 14 september 2016 1 / 30 Modelleren van LP en ILP problemen
TW2020 Optimalisering Hoorcollege 2 Leo van Iersel Technische Universiteit Delft 14 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 14 september 2016 1 / 30 Modelleren van LP en ILP problemen
3. Elke lijn van een graaf draagt twee bij tot de som van alle graden.
 Antwoorden Doeboek 4 Grafen.. De middelste en de rechtergraaf.. Een onsamenhangende graaf met vijf punten en vijf lijnen: Teken een vierhoek met één diagonaal. Het vijfde punt is niet verbonden met een
Antwoorden Doeboek 4 Grafen.. De middelste en de rechtergraaf.. Een onsamenhangende graaf met vijf punten en vijf lijnen: Teken een vierhoek met één diagonaal. Het vijfde punt is niet verbonden met een
Netwerkstroming. Algoritmiek
 Netwerkstroming Netwerkstroming Toepassingen in Logistiek Video-streaming Subroutine in algoritmen 2 Vandaag Netwerkstroming: wat was dat ook alweer? Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp
Netwerkstroming Netwerkstroming Toepassingen in Logistiek Video-streaming Subroutine in algoritmen 2 Vandaag Netwerkstroming: wat was dat ook alweer? Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp
V = {a, b, c, d, e} Computernetwerken: de knopen zijn machines in het netwerk, de kanten zijn communicatiekanalen.
 WIS14 1 14 Grafen 14.1 Grafen Gerichte grafen Voor een verzameling V is een binaire relatie op V een verzameling geordende paren van elementen van V. Voorbeeld: een binaire relatie op N is de relatie KleinerDan,
WIS14 1 14 Grafen 14.1 Grafen Gerichte grafen Voor een verzameling V is een binaire relatie op V een verzameling geordende paren van elementen van V. Voorbeeld: een binaire relatie op N is de relatie KleinerDan,
l e x e voor alle e E
 Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 2 Leo van Iersel Technische Universiteit Delft 9 september 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 september 2015 1 / 23 Huiswerk Huiswerk 1 is beschikbaar op
TW2020 Optimalisering Hoorcollege 2 Leo van Iersel Technische Universiteit Delft 9 september 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 september 2015 1 / 23 Huiswerk Huiswerk 1 is beschikbaar op
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 6 Leo van Iersel Technische Universiteit Delft 19 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 19 oktober 2016 1 / 20 Deze week Primal-Dual algoritmes voor:
TW2020 Optimalisering Hoorcollege 6 Leo van Iersel Technische Universiteit Delft 19 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 19 oktober 2016 1 / 20 Deze week Primal-Dual algoritmes voor:
1.2 Bomen Algemeen 1.2. BOMEN 7
 1.2. BOMEN 7 1.2 Bomen 1.2.1 Algemeen Beschouw eerst een niet-gerichte graaf. Een boom is een samenhangende graaf die geen kringen bevat. Een boom wordt meestal genoteerd met de letter T (tree). Een bos
1.2. BOMEN 7 1.2 Bomen 1.2.1 Algemeen Beschouw eerst een niet-gerichte graaf. Een boom is een samenhangende graaf die geen kringen bevat. Een boom wordt meestal genoteerd met de letter T (tree). Een bos
Netwerkstroming. Algoritmiek
 Netwerkstroming Vandaag Netwerkstroming: definitie en toepassing Het rest-netwerk Verbeterende paden Ford-Fulkerson algoritme Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp Toepassing: koppelingen
Netwerkstroming Vandaag Netwerkstroming: definitie en toepassing Het rest-netwerk Verbeterende paden Ford-Fulkerson algoritme Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp Toepassing: koppelingen
Twaalfde college complexiteit. 11 mei 2012. Overzicht, MST
 College 12 Twaalfde college complexiteit 11 mei 2012 Overzicht, MST 1 Agenda voor vandaag Minimum Opspannende Boom (minimum spanning tree) als voorbeeld van greedy algoritmen Overzicht: wat voor technieken
College 12 Twaalfde college complexiteit 11 mei 2012 Overzicht, MST 1 Agenda voor vandaag Minimum Opspannende Boom (minimum spanning tree) als voorbeeld van greedy algoritmen Overzicht: wat voor technieken
Tiende college algoritmiek. 14 april Gretige algoritmen
 College 10 Tiende college algoritmiek 1 april 011 Gretige algoritmen 1 Greedy algorithms Greed = hebzucht Voor oplossen van optimalisatieproblemen Oplossing wordt stap voor stap opgebouwd In elke stap
College 10 Tiende college algoritmiek 1 april 011 Gretige algoritmen 1 Greedy algorithms Greed = hebzucht Voor oplossen van optimalisatieproblemen Oplossing wordt stap voor stap opgebouwd In elke stap
Tiende college algoritmiek. 2 mei Gretige algoritmen, Dijkstra
 College 10 Tiende college algoritmiek mei 013 Gretige algoritmen, Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
College 10 Tiende college algoritmiek mei 013 Gretige algoritmen, Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
Tiende college algoritmiek. 26 april Gretige algoritmen
 Algoritmiek 01/10 College 10 Tiende college algoritmiek april 01 Gretige algoritmen 1 Algoritmiek 01/10 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag
Algoritmiek 01/10 College 10 Tiende college algoritmiek april 01 Gretige algoritmen 1 Algoritmiek 01/10 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag
Tiende college algoritmiek. 4 mei Gretige Algoritmen Algoritme van Dijkstra
 Tiende college algoritmiek mei 018 Gretige Algoritmen Algoritme van Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
Tiende college algoritmiek mei 018 Gretige Algoritmen Algoritme van Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
Benaderingsalgoritmen
 Benaderingsalgoritmen Eerste hulp bij NP-moeilijkheid 1 Herhaling NP-volledigheid (1) NP: er is een polynomiaal certificaat voor jainstanties dat in polynomiale tijd te controleren is Een probleem A is
Benaderingsalgoritmen Eerste hulp bij NP-moeilijkheid 1 Herhaling NP-volledigheid (1) NP: er is een polynomiaal certificaat voor jainstanties dat in polynomiale tijd te controleren is Een probleem A is
Tiende college algoritmiek. 13/21 april Gretige Algoritmen Algoritme van Dijkstra
 Algoritmiek 017/Gretige Algoritmen Tiende college algoritmiek 13/1 april 017 Gretige Algoritmen Algoritme van Dijkstra 1 Algoritmiek 017/Gretige Algoritmen Muntenprobleem Gegeven onbeperkt veel munten
Algoritmiek 017/Gretige Algoritmen Tiende college algoritmiek 13/1 april 017 Gretige Algoritmen Algoritme van Dijkstra 1 Algoritmiek 017/Gretige Algoritmen Muntenprobleem Gegeven onbeperkt veel munten
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 10 Leo van Iersel Technische Universiteit Delft 23 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 23 november 2016 1 / 40 Vraag Ik heb het deeltentamen niet
TW2020 Optimalisering Hoorcollege 10 Leo van Iersel Technische Universiteit Delft 23 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 23 november 2016 1 / 40 Vraag Ik heb het deeltentamen niet
Radboud Universiteit Nijmegen
 Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica L(,1)-labeling van grafen Naam: Studentnummer: Studie: Begeleider: Myrte klein Brink 4166140 Bachelor Wiskunde Dr.
Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica L(,1)-labeling van grafen Naam: Studentnummer: Studie: Begeleider: Myrte klein Brink 4166140 Bachelor Wiskunde Dr.
Kortste Paden. Algoritmiek
 Kortste Paden Toepassingen Kevin Bacon getal Six degrees of separation Heeft een netwerk de small-world eigenschap? TomTom / Google Maps 2 Kortste paden Gerichte graaf G=(N,A), en een lengte L(v,w) voor
Kortste Paden Toepassingen Kevin Bacon getal Six degrees of separation Heeft een netwerk de small-world eigenschap? TomTom / Google Maps 2 Kortste paden Gerichte graaf G=(N,A), en een lengte L(v,w) voor
Minimum Spanning Tree
 Minimum Spanning Tree Wat is MST? Minimum spanning tree De meest efficiënte manier vinden om een verbonden netwerk op te bouwen Wat is een tree/boom? Graaf G: een verzameling knopen (vertices): V een verzameling
Minimum Spanning Tree Wat is MST? Minimum spanning tree De meest efficiënte manier vinden om een verbonden netwerk op te bouwen Wat is een tree/boom? Graaf G: een verzameling knopen (vertices): V een verzameling
Grafen deel 2 8/9. Zesde college
 Grafen deel 2 8/9 Zesde college 1 Een Eulercircuit is een gesloten wandeling die elke lijn precies één keer bevat. traversable trail all edges distinct 8.5 rondwandeling zeven bruggenprobleem van Köningsbergen
Grafen deel 2 8/9 Zesde college 1 Een Eulercircuit is een gesloten wandeling die elke lijn precies één keer bevat. traversable trail all edges distinct 8.5 rondwandeling zeven bruggenprobleem van Köningsbergen
1 Vervangingsstrategie auto
 Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 28-03-2002 1 Vervangingsstrategie auto Onderdeel a Zij V = {0, 1, 2, 3, 4, 5, 6}, waarbij knoop i staat voor het einde
Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 28-03-2002 1 Vervangingsstrategie auto Onderdeel a Zij V = {0, 1, 2, 3, 4, 5, 6}, waarbij knoop i staat voor het einde
Optimaliseren in Netwerken
 Optimaliseren in Netwerken Kees Roos e-mail: C.Roos@tudelft.nl URL: http://www.isa.ewi.tudelft.nl/ roos Kaleidoscoop college Zaal D, Mekelweg 4, TU Delft 11 October, A.D. 2006 Optimization Group 1 Onderwerpen
Optimaliseren in Netwerken Kees Roos e-mail: C.Roos@tudelft.nl URL: http://www.isa.ewi.tudelft.nl/ roos Kaleidoscoop college Zaal D, Mekelweg 4, TU Delft 11 October, A.D. 2006 Optimization Group 1 Onderwerpen
Sommige praktische IP problemen kunnen worden geformuleerd als optimalisering op een netwerk.
 Netwerkanalyse (H3) Sommige praktische IP problemen kunnen worden geformuleerd als optimalisering op een netwerk. Deze problemen kunnen vaak als continu LP probleem worden opgelost. Door de speciale structuur
Netwerkanalyse (H3) Sommige praktische IP problemen kunnen worden geformuleerd als optimalisering op een netwerk. Deze problemen kunnen vaak als continu LP probleem worden opgelost. Door de speciale structuur
Week 1 20-02-2013. Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren.
 Combinatorische Optimalisatie, 2013 Week 1 20-02-2013 Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren. Opgave 1.16 Bewijs dat elke graaf een even aantal punten
Combinatorische Optimalisatie, 2013 Week 1 20-02-2013 Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren. Opgave 1.16 Bewijs dat elke graaf een even aantal punten
Universiteit Utrecht Betafaculteit. Examen Discrete Wiskunde op donderdag 13 april 2017, uur.
 Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde op donderdag 13 april 2017, 14.30-17.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde op donderdag 13 april 2017, 14.30-17.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Lege polygonen in een graaf.
 Uitwerking puzzel 94-2 Lege polygonen in een graaf. Lieke de Rooij Wobien Doyer We hebben n punten die al of niet met elkaar worden verbonden. De bedoeling is om met zo min mogelijk lijnen (=verbindingen)
Uitwerking puzzel 94-2 Lege polygonen in een graaf. Lieke de Rooij Wobien Doyer We hebben n punten die al of niet met elkaar worden verbonden. De bedoeling is om met zo min mogelijk lijnen (=verbindingen)
Uitwerkingen Sum of Us
 Instant Insanity Uitwerkingen Sum of Us Opgave A: - Opgave B: Voor elk van de vier kubussen kun je een graaf maken die correspondeert met de desbetreffende kubus. Elk van deze grafen bevat drie lijnen.
Instant Insanity Uitwerkingen Sum of Us Opgave A: - Opgave B: Voor elk van de vier kubussen kun je een graaf maken die correspondeert met de desbetreffende kubus. Elk van deze grafen bevat drie lijnen.
Universiteit Utrecht Betafaculteit. Examen Discrete Wiskunde II op donderdag 6 juli 2017, uur.
 Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde II op donderdag 6 juli 2017, 13.30-16.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde II op donderdag 6 juli 2017, 13.30-16.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Begrenzing van het aantal iteraties in het max-flow algoritme
 Begrenzing van het aantal iteraties in het max-flow algoritme Het oplossen van het maximum stroom probleem met behulp van stroomvermeerderende paden werkt, maar het aantal iteraties kan aardig de spuigaten
Begrenzing van het aantal iteraties in het max-flow algoritme Het oplossen van het maximum stroom probleem met behulp van stroomvermeerderende paden werkt, maar het aantal iteraties kan aardig de spuigaten
Hoofdstuk!7!Kortste!paden!
 oofdstukkortstepaden oofdstukkortstepaden In een gewogen graaf is men soms geïnteresseerd in het kortste pad tussen twee punten: dat is een pad, waarbij de som van de gewichten zo klein mogelijk is..inleiding
oofdstukkortstepaden oofdstukkortstepaden In een gewogen graaf is men soms geïnteresseerd in het kortste pad tussen twee punten: dat is een pad, waarbij de som van de gewichten zo klein mogelijk is..inleiding
Overzicht. 1. Definities. 2. Basisalgoritme. 3. Label setting methoden. 4. Label correcting methoden. 5. Ondergrenzen. 6.
 Overzicht 1. Definities 2. Basisalgoritme 3. Label setting methoden 4. Label correcting methoden 5. Ondergrenzen 6. Resultaten Kortste Pad Probleem 1 Definities Een graaf G = (V, E) bestaat uit een verzameling
Overzicht 1. Definities 2. Basisalgoritme 3. Label setting methoden 4. Label correcting methoden 5. Ondergrenzen 6. Resultaten Kortste Pad Probleem 1 Definities Een graaf G = (V, E) bestaat uit een verzameling
In dit gedeelte worden drie problemen genoemd die kunnen voorkomen in netwerken.
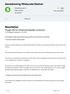 Aantekening Wiskunde Steiner Aantekening door D. 2086 woorden 25 mei 2016 2,1 1 keer beoordeeld Vak Wiskunde Resultaten Vragen bij het wetenschappelijk materiaal 9.1 Prototype example, p. 374-376 In dit
Aantekening Wiskunde Steiner Aantekening door D. 2086 woorden 25 mei 2016 2,1 1 keer beoordeeld Vak Wiskunde Resultaten Vragen bij het wetenschappelijk materiaal 9.1 Prototype example, p. 374-376 In dit
Transport-, Routing- en Schedulingproblemen. Wi4062TU / Wi487TU / a86g. Uitwerkingen
 Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 28-03-2003 1 Docenten Onderdeel a Er zijn 6 vakken V 1, V 2,..., V 6. Vak V j heeft een vraag b j = 1, voor j = 1, 2,...,
Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 28-03-2003 1 Docenten Onderdeel a Er zijn 6 vakken V 1, V 2,..., V 6. Vak V j heeft een vraag b j = 1, voor j = 1, 2,...,
Gerichte Grafen Boolese Algebra s &. Logische Netwerken
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 10 maart 2009 Gerichte Grafen Boolese Algebra s &. Logische Netwerken. Paragrafen
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 10 maart 2009 Gerichte Grafen Boolese Algebra s &. Logische Netwerken. Paragrafen
Heuristieken en benaderingsalgoritmen. Algoritmiek
 Heuristieken en benaderingsalgoritmen Wat te doen met `moeilijke optimaliseringsproblemen? Voor veel problemen, o.a. optimaliseringsproblemen is geen algoritme bekend dat het probleem voor alle inputs
Heuristieken en benaderingsalgoritmen Wat te doen met `moeilijke optimaliseringsproblemen? Voor veel problemen, o.a. optimaliseringsproblemen is geen algoritme bekend dat het probleem voor alle inputs
Elfde college algoritmiek. 21 april Dijkstra en Branch & Bound
 Algoritmiek 011/11 College 11 Elfde college algoritmiek 1 april 011 Dijkstra en Branch & Bound 1 Algoritmiek 011/11 Kortste paden Gegeven een graaf G met gewichten op de takken, en een beginknoop s. We
Algoritmiek 011/11 College 11 Elfde college algoritmiek 1 april 011 Dijkstra en Branch & Bound 1 Algoritmiek 011/11 Kortste paden Gegeven een graaf G met gewichten op de takken, en een beginknoop s. We
Discrete modellen in de toegepaste wiskunde (WISB136) Uitwerkingen proeftentamen.
 Discrete modellen in de toegepaste wiskunde (WISB6) Uitwerkingen proeftentamen. Docent: Rob H. Bisseling april 202. Begin met een matching M = {x y, x y, x 6 y 6 } aangegeven door de vette lijnen. x De
Discrete modellen in de toegepaste wiskunde (WISB6) Uitwerkingen proeftentamen. Docent: Rob H. Bisseling april 202. Begin met een matching M = {x y, x y, x 6 y 6 } aangegeven door de vette lijnen. x De
Transshipment problemen Simplex methode en netwerk optimalisatie algoritmes. Luuk van de Sande Begeleider: Judith Keijsper 20 januari 2013
 Transshipment problemen Simplex methode en netwerk optimalisatie algoritmes Luuk van de Sande Begeleider: Judith Keijsper 20 januari 2013 1 Inhoudsopgave 1 Transport problemen 3 2 Definities en stellingen
Transshipment problemen Simplex methode en netwerk optimalisatie algoritmes Luuk van de Sande Begeleider: Judith Keijsper 20 januari 2013 1 Inhoudsopgave 1 Transport problemen 3 2 Definities en stellingen
Elfde college algoritmiek. 18 mei Algoritme van Dijkstra, Heap, Heapify & Heapsort
 Algoritmiek 018/Algoritme van Dijkstra Elfde college algoritmiek 18 mei 018 Algoritme van Dijkstra, Heap, Heapify & Heapsort 1 Algoritmiek 018/Algoritme van Dijkstra Uit college 10: Voorb. -1- A B C D
Algoritmiek 018/Algoritme van Dijkstra Elfde college algoritmiek 18 mei 018 Algoritme van Dijkstra, Heap, Heapify & Heapsort 1 Algoritmiek 018/Algoritme van Dijkstra Uit college 10: Voorb. -1- A B C D
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2006 2007, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. 1. Verzamelingen:
Tweede bachelor Informatica Academiejaar 2006 2007, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. 1. Verzamelingen:
Uitwerking tentamen Analyse van Algoritmen, 29 januari
 Uitwerking tentamen Analyse van Algoritmen, 29 januari 2007. (a) De buitenste for-lus kent N = 5 iteraties. Na iedere iteratie ziet de rij getallen er als volgt uit: i rij na i e iteratie 2 5 4 6 2 2 4
Uitwerking tentamen Analyse van Algoritmen, 29 januari 2007. (a) De buitenste for-lus kent N = 5 iteraties. Na iedere iteratie ziet de rij getallen er als volgt uit: i rij na i e iteratie 2 5 4 6 2 2 4
definities recursieve datastructuren college 13 plaatjes soorten Graph = ( V, E ) V vertices, nodes, objecten, knopen, punten
 recursieve datastructuren college graphs definities Graph = ( V, E ) V vertices, nodes, objecten, knopen, punten E edges, arcs, kanten, pijlen, lijnen verbinding tussen knopen Voorbeelden steden en verbindingswegen
recursieve datastructuren college graphs definities Graph = ( V, E ) V vertices, nodes, objecten, knopen, punten E edges, arcs, kanten, pijlen, lijnen verbinding tussen knopen Voorbeelden steden en verbindingswegen
Discrete Wiskunde 2WC15, Lente Jan Draisma
 Discrete Wiskunde 2WC15, Lente 2010 Jan Draisma HOOFDSTUK 2 Gröbnerbases 1. Vragen We hebben gezien dat de studie van stelsels polynoomvergelijkingen in meerdere variabelen op natuurlijke manier leidt
Discrete Wiskunde 2WC15, Lente 2010 Jan Draisma HOOFDSTUK 2 Gröbnerbases 1. Vragen We hebben gezien dat de studie van stelsels polynoomvergelijkingen in meerdere variabelen op natuurlijke manier leidt
Tentamen combinatorische optimalisatie Tijd:
 Tentamen combinatorische optimalisatie 26-05-2014. Tijd: 9.00-11.30 Tentamen is met gesloten boek. Beschrijf bij elke opgave steeds het belangrijkste idee. Notatie en exacte formulering is van minder belang.
Tentamen combinatorische optimalisatie 26-05-2014. Tijd: 9.00-11.30 Tentamen is met gesloten boek. Beschrijf bij elke opgave steeds het belangrijkste idee. Notatie en exacte formulering is van minder belang.
Lineaire Algebra voor ST
 Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 9.3 email: J.C.M.Keijsper@tue.nl studiewijzer: http://www.win.tue.nl/wsk/onderwijs/2ds6 Technische Universiteit Eindhoven college 6 J.Keijsper (TUE)
Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 9.3 email: J.C.M.Keijsper@tue.nl studiewijzer: http://www.win.tue.nl/wsk/onderwijs/2ds6 Technische Universiteit Eindhoven college 6 J.Keijsper (TUE)
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2016 2017, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2016 2017, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Minimaal opspannende bomen
 Dit studiemateriaal is ontwikkeld door de kerngroep wiskunde D Delft en mag gratis gebruikt worden in het wiskundeonderwijs in het vo. Kerngroep wiskunde D Delft Liesbeth Bos Scala College Wim Caspers
Dit studiemateriaal is ontwikkeld door de kerngroep wiskunde D Delft en mag gratis gebruikt worden in het wiskundeonderwijs in het vo. Kerngroep wiskunde D Delft Liesbeth Bos Scala College Wim Caspers
Tentamen Discrete Wiskunde
 Discrete Wiskunde (WB011C) 22 januari 2016 Tentamen Discrete Wiskunde Schrijf op ieder ingeleverd blad duidelijk leesbaar je naam en studentnummer. De opgaven 1 t/m 6 tellen alle even zwaar. Je hoeft slechts
Discrete Wiskunde (WB011C) 22 januari 2016 Tentamen Discrete Wiskunde Schrijf op ieder ingeleverd blad duidelijk leesbaar je naam en studentnummer. De opgaven 1 t/m 6 tellen alle even zwaar. Je hoeft slechts
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2010 2011, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2010 2011, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Hoofdstuk 13: Integer Lineair Programmeren
 Hoofdstuk 13: Integer Lineair Programmeren Vandaag: Wat is Integer Lineair Programmeren (ILP)? Relatie tussen ILP en LP Voorbeeld 1: Minimum Spanning Tree (MST) Voorbeeld 2: Travelling Salesman Problem
Hoofdstuk 13: Integer Lineair Programmeren Vandaag: Wat is Integer Lineair Programmeren (ILP)? Relatie tussen ILP en LP Voorbeeld 1: Minimum Spanning Tree (MST) Voorbeeld 2: Travelling Salesman Problem
Tiende college algoritmiek. 14 april Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS
 Algoritmiek 2016/Dynamisch Programmeren Tiende college algoritmiek 14 april 2016 Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS 1 Algoritmiek 2016/Dynamisch Programmeren Houtzaagmolen
Algoritmiek 2016/Dynamisch Programmeren Tiende college algoritmiek 14 april 2016 Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS 1 Algoritmiek 2016/Dynamisch Programmeren Houtzaagmolen
Kortste Paden. Algoritmiek
 Kortste Paden Vandaag Kortste Paden probleem All pairs / Single Source / Single Target versies DP algoritme voor All Pairs probleem (Floyd s algoritme) Dijkstra s algoritme voor Single Source Negatieve
Kortste Paden Vandaag Kortste Paden probleem All pairs / Single Source / Single Target versies DP algoritme voor All Pairs probleem (Floyd s algoritme) Dijkstra s algoritme voor Single Source Negatieve
Vierde college complexiteit. 26 februari Beslissingsbomen en selectie Toernooimethode Adversary argument
 Complexiteit 2019/04 College 4 Vierde college complexiteit 26 februari 2019 Beslissingsbomen en selectie Toernooimethode Adversary argument 1 Complexiteit 2019/04 Zoeken: samengevat Ongeordend lineair
Complexiteit 2019/04 College 4 Vierde college complexiteit 26 februari 2019 Beslissingsbomen en selectie Toernooimethode Adversary argument 1 Complexiteit 2019/04 Zoeken: samengevat Ongeordend lineair
Toewijzingsprobleem Bachelorscriptie
 Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica Toewijzingsprobleem Bachelorscriptie Auteur: Veronique Rademaekers (s4155718) Begeleiders: Dr. W. Bosma en dr. H.
Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica Toewijzingsprobleem Bachelorscriptie Auteur: Veronique Rademaekers (s4155718) Begeleiders: Dr. W. Bosma en dr. H.
Optimalisering/Besliskunde 1. College 1 3 september, 2014
 Optimalisering/Besliskunde 1 College 1 3 september, 2014 Algemene informatie College: woensdag 9:00-10:45: Gorlaeus C1/C2, Leiden vrijdag: werkcollege Leiden en Delft Vier verplichte huiswerkopgaven Informatie
Optimalisering/Besliskunde 1 College 1 3 september, 2014 Algemene informatie College: woensdag 9:00-10:45: Gorlaeus C1/C2, Leiden vrijdag: werkcollege Leiden en Delft Vier verplichte huiswerkopgaven Informatie
8C080 deel BioModeling en bioinformatica
 Vijf algemene opmerkingen Tentamen Algoritmen voor BIOMIM, 8C080, 13 maart 2009, 09.00-12.00u. Het tentamen bestaat uit 2 delen, een deel van BioModeling & bioinformatics en een deel van BioMedische Beeldanalyse.
Vijf algemene opmerkingen Tentamen Algoritmen voor BIOMIM, 8C080, 13 maart 2009, 09.00-12.00u. Het tentamen bestaat uit 2 delen, een deel van BioModeling & bioinformatics en een deel van BioMedische Beeldanalyse.
Algoritmiek. 15 februari Grafen en bomen
 Algoritmiek 15 februari 2019 Grafen en bomen 1 Grafen (herhaling) Een graaf G wordt gedefinieerd als een paar (V,E), waarbij V een eindige verzameling is van knopen (vertices) en E een verzameling van
Algoritmiek 15 februari 2019 Grafen en bomen 1 Grafen (herhaling) Een graaf G wordt gedefinieerd als een paar (V,E), waarbij V een eindige verzameling is van knopen (vertices) en E een verzameling van
Algoritmen aan het werk
 Algoritmen aan het werk (Dag van de wiskunde 24/11/2018) Veerle Fack Universiteit Gent De bevers en de brug Vier bevers willen in het donker een brug oversteken. Ze kunnen de brug slechts alleen of met
Algoritmen aan het werk (Dag van de wiskunde 24/11/2018) Veerle Fack Universiteit Gent De bevers en de brug Vier bevers willen in het donker een brug oversteken. Ze kunnen de brug slechts alleen of met
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2008 2009, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Tweede bachelor Informatica Academiejaar 2008 2009, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Elfde college algoritmiek. 16 mei Dijkstra, Gretige algoritmen en Branch & Bound
 Algoritmiek 013/11 College 11 Elfde college algoritmiek 1 mei 013 Dijkstra, Gretige algoritmen en Branch & Bound 1 Algoritmiek 013/11 Voorbeeld -1- A B C D E F G H 9 7 5 A B C D E F G H 0 9 9 7 5 A B C
Algoritmiek 013/11 College 11 Elfde college algoritmiek 1 mei 013 Dijkstra, Gretige algoritmen en Branch & Bound 1 Algoritmiek 013/11 Voorbeeld -1- A B C D E F G H 9 7 5 A B C D E F G H 0 9 9 7 5 A B C
De volgende opgave gaat over de B-bomen van het college, waar sleutels zowel in de bladeren als ook in de interne knopen opgeslagen worden.
 . a) Een Fibonacci boom (niet te verwarren met een Fibonacci queue) van hoogte h is een AVL-boom van hoogte h met zo weinig mogelijk knopen. i. Geefvoorh =,,,,eenfibonacciboomvanhoogteh(eenboombestaande
. a) Een Fibonacci boom (niet te verwarren met een Fibonacci queue) van hoogte h is een AVL-boom van hoogte h met zo weinig mogelijk knopen. i. Geefvoorh =,,,,eenfibonacciboomvanhoogteh(eenboombestaande
Greedy algoritmes. Algoritmiek
 Greedy algoritmes Algoritmiek Algoritmische technieken Trucs, methoden, paradigma s voor het ontwerpen van algoritmen Dynamisch Programmeren Divide & Conquer Greedy 2 Greedy algoritme Bouwt de oplossing
Greedy algoritmes Algoritmiek Algoritmische technieken Trucs, methoden, paradigma s voor het ontwerpen van algoritmen Dynamisch Programmeren Divide & Conquer Greedy 2 Greedy algoritme Bouwt de oplossing
Vijfde college complexiteit. 21 februari Selectie Toernooimethode Adversary argument
 Complexiteit 2017/05 College 5 Vijfde college complexiteit 21 februari 2017 Selectie Toernooimethode Adversary argument 1 Complexiteit 2017/05 Opgave 28 Gegeven twee oplopend gesorteerde even lange rijen
Complexiteit 2017/05 College 5 Vijfde college complexiteit 21 februari 2017 Selectie Toernooimethode Adversary argument 1 Complexiteit 2017/05 Opgave 28 Gegeven twee oplopend gesorteerde even lange rijen
A.1 Grafentheorie 64 BIJLAGE A. OPLOSSING VAN DE VRAGEN A.1. GRAFENTHEORIE 65. dan heeft deze kring in ieder knooppunt een even aantal takken).
 64 BIJLAGE A. OPLOSSING VAN DE VRAGEN A. Grafentheorie Vraag. Neem drie knooppunten i, j en k. d(i, k) = het minimum aantal takken in een keten tussen i en k Vraag.2 het minimum aantal takken in een keten
64 BIJLAGE A. OPLOSSING VAN DE VRAGEN A. Grafentheorie Vraag. Neem drie knooppunten i, j en k. d(i, k) = het minimum aantal takken in een keten tussen i en k Vraag.2 het minimum aantal takken in een keten
Opdracht 3: De volhardende voetbalfan
 Opdracht 3: De volhardende voetbalfan Philippe Cara π-dag 2018 De volhardende voetbalfan Leo en Lambik willen de 16 voetbalstadions van onze eerste klasse bezoeken. Leo wil dat doen via een optimale rondrit
Opdracht 3: De volhardende voetbalfan Philippe Cara π-dag 2018 De volhardende voetbalfan Leo en Lambik willen de 16 voetbalstadions van onze eerste klasse bezoeken. Leo wil dat doen via een optimale rondrit
Activiteit 9. Modderstad Minimaal Opspannende Bomen. Samenvatting. Kerndoelen. Leeftijd. Vaardigheden. Materialen
 Activiteit 9 Modderstad Minimaal Opspannende Bomen Samenvatting Onze maatschappij is verbonden middels heel veel netwerken: telefoonnet, elektriciteitsnet, de riolering, computernetwerk, en het wegennet.
Activiteit 9 Modderstad Minimaal Opspannende Bomen Samenvatting Onze maatschappij is verbonden middels heel veel netwerken: telefoonnet, elektriciteitsnet, de riolering, computernetwerk, en het wegennet.
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2012 2013, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2012 2013, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
I.3 Functies. I.3.2 Voorbeeld. De afbeeldingen f: R R, x x 2 en g: R R, x x 2 zijn dus gelijk, ook al zijn ze gegeven door verschillende formules.
 I.3 Functies Iedereen is ongetwijfeld in veel situaties het begrip functie tegengekomen; vaak als een voorschrift dat aan elk getal een ander getal toevoegt, bijvoorbeeld de functie fx = x die aan elk
I.3 Functies Iedereen is ongetwijfeld in veel situaties het begrip functie tegengekomen; vaak als een voorschrift dat aan elk getal een ander getal toevoegt, bijvoorbeeld de functie fx = x die aan elk
Overzicht. Inleiding. Toepassingen. Verwante problemen. Modellering. Exacte oplosmethode: B&B. Insertie heuristieken. Local Search
 Overzicht Inleiding Toepassingen Verwante problemen Modellering Exacte oplosmethode: B&B Insertie heuristieken Local Search Handelsreizigersprobleem 1 Cyclische permutatie van steden b 3 77 a 93 21 42
Overzicht Inleiding Toepassingen Verwante problemen Modellering Exacte oplosmethode: B&B Insertie heuristieken Local Search Handelsreizigersprobleem 1 Cyclische permutatie van steden b 3 77 a 93 21 42
Vierde college complexiteit. 16 februari Beslissingsbomen en selectie
 Complexiteit 2016/04 College 4 Vierde college complexiteit 16 februari 2016 Beslissingsbomen en selectie 1 Complexiteit 2016/04 Zoeken: samengevat Ongeordend lineair zoeken: Θ(n) sleutelvergelijkingen
Complexiteit 2016/04 College 4 Vierde college complexiteit 16 februari 2016 Beslissingsbomen en selectie 1 Complexiteit 2016/04 Zoeken: samengevat Ongeordend lineair zoeken: Θ(n) sleutelvergelijkingen
Onderwerpen. Punten en lijnen, postbodes en handelsreizigers. Theorie. Theorie (2) Graaftheorie. Een mini-inleiding graaftheorie
 Onderwerpen Punten en lijnen, postbodes en handelsreizigers Een mini-inleiding graaftheorie Graaftheorie Herman Geuvers Euler en de postbode Radboud Universiteit Nijmegen 9 februari 2019 met dank aan Engelbert
Onderwerpen Punten en lijnen, postbodes en handelsreizigers Een mini-inleiding graaftheorie Graaftheorie Herman Geuvers Euler en de postbode Radboud Universiteit Nijmegen 9 februari 2019 met dank aan Engelbert
