Uitwerkingen Sum of Us
|
|
|
- Esmée de Vos
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Instant Insanity Uitwerkingen Sum of Us Opgave A: - Opgave B: Voor elk van de vier kubussen kun je een graaf maken die correspondeert met de desbetreffende kubus. Elk van deze grafen bevat drie lijnen. Er is een lijn tussen twee punten, wanneer de kubus de twee kleuren op twee overstaande vlakken heeft staan. Alles samenvoegen in één graaf geeft de volgende graaf: Opgave C: Een oplossing bestaat uit een duo deelgrafen, deze zijn hieronder naast elkaar weergeven. Eén van de volgende drie oplossingen is goed: Opgave D: Geef één van de tabellen van E. Afhankelijk van welke deelgrafen je in vraag C hebt genomen. Om van deelgrafen een oplossing te maken ga je als volgt te werk. We gaan er voor het gemak even vanuit dat de linkergraaf correspondeert met de voor en achterkant van de dobbelstenen en de rechter met de twee zijkanten (andersom zou je op hetzelfde antwoord uitkomen). We starten met de voor/achterkant, dus met de linkergraaf. Kubus heeft G en B op de voor of achterkant. We kiezen bijvoorbeeld dat groen op de voorkant zit en blauw op de achterkant. Kubus 2 heeft ook een blauw vlak, kies daarom bij kubus 2 een blauwe voorkant (de kleuren aan de voor en achterkant van de toren moeten immers verschillend zijn). Daardoor weten we dat de achterkant van kubus 2 rood moet zijn. Bepaal zo de voor en achterkanten van de toren en vul dit in, in de tabel. De verdeling van links en rechts is nu nog willekeurig. Omdat we de dobbelsteen nog kunnen draaien zonder dat de voor en achterkant veranderen. Bepaal nu op dezelfde wijze als net de invulling voor de zijvlakken. Vul deze invulling in, in de tabel.
2 Opgave E: Een van de onderstaande tabellen is al gegeven bij vraag D. De andere twee krijg je door vanuit een ander duo deelgrafen op dezelfde wijze de oplossing te bepalen. Let op! Wanneer voor/achterkant of linker/rechterkant zijn verwisseld zien we dit als dezelfde oplossing! In de onderstaande tabellen zijn de kolommen voorkant/achterkant en links/rechts verwisseld. In elke tabel staan acht weergaven van dezelfde oplossing. e voor achter links rechts voor achter links rechts k W R G B G B W R k 2 B G R R R R B G k 3 R B W G W G R B k 4 G W B W B W G W k W R B G B G W R k 2 B G R R R R B G k 3 R B G W G W R B k 4 G W W B W B G W k R W B G B G R W k2 G B R R R R G B k3 B R G W G W B R k4 W G W B W B W G k R W G B G B R W k2 G B R R R R G B k3 B R W G G W B R k4 W G B W W B W G 2e voor achter links rechts voor achter links rechts k G B R W R W G B k 2 B R G B G B B R k 3 W G B R B R W G k 4 R W W G W G R W k B G W R W R B G k2 R B B G B G R B k3 G W R B R B G W k4 W R G W G B W R k B G R W R W B G k2 R B G B G B R B k3 G W B R B R G W k4 W R W G W G W R k G B W R W R G B k2 B R G B B G B R k3 W G R B R B W G k4 R W G W G W R W 2
3 3e voor achter links rechts voor achter links rechts k W R G R G R W R k2 B G R B R B B G k3 R B W G W G R B k4 G W B W B W G W k W R R G R G W R k2 B G B R B R B G k3 R B G W G W R B k4 G W W B W G G W k R W R G R G R W k2 G B B R B R G B k3 B R G W G W B R k4 W G W B W B W G k R W G R G R R W k2 G B R B R B G B k3 B R W G W G B R k4 W G B W B W W G 3
4 2 Ticket to Ride Opgave 2A: De afbeelding hierboven geeft gevraagde de geïnduceerde graaf aan. De graaf bevat enkel de 2 gevraagde knopen én alle lijnen tussen die knopen. 4
5 Opgave 2B: Totale lengte = 22 Bovenstaande afbeelding is een van de mogelijke oplossingen. De graaf moet een boom zijn, want stel dat de graaf een cykel bevat, dan zorgt het weglaten van een lijn uit de cykel ervoor dat de kosten lager worden en aan de eisen is nog steeds voldaan. Verder moet de graaf samenhangend zijn, want elke knoop moet via een pad dat verbonden zijn met elke andere knoop. Opgave 2C: I = 9 (B = ) In dit algoritme bouw je de boom stap voor stap, dus je begint met de lege verzameling. Hieraan voeg je, verderop in het algoritme, elke keer een lijn aan toe tot je klaar bent. II = 5 (f(l) f(l ) voor alle l L) Dit betekent dat je een van de goedkoopste lijnen kiest. III = 6 ( B n ) Een boom bevat maximaal n lijnen. Een opspannende boom moet alle punten van de graaf met elkaar verbinden. Hiervoor zijn minimaal n lijnen nodig. Een minimaal opspannende boom bevat dus precies n lijnen. IV = (Voeg l toe aan B) De goedkoopste lijn uit de snede moet toegevoegd worden aan B. Door de lijnen steeds op deze manier te kiezen, kunnen er geen cykels ontstaan en heb je na het toevoegen van n lijnen, dus precies een opspannende boom gevonden. Omdat je steeds de goedkoopste lijn kiest, zijn de kosten van de opspannende boom minimaal. 5
6 Opgave 2D: Er zijn meerdere antwoorden mogelijk, maar hieronder staat een voorbeeld van een minimaal opspannende boom. Totale minimale lengte = 34 6
7 3 Sudoku Opgave 3A: {A, A3, C, C3} {A2, A4, C2, C4} {B2, B4, D2, D4} {B, B3, D, D3} {A, A4, B, B4} {A2, A3, B2, B3} {C2, C3, D2, D3} {C, C4, D, D4} {A, A2, B, B2, C, C2, D, D2} {A3, A4, B3, B4, C3, C4, D3, D4} Alle andere onvermijdelijke verzamelingen in de puzzel zijn verenigingen van bovenstaande onvermijdelijke verzamelingen. Opgave 3B: Dit is een minimale verzameling hints zodat de puzzel een unieke oplossing heeft. Deze hints hebben een niet-lege doorsnede met elke onvermijdelijke verzameling. De getallen in de onvermijdelijke verzamelingen liggen dan vast door de hints. Dus de puzzel heeft een unieke oplossing. Verder is het zo dat het verwijderen van een van de elementen uit de verzameling (een van de hints) ervoor zorgt dat er een onvermijdelijke verzameling is die een lege doorsnede heeft met de verzameling hints. De verzameling hints is dus minimaal. De getallen van die onvermijdelijke verzamelingen kun je dan op verschillende manieren invullen en dus heeft de puzzel geen unieke oplossing meer. Opgave 3C: Alle mogelijke oplossingen: {D6, E3} {C6, X} met X {A3, A5, A6, B5, B6, D5, D6, E3, E5, E6, F 5, F 6} Dit laatste betekent dat de rode hint gecombineerd moet worden met één van de blauwe hints. 7
8 4 Memory Opgave 4A: Het zijn 8 paren van 2 afbeeldingen. We gebruiken kennis van de combinatoriek om te zien dat het aantal het volgende is: 6! 2!2!2!2!2!2!2!2! = 6! 2! 8 Opgave 4B: We zien dat om aan de voorwaarden te kunnen voldoen, we het bord als volgt moeten opbouwen. ˆ Op de ene helft van het bord, als we het bord horizontaal doormidden delen, moeten de acht verschillende afbeeldingen liggen. ˆ de andere 8 tegels moeten zo geordend worden op de andere helft van het bord zodat als je het bord twee keer draait, het hetzelfde bord wordt. Deze helft ligt dus geheel vast ten opzichte van de eerste helft. Dit betekent dat we moeten uitrekenen op hoeveel manieren we de 8 verschillende tegels kunnen ordenen, hiermee hebben we het aantal borden uitgerekend. Dit is: Opgave 4C: Tactiek 2 Om het maximum te krijgen zul je zo veel mogelijk tegels tweemaal moeten omdraaien. Meer dan twee keer kan niet per tegel, omdat wanneer je weet waar een paar ligt, je deze direct omdraait. Om de eerste veertien tegels allemaal twee keer om te draaien, zal het spel als volgt gaan: De eerste twee tegels zijn verschillend. Vervolgens draai je elke beurt bij je eerste tegel een afbeelding om die je nog niet tegen bent gekomen, daarom zul je nog een tegel moeten omdraaien die je nog niet kent. De tweede tegel is een afbeelding waarvan je al wel weet waar de andere helft van het paar ligt (die heb je dus al eens omgedraaid in een eerdere beurt). Deze draai je in de beurt erna direct om, deze beide tegels heb je dan dus twee keer omgedraaid. Zo ga je het bord af, tot de laatste twee tegels, deze zijn in dit geval verschillend. 8! De laatste 2 tegels draai je echter maar keer om. Om dit in te zien bekijken we de verschillende opties: Als deze verschillend zijn, draai je de eerste tegel om en weet je al waar de andere helft van het paar ligt, omdat dit de laatste tegels zijn. De beurt daarna draai het laatste paar, dit zijn de laatste twee tegels. Als ze hetzelfde zijn, is dit het laatste paar en hoef je ze dus enkel om te draaien. Tactiek 3 Voor het eerste paar moeten we 8 tegels omdraaien. Want in het maximale geval zijn de eerste en laatste tegel een paar. Je zult dan dus eerst alle 6 tegels moeten omdraaien en daarna nog eens het paar. Vervolgens begin je opnieuw met de overige 4 tegels. Op dezelfde manier zien we dat je dan maximaal 6 tegels moet omdraaien voor het tweede paar. Dit gaat zo door. We bekijken het moment dat er nog 4 tegels over zijn. Ook in dit geval is het nog mogelijk dat je eerst alle tegels moet omdraaien voor je het paar hebt. We moeten hierbij onthouden dat je enkel de eerste tegel die je omdraait onthoudt en alleen kijkt of de volgende tegel 8
9 de andere helft van het paar is of niet. Dus dit betekent dat je eerst weer 4 tegels moet omdraaien en dan draai je het paar. Voor de laatste 2 tegels hoef je natuurlijk alleen die 2 tegels om te draaien, omdat dit een paar is. Tactiek Aantal tegels maximaal Tactiek 2 6+4=30 Tactiek =86 Opgave 4D: Om dit probleem te generaliseren gaan we er nu vanuit dat we in plaats van 6 tegels, 2n tegels hebben en dus n paren. We gebruiken wat we hebben gezien bij opgave 3a om dit uit te rekenen. Als je het nog niet helemaal ziet, probeer dan eens voor een ander aantal (bijvoorbeeld 0) om te vergelijken met de uitkomsten bij 6 tegels. Tactiek Aantal tegels maximaal Tactiek 2 2n Tactiek 2 2 (2n 2) + 2 Tactiek n 2 i=0 (2n + 2 2i) Natuurlijk zijn formules die er anders uitzien maar hetzelfde zijn (door plaatsing van haakjes) ook correct. 9
10 5 Cluedo Opgave 5A: ˆ Eerst moeten we de verwachte aantal kaarten bepalen voor 0 potjes. Verwacht Kamers Wapens Verdachten Bastiaan Willem Jasper ˆ Nu moeten we de grenswaarde bepalen. We weten dat het significantieniveau, namelijk 0%. Nu moeten we de vrijheidsgraden bepalen. Voor de rijen zien we dat als we weten hoeveel kaarten van de kamers en wapens Bastiaan bijvoorbeeld heeft gekregen, dan weten we hoeveel verdachten ze heeft gekregen. Dit omdat je weet hoeveel kaarten ieder krijgt (namelijk 6). Dit betekent dus dat er 2 vrijheidsgraden zijn in de rijen. Ook weet je van elke kaart (kamers, wapens en verdachten) hoeveel er in het spel zitten, dus als je weet hoeveel kamers bijvoorbeeld Bastiaan en Willem hebben, weet je hoeveel Jasper er heeft. Dit is dus ook 2 vrijheidsgraden in de kolommen. In totaal is dit dus 4 vrijheidsgraden. De grenswaarde is dan ˆ Daarna tellen we de waarnemingen op om te kijken wat er daadwerkelijk is waargenomen over die 0 potjes. Verwacht Kamers Wapens Verdachten Bastiaan Willem Jasper Om de χ 2 -waarde te berekenen moeten we de formule invullen. Voor het gemak berekenen we eerst de componenten (o ij e ij ) 2 e ij. Daarna zullen we die optellen. Nu berekenen we de χ 2 -waarde: Verwacht Kamers Wapens Verdachten Bastiaan Willem Jasper χ 2 = = Dus de χ 2 -waarde is dus ˆ Jasper speelt wel vals Opgave 5B: Om een verwachtingswaarde uit te rekenen moeten we de verschillende mogelijke situaties bedenken. We bekijken het geval dat Willem om een kamer vraagt, en de wapen en verdachte zelf op handen heeft. De andere twee gevallen gaan op een gelijke wijze. Er zijn 2 situaties mogelijk. Namelijk dat er geen kaart wordt getoond, (niemand heeft de gevraagde kamer in handen) of dat er wel een kaart wordt getoond. (iemand heeft de gevraagde kamer wel in handen.) Voor deze situaties bepalen we de RGI en de kans. 0
11 niet Voor de RGI vulen we de gegeven formule in. Vóór het uitspreken van het vermoeden wist Willem nog niets over 6 kamers (er zijn 9 kamers totaal en hij heeft er 3 in handen, die zijn het dus niet). In de teller komt nu ook 6. We zien dus: RGI =. De kans dat deze situatie zich voordoet is 6, dit is de kans dat precies de kamer die Willem vermoedt, in de envelop zit. De 3 die hij in handen heeft zitten er immers sowieso niet in. wel Ook nu rekenen we de RGI uit met de formule. In de noemer staat een 6 (zoals hierboven) en in de teller staat een. Dus: RGI = 6. De kans dat deze situatie zich voordoet is de kans dat een andere kamer dan de gevraagde kamer in de geheime envelop zit. Dit is dus 5 6. Voor het wapen en het verdachte gaat dit hetzelfde. Alleen staat steeds in de noemer steeds respectievelijk 4 (6 2) en 5 (6 ). Gekozen kaart Verwachtinswaarde van de RGI Kamer = Wapen = Verdachte = Conclusie: Willem kan het beste om een Wapen te vragen. Opgave 5C: We bekijken eerst het geval dat hij een kamer en verdachte vraagt. equivalent) Er zijn 4 situaties mogelijk. Namelijk (kamer en wapen is a. dat er niet een kaart wordt laten zien, (niemand heeft de gevraagde kamer én verdachte in handen) b. dat iemand de gevraagde kamer in handen heeft en de gevraagde verdachte in de envelop zit c. dat iemand de gevraagde verdachte in handen heeft en de gevraagde kamer in de envelop zit d. kamer en verdachte zitten beide NIET in de envelop (beide kaarten zitten in handen van de andere spelers) Voor deze situaties bepalen we de RGI en de kans. ad a. De kans dat deze situatie zich voordoet is 28. Voor de RGI vulen we de gegeven formule in. Vóór het uitspreken van het vermoeden wist Willem nog niets over 7 kamers en 4 verdachten. Voor beide weet hij nu dat ze in de envelop zitten. Dus RGI = + = 2. ad b. De kans dat deze situatie dit voordoet is Als je een kamer te zien krijgt kun je niet weten of de verdachte in de envelop zit, of dat deze nog bij een speler in handen zit. Je wint dus enkel informatie ten opzichte van de kamer. Dus RGI = 7. ad c. De kans dat deze situatie dit voordoet is Als je een verdachte te zien krijgt kun je niet weten of de kamer in de envelop zit, of dat deze nog bij een speler in handen zit. Je wint dus enkel informatie ten opzichte van de verdachte. Dus RGI = 4
12 ad d. De kans dat deze situatie dit voordoet is Voor de RGI moeten we even goed nadenken. We moeten hier apart een soort verwachting berekenen. Je krijgt namelijk maar kaart te zien, er zijn dus 2 verschillende situaties mogelijk. De kans dat je verdachte te zien krijgt is 2, een kamer is dan 2. Deze kansen moeten dan gecombineerd worden met de RGI per mogelijkheid ( 4 of 7 ). RGI = = 56 Voor de kamer en het wapen en verdachtre en het wapen gaat dit hetzelfde. Dat geeft de volgende tabel: Gekozen kaarten Verwachtinswaarde van de RGI Kamer en wapen Kamer en verdachte Verdachte en wapen Conclusie: Willem kan het beste om een wapen en verdachte te vragen. 2
Radboud Universiteit. Sum Of Us. Winkunde - Geluk of Strategie?
 Radboud Universiteit Sum Of Us Winkunde - Geluk of Strategie? September 2015 1 Sum of Us 2015 Winkunde Geluk of Strategie? Beste deelnemer aan het Wiskundetoernooi 2015, Als fanatieke spelers/wiskundigen
Radboud Universiteit Sum Of Us Winkunde - Geluk of Strategie? September 2015 1 Sum of Us 2015 Winkunde Geluk of Strategie? Beste deelnemer aan het Wiskundetoernooi 2015, Als fanatieke spelers/wiskundigen
Sum of Us Winkunde Geluk of strategie? 25 september 2015
 Sum of Us Winkunde Geluk of strategie? 25 september 2015 1 2 Sum of Us 2015 Winkunde Geluk of strategie? Beste deelnemers aan het Wiskundetoernooi 2015, Als fanatieke spelers/wiskundigen kunnen jullie
Sum of Us Winkunde Geluk of strategie? 25 september 2015 1 2 Sum of Us 2015 Winkunde Geluk of strategie? Beste deelnemers aan het Wiskundetoernooi 2015, Als fanatieke spelers/wiskundigen kunnen jullie
Radboud Universiteit
 Radboud Universiteit Voorbereidend materiaal Winkunde - Geluk of Strategie? Zie voor meer informatie onze Facebookpagina Wiskundetoernooi Nijmegen, de website www.ru.nl/wiskundetoernooi en onze Wiskundetoernooi-app.
Radboud Universiteit Voorbereidend materiaal Winkunde - Geluk of Strategie? Zie voor meer informatie onze Facebookpagina Wiskundetoernooi Nijmegen, de website www.ru.nl/wiskundetoernooi en onze Wiskundetoernooi-app.
Voorbereidendmateriaal Wiskundetoernooi 2015
 Voorbereidendmateriaal Wiskundetoernooi 2015 Beste deelnemer aan het Wiskundetoernooi 2015, Winkunde: geluk of strategie? is dit jaar het thema van het middagprogramma Sum of Us. In dit boekje vind je
Voorbereidendmateriaal Wiskundetoernooi 2015 Beste deelnemer aan het Wiskundetoernooi 2015, Winkunde: geluk of strategie? is dit jaar het thema van het middagprogramma Sum of Us. In dit boekje vind je
Tentamen Discrete Wiskunde 1 10 april 2012, 14:00 17:00 uur
 Tentamen Discrete Wiskunde 0 april 0, :00 7:00 uur Schrijf je naam op ieder blad dat je inlevert. Onderbouw je antwoorden, met een goede argumentatie zijn ook punten te verdienen. Veel succes! Opgave.
Tentamen Discrete Wiskunde 0 april 0, :00 7:00 uur Schrijf je naam op ieder blad dat je inlevert. Onderbouw je antwoorden, met een goede argumentatie zijn ook punten te verdienen. Veel succes! Opgave.
Radboud Universiteit
 Radboud Universiteit Sum of Us Winkunde - Geluk of Strategie? Masterscriptie Maartje Geurts, Giselle Loeffen en Rowan Reijtenbagh September 2015 Inhoudsopgave 1 Inleidend verslag 5 2 Voorbereidend Materiaal
Radboud Universiteit Sum of Us Winkunde - Geluk of Strategie? Masterscriptie Maartje Geurts, Giselle Loeffen en Rowan Reijtenbagh September 2015 Inhoudsopgave 1 Inleidend verslag 5 2 Voorbereidend Materiaal
Hebzucht loont niet altijd
 Thema Discrete wiskunde Hoe verbind je een stel steden met zo weinig mogelijk kilometers asfalt? Hoe maak je een optimaal computernetwerk met kabels die maar een beperkte capaciteit hebben? Veel van zulke
Thema Discrete wiskunde Hoe verbind je een stel steden met zo weinig mogelijk kilometers asfalt? Hoe maak je een optimaal computernetwerk met kabels die maar een beperkte capaciteit hebben? Veel van zulke
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober 2015 1 / 25 Definitie Een boom is een samenhangende
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober 2015 1 / 25 Definitie Een boom is een samenhangende
Spelregels IK BOX spel (3 of 4 personen)
 IK BOX spelregels Spelregels IK BOX spel (3 of 4 personen) Spelmateriaal 1 spelbord (binnenkant van de IK BOX) met aan de zijkanten de grote ZaaiGoedkaarten. 4 pionnen (Tess, Mo, Max en Kate). 4 bakjes.
IK BOX spelregels Spelregels IK BOX spel (3 of 4 personen) Spelmateriaal 1 spelbord (binnenkant van de IK BOX) met aan de zijkanten de grote ZaaiGoedkaarten. 4 pionnen (Tess, Mo, Max en Kate). 4 bakjes.
Uitwerking vierde serie inleveropgaven
 Uitwerking vierde serie inleveropgaven Opgave 1. Gegeven is dat G een permutatiegroep is; a is een willekeurig element. St(a) is de deelverzameling van G die alle permutaties π bevat waarvoor geldt π(a)
Uitwerking vierde serie inleveropgaven Opgave 1. Gegeven is dat G een permutatiegroep is; a is een willekeurig element. St(a) is de deelverzameling van G die alle permutaties π bevat waarvoor geldt π(a)
Gokautomaten (voor iedereen)
 Gokautomaten (voor iedereen) In een fruitautomaat draaien de schijven I, II en III onafhankelijk van elkaar. Door een hendel kan elke schijf tot stilstand worden gebracht. In de tabel zie je wat op elke
Gokautomaten (voor iedereen) In een fruitautomaat draaien de schijven I, II en III onafhankelijk van elkaar. Door een hendel kan elke schijf tot stilstand worden gebracht. In de tabel zie je wat op elke
Druk alle kartonnen delen uit de raampjes. Stel de pionnen samen door het kartonnen deel in het voetje te steken.
 spelregels Druk alle kartonnen delen uit de raampjes. Stel de pionnen samen door het kartonnen deel in het voetje te steken. Sorteer de kaarten in drie stapeltjes: Drakenkaarten Wapenkaarten Avonturenkaarten
spelregels Druk alle kartonnen delen uit de raampjes. Stel de pionnen samen door het kartonnen deel in het voetje te steken. Sorteer de kaarten in drie stapeltjes: Drakenkaarten Wapenkaarten Avonturenkaarten
Where innovation starts
 Kubussen stapelen Erjen Lefeber Nationale Wiskunde Dagen Noordwijkerhout, februari 08 Where innovation starts Ik neem aan dat puzzel is gedownload van http://mn.wtb.tue.nl/~lefeber/kubussenstapelen.pdf
Kubussen stapelen Erjen Lefeber Nationale Wiskunde Dagen Noordwijkerhout, februari 08 Where innovation starts Ik neem aan dat puzzel is gedownload van http://mn.wtb.tue.nl/~lefeber/kubussenstapelen.pdf
Week 1 20-02-2013. Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren.
 Combinatorische Optimalisatie, 2013 Week 1 20-02-2013 Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren. Opgave 1.16 Bewijs dat elke graaf een even aantal punten
Combinatorische Optimalisatie, 2013 Week 1 20-02-2013 Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren. Opgave 1.16 Bewijs dat elke graaf een even aantal punten
4.1 Negatieve getallen vermenigvuldigen [1]
![4.1 Negatieve getallen vermenigvuldigen [1] 4.1 Negatieve getallen vermenigvuldigen [1]](/thumbs/28/12962825.jpg) 4.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 x 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5 x -3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 x 3 = -15 Afspraak: In plaats
4.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 x 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5 x -3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 x 3 = -15 Afspraak: In plaats
http://www.kidzlab.nl/index2.php?option=com_content&task=vi...
 Veelvlakken De perfecte vorm Plato was een grote denker in de tijd van de Oude Grieken. Hij was een van de eerste die de regelmatige veelvlakken heel bijzonder vond. Hij hield ervan omdat ze zulke mooie,
Veelvlakken De perfecte vorm Plato was een grote denker in de tijd van de Oude Grieken. Hij was een van de eerste die de regelmatige veelvlakken heel bijzonder vond. Hij hield ervan omdat ze zulke mooie,
Wiskunde - MBO Niveau 4. Eerste- en tweedegraads verbanden
 Wiskunde - MBO Niveau 4 Eerste- en tweedegraads verbanden OPLEIDING: Noorderpoort MBO Niveau 4 DOCENT: H.J. Riksen LEERJAAR: Leerjaar 1 - Periode 2 UITGAVE: 2018/2019 Wiskunde - MBO Niveau 4 Eerste- en
Wiskunde - MBO Niveau 4 Eerste- en tweedegraads verbanden OPLEIDING: Noorderpoort MBO Niveau 4 DOCENT: H.J. Riksen LEERJAAR: Leerjaar 1 - Periode 2 UITGAVE: 2018/2019 Wiskunde - MBO Niveau 4 Eerste- en
START WISKUNDE-ESTAFETTE RU 2007 Je hebt 60 minuten voor 20 opgaven. Het totaal aantal te behalen punten is 600.
 START WISKUNDE-ESTAFETTE RU 2007 Je hebt 60 minuten voor 20 opgaven. Het totaal aantal te behalen punten is 600. Estafette-opgave 1 (20 punten, rest 580 punten) Vier bij vier. In een schema van vier maal
START WISKUNDE-ESTAFETTE RU 2007 Je hebt 60 minuten voor 20 opgaven. Het totaal aantal te behalen punten is 600. Estafette-opgave 1 (20 punten, rest 580 punten) Vier bij vier. In een schema van vier maal
3.1 Negatieve getallen vermenigvuldigen [1]
![3.1 Negatieve getallen vermenigvuldigen [1] 3.1 Negatieve getallen vermenigvuldigen [1]](/thumbs/101/149931282.jpg) 3.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5-3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 3 = -15 Voorbeeld 4: -5 3 9 2
3.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5-3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 3 = -15 Voorbeeld 4: -5 3 9 2
Stoomcursus. wiskunde A. Rekenregels voor vereenvoudigen. Voorbereidende opgaven VWO ( ) = = ( ) ( ) ( ) = ( ) ( ) = ( ) = = ( )
 Voorbereidende opgaven VWO Stoomcursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Voorbereidende opgaven VWO Stoomcursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Lege polygonen in een graaf.
 Uitwerking puzzel 94-2 Lege polygonen in een graaf. Lieke de Rooij Wobien Doyer We hebben n punten die al of niet met elkaar worden verbonden. De bedoeling is om met zo min mogelijk lijnen (=verbindingen)
Uitwerking puzzel 94-2 Lege polygonen in een graaf. Lieke de Rooij Wobien Doyer We hebben n punten die al of niet met elkaar worden verbonden. De bedoeling is om met zo min mogelijk lijnen (=verbindingen)
Bij het oplossen van een telprobleem zijn de volgende 2 dingen belangrijk: Is de volgorde van de gekozen dingen van belang?
 4. tellen & kansen 4.1 Tellen Herkennen Je kunt een vraag over telproblemen herkennen aan signaalwoorden: - hoeveel mogelijkheden, manieren, routes, volgordes etc. zijn er?, - bereken het aantal mogelijkheden/manieren
4. tellen & kansen 4.1 Tellen Herkennen Je kunt een vraag over telproblemen herkennen aan signaalwoorden: - hoeveel mogelijkheden, manieren, routes, volgordes etc. zijn er?, - bereken het aantal mogelijkheden/manieren
Hoofdstuk 1. Afspraken en notaties
 Hoofdstuk 1 Afspraken en notaties In deze tekst onderzoeken we een eenvoudig dobbelspel: twee spelers hebben een dobbelsteen, gooien deze, en wie het hoogst aantal ogen gooit wint. Er blijken setjes dobbelstenen
Hoofdstuk 1 Afspraken en notaties In deze tekst onderzoeken we een eenvoudig dobbelspel: twee spelers hebben een dobbelsteen, gooien deze, en wie het hoogst aantal ogen gooit wint. Er blijken setjes dobbelstenen
Uitwerkingen eerste serie inleveropgaven
 Uitwerkingen eerste serie inleveropgaven (1) Gegeven het 4 4 grid bestaande uit de 16 punten (i, j) met i, j = 0,..., 3. Bepaal het aantal driehoeken dat je kunt vinden zodanig dat ieder hoekpunt samenvalt
Uitwerkingen eerste serie inleveropgaven (1) Gegeven het 4 4 grid bestaande uit de 16 punten (i, j) met i, j = 0,..., 3. Bepaal het aantal driehoeken dat je kunt vinden zodanig dat ieder hoekpunt samenvalt
Excel 2013: Snelle analyse
 Excel 2013: Snelle analyse Handleiding van Auteur: CorVerm Juli 2015 Sinds Microsoft Office 2003 (en voorgaande versies) is er veel veranderd. Met weemoed denkt menig Office-gebruiker terug aan de menubalk
Excel 2013: Snelle analyse Handleiding van Auteur: CorVerm Juli 2015 Sinds Microsoft Office 2003 (en voorgaande versies) is er veel veranderd. Met weemoed denkt menig Office-gebruiker terug aan de menubalk
les 6 draaitabellen en draaigrafieken Herhaling Oefening 6.1
 draaitabellen en draaigrafieken Herhaling Oefening 6.1 a. Open de werkmap Draaitabel. b. Sorteer de gegevens Van A naar Z op de kolom Verkoper. c. Maak een Tabel bij alle gegevens van de verkoper De Koning.
draaitabellen en draaigrafieken Herhaling Oefening 6.1 a. Open de werkmap Draaitabel. b. Sorteer de gegevens Van A naar Z op de kolom Verkoper. c. Maak een Tabel bij alle gegevens van de verkoper De Koning.
Examencursus. wiskunde A. Rekenregels voor vereenvoudigen. Voorbereidende opgaven VWO kan niet korter
 Voorbereidende opgaven VWO Examencursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Voorbereidende opgaven VWO Examencursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Discrete Wiskunde, College 12. Han Hoogeveen, Utrecht University
 Discrete Wiskunde, College 12 Han Hoogeveen, Utrecht University Dynamische programmering Het basisidee is dat je het probleem stap voor stap oplost Het probleem moet voldoen aan het optimaliteitsprincipe
Discrete Wiskunde, College 12 Han Hoogeveen, Utrecht University Dynamische programmering Het basisidee is dat je het probleem stap voor stap oplost Het probleem moet voldoen aan het optimaliteitsprincipe
Elke groep van 3 leerlingen heeft een 9 setje speelkaarten nodig: 2 t/m 10, bijvoorbeeld alle schoppen, of alle harten kaarten.
 Versie 16 januari 2017 Sorteren unplugged Sorteren gebeurt heel veel. De namen van alle leerlingen in de klas staan vaak op alfabetische volgorde. De wedstrijden van een volleybal team staan op volgorde
Versie 16 januari 2017 Sorteren unplugged Sorteren gebeurt heel veel. De namen van alle leerlingen in de klas staan vaak op alfabetische volgorde. De wedstrijden van een volleybal team staan op volgorde
2. Optellen en aftrekken van gelijknamige breuken
 1. Wat is een breuk? Een breuk Een breuk is een verhoudingsgetal. Een breuk geeft aan hoe groot een deel is van een geheel. Stel een taart is verdeeld in stukken. Je neemt 2 stukken van de taart. Je hebt
1. Wat is een breuk? Een breuk Een breuk is een verhoudingsgetal. Een breuk geeft aan hoe groot een deel is van een geheel. Stel een taart is verdeeld in stukken. Je neemt 2 stukken van de taart. Je hebt
De teller geeft hoeveel stukken er zijn en de noemer zegt wat de 5. naam is van die stukken: 6 taart geeft dus aan dat de taart in 6
 Breuken Breuk betekent dat er iets gebroken is. Het is niet meer heel. Als je een meloen doormidden snijdt, is die niet meer heel, maar verdeeld in twee stukken. Eén zo n stuk is dan een halve meloen,
Breuken Breuk betekent dat er iets gebroken is. Het is niet meer heel. Als je een meloen doormidden snijdt, is die niet meer heel, maar verdeeld in twee stukken. Eén zo n stuk is dan een halve meloen,
Combinatorische Algoritmen: Binary Decision Diagrams, Deel III
 Combinatorische Algoritmen: Binary Decision Diagrams, Deel III Sjoerd van Egmond LIACS, Leiden University, The Netherlands svegmond@liacs.nl 2 juni 2010 Samenvatting Deze notitie beschrijft een nederlandse
Combinatorische Algoritmen: Binary Decision Diagrams, Deel III Sjoerd van Egmond LIACS, Leiden University, The Netherlands svegmond@liacs.nl 2 juni 2010 Samenvatting Deze notitie beschrijft een nederlandse
Opgaven Kunstmatige Intelligentie 1 maart 2017
 Opgaven Kunstmatige Intelligentie 1 maart 2017 Opgave 1. a. Denkt een schaakprogramma? b. Denkt een (Nederlands-Engels) vertaalprogramma? c. Denkt een C ++ -compiler? d. Denkt Watson, the IBM-computer
Opgaven Kunstmatige Intelligentie 1 maart 2017 Opgave 1. a. Denkt een schaakprogramma? b. Denkt een (Nederlands-Engels) vertaalprogramma? c. Denkt een C ++ -compiler? d. Denkt Watson, the IBM-computer
Wiskunde D Online uitwerking oefenopgaven 4 VWO blok 3 les 1
 Paragraaf De kansdefinitie Opgave a) Als de kikker verspringt, gaat hij van zwart naar wit, of andersom Hij zit dus afwisselend op een zwart en een wit veld Op een willekeurig moment is de kans even groot
Paragraaf De kansdefinitie Opgave a) Als de kikker verspringt, gaat hij van zwart naar wit, of andersom Hij zit dus afwisselend op een zwart en een wit veld Op een willekeurig moment is de kans even groot
Uitwerking tentamen Algoritmiek 10 juni :00 13:00
 Uitwerking tentamen Algoritmiek 10 juni 2014 10:00 13:00 1. Dominono s a. Toestanden: n x n bord met in elk hokje een O, een X of een -. Hierbij is het aantal X gelijk aan het aantal O of hooguit één hoger.
Uitwerking tentamen Algoritmiek 10 juni 2014 10:00 13:00 1. Dominono s a. Toestanden: n x n bord met in elk hokje een O, een X of een -. Hierbij is het aantal X gelijk aan het aantal O of hooguit één hoger.
REKENVAARDIGHEID BRUGKLAS
 REKENVAARDIGHEID BRUGKLAS Schooljaar 008/009 Inhoud Uitleg bij het boekje Weektaak voor e week: optellen en aftrekken Weektaak voor e week: vermenigvuldigen Weektaak voor e week: delen en de staartdeling
REKENVAARDIGHEID BRUGKLAS Schooljaar 008/009 Inhoud Uitleg bij het boekje Weektaak voor e week: optellen en aftrekken Weektaak voor e week: vermenigvuldigen Weektaak voor e week: delen en de staartdeling
Uitwerkingen Rekenen met cijfers en letters
 Uitwerkingen Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 2009 c Swier Garst - RGO Middelharnis 2 Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Uitwerkingen Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 2009 c Swier Garst - RGO Middelharnis 2 Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Breuken met letters WISNET-HBO. update juli 2013
 Breuken met letters WISNET-HBO update juli 2013 De bedoeling van deze les is het repeteren met pen en papier van het werken met breuken. Steeds wordt bij gebruik van letters verondersteld dat de noemers
Breuken met letters WISNET-HBO update juli 2013 De bedoeling van deze les is het repeteren met pen en papier van het werken met breuken. Steeds wordt bij gebruik van letters verondersteld dat de noemers
Twaalfde college complexiteit. 11 mei 2012. Overzicht, MST
 College 12 Twaalfde college complexiteit 11 mei 2012 Overzicht, MST 1 Agenda voor vandaag Minimum Opspannende Boom (minimum spanning tree) als voorbeeld van greedy algoritmen Overzicht: wat voor technieken
College 12 Twaalfde college complexiteit 11 mei 2012 Overzicht, MST 1 Agenda voor vandaag Minimum Opspannende Boom (minimum spanning tree) als voorbeeld van greedy algoritmen Overzicht: wat voor technieken
15 min. 1-4. NL Spelregels 1. 17996_ikleer_naar groep2_guide.indd 1 23-09-15 16:10
 4-5 15 min. 1-4 NL Spelregels 1 17996_ikleer_naar groep2_guide.indd 1 23-09-15 16:10 18 Leerzame spellen in 1 doos! Het alfabet leren & samenstellen van woorden 4 kruiswoordplaten, 90 letters en 1 alfabetbord
4-5 15 min. 1-4 NL Spelregels 1 17996_ikleer_naar groep2_guide.indd 1 23-09-15 16:10 18 Leerzame spellen in 1 doos! Het alfabet leren & samenstellen van woorden 4 kruiswoordplaten, 90 letters en 1 alfabetbord
Speel met spel ROOD!
 Speel met spel ROOD! Nabouwen Pak een kaart met een rode rand en bouw het voorbeeld op de kaart na. Patronen klikken Bedenk een patroon en maak dit met de klikkubussen. twee rode twee blauwe of: één rode
Speel met spel ROOD! Nabouwen Pak een kaart met een rode rand en bouw het voorbeeld op de kaart na. Patronen klikken Bedenk een patroon en maak dit met de klikkubussen. twee rode twee blauwe of: één rode
Theorie: Het maken van een verslag (Herhaling klas 2)
 Theorie: Het maken van een verslag (Herhaling klas 2) Onderdelen Een verslag van een experiment bestaat uit vier onderdelen: - inleiding: De inleiding is het administratieve deel van je verslag. De onderzoeksvraag
Theorie: Het maken van een verslag (Herhaling klas 2) Onderdelen Een verslag van een experiment bestaat uit vier onderdelen: - inleiding: De inleiding is het administratieve deel van je verslag. De onderzoeksvraag
Ruitjes vertellen de waarheid
 Ruitjes vertellen de waarheid Opdracht 1 Van fouten kun je leren Van fouten kun je leren, jazeker. Vooral als je héél goed weet wat er fout ging. Vandaag leer je handige formules begrijpen door kijken
Ruitjes vertellen de waarheid Opdracht 1 Van fouten kun je leren Van fouten kun je leren, jazeker. Vooral als je héél goed weet wat er fout ging. Vandaag leer je handige formules begrijpen door kijken
Les 1 - Brussels sprouts
 Les 1 - Brussels sprouts We doen een spel voor twee spelers. De eerste speler trekt rode lijnen, de tweede trekt groene lijnen. 1 Zet drie plustekens op papier. Elk plusteken heeft vier vije armen. 2 Om
Les 1 - Brussels sprouts We doen een spel voor twee spelers. De eerste speler trekt rode lijnen, de tweede trekt groene lijnen. 1 Zet drie plustekens op papier. Elk plusteken heeft vier vije armen. 2 Om
ANTWOORDEN blz. 1. d. 345 + 668 = 1013; 61 007 + 50 215 = 111 222; 102 240 30 628 = 71 612; 1 000 000 1 = 999 999
 ANTWOORDEN blz. 3 a. Zeer onwaarschijnlijk Zeer onwaarschijnlijk a. Dan heb je ergens een schuld uitstaan 86 Dan hadden beide een kopie van de kerfstok; om fraude te voorkomen a. MMXII, MCCCXXVII, DLXXXVI,
ANTWOORDEN blz. 3 a. Zeer onwaarschijnlijk Zeer onwaarschijnlijk a. Dan heb je ergens een schuld uitstaan 86 Dan hadden beide een kopie van de kerfstok; om fraude te voorkomen a. MMXII, MCCCXXVII, DLXXXVI,
Deze les heeft veel oefeningen. Om tijd te besparen kunt u eventueel de herhaling
 draaitabellen en draaigrafieken Herhaling Deze les heeft veel oefeningen. Om tijd te besparen kunt u eventueel de herhaling overslaan. Oefening 6.1 a. Open de werkmap Draaitabel. b. Sorteer de gegevens
draaitabellen en draaigrafieken Herhaling Deze les heeft veel oefeningen. Om tijd te besparen kunt u eventueel de herhaling overslaan. Oefening 6.1 a. Open de werkmap Draaitabel. b. Sorteer de gegevens
De Hongaarse kubus ontward
 De Hongaarse kubus ontward door Dick Grune, Aug. 1981 herzien Febr. 2007 Er zijn vele manieren om een in de war geraakte kubus weer te ontwarren. De bekendste worden gegeven door David Singmaster en Donald
De Hongaarse kubus ontward door Dick Grune, Aug. 1981 herzien Febr. 2007 Er zijn vele manieren om een in de war geraakte kubus weer te ontwarren. De bekendste worden gegeven door David Singmaster en Donald
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2006 2007, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. 1. Verzamelingen:
Tweede bachelor Informatica Academiejaar 2006 2007, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. 1. Verzamelingen:
2 REKENEN MET BREUKEN 3. 2.3 Optellen van breuken 6. 2.5 Aftrekken van breuken 9. 2.7 Vermenigvuldigen van breuken 11. 2.9 Delen van breuken 13
 REKENEN MET BREUKEN. De breuk. Opgaven. Optellen van breuken 6. Opgaven 8. Aftrekken van breuken 9.6 Opgaven 9.7 Vermenigvuldigen van breuken.8 Opgaven.9 Delen van breuken.0 Opgaven. Een deel van een deel.
REKENEN MET BREUKEN. De breuk. Opgaven. Optellen van breuken 6. Opgaven 8. Aftrekken van breuken 9.6 Opgaven 9.7 Vermenigvuldigen van breuken.8 Opgaven.9 Delen van breuken.0 Opgaven. Een deel van een deel.
Antwoorden. Magische vierkanten Vierkant voor Wiskunde Doeboek 8
 Antwoorden Magische vierkanten Vierkant voor Wiskunde Doeboek 8 1 6 1 8 7 5 3 2 9 4 2 De getallen 1 tot en met 9. 3 15. 15 en 15. De som van de getallen van elke rij is 15. 4 15. De som van de getallen
Antwoorden Magische vierkanten Vierkant voor Wiskunde Doeboek 8 1 6 1 8 7 5 3 2 9 4 2 De getallen 1 tot en met 9. 3 15. 15 en 15. De som van de getallen van elke rij is 15. 4 15. De som van de getallen
SNEL WERKEN MET EXCEL
 SNEL WERKEN MET EXCEL 2013 Computertraining voor 50-plussers PC50plus computertrainingen Eikbosserweg 52 1214AK Hilversum tel: 035 6213701 info@pc50plus.nl www.pc50plus.nl Snel werken met Excel C O M P
SNEL WERKEN MET EXCEL 2013 Computertraining voor 50-plussers PC50plus computertrainingen Eikbosserweg 52 1214AK Hilversum tel: 035 6213701 info@pc50plus.nl www.pc50plus.nl Snel werken met Excel C O M P
Discrete Structuren. Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Rekentijger - Groep 7 Tips bij werkboekje A
 Rekentijger - Groep 7 Tips bij werkboekje A Omtrek en oppervlakte (1) Werkblad 1 Van een rechthoek die mooi in het rooster past zijn lengte en breedte hele getallen. Lengte en breedte zijn samen gelijk
Rekentijger - Groep 7 Tips bij werkboekje A Omtrek en oppervlakte (1) Werkblad 1 Van een rechthoek die mooi in het rooster past zijn lengte en breedte hele getallen. Lengte en breedte zijn samen gelijk
11.1 Kansberekeningen [1]
![11.1 Kansberekeningen [1] 11.1 Kansberekeningen [1]](/thumbs/27/12038291.jpg) 11.1 Kansberekeningen [1] Kansdefinitie van Laplace: P(gebeurtenis) = Aantal gunstige uitkomsten/aantal mogelijke uitkomsten Voorbeeld 1: Wat is de kans om minstens 16 te gooien, als je met 3 dobbelstenen
11.1 Kansberekeningen [1] Kansdefinitie van Laplace: P(gebeurtenis) = Aantal gunstige uitkomsten/aantal mogelijke uitkomsten Voorbeeld 1: Wat is de kans om minstens 16 te gooien, als je met 3 dobbelstenen
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 27 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 27 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
Tentamen Discrete Wiskunde
 Discrete Wiskunde (WB011C) 22 januari 2016 Tentamen Discrete Wiskunde Schrijf op ieder ingeleverd blad duidelijk leesbaar je naam en studentnummer. De opgaven 1 t/m 6 tellen alle even zwaar. Je hoeft slechts
Discrete Wiskunde (WB011C) 22 januari 2016 Tentamen Discrete Wiskunde Schrijf op ieder ingeleverd blad duidelijk leesbaar je naam en studentnummer. De opgaven 1 t/m 6 tellen alle even zwaar. Je hoeft slechts
Basistechnieken Microsoft Excel in 15 minuten
 Basistechnieken Microsoft Excel in 15 minuten Microsoft Excel is een rekenprogramma. Je kan het echter ook heel goed gebruiken voor het maken van overzichten, grafieken, planningen, lijsten en scenario's.
Basistechnieken Microsoft Excel in 15 minuten Microsoft Excel is een rekenprogramma. Je kan het echter ook heel goed gebruiken voor het maken van overzichten, grafieken, planningen, lijsten en scenario's.
Sudoku s. Annelies Veen Noud Aldenhoven
 Sudoku s Annelies Veen Noud Aldenhoven Vierkant voor Wiskunde Zomerkamp A 2010 Voorwoord Het plaatje op de voorkant is een erg bijzondere puzzel, een soort sudoku. Sudoku s zijn puzzeltjes met hun eigen
Sudoku s Annelies Veen Noud Aldenhoven Vierkant voor Wiskunde Zomerkamp A 2010 Voorwoord Het plaatje op de voorkant is een erg bijzondere puzzel, een soort sudoku. Sudoku s zijn puzzeltjes met hun eigen
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 en 13 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 en 13 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ l.j.j.v.iersel@gmail.com
Examen VWO 2015. wiskunde C. tijdvak 2 woensdag 17 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Examen VWO 2015 tijdvak 2 woensdag 17 juni 13.30-16.30 uur wiskunde C Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 22 vragen. Voor dit examen zijn maximaal 79 punten te behalen. Voor
Examen VWO 2015 tijdvak 2 woensdag 17 juni 13.30-16.30 uur wiskunde C Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 22 vragen. Voor dit examen zijn maximaal 79 punten te behalen. Voor
Formeel Denken 2014 Uitwerkingen Tentamen
 Formeel Denken 2014 Uitwerkingen Tentamen (29/01/15) 1. Benader de betekenis van de volgende Nederlandse zin zo goed mogelijk (6 punten) door een formule van de propositielogica: Als het regent word ik
Formeel Denken 2014 Uitwerkingen Tentamen (29/01/15) 1. Benader de betekenis van de volgende Nederlandse zin zo goed mogelijk (6 punten) door een formule van de propositielogica: Als het regent word ik
het grote kerstdobbelspel
 het grote kerstdobbelspel leuk dat je dit leest Het grote kerstdobbelspel Een avondvullend programma vol actie, spanning en vooral plezier Dit spel is tot stand gekomen in samenwerking met dobbelspel.nl
het grote kerstdobbelspel leuk dat je dit leest Het grote kerstdobbelspel Een avondvullend programma vol actie, spanning en vooral plezier Dit spel is tot stand gekomen in samenwerking met dobbelspel.nl
Practicum hoogtemeting 3 e klas havo/vwo
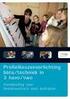 Deel (benaderbaar object) Om de hoogte van een bepaald object te berekenen hebben we geleerd dat je dat kunt doen als je in staat bent om een rechthoekige driehoek te bedenken waarvan je één zijde kunt
Deel (benaderbaar object) Om de hoogte van een bepaald object te berekenen hebben we geleerd dat je dat kunt doen als je in staat bent om een rechthoekige driehoek te bedenken waarvan je één zijde kunt
SYMMETRIEËN VAN RUIMTELIJKE FIGUREN. Prof. dr. Ronald Meester
 SYMMETRIEËN VAN RUIMTELIJKE FIGUREN Prof. dr. Ronald Meester Inleiding In dit college onderzoeken we symmetrie-eigenschappen van ruimtelijke figuren zoals driehoeken, vierkanten, kubussen en andere veelvlakken
SYMMETRIEËN VAN RUIMTELIJKE FIGUREN Prof. dr. Ronald Meester Inleiding In dit college onderzoeken we symmetrie-eigenschappen van ruimtelijke figuren zoals driehoeken, vierkanten, kubussen en andere veelvlakken
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
Sorteren, groeperen en totaliseren
 6 Sorteren, groeperen en totaliseren 6.1 Inleiding Een rapport maken begint met het selecteren van de tabellen en het plaatsen van de velden die u in uw rapport wilt afdrukken. Vervolgens sorteert, groepeert
6 Sorteren, groeperen en totaliseren 6.1 Inleiding Een rapport maken begint met het selecteren van de tabellen en het plaatsen van de velden die u in uw rapport wilt afdrukken. Vervolgens sorteert, groepeert
3. Elke lijn van een graaf draagt twee bij tot de som van alle graden.
 Antwoorden Doeboek 4 Grafen.. De middelste en de rechtergraaf.. Een onsamenhangende graaf met vijf punten en vijf lijnen: Teken een vierhoek met één diagonaal. Het vijfde punt is niet verbonden met een
Antwoorden Doeboek 4 Grafen.. De middelste en de rechtergraaf.. Een onsamenhangende graaf met vijf punten en vijf lijnen: Teken een vierhoek met één diagonaal. Het vijfde punt is niet verbonden met een
Excel reader. Beginner Gemiddeld. bas@excel-programmeur.nl
 Excel reader Beginner Gemiddeld Auteur Bas Meijerink E-mail bas@excel-programmeur.nl Versie 01D00 Datum 01-03-2014 Inhoudsopgave Introductie... - 3 - Hoofdstuk 1 - Databewerking - 4-1. Inleiding... - 5-2.
Excel reader Beginner Gemiddeld Auteur Bas Meijerink E-mail bas@excel-programmeur.nl Versie 01D00 Datum 01-03-2014 Inhoudsopgave Introductie... - 3 - Hoofdstuk 1 - Databewerking - 4-1. Inleiding... - 5-2.
TAFELTASJE. Tafeltasje is een rugzak met daarin allemaal leuke spelletjes om de maal- en deeltafels in te oefenen. juf Tessa
 TAFELTASJE Tafeltasje is een rugzak met daarin allemaal leuke spelletjes om de maal- en deeltafels in te oefenen. juf Tessa 0 INHOUD MAALTAFELBOEKJE... 2 SNELLE JELLE... 12 VIER OP EEN RIJ... 14 KRUISWOORDPUZZEL...
TAFELTASJE Tafeltasje is een rugzak met daarin allemaal leuke spelletjes om de maal- en deeltafels in te oefenen. juf Tessa 0 INHOUD MAALTAFELBOEKJE... 2 SNELLE JELLE... 12 VIER OP EEN RIJ... 14 KRUISWOORDPUZZEL...
Leest hij eerst de eerste kolom van boven naar beneden, dan de tweede enzovoorts, dan hoor je
 Estafette-opgave 1 (20 punten, rest 580 punten) Vier bij vier. In een schema van vier maal vier vierkantjes schrijft iemand letters. In iedere rij en in iedere kolom komt zo één A, één B en één C, zodat
Estafette-opgave 1 (20 punten, rest 580 punten) Vier bij vier. In een schema van vier maal vier vierkantjes schrijft iemand letters. In iedere rij en in iedere kolom komt zo één A, één B en één C, zodat
Activiteit 9. Modderstad Minimaal Opspannende Bomen. Samenvatting. Kerndoelen. Leeftijd. Vaardigheden. Materialen
 Activiteit 9 Modderstad Minimaal Opspannende Bomen Samenvatting Onze maatschappij is verbonden middels heel veel netwerken: telefoonnet, elektriciteitsnet, de riolering, computernetwerk, en het wegennet.
Activiteit 9 Modderstad Minimaal Opspannende Bomen Samenvatting Onze maatschappij is verbonden middels heel veel netwerken: telefoonnet, elektriciteitsnet, de riolering, computernetwerk, en het wegennet.
De schatkist wordt in het midden op tafel gezet, zodat elke speler er goed bij kan. Het rode kussen wordt er naast gelegd.
 Meisterdiebe Spelidee: In het juwelen wereldje barst de hel los! De juweliers proberen onechte juwelen (imitaties) kwijt te raken. De smokkelaars bundelen hun krachten om hun grote slag te slaan. En de
Meisterdiebe Spelidee: In het juwelen wereldje barst de hel los! De juweliers proberen onechte juwelen (imitaties) kwijt te raken. De smokkelaars bundelen hun krachten om hun grote slag te slaan. En de
5. Functies. In deze module leert u:
 5. Functies In deze module leert u: - Wat functies zijn; - Functies uitvoeren; - De verschillende functies van Calc kennen. - Naar een ander werkblad verwijzen. U kunt eenvoudige berekeningen, zoals aftrekken,
5. Functies In deze module leert u: - Wat functies zijn; - Functies uitvoeren; - De verschillende functies van Calc kennen. - Naar een ander werkblad verwijzen. U kunt eenvoudige berekeningen, zoals aftrekken,
Basisvaardigheden algebra. Willem van Ravenstein. 2012 Den Haag
 Basisvaardigheden algebra Willem van Ravenstein 2012 Den Haag 1. Variabelen Rekenenis het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken
Basisvaardigheden algebra Willem van Ravenstein 2012 Den Haag 1. Variabelen Rekenenis het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2010 2011, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2010 2011, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Basisvaardigheden Microsoft Excel
 Basisvaardigheden Microsoft Excel Met behulp van deze handleiding kun je de basisvaardigheden leren die nodig zijn om meetresultaten van een practicum te verwerken. Je kunt dan het verband tussen twee
Basisvaardigheden Microsoft Excel Met behulp van deze handleiding kun je de basisvaardigheden leren die nodig zijn om meetresultaten van een practicum te verwerken. Je kunt dan het verband tussen twee
Het leek ons wel een interessante opdracht, een uitdaging en een leuke aanvulling bij het hoofdstuk.
 Praktische-opdracht door een scholier 2910 woorden 3 mei 2000 5,2 46 keer beoordeeld Vak Wiskunde Wiskunde A1 - Praktische Opdracht Hoofdstuk 2 1. Inleiding We hebben de opdracht gekregen een praktische
Praktische-opdracht door een scholier 2910 woorden 3 mei 2000 5,2 46 keer beoordeeld Vak Wiskunde Wiskunde A1 - Praktische Opdracht Hoofdstuk 2 1. Inleiding We hebben de opdracht gekregen een praktische
Lesideeën beroepenkaarten WERKEND NEDERLANDS
 Lesideeën beroepenkaarten WERKEND NEDERLANDS Lesidee: Wat is weg? Speel dit spel met een klein groepje. Leg steeds vijf tot acht kaarten open op tafel. Geef de cursisten even de tijd om alle foto s in
Lesideeën beroepenkaarten WERKEND NEDERLANDS Lesidee: Wat is weg? Speel dit spel met een klein groepje. Leg steeds vijf tot acht kaarten open op tafel. Geef de cursisten even de tijd om alle foto s in
w e r k b o e k a n t w o o r d e n blok 225 + Hoeveel knikkers heeft Li? Teken op de getallenlijn en reken uit.
 jaargroep a n t w o o r d e n Zwijsen reken-wiskundemethode voor het basisonderwijs + blok = w e r k b o e k 00 0 300 Hoeveel knikkers heeft Li? Teken op de getallenlijn en reken uit. Les Overal getallen
jaargroep a n t w o o r d e n Zwijsen reken-wiskundemethode voor het basisonderwijs + blok = w e r k b o e k 00 0 300 Hoeveel knikkers heeft Li? Teken op de getallenlijn en reken uit. Les Overal getallen
Hoofdstuk 2: Grafieken en formules
 Hoofdstuk 2: Grafieken en formules Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 2: Grafieken en formules Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde
Hoofdstuk 2: Grafieken en formules Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 2: Grafieken en formules Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde
Universiteit Utrecht Betafaculteit. Examen Discrete Wiskunde II op donderdag 6 juli 2017, uur.
 Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde II op donderdag 6 juli 2017, 13.30-16.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde II op donderdag 6 juli 2017, 13.30-16.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Magidoku s en verborgen symmetrieën
 Uitwerking Puzzel 92-6 Magidoku s en verborgen symmetrieën Wobien Doyer Lieke de Rooij Een Latijns vierkant van orde n, is een vierkante matrix, gevuld met n verschillende symbolen waarvan elk precies
Uitwerking Puzzel 92-6 Magidoku s en verborgen symmetrieën Wobien Doyer Lieke de Rooij Een Latijns vierkant van orde n, is een vierkante matrix, gevuld met n verschillende symbolen waarvan elk precies
Mijn project noemt Het Wari-spel. De doelgroep van mijn programma is iedereen die houdt van strategische spelen.
 Voorstel project Mijn project noemt Het Wari-spel. De doelgroep van mijn programma is iedereen die houdt van strategische spelen. Het doel van mijn project is de spelers een ontspannende, plezierige en
Voorstel project Mijn project noemt Het Wari-spel. De doelgroep van mijn programma is iedereen die houdt van strategische spelen. Het doel van mijn project is de spelers een ontspannende, plezierige en
ROL, SCHUIF EN BEDEK. MEER DOBBELSTEENWERKBLADEN? Kijk op heutinkvoorthuis.nl AANTAL SPELERS: 2-4
 ROL, SCHUIF EN BEDEK AANTAL SPELERS: - JE HEBT NODIG: dobbelstenen in verschillende kleuren, fiches of iets om de plaatjes mee af te dekken. Eventueel een kookwekker. SPELREGELS: Rol om de beurt met de
ROL, SCHUIF EN BEDEK AANTAL SPELERS: - JE HEBT NODIG: dobbelstenen in verschillende kleuren, fiches of iets om de plaatjes mee af te dekken. Eventueel een kookwekker. SPELREGELS: Rol om de beurt met de
1.3 Rekenen met pijlen
 14 Getallen 1.3 Rekenen met pijlen 1.3.1 Het optellen van pijlen Jeweetnuwatdegetallenlijnisendat0nochpositiefnochnegatiefis. Wezullen nu een soort rekenen met pijlen gaan invoeren. We spreken af dat bij
14 Getallen 1.3 Rekenen met pijlen 1.3.1 Het optellen van pijlen Jeweetnuwatdegetallenlijnisendat0nochpositiefnochnegatiefis. Wezullen nu een soort rekenen met pijlen gaan invoeren. We spreken af dat bij
15. Tabellen. 1. wat rijen, kolommen en cellen zijn; 2. rijen en kolommen invoegen; 3. een tabel invoegen en weer verwijderen;
 15. Tabellen Misschien heeft u al eens geprobeerd om gegevens in een aantal kolommen te plaatsen door gebruik te maken van spaties, kolommen of tabs. Dat verloopt goed totdat u gegevens wilt wijzigen of
15. Tabellen Misschien heeft u al eens geprobeerd om gegevens in een aantal kolommen te plaatsen door gebruik te maken van spaties, kolommen of tabs. Dat verloopt goed totdat u gegevens wilt wijzigen of
Dossieropdracht 4. Analyse 1 - Didactiek
 Dossieropdracht 4 Analyse 1 - Didactiek Naam: Thomas Sluyter Nummer: 1018808 Jaar / Klas: 1e jaar Docent Wiskunde, deeltijd Datum: 27 november, 2007 Samenvatting Al eerder zijn de studenten bloot gesteld
Dossieropdracht 4 Analyse 1 - Didactiek Naam: Thomas Sluyter Nummer: 1018808 Jaar / Klas: 1e jaar Docent Wiskunde, deeltijd Datum: 27 november, 2007 Samenvatting Al eerder zijn de studenten bloot gesteld
Microsoft Publisher 2003
 Bureau voor Taal en Inform at ic a Werfkade 10 9601 LG Hoogezand 0598 390070 e-mail: bti@bbti.nl Microsoft Publisher 2003 www.bbti.nl bbti Hoogezand ,QKRXGVRSJDYH Introductie... 3 Persoonlijke informatie...
Bureau voor Taal en Inform at ic a Werfkade 10 9601 LG Hoogezand 0598 390070 e-mail: bti@bbti.nl Microsoft Publisher 2003 www.bbti.nl bbti Hoogezand ,QKRXGVRSJDYH Introductie... 3 Persoonlijke informatie...
Deel C. Breuken. vermenigvuldigen en delen
 Deel C Breuken vermenigvuldigen en delen - 0 Sprongen op de getallenlijn. De sprongen op de getallenlijn zijn even groot. Schrijf passende breuken of helen bij de deelstreepjes. 0 Welk eindpunt wordt bereikt
Deel C Breuken vermenigvuldigen en delen - 0 Sprongen op de getallenlijn. De sprongen op de getallenlijn zijn even groot. Schrijf passende breuken of helen bij de deelstreepjes. 0 Welk eindpunt wordt bereikt
Hieronder zie je hoe dat gaat. Opgave 3. Tel het aantal routes in de volgende onvolledige roosters van linksboven naar rechtsonder.
 Groepsopdracht 1: Volledige en onvolledige roosters Voor een volledig rooster kun je de driehoek van Pascal gebruiken om te weten te komen hoeveel routes er van A naar B zijn. Bij onvolledige roosters
Groepsopdracht 1: Volledige en onvolledige roosters Voor een volledig rooster kun je de driehoek van Pascal gebruiken om te weten te komen hoeveel routes er van A naar B zijn. Bij onvolledige roosters
Examen Datastructuren en Algoritmen II
 Tweede kandidatuur Informatica Academiejaar 2004 2005, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. 1. Binomiale
Tweede kandidatuur Informatica Academiejaar 2004 2005, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. 1. Binomiale
Workshop DisWis, De Start 13/06/2007 Bladzijde 1 van 7. Sudoku. Sudoku
 DisWis DisWis is een lessenserie discrete wiskunde die De Praktijk vorig jaar in samenwerking met prof.dr. Alexander Schrijver heeft opgezet. Gedurende vier weken komt een wiskundestudent twee blokuren
DisWis DisWis is een lessenserie discrete wiskunde die De Praktijk vorig jaar in samenwerking met prof.dr. Alexander Schrijver heeft opgezet. Gedurende vier weken komt een wiskundestudent twee blokuren
Handleiding Excel. bij. hoofdstuk 18 Cijfers in Orde Wageningse Methode
 Handleiding Excel bij hoofdstuk 18 Cijfers in Orde Wageningse Methode oktober 2008 1 Excel (Nederlandtalig) Excel is een programma dat snel allerlei berekeningen kan uitvoeren. Ook kan het programma gemakkelijk
Handleiding Excel bij hoofdstuk 18 Cijfers in Orde Wageningse Methode oktober 2008 1 Excel (Nederlandtalig) Excel is een programma dat snel allerlei berekeningen kan uitvoeren. Ook kan het programma gemakkelijk
7 2, 3, 5, 7, 11, 13, 17, 19, 29, 31,
 Hoofdstuk.0 INTRO De som is, of 0, of. Dat zijn de enige met vier mogelijkheden, zie eerste twee kolommen. Som Mogelijkheden Product Manieren om het product te schrijven + 8 + 7 + + 5 8 8 0 8 of 7 of 5
Hoofdstuk.0 INTRO De som is, of 0, of. Dat zijn de enige met vier mogelijkheden, zie eerste twee kolommen. Som Mogelijkheden Product Manieren om het product te schrijven + 8 + 7 + + 5 8 8 0 8 of 7 of 5
Estafette. De langste zijde wordt in twee ongelijke stukken verdeeld. Laat x de lengte van het ene stuk zijn, dan is het andere stuk 25 x.
 7 e Wiskundetoernooi Estafette 08 Uitwerking opgave e langste zijde wordt in twee ongelijke stukken verdeeld. Laat x de lengte van het ene stuk zijn, dan is het andere stuk 5 x. x 5 x at de twee rechthoeken
7 e Wiskundetoernooi Estafette 08 Uitwerking opgave e langste zijde wordt in twee ongelijke stukken verdeeld. Laat x de lengte van het ene stuk zijn, dan is het andere stuk 5 x. x 5 x at de twee rechthoeken
Credits. : Johan Beyens, Johannes Sneyers en Steven Redant. Uitgever Red Eyed Rabbit. Voor meer informatie, bezoek
 Credits Spelontwerp Spelontwikkeling Illustraties Grafische Vormgeving Eindredactie : Johan Beyens : Johan Beyens, Johannes Sneyers en Steven Redant : Joris Weyen : Erlend Van der haegen : Tom Pattyn Uitgever
Credits Spelontwerp Spelontwikkeling Illustraties Grafische Vormgeving Eindredactie : Johan Beyens : Johan Beyens, Johannes Sneyers en Steven Redant : Joris Weyen : Erlend Van der haegen : Tom Pattyn Uitgever
Begrenzing van het aantal iteraties in het max-flow algoritme
 Begrenzing van het aantal iteraties in het max-flow algoritme Het oplossen van het maximum stroom probleem met behulp van stroomvermeerderende paden werkt, maar het aantal iteraties kan aardig de spuigaten
Begrenzing van het aantal iteraties in het max-flow algoritme Het oplossen van het maximum stroom probleem met behulp van stroomvermeerderende paden werkt, maar het aantal iteraties kan aardig de spuigaten
rekentrainer jaargroep 7 Fietsen op Terschelling. Teken en vul in. Zwijsen naam: reken-wiskundemethode voor het basisonderwijs
 Zwijsen jaargroep 7 naam: reken-wiskundemethode voor het basisonderwijs Waar staat deze paddenstoel ongeveer? Teken op de kaart. Welke afstand of welke route fietsen de kinderen? naam route afstand Janna
Zwijsen jaargroep 7 naam: reken-wiskundemethode voor het basisonderwijs Waar staat deze paddenstoel ongeveer? Teken op de kaart. Welke afstand of welke route fietsen de kinderen? naam route afstand Janna
Uitwerkingen van geselecteerde opgaven (laatste update 4 Januari 2018) Zebra 50. De Wiskunde van Rubik s Kubus.
 Uitwerkingen van geselecteerde opgaven (laatste update 4 Januari 2018) Zebra 50. De Wiskunde van Rubik s Kubus. Opgave 1. Niet alle mogelijke posities zijn door middel van draaien te bereiken. Het is bijvoorbeeld
Uitwerkingen van geselecteerde opgaven (laatste update 4 Januari 2018) Zebra 50. De Wiskunde van Rubik s Kubus. Opgave 1. Niet alle mogelijke posities zijn door middel van draaien te bereiken. Het is bijvoorbeeld
