Vectoranalyse voor TG
|
|
|
- Michiel Groen
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 college 12 collegejaar college build slides Vandaag : : : : september ail Training Vessel 263 tad Amsterdam stelling van Gauss stelling van Green Conservatieve vectorvelden 1 VA intro
2 divergentie ection 16.8 finitie tel F (M 1, M 2,..., M n ) is een vectorveld op R n, waarvan de partiële afgeleiden van alle componentfuncties M i bestaan. divergentie van F is gedefinieerd als div F M 1 x 1 + M 2 x M n x n. In R 2 : als F (M, N ), dan div F M x + N y. In R 3 : als F (M, N, P), dan div F M x + N y + P z. diverentie is een functie van n variabelen. Alternatieve notatie voor de divergentie: div F F VA divergentie z k z r x y r + r F y O i j x Het rechthoekig blokvormig gebied D heeft hoekpunten r (x, y, z) en r + r (x + x, y + y, z + z). Het oppervlak is gedefinieerd als de rand van D. flux van F door het gesloten oppervlak is F n dσ VA
3 divergentie 1 2 k i j z x Pk y Nj F Mi Ontbind v in componenten: F M i + N j + P k. Iedere component is een vectorveld, dus F n dσ M i n dσ + + P k n dσ. N j n dσ Voor de eerste term geldt M i n dσ M 1 i n dσ + M 2 i n dσ omdat M i loodrecht staat op normaalvectoren van de andere zijvlakken van VA divergentie k k i j j 1 i 2 j i k normaal op is naar buiten gericht, dus op 1 geldt n i en op 2 geldt n i. M i n dσ M 2 i i dσ M 1 i i dσ M dσ M dσ VA
4 divergentie Onder de aanname dat x, y en z klein zijn geldt dat M constant is op zowel 1 als 2, dus op 1 geldt M (x) M (r) M (x, y, z) en op 2 geldt M (x) M (r + xi) M (x + x, y, z). Voor de flux-integraal van v x door 1 en 2 geldt M i n dσ M dσ M dσ 2 1 M (x + x, y, z) 1 dσ M (x, y, z) 1 dσ 2 1 M (x + x, y, z) opp 2 M (x, y, z) opp 1 ( ) M (x + x, y, z) M (x, y, z) y z M x (x, y, z) x y z VA divergentie Op soortgelijke wijze toon je aan dat N j n dσ N y x y z en P k n dσ P z x y z. Tel de resultaten op: F n dσ ( M x + N y + P ) x y z z divergentie is de flux per volume-eenheid: F n dσ lim M x, y, z x y z x + N y + P z divergentie heet ook wel fluxdichtheid. div F VA
5 divergentie van een laminaire stroming door een buis x y k L v snelheid v op positie x is v(x) P ( R 2 r 2) k 4ηL (,, P ( R 2 x 2 y 2)), 4ηL waarbij r de afstand tot de z-as is, waarbij P het drukverschil tussen begin en einde van de buis is, en waarbij η de dynamische viscositeit is. div F, de laminaire stroming is divergentievrij. z R R VA en rotatie telling tel F (M, N, P) is een vectorveld op R 3 en stel dat van M, N en P de tweede-orde partiële afgeleiden bestaan en continu zijn. Dan geldt div curl F. div curl F ( F ) ( P x y N ) + ( M z y z P ) + ( N x z x M ) y 2 P x y 2 N x z + 2 M y z 2 P y x + 2 N z x 2 M z y. ection 14.3, mixed derivative theorem VA
6 en rotatie Voorbeeld Toon aan dat het vectorveld F(x, y, z) ( xz, xyz, y 2) niet de rotatie van een vectorveld is, met andere woorden: er bestaat geen vectorveld G zodat F curl G. Als er een vectorveld G is waarvoor F curl G, dan div F div curl G. Er geldt echter div F (xz) x z + xz + + (xyz) y + ( y 2) z z + xz VA ection 16.8 telling Theorem 8 G is een enkelvoudig samenhangend gebied in R 3. rand van G is een naar buiten georiënteerd, enkelvoudig, gesloten, stuksgewijs glad oppervlak. Vectorveld F heeft continue partiële afgeleiden op een open omgeving van G. Dan geldt F n dσ G div F dv. wordt ook wel de stelling van Gauss genoemd VA
7 schets van een bewijs z n B 1 x 1 y B 2 n x 2 Voor een blokje B 1 met rand 1 geldt F n dσ div F x 1 y z Voor een tweede blokje B 2 met rand 2 geldt F (B 1 n F B 2 ) B 1 n dσ + F B 2 n dσ div F x 1 y z + div F x 2 y z integraal over het tussenvlak wordt twee keer meegeteld, maar zijn tegengesteld en vallen dus weg. Verdeel G in blokjes, bereken Riemannsommen. volgt door limieten te nemen VA Voorbeeld Gegeven is het vectorveld F(x, y, z) ( xy, y 2 +e xz2, sin(xy) ). Bereken F n dσ waarbij de rand is van het gebied G begrensd door het oppervlak z 1 x 2 en de vlakken z, y en y + z 2. Gebruik de. divergentie van F is div F x (xy) + (y 2 + e xz2) y + (sin xy) 3y. z G {(x, y, z) 1 x 1, z 1 x 2, y 2 z} VA
8 Voorbeeld (vervolg) F n dσ div F dv G 1 x 2 2 z 1 x 2 [ (2 z) 2 2 (2 z)3 3 G 3y dv y dy dz dx ] 1 x 2 (x 2 + 1) 3 8 dx dz dx dx x 6 + 3x 4 + 3x 2 7 dx VA Voorbeeld ection 16.8, example 3 Bereken de flux van F (xy, yz, xz) door de rand van de kubus D in het eerste octant met zijvlakken x 1, y 1 en z 1. rand van D bestaat uit 6 vierkanten, dus voor de berekening van de flux moet je zes oppervlakteintegralen berekenen. Oplossing: gebruik de. div F x (xy) + y (yz) + (xz) y + z + x. z Flux-integraal F n dσ div F dv D x + y + z dx dy dz D VA
9 Voorbeeld Bereken op twee manieren de flux van het vectorveld F (4x, 2y 2, x 2 z 2 ) door de rand van de cilinder G, met straal 2, begrensd door de vlakken z en z 3. Eerste manier: rechtstreeks F n dσ F 1 n dσ + F 2 n dσ + Gebruik voor de mantel 1 de parametrisering 3 F n dσ. r(θ, ζ) (2 cos θ, 2 sin θ, ζ) θ 2π, ζ VA Voorbeeld (vervolg) r θ ( 2 sin θ, 2 cos θ, ) en r ζ (,, 1). r θ r ζ (2 cos θ, 2 sin θ, ). F ( r(θ, ζ) ) (8 cos θ, 8 sin 2 θ, 4ζ 2 cos 2 θ). naar buiten georiënteerd F ( r(θ, ζ) ) (r θ r ζ ) 16 cos 2 θ 16 sin 3 θ. 3 2π F 1 n dσ 16 cos 2 θ 16 sin 3 θ dθ dζ dζ 2π 48π. 2π 16 cos 2 θ 16 sin 3 θ dθ 2π cos 2θ dθ cos 2 θ dcosθ [ 1 2 θ sin 2θ ] 2π + 48 [ cos θ 1 3 cos3 θ ] 2π VA
10 Voorbeeld (vervolg) Voor 2 nemen we de parametrisering r(r, θ) (r cos θ, r sin θ, 3) r 2, θ 2π. r r (cos θ, sin θ, ) en r θ ( r sin θ, r cos θ, ). r r r θ (,, r). naar boven georiënteerd F ( r(r, θ) ) (4r cos θ, 2r 2 sin 2 θ, 9r 2 cos 2 θ). F ( r(r, θ) ) (r r r θ ) 9r 3 cos 2 θ. 2π 2 F 2 n dσ 9r 3 cos 2 θ dr dθ π 2π 36π. cos 2 θ dθ 2 r 3 dr [ ] cos 2θ dθ 1 4 r 4 2 [ 1 2 θ sin 2θ ] 2π VA Voorbeeld (vervolg) Voor 3 geldt dus n (,, 1) en F(x, y, ) (4x, 2y 2, ), F(x, y, ) n, en daarmee geldt F 3 n dσ. Daarmee is de flux-integraal door gelijk aan F n dσ F 1 n dσ + F 2 n dσ + F 3 n dσ 48π + 36π + 84π VA
11 Voorbeeld (vervolg) Tweede manier: bereken de flux-integraal met behulp van de : div F(x, y, z) 4 4y + 2x 2 z. Gebruik cilindercoördinaten om G te beschrijven: x r cos θ, y r sin θ, z ζ. met r 2, θ 2π, ζ 3. Voor de divergentie geldt div F 4 4r sin θ + 2r 2 cos 2 θ ζ VA Voorbeeld (vervolg) F n dσ 3 2π 2 3 2π 3 2π π. G div F dv ( 4 4r sin θ + 2r 2 cos 2 θ ζ ) r dr dθ dζ [ 2r r 3 sin θ r 4 cos 2 θ ζ sin θ + 8 cos2 θ ζ dθ dζ ] 2 r [ ( ) ] 2π 8θ cos θ θ sin 2θ ζ dζ θ [ ] 16π + 8πζ dζ 16πζ + 4πζ 2 3 ζ dθ dζ VA
12 Eigenschappen telling tel het gesloten oppervlak 1 ligt geheel binnen het gesloten oppervlak 2. normaalvelden op 1 en 2 zijn naar buiten gericht. Als D het gebied is dat tussen 1 en 2 ligt, dan geldt div F dv F D 2 n dσ F 1 n dσ. Gevolg Als div F(x) voor alle x D, dan geldt F 2 n dσ F 1 n dσ VA Electrische velden Voorbeeld de wet van Gauss Blz. 996 In bevindt zich een electrische lading q. Het oppervlak is een enkelvoudig gesloten oppervlak dat q omvat. flux-integraal door van het electrisch veld veroorzaakt door q is gelijk aan q/ε. Het electrisch veld in x ten gevolge van q is E(x) q x 4πε x 3 (Wet van Coulomb). Er geldt: div E(x) voor alle x. tel B is een bol met middelpunt en straal a > zodat B binnen ligt, dan E n dσ E n dσ. B VA
13 Electrische velden Er geldt voor iedere x op de rand van B: E n q x 4πε x x 3 x q x x 4πε x 4 q 4πε 1 x 2 Hiermee leid je af E n dσ B B q 4πε a 2 dσ q 4πε a 2 opp(b) q 4πε a 2. E n dσ q 4πε a 2 1 dσ B q 4πε a 2 4πa2 q. ε Een andere formulering voor de wet van Gauss is: q ε E n dσ VA stelling van Green tel is een enkelvoudig samenhangend gebied met rand C. functies M (x, y) en N (x, y) zijn continu differentieerbaar op een open gebied dat omvat. finieer D {(x, y, z) (x, y), 1 2 z 1 2 }. Noem de bovenkant 1, de onderkant 2 en de zijwand W. normaal wijst naar buiten. finieer het vectorveld F(x, y, z) door F(x, y, z) ( N (x, y), M (x, y), ). div F(x, y, z) N x M y VA
14 stelling van Green D div F dv 1/2 1/2 N x M y ( N x M ) 1/2 1 dz da y 1/2 N x M y da. F n dσ D F 1 n dσ + F 2 n dσ + Op 1 geldt: F (N, M, ) (,, 1) n, dus 1 F n dσ. Op soortgelijke wijze volgt: 2 F n dσ. dz da W F n dσ VA stelling van Green tel r(t) ( x(t), y(t) ) met a t b is een parametrisering van C. Dan is r(t, z) ( x(t), y(t), z ) a t b en 1 2 z 1 2 met een parametrizering van W. r t r z (x, y, ) (,, 1) (y, x, ). F n dσ F n dσ D b 1/2 a b a 1/2 W (N, M, ) (y, x, ) dz dt N y + M x dt C M dx + N dy. Uit de volgt N M dx + N dy x M y da. C VA
15 Gesloten oppervlakken telling Voor een enkelvoudig gesloten oppervlak geldt curl F n dσ. Gebruik de. tel is de rand van E dan curl F n dσ div(curl F) dv. E Gevolg Voor twee een enkelvoudige oppervlakken 1 en 2 met gemeenschappelijke rand C en identieke oriëntatie geldt curl F 1 n dσ curl F 2 n dσ VA vlak niet vlak vlakke integralen lijnintegralen oppervlakteintegralen f (x) dx f (x, y) da f (x, y, z) dv van functies: f ds R 2 R 3 C van vectorvelden: F dr C C F n ds R 2 R 3 R 2 van functies: f dσ R 3 van vectorvelden: F n dσ R VA
16 Hoofdstelling van de calculus Hoofdstelling voor lijnintegralen telling van Green telling van tokes b a C F (x) dx F(b) F(a) f dr f ( r(b) ) f ( r(a) ) R R N x M y C da div F da C curl F n dσ F n ds; C F dr F dr stelling div F dv F n dσ D VA
Vectoranalyse voor TG
 college 11 collegejaar college build slides Vandaag : : : : 17-18 11 23 oktober 2017 35 De sterrennacht Vincent van Gogh, 1889 1 2 3 4 5 Verband met de stelling van n 1 VA intro ection 16.7 Definitie Equation
college 11 collegejaar college build slides Vandaag : : : : 17-18 11 23 oktober 2017 35 De sterrennacht Vincent van Gogh, 1889 1 2 3 4 5 Verband met de stelling van n 1 VA intro ection 16.7 Definitie Equation
Vectoranalyse voor TG
 college 1 collegejaar college build slides Vandaag : : : : 14-15 1 25 september 214 28 1 2 3 4 otatie Green De wet van Faraday 1 VA vandaag 4.5.6 ection 16.7 telling Vergeleijking (4.62) Theorem 6 Het
college 1 collegejaar college build slides Vandaag : : : : 14-15 1 25 september 214 28 1 2 3 4 otatie Green De wet van Faraday 1 VA vandaag 4.5.6 ection 16.7 telling Vergeleijking (4.62) Theorem 6 Het
Math D2 Gauss (Wiskunde leerlijn TOM) Deelnemende Modules: /FMHT/ / A. Oefententamen #2 Uitwerking
 Math D Gauss Wiskunde leerlijn TOM Deelnemende Modules: 14-144/FMHT/14161/14144-1A Oefententamen # Uitwerking Vraagstuk 1. tel de doorsnijding van de oppervlakken x + y + z 4 en z 1. Van bovenaf bekijkt
Math D Gauss Wiskunde leerlijn TOM Deelnemende Modules: 14-144/FMHT/14161/14144-1A Oefententamen # Uitwerking Vraagstuk 1. tel de doorsnijding van de oppervlakken x + y + z 4 en z 1. Van bovenaf bekijkt
Vectoranalyse voor TG
 college 6 collegejaar : 8-9 college : 6 build : 2 oktober 28 slides : 38 Vandaag Minecraft globe van remi993 2 erhaalde 3 4 intro VA Drievoudige integralen Section 5.5 Definitie Een rechthoekig blok is
college 6 collegejaar : 8-9 college : 6 build : 2 oktober 28 slides : 38 Vandaag Minecraft globe van remi993 2 erhaalde 3 4 intro VA Drievoudige integralen Section 5.5 Definitie Een rechthoekig blok is
Topologie in R n 10.1
 Topologie in R n 10.1 Lengte x = (x 1,..., x n ) = x 2 1 + x2 2 + + x2 n Bol B(x 0, r) = {x : x x 0 < r} x 0 r p 1 p 3 p 1 p 2 S p 1 heet uitwendig punt p 2 heet inwendig punt p 3 heet randpunt p 1 p 3
Topologie in R n 10.1 Lengte x = (x 1,..., x n ) = x 2 1 + x2 2 + + x2 n Bol B(x 0, r) = {x : x x 0 < r} x 0 r p 1 p 3 p 1 p 2 S p 1 heet uitwendig punt p 2 heet inwendig punt p 3 heet randpunt p 1 p 3
Vectoranalyse voor TG
 college 6 van een vectorveld collegejaar college build slides Vandaag : : : : 14-15 6 22 september 214 51 1 2 3 4 5 Gradiënt van een vectorveld 1 VA vandaag Section 16.2 Hoofdstu 4 Definitie Een vectorveld
college 6 van een vectorveld collegejaar college build slides Vandaag : : : : 14-15 6 22 september 214 51 1 2 3 4 5 Gradiënt van een vectorveld 1 VA vandaag Section 16.2 Hoofdstu 4 Definitie Een vectorveld
WI1708TH Analyse 3. College 5 23 februari Challenge the future
 WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
Faculteit Wiskunde en Informatica VECTORANALYSE
 12 Faculteit Wiskunde en Informatica Aanvulling 4 VECTOANALYE 2WA15 2006/2007 Hoofdstuk 4 De stelling van Gauss (divergentie-stelling) 4.1 Inleiding Dit hoofdstuk is gewijd aan slechts één stelling. De
12 Faculteit Wiskunde en Informatica Aanvulling 4 VECTOANALYE 2WA15 2006/2007 Hoofdstuk 4 De stelling van Gauss (divergentie-stelling) 4.1 Inleiding Dit hoofdstuk is gewijd aan slechts één stelling. De
Math D2 Gauss (Wiskunde leerlijn TOM) Deelnemende Modules: /FMHT/ / A. Oefententamen #1 Uitwerking.
 Math D Gauss Wiskunde leerlijn TOM) Deelnemende Modules: 14-144/FMHT/14161/14144-1A Oefententamen #1 Uitwerking Vraagstuk 1 Bereken de oppervlakte integraal F ˆn d, waarbij Fx, y, z) x î + y ĵ z ˆk en
Math D Gauss Wiskunde leerlijn TOM) Deelnemende Modules: 14-144/FMHT/14161/14144-1A Oefententamen #1 Uitwerking Vraagstuk 1 Bereken de oppervlakte integraal F ˆn d, waarbij Fx, y, z) x î + y ĵ z ˆk en
Vectoranalyse voor TG
 college 2 Ruimte en oppervlakken collegejaar : 18-19 college : 2 build : 5 september 2018 slides : 25 Vandaag Ruimte 1 Vectoren in R 3 recap 2 Oppervlakken 3 Ruimte 4 1 intro VA Voorkennis uit Ruimtewiskunde
college 2 Ruimte en oppervlakken collegejaar : 18-19 college : 2 build : 5 september 2018 slides : 25 Vandaag Ruimte 1 Vectoren in R 3 recap 2 Oppervlakken 3 Ruimte 4 1 intro VA Voorkennis uit Ruimtewiskunde
Faculteit Wiskunde en Informatica VECTORANALYSE
 2 Faculteit Wiskunde en Informatica Aanvulling 5 VECTORANALYE 2WA5 2006/2007 Hoofdstuk 5 De stellingen van tokes en Green 5. Inleiding In dit hoofdstuk worden de stellingen van tokes en van Green 2 behandeld.
2 Faculteit Wiskunde en Informatica Aanvulling 5 VECTORANALYE 2WA5 2006/2007 Hoofdstuk 5 De stellingen van tokes en Green 5. Inleiding In dit hoofdstuk worden de stellingen van tokes en van Green 2 behandeld.
Vectoranalyse voor TG
 college 4 en raakvlakken collegejaar : 16-17 college : 4 build : 19 september 2016 slides : 30 Vandaag Snowdon Mountain Railway (Wales) 1 De richtingsafgeleide 2 aan een grafiek 3 Differentieerbaarheid
college 4 en raakvlakken collegejaar : 16-17 college : 4 build : 19 september 2016 slides : 30 Vandaag Snowdon Mountain Railway (Wales) 1 De richtingsafgeleide 2 aan een grafiek 3 Differentieerbaarheid
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica
 TECHNICHE UNIVERITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Functies van meer variabelen (DE6) op maandag augustus 5, 4. 7. uur. De uitwerkingen van de opgaven dienen duidelijk geformuleerd
TECHNICHE UNIVERITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Functies van meer variabelen (DE6) op maandag augustus 5, 4. 7. uur. De uitwerkingen van de opgaven dienen duidelijk geformuleerd
Hertentamen WISN102 Wiskundige Technieken 2 Di 17 april 13:30 16:30
 Hertentamen WIN12 Wiskundige Technieken 2 Di 17 april 13:3 16:3 Normering voor 4 pt vragen (andere vragen naar rato): 4pt Goed begrepen en goed uitgevoerd met voldoende toelichting, eventueel enkele onbelangrijke
Hertentamen WIN12 Wiskundige Technieken 2 Di 17 april 13:3 16:3 Normering voor 4 pt vragen (andere vragen naar rato): 4pt Goed begrepen en goed uitgevoerd met voldoende toelichting, eventueel enkele onbelangrijke
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica
 TECHNISCHE UNIVERSITEIT EINHOVEN Faculteit Wiskunde en Informatica. Het gebied is een ringvormig gebied met als rand de twee cirkels met vergelijking x + y 9 respectievelijk x + y 5. Laat A lnx + y dxdy.
TECHNISCHE UNIVERSITEIT EINHOVEN Faculteit Wiskunde en Informatica. Het gebied is een ringvormig gebied met als rand de twee cirkels met vergelijking x + y 9 respectievelijk x + y 5. Laat A lnx + y dxdy.
Studiewijzer Vectorcalculus voor TN 2DN /13 Semester A kwartiel 2
 Studiewijzer Vectorcalculus voor TN 2DN13 2012/13 Semester A kwartiel 2 De actuele versie van deze studiewijzer is te vinden op http://www.win.tue.nl/ gprokert/wijzer2dn13.pdf Doelgroep: tweedejaars Bachelor
Studiewijzer Vectorcalculus voor TN 2DN13 2012/13 Semester A kwartiel 2 De actuele versie van deze studiewijzer is te vinden op http://www.win.tue.nl/ gprokert/wijzer2dn13.pdf Doelgroep: tweedejaars Bachelor
tentamen Analyse (deel 3) wi TH 21 juni 2006, uur
 Technische Universiteit Delft Technische Wiskunde Faculteit lektrotechniek, Wiskunde en Informatica Mekelweg 4, 68 CD DLFT tentamen Analyse (deel 3) wi 54 TH juni 6, 4. 7. uur Deelname aan dit tentamen
Technische Universiteit Delft Technische Wiskunde Faculteit lektrotechniek, Wiskunde en Informatica Mekelweg 4, 68 CD DLFT tentamen Analyse (deel 3) wi 54 TH juni 6, 4. 7. uur Deelname aan dit tentamen
Tentamen Vectorcalculus voor N (2DN06), dinsdag 24 januari 2006, uur.
 TEHNIHE UNIVERITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Vectorcalculus voor N (DN6), dinsdag 4 januari 6, 14.-17. uur. 1. Zij R 3 het deel van de grafiek van de functie f gegeven door
TEHNIHE UNIVERITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Vectorcalculus voor N (DN6), dinsdag 4 januari 6, 14.-17. uur. 1. Zij R 3 het deel van de grafiek van de functie f gegeven door
Mathematical Modelling
 1 / 94 Mathematical Modelling Ruud van Damme Creation date: 15-09-09 2 / 94 Overzicht 1 Herhaling 2 Deels oud, deels nieuw integreren 3 Lijnintegralen 3 / 94 Waarschuwing vooraf! Dit college heeft een
1 / 94 Mathematical Modelling Ruud van Damme Creation date: 15-09-09 2 / 94 Overzicht 1 Herhaling 2 Deels oud, deels nieuw integreren 3 Lijnintegralen 3 / 94 Waarschuwing vooraf! Dit college heeft een
Tentamen WISN102 Wiskundige Technieken 2 Ma 26 jan :30 16:30
 Tentamen WISN1 Wiskundige Technieken Ma 6 jan 14 13:3 16:3 Normering voor 4 pt vragen (andere vragen naar rato): 4pt Goed begrepen en goed uitgevoerd met voldoende toelichting, eventueel enkele onbelangrijke
Tentamen WISN1 Wiskundige Technieken Ma 6 jan 14 13:3 16:3 Normering voor 4 pt vragen (andere vragen naar rato): 4pt Goed begrepen en goed uitgevoerd met voldoende toelichting, eventueel enkele onbelangrijke
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.4, maandag K. P. Hart Faculteit EWI TU Delft Delft, 9 mei, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 40 Outline 1 f : [a, b] C f : C C Primitieven 2 K.
TW2040: Complexe Functietheorie week 4.4, maandag K. P. Hart Faculteit EWI TU Delft Delft, 9 mei, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 40 Outline 1 f : [a, b] C f : C C Primitieven 2 K.
Analyse I. 2. Formuleer en bewijs de formule van Taylor voor een functie f : R R. Stel de formules op voor de resttermen van Lagrange en Liouville.
 Academiejaar 006-007 1ste semester februari 007 Analyse I 1. Toon aan dat elke begrensde rij een convergente deelrij heeft. Geef de definitie van een Cauchy rij, en toon aan dat elke Cauchy rij begrensd
Academiejaar 006-007 1ste semester februari 007 Analyse I 1. Toon aan dat elke begrensde rij een convergente deelrij heeft. Geef de definitie van een Cauchy rij, en toon aan dat elke Cauchy rij begrensd
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.9, donderdag K. P. Hart Faculteit EWI TU Delft Delft, 16 juni, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 46 Outline III.7 Applications of the Residue Theorem
TW2040: Complexe Functietheorie week 4.9, donderdag K. P. Hart Faculteit EWI TU Delft Delft, 16 juni, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 46 Outline III.7 Applications of the Residue Theorem
TENTAMEN INFINITESIMAALREKENING 1C
 TENTAMEN INFINITESIMAALREKENING 1C onderdag 1 maart 1, 14. 17. uur. Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Shrijf je naam en studentnummer op elk vel dat je inlevert en op het
TENTAMEN INFINITESIMAALREKENING 1C onderdag 1 maart 1, 14. 17. uur. Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Shrijf je naam en studentnummer op elk vel dat je inlevert en op het
WI1708TH Analyse 3. College 2 12 februari Challenge the future
 WI1708TH Analyse 3 College 2 12 februari 2015 1 Programma Vandaag Partiële afgeleiden (14.3) Hogere orde partiële afgeleiden (14.3) Partiële differentiaal vergelijkingen (14.3) 2 Functies van twee variabelen
WI1708TH Analyse 3 College 2 12 februari 2015 1 Programma Vandaag Partiële afgeleiden (14.3) Hogere orde partiële afgeleiden (14.3) Partiële differentiaal vergelijkingen (14.3) 2 Functies van twee variabelen
Faculteit Wiskunde en Informatica VECTORANALYSE
 12 Faculteit Wiskunde en Informatica Aanvulling 2 VECTORANALYSE 2WA15 2006/2007 Hoofdstuk 2 Vectorvelden en lijnintegralen 2.1 De Euclidische ruimte E 3 Zij E 3 de (Euclidische) ruimte. iezen we in E 3
12 Faculteit Wiskunde en Informatica Aanvulling 2 VECTORANALYSE 2WA15 2006/2007 Hoofdstuk 2 Vectorvelden en lijnintegralen 2.1 De Euclidische ruimte E 3 Zij E 3 de (Euclidische) ruimte. iezen we in E 3
Vectoranalyse voor TG
 college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
college 5 De tweevoudige integrl collegejr : 8-9 college : 5 build : 27 ugustus 28 slides : 48 Vndg dubbel en De tweevoudige integrl en inhoud 2 Herhlde integrl 3 4 Poolcoördinten intro VA Wt is een integrl?
Analyse I. 1ste Bachelor Ingenieurswetenschappen Academiejaar ste semester 10 januari 2008
 ste Bachelor Ingenieurswetenschappen Academiejaar 007-008 ste semester 0 januari 008 Analyse I. Bewijs de stelling van Bolzano-Weierstrass: elke oneindige begrensde deelverzameling van R heeft minstens
ste Bachelor Ingenieurswetenschappen Academiejaar 007-008 ste semester 0 januari 008 Analyse I. Bewijs de stelling van Bolzano-Weierstrass: elke oneindige begrensde deelverzameling van R heeft minstens
(10 pnt) Bepaal alle punten waar deze functie een relatief extreem of een zadelpunt heeft. Opgave 3. Zij D het gebied gegeven door
 Calculus 3. Tentamen Calculus 3, 8 April 11 Opgave 1. Zij f(x, y, z) = xy z 3xz en g(x, y, z) = x 3 +z sin(y) y sin(z). i) (5 pnt) Laat zien dat p = (, 1, 1) op de oppervlakken {f(x, y, z)} = en {g(x,
Calculus 3. Tentamen Calculus 3, 8 April 11 Opgave 1. Zij f(x, y, z) = xy z 3xz en g(x, y, z) = x 3 +z sin(y) y sin(z). i) (5 pnt) Laat zien dat p = (, 1, 1) op de oppervlakken {f(x, y, z)} = en {g(x,
Opgaven Functies en Reeksen. E.P. van den Ban
 Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Analyse I. 1ste Bachelor Ingenieurswetenschappen Academiejaar 2005-2006 1ste semester 31 januari 2006
 1ste semester 31 januari 2006 Analyse I 1. Onderstel dat f : [a, b] R continu is, en dat f(a)f(b) < 0. Toon aan dat f minstens 1 nulpunt heeft gelegen in het interval (a, b). 2. Gegeven is een functie
1ste semester 31 januari 2006 Analyse I 1. Onderstel dat f : [a, b] R continu is, en dat f(a)f(b) < 0. Toon aan dat f minstens 1 nulpunt heeft gelegen in het interval (a, b). 2. Gegeven is een functie
Aanvullingen van de Wiskunde
 3de Bachelor EIT - de Bachelor Fysica Academiejaar 014-015 1ste semester 7 januari 015 Aanvullingen van de Wiskunde 1. Gegeven is een lineaire partiële differentiaalvergelijking van orde 1: a 1 (x 1,,
3de Bachelor EIT - de Bachelor Fysica Academiejaar 014-015 1ste semester 7 januari 015 Aanvullingen van de Wiskunde 1. Gegeven is een lineaire partiële differentiaalvergelijking van orde 1: a 1 (x 1,,
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.9, maandag K. P. Hart Faculteit EWI TU Delft Delft, 13 juni, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 41 Outline III.6 The Residue Theorem 1 III.6 The
TW2040: Complexe Functietheorie week 4.9, maandag K. P. Hart Faculteit EWI TU Delft Delft, 13 juni, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 41 Outline III.6 The Residue Theorem 1 III.6 The
Tussentoets Analyse 2. Natuur- en sterrenkunde.
 Tussentoets Analyse 2. Natuur- en sterrenkunde. Dinsdag 9 maart 2010, 9.00-11.00. Het gebruik van een rekenmachine is toegestaan. Motiveer elk antwoord dat je geeft d.m.v. een berekening of redenering.
Tussentoets Analyse 2. Natuur- en sterrenkunde. Dinsdag 9 maart 2010, 9.00-11.00. Het gebruik van een rekenmachine is toegestaan. Motiveer elk antwoord dat je geeft d.m.v. een berekening of redenering.
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica
 TECHNICHE UNIVERITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Functies van meer variabelen, deel B (YE6) op vrijdag juli 5, 9..3 uur. De uitwerkingen van de opgaven dienen duidelijk geformuleerd
TECHNICHE UNIVERITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Functies van meer variabelen, deel B (YE6) op vrijdag juli 5, 9..3 uur. De uitwerkingen van de opgaven dienen duidelijk geformuleerd
Mathematical Modelling
 1 / 104 Mathematical Modelling Ruud van Damme Creation date: 27-09-09 2 / 104 Waarschuwing vooraf Weer plaatjes dus opgelet! En: x F F x want anders worden de formules te lang... En: ik hoop dat ik consistent
1 / 104 Mathematical Modelling Ruud van Damme Creation date: 27-09-09 2 / 104 Waarschuwing vooraf Weer plaatjes dus opgelet! En: x F F x want anders worden de formules te lang... En: ik hoop dat ik consistent
1. Langere vraag over de theorie
 1. Langere vraag over de theorie a) Bereken, vertrekkend van de definitie van capaciteit, de capaciteit van een condensator die bestaat uit twee evenwijdige vlakke platen waarbij de afstand tussen de platen
1. Langere vraag over de theorie a) Bereken, vertrekkend van de definitie van capaciteit, de capaciteit van een condensator die bestaat uit twee evenwijdige vlakke platen waarbij de afstand tussen de platen
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Uitwerking Tentamen Calculus, 2DM10, maandag 22 januari 2007
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking Tentamen Calculus, DM, maandag januari 7. (a) Gevraagd is het polynoom f() + f () (x ) + f (x ). Een eenvoudige rekenpartij
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking Tentamen Calculus, DM, maandag januari 7. (a) Gevraagd is het polynoom f() + f () (x ) + f (x ). Een eenvoudige rekenpartij
De Riemannintegraal. Dan heet f(ξ ij, η ij ) A ij een Riemannsom bij f. May 9, I.A.M. Goddijn Faculteit EWI
 e Riemannintegraal Veronderstel dat f : R continu is, waarbij = [a, b] [c, d]. Laten a = x 0 < x 1 < x 2 < < x m 1 < x m = b en c = y 0 < y 1 < y 2 < < y n 1 < y n = d partities zijn van [a, b] en [c,
e Riemannintegraal Veronderstel dat f : R continu is, waarbij = [a, b] [c, d]. Laten a = x 0 < x 1 < x 2 < < x m 1 < x m = b en c = y 0 < y 1 < y 2 < < y n 1 < y n = d partities zijn van [a, b] en [c,
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.3, maandag K. P. Hart Faculteit EWI TU Delft Delft, 2 mei, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 34 Outline 1 Conforme afbeeldingen 2 K. P. Hart TW2040:
TW2040: Complexe Functietheorie week 4.3, maandag K. P. Hart Faculteit EWI TU Delft Delft, 2 mei, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 34 Outline 1 Conforme afbeeldingen 2 K. P. Hart TW2040:
Je mag Zorich deel I en II gebruiken, maar geen ander hulpmiddelen (zoals andere boeken, aantekeningen, rekenmachine etc.)!
 Tentamen Analyse II. Najaar 6 (.1.7) Toelicting: Je mag Zoric deel I en II gebruiken, maar geen ander ulpmiddelen (zoals andere boeken, aantekeningen, rekenmacine etc.)! Als je bekende stellingen gebruikt
Tentamen Analyse II. Najaar 6 (.1.7) Toelicting: Je mag Zoric deel I en II gebruiken, maar geen ander ulpmiddelen (zoals andere boeken, aantekeningen, rekenmacine etc.)! Als je bekende stellingen gebruikt
Ruimtewiskunde. college. Het inwendig- en het uitwendig product. Vandaag. Hoeken Orthogonaliteit en projecties. Toepassing: magnetische velden
 college 2 - en het uitwendig collegejaar college build slides Vandaag : : : : 6-7 2 30 mei 207 30 2 3 4 5 Hoeken Orthogonaliteit en projecties Toepassing: magnetische velden.6-7[2] vandaag meetkundig Section
college 2 - en het uitwendig collegejaar college build slides Vandaag : : : : 6-7 2 30 mei 207 30 2 3 4 5 Hoeken Orthogonaliteit en projecties Toepassing: magnetische velden.6-7[2] vandaag meetkundig Section
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 2013,
 Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.10, donderdag K. P. Hart Faculteit EWI TU Delft Delft, 23 juni, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 46 Outline 1 2 3 K. P. Hart TW2040: Complexe Functietheorie
TW2040: Complexe Functietheorie week 4.10, donderdag K. P. Hart Faculteit EWI TU Delft Delft, 23 juni, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 46 Outline 1 2 3 K. P. Hart TW2040: Complexe Functietheorie
dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π
![dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π](/thumbs/59/43623915.jpg) Analyse. (i) Bereken A = π sin d; +cos 2 (ii) * Bewijs dat voor elke f, continu ondersteld in [, a]: a f()d = a f(a )d (iii) Gebruik (i) en (ii) om de integraal J = π sin d te berekenen.(oef +cos 2 cursus)
Analyse. (i) Bereken A = π sin d; +cos 2 (ii) * Bewijs dat voor elke f, continu ondersteld in [, a]: a f()d = a f(a )d (iii) Gebruik (i) en (ii) om de integraal J = π sin d te berekenen.(oef +cos 2 cursus)
Huiswerk Hints&Tips Analyse 2, College 26
 Huiswerk Hints&Tips Analyse, College 6 [K..]. Tip : Toon aan dat er punten (x, y ) en (x, y ) en scalars m, M R bestaan zo dat m = f(x, y ) f(x, y) f(x, y ) = M. Laat dan zien dat m(b a)(d c) = m f M =
Huiswerk Hints&Tips Analyse, College 6 [K..]. Tip : Toon aan dat er punten (x, y ) en (x, y ) en scalars m, M R bestaan zo dat m = f(x, y ) f(x, y) f(x, y ) = M. Laat dan zien dat m(b a)(d c) = m f M =
Aanvullingen van de Wiskunde / Partiële Differentiaalvergelijkingen
 de Bachelor EIT 2de en de Bachelor Wiskunde Academiejaar 215-216 1ste semester 26 januari 216 Aanvullingen van de Wiskunde / Partiële Differentiaalvergelijkingen 1. Gegeven een homogene lineaire partiële
de Bachelor EIT 2de en de Bachelor Wiskunde Academiejaar 215-216 1ste semester 26 januari 216 Aanvullingen van de Wiskunde / Partiële Differentiaalvergelijkingen 1. Gegeven een homogene lineaire partiële
Tentamen WISN102 Wiskundige Technieken 2 Do 1 feb :00 12:00
 Normering Tentamen WISN02 Wiskundige Technieken 2 Do feb 207 9:00 2:00 voor 4 pt vragen (andere vragen naar rato): 4pt Goed begrepen en goed uitgevoerd met voldoende toelichting, eventueel enkele onbelangrijke
Normering Tentamen WISN02 Wiskundige Technieken 2 Do feb 207 9:00 2:00 voor 4 pt vragen (andere vragen naar rato): 4pt Goed begrepen en goed uitgevoerd met voldoende toelichting, eventueel enkele onbelangrijke
2 Kromming van een geparametriseerde kromme in het vlak. Veronderstel dat een kromme in het vlak gegeven is door een parametervoorstelling
 TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
Analyse I. 3. Formuleer en bewijs de formule van Taylor voor een functie f : R R. Stel de formules op voor de resttermen van Lagrange en Liouville.
 ste Bachelor Ingenieurswetenschappen Academiejaar 8-9 ste semester januari 9 Analyse I. Formuleer en bewijs de formule van Leibniz voor de n-de afgeleide van het product van twee functies f en g.. Onderstel
ste Bachelor Ingenieurswetenschappen Academiejaar 8-9 ste semester januari 9 Analyse I. Formuleer en bewijs de formule van Leibniz voor de n-de afgeleide van het product van twee functies f en g.. Onderstel
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Technische Natuurkunde Examen Elektromagnetisme 3 (3NC30) donderdag 5 juli 2012 van 14u00-17u00
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Technische Natuurkunde Examen Elektromagnetisme 3 (3NC30) donderdag 5 juli 202 van 4u00-7u00 Dit tentamen bestaat uit 5 opgaven met elk 3 onderdelen. Voor elk
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Technische Natuurkunde Examen Elektromagnetisme 3 (3NC30) donderdag 5 juli 202 van 4u00-7u00 Dit tentamen bestaat uit 5 opgaven met elk 3 onderdelen. Voor elk
Hoofdstuk 22 De Wet van Gauss
 Hoofdstuk 22 De Wet van Gauss Electrische Flux De Wet van Gauss Toepassingen van de Wet van Gauss Experimentele Basis van de Wetten van Gauss en Coulomb 22-1 Electrische Flux Electrische flux: Electrische
Hoofdstuk 22 De Wet van Gauss Electrische Flux De Wet van Gauss Toepassingen van de Wet van Gauss Experimentele Basis van de Wetten van Gauss en Coulomb 22-1 Electrische Flux Electrische flux: Electrische
Ruimtewiskunde. college 3 Lijnen, vlakken en oppervlakken in de ruimte. Vandaag
 college 3 Lijnen, vlakken en in de collegejaar : 16-17 college : 3 build : 6 juni 2017 slides : 37 Vandaag 1 Lijnen 2 Vlakken 3 4 Toepassing: perspectivische.16-17[3] 1 vandaag Lijnen in het platte vlak
college 3 Lijnen, vlakken en in de collegejaar : 16-17 college : 3 build : 6 juni 2017 slides : 37 Vandaag 1 Lijnen 2 Vlakken 3 4 Toepassing: perspectivische.16-17[3] 1 vandaag Lijnen in het platte vlak
Analyse I. 1. Toon aan dat een niet-dalende begrensde rij convergent is.
 ste Bacelor Ingenieurswetenscappen/ Wiskunde/Natuurkunde Academiejaar - ste semester, 7 januari Analyse I. Toon aan dat een niet-dalende begrensde rij convergent is.. Bescouw twee numerieke functies f
ste Bacelor Ingenieurswetenscappen/ Wiskunde/Natuurkunde Academiejaar - ste semester, 7 januari Analyse I. Toon aan dat een niet-dalende begrensde rij convergent is.. Bescouw twee numerieke functies f
Analyse I. 1ste Bachelor Ingenieurswetenschappen Academiejaar ste semester 12 januari 2010
 ste Bachelor Ingenieurswetenschappen Academiejaar 9- ste semester januari Analyse I. Formuleer en bewijs de formule van Leibniz voor de n-de afgeleide van het product van twee functies f en g.. Onderstel
ste Bachelor Ingenieurswetenschappen Academiejaar 9- ste semester januari Analyse I. Formuleer en bewijs de formule van Leibniz voor de n-de afgeleide van het product van twee functies f en g.. Onderstel
Eerste orde partiële differentiaalvergelijkingen
 Eerste orde partiële differentiaalvergelijkingen Vakgroep Differentiaalvergelijkingen 1995, 2001, 2002 1 Eerste orde golf-vergelijking De vergelijking au x + u t = 0, u = u(x, t), a ɛ IR (1.1) beschrijft
Eerste orde partiële differentiaalvergelijkingen Vakgroep Differentiaalvergelijkingen 1995, 2001, 2002 1 Eerste orde golf-vergelijking De vergelijking au x + u t = 0, u = u(x, t), a ɛ IR (1.1) beschrijft
Tentamen Functies en Reeksen
 Tentamen Functies en Reeksen 6 november 204, 3:30 6:30 uur Schrijf op ieder vel je naam en bovendien op het eerste vel je studentnummer, de naam van je practicumleider (Arjen Baarsma, KaYin Leung, Roy
Tentamen Functies en Reeksen 6 november 204, 3:30 6:30 uur Schrijf op ieder vel je naam en bovendien op het eerste vel je studentnummer, de naam van je practicumleider (Arjen Baarsma, KaYin Leung, Roy
Deeltoets II E&M & juni 2016 Velden en elektromagnetisme
 E&M Boller, Offerhaus, Dhallé Deeltoets II E&M 201300164 & 201300183 13 juni 2016 Velden en elektromagnetisme Aanwijzingen Voor de toets zijn 2 uren beschikbaar. Vul op alle ingeleverde vellen uw naam
E&M Boller, Offerhaus, Dhallé Deeltoets II E&M 201300164 & 201300183 13 juni 2016 Velden en elektromagnetisme Aanwijzingen Voor de toets zijn 2 uren beschikbaar. Vul op alle ingeleverde vellen uw naam
Voortgezette Analyse. H.A.W.M. Kneppers. april 2017
 Voortgezette Analyse H.A.W.M. Kneppers april 07 iteratuur [A] Robert A. Adams, Calculus, 8th edition, Addison-Wesley 00. [B] William E. Boyce & Richard C. DiPrima, Elementary Differential Equations and
Voortgezette Analyse H.A.W.M. Kneppers april 07 iteratuur [A] Robert A. Adams, Calculus, 8th edition, Addison-Wesley 00. [B] William E. Boyce & Richard C. DiPrima, Elementary Differential Equations and
Opgave a. We berekenen eerst een normaal v van V en een normaal w van W. v = (b a) (c a) = ((2)(1) ( 2)( 2), ( 2)( 1) ( 1)(1), ( 1)( 2) (2)( 1))
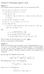 Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
Tussentijdse evaluatie Analyse I
 1ste Bachelor Wiskunde Academiejaar 1-1 1ste semester, november 1 Tussentijdse evaluatie Analyse I 1. Onderstel dat f : [a, b] R een continue functie is. (i) Bewijs dat er een x 1 en x in [a, b] bestaan
1ste Bachelor Wiskunde Academiejaar 1-1 1ste semester, november 1 Tussentijdse evaluatie Analyse I 1. Onderstel dat f : [a, b] R een continue functie is. (i) Bewijs dat er een x 1 en x in [a, b] bestaan
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica
 TECHNICHE UNIVERITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Functies van meer variabelen, deel A (2XE6) op maandag 2 mei 25, 9..3 uur. De uitwerkingen van de opgaven dienen duidelijk geformuleerd
TECHNICHE UNIVERITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Functies van meer variabelen, deel A (2XE6) op maandag 2 mei 25, 9..3 uur. De uitwerkingen van de opgaven dienen duidelijk geformuleerd
2015-2016 Laatste nieuws 2DN60 Lineaire algebra en vectorcalculus
 2015-2016 Laatste nieuws 2DN60 Lineaire algebra en vectorcalculus Kwartiel 2, week 7.b Op het college op donderdagochtend 7 januari is behandeld: - hoek tussen vectoren en cosinus regel - driehoeksongelijkheid
2015-2016 Laatste nieuws 2DN60 Lineaire algebra en vectorcalculus Kwartiel 2, week 7.b Op het college op donderdagochtend 7 januari is behandeld: - hoek tussen vectoren en cosinus regel - driehoeksongelijkheid
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Technische Natuurkunde Examen Elektromagnetisme 3 (3NC30) donderdag 30 juni 2011 van 14u00-17u00
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Technische Natuurkunde Examen Elektromagnetisme 3 (3NC30) donderdag 30 juni 20 van 4u00-7u00 Dit tentamen bestaat uit 5 opgaven met elk 3 onderdelen. Voor elk
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Technische Natuurkunde Examen Elektromagnetisme 3 (3NC30) donderdag 30 juni 20 van 4u00-7u00 Dit tentamen bestaat uit 5 opgaven met elk 3 onderdelen. Voor elk
5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm
 5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm x y + xy + (x ν )y = met ν R (1) heet een Bessel (differentiaal)vergelijking. De waarde van ν noemt men ook wel de orde
5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm x y + xy + (x ν )y = met ν R (1) heet een Bessel (differentiaal)vergelijking. De waarde van ν noemt men ook wel de orde
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
Relevante examenvragen , eerste examenperiode
 Relevante examenvragen 2007 2008, eerste examenperiode WAAR/VALS Zijn de volgende uitspraken waar of vals? Geef een korte argumentatie (bewijs) of een tegenvoorbeeld, eventueel aangevuld met een figuur.
Relevante examenvragen 2007 2008, eerste examenperiode WAAR/VALS Zijn de volgende uitspraken waar of vals? Geef een korte argumentatie (bewijs) of een tegenvoorbeeld, eventueel aangevuld met een figuur.
TENTAMEN ELEKTROMAGNETISME (3D020)
 TENTAMEN ELEKTROMAGNETIME (3D020) 21 juni 1999, 14.00 17.00 uur UITWERKING 1 Op de geleider bevindt zich een totale lading. De lengte van de geleider (een halve cirkel) is gelijk aan πr. y d ϕ R P x Voor
TENTAMEN ELEKTROMAGNETIME (3D020) 21 juni 1999, 14.00 17.00 uur UITWERKING 1 Op de geleider bevindt zich een totale lading. De lengte van de geleider (een halve cirkel) is gelijk aan πr. y d ϕ R P x Voor
2E HUISWERKOPDRACHT CONTINUE WISKUNDE 2
 2E HUISWERKOPDRACHT CONTINUE WISKUNDE 2 Inleverdatum 30 maart 207, uiterlijk :5 uur Je moet de hele uitwerking opschrijven en niet alleen het antwoord geven. Je mag de theorie gebruiken die op het college
2E HUISWERKOPDRACHT CONTINUE WISKUNDE 2 Inleverdatum 30 maart 207, uiterlijk :5 uur Je moet de hele uitwerking opschrijven en niet alleen het antwoord geven. Je mag de theorie gebruiken die op het college
Vectormeetkunde in R 3
 Vectormeetkunde in R Definitie. Een punt in R wordt gegeven door middel van drie coördinaten : P = (x, y, z). Een lijnstuk tussen twee punten P en Q voorzien van een richting noemen we een pijltje. Notatie
Vectormeetkunde in R Definitie. Een punt in R wordt gegeven door middel van drie coördinaten : P = (x, y, z). Een lijnstuk tussen twee punten P en Q voorzien van een richting noemen we een pijltje. Notatie
Tussentijdse evaluatie Analyse I
 ste Bachelor Wiskunde Academiejaar 4- ste semester 3 oktober 4 Tussentijdse evaluatie Analyse I. Toon aan dat een niet-stijgende begrensde rij convergent is.. Geef de definitie van een verdichtingspunt.
ste Bachelor Wiskunde Academiejaar 4- ste semester 3 oktober 4 Tussentijdse evaluatie Analyse I. Toon aan dat een niet-stijgende begrensde rij convergent is.. Geef de definitie van een verdichtingspunt.
Hoofdstuk 23 Electrische Potentiaal. Copyright 2009 Pearson Education, Inc.
 Hoofdstuk 23 Electrische Potentiaal Elektrische flux Een cilinder van een niet-geleidend materiaal wordt in een elektrisch veld gezet als geschetst. De totale elektrische flux door het oppervlak van de
Hoofdstuk 23 Electrische Potentiaal Elektrische flux Een cilinder van een niet-geleidend materiaal wordt in een elektrisch veld gezet als geschetst. De totale elektrische flux door het oppervlak van de
Examen G0O17D Wiskunde II (6sp) maandag 10 juni 2013, 8:30-12:30 uur
 Examen GO7D Wiskunde II (6sp maandag juni 3, 8:3-:3 uur Bachelor Biochemie & Biotechnologie Bachelor hemie, Bachelor Geologie Schakelprogramma Master Biochemie & Biotechnologie en Schakelprogramma Master
Examen GO7D Wiskunde II (6sp maandag juni 3, 8:3-:3 uur Bachelor Biochemie & Biotechnologie Bachelor hemie, Bachelor Geologie Schakelprogramma Master Biochemie & Biotechnologie en Schakelprogramma Master
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.6, maandag K. P. Hart Faculteit EWI TU Delft Delft, 30 mei, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 33 Outline 1 2 Algemeenheden Gedrag op de rand Machtreeksen
TW2040: Complexe Functietheorie week 4.6, maandag K. P. Hart Faculteit EWI TU Delft Delft, 30 mei, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 33 Outline 1 2 Algemeenheden Gedrag op de rand Machtreeksen
Modulen voor Calculus- en Analysevakken
 Modulen voor Calculus- en Analysevakken Versie juni 2005 Deze indeling in modulen is zoveel mogelijk onafhankelijk van enig leerboek. Echter, om de invulling ervan concreet te maken is er aangegeven waar
Modulen voor Calculus- en Analysevakken Versie juni 2005 Deze indeling in modulen is zoveel mogelijk onafhankelijk van enig leerboek. Echter, om de invulling ervan concreet te maken is er aangegeven waar
Ruimtewiskunde. college. De determinant en lineaire afbeeldingen. Vandaag. De determinant van een matrix. Toepassing: oppervlakte en inhoud
 college 6 en lineaire collegejaar college build slides Vandaag : : : : 6-7 6 9 juni 27 3 2 3 van een matrix Toepassing: oppervlakte en inhoud.6-7[6] vandaag van de 2 2-matrix a b c d is gelijk aan ad bc.
college 6 en lineaire collegejaar college build slides Vandaag : : : : 6-7 6 9 juni 27 3 2 3 van een matrix Toepassing: oppervlakte en inhoud.6-7[6] vandaag van de 2 2-matrix a b c d is gelijk aan ad bc.
7 College 01/12: Electrische velden, Wet van Gauss
 7 College 01/12: Electrische velden, Wet van Gauss Berekening van electrische flux Alleen de component van het veld loodrecht op het oppervlak draagt bij aan de netto flux. We definieren de electrische
7 College 01/12: Electrische velden, Wet van Gauss Berekening van electrische flux Alleen de component van het veld loodrecht op het oppervlak draagt bij aan de netto flux. We definieren de electrische
x a k of.x 1 a 1 / 2 + ::+.x n a n / 2 k 2 bol om a, straal k
 Punten, Vectoren in de R n Punten: a =.a 1 ; a 2 ; : : : ; a n / ; b =.b 1 ; b 2 ; : : : ; b n / Vectoren: a = a 1 ; a 2 ; : : : ; a n ; b = b 1 ; b 2 ; : : : ; b n lengte van a : a = a 2 1 + : : : + a2
Punten, Vectoren in de R n Punten: a =.a 1 ; a 2 ; : : : ; a n / ; b =.b 1 ; b 2 ; : : : ; b n / Vectoren: a = a 1 ; a 2 ; : : : ; a n ; b = b 1 ; b 2 ; : : : ; b n lengte van a : a = a 2 1 + : : : + a2
Examen Complexe Analyse (September 2008)
 Examen Complexe Analyse (September 2008) De examenvragen vind je op het einde van dit documentje. Omdat het hier over weinig studenten gaat, heb ik geen puntenverdeling meegegeven. Vraag. Je had eerst
Examen Complexe Analyse (September 2008) De examenvragen vind je op het einde van dit documentje. Omdat het hier over weinig studenten gaat, heb ik geen puntenverdeling meegegeven. Vraag. Je had eerst
Technische Universiteit Delft Tentamen Calculus TI1106M - Uitwerkingen. 2. Geef berekeningen en beargumenteer je antwoorden.
 Technische Universiteit elft Tentamen Calculus TI06M - Uitwerkingen Opmerkingen:. Het gebruik van de rekenmachine is NIET toegestaan.. Geef berekeningen en beargumenteer je antwoorden. 3. Bij iedere vraag
Technische Universiteit elft Tentamen Calculus TI06M - Uitwerkingen Opmerkingen:. Het gebruik van de rekenmachine is NIET toegestaan.. Geef berekeningen en beargumenteer je antwoorden. 3. Bij iedere vraag
Oefenzitting 2: Parametrisaties.
 Oefenzitting : Parametrisaties. Modeloplossingen Oefening.5:. Beschouw vooreerst de cirkel C in het xz-vlak met straal r en middelpunt (x, y, z) = (R,, ) (zie Figuur ). De parametrisatie van C wordt dan
Oefenzitting : Parametrisaties. Modeloplossingen Oefening.5:. Beschouw vooreerst de cirkel C in het xz-vlak met straal r en middelpunt (x, y, z) = (R,, ) (zie Figuur ). De parametrisatie van C wordt dan
Overzicht Fourier-theorie
 B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
Integratie voor meerdere variabelen
 Wiskunde 2 voor kunstmatige intelligentie, 27/28 Les 4 Integratie voor meerdere variabelen In deze les bekijken we het omgekeerde van de afgeleide, de integratie, en gaan na hoe we een integraal voor functies
Wiskunde 2 voor kunstmatige intelligentie, 27/28 Les 4 Integratie voor meerdere variabelen In deze les bekijken we het omgekeerde van de afgeleide, de integratie, en gaan na hoe we een integraal voor functies
1. (a) Gegeven z = 2 2i, w = 1 i 3. Bereken z w. (b) Bepaal alle complexe getallen z die voldoen aan z 3 8i = 0.
 Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
 2004 Gemeenschappelijke proef Algebra - Analyse - Meetkunde - Driehoeksmeting 14 vragen - 2:30 uur Reeks 1 Notatie: tan x is de tangens van de hoek x, cot x is de cotangens van de hoek x Vraag 1 In een
2004 Gemeenschappelijke proef Algebra - Analyse - Meetkunde - Driehoeksmeting 14 vragen - 2:30 uur Reeks 1 Notatie: tan x is de tangens van de hoek x, cot x is de cotangens van de hoek x Vraag 1 In een
Uitwerkingen toets emv
 Uitwerkingen toets emv 24 april 2012 1 (a) Bij aanwezigheid van een statische ladingsverdeling ρ(r) wordt het elektrische veld bepaald door E = 1 ρ(r ) 4π r 2 ˆrˆrˆr dτ, V waarin V het volume van de ladingsverdeling,
Uitwerkingen toets emv 24 april 2012 1 (a) Bij aanwezigheid van een statische ladingsverdeling ρ(r) wordt het elektrische veld bepaald door E = 1 ρ(r ) 4π r 2 ˆrˆrˆr dτ, V waarin V het volume van de ladingsverdeling,
34 HOOFDSTUK 1. EERSTE ORDE DIFFERENTIAALVERGELIJKINGEN
 34 HOOFDSTUK 1. EERSTE ORDE DIFFERENTIAALVERGELIJKINGEN 1.11 Vraagstukken Vraagstuk 1.11.1 Beschouw het beginwaardeprobleem = 2x (y 1), y(0) = y 0. Los dit beginwaardeprobleem op voor y 0 R en maak een
34 HOOFDSTUK 1. EERSTE ORDE DIFFERENTIAALVERGELIJKINGEN 1.11 Vraagstukken Vraagstuk 1.11.1 Beschouw het beginwaardeprobleem = 2x (y 1), y(0) = y 0. Los dit beginwaardeprobleem op voor y 0 R en maak een
== Uitwerkingen Tentamen Analyse 1, WI1600 == Maandag 10 januari 2011, u
 == en Tentamen Analyse, WI6 == Maandag januari, 4.-7.u Technische Universiteit Delft, Faculteit EWI. Gegeven is de functie + e + e arctan,, f = +, >. a Beargumenteer dat f continu is op R. b Bepaal de
== en Tentamen Analyse, WI6 == Maandag januari, 4.-7.u Technische Universiteit Delft, Faculteit EWI. Gegeven is de functie + e + e arctan,, f = +, >. a Beargumenteer dat f continu is op R. b Bepaal de
Wat kan er (niet) zonder ε-δ?
 Oneindig klein. Wat kan er (niet) zonder ε-δ? Michel Roelens University Colleges Leuven Limburg Maria-Boodschaplyceum Brussel Hilde Eggermont Sint-Pieterscollege Leuven Redactie Uitwiskeling Afgeleide
Oneindig klein. Wat kan er (niet) zonder ε-δ? Michel Roelens University Colleges Leuven Limburg Maria-Boodschaplyceum Brussel Hilde Eggermont Sint-Pieterscollege Leuven Redactie Uitwiskeling Afgeleide
Analyse I. f(x)dx + f(x)dx =
 1ste Bachelor Ingenieurswetenschappen/ Wiskunde/Natuurkunde Academiejaar 1-11 1ste semester, 18 januari 11 Analyse I 1. f en g zijn numerieke functies, f is differentieerbaar in a en g is differentieerbaar
1ste Bachelor Ingenieurswetenschappen/ Wiskunde/Natuurkunde Academiejaar 1-11 1ste semester, 18 januari 11 Analyse I 1. f en g zijn numerieke functies, f is differentieerbaar in a en g is differentieerbaar
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
1 ELECTROSTATICA: Recht toe, recht aan
 1 ELECTROSTATICA: Recht toe, recht aan We beschouwen eerst een oneindig lange lijnlading met uniforme ladingsdichtheid λ, langs de z-as van ons coördinatenstelsel. 1a Gebruik de wet van Gauss en beredeneer
1 ELECTROSTATICA: Recht toe, recht aan We beschouwen eerst een oneindig lange lijnlading met uniforme ladingsdichtheid λ, langs de z-as van ons coördinatenstelsel. 1a Gebruik de wet van Gauss en beredeneer
Krommen in de ruimte
 Krommen in de ruimte z Een ruimtekromme is de baan van een tijd-plaatsfunctie van een bewegend deeltje in de ruimte Na keuze van een rechthoekig assenstelsel Oxyz wordt die functie f gegeven door zijn
Krommen in de ruimte z Een ruimtekromme is de baan van een tijd-plaatsfunctie van een bewegend deeltje in de ruimte Na keuze van een rechthoekig assenstelsel Oxyz wordt die functie f gegeven door zijn
TENTAMEN ELEKTROMAGNETISME (8N010)
 TENTAMEN ELEKTROMAGNETISME (8N010) Opmerkingen: 1. Dit tentamen bestaat uit 4 vragen met in totaal 19 deelvragen. Elke deelvraag levert 3 punten op.. Het is toegestaan gebruik te maken van bijgeleverd
TENTAMEN ELEKTROMAGNETISME (8N010) Opmerkingen: 1. Dit tentamen bestaat uit 4 vragen met in totaal 19 deelvragen. Elke deelvraag levert 3 punten op.. Het is toegestaan gebruik te maken van bijgeleverd
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Technische Natuurkunde Examen Elektromagnetisme 3 (3NC30) donderdag 14 april 2011 van 9u00-12u00
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Technische Natuurkunde Examen Elektromagnetisme 3 (3NC30) donderdag 4 april 20 van 9u00-2u00 Dit tentamen bestaat uit 5 opgaven met elk 3 onderdelen. Voor elk
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Technische Natuurkunde Examen Elektromagnetisme 3 (3NC30) donderdag 4 april 20 van 9u00-2u00 Dit tentamen bestaat uit 5 opgaven met elk 3 onderdelen. Voor elk
Tussentijdse evaluatie Analyse I
 ste Bachelor Wiskunde Academiejaar 5-6 ste semester 9 oktober 5 Tussentijdse evaluatie Analyse I. Geef de definitie van een Cauchy rij. Toon aan dat elke Cauchy rij begrensd is. Toon aan dat een numerieke
ste Bachelor Wiskunde Academiejaar 5-6 ste semester 9 oktober 5 Tussentijdse evaluatie Analyse I. Geef de definitie van een Cauchy rij. Toon aan dat elke Cauchy rij begrensd is. Toon aan dat een numerieke
CALCULUS 2. najaar Wieb Bosma (naar aantekeningen van Arno van den Essen) Radboud Universiteit Nijmegen
 0 CALCULUS 2 najaar 2008 Wieb Bosma (naar aantekeningen van Arno van den Essen) Radboud Universiteit Nijmegen college 1: integratie Centrale vraag: hoe bereken je de bepaalde integraal Algemeen idee: b
0 CALCULUS 2 najaar 2008 Wieb Bosma (naar aantekeningen van Arno van den Essen) Radboud Universiteit Nijmegen college 1: integratie Centrale vraag: hoe bereken je de bepaalde integraal Algemeen idee: b
1 WGAM: overzicht definities, eigenschappen en stellingen. (Nuttig voor de WPO s)
 1 WGAM: overzicht definities, eigenschappen en stellingen. (Nuttig voor de WPO s) 1.1 Hoofdstuk 1: eeksen efinitie 1.1.1. Gegeven een rij (a n ) van reële getallen, dan noemen we een uitdrukking van de
1 WGAM: overzicht definities, eigenschappen en stellingen. (Nuttig voor de WPO s) 1.1 Hoofdstuk 1: eeksen efinitie 1.1.1. Gegeven een rij (a n ) van reële getallen, dan noemen we een uitdrukking van de
Opgaven Inleiding Analyse
 Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van iet dat y 0 y = 0. (b) Bewijs y 0 y 3 = 0 uit de definitie van iet. (c) Bewijs y 0 y 3
Opgaven Inleiding Analyse E.P. van den Ban Limieten en continuïteit Opgave. (a) Bewijs direct uit de definitie van iet dat y 0 y = 0. (b) Bewijs y 0 y 3 = 0 uit de definitie van iet. (c) Bewijs y 0 y 3
Uitwerking tentamen Analyse B
 Uitwerking tentamen Analyse B 30 juni 20, 7:00 20:00 uur De hieronder gegeven uitwerkingen moeten worden opgevat als voorbeelden van correcte oplossingen. In veel gevallen zijn andere correcte oplossingen
Uitwerking tentamen Analyse B 30 juni 20, 7:00 20:00 uur De hieronder gegeven uitwerkingen moeten worden opgevat als voorbeelden van correcte oplossingen. In veel gevallen zijn andere correcte oplossingen
