Prof. Pr, Ir. J.D. Pr. W.A.M. Brefnelrnana Dr. Is. F.P.T. Baaijens
|
|
|
- Stefan Janssen
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Afstudeerverslag Tatel : Doos : The-mo-vPs@g$lastisehe analyse voor een spuitgiet product J.P.H. verest juni, 1987 Prof. Pr, Ir. J.D. ~. Yanssen Pr. W.A.M. Brefnelrnana Dr. Is. F.P.T. Baaijens Rappmtnummer BFW
2 Inhoudsopsave Voorwoord O Samenvatting. 1 Inleiding Isotherm viscoelastisch materiaalgedrag bij verschillende waarden van de temperatuur. 2. I 2.1 Inleiding u Amorfe polymeren De typisch viscoëlastische fase : Tg < T < Tr Be rubberfase : T, < T < T, De glasfase : T < Tg Consistentie De invloed van de tijdafhankelijkheid der temperatuur op het materiaalgedrag Inleiding De I-dimensionale constitutieve vergelijking met : Tg < T(t) < Tr De 1-dimensionale constitutieve vergelijking met : T(t) < Tg De 3-dimensionale constitutieve vergelijking met : 3.5 T(t) < T. 3.9 Het bepa 4 en van de materiaaleigenschappen uit experimenten. 3.1Q 4 Het bepalen van de materiaaleigenschappen voor de 3-dimensionale formulering. 4.1 Inleiding. 4.2 De trekproef bij de referentietemperatuur To. 4.3 Een benadering voor C(t) bij de referentietemperatuur To. 4.4 Een numeriek voorbeeld. 4.5 De benadering van de glijdingsmodulus bij een temperatuur. 4.6 De experimenten. andere De simulatie van het experiment Inleiding Het experiment. di üe werkwijze van de rekenprocedure (VAX MARC KI) De instationaire energievergelijking Spanningen en vervormingen. 5.4
3 5.6 Confrontatie met het experiment. 6 Conclusies en aanbevelingen S. 1 Literatuur Bij lagen 1 Het niet lineaire l-dimensionale model van Schapery voor de relaxatie formulering. 2 De l-dimensionale spanningstoestand. 3 Een benadering voor G(t). 4 De experimenten. 5 Voorbeeld van een temperatuur en spanningsberekening. 6 Oplossing instationaire energievergelijking. 7 l-dimensionale viscoelastische berekeningen met MARC. 8 Berekeningen van de spanningen en vervormingen. I
4 Voorwoord Dit is het verslag van mijn afstudeerwerk verricht binnen de vakgroep WFW. Op deze plaats wil ik Marcel Brekelmans en Frank Baaijens bedanken voor de plezierige en uitstekende begeleiding. Leon Govaert bedank ik voor het uitvoeren van de metingen die noodzakelijk waren voor dit afstudeerwerk. Juni 1987, Han Verest
5 -0- Samenvattincr. Dit verslag handelt over de numerieke simulatie van een experiment met behulp van het eindige-elementenmethoden programma MARC. Een rotatie symmetrisch busje zit in een mal opgesloten bij een bepaalde hoge temperatuur. De mal met het busje wordt vervolgens onder gedefinieerde omstandigheden afgekoeld waarna het busje uit de mal wordt genomen. Getracht wordt de spanningen en vervormingen, van het busje, te berekenen die optreden tijdens de afkoeling en na het uitnemen. Hiervoor moet een instationaire energie vergelijking worden opgelost en er moet gerekend worden met thermo-viscoelastisch materiaalgedrag. De energievergelijking kan apart worden opgelost omdat de vervormingen en verplaatsingen klein zijn. Voor Bet beschrijven van het ;;lechanisch gedrag wordt Uitgegaan vari de 3-dimensionale isotrope lineair viscoelastische vergelijking volgens de relaxatie formulering bij een bepaalde referentietemperatuur. Om de invloed van de temperatuur in rekening te brengen wordt de 1-dimensionale constitutieve vergelijking gebruikt om een en ander toe te lichten. De gewenste 3-dimensionale formulering is een generalisatie van de 1-dimensionale formulering. Van de relaxatiefuncties wordt verondersteld dat deze uit een constant deel en een som van e-machten, tijdsafhankelijk deel, bestaan. Bij de 3-di ensiomalle ~ zijn de r ~~~~d~~~~~~~~~~~ ~ en ~ de ~ kompressiemodulus van belang. Van de kompressiemodulus wordt aangenomen dat deze niet tijdsafhankelijk is en uit het P-V-T diagram kan worden bepaald. De trekproef wordt gekozen om de glijdingsmodulus te bepalen. Omdat de kompressiemodulus bekend is kan uit de trekproef in principe de glijdingsmodulus worden berekend. Omdat dit zeer veel rekenwerk vergt wordt gebruik gemaakt van een benadering van de glijdingsmodulus. Uit 1-dimensionale testproblemen met MARC blijkt dat NARC niet de gewenste vergelijking oplost. Indien de materiaaleigenschappen van een bepaalde vorm zijn blijkt een juiste oplossing wel mogelijk. Voor de 3-dimensionale vergelijking wordt aangenomen dat hiervoor hetzelfde geldt. De materiaaleigenschappen worden in de gewenste vorm geschreven waarna de spanningen en vervormingen voor twee situaties worden berekend. In het eerste geval treden geen blijvende vervormingen op nadat het product uit de mal is genomen. Bij de tweede berekening treden blijvende vervormingen op nadat het product uit de mal is genomen.
6 Symbolen. 3 : verplaatsingsvector (P : Cauchy spanningstensor 6 : lineaire rektensor cd : deviatorische deel van de lineaire rektensor tr(a) : spoor van tensora II : eenheidstensor i : matesiele afgeleide van a ux, uy, uz : componenten van de verplaatsingsvector bij carthesische coördinaten ur, uz : componenten van de verplaatsingsvector bij cilinder coördinaten (rotatie-symmetrisch) Andere gebruikte symbolen worden in het verslag toegelicht.
7 -1.1- HOOFDSTUK 1 Inleidinu. Bij Philips loopt op dit moment een onderzoek naar het voorspellen van spanningen en vervormingen die ontstaan tijdens het afkoelen van kunststof producten die door middel van het spuitgiet proces worden gemaakt. Deze spanningen en vervormingen onstaan met name tijdens de nadrukfase. Dit is de laatste fase van het spuitgietproces waarbij onder hoge druk materiaal wordt toegevoerd om de krimp ten gevolge van de afkoeling te ondervangen. Het ligt in de bedoeling om deze nadrukfase in een laboratorium omgeving te simuleren. Hierbij wordt voor een zo eenvoudig mogelijke geometrie gekozen. Bij het experiment waarover dit verslag gaat is van een werkelijke nadrukzase geen spiiake. De hoeveelheid zateriaal (massa) tijdens de afkoeling blijft constant en de verplaatsingen en vervormingen die hierbij optreden zijn klein. Bij het betreffende experiment wordt een product (rotatie symmetrisch busje) opnieuw in een mal geplaatst en opgewarmd tot een bepaalde hoge temperatuur. Nadat de mal met product overal dezelfde temperatuur heeft bereikt en er in het product alleen sprake is van een homogene druk wordt de mal met product onder zo goed mogelijk gedefinieerde omstandigheden afgekoeld. Nadat de constructie volledig is afgekoeld wordt het product uit de mal verwijderd. De interesse bij dit experiment gaat uit naar de spanningen en vervormingen, van het kunstof product, die optreden tijdens de afkoeling en nadat het produkt uit de mal is genomen. Doel van dit afstudeerwerk is om tot een numerieke simulatie te komen van dit experiment met behulp van het eindige-elementenmethoden programma MARC. Centraal bij de numerieke simulatie staat het oplossen van de instationaire energie vergelijking en het rekenen met thermo-viscoëlastisch materiaalgedrag. Doordat de verplaatsingen en Vervormingen klein zijn kan de energie vergelijking apart worden opgelost. Dit komt neer op het oplossen van een diffusie vergelijking. Wat betreft de noodzakelijke constitutieve vergelijkingen, voor het mechanisch gedrag, dient als uitgangspunt de 3-dimensionale isotrope lineair viscoelastische relatie, welke een generalisering is van de 3-dimensionale isotrope lineair elastische vergelijking. In hoofdstuk 2 en 3 wordt aandacht besteedt aan het fomuleren van de constitutieve vergeìijkigen. De I-dimensionale situatie wordt hier gebruikt om de invloed van de temperatuur toe te lichten waarna de 3-aimensionale ~ ~ r ~ hierwan ~ ~ een ~ generalisatie j k L ~ wordt. ~ In hoofdstuk 4 komt het eenvoudigste experiment (trekproef) aan de orde om de materiaaleigenschappen te bepalen. Voor de 3-dimensionale vergelijking is de glijdingsmodulus en de kompressiemodulus van belang. Hoofdstuk 5 is een synthese waarbij de numerieke simulatie van het experiment met MARC centraal staat. Hoofdstuk 6 geeft een aantal conclusies.
8 -2.1- HOOFDSTUK 2 Isotherm viscoëlastisch materiaalqedraq bij verschillende waarden van de temperatuur. 2.1 Inleiding. Als uitgangspunt dienen de constitutieve vergelijkingen voor lineair viscoelastisch materiaalgedrag, bij een bepaalde constante temperatuur. Twee situaties worden hierbij onderscheiden, de lijnspanningstoestand en de 3-dimensionale spanningstoestand : De 1-dimensionale situatie. Dit is de equivalent van de 1-dimensionale wet van Hooke (u=ee) voor elastisch materiaal. De ondergrens van O- in de integraal wordt genomen om eventuele sprongen van de rek E(t) op tijdstip t=o te kunnen beschrijven. E( t 1 is de relaxatiemodulus, welke voortaan elasticiteitsmodulus of E-modulus wordt genoemd. Bij een sprong in de rek op t=o ter grootte E wordt de spanning o(t) gegeven door : O t-, figuur 2.1 de elasticiteitsmodulus t-*
9 De 3-dimensionale isotrope situatie. G(t) is de tijdsafhankelijke glijdingsmodulus, deze wordt voortaan glijdingsmodulus genoemd. Voor zuivere afschuiving zal bij een sprong van 8(t) op t=o de schuifspanning os(t) gegeven worden door : K(t) is de tijdsafhankelijke kompressiemodulus, deze wordt voortaan kompressiemodulus genoemd. Indien de volumerek EV(t)=tr(a(t)) op tijdstip t=o een sprong vertoont, wordt de hydrostatische druk p(t) gegeven door : ~ O t-, figuur 2.3 de kompressiemodulus. I t-,
10 -2.3- E(t1, G(t) en K(t) worden relaxatiefuncties genoemd. Voor de 1-dimensionale situatie is E(t) van belang en voor de 3-dimensionale situatie zijn G(t) en K(t) van belang. De 1-dimensionale en 3-dimensionale situatie zijn hier onafhankelijk gepresenteerd. In paragraaf 82.1 van bijlage 2 blijkt dat de 1-dimensionale spanningstoestand volgens (2.3) in een vorm als (2.1) kan worden geschreven. In het vervolg van dit hoofdstuk worden aannamen gedaan over de vorm van de relaxatiefuncties. Of de beide formuleringen consistent zijn komt aan het einde van dit hoofdstuk aan de orde. Beschouwd worden amorfe polymeren met lineair viscoelastisch materiaalgedrag. Nagegaan wordt wat de invloed is van de temperatuur op de relaxatiefuncties. In dit hoofdstuk wordt daarbij de temperatuur constant (geen functie van de tijd) verondersteld. E(t), G(t) en K(t) zijn de ralaxatiefuncties bij de referentietemperatuur To. De relaxatiefuncties bij temperatuur T zullen worden uitgedrukt in de relaxatiefuncties bij de referentietemperatuur. De tijdsafhankelijkheid van de kompressiemodulus wordt al snel verwaarloosd. 2.2 Amorfe polymeren. Amorfe polymeren bestaan uit lange lineaire of vertakte moleculen. De situatie waarbij de moleculen ineen gekronkeld zijn tot kluwen, die door elkaar heen liggen en verward zijn, is de amorfe toestand. Amorf zijn dus de niet gekristalliseerde polymeren of thermoharders, welke een netwerk van moleculen bezitten. Wordt op een amorf polymeer een trekproef uitgevoerd bij een bepaalde reksnelheid, zonder plastische vervorming, dan resulteert kwalitatief het volgende verband tussen de spanning u en de rek E : 1 E + figuur 2.4 de trekkromme voor een amorf polymeer. indien de trekproef bij verschillende temperaturen met de zelfde reksnelheid wordt uitgevoerd en de waarde U,/E~, met cl steeds hetzelfde,
11 -2.4- tegen de temperatuur wordt uitgezet dan is het onderstaande verband tussen u1/cl en de temperatuur typisch voor amorfe polymeren : Tg Tr TV figuur 2.5 ol/cl als functie van T. T + I I1 I11 IV Bij lage temperaturen gedragen de materialen zich glasachtig. Moleculair gezien is dit een ingevroren vloeistof toestand. Er is geen of nauwlijks ketenbeweeglijkheid. Relaxatie en kruip treedt in veel mindere mate op dan in gebied 11. Relaxatie en kruip zijn processen waarbij herstel van de molecuulconfiguraties optreedt. Het typische viscoëlastische gebied. De molecuulketens kunnen ten opzichte van elkaar bewegen. Met rubberachtige gebied. De keten beweeglijkheid is groot. De warpunten fungeren als dwarsverbindingen (cross-links). Bij rubbers worden deze dwars verbindingen gevormd door andere moleculen, bijv. door zwavelmoleculen. Het materiaal gedraagt zich steeds meer als een vloeistof. Er is volledige ketenbeweeglijkheid. De overgang van I naar I1 wordt gekenmerkt door de glastemperatuur (Tg). De overgang van TI naar I11 wordt bepaald door Tr, de rubbertemperatuur. Tv, de vloeitemperatuur, bepaalt de overgang van gebied IT1 naar IV. Deze overgangstemperaturen zijn in principe niet constant. In het vervolg wordt dit wel aangenomen.
12 ~~ Figuur 2.6 geeft kwantitatieve resultaten voor een aantal polymeren o T-Tg.I kl figuur 2-6 voorbeeld van figuur 2.5 Polycarbonaat (P.Cl en A.8.S zijn amorf. De andere polymeren zijn kristallijn. De reksnelheid en cl zijn onbekend. Wet betrekking tot de glastemperatuur wordt een nadere toelichting gegeven. karakteristiek voor amorfe polymeren is het volgende verloop van het specifiek volume (per massa eenheid) als functie van de temperatuur bij een bepaalde druk en afkoelsnelheid : Tg figuur 2.7 de glastemperatuur. De glastemperatuur Tg is de temperatuur waarbij de uitzettingscoëfficiënt een sprong vertoont. Boven T neemt vooral het vrije volume toe met het stijgen van de temperatuur. 8 et vrije volume is het totale volume (macroscopische volume) vermindert met het moleculaire volume (bezet volume). Wet de toename van het vrije volume neemt de beweeglijkheid van de molecuulsegmenten sterk toe. Dit is de oorzaak dat boven de T +
13 -2.6- glastemperatuur de relaxatietijden snel kleiner worden met toenemende temperatuur. De relaxatietijden zijn een maat voor de tijd waarin herstel van de molecuulconfiguraties optreedt. In figuur 2.5 blijkt dat de waarde al/&, sterk afneemt boven Tg met toenemende temperatuur. De volgende 3 gebieden worden in het vervolg nader bekeken : I1 Het gebied waarvoor geldt : Tg < T < Tr I11 Het gebied waarvoor geldt : Tr < T < Tv I Het gebied waarvoor geldt : T < Tg Deze volgorde wordt gekozen omdat gebied XI de minste problemen levert en gebied I de meeste om de invloed van de temperatuur op de relaxatiefuncties in rekening te brengen. Gebied IT komt niet nader aan de orde. 2.3 De typisch viscoëlastische fase: Tg < T < T,. Binnen de groep van amorfe polymeren, met lineair viscoelastisch materiaalgedrag, vertonen vele van deze een specifiek temperatuur afhankelijk materiaalgedrag, het zogenaamde thermo-rheologisch eenvoudig materiaalgedrag. Bit houdt in dat, indien een relaxatiefunctie (bij een bepaalde temperatuur To) wordt uitgezet tegen de tijd, de relaxatiefunctie een zuivere verschuiving naar links of rechts vertoont bij een andere konstante temperatuur T, in een grafiek met logaritmische tijdas. In onderstaande figuur is LT een van de relaxatiefuncties als functie van ln(t). LP figuur 2.8 thermo-rheologisch eenvoudig materiaalgedrag.
14 De 1-dimensionale situatie. ET(t) is de relaxatiefunctie bij temperatuur T. E (t) is de TO relaxatiefunctie bij temperatuur To. De verschuiving kan als volgt worden beschreven: f(t) heeft de volgende eigenschappen: 1. f(to) = O 2. d f o > O d T Indien T groter is dan To verschuift de relaxatiefunctie naar links en deze verschuift verder naar links bij nog hogere temperaturen. De elastische respons wordt niet beïnvloed door de temperatuur. In plaats van het gebruik van f(t) wordt de verschuiving nu op een andere manier beschreven. Definieer a(t) zodanig dat : Voor a(t) geldt dan : 1. a(to) = >o d T Voor ET(t) kan dan geschreven worden : ofwel : De gereduceerde tijd y wordt gedefinieerd als : y=ta(t), zodat : Wordt E (t) gekozen volgens : TO (2.11)
15 -2. a- dan geldt bij temperatuur T : (2.12) en met de definitie van y : (2.13) Een bekende vesachufvingsrege1 is de W-L-F vergelijking E53 : f(t) = ln(a(t)) = 40.0t T - T,) 51.6 i- T - Tg (2.14) Deze regel geldt in het gebied : Tg < T <T +loo, voor een groot aantal polymeren (To = T 1. De temperaturen zijn Eierbij gegeven in graden 9 Kelvin of Celsius. ET(0) is in dit gebied orden groter dan ET(") De 3-dimensionale situatie. De verschuivingsfactor a(t) volgens de W-L-F vergelijking geldt ook voor de glijdingsmodulus en de kompressiemodulus. Dus indien de glijdingsmodulus bij To gekozen word% volgens : (2.15) en de kompressiemodulus volgens : (2.16) dan geldt bij temperatuur T : (2.17)
16 -2.9- (2.18) (2.19) Ook hier geldt dat GT(O) orden groter is dan GT(-). Met de aanname dat het verschil in kompressiegedrag tussen een polymeer en een elastische stof veel kleiner is dan het verschil in afschuifgedrag tussen een polymeer en een elastische stof [5] kan de tijdsafhankelijkheid van de kompressiemodulus worden verwaarloosd. Volgens Pipkin [12] wordt in de meeste gevallen het materiaal gedrag voldoende nauwkeurig beschreven met deze aanname. Experimenten moeten echter aantonen of deze aanname gerechtvaardigd is. Relaxatie bij afschuiving wordt veroorzaakt door herstel van de plaatsconfiguraties van de molecuulsegmenten. Bij een toename van de druk neemt het vrije volume af en komen de atomen van de moleculen dichter op elkaar te zitten. Toename van de druk lijkt dus veel op verlaging van de temperatuur [8]. De uitzettingscoefflcient is in principe ook een functie van de tijd. Moleculair gezien zijn afschuiving en konaapsessie verschillende processeni waarbij het visceus gedrag bij kompressie vaak te verwaarlozen is ten op zichte van het visceus gedrag bij afschuiving. Boven de glastemperatuur is R constant (geen functie van de tijd (bovenstaande aanname)) en onafhankelijk van de temperatuur indien de verschuivingstheorie geldt, want volgens deze theorie wordt de elastische respons niet beïnvloed door de temperatuur. Met bovenstaande aanname krijgt de constitutieve vergelijking de volgende vorm : t m(t) =.f - 2G (a(t){t-rl)id(r)dr + Kgtr(a(t))ii =O TO (2.20) Kg is de kompressiemodulus boven de glastemperatuur. 2.4 De rubberfase : T, < T < T,. In dit gebied is het mogelijk dat een verschuiving (horizontaal) van de relaxatiefuncties niet voldoende is om de temperatuursinvloed in rekening te brengen. Volgens de theorie van de rubberelasticiteit zijn de E- modulus en de glijdingsmodulus evenredig met gt [6]. g is de dichtheid (=l/v). Opgemerkt moet worden dat een ideale rubber zich zuiver elastisch gedraagt en inkompressibel is. Met betrekking tot de elastische respons wordt voor de relaxatiefuncties in het rubberachtige gebied een correctie gemaakt worden door te veronderstellen dat Eo, Ei, Goen Gi evenredig zijn met OT C6l.
17 De l-dimensionale situatie. De elasticiteitsmodulus krijgt door de evenredigheid met pt de volgende vorm, waarbij in de lineaire theorie Q constant mag worden genomen zodat de vergelijkingen lineair blijven : (2.21) met y=ta(t) en E (t) volgens (2.11). Opmerkelijk is dat bij hogere TO temperaturen de elasticiteitsmodulus toeneemt De 3-dimensionale situatie. Voor de 3-dimensionale constitutieve vergelijking waarbij de glijdingsmodulus evenredig is met QT volgt : (2.22) met G (t) volgens (2.15). TO 2.5 Be glasfase : T < Tg De l-dimensionale situatie. Boven de glastemperatuur kan dus nu de invloed van de temperatuur op het materiaal gedrag worden beschreven m.b.v. bekende verschuivingsregels (voor een groot deel empirisch bepaald) en correcties op basis van de rubber theorie. Onder de glastemperatuur liggen de zaken anders. Door de overheersende vander Waalskrachten tussen de moleculen is de ketenbeweeglijkheid zeer gering of uitgesloten. Ver onder de glastemperatuur treedt praktisch geen herstel op in de periode dat de deformatie wordt opgelegd [5]. E(O1en E(-) verschillen weinig. De relaxatiemechanismen onder de glastemperatuur zijn anders van aard dan erboven. Zoals al is opgemerkt is de verhouding tussen E(O1 en E(-) onder de glastemperatuur veel kleiner dan boven de glastemperatuur. Indien ET (t) uitgedrukt moet worden in ET (t) dan is een verschuivingsfactor niet O voldoende daar met een verschuivingsfactor de verhouding tussen E(0) en E(-) niet beïnvloed wordt. Het model van Schapery [IS] biedt hier een oplossing. Het Schapery model is een enkelvoudige integraal formulering
18 voor niet lineair viscoëlastisch temperatuurafhankelijk materiaal gedrag. Dit model voldoet aan een aantal thermodynamische voorwaarden en heeft hiermee een vrij grote geldigheid. Aan de achtergronden van dit model wordt hier verder geen aandacht besteed. ïn de literatuur komt men dit model vaak alleen in de 1-dimensionale vorm tegen. Indien van dit model (zie bijlage 1) het niet lineaire gedeelte wordt weggelaten dan wordt, met E (t) volgens (2.111, ET(t) gegeven door : TO (2.23) vaarbij, voor de algemeenheid, voor de elasticiteitsmodulus een aparte verschuivingsfactor is gedefinieerd. Voor (2.23) wordt met een andere notatie, zoals gebruikelijk bij Schapery, geschreven : Voor T=To geldt dat fl(to)=l en f2(t0)=1. De eerste term in (2.24) stelt het constante deel van de relaxatiefunctie voor en de tweede term het tijdsafhankelijke deel. fl(t9 brengt de invloed van de temperatuur op Eo in rekening en f2(t) de invloed op Ei. ae (TI is de verschuivingsfactor voor de elasticiteitsmodulus. fl(t), f2(t) en ae(t) moeten experimenteel bepaald worden De 3-dimensionale situatie. Naar analogie van de elasticiteitsmodulus, volgens (2.241, wordt voor de glijdingsmodulus een zelfde beschrijving gekozen. GT(t) krijgt dan de volgende vorm : Voor T=To geldt hl(to)=l en h2(t0)=l. hl(t) brengt de invloed van de temperatuur op Go in rekening en h2(t) de invloed op Gi. ag(t) is de verschuivingsfactor voor de glijdingsmodulus. De constitutieve vergelijking wordt gegeven door : t a(t) = J {2hl(T)Go + 2h,(T)AG(a,rt-~})}~~(r)dr + K(T)tr($(t))H T=O- (2.26)
19 Consistentie. In paragraaf B2.1 van bijlage 2 blijkt dat de I-dimensionale spanningstoestand volgens de 3-dimensionale formulering (2.3) in de volgende vorm kan worden geschreven : (2.27) Beide formuleringen zijn consistent indien geldt : (2.28) Met het oog op het te simuleren experiment met het eindige elementenmethode programma MARC is gekozen voor relaxatiefuncties welke uit een constant deel en een reeks van e-machten (tijdsafhankelijke deel) bestaan. In paragraaf B2.2 van biylage*2 wordt, voor het geval dat 1 term (n=l) uit de reeks wordt meegenomen, E (t) berekend en nagegaan of voor de drie temperatuursgebieden de beide formuleringen consistent zijn. Uit de hoeveelheid rekenwerk die al nodig is voor dit geval lijkt een zelfde berekening voor n > 1 ondoenlijk. Voor n > 1 wordt dan ook geen uitspraak gedaan over consistentie.
20 -3.1- HOOFDSTUK 3 De invloed van de tiidafhankeliikheid der temperatuur OP het materiaal sedras. 3.1 Inleiding In het vorige hoofdstuk was de temperatuur geen functie van de tijd. Hierbij werd alleen bekeken hoe de relaxatiefuncties, behorend bij een referentietemperatuur, aangepast moesten worden voor een andere temperatuur. In dit hoofdstuk wordt bekeken hoe de constitutieve vergelijkingen er uitzien indien de temperatuur een bekesde functie var, de tijd is. In 3.2 wordt voor de 1-dimensionale vergelijking eerst de respons van de spanning op een stap van de rek op tijdstip t=o bepaald. Vervolgens wordt de respons op een willekeurig rekverloop bepaald. Voor T(t) geldt : T < T(t) < Tr In 3.3 komen de gebieden T(t) < T en T(t) > Tr voor de l-&mensionale situatie aan de orde, waarbij T(t7 > Tr als een speciaal geval van T(t) < T 9 wordt gezien. In 3.4 wordt de 3-dimensionale vergelijking, welke een generalisering van de 1-dimensionale vergelijking is, gegeven. Hierbij wordt alleen naar het gebied T(t) < Tg gekeken omdat de andere gebieden vereenvoudigingen hiervan zijn. De kompressiemodulus wordt tijdsonafankelijk verondersteld. Omdat de temperatuur verandert in de tijd moet de rek ten gevolge van uitzetting of krimp ook worden meegenomen. Aan consistentie van de 1-dimensionale situstie met de 3-dimensionale wordt geen aandacht meer besteed. 3.2 De 1-dimensionale constitutieve vergelijking met : Tg <T(t) < T, De respons van de spanning op een stap van de rek op t=o. Stel dat T(t) het onderstaande verloop heeft en gediscretiseerd (stuksgewijs constant) wordt via de punten ~i zoals hierbij ook is aangegeven. figuur 3.1 de temperatuur
21 -3.2- De relaxatiefuncties (E-modulus) voor de constante temperaturen Tj zijn hieronder getekend. figuur 3.2 relaxtiefuncties bij constante temperatuur Deze relaxatiefuncties kunnen op de volgende manier worden uitgedrukt in de relaxatiefunctie bij temperatuur To, indien To de referentietemperatuur is : ai is de in het vorige hoofdstuk geïntroduceerde verschuivingsfactor bij temperatuur Ti, zie (2.10). Vertoont de rek E(tl op t=o een sprong dan zal de spanning o(t) het volgende verloop hebben : Hierbij wordt geen temperatuursrek verondersteld. Voor de relaxatie functie Ea(t) moet een uitdrukking gevonden worden. T Verandert de temperatuur sprongsgewijs, zoals hiervoor aangegeven, dan volgt Ea(t) van tot TI de functie ET (tl. Na een sprong in de temperatuur op T~ T O wordt verondersteld dat E-(t) de verschoven functie ET (t) volgt. Wordt T 1 aangenomen dat bij een sprong in de temperatuur de spanning geen sprong vertoont dan moet ET (t) horizontaal worden verschoven (verschuiving heeft 1 hier een andere betekenis dan die bij de verschuivingsfactor). Omdat de verschuivigsfactor geen invloed op de waarde EA(-) heeft mag ET (t) niet T 1 verticaal worden verschoven. In de volgende figuur is het voorgaande weergegeven en doorgezet tot
22 -3.3- 'i t á 'i+ 1 figuur 3.3 constructie van E-(t) T In figuur 3.3 is vi de onbekende horizontale verschuiving van E.(t) en TI vi - vi-1 + A v ~ (3.3) (3.4) ET.(T~-v~) = E (aii'i-vi)) 1 TO (3.7) Uit (3.51, (3.6) en 13.7) volgt :
23 -3.4- {Ti-vilai = (3.8) Vergelijking (3.8) kan op de volgende manier worden herschreven : Met : ai - ai-? = Aai en vi - vi-l = Avi wordt vergelijking (3.12) : TiAai = viaai - aielavi (3.13) Door het verkleinen van de intervallen wordt T(t) steeds beter benaderd. In het limietgeval gaat de discrete variabele ~i over in de continue variabele T. Aai wordt da(t) en Avi wordt dv(t). ai-l krijgt de waarde a(t). In het limietgeval wordt vergelijking (3.13) : Tda = v(t)da + a(.r)dv (3.14) Hiervoor kan ook geschreven worden : Tda = dva (3.15) Integreren van (3.15) levert met v(o)=o: t f Tda = J dva = v(t)a(t) T=O 1 =O (3.16) Uit (3.16) kan v(t) worden opgelost : (3.17) (3.17) invullen in (3.4) geeft : t E-(t) = E (a(t)t- J Tda) T TO T=O (3.18)
24 -3.5- (3.18) kan ook op de volgende manier worden geschreven : L L (3.19) Ofwel : 4- L (3.20) De gereduceerde tijd y heeft nu de volgende vorm : (3.2t) De respons op een stap in de rek op t=o wordt hiermee : met y volgens (3.21). De gereduceerde tijd y wordt nader beschouwd. Indien ag de gemiddelde verschuivingsfactor in het interval (0,t) is dan geldt : (3.23) dus : y=agt (3.24) Vergelijking (3.21) wordt ook verkregen door te beseffen dat bij het gediscretiseerde temperatuursverloop (figuur 3.11 de lengte van een tijdsinterval ~ i- ~ i - ~ AT^# = bij temperatuur To gegeven wordt door : Ayi = aiari (3.25) Hierbij is ai de verschuivingsfactor bij de temperatuur in het interval AT^. Wordt de totale gereduceerde tijd gegeven door sommatie van de deelintervallen dan volgt : i i Y(T~) = E Ay, = r: aja-rj (3.26) j=l j= 1
25 -3.6- Bij limiet overgang wordt (3.26) : t Y(t9 = f a(t)dt T =O (3.27) De respons van de spanning op een willekeurig rek verloop. De thermische rek wordt nog niet meegenomen. Stel dat Eft) het onderstaande verloop heeft en gediscretiseerd wordt via de punten ~i zoals is aangegeven. Het bijbehorende temperatuursverloop is ook weergegeven. E(t1 I I *o= o Ti t+ figuur 3.4 I Bij een sprong in de rek op ~i ter grootte van A E geeft ~ de spanning (alleen ten gevolge van deze sprong) de volgende respons : ET(t) = E (agtt-ri}) TO (3.299 waarbij ag de gemiddelde verschuivingsfactor in het interval (~i,t) is : (3.30) zodat :
26 -3.7- De totale respons volgt door sommatie van alle deelresponsies : (3.32) Bij het nemen van de limiet gaat (3.32) over in : (3.339 t Y= I a q=o (3.34) T Be thermische rek op tijdstip T, i ac~{~>)t{q~d~, +)- met a de uitzettingscoëfficient welke een functie mag zijn van de temperatuur en niet van de tijd, kan nu ook worden meegenomen. in plaats van &(TI moet nu ;(T) - ~(T(T))T(T) in (3.33) worden ingevuld : (3.35) 3.3 De 1-dimensionale constitutieve vergelijking met : T(t) < Tg De volgende relatie voor de elasticiteitsmodulus bij temperatuur T (constant) werd in het vorige hoofdstuk gebruikt : (3.36) met y=aet, ae is de verschuivingsfactor voor de E-modulus. Naar analogie met het voorgaande kan ook nu de respons van de spanning op een stap in de rek ter grootte E op t=o worden bepaald, waarbij T=T(t) : (3.379
27 -3.8- met : en volgens (3.21) : (3.39) Aangenomen is dat : fl= fl(t(t)) en f2= fs(t(t)). Als de temperatuur nu een sprong vertoont dan zal de spanning ook een sprong vertonen omdat fl en f2 discontinu veranderen. De thermische rek wordt nog niet meegenomen. Bij een sprong in de rek op fi ter grootte Aei heeft de respons van de spanning, alleefi ten gevolge van deze reksprong, de volgende vorm : (3.40) met : (3.41) (3.42) Ook nu volgt de totale respons door sommatie van de deel responsies : en via een limietovergang : (3.44) De thermische rek kan nu ook worden meegenomen, (3.44) krijgt dan de volgende vorm :
28 -6'E- : qam
29 (3.50) waarbij $ en gegeven zijn door (3.49). Aangenomen is dat : hl= hl(t(t)) en ha= hs(t(t)). Voor temperaturen boven de glastemperatuur maar onder de rubbertemperatuur zijn de functies hl en h2 constant. In de rubber fase zijn deze functies evenredig met QT. De evenredigheid met Q kan In de linealre theorie verwaarloosd worden. 3.5 Het bepalen van aiateriaaleigenschappen uit experimenten. BiJ verschillende constante temperaturen is het mogelijk om uit een trekproef of afschuifproef de materiaaleigenschappen te bepalen. In 3.3 en 3.4 werd aangenomen dat, indien T=T(t) : fl= fl(t(t)), E2= f2(t(t1), hl= hl(t(t)) en ha= h2(t(t)). De meest eenvoudige experimenten, om aan te tonen of deze aannamen correct zijn, zijn zeer moeilijk uitvoerbaar, omdat hierbij de temperatuur op een gecontroleerde wijze moet veranderen in de tijd.
Eindhoven University of Technology MASTER. Thermo-viscoëlastische analyse voor een spuitgiet product. Verest, J.F.M.
 Eindhoven University of Technology MASTER Thermo-viscoëlastische analyse voor een spuitgiet product Verest, J.F.M. Award date: 1987 Link to publication Disclaimer This document contains a student thesis
Eindhoven University of Technology MASTER Thermo-viscoëlastische analyse voor een spuitgiet product Verest, J.F.M. Award date: 1987 Link to publication Disclaimer This document contains a student thesis
H O E D U U R I S L I M B U R G?
 H O E D U U R I S L I M B U R G? N AD E R E I N F O R M A T I E S T A T E N C O M M I S S I E S OV E R O N D E R AN D E R E A F V A L S T O F F E N H E F F I N G E N I N L I M B U R G 1 6 a u g u s t u
H O E D U U R I S L I M B U R G? N AD E R E I N F O R M A T I E S T A T E N C O M M I S S I E S OV E R O N D E R AN D E R E A F V A L S T O F F E N H E F F I N G E N I N L I M B U R G 1 6 a u g u s t u
Bepaling toezichtvorm gemeente Stein
 Bepaling toezichtvorm 2008-2011 gemeente Stein F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, juni 2 0 0 8 V e r d i e p i n g s o n d e r z o e k S t e i
Bepaling toezichtvorm 2008-2011 gemeente Stein F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, juni 2 0 0 8 V e r d i e p i n g s o n d e r z o e k S t e i
Buiging van een belaste balk
 Buiging van een belaste balk (Modelbouw III) G. van Delft Studienummer: 0480 E-mail: gerardvandelft@email.com Tel.: 06-49608704 4 juli 005 Doorbuigen van een balk Wanneer een men een balk op het uiteinde
Buiging van een belaste balk (Modelbouw III) G. van Delft Studienummer: 0480 E-mail: gerardvandelft@email.com Tel.: 06-49608704 4 juli 005 Doorbuigen van een balk Wanneer een men een balk op het uiteinde
( ) ( ) Bij welke karakteristieke afschuifsnelheid zijn de weerstanden voor beide materialen gelijk: dan moet gelden:
 Opgave 1: a) Enkele producteigenschappen die bepaald worden door de keuze voor PP of PS: 1 Stijfheid: PS is amorf, G = ca 1 GPa; PP is semi-kristallijn, G = ca.5 GPa. 2 Temperatuursbereik: Tg van PS is
Opgave 1: a) Enkele producteigenschappen die bepaald worden door de keuze voor PP of PS: 1 Stijfheid: PS is amorf, G = ca 1 GPa; PP is semi-kristallijn, G = ca.5 GPa. 2 Temperatuursbereik: Tg van PS is
L i mb u r g s e L a n d m a r k s
 L i mb u r g s e L a n d m a r k s P r o g r a m m a I n v e s t e r e n i n S t ed e n e n D o r p e n, l i j n 2 ; D e L i m b u r g s e I d e n t i t e i t v e r s i e 1. 0 D o c u m e n t h i s t o
L i mb u r g s e L a n d m a r k s P r o g r a m m a I n v e s t e r e n i n S t ed e n e n D o r p e n, l i j n 2 ; D e L i m b u r g s e I d e n t i t e i t v e r s i e 1. 0 D o c u m e n t h i s t o
TECHNISCHE UNIVERSITEIT EINDHOVEN FACULTEIT WERKTUIGBOUWKUNDE DIVISIE COMPUTATIONAL AND EXPERIMENTAL MECHANICS
 TECHNISCHE UNIVERSITEIT EINDHOVEN FACULTEIT WERKTUIGBOUWKUNDE DIVISIE COMPUTATIONAL AND EXPERIMENTAL MECHANICS Tentamen Polymeerverwerking (4K550) donderdag 5 juli 2007, 14:00-17:00. Bij het tentamen mag
TECHNISCHE UNIVERSITEIT EINDHOVEN FACULTEIT WERKTUIGBOUWKUNDE DIVISIE COMPUTATIONAL AND EXPERIMENTAL MECHANICS Tentamen Polymeerverwerking (4K550) donderdag 5 juli 2007, 14:00-17:00. Bij het tentamen mag
Tentamen Toegepaste elasticiteitsleer (4A450)
 Tentamen Toegepaste elasticiteitsleer (4A450) Datum: 3 juni 003 Tijd: 4:00 7:00 uur Locatie: Hal Matrixgebouw Dit tentamen bestaat uit drie opgaven. Het gebruik van het dictaat, oefeningenbundel en notebook
Tentamen Toegepaste elasticiteitsleer (4A450) Datum: 3 juni 003 Tijd: 4:00 7:00 uur Locatie: Hal Matrixgebouw Dit tentamen bestaat uit drie opgaven. Het gebruik van het dictaat, oefeningenbundel en notebook
NATUURKUNDE OLYMPIADE EINDRONDE 2013 PRAKTIKUMTOETS
 NATUURKUNDE OLYMPIADE EINDRONDE 13 PRAKTIKUMTOETS Opmerkingen 1. Schrijf bovenaan elk papier je naam.. Nummer elke bladzijde. 3. Schrijf op de eerste pagina het totale aantal bladen dat je inlevert. 4.
NATUURKUNDE OLYMPIADE EINDRONDE 13 PRAKTIKUMTOETS Opmerkingen 1. Schrijf bovenaan elk papier je naam.. Nummer elke bladzijde. 3. Schrijf op de eerste pagina het totale aantal bladen dat je inlevert. 4.
 EXAMEN Mechanische Eigenschappen Biologische Weefsels VAKCODE 8W200 DATUM 20 Maart 2007 14.00-17.00 u Bij dit examen mag gebruik worden gemaakt van het diktaat: Mechanical Properties of Living Tissues,
EXAMEN Mechanische Eigenschappen Biologische Weefsels VAKCODE 8W200 DATUM 20 Maart 2007 14.00-17.00 u Bij dit examen mag gebruik worden gemaakt van het diktaat: Mechanical Properties of Living Tissues,
THERMODYNAMICA 2 (WB1224)
 THERMODYNAMICA 2 (WB1224) dinsdag 21 januari 2003 14.00-17.00 u. AANWIJZINGEN Het tentamen bestaat uit twee open vragen en 15 meerkeuzevragen. Voor de beantwoording van de meerkeuzevragen is een formulier
THERMODYNAMICA 2 (WB1224) dinsdag 21 januari 2003 14.00-17.00 u. AANWIJZINGEN Het tentamen bestaat uit twee open vragen en 15 meerkeuzevragen. Voor de beantwoording van de meerkeuzevragen is een formulier
TENTAMEN. Thermodynamica en Statistische Fysica (TN )
 TENTAMEN Thermodynamica en Statistische Fysica (TN - 141002) 25 januari 2007 13:30-17:00 Het gebruik van het diktaat is NIET toegestaan Zet op elk papier dat u inlevert uw naam Begin iedere opgave bovenaan
TENTAMEN Thermodynamica en Statistische Fysica (TN - 141002) 25 januari 2007 13:30-17:00 Het gebruik van het diktaat is NIET toegestaan Zet op elk papier dat u inlevert uw naam Begin iedere opgave bovenaan
TRILLINGEN EN GOLVEN HANDOUT FOURIER
 TRILLINGEN EN GOLVEN HANDOUT FOURIER Cursusjaar 2009 / 2010 2 Inhoudsopgave 1 FOURIERANALYSE 5 1.1 INLEIDING............................... 5 1.2 FOURIERREEKSEN.......................... 5 1.3 CONSEQUENTIES
TRILLINGEN EN GOLVEN HANDOUT FOURIER Cursusjaar 2009 / 2010 2 Inhoudsopgave 1 FOURIERANALYSE 5 1.1 INLEIDING............................... 5 1.2 FOURIERREEKSEN.......................... 5 1.3 CONSEQUENTIES
Hertentamen Statistische en Thermische Fysica II Woensdag 14 februari 2007 Duur: 3 uur
 Hertentamen Statistische en Thermische Fysica II Woensdag 14 februari 2007 Duur: 3 uur Vermeld op elk blad duidelijk je naam, studierichting, en evt. collegekaartnummer! (TIP: lees eerst alle vragen rustig
Hertentamen Statistische en Thermische Fysica II Woensdag 14 februari 2007 Duur: 3 uur Vermeld op elk blad duidelijk je naam, studierichting, en evt. collegekaartnummer! (TIP: lees eerst alle vragen rustig
Schuifspanningen loodrecht op een cilindrisch gat
 Schuifspanningen loodrecht op een cilindrisch gat Colin van Weelden CT3000 Bachelor Eindwerk Begeleiders: 1379550 TU Delft P.C.J. Hoogenboom Delft, Juni 2010 C.B.M. Blom Voorwoord Dit rapport is het eindresultaat
Schuifspanningen loodrecht op een cilindrisch gat Colin van Weelden CT3000 Bachelor Eindwerk Begeleiders: 1379550 TU Delft P.C.J. Hoogenboom Delft, Juni 2010 C.B.M. Blom Voorwoord Dit rapport is het eindresultaat
R e g i o M i d d e n -L i m b u r g O o s t. G r e n z e l o o s w o n e n i n M i d d e n -L i m b u r g R e g i o n a l e W o o n v i s i e
 R e g i o M i d d e n -L i m b u r g O o s t G r e n z e l o o s w o n e n i n M i d d e n -L i m b u r g R e g i o n a l e W o o n v i s i e 4 o k t o b e r 2 0 0 6 P r o j e c t n r. 2 9 5 7. 7 2 B o
R e g i o M i d d e n -L i m b u r g O o s t G r e n z e l o o s w o n e n i n M i d d e n -L i m b u r g R e g i o n a l e W o o n v i s i e 4 o k t o b e r 2 0 0 6 P r o j e c t n r. 2 9 5 7. 7 2 B o
woensdag 6 augustus 2008, u Code: 8W020, BMT 1.3 Faculteit Biomedische Technologie Technische Universiteit Eindhoven
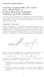 Tentamen Biomechanica woensdag 6 augustus 2008, 9.00-12.00 u Code: 8W020, BMT 1.3 Faculteit Biomedische Technologie Technische Universiteit Eindhoven Dit examen bestaat uit 6 opgaven. Het aantal punten
Tentamen Biomechanica woensdag 6 augustus 2008, 9.00-12.00 u Code: 8W020, BMT 1.3 Faculteit Biomedische Technologie Technische Universiteit Eindhoven Dit examen bestaat uit 6 opgaven. Het aantal punten
Practicum algemeen. 1 Diagrammen maken 2 Lineair verband en evenredig verband 3 Het schrijven van een verslag
 Practicum algemeen 1 Diagrammen maken 2 Lineair verband en evenredig verband 3 Het schrijven van een verslag 1 Diagrammen maken Onafhankelijke grootheid en afhankelijke grootheid In veel experimenten wordt
Practicum algemeen 1 Diagrammen maken 2 Lineair verband en evenredig verband 3 Het schrijven van een verslag 1 Diagrammen maken Onafhankelijke grootheid en afhankelijke grootheid In veel experimenten wordt
Tentamen Fundamentals of Deformation and Linear Elasticity (4A450)
 Tentamen Fundamentals of Deformation and Linear Elasticity (4A450) Datum: 22 november 2001 Tijd: 14:00 17:00 uur Locatie: Auditorium, zaal 9, 10, 15 en 16 Dit tentamen bestaat uit drie opgaven. Het gebruik
Tentamen Fundamentals of Deformation and Linear Elasticity (4A450) Datum: 22 november 2001 Tijd: 14:00 17:00 uur Locatie: Auditorium, zaal 9, 10, 15 en 16 Dit tentamen bestaat uit drie opgaven. Het gebruik
OVER HET WARMTETHEOREMA VANNERNST DOOR H. A. LORENTZ.
 OVER HE WARMEHEOREMA VANNERNS DOOR H. A. LORENZ. De thermodynamische stelling die eenige jaren geleden door Nernst werd opgesteld, komt hierop neer dat de entropieën van twee gecondenseerde, b.v. vaste
OVER HE WARMEHEOREMA VANNERNS DOOR H. A. LORENZ. De thermodynamische stelling die eenige jaren geleden door Nernst werd opgesteld, komt hierop neer dat de entropieën van twee gecondenseerde, b.v. vaste
H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W +
 H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W + D o e l m a t i g h e i d s t o e t s v o o r g e b i e d e n w a a r v o o r g e e n b o d e m b e h e e r p l a n i s v a s t g e s
H a n d l e i d i n g d o e l m a t i g h e i d s t o e t s M W W + D o e l m a t i g h e i d s t o e t s v o o r g e b i e d e n w a a r v o o r g e e n b o d e m b e h e e r p l a n i s v a s t g e s
10 Materie en warmte. Onderwerpen. 3.2 Temperatuur en warmte.
 1 Materie en warmte Onderwerpen - Temperatuur en warmte. - Verschillende temperatuurschalen - Berekening hoeveelheid warmte t.o.v. bepaalde temperatuur. - Thermische geleidbaarheid van een stof. - Warmteweerstand
1 Materie en warmte Onderwerpen - Temperatuur en warmte. - Verschillende temperatuurschalen - Berekening hoeveelheid warmte t.o.v. bepaalde temperatuur. - Thermische geleidbaarheid van een stof. - Warmteweerstand
Cover Page. The handle holds various files of this Leiden University dissertation.
 Cover Page The handle http://hdl.handle.net/1887/21709 holds various files of this Leiden University dissertation. Author: Siemens, Alexander Oltmann Nicolaas Title: Elasticity and plasticity : foams near
Cover Page The handle http://hdl.handle.net/1887/21709 holds various files of this Leiden University dissertation. Author: Siemens, Alexander Oltmann Nicolaas Title: Elasticity and plasticity : foams near
Nauwkeurige dieptemetingen
 Nauwkeurige dieptemetingen overwegingen & een methode drs. ir. Eric Weijters www.weijters.net Het inmeten van een wrakveld Een in onze Nederlandse wateren goed bruikbare methode om scheepswrakken in te
Nauwkeurige dieptemetingen overwegingen & een methode drs. ir. Eric Weijters www.weijters.net Het inmeten van een wrakveld Een in onze Nederlandse wateren goed bruikbare methode om scheepswrakken in te
Machten, exponenten en logaritmen
 Machten, eponenten en logaritmen Machten, eponenten en logaritmen Macht, eponent en grondtal Eponenten en logaritmen hebben alles met machtsverheffen te maken. Een macht als 4 is niets anders dan de herhaalde
Machten, eponenten en logaritmen Machten, eponenten en logaritmen Macht, eponent en grondtal Eponenten en logaritmen hebben alles met machtsverheffen te maken. Een macht als 4 is niets anders dan de herhaalde
Hoofdstuk 3: Tweede orde lineaire differentiaalvergelijkingen
 Hoofdstuk 3: Tweede orde lineaire differentiaalvergelijkingen De inhoud van hoofdstuk 3 zou grotendeels bekende stof moeten zijn. Deze stof is terug te vinden in Stewart, hoofdstuk 17. Daar staat alles
Hoofdstuk 3: Tweede orde lineaire differentiaalvergelijkingen De inhoud van hoofdstuk 3 zou grotendeels bekende stof moeten zijn. Deze stof is terug te vinden in Stewart, hoofdstuk 17. Daar staat alles
Bepaling toezichtvorm gemeente Meerlo-Wanssum
 Bepaling toezichtvorm 2007-2010 gemeente Meerlo-Wanssum F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k Provincie L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k M e e
Bepaling toezichtvorm 2007-2010 gemeente Meerlo-Wanssum F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k Provincie L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k M e e
Leeswijzer bij het college Functies en Reeksen
 Leeswijzer bij het college Functies en Reeksen Erik van den Ban Najaar 2012 Introductie eze leeswijzer bij het dictaat Functies en Reeksen (versie augustus 2011) heeft als doel een gewijzigde opbouw van
Leeswijzer bij het college Functies en Reeksen Erik van den Ban Najaar 2012 Introductie eze leeswijzer bij het dictaat Functies en Reeksen (versie augustus 2011) heeft als doel een gewijzigde opbouw van
TECHNISCHE UNIVERSITEIT EINDHOVEN FACULTEIT WERKTUIGBOUWKUNDE DIVISIE COMPUTATIONAL AND EXPERIMENTAL MECHANICS
 TECHNISCHE UNIVERSITEIT EINDHOVEN FACULTEIT WERKTUIGBOUWKUNDE DIVISIE COMPUTATIONAL AND EXPERIMENTAL MECHANICS Tentamen Polymeerverwerking (4K550) dinsdag 4 juli 2006, 14:00-17:00. Bij het tentamen mag
TECHNISCHE UNIVERSITEIT EINDHOVEN FACULTEIT WERKTUIGBOUWKUNDE DIVISIE COMPUTATIONAL AND EXPERIMENTAL MECHANICS Tentamen Polymeerverwerking (4K550) dinsdag 4 juli 2006, 14:00-17:00. Bij het tentamen mag
TECHNISCHE UNIVERSITEIT EINDHOVEN. Tentamen OGO Fysisch Experimenteren voor minor AP (3MN10) Tentamen Inleiding Experimentele Fysica (3AA10)
 TECHNISCHE UNIVERSITEIT EINDHOVEN Tentamen OGO Fysisch Experimenteren voor minor AP (3MN10) Tentamen Inleiding Experimentele Fysica (3AA10) d.d. 30 oktober 2009 van 9:00 12:00 uur Vul de presentiekaart
TECHNISCHE UNIVERSITEIT EINDHOVEN Tentamen OGO Fysisch Experimenteren voor minor AP (3MN10) Tentamen Inleiding Experimentele Fysica (3AA10) d.d. 30 oktober 2009 van 9:00 12:00 uur Vul de presentiekaart
Verrassende uitkomsten in stromingen
 Verrassende uitkomsten in stromingen Deel 2 G.A. Bruggeman De wiskundige theorie van de grondwaterstroming biedt nu en dan uitkomsten die opvallen door hun eenvoud of anderszins door hun bijzonder structuur,
Verrassende uitkomsten in stromingen Deel 2 G.A. Bruggeman De wiskundige theorie van de grondwaterstroming biedt nu en dan uitkomsten die opvallen door hun eenvoud of anderszins door hun bijzonder structuur,
Basic Creative Engineering Skills
 Mechanica: Sterkteleer Januari 2015 Theaterschool OTT-1 1 Sterkteleer Sterkteleer legt een relatie tussen uitwendige krachten (MEC1-A) en inwendige krachten Waarom lopen de balken taps toe? Materiaaleigenschappen
Mechanica: Sterkteleer Januari 2015 Theaterschool OTT-1 1 Sterkteleer Sterkteleer legt een relatie tussen uitwendige krachten (MEC1-A) en inwendige krachten Waarom lopen de balken taps toe? Materiaaleigenschappen
Solid Mechanics (4MB00) Toets 2 versie 1
 Solid Mechanics (4MB00) Toets 2 versie 1 Faculteit : Werktuigbouwkunde Datum : 1 april 2015 Tijd : 13.45-15.30 uur Locatie : Matrix Atelier Deze toets bestaat uit 3 opgaven. De opgaven moeten worden gemaakt
Solid Mechanics (4MB00) Toets 2 versie 1 Faculteit : Werktuigbouwkunde Datum : 1 april 2015 Tijd : 13.45-15.30 uur Locatie : Matrix Atelier Deze toets bestaat uit 3 opgaven. De opgaven moeten worden gemaakt
Tentamen Fundamentals of Deformation and Linear Elasticity (4A450)
 Tentamen Fundamentals of Deformation and Linear Elasticity (4A450) Datum: 6 maart 00 Tijd: 14:00 17:00 uur Locatie: Matrixgebouw, zaal 1.60 Dit tentamen bestaat uit drie opgaven. Het gebruik van het dictaat,
Tentamen Fundamentals of Deformation and Linear Elasticity (4A450) Datum: 6 maart 00 Tijd: 14:00 17:00 uur Locatie: Matrixgebouw, zaal 1.60 Dit tentamen bestaat uit drie opgaven. Het gebruik van het dictaat,
Bepaling energie en soortelijke warmte 2D-atoomrooster m.b.v. de Metropolis Monte Carlo methode
 Bepaling energie en soortelijke warmte 2D-atoomrooster m.b.v. de Metropolis Monte Carlo methode Verslag Computational Physics Sietze van Buuren Begeleider: Prof.Dr. H. de Raedt 29 december 25 Samenvatting
Bepaling energie en soortelijke warmte 2D-atoomrooster m.b.v. de Metropolis Monte Carlo methode Verslag Computational Physics Sietze van Buuren Begeleider: Prof.Dr. H. de Raedt 29 december 25 Samenvatting
T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M +
 T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M + A a n l e i d i n g I n d e St a t e nc o m m i s si e v o or R ui m t e e n G r o e n ( n u g e n o em d d e St at e n c
T I P S I N V U L L I N G E N H O O G T E T E G E N P R E S T A T I E S B O M + A a n l e i d i n g I n d e St a t e nc o m m i s si e v o or R ui m t e e n G r o e n ( n u g e n o em d d e St at e n c
Hoofdstuk 1: Inleiding
 Hoofdstuk 1: Inleiding 1.1. Richtingsvelden. Zie Stewart, 9.2. 1.2. Oplossingen van enkele differentiaalvergelijkingen. Zelf doorlezen. 1.3. Classificatie van differentiaalvergelijkingen. Differentiaalvergelijkingen
Hoofdstuk 1: Inleiding 1.1. Richtingsvelden. Zie Stewart, 9.2. 1.2. Oplossingen van enkele differentiaalvergelijkingen. Zelf doorlezen. 1.3. Classificatie van differentiaalvergelijkingen. Differentiaalvergelijkingen
Dune Ash een wiskundig model voor de verspreiding van een vulkanische aswolk werkbundel
 Dune Ash een wiskundig model voor de verspreiding van een vulkanische aswolk werkbundel Nele Cosemans en Greet Dockx, studenten SLO wiskunde KU Leuven VERKENNING Open het programma Dune Ash en lees de
Dune Ash een wiskundig model voor de verspreiding van een vulkanische aswolk werkbundel Nele Cosemans en Greet Dockx, studenten SLO wiskunde KU Leuven VERKENNING Open het programma Dune Ash en lees de
Samenvatting. Samenvatting
 Samenvatting Het tablet is om vele redenen een populaire toedieningsvorm van geneesmiddelen. Het gebruikersgemak en het gemak waarmee ze grootschalig kunnen worden geproduceerd zijn slechts twee van de
Samenvatting Het tablet is om vele redenen een populaire toedieningsvorm van geneesmiddelen. Het gebruikersgemak en het gemak waarmee ze grootschalig kunnen worden geproduceerd zijn slechts twee van de
Bepaling toezichtvorm gemeente Venray
 Bepaling toezichtvorm 2007-2010 gemeente Venray F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k V e n
Bepaling toezichtvorm 2007-2010 gemeente Venray F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, april 2 0 0 7 V e r d i e p i n g s o n d e r z o e k V e n
Deel 1. Basiskennis wiskunde
 & Geomatica 2 juli 2018 - reeks 1 - p. Deel 1. Basiskennis wiskunde Oefening 1 et gemiddelde van de getallen 1 2, 1 en 1 4 is (A) 1 27 (B) 1 4 (C) 1 (D) 1 6 Juist beantwoord: 81 %. Blanco: 0 %. Oefening
& Geomatica 2 juli 2018 - reeks 1 - p. Deel 1. Basiskennis wiskunde Oefening 1 et gemiddelde van de getallen 1 2, 1 en 1 4 is (A) 1 27 (B) 1 4 (C) 1 (D) 1 6 Juist beantwoord: 81 %. Blanco: 0 %. Oefening
V Kegelsneden en Kwadratische Vormen in R. IV.0 Inleiding
 V Kegelsneden en Kwadratische Vormen in R IV.0 Inleiding V. Homogene kwadratische vormen Een vorm als H (, ) = 5 4 + 8 heet een homogene kwadratische vorm naar de twee variabelen en. Een vorm als K (,
V Kegelsneden en Kwadratische Vormen in R IV.0 Inleiding V. Homogene kwadratische vormen Een vorm als H (, ) = 5 4 + 8 heet een homogene kwadratische vorm naar de twee variabelen en. Een vorm als K (,
Digitale systemen. Hoofdstuk 6. 6.1 De digitale regelaar
 Hoofdstuk 6 Digitale systemen Doelstellingen 1. Weten dat digitale systemen andere stabiliteitsvoorwaarden hebben In deze tijd van digitalisatie is het gebruik van computers in regelkringen alom.denk maar
Hoofdstuk 6 Digitale systemen Doelstellingen 1. Weten dat digitale systemen andere stabiliteitsvoorwaarden hebben In deze tijd van digitalisatie is het gebruik van computers in regelkringen alom.denk maar
94 Samenvatting te vervormen, wordt de huid bijzonder stijf bij grotere vervormingen. Uit onderzoek is gebleken dat deze eigenschap deels toe te schri
 Samenvatting De biofysica kan worden beschouwd als het grensgebied tussen de natuurkunde en de biologie. In dit vakgebied worden natuurkundige methoden gebruikt om biologische systemen te analyseren en
Samenvatting De biofysica kan worden beschouwd als het grensgebied tussen de natuurkunde en de biologie. In dit vakgebied worden natuurkundige methoden gebruikt om biologische systemen te analyseren en
Vrijdag 19 augustus, 9.30-12.30 uur
 EINDEXAMEN VOORBEREIDEND WETENSCHAPPELIJK ONDERWIJS IN 1977 Vrijdag 19 augustus, 9.30-12.30 uur NATUURKUNDE Zie ommezijde Deze opgaven zijn vastgesteld door de commissie bedoeld in artikel 24 van het Besluit
EINDEXAMEN VOORBEREIDEND WETENSCHAPPELIJK ONDERWIJS IN 1977 Vrijdag 19 augustus, 9.30-12.30 uur NATUURKUNDE Zie ommezijde Deze opgaven zijn vastgesteld door de commissie bedoeld in artikel 24 van het Besluit
Technische Universiteit Delft. ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW2030 Vrijdag 30 januari 2015,
 Technische Universiteit Delft Faculteit EWI ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW23 Vrijdag 3 januari 25, 4.-7. Dit tentamen bestaat uit 6 opgaven. Alle antwoorden dienen beargumenteerd
Technische Universiteit Delft Faculteit EWI ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW23 Vrijdag 3 januari 25, 4.-7. Dit tentamen bestaat uit 6 opgaven. Alle antwoorden dienen beargumenteerd
Stelsels differentiaalvergelijkingen
 Stelsels differentiaalvergelijkingen Stelsels homogene differentiaalvergelijkingen We bekijken in deze paragraaf stelsels homogene differentiaalvergelijkingen: x (t x (t x (t x (t x n(t A Voorbeeld x +
Stelsels differentiaalvergelijkingen Stelsels homogene differentiaalvergelijkingen We bekijken in deze paragraaf stelsels homogene differentiaalvergelijkingen: x (t x (t x (t x (t x n(t A Voorbeeld x +
Opdracht 1 bladzijde 8
 Opdrachten Opdracht bladzijde 8 Uit een stuk karton met lengte 45 cm en breedte 8 cm knip je in de vier hoeken vierkantjes af met zijde cm. Zo verkrijg je een open doos. 8 cm 45 cm Hoe groot is het volume
Opdrachten Opdracht bladzijde 8 Uit een stuk karton met lengte 45 cm en breedte 8 cm knip je in de vier hoeken vierkantjes af met zijde cm. Zo verkrijg je een open doos. 8 cm 45 cm Hoe groot is het volume
Hoofdstuk 10: Partiële differentiaalvergelijkingen en Fourierreeksen
 Hoofdstuk : Partiële differentiaalvergelijkingen en Fourierreeksen Partiële differentiaalvergelijkingen zijn vergelijkingen waarin een onbekende functie van twee of meer variabelen en z n partiële afgeleide(n)
Hoofdstuk : Partiële differentiaalvergelijkingen en Fourierreeksen Partiële differentiaalvergelijkingen zijn vergelijkingen waarin een onbekende functie van twee of meer variabelen en z n partiële afgeleide(n)
Tentamen Statistische Thermodynamica MST 19/6/2014
 Tentamen Statistische Thermodynamica MST 19/6/214 Vraag 1. Soortelijke warmte ( heat capacity or specific heat ) De soortelijke warmte geeft het vermogen weer van een systeem om warmte op te nemen. Dit
Tentamen Statistische Thermodynamica MST 19/6/214 Vraag 1. Soortelijke warmte ( heat capacity or specific heat ) De soortelijke warmte geeft het vermogen weer van een systeem om warmte op te nemen. Dit
Bepaling toezichtvorm gemeente Simpelveld
 Bepaling toezichtvorm 2008-2011 gemeente Simpelveld F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, j u n i 2 0 0 8 V e r d i e p i n g s o n d e r z o e k
Bepaling toezichtvorm 2008-2011 gemeente Simpelveld F i n a n c i e e l v e r d i e p i n g s o n d e r z o e k P r o v i n c i e L i m b u r g, j u n i 2 0 0 8 V e r d i e p i n g s o n d e r z o e k
Overgangsverschijnselen
 Hoofdstuk 5 Overgangsverschijnselen Doelstellingen 1. Overgangsverschijnselen van RC en RL ketens kunnen uitleggen waarbij de wiskundige afleiding van ondergeschikt belang is Als we een condensator of
Hoofdstuk 5 Overgangsverschijnselen Doelstellingen 1. Overgangsverschijnselen van RC en RL ketens kunnen uitleggen waarbij de wiskundige afleiding van ondergeschikt belang is Als we een condensator of
Vraag 1. F G = 18500 N F M = 1000 N k 1 = 100 kn/m k 2 = 77 kn/m
 Vraag 1 Beschouw onderstaande pickup truck met de afmetingen in mm zoals gegeven. F G is de massa van de wagen en bedraagt 18,5 kn. De volledige combinatie van wielen, banden en vering vooraan wordt voorgesteld
Vraag 1 Beschouw onderstaande pickup truck met de afmetingen in mm zoals gegeven. F G is de massa van de wagen en bedraagt 18,5 kn. De volledige combinatie van wielen, banden en vering vooraan wordt voorgesteld
Uitwerkingen Mei 2012. Eindexamen VWO Wiskunde B. Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek
 Uitwerkingen Mei 01 Eindexamen VWO Wiskunde B A B C Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek Onafhankelijkheid van a Opgave 1. We moeten aantonen dat F a een primitieve is van de
Uitwerkingen Mei 01 Eindexamen VWO Wiskunde B A B C Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek Onafhankelijkheid van a Opgave 1. We moeten aantonen dat F a een primitieve is van de
: Vermeld op alle bladen van uw werk uw naam. : Het tentamen bestaat uit 3 bladzijden inclusief dit voorblad.
 POST HBO-OPLEIDINGEN Betonconstructeur BV Staalconstructeur BmS Professional master of structural engineering Toegepaste mechanica Materiaalmodellen en niet-lineaire mechanica docent : dr. ir. P.C.J. Hoogenboom
POST HBO-OPLEIDINGEN Betonconstructeur BV Staalconstructeur BmS Professional master of structural engineering Toegepaste mechanica Materiaalmodellen en niet-lineaire mechanica docent : dr. ir. P.C.J. Hoogenboom
Opgave 1: waardering 20 punten... gebruik van MATLAB
 ~e 1 15 o EXAMEN VAKCODE DATUM Mechanische Eigenschappen Biologische Weefsels 4Q530 8 Maart 2000 14.00-17.00 u Bij dit examen mag gebruik worden gemaakt van het diktaat: Mechanical Properties of Living
~e 1 15 o EXAMEN VAKCODE DATUM Mechanische Eigenschappen Biologische Weefsels 4Q530 8 Maart 2000 14.00-17.00 u Bij dit examen mag gebruik worden gemaakt van het diktaat: Mechanical Properties of Living
Polymeren: Structuur en eigenschappen 4A580
 Polymeren: Structuur en eigenschappen 4A580 20 aart 2006 14.00-17.00 uur Dit tentamen bestaat uit 6 vragen met in totaal 20 deelvragen Tijdens het tentamen mag geen gebruik worden gemaakt van notebook,
Polymeren: Structuur en eigenschappen 4A580 20 aart 2006 14.00-17.00 uur Dit tentamen bestaat uit 6 vragen met in totaal 20 deelvragen Tijdens het tentamen mag geen gebruik worden gemaakt van notebook,
De studie van vlakke krommen gegeven in parametervorm. Lieve Lemmens en Andy Snoecx
 De studie van vlakke krommen gegeven in parametervorm Doelstellingen Lieve Lemmens en An Snoecx Deze tekst stelt een voorbeeld van de analyse van een kromme met de Texas TI-NSpire (en/of computersoftware)
De studie van vlakke krommen gegeven in parametervorm Doelstellingen Lieve Lemmens en An Snoecx Deze tekst stelt een voorbeeld van de analyse van een kromme met de Texas TI-NSpire (en/of computersoftware)
Trillingen en geluid wiskundig
 Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Radialen 3 Uitwijking van een harmonische trilling 4 Macht en logaritme 5 Geluidsniveau en amplitude 1 De sinus van een hoek Sinus van een hoek
Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Radialen 3 Uitwijking van een harmonische trilling 4 Macht en logaritme 5 Geluidsniveau en amplitude 1 De sinus van een hoek Sinus van een hoek
Tentamen Statistische Thermodynamica MS&T 27/6/08
 Tentamen Statistische Thermodynamica MS&T 27/6/08 Vraag 1. Toestandssom De toestandssom van een systeem is in het algemeen gegeven door de volgende uitdrukking: Z(T, V, N) = e E i/k B T. i a. Hoe is de
Tentamen Statistische Thermodynamica MS&T 27/6/08 Vraag 1. Toestandssom De toestandssom van een systeem is in het algemeen gegeven door de volgende uitdrukking: Z(T, V, N) = e E i/k B T. i a. Hoe is de
THERMODYNAMICA 2 (WB1224)
 THERMODYNAMICA 2 (WB1224) donderdag 27 januari 2005 14.00-17.00 u. AANWIJZINGEN Het tentamen bestaat uit twee of drie open vragen en 15 meerkeuzevragen. Voor de beantwoording van de meerkeuzevragen is
THERMODYNAMICA 2 (WB1224) donderdag 27 januari 2005 14.00-17.00 u. AANWIJZINGEN Het tentamen bestaat uit twee of drie open vragen en 15 meerkeuzevragen. Voor de beantwoording van de meerkeuzevragen is
TENTAMEN CHEMISCHE THERMODYNAMICA voor F2/MNW2. Vrijdag 23 december 2005
 TENTAMEN CHEMISCHE THERMODYNAMICA voor F/MNW Vrijdag 3 december 005 Bij het tentamen mag gebruik worden gemaakt van een GR. Mogelijk nodige constantes: Gasconstante R = 8.31447 Jmol 1 K 1 = 8.0574 10 L
TENTAMEN CHEMISCHE THERMODYNAMICA voor F/MNW Vrijdag 3 december 005 Bij het tentamen mag gebruik worden gemaakt van een GR. Mogelijk nodige constantes: Gasconstante R = 8.31447 Jmol 1 K 1 = 8.0574 10 L
Niet-lineaire mechanica datum: Algemeen 2 Vraag 1 3 Vraag 2 8 Vraag 3 11 Vraag 4 14 Vraag 5 17 Vraag 6 19
 Naam: Patrick Damen Datum: 17 juni 2003 INHOUDSOPGAVE Algemeen 2 Vraag 1 3 Vraag 2 8 Vraag 3 11 Vraag 4 14 Vraag 5 17 Vraag 6 19 pagina: 1 van 20 Algemeen Om de zestal vragen van de opgave niet-lineaire
Naam: Patrick Damen Datum: 17 juni 2003 INHOUDSOPGAVE Algemeen 2 Vraag 1 3 Vraag 2 8 Vraag 3 11 Vraag 4 14 Vraag 5 17 Vraag 6 19 pagina: 1 van 20 Algemeen Om de zestal vragen van de opgave niet-lineaire
2.1 Twee gekoppelde oscillatoren zonder aandrijving
 Hoofdstuk Twee gekoppelde oscillatoren.1 Twee gekoppelde oscillatoren zonder aandrijving We beschouwen als voorbeeld van een systeem van puntmassa s die gekoppeld zijn aan elkaar en aan twee vaste wanden
Hoofdstuk Twee gekoppelde oscillatoren.1 Twee gekoppelde oscillatoren zonder aandrijving We beschouwen als voorbeeld van een systeem van puntmassa s die gekoppeld zijn aan elkaar en aan twee vaste wanden
1 Het principe van d Alembert
 1 Het principe van d Alembert Gegeven een systeem, bestaande uit n deeltjes, elk met plaatscoördinaat r i en massa m i, i {1,, n}. Uit de tweede wet van Newton volgt onmiddellijk: p i F t i + f i, 1.1
1 Het principe van d Alembert Gegeven een systeem, bestaande uit n deeltjes, elk met plaatscoördinaat r i en massa m i, i {1,, n}. Uit de tweede wet van Newton volgt onmiddellijk: p i F t i + f i, 1.1
Tentamen numerieke analyse van continua I
 Tentamen numerieke analyse van continua I Donderdag 13 november 2008; 14.00-17.00 Code: 8W030, BMT 3.1 Faculteit Biomedische Technologie Technische Universiteit Eindhoven Het eamen is een volledig open
Tentamen numerieke analyse van continua I Donderdag 13 november 2008; 14.00-17.00 Code: 8W030, BMT 3.1 Faculteit Biomedische Technologie Technische Universiteit Eindhoven Het eamen is een volledig open
Experiment DutchBE (Belgium) Dansende korrels - Een model voor fase-overgangen en instabiliteiten
 Q2-1 Dansende korrels - Een model voor fase-overgangen en instabiliteiten (10 punten) Lees de algemene instructies in de aparte enveloppe voor je met het experiment begint. Introductie Fase-overgangen
Q2-1 Dansende korrels - Een model voor fase-overgangen en instabiliteiten (10 punten) Lees de algemene instructies in de aparte enveloppe voor je met het experiment begint. Introductie Fase-overgangen
Inhoud college 4 Basiswiskunde. 2.6 Hogere afgeleiden 2.8 Middelwaardestelling 2.9 Impliciet differentiëren 4.9 Linearisatie
 Inhoud college 4 Basiswiskunde 2.6 Hogere afgeleiden 2.8 Middelwaardestelling 2.9 Impliciet differentiëren 4.9 Linearisatie 2 Basiswiskunde_College_4.nb 2.6 Hogere afgeleiden De afgeleide f beschrijft
Inhoud college 4 Basiswiskunde 2.6 Hogere afgeleiden 2.8 Middelwaardestelling 2.9 Impliciet differentiëren 4.9 Linearisatie 2 Basiswiskunde_College_4.nb 2.6 Hogere afgeleiden De afgeleide f beschrijft
TECHNISCHE UNIVERSITEIT EINDHOVEN FACULTEIT WERKTUIGBOUWKUNDE DIVISIE COMPUTATIONAL AND EXPERIMENTAL MECHANICS
 TECHNISCHE UNIVERSITEIT EINDHOVEN FACULTEIT WERKTUIGBOUWKUNDE DIVISIE COMPUTATIONAL AND EXPERIMENTAL MECHANICS Tentamen Polymeerverwerking (4K550) vrijdag 2 juli 2004, 14:00-17:00. Bij het tentamen mag
TECHNISCHE UNIVERSITEIT EINDHOVEN FACULTEIT WERKTUIGBOUWKUNDE DIVISIE COMPUTATIONAL AND EXPERIMENTAL MECHANICS Tentamen Polymeerverwerking (4K550) vrijdag 2 juli 2004, 14:00-17:00. Bij het tentamen mag
Vergelijkingen met breuken
 Vergelijkingen met breuken WISNET-HBO update juli 2013 De bedoeling van deze les is het doorwerken van begin tot einde met behulp van pen en papier. 1 Oplossen van gebroken vergelijkingen Kijk ook nog
Vergelijkingen met breuken WISNET-HBO update juli 2013 De bedoeling van deze les is het doorwerken van begin tot einde met behulp van pen en papier. 1 Oplossen van gebroken vergelijkingen Kijk ook nog
R e s u l t a a t g e r i c h t h e i d e n c o m p e t e n t i e m a n a g e m e n t b i j d r i e o v e r h e i d s o r g a n i s a t i e s
 R e s u l t a a t g e r i c h t h e i d e n c o m p e t e n t i e m a n a g e m e n t b i j d r i e o v e r h e i d s o r g a n i s a t i e s O p le i d i n g: M a s t e r P u b l i c M a n a g e m e n
R e s u l t a a t g e r i c h t h e i d e n c o m p e t e n t i e m a n a g e m e n t b i j d r i e o v e r h e i d s o r g a n i s a t i e s O p le i d i n g: M a s t e r P u b l i c M a n a g e m e n
Vectoranalyse voor TG
 college 4 en raakvlakken collegejaar : 16-17 college : 4 build : 19 september 2016 slides : 30 Vandaag Snowdon Mountain Railway (Wales) 1 De richtingsafgeleide 2 aan een grafiek 3 Differentieerbaarheid
college 4 en raakvlakken collegejaar : 16-17 college : 4 build : 19 september 2016 slides : 30 Vandaag Snowdon Mountain Railway (Wales) 1 De richtingsafgeleide 2 aan een grafiek 3 Differentieerbaarheid
Wiskundige Technieken 1 Uitwerkingen Hertentamen 2 januari 2014
 Wiskundige Technieken Uitwerkingen Hertentamen januari 4 Normering voor 4 pt vragen (andere vragen naar rato): 4pt 3pt pt pt pt goed begrepen én goed uitgevoerd, eventueel met of onbelangrijke rekenfoutjes
Wiskundige Technieken Uitwerkingen Hertentamen januari 4 Normering voor 4 pt vragen (andere vragen naar rato): 4pt 3pt pt pt pt goed begrepen én goed uitgevoerd, eventueel met of onbelangrijke rekenfoutjes
De trekproef. De trekproef - inleiding. De trekproef - inleiding. De trekproef - inleiding. Principe. Bepalen van materiaaleigenschappen
 De trekproef Principe Materiaal inklemmen tussen klemmen welke met een constante snelheid uit elkaar bewegen Hoe belangrijk is het om materiaaleigenschappen te kennen? Uitvoering: volgens genormaliseerde
De trekproef Principe Materiaal inklemmen tussen klemmen welke met een constante snelheid uit elkaar bewegen Hoe belangrijk is het om materiaaleigenschappen te kennen? Uitvoering: volgens genormaliseerde
MODELBOUW eindopdrachten 6 november 2006
 MODELBOUW eindopdrachten 6 november 2006 Stefan problemen voor het bevriezen van water Als stilstaand water van een bepaalde constante temperatuur T m > 0 in een meer plotseling (zeg op tijdstip t = 0)
MODELBOUW eindopdrachten 6 november 2006 Stefan problemen voor het bevriezen van water Als stilstaand water van een bepaalde constante temperatuur T m > 0 in een meer plotseling (zeg op tijdstip t = 0)
Eindtoets 3BTX1: Thermische Fysica. Datum: 3 juli 2014 Tijd: uur Locatie: paviljoen study hub 2 vak c & d
 Eindtoets 3BTX1: Thermische Fysica Datum: 3 juli 2014 Tijd: 9.00-12.00 uur Locatie: paviljoen study hub 2 vak c & d Deze toets bestaat uit 3 opgaven die elk op een nieuwe pagina aanvangen. Maak de opgaven
Eindtoets 3BTX1: Thermische Fysica Datum: 3 juli 2014 Tijd: 9.00-12.00 uur Locatie: paviljoen study hub 2 vak c & d Deze toets bestaat uit 3 opgaven die elk op een nieuwe pagina aanvangen. Maak de opgaven
3. Beschouw een zeer goede thermische geleider ( k ) in de vorm van een cilinder met lengte L en straal a
 1. Op een vierkantig substraat bevinden zich 4 IC s (warmtebronnen), zoals op de bijgevoegde figuur. Als een van de warmtebronnen een vermogen van 1W dissipeert als warmte (en de andere geen vermogen dissiperen),
1. Op een vierkantig substraat bevinden zich 4 IC s (warmtebronnen), zoals op de bijgevoegde figuur. Als een van de warmtebronnen een vermogen van 1W dissipeert als warmte (en de andere geen vermogen dissiperen),
4. NUMERIEKE INTEGRATIE
 4. NUMERIEKE INTEGRATIE Uit het voorgaande is gebleken dat oppervlakken, volumina, zwaartepunten, statische momenten etc. een belangrijke rol spelen in de beschouwingen aangaande het evenwicht van drijvende
4. NUMERIEKE INTEGRATIE Uit het voorgaande is gebleken dat oppervlakken, volumina, zwaartepunten, statische momenten etc. een belangrijke rol spelen in de beschouwingen aangaande het evenwicht van drijvende
Vraag Antwoord Scores
 maximumscore Bij het consumeren van radioactieve melk is sprake van besmetting omdat het lichaam de ioniserende straling van binnenuit absorbeert / de bron zich in het lichaam bevindt. inzicht dat bij
maximumscore Bij het consumeren van radioactieve melk is sprake van besmetting omdat het lichaam de ioniserende straling van binnenuit absorbeert / de bron zich in het lichaam bevindt. inzicht dat bij
Cover Page. The handle http://hdl.handle.net/1887/32149 holds various files of this Leiden University dissertation.
 Cover Page The handle http://hdl.handle.net/1887/32149 holds various files of this Leiden University dissertation. Author: Renema, Jelmer Jan Title: The physics of nanowire superconducting single-photon
Cover Page The handle http://hdl.handle.net/1887/32149 holds various files of this Leiden University dissertation. Author: Renema, Jelmer Jan Title: The physics of nanowire superconducting single-photon
Een kogel die van een helling afrolt, ondervindt een constante versnelling. Deze versnelling kan berekend worden met de formule:
 Voorbeeldmeetrapport (eenparig versnelde beweging stopwatch en meetlat) Eenparig versnelde beweging stopwatch en meetlat. Doel van de proef Een kogel die van een helling afrolt, voert een eenparig versnelde
Voorbeeldmeetrapport (eenparig versnelde beweging stopwatch en meetlat) Eenparig versnelde beweging stopwatch en meetlat. Doel van de proef Een kogel die van een helling afrolt, voert een eenparig versnelde
VEILIGHEIDSVOORRADEN BEREKENEN
 VEILIGHEIDSVOORRADEN BEREKENEN 4 Soorten berekeningen 12 AUGUSTUS 2013 IR. PAUL DURLINGER Durlinger Consultancy Management Summary In dit paper worden vier methoden behandeld om veiligheidsvoorraden te
VEILIGHEIDSVOORRADEN BEREKENEN 4 Soorten berekeningen 12 AUGUSTUS 2013 IR. PAUL DURLINGER Durlinger Consultancy Management Summary In dit paper worden vier methoden behandeld om veiligheidsvoorraden te
XXX INTERNATIONALE NATUURKUNDE OLYMPIADE PADUA, ITALIË PRACTICUM-TOETS
 XXX INTERNATIONALE NATUURKUNDE OLYMPIADE PADUA, ITALIË PRACTICUM-TOETS 20 juli 1999 13.1 practicum toets ---63 De Torsieslinger In dit experiment bestuderen we een relatief complex mechanisch systeem een
XXX INTERNATIONALE NATUURKUNDE OLYMPIADE PADUA, ITALIË PRACTICUM-TOETS 20 juli 1999 13.1 practicum toets ---63 De Torsieslinger In dit experiment bestuderen we een relatief complex mechanisch systeem een
1 WAAM - Differentiaalvergelijkingen
 1 WAAM - Differentiaalvergelijkingen 1.1 Algemene begrippen Een (gewone) differentiaalvergelijking heeft naast de onafhankelijke veranderlijke (bijvoorbeeld genoteerd als x), eveneens een onbekende functie
1 WAAM - Differentiaalvergelijkingen 1.1 Algemene begrippen Een (gewone) differentiaalvergelijking heeft naast de onafhankelijke veranderlijke (bijvoorbeeld genoteerd als x), eveneens een onbekende functie
Het thermisch stemmen van een gitaar
 Het thermisch stemmen van een gitaar In dit experiment wordt bestudeerd hoe snaarinstrumenten beïnvloed kunnen worden door warmte. Door gebruik te maken van elektriciteit is het mogelijk om instrumenten
Het thermisch stemmen van een gitaar In dit experiment wordt bestudeerd hoe snaarinstrumenten beïnvloed kunnen worden door warmte. Door gebruik te maken van elektriciteit is het mogelijk om instrumenten
1. Orthogonale Hyperbolen
 . Orthogonale Hyperbolen a + b In dit hoofdstuk wordt de grafiek van functies van de vorm y besproken. Functies c + d van deze vorm noemen we gebroken lineaire functies. De grafieken van dit soort functies
. Orthogonale Hyperbolen a + b In dit hoofdstuk wordt de grafiek van functies van de vorm y besproken. Functies c + d van deze vorm noemen we gebroken lineaire functies. De grafieken van dit soort functies
Netwerkdiagram voor een project. AON: Activities On Nodes - activiteiten op knooppunten
 Netwerkdiagram voor een project. AON: Activities On Nodes - activiteiten op knooppunten Opmerking vooraf. Een netwerk is een structuur die is opgebouwd met pijlen en knooppunten. Bij het opstellen van
Netwerkdiagram voor een project. AON: Activities On Nodes - activiteiten op knooppunten Opmerking vooraf. Een netwerk is een structuur die is opgebouwd met pijlen en knooppunten. Bij het opstellen van
5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm
 5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm x y + xy + (x ν )y = met ν R (1) heet een Bessel (differentiaal)vergelijking. De waarde van ν noemt men ook wel de orde
5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm x y + xy + (x ν )y = met ν R (1) heet een Bessel (differentiaal)vergelijking. De waarde van ν noemt men ook wel de orde
Gaap, ja, nog een keer. In één variabele hebben we deze formule nu al een paar keer gezien:
 Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n
 Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n M w. d r s. E. L. J. E n g e l s ( P r o v i n c i e L i m b u r g ) M w. d r s.
Q u i c k -s c a n W M O i n L i m b u r g De e e r s t e e r v a r i n g e n v a n g e m e e n t e n e n c l i ë n t e n M w. d r s. E. L. J. E n g e l s ( P r o v i n c i e L i m b u r g ) M w. d r s.
Om een zo duidelijk mogelijk verslag te maken, hebben we de vragen onderverdeeld in 4 categorieën.
 Beste leerling, Dit document bevat het examenverslag voor leerlingen van het vak natuurkunde havo, tweede tijdvak (2018). In dit examenverslag proberen we een zo goed mogelijk antwoord te geven op de volgende
Beste leerling, Dit document bevat het examenverslag voor leerlingen van het vak natuurkunde havo, tweede tijdvak (2018). In dit examenverslag proberen we een zo goed mogelijk antwoord te geven op de volgende
S a m e nw e r k i n g e n s t r u c t u r e l e f o r m a t i e e x t e r n e v e i l i g h e id E i n d r a p p o r t a g e
 S a m e nw e r k i n g e n s t r u c t u r e l e f o r m a t i e e x t e r n e v e i l i g h e id E i n d r a p p o r t a g e P r o v i n c i e L i m b u r g 23 april 2 0 0 7 D e f i n i t i ef r a p p
S a m e nw e r k i n g e n s t r u c t u r e l e f o r m a t i e e x t e r n e v e i l i g h e id E i n d r a p p o r t a g e P r o v i n c i e L i m b u r g 23 april 2 0 0 7 D e f i n i t i ef r a p p
Niet-lineaire mechanica INHOUD LES 1. Niet-lineair materiaalgedrag: gewapend betonnen wanden en staalprofielen. Niet-lineair raamwerk-element
 INHOUD LES 1 Niet-lineair gedrag van een kabel-element Niet-lineair materiaalgedrag: gewapend betonnen wanden en staalprofielen Niet-lineair raamwerk-element Demonstratie van computerprogramma Dr.Frame
INHOUD LES 1 Niet-lineair gedrag van een kabel-element Niet-lineair materiaalgedrag: gewapend betonnen wanden en staalprofielen Niet-lineair raamwerk-element Demonstratie van computerprogramma Dr.Frame
Aanvullingen bij Hoofdstuk 8
 Aanvullingen bij Hoofdstuk 8 8.5 Definities voor matrices De begrippen eigenwaarde eigenvector eigenruimte karakteristieke veelterm en diagonaliseerbaar worden ook gebruikt voor vierkante matrices los
Aanvullingen bij Hoofdstuk 8 8.5 Definities voor matrices De begrippen eigenwaarde eigenvector eigenruimte karakteristieke veelterm en diagonaliseerbaar worden ook gebruikt voor vierkante matrices los
Eerste orde partiële differentiaalvergelijkingen
 Eerste orde partiële differentiaalvergelijkingen Vakgroep Differentiaalvergelijkingen 1995, 2001, 2002 1 Eerste orde golf-vergelijking De vergelijking au x + u t = 0, u = u(x, t), a ɛ IR (1.1) beschrijft
Eerste orde partiële differentiaalvergelijkingen Vakgroep Differentiaalvergelijkingen 1995, 2001, 2002 1 Eerste orde golf-vergelijking De vergelijking au x + u t = 0, u = u(x, t), a ɛ IR (1.1) beschrijft
13.1 De tweede afgeleide [1]
![13.1 De tweede afgeleide [1] 13.1 De tweede afgeleide [1]](/thumbs/40/20774591.jpg) 13.1 De tweede afgeleide [1] De functie is afnemend dalend tot het lokale minimum; Vanaf het lokale minimum tot punt A is de functie toenemend stijgend; Vanaf punt A tot het lokale maimum is de functie
13.1 De tweede afgeleide [1] De functie is afnemend dalend tot het lokale minimum; Vanaf het lokale minimum tot punt A is de functie toenemend stijgend; Vanaf punt A tot het lokale maimum is de functie
vwo: Het maken van een natuurkunde-verslag vs 21062011
 Het maken van een verslag voor natuurkunde, vwo versie Deze tekst vind je op www.agtijmensen.nl: Een voorbeeld van een verslag Daar vind je ook een po of pws verslag dat wat uitgebreider is. Gebruik volledige
Het maken van een verslag voor natuurkunde, vwo versie Deze tekst vind je op www.agtijmensen.nl: Een voorbeeld van een verslag Daar vind je ook een po of pws verslag dat wat uitgebreider is. Gebruik volledige
Statistiek voor Natuurkunde Opgavenserie 4: Lineaire regressie
 Statistiek voor Natuurkunde Opgavenserie 4: Lineaire regressie Inleveren: Uiterlijk 15 februari voor 16.00 in mijn postvakje Afspraken Overleg is toegestaan, maar iedereen levert zijn eigen werk in. Overschrijven
Statistiek voor Natuurkunde Opgavenserie 4: Lineaire regressie Inleveren: Uiterlijk 15 februari voor 16.00 in mijn postvakje Afspraken Overleg is toegestaan, maar iedereen levert zijn eigen werk in. Overschrijven
