6 Geconjungeerde gradienten

Transcriptie

1 6 GECONJUNGEERDE GRADIENTEN 59 6 Geconjungeerde gradienten Laat A IR n n een symmetrische positief definiete matrix zijn, d.w.z. A T = A en er is een γ > 0 zodat x T Ax γ x T x voor alle x IR n, (6.1) dan is het oplossen van het stelsel vergelijkingen Ax = b voor gegeven b IR n equivalent met het minimaliseren van de functie x F(x) := ( x x) T A ( x x), (6.2) waar x := A 1 b de oplossing is van Ax = b. Omdat A (strikt) positief definiet is, is F positief als x x. De functie F kunnen we ook anders schrijven, F(x) := (A 1 b x) T A (A 1 b x) = x T Ax 2b T x + b T A 1 b. (6.3) Omdat de derde term b T A 1 b constant is heeft deze geen invloed op de argument x dat F minimaliseert en mogen we deze term weglaten. In het vervolg gebruiken we dus de objectfunctie F(x) := x T Ax 2b T x. (6.4) We beschouwen de volge iteratieve algoritme (afdalings- of descentmethode) voor het minimaliseren van F: kies een startvector x 0 ; r 0 := b Ax 0 ; k := 0; while r k 0 do kies afdaalrichting p k en minimaliseer F langs de lijn x k + λp k d.w.z. kies λ k zo dat F(x k +λ k p k ) F(x k +λp k ) voor alle λ; x k+1 := x k + λ k p k ; r k+1 := b Ax k+1 = r k λ k Ap k ; k := k + 1; (6.5) x1 x x 3 x 4 3 Figure 12: Hoogtelijnen van de objectfunctie en opeenvolge iteranden en zoekrichtingen in een afdaalmethode. In deze algoritme kiezen we een beginpunt x 0 en een zoekrichting p 0 en we zoeken het minimum van de functie F langs de lijn x 0 + λp 0. Langs zo n lijn is de functie een eenvoudige parabool, waarvan we het minimum eenvoudig kunnen bepalen. In dit minimum is de functie uiteraard

2 6 GECONJUNGEERDE GRADIENTEN 60 kleiner dan in het startpunt. Dit gaat dan onze volge iterand zijn, van waaruit we de procedure herhalen. In de k-de slag zoeken we dus vanuit x k het minimum van λ F(x k + λp k ). Dit minimum λ k is eenvoudig te bepalen door te differentiëren 0 = d dλ F(x k + λp k ) = 2p T (A(x k + λp k ) b) zodat λ k = pt k (b Ax k) p T k Ap = pt k r k k p T k Ap k (6.6) Als volge iterand kiezen we dan x k+1 := x k + λ k p k. Aangezien we een oplossing van Ax = b zoeken, berekenen we ook het residu r k+1 := b Ax k+1, om te zien hoe ver we van ons doel verwijderd zijn. Voor het residu in (6.5) zijn twee (mathematisch) equivalente formules gegeven, het echte residu b Ax k+1 en het recursieve residu r k λ k Ap k. In de praktijk kan het recursieve residu door afroundfouten op den duur echter sterk van het echte residu gaan afwijken. Voor een zekere keuze van zoekrichtingen is het gedrag van een descentmethode geschetst in figuur 12. We zien, dat de lijn waarlangs we de functie minimaliseren in het minimum precies raakt aan de hoogtelijn (of niveaukromme) van de functie door dit minimum. Deze figuur suggereert, dat de methode wel zal convergeren als we de hoek tussen twee opeenvolge zoekrichtingen niet te klein nemen. Er blijft dus een enorme keuzevrijheid over, die we kunnen gebruiken voor het optimaliseren van de methode. Opgave 1: Bij de methode van Gauss Seidel (relaxatiemethode) splitsen we de matrix A in de diagonaal D, het strikte linksonderstuk L en het rechtsbovenstuk U, zodat A = D + L + U. De algoritme kun je dan op de volge manieren formuleren: kies een startvector y 0 ; v 0 := b U y 0 ; k := 0; while v k v k 1 0 do Los y k+1 op uit (D + L)y k+1 = v k ; v k+1 = b U y k+1 ; k := k + 1; kies een startvector y 0 ; r 0 := b Ay 0 ; k := 0; while r k 0 do Los u k op uit (D + L)u k = r k ; y k+1 := y k + u k ; r k+1 = U u k ; k := k + 1; Omdat D +L een onderdriehoeksmatrix is, kunnen we het stelsel (D +L)y k+1 = r k eenvoudig oplossen met een voorwaartse substitutie. Waarom is D + L niet singulier? Laat zien dat dit een descentmethode is, waarin de zoekrichtingen cyclisch de verzameling basisvectoren {e k k = 1 n} met (e j ) i = δ ij (Kroneckers delta) doorlopen: p k := e j(k) met j(k) = 1 + k mod n; als {x k } de rij iteranden is van de descentmethode (6.5) met startvector x 0 := y 0, dan geldt waar y j,i de i-de component is van y j. x nj+i = (y j+1,1,, y j+1,i, y j,i+1,, y j,n ) T In de gradiëntmethode kiezen we vanuit x k als zoekrichting de richting waarin de objectfunctie F het snelst daalt. Dit is de richting van de gradiënt, dus (6.7) p k = F x=xk = 2(b Ax k ) = 2r k. (6.8) De algoritme heeft dan de vorm: kies een startvector x 0 ; r 0 := b Ax 0 ; k := 0; while r k 0 do λ k = rt k r k r T k Ar ; {minimum langs afdaalrichting r k } k x k+1 := x k + λ k r k ; r k+1 := b Ax k+1 = r k λ k Ar k ; k := k + 1; (6.9)

3 6 GECONJUNGEERDE GRADIENTEN 61 De zoekrichting in k-de stap is in dit geval dus de richting van het residu r k. Vanwege de minimalisatie in de vorige (k 1 ste) stap is de afgeleide van F in x k in de richting r k 1 = p k 1 gelijk aan nul, zodat de nieuwe zoekrichting loodrecht staat op de vorig. Geconjungeerde zoekrichtingen. Bij de gradientmethode kiezen we, om vanuit x k de volge benadering te berekenen, als zoekrichting p de richting van de gradient, omdat F in die richting het snelst daalt (althans in x k ). De richting p is dus zo, dat F F(x k + tp) F(x k ) = lim = ( F)T p = 2(b Ax k) T p p x=xk t 0 t p p p (6.10) maximaal is. Hieruit volgt inderdaad, dat de maximalisere richting gelijk is aan de gradient van F in x k en dus loodrecht staat op het niveau-oppervlak {x IR n F(x) = F(x k )} van F door x k. Nu zijn deze niveau-oppervlakken in het algemeen ellipsoiden en geen bollen. De normaal in x k zal dus in het algemeen niet door het minimum van F gaan, tenzij x k een heel speciaal punt is. Alleen bij een bol gaat iedere normaal door het middelpunt. Alleen als de niveauoppervlakken bollen zijn hebben we aan één iteratie genoeg om het minimum van F te bepalen. Er is één metriek waarin de niveauoppervlakken van F bollen zijn en deze is gegeven door x x A := x T Ax met bijbehore bilineaire vorm (x, y) A x T Ay. (6.11) Omdat A symmetrisch en positief definiet is, is deze metriek niet gedegenereerd en is de bijbehore bilineaire vorm een inproduct in IR n. Uit (6.10) volgt dan dat de optimale zoekrichting t.o.v. deze metriek de richting is die de functionaal p 2(b Ax k) T p p T Ap maximaliseert. Deze wordt dus gegeven door p = A 1 (b Ax k ), maar hiervoor moeten we een stelsel van de vorm Ax = b oplossen. De steilste helling in de metriek (6.11) is dus niet te bepalen. We weten echter wel, dat deze steilste helling ligt in het (hyper-)vlak dat in x k A-loodrecht (in de zin van 6.11) staat op de vorige zoekrichting p k 1 en dat het gezochte minimum ook in dit loodvlak ligt. Dit betekent, dat we de verdere zoekactie kunnen beperken tot dit loodvlak en dus tot een deelruimte van kleinere dimensie. Als we de zoekrichting p k niet alleen A-loodrecht op de vorige zoekrichting maar op alle voorgaande zoekrichtingen kiezen, en dus als p T k Ap j = 0, j = 0,, k 1, (6.12) dan wordt de dimensie van de ruimte, waarin we het minimum zoeken, in iedere slag met één verlaagd, zodat we na n slagen het minimum gevonden hebben. Een stelsel vectoren {p 0,, p n 1 }, dat aan relatie (6.12) voldoet, heet een A-geconjungeerd stelsel. Aangezien A symmetrisch en positief definiet is, vormt een dergelijk stelsel vectoren een basis in IR n. Dit is het idee achter de stelling, dat algoritme (6.5) in hooguit n slagen naar de oplossing van Ax = b convergeert, als we achtereenvolgens de vectoren van het A-geconjungeerde stelsel {p 0,, p n 1 } als zoekrichtingen kiezen. Een preciese formulering van deze stelling is de volge: Stelling 6.1 Zij A IR n n een symmetrische positief definiete matrix, zij {p 0,, p n 1 } een A-geconjungeerd stelsel vectoren en zij x 0 IR n een willekeurige startvector voor de algoritme r 0 := b Ax 0 ; k := 0; while r k > 0 do λ k := pt k r k p T k Ap ; {minimum langs afdaalrichting p k } k x k+1 := x k + λ k p k ; r k+1 := b Ax k+1 = r k λ k Ap k ; k := k + 1;. (6.13)

4 6 GECONJUNGEERDE GRADIENTEN 62 Dan is de laatste iterand x k de gezochte oplossing van het stelsel vergelijkingen Ax = b. Bewijs: Laat x de oplossing zijn van Ax = b. Daar het stelsel {p 0,, p n 1 } een basis in IR n is, kunnen we x x 0 op unieke wijze schrijven als een lineaire combinatie van deze basisvectoren, Bijgevolg geldt: en dus vinden we x x 0 = x x 1 = n 1 i=0 n 1 i=1 α i p i en dus r 0 := b Ax 0 = A( x x 0 ) = λ 0 = pt 0 r 0 p T 0 Ap 0 = n 1 i=0 α i p T 0 Ap i p T 0 Ap 0 = α 0 α i p i {u IR n u T Ap 0 = 0} en r k = Analoog vinden we in alle stappen van de algoritme λ k = α k, x x k = en r k = n 1 i=k n 1 i=k n 1 i=k n 1 i=0 α i p i {u IR n u T Ap j = 0, j = 0 k 1} α i Ap i p j (j = 0 k 1). α i Ap i. (6.14) α i Ap i p 0. (6.15) Het is mogelijk, dat algoritme (6.13) stopt na minder dan n stappen, maar het residu is na n stappen zeker gelijk aan nul en als het residu nul is, dan is de bijbehore x k gelijk aan de oplossing x. Opmerking 6.2 : Uit (6.15) zien we dat x x k A-loodrecht staat op alle voorgaande zoekrichtingen, zoals al eerder opgemerkt, en dat r k (gewoon) loodrecht staat op alle voorgaande zoekrichtingen. We kunnen dus ook zeggen, dat de minimalisatie van F(x k + λp k ) in de k-de slag niet alleen het minimum geeft op de lijn door x k parallel aan p k, maar zelfs in de gehele affiene deelruimte (of lineaire variëteit) door x 0 parallel aan vect{p 0,, p k }. Met een A-geconjungeerd stelsel zoekrichtingen wordt de iteratieve methode (6.5) dus eindig. Als we daarbij echter het gehele A-geconjungeerde stelsel vooraf zouden moeten uitrekenen en in het geheugen moeten bewaren, dan zou de methode minstens zoveel tijd en geheugenruimte nodig hebben als een direkte methode zoals Gauss-eliminatie. Uit de algoritme zien we echter dat we de zoekrichting p k pas in de k+1 ste slag nodig hebben en dat we dus de keuze kunnen uitstellen tot deze slag. De enige beperking bij deze keuze is, dat p k A-loodrecht moet staan op alle voorgaande zoekrichtingen. De vraag is nu of we zo n zoekrichting kunnen vinden met weinig werk, en dus zonder alle orthogonalisaties expliciet uit te voeren. In (6.15) zagen we, dat r k (gewoon) loodrecht op alle voorgaande zoekrichtingen {p 0,, p k 1 } staat; we zullen laten zien, dat we een collectie zoekrichtingen kunnen vinden die zo is, dat r k ook A-loodrecht staat op al de voorgaande zoekrichtingen. Als we zo n collectie hebben, dan hoeven we r k slechts A-loodrecht op p k te zetten om een A-geconjungeerde zoekrichting te vinden voor de k+1 ste slag; we kiezen dan p k+1 := r k+1 rt k+1 Ap k p T k Ap k p k ( 0 als r k+1 0, omdat p k r k+1 ). (6.16) Veronderstel dat λ j 0 als j < k. (d.w.z. veronderstel r j 0). Uit (6.13) zien we dan r j+1 = r j λ j Ap j zodat Ap j = 1 λ j (r j r j+1 ). (6.17)

5 6 GECONJUNGEERDE GRADIENTEN 63 Voor het inproduct met r k vinden we dan r T k Ap j = 1 λ j r T k (r j r j+1 ). (6.18) Als r j een lineaire combinatie van {p 0,, p j } is, dan is het rechterlid van (6.18) nul voor j = 0,, k 1, omdat volgens (6.15) r T k p i = 0 voor i = 0,, k 1. Als we de keuze (6.16) in iedere stap hebben gedaan, is aan deze voorwaarde automatisch voldaan. Bovien impliceert deze keuze, dat r k = 0 en x k = x als λ k = 0, immers uit de definitie van λ k in (6.13) en de keuze (6.16) zien we: λ k = pt k r k p T k Ap k = rt k r k p T k Ap k omdat het inproduct p T k 1 r k = 0 volgens (6.15); λ k = 0 impliceert dus dat r k nul is en dat we de oplossing hebben gevonden. De afdalingsmethode (6.5) met zoekrichtingen gegeven door (6.16) heet de methode der geconjungeerde gradienten (Conjugate Gradients in het Engels). De algoritme luidt alsvolgt: Kies startvector x 0 ; r 0 := b Ax 0 ; k := 0; while r k > 0 do if k = 0 then p 0 := r 0 else µ k := rt k Ap k 1 p T k 1 Ap k 1 = r k 2 r k 1 2 ; p k := r k + µ k p k 1 ; λ k := pt k r k p T k Ap = r k 2 k p T k Ap ; x k+1 := x k + λ k p k ; k (c) r k+1 := b Ax k+1 = r k λ k Ap k ; (d) k := k + 1;. (a) (b) (6.19) Stelling 6.3 Zij A IR n n een symmetrische positief definiete matrix en zij x 0 IR n een willekeurige startvector voor de algoritme (6.19) dan is er m n zodat r m = 0 en x m = x. Bewijs: Een bewijs is hierboven gegeven; we zetten de elementen nog eens op een rijtje. Als k = 0 en r 0 0 dan maken we in (a) de vector p 0 = r 0 0 zodat r 0 vect{p 0 }. In (c d) vinden we dan λ 0 = r T 0 r 0/r T 0 Ar 0 0, x x 1 A {p 0 } en r 1 {p 0 }. Als k > 0 en r k 0 en als (bij inductieaanname) geldt: i. λ j 0 voor j = 0 k 1, ii. {p 0,, p k 1 } is een A-geconjungeerd stelsel, iii. vect{p 0,, p j } = vect{r 0,, r j } = K j+1 (A,r 0 ) := vect{r 0, Ar 0,, A j r j } voor j = 0 k 1, waar K k (A,r 0 ) de k-de Krylovruimte van A en r 0 genoemd wordt. iv. x x k A {p 0,, p k 1 } en r k {p 0,, p k 1 }, dan volgt in (b), dat p k 0 omdat r k p k 1 en dat bij constructie p k A-loodrecht staat op p k 1. Omdat λ j r T k Ap j = r T k (r j+1 r j ) = 0 voor j = 0 k 2 (zie 6.18), staat p k ook A-loodrecht op alle voorgaande zoekrichtingen, zodat {p 0,, p k } weer een A-geconjungeerd stelsel is met vect{p 0,, p k } = vect{r 0,, r k }. In (c-d) volgt tenslotte, dat x x k+1 A {p 0,, p k } en r k+1 {p 0,, p k }. Na hoogstens n slagen is het residu nul en is de oplossing bereikt.

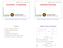
6 6 GECONJUNGEERDE GRADIENTEN 64 Opgave 2: Laat zien, dat we de getallen λ k en µ k in (6.19) ook kunnen berekenen met rt k r k λ k := p T k Ap k en µ k := rt k r k r T k 1 r. (6.20) k 1 Tesamen met de twee manieren om het residu (wel of niet recursief) geeft dit 8 (analytisch) equivalente manieren om de algoritme te implementeren. Bepaal voor ieder van deze manieren de hoeveelheid werk in termen van aantallen matrix-vector vermenigvuldigingen, inproducten en vector-updates (van de vorm x := x + αy). Deze algoritme, geïntroduceerd door Hestenes en Stiefel [1], geeft in theorie dus een eindige methode om de oplossing van Ax = b te berekenen. Deze methode is vooral geschikt voor ijle matrices, d.w.z. matrices waarvan de meeste elementen nul zijn zodat een matrix-vector vermenigvuldiging veel minder dan O(n 2 ) flops vraagt. Helaas is de eindigheid van de algoritme niet bestand tegen de eindige precisie van een computer. Door afrondfouten staat de bereke vector p k niet exact A-loodrecht op al zijn voorgangers. De afwijking t.o.v. de loodrechte stand tussen p k en p j wordt groter naarmate het verschil k j groter wordt. Figure 13: Het trampolinerooster met 8 knopen horizontaal en 6 verticaal. De randknopen zijn vast. Rond knoop (4,3) is het gebied geschetst waarvan de totale massa op deze knoop drukt. Voorbeeld: We willen de vorm van een trampoline (of bedspiraal) met afmetingen l b berekenen, als we deze belasten met een gewicht g(x, y) (per oppervlakte-eenheid). Modelleer de trampoline als een rechthoekig array van m n knopen, verbonden door veren van lengte h, zie fig. 13, zodat dus l = mh en b = nh. We kunnen de verticale kracht F i,j op knoop (i, j) schrijven als de som van de verticale krachten langs de vier veren. Deze krachten zijn evenredig met het hoogteverschil, zodat F i,j = S(u i,j 1 u i,j ) + S(u i,j+1 u i,j ) + S(u i 1,j u i,j + S(u i+1,j u i,j ), als u i,j de verticale uitwijking is in knoop (i, j), S de veerconstante is en als de verschillen in de uitwijkingen klein zijn t.o.v. h. Omdat de verticale kracht F i,j op knoop (i, j) evenredig is met het gewicht dat op een elementair vierkantje drukt en dus (ongeveer) evenredig is met h 2 maal g(ih, jh) vinden we de (benadere) vergelijking u i,j 1 + u i,j+1 + u i 1,j + u i+1,j 4u i,j = h2 g i,j S De rand van de trampoline zit vast, zodat met 0 < i < m en 0 < j < n. (6.21) u 0,j = u m,j = u i,0 = u i,n = 0.

7 6 GECONJUNGEERDE GRADIENTEN 65 In de andere punten van het rooster vinden we (n 1)(m 1) vergelijkingen voor evenveel onbeken. We ordenen de (niettriviale) onbeken en de bijbehore rechterleden in vectoren van lengte (m 1)(n 1), en stellen de bijbehore matrix op. Ga na, dat in het geval (m, n) = (5, 4) en lexicografische ordening van de knopen (begin linksonder en doorloop eerst alle knopen met dezelfde y-waarde) de matrix de volge vorm heeft: Dit is een typisch voorbeeld van een ijle matrix. Per rij zijn er hoogstens vijf elementen ongelijk aan nul, zodat een matrix-vectorvermenigvuldiging hoogstens 5(m 1)(n 1) flops vraagt als we voor deze matrix-vector vermenigvuldiging een routine schrijven die rekening houdt met de speciale vorm. Dit voorbeeld kan worden opgelost met de methode de geconjungeerde gradienten. In figuur 14 zijn de residunormen getek als functie van de iteratie-index. We zien dat het residu al tot de machineprecisie is gereduceerd lang voor het theoretische einde van het proces. We zien ook dat het echte residu (zoals verwacht) rond de machineprecisie blijft hangen terwijl het recursieve residu gewoon verder daalt en kennelijk geen relatie meer heeft met het echte residu. Ook zien we dat de A-orthogonaliteit van p 0 en p k met het klimmen van k volledig verdwijnt. De conclusie die we hieruit kunnen trekken is, dat CG niet moet worden gebruikt als direkte methode, maar als iteratieve, die na een aantal slagen, dat veel kleiner is dan de dimensie van het probleem, al een goede benadering van de oplossing geeft. Het was Reid [3] die als eerste in 1971 hierop wees. Opgave 3: Laat U k het k-de Chebyshev polynoom van tweede soort zijn (zie syllabus 7.c opgave 3). Laat zien dat de vector met componenten u k,j := U k 1 (ξ)u j 1 (η) een eigenvector is van de matrix in het linkerlid van (6.21) behor bij de eigenwaarde 2ξ + 2η 4, als ξ een nulpunt is van U m 1 en η een nulpunt van U n 1, en dat bijgevolg het conditiegetal (t.o.v. de Euklidische norm) van de matrix gelijk is aan κ 2 = 2 + cos π m + cos π n 2 cos π m cos π n 4n2 π 2 als n = m (6.22) Geconjungeerde gradienten als iteratieve methode. Om Geconjungeerde gradienten te kunnen vergelijken met andere iteratieve methoden herschrijven we (6.19) door de vectoren p k te elimineren met gebruik van (6.17): r k+1 = r k λ k Ap k = r k λ k A(r k + µ k p k 1 ) = r k λ k Ar k + λ kµ k λ k 1 (r k r k 1 ) zodat we effectief de drietermsrecursierelatie vinden: ( r k+1 = 1 + λ ) kµ k λ k A r k λ kµ k r k 1. (6.23) λ k 1 λ k 1 Als we de rij polynomen {p k } definiëren door de drietermsrecursie ( p k+1 (x) := 1 λ ) kµ k λ k x p k (x) + λ kµ k p k 1 (x) (k 2), λ k 1 λ k 1 p 0 (x) := 1 en p 1 (x) := 1 λ 0 x, (6.24)

8 6 GECONJUNGEERDE GRADIENTEN 66 residu-norm van Jacobi en CG voor nxn vierkant, n = cos v/d hoek tussen p(k) en p(0) bij echt residu Jacobi residu norm Chebyshev bovengrens cos v/d hoek tussen p(k) en p(0) bij recursief residu echt iteratie index Figure 14: Het oplosproces voor het stelsel vergelijkingen (6.21) met n = m = 41 zodat de dimensie van de oplosruimte 1600 is. Als functie van de iteratie-index zijn uitgezet: de norm van het residu van Jacobiiteratie en de normen van de residuen van geconjungeerde gradienten met echt met recursief residu. Voor beide varianten is ook de absolute waarde van de cosinus van de A-hoek tussen p 0 en p k uitgezet. dan geldt voor iedere k (ga na!): Op dezelfde manier elimineren we p k uit x k : r k = p k (A)r 0 en p k (0) = 1. (6.25) x k+1 = x k + λ k p k = x k + λ k (r k + µ k p k 1 ) = x k + λ k (b Ax k ) + λ kµ k λ k 1 (x k x k 1 ), x k+1 x = x k x λ k (Ax k A x) + λ kµ k λ k 1 ((x k x) (x k 1 x)) = p k (A)(x 0 x) = x 0 x + (p k (A) 1)A 1 A(x 0 x) = x 0 x + (1 p k (A))A 1 r 0. We vinden zo een polynoom q k van graad k 1 waarvoor geldt: x k+1 = x 0 + q k (A)r 0 met q k (x) := 1 p k(x) x We herschrijven de CG-algoritme (6.19) hiermee formeel alsvolgt: kies een startvector x 0 ; r 0 := b Ax 0 ; k := 0; while r k 0 do x k+1 := x 0 + q k (A)r 0 ; r k+1 := p k+1 (A)r 0 ; k := k + 1;. (6.26) (6.27)

9 6 GECONJUNGEERDE GRADIENTEN 67 We zien uit (6.25) dat r k en x k+1 x 0 elementen zijn van de k-de Krylov-ruimte S k van A en r 0 die opgespannen wordt door de vectoren r 0 A k r 0, S k := vect{r 0, Ar 0, A 2 r 0,, A k r 0 } (6.28) Ter vergelijking beschouwen we een ander proces in diezelfde Krylov-ruimte, successieve substitutie. We schrijven Ax = b als x = x + b Ax, we kiezen een startvector x 0 en de iteratie x n+1 = x n + b Ax n. Het residu is dan r n := b Ax n en r n+1 r n = Ax n+1 Ax n = Ar n. Alles bijeen vinden we dus: kies een startvector x 0 ; r 0 := b Ax 0 ; k := 0; while r k 0 do x k+1 := x k + r k ; r k+1 := (1 A)r k ; k := k + 1; We zien, dat r k := (1 A) k r 0 = p k (A)r 0 en k 1 x k = x 0 + r r k 1 = x 0 + (1 A) j r 0 = x 0 + (1 (1 A) k )A 1 r 0 = x 0 + q k (A)r 0, j=0 (6.29) met p k (x) := (1 x) k en q k (x) := (1 p k (x))/x. Deze methode heeft zo dus dezelfde vorm als (6.27). Convergentie treedt op als lim k (1 A) k = 0 in een of andere matrixnorm, d.w.z. als de absolute waarden van alle eigenwaarden van A strikt kleiner dan 1 zijn. Analoog aan Cesaro-sommatie kunnen we de door (6.29) voortgebrachte rij {x k } omzetten in een nieuwe rij {y k }, die sneller naar x convergeert, door voor y k een geschikte lineaire combinatie van {x 0 x k } te nemen, k y k := γ kj x j j=0 met k γ kj = 1. j=0 Als x 0 = x, dan geldt x k = x voor alle k; wegens de voorwaarde k j=0 γ kj = 1 geldt dan ook y k = x. Voor het residu s k := b Ay k betekent de voorwaarde op de som: k k k k s k := b γ kj Ax j = γ kj A( x x j ) = γ kj r j = γ kj (1 A) j r 0 =: π k (A)r 0, j=0 j=0 j=0 j=0 waar π k := k j=1 γ kj p j opnieuw een polynoom van graad k is dat voldoet aan π k (0) = 1 voor alle k vanwege de somconditie k j=0 γ kj = 1. We vinden analoog aan (6.26) het geassocieerde polynoom ϕ k waarvoor y k voldoet aan de relatie k k y k = x 0 + γ kj (x j x 0 ) = x 0 + γ kj q j (A)r 0 = x 0 + ϕ k (A)r 0 als ϕ k (x) := 1 π k(x) x j=0 j=1 Zonder referentie naar de oorspronkelijke rij {x k } kunnen we de recursie voor de nieuwe rij {y k } dan analoog aan (6.27) herschrijven als: kies een startvector y 0 ; r 0 := b Ay 0 ; s 0 := r 0 ; k := 0; while r k 0 do y k+1 := y 0 + ϕ k (A)r 0 ; s k+1 := π k+1 (A)r 0 ; k := k + 1;. (6.30)

10 6 GECONJUNGEERDE GRADIENTEN 68 De enige eis voor convergentie van (6.30) is: lim k π k (A) = 0. Voor iedere matrix A is er zo n rij polynomen te vinden, kies bijvoorbeeld alle p k met k n gelijk aan het karakteristieke polynoom Π A van A, dan geldt automatisch p k (A) = 0 (k n), zie (6.31). De constructie van het karakteristieke polynoom van A (voor grote n) en in het algemeen ook van een rij polynomen waarvoor (6.30) convergent is, is echter geen eenvoudige opgave. Voor het geval dat A symmetrisch en positief definiet is, hebben we echter zo n methode gevonden, nl. geconjungeerde gradienten (6.19). Zoals in (6.27) aangetoond, construeert deze methode (impliciet) een rij polynomen {p k }, waarvoor het schema (6.30) convergeert in eindig veel stappen. Bovien is deze methode optimaal. De geconjungeerde-gradientenmethode kiest in de k-de slag het polynoom p k zo, dat de functionaal x F(x) geminimaliseerd wordt in de ruimte x 0 +K k (A,r 0 ) (zie opmerking 6.2). Omdat voor het residu van CG geldt, dat r k = p k (A)r 0 K k+1 (A,r 0 ) en r k K k (A,r 0 ) (zie 6.15), is dit equivalent met minimalisatie van (A)r 0 over alle polynomen van graad k + 1 met (0) = 1. Het residu van CG is in iedere stap dus kleiner dan het residu verkregen met een andere iteratieve methoden van de vorm (6.30). Vegelijking CG met Chebyshev iteratie: We willen de convergentiesnelheid van CG schatten, dus we wensen een (goede) bovengrens te vinden voor de norm van het residu r k = p k (A)r 0 van CG. Als A een symmetrische matrix is dan heeft deze een eigenwaardeontbinding A = U Λ U 1, U = (u 1 u n ) en Au k = λ k u k (6.31) waarin Λ = diag(λ 1,, λ n ) een diagonaalmatrix is bestaande uit de eigenwaarden van A en waarin U een orthogonale matrix is, waarvan de kolommen de eigenvectoren zijn. Als p een polynoom is, dan geldt p(a) = U p(λ) U 1 met p(λ) = diag(p(λ 1 ),, p(λ n )). Als r 0 = n i=1 α i u i, dan is p(a)r 0 2 = n i=1 α 2 i p(λ i) 2. Een bovengrens voor deze norm hangt dus uitsluit af van de de waarden van het polynoom p op de eigenwaarden (het spectrum) van A. Om een bovengrens voor de norm van het residu p k (A)r 0 in de CG-methode te vinden zouden we de eigenwaarden van A moeten kennen en de waarden van p k op deze eigenwaarden. Dat is onbegonnen werk. We weten echter wel, dat CG optimaal is en dat dus iedere andere serie polynomen een grotere bovengrens geeft. Bovien weten we, dat A positief definiet is, zodat haar eigenwaarden in een interval 0 < a λ j (A) b liggen. We kunnen dan een bovengrens vinden met een rij polynomen die uniform klein zijn op het interval [a, b]. De optimale polynomen hiervoor zijn de Chebyshev polynomen. Het k-de Chebyshev polynoom is gedefinieerd door zodat T k voldoet aan de recurrente betrekking T k (cos t) := cos kt (6.32) T 0 = 1, T 1 (x) = x en T k+1 (x) + T k 1 (x) = 2xT k (x) voor k > 0. (6.33) De functie t cos kt heeft op het interval [0, π] precies k + 1 maxima en minima met waarden om en om +1 en 1. Aangezien de afbeelding t cos t het interval [0, π] een-euidig op [ 1, 1] afbeeldt, heeft T k dezelfde eigenschap op [ 1, 1]. Voor T k geldt de minimax eigenschap: Stelling 6.4 Als P een polynoom van graad k is met P(µ) = T k (µ) voor een zekere µ, µ > 1, dan geldt max P(x) max T k(x) 1. (6.34) 1 x 1 1 x 1

11 6 GECONJUNGEERDE GRADIENTEN 69 Bewijs: Stel P(x) γ < 1, dan kruist de grafiek van P die van T k minstens k maal, omdat T k k maal van +1 naar 1 gaat en terug en P tussen γ en γ blijft. P T k heeft dus (minstens) k nulpunten binnen het open interval ( 1, 1) en ook nog een er buiten (nl. µ). Omdat het een polynoom van graad k is, moet deze identiek nul zijn. Het optimale polynoom voor een uniform kleine bovengrens op [a, b] is dus Voor een bovengrens op [a, b] bewijzen we het volge lemma: Lemma 6.5 Als x > 1, dan geldt: k(x) := T k ( a + b 2x )/T k ( a + b b a b a ) (6.35) 1 2 (x + x 2 1) k T k (x) (x + x 2 1) k. (6.36) Bewijs: De oplossing van de recurrente betrekking (6.33) heeft de vorm T k (x) = αλ k 1 (x) + βλk 2 (x) waar λ 1,2 de wortels zijn van de karakteristieke vergelijking λ 2 2xλ + 1 = 0, zodat Omdat λ 1 = x + x 2 1 en λ 2 = x x = T 0 = α + β en x = T 1 (x) = α(x + x 2 1) + β(x x 2 1) volgt α = β = 1 2. Bijgevolg vinden we 1 2 (x + x 2 1) k T k (x) = 1 2 (x + x 2 1) k (x x 2 1) k (x + x 2 1) k. De teller in k is begrensd door 1 als x [a, b]. Met behulp van lemma 6.5 vinden we dus de schatting (b max k(x) 2 b + a ) k ( + a 2 ) k a x b b a a/b = 2 b a 1 + (6.37) a/b Als we a = λ min en b = λ max kiezen dan is κ := b/a het conditiegetal van de matrix (t.o.v. de Euclidische norm). Zo vinden we tenslotte: Stelling 6.6 Voor het residu van de geconjungeerde-gradientenmethode (6.19), geldt de volge schatting: ( ) k 1 1/κ r k 2 r (6.38) 1/κ waar κ het conditiegetal van A is. De Ritz-waarden We keren nu terug naar de drieterms-recursierelatie (6.23) en formuleren deze als Ar 0 = β 0 r 0 + α 1 r 1 en Ar k = α k+1 r k+1 + β k r k + γ k r k 1 (k 1) (6.39) met β 0 = α 1 := 1 λ 0, α k+1 := 1 λ k, γ k := µ k λ k 1 en β k := α k+1 γ k, voor k 1.

12 6 GECONJUNGEERDE GRADIENTEN 70 Als we alle residuen in de matrix R k := (r 0 r 1 r k 1 ) plaatsen en met T k de volge tridiagonale matrix aanduiden, β 0 γ 1 α 1 β 1 γ 2. α T k := , (6.40) γk 1 α k 1 β k 1 vinden we de relaties A R k = R k T k + α k r k e T k+1 en R T k A R k = T k. (6.41) De tweede relatie volgt uit het feit, dat r k loodrecht op de kolommen van de matrix R k staat. T k is dus de restrictie van A tot de tot de k-de Krylov-ruimte opgespannen door de residuen {r 0,, r k 1 }, te noteren met K k (A;r 0 ). Deze residuen vormen tesamen een orthogonale basis. De eigenwaarden van T k heten de Ritz-waarden van A met betrekking tot deze Krylov-ruimte. Opgave 4: Ga na dat de hoofddiagonaal van T k positief is, dat de neviagonalen negatief zijn en dat T k dus altijd omgezet kan worden in een symmetrische tridiagonale matrix door vermenigvuldiging met een diagonale matrix van links en met de inverse ervan van rechts. Laat ook zien dat voor alle k 1 de volge insluiting geldt van minimale en maximale eigenwaarden: λ min (A) λ min (T k ) λ min (T k 1 ) λ max (T k 1 ) λ max (T k ) λ max (A). (6.42) Aangezien ook {r 0,, A k 1 r 0 } ook een basis vormt van de k-de Krylovruimte (ga na!), bevat deze ruimte voor grote k dus een goede benadering van de eigenvector(en) van de grootste eigenwaarde(n) van A (en ook van de kleinste!). Als k voldo groot is (maar nog veel kleiner dan n), zullen de grootste en kleinste eigenwaarden van T k dus goede benaderingen geven van de grootste en kleinste eigenwaarden van A. De eigenwaarden van T k kunnen snel bepaald worden met QR-iteratie, Jacobi-iteratie of met speciale met bisectiemethoden voor (symmetrische) tridiagonale matrices. Deze combinatie van tridiagonalisatie in een Krylovruimte en de bepaling van de eigenwaarden van de (benadere) tridiagonaalmatrix heet de algoritme van Lanczos [2]. Het zal duidelijk zijn dat ook deze methode in de praktijk zwaar te lijden heeft onder de opbouw van afrondfouten. Desondanks kan de methode betrouwbaar geïmplementeerd worden voor de benadering van de extreme (grote en kleine) eigenwaarden van een symmetrische matrix. Als de eigenvectoren van de grootste en kleinste eigenwaarden van A goed benaderd worden in de Krylovruimte, mag je verwachten, dat de componenten van de CG-residu s in deze richtingen ook klein zullen zijn. Dus ook het bijbehore polynoom p k in (6.24) zal klein zijn op deze delen van het spectrum van A. Dat betekent, dat de convergentie op den duur veel sneller zal gaan dan de (pessimistische) bovengrens (6.38) verkregen door vergelijking met Chebyshev iteratie. We zien dit ook in fig. 14, waar de rechte met de kleinste helling de theoretische bovengrens voor de snelheid van Chebyshev iteratie geeft (met κ 2 = λ max /λ min ) en waarbij de andere rechte de helling geeft op grond van een κ die het quotient is van de op een na grootste en de op een na kleinste eigenwaarden van A. We zien in de figuur, dat het residu inderdaad steeds sneller afneemt, naarmate k groter wordt. Preconditionering We kunnen proberen de CG-iteratie te versnellen door de (uiterste) eigenwaarden van A dichter bij elkaar (en verder van nul) te brengen door A met een geschikte matrix te vermenigvuldigen. We kunnen een matrix P zoeken, een preconditioner genaamd, zodat λ max (PAP)/λ min (PAP) λ max (A)/λ min (A).

13 6 GECONJUNGEERDE GRADIENTEN 71 Het resultaat is dan weer een symmetrische matrix, waarop we de CG-algoritme kunnen toepassen als tevoren. Eenvoudiger wordt het echter, als we bedenken, dat we tot nu toe het standaard inproduct x T y gebruikt hebben zonder enige specifieke eigenschap ervan te gebruiken. We hadden evengoed het inproduct x, y := x T K y met een geschikte symmetrische positief definiete matrix K. Het is eenvoudig te verifiëren, dat K 1 A symmetrisch en positief definiet is t.o.v. dit nieuwe inproduct. We kunnen de reeds afgeleide CG-algoritme dus geheel volgen voor het oplossen van het gepreconditioneerde systeem K 1 Ax = K 1 b als we het nieuwe inproduct gebruiken. Preconditionering is voor het eerst beschreven in [4]. M&VdV kozen hiervoor een zogenaamde incomplete Cholesky ontbinding van A. Hierbij worden een onderdriehoeksmatrix L (met L kk = 1) en een diagonaalmatrix D gemaakt zo, dat L+L T hetzelfde ijlheidspatroon heeft als A, dwz. L ij 0 iff A ij 0, en zo, dat (L D L T ) ij = A ij voor alle (i, j) waarvoor A ij 0. Het idee hierachter is, dat deze incomplete Cholesky-factoren gelijken op de echte factoren en dat we zo een gemakkelijk te berekenen benadering van de inverse van A verkrijgen (A 1 is tenslotte de beste preconditioner).

14 REFERENCES 112 References [1] M. Hestenes & E. Stiefel, Methods of conjugate gradients for solving linear systems, J. Research NBS, 49, pp , [2] C. Lanczos, An iteration method for the solution of the eigenvalue problem of linear differential and integral operators, J. Research NBS, 45, pp , [3] J.K. Reid, On the method of conjugate gradients for the solution of large sparse systems of linear equations, Proc. Conf. on Large Sparse Sets of Linear Equations, Academic Press, New York, [4] J.A. Meijerink and H.A. van der Vorst, An iterative solution method for linear systems of which the coefficient matrix is a symmetric M-matrix, Math.of Comp., 31, pp , [5] G.H. Golub & C.F. Van Loan, Matrix Computations, The Johns Hopkins University Press, Baltimore, Maryland, USA, 1 ste druk, 1983, 2 de druk, 1988, 3 de druk, [6] R. Bulirsch & J. Stoer, Introduction to Numerical Analysis, Springer Verlag, Berlin, (Ook verkrijgbaar in een goedkope duitstalige pocketeditie). [7] D. Kincaid & W. Cheney, Numerical Analysis, Brooks & Cole Publishing Company, Pacific Grove, California, USA, 1991; 2de druk, 1996.