Zomercursus Wiskunde. Module 17 Integralen aan het werk (versie 22 augustus 2011)
|
|
|
- Andreas Bogaerts
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Katholieke Universiteit Leuven September 2011 Module 17 Integralen aan het werk (versie 22 augustus 2011)
2
3 Inhoudsopgave 1 Inleiding 1 2 Het integraalbegrip 1 3 De hoofdstelling van de integraalrekening 5 4 Evolutie van het waterpeil in een meer Probleemstelling Wiskundige formulering van het probleem Oplossing van het probleem Gemiddelde van functies Probleemstelling Oplossing Extra: CFK s onder controle? Probleemstelling Oplossing
4
5 Inleiding In deze module willen we het begrip integralen herhalen, en meteen in een aantal toepassingen aan het werk zetten. Telkens worden we geconfronteerd met één of ander probleem waarvan de wiskundige formulering een beroep zal doen op het integraalbegrip. Bij het oplossen van de problemen zal de hoofdstelling van de integraalrekening een prominente rol spelen. Bewust hebben we hier gekozen voor probleemsituaties waarbij voor de verschillende functies die erin voorkomen, geen concreet expliciet functievoorschrift voorhanden is. Zo focusseren we onze aandacht eerder op het conceptuele aspect dan op het (minder belangrijke) rekentechnische aspect van integralen. Bovendien is het ontbreken van expliciete functievoorschriften ook de dagdagelijkse realiteit in de meeste echte toepassingen. In zeer vele disciplines weet men immers wel dat één grootheid afhangt van, dus functie is van, een andere grootheid, maar de functie kent men slechts via een aantal metingen die men in een grafiek uitzet. 2 Het integraalbegrip Probleem 1: Als een begrensde functie f : [a,b] R + gegeven is, kunnen we dan de oppervlakte vinden onder deze grafiek? Y. f S =? a b X Probleem 2: Veronderstel dat we op elk ogenblik de snelheid van een rijdende auto kennen. Is er een manier om te bepalen hoeveel afstand deze auto aflegt tussen twee tijdstippen? Probleem 3: Het rendement van een zonnepaneel varieert in de tijd: zonnestralen vallen niet altijd onder dezelfde hoek op het paneel, er kan bewolking zijn, enzovoort. Als we gedurende een dag op elk tijdstip het vermogen van de invallende zonnestralen kennen, kunnen we dan berekenen hoeveel energie dat zonnepaneel op die dag levert? Al deze problemen kunnen worden opgelost dankzij integralen. We zullen het tweede probleem in detail uitwerken. Een auto rijdt op de snelweg. Op elk tijdstip t (gemeten
6 17-2 in seconden) heeft deze auto een bepaalde snelheid, die we noteren met v(t) (gemeten in meter per seconde). Op onderstaande grafiek kan je bijvoorbeeld aflezen dat op tijdstip t = 0 de auto rijdt met een snelheid van 10 m/s en dat tussen t = 10 en t = 15 de auto rijdt met een constante snelheid van 30 m/s. We zijn geïnteresseerd in de afgelegde afstand (genoteerd S) tussen t = 0 en t = 20. Kan je beredeneren welke afstand er werd afgelegd tussen de tijdstippen t = 10 en t = 15? Je merkt dat, wanneer de snelheid constant is, de afgelegde weg gelijk is aan de oppervlakte onder de grafiek. Dit zal ook nog waar zijn als de snelheid niet constant is: laten we, om dit in te zien, eerst de horizontale as onderverdelen in een aantal delen, bijvoorbeeld in 4 delen van 5 seconden. Bekijk dan de gearceerde oppervlakte in onderstaande figuur links, die bekomen werd door de laagste snelheid van elk tijdsinterval te nemen. Deze oppervlakte is duidelijk kleiner dan de gezochte afgelegde weg. Op gelijkaardige manier bekomen we de rechterfiguur door telkens de hoogste snelheid uit een tijdsinterval te gebruiken. De gearceerde oppervlakten uit de figuren links en rechts noemen we respectievelijk de onder- en bovensom horend bij deze onderverdeling van de horizontale as, we noteren ze respectievelijk S 1 en S 1. Je merkt dat er nog een behoorlijk groot verschil is tussen S 1 en S 1. Laten we daarom de onderverdeling wat verfijnen: we delen de horizontale as nu op in 20 delen van 1 seconde. Op dezelfde manier kunnen we ook voor deze verdeling de onder- en bovensom terugvinden, zie onderstaande figuur. We noteren deze ondersom met S 2, de bovensom met S 2. Met de notaties die we hebben ingevoerd, gelden volgende ongelijkheden. Ga goed na of je ze allemaal kan verklaren! S 1 S 2 S S 2 S 1
7 17-3 Je zal allicht wel vermoeden dat door de onderverdeling steeds verder te verfijnen, de onder- en bovensom steeds dichter bij elkaar zullen komen. Deze vaststelling leidt ons naar de definitie van integreerbaarheid en integraal. Definitie integraal Laat f : [a,b] R een begrensde functie zijn. Beschouw een rij van steeds fijner wordende onderverdelingen van [a,b]. Noteer telkens met S n de ondersom, en met S n de bovensom die hoort bij de n de onderverdeling. We noemen dan f integreerbaar over [a,b] als lim S n = lim S n. n n Wanneer dit geldt dan noemen we deze gemeenschappelijke limiet de integraal van f over [a,b], en we noteren dit getal met Opmerkingen b a f(t)dt. 1. Het symbool dt in b f(t)dt geeft aan dat t de integratievariable is, dus dat het a deze variabele is die bij het opstellen van de ondersommen en bovensommen de waarden op het interval [a, b] aanneemt. Merk op dat deze variabele niet voorkomt in de uitkomst van de integraal en dat we ze een andere naam kunnen geven zonder de uitkomst te veranderen: b f(t)dt = b f(u)du. a a 2. Het symbool dt herinnert er ook aan dat in de ondersommen en bovensommen de functiewaarden vermenigvuldigd worden met de breedte van kleine intervalletjes. De notatie suggereert eigenlijk een som over een oneindig fijne verdeling van
8 17-4 het interval [a, b]. Maar in een wiskundig exacte redenering wordt niet gewerkt met een oneindig fijne verdeling: er worden alleen sommen gemaakt over eindige verdelingen (de ondersommen en bovensommen hierboven) en van die sommen wordt een limiet beschouwd. Nadenken over een integraal als over een som van oneindig veel oneindig kleine bijdragen levert vaak wel nuttige intuïtie op voor het begrijpen van de toepassingen. 3. Bij toepassingen in de fysica helpt het symbool dt ook om de juiste fysische eenheden af te lezen. In het voorbeeld hierboven is f(t) een snelheid die we bijvoorbeeld in meter per seconde kunnen uitdrukken. Als we a en b (en in gedachten dt) dan in seconden uitdrukken, levert de integraal een resultaat in meter. Merk op dat we in fysische situaties ook moeten opletten met de al te letterlijke interpretatie van bepaalde integralen als oppervlaktes. Het gaat om een oppervlakte op de grafiek van f(t) als functie van t, maar als de grootheid op de horizontale as, zoals hier, wordt uitgedrukt in seconde, en de grootheid op de verticale as in meter per seconde, dan is deze oppervlakte in werkelijkheid een lengte: de afgelegde weg, uitgedrukt in meter. 4. Niet elke functie zal integreerbaar zijn. Dit is echter enkel een zorg voor wiskundigen. Men heeft immers aangetoond dat zeer veel functies integreerbaar zijn: bv. continue functies en functies met een eindig aantal discontinuïteitssprongen. Voor wat de toepassingen betreft zal de integreerbaarheid daarom zelden of nooit een probleem stellen.
9 17-5 Kijken we nu terug naar het voorbeeld van de rijdende auto, dan vinden we dat de afgelegde weg tussen t = 0 en t = 20 wordt gegeven door S = 20 0 v(t) dt. We hebben nu t = 20 gekozen als eindtijd, maar we hadden hiervoor natuurlijk ook een andere keuze kunnen maken. In het algemeen kunnen we zeggen dat de afgelegde weg tussen de tijdstippen t = 0 en t = x wordt gegeven door S(x) = x 0 v(t) dt. Het is dit type uitdrukkingen dat in de volgende paragraaf een belangrijke rol speelt. 3 De hoofdstelling van de integraalrekening In het bovenstaande inleidende voorbeeld vonden we dat de afstand die in een bepaald tijdsinterval door de auto wordt afgelegd, gegeven wordt door de integraal van de snelheidsfunctie over dat interval. Anderzijds werd bij de module over afgeleiden al vermeld dat de snelheid verkregen wordt door de positie (of afgelegde weg) af te leiden. Dit doet vermoeden dat afleiden en integreren in zekere zin elkaars omgekeerden zijn. De exacte formulering vinden we terug in de volgende stelling. Hoofdstelling Beschouw een continue functie f : [a,b] R. Definieer g : [a,b] R : x g(x) door g(x) = x a f(t)dt. Dan is g afleidbaar in ]a,b[ en g (x) = f(x) voor elke x ]a,b[. Deze stelling is zeer belangrijk, zowel conceptueel als rekentechnisch. Conceptueel, omdat ze het verband tussen integralen en afgeleiden rigoureus beschrijft. Vanuit rekentechnisch standpunt is ze interessant omdat ze ons toelaat eenvoudig integralen b a f(t)dt te berekenen voor een continue functie f waarvoor een primitieve1 F gekend is. Als rechtstreeks gevolg van de hoofdstelling leidt men immers volgende formule af: b a f(t)dt = F(b) F(a). Ook in berekeningen waarin functies voorkomen waarvoor geen concreet expliciet functievoorschrift gegeven is (zoals zo vaak het geval is in echte toepassingen) kan de hoofdstelling bijzonder nuttig zijn, zoals zal blijken uit de nu volgende toepassingen. 1 Een primitieve voor f is een afleidbare functie F zo dat F = f.
10 Evolutie van het waterpeil in een meer 4.1 Probleemstelling Een meer wordt gevoed door regen en instromende rivieren. Het debiet van het water dat het meer binnenstroomt hangt af van de tijd. Het tijdsgedrag van dit debiet beschrijven we met een functie b : R + R : t b(t) waarbij b(t) = de hoeveelheid water die per tijdseenheid het meer binnenstroomt (bv. gemeten in m 3 /dag) op het tijdstip t (gemeten in dagen vanaf een gekozen beginmoment 0). Het is realistisch te veronderstellen dat b een continue functie is. Uiteraard zal men in de praktijk geen concreet expliciet functievoorschrift kennen voor b; men zal b veeleer kennen via metingen die men op een grafiek uitzet. Typisch zal die grafiek eruit zien zoals op de tekening hieronder.. v. b t Anderzijds wordt het meer ook gebruikt om het omliggende land te irrigeren. Het waterverbruik zal ook afhangen van de tijd. We beschrijven het verbruik met een functie v : R + R : t v(t) waarbij v(t) = de hoeveelheid water die per tijdseenheid verbruikt wordt (bv. gemeten in m 3 /dag) op het tijdstip t (gemeten in dagen vanaf het beginmoment 0). Weer is het realistisch te veronderstellen dat v een continue functie is. De grafiek van v zou er kunnen uitzien zoals op de tekening hierboven. We kunnen ons dan volgende vragen stellen: Wanneer zal het waterpeil in het meer het hoogst staan, wanneer het laagst? Wat is het verschil in hoeveelheid water in het meer tussen hoogwaterstand en de daaropvolgende laagwaterstand?
11 Wiskundige formulering van het probleem We moeten de (lokale) extrema (d.i. minima en maxima) zoeken van de functie H : R + R : t H(t) waarin H(t) = hoeveelheid water in het meer (gemeten in m 3 ) op het ogenblik t (gemeten in dagen vanaf het beginmoment 0). We nemen aan dat het meer nooit droog komt te staan en nooit overloopt. Bovendien verwaarlozen we alle andere (secundaire) effecten die het waterpeil kunnen beïnvloeden (zoals verdamping,... ). Opdracht 1. Stel dat we de hoeveelheid water in het meer op het ogenblik 0 noteren met H 0. Bepaal dan het voorschrift voor H(t), waarbij je gebruik maakt van de functies v en b. Antwoord: de functie die het waterpeil weergeeft, wordt gegeven door H : R + R : t H(t) = Oplossing van het probleem Nu we een formule hebben gevonden voor de functie H, kunnen we de gestelde vragen beantwoorden. Aangezien gevraagd was naar het hoogste en laagste waterpeil, gaan we op zoek naar de lokale maxima en minima van H. Om deze te vinden gaan we de nulpunten van de afgeleide van H zoeken en een tekenonderzoek van de afgeleide functie H in de omgeving van die nulpunten uitvoeren. Opdracht 2. (a) Gebruik de hoofdstelling van de integraalrekening om de afgeleide H van H te berekenen. (b) Zoek de nulpunten van H. Lokaliseer die punten op de tekening met de grafieken van b en v. (c) Welke van die punten corresponderen met (lokale) maxima voor H, welke met lokale minima? Doe hiervoor een tekenonderzoek voor H. (d) Stemmen de resultaten die je gevonden hebt voor de momenten van extremale waterstand overeen met wat je intuïtief kon verwachten? (e) Vind een formule die het verschil in hoeveelheid water in het meer tussen twee opeenvolgende extremale waterstanden uitdrukt in termen van b en v.
12 Gemiddelde van functies 5.1 Probleemstelling Bij NASA wordt een nieuw type raket getest. Tijdens de eerste proefvlucht worden tientallen gegevens door de boordcomputer geregistreerd en on-line naar het vluchtcontrolecentrum doorgestuurd. Deze gegevens zijn uiteraard onmisbaar voor een verdere optimalisering van de raket. Zo is men bijzonder geïnteresseerd in de evolutie van het brandstofverbruik gedurende de hele lanceringsprocedure. De boordcomputer registreert het ogenblikkelijke brandstofverbruik (bv. in liter/sec) én het (tijds)gemiddelde brandstofverbruik (ook in liter/sec) sinds de ontsteking van de motor. Door een stomme fout in de software stuurt de boordcomputer enkel de gegevens over het gemiddeld brandstofverbruik door naar de aarde. De verantwoordelijke voor het departement Brandstof, Dr. Alfredo Pollo, verbleekt als hij op zijn computerscherm enkel de grafiek van dat gemiddeld brandstofverbruik ziet verschijnen. gemiddeld verbruik. tijd Moet Dr. Pollo met klamme handen bij zijn oversten gaan aankloppen met de vraag of ze alstublieft per toeval geen 10 miljoen dollar over hebben om het experiment nog eens opnieuw te doen, of kan hij (of jij?) met enige wiskundige creativiteit alsnog zijn baan redden door de gegevens voor het ogenblikkelijke verbruik uit de meting van het gemiddelde verbruik af te leiden? 5.2 Oplossing We noteren de (continue) functie die de evolutie van het ogenblikkelijke brandstofverbruik beschrijft met v, dus v : R + R : t v(t) waarbij v(t) = het ogenblikkelijke brandstofverbruik (gemeten in liter/sec) op het ogenblik t (gemeten in seconden vanaf het moment van de ontsteking van de motor). Het is deze functie waarin we uiteindelijk geïnteresseerd zijn, maar waar we geen rechtstreekse gegevens over hebben. We kennen wel de functie g : R + R : t g(t)
13 17-9 waarbij g(t) = het gemiddelde brandstofverbruik (gemeten in liter/sec) over het tijdsinterval [0,t]. Het is intuïtief vrij duidelijk dat g volledig bepaald is door v, d.w.z. hadden we v gekend, dan hadden we zeker g via berekening kunnen terugvinden. We verwachten dus dat er een formule moet zijn die g uitdrukt in termen van v. Het probleem waar Dr. Pollo echter mee geconfronteerd wordt, is eigenlijk het omgekeerde: is v volledig bepaald door g? Het antwoord op dit omgekeerde probleem is voor de modale intuïtie minder duidelijk. Om een antwoord te vinden gaan we als volgt te werk: we zoeken eerst een formule die g uitdrukt in termen van v; vervolgens onderzoeken we of we die formule kunnen inverteren tot een formule die v uitdrukt in termen van g. Opdrachten 3. Vind een formule die g uitdrukt in termen van v. Je vertrekt hiervoor best van de definitie van gemiddeld brandstofverbruik: g(t) = 1 t totaal brandstofverbruik in het tijdsinterval [0,t] en druk daarna het totaal brandstofverbruik in het interval [0, t] uit in termen van v. 4. Neem nu de afgeleide van beide leden van de formule die je in Opdracht 3 gevonden hebt. Zo vind je een formule die v uitdrukt in termen van g (en zijn afgeleide g, die in principe gekend is eens g gekend is), een formule waarvoor Dr. Pollo je minstens op een pint zal trakteren! 5. Maak bij wijze van toemaatje Dr. Pollo extra gelukkig door hem op het volgende te wijzen: op de momenten waar g een (lokaal) minimum of maximum bereikt, is het ogenblikkelijke brandstofverbruik onmiddellijk (dus zonder enige berekening) af te lezen uit de grafiek van g. Toon namelijk het volgende aan: als g een (lokaal) extremum bereikt op een tijdstip t 0 > 0, dan is v(t 0 ) = g(t 0 ). 6. In Opdracht 3 heb je een formule gevonden die het gemiddelde van v over het tijdsinterval [0,t] gaf. Hoe zou je dit kunnen abstraheren? M.a.w. als f : [a,b] R een (continue) functie is op een interval [a, b], welke definitie zou je voorstellen voor het gemiddelde van f over [a,b]? Confronteer je algemene abstracte definitie nu met volgende concrete situatie: de snelheid van een rijdende auto wordt als functie van de tijd beschreven door een (continue) functie v : R R : t v(t). Reproduceert je abstracte definitie de vertrouwde notie van gemiddelde snelheid nl. gemiddelde snelheid in een tijdsinterval = afstand afgelegd in dat tijdsinterval tijd verstreken om die afstand af te leggen?
14 Extra: CFK s onder controle? 6.1 Probleemstelling CFK s, die onder meer gebruikt worden in koelinstallaties en in drijfgassen, hebben een kwalijke reputatie. Zij zouden in hoge mate verantwoordelijk zijn voor de aantasting van de levensnoodzakelijke ozonlaag in de atmosfeer. CFK s vervallen omdat ze allerlei reacties en verbindingen aangaan. Zo n vervalproces kan zeer realistisch beschreven worden met een (dalende) exponentiële functie: als er nu een hoeveelheid c (bv. gemeten in kg) in de atmosfeer terecht komt, dan zal er na een tijd t (bv. gemeten in dagen) van die oorspronkelijke hoeveelheid nog c e αt overblijven. Hierin is α een positief reëel getal waarvan de waarde via metingen kan vastgesteld worden. Laat ons er nu van uitgaan dat die waarde gekend is. De evolutie van de uitstoot van CFK s in de atmosfeer beschrijven we met een functie u : R + R : t u(t) met u(t) = hoeveelheid uitgestoten per tijdseenheid (bv. gemeten in kg/dag) op het ogenblik t (bv. gemeten in dagen vanaf een gekozen beginmoment 0). De evolutie van de hoeveelheid CFK s in de atmosfeer modelleren we met een functie c : R + R : t c(t) met c(t) = hoeveelheid CFK s (gemeten in kg) op het ogenblik t (gemeten in dagen). We kunnen ons volgende vragen stellen: (a) Veronderstel dat men een prognose heeft voor de functie u. Kan men dan een prognose maken voor c? (b) Realisten merken op dat de uitstoot van CFK s wel nooit helemaal tot nul zal kunnen herleid worden. Uiteindelijk zal er steeds een zekere restuitstoot zijn. Veronderstel dat we dit modelleren door te stellen dat lim u(t) = r met r > 0. t + Betekent dit dan dat c onbeperkt zal blijven toenemen (want er komen steeds CFK s bij), m.a.w. voorspellen de realisten een uiteindelijke catastrofe? 6.2 Oplossing Probleem (a) komt eigenlijk op het volgende neer: kunnen we een formule vinden die c uitdrukt in termen van u? Eens we zo n formule gevonden hebben, kunnen we ook probleem (b) aanpakken. Kies een ogenblik t. We gaan op zoek naar een formule die c(t) uitdrukt in termen van u. Om die formule te vinden benaderen we eerst het continue uitstootproces door een
15 17-11 discreet proces. We verdelen het interval [0, t] in n deelintervallen, bijvoorbeeld alle met dezelfde lengte t = t/n. De hoeveelheid CFK s die uitgestoten worden in het k-de tijdsinterval [ k 1 n t, k n t] bedraagt dan benaderend met t k ] k 1 n t, k n t[. u(t k ) t, 0 t n (k 1)t n t k kt n (n 1)t n t Die hoeveelheid zal gedurende (ongeveer) (t t k ) dagen vervallen. Op het ogenblik t zal van die hoeveelheid, uitgestoten in het k-de interval, benaderend nog overblijven. Opdracht u(t k )e α(t t k) t 7. Vind een benadering voor c(t) door de benaderende bijdragen van elk van de deelintervallen op te tellen. Vergeet ook niet rekening te houden met de hoeveelheid CFK s, zeg c 0, die op het ogenblik 0 reeds in de atmosfeer aanwezig was. Deze benadering wordt exact als we de limiet n nemen. De som zal bij deze limiet overgaan naar een integraal. Zo vinden we t c(t) = c 0 e αt + e αt e αs u(s)ds. Hiermee is probleem (a) in principe opgelost. Nu zijn we gewapend voor probleem (b). Opdrachten 8. Veronderstel dat u constant is, bv. u(t) = r voor alle t R + (met r > 0). Bereken eerst c(t) voor alle t R + en vervolgens lim c(t). Resulteert een t + constante uitstoot, hoe klein ook, uiteindelijk in een doomsday-scenario? 9. Beschouw nu de situatie waarbij lim u(t) = r (met r > 0). Merk op dat dit de t + situatie van Opdracht 8 veralgemeent. Argumenteer dat in dit geval lim t + t 0 0 e αs u(s)ds = +. Je kunt nu via de regel van de l Hôpital lim c(t) berekenen. t +
16
(g 0 en n een heel getal) Voor het rekenen met machten geldt ook - (p q) a = p a q a
 Samenvatting wiskunde h4 hoofdstuk 3 en 6, h5 hoofdstuk 4 en 6 Hoofdstuk 3 Voorkennis Bij het rekenen met machten gelden de volgende rekenregels: - Bij een vermenigvuldiging van twee machten met hetzelfde
Samenvatting wiskunde h4 hoofdstuk 3 en 6, h5 hoofdstuk 4 en 6 Hoofdstuk 3 Voorkennis Bij het rekenen met machten gelden de volgende rekenregels: - Bij een vermenigvuldiging van twee machten met hetzelfde
11.0 Voorkennis. Optellen alleen bij gelijknamige termen: 3a 3 + 4a 3 = 7a 3. Bij macht van een macht exponenten vermenigvuldigen: (a 5 ) 4 = a 20
 .0 Voorkennis Herhaling rekenregels voor machten: Vermenigvuldigen is exponenten optellen: a 3 a 5 = a 8 Optellen alleen bij gelijknamige termen: 3a 3 + a 3 = 7a 3 Bij macht van een macht exponenten vermenigvuldigen:
.0 Voorkennis Herhaling rekenregels voor machten: Vermenigvuldigen is exponenten optellen: a 3 a 5 = a 8 Optellen alleen bij gelijknamige termen: 3a 3 + a 3 = 7a 3 Bij macht van een macht exponenten vermenigvuldigen:
Functieonderzoek. f(x) = x2 4 x 4 + 2. Igor Voulis. 9 december 2009. 1 De functie en haar definitiegebied 2. 2 Het tekenverloop van de functie 2
 Functieonderzoek f(x) = x2 4 x 4 + 2 Igor Voulis 9 december 2009 Inhoudsopgave 1 De functie en haar definitiegebied 2 2 Het tekenverloop van de functie 2 3 De asymptoten 3 4 De eerste afgeleide 3 5 De
Functieonderzoek f(x) = x2 4 x 4 + 2 Igor Voulis 9 december 2009 Inhoudsopgave 1 De functie en haar definitiegebied 2 2 Het tekenverloop van de functie 2 3 De asymptoten 3 4 De eerste afgeleide 3 5 De
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 2013,
 Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Begeleid Zelfstandig Leren (BZL)
 Begeleid Zelfstandig Leren (BZL) De Beaalde Integraal - Riemannsommen 1 Rijvariabelen u en v van het grafisch rekentoestel.... 1.1 Rijen.... 1. Odracht 1... 1.3 Rekentoestel... 3 1.4 Odracht... 4 1.5 Odracht
Begeleid Zelfstandig Leren (BZL) De Beaalde Integraal - Riemannsommen 1 Rijvariabelen u en v van het grafisch rekentoestel.... 1.1 Rijen.... 1. Odracht 1... 1.3 Rekentoestel... 3 1.4 Odracht... 4 1.5 Odracht
Reeksnr.: Naam: t 2. arcsin x f(t) = 2 dx. 1 x
 Calculus, 4//4. Gegeven de reële functie ft) met als voorschrift t arcsin x ft) = dx x a) Geef het domein van de functie ft). Op dit domein, bespreek waar de functie stijgt, daalt en bepaal de lokale extrema.
Calculus, 4//4. Gegeven de reële functie ft) met als voorschrift t arcsin x ft) = dx x a) Geef het domein van de functie ft). Op dit domein, bespreek waar de functie stijgt, daalt en bepaal de lokale extrema.
Werk het Practicum Functies en de [GR] door tot aan Families van functies. Onthoud alvast de uitdrukking karakteristieken van een functie.
![Werk het Practicum Functies en de [GR] door tot aan Families van functies. Onthoud alvast de uitdrukking karakteristieken van een functie. Werk het Practicum Functies en de [GR] door tot aan Families van functies. Onthoud alvast de uitdrukking karakteristieken van een functie.](/thumbs/48/23960977.jpg) 2 Domein en bereik Verkennen grafieken Domein en bereik Inleiding Verkennen Werk het Practicum Functies en de [GR] door tot aan Families van functies. Onthoud alvast de uitdrukking karakteristieken van
2 Domein en bereik Verkennen grafieken Domein en bereik Inleiding Verkennen Werk het Practicum Functies en de [GR] door tot aan Families van functies. Onthoud alvast de uitdrukking karakteristieken van
De dynamica van een hertenpopulatie. Verslag 1 Modellen en Simulatie
 De dynamica van een hertenpopulatie Verslag Modellen en Simulatie 8 februari 04 Inleiding Om de groei van een populatie te beschrijven, kunnen vele verschillende modellen worden gebruikt, en welke meer
De dynamica van een hertenpopulatie Verslag Modellen en Simulatie 8 februari 04 Inleiding Om de groei van een populatie te beschrijven, kunnen vele verschillende modellen worden gebruikt, en welke meer
Didactische wenken bij het onderdeel analyse
 Didactische wenken bij het onderdeel analyse Didactische wenken bij het onderdeel analyse 1/21 1. Eindtermen analyse Eindtermen ASO tweede graad ET 22 3 (4) aspecten van een functie ET 23 Standaardfuncties
Didactische wenken bij het onderdeel analyse Didactische wenken bij het onderdeel analyse 1/21 1. Eindtermen analyse Eindtermen ASO tweede graad ET 22 3 (4) aspecten van een functie ET 23 Standaardfuncties
Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 26 augustus 2010, , Examenzaal
 Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 26 augustus 2010, 14.00 17.00, Examenzaal Het gebruik van een rekenmachine en/of telefoon is niet toegestaan. U mag geen gebruik maken van het boek
Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 26 augustus 2010, 14.00 17.00, Examenzaal Het gebruik van een rekenmachine en/of telefoon is niet toegestaan. U mag geen gebruik maken van het boek
Wat kan er (niet) zonder ε-δ?
 Oneindig klein. Wat kan er (niet) zonder ε-δ? Michel Roelens University Colleges Leuven Limburg Maria-Boodschaplyceum Brussel Hilde Eggermont Sint-Pieterscollege Leuven Redactie Uitwiskeling Afgeleide
Oneindig klein. Wat kan er (niet) zonder ε-δ? Michel Roelens University Colleges Leuven Limburg Maria-Boodschaplyceum Brussel Hilde Eggermont Sint-Pieterscollege Leuven Redactie Uitwiskeling Afgeleide
Ijkingstoets 4 juli 2012
 Ijkingtoets 4 juli 2012 -vragenreeks 1 1 Ijkingstoets 4 juli 2012 Oefening 1 In de apotheek bezorgt de apotheker zijn assistent op verschillende tijdstippen van de dag een voorschrift voor een te bereiden
Ijkingtoets 4 juli 2012 -vragenreeks 1 1 Ijkingstoets 4 juli 2012 Oefening 1 In de apotheek bezorgt de apotheker zijn assistent op verschillende tijdstippen van de dag een voorschrift voor een te bereiden
Noordhoff Uitgevers bv
 5 bladzijde 9 ab f g h i j functie nr 5 Domein [ 0, 0, Bereik [ 0, [ 0, 0, c D k B k, 0 0, d Spiegelen in de -as geeft het tegengestelde bereik, dus, 0]. e u ( ) en yu ( ) u f D q, 0 0, ; B q 0, a [, b
5 bladzijde 9 ab f g h i j functie nr 5 Domein [ 0, 0, Bereik [ 0, [ 0, 0, c D k B k, 0 0, d Spiegelen in de -as geeft het tegengestelde bereik, dus, 0]. e u ( ) en yu ( ) u f D q, 0 0, ; B q 0, a [, b
Examenvragen Hogere Wiskunde I
 1 Examenvragen Hogere Wiskunde I Vraag 1. Zij a R willekeurig. Gegeven is dat voor alle r, s Q geldt dat a r+s = a r a s. Bewijs dat voor alle x, y R geldt dat a x+y = a x a y. Vraag 2. Gegeven 2 functies
1 Examenvragen Hogere Wiskunde I Vraag 1. Zij a R willekeurig. Gegeven is dat voor alle r, s Q geldt dat a r+s = a r a s. Bewijs dat voor alle x, y R geldt dat a x+y = a x a y. Vraag 2. Gegeven 2 functies
Definitie: Een functie f heeft een absoluut maximum f(x 0 ) in het punt. x 1 Domein(f) als voor alle x Domein(f) geldt:
 Definitie: Een functie f heeft een absoluut maximum f(x 0 ) in het punt x 0 Domein(f) als voor alle x Domein(f) geldt: f(x) f(x 0 ). Een functie f heeft een absoluut minimum f(x 1 ) in het punt x 1 Domein(f)
Definitie: Een functie f heeft een absoluut maximum f(x 0 ) in het punt x 0 Domein(f) als voor alle x Domein(f) geldt: f(x) f(x 0 ). Een functie f heeft een absoluut minimum f(x 1 ) in het punt x 1 Domein(f)
Riemannsommen en integralen
 Riemannsommen en integralen MET DE TI-NSPIRE Vervangt een deel van 0. uit VWO B deel gghm EEBII 0-0 Inhoud Oppervlakte onder de grafiek... Ondersom... 4 Bovensom... 4 Middensom... 4 Riemannsom... 5 Riemannsom
Riemannsommen en integralen MET DE TI-NSPIRE Vervangt een deel van 0. uit VWO B deel gghm EEBII 0-0 Inhoud Oppervlakte onder de grafiek... Ondersom... 4 Bovensom... 4 Middensom... 4 Riemannsom... 5 Riemannsom
Havo 4 - Practicumwedstrijd Versnelling van een karretje
 Havo 4 - Practicumwedstrijd Versnelling van een karretje Vandaag gaan jullie een natuurkundig experiment doen in een hele andere vorm dan je gewend bent, namelijk in de vorm van een wedstrijd. Leerdoelen
Havo 4 - Practicumwedstrijd Versnelling van een karretje Vandaag gaan jullie een natuurkundig experiment doen in een hele andere vorm dan je gewend bent, namelijk in de vorm van een wedstrijd. Leerdoelen
2. Hoelang moet de tweede faze duren om de hoeveelheid zout in de tank op het einde van de eerste faze, op de helft terug te brengen?
 Vraag Een vloeistoftank met onbeperkte capaciteit, bevat aanvankelijk V liter zuiver water. Tijdens de eerste faze stroomt water, dat zout bevat met een concentratie van k kilogram per liter, de tank binnen
Vraag Een vloeistoftank met onbeperkte capaciteit, bevat aanvankelijk V liter zuiver water. Tijdens de eerste faze stroomt water, dat zout bevat met een concentratie van k kilogram per liter, de tank binnen
Primitieve functie Als f : R --> R continu is op een interval, dan noemt men F : R --> R een primiteive functie of
 Enkelvoudige integralen Kernbegrippen Onbepaalde integralen Van onbepaalde naar bepaalde integraal Bepaalde integralen Integratiemethoden Standaardintegralen Integratie door splitsing Integratie door substitutie
Enkelvoudige integralen Kernbegrippen Onbepaalde integralen Van onbepaalde naar bepaalde integraal Bepaalde integralen Integratiemethoden Standaardintegralen Integratie door splitsing Integratie door substitutie
dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π
![dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π dx; (ii) * Bewijs dat voor elke f, continu ondersteld in [0, a]: dx te berekenen.(oef cursus) Gegeven is de bepaalde integraal I n = π](/thumbs/59/43623915.jpg) Analyse. (i) Bereken A = π sin d; +cos 2 (ii) * Bewijs dat voor elke f, continu ondersteld in [, a]: a f()d = a f(a )d (iii) Gebruik (i) en (ii) om de integraal J = π sin d te berekenen.(oef +cos 2 cursus)
Analyse. (i) Bereken A = π sin d; +cos 2 (ii) * Bewijs dat voor elke f, continu ondersteld in [, a]: a f()d = a f(a )d (iii) Gebruik (i) en (ii) om de integraal J = π sin d te berekenen.(oef +cos 2 cursus)
Het is niet toegestaan om een formulekaart of rekenmachine te gebruiken. f(x) = 9x(x 1) en g(x) = 9x 5. Figuur 1: De grafieken van de functies f en g.
 UNIVERSITEIT VAN AMSTERDAM FNWI Voorbeeld Toets Wiskunde A Het is niet toegestaan om een formulekaart of rekenmachine te gebruiken. 1. De twee functies f en g worden gegeven door f(x) = 9x(x 1) en g(x)
UNIVERSITEIT VAN AMSTERDAM FNWI Voorbeeld Toets Wiskunde A Het is niet toegestaan om een formulekaart of rekenmachine te gebruiken. 1. De twee functies f en g worden gegeven door f(x) = 9x(x 1) en g(x)
1 Limiet van een rij Het begrip rij Bepaling van een rij Expliciet voorschrift Recursief voorschrift 3
 HOOFDSTUK 6: RIJEN 1 Limiet van een rij 2 1.1 Het begrip rij 2 1.2 Bepaling van een rij 2 1.2.1 Expliciet voorschrift 2 1.2.2 Recursief voorschrift 3 1.2.3 Andere gevallen 3 1.2.4 Rijen met de grafische
HOOFDSTUK 6: RIJEN 1 Limiet van een rij 2 1.1 Het begrip rij 2 1.2 Bepaling van een rij 2 1.2.1 Expliciet voorschrift 2 1.2.2 Recursief voorschrift 3 1.2.3 Andere gevallen 3 1.2.4 Rijen met de grafische
y = 25 x y = 25 x y = 25 x 2 is het functievoorschrift dat bij de bovenste
 Hoofdstuk A: Integralen. I-. Hiernaast is een cirkel getekend met de oorsrong als middelunt en met een straal 5. Als je in de getekende driehoek de stelling van Pythagoras toeast, krijg je: + y = 5. Kwadrateren
Hoofdstuk A: Integralen. I-. Hiernaast is een cirkel getekend met de oorsrong als middelunt en met een straal 5. Als je in de getekende driehoek de stelling van Pythagoras toeast, krijg je: + y = 5. Kwadrateren
Werken met eenheden. Introductie 275. Leerkern 275
 Open Inhoud Universiteit Appendix B Wiskunde voor milieuwetenschappen Werken met eenheden Introductie 275 Leerkern 275 1 Grootheden en eenheden 275 2 SI-eenhedenstelsel 275 3 Tekenen en grafieken 276 4
Open Inhoud Universiteit Appendix B Wiskunde voor milieuwetenschappen Werken met eenheden Introductie 275 Leerkern 275 1 Grootheden en eenheden 275 2 SI-eenhedenstelsel 275 3 Tekenen en grafieken 276 4
V.4 Eigenschappen van continue functies
 V.4 Eigenschappen van continue functies We bestuderen een paar belangrijke stellingen over continue functies. Maxima en minima De stelling over continue functies die we in deze paragraaf bewijzen zegt
V.4 Eigenschappen van continue functies We bestuderen een paar belangrijke stellingen over continue functies. Maxima en minima De stelling over continue functies die we in deze paragraaf bewijzen zegt
Verbanden en functies
 Verbanden en functies 0. voorkennis Stelsels vergelijkingen Je kunt een stelsel van twee lineaire vergelijkingen met twee variabelen oplossen. De oplossing van het stelsel is het snijpunt van twee lijnen.
Verbanden en functies 0. voorkennis Stelsels vergelijkingen Je kunt een stelsel van twee lineaire vergelijkingen met twee variabelen oplossen. De oplossing van het stelsel is het snijpunt van twee lijnen.
8. Differentiaal- en integraalrekening
 Computeralgebra met Maxima 8. Differentiaal- en integraalrekening 8.1. Sommeren Voor de berekening van sommen kent Maxima de opdracht: sum (expr, index, laag, hoog) Hierbij is expr een Maxima-expressie,
Computeralgebra met Maxima 8. Differentiaal- en integraalrekening 8.1. Sommeren Voor de berekening van sommen kent Maxima de opdracht: sum (expr, index, laag, hoog) Hierbij is expr een Maxima-expressie,
IJkingstoets Industrieel Ingenieur. Wiskundevragen
 IJkingstoets Industrieel Ingenieur Wiskundevragen juli 8 Deel. Basiskennis wiskunde Vraag Het gemiddelde van de getallen 7 4 6, en 4 is Vraag en g met voorschrift g() =. Waaraan is Beschouw de functie
IJkingstoets Industrieel Ingenieur Wiskundevragen juli 8 Deel. Basiskennis wiskunde Vraag Het gemiddelde van de getallen 7 4 6, en 4 is Vraag en g met voorschrift g() =. Waaraan is Beschouw de functie
2.0 Voorkennis. Herhaling merkwaardige producten: (A + B) 2 = A 2 + 2AB + B 2 (A B) 2 = A 2 2AB + B 2 (A + B)(A B) = A 2 B 2
 .0 Voorkennis Herhaling merkwaardige producten: (A + B) = A + AB + B (A B) = A AB + B (A + B)(A B) = A B Voorbeeld 1: (5a) (a -3b) = 5a (4a 1ab + 9b ) = 5a 4a + 1ab 9b = 1a + 1ab 9b Voorbeeld : 4(x 7)
.0 Voorkennis Herhaling merkwaardige producten: (A + B) = A + AB + B (A B) = A AB + B (A + B)(A B) = A B Voorbeeld 1: (5a) (a -3b) = 5a (4a 1ab + 9b ) = 5a 4a + 1ab 9b = 1a + 1ab 9b Voorbeeld : 4(x 7)
1. Orthogonale Hyperbolen
 . Orthogonale Hyperbolen a + b In dit hoofdstuk wordt de grafiek van functies van de vorm y besproken. Functies c + d van deze vorm noemen we gebroken lineaire functies. De grafieken van dit soort functies
. Orthogonale Hyperbolen a + b In dit hoofdstuk wordt de grafiek van functies van de vorm y besproken. Functies c + d van deze vorm noemen we gebroken lineaire functies. De grafieken van dit soort functies
IJkingstoets Wiskunde-Informatica-Fysica september 2018: algemene feedback
 IJkingstoets wiskunde-informatica-fysica september 8 - reeks - p. IJkingstoets Wiskunde-Informatica-Fysica september 8: algemene feedback Positionering ten opzichte van andere deelnemers In totaal namen
IJkingstoets wiskunde-informatica-fysica september 8 - reeks - p. IJkingstoets Wiskunde-Informatica-Fysica september 8: algemene feedback Positionering ten opzichte van andere deelnemers In totaal namen
Uitwerkingen Mei 2012. Eindexamen VWO Wiskunde B. Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek
 Uitwerkingen Mei 01 Eindexamen VWO Wiskunde B A B C Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek Onafhankelijkheid van a Opgave 1. We moeten aantonen dat F a een primitieve is van de
Uitwerkingen Mei 01 Eindexamen VWO Wiskunde B A B C Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek Onafhankelijkheid van a Opgave 1. We moeten aantonen dat F a een primitieve is van de
Per nieuwe hoofdvraag een nieuwe bladzijde gebruiken. De vragen hoeven niet in de juiste volgorde te worden opgelost.
 SBC AMDG Ma 13/12/04 klas : 5WEWI8 5GRWI8 Van Hijfte D. toegelaten : grafisch rekentoestel Examen Wiskunde deel I (90p) Per nieuwe hoofdvraag een nieuwe bladzijde gebruiken. De vragen hoeven niet in de
SBC AMDG Ma 13/12/04 klas : 5WEWI8 5GRWI8 Van Hijfte D. toegelaten : grafisch rekentoestel Examen Wiskunde deel I (90p) Per nieuwe hoofdvraag een nieuwe bladzijde gebruiken. De vragen hoeven niet in de
Bespreking Examen Analyse 1 (Augustus 2007)
 Bespreking Examen Analyse 1 (Augustus 2007) Vooraf: Zoals het stilletjes aan een traditie is geworden, geef ik hier bedenkingen bij het examen van deze septemberzittijd. Ik zorg ervoor dat deze tekst op
Bespreking Examen Analyse 1 (Augustus 2007) Vooraf: Zoals het stilletjes aan een traditie is geworden, geef ik hier bedenkingen bij het examen van deze septemberzittijd. Ik zorg ervoor dat deze tekst op
{neem f(x) = 3} {haakjes uitwerken} {vereenvoudig}
 Wiskunde voor bachelor en master Deel Basiskennis en basisvaardigheden c 205, Synta Media, Utrecht www.syntamedia.nl Uitwerkingen hoofdstuk 2 2... We bepalen de afgeleide van f() 5 met de definitie van
Wiskunde voor bachelor en master Deel Basiskennis en basisvaardigheden c 205, Synta Media, Utrecht www.syntamedia.nl Uitwerkingen hoofdstuk 2 2... We bepalen de afgeleide van f() 5 met de definitie van
Wiskunde voor bachelor en master. Deel 1 Basiskennis en basisvaardigheden. c 2015, Syntax Media, Utrecht. Uitwerkingen hoofdstuk 9
 Wiskunde voor bachelor en master Deel Basiskennis en basisvaardigheden c 0, Sntax Media, Utrecht www.sntaxmedia.nl Uitwerkingen hoofdstuk 9 9.. = x = x 0 0 a. b. =, 0 0 = x + c. d. Uitwerkingen 9.. = x
Wiskunde voor bachelor en master Deel Basiskennis en basisvaardigheden c 0, Sntax Media, Utrecht www.sntaxmedia.nl Uitwerkingen hoofdstuk 9 9.. = x = x 0 0 a. b. =, 0 0 = x + c. d. Uitwerkingen 9.. = x
Zomercursus Wiskunde. Katholieke Universiteit Leuven Groep Wetenschap & Technologie. September 2008
 Katholieke Universiteit Leuven September 008 Algebraïsch rekenen (versie 7 juni 008) Inleiding In deze module worden een aantal basisrekentechnieken herhaald. De nadruk ligt vooral op het symbolisch rekenen.
Katholieke Universiteit Leuven September 008 Algebraïsch rekenen (versie 7 juni 008) Inleiding In deze module worden een aantal basisrekentechnieken herhaald. De nadruk ligt vooral op het symbolisch rekenen.
Gaap, ja, nog een keer. In één variabele hebben we deze formule nu al een paar keer gezien:
 Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
Polynomen. + 5x + 5 \ 3 x 1 = S(x) 2x x. 3x x 3x 2 + 2
 Lesbrief 3 Polynomen 1 Polynomen van één variabele Elke functie van de vorm P () = a n n + a n 1 n 1 + + a 1 + a 0, (a n 0), heet een polynoom of veelterm in de variabele. Het getal n heet de graad van
Lesbrief 3 Polynomen 1 Polynomen van één variabele Elke functie van de vorm P () = a n n + a n 1 n 1 + + a 1 + a 0, (a n 0), heet een polynoom of veelterm in de variabele. Het getal n heet de graad van
Voorbereidend Wetenschappelijk Onderwijs Tijdvak 1 Dinsdag 31 mei uur
 wiskunde B,2 Examen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Dinsdag 3 mei 3.30 6.30 uur 20 05 Voor dit examen zijn maximaal 89 punten te behalen; het examen bestaat uit 20 vragen. Voor elk
wiskunde B,2 Examen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Dinsdag 3 mei 3.30 6.30 uur 20 05 Voor dit examen zijn maximaal 89 punten te behalen; het examen bestaat uit 20 vragen. Voor elk
( ) Hoofdstuk 4 Verloop van functies. 4.1 De grafiek van ( ) 4.1.1 Spiegelen t.o.v. de x-as, y-as en de oorsprong
 Hoofdstuk 4 Verloop van functies Met DERIVE is het mogelijk om tal van eigenschappen van functies experimenteel te ontdekken. In een eerste paragraaf onderzoeken we het verband tussen de grafieken van
Hoofdstuk 4 Verloop van functies Met DERIVE is het mogelijk om tal van eigenschappen van functies experimenteel te ontdekken. In een eerste paragraaf onderzoeken we het verband tussen de grafieken van
V.2 Limieten van functies
 V.2 Limieten van functies Beschouw een deelverzameling D R, een functie f: D R en zij c R. We willen het gedrag van f in de buurt van c bestuderen. De functiewaarde in c is daarvoor niet belangrijk, de
V.2 Limieten van functies Beschouw een deelverzameling D R, een functie f: D R en zij c R. We willen het gedrag van f in de buurt van c bestuderen. De functiewaarde in c is daarvoor niet belangrijk, de
Inleiding tot de natuurkunde
 OBC Inleiding tot de Natuurkunde 01-08-2010 W.Tomassen Pagina 1 Hoofdstuk 1 : Hoe haal ik hoge cijfers. 1. Maak van elke paragraaf een samenvatting. (Titels, vet/schuin gedrukte tekst, opsommingen en plaatsjes.)
OBC Inleiding tot de Natuurkunde 01-08-2010 W.Tomassen Pagina 1 Hoofdstuk 1 : Hoe haal ik hoge cijfers. 1. Maak van elke paragraaf een samenvatting. (Titels, vet/schuin gedrukte tekst, opsommingen en plaatsjes.)
IJkingstoets Wiskunde-Informatica-Fysica 29 juni Nummer vragenreeks: 1
 IJkingstoets Wiskunde-Informatica-Fysica 29 juni 206 Nummer vragenreeks: IJkingstoets wiskunde-informatica-fysica 29 juni 206 - reeks - p. /0 Oefening Welke studierichting wil je graag volgen? (vraag
IJkingstoets Wiskunde-Informatica-Fysica 29 juni 206 Nummer vragenreeks: IJkingstoets wiskunde-informatica-fysica 29 juni 206 - reeks - p. /0 Oefening Welke studierichting wil je graag volgen? (vraag
Machten, exponenten en logaritmen
 Machten, eponenten en logaritmen Machten, eponenten en logaritmen Macht, eponent en grondtal Eponenten en logaritmen hebben alles met machtsverheffen te maken. Een macht als 4 is niets anders dan de herhaalde
Machten, eponenten en logaritmen Machten, eponenten en logaritmen Macht, eponent en grondtal Eponenten en logaritmen hebben alles met machtsverheffen te maken. Een macht als 4 is niets anders dan de herhaalde
Convergentie van een rij
 Hoofdstuk Convergentie van een rij. Basis. Bepaal de som van de volgende oneindige meetkundige rijen a) + 0. + 0.0 + 0.00 + 0.000 +... b) 6 + 8 + + 2 +, +... c) 8 + 2 + 2 + 8 +... 2. Schrijf de volgende
Hoofdstuk Convergentie van een rij. Basis. Bepaal de som van de volgende oneindige meetkundige rijen a) + 0. + 0.0 + 0.00 + 0.000 +... b) 6 + 8 + + 2 +, +... c) 8 + 2 + 2 + 8 +... 2. Schrijf de volgende
5.7. Boekverslag door P woorden 11 januari keer beoordeeld. Wiskunde B
 Boekverslag door P. 1778 woorden 11 januari 2012 5.7 103 keer beoordeeld Vak Methode Wiskunde B Getal en ruimte Wiskunde Hoofdstuk 1 Formules en Grafieken 1.1 Lineaire verbanden Van de lijn y=ax+b is de
Boekverslag door P. 1778 woorden 11 januari 2012 5.7 103 keer beoordeeld Vak Methode Wiskunde B Getal en ruimte Wiskunde Hoofdstuk 1 Formules en Grafieken 1.1 Lineaire verbanden Van de lijn y=ax+b is de
Wisnet-HBO. update maart. 2010
 Wat is Differentiëren? 1 Wat is differentiëren? Wisnet-HBO update maart. 2010 Differentiëren is eigenlijk het differentiaalquotient bepalen. Je begint met het delen van uiterst kleine verschillen op elkaar.
Wat is Differentiëren? 1 Wat is differentiëren? Wisnet-HBO update maart. 2010 Differentiëren is eigenlijk het differentiaalquotient bepalen. Je begint met het delen van uiterst kleine verschillen op elkaar.
Hoofdstuk 9 - exponentiele verbanden. [KC] exponentiële verbanden
![Hoofdstuk 9 - exponentiele verbanden. [KC] exponentiële verbanden Hoofdstuk 9 - exponentiele verbanden. [KC] exponentiële verbanden](/thumbs/92/109818709.jpg) Hoofdstuk 9 - exponentiele verbanden [KC] exponentiële verbanden 0. voorkennis Procenten en vermenigvuldigingsfactoren Procentuele toename met p%: g = 1 + p 100 p = ( g 1) 100 Procentuele afname met p%:
Hoofdstuk 9 - exponentiele verbanden [KC] exponentiële verbanden 0. voorkennis Procenten en vermenigvuldigingsfactoren Procentuele toename met p%: g = 1 + p 100 p = ( g 1) 100 Procentuele afname met p%:
Eindexamen wiskunde B1-2 vwo 2002-I
 Uit de kust Een kustlijn bestaat uit drie rechte stukken AB, BC en CD, die hoeken van 90 met elkaar maken. De lengte van elk recht stuk is 4 kilometer. Zie figuur. In de figuur zijn twee stippellijnen
Uit de kust Een kustlijn bestaat uit drie rechte stukken AB, BC en CD, die hoeken van 90 met elkaar maken. De lengte van elk recht stuk is 4 kilometer. Zie figuur. In de figuur zijn twee stippellijnen
Examen VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskunde B, (nieuwe stijl) Examen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Vrijdag 4 mei 3.30 6.30 uur 0 0 Voor dit examen zijn maximaal 86 punten te behalen; het examen bestaat uit 8 vragen.
Wiskunde B, (nieuwe stijl) Examen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Vrijdag 4 mei 3.30 6.30 uur 0 0 Voor dit examen zijn maximaal 86 punten te behalen; het examen bestaat uit 8 vragen.
Wiskundige functies. x is het argument of de (onafhankelijke) variabele
 Wiskundige functies Een (wiskundige) functie voegt aan ieder getal een ander getal toe. Bekijk bijv. de functie f() = 2 1 Aan het getal 2, d.w.z. = 2, wordt het getal 3 toegevoegd, want f(2) = 2 2 1 =
Wiskundige functies Een (wiskundige) functie voegt aan ieder getal een ander getal toe. Bekijk bijv. de functie f() = 2 1 Aan het getal 2, d.w.z. = 2, wordt het getal 3 toegevoegd, want f(2) = 2 2 1 =
Modelvragen ijkingstoets. 1 Redeneren
 Modelvragen ijkingtoets - KU Leuven, Groep W&T - versie 26 juni 2012 1 Modelvragen ijkingstoets Onderstaande vragen staan model voor de ijkingstoets georganiseerd door de groep wetenschap en technologie
Modelvragen ijkingtoets - KU Leuven, Groep W&T - versie 26 juni 2012 1 Modelvragen ijkingstoets Onderstaande vragen staan model voor de ijkingstoets georganiseerd door de groep wetenschap en technologie
maplev 2010/7/12 14:02 page 157 #159 Taylor-ontwikkelingen
 maplev 200/7/2 4:02 page 57 #59 Module 2 Taylor-ontwikkelingen Onderwerp Voorkennis Expressies Zie ook Taylor-ontwikkelingen van functies van éń of meer variabelen. Taylor-ontwikkelingen. taylor, convert(expressie,polynom),
maplev 200/7/2 4:02 page 57 #59 Module 2 Taylor-ontwikkelingen Onderwerp Voorkennis Expressies Zie ook Taylor-ontwikkelingen van functies van éń of meer variabelen. Taylor-ontwikkelingen. taylor, convert(expressie,polynom),
Korte handleiding Maple, bestemd voor gebruik bij de cursus Wiskunde
 Korte handleiding Maple, bestemd voor gebruik bij de cursus Wiskunde 3 voor B. Functies van twee variabelen.. Een functie fx, y) van twee variabelen kan analoog aan een functie van één variabele in Maple
Korte handleiding Maple, bestemd voor gebruik bij de cursus Wiskunde 3 voor B. Functies van twee variabelen.. Een functie fx, y) van twee variabelen kan analoog aan een functie van één variabele in Maple
Bepaalde Integraal (Training) Wat reken je uit als je een functie integreert
 Bepaalde Integraal (Training) WISNET-HBO update april 2009 Wat reken je uit als je een functie integreert De betekenis van de integraal is een optelling van uiterst kleine onderdelen. In dit voorbeeld
Bepaalde Integraal (Training) WISNET-HBO update april 2009 Wat reken je uit als je een functie integreert De betekenis van de integraal is een optelling van uiterst kleine onderdelen. In dit voorbeeld
Examen VWO. wiskunde B1,2 (nieuwe stijl)
 wiskunde B, (nieuwe stijl) Examen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Woensdag 3 juni 3.30 6.30 uur 0 04 Voor dit examen zijn maximaal 87 punten te behalen; het examen bestaat uit 9 vragen.
wiskunde B, (nieuwe stijl) Examen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Woensdag 3 juni 3.30 6.30 uur 0 04 Voor dit examen zijn maximaal 87 punten te behalen; het examen bestaat uit 9 vragen.
Wiskunde in het eerste bachelorjaar handelsingenieur
 Positie van wiskunde in de opleiding HIR Wiskunde in het eerste bachelorjaar handelsingenieur Wat en hoe? Departement Wiskunde, K.U.Leuven Lerarendag Wiskunde FEB, 6 mei 2010 Positie van wiskunde in de
Positie van wiskunde in de opleiding HIR Wiskunde in het eerste bachelorjaar handelsingenieur Wat en hoe? Departement Wiskunde, K.U.Leuven Lerarendag Wiskunde FEB, 6 mei 2010 Positie van wiskunde in de
Examen VWO. wiskunde B1,2
 wiskunde B1,2 Examen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak 2 Woensdag 22 juni 13.30 16.30 uur 20 05 Voor dit examen zijn maximaal 88 punten te behalen; het examen bestaat uit 19 vragen.
wiskunde B1,2 Examen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak 2 Woensdag 22 juni 13.30 16.30 uur 20 05 Voor dit examen zijn maximaal 88 punten te behalen; het examen bestaat uit 19 vragen.
IJkingstoets burgerlijk ingenieur-architect september 2018: feedback deel wiskunde
 IJkingstoets burgerlijk ingenieur-architect september 8: feedback deel wiskunde Positionering ten opzichte van andere deelnemers In totaal namen 5 studenten deel aan de ijkingstoets burgerlijk ingenieur-architect
IJkingstoets burgerlijk ingenieur-architect september 8: feedback deel wiskunde Positionering ten opzichte van andere deelnemers In totaal namen 5 studenten deel aan de ijkingstoets burgerlijk ingenieur-architect
IJkingstoets burgerlijk ingenieur-architect september 2018: feedback deel wiskunde
 IJkingstoets burgerlijk ingenieur-architect september 8: feedback deel wiskunde Positionering ten opzichte van andere deelnemers In totaal namen 5 studenten deel aan de ijkingstoets burgerlijk ingenieur-architect
IJkingstoets burgerlijk ingenieur-architect september 8: feedback deel wiskunde Positionering ten opzichte van andere deelnemers In totaal namen 5 studenten deel aan de ijkingstoets burgerlijk ingenieur-architect
Naam: Studierichting: Naam assistent:
 Naam: Tussentijdse Toets Wiskunde I ste bachelor Biochemie & Biotechnologie, Chemie, Geografie, Geologie, Informatica, Schakelprogramma Master Toegepaste Informatica, Master Chemie donderdag 4 november
Naam: Tussentijdse Toets Wiskunde I ste bachelor Biochemie & Biotechnologie, Chemie, Geografie, Geologie, Informatica, Schakelprogramma Master Toegepaste Informatica, Master Chemie donderdag 4 november
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
Inleiding tot de natuurkunde
 OBC Inleiding tot de Natuurkunde 01-09-2009 W.Tomassen Pagina 1 Inhoud Hoofdstuk 1 Rekenen.... 3 Hoofdstuk 2 Grootheden... 5 Hoofdstuk 3 Eenheden.... 7 Hoofdstuk 4 Evenredig.... 10 Inleiding... 10 Uitleg...
OBC Inleiding tot de Natuurkunde 01-09-2009 W.Tomassen Pagina 1 Inhoud Hoofdstuk 1 Rekenen.... 3 Hoofdstuk 2 Grootheden... 5 Hoofdstuk 3 Eenheden.... 7 Hoofdstuk 4 Evenredig.... 10 Inleiding... 10 Uitleg...
De bisectie methode uitgelegd met een makkelijk voorbeeld
 De Bisectie methode De bisectie methode uitgelegd met een makkelijk voorbeeld De bisectie methode is een recursieve methode om punten van een functie te gaan afschatten. Hierbij gaat men de functiewaarde
De Bisectie methode De bisectie methode uitgelegd met een makkelijk voorbeeld De bisectie methode is een recursieve methode om punten van een functie te gaan afschatten. Hierbij gaat men de functiewaarde
Eindexamen wiskunde B1-2 vwo 2005-I
 Inademen Bij controlemetingen aan de ademhaling wordt men gevraagd om diep uit te ademen en vervolgens gedurende vijf seconden zo diep mogelijk in te ademen. Tijdens het inademen is de hoeveelheid verse
Inademen Bij controlemetingen aan de ademhaling wordt men gevraagd om diep uit te ademen en vervolgens gedurende vijf seconden zo diep mogelijk in te ademen. Tijdens het inademen is de hoeveelheid verse
Numerieke berekening van integralen met DERIVE
 Numerieke berekening van integralen met DERIVE Dirk Danckaert Sint-Norbertusinstituut Duffel In deze tekst maak je kennis met enkele eenvoudige algoritmen voor de numerieke berekening van bepaalde integralen.
Numerieke berekening van integralen met DERIVE Dirk Danckaert Sint-Norbertusinstituut Duffel In deze tekst maak je kennis met enkele eenvoudige algoritmen voor de numerieke berekening van bepaalde integralen.
Inhoud college 5 Basiswiskunde Taylorpolynomen
 Inhoud college 5 Basiswiskunde 4.10 Taylorpolynomen 2 Basiswiskunde_College_5.nb 4.10 Inleiding Gegeven is een functie f met punt a in domein D f. Gezocht een eenvoudige functie, die rond punt a op f lijkt
Inhoud college 5 Basiswiskunde 4.10 Taylorpolynomen 2 Basiswiskunde_College_5.nb 4.10 Inleiding Gegeven is een functie f met punt a in domein D f. Gezocht een eenvoudige functie, die rond punt a op f lijkt
Trillingen en geluid wiskundig
 Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Radialen 3 Uitwijking van een harmonische trilling 4 Macht en logaritme 5 Geluidsniveau en amplitude 1 De sinus van een hoek Sinus van een hoek
Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Radialen 3 Uitwijking van een harmonische trilling 4 Macht en logaritme 5 Geluidsniveau en amplitude 1 De sinus van een hoek Sinus van een hoek
Hoofdstuk 7 - veranderingen. getal & ruimte HAVO wiskunde A deel 2
 Hoofdstuk 7 - veranderingen getal & ruimte HAVO wiskunde A deel 2 0. voorkennis Plotten, schetsen en tekenen Een grafiek plotten Een grafiek schetsen Een grafiek tekenen Na het invoeren van de formule
Hoofdstuk 7 - veranderingen getal & ruimte HAVO wiskunde A deel 2 0. voorkennis Plotten, schetsen en tekenen Een grafiek plotten Een grafiek schetsen Een grafiek tekenen Na het invoeren van de formule
Zomercursus Wiskunde. Module 10 De afgeleide functie: Rekenregels en Toepassingen (versie 22 augustus 2011)
 Katholieke Universiteit Leuven September 2011 Module 10 De afgeleide functie: Rekenregels en Toepassingen (versie 22 augustus 2011) Inhoudsopgave 1 Definitie Betekenis van de afgeleide 1 2 Standaardafgeleiden
Katholieke Universiteit Leuven September 2011 Module 10 De afgeleide functie: Rekenregels en Toepassingen (versie 22 augustus 2011) Inhoudsopgave 1 Definitie Betekenis van de afgeleide 1 2 Standaardafgeleiden
Uitwerkingen bij 1_0 Voorkennis: Machten en differentiëren
 Uitwerkingen bij _0 Voorkennis: Machten en differentiëren 3(x ) 6 3 6 (x ) 6 6-3 x 3 5 x - 6 43 x 6 x 3x 4 3 x 4 x 6 " $% & ' " $% & (& &( & ' " $% &( &&(& ' ) * '*, *-, *-, *-,, - VWO B deel 3 Analyse_
Uitwerkingen bij _0 Voorkennis: Machten en differentiëren 3(x ) 6 3 6 (x ) 6 6-3 x 3 5 x - 6 43 x 6 x 3x 4 3 x 4 x 6 " $% & ' " $% & (& &( & ' " $% &( &&(& ' ) * '*, *-, *-, *-,, - VWO B deel 3 Analyse_
Examen VWO. Wiskunde B1,2 (nieuwe stijl)
 Wiskunde B,2 (nieuwe stijl) Eamen VW Voorbereidend Wetenschappelijk nderwijs Tijdvak 2 Woensdag 8 juni 3.30 6.30 uur 20 03 Voor dit eamen zijn maimaal 84 punten te behalen; het eamen bestaat uit 7 vragen.
Wiskunde B,2 (nieuwe stijl) Eamen VW Voorbereidend Wetenschappelijk nderwijs Tijdvak 2 Woensdag 8 juni 3.30 6.30 uur 20 03 Voor dit eamen zijn maimaal 84 punten te behalen; het eamen bestaat uit 7 vragen.
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Uitwerking Tentamen Calculus, 2DM10, maandag 22 januari 2007
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking Tentamen Calculus, DM, maandag januari 7. (a) Gevraagd is het polynoom f() + f () (x ) + f (x ). Een eenvoudige rekenpartij
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking Tentamen Calculus, DM, maandag januari 7. (a) Gevraagd is het polynoom f() + f () (x ) + f (x ). Een eenvoudige rekenpartij
Exponentiële Functie: Toepassingen
 Exponentiële Functie: Toepassingen 1 Overgang tussen exponentiële functies en lineaire functies Wanneer we werken met de exponentiële functie is deze niet altijd gemakkelijk te herkennen. Daarom proberen
Exponentiële Functie: Toepassingen 1 Overgang tussen exponentiële functies en lineaire functies Wanneer we werken met de exponentiële functie is deze niet altijd gemakkelijk te herkennen. Daarom proberen
Zomercursus Wiskunde. Module 1 Algebraïsch rekenen (versie 22 augustus 2011)
 Katholieke Universiteit Leuven September 011 Module 1 Algebraïsch rekenen (versie augustus 011) Inhoudsopgave 1 Rekenen met haakjes 1.1 Uitwerken van haakjes en ontbinden in factoren............. 1. De
Katholieke Universiteit Leuven September 011 Module 1 Algebraïsch rekenen (versie augustus 011) Inhoudsopgave 1 Rekenen met haakjes 1.1 Uitwerken van haakjes en ontbinden in factoren............. 1. De
1.0 Voorkennis. Voorbeeld 1: Los op: 6x + 28 = 30 10x.
 1.0 Voorkennis Voorbeeld 1: Los op: 6x + 28 = 30 10x. 6x + 28 = 30 10x +10x +10x 16x + 28 = 30-28 -28 16x = 2 :16 :16 x = 2 1 16 8 Stappenplan: 1) Zorg dat alles met x links van het = teken komt te staan;
1.0 Voorkennis Voorbeeld 1: Los op: 6x + 28 = 30 10x. 6x + 28 = 30 10x +10x +10x 16x + 28 = 30-28 -28 16x = 2 :16 :16 x = 2 1 16 8 Stappenplan: 1) Zorg dat alles met x links van het = teken komt te staan;
Eenparig rechtlijnige beweging met de NXT
 Eenparig rechtlijnige beweging met de NXT Project tweede graad : VRIJ TECHNISCH INSTITUUT VEURNE Iepersesteenweg 90 8630 VEURNE e-mail: info@vtiveurne.be vzw Katholiek Secundair Onderwijs Veurne Nieuwpoort,
Eenparig rechtlijnige beweging met de NXT Project tweede graad : VRIJ TECHNISCH INSTITUUT VEURNE Iepersesteenweg 90 8630 VEURNE e-mail: info@vtiveurne.be vzw Katholiek Secundair Onderwijs Veurne Nieuwpoort,
TI83-werkblad. Vergelijkingen bij de normale verdeling
 TI83-werkblad Vergelijkingen bij de normale verdeling 1. Inleiding Een normale verdeling wordt bepaald door de constanten µ en σ. Dit blijkt uit het voorschrift van de verdelingsfunctie van de normale
TI83-werkblad Vergelijkingen bij de normale verdeling 1. Inleiding Een normale verdeling wordt bepaald door de constanten µ en σ. Dit blijkt uit het voorschrift van de verdelingsfunctie van de normale
Noordhoff Uitgevers bv
 V-a Hoofdstuk - Transformaties Voorkennis: Standaardfuncties bladzijde 70 f () = g () = sin h() = k () = log p () = m () = n () = b D f = [0, en B f = [0, ; D g = en B g =[, ] ; D h = en B h = 0, ; D k
V-a Hoofdstuk - Transformaties Voorkennis: Standaardfuncties bladzijde 70 f () = g () = sin h() = k () = log p () = m () = n () = b D f = [0, en B f = [0, ; D g = en B g =[, ] ; D h = en B h = 0, ; D k
Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Functies en grafieken. Een eigen samenvatting maken is nuttig.
 7 Totaalbeeld Samenvatten Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Functies en grafieken. Een eigen samenvatting maken is nuttig. Begrippenlijst: 21: functie invoerwaarde
7 Totaalbeeld Samenvatten Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Functies en grafieken. Een eigen samenvatting maken is nuttig. Begrippenlijst: 21: functie invoerwaarde
1. (a) Gegeven z = 2 2i, w = 1 i 3. Bereken z w. (b) Bepaal alle complexe getallen z die voldoen aan z 3 8i = 0.
 Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
Uitwerkingen Tentamen Gewone Differentiaalvergelijkingen
 Uitwerkingen Tentamen Gewone Differentiaalvergelijkingen Maandag 4 januari 216, 1: - 13: uur 1. Beschouw voor t > de inhomogene singuliere tweede orde vergelijking, t 2 ẍ + 4tẋ + 2x = f(t, (1 waarin f
Uitwerkingen Tentamen Gewone Differentiaalvergelijkingen Maandag 4 januari 216, 1: - 13: uur 1. Beschouw voor t > de inhomogene singuliere tweede orde vergelijking, t 2 ẍ + 4tẋ + 2x = f(t, (1 waarin f
Discrete Wiskunde 2WC15, Lente Jan Draisma
 Discrete Wiskunde 2WC15, Lente 2010 Jan Draisma HOOFDSTUK 3 De Nullstellensatz 1. De zwakke Nullstellensatz Stelling 1.1. Zij K een algebraïsch gesloten lichaam en zij I een ideaal in K[x] = K[x 1,...,
Discrete Wiskunde 2WC15, Lente 2010 Jan Draisma HOOFDSTUK 3 De Nullstellensatz 1. De zwakke Nullstellensatz Stelling 1.1. Zij K een algebraïsch gesloten lichaam en zij I een ideaal in K[x] = K[x 1,...,
Grafieken van veeltermfuncties
 (HOOFDSTUK 43, uit College Mathematics, door Frank Ayres, Jr. and Philip A. Schmidt, Schaum s Series, McGraw-Hill, New York; dit is de voorbereiding voor een uit te geven Nederlandse vertaling). Grafieken
(HOOFDSTUK 43, uit College Mathematics, door Frank Ayres, Jr. and Philip A. Schmidt, Schaum s Series, McGraw-Hill, New York; dit is de voorbereiding voor een uit te geven Nederlandse vertaling). Grafieken
Zomercursus Wiskunde. Katholieke Universiteit Leuven Groep Wetenschap & Technologie. September 2008
 Katholieke Universiteit Leuven September 2008 Minimum-Maimumproblemen (versie 11 augustus 2008) Inleiding In heel wat vraagstukken gaan we op zoek naar het maimum of het minimum van een zekere grootheid.
Katholieke Universiteit Leuven September 2008 Minimum-Maimumproblemen (versie 11 augustus 2008) Inleiding In heel wat vraagstukken gaan we op zoek naar het maimum of het minimum van een zekere grootheid.
Opdracht 1 bladzijde 8
 Opdrachten Opdracht bladzijde 8 Uit een stuk karton met lengte 45 cm en breedte 8 cm knip je in de vier hoeken vierkantjes af met zijde cm. Zo verkrijg je een open doos. 8 cm 45 cm Hoe groot is het volume
Opdrachten Opdracht bladzijde 8 Uit een stuk karton met lengte 45 cm en breedte 8 cm knip je in de vier hoeken vierkantjes af met zijde cm. Zo verkrijg je een open doos. 8 cm 45 cm Hoe groot is het volume
IJkingstoets Wiskunde-Informatica-Fysica juli 2018: algemene feedback
 IJkingstoets wiskunde-informatica-fysica juli 8 - reeks - p. IJkingstoets Wiskunde-Informatica-Fysica juli 8: algemene feedback Positionering ten opzichte van andere deelnemers In totaal namen 8 studenten
IJkingstoets wiskunde-informatica-fysica juli 8 - reeks - p. IJkingstoets Wiskunde-Informatica-Fysica juli 8: algemene feedback Positionering ten opzichte van andere deelnemers In totaal namen 8 studenten
Eindexamen wiskunde B1-2 vwo 2004-II
 Voedselbehoefte In een zeker gebied wordt een grote toename van de bevolking voorzien. Om de daarmee gepaard gaande problemen het hoofd te kunnen bieden, heeft men een schatting nodig van de grootte van
Voedselbehoefte In een zeker gebied wordt een grote toename van de bevolking voorzien. Om de daarmee gepaard gaande problemen het hoofd te kunnen bieden, heeft men een schatting nodig van de grootte van
0.25x. Het buitengebied - vanuit elk punt kun je twee raaklijnen tekenen - bevat twee oplossingen. De parabool zelf staat voor één oplossing.
 Uitwerkingen opgaven Zichtbaar maken van discriminantkrommen Opgave 1.1 a. Het binnengebied van de dalparabool oplossingen. y 0.5x, het holle deel, bevat geen Het buitengebied - vanuit elk punt kun je
Uitwerkingen opgaven Zichtbaar maken van discriminantkrommen Opgave 1.1 a. Het binnengebied van de dalparabool oplossingen. y 0.5x, het holle deel, bevat geen Het buitengebied - vanuit elk punt kun je
Statistiek voor Natuurkunde Opgavenserie 1: Kansrekening
 Statistiek voor Natuurkunde Opgavenserie 1: Kansrekening Inleveren: 12 januari 2011, VOOR het college Afspraken Serie 1 mag gemaakt en ingeleverd worden in tweetallen. Schrijf duidelijk je naam, e-mail
Statistiek voor Natuurkunde Opgavenserie 1: Kansrekening Inleveren: 12 januari 2011, VOOR het college Afspraken Serie 1 mag gemaakt en ingeleverd worden in tweetallen. Schrijf duidelijk je naam, e-mail
Ijkingstoets industrieel ingenieur aangeboden door UGent en VUB op 30 juni 2014: algemene feedback
 IJkingstoets juni 4 - reeks - p. / Ijkingstoets industrieel ingenieur aangeboden door UGent en VUB op juni 4: algemene feedback In totaal namen studenten deel aan deze ijkingstoets industrieel ingenieur
IJkingstoets juni 4 - reeks - p. / Ijkingstoets industrieel ingenieur aangeboden door UGent en VUB op juni 4: algemene feedback In totaal namen studenten deel aan deze ijkingstoets industrieel ingenieur
Noordhoff Uitgevers bv
 8 Voorkennis: Sinusfuncties ladzijde 9 V- Uit 8 radialen volgt 8 radialen Je krijgt dan de volgende tael: V-a V-a 8 graden 6 9 8 radialen O 6 6 7 8 9 Aflezen:,,,, c Aflezen:, d Aflezen:, e Aflezen: O Aflezen:,,,
8 Voorkennis: Sinusfuncties ladzijde 9 V- Uit 8 radialen volgt 8 radialen Je krijgt dan de volgende tael: V-a V-a 8 graden 6 9 8 radialen O 6 6 7 8 9 Aflezen:,,,, c Aflezen:, d Aflezen:, e Aflezen: O Aflezen:,,,
Enkele bedenkingen bij het examen Complexe Analyse
 Enkele bedenkingen bij het examen Complexe Analyse De examenvragen vind je op het einde van dit documentje. Eerst een paar algemene opmerkingen. Vele antwoorden zijn slordig opgeschreven wat het lezen
Enkele bedenkingen bij het examen Complexe Analyse De examenvragen vind je op het einde van dit documentje. Eerst een paar algemene opmerkingen. Vele antwoorden zijn slordig opgeschreven wat het lezen
Inhoud van een omwentelingslichaam
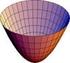 Inhoud van een omwentelingslichaam Wat is een omwentelingslichaam? Omwentelingslichamen ontstaan door het wentelen van een vlakdeel rond een rechte: de omwentelingsas Voorbeeld: volume van een (omwentelings)cilinder
Inhoud van een omwentelingslichaam Wat is een omwentelingslichaam? Omwentelingslichamen ontstaan door het wentelen van een vlakdeel rond een rechte: de omwentelingsas Voorbeeld: volume van een (omwentelings)cilinder
Significante cijfers en meetonzekerheid
 Inhoud Significante cijfers en meetonzekerheid... 2 Significante cijfers... 2 Wetenschappelijke notatie... 3 Meetonzekerheid... 3 Significante cijfers en meetonzekerheid... 4 Opgaven... 5 Opgave 1... 5
Inhoud Significante cijfers en meetonzekerheid... 2 Significante cijfers... 2 Wetenschappelijke notatie... 3 Meetonzekerheid... 3 Significante cijfers en meetonzekerheid... 4 Opgaven... 5 Opgave 1... 5
1. (a) Formuleer het Cauchy criterium voor de convergentie van een reeks
 Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 7 augustus 2015, 16:30 19:30 (20:30) Het gebruik van een rekenmachine, telefoon of tablet is niet toegestaan. U mag geen gebruik maken van het boek
Radboud Universiteit Nijmegen Tentamen Analyse 1 WP001B 7 augustus 2015, 16:30 19:30 (20:30) Het gebruik van een rekenmachine, telefoon of tablet is niet toegestaan. U mag geen gebruik maken van het boek
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
13.1 De tweede afgeleide [1]
![13.1 De tweede afgeleide [1] 13.1 De tweede afgeleide [1]](/thumbs/40/20774591.jpg) 13.1 De tweede afgeleide [1] De functie is afnemend dalend tot het lokale minimum; Vanaf het lokale minimum tot punt A is de functie toenemend stijgend; Vanaf punt A tot het lokale maimum is de functie
13.1 De tweede afgeleide [1] De functie is afnemend dalend tot het lokale minimum; Vanaf het lokale minimum tot punt A is de functie toenemend stijgend; Vanaf punt A tot het lokale maimum is de functie
Hoofdstuk 8 - Periodieke functies
 Havo B deel Uitwerkingen Moderne wiskunde Hoofdstuk 8 - Periodieke functies ladzijde 8 V-a c Na seconden = slagen per minuut ca., millivolt V-a Ja, met periode Nee Mogelijk, met periode = en amplitude
Havo B deel Uitwerkingen Moderne wiskunde Hoofdstuk 8 - Periodieke functies ladzijde 8 V-a c Na seconden = slagen per minuut ca., millivolt V-a Ja, met periode Nee Mogelijk, met periode = en amplitude
