Tentamen Gewone Differentiaal Vergelijkingen II
|
|
|
- Rosalia Kuiper
- 4 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Tentamen Gewone Differentiaal Vergelijkingen II Jullie mogen een willekeurige van de vier opgaven als bonusopgave bekijken. (Dus drie opgaven volledig en goed gedaan is al een 10.) Opgave 1 Bekijk de lineaire differentiaal vergelijking y y = 0. (a) Geef de algemene oplossing aan. (Expliciet, dus geen machtreeks!) (b) Bepaal de (unieke) oplossing die voldoet aan y(0) = 1, y (0) = y (0) = 0. (c) Los de differentiaalvergelijking door een machtreeks rond x = 0 op. Eerst algemeen en dan met de beginvoorwarden van (b). (d) Gebruik dit om 1 (3n)! te berekenen. (Geef een expliciete uitdrukking aan, maar je hoeft deze niet numeriek uit te rekenen.) Opgave Bepaal de Greense functie voor het randwaardeprobleem Hint: Substitueer x = e t. u + 1 u = f, u(1) = u() = 0. 4x Zie vervolg op achterkant!! 1
2 Opgave 3 (a) Bepaal de eigenwaarden 0 < λ 0 < λ 1 < en eigenfuncties voor het eigenwaarde probleem u + λu = 0 op [0, 1], u(0) = u (0), u(1) = 0. (b) Laat zien dat ( π λ n = n) + nπ + β, n = 0, 1,,..., waar βn 0. Opgave 4 Bekijk de differentiaalvergelijking van Legendre (α C vast): (z 1)u (z) + zu (z) α(α + 1)u(z) = 0. We zoeken een ontwikkeling voor de oplossing rond z = van de vorm u λ (z) = u k z λ k. (1) (a) Bepaal een inductivee conditie op de coëfficienten u k. (b) Laat zien dat λ {α, α 1}. (c) Bekijk het geval λ = α. Geef een expliciete formule voor u k. Gebruik hiervoor ( ) ( ) x x(x 1) (x n + 1) x :=, := 1, n n! 0 waar x C, n N. Welke conditie is er op α? (d) Bewijs dat de reeks (1) met λ = α voor z > 1 convergeert. (e) Laat zien dat u α een veelterm is als α N. (De Legendre polynomen.) (f) Als u α de boven bepaalde oplossing is, laat zien dat ook u α 1 een oplossing is. Wat is nu de conditie op α?
3 Oplossingen Oplossing 1 Dus: (a) Inzetten van y(x) = e kx levert k 3 = 1, en dus k 1 = 1, k = 1 + i 3, k 3 = 1 i 3 y(x) = c 1 e x + c e k x + c 3 e k 3x. = k. (b) De beginvoorwarden leveren de condities c 1 + c + c 3 = 1, c 1 + c k + c 3 k 3 = 0, c 1 + c (k ) + c 3 (k 3 ) = 0. Merk op dat (k ) = k 3 = k en (k 3 ) = k. Door optellen en van elkaar aftrekken van de tweede en derde vergelijking krijgen we c 1 + c (k + k ) + c 3 (k + k ) = 0, c (k k ) + c 3 (k k ) = 0. De tweede van deze levert c = c 3, en met k +k = 1 volgt uit de eerste dat c 1 c c 3 = c 1 c = 0, dus c 1 = c = c 3 en daarom c 1 = c = c 3 = 1/3. Dus y(x) = 1 ( e x + e kx + e ) k 3x 3 ( ( )) = 1 e x + e x 3 cos 3 x. () (c) Met geldt y(x) = a n x n y (x) = n(n 1)(n )a n x n 3 = (n + 3)(n + )(n + 1)a n+3 x n. n=3 Inzetten van de reeksen voor y en y in y = y en vergelijking van coefficienten geeft (n + 3)(n + )(n + 1)a n+3 = a n n N 0. We kunnen dus a 0, a 1, a willekeurig kiezen en verder geldt a 3n+k = k! (3n)! a k n 1, k {0, 1, }, ofwel a 3n = a 0 (3n)!, a 3n+1 = a 1 (3n)!, a 3n+ = a (3n)! 3 n 1.
4 Dus y(x) = a 0 x 3n (3n)! + a 1 ( x 3n+1 (3n + 1)! + a x + Natuurlijk geldt y(0) = a 0, y (0) = a 1, y (0) = a. De beginvoorwaarden van (b) leiden dus op (d) Met x = 1 krijgen we y(x) = x 3n (3n)!. 1 (3n)! = y(1), n=1 ) x 3n+. (3) (3n + )! waar y(x) de oplossing van y = y is die aan y(0) = 1, y (0) = y (0) = 0 voldoet. Door in () x = 1 te zetten krijgen we ( ( )) 1 (3n)! = e 1 3 cos. 3 (Dit is , wat op acht cijfers na de komma gelijk is aan 1 + 1/3! + 1/6! + 1/9!). Oplossing We zoeken eerst de algemene oplossing van u (x) + 1 u(x) = 0. 4x Met de substitutie x = e t, dus u(x) = v(t), hebben we du dx = dv dt dt dx = v (t) 1 x, d u dx = 1 x v (t) + 1 x v (t), dus v v et e + v = 0, t 4et of gewoon v v +v/4 = 0. De charakteristieke veelterm k k +1/4 heeft de dubbele nulpunt k = 1/, de oplossingen zijn dus v(t) = e t/ (c 1 + c t), Hiermee is u(x) = x(c 1 + c ln x). u(1) = c 1, u() = (c 1 + c ln ). De homogene randvoorwarden u(1) = u() = 0 leiden dus op c 1 = c = 0, er geldt dus eenduidigheid voor het inhomogene randwaardeprobleem. De oplossingen u 1 (x) = ln x x u (x) = (ln x ln ) x 4
5 voldoen aan u 1 (1) = u () = 0. De Wronski determinante u 1 u u 1u is gelijk aan ln, en dus is de Greensche functie G(x, ξ) = 1 { ln u1 (ξ)u (x) als 1 ξ x u 1 (x)u (ξ) als 1 x ξ { xξ (ln x ln ) ln ξ als 1 ξ x = ln (ln ξ ln ) ln x als 1 x ξ Oplossing 3 (a) De algemene oplossing van u + λu = 0 (waar λ > 0) is u(x) = c 1 cos( λx) + c sin( λx). Nu zijn u(0) = c 1 en u (0) = λc, dus moet c 1 = c, c = c. Dus u(x) = c( λ cos( λx) + sin( λx)). De voorwaarde u(1) = 0 leidt op λ cos( λ) + sin( λ) = 0, ofwel λ = tan λ. (b) We zoeken de oplossingen x 1, x,... van x = tan x. Op (0, π/) geldt tan x > 0 en bestaat dus geen oplossing. Een tekening van f 1 (x) = x, f (x) = tan x maakt duijdelijk dat x = tan x precies een oplossing x n in elk interval (π/ + nπ, 3π/ + nπ), n N 0 heeft, dus x n = π + nπ + β n met β n (0, π). Verder geldt dat x n voor n steeds dichter bij de linke rand van het interval (π/ + nπ, 3π/ + nπ) ligd, dus β n 0. De beweringen over λ n = x n volgenen meteen. Oplossing 4 (Alles resultaten) (a) Uit (1) volgt u λ (z) = u k (λ k)z λ k 1, u λ(z) = u k (λ k)(λ k 1)z λ k, en dus u k ((λ k)(λ k 1) + (λ k) α(α + 1)) z λ k u k ((λ k)(λ k 1))z λ k = 0. Door vergelijking van coefficienten krijgen we voor k = 0 en k = 1 en voor λ {, 3,...}: k= u 0 (λ(λ + 1) α(α + 1)) = 0, (4) u 1 ((λ 1)λ α(α + 1)) = 0, u k ((λ k)(λ k + 1) α(α + 1)) = u k (λ k + )(λ k + 1). (5) 5
6 (b) We kunnen u 0 en u 1 onafhankelijk kiezen. We kijken alleen naar de oplossing met u 0 = 1, u 1 = 0. (Een oplossing met u 0 = 0, u 1 = 1 kunnen we in een oplossing met u 0 = 1 transformeren als we λ door λ+1 vervangen.) Dan volgt uit (4) de conditie λ {α, α 1}. (c) Met λ = α wordt (5) Met u 0 = 1, u 1 = 0 krijgen we (α k + )(α k + 1) u k = u k ((α k)(α k + 1) α(α + 1)) (α k + )(α k + 1) = u k. k(α + 1 k) u(z) = i=0 z α i α(α ) (α i + )(α 1)(α 3) (α i + 1) ( i)( i ) ( )(α 1)(α 3) (α i + 1) We zijn dat α {1, 3,...} moet gelden. 6
168 HOOFDSTUK 5. REEKSONTWIKKELINGEN
 168 HOOFDSTUK 5. REEKSONTWIKKELINGEN 5.7 Vraagstukken Vraagstuk 5.7.1 Beschouw de differentiaalvergelijking d2 y d 2 = 2 y. (i) Schrijf y = a k k. Geef een recurrente betrekking voor de coëfficienten a
168 HOOFDSTUK 5. REEKSONTWIKKELINGEN 5.7 Vraagstukken Vraagstuk 5.7.1 Beschouw de differentiaalvergelijking d2 y d 2 = 2 y. (i) Schrijf y = a k k. Geef een recurrente betrekking voor de coëfficienten a
1 Eigenwaarden en eigenvectoren
 Eigenwaarden en eigenvectoren Invoeren van de begrippen eigenwaarde en eigenvector DEFINITIE Een complex (of reëel getal λ heet een eigenwaarde van de n n matrix A als er een vector x is met Ax = λx Dan
Eigenwaarden en eigenvectoren Invoeren van de begrippen eigenwaarde en eigenvector DEFINITIE Een complex (of reëel getal λ heet een eigenwaarde van de n n matrix A als er een vector x is met Ax = λx Dan
Hoofdstuk 3: Tweede orde lineaire differentiaalvergelijkingen
 Hoofdstuk 3: Tweede orde lineaire differentiaalvergelijkingen De inhoud van hoofdstuk 3 zou grotendeels bekende stof moeten zijn. Deze stof is terug te vinden in Stewart, hoofdstuk 17. Daar staat alles
Hoofdstuk 3: Tweede orde lineaire differentiaalvergelijkingen De inhoud van hoofdstuk 3 zou grotendeels bekende stof moeten zijn. Deze stof is terug te vinden in Stewart, hoofdstuk 17. Daar staat alles
Aanvullingen van de Wiskunde / Partiële Differentiaalvergelijkingen
 de Bachelor EIT 2de en de Bachelor Wiskunde Academiejaar 215-216 1ste semester 26 januari 216 Aanvullingen van de Wiskunde / Partiële Differentiaalvergelijkingen 1. Gegeven een homogene lineaire partiële
de Bachelor EIT 2de en de Bachelor Wiskunde Academiejaar 215-216 1ste semester 26 januari 216 Aanvullingen van de Wiskunde / Partiële Differentiaalvergelijkingen 1. Gegeven een homogene lineaire partiële
Hoofdstuk 1: Inleiding
 Hoofdstuk 1: Inleiding 1.1. Richtingsvelden. Zie Stewart, 9.2. 1.2. Oplossingen van enkele differentiaalvergelijkingen. Zelf doorlezen. 1.3. Classificatie van differentiaalvergelijkingen. Differentiaalvergelijkingen
Hoofdstuk 1: Inleiding 1.1. Richtingsvelden. Zie Stewart, 9.2. 1.2. Oplossingen van enkele differentiaalvergelijkingen. Zelf doorlezen. 1.3. Classificatie van differentiaalvergelijkingen. Differentiaalvergelijkingen
Hoofdstuk 10: Partiële differentiaalvergelijkingen en Fourierreeksen
 Hoofdstuk : Partiële differentiaalvergelijkingen en Fourierreeksen Partiële differentiaalvergelijkingen zijn vergelijkingen waarin een onbekende functie van twee of meer variabelen en z n partiële afgeleide(n)
Hoofdstuk : Partiële differentiaalvergelijkingen en Fourierreeksen Partiële differentiaalvergelijkingen zijn vergelijkingen waarin een onbekende functie van twee of meer variabelen en z n partiële afgeleide(n)
Stelsels differentiaalvergelijkingen
 Stelsels differentiaalvergelijkingen Stelsels homogene differentiaalvergelijkingen We bekijken in deze paragraaf stelsels homogene differentiaalvergelijkingen: x (t x (t x (t x (t x n(t A Voorbeeld x +
Stelsels differentiaalvergelijkingen Stelsels homogene differentiaalvergelijkingen We bekijken in deze paragraaf stelsels homogene differentiaalvergelijkingen: x (t x (t x (t x (t x n(t A Voorbeeld x +
11.3. Inhomogene randwaardeproblemen. We beschouwen eerst inhomogene Sturm- Liouville randwaardeproblemen van de vorm :
 11.3. Inhomogene randwaardeproblemen. We beschouwen eerst inhomogene Sturm- Liouville randwaardeproblemen van de vorm : L[y] := [p(x)y ] + q(x)y = µr(x)y + f(x), < x < 1 (1) a 1 y() + a 2 y () =, b 1 y(1)
11.3. Inhomogene randwaardeproblemen. We beschouwen eerst inhomogene Sturm- Liouville randwaardeproblemen van de vorm : L[y] := [p(x)y ] + q(x)y = µr(x)y + f(x), < x < 1 (1) a 1 y() + a 2 y () =, b 1 y(1)
Tentamenopgaven over hfdst. 1 t/m 4
 Ttamopgav over hfdst. 1 t/m 4 1. donderdag 31 oktober 1996 Bepaal de oplossing van het beginwaardeprobleem y + 4y = 4 cos 2x, y(0) = 1, y (0) = 0. 2. donderdag 31 oktober 1996 Bepaal de algeme oplossing
Ttamopgav over hfdst. 1 t/m 4 1. donderdag 31 oktober 1996 Bepaal de oplossing van het beginwaardeprobleem y + 4y = 4 cos 2x, y(0) = 1, y (0) = 0. 2. donderdag 31 oktober 1996 Bepaal de algeme oplossing
Bekijk nog een keer het stelsel van twee vergelijkingen met twee onbekenden x en y: { De tweede vergelijking van de eerste aftrekken geeft:
 Determinanten Invoeren van het begrip determinant Bekijk nog een keer het stelsel van twee vergelijkingen met twee onbekenden x en y: { a x + b y = c a 2 a 2 x + b 2 y = c 2 a Dit levert op: { a a 2 x
Determinanten Invoeren van het begrip determinant Bekijk nog een keer het stelsel van twee vergelijkingen met twee onbekenden x en y: { a x + b y = c a 2 a 2 x + b 2 y = c 2 a Dit levert op: { a a 2 x
== Hertentamen Analyse 1 == Dinsdag 25 maart 2008, u
 == Hertentamen Analyse == Dinsdag 5 maart 8, 4-7u Schrijf op ieder vel je naam en studentnummer, de naam van de docent (S Hille, O van Gaans) en je studierichting Geef niet alleen antwoorden, leg elke
== Hertentamen Analyse == Dinsdag 5 maart 8, 4-7u Schrijf op ieder vel je naam en studentnummer, de naam van de docent (S Hille, O van Gaans) en je studierichting Geef niet alleen antwoorden, leg elke
18.I.2010 Wiskundige Analyse I, theorie (= 60% van de punten)
 8.I.00 Wiskundige Analyse I, theorie 60% van de punten) Beantwoord elk van de vragen I,II,III en IV op één van de dubbele geruite bladen. Schrijf op elk van die dubbele geruite bladen, bovenaan de eerste
8.I.00 Wiskundige Analyse I, theorie 60% van de punten) Beantwoord elk van de vragen I,II,III en IV op één van de dubbele geruite bladen. Schrijf op elk van die dubbele geruite bladen, bovenaan de eerste
Technische Universiteit Delft. ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW2030 Vrijdag 30 januari 2015,
 Technische Universiteit Delft Faculteit EWI ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW23 Vrijdag 3 januari 25, 4.-7. Dit tentamen bestaat uit 6 opgaven. Alle antwoorden dienen beargumenteerd
Technische Universiteit Delft Faculteit EWI ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW23 Vrijdag 3 januari 25, 4.-7. Dit tentamen bestaat uit 6 opgaven. Alle antwoorden dienen beargumenteerd
Tentamen Functies en Reeksen
 Tentamen Functies en Reeksen 6 november 204, 3:30 6:30 uur Schrijf op ieder vel je naam en bovendien op het eerste vel je studentnummer, de naam van je practicumleider (Arjen Baarsma, KaYin Leung, Roy
Tentamen Functies en Reeksen 6 november 204, 3:30 6:30 uur Schrijf op ieder vel je naam en bovendien op het eerste vel je studentnummer, de naam van je practicumleider (Arjen Baarsma, KaYin Leung, Roy
OF (vermits y = dy. dx ) P (x, y) dy + Q(x, y) dx = 0
 Algemeen kunnen we een eerste orde differentiaalvergelijking schrijven als: y = Φ(x, y) OF (vermits y = dy dx ) P (x, y) dy + Q(x, y) dx = 0 Indien we dan P (x, y) en Q(x, y) kunnen schrijven als P (x,
Algemeen kunnen we een eerste orde differentiaalvergelijking schrijven als: y = Φ(x, y) OF (vermits y = dy dx ) P (x, y) dy + Q(x, y) dx = 0 Indien we dan P (x, y) en Q(x, y) kunnen schrijven als P (x,
Differentiaalvergelijkingen Technische Universiteit Delft
 Differentiaalvergelijkingen Technische Universiteit Delft Roelof Koekoek wi23wbmt Roelof Koekoek (TU Delft Differentiaalvergelijkingen wi23wbmt 1 / 12 Fourierreeksen van even en oneven functies a 2 + (
Differentiaalvergelijkingen Technische Universiteit Delft Roelof Koekoek wi23wbmt Roelof Koekoek (TU Delft Differentiaalvergelijkingen wi23wbmt 1 / 12 Fourierreeksen van even en oneven functies a 2 + (
ax + 2 dx con- vergent? n ln(n) ln(ln(n)), n=3 (d) y(x) = e 1 2 x2 e 1 2 t2 +t dt + 2
 Radboud Universiteit Nijmegen Tentamen Calculus NWI-NPB 8 januari 3, 8.3.3 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden. Maak uw redenering
Radboud Universiteit Nijmegen Tentamen Calculus NWI-NPB 8 januari 3, 8.3.3 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden. Maak uw redenering
Aanvullingen van de Wiskunde
 3de Bachelor EIT - de Bachelor Fysica Academiejaar 014-015 1ste semester 7 januari 015 Aanvullingen van de Wiskunde 1. Gegeven is een lineaire partiële differentiaalvergelijking van orde 1: a 1 (x 1,,
3de Bachelor EIT - de Bachelor Fysica Academiejaar 014-015 1ste semester 7 januari 015 Aanvullingen van de Wiskunde 1. Gegeven is een lineaire partiële differentiaalvergelijking van orde 1: a 1 (x 1,,
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN
 TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D020. Datum: Vrijdag 26 maart 2004. Tijd: 14.00 17.00 uur. Plaats: MA 1.41 Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D020. Datum: Vrijdag 26 maart 2004. Tijd: 14.00 17.00 uur. Plaats: MA 1.41 Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Uitwerking Tentamen Calculus, 2DM10, maandag 22 januari 2007
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking Tentamen Calculus, DM, maandag januari 7. (a) Gevraagd is het polynoom f() + f () (x ) + f (x ). Een eenvoudige rekenpartij
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Uitwerking Tentamen Calculus, DM, maandag januari 7. (a) Gevraagd is het polynoom f() + f () (x ) + f (x ). Een eenvoudige rekenpartij
3. Bepaal de convergentie-eigenschappen (absoluut convergent, voorwaardelijk convergent, divergent) van de volgende reeksen: n=1. ( 1) n (n + 1)x 2n.
 Radboud Universiteit Tentamen Calculus A NWI-WP025 25 januari 208, 8.30.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Tentamen Calculus A NWI-WP025 25 januari 208, 8.30.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm
 5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm x y + xy + (x ν )y = met ν R (1) heet een Bessel (differentiaal)vergelijking. De waarde van ν noemt men ook wel de orde
5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm x y + xy + (x ν )y = met ν R (1) heet een Bessel (differentiaal)vergelijking. De waarde van ν noemt men ook wel de orde
34 HOOFDSTUK 1. EERSTE ORDE DIFFERENTIAALVERGELIJKINGEN
 34 HOOFDSTUK 1. EERSTE ORDE DIFFERENTIAALVERGELIJKINGEN 1.11 Vraagstukken Vraagstuk 1.11.1 Beschouw het beginwaardeprobleem = 2x (y 1), y(0) = y 0. Los dit beginwaardeprobleem op voor y 0 R en maak een
34 HOOFDSTUK 1. EERSTE ORDE DIFFERENTIAALVERGELIJKINGEN 1.11 Vraagstukken Vraagstuk 1.11.1 Beschouw het beginwaardeprobleem = 2x (y 1), y(0) = y 0. Los dit beginwaardeprobleem op voor y 0 R en maak een
Analyse, Deel III Samenvatting Martijn Boussé
 Analyse, Deel III Inhoudsopgave I Lineaire Differentiaalvergelijkingen... 2 I.I Algemene theorie... 2 I.II Lineaire differentiaalvergelijkingen constante coëfficiënten... 3 I.III Lineaire differentiaalvergelijking
Analyse, Deel III Inhoudsopgave I Lineaire Differentiaalvergelijkingen... 2 I.I Algemene theorie... 2 I.II Lineaire differentiaalvergelijkingen constante coëfficiënten... 3 I.III Lineaire differentiaalvergelijking
A = b c. (b) Bereken de oppervlakte van het parallellogram dat opgespannen wordt door b en c. Voor welke p is deze oppervlakte minimaal?
 Oplossing Tussentijdse toets Wiskunde II Vraag Zij A de matrix met kolomvectoren met p een vast reëel getal A = a b c a =, b =, c = p a Voor welke p R zijn de vectoren lineair afhankelijk? b Bereken de
Oplossing Tussentijdse toets Wiskunde II Vraag Zij A de matrix met kolomvectoren met p een vast reëel getal A = a b c a =, b =, c = p a Voor welke p R zijn de vectoren lineair afhankelijk? b Bereken de
Wiskundige Technieken 1 Uitwerkingen Tentamen 4 november 2013
 Wiskundige Technieken Uitwerkingen Tentamen 4 november 0 Normering voor 4 pt vragen andere vragen naar rato): 4pt pt pt pt 0pt goed begrepen én goed uitgevoerd, eventueel met of onbelangrijke rekenfoutjes
Wiskundige Technieken Uitwerkingen Tentamen 4 november 0 Normering voor 4 pt vragen andere vragen naar rato): 4pt pt pt pt 0pt goed begrepen én goed uitgevoerd, eventueel met of onbelangrijke rekenfoutjes
1 WAAM - Differentiaalvergelijkingen
 1 WAAM - Differentiaalvergelijkingen 1.1 Algemene begrippen Een (gewone) differentiaalvergelijking heeft naast de onafhankelijke veranderlijke (bijvoorbeeld genoteerd als x), eveneens een onbekende functie
1 WAAM - Differentiaalvergelijkingen 1.1 Algemene begrippen Een (gewone) differentiaalvergelijking heeft naast de onafhankelijke veranderlijke (bijvoorbeeld genoteerd als x), eveneens een onbekende functie
Geef niet alleen antwoorden, maar bewijs al je beweringen.
 Tentamen Lineaire Algebra donderdag 29 januari 205, 9.00-2.00 uur Het is niet toegestaan telefoons, computers, grafische rekenmachines (wel een gewone), dictaten, boeken of aantekeningen te gebruiken.
Tentamen Lineaire Algebra donderdag 29 januari 205, 9.00-2.00 uur Het is niet toegestaan telefoons, computers, grafische rekenmachines (wel een gewone), dictaten, boeken of aantekeningen te gebruiken.
Hoofdstuk 10: Partiële differentiaalvergelijkingen en Fourierreeksen
 Hoofdstuk : Partiële differtiaalvergelijking Fourierreeks Partiële differtiaalvergelijking zijn vergelijking waarin e onbekde functie van twee of meer variabel z n partiële afgeleide(n) voorkom. Dit in
Hoofdstuk : Partiële differtiaalvergelijking Fourierreeks Partiële differtiaalvergelijking zijn vergelijking waarin e onbekde functie van twee of meer variabel z n partiële afgeleide(n) voorkom. Dit in
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
n 2 + 3n + 6 4n 3 3 n + 8n n + 3n + 16 n=1 Indien convergent, bepaal dan ook de waarde van de reeks.
 Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP004B januari 05,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP004B januari 05,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
n 2 + 2n + 4 3n 2 n + 4n n + 2n + 12 n=1
 Radboud Universiteit Nijmegen Tentamen Calculus 2 NWI-NP004B 6 april 205, 8.00 2.00 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten
Radboud Universiteit Nijmegen Tentamen Calculus 2 NWI-NP004B 6 april 205, 8.00 2.00 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten
Technische Universiteit Delft Uitwerking Tentamen Analyse 3, WI 2601 Maandag 11 januari 2010, 9.00-12.00
 Technische Universiteit Delft Uitwerking Tentamen Analyse 3, WI 6 Maandag januari, 9- Faculteit EWI Dit tentamen bestaat uit 6 opgaven Alle antwoorden dienen beargumenteerd te worden Normering: punten
Technische Universiteit Delft Uitwerking Tentamen Analyse 3, WI 6 Maandag januari, 9- Faculteit EWI Dit tentamen bestaat uit 6 opgaven Alle antwoorden dienen beargumenteerd te worden Normering: punten
Hoofdstuk 11: Randwaardeproblemen en Sturm-Liouville theorie
 Hoofdstuk : Randwaardeproblemen en Sturm-Liouville theorie.. Tweepunts randwaardeproblemen. Bij het oplossen van partiële differentiaalvergelijkingen met behulp van de methode van scheiden van variabelen
Hoofdstuk : Randwaardeproblemen en Sturm-Liouville theorie.. Tweepunts randwaardeproblemen. Bij het oplossen van partiële differentiaalvergelijkingen met behulp van de methode van scheiden van variabelen
Analyse I. f(x)dx + f(x)dx =
 1ste Bachelor Ingenieurswetenschappen/ Wiskunde/Natuurkunde Academiejaar 1-11 1ste semester, 18 januari 11 Analyse I 1. f en g zijn numerieke functies, f is differentieerbaar in a en g is differentieerbaar
1ste Bachelor Ingenieurswetenschappen/ Wiskunde/Natuurkunde Academiejaar 1-11 1ste semester, 18 januari 11 Analyse I 1. f en g zijn numerieke functies, f is differentieerbaar in a en g is differentieerbaar
Wiskunde: Voortgezette Analyse
 de Bach. IR Wet.: Architectuur Academiejaar 0-04 ste zittijd, januari 04 Wiskunde: Voortgezette Analyse. Gegeven is de reeks n x (x + ) n+ Toon aan dat de reeks puntsgewijs convergeert over R. Toon aan
de Bach. IR Wet.: Architectuur Academiejaar 0-04 ste zittijd, januari 04 Wiskunde: Voortgezette Analyse. Gegeven is de reeks n x (x + ) n+ Toon aan dat de reeks puntsgewijs convergeert over R. Toon aan
Eerste orde partiële differentiaalvergelijkingen
 Eerste orde partiële differentiaalvergelijkingen Vakgroep Differentiaalvergelijkingen 1995, 2001, 2002 1 Eerste orde golf-vergelijking De vergelijking au x + u t = 0, u = u(x, t), a ɛ IR (1.1) beschrijft
Eerste orde partiële differentiaalvergelijkingen Vakgroep Differentiaalvergelijkingen 1995, 2001, 2002 1 Eerste orde golf-vergelijking De vergelijking au x + u t = 0, u = u(x, t), a ɛ IR (1.1) beschrijft
Analyse I. 1ste Bachelor Ingenieurswetenschappen Academiejaar ste semester 10 januari 2008
 ste Bachelor Ingenieurswetenschappen Academiejaar 007-008 ste semester 0 januari 008 Analyse I. Bewijs de stelling van Bolzano-Weierstrass: elke oneindige begrensde deelverzameling van R heeft minstens
ste Bachelor Ingenieurswetenschappen Academiejaar 007-008 ste semester 0 januari 008 Analyse I. Bewijs de stelling van Bolzano-Weierstrass: elke oneindige begrensde deelverzameling van R heeft minstens
Oefensessie 1 Lineaire differentiaalvergelijkingen & MAPLE Modeloplossingen Versie
 Oefeningen Analyse III & Aanvullingen Wiskunde Oefensessie 1 Lineaire differentiaalvergelijkingen & MAPLE Modeloplossingen Versie 1-11 Leuven, Oktober 1 nico.scheerlinck@cs.kuleuven.be In deze bundel wordt
Oefeningen Analyse III & Aanvullingen Wiskunde Oefensessie 1 Lineaire differentiaalvergelijkingen & MAPLE Modeloplossingen Versie 1-11 Leuven, Oktober 1 nico.scheerlinck@cs.kuleuven.be In deze bundel wordt
TENTAMEN ANALYSE 1. dinsdag 3 april 2007,
 TENTAMEN ANALYSE. dinsdag april 2007, 4.00-7.00. Het tentamen bestaat uit twee gedeelten: de eerste vijf opgaven gaan over de stof van het eerste gedeelte van het college. De laatste vijf opgaven gaan
TENTAMEN ANALYSE. dinsdag april 2007, 4.00-7.00. Het tentamen bestaat uit twee gedeelten: de eerste vijf opgaven gaan over de stof van het eerste gedeelte van het college. De laatste vijf opgaven gaan
Tentamen Lineaire Algebra
 Tentamen Lineaire Algebra 3 januari 214, 8:3-11:3 uur - Bij dit tentamen mogen dictaten en boeken niet gebruikt worden - Een eenvoudige rekenmachine, hoewel niet nodig, is toegestaan, maar geen grafische
Tentamen Lineaire Algebra 3 januari 214, 8:3-11:3 uur - Bij dit tentamen mogen dictaten en boeken niet gebruikt worden - Een eenvoudige rekenmachine, hoewel niet nodig, is toegestaan, maar geen grafische
Lineaire dv van orde 2 met constante coefficienten
 Lineaire dv van orde 2 met constante coefficienten Homogene vergelijkingen We bekijken eerst homogene vergelijkingen van orde twee met constante coefficienten, d.w.z. dv s van de vorm a 0 y + a 1 y + a
Lineaire dv van orde 2 met constante coefficienten Homogene vergelijkingen We bekijken eerst homogene vergelijkingen van orde twee met constante coefficienten, d.w.z. dv s van de vorm a 0 y + a 1 y + a
x 1 (t) = ve rt = (a + ib) e (λ+iµ)t = (a + ib) e λt (cos µt + i sin µt) x 2 (t) = ve rt = e λt (a cos µt b sin µt) ie λt (a sin µt + b cos µt).
 76 Complexe eigenwaarden Ook dit hebben we reeds gezien bij Lineaire Algebra Zie: Lay, 57 Als xt ve rt een oplossing is van de homogene differentiaalvergelijking x t Axt, dan moet r een eigenwaarde van
76 Complexe eigenwaarden Ook dit hebben we reeds gezien bij Lineaire Algebra Zie: Lay, 57 Als xt ve rt een oplossing is van de homogene differentiaalvergelijking x t Axt, dan moet r een eigenwaarde van
Inhoud college 5 Basiswiskunde Taylorpolynomen
 Inhoud college 5 Basiswiskunde 4.10 Taylorpolynomen 2 Basiswiskunde_College_5.nb 4.10 Inleiding Gegeven is een functie f met punt a in domein D f. Gezocht een eenvoudige functie, die rond punt a op f lijkt
Inhoud college 5 Basiswiskunde 4.10 Taylorpolynomen 2 Basiswiskunde_College_5.nb 4.10 Inleiding Gegeven is een functie f met punt a in domein D f. Gezocht een eenvoudige functie, die rond punt a op f lijkt
Differentiaalvergelijkingen
 Notities bij de nascholing Differentiaalvergelijkingen Eekhoutcentrum 11 mei 2005 Bart Windels Differentiaalvergelijkingen 1 1 Algemeenheden Zij I een open interval van R (eventueel onbegrensd) en y :
Notities bij de nascholing Differentiaalvergelijkingen Eekhoutcentrum 11 mei 2005 Bart Windels Differentiaalvergelijkingen 1 1 Algemeenheden Zij I een open interval van R (eventueel onbegrensd) en y :
. Maak zelf een ruwe schets van f met A = 2, ω = 6π en ϕ = π 6. De som van twee trigonometrische polynomen is weer een trigonometrisch polynoom
 8. Fouriertheorie Periodieke functies. Veel verschijnselen en processen hebben een periodiek karakter. Na een zekere tijd, de periode, komt hetzelfde patroon terug. Denk maar aan draaiende of heen en weer
8. Fouriertheorie Periodieke functies. Veel verschijnselen en processen hebben een periodiek karakter. Na een zekere tijd, de periode, komt hetzelfde patroon terug. Denk maar aan draaiende of heen en weer
Doe de noodzakelijke berekeningen met de hand; gebruik Maple ter controle.
 De n-de term van de numerieke rij (t n ) (met n = 0,, 2,...) is het rekenkundig gemiddelde van zijn twee voorgangers. (a) Bepaal het Z-beeld F van deze numerieke rij en het bijhorende convergentiegebied.
De n-de term van de numerieke rij (t n ) (met n = 0,, 2,...) is het rekenkundig gemiddelde van zijn twee voorgangers. (a) Bepaal het Z-beeld F van deze numerieke rij en het bijhorende convergentiegebied.
Zelftest wiskunde voor Wiskunde, Fysica en Sterrenkunde
 In onderstaande zelftest zijn de vragen gebundeld die als voorbeeldvragen zijn opgenomen in de bijhorende overzichten van de verwachte voorkennis wiskunde. Naast de vragen over strikt noodzakelijke voorkennis,
In onderstaande zelftest zijn de vragen gebundeld die als voorbeeldvragen zijn opgenomen in de bijhorende overzichten van de verwachte voorkennis wiskunde. Naast de vragen over strikt noodzakelijke voorkennis,
Het vinden van een particuliere oplossing
 Het vind van e particuliere oplossing Voor e lineaire differtiaalvergelijking met constante (reële) coëfficiënt a 0 y (n) (t) + a 1 y (n 1) (t) +... + a n 1 y (t) + a n y(t) = g(t), a 0 0 (1) geldt, dat
Het vind van e particuliere oplossing Voor e lineaire differtiaalvergelijking met constante (reële) coëfficiënt a 0 y (n) (t) + a 1 y (n 1) (t) +... + a n 1 y (t) + a n y(t) = g(t), a 0 0 (1) geldt, dat
Tussentijdse Toets Wiskunde 2 1ste bachelor Biochemie & Biotechnologie, Chemie, Geografie, Geologie en Informatica april 2011
 Tussentijdse Toets Wiskunde ste bachelor Biochemie & Biotechnologie, Chemie, Geografie, Geologie en Informatica april Deze toets is bedoeld om u vertrouwd te maken met de wijze van ondervraging op het
Tussentijdse Toets Wiskunde ste bachelor Biochemie & Biotechnologie, Chemie, Geografie, Geologie en Informatica april Deze toets is bedoeld om u vertrouwd te maken met de wijze van ondervraging op het
== Uitwerkingen Tentamen Analyse 1, WI1600 == Maandag 10 januari 2011, u
 == en Tentamen Analyse, WI6 == Maandag januari, 4.-7.u Technische Universiteit Delft, Faculteit EWI. Gegeven is de functie + e + e arctan,, f = +, >. a Beargumenteer dat f continu is op R. b Bepaal de
== en Tentamen Analyse, WI6 == Maandag januari, 4.-7.u Technische Universiteit Delft, Faculteit EWI. Gegeven is de functie + e + e arctan,, f = +, >. a Beargumenteer dat f continu is op R. b Bepaal de
Combinatoriek groep 2
 Combinatoriek groep 2 Recursie Trainingsdag 3, 2 april 2009 Homogene lineaire recurrente betrekkingen We kunnen een rij getallen a 0, a 1, a 2,... op twee manieren definiëren: direct of recursief. Een
Combinatoriek groep 2 Recursie Trainingsdag 3, 2 april 2009 Homogene lineaire recurrente betrekkingen We kunnen een rij getallen a 0, a 1, a 2,... op twee manieren definiëren: direct of recursief. Een
I. Gewone lineaire differentiaalvergelijkingen.
 I. Gewone lineaire differentiaalvergelijkingen. In dit hoofdstuk bespreken we een aantal zaken m.b.t. gewone lineaire differentiaalvergelijkingen. Het gaat om vergelijkingen van het type p N (z)y (N) (z)
I. Gewone lineaire differentiaalvergelijkingen. In dit hoofdstuk bespreken we een aantal zaken m.b.t. gewone lineaire differentiaalvergelijkingen. Het gaat om vergelijkingen van het type p N (z)y (N) (z)
Oefenopgaven wi3097: Numerieke methoden voor differentiaalvergelijkingen
 Oefenopgaven wi3097: Numerieke methoden voor differentiaalvergelijkingen 1 Introductie Taylor polynoom, floating point getal, afrondfout Orde symbool Landau 1. Laat f(x) = x 3. Bepaal het tweede orde Taylor
Oefenopgaven wi3097: Numerieke methoden voor differentiaalvergelijkingen 1 Introductie Taylor polynoom, floating point getal, afrondfout Orde symbool Landau 1. Laat f(x) = x 3. Bepaal het tweede orde Taylor
Uitgewerkte oefeningen
 Uitgewerkte oefeningen Algebra Oefening 1 Gegeven is de ongelijkheid: 4 x. Welke waarden voor x voldoen aan deze ongelijkheid? A) x B) x [ ] 4 C) x, [ ] D) x, Oplossing We werken de ongelijkheid uit: 4
Uitgewerkte oefeningen Algebra Oefening 1 Gegeven is de ongelijkheid: 4 x. Welke waarden voor x voldoen aan deze ongelijkheid? A) x B) x [ ] 4 C) x, [ ] D) x, Oplossing We werken de ongelijkheid uit: 4
Technische Universiteit Delft Tentamen Calculus TI1106M - Uitwerkingen. 2. Geef berekeningen en beargumenteer je antwoorden.
 Technische Universiteit elft Tentamen Calculus TI06M - Uitwerkingen Opmerkingen:. Het gebruik van de rekenmachine is NIET toegestaan.. Geef berekeningen en beargumenteer je antwoorden. 3. Bij iedere vraag
Technische Universiteit elft Tentamen Calculus TI06M - Uitwerkingen Opmerkingen:. Het gebruik van de rekenmachine is NIET toegestaan.. Geef berekeningen en beargumenteer je antwoorden. 3. Bij iedere vraag
WI1708TH Analyse 2. College 5 24 november Challenge the future
 WI1708TH Analyse 2 College 5 24 november 2014 1 Programma Vandaag 2 e orde lineaire differentiaal vergelijking (17.1) 2 1 e orde differentiaal vergelijking Definitie Een 1 e orde differentiaal vergelijking
WI1708TH Analyse 2 College 5 24 november 2014 1 Programma Vandaag 2 e orde lineaire differentiaal vergelijking (17.1) 2 1 e orde differentiaal vergelijking Definitie Een 1 e orde differentiaal vergelijking
Actief gedeelte - Maken van oefeningen
 Actief gedeelte - Maken van oefeningen Algebra Oefening 1 Gegeven is de ongelijkheid: 4 x 2. Welke waarden voor x voldoen aan deze ongelijkheid? (A) x 2 (B) x 2 [ ] 4 (C) x, 2 [ ] 2 (D) x, 2 Oefening 2
Actief gedeelte - Maken van oefeningen Algebra Oefening 1 Gegeven is de ongelijkheid: 4 x 2. Welke waarden voor x voldoen aan deze ongelijkheid? (A) x 2 (B) x 2 [ ] 4 (C) x, 2 [ ] 2 (D) x, 2 Oefening 2
Tussentijdse evaluatie Analyse I
 ste Bachelor Wiskunde Academiejaar 6-7 ste semester november 6 Tussentijdse evaluatie Analyse I. Toon aan dat een niet-stijgende begrensde rij convergent is.. Onderstel dat f : [a, b] R continu is over
ste Bachelor Wiskunde Academiejaar 6-7 ste semester november 6 Tussentijdse evaluatie Analyse I. Toon aan dat een niet-stijgende begrensde rij convergent is.. Onderstel dat f : [a, b] R continu is over
De golfvergelijking in drie dimensies. Golfvergelijking in een dimensie: trillende snaar
 De golfvergelijking in drie dimensies In drie dimensies wordt de golfvergelijking 2 Ψ t 2 = c2 ( 2 ) Ψ x 2 + 2 Ψ y 2 + 2 Ψ z 2 waar c een constante is die de snelheid van de golven aangeeft. Dit is de
De golfvergelijking in drie dimensies In drie dimensies wordt de golfvergelijking 2 Ψ t 2 = c2 ( 2 ) Ψ x 2 + 2 Ψ y 2 + 2 Ψ z 2 waar c een constante is die de snelheid van de golven aangeeft. Dit is de
1E HUISWERKOPDRACHT CONTINUE WISKUNDE
 E HUISWERKOPDRACHT CONTINUE WISKUNDE Uiterste inleverdatum dinsdag oktober, voor het begin van het college N.B. Je moet de hele uitwerking opschrijven en niet alleen het antwoord geven. Je moet het huiswerk
E HUISWERKOPDRACHT CONTINUE WISKUNDE Uiterste inleverdatum dinsdag oktober, voor het begin van het college N.B. Je moet de hele uitwerking opschrijven en niet alleen het antwoord geven. Je moet het huiswerk
Tussentijdse evaluatie Analyse I
 ste Bachelor Wiskunde Academiejaar 4- ste semester 3 oktober 4 Tussentijdse evaluatie Analyse I. Toon aan dat een niet-stijgende begrensde rij convergent is.. Geef de definitie van een verdichtingspunt.
ste Bachelor Wiskunde Academiejaar 4- ste semester 3 oktober 4 Tussentijdse evaluatie Analyse I. Toon aan dat een niet-stijgende begrensde rij convergent is.. Geef de definitie van een verdichtingspunt.
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 2013,
 Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Opgave a. We berekenen eerst een normaal v van V en een normaal w van W. v = (b a) (c a) = ((2)(1) ( 2)( 2), ( 2)( 1) ( 1)(1), ( 1)( 2) (2)( 1))
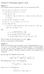 Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN
 TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D2. Datum: dinsdag 29 april 28. Tijd: 14: 17:. Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je naam en studentnummer
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D2. Datum: dinsdag 29 april 28. Tijd: 14: 17:. Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je naam en studentnummer
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
Examen Wiskundige Analyse I 1ste bach ir wet. dinsdag 5 januari Vraag 1.1. Waar of vals (1pt) Het beginvoorwaardenprobleem
 Examen Wiskundige Analyse I ste bach ir wet dinsdag 5 januari 206 Vraag.. Waar of vals (pt) Het beginvoorwaardenprobleem 32x 3 y = (y ) 3, y() = 2, y () = 4 bezit een unieke oplossing, die geldig is in
Examen Wiskundige Analyse I ste bach ir wet dinsdag 5 januari 206 Vraag.. Waar of vals (pt) Het beginvoorwaardenprobleem 32x 3 y = (y ) 3, y() = 2, y () = 4 bezit een unieke oplossing, die geldig is in
1 Stelsels lineaire vergelijkingen.
 Stelsels lineaire vergelijkingen Ter herinnering: in de tweede klas Havo/Atheneum leer je twee vergelijkingen met twee onbekenden oplossen Voorbeeld: { x + y = 5 x + y = 0 Twee keer de eerste vergelijking
Stelsels lineaire vergelijkingen Ter herinnering: in de tweede klas Havo/Atheneum leer je twee vergelijkingen met twee onbekenden oplossen Voorbeeld: { x + y = 5 x + y = 0 Twee keer de eerste vergelijking
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Tentamen Calculus C (2WCB1) op zaterdag 25 januari 2014, 9:00 12:00 uur
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Calculus C (WCB) op zaterdag 5 januari 04, 9:00 :00 uur Maak dit vel los van de rest van het tentamen. Vul uw naam etc. in op
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Calculus C (WCB) op zaterdag 5 januari 04, 9:00 :00 uur Maak dit vel los van de rest van het tentamen. Vul uw naam etc. in op
f even en g oneven = f g oneven. f(x) dx = 2 Stel dat f een even functie is en dat de Fourierreeks voor f gelijk is aan a n cos nπx + b n sin nπx )
 .4. Ev onev functies. E functie f heet ev als voor elke x in het domein van f ook x tot dat domein behoort f( x) = f(x) voor alle x in het domein van f. En e functie f heet onev als voor elke x in het
.4. Ev onev functies. E functie f heet ev als voor elke x in het domein van f ook x tot dat domein behoort f( x) = f(x) voor alle x in het domein van f. En e functie f heet onev als voor elke x in het
Examenvragen Wiskundige Analyse I, 1ste examenperiode
 Examenvragen Wiskundige Analyse I, ste examenperiode 24-25 Vraag (op 6pt) Vraag.. Waar of vals (.5pt) De Wronskiaanse determinant van twee LOF oplossingen y en y 2 van de differentiaalvergelijking cosh(x)y
Examenvragen Wiskundige Analyse I, ste examenperiode 24-25 Vraag (op 6pt) Vraag.. Waar of vals (.5pt) De Wronskiaanse determinant van twee LOF oplossingen y en y 2 van de differentiaalvergelijking cosh(x)y
Analyse I. 3. Formuleer en bewijs de formule van Taylor voor een functie f : R R. Stel de formules op voor de resttermen van Lagrange en Liouville.
 ste Bachelor Ingenieurswetenschappen Academiejaar 8-9 ste semester januari 9 Analyse I. Formuleer en bewijs de formule van Leibniz voor de n-de afgeleide van het product van twee functies f en g.. Onderstel
ste Bachelor Ingenieurswetenschappen Academiejaar 8-9 ste semester januari 9 Analyse I. Formuleer en bewijs de formule van Leibniz voor de n-de afgeleide van het product van twee functies f en g.. Onderstel
Functies van één veranderlijke
 Functies van één veranderlijke 952600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl /29 Elektrotechniek, Wiskunde en Informatica EWI UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde
Functies van één veranderlijke 952600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl /29 Elektrotechniek, Wiskunde en Informatica EWI UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde
TRILLINGEN EN GOLVEN HANDOUT FOURIER
 TRILLINGEN EN GOLVEN HANDOUT FOURIER Cursusjaar 2009 / 2010 2 Inhoudsopgave 1 FOURIERANALYSE 5 1.1 INLEIDING............................... 5 1.2 FOURIERREEKSEN.......................... 5 1.3 CONSEQUENTIES
TRILLINGEN EN GOLVEN HANDOUT FOURIER Cursusjaar 2009 / 2010 2 Inhoudsopgave 1 FOURIERANALYSE 5 1.1 INLEIDING............................... 5 1.2 FOURIERREEKSEN.......................... 5 1.3 CONSEQUENTIES
Bestaat er dan toch een wortel uit 1?
 Bestaat er dan toch een wortel uit 1? Complexe getallen en complexe functies Jan van de Craats Universiteit van Amsterdam, Open Universiteit CWI Vacantiecursus 2007 Wat zijn complexe getallen? Wat zijn
Bestaat er dan toch een wortel uit 1? Complexe getallen en complexe functies Jan van de Craats Universiteit van Amsterdam, Open Universiteit CWI Vacantiecursus 2007 Wat zijn complexe getallen? Wat zijn
== Modeluitwerking tentamen Analyse 1 == Maandag 14 januari 2008, u
 == Modeluitwerking tentmen Anlyse == Mndg 4 jnuri 8, 4.-7.u. Formuleer de Tussenwrdestelling. Als f :, b] R continu is en s R ligt tussen f en fb, dn bestt er een c, b] met fc = s. b Toon n, dt de vergelijking
== Modeluitwerking tentmen Anlyse == Mndg 4 jnuri 8, 4.-7.u. Formuleer de Tussenwrdestelling. Als f :, b] R continu is en s R ligt tussen f en fb, dn bestt er een c, b] met fc = s. b Toon n, dt de vergelijking
10.6. Andere warmteproblemen. We hebben warmteproblemen bekeken van de vorm. 0 < x < L, t > 0. w(0, t) = 0, w(l, t) = 0, t 0. u(x, 0) = f(x), 0 x L,
 .6. Andere warmteproblem. We hebb warmteproblem bekek van de vorm α 2 u xx = u t, < x u(, t) =, u(, t) =, t u(x, ) = f(x), x, waarbij de temperatuur aan de beide uiteind constant bovdi gelijk is.
.6. Andere warmteproblem. We hebb warmteproblem bekek van de vorm α 2 u xx = u t, < x u(, t) =, u(, t) =, t u(x, ) = f(x), x, waarbij de temperatuur aan de beide uiteind constant bovdi gelijk is.
HERTENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN
 HERTENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D. Datum: Vrijdag juli 3. Tijd: 9.. uur. Plaats: AUD 5. Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je naam en studentnummer
HERTENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D. Datum: Vrijdag juli 3. Tijd: 9.. uur. Plaats: AUD 5. Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je naam en studentnummer
6. Lineaire operatoren
 6. Lineaire operatoren Dit hoofdstukje is een generalisatie van hoofdstuk 2. De meeste dingen die we in hoofdstuk 2 met de R n deden, gaan we nu uitbreiden tot andere lineaire ruimten Definitie. Een lineaire
6. Lineaire operatoren Dit hoofdstukje is een generalisatie van hoofdstuk 2. De meeste dingen die we in hoofdstuk 2 met de R n deden, gaan we nu uitbreiden tot andere lineaire ruimten Definitie. Een lineaire
Overzicht Fourier-theorie
 B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.6, donderdag K. P. Hart Faculteit EWI TU Delft Delft, 2 juni, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 38 Outline 1 Rekenregels 2 K. P. Hart TW2040: Complexe
TW2040: Complexe Functietheorie week 4.6, donderdag K. P. Hart Faculteit EWI TU Delft Delft, 2 juni, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 38 Outline 1 Rekenregels 2 K. P. Hart TW2040: Complexe
Tentamen Numerieke Wiskunde dinsdag, 28 januari 2014,
 Tentamen Numerieke Wiskunde dinsdag, 8 januari 04, 3.30 6.30. Zet op ieder vel dat je inlevert je naam en op et eerste vel bovendien nog je studentnummer.. Je mag et dictaat gebruiken, de uitwerkingen
Tentamen Numerieke Wiskunde dinsdag, 8 januari 04, 3.30 6.30. Zet op ieder vel dat je inlevert je naam en op et eerste vel bovendien nog je studentnummer.. Je mag et dictaat gebruiken, de uitwerkingen
Complexe eigenwaarden
 Complexe eigenwaarden Tot nu toe hebben we alleen reële getallen toegelaten als eigenwaarden van een matrix Het is echter vrij eenvoudig om de definitie uit te breiden tot de complexe getallen Een consequentie
Complexe eigenwaarden Tot nu toe hebben we alleen reële getallen toegelaten als eigenwaarden van een matrix Het is echter vrij eenvoudig om de definitie uit te breiden tot de complexe getallen Een consequentie
Tentamen Differentiaalvergelijkingen, (wi1 909TH) woensdag 1 februari 2017, uur.
 Technische Universiteit Delft Faculteit Elektrotechniek, Wiskunde en Informatica Mekelweg 4, Delft Tentamen Differentiaalvergelijkingen, (wi1 909TH) woensdag 1 februari 2017, 18.30-20.30 uur. Het gebruik
Technische Universiteit Delft Faculteit Elektrotechniek, Wiskunde en Informatica Mekelweg 4, Delft Tentamen Differentiaalvergelijkingen, (wi1 909TH) woensdag 1 februari 2017, 18.30-20.30 uur. Het gebruik
Examen G0O17D Wiskunde II (6sp) maandag 10 juni 2013, 8:30-12:30 uur
 Examen GO7D Wiskunde II (6sp maandag juni 3, 8:3-:3 uur Bachelor Biochemie & Biotechnologie Bachelor hemie, Bachelor Geologie Schakelprogramma Master Biochemie & Biotechnologie en Schakelprogramma Master
Examen GO7D Wiskunde II (6sp maandag juni 3, 8:3-:3 uur Bachelor Biochemie & Biotechnologie Bachelor hemie, Bachelor Geologie Schakelprogramma Master Biochemie & Biotechnologie en Schakelprogramma Master
IJkingstoets Wiskunde-Informatica-Fysica 29 juni Nummer vragenreeks: 1
 IJkingstoets Wiskunde-Informatica-Fysica 29 juni 206 Nummer vragenreeks: IJkingstoets wiskunde-informatica-fysica 29 juni 206 - reeks - p. /0 Oefening Welke studierichting wil je graag volgen? (vraag
IJkingstoets Wiskunde-Informatica-Fysica 29 juni 206 Nummer vragenreeks: IJkingstoets wiskunde-informatica-fysica 29 juni 206 - reeks - p. /0 Oefening Welke studierichting wil je graag volgen? (vraag
Tentamen Numerieke Wiskunde (WISB251)
 1 Tentamen Numeriee Wisunde WISB51 Maa één opgave per vel en schrijf op ieder vel duidelij je naam en studentnummer. Laat duidelij zien hoe je aan de antwoorden omt. Onderstaande formules mag je zonder
1 Tentamen Numeriee Wisunde WISB51 Maa één opgave per vel en schrijf op ieder vel duidelij je naam en studentnummer. Laat duidelij zien hoe je aan de antwoorden omt. Onderstaande formules mag je zonder
Aanvullingen van de Wiskunde
 de Bachelor EIT Academiejaar -4 se semeser 8 januari 4 Aanvullingen van de Wiskunde. Gegeven een homogene lineaire parile differeniaalvergelijking van eerse orde: a x,, x n u x a n x,, x n u x n. a Wa
de Bachelor EIT Academiejaar -4 se semeser 8 januari 4 Aanvullingen van de Wiskunde. Gegeven een homogene lineaire parile differeniaalvergelijking van eerse orde: a x,, x n u x a n x,, x n u x n. a Wa
Lineaire Algebra voor W 2Y650
 Lineaire Algebra voor W 2Y650 Docent: L Habets HG 809, Tel: 040-2474230, Email: lcgjmhabets@tuenl http://wwwwintuenl/wsk/onderwijs/2y650 1 Herhaling: Oplossing homogene DV ẋ = Ax Aanname: A is diagonaliseerbaar
Lineaire Algebra voor W 2Y650 Docent: L Habets HG 809, Tel: 040-2474230, Email: lcgjmhabets@tuenl http://wwwwintuenl/wsk/onderwijs/2y650 1 Herhaling: Oplossing homogene DV ẋ = Ax Aanname: A is diagonaliseerbaar
Analyse I. 1ste Bachelor Ingenieurswetenschappen Academiejaar ste semester 12 januari 2010
 ste Bachelor Ingenieurswetenschappen Academiejaar 9- ste semester januari Analyse I. Formuleer en bewijs de formule van Leibniz voor de n-de afgeleide van het product van twee functies f en g.. Onderstel
ste Bachelor Ingenieurswetenschappen Academiejaar 9- ste semester januari Analyse I. Formuleer en bewijs de formule van Leibniz voor de n-de afgeleide van het product van twee functies f en g.. Onderstel
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op dinsdag 26 augustus 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op dinsdag 26 augustus 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
Examen Analyse 2 : Theorie (zonder Maple). (7 januari 2014)
 Examen Analyse 2 : Theorie (zonder Maple). (7 januari 204). Maclaurin reeksen. Geef met bewijs de Maclaurin reeksontwikkeling van de logaritmische functie ln( + x). Geef ook het convergentie-interval van
Examen Analyse 2 : Theorie (zonder Maple). (7 januari 204). Maclaurin reeksen. Geef met bewijs de Maclaurin reeksontwikkeling van de logaritmische functie ln( + x). Geef ook het convergentie-interval van
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Tentamen Basiswiskunde, 2DL03, woensdag 1 oktober 2008, uur.
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Basiswiskunde, DL3, woensdag oktober 8, 9.. uur. Geef op het eerste vel met uitwerkingen aan welk programma (Schakelprogramma
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Basiswiskunde, DL3, woensdag oktober 8, 9.. uur. Geef op het eerste vel met uitwerkingen aan welk programma (Schakelprogramma
Opgaven bij de cursus Relativiteitstheorie wiskunde voorkennis Najaar 2018 Docent: Dr. H. (Harm) van der Lek
 Opgaven bij de cursus Relativiteitstheorie wiskunde voorkennis Najaar 2018 Docent: Dr. H. (Harm) van der Lek Uitwerkingen worden beschikbaar gesteld op de dinsdagavond voorafgaande aan het volgende college
Opgaven bij de cursus Relativiteitstheorie wiskunde voorkennis Najaar 2018 Docent: Dr. H. (Harm) van der Lek Uitwerkingen worden beschikbaar gesteld op de dinsdagavond voorafgaande aan het volgende college
wiskunde B pilot vwo 2017-II
 Twee machten van maimumscore 5 f' ( ) = ln() + ln() Uit f' ( ) = volgt dat = Dus + = ( = ) Hieruit volgt = a+ a, met a =, moet minimaal zijn De vergelijking a = moet worden opgelost Dit geeft Hieruit volgt
Twee machten van maimumscore 5 f' ( ) = ln() + ln() Uit f' ( ) = volgt dat = Dus + = ( = ) Hieruit volgt = a+ a, met a =, moet minimaal zijn De vergelijking a = moet worden opgelost Dit geeft Hieruit volgt
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op dinsdag 6 januari 2009, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op dinsdag 6 januari 2009, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op donderdag 23 oktober 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op donderdag 23 oktober 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
Differentiaalvergelijkingen voor WbMT. wi2051wbmt. Dr. Roelof Koekoek
 Differentiaalvergelijkingen voor WbMT wi25wbmt Dr Roelof Koekoek Het boek William E Boyce & Richard C DiPrima Elementary Differential Equations and Boundary Value Problems Tenth Edition, Wiley, 22, ISBN
Differentiaalvergelijkingen voor WbMT wi25wbmt Dr Roelof Koekoek Het boek William E Boyce & Richard C DiPrima Elementary Differential Equations and Boundary Value Problems Tenth Edition, Wiley, 22, ISBN
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Uitwerking Tentamen Basiswiskunde, 2DL03, woensdag 3 oktober 2007.
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Algemeen deel. Bij het vermenigvuldigen met van de ongelijkheid moet u rekening houden met twee gevallen, te weten > 0 en < 0 en u moet
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Algemeen deel. Bij het vermenigvuldigen met van de ongelijkheid moet u rekening houden met twee gevallen, te weten > 0 en < 0 en u moet
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.10, donderdag K. P. Hart Faculteit EWI TU Delft Delft, 23 juni, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 46 Outline 1 2 3 K. P. Hart TW2040: Complexe Functietheorie
TW2040: Complexe Functietheorie week 4.10, donderdag K. P. Hart Faculteit EWI TU Delft Delft, 23 juni, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 46 Outline 1 2 3 K. P. Hart TW2040: Complexe Functietheorie
