Dubbelplaneten. Rainer Kaenders Radboud Universiteit Nijmegen
|
|
|
- Eva Bogaerts
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 pp Dubbelplaneten Rainer Kaenders Radboud Universiteit Nijmegen In 1695 heeft de Engelse astronoom Edmond Halley voorspeld dat de maanden (d.w.z. de omlooptijd van de maan rond de aarde) in de loop van de 600 jaar vóór zijn tijd ongeveer een tienduizendste uur korter zijn geworden [2]. Hoe kon hij met de middelen van toen een dergelijke uitspraak doen? Twee jaar eerder, in 1693, heeft Halley samen met een Oxfordse arabist de vertaling (door een zekere Plato Tiburtinus) van de observaties van de astronoom al-battani vanuit een vakdeskundig perspectief herzien [1]. De Arabier al-battani ( ), wiens naam door Halley tot Albategnius werd gelatiniseerd, beschreef verschillende maans- en zonsverduisteringen. Naar aanleiding hiervan beweerde Halley [2] dat hij aan kon tonen dat de maanden korter werden. De Utrechtse astronoom Frank Verbunt speculeert in [4], [6] hoe Halley tot deze conclusie gekomen zou kunnen zijn: Omdat zonsverduisteringen uitsluitend bij een nieuwe maan plaatsvinden moet er altijd een geheel aantal maanden tussen twee zonsverduisteringen zitten. Halley kende de lengte van een maand al enigszins nauwkeurig en kon dus terugrekenen wanneer en waar 800 jaar (oftewel ongeveer maanden) eerder al-battani een zonsverduistering gezien zou kunnen hebben. Stel nou dat Halley had berekend dat er toen een zonsverduistering in Alexandria plaats moest hebben gevonden terwijl al-battani een zonsverduistering op deze dag in Bagdad verslaat. Dit had Halley dan kunnen verklaren door aan te nemen dat de zonsverduistering een uur eerder plaatsvond dan hij had berekend, hetgeen betekent dat de doorsnee maandlengte tijdens deze 800 jaar met 10 4 uur langer was dan in zijn tijd. De derde wet van Kepler die we later nog zullen leren kennen, legt een verband tussen de omlooptijd en de afstand tussen aarde en maan en heeft tot gevolg dat met de lengte van de maanden ook de afstand tussen aarde en maan af moet nemen. Tegenwoordig weten wij echter door middel van lasermetingen aan de planeet Mars dat deze afstand tussen aarde en maan met 3,82 cm per jaar toeneemt en daarmee de maanden langer zouden moeten worden. Hoe is dit te verklaren? Had Halley gewoon ongelijk? Deze vraag van Halley is een vraag zoals die werkelijk in de wetenschap, of preciezer in de astrofysica speelt. De vraag oefent een fascinerende werking uit op astronomen maar ook op leerlingen, leraren en andere belangstellenden. Ook al spreken de metingen Halley tegen, toch is de vraag: Op grond waarvan heeft Halley zijn conclusie getrokken? Het antwoord is te vinden in de analyse van het achterliggende wiskundige model. aarde en maan vormen een zogenaamde dubbelplaneet en dubbelplaneten zijn weer draaiende systemen die onderhevig zijn aan de wet van behoud van impulsmoment (of
2 74 Rainer Kaenders Figuur 1. Edmond Halley ( ). draai-impuls). Dit is de natuurkundige notie om de hoeveelheid draaiing van een systeem te kwantificeren. Door een zorgvuldige analyse van deze wet voor aarde-maan is de constatering van Halley logisch te verklaren [4], [5], [6]. Naast de toename van de maandlengte heeft het behoud van impulsmoment namelijk ook een sterkere toename van de daglengte tot gevolg. Als de maanden in dagen worden gemeten dan worden zij daadwerkelijk korter en had Halley dus toch gelijk. Uiteindelijk kan door toepassing van de wet van behoud van impulsmoment de toekomst van de dubbelplaneten aarde-maan, Mars-Phobos en Neptunus-Triton worden voorspeld. Voor alle drie de dubbelplaneten geldt dezelfde wet maar toch gaat elk van hen een ander noodlot tegemoet. In deze bijdrage zullen we de wiskundige achtergronden belichten van begrippen als koppel en impulsmoment en daarmee de wet van behoud van impulsmoment afleiden. De wetten van Newton worden toegelicht en vormen de enige inbreng vanuit de natuurkunde de rest is wiskunde. Vectorfuncties, d.w.z. functies van R naar R 3, worden ingevoerd en de productregel voor inen uitproducten van zulke vectorfuncties afgeleid. Daarmee ligt de wet van behoud van impulsmoment al voor het oprapen. In het vervolg gaan we deze wet interpreteren. Daarvoor kijken wij naar zwaartepunten, hoeksnelheden, middelpuntzoekende krachten en traagheidsmomenten. Als loon voor deze moeite zullen we zien dat planeten in een vlak bewegen, de perkenwet van Kepler geldt en kunnen we het gyroscopisch effect begrijpen. De studie van het impulsmoment in ons zonnestelsel en in het bijzonder het antwoord op het probleem van Halley vormen een schoolvoorbeeld voor de kracht van wiskunde in de natuurwetenschap. De observaties leveren een tegenspraak op die alleen op te lossen is door een gepast wiskundig model dat in dit geval door de klassieke mechanica van Newton is gegeven. Met dit model wordt vervolgens puur wiskundig geredeneerd en dat levert uiteindelijk
3 Dubbelplaneten 75 Figuur 2. De dubbelplaneet aarde-maan. Zie pagina 137 voor een kleurenillustratie. resultaten op die naar de werkelijkheid terug kunnen worden vertaald. Daarmee zijn dan de paradoxaal lijkende observaties te verklaren. Zodra het probleem van Halley is doorgrond wordt duidelijk dat dit model veel meer dan een enkele vraag op kan lossen het maakt voorspellingen in uiteenlopende situaties mogelijk: de ene formule over behoud van impulsmoment levert uiteenlopende voorspellingen op in de drie gevallen aarde-maan, Mars-Phobos en Neptunus-Triton. Het probleem van Halley is een vraag die leerlingen toegang zou kunnen verlenen tot het cultuurgebied van wetenschap die berust op wis- en natuurkunde. Bijvoorbeeld het schoolboek [3] is een aanrader voor iedereen die op schoolniveau verder wil lezen over hemelmechanica en ruimtevaart. Deze bijdrage komt voort uit de samenwerking van het Regionale Steunpunt Wiskunde D in Nijmegen met Jan Kuijpers, hoogleraar astrofysica en decaan aan de Radboud Universiteit, en een kerngroep van negen wiskundedocenten: Mark van den Aarssen, Hanneke Abbenhuis, Herman Alink, Leon van den Broek, Bart Jordens, Maris van Haandel, Dolf van den Hombergh, Richard Klein Breteler en Jos Winkel. Ook op de universiteiten van Delft, Eindhoven en Twente is voor een soortgelijke aanpak gekozen (zie [7]). Inmiddels is er lesmateriaal in eerste versie geproduceerd dat beschikbaar wordt gesteld aan scholen en docenten die het domein Wiskunde in Wetenschap van wiskunde D in het zogenaamde samenwerkingsmodel aan gaan bieden (zie [8]). Het project en dit artikel zouden niet tot stand zijn gekomen zonder de zeer inspirerende bijdragen van Jan Kuijpers die ook het onderwerp naar aanleiding van [4], [5] en [6] in de samenwerking heeft aangedragen. Wij zijn hem hiervoor veel dank verschuldigd. Ten slotte geldt mijn dank Edith Verbeet, secretaresse op de Nijmeegse universitaire lerarenopleiding, die mij zoals zo vaak in de afgelopen jaren heeft geholpen mijn Nederlands op dat van een Nederlander te laten lijken.
4 76 Rainer Kaenders 1. Het wiskundig gereedschap De wiskunde die nodig is om dit hoofdstuk uit het boek van de astronomie te begrijpen is wat elementaire lineaire algebra en de notie van geparametriseerde krommen in het vlak en de ruimte en haar afgeleiden In s en out s van producten in R 3 We beginnen met een herinnering aan in- en uitproducten in R 3. De symbolen u, v, w en e, met of zonder indices, staan in deze paragraaf voor vectoren in R 3. Inproduct Het in(wendig)product van twee vectoren u = (a 1, a 2, a 3 ) en v = (b 1, b 2, b 3 ) uit R 3 is gedefinieerd als u, v = a 1 b 1 + a 2 b 2 + a 3 b 3. Wij spreken het inproduct uit als u in v en het is een voorschrift om uit twee vectoren een reëel getal te berekenen. Eenvoudig na te gaan is dat het inproduct symmetrisch (d.w.z. u, v = v, u ) en in beide argumenten lineair is dit noem je dan bilineair. Wij noemen u = u, u de norm van een vector u uit R 3 en met de stelling van Pythagoras ziet men dat de waarde van de norm gelijk is aan de lengte van de vector u. Als wij het pijltje van een vector u weglaten dan bedoelen wij de absolute waarde u = u van deze vector. Het inproduct is zeer geschikt om de projectie van een vector u op een vector v te berekenen. Er bestaat een op v loodrechte vector van de vorm u λ v. Het getal λ bepaal je door te eisen dat deze vector loodrecht staat op v. Met het inproduct betekent dit u λ v, v = 0 λ = u, v v 2. De projectievector en de loodvector van een vector u op een vector v worden gegeven door u, v u v := v 2 v en u u, v v := u v 2 v. Projectie- en loodvector geven aanleiding tot een ontbinding u = u v + u v van de vector u in een vector in de richting van v en een vector die loodrecht op v staat. Opgave: (i) Bewijs dat geldt u, v = u, v u = u v, v. (ii) De vectoren u en v spannen een parallellogram op. Laat zien dat de oppervlakte daarvan gelijk is aan u v v = v u u = u 2 v 2 u, v.
5 Dubbelplaneten 77 Figuur 3. De vectoren a, b en a b vormen een zogenaamd rechtshandig assenstelsel. Uitproduct In de natuurkunde en de techniek kom je vaak situaties tegen waar grootheden loodrecht op elkaar staan. Wij zoeken dus een manier om aan twee vectoren u en v in R 3 een derde vector u v uit R 3 toe te kennen zodat geldt als u 0 en v 0: (i) u v staat loodrecht op u en v, (ii) u, v en u v vormen een rechtshandig assenstelsel (zie Figuur 3), (iii) als u en v loodrecht op elkaar staan geldt: u v = u v, (iv) u v = u v u = u v v. Als één van de vectoren de nulvector is, dan is ook het uitproduct gelijk aan nul. Voor vectoren u en v geldt: u u = 0 en u v = u v. De tweede eigenschap volgt uit de toepassing van de eerste eigenschap op het uitproduct ( u + v) ( u + v). De eigenschappen hierboven maken duidelijk dat u v de eenduidig bepaalde vector is waarvoor geldt dat hij loodrecht staat op het door u en v opgespannen parallellogram, zijn lengte gelijk is aan het oppervlak (zie de opgave hierboven) van dat parallellogram, waarbij u, v en w georiënteerd zijn volgens de rechterhand-regel. Definitie: Wij noemen u v het uit(wendig)product van de vectoren u en v (spreek uit: u uit v). Opgave: Toon aan dat: u, v = u v cos θ en u v = u v sin θ, waarbij θ de hoek tussen u en v is. Bewijs dat voor vectoren u en v geldt: u ( v u) = u 2 v u, v u = u v u.
6 78 Rainer Kaenders Gegeven twee vectoren u = u v = a 1 a 2 a 3 b 1 b 2 b 3 a 1 a 2 a 3 en v = = b 1 b 2 b 3 a 2 b 3 b 2 a 3 a 1 b 3 + a 3 b 1 a 1 b 2 b 1 a 2 dan geldt: Het koppel Een andere toepassing voor het uitproduct is de definitie van het koppel. Als men een schroef wil schroeven dan gaat dat het beste met een arm die loodrecht staat op de schroef: een schroevensleutel. Hoe groter de afstand is tussen de schroef en het punt op de schroevensleutel waarop een kracht wordt uitgeoefend hoe beter de schroef te draaien zal zijn. Als de arm niet loodrecht staat dan is het enige wat voor het schroeven telt het loodrechte deel van de arm. (Bijvoorbeeld als iemand probeert te schroeven door de schroevensleutel in verlenging op de schroef erop te zetten dan is de schroefkracht kennelijk nul.) Op een punt van de arm wordt er bij het schroeven een kracht uitgeoefend en het enige wat er voor de schroefkracht toe doet is het gedeelte van de kracht dat loodrecht staat op de schroef en de schroevendraaier. De effectiviteit van het schroeven in een gegeven richting heeft te maken met enerzijds de lengte van de schroevensleutel en de mate waarin hij loodrecht staat op de schroef en anderzijds met de kracht die op een punt van de schroevensleutel wordt uitgeoefend en de mate waarin deze kracht loodrecht staat op de schroef en de schroevensleutel. We kunnen ook andersom redeneren. Gegeven een arm of hefboom, wiskundig voorgesteld door een vector r, en een krachtsvector F. Deze vectoren r en F leggen een richting vast waarin het beste geschroefd kan worden. Hoe sterker de kracht is en hoe langer de arm hoe effectiever er geschroefd kan worden. Uit de bovenste beschouwingen blijkt dat de mate en de richting waarin er effectief geschroefd kan worden gegeven wordt door het zogenaamde koppel ten opzichte van de oorsprong O dat wordt uitgedrukt door: N = r F. Als er een kracht werkt op een massadeeltje dan kunnen we het koppel van dat deeltje ten opzichte van elk willekeurig punt berekenen, hetgeen weergeeft in welke richting en hoe goed deze kracht toegepast op een hefboom naar dat willekeurig punt in staat zou zijn om een draaiing in gang te zetten Geparametriseerde ruimtekrommen In het vervolg kijken we naar afbeeldingen van R naar R 3 waarbij wij denken aan de beweging van puntmassa s in de driedimensionale ruimte. Zo n afbeelding F : R R 3 wordt gegeven door drie gewone differentieerbare functies:
7 Dubbelplaneten 79 F (t) = f 1 (t) f 2 (t) f 3 (t). De parameter noemen we meestal t omdat wij hierbij denken aan de tijd. Opgave: (i) Beschrijf met je handen de ruimtekromme die wordt gegeven door F (t) = cos(t) sin(t) t. (ii) Bedenk andere eenvoudige krommen in de ruimte en probeer er een voorschrift voor te vinden. De afgeleide van een dergelijke afbeelding kunnen we net als bij gewone functies verkrijgen door ( ) f1 (t+ t) f lim 1 (t) t 0 t ) df 1 ( ) (t) = lim F (t + t) F (t) = dt t 0 t lim t 0 ( f2 (t+ t) f 2 (t) t lim t 0 ( f3 (t+ t) f 3 (t) t Zodra men hierbij denkt aan de afgeleide naar de tijd geeft deze afbeelding voor elk moment de richting en de snelheid aan waarmee een denkbeeldig massapunt beweegt. Als het gaat om de tijd, schrijven wis- en natuurkundigen F (t) voor df ( ) dt. De uitdrukking t 1 F (t + t) F (t) waarin de vectoren F (t + t) en F 1 (t) worden vermenigvuldigd met het reële getal t schrijven wij soms ook als F (t+ t) F (t) t. Productregel voor in- en uitproduct van functies Met dergelijke afbeeldingen F en G kan men rekenen als met vectoren (waarbij wij denken dat ze met de tijd veranderen). Bijvoorbeeld: de afbeeldingen F G en F, G zijn gedefinieerd door F G(t) = F (t) G(t) en F, G (t) = F (t), G(t) waarbij aan de rechterkant voor elke t producten van gewone vectoren staan. De afgeleiden van deze afbeeldingen F G en F, G kunnen we net zo bepalen als wij dat kennen van gewone functies met de productregel. Het bewijs hiervoor is bijna letterlijk hetzelfde als bij de productregel ).
8 80 Rainer Kaenders voor gewone functies. 1 ( ) F G(t + t) F G(t) t = 1 ([ ] F (t + t) G(t + t) F (t + t) G(t) t [ ]) + F (t + t) G(t) F (t) G(t) ([ G(t = F (t + t) + t) G(t) ] [ ]) F (t + t) F (t) + G(t) t t. Als men nu t naar nul laat gaan blijkt dat ook voor het uitproduct de gewone productregel geldt: F G dt = d F dt G + F d G dt = F G + F G. Opgave: Formuleer en bewijs de productregel voor F, G. 2. Newton mechanica Het natuurkundige uitgangspunt voor alle wiskunde die nu volgt, wordt gegeven door de klassieke wetten van Newton. Laat r, r 1 en r 2 de positievectoren van deeltjes met massa s m, m 1, m 2 ten opzichte van O zijn. r, r 1 en r 2 zijn hierbij functies van de tijd t. (Wiskundig gezien gaat het hier om drie ruimtekrommen zoals we die hierboven hebben ingevoerd en drie positieve getallen m, m 1, m 2.) Dan zijn de bijbehorende snelheden v, v 1 en v 2. Hierbij horen impulsen P, P 1 en P 2 gegeven door P = m v = m r als ook P 1 = m 1 v 1 = m 1 r1 en P 2 = m 2 v 2 = m 2 r2 die kunnen worden opgevat als de hoeveelheid beweging. Newtons eerste wet Een lichaam blijft stil staan of beweegt eenparig (zonder versnelling) als er geen kracht op wordt uitgeoefend. Newtons tweede wet De versnelling die een lichaam ervaart is evenredig met de op hem werkende kracht en omgekeerd evenredig met de massa van het lichaam: a = 1 m F of F = m v = m r. Kort: F = P. Newtons derde wet (actio = reactio) Als twee lichamen onderling krachten op elkaar uitoefenen dan wordt er op beide lichamen een even grote kracht uigeoefend in tegengestelde richtingen. D.w.z. de som van de kracht F 12 op het eerste lichaam (1) vanuit het tweede lichaam (2) en de kracht F 21 op het tweede lichaam (2) vanuit het eerste lichaam (1) is gelijk aan nul, i.e. F 12 + F 21 = 0 oftewel F 12 = F 21. Newtons wet van universele gravitatie Verder heeft Newton de gravitatiewet geformuleerd die beschrijft hoe sterk de kracht is die een lichaam met massa m 1 uitoefent op een lichaam met massa m 2. Als we met r 21 = r 2 r 1 de vector tussen de twee lichamen aangeven met afstand d dan geldt voor deze kracht:
9 Dubbelplaneten 81 F = F 12 = G m 1m 2 d 2 r 21 d = Gm 1m 2 d 3 r 12. De constante G heet de gravitatieconstante. Haar waarde is 11 Nm2 G 6, kg Bewegen op een cirkel Voor cirkelvormige bewegingen is er een bijzondere middelpuntzoekende kracht nodig en de beschrijving van de snelheid van deze beweging kan het beste via de hoeksnelheid gebeuren. Middelpuntzoekende kracht We kijken nu naar cirkelvormige bewegingen in de ruimte. Stel dat r de positievector is van zulk een cirkelvormige beweging met constante absolute snelheid. Dan is r 2 = r, r constant en met de productregel vinden wij de eerste afgeleide naar de tijd: r, r + r, r = 2 r, r = 0. Dus r = v staat loodrecht op r. Omdat de snelheid van de beweging constant is, is v 2 = r, r constant. Daarom is de afgeleide hiervan nul waaruit volgt dat r dus weer loodrecht staat op r en dus in de richting van r of in de tegengestelde richting wijst. In de eerder gebruikte notatie betekent dit: r, r r, r r = r r = Differentiëren van r 2 r = r r. r r, r levert dan ook op r, r + r, r = 0. Anders geschreven vinden wij de uitdrukking voor de middelpuntzoekende versnelling: ( ) v r 2 r = r r.. Voor de grootte van de versnelling is dus a = v2 r r met a = Met de tweede wet van Newton is de centripetale kracht of middelpuntzoekende kracht gelijk aan F centripetaal = m v2 r r r en voor de grootte van deze kracht geldt: F centripetaal = m v2 r. Deze kracht is dus nodig om een deeltje op een cirkelbaan te laten bewegen.
10 82 Rainer Kaenders Hoeksnelheid De snelheid van een draaiing kan het beste worden weergegeven door de hoeksnelheid die aangeeft hoe een hoek θ (in radialen) met de tijd verandert, dus ω = dθ dt De hoeksnelheid is dus niet meer de snelheid van beweging maar wel de snelheid van een draaiing. Voor de snelheid zelf geldt dan v = ωr omdat voor de afgelegde afstand s geldt s = θr. Hiermee kan de centripetale kracht worden uitgedrukt door F centripetaal = mrω 2. Wij zien hieruit dat bij een gegeven hoeksnelheid de middelpuntzoekende kracht lineair groeit met de afstand naar het middelpunt. Het uitproduct geeft ons de mogelijkheid om voor een cirkelvormige beweging de snelheid en de richting van de draaiing in een enkele grootheid, de hoeksnelheidsvector, samen te vatten. De snelheidsvector v van een cirkelvormig rond een punt O bewegend deeltje kan als veralgemenisering van v = ωr worden uitgedrukt door v = ω r. Daarbij wijst de vector ω in de richting van de draaias en staat loodrecht op de positievector r en daarom geldt dan ook hier v = ωr met v = v, ω = ω en r = r. Wij zien dus dat de lengte ω van deze vector gelijk is aan de hoeksnelheid zoals boven weergegeven Impuls, koppel en impulsmoment In het vervolg leggen wij uit hoe uit de wetten van Newton het behoud van impuls en impulsmoment (draai-impuls) volgt. Impulsbehoud Laat r, r 1 en r 2 de positievectoren zijn van deeltjes met massa s m, m 1, m 2 ten opzichte van O. Deze drie positievectoren zijn hierbij functies van de tijd t en de bijbehorende impulsen zijn P, P 1 en P 2. Newtons derde wet (actio = reactio) zegt nu dat als twee lichamen krachten op elkaar uitoefenen, de som van de kracht F 12 op het tweede lichaam (2) vanuit het eerste lichaam (1) en de kracht F 21 op het eerste lichaam (1) vanuit het tweede lichaam (2) gelijk is aan nul, i.e. F12 + F 21 = 0. Hieruit volgt met de tweede wet dat P1 + P2 = 0. Dus is P 1 + P 2 constant (de wet van impulsbehoud). Hieruit kan men bijvoorbeeld rechtstreeks eenvoudige gevolgtrekkingen maken voor de botsing van twee deeltjes, zij het elastisch (dat ze weer uit elkaar vliegen) of inelastisch (dat ze samen blijven klonteren), die in natuurkundeboeken uitgebreid worden besproken. Impulsmoment of draai-impuls Laat r de positievector (als functie van de tijd t) van een deeltje met massa m ten opzichte van een willekeurig punt O zijn met impuls P. Dan heten J = r P het impulsmoment of de draai-impuls met betrekking tot oorsprong O (vaak gebruikt men ook de letter L resp. L), N = r F het koppel of draaimoment met betrekking tot oorsprong O (hiervoor wordt ook de letter τ resp. τ gebruikt).
11 Dubbelplaneten 83 Het impulsmoment kan worden opgevat als de hoeveelheid draaiing. STELLING 2.1 Voor een enkel massadeeltje geldt: d J dt = N. Opgave: Bewijs dit. Voor een deeltje waarop geen uitwendige kracht werkt, geldt dus dat J constant is. Hoe verhoudt zich dit tot de eerste wet van Newton? In het resterende gedeelte van deze bijdrage worden alleen nog maar conclusies uit deze stelling getrokken. Hier al enkele eenvoudige gevolgen voor een enkel massadeeltje. Als het deeltje in een centraal krachtenveld beweegt waarbij de oorsprong O in het centrum van dat krachtenveld ligt en alle krachtsvectoren naar de oorsprong wijzen, dan is N = r F = 0 omdat r en F in tegengestelde richting wijzen. Met de stelling volgt hieruit dat het impulsmoment J = r P = 0 blijft behouden. Dat betekent dus dat de met de tijd veranderende vector r altijd loodrecht staat op de vaste vector J. Dat betekent dat de vector r alleen nog maar in een vlak kan bewegen namelijk het vlak van alle vectoren die loodrecht staan op deze vaste vector J. Het feit dat J = r P constant is, betekent dat r v constant blijft. Als wij nu voor kleine tijdsintervallen t de afgeleide benaderen door r t dan is r r t = t 1 ( r r) voor kleine tijdsintervallen altijd even groot. De uitdrukking r r geeft twee keer de oppervlakte aan van de driehoek weer die wordt opgespannen door r en r. Bij benadering is dat de oppervlakte die de positievector r in de tijd t heeft bestreken. Als wij nu met A(t) de oppervlakte noteren die de positievector vanaf een tijdstip t 0 heeft bestreken dan volgt uit het bovenstaande A t 2 t 1 r r en 1 r daarom geldt: Ȧ = lim t 0 2 r t = 2m 1 J en dat is constant. Dus is de oppervlakte een lineaire functie in t. Uit het behoud van het impulsmoment in een centrale kracht (zonder dat er meer over bekend is) volgt de zogenaamde perkenwet van Kepler die ook bekend staat als zijn tweede wet en ook zonder de boven geschetste benaderingen worden afgeleid. De snelheid van een planeet in haar omloopbaan verandert zodanig dat in gelijke tijdsintervallen de oppervlakte, bestreken door de rechte lijn (voerstraal) tussen de zon en de planeet, gelijk is. Opmerking: Als het deeltje met massa m net als boven in een centraal krachtenveld beweegt dat ontstaat door de zwaartekracht vanuit een andere massa M in de oorsprong O, dan is de kracht dus bepaald door de universele gravitatiewet. Hieruit kan dan worden afgeleid dat het deeltje op een ellipsbaan beweegt. Dit is de eerste wet van Kepler en het was Isaac Newton die uit Kepler s wetten
12 84 Rainer Kaenders Figuur 4. De tweede wet van Kepler: de perkenwet. de universele gravitatiewet wist af te leiden. In het vervolg van dit stuk echter veronderstellen wij de planetenbanen als cirkelvormig. Gezien de kleine excentriciteiten van de beschouwde ellipsbanen blijft dit het gedrag van de dubbelplaneten goed beschrijven. Behoud van het totale impulsmoment Veel systemen bestaan uit meerdere puntmassa s: aan de ene kant kunnen bijvoorbeeld planeten worden opgevat als samenvoeging van afzonderlijke kleine puntmassa s en aan de andere kant kunnen systemen van meerdere planeten worden opgevat als puntmassa s die in hun zwaartepunten zijn geconcentreerd. In het eerste geval denken wij aan oneindig veel deeltjes en kunnen tot de limiet overgaan en in het tweede geval gaat het maar om enkele massadeeltjes. Gegeven N deeltjes met massa s m 1,..., m N en positievectoren r 1,..., r N vanuit een willekeurig punt O. Het totale impulsmoment van het systeem is dan gegeven door J tot = N i=1 r i P i en het totale koppel is N tot = N i=1 r i F i. De boven bewezen stelling heeft rechtstreeks de stelling hieronder tot gevolg. STELLING 2.2 Voor het totale impulsmoment en het totale koppel geldt: d J tot dt = N tot. Als het totale koppel verdwijnt, blijft ook het totale impulsmoment behouden. Op het i-de deeltje werkt een kracht F i die is samengesteld uit de krachten F ij die door de andere deeltjes worden uitgeoefend en een externe kracht F i,ext. Dus F i = N j=1 j i F ij + F i,ext. Het aandeel N j=1 j i F ij van de kracht F i noemen we de interne kracht F i,int op deeltje (i). Dus F i = F i,int + F i,ext op deeltje (i). STELLING 2.3 Als een aantal puntmassa s of zonder externe krachten of in een centraal krachtenveld beweegt, is het totale koppel gelijk aan nul en het totale impulsmoment blijft behouden.
13 Dubbelplaneten 85 Bewijs: In beide gevallen geldt voor de i-de puntmassa: r i F i,ext = 0. Als er geen externe kracht is geldt F i,ext = 0 en in een centraal krachtenveld wijzen r i en F i,ext in dezelfde richting, dus ook hier geldt: r i F i,ext = 0. N N = r i F N ( i = r i Fi,ext + F ) i,int i=1 i=1 N = r i N F i,ext + r i F i,int i=1 } {{ } i=1 =0 N = r i F ij = r i N F ij + r j F ji i=1 j i i<j i<j = ( r i r CM ) F ij r i F ij i<j i<j = i<j ( ri r j ) Fij = 0. Q.e.d. Rotaties Als we kijken naar een draaiende hoepel of een fietswiel met massa m vanuit het middelpunt dat wij ons voorstellen als bestaand uit kleine puntmassa s m 1,..., m N, dan is het totale impulsmoment N J = r i P i = N N = m i r i v i. i=1 i=1 De vectoren r i en v i staan altijd loodrecht op elkaar en daarom wijst r i v i in de richting van de draaias en heeft lengte r i v i = r v waarbij r en v de afstand van de puntmassa naar het middelpunt en de snelheid aangeven die voor elke puntmassa hetzelfde zijn. Dus J wijst in de richting van de draaias en J = m rv. Als wij de snelheid v met behulp van de hoeksnelheid ω uitdrukken, ν = ω r, dan vinden wij J = m r 2 ω. Hierdoor blijkt al dat hoe kleiner de straal r wordt hoe groter de snelheid ω van de draaiing wordt. Dit is een effect dat ook veelvuldig bij kunstschaatsers en op speeltuintoestellen te observeren is. Gyroscopisch effect Stel wij oefenen nu voor een korte tijd t een kracht in de richting van de rotatie-as uit op de rand (door bijvoorbeeld een slag of door een korte beweging van het stuur). De formule d J dt = N kunnen wij bij benadering lezen als: J = N t. Bij een dergelijke toepassing van het koppel N op het systeem wijst dus het verschil J van het impulsmoment in dezelfde richting
14 86 Rainer Kaenders als N (en niet in dezelfde richting als J want die wijst in de richting van de draaias). De draaias verandert dus met J van richting als N voor een moment t werkt. Dat is in een andere richting dan de uitoefening van de kracht doet vermoeden. Dit noemt men het gyroscopisch effect. Dit effect gaat bij veel mensen tegen de intuïtie in. Het verklaart waarom een tol niet kantelt; zodra de zwaartekracht hem naar beneden duwt zorgt dit effect ervoor dat hij in een zijwaartse beweging, de zogenaamde precessie, terechtkomt waardoor de bovenkant van de tol rondjes gaat draaien. 3. Impulsmoment verdelen op zwaartepunten Gegeven N deeltjes met massa s m 1,..., m N en positievectoren r 1,..., r N. Dan definiëren wij het zwaartepunt van deze N deeltjes door r CM = N m i i=1 m r i waarbij we m = N i=1 m i beschouwen als massa van het zwaartepunt (CM staat voor center of mass). Een zwaartepunt gedraagt zich in veel opzichten als een enkel massapunt. Daardoor zijn enkele grootheden die voor de afzonderlijke deeltjes bestaan ook zinvol te definiëren voor het zwaartepunt. Als wij met een homogeen lichaam met dichtheid ρ te maken hebben, is m = ρv waarbij V de inhoud van het lichaam weergeeft. Vaak stellen wij ons voor dat dit lichaam bestaat uit een groot aantal (N) kleine massadeeltjes met massa s m 1,..., m N. Een vast lichaam kan men opvatten als een verzameling van verschillende kleine massadeeltjes m 1,..., m N met positievectoren r 1,..., r N waarvoor geldt: m = m m N. De totale impuls is dan gelijk aan de impuls van het zwaartepunt: PCM = m r CM. Men kan hiermee het zwaartepunt opvatten als massapunt met massa m, positievector r CM en impuls P CM. Opgave: Laat aan de hand van de wetten van Newton zien dat als op het i-de deeltje een kracht F i werkt, dat dan met F ext = N i=1 Fi ook voor het zwaartepunt de tweede wet van Newton geldt, i.e. F ext = m r CM of F ext = P CM Impulsmoment van baan en spin De definitie van impulsmoment en koppel gelden met betrekking tot een willekeurig punt O. Hier kijken wij nu naar een systeem van N deeltjes en onderzoeken de grootheden in kwestie door ze zowel te relateren aan het punt O als ook aan het zwaartepunt. Bijvoorbeeld in systemen als de dubbelplaneet aarde-maan kan het zwaartepunt hiervan worden gerelateerd aan het impulsmoment gezien vanuit de zon. Gegeven N deeltjes met massa s m 1,..., m N en positievectoren r 1,..., r N vanuit een willekeurig punt O. Dan kunnen we het totale impulsmoment ten opzichte van O als volgt splitsen in impulsmoment van het zwaartepunt ten opzichte van O (baan-impulsmoment) en impulsmoment van alle deeltjes ten
15 Dubbelplaneten 87 opzichte van het zwaartepunt (spin-impulsmoment): N J = r i N P i = ( r i r CM ) P i + r CM P } {{ CM } i=1 i=1 } {{ } baan spin = J spin + r CM P CM. De vectoren r i r CM noemen we z i. Dan is J spin = N i=1 z i P i het spinimpulsmoment of de spin-draai-impuls het totale impulsmoment ten opzichte van het zwaartepunt en J baan is het impulsmoment van het zwaartepunt ten opzichte van O, het zogenaamde baan-impulsmoment of de baan-draai-impuls. Een vergelijkbare opsplitsing als bij het impulsmoment kan ook voor het totale koppel worden gemaakt. Dan is N = N int + N ext met N int = N i=1 z i F i en N ext = r CM F ext. Daarbij draagt F ext = N i=1 Fi zijn naam terecht want F ext is ook gelijk aan N i=1 Fi,ext, zoals wij boven bij de definitie van het zwaartepunt al hebben gezien. Opmerking: Als wij naar een dubbelplaneet kijken als bijvoorbeeld aarde-maan (met massa s m A en m M en totale massa m = m A + m M ) in het centraal krachtenveld van de zon met massa M, dan is het totale impulsmoment behouden. Wij kunnen het totale impulsmoment splitsen in een deel ten opzichte van de zon en een deel ten opzichte van het zwaartepunt van de dubbelplaneet. Het eerste impulsmoment van het zwaartepunt ten opzichte van de zon is J baan = r CM P CM en de afgeleide geeft: d J baan dt = r CM P CM + r CM F ext = r CM F ext. Deze vector F ext wijst niet noodzakelijk precies in de richting van r CM. De externe kracht op de dubbelplaneet is F ext = G Mm A r 3 A r A G Mm M rm 3 r M waarbij r A en r M de positievectoren van de zon naar aarde en maan zijn. Als wij echter veronderstellen dat r A r M ongeveer gelijk zijn aan r CM (de verschillen zijn verwaarloosbaar klein in verhouding met de grootte van r CM ) dan geldt F ext = G Mm ( ma r 3 m r A + m ) M m r M G Mm r r 3 CM en daarmee is dan dj baan dt = r CM F ext = 0. In de beschouwingen over dubbelplaneten zullen wij daarom ook veronderstellen dat het impulsmoment J J baan van de dubbelplaneet ten opzicht van het zwaartepunt van de dubbelplaneet behouden blijft Traagheidsmoment De laatste grootheid die wij hier invoeren is het traagheidsmoment. Stel je voor je hebt een hoepel met straal r en massa m. Als wij de hoepel opdelen
16 88 Rainer Kaenders in kleine stukjes met massa m i, die allemaal met dezelfde snelheid v = rω bewegen waar ω de hoeksnelheid weergeeft, dan is het impulsmoment ten opzichte van het zwaartepunt (spin-impulsmoment) gelijk aan J = i r i P i = i m i r i v i = i m i r 2 ω = mr 2 ω. De grootheid I = mr 2 hangt dus alleen af van het lichaam en niet van de snelheid ω van de draaiing (hoeksnelheid). I is het traagheidsmoment van de hoepel. Als we nu kijken naar een star lichaam, dan draaien alle delen van het lichaam weliswaar met verschillende absolute snelheden afhankelijk van de afstand naar de draaias maar met dezelfde hoeksnelheid ω. We kijken nu naar een massadeeltje met massa m, positievector r vanuit het zwaartepunt van het lichaam en snelheid v. Nu kunnen we de hoeksnelheid beschouwen als vector ω met lengte ω waarvoor geldt v= ω r. De hoeksnelheid ω wijst in de richting van de draaias. Hiermee zijn wij in staat om een uitdrukking voor het impulsmoment ten opzichte van het zwaartepunt te vinden die alleen afhangt van vorm en dichtheid van het lichaam en de hoeksnelheid ω. In principe gaat dit net als bij de hoepel. Het totale impulsmoment is in het algemeen J tot = i m i r i ( ω r i ). Net als bij de hoepel willen wij hieruit een uitdrukking afleiden waarin de hoeksnelheidsvector los staat van de rest van de uitdrukking die dan alleen nog maar afhangt van de eigenschappen van het lichaam. Bij een willekeurig lichaam leidt dit tot de definitie van de zogenaamde traagheidstensor. In het geval van een homogeen bolvormig lichaam met straal R en dichtheid ρ is dit echter niet veel moeilijker dan bij de hoepel. Hierbij herhalen wij in wezen het bewijs van de in opgave 1.1 te bewijzen formule u ( v u) = u 2 v u, v u = u v u voor vectoren u en v. Elke vector r i kunnen wij opsplitsen in een deel a i dat loodrecht staat op ω en een deel u i dat in dezelfde of in de tegengestelde richting van ω wijst. Dus r i = a i + u i met a i = ( r i ) ω en u i = ( r i ) ω. Dan berekenen wij J als volgt: J = i m i r i ( ω r i ) = i m i r i ( ω a i ) = i = i m i ( a i ( ω a i ) + u i ( ω a i )) m i ( a i 2 ω ω u i a i ) = i m i a i 2 ω ω i m i u i 2 a i. Het gedeelte ω i m i u i 2 a i echter verdwijnt bij een bolvormig lichaam omdat die zo in kleine massastukjes kan worden opgedeeld dat er een even aantal bijbehorende positievectoren r +1,..., r +N en r 1,..., r N ontstaat bestaande
17 Dubbelplaneten 89 uit paren van telkens twee vectoren r ±i = u i ± a i waar de loodrecht op ω staande delen elkaar opheffen. Voor een bolvormig lichaam houden we dus over: J = ω i m i a i 2 = I bol ω, waarbij I bol = i m i a i 2 het traagheidsmoment is. Hierbij kan m i worden gezien als ρv i met het bijbehorende deel V i van de inhoud V. Om het traagheidsmoment te berekenen delen wij de bol op in even grote schijfjes van dikte h. Op hoogte h heeft een dergelijke schijf breedte B, waarbij geldt: B = R 2 h 2. Deze schijfjes delen wij vervolgens op in ringen met een straal van b tot ( b + b en dikte h. Het traagheidsmoment voor zulk een ring is dan ρπ (b + b) 2 b 2) h b 2. Als we dit verder uitwerken krijgen we: ρπ ( 2b b b 2 b 2) h b 2 = ρπ2b b h b 2 ρπ b 2 h b 2. Nu nemen we de som over de ringen in de schijf met straal B. Dan wordt de som over b 2 h b 2 willekeurig klein als we b klein kiezen. Het impulsmoment van een dergelijke ring wordt dus gegeven door B ρπ h 2b 3 db = ρ π 0 2 hb4. Nu sommeren wij over alle schijven en vinden voor het traagheidsmoment: I bol = ρ π R ( 2 R R 2 h 2) 4 dh. Met de formule 4 3 πr 3 voor de inhoud van de bol is J = I bol ω, waarbij I bol het traagheidsmoment is van een bolvormig lichaam met straal R dat gegeven wordt door: I bol = 5 2mR2. 4. Behoud van impulsmoment bij dubbelplaneten Hier passen we de boven geschetste theorie toe op speciale gevallen die een rol spelen voor onze beschouwingen in de astrofysica. Wij hanteren hierbij de vereenvoudigende (en feitelijk gezien onjuiste) aanname dat de maan rond de aarde op een cirkelbaan beweegt. Eveneens veronderstellen wij dat het zwaartepunt van de twee niet beweegt Dubbelplaneten Hier hebben wij te maken met twee bolvormige vaste lichamen met massa s m 1 en m 2, positievectoren r 1 en r 2 vanuit het gemeenschappelijk zwaartepunt en onderlinge afstand r. Dan is de positievector van het zwaartepunt gelijk aan r CM = m 1 r 1 +m 2 r 2 m met m = m 1 + m 2 en er geldt r 1 = m 2 m ( r 1 r 2 ) en r 2 = m 1 m ( r 2 r 1 ). Daarmee liggen dus m 1 resp. m 2 op afstand r 1 = r 1 = m 2 m r resp. r 2 = r 2 = m 1 m r van het zwaartepunt. Nu kijken we naar de draaiing van de twee massa s rond het zwaartepunt en willen hiervoor de hoeksnelheid bepalen. Dit doen wij middels de derde wet van Newton door de centrifugale kracht en de gravitatiekracht aan elkaar gelijk te stellen. Op massa m 1 werkt in de richting r 2 r 1 de gravitatiekracht vanuit massa m 2 die zich op afstand r = r 2 r 1 van elkaar bevinden. Deze kracht is dus gelijk aan F gravitatie = G m 1m 2 ( r r 3 2 r 1 ). Tegelijkertijd werkt de centrifugale kracht op massa m 1 de andere kant op: Fcentrifugaal = m v 2 1 r 1 r ( r 2 r 1 ) = m 1 r 1 ω 2 ( r 2 r 1 ) r, waarbij
18 90 Rainer Kaenders ω de hoeksnelheid aangeeft met v = r 1 ω. Hiermee lukt het de hoeksnelheid te bepalen. G m 1m 2 r 3 = m 1 r 1 ω 2 ω = G (m 1 + m 2 ) r 3. Wij zien hieruit bijvoorbeeld dat de lichamen steeds sneller roteren naarmate ze dichter bij elkaar komen. Opmerking: Uit het evenwicht van gravitatiekracht en middelpuntzoekende kracht blijkt dat de omlooptijd T evenredig is met r 3 2. Dit staat in zijn algemene vorm bekend als de derde wet van Kepler, die een verband aangeeft tussen de afstand van de planeten en de omlooptijd. Behalve voor cirkelbanen geldt dit ook voor ellipsbanen (r is de halve lange as). Met de voorbereiding in de paragrafen hiervoor zijn wij nu in staat om het totale impulsmoment te berekenen. Omdat dubbelplaneten in een centraal krachtenveld ver weg van de zon bewegen, is het totale impulsmoment J ten opzichte van het zwaartepunt van de dubbelplaneet nagenoeg constant (zie opmerking 3.1). Wij splitsen J op in het impulsmoment ten opzichte van de zwaartepunten van elk van de planeten en de impulsmomenten van elk massadeeltje van een planeet ten opzichte van het zwaartepunt van deze planeet. r 1,i resp. r 2,i met impulsen P 1,i en P 2,i zijn de positievectoren van het i-de massadeeltje van planeet (1) resp. (2) met massa m 1,i resp. m 2,i. Voor de positievectoren vanuit de zwaartepunten van de planeten schrijven wij z 1,i = r 1,i r 1,CM en z 2,i = r 2,i r 2,CM. Dan vinden wij: J = i z 1,i P 1,i + i z 2,i P 2,i + i r 1,CM P 1,i + i r 2,CM P 1,i waarbij de positievectoren r 1,CM en r 2,CM uitgaan van het algehele zwaartepunt van de dubbelplaneet. P 1,i is gelijk aan ( P 1,i P 1,CM ) + P 1,CM en daarbij is P 1,i P 1,CM de impuls waarmee de i-de puntmassa rond het zwaartepunt van planeet (1) roteert. i z 1,i P 1,CM = ( i z 1,i) P 1,CM is gelijk aan nul als de bolvormige planeet op een symmetrische manier in massadeeltjes is opgedeeld waarbij er voor elke vector z 1,i zo n tegenovergestelde vector in de som i z 1,i te vinden is. Hetzelfde geldt voor planeet (2). Als we dit samenvatten, houden wij de volgende uitdrukking over: J = i z 1,i ( P 1,i P 1,CM ) + i z 2,i ( P 2,i P 2,CM ) + r 1,CM P 1,CM + r 2,CM P 2,CM. Met de berekeningen voor het traagheidsmoment vinden wij: ( ) J = I 1Ω1 + I 2Ω2 + m 1 r1 2 + m 2r2 2 ω oftewel (4.1)
19 Dubbelplaneten 91 J = I 1 Ω1 + I 2 Ω2 + µr 2 ω Hierbij is µ = m 1m 2 m 1 +m 2 de zogenaamde gereduceerde massa. Ω 1 en Ω 2 staan voor de rotatiesnelheden van de planeten (1) en (2). Opgave: Laat zien dat m 1 r m 2r 2 2 = µr2. Dit was het voorwerk. Met deze bagage zijn wij nu toegerust om diepere inzichten in bijvoorbeeld de eigenschappen van dubbelplaneten te verkrijgen Halley had toch gelijk Hoe zit het nu met het verhaal van Halley? Hiervoor gaan wij zorgvuldig kijken naar het totale impulsmoment van aarde en maan. De traagheidsmomenten van aarde I A = 5 2m ARA 2 en maan I M = 2 5 m M RM 2 zijn nogal verschillend van grootte: I A = 9, kg km 2 en I M = 8, kg km 2, d.w.z. I M is minder dan een duizendste van I A (zie tabel 1). De hoeksnelheid van aarde en maan wordt relatief tot de vaste sterren gemeten. Hierbij verwaarlozen wij het tollen van de aardas (precessie). Gezien vanuit de vaste sterren draait de aarde in 365,2564 dagen 366,2564 keer om haar eigen as. Daardoor geldt voor de hoeksnelheid Ω A = 2π 366, ,2564 dag 1 = 6, dag 1. De maan draait niet meer ten opzichte van de aarde maar wel ten opzichte van de vaste sterren. De maanden zoals wij die vanaf de aarde zien (de synodische maanden) zijn 29,53 dagen lang. Gezien vanuit de aarde draait de maand in één jaar dus 365, ,53 keer rond de aarde. Omdat het hele systeem 365, , ,2564 in een jaar rond de zon draait is Ω M = 2π geeft aan dat in de formule (4.1) het spin-impulsmoment van de maan kleiner dan een tienduizendste is van het spin-impulsmoment van de aarde. Daarom zullen wij het hier verwaarlozen. De draaiassen ω en Ω A wijzen in dezelfde richting. De wet van impulsbehoud geeft daarmee een verband tussen r en Ω A. Met m geven wij weer de totale massa aan: m = m A + m M. 1 dag = 0, dag. Dit J = µr 2 ω + I A Ω A = µ Gm r I A Ω A. (4.2) De tweede uitdrukking is afgeleid met behulp van de derde wet van Kepler ω = Gm r 3 2 (4.3) die de afhankelijkheid tussen r en ω aangeeft. De tweede vergelijking uit (4.2) kunnen wij ook schrijven als: Ω A = J I A µ I A Gm r 1 2. (4.4) Het is een feit dat de getijden de draaisnelheid Ω A van de aarde langzaam af laten nemen (zie [4], [5], [6]). Uit vergelijking (4.2) en het behoud van impulsmoment zien we dat daarmee r toe moet nemen. Dit is wat er ook werkelijk wordt geobserveerd. De afstand neemt met 3,82 cm per jaar toe.
20 92 Rainer Kaenders De vergelijkingen (4.3) en (4.4) geven aan hoe r, ω en Ω A van elkaar afhangen. Wij weten dat r langzaam toeneemt. Met name zijn we nu geïnteresseerd in de afhankelijkheid van de in dagen gemeten maandlengte van r. Wij noemen λ m (r) de lengte van een maand en λ d (r) de lengte van een dag zoals wij die op aarde bij een gegeven afstand r tussen aarde en maan zouden waarnemen (d.w.z. synodisch). Dan geeft λ m /λ d het aantal dagen aan in een maand. Wij willen nu aantonen dat λ m /λ d voor de dubbelplaneet aarde-maan als functie van de afstand r rond de werkelijke afstand r 0 = 3, km dalend is. Omdat deze afstand daadwerkelijk toeneemt weten we dan dat de maanden korter worden als zij in dagen worden gemeten. Hiervoor willen we eerst het verband formuleren tussen λ m en λ d aan de ene kant en ω en Ω A aan de andere kant die ten opzichte van de vaste sterren zijn gedefinieerd. Grootheden die ten opzichte van de vaste sterren worden bepaald, noemen we ook siderisch wat afkomstig is van het Latijnse woord sidus = ster. λ j staat voor de lengte van een jaar en die hangt dus niet af van r. De maan draait λ j /λ m keer per jaar rond de aarde, ( gezien ) vanuit de zon. λj Ten opzichte van de vaste sterren draait hij in één jaar λ m + 1 keer rond zijn eigen as. Hierbij gebruiken wij weer dat de maan ten opzichte van de aarde stilstaat en dus ten opzichte van de zon per maand een rondje om zichzelf draait. De siderische hoeksnelheid ω van de draaiende dubbelplaneet aarde-maan is dan λ j ( λ ω = 2π m = 2π + 1 ). λ j λ m λ j Willen we de afhankelijkheid van deze grootheden van r onderzoeken, dan kunnen wij hier de afgeleide naar r bestuderen die we met een accent aangeven, dus bijvoorbeeld ω = ω r. ω = 2π λ m λ 2. (4.5) m Net zo draait de aarde λ j /λ d keer per jaar rond haar eigen as, ( gezien vanuit ) λj de zon. Ten opzichte van de vaste sterren draait hij in één jaar λ + 1 keer d rond zijn eigen as. De siderische hoeksnelheid Ω A van de aarde is dan Ω A = 2π λ j ( λ + 1 d 1 = 2π + 1 ). λ j λ d λ j De afgeleide naar r geeft hier: Ω A = 2π λ d λ 2. (4.6) d Wij willen weten of λ m /λ d voor aarde-maan bij groter wordende r rond de werkelijke afstand r 0 daalt of stijgt. In ieder geval vertelt ons de quotiëntregel dat geldt:
21 Dubbelplaneten 93 ( λm λ d ) < 0 λ m λ d < λ m λ d. Hierbij moet wel veilig worden gesteld dat λ d > 0 is. Uit (4.4) volgt dat Ω A < 0 is en samen met (4.6) zien we λ d > 0. Uit de formules (4.5) en (4.6) concluderen wij λ m λ d = ω λ m λ m Ω A λ. d λ d De in dagen gemeten maanden worden dus daadwerkelijk korter als geldt: ω λ m Ω A λ < 1. (4.7) d Door de derde wet van Kepler te differentiëren volgt: ω = 3 2 Gm r 5 2. De wet van impulsbehoud geeft na differentiatie naar r: Ω A = µ 2I A Gm r 1 2. Dit ingevuld in de ongelijkheid (4.7) levert de conditie: ω λ m Ω A λ = 3 µ λ m r 2 < 1. d I A λ d Opgave: (i) Gebruik de data in Tabel 1 om te laten zien dat bij aarde-maan werkelijk aan dit criterium is voldaan. (ii) Wat gebeurt er als aarde en maan dichter bij elkaar zouden staan? 4.3. Twee andere dubbelplaneten nader bekeken Een en dezelfde formule (4.1) kan heel verschillende scenario s voor een dubbelplaneet tot gevolg hebben. Mars en Phobos De planeet Mars heeft twee manen Phobos en Deimos oftewel vrees en verschrikking. Wij kijken hier naar de dubbelplaneet Mars-Phobos. Mars draait langzamer om zijn eigen as dan zijn maan Phobos om hem heen draait. Dat betekent dat de hoeksnelheid van Mars Ω M en de hoekssnelheid van Phobos Ω P wel in dezelfde richting wijzen, maar dat geldt: Ω M < Ω P. De getijdewerking zorgt er dan voor dat Ω M toeneemt. De formule J = µr 2 ω + I M ΩM + I P ΩP
22 94 Rainer Kaenders Aarde Maan Straal 6371 km 1738 km Massa kg kg tijdseenheid siderische dag siderische maand siderisch jaar synodische maand synodische dag tijd 86164,1 seconde 27,32166 dag 365,2564 dag 29, dag 1 dag = 24 h verdere grootheden afstand aarde-maan 3, km toename per jaar 3,82 cm excentriciteit maanbaan 0,05490 Tabel 1. Belangrijke data voor aarde en maan. Figuur 5. Dubbelplaneet Mars-Phobos. Zie pagina 137 voor een kleurenillustratie. wordt met behulp van het verband tussen hoeksnelheid en afstand Mars- Phobos ω 2 r 3 = G(m M + m P ) tot de identiteit: J = µ (G(m M + m P )r) I M Ω M + I P Ω P. We zien dus dat het impulsmoment alleen kan worden behouden als met toenemende Ω M de afstand r afneemt. Mars en Phobos gaan dus langzaam naar elkaar toe totdat Phobos op Mars te pletter slaat.
23 Dubbelplaneten 95 Neptunus en Triton Triton is met afstand de grootste van 13 bekende manen van Neptunus. De kleinste drie van deze manen zijn pas sinds 2004 bekend en de allerkleinste heeft een doorsnede van maar 54 km. Triton is de langst bekende maan van Neptunus, waarvan het bestaan al een maand na de ontdekking van de planeet (1846) werd bevestigd. Pas in 1949 werd door de Amerikaanse astronoom van Nederlandse afkomst Gerard Kuiper ( ) de tweede maan Nereïde ontdekt. In de Griekse mythologie was Triton de oudste zoon van Poseidon die in de Romeinse mythologie Neptunus werd genoemd. Bijzonder aan de dubbelplaneet Neptunus-Triton is dat Neptunus om zijn eigen as draait maar tegelijkertijd draait zijn maan Triton tegen de draaiing van Neptunus in: Triton beweegt retrograde om Neptunus heen. Triton heeft, als enige grote maan in ons zonnestelsel, zo n retrograde baan. Daarnaast heeft de baan van Triton een opmerkelijk grote hoek (23 ) ten opzichte van de evenaar van Neptunus. Hieruit concludeert men dat Triton niet is ontstaan rond Neptunus, maar later is ingevangen door Neptunus. Het lijkt dan ook goed mogelijk dat Triton vroeger deel uitmaakte van de zogenaamde Kuipergordel, een gordel van vele miljarden komeetachtige, uit rots en ijs bestaande objecten, voorbij de baan van Neptunus, de achtste planeet van ons zonnestelsel. Ook bewegen Neptunus en Triton niet in hetzelfde vlak, al gaan we dit hier voor het gemak wel aannemen. Het is niet moeilijk het argument te nuanceren met de toevoeging dat de banen in een hoek van 23 staan. De retrograde beweging betekent dat de hoeksnelheid van Neptunus Ω N en de hoeksnelheid van Triton Ω T in tegengestelde richting wijzen. De getijdewerking zorgt er ook hier voor dat Ω N afneemt. De formule J = µr 2 ω + I M ΩM + I P ΩP wordt dan met behulp van het verband tussen hoeksnelheid en afstand Mars- Phobos ω 2 r 3 = G(m M + m P ) tot: J = µ (G(m N + m T )r) I N Ω N + I T Ω T. Het behoud van impulsmoment zegt ons nu dat als Ω T afneemt de afstand r eveneens af moet nemen. Dus ook Triton zal steeds dichter bij Neptunus komen totdat hij zo dichtbij komt dat hij door de getijden uiteen wordt gereten nadat hij de zogenaamde Rochelimiet heeft bereikt. Triton zal naar verwachting binnen 100 miljoen jaar op Neptunus neerstorten. Opgave: Vind een variant van het boven geschetste argument die rekening houdt met het feit dat de banen van Neptunus en Triton in vlakken liggen die een hoek van 23 met elkaar maken. Literatuur [1] E. HALLEY (1695). Some account of the ancient state of the city of Palmyra, with short remarks upon the inscriptions found there. Philosophical Transactions, XIX:
24 96 Rainer Kaenders Figuur 6. Neptunus met de drie grootste manen, opgenomen door het Hubble-ruimtetelescoop. Zie pagina 138 voor een kleurenillustratie. [2] E. HALLEY (1693). Emendationes ac notae in vetustas albatênii observationes astronomicas. Philosophical Transactions, XVII: [3] U. UFFRECHT & T. POPPE (2002). Himmelsmechanik und Raumfahrt. Stuttgart Düsseldorf Leipzig: Klett Verlag. [4] F. VERBUNT (2001). Van Halley tot lunar ranging, Zenit, april, [5] F. VERBUNT (2001). VLBI, zonsverduisteringen, schelpjes en modder, Zenit, juni, [6] F. VERBUNT (2002). The Earth and Moon: from Halley to lunar ranging and shells, verbunt/onderzoek/ earth.pdf. Webpagina s [7] T(R)U s, samenwerking van de regionale Wiskunde D steunpunten aan de universiteiten Delft, Eindhoven, Twente en Nijmegen, wiskundedsteun.nl/. [8] Commissie Toekomst WiskundeOnderwijs, ctwo, ministeriële vernieuwingscommissie wiskunde,
10 Had Halley gelijk: worden de maanden korter?
 10 Had Halley gelijk: worden de en korter? Dit is de laatste module. We kunnen nu (eindelijk!) terugkomen op de vraag waar we twee jaar geleden mee begonnen. Terugblik In 1695 had de Engelse astronoom
10 Had Halley gelijk: worden de en korter? Dit is de laatste module. We kunnen nu (eindelijk!) terugkomen op de vraag waar we twee jaar geleden mee begonnen. Terugblik In 1695 had de Engelse astronoom
Overzicht. Vandaag: Frank Verbunt Het heelal Nijmegen 2014
 Vandaag: Frank Verbunt Het heelal Nijmegen 2014 De aarde en de maan Boek: hoofdstuk 2.6 Overzicht Halley en de maan meting afstand van de Maan en verandering erin getijden: koppeling tussen lengte van
Vandaag: Frank Verbunt Het heelal Nijmegen 2014 De aarde en de maan Boek: hoofdstuk 2.6 Overzicht Halley en de maan meting afstand van de Maan en verandering erin getijden: koppeling tussen lengte van
1 Inleiding. Worden de maanden langer of korter?
 1 Inleiding Worden de maanden langer of korter? In 1695 had de Engelse astronoom Halley berekend dat in de loop van de laatste 800 jaar (vóór 1695) de maanden korter waren geworden. In zijn tijd zou een
1 Inleiding Worden de maanden langer of korter? In 1695 had de Engelse astronoom Halley berekend dat in de loop van de laatste 800 jaar (vóór 1695) de maanden korter waren geworden. In zijn tijd zou een
Krommen in de ruimte
 Krommen in de ruimte z Een ruimtekromme is de baan van een tijd-plaatsfunctie van een bewegend deeltje in de ruimte Na keuze van een rechthoekig assenstelsel Oxyz wordt die functie f gegeven door zijn
Krommen in de ruimte z Een ruimtekromme is de baan van een tijd-plaatsfunctie van een bewegend deeltje in de ruimte Na keuze van een rechthoekig assenstelsel Oxyz wordt die functie f gegeven door zijn
Hoofdstuk 8 Hemelmechanica. Gemaakt als toevoeging op methode Natuurkunde Overal
 Hoofdstuk 8 Hemelmechanica Gemaakt als toevoeging op methode Natuurkunde Overal 8.1 Gravitatie Geocentrisch wereldbeeld - Aarde middelpunt van heelal - Sterren bewegen om de aarde Heliocentrisch wereldbeeld
Hoofdstuk 8 Hemelmechanica Gemaakt als toevoeging op methode Natuurkunde Overal 8.1 Gravitatie Geocentrisch wereldbeeld - Aarde middelpunt van heelal - Sterren bewegen om de aarde Heliocentrisch wereldbeeld
Vectormeetkunde in R 3
 Vectormeetkunde in R Definitie. Een punt in R wordt gegeven door middel van drie coördinaten : P = (x, y, z). Een lijnstuk tussen twee punten P en Q voorzien van een richting noemen we een pijltje. Notatie
Vectormeetkunde in R Definitie. Een punt in R wordt gegeven door middel van drie coördinaten : P = (x, y, z). Een lijnstuk tussen twee punten P en Q voorzien van een richting noemen we een pijltje. Notatie
De wortel uit min één, Cardano, Kepler en Newton
 De wortel uit min één, Cardano, Kepler en Newton Van de middelbare school kent iedereen wel de a, b, c-formule (hier en daar ook wel het kanon genoemd) voor de oplossingen van de vierkantsvergelijking
De wortel uit min één, Cardano, Kepler en Newton Van de middelbare school kent iedereen wel de a, b, c-formule (hier en daar ook wel het kanon genoemd) voor de oplossingen van de vierkantsvergelijking
Hoofdstuk 1 Beweging in beeld. Gemaakt als toevoeging op methode Natuurkunde Overal
 Hoofdstuk 1 Beweging in beeld Gemaakt als toevoeging op methode Natuurkunde Overal 1.1 Beweging vastleggen Het verschil tussen afstand en verplaatsing De verplaatsing (x) is de netto verplaatsing en de
Hoofdstuk 1 Beweging in beeld Gemaakt als toevoeging op methode Natuurkunde Overal 1.1 Beweging vastleggen Het verschil tussen afstand en verplaatsing De verplaatsing (x) is de netto verplaatsing en de
Hoofdstuk 1 Beweging in beeld. Gemaakt als toevoeging op methode Natuurkunde Overal
 Hoofdstuk 1 Beweging in beeld Gemaakt als toevoeging op methode Natuurkunde Overal 1.4/1.5 Significantie en wiskundige vaardigheden Omrekenen van grootheden moet je kunnen. Onderstaande schema moet je
Hoofdstuk 1 Beweging in beeld Gemaakt als toevoeging op methode Natuurkunde Overal 1.4/1.5 Significantie en wiskundige vaardigheden Omrekenen van grootheden moet je kunnen. Onderstaande schema moet je
Uitwerkingen 1. ω = Opgave 1 a.
 Uitwerkingen Opgave π omtrek diameter Eén radiaal is de hoek, gemeten vanuit het middelpunt van een cirkel, waarbij de lengte van de boog gelijk is aan de straal. c. s ϕ r d. ϕ ω t Opgave π (dus ongeveer
Uitwerkingen Opgave π omtrek diameter Eén radiaal is de hoek, gemeten vanuit het middelpunt van een cirkel, waarbij de lengte van de boog gelijk is aan de straal. c. s ϕ r d. ϕ ω t Opgave π (dus ongeveer
VAK: Mechanica - Sterkteleer HWTK
 VAK: Mechanica - Sterkteleer HWTK Proeftoets Beschikbare tijd: 100 minuten Instructies voor het invullen van het antwoordblad. 1. Dit open boek tentamen bestaat uit 10 opgaven.. U mag tijdens het tentamen
VAK: Mechanica - Sterkteleer HWTK Proeftoets Beschikbare tijd: 100 minuten Instructies voor het invullen van het antwoordblad. 1. Dit open boek tentamen bestaat uit 10 opgaven.. U mag tijdens het tentamen
4. Maak een tekening:
 . De versnelling van elk deel van de trein is hetzelfde, dus wordt de kracht op de koppeling tussen de 3e en 4e wagon bepaald door de fractie van de massa die er achter hangt, en wordt dus gegeven door
. De versnelling van elk deel van de trein is hetzelfde, dus wordt de kracht op de koppeling tussen de 3e en 4e wagon bepaald door de fractie van de massa die er achter hangt, en wordt dus gegeven door
Begripsvragen: Cirkelbeweging
 Handboek natuurkundedidactiek Hoofdstuk 4: Leerstofdomeinen 4.2 Domeinspecifieke leerstofopbouw 4.2.1 Mechanica Begripsvragen: Cirkelbeweging 1 Meerkeuzevragen 1 [H/V] Een auto neemt een bocht met een
Handboek natuurkundedidactiek Hoofdstuk 4: Leerstofdomeinen 4.2 Domeinspecifieke leerstofopbouw 4.2.1 Mechanica Begripsvragen: Cirkelbeweging 1 Meerkeuzevragen 1 [H/V] Een auto neemt een bocht met een
vwo wiskunde b Baanversnelling de Wageningse Methode
 1 1 vwo wiskunde b Baanversnelling de Wageningse Methode 1 1 2 2 Copyright 2018 Stichting de Wageningse Methode Auteurs Leon van den Broek, Ton Geurtz, Maris van Haandel, Erik van Haren, Dolf van den Hombergh,
1 1 vwo wiskunde b Baanversnelling de Wageningse Methode 1 1 2 2 Copyright 2018 Stichting de Wageningse Methode Auteurs Leon van den Broek, Ton Geurtz, Maris van Haandel, Erik van Haren, Dolf van den Hombergh,
Formule afleiding opgaven bij de cursus Algemene relativiteitstheorie Docent: Dr. H. (Harm) van der Lek
 Formule afleiding opgaven bij de cursus Algemene relativiteitstheorie Docent: Dr. H. (Harm) van der Lek Dit document bevat aanwijzingen/aanmoedigingen voor het zelf doen van de afleidingen uit het curusmateriaal.
Formule afleiding opgaven bij de cursus Algemene relativiteitstheorie Docent: Dr. H. (Harm) van der Lek Dit document bevat aanwijzingen/aanmoedigingen voor het zelf doen van de afleidingen uit het curusmateriaal.
Theorie: Snelheid (Herhaling klas 2)
 Theorie: Snelheid (Herhaling klas 2) Snelheid en gemiddelde snelheid Met de grootheid snelheid geef je aan welke afstand een voorwerp in een bepaalde tijd aflegt. Over een langere periode is de snelheid
Theorie: Snelheid (Herhaling klas 2) Snelheid en gemiddelde snelheid Met de grootheid snelheid geef je aan welke afstand een voorwerp in een bepaalde tijd aflegt. Over een langere periode is de snelheid
Trillingen en geluid wiskundig
 Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Radialen 3 Uitwijking van een harmonische trilling 4 Macht en logaritme 5 Geluidsniveau en amplitude 1 De sinus van een hoek Sinus van een hoek
Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Radialen 3 Uitwijking van een harmonische trilling 4 Macht en logaritme 5 Geluidsniveau en amplitude 1 De sinus van een hoek Sinus van een hoek
3 Kermis aan de hemel
 3 Kermis aan de hemel In deze paragraaf onderzoeken en leren we over de beweging van de aarde om de zon, de draaiing van de aarde om haar as, de beweging van de maan rond de aarde, en hoe die bewegingen
3 Kermis aan de hemel In deze paragraaf onderzoeken en leren we over de beweging van de aarde om de zon, de draaiing van de aarde om haar as, de beweging van de maan rond de aarde, en hoe die bewegingen
V Kegelsneden en Kwadratische Vormen in R. IV.0 Inleiding
 V Kegelsneden en Kwadratische Vormen in R IV.0 Inleiding V. Homogene kwadratische vormen Een vorm als H (, ) = 5 4 + 8 heet een homogene kwadratische vorm naar de twee variabelen en. Een vorm als K (,
V Kegelsneden en Kwadratische Vormen in R IV.0 Inleiding V. Homogene kwadratische vormen Een vorm als H (, ) = 5 4 + 8 heet een homogene kwadratische vorm naar de twee variabelen en. Een vorm als K (,
Opdracht 3: Baanintegratie: Planeet in een dubbelstersysteem
 PLANETENSTELSELS - WERKCOLLEGE 3 EN 4 Opdracht 3: Baanintegratie: Planeet in een dubbelstersysteem In de vorige werkcolleges heb je je pythonkennis opgefrist. Je hebt een aantal fysische constanten ingelezen,
PLANETENSTELSELS - WERKCOLLEGE 3 EN 4 Opdracht 3: Baanintegratie: Planeet in een dubbelstersysteem In de vorige werkcolleges heb je je pythonkennis opgefrist. Je hebt een aantal fysische constanten ingelezen,
Opgave 3 - Uitwerking
 Mathrace 2014 Opgave 3 - Uitwerking Teken de rode hulplijntjes, en noem de lengte van dit lijntje y. Noem verder de lengte van een zijde van de gelijkzijdige driehoek x. Door de hoek van 45 graden in de
Mathrace 2014 Opgave 3 - Uitwerking Teken de rode hulplijntjes, en noem de lengte van dit lijntje y. Noem verder de lengte van een zijde van de gelijkzijdige driehoek x. Door de hoek van 45 graden in de
Uit: Niks relatief. Vincent Icke Contact, 2005
 Uit: Niks relatief Vincent Icke Contact, 2005 Dé formule Snappiknie kanniknie Waarschijnlijk is E = mc 2 de beroemdste formule aller tijden, tenminste als je afgaat op de meerderheid van stemmen. De formule
Uit: Niks relatief Vincent Icke Contact, 2005 Dé formule Snappiknie kanniknie Waarschijnlijk is E = mc 2 de beroemdste formule aller tijden, tenminste als je afgaat op de meerderheid van stemmen. De formule
Vlakke meetkunde. Module 6. 6.1 Geijkte rechte. 6.1.1 Afstand tussen twee punten. 6.1.2 Midden van een lijnstuk
 Module 6 Vlakke meetkunde 6. Geijkte rechte Beschouw een rechte L en kies op deze rechte een punt o als oorsprong en een punt e als eenheidspunt. Indien men aan o en e respectievelijk de getallen 0 en
Module 6 Vlakke meetkunde 6. Geijkte rechte Beschouw een rechte L en kies op deze rechte een punt o als oorsprong en een punt e als eenheidspunt. Indien men aan o en e respectievelijk de getallen 0 en
Fietsparadox Fietsen is een alledaagse activiteit. Desalniettemin zijn er redenen genoeg om het bewegen van een fiets nader te onderzoeken.
 Charles Mathy Fietsen is een alledaagse activiteit. Desalniettemin zijn er redenen genoeg om het bewegen van een fiets nader te onderzoeken. Natuurkunde is uit, het aantal studenten neemt af. En natuurkunde
Charles Mathy Fietsen is een alledaagse activiteit. Desalniettemin zijn er redenen genoeg om het bewegen van een fiets nader te onderzoeken. Natuurkunde is uit, het aantal studenten neemt af. En natuurkunde
Botsingen. N.G. Schultheiss
 1 Botsingen N.G. Schultheiss 1 Inleiding In de natuur oefenen voorwerpen krachten op elkaar uit. Dit kan bijvoorbeeld doordat twee voorwerpen met elkaar botsen. We kunnen hier denken aan grote samengestelde
1 Botsingen N.G. Schultheiss 1 Inleiding In de natuur oefenen voorwerpen krachten op elkaar uit. Dit kan bijvoorbeeld doordat twee voorwerpen met elkaar botsen. We kunnen hier denken aan grote samengestelde
TENTAMEN DYNAMICA (140302) 29 januari 2010, 9:00-12:30
 TENTAMEN DYNAMICA (14030) 9 januari 010, 9:00-1:30 Verzoek: begin de beantwoording van een nieuwe vraag op een nieuwe pagina. En schrijf duidelijk: alleen leesbaar en verzorgd werk kan worden nagekeken.
TENTAMEN DYNAMICA (14030) 9 januari 010, 9:00-1:30 Verzoek: begin de beantwoording van een nieuwe vraag op een nieuwe pagina. En schrijf duidelijk: alleen leesbaar en verzorgd werk kan worden nagekeken.
Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Complexe getallen. Een eigen samenvatting maken is nuttig.
 6 Totaalbeeld Samenvatten Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Complexe getallen. Een eigen samenvatting maken is nuttig. Begrippenlijst: 21: complex getal reëel deel
6 Totaalbeeld Samenvatten Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Complexe getallen. Een eigen samenvatting maken is nuttig. Begrippenlijst: 21: complex getal reëel deel
Vectoranalyse voor TG
 college 2 Ruimte en oppervlakken collegejaar : 18-19 college : 2 build : 5 september 2018 slides : 25 Vandaag Ruimte 1 Vectoren in R 3 recap 2 Oppervlakken 3 Ruimte 4 1 intro VA Voorkennis uit Ruimtewiskunde
college 2 Ruimte en oppervlakken collegejaar : 18-19 college : 2 build : 5 september 2018 slides : 25 Vandaag Ruimte 1 Vectoren in R 3 recap 2 Oppervlakken 3 Ruimte 4 1 intro VA Voorkennis uit Ruimtewiskunde
Naam:... Studentnummer:...
 AFDELING DER BEWEGINGSWETENSCHAPPEN, VRIJE UNIVERSITEIT AMSTERDAM INSTRUCTIE - Dit is een gesloten boek tentamen - Gebruik van een gewone (geen grafische) rekenmachine is toegestaan - Gebruik van enig
AFDELING DER BEWEGINGSWETENSCHAPPEN, VRIJE UNIVERSITEIT AMSTERDAM INSTRUCTIE - Dit is een gesloten boek tentamen - Gebruik van een gewone (geen grafische) rekenmachine is toegestaan - Gebruik van enig
Lineaire Algebra voor ST
 Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 9.31 email: J.C.M.Keijsper@tue.nl studiewijzer: http://www.win.tue.nl/wsk/onderwijs/2ds06 Technische Universiteit Eindhoven college 4 J.Keijsper
Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 9.31 email: J.C.M.Keijsper@tue.nl studiewijzer: http://www.win.tue.nl/wsk/onderwijs/2ds06 Technische Universiteit Eindhoven college 4 J.Keijsper
Maar het leidde ook tot een uitkomst die essentieel is in mijn werkstuk van een Stabiel Heelal.
 -09-5 Bijlage voor Stabiel Heelal. --------------------------------------- In deze bijlage wordt onderzocht hoe in mijn visie materie, ruimte en energie zich tot elkaar verhouden. Op zichzelf was de fascinatie
-09-5 Bijlage voor Stabiel Heelal. --------------------------------------- In deze bijlage wordt onderzocht hoe in mijn visie materie, ruimte en energie zich tot elkaar verhouden. Op zichzelf was de fascinatie
Mechanica - Sterkteleer - HWTK PROEFTOETS versie C - OPGAVEN en UITWERKINGEN.doc 1/16
 VAK: Mechanica - Sterkteleer HWTK Set Proeftoets 07-0 versie C Mechanica - Sterkteleer - HWTK PROEFTOETS- 07-0-versie C - OPGAVEN en UITWERKINGEN.doc 1/16 DIT EERST LEZEN EN VOORZIEN VAN NAAM EN LEERLINGNUMMER!
VAK: Mechanica - Sterkteleer HWTK Set Proeftoets 07-0 versie C Mechanica - Sterkteleer - HWTK PROEFTOETS- 07-0-versie C - OPGAVEN en UITWERKINGEN.doc 1/16 DIT EERST LEZEN EN VOORZIEN VAN NAAM EN LEERLINGNUMMER!
Samenvatting Natuurkunde Hoofdstuk 1
 Samenvatting Natuurkunde Hoofdstuk 1 Samenvatting door een scholier 1494 woorden 8 april 2014 7,8 97 keer beoordeeld Vak Methode Natuurkunde Systematische natuurkunde Grootheden en eenheden Kwalitatieve
Samenvatting Natuurkunde Hoofdstuk 1 Samenvatting door een scholier 1494 woorden 8 april 2014 7,8 97 keer beoordeeld Vak Methode Natuurkunde Systematische natuurkunde Grootheden en eenheden Kwalitatieve
Tentamen Mechanica ( )
 Tentamen Mechanica (20-12-2006) Achter iedere opgave is een indicatie van de tijdsbesteding in minuten gegeven. correspondeert ook met de te behalen punten, in totaal 150. Gebruik van rekenapparaat en
Tentamen Mechanica (20-12-2006) Achter iedere opgave is een indicatie van de tijdsbesteding in minuten gegeven. correspondeert ook met de te behalen punten, in totaal 150. Gebruik van rekenapparaat en
Uitwerkingen Tentamen Natuurkunde-1
 Uitwerkingen Tentamen Natuurkunde-1 5 november 2015 Patrick Baesjou Vraag 1 [17]: a. Voor de veerconstante moeten we de hoekfrequentie ω weten. Die wordt gegeven door: ω = 2π f ( = 62.8 s 1 ) Vervolgens
Uitwerkingen Tentamen Natuurkunde-1 5 november 2015 Patrick Baesjou Vraag 1 [17]: a. Voor de veerconstante moeten we de hoekfrequentie ω weten. Die wordt gegeven door: ω = 2π f ( = 62.8 s 1 ) Vervolgens
Toepassingen in de natuurkunde: snelheden, versnellingen, krachten.
 WIS8 8 Vectoren 8. Vectoren Vectoren Een vector met dimensie is een kolom bestaande uit twee reële getallen, bijvoorbeeld [ We kunnen deze meetkundig interpreteren als een pijl in het platte vlak van de
WIS8 8 Vectoren 8. Vectoren Vectoren Een vector met dimensie is een kolom bestaande uit twee reële getallen, bijvoorbeeld [ We kunnen deze meetkundig interpreteren als een pijl in het platte vlak van de
Vectoranalyse voor TG
 college 11 collegejaar college build slides Vandaag : : : : 17-18 11 23 oktober 2017 35 De sterrennacht Vincent van Gogh, 1889 1 2 3 4 5 Verband met de stelling van n 1 VA intro ection 16.7 Definitie Equation
college 11 collegejaar college build slides Vandaag : : : : 17-18 11 23 oktober 2017 35 De sterrennacht Vincent van Gogh, 1889 1 2 3 4 5 Verband met de stelling van n 1 VA intro ection 16.7 Definitie Equation
Theory Dutch (Netherlands) Lees eerst de algemene instructies uit de aparte enveloppe voordat je begint met deze opgave.
 Q1-1 Twee problemen uit de Mechanica (10 punten) Lees eerst de algemene instructies uit de aparte enveloppe voordat je begint met deze opgave. Deel A. De verborgen schijf (3.5 punten) We beschouwen een
Q1-1 Twee problemen uit de Mechanica (10 punten) Lees eerst de algemene instructies uit de aparte enveloppe voordat je begint met deze opgave. Deel A. De verborgen schijf (3.5 punten) We beschouwen een
Eindexamen vwo wiskunde B pilot 2014-I
 Eindeamen vwo wiskunde B pilot 04-I Formules Goniometrie sin( tu) sintcosu costsinu sin( tu) sintcosu costsinu cos( tu) costcosusintsinu cos( tu) costcosusintsinu sin( t) sintcost cos( t) cos tsin t cos
Eindeamen vwo wiskunde B pilot 04-I Formules Goniometrie sin( tu) sintcosu costsinu sin( tu) sintcosu costsinu cos( tu) costcosusintsinu cos( tu) costcosusintsinu sin( t) sintcost cos( t) cos tsin t cos
Tentamen Klassieke Mechanica, 29 Augustus 2007
 Tentamen Klassieke Mechanica, 9 Augustus 7 Dit tentamen bestaat uit vijf vragen, met in totaal negen onderdelen. Alle onderdelen, met uitzondering van 5.3, zijn onafhankelijk van elkaar te maken. Mocht
Tentamen Klassieke Mechanica, 9 Augustus 7 Dit tentamen bestaat uit vijf vragen, met in totaal negen onderdelen. Alle onderdelen, met uitzondering van 5.3, zijn onafhankelijk van elkaar te maken. Mocht
IJkingstoets Wiskunde-Informatica-Fysica 29 juni Nummer vragenreeks: 1
 IJkingstoets Wiskunde-Informatica-Fysica 29 juni 206 Nummer vragenreeks: IJkingstoets wiskunde-informatica-fysica 29 juni 206 - reeks - p. /0 Oefening Welke studierichting wil je graag volgen? (vraag
IJkingstoets Wiskunde-Informatica-Fysica 29 juni 206 Nummer vragenreeks: IJkingstoets wiskunde-informatica-fysica 29 juni 206 - reeks - p. /0 Oefening Welke studierichting wil je graag volgen? (vraag
Een model voor een lift
 Een model voor een lift 2 de Leergang Wiskunde schooljaar 213/14 2 Inhoudsopgave Achtergrondinformatie... 4 Inleiding... 5 Model 1, oriëntatie... 7 Model 1... 9 Model 2, oriëntatie... 11 Model 2... 13
Een model voor een lift 2 de Leergang Wiskunde schooljaar 213/14 2 Inhoudsopgave Achtergrondinformatie... 4 Inleiding... 5 Model 1, oriëntatie... 7 Model 1... 9 Model 2, oriëntatie... 11 Model 2... 13
PLANETENSTELSELS IN ONZE MELKWEG. Opgaven
 VOLKSSTERRENWACHT BEISBROEK VZW Zeeweg 96, 8200 Brugge - Tel. 050 39 05 66 www.beisbroek.be - E-mail: info@beisbroek.be PLANETENSTELSELS IN ONZE MELKWEG Opgaven Frank Tamsin en Jelle Dhaene De ster HR
VOLKSSTERRENWACHT BEISBROEK VZW Zeeweg 96, 8200 Brugge - Tel. 050 39 05 66 www.beisbroek.be - E-mail: info@beisbroek.be PLANETENSTELSELS IN ONZE MELKWEG Opgaven Frank Tamsin en Jelle Dhaene De ster HR
Gaap, ja, nog een keer. In één variabele hebben we deze formule nu al een paar keer gezien:
 Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
Van de opgaven met een letter en dus zonder nummer staat het antwoord achterin. De vragen met een nummer behoren tot het huiswerk. Spieken achterin helpt je niets in het beter snappen... 1 Stelling van
Theorie windmodellen 15.1
 Theorie windmodellen 15.1 15 THEORIE WINDMODELLEN 15.1 Inleiding Doordat er drukverschillen zijn in de atmosfeer waait er wind. Tengevolge van horizontale drukverschillen zal een luchtbeweging willen ontstaan
Theorie windmodellen 15.1 15 THEORIE WINDMODELLEN 15.1 Inleiding Doordat er drukverschillen zijn in de atmosfeer waait er wind. Tengevolge van horizontale drukverschillen zal een luchtbeweging willen ontstaan
Tentamen Natuurkunde A. 9.00 uur 12.00 uur woensdag 10 januari 2007 Docent Drs.J.B. Vrijdaghs. Vul Uw gegevens op het deelnameformulier in
 Tentamen Natuurkunde A 9. uur. uur woensdag januari 7 Docent Drs.J.B. Vrijdaghs Aanwijzingen: Vul Uw gegevens op het deelnameformulier in Dit tentamen omvat 8 opgaven met totaal deelvragen Maak elke opgave
Tentamen Natuurkunde A 9. uur. uur woensdag januari 7 Docent Drs.J.B. Vrijdaghs Aanwijzingen: Vul Uw gegevens op het deelnameformulier in Dit tentamen omvat 8 opgaven met totaal deelvragen Maak elke opgave
In het internationale eenhedenstelsel, ook wel SI, staan er negen basisgrootheden met bijbehorende grondeenheden. Dit is BINAS tabel 3A.
 Grootheden en eenheden Kwalitatieve en kwantitatieve waarnemingen Een kwalitatieve waarneming is wanneer je meet zonder bijvoorbeeld een meetlat. Je ziet dat een paard hoger is dan een muis. Een kwantitatieve
Grootheden en eenheden Kwalitatieve en kwantitatieve waarnemingen Een kwalitatieve waarneming is wanneer je meet zonder bijvoorbeeld een meetlat. Je ziet dat een paard hoger is dan een muis. Een kwantitatieve
Examen Algemene natuurkunde 1, oplossing
 Examen Algemene natuurkunde 1, oplossing Vraag 1 (6 ptn) De deeltjes m 1 en m 2 bewegen zich op eenzelfde rechte zoals in de figuur. Ze zitten op ramkoers want v 1 > v 2. v w m n Figuur 1: Twee puntmassa
Examen Algemene natuurkunde 1, oplossing Vraag 1 (6 ptn) De deeltjes m 1 en m 2 bewegen zich op eenzelfde rechte zoals in de figuur. Ze zitten op ramkoers want v 1 > v 2. v w m n Figuur 1: Twee puntmassa
NATUURKUNDE. Figuur 1
 NATUURKUNDE KLAS 5 PROEFWERK HOOFDSTUK 12-13: KRACHT EN BEWEGING OOFDSTUK 12-13: K 6/7/2009 Deze toets bestaat uit 5 opgaven (51 + 4 punten) en een uitwerkbijlage. Gebruik eigen grafische rekenmachine
NATUURKUNDE KLAS 5 PROEFWERK HOOFDSTUK 12-13: KRACHT EN BEWEGING OOFDSTUK 12-13: K 6/7/2009 Deze toets bestaat uit 5 opgaven (51 + 4 punten) en een uitwerkbijlage. Gebruik eigen grafische rekenmachine
Wiskundige vaardigheden
 Inleiding Bij het vak natuurkunde ga je veel rekenstappen zetten. Het is noodzakelijk dat je deze rekenstappen goed en snel kunt uitvoeren. In deze presentatie behandelen we de belangrijkste wiskundige
Inleiding Bij het vak natuurkunde ga je veel rekenstappen zetten. Het is noodzakelijk dat je deze rekenstappen goed en snel kunt uitvoeren. In deze presentatie behandelen we de belangrijkste wiskundige
Fysica: mechanica, golven en thermodynamica PROEFEXAMEN VAN 12 NOVEMBER 2008
 Fysica: mechanica, golven en thermodynamica Prof. J. Danckaert PROEFEXAMEN VAN 12 NOVEMBER 2008 OPGEPAST Veel succes! Dit proefexamen bestaat grotendeels uit meerkeuzevragen waarbij je de letter overeenstemmend
Fysica: mechanica, golven en thermodynamica Prof. J. Danckaert PROEFEXAMEN VAN 12 NOVEMBER 2008 OPGEPAST Veel succes! Dit proefexamen bestaat grotendeels uit meerkeuzevragen waarbij je de letter overeenstemmend
Wiskunde voor relativiteitstheorie
 Wiskunde voor relativiteitstheorie HOVO Utrecht Les 1: Goniometrie en vectoren Dr. Harm van der Lek vdlek@vdlek.nl Natuurkunde hobbyist Overzicht colleges 1. College 1 1. Goniometrie 2. Vectoren 2. College
Wiskunde voor relativiteitstheorie HOVO Utrecht Les 1: Goniometrie en vectoren Dr. Harm van der Lek vdlek@vdlek.nl Natuurkunde hobbyist Overzicht colleges 1. College 1 1. Goniometrie 2. Vectoren 2. College
Getaltheorie I. c = c 1 = 1 c (1)
 Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk
Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk
Opgave Zonnestelsel 2005/2006: 7. 7 Het viriaal theorema en de Jeans Massa: Stervorming. 7.1 Het viriaal theorema
 Opgave Zonnestelsel 005/006: 7 7 Het viriaal theorema en de Jeans Massa: Stervorming 7. Het viriaal theorema Het viriaal theorema is van groot belang binnen de sterrenkunde: bij stervorming, planeetvorming
Opgave Zonnestelsel 005/006: 7 7 Het viriaal theorema en de Jeans Massa: Stervorming 7. Het viriaal theorema Het viriaal theorema is van groot belang binnen de sterrenkunde: bij stervorming, planeetvorming
Dossier 4 VECTOREN. Dr. Luc Gheysens. bouwstenen van de lineaire algebra
 Dossier 4 VECTOREN bouwstenen van de lineaire algebra Dr. Luc Gheysens 1 Coördinaat van een vector In het vlak π 0 is het punt O de oorsprong en de punten E 1 en E 2 zijn zodanig gekozen dat OE 1 OE 2
Dossier 4 VECTOREN bouwstenen van de lineaire algebra Dr. Luc Gheysens 1 Coördinaat van een vector In het vlak π 0 is het punt O de oorsprong en de punten E 1 en E 2 zijn zodanig gekozen dat OE 1 OE 2
Tentamen Natuurkunde 1A 09.00 uur - 12.00 uur vrijdag 14 januari 2011 docent drs.j.b. Vrijdaghs
 Tentamen Natuurkunde 1A 09.00 uur - 12.00 uur vrijdag 14 januari 2011 docent drs.j.b. Vrijdaghs Aanwijzingen: Dit tentamen omvat 6 opgaven met totaal 20 deelvragen Begin elke opgave op een nieuwe kant
Tentamen Natuurkunde 1A 09.00 uur - 12.00 uur vrijdag 14 januari 2011 docent drs.j.b. Vrijdaghs Aanwijzingen: Dit tentamen omvat 6 opgaven met totaal 20 deelvragen Begin elke opgave op een nieuwe kant
7 College 01/12: Electrische velden, Wet van Gauss
 7 College 01/12: Electrische velden, Wet van Gauss Berekening van electrische flux Alleen de component van het veld loodrecht op het oppervlak draagt bij aan de netto flux. We definieren de electrische
7 College 01/12: Electrische velden, Wet van Gauss Berekening van electrische flux Alleen de component van het veld loodrecht op het oppervlak draagt bij aan de netto flux. We definieren de electrische
Krachten (4VWO) www.betales.nl
 www.betales.nl Grootheden Scalairen Vectoren - Grootte - Eenheid - Grootte - Eenheid - Richting Bv: m = 987 kg x = 10m (x = plaats) V = 3L Bv: F = 17N s = Δx (verplaatsing) v = 2km/h Krachten optellen
www.betales.nl Grootheden Scalairen Vectoren - Grootte - Eenheid - Grootte - Eenheid - Richting Bv: m = 987 kg x = 10m (x = plaats) V = 3L Bv: F = 17N s = Δx (verplaatsing) v = 2km/h Krachten optellen
Uitwerkingen Mei 2012. Eindexamen VWO Wiskunde B. Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek
 Uitwerkingen Mei 01 Eindexamen VWO Wiskunde B A B C Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek Onafhankelijkheid van a Opgave 1. We moeten aantonen dat F a een primitieve is van de
Uitwerkingen Mei 01 Eindexamen VWO Wiskunde B A B C Nederlands Mathematisch Instituut Voor Onderwijs en Onderzoek Onafhankelijkheid van a Opgave 1. We moeten aantonen dat F a een primitieve is van de
IJkingstoets burgerlijk ingenieur juni 2014: algemene feedback
 IJkingstoets burgerlijk ingenieur 30 juni 2014 - reeks 1 - p. 1 IJkingstoets burgerlijk ingenieur juni 2014: algemene feedback In totaal namen 716 studenten deel aan de ijkingstoets burgerlijk ingenieur
IJkingstoets burgerlijk ingenieur 30 juni 2014 - reeks 1 - p. 1 IJkingstoets burgerlijk ingenieur juni 2014: algemene feedback In totaal namen 716 studenten deel aan de ijkingstoets burgerlijk ingenieur
Klassieke Mechanica a (Tentamen 11 mei 2012) Uitwerkingen
 Klassieke Mechanica a (Tentamen mei ) Uitwerkingen Opgave. (Beweging in een conservatief krachtenveld) a. Een kracht is conservatief als r F =. Dit blijkt na invullen: (r F) x = @F z =@y @F y =@z = =,
Klassieke Mechanica a (Tentamen mei ) Uitwerkingen Opgave. (Beweging in een conservatief krachtenveld) a. Een kracht is conservatief als r F =. Dit blijkt na invullen: (r F) x = @F z =@y @F y =@z = =,
Inleiding Analyse 2009
 Inleiding Analyse 2009 Inleveropgaven A). Stel f(, y) = In (0, 0) is f niet gedefinieerd. We bestuderen y2 2 + y 4. lim f(, y). (,y) (0,0) 1. Bepaal de waarde van f(, y) op een willekeurige rechte lijn
Inleiding Analyse 2009 Inleveropgaven A). Stel f(, y) = In (0, 0) is f niet gedefinieerd. We bestuderen y2 2 + y 4. lim f(, y). (,y) (0,0) 1. Bepaal de waarde van f(, y) op een willekeurige rechte lijn
Trillingen en geluid wiskundig. 1 De sinus van een hoek 2 Uitwijking van een trilling berekenen 3 Macht en logaritme 4 Geluidsniveau en amplitude
 Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Uitwijking van een trilling berekenen 3 Macht en logaritme 4 Geluidsniveau en amplitude 1 De sinus van een hoek Eenheidscirkel In de figuur hiernaast
Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Uitwijking van een trilling berekenen 3 Macht en logaritme 4 Geluidsniveau en amplitude 1 De sinus van een hoek Eenheidscirkel In de figuur hiernaast
Deel 4: Krachten. 4.1 De grootheid kracht. 4.1.1 Soorten krachten
 Deel 4: Krachten 4.1 De grootheid kracht 4.1.1 Soorten krachten We kennen krachten uit het dagelijks leven: vul in welke krachten werkzaam zijn: trekkracht, magneetkracht, spierkracht, veerkracht, waterkracht,
Deel 4: Krachten 4.1 De grootheid kracht 4.1.1 Soorten krachten We kennen krachten uit het dagelijks leven: vul in welke krachten werkzaam zijn: trekkracht, magneetkracht, spierkracht, veerkracht, waterkracht,
Lessen over Cosmografie
 Lessen over Cosmografie Les 1 : Geografische coördinaten Meridianen en parallellen Orthodromen of grootcirkels Geografische lengte en breedte Afstand gemeten langs meridiaan en parallel Orthodromische
Lessen over Cosmografie Les 1 : Geografische coördinaten Meridianen en parallellen Orthodromen of grootcirkels Geografische lengte en breedte Afstand gemeten langs meridiaan en parallel Orthodromische
Achter het correctievoorschrift is een aanvulling op het correctievoorschrift opgenomen.
 Eamen VW 04 tijdvak dinsdag 0 mei 3.30-6.30 uur wiskunde B (pilot) chter het correctievoorschrift is een aanvulling op het correctievoorschrift opgenomen. Dit eamen bestaat uit 8 vragen. Voor dit eamen
Eamen VW 04 tijdvak dinsdag 0 mei 3.30-6.30 uur wiskunde B (pilot) chter het correctievoorschrift is een aanvulling op het correctievoorschrift opgenomen. Dit eamen bestaat uit 8 vragen. Voor dit eamen
Inleiding Astrofysica Tentamen 2009/2010: antwoorden
 Inleiding Astrofysica Tentamen 2009/200: antwoorden December 2, 2009. Begrippen, vergelijkingen, astronomische getallen a. Zie Kutner 0.3 b. Zie Kutner 23.5 c. Zie Kutner 4.2.6 d. Zie Kutner 6.5 e. Zie
Inleiding Astrofysica Tentamen 2009/200: antwoorden December 2, 2009. Begrippen, vergelijkingen, astronomische getallen a. Zie Kutner 0.3 b. Zie Kutner 23.5 c. Zie Kutner 4.2.6 d. Zie Kutner 6.5 e. Zie
2010-I. A heeft de coördinaten (4 a, 4a a 2 ). Vraag 1. Toon dit aan. Gelijkstellen: y= 4x x 2 A. y= ax
 00-I De parabool met vergelijking y = 4x x en de x-as sluiten een vlakdeel V in. De lijn y = ax (met 0 a < 4) snijdt de parabool in de oorsprong en in punt. Zie de figuur. y= 4x x y= ax heeft de coördinaten
00-I De parabool met vergelijking y = 4x x en de x-as sluiten een vlakdeel V in. De lijn y = ax (met 0 a < 4) snijdt de parabool in de oorsprong en in punt. Zie de figuur. y= 4x x y= ax heeft de coördinaten
Eindronde Natuurkunde Olympiade 2018 theorietoets deel 1
 Eindronde Natuurkunde Olympiade 2018 theorietoets deel 1 1. Spelen met water (3 punten) Water wordt aan de bovenkant met een verwaarloosbare snelheid in een dakgoot met lengte L = 100 cm gegoten en dat
Eindronde Natuurkunde Olympiade 2018 theorietoets deel 1 1. Spelen met water (3 punten) Water wordt aan de bovenkant met een verwaarloosbare snelheid in een dakgoot met lengte L = 100 cm gegoten en dat
Aanvullingen bij Hoofdstuk 8
 Aanvullingen bij Hoofdstuk 8 8.5 Definities voor matrices De begrippen eigenwaarde eigenvector eigenruimte karakteristieke veelterm en diagonaliseerbaar worden ook gebruikt voor vierkante matrices los
Aanvullingen bij Hoofdstuk 8 8.5 Definities voor matrices De begrippen eigenwaarde eigenvector eigenruimte karakteristieke veelterm en diagonaliseerbaar worden ook gebruikt voor vierkante matrices los
Vectoranalyse voor TG
 college 6 van een vectorveld collegejaar college build slides Vandaag : : : : 14-15 6 22 september 214 51 1 2 3 4 5 Gradiënt van een vectorveld 1 VA vandaag Section 16.2 Hoofdstu 4 Definitie Een vectorveld
college 6 van een vectorveld collegejaar college build slides Vandaag : : : : 14-15 6 22 september 214 51 1 2 3 4 5 Gradiënt van een vectorveld 1 VA vandaag Section 16.2 Hoofdstu 4 Definitie Een vectorveld
Samenvatting Natuurkunde Natuurkunde Samenvatting NOVA 3 vwo
 Samenvatting Natuurkunde Natuurkunde Samenvatting NOVA 3 vwo Samenvatting door N. 1441 woorden 9 oktober 2012 7,6 27 keer beoordeeld Vak Methode Natuurkunde Nova PARAGRAAF 1; KRACHT Krachten herkennen
Samenvatting Natuurkunde Natuurkunde Samenvatting NOVA 3 vwo Samenvatting door N. 1441 woorden 9 oktober 2012 7,6 27 keer beoordeeld Vak Methode Natuurkunde Nova PARAGRAAF 1; KRACHT Krachten herkennen
Opgave Zonnestelsel 2005/2006: 4. 4 Getijdekrachten. 4.1 Getijdeverhitting van Io
 Opgave Zonnestelsel 2005/2006: 4 4 Getijdekrachten 4.1 Getijdeverhitting van Io Io wordt verwarmd door de getijdewisselwerking met Jupiter: zo n 10 1 W. We zullen hier afleiden hoe deze verwarming in zijn
Opgave Zonnestelsel 2005/2006: 4 4 Getijdekrachten 4.1 Getijdeverhitting van Io Io wordt verwarmd door de getijdewisselwerking met Jupiter: zo n 10 1 W. We zullen hier afleiden hoe deze verwarming in zijn
Wiskunde voor relativiteitstheorie
 Wiskunde voor relativiteitstheorie Utrecht Les : Goniometrie en vectoren Dr. Harm van der Lek vdlek@vdlek.nl Natuurkunde hobbyist verzicht colleges. College. Goniometrie 2. Vectoren 2. College 2. Matrixen
Wiskunde voor relativiteitstheorie Utrecht Les : Goniometrie en vectoren Dr. Harm van der Lek vdlek@vdlek.nl Natuurkunde hobbyist verzicht colleges. College. Goniometrie 2. Vectoren 2. College 2. Matrixen
Kleine Mechanica van de Schaatsslag
 Kleine Mechanica van de Schaatsslag Kees Doets h.c.doets@gmail.com Samenvatting Hoe komt het dat je met schaatsen vooruit gaat door zijwaarts af te zetten? Dat mysterie wordt hier opgehelderd. Ook wordt
Kleine Mechanica van de Schaatsslag Kees Doets h.c.doets@gmail.com Samenvatting Hoe komt het dat je met schaatsen vooruit gaat door zijwaarts af te zetten? Dat mysterie wordt hier opgehelderd. Ook wordt
12.0 Voorkennis. Voorbeeld 1: Los de vergelijking sin(a) = 0 op. We zoeken nu de punten op de eenheidscirkel met y-coördinaat 0.
 12.0 Voorkennis Voorbeeld 1: Los de vergelijking sin(a) = 0 op. We zoeken nu de punten op de eenheidscirkel met y-coördinaat 0. Dit is in de punten (1,0) en (-1,0) (1,0) heeft draaiingshoek 0 (-1,0) heeft
12.0 Voorkennis Voorbeeld 1: Los de vergelijking sin(a) = 0 op. We zoeken nu de punten op de eenheidscirkel met y-coördinaat 0. Dit is in de punten (1,0) en (-1,0) (1,0) heeft draaiingshoek 0 (-1,0) heeft
Eindexamen vwo wiskunde B pilot 2013-I
 Eindeamen vwo wiskunde pilot 03-I Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin
Eindeamen vwo wiskunde pilot 03-I Formules Goniometrie sin( t u) sintcosu costsinu sin( t u) sintcosu costsinu cos( t u) costcosu sintsinu cos( t u) costcosu sintsinu sin( t) sintcost cos( t) cos t sin
x cos α y sin α . (1) x sin α + y cos α We kunnen dit iets anders opschrijven, namelijk als x x y sin α
 Lineaire afbeeldingen Rotatie in dimensie 2 Beschouw het platte vlak dat we identificeren met R 2 Kies een punt P in dit vlak met coördinaten (, y) Stel dat we het vlak roteren met de oorsprong (0, 0)
Lineaire afbeeldingen Rotatie in dimensie 2 Beschouw het platte vlak dat we identificeren met R 2 Kies een punt P in dit vlak met coördinaten (, y) Stel dat we het vlak roteren met de oorsprong (0, 0)
2 Pretpark aan de hemel
 2 Pretpark aan de hemel In deze paragraaf onderzoeken en leren we over de beweging van de aarde om de zon, de draaiing van de aarde om haar as, de beweging van de maan rond de aarde, en hoe die bewegingen
2 Pretpark aan de hemel In deze paragraaf onderzoeken en leren we over de beweging van de aarde om de zon, de draaiing van de aarde om haar as, de beweging van de maan rond de aarde, en hoe die bewegingen
Examen VWO. Wiskunde B Profi
 Wiskunde B Profi Eamen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Donderdag 25 mei 3.30 6.30 uur 20 00 Dit eamen bestaat uit 7 vragen. Voor elk vraagnummer is aangegeven hoeveel punten met een
Wiskunde B Profi Eamen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Donderdag 25 mei 3.30 6.30 uur 20 00 Dit eamen bestaat uit 7 vragen. Voor elk vraagnummer is aangegeven hoeveel punten met een
Examen H1B0 Toegepaste Mechanica 1
 16 augustus 2010, 8u30 naam :................................... Examen H1B0 Toegepaste Mechanica 1 Het verloop van het examen Uiterlijk om 12u30 geeft iedereen af. Lees de vragen grondig. De vraag begrijpen
16 augustus 2010, 8u30 naam :................................... Examen H1B0 Toegepaste Mechanica 1 Het verloop van het examen Uiterlijk om 12u30 geeft iedereen af. Lees de vragen grondig. De vraag begrijpen
Examen Klassieke Mechanica
 Examen Klassieke Mechanica Herbert De Gersem, Eef Temmerman 23 januari 2009, academiejaar 08-09 IW2 en BIW2 NAAM: RICHTING: vraag 1 (/4) vraag 2 (/4) vraag 3 (/5) vraag 4 (/4) vraag 5 (/3) TOTAAL (/20)
Examen Klassieke Mechanica Herbert De Gersem, Eef Temmerman 23 januari 2009, academiejaar 08-09 IW2 en BIW2 NAAM: RICHTING: vraag 1 (/4) vraag 2 (/4) vraag 3 (/5) vraag 4 (/4) vraag 5 (/3) TOTAAL (/20)
1. Orthogonale Hyperbolen
 . Orthogonale Hyperbolen a + b In dit hoofdstuk wordt de grafiek van functies van de vorm y besproken. Functies c + d van deze vorm noemen we gebroken lineaire functies. De grafieken van dit soort functies
. Orthogonale Hyperbolen a + b In dit hoofdstuk wordt de grafiek van functies van de vorm y besproken. Functies c + d van deze vorm noemen we gebroken lineaire functies. De grafieken van dit soort functies
Tweede huiswerkopdracht Lineaire algebra 1 Uitwerking en opmerkingen
 Tweede huiswerkopdracht Lineaire algebra 1 en opmerkingen November 10, 2009 Opgave 1 Gegeven een vectorruimte V met deelruimtes U 1 en U 2. Als er geldt dim U 1 = 7, dimu 2 = 9, en dim(u 1 U 2 ) = 4, wat
Tweede huiswerkopdracht Lineaire algebra 1 en opmerkingen November 10, 2009 Opgave 1 Gegeven een vectorruimte V met deelruimtes U 1 en U 2. Als er geldt dim U 1 = 7, dimu 2 = 9, en dim(u 1 U 2 ) = 4, wat
3 Cirkels, Hoeken en Bogen. Inversies.
 3 Cirkels, Hoeken en Bogen. Inversies. 3.1. Inleiding Het derde college betreft drie onderwerpen (hoeken, bogen en inversies), die in concrete meetkundige situaties vaak optreden. Dit hoofdstuk is bedoeld
3 Cirkels, Hoeken en Bogen. Inversies. 3.1. Inleiding Het derde college betreft drie onderwerpen (hoeken, bogen en inversies), die in concrete meetkundige situaties vaak optreden. Dit hoofdstuk is bedoeld
CIRKELBEWEGING & GRAVITATIE VWO
 CIRKELBEWEGING & GRAVITATIE VWO Foton is een opgavenverzameling voor het nieuwe eindexamenprogramma natuurkunde. Foton is gratis te downloaden via natuurkundeuitgelegd.nl/foton Uitwerkingen van alle opgaven
CIRKELBEWEGING & GRAVITATIE VWO Foton is een opgavenverzameling voor het nieuwe eindexamenprogramma natuurkunde. Foton is gratis te downloaden via natuurkundeuitgelegd.nl/foton Uitwerkingen van alle opgaven
Overzicht Fourier-theorie
 B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
B Overzicht Fourier-theorie In dit hoofdstuk geven we een overzicht van de belangrijkste resultaten van de Fourier-theorie. Dit kan als steun dienen ter voorbereiding op het tentamen. Fourier-reeksen van
Langere vraag over de theorie
 Langere vraag over de theorie (a) Magnetisch dipooloent Zoals het elektrisch dipooloent is het agnetisch dipooloent een vectoriële grootheid. Het agnetisch dipooloent wordt gedefinieerd voor een gesloten
Langere vraag over de theorie (a) Magnetisch dipooloent Zoals het elektrisch dipooloent is het agnetisch dipooloent een vectoriële grootheid. Het agnetisch dipooloent wordt gedefinieerd voor een gesloten
Opgave 2 Een kracht heeft een grootte, een richting en een aangrijpingspunt.
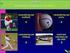 Uitwerkingen 1 Opgave 1 Het aangrijpingspunt van een kracht is de plaats waar de kracht op het voorwerp werkt. De werklijn van een kracht is de denkbeeldige (rechte) lijn die samenvalt met de bijbehorende
Uitwerkingen 1 Opgave 1 Het aangrijpingspunt van een kracht is de plaats waar de kracht op het voorwerp werkt. De werklijn van een kracht is de denkbeeldige (rechte) lijn die samenvalt met de bijbehorende
2 Kromming van een geparametriseerde kromme in het vlak. Veronderstel dat een kromme in het vlak gegeven is door een parametervoorstelling
 TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
Tussentoets Analyse 2. Natuur- en sterrenkunde.
 Tussentoets Analyse 2. Natuur- en sterrenkunde. Dinsdag 9 maart 2010, 9.00-11.00. Het gebruik van een rekenmachine is toegestaan. Motiveer elk antwoord dat je geeft d.m.v. een berekening of redenering.
Tussentoets Analyse 2. Natuur- en sterrenkunde. Dinsdag 9 maart 2010, 9.00-11.00. Het gebruik van een rekenmachine is toegestaan. Motiveer elk antwoord dat je geeft d.m.v. een berekening of redenering.
1. Overzicht Hemelmechanica 2. Elektromagnetische straling 3. Zonnestelsel(s) 4. Sterren: fysische eigenschappen 5. Sterren: struktuur + evolutie 6.
 Inleiding Astrofysica 1. Overzicht Hemelmechanica 2. Elektromagnetische straling 3. Zonnestelsel(s) 4. Sterren: fysische eigenschappen 5. Sterren: struktuur + evolutie 6. Sterren: stervorming, sterdood
Inleiding Astrofysica 1. Overzicht Hemelmechanica 2. Elektromagnetische straling 3. Zonnestelsel(s) 4. Sterren: fysische eigenschappen 5. Sterren: struktuur + evolutie 6. Sterren: stervorming, sterdood
Opgaven Functies en Reeksen. E.P. van den Ban
 Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Ruimtewiskunde. college. Het inwendig- en het uitwendig product. Vandaag. Hoeken Orthogonaliteit en projecties. Toepassing: magnetische velden
 college 2 - en het uitwendig collegejaar college build slides Vandaag : : : : 6-7 2 30 mei 207 30 2 3 4 5 Hoeken Orthogonaliteit en projecties Toepassing: magnetische velden.6-7[2] vandaag meetkundig Section
college 2 - en het uitwendig collegejaar college build slides Vandaag : : : : 6-7 2 30 mei 207 30 2 3 4 5 Hoeken Orthogonaliteit en projecties Toepassing: magnetische velden.6-7[2] vandaag meetkundig Section
Examen HAVO 2012. wiskunde B. tijdvak 1 donderdag 24 mei 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Examen HAVO 2012 tijdvak 1 donderdag 24 mei 13.30-16.30 uur wiskunde B Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 19 vragen. Voor dit examen zijn maximaal 80 punten te behalen. Voor
Examen HAVO 2012 tijdvak 1 donderdag 24 mei 13.30-16.30 uur wiskunde B Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 19 vragen. Voor dit examen zijn maximaal 80 punten te behalen. Voor
Inleiding tot de dynamica van atmosferen Krachten
 Inleiding tot de dynamica van atmosferen Krachten P. Termonia vakgroep wiskundige natuurkunde en sterrenkunde, UGent Inleiding tot de dynamica van atmosferen p.1/35 Inhoud 1. conventies: notatie 2. luchtdeeltjes
Inleiding tot de dynamica van atmosferen Krachten P. Termonia vakgroep wiskundige natuurkunde en sterrenkunde, UGent Inleiding tot de dynamica van atmosferen p.1/35 Inhoud 1. conventies: notatie 2. luchtdeeltjes
Eerste orde partiële differentiaalvergelijkingen
 Eerste orde partiële differentiaalvergelijkingen Vakgroep Differentiaalvergelijkingen 1995, 2001, 2002 1 Eerste orde golf-vergelijking De vergelijking au x + u t = 0, u = u(x, t), a ɛ IR (1.1) beschrijft
Eerste orde partiële differentiaalvergelijkingen Vakgroep Differentiaalvergelijkingen 1995, 2001, 2002 1 Eerste orde golf-vergelijking De vergelijking au x + u t = 0, u = u(x, t), a ɛ IR (1.1) beschrijft
te vermenigvuldigen, waarbij N het aantal geslagen Nederlandse munten en B het aantal geslagen buitenlandse munten zijn. Het resultaat is de vector
 Les 3 Matrix product We hebben gezien hoe we matrices kunnen gebruiken om lineaire afbeeldingen te beschrijven. Om het beeld van een vector onder een afbeelding te bepalen hebben we al een soort product
Les 3 Matrix product We hebben gezien hoe we matrices kunnen gebruiken om lineaire afbeeldingen te beschrijven. Om het beeld van een vector onder een afbeelding te bepalen hebben we al een soort product
BIOFYSICA: Toets I.4. Dynamica: Oplossing
 1 ste jaar Bachelor BIOMEDISCHE WETENSCHAPPEN Academiejaar 006-007 BIOFYSICA: Toets I.4. Dynamica: Oplossing 1 Opgave 1 Een blokje met massa 0, kg heeft onder aan een vlakke helling een snelheid van 7,
1 ste jaar Bachelor BIOMEDISCHE WETENSCHAPPEN Academiejaar 006-007 BIOFYSICA: Toets I.4. Dynamica: Oplossing 1 Opgave 1 Een blokje met massa 0, kg heeft onder aan een vlakke helling een snelheid van 7,
Ijkingstoets industrieel ingenieur aangeboden door UGent en VUB op 30 juni 2014: algemene feedback
 IJkingstoets juni 4 - reeks - p. / Ijkingstoets industrieel ingenieur aangeboden door UGent en VUB op juni 4: algemene feedback In totaal namen studenten deel aan deze ijkingstoets industrieel ingenieur
IJkingstoets juni 4 - reeks - p. / Ijkingstoets industrieel ingenieur aangeboden door UGent en VUB op juni 4: algemene feedback In totaal namen studenten deel aan deze ijkingstoets industrieel ingenieur
