Eerste orde partiële differentiaalvergelijkingen
|
|
|
- Esther van Doorn
- 5 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Eerste orde partiële differentiaalvergelijkingen Vakgroep Differentiaalvergelijkingen 1995, 2001, Eerste orde golf-vergelijking De vergelijking au x + u t = 0, u = u(x, t), a ɛ IR (1.1) beschrijft de beweging van een golf in één richting zonder dat de golf van vorm verandert. We zullen zien dat de konstante a de snelheid weergeeft waarmee de golf zich voortbeweegt. Vergelijking (1.1) staat ook wel bekend als de transport vergelijking. We lossen de partiële differentiaalvergelijking op door krommen in het xt-vlak te bepalen waarop (1.1) teruggebracht wordt tot een gewone differentiaalvergelijking. Laat C een geparametriseerde kromme (x(s), t(s)) in het xt-vlak zijn. Op C geldt dan Differentiatie naar s op C levert u(x, t) = u(x(s), t(s)). du ds = u dx x ds + u dt t ds. (1.2) Vergelijken we (1.2) met (1.1) dan zien we dat wanneer er geldt dx ds = a en dt ds = 1 (1.3) du = 0 op C. (1.4) ds Een kromme waarop (1.4) geldt heet een karakteristieke kromme of eenvoudigweg een karakteristiek van vergelijking (1.1), die in dit voorbeeld gedefinieerd wordt door (1.3). Uit (1.4) volgt dat de oplossing u van (1.1) konstant is op een karakteristiek. Uit (1.3) vinden we als oplossingen x(s) = as + x 0, t(s) = s + t 0, 1
2 waaruit na eliminatie van s volgt x = at + konstante. De karakteristieke krommen C zijn in dit geval rechte lijnen in het xt-vlak. De oplossing u(x, t) verandert alleen als we naar een andere karakteristiek overgaan, en is dus slechts afhankelijk van de waarde van x at. We schrijven dit met een willekeurige differentieerbare funktie F : u(x, t) = F (x at). (1.5) Dit wordt ook wel de algemene oplossing van (1.1) genoemd, omdat iedere oplossing van (1.1) van deze vorm moet zijn. Voor een unieke oplossing zijn kennelijk aanvullende gegevens of voorwaarden noodzakelijk. Een gebruikelijke voorwaarde is een voorschrift dat u(x, t) voor een zekere waarde van t, zeg t = 0, met een voorgeschreven continu differentieerbare funktie overeenkomt. Wanneer we aan (1.1) een dergelijke beginvoorwaarde toevoegen spreken we van een Cauchy-probleem: aux + u t = 0, x IR, t > 0, u(x, 0) = f(x), x IR. (1.6) t (x 0, t 0 ) (x 0 at 0, 0) x De waarde van u in (x 0, t 0 ) bepalen we door te bekijken op welke karakteristiek dit punt ligt. Aangezien de waarde op de karakteristiek konstant is, is zij gelijk aan de waarde voor t = 0. De karakteristiek door (x 0, t 0 ) snijdt de x-as in x 0 at 0, zodat Voorbeeld u(x 0, t 0 ) = u(x 0 at 0, 0) = f(x 0 at 0 ). (1.7) 2
3 In het beginwaardeprobleem u x + u t = 0, x IR, t > 0, u(x, 0) = x 2, x IR, is a = 1 en f(x) = 1. De oplossing wordt dan 1 + x2 u(x, t) = (x t) 2. De oplossing behoudt de vorm van de beginkromme en verplaatst zich langs de karakteristieken, de rechte lijnen x t = konstant. u t x = t u(x, 0) u(x, 1) u(x, 2) x = t + 1 x De voorwaarde waaronder u uit (1.7) een oplossing is van (1.6) is dat f continu differentieerbaar is. Dan namelijk zijn u x en u t continu. Dit type oplossing wordt wel een klassieke of sterke oplossing genoemd. Wanneer f slechts stuksgewijs continu differentieerbaar is, bijvoorbeeld 1 + x, 1 < x < 0, f(x) = 1 x, 0 x < 1, 0, elders, of zelfs slechts stuksgewijs continu, dan is het toch mogelijk om de oplossing u in nader te definiëren zin door middel van (1.7) te beschrijven. We gaan hier niet verder in op de vraag in welke zin u oplossing is, maar volstaan met op te merken dat we u in dit geval een zwakke of gegeneraliseerde oplossing noemen. Voorbeeld Het beginwaardeprobleem 3
4 heeft als gegeneraliseerde oplossing 2u x + u t = 0, x IR, t > 0, 0, x > 1, u(x, 0) = 1 x, x 1, 0, x > 1 t, u(x, t) = 1 x + 2t, 1 t < x < 1 t, 0, x < 1 t. Opgaven 1. Bereken de oplossing u(x, t) van het beginwaarde-probleem 2ux + u t = 0, x IR, t > 0, u(x, 0) = f(x), x IR, voor de volgende funkties f. oplossing, Geef aan of er sprake is van een sterke of zwakke (a) f(x) = e x2, x IR. (b) f(x) = e x, x IR. 0, x > 1, (c) f(x) = 1, x Gegeven het beginwaarde-probleem 3ux + u t = 5, x IR, t > 0, u(x, 0) = e x, x IR. Pas de transformatie u(x, t) = v(x, t)+5t toe en bereken de oplossing v(x, t). Bereken vervolgens u(x, t). 3. Gegeven het beginwaarde-probleem 4ux + u t = u, x IR, t > 0 u(x, 0) = cos x, x IR. Pas de transformatie u(x, t) = e t v(x, t) toe en bereken de oplossing v(x, t). Bereken vervolgens u(x, t). 4
5 2 Goed-gestelde problemen We hebben in 1.1 gezien dat de partiële differentiaalvergelijking au x + u t = 0 oneindig veel oplossingen heeft. Door een aanvullende voorwaarde op te leggen, in dit geval een beginwaarde, konden we tot een unieke oplossing komen. We noemen een probleem goed-gesteld wanneer het aan de volgende voorwaarden voldoet: 1. er bestaat een oplossing van het probleem (existentie), 2. er is precies één oplossing van het probleem (uniciteit), 3. de oplossing hangt continu af van de begin- en/of randvoorwaarden (stabiliteit). Wanneer we een model maken van een fysisch probleem met behulp van een partiële differentiaalvergelijking dan proberen we door middel van aanvullende voorwaarden een goedgesteld probleem te formuleren. Leggen we te weinig voorwaarden op dan kan de oplossing niet-uniek zijn, leggen we te veel voorwaarden op dan kan het zijn dat er geen oplossing bestaat. De stabiliteits-eis houdt bijvoorbeeld in dat een kleine meetfout in de beginwaarden geen grote verstoring in de oplossing kan veroorzaken. We komen op deze voorwaarde in de volgende hoofdstukken nog nader terug. We laten nu zien wat goed-gesteldheid inhoudt voor de transportvergelijking. Wanneer we de vergelijking op het gebied 0 < x < bekijken voor a > 0, aux + u t = 0, 0 < x <, t > 0 u(x, 0) = f(x), 0 < x <, (2.8) t x = at S 2 S 1 dan is de oplossing u(x, t) = f(x at) alleen gedefinieerd op het gebied S 1 = (x, t) x > at}. Voor S 2 = (x, t) 0 < x < at} is de oplossing onbepaald omdat er geen beginwaarde is gedefinieerd op karakteristieken met x at < 0. 5 x
6 Door de randwaarde op x = 0 vast te leggen kunnen we tot een goed-gesteld beginrandwaarde probleem komen: au x + u t = 0, 0 < x <, t > 0, u(x, 0) = f(x), 0 < x <, u(0, t) = g(t), t > 0. (2.9) In S 1 wordt de oplossing bepaald door de beginvoorwaarde, in S 2 door de randvoorwaarde: u(x, t) = f(x at), x > at, g(t x a ), 0 < x < at. (2.10) Wanneer a < 0 is, is het probleem (2.9) niet goed-gesteld. Voor een zekere x 0 > 0 liggen dan de punten (x 0, 0) en (0, x 0 ) op dezelfde karakteristiek. a t (0, x 0 a ) (x 0, 0) x De beginvoorwaarde geeft u(x 0, 0) = f(x 0 ), de randvoorwaarde u(0, x 0 a ) = g( x 0 ). Aangezien u konstant is op een karakteristiek moet dus a gelden f(x 0 ) = g( x 0 a ) voor willekeurige x 0 > 0. Voor willekeurige funkties f en g van het probleem (2.9) zal dit in het algemeen niet het geval zijn. Opgaven 1. Bereken de oplossing van het volgende begin-randwaardeprobleem. Maak een schets van de oplossing op de tijdstippen t = 0, 1 en 2. 6
7 u x + u t = 0, 0 < x <, t > 0, u(x, 0) = e x2, 0 < x <, u(0, t) = 1, t > Bereken de oplossing van het volgende begin-randwaardeprobleem. Maak een schets van de oplossing op de tijdstippen t = 0, 1 en 2. 3u x + u t = 0, 0 < x <, t > 0, u(x, 0) = 0, 0 < x <, t, 0 < t < 1, u(0, t) = 1, t Welke voorwaarden moeten we aan f en g van het probleem (2.9) opleggen wil de oplossing (2.10) continu differentieerbaar zijn? 3 Lineaire eerste orde vergelijkingen Wanneer een eerste orde partiële differentiaalvergelijking geschreven kan worden als a(u, x, t)u x + b(u, x, t)u t = c(u, x, t) (3.11) dan heet hij quasi-lineair. Een speciale klasse vormen de lineaire vergelijkingen, die geschreven kunnen worden als Als d 0 is dan heet de vergelijking homogeen. a(x, t)u x + b(x, t)u t = c(x, t)u + d(x, t). (3.12) We gaan nu voor het algemene lineaire beginwaarde-probleem a(x, t)ux + b(x, t)u t = c(x, t)u + d(x, t), x IR, t > 0, u(x, 0) = f(x), x IR (3.13) met behulp van de zogenaamde karakteristiekenmethode een oplossing construeren, op identieke wijze als voor het probleem (1.6). We hebben gezien dat oplossingen van vergelijking (1.1) gegeven konden worden met behulp van karakteristieken, de lijnen x at = konstant. De konstante noemen we λ. Hiermee hebben we een parameter gekregen waarmee we onderscheid kunnen maken tussen de verschillende karakteristieken. Een logische parametrisatie van de karakteristieken is dan x = as + λ, t = s. De parametrisatie is zodanig gekozen dat s de positie op de karakteristiek aangeeft terwijl s = 0 correspondeert met het snijpunt (λ, 0) in het xt-vlak van de karakteristiek met x-as. 7
8 u f t ruimtelijke karakteristiek s s = 0 x = λ x grondkarakteristiek We hebben hiermee ook direct een parametrisatie van de beginkromme gevonden, immers voor s = 0 is x(0) = λ, t(0) = 0, u(0) = f(λ)., λ IR, (3.14) Wanneer we van een algemene parametrisatie van de karakteristiek C λ uitgaan, x = x(s), t = t(s) op C λ, dan wordt aan (3.13) op C λ voldaan als x,t en u oplossing zijn van het karakteristieke stelsel dx ds = a(x, t), x(0) = x 0(λ), (1.15.a) dt ds = b(x, t), t(0) = t 0(λ), (1.15.b) du ds = c(x, t)u + d(x, t), u(0) = u 0(λ). (1.15.c) Doordat de funkties a en b niet van u afhangen kunnen de vergelijkingen (1.15.a) en (1.15.b) onafhankelijk van (1.15.c) opgelost worden. Oplossingen van deze vergelijkingen definiëren karakteristieken in het xt-vlak en heten ook wel grondkarakteristieken. Oplossingen van (1.15.a)-(1.15.c) definiëren zogeheten ruimtelijke karakteristieken. Bij iedere waarde van λ heeft dit stelsel een oplossing die een ruimtelijke karakteristiek voorstelt. Al deze karakteristieken samen beschrijven het oplossingsoppervlak u(x, t) in de xtu-ruimte, zij het door middel van de parameters s en λ: x = x(s, λ), t = t(s, λ), u = u(x(s, λ), t(s, λ)). (3.18) 8
9 Voorbeeld Het beginwaardeprobleem heeft als karakteristiek stelsel xux + u t = u, x IR, t > 0 u(x, 0) = sin(x), x IR, De parametrisatie van de oplossing is dx ds = x, x(0) = λ, dt ds = 1, t(0) = 0, du = ds u, u(0) = sin λ. x = λe s, t = s, u = e s sin λ. Merk op dat u(x, t) u(s, λ)! In het algemeen: u(x, t) = u(x(s, λ), t(s, λ)) = U(s, λ) Volgens de impliciete funktiestelling bestaan de inverse funkties s = s(x, t), λ = λ(x, t) in de omgeving van s = 0 als de Jacobiaan ongelijk aan nul is: (x, t) J(x, t) = (s, λ) = x s t s x λ t λ = x st λ x λ t s 0 (3.19) Deze voorwaarde betekent dat aan de beginkromme de eis gesteld wordt dat deze niet de karakteristieke richting heeft. Wanneer de beginwaarde is gedefinieerd op een willekeurige (differentieerbare) kromme in het xt-vlak betekent (3.19) dat de beginkromme in geen enkel punt de karakteristieke richting heeft. Voorbeeld Voor de parametrisatie uit het vorige voorbeeld is J(x, t) = λe s e s 1 0 = es 0 voor alle s. 9
10 Inverteren van x = λe s, t = s geeft s = t, λ = xe t, zodat de oplossing u gegeven wordt door u = u(x, t) = sin(xe t ) e t. Opgaven 1. Bepaal tot welke klasse (lineair, quasi-lineair,... ) de volgende vergelijkingen behoren, en geef aan of de vergelijking homogeen of inhomogeen is. (a) u x + tu t = 0 (b) u x + uu t = x (c) u x + tu t = u 2 (d) u x + sin x u t = x (e) u x + u 2 t = 0 2. Kan het volgende probleem met behulp van de karakteristieken-methode opgelost worden? Geef een verklaring. ux + u y = 0, x, y IR u(x, y) = 2, voor y = x 3. Bepaal met behulp van de karakteristieken methode de oplossing van de volgende beginwaarde problemen. Geef aan in welk gebied de oplossing geldig is. (a) (b) (c) ux + xu t = u 2, x > 0, t > 0 u(x, 0) = 1, x > 0. tux + u t = x, x IR, t > 0 u(x, 0) = x 2, x IR. xux tu t = 0, x IR, t > 0 u = x 2, op x = t. 4 Quasi-lineaire vergelijkingen De methode uit de vorige paragraaf kan uitgebreid worden naar quasi-lineaire partiële differentiaalvergelijkingen. Ook kunnen willekeurige beginkrommen worden beschouwd. We beschouwen het gegeneraliseerde beginwaardeprobleem: a(x, t, u)ux + b(x, t, u)u t = c(x, t, u), (x, t) ɛ D IR 2, x = x 0 (λ), t = t 0 (λ), u = u 0 (λ), λ ɛ Λ IR. (4.20) 10
11 De beginkromme B voor de quasi-lineaire vergelijking is een ruimtelijke kromme (x 0, t 0, u 0 ), die geparametriseerd wordt met λ. De oplossing u = u(x, t) stelt een oppervlak voor in de xtu-ruimte. De beginkromme B ligt geheel in dit oppervlak. De methode die we afleiden om dit oppervlak te bepalen zal sterk overeenkomen met die uit de vorige paragrafen. Eerst beschouwen we het vectorveld (a(x, t, u), b(x, t, u), c(x, t, u)). In ieder punt (x, t, u) van de xtu-ruimte definieert dit vectorveld een richting. We zoeken nu de krommen die in ieder punt (x, t, u) de richting van het vector-veld aannemen. Langs deze kromme C λ nemen we de parameter s, zodat we voor C λ de volgende parametrisering krijgen: (x(s), t(s), u(s)). We wensen dat deze kromme in ieder punt de richting van het vectorveld heeft. Er moet dan gelden dx ds = a(x(s), t(s), u(s)) dt ds = b(x(s), t(s), u(s)) (4.21) du ds = c(x(s), t(s), u(s)) De krommen die aan dit stelsel van gewone differentiaalvergelijkingen voldoen noemen we kortweg karakteristieken van vergelijking (4.20). We bekijken nu de verzameling van krommen die gaan door de punten van de beginkromme B(λ). Om dit te bereiken voegen we aan het stelsel (4.21) de volgende beginwaarden toe: x(0) = t(0) = u(0) = x 0 (λ) t 0 (λ) u 0 (λ) (4.22) De oplossing van het stelsel (4.21) met de beginwaarden (4.22) kunnen we formeel schrijven als Voorbeeld Het beginwaardeprobleem heeft als karakteristiek stelsel x = x(s, λ), t = t(s, λ), u = u(s, λ). (4.23) yux xu y = u, x > 0, y > 0, u = 1, op xy = 1, 11
12 dx = ds y, x(s = 0) = λ, dy ds = x, y(s = 0) = 1 λ, du = ds u, u(s = 0) = 1. De oplossing voor u is eenvoudig te berekenen: u = e s. De vergelijkingen voor x(s) en y(s) vormen een stelsel gekoppelde gewone differentiaalvergelijkingen, met als oplossing x(s, λ) = sin(s) + λ2 cos(s) λ, y(s, λ) = λ2 sin(s) cos(s) λ. Een expliciete relatie u = u(x, t) wordt gevonden als de inverse transformatie s = s(x, t), λ = λ(x, t) bepaald kan worden. Voorbeeld u(x, t) = U(s(x, t), λ(x, t)) (4.24) De Jacobiaan voor de funkties x(s, λ) en y(s, λ) uit het vorige voorbeeld is J = λ 2 sin(s) + cos(s) λ sin(s) + λ2 cos(s) λ 2 cos(s) sin(s) + λ2 cos(s) λ 2 2 sin(s) + λ2 sin(s) cos(s) λ 2 = λ4 1 λ 3. Aangezien x > 0 is, en dus ook λ > 0, hoeven we alleen voor λ = 1 problemen te verwachten. Het is in dit voorbeeld niet mogelijk s en λ als funkties van x en y te schrijven. Al met al hebben we in deze paragraaf een methode afgeleid voor het quasi-lineaire Cauchy probleem (4.20). De methode bestaat uit het oplossen van het karakteristieke stelsel (4.21), (4.22), en het uitdrukken van s en λ in funkties van x en t. Hierbij hebben we ons niet te veel bezig gehouden met de vraag wanneer het een en ander toepasbaar is! 12
13 Opgaven 1. Los het volgende quasi-lineaire beginwaardeprobleem op met hulp van de karakteristieken-methode, en geef aan waar de oplossing geldig is. x 2 u x + t 2 u t = u 2, x IR, t > 0, u(x, 4x) = 1, x IR. 2. Los de volgende beginwaardeproblemen op met hulp van de karakteristieken-methode. (a) (b) ux + u t = u, x IR, t > 1, u(x, 1) = e x2, x IR. xux + tu t = 1, x IR, t > 1 u(x, 1) = sin x, x IR. 3. We beschouwen de volgende coördinaten-transformatie: ξ = 3x + y η = e x (a) Bepaal ξ x, ξ y, η x en η y. Waarom is de transformatie inverteerbaar? (b) Bepaal x ξ, x η, y ξ en y η door impliciet differentiëren van de bovenstaande transformatieformules. (c) Druk x en y uit in ξ en η (bepaal de inverse transformatie). Controleer het antwoord bij (b). 13
1 WAAM - Differentiaalvergelijkingen
 1 WAAM - Differentiaalvergelijkingen 1.1 Algemene begrippen Een (gewone) differentiaalvergelijking heeft naast de onafhankelijke veranderlijke (bijvoorbeeld genoteerd als x), eveneens een onbekende functie
1 WAAM - Differentiaalvergelijkingen 1.1 Algemene begrippen Een (gewone) differentiaalvergelijking heeft naast de onafhankelijke veranderlijke (bijvoorbeeld genoteerd als x), eveneens een onbekende functie
Opgaven Functies en Reeksen. E.P. van den Ban
 Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Technische Universiteit Delft Uitwerking Tentamen Analyse 3, WI 2601 Maandag 11 januari 2010, 9.00-12.00
 Technische Universiteit Delft Uitwerking Tentamen Analyse 3, WI 6 Maandag januari, 9- Faculteit EWI Dit tentamen bestaat uit 6 opgaven Alle antwoorden dienen beargumenteerd te worden Normering: punten
Technische Universiteit Delft Uitwerking Tentamen Analyse 3, WI 6 Maandag januari, 9- Faculteit EWI Dit tentamen bestaat uit 6 opgaven Alle antwoorden dienen beargumenteerd te worden Normering: punten
Technische Universiteit Delft. ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW2030 Vrijdag 30 januari 2015,
 Technische Universiteit Delft Faculteit EWI ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW23 Vrijdag 3 januari 25, 4.-7. Dit tentamen bestaat uit 6 opgaven. Alle antwoorden dienen beargumenteerd
Technische Universiteit Delft Faculteit EWI ANTWOORDEN van Tentamen Gewone differentiaalvergelijkingen, TW23 Vrijdag 3 januari 25, 4.-7. Dit tentamen bestaat uit 6 opgaven. Alle antwoorden dienen beargumenteerd
WI1708TH Analyse 2. College 5 24 november Challenge the future
 WI1708TH Analyse 2 College 5 24 november 2014 1 Programma Vandaag 2 e orde lineaire differentiaal vergelijking (17.1) 2 1 e orde differentiaal vergelijking Definitie Een 1 e orde differentiaal vergelijking
WI1708TH Analyse 2 College 5 24 november 2014 1 Programma Vandaag 2 e orde lineaire differentiaal vergelijking (17.1) 2 1 e orde differentiaal vergelijking Definitie Een 1 e orde differentiaal vergelijking
Tentamenopgaven over hfdst. 1 t/m 4
 Ttamopgav over hfdst. 1 t/m 4 1. donderdag 31 oktober 1996 Bepaal de oplossing van het beginwaardeprobleem y + 4y = 4 cos 2x, y(0) = 1, y (0) = 0. 2. donderdag 31 oktober 1996 Bepaal de algeme oplossing
Ttamopgav over hfdst. 1 t/m 4 1. donderdag 31 oktober 1996 Bepaal de oplossing van het beginwaardeprobleem y + 4y = 4 cos 2x, y(0) = 1, y (0) = 0. 2. donderdag 31 oktober 1996 Bepaal de algeme oplossing
1e bachelor ingenieurswetenschappen Modeloplossing examen oefeningen analyse I, januari y = u sin(vt) dt. wordt voorgesteld door de matrix
 e bachelor ingenieurswetenschappen Modeloplossing examen oefeningen analyse I, januari 9. Opgave: Bereken dt ( q) als p = (, ), q = (, ) en p u+v x = e t dt T : (u, v) (x, y) : u y = u sin(vt) dt Oplossing:
e bachelor ingenieurswetenschappen Modeloplossing examen oefeningen analyse I, januari 9. Opgave: Bereken dt ( q) als p = (, ), q = (, ) en p u+v x = e t dt T : (u, v) (x, y) : u y = u sin(vt) dt Oplossing:
Hoofdstuk 10: Partiële differentiaalvergelijkingen en Fourierreeksen
 Hoofdstuk : Partiële differentiaalvergelijkingen en Fourierreeksen Partiële differentiaalvergelijkingen zijn vergelijkingen waarin een onbekende functie van twee of meer variabelen en z n partiële afgeleide(n)
Hoofdstuk : Partiële differentiaalvergelijkingen en Fourierreeksen Partiële differentiaalvergelijkingen zijn vergelijkingen waarin een onbekende functie van twee of meer variabelen en z n partiële afgeleide(n)
34 HOOFDSTUK 1. EERSTE ORDE DIFFERENTIAALVERGELIJKINGEN
 34 HOOFDSTUK 1. EERSTE ORDE DIFFERENTIAALVERGELIJKINGEN 1.11 Vraagstukken Vraagstuk 1.11.1 Beschouw het beginwaardeprobleem = 2x (y 1), y(0) = y 0. Los dit beginwaardeprobleem op voor y 0 R en maak een
34 HOOFDSTUK 1. EERSTE ORDE DIFFERENTIAALVERGELIJKINGEN 1.11 Vraagstukken Vraagstuk 1.11.1 Beschouw het beginwaardeprobleem = 2x (y 1), y(0) = y 0. Los dit beginwaardeprobleem op voor y 0 R en maak een
Hoofdstuk 3: Tweede orde lineaire differentiaalvergelijkingen
 Hoofdstuk 3: Tweede orde lineaire differentiaalvergelijkingen De inhoud van hoofdstuk 3 zou grotendeels bekende stof moeten zijn. Deze stof is terug te vinden in Stewart, hoofdstuk 17. Daar staat alles
Hoofdstuk 3: Tweede orde lineaire differentiaalvergelijkingen De inhoud van hoofdstuk 3 zou grotendeels bekende stof moeten zijn. Deze stof is terug te vinden in Stewart, hoofdstuk 17. Daar staat alles
1 Eigenwaarden en eigenvectoren
 Eigenwaarden en eigenvectoren Invoeren van de begrippen eigenwaarde en eigenvector DEFINITIE Een complex (of reëel getal λ heet een eigenwaarde van de n n matrix A als er een vector x is met Ax = λx Dan
Eigenwaarden en eigenvectoren Invoeren van de begrippen eigenwaarde en eigenvector DEFINITIE Een complex (of reëel getal λ heet een eigenwaarde van de n n matrix A als er een vector x is met Ax = λx Dan
Hoofdstuk 1: Inleiding
 Hoofdstuk 1: Inleiding 1.1. Richtingsvelden. Zie Stewart, 9.2. 1.2. Oplossingen van enkele differentiaalvergelijkingen. Zelf doorlezen. 1.3. Classificatie van differentiaalvergelijkingen. Differentiaalvergelijkingen
Hoofdstuk 1: Inleiding 1.1. Richtingsvelden. Zie Stewart, 9.2. 1.2. Oplossingen van enkele differentiaalvergelijkingen. Zelf doorlezen. 1.3. Classificatie van differentiaalvergelijkingen. Differentiaalvergelijkingen
Stelsels lineaire differentiaalvergelijkingen (homogeen)
 Stelsels lineaire differentiaalvergelijkingen (homogeen) Voorbeeld Voorbeeld ( 7., Opgave 22) Op t = 0 bevatten de vaten respectievelijk 25 en 5 oz (ounces) zout. 3 september 206 Onderzoeken we hoeveel
Stelsels lineaire differentiaalvergelijkingen (homogeen) Voorbeeld Voorbeeld ( 7., Opgave 22) Op t = 0 bevatten de vaten respectievelijk 25 en 5 oz (ounces) zout. 3 september 206 Onderzoeken we hoeveel
Analyse I. 2. Formuleer en bewijs de formule van Taylor voor een functie f : R R. Stel de formules op voor de resttermen van Lagrange en Liouville.
 Academiejaar 006-007 1ste semester februari 007 Analyse I 1. Toon aan dat elke begrensde rij een convergente deelrij heeft. Geef de definitie van een Cauchy rij, en toon aan dat elke Cauchy rij begrensd
Academiejaar 006-007 1ste semester februari 007 Analyse I 1. Toon aan dat elke begrensde rij een convergente deelrij heeft. Geef de definitie van een Cauchy rij, en toon aan dat elke Cauchy rij begrensd
Bekijk nog een keer het stelsel van twee vergelijkingen met twee onbekenden x en y: { De tweede vergelijking van de eerste aftrekken geeft:
 Determinanten Invoeren van het begrip determinant Bekijk nog een keer het stelsel van twee vergelijkingen met twee onbekenden x en y: { a x + b y = c a 2 a 2 x + b 2 y = c 2 a Dit levert op: { a a 2 x
Determinanten Invoeren van het begrip determinant Bekijk nog een keer het stelsel van twee vergelijkingen met twee onbekenden x en y: { a x + b y = c a 2 a 2 x + b 2 y = c 2 a Dit levert op: { a a 2 x
Tentamen Differentiaalvergelijkingen, (wi1 909TH) woensdag 1 februari 2017, uur.
 Technische Universiteit Delft Faculteit Elektrotechniek, Wiskunde en Informatica Mekelweg 4, Delft Tentamen Differentiaalvergelijkingen, (wi1 909TH) woensdag 1 februari 2017, 18.30-20.30 uur. Het gebruik
Technische Universiteit Delft Faculteit Elektrotechniek, Wiskunde en Informatica Mekelweg 4, Delft Tentamen Differentiaalvergelijkingen, (wi1 909TH) woensdag 1 februari 2017, 18.30-20.30 uur. Het gebruik
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op donderdag 25 oktober 2007, 9.00 2.00 uur. De uitwerkingen van de opgaven
Hoofdstuk 7: Stelsels eerste orde lineaire differentiaalvergelijkingen
 Hoofdstuk 7: Stelsels eerste orde lineaire differentiaalvergelijkingen Bij het vak Lineaire Algebra hebben we reeds kennis gemaakt met stelsels eerste orde lineaire differentiaalvergelijkingen We hebben
Hoofdstuk 7: Stelsels eerste orde lineaire differentiaalvergelijkingen Bij het vak Lineaire Algebra hebben we reeds kennis gemaakt met stelsels eerste orde lineaire differentiaalvergelijkingen We hebben
11.3. Inhomogene randwaardeproblemen. We beschouwen eerst inhomogene Sturm- Liouville randwaardeproblemen van de vorm :
 11.3. Inhomogene randwaardeproblemen. We beschouwen eerst inhomogene Sturm- Liouville randwaardeproblemen van de vorm : L[y] := [p(x)y ] + q(x)y = µr(x)y + f(x), < x < 1 (1) a 1 y() + a 2 y () =, b 1 y(1)
11.3. Inhomogene randwaardeproblemen. We beschouwen eerst inhomogene Sturm- Liouville randwaardeproblemen van de vorm : L[y] := [p(x)y ] + q(x)y = µr(x)y + f(x), < x < 1 (1) a 1 y() + a 2 y () =, b 1 y(1)
TENTAMEN ANALYSE 1. dinsdag 3 april 2007,
 TENTAMEN ANALYSE. dinsdag april 2007, 4.00-7.00. Het tentamen bestaat uit twee gedeelten: de eerste vijf opgaven gaan over de stof van het eerste gedeelte van het college. De laatste vijf opgaven gaan
TENTAMEN ANALYSE. dinsdag april 2007, 4.00-7.00. Het tentamen bestaat uit twee gedeelten: de eerste vijf opgaven gaan over de stof van het eerste gedeelte van het college. De laatste vijf opgaven gaan
Oefenopgaven wi3097: Numerieke methoden voor differentiaalvergelijkingen
 Oefenopgaven wi3097: Numerieke methoden voor differentiaalvergelijkingen 1 Introductie Taylor polynoom, floating point getal, afrondfout Orde symbool Landau 1. Laat f(x) = x 3. Bepaal het tweede orde Taylor
Oefenopgaven wi3097: Numerieke methoden voor differentiaalvergelijkingen 1 Introductie Taylor polynoom, floating point getal, afrondfout Orde symbool Landau 1. Laat f(x) = x 3. Bepaal het tweede orde Taylor
Functies van één veranderlijke
 Functies van één veranderlijke 952600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl /29 Elektrotechniek, Wiskunde en Informatica EWI UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde
Functies van één veranderlijke 952600 Docent : Anton Stoorvogel E-mail: A.A.Stoorvogel@utwente.nl /29 Elektrotechniek, Wiskunde en Informatica EWI UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde
Aanvullingen van de Wiskunde / Partiële Differentiaalvergelijkingen
 de Bachelor EIT 2de en de Bachelor Wiskunde Academiejaar 215-216 1ste semester 26 januari 216 Aanvullingen van de Wiskunde / Partiële Differentiaalvergelijkingen 1. Gegeven een homogene lineaire partiële
de Bachelor EIT 2de en de Bachelor Wiskunde Academiejaar 215-216 1ste semester 26 januari 216 Aanvullingen van de Wiskunde / Partiële Differentiaalvergelijkingen 1. Gegeven een homogene lineaire partiële
Tentamen Gewone Differentiaal Vergelijkingen II
 Tentamen Gewone Differentiaal Vergelijkingen II.0.007 Jullie mogen een willekeurige van de vier opgaven als bonusopgave bekijken. (Dus drie opgaven volledig en goed gedaan is al een 10.) Opgave 1 Bekijk
Tentamen Gewone Differentiaal Vergelijkingen II.0.007 Jullie mogen een willekeurige van de vier opgaven als bonusopgave bekijken. (Dus drie opgaven volledig en goed gedaan is al een 10.) Opgave 1 Bekijk
Vectoranalyse voor TG
 college 1 collegejaar college build slides Vandaag : : : : 14-15 1 25 september 214 28 1 2 3 4 otatie Green De wet van Faraday 1 VA vandaag 4.5.6 ection 16.7 telling Vergeleijking (4.62) Theorem 6 Het
college 1 collegejaar college build slides Vandaag : : : : 14-15 1 25 september 214 28 1 2 3 4 otatie Green De wet van Faraday 1 VA vandaag 4.5.6 ection 16.7 telling Vergeleijking (4.62) Theorem 6 Het
Complexe eigenwaarden
 Complexe eigenwaarden Tot nu toe hebben we alleen reële getallen toegelaten als eigenwaarden van een matrix Het is echter vrij eenvoudig om de definitie uit te breiden tot de complexe getallen Een consequentie
Complexe eigenwaarden Tot nu toe hebben we alleen reële getallen toegelaten als eigenwaarden van een matrix Het is echter vrij eenvoudig om de definitie uit te breiden tot de complexe getallen Een consequentie
Stelsels differentiaalvergelijkingen
 Stelsels differentiaalvergelijkingen Stelsels homogene differentiaalvergelijkingen We bekijken in deze paragraaf stelsels homogene differentiaalvergelijkingen: x (t x (t x (t x (t x n(t A Voorbeeld x +
Stelsels differentiaalvergelijkingen Stelsels homogene differentiaalvergelijkingen We bekijken in deze paragraaf stelsels homogene differentiaalvergelijkingen: x (t x (t x (t x (t x n(t A Voorbeeld x +
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking Proeftentamen 3 Functies van één veranderlijke (15126 De uitwerkingen van de opgaven dienen duidelijk geformuleerd en overzichtelijk
maplev 2010/9/8 17:01 page 349 #351
 maplev 00/9/8 7:0 page 49 5 Module Stabiliteit van evenwichten Onderwerp Voorkennis Expressies Bibliotheken Zie ook Stabiliteit van evenwichten van gewone differentiaalvergelijkingen. Gewone differentiaalvergelijkingen
maplev 00/9/8 7:0 page 49 5 Module Stabiliteit van evenwichten Onderwerp Voorkennis Expressies Bibliotheken Zie ook Stabiliteit van evenwichten van gewone differentiaalvergelijkingen. Gewone differentiaalvergelijkingen
Lineaire Algebra voor ST
 Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 9.3 email: J.C.M.Keijsper@tue.nl studiewijzer: http://www.win.tue.nl/wsk/onderwijs/2ds6 Technische Universiteit Eindhoven college 2 J.Keijsper (TUE)
Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 9.3 email: J.C.M.Keijsper@tue.nl studiewijzer: http://www.win.tue.nl/wsk/onderwijs/2ds6 Technische Universiteit Eindhoven college 2 J.Keijsper (TUE)
Uitwerking Proeftentamen Lineaire Algebra 1, najaar y y = 2x. P x. L(P ) y = x. 2/3 1/3 en L wordt t.o.v de standaardbasis gegeven door
 Uitwerking Proeftentamen Lineaire Algebra, najaar 007. Gegeven is de lineaire afbeelding L : R R, die een punt P = (x, y) langs de lijn y = x projecteert op de lijn y = x: y y = x P x L(P ) y = x Bepaal
Uitwerking Proeftentamen Lineaire Algebra, najaar 007. Gegeven is de lineaire afbeelding L : R R, die een punt P = (x, y) langs de lijn y = x projecteert op de lijn y = x: y y = x P x L(P ) y = x Bepaal
Hoofdstuk 9: Niet-lineaire differentiaalvergelijkingen en stabiliteit
 Hoofdstuk 9: Niet-lineaire differentiaalvergelijkingen en stabiliteit Hoewel we reeds vele methoden gezien hebben om allerlei typen differentiaalvergelijkingen op te lossen, zijn er toch nog veel differentiaalvergelijkingen
Hoofdstuk 9: Niet-lineaire differentiaalvergelijkingen en stabiliteit Hoewel we reeds vele methoden gezien hebben om allerlei typen differentiaalvergelijkingen op te lossen, zijn er toch nog veel differentiaalvergelijkingen
Aanvullingen van de Wiskunde
 3de Bachelor EIT - de Bachelor Fysica Academiejaar 014-015 1ste semester 7 januari 015 Aanvullingen van de Wiskunde 1. Gegeven is een lineaire partiële differentiaalvergelijking van orde 1: a 1 (x 1,,
3de Bachelor EIT - de Bachelor Fysica Academiejaar 014-015 1ste semester 7 januari 015 Aanvullingen van de Wiskunde 1. Gegeven is een lineaire partiële differentiaalvergelijking van orde 1: a 1 (x 1,,
Hertentamen WISN102 Wiskundige Technieken 2 Di 17 april 13:30 16:30
 Hertentamen WIN12 Wiskundige Technieken 2 Di 17 april 13:3 16:3 Normering voor 4 pt vragen (andere vragen naar rato): 4pt Goed begrepen en goed uitgevoerd met voldoende toelichting, eventueel enkele onbelangrijke
Hertentamen WIN12 Wiskundige Technieken 2 Di 17 april 13:3 16:3 Normering voor 4 pt vragen (andere vragen naar rato): 4pt Goed begrepen en goed uitgevoerd met voldoende toelichting, eventueel enkele onbelangrijke
Examen G0O17D Wiskunde II (6sp) maandag 10 juni 2013, 8:30-12:30 uur
 Examen GO7D Wiskunde II (6sp maandag juni 3, 8:3-:3 uur Bachelor Biochemie & Biotechnologie Bachelor hemie, Bachelor Geologie Schakelprogramma Master Biochemie & Biotechnologie en Schakelprogramma Master
Examen GO7D Wiskunde II (6sp maandag juni 3, 8:3-:3 uur Bachelor Biochemie & Biotechnologie Bachelor hemie, Bachelor Geologie Schakelprogramma Master Biochemie & Biotechnologie en Schakelprogramma Master
2 Kromming van een geparametriseerde kromme in het vlak. Veronderstel dat een kromme in het vlak gegeven is door een parametervoorstelling
 TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
Analyse I. 1ste Bachelor Ingenieurswetenschappen Academiejaar ste semester 12 januari 2010
 ste Bachelor Ingenieurswetenschappen Academiejaar 9- ste semester januari Analyse I. Formuleer en bewijs de formule van Leibniz voor de n-de afgeleide van het product van twee functies f en g.. Onderstel
ste Bachelor Ingenieurswetenschappen Academiejaar 9- ste semester januari Analyse I. Formuleer en bewijs de formule van Leibniz voor de n-de afgeleide van het product van twee functies f en g.. Onderstel
WI1708TH Analyse 3. College 2 12 februari Challenge the future
 WI1708TH Analyse 3 College 2 12 februari 2015 1 Programma Vandaag Partiële afgeleiden (14.3) Hogere orde partiële afgeleiden (14.3) Partiële differentiaal vergelijkingen (14.3) 2 Functies van twee variabelen
WI1708TH Analyse 3 College 2 12 februari 2015 1 Programma Vandaag Partiële afgeleiden (14.3) Hogere orde partiële afgeleiden (14.3) Partiële differentiaal vergelijkingen (14.3) 2 Functies van twee variabelen
Lineaire algebra I (wiskundigen)
 Lineaire algebra I (wiskundigen) Toets, donderdag 22 oktober, 2009 Oplossingen (1) Zij V het vlak in R 3 door de punten P 1 = (1, 2, 1), P 2 = (0, 1, 1) en P 3 = ( 1, 1, 3). (a) Geef een parametrisatie
Lineaire algebra I (wiskundigen) Toets, donderdag 22 oktober, 2009 Oplossingen (1) Zij V het vlak in R 3 door de punten P 1 = (1, 2, 1), P 2 = (0, 1, 1) en P 3 = ( 1, 1, 3). (a) Geef een parametrisatie
Je mag Zorich deel I en II gebruiken, maar geen ander hulpmiddelen (zoals andere boeken, aantekeningen, rekenmachine etc.)!
 Tentamen Analyse II. Najaar 6 (.1.7) Toelicting: Je mag Zoric deel I en II gebruiken, maar geen ander ulpmiddelen (zoals andere boeken, aantekeningen, rekenmacine etc.)! Als je bekende stellingen gebruikt
Tentamen Analyse II. Najaar 6 (.1.7) Toelicting: Je mag Zoric deel I en II gebruiken, maar geen ander ulpmiddelen (zoals andere boeken, aantekeningen, rekenmacine etc.)! Als je bekende stellingen gebruikt
Wiskundige Technieken
 1ste Bachelor Ingenieurswetenschappen 1ste Bachelor Fysica en Sterrenkunde Academiejaar 014-015 1ste semester 1 oktober 014 Wiskundige Technieken 1. Beschouw een scalaire functie f : R R en een vectorveld
1ste Bachelor Ingenieurswetenschappen 1ste Bachelor Fysica en Sterrenkunde Academiejaar 014-015 1ste semester 1 oktober 014 Wiskundige Technieken 1. Beschouw een scalaire functie f : R R en een vectorveld
2 Kromming van een geparametriseerde kromme in het vlak
 Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk 11. Daar worden deze begrippen echter
Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk 11. Daar worden deze begrippen echter
Lineaire dv van orde 2 met constante coefficienten
 Lineaire dv van orde 2 met constante coefficienten Homogene vergelijkingen We bekijken eerst homogene vergelijkingen van orde twee met constante coefficienten, d.w.z. dv s van de vorm a 0 y + a 1 y + a
Lineaire dv van orde 2 met constante coefficienten Homogene vergelijkingen We bekijken eerst homogene vergelijkingen van orde twee met constante coefficienten, d.w.z. dv s van de vorm a 0 y + a 1 y + a
TW2040: Complexe Functietheorie
 TW2040: Complexe Functietheorie week 4.3, maandag K. P. Hart Faculteit EWI TU Delft Delft, 2 mei, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 34 Outline 1 Conforme afbeeldingen 2 K. P. Hart TW2040:
TW2040: Complexe Functietheorie week 4.3, maandag K. P. Hart Faculteit EWI TU Delft Delft, 2 mei, 2016 K. P. Hart TW2040: Complexe Functietheorie 1 / 34 Outline 1 Conforme afbeeldingen 2 K. P. Hart TW2040:
De parabool en de cirkel raken elkaar in de oorsprong; bepaal ook de coördinaten van de overige snijpunten A 1 en A 2.
 BURGERLIJK INGENIEUR-ARCHITECT - 5 SEPTEMBER 2002 BLZ 1/10 1. We beschouwen de cirkel met vergelijking x 2 + y 2 2ry = 0 en de parabool met vergelijking y = ax 2. Hierbij zijn r en a parameters waarvoor
BURGERLIJK INGENIEUR-ARCHITECT - 5 SEPTEMBER 2002 BLZ 1/10 1. We beschouwen de cirkel met vergelijking x 2 + y 2 2ry = 0 en de parabool met vergelijking y = ax 2. Hierbij zijn r en a parameters waarvoor
Topologie in R n 10.1
 Topologie in R n 10.1 Lengte x = (x 1,..., x n ) = x 2 1 + x2 2 + + x2 n Bol B(x 0, r) = {x : x x 0 < r} x 0 r p 1 p 3 p 1 p 2 S p 1 heet uitwendig punt p 2 heet inwendig punt p 3 heet randpunt p 1 p 3
Topologie in R n 10.1 Lengte x = (x 1,..., x n ) = x 2 1 + x2 2 + + x2 n Bol B(x 0, r) = {x : x x 0 < r} x 0 r p 1 p 3 p 1 p 2 S p 1 heet uitwendig punt p 2 heet inwendig punt p 3 heet randpunt p 1 p 3
Vectoranalyse voor TG
 college 12 collegejaar college build slides Vandaag : : : : 17-18 12 4 september 217 3 ail Training Vessel 263 tad Amsterdam 1 2 3 4 stelling van Gauss stelling van Green Conservatieve vectorvelden 1 VA
college 12 collegejaar college build slides Vandaag : : : : 17-18 12 4 september 217 3 ail Training Vessel 263 tad Amsterdam 1 2 3 4 stelling van Gauss stelling van Green Conservatieve vectorvelden 1 VA
Wiskundige Technieken 1 Uitwerkingen Hertentamen 23 december 2014
 Wiskundige Technieken Uitwerkingen Hertentamen 3 december 04 Normering voor 4 pt vragen andere vragen naar rato: 4pt 3pt pt pt 0pt goed begrepen én goed uitgevoerd, eventueel met enkele onbelangrijke rekenfoutjes
Wiskundige Technieken Uitwerkingen Hertentamen 3 december 04 Normering voor 4 pt vragen andere vragen naar rato: 4pt 3pt pt pt 0pt goed begrepen én goed uitgevoerd, eventueel met enkele onbelangrijke rekenfoutjes
More points, lines, and planes
 More points, lines, and planes Make your own pictures! 1. Lengtes en hoeken In het vorige college hebben we het inwendig product (inproduct) gedefinieerd. Aan de hand daarvan hebben we ook de norm (lengte)
More points, lines, and planes Make your own pictures! 1. Lengtes en hoeken In het vorige college hebben we het inwendig product (inproduct) gedefinieerd. Aan de hand daarvan hebben we ook de norm (lengte)
x 1 (t) = ve rt = (a + ib) e (λ+iµ)t = (a + ib) e λt (cos µt + i sin µt) x 2 (t) = ve rt = e λt (a cos µt b sin µt) ie λt (a sin µt + b cos µt).
 76 Complexe eigenwaarden Ook dit hebben we reeds gezien bij Lineaire Algebra Zie: Lay, 57 Als xt ve rt een oplossing is van de homogene differentiaalvergelijking x t Axt, dan moet r een eigenwaarde van
76 Complexe eigenwaarden Ook dit hebben we reeds gezien bij Lineaire Algebra Zie: Lay, 57 Als xt ve rt een oplossing is van de homogene differentiaalvergelijking x t Axt, dan moet r een eigenwaarde van
Tentamen Functies en Reeksen
 Tentamen Functies en Reeksen 6 november 204, 3:30 6:30 uur Schrijf op ieder vel je naam en bovendien op het eerste vel je studentnummer, de naam van je practicumleider (Arjen Baarsma, KaYin Leung, Roy
Tentamen Functies en Reeksen 6 november 204, 3:30 6:30 uur Schrijf op ieder vel je naam en bovendien op het eerste vel je studentnummer, de naam van je practicumleider (Arjen Baarsma, KaYin Leung, Roy
Lineaire Algebra voor W 2Y650
 Lineaire Algebra voor W 2Y65 Docent: L Habets HG 89, Tel: 4-247423, Email: lcgjmhabets@tuenl http://wwwwintuenl/wsk/onderwijs/2y65 1 Herhaling: bepaling van eigenwaarden en eigenvectoren (1) Bepaal het
Lineaire Algebra voor W 2Y65 Docent: L Habets HG 89, Tel: 4-247423, Email: lcgjmhabets@tuenl http://wwwwintuenl/wsk/onderwijs/2y65 1 Herhaling: bepaling van eigenwaarden en eigenvectoren (1) Bepaal het
tentamen Analyse (deel 3) wi TH 21 juni 2006, uur
 Technische Universiteit Delft Technische Wiskunde Faculteit lektrotechniek, Wiskunde en Informatica Mekelweg 4, 68 CD DLFT tentamen Analyse (deel 3) wi 54 TH juni 6, 4. 7. uur Deelname aan dit tentamen
Technische Universiteit Delft Technische Wiskunde Faculteit lektrotechniek, Wiskunde en Informatica Mekelweg 4, 68 CD DLFT tentamen Analyse (deel 3) wi 54 TH juni 6, 4. 7. uur Deelname aan dit tentamen
WI1708TH Analyse 3. College 5 23 februari Challenge the future
 WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
WI1708TH Analyse 3 College 5 23 februari 2015 1 Programma Vandaag Richtingsafgeleide (14.6) Gradiënt (14.6) Maximalisatie richtingsafgeleide (14.6) Raakvlak voor niveauoppervlakken (14.6) 2 Richtingsafgeleide
7. Hamiltoniaanse systemen
 7. Hamiltoniaanse systemen In de moleculaire dynamica, maar ook in andere gebieden zoals de hemelmechanica of klassieke mechanica, worden oplossingen gezocht van het Hamiltoniaanse systeem van differentiaalvergelijkingen
7. Hamiltoniaanse systemen In de moleculaire dynamica, maar ook in andere gebieden zoals de hemelmechanica of klassieke mechanica, worden oplossingen gezocht van het Hamiltoniaanse systeem van differentiaalvergelijkingen
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 2013,
 Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Nijmegen Tentamen Calculus 1 NWI-NP003B 4 januari 013, 8.30 11.30 Het gebruik van een rekenmachine, telefoon en boek(en) is niet toegestaan. Geef precieze argumenten en antwoorden.
UITWERKINGEN d. Eliminatie van a geeft d. Eliminatie van b,
 UITWERKINGEN 1. Gegeven in R 3 zijn de punten P = (1, 1, ) t en Q = ( 2,, 1) t en het vlak V gegeven door de vergelijking 2x 1 x 2 + x 3 = 1. Zij l de lijn door P loodrecht op V en m de lijn door Q loodrecht
UITWERKINGEN 1. Gegeven in R 3 zijn de punten P = (1, 1, ) t en Q = ( 2,, 1) t en het vlak V gegeven door de vergelijking 2x 1 x 2 + x 3 = 1. Zij l de lijn door P loodrecht op V en m de lijn door Q loodrecht
Analyse 1 November 2011 Januari 2011 November 2010
 WI1330CT/CT1135-1/CTB1001-1 Januari 2013 November 2012 Januari 2012 Analyse 1 November 2011 Januari 2011 November 2010 Tentamenbundel Civiele Techniek Het Gezelschap "Practische Studie" TU DELFT, 2010
WI1330CT/CT1135-1/CTB1001-1 Januari 2013 November 2012 Januari 2012 Analyse 1 November 2011 Januari 2011 November 2010 Tentamenbundel Civiele Techniek Het Gezelschap "Practische Studie" TU DELFT, 2010
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op maandag 4 januari 2, 8.45.45 uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op maandag 4 januari 2, 8.45.45 uur. De uitwerkingen van de opgaven dienen
x a k of.x 1 a 1 / 2 + ::+.x n a n / 2 k 2 bol om a, straal k
 Punten, Vectoren in de R n Punten: a =.a 1 ; a 2 ; : : : ; a n / ; b =.b 1 ; b 2 ; : : : ; b n / Vectoren: a = a 1 ; a 2 ; : : : ; a n ; b = b 1 ; b 2 ; : : : ; b n lengte van a : a = a 2 1 + : : : + a2
Punten, Vectoren in de R n Punten: a =.a 1 ; a 2 ; : : : ; a n / ; b =.b 1 ; b 2 ; : : : ; b n / Vectoren: a = a 1 ; a 2 ; : : : ; a n ; b = b 1 ; b 2 ; : : : ; b n lengte van a : a = a 2 1 + : : : + a2
Relevante vragen , eerste examenperiode
 Relevante vragen 2006 2007, eerste examenperiode OEFENING y = x 2 2, y = x, z = x 2 + y 2, z = x + 6 omvatten, indien we ons tot het gedeelte binnen de parabolische cilinder beperken, twee verschillende
Relevante vragen 2006 2007, eerste examenperiode OEFENING y = x 2 2, y = x, z = x 2 + y 2, z = x + 6 omvatten, indien we ons tot het gedeelte binnen de parabolische cilinder beperken, twee verschillende
Opgave a. We berekenen eerst een normaal v van V en een normaal w van W. v = (b a) (c a) = ((2)(1) ( 2)( 2), ( 2)( 1) ( 1)(1), ( 1)( 2) (2)( 1))
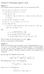 Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
Calculus 3. Uitwerking opgav 1 april. Opgave a. We berek eerst e normaal v van V e normaal w van W. Dus b a = 2, 4, 1 3, 2, 1 = 1, 2, 2, c a = 2,, 2 3, 2, 1 = 1, 2, 1, v = b a c a = 21 2 2, 2 1 11, 1 2
TENTAMEN LINEAIRE ALGEBRA 1 donderdag 23 december 2004,
 TENTAMEN LINEAIRE ALGEBRA donderdag december 004, 0.00-.00 Bij elke vraag dient een berekening of motivering worden opgeschreven. Het tentamen bestaat uit twee gedeelten: de eerste drie opgaven betreffen
TENTAMEN LINEAIRE ALGEBRA donderdag december 004, 0.00-.00 Bij elke vraag dient een berekening of motivering worden opgeschreven. Het tentamen bestaat uit twee gedeelten: de eerste drie opgaven betreffen
Vectoranalyse voor TG
 college 11 collegejaar college build slides Vandaag : : : : 17-18 11 23 oktober 2017 35 De sterrennacht Vincent van Gogh, 1889 1 2 3 4 5 Verband met de stelling van n 1 VA intro ection 16.7 Definitie Equation
college 11 collegejaar college build slides Vandaag : : : : 17-18 11 23 oktober 2017 35 De sterrennacht Vincent van Gogh, 1889 1 2 3 4 5 Verband met de stelling van n 1 VA intro ection 16.7 Definitie Equation
TRILLINGEN EN GOLVEN HANDOUT FOURIER
 TRILLINGEN EN GOLVEN HANDOUT FOURIER Cursusjaar 2009 / 2010 2 Inhoudsopgave 1 FOURIERANALYSE 5 1.1 INLEIDING............................... 5 1.2 FOURIERREEKSEN.......................... 5 1.3 CONSEQUENTIES
TRILLINGEN EN GOLVEN HANDOUT FOURIER Cursusjaar 2009 / 2010 2 Inhoudsopgave 1 FOURIERANALYSE 5 1.1 INLEIDING............................... 5 1.2 FOURIERREEKSEN.......................... 5 1.3 CONSEQUENTIES
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op dinsdag 6 januari 2009, 9.00 2.00 uur. De uitwerkingen van de opgaven
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (5260) op dinsdag 6 januari 2009, 9.00 2.00 uur. De uitwerkingen van de opgaven
5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm
 5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm x y + xy + (x ν )y = met ν R (1) heet een Bessel (differentiaal)vergelijking. De waarde van ν noemt men ook wel de orde
5.8. De Bessel differentiaalvergelijking. Een differentiaalvergelijking van de vorm x y + xy + (x ν )y = met ν R (1) heet een Bessel (differentiaal)vergelijking. De waarde van ν noemt men ook wel de orde
Krommen in de ruimte
 Krommen in de ruimte z Een ruimtekromme is de baan van een tijd-plaatsfunctie van een bewegend deeltje in de ruimte Na keuze van een rechthoekig assenstelsel Oxyz wordt die functie f gegeven door zijn
Krommen in de ruimte z Een ruimtekromme is de baan van een tijd-plaatsfunctie van een bewegend deeltje in de ruimte Na keuze van een rechthoekig assenstelsel Oxyz wordt die functie f gegeven door zijn
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie
 FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie Analyse A, deeltentamen Uitwerkingen maandag 1 november 2010, 9 11 uur Gebruik van een formuleblad of rekenmachine is niet toegestaan
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie Analyse A, deeltentamen Uitwerkingen maandag 1 november 2010, 9 11 uur Gebruik van een formuleblad of rekenmachine is niet toegestaan
10.6. Andere warmteproblemen. We hebben warmteproblemen bekeken van de vorm. 0 < x < L, t > 0. w(0, t) = 0, w(l, t) = 0, t 0. u(x, 0) = f(x), 0 x L,
 .6. Andere warmteproblem. We hebb warmteproblem bekek van de vorm α 2 u xx = u t, < x u(, t) =, u(, t) =, t u(x, ) = f(x), x, waarbij de temperatuur aan de beide uiteind constant bovdi gelijk is.
.6. Andere warmteproblem. We hebb warmteproblem bekek van de vorm α 2 u xx = u t, < x u(, t) =, u(, t) =, t u(x, ) = f(x), x, waarbij de temperatuur aan de beide uiteind constant bovdi gelijk is.
Vectoranalyse voor TG
 college 2 Ruimte en oppervlakken collegejaar : 18-19 college : 2 build : 5 september 2018 slides : 25 Vandaag Ruimte 1 Vectoren in R 3 recap 2 Oppervlakken 3 Ruimte 4 1 intro VA Voorkennis uit Ruimtewiskunde
college 2 Ruimte en oppervlakken collegejaar : 18-19 college : 2 build : 5 september 2018 slides : 25 Vandaag Ruimte 1 Vectoren in R 3 recap 2 Oppervlakken 3 Ruimte 4 1 intro VA Voorkennis uit Ruimtewiskunde
(10 pnt) Bepaal alle punten waar deze functie een relatief extreem of een zadelpunt heeft. Opgave 3. Zij D het gebied gegeven door
 Calculus 3. Tentamen Calculus 3, 8 April 11 Opgave 1. Zij f(x, y, z) = xy z 3xz en g(x, y, z) = x 3 +z sin(y) y sin(z). i) (5 pnt) Laat zien dat p = (, 1, 1) op de oppervlakken {f(x, y, z)} = en {g(x,
Calculus 3. Tentamen Calculus 3, 8 April 11 Opgave 1. Zij f(x, y, z) = xy z 3xz en g(x, y, z) = x 3 +z sin(y) y sin(z). i) (5 pnt) Laat zien dat p = (, 1, 1) op de oppervlakken {f(x, y, z)} = en {g(x,
6.0 Differentiëren Met het differentiequotiënt bereken je de gemiddelde verandering per tijdseenheid.
 6.0 Differentiëren Met het differentiequotiënt bereken je de gemiddelde verandering per tijdseenheid. f(x) = x x Differentiequotiënt van f(x) op [0, 3] = y f (3) f (0) 60 x 30 30 y x 1 Algemeen: Het differentiequotiënt
6.0 Differentiëren Met het differentiequotiënt bereken je de gemiddelde verandering per tijdseenheid. f(x) = x x Differentiequotiënt van f(x) op [0, 3] = y f (3) f (0) 60 x 30 30 y x 1 Algemeen: Het differentiequotiënt
Lineaire Algebra voor ST
 Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 93 email: JCMKeijsper@tuenl studiewijzer: http://wwwwintuenl/wsk/onderwijs/2ds06 Technische Universiteit Eindhoven college 3 JKeijsper (TUE) Lineaire
Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 93 email: JCMKeijsper@tuenl studiewijzer: http://wwwwintuenl/wsk/onderwijs/2ds06 Technische Universiteit Eindhoven college 3 JKeijsper (TUE) Lineaire
Faculteit Wiskunde en Informatica VECTORANALYSE
 12 Faculteit Wiskunde en Informatica Aanvulling 4 VECTOANALYE 2WA15 2006/2007 Hoofdstuk 4 De stelling van Gauss (divergentie-stelling) 4.1 Inleiding Dit hoofdstuk is gewijd aan slechts één stelling. De
12 Faculteit Wiskunde en Informatica Aanvulling 4 VECTOANALYE 2WA15 2006/2007 Hoofdstuk 4 De stelling van Gauss (divergentie-stelling) 4.1 Inleiding Dit hoofdstuk is gewijd aan slechts één stelling. De
Lineaire Afbeelding Stelsels differentiaalvergelijkingen. 6 juni 2006
 Lineaire Afbeelding Stelsels differentiaalvergelijkingen 6 juni 6 i ii Inhoudsopgave Stelsels differentiaalvergelijkingen Opgaven Stelsels differentiaalvergelijkingen In deze paragraaf passen we onze kennis
Lineaire Afbeelding Stelsels differentiaalvergelijkingen 6 juni 6 i ii Inhoudsopgave Stelsels differentiaalvergelijkingen Opgaven Stelsels differentiaalvergelijkingen In deze paragraaf passen we onze kennis
Wiskunde: Voortgezette Analyse
 de Bach. IR Wet.: Architectuur Academiejaar 0-04 ste zittijd, januari 04 Wiskunde: Voortgezette Analyse. Gegeven is de reeks n x (x + ) n+ Toon aan dat de reeks puntsgewijs convergeert over R. Toon aan
de Bach. IR Wet.: Architectuur Academiejaar 0-04 ste zittijd, januari 04 Wiskunde: Voortgezette Analyse. Gegeven is de reeks n x (x + ) n+ Toon aan dat de reeks puntsgewijs convergeert over R. Toon aan
Examenvragen Hogere Wiskunde I
 1 Examenvragen Hogere Wiskunde I Vraag 1. Zij a R willekeurig. Gegeven is dat voor alle r, s Q geldt dat a r+s = a r a s. Bewijs dat voor alle x, y R geldt dat a x+y = a x a y. Vraag 2. Gegeven 2 functies
1 Examenvragen Hogere Wiskunde I Vraag 1. Zij a R willekeurig. Gegeven is dat voor alle r, s Q geldt dat a r+s = a r a s. Bewijs dat voor alle x, y R geldt dat a x+y = a x a y. Vraag 2. Gegeven 2 functies
3. Bepaal de convergentie-eigenschappen (absoluut convergent, voorwaardelijk convergent, divergent) van de volgende reeksen: n=1. ( 1) n (n + 1)x 2n.
 Radboud Universiteit Tentamen Calculus A NWI-WP025 25 januari 208, 8.30.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
Radboud Universiteit Tentamen Calculus A NWI-WP025 25 januari 208, 8.30.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en antwoorden.
Differentiaalvergelijkingen
 Notities bij de nascholing Differentiaalvergelijkingen Eekhoutcentrum 11 mei 2005 Bart Windels Differentiaalvergelijkingen 1 1 Algemeenheden Zij I een open interval van R (eventueel onbegrensd) en y :
Notities bij de nascholing Differentiaalvergelijkingen Eekhoutcentrum 11 mei 2005 Bart Windels Differentiaalvergelijkingen 1 1 Algemeenheden Zij I een open interval van R (eventueel onbegrensd) en y :
Faculteit Wiskunde en Informatica VECTORANALYSE
 2 Faculteit Wiskunde en Informatica Aanvulling 5 VECTORANALYE 2WA5 2006/2007 Hoofdstuk 5 De stellingen van tokes en Green 5. Inleiding In dit hoofdstuk worden de stellingen van tokes en van Green 2 behandeld.
2 Faculteit Wiskunde en Informatica Aanvulling 5 VECTORANALYE 2WA5 2006/2007 Hoofdstuk 5 De stellingen van tokes en Green 5. Inleiding In dit hoofdstuk worden de stellingen van tokes en van Green 2 behandeld.
Gravitatie en kosmologie
 Gravitatie en kosmologie FEW cursus Jo van den Brand & Mark Beker Einsteinvergelijkingen: 7 oktober 009 Traagheid van gasdruk SRT: hoe hoger de gasdruk, des te moeilijker is het om het gas te versnellen
Gravitatie en kosmologie FEW cursus Jo van den Brand & Mark Beker Einsteinvergelijkingen: 7 oktober 009 Traagheid van gasdruk SRT: hoe hoger de gasdruk, des te moeilijker is het om het gas te versnellen
Hoofdstuk 10: Partiële differentiaalvergelijkingen en Fourierreeksen
 Hoofdstuk : Partiële differtiaalvergelijking Fourierreeks Partiële differtiaalvergelijking zijn vergelijking waarin e onbekde functie van twee of meer variabel z n partiële afgeleide(n) voorkom. Dit in
Hoofdstuk : Partiële differtiaalvergelijking Fourierreeks Partiële differtiaalvergelijking zijn vergelijking waarin e onbekde functie van twee of meer variabel z n partiële afgeleide(n) voorkom. Dit in
OF (vermits y = dy. dx ) P (x, y) dy + Q(x, y) dx = 0
 Algemeen kunnen we een eerste orde differentiaalvergelijking schrijven als: y = Φ(x, y) OF (vermits y = dy dx ) P (x, y) dy + Q(x, y) dx = 0 Indien we dan P (x, y) en Q(x, y) kunnen schrijven als P (x,
Algemeen kunnen we een eerste orde differentiaalvergelijking schrijven als: y = Φ(x, y) OF (vermits y = dy dx ) P (x, y) dy + Q(x, y) dx = 0 Indien we dan P (x, y) en Q(x, y) kunnen schrijven als P (x,
Opgaven bij de cursus Relativiteitstheorie wiskunde voorkennis Najaar 2018 Docent: Dr. H. (Harm) van der Lek
 Opgaven bij de cursus Relativiteitstheorie wiskunde voorkennis Najaar 2018 Docent: Dr. H. (Harm) van der Lek Uitwerkingen worden beschikbaar gesteld op de dinsdagavond voorafgaande aan het volgende college
Opgaven bij de cursus Relativiteitstheorie wiskunde voorkennis Najaar 2018 Docent: Dr. H. (Harm) van der Lek Uitwerkingen worden beschikbaar gesteld op de dinsdagavond voorafgaande aan het volgende college
Uitwerkingen Tentamen Gewone Differentiaalvergelijkingen
 Uitwerkingen Tentamen Gewone Differentiaalvergelijkingen Maandag 4 januari 216, 1: - 13: uur 1. Beschouw voor t > de inhomogene singuliere tweede orde vergelijking, t 2 ẍ + 4tẋ + 2x = f(t, (1 waarin f
Uitwerkingen Tentamen Gewone Differentiaalvergelijkingen Maandag 4 januari 216, 1: - 13: uur 1. Beschouw voor t > de inhomogene singuliere tweede orde vergelijking, t 2 ẍ + 4tẋ + 2x = f(t, (1 waarin f
Toets 3 Calculus 1 voor MST, 4051CALC1Y dinsdag 31 oktober 2017, 13:30 16:30 uur
 Toets 3 Calculus 1 voor MST, 4051CALC1Y dinsdag 31 oktober 2017, 13:30 16:30 uur Technische Universiteit Delft, Delft Institute of Applied Mathematics Naam: Groep (omcirkel): (Leids) studentnummer: A (Keijzer)
Toets 3 Calculus 1 voor MST, 4051CALC1Y dinsdag 31 oktober 2017, 13:30 16:30 uur Technische Universiteit Delft, Delft Institute of Applied Mathematics Naam: Groep (omcirkel): (Leids) studentnummer: A (Keijzer)
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Numerieke Methoden voor Werktuigbouwkunde (2N46) op maandag 23 Deel 1: Van 14 uur tot uiterlijk 153 uur Het gebruik van het
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Numerieke Methoden voor Werktuigbouwkunde (2N46) op maandag 23 Deel 1: Van 14 uur tot uiterlijk 153 uur Het gebruik van het
Hoofdstuk 11: Randwaardeproblemen en Sturm-Liouville theorie
 Hoofdstuk : Randwaardeproblemen en Sturm-Liouville theorie.. Tweepunts randwaardeproblemen. Bij het oplossen van partiële differentiaalvergelijkingen met behulp van de methode van scheiden van variabelen
Hoofdstuk : Randwaardeproblemen en Sturm-Liouville theorie.. Tweepunts randwaardeproblemen. Bij het oplossen van partiële differentiaalvergelijkingen met behulp van de methode van scheiden van variabelen
1. (a) Gegeven z = 2 2i, w = 1 i 3. Bereken z w. (b) Bepaal alle complexe getallen z die voldoen aan z 3 8i = 0.
 Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
Radboud Universiteit Nijmegen Tentamen Calculus NWI-NP003B 4 november 04,.30 5.30 Het gebruik van een rekenmachine/gr, telefoon, boek, aantekeningen e.d. is niet toegestaan. Geef precieze argumenten en
college 6: limieten en l Hôpital
 126 college 6: ieten en l Hôpital In dit college herhalen we enkele belangrijke definities van ieten, en geven we belangrijke technieken om ieten van functies (eigenlijk en oneigenlijk) te bepalen. In
126 college 6: ieten en l Hôpital In dit college herhalen we enkele belangrijke definities van ieten, en geven we belangrijke technieken om ieten van functies (eigenlijk en oneigenlijk) te bepalen. In
Faculteit Wiskunde en Informatica VECTORANALYSE
 12 Faculteit Wiskunde en Informatica Aanvulling 2 VECTORANALYSE 2WA15 2006/2007 Hoofdstuk 2 Vectorvelden en lijnintegralen 2.1 De Euclidische ruimte E 3 Zij E 3 de (Euclidische) ruimte. iezen we in E 3
12 Faculteit Wiskunde en Informatica Aanvulling 2 VECTORANALYSE 2WA15 2006/2007 Hoofdstuk 2 Vectorvelden en lijnintegralen 2.1 De Euclidische ruimte E 3 Zij E 3 de (Euclidische) ruimte. iezen we in E 3
7.9. Inhomogene lineaire stelsels. We keren nu weer terug naar de situatie
 79 Inhomogene lineaire selsels We keren nu weer erug naar de siuaie x ( A(x( + g(, ( waarbij A( een (n n-marix is en g( een vecor me n coördinaen Vergelijkbaar me de heorie voor gewone lineaire differeniaalvergelijking
79 Inhomogene lineaire selsels We keren nu weer erug naar de siuaie x ( A(x( + g(, ( waarbij A( een (n n-marix is en g( een vecor me n coördinaen Vergelijkbaar me de heorie voor gewone lineaire differeniaalvergelijking
Differentiaalvergelijkingen Technische Universiteit Delft
 Differentiaalvergelijkingen Technische Universiteit Delft Roelof Koekoek wi2030wbmt Roelof Koekoek (TU Delft) Differentiaalvergelijkingen wi2030wbmt 1 / 15 Even voorstellen... Dr. Roelof Koekoek Gebouw
Differentiaalvergelijkingen Technische Universiteit Delft Roelof Koekoek wi2030wbmt Roelof Koekoek (TU Delft) Differentiaalvergelijkingen wi2030wbmt 1 / 15 Even voorstellen... Dr. Roelof Koekoek Gebouw
w (n). w n+1 = w n+1 = w n + hf(w n ), w n+1 = w n + hf(w n+1 ), 1195w (n) [ ( 2) ( 2) =
 We bekijken het stelsel vergelijkingen { y 95y + 995y y 97y 997y, met als beginvoorwaarden { y (0) y (0) Op tijdsniveau t nh definieren we de vector w (n) w n+ w (n) Euler Voorwaarts is dan en Euler Achterwaarts
We bekijken het stelsel vergelijkingen { y 95y + 995y y 97y 997y, met als beginvoorwaarden { y (0) y (0) Op tijdsniveau t nh definieren we de vector w (n) w n+ w (n) Euler Voorwaarts is dan en Euler Achterwaarts
Technische Universiteit Delft Tentamen Calculus TI1106M - Uitwerkingen. 2. Geef berekeningen en beargumenteer je antwoorden.
 Technische Universiteit elft Tentamen Calculus TI06M - Uitwerkingen Opmerkingen:. Het gebruik van de rekenmachine is NIET toegestaan.. Geef berekeningen en beargumenteer je antwoorden. 3. Bij iedere vraag
Technische Universiteit elft Tentamen Calculus TI06M - Uitwerkingen Opmerkingen:. Het gebruik van de rekenmachine is NIET toegestaan.. Geef berekeningen en beargumenteer je antwoorden. 3. Bij iedere vraag
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN
 TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D. Datum: Donderdag 8 juli 4. Tijd: 14. 17. uur. Plaats: MA 1.44/1.46 Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D. Datum: Donderdag 8 juli 4. Tijd: 14. 17. uur. Plaats: MA 1.44/1.46 Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Lineaire Algebra en Lineaire Analyse (Y550/Y530), op donderdag 5 november 00, 9:00 :00 uur. De uitwerkingen van de opgaven dienen
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Lineaire Algebra en Lineaire Analyse (Y550/Y530), op donderdag 5 november 00, 9:00 :00 uur. De uitwerkingen van de opgaven dienen
Hertentamen WISN101 Wiskundige Technieken 1 Do 5 jan :30 16:30
 Hertentamen WISN0 Wiskundige Technieken Do 5 jan 207 3:30 6:30 Normering voor 4 pt vragen (andere vragen naar rato): 4pt Goed begrepen en goed uitgevoerd met voldoende toelichting, eventueel enkele onbelangrijke
Hertentamen WISN0 Wiskundige Technieken Do 5 jan 207 3:30 6:30 Normering voor 4 pt vragen (andere vragen naar rato): 4pt Goed begrepen en goed uitgevoerd met voldoende toelichting, eventueel enkele onbelangrijke
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica
 UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op dinsdag 26 augustus 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
UNIVERSITEIT TWENTE Faculteit Elektrotechniek, Wiskunde en Informatica Uitwerking tentamen Functies van één veranderlijke (526) op dinsdag 26 augustus 28, 9. 2. uur. De uitwerkingen van de opgaven dienen
