Hoofdstuk 8 - De normale verdeling
|
|
|
- Henriette Willemsen
- 9 jaren geleden
- Aantal bezoeken:
Transcriptie
1 ladzijde 216 1a Staafdiagram 3 want te verwachten is dat er elke maand ongeveer evenveel mensen jarig zijn. Dat is meteen ook de reden waarom de andere drie niet voldoen. Feruari estaat uit vier weken dus zal 2% van de in feruari georen mensen naar verwachting in de eerste week jarig zijn. c Decemer evat 31 dagen dus zal in de eerste week naar verwachting , 6 % 31 jarig zijn. 2a Iemand met een lengte van 177,3 cm valt in klasse C. y 30 percentage 2 1 c 10 x lengte in cm De lengte wordt afgerond naar hele centimeters. Een lengte van 167, tot 172, wordt afgerond van 168 tot en met 172. d Niet precies maar je mag er vanuit gaan dat de lengten regelmatig over deze klassen zijn verdeeld. e Deze klasse verloopt van 177, tot 182, en is dus vijf cm reed. Van 177, tot 181, is vier cm reed dus zal ij een gelijkmatige verdeling 4 deel van de mannen innen klasse C kleiner zijn dan 181, cm. f 2,7% + 8,6% + 16,6% , 6% 492, % zal naar verwachting kleiner zijn dan 181, cm. ladzijde 217 3a De klassengrenzen zijn 39, en 42,. De klasse is dus 3 cm reed. 0, = 1 deel , van de klasse dus 17% van de mannen uit de klasse cm heeft een schouderreedte van meer dan 42 cm. 017, mannen heen een schouderreedte meer dan 42 cm. c Van 39, tot 40, is 1 cm dus 1 deel ofwel ongeveer 33% van de mannen in klasse cm heeft een schouderreedte van minder dan 40, cm. 4a y 30 percentage x gewicht in kg Als klassenmidden van de eerste en laatste klasse is 0 en 80 gekozen. 128
2 c d De klasse waar 61,6 kg in ligt loopt van 7, tot 62, cm dus vijf reed. Het deel wat 61, 6 7, 41, minder weegt dan 61,6 kg is dan = = 082,. Het percentage vrouwen dat minder weegt is dan 13, 1+ 7, + 082, 262,, 3%. Het zal wat meer zijn omdat het percentage richting gemiddelde toeneemt. a voetlengte in cm percentage 1,1 2,6 61,3 11,6 0,4 y 70 percentage c d x voetlengte in cm 21, 2 19, 4 46 vrouwen heen een voetlengte van minder dan 21,2 cm. 21, 19, De doelgroep heeft dus een voetlengte van 21 tot 27 cm. Deze doelgroep evat = vrouwen , 9%van deze vrouwen valt innen de doelgroep. 000 ladzijde 218 6a Als de klassenreedte kleiner wordt gaat het staafdiagram meer op een erg lijken. Omdat het totaal aantal waarnemingen verdeeld wordt over meer staven zullen de staven minder hoog zijn. c Bij tien criminelen zul je waarschijnlijk geen evenwichtige verdeling krijgen. Bij 3000 criminelen is die kans wel heel groot. d m SD = 6, 2, 6= 629, en m+ SD = 6, + 2, 6= 681, Bij een lengte van 63 inch hoort een klasse van 62, tot 63,. Van deze klasse ligt 0,6 deel innen de grenzen. Van de klasse 67, tot 68, ligt ook 0,6 deel innen de grenzen. Dus tussen 62,9 en 68,1 zitten 06, , criminelen. Dat is = 69% ladzijde 219 7a 0% is langer dan het gemiddelde De langste % is groter dan = 187 cm. Dit komt doordat de klokvorm symmetrisch is. 8a c Het gemiddelde zit ij de top van de klokvorm en is ongeveer 141 mm. De frequenties tussen 141, = 13, mm en 141 +, = 146, mm zijn ongeveer = %. Dit klopt redelijk met de eerste vuistregel
3 d Het ziet er naar uit dat hier sprake is van een normale verdeling. Voor alle zekerheid zou je ook de tweede vuistregel moeten controleren. 9a Gemiddelde, mediaan en modus zijn ij een normale verdeling gelijk. A: Nee, je het uitschieters naar rechts (zeer hoge inkomens) B: Ja. C: Ja. D: Nee, je krijgt twee toppen. E: Nee, er zijn veel meer ay s dan 100-jarigen. ladzijde 2 10a lengte in cm 100, 101, 102, 103, 104, 10, 106, 107, 108, 109, percentage rollen 0, 0,7 1, 9, , 1, 12, 1, y 40 percentage x lengte in meters De kromme lijkt aardig op een klokvorm dus de verdeling kan normaal zijn. c Invoeren van de klassenmiddens en hun ijehorende frequenties op de GR geeft een gemiddelde van 10,6 meter en een standaarddeviatie van 1, meter (1,21124) d Tussen 104,1 en 107,1 ligt 09, , + 1, + 01, 12, 68% dus aan vuistregel één is voldaan. Tussen 102,6 en 108,6 ligt 04, 1, + 92, , + 1, + 12, + 06, 94% dus ook vuistregel twee voldoet redelijk. Je mag dus concluderen dat de lengte normaal verdeeld is. e Gemiddeld zit er 10,6 meter op één rol en dat is,6 meter teveel. Per dag zal er dus , = 0400 meter stof teveel worden afgeleverd. ladzijde De helft van de leerlingen heeft een cijfer lager dan,9 (het gemiddelde) wat aangeeft dat de verdeling symmetrisch is. Tussen 4,2 en 7,6 zitten 03, , 100 = 700 leerlingen dus 70%. Tussen 2, en 9,3 zitten , 1 = 946 leerlingen dus 9%. Aan eide vuistregels is redelijk voldaan dus mag je spreken van normale verdeling. 12a 130 Nee, want door de 37 ezoekers in klasse [170, 190] kan het frequentiepolygoon nooit symmetrisch zijn. Bij punt twee van de vorige ladzijde in je oek staat dat als het frequentiepolygoon geen klokvorm is, dat het zeker geen normale verdeling is.
4 13a De leeftijd waarop men dienstplichtig was verschilde. Vanaf 1986 is de dienstplicht opgeheven en kon men alleen vrijwillig in dienst. Je gaat er dan vanuit dat de lengtes gelijkmatig over de klasse zijn verdeeld. Dit is een redelijke veronderstelling. c 01, + 08, + 33, + 09, 11, 146, % is kleiner dan 174 cm in d Tussen 167,3 en 180,7 zit 044, 173, + 28, , + 024, 144, 66, 4%. Tussen 160,6 en 187,4 zit 078, 6+ 17, , + 27, , + 08, 4, 943, %. Aan eide vuistregels is redelijk voldaan dus mag je aannemen dat de lengte in 190 normaal verdeeld is. ladzijde a % zal een nettogewicht van meer dan gram heen. c Tussen 0 en 210 gram zit volgens vuistregel één 68%. Dus zal 32% 2= 16% een nettogewicht heen van minder dan 0 gram. d Het geied tussen 0 en gram wordt steeds groter. Tussen 0 en 2, gram zit dus minder dan 17%. Dit zal ongeveer 1% zijn. e Volgens vuistregel twee zal 2 1 % minder wegen dan 0 gram. 2 1 Volgens vuistregel één en de symmetrie ligt er tussen m en m s de helft van 68% dus 34%. Dat geldt ook voor het geied van m tot m+ s. Volgens vuistregel twee ligt 9% tussen m 2 s en m+ 2 s. Haal daar 68% vanaf en je houdt 27% over. Dus tussen m 2 s en m s en tussen m+ s en m+ 2 s ligt 1 27 = 13, %. Links van m 2 s en rechts van m+ 2 s lijft dus nog 1 = 2, % 2 2 over. ladzijde a m 1 s= 407, 1 0, 12 = 401,. Op ladzijde 222 kun je aflezen dat links van m 1 s ; , + 2, = 31% ligt. Tussen m 1 1 s en m+ 1 1 s ligt , 2 2, = 86 %. 2 2 c Ongeveer 29% zal een gewicht onder de 4,00 kg heen. 17a 38,21% is kleiner dan 0, , 21 = 61, 79% is groter dan 0,3 c 84,13% is kleiner dan 1,0 en 1,87% is kleiner dan 1,0 d Tussen 1,0 en 1,0 ligt 84, 13 1, 87 = 68, 26%. Dit komt overeen met vuistregel één. 131
5 18a Met vuistregel twee vind je dat 97,% van de leerlingen een temperatuur vindt van 2 C of lager. Uit de tael volgt dat 34,46% een lagere temperatuur vindt dus 6,24% vindt een hogere temperatuur dan 0,4 C. c 81, 9 24, = 7, 39% van de leerlingen vindt een temperatuur tussen 0,7 C en 0,9 C. d Tussen 0, C en 0, C ligt 69, 1 30, 8 = 38, 3%. ladzijde a 4,00 4,07 De ondergrens is nul en de ovengrens is vier kg. Je mag als ondergrens ook nemen. c TI: Normalcdf(0; 4; 4,07; 0,12)=0,2798 Casio : STAT-DIST-NORM-Ncd ; Lower = 0; Upper = 4; s = 0,2; m = 4,07 geeft pro=0, ,98% van de pakken heeft een gewicht minder dan 4,00 kg. ladzijde 22 a TI: normalcdf(-e99; 160; 181,3; 7)=0,0012 Casio: Ncd: Lower = -EXP99; Upper = 160; s = 7; m = 181,3 geeft pro=0,0012 0,12% was kleiner dan 160 cm. TI: normalcdf(0; E99; 181,3; 7)=0,0038 Casio: Ncd: Lower = 0; Upper = EXP99; s = 7; m = 181,3 geeft pro=0,0038 0,38% is groter dan 0 cm. c 100 0, 12 0, 38 = 99, %werd niet afgekeurd op hun lengte. 21a TI: normalcdf(49,9; 0,8; 0,6; 0,4)=0,614 Casio: Ncd: Lower = 49,9; Upper = 0,8; s = 0,4; m = 0,6 geeft pro=0,614 6,14% van de flesjes evat tussen 49,9 en 0,8 cl. TI: normalcdf(1; E99; 0,6; 0,4)=0,187 Casio: Ncd: Lower = 1; Upper = EXP99; s = 0,4; m = 0,6 geeft pro=0,187 1,87% van de flesjes evat minder dan 1cl. c TI: normalcdf(-e99; 0,1; 0,6; 0,4)=0,106 Casio: Ncd: Lower = -EXP99; Upper = 0,1; s = 0,4; m = 0,6 geeft pro=0,106 10,6% van de flesjes evat minder dan 0,1 cl. 132
6 22a Op grond van de redelijke klokvorm kun je eredeneren dat de longcapaciteit vrijwel normaal verdeeld is. TI: normalcdf(-e99; 2 900; 4 100; 400)=0,0013 Casio: Ncd: Lower = -EXP99; Upper = 2 900; s = 400; m = geeft pro=0,0013 0,13% van deze studenten zal een longcapaciteit kleiner dan cm 3 heen. c 0, dus gaat het om ongeveer twee studenten. d TI: normalcdf(2 300; 300; 4 100; 400)=0,9986 Casio: Ncd: Lower = 2 300; Upper = 300; s = 400; m = geeft pro=0, ,9% van de studenten heeft een longcapaciteit tussen en 300 cm 3. 23a TI: normalcdf(-e99; 797; 800; 2)=0,0668 Casio: Ncd: Lower = -EXP99; Upper = 797; s = 2; m = 800 geeft pro=0,0668 6,7% van de planken is onruikaar planken komt dan overeen met , = 93, 3%. Er moeten dus = 1072 planken gezaagd worden om goede over te houden. 93, 3 c Vanwege de symmetrie is ook 6,7% van de planken te lang dus zijn er 0, = 72 planken die op maat moeten worden gemaakt. Winst: , , = , - d TI: normalcdf(-e99; 797; 801; 2)=0,0228 Casio: Ncd: Lower = -EXP99; Upper = 797; s = 2; m = 801 geeft pro=0,0228 Er moeten dan dus = 1024 planken gezaagd worden. 97, 7 TI: normalcdf(803; E99; 801; 2)=0,187 Casio: Ncd: Lower = 803; Upper = EXP99; s = 2; m = 801 geeft pro=0,187 Er moeten dan dus 0, = 163 planken op maat worden gemaakt. Winst: ( ) 3, , = 3. 1, 0 dus is er meer winst en zijn er minder planken nodig. e TI: normalcdf(7-e99; 797; 902; 2)=0,0062 Casio : Ncd : Lower=-EXP99; Upper = 797; s = 2; m = 802 geeft pro=0,0062 In deze situatie moeten er = 1006 planken worden gezaagd. 99, 4 TI: normalcdf(803 ; E99 ; 802 ; 2)=0,308 Casio : Ncd : Lower = 803 ; Upper = EXP99 ; s = 2; m = 802 geeft pro=0,308 Er moeten nu 0, = 310 planken op maat worden gemaakt. Winst: ( ) 3, , = , - dus ij deze instelling wordt minder winst gemaakt. ladzijde a Na uur zal 0% moeten worden vervangen % g
7 c TI: Invnorm(0,10; 6 000; 00)= 39,2 Casio: Stat-Dist Norm InvN Area = 0,10; s = 00; m = geeft 39,2 Na 39 uur zal 10% van de lampen kapot zijn. ladzijde 227 2a TI: Invnorm(0,07; 6 000; 00)= 262,1 Casio: InvN: Area = 0,07; s = 00; m = geeft 262,1 Na 262 uur worden alle lampen vervangen. TI: Invnorm(0,1; 2 00; 0)=2 292,7 Casio: InvN: Area = 0,1; s = 0; m = 2 00 geeft 2 292,7 Na uur is 1% kapot. c Dat etekent dat 26% kapot is. TI: Invnorm(0,26; 2 00; 0)=2 371,3 Casio: InvN : Area = 0,26; s = 0; m = 2 00 geeft 2 371,3 Na uur randt nog maar 74%. 26a Als 13% van de pakken hoort ij het hoogtste vetgehalte heeft 87% een lager vetgehalte. TI: Invnorm(0,87; 3,0; 0,02)=3,22 Casio: InvN : Area = 0,87; s = 0,02; m = 3,0 geeft 3,22 13% van de pakken heft een vetgehalte van minstens 3,2%. TI: Invnorm(0,29; 3,0; 0,02)=3,4889 Casio: InvN : Area = 0,29; s = 0,02; m = 3,0 geeft 3, % van de pakken heft een vetgehalte minder dan 3,49%. c % 0,02 40% 40% g 1 3, g 2 TI: Invnorm(0,40; 3,0; 0,02)=3,4949 Casio: InvN : Area = 0,40; s = 0,02; m = 3,0 geeft 3,4949 De linkergrens is dus 3,49% vet en vanwege de symmetrie is de rechtergrens dus 3,1% vet. 27a Een redelijke schatting is natuurlijk 19,1 cm. TI: Normalcdf(19; 19,; 19,1; 1,06)=0,186 Casio: Ncd : Lower = 19; Upper = 19,; s = 1,06; m = 19,1 geeft pro=0,1863 0, leerlingen vinden een omtrek tussen 19,0 en 19, cm. c TI: Invnorm(0,4; 19,1; 1,06)=19,016 Casio: InvN : Area = 0,4; s = 1,06; m = 19,1 geeft 19,
8 De linkergrens is 19,02 cm en gezien de symmetrie moet de rechtergrens dan 19,28 cm zijn. De 10% leerlingen die het dichtst ij het gemiddelde zitten meten een omtrek van 19,02 tot 19,28 cm. d TI: Normalcdf(-E99; 17,1; 19,1; 1,06)=0,0296 Casio : Ncd : Lower = -EXP99 ; Upper = 17,1 ; s = 1,06; m = 19,1 geeft 0,0299 Vanwege de symmetrie meet ook 2,96% meer dan 21,1. 2 2, 96 = 92, % van de leerlingen moet de meting twee keer uitvoeren. e Deze kromme geeft aan hoe groot de fout is die ij een meting wordt gemaakt. f 1, a Als de gegevens alleen geheel zijn kan het frequentiepolygoon dus geen continue normaalkromme zijn. Door het grote aantal van kandidaten mag je de normale verdeling toch toepassen. c Je moet als grens 4, nemen. TI: normalcdf(-e99; 4,; 1; 16)=0,866 Casio : Ncd : Lower = -EXP99 ; Upper = 4, ; s = 16; m = 1 geeft 0,867 0, kandidaten ehaalden minder dan d TI: invnorm(0,93; 1; 16)=74,612 Casio: InvN : Area = 0,93; s = 16; m = 1 geeft 74,612 De este 7% haalden geen score van 7 of meer. ladzijde a TI: normalcdf(-e99; 800; 80; 38)=0,0941 Casio: Ncd : Lower = -EXP99; Upper = 800; s = 38; m = 80 geeft pro=0, ,41% van de flessen moeten opnieuw gevuld worden. gemiddelde percentage flessen minder dan 800 ml,72 4,36 3,27 2,42 1,76 1,26 0,89 c Bij een gemiddelde van 889 ml moet de farikant hoogstens 1% van de flessen opnieuw vullen. Bij een gemiddelde van 888 ml vind je nog 1,03%. ladzijde a Hoe kleiner de standaarddeviatie des te smaller en hoger de klokvorm, des te kleiner het percentage links van gram. 13
9 Standaarddeviatie 6, 6,4 6,3 6,2 6,1 6,0 Percentage 6,2,9,6,3,1 4,8 Uit de tael lijkt dat de standaarddeviatie 6,0 gram gekozen moet worden om te zorgen dat hoogstens % van de pakken minder dan gram evat. 31 S = 30 gram 1% m 80 Volgens de tweede vuistregel moet m kleiner zijn dan = 790. Gemiddelde Percentage 1, 1,4 1,3 1,2 1,1 0,98 Als het gemiddelde 780 gram wordt gekozen is niet meer dan 1% van de roden zwaarder dan 80 gram. 32a S = 1 ml 0,2% m 00 Volgens de tweede vuistregel moet m kleiner zijn dan = 470 ml. Gemiddelde Percentage 0,38 0,31 0,26 0,21 0,17 Als het gemiddelde 46 gram is zal minder dan 0,2% van de kuipjes overstromen. 4% Volgens vuistregel twee is de afstand tussen 40 en 46 ml minder dan twee keer de standaarddeviatie. Standaarddeviatie 3,1 3,2 3,3 3,4 3, Percentage 2,6 3,0 3, 3,9 4,3 De standaarddeviatie mag hoogstens 3,4 ml zijn. 136
10 33a TI: normalcdf(-e99; 0; 43,1; 6,6)=0,821 Casio: Ncd : Lower = -EXP99; Upper = 0; s = 6,6; m = 43,1 geeft 0,89 Inderdaad rijdt 8% niet harder dan 0 km/uur. TI: normalcdf(; E99; 43,1; 6,6)=0,037 Casio: Ncd : Lower = ; Upper = EXP99; s = 6,6; m = 43,1 geeft 0,03691 Bij 0, = 43 metingen mag je een snelheid van meer dan km/uur verwachten. c S = 2,1 8% m Gemiddelde 18,0 17,9 17,8 Percentage 0,830 0,841 0,83 De gemiddelde passeersnelheid ij dit type drempels is 17,8 km/uur. ladzijde a SD = 16 gram innenland export puree Binnenland: TI: normalcdf(30; 80; 72; 16)=0,6871 Casio: Ncd : Lower = 30; Upper = 80; s = 16; m = 72 geeft pro=0,68713 Puree: TI: normalcdf(-e99; 30; 72; 16)=0,0043 Casio : Ncd : Lower = -EXP99; Upper = 30; s = 16; m = 72 geeft pro=0,00433 Dus 0,43% is voor de puree, 68,71% is voor innelands geruik en , 6871, = 308, % is voor de export. Binnenland: TI: normalcdf(30; 80; 80; 16)=0,4991 Casio: Ncd : Lower = 30; Upper = 80; s = 16; m = 80 geeft pro=0,49911 Puree: TI: normalcdf(-e99; 30; 80; 16)=0,0009 Casio : Ncd : Lower = -EXP99; Upper = 30; s = 16; m = 80 geeft pro=0,00089 Nu is 0,09% voor de puree; 49,91% voor innenlands geruik en , 4991, = 0% is voor de export. 137
11 3a TI: normalcdf(8,7; 9,7; 9,2; 0,6)=0,93 Casio: Ncd : Lower = 8,7; Upper = 9,7; s = 0,6; m = 9,2 geeft pro=0,934 In = 60 jaar van een eeuw verwacht je een temperatuur die minder dan een halve graad afwijkt van het gemiddelde. TI: normalcdf(-e99; 8,; 9,2; 0,6)=0,1217 Casio: Ncd : Lower = -EXP99; Upper = 8,; s = 0,6; m = 9,2 geeft pro=0,12167 In 0, jaar verwacht je een temperatuur met een gemiddelde onder de 8, C. Dit is dus iets minder dan de dertien. c TI: normalcdf(10,3; E99; 9,2; 0,6)=0,0334 Casio : Ncd : Lower = 10,3; Upper - = EXP99 ; s = 0,6; m = 9,2 geeft pro=0, Je kunt per eeuw dus ongeveer 0, = 3 uitzonderlijke jaren verwachten. d 0,6 90% 10% 10,2 g 1 TI: Invnorm(0,9; 10,2; 0,6)=10,97 Casio: InvN : Area = 0,9; s = 0,6; m = 10,2 geeft x = 10,968. De 10% warmste jaren heen een gemiddelde temperatuur van meer dan 10,97 C. ladzijde a profieldiepte (mm) aantal percentage [1,33; 1,43> 2 1 [1,43; 1,3> 8 4 [1,3; 1,63> 2 12, [1,63; 1,73> [1,73; 1,83> 6 32, [1,83; 1,93> 27 13, [1,93; 2,03> 9 4, [2,03; 2,13> 1 0, [2,13; 2,23> 1 0, y 40 percentage x profieldiepte in mm 138 Met de klassenmiddens en de frequenties epaal je met de grafische rekenmachine dat het gemiddelde 1,73 mm en de standaarddeviatie 0,13 mm is. Vuistregel één: Tussen 1,60 en 1,86 ligt 03, 12, , + 03, 13, 71%. Vuistregel twee: Tussen 1,47 en 1,99 ligt 06, 4+ 12, , + 13, + 06, 4, 9, %. Er wordt redelijk aan de vuistregels voldaan.
12 c TI: normalcdf(1,6; 2,0 ; 1,7 ; 0,1)=0,9270 Casio : Ncd : Lower = 1,6 ; Upper = 2,0 ; s = 0,1; m = 1,7 geeft pro=0,92689 Dus 92,7% van de anden heeft een profile tussen 1,6 en 2,0 mm. d TI: normalcdf(-e99; 1,6; 1,7; 0,1)=0,0668 Casio : Ncd : Lower = -EXP99 ; Upper = 1,6 ; s = 0,1; m = 1,7 geeft pro=0, Na de test moet 6,7% afgekeurd worden. e TI: Invnomr(0,7; 1,7; 0,1)=1,82 Casio: InvN : Area = 0,7; s = 0,1; m = 1,7 geeft x = 1,8174 De este 2% anden heen een profile van minstens 1,82 mm. f Hier is sprake van een inomiale verdeling met n = 4 en p = 0,067 (zie onderdeel d). P(minstens één and wordt afgekeurd) = 1 P(geen enkele and wordt afgekeurd) = 4 1 0, 933 0, 2422 ladzijde 232 I-1a Je kunt aan het nummer zien dat het over 403 leerlingen gaat. De variaelen schoenmaat, lengte, taille, armspan, handspan, schedel en gewicht zijn lichaamsmaten. c De klassenreedte is 10 en er zijn 7 klassen. d In de klasse van 80 tot 90. e Je krijgt natuurlijk steeds meer en smallere staafjes. In het midden zitten de meeste waarnemingen. Hoe verder je vanuit het midden naar links of rechts gaat, des te minder waarnemingen per klasse. f De klasse loopt van 7,8 tot 79,. I-2a Alleen ij de variaele sexe zie je geen klokvorm. Naarmate de afstand tot het gemiddelde groter wordt neemt het aantal waarnemingen af. ladzijde 233 I-3a Als je werkt met 11 klassen en klassenmiddens 142; 147; ; 192, dan is het gemiddelde 166,26 en de standaarddeviatie 8,27. gem sd gem+sd gem-sd gem+2 sd gem-2 sd 166 8,3 174,3 17,7 182,6 149,4 19, 17, 7 174, 3 169, Tussen 17,7 en 174,3 liggen ( ) ( ) waarnemingen. Dat is %. 403 Tussen 149,4 en 182,6 liggen 01, 182, 6 179, ( ) waarnemingen. Dat is %. De vuistregels gelden hier. 403 I-4 Het gemiddelde is 7,2 en de standaardafwijking is 1,9. Tussen,3 en 9,1 liggen 07, , waarnemingen. Dat is %. 403 Tussen 3,4 en 11,0 liggen 06, waarnemingen. Dat is %. 403 Ook nu is redelijk aan de vuistregels voldaan. 139
13 I- De grafiek die hoort ij de normale enadering komt minder hoog maar is meer symmetrisch. I-6 Open hiervoor het estand dat hoort ij opdracht 2a. Voeg een kolom toe met de klassenmiddens dus 142, 147,. Kies onder OPTIES weer de normale enadering waarij je voor Waarnemingsgetallen de klassenmiddens kiest en voor Frequentie kies je Freq. Kies dan optie GRAFIEK en laat weer voor zowel de frequentie als de normale enadering een lijngrafiek plotten. Er is weinig verschil. De grafiek van de normale enadering is iets meer symmetrisch. ladzijde 234 I-7a TI: normalcdf(-e99; 2 800; 3 000; )=0,2119 Casio: Ncd : Lower = -EXP99; Upper = 2 800; s = ; m = 3000 geeft pro=0,2118. Dus 21,2% is kapot na uur. Op dezelfde manier vind je dat,% kapot is na uur. De kans links is inderdaad 0,048. c Door ij kans links 0,1 te kiezen krijg je als grens 2 679, Het duurt dus uur voordat 10% kapot is. ladzijde 23 I-8a Kies eerst voor twee grenzen. Kies dan als linkergrens 0 en als rechtergrens 190. De kans dat een leerling groter is dan 190 cm is dan 0, ,2% is dus langer dan 190 cm. Kies als linkergrens 160 en als rechtergrens 170. Bij Kansmidden staat dan 0,402. 4% van de leerlingen heeft een lengte tussen 160 en 170 cm. c Kies voor één grens en dan voor kans links 0,9. De 10% langste leerlingen zijn groter dan 176,6 cm. I-9a Kies voor twee grenzen. Kies als linkergrens nul en als rechtergrens 1. De kans is 0,187. Het percentage flesjes dat meer dan 1 cl cola evat is 1,9%. Kies als linkergrens 49,9 en als rechtergrens 0,8. Het gevraagde percentage is 6,1%. I-10a Kies voor één grens en als kans links 0,29. De 29% pakken met het laagste vetgehalte heen een vetgehalte van maximaal 3,49%. Kies nu voor kans links 0,87. Deze 13% pakken heen een vetgehalte van minstens 3,2%. I-11a Kies voor één grens en m = 4 en kans links 0,24. Schuif nu op de kromee de standaarddeviatie tot ij de grens 30 staat. De gevraagde standaarddeviatie is 21,2 punten. 140
14 Kies nu kans links 0,97 en schuif de standaarddeviatie tot ij de grens 7 staat. De gevraagde standaarddeviatie is 16,0. ladzijde 238 T-1a y 1 aantal koeien x 3 3, 4 4,, vetgehalte in % Deze klasse loopt van 3,7 tot 4,1%. Minder dan 4% is dan 4 3, = 62, %. 41, 3, 7 c Je gaat er vanuit dat de vetgehaltes gelijkmatig over de gehele klasse zijn verdeeld. Aangezien deze klasse veel gegevens evat is dit een redelijke veronderstelling. d Van deze 400 koeien gaven er ongeveer , 62 1 = 6 melk met een vetgehalte van minder dan 4%. 37, 3, 4 3 e 3,4% ligt in de klasse van 3,3 tot 3,7%. Uit deze klasse doet = deel mee. 37, 3, 3 4 4,7% ligt in de klasse van 4, tot 4,9%. Uit deze klasse doet de helft mee want 47, 4, = 1. 49, 4, 2 Het gaat dus over 07, koeien % van de koeien geeft melk met een vetgehalte tussen 3,4% en 4,7%. T-2a De grafiek is klokvormig. 166, + 1, 78 Het gemiddelde is = 172, meter. 2 c De standaarddeviatie is 172, 1, 66 = 006, meter. d Tussen 1,66 en 1,78 ligt 68%. De 32% die overlijft is vanwege de symmetrie gelijk verdeeld dus 16% is langer dan 1,78 m. e Het gemiddelde min twee keer de standaarddeviatie is 1,60 m. Volgens vuistregel twee is 2,% kleiner dan 1,60 m. 97,% van de vrouwen is dus groter dan 1,60 m. 27 T-3a 100 = 6, %van de onderzochte vrouwen heeft maat klassenmidden percentage 87 1,1 90 1,4 93 3,1 96,2, , ,4 108,2, , , , , , ,2 141
15 c percentage y x heupomvang in cm d Vuistregel één: Tussen 100 en 118 cm zit 0, 10, 4+ 14, +, , + 0, 13, 1 66, % Vuistregel twee: Tussen 91 en 127 zit 1 14, + 31, + 6, + 10, 4+ 14, +, , + 13, 1+ 7, 8 + 0, 28, 9, 4% 6 Aan eide vuistregels wordt redelijk voldaan. ladzijde 239 T-4a 34% 34% 2,% 13,% 13,% 2,% c d 49,9 0,2 0, 0,8 1,1 Uit de klokvorm is af te leiden dat 16% van de flessen een inhoud van meer dan 0,8 cl heeft. Uit de klokvorm lijkt dat 2,% van de flessen een inhoud heeft minder dan 49,9 cl. Net iets meer dan 2,% evat dus minder dan een halve liter. De gemiddelde inhoud per flesje is 0, cl. Per twintig flesjes kun je dus inderdaad 0, = 10 cl meer verwachten. T-a TI: normalcdf(7,4; E99; 7,4; 0,2)=0,4013 Casio : Ncd : Lower=7,4 ; Upper = EXP99 ;s = 0,2; m = 7,4 geeft pro=0,40129 Dus ongeveer 40% van de mensen heeft een ph-waarde van minstens 7,4. TI: normalcdf(-e99; 7,2; 7,4; 0,2)=0,2266 Casio: Ncd : Lower = -EXP99; Upper = 7,2; s = 0,2; m = 7,4 geeft pro=0, ,7% van de mensen heeft een ph-waarde kleiner dan 7,2. c TI: normalcdf(7,30; 7,; 7,4; 0,2)=0,4648 Casio : Ncd : Lower = 7,30 ; Upper = 7, ; s = 0,2; m = 7,4 geeft pro=0,46483 Bij 46,% van de mensen ligt de ph-waarde tussen 7,3 en 7,. 142
16 T-6a 9 3% 6 4,00 TI: invnorm(0,6; 6; 9)=68,47 Casio: InvN : Area = 0,6; s = 9; m = 6 geeft x = 68, 467 De 3% zwaarste vrouwen wegen 68, kg of meer. 40% SD = 9 g 1 6 g 2 TI: invnorm(0,3; 6; 9)=60,28 Casio: InvN : Area = 0,3; s = 9; m = 6 geeft x = 0,68. Vanwege de symmetrie geldt dan dat g 2 = 69, 72. De gewichten van de 40% vrouwen die rond het gemiddelde liggen lopen van 60,3 tot 69,7 kg. T-7a TI: normalcdf(-e99; 98 ; ; 12)=0,0668 Casio : Ncd : Lower = -EXP99; Upper = 98; s = 12; m = 1003 geeft pro=0, In 6,7% van de pakken zal minder dan 98 gram zitten. Deze farikant voldoet niet aan de EG-norm want dan mag slechts 2,% minder dan 98 gram evatten. c Dit gemiddelde zal volgens vuistregel twee net iets meer moeten zijn dan = gemiddelde 1009,1 1009,2 1009,3 1009,4 1009, 1009,6 1009,7 percentage 2,23 2,19 2,14 2,10 2,06 2,02 1,98 d Bij een gemiddelde van minstens 1 009,7 gram is aan de EG-norm voldaan. De afstand van 98 tot is 18 dus zal de standaarddeviatie ongeveer 9 zijn. standaarddeviatie 8,9 8,8 8,7 percentage 2,16 2,04 1,92 Bij een standaarddeviatie van hoogstens 8,7 gram is aan de EG-norm voldaan. 143
Hoofdstuk 4 Normale verdelingen
 V-1a c d V-2a Noordhoff Uitgevers v Moderne Wiskunde Uitwerkingen ij vwo C deel 3 Hoofdstuk 4 Normale verdelingen Hoofdstuk 4 Normale verdelingen ladzijde 92 De relatieve cumulatieve frequenties zijn de
V-1a c d V-2a Noordhoff Uitgevers v Moderne Wiskunde Uitwerkingen ij vwo C deel 3 Hoofdstuk 4 Normale verdelingen Hoofdstuk 4 Normale verdelingen ladzijde 92 De relatieve cumulatieve frequenties zijn de
Hoofdstuk 3 Verdelingen
 Hoofdstuk 3 Verdelingen Voorkennis: Statistische verwerking ladzijde 0 V-a inkomen in euro s cum. frequentie rel. cum. frequentie c d V-a [000; 000,9% [000; 00 9 7,0% [00; 000 38,0% [000; 000 0,0% [000;
Hoofdstuk 3 Verdelingen Voorkennis: Statistische verwerking ladzijde 0 V-a inkomen in euro s cum. frequentie rel. cum. frequentie c d V-a [000; 000,9% [000; 00 9 7,0% [00; 000 38,0% [000; 000 0,0% [000;
4.1 Eigenschappen van de normale verdeling [1]
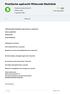
![4.1 Eigenschappen van de normale verdeling [1] 4.1 Eigenschappen van de normale verdeling [1]](/thumbs/62/48052723.jpg) 4.1 Eigenschappen van de normale verdeling [1] Relatief frequentiepolygoon van de lengte van mannen in 1968 1 4.1 Eigenschappen van de normale verdeling [1] In dit plaatje is een frequentiepolygoon getekend.
4.1 Eigenschappen van de normale verdeling [1] Relatief frequentiepolygoon van de lengte van mannen in 1968 1 4.1 Eigenschappen van de normale verdeling [1] In dit plaatje is een frequentiepolygoon getekend.
1 a Partij is een kwalitatieve variabele, kindertal een kwantitatieve, discrete variabele. b,c
 Hoofdstuk 8, Statistische maten 1 Hoofdstuk 8 Statistische maten Kern 1 Centrum- en spreidingsmaten 1 a Partij is een kwalitatieve variaele, kindertal een kwantitatieve, discrete variaele.,c d kindertal
Hoofdstuk 8, Statistische maten 1 Hoofdstuk 8 Statistische maten Kern 1 Centrum- en spreidingsmaten 1 a Partij is een kwalitatieve variaele, kindertal een kwantitatieve, discrete variaele.,c d kindertal
Hoofdstuk 6 Hypothesen toetsen
 Hoofdstuk 6 Hypothesen toetsen ladzijde 144 1a X is aantal autokopers die merk A aanschaffen. X is Bin(100; 0,30) verdeeld. 0,30 3 100 = 30, naar verwachting zullen dus 30 autokopers merk A aanschaffen.
Hoofdstuk 6 Hypothesen toetsen ladzijde 144 1a X is aantal autokopers die merk A aanschaffen. X is Bin(100; 0,30) verdeeld. 0,30 3 100 = 30, naar verwachting zullen dus 30 autokopers merk A aanschaffen.
8.1 Centrum- en spreidingsmaten [1]
![8.1 Centrum- en spreidingsmaten [1] 8.1 Centrum- en spreidingsmaten [1]](/thumbs/39/19316324.jpg) 8.1 Centrum- en spreidingsmaten [1] Gegeven zijn de volgende 10 waarnemingsgetallen: 1, 3, 3, 3, 4, 5, 6, 8, 8, 9 Het gemiddelde is: De mediaan is het middelste waarnemingsgetal als de getallen naar grootte
8.1 Centrum- en spreidingsmaten [1] Gegeven zijn de volgende 10 waarnemingsgetallen: 1, 3, 3, 3, 4, 5, 6, 8, 8, 9 Het gemiddelde is: De mediaan is het middelste waarnemingsgetal als de getallen naar grootte
Hoofdstuk 2 De normale verdeling. Kern 1 Normale verdelingen. 1 a
 Hoofdstuk De normale verdeling Kern Normale verdelingen a percentage 30 0 0 57 6 67 7 77 8 87 9 97 0 07 De polygoon heeft een klokvorm. b In totaal is 0, + 0,9 + 3,3 +,0 +,3 + 7,3= 50,5 procent van de
Hoofdstuk De normale verdeling Kern Normale verdelingen a percentage 30 0 0 57 6 67 7 77 8 87 9 97 0 07 De polygoon heeft een klokvorm. b In totaal is 0, + 0,9 + 3,3 +,0 +,3 + 7,3= 50,5 procent van de
Hoe verwerk je gegevens met de Grafische Rekenmachine?
 Hoe verwerk je gegevens met de Grafische Rekenmachine? Heb je een tabel met alleen gegevens? Kies STAT EDIT Vul L 1 met je gegevens (als de lijst niet leeg is, ga je met de pijltjes helemaal naar boven,
Hoe verwerk je gegevens met de Grafische Rekenmachine? Heb je een tabel met alleen gegevens? Kies STAT EDIT Vul L 1 met je gegevens (als de lijst niet leeg is, ga je met de pijltjes helemaal naar boven,
Hoofdstuk 9 De Normale Verdeling. Kern 1 Normale verdelingen. Netwerk, 4 Havo A, uitwerkingen Hoofdstuk 9, De Normale Verdeling Elleke van der Most
 Hoofdstuk 9 De Normale Verdeling Kern Normale verdelingen a percentage 30 0 0 57 6 67 7 77 8 87 9 97 0 07 De polygoon heeft een klokvorm. b De gemiddelde lengte valt in de klasse 80 84 cm. Omdat 8 precies
Hoofdstuk 9 De Normale Verdeling Kern Normale verdelingen a percentage 30 0 0 57 6 67 7 77 8 87 9 97 0 07 De polygoon heeft een klokvorm. b De gemiddelde lengte valt in de klasse 80 84 cm. Omdat 8 precies
Hoofdstuk 3 - Verdelingen
 Hoofdstuk - Verdelingen ladzijde 8 V-a De gemiddelde sore is ( 7 + 7 8 + 9 + + 8 ) : 0 = 0,8. Je kunt het ook invoeren op de rekenmahine. TI 8/8: L: 7, 8, 9, 0,..,7, 8 en L:, 7,..., -Var Stats L,L geeft
Hoofdstuk - Verdelingen ladzijde 8 V-a De gemiddelde sore is ( 7 + 7 8 + 9 + + 8 ) : 0 = 0,8. Je kunt het ook invoeren op de rekenmahine. TI 8/8: L: 7, 8, 9, 0,..,7, 8 en L:, 7,..., -Var Stats L,L geeft
34% 34% 2,5% 2,5% ,5% 13,5%
 C. von Schwartzenberg 1/16 1a Er is uitgegaan van de klassen: 1 < 160; 160 < 16; 16 < 170;... 18 < 190. 1b De onderzochte groep bestaat uit 1000 personen. 1c x = 17,3 (cm) en σ, 7 (cm). 1de 680 is 68%
C. von Schwartzenberg 1/16 1a Er is uitgegaan van de klassen: 1 < 160; 160 < 16; 16 < 170;... 18 < 190. 1b De onderzochte groep bestaat uit 1000 personen. 1c x = 17,3 (cm) en σ, 7 (cm). 1de 680 is 68%
Boek 2 hoofdstuk 8 De normale verdeling.
 52a. de groepen verschillen sterk in grootte b. 100 van de 5000 = 1 van de 50 dus 1 directielid, 90 winkelmedewerkers en 9 magazijnmedewerkers. Boek 2 hoofdstuk 8 De normale verdeling. 8.1 Vuistregels
52a. de groepen verschillen sterk in grootte b. 100 van de 5000 = 1 van de 50 dus 1 directielid, 90 winkelmedewerkers en 9 magazijnmedewerkers. Boek 2 hoofdstuk 8 De normale verdeling. 8.1 Vuistregels
G&R vwo A/C deel 2 8 De normale verdeling C. von Schwartzenberg 1/14. 3a 1 2
 G&R vwo A/C deel 8 De normale verdeling C. von Schwartzenberg 1/14 1a Gemiddelde startgeld x = 1 100000 + 4 4000 + 3000 = 13100 dollar. 10 1b Het gemiddelde wordt sterk bepaald door de uitschieter van
G&R vwo A/C deel 8 De normale verdeling C. von Schwartzenberg 1/14 1a Gemiddelde startgeld x = 1 100000 + 4 4000 + 3000 = 13100 dollar. 10 1b Het gemiddelde wordt sterk bepaald door de uitschieter van
13,5% 13,5% De normaalkromme heeft dezelfde vorm als A (even breed en even hoog), maar ligt meer naar links.
 G&R havo A deel C. von Schwartzenberg /8 a Er is uitgegaan van de klassen: < 60; 60 < 6; 6 < 70;... 8 < 90. b c De onderzochte groep bestaat uit 000 personen. (neem nog eens GRpracticum uit hoofdstuk 4
G&R havo A deel C. von Schwartzenberg /8 a Er is uitgegaan van de klassen: < 60; 60 < 6; 6 < 70;... 8 < 90. b c De onderzochte groep bestaat uit 000 personen. (neem nog eens GRpracticum uit hoofdstuk 4
Noordhoff Uitgevers bv
 bladzijde 9 a, 3 3000 = 8900 = 830, b 0, 07 000000 = 8000 = 80, c 300 700 = 6870000 = 690, 8 d 0, 000 0, 007 = 0, 00000 =, 0 6 e 6344, 78, 98 = 49604, 336 = 4960, 6 9 6 f, 0 + 4 0 = 74000000 =, 74 0 9
bladzijde 9 a, 3 3000 = 8900 = 830, b 0, 07 000000 = 8000 = 80, c 300 700 = 6870000 = 690, 8 d 0, 000 0, 007 = 0, 00000 =, 0 6 e 6344, 78, 98 = 49604, 336 = 4960, 6 9 6 f, 0 + 4 0 = 74000000 =, 74 0 9
De normale verdeling
 De normale verdeling Les 2 De klokvorm en de normale verdeling (Deze les sluit aan bij paragraaf 8 en 9 van Binomiale en normale verdelingen van de Wageningse Methode) De grafische rekenmachine Vooraf
De normale verdeling Les 2 De klokvorm en de normale verdeling (Deze les sluit aan bij paragraaf 8 en 9 van Binomiale en normale verdelingen van de Wageningse Methode) De grafische rekenmachine Vooraf
Hoofdstuk 8: De normale verdeling. 8.1 Centrum- en spreidingsmaten. Opgave 1:
 Hoofdstuk 8: De normale verdeling 8. Centrum- en spreidingsmaten Opgave : 00000 4 4000 5 3000 a. 300 dollar 0 b. 9 van de atleten verdienen minder dan de helft van het gemiddelde. Het gemiddelde is zo
Hoofdstuk 8: De normale verdeling 8. Centrum- en spreidingsmaten Opgave : 00000 4 4000 5 3000 a. 300 dollar 0 b. 9 van de atleten verdienen minder dan de helft van het gemiddelde. Het gemiddelde is zo
Keuzemenu - De standaardnormale verdeling
 ladzijde 4 a Volgens de vuistregels ligt 68% innen μ σ en μ + σ en ligt 95% innen μ σ en μ + σ. a c μ σ,5% 3,5% 34% 34% 3,5% μ σ μ De oppervlakte onder de klokvorm rechts van haar gewicht is,5%, dus daar
ladzijde 4 a Volgens de vuistregels ligt 68% innen μ σ en μ + σ en ligt 95% innen μ σ en μ + σ. a c μ σ,5% 3,5% 34% 34% 3,5% μ σ μ De oppervlakte onder de klokvorm rechts van haar gewicht is,5%, dus daar
De normale verdeling. Les 3 De Z-waarde (Deze les sluit aan bij de paragraaf 10 van Binomiale en normale verdelingen van de Wageningse Methode)
 De normale verdeling Les 3 De Z-waarde (Deze les sluit aan bij de paragraaf 10 van Binomiale en normale verdelingen van de Wageningse Methode) De grafische rekenmachine Vooraf In deze les ga je veel met
De normale verdeling Les 3 De Z-waarde (Deze les sluit aan bij de paragraaf 10 van Binomiale en normale verdelingen van de Wageningse Methode) De grafische rekenmachine Vooraf In deze les ga je veel met
Wiskunde D Online uitwerking 4 VWO blok 5 les 3
 Paragraaf 10 De standaard normale tabel Opgave 1 a Er geldt 20,1 16,6 = 3,5 C. Dit best wel een fors verschil, maar hoeft niet direct heel erg uitzonderlijk te zijn. b Er geldt 167 150 = 17. Dat valt buiten
Paragraaf 10 De standaard normale tabel Opgave 1 a Er geldt 20,1 16,6 = 3,5 C. Dit best wel een fors verschil, maar hoeft niet direct heel erg uitzonderlijk te zijn. b Er geldt 167 150 = 17. Dat valt buiten
UITWERKINGEN VOOR HET VWO NETWERK B13
 12 UITWERKINGEN VOOR HET VWO NETWERK B13 HOOFDSTUK 6 KERN 1 1a) Zie plaatje De polygoon heeft een klokvorm 1b) Ongeveer 50% 1c) 0,1 + 0,9 + 3,3 + 11,0 = 15,3% 2a) klokvorm 2b) geen klokvorm 2c) klokvorm
12 UITWERKINGEN VOOR HET VWO NETWERK B13 HOOFDSTUK 6 KERN 1 1a) Zie plaatje De polygoon heeft een klokvorm 1b) Ongeveer 50% 1c) 0,1 + 0,9 + 3,3 + 11,0 = 15,3% 2a) klokvorm 2b) geen klokvorm 2c) klokvorm
bijspijkercursus wiskunde voor psychologiestudenten bijeenkomst 9 de normale verdeling (niet in [PW])
![bijspijkercursus wiskunde voor psychologiestudenten bijeenkomst 9 de normale verdeling (niet in [PW]) bijspijkercursus wiskunde voor psychologiestudenten bijeenkomst 9 de normale verdeling (niet in [PW])](/thumbs/50/27198885.jpg) bijspijkercursus wiskunde voor psychologiestudenten bijeenkomst 9 de normale verdeling (niet in [PW]) vorige week: kansrekening de uitkomstvariabele was bijna altijd discreet aantal keer een vijf gooien
bijspijkercursus wiskunde voor psychologiestudenten bijeenkomst 9 de normale verdeling (niet in [PW]) vorige week: kansrekening de uitkomstvariabele was bijna altijd discreet aantal keer een vijf gooien
Hoofdstuk 4 - Normale verdelingen
 ladzijde 92 V-1a De relatieve umulatieve frequenties zijn de waarden van de umulatieve frequenties (somfrequenties) uitgedrukt in perentages. De laatste waarde (dat is de hoogste waarde) van de umulatieve
ladzijde 92 V-1a De relatieve umulatieve frequenties zijn de waarden van de umulatieve frequenties (somfrequenties) uitgedrukt in perentages. De laatste waarde (dat is de hoogste waarde) van de umulatieve
Wiskunde D Online uitwerking 4 VWO blok 6 les 2
 Paragraaf 8 De klokvorm Opgave 1 a De top van de grafiek van de PvdA ligt bij 30 %. Dus voor de PvdA wordt 30% voorspeld. b De grafiek loopt van ongeveer 27 tot 33, dus het percentage ligt met grote waarschijnlijkheid
Paragraaf 8 De klokvorm Opgave 1 a De top van de grafiek van de PvdA ligt bij 30 %. Dus voor de PvdA wordt 30% voorspeld. b De grafiek loopt van ongeveer 27 tot 33, dus het percentage ligt met grote waarschijnlijkheid
Antwoorden bij 4 - De normale verdeling vwo A/C (aug 2012)
 Antwoorden bij - De normale verdeling vwo A/C (aug 0) Opg. a Aflezen bij de 5,3 o C grafiek:,3% en bij de,9 o C grafiek: 33,3% b Het tweede percentage is 33,3 /,3 = 5, maal zo groot. c Bij de 5,3 o C grafiek
Antwoorden bij - De normale verdeling vwo A/C (aug 0) Opg. a Aflezen bij de 5,3 o C grafiek:,3% en bij de,9 o C grafiek: 33,3% b Het tweede percentage is 33,3 /,3 = 5, maal zo groot. c Bij de 5,3 o C grafiek
9.0 Voorkennis. Bij samengestelde kansexperimenten maak je gebruik van de productregel.
 9.0 Voorkennis Bij samengestelde kansexperimenten maak je gebruik van de productregel. Productregel: Voor de gebeurtenis G 1 bij het ene kansexperiment en de gebeurtenis G 2 bij het andere kansexperiment
9.0 Voorkennis Bij samengestelde kansexperimenten maak je gebruik van de productregel. Productregel: Voor de gebeurtenis G 1 bij het ene kansexperiment en de gebeurtenis G 2 bij het andere kansexperiment
4 De normale verdeling
 bladzijde 217 35 a X = het aantal vrouwen met osteoporose. P(X = 30) = binompdf(100, 1, 30) 0,046 4 b X = het aantal mannen met osteoporose. Y = het aantal vrouwen met osteoporose. P(2 met osteoporose)
bladzijde 217 35 a X = het aantal vrouwen met osteoporose. P(X = 30) = binompdf(100, 1, 30) 0,046 4 b X = het aantal mannen met osteoporose. Y = het aantal vrouwen met osteoporose. P(2 met osteoporose)
Hoofdstuk 5 - Hypothese toetsen
 V-1a 98 ladzijde 114 Niet iedereen heeft dezelfde kans om in deze steekproef te komen. Het zijn klanten van de winkel. Het zijn alleen vrouwen. Het zijn klanten die allemaal op hetzelfde tijdstip oodshappen
V-1a 98 ladzijde 114 Niet iedereen heeft dezelfde kans om in deze steekproef te komen. Het zijn klanten van de winkel. Het zijn alleen vrouwen. Het zijn klanten die allemaal op hetzelfde tijdstip oodshappen
11.0 Voorkennis. Wanneer je met binomcdf werkt, werk je dus altijd met een kans van de vorm P(X k)
 11.0 Voorkennis Let op: Cumulatieve binomiale verdeling: P(X k) = binomcdf(n,p,k) Wanneer je met binomcdf werkt, werk je dus altijd met een kans van de vorm P(X k) Voorbeeld 1: Binomiaal kanseperiment
11.0 Voorkennis Let op: Cumulatieve binomiale verdeling: P(X k) = binomcdf(n,p,k) Wanneer je met binomcdf werkt, werk je dus altijd met een kans van de vorm P(X k) Voorbeeld 1: Binomiaal kanseperiment
Rekenen met de normale verdeling (met behulp van grafisch rekentoestel)
 Rekenen met de normale verdeling (met behulp van grafisch rekentoestel) In 1947 werd in opdracht van N.V. Magazijn De Bijenkorf een statistisch onderzoek verricht naar de lichaamsafmetingen van de Nederlandse
Rekenen met de normale verdeling (met behulp van grafisch rekentoestel) In 1947 werd in opdracht van N.V. Magazijn De Bijenkorf een statistisch onderzoek verricht naar de lichaamsafmetingen van de Nederlandse
Kerstvakantiecursus. wiskunde A. Rekenregels voor vereenvoudigen. Voorbereidende opgaven HAVO kan niet korter
 Voorbereidende opgaven HAVO Kerstvakantiecursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk
Voorbereidende opgaven HAVO Kerstvakantiecursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk
Voorbeeld 1: kansverdeling discrete stochast discrete kansverdeling
 12.0 Voorkennis Voorbeeld 1: Yvette pakt vier knikkers uit een vaas waar er 20 inzitten. 9 van de knikkers zijn rood en 11 van de knikkers zijn blauw. X = het aantal rode knikkers dat Yvette pakt. Er zijn
12.0 Voorkennis Voorbeeld 1: Yvette pakt vier knikkers uit een vaas waar er 20 inzitten. 9 van de knikkers zijn rood en 11 van de knikkers zijn blauw. X = het aantal rode knikkers dat Yvette pakt. Er zijn
Hoofdstuk 3 Toetsen uitwerkingen
 Kern Kansen ij een normale verdeling a normalcdf(3.7,., 3,7) =,9 normalcdf(9, 9999,, 7) =,7 c normalcdf( 9999, 3,, ) =,978 a g = invnorm(.3, 8, 7) = 77,9 g = invnorm(.873,, ) = 97,9 c P(X < g μ = 8 en
Kern Kansen ij een normale verdeling a normalcdf(3.7,., 3,7) =,9 normalcdf(9, 9999,, 7) =,7 c normalcdf( 9999, 3,, ) =,978 a g = invnorm(.3, 8, 7) = 77,9 g = invnorm(.873,, ) = 97,9 c P(X < g μ = 8 en
Lesbrief de normale verdeling
 Lesbrief de normale verdeling 2010 Willem van Ravenstein Inhoudsopgave Inhoudsopgave... 1 Hoofdstuk 1 de normale verdeling... 2 Hoofdstuk 2 meer over de normale verdeling... 11 Hoofdstuk 3 de n-wet...
Lesbrief de normale verdeling 2010 Willem van Ravenstein Inhoudsopgave Inhoudsopgave... 1 Hoofdstuk 1 de normale verdeling... 2 Hoofdstuk 2 meer over de normale verdeling... 11 Hoofdstuk 3 de n-wet...
Paragraaf 9.1 : De Verwachtingswaarde
 Hoofdstuk 9 Kansverdelingen (V5 Wis A) Pagina 1 van 8 Paragraaf 9.1 : De Verwachtingswaarde Les 1 Verwachtingswaarde Definities : Verwachtingswaarde Verwachtingswaarde = { wat je verwacht } { gemiddelde
Hoofdstuk 9 Kansverdelingen (V5 Wis A) Pagina 1 van 8 Paragraaf 9.1 : De Verwachtingswaarde Les 1 Verwachtingswaarde Definities : Verwachtingswaarde Verwachtingswaarde = { wat je verwacht } { gemiddelde
c P( X 1249 of X 1751 µ = 1500 en σ = 100) = 1 P(1249 X 1751)
 Uitwerkingen Wiskunde A Netwerk VWO 6 Hoofdstuk 5 Toetsen www.uitwerkingensite.nl Hoofdstuk 5 Toetsen Kern Het principe van een toets a Nee, de waarneming,% wijkt erg sterk af van de verwachte,5%. Ja,,6%
Uitwerkingen Wiskunde A Netwerk VWO 6 Hoofdstuk 5 Toetsen www.uitwerkingensite.nl Hoofdstuk 5 Toetsen Kern Het principe van een toets a Nee, de waarneming,% wijkt erg sterk af van de verwachte,5%. Ja,,6%
Hoofdstuk 1 - Functies en de rekenmachine
 Hoofdstuk - Funties en de rekenmahine Voorkennis: Funties ladzijde V-a De formule is T = + 00, d Je moet oplossen + 00, d = dus dan geldt 00, d = en dan is d = : 00, 77 m V-a f( ) = = 0en f( ) = ( ) (
Hoofdstuk - Funties en de rekenmahine Voorkennis: Funties ladzijde V-a De formule is T = + 00, d Je moet oplossen + 00, d = dus dan geldt 00, d = en dan is d = : 00, 77 m V-a f( ) = = 0en f( ) = ( ) (
Samenvatting Wiskunde Samenvatting en stappenplan van hfst. 7 en 8
 Samenvatting Wiskunde Samenvatting en stappenplan van hfst. 7 en 8 Samenvatting door N. 1410 woorden 6 januari 2013 5,4 13 keer beoordeeld Vak Methode Wiskunde Getal en Ruimte 7.1 toenamediagrammen Interval
Samenvatting Wiskunde Samenvatting en stappenplan van hfst. 7 en 8 Samenvatting door N. 1410 woorden 6 januari 2013 5,4 13 keer beoordeeld Vak Methode Wiskunde Getal en Ruimte 7.1 toenamediagrammen Interval
Antwoorden door K woorden 14 augustus keer beoordeeld. Wiskunde A. Supersize me. Opgave 1: leerstof: Formules met meer variabelen.
 Antwoorden door K. 1901 woorden 14 augustus 2015 1 1 keer beoordeeld Vak Wiskunde A Supersize me Opgave 1: leerstof: Formules met meer variabelen. Formule energiebehoefte = =33,6 G 5000(kcal) = dagelijkse
Antwoorden door K. 1901 woorden 14 augustus 2015 1 1 keer beoordeeld Vak Wiskunde A Supersize me Opgave 1: leerstof: Formules met meer variabelen. Formule energiebehoefte = =33,6 G 5000(kcal) = dagelijkse
Paragraaf 9.1 : De Verwachtingswaarde
 Hoofdstuk 9 Kansverdelingen (V5 Wis A) Pagina 1 van 8 Paragraaf 9.1 : De Verwachtingswaarde Les 1 Verwachtingswaarde Definities : Verwachtingswaarde Verwachtingswaarde = { wat je verwacht } { gemiddelde
Hoofdstuk 9 Kansverdelingen (V5 Wis A) Pagina 1 van 8 Paragraaf 9.1 : De Verwachtingswaarde Les 1 Verwachtingswaarde Definities : Verwachtingswaarde Verwachtingswaarde = { wat je verwacht } { gemiddelde
14.1 Kansberekeningen [1]
![14.1 Kansberekeningen [1] 14.1 Kansberekeningen [1]](/thumbs/59/42966816.jpg) 14.1 Kansberekeningen [1] Herhaling kansberekeningen: Somregel: Als de gebeurtenissen G 1 en G 2 geen gemeenschappelijke uitkomsten hebben geldt: P(G 1 of G 2 ) = P(G 1 ) + P(G 2 ) B.v. P(3 of 4 gooien
14.1 Kansberekeningen [1] Herhaling kansberekeningen: Somregel: Als de gebeurtenissen G 1 en G 2 geen gemeenschappelijke uitkomsten hebben geldt: P(G 1 of G 2 ) = P(G 1 ) + P(G 2 ) B.v. P(3 of 4 gooien
5.0 Voorkennis. Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram:
 5.0 Voorkennis Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram: De lengte van de staven komt overeen met de hoeveelheid; De staven staan meestal los van
5.0 Voorkennis Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram: De lengte van de staven komt overeen met de hoeveelheid; De staven staan meestal los van
Eindexamen wiskunde A 1-2 havo 2003-II
 Eindexamen wiskunde A - havo 003-II 4 Antwoordmodel Wachtlijsten De mensen in de klassen C, D en E wachten tussen de 4 en 0 weken het aflezen van de cumulatieve percentages als (ongeveer) 38 en 58 het
Eindexamen wiskunde A - havo 003-II 4 Antwoordmodel Wachtlijsten De mensen in de klassen C, D en E wachten tussen de 4 en 0 weken het aflezen van de cumulatieve percentages als (ongeveer) 38 en 58 het
Werkbladen 3 Terugzoeken
 Werkbladen Terugzoeken We keren nu de vraag om. Bij een gegeven percentage (oppervlakte zoeken we de bijbehorende grenswaarde(n. Als voorbeeld zoeken we hoe groot een Nederlandse vrouw anno 97 moest zijn
Werkbladen Terugzoeken We keren nu de vraag om. Bij een gegeven percentage (oppervlakte zoeken we de bijbehorende grenswaarde(n. Als voorbeeld zoeken we hoe groot een Nederlandse vrouw anno 97 moest zijn
Extra oefening bij hoofdstuk 1
 Extra oefening ij hoofdstuk a Zij krijgt 8 67 8 960, euro. 6 Dat zijn 0, 87 06 64 kiezers. c Je het dan 0 4, 7 gram asterdsuiker nodig. 8 d In een jaar zitten 600 4 6 = 6 000 seconden. Er sterven per jaar
Extra oefening ij hoofdstuk a Zij krijgt 8 67 8 960, euro. 6 Dat zijn 0, 87 06 64 kiezers. c Je het dan 0 4, 7 gram asterdsuiker nodig. 8 d In een jaar zitten 600 4 6 = 6 000 seconden. Er sterven per jaar
Werkblad 1 Normale dichtheidsfunctie als benadering voor een klokvormig histogram
 Werkblad 1 Normale dichtheidsfunctie als benadering voor een klokvormig histogram Probeer zeker de opdrachten 1, 4 en 6 te maken. 1. In de tabel hieronder vind je gegevens over de borstomtrek van 5732
Werkblad 1 Normale dichtheidsfunctie als benadering voor een klokvormig histogram Probeer zeker de opdrachten 1, 4 en 6 te maken. 1. In de tabel hieronder vind je gegevens over de borstomtrek van 5732
Noordhoff Uitgevers bv
 Hoofdstuk - Meer variaelen ladzijde V-a Omdat het water met onstante snelheid uit de ak stroomt en de ak ilindervormig is, is de afname van de hoogte van de waterstand per tijdseenheid onstant. De hoogte
Hoofdstuk - Meer variaelen ladzijde V-a Omdat het water met onstante snelheid uit de ak stroomt en de ak ilindervormig is, is de afname van de hoogte van de waterstand per tijdseenheid onstant. De hoogte
Noordhoff Uitgevers bv
 Extra oefening ij hoofdstuk a Zij krijgt 8 67 8 960, euro. 6 Dat zijn 0, 87 06 64 kiezers. c Je het dan 0 4, 7 gram asterdsuiker nodig. 8 d In een jaar zitten 600 4 6 = 6 000 seconden. Er sterven per jaar
Extra oefening ij hoofdstuk a Zij krijgt 8 67 8 960, euro. 6 Dat zijn 0, 87 06 64 kiezers. c Je het dan 0 4, 7 gram asterdsuiker nodig. 8 d In een jaar zitten 600 4 6 = 6 000 seconden. Er sterven per jaar
5.0 Voorkennis. Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram:
 5.0 Voorkennis Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram: De lengte van de staven komt overeen met de hoeveelheid; De staven staan meestal los van
5.0 Voorkennis Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram: De lengte van de staven komt overeen met de hoeveelheid; De staven staan meestal los van
Blok 1 - Vaardigheden
 Blok - Vaardigheden Blok - Vaardigheden Etra oefening - Basis B-a h( ) = 000 00 = 00 h( 7 ) = 000 00 7 = 0 h(, ) = 000 00, = 70 000 00t = 00 00t = 00 t = B-a Invullen van geeft f ( ) = + 0 = +, maar de
Blok - Vaardigheden Blok - Vaardigheden Etra oefening - Basis B-a h( ) = 000 00 = 00 h( 7 ) = 000 00 7 = 0 h(, ) = 000 00, = 70 000 00t = 00 00t = 00 t = B-a Invullen van geeft f ( ) = + 0 = +, maar de
Steelbladdiagram In een steelbladdiagram staan alle leerlingen genoemd. Je kunt precies zien waar Wouter staat.
 2.1.3 Representaties In de voorbeelden kijken we steeds naar gewicht. Je gaat daarna zelf kijken naar de informatie over lengte en cijfergemiddelde. Voor alle opgaven geldt dat je deze zowel in de DWO
2.1.3 Representaties In de voorbeelden kijken we steeds naar gewicht. Je gaat daarna zelf kijken naar de informatie over lengte en cijfergemiddelde. Voor alle opgaven geldt dat je deze zowel in de DWO
Blok 3 - Vaardigheden
 B-a Extra oefening - Basis Ja, x en y zijn omgekeerd evenredig. Bij de tael hoort de formule x y = 70 of y = 70 of x = 70. x y Ja, x en y zijn omgekeerd evenredig. Bij de tael hoort de formule x y = 8
B-a Extra oefening - Basis Ja, x en y zijn omgekeerd evenredig. Bij de tael hoort de formule x y = 70 of y = 70 of x = 70. x y Ja, x en y zijn omgekeerd evenredig. Bij de tael hoort de formule x y = 8
Boek 1 hoofdstuk 4 Havo 4 Statistiek.
 Samenvatting statistiek havo4 boek 1 H4 Centrummaten: Modus (modaal) = wat het vaakst voorkomt, zowel kwalitatief als kwantitatief Mediaan = het middelste getal, in een rij getallen die op volgorde staat
Samenvatting statistiek havo4 boek 1 H4 Centrummaten: Modus (modaal) = wat het vaakst voorkomt, zowel kwalitatief als kwantitatief Mediaan = het middelste getal, in een rij getallen die op volgorde staat
Eindexamen wiskunde A 1-2 havo 2005-II
 Eindexamen wiskunde A - havo 005-II Het weer in september De frequenties zijn achtereenvolgens, 0, 3,, 7,, 6, 8, 6, 0, 8, 3,, en 0,5 3,5 7,0 7,5 de berekening 00 Het antwoord is 4 ( C) ( 4,05 4,03 4,0)
Eindexamen wiskunde A - havo 005-II Het weer in september De frequenties zijn achtereenvolgens, 0, 3,, 7,, 6, 8, 6, 0, 8, 3,, en 0,5 3,5 7,0 7,5 de berekening 00 Het antwoord is 4 ( C) ( 4,05 4,03 4,0)
2. In de klassen 2A en 2B is een proefwerk gemaakt. Je ziet de resultaten in de frequentietabel. 2A 2B
 1. (a) Bereken het gemiddelde salaris van de werknemers in de tabel hiernaast. (b) Bereken ook het mediale salaris. (c) Hoe groot is het modale salaris hier? salaris in euro s aantal werknemers 15000 1
1. (a) Bereken het gemiddelde salaris van de werknemers in de tabel hiernaast. (b) Bereken ook het mediale salaris. (c) Hoe groot is het modale salaris hier? salaris in euro s aantal werknemers 15000 1
2 Data en datasets verwerken
 Domein Statistiek en kansrekening havo A 2 Data en datasets verwerken 3 Frequentieverdelingen typeren 3.6 Geïntegreerd oefenen In opdracht van: Commissie Toekomst Wiskunde Onderwijs 3 Frequentieverdelingen
Domein Statistiek en kansrekening havo A 2 Data en datasets verwerken 3 Frequentieverdelingen typeren 3.6 Geïntegreerd oefenen In opdracht van: Commissie Toekomst Wiskunde Onderwijs 3 Frequentieverdelingen
Hoofdstuk 5 - Tabellen, grafieken, formules
 Hoofdstuk 5 - Taellen, grafieken, formules ladzijde 130 V-1a d De grafieken van de grond en de luht vertonen veel grotere temperatuurshommelingen dan de grafiek van het water. De grafiek van de grond omdat
Hoofdstuk 5 - Taellen, grafieken, formules ladzijde 130 V-1a d De grafieken van de grond en de luht vertonen veel grotere temperatuurshommelingen dan de grafiek van het water. De grafiek van de grond omdat
2.3 Frequentieverdelingen typeren
 2.3 Frequentieverdelingen typeren 2.3.1 Introductie Kijkend naar een datarepresentatie valt meestal al snel op hoe de verdeling van de tellingen/frequenties over de verschillende waarden eruitziet. Zitten
2.3 Frequentieverdelingen typeren 2.3.1 Introductie Kijkend naar een datarepresentatie valt meestal al snel op hoe de verdeling van de tellingen/frequenties over de verschillende waarden eruitziet. Zitten
directe invoer via OPTN Normal C.D kan ook direct worden aangeroepen, bijv. in het reken (RUN) menu.
 Normale verdeling A: berekenen van een kans In veel gevallen wordt uitdrukkelijk aangegeven dat iets normaal verdeeld is.de normale verdeling is in wezen een continue verdeling, in tegenstelling tot discrete
Normale verdeling A: berekenen van een kans In veel gevallen wordt uitdrukkelijk aangegeven dat iets normaal verdeeld is.de normale verdeling is in wezen een continue verdeling, in tegenstelling tot discrete
2 Data en datasets verwerken
 Domein Statistiek en kansrekening havo A 2 Data en datasets verwerken 1 Data presenteren 1.4 Oefenen In opdracht van: Commissie Toekomst Wiskunde Onderwijs 1.4 Oefenen Opgave 9 Bekijk de genoemde dataset
Domein Statistiek en kansrekening havo A 2 Data en datasets verwerken 1 Data presenteren 1.4 Oefenen In opdracht van: Commissie Toekomst Wiskunde Onderwijs 1.4 Oefenen Opgave 9 Bekijk de genoemde dataset
2.1.4 Oefenen. d. Je ziet hier twee weegschalen. Wat is het verschil tussen beide als het gaat om het aflezen van een gewicht?
 2.1.4 Oefenen Opgave 9 Bekijk de genoemde dataset GEGEVENS154LEERLINGEN. a. Hoe lang is het grootste meisje? En de grootste jongen? b. Welke lengtes komen het meeste voor? c. Is het berekenen van gemiddelden
2.1.4 Oefenen Opgave 9 Bekijk de genoemde dataset GEGEVENS154LEERLINGEN. a. Hoe lang is het grootste meisje? En de grootste jongen? b. Welke lengtes komen het meeste voor? c. Is het berekenen van gemiddelden
Eindexamen wiskunde A1 vwo 2002-II
 Eindexamen wiskunde A vwo 2002-II 4 Antwoordmodel Vliegen 8,7 groeifactor (,9) per 9 jaar 9,8 9 8,7 groeifactor, 074 per jaar 2 9,8 8,7,074 4 het antwoord: nee, want in 2003 zijn er meer dan 40 miljoen
Eindexamen wiskunde A vwo 2002-II 4 Antwoordmodel Vliegen 8,7 groeifactor (,9) per 9 jaar 9,8 9 8,7 groeifactor, 074 per jaar 2 9,8 8,7,074 4 het antwoord: nee, want in 2003 zijn er meer dan 40 miljoen
Noordhoff Uitgevers bv
 84 ladzijde 4 a Vul de gegevens in en lees af ij kans rehts : 0,22 Nadat je het olletje voor tweezijdigheid het aangeklikt en de linker en rehter grens het ingesteld lees je af ij kans midden 0,759. Het
84 ladzijde 4 a Vul de gegevens in en lees af ij kans rehts : 0,22 Nadat je het olletje voor tweezijdigheid het aangeklikt en de linker en rehter grens het ingesteld lees je af ij kans midden 0,759. Het
2 Data en datasets verwerken
 Domein Statistiek en kansrekening havo A 2 Data en datasets verwerken 1 Data presenteren 1.3 Representaties In opdracht van: Commissie Toekomst Wiskunde Onderwijs 1 Data presenteren 1.1 Introductie In
Domein Statistiek en kansrekening havo A 2 Data en datasets verwerken 1 Data presenteren 1.3 Representaties In opdracht van: Commissie Toekomst Wiskunde Onderwijs 1 Data presenteren 1.1 Introductie In
13.1 Kansberekeningen [1]
![13.1 Kansberekeningen [1] 13.1 Kansberekeningen [1]](/thumbs/53/31278159.jpg) 13.1 Kansberekeningen [1] Herhaling kansberekeningen: Somregel: Als de gebeurtenissen G 1 en G 2 geen gemeenschappelijke uitkomsten hebben geldt: P(G 1 of G 2 ) = P(G 1 ) + P(G 2 ) B.v. P(3 of 4 gooien
13.1 Kansberekeningen [1] Herhaling kansberekeningen: Somregel: Als de gebeurtenissen G 1 en G 2 geen gemeenschappelijke uitkomsten hebben geldt: P(G 1 of G 2 ) = P(G 1 ) + P(G 2 ) B.v. P(3 of 4 gooien
4 HAVO wiskunde A HOOFDSTUK voorkennis 1. soorten verdelingen 2. de normale verdeling 3. betrouwbaarheidsintervallen 4. groepen en kenmerken
 4 HAVO wiskunde A HOOFDSTUK 6 0. voorkennis 1. soorten verdelingen 2. de normale verdeling 3. betrouwbaarheidsintervallen 4. groepen en kenmerken 0. voorkennis Centrum- en spreidingsmaten Centrummaten:
4 HAVO wiskunde A HOOFDSTUK 6 0. voorkennis 1. soorten verdelingen 2. de normale verdeling 3. betrouwbaarheidsintervallen 4. groepen en kenmerken 0. voorkennis Centrum- en spreidingsmaten Centrummaten:
Blok 2 - Vaardigheden
 Moderne wiskunde 9e editie Havo A deel Blok - Vaardigheden ladzijde 0 a 6 f g h d, p, p p 0 5 p i e 6q 6q q q q 5 0 5a a 0a a 6 5 5 5 t t t t t t a Per weken is de groeifator 7,, 9 Een kwartaal heeft 5
Moderne wiskunde 9e editie Havo A deel Blok - Vaardigheden ladzijde 0 a 6 f g h d, p, p p 0 5 p i e 6q 6q q q q 5 0 5a a 0a a 6 5 5 5 t t t t t t a Per weken is de groeifator 7,, 9 Een kwartaal heeft 5
OEFENPROEFWERK HAVO A DEEL 2
 OEFENPROEFWERK HAVO A DEEL 2 HOOFDSTUK 6 STATISTIEK EN BESLISSINGEN OPGAVE 1 Hieronder zijn vier boxplots getekend. a Welke boxplot hoort bij een links-scheve verdeling? Licht toe. b Hoe ligt bij boxplot
OEFENPROEFWERK HAVO A DEEL 2 HOOFDSTUK 6 STATISTIEK EN BESLISSINGEN OPGAVE 1 Hieronder zijn vier boxplots getekend. a Welke boxplot hoort bij een links-scheve verdeling? Licht toe. b Hoe ligt bij boxplot
Praktische opdracht Wiskunde Statistiek
 Praktische opdracht Wiskunde Statistiek Praktische-opdracht door R. 3948 woorden 5 december 2016 2,8 3 keer beoordeeld Vak Wiskunde Scoreformulier: Statistisch onderzoek havo 4 wiskunde A Namen groepsleden:
Praktische opdracht Wiskunde Statistiek Praktische-opdracht door R. 3948 woorden 5 december 2016 2,8 3 keer beoordeeld Vak Wiskunde Scoreformulier: Statistisch onderzoek havo 4 wiskunde A Namen groepsleden:
Hoofdstuk 8 - Periodieke functies
 Havo B deel Uitwerkingen Moderne wiskunde Hoofdstuk 8 - Periodieke functies ladzijde 8 V-a c Na seconden = slagen per minuut ca., millivolt V-a Ja, met periode Nee Mogelijk, met periode = en amplitude
Havo B deel Uitwerkingen Moderne wiskunde Hoofdstuk 8 - Periodieke functies ladzijde 8 V-a c Na seconden = slagen per minuut ca., millivolt V-a Ja, met periode Nee Mogelijk, met periode = en amplitude
TI83-werkblad. Vergelijkingen bij de normale verdeling
 TI83-werkblad Vergelijkingen bij de normale verdeling 1. Inleiding Een normale verdeling wordt bepaald door de constanten µ en σ. Dit blijkt uit het voorschrift van de verdelingsfunctie van de normale
TI83-werkblad Vergelijkingen bij de normale verdeling 1. Inleiding Een normale verdeling wordt bepaald door de constanten µ en σ. Dit blijkt uit het voorschrift van de verdelingsfunctie van de normale
Werken met de grafische rekenmachine
 Werken met de grafische rekenmachine Plot de grafiek blz. Schets de grafiek of teken een globale grafiek blz. 3 Teken de grafiek blz. 4 Het berekenen van snijpunten blz. 3 5 Het berekenen van maxima en
Werken met de grafische rekenmachine Plot de grafiek blz. Schets de grafiek of teken een globale grafiek blz. 3 Teken de grafiek blz. 4 Het berekenen van snijpunten blz. 3 5 Het berekenen van maxima en
VB: De hoeveelheid neemt nu met 12% af. Hoeveel was de oorspronkelijke hoeveelheid? = 1655 oud = 1655 nieuw = 0,88 x 1655 = 1456
 Formules, grafieken en tabellen Procenten - altijd afronden op 1 decimaal tenzij anders vermeld VB: Een hoeveelheid neemt met 12% toe to 1456. Hoeveel was de oorspronkelijke hoeveelheid? Oud =? Nieuw =
Formules, grafieken en tabellen Procenten - altijd afronden op 1 decimaal tenzij anders vermeld VB: Een hoeveelheid neemt met 12% toe to 1456. Hoeveel was de oorspronkelijke hoeveelheid? Oud =? Nieuw =
Correctievoorschrift HAVO. Wiskunde A1,2 (nieuwe stijl)
 Wiskunde A, (nieuwe stijl) Correctievoorschrift HAVO Hoger Algemeen Voortgezet Onderwijs 0 03 Tijdvak Inzenden scores Vul de scores van de alfabetisch eerste vijf kandidaten per school in op de optisch
Wiskunde A, (nieuwe stijl) Correctievoorschrift HAVO Hoger Algemeen Voortgezet Onderwijs 0 03 Tijdvak Inzenden scores Vul de scores van de alfabetisch eerste vijf kandidaten per school in op de optisch
Antwoorden Hoofdstuk 1 Verschillen
 Antwoorden Hoofdstuk 1 Verschillen 1a. Niet sterk, want het is gebaseerd op slechts één zomer. b. Vriendinnen volgen is een vorm van groepsgedrag. Waar heeft Anneke het bericht gelezen? In een kwaliteitskrant
Antwoorden Hoofdstuk 1 Verschillen 1a. Niet sterk, want het is gebaseerd op slechts één zomer. b. Vriendinnen volgen is een vorm van groepsgedrag. Waar heeft Anneke het bericht gelezen? In een kwaliteitskrant
Hoofdstuk 4 - Machtsfuncties
 Hoofdstuk - Machtsfuncties Voorkennis: Functies en symmetrie ladzijde 9 V-a Kies als vensterinstelling voor je GR ijvooreeld X en Y en voer in Y = X X + Je krijgt: + = 0, dan D = ( ) = en = = = + = of
Hoofdstuk - Machtsfuncties Voorkennis: Functies en symmetrie ladzijde 9 V-a Kies als vensterinstelling voor je GR ijvooreeld X en Y en voer in Y = X X + Je krijgt: + = 0, dan D = ( ) = en = = = + = of
Eindexamen wiskunde A1-2 vwo 2004-I
 4 Beoordelingsmodel Examenresultaten aflezen in figuur : 77% heeft een score van 65 lager Dus 3% heeft een score hoger dan 65 Dat zijn (ongeveer) 59 kandidaten aflezen in figuur : 77% heeft een score van
4 Beoordelingsmodel Examenresultaten aflezen in figuur : 77% heeft een score van 65 lager Dus 3% heeft een score hoger dan 65 Dat zijn (ongeveer) 59 kandidaten aflezen in figuur : 77% heeft een score van
Hoofdstuk 4 Machtsverbanden
 Opstap Derdemachten O-1a I r r r 1 De inhoud van een kuus met r is 1 cm 3. Als I 7 geldt r 3 want 3 3 7. Een kuus met I 7 heeft een rie van 3 cm. c r in cm 1 3 d I in cm 3 1 7 6 1 l in cm 3 9 7 6 3 - -1-3
Opstap Derdemachten O-1a I r r r 1 De inhoud van een kuus met r is 1 cm 3. Als I 7 geldt r 3 want 3 3 7. Een kuus met I 7 heeft een rie van 3 cm. c r in cm 1 3 d I in cm 3 1 7 6 1 l in cm 3 9 7 6 3 - -1-3
GEGEVENS154LEERLINGEN
 2.4.4 Oefenen Voorbeeld Bekijk de dataset GEGEVENS154LEERLINGEN nog een keer. Je wilt nagaan of leerlingen die wiskunde B kiezen beter waren in wiskunde in de onderbouw dan leerlingen die wiskunde A kiezen.
2.4.4 Oefenen Voorbeeld Bekijk de dataset GEGEVENS154LEERLINGEN nog een keer. Je wilt nagaan of leerlingen die wiskunde B kiezen beter waren in wiskunde in de onderbouw dan leerlingen die wiskunde A kiezen.
Paragraaf 5.1 : Frequentieverdelingen
 Hoofdstuk 5 Beschrijvende statistiek (V4 Wis A) Pagina 1 van 7 Paragraaf 5.1 : verdelingen Les 1 Allerlei diagrammen = { Hoe vaak iets voorkomt } Relatief = { In procenten } Absoluut = { Echte getallen
Hoofdstuk 5 Beschrijvende statistiek (V4 Wis A) Pagina 1 van 7 Paragraaf 5.1 : verdelingen Les 1 Allerlei diagrammen = { Hoe vaak iets voorkomt } Relatief = { In procenten } Absoluut = { Echte getallen
Statistiek: Herhaling en aanvulling
 Statistiek: Herhaling en aanvulling 11 mei 2009 1 Algemeen Statistiek is de wetenschap die beschrijft hoe we gegevens kunnen verzamelen, verwerken en analyseren om een beter inzicht te krijgen in de aard,
Statistiek: Herhaling en aanvulling 11 mei 2009 1 Algemeen Statistiek is de wetenschap die beschrijft hoe we gegevens kunnen verzamelen, verwerken en analyseren om een beter inzicht te krijgen in de aard,
5. Lineaire verbanden.
 Uitwerkingen opgaven hoofdstuk 5 versie 15 5. Lineaire veranden. Opgave 5.1 Recht evenredig lineair verand F (N) 1 9 8 Uitrekking van een veer a = F 9 k = 37,5 x 4 = 7 6 5 4 F 9 N N k = = = 37,5 x 4 cm
Uitwerkingen opgaven hoofdstuk 5 versie 15 5. Lineaire veranden. Opgave 5.1 Recht evenredig lineair verand F (N) 1 9 8 Uitrekking van een veer a = F 9 k = 37,5 x 4 = 7 6 5 4 F 9 N N k = = = 37,5 x 4 cm
DOEN! - Praktische Opdracht Statistiek 4 Havo Wiskunde A
 DOEN! - Praktische Opdracht Statistiek 4 Havo Wiskunde A Docentenhandleiding 1. Voorwoord Doel van de praktische opdracht bij het hoofdstuk over statistiek 1 : Het doel van de praktische opdracht (PO)
DOEN! - Praktische Opdracht Statistiek 4 Havo Wiskunde A Docentenhandleiding 1. Voorwoord Doel van de praktische opdracht bij het hoofdstuk over statistiek 1 : Het doel van de praktische opdracht (PO)
Hoofdstuk 4 - Periodieke functies
 Hoofdstuk - Periodieke functies ladzijde 98 V-a Na seconden. Het hart klopt c, millivolt = slagen per minuut. V-a Ja, met periode ; nee; misschien met periode. Evenwichtsstand y = ; -; y =. Amplitude is
Hoofdstuk - Periodieke functies ladzijde 98 V-a Na seconden. Het hart klopt c, millivolt = slagen per minuut. V-a Ja, met periode ; nee; misschien met periode. Evenwichtsstand y = ; -; y =. Amplitude is
Centrummaten en klassen vmbo-kgt34
 Auteur Laatst gewijzigd Licentie Webadres VO-content 30 august 2017 CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie https://maken.wikiwijs.nl/74220 Dit lesmateriaal is gemaakt met Wikiwijs van
Auteur Laatst gewijzigd Licentie Webadres VO-content 30 august 2017 CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie https://maken.wikiwijs.nl/74220 Dit lesmateriaal is gemaakt met Wikiwijs van
3.1 Procenten [1] In 1994 zijn er 3070 groentewinkels in Nederland. In 2004 zijn dit er nog 1625.
![3.1 Procenten [1] In 1994 zijn er 3070 groentewinkels in Nederland. In 2004 zijn dit er nog 1625. 3.1 Procenten [1] In 1994 zijn er 3070 groentewinkels in Nederland. In 2004 zijn dit er nog 1625.](/thumbs/33/16051897.jpg) 3.1 Procenten [1] In 1994 zijn er 3070 groentewinkels in Nederland. In 2004 zijn dit er nog 1625. Absolute verandering = Aantal 2004 Aantal 1994 = 1625 3070 = -1445 Relatieve verandering = Nieuw Oud Aantal
3.1 Procenten [1] In 1994 zijn er 3070 groentewinkels in Nederland. In 2004 zijn dit er nog 1625. Absolute verandering = Aantal 2004 Aantal 1994 = 1625 3070 = -1445 Relatieve verandering = Nieuw Oud Aantal
3. Data verwerven. Boekje 3 havo wiskunde A, domein E: Statistiek. Uitwerkingen
 3. Data verwerven Boekje 3 havo wiskunde A, domein E: Statistiek Uitwerkingen 1 Verantwoording 2015, SLO (nationaal expertisecentrum leerplanontwikkeling), Enschede Dit lesmateriaal is ontwikkeld in het
3. Data verwerven Boekje 3 havo wiskunde A, domein E: Statistiek Uitwerkingen 1 Verantwoording 2015, SLO (nationaal expertisecentrum leerplanontwikkeling), Enschede Dit lesmateriaal is ontwikkeld in het
2 Data en datasets verwerken
 Domein Statistiek en kansrekening havo A 2 Data en datasets verwerken 4 Twee groepen vergelijken 4.4 Oefenen In opdracht van: Commissie Toekomst Wiskunde Onderwijs 4.4 Oefenen Voorbeeld Bekijk de dataset
Domein Statistiek en kansrekening havo A 2 Data en datasets verwerken 4 Twee groepen vergelijken 4.4 Oefenen In opdracht van: Commissie Toekomst Wiskunde Onderwijs 4.4 Oefenen Voorbeeld Bekijk de dataset
Vaardigheden. bladzijde 52. deel van 240 = 96 en 3 deel = 144. deel = ( 11 : 25 ) 2110 = 928, 40 euro en. deel = ( 14 : 25 ) 2110 = 1181,60 euro
 Vaardigheden ladzijde 5 a 7 f 8 0 g 8 0,96 h 9 d 9 i 0 e 8 j a 7,5 e 8 5 6 f 6 g 5, 0, = 0, 3 3 9 d 9 h = = =, 5 3a 8, = 3, 88 euro a 6, 365 = 58 dagen 6 3, = 3568, gram Drie dagen is 7 uur, dus 0, 7 =
Vaardigheden ladzijde 5 a 7 f 8 0 g 8 0,96 h 9 d 9 i 0 e 8 j a 7,5 e 8 5 6 f 6 g 5, 0, = 0, 3 3 9 d 9 h = = =, 5 3a 8, = 3, 88 euro a 6, 365 = 58 dagen 6 3, = 3568, gram Drie dagen is 7 uur, dus 0, 7 =
Centrummaten en klassen vmbo-kgt34. CC Naamsvermelding 3.0 Nederland licentie.
 Auteur VO-content Laatst gewijzigd Licentie Webadres 12 April 2016 CC Naamsvermelding 3.0 Nederland licentie http://maken.wikiwijs.nl/74220 Dit lesmateriaal is gemaakt met Wikiwijsleermiddelenplein. Wikiwijsleermiddelenplein
Auteur VO-content Laatst gewijzigd Licentie Webadres 12 April 2016 CC Naamsvermelding 3.0 Nederland licentie http://maken.wikiwijs.nl/74220 Dit lesmateriaal is gemaakt met Wikiwijsleermiddelenplein. Wikiwijsleermiddelenplein
Hoofdstuk 2 - De kettingregel
 Hoofdstuk - De kettingregel ladzijde V-a P ( ) 0 ( 0+ ) 0 0 + 0 0 + 0 60 W + + + a + t voor a 0 a a T u ( r ) r r 8 d R log + V-a u t wordt t en s t u t wordt t en s t 7 V-a A: t ( ) A: t ( ) ( ) 8 8 V-a
Hoofdstuk - De kettingregel ladzijde V-a P ( ) 0 ( 0+ ) 0 0 + 0 0 + 0 60 W + + + a + t voor a 0 a a T u ( r ) r r 8 d R log + V-a u t wordt t en s t u t wordt t en s t 7 V-a A: t ( ) A: t ( ) ( ) 8 8 V-a
Samenvattingen 5HAVO Wiskunde A.
 Samenvattingen 5HAVO Wiskunde A. Boek 1 H7, Boek 2 H7&8 [email protected] Boek 2: H7. Verbanden (Recht) Evenredig Verband ( 1) Omgekeerd Evenredig Verband ( 1) Hyperbolisch Verband ( 2) Machtsverband
Samenvattingen 5HAVO Wiskunde A. Boek 1 H7, Boek 2 H7&8 [email protected] Boek 2: H7. Verbanden (Recht) Evenredig Verband ( 1) Omgekeerd Evenredig Verband ( 1) Hyperbolisch Verband ( 2) Machtsverband
Eindexamen wiskunde A1-2 havo 2007-I
 Eindexamen wiskunde A- havo 007-I Beoordelingsmodel Marathon maximumscore 3 uur, 4 minuten en 55 seconden is 60 60 + 4 60 + 55 = 7495 seconden De gemiddelde snelheid is 495 5, 63 7495 m/s maximumscore
Eindexamen wiskunde A- havo 007-I Beoordelingsmodel Marathon maximumscore 3 uur, 4 minuten en 55 seconden is 60 60 + 4 60 + 55 = 7495 seconden De gemiddelde snelheid is 495 5, 63 7495 m/s maximumscore
Eindexamen wiskunde A1-2 havo 2006-I
 Eindexamen wiskunde A-2 havo 2006-I 4 Beoordelingsmodel Verdienen vrouwen minder? Het gemiddelde jaarinkomen is met 4200 0200 00% toegenomen 0200 2 Dit is ruim 39% 2 In 990 was het gemiddelde jaarinkomen
Eindexamen wiskunde A-2 havo 2006-I 4 Beoordelingsmodel Verdienen vrouwen minder? Het gemiddelde jaarinkomen is met 4200 0200 00% toegenomen 0200 2 Dit is ruim 39% 2 In 990 was het gemiddelde jaarinkomen
Eindexamen wiskunde A havo 2009 - I
 Beoordelingsmodel Autobanden maximumscore 4 De diameter van de velg is 4,54 = 35,56 (cm) De bandhoogte is 0,65 8,5 =,05 (cm) De bandhoogte is tweemaal nodig De diameter van de band is 35,56 +,05 = 59,6
Beoordelingsmodel Autobanden maximumscore 4 De diameter van de velg is 4,54 = 35,56 (cm) De bandhoogte is 0,65 8,5 =,05 (cm) De bandhoogte is tweemaal nodig De diameter van de band is 35,56 +,05 = 59,6
EXAMENTOETS TWEEDE PERIODE 5HAVO MLN/SNO
 EXAMENTOETS TWEEDE PERIODE 5HAVO wiskunde A MLN/SNO Onderwerp: Statistiek - Blok Datum: donderdag 1 januari 010 Tijd: 8.30-10.45 NB 1: Bij de beantwoording van de vragen ALTIJD JE BEREKENINGEN aangeven.
EXAMENTOETS TWEEDE PERIODE 5HAVO wiskunde A MLN/SNO Onderwerp: Statistiek - Blok Datum: donderdag 1 januari 010 Tijd: 8.30-10.45 NB 1: Bij de beantwoording van de vragen ALTIJD JE BEREKENINGEN aangeven.
