De Cantitruncated 600 cel
|
|
|
- Janne Mertens
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 De Cantitruncated 600 cel Afgeknotte icosahedrische prismatohexacosihecatonicosachoron Paul van de Veen januari 2013
2 I. De 5 Platonische lichamen In één dimensie bestaan alleen maar lijnen. Met meerdere lijnen kunnen we in het platte vlak, dus in twee dimensies verschillende figuren maken zoals driehoeken, vierkanten, vijfhoeken, zeshoeken, enz. Dit zijn regelmatige veelhoeken. In drie dimensies zoals onze wereld lijkt te zijn bestaan er ook regelmatige figuren. Met een aantal driehoeken kunnen we verschillende regelmatige ruimtelijke figuren, drie-dimensionale figuren maken. Het kan ook met vierkanten, met vijfhoeken. Maar niet met zeshoeken! Dat wisten de Grieken al. Zij zeiden: I. In een hoekpunt moeten altijd minstens drie vlakken samenkomen. Eén zijvlak per hoekpunt zou immers betekenen dat je een vlak hebt, en twee zijvlakken per hoekpunt levert nooit een volledig gesloten figuur op. II. In een hoekpunt moet de som van de hoeken altijd kleiner zijn dan 360. Want anders is er geen ruimte om te vouwen rond de hoek. Met deze twee gegevens kunnen we de regelmatige veelhoeken systematisch afgaan. Als we regelmatige veelvlakken met driehoeken willen maken hebben we nog maar drie mogelijkheden: 3, 4 of 5 driehoeken per hoekpunt. - Met drie driehoeken in een hoekpunt krijgen we de tetraëder. - Met vier driehoeken in een hoekpunt de octaëder. - Met vijf driehoeken de icosaëder. Als we regelmatige veelvlakken met vierhoeken willen maken hebben we maar één mogelijkheid, namelijk 3 vierhoeken per hoekpunt: de kubus. Als we regelmatige veelvlakken met vijfhoeken willen maken hebben we ook maar één mogelijkheid, namelijk 3 vijfhoeken per hoekpunt: de dodecaëder. Meer kan niet: 4 vijfhoeken levert een hoekensom van 4*108=432 graden. Te veel dus. Met drie zeshoeken gaat het gelijk al fout. De hoekensom is precies 360. Met de zeshoek kan er géén regelmatig veelvlak gemaakt worden met 3 zeshoeken per hoekpunt. De veelhoeken die op de zeshoek volgen hebben alleen nog maar grotere hoeken. Hiermee kunnen dus ook geen regelmatige veelvlakken gevormd worden. 1
3 En zo is het bewijs geleverd dat er in 3 dimensies slecht 5 regelmatige veel-vlakken bestaan. (in het Grieks poly-ëder), de tetraëder, de kubus, de octaëder, de dodecaëder en de icosaëder. Het 4-vlak (Tetraëder) 3 driehoeken in elk hoekpunt Het 6-vlak (Hexaëder) 3 vierkanten in elk hoekpunt Het 8-vlak (Octaëder) 4 driehoeken in elk hoekpunt Het 12-vlak Dodecaëder) 3 vijfhoeken in elk hoekpunt Het 20-vlak) (Icosaëder 5 driehoeken in elk hoekpunt Dat worden de Platonische veelvlakken genoemd. De Platonische veelvlakken hebben altijd een grote fascinatie op de mens uitgeoefend. Er zijn allerlei magische eigenschappen aan toegedicht. Ze hebben model gestaan voor de vier elementen en het heelal. Kubus Tetraëder Dodecaëder Icosaëder Octaëder Aarde Vuur Heelal Water Lucht 2
4 II. De Archimedische lichamen Uit de 5 Platonische figuren kunnen we andere figuren maken door hoekpunten af te snijden. Neem een Octaëder Begin de hoeken af te zagen. Dan ontstaat de Afgeknotte Octaëder met in elk hoekpunt 2 zeshoeken en 1 vierhoek Ga door met verder afzagen Dan ontstaat de Cubo-Octaëder met in elk hoekpunt 2 driehoeken en 2 vierhoeken. Ga door met verder afzagen Dan ontstaat de Afgeknotte Kubus met in elk hoekpunt 2 achthoeken en 1 driehoek Er blijft een Kubus over. De kubus en de Octaëder zijn dus met elkaar verbonden. Door hoeken af te snijden ontstaat de ene uit de andere. 3
5 We hadden ook met een Dodecaëder kunnen beginnen. Neem een Dodecaëder Begin de hoeken af te zagen. Dan ontstaat de Afgeknotte Dodecaëder met in elk hoekpunt 2 tienhoeken en 1 driehoek Ga door met verder afzagen Dan ontstaat de Icosidodecaëder met in elk hoekpunt 2 vijfhoeken en 2 driehoeken Ga door met verder afzagen Dan ontstaat de Afgeknotte Icosaëder met in elk hoekpunt 1 vijfhoeken en 2 zeshoeken En uiteindelijk houden we een Icosaëder over. De Octaëder en de Icosaëder zijn dus ook met elkaar verbonden. Door hoeken af te snijden ontstaat de ene uit de andere. 4
6 Door de hoeken af te zagen, af te knotten ( Truncation ) ontstaan uit de 5 Platonische lichamen de 13 Archimedische lichamen. Afgeknotte Icosaëder Icosidodecaëder Kleine Romben- Icosidodecaëder Grote romben- Icosidodecaëder Afgeknotte Dodecaëder Afgeknotte Tetraëder Cubo-Octaëder Stompe Kubus Afgeknotte Kubus Grote romben Cubo-Octaëder Stompe Dodecaëder Afgeknotte Octaëder Romben Cubo- Octaëder De Afgeknotte Icosaëder) is ook beroemd geworden onder de naam Buckminsterfullerene of Buckyball, een nieuwe moleculaire vorm van koolstof C60. In 1996 is de Nobelprijs in scheikunde toegekend aan de ontdekkers van deze nieuwe chemische verbindingen. 5
7 III. De vierde dimensie Driedimensionale objecten kunnen wij zien. Tenminste, de voorkant ervan want écht het hele voorwerp zien kunnen we niet. Maar uit wat we zien aan de voorkant van bijvoorbeeld een kubus begrijpen we wel zo n beetje hoe de achterkant er uit ziet. Vierdimensionale voorwerpen kunnen wij helemaal niet zien. Wat is de vierde dimensie? Daar is eigenlijk geen antwoord op te geven. In de wiskunde is het makkelijk om te praten over 1 dimensie, zoals een lijn, twee dimensies zoals een vlak, drie dimensies zoals een kubus, en dan gewoon doorgaan met vier dimensies zoals een hyperkubus. En we kunnen gewoon doorgaan! Vijf dimensies, zes dimensies, in de wiskunde bestaan ze. In de natuurkunde zou je kunnen zeggen dat de tijd een vierde dimensie is. Maar de tegenwoordige natuurkunde gaat er van uit dat onze wereld zelfs 11 of 13 dimensies heeft. Dat is helemaal onvoorstelbaar. Vierdimensionale voorwerpen kunnen wij niet zien. Bestaat iets eigenlijk wel als je het niet kunt zien of kunt voorstellen? Toen we nog als jagers rondtrokken telden we onze vangst: Vandaag 5 herten en 3 everzwijnen. Daar kon je mee thuiskomen. Iedereen kon zich daar veel bij voorstellen. Maar je was gek als je zei dat je daarvan 6 herten en 4 everzwijnen ging weggeven. Dat kon niet, dan hield je minder dan niets over, bij een negatief getal kon niemand zich iets voorstellen. Maar tegenwoordig vinden we het heel gewoon dat het 2 boven nul is en dat het s nachts nog 5 graden kouder zal worden. Dan wordt het die nacht -3. We zijn er helemaal aan gewend geraakt om met negatieve getallen te rekenen. Ook al kunnen we nooit 3 everzwijnen vangen! En pizza s kunnen we prima in tweeën of in drieën verdelen. Dan krijgt iedereen een 1 of 1 pizza. 2 3 Breuken zoals 1 en 1 konden de Babyloniërs 3000 jaar geleden al bij elkaar optellen = Maar de Grieken schrokken wel toen ze ontdekten dat de lengte van de diagonaal van een vierkant tussen de 7 en ligt maar dat er geen enkele breuk is die précies overeenkomt met die lengte. Die lengte is een vreemd getal. Het is geen heel getal, het is geen breuk, het is een nieuw soort getal en we noemen het de wortel uit 2 Ook dit getal kunnen we nooit zien, we kunnen het ons niet goed voorstellen, het is ongeveer 1, maar je kunt altijd nóg meer cijfers achter de komma opschrijven. Voorstellen kan je zo n getal niet maar er over nadenken kan wél! Als je het met zichzelf vermenigvuldigd bijvoorbeeld komt er 2 uit! En zo is het ook met de vierde dimensie. Zien kunnen we die niet maar er over denken kan wel! 6
8 IV. De hyperkubus en de Simplex Hoe kun je het dan wél voorstellen? Door analogie ofte wel door te kijken naar de overeenkomst. De 0 e dimensie is een punt. Als we dat punt oppakken en buiten die 0 e dimensie plaatsen en met het oorspronkelijke punt verbinden krijgen we een lijn. Die is 1-dimensionaal. Als we nu die lijn oppakken en buiten die 1 e dimensie plaatsen en met de oorspronkelijke eindpunten verbinden krijgen we een vlak. Dat is 2-dimensionaal Als we nu dat vlak oppakken en buiten die 2 e dimensie plaatsen en weer de nieuwe hoekpunten met de oorspronkelijke punten verbinden krijgen we een cel n.l. de kubus. Die is 3-dimensionaal. En als we de kubus oppakken en buiten die 3 e dimensie plaatsen en weer de nieuwe hoekpunten met de oorspronkelijke punten verbinden krijgen we een hyperkubus of Tesseract en die is 4- dimensionaal.. Dimensie 0 Dimensie 1 Dimensie 2 Dimensie 3 Dimensie 4 Zíen kunnen we die niet, vóórstellen wel. De hyperkubus móet wel 16 hoekpunten hebben, 32 ribben, 24 vlakken en 8 cellen hebben. Op dezelfde manier kunnen we ook een andere vierdimensionale figuur bedenken. De 0 e dimensie is een punt. Als we dat punt oppakken en buiten die 0 e dimensie plaatsen en met het oorspronkelijke punt verbinden krijgen we een lijn. Die is 1-dimensionaal. Als we nu een punt buiten die 1 e dimensie plaatsen en met de oorspronkelijke eindpunten verbinden krijgen we een vlak, een driehoek. Dat is 2-dimensionaal Als we nu een punt buiten die 2 e dimensie plaatsen en verbinden met de vorige drie krijgen we een cel n.l. de tetraëder. Die is 3-dimensionaal. En als we dit voortzetten krijgen we de vierdimensionale tetraëder, de Simplex of Pentachoron.. Dimensie 0 Dimensie 1 Dimensie 2 Dimensie 3 Dimensie 4 7
9 V. De zes 4-dimensionale Platonische objecten. In vier dimensies bestaan er nog meer regelmatige figuren. En ook die kunnen we ons een beetje voorstellen door te kijken naar analogie. De 5 Platonische lichamen maakten we door na te gaan hoeveel driehoeken, vierkanten, vijfhoeken en zeshoeken er rond een punt passen. - Drie driehoeken in een hoekpunt geeft de tetraëder. - Vier driehoeken in een hoekpunt geeft de octaëder. - Vijf driehoeken in een hoekpunt geeft de icosaëder. - Drie vierhoeken in een hoekpunt geeft de kubus - Drie vijfhoeken in een hoekpunt geeft de dodecaëder. Deze manier om figuren te maken kunnen we ook in vier-dimensies doen door na te gaan hoeveel en welk type cel rond een ribbe past. Er blijken dan 6 regelmatige vierdimensionale objecten te bestaan. Ze werden ontdekt door de Zwitserse wiskundige Ludwig Schläfli rond Drie tetraëders rond een ribbe geeft de 5-cel, de penta-choron, ook wel Simplex genoemd. - Drie kubussen rond een ribbe geeft de 8-cel, ook wel Hyperkubus genoemd. - Vier tetraëder rond een ribbe geeft de 16-cel, de hexadeca-choron, ook wel Kruisfiguur genoemd. - Drie octaëders rond een ribbe geeft de 24-cel, de icositetra-choron - Drie dodecaëders rond een ribbe geeft de 120-cel, de hecatonicosa-choron - Vijf tetraëders rond een ribbe geeft de 600-cel, de hexacosi-choron De zes 4-dimensionale lichamen en hun eigenschappen Naam Rond een ribbe: Vlakken Ribben Hoeken 5-cel Pentachoron 3 Tetraëders 10 driehoeken cel Hexadecachoron 4 Tetraëders 32 driehoeken cel Hexacosichoron 5 Tetraëders 1200 driehoeken cel Tesseract (Hyperkubus) 3 Kubussen 24 vierkanten cel Icositetrachoron 3 Octaëders 96 driehoeken cel Hecatonicosachoron 3 Dodecaëders 720 vijfhoeken Icosaëders Vooral de 120 cel en de 600 cel zijn spectaculair! Een simpele Hyperkubus heeft 8 cellen en 16 hoekpunten. Maar zo n 120-cel heeft maar liefst 600 hoekpunten! Als we naar ruimtes gaan kijken met 5 of meer dimensies, vinden we dat er telkens maar 3 regelmatige veelvlakken zijn. De eerste is de Simplex in hogere dimensies. Deze heeft n+1 hoekpunten waarbij n het aantal dimensies voorstelt. Het tweede regelmatige veelvlak is de Kubus. Deze heeft altijd 2n hoekpunten. Het derde regelmatige veelvlak is de 16-cel in hogere dimensies. Méér zijn er niet. De spannendste en rijkste dimensie is dus de vierde dimensie! Het wordt alleen maar simpeler naarmate je dimensies toevoegt! 8
10 VI. Centraal Projectie van vierdimensionale objecten. Eén van de manieren om een vierdimensionaal object toch te kunnen zien is door het te projecteren. Als we een kubus zouden willen laten zien aan een Platlander, een wezen dat alleen maar in twee kan waarnemen, dan zouden we een kubus tekenen op papier. We tekenen dan een projectie. Een kubus kan op verschillende manieren en vanuit verschillende hoeken geprojecteerd worden. Projectie met 3 verdwijnpunten Projectie met 2 verdwijnpunten Projectie met 1 verdwijnpunt (Centrale projectie) In Centrale projectie zien we een driedimensionale kubus geprojecteerd in twee dimensies als één centraal viervlak met daaromheen 4 afgeplatte viervlakken. Als we nu een vierdimensionale Hyperkubus in Centrale projectie afbeelden in onze driedimensionale wereld dan zien we een centrale kubus en daar omheen afgeplatte kubussen. 9
11 En als we een driedimensionale Dodecaëder willen laten zien aan een Platlander, zouden we door Centraal projectie in twee dimensies een vijfhoek zien met daaromheen 5 afgeplatte vijfhoeken. En precies zó zien we van een vierdimensionale 120-cel in Centrale projectie in drie dimensies eerst één centrale dodecaëder, daaromheen een laag van 12 dodecaëders, daaromheen een derde laag van 20 steeds sterker afgeplatte dodecaëders, een vierde laag van 12 bijna platte en een laatste laag van 30 dodecaëders die nu helemaal plat zijn. Laag1= 1 cel Laag 1+2= 13 cellen Laag 1+2+3= 33 cellen Laag = 45 cellen Laag = 75 cellen En na de buitenste laag gaat de projectie eigenlijk verder maar nu weer naar binnen. Laag 1 t/m 6 heeft 87 cellen, 1 t/m cellen, laag 1 t/m cellen en met de allerlaatste centrale cel komen we op 120 cellen. VII. De halfregelmatige vierdimensionale objecten. De 6 regelmatige vierdimensionale objecten zijn uit regelmatige driedimensionale cellen opgebouwd. De tetraëder, de kubus, de octaëder en de dodecaëder. Maar we kunnen van afgeknotte driedimensionale of algemener van half-regelmatige cellen uitgaan. Toen men dit eenmaal begreep in 1880 ontstond een wedloop wie als eerste alle half-regelmatige lichamen zou beschrijven. Die zoektocht gaat nog steeds door! Op dit moment zijn er 1849 vierdimensionale polychoron s bekend! Ze hebben de meest fantastische namen zoals Afgeknotte Pentachoron en Dubbel Afgeknotte Hyperkubus. Eén van de mooiste objecten is de Afgeknotte Icosahedrische prismatohexacosihecatonicosachoron of te wel de Cantitruncated 600 cel. Dit vierdimensionale object bestaat uit 120 afgeknotte icosaëders, 600 afgeknotte octaëders en 720 tienhoekige prisma s. Het telt 3600 vierkanten, 1440 vijfhoeken en 3600 zeshoeken. Het heeft ribben en 7200 vlakken. Er zijn onderdelen nodig! 1860 blauwe staafjes, 2400 gele staafjes, 2880 rode staafjes en 3660 witte kogels. 10
12 VIII. Opbouw: van de Cantitruncated 600 cel Centrale unit: 1 afgeknotte icosaëder 12 enigszins in elkaar gedrukte afgeknotte icosaëders 20 sterker in elkaar gedrukte afgeknotte icosaëders 12 bijna plat gedrukte afgeknotte dodecaëders 30 volledig platgedrukte afgeknotte icosaëders 11
13 IX. Geschiedenis van ontdekking Regelmatige convexe polytopen: 1852: Ludwig Schläfli bewees in zijn manuscript Theorie der vielfachen Kontinuität dat er precies 6 regelmatige polytopen in 4 dimensies bestaan en slechts 3 in 5 of meer dimensies. Regelmatige ster-polychora 1852: Ludwig Schläfli vond ook 4 van de 10 regelmatige sterpolychora, 1883: Edmund Hess voltooide de lijst van 10 niet-convexe regelmatige polychora. Half-regelmatige convexe polytopen 1900: Thorold Gosset stelde de lijst op van nonprismatische halfregelmatige convexe polytopen op. Convexe eenvormige polytopes: 1910: Alicia Boole Stott breidde in haar publicatie Meetkundige deductie van halfregelmatige polytopen de definitie uit door ook 4 dimensionale Archimedische polychora toe te staan. Zij had een uitzonderlijk vermogen om zich deze objecten voor te stellen. Zij introduceerde in 1910 het woord Polytoop en werkte samen met H.S.M. Coxeter. 1940: Het onderzoek werd uitgebreid door systematisch onderzoek van H.S.M. Coxeter in zijn publikatie Regelmatige en semi-regelmatige Polytopen. Convexe eenvormige polychora: 1965: De volledige lijst van convexe vormen werd definitief voltooid door John Horton Conway en Michael J.T. Kerel 1997: Een volledige opsomming van de namen en de elementen van convexe eenvormige polychora werd on-line gegeven door George Olshevsky 2004: Een bewijs dat de Conway-Kerel reeks volledig is werd gepubliceerd door Marco Möller in zijn verhandeling, Vierdimensionale Archimedische Polytope (in het Duits). De mogelijkheden om zulke polytopen af te beelden bleven beperkt. Door Paul S. Donchian werden in de jaren 30 enkele wireframes vervaardigd. In 1992 kwam het constructiesysteem Zometool op de markt. Door het 31-gaten systeem met slim gekozen hoeken en lengteverhoudingen (Gulden Snede!) bleek het mogelijk om Centraal Projecties te bouwen van alle 15 H4 polytopen
Een Rombicosidodecahedrische diprismatohexacosihecatonicosachoron op het Kottenpark
 Een Rombicosidodecahedrische diprismatohexacosihecatonicosachoron op het Kottenpark Deze Rombicosidodecahedrische diprismatohexacosihecatonicosachoron werd op 5 februari 2011 gebouwd door: Ninouk Akkerman,
Een Rombicosidodecahedrische diprismatohexacosihecatonicosachoron op het Kottenpark Deze Rombicosidodecahedrische diprismatohexacosihecatonicosachoron werd op 5 februari 2011 gebouwd door: Ninouk Akkerman,
Afgeknotte dodecahedrische diprismatohexacosihecatonicosachoron
 Afgeknotte dodecahedrische diprismatohexacosihecatonicosachoron Deze Afgeknotte dodecahedrische diprismatohexacosihecatonicosachoron werd op 3 en 4 februari 2012 gebouwd door: Jeffrey Hubert, Gijs Beernink,
Afgeknotte dodecahedrische diprismatohexacosihecatonicosachoron Deze Afgeknotte dodecahedrische diprismatohexacosihecatonicosachoron werd op 3 en 4 februari 2012 gebouwd door: Jeffrey Hubert, Gijs Beernink,
Een hecatonicosachoron op het Kottenpark
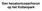 Een hecatonicosachoron op het Kottenpark Afgeknotte Hecatonicosachoron Deze schaduw van deze 4-dimensionale polytoop bestaat uit 120 afgeknotte dodecaëders en 600 tetraëders Gebouwd op 30 januari 2010
Een hecatonicosachoron op het Kottenpark Afgeknotte Hecatonicosachoron Deze schaduw van deze 4-dimensionale polytoop bestaat uit 120 afgeknotte dodecaëders en 600 tetraëders Gebouwd op 30 januari 2010
Veelvlak. Begrippenlijst
 Veelvlakken Tijdens dit project Veelvlakken ga je vooral veel zelf onderzoeken. Je zult veel aan het bouwen zijn met Polydron materiaal. Waarschijnlijk zul je naar aanleiding van je bevindingen zelf vragen
Veelvlakken Tijdens dit project Veelvlakken ga je vooral veel zelf onderzoeken. Je zult veel aan het bouwen zijn met Polydron materiaal. Waarschijnlijk zul je naar aanleiding van je bevindingen zelf vragen
Een ander zijvlak is het regelmatige vijfhoek met aantal zijden P=5. Hierbij moeten Q=3 zijvlakken samenkomen in een hoekpunt van het veelvlak.
 Praktische-opdracht door een scholier 1498 woorden 6 juni 2003 6,5 134 keer beoordeeld Vak Wiskunde Deelvraag 1: Wat is de definitie van een Platonische Lichaam / Platonisch Veelvlak? De definitie: Een
Praktische-opdracht door een scholier 1498 woorden 6 juni 2003 6,5 134 keer beoordeeld Vak Wiskunde Deelvraag 1: Wat is de definitie van een Platonische Lichaam / Platonisch Veelvlak? De definitie: Een
de Leuke En Uitdagende Wiskunde VEELVLAKKEN SAMENSTELLING: H. de Leuw
 SAMENSTELLING: H. de Leuw 1. VEELHOEKEN. Een veelvlak is een lichaam dat wordt begrensd door vlakke veelhoeken. Zo zijn balken en piramides wel veelvlakken, maar cilinders en bollen niet. Een veelhoek
SAMENSTELLING: H. de Leuw 1. VEELHOEKEN. Een veelvlak is een lichaam dat wordt begrensd door vlakke veelhoeken. Zo zijn balken en piramides wel veelvlakken, maar cilinders en bollen niet. Een veelhoek
Regelmatige en halfregelmatige veelvlakken
 Regelmatige en halfregelmatige veelvlakken Wiskunde & Cultuur 2-3 W.v.Ravenstein 2010-2011 aangepast Vandaag Platonische lichamen Regelmatig, halfregelmatig en andere naamgeving Waarom zijn er maar 5 Platonische
Regelmatige en halfregelmatige veelvlakken Wiskunde & Cultuur 2-3 W.v.Ravenstein 2010-2011 aangepast Vandaag Platonische lichamen Regelmatig, halfregelmatig en andere naamgeving Waarom zijn er maar 5 Platonische
Dimensies. een ruimtelijke tocht langs onbekende assen. Anne Lotte van der Kooi Jesse Krijthe Roderik Vogels Onder begeleiding van Aad Goddijn
 Dimensies een ruimtelijke tocht langs onbekende assen Anne Lotte van der Kooi Jesse Krijthe Roderik Vogels Onder begeleiding van Aad Goddijn Junior College Utrecht, Januari 7 Inhoud. Abstract.... Inleiding...5.
Dimensies een ruimtelijke tocht langs onbekende assen Anne Lotte van der Kooi Jesse Krijthe Roderik Vogels Onder begeleiding van Aad Goddijn Junior College Utrecht, Januari 7 Inhoud. Abstract.... Inleiding...5.
Platonische lichamen en andere reguliere polytopen
 Platonische lichamen en andere reguliere polytopen Bernd Souvignier Voorjaar 005 Inhoud De platonische lichamen. Reguliere veelhoeken.......................... Reguliere veelvlakken.........................
Platonische lichamen en andere reguliere polytopen Bernd Souvignier Voorjaar 005 Inhoud De platonische lichamen. Reguliere veelhoeken.......................... Reguliere veelvlakken.........................
Escher in Het Paleis. Wiskundepakket. Ruimtelijke figuren
 Escher in Het Paleis Wiskundepakket Ruimtelijke figuren Ruimtelijke figuren Escher maakt in EEN AANTAL prenten gebruik van wiskundig interessante ruimtelijke vormen, zoals Platonische lichamen en Möbiusbanden.
Escher in Het Paleis Wiskundepakket Ruimtelijke figuren Ruimtelijke figuren Escher maakt in EEN AANTAL prenten gebruik van wiskundig interessante ruimtelijke vormen, zoals Platonische lichamen en Möbiusbanden.
Caspar Bontenbal april 2015 WISKUNDE & KUNST. Eindverslag
 Caspar Bontenbal 0903785 24 april 2015 WISKUNDE & KUNST Eindverslag Table of Contents Les 1 - Introductie wiskunde & kunst... 2 Opdracht 1.1... 2 Opdracht 1.2... 2 Les 2 - Wiskunde met Verve bloemlezing
Caspar Bontenbal 0903785 24 april 2015 WISKUNDE & KUNST Eindverslag Table of Contents Les 1 - Introductie wiskunde & kunst... 2 Opdracht 1.1... 2 Opdracht 1.2... 2 Les 2 - Wiskunde met Verve bloemlezing
Handig met getallen 4 (HMG4), onderdeel Meetkunde
 Handig met getallen 4 (HMG4), onderdeel Meetkunde Erratum Meetkunde Je vindt hier de correcties voor Handig met getallen 4 (ISBN: 978 94 90681 005). Deze correcties zijn ook bedoeld voor het Rekenwerkboek
Handig met getallen 4 (HMG4), onderdeel Meetkunde Erratum Meetkunde Je vindt hier de correcties voor Handig met getallen 4 (ISBN: 978 94 90681 005). Deze correcties zijn ook bedoeld voor het Rekenwerkboek
Regelmaat in de ruimte
 Regelmaat in de ruimte . Regelmaat in de ruimte A.K. van der Vegt VSSD iv VSSD Eerste druk 1991, tweede druk 2002 Uitgave van: VSSD Leeghwaterstraat 42, 2628 CA Delft, The Netherlands tel. +31 15 27 82124,
Regelmaat in de ruimte . Regelmaat in de ruimte A.K. van der Vegt VSSD iv VSSD Eerste druk 1991, tweede druk 2002 Uitgave van: VSSD Leeghwaterstraat 42, 2628 CA Delft, The Netherlands tel. +31 15 27 82124,
Kernbegrippen Kennisbasis wiskunde Onderdeel meetkunde
 Kernbegrippen Kennisbasis wiskunde Onderdeel meetkunde Aanzicht Een ruimtelijk figuur kun je van verschillende kanten bekijken, je noemt dat aanzichten. Er zijn 5 aanzichten: Vooraanzicht (van voren).
Kernbegrippen Kennisbasis wiskunde Onderdeel meetkunde Aanzicht Een ruimtelijk figuur kun je van verschillende kanten bekijken, je noemt dat aanzichten. Er zijn 5 aanzichten: Vooraanzicht (van voren).
Figuur 3 PYTHAGORAS SEPTEMBER 2016
 In het juninummer zagen we hoe we met behulp van de piramidemethode en invarianten ruimtelijke figuren binnenstebuiten kunnen keren. Aan de invarianten stelden we voorwaarden, zoals dat alle vlakken zoveel
In het juninummer zagen we hoe we met behulp van de piramidemethode en invarianten ruimtelijke figuren binnenstebuiten kunnen keren. Aan de invarianten stelden we voorwaarden, zoals dat alle vlakken zoveel
Bouwen met veelhoeken
 Bouwen met veelhoeken Opdrachtbladen Jantine Bloemhof Inhoud De vormen........................ 1 Veelhoeken samenvoegen: van klein naar groot........... 2 Tegelpatronen....................... 6 Platonische
Bouwen met veelhoeken Opdrachtbladen Jantine Bloemhof Inhoud De vormen........................ 1 Veelhoeken samenvoegen: van klein naar groot........... 2 Tegelpatronen....................... 6 Platonische
Halve regelmaat (Archimedische of uniforme veelvlakken)
 30 3 Halve regelmaat (Archimedische of uniforme veelvlakken) 3.1. Algemeen In hoofdstuk 1 is de definitie van half-regelmatige of uniforme, ook Archimedische veelvlakken genoemd, al gegeven. Het zijn veelvlakken
30 3 Halve regelmaat (Archimedische of uniforme veelvlakken) 3.1. Algemeen In hoofdstuk 1 is de definitie van half-regelmatige of uniforme, ook Archimedische veelvlakken genoemd, al gegeven. Het zijn veelvlakken
Platonische transformatiegroepen
 Platonische transformatiegroepen Luc Van den Broeck 8 augustus 2015 Samenvatting In dit document worden de transformatiegroepen van de platonische lichamen bestudeerd. Zonder te vervallen in algebraïsche
Platonische transformatiegroepen Luc Van den Broeck 8 augustus 2015 Samenvatting In dit document worden de transformatiegroepen van de platonische lichamen bestudeerd. Zonder te vervallen in algebraïsche
Veelvlakken kleuren. Dion Gijswijt
 Stel, je wilt de zijvlakken van een veelvlak kleuren, en wel zo dat aangrenzende veelvlakken verschillende kleur krijgen. Hoeveel kleuren heb je dan minimaal nodig? Veelvlakken kleuren Dion Gijswijt De
Stel, je wilt de zijvlakken van een veelvlak kleuren, en wel zo dat aangrenzende veelvlakken verschillende kleur krijgen. Hoeveel kleuren heb je dan minimaal nodig? Veelvlakken kleuren Dion Gijswijt De
V el v'akk n kl ure. door Dion Gijswijt
 door Dion Gijswijt V el v'akk n kl ure Stel, je wilt de zijvlakken van een veelvlak kleuren, en wel zo dat aangrenzende veelvlakken verschillende kleur krijgen. Hoeveel kleuren heb je dan minimaal nodig?
door Dion Gijswijt V el v'akk n kl ure Stel, je wilt de zijvlakken van een veelvlak kleuren, en wel zo dat aangrenzende veelvlakken verschillende kleur krijgen. Hoeveel kleuren heb je dan minimaal nodig?
http://www.kidzlab.nl/index2.php?option=com_content&task=vi...
 Veelvlakken De perfecte vorm Plato was een grote denker in de tijd van de Oude Grieken. Hij was een van de eerste die de regelmatige veelvlakken heel bijzonder vond. Hij hield ervan omdat ze zulke mooie,
Veelvlakken De perfecte vorm Plato was een grote denker in de tijd van de Oude Grieken. Hij was een van de eerste die de regelmatige veelvlakken heel bijzonder vond. Hij hield ervan omdat ze zulke mooie,
Herhalingsles 2 Meetkunde 1 Weeroefeningen
 Herhalingsles Meetkunde Weeroefeningen HB. MK Kruis aan wat juist is. Deze figuur is een vierhoek, maar geen vierkant. een vierkant, maar geen ruit. een ruit, maar geen vierkant. een vierkant en een ruit.
Herhalingsles Meetkunde Weeroefeningen HB. MK Kruis aan wat juist is. Deze figuur is een vierhoek, maar geen vierkant. een vierkant, maar geen ruit. een ruit, maar geen vierkant. een vierkant en een ruit.
Les 2 Hoekpunten, ribben, vlakken
 ONTDEKKINGSTOCHT 2 Aanvullend op het artikel van Stephan Berendonk en Leon van den Broek hierbij het bijbehorende lesmateriaal. In dit document vindt u eerst het leelingmateriaal en verderop het materiaal
ONTDEKKINGSTOCHT 2 Aanvullend op het artikel van Stephan Berendonk en Leon van den Broek hierbij het bijbehorende lesmateriaal. In dit document vindt u eerst het leelingmateriaal en verderop het materiaal
Ruimte en tijd: overzicht
 Overzicht Contents 1 Inleiding 1 2 De klassieke ruimte 2 3 Klassieke mechanica 5 4 Hyperbolische meetkunde 7 5 Gekromde ruimten 11 6 De vierde dimensie 13 7 Ruimte en tijd in de moderne fysica 16 1 Inleiding
Overzicht Contents 1 Inleiding 1 2 De klassieke ruimte 2 3 Klassieke mechanica 5 4 Hyperbolische meetkunde 7 5 Gekromde ruimten 11 6 De vierde dimensie 13 7 Ruimte en tijd in de moderne fysica 16 1 Inleiding
De formule van Euler voor veelvlakken
 mc.vanhoorn@wxs.nl 1 Inhoudsopgave I. Verklaring van letters II. De formule III. Het bereik van de formule IV. Leonhard Euler V. Hoe bewijs je de geldigheid van de formule? VI. Regelmatige vlakvullingen
mc.vanhoorn@wxs.nl 1 Inhoudsopgave I. Verklaring van letters II. De formule III. Het bereik van de formule IV. Leonhard Euler V. Hoe bewijs je de geldigheid van de formule? VI. Regelmatige vlakvullingen
Bij de volgende vragen Bij een regelmatige veelhoek kun je het gemakkelijkst eerst de buitenhoeken berekenen en daarna pas de binnenhoeken.
 Rood-wit-blauw werkblad 1 Bij het hele werkblad: Alle rode getallen zijn deelbaar door hetzelfde getal. Elk wit getal is gelijk aan een rood getal + 1, elk blauw getal aan een rood getal + 2 Russisch vermenigvuldigen
Rood-wit-blauw werkblad 1 Bij het hele werkblad: Alle rode getallen zijn deelbaar door hetzelfde getal. Elk wit getal is gelijk aan een rood getal + 1, elk blauw getal aan een rood getal + 2 Russisch vermenigvuldigen
Diktaat Concrete Meetkunde Veelvlakken en alles wat daarbij komt kijken...
 Diktaat Concrete Meetkunde Veelvlakken en alles wat daarbij komt kijken... Anieke Brombacher 3230589 Auke Mollema 3233626 Patrick van Stiphout 3223604 24 april 2009 1 Inhoudsopgave 1 Inleiding 3 2 Regelmatige
Diktaat Concrete Meetkunde Veelvlakken en alles wat daarbij komt kijken... Anieke Brombacher 3230589 Auke Mollema 3233626 Patrick van Stiphout 3223604 24 april 2009 1 Inhoudsopgave 1 Inleiding 3 2 Regelmatige
Beeldende kunst PYTHAGORAS JUNI 2008
 wiskunde en kunst Beeldende kunst Sinds computers kleurenplaten van fractals kunnen maken, heeft iedereen op z n minst enig idee wat wiskundigen bedoelen met de schoonheid van hun vak. Ook sommige kunstenaars
wiskunde en kunst Beeldende kunst Sinds computers kleurenplaten van fractals kunnen maken, heeft iedereen op z n minst enig idee wat wiskundigen bedoelen met de schoonheid van hun vak. Ook sommige kunstenaars
2. Antwoorden meetkunde
 2. Antwoorden meetkunde In dit hoofdstuk zijn de antwoorden op de opgaven over Meetkunde opgenomen. Ze zijn kort en bondig per paragraaf gerangschikt. Dat betekent dat de antwoorden geen uitgebreide uitleg
2. Antwoorden meetkunde In dit hoofdstuk zijn de antwoorden op de opgaven over Meetkunde opgenomen. Ze zijn kort en bondig per paragraaf gerangschikt. Dat betekent dat de antwoorden geen uitgebreide uitleg
Uitwerkingen oefeningen hoofdstuk 4
 Uitwerkingen oefeningen hoofdstuk 4 4.4.1 Basis Lijnen en hoeken 1 Het assenstelsel met genoemde lijnen ziet er als volgt uit: 4 3 2 1 l k -4-3 -2-1 0 1 2 3 4-1 -2-3 n m -4 - Hieruit volgt: a Lijn k en
Uitwerkingen oefeningen hoofdstuk 4 4.4.1 Basis Lijnen en hoeken 1 Het assenstelsel met genoemde lijnen ziet er als volgt uit: 4 3 2 1 l k -4-3 -2-1 0 1 2 3 4-1 -2-3 n m -4 - Hieruit volgt: a Lijn k en
Fractale dimensie. Eline Sommereyns 6wwIi nr.9
 Fractale dimensie Eline Sommereyns 6wwIi nr.9 Inhoudstabel Inleiding... 3 Gehele dimensie... 4 Begrip dimensie... 4 Lengte, breedte, hoogte... 4 Tijd-ruimte... 4 Fractale dimensie... 5 Fractalen... 5 Wat?...
Fractale dimensie Eline Sommereyns 6wwIi nr.9 Inhoudstabel Inleiding... 3 Gehele dimensie... 4 Begrip dimensie... 4 Lengte, breedte, hoogte... 4 Tijd-ruimte... 4 Fractale dimensie... 5 Fractalen... 5 Wat?...
Steekkaart: nummer 5W
 Steekkaart: nummer 5W Onderwerp Ruimtefiguren herkennen in voorwerpen in de klas en hun eigenschappen benoemen Leeftijd/Doelgroep 5 e leerjaar Leergebied Wiskunde Organisatie Tijdsduur 50 minuten Beschrijving
Steekkaart: nummer 5W Onderwerp Ruimtefiguren herkennen in voorwerpen in de klas en hun eigenschappen benoemen Leeftijd/Doelgroep 5 e leerjaar Leergebied Wiskunde Organisatie Tijdsduur 50 minuten Beschrijving
WISKUNDE-ESTAFETTE Minuten voor 20 opgaven. Het totaal aantal te behalen punten is 500
 WISKUNDE-ESTFETTE 2014 60 Minuten voor 20 opgaven. Het totaal aantal te behalen punten is 00 1 (20 punten) Gegeven zijn drie aan elkaar rakende cirkels met straal 1. Hoe groot is de (donkergrijze) oppervlakte
WISKUNDE-ESTFETTE 2014 60 Minuten voor 20 opgaven. Het totaal aantal te behalen punten is 00 1 (20 punten) Gegeven zijn drie aan elkaar rakende cirkels met straal 1. Hoe groot is de (donkergrijze) oppervlakte
DE VIJFVOUDIGE OCTAEDER
 V DE VIJFVOUDIGE OCTAEDER Aan de buitenzijde van de dodecaëder zijn niet alleen de hoekpunten van een vijftal kubussen te zien, doch ook hun ribben. Van de bijbehorende 10 tetraëders echter, zien we nog
V DE VIJFVOUDIGE OCTAEDER Aan de buitenzijde van de dodecaëder zijn niet alleen de hoekpunten van een vijftal kubussen te zien, doch ook hun ribben. Van de bijbehorende 10 tetraëders echter, zien we nog
[Deze tekst komt ongeveer overeen met hoofdstukken 1 en 2 van het boekje Regelmaat in de Ruimte door A. K. van der Vegt]
![[Deze tekst komt ongeveer overeen met hoofdstukken 1 en 2 van het boekje Regelmaat in de Ruimte door A. K. van der Vegt] [Deze tekst komt ongeveer overeen met hoofdstukken 1 en 2 van het boekje Regelmaat in de Ruimte door A. K. van der Vegt]](/thumbs/50/26139651.jpg) [Deze tekst komt ongeveer overeen met hoofdstukken 1 en 2 van het boekje Regelmaat in de Ruimte door A. K. van der Vegt] Inleiding 1.1. Waar gaat het over? Vraag je aan iemand om een veelvlak te noemen,
[Deze tekst komt ongeveer overeen met hoofdstukken 1 en 2 van het boekje Regelmaat in de Ruimte door A. K. van der Vegt] Inleiding 1.1. Waar gaat het over? Vraag je aan iemand om een veelvlak te noemen,
Een les wiskunde: hoe Kepler naar de wereld keek (voorbeeldles voortgezet onderwijs)
 Een les wiskunde: hoe Kepler naar de wereld keek (voorbeeldles voortgezet onderwijs) Ab van der Roest Dit materiaal is onderdeel van het compendium christelijk leraarschap dat samengesteld is door het
Een les wiskunde: hoe Kepler naar de wereld keek (voorbeeldles voortgezet onderwijs) Ab van der Roest Dit materiaal is onderdeel van het compendium christelijk leraarschap dat samengesteld is door het
Wiskunde. Hoofdstuk 1 en hoofdstuk 5, paragraaf 5.1, 5.2 en 5.3 kennen en kunnen.
 Toetsstof In de toets weken moet je dit kunnen toepassen Hoofdstuk 1 en hoofdstuk 5, paragraaf 5.1, 5.2 en 5.3 kennen en kunnen. Periodetaak Maak een mooie mandala met passer en kleur hem leuk in. Ga naar
Toetsstof In de toets weken moet je dit kunnen toepassen Hoofdstuk 1 en hoofdstuk 5, paragraaf 5.1, 5.2 en 5.3 kennen en kunnen. Periodetaak Maak een mooie mandala met passer en kleur hem leuk in. Ga naar
Niet-euclidische meetkunde
 Keuzeonderdeel Wiskunde D Hans van Ballegooij Maaslandcollege, Oss Dictaat Versie: 20 februari 2013 Hans van Ballegooij Maaslandcollege Oss Inhoudsopgave 1 De elementen van Euclides 1 2 Niet-euclidische
Keuzeonderdeel Wiskunde D Hans van Ballegooij Maaslandcollege, Oss Dictaat Versie: 20 februari 2013 Hans van Ballegooij Maaslandcollege Oss Inhoudsopgave 1 De elementen van Euclides 1 2 Niet-euclidische
Het leek ons wel een interessante opdracht, een uitdaging en een leuke aanvulling bij het hoofdstuk.
 Praktische-opdracht door een scholier 2910 woorden 3 mei 2000 5,2 46 keer beoordeeld Vak Wiskunde Wiskunde A1 - Praktische Opdracht Hoofdstuk 2 1. Inleiding We hebben de opdracht gekregen een praktische
Praktische-opdracht door een scholier 2910 woorden 3 mei 2000 5,2 46 keer beoordeeld Vak Wiskunde Wiskunde A1 - Praktische Opdracht Hoofdstuk 2 1. Inleiding We hebben de opdracht gekregen een praktische
WISKUNDIG VOUWEN DE BUCKYBALL
 WISKUNDIG VOUWEN DE BUCKYBALL Wiskundig vouwen voor beginners Vaak wordt papiervouwen (origami) door mensen afgedaan als suf en zinloos. Het ziet er op zich best mooi uit, maar het blijft tenslotte toch
WISKUNDIG VOUWEN DE BUCKYBALL Wiskundig vouwen voor beginners Vaak wordt papiervouwen (origami) door mensen afgedaan als suf en zinloos. Het ziet er op zich best mooi uit, maar het blijft tenslotte toch
5 De ruimte in = 10 kogels. A = 56 kogels M M N. 11 cm 11 cm. 1 : cm. 2 cm 2 cm. 3 cm. even lang!
 31 32 1 2 5 e ruimte in 1 + 3 + 6 = 10 kogels N M M N A 1 + 36 + 10 + 15 + 21 = 56 kogels 11 cm 11 cm 1 : 150 4 cm 2 cm 2 cm 3 cm vooraanzicht bovenaanzicht even lang! vijfzijdig prisma wit Buitendiagonalen:
31 32 1 2 5 e ruimte in 1 + 3 + 6 = 10 kogels N M M N A 1 + 36 + 10 + 15 + 21 = 56 kogels 11 cm 11 cm 1 : 150 4 cm 2 cm 2 cm 3 cm vooraanzicht bovenaanzicht even lang! vijfzijdig prisma wit Buitendiagonalen:
Bij een pv kan men origineel en beeld continu in elkaar overvoeren. De `oriëntatie' blijft hierbij behouden. Er zijn dus twee soorten gt's: De directe
 Lesbrief 9 Meetkunde II 1 Puntvermenigvuldigingen Definitie 1.1 Een transformatie G van het vlak heet een gelijkvormigheidstransformatie (verder afgekort als gt) als er een constante f > 0 bestaat zo,
Lesbrief 9 Meetkunde II 1 Puntvermenigvuldigingen Definitie 1.1 Een transformatie G van het vlak heet een gelijkvormigheidstransformatie (verder afgekort als gt) als er een constante f > 0 bestaat zo,
By Tom Straub, : het visitekaartje van Jezus Christus een wiskundeboekje voor jonge denkers
 By Tom Straub, 1984 153: het visitekaartje van Jezus Christus De rij der rijen De sleutel tot het vinden van de rij der rijen is te vinden achterin het evangelie van Johannes, waarin wordt gesproken over
By Tom Straub, 1984 153: het visitekaartje van Jezus Christus De rij der rijen De sleutel tot het vinden van de rij der rijen is te vinden achterin het evangelie van Johannes, waarin wordt gesproken over
Voetbal(len) in de wiskundeles
 Voetbal(len) in de wiskundeles Item 1 --- Shot op doel Opdracht : a) figuur links boven (keeper op midden van de doellijn) Welke speler (B of D) maakt de grootste kans om te scoren? b) figuur rechtsboven
Voetbal(len) in de wiskundeles Item 1 --- Shot op doel Opdracht : a) figuur links boven (keeper op midden van de doellijn) Welke speler (B of D) maakt de grootste kans om te scoren? b) figuur rechtsboven
WETENSCHAPPEN oefeningen perspectief OEFENING 5. Arnout Van Vaerenbergh
 WETENSCHAPPEN oefeningen perspectief OEFENING 5 Arnout Van Vaerenbergh vorige oefening: 1/ contextsimulatie - Muziekles van Vermeer 2/ exacte input - objecten tekenen in perspectief 3/ exacte output -
WETENSCHAPPEN oefeningen perspectief OEFENING 5 Arnout Van Vaerenbergh vorige oefening: 1/ contextsimulatie - Muziekles van Vermeer 2/ exacte input - objecten tekenen in perspectief 3/ exacte output -
1 Vlaamse Wiskunde Olympiade : Tweede Ronde.
 1 Vlaamse Wiskunde Olympiade 1996 1997: Tweede Ronde e tweede ronde bestaat eveneens uit 0 meerkeuzevragen Het quoteringssysteem werkt (opnieuw) als volgt : een deelnemer start met 0 punten Per goed antwoord
1 Vlaamse Wiskunde Olympiade 1996 1997: Tweede Ronde e tweede ronde bestaat eveneens uit 0 meerkeuzevragen Het quoteringssysteem werkt (opnieuw) als volgt : een deelnemer start met 0 punten Per goed antwoord
handleiding pagina s 434 tot Handleiding 1.2 Huistaken huistaak 12: bladzijde Werkboek
 week 13 les 5 toets en foutenanalyse handleiding pagina s 434 tot 443 nuttige informatie 1 Handleiding 1.1 Kopieerbladen pagina s 374 en 375: vierhoeken pagina 376: eigenschappen van diagonalen in vierhoeken
week 13 les 5 toets en foutenanalyse handleiding pagina s 434 tot 443 nuttige informatie 1 Handleiding 1.1 Kopieerbladen pagina s 374 en 375: vierhoeken pagina 376: eigenschappen van diagonalen in vierhoeken
Gecijferdheid periode D Bijeenkomst 2 Hand-out: Meetkundige begrippen en vormen. Instap. Een opgave uit de oefentoets:
 Gecijferdheid periode D Bijeenkomst 2 Hand-out: Meetkundige begrippen en vormen Instap Een opgave uit de oefentoets: Van welke verpakkingen is de vorm een prisma? A. Pak spaghetti blikje chocomel doosje
Gecijferdheid periode D Bijeenkomst 2 Hand-out: Meetkundige begrippen en vormen Instap Een opgave uit de oefentoets: Van welke verpakkingen is de vorm een prisma? A. Pak spaghetti blikje chocomel doosje
Junior Wiskunde Olympiade : eerste ronde
 Junior Wiskunde lympiade 200-20: eerste ronde. Waaraan is xyz + xyz + xyz gelijk? () 3xyz () 27xyz () x 3 y 3 z 3 () 3x 3 y 3 z 3 () 27x 3 y 3 z 3 2. Welke van volgende ongelijkheden is waar? () 2 > 0,5
Junior Wiskunde lympiade 200-20: eerste ronde. Waaraan is xyz + xyz + xyz gelijk? () 3xyz () 27xyz () x 3 y 3 z 3 () 3x 3 y 3 z 3 () 27x 3 y 3 z 3 2. Welke van volgende ongelijkheden is waar? () 2 > 0,5
Vlaamse Wiskunde Olympiade : eerste ronde
 Vlaamse Wiskunde Olympiade 00-0: eerste ronde. e uitdrukking a b 4 is gelijk aan () ab () ab () ab 6 () ab 8 (E) ab 6. e uitdrukking (a b) is gelijk aan () a b () (b a) () a + b ab () a + b + ab (E) (a
Vlaamse Wiskunde Olympiade 00-0: eerste ronde. e uitdrukking a b 4 is gelijk aan () ab () ab () ab 6 () ab 8 (E) ab 6. e uitdrukking (a b) is gelijk aan () a b () (b a) () a + b ab () a + b + ab (E) (a
Inleiding 1. Onderzoeksvragen Reguliere polygonen en polyhedra 5
 Inhoudsopgave Inleiding 1 Onderzoeksvragen 3 1. Reguliere polygonen en polyhedra 5 1.1 polygonen 5 1.2 polyhedra 6 1.3 de formule van Euler in 3 dimensies 9 1.4 de formule van Euler in reguliere polyhedra
Inhoudsopgave Inleiding 1 Onderzoeksvragen 3 1. Reguliere polygonen en polyhedra 5 1.1 polygonen 5 1.2 polyhedra 6 1.3 de formule van Euler in 3 dimensies 9 1.4 de formule van Euler in reguliere polyhedra
Aan alle Wallabies, en aan hun leerkrachten, veel succes en, nog belangrijker, veel plezier!
 Noteer hier eventueel je naam: Aan alle Wallabies, en aan hun leerkrachten, veel succes en, nog belangrijker, veel plezier! Wiskunde leuk? Reken maar! wwwwiskundekangoeroebe c Vlaamse Wiskunde Olympiade
Noteer hier eventueel je naam: Aan alle Wallabies, en aan hun leerkrachten, veel succes en, nog belangrijker, veel plezier! Wiskunde leuk? Reken maar! wwwwiskundekangoeroebe c Vlaamse Wiskunde Olympiade
1 Vlaamse Wiskunde Olympiade : Eerste Ronde.
 Vlaamse Wiskunde Olympiade 99 99 : Eerste Ronde De eerste ronde bestaat uit 0 meerkeuzevragen, opgemaakt door de jury van VWO Het quoteringssysteem werkt als volgt : een deelnemer start met 0 punten Per
Vlaamse Wiskunde Olympiade 99 99 : Eerste Ronde De eerste ronde bestaat uit 0 meerkeuzevragen, opgemaakt door de jury van VWO Het quoteringssysteem werkt als volgt : een deelnemer start met 0 punten Per
Schaduwopgaven Verhoudingen
 Schaduwopgaven Verhoudingen bij 5 Een vierkant wordt verknipt in zeven driehoeken, zoals hiernaast. Het grijze driehoekje gooien we weg. Wat is de verhouding van de oppervlakte van de andere zes? na 10
Schaduwopgaven Verhoudingen bij 5 Een vierkant wordt verknipt in zeven driehoeken, zoals hiernaast. Het grijze driehoekje gooien we weg. Wat is de verhouding van de oppervlakte van de andere zes? na 10
1 Vlaamse Wiskunde Olympiade : tweede ronde
 1 Vlaamse Wiskunde Olympiade 005-006: tweede ronde Volgende benaderingen kunnen nuttig zijn bij het oplossen van sommige vragen 1,1 3 1,731 5,361 π 3,116 1 Als a 1 3 a 1 3 a m = a met a R + \{0, 1}, dan
1 Vlaamse Wiskunde Olympiade 005-006: tweede ronde Volgende benaderingen kunnen nuttig zijn bij het oplossen van sommige vragen 1,1 3 1,731 5,361 π 3,116 1 Als a 1 3 a 1 3 a m = a met a R + \{0, 1}, dan
De ruimte in de loop van de tijd
 De ruimte in de loop van de tijd Gert Vegter Instituut voor Wiskunde en Informatica (RUG) G.Vegter@rug.nl www.math.rug.nl/~gert HOVO, 17 maart 2009 GV () De ruimte in de loop van de tijd HOVO, 17/03/2009
De ruimte in de loop van de tijd Gert Vegter Instituut voor Wiskunde en Informatica (RUG) G.Vegter@rug.nl www.math.rug.nl/~gert HOVO, 17 maart 2009 GV () De ruimte in de loop van de tijd HOVO, 17/03/2009
a 2 +b 2 =c 2 www.stocs.nl patent pending / rights reserved / info@stocs.nl
 Bouwen met touwen spelend leren a 2 +b 2 =c 2 Met S TOCS kunnen kinderen spelenderwijs kennis maken met wiskunde, techniek en architectuur. STOCS bouwwerken bestaan uit lijnen, vlakken en hoeken. Wat zijn
Bouwen met touwen spelend leren a 2 +b 2 =c 2 Met S TOCS kunnen kinderen spelenderwijs kennis maken met wiskunde, techniek en architectuur. STOCS bouwwerken bestaan uit lijnen, vlakken en hoeken. Wat zijn
University of Groningen. Theory and history of geometric models Polo-Blanco, Irene
 University of Groningen Theory and history of geometric models Polo-Blanco, Irene IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite from it. Please
University of Groningen Theory and history of geometric models Polo-Blanco, Irene IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite from it. Please
Wiskunde Opdrachten Vlakke figuren
 Wiskunde Opdrachten Vlakke figuren Opdracht 1. Teken in de figuren hieronder alle symmetrieassen. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. Opdracht 2. A. Welke
Wiskunde Opdrachten Vlakke figuren Opdracht 1. Teken in de figuren hieronder alle symmetrieassen. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. Opdracht 2. A. Welke
1 Vlaamse Wiskunde Olympiade 2009-2010: tweede ronde
 Vlaamse Wiskunde Olympiade 009-00: tweede ronde Welke van de volgende vergelijkingen heeft als oplossing precies alle gehele veelvouden van π? () sinx = 0 (B) cos x = 0 (C) sinx = 0 (D) cosx = 0 (E) sinx
Vlaamse Wiskunde Olympiade 009-00: tweede ronde Welke van de volgende vergelijkingen heeft als oplossing precies alle gehele veelvouden van π? () sinx = 0 (B) cos x = 0 (C) sinx = 0 (D) cosx = 0 (E) sinx
5. C De routes langs A en C zijn even lang, dus is de route langs C ook 215 meter langer.
 ANTWOORDEN KANGOEROE 2001 BRUGKLAS en KLAS 2 1. E 2. E 18 doosjes voor de rode, 13 voor de blauwe: totaal 31 doosjes 3. C De ringen A, B en D zitten allemaal alleen door ring C. 4. B De twee getallen moeten
ANTWOORDEN KANGOEROE 2001 BRUGKLAS en KLAS 2 1. E 2. E 18 doosjes voor de rode, 13 voor de blauwe: totaal 31 doosjes 3. C De ringen A, B en D zitten allemaal alleen door ring C. 4. B De twee getallen moeten
ZESDE KLAS MEETKUNDE
 ZESDE KLAS MEETKUNDE maandag 1. Het vierkant. Eigenschappen. 2. Vierkanten tekenen met passer en lat vanuit zeshoek 3. Vierkanten tekenen met passer en lat binnen cirkel 4. Vierkanten tekenen met passer
ZESDE KLAS MEETKUNDE maandag 1. Het vierkant. Eigenschappen. 2. Vierkanten tekenen met passer en lat vanuit zeshoek 3. Vierkanten tekenen met passer en lat binnen cirkel 4. Vierkanten tekenen met passer
MEETKUNDE 120 PUNTEN, LIJNEN EN VLAKKEN
 120 PUNTEN, LIJNEN EN VLAKKEN een rechte lijn A het punt A a de rechte a een kromme lijn of een kromme een gebroken lijn a A b a B het lijnstuk [AB] evenwijdige rechten a // b een plat oppervlak of een
120 PUNTEN, LIJNEN EN VLAKKEN een rechte lijn A het punt A a de rechte a een kromme lijn of een kromme een gebroken lijn a A b a B het lijnstuk [AB] evenwijdige rechten a // b een plat oppervlak of een
1 Junior Wiskunde Olympiade : eerste ronde
 1 Junior Wiskunde Olympiade 2008-2009: eerste ronde 1 Hoeveel is 2 5 7? (A) 10 21 (B) 25 7 (C) 7 10 (D) 1 15 (E) 29 21 2 Welke van volgende sommen is gelijk aan 10? (A), + 5,555 (B) 2,222 + 6,666 (C),
1 Junior Wiskunde Olympiade 2008-2009: eerste ronde 1 Hoeveel is 2 5 7? (A) 10 21 (B) 25 7 (C) 7 10 (D) 1 15 (E) 29 21 2 Welke van volgende sommen is gelijk aan 10? (A), + 5,555 (B) 2,222 + 6,666 (C),
5.0 INTRO. Hoofdstuk 5 DE RUIMTE IN
 93 5.0 INTRO 1 Op het werkblad vind je vier bouwplaten. Knip ze uit en zet ze in elkaar. Je krijgt drie piramides en een kubusvormige doos zonder deksel. a De drie piramides passen precies in de doos.
93 5.0 INTRO 1 Op het werkblad vind je vier bouwplaten. Knip ze uit en zet ze in elkaar. Je krijgt drie piramides en een kubusvormige doos zonder deksel. a De drie piramides passen precies in de doos.
Wat is de som van de getallen binnen een cirkel? Geef alle mogelijke sommen!
 Estafette-opgave 1 (20 punten, rest 480 punten) Zeven gebieden Drie cirkels omheinen zeven gebieden. We verdelen de getallen 1 tot en met 7 over de zeven gebieden, in elk gebied één getal. De getallen
Estafette-opgave 1 (20 punten, rest 480 punten) Zeven gebieden Drie cirkels omheinen zeven gebieden. We verdelen de getallen 1 tot en met 7 over de zeven gebieden, in elk gebied één getal. De getallen
1. Het getal 200 9 = 1800 is even. De andere antwoorden zijn oneven: 2009, 2 + 0 + 0 + 9 = 11, 200 9 = 191, 200 + 9 = 209.
 1. Het getal 200 9 = 1800 is even. De andere antwoorden zijn oneven: 2009, 2 + 0 + 0 + 9 = 11, 200 9 = 191, 200 + 9 = 209. Kangoeroewedstrijd editie Wallabie: jaargang 2009, probleem 1; Kangoeroewedstrijd
1. Het getal 200 9 = 1800 is even. De andere antwoorden zijn oneven: 2009, 2 + 0 + 0 + 9 = 11, 200 9 = 191, 200 + 9 = 209. Kangoeroewedstrijd editie Wallabie: jaargang 2009, probleem 1; Kangoeroewedstrijd
1 Junior Wiskunde Olympiade : tweede ronde
 1 Junior Wiskunde Olympiade 005-006: tweede ronde Volgende benaderingen kunnen nuttig zijn bij het oplossen van sommige vragen 1,1 1,71 5,61 π,116 1 ls a a 17 a m = a 006, met a R + \{0, 1}, dan is m gelijk
1 Junior Wiskunde Olympiade 005-006: tweede ronde Volgende benaderingen kunnen nuttig zijn bij het oplossen van sommige vragen 1,1 1,71 5,61 π,116 1 ls a a 17 a m = a 006, met a R + \{0, 1}, dan is m gelijk
MEETKUNDE 120 PUNTEN, LIJNEN EN VLAKKEN
 120 PUNTEN, LIJNEN EN VLAKKEN een rechte lijn A het punt A a de rechte a een kromme lijn of een kromme een gebroken lijn a A b a B het lijnstuk [AB] evenwijdige rechten a // b een plat oppervlak of een
120 PUNTEN, LIJNEN EN VLAKKEN een rechte lijn A het punt A a de rechte a een kromme lijn of een kromme een gebroken lijn a A b a B het lijnstuk [AB] evenwijdige rechten a // b een plat oppervlak of een
Wiskunde D Online uitwerking 4 VWO blok 6 les 4
 Wiskunde Online uitwerking 4 VWO blok 6 les 4 Paragraaf 4 Het inproduct om hoeken te berekenen Opgave a e hoek is kleiner dan 4, want het dak zelf staat onder een hoek van 45, en de kilgoot loopt schuin
Wiskunde Online uitwerking 4 VWO blok 6 les 4 Paragraaf 4 Het inproduct om hoeken te berekenen Opgave a e hoek is kleiner dan 4, want het dak zelf staat onder een hoek van 45, en de kilgoot loopt schuin
SYMMETRIEËN VAN RUIMTELIJKE FIGUREN. Prof. dr. Ronald Meester
 SYMMETRIEËN VAN RUIMTELIJKE FIGUREN Prof. dr. Ronald Meester Inleiding In dit college onderzoeken we symmetrie-eigenschappen van ruimtelijke figuren zoals driehoeken, vierkanten, kubussen en andere veelvlakken
SYMMETRIEËN VAN RUIMTELIJKE FIGUREN Prof. dr. Ronald Meester Inleiding In dit college onderzoeken we symmetrie-eigenschappen van ruimtelijke figuren zoals driehoeken, vierkanten, kubussen en andere veelvlakken
1 Vlaamse Wiskunde Olympiade : Tweede ronde.
 1 Vlaamse Wiskunde Olympiade 1998-1999: Tweede ronde De tweede ronde bestaat eveneens uit 0 meerkeuzevragen Het quoteringssysteem is hetzelfde als dat voor de eerste ronde, dwz per goed antwoord krijgt
1 Vlaamse Wiskunde Olympiade 1998-1999: Tweede ronde De tweede ronde bestaat eveneens uit 0 meerkeuzevragen Het quoteringssysteem is hetzelfde als dat voor de eerste ronde, dwz per goed antwoord krijgt
B136. BIJLAGE H De verbinding met het 'On-eindige' vanuit het twaalf-, het ruitendertig- en het twintig-vlak. Het twaalfvlak of dodecaëder
 B136 De verbinding met het 'On-eindige' vanuit het twaalf-, het ruitendertig- en het twintig-vlak Het twaalfvlak of dodecaëder Een dodecaëder ligt besloten tussen 6 paren van evenwijdige vlakken. Als die
B136 De verbinding met het 'On-eindige' vanuit het twaalf-, het ruitendertig- en het twintig-vlak Het twaalfvlak of dodecaëder Een dodecaëder ligt besloten tussen 6 paren van evenwijdige vlakken. Als die
2.5 Regelmatige veelhoeken
 Regelmatige veelhoeken 81 2.5 Regelmatige veelhoeken Een regelmatige veelhoek is een figuur met zijden die allemaal even lang en hoekendieallemaalevengrootzijn. Wezijneraleenpaartegengekomen: de regelmatige
Regelmatige veelhoeken 81 2.5 Regelmatige veelhoeken Een regelmatige veelhoek is een figuur met zijden die allemaal even lang en hoekendieallemaalevengrootzijn. Wezijneraleenpaartegengekomen: de regelmatige
Leve de Wiskunde! 2011 W I N G O! Uw Wingo-master van vandaag: Jan Brandts Korteweg-de Vries Instituut voor Wiskunde Universiteit van Amsterdam
 Leve de Wiskunde! 2011 W I N G O! Uw Wingo-master van vandaag: Jan Brandts Korteweg-de Vries Instituut voor Wiskunde Universiteit van Amsterdam W I N G O = W I S K U N D E - B I N G O W I N G O 17 15 π
Leve de Wiskunde! 2011 W I N G O! Uw Wingo-master van vandaag: Jan Brandts Korteweg-de Vries Instituut voor Wiskunde Universiteit van Amsterdam W I N G O = W I S K U N D E - B I N G O W I N G O 17 15 π
= 3 1111 101 + 6 3 1111 101 + 2 1111 101 = (3 + 2) 1111 101 = 5 11
 . Bij A en E staan de benen van het poppetje loodrecht op elkaar. Bij C vormen de benen een scherpe hoek. Bij D vormen de benen een gestrekte hoek. Alleen bij B vormen de benen van het poppetje een stompe
. Bij A en E staan de benen van het poppetje loodrecht op elkaar. Bij C vormen de benen een scherpe hoek. Bij D vormen de benen een gestrekte hoek. Alleen bij B vormen de benen van het poppetje een stompe
Vlaamse Wiskunde Olympiade : eerste ronde
 608 875 Vlaamse Wiskunde Olympiade 07-08: eerste ronde. In een wijk staat een aantal interessante gebouwen, waarvan het bouwjaar is gegeven. Op welke van de volgende wandelingen kom je de gebouwen van
608 875 Vlaamse Wiskunde Olympiade 07-08: eerste ronde. In een wijk staat een aantal interessante gebouwen, waarvan het bouwjaar is gegeven. Op welke van de volgende wandelingen kom je de gebouwen van
Domein A: Inzicht en handelen
 Tussendoelen wiskunde onderbouw vo vmbo Preambule Domein A is een overkoepeld domein dat altijd in combinatie met de andere domeinen wordt toegepast (of getoetst). In domein A wordt benoemd: Vaktaal: het
Tussendoelen wiskunde onderbouw vo vmbo Preambule Domein A is een overkoepeld domein dat altijd in combinatie met de andere domeinen wordt toegepast (of getoetst). In domein A wordt benoemd: Vaktaal: het
Sum of Us 2014: Topologische oppervlakken
 Sum of Us 2014: Topologische oppervlakken Inleiding: topologische oppervlakken en origami Een topologisch oppervlak is, ruwweg gesproken, een tweedimensionaal meetkundig object. We zullen in deze tekst
Sum of Us 2014: Topologische oppervlakken Inleiding: topologische oppervlakken en origami Een topologisch oppervlak is, ruwweg gesproken, een tweedimensionaal meetkundig object. We zullen in deze tekst
HET IS EEN PRISMA, OF TOCH NIET...
 In dit artikel laten we zien hoe je een kubus, een rombendodecaëder en een afgeknotte octaëder kunt omvormen tot een. Om de constructie zelf uit te voeren, heb je de bouwtekeningen nodig die bij dit artikel
In dit artikel laten we zien hoe je een kubus, een rombendodecaëder en een afgeknotte octaëder kunt omvormen tot een. Om de constructie zelf uit te voeren, heb je de bouwtekeningen nodig die bij dit artikel
1 Junior Wiskunde Olympiade : tweede ronde
 Junior Wiskunde Olympiade 008-009: tweede ronde ( 7) = (A) 7 (B) 7 (C) 7 of + 7 (D) 7 (E) onbepaald Beschouw de rij opeenvolgende natuurlijke getallen beginnend met en eindigend met Wat is het middelste
Junior Wiskunde Olympiade 008-009: tweede ronde ( 7) = (A) 7 (B) 7 (C) 7 of + 7 (D) 7 (E) onbepaald Beschouw de rij opeenvolgende natuurlijke getallen beginnend met en eindigend met Wat is het middelste
Tussendoelen wiskunde onderbouw vo vmbo
 Tussendoelen wiskunde onderbouw vo vmbo Domein A: Inzicht en handelen Subdomein A1: Vaktaal wiskunde 1. vmbo passende vaktaal voor wiskunde herkennen en gebruiken voor het ordenen van het eigen denken
Tussendoelen wiskunde onderbouw vo vmbo Domein A: Inzicht en handelen Subdomein A1: Vaktaal wiskunde 1. vmbo passende vaktaal voor wiskunde herkennen en gebruiken voor het ordenen van het eigen denken
WISKUNDE-ESTAFETTE Minuten voor 20 opgaven. Het totaal aantal te behalen punten is 500
 WISKUNDE-ESTAFETTE 2012 60 Minuten voor 20 opgaven. Het totaal aantal te behalen punten is 500 1 (20 punten) Optellen De som van twee getallen van twee cijfers is een getal van drie cijfers (geen van deze
WISKUNDE-ESTAFETTE 2012 60 Minuten voor 20 opgaven. Het totaal aantal te behalen punten is 500 1 (20 punten) Optellen De som van twee getallen van twee cijfers is een getal van drie cijfers (geen van deze
24/11/2008. heel handig hulpvenster past zich voortdurend aan. Engelstalige handleiding van 63 blz. dag van de wiskunde 2e/3e graad 22 nov 2008
 Cabri 3D een voorstelling van de mogelijkheden dag van de wiskunde 2e/3e graad 22 nov 2008 Paul Decuypere, VVKSO cahier de brouillon interactif www.cabri.com 1985: eerste versie van Cabri I 1989: eerste
Cabri 3D een voorstelling van de mogelijkheden dag van de wiskunde 2e/3e graad 22 nov 2008 Paul Decuypere, VVKSO cahier de brouillon interactif www.cabri.com 1985: eerste versie van Cabri I 1989: eerste
1BK2 1BK6 1BK7 1BK9 2BK1
 Kern Subkern Leerdoel niveau BK begrippen vmbo waar in bettermarks 1.1.1. Je gebruikt positieve en negatieve getallen, breuken en decimale getallen in hun onderlinge samenhang en je ligt deze toe binnen
Kern Subkern Leerdoel niveau BK begrippen vmbo waar in bettermarks 1.1.1. Je gebruikt positieve en negatieve getallen, breuken en decimale getallen in hun onderlinge samenhang en je ligt deze toe binnen
Opgaven Kangoeroe vrijdag 17 maart 2000
 Opgaven Kangoeroe vrijdag 17 maart 2000 VBO en MAVO Klas 3 en 4 Vragen 1 t/m 10: voor elk goed antwoord +3 punten, voor elk fout antwoord -¾ punt. 1. Hiernaast zie je drie aanzichten (voor, boven, links)
Opgaven Kangoeroe vrijdag 17 maart 2000 VBO en MAVO Klas 3 en 4 Vragen 1 t/m 10: voor elk goed antwoord +3 punten, voor elk fout antwoord -¾ punt. 1. Hiernaast zie je drie aanzichten (voor, boven, links)
Uitwerkingen van de opgaven bij het vormen van ruimte: van Poincaré tot Perelman
 Uitwerkingen van de opgaven bij het vormen van ruimte: van Poincaré tot Perelman Roland van der Veen Inleiding Deze reeks opgaven is bedoeld voor de werkcolleges van de vakantiecursus Wiskunde in Wording,
Uitwerkingen van de opgaven bij het vormen van ruimte: van Poincaré tot Perelman Roland van der Veen Inleiding Deze reeks opgaven is bedoeld voor de werkcolleges van de vakantiecursus Wiskunde in Wording,
OPLOSSINGEN. Wallaroe Vlaamse Wiskunde Olympiade vzw
 OPLOSSINGEN Vlaamse Wiskunde Olympiade vzw Juist antwoord Geen antwoord Fout antwoord Wedstrijdduur Rekentoestel 5 punten 1 punt 0 punten 75 minuten niet toegelaten 1. Correct antwoord: A Wetellendehalvecirkels.Hetzijner6.
OPLOSSINGEN Vlaamse Wiskunde Olympiade vzw Juist antwoord Geen antwoord Fout antwoord Wedstrijdduur Rekentoestel 5 punten 1 punt 0 punten 75 minuten niet toegelaten 1. Correct antwoord: A Wetellendehalvecirkels.Hetzijner6.
handleiding pagina s 1005 tot 1015 1 Handleiding 1.2 Huistaken nihil 2 Werkboek 3 Posters 4 Scheurblokken bladzijden 122, 147, 150 en 156 5 Cd-rom
 week 32 les 2 toets en foutenanalyse handleiding pagina s 1005 tot 1015 nuttige informatie 1 Handleiding 11 Kopieerbladen pagina 812: gelijkvormig / vervormen pagina 813: patronen pagina 814: kubus pagina
week 32 les 2 toets en foutenanalyse handleiding pagina s 1005 tot 1015 nuttige informatie 1 Handleiding 11 Kopieerbladen pagina 812: gelijkvormig / vervormen pagina 813: patronen pagina 814: kubus pagina
Onmogelijke figuren. Geschreven door Judith Floor en Vivike Lapoutre. Herzien door Dieuwke van Wijk en Amarins van de Voorde
 Onmogelijke figuren Geschreven door Judith Floor en Vivike Lapoutre Herzien door Dieuwke van Wijk en Amarins van de Voorde Vierkant voor Wiskunde Zomerkamp A 2010 Voorwoord Je hebt vast wel eens een stripboek
Onmogelijke figuren Geschreven door Judith Floor en Vivike Lapoutre Herzien door Dieuwke van Wijk en Amarins van de Voorde Vierkant voor Wiskunde Zomerkamp A 2010 Voorwoord Je hebt vast wel eens een stripboek
1 Vlaamse Wiskunde Olympiade : tweede ronde
 1 Vlaamse Wiskunde Olympiade 006-007: tweede ronde 1 In een rechthoekige driehoek verdeelt de bissectrice uit een scherpe hoek de overstaande zijde in twee stukken met lengten 4 en 5 (zie figuur) De oppervlakte
1 Vlaamse Wiskunde Olympiade 006-007: tweede ronde 1 In een rechthoekige driehoek verdeelt de bissectrice uit een scherpe hoek de overstaande zijde in twee stukken met lengten 4 en 5 (zie figuur) De oppervlakte
1 Wiskunde, zeker. 1, 2, 3, 5, 6, 7. 8, 10, 11, 12 en 13 eurocent. duimstok Timmerman Hoe lang iets is.
 1 2 1 Wiskunde, zeker duimstok Timmerman Hoe lang iets is. Blokhaak: Timmerman Of een hoek haaks is. 1, 2, 3, 5, 6, 7. 8, 10, 11, 12 en 13 eurocent. Zeven munten: een van 1-eurocent, twee van 2-eurocent,
1 2 1 Wiskunde, zeker duimstok Timmerman Hoe lang iets is. Blokhaak: Timmerman Of een hoek haaks is. 1, 2, 3, 5, 6, 7. 8, 10, 11, 12 en 13 eurocent. Zeven munten: een van 1-eurocent, twee van 2-eurocent,
Naam:... Nr... SPRONG 5. a Kleur het juiste percentage van de figuren en vul in hoeveel percent er overblijft.
 Naam:... Nr.... SPRONG 5 G G 1 Percenten T a Kleur het juiste percentage van de figuren en vul in hoeveel percent er overblijft. Kleur 20 % blauw. 25 % maak je geel. 50 % krijgt een groene kleur. Er blijft
Naam:... Nr.... SPRONG 5 G G 1 Percenten T a Kleur het juiste percentage van de figuren en vul in hoeveel percent er overblijft. Kleur 20 % blauw. 25 % maak je geel. 50 % krijgt een groene kleur. Er blijft
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 2 Leo van Iersel Technische Universiteit Delft 9 september 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 september 2015 1 / 23 Huiswerk Huiswerk 1 is beschikbaar op
TW2020 Optimalisering Hoorcollege 2 Leo van Iersel Technische Universiteit Delft 9 september 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 september 2015 1 / 23 Huiswerk Huiswerk 1 is beschikbaar op
0. Warming Up. Opdracht 0.1 Classificeren. Voor iedereen: leg de juiste figuur op de juiste plaats
 0. Warming Up Opdracht 0.1 Classificeren Voor iedereen: leg de juiste figuur op de juiste plaats Workshops Meetkunde Voorbereiding Kennisbasistoets Rekenen Pagina 1 Opdracht 0.2 Classificeren Nog een keer
0. Warming Up Opdracht 0.1 Classificeren Voor iedereen: leg de juiste figuur op de juiste plaats Workshops Meetkunde Voorbereiding Kennisbasistoets Rekenen Pagina 1 Opdracht 0.2 Classificeren Nog een keer
Opgaven Kangoeroe vrijdag 17 maart 2000
 Opgaven Kangoeroe vrijdag 17 maart 2000 Brugklas en klas 2 Vragen 1 t/m 10: voor elk goed antwoord +3 punten, voor elk fout antwoord ¾ punt. 1. In de spiegel zien we een klok. Hoe laat is het? A) 9.45
Opgaven Kangoeroe vrijdag 17 maart 2000 Brugklas en klas 2 Vragen 1 t/m 10: voor elk goed antwoord +3 punten, voor elk fout antwoord ¾ punt. 1. In de spiegel zien we een klok. Hoe laat is het? A) 9.45
DE BINNENKANT VAN EEN TETRAËDER
 Heb je je ooit afgevraagd hoe de binnenkant van een tetraëder eruitziet? Waarschijnlijk niet. In dit artikel gaan we een tetraëder die op een bepaalde manier is gesneden binnenstebuiten vouwen. door William
Heb je je ooit afgevraagd hoe de binnenkant van een tetraëder eruitziet? Waarschijnlijk niet. In dit artikel gaan we een tetraëder die op een bepaalde manier is gesneden binnenstebuiten vouwen. door William
Hoofdstuk 2 : Som Hoekgrootten van een veelhoek (boek pag 34)
 - 39- Hoofdstuk 2 : Som Hoekgrootten van een veelhoek (boek pag 34) Som hoekgrootten van een driehoek ( boek pag 35) Stelling: Voor ABC geldt: A ˆ + Bˆ + Cˆ = 180 o Bewijs: Trek door het punt A een rechte
- 39- Hoofdstuk 2 : Som Hoekgrootten van een veelhoek (boek pag 34) Som hoekgrootten van een driehoek ( boek pag 35) Stelling: Voor ABC geldt: A ˆ + Bˆ + Cˆ = 180 o Bewijs: Trek door het punt A een rechte
De Riemann-hypothese
 De Riemann-hypothese Lars van den Berg 3 september 202 Laat ik je gelijk enthousiast maken om dit stukje te lezen: wie de Riemannhypothese oplost wint een miljoen. Wel zijn er waarschijnlijk eenvoudigere
De Riemann-hypothese Lars van den Berg 3 september 202 Laat ik je gelijk enthousiast maken om dit stukje te lezen: wie de Riemannhypothese oplost wint een miljoen. Wel zijn er waarschijnlijk eenvoudigere
1 Vlaamse Wiskunde Olympiade : Tweede Ronde.
 Vlaamse Wiskunde Olympiade 99-99 : Tweede Ronde De Vlaamse Wiskunde Olympiade vzw is een officiële foreign coordinator voor de welbekende AHSME-competitie (American High School Mathematics Examination
Vlaamse Wiskunde Olympiade 99-99 : Tweede Ronde De Vlaamse Wiskunde Olympiade vzw is een officiële foreign coordinator voor de welbekende AHSME-competitie (American High School Mathematics Examination
