Diktaat Concrete Meetkunde Veelvlakken en alles wat daarbij komt kijken...

Transcriptie

1 Diktaat Concrete Meetkunde Veelvlakken en alles wat daarbij komt kijken... Anieke Brombacher Auke Mollema Patrick van Stiphout april

2 Inhoudsopgave 1 Inleiding 3 2 Regelmatige veelvlakken Definities Bewijs Onregelmatige veelvlakken Inleiding Archimedische veelvlakken Dertien Archimedische veelvlakken Ontstaan Overige De formule van Euler Inleiding De formule Een bewijs van de formule van Euler Dualiteit 16 6 Symmetrie Definities Directe Symmetrie Tetraëder Hexaëder en Octaëder Dodecaëder en Icosaëder Indirecte symmetrie Referenties 25 2

3 1 Inleiding Regelmatige veelvlakken, de meest van jullie zullen die wel kennen. Ook de namen als tetraëder, kubus en octaëder zullen jullie wel eens gehoord hebben. Maar er is meer! In dit diktaat behandelen we de regelmatige veelvlakken maar ook de vervormingen daarvan. We zullen de middelpunten van de zijdes uitrekken en hoekpunten eraf snijden. Zo zullen we onregelmatige veelvlakken ontdekken en het verband tussen veelvlakken inzien. Tenslotte gaan we ook kijken naar symmetrieën binnen deze veelvlakken. Dit alles brengt ons tot het doel: Het enthousiast maken van de lezer voor dit onderwerp! 3

4 2 Regelmatige veelvlakken 2.1 Definities Voordat we naar de regelmatige veelvlakken gaan kijken, zullen we eerst een aantal definities behandelen en een aantal opmerkingen maken. Wanneer we naar een kubus kijken, valt het op dat deze alleen maar uit vierkanten bestaat. In het algemeen blijkt dat een regelmatig veelvlak bestaat uit zijvlakken die weer regelmatige veelhoeken zijn. Voor de grootte van een hoek in een regelmatige n-hoek (f(n)) geldt: f(n) = (n 2).180 o Opgave 1 Probeer figuurlijk in te zien waarom deze formule klopt. Tenslotte zullen we nog twee definities nodig hebben om een regelmatig veelvlak te kunen definiëren. Definitie 1 Onder de orde van een zijvlak van een veelvlak wordt verstaan het aantal ribben (of aantal hoekpunten) dat dat zijvlak begrenst. Definitie 2 Onder de orde van een hoekpunt wordt verstaan het aantal ribben (of aantal zijden) dat samenkomt in dat hoekpunt. Nu kunnen we met behulp van definities 1 en 2 en de gemaakte opmerkingen een regelmatig veelvlak definiëren: Definitie 3 De voorwaarden voor een regelmatig veelvlak zijn: De zijden zijn identieke regelmatige veelhoeken Convex... Opgave 2 Vul de tweede voorwaarde op de puntjes hierboven in (denk aan een kubus) en geef daarbij een voorbeeld waaruit blijkt dat die voorwaarde nodig is. 4

5 Figuur 1: De vijf regelmatige veelvlakken Dit alles geeft ons (een tabel met) 5 regelmatige veelvlakken: Naam Zijden Orde hoekpunt Orde zijde Tetraëder 4 driehoeken 3 3 Kubus 6 vierkanten 3 4 Octaëder 8 driehoeken 4 3 Dodecaëder 12 vijfhoeken 3 5 Icosaëder 20 driehoeken 5 3 Opmerking 1 Uit de tabel blijkt dat er vijf regelmatige veelvlakken zijn. Probeer voordat je verder leest te bedenken waarom er precies vijf zijn. 2.2 Bewijs Uit de vorige paragraaf bleek dat er vijf regelmatige veelvlakken zijn. We zullen nu een bewijs geven, waarom er hoogstens vijf regelmatige veelvlakken zijn. Dit doen we met de volgende aandachtspunten: Er zijn minimaal drie zijden nodig rond een hoekpunt; Een zijvlak heeft minimaal drie hoekpunten; De hoeken van elk zijvlak zijn even groot; Een regelmatig veelvlak bestaat maar uit één soort regelmatige veelhoek. 5

6 Stelling 1 Er zijn hoogstens vijf regelmatige veelvlakken. Bewijs: Aangezien we in een zijvlak minimaal drie hoeken nodig hebben om een zijvlak te kunnen maken en we drie zijvlakken nodig hebben in een hoekpunt beginnen we bij drie driehoeken in een hoekpunt. De hoeken in een gelijkbenige driehoek zijn 60 o graden, dus drie driehoeken levert 180 o. Dit geeft ons een tetraëder. Wanneer we vier driehoeken samen laten komen in een hoekpunt geeft dat een totaal van 240 o, de octaëder. Als we vijf driehoeken in een hoekpunt samen laten komen geeft dat een hoek van 300 o, de icosaëder. Tenslotte geeft zes driehoeken in een hoekpunt een regelmatige zeshoek en dus een plat vlak. Als we kijken naar de vierkanten en zo drie vierkanten in een hoekpunt samen laten komen geeft dat 270 o in een hoekpunt. Dit veelvlak heet ook wel een kubus. Laten we vier vierkanten samenkomen in een hoekpunt, dan krijgen we een groot vierkant verdeeld in vier kleine vierkantjes en dus een plat vlak (360 o ). Voor drie vijfhoeken (met een hoek van 108 o ) geeft 324 o in een hoekpunt. Zo ontstaat de dodecaëder. Vier vijfhoeken in een hoekpunt geeft meer dan 360 o en zal dus nooit een gesloten figuur worden. Tenslotte drie zeshoeken in een hoekpunt: voor de zeshoek geldt dat elke hoek 120 o is, dus drie zeshoeken geeft 360 o en dat is een plat vlak. Hier kan geen ruimtelijk figuur van gemaakt worden. Q.E.D. Opgave 3 Hebben we nu bewezen dat er vijf zijn? Zo nja, denk nog eens wat verder na. Zo nee, wat is het probleem nog? Zet het probleem en de oplossing uiteen in tenminste tien zinnen. Tenslotte zullen we ons nog iets meer verdiepen in de mogelijkheden van regelmatige veelvlakken door middel van twee opgaves. Opgave 4 Bekijk de dodecaëder. Kies daarop 8 hoekpunten die met elkaar verbonden een kubus opleveren. Hoeveel van die kubussen zijn er? Opgave 5 Bekijk nogmaals de dodecaëder en vind (net zoals in de vorige opgave) door middel van de hoekpunten te verbinden hoeveel tetraëders er in zitten. 6

7 3 Onregelmatige veelvlakken 3.1 Inleiding Naast regelmatige veelvlakken bestaan er ook onregelmatige veelvlakken. Onregelmatige veelvlakken zijn veelvlakken waarvoor onder andere één van de onderstaande gevallen geldt: Het veelvlak bestaat uit minimaal twee soorten regelmatige veelhoeken (met willekeurige orde van een hoekpunt); Het veelvlak bestaat uit één soort regelmatige veelhoek (met minstens twee verschillende ordes van de hoekpunten). Denk bij het laatste puntje nog even aan opgave twee van het vorige hoofdstuk. Een voorbeeld van een onregelmatig veelvlak is een prisma. Wanneer we kijken naar een prisma met een vijfhoek als basis en vierkanten als zijden dan hebben we het over een onregelmatig veelvlak. Andere voorbeelden van onregelmatige veelvlakken zijn de dertien Archimedische veelvlakken. Deze veelvlakken worden ook wel halfregematige veelvlakken genoemd. Aan de naam te zien ontstaat het vermoeden dat er toch enige regelmaat te ontdekken is, daarom zullen we deze vlakken apart behandelen. Opgave 6 Laat zien dat er oneindig veel onregelmatige veelvlakken zijn. 3.2 Archimedische veelvlakken Dertien Archimedische veelvlakken Er bestaan dertien Archimedische veelvlakken en ze hebben allen een bijpassende naam. We bekijken voorlopig alleen de Engelse namen. In die naam is verwerkt hoe ze zijn ontstaan: de meeste zijn namelijk ontstaan door een regelmatig veelvlak zo te veranderen dat hij niet meer regelmatig is maar de zijvlakken wel regelmatige veelhoeken zijn. Definitie 4 Een Archimedisch veelvlak is opgebouwd uit tenminste twee soorten regelmatige veelhoeken, in elk hoekpunt komt dezelfde groepering (in dezelfde volgorde) van veelhoeken voor en het is geen prisma of antiprisma. (Een antiprisma is een prisma waarbij het grondvlak en het bovenvlak niet precies boven elkaar staan, maar het bovenvlak gedraaid is ten opzicht van het ondervlak.) 7

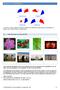
8 Figuur 2: De dertien Archimedische veelvlakken 1. Truncated Cube Great Rhombicuboctahedron 5. Rhombicuboctahedron 6. Truncated Dodecahedron 7. Icosidodecahedron 8. Truncated Icosahedron 9. Great Rhombicosidodecahedron 10. Rhombicosidodecahedron 11. Snub Cube 12. Snub Dodecahedron 13. Truncated Tetrahedron 8

9 Onderstaande tabel geeft het aantal en soort van de zijvlakken weer van de dertien Archimedische veelvlakken: Ontstaan Zijvlakken Drieh. Vierk. Vijfh. Zesh. Achth. Twaalfh Wanneer we naar een tetraëder kijken en op de één of andere manier de hoekpunten eraf snijden dan lijkt het wel of je de truncated tetrahedron krijgt. Als je nu kijkt naar de kubus en je pakt het midden van de vier zijden rondom en trekt dat midden omhoog op de één of andere manier dan krijg je de cub-octahedron. Hieruit blijkt dat je door regelmatige veelvlakken een beetje te verbouwen al een aantal van deze Archimedische veelvlakken krijgt. In het bijzonder bekijken we de verbouwingen afknotten en uitstulpen. Definitie 5 Afknotten betekent letterlijk dat je de hoekpunten van een veelvlak afsnijdt. Daarbij heeft de snijlijn overal dezelfde afstand tot het hoekpunt en de basis van het gedeelte dat je er afsnijdt is een regelmatige veelhoek. Daarbij geldt ook dat de zijdes die je overhoudt ook regelmatige veelhoeken moeten zijn. Definitie 6 Uitstulpen betekent dat je het midden van een zijde loodrecht omhoog trekt met gelijke afstand tussen het uitgetrokken hoekpunt en de hoekpunten van het zijvlak. Deze twee definities zullen we even illustreren met twee plaatjes. Hieronder zie je het principe van uitstulpen bij een kubus. De linker is niet goed maar de rechter is wel goed: Figuur 3: Uitstulpen, links fout en rechts goed. 9

10 En op de volgende pagina wordt een kubus afgeknot. Daarbij is weer het linker plaatje fout en het rechter plaatje goed. Wanneer je bij alle hoekpunten afknot zoals het rechterplaatje ontstaat de truncated cube. Daarbij is de zijde dus een regelmatige achthoek of een regelmatige driehoek: Figuur 4: Afknotten, links fout en rechts goed. Opvallend in de twee definities is dat we bij beide over de afstand praten tot het hoekpunt. Dit doen we omdat we zo een Archimedische veelvlak krijgen. Verder geldt bij het afknotten dat er een vlak bijkomt, een hoekpunt weggaat en er evenveel ribben als hoekpunten bijkomen. Iets waarvan we in het volgende hoofdstuk de regelmaat van zullen ontdekken. We eindigen dit hoofdstuk met een aantal plaatjes van het afknotten van 3 regelmatige veelvlakken: Figuur 5: Afknotten van een tetraëder geeft een octaëder Figuur 6: Afknotten van een kubus Figuur 7: Afknotten van een octaëder 10

11 Opgave 7 Zoals je ziet zijn bij het plaatje van de Archimedische veelvlakken twee namen weggevallen. Aangezien de naam veel vertelt over het veelvlak zijn die weggehaald. Probeer te achterhalen hoe die veelvlakken zijn ontstaan. Opgave 8 Welke veelvlakken ontstaan er bij het afknotten van de icosaëder en de dodecaëder? Opgave 9 De rhomb-cub-octahedron heeft zijvlakken gemeenschappelijk met drie andere van de tot nu toe behandelde veelvlakken. Welke? Opgave 10 De snub cube ofwel stompe kubus heeft zijvlakken gemeenschappelijk met de kubus en de octaëder. Leg uit waarom er geen snub tetrahedron is. Opgave 11 Welke twee Archimedische veelvlakken kunnen niet gemaakt worden door het afknotten van een regelmatig veelvlak? 3.3 Overige Deze paragraaf bestaat uit een aantal stellingen en een vraag. Kruis bij de stellingen aan of de stelling juist of onjuist is. Wanneer u juist aankruist probeer dan het onregelmatige veelvlak te tekenen. Wanneer we het hebben over een n-hoek dan is deze regelmatig. Je kan een onregelmatig veelvlak maken met 5 vierkanten en 2 vijfhoeken Juist / Onjuist Je kan een onregelmatig veelvlak maken met 2 vierkanten en 8 driehoeken Juist / Onjuist Je kan een onregelmatig veelvlak maken met een tienhoek, een vijfhoek, 5 vierkanten en 5 driehoeken Juist / Onjuist Je kan een onregelmatig veelvlak maken met 12 vijfhoeken Juist / Onjuist Opgave 12 Wanneer we kijken naar de icosaëder dan kunnen we gedeelten eraf snijden en dan een onregelmatig veelvlak overhouden (zie hieronder). Probeer door middel van snijden in het veelvlak (minimaal één keer) vier verschillende onregelmatige veelvlakken eruit te halen. Figuur 8: Afbeelding bij opgave 12 11

12 4 De formule van Euler 4.1 Inleiding Geschiedenis1 Leonhard Euler (Bazel, 15 april 1707 Sint-Petersburg, 18 september 1783) was een Zwitserse wiskundige en natuurkundige die het grootste deel van zijn leven doorbracht in Rusland en Duitsland. Hij was een van de meest productieve wiskundigen ooit; zo heeft Euler veel nieuwe concepten ontwikkeld en heeft hij zeer veel bijgedragen aan de moderne wiskundige notatie. Als we verschillende figuren met elkaar gaan vergelijken zien we dat de kubus acht hoekpunten, twaalf ribben en zes zijden heeft. Op dezelfde manier zien we dat de octaëder zes hoekpunten, twaalf ribben en acht zijden heeft en de tetraëder vier hoekpunten, zes ribben en vier zijden. Als we kijken naar de hoeveelheden blijkt steeds dat als we het aantal hoekputen en het aantal zijden optellen en er het aantal ribben vanaf halen, dat we dan twee eruit krijgen. Hierover heeft Euler een formule ontdekt. 4.2 De formule De formule van Euler gaat als volgt: Stelling 2 Het aantal hoeken + het aantal zijden - het aantal ribben = 2, m.a.w. H R + Z = 2 In de rest van dit dictaat is het aantal hoekpunten afgekort tot H, het aantal ribben afgekort tot R en het aantal zijvlakken afgekort tot Z. Zoals hieronder staat klopt het dus voor alle vijf regelmatige veelvlakken die hiervoor behandeld zijn. Zoals hieronder te zien is: Tetraëder: H R + Z = = 2 Kubus: H R + Z = = 2 Octaëder: H R + Z = = 2 Dodecaëder: H R + Z = = 2 Icosaëder: H R + Z = = 2 12

13 We gaan nu de formule van Euler na voor de volgende figuur: Figuur 9: La Grande Arche Geschiedenis2 Dit is La Grande Arche de la Fraternit ook wel bekend onder de naam l Arche de la Dense of Grande Arche. Het is een gebouw in de wijk La Dense in Parijs. De Deense architect Johann Otto von Spreckelsen ontwierp een 20e eeuwse versie van de Arc de Triomphe. Toen hij in 1987 overleed nam de Franse architect Paul Andreu het werk over. Het gebouw werd geopend op 14 juli 1989, 200 jaar na de bestorming van de Bastille. De Grande Arche is vrijwel kubusvormig en de binnenkant is open. Het heeft een hoogte van 110 meter (zo hoog dat de Notre-Dame erin zou passen), een lengte van 108 meter en een breedte van 112 meter. De Grand Arche heeft vier zijden aan de buitenkant, vier aan de voorkant, vier aan de achterkant en vier binnenin. Dat zijn dus 16 zijden. Verder zijn er 16 hoekpunten en 32 ribben. Als je dit invult in de formule van Euler krijg je: = 0. Blijkbaar geldt de Formule van Euler niet voor dit soort veelvlakken. Er zijn blijkbaar een aantal voorwaarden waar een veelvlak aan moet voldoen zodat de Formule van Euler klopt. De voorwaarden is dat het figuur enkelvoudig samenhangend moet zijn. Definitie 7 Een enkelvoudig veelvlak is een veelvlak dat niet doorboord is. Definitie 8 Een samenhangend veelvlak is een veelvlak dat uit één deel bestaat en dat niet uit twee losse delen bestaat. Wat we zien in figuur 9 is dat de La Grande Arche doorboord is; dit verklaart waarom de formule van Euler hier niet geldt. Opgave 13 We hebben gezien dat de formule niet klopt voor een kubus met een gat erin. Hier komt blijkbaar nul uit. Is dit toevallig of geldt dit voor alle veelvlakken waar een gat in zit? Kun je ook op 2 uitkomen? 13

14 4.3 Een bewijs van de formule van Euler Er zijn veel verschillende bewijzen van de formule van Euler. We bekijken het bewijs door Von Staudt: Bewijs: We kleuren een hoekpunt van een enkelvoudig samenhangend figuur rood. Dan kleuren we een ribben die aan dat hoekpunt grenst rood. Daardoor kleuren we dus weer een hoekpunt rood. Als we dit zolang blijven doen tot alle hoekpunten rood zijn, maar er geen gesloten paden ontstaan zijn we klaar. We kunnen zo alle hoekpunten bereiken, want de figuur is enkelvoudig samenhangend figuur. Als we met het inkleuren een hoekpunt overhouden, is die ook rood te kleuren. Omdat de figuur enkelvoudig samenhangend is bestaat er een ribbe die tussen een ongekleurd en een rood hoekpunt zit en deze kunnen we dan rood kleuren. Op deze manier kunnen we altijd ieder hoekpunt bereiken en we krijgen op deze manier nooit een gesloten vlak, want anders was het hoekpunt al rood gekleurd. Als we nu het rode pad uittekenen krijgen we een graaf. Dan zien we dat het aantal rode ribben gelijk is aan het aantal hoekpunten min één. Figuur 10: Een voorbeeld van een graaf Rr is hierbij het aantal rode ribben. Rr = H 1 (1) De ribben in de figuur die we niet rood kleurden, kleuren we nu groen. We stellen de zijvlakken nu voor als knopen, en tussen twee knopen tekenen we een boog als de desbetreffende zijvlakken verbonden zijn door groene ribben. De groene ribben kunnen geen cykel vormen, want als dat zou gebeuren kun je er een rood maken en dan zou de cykel worden doorbroken. Dus krijgen we een samenhangende graaf, want in de groene ribben zitten geen cykels. Wat we dan zien is dat het aantal bogen is het aantal knopen min één, dus: aantal bogen = aantal knopen - 1. Dit geld altijd, want als geldt dat een graaf samenhangend is en geen cykels heeft geldt altijd dat het aantal ribben gelijk is aan het aantal knopen min één. Als dit niet zo is, dan moet gelden dat de graaf uit 2 delen bestaat omdat dan komt er één knoop per deel bij komt. Om een aantal ribben 14

15 minimaal gelijk aan het aantal knopen te hebben, moet de graaf een cykel of gesloten pad bevatten. De bogen zijn de zijden en de knopen zijn de groene ribben, dus dan krijgen we dat het aantal groene ribben gelijk is aan het aantal zijden min één. Rg is hierbij het aantal groene ribben. Rg = Z 1 Het totale aantal ribben is gelijk aan het aantal groene ribben + het aantal rode ribben = Z H - 1. Dat kunnen we dan dus schrijven als R = Z + H - 2, wat we om kunnen schrijven als: H - R + Z = 2. Q.E.D. Dit bewijs gaat niet op voor de Grande Arche, omdat dit geen enkelvoudig samenhangend figuur is. We kunnen de ribben dus niet zo rood kleuren dat alle hoekpunten rood zijn, zonder dat de figuur gesloten is. Verder zien we dat de figuur niet in twee delen uiteen kan vallen. 15

16 5 Dualiteit We gaan eerst terug naar alles wat we al weten voordat we gaan kijken wat dualiteit inhoudt: Tetraëder: H R + Z = = 2 Kubus: H R + Z = = 2 Octaëder: H R + Z = = 2 Dodecaëder: H R + Z = = 2 Icosaëder: H R + Z = = 2 Als we van deze formules de orde van de zijde en de orde van de hoek bekijken. Tetraëder: Orde van de zijde: 3 Orde hoek: 3 Kubus: Orde van de zijde: 4 Orde hoek: 3 Octaëder: Orde van de zijde: 3 Orde hoek: 4 Dodecaëder: Orde van de zijde: 5 Orde hoek: 3 Icosaëder: Orde van de zijde: 3 Orde hoek: 5 Hieronder volgt een samenvattend schema: H R Z Orde zijde Orde hoek Tetraëder Kubus Octaëder Dodecaëder Icosaëder Wat opvalt is dat, als je naar kubus en de octaëder kijkt, zijn de aantallen hoeken en zijden omgedraaid. Hetzelfde geldt voor de dodecaëder en de icosaëder. Deze noemen we elkaars duale. De tetraëder is duaal met zichzelf. Stel K is het regelmatige veelvlak waarmee we beginnen, K is het duale veelvlak van K, en betekent de vorming van het duale veelvlak. Dan moet gelden: Als K K K en als geldt dat K = K, dan heet dit een operatie van dualiteit. 16

17 Ter illustratie volgt de volgende opdracht: Opgave 14 Neem een ballon en blaas deze op. Teken er met een watervaste stift vierkante blokken op, dit zijn landen. Pak van elk land het midden(de hoofdstad) en verbind de middens van de buurlanden met elkaar, met een andere kleur. We krijgen dan een nieuw netwerk van landen. Verbind nu weer de middens van deze landen. Wat valt je op? In de voorgaande tabel met de aantallen ribben, zijvlakken en hoekpunten per regelmatig veelvlak valt ons iets op: voor elk veelvlak bestaat een ander veelvlak waarvan het aantal ribben hetzelfde is, maar het aantal hoekpunten en zijvlakken precies is omgedraaid. Verder zien we bij dezelfde figuren dat de orde van de hoek en de orde van de zijden omgedraaid zijn. We vragen ons af of deze veelvlakken elkaars duale vormen kunnen zijn. Dit gaan we als volgt onderzoeken: We verbinden de middens van de zijvlakken van een veelvlak met elkaar. Deze middelpunten worden de hoekpunten in de nieuwe figuur: de aantallen zijvlakken en hoekpunten wordt dus omgewisseld. Als we nu in de nieuwe figuur weer de middens van de zijvlakken verbinden, zullen we de oorspronkelijke figuur terug krijgen. Het verbinden van middens van zijvlakken is dus een manier om een duale van een veelvlak te creëren. We zullen dit toepassen op de regelmatige veelvlakken. We bekijken eerst de tetraëder. Als we de middens van de vlakken met elkaar verbinden zien we dat we weer een tetraëder krijgen. De tetraëder is dus duaal met zichzelf: dit heet zelfduaal. Figuur 11: De middens van de zijden van de tetraëder met elkaar verbonden We bekijken nu de kubus en de octaëder: Figuur 12: Links: de middens van de zijden van de kubus met elkaar verbonden, rechts: de middens van de zijden van de octaëder met elkaar verbonden 17

18 Op dezelfde manier als bij de tetraëder is in te zien dat de kubus en de octaëder elkaars duale zijn. Als laatste de dodecaëder en icosaëder: De dodecaëder en de isocaëder zijn elkaars duale. Dit kun je hieronder zien: Figuur 13: Links: de middens van de zijden van de dodecaëder met elkaar verbonden, rechts: de middens van de zijden van de icosaëder met elkaar verbonden Voor al deze figuren geldt dus: K = K. Verder kunnen we dus zien dat we deze figuren uit de andere figuren kunnen krijgen als er gebruik wordt gemaakt van afknotten en uitstulpen. Dit zijn dan dus ook duale operaties. Opgave 15 Bepaal de dualel van een kubus waarbij in 1 hoek een stuk is afgeknot. Opgave 16 Is het verbinden van de middens van de ribben van veelvlakken een duale operatie? Laat zien. Een goed sluitende definitie noemen we niet. Hieronder volgt namelijk een tegenvoorbeeld waar je anders tegenaan loopt: Stel je hebt een tetraëder. Je kan delen van de tetraëder wegsnijden zodanig dat je een kubus overhoudt en van deze kubus kan je delen wegsnijden zodat je weer een tetraëder overhoudt. Er zou dan gelden: K = tetraëder, K = kubus en K = tetraëderen zouden de tetraëder en de kubus dus elkaars duale zijn. Dit klopt niet, want je voert namelijk niet twee maal precies dezelfde operatie uit. Uit dit alles blijkt dat we geen definitie van dualiteit willen noemen omdat je daar meer kennis voor nodig hebt, want je wilt dat je definitie alle uitzonderingen uitsluit. Ons doel was om in dit hoofdstuk puur de methode laten zien. 18

19 6 Symmetrie In n van de eerste colleges van deze cursus is het onderwerp symmetrie behandeld, toegepast op twee dimensies. Om symmetrie toe te kunnen passen op regelmatige veelvlakken zullen we met isometrieen in de derde dimensie moeten werken, maar deze zullen in veel opzichten weinig verschillen van de tweedimensionale varianten. We willen de symmetrie binnen regelmatige en halfregelmatige veelvlakken gaan beschrijven, dus daardoor zullen we niet alle isometrieën die bekend zijn van twee dimensies gebruiken: glijspiegelingen en translaties zullen bijvoorbeeld niet aan bod komen. De belangrijkste isometrieën zijn vandaag rotatie- en spiegelsymmetrie. 6.1 Definities We onderscheiden vandaag twee verschillende isometrieën: directe en indirecte symmetrie. zullen hier nu eerst formele definities van geven. We Definitie 9 Directe symmetrie is een beweging van een object die het object afbeeldt op een positie die niet te onderscheiden is van de beginpositie. Hierbij is het niet de beweging die de operatie interessant maakt, maar de relatie tussen begin- en eindpositie. Zo kunnen verschillende combinaties van operaties hetzelfde eindresultaat opleveren. Directe symmetrie is makkelijk te visualiseren door bijvoorbeeld een object vast te pakken en het in een nieuwe positie te draaien. In de praktijk zullen directe symmetrieën dan ook vaak rotatiesymmetrieën zijn. Definitie 10 Indirecte symmetrie is een operatie die een (driedimensionaal) object spiegelt in een denkbeeldige lijn of vlak. Deze isometrie wordt ook wel spiegelsymmetrie genoemd: de eindpositie wordt verkregen door een object te spiegelen in een lijn, of in het driedimensionale geval, een vlak. Indirecte symmetrie verschilt wezenlijk van directe symmetrie: het is vaak niet mogelijk om dezelfde eindpositie te creëren door een combinatie van rotaties. Dit kan makkelijk worden ingezien door de hoekpunten van het object te nummeren. Als we nu een indirecte symmetrie toepassen op het object kan men inzien dat de positie die hierdoor verkregen wordt niet gevormd kan worden door een combinatie van rotaties. 19

20 Figuur 14: Een octaëder met spiegelbeeld We zullen nu beide isometrieën toegepast op regelmatige veelvlakken uitgebreider beschreven, en we zullen inzien dat het begrip dualiteit een belangrijke rol zal spelen. 6.2 Directe Symmetrie Leonhard Euler toonde aan dat elke vorm van directe symmetrie binnen een willekeurig veelvlak een rotatie om een as is. We zullen daarom van nu af directe symmetrie aanduiden met rotatiesymmetrie. Om een rotatie te beschrijven zijn twee dingen nodig: een hoek en een as. In een veelvlak kunnen verschillende rotatieassen mogelijk zijn, en Euler bewees dat wanneer dit het geval is, deze assen elkaar snijden in het middelpunt van het veelvlak. Om de verschillende directe symmetrieën binnen een veelvlak goed te kunnen beschrijven, zullen we eerst de grootte van een willekeurige rotatie moeten beschrijven. Dit kan op twee manieren: we kunnen de grootte van de rotatiehoek gebruiken, of het aantal roaties dat nodig is voordat een object weer in zijn oorspronkelijke situatie is. We zullen vandaag de laatste vorm gebruiken: deze maakt het werken met regelmatige veelvlakken overzichtelijker. Stel dat er bij een bepaalde rotatie as n rotaties nodig zijn voordat het object weer terug is in zijn beginpositie, dan heet de rotatie n-voudig. De bijbehorende as heet een n-voudige as. Aan de hand van het aantal verschillende soorten rotatie- en spiegelsymmetrieën binnen een veelvlak kunnen we nu verschillende types van symmetrie onderscheiden, op zo n manier dat elk willekeurig veelvlak tot een van deze types behoort. We zullen dit illustreren aan de hand van de regelmatige veelvlakken. Tip: tijdens het lezen kan het handig zijn modellen van de veelvlakken bij de hand te houden. 20

21 6.2.1 Tetraëder We zien dat er vier symmetrieassen getekend kunnen worden door een hoekpunt van de tetraëder en het midden van de zijde tegenover dat hoekpunt (L). Over deze as zijn drie rotaties nodig om de tetraëder in de oorspronkelijke positie terug te zetten, dus deze rotaties zijn drievoudig. In totaal zijn er vier verschillende assen voor drievoudige symmetrie, door elk hoekpunt één. Ook is het mogelijk om een as te tekenen door de middens van twee overstaande ribben (K). De rotatie behorende bij deze assen is tweevoudig Hexaëder en Octaëder Figuur 15: De rotatie assen van een tetraëder We beginnen met de hexaëder (kubus). We zien dat hier n-voudige symmetrieën te vinden zijn voor drie verschillende waarden van n: Er zijn zes verschillende assen van tweevoudige symmetrie(m): deze assen gaan door de middens van twee overstaande ribben. Er zijn vier verschillende assen van drievoudige symmetrie (L): deze gaan door twee overstaande hoekpunten. Er zijn drie verschillende assen van viervoudige symmetrie (K): deze gaan door de middens van twee overstaande zijden. 21

22 Figuur 16: De rotatie assen van een kubus en een octaëder Een hexaëder en octaëder met een aantal symmetrie assen. De n behorende bij de as staat tussen haakjes aangegeven. Als we nu de octaëder gaan bekijken, zien we iets opvallends: Er zijn zes assen van tweevoudige symmetrie (M): de assen gaan door de middens van twee overstaande ribben. Er zijn vier assen van drievoudige symmetrie (L): de assen gaan door de middens van twee overstaande zijden. Er zijn drie assen van viervoudige symmetrie (K): de assen gaan door twee overstaande hoekpunten. De octaëder en hexaëder hebben dus dezelfde aantallen n-voudige symmetrie-assen, voor verschillende waarden van n Dodecaëder en Icosaëder Opgave 17 Zoek alle n-voudige symmetrie-assen van de dodecaëder en de icosaëder en vul deze in in de tabel. Wat valt je op? Hoe zou je dit kunnen verklaren? n Dodecaëder Icosaëder

23 6.3 Indirecte symmetrie Zoals al eerder gezegd is het vlak van een spiegelsymmetrie in de derde dimensie een vlak. Deze as is tweevoudig: door twee keer te spiegelen komen we terug in de beginsituatie. Omdat veel objecten ook spiegelsymmetrie hebben, zullen we hier rekening mee moeten houden wanneer we deze objecten op grond van hun symmetrie in klassen willen indelen. We zullen nu dan ook de verschillende spiegelsymmetrieën van de regelmatige veelvlakken gaan onderzoeken en deze aan hun klassen toevoegen. Tetraëder Er bestaat één soort spiegelsymmetrievlak voor de tetraëder: de vlakken van deze symmetrieën gaan door een ribbe van de tetraëder en het middelpunt van de ribbe hier tegenover. We laten het aan de lezer om al deze vlakken te identificeren. We kunnen nu de eerste symmetrieklasse definiëren: Definitie 11 De verzameling van alle objecten die dezelfde aantallen spiegelsymmetrie en n-voudige rotatiesymmetrie bezitten als de tetraëder voor alle verschillende waarden van n noemen we Tetraëder symmetrisch. Hexaëder en Octacaëder spiegelvlakken: Een hexaëder en dodecaëder hebben beide twee verschillende soorten Een vlak door twee overliggende ribben Een vlak door de middens van twee overliggende ribben en het midden van de ribbe die tussen deze ribben in ligt (hexaëder) of het hoekpunt dat tussen deze ribben in ligt (octaëder). We laten het weer aan de lezer om deze assen te identificeren. We zien nu dat de octaëder en hexaëder niet alleen dezelfde aantallen rotatiesymmetrieën hebben; ook hun spiegelsymmetrieën komen overeen. Deze twee veevlakken behoren dan ook tot dezefde symmetrieklasse: Definitie 12 De hexaëder- of octaëder symmetrieklasse bestaat uit alle objecten die precies dezelfde aantallen spiegelsymmetrie en n-voudige rotatiesymmetrie bezitten als de hexaëder en octaeder. Opgave 18 Construeer op dezelfde manier de verschillende assen voor de dodecaëder en icosaëder Het feit dat hexaëders en octaëders tot dezelfde klasse behoren, en dodecaëders en icosaëders ook, kan worden verklaard door dualiteit. De hexaëder en de octaëder zijn elkaars duale vorm, net als de dodecaëder en de icosaëder. Volgens de definitie van dualiteit ligt een hoekpunt van de ene vorm op het midden van een zijde van de andere vorm: als we dus een as tekenen door twee hoekpunten van de ene vorm, zal deze ook door de middens van twee overstaande zijden van de duale vorm gaan. Dit verklaart dezelfde aantallen vier- en drievoudige symmetrie. Wat lastiger, maar toch ook nog vrij duidelijk in te zien is dat een as die door de middens van twee overstaande ribben in de oorspronkelijke vorm gaat, ook door de middens van twee overstaande ribben in de duale vorm gaat. Hiermee wordt duidelijk dat het aantal twee-voudige assen in beide vormen hetzelfde is, en dus behoren beide duale vormen tot dezelfde klasse. Dit geldt ook voor alle spiegelassen van deze 23

24 veelvlakken. Hetzelfde verhaal geldt voor de dodecaëder en de octaëder. Deze twee zijn iets latiger te visualiseren, maar met een beetje fantasie lukt dit ook nog wel. De duale vorm van de tetraëder is de tetraëder zelf, daarom heeft dit regelmatige veelvlak een eigen klasse. De overige symmetrieklassen zullen we verder niet beschrijven, op één uitzondering na: de klassen zonder spiegelsymmetrie. Dit zijn een aantal verschillende klassen: objecten zonder spiegelsymmetrie kunnen immers verschillende rotatie symmetrieën hebben. Het bijzondere is hier dat één zo n klasse in twee groepen verdeeld kan worden. Hierbij is de ene groep het spiegelbeeld van de andere groep (denk bijvoorbeeld aan een kurkentrekker, deze kan linksdraaiend of rechtsdraaiend zijn). Een aantal halfregelmatige veelvlakken zijn goede voorbeelden van veelvlakken zonder spiegelsymmetrie, zie hieronder bijvoorbeeld de stompe dodecaëder: Figuur 17: De stompe dodecaëder Opgave 19 Onderzoek welke symmetrieën de stompe kubus heeft. a) Behoort dit veelvlak tot één van de typen Tetraëder-, Hexaëder- of Dodecaëder symmetrie? b) Heeft dit veelvlak spiegelsymmetrie? Zo ja, geef de assen, zo nee, teken twee bouplaten van de stompe kubus waarbij de ene bouwplaat (in elkaar gezet) het spiegelbeeld van de andere voorstelt. Het kan bij deze opdracht handig zijn een model van het veelvlak te maken, zie bijvoorbeeld Mathematica of de engelse site van Wikipedia voor een goed model. 24

25 7 Referenties Naast het enthousiasme van Aad hebben we de volgende bronnen gebruikt: Polyhedra Peter R. Cromwell De veelzijdigheid van bollen Martin Kindt en P. Boon 25