Didactisch gebruik van GeoGebra 3D in de lessen ruimtemeetkunde van de 3 de graad
|
|
|
- Karen van der Ven
- 6 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Didactisch gebruik van GeoGebra 3D in de lessen ruimtemeetkunde van de 3 de graad 0 Het opstarten van GeoGebra Om het programma GeoGebra 5.0 vast op je computer te installeren, ga je naar Kies voor Downloads en daarna voor Windows bij GeoGebra voor PC Je komt dan terecht in de GeoGebra 5 Setup Wizard, die je opent. Kies bij het installeren voor taal Nederlands. Bevestig dat je akkoord gaat met de licentievoorwaarden. Kies voor de standaardinstallatie en de knop Installeren. GeoGebra 5.0 wordt nu geïnstalleerd, waarna je het programma kan opstarten met Voltooien. - Om na te gaan over welke versie je beschikt, kan je het nummer opvragen via Help, About/Licentie. Bij mij was dit: - De ontwikkelaars voegen regelmatig nieuwe commando s toe aan de 3D-versie van GeoGebra. Je vindt die via de Release notes op de GeoGebra website: 1
2 1 Het gebruik van GeoGebra in de lessen ruimtemeetkunde Er zijn verschillende mogelijkheden om GeoGebra te gebruiken in de lessen. - De leraar demonstreert een stukje theorie aan de hand van een applet, gemaakt door de leraar (zie 4.1). - De leraar demonstreert de oplossing van een oefening aan de hand van een applet die hij zelf gemaakt heeft (zie 4.5). - De leerlingen controleren zelf de oplossing van een oefening aan de hand van een applet, gemaakt door de leraar (zie 4.3). - De leerlingen controleren zelf de oplossing van een oefening aan de hand van een applet, die ze zelf gemaakt hebben (zie 4.2). - De leerlingen maken een oefening door gebruik te maken van een applet, gemaakt door de leraar (zie 4.3 en 4.4). - De leerlingen maken een oefening door zelf een applet te maken (zie 4.6, 4.7 en 4.8) De opdrachten uit nr. 4 illustreren deze verschillende gebruiksmogelijkheden van GeoGebra. 2 Het 3D-tekenvenster 2.1 Overzicht - In de menubalk kun je via de knop Beeld het 3D-tekenvenster openen. Klikken we nu het 2D-tekenvenster en het algebravenster weg, dan krijgen we het volgende beeld. - Je hebt van boven naar beneden: - de klassieke menubalk. - de 3D-werkbalk of -knoppenbalk. 2
3 - de 3D-opmaakbalk - het 3D-tekenvenster - de invoerlijn 2.2 De 3D-werkbalk - Je vindt hier een aantal commando s terug van de 2D-werkbalk, naast een aantal typische 3D-commando s. De belangrijkste leggen we uit in nr. 3: Tools en commando s in het 3D-tekenvenster. Hier beperken we ons tot de laatste knop en de ikoontjes rechtsboven. Is deze knop actief, dan kun je door met een muisknop in het tekenvenster te klikken en de knop ingedrukt te houden, het beeld laten roteren. Je kan dit ook zonder deze knop door met de rechtermuisknop in het tekenvenster te klikken en de knop ingedrukt te houden. Is deze knop actief, dan kun je, door met de linkermuisknop in het tekenvenster te klikken en de knop ingedrukt te houden, het beeld laten verschuiven in horizontale richting. Door nog eens in het tekenvenster te klikken kun je het beeld ook laten verschuiven in verticale richting. Je kan dit ook zonder deze knop door de shift-toets ingedrukt te houden. Met deze knop kun je het beeld inzoomen door in het tekenvenster te klikken. Dit kan ook door aan het wieltje van de muis te draaien. Idem voor uitzoomen. Met de knop kun je verschillende aanzichten van een object creëren door op het juiste zijvlak te klikken. Met dit ikoontje kun je bewerkingen ongedaan maken. Met dit ikoontje kun je bewerkingen, die ongedaan gemaakt zijn, opnieuw doen uitvoeren. Hiermee kun je een aantal voorkeuren instellen. We leggen dit uit onder De 3D-opmaakbalk - Op de 3D-opmaakbalk vind je verscheidene knoppen: om de assen te tonen of te verbergen, om het rooster in het (x,y)-vlak te tonen of te verbergen, om het (x,y)-vlak te tonen of te verbergen, om terug te keren naar het standaardbeeld, om de punten al dan niet vast te maken aan het rooster, om het beeld al dan niet te laten roteren rond de z-as; de snelheid pas je aan met de schuifknop, 3
4 om het aanzicht te veranderen - geeft een projectie op het (x,y)-vlak, - geeft een projectie op het (x,z)-vlak, - geeft een projectie op het (y,z)-vlak, - met keer je terug naar het basisaanzicht na rotatie van het beeld om de clipping box aan en af te zetten en te vergroten of te verkleinen, om de projectie te kiezen: - geeft een loodrechte parallelprojectie ( parallel projection ), - geeft een perspectiefprojectie ( perspective projection ) - geeft anaglyphen of 3D-zicht, te bekijken met een 3D-bril ( projection for glasses ) - geeft een scheve parallelprojectie ( oblique projection ). - De combinatie van (projectie op het (y, z)-vlak) en (scheve parallelprojectie) geeft het klassieke orthonormale assenstelsel uit de ruimtemeetkunde van de 3 de graad. Hierbij wijst de x-as naar voor, de y-as naar rechts en de z-as naar boven. - Je kan dan nog de hoek tussen de x-as en de y-as aanpassen (zie verder). Standaard staat die hoek op Soms maken we gebruik van een ander klassiek assenstelsel in parallelprojectie. We verkrijgen dit door een combinatie van (projectie op het (x,z)-vlak) en (scheve parallelprojectie). In dit geval wijst de x-as naar rechts, de y-as naar achter en de z-as naar boven. Dit assenstelsel is compatibel met het assenstelsel in 2D. - Ook hier kan je de hoek tussen de x-as en de y-as aanpassen (zie verder). Standaard staat die hoek op 30. 4
5 2.4 De invoerlijn - Uiteraard is ook in 3D algebraïsche invoer mogelijk. Hiervoor beschik je over een aantal 3D-commando s naast de vertrouwde 2D-commando s. Een aantal van deze commando s leggen we uit in nr Let er echter op dat niet alle commando s uit 2D werken in 3D. Zo is het voorlopig niet mogelijk om in het 3D-tekenvenster te werken met schuifknoppen en actieknoppen of met de navigatiebalk. Dit kan echter omzeild worden door deze elementen te tonen in het 2D- tekenvenster. 2.5 Voorkeuren - Als je met de rechtermuisknop klikt in het tekenvenster, krijg je opnieuw een menu voor de opmaak van het 3D-tekenvenster. Ook hier kan je de assen, het rooster en het (x,y)-vlak tonen of verbergen. Je kunt ook de navigatiebalk tonen of verbergen. Met de optie Standaardbeeld kun je terugkeren naar het standaardbeeld na verplaatsing van het tekennvenster of na in- en uitzoomen. Met de optie Tekenvenster kom je in het menu Voorkeuren. Deze voorkeuren kan je ook oproepen door de knop bovenaan rechts aan te klikken. Het menu Voorkeuren bevat 6 deelmenu s:, resp. Objecten, 3D-tekenvenster, Lay-out, Standaard, Geavanceerd en Algebravenster. We beperken ons hier tot de deelmenu s Objecten, Standaard en 3D-tekenvenster. - In het deelmenu Objecten kun je de lay-out van de getekende objecten aanpassen. Dit kan je ook door met de rechter muisknop te klikken op de objecten. - In het deelmenu Standaard kun je de lay-out van punten, rechten, lijnstukken, halfrechten, veelhoekslijnen, vectoren, bepalen. Zo heb je voor punten - het tabblad Basis : hier kun je kiezen voor object tonen, spoor tonen, object fixeren en hulpobject, - het tabblad Kleur, waar je kan kiezen tussen 72 kleuren, - het tabblad Stijl, waar je de puntgrootte en de puntstijl kan instellen, - het tabblad Coördinaten, waar je kan kiezen tussen verschillende soorten coördinaten (cartesische coördinaten, poolcoördinaten, sferische coördinaten, ) en de stapgrootte kan instellen. - In het deelmenu 3D-tekenvenster kun je de hele opmaak van het 3D-venster aanpassen. - In het tabblad Basis kun je - de assen tonen of verbergen, - de y-as verticaal maken, - de navigatiebalk al dan niet tonen, - de achtergrondkleur wijzigen, - de Clipping box al dan niet gebruiken en tonen, - de grootte van de Clipping box aanpassen. 5
6 - In de tabbladen xas, yas en zas, kun je - al dan niet de assen tonen, - al dan niet de getallen op de assen tonen, - de volledige as of het positief gedeelte afbeelden, - de graduatie op de as wijzigen, - het label en de eenheid wijzigen. - In het tabblad Rooster kun je - het rooster al dan niet tonen, - de afstanden tussen de roosterlijnen aanpassen, zowel in de x- als in de y- richting. - In het tabblad Projectie kun je kiezen voor een - loodrechte parallelprojectie - perspectiefprojectie: hier kan je ook de afstand tot het scherm kiezen, - 3D-zicht: hier kan je de afstand tussen de ogen kiezen en al dan niet grijswaarden weergeven, - scheve parallelprojectie hier kan je de hoek en de schaalfactor (verkleiningsfactor) wijzigen. 6
7 3 Beperkt overzicht van tools en commando s in het 3D-tekenvenster Verplaatsen Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Verplaatsen Hiermee kan je objecten verslepen met de muis Punten Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Een nieuw punt tekenen in de ruimte (enkel 3D) Klik in het tekenvenster om een nieuw punt te creëren in het (x,y)-vlak. Je kan het punt nu verslepen in dit vlak. Klik op het punt met de linkermuisknop. Nu kan je de z-coördinaat van het punt wijzigen. Nogmaals klikken op het punt laat een horizontale verplaatsing toe in een vlak, evenwijdig met het (x,y)-vlak. P=(a,b,c) Creëert een punt P met coördinaat (a, b, c). Het midden van een lijnstuk bepalen 3.3 Rechten, lijnstukken, halfrechten en vectoren Een rechte bepalen door een punt en met een gegeven richtingsvector Selecteer twee punten of een lijnstuk en creëer het midden. Midden[<punt A>,<punt B>] Midden[<lijnstuk c>] A + B M = 2 Creëert het midden van het lijnstuk AB. Creëert het midden van het lijnstuk c. Creëert het midden M van de punten A en B. Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Selecteer een punt en een vector en Rechte[<punt A>,<vector v>] creëer een rechte door het punt en met de vector als richtingsvector. Creëert een rechte r door het punt A met richtingsvector v. 1 Alle constructies die uitgevoerd worden in het 2D-tekenvenster verschijnen automatisch in het (x, y)-vlak van het 3D-tekenvenster. Omgekeerd zullen elementen in het 3D-tekenvenster, die in het (x, y)-vlak liggen, ook verschijnen in het 2D-tekenvenster. 7
8 Een rechte door twee punten bepalen Een evenwijdige rechte bepalen Een loodlijn bepalen Een lijnstuk bepalen tussen twee punten Een vector bepalen tussen twee punten Een punt verschuiven over een vector Een vector bepalen met gegeven coördinaat Selecteer twee punten en creëer de rechte door die punten. Selecteer een punt en een rechte of een lijnstuk en creëer de evenwijdige door het punt aan de rechte of het lijnstuk. Selecteer een punt en een rechte of een lijnstuk en creëer de loodlijn vanuit het punt op de rechte of het lijnstuk. Selecteer een punt en een vlak en creëer de loodlijn vanuit het punt op het vlak Selecteer twee punten en creëer het lijnstuk tussen de twee punten. Selecteer twee punten en creëer de vector tussen deze punten. Selecteer een punt en een vector en creëer de vector, die gelijk is aan de gegeven vector en die het punt als beginpunt heeft. Rechte[<punt A>,<punt B>] Rechte[<punt A>,<rechte g>] Rechte[<punt A>,<lijnstuk l>] Loodlijn[<punt A>,<rechte r>] Loodlijn[<punt A>,<lijnstuk l>] Loodlijn[<punt A>,<vector v>] Loodlijn[<punt A>,<vlak α>] (enkel in 3D) Loodlijn[<punt A>,<richting b>, <richting c>] Loodlijn[<punt A>,<rechte r>, <vlak α>] (enkel in 3D) Loodlijn[<rechte a>,<rechte b>] Creëert een rechte r door A en B. In het algebravenster komt de vectoriële vergelijking. Creëert een rechte door het punt A evenwijdig met de rechte g. Creëert een rechte door het punt A evenwijdig met het lijnstuk l. Creëert een loodlijn door het punt A op de rechte r. Creëert een loodlijn door het punt A op het lijnstuk l. Creëert een loodlijn door het punt A op de vector v. Creëert een loodlijn door het punt A op het vlak α. Creëert een loodlijn door het punt A op het vlak, bepaald door de richtingen b en c (dit kunnen zowel rechten als vectoren zijn). Creëert een loodlijn door het punt A, loodrecht op de rechte r en evenwijdig met het vlak α. Creëert de gemeenschappelijke loodlijn van de rechten a en b. AB Lijnstuk[<punt A>,<punt B>] Creëert het lijnstuk Vector[<startpunt A>,<eindpunt B>] Vector[<punt A>] Punt[<punt A>,<vector v>] Creëert de vector AB met A als beginpunt en B als eindpunt. Creëert de vector OA met O als beginpunt en A als eindpunt. Verschuift het punt A over de vector v u=(a,b,c) Creëert een vector u met coördinaat (a, b, c). 8
9 3.4 Veelhoeken en veelhoekslijnen Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Selecteer minstens drie punten in hetzelfde Veelhoek[<punt A>,<punt vlak en klik daarna terug op het B>,...] eerste punt om een veelhoek te creëren. Veelhoek[<puntenlijst L>] Een veelhoek bepalen Een regelmatige veelhoek bepalen Veelhoek[<punt A>,<punt B>,<getal n>,<vlak α>] 3.5 Kegelsneden en meetkundige plaatsen Een cirkel door drie punten bepalen Veelhoek[<punt A>,<punt B>,<getal n>,<rechte r>] Veelhoek[<punt A>,<punt B>,<getal n>] Creëert een veelhoek met de gegeven punten als hoekpunten. Creëert een veelhoek met de punten uit lijst L als hoekpunten. Creëert een regelmatige n-hoek met [AB] als zijde en gelegen in een vlak, evenwijdig aan het vlak α (op voorwaarde dat AB//α). Creëert een regelmatige n-hoek met [AB] als zijde en gelegen in een vlak, loodrecht op de rechte r (op voorwaarde dat AB r). Creëert een regelmatige n-hoek met [AB] als zijde en gelegen in een vlak, evenwijdig aan het (x, y)-vlak (op voorwaarde dat AB evenwijdig is aan het (x, y)-vlak). Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Selecteer drie punten en creëer de cirkel Cirkel[<punt A>,<punt B>, door deze punten. <punt C>] 3.6 Vlakken Een vlak bepalen door drie gegeven punten (enkel in 3D) Creëert de cirkel door de punten A, B en C. Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Selecteer drie niet collineaire punten en Vlak[<punt A>,<punt B>,<punt creëer het vlak door die punten. C>] Een vlak bepalen door een punt en een rechte (enkel in 3D) Selecteer een punt en een rechte (die niet door het punt gaat) en creëer het vlak dat het punt en de rechte omvat. Vlak[<punt A>,<rechte a>] Creëert een vlak door de punten A, B en C. In het algebravenster komt de cartesiaanse vergelijking. Creëert een vlak door het punt A, dat de rechte a omvat. 9
10 Een vlak bepalen door twee snijdende of evenwijdige rechten (enkel in 3D) Een vlak tekenen met gegeven cartesiaanse vergelijking (enkel in 3D) Een evenwijdig vlak bepalen (enkel in 3D) Een loodvlak bepalen (enkel in 3D) Een middelloodvlak bepalen(enkel in 3D) Selecteer twee snijdende of evenwijdige rechten en creëer een vlak dat de twee rechten omvat. Vlak[<rechte a>,<rechte b>] Creëert een vlak dat de evenwijdige of snijdende rechten a en b omvat α:ax+by+cz=d Creëert het vlak α met vergelijking ax + by + cz = d. Selecteer een vlak en een punt en creëer het vlak dat door het punt gaat en evenwijdig is aan het gegeven vlak. Selecteer een rechte en een punt en creëer het loodvlak door het punt op de rechte. Vlak[<punt A>,<vlak α>] Loodvlak[<punt A>,<rechte a>] Loodvlak[<punt A>,<vector v>] Deelvlak[<punt A>,<punt B>] Deelvlak[<lijnstuk a>] Creëert een vlak door het punt A evenwijdig met het vlak α. Creëert een loodvlak op de rechte a door het punt A. Creëert een loodvlak op de vector v door het punt A. Creëert het middelloodvlak van het lijnstuk [AB] of het lijnstuk a. 3.7 Veelvlakken Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Selecteer een veelhoek (of de punten die Prisma[<punt A>,<punt B>,, de veelhoek bepalen) en een punt en <punt F>,<punt Q>] creëer een prisma met als grondvlak de Prisma[<veelhoek v>,<punt Q>] veelhoek en als bovenvlak een vlak door het punt. Sleep een veelhoek of selecteer een Prisma[<veelhoek v>,<getal h>] veelhoek en voer de hoogte in om een prisma te creëren. Een prisma bepalen (enkel in 3D) Een piramide bepalen (enkel in 3D) Selecteer een veelhoek (of de punten die de veelhoek bepalen) en een punt en creëer een piramide met als grondvlak de veelhoek en het punt als top. Sleep een veelhoek of selecteer een veelhoek en voer de hoogte in om een piramide te creëren. Piramide[<punt A>,<punt B>,,<punt F>,<top T>] Piramide[<veelhoek v>,<top T>] Piramide [<veelhoek v>,<hoogte h>] Creëert een prisma met grondvlak AB F en ribbe [AQ]. Creëert een prisma met als grondvlak de veelhoek v en Q als een punt van het bovenvlak. Creëert een prisma met grondvlak v en hoogte h. Creëert een piramide met grondvlak AB F en top T. Creëert een piramide met grondvlak v en top T. Creëert een piramide met grondvlak v en hoogte h. 10
11 Een kubus bepalen (enkel in 3D) Een octaëder of regelmatig achtvlak bepalen (enkel in 3D) Selecteer twee punten in het (x,y)-vlak en creëer een kubus die op dit vlak rust. of Selecteer een vlak en twee punten in dit vlak of in een evenwijdig vlak en creëer een kubus die rust op dit laatste vlak. Kubus[<punt A>,<punt B>, <richting r>] Kubus[<punt A>,<punt B>, <punt C>] Kubus[<punt A>,<punt B>] Achtvlak[<punt A>,<punt B>, <richting r>] Achtvlak[<punt A>,<punt B>, <punt C>] Achtvlak[<punt A>,<punt B>] Creëert een kubus met [AB] als ribbe. - Is de richting r een rechte, een halfrechte, een lijnstuk of een vector die loodrecht staat op [AB], dan heeft de kubus een zijvlak met ribbe [AB] en loodrecht op de richting. - Is de richting r een vlak evenwijdig aan [AB], dan heeft de kubus een zijvlak met ribbe [AB] en evenwijdig aan dit vlak. Creëert een kubus waarvan A, B en C in één zijvlak liggen, op voorwaarde dat die drie punten de hoekpunten kunnen zijn van een vierkant. Creëert een kubus waarvan [AB] een ribbe is. Het 3 de punt wordt automatisch gecreëerd op een cirkel zo dat de kubus kan draaien rond het lijnstuk [AB]. Deze cirkel heeft als middelpunt B, als straal AB en als as AB. Creëert een regelmatig achtvlak met [AB] als ribbe. - Is de richting r een rechte, een halfrechte, een lijnstuk of een vector die loodrecht staat op [AB], dan heeft de octaëder een zijvlak met ribbe [AB] en loodrecht op de richting. - Is de richting r een vlak evenwijdig aan [AB], dan heeft de octaëder een zijvlak met ribbe [AB] en evenwijdig aan dit vlak Creëert een regelmatig achtvlak waarvan A, B en C de hoekpunten zijn van één zijvlak, op voorwaarde dat die drie punten een gelijkzijdige driehoek vormen. Idem, maar het punt C wordt zo gecreëerd dat het met A en B een gelijkzijdige driehoek vormt. Door C te verplaatsen, kan je het achtvlak laten draaien rond het lijnstuk [AB]. 11
12 De ontvouwing van een veelvlak bepalen (enkel in 3D) Selecteer een veelvlak en creëer de ontvouwing. Ontvouwing[<veelvlak v>, <factor f>] Ontvouwing[<kubus k>,<factor f>,<zijvlak z>,<ribbe r>,<ribbe s>, ] Creëert de ontwikkeling van een prisma, een piramide of een regelmatig veelvlak v. De factor f, een getal tussen 0 en 1 geeft de graad aan van de ontwikkeling. Als f gelijk is aan 1, is het veelvlak volledig uitgevouwen. Creëert de ontwikkeling van een kubus k. De factor f, een getal tussen 0 en 1 geeft de graad aan van de ontwikkeling. Als f gelijk is aan 1, is het veelvlak volledig uitgevouwen. Het zijvlak z blijft op zijn plaats. Het veelvlak wordt doorgesneden volgens de ribben r, s, 3.8 Kwadrieken (cilinder, kegel en bol) Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Selecteer twee punten en een getal en Cilinder[<cirkel c>,<hoogte h>] creëer een cilinder. Het eerste punt is het middelpunt van het grondvlak, het tweede Cilinder[<punt M>,<punt N>, het middelpunt van het bovenvlak; het <straal r>] getal is de straal van het grondvlak en het bovenvlak. Sleep een cirkel of selecteer een cirkel en voer de hoogte in om een cilinder te creëren. Een cilinder bepalen (enkel in 3D) Een onbegrensde cilinder bepalen (enkel in 3D) Een kegel bepalen (enkel in 3D) OnbegrensdeCilinder[<rechte a>, <straal r>] Selecteer twee punten en een getal en creëer een kegel. Het eerste punt is het middelpunt van het grondvlak, het OnbegrensdeCilinder[<punt P>, <vector v>,<straal r>] OnbegrensdeCilinder[<Punt P>, <punt Q>,<straal r>] Kegel[<cirkel c>,<hoogte h>] Kegel[<middelpunt M>,<top T>, Creëert een cilinder met grondvlak c en hoogte h. Creëert een cilinder met straal r. M en N zijn resp. de middelpunten van het grondvlak en het bovenvlak. Creëert een onbegrensde cilinder met straal r en met de rechte a als symmetrieas. Creëert een onbegrensde cilinder met straal r, waarvan de symmetrieas door P gaat en evenwijdig is aan de vector v. Creëert een onbegrensde cilinder met straal r en met de rechte PQ als symmetrieas. Creëert een kegel met grondvlak c en hoogte h. Creëert een kegel met T als top en een 12
13 Een bol bepalen met gegeven middelpunt en door een punt (enkel in 3D) Een bol bepalen met gegeven middelpunt en straal (enkel in 3D) tweede de top, het getal is de straal van het grondvlak. Sleep een cirkel of selecteer een cirkel en voer de hoogte in om een kegel te creëren Selecteer twee punten en creëer een bol met het eerste punt als middelpunt en de afstand tussen de twee punten als straal. Selecteer een punt en voer een positief getal in om een bol te creëren met het punt als middelpunt en het getal als straal. <straal r>] Kegel[<top T>,<vector v>,<hoek α>] Bol[<punt M>,<punt A>] Bol[<punt M>,<getal r>] cirkel (M, r) als grondvlak. Creëert een kegel met T als top, as evenwijdig met de vector v en tophoek 2α. Creëert een bol met middelpunt M die door het punt A gaat. Creëert een bol met middelpunt M en straal r. 3.9 Doorsneden Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Klik achtereenvolgens op twee objecten Snijpunten[<object a>,<object b>] om de snijpunten van deze objecten te bepalen Snijpunt(en) van twee objecten bepalen De snijlijn van twee vlakken bepalen (enkel in 3D) De doorsnede van een kwadriek (cilinder, kegel, bol, ) met een vlak bepalen (enkel in 3D) Klik op twee vlakken en creëer zo de snijlijn van de twee vlakken. Klik op de kwadriek en op het vlak en creëer zo de doorsnede. Snijpunten[<vlak α>,<vlak β>] SnijpuntenPaden[<vlak α>,<vlak β>] Snijpunten[<vlak α>,<kwadriek k>] Kwadriekdoorsnede[<vlak α>, <kwadriek k>] Snijpuntenpaden[<vlak α>, <kwadriek k>] Creëert de snijpunten van 2 objecten a en b, bijv. - twee rechten, een rechte en een lijnstuk, een rechte en een veelhoek, een rechte en een kegelsnede, - twee kegelsneden, - een rechte en een vlak, een lijnstuk en een vlak, een veelhoek en een vlak, een kegelsnede en een vlak, Creëert de snijlijn van de vlakken α en β. Dit laat ook toe om de parametervergelijkingen van een rechte te bepalen, waarvan de cartesiaanse vergelijkingen gegeven zijn. Creëert de doorsnede van het vlak α met de kwadriek (cilinder, kegel, bol) k. 13
14 De doorsnede van twee bollen bepalen (enkel in 3D) De doorsnede bepalen van een veelvlak en een vlak (enkel in 3D) Klik op twee bollen en creëer zo de doorsnede. Klik op een veelvlak en op een vlak en creëer zo de doorsnede. Snijpunten[<bol b1>, bol b2] Kwadriekdoorsnede[<bol b1>,<bol b2>] Snijpunten[veelvlak a, vlak α] SnijpuntenPaden[veelvlak a, vlak α] Creëert de doorsnede van twee bollen b 1 en b 2. Creëert de doorsnede van het veelvlak a met het vlak α Hoek, lengte, oppervlakte en volume Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Hoeken bepalen 3 Selecteer drie punten en creëer de hoek bepaald door deze drie punten, waarvan het tweede het hoekpunt is. Afstanden bepalen De oppervlakte bepalen van een veelhoek of een kegelsnede Het volume bepalen van een ruimtefiguur (enkel 3D) Selecteer twee punten, een punt en een rechte of twee rechten en creëer de afstand tussen deze twee objecten. Selecteer een veelhoek en bereken de oppervlakte.. Selecteer een ruimtefiguur en bereken het volume. Hoek[<punt A>,<hoekpunt B>, <punt C>] Hoek[<punt A>,<hoekpunt B>, <punt C>,<richting r>] Hoek[<rechte r>,<vlak α>] Hoek[<vlak α>,<vlak β>] Afstand[<punt A>,<punt B>] Afstand[<punt A>,<rechte r>] Afstand[<rechte a>,<rechte b>] Oppervlakte[<veelhoek p>] Oppervlakte[<punt A>,<punt B>, ] Oppervlakte [<kegelsnede k>] Volume[<ruimtefiguur f>] Berekent en kleurt de hoek bepaald door de halfrechten [BA en [BC. Idem, maar houdt rekening met de plaats van waaruit de hoek bekeken wordt. Berekent en kleurt de hoek tussen de rechte r en het vlak α. Berekent en kleurt de hoek tussen de vlakken α en β. Berekent de afstand tussen twee punten A en B. Berekent de afstand tussen het punt A en de rechte r. Berekent de afstand tussen de rechten a en b. Berekent de oppervlakte van de veelhoek p. Berekent de oppervlakte van de veelhoek AB Berekent de oppervlakte van de kegelsnede k. Berekent het volume van de ruimtefiguur f. 2 Je kan de ware grootte van de doorsnede zichtbaar maken door met de rechtermuisknop op de veelhoek te klikken (in het algebravenster of het 3D tekenvenster) en te kiezen voor Toon veelhoek bij 2D venster. 3 Om de hoek tussen een rechte en een vlak te bepalen, kiezen we een punt op de rechte en bepalen we het voetpunt van de loodlijn vanuit dit punt op het vlak. 14
15 3.11 Transformaties Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Selecteer een object en een rechte en geef een rotatiehoek in. Je creëert het beeld door rotatie van het object rond de rechte over de gegeven hoek. Een rotatie uitvoeren met gegeven rotatie-as en gegeven rotatiehoek Een verschuiving uitvoeren 3.12 Krommen en oppervlakken Een kromme in de ruimte bepalen Selecteer een object en een vector en creëer het verschoven beeld van het object volgens de vector. Rotatie[<object o>,<hoek >, <rechte a>] Rotatie[<object o>,<hoek >, <punt A>,<richting r>] Rotatie[<object o>,<hoek >, <punt A>,<vlak α>] Verschuiving[<object o>, <vector v>] Roteert het object o over de hoek rond de rechte a. Roteert het object o over de hoek rond de rechte door het punt A met richting r. Roteert het object o over de hoek rond de rechte door het punt A en loodrecht op het vlak α. Verschuift het object o volgens de vector v. Begrip Invoer via de werkbalk (tools) Invoer via het invoerveld (commando s) Hoofdknop Deelmenu Wat gebeurt er? Commando Wat gebeurt er? Kromme [<expressie f(t)>, <expressie g(t)>,<expressie h(t)>,<parameter t>, <beginwaarde t1>,<eindwaarde t2>] tot t 2. Een oppervlak in de ruimte bepalen (enkel in 3D) Oppervlak[<expressie f(t,u)>, <expressie g(t,u)>,<expressie h(t,u)>,<parameter t>, <beginwaarde t1>,<eindwaarde t2>, <parameter u>,<beginwaarde u1>,<eindwaarde u2>] f(x, y) = Functie[<expressie f(u,v)>, <parameter u>,<startwaarde u1 >,<eindwaarde u2>, <parameter v>,<startwaarde v1>,<eindwaarde v2>] Creëert een kromme met als parametervergelijkingen x = f(t), y = g(t) en z = h(t) waarbij de parameter t gaat van t 1 Creëert een oppervlak met als parametervergelijkingen x = f(t, u) { y = g(t, u) z = h(t, u) waarbij de parameter t gaat van t 1 tot t 2 en de parameter u gaat van u 1 tot u 2. Creëert een oppervlak met als vergelijking z = f(x, y) Creëert een oppervlak, bepaald door de functie f(u, v), waarbij u verandert van u 1 tot u 2 en v verandert van v 1 tot v 2. 15
16 4 Oefeningen De parametervergelijkingen van een rechte Mogelijk gebruik in de klas De leraar illustreert de parametervergelijkingen van een rechte aan de hand van een applet, door hem gemaakt. Opbouw van de applet We illustreren de parametervergelijkingen van een rechte door een punt P en met richtingsvector d. - We tekenen eerst de oorsprong O met het commando O=(0,0,0). - Dan kiezen we 3 willekeurige getallen x 1, y 1 en z 1 en tekenen het punt P(x 1, y 1, z 1 ) met het commando P_1=(x_1,y_1,z_1). Als beginwaarden voor x 1, y 1 en z 1 kiezen we resp. 2, 3 en 4. We voorzien ook schuifknoppen om x 1, y 1 en z 1 gemakkelijk te kunnen wijzigen. We tekenen ook de vector OP 1 met het commando Vector[O,P_1]. - We kiezen opnieuw 3 willekeurige getallen a, b en c en tekenen de richtingsvector d (a, b, c) met het commando d=(a,b,c). Als beginwaarden voor a, b en c kiezen we resp. -1, -4 en 2. We voorzien ook schuifknoppen om a, b en c gemakkelijk te kunnen wijzigen. - We kiezen nu een willekeurig getal r. Als beginwaarde nemen r = 2. We voorzien ook r van een schuifknop. - We construeren nu de vector r. d met het commando rd=r*d. - Daarna construeren we het punt P zó dat OP = OP 1 + r. d. We doen dit met het commando P=P_1+r*d. We construeren ook de vector OP met het commando Vector[O,P]. Verder tekenen we het punt Q met Q=rd en het lijnstuk [QP]. - En ten slotte tekenen we de rechte l door P en met richtingsvector d. Dit doen we met het commando l=rechte[p,d]. In het algebravenster zien we de vectoriële vergelijking van de rechte l verschijnen. We brengen deze over naar het 2D-tekenvenster. Gebruik van de applet We kunnen d.m.v. deze applet heel wat illustreren. - Wijzigen we r d.m.v. de schuifknop, dan zien we P over de rechte l bewegen. 4 Tenzij anders aangegeven werken we met een assenstelsel, waarbij de x-as naar voor wijst, de y-as naar rechts en de z-as naar boven. De x-as en de y-as maken een hoek van 30 en de schaalfactor is 0,5. 16
17 - Wijzigen we x 1, y 1 of z 1 d.m.v. de schuifknoppen, dan zien we dat de rechte l evenwijdig met zichzelf beweegt. - Wijzigen we a, b of c d.m.v. de schuifknoppen, dan zien we dat de rechte van richting verandert. Nieuwe commando s - Een punt tekenen in de ruimte (zie 3.2) - Een schuifknop maken bij een getal - Een vector tekenen (zie 3.3) - Een rechte tekenen door een punt met een gegeven richting (zie 3.3). - Een lijnstuk tekenen (zie 3.3) 4.2 Schaduw van de piramide van Cheops Mogelijk gebruik in de klas De leerling maakt een oefening zonder GeoGebra en maakt tegelijkertijd een applet om het resultaat te illustreren. Een andere mogelijkheid is dat de leraar de oplossing d.m.v. een applet illustreert en de leerlingen aan de hand daarvan hun oplossing kunnen controleren. Opdracht voor de leerling De piramide van Cheops in Gizeh is het enige van de zeven klassieke wereldwonderen dat tot op de dag van vandaag bewaard is gebleven. De piramide heeft een hoogte van 147 meter en heeft als basis een vierkant met een zijde van 230 meter. In deze opdracht ligt één hoekpunt (A) van het grondvlak van de piramide in de oorsprong. De zijde [AB] van het grondvlak ligt langs de positieve x-as, waarbij de x-as naar het zuiden wijst. De zijde [AD] van het grondvlak ligt langs de positieve y-as, waarbij de y-as naar het oosten wijst. De richting van de zonnestralen wordt gegeven door de vector w ( 100, 100, 60). 1 Bepaal zonder GeoGebra de exacte plaats van de schaduw van de top op de grond. 2 Maak een applet van de piramide en van de schaduw van de piramide op de grond. Controleer op die manier je antwoord uit opdracht 1. 17
18 Opbouw van de applet - We construeren eerst het grondvlak van de piramide en de top. De hoekpunten van het grondvlak brengen we in als A=(0,0,0), B=(230,0,0), C=(230,230,0) en D=(0,230,0). De coördinaten van de top T zijn (115,115,147). De veelhoek vinden we met het commando ABCD=Veelhoek[A,B,C,D]. - De piramide Cheops tekenen we met het commando Cheops=Piramide[ABCD,T]. - De vector wordt getekend met het commando w=(-100,-100,-60). De straal door T vinden we met TT =Rechte[T,w]. - Het (x, y)-vlak vinden we met α:z=0. Het snijpunt van TT met α construeren we met T =Snijpunten[TT,α]. - En ten slotte construeren we de schaduw als een veelhoek met BADT =Veelhoek[B,A,D,T ]. Nieuwe commando s - Een veelhoek tekenen met gegeven hoekpunten (zie 3.4) - Een piramide tekenen (zie 3.7) - Een vlak tekenen, bepaald door een cartesiaanse vergelijking (zie 3.6) - Het snijpunt bepalen van een rechte en een vlak (zie 3.9) 4.3 Doorsnede van een kubus met een vlak In het 4 de jaar bestudeerden we de doorsnede van een kubus met een vlak. We behandelen nu een meer complexe situatie, waarbij het vlak α een gegeven rechte PQ omvat en evenwijdig is met een andere rechte HB. Mogelijk gebruik in de klas De leerlingen lossen de oefening analytisch op zonder GeoGebra. Na elke stap controleren ze hun oplossingen met GeoGebra op een gegeven applet. 18
19 Opdracht voor de leerling E F G Op de applet zie je de kubus ( A B C midden van [HG]. H ) met ribbe 4. P is het midden van [EH] en Q is het D 1 Zoek een cartesiaanse vergelijking van het vlak α dat de rechte PQ omvat en is evenwijdig met de rechte HB. 2 Teken het vlak op de gegeven applet. Controleer je antwoord uit 1. 3 Bereken de coördinaten van de hoekpunten van de doorsnede van de kubus met het vlak α. 4 Teken deze doorsnede op de applet. Controleer je antwoorden uit 3. 5 Teken de ware grootte van de doorsnede op de applet. Opbouw van de applet We tekenen een kubus k, bepaald door de punten A(4, 0, 0), B(4, 4, 0) en de z-as: k=kubus[a,b,zas]. We tekenen ook de punten P en Q en de rechten PQ en HB. Om het vlak α te tekenen zoeken we een derde punt van dit vlak, d.i. het punt R, zodanig dat OR = OP + HB. In GeoGebra vinden we R door het commando u = vector[h,b] en R = P + u. Het vlak zelf construeren we met het commando α = vlak[p, Q, R]. Om de doorsnede van α met de kubus te vinden, gebruiken we: Doorsnede = SnijpuntenPaden[k, α]. We tonen ook de ware grootte van de doorsnede door in het algebravenster met de rechter muisknop te klikken op Doorsnede en Toon Doorsnede bij 2D-venster te activeren. Nieuwe commando s - Een kubus tekenen (zie 3.7) - Het midden bepalen van twee punten (zie 3.2) - Een rechte tekenen door 2 punten (zie 3.3) - Een vlak tekenen, bepaald door 3 punten (zie 3.6) - De doorsnede bepalen van een kubus met een vlak (zie 3.9) - De ware grootte van een doorsnede bepalen (zie 3.9) 4.4 Een rechte, evenwijdig met een gegeven vlak en door een gegeven punt, die een gegeven rechte snijdt Gebruik maken van GeoGebra betekent niet dat de leerlingen niet moeten redeneren. Integendeel, door het gebruik van GeoGebra kun je verschillende oplossingsstrategieën laten uitproberen en de berekeningen aan de computer laten. Dit wordt geïllustreerd in het volgende voorbeeld. Opdracht voor de leerling Gegeven zijn het vlak α x + y + z = 5, het punt P (1, 2, 3) en de rechte a met parametervergelijkingen { y = 1 + r. x = 1 + 2r z = r Zoek vergelijkingen van de rechte b die evenwijdig is met het vlak α, door het punt P gaat en de rechte a snijdt. Er zijn verschillende strategieën mogelijk om de rechte b te bepalen, door telkens één voorwaarde weg te laten. Probeer verschillende oplossingsstrategieën uit. Maak tegelijk ook een applet om je oplossingen te illustreren. Je maakt daarbij best gebruik van een assenstelsel, waarbij de x-as naar rechts wijst, de y-as naar achter en de z-as naar boven. De x-as en de y-as snijden elkaar onder een hoek van 30. Om de vlakken beter te doen uitkomen maak je best ook gebruik van de clippingbox. 19
20 Mogelijk gebruik in de klas 1 De leerlingen proberen verschillende strategieën uit om dit probleem analytisch op te lossen. 2 De leerlingen illustreren hun oplossingen aan de hand van een gegeven applet. Op die manier kunnen ze ook hun analytische resultaten controleren. Een andere mogelijkheid is dat de leraar met een oplossingen-applet de verschillende strategieën illustreert. Strategieën en opbouw van de applet 1 We laten de eis dat b de rechte a moet snijden achterwege. Alle rechten die door het punt P gaan en evenwijdig zijn met het vlak α, liggen in het vlak α dat door P gaat en evenwijdig is met α. Dit vlak construeren we met het commando α =Vlak[P,α]. Zij S het snijpunt van dit vlak α met de rechte a (S=Snijpunten[a,α ], dan is de rechte b = SP (b=rechte[s,p]) de oplossing. 2 We laten de eis dat b evenwijdig is met het vlak α achterwege. Alle rechten die door het punt P gaan en de rechte a snijden liggen in het vlak β, bepaald door P en a. Dit vlak construeren we met het commando β=vlak[p,a]. De rechte b ligt ook in het vlak α dat door P gaat en evenwijdig is met α. De oplossing b is de snijlijn van de vlakken α en β (b=snijpuntenpaden[α,β]). Nieuwe commando s - Een vlak tekenen door een punt en evenwijdig met een gegeven vlak (zie 3.6) - Een vlak tekenen, bepaald door een punt en een rechte (zie 3.6) - De doorsnede bepalen van twee vlakken (zie 3.9) 20
21 4.5 Maximale inhoud van een balk in een piramide Mogelijk gebruik in de klas De leerlingen lossen de opdracht op zonder GeoGebra. De leraar demonstreert de oplossing d.m.v. een applet. Opdracht voor de leerling Van de piramide TABCD ligt de top T op hoogte 12 boven het grondvlak ABCD. Het grondvlak is een rechthoek waarbij AB = 12 en BC = 9. De hoogte van de piramide is TO. O ligt op [BD] zodanig dat BO = 2. DO. 1 Bepaal de coördinaten van A, B, C en D in het getekende orthonormaal assenstelsel. 2 Een vlak α z = h (0 < h < 12) snijdt de piramide volgens de rechthoek PQRS. PQRS is het bovenvlak van een balk PQRS EFGH waarbij EFGH in het grondvlak van de piramide ligt. Voor welke waarde van h is de inhoud van die balk maximaal? Hoeveel bedraagt die inhoud dan? Opbouw van de applet Volgens de stelling van Thales wordt [AB] door de x-as ook verdeeld in stukken die zich verhouden als 1:2, hetzelfde geldt voor [BC] en de y-as. Daaruit volgt: A(6, -4, 0), B(6, 8, 0), C(-3, 8, 0) en D(-3, -4, 0). We kunnen nu de piramide tekenen met de commando s: g = Veelhoek[A,B,C,D] en p = Piramide[g,T]. We kiezen nu voor h een willekeurige startwaarde (bijv. h = 5) en maken bij h een schuifknop, waarbij we h laten veranderen van 0 tot 12 met stappen van 0,1. Het bovenvlak PQRS van de balk ligt nu in het vlak α: z = h. PQRS zelf is de doorsnede van dit vlak met de piramide, dus PQRS = SnijpuntenPaden[α,p]. De balk zelf bepalen we nu met balk = Prisma[PQRS,-h] 21
22 Nu geldt: PQ AB = QT BT = MT = 12 h OT h Verder geldt: QR BC = QT BT = MT = 12 h OT h 12 h, en dus PQ = 12. = 12 h. 12, en dus QR = h 12 = 3 4 (12 h). De inhoud van de piramide is dus V = (12 h) (12 h). h = 3 4 h(12 h)2. We stellen de functie V(x) = 3 4 x(12 x)2 voor in het 2D-tekenvenster en beperken de functie tot het interval [0, 12] door het commando V_1=functie[V,0,12]. We bepalen de extrema van de functie V(x) met het commando Extrema[V] en vinden een maximum voor x = 4 en een minimum voor x = 12. Enkel het maximum is voor ons van belang. We vinden dat de inhoud van de balk maximaal is als de hoogte gelijk is aan 4. De inhoud is dan gelijk aan 192. Nieuwe commando s - Een prisma tekenen (zie 3.7) - De grafiek van een functie tekenen met gegeven voorschrift - De extrema van een veeltermfunctie bepalen 4.6 Een antiprisma Een regelmatig veelvlak is een convex veelvlak waarvan alle zijvlakken regelmatige veelhoeken zijn met evenveel zijden en waarbij in elk hoekpunt evenveel zijvlakken samenkomen. De beroemde filosoof Plato (ca. 427 v. Chr. 347 v.chr.) ontdekte reeds dat er slechts vijf dergelijke veelvlakken bestaan, de zogenaamde Platonische lichamen. 22
23 viervlak tetraëder zesvlak of kubus hexaëder achtvlak octaëder twaalfvlak dodecaëder twintigvlak icosaëder 4 zijvlakken 4 hoekpunten 6 ribben 6 zijvlakken 8 hoekpunten 12 ribben 8 zijvlakken 6 hoekpunten 12 ribben 12 zijvlakken 20 hoekpunten 30 ribben 20 vlakken 12 hoekpunten 30 ribben De vijf Platonische lichamen kunnen rechtstreeks met GeoGebra getekend worden (zie 3.7). Naast de regelmatige veelvlakken zijn er ook halfregelmatige veelvlakken. Daarbij moeten de zijvlakken nog steeds regelmatige veelhoeken zijn, maar ze hoeven niet allemaal evenveel zijden te tellen. Wel moeten alle hoekpunten op een bol liggen en moet er een zelfde patroon optreden in elk hoekpunt. De halfregelmatige veelvlakken vallen uiteen in 3 categorieën. - De (13) Archimedische lichamen Een typisch voorbeeld hiervan is de afgeknotte icosäeder, die we terugvinden op het leder of het plastic van een klassieke voetbal. Hierbij zijn de hoeken van de icosaëder afgeknot tot 12 regelmatige vijfhoeken zodanig dat er van elk van de 20 zijvlakken een regelmatige zeshoek overblijft. - De prisma s (oneindig veel mogelijkheden voor het aantal zijvlakken. - De antiprisma s, waarvan we hieronder een voorbeeld tekenen, waarbij zowel het grondvlak als het bovenvlak regelmatige zeshoeken zijn. 23
24 Mogelijk gebruik in de klas De leerling maakt zelf een applet om een halfregelmatig antiprisma te tekenen. Opdracht voor de leerling Bij een antiprisma zijn grond- en bovenvlak regelmatige veelhoeken. Deze veelhoeken zijn echter een weinig t.o.v. elkaar gedraaid zodat de zijvlakken gelijkzijdige driehoeken vormen. Tracht nu zelf om met GeoGebra een antiprisma met zeshoekig grond- en bovenvlak te construeren. Het moeilijkste daarbij is het bepalen van het hoekpunt G van het bovenvlak. Om dit punt te bepalen, kun je drie eigenschappen van dit punt gebruiken: - G ligt even ver van A als van B - De afstand van G tot de z-as is even groot als de afstand van A en B tot de z-as - G en B liggen even ver van A, Opbouw van de applet Het grondvlak is een regelmatige zeshoek. Nemen we als middelpunt van deze zeshoek het punt M(0, 0, 0), en als eerste hoekpunt A(1, 0, 0), dan vinden we het tweede hoekpunt door het commando B = Rotatie[A,60,zAs]. De zeshoek vinden we dan d.m.v. Grondvlak=Veelhoek[A,B,6,zAs]. Om G te bepalen maken we, zoals hierboven aangegeven, gebruik van drie eigenschappen van dit punt. Dit geeft ons resp. - G ligt in het middelloodvlak μ van [AB] (μ = Deelvlak[A,B]), - G ligt op de onbegrensde cilinder met de zas als as en MA = 1 als straal (Cilinder=OnbegrensdeCilinder[zAs,1]), - G ligt op een boloppervlak met A als middelpunt die door het punt B gaat (Bol = Bol[A,B]) De doorsnede van deze drie oppervlakken (Commando s p=intersectiepaden[μ,cilinder], k=intersectiepaden[μ,bol] en Snijpunten[p,k]) levert ons twee punten G en G op. We kiezen het punt met positieve z-coördinaat. Een tweede hoekpunt H van het bovenvlak vinden we dan weer door H=Rotatie[G,60,zAs] en het bovenvlak door Bovenvlak=Veelhoek[G,H,6,zAs]. Ten slotte moeten we dan nog het grondvlak en het bovenvlak verbinden door een netwerk van driehoeken. Nieuwe commando s - Een regelmatige veelhoek tekenen in een vlak (zie 3.4) - Een punt roteren rond een as (zie 3.11) - Een middelloodvlak (deelvlak) tekenen van een lijnstuk (zie 3.6) - Een onbegrensde cilinder tekenen (zie 3.8) - Doorsnede bepalen van een onbegrensde cilinder met een vlak (zie 3.9) - Een bol tekenen (zie 3.8) - Doorsnede bepalen van een vlak en een bol (zie 3.9) 4.7 Meetkundige plaats van de punten even ver van twee kruisende rechten Werktekst voor de leerlingen 1 We zoeken de verzameling van de punten die op gelijke afstand liggen van twee kruisende rechten x = r x = s l 1 { y = r en l 2 { y = s. z = 1 z = 1 De rechte l 1 is de rechte y = x van het (x,y)-vlak, verschoven over een afstand 1 naar onder, De rechte l 2 is de rechte y = -x van het (x,y)-vlak, verschoven over een afstand 1 naar boven. Is P (x, y, z) een punt van de oplossing, dan is d(p, l) = d(p, m). We zoeken dus de punten Q (r, r, -1) op l 1 en R (s, -s, 1) op l 2, zodanig dat PQ l 1, PQ l 2 en PQ = PR. 24
25 Leid daaruit af dat P(x, y, z) moet voldoen aan de vergelijking 2z xy = 0 of z = xy 2 x = r of { y = s z = rs Dit is geen vergelijking van een vlak, maar van een oppervlak in de ruimte. Teken dit oppervlak met GeoGebra. Leg de assen zo dat de x-as naar rechts wijst, de y-as naar achter en de z-as naar boven, en de hoek tussen de x-as en de y-as gelijk is aan 30. Omwille van de vorm noemt men dit oppervlak een zadelvlak. Uit de figuur hierboven vermoeden we dat de doorsnede van dit oppervlak met een vlak zowel een hyperbool als een parabool kan zijn. Vandaar ook de naam: hyperbolische paraboloïde. Bovendien zien we, aan de doorsneden van het oppervlak met de omhullende kubus, dat het oppervlak ook kan beschreven worden door rechten. Daarom spreken we van een regelvlak. We kunnen dit analytisch aantonen door de doorsneden te berekenen van het oppervlak met bepaalde vlakken. 3 Bepaal een parametervoorstelling van de doorsnede van het oppervlak met het vlak x = k, evenwijdig met het (y, z)-vlak. Teken deze doorsnede voor k gaande van -10 tot 10. Wat stelt elke doorsnede voor? 5 Deze afleiding gaat als volgt: De coordinaten van PQ en PR zijn resp. (r x, r y, 1 z) en (s x, s y, 1 z) d (1,1,0) 1 en d (1, 2 1,0) zijn resp. richtingsvectoren van l 1 en l 2. Daaruit volgt: PQ l 1 PQ. d 1 = 0 (r x). 1 + (r y). 1 = 0 x + y = 2r r = x+y. 2 PR l 2 PR. d 2 = 0 (s x). 1 + (s + y). 1 = 0 x y = 2s s = x y. 2 Verder geldt: PQ = RS PQ 2 = RS 2 (x r) 2 + (y r) 2 + (z + 1) 2 = (x s) 2 + (y + s) 2 + (z 1)² (1) Nu is x r = x x+y x y = s, x s = x = r en r + s = x. = x y 2 2 = x+y 2 2 Houden we daarmee rekening bij de uitwerking van (1), dan krijgen we: s² + (y r) 2 + (z + 1) 2 = r² + (y + 1) 2 + (z 1)² en verder: 2(r + s)y = 4z, waaruit volgt 2xy = 4z of z = xy 2. 25
26 4 Bepaal een parametervoorstelling van de doorsnede van het oppervlak met het vlak y = l, evenwijdig met het (x, z)-vlak. Teken deze doorsnede voor l gaande van -10 tot 10. Wat stelt elke doorsnede voor? 5 Bepaal een parametervoorstelling van de doorsnede van het oppervlak met het vlak z = m, evenwijdig met het (x, y)-vlak. Teken deze doorsnede voor verschillende waarden van m. Wat stelt elke doorsnede voor? 6 Bepaal een parametervoorstelling van de doorsnede van het oppervlak met het vlak x y = n. Teken deze doorsnede voor verschillende waarden van n. Wat stelt elke doorsnede voor? Opbouw van de applet 1 De rechte l 1 gaat door het punt A(0, 0, -1) en heeft als richtingsvector (1, d 1 1, 0), dus d_1=(1,1,0) en l_1=rechte[a,d_1]. De rechte l 2 gaat door het punt B(0, 0, 1) en heeft als richtingsvector (1, d 2 1, 0), dus d_2=(1,-1,0) en l_2=rechte[b,d_2]. 2 Het zadelvlak z = xy tekenen we met het commando a=oppervlak[r,s,r*s/2,r,-10,10,s,-10,10]. 2 3 Om de doorsnede van het zadelvlak met het vlak x = k te vinden, geven we k als beginwaarde 4. We creëren een schuifknop om k te kunnen veranderen van -10 tot 10. De doorsnede (een rechte) vinden we met het commando b=kromme[k,s,k*s/2,s,-10,10]. 4 Om de doorsnede van het zadelvlak met het vlak y = l te vinden, geven we l als beginwaarde -3. We creëren een schuifknop om l te kunnen veranderen van -10 tot 10. De doorsnede (een rechte) vinden we met het commando c=kromme[s,l,l*s/2,s,-10,10]. 5 Om de doorsnede van het zadelvlak met het vlak z = m te vinden, geven we m als beginwaarde 3. We creëren een schuifknop om m te kunnen veranderen van -10 tot 10. De doorsnede (een hyperbool) vinden we met het commando d=kromme[s,2m/s,m,s,-10,10]. 6 Om de doorsnede van het zadelvlak met het vlak x y = n te vinden, geven we n als beginwaarde 1. We creëren een schuifknop om m te kunnen veranderen van -10 tot 10. De doorsnede (een parabool) vinden we met het commando e=kromme[s,s-n,s(s-n)/2,s,-10,10]. Mogelijk gebruik in de klas De leerlingen maken een applet van de meetkundige plaats d.m.v. de werktekst. Deze oefening past goed in het maken van een onderzoeksopdracht, bijv. over afstanden. Nieuwe commando s 26
27 - Een oppervlak tekenen d.m.v de parametervoorstelling (zie 3.12) - Een kromme in de ruimte tekenen d.m.v. de parametervoorstelling (zie 3.12) 4.8 Viervlakken in een kubus Mogelijk gebruik in de klas De leerlingen lossen het probleem op door de applet te maken en daarop te redeneren. Voor de berekeningen kunnen ze eventueel gebruik maken van CAS. Opdracht voor de leerling Twee regelmatige viervlakken (tetraëders) T 1 en T 2 zitten in een kubus met volume 1. De hoekpunten van T 1 zijn de eindpunten van een diagonaal in het grondvlak van de kubus en van een diagonaal in het bovenvlak van de kubus. De overige hoekpunten van de kubus zijn die van T 2. Bereken het volume van T 1 U T 2. Illustreer met een applet. Het assenstelsel is klassiek: de x-as wijst naar voor, de y-as naar rechts en de z-as naar boven; de x-as wordt onder een hoek van 30 getekend. Opbouw van de applet We kiezen het punt D als oorsprong. De coördinaten van A en B zijn dan respectievelijk (1, 0, 0) en (1, 1, 0). De kubus vinden we dan met het commando Kubus[A,B,zAs]. De twee tetraëders vinden we dan resp. met de commando s: T1=Piramide[A,C,F,H] en T2=Piramide[B,D,E,G]. We zien dan op de applet dat de gevraagde inhoud gelijk is aan de som van de inhouden van deze twee viervlakken min de inhoud van de doorsnede. Die laatste is een octaëder, die we duidelijker zichtbaar kunnen maken met het commando O=Achtvlak[I,J,K]. Hierbij zijn I, J en K middens van zijvlakken van de kubus. Exacte berekening van het volume van T 1 U T 2 27
28 We berekenen eerst de inhoud van de viervlakken. - De zijde van het grondvlak van het viervlak is gelijk aan de diagonaal van een zijvlak van de kubus en is dus gelijk aan 2. De hoogte van een zijvlak van het viervlak is dan gelijk aan 2. sin 60 = 6. Daaruit volgt dat de oppervlakte gelijk is aan 12 = Op bovenstaande tekening zien we dat de hoogte HZ = HI = Dus in de inhoud van elk viervlak is gelijk aan = Daarna berekenen we de inhoud van de octaëder. Die is gelijk aan = En daaruit volgt dat het volume van T 1 U T 2 gelijk is aan = 1, d.i. de helft van de inhoud van de kubus Nieuwe commando s - Een octaëder of regelmatig achtvlak tekenen (zie 3.7) 2 28
GEOGEBRA 5. Ruimtemeetkunde in de eerste graad. R. Van Nieuwenhuyze. Oud-hoofdlector wiskunde aan Odisee, lerarenopleiding Brussel
 GEOGEBRA 5 Ruimtemeetkunde in de eerste graad R. Van Nieuwenhuyze Oud-hoofdlector wiskunde aan Odisee, lerarenopleiding Brussel Auteur Van Basis tot Limiet en auteur van Nando. roger.van.nieuwenhuyze@gmail.com
GEOGEBRA 5 Ruimtemeetkunde in de eerste graad R. Van Nieuwenhuyze Oud-hoofdlector wiskunde aan Odisee, lerarenopleiding Brussel Auteur Van Basis tot Limiet en auteur van Nando. roger.van.nieuwenhuyze@gmail.com
GEOGEBRA 5. Ruimtemeetkunde in de tweede en derde graad. R. Van Nieuwenhuyze. Hoofdlector wiskunde aan HUB, Brussel. Auteur Van Basis tot Limiet.
 GEOGEBRA 5 Ruimtemeetkunde in de tweede en derde graad R. Van Nieuwenhuyze Hoofdlector wiskunde aan HUB, Brussel Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@gmail.com GeoGebra in de tweede en derde
GEOGEBRA 5 Ruimtemeetkunde in de tweede en derde graad R. Van Nieuwenhuyze Hoofdlector wiskunde aan HUB, Brussel Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@gmail.com GeoGebra in de tweede en derde
GEOGEBRA 5. Ruimtemeetkunde in de tweede graad. R. Van Nieuwenhuyze. Hoofdlector wiskunde aan Odisee, Brussel. Auteur Van Basis tot Limiet.
 GEOGEBRA 5 Ruimtemeetkunde in de tweede graad R. Van Nieuwenhuyze Hoofdlector wiskunde aan Odisee, Brussel Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@gmail.com GeoGebra in de tweede graad Roger
GEOGEBRA 5 Ruimtemeetkunde in de tweede graad R. Van Nieuwenhuyze Hoofdlector wiskunde aan Odisee, Brussel Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@gmail.com GeoGebra in de tweede graad Roger
GEOGEBRA 6 IN DE eerste graad B
 GEOGEBRA 6 IN DE eerste graad B Heel tof? R. Van Nieuwenhuyze Oud-hoofdlector wiskunde aan Odisee, Brussel Auteur Van Basis tot Limiet en van Nando roger.van.nieuwenhuyze@gmail.com Roger Van Nieuwenhuyze
GEOGEBRA 6 IN DE eerste graad B Heel tof? R. Van Nieuwenhuyze Oud-hoofdlector wiskunde aan Odisee, Brussel Auteur Van Basis tot Limiet en van Nando roger.van.nieuwenhuyze@gmail.com Roger Van Nieuwenhuyze
Lesbrief GeoGebra. 1. Even kennismaken met GeoGebra (GG)
 Lesbrief GeoGebra Inhoud: 1. Even kennismaken met GeoGebra 2. Meetkunde: 2.1 Punten, lijnen, figuren maken 2.2 Loodlijn, deellijn, middelloodlijn maken 2.3 Probleem M1: De rechte van Euler 2.4 Probleem
Lesbrief GeoGebra Inhoud: 1. Even kennismaken met GeoGebra 2. Meetkunde: 2.1 Punten, lijnen, figuren maken 2.2 Loodlijn, deellijn, middelloodlijn maken 2.3 Probleem M1: De rechte van Euler 2.4 Probleem
INLEIDING TOT GEOGEBRA
 INLEIDING TOT GEOGEBRA Sven Mettepenningen, 28/02/2007 GEOGEBRA 1 EERSTE KENNISMAKING Het pakket Geogebra kan je downloaden op de site http://www.geogebra.at/ Eventueel is het ook nuttig van de laatste
INLEIDING TOT GEOGEBRA Sven Mettepenningen, 28/02/2007 GEOGEBRA 1 EERSTE KENNISMAKING Het pakket Geogebra kan je downloaden op de site http://www.geogebra.at/ Eventueel is het ook nuttig van de laatste
24/11/2008. heel handig hulpvenster past zich voortdurend aan. Engelstalige handleiding van 63 blz. dag van de wiskunde 2e/3e graad 22 nov 2008
 Cabri 3D een voorstelling van de mogelijkheden dag van de wiskunde 2e/3e graad 22 nov 2008 Paul Decuypere, VVKSO cahier de brouillon interactif www.cabri.com 1985: eerste versie van Cabri I 1989: eerste
Cabri 3D een voorstelling van de mogelijkheden dag van de wiskunde 2e/3e graad 22 nov 2008 Paul Decuypere, VVKSO cahier de brouillon interactif www.cabri.com 1985: eerste versie van Cabri I 1989: eerste
ICT. Meetkunde met GeoGebra. 2.7 deel 1 blz 78
 ICT Meetkunde met GeoGebra 2.7 deel 1 blz 78 Om de opdrachten van paragraaf 2.7 uit het leerboek te kunnen maken heb je het computerprogramma GeoGebra nodig. Je kunt het programma openen via de leerlingenkit
ICT Meetkunde met GeoGebra 2.7 deel 1 blz 78 Om de opdrachten van paragraaf 2.7 uit het leerboek te kunnen maken heb je het computerprogramma GeoGebra nodig. Je kunt het programma openen via de leerlingenkit
Dag van GeoGebra Probleemoplossende vaardigheden en onderzoekscompetentie wiskunde 28 mei 2011 Gent
 1 VERBORGEN FIGUREN 1.1 OPGAVE In heel wat klassieke opdrachten uit de meetkunde is het de bedoeling om een bepaalde figuur te tekenen indien een aantal punten gegeven zijn. De eigenschappen van deze figuur
1 VERBORGEN FIGUREN 1.1 OPGAVE In heel wat klassieke opdrachten uit de meetkunde is het de bedoeling om een bepaalde figuur te tekenen indien een aantal punten gegeven zijn. De eigenschappen van deze figuur
GeoGebra Quickstart. Snelgids voor GeoGebra. Vertaald door Beatrijs Versichel en Ivan De Winne
 GeoGebra Quickstart Snelgids voor GeoGebra Vertaald door Beatrijs Versichel en Ivan De Winne Dynamische meetkunde, algebra en analyse vormen de basis van GeoGebra, een educatief pakket, dat meetkunde en
GeoGebra Quickstart Snelgids voor GeoGebra Vertaald door Beatrijs Versichel en Ivan De Winne Dynamische meetkunde, algebra en analyse vormen de basis van GeoGebra, een educatief pakket, dat meetkunde en
héöéäëåéçéå=~äë=ãééíâìåçáöé=éä~~íëéå=ãéí=`~äêá= = hçéå=píìäéåë= = = = = = = =
 héöéäëåéçéå~äëãééíâìåçáöééä~~íëéåãéí`~äêá hçéåpíìäéåë De algemene vergelijking van een kegelsnede is van de vorm : 2 2 ax by 2cxy 2dx 2ey f 0 met a, b, c, d, e, f + + + + +. Indien je vijf punten van een
héöéäëåéçéå~äëãééíâìåçáöééä~~íëéåãéí`~äêá hçéåpíìäéåë De algemene vergelijking van een kegelsnede is van de vorm : 2 2 ax by 2cxy 2dx 2ey f 0 met a, b, c, d, e, f + + + + +. Indien je vijf punten van een
VOORAF. Een volledige versie is aan te kopen via
 CABRI 3D VOORAF De laatste jaren zijn enkele programma s voor ruimtemeetkunde op de softwaremarkt verschenen. Ook Cabri, waarvan het programma voor vlakke meetkunde al bestaat uit het DOS-tijdperk van
CABRI 3D VOORAF De laatste jaren zijn enkele programma s voor ruimtemeetkunde op de softwaremarkt verschenen. Ook Cabri, waarvan het programma voor vlakke meetkunde al bestaat uit het DOS-tijdperk van
Aan de slag met GeoGebra
 Aan de slag met GeoGebra De basis http://www.geogebra.org/ Wat je leert in deze powerpoint: Je kan GeoGebra opstarten Je kan de taal aanpassen Je kan je werk opslaan, fixeren en downloaden als afbeelding
Aan de slag met GeoGebra De basis http://www.geogebra.org/ Wat je leert in deze powerpoint: Je kan GeoGebra opstarten Je kan de taal aanpassen Je kan je werk opslaan, fixeren en downloaden als afbeelding
Open het programma Geogebra. Het beginscherm verschijnt. Klik voordat je verder gaat met je muis ergens in het
 Practicum I Opgave 1 Tekenen van een driehoek In de opgave gaan we op twee verschillende manieren een driehoek tekenen. We doen dit door gebruik te maken van de werkbalk (macrovenster) en van het invoerveld.
Practicum I Opgave 1 Tekenen van een driehoek In de opgave gaan we op twee verschillende manieren een driehoek tekenen. We doen dit door gebruik te maken van de werkbalk (macrovenster) en van het invoerveld.
7 Totaalbeeld. Samenvatten. Achtergronden. Testen
 7 Totaalbeeld Samenvatten Je hebt nu het onderwerp "Vectormeetkunde" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan... Ga na, of je al de bij dit onderwerp horende begrippen kent en weet
7 Totaalbeeld Samenvatten Je hebt nu het onderwerp "Vectormeetkunde" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan... Ga na, of je al de bij dit onderwerp horende begrippen kent en weet
Opgave 1 Bestudeer de Uitleg, pagina 1. Laat zien dat ook voor punten buiten lijnstuk AB maar wel op lijn AB geldt: x + 3y = 5
 2 Vergelijkingen Verkennen Meetkunde Vergelijkingen Inleiding Verkennen Beantwoord de vragen bij Verkennen. Uitleg Meetkunde Vergelijkingen Uitleg Opgave Bestudeer de Uitleg, pagina. Laat zien dat ook
2 Vergelijkingen Verkennen Meetkunde Vergelijkingen Inleiding Verkennen Beantwoord de vragen bij Verkennen. Uitleg Meetkunde Vergelijkingen Uitleg Opgave Bestudeer de Uitleg, pagina. Laat zien dat ook
de Leuke En Uitdagende Wiskunde VEELVLAKKEN SAMENSTELLING: H. de Leuw
 SAMENSTELLING: H. de Leuw 1. VEELHOEKEN. Een veelvlak is een lichaam dat wordt begrensd door vlakke veelhoeken. Zo zijn balken en piramides wel veelvlakken, maar cilinders en bollen niet. Een veelhoek
SAMENSTELLING: H. de Leuw 1. VEELHOEKEN. Een veelvlak is een lichaam dat wordt begrensd door vlakke veelhoeken. Zo zijn balken en piramides wel veelvlakken, maar cilinders en bollen niet. Een veelhoek
Vlakke meetkunde en geogebra
 Vlakke meetkunde en geogebra Open de geogebra-app. Kies het algebra- en tekenvenster. Aan de linkerkant zie je het algebravenster en rechts daarvan het tekenvenster met een x-as en een y-as. Om een rooster
Vlakke meetkunde en geogebra Open de geogebra-app. Kies het algebra- en tekenvenster. Aan de linkerkant zie je het algebravenster en rechts daarvan het tekenvenster met een x-as en een y-as. Om een rooster
Oefeningen analytische meetkunde
 Oefeningen analytische meetkunde ) orte herhaling. Zij gegeven twee vectoren P en Q. Bewijs dat de loodrechte projectie P' van P op Q gegeven wordt door: PQQ P'. Q. De cirkel c y 4y wordt gespiegeld om
Oefeningen analytische meetkunde ) orte herhaling. Zij gegeven twee vectoren P en Q. Bewijs dat de loodrechte projectie P' van P op Q gegeven wordt door: PQQ P'. Q. De cirkel c y 4y wordt gespiegeld om
Dag van de wiskunde 26/11/2005. R. Van Nieuwenhuyze. Docent wiskunde en statistiek aan Ehsal, Brussel. Auteur Van Basis tot Limiet.
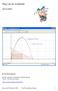 Dag van de wiskunde 26/11/2005 R. Van Nieuwenhuyze Docent wiskunde en statistiek aan Ehsal, Brussel. Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@skynet.be Dag van de Wiskunde 2005 Van Nieuwenhuyze
Dag van de wiskunde 26/11/2005 R. Van Nieuwenhuyze Docent wiskunde en statistiek aan Ehsal, Brussel. Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@skynet.be Dag van de Wiskunde 2005 Van Nieuwenhuyze
Stap 1: Ga naar Stap 3: Gebruik de pijltjes om te navigeren tussen de bladzijden.
 Stap 1: Ga naar www.wiskundewereld.be/bzl-ruimtemeetkunde.html Stap 2: Klik rechts op de witte knop. Stap 3: Gebruik de pijltjes om te navigeren tussen de bladzijden. Stap 4: Links zie je waar je je in
Stap 1: Ga naar www.wiskundewereld.be/bzl-ruimtemeetkunde.html Stap 2: Klik rechts op de witte knop. Stap 3: Gebruik de pijltjes om te navigeren tussen de bladzijden. Stap 4: Links zie je waar je je in
Handig met getallen 4 (HMG4), onderdeel Meetkunde
 Handig met getallen 4 (HMG4), onderdeel Meetkunde Erratum Meetkunde Je vindt hier de correcties voor Handig met getallen 4 (ISBN: 978 94 90681 005). Deze correcties zijn ook bedoeld voor het Rekenwerkboek
Handig met getallen 4 (HMG4), onderdeel Meetkunde Erratum Meetkunde Je vindt hier de correcties voor Handig met getallen 4 (ISBN: 978 94 90681 005). Deze correcties zijn ook bedoeld voor het Rekenwerkboek
Kaart 1: Kubus aanpassen Zet bij Beeld de assen uit en het rooster aan.
 Kaart 1: Kubus aanpassen Zet bij Beeld de assen uit en het rooster aan. Kies uit het menu Rechte door 2 punten voor lijnstuk tussen twee punten. Klik op een roosterpunt en punt A wordt getekend. Teken
Kaart 1: Kubus aanpassen Zet bij Beeld de assen uit en het rooster aan. Kies uit het menu Rechte door 2 punten voor lijnstuk tussen twee punten. Klik op een roosterpunt en punt A wordt getekend. Teken
2. Waar of vals: Als een rechte a evenwijdig is met een vlak α en dat vlak staat loodrecht op een vlak β dan staat a loodrecht op β.
 1 Synthetische RM 1. (a) Geef de definitie van de loodrechte stand van twee vlakken. (b) Geen stellingen die voorwaarden uitdrukken opdat twee vlakken orthogonaal zijn. (c) Steun op 1a of 1b om te bewijzen
1 Synthetische RM 1. (a) Geef de definitie van de loodrechte stand van twee vlakken. (b) Geen stellingen die voorwaarden uitdrukken opdat twee vlakken orthogonaal zijn. (c) Steun op 1a of 1b om te bewijzen
Nadat GeoGebra wordt opgestart zie je het hierna afgebeelde venster: Algebra Venster. Teken Venster. Invoerveld
 Vrije Ruimte Wiskunde GeoGebra Philip Bogaert GeoGebra 1. Inleiding GeoGebra is een (gratis) wiskundepakket dat meetkunde, algebra en analyse combineert. Het pakket werd ontwikkeld door Markus Hohenwarter
Vrije Ruimte Wiskunde GeoGebra Philip Bogaert GeoGebra 1. Inleiding GeoGebra is een (gratis) wiskundepakket dat meetkunde, algebra en analyse combineert. Het pakket werd ontwikkeld door Markus Hohenwarter
Analytische Meetkunde. Lieve Houwaer, Unit informatie, team wiskunde
 Analytische Meetkunde Lieve Houwaer, Unit informatie, team wiskunde . VECTOREN EN RECHTEN.. Vectoren... Het vectorbegrip De verzameling punten van het vlak noteren we door π. Kies in het vlak π een vast
Analytische Meetkunde Lieve Houwaer, Unit informatie, team wiskunde . VECTOREN EN RECHTEN.. Vectoren... Het vectorbegrip De verzameling punten van het vlak noteren we door π. Kies in het vlak π een vast
Vlakke meetkunde. Module 6. 6.1 Geijkte rechte. 6.1.1 Afstand tussen twee punten. 6.1.2 Midden van een lijnstuk
 Module 6 Vlakke meetkunde 6. Geijkte rechte Beschouw een rechte L en kies op deze rechte een punt o als oorsprong en een punt e als eenheidspunt. Indien men aan o en e respectievelijk de getallen 0 en
Module 6 Vlakke meetkunde 6. Geijkte rechte Beschouw een rechte L en kies op deze rechte een punt o als oorsprong en een punt e als eenheidspunt. Indien men aan o en e respectievelijk de getallen 0 en
Ruimtemeetkunde deel II. Cursus voor Latijn-Wiskunde, Wetenschappen-Wiskunde en Economie-Wiskunde
 Ruimtemeetkunde deel II Liliane Van Maldeghem Hendrik Van Maldeghem Cursus voor Latijn-Wiskunde, Wetenschappen-Wiskunde en Economie-Wiskunde 2 Hoofdstuk 1 De reële euclidische ruimte 1.1 De euclidische
Ruimtemeetkunde deel II Liliane Van Maldeghem Hendrik Van Maldeghem Cursus voor Latijn-Wiskunde, Wetenschappen-Wiskunde en Economie-Wiskunde 2 Hoofdstuk 1 De reële euclidische ruimte 1.1 De euclidische
Kernbegrippen Kennisbasis wiskunde Onderdeel meetkunde
 Kernbegrippen Kennisbasis wiskunde Onderdeel meetkunde Aanzicht Een ruimtelijk figuur kun je van verschillende kanten bekijken, je noemt dat aanzichten. Er zijn 5 aanzichten: Vooraanzicht (van voren).
Kernbegrippen Kennisbasis wiskunde Onderdeel meetkunde Aanzicht Een ruimtelijk figuur kun je van verschillende kanten bekijken, je noemt dat aanzichten. Er zijn 5 aanzichten: Vooraanzicht (van voren).
door: Bart Van den Bergh
 door: Bart Van den Bergh Inhoud 1. Inleiding...5 1.1. Wat is GeoGebra?... 5 1.2. Downloaden en installatie... 5 2. Basiscursus...7 2.1. Aan de slag... 7 2.1.1 Openen van het programma... 7 2.1.2 Lay-out...
door: Bart Van den Bergh Inhoud 1. Inleiding...5 1.1. Wat is GeoGebra?... 5 1.2. Downloaden en installatie... 5 2. Basiscursus...7 2.1. Aan de slag... 7 2.1.1 Openen van het programma... 7 2.1.2 Lay-out...
Proefexemplaar. ICT PraCTICumboek (1e graad / onderbouw) Filip Geeurickx Jan Thoelen Roger Van Nieuwenhuyze. GeoGebra
 ICT PraCTICumboek (1e graad / onderbouw) GeoGebra Filip Geeurickx Jan Thoelen Roger Van Nieuwenhuyze 3 ICT practicumboek > inhoud 1 Het pakket Geogebra 1.1 Het programma downloaden, 6 1.2 Vensters en icoontjes
ICT PraCTICumboek (1e graad / onderbouw) GeoGebra Filip Geeurickx Jan Thoelen Roger Van Nieuwenhuyze 3 ICT practicumboek > inhoud 1 Het pakket Geogebra 1.1 Het programma downloaden, 6 1.2 Vensters en icoontjes
6 Ligging. Verkennen. Uitleg
 6 Ligging Verkennen Ligging Inleiding Verkennen Door in de applet het assenstelsel te draaien kun je nagaan of twee lijnen een snijpunt hebben. Je kunt ook andere lijnen proberen door de punten A, B, C
6 Ligging Verkennen Ligging Inleiding Verkennen Door in de applet het assenstelsel te draaien kun je nagaan of twee lijnen een snijpunt hebben. Je kunt ook andere lijnen proberen door de punten A, B, C
GeoGebra voor starters. GeoGebradag 28 mei Riggy Van de Wiele
 GeoGebra voor starters GeoGebradag 28 mei 2011 Riggy Van de Wiele 1) GeoGebra installeren. GeoGebra voor starters. Ga naar de website www.geogebra.at Je krijgt er het volgende scherm te zien. Je drukt
GeoGebra voor starters GeoGebradag 28 mei 2011 Riggy Van de Wiele 1) GeoGebra installeren. GeoGebra voor starters. Ga naar de website www.geogebra.at Je krijgt er het volgende scherm te zien. Je drukt
1. Vlakke meetkunde. Geocadabra kan je downloaden op de website Opgave 1
 Geocadabra 1. Vlakke meetkunde Opgave 1 Geocadabra kan je downloaden op de website www.geocadabra.nl Teken de cirkel c met middelpunt M(2,1) en straal 5. Construeer de raaklijnen uit het punt P(-10,4)
Geocadabra 1. Vlakke meetkunde Opgave 1 Geocadabra kan je downloaden op de website www.geocadabra.nl Teken de cirkel c met middelpunt M(2,1) en straal 5. Construeer de raaklijnen uit het punt P(-10,4)
1 Middelpunten. Verkennen. Uitleg
 1 Middelpunten Verkennen Middelpunten Inleiding Verkennen Probeer vanuit drie gegeven punten (niet op één lijn) die op een cirkel moeten liggen het middelpunt van die cirkel te construeren. Je kunt hem
1 Middelpunten Verkennen Middelpunten Inleiding Verkennen Probeer vanuit drie gegeven punten (niet op één lijn) die op een cirkel moeten liggen het middelpunt van die cirkel te construeren. Je kunt hem
1. Exclusief aanvinken
 1. Exclusief aanvinken Hoe maak je meerkeuzevragen met exclusieve selectie? Het bestand 10_exclusiefhoe.ggb toont drie manieren om meerkeuzevragen te maken. 1.1 Aanvinkvakjes (voorlaatste knop) Op de aanvinkvakjes
1. Exclusief aanvinken Hoe maak je meerkeuzevragen met exclusieve selectie? Het bestand 10_exclusiefhoe.ggb toont drie manieren om meerkeuzevragen te maken. 1.1 Aanvinkvakjes (voorlaatste knop) Op de aanvinkvakjes
Integratie van de informatica in de wiskunde WIRIS 2.0
 Integratie van de informatica in de wiskunde WIRIS 2.0 9 Dynamische meetkunde met Wiris 9.1 Vlakke analytische meetkunde Het palet Meetkunde bevat een aantal gereedschappen voor het uitvoeren van meetkundige
Integratie van de informatica in de wiskunde WIRIS 2.0 9 Dynamische meetkunde met Wiris 9.1 Vlakke analytische meetkunde Het palet Meetkunde bevat een aantal gereedschappen voor het uitvoeren van meetkundige
uuur , DF en DB met kentallen. b) Laat zien door twee keer de stelling van Pythagoras in een rechthoekige uuur
 4 Van D naar 3D Verkennen Van D naar 3D Inleiding Verkennen Bekijk de applet. Met de rechter muisknop kun je het assenstelsel om de oorsprong draaien en de fig van alle kanten bekijken. Beantwoord nu de
4 Van D naar 3D Verkennen Van D naar 3D Inleiding Verkennen Bekijk de applet. Met de rechter muisknop kun je het assenstelsel om de oorsprong draaien en de fig van alle kanten bekijken. Beantwoord nu de
Willem-Jan van der Zanden
 Enkele praktische zaken: Altijd meenemen een schrift met ruitjespapier (1 cm of 0,5 cm) of losse blaadjes in een map. Bij voorkeur een groot schrift (A4); Geodriehoek: Deze kun je kopen in de winkel. Koop
Enkele praktische zaken: Altijd meenemen een schrift met ruitjespapier (1 cm of 0,5 cm) of losse blaadjes in een map. Bij voorkeur een groot schrift (A4); Geodriehoek: Deze kun je kopen in de winkel. Koop
Cabri-werkblad. Driehoeken, rechthoeken en vierkanten. 1. Eerst twee macro's
 Cabri-werkblad Driehoeken, rechthoeken en vierkanten 1. Eerst twee macro's Bij de opdrachten van dit werkblad zullen we vaak een vierkant nodig hebben waarvan alleen de beide eindpunten van een zijde gegeven
Cabri-werkblad Driehoeken, rechthoeken en vierkanten 1. Eerst twee macro's Bij de opdrachten van dit werkblad zullen we vaak een vierkant nodig hebben waarvan alleen de beide eindpunten van een zijde gegeven
Cursus Geogebra. Werkbladen voor vmbo en havo/vwo onderbouw. Docentencongres wiskunde: Aan de slag met ICT! Februari 2011
 Cursus Geogebra Docentencongres wiskunde: Aan de slag met ICT! Werkbladen voor vmbo en havo/vwo onderbouw Februari 2011 J. Manders Dominicus College Nijmegen jan.manders@dominicuscollege.nl 2 Introductie
Cursus Geogebra Docentencongres wiskunde: Aan de slag met ICT! Werkbladen voor vmbo en havo/vwo onderbouw Februari 2011 J. Manders Dominicus College Nijmegen jan.manders@dominicuscollege.nl 2 Introductie
Analytische Meetkunde
 Analytische Meetkunde Meetkunde met Geogebra en vergelijkingen van lijnen 2 Inhoudsopgave Achtergrondinformatie... 4 Meetkunde met Geogebra... 6 Stelling van Thales...... 7 3 Achtergrondinformatie Auteurs
Analytische Meetkunde Meetkunde met Geogebra en vergelijkingen van lijnen 2 Inhoudsopgave Achtergrondinformatie... 4 Meetkunde met Geogebra... 6 Stelling van Thales...... 7 3 Achtergrondinformatie Auteurs
MEETKUNDE 120 PUNTEN, LIJNEN EN VLAKKEN
 120 PUNTEN, LIJNEN EN VLAKKEN een rechte lijn A het punt A a de rechte a een kromme lijn of een kromme een gebroken lijn a A b a B het lijnstuk [AB] evenwijdige rechten a // b een plat oppervlak of een
120 PUNTEN, LIJNEN EN VLAKKEN een rechte lijn A het punt A a de rechte a een kromme lijn of een kromme een gebroken lijn a A b a B het lijnstuk [AB] evenwijdige rechten a // b een plat oppervlak of een
1 Cartesische coördinaten
 Cartesische coördinaten Verkennen www.math4all.nl MAThADORE-basic HAVO/VWO 4/5/6 VWO wi-d Analytische Meetkunde Cartesische coördinaten Inleiding Verkennen Beantwoord de vragen bij Verkennen. (Als je er
Cartesische coördinaten Verkennen www.math4all.nl MAThADORE-basic HAVO/VWO 4/5/6 VWO wi-d Analytische Meetkunde Cartesische coördinaten Inleiding Verkennen Beantwoord de vragen bij Verkennen. (Als je er
Creatief aan de slag met GeoGebra. Een tangram is een beroemde Chinese puzzel bestaande uit 7 puzzelstukjes: 1 vierkant, 1 parallellogram.
 18 Tangram puzzel Een tangram is een beroemde Chinese puzzel bestaande uit 7 puzzelstukjes: 5 gelijkbenige rechthoekige driehoeken van 3 verschillende grootten, 1 vierkant, 1 parallellogram. Aan het begin
18 Tangram puzzel Een tangram is een beroemde Chinese puzzel bestaande uit 7 puzzelstukjes: 5 gelijkbenige rechthoekige driehoeken van 3 verschillende grootten, 1 vierkant, 1 parallellogram. Aan het begin
Definitie van raaklijn aan cirkel: Stelling van raaklijn aan cirkel:
 13.0 Voorkennis Op de cirkel liggen alle punten met een Gelijke afstand tot het middelpunt van de cirkel. Voor een punt p op de cirkel geldt d(p, M) = r Definitie van raaklijn aan cirkel: Een raaklijn
13.0 Voorkennis Op de cirkel liggen alle punten met een Gelijke afstand tot het middelpunt van de cirkel. Voor een punt p op de cirkel geldt d(p, M) = r Definitie van raaklijn aan cirkel: Een raaklijn
Cabri werkblad. Meetkundige plaatsen
 Cabri werkblad Meetkundige plaatsen 1. Wat is een meetkundige plaats? We geven direct maar een Definitie Een meetkundige figuur heet meetkundige plaats van punten met een bepaalde eigenschap indien: 1.
Cabri werkblad Meetkundige plaatsen 1. Wat is een meetkundige plaats? We geven direct maar een Definitie Een meetkundige figuur heet meetkundige plaats van punten met een bepaalde eigenschap indien: 1.
Lijnen van betekenis meetkunde in 2hv
 Lijnen van betekenis meetkunde in 2hv Docentenhandleiding bij de DWO-module Lijnen van betekenis Deze handleiding bevat tips voor de docent bij het gebruiken van de module Lijnen van betekenis, een module
Lijnen van betekenis meetkunde in 2hv Docentenhandleiding bij de DWO-module Lijnen van betekenis Deze handleiding bevat tips voor de docent bij het gebruiken van de module Lijnen van betekenis, een module
Didactisch gebruik van GeoGebra in de eerste graad
 Didactisch gebruik van GeoGebra in de eerste graad 3 Het basisvenster 1 Downloaden van GeoGebra - GeoGebra is een gratis wiskundepakket dat meetkunde of geometrie en algebra combineert. Elk meetkundig
Didactisch gebruik van GeoGebra in de eerste graad 3 Het basisvenster 1 Downloaden van GeoGebra - GeoGebra is een gratis wiskundepakket dat meetkunde of geometrie en algebra combineert. Elk meetkundig
MEETKUNDE 120 PUNTEN, LIJNEN EN VLAKKEN
 120 PUNTEN, LIJNEN EN VLAKKEN een rechte lijn A het punt A a de rechte a een kromme lijn of een kromme een gebroken lijn a A b a B het lijnstuk [AB] evenwijdige rechten a // b een plat oppervlak of een
120 PUNTEN, LIJNEN EN VLAKKEN een rechte lijn A het punt A a de rechte a een kromme lijn of een kromme een gebroken lijn a A b a B het lijnstuk [AB] evenwijdige rechten a // b een plat oppervlak of een
Bijkomende Oefeningen: Les 1
 1 Inhoudstafel ijkomende Oefeningen: Les 1...2 ijkomende Oefeningen: Les 2...3 ijkomende Oefeningen: Les 3...4 ijkomende Oefeningen: Les 4...5 ijkomende Oefeningen: Les 5...6 ijkomende Oefeningen: Les
1 Inhoudstafel ijkomende Oefeningen: Les 1...2 ijkomende Oefeningen: Les 2...3 ijkomende Oefeningen: Les 3...4 ijkomende Oefeningen: Les 4...5 ijkomende Oefeningen: Les 5...6 ijkomende Oefeningen: Les
Dan is de afstand A B = lengte van lijnstuk [A B]: AB = x x )² + ( y ²
![Dan is de afstand A B = lengte van lijnstuk [A B]: AB = x x )² + ( y ² Dan is de afstand A B = lengte van lijnstuk [A B]: AB = x x )² + ( y ²](/thumbs/54/34123992.jpg) 1 Herhaling 1.1 Het vlak, punten, afstand, midden Opdracht: Teken in het vlak de punten: A ( 1, 2) B(3,6) C( 5,7) Bepaal de coördinaat van het midden van (lijnstuk) [A B]: M [B C ]: N Bepaal de afstand
1 Herhaling 1.1 Het vlak, punten, afstand, midden Opdracht: Teken in het vlak de punten: A ( 1, 2) B(3,6) C( 5,7) Bepaal de coördinaat van het midden van (lijnstuk) [A B]: M [B C ]: N Bepaal de afstand
Een ander zijvlak is het regelmatige vijfhoek met aantal zijden P=5. Hierbij moeten Q=3 zijvlakken samenkomen in een hoekpunt van het veelvlak.
 Praktische-opdracht door een scholier 1498 woorden 6 juni 2003 6,5 134 keer beoordeeld Vak Wiskunde Deelvraag 1: Wat is de definitie van een Platonische Lichaam / Platonisch Veelvlak? De definitie: Een
Praktische-opdracht door een scholier 1498 woorden 6 juni 2003 6,5 134 keer beoordeeld Vak Wiskunde Deelvraag 1: Wat is de definitie van een Platonische Lichaam / Platonisch Veelvlak? De definitie: Een
2 Vergelijkingen van lijnen
 2 Vergelijkingen van lijnen Verkennen Meetkunde Lijnen Inleiding Verkennen Beantwoord de vragen bij Verkennen. Gebruik de applet! Uitleg Meetkunde Lijnen Uitleg Opgave 1 Bestudeer de Uitleg. Laat zien
2 Vergelijkingen van lijnen Verkennen Meetkunde Lijnen Inleiding Verkennen Beantwoord de vragen bij Verkennen. Gebruik de applet! Uitleg Meetkunde Lijnen Uitleg Opgave 1 Bestudeer de Uitleg. Laat zien
Opgave 1 Bekijk de Uitleg, pagina 1. Bekijk wat een vectorvoorstelling van een lijn is.
 3 Lijnen en hoeken Verkennen Lijnen en hoeken Inleiding Verkennen Bekijk de applet en zie hoe de plaatsvector v ur van elk punt A op de lijn kan ur r ontstaan als som van twee vectoren: p + t r. Beantwoord
3 Lijnen en hoeken Verkennen Lijnen en hoeken Inleiding Verkennen Bekijk de applet en zie hoe de plaatsvector v ur van elk punt A op de lijn kan ur r ontstaan als som van twee vectoren: p + t r. Beantwoord
en een punt P BC zodat BP 2. CB.
 Oplossingen E F G H Gegeven is de kubus A C D en een punt P C zodat P C a) epaal het snijpunt van de rechte PH met het voorvlak AFE van de kubus De rechte PH ligt in het diagonaalvlak EHC van de kubus
Oplossingen E F G H Gegeven is de kubus A C D en een punt P C zodat P C a) epaal het snijpunt van de rechte PH met het voorvlak AFE van de kubus De rechte PH ligt in het diagonaalvlak EHC van de kubus
wiskunde B havo 2015-II
 Veilig vliegen De minimale en de maximale snelheid waarmee een vliegtuig veilig kan vliegen, zijn onder andere afhankelijk van de vlieghoogte. Deze hoogte wordt vaak weergegeven in de Amerikaanse eenheid
Veilig vliegen De minimale en de maximale snelheid waarmee een vliegtuig veilig kan vliegen, zijn onder andere afhankelijk van de vlieghoogte. Deze hoogte wordt vaak weergegeven in de Amerikaanse eenheid
Antwoorden De juiste ondersteuning
 ntwoorden De juiste ondersteuning a. De straal van de cirkel waarover het beweegt is 5. De maximale hoogte van het is dus 5. Het moet dus dm omhoog. b. Het van het tweede blok beweegt over een cirkel met
ntwoorden De juiste ondersteuning a. De straal van de cirkel waarover het beweegt is 5. De maximale hoogte van het is dus 5. Het moet dus dm omhoog. b. Het van het tweede blok beweegt over een cirkel met
Regelmatige en halfregelmatige veelvlakken
 Regelmatige en halfregelmatige veelvlakken Wiskunde & Cultuur 2-3 W.v.Ravenstein 2010-2011 aangepast Vandaag Platonische lichamen Regelmatig, halfregelmatig en andere naamgeving Waarom zijn er maar 5 Platonische
Regelmatige en halfregelmatige veelvlakken Wiskunde & Cultuur 2-3 W.v.Ravenstein 2010-2011 aangepast Vandaag Platonische lichamen Regelmatig, halfregelmatig en andere naamgeving Waarom zijn er maar 5 Platonische
Uitwerkingen oefeningen hoofdstuk 4
 Uitwerkingen oefeningen hoofdstuk 4 4.4.1 Basis Lijnen en hoeken 1 Het assenstelsel met genoemde lijnen ziet er als volgt uit: 4 3 2 1 l k -4-3 -2-1 0 1 2 3 4-1 -2-3 n m -4 - Hieruit volgt: a Lijn k en
Uitwerkingen oefeningen hoofdstuk 4 4.4.1 Basis Lijnen en hoeken 1 Het assenstelsel met genoemde lijnen ziet er als volgt uit: 4 3 2 1 l k -4-3 -2-1 0 1 2 3 4-1 -2-3 n m -4 - Hieruit volgt: a Lijn k en
1 Coördinaten in het vlak
 Coördinaten in het vlak Verkennen Meetkunde Coördinaten in het vlak Inleiding Verkennen Beantwoord de vragen bij Verkennen. (Als je er niet uitkomt, ga je gewoon naar de Uitleg, maar bekijk het probleem
Coördinaten in het vlak Verkennen Meetkunde Coördinaten in het vlak Inleiding Verkennen Beantwoord de vragen bij Verkennen. (Als je er niet uitkomt, ga je gewoon naar de Uitleg, maar bekijk het probleem
I n t r o d u c t i e
 I n t r o d u c t i e Wiskunde leer je door te doen, dat geldt ook voor GeoGebra. Deze reader is gebaseerd op een deel van mijn ervaringen met GeoGebra in de onderbouw havo/vwo de afgelopen twee jaar.
I n t r o d u c t i e Wiskunde leer je door te doen, dat geldt ook voor GeoGebra. Deze reader is gebaseerd op een deel van mijn ervaringen met GeoGebra in de onderbouw havo/vwo de afgelopen twee jaar.
EXAMENVRAGEN RUIMTEMEETKUNDE I (niet-analytische meetkunde)
 EXAMENVRAGEN RUIMTEMEETKUNDE I (niet-analytische meetkunde). (4 p) Geef drie verschillende mogelijkheden waardoor in de driedimensionale ruimte een rechte bepaald is? 2. (6 p) Wanneer zijn de snijlijnen
EXAMENVRAGEN RUIMTEMEETKUNDE I (niet-analytische meetkunde). (4 p) Geef drie verschillende mogelijkheden waardoor in de driedimensionale ruimte een rechte bepaald is? 2. (6 p) Wanneer zijn de snijlijnen
Didactisch gebruik van GeoGebra in de tweede graad
 Didactisch gebruik van GeoGebra in de tweede graad 3 Het basisvenster 1 Downloaden van GeoGebra - GeoGebra is een gratis wiskundepakket dat meetkunde of geometrie en algebra combineert. Elk meetkundig
Didactisch gebruik van GeoGebra in de tweede graad 3 Het basisvenster 1 Downloaden van GeoGebra - GeoGebra is een gratis wiskundepakket dat meetkunde of geometrie en algebra combineert. Elk meetkundig
ICT-LEERLIJN (met GeoGebra) Luc Gheysens WISKUNDIGE COMPETENTIES
 ICT-LEERLIJN (met GeoGebra) Luc Gheysens www.gnomon.bloggen.be WISKUNDIGE COMPETENTIES 1 Wiskundig denken 2 Wiskundige problemen aanpakken en oplossen 3 Wiskundig modelleren 4 Wiskundig argumenteren 5
ICT-LEERLIJN (met GeoGebra) Luc Gheysens www.gnomon.bloggen.be WISKUNDIGE COMPETENTIES 1 Wiskundig denken 2 Wiskundige problemen aanpakken en oplossen 3 Wiskundig modelleren 4 Wiskundig argumenteren 5
GEOGEBRA IN DE TWEEDE GRAAD. Kan dit wel? Roger Van Nieuwenhuyze Docent wiskunde en statistiek aan Ehsal, Brussel. Auteur Van Basis tot Limiet.
 GEOGEBRA Kan dit wel? IN DE TWEEDE GRAAD Roger Van Nieuwenhuyze Docent wiskunde en statistiek aan Ehsal, Brussel. Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@skynet.be Van Nieuwenhuyze Roger Geogebra
GEOGEBRA Kan dit wel? IN DE TWEEDE GRAAD Roger Van Nieuwenhuyze Docent wiskunde en statistiek aan Ehsal, Brussel. Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@skynet.be Van Nieuwenhuyze Roger Geogebra
27 Macro s voor de schijf van Poincaré
 27 Macro s voor de schijf van Poincaré 27.1 Inleiding In het secundair onderwijs zijn leerlingen vertrouwd met de Euclidische meetkunde. In het Euclidisch vlak geldt het beroemde 5 de parallellen postulaat:
27 Macro s voor de schijf van Poincaré 27.1 Inleiding In het secundair onderwijs zijn leerlingen vertrouwd met de Euclidische meetkunde. In het Euclidisch vlak geldt het beroemde 5 de parallellen postulaat:
GEOGEBRA IN DE EERSTE GRAAD. Kan dit wel? R. Van Nieuwenhuyze. Docent wiskunde en statistiek aan Ehsal, Brussel. Auteur Van Basis tot Limiet.
 GEOGEBRA Kan dit wel? IN DE EERSTE GRAAD R. Van Nieuwenhuyze Docent wiskunde en statistiek aan Ehsal, Brussel. Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@skynet.be Geogebra in de eerste graad
GEOGEBRA Kan dit wel? IN DE EERSTE GRAAD R. Van Nieuwenhuyze Docent wiskunde en statistiek aan Ehsal, Brussel. Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@skynet.be Geogebra in de eerste graad
1 Vlaamse Wiskunde Olympiade : Eerste ronde.
 1 Vlaamse Wiskunde Olympiade 1998-1999: Eerste ronde De eerste ronde bestaat uit 30 meerkeuzevragen Het quoteringssysteem werkt als volgt: per goed antwoord krijgt de deelnemer 5 punten, een blanco antwoord
1 Vlaamse Wiskunde Olympiade 1998-1999: Eerste ronde De eerste ronde bestaat uit 30 meerkeuzevragen Het quoteringssysteem werkt als volgt: per goed antwoord krijgt de deelnemer 5 punten, een blanco antwoord
11.1 De parabool [1]
![11.1 De parabool [1] 11.1 De parabool [1]](/thumbs/51/28339750.jpg) 11.1 De parabool [1] Algemeen: Het punt F heet het brandpunt van de parabool. De lijn l heet de richtlijn van de parabool. De afstand van F tot l heet de parameter van de parabool. Defintie van een parabool:
11.1 De parabool [1] Algemeen: Het punt F heet het brandpunt van de parabool. De lijn l heet de richtlijn van de parabool. De afstand van F tot l heet de parameter van de parabool. Defintie van een parabool:
1 Vlaamse Wiskunde Olympiade : eerste ronde
 1 Vlaamse Wiskunde Olympiade 2005-2006: eerste ronde 1 11 3 11 = () 11 2 3 () 11 5 6 () 11 1 12 11 1 4 11 1 6 2 ls a en b twee verschillende reële getallen verschillend van 0 zijn en 1 x + 1 b = 1, dan
1 Vlaamse Wiskunde Olympiade 2005-2006: eerste ronde 1 11 3 11 = () 11 2 3 () 11 5 6 () 11 1 12 11 1 4 11 1 6 2 ls a en b twee verschillende reële getallen verschillend van 0 zijn en 1 x + 1 b = 1, dan
Hoofdstuk 4: Meetkunde
 Hoofdstuk 4: Meetkunde Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 4: Meetkunde Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde Getallen Assenstelsel Lineair
Hoofdstuk 4: Meetkunde Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 4: Meetkunde Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde Getallen Assenstelsel Lineair
VISUALISATIE VAN KROMMEN EN OPPERVLAKKEN. 1. Inleiding
 VISUALISATIE VAN KROMMEN EN OPPERVLAKKEN IGNACE VAN DE WOESTNE. Inleiding In diverse wetenschappelijke disciplines maakt men gebruik van functies om fenomenen of processen te beschrijven. Hiervoor biedt
VISUALISATIE VAN KROMMEN EN OPPERVLAKKEN IGNACE VAN DE WOESTNE. Inleiding In diverse wetenschappelijke disciplines maakt men gebruik van functies om fenomenen of processen te beschrijven. Hiervoor biedt
Imaginary - van bol naar kubus
 Imaginary - van bol naar kubus Gommaar Maes en Tania Van Damme SLO Wiskunde - Universiteit Gent en Atheneum Mariakerke Inleiding: coördinaat en vergelijking. Vlak Coördinaat Als we werken binnen een orthonormaal
Imaginary - van bol naar kubus Gommaar Maes en Tania Van Damme SLO Wiskunde - Universiteit Gent en Atheneum Mariakerke Inleiding: coördinaat en vergelijking. Vlak Coördinaat Als we werken binnen een orthonormaal
Veelvlak. Begrippenlijst
 Veelvlakken Tijdens dit project Veelvlakken ga je vooral veel zelf onderzoeken. Je zult veel aan het bouwen zijn met Polydron materiaal. Waarschijnlijk zul je naar aanleiding van je bevindingen zelf vragen
Veelvlakken Tijdens dit project Veelvlakken ga je vooral veel zelf onderzoeken. Je zult veel aan het bouwen zijn met Polydron materiaal. Waarschijnlijk zul je naar aanleiding van je bevindingen zelf vragen
Help voor GeoGebra 2.6a
 Help voor GeoGebra 2.6a Markus Hohenwarter, www.geogebra.at Vertaald naar het Nederlands door: Beatrijs Versichel en Pedro Tytgat 16 augustus 2005 Inhoudsopgave Inhoudsopgave 2 1 Wat is GeoGebra? 5 2 Voorbeelden
Help voor GeoGebra 2.6a Markus Hohenwarter, www.geogebra.at Vertaald naar het Nederlands door: Beatrijs Versichel en Pedro Tytgat 16 augustus 2005 Inhoudsopgave Inhoudsopgave 2 1 Wat is GeoGebra? 5 2 Voorbeelden
PROBLEEMOPLOSSEND DENKEN MET
 PROBLEEMOPLOSSEND DENKEN MET Van onderzoekend leren naar leren onderzoeken in de tweede en derde graad Luc Gheysens DPB-Brugge 2012 PROBLEEM 1 Stelling van Pythagoras en gelijkvormige driehoeken Hieronder
PROBLEEMOPLOSSEND DENKEN MET Van onderzoekend leren naar leren onderzoeken in de tweede en derde graad Luc Gheysens DPB-Brugge 2012 PROBLEEM 1 Stelling van Pythagoras en gelijkvormige driehoeken Hieronder
Escher in Het Paleis. Wiskundepakket. Ruimtelijke figuren
 Escher in Het Paleis Wiskundepakket Ruimtelijke figuren Ruimtelijke figuren Escher maakt in EEN AANTAL prenten gebruik van wiskundig interessante ruimtelijke vormen, zoals Platonische lichamen en Möbiusbanden.
Escher in Het Paleis Wiskundepakket Ruimtelijke figuren Ruimtelijke figuren Escher maakt in EEN AANTAL prenten gebruik van wiskundig interessante ruimtelijke vormen, zoals Platonische lichamen en Möbiusbanden.
Lijst van alle opdrachten versie 13 mei 2014
 Lijst van alle opdrachten versie 13 mei 2014 Punt Pu1 Zorg dat Toon assen aan staat. Teken een punt in het vlak. Wijzig de naam naar X (hoofdletter!) (rechtsklikken op het punt voor openen snelmenu). Sleep
Lijst van alle opdrachten versie 13 mei 2014 Punt Pu1 Zorg dat Toon assen aan staat. Teken een punt in het vlak. Wijzig de naam naar X (hoofdletter!) (rechtsklikken op het punt voor openen snelmenu). Sleep
1 Vlaamse Wiskunde Olympiade : Eerste Ronde.
 1 Vlaamse Wiskunde Olympiade 199 1994 : Eerste Ronde De eerste ronde bestaat uit 0 meerkeuzevragen, opgemaakt door de jury van VWO Het quoteringssysteem werkt als volgt : een deelnemer start met 0 punten
1 Vlaamse Wiskunde Olympiade 199 1994 : Eerste Ronde De eerste ronde bestaat uit 0 meerkeuzevragen, opgemaakt door de jury van VWO Het quoteringssysteem werkt als volgt : een deelnemer start met 0 punten
Efficientie in de ruimte - leerlingmateriaal
 Junior College Utrecht Efficientie in de ruimte - leerlingmateriaal Versie 2 September 2012 Een project (ruimte-)meetkunde voor vwo-leerlingen Geschreven voor het Koningin Wilhelmina College Culemborg
Junior College Utrecht Efficientie in de ruimte - leerlingmateriaal Versie 2 September 2012 Een project (ruimte-)meetkunde voor vwo-leerlingen Geschreven voor het Koningin Wilhelmina College Culemborg
2. Antwoorden meetkunde
 2. Antwoorden meetkunde In dit hoofdstuk zijn de antwoorden op de opgaven over Meetkunde opgenomen. Ze zijn kort en bondig per paragraaf gerangschikt. Dat betekent dat de antwoorden geen uitgebreide uitleg
2. Antwoorden meetkunde In dit hoofdstuk zijn de antwoorden op de opgaven over Meetkunde opgenomen. Ze zijn kort en bondig per paragraaf gerangschikt. Dat betekent dat de antwoorden geen uitgebreide uitleg
GEOGEBRA 4. R. Van Nieuwenhuyze. Hoofdlector wiskunde, lerarenopleiding HUB, Brussel. Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@skynet.
 ? GEOGEBRA 4 R. Van Nieuwenhuyze Hoofdlector wiskunde, lerarenopleiding HUB, Brussel. Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@skynet.be Roger Van Nieuwenhuyze GeoGebra 4 Pagina 1 1. Schermen
? GEOGEBRA 4 R. Van Nieuwenhuyze Hoofdlector wiskunde, lerarenopleiding HUB, Brussel. Auteur Van Basis tot Limiet. roger.van.nieuwenhuyze@skynet.be Roger Van Nieuwenhuyze GeoGebra 4 Pagina 1 1. Schermen
8.0 Voorkennis. a De pijlen van O(0, 0) naar A(4, 2) en van A(4, 2) naar B(2, 3) zijn vectoren.
 8.0 Voorkennis De pijlen van O(0, 0) naar A(4, 2) en van A(4, 2) naar B(2, 3) zijn vectoren. 4 OA a 2 en AB 2 1 Het bovenste kengetal geeft aan hoeveel de vector naar links of rechts gaat. Het onderste
8.0 Voorkennis De pijlen van O(0, 0) naar A(4, 2) en van A(4, 2) naar B(2, 3) zijn vectoren. 4 OA a 2 en AB 2 1 Het bovenste kengetal geeft aan hoeveel de vector naar links of rechts gaat. Het onderste
E = mc². E = mc² E = mc² E = mc². E = mc² E = mc² E = mc²
 E = mc² E = mc² E = mc² E = mc² E = mc² E = mc² E = mc² E = mc² E = mc² De boom en het stokje staan loodrecht op de grond in het park. De boom is 3 en het stokje 1. Hoe lang is de schaduw van het stokje
E = mc² E = mc² E = mc² E = mc² E = mc² E = mc² E = mc² E = mc² E = mc² De boom en het stokje staan loodrecht op de grond in het park. De boom is 3 en het stokje 1. Hoe lang is de schaduw van het stokje
9.1 Vergelijkingen van lijnen[1]
![9.1 Vergelijkingen van lijnen[1] 9.1 Vergelijkingen van lijnen[1]](/thumbs/63/50068506.jpg) 9.1 Vergelijkingen van lijnen[1] y = -4x + 8 is de vergelijking van een lijn. Hier wordt y uitgedrukt in x. Algemeen: Van de lijn y = ax + b is de richtingscoëfficiënt a en het snijpunt met de y-as (0,
9.1 Vergelijkingen van lijnen[1] y = -4x + 8 is de vergelijking van een lijn. Hier wordt y uitgedrukt in x. Algemeen: Van de lijn y = ax + b is de richtingscoëfficiënt a en het snijpunt met de y-as (0,
Studie van functies en de analytische meetkunde in het vierde jaar van het ASO-TSO-KSO
 GeoGebra in het vierde jaar Studie van functies en de analytische meetkunde in het vierde jaar van het ASO-TSO-KSO R. Van Nieuwenhuyze Docent wiskunde aan HUB, Brussel Auteur Van Basis tot Limiet. Pedagogisch
GeoGebra in het vierde jaar Studie van functies en de analytische meetkunde in het vierde jaar van het ASO-TSO-KSO R. Van Nieuwenhuyze Docent wiskunde aan HUB, Brussel Auteur Van Basis tot Limiet. Pedagogisch
Snelstartgids FiloCAD2
 Snelstartgids FiloCAD2 Inleiding FiloCAD 2 Met deze korte inleiding leert u de belangrijkste functionaliteiten van het programma FiloCAD2 kennen. Als u een FiloCUT3 machine bezit en de licentie heeft ontvangen,
Snelstartgids FiloCAD2 Inleiding FiloCAD 2 Met deze korte inleiding leert u de belangrijkste functionaliteiten van het programma FiloCAD2 kennen. Als u een FiloCUT3 machine bezit en de licentie heeft ontvangen,
5.1 Punten, lijnen en vlakken [1]
![5.1 Punten, lijnen en vlakken [1] 5.1 Punten, lijnen en vlakken [1]](/thumbs/61/46167588.jpg) 5.1 Punten, lijnen en vlakken [1] Snijdende lijnen hebben een snijpunt. De snijdende lijnen FH en EG liggen in het vlak EFGH. Snijdende lijnen liggen altijd in één vlak. Een vlak is altijd plat en heeft
5.1 Punten, lijnen en vlakken [1] Snijdende lijnen hebben een snijpunt. De snijdende lijnen FH en EG liggen in het vlak EFGH. Snijdende lijnen liggen altijd in één vlak. Een vlak is altijd plat en heeft
A. Cooreman. 6 MV 3D volume, constructies en problemen
 A. Cooreman Ink ijke xe mp la ar MV 3D volume, constructies en problemen Leerjaar kk Groep 2 Remediëring 1 3 2 3 Naam: D/201/13280/ ISBN 9 7892 18 i.s.m 7 8 Klas: digitaal Legende iconen Leer dit vanbuiten.
A. Cooreman Ink ijke xe mp la ar MV 3D volume, constructies en problemen Leerjaar kk Groep 2 Remediëring 1 3 2 3 Naam: D/201/13280/ ISBN 9 7892 18 i.s.m 7 8 Klas: digitaal Legende iconen Leer dit vanbuiten.
Wiskunde D Online uitwerking 4 VWO blok 6 les 4
 Wiskunde Online uitwerking 4 VWO blok 6 les 4 Paragraaf 4 Het inproduct om hoeken te berekenen Opgave a e hoek is kleiner dan 4, want het dak zelf staat onder een hoek van 45, en de kilgoot loopt schuin
Wiskunde Online uitwerking 4 VWO blok 6 les 4 Paragraaf 4 Het inproduct om hoeken te berekenen Opgave a e hoek is kleiner dan 4, want het dak zelf staat onder een hoek van 45, en de kilgoot loopt schuin
1 Analytische meetkunde
 Domein Meetkunde havo B 1 Analytische meetkunde Inhoud 1.1. Coördinaten in het vlak 1.2. Vergelijkingen van lijnen 1.3. Vergelijkingen van cirkels 1.4. Snijden 1.5. Overzicht In opdracht van: Commissie
Domein Meetkunde havo B 1 Analytische meetkunde Inhoud 1.1. Coördinaten in het vlak 1.2. Vergelijkingen van lijnen 1.3. Vergelijkingen van cirkels 1.4. Snijden 1.5. Overzicht In opdracht van: Commissie
8.0 Voorkennis. Voorbeeld 1: Bereken het snijpunt van 3x + 2y = 6 en -2x + y = 3
 8.0 Voorkennis Voorbeeld 1: Bereken het snijpunt van 3x + 2y = 6 en -2x + y = 3 2x y 3 3 3x 2 y 6 2 Het vermenigvuldigen van de vergelijkingen zorgt ervoor dat in de volgende stap de x-en tegen elkaar
8.0 Voorkennis Voorbeeld 1: Bereken het snijpunt van 3x + 2y = 6 en -2x + y = 3 2x y 3 3 3x 2 y 6 2 Het vermenigvuldigen van de vergelijkingen zorgt ervoor dat in de volgende stap de x-en tegen elkaar
Hoofdstuk 2 : VLAKKE FIGUREN
 1 / 6 H2 Vlakke figuren Hoofdstuk 2 : VLAKKE FIGUREN 1. Wat moet ik leren? (handboek p. 46-74) 2.1 Herkennen van vlakke figuren In verband met een veelhoek: a) een veelhoek op de juiste wijze benoemen.
1 / 6 H2 Vlakke figuren Hoofdstuk 2 : VLAKKE FIGUREN 1. Wat moet ik leren? (handboek p. 46-74) 2.1 Herkennen van vlakke figuren In verband met een veelhoek: a) een veelhoek op de juiste wijze benoemen.
Practicum: De bolle lens
 Naam :.. Klas. nr : Datum: Vak: Wiskunde Leerkracht: Practicum: De bolle lens 1) Inleiding In dit practicum oefen je enkele reeds verworven vaardigheden met behulp van GeoGebra in. Omdat wiskunde en fysica
Naam :.. Klas. nr : Datum: Vak: Wiskunde Leerkracht: Practicum: De bolle lens 1) Inleiding In dit practicum oefen je enkele reeds verworven vaardigheden met behulp van GeoGebra in. Omdat wiskunde en fysica
De vergelijking van Antoine
 De vergelijking van Antoine Als een vloeistof een gesloten ruimte niet geheel opvult, dan verdampt een deel van de vloeistof. De damp oefent druk uit op de wanden van de gesloten ruimte: de dampdruk. De
De vergelijking van Antoine Als een vloeistof een gesloten ruimte niet geheel opvult, dan verdampt een deel van de vloeistof. De damp oefent druk uit op de wanden van de gesloten ruimte: de dampdruk. De
Bij een pv kan men origineel en beeld continu in elkaar overvoeren. De `oriëntatie' blijft hierbij behouden. Er zijn dus twee soorten gt's: De directe
 Lesbrief 9 Meetkunde II 1 Puntvermenigvuldigingen Definitie 1.1 Een transformatie G van het vlak heet een gelijkvormigheidstransformatie (verder afgekort als gt) als er een constante f > 0 bestaat zo,
Lesbrief 9 Meetkunde II 1 Puntvermenigvuldigingen Definitie 1.1 Een transformatie G van het vlak heet een gelijkvormigheidstransformatie (verder afgekort als gt) als er een constante f > 0 bestaat zo,
1 Junior Wiskunde Olympiade : tweede ronde . (D)
 Junior Wiskunde Olympiade 2006-2007: tweede ronde 9 is gelijk aan (A) 3 (B) 3 (C) 9 (D) 3 9 (E) 2 Het kwadraat van 3+ + 3 is gelijk aan (A) 2 (B) 6 (C) 0 (D) 2 2 (E) 4 3 Welk van volgende figuren is het
Junior Wiskunde Olympiade 2006-2007: tweede ronde 9 is gelijk aan (A) 3 (B) 3 (C) 9 (D) 3 9 (E) 2 Het kwadraat van 3+ + 3 is gelijk aan (A) 2 (B) 6 (C) 0 (D) 2 2 (E) 4 3 Welk van volgende figuren is het
Dossier 4 VECTOREN. Dr. Luc Gheysens. bouwstenen van de lineaire algebra
 Dossier 4 VECTOREN bouwstenen van de lineaire algebra Dr. Luc Gheysens 1 Coördinaat van een vector In het vlak π 0 is het punt O de oorsprong en de punten E 1 en E 2 zijn zodanig gekozen dat OE 1 OE 2
Dossier 4 VECTOREN bouwstenen van de lineaire algebra Dr. Luc Gheysens 1 Coördinaat van een vector In het vlak π 0 is het punt O de oorsprong en de punten E 1 en E 2 zijn zodanig gekozen dat OE 1 OE 2
Dag van GeoGebra 2013 Workshop creatieve toepassingen
 GeoGebra is een uitstekend gereedschap om zowat alle onderwerpen uit het leerplan wiskunde te exploreren, te demonstreren en te illustreren. Eén keer men het basisgebruik van GeoGebra beheerst kan men
GeoGebra is een uitstekend gereedschap om zowat alle onderwerpen uit het leerplan wiskunde te exploreren, te demonstreren en te illustreren. Eén keer men het basisgebruik van GeoGebra beheerst kan men
