Integratie van de informatica in de wiskunde WIRIS 2.0

Transcriptie

1 Integratie van de informatica in de wiskunde WIRIS Dynamische meetkunde met Wiris 9.1 Vlakke analytische meetkunde Het palet Meetkunde bevat een aantal gereedschappen voor het uitvoeren van meetkundige constructies. Andere pakketten voor dynamische meetkunde zoals Cabri en GeoGebra zijn uitermate geschikt voor het uitvoeren van meetkundige constructies met passer en liniaal. Wiris biedt niet alleen de mogelijkheid om deze meetkundige constructies uit te voeren, maar beschikt over een ingebouwd computer algebra systeem. Wiris bewijst vooral zijn nut in de analytische meetkunde. Vanaf versie 2 is er ook een module voor ruimtemeetkunde beschikbaar. Punten Opdracht punt Knop Bij het toekennen van dit object punt aan een variabele bekomt men in het eerste geval een vrij basispunt (DYNAMISCH). Dit punt A kan men in het grafiekvenster verslepen. Het punt B is een vast punt. Berekening van de coördinaatgetallen van een punt; Men kan ook de kleur van een punt wijzigen, de puntgrootte en ook de naam van het punt weergeven. 2OO4 [email protected] website 32

2 Rechten Opdracht rechte Knop In het grafiekvenster kan men deze rechte variëren door het verslepen van de vrije basispunten A en B. In het grafiekvenster kan men de naam, waarde en definitie van de rechte r opvragen. Alternatieven! Men kan een rechte ook ingeven m.b.v.; de vergelijking, met één punt en de richtingscoëfficiënt of met één punt en een richtingsvector. Notatie voor een vector met vierkante haakjes [, ] Berekening van de richtingscoëfficiënt van een rechte; Bepalen van een richtingsvector van een rechte; Lijnstukken Opdracht lijnstuk Knop 2OO7 [email protected] website 33

3 Driehoek, evenwijdige rechte, loodlijn en bissectrice Cirkels Opdracht cir of cirkel Knoppen Cirkel bepaald door middelpunt en straal Cirkel gaande door 3 punten Cirkel bepaald door middelpunt en punt op cirkel Opmerkingen Men mag i.p.v. de opdracht cirkel ook de afkorting cir gebruiken. De punten werden ingegeven als vrije basispunten. Men kan ook meerdere opdrachten op één opdrachtregel ingeven, gescheiden door. Indien men een opdracht niet onmiddellijk wil uitvoeren dan plaats men eveneens op het einde van de opdrachtregel 2OO7 [email protected] website 34

4 9.2 Een uitgewerkt voorbeeld; omgeschreven cirkel van een driehoek Gegeven zijn de drie hoekpunten A, B en C van een driehoek t. We bepalen het middelpunt van de omgeschreven cirkel, dit is het snijpunt van de middelloodlijnen van de driehoek. Dit zijn de Wiris-opdrachten en het eindresultaat 2OO7 [email protected] website 35

5 Wiris voorziet eveneens de mogelijkheid om het middelpunt en de straal van de omgeschreven cirkel te berekenen met de opdrachten mocir( ) en socir( ) 9.3 Punt met beperkte bewegingsvrijheid Het is mogelijk om de plaats van een punt te beperken tot een rechte, lijnstuk, cirkel en zelfs een kegelsnede met de opdracht beperking. Men tekent vooreerst een willekeurig vrij beweeglijk punt bvb P(.,.) en vervolgens een tweede punt Q:=beperking(object,P). Met deze opdracht beperkt men de locatie van P tot het object. Oefening: Constructie van een raaklijn in een punt van een cirkel. We tekenen een cirkel met als middelpunt de oorsprong (0,0) en als straal 5. We maken gebruik van het meetkundepalet en de knop voor het tekenen van een cirkel met gegeven middelpunt O en een tweede punt (5,0). De twee punten geven wij in als basispunten die men achteraf dynamisch kan verslepen. Het is handig om deze objecten toe te kennen aan een variabele. Bemerk de verschillende toekenningssymbolen. We definiëren vervolgens een punt P(3,4) (niet noodzakelijk) gelegen op de cirkel. Wij beperken de bewegingsvrijheid van dit punt tot de cirkel. 2OO7 [email protected] website 36

6 Tenslotte tekenen wij het lijnstuk dat O verbindt met T en de loodlijn in T op dit lijnstuk. Men bekomt een dynamische constructie. Men kan de punten O, P en T verslepen. Bovendien kan men de vergelijking van de cirkel en de raaklijn in T opvragen door in het grafiekvenster vooreerst de knop waarde aan te klikken en vervolgens de cirkel of de raaklijn aan te wijzen. 2OO7 [email protected] website 37

7 10 Bespreking van een rationale functie Gegeven is het voorschrift van een rationale functie; f( x) = x 2 4x+ 3 2x + 1 Bepaal het domein van deze functie Bepaal de nulpunten Voor welke x-waarden is de grafiek boven de X-as gelegen? Bepaal alle asymptoten Bepaal de eerste afgeleide van f en het tekenverloop van deze eerste afgeleide Zoek de eventuele extrema Bereken de x-waarden waarvoor de raaklijn in het overeenstemmend punt van de grafiek evenwijdig is met de eerste of tweede bissectrices. Voor deze vrij eenvoudige functie kan men Wiris gebruiken als controlemiddel. Het inschakelen van dit CAS is voor sommige opdrachten didactisch gezien overbodig. Dit voorbeeld wil enkel de mogelijkheden van Wiris illustreren waarbij ook een aantal opdrachten die niet beschikbaar zijn via de menubalk manueel moeten worden ingegeven. Start Wiris, definieer het functievoorschrift en sluit af met ENTER Naast de basisopdrachten die men kan ingeven via de menubalk en de paletten beschikt Wiris nog over een groot aantal opdrachten die men manueel kan ingeven bvb domein() Bepaal het domein van f met de opdracht domein(f(x)) en ENTER Laat de vorige opdracht uitvoeren via CTRL ENTER Voor het bepalen van de nulpunten maken we gebruik van de opdracht uit het palet Bewerkingen. Vul de plaatshouders aan. De mogelijkheid is ook voorzien om deze opdracht manueel in te geven via oplossen(f(x) 0) Hierbij wordt er gebruik gemaakt van een logisch =teken uit het palet Symbolen Het oplossen van een ongelijkheid gebeurt met de opdracht Spaties worden bij het manueel ingeven van opdrachten vervangen door een underscore. 2OO7 [email protected] website 38

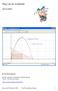
8 Omdat de graad van de teller groter is dan de graad van de noemer heeft deze functie geen horizontale asymptoten. Verticale asympoten vindt men via de polen van de functie, dit zijn de nulpunten noemer die geen nulpunten zijn van de teller. Berekening van de limiet, linkerlimiet en rechterlimiet via het Analysepalet. Bepalen van de schuine asymptoot kan via limietberekening. Maak gebruik van het toekenningssymbool Met behulp van dit toekenningssymbool is het mogelijk om de vergelijking van deze schuine asymptoot weer te geven als volgt met de variabele SA Laat ter controle Wiris de grafiek van f, de SA en ook de VA tekenen met de opdracht plot 2OO7 website 39

9 De vergelijking van de SA bekomt men ook als quotiënt van de Euclidische deling van de teller van f door de noemer van f. Gebruik hiervoor op het palet Bewerkingen de knop Bepalen van de eerste afgeleide, Analyse en of manueel afleiden(f(x),x) Het is handig om het voorschrift van de afgeleide functie van f te noteren als Df(x) Op deze wijze is het vrij eenvoudig om de rico van de raaklijn aan de grafiek van f te berekenen voor verschillende x-waarden. Nulpunten en tekenonderzoek van Df(x) 2OO7 [email protected] website 40

10 Het oplossen van deze ongelijkheid oplossen geeft een (in eerste instantie) eigenaardige bug? Deze ongelijkheid kan in dit geval niet symbolisch maar wel numeriek worden opgelost. Het volstaat om voor één der getallen in deze ongelijkheid de decimale notatie 10.0 in te geven. Raaklijn evenwijdig met de eerste of tweede bissectrice Het opstellen van de vergelijking van deze raaklijnen kan vrij snel door de x-waarden te kopiëren en te plakken. 2OO7 website 41

11 Analoog voor de vergelijking van de tweede raaklijn. Het onderzoek van de tweede afgeleide levert geen buigpunten op. De gevonden resultaten kan men ook controleren met de opdracht voorstelling(f(x)). 2OO7 website 42

12 10.1 Een toemaatje: het Wirisonline logo Na het doornemen van de gevorderde opties van Wiris blijkt dit CAS over heel wat mogelijkheden te beschikken om op een creatieve manier aan wiskunde te doen. De enige beperking is vaak ons eigen gebrek aan creativiteit. Als voorbeeld illustreren wij op welke wijze het Wirisonline-logo met behulp van Wiris kan gecreëerd worden. Met deze opdracht worden 10 cirkels met een veranderlijke straal getekend op een variabele afstand van de oorsprong. Bemerk het toevoegen van de attributen voor het kleuren en opvullen van de cirkelschijf. 2OO7 website 43

13 11 Ruimtemeetkunde met Wiris 11.1 inleidende voorbeelden. Vanaf versie 2 is er ook een module voor ruimtemeetkunde beschikbaar. Belangrijk om op te merken is het feit dat Wiris niet echt bedoeld is als Constructietool voor ruimtemeetkunde. Voor het illustratie van begrippen uit Analytische ruimtemeetkunde daarentegen, kan deze 3D-module van Wiris wel erg nuttig zijn. Wij illustreren de mogelijkheden aan de hand van twee concrete voorbeelden: Voorbeeld 1 Gegeven zijn de punten A(4,-1,3), B( 2,3,5) Bepaal de snijpunten van de rechte gaande door A en B met het xy-vlak, het xz-vlak en het yz-vlak. Voer de volgende opdrachtregels in. Gebruik hierbij de knoppen uit de ruimtemeetkundewerkbalk: = punt in de ruimte, = rechte en = doorsnede. Na berekening, krijg je: Als tussenresultaat kregen wij het stelsel van de 2 vergelijkingen van de rechte a. 2OO7 [email protected] website 44

14 Uiteraard willen wij deze resultaten ook voorstellen. Wij voegen daarom de volgende regel toe: Deze voorstelling is weinig of niets-zeggend behalve het feit dat de punten A, B, R, S en T op de rechte a gelegen zijn. Wij zullen vooreerst de 3 coördinaatvlakken in 3 verschillende kleuren voorstellen en vervolgens de punten A en B, de rechte a en de snijpunten R, S en T. Je kan deze voorstelling bewegen in de ruimte met de rechtermuisknop ofwel door te klikken op één van de knoppen links onderaan. 2OO7 [email protected] website 45

15 Het 3D-grafiekvenster Voor het bewegen met de rechtermuisknop gelden dezelfde principes, als voor het bewegen met de knoppen. Wij bespreken daarom eerst het gebruik van de knoppen. Rotatieknoppen de ruimtefiguur draait rond één van de 3 tafereelassen Groene Zoomknoppen Om te begrijpen hoe het bewegen in de ruimte gebeurt moet je je eerst realiseren dat een voorstelling in het 3D-grafiekvenster eigenlijk een perspectieftekening is, die de ruimte (gekoppled aan het afgebeelde assenstelsel) afbeeldt op een zogenaamd tafereel = het beeldscherm. Dit scherm heeft ook een driedimensionaal assenstelsel, dat niet wordt getoond. Dit laatste assenstelsel speelt echter een belangrijke rol bij het bewegen van de figuur. Het assenstelsel van het tafereel (beeldscherm) heeft twee assen in het beeldscherm en één as loodrecht op het beeldscherm. De assen in het beeldscherm liggen zoals gebruikelijk horizontaal en verticaal. Het assenstelsel van dit tafereel kan niet verplaatst worden, maar de ruimtelijke figuur kan wel gedraaid worden rond de assen van dit tafereelassenstelsel. De zes knoppen dienen om de ruimtefiguur te draaien rond één van deze tafereelassen. De ruimtefiguur draait rond de verticale tafereelas. De ruimtefiguur draait rond de horizontale tafereelas. De ruimtefiguur draait rond de tafereelas, die loodrecht op het beeldscherm staat. Indien men de ruimtelijke assen laat samenvallen met de tafereelassen, dan kan men de bewegingen duidelijker volgen. Dit gaat als volgt: Zorg er voor dat de ruimtefiguur in de positie staat zoals bij het openen van het grafiekvenster. Indien je de figuur ondertussen reeds gedraaid hebt, dan kan je de beginpositie opnieuw verkrijgen door op de knop te klikken. Zodoende wordt de figuur in het grafiekvenster opnieuw hertekend. Bij ingewikkelde figuren kan dit eventjes duren. In de beginpositie klik je tweemaal op de knop. De z-as is dan evenwijdig met het tafereel. Klik vervolgens vijfmaal op de knop. De x-as staat dan loodrecht op het tafereel en de y-as valt dan samen met de horizontale tafereelas. Indien je nu op één van de knoppen of klikt dan draait de figuur rond de x-as. Klik op één van de knoppen of en de figuur draait rond de y-as. 2OO7 [email protected] website 46

16 De werkbalk in het 3D-grafiekvenster is identiek aan de werkbalk van het 2D-grafiekvenster. In het voorbeeld hebben wij het commando plot3d gebruikt. Dit commando tekent driedimensionale objecten in een 3D-grafiekvenster. Je kan dit echter ook doen met het commando plot, op voorwaarde dat je eerst duidelijk maakt dat je in 3 dimensies wil werken. Dit kan met toevoegen van met de knop waarde de meetkunde_status overgaat naar 3D. Voorbeeld 2 Gegeven zijn twee punten A(2,1,7) en B(5,-4,-3). Bepaal het snijpunt van de rechte AB met het xy-vlak. Het volstaat nu om de coördinaten van A en B te wijzigen in het algebravenster en het grafiekvenster opnieuw te laten tekenen om verschillende situaties te onderzoeken. Omdat de rechte a en de doorsnede S met = werden gedefinieerd, is het grafiekvenster niet dynamisch. Bij het verslepen van de punten A en B, wijzigt de rechte a niet. 2OO7 [email protected] website 47

17 Het grafisch venster wordt wel dynamisch door de rechte a en het snijpunt S te definiëren met het toekenningssymbool : = De namen van de punten worden weergegeven door toevoeging van het attribuut aan het plotcommando. Bovendien kunnen de coördinaten van punten en vergelijkingen van rechten en vlakken in het grafiekvenster worden getoond (bij het aanwijzen van deze objecten) door toevoeging van het attribuut aan het plotvenster. Activeer hiertoe in het grafiekvenster de knop waarde en breng deze instelling van het grafiekvenster over naar het algebravenster met de knop Bij het verslepen van de basispunten A en B worden de resultaten in het grafiekvenster wel aangepast. (in Wiris 2 voorlopig nog niet in het algebravenster) 2OO7 [email protected] website 48

18 11.2 Vlakken in de ruimte Een vlak in de ruimte kan door verschillende gegevens bepaald worden; drie niet-collineaire punten, één punt en een normaalvector of één punt en twee richtingsvectoren Het commando vlak Met onderstaande gegevens, waarbij u en v (richtings)vectoren voorstellen kun je op verschillende manieren vlakken definiëren Vlak door drie punten Vlak door één punt en twee richtingsvectoren Vlak door een punt en bepaald door een normaalvector Vlak bepaald door twee snijdende rechten Uiteraard krijg je een foutmelding, indien de gegeven rechten niet snijdend maar kruisend zijn. OPMERKING! Dit is NIET het vlak dat het punt en de rechte bevat, maar WEL het vlak dat door het punt A gaat en loodrecht staat op de rechte. 2OO7 [email protected] website 49

19 Andere commando s die een vlak als resultaat opleveren Evenwijdig vlak aan een vlak door een punt Loodvlak commando loodrecht of orthogonaal In de oorspronkelijke versie van Wiris is er slechts één commando voor de Nederlandstalige tegenhangers: loodlijn, loodvlak, loodrecht e.d. Uiteindelijk werd loodrecht gekozen als het meest geschikte vertaling en werd orthogonaal behouden als synomiem. Bissectricevlak Bij evenwijdige vlakken bekomt men uiteraard een foutmelding. 2OO7 [email protected] website 50

20 11.3 Rechten in de ruimte Het commando rechte Met onderstaande gegevens kun jij op verschillende wijzen een rechte definiëren: Een rechte gaande door twee punten Een rechte gaande door één punt en bepaald door een richtingsvector Opmerking: Met de commando s punt en vector kun jij een basispunt en een richtingsvector van de rechte opvragen Een rechte bepaald door twee vergelijkingen (van vlakken) De dragers van de zijden van den driehoek of veelhoek 2OO7 [email protected] website 51

21 Andere commando s die een rechte als resultaat opleveren Evenwijdige Loodlijn Een bissectrice Resultaten na berekening Opmerking: Je kan ook de bissectrices van een driehoek laten berekenen De bijhorende vergelijkingen nemen vrij snel een gecompliceerde vorm aan. Het is dan aangewezen om minstens één coördinaatgetal van een hoekpunt in decimale vorm in te geven 2OO7 [email protected] website 52

22 11.4 Ruimtelijke objecten Veelvlakken In de werkbalk meetkunde vind je twee knoppen om veelvlakken te tekenen en De eerste knop geeft de functie veelvlak waarbij jij het aantal zijvlakken (4,6,8,12,of 20) en de lengte van de ribbe moet opgeven. De tweede knop opent een keuzelijst voor het aanmaken van regelmatige veelvlakken, prisma s en piramiden en benaderingen van omwentelingslichamen. Regelmatige veelvlakken Uit de keuzelijst kun jij één van de vijf Platonische lichamen kiezen. Jij moet niet meer opgeven hoeveel zijvlakken er zijn en bovendien bestaat de mogelijkheid om een ander middelpunt dan de oorsprong in te geven. Wil jij een draadmodel van de veelvlakken dan moet je aan de plotopdracht de attributen {wired=waar,vul=vals} meegeven. 2OO7 [email protected] website 53

23 Prisma s en piramiden De functie prisma kan gebruikt worden met de parameters grondvlak en hoogte Het grondvlak kan gelijk welke veelhoek zijn Benaderingen van omwentelingslichamen Het is (voorlopig) niet mogelijk om rechtstreeks omwentelingslichamen te definiëren, mar wel via een benadering met veelvlakken Ruimtekrommen Met de functie kromme3d kun je ook een ruimtekromme definiëren. Als eerste argument van de kromme moet een lijst met een stel parametervergelijkingen worden ingegeven, als tweede de parameter en als derde het bereik van deze parameter. 2OO7 [email protected] website 54

24 12 Analyse 12.1 Inleiding Om berekeningen uit de analyse te maken kan jij het best werken met het Analyse-palet Hierin vind jij een aantal knoppen i.v.m. afgeleiden, limieten en integralen. Knop Klikken op knop geeft: Een voorbeeld 2OO7 website 55

25 Wij illustreren een aantal mogelijkheden aan de hand van een voorbeeld Uitgewerkt voorbeeld: bespreking van een rationale functie Gegeven is het voorschrift van een rationale functie; f( x) = x 2 4x+ 3 2x + 1 Bepaal het domein van deze functie Bepaal de nulpunten Voor welke x-waarden is de grafiek boven de X-as gelegen? Bepaal alle asymptoten Bepaal de eerste afgeleide van f en het tekenverloop van deze eerste afgeleide Zoek de eventuele extrema Bereken de x-waarden waarvoor de raaklijn in het overeenstemmend punt van de grafiek evenwijdig is met de eerste of tweede bissectrices. Voor deze vrij eenvoudige functie kan men Wiris gebruiken als controlemiddel. Het inschakelen van dit CAS is voor sommige opdrachten didactisch gezien overbodig. Dit voorbeeld wil enkel de mogelijkheden van Wiris illustreren waarbij ook een aantal opdrachten die niet beschikbaar zijn via de menubalk manueel moeten worden ingegeven. Start Wiris, definieer het functievoorschrift en sluit af met ENTER Naast de basisopdrachten die men kan ingeven via de menubalk en de paletten beschikt Wiris nog over een groot aantal opdrachten die men manueel kan ingeven bvb domein() Bepaal het domein van f met de opdracht domein(f(x)) en ENTER Laat de vorige opdracht uitvoeren via CTRL ENTER Voor het bepalen van de nulpunten maken we gebruik van de opdracht uit het palet Bewerkingen. Vul de plaatshouders aan. De mogelijkheid is ook voorzien om deze opdracht manueel in te geven via oplossen(f(x) 0) Het oplossen van een ongelijkheid gebeurt met de opdracht Spaties worden bij het manueel ingeven van opdrachten vervangen door een underscore. 2OO7 [email protected] website 56

26 Omdat de graad van de teller groter is dan de graad van de noemer heeft deze functie geen horizontale asymptoten. Verticale asympoten vindt men via de polen van de functie, dit zijn de nulpunten noemer die geen nulpunten zijn van de teller. Berekening van de limiet, linkerlimiet en rechterlimiet via het Analysepalet. Bepalen van de schuine asymptoot kan via limietberekening. Maak gebruik van het toekenningssymbool Met behulp van dit toekenningssymbool is het mogelijk om de vergelijking van deze schuine asymptoot weer te geven als volgt met de variabele SA Laat ter controle Wiris de grafiek van f, de SA en ook de VA tekenen met de opdracht plot 2OO7 website 57

27 De vergelijking van de SA bekomt men ook als quotiënt van de Euclidische deling van de teller van f door de noemer van f. Gebruik hiervoor op het palet Bewerkingen de knop Bepalen van de eerste afgeleide, Analyse en of manueel afleiden(f(x),x) Het is handig om het voorschrift van de afgeleide functie van f te noteren als Df(x) Op deze wijze is het vrij eenvoudig om de rico van de raaklijn aan de grafiek van f te berekenen voor verschillende x-waarden. Nulpunten Df(x) 2OO7 [email protected] website 58

28 Tekenonderzoek van Df(x) Deze ongelijkheid kan in dit geval niet alleen symbolisch maar ook numeriek worden opgelost. Het volstaat om voor één der getallen in deze ongelijkheid de decimale notatie 10.0 in te geven. Raaklijn evenwijdig met de eerste of tweede bissectrice Het opstellen van de vergelijking van deze raaklijnen kan vrij snel door de x-waarden te kopiëren en te plakken. Analoog voor de vergelijking van de tweede raaklijn. 2OO7 website 59

29 Het onderzoek van de tweede afgeleide levert geen buigpunten op. De gevonden resultaten kan men ook controleren met de opdracht voorstelling(f(x)). 2OO7 website 60

30 12.3 Een toemaatje: het Wirisonline logo Na het doornemen van de gevorderde opties van Wiris blijkt dit CAS over heel wat mogelijkheden te beschikken om op een creatieve manier aan wiskunde te doen. De enige beperking is vaak ons eigen gebrek aan creativiteit. Als voorbeeld illustreren wij op welke wijze het Wirisonline-logo met behulp van Wiris kan gecreëerd worden. Met deze opdracht worden 10 cirkels met een veranderlijke straal getekend op een variabele afstand van de oorsprong. Bemerk het toevoegen van de attributen voor het kleuren en opvullen van de cirkelschijf. 2OO7 website 61

31 13 Lijsten en tabellen 13.1 Inleiding Lijsten zijn opsommingen ingesloten tussen 2 accolades. Merk op dat ondanks de notatie met accolades, lijsten geen verzamelingen zijn, omdat in een lijst een hetzelfde element meerdere keren mag voorkomen. Een lijst is een algemener begrip dan een verzameling. Een bereik a..b..c is een rekenkundige rij met als eerste term a en als stap b. De laatste term van de rij is niet noodzakelijk c maar wel de laatste term die kleiner dan of gelijk is aan c. Vectoren zijn opsommingen tussen rechte haakjes. Het onderscheid met een gewone lijst ligt in het feit dat vectoren de voorstelling zijn van wiskundige vectoren. Met vectoren kan je bewerkingen zoals het scalair product uitvoeren die niet mogelijk zijn met lijsten. De eenvoudigste manier om een lijst of een vector te genereren is met behulp van de Wiris met in constructie. Men kan het genereren van zo n lijst ook combineren met een bereik of een voorwaarde opleggen door gebruik te maken van met in waarbij 2OO7 [email protected] website 62

32 Men kan ook gebruikmaken van meerdere letters. Het volgende voorbeeld berekent alle Pythagorische drietallen onder de 10. Na sorteren van deze drietallen en eliminatie van de herhalingen bekomt men de gevraagde drietallen. Tabellen of matrices zijn vectoren waarvan de elementen ook vectoren zijn. Voorbeeld 1 De Vandermonde matrix en ontbonden vorm van de determinant Voorbeeld 2 De getallen van Pascal (Tartaglia) 2OO7 [email protected] website 63