Parametervrije toetsen
|
|
|
- Geert van de Brink
- 10 jaren geleden
- Aantal bezoeken:
Transcriptie
1 1 Inleiding Parametervrije toetsen Edward Omey Februari 2007 In de klassieke toetsingstheorie worden meestal speci eke veronderstellingen gemaakt over de populatie(s) waaruit steekproeven afkomstig zijn. Men veronderstelt bijvoorbeeld dat de (kans-)verdeling die de populatie beschrijft, op één of meerdere parameters na bekend is. Via een steekproef kan men dan hypothesen toetsen aangaande deze parameters. De klassieke t-toets en F-toets zijn daar voorbeelden van. In andere situaties is het niet steeds mogelijk of zinvol om veronderstellingen te maken over de onderliggende verdeling. In dit geval moeten toetsingsgrootheden geformuleerd worden waarvan de verdeling kan bepaald worden onafhankelijk van de onderliggende verdeling. Dergelijke toetsen worden verdelingsvrije of parametervrije toetsen genoemd. Verdelingsvrije toetsen worden soms gebruikt vanwege de eenvoud van de methode (terwijl er andere parametertoetsen beschikbaar zijn). In het volgend schema volgt een overzicht van veelgebruikte parametervrije toetsen. De indeling gebeurt op basis van het meetniveau en van het aantal dimensies. Het is uiteraard onmogelijk om al deze toetsen hier te bespreken. In de volgende paragrafen volgt de bespreking van enkele van deze toesen. 1.1 Nominaal Eén steekproef De binomiale test en de chikadraat test Twee steekproeven gepaard: McNemar test (chikwadraattoets) ongepaard: Fisher test en de chikwadraat test 1
2 1.1.3 k steekproeven gepaard: Cochran Q test ongepaard: chikwadraat test 1.2 Ordinaal Eén steekproef Kolmogorov-Smirnov test en de runs-test Twee steekproeven gepaard: tekentoets en Wilcoxon rangtest ongepaard: Mediaan test, Mann-Withney U test, Kolmogorov-Smirnov test, runs-tests k steekproeven gepaard: Friedman test ongepaard: Kruskal-Wallis test 1.3 Interval Eén steekproef Twee steekproeven gepaard: Walsh test ongepaard: randomization test k steekproeven 1.4 Correlatietoetsen nominaal de contingentie coe cient 2
3 1.4.2 Ordinaal Spearman rang correlatie, Kendall rangcorrelatie 2 De binomiaaltoets 2.1 Doel Deze toets wordt gebruikt in populaties met slechts twéé klassen: mannen - vrouwen; gehuwd - single; succes - mislukking; slagen - niet slagen; enzovoort. De toets is een toets omtrent aantallen of omtrent proporties van de vorm H 0 : p = p 0 versus H a : p 6= p 0 Hier kan uiteraard ook een eenzijdig alternatief staan. De toets zelf vormt de basis van vele andere toetsen. 2.2 Toetsingsgrootheid Via een steekproef van omvang n bepalen we het aantal successen N en/of de steekproefproportie bp = N=n. Als de nulhypothese correct is vinden we dat N s BIN(n; p 0 ) en kunnen kansen berekend worden. Voor grote steekproeven kan deze verdeling benaderd worden door een geschikte normale verdeling. 2.3 Voorbeelden Voorbeeld 1 Aan n = 18 mensen werden twee reclamepanelen A en B getoond en gevraagd naar hun voorkeur. Er waren N A = 3 mensen die A verkozen boven B. We toetsen hier of er een betekenisvolle voorkeur is voor B: H 0 : p B = 0; 5 versus H a : p B > 0; 5 Om te kiezen berekenen we de overschrijdingskans van N B = 15. We vinden P (N B 15) = 0; 003 Bij bijv. een betrouwbaarheid van 95% besluiten we dat er een betekenisvolle voorkeur is voor B. 3
4 Voorbeeld 2 Bij 144 hondenraces (8 honden in 8 banen) werd vastgesteld dat in 25 gevallen de hond die startte in baan 1 ook de winnaar werd. Is dit betekenisvol meer dan de verwachte 1/8? We toetsen hier H 0 : p 1 = 1=8 versus H a : p 1 > 1=8 De overschrijdingskans van het steekproefresultaat is hier P (N 1 25) = P (N 1 24; 5) Standardiseren geeft P (Z > 1; 637 = 0; 051. Bij = 0; 05 verwerpen we H 0 niet; bij = 0; 10 verwerpen we H 0 wel. 3 De tekentoets 3.1 Doel De tekentoets is een toets omtrent de centrale ligging van de variabele en als maatstaf gebruikt men de mediaan M e. Indien de verdeling symmetrisch is, dan is de mediaan uiteraard gelijk aan het gemiddelde. We willen hypothesen toetsen van de vorm H 0 : Me = a versus H a : Me 6= a UIteraard kan ook een eenzijdig alternatief geformuleerd worden. 3.2 Veronderstellingen We veronderstellen dat de onderliggende verdeling continu is 3.3 Toetsingsgrootheid Via een steekproef X 1 ; X 2 ; :::; X n bepalen we Z i als volgt: Z i = 1 als X i > a Z i = 0 als X i < a 4
5 Omdat X een continue t.v. is, is P (X = a) = 0. We kiezen dus Z i = 1 indien het teken van X i a positief is - vandaar de naam tekentoets!. Als toetsingsgrootheid hanteren we nu T n = Z 1 + Z 2 + ::: + Z n Onder H 0 bemerken we dat P (Z i = 1) = 1=2. Omdat het over een steeproef gaat, volgt hieruit dat T n v BIN(p = 1=2; n) en kunnen we kritieke grenzen bepalen en/of overschrijdingskansen berekenen. Voor kleine steekproeven zijn tabellen beschikbaar met daarin de kritieke grenzen. Voor grote steekproeven kunnen we de binomiale verdeling benaderen met een geschikte normale verdeling. 3.4 Voorbeelden Voorbeeld 1 Men wil nagaan of een bepaald middel het gewicht doet afnemen. Bij 20 proefpersonen vond men dat het gewicht bij 13 personen na het volgen van de kuur kleiner was geworden. We bekijken hier X = het gewicht voor de kuur, Y = het gewicht na de kuur en W = X Y. Het is wenselijk dat W positief is. We toetsen H 0 : Me(W ) = 0 versus H a : Me(W ) > 0 Onze toetsingsgrootheid is gelijk aan T n = 13. Indien H 0 correct is, dan is T n s BIN(p = 1=2; n = 20). We berekenen de overschrijdingskans van het steekproefresultaat en vinden P (T n 13) = 0; 14. Bij een signi cantieniveau van bijvoorbeeld = 10% verwerpen we H a. Voorbeeld 2 We meten het gehalte van een bepaalde stof in 10 monsters van een produkt. De meting is gedaan volgens 2 methoden A en B. We vinden: monsternummer meth. A meth. B teken verschil (A - B) 1 5,5 6,0-2 2,8 3,4-5
6 3 4,9 5,5-4 4,5 5,2-5 5,0 5,4-6 3,7 3, ,1 5,6-8 3,3 3,8-9 2,3 2, ,1 6,0 - We willen nagaan of er een verschil is tussen de twee methoden. De toetsingsgrootheid is hier T n = 2 en T n s BIN(p = 1=2; n = 10). De overschrijdingskans van 2 is gelijk aan P (T n 2) = 0; 054. Met bijvoorbeeld = 0; 10 is er geen betekenisvol verschil tussen de methoden. Opmerking Bij de tekentoets bekijken we enkelhet teken van het veschil. In andere toetsen kijkt men ook naar de grootte van de verschillen. Voorbeeld 3 Zie animatie EXCEL 4 Kolmogorov-Smirnov toets (1 st.pr) 4.1 Doel De KS (één steekproef) toets is een "goodness of t"- test waarbij nagegaan wordt in welk mate de empirische verdelingsfunctie (via een steekproef) aansluit bij een speci eke theoretische verdelingsfunctie. Hier toetsen we H 0 : de observaties zijn afkomstig van F t (x) H a : de observaties zijn niet afkomstig van F t (x) 4.2 Veronderstellingen Men veronderstelt meestal dat de theoretische verdelingsfunctie een continue functie is. In elk geval moet er een eenduidige transformatie zijn van F t (x) naar de uniforme verdelingsfunctie (dit is F u (x) = x; 0 x 1). Verder zijn de bekende kritische waarden alleen bruikbaar als F t (x) volledig gekend is (en dat er dus gvooraf geen parameters moeten geschat worden). 6
7 4.3 Toetsingsgrootheid De toetsingsgrootheid is de Kolmogorov-Smirnov statistiek KS = max jev F (x) x F t (x)j waarbij EV F (x) de empirische verdelingsfunctie is,dit is EV F (x) = 1 # fobservaties xg n Indien H 0 correct is, dan verwachten we dat er geen al te groot verschil is tussen de theoretische verdeling en de geöbserveerde empirische verdeling. Omgekeerd, indien KS "groot" is, dan verwachten we dat H 0 vals is. Voor kleine steekproeven zijn tabellen met kritische waarden beschikbaar. Voor grote steekproeven gebruiken we de kritische grens D() = p ( ln(=2))=2n Voor = 5% vinden we bijvoorbeeld D(5%) = 1:358= p n. 4.4 Voorbeeld ZIE EXCEL ANIMATIE Ik noteerde de dagelijkse return van een aandeel gedurende 2 jaar (582) dagen.. * histogram van de returns; * we testen of de return mag gemodelleerd worden met een normale N( = 0; = 0; 003) en vinden de EVF en TVF; * de berekende waarde van KS is KS = 0,16 en dit toont dat er een betekenisvol verschil is tussen de praktijk en de theorie. Opmerking Vooral het gedrag van de EVF in de buurt van 0 zorgt voor problemen: de return is heel dikwijls nul en dit is nietin overeenstemming met wat men volgens een normale verdeling kan verwachten. 5 Kolmogorov-Smirnov toets (2 onafh. stpr) 5.1 Doel De bedoeling is hier m na te gaan of twee onafhankelijke steekproeven al dan niet steekproeven zijn uit dezelfde populatie (verdeling). De toets is dus 7
8 een globale toets en er wordt niet alleen gekeken naar gemiddelden en/of varianties, maar ook naar de ligging en vorm. Hier toetsen we H 0 : de steekproeven zijn beide afkomstig van F t (x) H a : de steekproeven zijn niet beide afkomstig van F t (x) Er kunnen ook eenzijdige alternatieven geformuleerd worden maar in deze tekst geen we daar niet dieper op in. 5.2 Veronderstellingen Men veronderstelt meestal dat de theoretische verdelingsfunctie een continue functie is. In elk geval moet er een eenduidige transformatie zijn van F t (x) naar de uniforme verdelingsfunctie (dit is F u (x) = x; 0 x 1). 5.3 Toetsingsgrootheid De toetsingsgrootheid is de Kolmogorov-Smirnov statistiek KS = max jev F 1 (x) x EV F 2 (x)j waarbij EV F i (x); i = 1; 2 de empirische verdelingsfunctie is. Indien H 0 correct is, dan verwachten we dat er geen al te groot verschil is tussen de theoretische verdeling en de geöbserveerde empirische verdeling. Omgekeerd, indien KS "groot" is, dan verwachten we dat H 0 vals is. Voor kleine steekproeven zijn tabellen met kritische waarden beschikbaar. Voor grote steekproeven gebruiken we de volgende kristische grenzne r n1 + n 2 grens( = 0; 05) = 1; 36 n 1 n r 2 n1 + n 2 grens( = 0; 01) = 1; 63 n 1 n 2 Opmerking. Voor grote steekproeven kan men aantonen dat D = 4KS 2 n 1 n 2 n 1 + n 2 t 2 2 8
9 5.4 Voorbeeld ZIE EXCEL ANIMATIE Een aantal proefpersonen werden op basis van een psychologische test in twee groepen A en B verdeeld. Aan de groepen werd een reeks van 20 foto s van voorwerpen getoond. Later moesten alle deelnemers een lijst schrijven van voorwerpen die ze gezien hadden. Via een excelblad vinden we KS = 0; 72. Bij = 0; 05 vinden we de kritische grens 0; 269 wat wijst op een signi - cant verschil: 6 De rangtekentoets van Wilcoxon 6.1 Doel Zoals de tekentoets is deze toets een toets omtrent de centrale waarde van de onderliggende (continue) verdeling. De toets is een ver jning van de tekentoets We toetsen hier (bijvoorbeeld) H 0 : = a versus H a : 6= a Bij de tekentoets is enkel het teken van het verschil belangrijk. Bij de toets van Wilcoxon is ook de grootte-orde van de getallen belangrijk. 6.2 Toetsingsgrootheid Via een steekproef X 1 ; X 2 ; :::; X n bepalen we Z i als volgt: Z i = 1 als X i > a Z i = 0 als X i < a Omdat X een continue t.v. is, is P (X = a) = 0. Daarnaast berekenen we eveneens de absolute verschillen V i = jx i aj en rangschikken deze van klein naar groot. Vervolgens geven we in deze rangschikking aan elke uitkomst een rangnummer R i gaande van 1 tot en met n. We voorzien nu de rangnummers van het teken van het oorspronkelijke verschil en maken de som S van de positieve rangnummers: S = X R i Z i 9
10 Onder de nulhypothese is S symmetrisch verdeeld. De kleinste waarde is gelijk aan 0 en de grootste mogelijke waarde is gelijk aan n(n + 1)=2. Men kan aantonen dat E(S j H 0 ) = 1 n(n + 1) 4 V ar(s j H 0 ) = 1 n(n + 1)(2n + 1) 24 Voor kleine steekproeven zijn tabellen met kritische grenzen beschikbaar; voor grote steekproeven kan men werken met een geschikte normale benadering. ZIE EXCEL ANIMATIE Opmerkingen Soms gebruikt men in de plaats van S de toetsingsgrootheid S waarbij S = S = P R i Z i, waarbij Z i = +1 als X i > a en Z i = 1 als X i < a. Men kan controleren dat S = 2S n(n + 1)=2. Soms maakt men de som van de rangnummers bij de positieve verschillen en de som van de rangnummers bij de negatieve verschillen. Als toetsingsgrootheid neemt men nu de kleinste van deze twee rangsommen. 6.3 Voorbeeld Men test het reactievermogen van automobilisten voor en na het gebruik van een bepaalde hoeveelheid alcohol en men vond de volgende verschillen: 0; 1 0; 2 0; 35 0; 6 0; 4 1; 1 0; 3 0; 05 0; 45 0; 5 0; 8 0; De som van de positieve rangnummers is gelijk aan: = 66 De overschrijdingskans van dit getal is ongeveer 0,015 en we besluiten (bij = 5%) dat alcohol de reacties ernstig aantast. 7 De 2 steekproeventoets van Wilcoxon 7.1 Doel In deze toets wensen we na te gaan of twee ongepaarde steekproeven uit dezelfde populatie (verdeling) komen en meer speci ek of ze rond dezelfde 10
11 centrale waarde kunnen gesitueerd worden. Indien X en Y twee (onafhankelijke) continue t.v. zijn en als P (Y x) = P (X a x), dan toetsen we 7.2 Toetsingsgrootheid H 0 : a = 0 versus H a : a 6= 0 Via twee steekproeven X 1 ; X 2 ; :::; X n en Y 1 ; Y 2 ; :::; Y m vormen we één cijferreeks en rangschikken van klein naar groot. Vervolgens kennen we aan alle uitkomsten een rangnummer toe (gaande van 1 tot n + m). We berekenen nu S = som van de rangnummers van de X en of 1 U = S n(n + 1) 2 Indien de nulhypothese juist is kan men aantonen dat S een symmetrische verdeling heeft met E(S) = 1 n(n + m + 1) 2 V ar(s) = nm(n + m + 1) 12 Voor U kan men aantonen dat onder de nulhypothese, V ar(u) = V ar(s) en E(U) = nm=2. We kunnen kritische waarden vinden in tabellen (n klein) of via de normale benadering (n groot). 7.3 Voorbeeld zie EXCEL:twee voorbeelden 8 Mann-Whitney U test (onafh. stpr) 8.1 Doel Bij deze test gaan we na in hoeverre de scores in 2 groepen (de experimentele groep E en de controlegroep C) van elkaar verschillen. In de nulhypothese gaan we er van uit dat de scores steekproeven zijn uit dezelfde 11
12 populatie/verdeling. In het alternatief gaan we er van uit dat er een verschil (eenzijdig: de ene groep scoort hoger dan de andere groep; tweezijdig: er is een verschil). 8.2 Toetsingsgrootheid Stel dat we van 2 groepen C en E (van grootte m(c) n(e)) de scores krijgen. We groeperen alle data maar onthouden welk cijfer afkomstig is van welke groep. Vervolgens geven we een rangnummer aan alle cijfers (van klein naar groot). Vervolgens tellen we U(C) = aantal C-rangnummers kleiner dan E-rangnummers of U(E) = aantal E-rangnummers kleiner dan C-rangnummers We stellen U = min(u(e); U(C)) en V = max(u(e); U(C)). Eenvoudiger is om de volgende aantallen te tellen of R(E) = som van de rangnummers van de E-groep R(C) = som van de rangnummers van de C-groep Men kan aantonen dat U + V = U(E) + U(C) = n(c) n(e) en dat U(E) = n(e)n(c) + n(e)(n(e) + 1) 2 R(E) waarbij R(E) gelijk is aan de som van de rangnummers van de groep E. Een analoge uitdrukking geldt ook voor U(C). Wanneer de twee groepen gelijkaardig zijn (d.i. wanneer H 0 correct is) dan verwachten we dat hoge/lage scores mooi verdeeld liggen over de twee groepen. Voor kleine steekproeven zijn er tabellen met kritische waarden beschikbaar. Voor grote steekproeven kan men aantonen dat U(E) bij benadering normaal verdeeld is met = n(e)m(c) 2 2 n(e)n(c)(n(e) + n(c) + 1) = 12 12
13 8.3 Voorbeeld We beschikken over 2 groepen en de volgende scores: groep E: groep C: Rangschikken van klein naar groot geeft: score groep rangnummer 8 C 1 9 E 2 12 E 3 15 C 4 17 E 5 18 C 6 21 E 7 23 C 8 25 C 9 Bij de eerste rij zien we dat er geen enkele E komt voor C In de vierde rij zien we dat er 2 E-waarden komen voor C In de 6-de rij zien we dat er 3 E-waarden komen voor C in de 8-ste en 9-de rij zien we dat er 4 E-waarden komen voor C In totaal is U(E) = = 13. Op dezelfde manier vinden we dat U(C) = = 7 We vinden U = min(u(e); U(C)) = 7 en V = max(u(e); U(C)) = 13 zodat U + V = 20 = 4 5 Anderzijds is R(E) = = 17 en R(C) = = 28 en dit illustreert de formule n(e)(n(e) + 1) U(E) = n(e)n(c) + R(E) = = 13 2 In de tabellen vinden we dat P (U(C) 7) = 0; 278. Deze overschrijdingskans wijst niet op een signi cant verschil tussen de twee groepen. 9 Toets van Friedman (gepaard) 9.1 Doel Deze toets wordt gebruikt om na te gaan of m gepaarde steekproeven (van omvang k) van dezelfde populatie afkomstig zijn. We beschikken bijvoorbeeld 13
14 over k methoden om een bepaalde test of meting uit te voeren, en we voeren deze tests uit op m monsters. 9.2 Toetsingsgrootheid Per steekproef kennen we rangnummers (1; 2; :::; k) toe We berekenen dan R(i; j) = rangnummer van object j bij meting i R(j) = som van de rangnummers van object j R = gemiddelde van de rangsommen T = kx (R(j) j=1 R) 2 = toetsinsgrootheid Indien de "meningen" gelijklopend zijn, dan verwachten we dat T eerder klein zal zijn. Bij "uiteenlopende" meningen zal T eerder groot zijn. Opmerking. Als n > 3k en k > 7 kan men aantonen dat onder H 0 geldt dat 9.3 Voorbeeld D = 12T nk(k + 1) t 2 k 1 Bij een schoonheidswedstrijd worden k = 5 kandidaten (1, 2, 3, 4 en 5) gerangschikt door n = 7 juryleden. De meningen zijn de volgende: jurylid 1: jurylid 2: jurylid 3: jurylid 4: jurylid 5: jurylid 6: jurylid 7:
15 Volgens jurylid 1 is kandidaat 1 op de 2de plaats, kandidaat 2 op de 1ste plaats, kandidaat 3 op de 4de plaats enzovoort. De som van de rangnummers van de eerste kandidaat is R(1) = = 12 Voor de andere kandidaten vinden we De gemiddelde som is en nu vinden we R(2) = 12; R(3) = 24; R(4) = 27; R(5) = 30 R = 21 = 1 nk(k + 1)=k 2 T = = 288 Volgens de kritische waarde (tabellen) is T tabel (k = 5; n = 7; = 0; 05) = 167 en is er een signi cant verschil tussen de juryleden. 10 Toets van Kruskal en Wallis (onafh. stpr) 10.1 Doel Het doel van de toets van Kruskal en Wallis is na te gaan of 3 of meer onafhankelijke steekproeven afkomstig zijn uit dezelfde populatie (verdeling) Toetsingsgrootheid We vertrekken van k steekproeven van omvang n(1),n(2),..., n(k). Zoals bij Wilcoxon voegen we alle data bij elkaar en kennen een rangnummer toe aan elke waarneming. Vervolgens wordt voor elk van de verschillende steekproeven de som genomen van de rangnummers: R(i) = som van de rangnummers van steekproef i=1,2,...,k De toetsingsgrootheid is nu gelijk aan 12 kx T = n(n + 1) i=1 R 2 (i) n(i) 3(n + 1) waarbij n = n(1) + n(2) n(k). Voor k > 3 en n(i) > 4, kan de verdeling van T benaderd worden door een chikwadraatverdeling met parameter k
16 10.3 Voorbeeld zie EXCEL blad We krijgen 4 steekproeven A: B: C: D: We vinden R(1) = 40; R(2) = 55,5; R(3) = 97; R(4) = 60,5 Na rekenwerk vinden we T = 4,86.met een Okans van ongeveer 18%. 11 De runs-test van Wald-Wolfowitz 11.1 Doel De runs-test wordt gebruikt om na te gaan of 2 onafhankelijk genomen steekproeven afkomstig zijn van dezelfde continue populatie (verdeling). De toets is gevoelig voor de centrale ligging, voor de variantie en voor de vorm van de onderliggende verdeling(en) Toetsingsgrootheid Via twee steekproeven X 1 ; X 2 ; :::; X n (groep A) en Y 1 ; Y 2 ; :::; Y m (groep B) vormen we één cijferreeks en rangschikken van klein naar groot. We onthouden alleen uit welke groep elk resultaat afkomstig is. Vervolgens tellen we het aantal runs. Voorbeeld: groep A: groep B: Samenvoegen en rangschikken van klein naar groot: afkomstig uit resp. B B B A B A A We zien in dit voorbeeld eerst een run van B-waarden, dan een run van A, terug B en terug A. In totaal vinden we 4 runs. 16
17 De toetsingsgrootheid van Wald-Wolfowitz is gelijk aan R = het aantal runs Wanneer het aantal runs klein is, dan betekent dit dat er grote concentraties zijn van A en B-waarden en wijst dit op verschillen tussen de verdelingen. Voor kleine steekproeven zijn tabellen beschikbaar met kritische grenzen. Voor grote steekproeven kan men aantonen dat de verdeling van R kan benaderd worden door een normale verdeling met = 2nm n + m nm(2nm n m) = (n + m) 2 (n + m 1) Opmerking Naast runs kan men ook kijken naar "successen" en naar singles. Ook kan men de onafhankelijkheid afzwakken en verondertellen dat de opeenvolging van A een discrete Markovketen is Voorbeeld Zie excel In het voorbeeld vergelijk ik de (van nul verschillende) returns van een aandeel gedurende verschillende tijdsperiodes. De vraag rijst of de verdeling van deze returns verandert in de loop van de tijd. Het antwoord blijkt ja te zijn. 12 Referenties A. Grootenboer en A. Luiten (1978). Verdelingsvrije toetsen. Loghum Slaterus. Van Exploring Data Analysis: Hyperstat (on line cursus statistiek) B. Weaver (2002). Nonparametric Tests. 17
18 E. Omey en S. Van Gulck (2006). A Markov binomial dsitribution. Submitted. P. Sprent (1989). Applied nonparametric statistical methods. Chapman and Hall. S. Siegel en Castellan, N.J. (1988). Nonparametric statistics for the behavioral sciences. McGraw-Hill. 18
Statistiek 2 deel A 30 minuten over statistisch toetsen
 Statistiek 2 deel A 30 minuten over statistisch toetsen R.J. Baars, MSc Kruytgebouw N710 [email protected] februari 2014 Opbouw van statistiek Statistiek 1 (periode 2: vandaag) Dit college + zelfstudie +
Statistiek 2 deel A 30 minuten over statistisch toetsen R.J. Baars, MSc Kruytgebouw N710 [email protected] februari 2014 Opbouw van statistiek Statistiek 1 (periode 2: vandaag) Dit college + zelfstudie +
Hoofdstuk 5 Een populatie: parametrische toetsen
 Hoofdstuk 5 Een populatie: parametrische toetsen 5.1 Gemiddelde, variantie, standaardafwijking: De variantie is als het ware de gemiddelde gekwadrateerde afwijking van het gemiddelde. Hoe groter de variantie
Hoofdstuk 5 Een populatie: parametrische toetsen 5.1 Gemiddelde, variantie, standaardafwijking: De variantie is als het ware de gemiddelde gekwadrateerde afwijking van het gemiddelde. Hoe groter de variantie
Hoofdstuk 8 Het toetsen van nonparametrische variabelen
 Hoofdstuk 8 Het toetsen van nonparametrische variabelen 8.1 Non-parametrische toetsen: deze toetsen zijn toetsen waarbij de aannamen van normaliteit en intervalniveau niet nodig zijn. De aannamen zijn
Hoofdstuk 8 Het toetsen van nonparametrische variabelen 8.1 Non-parametrische toetsen: deze toetsen zijn toetsen waarbij de aannamen van normaliteit en intervalniveau niet nodig zijn. De aannamen zijn
HOOFDSTUK VI NIET-PARAMETRISCHE (VERDELINGSVRIJE) STATISTIEK
 HOOFDSTUK VI NIET-PARAMETRISCHE (VERDELINGSVRIJE) STATISTIEK 1 1. INLEIDING Parametrische statistiek: Normale Verdeling Niet-parametrische statistiek: Verdelingsvrij Keuze tussen de twee benaderingen I.
HOOFDSTUK VI NIET-PARAMETRISCHE (VERDELINGSVRIJE) STATISTIEK 1 1. INLEIDING Parametrische statistiek: Normale Verdeling Niet-parametrische statistiek: Verdelingsvrij Keuze tussen de twee benaderingen I.
Hoofdstuk 6 Twee populaties: parametrische toetsen
 Hoofdstuk 6 Twee populaties: parametrische toetsen 6.1 De t-toets voor het verschil tussen twee gemiddelden: In veel onderzoekssituaties zijn we vooral in de verschillen tussen twee populaties geïnteresseerd.
Hoofdstuk 6 Twee populaties: parametrische toetsen 6.1 De t-toets voor het verschil tussen twee gemiddelden: In veel onderzoekssituaties zijn we vooral in de verschillen tussen twee populaties geïnteresseerd.
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica. Tentamen Statistiek (2DD14) op vrijdag 17 maart 2006, 9.00-12.00 uur.
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Statistiek DD14) op vrijdag 17 maart 006, 9.00-1.00 uur. UITWERKINGEN 1. Methoden om schatters te vinden a) De aannemelijkheidsfunctie
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamen Statistiek DD14) op vrijdag 17 maart 006, 9.00-1.00 uur. UITWERKINGEN 1. Methoden om schatters te vinden a) De aannemelijkheidsfunctie
Inhoudsopgave. Deel I Schatters en toetsen 1
 Inhoudsopgave Deel I Schatters en toetsen 1 1 Hetschattenvanpopulatieparameters.................. 3 1.1 Inleiding:schatterversusschatting................. 3 1.2 Hetschattenvaneengemiddelde..................
Inhoudsopgave Deel I Schatters en toetsen 1 1 Hetschattenvanpopulatieparameters.................. 3 1.1 Inleiding:schatterversusschatting................. 3 1.2 Hetschattenvaneengemiddelde..................
Inhoud. Woord vooraf 13. Hoofdstuk 1. Inductieve statistiek in onderzoek 17. Hoofdstuk 2. Kansverdelingen en kansberekening 28
 Inhoud Woord vooraf 13 Hoofdstuk 1. Inductieve statistiek in onderzoek 17 1.1 Wat is de bedoeling van statistiek? 18 1.2 De empirische cyclus 19 1.3 Het probleem van de inductieve statistiek 20 1.4 Statistische
Inhoud Woord vooraf 13 Hoofdstuk 1. Inductieve statistiek in onderzoek 17 1.1 Wat is de bedoeling van statistiek? 18 1.2 De empirische cyclus 19 1.3 Het probleem van de inductieve statistiek 20 1.4 Statistische
Hiermee rekenen we de testwaarde van t uit: n. 10 ( x ) ,16
 modulus strepen: uitkomst > 0 Hiermee rekenen we de testwaarde van t uit: n 10 ttest ( x ) 105 101 3,16 n-1 4 t test > t kritisch want 3,16 >,6, dus 105 valt buiten het BI. De cola bevat niet significant
modulus strepen: uitkomst > 0 Hiermee rekenen we de testwaarde van t uit: n 10 ttest ( x ) 105 101 3,16 n-1 4 t test > t kritisch want 3,16 >,6, dus 105 valt buiten het BI. De cola bevat niet significant
Niet-Parametrische Statistiek
 10-11. Niet-Parametrische Statistiek I. Theorie : A Algemeen schema : 1 Steekproef willekeurige verdeling Teken-Toets symmetrische verdeling Wilcoxon-Rank-Toets 2 Steekproeven gepaarde waarnemingen Wilcoxon-Rank-Toets
10-11. Niet-Parametrische Statistiek I. Theorie : A Algemeen schema : 1 Steekproef willekeurige verdeling Teken-Toets symmetrische verdeling Wilcoxon-Rank-Toets 2 Steekproeven gepaarde waarnemingen Wilcoxon-Rank-Toets
Formules Excel Bedrijfsstatistiek
 Formules Excel Bedrijfsstatistiek Hoofdstuk 2 Data en hun voorstelling AANTAL.ALS vb: AANTAL.ALS(A1 :B6,H1) Telt hoeveel keer (frequentie) de waarde die in H1 zit in A1:B6 voorkomt. Vooral bedoeld voor
Formules Excel Bedrijfsstatistiek Hoofdstuk 2 Data en hun voorstelling AANTAL.ALS vb: AANTAL.ALS(A1 :B6,H1) Telt hoeveel keer (frequentie) de waarde die in H1 zit in A1:B6 voorkomt. Vooral bedoeld voor
Examen Statistiek I Januari 2010 Feedback
 Examen Statistiek I Januari 2010 Feedback Correcte alternatieven worden door een sterretje aangeduid. 1 Een steekproef van 400 personen bestaat uit 270 mannen en 130 vrouwen. Twee derden van de mannen
Examen Statistiek I Januari 2010 Feedback Correcte alternatieven worden door een sterretje aangeduid. 1 Een steekproef van 400 personen bestaat uit 270 mannen en 130 vrouwen. Twee derden van de mannen
Verklarende Statistiek: Toetsen. Zat ik nou in dat kritische gebied of niet?
 Verklarende Statistiek: Toetsen Zat ik nou in dat kritische gebied of niet? Toetsen, Overzicht Nulhypothese - Alternatieve hypothese (voorbeeld: toets voor p = p o in binomiale steekproef) Betrouwbaarheid
Verklarende Statistiek: Toetsen Zat ik nou in dat kritische gebied of niet? Toetsen, Overzicht Nulhypothese - Alternatieve hypothese (voorbeeld: toets voor p = p o in binomiale steekproef) Betrouwbaarheid
Data analyse Inleiding statistiek
 Data analyse Inleiding statistiek 1 Doel Beheersen van elementaire statistische technieken Toepassen van deze technieken op aardwetenschappelijke data 2 1 Leerstof Boek: : Introductory Statistics, door
Data analyse Inleiding statistiek 1 Doel Beheersen van elementaire statistische technieken Toepassen van deze technieken op aardwetenschappelijke data 2 1 Leerstof Boek: : Introductory Statistics, door
introductie Wilcoxon s rank sum toets Wilcoxon s signed rank toets introductie Wilcoxon s rank sum toets Wilcoxon s signed rank toets
 toetsende statistiek week 1: kansen en random variabelen week : de steekproevenverdeling week 3: schatten en toetsen: de z-toets week : het toetsen van gemiddelden: de t-toets week 5: het toetsen van varianties:
toetsende statistiek week 1: kansen en random variabelen week : de steekproevenverdeling week 3: schatten en toetsen: de z-toets week : het toetsen van gemiddelden: de t-toets week 5: het toetsen van varianties:
Oefenvragen bij Statistics for Business and Economics van Newbold
 Oefenvragen bij Statistics for Business and Economics van Newbold Hoofdstuk 1 1. Wat is het verschil tussen populatie en sample? De populatie is de complete set van items waar de onderzoeker in geïnteresseerd
Oefenvragen bij Statistics for Business and Economics van Newbold Hoofdstuk 1 1. Wat is het verschil tussen populatie en sample? De populatie is de complete set van items waar de onderzoeker in geïnteresseerd
Stochastiek 2. Inleiding in de Mathematische Statistiek 1 / 17
 Stochastiek 2 Inleiding in de Mathematische Statistiek 1 / 17 Statistische toetsen 2 / 17 Toetsen - algemeen - 1 Setting: observatie X in X, model {P θ : θ Θ}. Gegeven partitie Θ = Θ 0 Θ 1, met Θ 0 Θ 1
Stochastiek 2 Inleiding in de Mathematische Statistiek 1 / 17 Statistische toetsen 2 / 17 Toetsen - algemeen - 1 Setting: observatie X in X, model {P θ : θ Θ}. Gegeven partitie Θ = Θ 0 Θ 1, met Θ 0 Θ 1
Voorbeeldtentamen Statistiek voor Psychologie
 Voorbeeldtentamen Statistiek voor Psychologie 1) Vul de volgende uitspraak aan, zodat er een juiste bewering ontstaat: De verdeling van een variabele geeft een opsomming van de categorieën en geeft daarbij
Voorbeeldtentamen Statistiek voor Psychologie 1) Vul de volgende uitspraak aan, zodat er een juiste bewering ontstaat: De verdeling van een variabele geeft een opsomming van de categorieën en geeft daarbij
Toegepaste Statistiek, Week 3 1
 Toegepaste Statistiek, Week 3 1 In Week 2 hebben we toetsingstheorie besproken mbt een kwantitatieve (ordinale) variabele G, en met name over zijn populatiegemiddelde E(G). Er waren twee gevallen: Er is
Toegepaste Statistiek, Week 3 1 In Week 2 hebben we toetsingstheorie besproken mbt een kwantitatieve (ordinale) variabele G, en met name over zijn populatiegemiddelde E(G). Er waren twee gevallen: Er is
Examen Statistiek I Feedback
 Examen Statistiek I Feedback Bij elke vraag is alternatief A correct. Bij de trekking van een persoon uit een populatie beschouwt men de gebeurtenissen A (met bril), B (hooggeschoold) en C (mannelijk).
Examen Statistiek I Feedback Bij elke vraag is alternatief A correct. Bij de trekking van een persoon uit een populatie beschouwt men de gebeurtenissen A (met bril), B (hooggeschoold) en C (mannelijk).
Hoofdstuk 3 Statistiek: het toetsen
 Hoofdstuk 3 Statistiek: het toetsen 3.1 Schatten: Er moet een verbinding worden gelegd tussen de steekproefgrootheden en populatieparameters, willen we op basis van de een iets kunnen zeggen over de ander.
Hoofdstuk 3 Statistiek: het toetsen 3.1 Schatten: Er moet een verbinding worden gelegd tussen de steekproefgrootheden en populatieparameters, willen we op basis van de een iets kunnen zeggen over de ander.
Figuur 1: Voorbeelden van 95%-betrouwbaarheidsmarges van gemeten percentages.
 MARGES EN SIGNIFICANTIE BIJ STEEKPROEFRESULTATEN. De marges van percentages Metingen via een steekproef leveren een schatting van de werkelijkheid. Het toevalskarakter van de steekproef heeft als consequentie,
MARGES EN SIGNIFICANTIE BIJ STEEKPROEFRESULTATEN. De marges van percentages Metingen via een steekproef leveren een schatting van de werkelijkheid. Het toevalskarakter van de steekproef heeft als consequentie,
Wiskunde B - Tentamen 1
 Wiskunde B - Tentamen Tentamen 57 Wiskunde B voor CiT vrijdag januari 5 van 9. tot. uur Dit tentamen bestaat uit 6 opgaven, formulebladen en tabellen. Vermeld ook uw studentnummer op uw werk en tentamenbriefje.
Wiskunde B - Tentamen Tentamen 57 Wiskunde B voor CiT vrijdag januari 5 van 9. tot. uur Dit tentamen bestaat uit 6 opgaven, formulebladen en tabellen. Vermeld ook uw studentnummer op uw werk en tentamenbriefje.
+ ( 1 4 )2 σ 2 X σ2. 36 σ2 terwijl V ar[x] = 11. Aangezien V ar[x] het kleinst is, is dit rekenkundig gemiddelde de meest efficiënte schatter.
![+ ( 1 4 )2 σ 2 X σ2. 36 σ2 terwijl V ar[x] = 11. Aangezien V ar[x] het kleinst is, is dit rekenkundig gemiddelde de meest efficiënte schatter. + ( 1 4 )2 σ 2 X σ2. 36 σ2 terwijl V ar[x] = 11. Aangezien V ar[x] het kleinst is, is dit rekenkundig gemiddelde de meest efficiënte schatter.](/thumbs/48/24456561.jpg) STATISTIEK OPLOSSINGEN OEFENZITTINGEN 5 en 6 c D. Keppens 2004 5 1 (a) Zij µ de verwachtingswaarde van X. We moeten aantonen dat E[M i ] = µ voor i = 1, 2, 3 om te kunnen spreken van zuivere schatters.
STATISTIEK OPLOSSINGEN OEFENZITTINGEN 5 en 6 c D. Keppens 2004 5 1 (a) Zij µ de verwachtingswaarde van X. We moeten aantonen dat E[M i ] = µ voor i = 1, 2, 3 om te kunnen spreken van zuivere schatters.
Populatie: De gehele groep elementen waarover informatie wordt gewenst.
 Statistiek I Werkcollege 1 Populatie: De gehele groep elementen waarover informatie wordt gewenst. Steekproef: Gedeelte van de populatie dat feitelijk wordt onderzocht om informatie te vergaren. Eenheden:
Statistiek I Werkcollege 1 Populatie: De gehele groep elementen waarover informatie wordt gewenst. Steekproef: Gedeelte van de populatie dat feitelijk wordt onderzocht om informatie te vergaren. Eenheden:
SPSS Introductiecursus. Sanne Hoeks Mattie Lenzen
 SPSS Introductiecursus Sanne Hoeks Mattie Lenzen Statistiek, waarom? Doel van het onderzoek om nieuwe feiten van de werkelijkheid vast te stellen door middel van systematisch onderzoek en empirische verzamelen
SPSS Introductiecursus Sanne Hoeks Mattie Lenzen Statistiek, waarom? Doel van het onderzoek om nieuwe feiten van de werkelijkheid vast te stellen door middel van systematisch onderzoek en empirische verzamelen
Cursus TEO: Theorie en Empirisch Onderzoek. Practicum 2: Herhaling BIS 11 februari 2015
 Cursus TEO: Theorie en Empirisch Onderzoek Practicum 2: Herhaling BIS 11 februari 2015 Centrale tendentie Centrale tendentie wordt meestal afgemeten aan twee maten: Mediaan: de middelste waarneming, 50%
Cursus TEO: Theorie en Empirisch Onderzoek Practicum 2: Herhaling BIS 11 februari 2015 Centrale tendentie Centrale tendentie wordt meestal afgemeten aan twee maten: Mediaan: de middelste waarneming, 50%
Hoofdstuk 7: Statistische gevolgtrekkingen voor distributies
 Hoofdstuk 7: Statistische gevolgtrekkingen voor distributies 7.1 Het gemiddelde van een populatie Standaarddeviatie van de populatie en de steekproef In het vorige deel is bij de significantietoets uitgegaan
Hoofdstuk 7: Statistische gevolgtrekkingen voor distributies 7.1 Het gemiddelde van een populatie Standaarddeviatie van de populatie en de steekproef In het vorige deel is bij de significantietoets uitgegaan
We berekenen nog de effectgrootte aan de hand van formule 4.2 en rapporteren:
 INDUCTIEVE STATISTIEK VOOR DE GEDRAGSWETENSCHAPPEN OPLOSSINGEN BIJ HOOFDSTUK 4 1. Toets met behulp van SPSS de hypothese van Evelien in verband met de baardlengte van metalfans. Ga na of je dezelfde conclusies
INDUCTIEVE STATISTIEK VOOR DE GEDRAGSWETENSCHAPPEN OPLOSSINGEN BIJ HOOFDSTUK 4 1. Toets met behulp van SPSS de hypothese van Evelien in verband met de baardlengte van metalfans. Ga na of je dezelfde conclusies
Feedback proefexamen Statistiek I 2009 2010
 Feedback proefexamen Statistiek I 2009 2010 Het correcte antwoord wordt aangeduid door een sterretje. 1 Een steekproef van 400 personen bestaat uit 270 mannen en 130 vrouwen. Een derde van de mannen is
Feedback proefexamen Statistiek I 2009 2010 Het correcte antwoord wordt aangeduid door een sterretje. 1 Een steekproef van 400 personen bestaat uit 270 mannen en 130 vrouwen. Een derde van de mannen is
HOOFDSTUK 5 TOETSEN VAN HYPOTHESEN
 Toetsen van hypothesen 1 HOOFDSTUK 5 TOETSEN VAN HYPOTHESEN 1. Inleiding...2 2. Beslissingsregels...5 2.1. Beslissen op grond van kritische grenzen...5 2.1.1. Het α-risico...6 2.1.2. Het β-risico...7 2.2.
Toetsen van hypothesen 1 HOOFDSTUK 5 TOETSEN VAN HYPOTHESEN 1. Inleiding...2 2. Beslissingsregels...5 2.1. Beslissen op grond van kritische grenzen...5 2.1.1. Het α-risico...6 2.1.2. Het β-risico...7 2.2.
. Dan geldt P(B) = a. 1 4. d. 3 8
 Tentamen Statistische methoden 4052STAMEY juli 203, 9:00 2:00 Studienummers: Vult u alstublieft op het meerkeuzevragenformulier uw Delftse studienummer in (tbv automatische verwerking); en op het open
Tentamen Statistische methoden 4052STAMEY juli 203, 9:00 2:00 Studienummers: Vult u alstublieft op het meerkeuzevragenformulier uw Delftse studienummer in (tbv automatische verwerking); en op het open
Data analyse Inleiding statistiek
 Data analyse Inleiding statistiek 1 Terugblik - Inductieve statistiek Afleiden van eigenschappen van een populatie op basis van een beperkt aantal metingen (steekproef) Kennis gemaakt met kans & kansverdelingen»
Data analyse Inleiding statistiek 1 Terugblik - Inductieve statistiek Afleiden van eigenschappen van een populatie op basis van een beperkt aantal metingen (steekproef) Kennis gemaakt met kans & kansverdelingen»
Les 1: Waarschijnlijkheidrekening
 Les 1: Waarschijnlijkheidrekening A Men neemt een steekproef van 1000 appelen. Deze worden ingedeeld volgens gewicht en volgens symptomen van een bepaalde schimmel: geen, mild, gematigd of ernstig. Het
Les 1: Waarschijnlijkheidrekening A Men neemt een steekproef van 1000 appelen. Deze worden ingedeeld volgens gewicht en volgens symptomen van een bepaalde schimmel: geen, mild, gematigd of ernstig. Het
Samenvatting Statistiek
 Samenvatting Statistiek De hoofdstukken 1 t/m 3 gaan over kansrekening: het uitrekenen van kansen in een volledig gespecifeerd model, waarin de parameters bekend zijn en de kans op een gebeurtenis gevraagd
Samenvatting Statistiek De hoofdstukken 1 t/m 3 gaan over kansrekening: het uitrekenen van kansen in een volledig gespecifeerd model, waarin de parameters bekend zijn en de kans op een gebeurtenis gevraagd
Vandaag. Onderzoeksmethoden: Statistiek 3. Recap 2. Recap 1. Recap Centrale limietstelling T-verdeling Toetsen van hypotheses
 Vandaag Onderzoeksmethoden: Statistiek 3 Peter de Waal (gebaseerd op slides Peter de Waal, Marjan van den Akker) Departement Informatica Beta-faculteit, Universiteit Utrecht Recap Centrale limietstelling
Vandaag Onderzoeksmethoden: Statistiek 3 Peter de Waal (gebaseerd op slides Peter de Waal, Marjan van den Akker) Departement Informatica Beta-faculteit, Universiteit Utrecht Recap Centrale limietstelling
Verdelingsvrije statistiek
 Verdelingsvrije statistiek Inleiding In hoofdstuk II-5 (deel ) worden een aantal verdelingsvrije toetsen (ook wel niet-parametrische toetsen) besproken, die gebruikt worden als de te onderzoeken variabele
Verdelingsvrije statistiek Inleiding In hoofdstuk II-5 (deel ) worden een aantal verdelingsvrije toetsen (ook wel niet-parametrische toetsen) besproken, die gebruikt worden als de te onderzoeken variabele
INDUCTIEVE STATISTIEK VOOR DE GEDRAGSWETENSCHAPPEN OPLOSSINGEN BIJ HOOFDSTUK 5
 INDUCTIEVE STATISTIEK VOOR DE GEDRAGSWETENSCHAPPEN OPLOSSINGEN BIJ HOOFDSTUK 5 1. De onderzoekers van een preventiedienst vermoeden dat werknemers in een bedrijf zonder liften fitter zijn dan werknemers
INDUCTIEVE STATISTIEK VOOR DE GEDRAGSWETENSCHAPPEN OPLOSSINGEN BIJ HOOFDSTUK 5 1. De onderzoekers van een preventiedienst vermoeden dat werknemers in een bedrijf zonder liften fitter zijn dan werknemers
Statistiek II. 1. Eenvoudig toetsen. Onderdeel toetsen binnen de cursus: Toetsen en schatten ivm één statistiek of steekproef
 Statistiek II Onderdeel toetsen binnen de cursus: 1. Eenvoudig toetsen Toetsen en schatten ivm één statistiek of steekproef Via de z-verdeling, als µ onderzocht wordt en gekend is: Via de t-verdeling,
Statistiek II Onderdeel toetsen binnen de cursus: 1. Eenvoudig toetsen Toetsen en schatten ivm één statistiek of steekproef Via de z-verdeling, als µ onderzocht wordt en gekend is: Via de t-verdeling,
Toetsen van Hypothesen. Het vaststellen van de hypothese
 Toetsen van Hypothesen Wisnet-hbo update maart 2008 1. en Het vaststellen van de hypothese De nulhypothese en de Alternatieve hypothese. Het gaat in deze paragraaf puur alleen om de formulering. Er wordt
Toetsen van Hypothesen Wisnet-hbo update maart 2008 1. en Het vaststellen van de hypothese De nulhypothese en de Alternatieve hypothese. Het gaat in deze paragraaf puur alleen om de formulering. Er wordt
Statistische toetsen
 Statistische toetsen Een handleiding voor elke leerling die worstelt met het toetsen van zijn gegevens bij het PWS Hanna Bodde en Annalie Koerts Karla Thie Inhoudsopgave 1. Inleiding 3 2. Criteria voor
Statistische toetsen Een handleiding voor elke leerling die worstelt met het toetsen van zijn gegevens bij het PWS Hanna Bodde en Annalie Koerts Karla Thie Inhoudsopgave 1. Inleiding 3 2. Criteria voor
Toetsende Statistiek Week 5. De F-toets & Onderscheidend Vermogen
 M, M & C 7.3 Optional Topics in Comparing Distributions: F-toets 6.4 Power & Inference as a Decision 7.1 The power of the t-test 7.3 The power of the sample t- Toetsende Statistiek Week 5. De F-toets &
M, M & C 7.3 Optional Topics in Comparing Distributions: F-toets 6.4 Power & Inference as a Decision 7.1 The power of the t-test 7.3 The power of the sample t- Toetsende Statistiek Week 5. De F-toets &
11.0 Voorkennis. Wanneer je met binomcdf werkt, werk je dus altijd met een kans van de vorm P(X k)
 11.0 Voorkennis Let op: Cumulatieve binomiale verdeling: P(X k) = binomcdf(n,p,k) Wanneer je met binomcdf werkt, werk je dus altijd met een kans van de vorm P(X k) Voorbeeld 1: Binomiaal kanseperiment
11.0 Voorkennis Let op: Cumulatieve binomiale verdeling: P(X k) = binomcdf(n,p,k) Wanneer je met binomcdf werkt, werk je dus altijd met een kans van de vorm P(X k) Voorbeeld 1: Binomiaal kanseperiment
Les 7-8: Parameter- en Vergelijkingstoetsen
 Les 7-8: Parameter- en Vergelijkingstoetsen I Theorie : A. Algemeen :. Hypothese formuleren. H 0 : nul-hypothese H : alternatieve hypothese 2. teekproef nemen. x en 2 zijn te berekenen uit de steekproefresultaten.
Les 7-8: Parameter- en Vergelijkingstoetsen I Theorie : A. Algemeen :. Hypothese formuleren. H 0 : nul-hypothese H : alternatieve hypothese 2. teekproef nemen. x en 2 zijn te berekenen uit de steekproefresultaten.
G0N11a Statistiek en data-analyse: project Eerste zittijd Modeloplossing
 G0N11a Statistiek en data-analyse: project Eerste zittijd 2007-2008 Modeloplossing Opmerking vooraf: Deze modeloplossing is een heel volledig antwoord op de gestelde vragen. Om de maximumscore op een vraag
G0N11a Statistiek en data-analyse: project Eerste zittijd 2007-2008 Modeloplossing Opmerking vooraf: Deze modeloplossing is een heel volledig antwoord op de gestelde vragen. Om de maximumscore op een vraag
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica
 TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamenopgaven Statistiek 2DD71: UITWERKINGEN 1. Stroopwafels a De som S van de 12 gewichten is X 1 + X 2 + + X 12. Deze is normaal
TECHNISCHE UNIVERSITEIT EINDHOVEN Faculteit Wiskunde en Informatica Tentamenopgaven Statistiek 2DD71: UITWERKINGEN 1. Stroopwafels a De som S van de 12 gewichten is X 1 + X 2 + + X 12. Deze is normaal
15.1 Beslissen op grond van een steekproef [1]
![15.1 Beslissen op grond van een steekproef [1] 15.1 Beslissen op grond van een steekproef [1]](/thumbs/62/47072399.jpg) 15.1 Beslissen op grond van een steekproef [1] Voorbeeld 1: Een vulmachine vult flessen met een inhoud van X ml. X is normaal verdeeld met μ = 400 en σ = 4 Er wordt een steekproef genomen van 40 flessen.
15.1 Beslissen op grond van een steekproef [1] Voorbeeld 1: Een vulmachine vult flessen met een inhoud van X ml. X is normaal verdeeld met μ = 400 en σ = 4 Er wordt een steekproef genomen van 40 flessen.
Hoofdstuk 3 : Numerieke beschrijving van data. Marnix Van Daele. Vakgroep Toegepaste Wiskunde en Informatica Universiteit Gent
 Hoofdstuk 3 : Numerieke beschrijving van data Marnix Van Daele MarnixVanDaele@UGentbe Vakgroep Toegepaste Wiskunde en Informatica Universiteit Gent Numerieke beschrijving van data p 1/31 Beschrijvende
Hoofdstuk 3 : Numerieke beschrijving van data Marnix Van Daele MarnixVanDaele@UGentbe Vakgroep Toegepaste Wiskunde en Informatica Universiteit Gent Numerieke beschrijving van data p 1/31 Beschrijvende
Bijlage Bijlage 3. Statistische toetsing: werkwijze, toetsen, formules, toepassing
 Bijlage 3 Statistische toetsing: werkwijze, toetsen, formules, toepassing In dit boek wordt kennis van statistiek en statistische ( hypothese)toetsing in principe bekend verondersteld. Niettemin geven
Bijlage 3 Statistische toetsing: werkwijze, toetsen, formules, toepassing In dit boek wordt kennis van statistiek en statistische ( hypothese)toetsing in principe bekend verondersteld. Niettemin geven
Statistiek: Spreiding en dispersie 6/12/2013. dr. Brenda Casteleyn
 Statistiek: Spreiding en dispersie 6/12/2013 dr. Brenda Casteleyn dr. Brenda Casteleyn www.keu6.be Page 2 1. Theorie Met spreiding willen we in één getal uitdrukken hoe verspreid de gegevens zijn: in hoeveel
Statistiek: Spreiding en dispersie 6/12/2013 dr. Brenda Casteleyn dr. Brenda Casteleyn www.keu6.be Page 2 1. Theorie Met spreiding willen we in één getal uitdrukken hoe verspreid de gegevens zijn: in hoeveel
Kansrekening en statistiek wi2105in deel 2 16 april 2010, uur
 Kansrekening en statistiek wi205in deel 2 6 april 200, 4.00 6.00 uur Bij dit examen is het gebruik van een (evt. grafische) rekenmachine toegestaan. Tevens krijgt u een formuleblad uitgereikt na afloop
Kansrekening en statistiek wi205in deel 2 6 april 200, 4.00 6.00 uur Bij dit examen is het gebruik van een (evt. grafische) rekenmachine toegestaan. Tevens krijgt u een formuleblad uitgereikt na afloop
c Voorbeeldvragen, Methoden & Technieken, Universiteit Leiden TS: versie 1 1 van 6
 c Voorbeeldvragen, Methoden & Technieken, Universiteit Leiden TS: versie 1 1 van 6 1. Iemand kiest geblinddoekt 4 paaseitjes uit een mand met oneindig veel paaseitjes. De helft is melkchocolade, de andere
c Voorbeeldvragen, Methoden & Technieken, Universiteit Leiden TS: versie 1 1 van 6 1. Iemand kiest geblinddoekt 4 paaseitjes uit een mand met oneindig veel paaseitjes. De helft is melkchocolade, de andere
Toetsende Statistiek, Week 2. Van Steekproef naar Populatie: De Steekproevenverdeling
 Toetsende Statistiek, Week 2. Van Steekproef naar Populatie: De Steekproevenverdeling Moore, McCabe & Craig: 3.3 Toward Statistical Inference From Probability to Inference 5.1 Sampling Distributions for
Toetsende Statistiek, Week 2. Van Steekproef naar Populatie: De Steekproevenverdeling Moore, McCabe & Craig: 3.3 Toward Statistical Inference From Probability to Inference 5.1 Sampling Distributions for
Tabel 13.1. De verdeling van preferenties over vier automerken. Mercedes BMW Porsche Alfa Romeo Totaal
 13. NON-PARAMETRISCHE TOETSEN 13.1 Inleiding Wanneer de verzamelde gegevens niet op intervalniveau gemeten zijn, maar op ordinaal of nominaal niveau, of wanneer de verdeling van de scores verre van normaal
13. NON-PARAMETRISCHE TOETSEN 13.1 Inleiding Wanneer de verzamelde gegevens niet op intervalniveau gemeten zijn, maar op ordinaal of nominaal niveau, of wanneer de verdeling van de scores verre van normaal
Stochastiek 2. Inleiding in de Mathematische Statistiek 1 / 18
 Stochastiek 2 Inleiding in de Mathematische Statistiek 1 / 18 t-toetsen 2 / 18 Steekproefgemiddelde en -variantie van normale observaties Stelling. Laat X 1,..., X n o.o. zijn en N(µ, σ 2 )-verdeeld. Dan:
Stochastiek 2 Inleiding in de Mathematische Statistiek 1 / 18 t-toetsen 2 / 18 Steekproefgemiddelde en -variantie van normale observaties Stelling. Laat X 1,..., X n o.o. zijn en N(µ, σ 2 )-verdeeld. Dan:
Kansverdelingen Inductieve statistiek met Geogebra 4.2
 Kansverdelingen Inductieve statistiek met Geogebra 4.2 Brecht Dekeyser Pedic 20 november 2013 Gent 1 Inhoud Nieuw in Geogebra 4.2 Kansverdelingen: Berekeningen en grafische voorstellingen Manueel in rekenblad
Kansverdelingen Inductieve statistiek met Geogebra 4.2 Brecht Dekeyser Pedic 20 november 2013 Gent 1 Inhoud Nieuw in Geogebra 4.2 Kansverdelingen: Berekeningen en grafische voorstellingen Manueel in rekenblad
5.0 Voorkennis. Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram:
 5.0 Voorkennis Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram: De lengte van de staven komt overeen met de hoeveelheid; De staven staan meestal los van
5.0 Voorkennis Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram: De lengte van de staven komt overeen met de hoeveelheid; De staven staan meestal los van
Hoofdstuk 10 Eenwegs- en tweewegs-variantieanalyse
 Hoofdstuk 10 Eenwegs- en tweewegs-variantieanalyse 10.1 Eenwegs-variantieanalyse: Als we gegevens hebben verzameld van verschillende groepen en we willen nagaan of de populatiegemiddelden van elkaar verscihllen,
Hoofdstuk 10 Eenwegs- en tweewegs-variantieanalyse 10.1 Eenwegs-variantieanalyse: Als we gegevens hebben verzameld van verschillende groepen en we willen nagaan of de populatiegemiddelden van elkaar verscihllen,
Statistiek in de alfa en gamma studies. Aansluiting wiskunde VWO-WO 16 april 2018
 Statistiek in de alfa en gamma studies Aansluiting wiskunde VWO-WO 16 april 2018 Wie ben ik? Marieke Westeneng Docent bij afdeling Methoden en Statistiek Faculteit Sociale Wetenschappen Universiteit Utrecht
Statistiek in de alfa en gamma studies Aansluiting wiskunde VWO-WO 16 april 2018 Wie ben ik? Marieke Westeneng Docent bij afdeling Methoden en Statistiek Faculteit Sociale Wetenschappen Universiteit Utrecht
Examen G0N34 Statistiek
 Naam: Richting: Examen G0N34 Statistiek 8 september 2010 Enkele richtlijnen : Wie de vragen aanneemt en bekijkt, moet minstens 1 uur blijven zitten. Je mag gebruik maken van een rekenmachine, het formularium
Naam: Richting: Examen G0N34 Statistiek 8 september 2010 Enkele richtlijnen : Wie de vragen aanneemt en bekijkt, moet minstens 1 uur blijven zitten. Je mag gebruik maken van een rekenmachine, het formularium
Cursus Statistiek 2. Fellowonderwijs Opleiding Intensive Care. UMC St Radboud, Nijmegen
 Cursus Statistiek 2 Fellowonderwijs Opleiding Intensive Care UMC St Radboud, Nijmegen Cursus Statistiek 2 Steekproefgrootte en power berekening Vergelijken van gemiddelden (T-testen) Niet-parametrische
Cursus Statistiek 2 Fellowonderwijs Opleiding Intensive Care UMC St Radboud, Nijmegen Cursus Statistiek 2 Steekproefgrootte en power berekening Vergelijken van gemiddelden (T-testen) Niet-parametrische
HOOFDSTUK IV TOETSEN VAN STATISTISCHE HYPOTHESEN
 HOOFDSTUK IV TOETSEN VAN STATISTISCHE HYPOTHESEN 4.1 PARAMETERTOESTEN 1 A. Toetsen van het gemiddelde Beschouw een steekproef X 1, X,, X n van n onafhankelijke N(µ, σ) verdeelde kansveranderlijken Men
HOOFDSTUK IV TOETSEN VAN STATISTISCHE HYPOTHESEN 4.1 PARAMETERTOESTEN 1 A. Toetsen van het gemiddelde Beschouw een steekproef X 1, X,, X n van n onafhankelijke N(µ, σ) verdeelde kansveranderlijken Men
HOOFDSTUK 6: INTRODUCTIE IN STATISTISCHE GEVOLGTREKKINGEN
 HOOFDSTUK 6: INTRODUCTIE IN STATISTISCHE GEVOLGTREKKINGEN Inleiding Statistische gevolgtrekkingen (statistical inference) gaan over het trekken van conclusies over een populatie op basis van steekproefdata.
HOOFDSTUK 6: INTRODUCTIE IN STATISTISCHE GEVOLGTREKKINGEN Inleiding Statistische gevolgtrekkingen (statistical inference) gaan over het trekken van conclusies over een populatie op basis van steekproefdata.
Populaties beschrijven met kansmodellen
 Populaties beschrijven met kansmodellen Prof. dr. Herman Callaert Deze tekst probeert, met voorbeelden, inzicht te geven in de manier waarop je in de statistiek populaties bestudeert. Dat doe je met kansmodellen.
Populaties beschrijven met kansmodellen Prof. dr. Herman Callaert Deze tekst probeert, met voorbeelden, inzicht te geven in de manier waarop je in de statistiek populaties bestudeert. Dat doe je met kansmodellen.
HOOFDSTUK 7: STATISTISCHE GEVOLGTREKKINGEN VOOR DISTRIBUTIES
 HOOFDSTUK 7: STATISTISCHE GEVOLGTREKKINGEN VOOR DISTRIBUTIES 7.1 Het gemiddelde van een populatie Standaarddeviatie van de populatie en de steekproef In het vorige deel is bij de significantietoets uitgegaan
HOOFDSTUK 7: STATISTISCHE GEVOLGTREKKINGEN VOOR DISTRIBUTIES 7.1 Het gemiddelde van een populatie Standaarddeviatie van de populatie en de steekproef In het vorige deel is bij de significantietoets uitgegaan
Kansrekening en statistiek wi2105in deel 2 27 januari 2010, uur
 Kansrekening en statistiek wi2105in deel 2 27 januari 2010, 14.00 16.00 uur Bij dit examen is het gebruik van een (evt. grafische) rekenmachine toegestaan. Tevens krijgt u een formuleblad uitgereikt na
Kansrekening en statistiek wi2105in deel 2 27 januari 2010, 14.00 16.00 uur Bij dit examen is het gebruik van een (evt. grafische) rekenmachine toegestaan. Tevens krijgt u een formuleblad uitgereikt na
Interim Toegepaste Biostatistiek deel 1 14 december 2009 Versie A ANTWOORDEN
 Interim Toegepaste Biostatistiek deel december 2009 Versie A ANTWOORDEN C 2 B C A 5 C 6 B 7 B 8 B 9 D 0 D C 2 A B A 5 C Lever zowel het antwoordformulier als de interim toets in Versie A 2. Dit tentamen
Interim Toegepaste Biostatistiek deel december 2009 Versie A ANTWOORDEN C 2 B C A 5 C 6 B 7 B 8 B 9 D 0 D C 2 A B A 5 C Lever zowel het antwoordformulier als de interim toets in Versie A 2. Dit tentamen
Les 1: Waarschijnlijkheidrekening
 Les 1: Waarschijnlijkheidrekening A Men neemt een steekproef van 1000 appelen. Deze worden ingedeeld volgens gewicht en volgens symptomen van een bepaalde schimmel: geen, mild, gematigd of ernstig. Het
Les 1: Waarschijnlijkheidrekening A Men neemt een steekproef van 1000 appelen. Deze worden ingedeeld volgens gewicht en volgens symptomen van een bepaalde schimmel: geen, mild, gematigd of ernstig. Het
Hoeveel vertrouwen heb ik in mijn onderzoek en conclusie? Les 1
 Hoeveel vertrouwen heb ik in mijn onderzoek en conclusie? Les 1 1 Onderwerpen van de lessenserie: De Normale Verdeling Nul- en Alternatieve-hypothese ( - en -fout) Steekproeven Statistisch toetsen Grafisch
Hoeveel vertrouwen heb ik in mijn onderzoek en conclusie? Les 1 1 Onderwerpen van de lessenserie: De Normale Verdeling Nul- en Alternatieve-hypothese ( - en -fout) Steekproeven Statistisch toetsen Grafisch
Kansrekening en Statistiek
 Kansrekening en Statistiek College 14 Donderdag 28 Oktober 1 / 37 2 Statistiek Indeling: Hypothese toetsen Schatten 2 / 37 Vragen 61 Amerikanen werd gevraagd hoeveel % van de tijd zij liegen. Het gevonden
Kansrekening en Statistiek College 14 Donderdag 28 Oktober 1 / 37 2 Statistiek Indeling: Hypothese toetsen Schatten 2 / 37 Vragen 61 Amerikanen werd gevraagd hoeveel % van de tijd zij liegen. Het gevonden
Voorbeelden van gebruik van 5 VUSTAT-apps
 Voorbeelden van gebruik van 5 VUSTAT-apps Piet van Blokland Begrijpen van statistiek door simulaties en visualisaties Hoe kun je deze apps gebruiken bij het statistiek onderwijs? De apps van VUSTAT zijn
Voorbeelden van gebruik van 5 VUSTAT-apps Piet van Blokland Begrijpen van statistiek door simulaties en visualisaties Hoe kun je deze apps gebruiken bij het statistiek onderwijs? De apps van VUSTAT zijn
a. Wanneer kan men in plaats van de Pearson correlatie coefficient beter de Spearman rangcorrelatie coefficient berekenen?
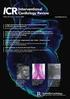 Opdracht 15a ------------ Spearman rangcorrelatie coefficient (non-parametrische tegenhanger van de Pearson correlatie coefficient) Wilcoxon symmetrie-toets (non-parametrische tegenhanger van de t-procedure
Opdracht 15a ------------ Spearman rangcorrelatie coefficient (non-parametrische tegenhanger van de Pearson correlatie coefficient) Wilcoxon symmetrie-toets (non-parametrische tegenhanger van de t-procedure
8. Analyseren van samenhang tussen categorische variabelen
 8. Analyseren van samenhang tussen categorische variabelen Er bestaat een samenhang tussen twee variabelen als de verdeling van de respons (afhankelijke) variabele verandert op het moment dat de waarde
8. Analyseren van samenhang tussen categorische variabelen Er bestaat een samenhang tussen twee variabelen als de verdeling van de respons (afhankelijke) variabele verandert op het moment dat de waarde
Ene variabele. Nonparametrische toetsen. Kolmogorov-Smirnov. Kolmogorov-Smirnov. Andere variabele. Onderzoekspracticum.
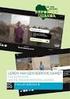 Nonparametrische Data Analyse (NPDA) Nonparametrische toetsen Andere variabele Onderzoekspracticum Sessie Gjalt-Jorn Peters [email protected] Ene variabele Dichotoom: afhankelijke Dichotoom: Meer dan twee Nominaal
Nonparametrische Data Analyse (NPDA) Nonparametrische toetsen Andere variabele Onderzoekspracticum Sessie Gjalt-Jorn Peters [email protected] Ene variabele Dichotoom: afhankelijke Dichotoom: Meer dan twee Nominaal
Statistiek I Samenvatting. Prof. dr. Carette
 Statistiek I Samenvatting Prof. dr. Carette Opleiding: bachelor of science in de Handelswetenschappen Academiejaar 2016 2017 Inhoudsopgave Hoofdstuk 1: Statistiek, gegevens en statistisch denken... 3 De
Statistiek I Samenvatting Prof. dr. Carette Opleiding: bachelor of science in de Handelswetenschappen Academiejaar 2016 2017 Inhoudsopgave Hoofdstuk 1: Statistiek, gegevens en statistisch denken... 3 De
Tentamen Mathematische Statistiek (2WS05), vrijdag 29 oktober 2010, van 14.00 17.00 uur.
 Technische Universiteit Eindhoven Faculteit Wiskunde en Informatica Tentamen Mathematische Statistiek (WS05), vrijdag 9 oktober 010, van 14.00 17.00 uur. Dit is een tentamen met gesloten boek. De uitwerkingen
Technische Universiteit Eindhoven Faculteit Wiskunde en Informatica Tentamen Mathematische Statistiek (WS05), vrijdag 9 oktober 010, van 14.00 17.00 uur. Dit is een tentamen met gesloten boek. De uitwerkingen
5.0 Voorkennis. Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram:
 5.0 Voorkennis Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram: De lengte van de staven komt overeen met de hoeveelheid; De staven staan meestal los van
5.0 Voorkennis Er zijn verschillende manieren om gegevens op een grafische wijze weer te geven: 1. Staafdiagram: De lengte van de staven komt overeen met de hoeveelheid; De staven staan meestal los van
Hoofdstuk 5: Steekproevendistributies
 Hoofdstuk 5: Steekproevendistributies Inleiding Statistische gevolgtrekkingen worden gebruikt om conclusies over een populatie of proces te trekken op basis van data. Deze data wordt samengevat door middel
Hoofdstuk 5: Steekproevendistributies Inleiding Statistische gevolgtrekkingen worden gebruikt om conclusies over een populatie of proces te trekken op basis van data. Deze data wordt samengevat door middel
11. Multipele Regressie en Correlatie
 11. Multipele Regressie en Correlatie Meervoudig regressie model Nu gaan we kijken naar een relatie tussen een responsvariabele en meerdere verklarende variabelen. Een bivariate regressielijn ziet er in
11. Multipele Regressie en Correlatie Meervoudig regressie model Nu gaan we kijken naar een relatie tussen een responsvariabele en meerdere verklarende variabelen. Een bivariate regressielijn ziet er in
Kansrekening en Statistiek
 Kansrekening en Statistiek College 11 Dinsdag 25 Oktober 1 / 27 2 Statistiek Vandaag: Hypothese toetsen Schatten 2 / 27 Schatten 3 / 27 Vragen: liegen 61 Amerikanen werd gevraagd hoeveel % van de tijd
Kansrekening en Statistiek College 11 Dinsdag 25 Oktober 1 / 27 2 Statistiek Vandaag: Hypothese toetsen Schatten 2 / 27 Schatten 3 / 27 Vragen: liegen 61 Amerikanen werd gevraagd hoeveel % van de tijd
1BA PSYCH Statistiek 1 Oefeningenreeks 3 1
 Juno KOEKELKOREN D.1.3. OEFENINGENREEKS 3 OEFENING 1 In onderstaande tabel vind je zes waarnemingen van twee variabelen (ratio meetniveau). Eén van de waarden van y is onbekend. Waarde x y 1 1 2 2 9 2
Juno KOEKELKOREN D.1.3. OEFENINGENREEKS 3 OEFENING 1 In onderstaande tabel vind je zes waarnemingen van twee variabelen (ratio meetniveau). Eén van de waarden van y is onbekend. Waarde x y 1 1 2 2 9 2
Opgaven hoofdstuk 16 Verdelingsvrije statistiek
 Opgaven hoofdstuk 16 Verdelingsvrije statistiek 16.1 Beschouw de volgende steekproef van 10 meetwaarden: LM15_4.DAT 8,4 16,9 15,8 10,3 4,9 12,9 9,8 23,7 7,3 Gebruik deze gegevens om elk van de volgende
Opgaven hoofdstuk 16 Verdelingsvrije statistiek 16.1 Beschouw de volgende steekproef van 10 meetwaarden: LM15_4.DAT 8,4 16,9 15,8 10,3 4,9 12,9 9,8 23,7 7,3 Gebruik deze gegevens om elk van de volgende
Vrije Universiteit 28 mei Gebruik van een (niet-grafische) rekenmachine is toegestaan.
 Afdeling Wiskunde Volledig tentamen Statistics Deeltentamen 2 Statistics Vrije Universiteit 28 mei 2015 Gebruik van een (niet-grafische) rekenmachine is toegestaan. Geheel tentamen: opgaven 1,2,3,4. Cijfer=
Afdeling Wiskunde Volledig tentamen Statistics Deeltentamen 2 Statistics Vrije Universiteit 28 mei 2015 Gebruik van een (niet-grafische) rekenmachine is toegestaan. Geheel tentamen: opgaven 1,2,3,4. Cijfer=
Statistiek II. Sessie 5. Feedback Deel 5
 Statistiek II Sessie 5 Feedback Deel 5 VPPK Universiteit Gent 2017-2018 Feedback Oefensessie 5 1 Statismex, gewicht en slaperigheid2 1. Lineair model: slaperigheid2 = β 0 + β 1 dosis + β 2 bd + ε H 0 :
Statistiek II Sessie 5 Feedback Deel 5 VPPK Universiteit Gent 2017-2018 Feedback Oefensessie 5 1 Statismex, gewicht en slaperigheid2 1. Lineair model: slaperigheid2 = β 0 + β 1 dosis + β 2 bd + ε H 0 :
Vandaag. Onderzoeksmethoden: Statistiek 2. Basisbegrippen. Theoretische kansverdelingen
 Vandaag Onderzoeksmethoden: Statistiek 2 Peter de Waal (gebaseerd op slides Peter de Waal, Marjan van den Akker) Departement Informatica Beta-faculteit, Universiteit Utrecht Theoretische kansverdelingen
Vandaag Onderzoeksmethoden: Statistiek 2 Peter de Waal (gebaseerd op slides Peter de Waal, Marjan van den Akker) Departement Informatica Beta-faculteit, Universiteit Utrecht Theoretische kansverdelingen
HOOFDSTUK VIII VARIANTIE ANALYSE (ANOVA)
 HOOFDSTUK VIII VARIANTIE ANALYSE (ANOVA) DATA STRUKTUUR Afhankelijke variabele: Eén kontinue variabele Onafhankelijke variabele(n): - één discrete variabele: één gecontroleerde factor - twee discrete variabelen:
HOOFDSTUK VIII VARIANTIE ANALYSE (ANOVA) DATA STRUKTUUR Afhankelijke variabele: Eén kontinue variabele Onafhankelijke variabele(n): - één discrete variabele: één gecontroleerde factor - twee discrete variabelen:
9. Lineaire Regressie en Correlatie
 9. Lineaire Regressie en Correlatie Lineaire verbanden In dit hoofdstuk worden methoden gepresenteerd waarmee je kwantitatieve respons variabelen (afhankelijk) en verklarende variabelen (onafhankelijk)
9. Lineaire Regressie en Correlatie Lineaire verbanden In dit hoofdstuk worden methoden gepresenteerd waarmee je kwantitatieve respons variabelen (afhankelijk) en verklarende variabelen (onafhankelijk)
Samenvatting Wiskunde A
 Bereken: Bereken algebraisch: Bereken exact: De opgave mag berekend worden met de hand of met de GR. Geef bij GR gebruik de ingevoerde formules en gebruikte opties. Kies op een examen in dit geval voor
Bereken: Bereken algebraisch: Bereken exact: De opgave mag berekend worden met de hand of met de GR. Geef bij GR gebruik de ingevoerde formules en gebruikte opties. Kies op een examen in dit geval voor
werkcollege 6 - D&P9: Estimation Using a Single Sample
 cursus 9 mei 2012 werkcollege 6 - D&P9: Estimation Using a Single Sample van frequentie naar dichtheid we bepalen frequenties van meetwaarden plot in histogram delen door totaal aantal meetwaarden > fracties
cursus 9 mei 2012 werkcollege 6 - D&P9: Estimation Using a Single Sample van frequentie naar dichtheid we bepalen frequenties van meetwaarden plot in histogram delen door totaal aantal meetwaarden > fracties
Hoofdstuk 12: Eenweg ANOVA
 Hoofdstuk 12: Eenweg ANOVA 12.1 Eenweg analyse van variantie Eenweg en tweeweg ANOVA Wanneer we verschillende populaties of behandelingen met elkaar vergelijken, dan zal er binnen de data altijd sprake
Hoofdstuk 12: Eenweg ANOVA 12.1 Eenweg analyse van variantie Eenweg en tweeweg ANOVA Wanneer we verschillende populaties of behandelingen met elkaar vergelijken, dan zal er binnen de data altijd sprake
Statistiek II. Sessie 1. Verzamelde vragen en feedback Deel 1
 Statistiek II Sessie 1 Verzamelde vragen en feedback Deel 1 VPPK Universiteit Gent 2017-2018 Feedback Oefensessie 1 1 Staafdiagram 1. Wat is de steekproefgrootte? Op de horizontale as vinden we de respectievelijke
Statistiek II Sessie 1 Verzamelde vragen en feedback Deel 1 VPPK Universiteit Gent 2017-2018 Feedback Oefensessie 1 1 Staafdiagram 1. Wat is de steekproefgrootte? Op de horizontale as vinden we de respectievelijke
Toetsende Statistiek Week 3. Statistische Betrouwbaarheid & Significantie Toetsing
 Toetsende Statistiek Week 3. Statistische Betrouwbaarheid & Significantie Toetsing M, M & C, Chapter 6, Introduction to Inference 6.1 Estimating with Confidence 6.2 Tests of Significance 6.3 Use and Abuse
Toetsende Statistiek Week 3. Statistische Betrouwbaarheid & Significantie Toetsing M, M & C, Chapter 6, Introduction to Inference 6.1 Estimating with Confidence 6.2 Tests of Significance 6.3 Use and Abuse
Sheets K&S voor INF HC 10: Hoofdstuk 12
 Sheets K&S voor INF HC 1: Hoofdstuk 12 Statistiek Deel 1: Schatten (hfdst. 1) Deel 2: Betrouwbaarheidsintervallen (11) Deel 3: Toetsen van hypothesen (12) Betrouwbaarheidsintervallen (H11) en toetsen (H12)
Sheets K&S voor INF HC 1: Hoofdstuk 12 Statistiek Deel 1: Schatten (hfdst. 1) Deel 2: Betrouwbaarheidsintervallen (11) Deel 3: Toetsen van hypothesen (12) Betrouwbaarheidsintervallen (H11) en toetsen (H12)
HOOFDSTUK IV TOETSEN VAN STATISTISCHE HYPOTHESEN
 HOOFDSTUK IV TOETSEN VAN STATISTISCHE HYPOTHESEN 4. VERGELIJKINGSTOETSEN A. Vergelijken van varianties Men beschouwt twee steekproeven uit normaal verdeelde populaties: X, X,, X n ~ N(µ, σ ) Y, Y,, Y n
HOOFDSTUK IV TOETSEN VAN STATISTISCHE HYPOTHESEN 4. VERGELIJKINGSTOETSEN A. Vergelijken van varianties Men beschouwt twee steekproeven uit normaal verdeelde populaties: X, X,, X n ~ N(µ, σ ) Y, Y,, Y n
Statistiek. Beschrijvend statistiek
 Statistiek Beschrijvend statistiek Verzameling van gegevens en beschrijvingen Populatie, steekproef Populatie = o de gehele groep ondervragen o parameter is een kerngetal Steekproef = o een onderdeel van
Statistiek Beschrijvend statistiek Verzameling van gegevens en beschrijvingen Populatie, steekproef Populatie = o de gehele groep ondervragen o parameter is een kerngetal Steekproef = o een onderdeel van
4 Domein STATISTIEK - versie 1.2
 USolv-IT - Boomstructuur DOMEIN STATISTIEK - versie 1.2 - c Copyrighted 42 4 Domein STATISTIEK - versie 1.2 (Op initiatief van USolv-IT werd deze boomstructuur mede in overleg met het Universitair Centrum
USolv-IT - Boomstructuur DOMEIN STATISTIEK - versie 1.2 - c Copyrighted 42 4 Domein STATISTIEK - versie 1.2 (Op initiatief van USolv-IT werd deze boomstructuur mede in overleg met het Universitair Centrum
