D A G 1 : T W E E D O M E I N E N
|
|
|
- Daniël Peter Smits
- 9 jaren geleden
- Aantal bezoeken:
Transcriptie
1 REKENEN 3F DAG 1 :TWEE DOMEINEN DAG 2 : TWEE DOMEINEN DAG 3: EXAMENTRAINING DAG 4:EXAMENTRAINING EN A FRONDING
2 Programma: Voorstellen uur uur Pauze: 15 minuten Theorie dag 1: Domein Getallen Domein Verhoudingen Theorie dag 2: Meten en Meetkunde Verbanden BEELDSCHERMEXAMEN: Datum: van 9-11 uur Hulpmiddelen: digitale rekenmachine, kladpapier, pen Digitale hulpmiddelen: licentie Rekenen op niveau van Edu Actief Werkwijze: Eerst instructie; daarna zelf aan de slag
3 Domein GETALLEN Wakker schudden: Rekenen bestaat uit afspraken maken Bij het vragen naar de leeftijd geeft elke deelnemer een afgerond getal op, terwijl niemand die dag jarig is HOE MOETEN WE VAN DE ONVOLDOENDE AFKOMEN? Standaardbewerkingen: met/zonder rekenmachine Uitkomsten schatten De betekenis van getallen/getal uitspreken: Voorbeeld: Afronden: één of meer decimalen
4 STRATEGIE: Eerst de duizendtallen Dan de honderdtallen OPTELLEN Vervolgens de tientallen en eenheden Bij een kommagetal: achter de, de getallen even lang maken = komma s onder elkaar zetten Voorbeeld: Zie digitaal bestand
5 AFTREKKEN Je leent 1 bij een grotere waarde Strategie: doortelmethode: Rond getal kiezen en daarna uitkomst aanpassen Voorbeeld: Zie digitaal bestand
6 VERMENIGVULDIGEN Herhaald optellen 0 x elk getal = 0 Totaal aantal komma s bij de te vermenigvuldigen getallen = totaal aantal cijfers achter de komma bij het totaal Voorbeeld: Zie digitaal bestand OEFENING: Tafeltjes van 1 t/m 10
7 DELEN Is het omgekeerde van vermenigvuldigen Methodes: Staartdeling Haakmethode Hapmethode
8 MACHTSVERHEFFEN Herhaald vermenigvuldigen 4³ = 4 x 4 x 4 = 64 4 is het grondtal 3 is de exponent 5º = 1 0³ = 0 Op de rekenmachine: 2⁵ = 32
9 WORTELTREKKEN Het omgekeerde van machtsverheffen ( = kwadrateren) 4 = 2, want 2 x 2 = 4 enz. tot en met 121 = 11, want 11 x 11 = 121
10 VOLGORDE VAN BEWERKINGEN Eerst haakjes wegwerken Daarna vermenigvuldigen en delen (van links naar rechts werken) Tenslotte optellen en aftrekken
11 STRATEGIËN OMKEREN: = = 33 VERANDEREN: = = 45 RIJGEN: = = 872 SCHAKELEN: = = 44 of = 44
12 REKENEN MET NEGATIEVE GETALLEN METHODE: Thermometermethode Rood staan op de betaalrekening gebruiken bij optellen en aftrekken ONTHOUDEN: bij vermenigvuldigen + x + = + + x - = - - x + = - - x - = +
13 VERVOLG NEGATIEVE GETALLEN ONTHOUDEN: bij delen + : + = + + : - = - - : + = - - : - = +
14 TEKENS < = kleiner dan > = groter dan = kleiner of gelijk aan = groter of gelijk aan
15 AFRONDEN Hangt samen met de gewenste nauwkeurigheid 4,0 is nauwkeuriger dan 4 Het eerste getal na het getal waarop afgerond moet worden is bepalend voor de uitkomst Is dit getal 5, dan wordt het laatste cijfer achter de komma met + 1 verhoogd Voorbeeld: 23,458 wordt 23,46 46,123 wordt 46,12 Afronden op een geheel getal, op 5 cent nauwkeurig
16 AFRONDING LIJST MET VERSTREKTE LICENTIES INLOGGEN WERKWIJZE
17 DOMEIN VERHOUDINGEN Procent = percentage = deel van 100 van voor begrip wil zeggen dat het begrip 100% is Eerst 1% uitrekenen Dan het gevraagde percentage uitrekenen Voorbeeld: 3% van 210,00
18 VERHOUDING 5% = 5/100 = 0,05 = 5 van de 100 = 1/20 deel = 1 van de 20 = (1 : 19) De prijs exclusief BTW = 100% De prijs inclusief BTW = 106% of 121%
19 PROMILLE Extra: PROMILLE = PROMILLAGE = DEEL VAN VOORBEELD: 15 van = 15/1000 x Eerst 1 uitrekenen. Dan het gevraagde promillage Komt voor bij het berekenen van de premie bij verzekeringen
20 VERHOUDINGEN De som van de verhoudingen = het totaalbedrag Voorbeeld: A : B : C = 1: 2 : 3 (verdeelsleutel) Totaal = (1) + (2) + (3) = (6) = 600,00
21 BREUKEN Uitkomsten schatten bij % en door gebruik te maken van bekende breuken: 10% = 10/100 = 0,1 = 1/10 deel 5% = 1/20 12,5% = 1/8 20% = 1/5 25% = ¼ 331/3 = 1/3 40% = 2/5 50% = ½ 66² 3 = 2/3
22 VERVOLG BREUKEN 13/25 13 is de teller 25 is de noemer Breuken altijd vereenvoudigen Voorbeeld: 16/42 = 8/21 Deelbaarheidsweetjes: zie stencil
23 BEWERKINGEN MET BREUKEN Bij optellen en aftrekken: de noemers gelijknamig maken De uitkomst altijd vereenvoudigen Bij vermenigvuldigen: de tellers met elkaar vermenigvuldigen Daarna de noemers met elkaar vermenigvuldigen Bij delen: de tweede breuk omdraaien en vervolgens de breuken met elkaar vermenigvuldigen Bijvoorbeeld: 5/7 : 2/3 = 5/7 x 3/2 = 15/14 = 1 1/14
24 DECIMALE EN GEWONE BREUKEN Breuken met een noemer van 10, 100, ¼ = 25/100 = 0,25 3/200 = 3 : 200 = 0,015
25 RENTEBEREKENINGEN 1 jaar = 4 kwartalen = 12 maanden = 360 dagen Bij delen van een maand wordt de eerste dag WEL meegeteld De laatste dag wordt NIET meegeteld Aan de slag
1. Optellen en aftrekken
 1. Optellen en aftrekken Om breuken op te tellen of af te trekken maak je de breuken gelijknamig. Gelijknamig maken wil zeggen dat je zorgt voor 'gelijke noemers': Om de breuken met 'derden' en 'vijfden'
1. Optellen en aftrekken Om breuken op te tellen of af te trekken maak je de breuken gelijknamig. Gelijknamig maken wil zeggen dat je zorgt voor 'gelijke noemers': Om de breuken met 'derden' en 'vijfden'
Decimaliseren. 1.1 Vereenvoudigen 2. 1.2 Verhoudingen omzetten 3. 1.3 Afronden 4. 1.4 Oefeningen 4
 Decimaliseren Samenvatting Decimaliseren is nodig, omdat alle apparaten voor hun instelling een decimaal getal nodig hebben. Bijvoorbeeld: een infuuspomp kan wel op 0,8 ml/min ingesteld worden, maar niet
Decimaliseren Samenvatting Decimaliseren is nodig, omdat alle apparaten voor hun instelling een decimaal getal nodig hebben. Bijvoorbeeld: een infuuspomp kan wel op 0,8 ml/min ingesteld worden, maar niet
Willem van Ravenstein
 Willem van Ravenstein 1. Variabelen Rekenen is het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken je de bewerkingen machtsverheffen en worteltrekken.
Willem van Ravenstein 1. Variabelen Rekenen is het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken je de bewerkingen machtsverheffen en worteltrekken.
Uitwerkingen Rekenen met cijfers en letters
 Uitwerkingen Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 2009 c Swier Garst - RGO Middelharnis 2 Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Uitwerkingen Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 2009 c Swier Garst - RGO Middelharnis 2 Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
3.2 Basiskennis. 3.2.1 De getallenlijn. 3.2.2 Symbolen, tekens en getallen. 92 Algebra. Inhoofdstuk1zijnaandeordegeweest: Het=teken. =staat.
 92 Algebra 3.2 Basiskennis Inhoofdstuk1zijnaandeordegeweest: 3.2.1 De getallenlijn... -5-4 -3-2 -1 0 1 2 3 4 5... 3.2.2 Symbolen, tekens en getallen Het=teken 5+2+3=10 = geeft aan dat wat links van = staat,
92 Algebra 3.2 Basiskennis Inhoofdstuk1zijnaandeordegeweest: 3.2.1 De getallenlijn... -5-4 -3-2 -1 0 1 2 3 4 5... 3.2.2 Symbolen, tekens en getallen Het=teken 5+2+3=10 = geeft aan dat wat links van = staat,
Hoofdstuk 1: Basisvaardigheden
 Hoofdstuk 1: Basisvaardigheden Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 1: Basisvaardigheden Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde Getallen
Hoofdstuk 1: Basisvaardigheden Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 1: Basisvaardigheden Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde Getallen
Basisvaardigheden algebra. Willem van Ravenstein. 2012 Den Haag
 Basisvaardigheden algebra Willem van Ravenstein 2012 Den Haag 1. Variabelen Rekenenis het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken
Basisvaardigheden algebra Willem van Ravenstein 2012 Den Haag 1. Variabelen Rekenenis het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken
INHOUDSOPGAVE. HOOFDSTUK 6 AFRONDEN Inleiding Cijfers Verstandig afronden 48 BLZ
 INHOUDSOPGAVE BLZ HOOFDSTUK 1 DOMEIN A: GETALLEN 15 1.1. Inleiding 15 1.2. Cijfers en getallen 15 1.3. Gebroken getallen 16 1.4. Negatieve getallen 17 1.5. Symbolen en vergelijken van getallen 19 HOOFDSTUK
INHOUDSOPGAVE BLZ HOOFDSTUK 1 DOMEIN A: GETALLEN 15 1.1. Inleiding 15 1.2. Cijfers en getallen 15 1.3. Gebroken getallen 16 1.4. Negatieve getallen 17 1.5. Symbolen en vergelijken van getallen 19 HOOFDSTUK
Het weetjesschrift. Weetjesschrift Galamaschool
 Het weetjesschrift Dit is het weetjesschrift. In dit schrift vind je heel veel weetjes over taal, rekenen en andere onderwerpen. Sommige weetjes zal je misschien al wel kennen en anderen leer je nog! Uiteindelijk
Het weetjesschrift Dit is het weetjesschrift. In dit schrift vind je heel veel weetjes over taal, rekenen en andere onderwerpen. Sommige weetjes zal je misschien al wel kennen en anderen leer je nog! Uiteindelijk
1 Rekenen met gehele getallen
 1 Inhoudsopgave 1 Rekenen met gehele getallen... 1.1 De gehele getallen... 1. Optellen... 1. Opgaven... 1. Aftrekken... 1. Opgaven... 1. Vermenigvuldigen... 1. Opgaven... 1.8 Delen... 9 1.9 Opgaven...9
1 Inhoudsopgave 1 Rekenen met gehele getallen... 1.1 De gehele getallen... 1. Optellen... 1. Opgaven... 1. Aftrekken... 1. Opgaven... 1. Vermenigvuldigen... 1. Opgaven... 1.8 Delen... 9 1.9 Opgaven...9
3.1 Haakjes wegwerken [1]
![3.1 Haakjes wegwerken [1] 3.1 Haakjes wegwerken [1]](/thumbs/53/31611347.jpg) 3.1 Haakjes wegwerken [1] Oppervlakte rechthoek (Manier 1): Opp. = l b = (a + b) c = (a + b)c Oppervlakte rechthoek (Manier 2): Opp. = Opp. Groen + Opp. Rood = l b + l b = a c + b c = ac + bc We hebben
3.1 Haakjes wegwerken [1] Oppervlakte rechthoek (Manier 1): Opp. = l b = (a + b) c = (a + b)c Oppervlakte rechthoek (Manier 2): Opp. = Opp. Groen + Opp. Rood = l b + l b = a c + b c = ac + bc We hebben
Rekentermen en tekens
 Rekentermen en tekens Erbij de som is hetzelfde, is evenveel, is gelijk aan Eraf het verschil, korting is niet hetzelfde, is niet evenveel Keer het product kleiner dan, minder dan; wijst naar het kleinste
Rekentermen en tekens Erbij de som is hetzelfde, is evenveel, is gelijk aan Eraf het verschil, korting is niet hetzelfde, is niet evenveel Keer het product kleiner dan, minder dan; wijst naar het kleinste
2A LEERLIJN. leerjaar 1. tellen. optellen en aftrekken GROEPEREN VERMENIGVULDIGEN EN DELEN. plaats en waarde. handig rekenen 1 ORDENEN EN UITSPREKEN
 2A LEERLIJN leerjaar 1. 1. tellen 1.1 Tellen in groepjes 1.2 Vooruittellen en terugtellen 7. optellen en aftrekken 7.1 Optellen 7.2 Aftrekken 2. GROEPEREN 2.1 Groeperen en inwisselen 2.2 Springen met grotere
2A LEERLIJN leerjaar 1. 1. tellen 1.1 Tellen in groepjes 1.2 Vooruittellen en terugtellen 7. optellen en aftrekken 7.1 Optellen 7.2 Aftrekken 2. GROEPEREN 2.1 Groeperen en inwisselen 2.2 Springen met grotere
Reken zeker: leerlijn kommagetallen
 Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde
![8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde](/thumbs/98/138669860.jpg) 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
SAMENVATTING BASIS & KADER
 SAMENVATTING BASIS & KADER Afronden Hoe je moet afronden hangt af van de situatie. Geldbedragen rond je meestal af op twee decimalen, 15,375 wordt 15,38. Grote getallen rondje meestal af op duizendtallen,
SAMENVATTING BASIS & KADER Afronden Hoe je moet afronden hangt af van de situatie. Geldbedragen rond je meestal af op twee decimalen, 15,375 wordt 15,38. Grote getallen rondje meestal af op duizendtallen,
2. Optellen en aftrekken van gelijknamige breuken
 1. Wat is een breuk? Een breuk Een breuk is een verhoudingsgetal. Een breuk geeft aan hoe groot een deel is van een geheel. Stel een taart is verdeeld in stukken. Je neemt 2 stukken van de taart. Je hebt
1. Wat is een breuk? Een breuk Een breuk is een verhoudingsgetal. Een breuk geeft aan hoe groot een deel is van een geheel. Stel een taart is verdeeld in stukken. Je neemt 2 stukken van de taart. Je hebt
Afspraken hoofdrekenen eerste tot zesde leerjaar
 24/04/2013 Afspraken hoofdrekenen eerste tot zesde leerjaar Sint-Ursula-Instituut Rekenprocedures eerste leerjaar Rekenen, hoe doe ik dat? 1. E + E = E 2 + 5 = 7 Ik heb er 2. Er komen er 5 bij. Dat is
24/04/2013 Afspraken hoofdrekenen eerste tot zesde leerjaar Sint-Ursula-Instituut Rekenprocedures eerste leerjaar Rekenen, hoe doe ik dat? 1. E + E = E 2 + 5 = 7 Ik heb er 2. Er komen er 5 bij. Dat is
Download gratis de PowerPoint rekenen domein getallen:
 Getallen Bron: Examenbladmbo.nl, SYLLABUS REKENEN 2F en 3F vo en mbo, Versie mei 2015 Download gratis de PowerPoint rekenen domein getallen: http://nielspicard.nl/download/powerpoint-rekenen-domein-getallen/
Getallen Bron: Examenbladmbo.nl, SYLLABUS REKENEN 2F en 3F vo en mbo, Versie mei 2015 Download gratis de PowerPoint rekenen domein getallen: http://nielspicard.nl/download/powerpoint-rekenen-domein-getallen/
Reken zeker: leerlijn kommagetallen
 Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
2 REKENEN MET BREUKEN 3. 2.3 Optellen van breuken 6. 2.5 Aftrekken van breuken 9. 2.7 Vermenigvuldigen van breuken 11. 2.9 Delen van breuken 13
 REKENEN MET BREUKEN. De breuk. Opgaven. Optellen van breuken 6. Opgaven 8. Aftrekken van breuken 9.6 Opgaven 9.7 Vermenigvuldigen van breuken.8 Opgaven.9 Delen van breuken.0 Opgaven. Een deel van een deel.
REKENEN MET BREUKEN. De breuk. Opgaven. Optellen van breuken 6. Opgaven 8. Aftrekken van breuken 9.6 Opgaven 9.7 Vermenigvuldigen van breuken.8 Opgaven.9 Delen van breuken.0 Opgaven. Een deel van een deel.
Domeinbeschrijving rekenen
 Domeinbeschrijving rekenen Discussiestuk ten dienste van de Expertgroep Doorlopende Leerlijnen Rekenen en Taal auteur: Jan van de Craats 11 december 2007 Inleiding Dit document bevat een beschrijving van
Domeinbeschrijving rekenen Discussiestuk ten dienste van de Expertgroep Doorlopende Leerlijnen Rekenen en Taal auteur: Jan van de Craats 11 december 2007 Inleiding Dit document bevat een beschrijving van
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde
![8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde](/thumbs/31/15201373.jpg) 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
Niveau 2F Lesinhouden Rekenen
 Niveau 2F Lesinhouden Rekenen LES 1 Begintest LES 2 Getallen Handig optellen en aftrekken Handig vermenigvuldigen en delen Schattend rekenen Negatieve getallen optellen en aftrekken Decimale getallen vermenigvuldigen
Niveau 2F Lesinhouden Rekenen LES 1 Begintest LES 2 Getallen Handig optellen en aftrekken Handig vermenigvuldigen en delen Schattend rekenen Negatieve getallen optellen en aftrekken Decimale getallen vermenigvuldigen
2.2 Ongelijknamige breuken en vereenvoudigde breuken 22. 2.3.1 Gemengde getallen optellen en aftrekken 26. 2.5 Van breuken naar decimale getallen 28
 Breuken Samenvatting Als je hele getallen deelt, kunnen er breuken ontstaan. Een breuk is een deel van iets. Je hebt iets in gelijke delen verdeeld. Wanneer je een kwart van een pizza hebt, dan heb je
Breuken Samenvatting Als je hele getallen deelt, kunnen er breuken ontstaan. Een breuk is een deel van iets. Je hebt iets in gelijke delen verdeeld. Wanneer je een kwart van een pizza hebt, dan heb je
LESFICHE 1. Handig rekenen. Lesfiche 1. 1 Procent & promille. 2 Afronden. Procent of percent (%) betekent letterlijk per honderd.
 Lesfiche 1 1 Procent & promille Handig rekenen Procent of percent (%) betekent letterlijk per honderd. 5 5 % is dus 5 per honderd. In breukvorm wordt dat of 0,05 als decimaal getal. Promille ( ) betekent
Lesfiche 1 1 Procent & promille Handig rekenen Procent of percent (%) betekent letterlijk per honderd. 5 5 % is dus 5 per honderd. In breukvorm wordt dat of 0,05 als decimaal getal. Promille ( ) betekent
Deel 1. het complete zakboek voor groep 7 & 8 deel 1 hele getallen, kommagetallen en breuken
 Deel 1 78 & het complete zakboek voor groep 7 & 8 deel 1 hele getallen, kommagetallen en breuken 2 DIT IS HET DiKiBO-BOEK VAN TIP PAS OP 2 HOE? hoi, ik ben DiKiBO samen met mijn vrienden help ik jou bij
Deel 1 78 & het complete zakboek voor groep 7 & 8 deel 1 hele getallen, kommagetallen en breuken 2 DIT IS HET DiKiBO-BOEK VAN TIP PAS OP 2 HOE? hoi, ik ben DiKiBO samen met mijn vrienden help ik jou bij
Aandachtspunten. blok 7, les 1 blok 7, les 3 blok 7, les 6 blok 7, les 8 blok 7, les 11 blok 9, les 1
 Aandachtspunten 291 Aandachtspuntenlijst 3, bij blok 7, 8 en 9 1 Getalbegrip. Het kind ziet de structuur niet tussen getallen boven en beneden 1 miljoen. uitspreken en opschrijven van grote getallen boven
Aandachtspunten 291 Aandachtspuntenlijst 3, bij blok 7, 8 en 9 1 Getalbegrip. Het kind ziet de structuur niet tussen getallen boven en beneden 1 miljoen. uitspreken en opschrijven van grote getallen boven
Hoofdstuk 3: NEGATIEVE GETALLEN
 1-6 H3. Negatieve getallen Hoofdstuk 3: NEGATIEVE GETALLEN 1. Wat moet ik leren? (handboek p. 96 123) 3.1 Positieve en negatieve getallen Het verschil verwoorden tussen positieve en negatieve getallen.
1-6 H3. Negatieve getallen Hoofdstuk 3: NEGATIEVE GETALLEN 1. Wat moet ik leren? (handboek p. 96 123) 3.1 Positieve en negatieve getallen Het verschil verwoorden tussen positieve en negatieve getallen.
Getallen 2. Doelgroep Rekenen en Wiskunde Getallen 2
 Getallen 2 Getallen 2 bestrijkt de uitbreiding van de basisvaardigheden van het rekenen, regels en vaardigheden die in het vmbo en de onderbouw van havo/vwo worden aangeleerd, geoefend en toegepast. Doelgroep
Getallen 2 Getallen 2 bestrijkt de uitbreiding van de basisvaardigheden van het rekenen, regels en vaardigheden die in het vmbo en de onderbouw van havo/vwo worden aangeleerd, geoefend en toegepast. Doelgroep
Het Breukenboekje. Alles over breuken
 Het Breukenboekje Alles over breuken breuken breukentaal tekening getal een hele 1 een halve een kwart een achtste ½ of ½ ¼ of ¼ ⅛ of ⅛ 3 breuken breukentaal tekening getal een vijfde ⅕ of ⅕ een tiende
Het Breukenboekje Alles over breuken breuken breukentaal tekening getal een hele 1 een halve een kwart een achtste ½ of ½ ¼ of ¼ ⅛ of ⅛ 3 breuken breukentaal tekening getal een vijfde ⅕ of ⅕ een tiende
Rekenen met cijfers en letters
 Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 009 c Swier Garst - RGO Middelharnis Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 009 c Swier Garst - RGO Middelharnis Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
5.1 Herleiden [1] Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) 2 = a 2 b 2
![5.1 Herleiden [1] Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) 2 = a 2 b 2 5.1 Herleiden [1] Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) 2 = a 2 b 2](/thumbs/72/66414323.jpg) Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) = a b 5.1 Herleiden [1] Voorbeeld 1: (a + 5)(a 6) (a + 5)(-a + 7) = a 6a + 5a 30 ( a + 14a 5a + 35) = a 6a + 5a 30
Herhaling haakjes wegwerken: a(b + c) = ab + ac (a + b)(c + d) = ac + ad + bc + bd (ab) = a b 5.1 Herleiden [1] Voorbeeld 1: (a + 5)(a 6) (a + 5)(-a + 7) = a 6a + 5a 30 ( a + 14a 5a + 35) = a 6a + 5a 30
Reken zeker: leerlijn breuken
 Reken zeker: leerlijn breuken B = breuk H = hele HB = hele plus breuk (1 1/4) Blauwe tekst is theorie uit het leerlingenboek. De breuknotatie in Reken zeker is - anders dan in deze handout - met horizontale
Reken zeker: leerlijn breuken B = breuk H = hele HB = hele plus breuk (1 1/4) Blauwe tekst is theorie uit het leerlingenboek. De breuknotatie in Reken zeker is - anders dan in deze handout - met horizontale
2 Meten 2.1 2.1 Kaarten 2.1 2.2 Materialen en technieken 2.3 2.3 Meten en schetsen 2.12 2.4 Praktijkopdrachten 2.16
 Inhoud Voorwoord v Het metrieke stelsel vii Inhoud ix Trefwoordenlijst x 1 Basis 1.1 1.1 Veel voorkomende berekeningen 1.1 1.2 Van punt tot vlak 1.4 1.3 Oppervlakten berekenen 1.12 1.4 Zelf tekenen 1.16
Inhoud Voorwoord v Het metrieke stelsel vii Inhoud ix Trefwoordenlijst x 1 Basis 1.1 1.1 Veel voorkomende berekeningen 1.1 1.2 Van punt tot vlak 1.4 1.3 Oppervlakten berekenen 1.12 1.4 Zelf tekenen 1.16
Getallen 2. Doelgroep Rekenen en Wiskunde Getallen 2. Omschrijving Rekenen en Wiskunde Getallen 2
 Getallen 2 Getallen 2 bestrijkt de uitbreiding van de basisvaardigheden van het rekenen, regels en vaardigheden die in het vmbo en de onderbouw van havo/vwo worden aangeleerd, geoefend en toegepast. Doelgroep
Getallen 2 Getallen 2 bestrijkt de uitbreiding van de basisvaardigheden van het rekenen, regels en vaardigheden die in het vmbo en de onderbouw van havo/vwo worden aangeleerd, geoefend en toegepast. Doelgroep
Leerlijnen groep 8 Wereld in Getallen
 Leerlijnen groep 8 Wereld in Getallen 1 2 3 4 REKENEN Boek 8a: Blok 1 - week 1 Oriëntatie - uitspreken en schrijven van getallen rond 1 miljoen - introductie miljard - helen uit een breuk halen 5/4 = -
Leerlijnen groep 8 Wereld in Getallen 1 2 3 4 REKENEN Boek 8a: Blok 1 - week 1 Oriëntatie - uitspreken en schrijven van getallen rond 1 miljoen - introductie miljard - helen uit een breuk halen 5/4 = -
WISNET-HBO. update aug. 2011
 Basiskennis van machten WISNET-HBO update aug. 0 Inleiding Deze les doorwerken met pen en papier! We noemen de uitdrukking a 4 (spreek uit: a tot de vierde macht) een macht van a (in dit geval de vierde
Basiskennis van machten WISNET-HBO update aug. 0 Inleiding Deze les doorwerken met pen en papier! We noemen de uitdrukking a 4 (spreek uit: a tot de vierde macht) een macht van a (in dit geval de vierde
INHOUDSTAFEL. inhoudstafel... 2
 INHOUDSTAFEL inhoudstafel... 2 getallenkennis waarde van cijfers in een getal... 6 grote getallen... 7 rekentaal... 8 rekentaal deel 2... 9 soorten getallen... 9 rekentaal deel 3... 10 de ongelijke verdeling...
INHOUDSTAFEL inhoudstafel... 2 getallenkennis waarde van cijfers in een getal... 6 grote getallen... 7 rekentaal... 8 rekentaal deel 2... 9 soorten getallen... 9 rekentaal deel 3... 10 de ongelijke verdeling...
Optellen en aftrekken kan: Uit je hoofd Op papier Met een rekenmachine (op je telefoon)
 1.1 Optellen en aftrekken Bedragen en aantallen bij elkaar optellen of van elkaar aftrekken doe je in de retail dagelijks. Meestal rekent een kassa, computer of rekenmachine de bedragen of aantallen voor
1.1 Optellen en aftrekken Bedragen en aantallen bij elkaar optellen of van elkaar aftrekken doe je in de retail dagelijks. Meestal rekent een kassa, computer of rekenmachine de bedragen of aantallen voor
8000-4000=4000 900-600=300 90-90 =0 7-8= 1 tekort! 4000 + 300+0-1 = 4299
 Rekenstrategieën Voor de basisbewerkingen optellen en aftrekken, vermenigvuldigen en delen en voor het rekenen met breuken en rekenen met decimale getallen, wordt een overzicht gegeven van rekenstrategieën
Rekenstrategieën Voor de basisbewerkingen optellen en aftrekken, vermenigvuldigen en delen en voor het rekenen met breuken en rekenen met decimale getallen, wordt een overzicht gegeven van rekenstrategieën
EXACT- Periode 1. Hoofdstuk Grootheden. 1.2 Eenheden.
 EXACT- Periode 1 Hoofdstuk 1 1.1 Grootheden. Een grootheid is in de natuurkunde en in de chemie en in de biologie: iets wat je kunt meten. Voorbeelden van grootheden (met bijbehorende symbolen): 1.2 Eenheden.
EXACT- Periode 1 Hoofdstuk 1 1.1 Grootheden. Een grootheid is in de natuurkunde en in de chemie en in de biologie: iets wat je kunt meten. Voorbeelden van grootheden (met bijbehorende symbolen): 1.2 Eenheden.
Hoofdstuk 9: NEGATIEVE GETALLEN
 1 H9. Negatieve getallen Hoofdstuk 9: NEGATIEVE GETALLEN 1. Wat moet ik leren? (handboek p. 53 57) 9.1 Getallen onder 0 Het verschil verwoorden tussen positieve en negatieve getallen. Weten dat we 0 zowel
1 H9. Negatieve getallen Hoofdstuk 9: NEGATIEVE GETALLEN 1. Wat moet ik leren? (handboek p. 53 57) 9.1 Getallen onder 0 Het verschil verwoorden tussen positieve en negatieve getallen. Weten dat we 0 zowel
Doe eenvoudige opgaven zonder een rekenmachine. XX. Gebruik een rekenmachine bij moeilijke opgaven. Controleer de berekening door te schatten.
 1.2 Vermenigvuldigen Binnen de retail gebruik je een rekenmachine om getallen of bedragen of aantallen te vermenigvuldigen of te delen. Daarnaast kun je met schatten controleren of de berekening klopt.
1.2 Vermenigvuldigen Binnen de retail gebruik je een rekenmachine om getallen of bedragen of aantallen te vermenigvuldigen of te delen. Daarnaast kun je met schatten controleren of de berekening klopt.
2.1 Bewerkingen [1] Video Geschiedenis van het rekenen ( 15 x 3 = 45
![2.1 Bewerkingen [1] Video Geschiedenis van het rekenen ( 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen ( 15 x 3 = 45](/thumbs/98/136422869.jpg) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
0,6 = 6 / 10 0,36 = 36 / 100 0,05 = 5 /100 2,02 = 2 gehelen en 2 / 100
 Breuken 8 teller breukstreep 9 noemer Breukvorm - kommagetal 0,6 6 / 10 0,36 36 / 100 0,05 5 /100 2,02 2 gehelen en 2 / 100 Breuken en gehelen 1) Hoeveel keer gaat de noemer in de teller? 2) Hoeveel is
Breuken 8 teller breukstreep 9 noemer Breukvorm - kommagetal 0,6 6 / 10 0,36 36 / 100 0,05 5 /100 2,02 2 gehelen en 2 / 100 Breuken en gehelen 1) Hoeveel keer gaat de noemer in de teller? 2) Hoeveel is
Onderstreep in elke opgave wat je eerst moet uitrekenen. Je hoeft de opdrachten niet uit te rekenen. 788 : (1 500 : 3)
 Blok 5 G/B vraag : volgorde van bewerkingen bepalen en correct uitvoeren Volgorde van bewerkingen Heel MoDerne PopMuziek Reken eerst uit wat tussen Haakjes staat. Daarna werk je verder van links naar rechts.
Blok 5 G/B vraag : volgorde van bewerkingen bepalen en correct uitvoeren Volgorde van bewerkingen Heel MoDerne PopMuziek Reken eerst uit wat tussen Haakjes staat. Daarna werk je verder van links naar rechts.
Onderstreep in elke opgave wat je eerst moet uitrekenen. Je hoeft de opdrachten niet uit te rekenen. 788 : (1 500 : 3)
 Blok G/B vraag : volgorde van bewerkingen bepalen en correct uitvoeren Volgorde van bewerkingen Heel MoDerne PopMuziek Reken eerst uit wat tussen Haakjes staat. Daarna werk je verder van links naar rechts.
Blok G/B vraag : volgorde van bewerkingen bepalen en correct uitvoeren Volgorde van bewerkingen Heel MoDerne PopMuziek Reken eerst uit wat tussen Haakjes staat. Daarna werk je verder van links naar rechts.
Getallen 1F Doelen Voorbeelden 2F Doelen Voorbeelden
 A Notatie en betekenis - Uitspraak, schrijfwijze en betekenis van, symbolen en relaties - Wiskundetaal gebruiken - de relaties groter/kleiner dan - breuknotatie met horizontale streep - teller, noemer,
A Notatie en betekenis - Uitspraak, schrijfwijze en betekenis van, symbolen en relaties - Wiskundetaal gebruiken - de relaties groter/kleiner dan - breuknotatie met horizontale streep - teller, noemer,
Leerstofoverzicht groep 6
 Leerstofoverzicht groep 6 Getallen en relaties Basisbewerkingen Leerlijn Groep 6 Uitspraak, schrijfwijze, kenmerken getallen boven 10 000 in cijfers schrijven haakjesnotatie deler en deeltal breuknotatie
Leerstofoverzicht groep 6 Getallen en relaties Basisbewerkingen Leerlijn Groep 6 Uitspraak, schrijfwijze, kenmerken getallen boven 10 000 in cijfers schrijven haakjesnotatie deler en deeltal breuknotatie
Elementaire rekenvaardigheden
 Hoofdstuk 1 Elementaire rekenvaardigheden De dingen die je niet durft te vragen, maar toch echt moet weten Je moet kunnen optellen en aftrekken om de gegevens van de patiënt nauwkeurig bij te kunnen houden.
Hoofdstuk 1 Elementaire rekenvaardigheden De dingen die je niet durft te vragen, maar toch echt moet weten Je moet kunnen optellen en aftrekken om de gegevens van de patiënt nauwkeurig bij te kunnen houden.
1.Tijdsduur. maanden:
 1.Tijdsduur 1 etmaal = 24 uur 1 uur = 60 minuten 1 minuut = 60 seconden 1 uur = 3600 seconden 1 jaar = 12 maanden 1 jaar = 52 weken 1 jaar = 365 (of 366 in schrikkeljaar) dagen 1 jaar = 4 kwartalen 1 kwartaal
1.Tijdsduur 1 etmaal = 24 uur 1 uur = 60 minuten 1 minuut = 60 seconden 1 uur = 3600 seconden 1 jaar = 12 maanden 1 jaar = 52 weken 1 jaar = 365 (of 366 in schrikkeljaar) dagen 1 jaar = 4 kwartalen 1 kwartaal
Instructie voor Docenten. Hoofdstuk 14 VERDER REKENEN MET KOMMAGETALLEN
 Instructie voor Docenten Hoofdstuk 14 VERDER REKENEN MET KOMMAGETALLEN Instructie voor docenten H14: VERDER REKENEN MET KOMMAGETALLEN DOELEN VAN DIT HOOFDSTUK: Leerlingen leren via verschillende manieren
Instructie voor Docenten Hoofdstuk 14 VERDER REKENEN MET KOMMAGETALLEN Instructie voor docenten H14: VERDER REKENEN MET KOMMAGETALLEN DOELEN VAN DIT HOOFDSTUK: Leerlingen leren via verschillende manieren
Wiskunde Werktuigbouwkunde & Metaal. Mechatronica
 Wiskunde 2-2016 Werktuigbouwkunde & Metaal Mechatronica Wiskunde 2-2016 Summa College Techniek Werktuigbouwkunde, Metaal en Mechatronica Auteurs: Ruud van Melis Jens Bijsterveld Inhoudsopgave 1. REKENEN...
Wiskunde 2-2016 Werktuigbouwkunde & Metaal Mechatronica Wiskunde 2-2016 Summa College Techniek Werktuigbouwkunde, Metaal en Mechatronica Auteurs: Ruud van Melis Jens Bijsterveld Inhoudsopgave 1. REKENEN...
2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45
![2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45](/thumbs/72/68043516.jpg) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
4.1 Negatieve getallen vermenigvuldigen [1]
![4.1 Negatieve getallen vermenigvuldigen [1] 4.1 Negatieve getallen vermenigvuldigen [1]](/thumbs/28/12962825.jpg) 4.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 x 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5 x -3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 x 3 = -15 Afspraak: In plaats
4.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 x 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5 x -3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 x 3 = -15 Afspraak: In plaats
Toetsen oefenen Rekenen deel 1. INZAGE EXEMPLAAR Groep 7&8
 Toetsen oefenen Rekenen deel 1 Getallen en Verhoudingen INZAGE EXEMPLAAR Groep 7&8 Oefenen met vragen (getallen en verhoudingen) voor LVS-, Entree-, Citotoetsen versie 1.0 Uitgave voor het basisonderwijs
Toetsen oefenen Rekenen deel 1 Getallen en Verhoudingen INZAGE EXEMPLAAR Groep 7&8 Oefenen met vragen (getallen en verhoudingen) voor LVS-, Entree-, Citotoetsen versie 1.0 Uitgave voor het basisonderwijs
ALBERDINGK THIJM COLLEGE REKENGIDS. Basis en afspraken rekenen
 ALBERDINGK THIJM COLLEGE REKENGIDS Basis en afspraken rekenen VOORWOORD Deze rekengids is bedoeld als overzichtelijk naslagwerk voor leerlingen, ouders, docenten en alle anderen die met rekenen te maken
ALBERDINGK THIJM COLLEGE REKENGIDS Basis en afspraken rekenen VOORWOORD Deze rekengids is bedoeld als overzichtelijk naslagwerk voor leerlingen, ouders, docenten en alle anderen die met rekenen te maken
INSIGHT Rekentoets. Spoorboekje. Tijd voor rekenen!
 INSIGHT Rekentoets Spoorboekje Tijd voor rekenen! Colofon Titel: Subtitel: Uitgave door: Adres: Insight Rekentoets Spoorboekje AMN b.v. Arnhem Oude Oeverstraat 120 6811 Arnhem Tel. 026-3557333 [email protected]
INSIGHT Rekentoets Spoorboekje Tijd voor rekenen! Colofon Titel: Subtitel: Uitgave door: Adres: Insight Rekentoets Spoorboekje AMN b.v. Arnhem Oude Oeverstraat 120 6811 Arnhem Tel. 026-3557333 [email protected]
Memoriseren: Een getal is deelbaar door 10 als het laatste cijfer een 0 is. Of: Een getal is deelbaar door 10 als het eindigt op 0.
 REKENEN VIJFDE KLAS en/of ZESDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Luc Cielen: Regels van deelbaarheid, grootste gemene deler en kleinste gemeen veelvoud 1 Deelbaarheid door 10, 100, 1000. Door
REKENEN VIJFDE KLAS en/of ZESDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Luc Cielen: Regels van deelbaarheid, grootste gemene deler en kleinste gemeen veelvoud 1 Deelbaarheid door 10, 100, 1000. Door
Rekensprong 5 boek A. Getallenkennis boek A sprong 1, 2 en 3
 Rekensprong 5 boek A Getallenkennis boek A sprong 1, 2 en 3 Sprong 1 les 2 natuurlijke getallen tot 100 000 Sprong 1 les 6 kommagetallen Sprong 2 les 14 de breuk als operator Sprong 2 les 19 de breuk als
Rekensprong 5 boek A Getallenkennis boek A sprong 1, 2 en 3 Sprong 1 les 2 natuurlijke getallen tot 100 000 Sprong 1 les 6 kommagetallen Sprong 2 les 14 de breuk als operator Sprong 2 les 19 de breuk als
Antwoorden bij Rekenen met het hoofd
 Antwoorden bij Rekenen met het hoofd Hoofdstuk Basisbewerkingen. Bewerkingen in beeld a. : splitsen in 5 en. Eerst min 5, dan min 0 en tenslotte nog min : splitsen in 5 en, die uitvoeren en dan nog stapsgewijs
Antwoorden bij Rekenen met het hoofd Hoofdstuk Basisbewerkingen. Bewerkingen in beeld a. : splitsen in 5 en. Eerst min 5, dan min 0 en tenslotte nog min : splitsen in 5 en, die uitvoeren en dan nog stapsgewijs
Onthoudboekje rekenen
 Onthoudboekje rekenen Inhoud 1. Hoofdrekenen: natuurlijke getallen tot 100 000 Optellen (p. 4) Aftrekken (p. 4) Vermenigvuldigen (p. 5) Delen (p. 5) Deling met rest (p. 6) 2. Hoofdrekenen: kommagetallen
Onthoudboekje rekenen Inhoud 1. Hoofdrekenen: natuurlijke getallen tot 100 000 Optellen (p. 4) Aftrekken (p. 4) Vermenigvuldigen (p. 5) Delen (p. 5) Deling met rest (p. 6) 2. Hoofdrekenen: kommagetallen
Startrekenen 1F. Leerwerkboek rekenen deel A SANDER HEEBELS IRENE LUGTEN JELTE FOLKERTSMA JASPER VAN ABSWOUDE
 Startrekenen 1F Leerwerkboek rekenen deel A SANDER HEEBELS IRENE LUGTEN JELTE FOLKERTSMA JASPER VAN ABSWOUDE SHARON TELKAMP MARK OOMEN SARI WOLTERS ROB LAGENDIJK RIEKE WYNIA Inhoudsopgave Startrekenen
Startrekenen 1F Leerwerkboek rekenen deel A SANDER HEEBELS IRENE LUGTEN JELTE FOLKERTSMA JASPER VAN ABSWOUDE SHARON TELKAMP MARK OOMEN SARI WOLTERS ROB LAGENDIJK RIEKE WYNIA Inhoudsopgave Startrekenen
Die moeilijke decibels.
 Die moeilijke decibels. Hoe werkt het en hoe moet ik er mee rekenen? PA FWN Met potlood en papier Er wordt zoveel mogelijk een rekenmethode toegepast, welke door zijn eenvoud met een simpele rekenmachine
Die moeilijke decibels. Hoe werkt het en hoe moet ik er mee rekenen? PA FWN Met potlood en papier Er wordt zoveel mogelijk een rekenmethode toegepast, welke door zijn eenvoud met een simpele rekenmachine
Tot het onderwijs in het vo horen naast de eerder genoemde getalsoorten ook nog machten, wortels en bijzondere getallen als π.
 De operationalisering voor Getallen Uit: Over de drempels met rekenen, Consolideren, onderhouden, gebruiken en verdiepen (zie voor het hele hoofdstuk en rapport: www.taalenrekenen.nl) Getallen 7.. Inleiding
De operationalisering voor Getallen Uit: Over de drempels met rekenen, Consolideren, onderhouden, gebruiken en verdiepen (zie voor het hele hoofdstuk en rapport: www.taalenrekenen.nl) Getallen 7.. Inleiding
1. REGELS VAN DEELBAARHEID.
 REKENEN VIJFDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Deelbaarheid door 10, 100, 1000 10: het laatste cijfer (= cijfer van de eenheden) is 0 100: laatste twee cijfers zijn 0 (cijfers van de eenheden
REKENEN VIJFDE KLAS Luc Cielen 1. REGELS VAN DEELBAARHEID. Deelbaarheid door 10, 100, 1000 10: het laatste cijfer (= cijfer van de eenheden) is 0 100: laatste twee cijfers zijn 0 (cijfers van de eenheden
Breuken. Tel.: Website:
 Breuken Leer- en oefenboek Versie - april 08 Auteur en uitgever: Klaas van der Veen Tel.: 00-700 E-mail: info@ [email protected] Website: www. www.meesterklaas.nl Inhoud Wat is een breuk Wat is groter:
Breuken Leer- en oefenboek Versie - april 08 Auteur en uitgever: Klaas van der Veen Tel.: 00-700 E-mail: info@ [email protected] Website: www. www.meesterklaas.nl Inhoud Wat is een breuk Wat is groter:
GETALLEN Onderdeel: Getalbegrip Doel: Je bewust zijn dat getallen verschillende betekenissen hebben.
 Leerroute 3 Jaargroep: 8 GETALLEN Onderdeel: Getalbegrip Doel: Je bewust zijn dat getallen verschillende betekenissen hebben. Je bewust zijn dat getallen verschillende betekenissen kunnen hebben. (hoeveelheidsgetal,
Leerroute 3 Jaargroep: 8 GETALLEN Onderdeel: Getalbegrip Doel: Je bewust zijn dat getallen verschillende betekenissen hebben. Je bewust zijn dat getallen verschillende betekenissen kunnen hebben. (hoeveelheidsgetal,
Kerstvakantiecursus. wiskunde B. Voorbereidende opgaven VWO. Haakjes. Machten
 Voorbereidende opgaven VWO Kerstvakantiecursus wiskunde B Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk
Voorbereidende opgaven VWO Kerstvakantiecursus wiskunde B Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk
OP WEG NAAR WISKUNDE. Plusboek uit de serie Het Grote Rekenboek Uitgeverij ScalaLeukerLeren.nl
 OP WEG NAAR WISKUNDE Plusboek uit de serie Het Grote Rekenboek Uitgeverij ScalaLeukerLeren.nl Voor kinderen die iets meer willen weten en begrijpen van wiskunde, bijvoorbeeld als voorbereiding op de middelbare
OP WEG NAAR WISKUNDE Plusboek uit de serie Het Grote Rekenboek Uitgeverij ScalaLeukerLeren.nl Voor kinderen die iets meer willen weten en begrijpen van wiskunde, bijvoorbeeld als voorbereiding op de middelbare
Vrijdag 3, maandag 6 en dinsdag 7 april Kinderen vrij ivm met Pasen en studiedag team
 Algemeen De kinderen van groep 1-2 en 3 hebben deze week een lentewandeling gemaakt. De narcissen en krokussen lieten zich zien. Het voorjaar gaat beginnen! Vandaag (vrijdag 13 maart) hebben we tijdens
Algemeen De kinderen van groep 1-2 en 3 hebben deze week een lentewandeling gemaakt. De narcissen en krokussen lieten zich zien. Het voorjaar gaat beginnen! Vandaag (vrijdag 13 maart) hebben we tijdens
Kommagetallen. Twee stukjes is
 Kommagetallen Een kommagetal is een getal dat niet heel is. Het is een breuk. Voor de komma staan de helen, achter de komma staat de breuk. De cijfers achter de komma staan voor de tienden, honderdsten,
Kommagetallen Een kommagetal is een getal dat niet heel is. Het is een breuk. Voor de komma staan de helen, achter de komma staat de breuk. De cijfers achter de komma staan voor de tienden, honderdsten,
handelingswijzer rekenen
 handelingswijzer rekenen Naslagwerk Voor leerlingen en ouders HANDELINGSWIJZER REKENEN INHOUD HANDELINGSWIJZER REKENEN... 1 1 INHOUD... 1 HOOFDBEWERKINGEN... 2 OPTELLEN... 3 AFTREKKEN... 3 VERMENIGVULDIGEN...
handelingswijzer rekenen Naslagwerk Voor leerlingen en ouders HANDELINGSWIJZER REKENEN INHOUD HANDELINGSWIJZER REKENEN... 1 1 INHOUD... 1 HOOFDBEWERKINGEN... 2 OPTELLEN... 3 AFTREKKEN... 3 VERMENIGVULDIGEN...
Exact periode = 1. h = 0, Js. h= 6, Js 12 * 12 = 1,4.10 2
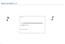 Exact periode 1.1 0 = 1 h = 0,000000000000000000000000000000000662607Js h= 6,62607. -34 Js 12 * 12 = 1,4. 2 1 Instructie gebruik CASIO fx-82ms 1. Instellingen resetten tot begininstellingen
Exact periode 1.1 0 = 1 h = 0,000000000000000000000000000000000662607Js h= 6,62607. -34 Js 12 * 12 = 1,4. 2 1 Instructie gebruik CASIO fx-82ms 1. Instellingen resetten tot begininstellingen
Voorkennis getallenverzamelingen en algebra. Introductie 213. Leerkern 214
 Open Inhoud Universiteit Appendix A Wiskunde voor milieuwetenschappen Voorkennis getallenverzamelingen en algebra Introductie Leerkern Natuurlijke getallen Gehele getallen 8 Rationele getallen Machten
Open Inhoud Universiteit Appendix A Wiskunde voor milieuwetenschappen Voorkennis getallenverzamelingen en algebra Introductie Leerkern Natuurlijke getallen Gehele getallen 8 Rationele getallen Machten
Hoofdstuk 1 : REKENEN
 1 / 6 H1 Rekenen Hoofdstuk 1 : REKENEN 1. Wat moet ik leren? (handboek p.3-34) 1.1 Het decimaal stelsel In verband met het decimaal stelsel: a) het grondtal van ons decimaal stelsel geven. b) benamingen
1 / 6 H1 Rekenen Hoofdstuk 1 : REKENEN 1. Wat moet ik leren? (handboek p.3-34) 1.1 Het decimaal stelsel In verband met het decimaal stelsel: a) het grondtal van ons decimaal stelsel geven. b) benamingen
Basiskennis van machten WISNET-HBO. update juli 2007
 Basiskennis van machten WISNET-HBO update juli 007 Inleiding Deze les doorwerken met pen en papier! We noemen de uitdrukking a 4 een macht van a (in dit geval de vierde macht van a). Het grondtal is a
Basiskennis van machten WISNET-HBO update juli 007 Inleiding Deze les doorwerken met pen en papier! We noemen de uitdrukking a 4 een macht van a (in dit geval de vierde macht van a). Het grondtal is a
De tiendeligheid van ons getalsysteem
 De tiendeligheid van ons getalsysteem Tiendeligheid is het principe dat telkens als je 10 keer iets hebt, je het kan vervangen door iets anders. Vb. 10E = 1T, 10T = 1H, Dat andere is dus telkens 10 keer
De tiendeligheid van ons getalsysteem Tiendeligheid is het principe dat telkens als je 10 keer iets hebt, je het kan vervangen door iets anders. Vb. 10E = 1T, 10T = 1H, Dat andere is dus telkens 10 keer
(o.a. voor 2F en 3F) Inhoud
 (o.a. voor 2F en 3F) Inhoud Optellen... 2 Aftrekken... 3 Vermenigvuldigen... 4 Delen... 5 Tot de macht... 6 Combinaties... 7 Wortels... 7 Afronden... 8 Breuken... 10 Procenten... 11 Verhoudingen... 12
(o.a. voor 2F en 3F) Inhoud Optellen... 2 Aftrekken... 3 Vermenigvuldigen... 4 Delen... 5 Tot de macht... 6 Combinaties... 7 Wortels... 7 Afronden... 8 Breuken... 10 Procenten... 11 Verhoudingen... 12
Blok 7 G/B vraag 1: natuurlijke getallen, kommagetallen en breuken structureren en op een getallenas situeren
 Blok 7 G/B vraag : natuurlijke getallen, kommagetallen en breuken structureren en op een getallenas situeren Natuurlijke getallen, kommagetallen en breuken structureren 0 2 0,5 0,75,25,8 2 3 4 en 4 Kijk
Blok 7 G/B vraag : natuurlijke getallen, kommagetallen en breuken structureren en op een getallenas situeren Natuurlijke getallen, kommagetallen en breuken structureren 0 2 0,5 0,75,25,8 2 3 4 en 4 Kijk
Blok 7 G/B vraag 1: natuurlijke getallen, kommagetallen en breuken structureren en op een getallenas situeren
 Blok 7 G/B vraag : natuurlijke getallen, kommagetallen en breuken structureren en op een getallenas situeren Natuurlijke getallen, kommagetallen en breuken structureren 0 2 0,5 0,75,25,8 2 3 4 en 4 Kijk
Blok 7 G/B vraag : natuurlijke getallen, kommagetallen en breuken structureren en op een getallenas situeren Natuurlijke getallen, kommagetallen en breuken structureren 0 2 0,5 0,75,25,8 2 3 4 en 4 Kijk
Extra oefeningen Hoofdstuk 8: Rationale getallen
 Extra oefeningen Hoofdstuk 8: Rationale getallen 1 Noteer met een breuk. a) Mijn stripverhaal is voor de helft uitgelezen. Een kamer is voor behangen. c) van de cirkel is gekleurd. 15 Gegeven : 18 teller
Extra oefeningen Hoofdstuk 8: Rationale getallen 1 Noteer met een breuk. a) Mijn stripverhaal is voor de helft uitgelezen. Een kamer is voor behangen. c) van de cirkel is gekleurd. 15 Gegeven : 18 teller
3.1 Negatieve getallen vermenigvuldigen [1]
![3.1 Negatieve getallen vermenigvuldigen [1] 3.1 Negatieve getallen vermenigvuldigen [1]](/thumbs/101/149931282.jpg) 3.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5-3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 3 = -15 Voorbeeld 4: -5 3 9 2
3.1 Negatieve getallen vermenigvuldigen [1] Voorbeeld 1: 5 3 = 15 (3 + 3 + 3 + 3 + 3 = 15) Voorbeeld 2: 5-3 = -15 (-3 +-3 +-3 +-3 +-3 = -3-3 -3-3 -3 = -15) Voorbeeld 3: -5 3 = -15 Voorbeeld 4: -5 3 9 2
Wiskunde klas 3. Vaardigheden. Inhoudsopgave. 1. Breuken 2. 2. Gelijksoortige termen samennemen 3. 3. Rekenen met machten 3. 4. Rekenen met wortels 4
 Vaardigheden Wiskunde klas Inhoudsopgave. Breuken. Gelijksoortige termen samennemen. Rekenen met machten. Rekenen met wortels. Algebraïsche producten 6. Ontbinden in factoren 6 7. Eerstegraads vergelijkingen
Vaardigheden Wiskunde klas Inhoudsopgave. Breuken. Gelijksoortige termen samennemen. Rekenen met machten. Rekenen met wortels. Algebraïsche producten 6. Ontbinden in factoren 6 7. Eerstegraads vergelijkingen
Groep 7, blok 1, week 1 Passende Perspectieven, leerroute 3
 Groep 7, blok 1, week 1 Passende Perspectieven, leerroute 3 LES 1 LES 2 LES 3 LES 4 LES 5 (tot 1000 en boven 1000 getallen herkennen, benoemen en noteren) (tot 1000) (1/10) (1/2 en 1/5) (10 cm = 0,10 m,
Groep 7, blok 1, week 1 Passende Perspectieven, leerroute 3 LES 1 LES 2 LES 3 LES 4 LES 5 (tot 1000 en boven 1000 getallen herkennen, benoemen en noteren) (tot 1000) (1/10) (1/2 en 1/5) (10 cm = 0,10 m,
De notatie van een berekening kan ook aangeven welke bewerking eerst moet = = 16
 Rekenregels De voorrangsregels van de hoofdbewerkingen geven aan wat als eerste moet worden uitgerekend. Voorrangsregels 1. Haakjes 2. Machtsverheffen en Worteltrekken. Vermenigvuldigen en Delen 4. Optellen
Rekenregels De voorrangsregels van de hoofdbewerkingen geven aan wat als eerste moet worden uitgerekend. Voorrangsregels 1. Haakjes 2. Machtsverheffen en Worteltrekken. Vermenigvuldigen en Delen 4. Optellen
Bijlage Cijfervaardigheid
 Bijlage Cijfervaardigheid 1 Inleiding De bedoeling van deze bijlage is in het kort de standaardrekenprocedures te herhalen. Je hebt in de vooropleiding ongetwijfeld rekenonderwijs genoten, maar vaak is
Bijlage Cijfervaardigheid 1 Inleiding De bedoeling van deze bijlage is in het kort de standaardrekenprocedures te herhalen. Je hebt in de vooropleiding ongetwijfeld rekenonderwijs genoten, maar vaak is
Tussendoelen domein GETALLEN, subdomein Getalbegrip
 Tussendoelen domein GETALLEN, subdomein Getalbegrip Eind groep 2 Eind groep 3 Eind groep 4 Eind groep 5 beheerst de doelen van groep 2, ook op het niveau van groep 3 HELE GETALLEN beheerst de doelen van
Tussendoelen domein GETALLEN, subdomein Getalbegrip Eind groep 2 Eind groep 3 Eind groep 4 Eind groep 5 beheerst de doelen van groep 2, ook op het niveau van groep 3 HELE GETALLEN beheerst de doelen van
Breuken volgens de rekenregels
 Breuken volgens de rekenregels Weeffout in het rekenonderwijs. Presentatie rekenidee volg: https://www.youtube.com/watch?v=azxqcuj7ole 7-5-2016 Terugrekenen Start + - Optellen of aftrekken (..) Haakjes
Breuken volgens de rekenregels Weeffout in het rekenonderwijs. Presentatie rekenidee volg: https://www.youtube.com/watch?v=azxqcuj7ole 7-5-2016 Terugrekenen Start + - Optellen of aftrekken (..) Haakjes
Hoe schrijf je de logaritmische waarden welke bij db s horen?
 Die moeilijke decibellen toch. PA0 FWN. Inleiding. Ondanks dat in Electron al vaak een artikel aan decibellen is geweid, en PA0 LQ in het verleden al eens een buitengewoon handige tabel publiceerde waar
Die moeilijke decibellen toch. PA0 FWN. Inleiding. Ondanks dat in Electron al vaak een artikel aan decibellen is geweid, en PA0 LQ in het verleden al eens een buitengewoon handige tabel publiceerde waar
Onderwijsassistent REKENEN BASISVAARDIGHEDEN
 Onderwijsassistent REKENEN BASISVAARDIGHEDEN Verhoudingstabel Wat zijn verhoudingen Rekenen met de verhoudingstabel Kruisprodukten Wat zijn verhoudingen * * * 2 Aantal rollen 1 2 12 Aantal beschuiten 18
Onderwijsassistent REKENEN BASISVAARDIGHEDEN Verhoudingstabel Wat zijn verhoudingen Rekenen met de verhoudingstabel Kruisprodukten Wat zijn verhoudingen * * * 2 Aantal rollen 1 2 12 Aantal beschuiten 18
1.1 Opbouw en naamgeving van decimale getallen. vijf honderd drie en twintig komma vier en twintig
 1 Rekenen met getallen decimaal getal kommagetal Onderwerpen - Opbouw en naamgeving van decimale getallen - Optellen en aftrekken - Negatieve getallen met toepassingen - Vermenigvuldigen en delen - Breuken,
1 Rekenen met getallen decimaal getal kommagetal Onderwerpen - Opbouw en naamgeving van decimale getallen - Optellen en aftrekken - Negatieve getallen met toepassingen - Vermenigvuldigen en delen - Breuken,
Rekenportfolio. Naam: cm 2. m 3 + = 1 _ 12
 Tytsjerksteradiel Rekenportfolio Naam: cm 2 1 5 7 + = 5 10 10 m 3 1 _ 12 X 5 1 + = 5 1 + Inhoudsopgave Voorwoord 3 Domein getallen 4 - Optellen, aftrekken, vermenigvuldigen en delen 5 - Breuken 6 - Rekenvolgorde
Tytsjerksteradiel Rekenportfolio Naam: cm 2 1 5 7 + = 5 10 10 m 3 1 _ 12 X 5 1 + = 5 1 + Inhoudsopgave Voorwoord 3 Domein getallen 4 - Optellen, aftrekken, vermenigvuldigen en delen 5 - Breuken 6 - Rekenvolgorde
Hoe maak je nu van breuken procenten? Voorbeeld: Opgave: hoeveel procent van de onderstaande tekening is zwart gekleurd?
 Procenten Zoals op de basisschool is aangeleerd kunnen we een taart verdelen in een aantal stukken. Hierbij krijgen we een breuk. We kunnen ditzelfde stuk taart ook aangegeven als een percentage. Procenten:
Procenten Zoals op de basisschool is aangeleerd kunnen we een taart verdelen in een aantal stukken. Hierbij krijgen we een breuk. We kunnen ditzelfde stuk taart ook aangegeven als een percentage. Procenten:
Wortels met getallen. 2 Voorbeeldenen met de vierkantswortel (Tweedemachts wortel)
 Wortels met getallen 1 Inleiding WISNET-HBO update sept 2009 Voorkennis voor deze les over Wortelvormen is de les over Machten. Voor de volledigheid staat aan het eind van deze les een overzicht van de
Wortels met getallen 1 Inleiding WISNET-HBO update sept 2009 Voorkennis voor deze les over Wortelvormen is de les over Machten. Voor de volledigheid staat aan het eind van deze les een overzicht van de
R.T. (fonsvendrik.nl 2017)
 Inhoud Rekenkunde. Nadruk verboden 1.1 Inleiding blz. 1 2.1 Positieve en negatieve getallen 3 2.2 Het gebruik van haakjes, accoladen, blokhaken, enz. 4 3.1 Vermenigvuldigen 7 3.2 Het vermenigvuldigen zowel
Inhoud Rekenkunde. Nadruk verboden 1.1 Inleiding blz. 1 2.1 Positieve en negatieve getallen 3 2.2 Het gebruik van haakjes, accoladen, blokhaken, enz. 4 3.1 Vermenigvuldigen 7 3.2 Het vermenigvuldigen zowel
De waarde van een plaats in een getal.
 Komma getallen. Toen je net op school leerde rekenen, wist je niet beter dan dat getallen heel waren. Dus een taart was een taart, een appel een appel en een peer een peer. Langzaam maar zeker werd dit
Komma getallen. Toen je net op school leerde rekenen, wist je niet beter dan dat getallen heel waren. Dus een taart was een taart, een appel een appel en een peer een peer. Langzaam maar zeker werd dit
Leerdoelen groep 7. Pluspunt rekenen
 Leerdoelen groep 7 Pluspunt rekenen NB. De leerdoelen van deze rekenmethode bieden wij de kinderen aan middels Denken in Doelen. Dat betekent dat we niet exact de blokken van de methode volgen, maar dat
Leerdoelen groep 7 Pluspunt rekenen NB. De leerdoelen van deze rekenmethode bieden wij de kinderen aan middels Denken in Doelen. Dat betekent dat we niet exact de blokken van de methode volgen, maar dat
Inhoud. 1 Ruimtefiguren 8. 4 Lijnen en hoeken 148. 2 Plaats bepalen 60. 5 Negatieve getallen 198. 3 Rekenen 100
 1 BK deel 1 Voorkennis 1 Aan de slag met wiskunde 6 1 Ruimtefiguren 8 1.1 Wiskundige ruimte guren 10 1.2 Vlakken, ribben en hoekpunten 14 1.3 Kubus en vierkant 17 1.4 Balk en rechthoek 24 1.5 Cilinder
1 BK deel 1 Voorkennis 1 Aan de slag met wiskunde 6 1 Ruimtefiguren 8 1.1 Wiskundige ruimte guren 10 1.2 Vlakken, ribben en hoekpunten 14 1.3 Kubus en vierkant 17 1.4 Balk en rechthoek 24 1.5 Cilinder
