Rekenvaardigheden op de basisschool
|
|
|
- Dirk van der Wolf
- 9 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Rekenvaardigheden op de basisschool Discussiestuk ten dienste van de Expertgroep Doorlopende Leerlijnen Rekenen en Taal auteur: Jan van de Craats 8 augustus 2007 Dit discussiestuk bevat in hoofdstuk 1 een overzicht van de minimaal gewenste rekenvaardigheden van leerlingen aan het einde van de basisschool (einde groep 8). Hoofdstuk 2 geeft achtergrondinformatie en commentaar. In een bijlage staan ter oriëntatie enige voorbeelden van toetsopgaven. 1 Rekenen op de basisschool In het primair onderwijs wordt gerekend met natuurlijke getallen, kommagetallen en breuken. Natuurlijke getallen zijn getallen waarmee je aantallen kunt weergeven: 5 vingers aan je hand, 12 appels op een schaal, 60 minuten in een uur, 16 miljoen Nederlanders, 0 euro in je portemonnee. Kommagetallen (decimale breuken, decimaalgetallen) zijn getallen zoals 354,27 en 0,067. Je gebruikt ze bijvoorbeeld bij het rekenen met euro s, bij schaalverdelingen, bij het bepalen van maten en gewichten of bij het rekenen met procenten. Breuken zijn getallen zoals 1 2, 5 8, en De rekenbewerkingen die op school worden geleerd, zijn optellen, aftrekken, vermenigvuldigen en delen. Worteltrekken en machtsverheffen staan in het primair onderwijs niet op het programma, evenmin als het rekenen met negatieve getallen. Hieronder wordt het streefniveau aan rekenvaardigheden beschreven voor het einde van de basisschool (kennis- en vaardigheidsdoelen). 1.1 Rekenen met natuurlijke getallen Leerlingen kennen de manier waarop ons decimale positiestelsel is opgebouwd. Zij kennen de betekenis van cijfers en hun plaats in getallen. Zo weten zij dat 6498 = Zij weten dat op die manier met behulp Prof.dr. J. van de Craats is lid van de Expertgroep, hoogleraar Wiskunde en Maatschappij aan de Universiteit van Amsterdam en hoogleraar Wiskunde, in het bijzonder Wiskunde-onderwijs, aan de Open Universiteit. [email protected], homepage craats. 1
2 van slechts tien cijfers (namelijk 0, 1, 2, 3, 4, 5, 6, 7, 8 en 9) elk natuurlijk getal kan worden weergegeven Hoofdrekenen Leerlingen kunnen vlot en zonder enige aarzeling de volgende berekeningen uit het hoofd uitvoeren: a. Twee getallen van één cijfer bij elkaar optellen. Voorbeelden: = 8, = 16, = 10. b. Een getal van één cijfer optellen bij een getal van twee cijfers. Voorbeelden: = 28, = 86, = 60. c. Twee getallen kleiner dan twintig van elkaar aftrekken (het kleinste van het grootste). Voorbeelden: 8 5 = 3, = 7, 17 9 = 8, 12 7 = 5. d. Twee getallen die elk bestaan uit één cijfer gevolgd door een aantal nullen, bij elkaar optellen. Voorbeelden: = 80, = 16000, = 280, = e. Twee getallen van één cijfer met elkaar vermenigvuldigen. Voorbeelden: 3 5 = 15, 7 9 = 63, 2 8 = 16. f. Een getal vermenigvuldigen met 10, 100, 1000, enzovoort. Voorbeelden: = 3450, = 5200, = g. Twee getallen die elk bestaan uit één cijfer gevolgd door een aantal nullen, met elkaar vermenigvuldigen. Voorbeelden: = 1500, = 63000, = 16000, = h. Een getal dat eindigt op een nul delen door 10, een getal dat eindigt op twee nullen delen door 100, enzovoort. Voorbeelden: 560 : 10 = 56, : 100 = 360, : 1000 = 606. i. Een deling, al dan niet met rest, uitvoeren als de deler een getal van één cijfer is, en het deeltal kleiner is dan tien maal de deler. Voorbeelden: 56 : 7 = 8, 36 : 9 = 4, 66 : 7 = 9 rest 3, 77 : 9 = 8 rest Rekenen met pen en papier Leerlingen kunnen met pen en papier de volgende rekenbewerkingen vlot uitvoeren. a. Optellen van twee of meer getallen (optellen onder elkaar). b. Aftrekken van een getal van een groter getal (aftrekken onder elkaar). c. Vermenigvuldigen van twee getallen (vermenigvuldigen onder elkaar). d. Delen met rest. 2
3 1.2 Rekenen met kommagetallen Leerlingen kennen de betekenis van kommagetallen en hun plaats op de getallenlijn. Ze kennen kommagetallen in tal van praktijksituaties, bijvoorbeeld bij het rekenen met geldbedragen of bij het gebruik van schaalverdelingen op linialen en andere meetinstumenten Hoofdrekenen Leerlingen kunnen vlot en zonder aarzelen de volgende rekenbewerkingen uit het hoofd uitvoeren. a. Een kommagetal vermenigvuldigen met 10, 100, 1000 enzovoort. b. Een kommagetal delen door 10, 100, 1000 enzovoort. c. Procenten omzetten in kommagetallen en omgekeerd. Voorbeeld: 15% = 0,15, 0,2% = 0,002, 235% = 2,35. d. Een kommagetal afronden op een gegeven aantal decimalen (plaatsen achter de komma) Rekenen met pen en papier Leerlingen kunnen met pen en papier de volgende rekenbewerkingen vlot uitvoeren. a. Optellen van twee of meer kommagetallen (optellen onder elkaar). b. Aftrekken van een kommagetal van een groter kommagetal (aftrekken onder elkaar). c. Vermenigvuldigen van twee kommagetallen (vermenigvuldigen onder elkaar). d. Het omzetten van een deling met kommagetallen in een deling waarbij de deler een natuurlijk getal is, vervolgens de deling uitvoeren, en ten slotte, indien gevraagd, het quotiënt afronden op een gegeven aantal decimalen. Voorbeeld: 1,452 : 0,17 = 145,2 : 17. Dit levert na uitvoering van de deling en afronden op twee decimalen als uitkomst 8, Toepassingen Leerlingen kunnen rekenen met kommagetallen in de volgende toepassingen (contexten). a. Rekenen met geldbedragen. b. Rekenen met percentages. c. Rekenen in het metrieke stelsel voor lengte, oppervlakte, inhoud en gewicht. d. Rekenen met tijd (uren, minuten, seconden) en snelheid (kilometers per uur en meters per seconde). 3
4 e. Omrekenen van meters per seconde naar kilometers per uur en omgekeerd. f. Omrekenen van valuta, bijvoorbeeld euro s naar dollars, bij een gegeven wisselkoers. Bij al deze toepassingen kunnen leerlingen de berekeningen in eenvoudige gevallen met de hand (pen en papier) uitvoeren. Leerlingen kunnen echter bij lastiger opgaven ook een rekenmachine gebruiken. In dat geval kunnen zij vooraf met pen en papier of uit het hoofd een schatting maken van de uitkomst. 1.3 Rekenen met breuken Leerlingen kunnen breuken visualiseren door middel van bijvoorbeeld pizzadiagrammen (taartdiagrammen). Daarnaast kunnen zij ook de plaats van een breuk aangeven op de getallenlijn. Zij kennen de betekenis van termen als teller, noemer en breukstreep. Naast de meest gebruikelijke notatie van een breuk met de horizontale breukstreep (zoals 3 4 ) kennen zij ook de notatie met een schuine breukstreep (zoals 3/4) Rekenen met pen en papier Leerlingen kunnen met pen en papier de volgende rekenbewerkingen voor breuken vlot uitvoeren. a. Een geheel getal als breuk schrijven (noemer 1). b. Een kommagetal als breuk schrijven (noemer 10, 100,...). c. Een breuk vereenvoudigen (teller en noemer delen door een gemeenschappelijke deler). d. Twee breuken onder één noemer brengen (gelijknamig maken). e. Twee breuken na gelijknamig maken bij elkaar optellen of van elkaar aftrekken. f. Twee breuken met elkaar vermenigvuldigen. g. Een breuk delen door een breuk. h. Een breuk met een teller die groter is dan de noemer, schrijven als gemengde breuk. Voorbeeld: 14 5 = Dit komt neer op delen met rest van de teller door de noemer: 14 : 5 = 2 rest 4, dus 14 5 = i. Een gemengde breuk schrijven als gewone breuk. j. Een breuk schrijven als een kommagetal, exact indien mogelijk, of anders afgerond op een gegeven aantal decimalen. Voorbeelden: 1 2 = 0,5, 3 4 = 0,75, 1 3 0,3333, 2 3 0,6667 (het teken, uitgesproken als is ongeveer gelijk aan betekent in dit verband dat de uitkomst is afgerond). Opmerking: vooral bij vermenigvuldigen en delen, maar vaak ook bij aftrekken, zijn gemengde breuken, erg onhandig. Het is daarom meestal beter om bij berekeningen gemengde breuken eerst om te zetten in gewone breuken. 4
5 2 Achtergronden en commentaar 2.1 Didactische controverses en de rol van de overheid Naast, of in plaats van de vanouds bekende standaardmethodes voor het rekenen met natuurlijke getallen worden thans op school ook wel andere methodes behandeld: kolomsgewijs rekenen voor optellen, aftrekken en vermenigvuldigen, en hapmethodes voor delen (in plaats van de staartdeling). De gepretendeerde verdiensten van die nieuwe methodes zijn inmiddels onderwerp van ernstige kritiek; zie bijvoorbeeld mijn artikel Waarom Daan en Sanne niet kunnen rekenen [1] voor een kritische bespreking van dit nieuwe rekenen en [3] voor een diepgaande analyse van strategieën van leerlingen bij delingsopgaven in de periodieke peilingen PPON 1997 en Een bloemlezing uit de reacties op [1] heb ik, samen met dat artikel, op mijn homepage craats geplaatst. Ze onderstrepen de ernst van de problematiek, niet alleen met betrekking tot het rekenen op de basisschool, maar evenzeer met betrekking tot het rekenonderwijs op de pabo. De overheid behoort echter uiterst terughoudend te zijn met betrekking tot dit soort didactische kwesties. Terecht kent zij de scholen ook op dit punt een grote autonomie toe. Ze dient er echter wel op toe te zien dat ook bij de nieuwe methodes de in het vorige hoofdstuk genoemde doelen worden bereikt, omdat anders aansluitingsproblemen naar het vervolgonderwijs onvermijdelijk zijn. 2.2 Minimumprogramma en doorstroming Hoofdstuk 1 is nadrukkelijk een minimaal programma, opgesteld met het oog op doorstroomrelevantie voor het voortgezet onderwijs. Vanzelfsprekend staat het scholen en boekenschrijvers vrij om meer te behandelen. Overigens zullen niet alle leerlingen bij dit kernprogramma hetzelfde niveau bereiken. Voor toekomstige havo- en vwo-leerlingen zal aan het einde van de basisschool bij rekentoetsen een beheersingsniveau van minstens negentig procent haalbaar en vereist zijn, terwijl bij toekomstige vmbo-leerlingen meestal een lager percentage gerealiseerd zal worden. Het is daarom van groot belang dat het rekenonderwijs op het vmbo en het mbo wordt voortgezet, zodat leerlingen daar hun rekenvaardigheid verder kunnen vergroten. Welke nieuwe onderwerpen op rekengebied in het vmbo en het mbo moeten worden behandeld (bijvoorbeeld negatieve getallen, machten, wortels, wetenschappelijke notatie van kommagetallen met machten van 10), zal afhangen van de specifieke richting. Opleidingen in de gezondheidszorg, de administratieve of de sociale sector zullen andere behoeftes hebben dan opleidingen met een exacte of een technische component. Alle mbo-studenten zullen echter uiteindelijk minstens het rekenniveau van hoofdstuk 1 moeten beheersen. Ook op havo en vwo moet de rekenvaardigheid worden bijgehouden en uitgebreid. Daarnaast komen meer specifiek wiskundige onderwerpen aan de orde zoals algebra, vergelijkingen en functies. Ook daarbij is overigens een grote rekenvaardigheid met getallen vereist. Aparte aandacht verdient het rekenen op de pabo. Natuurlijk moeten docenten 5
6 in het primair onderwijs het bovengeschetste niveau ruimschoots beheersen, maar daarnaast is het gewenst dat zij de nodige verdieping hebben bereikt en flink boven de stof staan die zij hun leerlingen onderwijzen. Het rekenonderwijs op de pabo dient daarom een veel grotere diepgang te hebben dan thans veelal het geval is. 2.3 Rekenen en wiskunde Ik heb me in het bovenstaande programma beperkt tot het rekenonderwijs, vooral omdat er juist op dit vlak in het basisonderwijs grote problemen liggen. Ze vormden, naast de problemen op taalgebied, de belangrijkste aanleiding tot de instelling van de Expertgroep. In de rekenlessen en in de boeken op de basisschool wordt echter ook aandacht besteed aan andere zaken met een wiskundig karakter: vlakke en ruimtelijke vormen, getallenpatronen, structuren, logica, puzzels enzovoort. Daarmee worden leerlingen intellectueel uitgedaagd, wordt exact talent opgespoord en gestimuleerd en wordt scherp redeneren bevorderd. Men moet op dit punt echter ook niet te veel verwachten: de vooral in wiskundige kringen veel gehoorde claim dat wiskunde ook in het algemeen het denken zou bevorderen, is nooit hard gemaakt. Bovendien is die pretentie grievend voor de grote groep mensen die ondanks matige of slechte resultaten bij het wiskundeonderwijs toch kritische en succesvolle leden van de maatschappij zijn geworden. Mede hierom ben ik van mening dat de Expertgroep zich voor wat betreft het programma voor de basisschool uitsluitend moet bezighouden met het in hoofdstuk 1 geschetste kernprogramma rekenen. Bijlage: voorbeelden van toetsopgaven Om een indicatie te geven van het streefnivau voor rekenvaardigheden aan het eind van de basisschool voor leerlingen die doorstromen naar havo en vwo geeft ik hieronder enige voorbeeldtoetsopgaven, voor een deel ontleend aan [2], pp Alle opgaven moeten zonder rekenmachione worden gemaakt. Natuurlijke getallen N N
7 N N N N Voer de volgende delingen met rest uit: N : 682 = N : 275 = Kommagetallen K.1 Bereken via optellen onder elkaar: 436, , , ,9 = K.2 Bereken via aftrekken onder elkaar: 4864, ,9651 = K.3 Bereken via vermenigvuldigen onder elkaar: 12,904 3,36 = K.4 Bereken het quotiënt van de deling 35 : 1,3 op vijf decimalen afgerond. K.5 Vul in: a. 5,03 hm = dm b. 87 km 2 = m 2 c. 321 cm 3 = mm 3 d. 4,08 hg = dg e. 21 m/s = km/u K.6 Bereken 14% van 25,50, afgerond op eurocent. K.7 Je krijgt iets dat normaal 350 euro kost voor 310 euro. Hoeveel procent korting krijg je dan? Rond af op gehele procenten. Breuken Geef de antwoorden van de volgende opgaven als een gewone breuk die je niet kunt vereenvoudigen. B.1 B.3 B = B = = B = : = B Schrijf de volgende kommagetallen als een gewone breuk die je niet kunt vereenvoudigen. B.7 32,75 B.8 0,075 = 7
8 B.9 12,9 B.10 1,035 Schrijf de volgende breuken als een kommagetal afgerond op 5 decimalen. B B Referenties: 1. Jan van de Craats, Waarom Daan en Sanne niet kunnen rekenen, Nieuw Archief voor Wiskunde, vijfde serie, jaargang 8, nr. 2, juni 2007, Jan van de Craats en Rob Bosch, Basisboek rekenen, Pearson Education, Amsterdam, C.M. van Putten en M. Hickendorff, Strategieën van leerlingen bij het beantwoorden van deelopgaven in de periodieke peilingen aan het eind van de basisschool van 2004 en 1997, Panama-post, jaargang 25, nummer 2, 2006, Jan van de Craats, Waarom Daan en Sanne niet kunnen rekenen Een bloemlezing van reacties per . Dit stuk is te lezen en te downloaden (in pdf) op mijn homepage craats. Daar staan ook mijn artikel [1] en grote delen uit het Basisboek Rekenen. 8
Domeinbeschrijving rekenen
 Domeinbeschrijving rekenen Discussiestuk ten dienste van de Expertgroep Doorlopende Leerlijnen Rekenen en Taal auteur: Jan van de Craats 11 december 2007 Inleiding Dit document bevat een beschrijving van
Domeinbeschrijving rekenen Discussiestuk ten dienste van de Expertgroep Doorlopende Leerlijnen Rekenen en Taal auteur: Jan van de Craats 11 december 2007 Inleiding Dit document bevat een beschrijving van
Hoofdrekenen als struikelblok
 Hoofdrekenen als struikelblok Jan van de Craats 18 oktober 2007 Op de basisschool neemt hoofdrekenen tegenwoordig een belangrijke plaats in. Daarbij gaat het vooral om sommen waarbij de manier waarop je
Hoofdrekenen als struikelblok Jan van de Craats 18 oktober 2007 Op de basisschool neemt hoofdrekenen tegenwoordig een belangrijke plaats in. Daarbij gaat het vooral om sommen waarbij de manier waarop je
Reken zeker: leerlijn kommagetallen
 Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
Reken zeker: leerlijn kommagetallen
 Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
Reken zeker: leerlijn kommagetallen De gebruikelijke didactische aanpak bij Reken Zeker is dat we eerst uitleg geven, vervolgens de leerlingen flink laten oefenen (automatiseren) en daarna het geleerde
Beter rekenonderwijs
 Beter rekenonderwijs Jan van de Craats Dit document geeft een systematische beschrijving van een wenselijk minimumniveau voor het vak rekenen op de basisschool, uitgesplitst naar verschillende domeinen.
Beter rekenonderwijs Jan van de Craats Dit document geeft een systematische beschrijving van een wenselijk minimumniveau voor het vak rekenen op de basisschool, uitgesplitst naar verschillende domeinen.
1. Optellen en aftrekken
 1. Optellen en aftrekken Om breuken op te tellen of af te trekken maak je de breuken gelijknamig. Gelijknamig maken wil zeggen dat je zorgt voor 'gelijke noemers': Om de breuken met 'derden' en 'vijfden'
1. Optellen en aftrekken Om breuken op te tellen of af te trekken maak je de breuken gelijknamig. Gelijknamig maken wil zeggen dat je zorgt voor 'gelijke noemers': Om de breuken met 'derden' en 'vijfden'
Een voorstel voor een alternatieve kennisbasis rekenen en wiskunde voor de pabo
 Stichting Goed Rekenonderwijs 1 Een voorstel voor een alternatieve kennisbasis rekenen en wiskunde voor de pabo 7 december 2009 Teachers cannot be expected to teach what they do not know National Mathematics
Stichting Goed Rekenonderwijs 1 Een voorstel voor een alternatieve kennisbasis rekenen en wiskunde voor de pabo 7 december 2009 Teachers cannot be expected to teach what they do not know National Mathematics
Tot het onderwijs in het vo horen naast de eerder genoemde getalsoorten ook nog machten, wortels en bijzondere getallen als π.
 De operationalisering voor Getallen Uit: Over de drempels met rekenen, Consolideren, onderhouden, gebruiken en verdiepen (zie voor het hele hoofdstuk en rapport: www.taalenrekenen.nl) Getallen 7.. Inleiding
De operationalisering voor Getallen Uit: Over de drempels met rekenen, Consolideren, onderhouden, gebruiken en verdiepen (zie voor het hele hoofdstuk en rapport: www.taalenrekenen.nl) Getallen 7.. Inleiding
2 REKENEN MET BREUKEN 3. 2.3 Optellen van breuken 6. 2.5 Aftrekken van breuken 9. 2.7 Vermenigvuldigen van breuken 11. 2.9 Delen van breuken 13
 REKENEN MET BREUKEN. De breuk. Opgaven. Optellen van breuken 6. Opgaven 8. Aftrekken van breuken 9.6 Opgaven 9.7 Vermenigvuldigen van breuken.8 Opgaven.9 Delen van breuken.0 Opgaven. Een deel van een deel.
REKENEN MET BREUKEN. De breuk. Opgaven. Optellen van breuken 6. Opgaven 8. Aftrekken van breuken 9.6 Opgaven 9.7 Vermenigvuldigen van breuken.8 Opgaven.9 Delen van breuken.0 Opgaven. Een deel van een deel.
SAMENVATTING BASIS & KADER
 SAMENVATTING BASIS & KADER Afronden Hoe je moet afronden hangt af van de situatie. Geldbedragen rond je meestal af op twee decimalen, 15,375 wordt 15,38. Grote getallen rondje meestal af op duizendtallen,
SAMENVATTING BASIS & KADER Afronden Hoe je moet afronden hangt af van de situatie. Geldbedragen rond je meestal af op twee decimalen, 15,375 wordt 15,38. Grote getallen rondje meestal af op duizendtallen,
Leerlijnen groep 8 Wereld in Getallen
 Leerlijnen groep 8 Wereld in Getallen 1 2 3 4 REKENEN Boek 8a: Blok 1 - week 1 Oriëntatie - uitspreken en schrijven van getallen rond 1 miljoen - introductie miljard - helen uit een breuk halen 5/4 = -
Leerlijnen groep 8 Wereld in Getallen 1 2 3 4 REKENEN Boek 8a: Blok 1 - week 1 Oriëntatie - uitspreken en schrijven van getallen rond 1 miljoen - introductie miljard - helen uit een breuk halen 5/4 = -
Instructie voor Docenten. Hoofdstuk 14 VERDER REKENEN MET KOMMAGETALLEN
 Instructie voor Docenten Hoofdstuk 14 VERDER REKENEN MET KOMMAGETALLEN Instructie voor docenten H14: VERDER REKENEN MET KOMMAGETALLEN DOELEN VAN DIT HOOFDSTUK: Leerlingen leren via verschillende manieren
Instructie voor Docenten Hoofdstuk 14 VERDER REKENEN MET KOMMAGETALLEN Instructie voor docenten H14: VERDER REKENEN MET KOMMAGETALLEN DOELEN VAN DIT HOOFDSTUK: Leerlingen leren via verschillende manieren
Kernbegrippen Kennisbasis wiskunde Onderdeel breuken
 Kernbegrippen Kennisbasis wiskunde Onderdeel breuken De omschreven begrippen worden expliciet genoemd in de Kennisbasis. De begrippen zijn in alfabetische volgorde opgenomen. Breuk Een breuk is een getal
Kernbegrippen Kennisbasis wiskunde Onderdeel breuken De omschreven begrippen worden expliciet genoemd in de Kennisbasis. De begrippen zijn in alfabetische volgorde opgenomen. Breuk Een breuk is een getal
Hoofdstuk 1: Basisvaardigheden
 Hoofdstuk 1: Basisvaardigheden Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 1: Basisvaardigheden Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde Getallen
Hoofdstuk 1: Basisvaardigheden Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 1: Basisvaardigheden Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde Getallen
0,6 = 6 / 10 0,36 = 36 / 100 0,05 = 5 /100 2,02 = 2 gehelen en 2 / 100
 Breuken 8 teller breukstreep 9 noemer Breukvorm - kommagetal 0,6 6 / 10 0,36 36 / 100 0,05 5 /100 2,02 2 gehelen en 2 / 100 Breuken en gehelen 1) Hoeveel keer gaat de noemer in de teller? 2) Hoeveel is
Breuken 8 teller breukstreep 9 noemer Breukvorm - kommagetal 0,6 6 / 10 0,36 36 / 100 0,05 5 /100 2,02 2 gehelen en 2 / 100 Breuken en gehelen 1) Hoeveel keer gaat de noemer in de teller? 2) Hoeveel is
Rekentermen en tekens
 Rekentermen en tekens Erbij de som is hetzelfde, is evenveel, is gelijk aan Eraf het verschil, korting is niet hetzelfde, is niet evenveel Keer het product kleiner dan, minder dan; wijst naar het kleinste
Rekentermen en tekens Erbij de som is hetzelfde, is evenveel, is gelijk aan Eraf het verschil, korting is niet hetzelfde, is niet evenveel Keer het product kleiner dan, minder dan; wijst naar het kleinste
Voorkennis : Breuken en letters
 Hoofdstuk 1 Getallen en Variabelen (V4 Wis A) Pagina 1 van 13 Voorkennis : Breuken en letters Les 1 : Breuken Bereken : a. 4 2 3 b. x 5 = c. 12 3 x a. 4 2 3 = 8 3 = 2 2 3 b. x 5 = 1 5 x c. 12 3 x = 12
Hoofdstuk 1 Getallen en Variabelen (V4 Wis A) Pagina 1 van 13 Voorkennis : Breuken en letters Les 1 : Breuken Bereken : a. 4 2 3 b. x 5 = c. 12 3 x a. 4 2 3 = 8 3 = 2 2 3 b. x 5 = 1 5 x c. 12 3 x = 12
Download gratis de PowerPoint rekenen domein getallen:
 Getallen Bron: Examenbladmbo.nl, SYLLABUS REKENEN 2F en 3F vo en mbo, Versie mei 2015 Download gratis de PowerPoint rekenen domein getallen: http://nielspicard.nl/download/powerpoint-rekenen-domein-getallen/
Getallen Bron: Examenbladmbo.nl, SYLLABUS REKENEN 2F en 3F vo en mbo, Versie mei 2015 Download gratis de PowerPoint rekenen domein getallen: http://nielspicard.nl/download/powerpoint-rekenen-domein-getallen/
3.2 Basiskennis. 3.2.1 De getallenlijn. 3.2.2 Symbolen, tekens en getallen. 92 Algebra. Inhoofdstuk1zijnaandeordegeweest: Het=teken. =staat.
 92 Algebra 3.2 Basiskennis Inhoofdstuk1zijnaandeordegeweest: 3.2.1 De getallenlijn... -5-4 -3-2 -1 0 1 2 3 4 5... 3.2.2 Symbolen, tekens en getallen Het=teken 5+2+3=10 = geeft aan dat wat links van = staat,
92 Algebra 3.2 Basiskennis Inhoofdstuk1zijnaandeordegeweest: 3.2.1 De getallenlijn... -5-4 -3-2 -1 0 1 2 3 4 5... 3.2.2 Symbolen, tekens en getallen Het=teken 5+2+3=10 = geeft aan dat wat links van = staat,
Voorkennis : Breuken en letters
 Hoofdstuk 1 Rekenregels en Verhoudingen (H4 Wis A) Pagina 1 van 11 Voorkennis : Breuken en letters Les 1 : Breuken Bereken : a. 4 2 3 b. x 5 = c. 12 3 x a. 4 2 3 = 8 3 = 2 2 3 b. x 5 = 1 5 x c. 12 3 x
Hoofdstuk 1 Rekenregels en Verhoudingen (H4 Wis A) Pagina 1 van 11 Voorkennis : Breuken en letters Les 1 : Breuken Bereken : a. 4 2 3 b. x 5 = c. 12 3 x a. 4 2 3 = 8 3 = 2 2 3 b. x 5 = 1 5 x c. 12 3 x
Onthoudboekje rekenen
 Onthoudboekje rekenen Inhoud 1. Hoofdrekenen: natuurlijke getallen tot 100 000 Optellen (p. 4) Aftrekken (p. 4) Vermenigvuldigen (p. 5) Delen (p. 5) Deling met rest (p. 6) 2. Hoofdrekenen: kommagetallen
Onthoudboekje rekenen Inhoud 1. Hoofdrekenen: natuurlijke getallen tot 100 000 Optellen (p. 4) Aftrekken (p. 4) Vermenigvuldigen (p. 5) Delen (p. 5) Deling met rest (p. 6) 2. Hoofdrekenen: kommagetallen
Uitwerkingen Rekenen met cijfers en letters
 Uitwerkingen Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 2009 c Swier Garst - RGO Middelharnis 2 Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Uitwerkingen Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 2009 c Swier Garst - RGO Middelharnis 2 Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Leerstofoverzicht groep 6
 Leerstofoverzicht groep 6 Getallen en relaties Basisbewerkingen Leerlijn Groep 6 Uitspraak, schrijfwijze, kenmerken getallen boven 10 000 in cijfers schrijven haakjesnotatie deler en deeltal breuknotatie
Leerstofoverzicht groep 6 Getallen en relaties Basisbewerkingen Leerlijn Groep 6 Uitspraak, schrijfwijze, kenmerken getallen boven 10 000 in cijfers schrijven haakjesnotatie deler en deeltal breuknotatie
Hoe is SmartRekenen opgebouwd?
 Hoe is SmartRekenen opgebouwd? Onderstaand figuur toont de opbouw van SmartRekenen: SmartRekenen 1F Instaptoets IT 2A 2F Referentieniveau Deel 1 Deel 3F Deel 2 Hoofdstuk 1 Paragraaf Eindtoets 2 Theorie
Hoe is SmartRekenen opgebouwd? Onderstaand figuur toont de opbouw van SmartRekenen: SmartRekenen 1F Instaptoets IT 2A 2F Referentieniveau Deel 1 Deel 3F Deel 2 Hoofdstuk 1 Paragraaf Eindtoets 2 Theorie
8000-4000=4000 900-600=300 90-90 =0 7-8= 1 tekort! 4000 + 300+0-1 = 4299
 Rekenstrategieën Voor de basisbewerkingen optellen en aftrekken, vermenigvuldigen en delen en voor het rekenen met breuken en rekenen met decimale getallen, wordt een overzicht gegeven van rekenstrategieën
Rekenstrategieën Voor de basisbewerkingen optellen en aftrekken, vermenigvuldigen en delen en voor het rekenen met breuken en rekenen met decimale getallen, wordt een overzicht gegeven van rekenstrategieën
Onderwijsassistent REKENEN BASISVAARDIGHEDEN
 Onderwijsassistent REKENEN BASISVAARDIGHEDEN Verhoudingstabel Wat zijn verhoudingen Rekenen met de verhoudingstabel Kruisprodukten Wat zijn verhoudingen * * * 2 Aantal rollen 1 2 12 Aantal beschuiten 18
Onderwijsassistent REKENEN BASISVAARDIGHEDEN Verhoudingstabel Wat zijn verhoudingen Rekenen met de verhoudingstabel Kruisprodukten Wat zijn verhoudingen * * * 2 Aantal rollen 1 2 12 Aantal beschuiten 18
Verdiepingsmodule Getallen Tweede bijeenkomst maandag 8 april 2013 monica wijers en vincent jonker
 Verdiepingsmodule Getallen Tweede bijeenkomst maandag 8 april 2013 monica wijers en vincent jonker Programma Breuken PPON Leerlijn Didactiek van bewerkingen Breuken en kommagetallen in het echt Kommagetallen
Verdiepingsmodule Getallen Tweede bijeenkomst maandag 8 april 2013 monica wijers en vincent jonker Programma Breuken PPON Leerlijn Didactiek van bewerkingen Breuken en kommagetallen in het echt Kommagetallen
Leerdoelen groep 7. Pluspunt rekenen
 Leerdoelen groep 7 Pluspunt rekenen NB. De leerdoelen van deze rekenmethode bieden wij de kinderen aan middels Denken in Doelen. Dat betekent dat we niet exact de blokken van de methode volgen, maar dat
Leerdoelen groep 7 Pluspunt rekenen NB. De leerdoelen van deze rekenmethode bieden wij de kinderen aan middels Denken in Doelen. Dat betekent dat we niet exact de blokken van de methode volgen, maar dat
Getallen 1 is een computerprogramma voor het aanleren van de basis rekenvaardigheden (getalbegrip).
 Getallen 1 Getallen 1 is een computerprogramma voor het aanleren van de basis rekenvaardigheden (getalbegrip). Doelgroep Rekenen en Wiskunde Getallen 1 Getallen 1 is geschikt voor groep 7 en 8 van de basisschool
Getallen 1 Getallen 1 is een computerprogramma voor het aanleren van de basis rekenvaardigheden (getalbegrip). Doelgroep Rekenen en Wiskunde Getallen 1 Getallen 1 is geschikt voor groep 7 en 8 van de basisschool
Rekentoetswijzer 3S. Voortgezet onderwijs. SLO nationaal expertisecentrum leerplanontwikkeling
 Rekentoetswijzer 3S Voortgezet onderwijs SLO nationaal expertisecentrum leerplanontwikkeling Rekentoetswijzer 3S December 2012 Verantwoording 2012 SLO (nationaal expertisecentrum leerplanontwikkeling),
Rekentoetswijzer 3S Voortgezet onderwijs SLO nationaal expertisecentrum leerplanontwikkeling Rekentoetswijzer 3S December 2012 Verantwoording 2012 SLO (nationaal expertisecentrum leerplanontwikkeling),
MYTHEN IN DE REKENDIDACTIEK
 Jan van de Craats (UvA, OU) MYTHEN IN DE REKENDIDACTIEK of: waarom Daan en Sanne niet kunnen rekenen Panama conferentie, 18 januari 2007 Jan van de Craats (UvA, OU) MYTHEN IN DE REKENDIDACTIEK of: Waarom
Jan van de Craats (UvA, OU) MYTHEN IN DE REKENDIDACTIEK of: waarom Daan en Sanne niet kunnen rekenen Panama conferentie, 18 januari 2007 Jan van de Craats (UvA, OU) MYTHEN IN DE REKENDIDACTIEK of: Waarom
Getallen 2. Doelgroep Rekenen en Wiskunde Getallen 2
 Getallen 2 Getallen 2 bestrijkt de uitbreiding van de basisvaardigheden van het rekenen, regels en vaardigheden die in het vmbo en de onderbouw van havo/vwo worden aangeleerd, geoefend en toegepast. Doelgroep
Getallen 2 Getallen 2 bestrijkt de uitbreiding van de basisvaardigheden van het rekenen, regels en vaardigheden die in het vmbo en de onderbouw van havo/vwo worden aangeleerd, geoefend en toegepast. Doelgroep
Antwoorden bij Rekenen met het hoofd
 Antwoorden bij Rekenen met het hoofd Hoofdstuk Basisbewerkingen. Bewerkingen in beeld a. : splitsen in 5 en. Eerst min 5, dan min 0 en tenslotte nog min : splitsen in 5 en, die uitvoeren en dan nog stapsgewijs
Antwoorden bij Rekenen met het hoofd Hoofdstuk Basisbewerkingen. Bewerkingen in beeld a. : splitsen in 5 en. Eerst min 5, dan min 0 en tenslotte nog min : splitsen in 5 en, die uitvoeren en dan nog stapsgewijs
Verhoudingen 1 is onderdeel van de Bundel Rekenen en Wiskunde 1. Deze bundel bevat ook Getallen 1, Meten en Meetkunde 1 en Verbanden 1.
 Verhoudingen 1 Verhoudingen 1 is onderdeel van de Bundel Rekenen en Wiskunde 1. Deze bundel bevat ook Getallen 1, Meten en Meetkunde 1 en Verbanden 1. Muiswerk Verhoudingen 1 bestrijkt de basisvaardigheden
Verhoudingen 1 Verhoudingen 1 is onderdeel van de Bundel Rekenen en Wiskunde 1. Deze bundel bevat ook Getallen 1, Meten en Meetkunde 1 en Verbanden 1. Muiswerk Verhoudingen 1 bestrijkt de basisvaardigheden
Kennis van de telrij De kinderen kunnen tellen en terugtellen tot 10 met sprongen van 1 en van 2.
 Rekenrijk doelen groep 1 en 2 De kinderen kunnen tellen en terugtellen tot 10 met sprongen van 1 en van 2. Aantallen kunnen tellen De kinderen kunnen kleine aantallen tellen. De kinderen kunnen eenvoudige
Rekenrijk doelen groep 1 en 2 De kinderen kunnen tellen en terugtellen tot 10 met sprongen van 1 en van 2. Aantallen kunnen tellen De kinderen kunnen kleine aantallen tellen. De kinderen kunnen eenvoudige
2.1 Bewerkingen [1] Video Geschiedenis van het rekenen ( 15 x 3 = 45
![2.1 Bewerkingen [1] Video Geschiedenis van het rekenen ( 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen ( 15 x 3 = 45](/thumbs/98/136422869.jpg) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
EXACT- Periode 1. Hoofdstuk Grootheden. 1.2 Eenheden.
 EXACT- Periode 1 Hoofdstuk 1 1.1 Grootheden. Een grootheid is in de natuurkunde en in de chemie en in de biologie: iets wat je kunt meten. Voorbeelden van grootheden (met bijbehorende symbolen): 1.2 Eenheden.
EXACT- Periode 1 Hoofdstuk 1 1.1 Grootheden. Een grootheid is in de natuurkunde en in de chemie en in de biologie: iets wat je kunt meten. Voorbeelden van grootheden (met bijbehorende symbolen): 1.2 Eenheden.
REKENTECHNIEKEN - OPLOSSINGEN
 REKENTECHNIEKEN - OPLOSSINGEN 1] 3,52 m + 13,6 cm =? 3,52 m 3,52 m - 2 13,6 cm 0,136 m - 3 3,656 m eindresultaat 3,66 m 2 cijfers na komma en afronden naar boven 3,52 m 352 cm - 0 13,6 cm 13,6 cm - 1 365,6
REKENTECHNIEKEN - OPLOSSINGEN 1] 3,52 m + 13,6 cm =? 3,52 m 3,52 m - 2 13,6 cm 0,136 m - 3 3,656 m eindresultaat 3,66 m 2 cijfers na komma en afronden naar boven 3,52 m 352 cm - 0 13,6 cm 13,6 cm - 1 365,6
INHOUDSOPGAVE. HOOFDSTUK 6 AFRONDEN Inleiding Cijfers Verstandig afronden 48 BLZ
 INHOUDSOPGAVE BLZ HOOFDSTUK 1 DOMEIN A: GETALLEN 15 1.1. Inleiding 15 1.2. Cijfers en getallen 15 1.3. Gebroken getallen 16 1.4. Negatieve getallen 17 1.5. Symbolen en vergelijken van getallen 19 HOOFDSTUK
INHOUDSOPGAVE BLZ HOOFDSTUK 1 DOMEIN A: GETALLEN 15 1.1. Inleiding 15 1.2. Cijfers en getallen 15 1.3. Gebroken getallen 16 1.4. Negatieve getallen 17 1.5. Symbolen en vergelijken van getallen 19 HOOFDSTUK
Het Breukenboekje. Alles over breuken
 Het Breukenboekje Alles over breuken breuken breukentaal tekening getal een hele 1 een halve een kwart een achtste ½ of ½ ¼ of ¼ ⅛ of ⅛ 3 breuken breukentaal tekening getal een vijfde ⅕ of ⅕ een tiende
Het Breukenboekje Alles over breuken breuken breukentaal tekening getal een hele 1 een halve een kwart een achtste ½ of ½ ¼ of ¼ ⅛ of ⅛ 3 breuken breukentaal tekening getal een vijfde ⅕ of ⅕ een tiende
Getallen 1F Doelen Voorbeelden 2F Doelen Voorbeelden
 A Notatie en betekenis - Uitspraak, schrijfwijze en betekenis van, symbolen en relaties - Wiskundetaal gebruiken - de relaties groter/kleiner dan - breuknotatie met horizontale streep - teller, noemer,
A Notatie en betekenis - Uitspraak, schrijfwijze en betekenis van, symbolen en relaties - Wiskundetaal gebruiken - de relaties groter/kleiner dan - breuknotatie met horizontale streep - teller, noemer,
Programma: De rekendocent voor het MBO
 Rekenen op Rekenen Didactische training tot rekendocent [email protected] http://www.rekenenoprekenen.nl Programma: De rekendocent voor het MBO Doel: zelfstandig rekenonderwijs kunnen verzorgen
Rekenen op Rekenen Didactische training tot rekendocent [email protected] http://www.rekenenoprekenen.nl Programma: De rekendocent voor het MBO Doel: zelfstandig rekenonderwijs kunnen verzorgen
Rekenportfolio. Naam: cm 2. m 3 + = 1 _ 12
 Tytsjerksteradiel Rekenportfolio Naam: cm 2 1 5 7 + = 5 10 10 m 3 1 _ 12 X 5 1 + = 5 1 + Inhoudsopgave Voorwoord 3 Domein getallen 4 - Optellen, aftrekken, vermenigvuldigen en delen 5 - Breuken 6 - Rekenvolgorde
Tytsjerksteradiel Rekenportfolio Naam: cm 2 1 5 7 + = 5 10 10 m 3 1 _ 12 X 5 1 + = 5 1 + Inhoudsopgave Voorwoord 3 Domein getallen 4 - Optellen, aftrekken, vermenigvuldigen en delen 5 - Breuken 6 - Rekenvolgorde
2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45
![2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 = 45](/thumbs/72/68043516.jpg) 15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
15 x 3 = 45 2.1 Bewerkingen [1] Video Geschiedenis van het rekenen (http://www.youtube.com/watch?v=cceqwwj6vrs) 15 x 3 is een product. 15 en 3 zijn de factoren van het product. 15 : 3 = 5 15 : 3 is een
Leerlijnen groep 7 Wereld in Getallen
 Leerlijnen groep 7 Wereld in Getallen 1 2 REKENEN Boek 7a: Blok 1 - week 1 in geldcontext 2 x 2,95 = / 4 x 2,95 = Optellen en aftrekken tot 10.000 - ciferend; met 2 of 3 getallen 4232 + 3635 + 745 = 1600
Leerlijnen groep 7 Wereld in Getallen 1 2 REKENEN Boek 7a: Blok 1 - week 1 in geldcontext 2 x 2,95 = / 4 x 2,95 = Optellen en aftrekken tot 10.000 - ciferend; met 2 of 3 getallen 4232 + 3635 + 745 = 1600
Getallen 2. Doelgroep Rekenen en Wiskunde Getallen 2. Omschrijving Rekenen en Wiskunde Getallen 2
 Getallen 2 Getallen 2 bestrijkt de uitbreiding van de basisvaardigheden van het rekenen, regels en vaardigheden die in het vmbo en de onderbouw van havo/vwo worden aangeleerd, geoefend en toegepast. Doelgroep
Getallen 2 Getallen 2 bestrijkt de uitbreiding van de basisvaardigheden van het rekenen, regels en vaardigheden die in het vmbo en de onderbouw van havo/vwo worden aangeleerd, geoefend en toegepast. Doelgroep
Rekentoetswijzer 2F. Eindversie
 Rekentoetswijzer 2F Eindversie Voorwoord De rekentoetswijzer stelt docenten in staat zich een beeld te vormen van wat er in de rekentoetsen rekenen 2F voor het voortgezet onderwijs wel en niet gevraagd
Rekentoetswijzer 2F Eindversie Voorwoord De rekentoetswijzer stelt docenten in staat zich een beeld te vormen van wat er in de rekentoetsen rekenen 2F voor het voortgezet onderwijs wel en niet gevraagd
Aandachtspunten. blok 7, les 1 blok 7, les 3 blok 7, les 6 blok 7, les 8 blok 7, les 11 blok 9, les 1
 Aandachtspunten 291 Aandachtspuntenlijst 3, bij blok 7, 8 en 9 1 Getalbegrip. Het kind ziet de structuur niet tussen getallen boven en beneden 1 miljoen. uitspreken en opschrijven van grote getallen boven
Aandachtspunten 291 Aandachtspuntenlijst 3, bij blok 7, 8 en 9 1 Getalbegrip. Het kind ziet de structuur niet tussen getallen boven en beneden 1 miljoen. uitspreken en opschrijven van grote getallen boven
Duizend 3 getallen achter de komma 230 duizend 230 000 46 duizend 46 000 Andersom 345 600 345,6 duizend 24 500 24,5 duizend
 Hoofdstuk 5 5A Grote getallen Duizend 3 getallen achter de komma 230 duizend 230 000 46 duizend 46 000 Andersom 345 600 345,6 duizend 24 500 24,5 duizend Miljoen 6 getallen achter de komma 230 miljoen
Hoofdstuk 5 5A Grote getallen Duizend 3 getallen achter de komma 230 duizend 230 000 46 duizend 46 000 Andersom 345 600 345,6 duizend 24 500 24,5 duizend Miljoen 6 getallen achter de komma 230 miljoen
Mythen in de rekendidactiek
 Mythen in de rekendidactiek Waarom Daan en Sanne niet kunnen rekenen Rekensymposium De Rekenacademie Leopoldsburg, België, 8 mei 2014 Jan van de Craats Universiteit van Amsterdam Reken mee (pen en papier
Mythen in de rekendidactiek Waarom Daan en Sanne niet kunnen rekenen Rekensymposium De Rekenacademie Leopoldsburg, België, 8 mei 2014 Jan van de Craats Universiteit van Amsterdam Reken mee (pen en papier
De teller geeft hoeveel stukken er zijn en de noemer zegt wat de 5. naam is van die stukken: 6 taart geeft dus aan dat de taart in 6
 Breuken Breuk betekent dat er iets gebroken is. Het is niet meer heel. Als je een meloen doormidden snijdt, is die niet meer heel, maar verdeeld in twee stukken. Eén zo n stuk is dan een halve meloen,
Breuken Breuk betekent dat er iets gebroken is. Het is niet meer heel. Als je een meloen doormidden snijdt, is die niet meer heel, maar verdeeld in twee stukken. Eén zo n stuk is dan een halve meloen,
Klok dag en nacht. Hulpkaart OPTELLEN/AFTREKKEN
 OPTELLEN/AFTREKKEN Zet de getallen onder elkaar in je schrift eerst zelf proberen uit te rekenen bij aftrekken: denk om lenen bij optellen: denk om doorschuiven geen vergissingen? bij lang nadenken: rekenmachine
OPTELLEN/AFTREKKEN Zet de getallen onder elkaar in je schrift eerst zelf proberen uit te rekenen bij aftrekken: denk om lenen bij optellen: denk om doorschuiven geen vergissingen? bij lang nadenken: rekenmachine
Getallen 1 is een programma voor het aanleren van de basis rekenvaardigheden (getalbegrip).
 Getallen 1 Getallen 1 is een programma voor het aanleren van de basis rekenvaardigheden (getalbegrip). Doelgroep Rekenen en Wiskunde Getallen 1 Getallen 1 is geschikt voor groep 7 en 8 van de basisschool
Getallen 1 Getallen 1 is een programma voor het aanleren van de basis rekenvaardigheden (getalbegrip). Doelgroep Rekenen en Wiskunde Getallen 1 Getallen 1 is geschikt voor groep 7 en 8 van de basisschool
Dossier opdracht 2. Analyse 1 - Didactiek
 Dossier opdracht 2 Analyse 1 - Didactiek Naam: Thomas Sluyter Nummer: 1018808 Jaar / Klas: 1e jaar Docent Wiskunde, deeltijd Datum: 21 november, 2007 Samenvatting Uit onderzoek van CITO blijkt dat veel
Dossier opdracht 2 Analyse 1 - Didactiek Naam: Thomas Sluyter Nummer: 1018808 Jaar / Klas: 1e jaar Docent Wiskunde, deeltijd Datum: 21 november, 2007 Samenvatting Uit onderzoek van CITO blijkt dat veel
Bijlage Wiskunde vmbo
 Bijlage Wiskunde vmbo IJking Referentiekader Rekenen versus Examenprogramma's Victor Schmidt April 2010 Verantwoording 2010 Stichting leerplanontwikkeling (SLO), Enschede Alle rechten voorbehouden. Mits
Bijlage Wiskunde vmbo IJking Referentiekader Rekenen versus Examenprogramma's Victor Schmidt April 2010 Verantwoording 2010 Stichting leerplanontwikkeling (SLO), Enschede Alle rechten voorbehouden. Mits
Uit De Ophaalbrug, werkmateriaal bij de overstap basisonderwijs voortgezet onderwijs, sept. 2003
 Uit De Ophaalbrug, werkmateriaal bij de overstap basisonderwijs voortgezet onderwijs, sept. 2003 REKENEN-WISKUNDE VERSLAG Samenstelling De BOVO-kwaliteitsgroep rekenen-wiskunde bestond uit: Sira Kamermans,
Uit De Ophaalbrug, werkmateriaal bij de overstap basisonderwijs voortgezet onderwijs, sept. 2003 REKENEN-WISKUNDE VERSLAG Samenstelling De BOVO-kwaliteitsgroep rekenen-wiskunde bestond uit: Sira Kamermans,
Cursus voor Rekenondersteuners rekenen de 3 e slag. Bijeenkomst 3 28 februari 2012 Ceciel Borghouts & Monica Wijers Freudenthal Instituut
 Cursus voor Rekenondersteuners rekenen de 3 e slag Bijeenkomst 3 28 februari 2012 Ceciel Borghouts & Monica Wijers Freudenthal Instituut deel 0 EVEN DE KRANT 1. Huiswerk Programma 16 februari doen
Cursus voor Rekenondersteuners rekenen de 3 e slag Bijeenkomst 3 28 februari 2012 Ceciel Borghouts & Monica Wijers Freudenthal Instituut deel 0 EVEN DE KRANT 1. Huiswerk Programma 16 februari doen
Deel 1: Getallenkennis
 Deel 1: Getallenkennis 1 Natuurlijke getallen 10 1.1 De waarde van cijfers in natuurlijke getallen 10 Les 1: Natuurlijke getallen kleiner dan 10 000 10 Les 2: Natuurlijke getallen kleiner dan 100 000 13
Deel 1: Getallenkennis 1 Natuurlijke getallen 10 1.1 De waarde van cijfers in natuurlijke getallen 10 Les 1: Natuurlijke getallen kleiner dan 10 000 10 Les 2: Natuurlijke getallen kleiner dan 100 000 13
wat is de som zie ik een instinker bij de antwoorden? het goede antwoord aan
 e it re st r st 1. ik lees de opgave 2. ik kijk naar het plaatje 3. wat is de som die schrijf ik op kladpapier 4. ik kijk naar de antwoorden, antwoorden die niet kunnen streep ik in mijn hoofd weg! 5.
e it re st r st 1. ik lees de opgave 2. ik kijk naar het plaatje 3. wat is de som die schrijf ik op kladpapier 4. ik kijk naar de antwoorden, antwoorden die niet kunnen streep ik in mijn hoofd weg! 5.
Begin situatie Wiskunde/Rekenen. VMBO BB leerling
 VMBO BB leerling Verbanden en Hoge -bewerkingen onder 100 -tafels t/m 10 (x:) -bewerkingen met eenvoudige grote en -makkelijk rekenen -vergelijken/ordenen op getallenlijn -makkelijke breuken omzetten -deel
VMBO BB leerling Verbanden en Hoge -bewerkingen onder 100 -tafels t/m 10 (x:) -bewerkingen met eenvoudige grote en -makkelijk rekenen -vergelijken/ordenen op getallenlijn -makkelijke breuken omzetten -deel
1 Basisrekenen en letterrekenen.
 Uitwerkingen versie 0 Basisrekenen en letterrekenen. Opgave. Opbouw van getallen. a 605 6 00 + 5 b 3.78 3 000+ 00+ 7 0+ 8 c 56.890 56 000+ 8 00+ 9 0+ 0 d 900.30 900 000+ 00+ 0+ 0 e 3.56.675 3.000.000+
Uitwerkingen versie 0 Basisrekenen en letterrekenen. Opgave. Opbouw van getallen. a 605 6 00 + 5 b 3.78 3 000+ 00+ 7 0+ 8 c 56.890 56 000+ 8 00+ 9 0+ 0 d 900.30 900 000+ 00+ 0+ 0 e 3.56.675 3.000.000+
Op stap naar 1 B Minimumdoelen wiskunde
 Campus Zuid Boomsesteenweg 265 2020 Antwerpen Tel. (03) 216 29 38 Fax (03) 238 78 31 www.vclbdewisselantwerpen.be VCLB De Wissel - Antwerpen Vrij Centrum voor Leerlingenbegeleiding Op stap naar 1 B Minimumdoelen
Campus Zuid Boomsesteenweg 265 2020 Antwerpen Tel. (03) 216 29 38 Fax (03) 238 78 31 www.vclbdewisselantwerpen.be VCLB De Wissel - Antwerpen Vrij Centrum voor Leerlingenbegeleiding Op stap naar 1 B Minimumdoelen
Blok 4 G/B vraag 1: een kommagetal cijferend delen door een natuurlijk getal < 100
 Blok 4 G/B vraag 1: een kommagetal cijferend delen door een natuurlijk getal < 100 Een kommagetal cijferend delen door een natuurlijk getal < 100 510,8 : 23 =? Ik schat 500 : 20 = 25 Ik noteer de rekenhulp.
Blok 4 G/B vraag 1: een kommagetal cijferend delen door een natuurlijk getal < 100 Een kommagetal cijferend delen door een natuurlijk getal < 100 510,8 : 23 =? Ik schat 500 : 20 = 25 Ik noteer de rekenhulp.
Bijlage 11 - Toetsenmateriaal
 Bijlage - Toetsenmateriaal Toets Module In de eerste module worden de getallen behandeld: - Natuurlijke getallen en talstelsels - Gemiddelde - mediaan - Getallenas en assenstelsel - Gehele getallen met
Bijlage - Toetsenmateriaal Toets Module In de eerste module worden de getallen behandeld: - Natuurlijke getallen en talstelsels - Gemiddelde - mediaan - Getallenas en assenstelsel - Gehele getallen met
Getal en Ruimte wi 1 havo/vwo deel 1 hoofdstuk 4 Didactische analyse door Lennaert van den Brink (1310429)
 Getal en Ruimte wi 1 havo/vwo deel 1 hoofdstuk 4 Didactische analyse door Lennaert van den Brink (1310429) - een lijst met operationele en concrete doelen van de lessenserie, indien mogelijk gerelateerd
Getal en Ruimte wi 1 havo/vwo deel 1 hoofdstuk 4 Didactische analyse door Lennaert van den Brink (1310429) - een lijst met operationele en concrete doelen van de lessenserie, indien mogelijk gerelateerd
REKENEN Hfst 1-3 PROCENTEN. Procenten betekent per honderd.
 REKENEN Hfst 1-3 PROCENTEN Procenten betekent per honderd. Percentage Groeifactor 1% 1/100 0,01 2% 2/100 0,02 10% 10/100 0,10 99% 99/100 0,99 104% 104/100 1,04 150% 150/100 1,50 Rekenen met procenten:
REKENEN Hfst 1-3 PROCENTEN Procenten betekent per honderd. Percentage Groeifactor 1% 1/100 0,01 2% 2/100 0,02 10% 10/100 0,10 99% 99/100 0,99 104% 104/100 1,04 150% 150/100 1,50 Rekenen met procenten:
Blok 4 G/B vraag 1: een kommagetal cijferend delen door een natuurlijk getal < 100
 Blok 4 G/B vraag 1: een kommagetal cijferend delen door een natuurlijk getal < 100 Een kommagetal cijferend delen door een natuurlijk getal < 100 510,8 : 23 =? Ik schat 500 : 20 = 25 Ik noteer de rekenhulp.
Blok 4 G/B vraag 1: een kommagetal cijferend delen door een natuurlijk getal < 100 Een kommagetal cijferend delen door een natuurlijk getal < 100 510,8 : 23 =? Ik schat 500 : 20 = 25 Ik noteer de rekenhulp.
Reken zeker: leerlijn breuken
 Reken zeker: leerlijn breuken B = breuk H = hele HB = hele plus breuk (1 1/4) Blauwe tekst is theorie uit het leerlingenboek. De breuknotatie in Reken zeker is - anders dan in deze handout - met horizontale
Reken zeker: leerlijn breuken B = breuk H = hele HB = hele plus breuk (1 1/4) Blauwe tekst is theorie uit het leerlingenboek. De breuknotatie in Reken zeker is - anders dan in deze handout - met horizontale
INHOUDSTAFEL. inhoudstafel... 2
 INHOUDSTAFEL inhoudstafel... 2 getallenkennis waarde van cijfers in een getal... 6 grote getallen... 7 rekentaal... 8 rekentaal deel 2... 9 soorten getallen... 9 rekentaal deel 3... 10 de ongelijke verdeling...
INHOUDSTAFEL inhoudstafel... 2 getallenkennis waarde van cijfers in een getal... 6 grote getallen... 7 rekentaal... 8 rekentaal deel 2... 9 soorten getallen... 9 rekentaal deel 3... 10 de ongelijke verdeling...
2.1 Kennismaken met breuken. 2.1.1 Deel van geheel. Opdracht 1 Welk deel van deze cirkel is zwart ingekleurd?
 Oefenopdrachten hoofdstuk Gebroken getallen RekenWijzer, oefenopdrachten hoofdstuk Gebroken getallen. Kennismaken met breuken.. eel van geheel Opdracht Welk deel van deze cirkel is zwart ingekleurd? deel
Oefenopdrachten hoofdstuk Gebroken getallen RekenWijzer, oefenopdrachten hoofdstuk Gebroken getallen. Kennismaken met breuken.. eel van geheel Opdracht Welk deel van deze cirkel is zwart ingekleurd? deel
De laatste loodjes...
 De laatste loodjes... Hieronder vindt je een uittreksel van alles dat we met rekenen hebben geoefend. En nog een paar herhaalsommetjes. Om als laatste nog even door te lezen om te zien of je alles nog
De laatste loodjes... Hieronder vindt je een uittreksel van alles dat we met rekenen hebben geoefend. En nog een paar herhaalsommetjes. Om als laatste nog even door te lezen om te zien of je alles nog
Referentieniveaus uitgelegd. 1S - rekenen Vaardigheden referentieniveau 1S rekenen. 1F - rekenen Vaardigheden referentieniveau 1F rekenen
 Referentieniveaus uitgelegd De beschrijvingen zijn gebaseerd op het Referentiekader taal en rekenen'. In 'Referentieniveaus uitgelegd' zijn de niveaus voor de verschillende sectoren goed zichtbaar. Door
Referentieniveaus uitgelegd De beschrijvingen zijn gebaseerd op het Referentiekader taal en rekenen'. In 'Referentieniveaus uitgelegd' zijn de niveaus voor de verschillende sectoren goed zichtbaar. Door
REKENTOETS VMBO BB/KB/TL-GL
 rekentoets vmbo BB/KB/TL-GL vakinformatie staatsexamen 2020 REKENTOETS VMBO BB/KB/TL-GL VAKINFORMATIE STAATSEXAMEN 2020 Versie: 22 maart 2019 pagina 1 van 7 rekentoets vmbo BB/KB/TL-GL vakinformatie staatsexamen
rekentoets vmbo BB/KB/TL-GL vakinformatie staatsexamen 2020 REKENTOETS VMBO BB/KB/TL-GL VAKINFORMATIE STAATSEXAMEN 2020 Versie: 22 maart 2019 pagina 1 van 7 rekentoets vmbo BB/KB/TL-GL vakinformatie staatsexamen
Leerlijnen rekenen: De wereld in getallen
 Leerlijnen rekenen: De wereld in getallen Groep 7(eerste helft) Getalbegrip - Telrij tot en met 1 000 000 - Uitspraak en schrijfwijze van de getallen (800 000 en 0,8 miljoen) - De opbouw en positiewaarde
Leerlijnen rekenen: De wereld in getallen Groep 7(eerste helft) Getalbegrip - Telrij tot en met 1 000 000 - Uitspraak en schrijfwijze van de getallen (800 000 en 0,8 miljoen) - De opbouw en positiewaarde
Hoofdstuk 5 gaat over rekenen. Deel 2 is eigenlijk herhaling van alle stof. Trainen voor het examen.
 Hoofdstuk 5 gaat over rekenen. Deel 2 is eigenlijk herhaling van alle stof. Trainen voor het examen. Het werkt als volgt, Je maakt een opgave bijv. opgave 1. Hoe gaat het ook al weer denk je dan. Nou,
Hoofdstuk 5 gaat over rekenen. Deel 2 is eigenlijk herhaling van alle stof. Trainen voor het examen. Het werkt als volgt, Je maakt een opgave bijv. opgave 1. Hoe gaat het ook al weer denk je dan. Nou,
DE basis WISKUNDE VOOR DE LAGERE SCHOOL
 Inhoud GETALLENKENNIS 13 1 Getallen 13 2 Het decimale talstelsel 14 3 Breuken 16 Begrippen 16 Soorten breuken 16 Een breuk vereenvoudigen 17 4 Breuken, percenten, kommagetallen 18 Breuk omzetten in een
Inhoud GETALLENKENNIS 13 1 Getallen 13 2 Het decimale talstelsel 14 3 Breuken 16 Begrippen 16 Soorten breuken 16 Een breuk vereenvoudigen 17 4 Breuken, percenten, kommagetallen 18 Breuk omzetten in een
D A G 1 : T W E E D O M E I N E N
 REKENEN 3F DAG 1 :TWEE DOMEINEN DAG 2 : TWEE DOMEINEN DAG 3: EXAMENTRAINING DAG 4:EXAMENTRAINING EN A FRONDING Programma: Voorstellen 13.30 uur 16.15 uur Pauze: 15 minuten Theorie dag 1: Domein Getallen
REKENEN 3F DAG 1 :TWEE DOMEINEN DAG 2 : TWEE DOMEINEN DAG 3: EXAMENTRAINING DAG 4:EXAMENTRAINING EN A FRONDING Programma: Voorstellen 13.30 uur 16.15 uur Pauze: 15 minuten Theorie dag 1: Domein Getallen
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde
![8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde](/thumbs/98/138669860.jpg) 8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
8.1 Herleiden [1] Herleiden bij vermenigvuldigen: -5 3a 6b 8c = -720abc 1) Vermenigvuldigen cijfers (let op teken) 2) Letters op alfabetische volgorde Optellen: 5a + 3b + 2a + 6b = 7a + 9b 1) Alleen gelijksoortige
Instructie voor Docenten. Hoofdstuk19 KOMMAGETALLEN - BASIS
 Instructie voor Docenten Hoofdstuk9 KOMMAGETALLEN - BASIS Instructie voor docenten H9: KOMMAGETALLEN DE BASIS DOELEN VAN DE LES: Leerlingen weten dat getallen in de plaatswaarde kaart een bepaalde waarde
Instructie voor Docenten Hoofdstuk9 KOMMAGETALLEN - BASIS Instructie voor docenten H9: KOMMAGETALLEN DE BASIS DOELEN VAN DE LES: Leerlingen weten dat getallen in de plaatswaarde kaart een bepaalde waarde
1.Tijdsduur. maanden:
 1.Tijdsduur 1 etmaal = 24 uur 1 uur = 60 minuten 1 minuut = 60 seconden 1 uur = 3600 seconden 1 jaar = 12 maanden 1 jaar = 52 weken 1 jaar = 365 (of 366 in schrikkeljaar) dagen 1 jaar = 4 kwartalen 1 kwartaal
1.Tijdsduur 1 etmaal = 24 uur 1 uur = 60 minuten 1 minuut = 60 seconden 1 uur = 3600 seconden 1 jaar = 12 maanden 1 jaar = 52 weken 1 jaar = 365 (of 366 in schrikkeljaar) dagen 1 jaar = 4 kwartalen 1 kwartaal
1 Rekenen met gehele getallen
 1 Inhoudsopgave 1 Rekenen met gehele getallen... 1.1 De gehele getallen... 1. Optellen... 1. Opgaven... 1. Aftrekken... 1. Opgaven... 1. Vermenigvuldigen... 1. Opgaven... 1.8 Delen... 9 1.9 Opgaven...9
1 Inhoudsopgave 1 Rekenen met gehele getallen... 1.1 De gehele getallen... 1. Optellen... 1. Opgaven... 1. Aftrekken... 1. Opgaven... 1. Vermenigvuldigen... 1. Opgaven... 1.8 Delen... 9 1.9 Opgaven...9
Deel 1: Getallenkennis
 Deel 1: Getallenkennis 1 Natuurlijke getallen 10 1.1 De waarde van cijfers in natuurlijke getallen 10 Les 1: Natuurlijke getallen kleiner dan 100 000 10 Les 2: Natuurlijke getallen kleiner dan 1 000 000
Deel 1: Getallenkennis 1 Natuurlijke getallen 10 1.1 De waarde van cijfers in natuurlijke getallen 10 Les 1: Natuurlijke getallen kleiner dan 100 000 10 Les 2: Natuurlijke getallen kleiner dan 1 000 000
Deel 1: Getallenkennis
 Deel 1: Getallenkennis 1 Natuurlijke getallen 10 1.1 De waarde van cijfers in natuurlijke getallen 10 Les 1: Natuurlijke getallen kleiner dan 10 000 10 Les 2: Natuurlijke getallen kleiner dan 100 000 13
Deel 1: Getallenkennis 1 Natuurlijke getallen 10 1.1 De waarde van cijfers in natuurlijke getallen 10 Les 1: Natuurlijke getallen kleiner dan 10 000 10 Les 2: Natuurlijke getallen kleiner dan 100 000 13
WISKUNDE 1. Aansluitmodule wiskunde MBO-HBO
 WISKUNDE 1 Aansluitmodule wiskunde MBO-HBO Wat moet je aanschaffen? Basisboek wiskunde tweede editie Jan van de Craats en Rob Bosch isbn:978-90-430-1673-5 Dit boek gebruikt men ook op de Hanze bij engineering.
WISKUNDE 1 Aansluitmodule wiskunde MBO-HBO Wat moet je aanschaffen? Basisboek wiskunde tweede editie Jan van de Craats en Rob Bosch isbn:978-90-430-1673-5 Dit boek gebruikt men ook op de Hanze bij engineering.
REKENTOETSWIJZER 3F 2015 REKENTOETS VO 2015
 REKENTOETSWIJZER 3F 2015 REKENTOETS VO 2015 pagina 2 van 16 Inhoud Voorwoord 5 Vooraf 6 1 Inleiding 7 1.1 Wat is een rekentoetswijzer? 7 1.2 De rekentoets 3F 7 1.3 Uitgangspunten bij de constructie van
REKENTOETSWIJZER 3F 2015 REKENTOETS VO 2015 pagina 2 van 16 Inhoud Voorwoord 5 Vooraf 6 1 Inleiding 7 1.1 Wat is een rekentoetswijzer? 7 1.2 De rekentoets 3F 7 1.3 Uitgangspunten bij de constructie van
Willem van Ravenstein
 Willem van Ravenstein 1. Variabelen Rekenen is het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken je de bewerkingen machtsverheffen en worteltrekken.
Willem van Ravenstein 1. Variabelen Rekenen is het werken met getallen. Er zijn vier hoofdbewerkingen: optellen, aftrekken, vermenigvuldigen en delen. Verder ken je de bewerkingen machtsverheffen en worteltrekken.
Verhoudingen. de deel geheel relatie: 4 als 3 van de 4 delen van een geheel ( 4 taart);
 De operationalisering voor Verhoudingen Uit: Over de drempels met rekenen, Consolideren, onderhouden, gebruiken en verdiepen (zie voor het hele hoofdstuk en rapport: www.taalenrekenen.nl) Verhoudingen
De operationalisering voor Verhoudingen Uit: Over de drempels met rekenen, Consolideren, onderhouden, gebruiken en verdiepen (zie voor het hele hoofdstuk en rapport: www.taalenrekenen.nl) Verhoudingen
Rekensprong 5 boek A. Getallenkennis boek A sprong 1, 2 en 3
 Rekensprong 5 boek A Getallenkennis boek A sprong 1, 2 en 3 Sprong 1 les 2 natuurlijke getallen tot 100 000 Sprong 1 les 6 kommagetallen Sprong 2 les 14 de breuk als operator Sprong 2 les 19 de breuk als
Rekensprong 5 boek A Getallenkennis boek A sprong 1, 2 en 3 Sprong 1 les 2 natuurlijke getallen tot 100 000 Sprong 1 les 6 kommagetallen Sprong 2 les 14 de breuk als operator Sprong 2 les 19 de breuk als
Rekenen met cijfers en letters
 Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 009 c Swier Garst - RGO Middelharnis Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
Rekenen met cijfers en letters Maerlant College Brielle 5 oktober 009 c Swier Garst - RGO Middelharnis Inhoudsopgave Rekenen met gehele getallen 7. De gehele getallen.....................................
6 Breuken VOORBEELDPAGINA S. Bestelnr Het grote rekenboek - overzicht - Hoofdstuk Breuken
 Bestelnr. Het grote rekenboek - overzicht - Hoofdstuk Breuken K-Publisher B.V. Prins Hendrikstraat NL- CS Bodegraven Telefoon +(0)- 0 Telefax +(0)- [email protected] www.k-publisher.nl Breuken Breuk
Bestelnr. Het grote rekenboek - overzicht - Hoofdstuk Breuken K-Publisher B.V. Prins Hendrikstraat NL- CS Bodegraven Telefoon +(0)- 0 Telefax +(0)- [email protected] www.k-publisher.nl Breuken Breuk
Overig nieuws Hulp ouders bij rekenen deel 3.
 Overig nieuws Hulp ouders bij rekenen deel 3. Het rekenonderwijs van tegenwoordig ziet er anders uit dan vroeger. Dat komt omdat er nieuwe inzichten zijn over hoe kinderen het beste leren. Vroeger lag
Overig nieuws Hulp ouders bij rekenen deel 3. Het rekenonderwijs van tegenwoordig ziet er anders uit dan vroeger. Dat komt omdat er nieuwe inzichten zijn over hoe kinderen het beste leren. Vroeger lag
INSIGHT Rekentoets. Spoorboekje. Tijd voor rekenen!
 INSIGHT Rekentoets Spoorboekje Tijd voor rekenen! Colofon Titel: Subtitel: Uitgave door: Adres: Insight Rekentoets Spoorboekje AMN b.v. Arnhem Oude Oeverstraat 120 6811 Arnhem Tel. 026-3557333 [email protected]
INSIGHT Rekentoets Spoorboekje Tijd voor rekenen! Colofon Titel: Subtitel: Uitgave door: Adres: Insight Rekentoets Spoorboekje AMN b.v. Arnhem Oude Oeverstraat 120 6811 Arnhem Tel. 026-3557333 [email protected]
Exact periode = 1. h = 0, Js. h= 6, Js 12 * 12 = 1,4.10 2
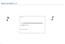 Exact periode 1.1 0 = 1 h = 0,000000000000000000000000000000000662607Js h= 6,62607. -34 Js 12 * 12 = 1,4. 2 1 Instructie gebruik CASIO fx-82ms 1. Instellingen resetten tot begininstellingen
Exact periode 1.1 0 = 1 h = 0,000000000000000000000000000000000662607Js h= 6,62607. -34 Js 12 * 12 = 1,4. 2 1 Instructie gebruik CASIO fx-82ms 1. Instellingen resetten tot begininstellingen
Deel 12 en 13 van De Wiskanjers Zorg: Curriculumdifferentiatie
 Deel 12 en 13 van De Wiskanjers Zorg: Curriculumdifferentiatie Deze mappen willen wegwijzers aanreiken om vanuit begrip en respect het beste te halen uit die leerlingen die de basis wiskundeleerstof uit
Deel 12 en 13 van De Wiskanjers Zorg: Curriculumdifferentiatie Deze mappen willen wegwijzers aanreiken om vanuit begrip en respect het beste te halen uit die leerlingen die de basis wiskundeleerstof uit
Dit betekent. noodzakelijk.
 Doelenlijsten 6 t/m 7: Verhoudingen Legenda De cel in de kolom Leerroute 2 po/s(b)o heeft als kleur In de bijborende kolommen Leerroute vmbo 2F of vmbo- bb 2A staat In de cel staat of. De cel heeft een
Doelenlijsten 6 t/m 7: Verhoudingen Legenda De cel in de kolom Leerroute 2 po/s(b)o heeft als kleur In de bijborende kolommen Leerroute vmbo 2F of vmbo- bb 2A staat In de cel staat of. De cel heeft een
3.1 Haakjes wegwerken [1]
![3.1 Haakjes wegwerken [1] 3.1 Haakjes wegwerken [1]](/thumbs/53/31611347.jpg) 3.1 Haakjes wegwerken [1] Oppervlakte rechthoek (Manier 1): Opp. = l b = (a + b) c = (a + b)c Oppervlakte rechthoek (Manier 2): Opp. = Opp. Groen + Opp. Rood = l b + l b = a c + b c = ac + bc We hebben
3.1 Haakjes wegwerken [1] Oppervlakte rechthoek (Manier 1): Opp. = l b = (a + b) c = (a + b)c Oppervlakte rechthoek (Manier 2): Opp. = Opp. Groen + Opp. Rood = l b + l b = a c + b c = ac + bc We hebben
Bijlage Cijfervaardigheid
 Bijlage Cijfervaardigheid 1 Inleiding De bedoeling van deze bijlage is in het kort de standaardrekenprocedures te herhalen. Je hebt in de vooropleiding ongetwijfeld rekenonderwijs genoten, maar vaak is
Bijlage Cijfervaardigheid 1 Inleiding De bedoeling van deze bijlage is in het kort de standaardrekenprocedures te herhalen. Je hebt in de vooropleiding ongetwijfeld rekenonderwijs genoten, maar vaak is
