INHOUDSOPGAVE MAGNETISME
|
|
|
- Camiel Lemmens
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 INHOUDSOPGAVE MAGNETISME 1. HET ELEKTRISCH VELD Veldlijnen rondom elektrische ladingen De Elektrische veldsterkte E Krachten op elektrische ladingen Wet van Coulomb Spanningspotentialen in elektrische velden De spanning in een elektrisch veld Spanning U tussen twee gelijke ladingen op een afstand l Ladingen in een condensator Isoleerstoffen in het elektrisch veld Ladingsverschuiving in isoleerstoffen Veld- of diëlectrische konstante Capaciteit van een plaatcondensator Schakelen van condensatoren Serieschakeling Parallelschakeling Gemengde schakeling In- en uitschakelgedrag van condensatoren Inschakelen (laden) Uitschakelen (ontladen) 24 KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -A-
2 2. HET MAGNETISCH VELD Voorkomende magnetische velden Het magnetisch veld rondom een permanente magneet Het magnetisch veld rondom een stroomvoerende geleider Het magnetisch veld rondom een stroomvoerende spoel Grootheden van magnetische velden De magnetische poolsterkte De magnetische flux Fluxdichtheid of magnetische inductie B De magnetische veldsterkte Verband tussen magnetische veldsterkte en stroomsterkte De wet van Maxwell De veldsterkte binnen een luchtspoel Veldsterkte binnen een spoel met een homogeen ferromagneticum Veldsterkte binnen een spoel met een niet homogeen ferromagneticum Veldsterkte op afstand s van een rechte geleider Veldsterkte in een spoel als l d Verband tussen magnetische veldsterkte en magnetische inductie inductie B = f(h) voor een luchtspoel B = f(h) voor een spoel met ferromagnetisch materiaal De Hysteresislus Verschillende hysteresislussen Magnetiseringsarbeid- en verlies Het magnetisch circuit Wet van Hopkinson De magnetische spanning De magnetische weerstand Voorbeelden Krachten in het magnetisch veld Inleiding Kracht op een bewegend elektron in een magnetisch veld Kracht op een stroomvoerende geleider in een magnetisch veld Kracht tussen twee evenwijdige stroomvoerende geleiders Toepassingen van magnetische krachtwerking Elektromagnetische inductie Inleiding De wet van Lenz De inductiewet van Faraday Beweging van magneet naar- of van een spoel Berwegende winding in een homogeen veld Roterende winding in een homogeen veld Spanning van zelfinductie Spanning van wederzijdse inductie In- en uitschakelen van een RL - combinatie 84 KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -B-
3 Magnetisme KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -C-
4 1. HET ELEKTRISCH VELD 1.1 Veldlijnen rondom elektrische ladingen Een voorwerp is elektrisch geladen als het te veel of te weinig elektronen heeft. Een teveel aan elektronen resulteert in een negatieve lading (-), een tekort aan elektronen (teveel positieve kernen) in een positieve lading. Proefondervindelijk kan vastgesteld worden dat ladingen met hetzelfde teken elkaar afstoten, ladingen met een verschillend teken trekken elkaar aan. In de omgeving van een lading heerst dus een krachtenveld, dat elektrisch veld genoemd wordt. Dit krachtenveld kan voorgesteld worden door denkbeeldige krachtlijnen of veldlijnen te tekenen. Deze veldlijnen zijn in feite de banen die een vrij bewegende positieve of negatieve lading zou volgen in het elektrische veld. De zin van de veldlijnen wijst steeds van + naar -. Veldlijnen snijden elkaar nooit, en ze staan steeds loodrecht op het oppervlak van het voorwerp waarop ze toekomen of van waaruit ze vertrekken. Omdat het veld in onderstaande figuur veroorzaakt wordt door stilstaande ladingen, noemen we het ook wel een elektrostatisch veld. figuur 1.A Elektrisch veld rond een lading Indien de veldlijnen uniform verdeeld zijn over de ruimte tussen twee ladingen, kunnen we zoals in volgende figuur spreken van een homogeen veld. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -A-
5 figuur 1.B Homogeen en niet homogeen veld 1.2 De Elektrische veldsterkte E figuur 1.C : elektrische veldsterkte De elektrische veldsterkte in een niet homogeen veld is E = U l in een homogeen veld geeft dit : E = U l waarin : E = veldsterkte U = l = spanningsverschil tussen + en - lading afstand tussen + en - lading evenwijdig met de veldlijnen gemeten. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -B-
6 De eenheid van elektrische veldsterkte E is : [ V m ( Volt meter )] C In het verdere verloop van de kursus veronderstellen we steeds, tenzij uitdrukkelijk vermeld, dat we te maken hebben met homogene velden. voorbeeld 1. Bereken de veldsterkte tussen een hoogspanningsleiding van 380kV en de aarde (0 V) als deze leiding 25m boven de aarde hangt. E = U l = V m = V m = 15,2 kv m 1.3 Krachten op elektrische ladingen Elektrische stroom in een stroomkring is een verplaatsing van vrije elektronen. Deze verplaatsing wordt veroorzaakt doordat het elektrische veld een kracht uitoefent op deze vrije elektronen. In formulevorm kunnen we schrijven dat : Veldsterkte = kracht lading _ E = F Q Als we hierop een eenheidskontrole doen vinden we : [E = F Q = N A. s = W. s m A. s = V. A A. m = V m ] KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -C-
7 1.3.1 Wet van Coulomb De wet van coulomb geeft de kracht tussen twee ladingen Q 1 en Q 2 die zich op een afstand r van elkaar in de lucht of het luchtledige bevinden. figuur 1.D kracht tussen twee ladingen F = Q. Q π. r. ε 0 waarin : 4πr 2 = oppervlakte van een bol ε 0H = evenredigheidskonstante = 8, A. s V. m I Q 1 en Q 2 : de grootte van de ladingen (in A.s) Ladingen met gelijk teken stoten elkaar af, ladingen met een verschillend teken trekken elkaar aan. Dit heeft tot gevolg dat : Als de kracht F positief is stoten de elektronen elkaar af, als de kracht negatief is trekken ze elkaar aan. Ook hier kunnen we een eenheidskontrole uitvoeren : [F = A. s. A. s = A. s V. m. m 2 V. A. s m = W. s m = N. m m = N] voorbeeld 2. Bereken de kracht tussen twee elektronen die zich op een afstand r van 1µm van elkaar bevinden. Q e = 1, A.s r = 1µm = m F = , , π. (1. 10 ).8, = 2,3. 10 N F is positief, dus : afstoting KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -D-
8 1.4 Spanningspotentialen in elektrische velden De spanning in een elektrisch veld De veldsterkte werd eerder gedefinieerd als spanning per veldlijnlengte. Voor een deel van deze veldlijnlengte zal dus ook een deel van deze spanning gelden. Als bewijs kunnen we het spanningsverschil meten in de ruimte tussen twee metaalplaten die op een verschillend potentiaal staan. Tussen deze platen hebben we een homogeen verdeeld veld. (zie figuur) figuur 1.E spanning in een elektrisch veld We kunnen zo constateren dat : U 12 = U 13 = U 14 = U 15 = U 42 = U 43 = U 45 U 14 = U 23 = U 35 = 0 De grootte van de spanning is dus evenredig met de veldlijnlengte tussen twee punten. Als al de punten op dezelfde potentiaal met elkaar verbonden worden, krijgen we equipotentiaallijnen. Deze equipotentiaallijnen staan loodrecht op de veldlijnen. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -E-
9 1.4.2 Spanning U tussen twee gelijke ladingen op een afstand l Voor twee ladingen Q op een afstand L van elkaar kunnen we schrijven dat : E U = en E = l F Q U l = F Q U = l. F Q met de wet van Coulomb F = Q. Q π. l. ε vinden we : U F = l. = l. Q Q. Q π. l. ε 0 Q U = Q 4. π. l. ε 0 Eenheidskontrole op deze formule geeft : [U = A. s A. s V. m. m = 1 1 V = V(Volt)] KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -F-
10 KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -Gvoorbeeld 3. figuur 1.F voorbeeld spanningspotentialen in elektrisch veld gegeven : l = mm U = 100 V gevraagd: U 13, U 45, U 36, U 72, U 51 oplossing : E = U l = 100V 31,25mm = 3,2 V mm U = E. l = 3,2 V mm.10mm = 32V U = E. l = 3,2 V mm = 16V mm U = E. l = 3,2 V mm.0mm = 0V U = E. l = - 3,2 V mm.20mm = - 64V De spanning U51 is tegengesteld aan de veldlijnrichting! voorbeeld 4. Twee elektrische ladingen van Q = 0, C worden tot op een afstand van 1 cm naar elkaar gebracht. Bereken de opgebouwde spanning. U = Q 4πl ε 0 = -19 0, π.0,01.9, = 449,59V
11 1.5 Ladingen in een condensator A B + s - l figuur 1.G principe-opbouw condensator Een condensator is een toestel dat bestaat uit twee geleidende oppervlakken gescheiden door een isolator. De isolatiestof wordt het diëlectricum genoemd. Als we de schakelaar s in bovenstaande figuur sluiten vloeien er elektronen van de negatieve klem naar plaat B : B wordt negatief geladen, A zal negatief geladen worden. De lading op plaat A en B zal gelijk zijn als de condensator geladen is. ( vb. A = +Q en B = -Q) Bij een geladen condensator is de condensatorspanning gelijk aan de bronspanning. Tijdens het laden worden voortdurend elektronen toegevoerd naar een van de condensatorplaten. Hierdoor verandert voortdurend de condensatorspanning en de laadstroom. Men spreekt voor deze stroom dan ook van een ogenblikkelijke waarde. De ogenblikkelijke grootte van de laadstroom kunnen we bepalen uit : i = Q t terwijl ook geldt dat de totale lading van de condensator kan gevonden worden uit : i = Q t Q = I gem. t KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -H-
12 Proefondervindelijk kan vastgesteld worden dat als de spanning U over een condensator stijgt de hoeveelheid lading in de condensator evenredig zal stijgen. De capaciteit van een condensator is de -konstante- verhouding tussen lading en spanning : C = Q U = A. s V = F (Farad) figuur 1.H verband tussen U en C bij condensatoren voor de ogenblikkelijke laadstroom kunnen we zo berekenen dat : i = Q t U = C. t = i De laadstroom heeft dus op elk tijdstip een andere waarde, maar is wel afhankelijk van de condensatorwaarde C. In een later volgende paragraaf zal deze formule verder uitgediept en aan de praktijk getoetst worden. voorbeeld 5 Bij het laden van een condensator wordt een hoeveelheid lading Q = C in een tijdsinterval van t = 1 ms verplaatst. Bereken de ogenblikkelijke waarde van de stroom tijdens dit interval. i = Q t = = 1A - KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -I-
13 KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -Jvoorbeeld 6 De spanningstoename van een condensator met capaciteit C = 10 µf bedraagt 5 V/ms = U/ t. Bereken de stroomsterkte op dit ogenblik. U i = C. t 5-6 = i = 50mA -3-3 = A 1.6 Isoleerstoffen in het elektrisch veld Ladingsverschuiving in isoleerstoffen figuur 1.9 geeft een condensator weer met tussen de platen een vaste isolator in plaats van lucht Figuur 1.9 Condensator met isolator tussen de platen Onder invloed van het elektrisch veld treedt ladingsverschuiving op. Deze ladingsverschuiving beïnvloedt de capaciteit van de condensator. verklaring : We weten dat de atomen van elke stof opgebouwd zijn uit een positieve kern met daaromheen negatieve elektronen. De elektronen worden door de positieve plaat van de condensator aangetrokken, terwijl de positieve kernen een weinig naar de negatieve plaat verschuiven. Het gevolg is dat sommige atomen polair worden. Een polair atoom wordt ook wel dipool genoemd. (zie figuur 1.9 )
14 Deze dipolen neutraliseren een gedeelte van de werking van de lading op de platen. Door het neutraliseren van de lading zou de potentiaal van de platen afnemen indien het 'tekort' aan ladingen niet onmiddellijk door de bron zou aangevuld worden. Als gevolg van het polariseren wordt op de platen van de condensator bij eenzelfde bronspanning meer lading gebracht Veld- of diëlectrische konstante Als ten gevolge van het polariseren de lading van de condensator stijgt, zal de ladingsdichtheid D = Q A A ook toenemen. De veldsterkte E = U l A daarentegen blijft constant figuur 1.J diëlectrische konstante A Hieruit kunnen we berekenen dat : D = Q A met Q = C.U = C.U A met U = E. l D = C. l A. E D E = C. l A = Constante KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -K-
15 Naarmate D/E groter is, kan men zeggen dat er meer dipolen gevormd zijn. De ervaring leert dat D/E voor ieder diëlectricum een bepaalde constante is. Deze constante wordt de diëlectrische konstante of permittiviteit ε D genoemd. ε = D E = c. l A Als eenheid kunnen we schrijven: A. s. m ε : [ 2 V. m = A. s V. m = F m ] We kunnen nu ook de relatieve permittiviteit definiëren : ε = ε. ε 0 r waarbij: ε 0-12 = 8, = diâlectrische konstante van het vacuum en ε r = relatieve diâlectrische konstante De relatieve diëlectrische konstante is dus een onbenoemd getal dat aangeeft hoeveel maal de permittiviteit van een isolatiestof groter is dan die van het luchtledige. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -L-
16 Diëlektrica ε r (onbenoemd) ε (F/m) baketiet 3,5 30, eboniet 2,8 24, Glas 7 61, lucht 1 8, magnesiumtitanaat ,25-354, natriumtitanaat , mica 7 61, olie 3 26, papier 3,5 30, paraffine 2 17, polyetheen 3,5 30, porselein 3,2 28, p.v.c. 2,25 19, rubber 3 26, figuur 1.K dielectrische constante van enkele materialen De wet van Coulomb kan men nu schrijven voor verschillende isolatoren in de middenstof. F = Q. Q π r. ε. ε 0 r voorbeeld 7 geg : condensator met A = 6 cm, l = 1 mm, U = 500 V, = 30, F 2-12 ε m gevr : C, Q, D, E oplossing: -4 A C = ε = 30, = 185, = 18,6 pf l Q = C. U = 18, = 92, C D = Q A = 15, C -6 2 m E = U l = V 5 m KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -M-
17 1.6.3 Capaciteit van een plaatcondensator Uit ε = C. l J vinden we : A C = ε. A l met : ε = ε. ε 0 r K C = ε.. A 0 ε r l met : A = plaatoppervlak in m 2 en l = plaatafstand in m figuur 1.L capaciteit van een plaatcondensator voorbeeld 8 a. Bereken de capaciteit van een plaatcondensator met als diëlectricum lucht. De oppervlakte van de platen (A) is 1 m 2 en ze staan op een afstand van 1 mm van elkaar. b. Hoe groot zal de capaciteit zijn als het diëlectricum olie is? A 1-12 a. C = ε 0. ε r = 8, l 10 b. ε van olie : zie tabel C = ε.. A 0 ε r l r 1-12 = 8, = 8,85nF = 26nF KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -N-
18 1.7 Schakelen van condensatoren Serieschakeling figuur 1.M serieschakeling van condensatoren Bij een serieschakeling van condensatoren hebben alle platen, afgezien van het teken, dezelfde lading Q, zodat geldt : Q 1 = Q 2 = Q 3 = Q = I.t waarbij I de gemeenschappelijke stroom naar de serieschakeling is. Volgens de tweede wet van Kirchoff geldt bovendien : U 1 + U 2 + U 3 = U zodat we kunnen schrijven : of algemeen U = Q C + Q C + Q C = Q. ( 1 C + 1 C + 1 C ) = Q. ( 1 C ) v waarbij C de vervangingscapaciteit is. v geeft 1 C = 1 C + 1 C + 1 C v C = 1 C v n KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -O-
19 Evenals bij de parallelschakeling van weerstanden geeft de serieschakeling van condensatoren steeds een vervangingswaarde die kleiner is dan het kleinste in de schakeling opgenomen element. Voor twee condensatoren kunnen we uit bovenstaande formule afleiden dat : 1 2 C v = C. C C + C P Parallelschakeling figuur 1.N parallelschakeling van condensatoren De stroom I verdeelt zich in een deelstroom naar elk van de condensatoren toe. De aangebrachte lading is dus de som van de ladingen die elke condensator bevat. Q = Q + Q + Q met: t U = U = U = U zodat: Q = C.U 1 1 Q = C.U 2 2 Q = C.U 3 3 Q = C.U t v geeft : C.U = C.U + C.U + C.U v C = C + C + C v KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -P-
20 KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -Qof algemeen : C = C v n Bij een parallelschakeling van condensatoren is dus de vervangingscapaciteit gelijk aan de som van de capaciteiten van alle condensatoren. voorbeeld 9 Vier condensatoren met waarden C 1 = 1µF, C 2 = 0,5µF, C 3 = 400nF, C 4 = 2µF worden in serie geschakeld. Bereken de vervangingscapaciteit. 1 = 1 C C + 1 C + 1 C + 1 v C4 = 1 1 F + 1 0,5 F + 1 0,4 F + 1 µ µ µ 2µ F = 6 1µ F = 0,16 µ F voorbeeld 10 Vier condensatoren met waarden C 1 = 18 pf, C 2 = 0,08 nf, C 3 = F, C 4 = 0, F worden parallel geschakeld. Bereken de vervangingscapaciteit. C v = C 1 + C 2 + C 3 + C4 = ( )pF = 153pF
21 1.7.3 Gemengde schakeling Een gemengde schakeling kan beschouwd worden als een combinatie van serie- en parallelschakelingen. voorbeeld 11 gegeven : figuur 1.O Gemengde schakeling C 1 = 1µF, C 2 = 2µF, C 3 = 3µF, C 4 = 4µF, C 5 = 5µF gevraagd : C v = C 14 oplossing : C = C + C = = 7 µ F : parallelschakeling C = 234 C 2. C34 C 2 + C = = 1,55µ F : serieschakeling C = C + C = 1, = 6,55 µ F : parallelschakeling C = C + C C 1 + C = 1.6, ,55 = 0,867 µ F : serieschakeling KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -R-
22 1.8 In- en uitschakelgedrag van condensatoren Inschakelen (laden) figuur 1.P laden van een condensator Als we de schakelaar s sluiten zal de condensator worden opgeladen. De condensatorspanning neemt toe volgens een exponentiële functie en de spanning over de weerstand neemt af. We kunnen op elk ogenblik tijdens het laden zeggen dat : u c + u r = U b waarin : u c = momentele waarde van de condensatorspanning u r = momentele waarde van de weerstandsspanning U b = bronspanning vullen we hierin in dat u r = i.r met i = momentele waarde van de stroom in de kring) dan vinden we : U = u + u = i. R + u b r c c u met i = C. t c u U b = R. c. t c + u c waarin R. C = Τ = tijdskonstante (eenheid [ V A. A. s v = s]) KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -S-
23 Het spanningsverloop over de condensator kunnen we vinden uit de differentiaalvergelijking u u c = U b - R. C. t met als oplossing : c c b -t τ u = U. (1 - e ) met e = exponentiële functie = 2, het stroomverloop kunnen we berekenen uit : U = i. R + u b c en u = U - U. e c b b -t τ geeft U = i. R + U - U. e b b b -t τ waaruit: b i = U R. e -t τ of : i = I. e -t max τ Besluit : tijdens het laden van een condensator neemt de spanning over de condensator toe volgens een exponentiële functie, de stroom in de kring neemt af volgens een exponentiële functie. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -T-
24 100% 90% 80% U c in % van U b i c in % van U b /R 86,5% 95% 98,2% 99,3% 99,8% 99,93% 70% 60% 50% 40% 63,2% 36,8% u c =f(t) i=f(t) i u 30% 20% 10% 0 13,5% 5% 1,8% 0,7% 0,2% 0,07% t/τ figuur 1.Q laden v.e.condensator -stroom- en spanningsverloop KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -Uvoorbeeld 12 Een condensator met capaciteit van 1 µf wordt door een spanningsbron van 10V via een weerstand van 10kΩ opgeladen. C = 1µF, R = 10kΩ, U b = 10V Bereken het verloop van de spanning over de condensator en de laadstroom in functie van de tijd. U c = f(t) en i = f(t) Oplossing : c met τ = R. C = = s = 10ms het verloop van de condensatorspanning en de stroom wordt nu : -t τ u = U(1 - e ) b -t i = U R e = 10 τ c t 10 ms - t 10 ms u = 10(1 - e ) -t 10 ms. e = 1. e [ma] met t in ms
25 KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -Vberekeningen met deze formules geven : t(ms) t/τ 0 0, u c (V) 0 3,93 6,32 8,64 9,5 9,81 9,93 9,97 u c (%) 0% 39,3% 63,2% 86,4% 95% 98,1% 99,3% 99,7% i c (ma) 1 0,6 0,367 0,135 0,049 0,018 0,006 0,002 i c (%) 100% 60% 36,7% 13,5% 4,9% 1,8% 0,6% 0,2% besluit : - na t = τ heeft de condensatorspanning 63,2% van haar eindwaarde. - na t = τ is de laadstroom gedaald tot 37 % van zijn beginwaarde. - na t = 5τ kan men het laadproces als beëindigd beschouwen. - Schakeltechnisch gedraagt een ongeladen condensator zich op het inschakelogenblik als een kortsluiting (i=max, U c = 0). Op het einde van het laadproces is i=0a zodat de condensator zich als een oneindig grote weerstand gedraagt.in grafiek geeft dit :
26 10 V 9 V 8 V U c 8,65V 9,5V 9,8V 9,9V 9,98 9,99V 7 V 6 V 5 V 4 V 3 V 2 V 6,3V raaklijn u c =f(t) 1 V 0 τ t (ms) 1mA i c in ma raaklijn 0,5mA 0,37 i=f(t) 0,1mA 0 0,13% 0,05mA 0,02mA 0, t/τ figuur 1.R laadstroom en spanningsverloop bij laden v.e. condensator KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -W-
27 1.8.2 Uitschakelen (ontladen) Theoretisch is een geladen condensator een vat met ladingen dat niet leeg loopt. Dit betekent dat hij zijn spanning zou behouden. Praktisch gezien zal de condensator wel langzaam ontladen door 'lekstromen' in het diëlectricum. Snel ontladen kan door een weerstand R parallel te schakelen met de condensator C. figuur 1.S ontladen van een condensator Als we de schakelaar s sluiten zal de condensator worden ontladen. Tijdens het ontladen kunnen we de condensator beschouwen als een spanningsbron, let dus op de richting van de stroom i. De condensatorspanning (u c ) en de spanning over de weerstand (u r ) nemen af volgens een exponentiële functie. We kunnen op elk ogenblik tijdens het ontladen zeggen dat : u c = u r = i.r waarin : u c = momentele waarde van de condensatorspanning u r = momentele waarde van de weerstandsspanning i = momentele waarde van de ontlaadstroom vullen we hierin in dat u i = C. t c waarin : U c = de beginspanning van de geladen condensator KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -X-
28 KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -Ydan vinden we na oplossen van de differentiaalvergelijking : u = U. e c c -t τ met τ = tijdsconstante R. C het stroomverloop kunnen we berekenen uit : c -t -t max τ i = U R. e τ = I. e met I max = de maximale stroom bij het begin van het ontladen. Besluit : tijdens het ontladen van een condensator neemt de spanning over de condensator af volgens een exponentiële functie, de stroom in de kring neemt eveneens af volgens een exponentiële functie.
29 100% u c in % van U b raaklijn 50% 36,8% u c =f(t) 10% 0 12,5% 5% 1,8% 0,7% t/τ 100% i c in % van I max = U b /R raaklijn 50% 36,8% i=f(t) 10% 0 12,5% 5% 1,8% 0,7% t/τ figuur 1.T ontladen condensator -stroom- en spanningsverloop KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -Z-
30 KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -AAvoorbeeld 13 Een condensator met capaciteit van 100 µf is door een spanningsbron tot 10V opgeladen. C = 100µF R = 1kΩ U b = 10V Bereken het verloop van de spanning over de condensator en de laadstroom in functie van de tijd. U c = f(t) i = f(t) Oplossing : c 3-6 met = R. C = = 100ms τ c u = U. e -t 100ms -t τ u = 10. e met t in ms i = I max. e -t τ met I = U R = 10 max i = 10. e 3 -t 100ms = 10mA berekeningen met deze formules geven : t(ms) t/τ 0 0, u c (V) ,67 1,35 0,49 0,18 0,06 0,02 u c (%) 100% 60% 36,7% 13,5% 4,9% 1,8% 0,6% 0,2% i c (ma) ,67 1,35 0,49 0,18 0,06 0,02 i c (%) 100% 60% 36,7% 13,5% 4,9% 1,8% 0,6% 0,2%
31 In grafiek geeft dit : 10V u c raaklijn 5V 3,68V u c =f(t) 1V =τ 1,25V 0,5V 0,18V 0,07V =5τ t (ms) 10mA i c raaklijn 5mA 3,68mA i=f(t) 1mA 0 1,25mA 0,5mA 0,18mA 0,07mA t/τ figuur 1.Ulaadstroom en spanningsverloop bij laden v.e. condensator KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -BB-
32 2. Het magnetisch veld 2.1 Voorkomende magnetische velden Een magneet is een lichaam dat op stalen voorwerpen krachten kan uitoefenen. We onderscheiden twee soorten magneten : - Permanente magneten - Elektromagneten Het magnetisch veld rondom een permanente magneet figuur 2.A veldlijnen rond een permanente magneet De Noordpool van de magneet is die zijde van de magneet die naar het geografische noorden wijst. De Zuidpool is dan de zijde die naar het geografische zuiden wijst. We kunnen nu lijnen construeren die in elk punt van het veld door hun raaklijn aldaar de richting aangeven, waarin een magneetnaaldje onder invloed van het magnetisch veld is gaan staan. Deze lijnen worden veld- of krachtlijnen genoemd. Het blijkt dus dat ongelijknamige polen elkaar aantrekken en gelijknamige polen elkaar afstoten. De veldlijnen gaan van de noordpool naar de zuidpool buiten de magneet en van de zuidpool naar de noordpool in de magneet. Magnetische veldlijnen zijn in zichzelf gesloten. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -CC-
33 2.1.2 Het magnetisch veld rondom een stroomvoerende geleider Rond een stroomvoerende geleider ontstaat een magnetisch veld. Het magneetveld kan voorgesteld worden door concentrische cirkels met de geleider als middelpunt. De richting van de veldlijnen is afhankelijk van de stroomrichting in de geleider. De richting van de veldlijnen kunnen we bepalen met de zogenaamde kurketrekkerregel: - De richting van de elektrische stroom behoort bij de voortgaande beweging van de kurketrekker ( schroef). - De richting van de veldlijnen behoort bij de draaiende beweging van de kurketrekker ( schroef ). figuur 2.B Magnetisch veld rond een stroomvoerende geleider Kijken we op de doorsnede van een geleider en is de stroomrichting van ons afgekeerd, dan wordt dit aangegeven met een kruisje. Is de stroomrichting naar ons toe, dan plaatsen we een punt in de geleider. figuur 2.C stroom in het vlak - stroom uit het vlak KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -DD-
34 2.1.3 Het magnetisch veld rondom een stroomvoerende spoel Hebben we een geleider in de vorm van een rechte spoel, ook wel solenoïde genoemd, dan ontstaat er bij een stroomdoorgang eveneens een magnetisch veld. De richting van het veld kan met de kurketrekkerregel gevonden worden. figuur 2.D Magnetisch veld rond een solenoïde Analoog als bij de kurketrekkerregel kunnen we door middel van de Rechter Hand Regel (RHR) de richting van het veld vinden. - Omvat de spoel met de rechterhand zodat de vingers in de stroomrichting wijzen, dan duidt de duim de richting van het veld aan. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -EE-
35 2.2 Grootheden van magnetische velden De magnetische poolsterkte Magneetpolen die in elkaars nabijheid gebracht worden oefenen een kracht F op elkaar uit. Deze kracht hangt af van de "sterkte" van elke magneetpool ( kortom : poolsterkte, m ) en de eigenschappen van de stof die zich tussen de twee magneetpolen bevindt en de afstand tussen de polen ( r ) 1 2 F = m. m 2 k. r [N] Waarin : m 1 en m 2 : resp. poolsterkten r : afstand tussen de polen k : materiaalkonstante middenstof F : kracht in N ( Newton ) De eenheid van magnetische poolsterkte is Vs of Wb ( Weber ). De invloed van twee magneetpolen, of een stroomvoerende geleider of een stoomvoerende spoel kunnen we voorstellen als magnetische veldlijnen De magnetische flux Het geheel van alle veldlijnen door de winding omvat wordt de magnetische flux genoemd. Magnetische flux: Φ [Vs of Wb] figuur 2.E De magnetische flux KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -FF-
36 2.2.3 Fluxdichtheid of magnetische inductie B Onder de fluxdichtheid verstaat men de magnetische flux gedeeld door het beschikbare oppervlak A loodrecht op de fluxrichting. Φ B = A [ Wb m = Vs 2 2 m = T (Tesla)] Voorbeeld 1 De spoeldoormeter van een ringspoel is d = 1 cm. De doorsnede van de kern is cirkelvormig. De magnetische flux van de spoel is 0,05 Wb. Bereken de fluxdichtheid of magnetische inductie. A = 1 π. d = π m 4 = 0, m -4 2 Φ B = = A 1 1 0,05Wb , m = 636,94 T Hoe groot zal B zijn als de diameter verdubbeld d = 2 cm? A = 2 π. d = π m 4 = 3, m -4 2 Φ B = = A 2 2 0,05Wb , m = 159,15 T Besluit B 2 is 4 maal kleiner geworden. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -GG-
37 2.2.4 De magnetische veldsterkte De magnetische veldsterkte is de kracht die het veld uitoefent op de eenheid van flux ( poolsterkte ). H = F [ A m ] Φ Eenheidscontrole N wb = N. m wb. m = J V. s. m V. A. s = V. s. m = A m Soorten magnetische velden zijn : - Homogeen veld : Als de veldsterkte in elk punt van het magnetisch veld even groot en gelijk gericht is. - Heterogeen veld : Als de veldsterkte niet in elk punt even groot en / of gericht is. - Lekveld : Gedeelte van het veld dat niet door de kern van een magnetisch circuit gaat, maar zichzelf sluit door de lucht. figuur 2.F Spoel met zachtstalen circuit Als we het lekveld buiten beschouwing laten is: H 1 = H 2 = H 3 = H 4 = H = Homogeen veld voorbeeld 2 Een magneetnaaldje, dat zelf een flux bezit van Wb bevindt zich in een magnetisch veld en ondervindt hiervan een kracht van 0,1 N. Bereken de veldsterkte ter plaatse van het magneetnaaldje. H = F = Φ 0,1. N Wb = A m KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -HH-
38 2.3 Verband tussen magnetische veldsterkte en stroomsterkte De wet van Maxwell figuur 2.G De wet van Maxwell Rond twee stroomvoerende geleiders ontstaat een heterogeen veld. Van dit veld is één veldlijn weergegeven die beide geleiders omsluit. We verdelen de veldlijn in vele stukjes l met elk hun veldsterkte H. Dan kunnen we zeggen : H. l + H. l + H. l +... = H. l a b c De engelse wis- en natuurkundige maxwell heeft aangetoond dat voor een veldlijn, die stroomvoerende geleiders omsluit, de volgende betrekking geldt: H. l = I Voor een veldlijn die stroomvoerende geleiders omsluit geldt dat de som van de veldsterkte -wegproduktjes, gerekend over een gehele veldlijn, gelijk is aan de algebraïsche som van de door de veldlijn omvatte stromen. Met behulp van de wet van Maxwell kunnen we nu in een aantal gevallen op eenvoudige wijze de veldsterkte bepalen. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -II-
39 2.3.2 De veldsterkte binnen een luchtspoel figuur 2.H H in een luchtspoel We veronderstellen dat de spoellengte groot is ten opzichte van de spoeldoorsnede : l >> d. Volgens Maxwell ΣH. l = ΣI We kunnen de veldlijnen opslitsen in een deel dat binnen de spoel verloopt en een deel buiten de spoel. H. l = H. l + H. l binnen Door de spreiding van het veld buiten de spoel is bij een lange dunne spoel de veldsterkte te verwaarlozen ten opzichte van de veldsterkte binnen de spoel. H. l = H. l binnen buiten Het veld binnen de spoel is homogeen: H 1 =H 2 =H 3 =H H. l binnen = H 1. l + H 2. l+... = H. ( l + l+... ) H. l = H. L ( l = spoellengte ) Bezit de spoel N windingen dan wordt door de veldlijn N maal de stroom I omvat. I = N. I Volgens Maxwell geeft dit dan: H = N. I l of H = l θ I : stroom door de spoel in [ A ] N : aantal windingen l : lengte van de spoel in [ m ] H : veldsterkte in [ A/m ] θ : magnetische spanning in [ A ] KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -JJ-
40 2.3.3 Veldsterkte binnen een spoel met een homogeen ferromagneticum. We gaan met behulp van de wet van Maxwell de veldsterkte in een spoel berekenen. De spoel bevindt zich rond een kern die overal uit hetzelfde materiaal bestaat. Volgens Maxwell : H. l = I H. l = H 1. l + H 2. l+... met H 1 = H 2 =....= H : homogene keten H. l = H. ( l + l+... ) Veldsterkte x de gem. lengte v.d. veldlijnen I = N. I Volgens Maxwell: H. l = N. I gem H = N. I l gem θ = l gem figuur 2.I Homogeen ferromagneticum KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -KK-
41 2.3.4 Veldsterkte binnen een spoel met een niet homogeen ferromagneticum We gaan met behulp van de wet van Maxwell de veldsterkte in een spoel berekenen. De spoel bevindt zich rond een kern die uit verschillende materialen bestaat. Volgens Maxwell : H. l = I H. l = H 1. l + H 2. l + H 3. l. H 4. l H. l = H 1. l 1 + H 2. l 2 + H 3. l 3 + H 4. l4 I = N. I met H1 H 2 H 3 H 4 N. I = θ = H 1. l 1 + H 2. l 2 + H 3. l 3 + H 4. l 4 figuur 2.J Niet homogeen ferromagneticum KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -LL-
42 2.3.5 Veldsterkte op afstand s van een rechte geleider figuur 2.K H rond geleider In de bovenstaande figuur is de afstand van elk punt van de veldlijn tot de geleider gelijk; immers de veldlijn is een cirkel met de geleider als middelpunt. Uit de symmetrie - overweging volgt nu dat de veldsterkte in ieder punt op de cirkelvormige veldlijn dezelfde is. H 1 = H 2 = H 3 = H 4 = H Volgens maxwell : ofwel : H. l = I H 1. l + H 2. l+... = I H. ( l + l+... ) = I ( omtrek van een cirkel = 2.π.s ) H.2. π. s = I Voor de veldsterkte H op afstand s van en stroomvoerende (I) geleider vinden we dan : H = I 2. π. s I : [ A ] s : [ m ] H : [ A/m ] KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -MM-
43 2.3.6 Veldsterkte in een spoel als l d H = N. I 2 2 L + D l : lengte van de spoel [ m ] D : diameter van de spoel [ m ] 2.4 Verband tussen magnetische veldsterkte en magnetische inductie µ = µ. µ o r De magnetische veldconstante µ µ o = veldconstante voor lucht of vacuüm ( permeabiliteit ) = 4.π.10-7 Vs/Am µ r = De relatieve permeabiliteit : een onbenoemd getal dat aangeeft hoeveel maal zo groot de permeabiliteit van een magneticum is ten opzichte van die van het vacuüm. fluxdichtheid De verhouding wordt permeabiliteit genoemd. veldsterkte µ = B µ µ H ofwel B =.. H Diamagnetische stoffen : µ r iets kleiner dan 1 vb. koper, bismut, waterstof, lucht,... o r Paramagnetische stoffen : µ r iets groter dan 1 vb. glas, aluminium, silicium, zuurstof,... Ferromagnetische stoffen :µ r veel groter dan 1 vb. zacht staal, kobalt, nikkel,... KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -NN-
44 Magnetisch harde materialen : materiaal dat moeilijk te magnetiseren en te ontmagnetiseren is. Dit materiaal wordt gebruikt voor permanente magneten. Magnetisch zachte materialen : materiaal dat gemakkelijk te magnetiseren en te ontmagnetiseren is. Dit materiaal wordt gebruikt als kern bij een elektromagneet of als kernmateriaal van spoelen en transfo's inductie B = f(h) voor een luchtspoel B = µ o.µ r.h µ r voor lucht = 1 B = µ o.h Dit is de vergelijking van een rechte y = a.x met een zeer kleine helling. B -7-6 tg α = = µ o = 4. π. 10 _ α = 1, H B (T) α H (ka/m) figuur 2.L B=f(H) voor een luchtspoel KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -OO-
45 2.4.2 B = f(h) voor een spoel met ferromagnetisch materiaal Plaatsen we een ferromagnetische stof (µ r >> 1) in een magnetisch veld, waarvan de veldsterkte regelbaar is, dan verloopt de fluxdichtheid B volgens onderstaande figuur. figuur 2.M B=f(H) voor spoel met ferromagetisch materiaal Is de stof niet magnetisch, met andere woorden vertoond de stof geen uitwendig magnetisch veld, dan betekent dit naar buiten gezien dat alle weisscomplexen elkaar opheffen. Deze toestand geeft fig 2.13 a schematisch weer (weisscomplexen of weissgebieden zijn gebiedjes van spontane magnetisatie ten gevolge van groepen atomen waarvan de elementaire magneetjes gelijk gericht zijn). Wordt het magneticum in een magnetisch veld gebracht, dan zullen de weissgebiedjes die al bijna in de veldrichting staan worden bijgericht. fig 2.13 b het voorgaande vindt plaats tot aan punt A van de magnetiseringskromme. Bij verdere toename van de veldsterkte gaan de weissgebiedjes met niet al te sterk afwijkende richting draaien en komen hierdoor eveneens in de veldrichting te staan (Barkhouseneffect). Bij Hb wordt de toestand bereikt zoals fig 2.13 c vertoont. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -PP-
46 Om tenslotte de weissgebiedjes met sterk afwijkende richting om te klappen is naar verhouding een veel sterker veld nodig, hetgeen tot uiting komt in het ombuigen van de magnetiseringskromme over het traject B-C. Bij een veldsterkte Hc ( fig ) liggen alle weissgebiedjes in de richting van het veld. Fig d geeft dit schematisch weer. We zeggen nu dat het magneticum magnetisch verzadigd is. Bij verdere toename van de velsterkte (H) krijgen we geen toename meer van de fluxdichtheid (B). In fig 2.13 loopt de magnetiseringskromme na punt c dan ook vrijwel evenwijdig met de H-as. B µ = α H = tg De permeabiliteit (µ) van een ferromagnetische stof is niet constant, doch hangt af van de veldsterkte. figuur 2.N Permeabiliteit i.f.v. veldsterkte Bij H o, B o is α max dus ook µ maximaal ( fig.2.14) We zullen voor elk ander materiaal een ander verloop krijgen van de magnetiseringskromme. Fig 2.15 geeft voor enige ferromagnetische materialen de fluxdichtheid en permeabiliteit als functie van de velsterkte. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -QQ-
47 figuur 2.O Tabel : permeabiliteit en veldsterkte i.f.v. B voor gietijzer, zachtstaal en dynamostaal KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -RR-
48 figuur 2.P Grafiek B=f(H) KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -SS-
49 Voorbeeld 4 Een ringspoel met vierkante doorsnede heeft de afmetingen volgens onderstaande figuur. De kern is uit zachtstaal. Bereken de veldsterkte, de fluxdichtheid en de flux in de kern. I=2A N=50 Φ d u =30cm d i =20cm a a figuur 2.Q ringspoel van vb 4 a = d - d = a i = 5cm A = opp = a. a = 25 cm = m H = N. I l = , = 127,4 A m l : gem. magnetische weg van de krachtlijnen. l =. ( d + d π a i ) = π. ( ) = 78,5 cm = 78, m 2 2 Uit de tabel : H = 128 A/m -> B = 0,5 T -4 Φ = B. A = 0, = 1,25 mwb KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -TT-
50 Voorbeeld 5 Uit welk materiaal bestaat volgende kern als de magnetische inductie gelijk is aan 1 T en de stroom I door de spoel gelijk is aan 0,89 A. figuur 2. R -3 l gem = [(80-10) + (100-10)].2 = 320 mm = m H = N. I l gem = 100.0, = 278 A m Uit de tabel vinden we voor H = 280 A/m en B = 1 T,dat het materiaal dynamostaal is De Hysteresislus Vloeit door een spoel een wisselstroom, dan verandert de veldsterkte binnen de spoel overeenkomstig de stroom door de spoel. H = N. I met N als constante l l figuur 2.S Verloop van de veldsterkte bij een wisselstroom I KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -UU-
51 Het verloop van de fluxdichtheid B als functie van de veldsterkte H heet de hysteresislus. (Zie figuur 2.t ) figuur 2.T Hysteresislus Wordt de kern in de spoel voor de eerst maal gemagnetiseerd dan neemt B toe volgens de kromme OB 1. Deze kromme heet ook wel de aanvangskromme. Na tijdstip t 1 in 19 zijn de stroom en de veldsterkte hun maximale positieve waarden gepasseerd en neemt B af volgens de kromme B 1 - B 2. Op tijdstip t 2, waarbij I = 0, H = 0 en B = B r. Deze B r wordt veroorzaakt doordat een aantal weissgebiedjes nog in de oorspronkelijke veldrichting werken. Het magneticum vertoont hierdoor een remanent magnetisme. De fluxdichtheid B r is hiervoor een maat. Na t 2 verandert de veldsterkte van richting. Bij een veldsterkte - H c is B = 0. De kern is dan ontmagnetiseerd. De negatieve veldsterkte, nodig om de kern te ontmagnetiseren, heet coërcitieve veldsterkte (H c ). Bij verdere toename van de veldsterkte in negatieve zin zal het magneticum opnieuw worden gemagnetiseerd. Op tijdstip t 3 bereikt de fluxdichtheid een waarde -B 2 bij een veldsterkte - H max. Ten tijde t 4, als I=0 en H=0, vertoont de kern remanent magnetisme in negatieve richting, waarbij dan een fluxdichtheid van -B r optreedt. Hierna gaat de stroom weer van richting veranderen, waardoor de kern opnieuw ontmagnetiseerd wordt. Het magneticum is weer ontmagnetiseerd indien de veldsterkte in KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -VV-
52 KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -WWpositieve richting de waarde H c heeft bereikt. Bij verdere toename van de veldsterkte in positieve richting wordt de kern weer gemagnetiseerd van B r naar B 1. De fluxdichtheid B 1 wordt weer bereikt op tijdstip t 5, dus bij een veldsterkte van H max. Gerekend van t 1 tot t 5 wordt de hysteresislus in aangegeven pijlrichting doorlopen. We spreken dan van magnetische kringloop. Het tijdsinterval t 5 -t 1 = T komt overeen met 1 periode van de wisselstroom Verschillende hysteresislussen De hysteresislus van magnetisch zacht materiaal: B r klein. Als B r klein is hebben we een materiaal met een klein remanent magnetisme. figuur 2.U Magnetisch zacht materiaal De hysteresislus van magnetisch hard materiaal: B r groot. Als B r groot is hebben we een materiaal met een groot remanent magnetisme. figuur 2.V Magnetisch hard materiaal
53 De hysteresislus van een magnetisch zeer hard materiaal: B r zeer groot. Dit materiaal wordt gebruikt voor permanente magneten. figuur 2.W Magnetisch zeer hard materiaal De waarde van H c bepaalt hoe gemakkelijk of moeilijk een kern van dat materiaal te demagnetiseren is ( B=0 ). De waarde van B r bepaalt hoe sterk het remanent magnetisme is na het wegnemen van de bekrachtigingsspoel rond de kern Magnetiseringsarbeid- en verlies Het magnetiseren en ontmagnetiseren gaat gepaard met het warm worden van de kern. Voor het voortdurend van richting veranderen van de weissgebiedjes is energie nodig; het oppervlak, ingesloten door de hysteresislus, blijkt hiervoor een maat te zijn. Deze energie wordt uiteindelijk geheel in warmte omgezet. We nemen een kleine B = B 2 - B 1, dan krijgen we een rechthoekje met oppervlakte (B 2 -B 1 ).(H 2 -H 1 ) T. A/m Wb/m 2. A/m Vs/m 2. A/m VAs/m 3 J/m 3 Arbeid per volume eenheid. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -XX-
54 Het totale oppervlak, van de hysteresislus bestaat uit de som van een groot aantal van dergelijke strookjes en stelt de energie per m 3 voor, nodig om de hysteresislus éénmaal te doorlopen. figuur 2.X Hysteresisverliezen Onder hysteresisverliezen verstaat men de energie, die per seconde nodig is voor het magnetiseren en ontmagnetiseren [ J/s of Watt ]. Om deze energie zo klein mogelijk te houden, kiest men een magneticum met smalle hysteresislus en beperkt men zoveel mogelijk het volume van het magneticum. Bevindt zich een metaal in een veranderlijk magnetisch veld, dan wordt in dit magneticum een spanning geïnduceerd. Deze spanning doet stroompjes ontstaan van moeilijk te bepalen richting. Deze stroompjes noemen we wervelstromen of foucault stromen. Is I f de som van de wervelstromen en R de ohmse weerstand van het magneticum -> I 2 f.r.t is de energie die in warmte wordt omgezet. ( met t = de tijd in s ) We spreken van wervelstroomverliezen. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -YY-
55 Om de wervelstroomverliezen te beperken moeten we I f zo klein mogelijk houden of m.a.w. de soortelijke weerstand zo groot mogelijk. Dit kunnen we bekomen door de kern te lamelleren evenwijdig met de fluxrichting. De magnetische flux ondervindt dan geen weerstand, de werverlstromen daarentegen een zeer grote R. In elektrische machines treden altijd hysteresisverliezen en wervelstroomverliezen tegelijk op. Beide verliezen worden omgezet in warmte. Het is moeilijk deze verliezen afzonderlijk te bepalen. Daarom worden ze in het algemeen samen genomen en spreken we van yzerverliezen. Yzerverliezen = Hysteresisverlies + Wervelstroomverlies. P fe = P h + P f Een maat voor de yzerverliezen is het zogenaamd verliesgetal V. Onder verliesgetal verstaan we het aantal watt per kg yzer dat bij een fluxdichtheid Bv = 1 T en een frequentie van 50 Hz bij een plaatdikte van 0,5 mm als gevolg van yzerverliezen in warmte wordt omgezet. P = V. ( B B ). m fe v 2 V in W/kg ;m in kg ;P fe in W ;B in T ;Bv = 1 T Voorbeeld 6 De massa van een magnetisch circuit van een transformator is 70 kg. Het verliesgetal is 1,6 W/kg. Bereken P fe bij 50 Hz en een fluxdichtheid van B =1,2 T. 2 2 P fe = V. ( B B ). m = 1,6 W kg. ( 1,6 ).70 kg = 161,28 W 1 v KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -ZZ-
56 2.5 Het magnetisch circuit Wet van Hopkinson Een magnetisch circuit is opgebouwd uit ferromagnetisch materiaal bv. dynamoblik. Om de kern is een spoel aangebracht met N windingen, waarvan een stroom van I ampère vloeit. Laten we een magnetisch lek buiten beschouwing, dan verloopt de gehele flux door het ferromagneisch circuit. Volgens Maxwell is H = N. I l gem en B = µ. H = µ. N. I l Φ = B. A = µ. N. I. A l Φ = N. I l gem µ. A gem θ => Φ = R gem m θ = N. I = magnetische spanning [ A ] R = m l µ. A gem -1 = magnetische weerstand of reluctantie [ H ] figuur 2.Y Wet van Hopkinson KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -AAA-
57 2.5.2 De magnetische spanning Evenals bij een gelijkstroomketen kan men een magnetische keten beschouwen, bestaande uit een bron met een bepaalde magnetische spanning en een aantal magnetische weerstanden. Nemen we als voorbeeld een spoel met N windingen, welke doorlopen wordt door een stroomsterkte I. Een werkelijke spoel heeft een weerstand R. Als we een spanning U aanleggen aan de spoel krijgen we een stroom I = U/R. Deze stroom zorgt voor de magnetische flux. I is bepalend voor de grootte en de richting van de flux. De flux is eveneens afhankelijk van het aantal windingen. figuur 2.Z Magnetische spanning De magnetische spanning als oorzaak van de flux is gelijk aan het product van stroom en aantal windingen. θ = N. I θ = (thäta) : [A] of [Ampäre windingen] In een gelijkstroomketen spreekt men van spanningsvallen over weerstanden of verbruikers. Een gelijkaardige redenering kan men opbouwen voor twee spoelen die elk een deel van de magnetische flux opwekken. De deelspanningen in de magnetische keten noemen we V 1, V 2 enz. De totale magnetische spanning noemen we θ (thèta). θ = N. I + N. I +... = V + V KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -BBB-
58 figuur 2.AA Analogie tussen een elektrische- en een magnetische keten Voorbeeld 3 Een spoel met een doorsnede van 2 cm 2 en 100 windingen wordt doorlopen door een stroom van 1 A. Hoe groot is de magnetische spanning. θ = N.I = = 100 A windingen De magnetische weerstand Om tot een volledig vergelijk te komen met de gelijkstroomketen ontbreekt ons nog een overeenkomst tussen elektrische- en magnetische weerstand. Dat we de veldlijnen kunnen beïnvloeden kunnen we aantonen aan de hand van een kleine proefopstelling. Eenerzijds hebben we een magnetisch veld in lucht en anderzijds gaan we een blokje ijzer in de veldlijnen brengen. figuur 2.BB Ongestoord- en verstoord veld KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -CCC-
59 Door het aanbrengen van het blokje ijzer, concentreren de veldlijnen zich bijna volledig door het stuk ijzer. Men kan dus zeggen dat de magnetische weerstand van het ijzer kleiner is dan deze van lucht. De materialen met een kleine magnetische weerstand noemen we ferromagnetische materialen. Analoog als voor een gelijkstroomketen kunnen we deze magnetische weerstand berekenen. R = U θ R m = = N. I [ A I Φ Φ VS ] R = ρ. l A Rm = l µ. A R m : magnetische weerstand A/Vs l : gem lengte van de veldlijnen in m A : oppervlakte loodrecht op de veldlijnen µ : magnetische velconstante Vs/Am Voorbeelden 1. Ringspoel zonder kern. figuur 2.CC ringspoel zonder kern KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -DDD-
60 2. Spoel met gesloten kern figuur 2.DD spoel met kern 3. luchtspoel figuur 2.EE luchtspoel Opmerkingen * Indien er lekfluxen optreden is de flux niet constant in de gehele magnetische kring. We dienen daar rekening mee te houden. * Indien we een luchtspoel hebben in de magnetische kring krijgen we een spreiding van de veldlijnen. De oppervlakte A lucht zal dan groter zijn dan A magneticum We kunnen de spreiding aangeven door een getal; Vb. spreiding van 20 %. Dit wil zeggen dan A lucht gelijk is aan 1,2 x A fe Ofwel bereken we de spreiding met behulp van de formule; A lucht = (a+l).(b+l) Met l de lengte van de luchtspleet. KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -EEE-
61 2.5.4 Voorbeelden Voorbeeld 7 Een spoel met 720 windingen bevindt zich op een ferromagnetisch circuit met een doorsnede van 5 cm x 5 cm en een gemiddelde veldlijnweg van 60 cm. Bereken de opgenomen stroomsterkte, wanneer in het magnetisch circuit een flux optreedt van 3,75 mwb. Geg.:A = 5*5=25 cm 2 = m 2 Gevr.: I =? N = 720 l gem = 0,6 m Φ = 3, Wb Opl.: Eerste methode Φ B = = A 3, = 1,5 T Uit de B=f(H) tabel vinden we voor dynamoblik: B = 1,5 T --> H = 2000 A/m H = N. I l gem _ I = H. l N gem = ,6 720 = 1,67 A Opl.: Tweede methode Volgens de tabel is voor B = 1,5 T --> µ = H/m R = m l gem. A = 0,6 µ = 3,2. 10 H 5-1 θ = N. I = Φ. R = 3, m.3,2. 10 = 1200 A -3 5 I = Φ. R N m = = 1,67 A KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -FFF-
62 Voorbeeld 8 Een gietstalen ring met een vierkante doorsnede heeft een buitendiameter van 100 mm en een binnendiameter van 60 mm. De ring bezit een spoel met 100 windingen. 1. Hoe groot is de stroomsterkte, die bij een relatieve permeabiliteit µ r van 2000 een magnetische flux van 2, Wb veroorzaakt? 2. Als het circuit een luchtspleet van 1 mm heeft hoe groot moet dan de stroomsterkte zijn om dezelfde flux te laten optreden. We verwaarlozen de spreiding van de veldlijnen in de lucht. 1. zonder luchtspleet l = π. D = π. ( gem gem )mm = 251,3 mm = 251,3. 10 m De dikte van de ring is (100+60)/2 = 20 mm De oppervlakte wordt dus: A = 20 x 20 = 400 mm 2 = m 2 R = m l µ µ π -3 gem -7-4 o. r. A = = 2,5. 10 H θ = N. I = Φ. R = 2, ,5. 10 = 60 A m I = θ N = = 0,6 A 2. met luchtspleet l gem in staal = 251,3 mm - 1 mm = 250, m = l gem1 R 1 = m -3 l gem 1.. A = 250,3. 10 µ µ 4. π o r -7-4 = 2, H 5-1 R 2 = m -3 l gem = µ. A 4. π o -7-4 = 19, H 5-1 R = R 1 + R 2 = 2, , = 22, H m m m θ -4 5 = N. I = Φ. R = 2, , = 537 A m I = θ N = = 5,37 A KHLim dep IWT basis-elektriciteit graduaat EM/EL Magnetisme -GGG-
1. Weten wat potentiaal en potentiaalverschil is 2. Weten wat capaciteit en condensator is 3. Kunnen berekenen van een vervangingscapaciteit
 Hoofdstuk 2 Elektrostatica Doelstellingen 1. Weten wat potentiaal en potentiaalverschil is 2. Weten wat capaciteit en condensator is 3. Kunnen berekenen van een vervangingscapaciteit 2.1 Het elektrisch
Hoofdstuk 2 Elektrostatica Doelstellingen 1. Weten wat potentiaal en potentiaalverschil is 2. Weten wat capaciteit en condensator is 3. Kunnen berekenen van een vervangingscapaciteit 2.1 Het elektrisch
Magnetische toepassingen in de motorvoertuigentechniek (1)
 Magnetische toepassingen in de motorvoertuigentechniek (1) E. Gernaat, ISBN 978-90-808907-3-2 1 Magnetisme 1.1 Het magnetische veld Voor de beschrijving van een magnetisch veld gaan we uit van een staafvormige
Magnetische toepassingen in de motorvoertuigentechniek (1) E. Gernaat, ISBN 978-90-808907-3-2 1 Magnetisme 1.1 Het magnetische veld Voor de beschrijving van een magnetisch veld gaan we uit van een staafvormige
Magnetisme - magnetostatica
 Hoofdstuk 6. Magnetisme - magnetostatica 1 Algemene inleiding 1.1 Inleiding. Magnetostatica is de leer van de magneten in rust. Het moet niet verward worden met gravitatie, noch met elektrostatica. Gravitatiewerking:
Hoofdstuk 6. Magnetisme - magnetostatica 1 Algemene inleiding 1.1 Inleiding. Magnetostatica is de leer van de magneten in rust. Het moet niet verward worden met gravitatie, noch met elektrostatica. Gravitatiewerking:
Elektro-magnetisme Q B Q A
 Elektro-magnetisme 1. Een lading QA =4Q bevindt zich in de buurt van een tweede lading QB = Q. In welk punt zal de resulterende kracht op een kleine positieve lading QC gelijk zijn aan nul? X O P Y
Elektro-magnetisme 1. Een lading QA =4Q bevindt zich in de buurt van een tweede lading QB = Q. In welk punt zal de resulterende kracht op een kleine positieve lading QC gelijk zijn aan nul? X O P Y
Vak: Elektromagnetisme ELK Docent: ir. P.den Ouden nov 2005
 Onderstaande opgaven lijken op de de verwachten tentamenvragen. Getallen bij beweringen kunnen zijn afgerond, om te voldoen aan de juiste significantie. BEGIN TOETS 1 Een magnetisch veld kan worden voorgesteld
Onderstaande opgaven lijken op de de verwachten tentamenvragen. Getallen bij beweringen kunnen zijn afgerond, om te voldoen aan de juiste significantie. BEGIN TOETS 1 Een magnetisch veld kan worden voorgesteld
1. Twee lichamen zijn op een afstand van 30 cm van elkaar opgesteld. Het ene lichaam is negatief geladen met een lading van
 Vraagstukken Theoretische Elektriciteitsleer Elektronica Technicus (Rens & Rens) 1. Twee lichamen zijn op een afstand van 30 cm van elkaar opgesteld. Het ene lichaam is negatief geladen met een lading
Vraagstukken Theoretische Elektriciteitsleer Elektronica Technicus (Rens & Rens) 1. Twee lichamen zijn op een afstand van 30 cm van elkaar opgesteld. Het ene lichaam is negatief geladen met een lading
Newton - HAVO. Elektromagnetisme. Samenvatting
 Newton - HAVO Elektromagnetisme Samenvatting Het magnetisch veld Een permanente magneet is een magneet waarvan de magnetische werking niet verandert Een draaibare kompasnaald draait met zijn noordpool
Newton - HAVO Elektromagnetisme Samenvatting Het magnetisch veld Een permanente magneet is een magneet waarvan de magnetische werking niet verandert Een draaibare kompasnaald draait met zijn noordpool
Magnetisme. Hoofdstuk 4. 4.1 Inleiding. Doelstellingen
 Hoofdstuk 4 Magnetisme Doelstellingen 1. Weten welke magnetische grootheden bestaan en de verbanden ertussen kennen 2. Weten dat er verschillende soorten magnetisme bestaan 3. Weten wat inductie is 4.
Hoofdstuk 4 Magnetisme Doelstellingen 1. Weten welke magnetische grootheden bestaan en de verbanden ertussen kennen 2. Weten dat er verschillende soorten magnetisme bestaan 3. Weten wat inductie is 4.
Magnetische toepassingen in de motorvoertuigentechniek (2)
 Magnetische toepassingen in de motorvoertuigentechniek () E. Gernaat, ISBN 97-9-97-3- 1 Inductiespanning 1.1 Introductie Eén van de belangrijkste ontdekkingen op het gebied van de elektriciteit was het
Magnetische toepassingen in de motorvoertuigentechniek () E. Gernaat, ISBN 97-9-97-3- 1 Inductiespanning 1.1 Introductie Eén van de belangrijkste ontdekkingen op het gebied van de elektriciteit was het
TENTAMEN ELEKTROMAGNETISME (3D020)
 TENTAMEN ELEKTROMAGNETISME (3D020) 10 augustus 1999, 14.00 17.00 uur UITWERKING 1 a) De totale weerstand in de keten wor gegeven door de som van de weerstanden van 1 Ω, 5Ω, de parallelschakeling van 30
TENTAMEN ELEKTROMAGNETISME (3D020) 10 augustus 1999, 14.00 17.00 uur UITWERKING 1 a) De totale weerstand in de keten wor gegeven door de som van de weerstanden van 1 Ω, 5Ω, de parallelschakeling van 30
TENTAMEN ELEKTROMAGNETISME
 TENTMEN ELEKTROMGNETISME 23 juni 2003, 14.00 17.00 uur Dit tentamen bestaat uit 4 opgaven. OPGVE 1 Gegeven is een zeer dunne draad B waarop zch een elektrische lading Q bevindt die homogeen over de lengte
TENTMEN ELEKTROMGNETISME 23 juni 2003, 14.00 17.00 uur Dit tentamen bestaat uit 4 opgaven. OPGVE 1 Gegeven is een zeer dunne draad B waarop zch een elektrische lading Q bevindt die homogeen over de lengte
Magnetische materialen
 1 Hoofdstuk 1: Fysische beschouwingen 1. Inleiding magnetische afstandswerking = afstandswerking tussen bewegende ladingen Om de krachtwerking tussen twee stroomvoerende geleiders te beschrijven voeren
1 Hoofdstuk 1: Fysische beschouwingen 1. Inleiding magnetische afstandswerking = afstandswerking tussen bewegende ladingen Om de krachtwerking tussen twee stroomvoerende geleiders te beschrijven voeren
We willen dat de magnetische inductie in het punt K gelijk aan rul zou worden. Daartoe moet men door de draad AB een stroom sturen die gelijk is aan
 jaar: 1995 nummer: 28 Twee zeer lange draden zijn evenwijdig opgesteld. De stroom door de linkse draad ( zie figuur) is in grootte gelijk aan 30 A en de zin ervan wordt aangegeven door de pijl. We willen
jaar: 1995 nummer: 28 Twee zeer lange draden zijn evenwijdig opgesteld. De stroom door de linkse draad ( zie figuur) is in grootte gelijk aan 30 A en de zin ervan wordt aangegeven door de pijl. We willen
3.3.2 Moment op een rechthoekige winding in een magnetisch. veld... 10
 Contents 1 Electrostatica 3 1.1 Wet van Coulomb......................... 3 1.2 Elektrische veldsterkte...................... 3 1.3 Arbeid in het electrisch veld................... 3 1.4 Beweging van lading
Contents 1 Electrostatica 3 1.1 Wet van Coulomb......................... 3 1.2 Elektrische veldsterkte...................... 3 1.3 Arbeid in het electrisch veld................... 3 1.4 Beweging van lading
1 Overzicht theorievragen
 1 Overzicht theorievragen 1. Wat is een retrograde beweging? Vergelijk de wijze waarop Ptolemaeus deze verklaarde met de manier waarop Copernicus deze verklaarde. 2. Formuleer de drie wetten van planeetbeweging
1 Overzicht theorievragen 1. Wat is een retrograde beweging? Vergelijk de wijze waarop Ptolemaeus deze verklaarde met de manier waarop Copernicus deze verklaarde. 2. Formuleer de drie wetten van planeetbeweging
Opgave 1. Voor de grootte van de magnetische veldsterkte in de spoel geldt: = l
 Opgave 1 Een kompasnaald staat horizontaal opgesteld en geeft de richting aan van de horizontale r component Bh van de magnetische veldsterkte van het aardmagnetische veld. Een spoel wordt r evenwijdig
Opgave 1 Een kompasnaald staat horizontaal opgesteld en geeft de richting aan van de horizontale r component Bh van de magnetische veldsterkte van het aardmagnetische veld. Een spoel wordt r evenwijdig
TENTAMEN ELEKTROMAGNETISME (3D020)
 TENTAMEN ELEKTROMAGNETIME (3D020) 21 juni 1999, 14.00 17.00 uur UITWERKING 1 Op de geleider bevindt zich een totale lading. De lengte van de geleider (een halve cirkel) is gelijk aan πr. y d ϕ R P x Voor
TENTAMEN ELEKTROMAGNETIME (3D020) 21 juni 1999, 14.00 17.00 uur UITWERKING 1 Op de geleider bevindt zich een totale lading. De lengte van de geleider (een halve cirkel) is gelijk aan πr. y d ϕ R P x Voor
1. Langere vraag over de theorie
 . Langere vraag over de theorie. Bereken het magneetveld dat veroorzaakt wordt door een lange, cilindervormige stroomvoerende geleider met straal R en stroom (uniforme stroomdichtheid) en dit zowel binnen
. Langere vraag over de theorie. Bereken het magneetveld dat veroorzaakt wordt door een lange, cilindervormige stroomvoerende geleider met straal R en stroom (uniforme stroomdichtheid) en dit zowel binnen
MAGNETISME & ELEKTRICITEIT
 Hoofdstuk 1 MAGNETISME & ELEKTRICITEIT 1.1 Doelstelling In tegenstelling tot praktisch alle handboeken start je met elektromagnetisme. De reden is eenvoudig omdat alle elektrische toepassingen steeds gepaard
Hoofdstuk 1 MAGNETISME & ELEKTRICITEIT 1.1 Doelstelling In tegenstelling tot praktisch alle handboeken start je met elektromagnetisme. De reden is eenvoudig omdat alle elektrische toepassingen steeds gepaard
I A (papier in) 10cm 10 cm X
 Tentamen: Fysica en Medische Fysica 2 Tijd: 15:15-18:00 uur, donderdag 28 mei 2009 Plaats: TenT blok 4 (met bijlage van formules, handrekenmachine is toegestaan) Docent: Dr. K.S.E. Eikema Puntentelling:
Tentamen: Fysica en Medische Fysica 2 Tijd: 15:15-18:00 uur, donderdag 28 mei 2009 Plaats: TenT blok 4 (met bijlage van formules, handrekenmachine is toegestaan) Docent: Dr. K.S.E. Eikema Puntentelling:
Tentamen Fysica: Elektriciteit en Magnetisme (MNW en SBI)
 Tentamen Fysica: Elektriciteit en Magnetisme (MNW en SBI) Tijd: 2 Juni 217, 12: 14: uur Plaats: WN zalen S67; P647; P663; S 623, S 631, S 655; M 639, M 655 Bij dit tentamen zit aan het eind een formuleblad.
Tentamen Fysica: Elektriciteit en Magnetisme (MNW en SBI) Tijd: 2 Juni 217, 12: 14: uur Plaats: WN zalen S67; P647; P663; S 623, S 631, S 655; M 639, M 655 Bij dit tentamen zit aan het eind een formuleblad.
V 10.10.23 M.JACOBS INHAALCURSUS SLPL Paardenmarkt Antwerpen
 Magnetisme p. 2 INHOUD 17. Magnetisme... 3 17.1. Natuurlijke en kunstmatige magneten... 3 17.2. Soorten magneten... 3 17.3. Enkele begrippen... 4 17.4. Krachtwerking van een magneet... 4 17.5. Magnetisch
Magnetisme p. 2 INHOUD 17. Magnetisme... 3 17.1. Natuurlijke en kunstmatige magneten... 3 17.2. Soorten magneten... 3 17.3. Enkele begrippen... 4 17.4. Krachtwerking van een magneet... 4 17.5. Magnetisch
TENTAMEN ELEKTROMAGNETISME (8N010)
 TENTAMEN ELEKTROMAGNETISME (8N010) Opmerkingen: 1. Dit tentamen bestaat uit 4 vragen met in totaal 19 deelvragen. Elke deelvraag levert 3 punten op.. Het is toegestaan gebruik te maken van bijgeleverd
TENTAMEN ELEKTROMAGNETISME (8N010) Opmerkingen: 1. Dit tentamen bestaat uit 4 vragen met in totaal 19 deelvragen. Elke deelvraag levert 3 punten op.. Het is toegestaan gebruik te maken van bijgeleverd
Elektrische stroomnetwerken
 ntroductieweek Faculteit Bewegings- en evalidatiewetenschappen 25 29 Augustus 2014 Elektrische stroomnetwerken Dr. Pieter Neyskens Monitoraat Wetenschappen pieter.neyskens@wet.kuleuven.be Assistent: Erik
ntroductieweek Faculteit Bewegings- en evalidatiewetenschappen 25 29 Augustus 2014 Elektrische stroomnetwerken Dr. Pieter Neyskens Monitoraat Wetenschappen pieter.neyskens@wet.kuleuven.be Assistent: Erik
Langere vraag over de theorie
 Langere vraag over de theorie a) Bereken de potentiaal van een uniform geladen ring met straal R voor een punt dat gelegen is op een afstand x van het centrum van de ring op de as loodrecht op het vlak
Langere vraag over de theorie a) Bereken de potentiaal van een uniform geladen ring met straal R voor een punt dat gelegen is op een afstand x van het centrum van de ring op de as loodrecht op het vlak
Hoofdstuk 6: Elektromagnetisme
 Hoofdstuk 6: lektromagnetisme Natuurkunde VWO 2011/2012 www.lyceo.nl Hoofdstuk 6: lektromagnetisme Natuurkunde 1. Mechanica 2. Golven en straling 3. lektriciteit en magnetisme 4. Warmteleer Rechtlijnige
Hoofdstuk 6: lektromagnetisme Natuurkunde VWO 2011/2012 www.lyceo.nl Hoofdstuk 6: lektromagnetisme Natuurkunde 1. Mechanica 2. Golven en straling 3. lektriciteit en magnetisme 4. Warmteleer Rechtlijnige
Mkv Magnetisme. Vraag 1 Twee lange, rechte stroomvoerende geleiders zijn opgehangen in hetzelfde verticale vlak, op een afstand d van elkaar.
 Mkv Magnetisme Vraag 1 Twee lange, rechte stroomvoerende geleiders zijn opgehangen in hetzelfde verticale vlak, op een afstand d van elkaar. In een punt P op een afstand d/2 van de rechtse geleider is
Mkv Magnetisme Vraag 1 Twee lange, rechte stroomvoerende geleiders zijn opgehangen in hetzelfde verticale vlak, op een afstand d van elkaar. In een punt P op een afstand d/2 van de rechtse geleider is
oefen vt vwo5 h6 Elektromagnetisme Opgaven en uitwerkingen vind je op www.agtijmensen.nl Oefen vt vwo5 h6 Elektromagnetisme Opgave 1.
 Opgaven en uitwerkingen vind je op www.agtijmensen.nl Oefen vt vwo5 h6 Elektromagnetisme Opgave 1. Elektrisch veld In de vacuüm gepompte beeldbuis van een TV staan twee evenwijdige vlakke metalen platen
Opgaven en uitwerkingen vind je op www.agtijmensen.nl Oefen vt vwo5 h6 Elektromagnetisme Opgave 1. Elektrisch veld In de vacuüm gepompte beeldbuis van een TV staan twee evenwijdige vlakke metalen platen
3.4.3 Plaatsing van de meters in een stroomkring
 1 De stroom- of ampèremeter De ampèremeter is een meetinstrument om elektrische stroom te meten. De sterkte van een elektrische stroom wordt uitgedrukt in ampère, vandaar de naam ampèremeter. Voorstelling
1 De stroom- of ampèremeter De ampèremeter is een meetinstrument om elektrische stroom te meten. De sterkte van een elektrische stroom wordt uitgedrukt in ampère, vandaar de naam ampèremeter. Voorstelling
Uitwerkingen VWO deel 1 H2 (t/m par. 2.5)
 Uitwerkingen VWO deel 1 H2 (t/m par. 2.5) 2.1 Inleiding 1. a) Warmte b) Magnetische Energie c) Bewegingsenergie en Warmte d) Licht (stralingsenergie) en warmte e) Stralingsenergie 2. a) Spanning (Volt),
Uitwerkingen VWO deel 1 H2 (t/m par. 2.5) 2.1 Inleiding 1. a) Warmte b) Magnetische Energie c) Bewegingsenergie en Warmte d) Licht (stralingsenergie) en warmte e) Stralingsenergie 2. a) Spanning (Volt),
HOOFDSTUK 2: Elektrische netwerken
 HOOFDSTUK 2: Elektrische netwerken 1. Netwerken en netwerkelementen elektrische netwerken situering brug tussen fysica en informatieverwerkende systemen abstractie maken fysische verschijnselen vb. velden
HOOFDSTUK 2: Elektrische netwerken 1. Netwerken en netwerkelementen elektrische netwerken situering brug tussen fysica en informatieverwerkende systemen abstractie maken fysische verschijnselen vb. velden
1 Begrip magnetisatie.
 Hoofdstuk 8. 1 Begrip magnetisatie. 1.1 Verklaring van de magnetisatie Magnetisatie. De franse fysicus Pierre Weiss stelde, rond 1900, een theorie op die het magnetiseren van bepaalde stoffen moest verklaren.
Hoofdstuk 8. 1 Begrip magnetisatie. 1.1 Verklaring van de magnetisatie Magnetisatie. De franse fysicus Pierre Weiss stelde, rond 1900, een theorie op die het magnetiseren van bepaalde stoffen moest verklaren.
Schriftelijk examen: theorie en oefeningen Fysica: elektromagnetisme
 Schriftelijk eamen: theorie en oefeningen 2010-2011 Naam en studierichting: Aantal afgegeven bladen, deze opgavebladen niet meegerekend: Gebruik voor elke nieuwe vraag een nieuw blad. Zet op elk blad de
Schriftelijk eamen: theorie en oefeningen 2010-2011 Naam en studierichting: Aantal afgegeven bladen, deze opgavebladen niet meegerekend: Gebruik voor elke nieuwe vraag een nieuw blad. Zet op elk blad de
Langere vraag over de theorie
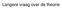 Langere vraag over de theorie (a) Arbeid om de condensator op te laden Bij het opladen van een condensator moet arbeid geleverd worden om lading te verplaatsen van de ene plaat naar de andere. Als er nog
Langere vraag over de theorie (a) Arbeid om de condensator op te laden Bij het opladen van een condensator moet arbeid geleverd worden om lading te verplaatsen van de ene plaat naar de andere. Als er nog
Condensator. Het hellingsgetal a is constant. Dit hellingsgetal noemen we de capaciteit van de condensator C. Er geldt dus: C = Q U
 Inhoud Condensator... 2 Het laden van een condensator... 3 Het ontladen van een condensator... 6 Het gedrag van een condensator in een schakeling... 7 Opgaven... 8 Opgave: Alarminstallatie... 8 Opgave:
Inhoud Condensator... 2 Het laden van een condensator... 3 Het ontladen van een condensator... 6 Het gedrag van een condensator in een schakeling... 7 Opgaven... 8 Opgave: Alarminstallatie... 8 Opgave:
Materialen en onderdelen. Nadruk verboden 1
 Materialen en onderdelen. Nadruk verboden 1 Opgaven 1. Bereken de weerstand van koperdraad waarvan de diameter 2 mm. en de lengte 30 m. bedraagt. 2. Bereken de weerstand van een aluminiumdraad met een
Materialen en onderdelen. Nadruk verboden 1 Opgaven 1. Bereken de weerstand van koperdraad waarvan de diameter 2 mm. en de lengte 30 m. bedraagt. 2. Bereken de weerstand van een aluminiumdraad met een
Hoofdstuk 24 Condensatoren, Diëlektrika, Electrische Energie Opslag. Copyright 2009 Pearson Education, Inc.
 Hoofdstuk 24 Condensatoren, Diëlektrika, Electrische Energie Opslag Onderdelen van Hoofdstuk 24 Condensatoren Bepaling van Capaciteit Condensatoren in Serie en Parallel Electrische Energie Opslag Dielectrica
Hoofdstuk 24 Condensatoren, Diëlektrika, Electrische Energie Opslag Onderdelen van Hoofdstuk 24 Condensatoren Bepaling van Capaciteit Condensatoren in Serie en Parallel Electrische Energie Opslag Dielectrica
4,1. Samenvatting door L. 836 woorden 21 november keer beoordeeld. Natuurkunde. Natuurkunde samenvattingen Havo 4 periode 2.
 Samenvatting door L. 836 woorden 21 november 2012 4,1 51 keer beoordeeld Vak Methode Natuurkunde Pulsar Natuurkunde samenvattingen Havo 4 periode 2. Hoofdstuk 3 Stroom, spanning en weerstand. * Elektrische
Samenvatting door L. 836 woorden 21 november 2012 4,1 51 keer beoordeeld Vak Methode Natuurkunde Pulsar Natuurkunde samenvattingen Havo 4 periode 2. Hoofdstuk 3 Stroom, spanning en weerstand. * Elektrische
Overgangsverschijnselen
 Hoofdstuk 5 Overgangsverschijnselen Doelstellingen 1. Overgangsverschijnselen van RC en RL ketens kunnen uitleggen waarbij de wiskundige afleiding van ondergeschikt belang is Als we een condensator of
Hoofdstuk 5 Overgangsverschijnselen Doelstellingen 1. Overgangsverschijnselen van RC en RL ketens kunnen uitleggen waarbij de wiskundige afleiding van ondergeschikt belang is Als we een condensator of
Repetitie magnetisme voor 3HAVO (opgavenblad met waar/niet waar vragen)
 Repetitie magnetisme voor 3HAVO (opgavenblad met waar/niet waar vragen) Ga na of de onderstaande beweringen waar of niet waar zijn (invullen op antwoordblad). 1) De krachtwerking van een magneet is bij
Repetitie magnetisme voor 3HAVO (opgavenblad met waar/niet waar vragen) Ga na of de onderstaande beweringen waar of niet waar zijn (invullen op antwoordblad). 1) De krachtwerking van een magneet is bij
Fiche 7 (Analyse): Begrippen over elektriciteit
 Fiche 7 (Analyse): Begrippen over elektriciteit 1. Gelijkstroomkringen (DC) De verschillende elektrische grootheden bij gelijkstroom zijn: Elektrische spanning (volt) definitie: verschillend potentiaal
Fiche 7 (Analyse): Begrippen over elektriciteit 1. Gelijkstroomkringen (DC) De verschillende elektrische grootheden bij gelijkstroom zijn: Elektrische spanning (volt) definitie: verschillend potentiaal
Hoofdstuk 13 Magnetische velden. Gemaakt als toevoeging op methode Natuurkunde Overal
 Hoofdstuk 13 Magnetische velden Gemaakt als toevoeging op methode Natuurkunde Overal 13.1 Magnetisme Magneten Z N Z Magnetische veldlijnen: Gaat van N naar Z Als er veel veldlijnen bij elkaar zijn is het
Hoofdstuk 13 Magnetische velden Gemaakt als toevoeging op methode Natuurkunde Overal 13.1 Magnetisme Magneten Z N Z Magnetische veldlijnen: Gaat van N naar Z Als er veel veldlijnen bij elkaar zijn is het
Schriftelijk examen 2e Ba Biologie Fysica: elektromagnetisme 2011-2012
 - Biologie Schriftelijk examen 2e Ba Biologie 2011-2012 Naam en studierichting: Aantal afgegeven bladen, deze opgaven niet meegerekend: Gebruik voor elke nieuwe vraag een nieuw blad. Zet op elk blad de
- Biologie Schriftelijk examen 2e Ba Biologie 2011-2012 Naam en studierichting: Aantal afgegeven bladen, deze opgaven niet meegerekend: Gebruik voor elke nieuwe vraag een nieuw blad. Zet op elk blad de
o a. onveranderd blijven o b. verdubbelen tot -360 kv. o c. stijgen tot een waarde van OV. o d. positief worden tot een waarde van 720 kv.
 jaar: 1989 nummer: 07 In ieder hoekpunt van een driehoek ABC bevindt zich een lading. In A en C is dit een lading van - 6.10-6 C. In B is dit +10.10-6 C. Beschouwen we het punt P gelegen op 30 cm van A
jaar: 1989 nummer: 07 In ieder hoekpunt van een driehoek ABC bevindt zich een lading. In A en C is dit een lading van - 6.10-6 C. In B is dit +10.10-6 C. Beschouwen we het punt P gelegen op 30 cm van A
Theorie Stroomtransformatoren. Tjepco Vrieswijk Hamermolen Ugchelen, 22 november 2011
 Theorie Stroomtransformatoren Tjepco Vrieswijk Hamermolen Ugchelen, 22 november 2011 Theorie Stroomtransformatoren 22 november 2011 Onderwerpen: - Theorie stroomtransformatoren - Vervangingsschema CT -
Theorie Stroomtransformatoren Tjepco Vrieswijk Hamermolen Ugchelen, 22 november 2011 Theorie Stroomtransformatoren 22 november 2011 Onderwerpen: - Theorie stroomtransformatoren - Vervangingsschema CT -
Samenvatting Natuurkunde Hoofdstuk 4
 Samenvatting Natuurkunde Hoofdstuk 4 Samenvatting door Roy 1370 woorden 5 maart 2017 6,8 14 keer beoordeeld Vak Methode Natuurkunde Nova Samenvatting h4 NaSk1 4.1 Elke keer dat je een apparaat aanzet,
Samenvatting Natuurkunde Hoofdstuk 4 Samenvatting door Roy 1370 woorden 5 maart 2017 6,8 14 keer beoordeeld Vak Methode Natuurkunde Nova Samenvatting h4 NaSk1 4.1 Elke keer dat je een apparaat aanzet,
Samenvatting Natuurkunde Hoofdstuk 2 (elektriciteit)
 Samenvatting Natuurkunde Hoofdstuk 2 (elektriciteit) Samenvatting door een scholier 1671 woorden 2 december 2012 5,6 55 keer beoordeeld Vak Methode Natuurkunde Natuurkunde overal Natuurkunde H2 elektriciteit
Samenvatting Natuurkunde Hoofdstuk 2 (elektriciteit) Samenvatting door een scholier 1671 woorden 2 december 2012 5,6 55 keer beoordeeld Vak Methode Natuurkunde Natuurkunde overal Natuurkunde H2 elektriciteit
Chapter 28 Bronnen van Magnetische Velden. Copyright 2009 Pearson Education, Inc.
 Chapter 28 Bronnen van Magnetische Velden Magnetisch Veld van een Stroomdraad Magneetveld omgekeerd evenredig met afstand tot draad : Constante μ 0 is de permeabiliteit van het vacuum: μ 0 = 4π x 10-7
Chapter 28 Bronnen van Magnetische Velden Magnetisch Veld van een Stroomdraad Magneetveld omgekeerd evenredig met afstand tot draad : Constante μ 0 is de permeabiliteit van het vacuum: μ 0 = 4π x 10-7
Hoofdstuk 29 Electromagnetische Inductie en de wet van Faraday. Copyright 2009 Pearson Education, Inc.
 Hoofdstuk 29 Electromagnetische Inductie en de wet van Faraday Onderwerpen van H 29 Geinduceerde EMF Faraday s Inductie wet; de wet van Lenz EMF Geinduceerd in een Bewegende Geleider Electrische Generatoren
Hoofdstuk 29 Electromagnetische Inductie en de wet van Faraday Onderwerpen van H 29 Geinduceerde EMF Faraday s Inductie wet; de wet van Lenz EMF Geinduceerd in een Bewegende Geleider Electrische Generatoren
Tentamen Fysica: Elektriciteit en Magnetisme (MNW)
 Tentamen Fysica: Elektriciteit en Magnetisme (MNW) Tijd: 27 mei 12.-14. Plaats: WN-C147 A t/m K WN-D17 L t/m W Bij dit tentamen zit aan het eind een formuleblad. Eenvoudige handrekenmachine is toegestaan
Tentamen Fysica: Elektriciteit en Magnetisme (MNW) Tijd: 27 mei 12.-14. Plaats: WN-C147 A t/m K WN-D17 L t/m W Bij dit tentamen zit aan het eind een formuleblad. Eenvoudige handrekenmachine is toegestaan
Hoofdstuk 12 Elektrische velden. Gemaakt als toevoeging op methode Natuurkunde Overal
 Hoofdstuk 12 Elektrische velden Gemaakt als toevoeging op methode Natuurkunde Overal 12.1 Elektrische kracht en lading Elektrische krachten F el + + F el F el F el r F el + F el De wet van Coulomb q Q
Hoofdstuk 12 Elektrische velden Gemaakt als toevoeging op methode Natuurkunde Overal 12.1 Elektrische kracht en lading Elektrische krachten F el + + F el F el F el r F el + F el De wet van Coulomb q Q
Uitwerkingen opgaven hoofdstuk Het magnetisch veld
 Uitwerkingen opgaven hoofdstuk 4 4.1 Het magnetisch veld Opgave 1 a Het koperen staafje is het staafje dat geen van de andere staafjes aantrekt en niet door de andere staafjes wordt aangetrokken. Het is
Uitwerkingen opgaven hoofdstuk 4 4.1 Het magnetisch veld Opgave 1 a Het koperen staafje is het staafje dat geen van de andere staafjes aantrekt en niet door de andere staafjes wordt aangetrokken. Het is
Vrijdag 19 augustus, 9.30-12.30 uur
 EINDEXAMEN VOORBEREIDEND WETENSCHAPPELIJK ONDERWIJS IN 1977 Vrijdag 19 augustus, 9.30-12.30 uur NATUURKUNDE Zie ommezijde Deze opgaven zijn vastgesteld door de commissie bedoeld in artikel 24 van het Besluit
EINDEXAMEN VOORBEREIDEND WETENSCHAPPELIJK ONDERWIJS IN 1977 Vrijdag 19 augustus, 9.30-12.30 uur NATUURKUNDE Zie ommezijde Deze opgaven zijn vastgesteld door de commissie bedoeld in artikel 24 van het Besluit
NATUURKUNDE KLAS 5. PROEFWERK H8 JUNI 2010 Gebruik eigen rekenmachine en BINAS toegestaan. Totaal 29 p
 NATUURKUNDE KLAS 5 PROEFWERK H8 JUNI 2010 Gebruik eigen rekenmachine en BINAS toegestaan. Totaal 29 p Opgave 1: alles heeft een richting (8p) Bepaal de richting van de gevraagde grootheden. Licht steeds
NATUURKUNDE KLAS 5 PROEFWERK H8 JUNI 2010 Gebruik eigen rekenmachine en BINAS toegestaan. Totaal 29 p Opgave 1: alles heeft een richting (8p) Bepaal de richting van de gevraagde grootheden. Licht steeds
TENTAMEN ELEKTROMAGNETISME (8N010)
 TENTAMEN ELEKTROMAGNETISME (8N010) 25 april, 2008, 14.00-17.00 uur Opmerkingen: 1. Dit tentamen bestaat uit 4 vragen met in totaal 18 deelvragen. 2. Het is toegestaan gebruik te maken van bijgeleverd formuleblad
TENTAMEN ELEKTROMAGNETISME (8N010) 25 april, 2008, 14.00-17.00 uur Opmerkingen: 1. Dit tentamen bestaat uit 4 vragen met in totaal 18 deelvragen. 2. Het is toegestaan gebruik te maken van bijgeleverd formuleblad
QUARK_5-Thema-01-elektrische kracht Blz. 1
 QUARK_5-Thema-01-elektrische kracht Blz. 1 THEMA 1: elektrische kracht Elektriciteit Elektrische lading Lading van een voorwerp Fenomeen: Sommige voorwerpen krijgen een lading door wrijving. Je kan aan
QUARK_5-Thema-01-elektrische kracht Blz. 1 THEMA 1: elektrische kracht Elektriciteit Elektrische lading Lading van een voorwerp Fenomeen: Sommige voorwerpen krijgen een lading door wrijving. Je kan aan
. Vermeld je naam op elke pagina.
 Tentamen: Elektriciteit en Magnetisme Docent: J. F. J. van den Brand R. J. Wijngaarden Datum: 30 Mei 2006 Zaal: Q112/M143 Tijd: 15:15-18.00 uur. Vermeld je naam op elke pagina.. Vermeld je collegenummer..
Tentamen: Elektriciteit en Magnetisme Docent: J. F. J. van den Brand R. J. Wijngaarden Datum: 30 Mei 2006 Zaal: Q112/M143 Tijd: 15:15-18.00 uur. Vermeld je naam op elke pagina.. Vermeld je collegenummer..
Impedantie V I V R R Z R
 Impedantie Impedantie (Z) betekent: wisselstroom-weerstand. De eenheid is (met als gelijkstroom-weerstand) Ohm. De weerstand geeft aan hoe goed de stroom wordt tegengehouden. We kennen de formules I R
Impedantie Impedantie (Z) betekent: wisselstroom-weerstand. De eenheid is (met als gelijkstroom-weerstand) Ohm. De weerstand geeft aan hoe goed de stroom wordt tegengehouden. We kennen de formules I R
Rekenkunde, eenheden en formules voor HAREC. 10 april 2015 presentator : ON5PDV, Paul
 Rekenkunde, eenheden en formules voor HAREC 10 april 2015 presentator : ON5PDV, Paul Vooraf : expectation management 1. Verwachtingen van deze presentatie (inhoud, diepgang) U = R= R. I = 8 Ω. 0,5 A =
Rekenkunde, eenheden en formules voor HAREC 10 april 2015 presentator : ON5PDV, Paul Vooraf : expectation management 1. Verwachtingen van deze presentatie (inhoud, diepgang) U = R= R. I = 8 Ω. 0,5 A =
Uitwerking LES 5 N CURSSUS
 1) C De letter C wordt in de elektronica gebruikt voor een: A) spoel (symbool L, eenheid Henry) B) weerstand (symbool R, eenheid Ohm Ω) C) condensator (symbool C, eenheid Farad, 2 geleiders gescheiden
1) C De letter C wordt in de elektronica gebruikt voor een: A) spoel (symbool L, eenheid Henry) B) weerstand (symbool R, eenheid Ohm Ω) C) condensator (symbool C, eenheid Farad, 2 geleiders gescheiden
Condensator = passieve component bestaande uit 2 geleiders (platen) met een isolator/diëlectricum(lucht, papier, kunststoffen) tussen.
 H2: Condensatoren: Opbouw: Condensator = passieve component bestaande uit 2 geleiders (platen) met een isolator/diëlectricum(lucht, papier, kunststoffen) tussen. Opgelet: 2 draden/printbanen kort naast
H2: Condensatoren: Opbouw: Condensator = passieve component bestaande uit 2 geleiders (platen) met een isolator/diëlectricum(lucht, papier, kunststoffen) tussen. Opgelet: 2 draden/printbanen kort naast
Voorbereiding toelatingsexamen arts/tandarts. Fysica: Elektrostatica. 25 juli 2015. dr. Brenda Casteleyn
 Voorbereiding toelatingsexamen arts/tandarts Fysica: Elektrostatica 25 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
Voorbereiding toelatingsexamen arts/tandarts Fysica: Elektrostatica 25 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
Hoofdstuk 8 Elektrostatica
 Hoofdstuk 8 Elektrostatica Alain Risack Elektriseren Elektriseren door wrijving. Elektriseren door contact. Een vlierpit bolletje: 8 Elektrostatica Elektriseren. Verklaar wat er gebeurt. Wat wordt er hiermee
Hoofdstuk 8 Elektrostatica Alain Risack Elektriseren Elektriseren door wrijving. Elektriseren door contact. Een vlierpit bolletje: 8 Elektrostatica Elektriseren. Verklaar wat er gebeurt. Wat wordt er hiermee
NATUURKUNDE 8 29/04/2011 KLAS 5 INHAALPROEFWERK HOOFDSTUK
 NATUURKUNDE KLAS 5 INHAALPROEFWERK HOOFDSTUK 8 29/04/2011 Deze toets bestaat uit 3 opgaven (32 punten). Gebruik eigen grafische rekenmachine en BINAS toegestaan. Veel succes! Opgave 1: Afbuigen van geladen
NATUURKUNDE KLAS 5 INHAALPROEFWERK HOOFDSTUK 8 29/04/2011 Deze toets bestaat uit 3 opgaven (32 punten). Gebruik eigen grafische rekenmachine en BINAS toegestaan. Veel succes! Opgave 1: Afbuigen van geladen
Condensator. Het hellingsgetal a is constant. Dit hellingsgetal noemen we de capaciteit van de condensator C. Er geldt dus: C = Q U
 Inhoud Condensator... 2 Het laden van een condensator... 3 Het ontladen van een condensator... 5 Opgaven... 6 Opgave: Alarminstallatie... 6 Opgave: Gelijkrichtschakeling... 6 Opgave: Boormachine... 7 1/7
Inhoud Condensator... 2 Het laden van een condensator... 3 Het ontladen van een condensator... 5 Opgaven... 6 Opgave: Alarminstallatie... 6 Opgave: Gelijkrichtschakeling... 6 Opgave: Boormachine... 7 1/7
Begripsvragen: Elektrisch veld
 Handboek natuurkundedidactiek Hoofdstuk 4: Leerstofdomeinen 4.2 Domeinspecifieke leerstofopbouw 4.2.4 Elektriciteit en magnetisme Begripsvragen: Elektrisch veld 1 Meerkeuzevragen Elektrisch veld 1 [V]
Handboek natuurkundedidactiek Hoofdstuk 4: Leerstofdomeinen 4.2 Domeinspecifieke leerstofopbouw 4.2.4 Elektriciteit en magnetisme Begripsvragen: Elektrisch veld 1 Meerkeuzevragen Elektrisch veld 1 [V]
8 College 08/12: Magnetische velden, Wet van Ampere
 8 College 08/12: Magnetische velden, Wet van Ampere Enkele opmerkingen: Permanente magneten zijn overal om ons heen. Magnetisme is geassociëerd met bewegende electrische ladingen. Magnetisme: gebaseerd
8 College 08/12: Magnetische velden, Wet van Ampere Enkele opmerkingen: Permanente magneten zijn overal om ons heen. Magnetisme is geassociëerd met bewegende electrische ladingen. Magnetisme: gebaseerd
Fundamentele elektriciteit
 KONNKLJKE MLTARE CHOOL Leerstoel Elektriciteit 1 oktober 2002 11 TAW Fundamentele elektriciteit Praktisch werk 6 Oplossingen 1. Twee identieke permanente magneten hebben elk een magnetisch veld van 2 T
KONNKLJKE MLTARE CHOOL Leerstoel Elektriciteit 1 oktober 2002 11 TAW Fundamentele elektriciteit Praktisch werk 6 Oplossingen 1. Twee identieke permanente magneten hebben elk een magnetisch veld van 2 T
Deze toets bestaat uit 3 opgaven (34 punten). Gebruik eigen grafische rekenmachine en BINAS toegestaan. Veel succes!
 NATUURKUNDE KLAS 5 PROEFWERK HOOFDSTUK OOFDSTUK 8 03/05/2010 Deze toets bestaat uit 3 opgaven (34 punten). Gebruik eigen grafische rekenmachine en BINAS toegestaan. Veel succes! Opgave 1: Eerste elektromotor
NATUURKUNDE KLAS 5 PROEFWERK HOOFDSTUK OOFDSTUK 8 03/05/2010 Deze toets bestaat uit 3 opgaven (34 punten). Gebruik eigen grafische rekenmachine en BINAS toegestaan. Veel succes! Opgave 1: Eerste elektromotor
1. Langere vraag over de theorie
 1. Langere vraag over de theorie a) Bereken, vertrekkend van de definitie van capaciteit, de capaciteit van een condensator die bestaat uit twee evenwijdige vlakke platen waarbij de afstand tussen de platen
1. Langere vraag over de theorie a) Bereken, vertrekkend van de definitie van capaciteit, de capaciteit van een condensator die bestaat uit twee evenwijdige vlakke platen waarbij de afstand tussen de platen
3.1 Magneten en elektromagneten
 3.1 Magneten en elektromagneten 1 a De punt van de magneet die naar het geografische noorden wijst, heet de magnetische noordpool van de magneet. Dat is afspraak. Hij wordt aangetrokken door een ongelijke
3.1 Magneten en elektromagneten 1 a De punt van de magneet die naar het geografische noorden wijst, heet de magnetische noordpool van de magneet. Dat is afspraak. Hij wordt aangetrokken door een ongelijke
Opgave 5 Een verwarmingselement heeft een weerstand van 14,0 Ω en is opgenomen in de schakeling van figuur 3.
 Opgave 5 Een verwarmingselement heeft een weerstand van 14,0 Ω en is opgenomen in de schakeling van figuur 3. figuur 3 De schuifweerstand is zo ingesteld dat de stroomsterkte 0,50 A is. a) Bereken het
Opgave 5 Een verwarmingselement heeft een weerstand van 14,0 Ω en is opgenomen in de schakeling van figuur 3. figuur 3 De schuifweerstand is zo ingesteld dat de stroomsterkte 0,50 A is. a) Bereken het
Voorbereiding toelatingsexamen arts/tandarts. Fysica: Elektromagnetisme. 4 november Brenda Casteleyn, PhD
 Voorbereiding toelatingsexamen arts/tandarts Fysica: Elektromagnetisme 4 november 2017 Brenda Casteleyn, PhD Met dank aan: Atheneum van Veurne, Leen Goyens (http://users.telenet.be/toelating) 1. Inleiding
Voorbereiding toelatingsexamen arts/tandarts Fysica: Elektromagnetisme 4 november 2017 Brenda Casteleyn, PhD Met dank aan: Atheneum van Veurne, Leen Goyens (http://users.telenet.be/toelating) 1. Inleiding
Magnetische toepassingen in de motorvoertuigentechniek (3)
 Magnetische toepassingen in de motorvoertuigentechniek (3) E. Gernaat, ISBN 978-90-808907-3-2 1 Theorie wisselspanning 1.1 De inductieve spoelweerstand (X L ) Wanneer we een spoel op een wisselspanning
Magnetische toepassingen in de motorvoertuigentechniek (3) E. Gernaat, ISBN 978-90-808907-3-2 1 Theorie wisselspanning 1.1 De inductieve spoelweerstand (X L ) Wanneer we een spoel op een wisselspanning
TENTAMEN ELEKTROMAGNETISME (8N010)
 TENTAMEN ELEKTROMAGNETISME (8N010) 2 Juli, 2010, 14:00 17:00 uur Opmerkingen: 1. Dit tentamen bestaat uit 4 vragen met in totaal 19 deelvragen. 2. Werk nauwkeurig en netjes. Als ik het antwoord niet kan
TENTAMEN ELEKTROMAGNETISME (8N010) 2 Juli, 2010, 14:00 17:00 uur Opmerkingen: 1. Dit tentamen bestaat uit 4 vragen met in totaal 19 deelvragen. 2. Werk nauwkeurig en netjes. Als ik het antwoord niet kan
Oplossing examenoefening 2 :
 Oplossing examenoefening 2 : Opgave (a) : Een geleidende draad is 50 cm lang en heeft een doorsnede van 1 cm 2. De weerstand van de draad bedraagt 2.5 mω. Wat is de geleidbaarheid van het materiaal waaruit
Oplossing examenoefening 2 : Opgave (a) : Een geleidende draad is 50 cm lang en heeft een doorsnede van 1 cm 2. De weerstand van de draad bedraagt 2.5 mω. Wat is de geleidbaarheid van het materiaal waaruit
Deeltoets II E&M & juni 2016 Velden en elektromagnetisme
 E&M Boller, Offerhaus, Dhallé Deeltoets II E&M 201300164 & 201300183 13 juni 2016 Velden en elektromagnetisme Aanwijzingen Voor de toets zijn 2 uren beschikbaar. Vul op alle ingeleverde vellen uw naam
E&M Boller, Offerhaus, Dhallé Deeltoets II E&M 201300164 & 201300183 13 juni 2016 Velden en elektromagnetisme Aanwijzingen Voor de toets zijn 2 uren beschikbaar. Vul op alle ingeleverde vellen uw naam
VLAKKE PLAATCONDENSATOR
 H Electrostatica PUNTLADINGEN In een ruimte bevinden zich de puntladingen A en B. De lading van A is 6,010 9 C en die van B is +6,010 9 C. Om een idee van afstanden te hebben is in het vlak een rooster
H Electrostatica PUNTLADINGEN In een ruimte bevinden zich de puntladingen A en B. De lading van A is 6,010 9 C en die van B is +6,010 9 C. Om een idee van afstanden te hebben is in het vlak een rooster
7 College 01/12: Electrische velden, Wet van Gauss
 7 College 01/12: Electrische velden, Wet van Gauss Berekening van electrische flux Alleen de component van het veld loodrecht op het oppervlak draagt bij aan de netto flux. We definieren de electrische
7 College 01/12: Electrische velden, Wet van Gauss Berekening van electrische flux Alleen de component van het veld loodrecht op het oppervlak draagt bij aan de netto flux. We definieren de electrische
hoofdstuk 1 Elektriciteit.
 hoofdstuk 1 Elektriciteit. 1.1 Lading. Veel toestellen op het laboratorium werken met elektriciteit. De werking van deze toestellen berust op elektrische lading die stroomt. We kennen twee soorten lading:
hoofdstuk 1 Elektriciteit. 1.1 Lading. Veel toestellen op het laboratorium werken met elektriciteit. De werking van deze toestellen berust op elektrische lading die stroomt. We kennen twee soorten lading:
Opgave 3 Staafmagneten, hoefijzermagneten, naaldmagneten en schijfmagneten.
 Uitwerkingen 1 Opgave 1 IJzer, nikkel en kobalt. Opgave 2 ermanente magneten zijn blijvend magnetisch. Opgave 3 Staafmagneten, hoefijzermagneten, naaldmagneten en schijfmagneten. Opgave 4 Weekijzer is
Uitwerkingen 1 Opgave 1 IJzer, nikkel en kobalt. Opgave 2 ermanente magneten zijn blijvend magnetisch. Opgave 3 Staafmagneten, hoefijzermagneten, naaldmagneten en schijfmagneten. Opgave 4 Weekijzer is
2 Elektriciteit Elektriciteit. 1 A De aal heeft ca 4000 elektrische cellen van 0,15 volt, die in serie geschakeld zijn.
 2 Elektriciteit 1 2.1 Elektriciteit 1 A De aal heeft ca 4000 elektrische cellen van 0,15 volt, die in serie geschakeld zijn. 2 mp3-speler dynamo fiets accu lamp op je kamer stopcontact auto batterij 3
2 Elektriciteit 1 2.1 Elektriciteit 1 A De aal heeft ca 4000 elektrische cellen van 0,15 volt, die in serie geschakeld zijn. 2 mp3-speler dynamo fiets accu lamp op je kamer stopcontact auto batterij 3
TENTAMEN ELEKTROMAGNETISME (3D020)
 TENTAMEN ELEKTOMAGNETISME (3D2) 11 augustus 23, 14. 17. uur UITWEKING 1 Op de geleider bevin zich een totale lading. De lengte van de geleider (een halve cirkel) is gelijk aan π. y d ϕ P x Voor de ladingsdichtheid
TENTAMEN ELEKTOMAGNETISME (3D2) 11 augustus 23, 14. 17. uur UITWEKING 1 Op de geleider bevin zich een totale lading. De lengte van de geleider (een halve cirkel) is gelijk aan π. y d ϕ P x Voor de ladingsdichtheid
7 Elektriciteit en magnetisme.
 7 Elektriciteit en magnetisme. itwerkingen Opgae 7. aantal 6, 0 9,60 0 8 elektronen Opgae 7. aantal,0 0,0 0 A,60 0 s 9,5 0 6 elektronen/s Opgae 7. O-atoom : +8-8 0 O-ion : +8-0 - Lading O-ion - x,6 0-9
7 Elektriciteit en magnetisme. itwerkingen Opgae 7. aantal 6, 0 9,60 0 8 elektronen Opgae 7. aantal,0 0,0 0 A,60 0 s 9,5 0 6 elektronen/s Opgae 7. O-atoom : +8-8 0 O-ion : +8-0 - Lading O-ion - x,6 0-9
Hoofdstuk 8 Elektrostatica
 Hoofdstuk 8 Elektrostatica Alain Risack Elektriseren. Verklaar wat er gebeurt. Wat wordt er hiermee aangetoond? Elektriseren Elektriseren door wrijving. Elektriseren door contact. Een vlierpit bolletje:
Hoofdstuk 8 Elektrostatica Alain Risack Elektriseren. Verklaar wat er gebeurt. Wat wordt er hiermee aangetoond? Elektriseren Elektriseren door wrijving. Elektriseren door contact. Een vlierpit bolletje:
Langere vraag over de theorie
 Naam (in drukletters): Studentennummer: Langere vraag over de theorie (a) Bereken de elektrische potentiaal voor een uniform geladen ring en dit voor een punt dat ligt op de as die loodrecht staat op de
Naam (in drukletters): Studentennummer: Langere vraag over de theorie (a) Bereken de elektrische potentiaal voor een uniform geladen ring en dit voor een punt dat ligt op de as die loodrecht staat op de
EXAMEN VOORBEREIDEND WETENSCHAPPELUK ONDERWIJS IN 1979 , I. Dit examen bestaat uit 4 opgaven. " '"of) r.. I r. ',' t, J I i I.
 .o. EXAMEN VOORBEREDEND WETENSCHAPPELUK ONDERWJS N 1979 ' Vrijdag 8 juni, 9.00-12.00 uur NATUURKUNDE.,, Dit examen bestaat uit 4 opgaven ',", "t, ', ' " '"of) r.. r ',' t, J i.'" 'f 1 '.., o. 1 i Deze
.o. EXAMEN VOORBEREDEND WETENSCHAPPELUK ONDERWJS N 1979 ' Vrijdag 8 juni, 9.00-12.00 uur NATUURKUNDE.,, Dit examen bestaat uit 4 opgaven ',", "t, ', ' " '"of) r.. r ',' t, J i.'" 'f 1 '.., o. 1 i Deze
LES1: ELEKTRISCHE LADING DE WET VAN COULOMB. H21: Elektrische lading en elektrische velden
 LES1: ELEKTRISCHE LADING DE WET VAN COULOMB ELEKTROSTATICA Studie van ladingen in rust in een intertiaalstelsel. ELEKTRISCH GELADEN LICHAMEN Een massa is steeds positief. H21: Elektrische lading en elektrische
LES1: ELEKTRISCHE LADING DE WET VAN COULOMB ELEKTROSTATICA Studie van ladingen in rust in een intertiaalstelsel. ELEKTRISCH GELADEN LICHAMEN Een massa is steeds positief. H21: Elektrische lading en elektrische
Geleider: (metaal) hierin kunnen elektronen bewegen, omdat de buitenste elektronen maar zwak aangetrokken worden tot de kern (vrije elektronen)
 Boekverslag door B. 1240 woorden 16 juni 2015 7.6 10 keer beoordeeld Vak Methode Natuurkunde Pulsar Hoofdstuk 3, Elektriciteit 1 1 Lading en stroom Elektrische lading kan positief of negatief zijn. Gelijke
Boekverslag door B. 1240 woorden 16 juni 2015 7.6 10 keer beoordeeld Vak Methode Natuurkunde Pulsar Hoofdstuk 3, Elektriciteit 1 1 Lading en stroom Elektrische lading kan positief of negatief zijn. Gelijke
-Zoek de eventuele benodigde gegevens op in het tabellenboek. -De moeilijkere opgaven hebben een rood opgavenummer.
 Extra opgaven hoofdstuk 7 -Zoek de eventuele benodigde gegevens op in het tabellenboek. -De moeilijkere opgaven hebben een rood opgavenummer. Gebruik eventueel gegevens uit tabellenboek. Opgave 7.1 Door
Extra opgaven hoofdstuk 7 -Zoek de eventuele benodigde gegevens op in het tabellenboek. -De moeilijkere opgaven hebben een rood opgavenummer. Gebruik eventueel gegevens uit tabellenboek. Opgave 7.1 Door
hoofdstuk 1 Elektriciteit.
 spanning 2007-2008 hoofdstuk 1 Elektriciteit. 1.1 Lading. Veel toestellen op het laboratorium werken met elektriciteit. De werking van deze toestellen berust op van elektrische lading die stroomt. We kennen
spanning 2007-2008 hoofdstuk 1 Elektriciteit. 1.1 Lading. Veel toestellen op het laboratorium werken met elektriciteit. De werking van deze toestellen berust op van elektrische lading die stroomt. We kennen
NATIONALE NATUURKUNDE OLYMPIADE. Tweede ronde - theorie toets. 21 juni beschikbare tijd : 2 x 2 uur
 NATIONALE NATUURKUNDE OLYMPIADE Tweede ronde - theorie toets 21 juni 2000 beschikbare tijd : 2 x 2 uur 52 --- 12 de tweede ronde DEEL I 1. Eugenia. Onlangs is met een telescoop vanaf de Aarde de ongeveer
NATIONALE NATUURKUNDE OLYMPIADE Tweede ronde - theorie toets 21 juni 2000 beschikbare tijd : 2 x 2 uur 52 --- 12 de tweede ronde DEEL I 1. Eugenia. Onlangs is met een telescoop vanaf de Aarde de ongeveer
Opgave 3 Staafmagneten, hoefijzermagneten, naaldmagneten en schijfmagneten.
 Uitwerkingen 1 Opgave 1 IJzer, nikkel en kobalt. Opgave 2 ermanente magneten zijn blijvend magnetisch. Opgave 3 Staafmagneten, hoefijzermagneten, naaldmagneten en schijfmagneten. Opgave 4 Weekijzer is
Uitwerkingen 1 Opgave 1 IJzer, nikkel en kobalt. Opgave 2 ermanente magneten zijn blijvend magnetisch. Opgave 3 Staafmagneten, hoefijzermagneten, naaldmagneten en schijfmagneten. Opgave 4 Weekijzer is
Voorbereiding toelatingsexamen arts/tandarts. Fysica: Elektrodynamica. 25 juli 2015 dr. Brenda Casteleyn
 Voorbereiding toelatingsexamen arts/tandarts Fysica: Elektrodynamica 25 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
Voorbereiding toelatingsexamen arts/tandarts Fysica: Elektrodynamica 25 juli 2015 dr. Brenda Casteleyn Met dank aan: Atheneum van Veurne (http://www.natuurdigitaal.be/geneeskunde/fysica/wiskunde/wiskunde.htm),
1. Weten wat elektrische stroom,spanning en vemogen is en het verband ertussen kennen 2. Elektrische netwerken kunnen oplossen
 Hoofdstuk 3 Elektrodynamica Doelstellingen 1. Weten wat elektrische stroom,spanning en vemogen is en het verband ertussen kennen 2. Elektrische netwerken kunnen oplossen Elektrodynamica houdt de studie
Hoofdstuk 3 Elektrodynamica Doelstellingen 1. Weten wat elektrische stroom,spanning en vemogen is en het verband ertussen kennen 2. Elektrische netwerken kunnen oplossen Elektrodynamica houdt de studie
HOGERE ZEEVAARTSCHOOL ANTWERPEN SCHEEPSWERKTUIGKUNDE. Basiselektriciteit. Author: Willem MAES
 HOGERE ZEEVAARTSCHOOL ANTWERPEN SCHEEPSWERKTUIGKUNDE Basiselektriciteit Author: Willem MAES December 6, 2010 Contents 0.1 INLEIDING............................. 5 0.1.1 Voorkennis.........................
HOGERE ZEEVAARTSCHOOL ANTWERPEN SCHEEPSWERKTUIGKUNDE Basiselektriciteit Author: Willem MAES December 6, 2010 Contents 0.1 INLEIDING............................. 5 0.1.1 Voorkennis.........................
TENTAMEN ELEKTROMAGNETISME (8N010)
 TENTAMEN ELEKTROMAGNETISME (8N010) Opmerkingen: 1. Dit tentamen bestaat uit 4 vragen met in totaal 19 deelvragen. Elke deelvraag levert 3 punten op. 2. Het is toegestaan gebruik te maken van bijgeleverd
TENTAMEN ELEKTROMAGNETISME (8N010) Opmerkingen: 1. Dit tentamen bestaat uit 4 vragen met in totaal 19 deelvragen. Elke deelvraag levert 3 punten op. 2. Het is toegestaan gebruik te maken van bijgeleverd
Oefeningenexamen Fysica 2 1ste zit 2006-2007
 Oefeningenexamen 2006-2007 12 januari 2007 Naam en groep: Aantal afgegeven bladen, dit blad niet meegerekend: Gebruik voor elke nieuwe vraag een nieuw blad. Zet op elk blad de vermelding 12/01/2007 alsook
Oefeningenexamen 2006-2007 12 januari 2007 Naam en groep: Aantal afgegeven bladen, dit blad niet meegerekend: Gebruik voor elke nieuwe vraag een nieuw blad. Zet op elk blad de vermelding 12/01/2007 alsook
