Hoofdstuk 1 - Functies differentiëren
|
|
|
- Benjamin Leopold Vedder
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 V-a V-a Hoostuk - Funtis irntiërn lazij Na sonn h in m A 0 0 t in s m/s t 0 : h m/s t t 80 : h , m/s t O, 00 0, 7 0, 00 Voor n voor is hlling 0, 7. ( ) n us ( ) lazij V-a ( ) g ( p) p 8p h ( ) 0 l ( ) k ( a) 0 0, 0a a m ( ) 0
2 V-a s ( t) t t t, t 0t s t s ( t ) t, s t 0 t t s ( t ) t, s t 0 s ( t )( t ) t t t 9 t 9, s t 0 t t s ( t) ( t)( t) t t t t t V-a, h 0, 9 t 9, 8t n h 9, 8 9, m/s t t t Na sonn is valsnlhi van stn 9, m/s ( stn valt naar nn, vanaar ht mintkn). h 0 oplossn: 0, 9t 0 gt 0, 9t waaruit volgt t 0 0, n us, 9 sonn. D ngativ oplossing is nit van topassing. Conlusi: na, sonn is stn op gron gvalln. h 9, 8,, m/s t t, V-a ( ), ( ) 0 oplossn: 0 gt n us o. 0 O 0 0 Hoostuk - Funtis irntiërn s 0 t 8t t 0,, 9 Voor n glt ( ) 0, at wil zggn voor n is hlling van graik van glijk aan 0. Mt graik volgt an at graik an n top ht. Dus n zijn -oörinatn van toppn van graik van. Maimum: ( ) 8 8 n minimum: ( ) ( ) 8
3 Hoostuk - Funtis irntiërn V-7a g ( ) 0, 7, g ( ) 0 oplossn: 0 gt ( ) 0 waaruit volgt 0 o 0 n us 0 o O Voor ht graik van g n top, voor 0 nit. D uitrst waar van g is n minimum: g( ), V-8a h ( t) t 8t, h ( t) 0 oplossn: 8t 0 gt 8t n us t. h( ) ( ) ( ) D uitrst waar van h is n minimum:. a a lazij 7 O is vrtial asmptoot. Dan is nomr glijk aan 0 n tllr nit. is horizontal asmptoot. h( ) 0 is vrtial asmptoot n is horizontal asmptoot. A( t) t t t t t t t 0 is vrtial asmptoot n A is horizontal asmptoot.
4 a p p p p p p W( p) p p p p p p,,,, q q q q N( q) q q q q q P( k) k 0k k 0k k k k k k k 0, q ( q 8) q q q q w( q) q q q q q q q q,, a is vrtial asmptoot. Dan is nomr glijk aan 0 n tllr nit. D graik van ht gn horizontal asmptotn. 0, 0 gt ( 0, ) 0 waaruit volgt 0 o 0, 0. D laatst vrglijking gt 0, n us. a ( ) tllr nomr, ( ) 0 als tllr van glijk aan nul is, at wil zggn als 0, 0 ( vrglijking i j ij opraht opglost ht). lazij O Voor 0 staat unti g nit. D graik ht gn vrtial asmptoot voor z waar van. g( ) 0 als glt 0. Dit gt ( ) 0 n us 0 o 0 waaruit volgt n us. Conlusi: g( ) 0 voor. (D oplossing 0 valt wg, omat nomr van g an ook glijk aan nul is, zi vntul ook graik van g.) k Hoostuk - Funtis irntiërn 7
5 8 a 7a Hoostuk - Funtis irntiërn 0 als 0 n 0. Dit gt 0. P 0 als P 0 n P 0. Dit gt P n us P P ( w )( w ) 0 als ( w )( w ) 0 n w 0. D vrglijking gt w w 0 n w 0, waaruit volgt w n w. Omat w is oplossing w. a 8a 0 als a 8a 0 n a 0. D vrglijking gt a( a 8) 0, waaruit a volgt a 0 n a 8 0 n us a 8. ( q )( q ) 0 als ( q )( q ) 0 n q 0. D vrglijking gt q q 0 n q 0. D rst vrglijking gt q n us q o q. D tw vrglijking gt q. Omat q zijn oplossingn i ovrlijvn q n q. B 8 0 als B B 8 0 n B 0. D vrglijking gt B ( B )( B ) 0, waaruit volgt B n B. Omat B is oplossing i ovrlijt B. D graik van GK ht n vrtial asmptoot q 0. Dz asmptoot is nit van lang voor prount om hij gn ngati aantal shaatsn kan prourn. GK 00 is horizontal asmptoot. Dit tknt at prijs voor n paar klapshaatsn nit onr 00 uro komt GK( 0), uro pr paar shaatsn TK( 0) GK( 0) 0, , 7 uro 00q 000q TK GK q q 0 8a TK 000 oplossn mt hulp van rknmahin. Vor in Y ( 00X ^ 000X) / ( X 0) n Y 000. D opti intrst gt q 80,, us prount kan 80 paar shaatsn prourn. lazij Mt hulp van opti /. :, :, : 9 ( ) Klopt.
6 9a 0,7 0,07 0,0 g ( ) g() 0,7 0,07 0,0 Dz tal komt ovrn mt tal van opraht a. 0a, h ( ) 0, 7 0 h() 0,7 0,9 0,0 0, 0, 0,09 D unti van opraht a kan agli van h zijn., a ( ), TK ( q) 0, q q q q 7 0,,,, P ( t) 0, 8t, t 0, 7, 0, 7,, 8, 8 A,, 0 0, g g 0g g g 9 9 N,, p 0 8, p p lazij 7, a ( ) 0 ( ) 0, 0,,, 0, 0, g( ) g ( ) Hoostuk - Funtis irntiërn 9
7 0 Hoostuk - Funtis irntiërn a S( p), p p 0, 0, 0,, S ( p) 0, p, p p,, g( ),,, g ( ),,,, q q q q q q GK( q) q q, GK ( q) q 0 q q q q q TW( q) q q q q 0, 0, 0,, p( t) t, p ( t) t t t t 0, g A p 0, p p, A p 0, p p 0, p 0, p p p p h K t t 0,, t t t t t, K, t t,, t t t t t, a TW TO TK 0 7 ( 00 7 ) 9, 77 uro TW TO TK 0 q ( 00 q ) 0q 00 q ,, q Voor q is winst maimaal, namlijk 88 uro. TW ( q) 0 0, q 0, q 0, 0, TW ( q) 0 mt hulp van rknmahin oplossn (Y 0. q ^ 0. n vrvolgns opti zro) lvrt q.,, GK q TK 00 q q ( ) 00 00q q q q q q GK ( q) 00 q 0, q 00q 0, q 0, 0, 0, GK ( q) 0 mt hulp van rknmahin oplossn TW ( q) 0, q 0, q, q q 0, 7 0, 0, 7 0, (Y 00q ^ 0. q ^ 0. n vrvolgns opti zro) lvrt q, 7.
8 a Als lngt AB mtr is, is rt BC glijk aan mtr. Total lngt: 0 0 mtr. Total rt: 0 mtr. D hovlhi gron i noig is, is m. O( ) lngt rt ( 0 )( ) ( )( ) 0 8 O ( ) O ( ) 0 gt 8, waaruit volgt 8 n us 7 o 7. In z situati gaat ht om oplossing 7, us minimal amtingn van ht stuk gron zijn mtr voor lngt n 0 mtr 7 voor rt. lazij 8 a p ( ), z uitkomst klopt nit mt waar in tal. p( ) ( ), p ( ) 0 p () Dz waarn kloppn mt tal in ht ok. 7a l ( t) t n l ( ). D hlling is positi, us lngt nmt to. ( t) t n ( ). D hlling is positi, us rt nmt to. l l(, ) l( ) (,, ) ( ) 0, 09 (, ) ( ) (,, ) ( ) 0, 9 O lngt rt, t, : O, 09, 9 7,, t : O, us O 7,, O staan rhthok liggn rhthok klin rhthok l l l O l l l 0, 09 0, 9 0, 09 0, 9, g O, t 0, m / s, Als j n hl klin tijsintrval kijkt, zijn zowl l als hl klin. D vrmnigvuliging l wort an nog klinr, waaroor ling l t t vrwaarlozn is. Hoostuk - Funtis irntiërn
9 h 8a Hoostuk - Funtis irntiërn Als j voor t n hl klin gtal kist, nart O tot O O ( t). t t Als j voor t n hl klin gtal kist nart l l l tot t t t t l ( t) ( t) l( t) ( t) (waarij laatst trm wgvalt, zi opraht g). Conlusi: O ( t) l ( t) ( t) l( t) ( t) i O ( t) l ( t) ( t) l( t) ( t) ( t )( t t ) ( t t )( t ) O ( ) ( )( ) ( )( ) lazij 9 ( ) ( )( 0) 0 0 0, Bi antwoorn zijn glijk. 9a ( ) ( ) A ( t) ( t ) t t t t 8t P ( )( ) ( ) 0 ( 8) ( )( ) l ( q) ( q ) ( q 7) 0q 0q 0q 70q 0q 0 70q M ( p )( p) ( p p ) p 8p p 9p p 7p p 0 0a k( t) t( t t) t, k ( t) t p 8 A ( p) ( p )( p ) ( p p) 0p 8p p p p p p q( q ) q 0q q 0q TK( q) q 0, TK ( q) q q q q q S( t) ( t )( t ) t t t t, S ( t) t k( ) ( ) 0, k ( ) ( ) ( )( 0) ( ) P( ), P ( ) 0 0 ( ) 0
10 a TK p q ( 0 ) TK( ) a 00 uro, TK( ) uro TK Hoostuk - Funtis irntiërn TK ( ) TK ( ) 0 gt , waaruit volgt 000 n us o. 00 In z situati is alln oplossing van topassing. Conlusi: ij opprvlakt TK a lazij 0, m zijn total kostn minimaal. uro n q 00 ( ) 7 postrs ( ), ( ) 0 g( ), g ( ) 0 J kunt unti g( ) nit shrijvn als n som van mahtsuntis want nomr staat uit tw trmn. 0, 0, 0,080 ( ) g ( ) ( ) ( ) ( ) g ( ) 0, 0, 0,080 Dz waarn komn ovrn mt tal ij opraht. ( ) ( ) ( ) ( ) g ( ) ( )
11 Hoostuk - Funtis irntiërn lazij ( ) ( ) a A ( ) 7 ( ) ( ) ( ) a ( q ) ( q 8) q q q q TK ( q) q q ( q ) ( q ) ( q ) ( ) 0 ( ) 0 ( ) ( ) ( t ) ( t ) t B ( t) t t t t t ( t ) ( t ) ( t ) a p p p p A( p) p, A p p p p A( p) p p, p A p p A ( p ) 0 7 p p p ( p ) ( p ) A ( p ) 0 p ( p ) ( p ) K K A D graik is stijgn, us kostn nmn to als ht wrktmpo hogr wort. D unti K staat uit n tllr n n nomr. Als A grotr wort, wort tllr grotr n nomr klinr. Als ghl wort uitkomst van ling an grotr. K 7A 7 00 A K ( 00 A) 7 ( 7A 7) 00 7A 7A 7 7 A ( 00 A) ( 00 A) ( 00 A) Als kostn voor A 70 tw kr zo snl stijgn als voor A zou motn gln: K ( 70) K ( ). K ( ),, 70 n K ( 70), 98, us kostn stijgn nit tw kr zo snl.
12 ( t ) 8 8t t 7a C ( t) 8t t ( t ) ( t ) 8t ( t ) C ( t) 8t 0 als 8t 0. Dit gt t n us t o t. ( t ) Conlusi: na tw uur is onntrati in ht lo maimaal. C ( 0) 8 0 mg/litr/uur C ( ) 8 0, mg/litr/uur ( ) 8a C, 0, C t D onntrati van ht gnsmil nart na vrloop van tij tot nul. D vrglijking 8t mt GR oplossn (Y X X t ( 8 ) / ( ^ ), Y n an opti intrst) lvrt ht tijstip t 7, uur. Conlusi: na ongvr 7, uur mot r n tw injti ggvn worn. lazij O D toppn liggn ij, 0 n. ( ) ( ) 0 oplossn gt 0 waaruit volgt ( ) 0 n us 0 o 0. Dit gt oplossingn 0, n. D graik van aalt voor < n voor 0 < <. D graik van stijgt voor < < 0 n voor >. Hoostuk - Funtis irntiërn
13 Hoostuk - Funtis irntiërn 9a Domin: Uit 0 volgt n us. Brik: 0. D graik ht aar n vrtial raaklijn., ; 7, 08 n, D graik van g ht voor 0, n vrtial raaklijn. 0a D unti staat nit voor, omat voor z waar nomr glijk is aan nul. ( ) 0 ( ) ( ) ( ) ( 0, 9) 00 n (, ) 00. Voor ht graik van n vrtial asmptoot. ( ). D tllr is altij ngati n nomr is vanwg ht kwaraat ( ) altij positi. Als ghl is ht rsultaat altij ngati. Als ( ) altij ngati is, aalt graik van links van n rhts van. Mrk op at ht ghl NIET aln is. lazij a I 0 D tllr is onstant n nomr wort sts grotr. Als ghl ( 0, 0t ) wort ht rsultaat van ling us sts klinr, at wil zggn inhou nmt a. P ( ) 0, I ( 0, 00t 0, t ) 0 0 ( 0, 00t 0, ) 0, t t ( 0, 00t 0, t ) ( 0, 00t 0, t ) Als inhou van ht rsrvoir sts langzamr anmt, mot agli altij ngati zijn n sts ihtr tot nul narn. (Anmn aln) Voor agli glt at tllr altij ngati is n sts klinr wort n at nomr altij positi is (vanwg ht kwaraat) n sts grotr wort. Als ghl is agli us altij ngati n nart agli voor grot waarn van t tot nul. a Domin: 0, rik: ( ), omin: > 0. ( 0, ), 8, ( 0, 0) n ( 0, 00), 8 D raaklijn aan graik van in ht punt ( 0, ) loopt vrtiaal. a ht tw nulpuntn. Vrr kun j aan graik van zin at links van ht rst nulpunt graik van aalt, at tussn i nulpuntn graik van stijgt n rhts van ht tw nulpunt graik van aalt. D uitspraak is us waar. ( ) is voor maimaal, uitspraak is us waar. ( ) is n paraool, aar hoort n kwaratish unti ij. D unti is us n rmahtsunti. En rmahtsunti ht, o nulpuntn. D uitspraak kan us waar zijn.
14 a D uitspraak kan waar zijn (zi opraht ). D uitspraak is nit waar (zi opraht ). O 8 7 O g lazij 7 8 a t t t t t ( ) t t p G( p) p p p p p p p p, G p p p ( ) p p p q( q ) ( q q ) q q q q q TK ( q) q q q q K ( ) ( )( ) ( ) 0 l( n) n( n ) n ( n ) n n, l ( n) n n n n n ( q )( q ) ( q q) q q q q q q q g M ( q) ( q ) ( q ) ( q ) o Hoostuk - Funtis irntiërn O 7 n 7
15 a D lngt nmt n uitrst waar aan, want ht is n kwaratish unti. D rt nit want at is n linair unti. l ( t) t, l ( t) 0 oplossn gt t 0 us t. D uitrst waar is l( ). 8 O( t) l( t) ( t) ( t t )( t ) t t t t t t t D opprvlakt nmt n uitrst waar aan. O ( t) t, O ( t) 0 oplossn gt t 0 waaruit volgt t. 7a Hoostuk - Funtis irntiërn Dit lvrt t n us t o t. D uitrst waar is O( ), 9 D tijstippn komn nit ovrn. ( ). Snlhi astan 000 8, km/uur tij 9 TK BK PK 0v 000 t 0v v TK( ) uro TK( 0) uro 0 TK( 8, ) 0 ( 8, ) uro 8, TK( v) BK PK 0v 000 t 0v v v 7 TK v v v ( ) v 0 v TK ( v) 0 oplossn 7 00v 0 0 v 00v 0 7 v 00v , 00 v 7 v 89, 0, km/uur TK( 0, ) 8 88 uro 7 0 v 7
16 lazij 0, , 00 8a K 000 0, P 0, 8 0, 8 P P T-a K K nmt a als P tonmt. K O n O 70, us oplossn mt hulp van rknmahin. 0 8 P, D opti intrst lvrt P 89 ton pr jaar. W O K 70P 000P 0, O W D winst stijgt als prouti tonmt. Conlusi: prount kan zijn prouti ht st grootshalig inrihtn. lazij O D unti staat nit voor 0 n, omat nomr an nul is. D graik van ht vrtial asmptoot als 9 0 n ( ) 0. D vrglijking gt 9 n us ( ) o. D onglijkhi gt 0 n. D oplossing i ovrlijt is. ( )( ) ( ) 9 (mt 0 n ) ( ) ( ) D lijn. Hoostuk - Funtis irntiërn 9
17 T-a ( ) 0,, ( ) ( ),, ( ), ( ), ( ) ( ), ( ) ( ) 0, 7, 0, 8 Hoostuk - Funtis irntiërn 0, 0, ( ), ( ) T-a ( ) ( ) ( )( ) ( ) ( ) 0 ( ) ( )( ) ( ) ( ) ( )( ) ( ) ( ) ( ) T-a A ( ) 7 ( ) ( ) ( ) ( k)( k ) ( k k) A ( k) k k k k k k k ( k) ( k) ( k) ( q ) 0 q 8q P ( q) ( q ) ( q ) v ( v ) ( v ) v S ( v) v v v v v ( v ) v v v ( ) ( ) h ( ) ( ) ( ) ( ) ( ) ( t) t t ( t) t t t t t t t t t t t
18 lazij 9 T-a Domin: 0 0 O n zijn nulpuntn van, voor ht graik van n top. ( ) 0, 0, 0,, ( ) 0, 0, D graik ht aar n horizontal raaklijn. In uurt van (0, 0) is nit t zin at graik aar n horizontal raaklijn ht. 000 T-a Groningn: 7, N Harn: 800 9, N Groningn-Harn:, N Conlusi: n gmntlijk hrinling zou voor Harn nalig gvolgn hn. Dz gmnt mot an namlijk mr lrlingn op n shool hn an in ou situati om shool opn t houn. ( 8 ) 0 0 N ( ) ( 8 ) ( 8 ) ( 8 ) D tllr n nomr van N ( ) zijn i positi, us N ( ) is positi. Dat N ( ) positi is tknt at hlling van graik van N grotr an nul is. Conlusi: graik van N is stijgn op [ 0,. D lijn N 0 is horizontal asmptoot. Dit tknt at ophingsnorm nooit hogr an 0 lrlingn is. Hoostuk - Funtis irntiërn
19 T-7a Hoostuk - Funtis irntiërn Voorl : n gmnt mt opprvlakt 00 km n 000 lrlingn ht n lrlingnihthi van 0 lrlingn pr km. D ophingsnorm is an N Als r 0 lrlingn ij komn vranrt lrlingnihthi, maar ophingsnorm lijt htzl. Htzl glt als r 00 lrlingn ij komn. Dz paar tra lrlingn kunnn shool rn. Voorl : n gmnt mt n opprvlakt van 0 km n 00 lrlingn ht n lrlingnihthi van 0 lrlingn pr km. D ophingsnorm is an N Als r 0 lrlingn ijkomn vranrt zowl lrlingnihthi als ophingsnorm. Er glt an namlijk N 8. Dz tra lrlingn vrhogn us ophingsnorm, wat situati ongunstigr maakt. Conlusi: uitspraak klopt. Voor onvn waarn van n. Na irntiërn is maht van an vn n at tknt at ( ) an grotr o glijk aan nul is. Zi ijvoorl oprahtn a,, T-a. In ht algmn: als j n quotiëntunti gmakklijk als (som van) mahtsunti(s) kunt shrijvn.
Hoofdstuk 1 - Functies differentiëren
Hoostuk - Funtis irntiërn lazij V-a Na sonn h in m 000 900 A 800 0 0 t in s 80 97 m/s t 0 : h 00 000 00 7 m/s t 0 0 0 t 80 : h 0 00 00, m/s t 80 00 80 V-a O, 00 0, 7 0, 00 Voor n voor is hlling 0, 7. (
Hoofdstuk 12A - Breuken en functies
Hoostuk A - Brukn n untis Hoostuk A - Brukn n untis Voorknnis V-a g 9 h 9 9 i 0 j 9 0 0 V-a 0 nt is 0,0. J trkt ht aantal likjs kr 0,0 van uro a. W(0) 0,0 0 Z ht nog uro op klantnkaart staan. 0,0 0,0 :
Noordhoff Uitgevers bv
Vriping - Bwijs van a-formul a D zij van ht klin virkant wort an = D opprvlakt van ht grot virkant wort an = D opprvlakt van ht klin virkant wort an = D opprvlakt van i virkantn samn is + = a D vrglijking
Hoofdstuk 6 Machtsfuncties. Kern 1 Even en oneven exponenten. 4VWO B, uitwerkingen Hoofdstuk 6, Machtsfuncties1
VWO B, uitwrkingn Hoostuk, Mahtsuntis Hoostuk Mahtsuntis Krn Evn n onvn ponntn a Ht gwiht van kuus staat uit ht gwiht van rin. Er zijn rin. Als ri r m lang is, an wgt ir ri 0, r gram. Ht total gwiht wort
Hoofdstuk 6 - Formules met breuken en machten
Morn wiskun 9 iti Havo A l Hoofstuk - Formuls mt rukn n mahtn lazij 4 V-a 4 774, us 4 774 Dit laatst antwoor kun j ook shrijvn als 7, 74 7, 74, 7, 9 7 : 9 4 9, 44 9 is n hl klin gtal, namlijk, mt nulln
Hoofdstuk 6 - Formules met breuken en machten
Morn wiskun 9 iti Havo A l Hoofstuk 6 - Formuls mt rukn n mahtn lazij 46 V-a 4 6 = 774, us 4 6 = 774 Dit laatst antwoor kun j ook shrijvn als 7, 74 = 7, 74 6, 7, 9 7 : 9 = 9, 644 4, 9 is n hl klin gtal,
Oplossingen. (2): y = ,50 x. 8 a (1): y = 10,50x Algebraïsche verbanden (blz. 21) 1 a a, d, f. meer dan 10 beurten.
= Oplossinn.. Alraïsh vrann (lz. ) a a i h a i h in 00 aantal o n zwaarwon itsslahtors op 00 rnn a april novmr n mr januari 000 uro winst a Ilk is zwaarr an mst zls zwaarlijvi ay's ja (zi raik) nooit 6
getal en ruimte wi 1 vwo deel2 Uitwerkingen
tal n ruimt wi 1 vwo l Uitwrkinn Gtal n ruimt 1VWO l - Hst 6 6.1 Kwaratn 1 40 x 40 = 1600 m 3 x 1600 4800. D kwkr poot 4800 ahlia's. tal 1 3 4 5 6 7 8 9 10 11 1 13 14 15 0 5 kwaraat 1 4 9 16 5 36 49 64
Noordhoff Uitgevers bv
172 Vriping - Gin 1a ll puntn op milloolijn van liggn vn vr van punt als van punt. ll puntn i ihtr ij punt liggn, zulln us aan n kant van milloolijn liggn n all puntn i ihtr ij punt liggn, zulln aan anr
Oplossingen vbtl 5 analyse 1, leerweg 6-8
= Oplossingn vtl analys lrwg -8. Vltrmuntis (lz. ) (); (); (0); g(); () a gn 0 g 0 + i gn 0 a + + + + ; 0; a 9 + C A A + A A A A < F A A A a ovn: A A + onr: A A nn uur; 8 m m uur top : () ; () al : (0)
20 m/s. 11 m/s. 20km h. 5,6 m/s op t = 4,0 s is de plaats: 5,6 4,0 22 m. 58 [W] Experiment. 59 [W] Experiment: Versnellend karretje
![20 m/s. 11 m/s. 20km h. 5,6 m/s op t = 4,0 s is de plaats: 5,6 4,0 22 m. 58 [W] Experiment. 59 [W] Experiment: Versnellend karretje](/thumbs/93/111671772.jpg "20 m/s. 11 m/s. 20km h. 5,6 m/s op t = 4,0 s is de plaats: 5,6 4,0 22 m. 58 [W] Experiment. 59 [W] Experiment: Versnellend karretje")
58 [W] Exprimnt 59 [W] Exprimnt: Vrsnlln krrtj 60 [W] Exprimnt: Knikkrn 61 [W] Drgrr 62 [W] Exprimnt: En ign wging 63 [W] Wissln op stftt 64 Wr of nit wr? Nit wr: ht v,t-igrm vn n nprig vrsnl wging is
Uitwerkingen H9 van vwo B deel 3 Exponentiële functies en logaritmische functies
Uitwrkingn H9 van vwo B dl Eponntiël functis n logaritmisch functis. y log( + 5) y log() + log (5) n y log (5) Uit d tabl blijkt dat y n y htzlfd zijn. log() + log(5) log(5) Vor in : y log( 5) ; y log()
Hoofdstuk 1 Maten omrekenen
Hoostuk 1 Matn omrknn Opstap Enhn n hanig matn O-1a O-2a Ht gwiht van n puppy is 325 gram. Elln loopt 100 mtr in 15,3 sonn. D lngt van kantin is 27,3 mtr. D inhou van n pak mlk is 1,5 litr. En hoolarp
De Wageningse Methode 5&6 VWO wiskunde B Uitgebreidere antwoorden Hoofdstuk 5 Exponentiële functies
D Wagnings Mthod 5&6 VWO wiskund B Uitgbridr antwoordn Hoofdstuk 5 Eponntiël functis Paragraaf Eponntiël functis a. J mag wl van n artikl van 00 uro uitgaan. Bij d n krijg j: 00 0 0 99 Bij d andr: 00 90
Statistiek. Waar gaat het om? S 3.1 Steekproeven. Dit is waarschijnlijk representatief als de steek- proef groot genoeg is.
1 1 Statistik S 3 I II a Waar gaat ht om? Statistik is n onrl van wiskun waarij ht gaat om ht ornn n intrprtrn van grot hovlhn ggvns. En statistik is ook wl n tal o n iagram mt ggvns. 4 nt Dit is waarshijnlijk
Uitwerkingen extra opgaven hoofdstuk 5 Functieonderzoek: toepassing van de differentiaalrekening ( ) ( )( ) ( ) ( )( )
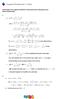Uitwrkingn tra opgavn hoofdstuk 5 Functiondrzok: topassing van d diffrntiaalrkning. a. g( ) ( ) - 4 = Þ + - 6 ( + - 6) - ( - 4)( + ) ( + - 6) + - - ( - 8 + - 4) ( + - 6) g = = = = ( + )( - ) ( - ) ( +
4 a. b 9 d. 5 a Õ b Œ c Œ. 6 a C d C f Ç b C e Ç h C c Ç f Ç i C. 7 a 3 C N d 0,25 C Q + 3 Ç Z e 7. gemengd repeterend.
= Oplossinn. Rational talln (lz. 9) a -7-6 0,000, -7-6 -, i a 9 9-8 a Õ Œ Œ - a 6 6-8 i a - 7,6 - -6-0 i - 0 - - - 0 8 6 a C C Ç C Ç C Ç Ç i C 7 a C N 0, C Q + Ç Z 7 8 C Q+ - C Q - C Z- 8 imal vorm zuivr
Extra oefening hoofdstuk 1
Etra ofning hoofdstuk = ( ) = = v v v dr 7 7 7 v a = + v als v 7 v v dus als = 7 7 7 7 dv waaruit volgt dat v = 7 km/uur. v = 7 gft R = 7, 7 mg/min. a f ' = = ' = + = ( + ) ' = = ( ) = f f d f ' ln ln
Hoeveel warmte heb je nodig om een stof op te warmen? Water is erg geschikt om warmte in op te slaan?
1 Wrmtr. Oprht 1.1 Hov wrmt h j noig om n stof op t wrmn? =,5 5,= 1,1 1 = 1 15= 6, 1 1 1 T = T = =,9,1 18, 1 = 1, 9 kg 9 Opgv 1. Wtr is rg gshikt om wrmt in op t sn? Om 1 kg ijs 1 op t wrmn h j 6 noig.
Hoofdstuk 6 - Differentiaalvergelijkingen oplossen
Hoofsuk 6 - Diffrniaalvrglijkingn oplossn 6 Shin van varialn lazij a, 5 (, 5) us (, 5 ), 5 us volo D kromm gaa oor (0, ) us, 5, 5 0, 5, klop H onrs l van kromm vanaf pun (, 5; 0 ) a Als j a iffrnir, an
Bij de toepassing van de in paraplubestemmingsplan bedoelde ontheffing wordt verstaan onder:
HOOFDSTUK 2. REGELS PARAGRAAF 1 TOEPASSINGSREGELS Artikl 1 Topssingsrik Inin nit op gron vn nr plingn vn in ijlg 1 gnom stmmingsplnnn vrijstlling/onthffing kn worn vrln zijn urgmstr n wthours vog onthffing
Negatieve getallen in een assenstelsel
G Ngtiv gtlln in n ssnstlsl 98 kijk ht ssnstlsl n los vrgn op. Gf oörint vn puntn, n. 2 4 (...,...) (...,...) 2 (...,...) Tkn in ht ssnstlsl puntn D(, 2), ( 4,) n (2, ). Klur ht glt vn ht ssnstlsl gron
Hoofdstuk 1 Algemene bepalingen
Bviligingshnok GBA Gmnt Brgmht 2011 Burgmstr n wthours vn gmnt Brgmht, Glt op rtikl 14 vn Wt gmntlijk sisministrti prsoonsggvns; Bsluitn vst t stlln Bhrrgling gmntlijk sisministrti prsoonsggvns 2011: Hoostuk
Oplossingen analyse 2 (leerweg 4)
= Oplossingn analys (lwg ). Limit van n unti (lz. ) a 8 8 08 0 g h a L.L. = ; R.L. = + L.L. = + ; R.L. = L.L. = ; R.L. = L.L. = + ; R.L. = L.L. = + ; R.L. = L.L. = + ; R.L. = + g L.L. = 8; R.L. = 8 h L.L.
In figuur 5-1 zie je een afbeelding van de snelheidsmeter en de kilometerteller van een nieuwe auto.
Opgvn Vrkr In ht vrkr spln snlhi n krht n lngrijk rol. W zulln topssingn kijkn wrij voorl ook vilighi in ht vrkr n o zl komn. Opgv 1 In figuur 5-1 zi j n fling vn snlhismtr n kilomtrtllr vn n niuw uto.
Hoofdstuk 1 - Exponentiële en logaritmische functies
Hoofsuk - Eponniël n logarimish funis Voorknnis: Eponnn n logarimn lazij V-a Elk jaar wor h aanal hilauwjs vrmnigvulig m n vas gal. Di gal lig ussn n, us is r sprak van ponniël afnam. g pr jaar 88, g pr
Machten. Inhoud Machten
Mchtn Inhoud Mchtn Mchtn n mchtsvrhffn Evn n onvn mchtn Vrmnigvuldign vn mchtn Dln vn mchtn Mcht vn n mcht Mchtn vn productn 7 Mchtn vn rukn Sustiturn vrvngn vn n lttr door n gtl Wortls n mchtn mt grokn
Antwoordblad. Hoofdstuk 2 Dansen door de eeuwen heen. 2.1 De dans. (melodie van de blazers)
Antwoorla Hoofstuk 2 Dansn oor uwn hn 2.1 D ans 03 Maat 36, 44 (vanaf tw tl), 64 (vanaf tw tl). 04 a In maat 5 n 7: tw ahtst van tw n vir tl. Maathakn (maat 12, 13): rst kr spl j tot n mt rst maathaak,
NEVAC examen Elementaire Vacuümtechniek Vrijdag 11 april 2003, 14:00-16:30 uur. Vraagstuk 1 (EV-03-1) (25 punten)
NEVAC xmn Elmntir Vuümthnik Vrijg 11 pril 2003, 14:00-16:30 uur Vrgstuk 1 (EV-03-1) (25 puntn) En vuümsystm wort gëvur mt n olivrij pompsystm, t stt uit n voorvuümpomp n n turomolulirpomp. D pompsnlhi
Gelijknamige breuken kun je eenvoudig bij elkaar optellen of van elkaar aftrekken:
Brukn optlln n ftrkkn Vrknnn Opgv 1 Ton n Hns stlln smn n grot pizz. Ton t d hlft vn d pizz op, Hns t 3 dl vn d pizz. 8 Wlk dl vn d pizz tn z smn op? Wlk dl vn d pizz t Ton mr op dn Hns? nm: Imgs/R1003.jpg
Noordhoff Uitgevers bv
a lok - Kuznu Vriping Voorwaarlik kansn Er zin 927 annn onrzoht. En r zin 7 vrouwn onrzoht. Er zin 72 annn klurnlin. En r zin vrouwn klurnlin. 2a aantal 927 72 prntag 00 0,00 8,0 Van onrzoht annn is ongvr
UITWERKINGEN. Wiskunde. voor het hoger onderwijs. Deel A. Sieb Kemme Wim Groen Harmen Timmer Chris Ultzen Jan Walter. Gewijzigde vijfde editie
UITWERKINGEN Dl A Wiskun voor t or onrwijs Si Kmm Wim Gron Harmn Timmr Cris Ultzn Jan Waltr Gwijzi vij iti Wiskun voor t or onrwijs Dl A Uitwrkinn Wiskun voor t or onrwijs Dl A Uitwrkinn Si Kmm Wim Gron
Eindexamen wiskunde B1 vwo 2008-I
Eindamn wiskund B vwo 008-I Boordlingsmodl Vraag Antwoord Scors Landing maimumscor 4 y' 4,8 0 3 + 4,8 0 5 y '(0) 0 (dus in (0, 8) hft ht vligtuig n horizontal bwgingsrichting) y '(00) 0,48+ 0,48 0 (dus
13 Afgeleide en tweede afgeleide
Afglid n twd afglid a f ( + gft f ( + + + ( + f ( gft ( - - + ƒ ma is f ( B f, ] b f ( + + ( + ( + + f ( gft ( + + + f ( dus ht buigunt is, c f ( Zi d figuur + a hft één olossing voor a a a ƒ d b( + hft
Ajodakt Hoofdrekenen groep 5-6
Ajokt Hoofrknn grop - Dln t/m 0 n hogr, mt n zonr rst Colofon ũžěăŭƚ ŵăăŭƚ ĚĞĞů Ƶŝƚ ǀĂŶ ŚŝĞŵĞDĞƵůĞŶŚŽī ĞůĨƐƚĂŶĚŝŐ ǁĞƌŬĞŶ ŝƚ ďğɛƚăăƚ Ƶŝƚ ĞĞŶ ŐƌŽŽƚ ĂƐƐŽƌƟ ŵğŷƚ ůğğƌŵŝěěğůğŷ ǀŽŽƌ ĂůůĞ ůğğƌũăƌğŷ Op onz Z-sit
De Wageningse Methode 5&6 VWO wiskunde B Uitgebreidere antwoorden Hoofdstuk 8 Integralen toepassen
D Wagnings Mtod & VWO wiskund B Uitgbridr antwoordn Hoofdstuk Intgraln topassn Paragraaf Inoud n intgraal f d ( ) d ( ) d a Ht 'topj' van d piramid is glijkvormig mt d l piramid mt factor f, dus O()f b
Getal en Ruimte 1VWO deel 2
Gtal n Rumt 1VWO l 2 MA2N Hoostuk 8 Utwrknn m / 2 Gtal n rumt 1VWO l 2 - Hst 8 8.1 Hrln 1a 6a + 2a = 8a 7p p = 6p 3p + 3q = kan nt 4a 7 = 28a 2a 5a = 10a² j 2 3a = 6a 3a + 2 + 5a = 8a + 2 2a 5 + 7 a =
Evaluatievragen Algemene economie reeks 1 (Thema 1, 1.1 De prijsvorming op competitieve markten)
Evlutivrgn Algmn onomi rks 1 (Thm 1, 1.1 D prijsvorming op omptitiv mrktn) 1 Kruis torn n i n invlo hn op vrg nr n prout. O ht inkomn vn onsumnt O gprour hovlhi O prijs vn nr proutn O hotn vn onsumnt O
8 Elektromotor en dynamo
8 Elktromotor n ynmo Elktromgntish vl vwo Uitwrking sisok 8.1 INTRODUCTIE 1 [W] Exprimnt: Mgntn, spijkrs n kompssn 2 [W] Exprimnt: Rlis 3 [W] Exprimnt: Frromgnt n ntifrromgnt 4 Wr of nit wr? f g h Nit
Algebra Pijlen - hv. Opdracht 2 Je ziet hieronder een ander voorbeeld. Bouw ook dit schema na. Vul bij invoer de waarde 10 in. Wat komt er uit?
9 Psl Algr Pijln - hv A Bwrkingn mt Algr Pijln D shm s in pplt Algr pijln nomn w rknshm s. Oprht 1 Gruik pplt Algr Pijln. J ht ht shm uit ht voorl ngouw. Vul ij invor wr 18 in. Wt komt r uit? Voor kommgtlln
Welke drie redenen kun je noemen voor het feit dat hun aantal in Zuid-Afrika achteruit is gegaan?
Rout B 1 Zwrtvotpinguïns Zwrtvotpinguïns zijn ngpst n ht wtrlvn. Doort hun kort vrn iht tgn lkr zittn, zijn z shrm tgn ht kou wtr. Bovnin hn z onr hun hui n ikk vtlg. Zwrtvotpinguïns mkn l uit vn volgn
5. Exponentiële en logaritmische functies.
uitwrkingn ponntiël n logritmish funtis Vrvoort Bokn,,,9 : fgron,,, : :,, fgron t, 9,9, : : 9,9 fgron t,,,,,,,9,,,,, 9 9 9 Uitwrkingn hoofstuk. Eponntiël n logritmish funtis. Opgv. Bsisrkningn mt logritmn,
Aanvraagformulier Persoonsgebonden Budget Verpleging en Verzorging
Anvrgormulir Prsoonsgonn Bugt Vrplging n Vrzorging DEEL 3: Bugtpln Dit ugtpln wort oor vrzkr o wttlijk vrtgnwoorigr ingvul. 1 (En tolihting op ht ormulir stt in ijlg) 1. Grssr Dit ormulir is stm voor:
Inhoud. 2 Symmetrie Lijnsymmetrie Puntsymmetrie Draaisymmetrie Driehoeken Vierhoeken 28 2.
Wiskun voor 2 vwo Dl 1, Antwoornok Vrsi 2013 Samnstllr 2013 Ht autursrht op it lsmatriaal rust ij Stihting Math4All. Math4All is rhalv rhthn zoals ol in hironr vrml rativ ommons linti. Ht lsmatriaal is
F z. hoe merk je dat?
4 Sport n vrkr Krhtn VWO Uitwrkingn sisok 41 INTRODUCTIE 1 [W] Wt wt j nog ovr krhtn? 2 [W] Wt on krhtn? 3 [W] Voorknnistst 4 [W] Extr opgvn 5 Wr of nit wr? Wr Wl n nit wr: nttokrht is n lijft 0 ij n nprig
Inhoud. 6 Veranderingen In grafieken Differentiequotiënt Totaalbeeld 60
Wiskun A voor 4/5 havo Dl 1, Antwoornok Vrsi 2013 Samnstllr 2013 Ht autursrht op it lsmatriaal rust ij Stihting Math4All. Math4All is rhalv rhthn zoals ol in hironr vrml rativ ommons linti. Ht lsmatriaal
Voorbereiding toelatingsexamen arts/tandarts. Wiskunde: integralen en afgeleiden. 16 september dr. Brenda Casteleyn
Voorbriding tolatingsamn arts/tandarts Wiskund: intgraln n afglidn 16 sptmbr 017 dr. Brnda Castlyn Mt dank aan: Athnum van Vurn Ln Goyns (http://usrs.tlnt.b/tolating) 1. Inliding Dit ofningnovrzicht is
Hoofdstuk 5 - Verbanden herkennen
V-a V-a Hoofstuk - Veranen herkennen Hoofstuk - Veranen herkennen Voorkennis O A B De grafiek ij tael A is een rehte lijn, want telkens als in e tael met toeneemt neemt met toe. Het startgetal is en het
Antwoorden Leereenhedentoets Module 13 Financieel beleid nietcommerciële
Antwoordn Lrnhdntots Modul 13 Financil blid nitcommrciël organisatis (nco) 13.1 Liquidititsbgroting n kassaldo nco KASSALDO BUURTVERENIGING STADSPLEIN a 2p D omvang van d liquid middln op 31 dcmbr 2013
Oplossingen matrices en stelsels 5/6, beknopt
Oplossingn matris n stlsls /6 knopt. rminologi n wrkingn (lz. 8) 0 6 9 6 0 6 0 7 a u n v u 4 v n w x n y 4 B: 4 x ; C: x ; D: x ; E: 4 x 6 ; F: 4 x 7 4 0 7 6+ 0 4 6 6 0 9 6 a 0 4 4 8 < 0 4 7 8 7 nit zinvol
Niet waar: Een schildpad heeft een grotere massa, dus ook een grotere traagheid dan een slak.
2.3 VERSNELLEN EN VERTRAGEN 32 [W] Wstrijj vrsnlln 33 Wr o nit wr? Wr Nit wr: Bij n onstnt vrtrging is voorwrts krht klinr n tgnwrkn krhtn. Wr Nit wr: En shilp ht n grotr mss, us ook n grotr trghi n n
Noordhoff Uitgevers bv
b 9 Blzij 0 8 mtr 08 b HA in mtrs 0 7 08 D in mtrs,7 8,89 J ; ngglir gt in n rt lijn nr bnn. J omt r tussn HA n D n linir vrbn bstt. D f 0 0 g O 0 0 0 80 00 0 HA D grfik gt oor (0, 0). 08 9 9 Blzij D vnrigisonstnt
Hoofdstuk 2 Limieten toepassen
Hoofdstuk Liit topass. Covrgti ladzijd a Er ot gld dat u > u dus u u >. u u ( ) >, wat ( ) ( ) ( ) u adrt aar voor Uit, 999 volgt dus vaaf zij d tr grotr da,999. a ( ) voor dus u D klist is u d grootst
Hoofdstuk 5 - Evenredigheden
Hvo D l Uitwrkingn Morn wiskun Hoofstuk - Evnrign Blzij 0 6 8 mtr 08 b HA in mtrs 0 7 08 D in mtrs,67 8,89 6 J ; ngglir gt in n rt lijn nr bnn. J omt r tussn HA n D n linir vrbn bstt. D 0 0 O 0 0 60 80
Getal en Ruimte 1VWO deel 2
Gtal n Ruimt 1VWO l 2 MA2N Hoofstuk 10 Uitwrkingn gghm / 2 Gtal n ruimt 1VWO l 2 - Hfst 10 10.1 Omgaan mt grafikn 1a In 1995 uur ht groisizon ongvr 285 agn. In 1965 was ht groisizon ht kortst; ongvr 250
Hoofdstuk 6 Goniometrie
Opstap Tangens O-1a EF!1044 32,3 m zije kwaraat zije kwaraat KL 30 m 900 ST 20 m 400 LM 15 m 225 TW? 225 KM? 1125 SW 25 m 625 KM!1125 33,5 m TW!225 15 m O-2a Driehoek PQR is een rehthoekige riehoek omat
Wiskunde voor 2 havo. Deel 2. Versie 2013. Samensteller
Wiskun voor 2 hvo Dl 2 Vrsi 2013 Smnstllr 2013 Ht utursrht op it lsmtril rust ij Stihting Mth4All. Mth4All is rhlv rhthn zols ol in hironr vrml rtiv ommons linti. Ht lsmtril is mt zorg smngstl n gtst.
4.3. Toepassingen van logaritmische en exponentiële functies
4.3. Topassingn van logaritmisch n ponntiël functis 4.3.. Limitn van logaritmisch n ponntiël functis Voorbld : a b a b H lna a lna lnb b lnb b log a Voorbld : Dit is n niuw onbpaald vorm! W wtn wl dat
Hoofdstuk 6 - Differentiëren
Havo D eel Uitwerkingen Moerne wiskune Hoofstuk - Differentiëren Blazije a Het water steeg het harst op e tijstippen waarij e grafiek het steilst loopt. Dat is om ongeveer 7 uur s ohtens en om 7 uur s
Wiskunde voor 2 vwo. Deel 2. Versie 2013. Samensteller
Wiskun voor 2 vwo Dl 2 Vrsi 2013 Smnstllr 2013 Ht utursrht op it lsmtril rust ij Stihting Mth4All. Mth4All is rhlv rhthn zols ol in hironr vrml rtiv ommons linti. Ht lsmtril is mt zorg smngstl n gtst.
Hoofdstuk 2 - Veranderingen
lazije 6 V-1a 1 m, want ij een massa van kg lees je in e grafiek e lengte van 1 m af. Veer B is stugger, want in e grafiek kan je aflezen at wanneer je aan eie veren evenveel gewiht hangt, veer B korter
= Oplossingen vbtl 5 analyse 1, leerweg 4
OPLOSSINGEN = Olossingn vtl nlys lrwg. D uliish ling (lz. ) + 7 + + 8 8 0 8 9 9 _ + i + _ i + _ + i 7 8 7 _ + i + _ i + _ + i + _ 8i _ + i + _ + i + 8 0 g ( _ + i + _ i + _ + i ) h 9 + + 9 0 i + 8 + +
Algebra Pijlen - vm. Opdracht 2 Je ziet hieronder een ander voorbeeld. Bouw ook dit schema na. Vul bij invoer de waarde 10 in. Wat komt er uit?
9 Psl Algr Pijln - vm A Bwrkingn mt Algr Pijln D shm s in pplt Algr pijln nomn w rknshm s. Oprht 1 Gruik pplt Algr Pijln. J ht ht shm uit ht voorl ngouw. Vul ij invor wr 18 in. Wt komt r uit? Voor kommgtlln
Oefenopgaven Schoolexamen 1 Scheikunde 6 VWO 1/5
Ofnopgavn Schoolxamn 1 Schikun 6 VWO 1/5 Hoofstuk 10 nrgi n vnwicht 1 Eén van ractis i plaatsvint in n zwavlzuurfabrik, is racti tussn zwavlioxi n zuurstof uit lucht. Hirbij wort zwavltrioxi gvorm. All
Hoofdstuk 4 De afgeleide
Havo B eel Uitwerkingen Moerne wiskune Hoofstuk De afgeleie lazije 9 V-a 8 8 8 kg Lengte in m Gewiht in kg 8 7 8 9 8 gewiht 8 8 lengte m weegt 8 kg us m weegt 8 : 8 kg. e 8 m 8 8 is het startgetal en 8
Noordhoff Uitgevers bv
0 Voorkennis: Differentiëren en rekenregels lazije 0 V-a h ( ) 0 f () t 6 t + t 0 t + t n () t t t 7 t 6t e k ( p) p p + 0 0p 7 p g ( ) + 08 V-a f( ) ( + ) 6 f ( ) 6 h ( ) ( + 9) 8 gt () tt ( + t ) t +
Hoofdstuk 4 De afgeleide
Hoofstuk De afgeleie lazije 9 V-a 8 8 8 kg lengte in m gewiht in kg 8 7 8 9 8 gewiht 8 8 lengte m weegt 8 kg us m weegt 8 : 8 kg. e 8 m 8 8 is het startgetal en 8 is het hellingsgetal. V-a ();(); ();(
Noordhoff Uitgevers bv
Hoofstuk De afgeleie lazije 9 V-a, 8, 8 8 kg lengte in m gewiht in kg,8,, 7, 8 9,,8 gewiht 8 8 lengte m weegt 8 kg us m weegt 8 : 8, kg. e, 8,, m 8,,8 is het startgetal en,8 is het hellingsgetal. V-a (,);(,);
Eigen mening op grond van bijvoorbeeld: de uitvoeringspraktijk, opzwepend ritme, hoog tempo, opgewekt karakter.
Antwoorla Hoofstuk 7 Blu Nots, Swing n Changs 7.1 Blus 04 a A A B B A D rhtrhan gint n otaaf hogr. Knmrkn van ragtim: D rag wort op piano gspl. D gsynopr mloi gominr mt strakk gliing op tl ( ragg tim ).
Integralen. onbepaalde integralen. oneigenlijke integralen. gemiddelde functiewaarde op een interval
Intgrln onld intgrln onignlijk intgrln gmiddld funtiwrd o n intrvl Onld intgrl En onld intgrl wordt ogshrvn ls: f ( d ) wrin f() n willkurig funti is. En r gldt: f ( d ) = F( ) + Wrij F() d rimitiv funti
Hoofdstuk 11 Verbanden
Opstap Remweg O- De rie remwegen zullen vershillen zijn. Algemeen gelt at ij e hoogste snelhei e langste remweg hoort. O- De remparahute geeft nog meer remkraht. O- De remweg wort langer op een sleht of
e De omvang van de partij is van een lage bes tot een hoge d. De lage bes valt volgens het overzicht van opdracht 2c buiten het bereik.
Antwoorla Hoostuk 1 Ht lang lvn van ht li 1.1 Ht li 02 Eign antwoor Eign antwoor 04 Omirkl: = 145 145 kwartnotn pr minuut D omvang van partij is van n lag s tot n hog. D lag s valt volgns ht ovrziht van
Standaardantwoorden bij Recht op de praktijk af, Opgaven
Stanaarantwoorn ij Rht op praktijk af, Opgavn C.M. Vrka Woltrs-Noorhoff Groningn/Houtn Evntul op- n aanmrkingn ovr z of anr uitgavn kunt u rihtn aan: Woltrs-Noorhoff v, Afling Hogr Onrwijs, Antwoornummr
Nieuw voorinkoop contract. Nieuw voorverkoopcontract
Smnvtting oor E. 1185 woorn 14 novmr 2013 5.8 4 kr oorl Vk Mtho M&O In lns Hoofstuk 21 Voorrwrring 21.1 Economisch n tchnisch voorr Brutowinst is ht vrschil tussn vrkoopprijs vn vrkocht rtikln n inkoopprijs