Escher in Het Paleis. Wiskundepakket. Onmogelijke figuren
|
|
|
- Stefan Martens
- 7 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Escher in Het Paleis Wiskundepakket Onmogelijke figuren
2 Onmogelijke figuren Een onmogelijk figuur is een tweedimensionale weergave van een object dat in drie dimensies onmogelijk lijkt te kunnen bestaan. Het is een vorm van gezichtsbedrog. De menselijke hersenen zijn er aan gewend om een tweedimensionale weergave van een object te interpreteren als een driedimensionaal object. Daarbij wordt in eerste instantie gelet op details, dan op de grote vorm, waarna de hersenen razendsnel met een interpretatie komen. De hersenen nemen niet de moeite om de informatie over alle details te combineren met de informatie over de grote vorm. Een goede tekenaar kan de hersenen daardoor makkelijk in de luren leggen. De volgende foto laat zien dat er wel degelijk ruimtelijke vormen zijn, die er uit kunnen zien als een onmogelijk figuur. Dit beeld ziet er echter maar vanaf één punt uit als een onmogelijk figuur, vanaf alle andere punten zie je drie balken die rechte hoeken met elkaar maken! Dat is ook de informatie die je krijgt als je alleen let op de hoekpunten. Deze informatie strookt niet met de grote vorm die het beeld, vanuit dit gezichtspunt, suggereert: een gesloten driehoek. Het beeld is knap gemaakt omdat je niet ziet dat de linkerbalk los staat van de rechterbalk. Behoort het grijze blok bovenin bij de linker- of bij de rechterbalk? Kan jij het zien? Het beeld staat op een camping bij het Oostenrijkse Gotschuchen, als je ter plekke wilt gaan kijken.
3 De hierboven besproken vorm wordt wel Penrose-driehoek genoemd. Roger Penrose was een wiskundige die in 1958 een artikel publiceerde over onmogelijke figuren. Het idee was al in 1934 bedacht en gebruikt door de Zweedse kunstenaar Oscar Reutersvärd. Penrose was geïnteresseerd in het werk van Escher en zij werden vrienden. Het was Penrose die Escher op het idee bracht om onmogelijke figuren te verwerken in zijn prenten. Escher gebruikte drie Penrose-driehoeken in zijn prent waterval uit Behalve een visuele illusie, verbeeldde Escher hier tevens een fysische illusie: het idee van een perpetuum mobile, een beweging die, zonder er energie aan toe te voegen, oneindig lang doorgaat. Het rad blijft eeuwig draaien door de kracht van het rond stromende water. Waterval werd een van de bekendste prenten van Escher.
4 Voor zijn prent Belvedere, die Escher bij voorstudies consequent betitelde als het spookhuis, verwerkte hij het thema van de onmogelijke kubus. Op de tekening die, schijnbaar nonchalant gevallen, op de tegelvloer ligt, wordt het idee dat ten grondslag ligt aan onmogelijke kubussen aangegeven door middel van kringetjes om de schijnbare snijpunten van de ribben van de kubus. In deze projectie is niet aan te geven welke ribben vóór en welke ribben achter ligt. Als de ribben echter gepresenteerd worden als balkjes kan je zien welke voor en welke achter ligt. Tenzij de informatie die van de twee schijnbare snijpunten afkomstig is zichzelf tegenspreekt. Dat is het geval bij de onmogelijke kubus waar de man op het bankje zit te staren! Maar het is tevens het geval voor het hele gebouw achter hem. Alhoewel de bovenverdieping helemaal normaal is, bestaat de middelste verdieping in feite uit twee (of drie.) onmogelijke kubussen, waarvan de verticale ribben gevormd worden door de pilaren. Merkwaardig is ook dat niet meer vast te stellen is wat binnen en buiten is. De ladder staat, vanuit de middelste verdieping bekeken binnen en vanuit de bovenste verdieping buiten. Thema s uit Escher s eerder werk, zoals hol en bol en het niet bestaan van boven/onder van de Möbius banden, komen in deze prent samen.
5 De wiskundige Penrose stuurde Escher ook een schets van een onmogelijke trap. In eerste instantie lijkt deze trap volkomen normaal. Maar bij nadere beschouwing is er echter iets erg vreemds aan de hand: de trap blijft steeds stijgen! Dit idee verwerkte Escher in zijn beroemd geworden prent stijgen en dalen Het eindeloze proces van stijgen en dalen wordt hier benadrukt door de traplopende monniken en de persoon op het balkon die dit observeert. Terloops paste Escher op heel natuurlijke wijze het driepuntsperspectief toe.
6 Wiskundig gezien is de truc van de onmogelijke trap eenvoudig te realiseren. In de tekening hier linksonder zie je een correct weergegeven trap. Door het tekenen en weglaten van enkele lijnstukjes krijg je de onmogelijke trap in het rechterfiguur. Dat de onmogelijke figuren van Escher in werkelijkheid wel degelijk kunnen bestaan, maar er dan héél anders uitzien dan de prenten suggereren kan je bijvoorbeeld op de volgende website zien: Van een prent als relativiteit wordt ook wel beweert dat het een onmogelijk figuur is. Wiskundig gezien is dat niet juist. Er wordt knap gebruik gemaakt van driepuntsperspectief en de wetten van de zwaartekracht worden getrotseerd, maar dit model is zelfs met lego te realiseren!
Escher in Het Paleis. Wiskundepakket. Perspectief
 Escher in Het Paleis Wiskundepakket Perspectief Perspectief We leven in een driedimensionale wereld. Deze wereld nemen we echter waar door projecties op tweedimensionale vlakken of gebogen vlakken. In
Escher in Het Paleis Wiskundepakket Perspectief Perspectief We leven in een driedimensionale wereld. Deze wereld nemen we echter waar door projecties op tweedimensionale vlakken of gebogen vlakken. In
Onmogelijke figuren. Geschreven door Judith Floor en Vivike Lapoutre. Herzien door Dieuwke van Wijk en Amarins van de Voorde
 Onmogelijke figuren Geschreven door Judith Floor en Vivike Lapoutre Herzien door Dieuwke van Wijk en Amarins van de Voorde Vierkant voor Wiskunde Zomerkamp A 2010 Voorwoord Je hebt vast wel eens een stripboek
Onmogelijke figuren Geschreven door Judith Floor en Vivike Lapoutre Herzien door Dieuwke van Wijk en Amarins van de Voorde Vierkant voor Wiskunde Zomerkamp A 2010 Voorwoord Je hebt vast wel eens een stripboek
Escher in Het Paleis. Wiskundepakket. Ruimtelijke figuren
 Escher in Het Paleis Wiskundepakket Ruimtelijke figuren Ruimtelijke figuren Escher maakt in EEN AANTAL prenten gebruik van wiskundig interessante ruimtelijke vormen, zoals Platonische lichamen en Möbiusbanden.
Escher in Het Paleis Wiskundepakket Ruimtelijke figuren Ruimtelijke figuren Escher maakt in EEN AANTAL prenten gebruik van wiskundig interessante ruimtelijke vormen, zoals Platonische lichamen en Möbiusbanden.
Escher in Het Paleis. Wiskundepakket. Inleiding. M.C. Escher en Wiskunde. De wiskunde educatie van Escher in Het Paleis
 Escher in Het Paleis Wiskundepakket Inleiding M.C. Escher en Wiskunde De wiskunde educatie van Escher in Het Paleis M.C. Escher en Wiskunde Hieronder volgt de inleiding van de wiskunde educatie voor middelbare
Escher in Het Paleis Wiskundepakket Inleiding M.C. Escher en Wiskunde De wiskunde educatie van Escher in Het Paleis M.C. Escher en Wiskunde Hieronder volgt de inleiding van de wiskunde educatie voor middelbare
Sum of Us 2014: Topologische oppervlakken
 Sum of Us 2014: Topologische oppervlakken Inleiding: topologische oppervlakken en origami Een topologisch oppervlak is, ruwweg gesproken, een tweedimensionaal meetkundig object. We zullen in deze tekst
Sum of Us 2014: Topologische oppervlakken Inleiding: topologische oppervlakken en origami Een topologisch oppervlak is, ruwweg gesproken, een tweedimensionaal meetkundig object. We zullen in deze tekst
Presentatie Wiskunde Escher
 Presentatie Wiskunde Escher Presentatie door M. 2448 woorden 14 januari 2017 4,8 9 keer beoordeeld Vak Wiskunde Maurits Cornelis Escher Goeiemorgen! Iedereen heeft het waarschijnlijk wel eens meegemaakt:
Presentatie Wiskunde Escher Presentatie door M. 2448 woorden 14 januari 2017 4,8 9 keer beoordeeld Vak Wiskunde Maurits Cornelis Escher Goeiemorgen! Iedereen heeft het waarschijnlijk wel eens meegemaakt:
Escher in Het Paleis. Wiskundepakket. Regelmatige vlakvullingen
 Escher in Het Paleis Wiskundepakket Regelmatige vlakvullingen Regelmatige vlakvullingen Een regelmatige vlakvulling is een manier om een vlak te vullen doormiddel van een zich steeds herhalend patroon.
Escher in Het Paleis Wiskundepakket Regelmatige vlakvullingen Regelmatige vlakvullingen Een regelmatige vlakvulling is een manier om een vlak te vullen doormiddel van een zich steeds herhalend patroon.
inh oud 1. Inleiding 3 2. Kijken en zien 4 3. Proefjes 4. Hoogte, breedte en diepte 5. Gefopt door licht en donker 6. Gefopt door schuine lijnen
 Je ogen bedrogen inhoud 1. Inleiding 3 2. Kijken en zien 4 3. Proefjes 5 4. Hoogte, breedte en diepte 6 5. Gefopt door licht en donker 7 6. Gefopt door schuine lijnen 7 6. Gefopt door kleur 8 7. Gefopt
Je ogen bedrogen inhoud 1. Inleiding 3 2. Kijken en zien 4 3. Proefjes 5 4. Hoogte, breedte en diepte 6 5. Gefopt door licht en donker 7 6. Gefopt door schuine lijnen 7 6. Gefopt door kleur 8 7. Gefopt
Beeldende kunst PYTHAGORAS JUNI 2008
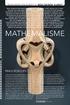 wiskunde en kunst Beeldende kunst Sinds computers kleurenplaten van fractals kunnen maken, heeft iedereen op z n minst enig idee wat wiskundigen bedoelen met de schoonheid van hun vak. Ook sommige kunstenaars
wiskunde en kunst Beeldende kunst Sinds computers kleurenplaten van fractals kunnen maken, heeft iedereen op z n minst enig idee wat wiskundigen bedoelen met de schoonheid van hun vak. Ook sommige kunstenaars
88 Optische illusies verzameld door meester Jan
 88 Optische illusies verzameld door meester Jan 01 Punten Zijn de punten nu zwart of wit? 02 Rekenen Voer de onderstaande berekening, uit het hoofd, zo snel uit als je kunt (dus zonder pen en papier en
88 Optische illusies verzameld door meester Jan 01 Punten Zijn de punten nu zwart of wit? 02 Rekenen Voer de onderstaande berekening, uit het hoofd, zo snel uit als je kunt (dus zonder pen en papier en
Werkstuk van Suzanne groep 7a
 Werkstuk van Suzanne groep 7a Inhoud: Waarom doe ik mijn werkstuk over Escher? 3 Wie is Escher 3 Het leven van Escher 4 De jeugd van Escher Reizen Geldzorgen Houtsnede en litho s 6 Houdsneden Litho s Optische
Werkstuk van Suzanne groep 7a Inhoud: Waarom doe ik mijn werkstuk over Escher? 3 Wie is Escher 3 Het leven van Escher 4 De jeugd van Escher Reizen Geldzorgen Houtsnede en litho s 6 Houdsneden Litho s Optische
Schaduwopgaven Verhoudingen
 Schaduwopgaven Verhoudingen bij 5 Een vierkant wordt verknipt in zeven driehoeken, zoals hiernaast. Het grijze driehoekje gooien we weg. Wat is de verhouding van de oppervlakte van de andere zes? na 10
Schaduwopgaven Verhoudingen bij 5 Een vierkant wordt verknipt in zeven driehoeken, zoals hiernaast. Het grijze driehoekje gooien we weg. Wat is de verhouding van de oppervlakte van de andere zes? na 10
TEKENEN. beeldende vorming. Vlakvullingen. hoofdstuk 13: vlakvulling
 Vlakvullingen Tekeningen zoals hierboven heb je vast weleens eerder gezien, bijvoorbeeld op één van de posters in de wiskundelokalen. Het is het werk van Escher.Je kent hem misschien ook wel van de onmogelijke
Vlakvullingen Tekeningen zoals hierboven heb je vast weleens eerder gezien, bijvoorbeeld op één van de posters in de wiskundelokalen. Het is het werk van Escher.Je kent hem misschien ook wel van de onmogelijke
WISKUNDIG DOOR DE BOCHT
 WISKUNDE B-DAG 2003 28 november 2003 WISKUNDIG DOOR DE BOCHT De Wiskunde B-dag wordt gesponsord door Texas instruments -1- Inleiding Soms dringt wiskunde zich spontaan op, bijvoorbeeld in een stukje speelgoed.
WISKUNDE B-DAG 2003 28 november 2003 WISKUNDIG DOOR DE BOCHT De Wiskunde B-dag wordt gesponsord door Texas instruments -1- Inleiding Soms dringt wiskunde zich spontaan op, bijvoorbeeld in een stukje speelgoed.
Antwoorden Vorm en Ruimte herhaling. Verhoudingen
 Antwoorden Vorm en Ruimte herhaling Verhoudingen 1. a. Tegenover elke 4 eenheden A staan 5 eenheden B en omgekeerd. b. 125 ; 80 c. A bevat 800 exemplaren, B bevat 1000 exemplaren. d. x ; y 2. a. 3 : 2
Antwoorden Vorm en Ruimte herhaling Verhoudingen 1. a. Tegenover elke 4 eenheden A staan 5 eenheden B en omgekeerd. b. 125 ; 80 c. A bevat 800 exemplaren, B bevat 1000 exemplaren. d. x ; y 2. a. 3 : 2
Escher in Het Paleis. Wiskundepakket. Oneindigheid
 Escher in Het Paleis Wiskundepakket Oneindigheid Oneindigheid Wiskundigen hebben weinig moeite met het begrip oneindigheid. Er zijn bijvoorbeeld oneindig veel getallen, een lijn is oneindig lang en oneindig
Escher in Het Paleis Wiskundepakket Oneindigheid Oneindigheid Wiskundigen hebben weinig moeite met het begrip oneindigheid. Er zijn bijvoorbeeld oneindig veel getallen, een lijn is oneindig lang en oneindig
HET IS EEN PRISMA, OF TOCH NIET...
 In dit artikel laten we zien hoe je een kubus, een rombendodecaëder en een afgeknotte octaëder kunt omvormen tot een. Om de constructie zelf uit te voeren, heb je de bouwtekeningen nodig die bij dit artikel
In dit artikel laten we zien hoe je een kubus, een rombendodecaëder en een afgeknotte octaëder kunt omvormen tot een. Om de constructie zelf uit te voeren, heb je de bouwtekeningen nodig die bij dit artikel
1. C De derde zijde moet meer dan 5-2=3 zijn en minder dan 5+2=7 (anders heb je geen driehoek).
 Uitwerkingen wizprof 08. C De derde zijde moet meer dan 5-=3 zijn en minder dan 5+=7 (anders heb je geen driehoek).. C De rode ringen zitten in elkaar, de groene liggen onder de rode ringen en zijn er
Uitwerkingen wizprof 08. C De derde zijde moet meer dan 5-=3 zijn en minder dan 5+=7 (anders heb je geen driehoek).. C De rode ringen zitten in elkaar, de groene liggen onder de rode ringen en zijn er
Een ander zijvlak is het regelmatige vijfhoek met aantal zijden P=5. Hierbij moeten Q=3 zijvlakken samenkomen in een hoekpunt van het veelvlak.
 Praktische-opdracht door een scholier 1498 woorden 6 juni 2003 6,5 134 keer beoordeeld Vak Wiskunde Deelvraag 1: Wat is de definitie van een Platonische Lichaam / Platonisch Veelvlak? De definitie: Een
Praktische-opdracht door een scholier 1498 woorden 6 juni 2003 6,5 134 keer beoordeeld Vak Wiskunde Deelvraag 1: Wat is de definitie van een Platonische Lichaam / Platonisch Veelvlak? De definitie: Een
Handig met getallen 4 (HMG4), onderdeel Meetkunde
 Handig met getallen 4 (HMG4), onderdeel Meetkunde Erratum Meetkunde Je vindt hier de correcties voor Handig met getallen 4 (ISBN: 978 94 90681 005). Deze correcties zijn ook bedoeld voor het Rekenwerkboek
Handig met getallen 4 (HMG4), onderdeel Meetkunde Erratum Meetkunde Je vindt hier de correcties voor Handig met getallen 4 (ISBN: 978 94 90681 005). Deze correcties zijn ook bedoeld voor het Rekenwerkboek
Het brein. Jouw werkbladen. In de klas. Ontdek zélf hoe de wereld werkt! Mijn naam: Het brein Groep 7-8 Leerlingen In de klas versie 04-2014 1
 Het brein Jouw werkbladen In de klas Mijn naam: Mijn school: Ik zit in groep: Ontdek zélf hoe de wereld werkt! Het brein Groep 7-8 Leerlingen In de klas versie 04-2014 1 Het brein Hersenen zijn ontzettend
Het brein Jouw werkbladen In de klas Mijn naam: Mijn school: Ik zit in groep: Ontdek zélf hoe de wereld werkt! Het brein Groep 7-8 Leerlingen In de klas versie 04-2014 1 Het brein Hersenen zijn ontzettend
Exploraties met GeoGebra
 9 Fractalen Exploraties met GeoGebra Een fractaal is een meetkundige figuur waarin een zelfde motief zich steeds op kleinere schaal herhaalt. Men spreekt in dat verband over de bloemkoolstructuur of de
9 Fractalen Exploraties met GeoGebra Een fractaal is een meetkundige figuur waarin een zelfde motief zich steeds op kleinere schaal herhaalt. Men spreekt in dat verband over de bloemkoolstructuur of de
1 Wiskunde, zeker. 1, 2, 3, 5, 6, 7. 8, 10, 11, 12 en 13 eurocent. duimstok Timmerman Hoe lang iets is.
 1 2 1 Wiskunde, zeker duimstok Timmerman Hoe lang iets is. Blokhaak: Timmerman Of een hoek haaks is. 1, 2, 3, 5, 6, 7. 8, 10, 11, 12 en 13 eurocent. Zeven munten: een van 1-eurocent, twee van 2-eurocent,
1 2 1 Wiskunde, zeker duimstok Timmerman Hoe lang iets is. Blokhaak: Timmerman Of een hoek haaks is. 1, 2, 3, 5, 6, 7. 8, 10, 11, 12 en 13 eurocent. Zeven munten: een van 1-eurocent, twee van 2-eurocent,
Hoofdstuk 2: Kijken. Vraag 2 a) Zevende traptrede van onderen. b) Eén optrede is ongeveer 20 cm, dus het oog was ongeveer 140 cm boven de vloer.
 1 Hoofdstuk 2: Kijken Vraag 1 a) Op de hoogte van de horizon. Ongeveer op de hoogte van de vierde rij ramen van het rechter gebouw. b) Ongeveer 4 etages van 3 meter = 12 meter. De pilaar van het rechter
1 Hoofdstuk 2: Kijken Vraag 1 a) Op de hoogte van de horizon. Ongeveer op de hoogte van de vierde rij ramen van het rechter gebouw. b) Ongeveer 4 etages van 3 meter = 12 meter. De pilaar van het rechter
Extra oefenmateriaal H10 Kegelsneden
 Deel 1 Extra oefenmateriaal H10 Kegelsneden 1. Bereken de inhoud van de volgende twee afgeknotte figuren. 2. Hiernaast zie je een afgeknot zeszijdig prisma. Het grondvlak is een regelmatige zeshoek met
Deel 1 Extra oefenmateriaal H10 Kegelsneden 1. Bereken de inhoud van de volgende twee afgeknotte figuren. 2. Hiernaast zie je een afgeknot zeszijdig prisma. Het grondvlak is een regelmatige zeshoek met
Paul Cezánne, de vader van de moderne kunst.
 Paul Cezánne, de vader van de moderne kunst. Post Impressionist, vereenvoudigde onderwerpen tot geometrische vormen, was revolutionair met zijn Nature morte avec pommes et pêches in 1905, Schilderde in
Paul Cezánne, de vader van de moderne kunst. Post Impressionist, vereenvoudigde onderwerpen tot geometrische vormen, was revolutionair met zijn Nature morte avec pommes et pêches in 1905, Schilderde in
Wisknutselen in de klas: creatief met wiskunde
 Wisknutselen in de klas: creatief met wiskunde Florine Meijer, Wisknutsels Inleiding Creativiteit en wiskunde, gaat dat samen? Kan je wiskunde doen en tegelijk knippen en plakken, of haken, breien en borduren?
Wisknutselen in de klas: creatief met wiskunde Florine Meijer, Wisknutsels Inleiding Creativiteit en wiskunde, gaat dat samen? Kan je wiskunde doen en tegelijk knippen en plakken, of haken, breien en borduren?
Steekkaart: nummer 5W
 Steekkaart: nummer 5W Onderwerp Ruimtefiguren herkennen in voorwerpen in de klas en hun eigenschappen benoemen Leeftijd/Doelgroep 5 e leerjaar Leergebied Wiskunde Organisatie Tijdsduur 50 minuten Beschrijving
Steekkaart: nummer 5W Onderwerp Ruimtefiguren herkennen in voorwerpen in de klas en hun eigenschappen benoemen Leeftijd/Doelgroep 5 e leerjaar Leergebied Wiskunde Organisatie Tijdsduur 50 minuten Beschrijving
en een punt P BC zodat BP 2. CB.
 Oplossingen E F G H Gegeven is de kubus A C D en een punt P C zodat P C a) epaal het snijpunt van de rechte PH met het voorvlak AFE van de kubus De rechte PH ligt in het diagonaalvlak EHC van de kubus
Oplossingen E F G H Gegeven is de kubus A C D en een punt P C zodat P C a) epaal het snijpunt van de rechte PH met het voorvlak AFE van de kubus De rechte PH ligt in het diagonaalvlak EHC van de kubus
Kernbegrippen Kennisbasis wiskunde Onderdeel meetkunde
 Kernbegrippen Kennisbasis wiskunde Onderdeel meetkunde Aanzicht Een ruimtelijk figuur kun je van verschillende kanten bekijken, je noemt dat aanzichten. Er zijn 5 aanzichten: Vooraanzicht (van voren).
Kernbegrippen Kennisbasis wiskunde Onderdeel meetkunde Aanzicht Een ruimtelijk figuur kun je van verschillende kanten bekijken, je noemt dat aanzichten. Er zijn 5 aanzichten: Vooraanzicht (van voren).
Beetle Blocks Startgids
 Beetle Blocks Startgids 1. Verplaats en draai Klik op de verplaats en draai blokken om de kever te bewegen 2. Maak een stapel en voeg een vorm toe Maak de blokken verplaats en draai aan elkaar en klik
Beetle Blocks Startgids 1. Verplaats en draai Klik op de verplaats en draai blokken om de kever te bewegen 2. Maak een stapel en voeg een vorm toe Maak de blokken verplaats en draai aan elkaar en klik
handleiding pagina s 434 tot Handleiding 1.2 Huistaken huistaak 12: bladzijde Werkboek
 week 13 les 5 toets en foutenanalyse handleiding pagina s 434 tot 443 nuttige informatie 1 Handleiding 1.1 Kopieerbladen pagina s 374 en 375: vierhoeken pagina 376: eigenschappen van diagonalen in vierhoeken
week 13 les 5 toets en foutenanalyse handleiding pagina s 434 tot 443 nuttige informatie 1 Handleiding 1.1 Kopieerbladen pagina s 374 en 375: vierhoeken pagina 376: eigenschappen van diagonalen in vierhoeken
Les 8 ruimtelijke patronen
 Les 8 ruimtelijke patronen Kern van de les - Leerlingen verkennen patronen op en van ruimtelijke objecten en redeneren erover. - Ze onderzoeken hoe een patroon dat ze ontwerpen op de uitslag van het balkje
Les 8 ruimtelijke patronen Kern van de les - Leerlingen verkennen patronen op en van ruimtelijke objecten en redeneren erover. - Ze onderzoeken hoe een patroon dat ze ontwerpen op de uitslag van het balkje
5.7. Boekverslag door P woorden 11 januari keer beoordeeld. Wiskunde B
 Boekverslag door P. 1778 woorden 11 januari 2012 5.7 103 keer beoordeeld Vak Methode Wiskunde B Getal en ruimte Wiskunde Hoofdstuk 1 Formules en Grafieken 1.1 Lineaire verbanden Van de lijn y=ax+b is de
Boekverslag door P. 1778 woorden 11 januari 2012 5.7 103 keer beoordeeld Vak Methode Wiskunde B Getal en ruimte Wiskunde Hoofdstuk 1 Formules en Grafieken 1.1 Lineaire verbanden Van de lijn y=ax+b is de
Optische illusies : wat je ziet is niet altijd de werkelijkheid!
 Optische illusies : wat je ziet is niet altijd de werkelijkheid! Deze tekst is aanvullende stof bij hoofdstuk 10. Sommige illusies zijn te verklaren aan de hand van de theorie met betrekking tot selectie,
Optische illusies : wat je ziet is niet altijd de werkelijkheid! Deze tekst is aanvullende stof bij hoofdstuk 10. Sommige illusies zijn te verklaren aan de hand van de theorie met betrekking tot selectie,
Tussendoelen wiskunde onderbouw vo vmbo
 Tussendoelen wiskunde onderbouw vo vmbo Domein A: Inzicht en handelen Subdomein A1: Vaktaal wiskunde 1. vmbo passende vaktaal voor wiskunde herkennen en gebruiken voor het ordenen van het eigen denken
Tussendoelen wiskunde onderbouw vo vmbo Domein A: Inzicht en handelen Subdomein A1: Vaktaal wiskunde 1. vmbo passende vaktaal voor wiskunde herkennen en gebruiken voor het ordenen van het eigen denken
IJkingstoets Wiskunde-Informatica-Fysica 1 juli 2015 Oplossingen
 IJkingstoets Wiskunde-Informatica-Fysica 1 juli 15 Oplossingen IJkingstoets wiskunde-informatica-fysica 1 juli 15 - p. 1/1 Oefening 1 Welke studierichting wil je graag volgen? (vraag zonder score, wel
IJkingstoets Wiskunde-Informatica-Fysica 1 juli 15 Oplossingen IJkingstoets wiskunde-informatica-fysica 1 juli 15 - p. 1/1 Oefening 1 Welke studierichting wil je graag volgen? (vraag zonder score, wel
1 Vlaamse Wiskunde Olympiade : tweede ronde
 1 Vlaamse Wiskunde Olympiade 005-006: tweede ronde Volgende benaderingen kunnen nuttig zijn bij het oplossen van sommige vragen 1,1 3 1,731 5,361 π 3,116 1 Als a 1 3 a 1 3 a m = a met a R + \{0, 1}, dan
1 Vlaamse Wiskunde Olympiade 005-006: tweede ronde Volgende benaderingen kunnen nuttig zijn bij het oplossen van sommige vragen 1,1 3 1,731 5,361 π 3,116 1 Als a 1 3 a 1 3 a m = a met a R + \{0, 1}, dan
Let s play baseball! Let s get ready! Voorkennis: Sprites, Lopen, Variabelen, Scores, xy. Leerdoelen: 3D illusie, Klonen
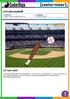 Let s play baseball! Voorkennis: Sprites, Lopen, Variabelen, Scores, xy Leerdoelen: 3D illusie, Klonen Let s get ready! Jullie weten ongetwijfeld wat het belangrijkste is van het succes van elk goed spel
Let s play baseball! Voorkennis: Sprites, Lopen, Variabelen, Scores, xy Leerdoelen: 3D illusie, Klonen Let s get ready! Jullie weten ongetwijfeld wat het belangrijkste is van het succes van elk goed spel
Inhoud. Het leven van Escher. Weiland wordt vogel. Kringloop metamorfose. De wereld op z n kop.
 Inhoud. Blz. 1. Blz. 2. Blz. 3. Blz. 4. Blz. 5. Blz. 6. Blz. 7. Blz. 8. Blz. 9. Blz. 10. Blz. 11. Kaft Inhoud Het leven van Escher. Moeilijke jaren. Weiland wordt vogel. Kringloop metamorfose. De wereld
Inhoud. Blz. 1. Blz. 2. Blz. 3. Blz. 4. Blz. 5. Blz. 6. Blz. 7. Blz. 8. Blz. 9. Blz. 10. Blz. 11. Kaft Inhoud Het leven van Escher. Moeilijke jaren. Weiland wordt vogel. Kringloop metamorfose. De wereld
PROJECTIEMETHODEN. Labine Coskun ; ; CC Naamsvermelding 3.0 Nederland licentie.
 Auteurs Laatst gewijzigd Licentie Webadres Labine Coskun ; ; 30 June 2016 CC Naamsvermelding 3.0 Nederland licentie http://maken.wikiwijs.nl/75861 Dit lesmateriaal is gemaakt met Wikiwijsleermiddelenplein.
Auteurs Laatst gewijzigd Licentie Webadres Labine Coskun ; ; 30 June 2016 CC Naamsvermelding 3.0 Nederland licentie http://maken.wikiwijs.nl/75861 Dit lesmateriaal is gemaakt met Wikiwijsleermiddelenplein.
http://www.kidzlab.nl/index2.php?option=com_content&task=vi...
 Veelvlakken De perfecte vorm Plato was een grote denker in de tijd van de Oude Grieken. Hij was een van de eerste die de regelmatige veelvlakken heel bijzonder vond. Hij hield ervan omdat ze zulke mooie,
Veelvlakken De perfecte vorm Plato was een grote denker in de tijd van de Oude Grieken. Hij was een van de eerste die de regelmatige veelvlakken heel bijzonder vond. Hij hield ervan omdat ze zulke mooie,
Figuratief. Een figuratieve afbeelding vertoont duidelijke overeenkomsten met de werkelijkheid. Het is afgebeeld zoals het is.
 Figuratief Een figuratieve afbeelding vertoont duidelijke overeenkomsten met de werkelijkheid. Het is afgebeeld zoals het is. Realistisch Manier van werken waarbij de werkelijkheid zo nauwkeurig mogelijk
Figuratief Een figuratieve afbeelding vertoont duidelijke overeenkomsten met de werkelijkheid. Het is afgebeeld zoals het is. Realistisch Manier van werken waarbij de werkelijkheid zo nauwkeurig mogelijk
Werkbladen voor leerlingen
 Magneetpolen Leerdoel: Begrijpen hoe de positieve en negatieve magnetische polen duw- en trekkrachten kunnen aantonen. 1 1. Noem vijf voorwerpen die een magneet aantrekt. 2. Hoe worden de uiteinden van
Magneetpolen Leerdoel: Begrijpen hoe de positieve en negatieve magnetische polen duw- en trekkrachten kunnen aantonen. 1 1. Noem vijf voorwerpen die een magneet aantrekt. 2. Hoe worden de uiteinden van
Domein A: Inzicht en handelen
 Tussendoelen wiskunde onderbouw vo vmbo Preambule Domein A is een overkoepeld domein dat altijd in combinatie met de andere domeinen wordt toegepast (of getoetst). In domein A wordt benoemd: Vaktaal: het
Tussendoelen wiskunde onderbouw vo vmbo Preambule Domein A is een overkoepeld domein dat altijd in combinatie met de andere domeinen wordt toegepast (of getoetst). In domein A wordt benoemd: Vaktaal: het
IJkingstoets burgerlijk ingenieur juli 2015: algemene feedback
 IJkingstoets burgerlijk ingenieur juli 5 - reeks - p. IJkingstoets burgerlijk ingenieur juli 5: algemene feedback In totaal namen 79 studenten deel aan de ijkingstoets burgerlijk ingenieur die aangeboden
IJkingstoets burgerlijk ingenieur juli 5 - reeks - p. IJkingstoets burgerlijk ingenieur juli 5: algemene feedback In totaal namen 79 studenten deel aan de ijkingstoets burgerlijk ingenieur die aangeboden
IJkingstoets burgerlijk ingenieur juli 2015: algemene feedback
 IJkingstoets burgerlijk ingenieur juli 5 - reeks 4 - p. IJkingstoets burgerlijk ingenieur juli 5: algemene feedback In totaal namen 79 studenten deel aan de ijkingstoets burgerlijk ingenieur die aangeboden
IJkingstoets burgerlijk ingenieur juli 5 - reeks 4 - p. IJkingstoets burgerlijk ingenieur juli 5: algemene feedback In totaal namen 79 studenten deel aan de ijkingstoets burgerlijk ingenieur die aangeboden
Doelenlijst 10: MEETKUNDE
 Doelenlijst 10: MEETKUNDE Doel: Oriëntatiebegrippen kennen 93 Passende Perspectieven rekenen Doelenlijst 10: Meetkunde Kunnen toepassen van ruimtelijke oriënteringsbegrippen als links, rechts, onder, boven,
Doelenlijst 10: MEETKUNDE Doel: Oriëntatiebegrippen kennen 93 Passende Perspectieven rekenen Doelenlijst 10: Meetkunde Kunnen toepassen van ruimtelijke oriënteringsbegrippen als links, rechts, onder, boven,
1 Junior Wiskunde Olympiade : tweede ronde
 Junior Wiskunde Olympiade 008-009: tweede ronde ( 7) = (A) 7 (B) 7 (C) 7 of + 7 (D) 7 (E) onbepaald Beschouw de rij opeenvolgende natuurlijke getallen beginnend met en eindigend met Wat is het middelste
Junior Wiskunde Olympiade 008-009: tweede ronde ( 7) = (A) 7 (B) 7 (C) 7 of + 7 (D) 7 (E) onbepaald Beschouw de rij opeenvolgende natuurlijke getallen beginnend met en eindigend met Wat is het middelste
d = 8 cm 2 6 A: = 26 m 2 B: = 20 m 2 C: = 18 m 2 D: 20 m 2 E: 26 m 2
 H17 PYTHAGORAS 17.1 INTRO 1 b c d 1 4 4 = 8 cm 6 A: 6 1 5 1 4 = 6 m B: 6 1 4 4 = 0 m C: 6 1 3 3 4 = 18 m D: 0 m E: 6 m 7 a A:, cm B: 5,0 cm C: 3, cm D: 4,1 cm b Voor elke zijde geldt dat het de schuine
H17 PYTHAGORAS 17.1 INTRO 1 b c d 1 4 4 = 8 cm 6 A: 6 1 5 1 4 = 6 m B: 6 1 4 4 = 0 m C: 6 1 3 3 4 = 18 m D: 0 m E: 6 m 7 a A:, cm B: 5,0 cm C: 3, cm D: 4,1 cm b Voor elke zijde geldt dat het de schuine
Antwoordmodel - In de ruimte
 Antwoordmodel - In de ruimte Vraag 1 Welke ruimtefiguren (of delen van) herken je op de volgende foto s? a Foto 1. Balk, prisma, cilinder en kubus. b Foto 2. Cilinder, balk, kubus en prisma c Foto 3. Balk,
Antwoordmodel - In de ruimte Vraag 1 Welke ruimtefiguren (of delen van) herken je op de volgende foto s? a Foto 1. Balk, prisma, cilinder en kubus. b Foto 2. Cilinder, balk, kubus en prisma c Foto 3. Balk,
Ijkingstoets 4 juli 2012
 Ijkingtoets 4 juli 2012 -vragenreeks 1 1 Ijkingstoets 4 juli 2012 Oefening 1 In de apotheek bezorgt de apotheker zijn assistent op verschillende tijdstippen van de dag een voorschrift voor een te bereiden
Ijkingtoets 4 juli 2012 -vragenreeks 1 1 Ijkingstoets 4 juli 2012 Oefening 1 In de apotheek bezorgt de apotheker zijn assistent op verschillende tijdstippen van de dag een voorschrift voor een te bereiden
de Leuke En Uitdagende Wiskunde VEELVLAKKEN SAMENSTELLING: H. de Leuw
 SAMENSTELLING: H. de Leuw 1. VEELHOEKEN. Een veelvlak is een lichaam dat wordt begrensd door vlakke veelhoeken. Zo zijn balken en piramides wel veelvlakken, maar cilinders en bollen niet. Een veelhoek
SAMENSTELLING: H. de Leuw 1. VEELHOEKEN. Een veelvlak is een lichaam dat wordt begrensd door vlakke veelhoeken. Zo zijn balken en piramides wel veelvlakken, maar cilinders en bollen niet. Een veelhoek
Fractale dimensie. Eline Sommereyns 6wwIi nr.9
 Fractale dimensie Eline Sommereyns 6wwIi nr.9 Inhoudstabel Inleiding... 3 Gehele dimensie... 4 Begrip dimensie... 4 Lengte, breedte, hoogte... 4 Tijd-ruimte... 4 Fractale dimensie... 5 Fractalen... 5 Wat?...
Fractale dimensie Eline Sommereyns 6wwIi nr.9 Inhoudstabel Inleiding... 3 Gehele dimensie... 4 Begrip dimensie... 4 Lengte, breedte, hoogte... 4 Tijd-ruimte... 4 Fractale dimensie... 5 Fractalen... 5 Wat?...
Hoofdstuk 2: Kijken. Vraag 2 a) Zevende traptrede van onderen. b) Eén optrede is ongeveer 20 cm, dus het oog was ongeveer 140 cm boven de vloer.
 1 Hoofdstuk 2: Kijken Vraag 1 a) Op de hoogte van de horizon. Ongeveer op de hoogte van de vierde rij ramen van het rechter gebouw. b) Ongeveer 4 etages van 3 meter = 12 meter. De pilaar van het rechter
1 Hoofdstuk 2: Kijken Vraag 1 a) Op de hoogte van de horizon. Ongeveer op de hoogte van de vierde rij ramen van het rechter gebouw. b) Ongeveer 4 etages van 3 meter = 12 meter. De pilaar van het rechter
Aan alle Wallabies, en aan hun leerkrachten, veel succes en, nog belangrijker, veel plezier!
 Noteer hier eventueel je naam: Aan alle Wallabies, en aan hun leerkrachten, veel succes en, nog belangrijker, veel plezier! Wiskunde leuk? Reken maar! wwwwiskundekangoeroebe c Vlaamse Wiskunde Olympiade
Noteer hier eventueel je naam: Aan alle Wallabies, en aan hun leerkrachten, veel succes en, nog belangrijker, veel plezier! Wiskunde leuk? Reken maar! wwwwiskundekangoeroebe c Vlaamse Wiskunde Olympiade
Thinking of Art Stijldocument
 Thinking of Art Stijldocument Niels de Jong GDD1A Inspiratie: M.C. Escher Inhoudsopgave Inleiding...2 1 Moodboard / stijlinspiratie kiezen...2 Kiezen stijlinspiratie...3 Beeldmateriaal in Moodboards...4
Thinking of Art Stijldocument Niels de Jong GDD1A Inspiratie: M.C. Escher Inhoudsopgave Inleiding...2 1 Moodboard / stijlinspiratie kiezen...2 Kiezen stijlinspiratie...3 Beeldmateriaal in Moodboards...4
27 Macro s voor de schijf van Poincaré
 27 Macro s voor de schijf van Poincaré 27.1 Inleiding In het secundair onderwijs zijn leerlingen vertrouwd met de Euclidische meetkunde. In het Euclidisch vlak geldt het beroemde 5 de parallellen postulaat:
27 Macro s voor de schijf van Poincaré 27.1 Inleiding In het secundair onderwijs zijn leerlingen vertrouwd met de Euclidische meetkunde. In het Euclidisch vlak geldt het beroemde 5 de parallellen postulaat:
wiskunde CSE GL en TL
 Examen VMBO-GL en TL 2012 tijdvak 1 maandag 21 mei 13.30-15.30 uur wiskunde CSE GL en TL Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 23 vragen. Voor dit examen zijn maximaal 75 punten
Examen VMBO-GL en TL 2012 tijdvak 1 maandag 21 mei 13.30-15.30 uur wiskunde CSE GL en TL Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 23 vragen. Voor dit examen zijn maximaal 75 punten
Ruimtelijke projectie. Cirkels tekenen. Aanwijzingen bij het gebruik van dit PDF-bestand.
 Inhoudsopgave Ruimtelijke projectie Blz. 1 Blz. 2 Blz. 3 Blz. 4 Wiskundige manier Axonometrie Isometrie Cirkels tekenen Ronde vormen Aanwijzingen bij het gebruik van dit PDF-bestand. Dit bestand bevat
Inhoudsopgave Ruimtelijke projectie Blz. 1 Blz. 2 Blz. 3 Blz. 4 Wiskundige manier Axonometrie Isometrie Cirkels tekenen Ronde vormen Aanwijzingen bij het gebruik van dit PDF-bestand. Dit bestand bevat
24/11/2008. heel handig hulpvenster past zich voortdurend aan. Engelstalige handleiding van 63 blz. dag van de wiskunde 2e/3e graad 22 nov 2008
 Cabri 3D een voorstelling van de mogelijkheden dag van de wiskunde 2e/3e graad 22 nov 2008 Paul Decuypere, VVKSO cahier de brouillon interactif www.cabri.com 1985: eerste versie van Cabri I 1989: eerste
Cabri 3D een voorstelling van de mogelijkheden dag van de wiskunde 2e/3e graad 22 nov 2008 Paul Decuypere, VVKSO cahier de brouillon interactif www.cabri.com 1985: eerste versie van Cabri I 1989: eerste
Wiskunde. Hoofdstuk 1 en hoofdstuk 5, paragraaf 5.1, 5.2 en 5.3 kennen en kunnen.
 Toetsstof In de toets weken moet je dit kunnen toepassen Hoofdstuk 1 en hoofdstuk 5, paragraaf 5.1, 5.2 en 5.3 kennen en kunnen. Periodetaak Maak een mooie mandala met passer en kleur hem leuk in. Ga naar
Toetsstof In de toets weken moet je dit kunnen toepassen Hoofdstuk 1 en hoofdstuk 5, paragraaf 5.1, 5.2 en 5.3 kennen en kunnen. Periodetaak Maak een mooie mandala met passer en kleur hem leuk in. Ga naar
Dimensies. een ruimtelijke tocht langs onbekende assen. Anne Lotte van der Kooi Jesse Krijthe Roderik Vogels Onder begeleiding van Aad Goddijn
 Dimensies een ruimtelijke tocht langs onbekende assen Anne Lotte van der Kooi Jesse Krijthe Roderik Vogels Onder begeleiding van Aad Goddijn Junior College Utrecht, Januari 7 Inhoud. Abstract.... Inleiding...5.
Dimensies een ruimtelijke tocht langs onbekende assen Anne Lotte van der Kooi Jesse Krijthe Roderik Vogels Onder begeleiding van Aad Goddijn Junior College Utrecht, Januari 7 Inhoud. Abstract.... Inleiding...5.
1 Vlaamse Wiskunde Olympiade : tweede ronde
 1 Vlaamse Wiskunde Olympiade 00-005: tweede ronde De tweede ronde bestaat uit 0 meerkeuzevragen Het quoteringssysteem werkt als volgt: per goed antwoord krijgt de deelnemer 5 punten, een blanco antwoord
1 Vlaamse Wiskunde Olympiade 00-005: tweede ronde De tweede ronde bestaat uit 0 meerkeuzevragen Het quoteringssysteem werkt als volgt: per goed antwoord krijgt de deelnemer 5 punten, een blanco antwoord
1 Vlaamse Wiskunde Olympiade : tweede ronde
 Vlaamse Wiskunde Olympiade 2003-2004: tweede ronde De tweede ronde bestaat uit 30 meerkeuzevragen Het quoteringssysteem werkt als volgt: per goed antwoord krijgt de deelnemer 5 punten, een blanco antwoord
Vlaamse Wiskunde Olympiade 2003-2004: tweede ronde De tweede ronde bestaat uit 30 meerkeuzevragen Het quoteringssysteem werkt als volgt: per goed antwoord krijgt de deelnemer 5 punten, een blanco antwoord
Vraag Antwoord Scores. 2 maximumscore 3 Laatste rij in tabel verder invullen tot totaal aantal vierkanten 19 is 2. Het rijnummer is 9 1 ).
 BEOORDELINGSMODEL VMBO KB 003-II Vraag Antwoord Scores VIERKANTEN LEGGEN maximumscore 4 rijnummer 3 4 5 aantal witte vierkanten in de rij 3 5 7 9 aantal grijze vierkanten in de rij totaal aantal vierkanten
BEOORDELINGSMODEL VMBO KB 003-II Vraag Antwoord Scores VIERKANTEN LEGGEN maximumscore 4 rijnummer 3 4 5 aantal witte vierkanten in de rij 3 5 7 9 aantal grijze vierkanten in de rij totaal aantal vierkanten
OPLOSSINGEN. Wallaroe Vlaamse Wiskunde Olympiade vzw
 OPLOSSINGEN Vlaamse Wiskunde Olympiade vzw Juist antwoord Geen antwoord Fout antwoord Wedstrijdduur Rekentoestel 5 punten 1 punt 0 punten 75 minuten niet toegelaten 1. Correct antwoord: A Wetellendehalvecirkels.Hetzijner6.
OPLOSSINGEN Vlaamse Wiskunde Olympiade vzw Juist antwoord Geen antwoord Fout antwoord Wedstrijdduur Rekentoestel 5 punten 1 punt 0 punten 75 minuten niet toegelaten 1. Correct antwoord: A Wetellendehalvecirkels.Hetzijner6.
Estafette. 26 e Wiskundetoernooi
 6 e Wiskundetoernooi Estafette 07 Opgave rnoud is geboren tussen 900 en 980. Het getal dat wordt gevormd door de laatste twee cijfers van het geboortejaar van rnoud is een kwadraat. Toen rnoud in 07 jarig
6 e Wiskundetoernooi Estafette 07 Opgave rnoud is geboren tussen 900 en 980. Het getal dat wordt gevormd door de laatste twee cijfers van het geboortejaar van rnoud is een kwadraat. Toen rnoud in 07 jarig
Ziet uw kubus er op dit moment niet zo uit? Maar wilt u hem wel zo krijgen? Dan zit u hier goed!
 Ziet uw kubus er op dit moment niet zo uit? Maar wilt u hem wel zo krijgen? Dan zit u hier goed! Stap voor stap uitgelegd hoe u uw kubus van Rubik weer goed krijgt. Orginele versie http://rubik.tormentil.nl/
Ziet uw kubus er op dit moment niet zo uit? Maar wilt u hem wel zo krijgen? Dan zit u hier goed! Stap voor stap uitgelegd hoe u uw kubus van Rubik weer goed krijgt. Orginele versie http://rubik.tormentil.nl/
Inhoudsopgave. Introductie Escher 4. Escher biografie 5. Escher van toen... 7. Escher stijl 8. Escher werk 10. Escher van nu... 14.
 Inhoudsopgave Introductie Escher 4 Escher biografie 5 Escher van toen... 7 Escher stijl 8 Escher werk 10 Escher van nu... 14 Museum 16 Escher zelf... 18 Colofon 19 03 Introductie Escher Maurits Cornelis
Inhoudsopgave Introductie Escher 4 Escher biografie 5 Escher van toen... 7 Escher stijl 8 Escher werk 10 Escher van nu... 14 Museum 16 Escher zelf... 18 Colofon 19 03 Introductie Escher Maurits Cornelis
Bereken hoeveel populieren hiervoor gebruikt zijn. Schrijf je berekening op.
 Lucifers Lucifers worden meestal gemaakt van het hout van de ratelpopulier. Van één populier worden gemiddeld 6 miljoen lucifers gemaakt. In een luciferdoosje zitten gemiddeld 60 lucifers. 3p 1 Het bedrijf
Lucifers Lucifers worden meestal gemaakt van het hout van de ratelpopulier. Van één populier worden gemiddeld 6 miljoen lucifers gemaakt. In een luciferdoosje zitten gemiddeld 60 lucifers. 3p 1 Het bedrijf
Eindexamen wiskunde B havo I (oude stijl)
 Een functie Voor 0 < = x < = 2π is gegeven de functie figuur 1 f(x) = 2sin(x + 1 6 π). In figuur 1 is de grafiek van f getekend. y 1 f 4 p 1 Los op: f(x) < 1. De lijn l raakt de grafiek van f in het punt
Een functie Voor 0 < = x < = 2π is gegeven de functie figuur 1 f(x) = 2sin(x + 1 6 π). In figuur 1 is de grafiek van f getekend. y 1 f 4 p 1 Los op: f(x) < 1. De lijn l raakt de grafiek van f in het punt
Efficientie in de ruimte - leerlingmateriaal
 Junior College Utrecht Efficientie in de ruimte - leerlingmateriaal Versie 2 September 2012 Een project (ruimte-)meetkunde voor vwo-leerlingen Geschreven voor het Koningin Wilhelmina College Culemborg
Junior College Utrecht Efficientie in de ruimte - leerlingmateriaal Versie 2 September 2012 Een project (ruimte-)meetkunde voor vwo-leerlingen Geschreven voor het Koningin Wilhelmina College Culemborg
Examen VMBO-KB. wiskunde CSE KB. tijdvak 1 maandag 21 mei 13.30-15.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Examen VMBO-KB 2012 tijdvak 1 maandag 21 mei 13.30-15.30 uur wiskunde CSE KB Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 25 vragen. Voor dit examen zijn maximaal 75 punten te behalen.
Examen VMBO-KB 2012 tijdvak 1 maandag 21 mei 13.30-15.30 uur wiskunde CSE KB Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 25 vragen. Voor dit examen zijn maximaal 75 punten te behalen.
TOT de graphici in ons land, wier werk betrekkelijk onbekend is,
 NIEUW WERK VAN M. C. ESCHER DOOR G. H. 's GRAVESANDE TOT de graphici in ons land, wier werk betrekkelijk onbekend is, behoort M. C. Escher.*) Hij is een werker, die een eigen stijl heeft; hij is een rusteloos
NIEUW WERK VAN M. C. ESCHER DOOR G. H. 's GRAVESANDE TOT de graphici in ons land, wier werk betrekkelijk onbekend is, behoort M. C. Escher.*) Hij is een werker, die een eigen stijl heeft; hij is een rusteloos
13 Vlaamse Wiskunde Olympiade : Tweede ronde.
 13 Vlaamse Wiskunde Olympiade 1999-000: Tweede ronde De tweede ronde bestaat eveneens uit 30 meerkeuzevragen Het quoteringssysteem is hetzelfde als dat voor de eerste ronde, dwz per goed antwoord krijgt
13 Vlaamse Wiskunde Olympiade 1999-000: Tweede ronde De tweede ronde bestaat eveneens uit 30 meerkeuzevragen Het quoteringssysteem is hetzelfde als dat voor de eerste ronde, dwz per goed antwoord krijgt
1. INLEIDING... 3 2. PERSPECTIEVEN... 4 3. PROJECTIEMETHODEN... 8 4. AANZICHTEN TEKENEN... 10 5. PERSPECTIEF TEKENEN... 14 6. BRONVERMELDING...
 1. INLEIDING... 3 2. PERSPECTIEVEN... 4 3. PROJECTIEMETHODEN... 8 4. AANZICHTEN TEKENEN... 10 5. PERSPECTIEF TEKENEN... 14 6. BRONVERMELDING... 22 Leerplandoelstellingen Perspectieftekenen 9. De afgewerkte
1. INLEIDING... 3 2. PERSPECTIEVEN... 4 3. PROJECTIEMETHODEN... 8 4. AANZICHTEN TEKENEN... 10 5. PERSPECTIEF TEKENEN... 14 6. BRONVERMELDING... 22 Leerplandoelstellingen Perspectieftekenen 9. De afgewerkte
1. Ik kan vormen en figuren herkennen en gebruiken met bijbehorende wiskundige vaktaal.
 LEERLIJN WISKUNDE VMBO-BKTG (Leerjaar 1-periode 1) VMBO BKTG LJ1 Vmbo BKTG Periode 1 Wat ga ik leren? Wanneer? Welke inhoud heb ik nodig? Wat ga ik doen om dit te leren? Hoe bewijs ik dat ik dit geleerd
LEERLIJN WISKUNDE VMBO-BKTG (Leerjaar 1-periode 1) VMBO BKTG LJ1 Vmbo BKTG Periode 1 Wat ga ik leren? Wanneer? Welke inhoud heb ik nodig? Wat ga ik doen om dit te leren? Hoe bewijs ik dat ik dit geleerd
uuur , DF en DB met kentallen. b) Laat zien door twee keer de stelling van Pythagoras in een rechthoekige uuur
 4 Van D naar 3D Verkennen Van D naar 3D Inleiding Verkennen Bekijk de applet. Met de rechter muisknop kun je het assenstelsel om de oorsprong draaien en de fig van alle kanten bekijken. Beantwoord nu de
4 Van D naar 3D Verkennen Van D naar 3D Inleiding Verkennen Bekijk de applet. Met de rechter muisknop kun je het assenstelsel om de oorsprong draaien en de fig van alle kanten bekijken. Beantwoord nu de
Stap 1. M o n t a g e h a n d l e i d i n g S p e e l J u w e e l
 Stap 1 Benodigdheden: - 2 balken van 4,5 x 9 x 180 cm - 2 balken van 4,5 x 9 x 171 cm - 4 schroeven van 6 x 100 mm Uitleg: 1. Leg de balken neer zoals op de tekening is aangegeven. 2. Schroef in elke hoek
Stap 1 Benodigdheden: - 2 balken van 4,5 x 9 x 180 cm - 2 balken van 4,5 x 9 x 171 cm - 4 schroeven van 6 x 100 mm Uitleg: 1. Leg de balken neer zoals op de tekening is aangegeven. 2. Schroef in elke hoek
Niet meer dan drie tetraëders in één kubus
 Niet meer dan drie tetraëders in één kubus or Hurkens januari 008 Samenvatting Een opgave door Jan van de raats gesteld luidt als volgt: Hoeveel tetraëders met zijde een kun je stapelen in een eenheidskubus?
Niet meer dan drie tetraëders in één kubus or Hurkens januari 008 Samenvatting Een opgave door Jan van de raats gesteld luidt als volgt: Hoeveel tetraëders met zijde een kun je stapelen in een eenheidskubus?
B136. BIJLAGE H De verbinding met het 'On-eindige' vanuit het twaalf-, het ruitendertig- en het twintig-vlak. Het twaalfvlak of dodecaëder
 B136 De verbinding met het 'On-eindige' vanuit het twaalf-, het ruitendertig- en het twintig-vlak Het twaalfvlak of dodecaëder Een dodecaëder ligt besloten tussen 6 paren van evenwijdige vlakken. Als die
B136 De verbinding met het 'On-eindige' vanuit het twaalf-, het ruitendertig- en het twintig-vlak Het twaalfvlak of dodecaëder Een dodecaëder ligt besloten tussen 6 paren van evenwijdige vlakken. Als die
1. C In elk van de wolken A, B, D en E staat het oneven getal 3. In wolk C staan de getallen 2, 10, 34 en 58 die allemaal even zijn.
 Uitwerkingen wizbrain 019 1. C In elk van de wolken A, B, D en E staat het oneven getal 3. In wolk C staan de getallen, 10, 34 en 58 die allemaal even zijn.. A Een uur heeft vier kwartier, dus tien kwartier
Uitwerkingen wizbrain 019 1. C In elk van de wolken A, B, D en E staat het oneven getal 3. In wolk C staan de getallen, 10, 34 en 58 die allemaal even zijn.. A Een uur heeft vier kwartier, dus tien kwartier
6 A: 6 2 2 1 5 1 4 = 26 m 2 B: 6 2 2 1 4 2 4 = 20 m 2 C: 6 2 1 2
 Hoofdstuk 17 PYTHAGORAS HAVO 17.1 INTRO 1 b c 6 A: 6 1 5 1 4 = 6 m B: 6 1 4 4 = 0 m C: 6 1 3 3 4 = 18 m D: 0 m E: 6 m 7 a A:, cm B: 5,0 cm C: 3, cm D: 4,1 cm b Voor elke zijde geldt dat het de schuine
Hoofdstuk 17 PYTHAGORAS HAVO 17.1 INTRO 1 b c 6 A: 6 1 5 1 4 = 6 m B: 6 1 4 4 = 0 m C: 6 1 3 3 4 = 18 m D: 0 m E: 6 m 7 a A:, cm B: 5,0 cm C: 3, cm D: 4,1 cm b Voor elke zijde geldt dat het de schuine
Bereken hoeveel populieren hiervoor gebruikt zijn. Schrijf je berekening op.
 Lucifers Lucifers worden meestal gemaakt van het hout van de ratelpopulier. Van één populier worden gemiddeld 6 miljoen lucifers gemaakt. In een luciferdoosje zitten gemiddeld 60 lucifers. 2p 1 Bereken
Lucifers Lucifers worden meestal gemaakt van het hout van de ratelpopulier. Van één populier worden gemiddeld 6 miljoen lucifers gemaakt. In een luciferdoosje zitten gemiddeld 60 lucifers. 2p 1 Bereken
Als je het programma opent krijg je een scherm te zien met promotie van Sketchup. Klik nu op het driehoekje voor: template
 Hierbij dan de cursus (in stukjes): Een gebouw namaken in in Sketchup vanaf een foto. Als eerste heb je het programma Sketchup nodig. Op: http://www.sketchup.com/ kun je het programma downloaden. De demoversie
Hierbij dan de cursus (in stukjes): Een gebouw namaken in in Sketchup vanaf een foto. Als eerste heb je het programma Sketchup nodig. Op: http://www.sketchup.com/ kun je het programma downloaden. De demoversie
1 Vlaamse Wiskunde Olympiade : eerste ronde
 1 Vlaamse Wiskunde Olympiade 008-009: eerste ronde 1 Welke van volgende sommen is gelijk aan 10? () 4,444 + 5,555 (B), + 6,666 (C), + 7,777 (D) 5,555 +, (E) 9,999 + 1,111 Voor hoeveel natuurlijke getallen
1 Vlaamse Wiskunde Olympiade 008-009: eerste ronde 1 Welke van volgende sommen is gelijk aan 10? () 4,444 + 5,555 (B), + 6,666 (C), + 7,777 (D) 5,555 +, (E) 9,999 + 1,111 Voor hoeveel natuurlijke getallen
(1) (2) (3) (4) (5) TAL-bovenbouw Lesbeschrijving
 Het doorsnijden van een kubus lesbeschrijving lesdoelen 1. Leerlingen leren wat een doorsnede is. Ze doen praktische ervaring op met het maken van doorsneden van een balk en een kubus. Ze systematiseren
Het doorsnijden van een kubus lesbeschrijving lesdoelen 1. Leerlingen leren wat een doorsnede is. Ze doen praktische ervaring op met het maken van doorsneden van een balk en een kubus. Ze systematiseren
Gezichtsbedrog hv12. CC Naamsvermelding-GelijkDelen 3.0 Nederland licentie. https://maken.wikiwijs.nl/62517
 Auteur Laatst gewijzigd Licentie Webadres VO-content 30 mei 2017 CC Naamsvermelding-GelijkDelen 3.0 Nederland licentie https://maken.wikiwijs.nl/62517 Dit lesmateriaal is gemaakt met Wikiwijs van Kennisnet.
Auteur Laatst gewijzigd Licentie Webadres VO-content 30 mei 2017 CC Naamsvermelding-GelijkDelen 3.0 Nederland licentie https://maken.wikiwijs.nl/62517 Dit lesmateriaal is gemaakt met Wikiwijs van Kennisnet.
Inhoud. 1 Ruimtefiguren 8. 4 Lijnen en hoeken 148. 2 Plaats bepalen 60. 5 Negatieve getallen 198. 3 Rekenen 100
 1 BK deel 1 Voorkennis 1 Aan de slag met wiskunde 6 1 Ruimtefiguren 8 1.1 Wiskundige ruimte guren 10 1.2 Vlakken, ribben en hoekpunten 14 1.3 Kubus en vierkant 17 1.4 Balk en rechthoek 24 1.5 Cilinder
1 BK deel 1 Voorkennis 1 Aan de slag met wiskunde 6 1 Ruimtefiguren 8 1.1 Wiskundige ruimte guren 10 1.2 Vlakken, ribben en hoekpunten 14 1.3 Kubus en vierkant 17 1.4 Balk en rechthoek 24 1.5 Cilinder
Errata Moderne wiskunde 9e editie VWO B deel 2 hoofdboek
 Onderstaande verbeteringen zijn gebaseerd op de eerste druk van deze titel. In bijdrukken worden fouten hersteld. Het is dus goed mogelijk, dat hier verbeteringen staan, die bij een nieuwe druk al zijn
Onderstaande verbeteringen zijn gebaseerd op de eerste druk van deze titel. In bijdrukken worden fouten hersteld. Het is dus goed mogelijk, dat hier verbeteringen staan, die bij een nieuwe druk al zijn
Peuters - 1K 2K 3K. Basismateriaal. Aanbod peuters 1K indien nodig
 Peuters - 1K 2K 3K puzzelhoek Materialen Insteekblokken: meetkundige lichamen, kubus, cilinder, Inlegplank met en zonder knoppen - Per inlegruimte één persoon, dier of voorwerp - Per inlegruimte enkele
Peuters - 1K 2K 3K puzzelhoek Materialen Insteekblokken: meetkundige lichamen, kubus, cilinder, Inlegplank met en zonder knoppen - Per inlegruimte één persoon, dier of voorwerp - Per inlegruimte enkele
Opgaven bij het vormen van ruimte: van Poincaré tot Perelman
 Opgaven bij het vormen van ruimte: van Poincaré tot Perelman Roland van der Veen Inleiding Deze reeks opgaven is bedoeld voor de werkcolleges van de vakantiecursus Wiskunde in Wording, Augustus 2013. 1
Opgaven bij het vormen van ruimte: van Poincaré tot Perelman Roland van der Veen Inleiding Deze reeks opgaven is bedoeld voor de werkcolleges van de vakantiecursus Wiskunde in Wording, Augustus 2013. 1
Stap 1: Ga naar Stap 3: Gebruik de pijltjes om te navigeren tussen de bladzijden.
 Stap 1: Ga naar www.wiskundewereld.be/bzl-ruimtemeetkunde.html Stap 2: Klik rechts op de witte knop. Stap 3: Gebruik de pijltjes om te navigeren tussen de bladzijden. Stap 4: Links zie je waar je je in
Stap 1: Ga naar www.wiskundewereld.be/bzl-ruimtemeetkunde.html Stap 2: Klik rechts op de witte knop. Stap 3: Gebruik de pijltjes om te navigeren tussen de bladzijden. Stap 4: Links zie je waar je je in
Een hecatonicosachoron op het Kottenpark
 Een hecatonicosachoron op het Kottenpark Afgeknotte Hecatonicosachoron Deze schaduw van deze 4-dimensionale polytoop bestaat uit 120 afgeknotte dodecaëders en 600 tetraëders Gebouwd op 30 januari 2010
Een hecatonicosachoron op het Kottenpark Afgeknotte Hecatonicosachoron Deze schaduw van deze 4-dimensionale polytoop bestaat uit 120 afgeknotte dodecaëders en 600 tetraëders Gebouwd op 30 januari 2010
Meetkunst Les 4 Spelen met perspectief
 Meetkunst Les 4 Spelen met perspectief Vervreemding door optische illusies Niet alle kunstenaars houden zich aan de regels van perspectief, standpunt, onderlinge verhoudingen etc. Zij overtreden moedwillig
Meetkunst Les 4 Spelen met perspectief Vervreemding door optische illusies Niet alle kunstenaars houden zich aan de regels van perspectief, standpunt, onderlinge verhoudingen etc. Zij overtreden moedwillig
Praktische opdracht Wiskunde B Fractals
 Praktische opdracht Wiskunde B Fractals Praktische-opdracht door een scholier 2136 woorden 4 juli 2004 4,9 36 keer beoordeeld Vak Wiskunde B Inleiding Voor wiskunde B-1 moesten we in groepjes van 2 of
Praktische opdracht Wiskunde B Fractals Praktische-opdracht door een scholier 2136 woorden 4 juli 2004 4,9 36 keer beoordeeld Vak Wiskunde B Inleiding Voor wiskunde B-1 moesten we in groepjes van 2 of
Wiskundeonderwijs en visuele problemendetectie bij leerlingen
 Dyslexie, dyscalcie en nu is er ook nog fixatie disparatie. Het grote voordeel van fixatie disparatie is echter dat dit te verhelpen is. Als wiskundedocent kun je fixatie disparatie op het spoor komen
Dyslexie, dyscalcie en nu is er ook nog fixatie disparatie. Het grote voordeel van fixatie disparatie is echter dat dit te verhelpen is. Als wiskundedocent kun je fixatie disparatie op het spoor komen
Examen HAVO en VHBO. Wiskunde B
 Wiskunde B Examen HAVO en VHBO Hoger Algemeen Voortgezet Onderwijs Vooropleiding Hoger Beroeps Onderwijs HAVO Tijdvak 1 VHBO Tijdvak 2 Dinsdag 23 mei 13.30 16.30 uur 00 Dit examen bestaat uit 19 vragen.
Wiskunde B Examen HAVO en VHBO Hoger Algemeen Voortgezet Onderwijs Vooropleiding Hoger Beroeps Onderwijs HAVO Tijdvak 1 VHBO Tijdvak 2 Dinsdag 23 mei 13.30 16.30 uur 00 Dit examen bestaat uit 19 vragen.
1BK2 1BK6 1BK7 1BK9 2BK1
 Kern Subkern Leerdoel niveau BK begrippen vmbo waar in bettermarks 1.1.1. Je gebruikt positieve en negatieve getallen, breuken en decimale getallen in hun onderlinge samenhang en je ligt deze toe binnen
Kern Subkern Leerdoel niveau BK begrippen vmbo waar in bettermarks 1.1.1. Je gebruikt positieve en negatieve getallen, breuken en decimale getallen in hun onderlinge samenhang en je ligt deze toe binnen
