Complexiteit van berekeningen
|
|
|
- Nele Visser
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Logica in actie H O O F D S T U K 7 Complexiteit van berekeningen We hebben nu al een paar keer gezien dat logica nauw verbonden is met processen die informatie bewerken en overdragen. Het proces bij uitstek met deze informatieve functie is rekenen, en daarom gaan we deze connectie in dit hoofdstuk eens wat preciezer aan het licht brengen. Niet alleen omdat het onderwerp praktisch van belang is in de informatietechnologie, maar ook omdat dit samenhangt met diepe vragen over complexiteit van processen van de meest uiteenlopende aard. Redeneren en rekenen liggen dicht bij elkaar. De twintigste eeuwse contacten tussen logica en informatica gaan terug op een oudere historische traditie van redeneermachines. Zo werken de digitale circuits van een moderne computer in wezen volgens de negentiende eeuwse propositielogica van George Boole. Maar naast dit rekenaspect is er nog een tweede kant aan het contact tussen logica en informatica. De logische talen die we gezien hebben geven manieren om diverse soorten van informatie exact uit te drukken: propositioneel, met kwantoren, en modaal (en er zijn nog vele andere mogelijkheden). Daarmee wordt die informatie voor berekening vatbaar. In dit hoofdstuk staat dat genre van berekening centraal. In de informatica gaat het om het juiste samenspel tussen de geschikte weergave of representatie van informatie (in getalstructuren, gegevensbanken, of andere vormen) en efficiënte berekening met die gegevens, met andere woorden om de interactie tussen, in het Engels: representation + computation. En in ons cognitief gedrag vindt een vergelijkbaar samenspel plaats van informatieverwerking met een beperkte hoeveelheid tijd en aandacht. Deze balans kan men goed bestuderen in het gedrag van logische systemen, die een evenwicht moeten vinden tussen logische uitdrukkingskracht en rekencomplexiteit. In het algemeen geldt: hoe rijker de taal, hoe moeilijker het rekenproces voor de centrale logische taken. De bedoeling van dit hoofdstuk is om enig inzicht te geven in deze balans, die vooral typerend is voor logische systemen die ontwikkeld zijn in de buurt van de informatica. In paragraaf 7.1 introduceren we de relevante logische taken: bewijzen, vervullen, evalueren en vergelijken. In de paragrafen 7.2 en 7.3 geven we 1
2 enige voorbeelden van de complexiteit van taken in de standaard logische systemen die we gezien hebben. 7.1 Bewijzen, vervullen, evalueren en vergelijken In dit boek zijn heel uiteenlopende logische taken besproken. Het berekenen van een waarheidswaarde van een formule in een gegeven model is zo n taak, maar ook het vinden van een model voor een gegeven stel formules. We zetten een aantal van deze taken nog eens iets uitvoeriger op een rij. Om te beginnen hebben we bewijstaken. Bewijstaken Veel theoretische en praktische problemen komen erop neer dat bepaald (theorem proving) moet worden of een bewering uit een andere volgt. We kunnen dit bijvoorbeeld zien bij het automatisch vinden van wiskundige stellingen die volgen uit gegeven axioma s. Zo kunnen we een bewijs van de stelling van Pythagoras (hoofdstuk 1) in principe mechanisch vinden gegeven een aantal basisaannames (de postulaten van Euclides) en de afleidingsregel modus ponens (ϕ, ϕ ψ ψ). Dit soort logische geldigheidsvragen wordt gesteld binnen het kader van een formeel bewijssysteem en de gangbare term hiervoor is stellingbewijzen (in het Engels: theorem proving ). Aan de complexiteit van bewijzen besteden we geen aandacht, behoudens een voorbeeld. VOORBEELD 7.1 Vervulbaarheidstaken (satisfiability) Als p bekend is dan kunnen we met twee implicaties p q en q r, en de modus ponens regel bewijzen dat r. Eerst volgt uit p en p q dat q, en uit q en q r volgt dan r. Dat zijn maar twee stappen, lekker snel dus en niet zo complex. Een probleem in zo n bewijs is dat q niet voorkomt in de aanname p en ook niet in de te bewijzen conclusie r, en dat het daarom toch heel complex kan worden, namelijk omdat we uit meerdere beschikbare implicaties nu juist p q en q r moeten selecteren, en niet twee van tienduizenden andere beschikbare implicaties p q 1, p q 2,... De complexiteit van bewijzen heeft dus niet alleen te maken met de lengte van het bewijs dat we uiteindelijk vinden, maar ook (en zelfs vooral) met de duur van de zoektocht naar zo n bewijs. Een ander kort bewijs is dat van p r p q: uit p r volgt p, en uit p volgt de zwakkere disjunctie p q. In dit bewijs is de tussenstap p een deelformule van het uitgangspunt en een deelformule van de te bewijzen conclusie. Als we bij het zoeken naar bewijzen zo n restrictie kunnen aannemen, is het zoeken veel sneller te verrichten. Zulke bewijzen heten cut free (zonder snede), de stap p q, q r p r waarin propositieletter q links wel staat maar rechts niet kunnen we zien als het wegsnijden van q. In gewone conversatie bewijzen we zelden formeel. Het gaat er dan meer om, consistente informatie te verstrekken. Dit consistency management heeft als logische kernvraag of een gegeven verzameling beweringen een model heeft. Dit is de zogenaamde vervulbaarheid van die verzameling, in 2
3 Evaluatietaken (model checking) VOORBEELD 7.2 Vergelijkingstaken (model comparison) VOORBEELD 7.3 het Engels: satisfiability. Dezelfde vraag doet zich in een ander jasje voor bij ontwerpen, bijvoorbeeld het ontwerp van een digitaal circuit dat moet voldoen aan vooraf gegeven Boolese specificaties, of dat van een multiactorsysteem dat moet voldoen aan vooraf gegeven kennislogische eisen. In wezen eenvoudiger dan vervulbaarheidstaken, maar ook zeer nuttig, zijn evaluatietaken (ook wel bekend onder de naam verificatietaken). Hoe bepalen we de waarheidswaarde van een formule in een model? Dit is de controle of een gegeven structuur voldoet aan zekere eisen die we van tevoren hebben gesteld. In het Engels: model checking. Het checken van specificaties voor een gegeven proces is van deze aard, evenals het bepalen van eigenschappen van een circuit van Boolese schakelingen. Logische taken kunnen ook tezamen voorkomen in eenzelfde situatie. Zo moet in de rechtszaal de aanklager bewijzen dat de beklaagde schuldig is: een bewijstaak voor een conclusie uit de voorliggende gegevens. Maar de verdediger heeft slechts de vervulbaarheidstaak om een scenario te schetsen dat past bij die gegevens, maar waarin zijn cliënt onschuldig is. Ook evaluatietaken kunnen voorkomen, namelijk bij het vaststellen van het toelaatbare bewijsmateriaal. Er zijn nog heel andere genres taken. Heel belangrijk zijn bijvoorbeeld vergelijkingstaken. Wanneer zijn twee Boolese circuits equivalent, of twee modellen voor de predikaatlogica, of twee multi actorsystemen in die zin dat ze dezelfde formules van de relevante taal waar maken? Dit soort informatie is cruciaal bij het vereenvoudigen van voorgestelde machines of informatieprocessen. De onderstaande figuur bevat twee verschillende modellen, die toch dezelfde informatie uitdrukken, namelijk dat zowel actor a als actor b niet weet of p (en dat ze dit ook van elkaar weten, enzovoort). We kunnen dit inzien door bijvoorbeeld in de p situatie linksboven te beginnen, en dan met een a pijl naar de p situatie rechtsboven te gaan. In de rechterfiguur kunnen we zo n overgang simuleren door in de p situatie onder te beginnen, en naar de p situatie boven te gaan met een a pijl. Dit kunnen we vanuit iedere situatie doen, voor a pijlen en b pijlen, waarbij we bovendien ervoor blijven zorgen dat de waarheidswaarde van p blijft corresponderen: of allebei waar, of allebei onwaar. Evenzo kunnen we een stap die we eerst rechts maken links simuleren. Zo n simulatie twee kanten 3
4 op heet een bisimulatie. Als dit kan, dan volgt hieruit dat iedere kennislogische formule die rechts waar is, ook links waar is, en andersom. De modellen hebben dus dezelfde informatie inhoud: we kunnen ze niet van elkaar onderscheiden in de taal van de kennislogica. 7.2 Hoe moeilijk zijn logische taken? Onze volgende vraag betreft de moeilijkheid van deze logische taken. Een evaluatietaak in de propositielogica, dat wil zeggen het uitrekenen van een waarheidswaarde in een waarheidstabel, lijkt op het eerste gezicht eenvoudig, en gelukkig is dat ook inderdaad zo. Een rij in een waarheidstabel komt overeen met een propositielogische waardering. In die rij vullen we één voor één de waarheidswaarden in voor alle subformules van een gegeven formule. Dit kost ons evenveel tijd (stappen) als het aantal subformules van die formule. En het aantal subformules is weer ongeveer gelijk aan de lengte van die formule: het aantal symbolen. Men zegt wel dat deze evaluatietaak in de orde van grootte is van de lengte van de formule. Evaluatie in de propositielogica kost dus zogenaamde lineaire tijd, gemeten in de lengte van de invoerformule. Daarentegen is het is veel lastiger om te bepalen of een formule een model heeft (satisfiability), omdat we nu in het ergste geval alle rijen in de waarheidstabel zullen moeten nagaan. Dit is een exponentieel aantal, namelijk alle combinaties van nullen en enen voor de propositieletters in de formule. VOORBEELD 7.4 We kijken nog eens naar de waarheidstabel voor de formule p q van voorbeeld 3.4 p q p q Hierin komen twee propositieletters voor. Deze formule is vervulbaar want er is een waardering waarvoor de formule waar is, namelijk als p waar is en q onwaar. Om te bepalen of een formule waarin twee propositieletters voorkomen vervulbaar is, moeten we in het ergste geval vier rijen (namelijk twee tot de macht van deze twee propositieletters) van de waarheidstabel onderzoeken. Maar voor deze formule zijn we bij de tweede rij al klaar! Complexiteitsanalyses gaan altijd uit van het ergste dat ons kan overkomen. In de praktijk kan het meevallen. 4
5 Om te bepalen dat de waardering waarin p waar en q onwaar is, een model is van de formule ( model checking ) moeten we één keer de waarde van een negatie bepalen, namelijk de negatie van q, en één keer de waarde van een conjunctie, die van p en q. De lengte van een formule is het aantal symbolen waar de formule uit bestaat. De formule p q bestaat uit vier symbolen, of zes, als we de haakjes van de conjunctie meetellen, als in (p q). Een formule kan natuurlijk nooit meer logische connectieven hebben dan het aantal symbolen. In het ergste geval is het aantal symbolen de lengte van de formule min één, zoals in p. Daarom kost een evaluatietaak in de propositielogica lineaire tijd. VOORBEELD 7.5 Nu willen we bepalen of de formule p 1 p 2... p 99 (p 100 p 100 ) vervulbaar is. Hierin komen 100 propositieletters voor. Als we blind gaan zoeken, moeten we dus een waarheidstabel met rijen gaan aflopen; is ongeveer (want 2 10 = 1024) dus met een minuut rekentijd per rij komen we dan met gemak boven de ouderdom van het heelal uit. Niettemin ziet u meteen dat de formule onvervulbaar is, vanwege de contradictie p 100 p 100 aan het eind. En dit zien is ook met geringe mechanische moeite uit te voeren. Er zijn vele methoden om sneller vervulbaarheid te bepalen. Dit is zelfs een belangrijk specialisme in de informatica (Boolean satisfiability checking, SAT checking). Soortgelijke vragen rijzen bij de rijkere taal van de predikaatlogica. Hoe moeilijk is het bijvoorbeeld om voor een formule x y R(x, y) met twee kwantoren te bepalen of deze waar is in een gegeven model van n objecten? Op het eerste gezicht is het antwoord hierop: dit duurt n 2 stappen. In het ergste geval moeten we namelijk alle (n) objecten één voor één voor x invullen, en voor elk daarvan weer alle (n) objecten proberen als mogelijke y. In het algemeen verwachten we dus exponentiële tijd voor de evaluatie van een formule met kwantoren, als we het model en die formule als invoerparameters nemen: namelijk het aantal objecten van het model tot de macht van de grootste nesting van kwantoren in de formule. Maar ook hier kunnen verrassingen optreden die tot lagere complexiteit leiden! Het nu volgende voorbeeld bevat zo n verrassing. VOORBEELD 7.6 Vind de beroemdheid Dit instructieve voorbeeld is van Anne Kaldewaij. Een beroemdheid is iemand die niemand anders kent, maar wel door ieder ander wordt gekend. Hoe bepalen we zo snel mogelijk of een groep een beroemdheid heeft, en wie dat is? Het gaat hier om de vraag of in een gegeven model de predikaatlogische formule x y (y x (K(y, x) K(x, y))) waar is. Omdat er een stapeling van twee kwantoren is, zou men verwachten dat dit kwadratische tijd kost. Het kan echter lineair! We geven daartoe aan iedereen een rood balletje, voor potentiële beroemdheid. Nu herhalen we de volgende procedure: 5
6 Zolang er nog minstens twee mensen met rode balletjes zijn, pak er dan twee, zeg x en y, en kijk of x de persoon y kent. Zo ja, neem dan x het rode balletje af, zo nee, neem y het balletje af. De unieke overblijver met een balletje wordt nu nog even getest op de eigenschap beroemdheid te zijn. Dit hele proces loopt hoogstens drie keer door het domein: namelijk twee keer om de overblijver met het rode balletje te bepalen (twee objecten kiezen, net zo vaak als het aantal objecten), en één keer om voor alle anderen te testen of zij die overblijver kennen en de overblijver hen niet kent. Daarmee is de complexiteit lineair. Van de complexiteit van vergelijkingstaken geven we geen concreet voorbeeld. We formuleren nog eens de drie besproken typische taken van een logische taal: Model checking (verificatie/evaluatie): Gegeven een model en een formule, is de formule waar in het model? Satisfiability (vervulbaarheid): Gegeven een formule, is er een model dat de formule waarmaakt? Model comparison (vergelijking): Gegeven twee modellen, maken deze dezelfde formules waar? Als we de precieze rekencomplexiteit van al deze taken kennen, dan hebben we een redelijk profiel van het computationele gedrag van zo n logisch systeem. We zullen alleen wat voorbeelden geven van de complexiteit van dit soort kwesties voor de logische talen van dit boek. Maar voordat we dat kunnen doen, moeten we natuurlijk wel iets preciezer zijn over wat we bedoelen met rekencomplexiteit! Dit is op zich al een belangrijk vakspecialisme in de praktische en theoretische informatica. 7.3 Computationale complexiteit Een taak is effectief opgelost als je er een algoritme voor kunt schrijven, misschien als programma in een of andere programmeertaal. Bij een JA/NEE vraag P? wordt de bewering P als invoer aan een mechanische procedure gegeven die na een eindig aantal stappen steeds het juiste antwoord geeft. Een voorbeeld van zo n vraag is: kunnen we uit een beginsituatie een gewenste eindsituatie bereiken via een eindig aantal stappen? Heel veel taken in de informatica, zoals het bevragen van gegevensbanken, of zoektaken in de kunstmatige intelligentie, komen neer op het bepalen van dergelijke bereikbaarheid van een doel uit een beginpunt. VOORBEELD 7.7 Graph reachability (bereikbaarheid in een graaf) Gegeven is een eindige gerichte graaf G en twee knopen s ( beginknoop ) en t ( eindknoop ). Is er een pad van s naar t? Deze vraag is te beantwoorden met het volgende algoritme: 6
7 R wordt de verzameling rode knopen. Kleur om te beginnen alleen s rood. B wordt de verzameling blauwe knopen. Deze is in eerste instantie leeg. Herhaal nu de volgende procedure: pak een rode knoop uit R, verf deze blauw (voeg deze aan B toe), en vervang die knoop in R door al zijn (directe) opvolgers in de graaf, tenzij je ze al gehad hebt, dat wil zeggen: tenzij ze al rood of blauw zijn. Met andere woorden: verf alle niet gekleurde opvolgers rood. Als er niet zulke opvolgers zijn, dan krimpt R dus. Stop als R leeg is. Als t nu blauw is, dan is t bereikbaar uit s, en anders niet. Dit algoritme is correct en eindigt in kwadratische tijd ten opzichte van het aantal knopen van de graaf. Dit kunnen we als volgt inzien. Stel n is het aantal knopen in de graaf. Ten hoogste iedere knoop verkleurt een keer van rood naar blauw, ieder van die knopen heeft ten hoogste alle andere knopen als opvolger, en aan het eind moeten we nog even de verzameling B doorlopen, die ten hoogste alle knopen bevat. In totaal zijn dit hooguit n(n 1) + n stappen. Omdat voor grote n de lineaire factoren verwaarloosbaar zijn ten opzichte van kwadraten, en n en n 1 dan bijna hetzelfde zijn, zeggen we: de orde van grootte is n 2. De kunst van efficiënt programmeren loopt via dergelijke slimme representaties met lage complexiteit. Vergelijk dit ook met voorbeeld 7.6 van vind de beroemdheid. Graden van groei Als een antwoord op een JA/NEE vraag P? altijd in eindig veel stappen puur mechanisch bepaald kan worden noemen we het probleem beslisbaar. Het is dan immers te beslissen (uit te maken) of het antwoord op deze vraag JA dan wel NEE is. De complexiteit van zo n beslisbare procedure is een functie van de lengte van de invoer van die procedure (zoals bij een propositielogische formule: het aantal symbolen). Daarbij speelt het aantal rekenstappen een belangrijke rol. Dit wordt de tijdscomplexiteit van het probleem genoemd. We hebben al gezien dat het aantal rekenstappen lineair kan zijn in de invoer, en ook dat het een groter polynoom kan zijn dan lineair, bijvoorbeeld kwadratisch, zoals in voorbeeld 7.7. Beide noemen we van polynomiale complexiteit. Als de rekencomplexiteit polynomiaal is ten opzichte van de invoer noemen we een probleem in de klasse P (waarbij P inderdaad voor polynomiaal staat). Als x de invoerlengte is, dan is bijvoorbeeld ax + b lineair en ax 3 derdegraads, en beide zijn polynomen, dus deze problemen zitten allebei in P. Als de rekencomplexiteit daarentegen exponentieel is als functie van de invoerlengte vinden we het heel complex. Deze klasse noemen we Exptime: deze exponentiële tijd ziet er ten minste uit als a x. Oudere lezers herinneren zich nog de groeigrafieken van de Club van Rome in de zeventiger jaren, die aangaven hoe vervuiling en andere doemscenario s op deze akelig snelle manier toenamen. En het kan zelfs 2 nog erger dan Exptime, zoals bijvoorbeeld in x! en in 2 x. Er zitten ook nog complexiteitsklassen tussen polynomiaal en exponentieel, maar daar gaan we niet op in. 7
8 VOORBEELD 7.8 Graph reachability, GR, is in P, omdat voor een gegeven graaf G de procedure altijd eindigt na hooguit een aantal stappen van een kwadratische orde van grootte (namelijk n(n 1) + n). Een logische analogie kan helpen deze begrippen nog iets beter te begrijpen. Hiervoor zagen we al dat propositielogische evaluatie in P zit. Testen op propositielogische vervulbaarheid leek exponentiële complexiteit te hebben maar zit in feite in een lagere complexiteitsklasse, tussen P en Exptime in. Zelfs als een taak in P zit, blijft een algoritme van lineaire tijd prettiger dan één van kwadratische tijd, enzovoorts: een polynoom van lagere graad is altijd weer beter dan een van hogere graad. De kunst van het programmeren bestaat doorgaans uit het geschikt kiezen van datastructuren en instructies, om zo laag mogelijk in rekencomplexiteit uit te komen. Problemen in P gelden als doenlijk (in het Engels: tractable ) en alles daarbuiten als ondoenlijk ( intractable ), hetgeen overigens niemand verhindert allerlei speciale gevallen toch op de computer op te lossen. Onbeslisbaarheid VOORBEELD 7.9 Het kan dus, zoals we al zagen, nog veel erger qua complexiteit. En sommige problemen zijn helemaal niet met een algoritmische methode op te lossen: deze heten onbeslisbaar. Wie zou niet graag willen kunnen vermijden dat zijn computer vastloopt? Dit is het Stopprobleem: Bepaal bij een willekeurig programma en willekeurige invoer, of het programma voor die invoer termineert. In het Engels is het probleem bekend als het Halting problem. Het is nu een feit dat dit Stopprobleem onbeslisbaar is. Dit feit werd bewezen door Alan Turing in Er zijn dus geen wondermiddelen die automatisch ongewenst gedrag van onze computers detecteren. Nog zo n onbeslisbare vraag is bijvoorbeeld die naar de equivalentie van twee gegeven programma s, bijvoorbeeld in een eenvoudige imperatieve programmeertaal: geven ze op alle invoer dezelfde waarden? De oudste voorbeelden van onbeslisbare problemen komen uit de logica. Predikaatlogica is onbeslisbaar In de propositielogica hebben we een beslissingsprocedure om te bepalen of een gegeven formule een tautologie is, of niet: maak de waarheidstabel, loop alle waarderingen langs en bepaal de waarde van de hele formule voor die waardering, en als er overal énen staan, is het een tautologie. Maar in de predikaatlogica bestaat zo n procedure niet. (We laten details achterwege.) Het resultaat dat de predikaatlogica onbeslisbaar is danken we aan Alonzo Church, die hiertoe gebruik maakte van de beroemde Stelling van Gödel. Hoe zit het dan met bijvoorbeeld onze kennislogica, die qua kracht in lag tussen de propositielogica en de predikaatlogica? Deze blijkt weer beslisbaar, maar wel met een wezenlijk complexer algoritme dan voor de propositielogica. 8
9 De algemene moraal is deze: niet elk eenvoudig formuleerbaar probleem inzake redeneren, rekenen of informatieverwerking heeft een mechanische oplossing! Ook hier merken we weer op dat de praktijk toch enig optimisme wettigt. Zelfs onbeslisbare problemen kunnen systematisch worden aangepakt. Er zijn namelijk allerlei bewijsmethodes voor de predikaatlogica, waarmee we meestal wel uit de voeten kunnen. In dit verband maken we nog een opmerking. Onze voorbeelden in dit hoofdstuk geven slechts bovengrenzen: hoeveel tijd of ruimtestappen hebben we hoogstens nodig, in het ergste geval? Om een probleem precies te plaatsen in de complexiteitshiërarchie moeten we ook een ondergrens geven: hoeveel stappen kan de oplossing minstens vergen, wat is de minimale complexiteit? Maar in het algemeen wordt het gedrag van een algoritme in de praktijk bepaald door rekentijd op willekeurige invoer, zodat we eerder zouden moeten spreken over een gemiddelde complexiteit. Deze verdere kwesties laten we hier terzijde. Tegen deze achtergrond eindigen we met een meer theoretische kwestie. Hoe moeilijk is het vervulbaarheids of geldigheidsprobleem van de propositielogica nu werkelijk? Moet het exponentieel, of wordt er wellicht toch nog een slim algoritme gevonden dat het in polynomiale tijd afkan? Deze vraag staat bekend als het P = NP probleem, dat voorkomt op de lijst van Tien Meest Beroemde Open Vragen van de Wiskunde, in 2000 gepubliceerd door het Cray Institute. Het is opmerkelijk dat een zo eenvoudig logisch systeem als de propositielogica, in wezen al bekend sinds de Klassieke Oudheid, nog zulke nieuwe vragen weet op te werpen. 9
10 Samenvatting Een probleem is beslisbaar als een antwoord op een JA/NEE vraag P? altijd in eindig veel stappen puur mechanisch bepaald kan worden. De complexiteit van zo n beslissingsprocedure is een functie van de lengte van de invoer van die procedure. Daarbij speelt het aantal rekenstappen (tijdscomplexiteit) een rol. Wat betreft het aantal rekenstappen is lineair minder complex dan (vanaf tweedegraads) polynomiaal, en polynomiaal minder complex dan exponentieel. Al deze genres complexiteit komen voor in de propositielogica, en overigens ook in de kennislogica van hoofdstuk 6. Sommige belangrijke problemen zijn zelfs onbeslisbaar, dat wil zeggen dat geen enkel programmeerbaar algoritme, hoe ingewikkeld ook, ze kan oplossen. Bijvoorbeeld, het is onbeslisbaar of bij een willekeurig programma en willekeurige invoer, het programma voor die invoer termineert. Dit staat bekend als het Stopprobleem. Maar ook logische geldigheid in systemen als de predikaatlogica is van deze hoge complexiteit. Dit document bevat hoofdstuk 7 van de cursus Logica in actie. De volledige cursus is beschikbaar op Open Universiteit Nederland; Uitgeverij: Sdu Uitgevers, s Gravenhage. Dit materiaal is gelicentieerd onder een Creative Commons Licentie. Zie de licentie voor details. The content on this site is licensed under a Creative Commons Licentie. See licence for more details. 10
11 Opgaven OPGAVE 7.1 Voer het graph reachability algoritme van voorbeeld 7.7 uit voor de volgende graaf. Als beginknoop s neemt u knoop 1 in de figuur. Als eindknoop t neemt u knoop 4. OPGAVE 7.2 Voer het vind de bekendheid algoritme van voorbeeld 7.6 uit voor de volgende graaf. 11
12 Uitwerkingen van de opgaven bij hoofdstuk We voeren het graph reachability algoritme van voorbeeld 7.7 uit voor de gegeven graaf, met s als beginknoop en t als eindknoop. R is de verzamelingen rode knopen, B is de verzameling blauwe knopen. Om te beginnen is R = {1} en B =. De handeling waarbij we een rode knoop uit R selecteren, blauw maken, en zijn opvolgers rood, noemen we een stap. Merk op dat de selectie van een rode knoop in een stap nondeterministisch (onbepaald) is. We kiezen dus gewoon een rode knoop niet per se de eerste als we de elementen van de verzamelingen R van links naar rechts lezen. Het is mogelijk dat u in uw antwoord een andere keuze gemaakt heeft, maar dat uw antwoord toch goed is. R = {1} B = R = {2, 3, 7} B = {1} R = {3, 4, 7} B = {1, 2} R = {4, 5, 6, 7} B = {1, 2, 3} R = {4, 5, 7} B = {1, 2, 3, 6} R = {5, 7} B = {1, 2, 3, 4, 6} R = {5} B = {1, 2, 3, 4, 6, 7} R = B = {1, 2, 3, 4, 5, 6, 7} Kies 1, de opvolgers zijn 2, 3 en 7. Kies 2, de opvolgers zijn 1, 3, en 4; 4 heeft geen kleur. Kies 3, de opvolgers zijn 2, 4, 5, en 6; 5 en 6 hebben geen kleur. Kies 6, alle knopen zijn inmiddels gekleurd. Kies 4. Kies 7. Kies 5. De knoop t = 4 maakt deel uit van de verzameling B. Dus t is vanuit s bereikbaar. Merk op dat we het algoritme niet stoppen op het moment dat 4 in de verzameling B komt, maar dat het algoritme volgens afspraak pas termineert als de verzameling R leeg is. 7.2 We voeren het vind de bekendheid algoritme van voorbeeld 7.6 uit voor de gegeven graaf. De verzameling punten (of mensen) met rode balletjes is R. De keuze voor twee uit R is non deterministisch (net als in de vorige opgave). We geven de keuze aan in het overzicht hierna u heeft wellicht een andere keuze gemaakt! R = {1, 2, 3, 4} R = {1, 2, 3} Kies 2 en 4, 2 kent 4 niet, neem dus 4 rood af. 12
13 R = {2, 3} R = {3} Kies 1 en 3, 1 kent 3, neem dus 1 rood af. Kies 2 en 3, 2 kent 3, neem dus 2 rood af. We moeten nu testen of de unieke overblijver (er is altijd een unieke overblijver!) een beroemdheid is. Dit is zo, want (1, 3), (2, 3), (4, 3) zitten alledrie in K, maar (3, 3) zit niet in K. 13
Credit cards, computationele complexiteit en consistentie uitspraken
 Credit cards, computationele complexiteit en consistentie uitspraken Joost J. Joosten 14 december 2005 Praag en bier Sinds enkele maanden werk ik als post-doc aan de Czech Academy of Sciences in Praag.
Credit cards, computationele complexiteit en consistentie uitspraken Joost J. Joosten 14 december 2005 Praag en bier Sinds enkele maanden werk ik als post-doc aan de Czech Academy of Sciences in Praag.
REDENEREN, REKENEN, EN COMPLEXITEIT
 REDENEREN, REKENEN, EN COMPLEXITEIT 1 Redeneren is rekenen is redeneren In het abstracte perspectief van de logicus zijn gevolgtrekkingen in wezen slechts symbolische configuraties: en wel rijtjes symbolen
REDENEREN, REKENEN, EN COMPLEXITEIT 1 Redeneren is rekenen is redeneren In het abstracte perspectief van de logicus zijn gevolgtrekkingen in wezen slechts symbolische configuraties: en wel rijtjes symbolen
Wie A zegt moet B zeggen
 Logica in actie H O O F D S T U K 3 Wie A zegt moet B zeggen Logici ontwerpen niet alleen systemen om bestaande vormen van redeneren te analyseren, ze bestuderen ook de eigenschappen van die systemen op
Logica in actie H O O F D S T U K 3 Wie A zegt moet B zeggen Logici ontwerpen niet alleen systemen om bestaande vormen van redeneren te analyseren, ze bestuderen ook de eigenschappen van die systemen op
Negende college complexiteit. 9 april NP-volledigheid I: introductie
 College 9 Negende college complexiteit 9 april 2019 NP-volledigheid I: introductie 1 Handelbaar/onhandelbaar -1- N 10 50 100 300 1000 log 2 N 3 5 6 8 9 5N 50 250 500 1500 5000 N log 2 N 33 282 665 2469
College 9 Negende college complexiteit 9 april 2019 NP-volledigheid I: introductie 1 Handelbaar/onhandelbaar -1- N 10 50 100 300 1000 log 2 N 3 5 6 8 9 5N 50 250 500 1500 5000 N log 2 N 33 282 665 2469
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 11 Leo van Iersel Technische Universiteit Delft 25 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 25 november 2015 1 / 28 Vandaag Vraag Voor welke problemen
TW2020 Optimalisering Hoorcollege 11 Leo van Iersel Technische Universiteit Delft 25 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 25 november 2015 1 / 28 Vandaag Vraag Voor welke problemen
Logic for Computer Science
 Logic for Computer Science 06 Normaalvormen en semantische tableaux Wouter Swierstra University of Utrecht 1 Vorige keer Oneindige verzamelingen 2 Vandaag Wanneer zijn twee formules hetzelfde? Zijn er
Logic for Computer Science 06 Normaalvormen en semantische tableaux Wouter Swierstra University of Utrecht 1 Vorige keer Oneindige verzamelingen 2 Vandaag Wanneer zijn twee formules hetzelfde? Zijn er
Predikaatlogica, modellen en programma s
 Logica in actie H O O F D S T U K 4 Predikaatlogica, modellen en programma s De taal van de propositielogica is voor veel toepassingen te arm. Dat bleek al in de Klassieke Oudheid, waar logici allerlei
Logica in actie H O O F D S T U K 4 Predikaatlogica, modellen en programma s De taal van de propositielogica is voor veel toepassingen te arm. Dat bleek al in de Klassieke Oudheid, waar logici allerlei
Uitwerking tentamen Analyse van Algoritmen, 29 januari
 Uitwerking tentamen Analyse van Algoritmen, 29 januari 2007. (a) De buitenste for-lus kent N = 5 iteraties. Na iedere iteratie ziet de rij getallen er als volgt uit: i rij na i e iteratie 2 5 4 6 2 2 4
Uitwerking tentamen Analyse van Algoritmen, 29 januari 2007. (a) De buitenste for-lus kent N = 5 iteraties. Na iedere iteratie ziet de rij getallen er als volgt uit: i rij na i e iteratie 2 5 4 6 2 2 4
Uitgebreide uitwerking Tentamen Complexiteit, mei 2007
 Uitgebreide uitwerking Tentamen Complexiteit, mei 007 Opgave. a. Een beslissingsboom beschrijft de werking van het betreffende algoritme (gebaseerd op arrayvergelijkingen) op elke mogelijke invoer. In
Uitgebreide uitwerking Tentamen Complexiteit, mei 007 Opgave. a. Een beslissingsboom beschrijft de werking van het betreffende algoritme (gebaseerd op arrayvergelijkingen) op elke mogelijke invoer. In
Propositielogica, waarheid en classificeren
 Logica in actie H O O F D S T U K 2 Propositielogica, waarheid en classificeren We hebben al gezien dat voor een logicus het verhevene heel dicht kan liggen bij het alledaagse. Misschien beter gezegd:
Logica in actie H O O F D S T U K 2 Propositielogica, waarheid en classificeren We hebben al gezien dat voor een logicus het verhevene heel dicht kan liggen bij het alledaagse. Misschien beter gezegd:
Kennis en communicatie
 Logica in actie H O O F D S T U K 6 Kennis en communicatie De traditionele logica richtte zich voornamelijk op producten van menselijk activiteit, zoals formules, formele gevolgtrekkingen, of bewijzen.
Logica in actie H O O F D S T U K 6 Kennis en communicatie De traditionele logica richtte zich voornamelijk op producten van menselijk activiteit, zoals formules, formele gevolgtrekkingen, of bewijzen.
Inleiding Wiskundige Logica
 Inleiding Wiskundige Logica Yde Venema 2017/2018 c YV 2018 Institute for Logic, Language and Computation, University of Amsterdam, Science Park 904, NL 1098XH Amsterdam E-mail: yvenema@uvanl Voorwoord
Inleiding Wiskundige Logica Yde Venema 2017/2018 c YV 2018 Institute for Logic, Language and Computation, University of Amsterdam, Science Park 904, NL 1098XH Amsterdam E-mail: yvenema@uvanl Voorwoord
Wiskundige beweringen en hun bewijzen
 Wiskundige beweringen en hun bewijzen Analyse (en feitelijk de gehele wiskunde) gaat over het bewijzen van beweringen (proposities), d.w.z. uitspraken waaraan de karakterisering waar of onwaar toegekend
Wiskundige beweringen en hun bewijzen Analyse (en feitelijk de gehele wiskunde) gaat over het bewijzen van beweringen (proposities), d.w.z. uitspraken waaraan de karakterisering waar of onwaar toegekend
(On)Doenlijke problemen
 Fundamentele Informatica In3 005 Deel 2 College 1 Cees Witteveen Parallelle en Gedistribueerde Systemen Faculteit Informatie Technologie en Systemen Overzicht Inleiding - Relatie Deel 1 en Deel 2 - Doenlijke
Fundamentele Informatica In3 005 Deel 2 College 1 Cees Witteveen Parallelle en Gedistribueerde Systemen Faculteit Informatie Technologie en Systemen Overzicht Inleiding - Relatie Deel 1 en Deel 2 - Doenlijke
Caleidoscoop: Logica
 Caleidoscoop: Logica Non impeditus ab ulla scientia K. P. Hart Faculteit EWI TU Delft Delft, 3 October, 2007 Overzicht 1 2 Negaties We gaan rekenen met proposities (beweringen). Bedenker: George Boole
Caleidoscoop: Logica Non impeditus ab ulla scientia K. P. Hart Faculteit EWI TU Delft Delft, 3 October, 2007 Overzicht 1 2 Negaties We gaan rekenen met proposities (beweringen). Bedenker: George Boole
Uitgebreide uitwerking Tentamen Complexiteit, juni 2017
 Uitgebreide uitwerking Tentamen Complexiteit, juni 017 Opgave 1. a. Een pad van de wortel naar een blad stelt de serie achtereenvolgende arrayvergelijkingen voor die het algoritme doet op zekere invoer.
Uitgebreide uitwerking Tentamen Complexiteit, juni 017 Opgave 1. a. Een pad van de wortel naar een blad stelt de serie achtereenvolgende arrayvergelijkingen voor die het algoritme doet op zekere invoer.
Tegenvoorbeeld. TI1300: Redeneren en Logica. De truc van Gauss. Carl Friedrich Gauss, 7 jaar oud (omstreeks 1785)
 Tegenvoorbeeld TI1300: Redeneren en Logica College 3: Bewijstechnieken & Propositielogica Tomas Klos Definitie (Tegenvoorbeeld) Een situatie waarin alle premissen waar zijn, maar de conclusie niet Algoritmiek
Tegenvoorbeeld TI1300: Redeneren en Logica College 3: Bewijstechnieken & Propositielogica Tomas Klos Definitie (Tegenvoorbeeld) Een situatie waarin alle premissen waar zijn, maar de conclusie niet Algoritmiek
8. Complexiteit van algoritmen:
 8. Complexiteit van algoritmen: Voorbeeld: Een gevaarlijk spel 1 Spelboom voor het wespenspel 2 8.1 Complexiteit 4 8.2 NP-problemen 6 8.3 De oplossing 7 8.4 Een vuistregel 8 In dit hoofdstuk wordt het
8. Complexiteit van algoritmen: Voorbeeld: Een gevaarlijk spel 1 Spelboom voor het wespenspel 2 8.1 Complexiteit 4 8.2 NP-problemen 6 8.3 De oplossing 7 8.4 Een vuistregel 8 In dit hoofdstuk wordt het
Logica voor Informatica. Propositielogica. Normaalvormen en Semantische tableaux. Mehdi Dastani
 Logica voor Informatica Propositielogica Normaalvormen en Semantische tableaux Mehdi Dastani m.m.dastani@uu.nl Intelligent Systems Utrecht University Literals Een literal is een propositieletter, of de
Logica voor Informatica Propositielogica Normaalvormen en Semantische tableaux Mehdi Dastani m.m.dastani@uu.nl Intelligent Systems Utrecht University Literals Een literal is een propositieletter, of de
Gödels theorem An Incomplete Guide to Its Use and Abuse, Hoofdstuk 3
 Gödels theorem An Incomplete Guide to Its Use and Abuse, Hoofdstuk 3 Koen Rutten, Aris van Dijk 30 mei 2007 Inhoudsopgave 1 Verzamelingen 2 1.1 Definitie................................ 2 1.2 Eigenschappen............................
Gödels theorem An Incomplete Guide to Its Use and Abuse, Hoofdstuk 3 Koen Rutten, Aris van Dijk 30 mei 2007 Inhoudsopgave 1 Verzamelingen 2 1.1 Definitie................................ 2 1.2 Eigenschappen............................
Mededelingen. TI1300: Redeneren en Logica. Waarheidstafels. Waarheidsfunctionele Connectieven
 Mededelingen TI1300: Redeneren en Logica College 4: Waarheidstafels, Redeneringen, Syntaxis van PROP Tomas Klos Algoritmiek Groep Voor de Fibonacci getallen geldt f 0 = f 1 = 1 (niet 0) Practicum 1 Practicum
Mededelingen TI1300: Redeneren en Logica College 4: Waarheidstafels, Redeneringen, Syntaxis van PROP Tomas Klos Algoritmiek Groep Voor de Fibonacci getallen geldt f 0 = f 1 = 1 (niet 0) Practicum 1 Practicum
Predikaatlogica en informatica
 Logica in actie H O O F D S T U K 5 Predikaatlogica en informatica Wanneer is een predikaatlogische formule waar? Om de gedachten te bepalen, beschouwen we nog eens de formule: x (P(x) y (P(y) y > x))
Logica in actie H O O F D S T U K 5 Predikaatlogica en informatica Wanneer is een predikaatlogische formule waar? Om de gedachten te bepalen, beschouwen we nog eens de formule: x (P(x) y (P(y) y > x))
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl. 9 februari 2009 BEWIJZEN
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 9 februari 2009 BEWIJZEN Discrete Structuren Week1 : Bewijzen Onderwerpen Puzzels
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 9 februari 2009 BEWIJZEN Discrete Structuren Week1 : Bewijzen Onderwerpen Puzzels
Inleiding logica Inleveropgave 3
 Inleiding logica Inleveropgave 3 Lientje Maas 30 september 2013 Ik (Rijk) heb verbeteringen in rood vermeld. Deze verbeteringen meegenomen zijn dit correcte uitwerkingen van de derde inleveropgaven. 1
Inleiding logica Inleveropgave 3 Lientje Maas 30 september 2013 Ik (Rijk) heb verbeteringen in rood vermeld. Deze verbeteringen meegenomen zijn dit correcte uitwerkingen van de derde inleveropgaven. 1
V = {a, b, c, d, e} Computernetwerken: de knopen zijn machines in het netwerk, de kanten zijn communicatiekanalen.
 WIS14 1 14 Grafen 14.1 Grafen Gerichte grafen Voor een verzameling V is een binaire relatie op V een verzameling geordende paren van elementen van V. Voorbeeld: een binaire relatie op N is de relatie KleinerDan,
WIS14 1 14 Grafen 14.1 Grafen Gerichte grafen Voor een verzameling V is een binaire relatie op V een verzameling geordende paren van elementen van V. Voorbeeld: een binaire relatie op N is de relatie KleinerDan,
Logica voor Informatica. Propositielogica. Syntax & Semantiek. Mehdi Dastani Intelligent Systems Utrecht University
 Logica voor Informatica Propositielogica Syntax & Semantiek Mehdi Dastani m.m.dastani@uu.nl Intelligent Systems Utrecht University Wat is Logica? Afleiden van conclusies uit aannames Jan Sara Petra Schuldig
Logica voor Informatica Propositielogica Syntax & Semantiek Mehdi Dastani m.m.dastani@uu.nl Intelligent Systems Utrecht University Wat is Logica? Afleiden van conclusies uit aannames Jan Sara Petra Schuldig
Practicumopgave 3: SAT-solver
 Practicumopgave 3: SAT-solver Modelleren en Programmeren 2015/2016 Deadline: donderdag 7 januari 2016, 23:59 Introductie In het vak Inleiding Logica is onder andere de propositielogica behandeld. Veel
Practicumopgave 3: SAT-solver Modelleren en Programmeren 2015/2016 Deadline: donderdag 7 januari 2016, 23:59 Introductie In het vak Inleiding Logica is onder andere de propositielogica behandeld. Veel
NP-Volledigheid. Wil zo snel mogelijke algoritmes om problemen op te lossen. De looptijd is polynomiaal: O n k - dat is heel erg mooi
 NP-Volledigheid Wil zo snel mogelijke algoritmes om problemen op te lossen Gezien: selectie [O(n)], DFS [O(n + m)], MaxFlow [O nm n + m ], MST [O(n + m)], etc De looptijd is polynomiaal: O n k - dat is
NP-Volledigheid Wil zo snel mogelijke algoritmes om problemen op te lossen Gezien: selectie [O(n)], DFS [O(n + m)], MaxFlow [O nm n + m ], MST [O(n + m)], etc De looptijd is polynomiaal: O n k - dat is
Elfde college complexiteit. 23 april NP-volledigheid III
 college 11 Elfde college complexiteit 23 april 2019 NP-volledigheid III 1 TSP Als voorbeeld bekijken we het Travelling Salesman/person Problem, ofwel het Handelsreizigersprobleem TSP. Hiervoor geldt: TSP
college 11 Elfde college complexiteit 23 april 2019 NP-volledigheid III 1 TSP Als voorbeeld bekijken we het Travelling Salesman/person Problem, ofwel het Handelsreizigersprobleem TSP. Hiervoor geldt: TSP
Inhoud leereenheid 1. Inleiding. Introductie 13. Leerkern 13. 1.1 Wat is logica? 13 1.2 Logica en informatica 13
 Inhoud leereenheid 1 Inleiding Introductie 13 Leerkern 13 1.1 Wat is logica? 13 1.2 Logica en informatica 13 12 Leereenheid 1 Inleiding I N T R O D U C T I E Studeeraanwijzing Deze leereenheid is een leesleereenheid.
Inhoud leereenheid 1 Inleiding Introductie 13 Leerkern 13 1.1 Wat is logica? 13 1.2 Logica en informatica 13 12 Leereenheid 1 Inleiding I N T R O D U C T I E Studeeraanwijzing Deze leereenheid is een leesleereenheid.
Module Limieten van de berekenbaarheid : antwoorden
 Module Limieten van de berekenbaarheid : antwoorden Gilles Coremans 2018 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license. Dit werk is gebaseerd
Module Limieten van de berekenbaarheid : antwoorden Gilles Coremans 2018 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license. Dit werk is gebaseerd
Bijzondere kettingbreuken
 Hoofdstuk 15 Bijzondere kettingbreuken 15.1 Kwadratische getallen In het vorige hoofdstuk hebben we gezien dat 2 = 1, 2, 2, 2, 2, 2, 2,.... Men kan zich afvragen waarom we vanaf zeker moment alleen maar
Hoofdstuk 15 Bijzondere kettingbreuken 15.1 Kwadratische getallen In het vorige hoofdstuk hebben we gezien dat 2 = 1, 2, 2, 2, 2, 2, 2,.... Men kan zich afvragen waarom we vanaf zeker moment alleen maar
De Resolutiemethode (Logica, hoofdstuk 15) Robinson (1965) TI1300 Redeneren en Logica
 De Resolutiemethode (Logica, hoofdstuk 15) Robinson (1965) TI1300 Redeneren en Logica College 7: Resolutie Tomas Klos Algoritmiek Groep De Resolutiemethode De resolutiemethode is een methode waarmee je
De Resolutiemethode (Logica, hoofdstuk 15) Robinson (1965) TI1300 Redeneren en Logica College 7: Resolutie Tomas Klos Algoritmiek Groep De Resolutiemethode De resolutiemethode is een methode waarmee je
Automaten. Informatica, UvA. Yde Venema
 Automaten Informatica, UvA Yde Venema i Inhoud Inleiding 1 1 Formele talen en reguliere expressies 2 1.1 Formele talen.................................... 2 1.2 Reguliere expressies................................
Automaten Informatica, UvA Yde Venema i Inhoud Inleiding 1 1 Formele talen en reguliere expressies 2 1.1 Formele talen.................................... 2 1.2 Reguliere expressies................................
1 Delers 1. 3 Grootste gemene deler en kleinste gemene veelvoud 12
 Katern 2 Getaltheorie Inhoudsopgave 1 Delers 1 2 Deelbaarheid door 2, 3, 5, 9 en 11 6 3 Grootste gemene deler en kleinste gemene veelvoud 12 1 Delers In Katern 1 heb je geleerd wat een deler van een getal
Katern 2 Getaltheorie Inhoudsopgave 1 Delers 1 2 Deelbaarheid door 2, 3, 5, 9 en 11 6 3 Grootste gemene deler en kleinste gemene veelvoud 12 1 Delers In Katern 1 heb je geleerd wat een deler van een getal
Over Plantinga s argument voor de existentie van een noodzakelijk bestaand individueel ding. G.J.E. Rutten
 1 Over Plantinga s argument voor de existentie van een noodzakelijk bestaand individueel ding G.J.E. Rutten Introductie In dit artikel wil ik het argument van de Amerikaanse filosoof Alvin Plantinga voor
1 Over Plantinga s argument voor de existentie van een noodzakelijk bestaand individueel ding G.J.E. Rutten Introductie In dit artikel wil ik het argument van de Amerikaanse filosoof Alvin Plantinga voor
Twaalfde college complexiteit. 7 mei NP-volledigheid IV Cook-Levin Savitch 1
 college 12 Twaalfde college complexiteit 7 mei 2019 NP-volledigheid IV Cook-Levin Savitch 1 Turing machine {0 n 1 n n 0} q Y 0/b, +1 b/b, 0 q N 0/0, +1 1/1, +1 b/b, 1 q 1 q 2 q 0 1/1, 0 b/b, +1 0/0, 0
college 12 Twaalfde college complexiteit 7 mei 2019 NP-volledigheid IV Cook-Levin Savitch 1 Turing machine {0 n 1 n n 0} q Y 0/b, +1 b/b, 0 q N 0/0, +1 1/1, +1 b/b, 1 q 1 q 2 q 0 1/1, 0 b/b, +1 0/0, 0
Tentamen Discrete Wiskunde 1 10 april 2012, 14:00 17:00 uur
 Tentamen Discrete Wiskunde 0 april 0, :00 7:00 uur Schrijf je naam op ieder blad dat je inlevert. Onderbouw je antwoorden, met een goede argumentatie zijn ook punten te verdienen. Veel succes! Opgave.
Tentamen Discrete Wiskunde 0 april 0, :00 7:00 uur Schrijf je naam op ieder blad dat je inlevert. Onderbouw je antwoorden, met een goede argumentatie zijn ook punten te verdienen. Veel succes! Opgave.
Hoofdstuk 15. In dit hoofdstuk geven we een inleiding op het gebied van het automatisch bewijzen
 Resolutie in de Propositielogica Hoofdstuk 15 In dit hoofdstuk geven we een inleiding op het gebied van het automatisch bewijzen van theorema's. Het idee daarbij is dat een computerprogramma nagaat of
Resolutie in de Propositielogica Hoofdstuk 15 In dit hoofdstuk geven we een inleiding op het gebied van het automatisch bewijzen van theorema's. Het idee daarbij is dat een computerprogramma nagaat of
Propositielogica. Evert De Nolf Delphine Draelants Kirsten Storms Evelien Weyn. 24 augustus Universiteit Antwerpen
 Propositielogica Evert De Nolf Delphine Draelants Kirsten Storms Evelien Weyn Universiteit Antwerpen 24 augustus 2006 Propositionele connectoren Negatie Conjunctie Disjunctie Implicatie Equivalentie Propositionele
Propositielogica Evert De Nolf Delphine Draelants Kirsten Storms Evelien Weyn Universiteit Antwerpen 24 augustus 2006 Propositionele connectoren Negatie Conjunctie Disjunctie Implicatie Equivalentie Propositionele
Tentamen TI1300 en IN1305-A (Redeneren en) Logica
 TECHNISCHE UNIVERSITEIT DELFT Faculteit Elektrotechniek, Wiskunde en Informatica Tentamen TI1300 en IN1305-A (Redeneren en) Logica 21 Januari 2011, 8.30 11.30 uur LEES DEZE OPMERKINGEN AANDACHTIG DOOR
TECHNISCHE UNIVERSITEIT DELFT Faculteit Elektrotechniek, Wiskunde en Informatica Tentamen TI1300 en IN1305-A (Redeneren en) Logica 21 Januari 2011, 8.30 11.30 uur LEES DEZE OPMERKINGEN AANDACHTIG DOOR
Formeel Denken 2014 Uitwerkingen Tentamen
 Formeel Denken 2014 Uitwerkingen Tentamen (29/01/15) 1. Benader de betekenis van de volgende Nederlandse zin zo goed mogelijk (6 punten) door een formule van de propositielogica: Als het regent word ik
Formeel Denken 2014 Uitwerkingen Tentamen (29/01/15) 1. Benader de betekenis van de volgende Nederlandse zin zo goed mogelijk (6 punten) door een formule van de propositielogica: Als het regent word ik
Formeel Denken 2013 Uitwerkingen Tentamen
 Formeel Denken 201 Uitwerkingen Tentamen (29/01/1) 1. Benader de betekenis van de volgende Nederlandse zin zo goed mogelijk (6 punten) door een formule van de propositielogica: Het is koud, maar er ligt
Formeel Denken 201 Uitwerkingen Tentamen (29/01/1) 1. Benader de betekenis van de volgende Nederlandse zin zo goed mogelijk (6 punten) door een formule van de propositielogica: Het is koud, maar er ligt
Getaltheorie I. c = c 1 = 1 c (1)
 Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk
Lesbrief 1 Getaltheorie I De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder, van natuurlijke getallen. In de getaltheorie is het gebruikelijk
Helden van de wiskunde: L.E.J. Brouwer Brouwers visie vanuit een logica-informatica perspectief
 Helden van de wiskunde: L.E.J. Brouwer Brouwers visie vanuit een logica-informatica perspectief Herman Geuvers Radboud Universiteit Nijmegen Technische Universiteit Eindhoven 1 Helden van de wiskunde:
Helden van de wiskunde: L.E.J. Brouwer Brouwers visie vanuit een logica-informatica perspectief Herman Geuvers Radboud Universiteit Nijmegen Technische Universiteit Eindhoven 1 Helden van de wiskunde:
Gödels Onvolledigheidsstellingen
 Gödels Onvolledigheidsstellingen Jaap van Oosten Department Wiskunde, Universiteit Utrecht Symposium A-eskwadraat, 11 december 2014 De Onvolledigheidsstellingen van Gödel zijn verreweg de beroemdste resultaten
Gödels Onvolledigheidsstellingen Jaap van Oosten Department Wiskunde, Universiteit Utrecht Symposium A-eskwadraat, 11 december 2014 De Onvolledigheidsstellingen van Gödel zijn verreweg de beroemdste resultaten
FLIPIT 5. (a i,j + a j,i )d i d j = d j + 0 = e d. i<j
 FLIPIT JAAP TOP Een netwerk bestaat uit een eindig aantal punten, waarbij voor elk tweetal ervan gegeven is of er wel of niet een verbinding is tussen deze twee. De punten waarmee een gegeven punt van
FLIPIT JAAP TOP Een netwerk bestaat uit een eindig aantal punten, waarbij voor elk tweetal ervan gegeven is of er wel of niet een verbinding is tussen deze twee. De punten waarmee een gegeven punt van
Twaalfde college complexiteit. 11 mei 2012. Overzicht, MST
 College 12 Twaalfde college complexiteit 11 mei 2012 Overzicht, MST 1 Agenda voor vandaag Minimum Opspannende Boom (minimum spanning tree) als voorbeeld van greedy algoritmen Overzicht: wat voor technieken
College 12 Twaalfde college complexiteit 11 mei 2012 Overzicht, MST 1 Agenda voor vandaag Minimum Opspannende Boom (minimum spanning tree) als voorbeeld van greedy algoritmen Overzicht: wat voor technieken
NP-volledigheid. Algoritmiek
 NP-volledigheid Polynomiale algoritmen of moeilijke problemen? Algoritme A is polynomiaal, als er een constante c bestaat, zodat het algoritme bij inputs van formaat n O(n c ) tijd gebruikt. Sommige problemen
NP-volledigheid Polynomiale algoritmen of moeilijke problemen? Algoritme A is polynomiaal, als er een constante c bestaat, zodat het algoritme bij inputs van formaat n O(n c ) tijd gebruikt. Sommige problemen
Samenvatting. TI1306 Redeneren & Logica Review Guide 2014 Door: David Alderliesten. Disclaimer
 Samenvatting TI1306 Redeneren & Logica Review Guide 2014 Door: David Alderliesten Disclaimer De informatie in dit document is afkomstig van derden. W.I.S.V. Christiaan Huygens betracht de grootst mogelijke
Samenvatting TI1306 Redeneren & Logica Review Guide 2014 Door: David Alderliesten Disclaimer De informatie in dit document is afkomstig van derden. W.I.S.V. Christiaan Huygens betracht de grootst mogelijke
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 26 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 26 oktober 2016 1 / 28 Deze week: analyseren van algoritmes Hoe
TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 26 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 26 oktober 2016 1 / 28 Deze week: analyseren van algoritmes Hoe
Puzzels en wiskunde. Inleiding. Algoritme. Sudoku. 22 Puzzels en wiskunde
 Een miljoen dollar verdienen in de kerstvakantie? Het enige dat u hoeft te doen, is een polynomiaal algoritme te vinden om een sudoku mee op te lossen. Niels Oosterling schetst waar u dan rekening mee
Een miljoen dollar verdienen in de kerstvakantie? Het enige dat u hoeft te doen, is een polynomiaal algoritme te vinden om een sudoku mee op te lossen. Niels Oosterling schetst waar u dan rekening mee
Logica voor Informatica. Propositielogica. Bewijssystemen voor propositielogica. Mehdi Dastani
 Logica voor Informatica Propositielogica Bewijssystemen voor propositielogica Mehdi Dastani mmdastani@uunl Intelligent Systems Utrecht University Deductie Tot nu toe voornamelijk semantisch naar logica
Logica voor Informatica Propositielogica Bewijssystemen voor propositielogica Mehdi Dastani mmdastani@uunl Intelligent Systems Utrecht University Deductie Tot nu toe voornamelijk semantisch naar logica
start -> id (k (f c s) (g s c)) -> k (f c s) (g s c) -> f c s -> s c
 Een Minimaal Formalisme om te Programmeren We hebben gezien dat Turing machines beschouwd kunnen worden als universele computers. D.w.z. dat iedere berekening met natuurlijke getallen die met een computer
Een Minimaal Formalisme om te Programmeren We hebben gezien dat Turing machines beschouwd kunnen worden als universele computers. D.w.z. dat iedere berekening met natuurlijke getallen die met een computer
Hoorcollege Logica. Hans-Dieter A. Hiep
 Hoorcollege Logica Hans-Dieter A. Hiep Agenda 1. Horn-formules 2. Vervulbaarheidsprobleem Validiteit en vervulbaarheid Gegeven een formule φ in de (klassieke) propositielogica. Definitie φ is valide voor
Hoorcollege Logica Hans-Dieter A. Hiep Agenda 1. Horn-formules 2. Vervulbaarheidsprobleem Validiteit en vervulbaarheid Gegeven een formule φ in de (klassieke) propositielogica. Definitie φ is valide voor
Hebzucht loont niet altijd
 Thema Discrete wiskunde Hoe verbind je een stel steden met zo weinig mogelijk kilometers asfalt? Hoe maak je een optimaal computernetwerk met kabels die maar een beperkte capaciteit hebben? Veel van zulke
Thema Discrete wiskunde Hoe verbind je een stel steden met zo weinig mogelijk kilometers asfalt? Hoe maak je een optimaal computernetwerk met kabels die maar een beperkte capaciteit hebben? Veel van zulke
Handout Natuurlijke Deductie
 Handout Natuurlijke Deductie Peter van Ormondt 4 februari 2017 1 Inleiding In Van Benthem et al (2016, Hoofdstuk 2), hebben we redeneringen bestudeerd door te kijken naar de semantiek of betekenis van
Handout Natuurlijke Deductie Peter van Ormondt 4 februari 2017 1 Inleiding In Van Benthem et al (2016, Hoofdstuk 2), hebben we redeneringen bestudeerd door te kijken naar de semantiek of betekenis van
PROPOSITIELOGICA. fundament voor wiskundig redeneren. Dr. Luc Gheysens
 PROPOSITIELOGICA fundament voor wiskundig redeneren Dr. Luc Gheysens PROPOSITIELOGICA Een propositie of logische uitspraak, verder weergegeven door een letter p, q, r is een uitspraak die in een vastgelegde
PROPOSITIELOGICA fundament voor wiskundig redeneren Dr. Luc Gheysens PROPOSITIELOGICA Een propositie of logische uitspraak, verder weergegeven door een letter p, q, r is een uitspraak die in een vastgelegde
Grafen. Indien de uitgraad van ieder punt 1 is, dan bevat de graaf een cykel. Indien de ingraad van ieder punt 1 is, dan bevat de graaf een cykel.
 Grafen Grafen Een graaf bestaat uit een verzameling punten (ook wel knopen, of in het engels vertices genoemd) en een verzameling kanten (edges) of pijlen (arcs), waarbij de kanten en pijlen tussen twee
Grafen Grafen Een graaf bestaat uit een verzameling punten (ook wel knopen, of in het engels vertices genoemd) en een verzameling kanten (edges) of pijlen (arcs), waarbij de kanten en pijlen tussen twee
opgaven formele structuren deterministische eindige automaten
 opgaven formele structuren deterministische eindige automaten Opgave. De taal L over het alfabet {a, b} bestaat uit alle strings die beginnen met aa en eindigen met ab. Geef een reguliere expressie voor
opgaven formele structuren deterministische eindige automaten Opgave. De taal L over het alfabet {a, b} bestaat uit alle strings die beginnen met aa en eindigen met ab. Geef een reguliere expressie voor
Week 1 20-02-2013. Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren.
 Combinatorische Optimalisatie, 2013 Week 1 20-02-2013 Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren. Opgave 1.16 Bewijs dat elke graaf een even aantal punten
Combinatorische Optimalisatie, 2013 Week 1 20-02-2013 Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren. Opgave 1.16 Bewijs dat elke graaf een even aantal punten
Andere grote namen van wiskundigen en/of filosofen: Plato, Socrates, Descartes (Cartesius), Spinoza, Kant, Russell, Hilbert, Tarski en Brouwer
 Formele Logica Grondlegger Aristoteles (384/322 voor Chr.), filosoof. Andere grote namen van wiskundigen en/of filosofen: Plato, Socrates, Descartes (Cartesius), Spinoza, Kant, Russell, Hilbert, Tarski
Formele Logica Grondlegger Aristoteles (384/322 voor Chr.), filosoof. Andere grote namen van wiskundigen en/of filosofen: Plato, Socrates, Descartes (Cartesius), Spinoza, Kant, Russell, Hilbert, Tarski
Diophantische vergelijkingen
 Diophantische vergelijkingen 1 Wat zijn Diophantische vergelijkingen? Een Diophantische vergelijking is een veeltermvergelijking waarbij zowel de coëfficiënten als de oplossingen gehele getallen moeten
Diophantische vergelijkingen 1 Wat zijn Diophantische vergelijkingen? Een Diophantische vergelijking is een veeltermvergelijking waarbij zowel de coëfficiënten als de oplossingen gehele getallen moeten
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 21 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 21 oktober 2015 1 / 20 Deze week: algoritmes en complexiteit
TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 21 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 21 oktober 2015 1 / 20 Deze week: algoritmes en complexiteit
De partitieformule van Euler
 De partitieformule van Euler Een kennismaking met zuivere wiskunde J.H. Aalberts-Bakker 29 augustus 2008 Doctoraalscriptie wiskunde, variant Communicatie en Educatie Afstudeerdocent: Dr. H. Finkelnberg
De partitieformule van Euler Een kennismaking met zuivere wiskunde J.H. Aalberts-Bakker 29 augustus 2008 Doctoraalscriptie wiskunde, variant Communicatie en Educatie Afstudeerdocent: Dr. H. Finkelnberg
Modelleren en Programmeren voor KI
 Modelleren en Programmeren voor KI Practicumopdracht 4: SAT Solver Tomas Klos Het SAT probleem Parvulae Logicales: Propositielogica, Hoofdstuk 6 (Semantiek), p. 62: Het SAT probleem Ik geef je een propositielogische
Modelleren en Programmeren voor KI Practicumopdracht 4: SAT Solver Tomas Klos Het SAT probleem Parvulae Logicales: Propositielogica, Hoofdstuk 6 (Semantiek), p. 62: Het SAT probleem Ik geef je een propositielogische
Introductie tot de cursus
 Introductie tot de cursus 1 Plaats en functie van de cursus 7 1.1 Positie in de opleiding 7 1.2 Functie 7 2 Cursusmateriaal 8 2.1 Tekstboek 8 2.2 Werkboek 8 2.3 Software 9 2.4 Cursussite 9 3 Planning 10
Introductie tot de cursus 1 Plaats en functie van de cursus 7 1.1 Positie in de opleiding 7 1.2 Functie 7 2 Cursusmateriaal 8 2.1 Tekstboek 8 2.2 Werkboek 8 2.3 Software 9 2.4 Cursussite 9 3 Planning 10
Geldwisselprobleem van Frobenius
 Geldwisselprobleem van Frobenius Karin van de Meeberg en Dieuwertje Ewalts 12 december 2001 1 Inhoudsopgave 1 Inleiding 3 2 Afspraken 3 3 Is er wel zo n g? 3 4 Eén waarde 4 5 Twee waarden 4 6 Lampenalgoritme
Geldwisselprobleem van Frobenius Karin van de Meeberg en Dieuwertje Ewalts 12 december 2001 1 Inhoudsopgave 1 Inleiding 3 2 Afspraken 3 3 Is er wel zo n g? 3 4 Eén waarde 4 5 Twee waarden 4 6 Lampenalgoritme
3 De stelling van Kleene
 18 3 De stelling van Kleene Definitie 3.1 Een formele taal heet regulier als hij wordt herkend door een deterministische eindige automaat. Talen van de vorm L(r) met r een reguliere expressie noemen we
18 3 De stelling van Kleene Definitie 3.1 Een formele taal heet regulier als hij wordt herkend door een deterministische eindige automaat. Talen van de vorm L(r) met r een reguliere expressie noemen we
Semantiek 1 college 4. Jan Koster
 Semantiek 1 college 4 Jan Koster 1 Uitgangspunt sinds vorige week Semantiek is representationeel (en niet referentieel), gebaseerd op interpretaties van sprekers en hoorders Geen scherpe scheiding tussen
Semantiek 1 college 4 Jan Koster 1 Uitgangspunt sinds vorige week Semantiek is representationeel (en niet referentieel), gebaseerd op interpretaties van sprekers en hoorders Geen scherpe scheiding tussen
Propositielogica Het maken van een waarheidstabel
 Informatiekunde naam datum Propositielogica Het maken van een waarheidstabel Eindhoven, 4 juni 2011 De propositielogica Zoekopdrachten met de operatoren AND, OR en zijn zogenaamde Booleaanse expressies.
Informatiekunde naam datum Propositielogica Het maken van een waarheidstabel Eindhoven, 4 juni 2011 De propositielogica Zoekopdrachten met de operatoren AND, OR en zijn zogenaamde Booleaanse expressies.
Diophantische vergelijkingen in het kerstpakket
 Diophantische vergelijkingen in het kerstpakket Benne de Weger b.m.m.d.weger@tue.nl Faculteit Wiskunde en Informatica Technische Universiteit Eindhoven versie.0, 3 december 00 De TU/e viert een feestje
Diophantische vergelijkingen in het kerstpakket Benne de Weger b.m.m.d.weger@tue.nl Faculteit Wiskunde en Informatica Technische Universiteit Eindhoven versie.0, 3 december 00 De TU/e viert een feestje
The knight s tour. Het paard in schaken beweegt als volgt: Steeds 1 vakje in een richting en 2 in een andere richting, of omgekeerd.
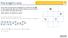 The knight s tour In het Engels heet een paard uit schaken een Knight (Ridder). In het begin zaten er namelijk ridders op de paarden. (link wiki) Stel, je bent een paard uit het schaakspel en je staat
The knight s tour In het Engels heet een paard uit schaken een Knight (Ridder). In het begin zaten er namelijk ridders op de paarden. (link wiki) Stel, je bent een paard uit het schaakspel en je staat
Uitgebreide uitwerking Tentamen Complexiteit, juni 2018
 Uitgebreide uitwerking Tentamen Complexiteit, juni 018 Opgave 1. a. Een pad van de wortel naar een blad stelt de serie achtereenvolgende arrayvergelijkingen voor die het algoritme doet op zekere invoer.
Uitgebreide uitwerking Tentamen Complexiteit, juni 018 Opgave 1. a. Een pad van de wortel naar een blad stelt de serie achtereenvolgende arrayvergelijkingen voor die het algoritme doet op zekere invoer.
Aanvullingen bij Hoofdstuk 8
 Aanvullingen bij Hoofdstuk 8 8.5 Definities voor matrices De begrippen eigenwaarde eigenvector eigenruimte karakteristieke veelterm en diagonaliseerbaar worden ook gebruikt voor vierkante matrices los
Aanvullingen bij Hoofdstuk 8 8.5 Definities voor matrices De begrippen eigenwaarde eigenvector eigenruimte karakteristieke veelterm en diagonaliseerbaar worden ook gebruikt voor vierkante matrices los
vandaag is Annie twee jaar jonger dan Ben en Cees samen
 Hoofdstuk I Lineaire Algebra Les 1 Stelsels lineaire vergelijkingen Om te beginnen is hier een puzzeltje: vandaag is Annie twee jaar jonger dan Ben en Cees samen over vijf jaar is Annie twee keer zo oud
Hoofdstuk I Lineaire Algebra Les 1 Stelsels lineaire vergelijkingen Om te beginnen is hier een puzzeltje: vandaag is Annie twee jaar jonger dan Ben en Cees samen over vijf jaar is Annie twee keer zo oud
Getallensystemen, verzamelingen en relaties
 Hoofdstuk 1 Getallensystemen, verzamelingen en relaties 1.1 Getallensystemen 1.1.1 De natuurlijke getallen N = {0, 1, 2, 3,...} N 0 = {1, 2, 3,...} 1.1.2 De gehele getallen Z = {..., 4, 3, 2, 1, 0, 1,
Hoofdstuk 1 Getallensystemen, verzamelingen en relaties 1.1 Getallensystemen 1.1.1 De natuurlijke getallen N = {0, 1, 2, 3,...} N 0 = {1, 2, 3,...} 1.1.2 De gehele getallen Z = {..., 4, 3, 2, 1, 0, 1,
Toeristen stad Dominerende verzamelingen
 Activiteit 14 Toeristen stad Dominerende verzamelingen Samenvatting Veel situaties uit het dagelijks leven kunnen weergegeven worden in de vorm van een netwerk of graaf, zoals gebruikt bij de kleuropdracht
Activiteit 14 Toeristen stad Dominerende verzamelingen Samenvatting Veel situaties uit het dagelijks leven kunnen weergegeven worden in de vorm van een netwerk of graaf, zoals gebruikt bij de kleuropdracht
De huwelijksstelling van Hall
 Thema Discrete wiskunde In de vorige twee afleveringen heb je al kennis kunnen maken met het begrip graaf en hoe grafen worden gebruikt door Google s zoekmachine en door de NS bij het maken van een optimale
Thema Discrete wiskunde In de vorige twee afleveringen heb je al kennis kunnen maken met het begrip graaf en hoe grafen worden gebruikt door Google s zoekmachine en door de NS bij het maken van een optimale
Logica voor Informatici najaar 2000 Opgaven en Oplossingen Hoofdstuk 2
 Logica voor Informatici najaar 2000 Opgaven en Oplossingen Hoofdstuk 2 2.1 Geef de volgende zinnen weer in propositionele notatie: i Als de bus niet komt, komen de tram en de trein We voeren de volgende
Logica voor Informatici najaar 2000 Opgaven en Oplossingen Hoofdstuk 2 2.1 Geef de volgende zinnen weer in propositionele notatie: i Als de bus niet komt, komen de tram en de trein We voeren de volgende
Les B-08 Kunstmatige intelligentie en logica
 2004, David Lans Les B-08 Kunstmatige intelligentie en logica 8.1 De Turing test Toen halverwege de 20 e eeuw de computer zijn intrede deed, stelde de Brit Alan Turing (1912-1953) in een wetenschappelijke
2004, David Lans Les B-08 Kunstmatige intelligentie en logica 8.1 De Turing test Toen halverwege de 20 e eeuw de computer zijn intrede deed, stelde de Brit Alan Turing (1912-1953) in een wetenschappelijke
Mededelingen. TI1300: Redeneren en Logica. Metavariabelen Logica, p Minder connectieven nodig
 Mededelingen TI1300: Redeneren en Logica College 5: Semantiek van de Propositielogica Tomas Klos Algoritmiek Groep Tip: Als ik je vraag de recursieve definitie van een functie over PROP op te schrijven,
Mededelingen TI1300: Redeneren en Logica College 5: Semantiek van de Propositielogica Tomas Klos Algoritmiek Groep Tip: Als ik je vraag de recursieve definitie van een functie over PROP op te schrijven,
4 Beschouw de volgende formuleverzameling S: {"x "y ((Rxy Æ "z (Rxz Æ y = z)), "x "y (Ryx Æ "z (Rzx Æ y = z)),
 T E N T A M E N L O G I C A 1 1 Bepaal met behulp van een waarheidstabel een disjunctieve normaalvorm voor de formule (p (q Ÿ ( r Æ (p Ÿ q)))). Is er een eenvoudiger formule waarmee de gevonden formule
T E N T A M E N L O G I C A 1 1 Bepaal met behulp van een waarheidstabel een disjunctieve normaalvorm voor de formule (p (q Ÿ ( r Æ (p Ÿ q)))). Is er een eenvoudiger formule waarmee de gevonden formule
Semantiek 1 college 10. Jan Koster
 Semantiek 1 college 10 Jan Koster 1 Vandaag Vorige keer: conceptuele structuur en semantische decompositie Vandaag: inleiding in de formele semantiek Gebruikt notaties uit formele logica plus de daar gehanteerde
Semantiek 1 college 10 Jan Koster 1 Vandaag Vorige keer: conceptuele structuur en semantische decompositie Vandaag: inleiding in de formele semantiek Gebruikt notaties uit formele logica plus de daar gehanteerde
Modulewijzer InfPbs00DT
 Modulewijzer InfPbs00DT W. Oele 0 juli 008 Inhoudsopgave Inleiding 3 Waarom wiskunde? 3. Efficiëntie van computerprogramma s............... 3. 3D-engines en vectoranalyse................... 3.3 Bewijsvoering
Modulewijzer InfPbs00DT W. Oele 0 juli 008 Inhoudsopgave Inleiding 3 Waarom wiskunde? 3. Efficiëntie van computerprogramma s............... 3. 3D-engines en vectoranalyse................... 3.3 Bewijsvoering
Formeel Denken. Herfst 2004
 Formeel Denken Herman Geuvers Deels gebaseerd op het herfst 2002 dictaat van Henk Barendregt en Bas Spitters, met dank aan het Discrete Wiskunde dictaat van Wim Gielen Herfst 2004 Contents 1 Propositielogica
Formeel Denken Herman Geuvers Deels gebaseerd op het herfst 2002 dictaat van Henk Barendregt en Bas Spitters, met dank aan het Discrete Wiskunde dictaat van Wim Gielen Herfst 2004 Contents 1 Propositielogica
Eigenschap (Principe van welordening) Elke niet-lege deelverzameling V N bevat een kleinste element.
 Hoofdstuk 2 De regels van het spel 2.1 De gehele getallen Grof gezegd kunnen we de (elementaire) getaltheorie omschrijven als de wiskunde van de getallen 1, 2, 3, 4,... die we ook de natuurlijke getallen
Hoofdstuk 2 De regels van het spel 2.1 De gehele getallen Grof gezegd kunnen we de (elementaire) getaltheorie omschrijven als de wiskunde van de getallen 1, 2, 3, 4,... die we ook de natuurlijke getallen
Referentieniveaus uitgelegd. 1S - rekenen Vaardigheden referentieniveau 1S rekenen. 1F - rekenen Vaardigheden referentieniveau 1F rekenen
 Referentieniveaus uitgelegd De beschrijvingen zijn gebaseerd op het Referentiekader taal en rekenen'. In 'Referentieniveaus uitgelegd' zijn de niveaus voor de verschillende sectoren goed zichtbaar. Door
Referentieniveaus uitgelegd De beschrijvingen zijn gebaseerd op het Referentiekader taal en rekenen'. In 'Referentieniveaus uitgelegd' zijn de niveaus voor de verschillende sectoren goed zichtbaar. Door
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 22 februari 2009 INDUCTIE & RECURSIE Paragrafen 4.3-4.6 Discrete Structuren Week 3:
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter piter@math.rug.nl 22 februari 2009 INDUCTIE & RECURSIE Paragrafen 4.3-4.6 Discrete Structuren Week 3:
Waarmaken van Leibniz s droom
 Waarmaken van Leibniz s droom Artificiële intelligentie Communicatie & internet Operating system Economie Computatietheorie & Software Efficiënt productieproces Hardware architectuur Electronica: relais
Waarmaken van Leibniz s droom Artificiële intelligentie Communicatie & internet Operating system Economie Computatietheorie & Software Efficiënt productieproces Hardware architectuur Electronica: relais
Stelling. SAT is NP-compleet.
 Het bewijs van de stelling van Cook Levin zoals gegeven in het boek van Sipser gebruikt niet-deterministische turing machines. Het is inderdaad mogelijk de klasse NP op een alternatieve wijze te definiëren
Het bewijs van de stelling van Cook Levin zoals gegeven in het boek van Sipser gebruikt niet-deterministische turing machines. Het is inderdaad mogelijk de klasse NP op een alternatieve wijze te definiëren
College Logica voor CKI
 College Logica voor CKI Albert Visser Department of Philosophy, Faculty Humanities, Utrecht University 15 oktober, 2012 1 Overview 2 Overview 2 Overview 2 Overview 3 Syntaxis De eerste ronde: Constanten:
College Logica voor CKI Albert Visser Department of Philosophy, Faculty Humanities, Utrecht University 15 oktober, 2012 1 Overview 2 Overview 2 Overview 2 Overview 3 Syntaxis De eerste ronde: Constanten:
Logica voor Informatici najaar 2000 Opgaven en Oplossingen Hoofdstuk 3
 Logica voor Informatici najaar 2000 Opgaven en Oplossingen Hoofdstuk 3 3.1 Stel ϕ, ψ α, β γ, en ψ, α, γ χ. Indien nu bovendien bekend wordt dat χ onwaar is, maar ψ en β waar, wat weet u dan over ϕ? oplossing:
Logica voor Informatici najaar 2000 Opgaven en Oplossingen Hoofdstuk 3 3.1 Stel ϕ, ψ α, β γ, en ψ, α, γ χ. Indien nu bovendien bekend wordt dat χ onwaar is, maar ψ en β waar, wat weet u dan over ϕ? oplossing:
Logica Les 1 Definities en waarheidstabellen. (Deze les sluit aan bij les 1 van de syllabus Logica WD_online)
 Logica Les 1 Definities en waarheidstabellen (Deze les sluit aan bij les 1 van de syllabus Logica WD_online) Definities Een propositie is een bewering die waar of onwaar is (er is geen derde mogelijkheid).
Logica Les 1 Definities en waarheidstabellen (Deze les sluit aan bij les 1 van de syllabus Logica WD_online) Definities Een propositie is een bewering die waar of onwaar is (er is geen derde mogelijkheid).
Radboud Universiteit Nijmegen
 Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica L(,1)-labeling van grafen Naam: Studentnummer: Studie: Begeleider: Myrte klein Brink 4166140 Bachelor Wiskunde Dr.
Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica L(,1)-labeling van grafen Naam: Studentnummer: Studie: Begeleider: Myrte klein Brink 4166140 Bachelor Wiskunde Dr.
Propositionele logica
 Logic is the beginning of wisdom, not the end. Captain Spock, Star Trek VI (1991) Hoofdstuk 1 ropositionele logica 1.1 Uitspraken Het begrip uitspraak. We geven hier geen definitie van het begrip uitspraak
Logic is the beginning of wisdom, not the end. Captain Spock, Star Trek VI (1991) Hoofdstuk 1 ropositionele logica 1.1 Uitspraken Het begrip uitspraak. We geven hier geen definitie van het begrip uitspraak
Logica voor Informatica
 Logica voor Informatica 10 Predikatenlogica Wouter Swierstra University of Utrecht 1 Vorige keer Syntax van predikatenlogica Alfabet Termen Welgevormde formulas (wff) 2 Alfabet van de predikatenlogica
Logica voor Informatica 10 Predikatenlogica Wouter Swierstra University of Utrecht 1 Vorige keer Syntax van predikatenlogica Alfabet Termen Welgevormde formulas (wff) 2 Alfabet van de predikatenlogica
Workshop DisWis, De Start 13/06/2007 Bladzijde 1 van 7. Sudoku. Sudoku
 DisWis DisWis is een lessenserie discrete wiskunde die De Praktijk vorig jaar in samenwerking met prof.dr. Alexander Schrijver heeft opgezet. Gedurende vier weken komt een wiskundestudent twee blokuren
DisWis DisWis is een lessenserie discrete wiskunde die De Praktijk vorig jaar in samenwerking met prof.dr. Alexander Schrijver heeft opgezet. Gedurende vier weken komt een wiskundestudent twee blokuren
Tiende college algoritmiek. 14 april Gretige algoritmen
 College 10 Tiende college algoritmiek 1 april 011 Gretige algoritmen 1 Greedy algorithms Greed = hebzucht Voor oplossen van optimalisatieproblemen Oplossing wordt stap voor stap opgebouwd In elke stap
College 10 Tiende college algoritmiek 1 april 011 Gretige algoritmen 1 Greedy algorithms Greed = hebzucht Voor oplossen van optimalisatieproblemen Oplossing wordt stap voor stap opgebouwd In elke stap
Opgave 1b: Toon ook aan dat meer algemeen geldt: Als het lukt met n = a munten in w keer wegen, dan lukt het voor a < n 2a in w + 1 keer wegen.
 Uitwerking Puzzel 92-7 Allemaal gelijk? Wobien Doyer Lieke de Rooij Er zijn veel puzzels over het opsporen van één valse munt tussen een aantal goede munten met hulp van een balans. Bij deze puzzel is
Uitwerking Puzzel 92-7 Allemaal gelijk? Wobien Doyer Lieke de Rooij Er zijn veel puzzels over het opsporen van één valse munt tussen een aantal goede munten met hulp van een balans. Bij deze puzzel is
