13 Hidden Markov Modellen.
|
|
|
- Gerda de Veer
- 4 jaren geleden
- Aantal bezoeken:
Transcriptie
1 3 Hidden Markov Modellen. 3. Inleiding. In dit Hoofdstuk bekijken we Markov modellen waarvan we de toestanden niet met zekerheid kunnen waarnemen. In plaats daarvan gaan we ervan uit dat toestand i met kans b iα tot waarneming α leidt. Zo n Hidden Markov Model wordt dus beschreven door de volgende gegevens: Een collectie van N mogelijk toestanden. Een collectie van V mogelijke waarnemingen. Een N-vector (π) waar π i de kans aangeeft dat de eerste toestand van het model toestand i is. Een N N-matrix (a) waar a ij de kans aangeeft dat het model van toestand i in toestand j overgaat. Een N V -matrix b waar b iα de zogenaamde emissie-kans aangeeft dat we toestand i als waarneming α registreren. Er is dus sprake van een kansrij X, X 2,... van verborgen toestanden, en een kansrij Y, Y 2,... van waarnememingen waarbij geldt dat p(x = i) = π i p(x n = j X n = i, X n 2 = i n 2,... ) = a ij p(y n = α X n = i,... ) = b iα We kunnen de be-invloedingen schematisch zo weergeven: a X n X a n b b X n+ Y n Y n Y n+ b We proberen in dit Hoofdstuk een relatie te leggen tussen een rij van T verborgen toestanden X, X 2,..., X T en de bijbehorende observaties Y,..., Y T. We doen dat aan de hand van het volgende mini rekenvoorbeeld, afkomstig van Jacob Eisner. Stel in het jaar AD 2700 wil iemand bestuderen hoe in de 2-ste eeuw het klimaat is veranderd. Helaas zijn de directe meetgegevens verloren gegaan. Wat nog wel beschikbaar is, is het dagboek van Jacob Eisner, waarin staat genoteerd hoeveel ijsjes Jacob op elke dag verorberde. De details van het model zijn als volgt: Er zijn 2 mogelijke verborgen toestanden: de dag is warm of koud.
2 2 3 HIDDEN MARKOV MODELLEN. Er zijn 3 mogelijke waarnemingen: Jacob at die dag, 2 of 3 ijsjes. De eerste dag was met 80% kans warm en met 20% kans koud. Na een warme dag komt met 70% kans weer een warme dag en met 30% kans een koude. Na een koude dag komt met 60% kans weer een koude dag en met 40% kans een warme. Op een warme dag eet Jacob met 20% kans één ijsje, met 40% kans twee ijsjes en met 40% kans drie ijsjes. Op een koude dag eet Jacob met 50% kans één ijsje, met 40% kans twee ijsjes en met 0% kans drie ijsjes. We stellen ons bij een HMM model in het algemeen drie vragen, van oplopende moeilijkheids-graad:. Wat is de kans op een bepaalde rij waarnemingen (o, o 2,..., o T ), gegeven de structuur van het model, en gegeven de parameters (π), (a) en (b) van het model. Deze vraag wordt beantwoord door het zogenaamde forward-algoritme, wat we straks gaan bespreken. We bespreken ook een variant hiervan, het zogenaamde backward-algoritme. 2. Wat is de meest waarschijnlijke rij verborgen toestanden (i, i 2,..., i T ), gegeven de structuur van het model en zijn parameters, en gegeven rij waarnemingen (o, o 2,..., o T ). Deze vraag wordt beantwoord door het zogenaamde Viterbi algoritme, wat we ook straks gaan bespreken. 3. Wat is de meest waarschijnlijke waarde voor de parameters van het model, gegeven de structuur van het model, en gegeven een voldoende grote rij waarnemingen. Dit noemt men het trainen van het model. Deze vraag wordt beantwoord door het zogenaamde Baum-Welch-algoritme, wat we ook nog gaan bespreken. 3.2 Het Forward algoritme. De kans p(y = o,..., Y T = o T ) op een rij waarnemingen (o,..., o T ) is in principe te berekenen als de som over de bijdragen van alle rijtjes (i,..., i T )
3 3.2 Het Forward algoritme. 3 van verborgen toestanden: p(y = o,..., Y T = o T ) p(y = o,..., Y T = o T, X = i,..., X T = i T ) p(y = o,..., Y T = o T X = i,..., X T = i T ) (i,...,i T ) (i,...,i T ) (i,...,i T ) p(x = i,..., x T = i T ) p(y = o X = i ) p(y T = o T X T = i T ) p(x T = i t X T = i T ) p(x 2 = i 2 X = i ) p(x = i ) b i,o b it,o T a it,i T a i,i 2 π i Het probleem hierbij is dat hier een som staat van N T vele rijtjes wat voor realistische N en T al gauw uit de hand loopt. Een sleutel tot de oplossing van het probleem wordt geleverd door de constatering dat in een heleboel termen van deze som producten voorkomen met eenzelfde beginstuk. We kunnen dus veel werk voorkomen door die beginstukken niet steeds opnieuw uit te rekenen maar slechts één keer, en de uitkomsten op te slaan. We definiëren daarom α n (j) als α (j) = π j b j,o N α n (j) = α n (i) a ij b j,on i= Men rekent gemakkelijk na dat dan geldt: voor n = 2,..., T () p(y = o,..., Y T = o T ) i α T (i) (2) en we hoeven slechts NT uitdrukkingen α n (j) uit te rekenen, die elk N termen hebben, voor een totaal van N 2 T termen. Meer algemeen heb je p(y = o,..., Y T = o t, X t = j) = α t (j) wat betekent dat de α n (j) een zinvolle interpretatie hebben als de kans op waarnemingen (o,..., o n ) veroorzaakt door een zekere rij verborgen toestanden (i,..., i n ) met i n = j. We kunnen het algoritme dat door formules () en (2) wordt beschreven als volgt in een diagram beschrijven. Horizontaal komen de tijdstippen n =,..., T, voorafgegaan door een beginpunt, en gevolgd door een eindpunt. Verticaal komen de toestanden j =,..., N. Op het kruispunt (n, j)
4 4 3 HIDDEN MARKOV MODELLEN. gaan we de waarde van α n (j) invullen. Bij elk kruispunt (n, i) zijn er uitgaande pijlen naar de kruispunten (n, j) voor alle mogelijke j; boven de pijl noteren we de kans op de overgang van i naar j, eronder de kans dat toestand j waarneming o n oplevert. Om een plek in het diagram in te vullen vermenigvuldig je voor elke binnenkomende pijl de getallen boven en onder de pijl met het getal aan de bron van de pijl, en je telt die producten op. We demonstreren nu het bovenstaande aan de hand van ons rekenvoorbeeld. We bepalen de kans op de rij waarnemingen (3,, 3). 0.7 warm koud begin 3 ijsjes ijsje 3 ijsjes einde Dus bijvoorbeeld α 2 (w) = α (w) a ww b w + α (k) a kw b w = = = waar w staat voor de verborgen toestand warm, en k voor koud. 3.3 Het backward algoritme. Dit algoritme is gebaseerd op de constatering dat in de som van N T termen veel producten voorkomen met hetzelfde eindstuk. We definiëren daarom β n (j) als β T (j) = N β n (i) = β n+ (j) a ij b j,on+ j= Weer rekent men gemakkelijk na dat dan geldt: p(y = o,..., Y T = o T ) = N π j b j,o β (j) en weer hoeven we slechts NT uitdrukkingen α n (j) uit te rekenen, die elk N termen hebben. De grootheid β n (i) beschrijft de kans dat we op tijdstip j=
5 3.4 Het Viterbi Algoritme. 5 n in toestand i zijn en bovendien de waarnemingen (o n+,..., o T ) te zien krijgen. We kunnen dit algoritme weer beschrijven door een diagram als eerder. Op plek (n, i) vullen we de waarde van β n (i) in, en deze wordt weer berekend als som van producten behorende bij binnenkomende pijlen. Het verschil is echter dat de pijlen allen in de andere richting wijzen. Ze zijn echter wel versierd met dezelfde factoren! We illustreren dit door ons rekenvoorbeeld: warm koud begin 3 ijsjes ijsje 3 ijsjes einde 3.4 Het Viterbi Algoritme. In de beschrijving van het forward en backward algoritme hebben we gebruik gemaakt van een diagram. Een mogelijk rijtje I = (i,..., i T ) van verborgen toestanden die het opgetreden rijtje waarnemingen O = (o,..., o T ) zou kunnen verklaren is voor te stellen als een pad door dat diagram dat begin en eind verbindt. Elk pad heeft een zekere waarde w(i), namelijk de kans dat de waarnemingen O gerealiseerd worden, gegeven dat rijtje I. We zoeken nu onder alle paden I het pad waarvoor die waarde w(i) maximaal is, een zogenaamd optimaal pad. In principe zouden we die kans voor elk rijtje (i,..., i T ) kunnen uitrekenen, om daar dan de beste uit te plukken. Maar dat zou betekenen dat er N T berekeningen moeten worden uitgevoerd, wat niet erg praktisch is. Ook hier kunnen we echter het werk drastisch inkorten door gebruik te maken een speciale eigenschap van de waarde-functie w, namelijk: De waarde van een pad I door een punt p hangt alleen af van de waarde van het beginstuk van het pad (van begin tot p) en de waarde van het eindstuk van het pad (van p tot het eind). Bovendien zijn beide afhankelijkheden stijgend. Onder deze omstandigheden geldt het volgende Bellman principe : Als I een optimaal pad is dat door p gaat dan moet het beginstuk van I optimaal zijn en ook het eindstuk van I optimaal zijn. Immers als bijvoorbeeld het beginstuk van I niet optimaal is dan kunnen we het vervangen door een andere met grotere waarde, en als we die andere combineren met het oude eindstuk dan krijgen we een volledig pad met een grotere waarde.
6 6 3 HIDDEN MARKOV MODELLEN. We kunnen dit principe verwerken in een algoritme door bij elk punt p = (n, j) van het forward diagram niet alleen de kans α n (j) op te slaan maar ook een optimaal pad van het beginpunt naar p. We bepalen het optimale pad naar p = (n, j) als volgt: We bekijken alle mogelijke voorgangers q i = (n, i). Voor die q i kennen we de bijdrage aan α n (j) namelijk α n (i) a ij b j,on. Kies de i waarvoor die bijdrage maximaal is. Verleng het optimale pad van het begin naar q i met de stap van i j. We illustreren dit weer aan ons rekenvoorbeeld: Het pad (begin,w) is optimaal voor het punt (, w) omdat het het enige pad is naar dat punt. Het pad (begin,k) is optimaal voor het punt (, k) omdat het het enige pad is naar dat punt. Punt (, w) geeft bijdrage α (w) a w,w b w,2 = aan α 2 (w). Punt (, k) geeft bijdrage α (k) a k,w b w,2 = aan α 2 (w). Het pad (begin,w,w) is dus optimaal voor het punt (2, w). Punt (, w) geeft bijdrage α (w) a w,k b k,2 = aan α 2 (k). Punt (, k) geeft bijdrage α (k) a k,k b k,2 = aan α 2 (k). Het pad (begin,w,k) is dus optimaal voor het punt (2, k). Punt (2, w) geeft bijdrage α 2 (w) a w,w b w,3 = aan α 3,w. Punt (2, k) geeft bijdrage α 2 (k) a k,w b w,3 = aan α 3,w. Het pad (begin,w,w,w) is dus optimaal voor het punt (3, w). Punt (2, w) geeft bijdrage α 2 (w) a w,k b k,3 = aan α 3,k. Punt (2, k) geeft bijdrage α 2 (k) a k,k b k,3 = aan α 3,k. Het pad (begin,w,w,k) is dus optimaal voor het punt (3, k). Punt (3, w) geeft bijdrage α 3,w = Punt (3, k) geeft bijdrage α 3,k = Het pad (begin,w,w,w,eind) is dus optimaal van begin tot eind. Tenslotte merken we op dat er een efficiënte manier is om voor elk punt het optimale pad op te slaan: het volstaat om een verwijzing op te slaan
7 3.5 Het Baum-Welch algoritme. 7 naar de voorganger in het optimale pad; in feite dus de toestand van die voorganger. warm koud Het diagram hierboven illustreert dit voor ons rekenvoorbeeld. 3.5 Het Baum-Welch algoritme. We proberen nu om, gegeven de structuur van het model, de parameters zó te kiezen dat ze de serie waarnemingen in de training zo goed mogelijk verklaren d.w.z. een zo groot mogelijke waarschijnlijkheid geven. Dit probleem heeft een iets ander karakter dan de twee voorgaande problemen. Daar ging het er om een groot aantal optellingen en vermenigvuldigingen zo efficiënt mogelijk uit te voeren. Hier gaat het erom een aantal (grote) vergelijkingen op te lossen. Omdat die vergelijkingen niet lineair zijn is het beste wat we kunnen hopen een benaderingsproces: Je begint met een niet heel slecht stel waarden voor de parameters, Daaruit bereken je een betere keuze voor de parameters En nog eens... En je hoopt dat die keuzes redelijk snel naar een limiet convergeren. Uit de vorige deelhoofdstukjes hebben het vertrwouwen gewekt dat we bij gegeven waardes van de parameters kunnen inschatten welke toestand op een zeker tijdstip n gedurende de training is opgetreden. Omdat we dat voor elke n kunnen doen krijgen we zo een schatting van de frequenties van de diverse toestanden, en ook van de frequenties van de overgangen tussen toestanden. Door deze twee frequenties op elkaar te delen krijgen we een schatting van de waarschijnlijkheden van de diverse overgangen d.w.z. nieuwe waardes van de parameters: de elementen van de matrices (a) en (b). Men kan laten zien dat deze waardes inderdaad beter zijn. We werken nu uit hoe we bovengenoemde frequenties bepalen. We hebben eerder gezien dat p(y = o,..., Y T = o T ) i,...,i T π i a i,i 2 a i2,i 3... a it,i T b i,o b i2,o 2... b it,o T
8 8 3 HIDDEN MARKOV MODELLEN. Op dezelfde manier zie je dat p(y = o,..., Y T = o T, X n = j) = π i a i,i 2 a i2,i 3... a in,ja j,in+... a it,i T i,...,i n,i n+,...,i T b i,o b i2,o 2... b j,on... b it,o T Vergelijken we dat met de formules voor α en β α n (j) =p(y = o,..., Y n = o n, X n = j) i,...,i n π i a i,i 2 a i2,i 3... a in,j b i,o b i2,o 2... b j,on β n (j) =p(y n+ = o n+,..., Y T = o T, X n = j) dan zien we dat i n+,...,i T a j,in+... a it,i T b in+,o n+... b it,o T p(y = o,..., Y T = o T, X n = j) = α n (j)β n (j) p(y = o,..., Y T = o T ) j α n (j)β n (j) De kans dat op tijdstip n toestand j is opgetreden, gegeven de waarnemingen (o,..., o T ) is dus γ n (j) = p(x n = j ; Y = o,..., Y T = o T ) = p(x n = j, Y = o,..., Y T = o T ) p(y = o,..., Y T = o T ) = α n(j) β n (j) k α n(k)β n (k) Op dezelfde manier zien we dat de kans dat in de stap n n+ de overgang van toestand i naar j is opgetreden gelijk is aan ξ n (i, j) = p(x n = i, X n+ = j ; Y = o,..., Y T = o T ) = p(x n = i, X n+ = j, Y = o,..., Y T = o T ) p(y = o,..., Y T = o T ) = α n(i) a ij b j,on+ β n (j) k α n(k)β n (k) Onze beste schatting van het aantal keren dat toestand j is opgetreden is dus T n= γ n(j), en onze beste schatting van het aantal keren dat de overgang van i naar j is opgetreden is dus T n= ξ n(i, j). Dit geeft ons de nieuwe waarden van de parameters: a i,j = n ξ n(i, j) n γ n(i), b i,o = n met o n=o γ n(i) n γ n(i)
9 3.6 De Levenshtein afstand De Levenshtein afstand. We bespreken nu een andere toepasing van Bellman s principe, en wel het bepalen van de mate van verschil tussen twee reeksen van symbolen. Een mogelijke maat daarvoor is de Edit afstand, die naar een van de uitvinders Levenshtein afstand heet. Het idee is daarbij dat je de ene reeks x x 2... x N in de andere reeks y y 2... y M probeert over te voeren door een aantal elementaire ingrepen, die elk met zekere kosten gepaard gaan. De Levenshtein afstand tussen de twee reeksen is dan het minimale totaal aan kosten waarmee dat lukt. De elementaire ingrepen zouden bijvoorbeeld kunnen zijn: Vervangen (substitution) van een symbool, bijvoorbeeld hard hart. Invoegen (insertion) van een symbool, bijvoorbeeld hard haard. Weglaten (deletion) van een symbool, bijvoorbeeld haard hard. Zeg dat de kosten van deze ingrepen respectievelijk k s, k i en k d zijn. Volgens Bellman s principe is het nuttig om te bepalen wat de prijs D(i, j) is van het transformeren van een beginstuk x x 2... x i van de ene reeks in een beginstuk y y 2... y j van de andere reeks. Dat levert de volgende formules: ) D(i, j) = min (D(i, j ) + v(i, j) k s, D(i, j ) + k i, D(i, j) + k d { 0 als i = j waar v(i, j) = en D(i, 0) = i k d en D(0, j) = j k i als i j De gevraagde afstand is dan D(N, M). Het schema hieronder illustreert deze berekening voor x = KUNSTMATIGE en y = INTELLIGENTIE in het geval k s = 5, k i = 3, k d = 4. I N T E L L I G E N T I E K U N S T M A T I G E
10 0 3 HIDDEN MARKOV MODELLEN. We zien dat de afstand van KUNSTMATIGE naar INTELLIGENTIE gelijk is aan 40, maar ook dat de afstand van KUNST naar INTELLIGENT gelijk is aan 35. De tabel wordt opgesteld door eerst de eerste rij en eerste kolom in te vullen, en vervolgens van links boven naar rechts onder te werken: op elke plek wordt het getal bepaald door het al dan niet gelijk zijn van het symbool van de rij en het symbool van de kolom, en door de drie getallen links, boven, en linksboven. Om een route te vinden die minimale kosten oplevert hoeven we alleen bij elk knooppunt (i, j) op te slaan welke van zijn drie voorgangers (i, j ) en (i, j) en (i, j ) het minimum in de formule voor D(i, j) oplevert (dat kunnen er meer dan één zijn). In het voorbeeld is dat aangegeven door de getallen te onderstrepen, en is een route als volgt: KU N S T M A T I G E d,s d s s s i,i,i,i I N T E L L I G EN T I E Hier staan d, s, i voor de drie soorten ingrepen, en de onderste rij geeft de bijdrage aan de totale kosten.
Bekijk nog een keer het stelsel van twee vergelijkingen met twee onbekenden x en y: { De tweede vergelijking van de eerste aftrekken geeft:
 Determinanten Invoeren van het begrip determinant Bekijk nog een keer het stelsel van twee vergelijkingen met twee onbekenden x en y: { a x + b y = c a 2 a 2 x + b 2 y = c 2 a Dit levert op: { a a 2 x
Determinanten Invoeren van het begrip determinant Bekijk nog een keer het stelsel van twee vergelijkingen met twee onbekenden x en y: { a x + b y = c a 2 a 2 x + b 2 y = c 2 a Dit levert op: { a a 2 x
vandaag is Annie twee jaar jonger dan Ben en Cees samen
 Hoofdstuk I Lineaire Algebra Les 1 Stelsels lineaire vergelijkingen Om te beginnen is hier een puzzeltje: vandaag is Annie twee jaar jonger dan Ben en Cees samen over vijf jaar is Annie twee keer zo oud
Hoofdstuk I Lineaire Algebra Les 1 Stelsels lineaire vergelijkingen Om te beginnen is hier een puzzeltje: vandaag is Annie twee jaar jonger dan Ben en Cees samen over vijf jaar is Annie twee keer zo oud
FLIPIT 5. (a i,j + a j,i )d i d j = d j + 0 = e d. i<j
 FLIPIT JAAP TOP Een netwerk bestaat uit een eindig aantal punten, waarbij voor elk tweetal ervan gegeven is of er wel of niet een verbinding is tussen deze twee. De punten waarmee een gegeven punt van
FLIPIT JAAP TOP Een netwerk bestaat uit een eindig aantal punten, waarbij voor elk tweetal ervan gegeven is of er wel of niet een verbinding is tussen deze twee. De punten waarmee een gegeven punt van
Netwerkdiagram voor een project. AON: Activities On Nodes - activiteiten op knooppunten
 Netwerkdiagram voor een project. AON: Activities On Nodes - activiteiten op knooppunten Opmerking vooraf. Een netwerk is een structuur die is opgebouwd met pijlen en knooppunten. Bij het opstellen van
Netwerkdiagram voor een project. AON: Activities On Nodes - activiteiten op knooppunten Opmerking vooraf. Een netwerk is een structuur die is opgebouwd met pijlen en knooppunten. Bij het opstellen van
0.97 0.03 0 0 0.008 0.982 0.01 0 0.02 0 0.975 0.005 0.01 0 0 0.99
 COHORTE MODELLEN Markov ketens worden vaak gebruikt bij de bestudering van een groep van personen of objecten. We spreken dan meestal over Cohorte modellen. Een voorbeeld van zo n situatie is het personeelsplanning
COHORTE MODELLEN Markov ketens worden vaak gebruikt bij de bestudering van een groep van personen of objecten. We spreken dan meestal over Cohorte modellen. Een voorbeeld van zo n situatie is het personeelsplanning
Netwerkdiagram voor een project. AOA: Activities On Arrows - activiteiten op de pijlen.
 Netwerkdiagram voor een project. AOA: Activities On Arrows - activiteiten op de pijlen. Opmerking vooraf. Een netwerk is een structuur die is opgebouwd met pijlen en knooppunten. Bij het opstellen van
Netwerkdiagram voor een project. AOA: Activities On Arrows - activiteiten op de pijlen. Opmerking vooraf. Een netwerk is een structuur die is opgebouwd met pijlen en knooppunten. Bij het opstellen van
Combinatoriek groep 1 & 2: Recursie
 Combinatoriek groep 1 & : Recursie Trainingsweek juni 008 Inleiding Bij een recursieve definitie van een rij wordt elke volgende term berekend uit de vorige. Een voorbeeld van zo n recursieve definitie
Combinatoriek groep 1 & : Recursie Trainingsweek juni 008 Inleiding Bij een recursieve definitie van een rij wordt elke volgende term berekend uit de vorige. Een voorbeeld van zo n recursieve definitie
te vermenigvuldigen, waarbij N het aantal geslagen Nederlandse munten en B het aantal geslagen buitenlandse munten zijn. Het resultaat is de vector
 Les 3 Matrix product We hebben gezien hoe we matrices kunnen gebruiken om lineaire afbeeldingen te beschrijven. Om het beeld van een vector onder een afbeelding te bepalen hebben we al een soort product
Les 3 Matrix product We hebben gezien hoe we matrices kunnen gebruiken om lineaire afbeeldingen te beschrijven. Om het beeld van een vector onder een afbeelding te bepalen hebben we al een soort product
De partitieformule van Euler
 De partitieformule van Euler Een kennismaking met zuivere wiskunde J.H. Aalberts-Bakker 29 augustus 2008 Doctoraalscriptie wiskunde, variant Communicatie en Educatie Afstudeerdocent: Dr. H. Finkelnberg
De partitieformule van Euler Een kennismaking met zuivere wiskunde J.H. Aalberts-Bakker 29 augustus 2008 Doctoraalscriptie wiskunde, variant Communicatie en Educatie Afstudeerdocent: Dr. H. Finkelnberg
P (X n+1 = j X n = i, X n 1,..., X 0 ) = P (X n+1 = j X n = i). P (X n+1 = j X n = i) MARKOV KETENS. Definitie van Markov keten:
 Definitie van Markov keten: MARKOV KETENS Een stochastisch proces {X n, n 0} met toestandsruimte S heet een discrete-tijd Markov keten (DTMC) als voor alle i en j in S geldt P (X n+ = j X n = i, X n,...,
Definitie van Markov keten: MARKOV KETENS Een stochastisch proces {X n, n 0} met toestandsruimte S heet een discrete-tijd Markov keten (DTMC) als voor alle i en j in S geldt P (X n+ = j X n = i, X n,...,
Werkblad havo 4 natuurkunde Basisvaardigheden
 Werkblad havo 4 natuurkunde Basisvaardigheden Grootheden en eenheden Bij het vak natuurkunde spelen grootheden en eenheden een belangrijke rol. Wat dat zijn, grootheden en eenheden? Een grootheid is een
Werkblad havo 4 natuurkunde Basisvaardigheden Grootheden en eenheden Bij het vak natuurkunde spelen grootheden en eenheden een belangrijke rol. Wat dat zijn, grootheden en eenheden? Een grootheid is een
Genererende Functies K. P. Hart
 genererende_functies.te 27--205 Z Hoe kun je een rij getallen zo efficiënt mogelijk coderen? Met behulp van functies. Genererende Functies K. P. Hart Je kunt rijen getallen op diverse manieren weergeven
genererende_functies.te 27--205 Z Hoe kun je een rij getallen zo efficiënt mogelijk coderen? Met behulp van functies. Genererende Functies K. P. Hart Je kunt rijen getallen op diverse manieren weergeven
1 Eigenwaarden en eigenvectoren
 Eigenwaarden en eigenvectoren Invoeren van de begrippen eigenwaarde en eigenvector DEFINITIE Een complex (of reëel getal λ heet een eigenwaarde van de n n matrix A als er een vector x is met Ax = λx Dan
Eigenwaarden en eigenvectoren Invoeren van de begrippen eigenwaarde en eigenvector DEFINITIE Een complex (of reëel getal λ heet een eigenwaarde van de n n matrix A als er een vector x is met Ax = λx Dan
Basiskennis lineaire algebra
 Basiskennis lineaire algebra Lineaire algebra is belangrijk als achtergrond voor lineaire programmering, omdat we het probleem kunnen tekenen in de n-dimensionale ruimte, waarbij n gelijk is aan het aantal
Basiskennis lineaire algebra Lineaire algebra is belangrijk als achtergrond voor lineaire programmering, omdat we het probleem kunnen tekenen in de n-dimensionale ruimte, waarbij n gelijk is aan het aantal
Hoofdstuk 1 : Vectoren (A5D)
 1 Hoofdstuk 1 : Vectoren (A5D) Hoofdstuk 1 : Vectoren (A5D) Les 1 : Stelsels en Echelon vorm DOEL : WE GAAN EEN AANTAL VERGELIJKINGEN MET EEN AANTAL VARIABELEN PROBEREN OP TE LOSSEN. Definities Stelsel
1 Hoofdstuk 1 : Vectoren (A5D) Hoofdstuk 1 : Vectoren (A5D) Les 1 : Stelsels en Echelon vorm DOEL : WE GAAN EEN AANTAL VERGELIJKINGEN MET EEN AANTAL VARIABELEN PROBEREN OP TE LOSSEN. Definities Stelsel
Mengsel mix. Elieke van Sark en Liza Fredriks
 Mengsel mix Elieke van Sark en Liza Fredriks 2 oktober 29 Inleiding Een chemisch bedrijf is naar ons toe gekomen met een aantal vragen over het reageren van stoffen tot andere stoffen Hierbij gaat het
Mengsel mix Elieke van Sark en Liza Fredriks 2 oktober 29 Inleiding Een chemisch bedrijf is naar ons toe gekomen met een aantal vragen over het reageren van stoffen tot andere stoffen Hierbij gaat het
Combinatoriek groep 2
 Combinatoriek groep 2 Recursie Trainingsdag 3, 2 april 2009 Homogene lineaire recurrente betrekkingen We kunnen een rij getallen a 0, a 1, a 2,... op twee manieren definiëren: direct of recursief. Een
Combinatoriek groep 2 Recursie Trainingsdag 3, 2 april 2009 Homogene lineaire recurrente betrekkingen We kunnen een rij getallen a 0, a 1, a 2,... op twee manieren definiëren: direct of recursief. Een
Geldwisselprobleem van Frobenius
 Geldwisselprobleem van Frobenius Karin van de Meeberg en Dieuwertje Ewalts 12 december 2001 1 Inhoudsopgave 1 Inleiding 3 2 Afspraken 3 3 Is er wel zo n g? 3 4 Eén waarde 4 5 Twee waarden 4 6 Lampenalgoritme
Geldwisselprobleem van Frobenius Karin van de Meeberg en Dieuwertje Ewalts 12 december 2001 1 Inhoudsopgave 1 Inleiding 3 2 Afspraken 3 3 Is er wel zo n g? 3 4 Eén waarde 4 5 Twee waarden 4 6 Lampenalgoritme
Kwantummechanica Donderdag, 13 oktober 2016 OPGAVEN SET HOOFDSTUK 4. Bestudeer Appendix A, bladzijden van het dictaat.
 1 Kwantummechanica Donderdag, 1 oktober 016 OPGAVEN SET HOOFDSTUK 4 VECTOREN OVER DE REËLE RUIMTE DUS DE ELEMENTEN ZIJN REËLE GETALLEN Bestudeer Appendix A, bladzijden 110-114 van het dictaat. Opgave 1:
1 Kwantummechanica Donderdag, 1 oktober 016 OPGAVEN SET HOOFDSTUK 4 VECTOREN OVER DE REËLE RUIMTE DUS DE ELEMENTEN ZIJN REËLE GETALLEN Bestudeer Appendix A, bladzijden 110-114 van het dictaat. Opgave 1:
P (X n+1 = j X n = i, X n 1,..., X 0 ) = P (X n+1 = j X n = i). P (X n+1 = j X n = i) MARKOV KETENS. Definitie van Markov keten:
 Definitie van Markov keten: MARKOV KETENS Een stochastisch proces {X n, n 0} met toestandsruimte S heet een discrete-tijd Markov keten (DTMC) als voor alle i en j in S geldt P (X n+1 = j X n = i, X n 1,...,
Definitie van Markov keten: MARKOV KETENS Een stochastisch proces {X n, n 0} met toestandsruimte S heet een discrete-tijd Markov keten (DTMC) als voor alle i en j in S geldt P (X n+1 = j X n = i, X n 1,...,
Opgave 1b: Toon ook aan dat meer algemeen geldt: Als het lukt met n = a munten in w keer wegen, dan lukt het voor a < n 2a in w + 1 keer wegen.
 Uitwerking Puzzel 92-7 Allemaal gelijk? Wobien Doyer Lieke de Rooij Er zijn veel puzzels over het opsporen van één valse munt tussen een aantal goede munten met hulp van een balans. Bij deze puzzel is
Uitwerking Puzzel 92-7 Allemaal gelijk? Wobien Doyer Lieke de Rooij Er zijn veel puzzels over het opsporen van één valse munt tussen een aantal goede munten met hulp van een balans. Bij deze puzzel is
Ruimtemeetkunde deel 1
 Ruimtemeetkunde deel 1 1 Punten We weten reeds dat Π 0 het meetkundig model is voor de vectorruimte R 2. We definiëren nu op dezelfde manier E 0 als meetkundig model voor de vectorruimte R 3. De elementen
Ruimtemeetkunde deel 1 1 Punten We weten reeds dat Π 0 het meetkundig model is voor de vectorruimte R 2. We definiëren nu op dezelfde manier E 0 als meetkundig model voor de vectorruimte R 3. De elementen
Combinatoriek groep 1
 Combinatoriek groep 1 Recursie Trainingsweek, juni 009 Stappenplan homogene lineaire recurrente betrekkingen Even herhalen: het stappenplan om een recurrente betrekking van orde op te lossen: Stap 1. Bepaal
Combinatoriek groep 1 Recursie Trainingsweek, juni 009 Stappenplan homogene lineaire recurrente betrekkingen Even herhalen: het stappenplan om een recurrente betrekking van orde op te lossen: Stap 1. Bepaal
Toegepaste Wiskunde 2: Het Kalman-filter
 Toegepaste Wiskunde 2: Het Kalman-filter 25 februari, 2008 Hans Maassen 1. Inleiding Het Kalman filter schat de toestand van een systeem op basis van een reeks, door ruis verstoorde waarnemingen. Een meer
Toegepaste Wiskunde 2: Het Kalman-filter 25 februari, 2008 Hans Maassen 1. Inleiding Het Kalman filter schat de toestand van een systeem op basis van een reeks, door ruis verstoorde waarnemingen. Een meer
D-dag 2014 Vrijeschool Zutphen VO. D -DAG 13 februari 2014: 1+ 1 = 2. (en hoe nu verder?) 1 = 2en hoe nu verder?
 D -DAG 13 februari 2014: 1+ 1 = 2 (en hoe nu verder?) 1 = 2en hoe nu verder? 1 Inleiding Snel machtsverheffen Stel je voor dat je 7 25 moet uitrekenen. Je weet dat machtsverheffen herhaald vermenigvuldigen
D -DAG 13 februari 2014: 1+ 1 = 2 (en hoe nu verder?) 1 = 2en hoe nu verder? 1 Inleiding Snel machtsverheffen Stel je voor dat je 7 25 moet uitrekenen. Je weet dat machtsverheffen herhaald vermenigvuldigen
ProefToelatingstoets Wiskunde B
 Uitwerking ProefToelatingstoets Wiskunde B Hulpmiddelen :tentamenpapier,kladpapier, een eenvoudige rekenmachine (dus geen grafische of programmeerbare rekenmachine) De te bepalen punten per opgave staan
Uitwerking ProefToelatingstoets Wiskunde B Hulpmiddelen :tentamenpapier,kladpapier, een eenvoudige rekenmachine (dus geen grafische of programmeerbare rekenmachine) De te bepalen punten per opgave staan
Uitwerkingen Lineaire Algebra I (wiskundigen) 22 januari, 2015
 Uitwerkingen Lineaire Algebra I (wiskundigen) januari, 5 In deze uitwerkingen is hier en daar een berekening weggelaten (bijvoorbeeld het bepalen van de kern van een matrix) die uiteraard op het tentamen
Uitwerkingen Lineaire Algebra I (wiskundigen) januari, 5 In deze uitwerkingen is hier en daar een berekening weggelaten (bijvoorbeeld het bepalen van de kern van een matrix) die uiteraard op het tentamen
Supplement Wiskunde 2017/2018. Inhoudsopgave
 Inhoudsopgave Hoofdstuk 1: Missende stof in de verslagen... 2 Hoofdstuk 2: Overbodige stof in de verslagen... 7 Hoofdstuk 3: Fouten in de verslagen... 8 Tentamen halen? www.rekenmaarverslagen.nl 1 Hoofdstuk
Inhoudsopgave Hoofdstuk 1: Missende stof in de verslagen... 2 Hoofdstuk 2: Overbodige stof in de verslagen... 7 Hoofdstuk 3: Fouten in de verslagen... 8 Tentamen halen? www.rekenmaarverslagen.nl 1 Hoofdstuk
Antwoorden. Magische vierkanten Vierkant voor Wiskunde Doeboek 8
 Antwoorden Magische vierkanten Vierkant voor Wiskunde Doeboek 8 1 6 1 8 7 5 3 2 9 4 2 De getallen 1 tot en met 9. 3 15. 15 en 15. De som van de getallen van elke rij is 15. 4 15. De som van de getallen
Antwoorden Magische vierkanten Vierkant voor Wiskunde Doeboek 8 1 6 1 8 7 5 3 2 9 4 2 De getallen 1 tot en met 9. 3 15. 15 en 15. De som van de getallen van elke rij is 15. 4 15. De som van de getallen
Hoofdstuk!7!Kortste!paden!
 oofdstukkortstepaden oofdstukkortstepaden In een gewogen graaf is men soms geïnteresseerd in het kortste pad tussen twee punten: dat is een pad, waarbij de som van de gewichten zo klein mogelijk is..inleiding
oofdstukkortstepaden oofdstukkortstepaden In een gewogen graaf is men soms geïnteresseerd in het kortste pad tussen twee punten: dat is een pad, waarbij de som van de gewichten zo klein mogelijk is..inleiding
P = LIMIETGEDRAG VAN MARKOV KETENS Limietverdeling van irreducibele, aperiodieke Markov keten:
 LIMIETGEDRAG VAN MARKOV KETENS Limietverdeling van irreducibele, aperiodieke Markov keten: Voorbeeld: Zoek de unieke oplossing van het stelsel π = π P waarvoor bovendien geldt dat i S π i = 1. P = 0 1/4
LIMIETGEDRAG VAN MARKOV KETENS Limietverdeling van irreducibele, aperiodieke Markov keten: Voorbeeld: Zoek de unieke oplossing van het stelsel π = π P waarvoor bovendien geldt dat i S π i = 1. P = 0 1/4
1 Rekenen met gehele getallen
 1 Inhoudsopgave 1 Rekenen met gehele getallen... 1.1 De gehele getallen... 1. Optellen... 1. Opgaven... 1. Aftrekken... 1. Opgaven... 1. Vermenigvuldigen... 1. Opgaven... 1.8 Delen... 9 1.9 Opgaven...9
1 Inhoudsopgave 1 Rekenen met gehele getallen... 1.1 De gehele getallen... 1. Optellen... 1. Opgaven... 1. Aftrekken... 1. Opgaven... 1. Vermenigvuldigen... 1. Opgaven... 1.8 Delen... 9 1.9 Opgaven...9
Opgaven bij de cursus Relativiteitstheorie wiskunde voorkennis Najaar 2018 Docent: Dr. H. (Harm) van der Lek
 Opgaven bij de cursus Relativiteitstheorie wiskunde voorkennis Najaar 2018 Docent: Dr. H. (Harm) van der Lek Uitwerkingen worden beschikbaar gesteld op de dinsdagavond voorafgaande aan het volgende college
Opgaven bij de cursus Relativiteitstheorie wiskunde voorkennis Najaar 2018 Docent: Dr. H. (Harm) van der Lek Uitwerkingen worden beschikbaar gesteld op de dinsdagavond voorafgaande aan het volgende college
a) Bepaal punten a l en b m zó dat de lijn door a en b parallel is met n.
 . Oefen opgaven Opgave... Gegeven zijn de lijnen l : 2 + λ m : 2 2 + λ 3 n : 3 6 4 + λ 3 6 4 a) Bepaal punten a l en b m zó dat de lijn door a en b parallel is met n. b) Bepaal de afstand tussen die lijn
. Oefen opgaven Opgave... Gegeven zijn de lijnen l : 2 + λ m : 2 2 + λ 3 n : 3 6 4 + λ 3 6 4 a) Bepaal punten a l en b m zó dat de lijn door a en b parallel is met n. b) Bepaal de afstand tussen die lijn
Examen Complexe Analyse (September 2008)
 Examen Complexe Analyse (September 2008) De examenvragen vind je op het einde van dit documentje. Omdat het hier over weinig studenten gaat, heb ik geen puntenverdeling meegegeven. Vraag. Je had eerst
Examen Complexe Analyse (September 2008) De examenvragen vind je op het einde van dit documentje. Omdat het hier over weinig studenten gaat, heb ik geen puntenverdeling meegegeven. Vraag. Je had eerst
Toepassingen in de natuurkunde: snelheden, versnellingen, krachten.
 WIS8 8 Vectoren 8. Vectoren Vectoren Een vector met dimensie is een kolom bestaande uit twee reële getallen, bijvoorbeeld [ We kunnen deze meetkundig interpreteren als een pijl in het platte vlak van de
WIS8 8 Vectoren 8. Vectoren Vectoren Een vector met dimensie is een kolom bestaande uit twee reële getallen, bijvoorbeeld [ We kunnen deze meetkundig interpreteren als een pijl in het platte vlak van de
Trillingen en geluid wiskundig
 Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Radialen 3 Uitwijking van een harmonische trilling 4 Macht en logaritme 5 Geluidsniveau en amplitude 1 De sinus van een hoek Sinus van een hoek
Trillingen en geluid wiskundig 1 De sinus van een hoek 2 Radialen 3 Uitwijking van een harmonische trilling 4 Macht en logaritme 5 Geluidsniveau en amplitude 1 De sinus van een hoek Sinus van een hoek
WISKUNDE-ESTAFETTE RU 2005 Uitwerkingen
 WISKUNDE-ESTAFETTE RU 2005 Uitwerkingen 1 We proberen alle mogelijkheden van klein naar groot: p = 1 is uitgesloten: dan zou elke dag hetzelfde resultaat geven. p = 2 is uitgesloten: dan zouden dag 1 en
WISKUNDE-ESTAFETTE RU 2005 Uitwerkingen 1 We proberen alle mogelijkheden van klein naar groot: p = 1 is uitgesloten: dan zou elke dag hetzelfde resultaat geven. p = 2 is uitgesloten: dan zouden dag 1 en
Bijzondere kettingbreuken
 Hoofdstuk 15 Bijzondere kettingbreuken 15.1 Kwadratische getallen In het vorige hoofdstuk hebben we gezien dat 2 = 1, 2, 2, 2, 2, 2, 2,.... Men kan zich afvragen waarom we vanaf zeker moment alleen maar
Hoofdstuk 15 Bijzondere kettingbreuken 15.1 Kwadratische getallen In het vorige hoofdstuk hebben we gezien dat 2 = 1, 2, 2, 2, 2, 2, 2,.... Men kan zich afvragen waarom we vanaf zeker moment alleen maar
3 De duale vectorruimte
 3 De duale vectorruimte We brengen de volgende definitie in de herinnering. Definitie 3.1 (hom K (V, W )) Gegeven twee vectorruimtes (V, K) en (W, K) over K noteren we de verzameling van alle lineaire
3 De duale vectorruimte We brengen de volgende definitie in de herinnering. Definitie 3.1 (hom K (V, W )) Gegeven twee vectorruimtes (V, K) en (W, K) over K noteren we de verzameling van alle lineaire
168 HOOFDSTUK 5. REEKSONTWIKKELINGEN
 168 HOOFDSTUK 5. REEKSONTWIKKELINGEN 5.7 Vraagstukken Vraagstuk 5.7.1 Beschouw de differentiaalvergelijking d2 y d 2 = 2 y. (i) Schrijf y = a k k. Geef een recurrente betrekking voor de coëfficienten a
168 HOOFDSTUK 5. REEKSONTWIKKELINGEN 5.7 Vraagstukken Vraagstuk 5.7.1 Beschouw de differentiaalvergelijking d2 y d 2 = 2 y. (i) Schrijf y = a k k. Geef een recurrente betrekking voor de coëfficienten a
MACHINES. ... en kralenkettingen. Onderzoeksprogramma Vierkant voor Wiskunde. Wiskundeclubs. Tristan Cranendonk & Joost Langeveld
 MACHINES... en kralenkettingen. Onderzoeksprogramma Vierkant voor Wiskunde Wiskundeclubs Tristan Cranendonk & Joost Langeveld Kralenketting machines 1 Uitleg van de gebruikte symbolen: In de kantlijn staan
MACHINES... en kralenkettingen. Onderzoeksprogramma Vierkant voor Wiskunde Wiskundeclubs Tristan Cranendonk & Joost Langeveld Kralenketting machines 1 Uitleg van de gebruikte symbolen: In de kantlijn staan
MARKOV KETENS, OF: WAT IS DE KANS DAT MEVROUW DE VRIES NAT ZAL WORDEN?
 MARKOV KETENS, OF: WAT IS DE KANS DAT MEVROUW DE VRIES NAT ZAL WORDEN? KARMA DAJANI In deze lezing gaan we over een bijzonder model in kansrekening spreken Maar eerst een paar woorden vooraf Wat doen we
MARKOV KETENS, OF: WAT IS DE KANS DAT MEVROUW DE VRIES NAT ZAL WORDEN? KARMA DAJANI In deze lezing gaan we over een bijzonder model in kansrekening spreken Maar eerst een paar woorden vooraf Wat doen we
Stelsels Vergelijkingen
 Hoofdstuk 5 Stelsels Vergelijkingen Eén van de motiverende toepassingen van de lineaire algebra is het bepalen van oplossingen van stelsels lineaire vergelijkingen. De belangrijkste techniek bestaat uit
Hoofdstuk 5 Stelsels Vergelijkingen Eén van de motiverende toepassingen van de lineaire algebra is het bepalen van oplossingen van stelsels lineaire vergelijkingen. De belangrijkste techniek bestaat uit
RSA. F.A. Grootjen. 8 maart 2002
 RSA F.A. Grootjen 8 maart 2002 1 Delers Eerst wat terminologie over gehele getallen. We zeggen a deelt b (of a is een deler van b) als b = qa voor een of ander geheel getal q. In plaats van a deelt b schrijven
RSA F.A. Grootjen 8 maart 2002 1 Delers Eerst wat terminologie over gehele getallen. We zeggen a deelt b (of a is een deler van b) als b = qa voor een of ander geheel getal q. In plaats van a deelt b schrijven
Om nu te berekenen hoeveel koelwater er per uur door een leiding stroomt, heb je een vergelijking of formule nodig. Je gebruikt de volgende formule:
 Een vergelijking (1) In je dagelijkse werk reken je onbewust vaak met behulp van vergelijkingen of formules. Stel je voor dat je graag wilt weten hoeveel koelwater er per uur door een leiding stroomt.
Een vergelijking (1) In je dagelijkse werk reken je onbewust vaak met behulp van vergelijkingen of formules. Stel je voor dat je graag wilt weten hoeveel koelwater er per uur door een leiding stroomt.
Optimalisering en Complexiteit, College 11. Complementaire speling; duale Simplex methode. Han Hoogeveen, Utrecht University
 Optimalisering en Complexiteit, College 11 Complementaire speling; duale Simplex methode Han Hoogeveen, Utrecht University Duale probleem (P) (D) min c 1 x 1 + c 2 x 2 + c 3 x 3 max w 1 b 1 + w 2 b 2 +
Optimalisering en Complexiteit, College 11 Complementaire speling; duale Simplex methode Han Hoogeveen, Utrecht University Duale probleem (P) (D) min c 1 x 1 + c 2 x 2 + c 3 x 3 max w 1 b 1 + w 2 b 2 +
Hoofdstuk 2: Grafieken en formules
 Hoofdstuk 2: Grafieken en formules Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 2: Grafieken en formules Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde
Hoofdstuk 2: Grafieken en formules Wiskunde VMBO 2011/2012 www.lyceo.nl Hoofdstuk 2: Grafieken en formules Wiskunde 1. Basisvaardigheden 2. Grafieken en formules 3. Algebraïsche verbanden 4. Meetkunde
In het internationale eenhedenstelsel, ook wel SI, staan er negen basisgrootheden met bijbehorende grondeenheden. Dit is BINAS tabel 3A.
 Grootheden en eenheden Kwalitatieve en kwantitatieve waarnemingen Een kwalitatieve waarneming is wanneer je meet zonder bijvoorbeeld een meetlat. Je ziet dat een paard hoger is dan een muis. Een kwantitatieve
Grootheden en eenheden Kwalitatieve en kwantitatieve waarnemingen Een kwalitatieve waarneming is wanneer je meet zonder bijvoorbeeld een meetlat. Je ziet dat een paard hoger is dan een muis. Een kwantitatieve
De inverse van een matrix
 De inverse van een matrix Laat A een n n matrix zijn. Veronderstel dat de matrixvergelijking A X = I n de oplossing X = C heeft. Merk op dat [ A I n ] rijoperaties [ I n C ] [ I n A] inverse rijoperaties
De inverse van een matrix Laat A een n n matrix zijn. Veronderstel dat de matrixvergelijking A X = I n de oplossing X = C heeft. Merk op dat [ A I n ] rijoperaties [ I n C ] [ I n A] inverse rijoperaties
2.1 Lineaire functies [1]
![2.1 Lineaire functies [1] 2.1 Lineaire functies [1]](/thumbs/65/53276356.jpg) 2.1 Lineaire functies [1] De lijn heeft een helling (richtingscoëfficiënt) van 1; De lijn gaat in het punt (0,2) door de y-as; In het plaatje is de lijn y = x + 2 getekend. Omdat de grafiek een rechte
2.1 Lineaire functies [1] De lijn heeft een helling (richtingscoëfficiënt) van 1; De lijn gaat in het punt (0,2) door de y-as; In het plaatje is de lijn y = x + 2 getekend. Omdat de grafiek een rechte
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie
 FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie Lineaire Algebra, tentamen Uitwerkingen vrijdag 4 januari 0, 9 uur Gebruik van een formuleblad of rekenmachine is niet toegestaan. De
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE Afdeling Kwantitatieve Economie Lineaire Algebra, tentamen Uitwerkingen vrijdag 4 januari 0, 9 uur Gebruik van een formuleblad of rekenmachine is niet toegestaan. De
Werkwijzers. 1 Wetenschappelijke methode 2 Practicumverslag 3 Formules 4 Tabellen en grafieken 5 Rechtevenredigheid 6 Op zijn kop optellen
 Werkwijzers 1 Wetenschappelijke methode 2 Practicumverslag 3 ormules 4 Tabellen en grafieken 5 Rechtevenredigheid 6 Op zijn kop optellen Werkwijzer 1 Wetenschappelijke methode Als je de natuur onderzoekt
Werkwijzers 1 Wetenschappelijke methode 2 Practicumverslag 3 ormules 4 Tabellen en grafieken 5 Rechtevenredigheid 6 Op zijn kop optellen Werkwijzer 1 Wetenschappelijke methode Als je de natuur onderzoekt
Dossier 4 VECTOREN. Dr. Luc Gheysens. bouwstenen van de lineaire algebra
 Dossier 4 VECTOREN bouwstenen van de lineaire algebra Dr. Luc Gheysens 1 Coördinaat van een vector In het vlak π 0 is het punt O de oorsprong en de punten E 1 en E 2 zijn zodanig gekozen dat OE 1 OE 2
Dossier 4 VECTOREN bouwstenen van de lineaire algebra Dr. Luc Gheysens 1 Coördinaat van een vector In het vlak π 0 is het punt O de oorsprong en de punten E 1 en E 2 zijn zodanig gekozen dat OE 1 OE 2
Lights Out. 1 Inleiding
 Lights Out 1 Inleiding Het spel Lights Out is een elektronisch spel dat gelanceerd werd in 1995 door Tiger Electronics. Het originele spel heeft een bord met 25 lampjes in een rooster van 5 rijen en 5
Lights Out 1 Inleiding Het spel Lights Out is een elektronisch spel dat gelanceerd werd in 1995 door Tiger Electronics. Het originele spel heeft een bord met 25 lampjes in een rooster van 5 rijen en 5
Discrete Wiskunde 2WC15, Lente Jan Draisma
 Discrete Wiskunde 2WC15, Lente 2010 Jan Draisma HOOFDSTUK 2 Gröbnerbases 1. Vragen We hebben gezien dat de studie van stelsels polynoomvergelijkingen in meerdere variabelen op natuurlijke manier leidt
Discrete Wiskunde 2WC15, Lente 2010 Jan Draisma HOOFDSTUK 2 Gröbnerbases 1. Vragen We hebben gezien dat de studie van stelsels polynoomvergelijkingen in meerdere variabelen op natuurlijke manier leidt
Ter Leering ende Vermaeck
 Ter Leering ende Vermaeck 15 december 2011 1 Caleidoscoop 1. Geef een relatie op Z die niet reflexief of symmetrisch is, maar wel transitief. 2. Geef een relatie op Z die niet symmetrisch is, maar wel
Ter Leering ende Vermaeck 15 december 2011 1 Caleidoscoop 1. Geef een relatie op Z die niet reflexief of symmetrisch is, maar wel transitief. 2. Geef een relatie op Z die niet symmetrisch is, maar wel
VU University Amsterdam 2018, juli 11.
 Department of Mathematics Herexamen: Voortgezette biostatistiek VU University Amsterdam 018, juli 11. c Dept. of Mathematics, VU University Amsterdam NB. Geef een duidelijke toelichting bij de antwoorden.
Department of Mathematics Herexamen: Voortgezette biostatistiek VU University Amsterdam 018, juli 11. c Dept. of Mathematics, VU University Amsterdam NB. Geef een duidelijke toelichting bij de antwoorden.
MARKOV MODEL MET KOSTEN In Markov modellen zijn we vaak geïnteresseerd in kostenberekeningen.
 MARKOV MODEL MET KOSTEN In Markov modellen zijn we vaak geïnteresseerd in kostenberekeningen. voorraadmodel: voorraadkosten personeelsplanningmodel: salariskosten machineonderhoudsmodel: reparatiekosten
MARKOV MODEL MET KOSTEN In Markov modellen zijn we vaak geïnteresseerd in kostenberekeningen. voorraadmodel: voorraadkosten personeelsplanningmodel: salariskosten machineonderhoudsmodel: reparatiekosten
Vierde huiswerkopdracht Lineaire algebra 1
 Vierde huiswerkopdracht Lineaire algebra December, 00 Opgave : Voor positieve gehele getallen m, n schrijven we Mat(m n, R) voor de vectorruimte van alle m n matrices, met de gebruikelijke optelling en
Vierde huiswerkopdracht Lineaire algebra December, 00 Opgave : Voor positieve gehele getallen m, n schrijven we Mat(m n, R) voor de vectorruimte van alle m n matrices, met de gebruikelijke optelling en
3.2 Vectoren and matrices
 we c = 6 c 2 = 62966 c 3 = 32447966 c 4 = 72966 c 5 = 2632833 c 6 = 4947966 Sectie 32 VECTOREN AND MATRICES Maar het is a priori helemaal niet zeker dat het stelsel vergelijkingen dat opgelost moet worden,
we c = 6 c 2 = 62966 c 3 = 32447966 c 4 = 72966 c 5 = 2632833 c 6 = 4947966 Sectie 32 VECTOREN AND MATRICES Maar het is a priori helemaal niet zeker dat het stelsel vergelijkingen dat opgelost moet worden,
Department of Mathematics Exam: Voortgezette biostatistiek / Biomedische wiskunde VU University Amsterdam 2017, Maart 28
 Department of Mathematics Exam: Voortgezette biostatistiek / Biomedische wiskunde VU University Amsterdam 07, Maart 8 c Dept. of Mathematics, VU University Amsterdam NB. Geef een duidelijke toelichting
Department of Mathematics Exam: Voortgezette biostatistiek / Biomedische wiskunde VU University Amsterdam 07, Maart 8 c Dept. of Mathematics, VU University Amsterdam NB. Geef een duidelijke toelichting
3. Stelsels van vergelijkingen
 . Stelsels van vergelijkingen We gaan de theorie van de voorgaande hoofdstukken toepassen op stelsels van lineaire vergelijkingen. Een voorbeeld: bepaal alle oplossingen (x,, ) van het stelsel vergelijkingen
. Stelsels van vergelijkingen We gaan de theorie van de voorgaande hoofdstukken toepassen op stelsels van lineaire vergelijkingen. Een voorbeeld: bepaal alle oplossingen (x,, ) van het stelsel vergelijkingen
Wanneer zijn veelvouden van proniks proniks?
 1 Uitwerking puzzel 92-1 Wanneer zijn veelvouden van proniks proniks? Harm Bakker noemde het: pro-niks voor-niks De puzzel was voor een groot deel afkomstig van Frits Göbel. Een pronik is een getal dat
1 Uitwerking puzzel 92-1 Wanneer zijn veelvouden van proniks proniks? Harm Bakker noemde het: pro-niks voor-niks De puzzel was voor een groot deel afkomstig van Frits Göbel. Een pronik is een getal dat
4.1 Cijfermateriaal. In dit getal komen zes nullen voor. Om deze reden geldt: 1.000.000 = 10 6
 Voorbeeld 1: 1 miljoen = 1.000.000 4.1 Cijfermateriaal In dit getal komen zes nullen voor. Om deze reden geldt: 1.000.000 = 10 6 Voorbeeld 2: 1 miljard = 1.000.000.000 In dit getal komen negen nullen voor.
Voorbeeld 1: 1 miljoen = 1.000.000 4.1 Cijfermateriaal In dit getal komen zes nullen voor. Om deze reden geldt: 1.000.000 = 10 6 Voorbeeld 2: 1 miljard = 1.000.000.000 In dit getal komen negen nullen voor.
Hertentamen Biostatistiek 3 / Biomedische wiskunde
 Hertentamen Biostatistiek 3 / Biomedische wiskunde 2 juni 2014; 18:30-20:30 NB. Geef een duidelijke toelichting bij de antwoorden. Na correctie liggen de tentamens ter inzage bij het onderwijsbureau. Het
Hertentamen Biostatistiek 3 / Biomedische wiskunde 2 juni 2014; 18:30-20:30 NB. Geef een duidelijke toelichting bij de antwoorden. Na correctie liggen de tentamens ter inzage bij het onderwijsbureau. Het
Samenvatting wiskunde havo 4 hoofdstuk 5,7,8 en vaardigheden 3 en 4 en havo 5 hoofdstuk 3 en 5 Hoofdstuk 5 afstanden en hoeken Voorkennis Stelling van
 Samenvatting wiskunde havo 4 hoofdstuk 5,7,8 en vaardigheden 3 en 4 en havo 5 hoofdstuk 3 en 5 Hoofdstuk 5 afstanden en hoeken Stelling van Kan alleen bij rechthoekige driehoeken pythagoras a 2 + b 2 =
Samenvatting wiskunde havo 4 hoofdstuk 5,7,8 en vaardigheden 3 en 4 en havo 5 hoofdstuk 3 en 5 Hoofdstuk 5 afstanden en hoeken Stelling van Kan alleen bij rechthoekige driehoeken pythagoras a 2 + b 2 =
Krulgetallen en een heel langzaam stijgende rij. D. C. Gijswijt
 krulgetal.tex 11 oktober 2015 ²J1 Krulgetallen en een heel langzaam stijgende rij. D. C. Gijswijt Krulgetallen Bekijk eens het volgende rijtje: 2, 1, 2, 3, 2, 3, 1, 2, 3, 2, 3, 1, 2, 3, 2, 3. Dit rijtje
krulgetal.tex 11 oktober 2015 ²J1 Krulgetallen en een heel langzaam stijgende rij. D. C. Gijswijt Krulgetallen Bekijk eens het volgende rijtje: 2, 1, 2, 3, 2, 3, 1, 2, 3, 2, 3, 1, 2, 3, 2, 3. Dit rijtje
VAARDIGHEDEN EXCEL. MEETWAARDEN INVULLEN In de figuur hieronder zie je twee keer de ingevoerde meetwaarden, eerst ruw en daarna netjes opgemaakt.
 VAARDIGHEDEN EXCEL Excel is een programma met veel mogelijkheden om meetresultaten te verwerken, maar het was oorspronkelijk een programma voor boekhouders. Dat betekent dat we ons soms in bochten moeten
VAARDIGHEDEN EXCEL Excel is een programma met veel mogelijkheden om meetresultaten te verwerken, maar het was oorspronkelijk een programma voor boekhouders. Dat betekent dat we ons soms in bochten moeten
Functies van vectoren
 Functies van vectoren Alexander Ly Psychological Methods University of Amsterdam 15 September 2014 Overview 1 Notatie 2 Overview 1 Notatie 2 Matrices Een matrix schrijven we vaak met een hoofdletter A.
Functies van vectoren Alexander Ly Psychological Methods University of Amsterdam 15 September 2014 Overview 1 Notatie 2 Overview 1 Notatie 2 Matrices Een matrix schrijven we vaak met een hoofdletter A.
kun je op verschillende manieren opschrijven of uitspreken: XX Daarnaast kun je een breuk ook opschrijven als een decimaal getal.
 . Breuken Je kunt breuken gebruiken om een verhouding weer te geven. Een breuk schrijf je als een streepje met een getal erboven (de teller) en een getal eronder (de noemer), bijvoorbeeld. De streep zelf
. Breuken Je kunt breuken gebruiken om een verhouding weer te geven. Een breuk schrijf je als een streepje met een getal erboven (de teller) en een getal eronder (de noemer), bijvoorbeeld. De streep zelf
6 Modellen in de scheikunde
 In dit hoofdstuk komen modellen aan de orde die de vorming of verspreiding van chemische stoffen beschrijven. In "reactievergelijkingen" wordt een model opgesteld voor de vorming van stoffen bij een gegeven
In dit hoofdstuk komen modellen aan de orde die de vorming of verspreiding van chemische stoffen beschrijven. In "reactievergelijkingen" wordt een model opgesteld voor de vorming van stoffen bij een gegeven
Opgaven Functies en Reeksen. E.P. van den Ban
 Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Opgaven Functies en Reeksen E.P. van den Ban c Mathematisch Instituut Universiteit Utrecht Augustus 2014 1 Opgaven bij Hoofdstuk 1 Opgave 1.1 Zij f : R n R partieel differentieerbaar naar iedere variabele
Modulewijzer InfPbs00DT
 Modulewijzer InfPbs00DT W. Oele 0 juli 008 Inhoudsopgave Inleiding 3 Waarom wiskunde? 3. Efficiëntie van computerprogramma s............... 3. 3D-engines en vectoranalyse................... 3.3 Bewijsvoering
Modulewijzer InfPbs00DT W. Oele 0 juli 008 Inhoudsopgave Inleiding 3 Waarom wiskunde? 3. Efficiëntie van computerprogramma s............... 3. 3D-engines en vectoranalyse................... 3.3 Bewijsvoering
1.1 Lineaire vergelijkingen [1]
![1.1 Lineaire vergelijkingen [1] 1.1 Lineaire vergelijkingen [1]](/thumbs/62/47724253.jpg) 1.1 Lineaire vergelijkingen [1] Voorbeeld: Los de vergelijking 4x + 3 = 2x + 11 op. Om deze vergelijking op te lossen moet nu een x gevonden worden zodat 4x + 3 gelijk wordt aan 2x + 11. = x kg = 1 kg
1.1 Lineaire vergelijkingen [1] Voorbeeld: Los de vergelijking 4x + 3 = 2x + 11 op. Om deze vergelijking op te lossen moet nu een x gevonden worden zodat 4x + 3 gelijk wordt aan 2x + 11. = x kg = 1 kg
Hoofdstuk 3 : Determinanten
 (A5D) Hoofdstuk 3 : Determinanten Les : Determinanten Definitie 3. De determinant van de [2 x 2]-matrix A = ( a c det(a) = ad bc. b ) is een getal met waarde d a b Notatie : det(a) = = ad bc c d Voorbeeld
(A5D) Hoofdstuk 3 : Determinanten Les : Determinanten Definitie 3. De determinant van de [2 x 2]-matrix A = ( a c det(a) = ad bc. b ) is een getal met waarde d a b Notatie : det(a) = = ad bc c d Voorbeeld
9.1 Recursieve en directe formules [1]
![9.1 Recursieve en directe formules [1] 9.1 Recursieve en directe formules [1]](/thumbs/61/45664687.jpg) 9.1 Recursieve en directe formules [1] Voorbeeld: 8, 12, 16, 20, 24, is een getallenrij. De getallen in de rij zijn de termen. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is
9.1 Recursieve en directe formules [1] Voorbeeld: 8, 12, 16, 20, 24, is een getallenrij. De getallen in de rij zijn de termen. 8 is de eerste term (startwaarde, u 0 ) 12 is de tweede term (u 1 ) 24 is
Examencursus. wiskunde A. Rekenregels voor vereenvoudigen. Voorbereidende opgaven VWO kan niet korter
 Voorbereidende opgaven VWO Examencursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Voorbereidende opgaven VWO Examencursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
LOPUC. Een manier om problemen aan te pakken
 LOPUC Een manier om problemen aan te pakken LOPUC Lees de opgave goed, zodat je precies weet wat er gevraagd wordt. Zoek naar grootheden en eenheden. Schrijf de gegevens die je nodig denkt te hebben overzichtelijk
LOPUC Een manier om problemen aan te pakken LOPUC Lees de opgave goed, zodat je precies weet wat er gevraagd wordt. Zoek naar grootheden en eenheden. Schrijf de gegevens die je nodig denkt te hebben overzichtelijk
Combinatoriek en rekenregels
 Combinatoriek en rekenregels Les 2: Roosters en ongeordende grepen (deze les sluit aan bij de paragrafen 3 en 4 van Hoofdstuk 1 Combinatoriek en Rekenregels van de Wageningse Methode, http://www.wageningsemethode.nl/methode/het-lesmateriaal/?s=y456v-d)
Combinatoriek en rekenregels Les 2: Roosters en ongeordende grepen (deze les sluit aan bij de paragrafen 3 en 4 van Hoofdstuk 1 Combinatoriek en Rekenregels van de Wageningse Methode, http://www.wageningsemethode.nl/methode/het-lesmateriaal/?s=y456v-d)
3.0 Voorkennis. Voorbeeld 1: Los op: 6x + 28 = 30 10x.
 3.0 Voorkennis Voorbeeld 1: Los op: 6x + 28 = 30 10x. 6x + 28 = 30 10x +10x +10x 16x + 28 = 30-28 -28 16x = 2 :16 :16 x = 2 1 16 8 Stappenplan: 1) Zorg dat alles met x links van het = teken komt te staan;
3.0 Voorkennis Voorbeeld 1: Los op: 6x + 28 = 30 10x. 6x + 28 = 30 10x +10x +10x 16x + 28 = 30-28 -28 16x = 2 :16 :16 x = 2 1 16 8 Stappenplan: 1) Zorg dat alles met x links van het = teken komt te staan;
Stoomcursus. wiskunde A. Rekenregels voor vereenvoudigen. Voorbereidende opgaven VWO ( ) = = ( ) ( ) ( ) = ( ) ( ) = ( ) = = ( )
 Voorbereidende opgaven VWO Stoomcursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Voorbereidende opgaven VWO Stoomcursus wiskunde A Tips: Maak de voorbereidende opgaven voorin in een van de A4-schriften die je gaat gebruiken tijdens de cursus. Als een opdracht niet lukt, werk hem dan
Examen VWO. Wiskunde B Profi
 Wiskunde B Profi Eamen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Donderdag 25 mei 3.30 6.30 uur 20 00 Dit eamen bestaat uit 7 vragen. Voor elk vraagnummer is aangegeven hoeveel punten met een
Wiskunde B Profi Eamen VWO Voorbereidend Wetenschappelijk Onderwijs Tijdvak Donderdag 25 mei 3.30 6.30 uur 20 00 Dit eamen bestaat uit 7 vragen. Voor elk vraagnummer is aangegeven hoeveel punten met een
Utrecht, 25 november Numerieke Wiskunde. Gerard Sleijpen Department of Mathematics.
 Utrecht, 25 november 2014 Numerieke Wiskunde Gerard Sleijpen Department of Mathematics http://www.staff.science.uu.nl/ sleij101/ [a, b] R, : [a, b] R Benader f door eenvoudige functies Voorbeelden eenvoudige
Utrecht, 25 november 2014 Numerieke Wiskunde Gerard Sleijpen Department of Mathematics http://www.staff.science.uu.nl/ sleij101/ [a, b] R, : [a, b] R Benader f door eenvoudige functies Voorbeelden eenvoudige
Uitwerking tentamen Algoritmiek 10 juni :00 13:00
 Uitwerking tentamen Algoritmiek 10 juni 2014 10:00 13:00 1. Dominono s a. Toestanden: n x n bord met in elk hokje een O, een X of een -. Hierbij is het aantal X gelijk aan het aantal O of hooguit één hoger.
Uitwerking tentamen Algoritmiek 10 juni 2014 10:00 13:00 1. Dominono s a. Toestanden: n x n bord met in elk hokje een O, een X of een -. Hierbij is het aantal X gelijk aan het aantal O of hooguit één hoger.
Netwerkstroming. Algoritmiek
 Netwerkstroming Vandaag Netwerkstroming: definitie en toepassing Het rest-netwerk Verbeterende paden Ford-Fulkerson algoritme Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp Toepassing: koppelingen
Netwerkstroming Vandaag Netwerkstroming: definitie en toepassing Het rest-netwerk Verbeterende paden Ford-Fulkerson algoritme Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp Toepassing: koppelingen
Tentamen Lineaire Algebra 2
 Lineaire algebra (NP010B) januari 013 Tentamen Lineaire Algebra Vermeld op ieder blad je naam en studentnummer. Lees eerst de opgaven voordat je aan de slag gaat. Schrijf leesbaar en geef uitleg over je
Lineaire algebra (NP010B) januari 013 Tentamen Lineaire Algebra Vermeld op ieder blad je naam en studentnummer. Lees eerst de opgaven voordat je aan de slag gaat. Schrijf leesbaar en geef uitleg over je
Lineaire afbeeldingen
 Les 2 Lineaire afbeeldingen Als een robot bij de robocup (het voetbaltoernooi voor robots een doelpunt wil maken moet hij eerst in de goede positie komen, d.w.z. geschikt achter de bal staan. Hiervoor
Les 2 Lineaire afbeeldingen Als een robot bij de robocup (het voetbaltoernooi voor robots een doelpunt wil maken moet hij eerst in de goede positie komen, d.w.z. geschikt achter de bal staan. Hiervoor
eerste en laatste cijfers Jaap Top
 eerste en laatste cijfers Jaap Top JBI-RuG & DIAMANT j.top@rug.nl 3-10 april 2013 (Collegecarrousel, Groningen) 1 laatste, eerste?! over getallen 2,..., 101,..., 2014,...... laatste cijfers hiervan: 2,...,
eerste en laatste cijfers Jaap Top JBI-RuG & DIAMANT j.top@rug.nl 3-10 april 2013 (Collegecarrousel, Groningen) 1 laatste, eerste?! over getallen 2,..., 101,..., 2014,...... laatste cijfers hiervan: 2,...,
Hebzucht loont niet altijd
 Thema Discrete wiskunde Hoe verbind je een stel steden met zo weinig mogelijk kilometers asfalt? Hoe maak je een optimaal computernetwerk met kabels die maar een beperkte capaciteit hebben? Veel van zulke
Thema Discrete wiskunde Hoe verbind je een stel steden met zo weinig mogelijk kilometers asfalt? Hoe maak je een optimaal computernetwerk met kabels die maar een beperkte capaciteit hebben? Veel van zulke
Meetkunde en lineaire algebra
 Meetkunde en lineaire algebra Daan Pape Universiteit Gent 7 juni 2012 1 1 Möbius transformaties De mobiustransformatie wordt gegeven door: z az + b cz + d (1) Als we weten dat het drietal (x 1, x 2, x
Meetkunde en lineaire algebra Daan Pape Universiteit Gent 7 juni 2012 1 1 Möbius transformaties De mobiustransformatie wordt gegeven door: z az + b cz + d (1) Als we weten dat het drietal (x 1, x 2, x
Hertentamen Voortgezette biostatistiek / Biomedische wiskunde
 Hertentamen Voortgezette biostatistiek / Biomedische wiskunde 3 juni 5; 8:3-:3 NB. Geef een duidelijke toelichting bij de antwoorden. Na correctie liggen de tentamens ter inzage bij het onderwijsbureau.
Hertentamen Voortgezette biostatistiek / Biomedische wiskunde 3 juni 5; 8:3-:3 NB. Geef een duidelijke toelichting bij de antwoorden. Na correctie liggen de tentamens ter inzage bij het onderwijsbureau.
Examen VWO 2015. wiskunde C. tijdvak 2 woensdag 17 juni 13.30-16.30 uur. Bij dit examen hoort een uitwerkbijlage.
 Examen VWO 2015 tijdvak 2 woensdag 17 juni 13.30-16.30 uur wiskunde C Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 22 vragen. Voor dit examen zijn maximaal 79 punten te behalen. Voor
Examen VWO 2015 tijdvak 2 woensdag 17 juni 13.30-16.30 uur wiskunde C Bij dit examen hoort een uitwerkbijlage. Dit examen bestaat uit 22 vragen. Voor dit examen zijn maximaal 79 punten te behalen. Voor
Practicum hoogtemeting 3 e klas havo/vwo
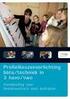 Deel (benaderbaar object) Om de hoogte van een bepaald object te berekenen hebben we geleerd dat je dat kunt doen als je in staat bent om een rechthoekige driehoek te bedenken waarvan je één zijde kunt
Deel (benaderbaar object) Om de hoogte van een bepaald object te berekenen hebben we geleerd dat je dat kunt doen als je in staat bent om een rechthoekige driehoek te bedenken waarvan je één zijde kunt
Linalg.nb 1. Werk het notebook aandachtig door en maak de (genummerde) oefeningen aan het einde van elke sectie. Succes!
 Linalg.nb Lineaire Algebra Andr Heck AMSTEL Instituut, Universiteit van Amsterdam Werk het notebook aandachtig door en maak de (genummerde) oefeningen aan het einde van elke sectie. Succes! Å Introductie
Linalg.nb Lineaire Algebra Andr Heck AMSTEL Instituut, Universiteit van Amsterdam Werk het notebook aandachtig door en maak de (genummerde) oefeningen aan het einde van elke sectie. Succes! Å Introductie
Tentamen Numerieke Wiskunde dinsdag, 28 januari 2014,
 Tentamen Numerieke Wiskunde dinsdag, 8 januari 04, 3.30 6.30. Zet op ieder vel dat je inlevert je naam en op et eerste vel bovendien nog je studentnummer.. Je mag et dictaat gebruiken, de uitwerkingen
Tentamen Numerieke Wiskunde dinsdag, 8 januari 04, 3.30 6.30. Zet op ieder vel dat je inlevert je naam en op et eerste vel bovendien nog je studentnummer.. Je mag et dictaat gebruiken, de uitwerkingen
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN
 TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D2. Datum: dinsdag 29 april 28. Tijd: 14: 17:. Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je naam en studentnummer
TENTAMEN WISKUNDIGE BEELDVERWERKINGSTECHNIEKEN Vakcode: 8D2. Datum: dinsdag 29 april 28. Tijd: 14: 17:. Lees dit vóórdat je begint! Maak iedere opgave op een apart vel. Schrijf je naam en studentnummer
6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen:
![6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen: 6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen:](/thumbs/101/148944451.jpg) 6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen: 1) Haakjes wegwerken 2) Vermenigvuldigen en delen van links naar rechts 3) Optellen en aftrekken van links naar rechts Schrijf ALLE stappen ONDER
6.1 Kwadraten [1] HERHALING: Volgorde bij berekeningen: 1) Haakjes wegwerken 2) Vermenigvuldigen en delen van links naar rechts 3) Optellen en aftrekken van links naar rechts Schrijf ALLE stappen ONDER
Opgaven Getaltheorie en Cryptografie (deel 4) Inleverdatum: 13 mei 2002
 Opgaven Getaltheorie en Cryptografie (deel 4) Inleverdatum: 13 mei 2002 19.a) Laat zien dat 5 een voortbrenger is van F 37. b) In het sleuteldistributiesysteem van Diffie en Hellman (met G = F 37, α =
Opgaven Getaltheorie en Cryptografie (deel 4) Inleverdatum: 13 mei 2002 19.a) Laat zien dat 5 een voortbrenger is van F 37. b) In het sleuteldistributiesysteem van Diffie en Hellman (met G = F 37, α =
Workshop DisWis, De Start 13/06/2007 Bladzijde 1 van 7. Sudoku. Sudoku
 DisWis DisWis is een lessenserie discrete wiskunde die De Praktijk vorig jaar in samenwerking met prof.dr. Alexander Schrijver heeft opgezet. Gedurende vier weken komt een wiskundestudent twee blokuren
DisWis DisWis is een lessenserie discrete wiskunde die De Praktijk vorig jaar in samenwerking met prof.dr. Alexander Schrijver heeft opgezet. Gedurende vier weken komt een wiskundestudent twee blokuren
