Hoofdstuk 5 Oneigenlijke integralen
|
|
|
- Hilde de Valk
- 8 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Anlys Plus rdr Hoofdsuk 5 Hoofdsuk 5 Onignlijk ingrln Inhoud Hoofdsuk 5 Onignlijk ingrln Inliding Ni grnsd ingri-inrvlln Disconinu o h ingri-inrvl Gmngd ogvn Hogschool Rordm 4 Lrrnoliding Wiskund
2 Anlys Plus rdr Hoofdsuk 5 5. Inliding. W kijkn d ingrl - 4 d. Als w, zondr ons f vrgn of h ignlijk mg, d ingrl gn rknn vindn h volgnd nwoord: é ù d= 4 ê- ú =- - =- - ë û H nwoord is ngif. - D is vrmd, wn d grfik vn f ( ) = lig in zijn ghl ovn d -s n kn dus ni 4 ngif zijn. H rolm is d h ingri-inrvl ni volldig gdfinird is o h domin vn f. D grfik vn f v nmlijk n vricl symoo voor =. En disconinuïi o n ingri-inrvl is n voorld vn n onignlijk ingrl. To nu o hn w ingrln f ( )d rknd, wrij f n coninu funci is o h grnsd inrvl [ ],. In di hoofdsuk gn w kijkn nr ingrln wrvn h ingriinrvl ni grnsd is n/of d ingrn disconinu is o h ingri-inrvl. Hogschool Rordm 4 Lrrnoliding Wiskund
3 Anlys Plus rdr Hoofdsuk 5 5. Ni grnsd ingri-inrvlln. In dz rgrf kijkn w nr ingrln di gn rciz ondr- n/of ovngrns knnn. W kunnn dri gvlln ondrschidn:. En ni-grnsd ovngrns: ingri-inrvl =[,. En ni-grnsd ondrgrns: ingri-inrvl =,]. En ni-grnsd ondr- n ovngrns: ingri-inrvl = In gvl rknn w d ingrl f ( )d= lim f ( )d In gvl rknn w d ingrl f ( )d= lim f ( )d - - In gvl rknn w d ingrl f ( )d= lim f ( )d+ lim f ( )d c s - s c wrij c n willkurig gkozn gl is. Msl word hir gkozn. Als d limin sn dn zl d onignlijk ingrl convrgrn nr d limiwrd (in gvl convrgr d ingrl nr d som vn d limiwrdn). Als n limi ni s, dn zl d ingrl divrgrn. Voorld Brkn, indin moglijk Olossing: - d d= lim d= limé ë- ù û = lim( - -- ) = + = Voorld Brkn, indin moglijk d - - Olossing: - ( ) d= lim - d= lim - - = lim = ë û - - ( ) é ( ) ù ( ) D limi s ni, dus d ingrl divrgr. Hogschool Rordm 4 Lrrnoliding Wiskund
4 Anlys Plus rdr Hoofdsuk 5 Sommig limin zijn ni gmkklijk rknn. J kun dn gruik mkn vn d insluislling of sndrdlimin (zi Anlys: Rijn n limin). J mg zondr wijs gruik mkn vn: (hirij zijn n k consns) lim = m k³ k lim = m > k lim = m > æ ö limç + = m Î R è ø ln( k) lim = m k > k Ogv Brkn indin moglijk d volgnd ingrln. -. d - -. d - + c. d d. ln(8) d. f. - - d - d Hogschool Rordm 4 Lrrnoliding Wiskund
5 Anlys Plus rdr Hoofdsuk 5 5. Disconinu o h ingri-inrvl En grfik kn o n inrvl [, ] o w vrschillnd mnirn disconinu zijn. Er kn zich nmlijk n vricl symoo o h inrvl vindn of n srong. In d figuur hirns kun j zin d in gvl vn n srong j h ingri-inrvl nvoudig kun odln. D ol ingrl is dn glijk n d som vn d w dl-ingrln. W zulln ons drom lln rkn o d ingrln wro zich n symoo o h ingri-inrvl vind. In h gvl vn d vricl symoo kunnn w vir siuis ondrschidn. Siui : D symoo vind zich in d ovngrns. ( ) d= lim f f ( ) d Siui : D symoo vind zich in d ondrgrns. f ( ) d= lim f ( ) d Siui : D ingrn hf n symoo in zowl d ondr- ls ovngrns. ) d= lim f ( ) d+ c f ( lim f ( ) d m < c< c Siui 4: D symoo vind zich in = d m < d<. d f ( ) d= lim f ( ) d+ lim f ( ) d d d Als d limin sn dn convrgr d ingrl nr d limiwrd in gvl n. In d gvlln n 4 convrgr d ingrl nr d som vn d limiwrdn. Voorld Brkn, indin moglijk d. Olossing D funci f ( ) = hf n vricl symoo in =, vrdr is d funci coninu voor osiiv wrdn vn. d= lim d = lim [ ] = lim( - ) = Hogschool Rordm 44 Lrrnoliding Wiskund
6 Anlys Plus rdr Hoofdsuk 5 Ook ij dz ingrln is r n nl sndrdlimin inzr: sin lim = n lim = - lim = ln( + ) lim = lim lim ln( ) = m Î, wrij n consn voorsl. + - = m Î + Voorld Brkn, indin moglijk ( + ) Olossing: ln( ) d æ ö ç è ø ( + ln( )) d = d + lim ln( )d [ ] lim [ ln( )] d = + - = [ ] - lim[ ln( ) ] -[ ] = lim( ln( )- ln( ) ) = - = Voorld W rkn nogmls d ingrl ui d inliding: - 4 d. Olossing: - 4 d = lim d + lim d = limé ë- ù û + limé ë- ù û æ = lim ç- è -+ ö æ + lim ç- ø è - ö =+ (mrk o d ngif is) ø D ingrl divrgr. Hogschool Rordm 45 Lrrnoliding Wiskund
7 Anlys Plus rdr Hoofdsuk 5 Ogv Brkn, indin moglijk d volgnd ingrln 4. d d. 4 d f d c. d g. ln - d d. - d h. - d - Ogv - + Bschouw d funci f ( ) =. Zi ook d grfik hirns. W gn d orvlk ondr d grfik vn f rknn o h inrvl - ln(),ln(). [ ]. Dl rs d grokn funci ui n hrschrijf f().. Brkn d door slchs ml gruik mkn vn ril ingri. Kijk god nr d ingrl di j ovrhoud. c. Gruik h rsul vn om d gvrgd orvlk c rknn. d. Wrom vind j hzlfd nwoord ls j gn limi gruik? Hogschool Rordm 46 Lrrnoliding Wiskund
8 Anlys Plus rdr Hoofdsuk 5 5. Gmngd ogvn Bij d volgnd ogvn wordn d vrschillnd chnikn door lkr gvrgd. Ogv 4 Primiivr d volgnd funcis:. f ( ) = n() 6-. g ( ) = -6 c. h( ) = ln(5- ) d.. f. g. ln (5- ) k ( ) = l( ) = 8 m ( ) = 9- (+ 5) sin n( ) = cos h. ( ) = sin (i: gruik ml susiui n dn ril) Ogv 5 Brkn c, indin moglijk.. + 9d. sin cos d c. d. - ln( ) d d 5-. d æ n n f. d ö ç - + è ø i: Gruik ogv Hogschool Rordm 47 Lrrnoliding Wiskund
Analyse Plus reader Hoofdstuk 5. Als we, zonder ons af te vragen of het eigenlijk mag, de integraal gaan berekenen vinden het volgende antwoord:
 5. Inleiding. We ekijken de inegrl - 4 d. Als we, zonder ons f e vrgen of he eigenlijk mg, de inegrl gn erekenen vinden he volgende nwoord: é ù d= ê- ú =- - =- 4 - ë û- He nwoord is negief. D is vreemd,
5. Inleiding. We ekijken de inegrl - 4 d. Als we, zonder ons f e vrgen of he eigenlijk mg, de inegrl gn erekenen vinden he volgende nwoord: é ù d= ê- ú =- - =- 4 - ë û- He nwoord is negief. D is vreemd,
Integralen. onbepaalde integralen. oneigenlijke integralen. gemiddelde functiewaarde op een interval
 Intgrln onld intgrln onignlijk intgrln gmiddld funtiwrd o n intrvl Onld intgrl En onld intgrl wordt ogshrvn ls: f ( d ) wrin f() n willkurig funti is. En r gldt: f ( d ) = F( ) + Wrij F() d rimitiv funti
Intgrln onld intgrln onignlijk intgrln gmiddld funtiwrd o n intrvl Onld intgrl En onld intgrl wordt ogshrvn ls: f ( d ) wrin f() n willkurig funti is. En r gldt: f ( d ) = F( ) + Wrij F() d rimitiv funti
Gelijknamige breuken kun je eenvoudig bij elkaar optellen of van elkaar aftrekken:
 Brukn optlln n ftrkkn Vrknnn Opgv 1 Ton n Hns stlln smn n grot pizz. Ton t d hlft vn d pizz op, Hns t 3 dl vn d pizz. 8 Wlk dl vn d pizz tn z smn op? Wlk dl vn d pizz t Ton mr op dn Hns? nm: Imgs/R1003.jpg
Brukn optlln n ftrkkn Vrknnn Opgv 1 Ton n Hns stlln smn n grot pizz. Ton t d hlft vn d pizz op, Hns t 3 dl vn d pizz. 8 Wlk dl vn d pizz tn z smn op? Wlk dl vn d pizz t Ton mr op dn Hns? nm: Imgs/R1003.jpg
Toegepaste Wiskunde deel 1
 Togpas Wiskund dl Era opgavn hoofdsuk Limin n diffrniaalrkning. H ibgrip n. H brknn van in. Ggvn d funci m voorschrif f( ). Bpaal f( ) n f( ). Wa bkn di voor d grafik van.. Brkn, indin moglijk, d volgnd
Togpas Wiskund dl Era opgavn hoofdsuk Limin n diffrniaalrkning. H ibgrip n. H brknn van in. Ggvn d funci m voorschrif f( ). Bpaal f( ) n f( ). Wa bkn di voor d grafik van.. Brkn, indin moglijk, d volgnd
Machten. Inhoud Machten
 Mchtn Inhoud Mchtn Mchtn n mchtsvrhffn Evn n onvn mchtn Vrmnigvuldign vn mchtn Dln vn mchtn Mcht vn n mcht Mchtn vn productn 7 Mchtn vn rukn Sustiturn vrvngn vn n lttr door n gtl Wortls n mchtn mt grokn
Mchtn Inhoud Mchtn Mchtn n mchtsvrhffn Evn n onvn mchtn Vrmnigvuldign vn mchtn Dln vn mchtn Mcht vn n mcht Mchtn vn productn 7 Mchtn vn rukn Sustiturn vrvngn vn n lttr door n gtl Wortls n mchtn mt grokn
In figuur 5-1 zie je een afbeelding van de snelheidsmeter en de kilometerteller van een nieuwe auto.
 Opgvn Vrkr In ht vrkr spln snlhi n krht n lngrijk rol. W zulln topssingn kijkn wrij voorl ook vilighi in ht vrkr n o zl komn. Opgv 1 In figuur 5-1 zi j n fling vn snlhismtr n kilomtrtllr vn n niuw uto.
Opgvn Vrkr In ht vrkr spln snlhi n krht n lngrijk rol. W zulln topssingn kijkn wrij voorl ook vilighi in ht vrkr n o zl komn. Opgv 1 In figuur 5-1 zi j n fling vn snlhismtr n kilomtrtllr vn n niuw uto.
Opleidingsplan. : Almelo, De Sumpel
 Oplidingsplan Opliding : ICT- n mdiabhr Crbo opliding : 95320 Uisroomdiffrniais : Nwrkbhrdr Crbo uisroom 95323 Cohor : 2014-2016 Nivau : 4 Lrwg : BBL Locai : Almlo, D Sumpl Ho zi j opliding rui Algmn oplidingsggvns
Oplidingsplan Opliding : ICT- n mdiabhr Crbo opliding : 95320 Uisroomdiffrniais : Nwrkbhrdr Crbo uisroom 95323 Cohor : 2014-2016 Nivau : 4 Lrwg : BBL Locai : Almlo, D Sumpl Ho zi j opliding rui Algmn oplidingsggvns
4.3. Toepassingen van logaritmische en exponentiële functies
 4.3. Topassingn van logaritmisch n ponntiël functis 4.3.. Limitn van logaritmisch n ponntiël functis Voorbld : a b a b H lna a lna lnb b lnb b log a Voorbld : Dit is n niuw onbpaald vorm! W wtn wl dat
4.3. Topassingn van logaritmisch n ponntiël functis 4.3.. Limitn van logaritmisch n ponntiël functis Voorbld : a b a b H lna a lna lnb b lnb b log a Voorbld : Dit is n niuw onbpaald vorm! W wtn wl dat
Opleidingsplan. : Almelo, De Sumpel
 Oplidingsplan Opliding : ICT- n mdiabhr Crbo opliding : 95320 Uisroomdiffrniais : ICT-bhrdr Crbo uisroom 95321 Cohor : 2014-2016 Nivau : 4 Lrwg : BBL Locai : Almlo, D Sumpl Ho zi j opliding rui Algmn oplidingsggvns
Oplidingsplan Opliding : ICT- n mdiabhr Crbo opliding : 95320 Uisroomdiffrniais : ICT-bhrdr Crbo uisroom 95321 Cohor : 2014-2016 Nivau : 4 Lrwg : BBL Locai : Almlo, D Sumpl Ho zi j opliding rui Algmn oplidingsggvns
NEVAC examen Elementaire Vacuümtechniek Vrijdag 11 april 2003, 14:00-16:30 uur. Vraagstuk 1 (EV-03-1) (25 punten)
 NEVAC xmn Elmntir Vuümthnik Vrijg 11 pril 2003, 14:00-16:30 uur Vrgstuk 1 (EV-03-1) (25 puntn) En vuümsystm wort gëvur mt n olivrij pompsystm, t stt uit n voorvuümpomp n n turomolulirpomp. D pompsnlhi
NEVAC xmn Elmntir Vuümthnik Vrijg 11 pril 2003, 14:00-16:30 uur Vrgstuk 1 (EV-03-1) (25 puntn) En vuümsystm wort gëvur mt n olivrij pompsystm, t stt uit n voorvuümpomp n n turomolulirpomp. D pompsnlhi
Hoofdstuk 6 - Differentiaalvergelijkingen oplossen
 Hoofsuk 6 - Diffrniaalvrglijkingn oplossn 6 Shin van varialn lazij a, 5 (, 5) us (, 5 ), 5 us volo D kromm gaa oor (0, ) us, 5, 5 0, 5, klop H onrs l van kromm vanaf pun (, 5; 0 ) a Als j a iffrnir, an
Hoofsuk 6 - Diffrniaalvrglijkingn oplossn 6 Shin van varialn lazij a, 5 (, 5) us (, 5 ), 5 us volo D kromm gaa oor (0, ) us, 5, 5 0, 5, klop H onrs l van kromm vanaf pun (, 5; 0 ) a Als j a iffrnir, an
Hoofdstuk 9: Exponentiële en logaritmische functies. 9.1 Logaritmische en exponentiële vergelijkingen. Opgave 1: a. y2 b. y2 c. y1. Opgave 2: c.
 Hoodstk 9: Eonntiël n ritmisch nctis 9. Logritmisch n onntiël vrglijkingn Ogv :. y n y b. y n y c. y n y Ogv :. 6 6 b. 6 c. 9 d. 8 8 7. 6 6 6 6. Ogv :. 6 8 b. 8 8 c. d. 9. 6 8 6 7 7. Ogv :. 6 9 b. c. 7
Hoodstk 9: Eonntiël n ritmisch nctis 9. Logritmisch n onntiël vrglijkingn Ogv :. y n y b. y n y c. y n y Ogv :. 6 6 b. 6 c. 9 d. 8 8 7. 6 6 6 6. Ogv :. 6 8 b. 8 8 c. d. 9. 6 8 6 7 7. Ogv :. 6 9 b. c. 7
Christmas time 2.0! Lesbrief
 Lsbrif Christms tim 2.0! En updt vn ht succsvoll Tumult krstspl vn vorig jr. In smnwrking mt Musicbox is d muzikrond nu n krstmuzikquiz gwordn di j klssikl ls fsluiting vn ht spl dot: vl plzir n lvst hl
Lsbrif Christms tim 2.0! En updt vn ht succsvoll Tumult krstspl vn vorig jr. In smnwrking mt Musicbox is d muzikrond nu n krstmuzikquiz gwordn di j klssikl ls fsluiting vn ht spl dot: vl plzir n lvst hl
Ajodakt Hoofdrekenen groep 5-6
 Ajokt Hoofrknn grop - Dln t/m 0 n hogr, mt n zonr rst Colofon ũžěăŭƚ ŵăăŭƚ ĚĞĞů Ƶŝƚ ǀĂŶ ŚŝĞŵĞDĞƵůĞŶŚŽī ĞůĨƐƚĂŶĚŝŐ ǁĞƌŬĞŶ ŝƚ ďğɛƚăăƚ Ƶŝƚ ĞĞŶ ŐƌŽŽƚ ĂƐƐŽƌƟ ŵğŷƚ ůğğƌŵŝěěğůğŷ ǀŽŽƌ ĂůůĞ ůğğƌũăƌğŷ Op onz Z-sit
Ajokt Hoofrknn grop - Dln t/m 0 n hogr, mt n zonr rst Colofon ũžěăŭƚ ŵăăŭƚ ĚĞĞů Ƶŝƚ ǀĂŶ ŚŝĞŵĞDĞƵůĞŶŚŽī ĞůĨƐƚĂŶĚŝŐ ǁĞƌŬĞŶ ŝƚ ďğɛƚăăƚ Ƶŝƚ ĞĞŶ ŐƌŽŽƚ ĂƐƐŽƌƟ ŵğŷƚ ůğğƌŵŝěěğůğŷ ǀŽŽƌ ĂůůĞ ůğğƌũăƌğŷ Op onz Z-sit
Eindexamen wiskunde B1 vwo 2008-I
 Eindamn wiskund B vwo 008-I Boordlingsmodl Vraag Antwoord Scors Landing maimumscor 4 y' 4,8 0 3 + 4,8 0 5 y '(0) 0 (dus in (0, 8) hft ht vligtuig n horizontal bwgingsrichting) y '(00) 0,48+ 0,48 0 (dus
Eindamn wiskund B vwo 008-I Boordlingsmodl Vraag Antwoord Scors Landing maimumscor 4 y' 4,8 0 3 + 4,8 0 5 y '(0) 0 (dus in (0, 8) hft ht vligtuig n horizontal bwgingsrichting) y '(00) 0,48+ 0,48 0 (dus
Examen VWO. wiskunde B. tijdvak 2 woensdag 20 juni uur
 Emen VW 018 ijdvk woensdg 0 juni 1.0-16.0 uur wiskunde B Di emen bes ui 16 vrgen. Voor di emen zijn miml 77 punen e behlen. Voor elk vrgnummer s hoeveel punen me een goed nwoord behld kunnen worden. Als
Emen VW 018 ijdvk woensdg 0 juni 1.0-16.0 uur wiskunde B Di emen bes ui 16 vrgen. Voor di emen zijn miml 77 punen e behlen. Voor elk vrgnummer s hoeveel punen me een goed nwoord behld kunnen worden. Als
Uitwerkingen H9 van vwo B deel 3 Exponentiële functies en logaritmische functies
 Uitwrkingn H9 van vwo B dl Eponntiël functis n logaritmisch functis. y log( + 5) y log() + log (5) n y log (5) Uit d tabl blijkt dat y n y htzlfd zijn. log() + log(5) log(5) Vor in : y log( 5) ; y log()
Uitwrkingn H9 van vwo B dl Eponntiël functis n logaritmisch functis. y log( + 5) y log() + log (5) n y log (5) Uit d tabl blijkt dat y n y htzlfd zijn. log() + log(5) log(5) Vor in : y log( 5) ; y log()
Bij de toepassing van de in paraplubestemmingsplan bedoelde ontheffing wordt verstaan onder:
 HOOFDSTUK 2. REGELS PARAGRAAF 1 TOEPASSINGSREGELS Artikl 1 Topssingsrik Inin nit op gron vn nr plingn vn in ijlg 1 gnom stmmingsplnnn vrijstlling/onthffing kn worn vrln zijn urgmstr n wthours vog onthffing
HOOFDSTUK 2. REGELS PARAGRAAF 1 TOEPASSINGSREGELS Artikl 1 Topssingsrik Inin nit op gron vn nr plingn vn in ijlg 1 gnom stmmingsplnnn vrijstlling/onthffing kn worn vrln zijn urgmstr n wthours vog onthffing
Examen VWO. wiskunde B. tijdvak 2 woensdag 20 juni uur
 Emen VW 018 ijdvk woensdg 0 juni 1.0-16.0 uur wiskunde B Di emen bes ui 16 vrgen. Voor di emen zijn miml 77 punen e behlen. Voor elk vrgnummer s hoeveel punen me een goed nwoord behld kunnen worden. Als
Emen VW 018 ijdvk woensdg 0 juni 1.0-16.0 uur wiskunde B Di emen bes ui 16 vrgen. Voor di emen zijn miml 77 punen e behlen. Voor elk vrgnummer s hoeveel punen me een goed nwoord behld kunnen worden. Als
Sports Center. 22 juni 2011
 Titl procs: Klachtnblid Tilburg Univrsity Procsignaar: Ing Schprs Paraaf kwalititsfunctionaris Vrsi nr.: 2 Bsprokn mt: M.T. d.d. 13 april 2011 Vastgstld in M.T. d.d. 22 juni 2011 Pndragon d.d. 10 aug.
Titl procs: Klachtnblid Tilburg Univrsity Procsignaar: Ing Schprs Paraaf kwalititsfunctionaris Vrsi nr.: 2 Bsprokn mt: M.T. d.d. 13 april 2011 Vastgstld in M.T. d.d. 22 juni 2011 Pndragon d.d. 10 aug.
Voorbereiding toelatingsexamen arts/tandarts. Wiskunde: integralen en afgeleiden. 16 september dr. Brenda Casteleyn
 Voorbriding tolatingsamn arts/tandarts Wiskund: intgraln n afglidn 16 sptmbr 017 dr. Brnda Castlyn Mt dank aan: Athnum van Vurn Ln Goyns (http://usrs.tlnt.b/tolating) 1. Inliding Dit ofningnovrzicht is
Voorbriding tolatingsamn arts/tandarts Wiskund: intgraln n afglidn 16 sptmbr 017 dr. Brnda Castlyn Mt dank aan: Athnum van Vurn Ln Goyns (http://usrs.tlnt.b/tolating) 1. Inliding Dit ofningnovrzicht is
Hoofdstuk 7 - DM Toepassingen
 Hoofdsuk 7 - DM Toepssingen ldzijde 7 Vul in op je rekenmhine nmin 0, u(n)0+0,u(n-) en u(nmin). Vul ook in (n) 0+0,(n-) en (nmin)0. Neem Xmin 0, Xm 0, Ymin 0 en Ym 0. Bij een openingskoers n euro krijg
Hoofdsuk 7 - DM Toepssingen ldzijde 7 Vul in op je rekenmhine nmin 0, u(n)0+0,u(n-) en u(nmin). Vul ook in (n) 0+0,(n-) en (nmin)0. Neem Xmin 0, Xm 0, Ymin 0 en Ym 0. Bij een openingskoers n euro krijg
Derde editie. Tweede Fase. du français garan
 r z j i w mthod Drd diti Twd Fas aîtris m n n o b n U! d D accor ti! du français garan Drd diti Twd Fas lrn voor d praktijk én succs op d xamns. Mt d niuw, drd diti van wrkn lrlingn daar nog dolgrichtr
r z j i w mthod Drd diti Twd Fas aîtris m n n o b n U! d D accor ti! du français garan Drd diti Twd Fas lrn voor d praktijk én succs op d xamns. Mt d niuw, drd diti van wrkn lrlingn daar nog dolgrichtr
LEERJAAR 3 MUZISCHE VORMING
 VOORBEELDMATERIAAL HOEKENBOX LEERJAAR 3 MUZISCHE VORMING P. 02-03 Bldopvoding STOELEN D lrlingn ontwrpn n stol voor n figuur uit n sprookj. P. 04-05 Dramatisch Spl TABLEAU VIVANT mt KEITH HARING D lrlingn
VOORBEELDMATERIAAL HOEKENBOX LEERJAAR 3 MUZISCHE VORMING P. 02-03 Bldopvoding STOELEN D lrlingn ontwrpn n stol voor n figuur uit n sprookj. P. 04-05 Dramatisch Spl TABLEAU VIVANT mt KEITH HARING D lrlingn
Uitwerkingen extra opgaven hoofdstuk 5 Functieonderzoek: toepassing van de differentiaalrekening ( ) ( )( ) ( ) ( )( )
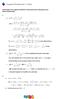 Uitwrkingn tra opgavn hoofdstuk 5 Functiondrzok: topassing van d diffrntiaalrkning. a. g( ) ( ) - 4 = Þ + - 6 ( + - 6) - ( - 4)( + ) ( + - 6) + - - ( - 8 + - 4) ( + - 6) g = = = = ( + )( - ) ( - ) ( +
Uitwrkingn tra opgavn hoofdstuk 5 Functiondrzok: topassing van d diffrntiaalrkning. a. g( ) ( ) - 4 = Þ + - 6 ( + - 6) - ( - 4)( + ) ( + - 6) + - - ( - 8 + - 4) ( + - 6) g = = = = ( + )( - ) ( - ) ( +
Kennismaking met Photoshop
 Hoofdstuk Knnismaking mt Photoshop Hoofdstuk, ht bgin van onz boind tocht doorhn Photoshop. Waarschijnlijk was j tot nu to gwoon om mt programma s van Microsoft t wrkn. Z hbbn allmaal n zlfd look n fl.
Hoofdstuk Knnismaking mt Photoshop Hoofdstuk, ht bgin van onz boind tocht doorhn Photoshop. Waarschijnlijk was j tot nu to gwoon om mt programma s van Microsoft t wrkn. Z hbbn allmaal n zlfd look n fl.
VOORBEELDEN TOELATINGSONDERZOEK WISKUNDE
 VOORBEELDEN TOELATINGSONDERZOEK WISKUNDE MET UITWERKINGEN Omrkingn H gbruik van n zakrknmachin vnul m grafich, maar zondr mbolich rknmoglijkhdn i ogaan Mn din alijd d anwoordn volldig o lichn n d unan
VOORBEELDEN TOELATINGSONDERZOEK WISKUNDE MET UITWERKINGEN Omrkingn H gbruik van n zakrknmachin vnul m grafich, maar zondr mbolich rknmoglijkhdn i ogaan Mn din alijd d anwoordn volldig o lichn n d unan
5. Exponentiële en logaritmische functies.
 uitwrkingn ponntiël n logritmish funtis Vrvoort Bokn,,,9 : fgron,,, : :,, fgron t, 9,9, : : 9,9 fgron t,,,,,,,9,,,,, 9 9 9 Uitwrkingn hoofstuk. Eponntiël n logritmish funtis. Opgv. Bsisrkningn mt logritmn,
uitwrkingn ponntiël n logritmish funtis Vrvoort Bokn,,,9 : fgron,,, : :,, fgron t, 9,9, : : 9,9 fgron t,,,,,,,9,,,,, 9 9 9 Uitwrkingn hoofstuk. Eponntiël n logritmish funtis. Opgv. Bsisrkningn mt logritmn,
In de wijk Zesgehuchten in Geldrop, dichtbij het centrum en station komen 6 starterswoningen vanaf 169.900 v.o.n.! Hoog tijd voor je eigen huis
 In d wijk Zshuchn in ldrp, dichbij h cnrum n sin kmn 6 srrswninn vnf 169.900 v..n.! H ijd vr j in huis Mirl 3 km Eindhvn 2 km Eindh vnsw sw irl M wnd l Cnrum (Winkls & Hrc) S r sr in dij k iv ld S. Ann
In d wijk Zshuchn in ldrp, dichbij h cnrum n sin kmn 6 srrswninn vnf 169.900 v..n.! H ijd vr j in huis Mirl 3 km Eindhvn 2 km Eindh vnsw sw irl M wnd l Cnrum (Winkls & Hrc) S r sr in dij k iv ld S. Ann
F G H I J. 5480
 () Nm : Kls: Dtum: A. 06 Uit ln + ln( ) = ln volgt dt gelijk is n ) ) ) ) ) g.v.d.v. B. 77 + b ) b ) (+ is gelijk n b ) ) b) ).b b F. 7 kn ook geschreven worden ls ) e ) e ) e ( ) ln e ) ) e G. 7 9 Als
() Nm : Kls: Dtum: A. 06 Uit ln + ln( ) = ln volgt dt gelijk is n ) ) ) ) ) g.v.d.v. B. 77 + b ) b ) (+ is gelijk n b ) ) b) ).b b F. 7 kn ook geschreven worden ls ) e ) e ) e ( ) ln e ) ) e G. 7 9 Als
Verdeling van personen volgens rijbewijsbezit
 2 Rijbwijsbzit Tabl. Vrdling van prsonn volgns rijbwijsbzit Cumulativ Cumulativ RYBEWYS Frquncy Prcnt Frquncy Prcnt ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ ja 50.3 67.7 50.3 67.7 nn 243.739
2 Rijbwijsbzit Tabl. Vrdling van prsonn volgns rijbwijsbzit Cumulativ Cumulativ RYBEWYS Frquncy Prcnt Frquncy Prcnt ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ ja 50.3 67.7 50.3 67.7 nn 243.739
Extra oefening hoofdstuk 1
 Etra ofning hoofdstuk = ( ) = = v v v dr 7 7 7 v a = + v als v 7 v v dus als = 7 7 7 7 dv waaruit volgt dat v = 7 km/uur. v = 7 gft R = 7, 7 mg/min. a f ' = = ' = + = ( + ) ' = = ( ) = f f d f ' ln ln
Etra ofning hoofdstuk = ( ) = = v v v dr 7 7 7 v a = + v als v 7 v v dus als = 7 7 7 7 dv waaruit volgt dat v = 7 km/uur. v = 7 gft R = 7, 7 mg/min. a f ' = = ' = + = ( + ) ' = = ( ) = f f d f ' ln ln
Aanvraagformulier Persoonsgebonden Budget Verpleging en Verzorging
 Anvrgormulir Prsoonsgonn Bugt Vrplging n Vrzorging DEEL 3: Bugtpln Dit ugtpln wort oor vrzkr o wttlijk vrtgnwoorigr ingvul. 1 (En tolihting op ht ormulir stt in ijlg) 1. Grssr Dit ormulir is stm voor:
Anvrgormulir Prsoonsgonn Bugt Vrplging n Vrzorging DEEL 3: Bugtpln Dit ugtpln wort oor vrzkr o wttlijk vrtgnwoorigr ingvul. 1 (En tolihting op ht ormulir stt in ijlg) 1. Grssr Dit ormulir is stm voor:
Algebra Pijlen - vm. Opdracht 2 Je ziet hieronder een ander voorbeeld. Bouw ook dit schema na. Vul bij invoer de waarde 10 in. Wat komt er uit?
 9 Psl Algr Pijln - vm A Bwrkingn mt Algr Pijln D shm s in pplt Algr pijln nomn w rknshm s. Oprht 1 Gruik pplt Algr Pijln. J ht ht shm uit ht voorl ngouw. Vul ij invor wr 18 in. Wt komt r uit? Voor kommgtlln
9 Psl Algr Pijln - vm A Bwrkingn mt Algr Pijln D shm s in pplt Algr pijln nomn w rknshm s. Oprht 1 Gruik pplt Algr Pijln. J ht ht shm uit ht voorl ngouw. Vul ij invor wr 18 in. Wt komt r uit? Voor kommgtlln
Maatregel 7 - Het verhalen van de schade op de dader
 Maagl 7 - H vhaln van d schad op d dad Waaom? Bij agssi n gwld onsaa vaak schad schad aan godn van d wknm of wkgv, bijvoobld n auo. Maa ook onsaa vl pijn n ld, immaiël schad of is gvolgschad. H klink bijna
Maagl 7 - H vhaln van d schad op d dad Waaom? Bij agssi n gwld onsaa vaak schad schad aan godn van d wknm of wkgv, bijvoobld n auo. Maa ook onsaa vl pijn n ld, immaiël schad of is gvolgschad. H klink bijna
Rekenen met procenten
 W4 Rknn mt procntn Dolstllingn Na ht doorlopn van dz modul kan d studnt rknn mt procntn, zoals: d btw n d brutoprijs brknn bij n ggvn nttoprijs; bpaln hovl procnt n bdrag is van n andr bdrag; d procntul
W4 Rknn mt procntn Dolstllingn Na ht doorlopn van dz modul kan d studnt rknn mt procntn, zoals: d btw n d brutoprijs brknn bij n ggvn nttoprijs; bpaln hovl procnt n bdrag is van n andr bdrag; d procntul
Hoofdstuk 1 Algemene bepalingen
 Bviligingshnok GBA Gmnt Brgmht 2011 Burgmstr n wthours vn gmnt Brgmht, Glt op rtikl 14 vn Wt gmntlijk sisministrti prsoonsggvns; Bsluitn vst t stlln Bhrrgling gmntlijk sisministrti prsoonsggvns 2011: Hoostuk
Bviligingshnok GBA Gmnt Brgmht 2011 Burgmstr n wthours vn gmnt Brgmht, Glt op rtikl 14 vn Wt gmntlijk sisministrti prsoonsggvns; Bsluitn vst t stlln Bhrrgling gmntlijk sisministrti prsoonsggvns 2011: Hoostuk
Derde editie. onderbouw
 r z j i w mthod Drd diti ondrbouw ir! la f t m d o h t En m municrn mt n m Motivrn n lrn co modrn n h sc ti ak pr op t ch mthod gri Drd diti ondrbouw D mthod is vrdr ontwikkld n aangpast. Dat is t zin
r z j i w mthod Drd diti ondrbouw ir! la f t m d o h t En m municrn mt n m Motivrn n lrn co modrn n h sc ti ak pr op t ch mthod gri Drd diti ondrbouw D mthod is vrdr ontwikkld n aangpast. Dat is t zin
En wat gaan we doen? Vakantiewerking. Vakantiewerking. Geetbets. Geetbets 2014. l e. ppe n
 En wat gaan w don? 30/6 30/6 04/07: Muzik n dans Zingn mt K3, dansn mt mvrouw d pauw, springn tot w r bij nr valln, bwgn, luistrn naar mooi muzikal sprookjs n vrtlln, fantasrn, musicals makn,... Vakantiwrking
En wat gaan w don? 30/6 30/6 04/07: Muzik n dans Zingn mt K3, dansn mt mvrouw d pauw, springn tot w r bij nr valln, bwgn, luistrn naar mooi muzikal sprookjs n vrtlln, fantasrn, musicals makn,... Vakantiwrking
Voorbeeld ISSO-publicatie 53
 Voorbld ISSO-publicati 53 6. VOORBEELD Ht (kantoorgbouw is wrggvn in figuur 6.1. Fig. 6.1 Gvlaanzicht n plattgrond van ht kantoorgbouw. Ht (kantoorgbouw kan wordn bstmpld als n middlgroot modulnkantoor.
Voorbld ISSO-publicati 53 6. VOORBEELD Ht (kantoorgbouw is wrggvn in figuur 6.1. Fig. 6.1 Gvlaanzicht n plattgrond van ht kantoorgbouw. Ht (kantoorgbouw kan wordn bstmpld als n middlgroot modulnkantoor.
CBS Nije-Kroost 18 april 2013 www.cbsnijekroost.nl
 CBS Nij-Kroost 18 april 2013 www.cbsnijkroost.nl Vanuit d gropn Niuw lrlingn: in grop 1/2c: Rol Vnmans Gropn 1 n 2 Wi wil in d mivakanti ons poppnmubilair schildrn? Graag vn contact opnmn mt juf Lia. Op
CBS Nij-Kroost 18 april 2013 www.cbsnijkroost.nl Vanuit d gropn Niuw lrlingn: in grop 1/2c: Rol Vnmans Gropn 1 n 2 Wi wil in d mivakanti ons poppnmubilair schildrn? Graag vn contact opnmn mt juf Lia. Op
De Wageningse Methode 5&6 VWO wiskunde B Uitgebreide antwoorden Hoofdstuk 6 De integraal
 D Wgnings Mthod & VWO wiskund B Uitgrid ntwoordn Hoofdstuk D intgrl Prgrf Opprvlkt ondr n grfik. km. ls t< : w(t t ls t< : in uur km glopn n t uur km/u, dus (t glopn, dus w(t t ls t : w(t (t t c., n. t
D Wgnings Mthod & VWO wiskund B Uitgrid ntwoordn Hoofdstuk D intgrl Prgrf Opprvlkt ondr n grfik. km. ls t< : w(t t ls t< : in uur km glopn n t uur km/u, dus (t glopn, dus w(t t ls t : w(t (t t c., n. t
de nationale E-bike verzekering
 Ht comfort gaat altijd door mt d national E-bik vrzkring D spcial n voordlig vrzkring voor all lktrisch trapondrstund fitsn Dri, vir of vijf ar vrzkrd tgn difstal of cascoschad (incl. difstal) voor n nmalig
Ht comfort gaat altijd door mt d national E-bik vrzkring D spcial n voordlig vrzkring voor all lktrisch trapondrstund fitsn Dri, vir of vijf ar vrzkrd tgn difstal of cascoschad (incl. difstal) voor n nmalig
Negatieve getallen in een assenstelsel
 G Ngtiv gtlln in n ssnstlsl 98 kijk ht ssnstlsl n los vrgn op. Gf oörint vn puntn, n. 2 4 (...,...) (...,...) 2 (...,...) Tkn in ht ssnstlsl puntn D(, 2), ( 4,) n (2, ). Klur ht glt vn ht ssnstlsl gron
G Ngtiv gtlln in n ssnstlsl 98 kijk ht ssnstlsl n los vrgn op. Gf oörint vn puntn, n. 2 4 (...,...) (...,...) 2 (...,...) Tkn in ht ssnstlsl puntn D(, 2), ( 4,) n (2, ). Klur ht glt vn ht ssnstlsl gron
8 Elektromotor en dynamo
 8 Elktromotor n ynmo Elktromgntish vl vwo Uitwrking sisok 8.1 INTRODUCTIE 1 [W] Exprimnt: Mgntn, spijkrs n kompssn 2 [W] Exprimnt: Rlis 3 [W] Exprimnt: Frromgnt n ntifrromgnt 4 Wr of nit wr? f g h Nit
8 Elktromotor n ynmo Elktromgntish vl vwo Uitwrking sisok 8.1 INTRODUCTIE 1 [W] Exprimnt: Mgntn, spijkrs n kompssn 2 [W] Exprimnt: Rlis 3 [W] Exprimnt: Frromgnt n ntifrromgnt 4 Wr of nit wr? f g h Nit
Werkcollege 2 - Lokaal plooien en classificatie van doorsneden
 Wkollg - Lokaal plooin n lassiiai van doosndn Opgav : Klass van n monosmmis kokdoosnd In kollg 'Gondslagn voo d kning van saalonsuis' d d ligging van d lasis n d plasis nual as ij uiging om d sk as van
Wkollg - Lokaal plooin n lassiiai van doosndn Opgav : Klass van n monosmmis kokdoosnd In kollg 'Gondslagn voo d kning van saalonsuis' d d ligging van d lasis n d plasis nual as ij uiging om d sk as van
Algebra Pijlen - hv. Opdracht 2 Je ziet hieronder een ander voorbeeld. Bouw ook dit schema na. Vul bij invoer de waarde 10 in. Wat komt er uit?
 9 Psl Algr Pijln - hv A Bwrkingn mt Algr Pijln D shm s in pplt Algr pijln nomn w rknshm s. Oprht 1 Gruik pplt Algr Pijln. J ht ht shm uit ht voorl ngouw. Vul ij invor wr 18 in. Wt komt r uit? Voor kommgtlln
9 Psl Algr Pijln - hv A Bwrkingn mt Algr Pijln D shm s in pplt Algr pijln nomn w rknshm s. Oprht 1 Gruik pplt Algr Pijln. J ht ht shm uit ht voorl ngouw. Vul ij invor wr 18 in. Wt komt r uit? Voor kommgtlln
RAADSBESLUIT. 1047311 Wildemors, Chantal SAM-MO Erik Lievers. Tarievenverordening sportaccommodaties 2015
 RAADSBESLUIT ZAAKNUMMER BEHANDELEND AMBTENAAR SECTOR PORT. HOUDER 1047311 Wildmors, Chantal SAM-MO Erik Livrs ONDERWERP Tarivnvrordning sportaccommodatis 2015 DE RAAD VAN DE GEMEENTE HENGELO BESLUIT: Vaststlln
RAADSBESLUIT ZAAKNUMMER BEHANDELEND AMBTENAAR SECTOR PORT. HOUDER 1047311 Wildmors, Chantal SAM-MO Erik Livrs ONDERWERP Tarivnvrordning sportaccommodatis 2015 DE RAAD VAN DE GEMEENTE HENGELO BESLUIT: Vaststlln
Duco geeft op een natuurlijke manier. zuurstof aan ieder gebouw. Verse. lucht rechtstreeks via de gevel. binnenbrengen, zonder complexe
 RAAMvntilati nl Tchnisch Waardntabl HOME OF OXYGEN Duco gft op n natuurlijk manir zuurstof aan idr gbouw. Vrs lucht rchtstrks via d gvl binnnbrngn, zondr complx tovorkanaln, is d ultim garanti voor n gzond
RAAMvntilati nl Tchnisch Waardntabl HOME OF OXYGEN Duco gft op n natuurlijk manir zuurstof aan idr gbouw. Vrs lucht rchtstrks via d gvl binnnbrngn, zondr complx tovorkanaln, is d ultim garanti voor n gzond
Toebehoren voor bekisting Bekistingsafstandhouders
 Tobhorn voor bkisting Bkistingsafstandhoudrs Buizn, conisch uitindn & stoppn in PVC Constructi voor ht btonnrn Rond buizn in PVC Ø Afwrking Ruw afwrking RS6602 14 19 Glad RS6406 20 24 Ruw RS6400 22 26
Tobhorn voor bkisting Bkistingsafstandhoudrs Buizn, conisch uitindn & stoppn in PVC Constructi voor ht btonnrn Rond buizn in PVC Ø Afwrking Ruw afwrking RS6602 14 19 Glad RS6406 20 24 Ruw RS6400 22 26
Rechtsbijstandverzekering
 Rchtsbijstandvrzkring Ht kan hoog oplopn En uit d hand glopn ruzi mt d burn. En conflict mt uw wrkgvr. En lvrancir di zijn blofts nit waar kan makn. En huisbaas di ht nit zo nauw nmt mt ht ondrhoud van
Rchtsbijstandvrzkring Ht kan hoog oplopn En uit d hand glopn ruzi mt d burn. En conflict mt uw wrkgvr. En lvrancir di zijn blofts nit waar kan makn. En huisbaas di ht nit zo nauw nmt mt ht ondrhoud van
Calamiteitenprotocol instellingen zorg voor jeugd, de gemeenten in de provincie Utrecht en de gemeenten Weesp en Wijdemeren
 Calamititnprotocol instllingn zorg voor jugd, d gmntn in d provinci Utrcht n d gmntn Wsp n Wijdmrn Inliding Calamititn in d jugdhulp kunnn hlaas nit altijd voorkomn wordn. Z hbbn n grot impact op btrokknn
Calamititnprotocol instllingn zorg voor jugd, d gmntn in d provinci Utrcht n d gmntn Wsp n Wijdmrn Inliding Calamititn in d jugdhulp kunnn hlaas nit altijd voorkomn wordn. Z hbbn n grot impact op btrokknn
Lijst van gewenste wiskunde-onderwerpen als basis voor een universitaire studie economie en/of bedrijfskunde.
 Lijst v gwst wiskud-odrwrp ls sis voor uivrsitir studi coomi /of drijfskud. BASIS -WISKUNDE (mt m: Algr) Ghl gtll, rtiol gtll rël gtll. Ghl pot: ( fctor) 0 p q q p Grok pot: ( > 0 ) Rgls voor pot: m m
Lijst v gwst wiskud-odrwrp ls sis voor uivrsitir studi coomi /of drijfskud. BASIS -WISKUNDE (mt m: Algr) Ghl gtll, rtiol gtll rël gtll. Ghl pot: ( fctor) 0 p q q p Grok pot: ( > 0 ) Rgls voor pot: m m
Een uitgave van katholieke basisschool De Kinderarcke. Deze wordt eens in de twee weken verstuurd aan alle ouders.
 UIT DE SCHOOL GEKLAPT NUMMER 2 Dondrdag 18 sptmbr 2014 En uitgav van katholik basisschool D Kindrarck. Dz wordt ns in d tw wkn vrstuurd aan all oudrs. DE KOP IS ER AF Wat n zindrnd n inspirrnd bgin van
UIT DE SCHOOL GEKLAPT NUMMER 2 Dondrdag 18 sptmbr 2014 En uitgav van katholik basisschool D Kindrarck. Dz wordt ns in d tw wkn vrstuurd aan all oudrs. DE KOP IS ER AF Wat n zindrnd n inspirrnd bgin van
Duco geeft op een natuurlijke manier. zuurstof aan ieder gebouw. Verse. lucht rechtstreeks via de gevel. binnenbrengen, zonder complexe
 RAAMVENTILATIE nl HOME OF OXYGEN Duco gft op n natuurlijk manir zuurstof aan idr gbouw. Vrs lucht rchtstrks via d gvl binnnbrngn, zondr complx tovorkanaln, is d ultim garanti voor n gzond binnnklimaat.
RAAMVENTILATIE nl HOME OF OXYGEN Duco gft op n natuurlijk manir zuurstof aan idr gbouw. Vrs lucht rchtstrks via d gvl binnnbrngn, zondr complx tovorkanaln, is d ultim garanti voor n gzond binnnklimaat.
Deel 1 Vijfde, herziene druk
 drs. J.H. Blanksoor drs. C. d Jood ir. A. Sluijtr Togast Wiskund voor ht hogr brosondrwijs Dl Vijfd, hrzin druk Uitwrking hrhalingsogavn hoofdstuk 6 ThimMulnhoff, Amrsfoort, Togast Wiskund, dl Uitwrking
drs. J.H. Blanksoor drs. C. d Jood ir. A. Sluijtr Togast Wiskund voor ht hogr brosondrwijs Dl Vijfd, hrzin druk Uitwrking hrhalingsogavn hoofdstuk 6 ThimMulnhoff, Amrsfoort, Togast Wiskund, dl Uitwrking
DE NAAKTE WAARHEID EEN GEKNIPT PRELEIDINGSVORMINGSPEL
 K RH GKP PRLGSVORMGSPL nldn n kn rldnvrmnl. ndrdd! H n d j n m dn krj uknn n dn j n kn-n-klr l d rn vr n luk l m j l vr Cr n ldn wrdn/zjn. Zkr dn! n d jl kn j l w ul vndn vr rldnvrmn n wrm w z lnrjk vndn
K RH GKP PRLGSVORMGSPL nldn n kn rldnvrmnl. ndrdd! H n d j n m dn krj uknn n dn j n kn-n-klr l d rn vr n luk l m j l vr Cr n ldn wrdn/zjn. Zkr dn! n d jl kn j l w ul vndn vr rldnvrmn n wrm w z lnrjk vndn
Ventilatie vraagt om een totaalconcept!
 Vntilati vraagt om n totaalconcpt! Vrbtring van vntilati n vrmindring van nrgivrbruik is in d bstaand woningvoorraad van cruciaal blang. aarbij strft uco naar d kwalititsisn di ook bij niuwbouw gldn. at
Vntilati vraagt om n totaalconcpt! Vrbtring van vntilati n vrmindring van nrgivrbruik is in d bstaand woningvoorraad van cruciaal blang. aarbij strft uco naar d kwalititsisn di ook bij niuwbouw gldn. at
Ajodakt. Rekenen. Cijferen Mix. Cijferen groep 8. Colofon. Zelfstandig werken. Antwoorden. Rekenen. Groep 8
 Cijn Mix Ajokt Coloon Rknn Cijn gop Autus Mjnn vn Gmn Cokky Stolz ThimMulnho ontwikklt lmiln voo Pimi Onwijs, Vootgzt Onwijs, Bopsonwijs n Volwssnnuti n Hog Onwijs Zlstnig wkn Rknn Gop Antwoon Dit ntwoonokj
Cijn Mix Ajokt Coloon Rknn Cijn gop Autus Mjnn vn Gmn Cokky Stolz ThimMulnho ontwikklt lmiln voo Pimi Onwijs, Vootgzt Onwijs, Bopsonwijs n Volwssnnuti n Hog Onwijs Zlstnig wkn Rknn Gop Antwoon Dit ntwoonokj
Noordhoff Uitgevers bv
 172 Vriping - Gin 1a ll puntn op milloolijn van liggn vn vr van punt als van punt. ll puntn i ihtr ij punt liggn, zulln us aan n kant van milloolijn liggn n all puntn i ihtr ij punt liggn, zulln aan anr
172 Vriping - Gin 1a ll puntn op milloolijn van liggn vn vr van punt als van punt. ll puntn i ihtr ij punt liggn, zulln us aan n kant van milloolijn liggn n all puntn i ihtr ij punt liggn, zulln aan anr
H. 9 Het getal e / Logaritmen
 H. 9 Ht tal / Loaritmn 9.1 Ht tal Ht tal is n spciaal tal in d wiskund, nt zoals ht tal π. Ht is als volt dfinird: 1 1 1 1 1 1 = + + + + + + 1 1 1 14 145 Als w dit uitrknn, dan wordt d waard van ht tal
H. 9 Ht tal / Loaritmn 9.1 Ht tal Ht tal is n spciaal tal in d wiskund, nt zoals ht tal π. Ht is als volt dfinird: 1 1 1 1 1 1 = + + + + + + 1 1 1 14 145 Als w dit uitrknn, dan wordt d waard van ht tal
De Wageningse Methode 5&6 VWO wiskunde B Uitgebreidere antwoorden Hoofdstuk 8 Integralen toepassen
 D Wagnings Mtod & VWO wiskund B Uitgbridr antwoordn Hoofdstuk Intgraln topassn Paragraaf Inoud n intgraal f d ( ) d ( ) d a Ht 'topj' van d piramid is glijkvormig mt d l piramid mt factor f, dus O()f b
D Wagnings Mtod & VWO wiskund B Uitgbridr antwoordn Hoofdstuk Intgraln topassn Paragraaf Inoud n intgraal f d ( ) d ( ) d a Ht 'topj' van d piramid is glijkvormig mt d l piramid mt factor f, dus O()f b
Onomatopeeën. Inleiding. Doelgroep. Uitleg. Opzet van de lesbrief. Door Jan de Waard
 Door Jn Wr Onomtopën Inliing Vrooom! Mt loin motor shur ovrvllr rvnoor. Png, png, png! klonkn pistoolshotn htr hm. Zlfs ht rttttt! vn n mhingwr klonk oor vrr lg strt! Pok! Pok! hoor hij kogls insln in
Door Jn Wr Onomtopën Inliing Vrooom! Mt loin motor shur ovrvllr rvnoor. Png, png, png! klonkn pistoolshotn htr hm. Zlfs ht rttttt! vn n mhingwr klonk oor vrr lg strt! Pok! Pok! hoor hij kogls insln in
Inhoud college 7 Basiswiskunde
 Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
Inhoud college 7 Bsiswiskunde 3.3 De ntuurlijke logritme en de exponentiële functie (zie college 6) 5.1/3 Introductie Integrlen 5.4 Eigenschppen vn de eplde integrl 5.5 De hoofdstelling vn Clculus 2.10
BESCHRIJVING PROCEDURE
 Wrkinstructi : HSEW Blz. : 1 van 7 INDEX 1 SCOPE 2 DOEL 3 BESCHRIJVING PROCEDURE 3.1 Introducti 3.2 Vrpakking radioactiv matrialn 3.2.1 Radioactif bsmtt installati-ondrdln 3.2.2 Radioactif afval: 3.2.3
Wrkinstructi : HSEW Blz. : 1 van 7 INDEX 1 SCOPE 2 DOEL 3 BESCHRIJVING PROCEDURE 3.1 Introducti 3.2 Vrpakking radioactiv matrialn 3.2.1 Radioactif bsmtt installati-ondrdln 3.2.2 Radioactif afval: 3.2.3
20 m/s. 11 m/s. 20km h. 5,6 m/s op t = 4,0 s is de plaats: 5,6 4,0 22 m. 58 [W] Experiment. 59 [W] Experiment: Versnellend karretje
![20 m/s. 11 m/s. 20km h. 5,6 m/s op t = 4,0 s is de plaats: 5,6 4,0 22 m. 58 [W] Experiment. 59 [W] Experiment: Versnellend karretje 20 m/s. 11 m/s. 20km h. 5,6 m/s op t = 4,0 s is de plaats: 5,6 4,0 22 m. 58 [W] Experiment. 59 [W] Experiment: Versnellend karretje](/thumbs/93/111671772.jpg) 58 [W] Exprimnt 59 [W] Exprimnt: Vrsnlln krrtj 60 [W] Exprimnt: Knikkrn 61 [W] Drgrr 62 [W] Exprimnt: En ign wging 63 [W] Wissln op stftt 64 Wr of nit wr? Nit wr: ht v,t-igrm vn n nprig vrsnl wging is
58 [W] Exprimnt 59 [W] Exprimnt: Vrsnlln krrtj 60 [W] Exprimnt: Knikkrn 61 [W] Drgrr 62 [W] Exprimnt: En ign wging 63 [W] Wissln op stftt 64 Wr of nit wr? Nit wr: ht v,t-igrm vn n nprig vrsnl wging is
