Examen Datastructuren en Algoritmen II
|
|
|
- Evelien Gerritsen
- 9 jaren geleden
- Aantal bezoeken:
Transcriptie
1 Tweede kandidatuur Informatica Academiejaar , eerste zittijd Examen Datastructuren en Algoritmen II Naam : Binomiale prioriteitswachtlijnen: Stel dat het bekend is hoe twee binomiale prioriteitswachtlijnen moeten gemerged worden. Beschrijf hoe elementen worden toegevoegd en hoe het kleinste element wordt verwijderd. Merge de volgende twee binomiale prioriteitswachtlijnen:
2 bomen: Wat is de definitie van een 2-3-boom? Welke van de volgende bomen voldoet niet aan deze definitie en waarom niet? ) 2.) Voeg de volgende reeks van getallen toe aan een initieel lege 2-3-boom: 15, 20, 30, 40, 35, 6, 10. Verwijder ten slotte de sleutel 40.
3 3. Dynamisch programmeren: Beschrijf een algoritme met dynamisch programmeren voor het wisselgeldprobleem en toon aan hoe het werkt voor het voorbeeld 1,73 euro met de normale euromunten (1, 2, 5, 10, 20 en 50 cent en 1 en 2 euro).
4 4. Benaderende algoritmen: Deze oefening gaat over off-line algoritmen voor het inpakprobleem: Geef een voorbeeld waar first-fit dalend beter presteert dan best-fit dalend. Geef een voorbeeld waar best-fit dalend beter presteert dan first-fit dalend. Geef een oneindige reeks van voorbeelden (dus een reeks die afhankelijk is van bijvoorbeeld k) waar best-fit dalend en first-fit dalend allebei niet het optimum vinden.
5 5. Tonen dat iets arbitrair slecht presteert: Een Greedy-algoritme voor het (gewone) TSP kan bijvoorbeeld zo werken: Begin met de goedkoopste boog en maak het pad altijd langer (zoals in de cursus) maar kies altijd de goedkoopste boog, die het pad verlengt. Toon dat dit algoritme arbitrair slechte resultaten kan opleveren. Dus: toon dat er voor elk getal k TSP s zijn, zodat dit algoritme Hamiltoniaanse cykels berekent die tenminste k keer duurder zijn, dan de goedkoopste.
6 6. Een probleem vertalen: Een vertegenwoordiger moet n steden bezoeken en zoekt de snelste manier om dat te doen en terug te komen. Voor elk paar a,b van steden is de tijd bekend die nodig is om van a naar b te rijden zonder door één van de andere steden te gaan. Als het belangrijk is dat hij elke stad precies één keer bezoekt (bijvoorbeeld als hij echt slechte produkten verkoopt... ) dan is dit probleem equivalent met het handelsreizigersprobleem. Maar normaal is dat voor hem niet belangrijk hij zoekt gewoon de kortste rondreis waarin elke stad tenminste één keer wordt bezocht. Vertaal dit probleem naar het normale TSP. Schets een polynomiaal algoritme dat als resultaat een input voor het normale TSP heeft, zodat als wij de lengte van een kortste Hamiltoniaanse cykel in dit TSP kennen, wij ook de lengte van een kortste rondreis voor de vertegenwoordiger kennen. Toon aan dat jouw algoritme aan de eisen voldoet.
7 7. Spelstrategieën: Een wisselgeldspel: Gegeven een bedrag b van eurocent en een getal m dat het maximale aantal zetten bepaalt. De regels zijn als volgt: In het begin ligt 0 cent op tafel. Speler X begint. Als een speler aan de beurt is en er ligt al een bedrag van t < b cent op tafel, moet hij er precies één munt bijleggen zodanig dat nog steeds ten hoogste een bedrag van b op tafel ligt (1 euro telt natuurlijk als 100 cent, etc). Het spel is gedaan als er b cent op tafel ligt. Als er op dit moment ten hoogste m munten liggen, mag speler X het bedrag houden, anders speler Y. De winst is natuurlijk, wat de andere speler op tafel legde. Stel nu dat alleen maar munten van 1, 2 en 10 cent toegelaten zijn (anders wordt de vertakking gewoon te groot om het op papier te doen). Wat is de waarde van het spel met b = 15 en m = 5. Misschien kan je hier ook branch and bound en dynamisch programmeren toepassen om niet de hele spelboom te moeten uitwerken...
8 8. Gerandomiseerde algoritmen: Gegeven is een random-number-generator, die getallen 1,...,k allemaal met kans 1/k genereert maar het getal k is niet bekend. Beschrijf een algoritme, dat de random-number-generator gebruikt en een getal k berekent dat met grote kans een goede bovengrens is, of precies: waarvoor met kans 99.9% geldt dat k <= k <= (10/9) k. Toon aan dat jouw algoritme aan de eisen voldoet.
Oefeningen voor de oefeningenles. Oefening 1
 Oefeningen voor de oefeningenles Oefening 1 Gegeven een arbitraire binaire zoekboom T met n toppen en een (andere of gelijke) binaire zoekboom T die ook n sleutels bevat. Beschrijf een algoritme dat in
Oefeningen voor de oefeningenles Oefening 1 Gegeven een arbitraire binaire zoekboom T met n toppen en een (andere of gelijke) binaire zoekboom T die ook n sleutels bevat. Beschrijf een algoritme dat in
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2008 2009, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Tweede bachelor Informatica Academiejaar 2008 2009, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2010 2011, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2010 2011, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2016 2017, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2016 2017, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2008 2009, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Tweede bachelor Informatica Academiejaar 2008 2009, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2014 2015, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2014 2015, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2012 2013, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2012 2013, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2009 2010, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2009 2010, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Examen Algoritmen en Datastructuren III
 Derde bachelor Informatica Academiejaar 2006 2007, eerste zittijd Examen Algoritmen en Datastructuren III Naam :.............................................................................. 1. (2 pt)
Derde bachelor Informatica Academiejaar 2006 2007, eerste zittijd Examen Algoritmen en Datastructuren III Naam :.............................................................................. 1. (2 pt)
Tiende college algoritmiek. 2 mei Gretige algoritmen, Dijkstra
 College 10 Tiende college algoritmiek mei 013 Gretige algoritmen, Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
College 10 Tiende college algoritmiek mei 013 Gretige algoritmen, Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
Discrete Structuren. Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter [email protected] 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter [email protected] 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Examen Algoritmen en Datastructuren III
 Derde bachelor Informatica Academiejaar 2006 2007, tweede zittijd Examen Algoritmen en Datastructuren III Naam :.............................................................................. 1. (2 pt)
Derde bachelor Informatica Academiejaar 2006 2007, tweede zittijd Examen Algoritmen en Datastructuren III Naam :.............................................................................. 1. (2 pt)
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter [email protected] 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter [email protected] 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
Tiende college algoritmiek. 26 april Gretige algoritmen
 Algoritmiek 01/10 College 10 Tiende college algoritmiek april 01 Gretige algoritmen 1 Algoritmiek 01/10 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag
Algoritmiek 01/10 College 10 Tiende college algoritmiek april 01 Gretige algoritmen 1 Algoritmiek 01/10 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 11 Leo van Iersel Technische Universiteit Delft 25 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 25 november 2015 1 / 28 Vandaag Vraag Voor welke problemen
TW2020 Optimalisering Hoorcollege 11 Leo van Iersel Technische Universiteit Delft 25 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 25 november 2015 1 / 28 Vandaag Vraag Voor welke problemen
Tiende college algoritmiek. 13/21 april Gretige Algoritmen Algoritme van Dijkstra
 Algoritmiek 017/Gretige Algoritmen Tiende college algoritmiek 13/1 april 017 Gretige Algoritmen Algoritme van Dijkstra 1 Algoritmiek 017/Gretige Algoritmen Muntenprobleem Gegeven onbeperkt veel munten
Algoritmiek 017/Gretige Algoritmen Tiende college algoritmiek 13/1 april 017 Gretige Algoritmen Algoritme van Dijkstra 1 Algoritmiek 017/Gretige Algoritmen Muntenprobleem Gegeven onbeperkt veel munten
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 27 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ [email protected]
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 27 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ [email protected]
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 12 Leo van Iersel Technische Universiteit Delft 7 december 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 december 2016 1 / 25 Volgende week: Study guide Vragenuurtje
TW2020 Optimalisering Hoorcollege 12 Leo van Iersel Technische Universiteit Delft 7 december 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 december 2016 1 / 25 Volgende week: Study guide Vragenuurtje
Uitwerkingen Sum of Us
 Instant Insanity Uitwerkingen Sum of Us Opgave A: - Opgave B: Voor elk van de vier kubussen kun je een graaf maken die correspondeert met de desbetreffende kubus. Elk van deze grafen bevat drie lijnen.
Instant Insanity Uitwerkingen Sum of Us Opgave A: - Opgave B: Voor elk van de vier kubussen kun je een graaf maken die correspondeert met de desbetreffende kubus. Elk van deze grafen bevat drie lijnen.
Discrete Wiskunde, College 13. Han Hoogeveen, Utrecht University
 Discrete Wiskunde, College 13 Han Hoogeveen, Utrecht University Algoritme van Kruskal (1) Sorteer de kanten in E op volgorde van lengte; hernummer de kanten zodanig dat c(e 1 ) c(e 2 )... c(e m ) Bij twee
Discrete Wiskunde, College 13 Han Hoogeveen, Utrecht University Algoritme van Kruskal (1) Sorteer de kanten in E op volgorde van lengte; hernummer de kanten zodanig dat c(e 1 ) c(e 2 )... c(e m ) Bij twee
Opgaven Kunstmatige intelligentie 4 mei 2012
 Opgaven Kunstmatige intelligentie 4 mei 2012 Opgave 28. (opgave tentamen 12 augustus 2002) Stel dat we een handelsreizigersprobleem op willen lossen, en dat we dat met een genetisch algoritme willen doen.
Opgaven Kunstmatige intelligentie 4 mei 2012 Opgave 28. (opgave tentamen 12 augustus 2002) Stel dat we een handelsreizigersprobleem op willen lossen, en dat we dat met een genetisch algoritme willen doen.
Overzicht. Inleiding. Toepassingen. Verwante problemen. Modellering. Exacte oplosmethode: B&B. Insertie heuristieken. Local Search
 Overzicht Inleiding Toepassingen Verwante problemen Modellering Exacte oplosmethode: B&B Insertie heuristieken Local Search Handelsreizigersprobleem 1 Cyclische permutatie van steden b 3 77 a 93 21 42
Overzicht Inleiding Toepassingen Verwante problemen Modellering Exacte oplosmethode: B&B Insertie heuristieken Local Search Handelsreizigersprobleem 1 Cyclische permutatie van steden b 3 77 a 93 21 42
Universiteit Utrecht Betafaculteit. Examen Discrete Wiskunde II op donderdag 6 juli 2017, uur.
 Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde II op donderdag 6 juli 2017, 13.30-16.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde II op donderdag 6 juli 2017, 13.30-16.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
dieren-geldspel de rekenhoek Uitleg dieren-geldspel Kaart 1: ronde bedragen tot 20 euro Kaart 2: ronde bedragen tot 30 euro
 Uitleg dieren-geldspel dieren-geldspel Benodigdheden: - Speelkaart 1, 2 of 3 - Geldkaartjes. Bij elke speelkaart horen andere geldkaartjes. - Geld: 10 munten van 2 euro en 10 munten van 1 euro. Bij drie
Uitleg dieren-geldspel dieren-geldspel Benodigdheden: - Speelkaart 1, 2 of 3 - Geldkaartjes. Bij elke speelkaart horen andere geldkaartjes. - Geld: 10 munten van 2 euro en 10 munten van 1 euro. Bij drie
Formeel Denken 2014 Uitwerkingen Tentamen
 Formeel Denken 2014 Uitwerkingen Tentamen (29/01/15) 1. Benader de betekenis van de volgende Nederlandse zin zo goed mogelijk (6 punten) door een formule van de propositielogica: Als het regent word ik
Formeel Denken 2014 Uitwerkingen Tentamen (29/01/15) 1. Benader de betekenis van de volgende Nederlandse zin zo goed mogelijk (6 punten) door een formule van de propositielogica: Als het regent word ik
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 10 Leo van Iersel Technische Universiteit Delft 23 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 23 november 2016 1 / 40 Vraag Ik heb het deeltentamen niet
TW2020 Optimalisering Hoorcollege 10 Leo van Iersel Technische Universiteit Delft 23 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 23 november 2016 1 / 40 Vraag Ik heb het deeltentamen niet
Uitwerking tentamen Algoritmiek 9 juli :00 13:00
 Uitwerking tentamen Algoritmiek 9 juli 0 0:00 :00. (N,M)-game a. Toestanden: Een geheel getal g, waarvoor geldt g N én wie er aan de beurt is (Tristan of Isolde) b. c. Acties: Het noemen van een geheel
Uitwerking tentamen Algoritmiek 9 juli 0 0:00 :00. (N,M)-game a. Toestanden: Een geheel getal g, waarvoor geldt g N én wie er aan de beurt is (Tristan of Isolde) b. c. Acties: Het noemen van een geheel
Branch-and-Bound en Cutting Planes
 Branch-and-Bound en Cutting Planes Vandaag: Er is nog geen algoritme om ILP s in polynomiale tijd op te lossen. Twee opties: 1 Exponentiëel algoritme dat optimale oplossing geeft 2 Polynomiaal algoritme
Branch-and-Bound en Cutting Planes Vandaag: Er is nog geen algoritme om ILP s in polynomiale tijd op te lossen. Twee opties: 1 Exponentiëel algoritme dat optimale oplossing geeft 2 Polynomiaal algoritme
Discrete Wiskunde, College 12. Han Hoogeveen, Utrecht University
 Discrete Wiskunde, College 12 Han Hoogeveen, Utrecht University Dynamische programmering Het basisidee is dat je het probleem stap voor stap oplost Het probleem moet voldoen aan het optimaliteitsprincipe
Discrete Wiskunde, College 12 Han Hoogeveen, Utrecht University Dynamische programmering Het basisidee is dat je het probleem stap voor stap oplost Het probleem moet voldoen aan het optimaliteitsprincipe
Uitwerking tentamen Algoritmiek 10 juni :00 13:00
 Uitwerking tentamen Algoritmiek 10 juni 2014 10:00 13:00 1. Dominono s a. Toestanden: n x n bord met in elk hokje een O, een X of een -. Hierbij is het aantal X gelijk aan het aantal O of hooguit één hoger.
Uitwerking tentamen Algoritmiek 10 juni 2014 10:00 13:00 1. Dominono s a. Toestanden: n x n bord met in elk hokje een O, een X of een -. Hierbij is het aantal X gelijk aan het aantal O of hooguit één hoger.
Heuristieken en benaderingsalgoritmen. Algoritmiek
 Heuristieken en benaderingsalgoritmen Wat te doen met `moeilijke optimaliseringsproblemen? Voor veel problemen, o.a. optimaliseringsproblemen is geen algoritme bekend dat het probleem voor alle inputs
Heuristieken en benaderingsalgoritmen Wat te doen met `moeilijke optimaliseringsproblemen? Voor veel problemen, o.a. optimaliseringsproblemen is geen algoritme bekend dat het probleem voor alle inputs
Minimum Opspannende Bomen. Algoritmiek
 Minimum Opspannende Bomen Inhoud Het minimum opspannende bomen probleem Een principe om een minimum opspannende boom te laten groeien Twee greedy algoritmen + tijd en datastructuren: Het algoritme van
Minimum Opspannende Bomen Inhoud Het minimum opspannende bomen probleem Een principe om een minimum opspannende boom te laten groeien Twee greedy algoritmen + tijd en datastructuren: Het algoritme van
Universiteit Gent. Academiejaar Discrete Wiskunde. 1ste kandidatuur Informatica. Collegenota s. Prof. Dr.
 Universiteit Gent Academiejaar 2001 2002 Discrete Wiskunde 1ste kandidatuur Informatica Collegenota s Prof. Dr. Frank De Clerck Herhalingsoefeningen 1. Bepaal het quotiënt en de rest van de deling van
Universiteit Gent Academiejaar 2001 2002 Discrete Wiskunde 1ste kandidatuur Informatica Collegenota s Prof. Dr. Frank De Clerck Herhalingsoefeningen 1. Bepaal het quotiënt en de rest van de deling van
Tiende college algoritmiek. 14 april Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS
 Algoritmiek 2016/Dynamisch Programmeren Tiende college algoritmiek 14 april 2016 Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS 1 Algoritmiek 2016/Dynamisch Programmeren Houtzaagmolen
Algoritmiek 2016/Dynamisch Programmeren Tiende college algoritmiek 14 april 2016 Dynamisch Programmeren, Gretige Algoritmen, Kortste Pad met BFS 1 Algoritmiek 2016/Dynamisch Programmeren Houtzaagmolen
Begrenzing van het aantal iteraties in het max-flow algoritme
 Begrenzing van het aantal iteraties in het max-flow algoritme Het oplossen van het maximum stroom probleem met behulp van stroomvermeerderende paden werkt, maar het aantal iteraties kan aardig de spuigaten
Begrenzing van het aantal iteraties in het max-flow algoritme Het oplossen van het maximum stroom probleem met behulp van stroomvermeerderende paden werkt, maar het aantal iteraties kan aardig de spuigaten
Elke groep van 3 leerlingen heeft een 9 setje speelkaarten nodig: 2 t/m 10, bijvoorbeeld alle schoppen, of alle harten kaarten.
 Versie 16 januari 2017 Sorteren unplugged Sorteren gebeurt heel veel. De namen van alle leerlingen in de klas staan vaak op alfabetische volgorde. De wedstrijden van een volleybal team staan op volgorde
Versie 16 januari 2017 Sorteren unplugged Sorteren gebeurt heel veel. De namen van alle leerlingen in de klas staan vaak op alfabetische volgorde. De wedstrijden van een volleybal team staan op volgorde
Activiteit 9. Modderstad Minimaal Opspannende Bomen. Samenvatting. Kerndoelen. Leeftijd. Vaardigheden. Materialen
 Activiteit 9 Modderstad Minimaal Opspannende Bomen Samenvatting Onze maatschappij is verbonden middels heel veel netwerken: telefoonnet, elektriciteitsnet, de riolering, computernetwerk, en het wegennet.
Activiteit 9 Modderstad Minimaal Opspannende Bomen Samenvatting Onze maatschappij is verbonden middels heel veel netwerken: telefoonnet, elektriciteitsnet, de riolering, computernetwerk, en het wegennet.
Fundamentele Informatica
 Fundamentele Informatica (IN3120 en IN3005 DOI nwe stijl) 20 augustus 2004, 9.00 11.00 uur Het tentamen IN3120 bestaat uit 10 meerkeuzevragen en 2 open vragen. Voor de meerkeuzevragen kunt u maximaal 65
Fundamentele Informatica (IN3120 en IN3005 DOI nwe stijl) 20 augustus 2004, 9.00 11.00 uur Het tentamen IN3120 bestaat uit 10 meerkeuzevragen en 2 open vragen. Voor de meerkeuzevragen kunt u maximaal 65
groep 8 blok 7 antwoorden Malmberg s-hertogenbosch
 blok 7 groep 8 antwoorden Malmberg s-hertogenbosch blok 7 les 3 3 Reken de omtrek en de oppervlakte van de figuren uit. Gebruik m en m 2. 1 m C Omtrek figuur C 20 m Oppervlakte figuur C 22 m 2 A B Omtrek
blok 7 groep 8 antwoorden Malmberg s-hertogenbosch blok 7 les 3 3 Reken de omtrek en de oppervlakte van de figuren uit. Gebruik m en m 2. 1 m C Omtrek figuur C 20 m Oppervlakte figuur C 22 m 2 A B Omtrek
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 13 Leo van Iersel Technische Universiteit Delft 9 december 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 december 2015 1 / 13 Vraag Wat moet ik kennen en kunnen voor
TW2020 Optimalisering Hoorcollege 13 Leo van Iersel Technische Universiteit Delft 9 december 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 december 2015 1 / 13 Vraag Wat moet ik kennen en kunnen voor
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober 2015 1 / 25 Definitie Een boom is een samenhangende
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober 2015 1 / 25 Definitie Een boom is een samenhangende
Tentamen combinatorische optimalisatie Tijd:
 Tentamen combinatorische optimalisatie 26-05-2014. Tijd: 9.00-11.30 Tentamen is met gesloten boek. Beschrijf bij elke opgave steeds het belangrijkste idee. Notatie en exacte formulering is van minder belang.
Tentamen combinatorische optimalisatie 26-05-2014. Tijd: 9.00-11.30 Tentamen is met gesloten boek. Beschrijf bij elke opgave steeds het belangrijkste idee. Notatie en exacte formulering is van minder belang.
Uitwerking tentamen Analyse van Algoritmen, 29 januari
 Uitwerking tentamen Analyse van Algoritmen, 29 januari 2007. (a) De buitenste for-lus kent N = 5 iteraties. Na iedere iteratie ziet de rij getallen er als volgt uit: i rij na i e iteratie 2 5 4 6 2 2 4
Uitwerking tentamen Analyse van Algoritmen, 29 januari 2007. (a) De buitenste for-lus kent N = 5 iteraties. Na iedere iteratie ziet de rij getallen er als volgt uit: i rij na i e iteratie 2 5 4 6 2 2 4
Oude tentamens Kunstmatige intelligentie Universiteit Leiden Informatica 2005
 Oude tentamens Kunstmatige intelligentie Universiteit Leiden Informatica 2005 Opgave 1. A* (20/100 punten; tentamen 1 juni 2001) a. (5 punten) Leg het A*-algoritme uit. b. (2 punten) Wanneer heet een heuristiek
Oude tentamens Kunstmatige intelligentie Universiteit Leiden Informatica 2005 Opgave 1. A* (20/100 punten; tentamen 1 juni 2001) a. (5 punten) Leg het A*-algoritme uit. b. (2 punten) Wanneer heet een heuristiek
In dit gedeelte worden drie problemen genoemd die kunnen voorkomen in netwerken.
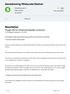 Aantekening Wiskunde Steiner Aantekening door D. 2086 woorden 25 mei 2016 2,1 1 keer beoordeeld Vak Wiskunde Resultaten Vragen bij het wetenschappelijk materiaal 9.1 Prototype example, p. 374-376 In dit
Aantekening Wiskunde Steiner Aantekening door D. 2086 woorden 25 mei 2016 2,1 1 keer beoordeeld Vak Wiskunde Resultaten Vragen bij het wetenschappelijk materiaal 9.1 Prototype example, p. 374-376 In dit
l e x e voor alle e E
 Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
Kosten. Computationale Intelligentie. Een zoekprobleem met stapkosten. Een voorbeeld: het vinden van een route. Zoeken met kosten.
 Kosten omputationale Intelligentie Zoeken met kosten Veel zoekproblemen omvatten kosten: een afstand in kilometers; een geldbedrag; een hoeveelheid tijd;... Voorbeelden van dergelijke problemen zijn: het
Kosten omputationale Intelligentie Zoeken met kosten Veel zoekproblemen omvatten kosten: een afstand in kilometers; een geldbedrag; een hoeveelheid tijd;... Voorbeelden van dergelijke problemen zijn: het
Benaderingsalgoritmen
 Benaderingsalgoritmen Eerste hulp bij NP-moeilijkheid 1 Herhaling NP-volledigheid (1) NP: er is een polynomiaal certificaat voor jainstanties dat in polynomiale tijd te controleren is Een probleem A is
Benaderingsalgoritmen Eerste hulp bij NP-moeilijkheid 1 Herhaling NP-volledigheid (1) NP: er is een polynomiaal certificaat voor jainstanties dat in polynomiale tijd te controleren is Een probleem A is
Universiteit Utrecht Betafaculteit. Examen Discrete Wiskunde op donderdag 13 april 2017, uur.
 Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde op donderdag 13 april 2017, 14.30-17.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde op donderdag 13 april 2017, 14.30-17.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Modeluitwerking Tentamen Computationele Intelligentie Universiteit Leiden Informatica Vrijdag 11 Januari 2013
 Modeluitwerking Tentamen Computationele Intelligentie Universiteit Leiden Informatica Vrijdag Januari 20 Opgave. Python Gegeven is de volgende (slechte) Python code:. def t(x): 2. def p(y):. return x*y
Modeluitwerking Tentamen Computationele Intelligentie Universiteit Leiden Informatica Vrijdag Januari 20 Opgave. Python Gegeven is de volgende (slechte) Python code:. def t(x): 2. def p(y):. return x*y
Radboud Universiteit Nijmegen
 Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica L(,1)-labeling van grafen Naam: Studentnummer: Studie: Begeleider: Myrte klein Brink 4166140 Bachelor Wiskunde Dr.
Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica L(,1)-labeling van grafen Naam: Studentnummer: Studie: Begeleider: Myrte klein Brink 4166140 Bachelor Wiskunde Dr.
Datastructuren Uitwerking jan
 Datastructuren Uitwerking jan 2015 1 1a. Een abstracte datastructuur is een beschrijving van een datastructuur, met de specificatie van wat er opgeslagen wordt (de data en hun structuur) en welke operaties
Datastructuren Uitwerking jan 2015 1 1a. Een abstracte datastructuur is een beschrijving van een datastructuur, met de specificatie van wat er opgeslagen wordt (de data en hun structuur) en welke operaties
w e r k b o e k a n t w o o r d e n blok Teken de versiering op de taart.
 j aargroep 6 a n t w o o r d e n Zwijsen reken-wiskundemethode voor het basisonderwijs De helft met aardbeien. Een vierde deel met appels. Een achtste deel met kersen. De rest met bessen. blok w e r k
j aargroep 6 a n t w o o r d e n Zwijsen reken-wiskundemethode voor het basisonderwijs De helft met aardbeien. Een vierde deel met appels. Een achtste deel met kersen. De rest met bessen. blok w e r k
WISKUNDE 5 PERIODEN. DATUM : 4 juni 2010. Formuleboekje voor de Europese scholen Niet-programmeerbare, niet-grafische rekenmachine
 EUROPEES BACCALAUREAAT 2010 WISKUNDE 5 PERIODEN DATUM : 4 juni 2010 DUUR VAN HET EXAMEN : 4 uur (240 minuten) TOEGESTANE HULPMIDDELEN : Formuleboekje voor de Europese scholen Niet-programmeerbare, niet-grafische
EUROPEES BACCALAUREAAT 2010 WISKUNDE 5 PERIODEN DATUM : 4 juni 2010 DUUR VAN HET EXAMEN : 4 uur (240 minuten) TOEGESTANE HULPMIDDELEN : Formuleboekje voor de Europese scholen Niet-programmeerbare, niet-grafische
Paradox van zelfreproductie. IN2505-II Berekenbaarheidstheorie. Zelfreproductie? Programma s en zelfreproductie. College 11.
 Paradox van zelfreproductie College 11 Algoritmiekgroep Faculteit EWI TU Delft 27 mei 2009 1 Levende wezens zijn machines. 2 Levende wezens kunnen zich reproduceren. 3 Machines kunnen zich niet reproduceren.
Paradox van zelfreproductie College 11 Algoritmiekgroep Faculteit EWI TU Delft 27 mei 2009 1 Levende wezens zijn machines. 2 Levende wezens kunnen zich reproduceren. 3 Machines kunnen zich niet reproduceren.
V = {a, b, c, d, e} Computernetwerken: de knopen zijn machines in het netwerk, de kanten zijn communicatiekanalen.
 WIS14 1 14 Grafen 14.1 Grafen Gerichte grafen Voor een verzameling V is een binaire relatie op V een verzameling geordende paren van elementen van V. Voorbeeld: een binaire relatie op N is de relatie KleinerDan,
WIS14 1 14 Grafen 14.1 Grafen Gerichte grafen Voor een verzameling V is een binaire relatie op V een verzameling geordende paren van elementen van V. Voorbeeld: een binaire relatie op N is de relatie KleinerDan,
Surinaamse Wiskunde Olympiade
 Surinaamse Wiskunde Olympiade SUCCES! Calculator is niet toegestaan Klad papier is wel toegestaan Je hebt 90 minuten de tijd De uitslag wordt eind juni bekend gemaakt Voor 3 e klas Mulo 1. Gegeven het
Surinaamse Wiskunde Olympiade SUCCES! Calculator is niet toegestaan Klad papier is wel toegestaan Je hebt 90 minuten de tijd De uitslag wordt eind juni bekend gemaakt Voor 3 e klas Mulo 1. Gegeven het
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 21 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 21 oktober 2015 1 / 20 Deze week: algoritmes en complexiteit
TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 21 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 21 oktober 2015 1 / 20 Deze week: algoritmes en complexiteit
D-dag 2014 Vrijeschool Zutphen VO. D -DAG 13 februari 2014: 1+ 1 = 2. (en hoe nu verder?) 1 = 2en hoe nu verder?
 D -DAG 13 februari 2014: 1+ 1 = 2 (en hoe nu verder?) 1 = 2en hoe nu verder? 1 Inleiding Snel machtsverheffen Stel je voor dat je 7 25 moet uitrekenen. Je weet dat machtsverheffen herhaald vermenigvuldigen
D -DAG 13 februari 2014: 1+ 1 = 2 (en hoe nu verder?) 1 = 2en hoe nu verder? 1 Inleiding Snel machtsverheffen Stel je voor dat je 7 25 moet uitrekenen. Je weet dat machtsverheffen herhaald vermenigvuldigen
Universiteit Utrecht Faculteit Wiskunde en Informatica. Examen Optimalisering op maandag 18 april 2005, uur.
 Universiteit Utrecht Faculteit Wiskunde en Informatica Examen Optimalisering op maandag 18 april 2005, 9.00-12.00 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf
Universiteit Utrecht Faculteit Wiskunde en Informatica Examen Optimalisering op maandag 18 april 2005, 9.00-12.00 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf
TOELICHTING BETEKENIS GEVEN AAN PROCENTEN
 TOELICHTING BETEKENIS GEVEN AAN PROCENTEN LEERSTAP 1 LEERSTAP 2 LEERSTAP 3 Rekenvlinder_betekenis_geven_aan_procenten.indd 2 27-06-13 21:23 LEERSTAP 4 LEERSTAP 5 LEERSTAP 6 Rekenvlinder_betekenis_geven_aan_procenten.indd
TOELICHTING BETEKENIS GEVEN AAN PROCENTEN LEERSTAP 1 LEERSTAP 2 LEERSTAP 3 Rekenvlinder_betekenis_geven_aan_procenten.indd 2 27-06-13 21:23 LEERSTAP 4 LEERSTAP 5 LEERSTAP 6 Rekenvlinder_betekenis_geven_aan_procenten.indd
Uitwerking Puzzel 93-1, Doelloos
 Uitwerking Puzzel 93-1, Doelloos Wobien Doyer Lieke de Rooij Volgens de titel is deze puzzel zonder doel, dus zonder bekende toepassing. Het doel is echter nul en dat is zeker in de wiskunde niet niks.
Uitwerking Puzzel 93-1, Doelloos Wobien Doyer Lieke de Rooij Volgens de titel is deze puzzel zonder doel, dus zonder bekende toepassing. Het doel is echter nul en dat is zeker in de wiskunde niet niks.
Hoofdstuk 8: Algoritmen en Complexiteit
 Hoofdstuk 8: Algoritmen en Complexiteit Vandaag: Hoe meten we de performance van algoritmen? Waar ligt de grens tussen een goed en een slecht algoritme? 22 oktober 2014 1 Vandaag: Hoe meten we de performance
Hoofdstuk 8: Algoritmen en Complexiteit Vandaag: Hoe meten we de performance van algoritmen? Waar ligt de grens tussen een goed en een slecht algoritme? 22 oktober 2014 1 Vandaag: Hoe meten we de performance
Opgaven voor Kansrekening
 Opgaven voor Kansrekening Opgave 1. Je hebt 4 verschillende wiskunde boeken, 6 psychologie boeken en 2 letterkundige boeken. Hoeveel manieren zijn er om deze twaalf boeken op een boord te plaatsen als:
Opgaven voor Kansrekening Opgave 1. Je hebt 4 verschillende wiskunde boeken, 6 psychologie boeken en 2 letterkundige boeken. Hoeveel manieren zijn er om deze twaalf boeken op een boord te plaatsen als:
Zwijsen. a n t w o o r d e n. reken-wiskundemethode voor het basisonderwijs. blok. o e f e n b o e k
 jaargroep a n t w o o r d e n Zwijsen reken-wiskundemethode voor het basisonderwijs liter liter blok o e f e n b o e k Kleur eerst liter en liter en maak daarna vast. Les Overal getallen Tienen en enen.
jaargroep a n t w o o r d e n Zwijsen reken-wiskundemethode voor het basisonderwijs liter liter blok o e f e n b o e k Kleur eerst liter en liter en maak daarna vast. Les Overal getallen Tienen en enen.
Transport-, Routing- en Schedulingproblemen. Wi4062TU / Wi487TU / a86g. Uitwerkingen 08-04-2005
 Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 08-04-2005 1 Transportprobleem Onderdeel a Fabriek 1 kan 120 ton staal fabriceren in 40 uur. Voor fabriek 2 is dit 150
Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 08-04-2005 1 Transportprobleem Onderdeel a Fabriek 1 kan 120 ton staal fabriceren in 40 uur. Voor fabriek 2 is dit 150
Grafen. Indien de uitgraad van ieder punt 1 is, dan bevat de graaf een cykel. Indien de ingraad van ieder punt 1 is, dan bevat de graaf een cykel.
 Grafen Grafen Een graaf bestaat uit een verzameling punten (ook wel knopen, of in het engels vertices genoemd) en een verzameling kanten (edges) of pijlen (arcs), waarbij de kanten en pijlen tussen twee
Grafen Grafen Een graaf bestaat uit een verzameling punten (ook wel knopen, of in het engels vertices genoemd) en een verzameling kanten (edges) of pijlen (arcs), waarbij de kanten en pijlen tussen twee
Getallensystemen, verzamelingen en relaties
 Hoofdstuk 1 Getallensystemen, verzamelingen en relaties 1.1 Getallensystemen 1.1.1 De natuurlijke getallen N = {0, 1, 2, 3,...} N 0 = {1, 2, 3,...} 1.1.2 De gehele getallen Z = {..., 4, 3, 2, 1, 0, 1,
Hoofdstuk 1 Getallensystemen, verzamelingen en relaties 1.1 Getallensystemen 1.1.1 De natuurlijke getallen N = {0, 1, 2, 3,...} N 0 = {1, 2, 3,...} 1.1.2 De gehele getallen Z = {..., 4, 3, 2, 1, 0, 1,
Tentamen Kansrekening en Statistiek (2WS04), dinsdag 17 juni 2008, van uur.
 Technische Universiteit Eindhoven Faculteit Wiskunde en Informatica Tentamen Kansrekening en Statistiek (2WS4, dinsdag 17 juni 28, van 9. 12. uur. Dit is een tentamen met gesloten boek. De uitwerkingen
Technische Universiteit Eindhoven Faculteit Wiskunde en Informatica Tentamen Kansrekening en Statistiek (2WS4, dinsdag 17 juni 28, van 9. 12. uur. Dit is een tentamen met gesloten boek. De uitwerkingen
Hoofdstuk 13: Integer Lineair Programmeren
 Hoofdstuk 13: Integer Lineair Programmeren Vandaag: Wat is Integer Lineair Programmeren (ILP)? Relatie tussen ILP en LP Voorbeeld 1: Minimum Spanning Tree (MST) Voorbeeld 2: Travelling Salesman Problem
Hoofdstuk 13: Integer Lineair Programmeren Vandaag: Wat is Integer Lineair Programmeren (ILP)? Relatie tussen ILP en LP Voorbeeld 1: Minimum Spanning Tree (MST) Voorbeeld 2: Travelling Salesman Problem
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 26 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 26 oktober 2016 1 / 28 Deze week: analyseren van algoritmes Hoe
TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 26 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 26 oktober 2016 1 / 28 Deze week: analyseren van algoritmes Hoe
OPZOEKEN IN HET WOORDENBOEK (1)
 OPZOEKEN IN HET WOORDENBOEK (1) In de les leer je vaak nieuwe woorden. Je docent kan je helpen, maar je kan nieuwe woorden ook in het woordenboek opzoeken. Wat moet je doen? 1. Neem een woordenboek en
OPZOEKEN IN HET WOORDENBOEK (1) In de les leer je vaak nieuwe woorden. Je docent kan je helpen, maar je kan nieuwe woorden ook in het woordenboek opzoeken. Wat moet je doen? 1. Neem een woordenboek en
Greedy algoritmes. Algoritmiek
 Greedy algoritmes Algoritmiek Algoritmische technieken Trucs, methoden, paradigma s voor het ontwerpen van algoritmen Dynamisch Programmeren Divide & Conquer Greedy 2 Greedy algoritme Bouwt de oplossing
Greedy algoritmes Algoritmiek Algoritmische technieken Trucs, methoden, paradigma s voor het ontwerpen van algoritmen Dynamisch Programmeren Divide & Conquer Greedy 2 Greedy algoritme Bouwt de oplossing
Zwijsen. jaargroep 4. naam: reken-wiskundemethode voor het basisonderwijs. rekentrainer. jij. Bezoek alle leuke dingen. Teken de weg.
 Zwijsen jaargroep naam: reken-wiskundemethode voor het basisonderwijs! jij rekentrainer Bezoek alle leuke dingen. Teken de weg. Groep blad 1 Hoe komt de hond bij het bot? Teken. Kleur de tegels. Kleur
Zwijsen jaargroep naam: reken-wiskundemethode voor het basisonderwijs! jij rekentrainer Bezoek alle leuke dingen. Teken de weg. Groep blad 1 Hoe komt de hond bij het bot? Teken. Kleur de tegels. Kleur
Uitwerkingen eerste serie inleveropgaven
 Uitwerkingen eerste serie inleveropgaven (1) Gegeven het 4 4 grid bestaande uit de 16 punten (i, j) met i, j = 0,..., 3. Bepaal het aantal driehoeken dat je kunt vinden zodanig dat ieder hoekpunt samenvalt
Uitwerkingen eerste serie inleveropgaven (1) Gegeven het 4 4 grid bestaande uit de 16 punten (i, j) met i, j = 0,..., 3. Bepaal het aantal driehoeken dat je kunt vinden zodanig dat ieder hoekpunt samenvalt
9. Strategieën en oplossingsmethoden
 9. Strategieën en oplossingsmethoden In dit hoofdstuk wordt nog even terug gekeken naar alle voorgaande hoofdstukken. We herhalen globaal de structuren en geven enkele richtlijnen voor het ontwerpen van
9. Strategieën en oplossingsmethoden In dit hoofdstuk wordt nog even terug gekeken naar alle voorgaande hoofdstukken. We herhalen globaal de structuren en geven enkele richtlijnen voor het ontwerpen van
Wat betekenen de getallen? Samen bespreken. Kies uit kilometer, meter, decimeter of centimeter.
 70 blok 5 les 23 C 1 Wat betekenen de getallen? Samen bespreken. 10 20 30 40 50 60 70 80 90 100 60 981 540 C 2 Welke maten horen erbij? Samen bespreken. Kies uit kilometer, meter, decimeter of centimeter.
70 blok 5 les 23 C 1 Wat betekenen de getallen? Samen bespreken. 10 20 30 40 50 60 70 80 90 100 60 981 540 C 2 Welke maten horen erbij? Samen bespreken. Kies uit kilometer, meter, decimeter of centimeter.
Programmeren in C++ Efficiënte zoekfunctie in een boek
 Examen Software Ontwikkeling I 2e Bachelor Informatica Faculteit Wetenschappen Academiejaar 2010-2011 21 januari, 2011 **BELANGRIJK** 1. Lees eerst de volledige opgave (inclusief de hints/opmerkingen)!
Examen Software Ontwikkeling I 2e Bachelor Informatica Faculteit Wetenschappen Academiejaar 2010-2011 21 januari, 2011 **BELANGRIJK** 1. Lees eerst de volledige opgave (inclusief de hints/opmerkingen)!
Breukenpizza! Ga je mee om de wonderlijke wereld van de breuken te ontdekken? Bedacht en ontwikkeld door Linda van de Weerd. www.klasvanjuflinda.
 Breukenpizza! Ga je mee om de wonderlijke wereld van de breuken te ontdekken? Bedacht en ontwikkeld door Linda van de Weerd. www.klasvanjuflinda.nl Breukenpizza! 1. Knijpkaart 2. Decimalen 3. Domino 4.
Breukenpizza! Ga je mee om de wonderlijke wereld van de breuken te ontdekken? Bedacht en ontwikkeld door Linda van de Weerd. www.klasvanjuflinda.nl Breukenpizza! 1. Knijpkaart 2. Decimalen 3. Domino 4.
1 Complexiteit. of benadering en snel
 1 Complexiteit Het college van vandaag gaat over complexiteit van algoritmes. In het boek hoort hier hoofdstuk 8.1-8.5 bij. Bij complexiteitstheorie is de belangrijkste kernvraag: Hoe goed is een algoritme?
1 Complexiteit Het college van vandaag gaat over complexiteit van algoritmes. In het boek hoort hier hoofdstuk 8.1-8.5 bij. Bij complexiteitstheorie is de belangrijkste kernvraag: Hoe goed is een algoritme?
Les 1 - Brussels sprouts
 Les 1 - Brussels sprouts We doen een spel voor twee spelers. De eerste speler trekt rode lijnen, de tweede trekt groene lijnen. 1 Zet drie plustekens op papier. Elk plusteken heeft vier vije armen. 2 Om
Les 1 - Brussels sprouts We doen een spel voor twee spelers. De eerste speler trekt rode lijnen, de tweede trekt groene lijnen. 1 Zet drie plustekens op papier. Elk plusteken heeft vier vije armen. 2 Om
