2WO12: Optimalisering in Netwerken
|
|
|
- Katrien van der Velde
- 10 jaren geleden
- Aantal bezoeken:
Transcriptie
1 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 27 februari Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
2 Overzicht Tot nog toe: grafen, kleuren en routeren graafrepresentaties en complexiteit kortste pad algoritmes Vandaag minimum opspannende bomen Prüfer reeksen fylogenetische bomen Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
3 Definitie Een bos is een graaf zonder circuits. Definitie Een boom is een samenhangend bos. Laat G = (V, E) een graaf zijn. Een opspannende boom (spanning tree) van G is een boom T = (V, F ) met F E. Anders gezegd, een opspannende boom van G is een deelgraaf van G die alle punten van G opspant (verbindt) en geen circuits bevat. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
4 Voorbeeld Een opspannende boom van de Petersen graaf (in zwart): Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
5 Voorbeeld Een andere opspannende boom van de Petersen graaf (in zwart): Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
6 Probleem Minimum Opspannende Boom (Minimum Spanning Tree) Gegeven: samenhangende graaf G = (V, E) en lengtefunctie l : E R Vind: een opspannende boom T = (V, F ) van G met minimale lengte l(e) e F Elke samenhangende graaf heeft een opspannende boom. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
7 Prim-Dijkstra methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) en lengtefunctie l : E R Definitie δ(u) is de verzameling lijnen die precies één eindpunt in U hebben Algoritme Kies willekeurig punt v 1 U 1 := {v 1 } F 1 := Voor k = 1, 2,..., V 1 Kies een lijn ek δ(u k ) met minimale lengte Stelling Uk+1 := U k e k Fk+1 := F k {e k } (V, F V ) is een minimum opspannende boom van G Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
8 Voorbeeld Vind een minimum opspannende boom in de volgende graaf m.b.v. de Prim-Dijkstra methode: Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
9 Lemma (1) De volgende uitspraken zijn equivalent voor een graaf G = (V, E): 1 G is een boom (is samenhangend en bevat geen circuit) 2 G is samenhangend en E = V 1 3 G bevat geen circuit en E = V 1 4 G bevat een uniek pad tussen elk tweetal punten Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
10 Lemma (2) Als G = (V, E) samenhangend is, (V, F ) een opspannende boom van G en e E \ F dan zijn de volgende twee uitspraken waar: 1 F {e} bevat een uniek circuit C 2 als f een lijn is van C, dan is F \ {f } {e} een opspannende boom van G e Voorbeeld: lijn e toevoegen geeft een uniek circuit; lijn f weglaten geeft weer een opspannende boom. f Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
11 Definitie (V, F ) is een bos van G = (V, E) als F E en (V, F ) een bos is. Definitie Een bos (V, F ) van G heet gulzig (greedy) als er een opspannende boom van minimale lengte bestaat die alle lijnen van F bevat. Een opspannende boom die gulzig is heeft dus minimale lengte Stelling (1.11) Laat (V, F ) een gulzig bos zijn van G = (V, E) en U een component van (V, F ). Als e een lijn met minimale lengte is over alle lijnen in δ(u), dan is (V, F {e}) weer een gulzig bos. Stelling Het algoritme van Prim-Dijkstra vindt een minimum opspannende boom. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
12 Stelling Het algoritme van Prim-Dijkstra vindt een minimum opspannende boom in tijd O( V 2 ). Bewijs Stelling Houd voor elk punt v V \ U k de lengte f (v) bij van een kortste lijn {u, v} met u U k. Er zijn V iteraties. In elke iteratie is er O( V ) tijd nodig om een punt v V \ U k met minimale f (v) te vinden. In elke iteratie is er O( V ) tijd nodig om de labels van de buren van dit punt v aan te passen. Het algoritme van Prim-Dijkstra geïmplementeerd met Fibonacci Heaps lost het minimum opspannende boom probleem op in tijd O( E + V log( V )). Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
13 Kruskals methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) met lengtefunctie l : E R. Algoritme Stelling F := Voor k = 1, 2,..., V 1 Kies een lijn e k E \ F met minimale lengte waarvoor (V, F {e k }) een bos is F := F {ek } Kruskals algoritme vindt een minimum opspannende boom (V, F ) van G. Stelling Kruskals algoritme kan geïmplementeerd worden zodat de looptijd O( E log( V )) is. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
14 Voorbeeld Vind een opspannende boom in de volgende graaf m.b.v. Kruskals algoritme: Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
15 Borůvka s methode voor het vinden van een minimum opspannende boom van een samenhangende graaf G = (V, E) met lengtefunctie l : E R. Neem voor het gemak aan dat alle lijnen verschillende lengtes hebben. Algoritme Stelling F := while F < V 1 laat U1,..., U k de componenten van (V, F ) zijn voor i = 1,..., k kies een lijn e i δ(u i ) van minimum lengte F := F {e1,..., e k } Borůvka s algoritme vindt een minimum opspannende boom (V, F ) van G. Stelling Borůvka s algoritme kan geïmplementeerd worden zodat de looptijd O( E log( V )) is. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
16 Voorbeeld Vind een opspannende boom in de volgende graaf m.b.v. Borůvka s methode: Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
17 Lemma (cut property) Als G = (V, E) een graaf is, l : E R, U V en e een lijn met l(e) < l(f ) f δ(u) met f e dan bevat elke minimum opspannende boom voor G de lijn e. Lemma (cycle property) Als G = (V, E) een graaf is, l : E R en e een lijn in een circuit C met l(e) > l(f ) f in C met f e dan bevat geen enkele minimum opspannende boom voor G de lijn e. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
18 Probleem Minimum Bottleneck Opspannende Boom Gegeven: samenhangende graaf G = (V, E) en lengtefunctie l : E R Vind: een opspannende boom T = (V, F ) van G waarvoor max e F l(e) minimaal is. Stelling Elke minimum opspannende boom is een minimum bottleneck opspannende boom. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
19 Stelling (Formule van Cayley) Het aantal verschillende bomen met n gelabelde punten is n n 2. Alle = 1 bomen met 2 punten, alle = 3 bomen met 3 punten en alle = 16 bomen met 4 punten. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
20 Definitie Een Prüfer reeks is een reeks van lengte n 2 bestaande uit getallen uit {1,..., n} Gegeven een gelabelde boom T, kun je als volgt een unieke Prüfer reeks bepalen: Laat 1, 2,..., n de labels van de punten van T zijn. Een blad is een punt met graad één. Algoritme Vind het blad b met kleinste label; voeg de buur van b toe aan de Prüfer reeks; verwijder b uit de boom; herhaal de voorgaande stappen totdat er twee punten over zijn. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
21 Algoritme Vind het blad b met kleinste label; voeg de buur van b toe aan de Prüfer reeks; verwijder b uit de boom; herhaal de voorgaande stappen totdat er twee punten over zijn. Voorbeeld Vind de Prüfer reeks van de onderstaande boom Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34 7
22 Gegeven een Prüfer reeks a = (a 1, a 2,..., a n 2 ), kun je als volgt een unieke gelabelde boom bepalen: Algoritme L := (1, 2,..., n) Creëer punten met labels 1, 2,..., n Herhaal de volgende stappen totdat L = 2 Laat l het eerste label in L zijn dat niet in a voor komt Laat a1 het eerste element van a zijn Verbind het punt met label l met het punt met label a1 Verwijder l uit L en a1 uit a Laat L = {l 1, l 2 } Verbind het punt met label l 1 met het punt met label l 2 Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
23 Stelling Er is een bijectie tussen bomen met puntlabels 1,..., n en Prüfer reeksen van lengte n 2. Stelling (Formule van Cayley) Het aantal verschillende bomen met n gelabelde punten is n n 2. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
24 Fylogenetische bomen en splits Definitie Gegeven een verzameling labels X, een fylogenetische boom T op X is een boom zonder punten van graad 2 waarvan de bladeren bijectief zijn gelabelled met de elementen van X. Definitie A B is een split over X als {A, B} een partitie van X is, d.w.z. als A B = en A B = X. A B = B A Definitie Laat e een lijn zijn van een fylogenetische boom T op X. Split A B is de split geassocieerd met e als A en B de labels zijn van de bladeren in de twee componenten die verkregen worden als e uit T verwijderd wordt. Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
25 Notatie: Σ(T ) is de verzameling van alle splits geassocieerd met lijnen van T Voorbeeld: e a b c d Σ(T ) = {ab cde, abc de, a bcde, b acde, c abde, d abce, e abcd} Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
26 Stelling (split equivalence) Laat Σ een verzameling splits over X zijn. Dan zijn de volgende twee uitspraken equivalent: 1 er bestaat een fylogenetische boom T op X met Σ = Σ(T ) 2 voor elke twee splits A 1 B 1 en A 2 B 2 in Σ is tenminste één van de volgende vier doorsnedes leeg A1 A 2 A1 B 2 B1 A 2 B1 B 2 Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
27 Voorbeeld Voor de onderstaande boom T geldt: Σ(T ) = {ab cdefg, abfg cde, abcde fg, abcfg de} Plus alle splits die één blad afsplitsen van de rest. b a c f d e g Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
28 Het vinden van T aan de hand van Σ(T ): Creëer een boom voor de eerste split. Σ(T ) = {ab cdefg, abfg cde, abcde fg, abcfg de} a,b c,d,e,f,g Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
29 Het vinden van T aan de hand van Σ(T ): Voeg de tweede split toe. Σ(T ) = {ab cdefg, abfg cde, abcde fg, abcfg de} a,b f,g c,d,e Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
30 Het vinden van T aan de hand van Σ(T ): Voeg de derde split toe. Σ(T ) = {ab cdefg, abfg cde, abcde fg, abcfg de} a,b f,g c,d,e Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
31 Het vinden van T aan de hand van Σ(T ): Voeg de vierde split toe. Σ(T ) = {ab cdefg, abfg cde, abcde fg, abcfg de} a,b f,g c d,e Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
32 Het vinden van T aan de hand van Σ(T ): Voeg alle splits toe die één blad afsplitsen van de rest. b a c f g d e Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
33 Fylogenetische bomen met lengtes Definitie Laat T = (V, E) een fylogenetische boom op X zijn en l : E R + een lengtefunctie. Voor twee bladeren met labels a en b is d T,l (a, b) := e P l(e) met P het unieke pad tussen de bladeren met labels a en b in T. Definitie Een metriek op X is een functie d : X X R + waarvoor geldt: d(x, y) = 0 x = y d(x, y) = d(y, x) (symmetrie) d(x, y) d(x, z) + d(z, y) (driehoeksongelijkheid) Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
34 Stelling (4-point condition) Laat d : X X R + een metriek op X zijn. Dan zijn de volgende twee uitspraken equivalent: 1 er bestaat een fylogenetische boom T op X met lengtefunctie l : E R + waarvoor d(x, y) = d T,l (x, y) voor alle x, y X ; 2 voor elke vier A, B, C, D X geldt: { d(a, C) + d(b, D) d(a, B) + d(c, D) max d(a, D) + d(b, C). Charles Semple and Mike Steel, Phylogenetics, Oxford University Press, Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in Netwerken 27 februari / 34
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober 2015 1 / 25 Definitie Een boom is een samenhangende
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 28 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 28 oktober 2015 1 / 25 Definitie Een boom is een samenhangende
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
TW2020 Optimalisering Hoorcollege 8 Leo van Iersel Technische Universiteit Delft 2 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 2 november 2016 1 / 28 Minimum Opspannende Boom (Minimum Spanning
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TUE) en Centrum Wiskunde & Informatica (CWI) 3 en 6 februari 2014 Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TUE) en Centrum Wiskunde & Informatica (CWI) 3 en 6 februari 2014 Leo van Iersel (TUE/CWI) 2WO12: Optimalisering in
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 maart 2014 http://homepages.cwi.nl/~iersel/2wo12/ [email protected]
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 maart 2014 http://homepages.cwi.nl/~iersel/2wo12/ [email protected]
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 en 13 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ [email protected]
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 10 en 13 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ [email protected]
Discrete Wiskunde, College 12. Han Hoogeveen, Utrecht University
 Discrete Wiskunde, College 12 Han Hoogeveen, Utrecht University Dynamische programmering Het basisidee is dat je het probleem stap voor stap oplost Het probleem moet voldoen aan het optimaliteitsprincipe
Discrete Wiskunde, College 12 Han Hoogeveen, Utrecht University Dynamische programmering Het basisidee is dat je het probleem stap voor stap oplost Het probleem moet voldoen aan het optimaliteitsprincipe
Discrete Structuren. Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter [email protected] 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Discrete Structuren Piter Dykstra Sietse Achterop Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter [email protected] 3 maart 2008 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren
Minimum Opspannende Bomen. Algoritmiek
 Minimum Opspannende Bomen Inhoud Het minimum opspannende bomen probleem Een principe om een minimum opspannende boom te laten groeien Twee greedy algoritmen + tijd en datastructuren: Het algoritme van
Minimum Opspannende Bomen Inhoud Het minimum opspannende bomen probleem Een principe om een minimum opspannende boom te laten groeien Twee greedy algoritmen + tijd en datastructuren: Het algoritme van
Discrete Structuren. Piter Dykstra Opleidingsinstituut Informatica en Cognitie
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter [email protected] 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter [email protected] 23 februari 2009 GRAFEN & BOMEN Paragrafen 6.1-6.4 Discrete Structuren Week 3 en 4:
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 11 Leo van Iersel Technische Universiteit Delft 25 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 25 november 2015 1 / 28 Vandaag Vraag Voor welke problemen
TW2020 Optimalisering Hoorcollege 11 Leo van Iersel Technische Universiteit Delft 25 november 2015 Leo van Iersel (TUD) TW2020 Optimalisering 25 november 2015 1 / 28 Vandaag Vraag Voor welke problemen
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 12 Leo van Iersel Technische Universiteit Delft 7 december 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 december 2016 1 / 25 Volgende week: Study guide Vragenuurtje
TW2020 Optimalisering Hoorcollege 12 Leo van Iersel Technische Universiteit Delft 7 december 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 december 2016 1 / 25 Volgende week: Study guide Vragenuurtje
Tentamen Discrete Wiskunde 1 10 april 2012, 14:00 17:00 uur
 Tentamen Discrete Wiskunde 0 april 0, :00 7:00 uur Schrijf je naam op ieder blad dat je inlevert. Onderbouw je antwoorden, met een goede argumentatie zijn ook punten te verdienen. Veel succes! Opgave.
Tentamen Discrete Wiskunde 0 april 0, :00 7:00 uur Schrijf je naam op ieder blad dat je inlevert. Onderbouw je antwoorden, met een goede argumentatie zijn ook punten te verdienen. Veel succes! Opgave.
Grafen. Indien de uitgraad van ieder punt 1 is, dan bevat de graaf een cykel. Indien de ingraad van ieder punt 1 is, dan bevat de graaf een cykel.
 Grafen Grafen Een graaf bestaat uit een verzameling punten (ook wel knopen, of in het engels vertices genoemd) en een verzameling kanten (edges) of pijlen (arcs), waarbij de kanten en pijlen tussen twee
Grafen Grafen Een graaf bestaat uit een verzameling punten (ook wel knopen, of in het engels vertices genoemd) en een verzameling kanten (edges) of pijlen (arcs), waarbij de kanten en pijlen tussen twee
Week 1 20-02-2013. Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren.
 Combinatorische Optimalisatie, 2013 Week 1 20-02-2013 Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren. Opgave 1.16 Bewijs dat elke graaf een even aantal punten
Combinatorische Optimalisatie, 2013 Week 1 20-02-2013 Hier vind je uitwerkingen van enkele opgaven uit het dictaat Grafen: Kleuren en Routeren. Opgave 1.16 Bewijs dat elke graaf een even aantal punten
Kortste Paden. Algoritmiek
 Kortste Paden Toepassingen Kevin Bacon getal Six degrees of separation Heeft een netwerk de small-world eigenschap? TomTom / Google Maps 2 Kortste paden Gerichte graaf G=(N,A), en een lengte L(v,w) voor
Kortste Paden Toepassingen Kevin Bacon getal Six degrees of separation Heeft een netwerk de small-world eigenschap? TomTom / Google Maps 2 Kortste paden Gerichte graaf G=(N,A), en een lengte L(v,w) voor
In dit gedeelte worden drie problemen genoemd die kunnen voorkomen in netwerken.
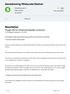 Aantekening Wiskunde Steiner Aantekening door D. 2086 woorden 25 mei 2016 2,1 1 keer beoordeeld Vak Wiskunde Resultaten Vragen bij het wetenschappelijk materiaal 9.1 Prototype example, p. 374-376 In dit
Aantekening Wiskunde Steiner Aantekening door D. 2086 woorden 25 mei 2016 2,1 1 keer beoordeeld Vak Wiskunde Resultaten Vragen bij het wetenschappelijk materiaal 9.1 Prototype example, p. 374-376 In dit
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 21 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 21 oktober 2015 1 / 20 Deze week: algoritmes en complexiteit
TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 21 oktober 2015 Leo van Iersel (TUD) TW2020 Optimalisering 21 oktober 2015 1 / 20 Deze week: algoritmes en complexiteit
1.2 Bomen Algemeen 1.2. BOMEN 7
 1.2. BOMEN 7 1.2 Bomen 1.2.1 Algemeen Beschouw eerst een niet-gerichte graaf. Een boom is een samenhangende graaf die geen kringen bevat. Een boom wordt meestal genoteerd met de letter T (tree). Een bos
1.2. BOMEN 7 1.2 Bomen 1.2.1 Algemeen Beschouw eerst een niet-gerichte graaf. Een boom is een samenhangende graaf die geen kringen bevat. Een boom wordt meestal genoteerd met de letter T (tree). Een bos
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2010 2011, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2010 2011, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2008 2009, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
Tweede bachelor Informatica Academiejaar 2008 2009, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees elke
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 26 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 26 oktober 2016 1 / 28 Deze week: analyseren van algoritmes Hoe
TW2020 Optimalisering Hoorcollege 7 Leo van Iersel Technische Universiteit Delft 26 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 26 oktober 2016 1 / 28 Deze week: analyseren van algoritmes Hoe
Radboud Universiteit Nijmegen
 Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica L(,1)-labeling van grafen Naam: Studentnummer: Studie: Begeleider: Myrte klein Brink 4166140 Bachelor Wiskunde Dr.
Radboud Universiteit Nijmegen Faculteit der Natuurwetenschappen, Wiskunde en Informatica L(,1)-labeling van grafen Naam: Studentnummer: Studie: Begeleider: Myrte klein Brink 4166140 Bachelor Wiskunde Dr.
Netwerkstroming. Algoritmiek
 Netwerkstroming Netwerkstroming Toepassingen in Logistiek Video-streaming Subroutine in algoritmen 2 Vandaag Netwerkstroming: wat was dat ook alweer? Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp
Netwerkstroming Netwerkstroming Toepassingen in Logistiek Video-streaming Subroutine in algoritmen 2 Vandaag Netwerkstroming: wat was dat ook alweer? Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp
Greedy algoritmes. Algoritmiek
 Greedy algoritmes Algoritmiek Algoritmische technieken Trucs, methoden, paradigma s voor het ontwerpen van algoritmen Dynamisch Programmeren Divide & Conquer Greedy 2 Greedy algoritme Bouwt de oplossing
Greedy algoritmes Algoritmiek Algoritmische technieken Trucs, methoden, paradigma s voor het ontwerpen van algoritmen Dynamisch Programmeren Divide & Conquer Greedy 2 Greedy algoritme Bouwt de oplossing
Tentamen combinatorische optimalisatie Tijd:
 Tentamen combinatorische optimalisatie 26-05-2014. Tijd: 9.00-11.30 Tentamen is met gesloten boek. Beschrijf bij elke opgave steeds het belangrijkste idee. Notatie en exacte formulering is van minder belang.
Tentamen combinatorische optimalisatie 26-05-2014. Tijd: 9.00-11.30 Tentamen is met gesloten boek. Beschrijf bij elke opgave steeds het belangrijkste idee. Notatie en exacte formulering is van minder belang.
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 5 Leo van Iersel Technische Universiteit Delft 12 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 12 oktober 2016 1 / 31 Dualiteit Dualiteit: Elk LP probleem heeft
TW2020 Optimalisering Hoorcollege 5 Leo van Iersel Technische Universiteit Delft 12 oktober 2016 Leo van Iersel (TUD) TW2020 Optimalisering 12 oktober 2016 1 / 31 Dualiteit Dualiteit: Elk LP probleem heeft
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 13 Leo van Iersel Technische Universiteit Delft 9 december 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 december 2015 1 / 13 Vraag Wat moet ik kennen en kunnen voor
TW2020 Optimalisering Hoorcollege 13 Leo van Iersel Technische Universiteit Delft 9 december 2015 Leo van Iersel (TUD) TW2020 Optimalisering 9 december 2015 1 / 13 Vraag Wat moet ik kennen en kunnen voor
Begrenzing van het aantal iteraties in het max-flow algoritme
 Begrenzing van het aantal iteraties in het max-flow algoritme Het oplossen van het maximum stroom probleem met behulp van stroomvermeerderende paden werkt, maar het aantal iteraties kan aardig de spuigaten
Begrenzing van het aantal iteraties in het max-flow algoritme Het oplossen van het maximum stroom probleem met behulp van stroomvermeerderende paden werkt, maar het aantal iteraties kan aardig de spuigaten
Benaderingsalgoritmen
 Benaderingsalgoritmen Eerste hulp bij NP-moeilijkheid 1 Herhaling NP-volledigheid (1) NP: er is een polynomiaal certificaat voor jainstanties dat in polynomiale tijd te controleren is Een probleem A is
Benaderingsalgoritmen Eerste hulp bij NP-moeilijkheid 1 Herhaling NP-volledigheid (1) NP: er is een polynomiaal certificaat voor jainstanties dat in polynomiale tijd te controleren is Een probleem A is
3. Elke lijn van een graaf draagt twee bij tot de som van alle graden.
 Antwoorden Doeboek 4 Grafen.. De middelste en de rechtergraaf.. Een onsamenhangende graaf met vijf punten en vijf lijnen: Teken een vierhoek met één diagonaal. Het vijfde punt is niet verbonden met een
Antwoorden Doeboek 4 Grafen.. De middelste en de rechtergraaf.. Een onsamenhangende graaf met vijf punten en vijf lijnen: Teken een vierhoek met één diagonaal. Het vijfde punt is niet verbonden met een
2WO12: Optimalisering in Netwerken
 2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 20 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ [email protected]
2WO12: Optimalisering in Netwerken Leo van Iersel Technische Universiteit Eindhoven (TU/E) en Centrum Wiskunde & Informatica (CWI) 20 februari 2014 http://homepages.cwi.nl/~iersel/2wo12/ [email protected]
Tentamen Discrete Wiskunde
 Discrete Wiskunde (WB011C) 22 januari 2016 Tentamen Discrete Wiskunde Schrijf op ieder ingeleverd blad duidelijk leesbaar je naam en studentnummer. De opgaven 1 t/m 6 tellen alle even zwaar. Je hoeft slechts
Discrete Wiskunde (WB011C) 22 januari 2016 Tentamen Discrete Wiskunde Schrijf op ieder ingeleverd blad duidelijk leesbaar je naam en studentnummer. De opgaven 1 t/m 6 tellen alle even zwaar. Je hoeft slechts
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2016 2017, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2016 2017, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 5 Leo van Iersel Technische Universiteit Delft 2 oktober 206 Leo van Iersel (TUD) TW2020 Optimalisering 2 oktober 206 / 3 Dualiteit Dualiteit: Elk LP probleem heeft een
TW2020 Optimalisering Hoorcollege 5 Leo van Iersel Technische Universiteit Delft 2 oktober 206 Leo van Iersel (TUD) TW2020 Optimalisering 2 oktober 206 / 3 Dualiteit Dualiteit: Elk LP probleem heeft een
Transport-, Routing- en Schedulingproblemen. Wi4062TU / Wi487TU / a86g. Uitwerkingen 08-04-2005
 Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 08-04-2005 1 Transportprobleem Onderdeel a Fabriek 1 kan 120 ton staal fabriceren in 40 uur. Voor fabriek 2 is dit 150
Transport-, Routing- en Schedulingproblemen Wi4062TU / Wi487TU / a86g Uitwerkingen 08-04-2005 1 Transportprobleem Onderdeel a Fabriek 1 kan 120 ton staal fabriceren in 40 uur. Voor fabriek 2 is dit 150
Discrete modellen in de toegepaste wiskunde (WISB136) Uitwerkingen proeftentamen.
 Discrete modellen in de toegepaste wiskunde (WISB6) Uitwerkingen proeftentamen. Docent: Rob H. Bisseling april 202. Begin met een matching M = {x y, x y, x 6 y 6 } aangegeven door de vette lijnen. x De
Discrete modellen in de toegepaste wiskunde (WISB6) Uitwerkingen proeftentamen. Docent: Rob H. Bisseling april 202. Begin met een matching M = {x y, x y, x 6 y 6 } aangegeven door de vette lijnen. x De
l e x e voor alle e E
 Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
Geselecteerde uitwerkingen Werkcollege Introduceer beslissingsvariabelen x e met x e = als lijn e in de boom zit en anders x e = 0. De doelfunctie wordt: min e E l e x e Voor elke deelverzameling S V met
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 1 Leo van Iersel Technische Universiteit Delft 7 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 september 2016 1 / 40 Opzet vak Woensdag: hoorcollege 13:45-15:30
TW2020 Optimalisering Hoorcollege 1 Leo van Iersel Technische Universiteit Delft 7 september 2016 Leo van Iersel (TUD) TW2020 Optimalisering 7 september 2016 1 / 40 Opzet vak Woensdag: hoorcollege 13:45-15:30
Universiteit Utrecht Betafaculteit. Examen Discrete Wiskunde II op donderdag 6 juli 2017, uur.
 Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde II op donderdag 6 juli 2017, 13.30-16.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde II op donderdag 6 juli 2017, 13.30-16.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Activiteit 9. Modderstad Minimaal Opspannende Bomen. Samenvatting. Kerndoelen. Leeftijd. Vaardigheden. Materialen
 Activiteit 9 Modderstad Minimaal Opspannende Bomen Samenvatting Onze maatschappij is verbonden middels heel veel netwerken: telefoonnet, elektriciteitsnet, de riolering, computernetwerk, en het wegennet.
Activiteit 9 Modderstad Minimaal Opspannende Bomen Samenvatting Onze maatschappij is verbonden middels heel veel netwerken: telefoonnet, elektriciteitsnet, de riolering, computernetwerk, en het wegennet.
Tiende college algoritmiek. 2 mei Gretige algoritmen, Dijkstra
 College 10 Tiende college algoritmiek mei 013 Gretige algoritmen, Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
College 10 Tiende college algoritmiek mei 013 Gretige algoritmen, Dijkstra 1 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag van n (n 0) eurocent. Alle
Netwerkstroming. Algoritmiek
 Netwerkstroming Vandaag Netwerkstroming: definitie en toepassing Het rest-netwerk Verbeterende paden Ford-Fulkerson algoritme Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp Toepassing: koppelingen
Netwerkstroming Vandaag Netwerkstroming: definitie en toepassing Het rest-netwerk Verbeterende paden Ford-Fulkerson algoritme Minimum Snede Maximum Stroming Stelling Variant: Edmonds-Karp Toepassing: koppelingen
V = {a, b, c, d, e} Computernetwerken: de knopen zijn machines in het netwerk, de kanten zijn communicatiekanalen.
 WIS14 1 14 Grafen 14.1 Grafen Gerichte grafen Voor een verzameling V is een binaire relatie op V een verzameling geordende paren van elementen van V. Voorbeeld: een binaire relatie op N is de relatie KleinerDan,
WIS14 1 14 Grafen 14.1 Grafen Gerichte grafen Voor een verzameling V is een binaire relatie op V een verzameling geordende paren van elementen van V. Voorbeeld: een binaire relatie op N is de relatie KleinerDan,
Universiteit Utrecht Betafaculteit. Examen Discrete Wiskunde op donderdag 13 april 2017, uur.
 Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde op donderdag 13 april 2017, 14.30-17.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Universiteit Utrecht Betafaculteit Examen Discrete Wiskunde op donderdag 13 april 2017, 14.30-17.30 uur. De opgaven dienen duidelijk uitgewerkt te zijn en netjes ingeleverd te worden. Schrijf op elk ingeleverd
Tiende college algoritmiek. 26 april Gretige algoritmen
 Algoritmiek 01/10 College 10 Tiende college algoritmiek april 01 Gretige algoritmen 1 Algoritmiek 01/10 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag
Algoritmiek 01/10 College 10 Tiende college algoritmiek april 01 Gretige algoritmen 1 Algoritmiek 01/10 Muntenprobleem Gegeven onbeperkt veel munten van d 1,d,...d m eurocent, en een te betalen bedrag
Examen Datastructuren en Algoritmen II
 Tweede kandidatuur Informatica Academiejaar 2004 2005, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. 1. Binomiale
Tweede kandidatuur Informatica Academiejaar 2004 2005, eerste zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. 1. Binomiale
Uitwerkingen Sum of Us
 Instant Insanity Uitwerkingen Sum of Us Opgave A: - Opgave B: Voor elk van de vier kubussen kun je een graaf maken die correspondeert met de desbetreffende kubus. Elk van deze grafen bevat drie lijnen.
Instant Insanity Uitwerkingen Sum of Us Opgave A: - Opgave B: Voor elk van de vier kubussen kun je een graaf maken die correspondeert met de desbetreffende kubus. Elk van deze grafen bevat drie lijnen.
Gerichte Grafen Boolese Algebra s &. Logische Netwerken
 Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter [email protected] 10 maart 2009 Gerichte Grafen Boolese Algebra s &. Logische Netwerken. Paragrafen
Discrete Structuren Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.math.rug.nl/~piter [email protected] 10 maart 2009 Gerichte Grafen Boolese Algebra s &. Logische Netwerken. Paragrafen
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 10 Leo van Iersel Technische Universiteit Delft 23 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 23 november 2016 1 / 40 Vraag Ik heb het deeltentamen niet
TW2020 Optimalisering Hoorcollege 10 Leo van Iersel Technische Universiteit Delft 23 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 23 november 2016 1 / 40 Vraag Ik heb het deeltentamen niet
Examen Datastructuren en Algoritmen II
 Tweede bachelor Informatica Academiejaar 2012 2013, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Tweede bachelor Informatica Academiejaar 2012 2013, tweede zittijd Examen Datastructuren en Algoritmen II Naam :.............................................................................. Lees de hele
Divide & Conquer: Verdeel en Heers vervolg. Algoritmiek
 Divide & Conquer: Verdeel en Heers vervolg Algoritmiek Algoritmische technieken Vorige keer: Divide and conquer techniek Aantal toepassingen van de techniek Analyse met Master theorem en substitutie Vandaag:
Divide & Conquer: Verdeel en Heers vervolg Algoritmiek Algoritmische technieken Vorige keer: Divide and conquer techniek Aantal toepassingen van de techniek Analyse met Master theorem en substitutie Vandaag:
Optimaliseren in Netwerken
 Optimaliseren in Netwerken Kees Roos e-mail: [email protected] URL: http://www.isa.ewi.tudelft.nl/ roos Kaleidoscoop college Zaal D, Mekelweg 4, TU Delft 11 October, A.D. 2006 Optimization Group 1 Onderwerpen
Optimaliseren in Netwerken Kees Roos e-mail: [email protected] URL: http://www.isa.ewi.tudelft.nl/ roos Kaleidoscoop college Zaal D, Mekelweg 4, TU Delft 11 October, A.D. 2006 Optimization Group 1 Onderwerpen
Talen & Automaten. Wim Hesselink Piter Dykstra Opleidingsinstituut Informatica en Cognitie 9 mei 2008
 Talen & Automaten Wim Hesselink Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.cs.rug.nl/~wim 9 mei 2008 Talen & automaten Week 1: Inleiding Dit college Talen Automaten Berekenbaarheid Weekoverzicht
Talen & Automaten Wim Hesselink Piter Dykstra Opleidingsinstituut Informatica en Cognitie www.cs.rug.nl/~wim 9 mei 2008 Talen & automaten Week 1: Inleiding Dit college Talen Automaten Berekenbaarheid Weekoverzicht
Heuristieken en benaderingsalgoritmen. Algoritmiek
 Heuristieken en benaderingsalgoritmen Wat te doen met `moeilijke optimaliseringsproblemen? Voor veel problemen, o.a. optimaliseringsproblemen is geen algoritme bekend dat het probleem voor alle inputs
Heuristieken en benaderingsalgoritmen Wat te doen met `moeilijke optimaliseringsproblemen? Voor veel problemen, o.a. optimaliseringsproblemen is geen algoritme bekend dat het probleem voor alle inputs
Tiende college algoritmiek. 13/21 april Gretige Algoritmen Algoritme van Dijkstra
 Algoritmiek 017/Gretige Algoritmen Tiende college algoritmiek 13/1 april 017 Gretige Algoritmen Algoritme van Dijkstra 1 Algoritmiek 017/Gretige Algoritmen Muntenprobleem Gegeven onbeperkt veel munten
Algoritmiek 017/Gretige Algoritmen Tiende college algoritmiek 13/1 april 017 Gretige Algoritmen Algoritme van Dijkstra 1 Algoritmiek 017/Gretige Algoritmen Muntenprobleem Gegeven onbeperkt veel munten
Meetkundige Ongelijkheden Groep 2
 Meetkundige Ongelijkheden Groep Trainingsweek Juni 009 1 Introductie We werken hier met ongeoriënteerde lengtes en voor het gemak laten we de absoluutstrepen weg. De lengte van een lijnstuk XY wordt dus
Meetkundige Ongelijkheden Groep Trainingsweek Juni 009 1 Introductie We werken hier met ongeoriënteerde lengtes en voor het gemak laten we de absoluutstrepen weg. De lengte van een lijnstuk XY wordt dus
Algoritmiek. 15 februari Grafen en bomen
 Algoritmiek 15 februari 2019 Grafen en bomen 1 Grafen (herhaling) Een graaf G wordt gedefinieerd als een paar (V,E), waarbij V een eindige verzameling is van knopen (vertices) en E een verzameling van
Algoritmiek 15 februari 2019 Grafen en bomen 1 Grafen (herhaling) Een graaf G wordt gedefinieerd als een paar (V,E), waarbij V een eindige verzameling is van knopen (vertices) en E een verzameling van
Doorzoeken van grafen. Algoritmiek
 Doorzoeken van grafen Algoritmiek Vandaag Methoden om door grafen te wandelen Depth First Search Breadth First Search Gerichte Acyclische Grafen en topologische sorteringen 2 Doolhof start eind 3 Depth
Doorzoeken van grafen Algoritmiek Vandaag Methoden om door grafen te wandelen Depth First Search Breadth First Search Gerichte Acyclische Grafen en topologische sorteringen 2 Doolhof start eind 3 Depth
Lineaire algebra I (wiskundigen)
 Lineaire algebra I (wiskundigen) Toets, donderdag 22 oktober, 2009 Oplossingen (1) Zij V het vlak in R 3 door de punten P 1 = (1, 2, 1), P 2 = (0, 1, 1) en P 3 = ( 1, 1, 3). (a) Geef een parametrisatie
Lineaire algebra I (wiskundigen) Toets, donderdag 22 oktober, 2009 Oplossingen (1) Zij V het vlak in R 3 door de punten P 1 = (1, 2, 1), P 2 = (0, 1, 1) en P 3 = ( 1, 1, 3). (a) Geef een parametrisatie
TW2020 Optimalisering
 TW2020 Optimalisering Hoorcollege 9 Leo van Iersel Technische Universiteit Delft 16 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 16 november 2016 1 / 28 Vandaag Integer Linear Programming (ILP)
TW2020 Optimalisering Hoorcollege 9 Leo van Iersel Technische Universiteit Delft 16 november 2016 Leo van Iersel (TUD) TW2020 Optimalisering 16 november 2016 1 / 28 Vandaag Integer Linear Programming (ILP)
Gegevens invullen in HOOFDLETTERS en LEESBAAR, aub. Belgische Olympiades in de Informatica (duur : maximum 1u15 )
 OI 2010 Finale 12 Mei 2010 Gegevens invullen in HOOFDLETTERS en LEESBAAR, aub VOORNAAM :....................................................... NAAM :..............................................................
OI 2010 Finale 12 Mei 2010 Gegevens invullen in HOOFDLETTERS en LEESBAAR, aub VOORNAAM :....................................................... NAAM :..............................................................
Vierde college complexiteit. 26 februari Beslissingsbomen en selectie Toernooimethode Adversary argument
 Complexiteit 2019/04 College 4 Vierde college complexiteit 26 februari 2019 Beslissingsbomen en selectie Toernooimethode Adversary argument 1 Complexiteit 2019/04 Zoeken: samengevat Ongeordend lineair
Complexiteit 2019/04 College 4 Vierde college complexiteit 26 februari 2019 Beslissingsbomen en selectie Toernooimethode Adversary argument 1 Complexiteit 2019/04 Zoeken: samengevat Ongeordend lineair
Elke gelijkenis met bestaande gebeurtenissen en/of personen berust op louter toeval.
 Leo is een hevige fan van het Belgisch voetbal. Behalve een vurige fan van Blauw Zwart, is hij ook geïnteresseerd in de voetbaltempels van de eersteklassevoetbalclubs. Daarom wil hij, samen met zijn kameraad
Leo is een hevige fan van het Belgisch voetbal. Behalve een vurige fan van Blauw Zwart, is hij ook geïnteresseerd in de voetbaltempels van de eersteklassevoetbalclubs. Daarom wil hij, samen met zijn kameraad
Grafen. Grafen, toppen en bogen
 Grafen Het zijn configuraties van knoppen en verbindingen, waar we de knoppen toppen noemen en de verbindingen tussen 2 toppen noemen we een boog. Toppen en bogen kunnen bijkomende attributen hebben, zoals
Grafen Het zijn configuraties van knoppen en verbindingen, waar we de knoppen toppen noemen en de verbindingen tussen 2 toppen noemen we een boog. Toppen en bogen kunnen bijkomende attributen hebben, zoals
I.3 Functies. I.3.2 Voorbeeld. De afbeeldingen f: R R, x x 2 en g: R R, x x 2 zijn dus gelijk, ook al zijn ze gegeven door verschillende formules.
 I.3 Functies Iedereen is ongetwijfeld in veel situaties het begrip functie tegengekomen; vaak als een voorschrift dat aan elk getal een ander getal toevoegt, bijvoorbeeld de functie fx = x die aan elk
I.3 Functies Iedereen is ongetwijfeld in veel situaties het begrip functie tegengekomen; vaak als een voorschrift dat aan elk getal een ander getal toevoegt, bijvoorbeeld de functie fx = x die aan elk
Oefeningen Discrete Wiskunde - Hoofdstuk 6 - Peter Vandendriessche Fouten, opmerkingen of alternatieve methodes? me:
 Oefeningen Discrete Wiskunde - Hoofdstuk 6 - Peter Vandendriessche Fouten, opmerkingen of alternatieve methodes? Email me: [email protected] 1. Het aantal knoop-tak overgangen is altijd even. De totaalsom
Oefeningen Discrete Wiskunde - Hoofdstuk 6 - Peter Vandendriessche Fouten, opmerkingen of alternatieve methodes? Email me: [email protected] 1. Het aantal knoop-tak overgangen is altijd even. De totaalsom
2 Kromming van een geparametriseerde kromme in het vlak. Veronderstel dat een kromme in het vlak gegeven is door een parametervoorstelling
 TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
TU/e technische universiteit eindhoven Kromming Extra leerstof bij het vak Wiskunde voor Bouwkunde (DB00) 1 Inleiding De begrippen kromming en kromtestraal worden in het boek Calculus behandeld in hoofdstuk
2 beslissen in netwerken. Wiskunde D. Keuzevak beslissen onderdeel: beslissen in netwerken. versie 4 vrijdag 16 november 2007
 eslissen beslissen in netwerken Wiskunde Keuzevak beslissen onderdeel: beslissen in netwerken versie vrijdag november 00 Samenstelling Jan ssers ism Kerngroep Wiskunde indhoven ontys voorkennis: optimaliseren.
eslissen beslissen in netwerken Wiskunde Keuzevak beslissen onderdeel: beslissen in netwerken versie vrijdag november 00 Samenstelling Jan ssers ism Kerngroep Wiskunde indhoven ontys voorkennis: optimaliseren.
Lineaire Algebra voor ST
 Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 9.3 email: [email protected] studiewijzer: http://www.win.tue.nl/wsk/onderwijs/2ds6 Technische Universiteit Eindhoven college 6 J.Keijsper (TUE)
Lineaire Algebra voor ST docent: Judith Keijsper TUE, HG 9.3 email: [email protected] studiewijzer: http://www.win.tue.nl/wsk/onderwijs/2ds6 Technische Universiteit Eindhoven college 6 J.Keijsper (TUE)
Ter Leering ende Vermaeck
 Ter Leering ende Vermaeck 15 december 2011 1 Caleidoscoop 1. Geef een relatie op Z die niet reflexief of symmetrisch is, maar wel transitief. 2. Geef een relatie op Z die niet symmetrisch is, maar wel
Ter Leering ende Vermaeck 15 december 2011 1 Caleidoscoop 1. Geef een relatie op Z die niet reflexief of symmetrisch is, maar wel transitief. 2. Geef een relatie op Z die niet symmetrisch is, maar wel
Je hebt twee uur de tijd voor het oplossen van de vraagstukken. µkw uitwerkingen. 12 juni 2015
 Je hebt twee uur de tijd voor het oplossen van de vraagstukken. Elk vraagstuk is maximaal 10 punten waard. Begin elke opgave op een nieuw vel papier. µkw uitwerkingen 12 juni 2015 Vraagstuk 1. We kunnen
Je hebt twee uur de tijd voor het oplossen van de vraagstukken. Elk vraagstuk is maximaal 10 punten waard. Begin elke opgave op een nieuw vel papier. µkw uitwerkingen 12 juni 2015 Vraagstuk 1. We kunnen
Radboud Universiteit Nijmegen
 Radboud Universiteit Nijmegen Faculteit der natuurwetenschappen, wiskunde en informatica juli 07 Matchingtheorie op grafen Jorrit Bastings S6556 Begeleider: Wieb Bosma Inhoudsopgave Het huwelijksprobleem
Radboud Universiteit Nijmegen Faculteit der natuurwetenschappen, wiskunde en informatica juli 07 Matchingtheorie op grafen Jorrit Bastings S6556 Begeleider: Wieb Bosma Inhoudsopgave Het huwelijksprobleem
Algoritmen aan het werk
 Algoritmen aan het werk (Dag van de wiskunde 24/11/2018) Veerle Fack Universiteit Gent De bevers en de brug Vier bevers willen in het donker een brug oversteken. Ze kunnen de brug slechts alleen of met
Algoritmen aan het werk (Dag van de wiskunde 24/11/2018) Veerle Fack Universiteit Gent De bevers en de brug Vier bevers willen in het donker een brug oversteken. Ze kunnen de brug slechts alleen of met
Vierde college complexiteit. 14 februari Beslissingsbomen
 College 4 Vierde college complexiteit 14 februari 2017 Restant zoeken Beslissingsbomen 1 Binair zoeken Links := 1; Rechts := n; while Links Rechts do Midden := Links + Rechts 2 ; if X = A[Midden] then
College 4 Vierde college complexiteit 14 februari 2017 Restant zoeken Beslissingsbomen 1 Binair zoeken Links := 1; Rechts := n; while Links Rechts do Midden := Links + Rechts 2 ; if X = A[Midden] then
